Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
|
|
|
- Νίκη Κοντολέων
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig. H μζκοδοσ αυτι αποτελεί μια αλγεβρικι επαναλθπτικι διαδικαςία θ οποία επιλφει ακριβϊσ, κάκε πρόβλθμα γραμμικοφ προγραμματιςμοφ, ςε ζνα πεπεραςμζνο πλικοσ βθμάτων. Τα βιματα αυτά κα αναφερκοφν αναλυτικά παρακάτω αφοφ πρϊτα ορίςουμε κάποιεσ ζννοιεσ. Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν: i) H αντικειμενικι ςυνάρτθςθ ηθτείται να μεγιςτοποιθκεί. ii) Οι μεταβλθτζσ είναι όλεσ μθ αρνθτικζσ, δθλαδι, μεγαλφτερεσ ι ίςεσ του μθδενόσ. iii) Στουσ περιοριςμοφσ, οι γραμμικζσ εκφράςεισ που περιζχουν τισ μεταβλθτζσ είναι μικρότερεσ ι ίςεσ από μία μθ αρνθτικι ςτακερά, δθλαδι είναι τθσ μορφισ: (γραμμικό πολυϊνυμο) α, όπου α 0 Παράδειγμα κανονικής μορφής : Μεγιςτοποίθςθ τθσ m=6x+8y υπό τουσ περιοριςμοφσ x+y 10, 2x+3y 12, x 0 και y 0 Μία μεταβλθτι ονομάηεται χαλαρι, όταν παριςτάνει τθ διαφορά μεταξφ μιασ διακζςιμθσ ποςότθτασ και τθσ ποςότθτασ που πράγματι χρθςιμοποιείται. Παράδειγμα χαλαρισ μεταβλθτισ : ίνεται θ ανιςότθτα 2x+y 10 Θα ορίςουμε τθ χαλαρι μεταβλθτι s1 ζτςι ϊςτε 2x+y+s1 = 10 Η τυποποιθμζνθ μορφι τθσ αντικειμενικισ ςυνάρτθςθσ δθμιουργείται όταν ταξινομοφμε τουσ όρουσ τθσ ζτςι ϊςτε να ζχει τθν ίδια μορφι εξίςωςθσ με τουσ περιοριςμοφσ. Παράδειγμα τυποποιθμζνθσ μορφισ : ίνεται θ αντικειμενικι ςυνάρτθςθ m=6x+8y. Η τυποποιθμζνθ μορφι τθσ κα είναι -6x-8y+m=0 Αρχικόσ Simplex πίνακασ καλείται ο επαυξθμζνοσ πίνακασ ο οποίοσ αποτελείται από ςειρζσ με ςτοιχεία τουσ ςυντελεςτζσ των μεταβλθτϊν των εξιςϊςεων των περιοριςμϊν, θ τελευταία του ςειρά αποτελείται από τουσ ςυντελεςτζσ τθσ αντικειμενικισ ςυνάρτθςθσ και θ τελευταία του ςτιλθ από τισ ςτακερζσ τουσ. Παράδειγμα αρχικοφ Simplex πίνακα:
2 Εικόνα 11 Από αυτά τα δεδομζνα προκφπτει ο πίνακασ Εικόνα 12 Μία ςτιλθ βρίςκεται ςε βαςικι μορφι όταν μόνο ζνα ςτοιχείο τθσ είναι ίςο με το 1 και όλα τα υπόλοιπα είναι 0. Η μεταβλθτι ςτθν οποία αντιςτοιχεί ονομάηεται βαςικι μεταβλθτι.οι υπόλοιπεσ μεταβλθτζσ ονομάηονται μθ-βαςικζσ. Τθν βαςικι εφικτι λφςθ τθν παίρνουμε όταν ςτον αρχικό Simplex πίνακα κζςουμε τισ μθβαςικζσ μεταβλθτζσ ίςεσ με 0, οπότε αντιςτοιχίηομαι τισ βαςικζσ μεταβλθτζσ με τα ςτακερά ςτοιχεία τθσ τελευταίασ ςτιλθσ. Παράδειγμα εφρεςθσ βαςικισ λφςθσ : Εικόνα 13 Οι ςτιλεσ που βρίςκονται ςε βαςικι μορφι είναι θ δεφτερθ, Τρίτθ και πζμπτθ. Οι βαςικζσ μεταβλθτζσ είναι θ y, s1, m και θ βαςικι εφικτι λφςθ, αν κζςουμε x= s2 =0, είναι y=5, s1 =2, m=15. Κάκε αρχικόσ Simplex πίνακασ ζχει περιςςότερεσ ςτιλεσ από ότι ςειρζσ, ϊςτε το ςφςτθμα να ζχει άπειρο αρικμό λφςεων. Ποια είναι θ καλφτερθ εφικτι λφςθ κα εξαρτθκεί από τθν μορφι του πίνακα και τθν εφαρμογι του ελζγχου μζγιςτθσ λφςθσ που λζει: Ο αρχικόσ
3 Simplex πίνακασ κα δϊςει τθν βζλτιςτθ λφςθ αν και μόνο αν θ τελευταία ςειρά, θ οποία αναφζρεται ςτθν αντικειμενικι ςυνάρτθςθ, περιλαμβάνει μόνο μθ αρνθτικά ςτοιχεία. Η ςτιλθ που ζχει το πιο αρνθτικό ςτοιχείο ςτθν τελευταία ςειρά ονομάηεται ςτιλθ οδθγόσ. Η μεταβλθτι που αντιςτοιχεί ςτθν ςτιλθ αυτι καλείται ειςερχομζνθ μεταβλθτι. Αν υπάρχουν δφο ι περιςςότερα ίςα και αρνθτικά ςτοιχεία, τότε μποροφμε να επιλζξουμε οποιαδιποτε από τισ ςτιλεσ που τουσ αντιςτοιχοφν. Όταν επιλεγεί θ ςτιλθ οδθγόσ, αναηθτάμε τθ ςειρά οδθγό ωσ εξισ: Για κάκε ςειρά, εκτόσ από τθν τελευταία, με κετικι καταχϊριςθ ςτθν ςτιλθ οδθγό, υπολογίηουμε τον λόγο του ςτοιχείου ςτθν τελευταία ςτιλθ προσ το ςτοιχείο ςτθν ςτιλθ οδθγό. Αν προκφψουν δφο ι περιςςότερεσ ςειρζσ με τον ίδιο λόγο, τότε μποροφμε να χρθςιμοποιιςουμε οποιαδιποτε ςειρά αλλιϊσ το ςτοιχείο που αντιςτοιχεί ςτθν ςειρά με τον μικρότερο κετικό λόγο ονομάηεται ςτοιχείο οδθγόσ. Το ςτοιχείο αυτό κα γίνει 1 και τα υπόλοιπα τθσ ςτιλθσ του 0 φςτερα από μία ςειρά εργαςιϊν ςτισ ςειρζσ που κα πραγματοποιθκεί, προκειμζνου να μετατραπεί θ ςτιλθ άξονασ ςε βαςικι μορφι. Αυτι θ διαδικαςία ονομάηεται οδιγθςθ. Εικόνα 14 Ο ζλεγχοσ μζγιςτθσ λφςθσ αποτυγχάνει αφοφ υπάρχει αρνθτικό ςτοιχείο ςτθν τελευταία ςειρά. Η δεφτερθ ςτιλθ είναι θ ςτιλθ άξονασ και θ y θ ειςερχόμενθ μεταβλθτι. Μετά από υπολογιςμό του λόγου τθσ πρϊτθσ ςειράσ 26/2 και τθσ δεφτερθσ ςειράσ 10/1 προκφπτει ότι θ δεφτερθ ςειρά είναι ςειρά άξονασ και θ καταχϊριςθ άξονα κα είναι ίςθ με το ςτοιχείο(2,2)=1. Στθ ςυνζχεια μζςα από τισ ακόλουκεσ πράξεισ ςειρϊν μετατρζπουμε το πίνακα μασ ςε βαςικι μορφι Εικόνα 15 Και από όπου προκφπτει θ μζγιςτθ εφικτι λφςθ x=6, y=10, m=32 Να ςθμειωκεί εδϊ ότι θ διαδικαςία αυτι επαναλαμβάνεται όςεσ φορζσ χρειαςτεί προκειμζνου ο πίνακασ που κα προκφψει τελικά να ζχει τελευταία ςειρά με μθ αρνθτικά ςτοιχεία. Αφοφ ορίςαμε όλεσ τισ ζννοιεσ, μποροφμε ςε αυτό το ςθμείο να δϊςουμε τα βιματα για τθν επίλυςθ προβλθμάτων με τθ μζκοδο Simplex τα οποία βρίςκονται ςε κανονικι μορφι. H Μζθοδος Simplex για Προβλήματα σε Κανονική Μορφή.
4 1. Ανάγουμε τουσ περιοριςμοφσ που εκφράηονται με ανιςϊςεισ ςε εξιςϊςεισ, ειςάγοντασ νζεσ μθ αρνθτικζσ μεταβλθτζσ, οι οποίεσ ονομάηονται χαλαρζσ μεταβλθτζσ και εκφράηουμε τθν αντικειμενικι ςυνάρτθςθ ςε κατάλλθλθ μορφι. 2. Καταςκευάηουμε τον αρχικό Simplex πίνακα. 3. Εφαρμόηουμε τον ζλεγχο τθσ μζγιςτθσ λφςθσ. Αν θ βαςικι εφικτι λφςθ είναι μζγιςτθ, τότε το πρόβλθμα ζχει λυκεί. Αν όχι τότε προχωράμε ςτο επόμενο βιμα. 4. Καταςκευάηουμε ζνα νζο Simplex πίνακα ακολουκϊντασ τθν εξισ διαδικαςία: a) Επιλζγουμε τθν ςτιλθ άξονα b) Επιλζγουμε τθν ςειρά άξονα c) Εφαρμόηουμε τθ διαδικαςία οδιγθςθσ γφρω από τθν καταχϊριςθ άξονα. 5. Επαναλαμβάνουμε το βιμα 3. Εκτόσ όμωσ από τα προβλιματα αυτά, θ μζκοδοσ Simplex μπορεί να εφαρμοςτεί και ςε προβλιματα που δεν βρίςκονται ςε κανονικι μορφι, δθλαδι, ςυμβαίνει τουλάχιςτον ζνα από τα παρακάτω: i) Ζθτείται θ αντικειμενικι ςυνάρτθςθ να ελαχιςτοποιθκεί. ii) Στουσ περιοριςμοφσ, οι γραμμικζσ εκφράςεισ που περιζχουν τισ μεταβλθτζσ είναι μεγαλφτερεσ από μία μθ αρνθτικι ςτακερά, δθλαδι είναι τθσ μορφισ: (γραμμικό πολυϊνυμο) α, όπου α 0 Και ςτα προβλιματα αυτά ςυνεχίηει να ιςχφει ότι οι μεταβλθτζσ είναι όλεσ μθ αρνθτικζσ, δθλαδι, μεγαλφτερεσ ι ίςεσ του μθδενόσ. Στισ περιπτϊςεισ αυτζσ τα βιματα που ακολουκοφμε για τθν επίλυςθ προβλθμάτων με τθ μζκοδο Simplex τα οποία βρίςκονται ςε μθ-κανονικι μορφι είναι τα εξισ : H Μζθοδος Simplex για Προβλήματα σε Μη-Κανονική Μορφή 1. Αν το πρόβλθμα ηθτά τθν ελαχιςτοποίθςθ τθσ m, τότε δουλεφουμε με το πρόβλθμα τθσ μεγιςτοποίθςθσ τθσ m. 2. Αν οι περιοριςμοί είναι τθσ μορφισ ( γραμμικό πολυϊνυμο ) α, όπου α 0 τότε πολλαπλαςιάηοντασ επί -1 λαμβάνουμε τθν επικυμθτι μορφι. 3. Αν δεν εμφανιςτεί αρνθτικόσ αρικμόσ ςτθν τελευταία ςτιλθ,εκτόσ από το τελευταίο τθσ ςτοιχείο, τότε πθγαίνουμε κατευκείαν ςτο βιμα 6, αλλιϊσ ςυνεχίηουμε ςτο επόμενο βιμα. 4. Μετατρζπουμε τον αρνθτικό αρικμό ςε κετικό με τον ακόλουκο τρόπο: a) ιαλζγουμε ζνα αρνθτικό ςτοιχείο που βρίςκεται ςτθν ίδια ςειρά με τον αρνθτικό αρικμό τθσ τελευταίασ ςτιλθσ.η ςτιλθ του κα γίνει ςτιλθ οδθγόσ. b) Υπολογίηουμε όλουσ τουσ λόγουσ, ςυμπεριλαμβανομζνων και αυτϊν που αντιςτοιχοφν ςτουσ αρνθτικοφσ αρικμοφσ τθσ ςτιλθσ οδθγό.τότε θ ςειρά οδθγόσ κα είναι αυτι με το μικρότερο κετικό λόγο. c) Εφαρμόηουμε τθ διαδικαςία οδιγθςθσ γφρω από το ςτοιχείο οδθγό. 5. Επαναλαμβάνουμε το βιμα 3 εϊσ ότου να μθν υπάρχει άλλθ αρνθτικι καταχϊριςθ ςτθν τελευταία ςτιλθ.
5 6. Τελικά ο πίνακασ που προκφπτει είναι ςε κανονικι μορφι και χρθςιμοποιοφμε κατά τα γνωςτά τθ μζκοδο Simplex για τθν επίλυςθ προβλιματοσ ςε κανονικι μορφι. Παράδειγμα προβλιματοσ ςε μθ-κανονικι μορφι : Εικόνα 16 Οπότε ακολουκϊντασ τα βιματα ηθτάμε τθν μεγιςτοποίθςθ τθσ -m= -x-y Υπό περιοριςμοφσ -2x+y -30 x-y -50 O αρχικόσ Simplex πίνακασ κα είναι Εικόνα 17 Υπάρχουν 2 αρνθτικοί αρικμοί ςτθν τελευταία ςτιλθ επιλζγουμε τυχαία τον -50 τθσ δεφτερθσ ςειράσ.τότε θ δεφτερθ ςτιλθ γίνεται ςτιλθ άξονασ λόγω τθσ φπαρξθσ του -1 και οι λόγοι κα είναι ίςοι με -80/(-1) για τθν πρϊτθ ςειρά και 50/(-1) για τθν δεφτερθ ςειρά.οπότε το ςτοιχείο άξονασ κα είναι το (2,2)= -1. Με πράξεισ κα προκφψει ο πίνακασ Εικόνα 18
6 Εικόνα 19 Παρατθροφμε ότι πάλι εμφανίηεται αρνθτικόσ αρικμόσ -80 ςτθν τελευταία ςτιλθ, οπότε με επανάλθψθ των παραπάνω βθμάτων κα καταλιξουμε ςτον πίνακα Εικόνα 20 Ανακεφαλαιϊνοντασ είδαμε πωσ μποροφμε με τθ μζκοδο Simplex να επιλφςουμε προβλιματα γραμμικοφ προγραμματιςμοφ ςε κανονικι και μθ-κανονικι μορφι. Η μζκοδοσ αυτι υπεριςχφει ζναντι τθσ γεωμετρικισ προςζγγιςθσ και αυτό οφείλεται ςτο ότι : 1) H μζκοδοσ Simplex μπορεί να χειριςτεί πολλζσ εξιςϊςεισ και μεταβλθτζσ, ενϊ θ γεωμετρικι μζκοδοσ μπορεί μόνο 2 μεταβλθτζσ. 2) Η μζκοδοσ Simplex είναι μθχανικι και δεν βαςίηεται ςε οπτικζσ ι γεωμετρικζσ ερμθνείεσ των δεδομζνων. Έτςι είναι ευκολότερο να προγραμματιςτεί ζνασ υπολογιςτισ να κάνει τουσ υπολογιςμοφσ.
ςυςτιματα γραμμικϊν εξιςϊςεων
 κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R
 Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 5 η : Η Μζθοδοσ Simplex Παρουςίαςη τησ μεθόδου Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 5 η : Η Μζθοδοσ Simplex Παρουςίαςη τησ μεθόδου Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Παράςταςη ςυμπλήρωμα ωσ προσ 1
 Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4.1
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4. Να γίνει πρόγραμμα το οποίο να επιλφει το Διαγώνιο Σφςτθμα: A ι το ςφςτθμα : ι ςε μορφι εξιςώςεων το ςφςτθμα : Αλγόρικμοσ m(). Διαβάηουμε τθν τιμι του ( θ διάςταςθ του Πίνακα Α )..
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4. Να γίνει πρόγραμμα το οποίο να επιλφει το Διαγώνιο Σφςτθμα: A ι το ςφςτθμα : ι ςε μορφι εξιςώςεων το ςφςτθμα : Αλγόρικμοσ m(). Διαβάηουμε τθν τιμι του ( θ διάςταςθ του Πίνακα Α )..
8 τριγωνομετρία. βαςικζσ ζννοιεσ. γ ςφω. εφω και γ. κεφάλαιο
 κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R
 Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 6 η : Η Μζθοδοσ Μ και η Μζθοδοσ των Δφο Φάςεων Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 6 η : Η Μζθοδοσ Μ και η Μζθοδοσ των Δφο Φάςεων Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium V
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Πανεπιςτιμιο Κφπρου ΟΙΚ 223: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων:
 Πανεπιςτιμιο Κφπρου ΟΙΚ 3: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων: Φάμπιο Αντωνίου τοιχεία Επικοινωνίασ: email: fantoniou@aueb.gr ; fabio@ucy.ac.cy Σθλ:893683 Προςωπικι Ιςτοςελίδα: fantoniou.wordpress.com
Πανεπιςτιμιο Κφπρου ΟΙΚ 3: Μακθματικά για οικονομολόγουσ ΙΙ Διδάςκων: Φάμπιο Αντωνίου τοιχεία Επικοινωνίασ: email: fantoniou@aueb.gr ; fabio@ucy.ac.cy Σθλ:893683 Προςωπικι Ιςτοςελίδα: fantoniou.wordpress.com
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
ΑΝΣΙΣΡΟΦΗ ΤΝΑΡΣΗΗ. f y x y f A αντιςτοιχίηεται ςτο μοναδικό x A για το οποίο. Παρατθριςεισ Ιδιότθτεσ τθσ αντίςτροφθσ ςυνάρτθςθσ 1. Η. f A τθσ f.
 .. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
.. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα
 Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO
 ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO Το Micro Worlds Pro είναι ζνα ολοκλθρωμζνο περιβάλλον προγραμματιςμοφ. Χρθςιμοποιεί τθ γλϊςςα προγραμματιςμοφ Logo (εξελλθνιςμζνθ) Το Micro Worlds Pro περιλαμβάνει
ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO Το Micro Worlds Pro είναι ζνα ολοκλθρωμζνο περιβάλλον προγραμματιςμοφ. Χρθςιμοποιεί τθ γλϊςςα προγραμματιςμοφ Logo (εξελλθνιςμζνθ) Το Micro Worlds Pro περιλαμβάνει
Ηλεκτρονικι Επιχειρθςιακι Δράςθ Εργαςτιριο 1
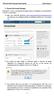 1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
Διάδοση θερμότητας σε μία διάσταση
 Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Διάδοση θερμότητας σε μία διάσταση Η θεωρητική μελζτη που ακολουθεί πραγματοποιήθηκε με αφορμή την εργαςτηριακή άςκηςη μζτρηςησ του ςυντελεςτή θερμικήσ αγωγιμότητασ του αλουμινίου, ςτην οποία διαγωνίςτηκαν
Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων. (v.1.0.7)
 Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων (v.1.0.7) 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ ςτθλών βιβλίου Εςόδων - Εξόδων.
Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων (v.1.0.7) 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ ςτθλών βιβλίου Εςόδων - Εξόδων.
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R
 Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 2 η : Ειςαγωγή ςτον Γραμμικό Προγραμματιςμό Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Επιχειρηςιακή Ζρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 2 η : Ειςαγωγή ςτον Γραμμικό Προγραμματιςμό Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό. μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ
 Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Άςκθςθ 1θ: Να γραφεί αλγόρικμοσ που κα δθμιουργεί με τθ βοικεια διπλοφ επαναλθπτικοφ βρόχου, τον ακόλουκο διςδιάςτατο πίνακα:
 2 ο Σετ Ασκήσεων Δομές Δεδομένων - Πίνακες Άςκθςθ 1θ: Να γραφεί αλγόρικμοσ που κα δθμιουργεί με τθ βοικεια διπλοφ επαναλθπτικοφ βρόχου, τον ακόλουκο διςδιάςτατο πίνακα: 2 3 4 5 3 4 5 6 4 5 6 7 5 6 7 8
2 ο Σετ Ασκήσεων Δομές Δεδομένων - Πίνακες Άςκθςθ 1θ: Να γραφεί αλγόρικμοσ που κα δθμιουργεί με τθ βοικεια διπλοφ επαναλθπτικοφ βρόχου, τον ακόλουκο διςδιάςτατο πίνακα: 2 3 4 5 3 4 5 6 4 5 6 7 5 6 7 8
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
17. Πολυδιάςτατοι πίνακεσ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 17. Πολυδιάςτατοι πίνακεσ Ιωάννθσ Κατάκθσ Πολυδιάςτατοι πίνακεσ o Μζχρι τϊρα μιλοφςαμε για μονοδιάςτατουσ πίνακεσ ι int age[5]= 31,28,31,30,31; o Για παράλλθλουσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 17. Πολυδιάςτατοι πίνακεσ Ιωάννθσ Κατάκθσ Πολυδιάςτατοι πίνακεσ o Μζχρι τϊρα μιλοφςαμε για μονοδιάςτατουσ πίνακεσ ι int age[5]= 31,28,31,30,31; o Για παράλλθλουσ
Δείκτεσ απόδοςθσ υλικών
 Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
Δείκτεσ απόδοςθσ υλικών Κάκε ςυνδυαςμόσ λειτουργίασ, περιοριςμϊν και ςτόχων, οδθγεί ςε ζνα μζτρο τθσ απόδοςθσ τθσ λειτουργίασ του εξαρτιματοσ και περιζχει μια ομάδα ιδιοτιτων των υλικϊν. Αυτι θ ομάδα των
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 5: Γνωριμία με το λογιςμικό του υπολογιςτι
 ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 5: Γνωριμία με το λογιςμικό του υπολογιςτι Λογιςμικό (Software), Πρόγραμμα (Programme ι Program), Προγραμματιςτισ (Programmer), Λειτουργικό Σφςτθμα (Operating
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 5: Γνωριμία με το λογιςμικό του υπολογιςτι Λογιςμικό (Software), Πρόγραμμα (Programme ι Program), Προγραμματιςτισ (Programmer), Λειτουργικό Σφςτθμα (Operating
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Διαχείριςθ του φακζλου "public_html" ςτο ΠΣΔ
 Διαχείριςθ του φακζλου "public_html" ςτο ΠΣΔ Οι παρακάτω οδθγίεσ αφοροφν το χριςτθ webdipe. Για διαφορετικό λογαριαςμό χρθςιμοποιιςτε κάκε φορά το αντίςτοιχο όνομα χριςτθ. = πατάμε αριςτερό κλικ ςτο Επιςκεφκείτε
Διαχείριςθ του φακζλου "public_html" ςτο ΠΣΔ Οι παρακάτω οδθγίεσ αφοροφν το χριςτθ webdipe. Για διαφορετικό λογαριαςμό χρθςιμοποιιςτε κάκε φορά το αντίςτοιχο όνομα χριςτθ. = πατάμε αριςτερό κλικ ςτο Επιςκεφκείτε
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων
 Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 5 η : Μερικι Παράγωγοσ Ι Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 5 η : Μερικι Παράγωγοσ Ι Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Η θεωρία τησ ςτατιςτικήσ ςε ερωτήςεισ-απαντήςεισ Μέροσ 1 ον (έωσ ομαδοποίηςη δεδομένων)
 1)Πώσ ορύζεται η Στατιςτικό επιςτόμη; Στατιςτικι είναι ζνα ςφνολο αρχϊν και μεκοδολογιϊν για: το ςχεδιαςμό τθσ διαδικαςίασ ςυλλογισ δεδομζνων τθ ςυνοπτικι και αποτελεςματικι παρουςίαςι τουσ τθν ανάλυςθ
1)Πώσ ορύζεται η Στατιςτικό επιςτόμη; Στατιςτικι είναι ζνα ςφνολο αρχϊν και μεκοδολογιϊν για: το ςχεδιαςμό τθσ διαδικαςίασ ςυλλογισ δεδομζνων τθ ςυνοπτικι και αποτελεςματικι παρουςίαςι τουσ τθν ανάλυςθ
ΑΝΑΠΣΤΞΘ ΕΦΑΡΜΟΓΩΝ Ε ΠΡΟΓΡΑΜΜΑΣΙΣΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 3 ο ΓΕΝΙΚΟ ΛΤΚΕΙΟ Ν. ΜΤΡΝΘ- ΕΠΙΜΕΛΕΙΑ: ΠΤΡΙΔΑΚΘ Λ.
 Ερωτήςεισ Προβλήματα Α. Σημειώςτε δεξιά από κάθε πρόταςη το γράμμα Σ αν η πρόταςη είναι ςωςτή και το γράμμα Λ αν είναι λάθοσ. 1. Θ περατότθτα ενόσ αλγορίκμου αναφζρεται ςτο γεγονόσ ότι καταλιγει ςτθ λφςθ
Ερωτήςεισ Προβλήματα Α. Σημειώςτε δεξιά από κάθε πρόταςη το γράμμα Σ αν η πρόταςη είναι ςωςτή και το γράμμα Λ αν είναι λάθοσ. 1. Θ περατότθτα ενόσ αλγορίκμου αναφζρεται ςτο γεγονόσ ότι καταλιγει ςτθ λφςθ
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 11 η : Μζγιςτα και Ελάχιςτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 11 η : Μζγιςτα και Ελάχιςτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΧΗΥΙΑΚΟ ΔΚΠΑΙΔΔΤΣΙΚΟ ΒΟΗΘΗΜΑ «ΥΤΙΚΗ ΘΔΣΙΚΗ ΚΑΙ ΣΔΦΝΟΛΟΓΙΚΗ ΚΑΣΔΤΘΤΝΗ» ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΑΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΑΤΔΥΘΥΝΣΗΣ ΘΔΜΑ Α ΘΔΜΑ Β
 4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
4 o ΔΙΓΩΝΙΜ ΠΡΙΛΙΟ 04: ΔΝΔΔΙΚΣΙΚΔ ΠΝΣΗΔΙ ΦΥΣΙΚΗ ΘΔΤΙΚΗΣ ΚΙ ΤΔΧΝΟΛΟΓΙΚΗΣ ΚΤΔΥΘΥΝΣΗΣ 4 ο ΔΙΓΩΝΙΣΜ ΔΝΔΔΙΚΤΙΚΔΣ ΠΝΤΗΣΔΙΣ ΘΔΜ. β. β 3. α 4. γ 5. α.σ β.σ γ.λ δ.σ ε.λ. ΘΔΜ Β Σωςτι είναι θ απάντθςθ γ. Έχουμε ελαςτικι
Επιχειρθςιακι Ζρευνα και εφαρμογζσ με τθν χριςθ του λογιςμικοφ R
 Επιχειρθςιακι Ζρευνα και εφαρμογζσ με τθν χριςθ του λογιςμικοφ R Ενότθτα 3 θ : Γραφικι Επίλυςθ και Ανάλυςθ Ευαιςκθςίασ Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Επιχειρθςιακι Ζρευνα και εφαρμογζσ με τθν χριςθ του λογιςμικοφ R Ενότθτα 3 θ : Γραφικι Επίλυςθ και Ανάλυςθ Ευαιςκθςίασ Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ
Ιδιότθτεσ πεδίων Γενικζσ.
 Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Παπαδρακάκθσ Μανόλθσ Θζμα ΙI Στατικι ΙΙΙ Καρακίτςιοσ Παναγιϊτθσ. Εθνικό Μετςόβιο Πολυτεχνείο Ακαδημαϊκό ζτοσ χολή Πολιτικϊν Μηχανικϊν
 Εθνικό Μετςόβιο Πολυτεχνείο Ακαδημαϊκό ζτοσ 2010-2011 χολή Πολιτικϊν Μηχανικϊν 6 ο εξάμηνο Σομζασ Δομοςτατικήσ Μάθημα: τατική ΙΙΙ (Ανάλυςη Ραβδωτϊν Φορζων φγχρονεσ Μζθοδοι) Παπαδρακάκησ Μανόλησ Καθηγητήσ
Εθνικό Μετςόβιο Πολυτεχνείο Ακαδημαϊκό ζτοσ 2010-2011 χολή Πολιτικϊν Μηχανικϊν 6 ο εξάμηνο Σομζασ Δομοςτατικήσ Μάθημα: τατική ΙΙΙ (Ανάλυςη Ραβδωτϊν Φορζων φγχρονεσ Μζθοδοι) Παπαδρακάκησ Μανόλησ Καθηγητήσ
Ενδεικτικζσ Λφςεισ Θεμάτων
 c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
c AM (t) x(t) ΤΕΙ Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σειρά Β Ειςηγητήσ: Δρ Απόςτολοσ Γεωργιάδησ ΕΠΙΚΟΙΝΩΝΙΕΣ Ι Ενδεικτικζσ Λφςεισ Θεμάτων Θζμα 1 ο (1 μον.) Ζςτω περιοδικό ςιμα πλθροφορίασ με περίοδο.
x n D 2 ENCODER m - σε n (m 2 n ) x 1 Παραδείγματα κωδικοποιθτϊν είναι ο κωδικοποιθτισ οκταδικοφ ςε δυαδικό και ο κωδικοποιθτισ BCD ςε δυαδικό.
 Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
ΕΝΟΤΘΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΘ. ΚΕΦΑΛΑΙΟ 6: Θ «Βοικεια» ςτον Υπολογιςτι
 ΕΝΟΤΘΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΘ ΚΕΦΑΛΑΙΟ 6: Θ «Βοικεια» ςτον Υπολογιςτι Βοικεια (Help), Ευρετιριο, Κόμβοσ, Λζξθ κλειδί, Σφνδεςμόσ, Υπερκείμενο Τι είναι θ «Βοικεια» ςτουσ υπολογιςτζσ; Πώσ ενεργοποιοφμε
ΕΝΟΤΘΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΘ ΚΕΦΑΛΑΙΟ 6: Θ «Βοικεια» ςτον Υπολογιςτι Βοικεια (Help), Ευρετιριο, Κόμβοσ, Λζξθ κλειδί, Σφνδεςμόσ, Υπερκείμενο Τι είναι θ «Βοικεια» ςτουσ υπολογιςτζσ; Πώσ ενεργοποιοφμε
Πειραματικι Ψυχολογία (ΨΧ66)
 Πειραματικι Ψυχολογία (ΨΧ66) Διάλεξη 7 Σεχνικζσ για τθν επίτευξθ ςτακερότθτασ Πζτροσ Ροφςςοσ Μζθοδοι για την επίτευξη του ελζγχου Μζςω του κατάλλθλου ςχεδιαςμοφ του πειράματοσ (ςτόχοσ είναι θ εξάλειψθ
Πειραματικι Ψυχολογία (ΨΧ66) Διάλεξη 7 Σεχνικζσ για τθν επίτευξθ ςτακερότθτασ Πζτροσ Ροφςςοσ Μζθοδοι για την επίτευξη του ελζγχου Μζςω του κατάλλθλου ςχεδιαςμοφ του πειράματοσ (ςτόχοσ είναι θ εξάλειψθ
ΔΟΜΗ ΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αςκήςεισ με ψευδογλώςςα/ διάγραμμα ροήσ. Αντώνης Μαϊργιώτης
 ΔΟΜΗ ΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αςκήςεισ με ψευδογλώςςα/ διάγραμμα ροήσ Αντώνης Μαϊργιώτης Να γραφεί αλγόριθμοσ με τη βοήθεια διαγράμματοσ ροήσ, που να υπολογίζει το εμβαδό Ε ενόσ τετραγώνου με μήκοσ Α. ΑΡΧΗ ΔΙΑΒΑΣΕ
ΔΟΜΗ ΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Αςκήςεισ με ψευδογλώςςα/ διάγραμμα ροήσ Αντώνης Μαϊργιώτης Να γραφεί αλγόριθμοσ με τη βοήθεια διαγράμματοσ ροήσ, που να υπολογίζει το εμβαδό Ε ενόσ τετραγώνου με μήκοσ Α. ΑΡΧΗ ΔΙΑΒΑΣΕ
Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ
 Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ διαδικαςίασ αυτόματησ δημιουργίασ ςτηλών και αντιςτοίχιςησ
Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ διαδικαςίασ αυτόματησ δημιουργίασ ςτηλών και αντιςτοίχιςησ
Δυναμικι Μθχανϊν I. Διάλεξθ 16. Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ
 Δυναμικι Μθχανϊν I Διάλεξθ 16 Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ 1 Ανακοινϊςεισ Office Hours: Δευτζρα 1-3 μμ, Εργαςτιριο Εμβιομθχανικισ, Ιςόγειο Κτθρίου Μ (210 772-1516) DMmeche2013@gmail.com
Δυναμικι Μθχανϊν I Διάλεξθ 16 Χειμερινό Εξάμθνο 2013 Τμιμα Μθχανολόγων Μθχ., ΕΜΠ 1 Ανακοινϊςεισ Office Hours: Δευτζρα 1-3 μμ, Εργαςτιριο Εμβιομθχανικισ, Ιςόγειο Κτθρίου Μ (210 772-1516) DMmeche2013@gmail.com
Απάντηση ΘΕΜΑ1 ΘΕΜΑ2. t=t 1 +T/2. t=t 1 +3T/4. t=t 1 +T ΔΙΑΓΩΝΙΣΜΑ ΣΕ ΤΑΛΑΝΤΩΣΕΙΣ-ΚΥΜΑΤΑ 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ).
 Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Απάντηση ΘΕΜΑ1 1) (Β), 2. (Γ), 3. (Γ), 4. (Γ), 5. (Δ). ΘΕΜΑ2 Α)Ανάκλαςθ ςε ακίνθτο άκρο. Το προςπίπτον κφμα ςε χρόνο Τ/2 κα ζχει μετακινθκεί προσ τα δεξιά κατά 2 τετράγωνα όπωσ φαίνεται ςτο ςχιμα. Για
Διαχείριςη Αριθμοδεικτών (v.1.0.7)
 Διαχείριςη Αριθμοδεικτών (v.1.0.7) Περιεχόμενα 1. Μενοφ... 5 1.1 Αρικμοδείκτεσ.... 5 1.1.1 Δθμιουργία Αρικμοδείκτθ... 6 1.1.2 Αντιγραφι Αρικμοδείκτθ... 11 2. Παράμετροι... 12 2.1.1 Κατθγορίεσ Αρικμοδεικτϊν...
Διαχείριςη Αριθμοδεικτών (v.1.0.7) Περιεχόμενα 1. Μενοφ... 5 1.1 Αρικμοδείκτεσ.... 5 1.1.1 Δθμιουργία Αρικμοδείκτθ... 6 1.1.2 Αντιγραφι Αρικμοδείκτθ... 11 2. Παράμετροι... 12 2.1.1 Κατθγορίεσ Αρικμοδεικτϊν...
Αυτόνομοι Πράκτορες. Αναφορά Εργασίας Εξαμήνου. Το αστέρι του Aibo και τα κόκαλα του
 Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
Αυτόνομοι Πράκτορες Αναφορά Εργασίας Εξαμήνου Το αστέρι του Aibo και τα κόκαλα του Jaohar Osman Η πρόταςθ εργαςίασ που ζκανα είναι το παρακάτω κείμενο : - ξ Aibo αγαπάει πάρα πξλύ ρα κόκαλα και πάμρα ρα
Ιςίδωροσ Ροδομαγουλάκθσ Αλγόρικμοι Δικτφων και Πολυπλοκότθτα K-median
 Ιςίδωροσ Ροδομαγουλάκθσ Αλγόρικμοι Δικτφων και Πολυπλοκότθτα 00-0 K-median Επιςκόπθςθ του κεφαλαίου 5 από το βιβλίο «Approximation algorithms» του V. Vazirani 56 c c 6 c c Metric Uncapacitated Facility
Ιςίδωροσ Ροδομαγουλάκθσ Αλγόρικμοι Δικτφων και Πολυπλοκότθτα 00-0 K-median Επιςκόπθςθ του κεφαλαίου 5 από το βιβλίο «Approximation algorithms» του V. Vazirani 56 c c 6 c c Metric Uncapacitated Facility
Ανάλυςη κλειςτϊν δικτφων
 Ανάλυςη κλειςτϊν δικτφων Θ ανάλυςθ κλειςτϊν δικτφων ςτθρίηεται ςτθ διατιρθςθ τθσ μάηασ και τθσ ενζργειασ. Σε ζνα τυπικό βρόχο ABCDA υπάρχει ζνασ αρικμόσ από κόμβουσ, εδϊ A,B,C,D, ςτουσ οποίουσ ιςχφει θ
Ανάλυςη κλειςτϊν δικτφων Θ ανάλυςθ κλειςτϊν δικτφων ςτθρίηεται ςτθ διατιρθςθ τθσ μάηασ και τθσ ενζργειασ. Σε ζνα τυπικό βρόχο ABCDA υπάρχει ζνασ αρικμόσ από κόμβουσ, εδϊ A,B,C,D, ςτουσ οποίουσ ιςχφει θ
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
1. Εγκατάςταςη κειμενογράφου JCE
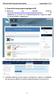 1. Εγκατάςταςη κειμενογράφου JCE 1.1. Πθγαίνουμε ςτθν ακόλουκθ διεφκυνςθ https://www.joomlacontenteditor.net/downloads/editor/joomla-3 και κατεβάηουμε τον JCE Editor 2.5.8. Εναλλακτικά βρίςκουμε το αρχείο
1. Εγκατάςταςη κειμενογράφου JCE 1.1. Πθγαίνουμε ςτθν ακόλουκθ διεφκυνςθ https://www.joomlacontenteditor.net/downloads/editor/joomla-3 και κατεβάηουμε τον JCE Editor 2.5.8. Εναλλακτικά βρίςκουμε το αρχείο
Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία).
 Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία). Από τθν τράπεηα κεμάτων Α_ΧΘΜ_0_20651 Διακζτουμε υδατικό διάλυμα (Δ1) KOH 0,1 Μ. α)να υπολογίςετε τθν % w/v περιεκτικότθτα του
Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία). Από τθν τράπεηα κεμάτων Α_ΧΘΜ_0_20651 Διακζτουμε υδατικό διάλυμα (Δ1) KOH 0,1 Μ. α)να υπολογίςετε τθν % w/v περιεκτικότθτα του
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ. Φιλιοποφλου Ειρινθ
 ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
Γράφοι. Δομζσ Δεδομζνων Διάλεξθ 9
 Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
Γράφοι Δομζσ Δεδομζνων Διάλεξθ 9 Περιεχόμενα Γράφοι Γενικζσ ζννοιεσ, οριςμόσ, κτλ Παραδείγματα Γράφων Αποκικευςθ Γράφων Βαςικοί Οριςμοί Γράφοι και Δζντρα Διάςχιςθ Γράφων Περιοδεφων Πωλθτισ Γράφοι Οριςμόσ:
Πολυπλέκτες. 0 x 0 F = S x 0 + Sx 1 1 x 1
 Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Γενικά Μακθματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Ενότθτα 8 θ : Σειρζσ Taylor και Πεπλεγμζνεσ Συναρτιςεισ Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χριςθσ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Ενότθτα 8 θ : Σειρζσ Taylor και Πεπλεγμζνεσ Συναρτιςεισ Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χριςθσ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΜΑ032: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Εαρινό εξάμηνο , Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, 21 Μαρτίου, 2012 Διάρκεια: 2 ώρεσ
 ΜΑ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Εαρινό εξάμηνο -, Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Μαρτίου, Διάρκεια: ώρεσ ΟΝΟΜΑ: Αρ. Πολ. Σαυτ. Πρόβλημα. Θεωροφμε τα διανφςματα u =,,,, v =,,,4, w =,,,, (α) Υπολογίςτε
ΜΑ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Εαρινό εξάμηνο -, Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Μαρτίου, Διάρκεια: ώρεσ ΟΝΟΜΑ: Αρ. Πολ. Σαυτ. Πρόβλημα. Θεωροφμε τα διανφςματα u =,,,, v =,,,4, w =,,,, (α) Υπολογίςτε
Μετατροπι Αναλογικοφ Σιματοσ ςε Ψθφιακό. Διάλεξθ 10
 Μετατροπι Αναλογικοφ Σιματοσ ςε Ψθφιακό Διάλεξθ 10 Γενικό Σχιμα Μετατροπζασ Αναλογικοφ ςε Ψθφιακό Ψθφιακό Τθλεπικοινωνιακό Κανάλι Μετατροπζασ Ψθφιακοφ ςε Αναλογικό Τα αναλογικά ςιματα μετατρζπονται ςε
Μετατροπι Αναλογικοφ Σιματοσ ςε Ψθφιακό Διάλεξθ 10 Γενικό Σχιμα Μετατροπζασ Αναλογικοφ ςε Ψθφιακό Ψθφιακό Τθλεπικοινωνιακό Κανάλι Μετατροπζασ Ψθφιακοφ ςε Αναλογικό Τα αναλογικά ςιματα μετατρζπονται ςε
ΧΡΟΝΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ ΧΟΝΙΚΟΣ ΡΟΓΑΜΜΑΤΙΣΜΟΣ
 ΧΡΟΝΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ ΧΟΝΙΚΟΣ ΡΟΓΑΜΜΑΤΙΣΜΟΣ 1 Συςτήματα Παραγωγήσ Θςμάζηε ηεν ηαξινόμεζε ηων ζςζηεμάηων παπαγωγήρ; Για κάκε κατθγορία ςυςτθμάτων, εκτόσ από το ςτρατθγικό πρόβλθμα του μακροπρόκεςμου ςχεδιαςμοφ
ΧΡΟΝΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ ΧΟΝΙΚΟΣ ΡΟΓΑΜΜΑΤΙΣΜΟΣ 1 Συςτήματα Παραγωγήσ Θςμάζηε ηεν ηαξινόμεζε ηων ζςζηεμάηων παπαγωγήρ; Για κάκε κατθγορία ςυςτθμάτων, εκτόσ από το ςτρατθγικό πρόβλθμα του μακροπρόκεςμου ςχεδιαςμοφ
Ενδεικτική Οργάνωςη Ενοτήτων. Α Σάξη. Διδ. 1 ΕΝΟΣΗΣΑ 1. 6 Ομαδοποίθςθ, Μοτίβα,
 Ενδεικτική Οργάνωςη Ενοτήτων Α Σάξη Α/ Μαθηματικό περιεχόμενο Δείκτεσ Επιτυχίασ Ώρεσ Α Διδ. 1 ΕΝΟΣΗΣΑ 1 Αλ1.1 υγκρίνουν και ταξινομοφν αντικείμενα ςφμφωνα με κάποιο χαρακτθριςτικό/κριτιριο/ιδιότθτά Ομαδοποίθςθ,
Ενδεικτική Οργάνωςη Ενοτήτων Α Σάξη Α/ Μαθηματικό περιεχόμενο Δείκτεσ Επιτυχίασ Ώρεσ Α Διδ. 1 ΕΝΟΣΗΣΑ 1 Αλ1.1 υγκρίνουν και ταξινομοφν αντικείμενα ςφμφωνα με κάποιο χαρακτθριςτικό/κριτιριο/ιδιότθτά Ομαδοποίθςθ,
Αςφάλεια και Προςταςία Δεδομζνων
 Αςφάλεια και Προςταςία Δεδομζνων Κρυπτογράφθςθ υμμετρικι και Αςφμμετρθ Κρυπτογραφία Αλγόρικμοι El Gamal Diffie - Hellman Σςιρόπουλοσ Γεώργιοσ ΣΙΡΟΠΟΤΛΟ ΓΕΩΡΓΙΟ 1 υμμετρικι Κρυπτογραφία υμμετρικι (Κλαςικι)
Αςφάλεια και Προςταςία Δεδομζνων Κρυπτογράφθςθ υμμετρικι και Αςφμμετρθ Κρυπτογραφία Αλγόρικμοι El Gamal Diffie - Hellman Σςιρόπουλοσ Γεώργιοσ ΣΙΡΟΠΟΤΛΟ ΓΕΩΡΓΙΟ 1 υμμετρικι Κρυπτογραφία υμμετρικι (Κλαςικι)
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 13 η : Επαναλθπτικι Ενότθτα Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Ειςαγωγι ςτθν Τεχνολογία Αυτοματιςμοφ
 ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑIΟΤ & ΑΕΙ ΠΕΙΡΑΙΑ Σ.Σ. Σμήματα Ναυτιλίας και Επιχειρηματικών Τπηρεσιών & Μηχ. Αυτοματισμού ΣΕ Ειςαγωγι ςτθν Τεχνολογία Αυτοματιςμοφ Ενότθτα # 7: Συςτιματα Ελζγχου Μόνιμο ςφάλμα Ευςτάκεια
ΠΑΝΕΠΙΣΗΜΙΟ ΑΙΓΑIΟΤ & ΑΕΙ ΠΕΙΡΑΙΑ Σ.Σ. Σμήματα Ναυτιλίας και Επιχειρηματικών Τπηρεσιών & Μηχ. Αυτοματισμού ΣΕ Ειςαγωγι ςτθν Τεχνολογία Αυτοματιςμοφ Ενότθτα # 7: Συςτιματα Ελζγχου Μόνιμο ςφάλμα Ευςτάκεια
ΕΦΑΡΜΟΓΖσ ΒΆΕΩΝ ΔΕΔΟΜΖΝΩΝ ΚΑΙ ΔΙΑΔΙΚΣΥΟΤ. Ειρινθ Φιλιοποφλου
 ΕΦΑΡΜΟΓΖσ ΒΆΕΩΝ ΔΕΔΟΜΖΝΩΝ ΚΑΙ ΔΙΑΔΙΚΣΥΟΤ Ειρινθ Φιλιοποφλου Ειςαγωγι Ο Παγκόςμιοσ Ιςτόσ (World Wide Web - WWW) ι πιο απλά Ιςτόσ (Web) είναι μία αρχιτεκτονικι για τθν προςπζλαςθ διαςυνδεδεμζνων εγγράφων
ΕΦΑΡΜΟΓΖσ ΒΆΕΩΝ ΔΕΔΟΜΖΝΩΝ ΚΑΙ ΔΙΑΔΙΚΣΥΟΤ Ειρινθ Φιλιοποφλου Ειςαγωγι Ο Παγκόςμιοσ Ιςτόσ (World Wide Web - WWW) ι πιο απλά Ιςτόσ (Web) είναι μία αρχιτεκτονικι για τθν προςπζλαςθ διαςυνδεδεμζνων εγγράφων
ΑΡΙΘΜΗΣΙΚΕ ΜΕΘΟΔΟΙ ΤΨΗΛΗ ΣΑΞΗ ΓΙΑ ΣΗΝ ΕΠΙΛΤΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΩΕΩΝ ΚΑΙ ΤΣΗΜΑΣΩΝ ΕΚΣΙΜΗΗ ΦΑΛΜΑΣΩΝ ΕΦΑΡΜΟΓΕ ΜΕ ΠΡΟΓΡΑΜΜΑΣΑ Ε MATLAB
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΣΜΗΜΑ ΜΑΘΗΜΑΣΙΚΩΝ ΜΕΣΑΠΣΤΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΠΟΤΔΩΝ ΘΕΩΡΗΣΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ & ΘΕΩΡΙΑ ΤΣΗΜΑΣΩΝ ΚΑΙ ΕΛΕΓΧΟΤ ΑΡΙΘΜΗΣΙΚΕ ΜΕΘΟΔΟΙ ΤΨΗΛΗ ΣΑΞΗ ΓΙΑ ΣΗΝ ΕΠΙΛΤΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΩΕΩΝ ΚΑΙ
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΣΜΗΜΑ ΜΑΘΗΜΑΣΙΚΩΝ ΜΕΣΑΠΣΤΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΠΟΤΔΩΝ ΘΕΩΡΗΣΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ & ΘΕΩΡΙΑ ΤΣΗΜΑΣΩΝ ΚΑΙ ΕΛΕΓΧΟΤ ΑΡΙΘΜΗΣΙΚΕ ΜΕΘΟΔΟΙ ΤΨΗΛΗ ΣΑΞΗ ΓΙΑ ΣΗΝ ΕΠΙΛΤΗ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΩΕΩΝ ΚΑΙ
ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΙΚΗΣ ΛΟΓΙΚΗΣ
 ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΙΚΗΣ ΛΟΓΙΚΗΣ Λογικι πρόταςθ: Με τον όρο λογικι πρόταςθ (ι απλά πρόταςθ) ςτα μακθματικά, εννοοφμε μια ζκφραςθ με πλιρεσ νόθμα που δζχεται τον χαρακτθριςμό ι μόνο αλθκισ ι μόνο ψευδισ. Παραδείγματα:
ΣΤΟΙΧΕΙΑ ΜΑΘΗΜΑΤΙΚΗΣ ΛΟΓΙΚΗΣ Λογικι πρόταςθ: Με τον όρο λογικι πρόταςθ (ι απλά πρόταςθ) ςτα μακθματικά, εννοοφμε μια ζκφραςθ με πλιρεσ νόθμα που δζχεται τον χαρακτθριςμό ι μόνο αλθκισ ι μόνο ψευδισ. Παραδείγματα:
Τμήματα Μνήμησ Υπολογιςμόσ Φυςικών διευθύνςεων. Εκπαιδεφτρια: Μαρία Πολίτθ
 Τμήματα Μνήμησ Υπολογιςμόσ Φυςικών διευθύνςεων Εκπαιδεφτρια: Μαρία Πολίτθ Σύνδεςη με προηγούμενα Κάκε μονάδα ενόσ υπολογιςτι που χρθςιμεφει για τθ μόνιμθ ι προςωρινι αποκικευςθ δεδομζνων ανικει ςτθ μνήμη
Τμήματα Μνήμησ Υπολογιςμόσ Φυςικών διευθύνςεων Εκπαιδεφτρια: Μαρία Πολίτθ Σύνδεςη με προηγούμενα Κάκε μονάδα ενόσ υπολογιςτι που χρθςιμεφει για τθ μόνιμθ ι προςωρινι αποκικευςθ δεδομζνων ανικει ςτθ μνήμη
Modellus 4.01 Συ ντομοσ Οδηγο σ
 Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Μθχανζσ Διανυςμάτων Υποςτιριξθσ Support Vector Machines. Κϊςτασ Διαμαντάρασ Τμιμα Ρλθροφορικισ ΤΕΙ Θεςςαλονίκθσ
 Μθχανζσ Διανυςμάτων Υποςτιριξθσ Support Vector Machines Κϊςτασ Διαμαντάρασ Τμιμα Ρλθροφορικισ ΤΕΙ Θεςςαλονίκθσ Γραμμικόσ διαχωριςμόσ κλάςεων Ξαναμελετάμε το πρόβλθμα του γραμμικοφ διαχωριςμοφ κλάςεων C,
Μθχανζσ Διανυςμάτων Υποςτιριξθσ Support Vector Machines Κϊςτασ Διαμαντάρασ Τμιμα Ρλθροφορικισ ΤΕΙ Θεςςαλονίκθσ Γραμμικόσ διαχωριςμόσ κλάςεων Ξαναμελετάμε το πρόβλθμα του γραμμικοφ διαχωριςμοφ κλάςεων C,
Γ' ΛΥΚΕΙΟΥ Η ΤΑΞΗ ΤΗΣ ΤΕΛΙΚΗΣ ΕΠΙΛΟΓΗΣ. Στθ ΓϋΛυκείου οι Ομάδεσ Προςανατολιςμοφ είναι τρεισ:
 Γ' ΛΥΚΕΙΟΥ Η ΤΑΞΗ ΤΗΣ ΤΕΛΙΚΗΣ ΕΠΙΛΟΓΗΣ Στθ ΓϋΛυκείου οι Ομάδεσ Προςανατολιςμοφ είναι τρεισ: 1. Ομάδα Ανκρωπιςτικών Σπουδών 2. Ομάδα Οικονομικών, Πολιτικών, Κοινωνικών & Παιδαγωγικών Σπουδών 3. Ομάδα Θετικών
Γ' ΛΥΚΕΙΟΥ Η ΤΑΞΗ ΤΗΣ ΤΕΛΙΚΗΣ ΕΠΙΛΟΓΗΣ Στθ ΓϋΛυκείου οι Ομάδεσ Προςανατολιςμοφ είναι τρεισ: 1. Ομάδα Ανκρωπιςτικών Σπουδών 2. Ομάδα Οικονομικών, Πολιτικών, Κοινωνικών & Παιδαγωγικών Σπουδών 3. Ομάδα Θετικών
Megatron ERP Βάςη δεδομζνων Π/Φ - κατηγοριοποίηςη Databox
 Megatron ERP Βάςη δεδομζνων Π/Φ - κατηγοριοποίηςη Databox 03 05 ΙΛΤΔΑ ΠΛΗΡΟΦΟΡΙΚΗ Α.Ε. αρμά Ιηαμπζλλα Βαρλάμθσ Νίκοσ Ειςαγωγι... 1 Σι είναι το Databox...... 1 Πότε ανανεϊνεται...... 1 Μπορεί να εφαρμοςτεί
Megatron ERP Βάςη δεδομζνων Π/Φ - κατηγοριοποίηςη Databox 03 05 ΙΛΤΔΑ ΠΛΗΡΟΦΟΡΙΚΗ Α.Ε. αρμά Ιηαμπζλλα Βαρλάμθσ Νίκοσ Ειςαγωγι... 1 Σι είναι το Databox...... 1 Πότε ανανεϊνεται...... 1 Μπορεί να εφαρμοςτεί
Ονοματεπϊνυμο.. ΔΙΑΓΩΝΙΣΜΑ ΑΕΠΠ
 Ονοματεπϊνυμο.. ΔΙΑΓΩΝΙΣΜΑ ΑΕΠΠ ΘΕΜΑ 1 Ο Α) Ερωτισεις τφπου ωστοφ-λάκους 1. Κάκε βρόχος Για μπορεί να μετατραπεί σε Όσο 2. Κάκε βρόχος που υλοποιείται με τθν εντολι Όσο...επανάλαβε μπορεί να γραφεί και
Ονοματεπϊνυμο.. ΔΙΑΓΩΝΙΣΜΑ ΑΕΠΠ ΘΕΜΑ 1 Ο Α) Ερωτισεις τφπου ωστοφ-λάκους 1. Κάκε βρόχος Για μπορεί να μετατραπεί σε Όσο 2. Κάκε βρόχος που υλοποιείται με τθν εντολι Όσο...επανάλαβε μπορεί να γραφεί και
Virtualization. Στο ςυγκεκριμζνο οδηγό, θα παρουςιαςτεί η ικανότητα δοκιμήσ τησ διανομήσ Ubuntu 9.04, χωρίσ την ανάγκη του format.
 Virtualization Στο ςυγκεκριμζνο οδηγό, θα παρουςιαςτεί η ικανότητα δοκιμήσ τησ διανομήσ Ubuntu 9.04, χωρίσ την ανάγκη του format. Το virtualization πρόκειται για μια τεχνολογία, θ οποία επιτρζπει το διαχωριςμό
Virtualization Στο ςυγκεκριμζνο οδηγό, θα παρουςιαςτεί η ικανότητα δοκιμήσ τησ διανομήσ Ubuntu 9.04, χωρίσ την ανάγκη του format. Το virtualization πρόκειται για μια τεχνολογία, θ οποία επιτρζπει το διαχωριςμό
Γενικά Μαθηματικά ΙΙ
 ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 4 η : Όρια και Συνζχεια Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΟΣΕΛΕΙΟ ΠΑΝΕΠΙΣΗΜΙΟ ΘΕΑΛΟΝΙΚΗ ΑΝΟΙΚΣΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΣΑ Γενικά Μαθηματικά ΙΙ Ενότητα 4 η : Όρια και Συνζχεια Λουκάσ Βλάχοσ Κακθγθτισ Αςτροφυςικισ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται
Λαμβάνοντασ υπόψη ότι κατά την πρόςθεςη δφο δυαδικϊν ψηφίων ιςχφει: Κρατοφμενο
 Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Βάςεισ Δεδομζνων Ι. Ενότητα 12: Κανονικοποίηςη. Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ
 Βάςεισ Δεδομζνων Ι Ενότητα 12: Κανονικοποίηςη Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό
Βάςεισ Δεδομζνων Ι Ενότητα 12: Κανονικοποίηςη Δρ. Τςιμπίρθσ Αλκιβιάδθσ Τμιμα Μθχανικών Πλθροφορικισ ΤΕ Άδειεσ Χρήςησ Το παρόν εκπαιδευτικό υλικό υπόκειται ςε άδειεσ χριςθσ Creative Commons. Για εκπαιδευτικό
 Θ διαδικαςία κοςτολόγθςθσ εφρεςθσ του κόςτουσ παραγωγισ των προϊόντων χωρίηεται ςε διαφορετικζσ τεχνικζσ μεκόδουσ: Α) Την απορροφητική ή πλήρη κοςτολόγηςη Β) Την οριακή ή άμεςη κοςτολόγηςη Απορροφητική
Θ διαδικαςία κοςτολόγθςθσ εφρεςθσ του κόςτουσ παραγωγισ των προϊόντων χωρίηεται ςε διαφορετικζσ τεχνικζσ μεκόδουσ: Α) Την απορροφητική ή πλήρη κοςτολόγηςη Β) Την οριακή ή άμεςη κοςτολόγηςη Απορροφητική
Ανάπτυξη Εφαρμογών με Σχεςιακέσ Βάςεισ Δεδομένων
 Ανάπτυξη Εφαρμογών με Σχεςιακέσ Βάςεισ Δεδομένων Δρ. Θεοδώρου Παύλοσ theodorou@uoc.gr Περιεχόμενα Τι είναι οι Βάςεισ Δεδομζνων (DataBases) Τι είναι Σφςτθμα Διαχείριςθσ Βάςεων Δεδομζνων (DBMS) Οι Στόχοι
Ανάπτυξη Εφαρμογών με Σχεςιακέσ Βάςεισ Δεδομένων Δρ. Θεοδώρου Παύλοσ theodorou@uoc.gr Περιεχόμενα Τι είναι οι Βάςεισ Δεδομζνων (DataBases) Τι είναι Σφςτθμα Διαχείριςθσ Βάςεων Δεδομζνων (DBMS) Οι Στόχοι
Αναφορά Εργαςίασ Nim Game
 Αναφορά Εργαςίασ Nim Game Αυτόνομοι Πράκτορεσ (ΠΛΗ 513) Βαγενάσ Σωτιριοσ 2010030034 Ειςαγωγή Για τθν εργαςία του μακιματοσ αςχολικθκα με το board game Nim. Ρρόκειται για ζνα παιχνίδι δφο παιχτϊν (2-player
Αναφορά Εργαςίασ Nim Game Αυτόνομοι Πράκτορεσ (ΠΛΗ 513) Βαγενάσ Σωτιριοσ 2010030034 Ειςαγωγή Για τθν εργαςία του μακιματοσ αςχολικθκα με το board game Nim. Ρρόκειται για ζνα παιχνίδι δφο παιχτϊν (2-player
ΠΡΟΦΟΡΑ ΖΗΣΗΗ ΚΡΑΣΘΚΗ ΠΑΡΕΜΒΑΗ
 ΠΡΟΦΟΡΑ ΖΗΣΗΗ ΚΡΑΣΘΚΗ ΠΑΡΕΜΒΑΗ 1 Ειςαγωγι: Οι αγοραίεσ δυνάµεισ τθσ προςφοράσ και ηιτθςθσ Προσφορά και Ζήτηση είναι οι πιο γνωςτοί οικονοµικοί όροι. Η λειτουργία των αγορϊν προςδιορίηεται από δφο βαςικζσ
ΠΡΟΦΟΡΑ ΖΗΣΗΗ ΚΡΑΣΘΚΗ ΠΑΡΕΜΒΑΗ 1 Ειςαγωγι: Οι αγοραίεσ δυνάµεισ τθσ προςφοράσ και ηιτθςθσ Προσφορά και Ζήτηση είναι οι πιο γνωςτοί οικονοµικοί όροι. Η λειτουργία των αγορϊν προςδιορίηεται από δφο βαςικζσ
ΗΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ Παράςταςη ςταθεροφ ςημείου Παράςταςη αριθμών κινητοφ ςημείου 2 Παράςταςη ςταθεροφ ςημείου Στθν παράςταςθ αρικμϊν ςτακεροφ ςθμείου (Fixed
Παράςταςη κινητήσ υποδιαςτολήσ Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ Παράςταςη ςταθεροφ ςημείου Παράςταςη αριθμών κινητοφ ςημείου 2 Παράςταςη ςταθεροφ ςημείου Στθν παράςταςθ αρικμϊν ςτακεροφ ςθμείου (Fixed
Slide 1. Εισαγωγή στη ψυχρομετρία
 Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
Slide 1 Εισαγωγή στη ψυχρομετρία 1 Slide 2 Σφντομη ειςαγωγή ςτη ψυχρομετρία. Διάγραμμα Mollier (πίεςησ-ενθαλπίασ P-H) Σο διάγραμμα Mollier είναι μία γραφικι παράςταςθ ςε ζναν άξονα ςυντεταγμζνων γραμμϊν
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε)
 ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε) Γραφικό Περιβάλλον Επικοινωνίασ Περιβάλλον Εντολϊν Γραμμισ (Graphical User Interface/GUI), (Command Line Interface),
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε) Γραφικό Περιβάλλον Επικοινωνίασ Περιβάλλον Εντολϊν Γραμμισ (Graphical User Interface/GUI), (Command Line Interface),
α) Στο μιγαδικό επίπεδο οι εικόνεσ δφο ςυηυγϊν μιγαδικϊν είναι ςθμεία ςυμμετρικά ωσ προσ τον πραγματικό άξονα
 ΘΕΜΑ Α ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΚΑΙ ΕΠΑΛ ΟΜΑΔΑ Β ΔΕΤΣΕΡΑ 8 ΜΑΪΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΘΕΣΙΚΗ ΚΑΙ ΣΕΧΝΟΛΟΓΙΚΗ ΚΑΣΕΤΘΤΝΗ ΤΝΟΛΟ ΕΛΙΔΩΝ: ΣΕΕΡΙ A. Ζςτω μια ςυνάρτθςθ f θ
ΘΕΜΑ Α ΠΑΝΕΛΛΗΝΙΕ ΕΞΕΣΑΕΙ Γ ΣΑΞΗ ΗΜΕΡΗΙΟΤ ΓΕΝΙΚΟΤ ΛΤΚΕΙΟΤ ΚΑΙ ΕΠΑΛ ΟΜΑΔΑ Β ΔΕΤΣΕΡΑ 8 ΜΑΪΟΤ ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΣΙΚΑ ΘΕΣΙΚΗ ΚΑΙ ΣΕΧΝΟΛΟΓΙΚΗ ΚΑΣΕΤΘΤΝΗ ΤΝΟΛΟ ΕΛΙΔΩΝ: ΣΕΕΡΙ A. Ζςτω μια ςυνάρτθςθ f θ
16. Πίνακεσ και Συναρτήςεισ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ
 ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ Οδηγός Χρήσης Εφαρμογής Ελέγχου Προσφορών Αφοφ πιςτοποιθκεί ο λογαριαςμόσ που δθμιουργιςατε ςτο πρόγραμμα ωσ Πάροχοσ Προςφορϊν, κα λάβετε ζνα e-mail με
ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ Οδηγός Χρήσης Εφαρμογής Ελέγχου Προσφορών Αφοφ πιςτοποιθκεί ο λογαριαςμόσ που δθμιουργιςατε ςτο πρόγραμμα ωσ Πάροχοσ Προςφορϊν, κα λάβετε ζνα e-mail με
ΜΑ270: ΑΡΙΘΜΗΣΙΚΗ ΑΝΑΛΤΗ Ι Χειμερινό εξάμθνο , Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Διάρκεια: 2 ώρεσ 21 Νοεμβρίου, 2009
 ΜΑ270: ΑΡΙΘΜΗΣΙΚΗ ΑΝΑΛΤΗ Ι Χειμερινό εξάμθνο 2009-200, Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Διάρκεια: 2 ώρεσ 2 Νοεμβρίου, 2009 ΟΝΟΜΑ: Αρ. Πολ. Σαυτ. Πρόβλθμα Διατυπϊςτε τουσ οριςμοφσ των πιο κάτω:
ΜΑ270: ΑΡΙΘΜΗΣΙΚΗ ΑΝΑΛΤΗ Ι Χειμερινό εξάμθνο 2009-200, Διδάςκων: Γιώργοσ Γεωργίου ΕΝΔΙΑΜΕΗ ΕΞΕΣΑΗ, Διάρκεια: 2 ώρεσ 2 Νοεμβρίου, 2009 ΟΝΟΜΑ: Αρ. Πολ. Σαυτ. Πρόβλθμα Διατυπϊςτε τουσ οριςμοφσ των πιο κάτω:
ΜΑ270: ΑΡΙΘΜΗΣΙΚΗ ΑΝΑΛΤΗ Ι Χειμερινό εξάμηνο
 ΜΑ7: ΑΡΙΘΜΗΣΙΚΗ ΑΝΑΛΤΗ Ι Χειμερινό εξάμηνο 9- η Τπολογιςτική Άςκηςη. Θεωροφμε τθν εξίςωςθ + = (α) Δείξτε γραφικά ότι θ εξίςωςθ ζχει ακριβϊσ μία ρίηα. (β) Τι ςυμβολίηει θ μοναδικι ρίηα τθσ εξίςωςθσ; (γ)
ΜΑ7: ΑΡΙΘΜΗΣΙΚΗ ΑΝΑΛΤΗ Ι Χειμερινό εξάμηνο 9- η Τπολογιςτική Άςκηςη. Θεωροφμε τθν εξίςωςθ + = (α) Δείξτε γραφικά ότι θ εξίςωςθ ζχει ακριβϊσ μία ρίηα. (β) Τι ςυμβολίηει θ μοναδικι ρίηα τθσ εξίςωςθσ; (γ)
HY220 Εργαςτόριο Ψηφιακών Κυκλωμϊτων
 HY220 Εργαςτόριο Ψηφιακών Κυκλωμϊτων Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Κουναλϊκησ, Π. Ματτθαιϊκησ, Δ. Τςαλιαγκόσ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Ρολυδιάςτατοσ Δυαδικόσ Χϊροσ Δυαδικζσ Συναρτιςεισ
HY220 Εργαςτόριο Ψηφιακών Κυκλωμϊτων Διδϊςκων: Χ. Σωτηρύου, Βοηθού: Ε. Κουναλϊκησ, Π. Ματτθαιϊκησ, Δ. Τςαλιαγκόσ http://www.csd.uoc.gr/~hy220 1 Περιεχόμενα Ρολυδιάςτατοσ Δυαδικόσ Χϊροσ Δυαδικζσ Συναρτιςεισ
Επιχειρηςιακή Έρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R
 Επιχειρηςιακή Έρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 10 η : Ακζραιοσ Προγραμματιςμόσ Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ Σχολι
Επιχειρηςιακή Έρευνα και εφαρμογζσ με την χρήςη του λογιςμικοφ R Ενότητα 10 η : Ακζραιοσ Προγραμματιςμόσ Κων/νοσ Κουνετάσ, Επίκουροσ Κακθγθτισ Νίκοσ Χατηθςταμοφλου, Υπ. Δρ. Οικονομικισ Επιςτιμθσ Σχολι
ΚΩΝΣΑΝΣΙΝΟ ΑΛ. ΝΑΚΟ ΜΑΘΗΜΑΣΙΚΟ M.Sc ΧΟΛΙΚΟ ΤΜΒΟΤΛΟ Πτυχ. ΚΟΙΝΩΝΙΚΗ ΟΙΚΟΝΟΜΙΑ
 1 ΚΩΝΣΑΝΣΙΝΟ ΑΛ. ΝΑΚΟ ΜΑΘΗΜΑΣΙΚΟ M.Sc ΧΟΛΙΚΟ ΤΜΒΟΤΛΟ Πτυχ. ΚΟΙΝΩΝΙΚΗ ΟΙΚΟΝΟΜΙΑ.ΣΙΡΚΑ 8 και ΑΝΣΤΠΑ 30100 ΑΓΡΙΝΙΟ Email: nakosk@sch.gr Σηλ 64105400 κι.69749695 ΜΕΓΙΣΑ-ΕΛΑΧΙΣΑ ΧΩΡΙ ΠΑΡΑΓΩΓΟΤ 3 ΕΙΣΑΓΩΓΗ Σα
1 ΚΩΝΣΑΝΣΙΝΟ ΑΛ. ΝΑΚΟ ΜΑΘΗΜΑΣΙΚΟ M.Sc ΧΟΛΙΚΟ ΤΜΒΟΤΛΟ Πτυχ. ΚΟΙΝΩΝΙΚΗ ΟΙΚΟΝΟΜΙΑ.ΣΙΡΚΑ 8 και ΑΝΣΤΠΑ 30100 ΑΓΡΙΝΙΟ Email: nakosk@sch.gr Σηλ 64105400 κι.69749695 ΜΕΓΙΣΑ-ΕΛΑΧΙΣΑ ΧΩΡΙ ΠΑΡΑΓΩΓΟΤ 3 ΕΙΣΑΓΩΓΗ Σα
ΜΑΘΗΜΑΣΙΚΑ Γ ΓΕΝΙΚΗ ( ΑΠΟ ΘΕΜΑΣΑ ΛΤΚΕΙΩΝ ) ΕΡΩΣΗΕΙ ΩΣΟΤ ΛΑΘΟΤ ΑΝΑΛΤΗ
 ΜΑΘΗΜΑΣΙΚΑ Γ ΓΕΝΙΚΗ ( ΑΠΟ ΘΕΜΑΣΑ ΛΤΚΕΙΩΝ ) ΕΡΩΣΗΕΙ ΩΣΟΤ ΛΑΘΟΤ ΑΝΑΛΤΗ 1. Αν οι ςυναρτιςεισ f και g ζχουν όρια ςτο x πραγματικοφσ αρικμοφσ, δθλαδι lim f( x) l 1 και lim g( x) l 2 με l 1, l 2 IR, τότε lim
ΜΑΘΗΜΑΣΙΚΑ Γ ΓΕΝΙΚΗ ( ΑΠΟ ΘΕΜΑΣΑ ΛΤΚΕΙΩΝ ) ΕΡΩΣΗΕΙ ΩΣΟΤ ΛΑΘΟΤ ΑΝΑΛΤΗ 1. Αν οι ςυναρτιςεισ f και g ζχουν όρια ςτο x πραγματικοφσ αρικμοφσ, δθλαδι lim f( x) l 1 και lim g( x) l 2 με l 1, l 2 IR, τότε lim
Εγκατάσταση «Μισθός 2005»
 Εγκατάσταση «Μισθός 2005» Έκδοση 8.5 ΟΔΗΓΙΕΣ ΕΓΚΑΤΑΣΤΑΣΗΣ Βιμα 1 ο. Κάνουμε φφλαξθ των αρχείων από τθν προθγοφμενθ ζκδοςθ του προγράμματοσ. Εργαλεία Φφλαξθ c:\msteuro\20111001 *Εντάξει+ Όποσ: 20111001
Εγκατάσταση «Μισθός 2005» Έκδοση 8.5 ΟΔΗΓΙΕΣ ΕΓΚΑΤΑΣΤΑΣΗΣ Βιμα 1 ο. Κάνουμε φφλαξθ των αρχείων από τθν προθγοφμενθ ζκδοςθ του προγράμματοσ. Εργαλεία Φφλαξθ c:\msteuro\20111001 *Εντάξει+ Όποσ: 20111001
GNSS Solutions guide. 1. Create new Project
 GNSS Solutions guide 1. Create new Project 2. Import Raw Data Αναλόγωσ τον τφπο των δεδομζνων επιλζγουμε αντίςτοιχα το Files of type. παράδειγμα ζχουν επιλεγεί για ειςαγωγι αρχεία τφπου RINEX. το Με τθν
GNSS Solutions guide 1. Create new Project 2. Import Raw Data Αναλόγωσ τον τφπο των δεδομζνων επιλζγουμε αντίςτοιχα το Files of type. παράδειγμα ζχουν επιλεγεί για ειςαγωγι αρχεία τφπου RINEX. το Με τθν
Εφδοξοσ+ Συνδεκείτε ςτθν Εφαρμογι Φοιτθτϊν και μεταβείτε ςτθ ςελίδα «Ανταλλαγι Βιβλίων (Εφδοξοσ+)».
 Εφδοξοσ+ Διαθζτοντασ βιβλία μζςω του «Εφδοξοσ+» Συνδεκείτε ςτθν Εφαρμογι Φοιτθτϊν και μεταβείτε ςτθ ςελίδα «Ανταλλαγι Βιβλίων (Εφδοξοσ+)». Εμφανίηεται θ λίςτα με όλα ςασ τα βιβλία. Από εδϊ μπορείτε: -
Εφδοξοσ+ Διαθζτοντασ βιβλία μζςω του «Εφδοξοσ+» Συνδεκείτε ςτθν Εφαρμογι Φοιτθτϊν και μεταβείτε ςτθ ςελίδα «Ανταλλαγι Βιβλίων (Εφδοξοσ+)». Εμφανίηεται θ λίςτα με όλα ςασ τα βιβλία. Από εδϊ μπορείτε: -
ΥΡΟΝΣΙ ΣΗΡΙΟ Μ. Ε. ΚΑΙ ΚΕΝΣΡΟ ΙΔΙΑΙΣΕΡΩΝ ΜΑΘΗΜΑΣΩΝ «ΚΤΡΙΣ Η» ΔΙΑΓΩΝΙ ΜΑ ΑΕΠΠ
 ΥΡΟΝΣΙ ΣΗΡΙΟ Μ. Ε. ΚΑΙ ΚΕΝΣΡΟ ΙΔΙΑΙΣΕΡΩΝ ΜΑΘΗΜΑΣΩΝ «ΚΤΡΙΣ Η» ΔΙΑΓΩΝΙ ΜΑ ΘΕΜΑΣΑ Β ΛΤΚΕΙΟΤ ΑΠΡΙΛΙΟ 2018 ΚΑΘΗΓΗΤΗΣ: Γιώργος Πασσαλίδης ΑΕΠΠ ΟΝΟΜΑΣΕΠΩΝΤΜΟ: ΒΑΘΜΟ : ΘΕΜΑ Α Α1. Για κακεμία από τισ παρακάτω προτάςεισ
ΥΡΟΝΣΙ ΣΗΡΙΟ Μ. Ε. ΚΑΙ ΚΕΝΣΡΟ ΙΔΙΑΙΣΕΡΩΝ ΜΑΘΗΜΑΣΩΝ «ΚΤΡΙΣ Η» ΔΙΑΓΩΝΙ ΜΑ ΘΕΜΑΣΑ Β ΛΤΚΕΙΟΤ ΑΠΡΙΛΙΟ 2018 ΚΑΘΗΓΗΤΗΣ: Γιώργος Πασσαλίδης ΑΕΠΠ ΟΝΟΜΑΣΕΠΩΝΤΜΟ: ΒΑΘΜΟ : ΘΕΜΑ Α Α1. Για κακεμία από τισ παρακάτω προτάςεισ
ΟΔΗΓΙΕ ΓΙΑ ΣΗΝ ΕΙΑΓΩΓΗ ΕΚΔΡΟΜΩΝ & ΝΕΩΝ - ΑΝΑΚΟΙΝΩΕΩΝ ΣΗΝ ΙΣΟΕΛΙΔΑ ΣΗ Δ.Δ.Ε. ΘΕΠΡΩΣΙΑ
 ΟΔΗΓΙΕ ΓΙΑ ΣΗΝ ΕΙΑΓΩΓΗ ΕΚΔΡΟΜΩΝ & ΝΕΩΝ - ΑΝΑΚΟΙΝΩΕΩΝ ΣΗΝ ΙΣΟΕΛΙΔΑ ΣΗ Δ.Δ.Ε. ΘΕΠΡΩΣΙΑ ΕΙΑΓΩΓΗ Ο νζοσ δικτυακόσ τόποσ τθσ Δ.Δ.Ε. Θεςπρωτίασ παρζχει πλζον τθ δυνατότθτα τθσ καταχϊρθςθσ νζων, ειδιςεων και
ΟΔΗΓΙΕ ΓΙΑ ΣΗΝ ΕΙΑΓΩΓΗ ΕΚΔΡΟΜΩΝ & ΝΕΩΝ - ΑΝΑΚΟΙΝΩΕΩΝ ΣΗΝ ΙΣΟΕΛΙΔΑ ΣΗ Δ.Δ.Ε. ΘΕΠΡΩΣΙΑ ΕΙΑΓΩΓΗ Ο νζοσ δικτυακόσ τόποσ τθσ Δ.Δ.Ε. Θεςπρωτίασ παρζχει πλζον τθ δυνατότθτα τθσ καταχϊρθςθσ νζων, ειδιςεων και
ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 5: Αρχεία - Φάκελοι
 ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Αρχείο (File) Φάκελοσ (Folder) Διαχειριςτισ Αρχείων (File Manager) Τφποι Αρχείων Σε τι εξυπθρετεί θ οργάνωςθ των εργαςιϊν μασ ςτουσ υπολογιςτζσ; Πϊσ κα οργανϊςουμε
ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Αρχείο (File) Φάκελοσ (Folder) Διαχειριςτισ Αρχείων (File Manager) Τφποι Αρχείων Σε τι εξυπθρετεί θ οργάνωςθ των εργαςιϊν μασ ςτουσ υπολογιςτζσ; Πϊσ κα οργανϊςουμε
