Positive dispersion: 2 n. ω > 0, 2 n. Negative dispersion: ω < 0, 2 n
|
|
|
- Κλυμένη Φωτόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1
2 Positive dispersion: 2 n ω > 0, 2 n 2 λ > 0 2 Negative dispersion: 2 n ω < 0, 2 n 2 λ < 0 2
3 φ(z,ω) = k ( n ω )z E( z,t)= 1 2π E ( z = 0,ω )e iωt iφ z,ω e ( ) dω
4 φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0 ( ) dφω ( ) E( z,t)= 1 2π dω + ω0 E ( z = 0,ω )e iωt iφ z,ω e ( ) dω ( ) 2 d 2 φω ( ) 1 2! ω ω 0 dω ω0 ω 0
5 φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0 ( ) dφω ( ) E( z,t)= 1 2π dω + ω0 E ( z = 0,ω )e iωt iφ z,ω e ( ) dω ( ) 2 d 2 φω ( ) 1 2! ω ω 0 dω ω0 ω 0
6 φ(z,ω) = k ( n ω )z φ( ω )= φ 0 + ω ω 0 ( ) dφω ( ) E( z,t)= 1 2π dω + ω0 E ( z = 0,ω )e iωt iφ z,ω e ( ) dω ( ) 2 d 2 φω ( ) 1 2! ω ω 0 dω ω0 ω 0
7 t p (0) t p (z) t t τ p ( z) τ p ( 0) = 1 + 4ln2 d 2 φ dω 2 τ 2 p ( 0) 2 d 2 φ dω >> τ 2 2 p( 0) τ p () z d 2 φ dω Δω 2 p
8 p τ τ d 4ln2 d 1 p p ϕ ω τ τ τ = +
9 n 2 1 = B k λ 2 Positive dispersion: 2 n ω 2 > 0, 2 n λ 2 > 0 k λ 2 C k up-chirped dω dt > 0 B 1 = , C 1 =(65 nm) 2, B 2 = , and C 2 =(132 nm) 2
10 τ p () z d 2 φ dω Δω 2 p
11 n= n() λ
12 Dispersion of material n() Snellius Law: Refraction is frequency dependent d.h. = ()
13 t t
14
15
16 J. A. Valdmanis et al., Opt. Lett. 10, 131, 1985
17 Pump-Laser Ti:Saphir Kristall (2.3 mm, 0.25 wt.%) M 2 M 3 M 4 SESAM M 1 M 7 M 5 M 6 Quartzprismen Auskoppel- Spiegel
18 θ 1 ( λ 0 )= θ 2 ( λ 0 )= α 2 tanθ B = n 2 = n, and θ B + θ B = 90 o n 1 α = 180 o 2θ B = π 2θ B
19 n n = sin αδ ( min )+ δ min 2 ( ) sin αδ min 2
20 θ 1 ( λ 0 )= θ 2 ( λ 0 )= α 2 tanθ B = n 2 = n, and θ B + θ B = 90 o n 1 θ 2 ( λ)= arcsin( nsin θ 2 )= arcsin n( λ)sin π 2θ B arcsin sinθ B n( λ) α = 180 o 2θ B = π 2θ B
21 C θ 2 G H A β L P = 2 CDE opt = 2 AB = 2Lcosβ β θ 2 D E F s h B φ p = kp ( λ)= 2π λ P ( λ) d 2 φ P dω 2 = λ 3 2π c 2 d 2 P dλ 2 d 2 P dλ 2 = P β 2 n β λ 2 n + 2 β n n 2 λ 2 + β n n 2 d 2 P λ dβ 2 β = 0 d 2 P dλ = 2 θ 2 2 n n λ 2 L 8 dn dλ 2 L < 0
22 EFG = BH CDE = AB = L cosβ E F G = BH= BH C D E = AB= L cos β dφ P dω = d dω kp(ω ) ( )= 2L c cosβ 2ω L c sinβ dβ dω, dβ dω < 0
23 Fused Quartz 0 SF10 d 2 φ/dω 2 [fs 2 ] d 2 φ/dω 2 [fs 2 ] L [m] L [m]
24 d 2 φ dω >> τ 2 2 p( 0) Fused Quartz SF10 d 2 φ/dω 2 [fs 2 ] d 2 φ/dω 2 [fs 2 ] d 3 φ dω 3 >> τ p d 3 φ/dω 3 [fs 3 ] ( ) L [m] Fused Quartz d 3 φ/dω 3 [fs 3 ] L [m] 0.3 SF x L [m] L [m]
25 mm Fused Silica Prisms 35 cm apex separation 1000 adjustable negative GDD allows compensation of material dispersion strong higher-order contributions mm Wavelength (nm) 1000
26 λ < λ h λ > λ h Any wavelength < h will not be refracted by the second prism and will be lost during propagation through the prism pair. λ h
27 Ti:S-gain Prism + Ti:S-Crystal 0.8 GDD, fs x Standard Mirror (measured) Total Dispersion Spektrum x Chirped Mirror Wavelength, nm Goals: ---> High Reflectivity from 650 nm nm ---> Constant Total GDD from 650 nm nm
28 Ti:S-gain Prism + Ti:S-Crystal 0.8 GDD, fs x Standard Mirror (measured) Total Dispersion Spektrum x Chirped Mirror Wavelength, nm λ < λ h λ > λ h λ h
29
30 Λ ν x,m = m 1 Λ θ x,m m λ Λ t t t t
31
32 sinθ m = m λ Λ + sinθ i where m = 0, ± 1, ± 2,... x φ g ( x)= π m x Λ 2π
33 z L g x B θ i P' P Q b θ m A x sinθ m = m λ Λ + sinθ i where m = 0, ± 1, ± 2,... Beugungsgitter z.b. Blaze-Gitter φ = ω c L + φ g ( x), with x = L g tan( θ m ) φ g ( x)= π m 2π Λ x ( ) L = PABQ = PA+ b = b 1 + cos θ m + θ i = L g cosθ m ( ) 1+ cos θ m + θ i
34 sinθ m = m λ Λ + sinθ i L g d 2 φ dω = m2 λ 3 L g 2 2πc 2 Λ 1 m λ 2 Λ sinθ i 2 3/2 d 2 φ dω 2 L g angle of incidence angle of incidence 1200 lines/mm 300 lines/mm Λ 830 nm Λ 3.3 μm
35 L f stretcher something a Treacy grating pair cannot do! L f compressor like the Treacy grating pair
36
37 L f E out ( ω )= h ( ω ) E in ( ω )
38
39 A. M. Weiner, Rev. Sci. Instrum. 71, 1929 (2000) f = 300 mm knife-edge f = 300 mm SLM 640 pixels 300 l/mm grating 300 l/mm grating Possible bandwidth through Spatial Light Modulator: nm
40
41
42
43
44
45
46
47
48 R = 100% b AR-Coating R t R R GTI R GTI = 1 and R GTI = exp i2φ GTI ( ) d Glass substrate Air gap (non-absorbing spacer layer) r GTI exp( iφ GTI )= r 12 + r 23 e i2ϕ 1 + r 12 r 23 e = R t e i2ϕ i2ϕ 1 R t e i2ϕ t 0 t 0 = 2nd c ϕ = nkd = n ω c d ωt 0 2 dϕ dω t 0 2 tanφ GTI = Im r GTI Re r GTI ( ) ( ) = 1 R t ( )sin2ϕ 2 R t ( 1 + R t )cos2ϕ and d dω tanφ = ( 1+ tan2 φ) dφ dω ( ) R t sinωt 0 dt g dω = d 2 φ GTI = 2t R t dω 2 1+ R t 2 R t cosωt 0 ( ) 2
49 R = 100% b R t AR-Coating R R GTI dt g dω d 2 d Glass substrate Air gap (non-absorbing spacer layer) Bandwidth of dt g dω 1 d Example: d = 2.25 μm, R t = 4% Example: d = 80 μm, R t = 4%
50 t p (0) t p (z) t t L Substrate
51 Bragg-Mirror: SiO 2 - Substrate TiO / SiO 2 2 B - Layers 4 AIR Intensity Reflexion Phase Wavelength (μm) Wavelength (μm) 1.4
52 R λ/4 stack Substrate T Refr. index n H n S n I n L Physical distance r = ( n H n L ) ( n H + n L ) Δω ω B = 4 π arcsin( r) R 0 ( λ B )= 1 aqpm aqp m 1 2 p = n I n H q = n L n H a = n L n S
53 μ μ dt g dλ > 0 dt g dω < 0
54 λ Bragg Substrate Chirp Bragg wavelength wavelength-dependent penetration depth engineerable dispersion compensation of arbitrary material dispersion increased high-reflection bandwidth Group Delay (fs) Szipöcs et al., Opt. Lett. 19, 201 (1994) λ 4 λ 3 λ 2 GDD = 30 fs 2 (3.5 μm thick λ 1 mirror stack) Wavelength (nm)
55 Substrate Gires-Tournois High Partial R = 5% Interferometer (GTI) Reflector Reflector Group Delay (fs) Wavelength (nm) GTI desired
56 Substrate Substrate AR Anti-reflection coating matches first-layer impedance to air Kärtner et al., Opt. Lett. 22, 831 (1997) Matuschek et al., IEEE J. Sel. Top. Quantum Electron. 4, 197 (1998)
57 k B,min = 2π 600 nm k B,max = 2π 900 nm
58 0 prism pair: tunability, better DCM designs (GDD= T g / ) 0 20 Double-Chirped Mirrors: trade off: bandwidth vs. GDD oscillations non-normal incidence: smoother average GDD (average of several DCMs) ) 2x 20 Wavelength (nm)
59 (a) Bragg Mirror: SiO 2 Substrate TiO / SiO 2 2 λ /4-Layers B Air (b) Simple-Chirped Mirror: Bragg Wavelength λ Chirped SiO 2 Substrate B λ 1 λ 2 Negative Dispersion: λ λ 2 > 1 GTI (c) Double-Chirped Mirror: Bragg Wavelength and Coupling Chirped SiO 2 Substrate AR Coating Air { Impedance Matching (n d < h h < n d ) l l
60 Δλ = 230 nm Wavelength (nm) With AR Without AR R AR < Wavelength (nm) 1000 cannot make arbitrarily low reflectivity and arbitrarily broad bandwidth at the same time J.A. Dobrowolski et al., Appl. Opt. 35, 644 (1996)
61 Substrate Perfect impedance matching with double-chirp and n substrate = n first layer Front-reflection from substrate is not interfering with wave from mirror stack (by geometry) AR coating required only for loss reduction
62 BASIC DCM: Target Design conventional DCM: Target Design Wavelength (nm) Wavelength (nm) BASIC conventional Wavelength (nm) 1400 R > 99.7% ( nm) T g variations = 0.3 fs rms GDD var. = 3.8 fs 2 rms 260 THz bandwidth
63 Error simulations Measured GDD Design Layer deposition error: 0.2 nm rms Wavelength (nm) 1000 future Error simulations Measured GDD Design Layer deposition error: 0.1 nm rms Wavelength (nm) 1000
64 N. Matuschek: Theory and design of double-chirped mirrors, Ph.D. Thesis, ETH Zurich (1999) Hartung-Gorre Verlag, ISBN
65 [ ] n o,k o = kn o, and ω,ω a,ω b ω 0 ± Δω k A,ω A n e, k e = kn e ω o + ω A = ω e, because ω A << ω ω o ω e k o + k A = k e k( n e n o )= k A = ω A υ A
66
67 + S ( Δt)= R E S * ()E t R ( t Δt)dt K. Naganuma, K. Mogi, H. Yamada, Opt. Lett. 15, (1990).
68 + S( Δt)= R E S ()E t * R ( t Δt)dt K. Naganuma, K. Mogi, H. Yamada, Opt. Lett. 15, (1990).
69 ϕω ( ) + S ( Δt)= R E S * ()E t R ( t Δt)dt K. Naganuma, K. Mogi, H. Yamada, Opt. Lett. 15, (1990). GDD = d 2 ϕω ( ) dω 2 ϕω ( )
70 + S ( Δt)= R E S * ()E t R ( t Δt)dt K. Naganuma, K. Mogi, H. Yamada, Opt. Lett. 15, (1990). GDD = d 2 ϕω ( ) dω 2 ϕω ( )
71
72
73
6.4 Superposition of Linear Plane Progressive Waves
 .0 - Marine Hydrodynamics, Spring 005 Lecture.0 - Marine Hydrodynamics Lecture 6.4 Superposition of Linear Plane Progressive Waves. Oblique Plane Waves z v k k k z v k = ( k, k z ) θ (Looking up the y-ais
.0 - Marine Hydrodynamics, Spring 005 Lecture.0 - Marine Hydrodynamics Lecture 6.4 Superposition of Linear Plane Progressive Waves. Oblique Plane Waves z v k k k z v k = ( k, k z ) θ (Looking up the y-ais
 Problem 7.19 Ignoring reflection at the air soil boundary, if the amplitude of a 3-GHz incident wave is 10 V/m at the surface of a wet soil medium, at what depth will it be down to 1 mv/m? Wet soil is
Problem 7.19 Ignoring reflection at the air soil boundary, if the amplitude of a 3-GHz incident wave is 10 V/m at the surface of a wet soil medium, at what depth will it be down to 1 mv/m? Wet soil is
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Note: Please use the actual date you accessed this material in your citation.
 MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
MIT OpenCourseWare http://ocw.mit.edu 6.03/ESD.03J Electromagnetics and Applications, Fall 005 Please use the following citation format: Markus Zahn, 6.03/ESD.03J Electromagnetics and Applications, Fall
Tunable Diode Lasers. Turning Laser Diodes into Diode Lasers. Mode selection. Laser diodes
 Tunable Diode Lasers Turning Laser Diodes into Diode Lasers Laser diodes Mode selection FP diodes high power at low cost AR diodes for best performance Compact and robust Littrow setup Highest power from
Tunable Diode Lasers Turning Laser Diodes into Diode Lasers Laser diodes Mode selection FP diodes high power at low cost AR diodes for best performance Compact and robust Littrow setup Highest power from
γ c = rl = lt R ~ e (g l)t/t R Intensität 0 e γ c t Zeit, ns
 There is however one main difference in this chapter compared to many other chapters. All loss and gain coefficients are given for the intensity and not the amplitude and are therefore a factor of 2 larger!
There is however one main difference in this chapter compared to many other chapters. All loss and gain coefficients are given for the intensity and not the amplitude and are therefore a factor of 2 larger!
4.4 Superposition of Linear Plane Progressive Waves
 .0 Marine Hydrodynamics, Fall 08 Lecture 6 Copyright c 08 MIT - Department of Mechanical Engineering, All rights reserved..0 - Marine Hydrodynamics Lecture 6 4.4 Superposition of Linear Plane Progressive
.0 Marine Hydrodynamics, Fall 08 Lecture 6 Copyright c 08 MIT - Department of Mechanical Engineering, All rights reserved..0 - Marine Hydrodynamics Lecture 6 4.4 Superposition of Linear Plane Progressive
wave energy Superposition of linear plane progressive waves Marine Hydrodynamics Lecture Oblique Plane Waves:
 3.0 Marine Hydrodynamics, Fall 004 Lecture 0 Copyriht c 004 MIT - Department of Ocean Enineerin, All rihts reserved. 3.0 - Marine Hydrodynamics Lecture 0 Free-surface waves: wave enery linear superposition,
3.0 Marine Hydrodynamics, Fall 004 Lecture 0 Copyriht c 004 MIT - Department of Ocean Enineerin, All rihts reserved. 3.0 - Marine Hydrodynamics Lecture 0 Free-surface waves: wave enery linear superposition,
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
A. Two Planes Waves, Same Frequency Visible light
 Interference 1 A. Two Planes Waves, Same Frequency EE 1 rr, tt = EE 0,1 cccccc αα 1 ωω tt αα 1 kk 1. rr + εε 1 EE 2 rr, tt = EE 0,2 cccccc αα 2 ωω tt αα 2 kk 2. rr + εε 2 ωω = 4.3 7.5 10 14 HHHH Visible
Interference 1 A. Two Planes Waves, Same Frequency EE 1 rr, tt = EE 0,1 cccccc αα 1 ωω tt αα 1 kk 1. rr + εε 1 EE 2 rr, tt = EE 0,2 cccccc αα 2 ωω tt αα 2 kk 2. rr + εε 2 ωω = 4.3 7.5 10 14 HHHH Visible
Lifting Entry (continued)
 ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
Magnetically Coupled Circuits
 DR. GYURCSEK ISTVÁN Magnetically Coupled Circuits Sources and additional materials (recommended) Dr. Gyurcsek Dr. Elmer: Theories in Electric Circuits, GlobeEdit, 2016, ISBN:978-3-330-71341-3 Ch. Alexander,
DR. GYURCSEK ISTVÁN Magnetically Coupled Circuits Sources and additional materials (recommended) Dr. Gyurcsek Dr. Elmer: Theories in Electric Circuits, GlobeEdit, 2016, ISBN:978-3-330-71341-3 Ch. Alexander,
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Review of Single-Phase AC Circuits
 Single-Phase AC Circuits in a DC Circuit In a DC circuit, we deal with one type of power. P = I I W = t2 t 1 Pdt = P(t 2 t 1 ) = P t (J) DC CIRCUIT in an AC Circuit Instantaneous : p(t) v(t)i(t) i(t)=i
Single-Phase AC Circuits in a DC Circuit In a DC circuit, we deal with one type of power. P = I I W = t2 t 1 Pdt = P(t 2 t 1 ) = P t (J) DC CIRCUIT in an AC Circuit Instantaneous : p(t) v(t)i(t) i(t)=i
ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL (SMAC) I
 ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL SMAC) I Dynamicresponseof 2 nd ordersystem Prof.SongZhangMEG088) Solutions to ODEs Forann@thorderLTIsystem a n yn) + a n 1 y n 1) ++ a 1 "y + a 0 y = b m u m)
ME 365: SYSTEMS, MEASUREMENTS, AND CONTROL SMAC) I Dynamicresponseof 2 nd ordersystem Prof.SongZhangMEG088) Solutions to ODEs Forann@thorderLTIsystem a n yn) + a n 1 y n 1) ++ a 1 "y + a 0 y = b m u m)
Lifting Entry 2. Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYLAND U N I V E R S I T Y O F
 ifting Entry Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYAN 1 010 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu ifting Atmospheric
ifting Entry Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYAN 1 010 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu ifting Atmospheric
Calculating the propagation delay of coaxial cable
 Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Your source for quality GNSS Networking Solutions and Design Services! Page 1 of 5 Calculating the propagation delay of coaxial cable The delay of a cable or velocity factor is determined by the dielectric
Oscillatory Gap Damping
 Oscillatory Gap Damping Find the damping due to the linear motion of a viscous gas in in a gap with an oscillating size: ) Find the motion in a gap due to an oscillating external force; ) Recast the solution
Oscillatory Gap Damping Find the damping due to the linear motion of a viscous gas in in a gap with an oscillating size: ) Find the motion in a gap due to an oscillating external force; ) Recast the solution
Review Test 3. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
レーザ結晶. Altechna 社. Laser Crystals. Ti:Sapphire crystals. High damage threshold Strong Kerr effect
 Ti:Sapphire crystals Features Large gain-bandwidth Very large emission bandwidth Excellent thermal conductivity Short upper-state lifetime (3.2 μs) High saturation power Relatively high laser cross-sections
Ti:Sapphire crystals Features Large gain-bandwidth Very large emission bandwidth Excellent thermal conductivity Short upper-state lifetime (3.2 μs) High saturation power Relatively high laser cross-sections
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
6.003: Signals and Systems. Modulation
 6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
 ω α β χ φ() γ Γ θ θ Ξ Μ ν ν ρ σ σ σ σ σ σ τ ω ω ω µ υ ρ α Coefficient of friction Coefficient of friction 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 5 10 15 20 0.90 0.80 0.70 0.60 0.50 0.40 0.30
ω α β χ φ() γ Γ θ θ Ξ Μ ν ν ρ σ σ σ σ σ σ τ ω ω ω µ υ ρ α Coefficient of friction Coefficient of friction 1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 5 10 15 20 0.90 0.80 0.70 0.60 0.50 0.40 0.30
A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3
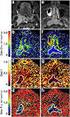 大阪電気通信大学研究論集 ( 自然科学編 ) 第 51 号 A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3 Takuya IWATA and Kiyoshi
大阪電気通信大学研究論集 ( 自然科学編 ) 第 51 号 A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3 Takuya IWATA and Kiyoshi
Sampling Basics (1B) Young Won Lim 9/21/13
 Sampling Basics (1B) Copyright (c) 2009-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
Sampling Basics (1B) Copyright (c) 2009-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any
MathCity.org Merging man and maths
 MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
Section 7.7 Product-to-Sum and Sum-to-Product Formulas
 Section 7.7 Product-to-Sum and Sum-to-Product Fmulas Objective 1: Express Products as Sums To derive the Product-to-Sum Fmulas will begin by writing down the difference and sum fmulas of the cosine function:
Section 7.7 Product-to-Sum and Sum-to-Product Fmulas Objective 1: Express Products as Sums To derive the Product-to-Sum Fmulas will begin by writing down the difference and sum fmulas of the cosine function:
Spectrum Representation (5A) Young Won Lim 11/3/16
 Spectrum (5A) Copyright (c) 2009-2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Spectrum (5A) Copyright (c) 2009-2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
 φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
φ(t) TE 0 φ(z) φ(z) φ(z) φ(z) η(λ) G(z,λ) λ φ(z) η(λ) η(λ) = t CIGS 0 G(z,λ)φ(z)dz t CIGS η(λ) φ(z) 0 z
Contents 1. Introduction Theoretical Background Theoretical Analysis of Nonlinear Interactions... 35
 Contents 1. Introduction...1 1.1 Nonlinear Optics and Nonlinear-Optic Instruments...1 1.2 Waveguide and Integrated Optics...2 1.3. Historical Perspectives on Waveguide NLO Devices...3 1.4. Future Prospects...6
Contents 1. Introduction...1 1.1 Nonlinear Optics and Nonlinear-Optic Instruments...1 1.2 Waveguide and Integrated Optics...2 1.3. Historical Perspectives on Waveguide NLO Devices...3 1.4. Future Prospects...6
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
BandPass (4A) Young Won Lim 1/11/14
 BandPass (4A) Copyright (c) 22 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later version
BandPass (4A) Copyright (c) 22 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later version
ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ
 ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ ΤΙ ΕΞΕΤΑΖΟΥΜΕ? ΤΟ ΦΩΣ ΙΑ Ι ΕΤΑΙ ΣΕ ΕΝΑ ΜΕΣΟ (ΓΥΑΛΙ, κα) ΑΠΑΙΤΕΙΤΑΙ ΜΕΛΕΤΗ ΤΗΣ ΙΑ ΟΣΗΣ ΣΤΟ ΜΕΣΟ ΕΦΑΡΜΟΓΗ ΣΥΝΟΡΙΑΚΩΝ ΣΥΝΘΗΚΩΝ ευθύγραµµη διάδοσητου φωτός Πυθαγόρας, ηµόκριτος, Εµπεδοκλής,
ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ ΤΙ ΕΞΕΤΑΖΟΥΜΕ? ΤΟ ΦΩΣ ΙΑ Ι ΕΤΑΙ ΣΕ ΕΝΑ ΜΕΣΟ (ΓΥΑΛΙ, κα) ΑΠΑΙΤΕΙΤΑΙ ΜΕΛΕΤΗ ΤΗΣ ΙΑ ΟΣΗΣ ΣΤΟ ΜΕΣΟ ΕΦΑΡΜΟΓΗ ΣΥΝΟΡΙΑΚΩΝ ΣΥΝΘΗΚΩΝ ευθύγραµµη διάδοσητου φωτός Πυθαγόρας, ηµόκριτος, Εµπεδοκλής,
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
レーザ結晶. Altechna 社. Laser Crystals. Ti:Sapphire crystals. High damage threshold Strong Kerr effect
 Ti:Sapphire crystals Features Large gain-bandwidth Very large emission bandwidth Excellent thermal conductivity Short upper-state lifetime (3. μs) High saturation power Relatively high laser cross-sections
Ti:Sapphire crystals Features Large gain-bandwidth Very large emission bandwidth Excellent thermal conductivity Short upper-state lifetime (3. μs) High saturation power Relatively high laser cross-sections
Differential equations
 Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
= 0.927rad, t = 1.16ms
 P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
ΘΕΜΑ 1. Στο φορέα του σχήματος ζητούνται να χαραχθούν τα διαγράμματα M, Q, N. (3 μονάδες)
 ΘΕΜΑ ΔΕΔΟΜΕΝΑ: Στο φορέα του σχήματος ζητούνται να χαραχθούν τα διαγράμματα M, Q, N. (3 μονάδες) ΕΠΙΛΥΣΗ: Ο φορέας χωρίζεται στα τμήματα Α και Β. Το τμήμα Α είναι τριαρθρωτό τόξο. Απομονώνοντας το Α και
ΘΕΜΑ ΔΕΔΟΜΕΝΑ: Στο φορέα του σχήματος ζητούνται να χαραχθούν τα διαγράμματα M, Q, N. (3 μονάδες) ΕΠΙΛΥΣΗ: Ο φορέας χωρίζεται στα τμήματα Α και Β. Το τμήμα Α είναι τριαρθρωτό τόξο. Απομονώνοντας το Α και
(1) Describe the process by which mercury atoms become excited in a fluorescent tube (3)
 Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
Q1. (a) A fluorescent tube is filled with mercury vapour at low pressure. In order to emit electromagnetic radiation the mercury atoms must first be excited. (i) What is meant by an excited atom? (1) (ii)
AREAS AND LENGTHS IN POLAR COORDINATES. 25. Find the area inside the larger loop and outside the smaller loop
 SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
What happens when two or more waves overlap in a certain region of space at the same time?
 Wave Superposition What happens when two or more waves overlap in a certain region of space at the same time? To find the resulting wave according to the principle of superposition we should sum the fields
Wave Superposition What happens when two or more waves overlap in a certain region of space at the same time? To find the resulting wave according to the principle of superposition we should sum the fields
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
TIME SWITCHES AND TWILIGHT SWITCHES
 W ANALOG DIN-RAIL TIME SWITCH QUARTZ, SERIES TEMPUS ANALOG 244 W SCHRACK-INFO Analogue time switch 1 channel Daily program With power reserve (NiMH rechargeable battery) Synchronised with mains Shortest
W ANALOG DIN-RAIL TIME SWITCH QUARTZ, SERIES TEMPUS ANALOG 244 W SCHRACK-INFO Analogue time switch 1 channel Daily program With power reserve (NiMH rechargeable battery) Synchronised with mains Shortest
PMD Compensator and PMD Emulator * * * Yu Mimura Kazuhiro Ikeda Tatsuya Hatano * * * Takesi Takagi Sugio Wako Hiroshi Matsuura
 PMD PMD PMD Compensator and PMD Emulator * * * Yu Mimura Kazuhiro Ikeda Tatsuya Hatano * * * Takesi Takagi Sugio Wako Hiroshi Matsuura D- WDM: Dense-Wavelength Division Multiplexing 4 Gbps Polarization
PMD PMD PMD Compensator and PMD Emulator * * * Yu Mimura Kazuhiro Ikeda Tatsuya Hatano * * * Takesi Takagi Sugio Wako Hiroshi Matsuura D- WDM: Dense-Wavelength Division Multiplexing 4 Gbps Polarization
Current Status of PF SAXS beamlines. 07/23/2014 Nobutaka Shimizu
 Current Status of PF SAXS beamlines 07/23/2014 Nobutaka Shimizu BL-6A Detector SAXS:PILATUS3 1M WAXD:PILATUS 100K Wavelength 1.5Å (Fix) Camera Length 0.25, 0.5, 1.0, 2.0, 2.5 m +WAXD Chamber:0.75, 1.0,
Current Status of PF SAXS beamlines 07/23/2014 Nobutaka Shimizu BL-6A Detector SAXS:PILATUS3 1M WAXD:PILATUS 100K Wavelength 1.5Å (Fix) Camera Length 0.25, 0.5, 1.0, 2.0, 2.5 m +WAXD Chamber:0.75, 1.0,
Κλασσική Θεωρία Ελέγχου
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 5: Ο μετασχηματισμός Laplace Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Topic 4. Linear Wire and Small Circular Loop Antennas. Tamer Abuelfadl
 Topic 4 Linear Wire and Small Circular Loop Antennas Tamer Abuelfadl Electronics and Electrical Communications Department Faculty of Engineering Cairo University Tamer Abuelfadl (EEC, Cairo University)
Topic 4 Linear Wire and Small Circular Loop Antennas Tamer Abuelfadl Electronics and Electrical Communications Department Faculty of Engineering Cairo University Tamer Abuelfadl (EEC, Cairo University)
High Performance Voltage Controlled Amplifiers Typical and Guaranteed Specifications 50 Ω System
 High Performance Voltage Controlled Amplifiers Typical and Guaranteed Specifications 50 Ω System Typical and guaranteed specifications vary versus frequency; see detailed data sheets for specification
High Performance Voltage Controlled Amplifiers Typical and Guaranteed Specifications 50 Ω System Typical and guaranteed specifications vary versus frequency; see detailed data sheets for specification
+85 C Snap-Mount Aluminum Electrolytic Capacitors. High Voltage Lead free Leads Rugged Design. -40 C to +85 C
 +85 C Snap-Mount Capacitors FEATURES High ripple Current Ratings Large Case Size Selection Extended Life High Voltage Lead free Leads Rugged Design SPECIFICATIONS Tolerance ±20% at 120Hz, 20 C Operating
+85 C Snap-Mount Capacitors FEATURES High ripple Current Ratings Large Case Size Selection Extended Life High Voltage Lead free Leads Rugged Design SPECIFICATIONS Tolerance ±20% at 120Hz, 20 C Operating
14.5mm 14.5mm
 This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 1.119/JETCAS.218.289582,
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 1.119/JETCAS.218.289582,
December 18, I T = I 0 e α(ω)x (1) I R = I 0 I T (2) N i = (3) g k
 Φασματοσκοπία Doppler Limited 2 Χειμερινό εξάμηνο 2016 December 18, 2016 1 Μέθοδοι αυξημένης ευαισθησίας Η γενική μέθοδος για τη μέτρηση της απορρόφησης ενός δείγματος είναι η μέτρηση σου συντελεστή απορρόφησης
Φασματοσκοπία Doppler Limited 2 Χειμερινό εξάμηνο 2016 December 18, 2016 1 Μέθοδοι αυξημένης ευαισθησίας Η γενική μέθοδος για τη μέτρηση της απορρόφησης ενός δείγματος είναι η μέτρηση σου συντελεστή απορρόφησης
X-Y COUPLING GENERATION WITH AC/PULSED SKEW QUADRUPOLE AND ITS APPLICATION
 X-Y COUPLING GENERATION WITH AC/PULSED SEW QUADRUPOLE AND ITS APPLICATION # Takeshi Nakamura # Japan Synchrotron Radiation Research Institute / SPring-8 Abstract The new method of x-y coupling generation
X-Y COUPLING GENERATION WITH AC/PULSED SEW QUADRUPOLE AND ITS APPLICATION # Takeshi Nakamura # Japan Synchrotron Radiation Research Institute / SPring-8 Abstract The new method of x-y coupling generation
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
& : $!" # RC : ) %& & '"( RL : ), *&+ RLC : - # ( : $. %! & / 0!1& ( :
 : : C : : C : : : .. ).. (................... ٢ ( - ). :.... S MP. T S..... -. (... ) :. :. : :. - - - - ٣ sweep :X. :Y. :. CCD.. ( - ) ( - ) ( - ) ( ) ( ) ( ) X : gnd -.... ٤ DC AC - AC DC DC - Y ( )
: : C : : C : : : .. ).. (................... ٢ ( - ). :.... S MP. T S..... -. (... ) :. :. : :. - - - - ٣ sweep :X. :Y. :. CCD.. ( - ) ( - ) ( - ) ( ) ( ) ( ) X : gnd -.... ٤ DC AC - AC DC DC - Y ( )
Trigonometry (4A) Trigonometric Identities. Young Won Lim 1/2/15
 Trigonometry (4 Trigonometric Identities 1//15 Copyright (c 011-014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Trigonometry (4 Trigonometric Identities 1//15 Copyright (c 011-014 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License,
Low Frequency Plasma Conductivity in the Average-Atom Approximation
 Low Frequency Plasma Conductivity in the Average-Atom Approximation Walter Johnson & Michael Kuchiev Physical Review E 78, 026401 (2008) 1. Review of Average-Atom Linear Response Theory 2. Demonstration
Low Frequency Plasma Conductivity in the Average-Atom Approximation Walter Johnson & Michael Kuchiev Physical Review E 78, 026401 (2008) 1. Review of Average-Atom Linear Response Theory 2. Demonstration
Fourier Analysis of Waves
 Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
Handbook of Electrochemical Impedance Spectroscopy
 Handbook of Electrochemical Impedance Spectroscopy A B D Im Y * Im Y * Im Y * Im Y * e Y * e Y * e Y * e Y * IUITS made of ESISTOS, INDUTOS and APAITOS E@SE/EPMI J.-P. Diard, B. e Gorrec,. Montella Hosted
Handbook of Electrochemical Impedance Spectroscopy A B D Im Y * Im Y * Im Y * Im Y * e Y * e Y * e Y * e Y * IUITS made of ESISTOS, INDUTOS and APAITOS E@SE/EPMI J.-P. Diard, B. e Gorrec,. Montella Hosted
If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2
![If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2 If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2](/thumbs/53/31933086.jpg) Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Handbook of Electrochemical Impedance Spectroscopy
 Handbook of Electrochemical Impedance Spectroscopy Im Z u c T u c T Re Z CIRCUITS made of RESISTORS and INDUCTORS ER@SE/LEPMI J.-P. Diard, B. Le Gorrec, C. Montella Hosted by Bio-Logic @ www.bio-logic.info
Handbook of Electrochemical Impedance Spectroscopy Im Z u c T u c T Re Z CIRCUITS made of RESISTORS and INDUCTORS ER@SE/LEPMI J.-P. Diard, B. Le Gorrec, C. Montella Hosted by Bio-Logic @ www.bio-logic.info
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Data sheet Thick Film Chip Resistor 5% - RS Series 0201/0402/0603/0805/1206
 Data sheet Thick Film Chip Resistor 5% - RS Series 0201/0402/0603/0805/1206 Scope -This specification applies to all sizes of rectangular-type fixed chip resistors with Ruthenium-base as material. Features
Data sheet Thick Film Chip Resistor 5% - RS Series 0201/0402/0603/0805/1206 Scope -This specification applies to all sizes of rectangular-type fixed chip resistors with Ruthenium-base as material. Features
38 Te(OH) 6 2NH 4 H 2 PO 4 (NH 4 ) 2 HPO 4
 Fig. A-1-1. Te(OH) NH H PO (NH ) HPO (TAAP). Projection of the crystal structure along the b direction [Ave]. 9 1. 7.5 ( a a )/ a [1 ] ( b b )/ b [1 ] 5..5 1.5 1 1.5 ( c c )/ c [1 ].5 1. 1.5. Angle β 1.
Fig. A-1-1. Te(OH) NH H PO (NH ) HPO (TAAP). Projection of the crystal structure along the b direction [Ave]. 9 1. 7.5 ( a a )/ a [1 ] ( b b )/ b [1 ] 5..5 1.5 1 1.5 ( c c )/ c [1 ].5 1. 1.5. Angle β 1.
If we restrict the domain of y = sin x to [ π 2, π 2
 Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
..,..,..,..,..,.. $#'().. #*#'!# !" #$% &'( )*%!"( %+
 !" #$% &'( )*%!"( %+,--%. )!%/%#-%. %% (*%!%!)..,..,..,..,..,..!" #$#%$"& $#% $#'().. #*#'!# -0 --%0 % %--/%#-%0 %%0 () - %)!" %1 -# #( )%+!"&/ #$%+/,!% 1%/!"& )(00& 3 ) %4%)!% "% %-" ) )!%1 )(-% 3 651300
!" #$% &'( )*%!"( %+,--%. )!%/%#-%. %% (*%!%!)..,..,..,..,..,..!" #$#%$"& $#% $#'().. #*#'!# -0 --%0 % %--/%#-%0 %%0 () - %)!" %1 -# #( )%+!"&/ #$%+/,!% 1%/!"& )(00& 3 ) %4%)!% "% %-" ) )!%1 )(-% 3 651300
Chapter 6 BLM Answers
 Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
Chapter 7 Transformations of Stress and Strain
 Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
is like multiplying by the conversion factor of. Dividing by 2π gives you the
 Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Part 4 RAYLEIGH AND LAMB WAVES
 Part 4 RAYLEIGH AND LAMB WAVES Rayleigh Surfae Wave x x 1 x 3 urfae wave x 1 x 3 Partial Wave Deompoition Diplaement potential: u = ϕ + ψ Wave equation: 1 ϕ 1 ψ ϕ = = k ϕ an ψ = = k t t ψ Wave veloitie:
Part 4 RAYLEIGH AND LAMB WAVES Rayleigh Surfae Wave x x 1 x 3 urfae wave x 1 x 3 Partial Wave Deompoition Diplaement potential: u = ϕ + ψ Wave equation: 1 ϕ 1 ψ ϕ = = k ϕ an ψ = = k t t ψ Wave veloitie:
Solar Neutrinos: Fluxes
 Solar Neutrinos: Fluxes pp chain Sun shines by : 4 p 4 He + e + + ν e + γ Solar Standard Model Fluxes CNO cycle e + N 13 =0.707MeV He 4 C 1 C 13 p p p p N 15 N 14 He 4 O 15 O 16 e + =0.997MeV O17
Solar Neutrinos: Fluxes pp chain Sun shines by : 4 p 4 He + e + + ν e + γ Solar Standard Model Fluxes CNO cycle e + N 13 =0.707MeV He 4 C 1 C 13 p p p p N 15 N 14 He 4 O 15 O 16 e + =0.997MeV O17
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Integrals in cylindrical, spherical coordinates (Sect. 15.7)
 Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
CORDIC Background (2A)
 CORDIC Background 2A Copyright c 20-202 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
CORDIC Background 2A Copyright c 20-202 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version.2 or any later
Sum of Two Sinusoids by Richard (Rick) Lyons
 Sum of Two Sinusoids by Richard (Rick) Lyons Several months ago I reviewed the manuscript of a book being considered by the IEEE Press for possible publication. In that manuscript the author presented
Sum of Two Sinusoids by Richard (Rick) Lyons Several months ago I reviewed the manuscript of a book being considered by the IEEE Press for possible publication. In that manuscript the author presented
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Computing the Macdonald function for complex orders
 Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
+85 C Screw Terminal Aluminum Electrolytic Capacitors. For filtering applications. Capacitance change Dissipation factor Leakage current
 For filtering applications FEATURES High ripple current High reiability range: 270µF to 680,000µF Voltage range: 6.3 to 450 SPECIFICATIONS Tolerance ±20% at 120 Hz, 25 C Operating Temperature Range Dissipation
For filtering applications FEATURES High ripple current High reiability range: 270µF to 680,000µF Voltage range: 6.3 to 450 SPECIFICATIONS Tolerance ±20% at 120 Hz, 25 C Operating Temperature Range Dissipation
Derivation of Optical-Bloch Equations
 Appendix C Derivation of Optical-Bloch Equations In this appendix the optical-bloch equations that give the populations and coherences for an idealized three-level Λ system, Fig. 3. on page 47, will be
Appendix C Derivation of Optical-Bloch Equations In this appendix the optical-bloch equations that give the populations and coherences for an idealized three-level Λ system, Fig. 3. on page 47, will be
Microwave Sintering of Electronic Ceramics
 25,,, Microwave Sintering of Electronic Ceramics Hideoki Fukushima, Goro Watanabe, Hiroyuki Mori, Masao Matsui ZnO PZT ZnO PZT Microwave heating offers advantages over conventional technologies such as
25,,, Microwave Sintering of Electronic Ceramics Hideoki Fukushima, Goro Watanabe, Hiroyuki Mori, Masao Matsui ZnO PZT ZnO PZT Microwave heating offers advantages over conventional technologies such as
( ) Sine wave travelling to the right side
 SOUND WAVES (1) Sound wave: Varia2on of density of air Change in density at posi2on x and 2me t: Δρ(x,t) = Δρ m sin kx ωt (2) Sound wave: Varia2on of pressure Bulk modulus B is defined as: B = V dp dv
SOUND WAVES (1) Sound wave: Varia2on of density of air Change in density at posi2on x and 2me t: Δρ(x,t) = Δρ m sin kx ωt (2) Sound wave: Varia2on of pressure Bulk modulus B is defined as: B = V dp dv
ITU-R P (2012/02) khz 150
 (0/0) khz 0 P ii (IPR) (ITU-T/ITU-R/ISO/IEC) ITU-R http://www.itu.int/itu-r/go/patents/en http://www.itu.int/publ/r-rec/en BO BR BS BT F M P RA RS S SA SF SM SNG TF V ITU-R 0 ITU 0 (ITU) khz 0 (0-009-00-003-00-994-990)
(0/0) khz 0 P ii (IPR) (ITU-T/ITU-R/ISO/IEC) ITU-R http://www.itu.int/itu-r/go/patents/en http://www.itu.int/publ/r-rec/en BO BR BS BT F M P RA RS S SA SF SM SNG TF V ITU-R 0 ITU 0 (ITU) khz 0 (0-009-00-003-00-994-990)
5.0 DESIGN CALCULATIONS
 5.0 DESIGN CALCULATIONS Load Data Reference Drawing No. 2-87-010-80926 Foundation loading for steel chimney 1-00-281-53214 Boiler foundation plan sketch : Figure 1 Quantity Unit Dia of Stack, d 6.00 m
5.0 DESIGN CALCULATIONS Load Data Reference Drawing No. 2-87-010-80926 Foundation loading for steel chimney 1-00-281-53214 Boiler foundation plan sketch : Figure 1 Quantity Unit Dia of Stack, d 6.00 m
CSR series. Thick Film Chip Resistor Current Sensing Type FEATURE PART NUMBERING SYSTEM ELECTRICAL CHARACTERISTICS
 FEATURE Operating Temperature: -55 ~ +155 C 3 Watts power rating in 1 Watt size, 1225 package High purity alumina substrate for high power dissipation Long side terminations with higher power rating PART
FEATURE Operating Temperature: -55 ~ +155 C 3 Watts power rating in 1 Watt size, 1225 package High purity alumina substrate for high power dissipation Long side terminations with higher power rating PART
10.7 Performance of Second-Order System (Unit Step Response)
 Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Lecture Notes on Control Systems/D. Ghose/0 57 0.7 Performance of Second-Order System (Unit Step Response) Consider the second order system a ÿ + a ẏ + a 0 y = b 0 r So, Y (s) R(s) = b 0 a s + a s + a
Homework#13 Trigonometry Honors Study Guide for Final Test#3
 Homework#13 Trigonometry Honors Study Guide for Final Test#3 1. Στο παρακάτω σχήμα δίνεται ο μοναδιαίος κύκλος: Να γράψετε τις συντεταγμένες του σημείου ή το όνομα του άξονα: 1. (ε 1) είναι ο άξονας 11.
Homework#13 Trigonometry Honors Study Guide for Final Test#3 1. Στο παρακάτω σχήμα δίνεται ο μοναδιαίος κύκλος: Να γράψετε τις συντεταγμένες του σημείου ή το όνομα του άξονα: 1. (ε 1) είναι ο άξονας 11.
University of Illinois at Urbana-Champaign ECE 310: Digital Signal Processing
 University of Illinois at Urbana-Champaign ECE : Digital Signal Processing Chandra Radhakrishnan PROBLEM SET : SOLUTIONS Peter Kairouz Problem Solution:. ( 5 ) + (5 6 ) + ( ) cos(5 ) + 5cos( 6 ) + cos(
University of Illinois at Urbana-Champaign ECE : Digital Signal Processing Chandra Radhakrishnan PROBLEM SET : SOLUTIONS Peter Kairouz Problem Solution:. ( 5 ) + (5 6 ) + ( ) cos(5 ) + 5cos( 6 ) + cos(
UDZ Swirl diffuser. Product facts. Quick-selection. Swirl diffuser UDZ. Product code example:
 UDZ Swirl diffuser Swirl diffuser UDZ, which is intended for installation in a ventilation duct, can be used in premises with a large volume, for example factory premises, storage areas, superstores, halls,
UDZ Swirl diffuser Swirl diffuser UDZ, which is intended for installation in a ventilation duct, can be used in premises with a large volume, for example factory premises, storage areas, superstores, halls,
Advanced operation schemes: two-color, split & delay
 Advanced operation schemes: two-color, split & delay Production of two FEL pulses of different wavelengths with a controllable temporal delay (and) Splitting the FEL pulse into two sequential pulses at
Advanced operation schemes: two-color, split & delay Production of two FEL pulses of different wavelengths with a controllable temporal delay (and) Splitting the FEL pulse into two sequential pulses at
