9. ιαµόρφωση περιγράµµατος και αποστάσεων
|
|
|
- Ἀγλαΐη Ζυγομαλάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 9. ιαµόρφωση περιγράµµατος και αποστάσεων 9.1 Περίγραµµα (1) Οι πινακίδες που έχουν υπόβαθρο πρασίνου χρώµατος έχουν σαν πλαίσιο ένα λευκό περίγραµµα. Το πλάτος του περιγράµµατος εξαρτάται από το µήκος της διαγωνίου της πινακίδας (πριν από τη στρογγύλευση των γωνιών) σύµφωνα µε τον πίνακα 13. (2) Αν µια πινακίδα αποτελείται από δυο επιµέρους πινακίδες, τότε: α) Αν ο διαχωρισµός γίνεται κατακόρυφα (π.χ. πινακίδες διακλαδώσεων, Σχήµατα 25, 26 και 27), τότε το πλάτος του περιγράµµατος προκύπτει από τις διαστάσεις (διαγωνίους) των επιµέρους πινακίδων. Αν προκύπτουν διαφορετικά πλάτη περιγραµµάτων, τότε επιλέγεται για το σύνολο της πινακίδας το µεγαλύτερο εξ αυτών. Το ίδιο πλάτος έχει και η λευκή διαχωριστική γραµµή, η ο- ποία φθάνει µέχρι το περίγραµµα και πάνω και κάτω. β) Αν ο διαχωρισµός γίνεται οριζόντια διακρίνουµε τις εξής περιπτώσεις: β.1) Αν πρόκειται για επιβεβαιωτική πινακίδα αποστάσεων (π.χ. Σχήµα 13), τότε το περίγραµµα της πινακίδας διαστασιολογείται από τη διαγώνιο της όλης πινακίδας και η λευκή διαχωριστική γραµµή έχει πλάτος mm. H διαχωριστική γραµµή δεν φθάνει µέχρι το περίγραµµα, αλλά αφήνει απόσταση απ αυτό (και δεξιά, και αριστερά) όσο οι αναγραφές. β.2) Αν πρόκειται για πινακίδα διπλής αναγγελίας προσέγγισης σε κόµβους. (βλ. κατωτέρω παράγρ ), τότε ανάλογα µε την περίπτωση: ή εφαρµόζεται το ανωτέρω εδάφιο (α) (στις περιπτώσεις (1) και (2.α) της παραγρ ) αλλά µε πλάτος της διαχωριστικής γραµµής 50 mm και ελάχιστο πλάτος περιγράµµατος επίσης 50 mm ή εφαρµόζεται το ανωτέρω εδάφιο (β.1) (στις περιπτώσεις (3) και (4) της παραγρ ) β.3) Στις υπόλοιπες περιπτώσεις επί µέρους πινακίδων εφαρµόζεται αντίστοιχα είτε το εδάφιο (α), είτε το εδάφιο (β.1), ανάλογα µε το αν τα αναγραφόµενα των δυο επιµέρους πινακίδων είναι ανεξάρτητα µεταξύ τους ή έχουν εννοιολογική ή κυκλοφοριακή σχέση. (3) Οι γωνίες των πινακίδων στρογγυλεύονται µε ελάχιστη ακτίνα στρογγύλευσης R= mm. Ανάλογα µε το µέγεθος της πινακίδας οι ακτίνες στρογγύλευσης των ορθογώνιων ή οξειών γωνιών προκύπτουν µε βάση τον πίνακα 13. Γωνίες που δεν εντάσσονται στις παραπάνω κατηγορίες διαµορφώνονται µε βάση τα εκάστοτε ι- σχύοντα κατασκευαστικά σχέδια. 75
2 Πίνακας 13: Πλάτος περιγράµµατος / ακτίνα στρογγύλευσης ιαγώνιος πινακίδας [m] Πλάτος περιγράµµατος [mm] Εξωτερική ακτίνα στρογγύλευσης [mm] 0,75 >0,75-1,15 >1,15-1,55 >1,55-1,95 >1,95-2,35 >2,35-2,75 >2,75-3,35 >3,35-4,10 >4,10-4,90 >4,90-5,70 >5,70-6,50 >6,50-7,30 >7, Αποστάσεις µεταξύ των στοιχείων διαµόρφωσης των πινακίδων Γενικά (1) Οι αποστάσεις, που αναφέρονται στις παρούσες οδηγίες εξαρτώνται από το ύψος των χαρακτήρων (h). Λόγω της απαιτούµενης διάταξης του κάθε µεµονωµένου στοιχείου σε σχέση µε τα υπόλοιπα, για τις µεταξύ τους αποστάσεις πρέπει να τηρούνται οι αναγραφόµενες τιµές, προκειµένου να εξασφαλίζεται η καλή αναγνωσι- µότητα και η αρµονική εµφάνιση του συνόλου της πινακίδας. Στα κατασκευαστικά σχέδια που ακολουθούν, οι αποστάσεις δίνονται σε µονάδες (Ε). Σαν µονάδα (Ε) ορίζεται το 1/7 του ύψους των χαρακτήρων (Ε=1/7 h). (2) Αν για δύο γειτονικά στοιχεία διαµόρφωσης δίνονται διαφορετικές αποστάσεις, τότε επιλέγεται η µικρότερη από τις δύο. Από τον κανόνα αυτό εξαιρούνται, στις ορθογώνιες πινακίδες, οι αποστάσεις από το περίγραµµα. (βλ. παρ ). (3) Τα κατασκευαστικά σχέδια για τις διάφορες πινακίδες που περιλαµβάνονται στις παρούσες οδηγίες έχουν διαστασιολογηθεί κατά τέτοιο τρόπο, ώστε οι µεταβλητές διαστάσεις να χαρακτηρίζονται µε το σύµβολο " " Γραφή (βλ. και Πίνακα 1, παραγρ.7.2) (1) Η απόσταση µεταξύ των κεφαλαίων χαρακτήρων δύο γραµµών (διάκενο γραµµών) ανέρχεται σε 4Ε. 76
3 (2) Αν, µε δεδοµένο το 4Ε σαν διάκενο γραµµών, το ύψος της πινακίδας που προκύπτει είναι κατά 6Ε µικρότερο από το ύψος πινακίδας που προκύπτει από άλλους λόγους (π.χ. ίσο ύψος πινακίδων σε γέφυρα σήµανσης), τότε σαν απόσταση διακένου γραµµών λαµβάνεται το 6Ε. Τυχόν παραµένοντα υπόλοιπα στις διαστάσεις προστίθενται ισόποσα στις θέσεις εκείνες, που χαρακτηρίζονται µε το σύµβολο " ". (3) Στην περίπτωση διαφορετικών µεγεθών γραφής υπολογίζεται η απόσταση µεταξύ δύο γραµµών ως ο µέσος όρος των αποστάσεων, που αντιστοιχούν σε κάθε µέγεθος γραφής. Το διάκενο των γραµµών δηλαδή κατά κανόνα προκύπτει σαν άθροισµα του 2Ε του µικρότερου µεγέθους και του 2Ε του µεγαλύτερου µεγέθους γραφής. (4) Η απόσταση µεταξύ των λέξεων κατά την οριζόντια έννοια για προορισµούς όπως Αγ. Βασίλειος, ανέρχεται στη στενή γραφή 4Ε στην κανονική γραφή 5Ε ε λαµβάνονται υπόψη οι τυχόν υπάρχουσες τελείες συντοµογραφιών. Οι ίδιες αποστάσεις εφαρµόζονται και µεταξύ του τελευταίου γράµµατος ενός προορισµού και του πρώτου ψηφίου της αναγραφόµενης δίπλα σ αυτόν απόστασης. (5) Όταν αναγράφονται δύο ανεξάρτητοι µεταξύ τους προορισµοί στην ίδια γραµµή, ο ένας δίπλα στον άλλο, όπως π.χ. «Λαµία Χαλκίδα», τότε αυξάνεται η µεταξύ των λέξεων απόσταση κατά 2Ε. Αν χρησιµοποιούνται και άλλα στοιχεία στην ίδια γραµµή µαζί µε τους προορισµούς (π.χ. προορισµός και ακολουθεί έµβληµα), τότε επιλέγονται και για τα στοιχεία αυτά οι ίδιες αποστάσεις όπως µεταξύ λέξεων. (6) Στις αναγραφές αποστάσεων, η απόσταση µεταξύ του τελευταίου ψηφίου της αναγραφόµενης απόστασης και της διάστασης km ή m ανέρχεται σε 2Ε στη στενή γραφή και 3Ε στην κανονική γραφή. Η ίδια απόσταση ισχύει και µεταξύ αριθµού και της µονάδας h (ώρες). Σε περίπτωση που η µονάδα είναι t (τόνο), η απόσταση αυτή µειώνεται κατά 2h/112 ή κατά 4h/112 αντίστοιχα (σε mm). (7) Οι αποστάσεις µεταξύ των οµάδων των προορισµών διαφόρων κατευθύνσεων δίνονται αναλυτικά στα κατασκευαστικά σχέδια. Για τις περιπτώσεις εκείνες που δεν γίνεται αναφορά ή δεν προκύπτουν από τα υπάρχοντα σχέδια, επιλέγεται η απόσταση 15Ε Έγχρωµα ένθετα (1) Αν βρίσκεται µια γραµµή λέξεων, µια οµάδα προορισµών ή ένα άλλο στοιχείο διαµόρφωσης µέσα σε έγχρωµο ένθετο, τότε λαµβάνεται σαν απόσταση µέχρι τις πλευρές του ένθετου, προς όλες τις κατευθύνσεις, η απόσταση 3Ε. (2) Οι αποστάσεις προς άλλα στοιχεία διαµόρφωσης µετρούνται από τις πλευρές του ένθετου. (3) Ειδικά οι αναγραφές σε λευκό ένθετο γίνονται µε ύψος χαρακτήρων h w = h 70, όπου h το καθοριστικό µέγεθος των χαρακτήρων της πινακίδας. Οταν χρησιµοποιείται και γραφικό σύµβολο αυτό σχεδιάζεται χωρίς πλαίσιο. ηλαδή σε µια 77
4 πλευρική πινακίδα όπου το καθοριστικό µέγεθος των χαρακτήρων είναι h = 350, είναι h w = 280 (βλέπε επόµενο σχήµα). 1Ε w =1/7 h w, h w = Μέγεθος χαρακτήρων σε λευκό ένθετο Εµβλήµατα Αριθµοί κόµβων Σύµβολα κρατών Εµβλήµατα (1) Η απόσταση µεταξύ των εµβληµάτων (αριθµός αυτοκινητοδρόµου, αριθµός E-road ή εθνικής οδού) και των άλλων στοιχείων διαµόρφωσης της πινακίδας ανέρχεται σε 5Ε προς τα πλάγια και 4Ε προς τα άνω και προς τα κάτω. (2) Σε διπλές αριθµήσεις (π.χ. Ε96 Ε43), η απόσταση των άλλων στοιχείων της πινακίδας από αυτή τη διπλή αρίθµηση ανέρχεται σε 4Ε προς όλες τις πλευρές. (3) Η απόσταση µεταξύ ίδιων εµβληµάτων ανέρχεται στα 2/7 του ύψους των στοιχείων του εµβλήµατος, όταν τα εµβλήµατα διατάσσονται το ένα δίπλα στο άλλο ή το ένα πάνω από το άλλο. (4) Η ειδική διάταξη και η διαµόρφωση των αποστάσεων στις διπλές αριθµήσεις των Ε- αριθµών και των Α-αριθµών καθορίζεται στα Σχήµατα 13(Α) έως 13( ), παράγρ Αριθµοί κόµβων Η απόσταση του κυκλικού περιγράµµατος ενός αριθµού κόµβου από τα άλλα στοιχεία διαµόρφωσης της πινακίδας ανέρχεται σε 5Ε κατά την οριζόντια έννοια και σε 4Ε κατά την κατακόρυφη έννοια Σύµβολα κρατών Για τη σύµβολα κρατών ισχύουν οι ίδιοι κανόνες αποστάσεων που ισχύουν για τα εµβλή- µατα, τόσο για τις αποστάσεις µεταξύ τους, όσο και για τις αποστάσεις προς άλλα στοιχεία διαµόρφωσης της πινακίδας. Οι χαρακτήρες που προσδιορίζουν το κράτος, (βλ. παράγρ.7.5 (4)) αναγράφονται εντός του ορθογωνίου που δείχνεται στο επόµενο σχήµα. 78
5 N=1/7z z=το ύψος των χαρακτήρων Σύµβολα βελών Η απόσταση των βελών από τα υπόλοιπα στοιχεία διαµόρφωσης εφαρµόζεται σύµφωνα µε τα επόµενα: Γραφικά σύµβολα (πικτογράµµατα) (1) Η απόσταση των γραφικών συµβόλων από τα υπόλοιπα στοιχεία διαµόρφωσης ανέρχεται σε 5Ε. Σε περίπτωση που το γραφικό σύµβολο τοποθετείται σε πλαίσιο, η απόσταση 5Ε µετράται από τις πλευρές του πλαισίου. (2) Αν σε µια πινακίδα υπάρχουν µόνο γραφικά σύµβολα, χωρίς κείµενο, τότε η απόσταση µεταξύ τους δεν πρέπει να είναι µικρότερη από το 25% του µήκους της κατακόρυφης πλευράς του πλαισίου του γραφικού συµβόλου Απόσταση από το περίγραµµα (1) Η απόσταση των στοιχείων διαµόρφωσης από το περίγραµµα ανέρχεται σε 6Ε κατά την οριζόντια έννοια και σε 5Ε κατά την κατακόρυφη έννοια. Οι αποστάσεις αυτές υπερισχύουν των αποστάσεων που αναφέρονται στις προηγούµενες παραγράφους (π.χ. στην παράγρ.9.2.5), πλην της κατακόρυφης απόστασης του κυκλικού περιγράµµατος αριθµού κόµβου από το περίγραµµα της πινακίδας, που είναι 4Ε (βλ. παραγρ ). (2) Σε πινακίδες µε γραφικά σύµβολα χωρίς κείµενο επιλέγεται η απόσταση σύµφωνα µε τα αναφερόµενα στο εδάφιο (2) της παραγράφου Αποστάσεις σε πινακίδες µορφής βέλους (βλ. Σχήµα 12) Λόγω της ειδικής διαµόρφωσης της πινακίδας η εφαρµογή των παραπάνω αναφερθεισών αποστάσεων γίνεται κάτω από προϋποθέσεις. Κάθε φορά πρέπει να ελέγχεται η αρµονική γραφική διαµόρφωση της πινακίδας. Στην περίπτωση αυτή µπορεί να θεωρη- 79
6 θεί σκόπιµη η µείωση της απόστασης µεταξύ των στοιχείων διαµόρφωσης και από την άνω ή κάτω πλευρά της πινακίδας σε 3Ε περίπου. Σε καµία περίπτωση όµως η οριζόντια απόσταση από την πλευρά (περίγραµµα) της πινακίδας δεν πρέπει να είναι µικρότερη από 4Ε (βλ. και Σχήµα 48, παράγρ ). 80
8. ιαµόρφωση συµβόλων και εµβληµάτων
 8. ιαµόρφωση συµβόλων και εµβληµάτων 8.1 Σύµβολα βελών 8.1.1 Τύποι βελών (1) Τα σύµβολα των βελών χρησιµοποιούνται µε αναφορά στις λωρίδες κυκλοφορίας και στις κατευθύνσεις. Συνδέουν τον προορισµό και
8. ιαµόρφωση συµβόλων και εµβληµάτων 8.1 Σύµβολα βελών 8.1.1 Τύποι βελών (1) Τα σύµβολα των βελών χρησιµοποιούνται µε αναφορά στις λωρίδες κυκλοφορίας και στις κατευθύνσεις. Συνδέουν τον προορισµό και
16. Σήµανση σε δευτερεύουσες οδούς προς αυτοκινητόδροµο
 16. Σήµανση σε δευτερεύουσες οδούς προς αυτοκινητόδροµο 16.1 Πληροφοριακή σήµανση προς δευτερεύοντες ανισόπεδους κόµβους 16.1.1 Γενικά (1) Την καθοδήγηση προς τους δευτερεύοντες ανισόπεδους κόµβους αναλαµβάνουν
16. Σήµανση σε δευτερεύουσες οδούς προς αυτοκινητόδροµο 16.1 Πληροφοριακή σήµανση προς δευτερεύοντες ανισόπεδους κόµβους 16.1.1 Γενικά (1) Την καθοδήγηση προς τους δευτερεύοντες ανισόπεδους κόµβους αναλαµβάνουν
10. Σήµανση κόµβων ΥΠΕΧΩ Ε ΓΓ Ε. Οδηγίες Μελετών Οδικών Εργων Κατακόρυφη Σήµανση Αυτοκινητοδρόµων (ΟΜΟΕ - ΚΣΑ) Μέρος 1: Πληροφοριακή Σήµανση
 Μέρος 1: Πληροφοριακή Σήµανση 10. Σήµανση κόµβων (1) Το κεφάλαιο αυτό περιλαµβάνει σχέδια της τυπικής διάταξης των πινακίδων σε δευτερεύοντες ανισόπεδους κόµβους και σε διασταυρώσεις και συµβολές αυτοκινητοδρόµων
Μέρος 1: Πληροφοριακή Σήµανση 10. Σήµανση κόµβων (1) Το κεφάλαιο αυτό περιλαµβάνει σχέδια της τυπικής διάταξης των πινακίδων σε δευτερεύοντες ανισόπεδους κόµβους και σε διασταυρώσεις και συµβολές αυτοκινητοδρόµων
2. οµή πληροφοριακής σήµανσης
 2. οµή πληροφοριακής σήµανσης 2.1 Συστατικά µέρη του συστήµατος 2.1.1 Γενικά Τα σπουδαιότερα χαρακτηριστικά της κυκλοφοριακής καθοδήγησης στην πληροφοριακή σήµανση των αυτοκινητοδρόµων είναι ο αριθµός
2. οµή πληροφοριακής σήµανσης 2.1 Συστατικά µέρη του συστήµατος 2.1.1 Γενικά Τα σπουδαιότερα χαρακτηριστικά της κυκλοφοριακής καθοδήγησης στην πληροφοριακή σήµανση των αυτοκινητοδρόµων είναι ο αριθµός
ΠΑΡΑΡΤΗΜΑ I. Κατάλογος πληροφοριακών πινακίδων
 ΠΑΡΑΡΤΗΜΑ I Κατάλογος πληροφοριακών πινακίδων I-1 I-2 Πλευρική πινακίδα αναγγελίας προσέγγισης, σε δευτερεύοντα ανισόπεδο κόµβο Σχήµα 1 Π-80.1 Πινακίδα αναγγελίας προσέγγισης, σε πρόβολο, σε δευτερεύοντα
ΠΑΡΑΡΤΗΜΑ I Κατάλογος πληροφοριακών πινακίδων I-1 I-2 Πλευρική πινακίδα αναγγελίας προσέγγισης, σε δευτερεύοντα ανισόπεδο κόµβο Σχήµα 1 Π-80.1 Πινακίδα αναγγελίας προσέγγισης, σε πρόβολο, σε δευτερεύοντα
5. Σήµανση σε ειδικές περιπτώσεις
 5. Σήµανση σε ειδικές περιπτώσεις 5.1 Κόµβοι αυτοκινητοδρόµων µε µικρή απόσταση µεταξύ τους (βλ. και παραγρ. 10.4) 5.1.1 Γενικά (1) Στην περίπτωση που κόµβοι αυτοκινητοδρόµων (δευτερεύοντες και πρωτεύοντες
5. Σήµανση σε ειδικές περιπτώσεις 5.1 Κόµβοι αυτοκινητοδρόµων µε µικρή απόσταση µεταξύ τους (βλ. και παραγρ. 10.4) 5.1.1 Γενικά (1) Στην περίπτωση που κόµβοι αυτοκινητοδρόµων (δευτερεύοντες και πρωτεύοντες
12. Σήµανση παρόδιων εγκαταστάσεων
 12. Σήµανση παρόδιων εγκαταστάσεων 12.1 Γενικά (1) Παρόδιες εγκαταστάσεις σε σταθµούς εξυπηρέτησης αυτοκινητιστών (Σ.Ε.Α.) σε αυτοκινητόδροµους είναι: πρατήρια βενζίνης αυτοκινητοδρόµων σταθµοί εξυπηρέτησης
12. Σήµανση παρόδιων εγκαταστάσεων 12.1 Γενικά (1) Παρόδιες εγκαταστάσεις σε σταθµούς εξυπηρέτησης αυτοκινητιστών (Σ.Ε.Α.) σε αυτοκινητόδροµους είναι: πρατήρια βενζίνης αυτοκινητοδρόµων σταθµοί εξυπηρέτησης
4. Βασικοί κανόνες τοποθέτησης των πινακίδων
 4. Βασικοί κανόνες τοποθέτησης των πινακίδων 4.1 Γενικά (1) Η σωστή επιλογή της θέσης των πληροφοριακών πινακίδων είναι βασικής σηµασίας για την έγκαιρη παρατήρηση της πληροφοριακής σήµανσης καθώς επίσης
4. Βασικοί κανόνες τοποθέτησης των πινακίδων 4.1 Γενικά (1) Η σωστή επιλογή της θέσης των πληροφοριακών πινακίδων είναι βασικής σηµασίας για την έγκαιρη παρατήρηση της πληροφοριακής σήµανσης καθώς επίσης
ή 7β ή µε µεγάλους κυκλοφοριακούς φόρτους από την πρόσβαση 1 Σχέδιο 18: Περιοχή πλέξης χωρίς διερχόµενο διανεµητήριο οδόστρωµα - Άνω διάβαση
 7α ή 7β ή µε µεγάλους κυκλοφοριακούς φόρτους από την πρόσβαση 1 β γ α 7γ 6 5 4 1 2 3 Σχέδιο 18: Περιοχή πλέξης χωρίς διερχόµενο διανεµητήριο οδόστρωµα - Άνω διάβαση 113 8 7 6 5 4 1 2 3 Σχέδιο 19: Περιοχή
7α ή 7β ή µε µεγάλους κυκλοφοριακούς φόρτους από την πρόσβαση 1 β γ α 7γ 6 5 4 1 2 3 Σχέδιο 18: Περιοχή πλέξης χωρίς διερχόµενο διανεµητήριο οδόστρωµα - Άνω διάβαση 113 8 7 6 5 4 1 2 3 Σχέδιο 19: Περιοχή
Σήµατα Τροχονόµων και Οδηγών
 Οδική σήµανση και σηµατοδότηση Κατακόρυφη σήµανση 1. Φωτεινοί Σηµατοδότες ( Φανάρια) 2. Πινακίδες Σήµανσης Οριζόντια σήµανση Κυκλοφοριακά Βοηθήµατα ιαγραµµίσεις στους δρόµους Σήµατα Τροχονόµων και Οδηγών
Οδική σήµανση και σηµατοδότηση Κατακόρυφη σήµανση 1. Φωτεινοί Σηµατοδότες ( Φανάρια) 2. Πινακίδες Σήµανσης Οριζόντια σήµανση Κυκλοφοριακά Βοηθήµατα ιαγραµµίσεις στους δρόµους Σήµατα Τροχονόµων και Οδηγών
Συστηματοποίηση Δυναμικής Σήμανσης Σήμανση στις προσβάσεις σηράγγων
 Συστηματοποίηση Δυναμικής Σήμανσης Σήμανση στις προσβάσεις σηράγγων 1 Για τη σήμανση των προσβάσεων στην Ελλάδα εφαρμόζεται το κεφάλαιο 20 των ΟΜΟΕ-ΚΣΑ, μέρος 1 Με αυτές τις οδηγίες αντιμετωπίζεται η σήμανση
Συστηματοποίηση Δυναμικής Σήμανσης Σήμανση στις προσβάσεις σηράγγων 1 Για τη σήμανση των προσβάσεων στην Ελλάδα εφαρμόζεται το κεφάλαιο 20 των ΟΜΟΕ-ΚΣΑ, μέρος 1 Με αυτές τις οδηγίες αντιμετωπίζεται η σήμανση
ιαστασιολόγηση Περιεχόμενα Ορισμός Μηχανολογικός Σχεδιασμός Εισαγωγή Στοιχεία διαστασιολόγησης ιαστασιολόγηση χαρακτηριστικών αντικειμένων
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή ιαστασιολόγηση η Στοιχεία διαστασιολόγησης ιαστασιολόγηση χαρακτηριστικών αντικειμένων Πρακτική διαστασιολόγησης Μηχανολογικός
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ναυπηγών Μηχανολόγων Μηχανικών Περιεχόμενα Εισαγωγή ιαστασιολόγηση η Στοιχεία διαστασιολόγησης ιαστασιολόγηση χαρακτηριστικών αντικειμένων Πρακτική διαστασιολόγησης Μηχανολογικός
3. Αναγραφές προορισµών
 3. Αναγραφές προορισµών 3.1 Κανόνες (1) Οι αναγραφές των προορισµών εξυπηρετούν το γεωγραφικό προσανατολισµό στο οδικό δίκτυο, καθώς και τον εντοπισµό του προορισµού. Ως προορισµοί επιλέγονται τοπωνύµια
3. Αναγραφές προορισµών 3.1 Κανόνες (1) Οι αναγραφές των προορισµών εξυπηρετούν το γεωγραφικό προσανατολισµό στο οδικό δίκτυο, καθώς και τον εντοπισµό του προορισµού. Ως προορισµοί επιλέγονται τοπωνύµια
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΑΡΑΡΤΗΜΑ Τεχνικές διατάξεις σχετικά με το πρότυπο λογοτύπου, σφραγίδων και εγγράφων του Α.Π.Θ. Έκδοση 1.0 Σεπτέμβριος 2005 1. Εισαγωγή Το Αριστοτέλειο Πανεπιστήμιο
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΑΡΑΡΤΗΜΑ Τεχνικές διατάξεις σχετικά με το πρότυπο λογοτύπου, σφραγίδων και εγγράφων του Α.Π.Θ. Έκδοση 1.0 Σεπτέμβριος 2005 1. Εισαγωγή Το Αριστοτέλειο Πανεπιστήμιο
ΡΥΘΜΙΣΤΙΚΕΣ ΠΙΝΑΚΙ ΕΣ (Ρ)
 ΡΥΘΜΙΣΤΙΚΕΣ ΠΙΝΑΚΙ ΕΣ (Ρ) Made by Nikouba!!! Οι ρυθµιστικές πινακίδες επιβάλλουν στον οδηγό την τήρηση ορισµένων κανόνων κυκλοφορίας (π.χ. απαγόρευση στροφής, υποχρεωτική πορεία, όριο ταχύτητας κλπ.).
ΡΥΘΜΙΣΤΙΚΕΣ ΠΙΝΑΚΙ ΕΣ (Ρ) Made by Nikouba!!! Οι ρυθµιστικές πινακίδες επιβάλλουν στον οδηγό την τήρηση ορισµένων κανόνων κυκλοφορίας (π.χ. απαγόρευση στροφής, υποχρεωτική πορεία, όριο ταχύτητας κλπ.).
Οδηγίες Συντήρησης Αυτοκινητοδρόµων ΤΕΥΧΟΣ 2
 Οδηγίες Συντήρησης Αυτοκινητοδρόµων ΤΕΥΧΟΣ 2 Μητρώο Αυτοκινητοδρόµου για τη Στοιχειώδη Συντήρηση 1. Εισαγωγή Το τεύχος αυτό αναφέρεται στο µητρώο αυτοκινητοδρόµου, η τήρηση του οποίου είναι απαραίτητη
Οδηγίες Συντήρησης Αυτοκινητοδρόµων ΤΕΥΧΟΣ 2 Μητρώο Αυτοκινητοδρόµου για τη Στοιχειώδη Συντήρηση 1. Εισαγωγή Το τεύχος αυτό αναφέρεται στο µητρώο αυτοκινητοδρόµου, η τήρηση του οποίου είναι απαραίτητη
Επίσηµη Εφηµερίδα της Ευρωπαϊκής Ένωσης ΑΠΟΦΑΣΕΙΣ
 14.10.2015 L 267/5 ΑΠΟΦΑΣΕΙΣ ΕΚΤΕΛΕΣΤΙΚΗ ΑΠΟΦΑΣΗ (ΕΕ) 2015/1842 ΤΗΣ ΕΠΙΤΡΟΠΗΣ της 9ης Οκτωβρίου 2015 σχετικά με τις τεχνικές προδιαγραφές για τη διάταξη, τον σχεδιασμό και το σχήμα των συνδυασμένων προειδοποιήσεων
14.10.2015 L 267/5 ΑΠΟΦΑΣΕΙΣ ΕΚΤΕΛΕΣΤΙΚΗ ΑΠΟΦΑΣΗ (ΕΕ) 2015/1842 ΤΗΣ ΕΠΙΤΡΟΠΗΣ της 9ης Οκτωβρίου 2015 σχετικά με τις τεχνικές προδιαγραφές για τη διάταξη, τον σχεδιασμό και το σχήμα των συνδυασμένων προειδοποιήσεων
Μπορούμε να χρησιμοποιήσουμε τις παρακάτω μορφές συντεταγμένων με οποιοδήποτε συνδυασμό θέλουμε. Καρτεσιανές συντεταγμένες
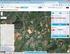 ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
ΣΥΝΤΕΤΑΓΜΕΝΕΣ Όταν σχεδιάζουμε, πρέπει να προσδιορίζουμε σημεία πάνω σε ένα επίπεδο. Μπορούμε να εντοπίσουμε οποιοδήποτε σημείο στο χώρο, αν ορίσουμε πρώτα ένα απόλυτο, σταθερό σημείο και να μετρήσουμε
1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα)
 20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
20 1.3 Σχεδίαση µε ελεύθερο χέρι (Σκαρίφηµα) 1.3.1 Ορισµός- Είδη - Χρήση Σκαρίφηµα καλείται η εικόνα ενός αντικειµένου ή εξαρτήµατος που µεταφέρεται σε χαρτί µε ελεύθερο χέρι (χωρίς όργανα σχεδίασης ή
Tυποποίηση σήμανσης. Κόμβων και οδικού δικτυού πλην αυτοκινητοδρόμων ευα κασαπη νοεμβρης 2008 Τρίπολης
 Tυποποίηση σήμανσης Κόμβων και οδικού δικτυού πλην αυτοκινητοδρόμων ευα κασαπη νοεμβρης 2008 Τρίπολης η σήμανση πρέπει να είναι: Αντιληπτή και εύκολα κατανοητή. Οφείλει να ανταποκρίνεται στις απαιτήσεις
Tυποποίηση σήμανσης Κόμβων και οδικού δικτυού πλην αυτοκινητοδρόμων ευα κασαπη νοεμβρης 2008 Τρίπολης η σήμανση πρέπει να είναι: Αντιληπτή και εύκολα κατανοητή. Οφείλει να ανταποκρίνεται στις απαιτήσεις
Σχέδιο 5: ιασταύρωση αυτοκινητοδρόµων 2x2 λωρίδων
 Μέρος 1: Πληροφοριακ Σµανση µονόιχνη έξοδος µε δίιχνη έξοδος µε 5 4 3 2 1 Η θέση Σ.Α.1 πρέπει να βρίσκεται πάντα σε απόσταση 70 m από την αρχ του taper το οποίο πρέπει να έχει µκος 60 m Σ.Α. = Σηµείο αναφοράς
Μέρος 1: Πληροφοριακ Σµανση µονόιχνη έξοδος µε δίιχνη έξοδος µε 5 4 3 2 1 Η θέση Σ.Α.1 πρέπει να βρίσκεται πάντα σε απόσταση 70 m από την αρχ του taper το οποίο πρέπει να έχει µκος 60 m Σ.Α. = Σηµείο αναφοράς
ΠΑΡΑΡΤΗΜΑ Γ. Τυπικά Σχέδια. ιατάξεων Σήµανσης Εκτελούµενων Εργων ΥΠΕΧΩ Ε ΓΓ Ε
 ΠΑΡΑΡΤΗΜΑ Γ Τυπικά Σχέδια ιατάξεων Σήµανσης Εκτελούµενων Εργων Γ-1 Κενή Σελίδα Γ-2 ΑΥΤΟΚΙΝΗΤΟ ΡΟΜΟΙ Εργοτάξια µακράς διάρκειας 1.1.1 Στένωση Λωρίδων 1.1.2 Αποκλεισµός Λωρίδας 1.1.3α Κλείσιµο λωρίδων µε
ΠΑΡΑΡΤΗΜΑ Γ Τυπικά Σχέδια ιατάξεων Σήµανσης Εκτελούµενων Εργων Γ-1 Κενή Σελίδα Γ-2 ΑΥΤΟΚΙΝΗΤΟ ΡΟΜΟΙ Εργοτάξια µακράς διάρκειας 1.1.1 Στένωση Λωρίδων 1.1.2 Αποκλεισµός Λωρίδας 1.1.3α Κλείσιµο λωρίδων µε
2.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΟΙ ΑΡΙΘΜΟΙ 30 Ο 45 Ο 60 Ο
 .4 ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ 0 Ο 45 Ο 60 Ο ΘΕΩΡΙ. Τριγωνοµετρικοί αριθµοί 0 ο, 45 ο, 60 ο : ηµίτονο συνηµίτονο εφαπτοµένη 0 ο 45 ο 60 ο ΣΚΗΣΕΙΣ. Στο διπλανό πίνακα, σε κάθε πληροφορία της στήλης, να επιλέξετε
.4 ΤΡΙΩΝΟΜΕΤΡΙΚΟΙ ΡΙΘΜΟΙ 0 Ο 45 Ο 60 Ο ΘΕΩΡΙ. Τριγωνοµετρικοί αριθµοί 0 ο, 45 ο, 60 ο : ηµίτονο συνηµίτονο εφαπτοµένη 0 ο 45 ο 60 ο ΣΚΗΣΕΙΣ. Στο διπλανό πίνακα, σε κάθε πληροφορία της στήλης, να επιλέξετε
Παρατηρήσεις για τη χρήση ενός κυκλικού διαγράμματος
 Παρατηρήσεις για τη χρήση ενός κυκλικού διαγράμματος Χρησιμοποιείται μόνο όταν οι τιμές της μεταβλητής έχουν ένα σταθερό άθροισμα (συνήθως 100%, όταν μιλάμε για σχετικές συχνότητες) Είναι χρήσιμο μόνο
Παρατηρήσεις για τη χρήση ενός κυκλικού διαγράμματος Χρησιμοποιείται μόνο όταν οι τιμές της μεταβλητής έχουν ένα σταθερό άθροισμα (συνήθως 100%, όταν μιλάμε για σχετικές συχνότητες) Είναι χρήσιμο μόνο
16REQ
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΜΟΣ ΑΜΠΕΛΟΚΗΠΩΝ- ΜΕΝΕΜΕΝΗΣ ΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΠΟΛΕΟ ΟΜΙΑΣ-ΚΑΘΑΡΙΟΤΗΤΑΣ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΜΕΛΕΤΩΝ-ΚΑΤΑΣΚΕΥΩΝ ΚΑΙ ΠΟΛΕΟ ΟΜΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΕΡΓΟ: «ΠΡΟΜΗΘΕΙΑ
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΝΟΜΟΣ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΜΟΣ ΑΜΠΕΛΟΚΗΠΩΝ- ΜΕΝΕΜΕΝΗΣ ΙΕΥΘΥΝΣΗ ΤΕΧΝΙΚΩΝ ΥΠΗΡΕΣΙΩΝ ΠΟΛΕΟ ΟΜΙΑΣ-ΚΑΘΑΡΙΟΤΗΤΑΣ & ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΤΜΗΜΑ ΜΕΛΕΤΩΝ-ΚΑΤΑΣΚΕΥΩΝ ΚΑΙ ΠΟΛΕΟ ΟΜΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΕΡΓΟ: «ΠΡΟΜΗΘΕΙΑ
ΔΙΑΣΤΑΣΕΙΣ. Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων
 ΔΙΑΣΤΑΣΕΙΣ Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων Η Σωστή τοποθετηση Διαστασεων στο Μηχανολογικο Σχεδιο ειναι απαραιτητη για τη Σωστή Κατασκευή Εχετε κατι να παρατηρησετε;
ΔΙΑΣΤΑΣΕΙΣ Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων Η Σωστή τοποθετηση Διαστασεων στο Μηχανολογικο Σχεδιο ειναι απαραιτητη για τη Σωστή Κατασκευή Εχετε κατι να παρατηρησετε;
Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει:
 ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να αναγνωρίζει και να κατονομάζει τα διάφορα είδη προβολών. 2. Να αναγνωρίζει και να κατονομάζει
ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΟΡΘΟΓΡΑΦΙΚΗ ΠΡΟΒΟΛΗ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να αναγνωρίζει και να κατονομάζει τα διάφορα είδη προβολών. 2. Να αναγνωρίζει και να κατονομάζει
Χάραξη κόμβου. 10/11/09 Μάθημα Θέμα Οδοποιίας
 Χάραξη κόμβου 10/11/09 Μάθημα Θέμα Οδοποιίας 1 Τύποι ισόπεδων κόμβων Με τρία σκέλη Με τέσσερα σκέλη Με πάνω από τέσσερα σκέλη 10/11/09 Μάθημα Θέμα Οδοποιίας 2 Απλή διασταύρωση τύπου Τ Προσφέρεται όταν
Χάραξη κόμβου 10/11/09 Μάθημα Θέμα Οδοποιίας 1 Τύποι ισόπεδων κόμβων Με τρία σκέλη Με τέσσερα σκέλη Με πάνω από τέσσερα σκέλη 10/11/09 Μάθημα Θέμα Οδοποιίας 2 Απλή διασταύρωση τύπου Τ Προσφέρεται όταν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΥΠΟΔΟΜΩΝ ΚΑΙ ΜΕΤΑΦΟΡΩΝ ΓΕΝ. ΓΡΑΜ. ΥΠΟΔΟΜΩΝ Δ/ΝΣΗ ΟΔΙΚΩΝ ΥΠΟΔΟΜΩΝ (Δ.Ο.Υ.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΥΠΟΔΟΜΩΝ ΚΑΙ ΜΕΤΑΦΟΡΩΝ ΓΕΝ. ΓΡΑΜ. ΥΠΟΔΟΜΩΝ Δ/ΝΣΗ ΟΔΙΚΩΝ ΥΠΟΔΟΜΩΝ (Δ.Ο.Υ./Δ13) ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΚΥΚΛΟΦΟΡΙΑΣ & ΜΗΤΡΩΟΥ ΟΔΙΚΩΝ ΥΠΟΔΟΜΩΝ ΓΕΝΙΚΕΣ ΚΑΤΕΥΘΥΝΤΗΡΙΕΣ ΟΔΗΓΙΕΣ, ΠΟΥ ΑΦΟΡΟΥΝ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΥΠΟΔΟΜΩΝ ΚΑΙ ΜΕΤΑΦΟΡΩΝ ΓΕΝ. ΓΡΑΜ. ΥΠΟΔΟΜΩΝ Δ/ΝΣΗ ΟΔΙΚΩΝ ΥΠΟΔΟΜΩΝ (Δ.Ο.Υ./Δ13) ΤΜΗΜΑ ΔΙΑΧΕΙΡΙΣΗΣ ΚΥΚΛΟΦΟΡΙΑΣ & ΜΗΤΡΩΟΥ ΟΔΙΚΩΝ ΥΠΟΔΟΜΩΝ ΓΕΝΙΚΕΣ ΚΑΤΕΥΘΥΝΤΗΡΙΕΣ ΟΔΗΓΙΕΣ, ΠΟΥ ΑΦΟΡΟΥΝ
Οδηγίες Συντήρησης Αυτοκινητοδρόµων ΤΕΥΧΟΣ 3
 Οδηγίες Συντήρησης Αυτοκινητοδρόµων ΤΕΥΧΟΣ 3 Μητρώο Αυτοκινητοδρόµου για τη Στοιχειώδη Συντήρηση Συντακτική οµάδα - Επιµέλεια:, Επιµέλεια: Ιωάννα Καρακαϊδού, Αναπληρωτής ιευθυντής ιεύθυνσης Υποστήριξης
Οδηγίες Συντήρησης Αυτοκινητοδρόµων ΤΕΥΧΟΣ 3 Μητρώο Αυτοκινητοδρόµου για τη Στοιχειώδη Συντήρηση Συντακτική οµάδα - Επιµέλεια:, Επιµέλεια: Ιωάννα Καρακαϊδού, Αναπληρωτής ιευθυντής ιεύθυνσης Υποστήριξης
Οδηγßεò Μελετþν Οδικþν Εργων (ΟΜΟΕ) Τεýχοò 6 Κατακόρυφη Σήµανση Αυτοκινητοδρόµων (ΟΜΟΕ-ΚΣΑ)
 Υ. ΠΕ. ΧΩ.. Ε. ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΗΜΟΣΙΩΝ ΕΡΓΩΝ Οδηγßεò Μελετþν Οδικþν Εργων (ΟΜΟΕ) Τεýχοò 6 Κατακόρυφη Σήµανση Αυτοκινητοδρόµων (ΟΜΟΕ-ΚΣΑ) Μέρος Μέρος 2: 2: Πινακίδες Πινακίδες σταθερού σταθερού περιεχοµένου
Υ. ΠΕ. ΧΩ.. Ε. ΓΕΝΙΚΗ ΓΡΑΜΜΑΤΕΙΑ ΗΜΟΣΙΩΝ ΕΡΓΩΝ Οδηγßεò Μελετþν Οδικþν Εργων (ΟΜΟΕ) Τεýχοò 6 Κατακόρυφη Σήµανση Αυτοκινητοδρόµων (ΟΜΟΕ-ΚΣΑ) Μέρος Μέρος 2: 2: Πινακίδες Πινακίδες σταθερού σταθερού περιεχοµένου
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2015 Πανεπιστήμιο Αθηνών, Εργαστήριο Φυσικών Επιστημών, Τεχνολογίας, Περιβάλλοντος
 Γ Λυκείου 7 Μαρτίου 2015 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα
Γ Λυκείου 7 Μαρτίου 2015 ΟΔΗΓΙΕΣ: 1. Η επεξεργασία των θεμάτων θα γίνει γραπτώς σε χαρτί Α4 ή σε τετράδιο που θα σας δοθεί (το οποίο θα παραδώσετε στο τέλος της εξέτασης). Εκεί θα σχεδιάσετε και όσα γραφήματα
Σχέδιο ΚΑΝΟΝΙΣΜΟΣ (ΕΕ) ΑΡΙΘ. /.. ΤΗΣ ΕΠΙΤΡΟΠΗΣ
 ΕΥΡΩΠΑΪΚΗ ΕΠΙΤΡΟΠΗ ΣΧΕ ΙΟ Έκδοση 9.00 της 31ης Μαρ. 2010 Σχέδιο ΚΑΝΟΝΙΣΜΟΣ (ΕΕ) ΑΡΙΘ. /.. ΤΗΣ ΕΠΙΤΡΟΠΗΣ της σχετικά µε τις απαιτήσεις έγκρισης τύπου για το χώρο τοποθέτησης και τη στερέωση των οπίσθιων
ΕΥΡΩΠΑΪΚΗ ΕΠΙΤΡΟΠΗ ΣΧΕ ΙΟ Έκδοση 9.00 της 31ης Μαρ. 2010 Σχέδιο ΚΑΝΟΝΙΣΜΟΣ (ΕΕ) ΑΡΙΘ. /.. ΤΗΣ ΕΠΙΤΡΟΠΗΣ της σχετικά µε τις απαιτήσεις έγκρισης τύπου για το χώρο τοποθέτησης και τη στερέωση των οπίσθιων
5. Τα μήκη των βάσεων ενός τραπεζίου είναι 8 cm και 12 cm και το ύψος του είναι 7. Να βρείτε το εμβαδό του.
 1 ΑΣΚΗΣΕΙΣ 1. Ένα παραλληλόγραμμο ΑΒΓΔ έχει μια πλευρά ίση με 48 και το αντίστοιχο σε αυτή την πλευρά ύψος είναι 4,5 dm. Να βρείτε το εμβαδό του παραλληλογράμμου 2. Ένα παραλληλόγραμμο έχει εμβαδό 72 2
1 ΑΣΚΗΣΕΙΣ 1. Ένα παραλληλόγραμμο ΑΒΓΔ έχει μια πλευρά ίση με 48 και το αντίστοιχο σε αυτή την πλευρά ύψος είναι 4,5 dm. Να βρείτε το εμβαδό του παραλληλογράμμου 2. Ένα παραλληλόγραμμο έχει εμβαδό 72 2
Oδηγοί - Eγχειρίδια. «Προδιαγραφές γραφικής απεικόνισης του ευρωπαϊκού συµβόλου», Eυρωπαϊκή Eπιτροπή
 Oδηγοί - Eγχειρίδια 5. «Προδιαγραφές γραφικής απεικόνισης του ευρωπαϊκού συµβόλου», Eυρωπαϊκή Eπιτροπή 169 ΠΛHPOΦOPHΣH & HMOΣIOTHTA ΣTO KΠΣ 2000-2006: Oδηγοί - Eγχειρίδια «Προδιαγραφές γραφικής απεικόνισης
Oδηγοί - Eγχειρίδια 5. «Προδιαγραφές γραφικής απεικόνισης του ευρωπαϊκού συµβόλου», Eυρωπαϊκή Eπιτροπή 169 ΠΛHPOΦOPHΣH & HMOΣIOTHTA ΣTO KΠΣ 2000-2006: Oδηγοί - Eγχειρίδια «Προδιαγραφές γραφικής απεικόνισης
1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων
 1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων 1.4.1 Κλίµακες σχεδίασης Στο µηχανολογικό σχέδιο είναι επιθυµητό να σχεδιάζεται ένα αντικείµενο σε φυσικό µέγεθος, γιατί έτσι παρουσιάζεται η αληθινή
1.4 Κλίµακες σχεδίασης και κανόνες τοποθέτησης διαστάσεων 1.4.1 Κλίµακες σχεδίασης Στο µηχανολογικό σχέδιο είναι επιθυµητό να σχεδιάζεται ένα αντικείµενο σε φυσικό µέγεθος, γιατί έτσι παρουσιάζεται η αληθινή
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
Μέρος 3: Συλλογή εδοµένων Γενικοί Κανόνες Καταγραφής
 Μέρος 3: Συλλογή εδοµένων Γενικοί Κανόνες Καταγραφής ΣΥΛΛΟΓΗ Ε ΟΜΕΝΩΝ, ΓΕΝΙΚΟΙ ΚΑΝΟΝΕΣ ΚΑΤΑΓΡΑΦΗΣ 3.1 Γενικά Στο µέρος αυτό δίδονται κατευθυντήριες οδηγίες και γενικοί κανόνες για τη συλλογή και καταγραφή
Μέρος 3: Συλλογή εδοµένων Γενικοί Κανόνες Καταγραφής ΣΥΛΛΟΓΗ Ε ΟΜΕΝΩΝ, ΓΕΝΙΚΟΙ ΚΑΝΟΝΕΣ ΚΑΤΑΓΡΑΦΗΣ 3.1 Γενικά Στο µέρος αυτό δίδονται κατευθυντήριες οδηγίες και γενικοί κανόνες για τη συλλογή και καταγραφή
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 5 η ΕΚΑ Α
 1 ΣΚΗΣΕΙΣ ΕΠΝΛΗΨΗΣ 5 η ΕΚ 1. Οι πλευρές ενός τριγώνου σε cm είναι = 3x 3, = 3x + 1 και = x και η περίµετρος Π του τριγώνου είναι Π = 8cm. Να βρείτε τα µήκη των πλευρών του τριγώνου. Να δείξτε ότι το τρίγωνο
1 ΣΚΗΣΕΙΣ ΕΠΝΛΗΨΗΣ 5 η ΕΚ 1. Οι πλευρές ενός τριγώνου σε cm είναι = 3x 3, = 3x + 1 και = x και η περίµετρος Π του τριγώνου είναι Π = 8cm. Να βρείτε τα µήκη των πλευρών του τριγώνου. Να δείξτε ότι το τρίγωνο
Άσκηση 4η Να βρεθεί ο τριψήφιος αριθμός που τα ψηφία του είναι ανάλογα των αριθμών 1, 2, 3 κατά σειρά και διαιρείται από το 9. Άσκηση 7η.
 Άσκηση 1η Αν η εξίσωση είναι αόριστη, τότε: α) Να δειχθεί ότι η εξίσωση είναι αδύνατη β) Να λυθεί η ανίσωση γ) Αν ισχύει ότι να βρεθεί ο αριθμός Α Άσκηση 2η Αν η εξίσωση έχει λύση μεγαλύτερη του και η
Άσκηση 1η Αν η εξίσωση είναι αόριστη, τότε: α) Να δειχθεί ότι η εξίσωση είναι αδύνατη β) Να λυθεί η ανίσωση γ) Αν ισχύει ότι να βρεθεί ο αριθμός Α Άσκηση 2η Αν η εξίσωση έχει λύση μεγαλύτερη του και η
Δύο κύριοι τρόποι παρουσίασης δεδομένων. Παράδειγμα
 Δύο κύριοι τρόποι παρουσίασης δεδομένων Παράδειγμα Με πίνακες Με διαγράμματα Ονομαστικά δεδομένα Εδώ τα περιγραφικά μέτρα (μέσος, διάμεσος κλπ ) δεν έχουν νόημα Πήραμε ένα δείγμα από 25 άτομα και τα ρωτήσαμε
Δύο κύριοι τρόποι παρουσίασης δεδομένων Παράδειγμα Με πίνακες Με διαγράμματα Ονομαστικά δεδομένα Εδώ τα περιγραφικά μέτρα (μέσος, διάμεσος κλπ ) δεν έχουν νόημα Πήραμε ένα δείγμα από 25 άτομα και τα ρωτήσαμε
ΠΡΟΒΛΗΜΑ ΔΙΑΓΩΝΙΟΥ. Εξετάζουμε ενδεικτικά ορισμένες περιπτώσεις: 1 ο 2 ο. 3 ο 4 ο
 ΠΡΟΒΛΗΜΑ ΔΙΑΓΩΝΙΟΥ Δίνεται ορθογώνιο παραλληλόγραμμο διάστασης m n όπου m,n φυσικοί αριθμοί, το οποίο είναι διαιρεμένο σε τετράγωνα που το καθένα ισούται με την μονάδα μέτρησης του εμβαδού του. Να βρεθεί
ΠΡΟΒΛΗΜΑ ΔΙΑΓΩΝΙΟΥ Δίνεται ορθογώνιο παραλληλόγραμμο διάστασης m n όπου m,n φυσικοί αριθμοί, το οποίο είναι διαιρεμένο σε τετράγωνα που το καθένα ισούται με την μονάδα μέτρησης του εμβαδού του. Να βρεθεί
ΚΑΝΟΝΙΣΜΟΙ. L 291/22 Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης
 L 291/22 Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης 9.11.2010 ΚΑΝΟΝΙΣΜΟΙ ΚΑΝΟΝΙΣΜΟΣ (ΕΕ) αριθ. 1003/2010 ΤΗΣ ΕΠΙΤΡΟΠΗΣ της 8ης Νοεμβρίου 2010 σχετικά με τις απαιτήσεις έγκρισης τύπου για το χώρο τοποθέτησης
L 291/22 Επίσημη Εφημερίδα της Ευρωπαϊκής Ένωσης 9.11.2010 ΚΑΝΟΝΙΣΜΟΙ ΚΑΝΟΝΙΣΜΟΣ (ΕΕ) αριθ. 1003/2010 ΤΗΣ ΕΠΙΤΡΟΠΗΣ της 8ης Νοεμβρίου 2010 σχετικά με τις απαιτήσεις έγκρισης τύπου για το χώρο τοποθέτησης
ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ. ΔΙΑΡΚΕΙΑ: 1 περιόδους. 28/9/2008 12:48 Όνομα: Λεκάκης Κωνσταντίνος καθ.
 ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ ΔΙΑΡΚΕΙΑ: 1 περιόδους 28/9/2008 12:48 καθ. Τεχνολογίας 28/9/2008 12:57 Προοπτικό σχέδιο με 2 Σημεία Φυγής Σημείο φυγής 1 Σημείο φυγής 2 Γωνία κτιρίου
ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ ΔΙΑΡΚΕΙΑ: 1 περιόδους 28/9/2008 12:48 καθ. Τεχνολογίας 28/9/2008 12:57 Προοπτικό σχέδιο με 2 Σημεία Φυγής Σημείο φυγής 1 Σημείο φυγής 2 Γωνία κτιρίου
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ 3 η ΕΚΑ Α
 1 ΣΚΗΣΙΣ ΠΝΛΗΨΗΣ 3 η Κ 1. Στο διπλανό σχήµα το τετράπλευρο παριστάνει µία τετράγωνη πλατεία και τα τετράπλευρα ΚΛΘ και ΗΜΡΖ παριστάνουν δύο κήπους. Η πλευρά του είναι 30m και η απόσταση των ΚΛ και ΡΜ είναι
1 ΣΚΗΣΙΣ ΠΝΛΗΨΗΣ 3 η Κ 1. Στο διπλανό σχήµα το τετράπλευρο παριστάνει µία τετράγωνη πλατεία και τα τετράπλευρα ΚΛΘ και ΗΜΡΖ παριστάνουν δύο κήπους. Η πλευρά του είναι 30m και η απόσταση των ΚΛ και ΡΜ είναι
Ενδεικτικό Φύλλο Εργασίας 1. Ορθογώνιο Παραλληλεπίπεδο - Κύβος
 Διδακτική των Μαθηματικών με Τ.Π.Ε Σελίδα 1 από 6 Ενδεικτικό Φύλλο Εργασίας 1. Ορθογώνιο Παραλληλεπίπεδο - Κύβος Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:... Όλες οι εφαρμογές που καλείσθε να χρησιμοποιήσετε
Διδακτική των Μαθηματικών με Τ.Π.Ε Σελίδα 1 από 6 Ενδεικτικό Φύλλο Εργασίας 1. Ορθογώνιο Παραλληλεπίπεδο - Κύβος Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:... Όλες οι εφαρμογές που καλείσθε να χρησιμοποιήσετε
Γράμματα και αριθμοί
 5 Γράμματα και αριθμοί 5.1 Γενικά Στα τεχνικά σχέδια χρησιμοποιούμε γράμματα και αριθμούς, όταν θέλουμε να δώσουμε περισσότερες πληροφορίες, όπως να χαρακτηρίσουμε χώρους ή υλικά, να δείξουμε την πορεία
5 Γράμματα και αριθμοί 5.1 Γενικά Στα τεχνικά σχέδια χρησιμοποιούμε γράμματα και αριθμούς, όταν θέλουμε να δώσουμε περισσότερες πληροφορίες, όπως να χαρακτηρίσουμε χώρους ή υλικά, να δείξουμε την πορεία
25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: ΜΟΝΑΔΕΣ:
 ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗ 25 Ιανουαρίου 2014 ΛΥΚΕΙΟ:..... ΟΜΑΔΑ ΜΑΘΗΤΩΝ: 1.. 2..... 3..... ΜΟΝΑΔΕΣ: Το πρόβλημα Ένας φίλος σας βρήκε ένα μικρό, πολύ όμορφο τεμάχιο διαφανούς στερεού και ζητά τη γνώμη
ΕΚ ΟΣΗ ΚΑΙ ΠΑΡΑ ΟΣΗ ΑΠΟΤΕΛΕΣΜΑΤΩΝ
 Κωδικός:.540 Αρ. Έκδοσης: 3 Ηµ/νία: 01-02-2012 Σελ 1 από 5 1. ΕΙΣΑΓΩΓΗ Η παρούσα ιαδικασία περιγράφει τον τρόπο µε τον οποίο το ΕΣΕΑΠ εκδίδει και παραδίδει τα αποτελέσµατα του εξωτερικού ελέγχου ποιότητας
Κωδικός:.540 Αρ. Έκδοσης: 3 Ηµ/νία: 01-02-2012 Σελ 1 από 5 1. ΕΙΣΑΓΩΓΗ Η παρούσα ιαδικασία περιγράφει τον τρόπο µε τον οποίο το ΕΣΕΑΠ εκδίδει και παραδίδει τα αποτελέσµατα του εξωτερικού ελέγχου ποιότητας
Β. Ψαριανός, Καθηγ. ΕΜΠ ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΠΑΡΑΤΗΡΗΤΗΡΙΟ ΟΔΙΚΗΣ ΑΣΦΑΛΕΙΑΣ. Ημερίδα Οδικής Ασφάλειας ΤΡΙΠΟΛΗ
 Β. Ψαριανός, Καθηγ. ΕΜΠ ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΠΑΡΑΤΗΡΗΤΗΡΙΟ ΟΔΙΚΗΣ ΑΣΦΑΛΕΙΑΣ Ημερίδα Οδικής ΤΡΙΠΟΛΗ 22.11.2008 -22.11.2008 2 -22.11.2008 3 -22.11.2008 4 -22.11.2008 5 -22.11.2008 6 ΚΑΙΡΙΚΕΣ ΣΥΝΘΗΚΕΣ
Β. Ψαριανός, Καθηγ. ΕΜΠ ΤΕΧΝΙΚΟ ΕΠΙΜΕΛΗΤΗΡΙΟ ΕΛΛΑΔΑΣ ΠΑΡΑΤΗΡΗΤΗΡΙΟ ΟΔΙΚΗΣ ΑΣΦΑΛΕΙΑΣ Ημερίδα Οδικής ΤΡΙΠΟΛΗ 22.11.2008 -22.11.2008 2 -22.11.2008 3 -22.11.2008 4 -22.11.2008 5 -22.11.2008 6 ΚΑΙΡΙΚΕΣ ΣΥΝΘΗΚΕΣ
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με πέντε (5) αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΤΡΙΤΗ 21 ΙΟΥΝΙΟΥ 2016 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με πέντε (5) αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΔΙΑΣΤΑΣΕΙΣ - ΤΟΜΕΣ
 ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΔΙΑΣΤΑΣΕΙΣ - ΤΟΜΕΣ Διαστασιολόγηση Μια από τις σημαντικότερες εργασίες του σχεδιαστή, αλλά και η πιο δύσκολη και υπεύθυνη, είναι η σωστή τοποθέτηση διαστάσεων
ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΔΙΑΣΤΑΣΕΙΣ - ΤΟΜΕΣ Διαστασιολόγηση Μια από τις σημαντικότερες εργασίες του σχεδιαστή, αλλά και η πιο δύσκολη και υπεύθυνη, είναι η σωστή τοποθέτηση διαστάσεων
ΕΠΙΤΡΟΠΗ ΤΩΝ ΕΥΡΩΠΑΪΚΩΝ ΚΟΙΝΟΤΗΤΩΝ. Πρόταση ΟΔΗΓΙΑΣ ΤΟΥ ΕΥΡΩΠΑΪΚΟΥ ΚΟΙΝΟΒΟΥΛΙΟΥ ΚΑΙ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ
 ΕΠΙΤΡΟΠΗ ΤΩΝ ΕΥΡΩΠΑΪΚΩΝ ΚΟΙΝΟΤΗΤΩΝ Βρυξέλλες, 5.9.2006 COM(2006) 478 τελικό 2006/0161 (COD) Πρόταση ΟΔΗΓΙΑΣ ΤΟΥ ΕΥΡΩΠΑΪΚΟΥ ΚΟΙΝΟΒΟΥΛΙΟΥ ΚΑΙ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ σχετικά με τη θέση προσαρμογής της οπίσθιας πινακίδας
ΕΠΙΤΡΟΠΗ ΤΩΝ ΕΥΡΩΠΑΪΚΩΝ ΚΟΙΝΟΤΗΤΩΝ Βρυξέλλες, 5.9.2006 COM(2006) 478 τελικό 2006/0161 (COD) Πρόταση ΟΔΗΓΙΑΣ ΤΟΥ ΕΥΡΩΠΑΪΚΟΥ ΚΟΙΝΟΒΟΥΛΙΟΥ ΚΑΙ ΤΟΥ ΣΥΜΒΟΥΛΙΟΥ σχετικά με τη θέση προσαρμογής της οπίσθιας πινακίδας
Σχεδίαση τομών Συνήθη σφάλματα και Παραδείγματα. Πότε;
 Σχεδίαση τομών... Πότε;...Συνήθη σφάλματα και Παραδείγματα Οταν 5 η Διάλεξη οι οψεις Τομές δημιουργουν συγχυση και δεν εμφανιζουν αμεσα το εσωτερικο των αντικειμένων Ι.Ν. ΑΓ. ΔΗΜΗΤΡΙΟΥ, ΗΠΕΙΡΟΣ Διαδικασία
Σχεδίαση τομών... Πότε;...Συνήθη σφάλματα και Παραδείγματα Οταν 5 η Διάλεξη οι οψεις Τομές δημιουργουν συγχυση και δεν εμφανιζουν αμεσα το εσωτερικο των αντικειμένων Ι.Ν. ΑΓ. ΔΗΜΗΤΡΙΟΥ, ΗΠΕΙΡΟΣ Διαδικασία
ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΟΜΕΣ - ΔΙΑΣΤΑΣΕΙΣ
 ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΟΜΕΣ - ΔΙΑΣΤΑΣΕΙΣ Τομές Η σχεδίαση σε τομή είναι απαραίτητη όταν θέλουμε να αποδώσουμε το εσωτερικό ενός αντικειμένου ή ενός μηχανήματος. Η σχεδίαση σε τομή
ΕΙΣΑΓΩΓΗ ΣΤΟ ΣΧΕΔΙΑΣΜΟ ΤΕΧΝΟΛΟΓΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΟΜΕΣ - ΔΙΑΣΤΑΣΕΙΣ Τομές Η σχεδίαση σε τομή είναι απαραίτητη όταν θέλουμε να αποδώσουμε το εσωτερικό ενός αντικειμένου ή ενός μηχανήματος. Η σχεδίαση σε τομή
w w w.k z a c h a r i a d i s.g r
 Πως αποδεικνύουμε ότι ένα σώμα εκτεί απλή αρμονική ταλάντωση Μεθοδολογία i) Βρίσκουμε την θέση ισορροπίας του σώματος και σχεδιάζουμε το σώμα σε αυτή την θέση. ii) Σχεδιάζουμε τις δυνάμεις που ενεργούν
Πως αποδεικνύουμε ότι ένα σώμα εκτεί απλή αρμονική ταλάντωση Μεθοδολογία i) Βρίσκουμε την θέση ισορροπίας του σώματος και σχεδιάζουμε το σώμα σε αυτή την θέση. ii) Σχεδιάζουμε τις δυνάμεις που ενεργούν
8. Σύνθεση και ανάλυση δυνάμεων
 8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
8. Σύνθεση και ανάλυση δυνάμεων Βασική θεωρία Σύνθεση δυνάμεων Συνισταμένη Σύνθεση δυνάμεων είναι η διαδικασία με την οποία προσπαθούμε να προσδιορίσουμε τη δύναμη εκείνη που προκαλεί τα ίδια αποτελέσματα
Εισαγωγή στο Word 2007 Ν. Παπαδόπουλος
 Εισαγωγή στο Word 2007 Ν. Παπαδόπουλος Πληκτρολογώ το διπλανό κείµενο. Επειδή το κείµενο αποτελείται από δύο παραγράφους πατάω το Enter µόνο στο τέλος της κάθε παραγράφου και όχι σε κάθε γραµµή 1. δηµιουργία
Εισαγωγή στο Word 2007 Ν. Παπαδόπουλος Πληκτρολογώ το διπλανό κείµενο. Επειδή το κείµενο αποτελείται από δύο παραγράφους πατάω το Enter µόνο στο τέλος της κάθε παραγράφου και όχι σε κάθε γραµµή 1. δηµιουργία
ΣΧΕ ΙΟ ΜΑΘΗΜΑΤΟΣ : Μαθηµατικά Θετικής και Τεχνολογικής κατεύθυνσης : Β Ενιαίου Λυκείου
 ΜΑΘΗΜΑ ΤΑΞΗ ΕΝΟΤΗΤΑ ΕΙΣΗΓΗΤΗΣ : Μαθηµατικά Θετικής και Τεχνολογικής κατεύθυνσης : Β Ενιαίου Λυκείου : Υπερβολή : Λυµπερόπουλος Ιωάννης. Σκοπός : Οι µαθητές να γνωρίζουν : α) Τον ορισµό της υπερβολής. β)
ΜΑΘΗΜΑ ΤΑΞΗ ΕΝΟΤΗΤΑ ΕΙΣΗΓΗΤΗΣ : Μαθηµατικά Θετικής και Τεχνολογικής κατεύθυνσης : Β Ενιαίου Λυκείου : Υπερβολή : Λυµπερόπουλος Ιωάννης. Σκοπός : Οι µαθητές να γνωρίζουν : α) Τον ορισµό της υπερβολής. β)
Εργαστήριο Εισαγωγή στο Σχεδιασμό Τεχνολογικών Συστημάτων Τομές & Διαστάσεις
 Εργαστήριο Εισαγωγή στο Σχεδιασμό Τεχνολογικών Συστημάτων Τομές & Διαστάσεις Τομές Οι τομές είναι όψεις στις οποίες έχει γίνει μια νοερή τομή σε ένα επίπεδο κάθετο στο επίπεδο σχεδίασης. Το τμήμα του αντικειμένου
Εργαστήριο Εισαγωγή στο Σχεδιασμό Τεχνολογικών Συστημάτων Τομές & Διαστάσεις Τομές Οι τομές είναι όψεις στις οποίες έχει γίνει μια νοερή τομή σε ένα επίπεδο κάθετο στο επίπεδο σχεδίασης. Το τμήμα του αντικειμένου
Προδιαγραφές για την κατασκευή χώρων στάθµευσης αυτοκινήτων που εξυπηρετούν τα κτίρια. (ΦΕΚ 167/ /2-3-93)
 ΥΠΟΥΡΓΙΚΗ ΑΠΟΦΑΣΗ: Αριθµός 98728/7722/93 Προδιαγραφές για την κατασκευή χώρων στάθµευσης αυτοκινήτων που εξυπηρετούν τα κτίρια. (ΦΕΚ 167/ /2-3-93) Ο ΥΠΟΥΡΓΟΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΧΩΡΟΤΑΞΙΑΣ ΚΑΙ ΗΜΟΣΙΩΝ ΕΡΓΩΝ
ΥΠΟΥΡΓΙΚΗ ΑΠΟΦΑΣΗ: Αριθµός 98728/7722/93 Προδιαγραφές για την κατασκευή χώρων στάθµευσης αυτοκινήτων που εξυπηρετούν τα κτίρια. (ΦΕΚ 167/ /2-3-93) Ο ΥΠΟΥΡΓΟΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΧΩΡΟΤΑΞΙΑΣ ΚΑΙ ΗΜΟΣΙΩΝ ΕΡΓΩΝ
α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση
 Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Κεφάλαιο 15 Κίνηση Κυµάτων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
Κεφάλαιο 15 Κίνηση Κυµάτων Περιεχόµενα Κεφαλαίου 15 Χαρακτηριστικά των Κυµάτων Είδη κυµάτων: Διαµήκη και Εγκάρσια Μεταφορά ενέργειας µε κύµατα Μαθηµατική Περιγραφή της Διάδοσης κυµάτων Η Εξίσωση του Κύµατος
1. 3 3cm 2. E( ) 24 3cm 3. E( ) 12 3cm ) 1. 8cm 2. 18cm 3. E 56 3 cm 4. E 20 3 cm. 6cm, cm, 3 6 cm, E cm )
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( 1) 3( ) 5( 3). 4 ( 3) 6 3. 3(4 ) 5( 1) 1 3(1 ) 3( ) 4 3 4. 1 5. 4 6 3 1 1 4( ) 1 1 3 6. 1 7. 1 3 6 3 4 3 3 1
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( 1) 3( ) 5( 3). 4 ( 3) 6 3. 3(4 ) 5( 1) 1 3(1 ) 3( ) 4 3 4. 1 5. 4 6 3 1 1 4( ) 1 1 3 6. 1 7. 1 3 6 3 4 3 3 1
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΟΛ. ΕΡΓΩΝ ΥΠΟ ΟΜΗΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΟΛ. ΕΡΓΩΝ ΥΠΟ ΟΜΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: «ΑΡΧΕΣ ΣΧΕ ΙΑΣΜΟΥ ΙΣΟΠΕ ΩΝ ΚΟΜΒΩΝ» ΕΙΣΗΓΗΤΗΣ: ρ. Μηχ. ΑΝΑΣΤΑΣΙΟΣ ΜΑΝΙΑΤΗΣ ΣΠΟΥ ΑΣΤΡΙΕΣ: ΦΤΕΡΓΙΩΤΗ ΑΝΝΑ του
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΟΛ. ΕΡΓΩΝ ΥΠΟ ΟΜΗΣ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΘΕΜΑ: «ΑΡΧΕΣ ΣΧΕ ΙΑΣΜΟΥ ΙΣΟΠΕ ΩΝ ΚΟΜΒΩΝ» ΕΙΣΗΓΗΤΗΣ: ρ. Μηχ. ΑΝΑΣΤΑΣΙΟΣ ΜΑΝΙΑΤΗΣ ΣΠΟΥ ΑΣΤΡΙΕΣ: ΦΤΕΡΓΙΩΤΗ ΑΝΝΑ του
1. Εύρεση µήκους ενός κύκλου : Για να βρω το µήκος ενός κύκλου βρίσκω την ακτίνα του κύκλου και εφαρµόζω τον τύπο
 1 3.3 ΜΗΚΟΣ ΚΥΚΛΟΥ ΘΕΩΡΙ 1. Μήκος κύκλου ακτίνας ρ : Το µήκος L ενός κύκλου δίνεται από τον τύπο L = 2πρ ή L = πδ όπου δ η διάµετρος του κύκλου και π ένας άρρητος αριθµός του οποίου προσέγγιση µε δύο δεκαδικά
1 3.3 ΜΗΚΟΣ ΚΥΚΛΟΥ ΘΕΩΡΙ 1. Μήκος κύκλου ακτίνας ρ : Το µήκος L ενός κύκλου δίνεται από τον τύπο L = 2πρ ή L = πδ όπου δ η διάµετρος του κύκλου και π ένας άρρητος αριθµός του οποίου προσέγγιση µε δύο δεκαδικά
ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: α. Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών. Αναπληρωτής Καθηγητής ΤΕΧΝΙΚΟ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟ ΣΧΕΔΙΟ Ι ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
Σχήμα 8.46: Δίκτυο αεραγωγών παραδείγματος.
 Παράδειγμα 8.8 Διαστασιολόγηση και υπολογισμός δικτύου αεραγωγών με τη μέθοδο της σταθερής ταχύτητας Να υπολογιστούν οι διατομές των αεραγωγών και η συνολική πτώση πίεσης στους κλάδους του δικτύου αεραγωγών
Παράδειγμα 8.8 Διαστασιολόγηση και υπολογισμός δικτύου αεραγωγών με τη μέθοδο της σταθερής ταχύτητας Να υπολογιστούν οι διατομές των αεραγωγών και η συνολική πτώση πίεσης στους κλάδους του δικτύου αεραγωγών
2. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 και του 100 αυξάνονται κατά 9 μονάδες, όταν αντιστραφούν τα ψηφία τους; Γ. Αν, Δ. Αν, τότε. τότε.
 11η Κυπριακή Μαθηματική Ολυμπιάδα πρίλιος 010 Χρόνος: 60 λεπτά ΛΥΚΕΙΟΥ 1. Το τελευταίο ψηφίο του αριθμού 1 3 5 Ε 9 7. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 του 100 αυξάνονται κατά 9 μονάδες όταν αντιστραφούν
11η Κυπριακή Μαθηματική Ολυμπιάδα πρίλιος 010 Χρόνος: 60 λεπτά ΛΥΚΕΙΟΥ 1. Το τελευταίο ψηφίο του αριθμού 1 3 5 Ε 9 7. Πόσοι ακέραιοι αριθμοί μεταξύ του 10 του 100 αυξάνονται κατά 9 μονάδες όταν αντιστραφούν
ΥΔΡΟΣΤΑΤΙΚΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΕΠΙΠΕΔΕΣ ΕΠΙΦΑΝΕΙΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΚΑΜΠΥΛΕΣ ΕΠΙΦΑΝΕΙΕΣ ΕΠΙΠΛΕΥΣΗ
 ΥΔΡΟΣΤΑΤΙΚΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΕΠΙΠΕΔΕΣ ΕΠΙΦΑΝΕΙΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΚΑΜΠΥΛΕΣ ΕΠΙΦΑΝΕΙΕΣ ΕΠΙΠΛΕΥΣΗ ΔΎΝΑΜΗ ΣΕ ΕΠΙΦΆΝΕΙΑ Μέτρο υδροστατικής δύναμης σε βυθισμένη επιφάνεια ΘΑ ΑΠΟΔΕΙΧΘΕΙ ΟΤΙ: ΘΈΣΗ
ΥΔΡΟΣΤΑΤΙΚΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΕΠΙΦΑΝΕΙΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΕΠΙΠΕΔΕΣ ΕΠΙΦΑΝΕΙΕΣ ΔΥΝΑΜΕΙΣ ΣΕ ΚΑΜΠΥΛΕΣ ΕΠΙΦΑΝΕΙΕΣ ΕΠΙΠΛΕΥΣΗ ΔΎΝΑΜΗ ΣΕ ΕΠΙΦΆΝΕΙΑ Μέτρο υδροστατικής δύναμης σε βυθισμένη επιφάνεια ΘΑ ΑΠΟΔΕΙΧΘΕΙ ΟΤΙ: ΘΈΣΗ
Οπτικοποίηση και Χαρτογραφικός Σχεδιασµός
 ΠΜΣ «Πληροφορική» Τµήµα Πληροφορικής Πανεπιστήµιο Πειραιώς ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ (Introduction to GeoInformatics) Οπτικοποίηση και Χαρτογραφικός Σχεδιασµός Μαργαρίτα Κόκλα Ορισµοί του χάρτη Μια αναπαράσταση,
ΠΜΣ «Πληροφορική» Τµήµα Πληροφορικής Πανεπιστήµιο Πειραιώς ΕΙΣΑΓΩΓΗ ΣΤΗ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗ (Introduction to GeoInformatics) Οπτικοποίηση και Χαρτογραφικός Σχεδιασµός Μαργαρίτα Κόκλα Ορισµοί του χάρτη Μια αναπαράσταση,
ΔΙΑΣΤΑΣΕΙΣ ΣΧΕΔΙΟΥ. Αναγκαιότητα τοποθέτησης διαστάσεων. 29/10/2015 Πολύζος Θωμάς
 Αναγκαιότητα τοποθέτησης διαστάσεων 29/10/2015 Πολύζος Θωμάς 1 Αναγκαιότητα τοποθέτησης διαστάσεων Σφάλμα μέτρησης που οφείλεται: Σε υποκειμενικό λάθος εκείνου που κάνει την μέτρηση. Σε σφάλμα του οργάνου
Αναγκαιότητα τοποθέτησης διαστάσεων 29/10/2015 Πολύζος Θωμάς 1 Αναγκαιότητα τοποθέτησης διαστάσεων Σφάλμα μέτρησης που οφείλεται: Σε υποκειμενικό λάθος εκείνου που κάνει την μέτρηση. Σε σφάλμα του οργάνου
Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
 Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Ασκήσεις σχολικού βιβλίου σελίδας
 ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Ασκήσεις σχολικού βιβλίου σελίδας 07 3. Να αποδείξετε την ταυτότητα + + αβ βγ γα = Να αποδείξετε ότι για όλους τους α, β, γ ισχύει + + αβ + βγ + γα Πότε ισχύει ισότητα; = = + + =
ΑΣΚΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Ασκήσεις σχολικού βιβλίου σελίδας 07 3. Να αποδείξετε την ταυτότητα + + αβ βγ γα = Να αποδείξετε ότι για όλους τους α, β, γ ισχύει + + αβ + βγ + γα Πότε ισχύει ισότητα; = = + + =
Ενδεικτικό Φύλλο Εργασίας 1. Ορθογώνιο Παραλληλεπίπεδο - Κύβος
 Διδακτική των Μαθηματικών με Τ.Π.Ε Σελίδα 1 από 6 Ενδεικτικό Φύλλο Εργασίας 1. Ορθογώνιο Παραλληλεπίπεδο - Κύβος Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:... Κάντε κλικ στο URL https://www.geogebra.org/m/msrbdbc5.
Διδακτική των Μαθηματικών με Τ.Π.Ε Σελίδα 1 από 6 Ενδεικτικό Φύλλο Εργασίας 1. Ορθογώνιο Παραλληλεπίπεδο - Κύβος Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:... Κάντε κλικ στο URL https://www.geogebra.org/m/msrbdbc5.
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
Chess Academy Free Lessons Ακαδημία Σκάκι Δωρεάν Μαθήματα. Οι κινήσεις των κομματιών Σκοπός της παρτίδας, το Ματ Πατ Επιμέλεια: Γιάννης Κατσίρης
 Οι κινήσεις των κομματιών Σκοπός της παρτίδας, το Ματ Πατ Επιμέλεια: Γιάννης Κατσίρης Παρατήρηση: Μόνο σε αυτό το μάθημα όταν λέμε κομμάτι εννοούμε κομμάτι ή πιόνι και όταν λέμε κομμάτια εννοούμε κομμάτια
Οι κινήσεις των κομματιών Σκοπός της παρτίδας, το Ματ Πατ Επιμέλεια: Γιάννης Κατσίρης Παρατήρηση: Μόνο σε αυτό το μάθημα όταν λέμε κομμάτι εννοούμε κομμάτι ή πιόνι και όταν λέμε κομμάτια εννοούμε κομμάτια
1. 3 3cm 2. E( ) 24 3cm 3. E( ) 12 3cm ) 1. 8cm 2. 18cm 3. E 56 3 cm 4. E 20 3 cm. 6cm, cm, 3 6 cm, E cm )
 ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( x 1) 3( x) 5( x 3). 4x ( x 3) 6 x 3. x 3(4 x) x 5( x 1) x 1 3(1 x) x 3( x) x 4 3x 4. 1 x 5. x 4 6 3 1 1 4( )
ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Β ΓΥΜΝΑΣΙΟΥ Α. Να λυθούν οι παρακάτω εξισώσεις: 1. ( x 1) 3( x) 5( x 3). 4x ( x 3) 6 x 3. x 3(4 x) x 5( x 1) x 1 3(1 x) x 3( x) x 4 3x 4. 1 x 5. x 4 6 3 1 1 4( )
ΠΡΟΒΛΗΜΑ 1. Αν x=-3, με τι ισούται το -3x; Α. -9 Β. -6 Γ. -1 Δ. 1 Ε. 9 ΠΡΟΒΛΗΜΑ 2
 ΠΡΟΒΛΗΜΑ 1 Αν x=-3, με τι ισούται το -3x; Α. -9 Β. -6 Γ. -1 Δ. 1 Ε. 9 ΠΡΟΒΛΗΜΑ 2 Τα αντικείμενα της παρακάτω ζυγαριάς ισορροπούν τέλεια. Στην αριστερή πλευρά υπάρχει ένα δοχείο 1 κιλού και μισό τούβλο.
ΠΡΟΒΛΗΜΑ 1 Αν x=-3, με τι ισούται το -3x; Α. -9 Β. -6 Γ. -1 Δ. 1 Ε. 9 ΠΡΟΒΛΗΜΑ 2 Τα αντικείμενα της παρακάτω ζυγαριάς ισορροπούν τέλεια. Στην αριστερή πλευρά υπάρχει ένα δοχείο 1 κιλού και μισό τούβλο.
5ο Μάθημα ΜΕΤΡΗΣΗ ΕΠΙΦΑΝΕΙΑΣ ΚΑΙ ΟΓΚΟΥ
 5ο Μάθημα ΜΕΤΡΗΣΗ ΕΠΙΦΑΝΕΙΑΣ ΚΑΙ ΟΓΚΟΥ Μετρούμε αλλά και υπολογίζουμε Στο προηγούμενο μάθημα χρησιμοποιήσαμε το μέτρο, αλλά και άλλα όργανα με τα οποία μετρούμε το μήκος. Το σχήμα που μετρούμε με το μέτρο
5ο Μάθημα ΜΕΤΡΗΣΗ ΕΠΙΦΑΝΕΙΑΣ ΚΑΙ ΟΓΚΟΥ Μετρούμε αλλά και υπολογίζουμε Στο προηγούμενο μάθημα χρησιμοποιήσαμε το μέτρο, αλλά και άλλα όργανα με τα οποία μετρούμε το μήκος. Το σχήμα που μετρούμε με το μέτρο
ΣΥΝΘΕΣΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΥΝΑΜΕΩΝ
 ΣΥΝΘΕΣΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΥΝΑΜΕΩΝ Συνισταμένη δυο ή περισσοτέρων δυνάμεων οι οποίες ενεργούν ταυτόχρονα σε ένα σώμα λέγεται η δύναμη που επιέρει τα ίδια μηχανικά αποτελέσματα που επιέρουν όλες μαζί Τις δυνάμεις,f,...
ΣΥΝΘΕΣΗ ΚΑΙ ΑΝΑΛΥΣΗ ΔΥΝΑΜΕΩΝ Συνισταμένη δυο ή περισσοτέρων δυνάμεων οι οποίες ενεργούν ταυτόχρονα σε ένα σώμα λέγεται η δύναμη που επιέρει τα ίδια μηχανικά αποτελέσματα που επιέρουν όλες μαζί Τις δυνάμεις,f,...
14 Εφαρµογές των ολοκληρωµάτων
 14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
ΓΕΩΜΕΤΡΙΚΟΣ ΣΧΕ ΙΑΣΜΟΣ ΑΝΙΣΟΠΕ ΩΝ ΚΟΜΒΩΝ
 ΓΕΩΜΕΤΡΙΚΟΣ ΣΧΕ ΙΑΣΜΟΣ ΑΝΙΣΟΠΕ ΩΝ ΚΟΜΒΩΝ Β. Ψαριανός Ακαδ. Έτος 2002-2003 ΕΡΓΑΣΤΗΡΙΟ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΤΕΧΝΙΚΗΣ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ Βασικές Αρχές ιαµόρφωσης Ανισόπεδων Κόµβων Όλες οι
ΓΕΩΜΕΤΡΙΚΟΣ ΣΧΕ ΙΑΣΜΟΣ ΑΝΙΣΟΠΕ ΩΝ ΚΟΜΒΩΝ Β. Ψαριανός Ακαδ. Έτος 2002-2003 ΕΡΓΑΣΤΗΡΙΟ ΣΥΓΚΟΙΝΩΝΙΑΚΗΣ ΤΕΧΝΙΚΗΣ ΣΧΟΛΗ ΑΓΡΟΝΟΜΩΝ ΤΟΠΟΓΡΑΦΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ Βασικές Αρχές ιαµόρφωσης Ανισόπεδων Κόµβων Όλες οι
ΜΑΘΗΜΑΤΙΚΑ MATHEMATICS
 ΜΑΘΗΜΑΤΙΚΑ MATHEMATICS LEVEL: 9 10 (Γ Γυμνασίου Α Λυκείου) 10:00 11:00, 20 March 2010 THALES FOUNDATION 1 3 βαθμοί 1. Ποιο από τα ακόλουθα είναι το αποτέλεσμα της διαίρεσης του αριθμού 20102010 με τον
ΜΑΘΗΜΑΤΙΚΑ MATHEMATICS LEVEL: 9 10 (Γ Γυμνασίου Α Λυκείου) 10:00 11:00, 20 March 2010 THALES FOUNDATION 1 3 βαθμοί 1. Ποιο από τα ακόλουθα είναι το αποτέλεσμα της διαίρεσης του αριθμού 20102010 με τον
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση του στόχου αυτού θα μπορείτε να: Σχεδιάζετε τρίγωνα, τετράπλευρα και πολύγωνα.
 ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση του στόχου αυτού θα μπορείτε να: Σχεδιάζετε τρίγωνα, τετράπλευρα και πολύγωνα. ΓΕΝΙΚΑ: Οι γεωμετρικές κατασκευές εφαρμόζονται στην επίλυση σχεδιαστικών προβλημάτων
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση του στόχου αυτού θα μπορείτε να: Σχεδιάζετε τρίγωνα, τετράπλευρα και πολύγωνα. ΓΕΝΙΚΑ: Οι γεωμετρικές κατασκευές εφαρμόζονται στην επίλυση σχεδιαστικών προβλημάτων
1. ** Σε ορθό τριγωνικό πρίσµα µε βάση ορθογώνιο τρίγωνο ΑΒΓ (A = 90 ) και πλευρές ΑΓ = 3 cm, ΒΓ = 5 cm, η παράπλευρη ακµή του είναι 7 cm.
 Ερωτήσεις ανάπτυξης 1. ** Σε ορθό τριγωνικό πρίσµα µε βάση ορθογώνιο τρίγωνο (A = 90 ) και πλευρές = 3 cm, = 5 cm, η παράπλευρη ακµή του είναι 7 cm. Να βρείτε: α) Το εµβαδό Ε Π της παράπλευρης επιφάνειας.
Ερωτήσεις ανάπτυξης 1. ** Σε ορθό τριγωνικό πρίσµα µε βάση ορθογώνιο τρίγωνο (A = 90 ) και πλευρές = 3 cm, = 5 cm, η παράπλευρη ακµή του είναι 7 cm. Να βρείτε: α) Το εµβαδό Ε Π της παράπλευρης επιφάνειας.
Ενδεικτικό Φύλλο Εργασίας 1. Επίπεδα και Ευθείες Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:...
 Διδακτική των Μαθηματικών με Τ.Π.Ε Σελίδα 1 από 13 Ενδεικτικό Φύλλο Εργασίας 1. Επίπεδα και Ευθείες Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:... Όλες οι εφαρμογές που καλείσθε να χρησιμοποιήσετε είναι
Διδακτική των Μαθηματικών με Τ.Π.Ε Σελίδα 1 από 13 Ενδεικτικό Φύλλο Εργασίας 1. Επίπεδα και Ευθείες Ονοματεπώνυμο:... Τάξη Τμήμα:... Ημερομηνία:... Όλες οι εφαρμογές που καλείσθε να χρησιμοποιήσετε είναι
A3. Στο στιγμιότυπο αρμονικού μηχανικού κύματος του Σχήματος 1, παριστάνονται οι ταχύτητες ταλάντωσης δύο σημείων του.
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 15 ΙΟΥΝΙΟΥ 2015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 15 ΙΟΥΝΙΟΥ 2015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Στις ερωτήσεις Α1-Α4 να γράψετε στο
ΚΑΤΑΣΚΕΥΗ ΠΙΝΑΚΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΣΤΟ ΔΟΚΙΜΙΟ ΕΡΕΥΝΗΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: Μερικές χρήσιμες(;) υποδείξεις. Βασίλης Παυλόπουλος
 ΚΑΤΑΣΚΕΥΗ ΠΙΝΑΚΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΣΤΟ ΔΟΚΙΜΙΟ ΕΡΕΥΝΗΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: Μερικές χρήσιμες(;) υποδείξεις Βασίλης Παυλόπουλος Διάγραμμα της παρουσίασης Πότε (δεν) χρειάζονται πίνακες και σχήματα σε μια ερευνητική
ΚΑΤΑΣΚΕΥΗ ΠΙΝΑΚΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΣΤΟ ΔΟΚΙΜΙΟ ΕΡΕΥΝΗΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: Μερικές χρήσιμες(;) υποδείξεις Βασίλης Παυλόπουλος Διάγραμμα της παρουσίασης Πότε (δεν) χρειάζονται πίνακες και σχήματα σε μια ερευνητική
Ενότητα 1: Απλές εντολές γραφικών
 Ενότητα 1: Απλές εντολές γραφικών ΣΤΚ: Στυλό Κάτω ΣΒΓ: Σβήσε Γραφικά (Σβήνει όλα τα σχέδια και φέρνει τη χελώνα στην αρχή με το κεφάλι προς τα πάνω) Εντολές Κίνησης: Εντολές Παραδείγματα σύνταξης Εντολή
Ενότητα 1: Απλές εντολές γραφικών ΣΤΚ: Στυλό Κάτω ΣΒΓ: Σβήσε Γραφικά (Σβήνει όλα τα σχέδια και φέρνει τη χελώνα στην αρχή με το κεφάλι προς τα πάνω) Εντολές Κίνησης: Εντολές Παραδείγματα σύνταξης Εντολή
Πίνακες, περιγράµµατα και σκίαση
 Πίνακες, περιγράµµατα και σκίαση Οι πίνακες Οι πίνακες είναι ορθογώνια πλαίσια που χωρίζονται σε γραµµές και στήλες. Η τοµή µιας γραµµής µε µια στήλη προσδιορίζει ένα κελί. Τα στοιχεία, που παρουσιάζουµε,
Πίνακες, περιγράµµατα και σκίαση Οι πίνακες Οι πίνακες είναι ορθογώνια πλαίσια που χωρίζονται σε γραµµές και στήλες. Η τοµή µιας γραµµής µε µια στήλη προσδιορίζει ένα κελί. Τα στοιχεία, που παρουσιάζουµε,
Εργαστήριο 1: Σχέδια από την οικοδομική άδεια ενός κτηνοτροφικού κτηρίου
 Εργαστήριο 1: Σχέδια από την οικοδομική άδεια ενός κτηνοτροφικού κτηρίου Περιεχόμενα 1. Στόχος του εργαστηρίου... 3 2. ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ... 3 2.1 Εξοπλισμός σχεδίασης... 3 2.1.1 Μολύβια... 3 2.1.2. Επιφάνεια
Εργαστήριο 1: Σχέδια από την οικοδομική άδεια ενός κτηνοτροφικού κτηρίου Περιεχόμενα 1. Στόχος του εργαστηρίου... 3 2. ΘΕΩΡΗΤΙΚΟ ΥΠΟΒΑΘΡΟ... 3 2.1 Εξοπλισμός σχεδίασης... 3 2.1.1 Μολύβια... 3 2.1.2. Επιφάνεια
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΔΕΥΤΕΡΟΒΑΘΜΙΕΣ ΕΞΙΣΩΣΕΙΣ
 1. Να λύσετε τις εξισώσεις ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΔΕΥΤΕΡΟΒΑΘΜΙΕΣ ΕΞΙΣΩΣΕΙΣ 3 50 3 5 0 0 ή 3 5 0 0 ή 3 5 0 ή 8 50 8 5 αδύνατη 3 60 3 6 6 3 3 4 510, α = 4, β = -5 και γ = 1 Δ = 4 5 4 4 15169 5 9 4 53 8 1 ή 4 410
1. Να λύσετε τις εξισώσεις ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΔΕΥΤΕΡΟΒΑΘΜΙΕΣ ΕΞΙΣΩΣΕΙΣ 3 50 3 5 0 0 ή 3 5 0 0 ή 3 5 0 ή 8 50 8 5 αδύνατη 3 60 3 6 6 3 3 4 510, α = 4, β = -5 και γ = 1 Δ = 4 5 4 4 15169 5 9 4 53 8 1 ή 4 410
Σημειώσεις του μαθήματος Μητρωϊκή Στατική
 ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Σημειώσεις του μαθήματος Μητρωϊκή Στατική Π. Γ. Αστερής Αθήνα, Μάρτιος 017 Περιεχόμενα Κεφάλαιο 1 Ελατήρια σε σειρά... 1.1 Επιλογή μονάδων και καθολικού
ΑΝΩΤΑΤΗ ΣΧΟΛΗ ΠΑΙΔΑΓΩΓΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Σημειώσεις του μαθήματος Μητρωϊκή Στατική Π. Γ. Αστερής Αθήνα, Μάρτιος 017 Περιεχόμενα Κεφάλαιο 1 Ελατήρια σε σειρά... 1.1 Επιλογή μονάδων και καθολικού
1.4 ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ
 1 1.4 ΠΥΘΑΟΡΕΙΟ ΘΕΩΡΗΜΑ ΘΕΩΡΙΑ 1. Πυθαγόρειο θεώρηµα : Σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο µε το άθροισµα των τετραγώνων των καθέτων πλευρών. γ α α = β + γ β. Αντίστροφο Πυθαγορείου
1 1.4 ΠΥΘΑΟΡΕΙΟ ΘΕΩΡΗΜΑ ΘΕΩΡΙΑ 1. Πυθαγόρειο θεώρηµα : Σε κάθε ορθογώνιο τρίγωνο το τετράγωνο της υποτείνουσας είναι ίσο µε το άθροισµα των τετραγώνων των καθέτων πλευρών. γ α α = β + γ β. Αντίστροφο Πυθαγορείου
Πανελλήνιος Σύλλογος Εκπαιδευτών Οδήγησης & Κυκλοφοριακής Αγωγής
 Πανελλήνιος Σύλλογος Εκπαιδευτών Οδήγησης & Κυκλοφοριακής Αγωγής Ένα τυχαίο περιστατικό Υπάρχουν λανθασμένες συμπεριφορές ; Κώδικας Οδικής Κυκλοφορίας Είναι οι κανόνες που πρέπει να ακολουθούν όλοι όσοι
Πανελλήνιος Σύλλογος Εκπαιδευτών Οδήγησης & Κυκλοφοριακής Αγωγής Ένα τυχαίο περιστατικό Υπάρχουν λανθασμένες συμπεριφορές ; Κώδικας Οδικής Κυκλοφορίας Είναι οι κανόνες που πρέπει να ακολουθούν όλοι όσοι
Άσκηση 8 9. Ιδια με την άσκηση 8, αλλά τώρα η συνισταμένη έχει αντίθετη κατεύθυνση.
 1. Επιλέξτε τη σωστή απάντηση: Η συνισταμένη δύο δυνάμεων είναι μία δύναμη που a. έχει μέτρο ίσο με το άθροισμα των μέτρων των δύο δυνάμεων. b. έχει μέτρο πάντα μεγαλύτερο από το μέτρο της κάθε επί μέρους
1. Επιλέξτε τη σωστή απάντηση: Η συνισταμένη δύο δυνάμεων είναι μία δύναμη που a. έχει μέτρο ίσο με το άθροισμα των μέτρων των δύο δυνάμεων. b. έχει μέτρο πάντα μεγαλύτερο από το μέτρο της κάθε επί μέρους
ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος
 Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Ο1 ΘΕΩΡΗΤΙΚΗ ΑΣΚΗΣΗ ιάθλαση µέσω πρίσµατος Φασµατοσκοπικά χαρακτηριστικά πρίσµατος 1. Εισαγωγή Όταν δέσµη λευκού φωτός προσπέσει σε ένα πρίσµα τότε κάθε µήκος κύµατος διαθλάται σύµφωνα µε τον αντίστοιχο
Πόσες µαύρες τελείες βλέπετε ; Οι οριζόντιες γραµµές δείχνουν να είναι παράλληλες ;
 Πόσες µαύρες τελείες βλέπετε ; Οι οριζόντιες γραµµές δείχνουν να είναι παράλληλες ; και όµως είναι! 1 Το παρακάτω σχήµα δείχνει για ελικοειδές ; και όµως δεν είναι! Οι κύκλοι είναι ανεξάρτητοι. Πόσα χρώµατα
Πόσες µαύρες τελείες βλέπετε ; Οι οριζόντιες γραµµές δείχνουν να είναι παράλληλες ; και όµως είναι! 1 Το παρακάτω σχήµα δείχνει για ελικοειδές ; και όµως δεν είναι! Οι κύκλοι είναι ανεξάρτητοι. Πόσα χρώµατα
