omponentni ni sistemi- RASTVORI 9.1. Potpuno mešljive tečnosti itisak-sastavsastav emperatura-sastav Dijagram pritisakp Dijagram temperaturt
|
|
|
- Νατάσα Δεσποτόπουλος
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Fazni dijagram 9. DvokD vokomonent omonentni ni sistemi- RASTVORI 9.. Potuno mešljive tečnosti Tečnost nost-ara,, Idealni rastvori-raulov zakon - Dijagram ritisak itisak-sastavsastav - Dijagram temeraturt emeratura-sastav Tečnost nost-ara,, NeidealniN Dijagram ritisak itisak-sastavsastav Dijagram temeraturt emeratura-sastav Dijagram tečnost nost-tečnost - Delimična mešljivost - Potuna nemešljivost
2 teč. ara ravn.. u binarnoj smeši I tečnost i ara su binarne smeše A() i B(2). x, x 2 su molske frakcije u tečnosti nosti. y A (x ), y B (x 2 ) su molske frakcije u ari. A, B su arcijalni ritisci.
3 Molekularna osnova idealnih rastvora U čistoj tečnosti A, ostoje samo A-A interakcije. U čistoj tečnosti B, ostoje samo B-B interakci cije. U rastvoru A i B, ostoje i A-B interakci cije. H mešanja anja= = i V mešanja anja= = znači i da su sve interakcije iste jačine ine.
4 Idealni rastvori Idealni tečni rastvori se mogu definisati kao oni kod kojih meñumolekulske interakcije ostoje, ali su ribližno iste izmeñu molekula u čistom stanju kao i u smeši,, tj. F A-A F B-B F A-B. Obrazovanje ovakvih idealnih rastvora, ri bilo kom kvantitativnom odnosu izmeñu komonenata, nije raćeno ni romenom zaremine ( V meš = ) ni nekim tolotnim efektom ( H meš = ). Ovakvo onašanje anje okazuje manji broj smeša komonenata koje su sličnih hemijskih i fizičkih osobina, kao na rimer izotoa i izotoskih jedinjenja (sem vodonika i helijuma), izomernih jedinjenja, otičkih antioda kao i nekih drugih jedinjenja kao što su n-heksan i n-hetan, etilbromid i etiljodid ili n-butilhlorid i n-butilbromid i slično no. F=2-2+2=22+2=2 (T i x i ) =f(x Nezavisno romenjljive f(x i ) za svako T 4
5 Raulov zakon Binerni tečni sistemi, kod kojih ostoji ravnoteža izmeñu gasovite i tečne faze, imaju dva steena slobode, što znači da naon are nad rastvorom zavisi od temerature i sastava rastvora,, a ri konstantnoj temeraturi samo od sastava rastvora. Vezu izmeñu naona are i sastava rastvora utvrdio je francuski hemičar Raul (886) ekserimentalnim merenjima, koristeći smeše hemijski sličnih komonenata Francois Marie Raoult (83-9) 5
6 Raulov zakon Raulov zakon: arcijalni naon are svake komonente nad rastvorom,, i, jednak je roizvodu iz molske frakcije komonente u rastvoru,, x i i njenog naona are u čistom stanju,, i, ri istoj temeraturi i ritisku. = i U egzaktnom termodinamičkom obliku Raulovog zakona se umesto ritisaka koriste fugasnosti komonenata: f = i x gde je f i fugasnost komonente u ari ili rastvoru sa kojim je ara u ravnoteži,, a f i je fugasnostčiste komonente na istoj temeraturi i ritisku. Tečni rastvori koji se okoravaju Raulovom zakonu u čitavom osegu koncentracija tj. od čiste komonente do čiste komonente 2 i ri svim temeraturama i ritiscima, nazivaju se idealnim rastvorima. i x f i i i 6
7 Idealni rastvori-raulov zakon Može e se okazati termodinamički da ako Raulov zakon važi i za jednu komonentu rastvora, mora važiti i za drugu. Takoñe se može e okazati da su ukuniu tolotni sadržaj aj (odnosno zaremina) smeše jednaki sumi tolotnih sadržaja aja (odnosno zaremina)čistih istih konstituenata, tako da se u tom ogledu idealni rastvor onaša kao smeša idealnih gasova. 7
8 Idealni rastvori-dijagram stanja Dijagram stanja za ravnotežu gasovite i tečne faze idealnog rastvora, ri konstantnoj temeraturi, redstavlja zavisnost arcijalnog ritiska komonenata i 2 u gasnoj fazi, od sastava tečne faze, izražene u molskim frakcijama komonenata.. Ova zavisnost je ravolinijska, jer se komonente moraju okoravati Raulovom zakonu: = x 2 = x 2 2 Ukuni naon are nad rastvorom, koji je rema Daltonovom zakonu jednak zbiru arcijalnih ritiskaka, je stoga: = + 2 = x + x 2 2 = x ( 2 ) + 2 takoñe linearna funkcija sastava rastvora. 8
9 Idealni rastvori-dijagram stanja T= const. 2 l v 2 = = x 2 x22 = + 2 = x + x 2 2 = x = x = 2 x 2 x x ' x 2= x = =x ( 2 ) + 2 9
10 Benzol i toluol
11 Naon are benzb enzol-toluol mix benz
12 Molekulska interretacija Raulovog zakona Raulov zakon reflektuje činjenicu da risustvo druge komonente smanjuje brzinu kojom molekuli nauštaju ovršinu tečnosti ali ne utiče e na brzinu kojom se vraćaju aju tj. na brzinu kondenzacije. brzina isaravanja=kx brzina kondenzacije=k kx =k u ravnoteži k = x = x = k' k k' 2
13 Sastavi tečnosti i are se razlikuju X b va =.7 X t va =.29 Para iznad tečnosti koja ključa X b =.5 X t =.5 P bo = 92 Torr P to = 38 Torr Tečnost na tački ključanja 3
14 Zavisnost naona are od sastava are Do zavisnosti naona are od sastava are se dolazi uz retostavku da se ara može smatrati kao smeša idealnih gasova, ričemu je arcijalni ritisak svake od komonenata izražen reko jednačine idealnog gasnog stanja: ' ' n n2 = RT, 2 = RT V V n i n 2 su brojevi molova komonenata u arnoj fazi = + 2 = + ( ' ' ) RT n n V 2 x ' = = x x ' 2 2 = = x 2 2 4
15 Izračunavanje sastava are P o toluola ola = 38 Torr; ; P o benzola = 92 Torr Uzećemo emo X b =X t =.5 P a =X a P o a Raoult-ov ov zakon P b = (92 Torr)(.5)=46 Torr; P t =(38 Torr)(.5)=9 Torr P total = = 65 Torr X va a = P a /P tot X va b =46 Torr/65 Torr =.7 Torr X va t =..7 =.29 Torr 5
16 Zavisnost naona are od sastava are Zavisnost naona are od sastava arne faze može se naći u dijagramu faza ako se kroz tačku koja odgovara naonu are tečnog rastvora (l) odreñenog sastava (x ) ovuče izobara (jer ara i tečnost u ravnoteži imaju istu temeraturu i ritisak). Zatim se iz tačke na ascisi koja odgovara sastavu are ovuče vertikala čiji resek sa izobarom daje ritisak zasićene ' are (v).( l). ' x x x = x 2 ( ) + 2 x = x ' 2 2 x = x = ( ) + 2 = T= const. l v x 2 x x ' x 2= x = + ( ) x ' 6
17 Zavisnost naona are od sastava are x x ' ' = x 2 = x( 2) + 2 x ' Molska frakcija A u ari U svim slučajevima je x >x (ara je bogatija isarljivijom komonentom). Ako je kom.. 2 neisarljiva 2 =, x 2 =. = 2 + ( ) x 2 ' Ukuni ritisak A / a Molska frakcija A u tečnosti Što se komonente više e razlikuju u isarljivosti to će e se viñe razlikovati sastav tečne od sastava arne faze! Molska frakcija A u ari 7
18 -y dijagram za idealan rastvor Gornja linija je tečnost nost- sastav linija. Donja linija je ara-sastav linija. Pravilo faza: : F = C-P+2C Za konstantnu temeraturu i 2 komonente F = 3 - P Iznad gornje linije tečnosti ili isod donje za aru,, F = 2 Izmeñu linija,, F = Za bilo koji, i x A i y A su fiksirani. Relativna količina ina dve faze može e varirati. Tečnost Para 8
19 Kretanje duž izolete Izolet oleta je linija konstantnog sastava. Na -z ili T-z dijagram agramu u za dvokomonentni sistem, izoleta je vertikalna linija. Na a je risutna samo tečnost nost. Na a očinje da se formira ara Sastav ove are = a Na a 3 nestaje tečnost nost. Sastav ove tečnosti je = a 3 tečnost izobara ara izoleta 9
20 Fizička slika rocesa Jedan način smanjivanja ritiska je odizanje klia. Pri dovoljno visokom ritisku (nije rikazan), risutna je samo tečnost nost. (a) Nešto are se ojavilo. (b) Samo malo tečnosti je ostalo. (c) Samo je ara risutna. Fig. 8.,. 97 2
21 Sojna linija i ravilo oluge Linija koja ide kroz dvofaznu oblast i saja dve faze u ravnoteži i je sojna linija. Prema ravilu oluge, n α l α = n β l β Što je ukuni sastav bliži liniji tečnost nost-sastav sastav to je risutno više e tečnosti u dvofaznoj oblasti. 2
22 Tačka ključanja idealnih rastvora Za raktične svrhe mnogo je značajnije ajnije osmatrati ravnotežu izmeñu tečne i arne faze ri uslovima konstantnog ritiska, najčešće od bara.. U tom slučaju se osmatra temeratura ri kojoj su tečnost i ara u ravnoteži za svaki sastav rastvora.. Ova temeratura redstavlja tačku ključanja datog rastvora i ona je za rastvor svakog ojedinog sastava drukčija ija, tako da se na osnovu ovih odataka formira zavisnosti tačke ključanja od sastava tečne i arne faze na istom faznom dijagramu. 22
23 Tačka ključanja idealnih rastvora bar O θ/( C) x vode x vode / (kpa) Gornji 3 2 Gornji deo slike okazuje orast ukunog naona are idealnog rastvora sa temeraturom. Preseci ravih naona are sa izobarom ri kpa, odgovaraju tačkama ključanja rastvora različitih itih sastava. Iz očitanih vrednosti temeratura i sastava može se dobiti donji dijagram zavisnosti tačke ključanja od sastava za idealan binerni tečni sistem kako je rikazano na donjem delu slike. Iz zavisnosti naona are od sastava arne faze može e se dobiti drugi deo dijagrama zavisnost tačke ključanja od sastava arne faze. 23
24 T u funkciji sastava za idealni rastvor Dobijen komletni dijagram rikazan je na slici ( A * > B *) Uočimo da je ovde kriva ara-sastav iznad krive tečnost nost-sastavsastav Ovde se ritisak drži konstantnim. Sastav are Temeratura ključanja tečnosti 24
25 Tačka ključanja idealnih rastvora Oblast izmeñu linija F=, sastav svake faze je fiksiran na datoj temeraturi. Oblast izvan linija, F=2, temeratura i sastav su romenjljivi. a :tečnost se zagreva i ključa a na T 2 sa sastavom a =a 2 a ara a 2 a 3 : ara je ohlañena i kondenzat je bogatiji isaarljivijom komonentom a 4 : ara je izdvojena i ohlañena,, kondenzat je veoma bogat komonentom Ciklusi isaravanja i kondenzacije se nazivaju frakcionom destilacijom. A isarljivija kom. sastav are Temeratura ključanja tečnosti 25
26 Sastav tečnosti i are za rastvor toluola ola i benzb enzila 26
27 Dijagram destilacije Dijagram desno okazuje uslove destilacije. Na slici od (a) ostoje 3 teoriska latoa, koja odgovaraju trima isaravanjima i kondenzaciji. Na slici od (b) ostroji 5 terijskih latoa. Skoro čisto B može e da se izdvoji u destilatu i skoro čisto A u ostatku. 27
28 T T O Frakciona destilacija ara v 3 v' v 2 B C A l v 2 2 l te~ nost l 3 l' T 2 O T' T 3 T 2 %, x x 2 %, 2 a) D T T T 2 T 3 b) Za razdvajanje komonenata koristi se frakciona destilacija u kojoj se jedan korak onavlja, tako što se tečnost dobijena kondenzovanjem izdvojene are onovo zagreva do ključanja anja,, nova količina ina are koja je još bogatija isarljivijom komonentom oet kondenzuje, onovo isarava, ričemu tečnost iz koje se ara izdvaja ostaje bogatija manje isarljivom komonentom.. Na taj način se ostukom steenastog kretanja kroz fazni dijagram konačno no osle odreñenog broja koraka dolazi raktično do razdvajanja komonenata iz rastvora. Metodom frakcione destilacije moguće je izvršiti iti razdvajanječistih komonenata iz rastvora. 28
29 Aarat za destilaciju Izlaz vode Ulaz vode Kolona za destilaciju Destilat Smeša a koja se razdvaja 29
30 Zavisnost naona are od sastava dve isarljive tečnosti nosti-neidealni neidealni rastvori Ako je F A A >F A B <F B B, kada su komonente u čistom tečnom stanju asosovane, tadaće težnja komonenata ka isaravanju biti veća iz rastvora i arcijalni naon are će za svaku od komonenata biti veći od onog rema Raulovom zakonu a će se javiti ozitivna odstuanja od Raulovog zakona Ako je F A A <F A B >F B B, osebno ako je to osledica stvaranja jedinjenja izmeñu komonenti u rastvoru, tadaće težnja ka isaravanju komonenata u rastvoru biti manja nego u čistom tečnom stanju i sistem će okazivati negativna odstuanja od Raulovog zakona
31 Pozitivna odstuanja od Raulovog zakona Može se okazati da ako jedna od komonenata okazuje ozitivno odstuanje od idealniog onašanja anja, tada i druga komonenta mora takoñe okazivati ozitivno odstuanje. Pri velikim ozitivnim odstuanjima od Raulovog zakona ukuna kriva naona are okazuje maksimum. Najveći broj binernih tečnih sistema okazuje baš ozitivna odstuanja. Primeri tečnih smeša sa ozitivnim odstuanjima su: aceton- ugljendisulfid, hetan-etilalkohol etilalkohol kao i smeše vode i rimarnih alkohola. 3
32 Negativno odstuanje od Raulovog zakona Primeri za negativno odstuanje su: iridin-mravlja mravlja, sirćetna ili roionska kiselina (bazni i kiseli sastojak), smeše halometana, nr. hloroforma sa kiseoničnim nim ili azotnim jedinjenjem nr. keton, etar, estar ili amin.. U svim ovim rimerima dolazi do grañenja vodonične ne veze izmeñu dva različita ita molekula. Negativna odstuanja se javljaju i u smešama lako isarljivih kiselina nr. halogenih, azotne ili erhlorne sa vodom. 32
33 Krive se ribližavaju idealnim sa ribližavanjem sistemačistoj istoj komoneti ili 2. To znači da u slučaju ribližavanja sastavučiste komonete, ona očinje da se onaša kao rastvarač jer je u velikom višku ku,, a stoga očinje da se okorava Raulovom zakonu, dok je tada komonenta 2 risutna u maloj koncentraciji i onaša se kao rastvorena sustancija za koju važi Henrijev zakon ( i = k i x i ). To znači da u idealno razblaženom rastvoru se rastvarač okorava Raulovom zakonu,, a rastvorak se onaša o Henrijevom zakonu. 33
34 Neidealni rastvori I Ako se rikaže fazni dijagram u kome je tačka ključanja rikazana u funkciji sastava, ondaće sistem sa negativnim odstuanjima imati zavisnost kao na slici i kriva okazuje maksimum Dijagram -z će e okazivati minimum. U maksimumu je sastav atzeotrone smeše e za koji je x A = x A. 34
35 Neidealni rastvori II Ponekad ovoljne interakcije izmeñu molekula snižavaju naon are isod idealne vrednosti, tj. interakcija A-B A B stabilizuje tečnu fazu, rimer : roanon-trihlormetan, azotna kiselina-voda Sastav a se greje do ključanja, ara (a( 2 )) bogatija sa A, reostala tečnost bogatija sa B, tečnost a 3 u ravnoteži i sa arom a 3 ara uklonjena, sastav tečnosti se omera do a 4 a ara sastava a 4 Sastav reostale tečnosi se omera do b jer je komonenta A udaljena, ara je bogatija sa B Konačno no ri sastavu b ara i tečnost su istog sastava Isaravanje se dešava bez romene sastava, smeša se naziva azeotroska (ključanje bez izmene) destilacija ne može e da omogući i razdvajanje komonenata 35
36 Neidealni rastvori III Desno je T-z dijagram za sistem koji okazuje ozitivno odstuanje od Raulovog zakona. Dijagram -z će e okazivati maks ksimum. U minimumu u je sastav azeotrone smeše za koju je x A = y A. Azeotroska smeša a je destabilizovana u odnosu na idealan rastvor Primer: dioksan-voda, etanol-voda Počinje u a, ključa a u a 2 sa arom sastava a 2 Para kondenzuje do a 3, ara je sastava a 3 kondenzacija daje a 4 Azeotrona smeša a je sastava b Azeotroske smeše e mogu biti razorene dodavanjem treće e sustancije. Benzen se koristi za tu svrhu 36
37 Delimično mešljive tečnosti Ako se krive naona are od sastava za tečnosti koje okazuju ozitivna odstuanja od Raulovog zakona rikažu za različite ite temerature kao na slici, tadaće odstuanja biti sve veća sa oadanjem temerature i ri dovoljno niskoj temeraturi T 3 odstuanjaće biti tako velika daće doći do rekida mešljivosti ovih komonenata. Pri toj temeraturi na osnovu krive na slici očekivala bi se tri tečna sloja u ravnoteži. Da a bi se definisalo stanje dvokomonentnog sistema,, bio bi otreban bar jedan steen slobode: : = 2 P + 2, tj.. P = 3. To znači da ored are mogu u ravnoteži biti još samo dva tečna sloja. Deo krive abc nije realan. a T 3 T 2 T b T> T> T 2 3 x c 37
38 Parcijal alno mešljive tečnosti Desno je dijagram mešljivosti heks ksana a i nitrobenzena. Smeša a na 29 i ri ukunom sastavu rikazanom vertikalnom linijom razdvaja se u dva sloja. Sastav svakog sloja može e da se očita o iz krajeva sojne linije. Na 292 K sloj heks ksana nestaje. 38
39 Kritične temerature smeša Temeratura a iznad koje heks ksan i nitrobenzen (rethodni slajd) su mešljivi je gornja kritična temeratura. Neki sistemi (nr. nr., voda- trietilamin lamin) imaju donju kritičnu temeraturu. Ponekad (nr. nr., nikotin otin- voda) ostoji i donja i gornja kritična temeratura. Fig. 8.24,
40 Potuno nemešljive tečnosti Kada se dve nemešljive tečnosti mućkaju zajedno,, the ukuni naon are je = A * + B *. OBE će e ključati kada je ukuni ritisak = atmosferski ritisak itisak. Da bi se to desilo mora da bude intenzivno mešanje tečnosti kao na (a), ali NE na (b). 4
41 Destilacija arom Činjenica da je = A * + B * za nemešljive tečnosti je osnov destilacije arom. Destilacija arom omogućava da se ulje i druga sa vodom nemešljiva organska jedinjenja destiluju na nižoj temeraturi od normalne tačke ključanja anja. Mnoga organska jedinjenja su termički nestabilna i mogu se rasadati re ključanja anja. Nedostatak je što je sastav destilata roorcionalan naonu are komonenata. 4
42 Delimično mešljive tečnosti često formiraju azeotrone smeše e sa minimumom tačke ključanja anja. Ako je gornja kritična temeratura isod tačke ključanja javiće e se dijagram kao na slici. Fig. 8.25,
43 Zakon rasodele i ekstrakcija Ako se sistemu od dve nemešljive ili slabo mešljive tečnosti doda odreñena količina ina neke treće sustancije, ona će se rastvoriti u oba tečna sloja, tako da će odnos ravnotežnih nih koncentracija te sustancije u I i II sloju biti konstantan na bilo kojoj temeraturi: C C I II = bez obzira na vrednosti ravnotežnih nih koncentracija, gde je K konstanta rasodele.. Ova relacija je oznata kao Nernstov (Nernst,, 89) zakon rasodele. K 43
44 44 I I I a RTln =µ + µ II II II a RTln =µ + µ RT a a I II II I ln µ µ = K a a II I = K x x II I = K C C II I = Idealni Idealni Razbla Razblaženi eni K C C II II I I = ) α ( ) α ( Neidealni Neidealni
45 Ekstrakcija Organske sustancije kao više rastvorljive u organskim rastvaračima nego u vodi mogu se ekstrahovati iz vodenih rastvora.. Kao organski rastvarači najčešće se koriste etar, hloroform, ugljentetrahlorid ili benzen. 45
46 m / V ( m m) / l = K m = m Kv Kv+ l m 2 KV KV 2 = m = m KV + l KV + l m n = m KV KV + l n 46
9. DvokD. vokomponent. omponentni ni sistemi- RASTVORI 9.1. Potpuno mešljive tečnosti. Dijagram tečnost. Dijagram pritisakp Dijagram temperaturt
 Fazni dijagram 9. DvokD vokomonent omonentni ni sistemi- RASTVORI 9.. Potuno mešljive tečnosti Tečnost nost-ara,, Idealni rastvori-raulov zakon - Dijagram ritisak itisak-sastavsastav - Dijagram temeraturt
Fazni dijagram 9. DvokD vokomonent omonentni ni sistemi- RASTVORI 9.. Potuno mešljive tečnosti Tečnost nost-ara,, Idealni rastvori-raulov zakon - Dijagram ritisak itisak-sastavsastav - Dijagram temeraturt
RAVNOTEŽA TEČNO-PARA
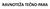 RAVNOTEŽA TEČNO-PARA Smeša dve isparljive komponente (dve tečnosti) koje se mešaju u svim odnosima: f = c p + 2 = 2 2 + 2 = 2 tečna homogena smeša+para iznad tečnosti Ako su te dve nezavisno promenjive
RAVNOTEŽA TEČNO-PARA Smeša dve isparljive komponente (dve tečnosti) koje se mešaju u svim odnosima: f = c p + 2 = 2 2 + 2 = 2 tečna homogena smeša+para iznad tečnosti Ako su te dve nezavisno promenjive
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Slično važi i za bilo koje druge kombinacije nekondenzujućih ( O
 8. Vlažni gasovi 8.1 Uvod - smeše realnog i idealnog gasa - smeše kondenzujućeg i nekondenzujućeg gasa - arno gasne smeše - najoznatiji redstavnik ažan vazduh - smeša (suvog) vazduha idealnog gasa i age
8. Vlažni gasovi 8.1 Uvod - smeše realnog i idealnog gasa - smeše kondenzujućeg i nekondenzujućeg gasa - arno gasne smeše - najoznatiji redstavnik ažan vazduh - smeša (suvog) vazduha idealnog gasa i age
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Tako se dobivaju linije kondenzacije i linije ključanja tekuće smjese
 DESTILCIJ Je tehnološka oeracija kojom se tekuća smjesa hlaivih komonenata isaravanjem i naknadnim ukaljivanjem ara razdvaja na relativno čiste komonente Destilacija se zasniva na različitoj hlaivosti
DESTILCIJ Je tehnološka oeracija kojom se tekuća smjesa hlaivih komonenata isaravanjem i naknadnim ukaljivanjem ara razdvaja na relativno čiste komonente Destilacija se zasniva na različitoj hlaivosti
DAMIR&SILVANA DESTILACIJA. Title goes here
 DMIR&SILVN DESTILCIJ Je tehnološka oeracija kojom se tekuća smjesa hlaivih komonenata isaravanjem i naknadnim ukaljivanjem ara razdvaja na relativno čiste komonente Destilacija se zasniva na različitoj
DMIR&SILVN DESTILCIJ Je tehnološka oeracija kojom se tekuća smjesa hlaivih komonenata isaravanjem i naknadnim ukaljivanjem ara razdvaja na relativno čiste komonente Destilacija se zasniva na različitoj
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Trigonometrijske nejednačine
 Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Rastvor predstavlja homogenu smešu dve ili više komponenti. Uslovna podela komponenata na rastvorak i rastvarač:
 RASTVORI 1 Rastvor predstavlja homogenu smešu dve ili više komponenti. Uslovna podela komponenata na rastvorak i rastvarač: Rastvarač je komponenta koja ima isto agregatno stanje kao i dobijeni rastvor.
RASTVORI 1 Rastvor predstavlja homogenu smešu dve ili više komponenti. Uslovna podela komponenata na rastvorak i rastvarač: Rastvarač je komponenta koja ima isto agregatno stanje kao i dobijeni rastvor.
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
BROJ NEZAVISNIH KOMPONENTI
 RAVNOTEŽA FAZA FAZA p-homogeni deo nekog heterogenog sistema, uniforman po svojim fizičkim osobinama i hemijskom sastavu u celoj zapremini a koji je od ostalih delova sistema odvojen granicom faza. Granica
RAVNOTEŽA FAZA FAZA p-homogeni deo nekog heterogenog sistema, uniforman po svojim fizičkim osobinama i hemijskom sastavu u celoj zapremini a koji je od ostalih delova sistema odvojen granicom faza. Granica
2log. se zove numerus (logaritmand), je osnova (baza) log. log. log =
 ( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: S čvrsto < S tečno << S gas
 ,4,4, Odreñivanje promene entropije,4,4,, romena entropije pri promeni faza Molekular ularna interpretacija entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: čvrsto
,4,4, Odreñivanje promene entropije,4,4,, romena entropije pri promeni faza Molekular ularna interpretacija entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: čvrsto
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije a + b + c je parabola. Najpre ćemo naučiti kako izgleda
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije a + b + c je parabola. Najpre ćemo naučiti kako izgleda
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Matematika 4. t x(u)du + 4. e t u y(u)du, t e u t x(u)du + Pismeni ispit, 26. septembar e x2. 2 cos ax dx, a R.
 Matematika 4 zadaci sa pro²lih rokova, emineter.wordpress.com Pismeni ispit, 26. jun 25.. Izra unati I(α, β) = 2. Izra unati R ln (α 2 +x 2 ) β 2 +x 2 dx za α, β R. sin x i= (x2 +a i 2 ) dx, gde su a i
Matematika 4 zadaci sa pro²lih rokova, emineter.wordpress.com Pismeni ispit, 26. jun 25.. Izra unati I(α, β) = 2. Izra unati R ln (α 2 +x 2 ) β 2 +x 2 dx za α, β R. sin x i= (x2 +a i 2 ) dx, gde su a i
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
POGON SA ASINHRONIM MOTOROM
 OGON SA ASNHRON OTORO oučavaćemo amo ogone a tofaznim motoom. Najčešće koišćeni ogon. Ainhoni moto: - ota kontukcija; - jeftin; - efikaan. ETALN RSTEN LANRANO JEZGRO BAKARNE ŠKE KAVEZN ROTOR NAOTAJ LANRANO
OGON SA ASNHRON OTORO oučavaćemo amo ogone a tofaznim motoom. Najčešće koišćeni ogon. Ainhoni moto: - ota kontukcija; - jeftin; - efikaan. ETALN RSTEN LANRANO JEZGRO BAKARNE ŠKE KAVEZN ROTOR NAOTAJ LANRANO
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Pismeni dio ispita iz Matematike Riješiti sistem jednačina i diskutovati rješenja u zavisnosti od parametra a:
 Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
GASNO STANJE.
 GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Ispit održan dana i tačka A ( 3,3, 4 ) x x + 1
 Ispit održan dana 9 0 009 Naći sve vrijednosti korjena 4 z ako je ( ) 8 y+ z Data je prava a : = = kroz tačku A i okomita je na pravu a z = + i i tačka A (,, 4 ) Naći jednačinu prave b koja prolazi ( +
Ispit održan dana 9 0 009 Naći sve vrijednosti korjena 4 z ako je ( ) 8 y+ z Data je prava a : = = kroz tačku A i okomita je na pravu a z = + i i tačka A (,, 4 ) Naći jednačinu prave b koja prolazi ( +
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
1 Afina geometrija. 1.1 Afini prostor. Definicija 1.1. Pod afinim prostorom nad poljem K podrazumevamo. A - skup taqaka
 1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
