Doc. Dr Radomir Naumović. Klinika za nefrologiju, KCS Medicinski fakultet u Beogradu
|
|
|
- Κρίος Κολιάτσος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Doc. Dr Radomir Naumović Klinika za nefrologiju, KCS Medicinski fakultet u Beogradu
2 Transplantacija bubrega Terapija izbora Najbolje preţivljavanje Najbolji kvalitet ţivota Naj ekonomičnija
3 Tolerancija vs. Odbacivanje Tolerancija zavisi od lokalnog prisustva T reg
4 Hronična nefropatija alokalema (CAN) Akutno odbacivanje DGF Dugotrajno preţivljavanje bez promena Odlično jednogodišnje preţivljavanje Meier-Kriesche H-U, et al. Am J Transplant 2004.
5 ZLATNI STANDARD: BIOPSIJA!
6 Razlozi za određivanje biomarkera Neinvazivna dijagnoza poremećaja funkcije Izbegavanje biopsije Anticipacija AO pre nastanka tkivnog oštećenja Prognoza ishoda odvacivanja i odgovora na Th Predviđanje funkcije kalema nakon odbacivanja Davanje specifične terapije Individualizacija i optimizacija terapije Gruber SA et al. Transplantation 2008.
7 Uslovi da da bi nešto bilo biomarker Visoka specifičnost i senzitivnost za datu patologiju Rapidno pojavljivanje u serumu Jasna povezanost sa oštećenjem Dijagnoza, prognoza, odluka o terapiji
8 Krv Urin Imunološki monitoring: Šta i kako pratiti? Biopsija Transkripcija gena (mdna i mlrna) Jedan gen RT PCR Više gena Microarray Proteinski markeri Pojedinačni proteini: ELISA/Western blot Više proteina: delovi proteina Limfocitni markeri/aktivnost Proliferacija Kvantitativna protočna citometrija CFSE Analiza citokina ELISPOT ATP nivo u aktivisanim T ćelijama Aloantitela (DSA i nondsa; HLA i nonhla antitela) Testiranje ćelija Citotoksićnost (CDCC) Protočna citometrija Testiranje solubilnih antigena ELISA Protočna citometrija (Flow PRA) Luminex Virusna aktivnost DNA i mrna
9 Odloţena funkcija kalema DGF 4-10% nakon ŢTx 5-50% nakon KTx Predispozicija za AO DGF Predispozicija za HO Suboptimalna funkcija DGF Gubitak grafta Salahudeen AK, et al. Kidney Int Jacobs SC, et al. J Urol 2004.
10 Biomarkeri DGF (urin, serum, tkivo..) ICAM1 VCAM1 NGAL IL-18 sgp130 TGFβ DGF ATN sca TNF β2mg KIM1 IL-6
11 Neutrofilna gelatinaza vezana za lipokalin - NGAL Gen za NGAL je najaktiviraniji u bubregu nakon ishemije Povećana produkcija NGAL u tubulskim ćelijama u ranom periodu nakon ishemije Lako ga je detektovati u urinu nakon ishemije Biomarkeri za AKI nakon kardio-hirurških operacija Salahudeen AK, et al. Kidney Int Jacobs SC, et al. J Urol 2004.
12 NGAL: prediktor DGF ŢTx KTx KTx-DGF Parikh CR, et al. Am J Transplant 2006.
13 Interleukin-18 Pripada IL-1 superfamiliji Dominatno ga produkuju makrofagi Indukuje ćelijski imunitet u odgovoru na infekciju Medijator ishimejske ATN (eksperimentalno) Marker oštećenja proksimalnih tubula tokom ATN Lako ga je detektovati u urinu Parikh CR, et al. Am J kidney Dis 2004.
14 IL-18: prediktor DGF PGF DGF Parikh CR, et al. Am J kidney Dis Parikh CR, et al. Am J Transplant 2006.
15 Akutno odbacivanje Akutno odbacivanje 35% bolesnika ima AO tokom prve godine nakon Tx Akutno odbacivanje 20% manje jednogodišnje preţivljavanje grafta Akutno odbacivanje Smanjenje dugotrajnog preţivljavanja grafta Cecka JM and Terasaki PI (eds). Clinical Transplant Naumovic R et al. Transpl Int
16 Biomarkeri AO (urin, serum, tkivo) Antitela Perforin Granzim B CD 20 + MCP1 AO CD 30 + mrna IL-4 mrna IFNγ mrna IL-6 mrna IL-5
17 Akutno celularno odbacivanje Citotoksične ćelije Perforin Granzim B
18 Citotoksične efektorne ćelije Perforin (u granulama CTĆ) Granzyme B (aktivisane CTĆ) Stvara pore na membranama ćelija Defragmentacija DNA (aktivacija kaptaze) Smrt ćelije
19 Nivoi mrna u urinu bolesnika sa AO Tip mrna Akutno odbacivanj e (N=24) Ostali PH nalazi (N=15) CAN (N=5) Strabilna f grafta (N=107) p Fg mrna/µg ukupne RNA Perforin 1,4 ± 0,3-0,8 ± 0,5-0,7 ± 0,8-0,6 ± 0,2 <0.001 Granzyme B 1,2 ± 0,3-0,7 ± 0,5-0,3 ± 0,7-0,9 ± 0,2 <0.001 Cyclophilin B 2,3 ± 0,3 2,4 ± 0,3 2,7 ± 0,6 2,5 ± 0, Li B, et al. NEJM 2001; 344:
20 Li B, et al. NEJM 2001.
21 Akutno humoralno odbacivanje Citotoksična antitela Donor specifična antitela Sistem komplemeta (C4d) Peritubularni kapilari Colvin RB. AJT 2010.
22 AHO - Donor specifična antitela Povezanost sa AHO Loša prognoza Jednogodišnje preţivljavanje 15 50% % bolesnika sa DSA ima AO 98% bolesnika sa DSA ima i C4d pozitivnost Crespo M, et al. Transplantation 2001.
23 FOXP3 prediktor ishoda AO Muthukumar T et al.n Engl J Med 2005.
24 CAN Uzrok gubitka kalema u više od 50% slučajeva CAN Vraćanje na dijalizu Trostruko veći rizik za smrt CAN Lošiji kvalitet ţivota Ĉetvorostruko skuplje lečenje
25 CAN CAN Pogoršanje funkcije IF/TA Proteinurija Glomeruloskleroza Hipertenzija Okluzija krvnih sudova Racusen LC et al: Banff 97. KI 1999.
26 CAN...Ne specifičan termin! Podrazumeva sve uzroke CAD sa IF/TA Nije precizna dijagnoza Ne pruţa mogućnost za odluku o Th Uloga antitela u hroničnim dešavanjima! CAAR Solez K, et al. Banff 05 meeting report. Am J Transplant 2007.
27 Biomarkeri HO (urin, serum, tkivo..) TNF DSA HLA At NGAL E selektin AO IL-4 IL-1β ICAM 1 IL-2 IL-6
28 Značaj humoralnog imuniteta za nastanak CAN 30% bolesnika sa CAN imaju anti HLA At 31% bolesnika sa CAN ima DSA DSA anti klasa II su povezana sa ACO Bolesnici sa DSA imaju lošiju prognozu Solez K, et al. Banff 05 meeting report. Am J Transplant 2007.
29 Mass spektrometrija: određivanje urinarnih polipeptida bolesnika sa IF/TA i CAAR IF/TA CAAR Quintana LF, et al. JASN 2009.
30 TOLERANCIJA Stabilna, dobra funkcija alokalema koja se odrţava bez IS lekova Dugotrajna funkcija kalema zavisi od stalne IS terapije KV bolesti, oportunističke infekcije, maligniteti Kako identifikovati bolesnike koji će razviti toleranciju? Roussey-Kesler G, et al. AJT 2006.
31 Multicentrična studija Procena imunoloških osobina koje dovode do tolerancije Stabilna funkcija, bez IS, bez porasta scr (1god <10%) Grupe: 1. Tol-DF 2. slp: stabilna F, <10mg prednisona 3. s-ncni: nikada nisu dobijala CNI 4. s-cni: standardna Th sa CNI 5. CR: biopsijom potvrđeno hronično odbacivanje 6. HCs: zdrave kontrole Sagoo P, et al. J Clin Invest 2010.
32 Bolesnici koji su razvili toleranciju imaju veći % B ćelija Sagoo P, et al. J Clin Invest 2010.
33 Bolesnici koji su razvili toleranciju imaju veći % NK ćelija Sagoo P, et al. J Clin Invest 2010.
34 Bolesnici koji su razvili toleranciju imaju manji % cirkulišućih T ćelija
35 Odnos % zastupljenosti B i T ćelija Sagoo P, et al. J Clin Invest 2010.
36 Bolesnici koji su razvili toleranciju Redistribucija subseta B ćelija Smanjenje memorijskih B ćelija Povećanje tranzicionih i nevinih B ćelija In vitro stimulacija: TGFβ IL-10 ili IFNγ Sagoo P, et al. J Clin Invest 2010.
37 Bolesnici koji su razvili toleranciju imaju manji % cirkulišućih CD4 + CD25 int T ćelija Sagoo P, et al. J Clin Invest 2010.
38 Odnos ekspresije gena za FoxP3/ α-1,2-manosidase u perifernoj krvi Sagoo P, et al. J Clin Invest 2010.
39 Bolesnici koji su razvili toleranciju nemaju DSA Sagoo P, et al. J Clin Invest 2010.
40 Biopsija kalema? Biomarkeri
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
I.Ν.Μπολέτης. Νεφρολογική Κλινική & Μονάδα Μεταμόσχευσης Νεφρού, Ιατρική Σχολή ΕΚΠΑ, ΓΝΑ «Λαϊκό»
 I.Ν.Μπολέτης Νεφρολογική Κλινική & Μονάδα Μεταμόσχευσης Νεφρού, Ιατρική Σχολή ΕΚΠΑ, ΓΝΑ «Λαϊκό» 20 ο Πανελλήνιο Συνέδριο Νεφρολογίας Αθήνα, 3 6 Μαΐου 2018 Αναμενόμενα έτη επιβίωσης ανάλογα με την ηλικία
I.Ν.Μπολέτης Νεφρολογική Κλινική & Μονάδα Μεταμόσχευσης Νεφρού, Ιατρική Σχολή ΕΚΠΑ, ΓΝΑ «Λαϊκό» 20 ο Πανελλήνιο Συνέδριο Νεφρολογίας Αθήνα, 3 6 Μαΐου 2018 Αναμενόμενα έτη επιβίωσης ανάλογα με την ηλικία
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Izbor statističkih testova Ana-Maria Šimundić
 Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Αύξηση της δωρεάς από ζώντες δότες νεφρού
 Αύξηση της δωρεάς από ζώντες δότες νεφρού I.Ν.Μπολέτης Νεφρολογική Κλινική & Μονάδα Μεταμόσχευσης Νεφρού, Ιατρική Σχολή ΕΚΠΑ, ΓΝΑ «Λαϊκό» 20 ο Πανελλήνιο Συνέδριο Νεφρολογίας Αθήνα, 3 6 Μαΐου 2018 Αναμενόμενα
Αύξηση της δωρεάς από ζώντες δότες νεφρού I.Ν.Μπολέτης Νεφρολογική Κλινική & Μονάδα Μεταμόσχευσης Νεφρού, Ιατρική Σχολή ΕΚΠΑ, ΓΝΑ «Λαϊκό» 20 ο Πανελλήνιο Συνέδριο Νεφρολογίας Αθήνα, 3 6 Μαΐου 2018 Αναμενόμενα
SUPPLEMENTAL INFORMATION. Fully Automated Total Metals and Chromium Speciation Single Platform Introduction System for ICP-MS
 Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Electronic Supplementary Material (ESI) for Journal of Analytical Atomic Spectrometry. This journal is The Royal Society of Chemistry 2018 SUPPLEMENTAL INFORMATION Fully Automated Total Metals and Chromium
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Ο ρόλος της αιμαφαίρεσης στην ΑΒΟ ασύμβατη μεταμόσχευση νεφρού και στη νεφρική απόρριψη
 Ο ρόλος της αιμαφαίρεσης στην ΑΒΟ ασύμβατη μεταμόσχευση νεφρού και στη νεφρική απόρριψη Μελεξοπούλου Χριστίνα Νεφρολογική Κλινική και Μονάδα Μεταμόσχευσης Νεφρού Ιατρική Σχολή, ΕΚΠΑ, Γ.Ν.Α. «Λαϊκό» Page
Ο ρόλος της αιμαφαίρεσης στην ΑΒΟ ασύμβατη μεταμόσχευση νεφρού και στη νεφρική απόρριψη Μελεξοπούλου Χριστίνα Νεφρολογική Κλινική και Μονάδα Μεταμόσχευσης Νεφρού Ιατρική Σχολή, ΕΚΠΑ, Γ.Ν.Α. «Λαϊκό» Page
LANCI & ELEMENTI ZA KAČENJE
 LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Implementacija HE4 i ROMA indeksa u Klinici za tumore Centru za maligne bolesti KBCSM
 Implementacija HE4 i ROMA indeksa u Klinici za tumore Centru za maligne bolesti KBCSM Dr.sc. Ljiljana Mayer, spec.med.biokemije Zagreb, 18. ožujka 2017. Klinika za tumore Centar za maligne bolesti, KBCSM
Implementacija HE4 i ROMA indeksa u Klinici za tumore Centru za maligne bolesti KBCSM Dr.sc. Ljiljana Mayer, spec.med.biokemije Zagreb, 18. ožujka 2017. Klinika za tumore Centar za maligne bolesti, KBCSM
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Η Πλασμαφαίρεση στην αντιμετώπιση της Αντισωματικού Τύπου Απόρριψης του Νεφρικού Μοσχεύματος.
 Η Πλασμαφαίρεση στην αντιμετώπιση της Αντισωματικού Τύπου Απόρριψης του Νεφρικού Μοσχεύματος. Μάριος Παπασωτηρίου mpapasotiriou@yahoo.com Η Πλασμαφαίρεση στην ΑMR Βασικά στοιχεία της αντισωματικού τύπου
Η Πλασμαφαίρεση στην αντιμετώπιση της Αντισωματικού Τύπου Απόρριψης του Νεφρικού Μοσχεύματος. Μάριος Παπασωτηρίου mpapasotiriou@yahoo.com Η Πλασμαφαίρεση στην ΑMR Βασικά στοιχεία της αντισωματικού τύπου
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Sistemi veštačke inteligencije primer 1
 Sistemi veštačke inteligencije primer 1 1. Na jeziku predikatskog računa formalizovati rečenice: a) Miloš je slikar. b) Sava nije slikar. c) Svi slikari su umetnici. Uz pomoć metode rezolucije dokazati
Sistemi veštačke inteligencije primer 1 1. Na jeziku predikatskog računa formalizovati rečenice: a) Miloš je slikar. b) Sava nije slikar. c) Svi slikari su umetnici. Uz pomoć metode rezolucije dokazati
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
ΜΕΤΑΜΟΣΧΕΥΣΗ ΝΕΦΡΟΥ: Η ΕΠΙΔΡΑΣΗ ΤΗΣ ΠΑΡΟΥΣΙΑΣ DSA ΚΑΙ HLA ΑΣΥΜΒΑΤΟΤΗΤΩΝ ΣΤΗΝ ΕΚΒΑΣΗ
 ΜΕΤΑΜΟΣΧΕΥΣΗ ΝΕΦΡΟΥ: Η ΕΠΙΔΡΑΣΗ ΤΗΣ ΠΑΡΟΥΣΙΑΣ DSA ΚΑΙ HLA ΑΣΥΜΒΑΤΟΤΗΤΩΝ ΣΤΗΝ ΕΚΒΑΣΗ Μ. Δαρεμά 1, Α. Βιττωράκη 2, Κ. Δρούζας 1, Ι. Τσουμπού 1, Ι. Γαβαλάς 1, Α. Σιόρεντα 2, Ι. Μπόκος 3, Γ. Ζαββός 3, Α. Ινιωτάκη
ΜΕΤΑΜΟΣΧΕΥΣΗ ΝΕΦΡΟΥ: Η ΕΠΙΔΡΑΣΗ ΤΗΣ ΠΑΡΟΥΣΙΑΣ DSA ΚΑΙ HLA ΑΣΥΜΒΑΤΟΤΗΤΩΝ ΣΤΗΝ ΕΚΒΑΣΗ Μ. Δαρεμά 1, Α. Βιττωράκη 2, Κ. Δρούζας 1, Ι. Τσουμπού 1, Ι. Γαβαλάς 1, Α. Σιόρεντα 2, Ι. Μπόκος 3, Γ. Ζαββός 3, Α. Ινιωτάκη
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Appendix B Table of Radionuclides Γ Container 1 Posting Level cm per (mci) mci
 3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)
3 H 12.35 Y β Low 80 1 - - Betas: 19 (100%) 11 C 20.38 M β+, EC Low 400 1 5.97 13.7 13 N 9.97 M β+ Low 1 5.97 13.7 Positrons: 960 (99.7%) Gaas: 511 (199.5%) Positrons: 1,199 (99.8%) Gaas: 511 (199.6%)
Βιολογία Γενικής Παιδείας Β Λυκείου
 Απρίλιος Μάιος 12 Βιολογία Γενικής Παιδείας Β Λυκείου Δημοσθένης Καρυοφύλλης Βιολογία Γενικής Παιδείας Β Λυκείου (Ερωτήσεις που παρουσιάζουν ενδιαφέρον) 1. Τι είναι τα βιομόρια και ποια είναι τα βασικά
Απρίλιος Μάιος 12 Βιολογία Γενικής Παιδείας Β Λυκείου Δημοσθένης Καρυοφύλλης Βιολογία Γενικής Παιδείας Β Λυκείου (Ερωτήσεις που παρουσιάζουν ενδιαφέρον) 1. Τι είναι τα βιομόρια και ποια είναι τα βασικά
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Η άλλη προσέγγιση Πρώτη η Περιτοναϊκή Κάθαρση. Β. Λιακόπουλος Επ. Καθηγητής Νεφρολογίας Παν/μίου Θεσσαλίας
 Η άλλη προσέγγιση Πρώτη η Περιτοναϊκή Κάθαρση Β. Λιακόπουλος Επ. Καθηγητής Νεφρολογίας Παν/μίου Θεσσαλίας Κριτήρια επιλογής Επίδραση στην επιβίωση και ποιότητα ζωής Πιθανή επίδραση στην επόμενη μέθοδο
Η άλλη προσέγγιση Πρώτη η Περιτοναϊκή Κάθαρση Β. Λιακόπουλος Επ. Καθηγητής Νεφρολογίας Παν/μίου Θεσσαλίας Κριτήρια επιλογής Επίδραση στην επιβίωση και ποιότητα ζωής Πιθανή επίδραση στην επόμενη μέθοδο
Usluge koje se rade na lični zahtev
 Usluge koje se rade na lični zahtev Redni broj Naziv usluge 1 Uzorkovanje krvi (venepunkcija) 2 Uzorkovanje krvi (mikrouzorkovanje) 3 Specijalistički pregled prvi 4 Specijalistički pregled kontrolni 5
Usluge koje se rade na lični zahtev Redni broj Naziv usluge 1 Uzorkovanje krvi (venepunkcija) 2 Uzorkovanje krvi (mikrouzorkovanje) 3 Specijalistički pregled prvi 4 Specijalistički pregled kontrolni 5
ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Autoriteti. Svetska zdravstvena organizacija (SZO) American Diabetes Association (ADA) Srbija: Nacionalni vodič
 Autoriteti Svetska zdravstvena organizacija (SZO) American Diabetes Association (ADA) Srbija: Nacionalni vodič 1 Klasifikacija DM Tip 1 dijabetesa Tip 2 dijabetesa Drugi specifični tipovi dijabetesa Gestacijiski
Autoriteti Svetska zdravstvena organizacija (SZO) American Diabetes Association (ADA) Srbija: Nacionalni vodič 1 Klasifikacija DM Tip 1 dijabetesa Tip 2 dijabetesa Drugi specifični tipovi dijabetesa Gestacijiski
STVARANJE VEZE C-C POMO]U ORGANOBORANA
![STVARANJE VEZE C-C POMO]U ORGANOBORANA STVARANJE VEZE C-C POMO]U ORGANOBORANA](/thumbs/55/37829094.jpg) STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
PRAVAC. riješeni zadaci 1 od 8 1. Nađite parametarski i kanonski oblik jednadžbe pravca koji prolazi točkama. i kroz A :
 PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
Cenovnik zdravstvenih usluga na lični zahtev
 Institut za transfuziju krvi Srbije Br.1/9/1.5 Beograd, 24.12.2015. Cenovnik zdravstvenih usluga na lični zahtev Redni 1 1-000026 Uzorkovanje krvi (venepunkcija) 120,00 2 1-000018 Uzorkovanje krvi (mikrouzorkovanje)
Institut za transfuziju krvi Srbije Br.1/9/1.5 Beograd, 24.12.2015. Cenovnik zdravstvenih usluga na lični zahtev Redni 1 1-000026 Uzorkovanje krvi (venepunkcija) 120,00 2 1-000018 Uzorkovanje krvi (mikrouzorkovanje)
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ ο Γυμνάσιο Αγ. Παρασκευής
 ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
ΠΕΡΙΟΔΙΚΟ ΣΥΣΤΗΜΑ ΤΩΝ ΣΤΟΙΧΕΙΩΝ (1) Ηλία Σκαλτσά ΠΕ04.01 5 ο Γυμνάσιο Αγ. Παρασκευής Όπως συμβαίνει στη φύση έτσι και ο άνθρωπος θέλει να πετυχαίνει σπουδαία αποτελέσματα καταναλώνοντας το λιγότερο δυνατό
Παρουσίαση ενδιαφέροντος περιστατικού. Νεφρολογική Κλινική ΑΠΘ. Λαμπροπούλου Ιωάννα Ειδικευόμενη Νεφρολόγος
 Παρουσίαση ενδιαφέροντος περιστατικού Νεφρολογική Κλινική ΑΠΘ Λαμπροπούλου Ιωάννα Ειδικευόμενη Νεφρολόγος ΑΙΤΙΟΛΟΓΙΑ ΕΙΣΟΔΟΥ Γυναίκα 71 ετών εισήχθει στη Νεφρολογική Κλινική (10/2011) I. οιδήματα κάτω
Παρουσίαση ενδιαφέροντος περιστατικού Νεφρολογική Κλινική ΑΠΘ Λαμπροπούλου Ιωάννα Ειδικευόμενη Νεφρολόγος ΑΙΤΙΟΛΟΓΙΑ ΕΙΣΟΔΟΥ Γυναίκα 71 ετών εισήχθει στη Νεφρολογική Κλινική (10/2011) I. οιδήματα κάτω
Trigonometrijske nejednačine
 Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1
 Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής
 ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Οξεία βρογχίτιδα. Ιωάννης Γαροφαλάκης Παθολόγος
 Οξεία βρογχίτιδα Ιωάννης Γαροφαλάκης Παθολόγος Παρουσίαση τυπικού περιστατικού [1] Άνδρας 38 ετών, χωρίς ιστορικό πνευμονικής νόσου. Από 7-ημέρου, ήπια δύσπνοια κατά την άσκηση με συνοδό παραγωγικό βήχα
Οξεία βρογχίτιδα Ιωάννης Γαροφαλάκης Παθολόγος Παρουσίαση τυπικού περιστατικού [1] Άνδρας 38 ετών, χωρίς ιστορικό πνευμονικής νόσου. Από 7-ημέρου, ήπια δύσπνοια κατά την άσκηση με συνοδό παραγωγικό βήχα
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
ΜΕΛΕΤΗ ΤΗΣ ΥΝΑΤΟΤΗΤΑΣ ΑΞΙΟΠΟΙΗΣΗΣ ΤΟΥ ΓΕΩΘΕΡΜΙΚΟΥ ΠΕ ΙΟΥ ΘΕΡΜΩΝ ΝΙΓΡΙΤΑΣ (Ν. ΣΕΡΡΩΝ)
 ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
ελτίο της Ελληνικής Γεωλογικής Εταιρίας τοµ. XXXVI, 2004 Πρακτικά 10 ου ιεθνούς Συνεδρίου, Θεσ/νίκη Απρίλιος 2004 Bulletin of the Geological Society of Greece vol. XXXVI, 2004 Proceedings of the 10 th
Pismeni dio ispita iz Matematike Riješiti sistem jednačina i diskutovati rješenja u zavisnosti od parametra a:
 Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ
 ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
!"#$%&' ()*%!&"' «$+,-./0µ12 3410567/8+9 5+9 :1/.;./:69 <.5-8+9: $=5-.>057=9/7/=9» !"#$%&$'( trafficking %)*+!,,-.$. /0"1%µ$)$ 2"(%3$)*4 5"67+$4
 1!"#$%&' ()*%!&"' «$+,-./0µ12 3410567/8+9 5+9 :1/.;./:69 057=9/7/=9»!"#$%$&"'$ «NOVOTEL» ()*. +,-. 4-6, /01#/ 14 & 15 /23)4567 2011!"#$%&$'( trafficking %)*+!,,-.$. /0"1%µ$)$ 2"(%3$)*4 5"67+$4
1!"#$%&' ()*%!&"' «$+,-./0µ12 3410567/8+9 5+9 :1/.;./:69 057=9/7/=9»!"#$%$&"'$ «NOVOTEL» ()*. +,-. 4-6, /01#/ 14 & 15 /23)4567 2011!"#$%&$'( trafficking %)*+!,,-.$. /0"1%µ$)$ 2"(%3$)*4 5"67+$4
Η ΕΦΑΡΜΟΓΗ ΘΕΡΑΠΕΥΤΙΚΗΣ ΑΦΑΙΡΕΣΗΣ ΣΤΗΝ ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΑΒΟ-ΑΣΥΜΒΑΤΗ ΜΕΤΑΜΟΣΧΕΥΣΗ ΚΑΙ ΣΤΗΝ ΑΠΕΥΑΙΣΘΗΤΟΠΟΙΗΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΛΗΠΤΩΝ ΦΙΛΙΟΠΟΥΛΟΣ ΒΑΣΙΛΗΣ
 Η ΕΦΑΡΜΟΓΗ ΘΕΡΑΠΕΥΤΙΚΗΣ ΑΦΑΙΡΕΣΗΣ ΣΤΗΝ ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΑΒΟ-ΑΣΥΜΒΑΤΗ ΜΕΤΑΜΟΣΧΕΥΣΗ ΚΑΙ ΣΤΗΝ ΑΠΕΥΑΙΣΘΗΤΟΠΟΙΗΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΛΗΠΤΩΝ ΦΙΛΙΟΠΟΥΛΟΣ ΒΑΣΙΛΗΣ Νεφρολογική Κλινική και Μονάδα Μεταμόσχευσης Νεφρού,
Η ΕΦΑΡΜΟΓΗ ΘΕΡΑΠΕΥΤΙΚΗΣ ΑΦΑΙΡΕΣΗΣ ΣΤΗΝ ΠΡΟΕΤΟΙΜΑΣΙΑ ΓΙΑ ΑΒΟ-ΑΣΥΜΒΑΤΗ ΜΕΤΑΜΟΣΧΕΥΣΗ ΚΑΙ ΣΤΗΝ ΑΠΕΥΑΙΣΘΗΤΟΠΟΙΗΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΛΗΠΤΩΝ ΦΙΛΙΟΠΟΥΛΟΣ ΒΑΣΙΛΗΣ Νεφρολογική Κλινική και Μονάδα Μεταμόσχευσης Νεφρού,
Η ΕΠΙ ΡΑΣΗ ΙΝΩΤΙΚΩΝ ΠΑΡΑΓΟΝΤΩΝ ΣΤΟΝ ΕΝΤΕΡΙΚΟ ΒΛΕΝΝΟΓΟΝΟ ΩΣ ΣΤΟΧΟΣ ΘΕΡΑΠΕΥΤΙΚΩΝ ΣΤΡΑΤΗΓΙΚΩΝ ΣΤΗ ΝΟΣΟ ΤΟΥ CROHN
 ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΙΑΤΡΙΚΗΣ ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Κλινική Φαρµακολογία και Θεραπευτική» Η ΕΠΙ ΡΑΣΗ ΙΝΩΤΙΚΩΝ ΠΑΡΑΓΟΝΤΩΝ ΣΤΟΝ ΕΝΤΕΡΙΚΟ ΒΛΕΝΝΟΓΟΝΟ ΩΣ ΣΤΟΧΟΣ ΘΕΡΑΠΕΥΤΙΚΩΝ
ΗΜΟΚΡΙΤΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΡΑΚΗΣ ΤΜΗΜΑ ΙΑΤΡΙΚΗΣ ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Κλινική Φαρµακολογία και Θεραπευτική» Η ΕΠΙ ΡΑΣΗ ΙΝΩΤΙΚΩΝ ΠΑΡΑΓΟΝΤΩΝ ΣΤΟΝ ΕΝΤΕΡΙΚΟ ΒΛΕΝΝΟΓΟΝΟ ΩΣ ΣΤΟΧΟΣ ΘΕΡΑΠΕΥΤΙΚΩΝ
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
IL - 13 /IL - 18 ELISA PCR RT - PCR. IL - 13 IL - 18 mrna. 13 IL - 18 mrna IL - 13 /IL Th1 /Th2
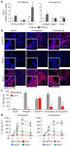 344 IL - 13 /IL - 18 1 2 1 2 1 2 1 2 1 2 3 1 2 13 18 IL - 13 /IL - 18 10% / OVA /AL OH 3 5% 16 ~ 43 d 44 d ELISA BALF IL - 13 IL - 18 PCR RT - PCR IL - 13 IL - 18 mrna IL - 13 mrna 0. 01 IL - 18 mrna 0.
344 IL - 13 /IL - 18 1 2 1 2 1 2 1 2 1 2 3 1 2 13 18 IL - 13 /IL - 18 10% / OVA /AL OH 3 5% 16 ~ 43 d 44 d ELISA BALF IL - 13 IL - 18 PCR RT - PCR IL - 13 IL - 18 mrna IL - 13 mrna 0. 01 IL - 18 mrna 0.
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Ovo nam govori da funkcija nije ni parna ni neparna, odnosno da nije simetrična ni u odnosu na y osu ni u odnosu na
 . Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
. Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
Ankylosing Spondylitis AS. NSAIDs. NSAIDs 100% B27 NSAID ~ 90% FDA EMA
 2016 12 12 Ankylosing Spondylitis AS human leukocyte antigen HLA- AS NSAIDs NSAIDs B27 100% NSAIDs NSAIDs 90% NSAID ~ AS 0.25% 2~3 1 100% 1 AS CFDA FDA EMA 14 AS NSAIDs 2 CFDA non-ster- AS 1 oidal anti-inflammatory
2016 12 12 Ankylosing Spondylitis AS human leukocyte antigen HLA- AS NSAIDs NSAIDs B27 100% NSAIDs NSAIDs 90% NSAID ~ AS 0.25% 2~3 1 100% 1 AS CFDA FDA EMA 14 AS NSAIDs 2 CFDA non-ster- AS 1 oidal anti-inflammatory
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med =
 100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Αλληλεπίδραση ακτίνων-χ με την ύλη
 Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Η στεφανιαία νόσος : πρώτη αιτία θανάτου στις Δυτικές Κοινωνίες
 Η επίδραση του πολυμορφισμού 3872 Α>G του γονιδίου της C-αντιδρώσας πρωτεΐνης στους μηχανισμούς φλεγμονής και θρόμβωσης σε ασθενείς με σταθερή στεφανιαία νόσο Γ. Χατζής, Δ. Τούσουλης, Ν. Παπαγεωργίου,
Η επίδραση του πολυμορφισμού 3872 Α>G του γονιδίου της C-αντιδρώσας πρωτεΐνης στους μηχανισμούς φλεγμονής και θρόμβωσης σε ασθενείς με σταθερή στεφανιαία νόσο Γ. Χατζής, Δ. Τούσουλης, Ν. Παπαγεωργίου,
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
ΠΑΡΑΡΤΗΜΑ V. Πρότυπα δυναμικά αναγωγής ( ) ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 25 o C. Ημιαντιδράσεις αναγωγής , V. Antimony. Bromine. Arsenic.
 ΠΑΡΑΡΤΗΜΑ V. ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C ΠΑΡΑΡΤΗΜΑ V. Πρότυπα δυναμικά αναγωγής ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C, V, V Auminum Bervium A ( H ) e A H. 0 Be e Be H. 1 ( ) [ ] e A F. 09 AF
ΠΑΡΑΡΤΗΜΑ V. ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C ΠΑΡΑΡΤΗΜΑ V. Πρότυπα δυναμικά αναγωγής ΠΡΟΤΥΠΑ ΔΥΝΑΜΙΚΑ ΑΝΑΓΩΓΗΣ ΣΤΟΥΣ 5 o C, V, V Auminum Bervium A ( H ) e A H. 0 Be e Be H. 1 ( ) [ ] e A F. 09 AF
