E-Companion: Stakeholder Perspectives on E-waste Take-Back Legislation
|
|
|
- Οκυροη Ρέντης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 E-Compaio: Stakeholder Perspectives o E-waste Take-Back Legislatio Atalay Atasu atalayatasu@mgtgatechedu College of Maagemet, Georgia Istitute of Techology 800, West Peachtree Street, Atlata, GA Özur Özdemir, oozdemir@rsml RSM, Erasmus Uiversity Rotterdam, Postbus 1738, Rotterdam, Netherlads Luk N Va Wassehove, lukva-wassehove@iseadedu INSEAD, Boulevard de Costace, Fotaiebleau, Frace Jauary 1, 01 1 Tax or Rate? We cosider a market for a sigle product, with three sets of decisio makers: cosumers, maufacturers ad a social plaer The decisio makig process occurs sequetially First, the social plaer decides o the policy implemetatio model ad parameters The the maufacturers determie prices/sales quatities, give the costs they icur uder the selected policy parameters Fially, give the maufacturers decisios, cosumers make the purchasig decisio assume that cosumer utilities (υ) from purchasig a product are uiformly distributed betwee 0 ad 1 ad market size is ormalized to 1 Hece, a cosumer with utility υ j purchases the product if υ j p, the price of the product We assume idetical maufacturers competig i a Courot settig Maufacturers select their sales quatities (q i ), which determie the price i the market, ie, p =1 i=1 q i The social plaer makes a choice betwee the two differet models (see Figure EC1): We 1
2 Tax Model (T ): I this model, the social plaer udertakes the take-back task, ie, collectio ad recyclig, to divert a fractio c of products from ladfill, ad charges a recovery fee (tax) τ to the maufacturers Take-back Rate Model (R): I this model, the social plaer determies a take-back rate (c) ad requires the maufacturers to esure this rate SOCIAL PLANNER MANUFACTURER qc SOCIAL PLANNER c MANUFACTURER q CONSUMERS q CONSUMERS qc TAX MODEL RATE MODEL Figure EC1: Take-back Legislatio Models The maufacturers uit cost of productio is μ The take-back cost icurred by the maufacturers depeds o the policy tool The party resposible for product take-back (ie, the operatig party) icurs a uit take-back cost of χ>0 We assume that χ+μ <1 so that the maufacturers ca operate at a positive profit margi Give these costs ad k (T,R) deotig the policy implemetatio model of the social plaer, maufacturer i maximizes his profit max q i Π Mi (k) =q i (p μ) q i ρ k (τ,c) where, τ, if k = T ; ρ k (τ,c) = cχ, if k = R (1) is the effective per uit cost of take-back to the maufacturer From the objective fuctio of maufacturer i, it is easy to show that the equilibrium is at qi = 1 μ ρ k(τ,c),aditur, p = 1+(μ+ρ k(τ,c)) By aticipatig the maufacturers choices, the social plaer ca focus o its ow objective Sice a stadard approach to determiig the appropriateess of alterative
3 forms of regulatio is to focus o a first-best socially optimal solutio, we assume the social plaer maximizes the social welfare, which cosists of maufacturer profits, cosumer surplus (followig the traditioal defiitio i ecoomics, eg, Barett 1980, Fishma ad Rob 000, ad Plambeck ad Wag 009 to ame a few) ad other exteralities I particular, we cosider the followig: Total Maufacturer Profit: Π M (k) = i=1 Π M i (k) =(q i (p μ ρ k (τ,c)) = ( 1 μ ρ k(τ,c) ) Total Cosumer Surplus: Π C (k) =(1 p )q i / = ((1 μ ρ k(τ,c))) () Note that Π C (k) = Π M (k) Evirometal Impact: We focus o the level of ladfill aversio as a evirometal objective, which is oe of the mai goals of the curret practice of product take-back legislatio, alog with providig recyclable product desig icetives As our focus is o ladfill diversio, we assume there exists a uit evirometal cost associated with each ladfilled product, deoted by ɛ We assume that the total evirometal impact of ot takig back (1 c) proportio of total sales is Π E (k) = ɛ(1 c)qi = ɛ(1 c) 1 μ ρ k(τ,c) Depedig o the particular policy model chose, the social plaer will either collect taxes from the maufacturers ad take resposibility of take-back herself or impose a take-back rate o the maufacturers Hece, give the policy model (k), the social plaer s objective icludes the followig term; qi (τ cχ), if k=t; φ k (τ,c)= 0, if k=r () The total social welfare is the writte as; SW(k) =Π M (k)+π C (k)+π E (k)+φ k (τ,c) (3) The social plaer maximizes SW(k) by decidig o the tax (τ) ad the take-back rate (c) i the tax model ad oly the take-back rate i the rate model A summary of otatio is give i Table EC1 3
4 Parameters μ χ ɛ k Uit productio cost Uit take-back cost Uit evirometal cost Number of maufacturers Policy model, k {T,R} Decisio variables c τ q i q p Take-back rate Uit recovery fee (tax) Sales quatity of maufacturer i Total sales quatity Uit price Objectives Π M Π C Π E SW Total maufacturig profit Cosumer surplus Evirometal impact Social welfare Table EC1: Notatio Impact o Stakeholders 1 Social Plaer Perspective 11 Rate Model I this case, the objective fuctio of maufacturer i is Sice max q i Π Mi = (p μ)q i cχq i (4) where p = 1 q i (5) i=1 Π Mi q i =1 ( +1)q i μ cχ ad Π Mi q i = ( +1) the maufacturer i s objective fuctio is cocave i q i By the first order coditios, the optimal sales quatity for each maufacturer (qi ) ad the optimal price (p )aregiveas 1 μ cχ ad 4
5 1+(cχ+μ), respectively Give this, Π M = Π Mi = i=1 (cχ + μ 1) ( +1) Π C = (cχ + μ 1) ( +1) ɛ(c 1)(cχ + μ 1) Π E = +1 Propositio 1 (Rate Model) Table EC summarizes the optimal decisio of the social plaer for the take-back rate model The optimal take-back rate icreases i the degree of the competitio () ad the evirometal cost (ɛ) 0 <ɛ (1 μ)χ ) (1 μ)χ c 0 q (1 μ) ) <ɛ<χ( + ) ɛ χ( + ɛ(μ 1)() χ(ɛ()+(μ 1)(+)) χ(χ(+) ɛ()) 1 ɛ(χ+μ 1) χ(+) ɛ() ) ( χ μ+1) (μ 1) Π ɛ (χ+μ 1) (χ+μ 1) M () (χ(+) ɛ()) () Π E ɛ(1 μ) ɛ (χ+μ 1) (ɛ+ɛ χ(+)) χ(χ(+) ɛ()) 0 (μ 1) Π ɛ (χ+μ 1) (χ+μ 1) C () (χ(+) ɛ()) () SW (μ 1)(ɛ()+(μ 1)(+)) () ɛ (χ+μ 1) χ(χ(+) ɛ()) Table EC: The optimal solutio for the rate model (χ+μ 1) (+) () Proof Takig the sum of Π M,Π C ad Π E, the social plaer s problem is writte as; max c SW = (cχ + μ 1)(ɛ( +1)+(μ 1)( +)+c(χ( +) ɛ( + 1))) ( +1) (6) st 0 c 1 (7) The first ad the secod order derivatives of the objective with respect to c are; SW c SW c = = ( c( +)χ + ((1 c)ɛ( +1)+(μ 1)( +))χ ɛ(μ 1)( +1) ) ( +1) (8) χ(χ( +) ɛ( +1)) ( +1) (9) SW c < 0, if χ( +) ɛ> ( +1) ; (10) SW c =0, if χ( +) ɛ = ( +1) ; (11) SW c > 0, if χ( +) ɛ< ( +1) (1) 5
6 I (10), SW is cocave i c From the first order coditios, c = ɛ(μ 1)() χ(ɛ()+(μ 1)(+)) χ(χ(+) ɛ()) if ɛ χ( + ), c 1, thus the optimal c (c )issetto1 if (1 μ)χ if χ(+) () ) <ɛ<χ( + ), 0 <c<1, thus c = ɛ(μ 1)() χ(ɛ()+(μ 1)(+)) χ(χ(+) ɛ()) <ɛ (1 μ)χ ), c 0, thus c =0 I (11), SW is liear ad decreasig i c Hece, c =0 I (1), SW is covex i c We compare the two boudary solutios: SW c=0 ad SW c=1 The root of SW c=0 SW c=1 =0isɛ = χ(χ+μ )(+) (μ 1)() SW c=0 >SW c=1 whe ɛ is smaller tha this root This root is greater tha χ(+) () (the upper boud o ɛ for covexity): Sice by assumptio χ + μ<1, χ(χ +μ )( +) (μ 1)( +1) (χ +μ ) (μ 1) ( μ χ) (1 μ) χ (1 μ) χ( +) ( +1) (13) 1 (14) 1 (15) 1 (16) χ < 1 Hece, (17) (1 μ) χ (1 μ) > 1 (18) Thus, give the covexity coditio SW c=0 is always greater tha SW c=1 ad c =0 Give these results, the optimal decisios of the social plaer i the rate model ca be summarized as i Table EC To show the secod part of the propositio, first ote that as ɛ icreases, the optimal solutio occurs at higher take-back rate itervals, this is obvious from the table The we check the chage of the iterval bouds i Table EC with These bouds decrease with the degree of competitio (): Moreover; ( (1 μ)χ )) = χ(μ 1) (χ μ +1)( +1) ( (1 μ)χ )) > )) < 0 ad (χ( + (χ( + )) χ = ( +1) < 0 This implies that as icreases the zero ad the partial take-back itervals get smaller while the perfect take-back iterval elarges Also the iterior take-back rate icreases with ad ɛ: ( ) ɛ(μ 1)() χ(ɛ()+(μ 1)(+)) χ(χ(+) ɛ()) ɛ(1 χ μ) = (χ( +) ɛ( +1)) > 0 6
7 ( ) ɛ(μ 1)() χ(ɛ()+(μ 1)(+)) χ(χ(+) ɛ()) (1 χ μ)( +1)( +) = ɛ (χ( +) ɛ( +1)) > 0 Hece, we ca coclude that the optimal take-back rate icreases with the degree of competitio () ad the evirometal impact (ɛ) 1 Tax Model The problem of each maufacturer is max q i Π Mi = (p μ τ)q i (19) where p = 1 q i (0) Sice Π Mi =1 ( +1)q i μ τ ad Π Mi q i qi = ( +1) the maufacturer i s objective fuctio is cocave i q i By the first order coditios, the optimal sales quatity for each maufacturer qi = 1 μ τ ad the optimal price p = 1+(μ+τ) Whewe substitute these expressios i Π M,Π C,adΠ E,weget Π M = Π Mi = i=1 i=1 (μ + τ 1) ( +1) Π C = (μ + τ 1) ( +1) (c 1)ɛ(μ + τ 1) Π E = +1 Propositio (Tax Model) The optimal decisios of the social plaer uder the tax model are give i Table EC3 The optimal tax is o-decreasig i the take-back cost (χ) adthe evirometal cost (ɛ), ad icreasig i the degree of competitio () Proof The social plaer s problem is writte as, max c,τ SW = SW is cocave i τ sice (μ + τ 1)(c(χ ɛ)( +1)+ɛ( +1)+(μ 1)( +) τ) ( +1) (1) SW τ = st 0 c 1 () 0 τ 1 μ (3) (ɛ + ɛ + μ + c(χ ɛ)( +1) τ 1) ( +1) (4) SW τ = ( +1) < 0 (5) 7
8 0 <ɛ 1 μ ɛ χ 1 μ 1 μ <ɛ<1 μ 0 <χ ɛ>χ 1 μ <χ<1 μ c τ 0 q (1 μ) 1 μ ɛ (μ 1) Π (1 ɛ μ) M () Π E 1+()ɛ+μ 0 (1 μ) 1+()χ+μ 1 μ χ (μ 1) (1 χ μ) () ɛ(1 μ) ɛ(1 ɛ μ) 0 0 Π (μ 1) (1 ɛ μ) C () SW (μ 1)(ɛ()+(μ 1)(+)) (1 ɛ μ) () (μ 1) (1 χ μ) () (μ 1)(χ()+(μ 1)(+)) (1 χ μ) () Table EC3: The optimal solutio for the tax model From the the first order coditios, SW τ =0 τ = SW is liear i c sice SW c = ɛ + ɛ + μ + c(χ ɛ)( +1) 1 (χ ɛ)(μ + τ 1) +1 SW c = 0 (8) Hece, the optimal c (c ) takes a boudary value (either 0 or 1) I the tax model, τ + μ 1 should hold so that the maufacturers have oegative profit τ =1 μ is a special case where there is o productio (qi =0)adSW = 0 But this solutio ca ever be optimal, hece we igore it Whe μ + τ < 1, the value of c depeds o the relatio betwee ɛ ad χ ad substitutig c i τ = ɛ+ɛ+μ+c(χ ɛ)() 1, we fid ( 0, 1+()ɛ+μ) (c, if χ ɛ;,τ)= ( 1, 1+()χ+μ) (9), if χ<ɛ Uit tax should always be oegative ad lower tha 1 μ so that there is always positive productio i the market as metioed above Hece, we eed to check whether the τ values foud above satisfy these coditios τ c=0 isgreatertha0ifɛ> 1 μ ad lower tha 1 μ if ɛ<1 μ Siceɛ χ i this case ad χ<1 μ by assumptio (see page ), ɛ<1 μ is always satisfied Hece, for c =0,optimalτ (τ )is0wheɛ 1 μ 1+()ɛ+μ,ad Similarly, τ c=1 isgreatertha0ifχ> 1 μ (6) (7) whe ɛ> 1 μ ad lower tha 1 μ whe χ<1 μ By assumptio χ<1 μ Thus,forc =1,optimalτ is 0 whe χ 1 μ 1+()χ+μ ad aresummarizeditableec3 To show the secod part of the propositio, ote that 8 whe χ> 1 μ These
9 i the iterval ɛ χ, uptothethresholdof 1 μ, the optimal tax is always 0, hece ot affected by ɛ After this threshold, sice τ ɛ =()/ > 0, the optimal tax is icreasig i ɛ These two observatios prove that the optimal tax is o-decreasig i the evirometal cost (ɛ) i the iterval ɛ>χ,uptothethresholdof 1 μ, the optimal tax is always 0, hece ot affected by χ After this threshold, sice τ χ =( +1)/ > 0 the optimal tax is icreasig i χ These observatios prove that the optimal tax is o-decreasig i the take-back cost (χ) the itervals where the optimal tax is 0 get smaller as icreases This is because the upper boud o these itervals ( 1 μ ) decreases as icreases Also i the itervals where the optimal tax is positive, τ icreases as icreases: ( ( 1+()ɛ)+μ ) ( ( 1+()χ)+μ ) = ɛ + μ 1 > 0siceɛ<1 μ i the associated iterval (30) = χ + μ 1 > 0siceχ<1 μ by assumptio (31) Give these, we ca coclude that τ is icreasig i the degree of competitio () Corollary 1 SW(T ) SW(R), ie, the social welfare uder the tax model is better tha or equal to that uder the rate model (see Table EC4) Furthermore, icreased competitio () reiforces the domiace of the tax model from the social plaer s perspective 0 <ɛ 1 μ SW(T )=SW(R) ɛ χ χ<ɛ< (+)(1 μ) 1 μ <ɛ<1 μ 0 <χ<1 μ SW(T ) >SW(R) Table EC4: Social plaer prefereces (+)(1 μ) ɛ Proof Cosiderig the solutio itervals of the two models, we evaluate the two models i terms of the social welfare uder three cases; whe ɛ χ, χ<ɛ< (+)(1 μ) ad (+)(1 μ) ɛ Whe ɛ χ: I the iterval of ɛ 1 μ, The optimal solutio for the tax model is c =0adτ = 0 ad the optimal social welfare is SW(T )= (μ 1)(ɛ()+(μ 1)(+)) () 9
10 The optimal solutio for the rate model is c = 0 ad the optimal social welfare is SW(R) = (μ 1)(ɛ()+(μ 1)(+)) () Hece, SW(T ) =SW(R) I the iterval of ɛ> 1 μ, The optimal solutio for the tax model is c =0adτ = 1+()ɛ+μ ad SW(T )= (1 ɛ μ) For the rate model there are two feasible optima: (1) whe ɛ (1 μ)χ ad SW(R) = (μ 1)(ɛ()+(μ 1)(+)),()whe (1 μ)χ () c (0, 1) ad SW(R) = ɛ (χ+μ 1) χ(χ(+) ɛ()) ), c =0 ) <ɛ<χ( + ), I case (1) we compare SW(T )= (1 ɛ μ) vs SW(R) = (μ 1)(ɛ()+(μ 1)(+)) () (1 ɛ μ) (μ 1)(ɛ( +1)+(μ 1)( +)) ( +1) (3) (ɛ + μ 1) ( +1) (μ 1)(ɛ( +1)+(μ 1)( + )) (33) ɛ ( +1) +(μ 1) ( +1) +ɛ(μ 1)( +1) (μ 1)ɛ( +1)+(μ 1) ( + ) (34) ( +1) ɛ +(μ 1) +ɛ(μ 1)( +1) 0 (35) (( +1)ɛ +(μ 1)) > 0 (36) Hece, we ca coclude that SW(T ) >SW(R) I case () we compare SW(T ) = (1 ɛ μ) vs SW(R) = ɛ (χ+μ 1) χ(χ(+) ɛ()) compariso iterval ca be writte as max( 1 μ, (1 μ)χ χ<χ( + (1 μ)χ )ad ) > 1 μ as (1 μ)χ The )) < ɛ mi(χ, χ( + )) Hece, the compariso iterval ca be summarized ) <ɛ χ IfwesolveSW(T ) SW(R) = 0, the roots are ɛ 1 = (μ 1) χ(+)(μ 1)+ (μ 1) ( 4(+)χ 4(μ 1)(+)χ+(μ 1) ) 4χ() (37) ɛ = (μ 1) χ(+)(μ 1) (μ 1) ( 4(+)χ 4(μ 1)(+)χ+(μ 1) ) 4χ() (38) ɛ 3 = χ (39) Note that ɛ 3 is already equal to the upper boud of the iterval Also ɛ < (1 μ)χ ) < χ<ɛ 1 give all the restrictios o parameters 1 Hece, oe of the roots exist i the compariso iterval This implies that SW(T ) SW(R) ever hits 0 i the give iterval ad the sig of SW(T ) SW(R) does ot chage withi the iterval Hece, to fid the sig of the differece throughout the iterval, it is sufficiet to determie the sig at a arbitrary poit Let s cosider the parameter istace, {χ =9/64,μ =1/8, =31} 1 The complexity of the expressios for ɛ 1 ad ɛ ad the iterval restrictios make the compariso betwee ɛ 1 ad ɛ tedious Hece, the required computatios for the proof have bee performed i Mathematica, which allows for symbolic computatios The Mathematica code is available from the authors 10
11 for which the value iterval for ɛ is computed as (079/16640, 9/64] We choose 1/8 (079/16640, 9/64] For this particular poit SW(T ) SW(R) = 1181/47680 > 0 This implies that SW(T ) > SW(R) i the etire iterval Whe χ<ɛ< (+)(1 μ) : I the iterval of 0 <χ 1 μ, The optimal solutio for the tax model is c =1adτ =0ad SW(T )= (μ 1)(χ()+(μ 1)(+)) () For the rate model there are three feasible optima: (1) whe χ ɛ() +, c =1 ad SW(R) = (χ+μ 1) (+),()whe ɛ() () + <χ< ɛ(1 μ)( 1) ɛ() (1 μ)(+), c (0, 1) ad SW(R) = ɛ (χ+μ 1) ɛ(1 μ)( 1), ad (3) whe χ, c =0ad χ(χ(+) ɛ()) ɛ() (1 μ)(+) SW(R) = (μ 1)(ɛ()+(μ 1)(+)) () I Case (1), we compare SW(T ) = (μ 1)(χ()+(μ 1)(+)) () vs SW(R) = (χ+μ 1) (+) () (μ 1)(χ( +1)+(μ 1)( +)) ( +1) (χ + μ 1) ( +) ( +1) (40) (μ 1)χ( +1)+(μ 1) ( +) (μ 1) ( +)+χ ( +)+(μ 1)χ( + ) (41) (1 μ) + > 1 μ (μ 1)χ( +1) χ ( +)+(μ 1)χ( + ) (4) (1 μ)χ χ ( + ) (43) (1 μ) + χ (44) (the upper boud o χ i the give iterval), thus χ< (1 μ) + i the give iterval This implies that SW(T ) > SW(R) I case (), we compare SW(T )= (μ 1)(χ()+(μ 1)(+)) () vs SW(R) = ɛ (χ+μ 1) χ(χ(+) ɛ()) IthisitervalSW(T) >SW(R) give all the bouds o the parameters I case (3), we compare SW(T )= (μ 1)(χ()+(μ 1)(+)) () vs SW(R) = (μ 1)(ɛ()+(μ 1)(+)) () This compariso is quite easy Sice χ<ɛi this iterval ad sice the coefficiet of χ ad ɛ i SW(T )adsw(r) ( (μ 1) <0 ) is egative, SW(T ) >SW(R) I the iterval of 1 μ <χ<1 μ, The optimal solutio for the tax model is c =1adτ = 1+()χ+μ ad SW(T )= (1 χ μ) The expressios ad the iterval bouds have complicated structures which makes this proof tedious Hece, the required computatios for the proof have bee performed i Mathematica The Mathematica code is available from the authors 11
12 For the rate model there are two feasible optima depedig o the value of χ: (1) whe χ ɛ() +, c =1adSW(R) = (χ+μ 1) (+) ad () whe ɛ() + <χ< ɛ(1 μ)( 1) ɛ() (1 μ)(+), c (0, 1) ad SW(R) = ɛ () (χ+μ 1) χ(χ(+) ɛ()) I case (1), we compare SW(T )= (1 χ μ) vs SW(R) = (χ+μ 1) (+) () This implies that SW(T ) >SW(R) (1 χ μ) (χ + μ 1) ( +) ( +1) (45) 1 ( +) ( +1) (46) ( +1) ( + ) (47) 1 > 0 (48) I case (), we compare SW(T )= (1 χ μ) vs SW(R) = ɛ (χ+μ 1) χ(χ(+) ɛ()) This compariso iterval ca be writte as max( 1 μ, ɛ() + ) <χ<mi(ɛ, 1 ɛ(1 μ)( 1) μ, ɛ() (1 μ)(+) ) If we solve SW(T ) SW(R) = 0, we fid 4 roots: χ 1 = ɛ (49) χ,3 = 1 μ (50) χ 4 = ɛ + (51) χ 1 ad χ,3 are already equal to the upper bouds of the compariso iterval Hece, they are out of the compariso iterval χ 4 = ɛ + < ɛ() +, hece this root is also out of the iterval Thus, there are o roots i the compariso iterval This implies that SW(T ) SW(R) ever hits 0 ad the sig of the differece does ot chage i the compariso iterval To determie the sig of SW(T ) SW(R) throughout the iterval, it is sufficiet to determie the sig at a arbitrary poit of the iterval Cosider the poit {ɛ = 301/4096,μ = 13/16, = } i the iterval For this data istace the value iterval for χ ca be computed as (1/16, 301/4096) We select 9/18 (1/16, 301/4096) from this iterval ad at this particular poit SW(T ) SW(R) = 89375/ > 0 This shows that SW(T ) >SW(R) i the give iterval Whe (+)(1 μ) ɛ: This case is very similar to the secod case (ie, χ<ɛ< (+)(1 μ) ) with respect to the compariso itervals ad the optimal SW values i the relevat itervals The oly differece is that there exists oly oe feasible optima for the rate model Both i the iterval of 0 <χ 1 μ model is c = 1, ad the optimal SW(R) = (χ+μ 1) (+) () 1 μ ad <χ<1 μ, the optimal solutio for the rate 1
13 Similar to the previous case, the optimal social welfare for the tax model is SW(T )= (μ 1)(χ()+(μ 1)(+)) () whe 0 <χ 1 μ (1 χ μ),adsw(t)= whe 1 μ <χ Hece, the comparisos give i the secod case hold for this case as well ad we ca coclude that SW(T ) >SW(R) Give this aalysis, we ca coclude that SW(T )=SW(R) oly whe ɛ 1 μ ad SW(T ) >SW(R) otherwise as show i Table EC4 ad ɛ χ, To show the secod part of the corollary ote that as the degree of competitio () icreases, the upper boud ( 1 μ ) o the equality regio decreases ( 1 μ ) < 0 (5) This implies that as icreases the equality regio gets smaller while the regio where the tax model domiates elarges I other words, the social plaer prefers the tax model i a wider rage of ɛ values Hece, icreased competitio () reiforces the domiace of the tax model from the perspective of the social plaer Maufacturer ad Cosumer Perspectives We compare the two polices with respect to the total maufacturer profit ad the evirometal impact The comparisos with respect to the cosumer surplus parallel those for the total maufacturer profit i this settig because the cosumer surplus is always equal to a costat ( ) times the total maufacturer profit Hece, we do ot make a separate compariso for the cosumer surplus However, we ote that this is ot the case whe operatig cost exteralities are take ito accout, as illustrated i 31 Corollary If 1 μ (+)(1 μ) <ɛ< () ad ɛ χ, theπ M (R) > Π M (T ) ad Π C (R) > Π C (T ), ie, the rate model is preferred by the maufacturers ad the cosumers Otherwise, Π M (R) Π M (T ) ad Π C (R) Π C (T ), ie, the tax model is at least as good as the rate model (see Table EC5) Furthermore, with more itese competitio () the rate model is preferred by the maufacturers ad the cosumers for lower ɛ values ɛ 1 μ ɛ χ 1 μ (+)(1 μ) <ɛ< () χ<ɛ< (+)(1 μ) (+)(1 μ) () ɛ<1 μ χ< χ χ χ 1 μ (+)(1 μ) ɛ 1 μ <χ<1 μ 0 <χ<1 μ Π M (T )=Π M (R) Π M (T ) < Π M (R) Π M (T ) Π M (R) Π M (T )=Π M (R) Π M (T ) > Π M (R) Table EC5: Compariso of the total maufacturer profit betwee the two models Proof Similar to the social welfare compariso, we ca evaluate the two models i terms of the maufacturer profit uder three cases; whe ɛ χ, χ<ɛ< (+)(1 μ) ad (+)(1 μ) ɛ 13
14 Whe ɛ χ: I the iterval of ɛ 1 μ, The optimal solutio for tax model is c =0adτ = 0 ad the optimal total maufacturer profit is Π M (T )= (μ 1) () Similarly, the optimal solutio for the rate model is c = 0 ad the optimal Π M (R) = (μ 1) () Hece, it is obvious that Π M (T )=Π M (R) ithisiterval I the iterval of ɛ> 1 μ, The optimal solutio for the tax model is c =0adτ = 1+()ɛ+μ,adΠ M (T )= (1 ɛ μ) For the rate model there are two feasible optima depedig o the value of ɛ: (1) whe ɛ (1 μ)χ ), c =0adΠ M(R) = (μ 1),()whe (1 μ)χ () ) < ɛ<χ( (+) ), optimal c (0, 1) ad Π M(R) = ɛ (χ+μ 1) (χ(+) ɛ()) I case (1) we compare Π M (T )= (1 ɛ μ) vs Π M (R) = (μ 1) () The compar- ( ) iso iterval ca be writte as 1 μ <ɛ<mi χ, (1 μ)χ ) χ> (1 μ)χ ), hece the tightest compariso iterval ca be summarized as 1 μ (1 μ)χ <ɛ< ) If we solve we fid roots: Π M (T ) Π M (R) = 0 (53) (1 ɛ μ) (μ 1) ( +1) = 0 (54) ɛ 1 = 1 μ +1 (μ 1)( +1) ɛ = +1 (55) (56) ɛ 1 is out of the compariso iterval because 1 μ <ɛi this iterval To see that ɛ is also out of the iterval, we compare ɛ with (1 μ)χ ) (the upper boud of the iterval): (μ 1)( +1) (1 μ)χ + ( +1 1 μ + χ +1 ) (57) ( + 1)(1 μ + χ) χ( + ) (58) χ + χ +( + 1)(1 μ) χ +χ (59) χ χ ( + 1)(1 μ) (60) χ( 1) ( + 1)(1 μ) (61) 14
15 Sice 1adμ<1 by assumptio, the right-had side of (61) is (-) Thus, the iequality holds with (>) which meas that ɛ is greater tha the upper boud ad out of the compariso iterval Hece, o roots exist i the compariso iterval ad this implies that Π M (T ) Π M (R) ever hits 0 ad the sig of the differece does ot chage withi the compariso iterval To determie the sig of Π M (T ) Π M (R), it is sufficiet to determie the sig at a arbitrary poit i the iterval Cosider the parameter istace { χ = 11 3,μ= 1 4,ɛ = 1 4,=9} At this parameter istace, the value iterval for ɛ is (3/40, 363/1400) We choose ɛ =1/4 (3/40, 363/1400) ad compute Π M (T ) Π M (R) = 39/14400 < 0 which implies that Π M (T ) < Π M (R) throughout this compariso iterval I case () we compare Π M (T )= (1 ɛ μ) vs Π M (R) = ɛ (χ+μ 1) Takig (χ(+) ɛ()) ito accout all the upper ad the lower bouds o ɛ the tightest compariso iterval ca be writte as (1 μ)χ ) <ɛ χ (for detailed aalysis please see Case () o page 10 which refers to the same compariso iterval) If we solve (1 ɛ μ) Π M (T ) Π M (R) = 0 (6) ɛ (χ + μ 1) (χ( +) ɛ( +1)) = 0 (63) we fid 4 roots ɛ 1 = ((μ 1)(3+) χ) +8χ(μ 1)()(+)+χ (μ 1)(3+) ɛ = ((μ 1)(3+) χ) +8χ(μ 1)()(+) χ+(μ 1)(3+) 4() (64) 4() (65) ɛ 3 = ( + )(1 μ) ( +1) (66) ɛ 4 = χ (67) ɛ < (1 μ)χ ) <ɛ 4 = χ<ɛ 1, hece the roots ɛ 1, ɛ,adɛ 4 are out of the compariso iterval 3 Olyɛ 3 ca be located i the compariso iterval ad split the compariso iterval ito Hece, ɛ 3 istheolyrootatwhichπ M (T ) Π M (R) hits 0 ad chages sig i the compariso iterval The to determie the sig of Π M (T ) Π M (R) (thus the greater Π M )whe (1 μ)χ ) <ɛ<ɛ 3 ad ɛ 3 < ɛ χ, we take two arbitrary poits i each subiterval Cosider the parameter istace {μ =1/4,χ =3/5, =6} for which the value iterval for ɛ i the first subiterval ca be writte as (8/1, 9/1) ad i the secod oe as (9/1, 3/5] We choose ɛ =17/4 from the first subiterval ad compute Π M (T ) Π M (R) = 3 The compariso of the roots withi the iterval bouds is complicated ad tedious Hece, the proof that these roots are outside the compariso iterval has bee performed i Mathematica The Mathematica code is available from the authors 15
16 8569/ < 0 From thesecod subitervalwe chooseɛ = 5/4 ad calculate Π M (T ) Π M (R) = 341/13604 > 0 This aalysis proves that Π M (T ) < Π M (R) whe (1 μ)χ ) <ɛ<ɛ 3 (68) Π M (T ) > Π M (R) whe ɛ 3 <ɛ χ (69) Π M (T )=Π M (R) whe ɛ = ɛ 3 (70) Give these results ad the results of Case (1), we ca coclude that Π M (T ) < Π M (R) whe 1 μ (+)(1 μ) () <ɛ () (71) Π M (T ) > Π M (R) whe (+)(1 μ) () <ɛ<1 μ (7) Π M (T )=Π M (R) whe ɛ = (+)(1 μ) () (73) Note that at the poit ɛ = (+)(1 μ) (), the maufacturer profits are equal uder the two models For the ease of presetatio we do ot show the equality poit separately i Table EC5 ad combie it with the secod case as: whe (+)(1 μ) () ɛ<1 μ, Π M (T ) Π M (R) Whe χ<ɛ< (+)(1 μ) : I the iterval of 0 <χ 1 μ, The optimal solutio for the tax model is c =1adτ =0adΠ M (T )= (μ 1) () For the rate model depedig o the value of χ there are 3 feasible optima: (1) whe χ ()ɛ (+), c =1adΠ M(R) = (χ+μ 1),()whe ɛ() + <χ< χ = () ɛ(1 μ)( 1) ɛ() (1 μ)(+), c (0, 1) ad Π M (R) = χ χ, c =0adΠ M (R) = (μ 1) () I case (1) we compare Π M (T )= (μ 1) () (μ 1) ( +1) ɛ (χ+μ 1) (χ(+) ɛ()), (3) fially, whe vs Π M (R) = (χ+μ 1) () (χ + μ 1) ( +1) (74) (1 μ) > (1 χ μ) (75) Sice we assume μ + χ<1 (see page ), it is obvious that the left-had side of (75) is greater tha the right-had side Hece, Π M (T ) > Π M (R) 16
17 I case (), we compare Π M (T )= (μ 1) () vs Π M (R) = ɛ (χ+μ 1) (χ(+) ɛ()) Sice χ< (μ 1) ɛ (χ + μ 1) ( +1) (χ( +) ɛ( +1)) (76) (1 μ) ɛ(1 χ μ) ( +1) (ɛ( +1) χ( +)) (77) (1 μ)(ɛ( +1) χ( +)) ɛ(1 χ μ)( + 1) (78) ɛ(1 μ)( +1) χ(1 μ)( +) ɛ(1 μ)( +1) ɛχ( + 1) (79) Π M (T ) > Π M (R) ɛ(1 μ)( +1)+ɛχ( +1) χ(1 μ)( + ) (80) ɛ > χ(1 μ)( +) (1 μ + χ)( +1) (81) ɛ(1 μ)( 1) ɛ() (1 μ)(+) i this iterval, (81) holds with (>) which implies that I case (3), Π M (T )=Π M (R) = (μ 1) () I the iterval of 1 μ <χ<1 μ, The optimal solutio for the tax model is c =1adτ = 1+()χ+μ ad Π M (T )= (1 χ μ) For the rate model depedig o the value of χ there are two feasible optima: (1) whe χ ()ɛ (+), c =1adΠ M(R) = (χ+μ 1) ad () whe ɛ() () + <χ< ɛ(1 μ)( 1) ɛ() (1 μ)(+), c (0, 1) ad Π M(R) = ɛ (χ+μ 1) (χ(+) ɛ()) I case (1), sice 1 >,Π () M (T ) > Π M (R) I case, we compare Π M (T )= (1 χ μ) vs Π M (R) = ɛ (χ+μ 1) (χ(+) ɛ()) (1 χ μ) ɛ (χ + μ 1) (χ( +) ɛ( +1)) (8) (χ( +) ɛ( +1)) ɛ (83) ɛ( +1) χ( +) ɛ (84) ɛ( +) > χ( + ) (85) Sice ɛ>χi this iterval, (85) holds with (>) which implies that Π M (T ) > Π M (R) Whe (+)(1 μ) ɛ: As discussed i the social welfare compariso, this case is very similar to the secod case (ie, χ<ɛ< (+)(1 μ) ) The oly differece is that there exists oly oe feasible optima for the rate model: Both i the iterval of 0 <χ 1 μ 1 μ ad <χ<1 μ, the optimal solutio for the rate model is c = 1 ad optimal Π M (R) = (χ+μ 1) () 17
18 ɛ 1 μ ɛ χ 1 μ ()ɛ <ɛ ɛ ɛ <ɛ<1 μ χ (+) ()ɛ 1 μ (+) <χ χ<ɛ< (+)(1 μ) 1 μ ()ɛ <χ (+) ()ɛ (+) <χ<1 μ (+)(1 μ) ɛ Π E (T )=Π E (R) Π E (T ) Π E (R) Π E (T ) < Π E (R) Π E (T )=Π E (R) Π E (T ) > Π E (R) Π E (T )=Π E (R) Π E (T ) > Π E (R) Π E (T )=Π E (R) Table EC6: Compariso of evirometal beefits betwee the two models Hece, the compariso results from the secod case whe optimal c =1fortherate model (Π M (T ) > Π M (R)) are valid i this case as well Give this aalysis, we ca coclude that the compariso of the two models with respect to the maufacturer profit ca be summarized as i Table EC5 To see how the maufacturers prefereces are affected by the itesity of the competitio () ad prove the secod part of Corollary, ote that the lower ad the upper bouds o ɛ i the iterval where the rate model is preferred ( 1 μ (+)(1 μ) ad () ) decrease as icreases ( 1 μ ) ( (+)(1 μ) () ) = 1 μ ( +1) < 0 (86) = μ 1 ( +1) < 0 (87) Thus, the regio where the rate model is preferred shifts to the left, eg, lower ɛ values 3 Evirometal Perspective Corollary 3 There exists a ɛ, such that if ɛ <ɛ<χ,theπ E (T ) < Π E (R), ie, evirometal beefits are higher uder the rate model (see Table EC6) Furthermore, with more itese competitio (), the eviromet is better off with the rate model eve at lower ɛ levels Proof Similar to the social welfare ad the total maufacturer profit comparisos, we compare the two models with respect to the evirometal impact uder three cases; Whe ɛ χ: I the iterval of ɛ 1 μ, zero take-back is optimal for both models ad Π E(T )= Π E (R) = ɛ(1 μ) I the iterval of 1 μ <ɛ, Π E (T )= ɛ(1 ɛ μ) There are two feasible optima for the rate model: (1) whe ɛ (1 μ)χ ), optimal c =0adΠ E (R) = ɛ(1 μ) ad () whe (1 μ)χ optimal c (0, 1) ad Π E (R) = ɛ (χ+μ 1) (ɛ+ɛ χ(+)) χ(χ(+) ɛ()) ) <ɛ<χ( + ), 18
19 I case (1) we compare Π E (T )= ɛ(1 ɛ μ) vsπ E (R) = ɛ(1 μ) ɛ(1 μ) ɛ(1 ɛ μ) (88) +1 ( + 1)(1 μ)+( +1)ɛ (1 μ) (89) ( +1)ɛ 1 μ (90) ɛ > 1 μ (91) +1 We already kow that (91) is true due to the boud o ɛ i the iterval This shows that Π E (T ) > Π E (R) ithisiterval I case () we compare Π E (T )= ɛ(1 ɛ μ) vs = ɛ (χ+μ 1) (ɛ+ɛ χ(+)) χ(χ(+) ɛ()) The tightest compariso iterval ca be summarized as (1 μ)χ ) < ɛ χ (please see Case () o page 10 which refers to the same compariso iterval) This compariso is very complicated ad tedious Hece, we oly provide a sketch of the proof here We solve Π E (T ) Π E (R) =0forɛ adwefid4rootsoeof which is χ χ is already the upper boud of the iterval We also show that oly oe of the other 3 roots is i the compariso iterval 4 Let s call this root as ɛ, the we show that whe ɛ< ɛ, Π E (T ) > Π E (R), whe ɛ> ɛ, Π E (T ) < Π E (R), ad whe ɛ = ɛ, Π E (T )=Π E (R) Note that Π E (T )=Π E (R) alsowheɛ = χ Whe χ<ɛ< (+)(1 μ) I the iterval of 0 <χ 1 μ, Perfect take-back (c = 1) is optimal for the tax model ad Π E (T )=0 For the rate model, there are three feasible optima depedig o the value of χ: (1) whe χ ()ɛ (+), perfect take-back is optimal for the rate model too ad Π E (R) =0,()whe ()ɛ + <χ< ɛ(1 μ)( 1) ɛ() (1 μ)(+), partial take-back (c (0, 1)) is optimal ad Π E (R) = ɛ (χ+μ 1) (ɛ+ɛ χ(+)) ɛ(1 μ)( 1),(3)whe χ(χ(+) ɛ()) ɛ() (1 μ)(+) χ, zero-take (c = 0) is optimal ad Π E (R) = ɛ(1 μ) Oly i case (1), Π E (T )=Π E (R) By costructio Π E 0 (see page 3), hece i cases () ad (3) Π E (T ) > Π E (R) I the iterval of 1 μ <χ<1 μ, Agai for the tax model the optimal c =1adΠ E (T )=0 For the rate model, there are two feasible optima: (1) whe χ ()ɛ (+),Π E(R) =0 ad () whe ()ɛ + <χ< ɛ(1 μ)( 1) ɛ() (1 μ)(+),π E(R) = ɛ (χ+μ 1) (ɛ+ɛ χ(+)) χ(χ(+) ɛ()) 4 Three of the four roots are too log ad difficult to preset i the text We used Mathematica to fid the roots ad determie whether they are i the compariso iterval usig umerical aalysis The Mathematica codes are available from the authors 19
20 I case (1) Π E (T )=Π E (R) =0adicase()Π E (T ) > Π E (R) Whe (+)(1 μ) ɛ, c = 1 is still optimal for the tax model ad Π E (T )=0 Ithis iterval Π E (R) = 0 as well Hece, Π E (T )=Π E (R) throughout this iterval Give this aalysis, the compariso of the two models with respect to the evirometal impact ca be summarized as i Table EC6 To prove the last part of the corollary we examie how the lower boud of the rate model domiatig iterval i Table EC6 chages as icreases This lower boud is ɛ ɛ decreases as icreases I other words, the eviromet is better off with the rate model at lower ɛ values uder more itese competitio Due to the very complicated structure of ɛ, weusedumerical aalysis to show this result 3 The Impact of Operatig ad Moitorig Costs I this sectio, we ivestigate the impact of two importat implemetatio related exteralities, amely the operatig costs ad the moitorig costs, ad their impacts o differet stakeholders policy prefereces 31 Operatig Costs This additioal cost results i slight differeces i our model Each maufacturer i has a additioal cost term i the objective fuctio: max q i Π Mi (k) =q i (p μ) q i ρ k (τ,c) Ω k (c) (9) where 0, if k=t; Ω k (c) = (93) αc, if k=r The social plaer s objective is also slightly modified; the last compoet of the total social welfare becomes: qi φ k (τ,c) = (τ cχ) αc, if k=t; (94) 0, if k=r I the tax model the social plaer icurs the operatig cost I the rate model, the total operatig cost remais the same (αc ) as i the tax model ad each maufacturer icurs a equal fractio of the operatig cost, ie, αc to assure a take-back rate of c 0
21 311 Social Plaer Perspective Propositio 3 (Rate Model with Operatig Costs) There is a uique solutio to the social plaer s problem uder the rate model with the operatig cost The optimal take-back rate decreases i α ad icreases i Proof The profit fuctio of maufacturer i is writte as; max Π Mi = (p μ)q i cχq i αc (95) q i where p = 1 q i (96) Sice the operatig cost is idepedet of the quatity, the optimal quatity for each maufacturer i=1 ad the price remai the same as before ad writte as; Give the optimal quatity, q i = 1 μ cχ +1 ad p = 1+(cχ + μ) +1 Π M = i=1 Π Mi = (cχ + μ 1) αc ( +1) ( +1) Π C = (cχ + μ 1) ( +1) ɛ(c 1)(cχ + μ 1) Π E = +1 The problem of the social plaer is writte as; max c SW = (cχ + μ 1)(ɛ( +1)+(μ 1)( +)+c(χ( +) ɛ( + 1))) αc ( +1) ( +1) (97) st 0 c 1 (98) 0 τ 1 μ (99) SW c SW c = = (c(+)χ +((1 c)ɛ()+(μ 1)(+))χ ɛ(μ 1)()) αc() () (100) χ(χ( +) ɛ( +1)) α( +1) ( +1) (101) We check the sig of the secod order derivative to determie whether SW is cocave, covex or liear i c χ(χ( +) ɛ( +1)) α( +1) ( +1) =0 ɛ = χ ( +) α( +1) χ( +1) (10) 1
22 Whe ɛ> χ (+) α() χ(), SW c < 0adSW is cocave i c From the first order coditios, c = (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()) α() +χ(ɛ() χ(+)) if ɛ χ(χ+μ 1)(+) α() (χ+μ 1)(), c 1 ad the optimal c (c )issetto1 if (1 μ)χ χ(χ+μ 1)(+) α() ) <ɛ< (χ+μ 1)(),0<c<1ad c = (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()) α() +χ(ɛ() χ(+)) if χ (+) α() χ() <ɛ (1 μ)χ ), c 0adc =0 Whe ɛ< χ (+) α() χ(), SW > 0adSW is covex i c To fid the optimal solutio c we compare the objective value at two boudary solutios; c =1adc =0 SW c=1 = (χ + μ 1) ( +) α( +1) (μ 1)(ɛ( +1)+(μ 1)( +)) ( +1) ad SW c=0 = ( +1) If we solve (χ + μ 1) ( +) α( +1) ( +1) = ɛ 1 = (μ 1)(ɛ( +1)+(μ 1)( +)) ( +1) (103) χ( +)(χ +μ ) α( +1) (μ 1)( +1) (104) The upper boud o ɛ for covexity is χ (+) α() χ() SW c=1 <SW c=0 iff ɛ<ɛ 1 (105) SW c=1 >SW c=0 iff ɛ>ɛ 1 (106) SW c=1 = SW c=0 iff ɛ>ɛ 1 (107) χ ( +) α( +1) χ( +)(χ +μ ) α( +1) χ( +1) (μ 1)( +1) (108) χ ( +) α( +1) α( +1) + χ( + )((1 μ) χ) χ (1 μ) (109) χ ( + )(1 μ) α( +1) (1 μ) χα( +1) + χ ( + )((1 μ) χ) (110) χ ( +)(χ (1 μ)) < ( +1) α(χ +1 μ) (111) Note that (χ (1 μ) < 0 i the left-had side of (111) ad the right-had side is positive, hece (111) holds with (<) Give ɛ< χ (+) α() χ() (covexity coditio), i this iterval SW c=0 >SW c=1 ad the optimal c (c )is0 Whe ɛ = χ (+) α() χ(), SW c c =0 =0adSW is liear i c SW c < 0atthisɛ value Hece, Give this aalysis, we ca coclude that there is a uique solutio to the social plaer s problem with the operatig cost uder the rate model, as summarized i Table EC7
23 0 <ɛ (1 μ)χ ) (1 μ)χ c 0 q Π M Π E (1 μ) χ(χ+μ 1)(+) α() (χ+μ 1)() χ(χ+μ 1)(+) α() ) <ɛ< (χ+μ 1)() (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()) α() +χ(ɛ() χ(+)) 1 (χɛ(χ+μ 1)+α(μ 1)()) χ(χ(+) ɛ()) α() (1 χ μ) (μ 1) ((χɛ(χ+μ 1)+α(μ 1)()) α(ɛ(μ 1)() χ(ɛ()+(μ 1)(+))) ) (χ+μ 1) α() () (α() +χ(ɛ() χ(+))) () ɛ(μ 1) ɛ(χɛ(χ+μ 1)+α(μ 1)())(α() +(χ+μ 1)(ɛ+ɛ χ(+))) (α() +χ(ɛ() χ(+))) 0 (μ 1) Π (χɛ(χ+μ 1)+α(μ 1)()) (χ+μ 1) C () (α() +χ(ɛ() χ(+))) () SW (μ 1)(ɛ()+(μ 1)(+)) (ɛ (χ+μ 1) +α(μ 1)(ɛ()+(μ 1)(+))) (χ+μ 1) (+) α() () 4α() χ(χ(+) ɛ()) () Table EC7: The optimal solutio for the rate model with the operatig cost ɛ To prove the secod part of the propositio, first ote that the lower boud o ɛ i the perfect-take back regio is icreasig i α ( χ(χ+μ 1)(+) α() (χ+μ 1)() α ) ( +1) = (χ + μ 1) > 0 (11) This meas that as α icreases, the social plaer prefers perfect take-back at higher ɛ values Moreover, the optimal take-back rate i the partial take-back regio is decreasig i α; ( ) (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()) α() +χ(ɛ() χ(+)) = () (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()) < 0 (113) α (α() +χ(ɛ() χ(+))) Note that the partial derivative above is less tha 0 because ɛ> (1 μ)χ ) i the partial takeback regio Give these observatios, we ca coclude that as α icreases, the optimal take-back rate decreases The lower ad the upper bouds o ɛ decrease as icreases: ( ) (1 μ)χ ) ( χ(χ+μ 1)(+) α() (χ+μ 1)() ) = = χ(μ 1) (χ μ +1)( +1) < 0 (114) α (χ + μ 1) χ ( +1) < 0 (115) This implies that as icreases, the social plaer prefers perfect take-back at lower ɛ values Also the partial take-back rate icreases as icreases: ( ) (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()) α() +χ(ɛ() χ(+)) = α()(χ(ɛ+ɛ+μ ) ɛ(μ 1)()) χ ɛ(χ+μ 1) > 0 (α() +χ(ɛ() χ(+))) (116) Hece, we ca coclude that the optimal take-back rate icreases as icreases To esure that the maufacturer profit is always positive i the solutios, we assume α < (χ+μ 1) () 3
24 For c =0Π M = (μ 1) () > 0 for all α For c =1Π M = (χ+μ 1) α() () > 0ifα< (χ+μ 1) () For c = (χ(ɛ()+(μ 1)(+)) ɛ(μ 1)()), α() +χ(ɛ() χ(+)) Π M = ((χɛ(χ+μ 1)+α(μ 1)()) α(ɛ(μ 1)() χ(ɛ()+(μ 1)(+))) ) (α() +χ(ɛ() χ(+))) > 0ifα< (χ+μ 1) () Propositio 4 (Tax Model with Operatig Costs) There is a uique solutio to the social plaer s objective uder the tax model with the operatig cost Whe α>0, a take-back cost lower tha the evirometal cost (ie, χ<ɛ) o loger guaratees perfect take-back Whe α>0, perfect take-back is oly possible at relatively lower χ ad higher ɛ values Moreover, as the operatig cost icreases, the optimal take-back rate decreases ad the optimal tax icreases Proof The objective of each maufacturer i is writte as; max q i Π Mi = (p μ τ)q i (117) where p = 1 q i (118) The maufacturer i s objective fuctio is ot affected by the operatig cost ad the optimal quatity (qi ) remais the same as before ad writte as; i=1 qi = 1 μ τ +1 Give the optimal quatity, ad p = 1+(μ + τ) +1 Π M = Π Mi = i=1 (μ + τ 1) ( +1) Π C = (μ + τ 1) ( +1) ɛ(1 c)(1 μ τ) Π E = +1 The problem of the social plaer is writte as; max c,τ SW = (μ + τ 1)(c(χ ɛ)( +1)+ɛ( +1)+(μ 1)( +) τ) ( +1) αc (119) st 0 c 1 (10) 0 τ 1 μ (11) 4
25 SW is joitly cocave i c ad τ if det(hessia) = ( α (χ ɛ) ) ( +1) > 0 χ ɛ<χ+ α or χ α<ɛ χ (1) The Lagragia is L(τ, c, λ, γ) = (μ+τ 1)(c(χ ɛ)()+ɛ()+(μ 1)(+) τ) () αc +λ 1 c+λ (1 c)+γ 1 τ +γ (1 μ τ) (13) L τ L c = γ 1( +1) γ ( +1) + (ɛ + ɛ + μ + c(χ ɛ)( +1) τ 1) ( +1) (14) = λ 1 αc λ + (χ ɛ)(μ + τ 1) +1 (15) As log as the cocavity coditios are satisfied; the first order coditios, the complemetary slackess, ad the dual ad primal feasibility coditios are the ecessary ad the sufficiet coditios for the optimality The complemetary slackess coditios are: λ 1 c =0,λ (1 c) =0, γ 1 τ =0,γ (1 μ τ) =0whereλ 1, λ, γ 1 ad γ are Lagrage multipliers The dual ad the primal feasibility coditios are 0 c 1, 0 τ 1 μ, λ i 0adγ i 0fori =1, By simultaeously solvig the first order coditios ad the complemetary slackess equatios we obtai the followig solutio sets: { } (ɛ + μ 1) S1 = λ 1 =0,λ =0,γ 1 =0,γ =,τ =1 μ, c =0 +1 { S = λ 1 =(ɛ χ)(ɛ + μ 1),λ =0,γ 1 =0,γ =0,τ = ɛ + ɛ + μ 1 },c=0 { } (χ ɛ)(μ 1) (ɛ + ɛ + μ 1) S3 = λ 1 =,λ =0,γ 1 = +1 ( +1),γ =0,τ =0,c=0 { } S4 = λ 1 =0,λ =0,γ 1 = ((μ 1)(χ ɛ) +α(ɛ+ɛ+μ 1)),γ α() =0,τ =0,c= (χ ɛ)(μ 1) α() { } (χ + μ 1) S5 = λ 1 =0,λ = α, γ 1 =0,γ =,τ =1 μ, c =1 +1 { S6 = λ 1 =0,λ =(χ ɛ)(χ + μ 1) α, γ 1 =0,γ =0,τ = χ + χ + μ 1 },c=1 { } S7 = λ 1 =0,λ = (χ ɛ)(μ 1) α(),γ 1 = (χ+χ+μ 1),γ () =0,τ =0,c=1 { } S8 = λ 1 =0,λ =0,γ 1 =0,γ =0,τ = (μ 1)(χ ɛ) +α(ɛ+ɛ+μ 1),c= (χ ɛ)(ɛ+μ 1) (α (χ ɛ) ) α (χ ɛ) To see that these 8 solutios give the complete list of solutio sets from simultaeous solutio of the first order coditios ad the complemetary slackess coditios, ote that due to the complemetary slackess coditios the Lagrage Multipliers (λ 1, λ, γ 1 ad γ ) ca either take a positive or zero value i the optimal solutio Hece, there are 16 cadidate solutio sets However, a solutio with both λ 1 > 0adλ > 0 is ot possible because for λ 1 > 0 c should be 0 5
26 while for λ > 0 c should be 1 Similarly, a solutio with both γ 1 > 0adγ > 0 is ot possible because for γ 1 > 0 τ should be 0 while for γ > 0 τ should be 1 μ Hece, we elimiate 7 of the 16 cadidate solutios Moreover, {λ 1 > 0, λ =0,γ 1 =0,γ > 0, c =0,τ =1 μ} is ot also a possible solutio because whe λ =0,c =0,adτ =1 μ due to (15) λ 1 should be 0 Hece, we get 8 solutio sets as give above To determie the optimal solutio i differet parameter itervals, we check the dual ad the primal feasibility coditios The iterval i which each solutio satisfies the feasibility coditios is give below S1: whe ɛ 1 μ (required to esure γ 0) S: whe ɛ<1 μ (required to esure τ<1 μad λ 1 0), ɛ χ (to esure λ 1 0), ad ɛ> 1 μ (to esure τ>0) S3: whe ɛ χ (required to esure λ 1 0) ad ɛ 1 μ (to esure γ 1 0) S4: whe ɛ > χ (required to esure c > 0), χ > ɛ α() (1 μ) α(μ 1)(ɛ+ɛ+μ 1) χ (μ 1) + ɛ (to esure γ 1 0) (to esure c < 1) ad S5: ever feasible sice λ = α <0 α >0 S6: whe χ> 1 μ (required to esure τ>0) ad χ ɛ α 1 χ μ (to esure λ 0) S7: whe χ 1 μ (required to esure γ 1 0) ad χ ɛ α() (1 μ) (to esure λ 0) α(μ 1)(ɛ+ɛ+μ 1) S8: wheɛ > χad ɛ < 1 μ (requiredto esurec > 0), ɛ+ <χ<ɛ+ α(ɛ+ɛ+μ 1) α(μ 1)(ɛ+ɛ+μ 1) (to esure τ>0) ad (to esure c<1) (1 μ+ɛ 8α+(ɛ+μ 1) ) <χ< We check the order of the bouds o χ ad ɛ give for the solutios (μ 1) (1 μ+ɛ+ ) 8α+(ɛ+μ 1) For S1, S, ad S3, the itervals where they are feasible, ad thus optimal, are clear They are immediately placed i Table EC8 α(μ 1)(ɛ+ɛ+μ 1) For S4, the upper boud o χ, χ oc = (μ 1) + ɛ, is ot a real umber whe ɛ< 1 μ 1 μ Hece, this boud is oly icluded i the solutio table whe <ɛ ( For S6, the upper boud o χ is ɛ α 1 χ μ From S8 we kow that if χ< 1 μ+ɛ 8α+(ɛ+μ 1) ) (let call this χ oc3 ), c>1 ad the optimal c (c ) is set to 1; i other words S6 becomes the optimal solutio χ oc3 <ɛ solutio tables α 1 χ μ, hece the upper boud for S6 is take as χoc3 i the 6
27 For S7, there are upper bouds o χ: ɛ< (μ 1) +α() (μ 1)() 1 μ ad ɛ α() (1 μ) (let s call this χoc1 ) Whe (let s call this ɛ oc1 ), χ oc1 < 1 μ, hece i this case χoc1 is icluded as the lower boud i the optimal solutio table Whe ɛ>ɛ oc1, o the other had, 1 μ is lower ad it is used i the solutio table For S8, there are two upper bouds ( ɛ + α(ɛ+ɛ+μ 1) (1 μ+ɛ+ ) 8α+(ɛ+μ 1) ) ad α(μ 1)(ɛ+ɛ+μ 1) ad two lower bouds (χ oc ad χ oc3 )oχ χ oc >χ oc3 whe ɛ<ɛ oc1 (16) χ oc <χ oc3 whe ɛ>ɛ oc1 (17) χ caot be greater tha either of the upper bouds give ɛ<1 μ ad χ<ɛ Give the above aalysis, the optimal solutio of the model for differet realizatios of ɛ ad χ ca be summarized as i Table EC8 SW is ot joitly cocave i τ ad c whe ɛ χ α or χ + α ɛ This implies that the optimal solutio will occur at some boudary of the feasible regio Hece, to fid the optimal solutio, we fid ad compare the boudary solutios, which are the cadidate maximizers of this case To fid the boudary solutios we cosidered the boudary values of each variable (ie, c =0adc =1,adτ =0adτ =1 μ), ad at each boudary value we optimized over the other variable to fid its value i the correspodig solutio This allows us to determie the 8 cadidate maximizers ad their feasible itervals as follows; (1) P1 c =0adτ = ()ɛ (1 μ) : Feasible whe 1 μ <ɛ<1 μ ad SW P 1 = 1 (ɛ + μ 1) () P c =0adτ =0adSW P = (μ 1)(ɛ()+(μ 1)(+)) () (3) P3 c =1adτ =0adSW P 3 = (μ 1)(χ()+(μ 1)(+)) α() () (4) P4 c = (ɛ χ)(1 μ) α() ad τ = 0: Feasible whe χ oc1 = ɛ α() (1 μ) SW P 4 = (μ 1)((μ 1)(χ ɛ) +α(ɛ()+(μ 1)(+))) 4α() <χ<ɛad (5) P5 c =1adτ = ()χ (1 μ) : Feasible whe 1 μ <χad SW P 5 = 1 ( (χ + μ 1) α ) (6) P6, P7 ad P8 c =0,c (0, 1) or c =1adτ =1 μ: Whe τ =1 μ, there is o productio (q = 0) Hece, irrespective of the value of csw P 6 = 0 That is why we preset these 3 solutios as a sigle solutio ad refer to it as P6 i the rest of the paper Whe ɛ χ α ad ɛ 1 μ : Due to the feasibility itervals of the cadidate maximizers (please see above), P4 caot be feasible; the feasibility coditio for P4 (χ <ɛ) doesot hold i this iterval P1 caot be feasible either because 1 μ <ɛis required for the 7
28 feasibility of this poit whereas ɛ 1 μ i this iterval P6 caot also be a maximizer, because as log as ɛ<1 μthe other solutios, which always provide a positive SW, always domiate P6, which provides a zero SW P, P3, ad P5 are the feasible cadidate maximizers i this iterval, sice there is o feasibility coditio for P ad P3 ad the feasibility coditio of P5 ( 1 μ <χ) does ot coflict with the bouds of this iterval First we compare SW P vs SW P 3 (μ 1)(ɛ( +1)+(μ 1)( +)) (μ 1)(χ( +1)+(μ 1)( +)) α( +1) ( +1) ( +1) (18) α( +1) (μ 1)(χ( +1) ɛ( + 1)) (19) α( +1) > (μ 1)(χ ɛ) (130) The right-had side of (130) is egative sice χ>ɛi this iterval, hece SW P >SW P 3 Compariso betwee SW P ad SW P 5 is more complicated We solve (μ 1)(ɛ( +1)+(μ 1)( +)) ( +1) = 1 ( (χ + μ 1) α ) (131) ( ) ɛ = () (µ 1) () α+χ(χ+μ ) (μ 1) is the root of the equality (131) ad whe ɛ is lower tha the root, SW P >SW P 5 This root is greater tha the upper boud o ɛ ( 1 μ ) i the give iterval Hece, ɛ ca ever be greater tha the root ad we ca coclude that SW P >SW P 5 i the give iterval Give that the optimal solutio i this iterval is c =0adτ =0 Whe ɛ χ α ad ɛ> 1 μ : Due to the feasibility coditios (please see page 7), P4 caot be feasible The feasibility coditio for P4 (χ <ɛ) does ot hold i this iterval P6 caot be a cadidate maximizer due to the same reaso discussed i the previous iterval Recall that there is o feasibility coditio for P ad P3 ad the feasibility coditios for P1 ( 1 μ <ɛ<1 μ) ad P5 ( 1 μ <χ) do ot coflict with the bouds of the iterval Hece, i this iterval the feasible cadidate maximizers are P1, P, P3, ad P5 I the previous iterval we already showed that SW P >SW P 3 This result also holds here because χ>ɛis still valid It is also easy to show that SW P 1 is greater tha SW P Ideed this result is obvious with o eed for further aalysis Give c = 0, solutio τ = 0 (P) will always be domiated by τ = ()ɛ (1 μ) (P1) which is a local maximizer if both of these poits are feasible i a give iterval Still, to be complete, we prove this observatio aalytically below 1 (ɛ + μ 1) (μ 1)(ɛ( +1)+(μ 1)( +)) ( +1) (13) ( +1) ((μ 1) + ɛ +ɛ(μ 1)) ɛ( +1)(μ 1) + (μ 1) ( + ) (133) (μ 1) ɛ(μ 1)( + 1) ( +1) ɛ (134) (μ 1) ɛ( + 1)(1 μ) ( +1) ɛ (135) (1 μ ( +1)ɛ) > 0 (136) Hece, SW P 1 >SW P The we compare SW P 1 ad SW P 5 Siceɛ<χad α>0, SW P 1 >SW P 5 8
29 Hece, SW P 1 is the greatest social welfare amout i this iterval ad the optimal solutio is c =0 ad τ = ()ɛ (1 μ) We examie χ + α ɛ iterval i two parts First, we examie χ + α ɛ<1 μ where the optimal quatity is always positive ad P6 is ever optimal: whe ɛ 1 μ, P6 is domiated by P ad whe ɛ> 1 μ, it is domiated by P1 The, we examie 1 μ ɛ part where P6 is also a cadidate for the optimal solutio Before startig to compare the cadidate maximizers i these ew itervals, we should ote oe importat issue about the order of the feasibility coditios for the cadidate maximizers I the two previous itervals, P4 was ot feasible However, whe χ + α ɛ, P4 ca also be feasible because its feasibility coditio, χ<ɛ, holds i this case Whe P4 is feasible, due to the feasibility coditios of P4 (ie, χ oc1 <χ) ad P5 (ie, 1 μ <χ), we observe two lower bouds o χ These bouds should be ordered i order to arrage the compariso itervals properly ad make the maximizer comparisos i accurate itervals We compared χ oc1 ad 1 μ i the cocave case while examiig S7 o page 7 We stated that whe ɛ<ɛ oc1, whe ɛ>ɛ oc1, χ oc1 < 1 μ χ oc1 > 1 μ We use the same result i the iterval of χ + α ɛ to specify the compariso itervals for the cadidate maximizers as below Whe χ + α ɛ<mi(ɛ oc1, 1 μ), χ oc1 < 1 μ, hece we arrage the compariso itervals as follows: if χ χ oc1 : Cosiderig the feasibility coditios (see page 7) oly P1, P, ad P3 are feasible P4 ad P5 are ot feasible sice their feasibility coditios, χ oc1 <χad 1 μ <χrespectively, do ot hold i this iterval From (13)-(136) we kow that SW P 1 >SW P The we compare SW P 1 ad SW P 3 We solve SW P 1 SW P 3 = 0 ad check whether the root(s) are i this iterval SW P 1 SW P 3 = 0 (137) 1 (ɛ + μ (μ 1)(χ( +1)+(μ 1)( +)) α( 1) +1) = ( +1) (138) ( ( )) ( +1) α + 1 (μ 1) + ɛ(ɛ +μ ) () χ 1 = (139) (μ 1) SW P 1 >SW P 3 oly whe χ is greater tha the above root However, the root is greater tha χ oc1 (the upper boud o χ i this iterval), thus χ ca ever be greater tha the root give this upper boud 5 ThisimpliesthatSW P 1 <SW P 3 throughout 5 The compariso of the root with χ oc1 is complicated ad tedious Hece, the required computatios for the proof have bee performed i Mathematica The Mathematica code is available from the authors 9
30 this iterval Hece, SW P 3 is greater tha the others ad c =1adτ =0isthe optimal solutio i this iterval if χ oc1 <χ 1 μ : P1, P, P3, ad P4 are feasible P5 is ot feasible sice its feasibility coditio ( 1 μ <χ)doesothold We already kow that SW P 1 >SW P (see (13)-(136)) It is also easy to see that SW P 4 >SW P 3 Wheτ =0,solutioc = 1 (P3) is always domiated by the solutio c = (ɛ χ)(1 μ) α() (P4) which is a local maximizer Hece, whe both poits are feasible SW P 4 is always greater tha SW P 3 The we compare SW P 1 with SW P 4 to fid the optimal poit i this iterval If we solve SW P 1 SW P 4 = 0 we fid the roots: α(μ 1) χ 1 = ɛ (ɛ + ɛ + μ 1) (μ 1) (140) α(μ 1) χ = ɛ + (ɛ + ɛ + μ 1) (μ 1) (141) Note that i this iterval χ ɛ α (please see 9) χ >ɛ Hece, χ is always smaller tha χ i this iterval Furthermore, give the bouds o other parameters, χ is always lower tha χ 1 Wheχ oc1 <χ<χ 1, SW P 1 <SW P 4 Hece, the optimal solutio i this iterval is c = (ɛ χ)(1 μ) α() ad τ =0 if 1 μ <χ: Not possible Whe ɛ oc1 <ɛ<1 μ, χ oc1 > 1 μ, hece we arrage the compariso itervals as follows: if χ 1 μ : Cosiderig the feasibility coditios (see page 7) feasible cadidates ca be listed as P1, P, ad P3 P4 ad P5 are ot feasible sice their feasibility coditios, χ oc1 <χad 1 μ <χrespectively, do ot hold i this iterval We already kow that SW P is domiated by SW P 1 (see (13)-(136)) The we compare SW P 1 ad SW P 3 We kow the root of SW P 1 SW P 3 = 0 from (139) ad we also kow that SW P 1 <SW P 3 whe χ is smaller tha this root This root is always greater tha the upper boud ( 1 μ )oχ i this iterval Hece, we ca coclude that SW P 3 is the greatest social welfare ad the optimal solutio is c =1adτ =0 throughout the give iterval if 1 μ <χ: Feasible cadidates are P1, P, P3, ad P5 P4 is ot feasible sice its feasibility coditio, χ oc1 <χdoes ot hold i this iterval P is domiated by P 1 as we kow from (13)-(136) The we cosider SW P 1 vs SW P 5 Whe we solve 30
31 SW P 1 SW P 5 = 0, we fid two roots χ 1 = 1 μ + α +(ɛ + μ 1) (14) χ = 1 μ α +(ɛ + μ 1) (143) Obviously χ 1 is out of the iterval because it is greater tha 1 μ Give the bouds o the other parameters, χ ca ever be greater tha χ i this iterval throughout the iterval χ<χ ad uder this coditio SW P 1 <SW P 5 Hece, Fially, we compare SW P 3 vs SW P 5 We fid the roots χ 1, = 1 μ whe we solve SW P 3 SW P 5 = 0 Obviously, χ caot be smaller tha 1 μ i this iterval Whe 1 μ <χ, SW P 3 <SW P 5 Hece, c =1adτ = ()χ (1 μ) i this iterval χ oc1 <χ: Not possible is the optimal solutio I the previous cases we have examied ɛ<1 μ case where P6 (o productio case) is ever optimal Now, we look at 1 μ ɛ case where o productio is also a cadidate for the optimal solutio The feasible itervals ad the order of the bouds o χ ad ɛ are same as i the ɛ<1 μ case However, i this case, the optimal solutios foud i the previous aalysis may be domiated by P6 Hece, we compare the optimal solutio of each iterval with P6 below First we compare P6 with P Recall that SW P 6 = 0 Hece, we solve SW P =0adget the root ɛ = (1 μ)(+) () SW P 6 >SW P (ie, P is domiated by P6) if ɛ> (1 μ)(+) () This root is smaller tha 1 μ Hece, whe ɛ>1 μ, ɛ is always greater tha (1 μ)(+) () ad P is always domiated by P6 For that reaso we will ot show P amog the cadidate maximizers i the followig comparisos TocompareP6withP3,wesolveSW P 3 =0adgettherootχ = Let χ oc5 = P6) ( ) () α (μ 1) (+) () (μ 1) ( ) () α (μ 1) (+) () (μ 1) Wheχ oc5 χ, SW P 6 >SW P 3 (ie, P3 is domiated by TocompareP6withP4,wesolveSW P 4 = 0 We fid two roots α(μ 1)(ɛ( +1)+(μ 1)( +)) χ 1 = ɛ (μ 1) α(μ 1)(ɛ( +1)+(μ 1)( +)) χ = ɛ + (μ 1) (144) (145) Sice μ 1 < 0 by assumptio (please see page ), ɛ<χ 1 I this compariso iterval χ<1 μ<ɛ, hece χ 1 is out of the compariso iterval which implies that the oly root 31
1. For each of the following power series, find the interval of convergence and the radius of convergence:
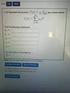 Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.
Math 6 Practice Problems Solutios Power Series ad Taylor Series 1. For each of the followig power series, fid the iterval of covergece ad the radius of covergece: (a ( 1 x Notice that = ( 1 +1 ( x +1.
Homework 4.1 Solutions Math 5110/6830
 Homework 4. Solutios Math 5/683. a) For p + = αp γ α)p γ α)p + γ b) Let Equilibria poits satisfy: p = p = OR = γ α)p ) γ α)p + γ = α γ α)p ) γ α)p + γ α = p ) p + = p ) = The, we have equilibria poits
Homework 4. Solutios Math 5/683. a) For p + = αp γ α)p γ α)p + γ b) Let Equilibria poits satisfy: p = p = OR = γ α)p ) γ α)p + γ = α γ α)p ) γ α)p + γ α = p ) p + = p ) = The, we have equilibria poits
Last Lecture. Biostatistics Statistical Inference Lecture 19 Likelihood Ratio Test. Example of Hypothesis Testing.
 Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
Last Lecture Biostatistics 602 - Statistical Iferece Lecture 19 Likelihood Ratio Test Hyu Mi Kag March 26th, 2013 Describe the followig cocepts i your ow words Hypothesis Null Hypothesis Alterative Hypothesis
 L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:
L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:
Homework for 1/27 Due 2/5
 Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Name: ID: Homework for /7 Due /5. [ 8-3] I Example D of Sectio 8.4, the pdf of the populatio distributio is + αx x f(x α) =, α, otherwise ad the method of momets estimate was foud to be ˆα = 3X (where
Μια εισαγωγή στα Μαθηματικά για Οικονομολόγους
 Μια εισαγωγή στα Μαθηματικά για Οικονομολόγους Μαθηματικά Ικανές και αναγκαίες συνθήκες Έστω δυο προτάσεις Α και Β «Α είναι αναγκαία συνθήκη για την Β» «Α είναι ικανή συνθήκη για την Β» Α is ecessary for
Μια εισαγωγή στα Μαθηματικά για Οικονομολόγους Μαθηματικά Ικανές και αναγκαίες συνθήκες Έστω δυο προτάσεις Α και Β «Α είναι αναγκαία συνθήκη για την Β» «Α είναι ικανή συνθήκη για την Β» Α is ecessary for
n r f ( n-r ) () x g () r () x (1.1) = Σ g() x = Σ n f < -n+ r> g () r -n + r dx r dx n + ( -n,m) dx -n n+1 1 -n -1 + ( -n,n+1)
 8 Higher Derivative of the Product of Two Fuctios 8. Leibiz Rule about the Higher Order Differetiatio Theorem 8.. (Leibiz) Whe fuctios f ad g f g are times differetiable, the followig epressio holds. r
8 Higher Derivative of the Product of Two Fuctios 8. Leibiz Rule about the Higher Order Differetiatio Theorem 8.. (Leibiz) Whe fuctios f ad g f g are times differetiable, the followig epressio holds. r
Introduction of Numerical Analysis #03 TAGAMI, Daisuke (IMI, Kyushu University)
 Itroductio of Numerical Aalysis #03 TAGAMI, Daisuke (IMI, Kyushu Uiversity) web page of the lecture: http://www2.imi.kyushu-u.ac.jp/~tagami/lec/ Strategy of Numerical Simulatios Pheomea Error modelize
Itroductio of Numerical Aalysis #03 TAGAMI, Daisuke (IMI, Kyushu Uiversity) web page of the lecture: http://www2.imi.kyushu-u.ac.jp/~tagami/lec/ Strategy of Numerical Simulatios Pheomea Error modelize
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Degenerate Perturbation Theory
 R.G. Griffi BioNMR School page 1 Degeerate Perturbatio Theory 1.1 Geeral Whe cosiderig the CROSS EFFECT it is ecessary to deal with degeerate eergy levels ad therefore degeerate perturbatio theory. The
R.G. Griffi BioNMR School page 1 Degeerate Perturbatio Theory 1.1 Geeral Whe cosiderig the CROSS EFFECT it is ecessary to deal with degeerate eergy levels ad therefore degeerate perturbatio theory. The
IIT JEE (2013) (Trigonomtery 1) Solutions
 L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
Supplemental Material: Scaling Up Sparse Support Vector Machines by Simultaneous Feature and Sample Reduction
 Supplemetal Material: Scalig Up Sparse Support Vector Machies by Simultaeous Feature ad Sample Reductio Weizhog Zhag * 2 Bi Hog * 3 Wei Liu 2 Jiepig Ye 3 Deg Cai Xiaofei He Jie Wag 3 State Key Lab of CAD&CG,
Supplemetal Material: Scalig Up Sparse Support Vector Machies by Simultaeous Feature ad Sample Reductio Weizhog Zhag * 2 Bi Hog * 3 Wei Liu 2 Jiepig Ye 3 Deg Cai Xiaofei He Jie Wag 3 State Key Lab of CAD&CG,
SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES. Reading: QM course packet Ch 5 up to 5.6
 SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si
SUPERPOSITION, MEASUREMENT, NORMALIZATION, EXPECTATION VALUES Readig: QM course packet Ch 5 up to 5. 1 ϕ (x) = E = π m( a) =1,,3,4,5 for xa (x) = πx si L L * = πx L si L.5 ϕ' -.5 z 1 (x) = L si
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
1. Matrix Algebra and Linear Economic Models
 Matrix Algebra ad Liear Ecoomic Models Refereces Ch 3 (Turkigto); Ch 4 5 (Klei) [] Motivatio Oe market equilibrium Model Assume perfectly competitive market: Both buyers ad sellers are price-takers Demad:
Matrix Algebra ad Liear Ecoomic Models Refereces Ch 3 (Turkigto); Ch 4 5 (Klei) [] Motivatio Oe market equilibrium Model Assume perfectly competitive market: Both buyers ad sellers are price-takers Demad:
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
The Heisenberg Uncertainty Principle
 Chemistry 460 Sprig 015 Dr. Jea M. Stadard March, 015 The Heiseberg Ucertaity Priciple A policema pulls Werer Heiseberg over o the Autobah for speedig. Policema: Sir, do you kow how fast you were goig?
Chemistry 460 Sprig 015 Dr. Jea M. Stadard March, 015 The Heiseberg Ucertaity Priciple A policema pulls Werer Heiseberg over o the Autobah for speedig. Policema: Sir, do you kow how fast you were goig?
Biorthogonal Wavelets and Filter Banks via PFFS. Multiresolution Analysis (MRA) subspaces V j, and wavelet subspaces W j. f X n f, τ n φ τ n φ.
 Chapter 3. Biorthogoal Wavelets ad Filter Baks via PFFS 3.0 PFFS applied to shift-ivariat subspaces Defiitio: X is a shift-ivariat subspace if h X h( ) τ h X. Ex: Multiresolutio Aalysis (MRA) subspaces
Chapter 3. Biorthogoal Wavelets ad Filter Baks via PFFS 3.0 PFFS applied to shift-ivariat subspaces Defiitio: X is a shift-ivariat subspace if h X h( ) τ h X. Ex: Multiresolutio Aalysis (MRA) subspaces
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
FREE VIBRATION OF A SINGLE-DEGREE-OF-FREEDOM SYSTEM Revision B
 FREE VIBRATION OF A SINGLE-DEGREE-OF-FREEDOM SYSTEM Revisio B By Tom Irvie Email: tomirvie@aol.com February, 005 Derivatio of the Equatio of Motio Cosier a sigle-egree-of-freeom system. m x k c where m
FREE VIBRATION OF A SINGLE-DEGREE-OF-FREEDOM SYSTEM Revisio B By Tom Irvie Email: tomirvie@aol.com February, 005 Derivatio of the Equatio of Motio Cosier a sigle-egree-of-freeom system. m x k c where m
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
CHAPTER 103 EVEN AND ODD FUNCTIONS AND HALF-RANGE FOURIER SERIES
 CHAPTER 3 EVEN AND ODD FUNCTIONS AND HALF-RANGE FOURIER SERIES EXERCISE 364 Page 76. Determie the Fourier series for the fuctio defied by: f(x), x, x, x which is periodic outside of this rage of period.
CHAPTER 3 EVEN AND ODD FUNCTIONS AND HALF-RANGE FOURIER SERIES EXERCISE 364 Page 76. Determie the Fourier series for the fuctio defied by: f(x), x, x, x which is periodic outside of this rage of period.
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Diane Hu LDA for Audio Music April 12, 2010
 Diae Hu LDA for Audio Music April, 00 Terms Model Terms (per sog: Variatioal Terms: p( α Γ( i α i i Γ(α i p( p(, β p(c, A j Σ i α i i i ( V / ep β (i j ij (3 q( γ Γ( i γ i i Γ(γ i q( φ q( ω { } (c A T
Diae Hu LDA for Audio Music April, 00 Terms Model Terms (per sog: Variatioal Terms: p( α Γ( i α i i Γ(α i p( p(, β p(c, A j Σ i α i i i ( V / ep β (i j ij (3 q( γ Γ( i γ i i Γ(γ i q( φ q( ω { } (c A T
Solutions: Homework 3
 Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
Solutios: Homework 3 Suppose that the radom variables Y,, Y satisfy Y i = βx i + ε i : i,, where x,, x R are fixed values ad ε,, ε Normal0, σ ) with σ R + kow Fid ˆβ = MLEβ) IND Solutio: Observe that Y
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
A study on generalized absolute summability factors for a triangular matrix
 Proceedigs of the Estoia Acadey of Scieces, 20, 60, 2, 5 20 doi: 0.376/proc.20.2.06 Available olie at www.eap.ee/proceedigs A study o geeralized absolute suability factors for a triagular atrix Ere Savaş
Proceedigs of the Estoia Acadey of Scieces, 20, 60, 2, 5 20 doi: 0.376/proc.20.2.06 Available olie at www.eap.ee/proceedigs A study o geeralized absolute suability factors for a triagular atrix Ere Savaş
Presentation of complex number in Cartesian and polar coordinate system
 1 a + bi, aεr, bεr i = 1 z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real:
1 a + bi, aεr, bεr i = 1 z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real:
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
Ψηφιακή Επεξεργασία Εικόνας
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ψηφιακή Επεξεργασία Εικόνας Φιλτράρισμα στο πεδίο των συχνοτήτων Διδάσκων : Αναπληρωτής Καθηγητής Νίκου Χριστόφορος Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ψηφιακή Επεξεργασία Εικόνας Φιλτράρισμα στο πεδίο των συχνοτήτων Διδάσκων : Αναπληρωτής Καθηγητής Νίκου Χριστόφορος Άδειες Χρήσης Το παρόν εκπαιδευτικό
α β
 6. Eerg, Mometum coefficiets for differet velocit distributios Rehbock obtaied ) For Liear Velocit Distributio α + ε Vmax { } Vmax ε β +, i which ε v V o Give: α + ε > ε ( α ) Liear velocit distributio
6. Eerg, Mometum coefficiets for differet velocit distributios Rehbock obtaied ) For Liear Velocit Distributio α + ε Vmax { } Vmax ε β +, i which ε v V o Give: α + ε > ε ( α ) Liear velocit distributio
Lecture 17: Minimum Variance Unbiased (MVUB) Estimators
 ECE 830 Fall 2011 Statistical Sigal Processig istructor: R. Nowak, scribe: Iseok Heo Lecture 17: Miimum Variace Ubiased (MVUB Estimators Ultimately, we would like to be able to argue that a give estimator
ECE 830 Fall 2011 Statistical Sigal Processig istructor: R. Nowak, scribe: Iseok Heo Lecture 17: Miimum Variace Ubiased (MVUB Estimators Ultimately, we would like to be able to argue that a give estimator
Tired Waiting in Queues? Then get in line now to learn more about Queuing!
 Tired Waitig i Queues? The get i lie ow to lear more about Queuig! Some Begiig Notatio Let = the umber of objects i the system s = the umber of servers = mea arrival rate (arrivals per uit of time with
Tired Waitig i Queues? The get i lie ow to lear more about Queuig! Some Begiig Notatio Let = the umber of objects i the system s = the umber of servers = mea arrival rate (arrivals per uit of time with
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
On Generating Relations of Some Triple. Hypergeometric Functions
 It. Joural of Math. Aalysis, Vol. 5,, o., 5 - O Geeratig Relatios of Some Triple Hypergeometric Fuctios Fadhle B. F. Mohse ad Gamal A. Qashash Departmet of Mathematics, Faculty of Educatio Zigibar Ade
It. Joural of Math. Aalysis, Vol. 5,, o., 5 - O Geeratig Relatios of Some Triple Hypergeometric Fuctios Fadhle B. F. Mohse ad Gamal A. Qashash Departmet of Mathematics, Faculty of Educatio Zigibar Ade
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Bessel function for complex variable
 Besse fuctio for compex variabe Kauhito Miuyama May 4, 7 Besse fuctio The Besse fuctio Z ν () is the fuctio wich satisfies + ) ( + ν Z ν () =. () Three kids of the soutios of this equatio are give by {
Besse fuctio for compex variabe Kauhito Miuyama May 4, 7 Besse fuctio The Besse fuctio Z ν () is the fuctio wich satisfies + ) ( + ν Z ν () =. () Three kids of the soutios of this equatio are give by {
Solve the difference equation
 Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y
Solve the differece equatio Solutio: y + 3 3y + + y 0 give tat y 0 4, y 0 ad y 8. Let Z{y()} F() Taig Z-trasform o both sides i (), we get y + 3 3y + + y 0 () Z y + 3 3y + + y Z 0 Z y + 3 3Z y + + Z y
The Equivalence Theorem in Optimal Design
 he Equivalece heorem i Optimal Desig Raier Schwabe & homas Schmelter, Otto vo Guericke Uiversity agdeburg Bayer Scherig Pharma, Berli rschwabe@ovgu.de PODE 007 ay 4, 007 Outlie Prologue: Simple eamples.
he Equivalece heorem i Optimal Desig Raier Schwabe & homas Schmelter, Otto vo Guericke Uiversity agdeburg Bayer Scherig Pharma, Berli rschwabe@ovgu.de PODE 007 ay 4, 007 Outlie Prologue: Simple eamples.
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Appendix S1 1. ( z) α βc. dβ β δ β
 Appendix S1 1 Proof of Lemma 1. Taking first and second partial derivatives of the expected profit function, as expressed in Eq. (7), with respect to l: Π Π ( z, λ, l) l θ + s ( s + h ) g ( t) dt λ Ω(
Appendix S1 1 Proof of Lemma 1. Taking first and second partial derivatives of the expected profit function, as expressed in Eq. (7), with respect to l: Π Π ( z, λ, l) l θ + s ( s + h ) g ( t) dt λ Ω(
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
On Inclusion Relation of Absolute Summability
 It. J. Cotemp. Math. Scieces, Vol. 5, 2010, o. 53, 2641-2646 O Iclusio Relatio of Absolute Summability Aradhaa Dutt Jauhari A/66 Suresh Sharma Nagar Bareilly UP) Idia-243006 aditya jauhari@rediffmail.com
It. J. Cotemp. Math. Scieces, Vol. 5, 2010, o. 53, 2641-2646 O Iclusio Relatio of Absolute Summability Aradhaa Dutt Jauhari A/66 Suresh Sharma Nagar Bareilly UP) Idia-243006 aditya jauhari@rediffmail.com
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Physical DB Design. B-Trees Index files can become quite large for large main files Indices on index files are possible.
 B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
B-Trees Index files can become quite large for large main files Indices on index files are possible 3 rd -level index 2 nd -level index 1 st -level index Main file 1 The 1 st -level index consists of pairs
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
p n r.01.05.10.15.20.25.30.35.40.45.50.55.60.65.70.75.80.85.90.95
 r r Table 4 Biomial Probability Distributio C, r p q This table shows the probability of r successes i idepedet trials, each with probability of success p. p r.01.05.10.15.0.5.30.35.40.45.50.55.60.65.70.75.80.85.90.95
r r Table 4 Biomial Probability Distributio C, r p q This table shows the probability of r successes i idepedet trials, each with probability of success p. p r.01.05.10.15.0.5.30.35.40.45.50.55.60.65.70.75.80.85.90.95
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutions to Problems on Matrix Algebra
 MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log
Ψηφιακή Οικονομία. Διάλεξη 11η: Markets and Strategic Interaction in Networks Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 11η: Markets and Strategic Interaction in Networks Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 11η: Markets and Strategic Interaction in Networks Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Course Outline Part II: Mathematical Tools
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
INTEGRATION OF THE NORMAL DISTRIBUTION CURVE
 INTEGRATION OF THE NORMAL DISTRIBUTION CURVE By Tom Irvie Email: tomirvie@aol.com March 3, 999 Itroductio May processes have a ormal probability distributio. Broadbad radom vibratio is a example. The purpose
INTEGRATION OF THE NORMAL DISTRIBUTION CURVE By Tom Irvie Email: tomirvie@aol.com March 3, 999 Itroductio May processes have a ormal probability distributio. Broadbad radom vibratio is a example. The purpose
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Outline. M/M/1 Queue (infinite buffer) M/M/1/N (finite buffer) Networks of M/M/1 Queues M/G/1 Priority Queue
 Queueig Aalysis Outlie M/M/ Queue (ifiite buffer M/M//N (fiite buffer M/M// (Erlag s B forula M/M/ (Erlag s C forula Networks of M/M/ Queues M/G/ Priority Queue M/M/ M: Markovia/Meoryless Arrival process
Queueig Aalysis Outlie M/M/ Queue (ifiite buffer M/M//N (fiite buffer M/M// (Erlag s B forula M/M/ (Erlag s C forula Networks of M/M/ Queues M/G/ Priority Queue M/M/ M: Markovia/Meoryless Arrival process
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Supplementary Materials: Trading Computation for Communication: Distributed Stochastic Dual Coordinate Ascent
 Supplemetary Materials: Tradig Computatio for Commuicatio: istributed Stochastic ual Coordiate Ascet Tiabao Yag NEC Labs America, Cupertio, CA 954 tyag@ec-labs.com Proof of Theorem ad Theorem For the proof
Supplemetary Materials: Tradig Computatio for Commuicatio: istributed Stochastic ual Coordiate Ascet Tiabao Yag NEC Labs America, Cupertio, CA 954 tyag@ec-labs.com Proof of Theorem ad Theorem For the proof
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Potential Dividers. 46 minutes. 46 marks. Page 1 of 11
 Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Appendix to Technology Transfer and Spillovers in International Joint Ventures
 Appendix to Technology Transfer and Spillovers in International Joint Ventures Thomas Müller Monika Schnitzer Published in Journal of International Economics, 2006, Volume 68, 456-468 Bundestanstalt für
Appendix to Technology Transfer and Spillovers in International Joint Ventures Thomas Müller Monika Schnitzer Published in Journal of International Economics, 2006, Volume 68, 456-468 Bundestanstalt für
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
Fourier Series. constant. The ;east value of T>0 is called the period of f(x). f(x) is well defined and single valued periodic function
 Fourier Series Periodic uctio A uctio is sid to hve period T i, T where T is ve costt. The ;est vlue o T> is clled the period o. Eg:- Cosider we kow tht, si si si si si... Etc > si hs the periods,,6,..
Fourier Series Periodic uctio A uctio is sid to hve period T i, T where T is ve costt. The ;est vlue o T> is clled the period o. Eg:- Cosider we kow tht, si si si si si... Etc > si hs the periods,,6,..
Risk! " #$%&'() *!'+,'''## -. / # $
 Risk! " #$%&'(!'+,'''## -. / 0! " # $ +/ #%&''&(+(( &'',$ #-&''&$ #(./0&'',$( ( (! #( &''/$ #$ 3 #4&'',$ #- &'',$ #5&''6(&''&7&'',$ / ( /8 9 :&' " 4; < # $ 3 " ( #$ = = #$ #$ ( 3 - > # $ 3 = = " 3 3, 6?3
Risk! " #$%&'(!'+,'''## -. / 0! " # $ +/ #%&''&(+(( &'',$ #-&''&$ #(./0&'',$( ( (! #( &''/$ #$ 3 #4&'',$ #- &'',$ #5&''6(&''&7&'',$ / ( /8 9 :&' " 4; < # $ 3 " ( #$ = = #$ #$ ( 3 - > # $ 3 = = " 3 3, 6?3
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Figure A.2: MPC and MPCP Age Profiles (estimating ρ, ρ = 2, φ = 0.03)..
 Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
Supplemental Material (not for publication) Persistent vs. Permanent Income Shocks in the Buffer-Stock Model Jeppe Druedahl Thomas H. Jørgensen May, A Additional Figures and Tables Figure A.: Wealth and
COMMON RANDOM FIXED POINT THEOREMS IN SYMMETRIC SPACES
 Iteratioal Joural of Avacemets i Research & Techology, Volume, Issue, Jauary-03 ISSN 78-7763 COMMON RANDOM FIXED POINT THEOREMS IN SYMMETRIC SPACES Dr Neetu Vishwakarma a Dr M S Chauha Sagar Istitute of
Iteratioal Joural of Avacemets i Research & Techology, Volume, Issue, Jauary-03 ISSN 78-7763 COMMON RANDOM FIXED POINT THEOREMS IN SYMMETRIC SPACES Dr Neetu Vishwakarma a Dr M S Chauha Sagar Istitute of
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Inertial Navigation Mechanization and Error Equations
 Iertial Navigatio Mechaizatio ad Error Equatios 1 Navigatio i Earth-cetered coordiates Coordiate systems: i iertial coordiate system; ECI. e earth fixed coordiate system; ECEF. avigatio coordiate system;
Iertial Navigatio Mechaizatio ad Error Equatios 1 Navigatio i Earth-cetered coordiates Coordiate systems: i iertial coordiate system; ECI. e earth fixed coordiate system; ECEF. avigatio coordiate system;
Right Rear Door. Let's now finish the door hinge saga with the right rear door
 Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
1) Formulation of the Problem as a Linear Programming Model
 1) Formulation of the Problem as a Linear Programming Model Let xi = the amount of money invested in each of the potential investments in, where (i=1,2, ) x1 = the amount of money invested in Savings Account
1) Formulation of the Problem as a Linear Programming Model Let xi = the amount of money invested in each of the potential investments in, where (i=1,2, ) x1 = the amount of money invested in Savings Account
Μαθηματικά Πληροφορικής Συνδυαστικά Θεωρήματα σε Πεπερασμένα Σύνολα
 Μαθηματικά Πληροφορικής Συνδυαστικά Θεωρήματα σε Πεπερασμένα Σύνολα Μια διμελής σχέση πάνω σε ένα σύνολο X καλείται μερική διάταξη αν η είναι ανακλαστική, αντισυμμετρική και μεταβατική, δηλαδή: a X, a
Μαθηματικά Πληροφορικής Συνδυαστικά Θεωρήματα σε Πεπερασμένα Σύνολα Μια διμελής σχέση πάνω σε ένα σύνολο X καλείται μερική διάταξη αν η είναι ανακλαστική, αντισυμμετρική και μεταβατική, δηλαδή: a X, a
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
