Εξαγωγή Χαρακτηριστικών
|
|
|
- Δανάη Γλυκύς
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Μάθηµα 7 Εξαγωγή Χαρακτηριστικών Το στάδιο της εξαγωγής χαρακτηριστικών αφορά το πρώτο βήµα για την αναγνώριση των χαρακτήρων και περιλαµβάνει την µετατροπή κάθε χαρακτήρα σε διάνυσµα χαρακτηριστικών µικρής διάστασης το οποίο αποτελεί και την ταυτότητά του. Κάθε χαρακτηριστικό µπορεί να έχει συγκεκριµένη κανονικοποιηµένη τιµή, π.χ. περίµετρος του χαρακτήρα, ποσοστό κάλυψης από µαύρα pixels ή να έχει τιµή 0 ή 1 ανάλογα αν πληροί ή όχι κάποια ιδιότητα, π.χ. ύπαρξη οπής, ύπαρξη τελικού σηµείου σε κάποιο τεταρτηµόριο του χαρακτήρα. Η εξαγωγή χαρακτηριστικών χρησιµοποιείται τόσο στο στάδιο της εκπαίδευσης όσο και στο στάδιο της αναγνώρισης. Στο στάδιο της εκπαίδευσης, ένα σύνολο χαρακτήρων κανονικοποιείται ως προς το µέγεθος, µετατρέπεται σε διανύσµατα χαρακτηριστικών και συνδυάζεται µε την αντίστοιχη ASCII κωδικοποίησή του για την εκπαίδευση του ταξινοµητή αναγνώρισης (σχήµα 7.1α). Στο στάδιο αναγνώρισης, κάθε περιοχη της εικόνας που έχει εντοπιστεί ότι περιέχει χαρακτήρα, κανονικοποιείται, µετατρέπεται σε διάνυσµα χαρακτηριστικών και στη συνέχεια αντιστοιχίζεται σε ένα από τους γνωστούς χαρακτήρες µε τη βοήθεια του ταξινοµητή αναγνώρισης (σχήµα 7.1β). (α) (β) Σχήµα 7.1. Οπτική αναγνώριση χαρακτήρων. (α) Στάδιο εκπαίδευσης. (β) Στάδιο αναγνώρισης.
2 Ένα σύνολο ικανοποιητικών χαρακτηριστικών πρέπει να πληροί ορισµένες προϋποθέσεις όπως: ιακριτική ικανότητα. Τα χαρακτηριστικά πρέπει να έχουν αρκετά διαφορετικές τιµές για χαρακτήρες οι οποίοι ανήκουν σε διαφορετικές κλάσεις. Αξιοπιστία. Τα χαρακτηριστικά πρέπει να έχουν παραπλήσιες τιµές για χαρακτήρες οι οποίοι ανήκουν στην ίδια κλάση. Ανεξαρτησία. Τα χαρακτηριστικά δεν πρέπει να επικαλύπτονται µεταξύ τους. Μικρό µέγεθος. Ο αριθµός των χαρακτηριστικών πρέπει να είναι µικρός ώστε η αναγνώριση να γίνεται απλά και γρήγορα. Μικρό υπολογιστικό κόστος. Μικρή πολυπλοκότητα εξαγωγής. Επίσης, τα χαρακτηριστικά θα πρέπει να µένουν αναλλοίωτα όταν ο χαρακτήρας εµφανίζει: Θόρυβο Μετακίνηση Αλλαγή στο µέγεθος Στροφή Κλίση Παραµόρφωση Οι παραπάνω µετασχηµατισµοί του χαρακτήρα για τους οποίους θέλουµε τα χαρακτηριστικά να µένουν αναλλοίωτα φαίνονται στο σχήµα 7.2. (α) (β) (γ) (δ) (ε) (ζ) Σχήµα 7.2. Μετασχηµατισµοί του χαρακτήρα για του οποίους θέλουµε τα χαρακτηριστικά να παραµένουν αναλλοίωτα. (α)θόρυβος. (β) Μετακίνηση. (γ) Αλλαγή στο µέγεθος. (δ) Στροφή. (ε) Κλίση. (ζ) Παραµόρφωση.
3 Η εξαγωγή χαρακτηριστικών µπορεί να βασίζεται στο σώµα, στο περίγραµµα ή στο σκελετό του χαρακτήρα (Trier 1996). Στη συνέχεια, θα περιγραφεί το στάδιο της κανονικοποίησης των χαρακτήρων και θα αναλυθούν οι κυριότερες µέθοδοι που βασίζονται στις παραπάνω κατηγορίες. 7.1 Κανονικοποίηση χαρακτήρων Η κανονικοποίηση των χαρακτήρων ως προς το µέγεθος είναι ένα βασικό στάδιο προεπεξεργασίας πριν την εξαγωγή χαρακτηριστικών και την αναγνώριση. Το στάδιο αυτό είναι απαραίτητο γιατί θα πρέπει οι χαρακτήρες που θα συγκριθούν µε τους χαρακτήρες της βάσης αναγνώρισης να έχουν το ίδιο µέγεθος. Συνήθως, γίνεται κανονικοποίηση των χαρακτήρων σε πίνακες των οποίων το ύψος είναι σχεδόν διπλάσιο από το πλάτος, π.χ. 24x48. Οι διαστάσεις του παραθύρου κανονικοποίησης εξαρτώνται και από την µέθοδο εξαγωγής χαρακτηριστικών που θα χρησιµοποιήσουµε. Για παράδειγµα, αν θα χρησιµοποιήσουµε τον χωρισµό των χαρακτήρων σε παράθυρα διαστάσεων 5x10 τότε το παράθυρο κανονικοποίησης θα πρέπει να έχει πλάτος πολλαπλάσιο του 5 και ύψος πολλαπλάσιο του 10, π.χ. 30x60. Για να προχωρήσουµε σε σωστή κανονικοποίηση κάθε χαρακτήρα θα πρέπει να χρησιµοποιήσουµε τις πληροφορίες τόσο για την οριοθέτηση του χαρακτήρα στην γραµµή του κειµένου όσο και για την οριοθέτηση της γραµµής του κειµένου στην συνολική εικόνα (σχήµα 7.3). Το αριστερό και δεξί όριο του χαρακτήρα θεωρείται το όριο διαχωρισµού από το προηγούµενο και το επόµενο γράµµα. Το πάνω και κάτω όριο του χαρακτήρα θα πρέπει να είναι το πάνω και κάτω όριο της αντίστοιχης γραµµής κειµένου. Αυτό γίνεται για να διαχωριστούν τα κεφαλαία από τα µικρά γράµµατα (π.χ. «ο» - «Ο») και οι χαρακτήρες που εξαρτώνται από την θέση τους στην γραµµή του κειµένου (π.χ. «.» - ). Εναλλακτικά, µπορούµε να κανονικοποιήσουµε κάθε χαρακτήρα στα όρια του, όµως θα πρέπει να αποθηκεύσουµε κάποια επιπλέον πληροφορία την οποία θα την χρησιµοποιήσουµε στην ταξινόµηση και αφορά το µέγεθος και την θέση των χαρακτήρων ως προς την γραµµή του κειµένου. Σχήµα 7.3. Παράδειγµα κανονικοποίησης χαρακτήρων.
4 7.2 Χρησιµοποιώντας το σώµα των χαρακτήρων Οι βασικότεροι µέθοδοι εξαγωγής χαρακτηριστικών που βασίζονται στην πληροφορία που υπάρχει στο συνολικό σώµα των χαρακτήρων είναι οι µέθοδοι απευθείας σύγκρισης (template matching), ο χωρισµός σε ζώνες, οι γεωµετρικές ροπές και οι προβολές, Επιπροσθέτως, από το σώµα των χαρακτήρων µπορούµε να εξάγουµε χαρακτηριστικά που αφορούν το ποσοστό κάλυψης των µαύρων pixels, τον αριθµό των σηµείων τοµής µε ευθείες (crossing points), την θέση του χαρακτήρα ως προς την γραµµή κειµένου καθώς και την ύπαρξη οπών. Απευθείας σύγκριση (template matching) Η µεθοδολογία της απευθείας σύγκρισης (template matching) θεωρεί ότι τα pixels της εικόνας του χαρακτήρα είναι και το διάνυσµα των χαρακτηριστικών του (Pratt 1991). Αν θέλουµε να συγκρίνουµε δύο χαρακτήρες X,Y (X είναι το πρότυπο και Y ο χαρακτήρας που εξετάζουµε) οι οποίοι έχουν κανονικοποιηθεί στις ίδιες διαστάσεις και αποτελούνται από n σηµεία, τότε ο αριθµός n ij των σηµείων όπου ο χαρακτήρας X έχει τιµή i και ο χαρακτήρας Y έχει τιµή j, µε i,j є {0,1} δίδεται από τον τύπο: όπου n ij = n δ ( i, j) (7.1) m m= 1 1, if ( xm = i) ( ym = j) δ m( i, j) = 0, otherwise (7.2) και x m και y m είναι τα m-ιοστά σηµεία των προς σύγκριση χαρακτήρων Χ και Y. Χρησιµοποιώντας την απευθείας σύγκριση των pixels έχουν προταθεί οι παρακάτω βασικές τεχνικές για τον εντοπισµό της απόστασης µεταξύ δύο χαρακτήρων (Tubbs 1989): XOR µεταξύ των δύο πινάκων: D = n 10 +n 01 (7.3) Όσο µεγαλύτερη είναι η απόσταση D τόσο πιο µακριά είναι οι δύο χαρακτήρες. Οι αποστάσεις Jaccard και Yule: d n11 = J n + n + n (7.4) n11n00 n d Y = n n + n n n (7.5) Οι παραπάνω αποστάσεις όσο πιο κοντά στο 1 είναι τόσο κοντύτερα είναι οι δύο χαρακτήρες. Στο παράδειγµα του πίνακα 7.1 υπολογίζονται οι παραπάνω αποστάσεις για την απευθείας σύγκριση ενός προτύπου µε τρεις χαρακτήρες. Η χρήση βαρών: Ο τύπος υπολογισµού του n ij γίνεται: n ij = n m= 1 p ( k / i) δ ( i, j) (7.6) m m
5 όπου p m (k/i) είναι η πιθανότητα η εικόνα Y να ταιριάζει µε το πρότυπο X k, δεδοµένου ότι το m- ιοστό σηµείο του προτύπου X k είναι i. Η τιµή του p m (k/i) προσεγγίζεται σαν ο αριθµός των προτύπων που έχουν την ίδια m-ιοστή τιµή σηµείου όπως το πρότυπο X k δια τον συνολικό αριθµό των προτύπων. Η χρήση βαρών βοηθάει στο να δίνουµε µεγαλύτερη βαρύτητα στα pixels τα οποία ανήκουν µε µεγαλύτερη σιγουριά σε συγκεκριµένη κλάση χαρακτήρα. Στο σχήµα 7.4 δίδεται παράδειγµα υπολογισµού των πιθανοτήτων p m (k/i) για κλάση χαρακτήρων η οποία αποτελείται από 3 πρότυπα. Στο συγκεκριµένο παράδειγµα, το n 11 της σύγκρισης µε τον πρώτο χαρακτήρα από 11 γίνεται (9*1+2*2/3) = 10,33 Πίνακας 7.1. Εντοπισµός της απόστασης χρησιµοποιώντας απευθείας σύγκριση (template matching). D η απόσταση βάσει του XOR, d J η Jaccard απόσταση και d Y η Yule απόσταση. n n n n ,846 0,769 0,769 0,913 0,818 0,818 (α) (β) Σχήµα 7.4 Παράδειγµα υπολογισµού των πιθανοτήτων p m (k/i) για κλάση χαρακτήρων η οποία αποτελείται από 3 πρότυπα. (α) Η πιθανότητα p 1 (k/0) είναι 0/3 γιατί δεν έχουµε κανένα πρότυπο που να έχει 0 στην θέση 1 (πάνω αριστερό pixel). Οµοίως υπολογίζονται οι όλα τα p m (k/i). (β) Οι τελικές τιµές για τα p m (k/0)και p m (k/1) της συγκεκριµένης κλάσης προτύπων.
6 Χωρισµός σε ζώνες Σύµφωνα µε την προσέγγιση χωρισµού σε ζώνες, υπολογίζεται η κατανοµή των µαύρων pixels σε διάφορες ζώνες στις οποίες χωρίζουµε τον χαρακτήρα (Bokser 1992). Για την εξαγωγή χαρακτηριστικών µε χρήση των ζωνών του χαρακτήρα, η πιο απλή εφαρµογή είναι ο χωρισµός του χαρακτήρα σε nxm ζώνες και ο υπολογισµός της πυκνότητας των pixels σε κάθε ζώνη. Στο παράδειγµα του σχήµατος 7.5 υπολογίζεται η πυκνότητα των pixels σε 16 ζώνες καθώς και σε 9 ζώνες που επικαλύπτουν τις πρώτες στις οποίες έχουµε χωρίσει τον χαρακτήρα. Εναλλακτικά, µπορούµε να δώσουµε βάρη στα pixels κάθε παραθύρου που έχουµε χωρίσει τον χαρακτήρα τονίζοντας περισσότερο τα pixels που βρίσκονται στο κέντρο του παραθύρου (σχήµα 7.6) (Gatos 1993). Με αυτό τον τρόπο επιτυγχάνουµε µεγαλύτερη αντοχή στον θόρυβο. (α) (β) Σχήµα 7.5 Υπολογισµός της πυκνότητας των pixels σε ζώνες στις οποίες έχουµε χωρίσει τον χαρακτήρα. (α) 16 ζώνες. (β) 9 ζώνες που επικαλύπτουν τις πρώτες. (α) (β) Σχήµα 7.6 Χρήση βαρών για τον υπολογισµό της πυκνότητας των pixels σε κάθε παράθυρο. (α) Τα βάρη σε κάθε παράθυρο. (β) Οι τιµές των χαρακτηριστικών που προκύπτουν.
7 Προβολές Οι προβολές σε οριζόντια και κάθετη διεύθυνση συνήθως χρησιµοποιούνται για την κατάτµηση των εγγράφων σε γραµµές κειµένου, λέξεις, χαρακτήρες κ.λ.π. καθώς και για τον εντοπισµό της στροφής των εγγράφων. Όµως έχουν προταθεί για την εξαγωγή χαρακτηριστικών από το 1956 (Glauberman 1956). Ένα παράδειγµα οριζόντιας και κάθετης προβολής ενός χαρακτήρα δίδεται στο σχήµα 7.7. Το ιστόγραµµα της προβολής συνήθως κανονικοποιείται µε την οµαδοποίηση γειτονικών γραµµών ή στηλών ώστε να χρησιµοποιείται σταθερός αριθµός περιοχών σε οριζόντια και κάθετη διεύθυνση. Όµως, οι προβολές είναι πολύ ευαίσθητες στην στροφή και στον τύπο γραψίµατος. Επιπροσθέτως, βασική πληροφορία σχετικά µε την µορφή του χαρακτήρα χάνεται. Η κάθετη προβολή y(x i ) αντιστοιχεί στον αριθµό των pixels για το οποία ισχύει x=x i. Για να µετρήσουµε την οµοιότητα µεταξύ δύο ιστογραµµάτων αρκεί να υπολογίσουµε το: d = n i= 1 y1 ( xi ) y2( x i ) (7.7) όπου n ο αριθµός των υποδιαιρέσεων της οριζόντιας διάστασης του χαρακτήρα και y 1 και y 2 είναι τα δύο ιστογράµµατα που θέλουµε να συγκρίνουµε. Συνήθως, χρησιµοποιούµε το αθροιστικό ιστόγραµµα Υ το οποίο αθροίζει τις k πρώτες τιµές του ιστογράµµατος: k Y ( x ) = y( ) (7.8) k x i i= 1 Η απόσταση µεταξύ των δύο ιστογραµµάτων γίνεται: D = n i= 1 Y1 ( xi ) Y2( x i ) (7.9) Η απόσταση D δεν είναι τόσο ευαίσθητη σε τυχών µετατοπίσεις των επικρατέστερων κορυφών των οριζόντιων και κάθετων προβολών. Σχήµα 7.7 Εξαγωγή χαρακτηριστικών που βασίζεται στις οριζόντιες και κάθετες προβολές του χαρακτήρα.
8 Γεωµετρικές ροπές (geometric moments) Οι αναλλοίωτες ροπές έχουν προταθεί σαν χαρακτηριστικά για την αναγνώριση προτύπων από την δεκαετία του 1960 (Hu 1962). Με την χρήση των ροπών µπορούµε να εξάγουµε χαρακτηριστικά των αντικειµένων τα οποία µπορεί να είναι αναλλοίωτα ως προς την µετακίνηση, το µέγεθος και την στροφή. Οι κανονικές ροπές (regular moments) τάξης (p+q) ορίζονται για µια ασπρόµαυρη εικόνα ως εξής: m pq = M i= 1 i p i q ( x ) ( y ) (7.10) όπου Μ είναι το σύνολο των σηµείων της εικόνας και (x i,y i ) οι συντεταγµένες κάθε σηµείου. Οι κεντρικές ροπές (central moments) οι οποίες είναι ανεξάρτητες µετακίνησης δίδονται από το τύπο: M µ = ( x x) ( y y) (7.11) pq i = 1 i p i q m10 m x =, y = m m (7.12) Οι κανονικοποιηµένες κεντρικές ροπές (normalized central moments) οι οποίες είναι ανεξάρτητες της µετακίνησης και του µεγέθους δίδονται από τον τύπο: n pq µ pq p + q =, γ = + 1, p + q = 2,3,... γ µ 2 (7.13) 00 Τέλος, οι αναλλοίωτες ροπές Hu (Hu moments invariants) οι οποίες είναι ανεξάρτητες µετακίνησης, µεγέθους και στροφής, δίδονται από τους τύπους (οι ροπές δεύτερης τάξης): Φ Φ 1 = n 20 + n = n 20 n02) + 4 ( n 2 11 (7.14) Στο σχήµα 7.8 δίδεται παράδειγµα υπολογισµού των κανονικών ροπών, των κεντρικών ροπών, των κανονικοποιηµένων κεντρικών ροπών και των αναλλοίωτων ροπών Hu, για χαρακτήρα οποίος έχει υποστεί µετακίνηση, µεγέθυνση και στροφή. Παρατηρούµε ότι οι κεντρικές ροπές έχουν ίδιες τιµές για τους δύο πρώτους χαρακτήρες (αναλλοίωτες σε µετακίνηση), οι κανονικοποιηµένες κεντρικές ροπές έχουν ίδιες τιµές για τους τρεις πρώτους χαρακτήρες (αναλλοίωτες σε µετακίνηση και αλλαγή στο µέγεθος) ενώ οι αναλλοίωτες ροπές Hu έχουν περίπου ίδιες τιµές για όλους τους χαρακτήρες (αναλλοίωτες σε µετακίνηση, αλλαγή στο µέγεθος και περιστροφή). Ποσοστό κάλυψης των µαύρων pixels Το ποσοστό κάλυψης των µαύρων pixels για έναν χαρακτήρα δίδεται από τον τύπο: P = X Y x= 1 y = 1 f ( x, y) (7.15) XY όπου XxY είναι οι διαστάσεις του κανονικοποιηµένου παραθύρου του χαρακτήρα και f(x,y) η εικόνα του χαρακτήρα µε τιµές 1 για τα µαύρα pixels και 0 για τα pixels φόντου. Το ποσοστό
9 κάλυψης των µαύρων pixels είναι στατιστικό χαρακτηριστικό το οποίο είναι αναλλοίωτο κυρίως ως προς την µετακίνηση και την στροφή. Μπορεί να χρησιµοποιηθεί σαν ένα κριτήριο διαχωρισµού των χαρακτήρων σε βασικές κατηγορίες. Σηµεία τοµής µε ευθείες (crossing points) Αν µετρήσουµε τις εναλλαγές 01 και 10 στις οριζόντιες και κάθετες µεσοκάθετους στο κανονικοποιηµένο παράθυρο του χαρακτήρα τότε τα σηµεία τοµής µε τις δύο µεσοκάθετους προκύπτουν αν διαιρέσουµε τις εναλλαγές δια 2 (σχήµα 7.9). Ο αριθµό των σηµείων τοµής µε τις µεσοκάθετους χρησιµοποιείται σαν χαρακτηριστικό (Impedovo 1991) το οποίο είναι αναλλοίωτο κυρίως ως προς τον θόρυβο, την µετατόπιση, το µέγεθος και την παραµόρφωση. Χρησιµοποιείται κυρίως σαν ένα κριτήριο διαχωρισµού των χαρακτήρων σε βασικές κατηγορίες. Σχήµα 7.8 Υπολογισµός των κανονικών ροπών, των κεντρικών ροπών, των κανονικοποιηµένων κεντρικών ροπών και των αναλλοίωτων ροπών Hu, για χαρακτήρα οποίος έχει υποστεί µετακίνηση, µεγέθυνση και στροφή. Σχήµα 7.9 Υπολογισµός των σηµείων τοµής µε τις οριζόντιες και κάθετες µεσοκάθετους.
10 Ύπαρξη οπών Οι οπές που υπάρχουν στην εικόνα του χαρακτήρα µπορούν να υπολογιστούν µε τον παρακάτω αλγόριθµο ο οποίος βασίζεται στα διαδοχικά σηµεία φόντου (white runs) της ασπρόµαυρης εικόνας. Βήµα 1. Όλα τα οριζόντια και κάθετα διαδοχικά σηµεία φόντου που συνορεύουν µε τα όρια της εικόνας µαρκάρονται. Βήµα 2. Όλα τα οριζόντια και κάθετα διαδοχικά µη µαρκαρισµένα σηµεία φόντου που συνορεύουν µε µαρκαρισµένα σηµεία του βήµατος 1 µαρκάρονται επίσης. Βήµα 3. Επαναλαµβάνουµε το βήµα 2 µέχρι να µην υπάρχουν άλλα σηµεία για µαρκάρισµα στην τελευταία επανάληψη. Βήµα 4. Όλα τα µη µαρκαρισµένα σηµεία φόντου ανήκουν σε οπές. Χρησιµοποιώντας ονοµατισµό των συνδεδεµένων συστατικών για τα σηµεία αυτά µπορούµε να εντοπίσουµε τον αριθµό και την θέση των οπών. Παράδειγµα του παραπάνω αλγορίθµου δίδεται στο σχήµα Ο αριθµό των οπών χρησιµοποιείται σαν χαρακτηριστικό το οποίο είναι αναλλοίωτο ως προς τους περισσότερους δυνατούς µετασχηµατισµούς του χαρακτήρα. Χρησιµοποιείται κυρίως σαν ένα κριτήριο διαχωρισµού των χαρακτήρων σε βασικές κατηγορίες. (α) (β) (γ) (δ) (ε) Σχήµα 7.10 Εντοπισµός οπών σε εικόνα. (α) Αρχική εικόνα. (β)-(ε) Αποτελέσµατα µετά από 1,2,5 και 19 επαναλήψεις αντίστοιχα. Θέση ως προς στην γραµµή κειµένου Αφού εντοπιστούν οι τρεις ζώνες (πάνω, µεσαία, κάτω) από τις οποίες αποτελείται η γραµµή του κειµένου (σχήµα 7.11), υπολογίζουµε αν ο χαρακτήρας έχει τµήµα του σε κάθε µία από αυτές τις ζώνες (Gatos 1997). Τα όρια των τριών ζωνών των γραµµών κειµένου αντιστοιχούν στα τοπικά ελάχιστα της οριζόντιας προβολής της γραµµής κειµένου. Η θέση του χαρακτήρα ως προς την γραµµή κειµένου χρησιµοποιείται σαν χαρακτηριστικό το οποίο είναι αναλλοίωτο ως προς τους περισσότερους δυνατούς µετασχηµατισµούς του χαρακτήρα. Χρησιµοποιείται κυρίως σαν ένα κριτήριο διαχωρισµού των χαρακτήρων σε βασικές κατηγορίες. Σχήµα 7.11 Οι τρεις ζώνες από τις οποίες αποτελείται η γραµµή κειµένου.
11 7.2 Χρησιµοποιώντας το περίγραµµα των χαρακτήρων Οι βασικότεροι µέθοδοι εξαγωγής χαρακτηριστικών που βασίζονται στην επεξεργασία του περιγράµµατος είναι οι προβολές του περιγράµµατος, ο χωρισµός του περιγράµµατος σε ζώνες και οι Fourier περιγραφείς (Fourier Descriptors). Επιπροσθέτως, σαν χαρακτηριστικό µπορούµε να θεωρήσουµε και το µήκος του περιγράµµατος κάθε χαρακτήρα. Προβολές του περιγράµµατος Το κίνητρο για την χρήση των προβολών του περιγράµµατος είναι ότι κάθε µισό του περιγράµµατος (σχήµα 7.12) µπορεί να προσεγγιστεί µε ξεχωριστή συνάρτηση ως προς x ή y. Μπορούµε να χρησιµοποιήσουµε οριζόντιες και κάθετες, εσωτερικές ή εξωτερικές προβολές του περιγράµµατος των χαρακτήρων. Για να υπολογίσουµε τις οριζόντιες προβολές του περιγράµµατος, πρώτα υπολογίζουµε το ανώτατο και κατώτατο σηµείο του περιγράµµατος του γράµµατος (σχήµα 7.13α). Το περίγραµµα χωρίζεται στα δύο σύµφωνα µε τα δύο αυτά σηµεία. Για να εξάγουµε τις εξωτερικές προβολές του περιγράµµατος, για κάθε τιµή του y, επιλέγουµε τα σηµεία του περιγράµµατος µε τις περισσότερο προς τα έξω τιµές για κάθε µισό του περιγράµµατος (σχήµα 7.13β). Για να εξάγουµε τις εσωτερικές προβολές του περιγράµµατος, για κάθε τιµή του y, επιλέγουµε τα σηµεία του περιγράµµατος µε τις περισσότερο προς τα µέσα µεγαλύτερες τιµές για κάθε µισό του περιγράµµατος (σχήµα 7.13γ). Τα χαρακτηριστικά που προκύπτουν έχουν αρκετή ανεξαρτησία ως προς τον θόρυβο και την παραµόρφωση, όµως εξαρτώνται από την στροφή του χαρακτήρα. Σχήµα 7.12 Η προβολή προς τα αριστερά και προς τα δεξιά του περιγράµµατος του χαρακτήρα. (α) (β) (γ) Σχήµα 7.13 Εξωτερικές και εσωτερικές προβολές του περιγράµµατος. (α) Χωρισµός του περιγράµµατος σε δύο τµήµατα εντοπίζοντας το ανώτατο και κατώτατο σηµείο του. (β) Οι εξωτερικές προβολές του αριστερού µέρους των οριζόντιων προβολών του περιγράµµατος. (γ) Οι αντίστοιχες εσωτερικές προβολές.
12 Χωρισµός του περιγράµµατος σε ζώνες Ο χωρισµός του περιγράµµατος σε ζώνες έχει χρησιµοποιηθεί µε επιτυχία για την εξαγωγή χαρακτηριστικών (Kimura 1991). Σε κάθε ζώνη, τα ευθύγραµµα τµήµατα ανάµεσα σε διαδοχικά σηµεία του περιγράµµατος οµαδοποιούνται ανάλογα µε την κλίση τους: Οριζόντια κλίση (0 0 ), κάθετη κλίση (90 0 ) και δύο διαγώνιες κλίσεις (45 0, ). Τα χαρακτηριστικά προκύπτουν από τον συνολικό αριθµό των τµηµάτων κάθε οµάδας. Αν και τα χαρακτηριστικά που προκύπτουν έχουν αρκετή ανεξαρτησία ως προς τον θόρυβο και την παραµόρφωση, όµως εξαρτώνται από την στροφή του χαρακτήρα. (α) (β) (γ) Σχήµα 7.14 Χωρισµός του περιγράµµατος σε ζώνες. (α) Χωρισµός σε 16 ζώνες. (β) Τα διαδοχικά σηµεία του περιγράµµατος για την πάνω δεξιά ζώνη. (γ) Τα χαρακτηριστικά που προκύπτουν ανάλογα µε τις κλίσεις των σηµείων. Περιγραφείς Fourier (Fourier Descriptors) Αν προσεγγίσουµε το περίγραµµα των χαρακτήρων µε κάποια συνάρτηση, τότε οι συντελεστές της συνάρτησης αυτής µπορούν να χρησιµοποιηθούν ως χαρακτηριστικά. Η ακολουθία των σηµείων του κλειστού περιγράµµατος των χαρακτήρων µπορεί να προσεγγιστεί µε χρήση κάποιας περιοδικής συνάρτησης. Οι σειρές Fourier έχουν χρησιµοποιηθεί µε επιτυχία για τον σκοπό αυτό (Kuhl 1982). Το κλειστό περίγραµµα, (x(t),y(t)), t=1,,m, προσεγγίζεται ως εξής: (7.16) όπου Τ είναι το συνολικό µήκος του περιγράµµατος και, όταν. Οι συντελεστές είναι:
13 (7.17) Οι συναρτήσεις x(t) και y(t) µπορούν να οριστούν χρησιµοποιώντας αθροίσµατα αντί για ολοκληρώµατα στον υπολογισµό των συντελεστών. Οι συντελεστές a n, b n, c n και d n οι οποίοι είναι και τα εξαγόµενα χαρακτηριστικά, µπορούν να οριστούν ως εξής: (7.18) όπου (7.19) και m είναι ο αριθµός των σηµείων του περιγράµµατος. Επειδή η επιλογή του αρχικού σηµείου (x 1,y 1 ) επηρεάζει τις τιµές των χαρακτηριστικών, υπολογίζουµε την γωνία µετατόπισης από τον πρώτο κύριο άξονα: (7.20) Οι συντελεστές οι οποίοι είναι ανεξάρτητοι από την επιλογή του αρχικού σηµείου υπολογίζονται ως εξής:
14 (7.21) Για να υπολογίσουµε συντελεστές ανεξάρτητους από την γωνία στροφής του αντικειµένου, αρχικά υπολογίζουµε την γωνία του κεντρικού άξονα του αντικειµένου (σχήµα 7.15): (7.22) Τα νέα χαρακτηριστικά τα οποία είναι ανεξάρτητα από την στροφή του αντικειµένου δίδονται από τον τύπο: (7.23) Για να έχουµε επιπλέον ανεξαρτησία από το µέγεθος, αρκεί να διαιρέσουµε του συντελεστές µε την ποσότητα E: (7.24) Στο σχήµα 7.16 δίδονται δύο παραδείγµατα αναδηµιουργίας των χαρακτήρων χρησιµοποιώντας τους συντελεστές Fourier n τάξης. Χρησιµοποιώντας τους συντελεστές τάξης 3 ή 4 σαν χαρακτηριστικά µπορούµε να δηµιουργήσουµε ταξινοµητή µε ικανοποιητική διαχωριστική ικανότητα. (α) (β) Σχήµα 7.15 Η στροφή των ελλείψεων πρώτης τάξης που χρησιµοποιούνται στους Fourier περιγραφείς ώστε να πετύχουµε ανεξαρτησία από στροφή. (α) Πριν την στροφή. (β) Μετά την στροφή.
15 Σχήµα 7.16 Αναδηµιουργία χαρακτήρων χρησιµοποιώντας τους περιγραφείς Fourier τάξης 1,2,3,4,5,6,7,8,9,10,15,20,30,40,50 και 100. Στο αριστερό µέρος είναι οι αρχικοί χαρακτήρες «4» και «5». Χρησιµοποιώντας τους συντελεστές τάξης 3 ή 4 σαν χαρακτηριστικά µπορούµε να περιγράψουµε ικανοποιητικά τους χαρακτήρες. 7.3 Χρήση σκελετού Ο σκελετός ενός αντικειµένου ορίζεται σαν ο γεωµετρικός τόπος των κέντρων των µέγιστων κυκλικών δίσκων που περιέχονται µέσα στο αντικείµενο (Choi 2003) (σχήµα 7.17). Για τον εντοπισµό του σκελετού αρκεί να εντοπίσουµε τους κυκλικούς δίσκους οι οποίοι έχουν τουλάχιστον δύο σηµεία επαφής µε το περίγραµµα του αντικειµένου. Σχήµα 7.17 Ορισµός του σκελετού ενός αντικειµένου.
16 Αν οι γειτονίες γύρω από ένα pixel p1 ορίζονται από το σχήµα 7.18, ένας απλός αλγόριθµος υπολογισµού του σκελετού είναι ο ακόλουθος (Gonzalez 1997): BHMA 1: Ένα pixel µαρκάρεται για αποµάκρυνση αν: (α) 2<=Ν(p1)<=6 (β) S(p1)=1 (γ) p2 p4 p6 = 0 (δ) p4 p6 p8 = 0 όπου N(p1) ο αριθµός των µη µηδενικών γειτόνων του p1 και S(p1) ο αριθµός των 0-1 µεταπτώσεων των διαδοχικών pixels p1,p2,,p9. BHMA 2: Μετά την πρώτη από πάνω προς τα κάτω σάρωση σβήνονται τα µαρκαρισµένα pixels και επαναλαµβάνεται η διαδικασία µε: (γ) p2 p4 p8 = 0 (δ) p2 p6 p8 = 0 BHMA 3: H παραπάνω διαδικασία επαναλαµβάνεται µέχρι να µην υπάρχει αλλαγή σε pixel. Ένα αποτέλεσµα του παραπάνω αλγορίθµου σκελετοποίησης δίδεται στο σχήµα Σχήµα 7.18 Οι γειτονίες γύρω από ένα pixel p1 Σχήµα 7.19 Σκελετός αντικειµένου χρησιµοποιώντας τον αλγόριθµο του (Gonzalez 1997).
17 Αν έχουµε εξάγει τον σκελετό του γράµµατος, τότε µπορούµε να χρησιµοποιήσουµε σαν χαρακτηριστικά την θέση των τελικών σηµείων και των σηµείων διακλάδωσης του σκελετού. Ένα σηµείο του σκελετού είναι τελικό αν ισχύει: Ένα σηµείο του σκελετού είναι σηµείο διακλάδωσης αν ισχύει: N(p1)=1 (7.25) N(p1)>=3 (7.26) Παραδείγµατα τελικών σηµείων και σηµείων διακλάδωσης δίδονται στο σχήµα Συνήθως ως χαρακτηριστικά χρησιµοποιoύνται ο αριθµός και η ύπαρξη των σηµείων αυτών στα 4 τεταρτηµόρια του χαρακτήρα (Gatos 1997). Σχήµα 7.20 Εντοπισµός τελικών σηµείων και σηµείων διακλάδωσης στον σκελετό των χαρακτήρων. Σχήµα 7.20 Εντοπισµός τελικών σηµείων και σηµείων διακλάδωσης στα 4 τεταρτηµόρια του χαρακτήρα.
18 Βιβλιογραφία (Bokser 1992) Bokser, M.: Omnidocument technologies. Proc. IEEE 80 (1992) (Choi 2003) Choi, W., Lam, K., Siu, W.: Extraction of the Euclidean skeleton based on a connectivity criterion. Pattern Recognition 36 (2003) (Gatos 1993) Gatos, B., Karras, D., Perantonis, S.: Optical Character Recognition Using Novel Feature Extraction & Neural Network Classification Techniques. Proc. of the Workshop on Neural Network Application and Tools, IEEE Computer Society Press (1993) (Gatos 1997) Gatos, B., Papamarkos N., Chamzas, C.: A binary tree based OCR technique for machine printed characters", Engineering Applications of Artificial Intelligence, vol. 10, No. 4 (1997) (Glauberman 1956) Glauberman, M.H.: Character Recognition for Business Machines, Electronics (1956) (Gonzalez 1997) Gonzalez, R.C.: Digital Image Processing, Second Edition (1997) (Hu 1962) Hu, M.K.: Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 8 (1962) (Impedovo 1991) Impedovo, S., Ottaviano, L., Occhinegro, S.: Optical Character Recognition A survey. International Journal of Pattern Recognition and Artificial Intelligence, Vol. 5 (1991) 1-23 (Kimura 1991) Kimura, F., Shridhar, M.: Handwritten numerical recognition based on multiple algorithms. Pattern Recognition, No. 24, Vol. 10 (1991) (Kuhl 1982) Kuhl, F.P., Giardina, C.R.: Elliptic Fourier features of a closed contour. Comput. Vis. Graphics Image Process. 18 (1982) (Pratt 1991) Pratt, W.K.: Digital Image Processing, 2 nd edn. Wiley, New York (1991) (Trier 1996) Trier, O.D., Jain, A.K., Taxt, T.: Feature Extraction Methods for Character Recognition A Survey. Pattern Recognition, Vol. 29, No. 4 (1996) (Tubbs 1989) Tubbs, J.D.: A note on binary template matching. Pattern Recognition, Vol. 22, No. 4 (1989)
Εργασίες στο µάθηµα Ψηφιακής Επεξεργασίας και Αναγνώρισης Εγγράφων
 Εργασίες στο µάθηµα Ψηφιακής Επεξεργασίας και Αναγνώρισης Εγγράφων Μάθηµα 2: υαδική Μετατροπή 1. Βελτιωµένη µέθοδος προσαρµοσµένης κατωφλίωσης βάσει του πλάτους των γραµµών των χαρακτήρων (Απαλλακτική
Εργασίες στο µάθηµα Ψηφιακής Επεξεργασίας και Αναγνώρισης Εγγράφων Μάθηµα 2: υαδική Μετατροπή 1. Βελτιωµένη µέθοδος προσαρµοσµένης κατωφλίωσης βάσει του πλάτους των γραµµών των χαρακτήρων (Απαλλακτική
Β. Γάτος, Ψηφιακή Επεξεργασία και Αναγνώριση Εγγράφων. 3.1 Προβλήµατα στην ποιότητα των δυαδικών εικόνων
 Μάθηµα 3 Βελτίωση ποιότητας 3.1 Προβλήµατα στην ποιότητα των δυαδικών εικόνων Οι δυαδικές εικόνες των εγγράφων συνήθως χρειάζονται ένα στάδιο προεπεξεργασίας για την βελτίωση της ποιότητάς τους. Στο στάδιο
Μάθηµα 3 Βελτίωση ποιότητας 3.1 Προβλήµατα στην ποιότητα των δυαδικών εικόνων Οι δυαδικές εικόνες των εγγράφων συνήθως χρειάζονται ένα στάδιο προεπεξεργασίας για την βελτίωση της ποιότητάς τους. Στο στάδιο
Μέθοδοι Αναπαράστασης Περιοχών
 KEΣ 3 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Μέθοδοι Αναπαράστασης Περιοχών ΤµήµαΕπιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Εισαγωγή Χαρακτηριστικά χώρου Χαρακτηριστικά από µετασχηµατισµό
KEΣ 3 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Μέθοδοι Αναπαράστασης Περιοχών ΤµήµαΕπιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Εισαγωγή Χαρακτηριστικά χώρου Χαρακτηριστικά από µετασχηµατισµό
Εντοπισµός χαρακτήρων
 Μάθηµα 6 Εντοπισµός χαρακτήρων Το στάδιο του εντοπισµού των χαρακτήρων αφορά την επεξεργασία τµηµάτων κειµένου ώστε να αποµονωθούν οι χαρακτήρες που υπάρχουν σε αυτά. Το στάδιο αυτό επηρεάζει σηµαντικά
Μάθηµα 6 Εντοπισµός χαρακτήρων Το στάδιο του εντοπισµού των χαρακτήρων αφορά την επεξεργασία τµηµάτων κειµένου ώστε να αποµονωθούν οι χαρακτήρες που υπάρχουν σε αυτά. Το στάδιο αυτό επηρεάζει σηµαντικά
Β. Γάτος, Ψηφιακή Επεξεργασία και Αναγνώριση Εγγράφων
 Μάθηµα 8 Ταξινόµηση Το στάδιο της ταξινόµησης αφορά την τελική αναγνώριση των χαρακτήρων και αντιστοίχισή τους σε κάποια ASCII κωδικοποίηση. Αποτελείται από: την φάση της εκπαίδευσης όπου ένα σύνολο χαρακτήρων
Μάθηµα 8 Ταξινόµηση Το στάδιο της ταξινόµησης αφορά την τελική αναγνώριση των χαρακτήρων και αντιστοίχισή τους σε κάποια ASCII κωδικοποίηση. Αποτελείται από: την φάση της εκπαίδευσης όπου ένα σύνολο χαρακτήρων
ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΑΠΟ ΤΗ ΘΕΩΡΙΑ ΑΝΑΛΥΣΗΣ ΕΙΚΟΝΑΣ (ΓΙΑ ΤΗΝ ΑΝΑ ΕΙΞΗ ΟΥΣΙΩ ΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΕΙΚΟΝΑΣ) ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ
 ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΑΠΟ ΤΗ ΘΕΩΡΙΑ ΑΝΑΛΥΣΗΣ ΕΙΚΟΝΑΣ (ΓΙΑ ΤΗΝ ΑΝΑ ΕΙΞΗ ΟΥΣΙΩ ΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΕΙΚΟΝΑΣ) Τµήµα από το µάθηµα ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΒΙΒΛΙΟΓΡΑΦΙΑ Η καλύτερη προσέγγιση της ύλης του µαθήµατος 1.R.C.
ΕΙ ΙΚΑ ΚΕΦΑΛΑΙΑ ΑΠΟ ΤΗ ΘΕΩΡΙΑ ΑΝΑΛΥΣΗΣ ΕΙΚΟΝΑΣ (ΓΙΑ ΤΗΝ ΑΝΑ ΕΙΞΗ ΟΥΣΙΩ ΩΝ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΕΙΚΟΝΑΣ) Τµήµα από το µάθηµα ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΒΙΒΛΙΟΓΡΑΦΙΑ Η καλύτερη προσέγγιση της ύλης του µαθήµατος 1.R.C.
Β. Γάτος, Ψηφιακή Επεξεργασία και Αναγνώριση Εγγράφων. 4.1 Το πρόβληµα της στροφής των εγγράφων
 Μάθηµα 4 ιόρθωση στροφής 4. Το πρόβληµα της στροφής των εγγράφων Ένα από τα βασικά βήµατα της προεπεξεργασίας του εγγράφου είναι ο εντοπισµός και η διόρθωση της στροφής του (σχήµα 4.). Η στροφή αυτή συνήθως
Μάθηµα 4 ιόρθωση στροφής 4. Το πρόβληµα της στροφής των εγγράφων Ένα από τα βασικά βήµατα της προεπεξεργασίας του εγγράφου είναι ο εντοπισµός και η διόρθωση της στροφής του (σχήµα 4.). Η στροφή αυτή συνήθως
α) Κύκλος από δύο δοσµένα σηµεία Α, Β. Το ένα από τα δύο σηµεία ορίζεται ως κέντρο αν το επιλέξουµε πρώτο. β) Κύκλος από δοσµένο σηµείο και δοσµένο ευ
 ΕΙΣΑΓΩΓΗ ΣΤΟ ΛΟΓΙΣΜΙΚΟ SKETCHPAD ΜΕΡΟΣ Α Μιλώντας για ένα λογισµικό δυναµικής γεωµετρίας καλό θα ήταν να διακρίνουµε αρχικά 3 οµάδες εργαλείων µε τα οποία µπορούµε να εργαστούµε µέσα στο συγκεκριµένο περιβάλλον.
ΕΙΣΑΓΩΓΗ ΣΤΟ ΛΟΓΙΣΜΙΚΟ SKETCHPAD ΜΕΡΟΣ Α Μιλώντας για ένα λογισµικό δυναµικής γεωµετρίας καλό θα ήταν να διακρίνουµε αρχικά 3 οµάδες εργαλείων µε τα οποία µπορούµε να εργαστούµε µέσα στο συγκεκριµένο περιβάλλον.
2 + 0.5 2 + 0.25 + 1 + 0.5 2 + 0.25 + 1 + 0.5 2 + 0.25 2 + 0.5 0 0.125 + 1 + 0.5 1 0.125 + 1 + 0.75 1 0.125 1/5
 IOYNIOΣ 23 Δίνονται τα εξής πρότυπα: x! = 2.5 Άσκηση η (3 µονάδες) Χρησιµοποιώντας το κριτήριο της οµοιότητας να απορριφθεί ένα χαρακτηριστικό µε βάση το συντελεστή συσχέτισης. Γράψτε εδώ το χαρακτηριστικό
IOYNIOΣ 23 Δίνονται τα εξής πρότυπα: x! = 2.5 Άσκηση η (3 µονάδες) Χρησιµοποιώντας το κριτήριο της οµοιότητας να απορριφθεί ένα χαρακτηριστικό µε βάση το συντελεστή συσχέτισης. Γράψτε εδώ το χαρακτηριστικό
Μέθοδοι Αναπαράστασης Περιγραµµάτων
 KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Μέθοδοι Αναπαράστασης Περιγραµµάτων Τµήµα Επιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Μέθοδοι Αναπαράστασης Περιγραµµάτων Τµήµα Επιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
Κατάτµηση σελίδας εγγράφου
 Μάθηµα 5 Κατάτµηση σελίδας εγγράφου 5.1 Το στάδιο της κατάτµησης της σελίδας του εγγράφου Το στάδιο της κατάτµησης της σελίδας των εγγράφων είναι από τα πιο σηµαντικά στάδια στην επεξεργασία και κατανόηση
Μάθηµα 5 Κατάτµηση σελίδας εγγράφου 5.1 Το στάδιο της κατάτµησης της σελίδας του εγγράφου Το στάδιο της κατάτµησης της σελίδας των εγγράφων είναι από τα πιο σηµαντικά στάδια στην επεξεργασία και κατανόηση
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
Μάθημα 10 ο. Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1
 Μάθημα 10 ο Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Η περιγραφή μίας περιοχής μπορεί να γίνει: Με βάση τα εξωτερικά χαρακτηριστικά (ακμές, όρια). Αυτή η περιγραφή προτιμάται όταν μας ενδιαφέρουν
Μάθημα 10 ο Περιγραφή Σχήματος ΤΜΗΥΠ / ΕΕΣΤ 1 Εισαγωγή (1) Η περιγραφή μίας περιοχής μπορεί να γίνει: Με βάση τα εξωτερικά χαρακτηριστικά (ακμές, όρια). Αυτή η περιγραφή προτιμάται όταν μας ενδιαφέρουν
11 Το ολοκλήρωµα Riemann
 Το ολοκλήρωµα Riem Το πρόβληµα υπολογισµού του εµβαδού οποιασδήποτε επιφάνειας ( όπως κυκλικοί τοµείς, δακτύλιοι και δίσκοι, ελλειπτικοί δίσκοι, παραβολικά και υπερβολικά χωρία κτλ) είναι γνωστό από την
Το ολοκλήρωµα Riem Το πρόβληµα υπολογισµού του εµβαδού οποιασδήποτε επιφάνειας ( όπως κυκλικοί τοµείς, δακτύλιοι και δίσκοι, ελλειπτικοί δίσκοι, παραβολικά και υπερβολικά χωρία κτλ) είναι γνωστό από την
14 Εφαρµογές των ολοκληρωµάτων
 14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
14 Εφαρµογές των ολοκληρωµάτων 14.1 Υπολογισµός εµβαδών µε την µέθοδο των παράλληλων διατοµών Θεωρούµε µια ϕραγµένη επίπεδη επιφάνεια A µε οµαλό σύνορο, δηλαδή που περιγράφεται από µια συνεχή συνάρτηση.
ΕΡΕΥΝΗΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΑΡΧΙΜΗΔΗΣ ΕΝΙΣΧΥΣΗ ΕΡΕΥΝΗΤΙΚΩΝ ΟΜΑΔΩΝ ΣΤΟ ΤΕΙ ΣΕΡΡΩΝ. Ενέργεια. 2.2.3.στ ΘΕΜΑ ΕΡΕΥΝΑΣ: ΔΙΑΡΘΡΩΣΗ ΠΕΡΙΕΧΟΜΕΝΟΥ ΕΧΡΩΜΩΝ ΕΓΓΡΑΦΩΝ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ (Τ.Ε.Ι.) ΣΕΡΡΩΝ Τμήμα ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΡΕΥΝΗΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΑΡΧΙΜΗΔΗΣ ΕΝΙΣΧΥΣΗ ΕΡΕΥΝΗΤΙΚΩΝ ΟΜΑΔΩΝ ΣΤΟ ΤΕΙ ΣΕΡΡΩΝ Ενέργεια. 2.2.3.στ ΘΕΜΑ ΕΡΕΥΝΑΣ: ΔΙΑΡΘΡΩΣΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ (Τ.Ε.Ι.) ΣΕΡΡΩΝ Τμήμα ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΡΕΥΝΗΤΙΚΑ ΠΡΟΓΡΑΜΜΑΤΑ ΑΡΧΙΜΗΔΗΣ ΕΝΙΣΧΥΣΗ ΕΡΕΥΝΗΤΙΚΩΝ ΟΜΑΔΩΝ ΣΤΟ ΤΕΙ ΣΕΡΡΩΝ Ενέργεια. 2.2.3.στ ΘΕΜΑ ΕΡΕΥΝΑΣ: ΔΙΑΡΘΡΩΣΗ
Κατάτµηση εικόνας σε οµοιόµορφες περιοχές
 KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση εικόνας σε οµοιόµορφες περιοχές ΤµήµαΕπιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Εισαγωγή Κατάτµηση µε πολυκατωφλίωση Ανάπτυξη
KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση εικόνας σε οµοιόµορφες περιοχές ΤµήµαΕπιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Εισαγωγή Κατάτµηση µε πολυκατωφλίωση Ανάπτυξη
ΒΙΟΜΗΧΑΝΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
 ΒΙΟΜΗΧΑΝΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Συµπληρωµατικές Σηµειώσεις Προχωρηµένο Επίπεδο Επεξεργασίας Εικόνας Σύνθεση Οπτικού Μωσαϊκού ρ. Γ. Χ. Καρράς Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τοµέας Μηχανολογικών
ΒΙΟΜΗΧΑΝΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Συµπληρωµατικές Σηµειώσεις Προχωρηµένο Επίπεδο Επεξεργασίας Εικόνας Σύνθεση Οπτικού Μωσαϊκού ρ. Γ. Χ. Καρράς Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τοµέας Μηχανολογικών
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Ακμές και περιγράμματα Ακμές και περιγράμματα Γενικά Μεγάλο τμήμα της πληροφορίας που γίνεται αντιληπτή
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Ακμές και περιγράμματα Ακμές και περιγράμματα Γενικά Μεγάλο τμήμα της πληροφορίας που γίνεται αντιληπτή
Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση
 Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση Εντοπισμός ενός σήματος STOP σε μια εικόνα. Περιγράψτε τη διαδικασία με την οποία μπορώ να εντοπίσω απλά σε μια εικόνα την ύπαρξη του παρακάτω
Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση Εντοπισμός ενός σήματος STOP σε μια εικόνα. Περιγράψτε τη διαδικασία με την οποία μπορώ να εντοπίσω απλά σε μια εικόνα την ύπαρξη του παρακάτω
ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής
 ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής Το πρόβληµα Το πρόβληµα που καλείται ο υποψήφιος διδάκτορας να επιλύσει είναι η εξαγωγή χαρακτηριστικών (feature extraction) από ένα 3 αντικείµενο,
ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής Το πρόβληµα Το πρόβληµα που καλείται ο υποψήφιος διδάκτορας να επιλύσει είναι η εξαγωγή χαρακτηριστικών (feature extraction) από ένα 3 αντικείµενο,
Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ
 ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΟ ΛΟΓΙΣΜΙΚΟ GEOGEBRA Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ Η ΠΡΩΤΗ ΓΝΩΡΙΜΙΑ ΜΕ ΤΗΝ ΓΕΩΜΕΤΡΙΑ ΤΟΥ GEOGEBRA 1. ΓΕΝΙΚΑ Με το λογισµικό Geogebra µπορούµε να κατασκευάσουµε όλα σχεδόν τα γεωµετρικά επίπεδα
ΜΑΘΗΜΑΤΙΚΑ ΜΕ ΤΟ ΛΟΓΙΣΜΙΚΟ GEOGEBRA Ο ΗΓΟΣ ΧΡΗΣΗΣ ΓΕΩΜΕΤΡΙΑ Η ΠΡΩΤΗ ΓΝΩΡΙΜΙΑ ΜΕ ΤΗΝ ΓΕΩΜΕΤΡΙΑ ΤΟΥ GEOGEBRA 1. ΓΕΝΙΚΑ Με το λογισµικό Geogebra µπορούµε να κατασκευάσουµε όλα σχεδόν τα γεωµετρικά επίπεδα
Ενότητα 2: Οι Θεµελιώδεις Αρχές των Ψηφιακών Εικόνων
 Ενότητα 2: Οι Θεµελιώδεις Αρχές των Ψηφιακών Εικόνων Δειγµατοληψία και Κβαντισµός: Μια εικόνα (µπορεί να) είναι συνεχής τόσο ως προς τις συντεταγµένες x, y όσο και ως προς το πλάτος. Για να τη µετατρέψουµε
Ενότητα 2: Οι Θεµελιώδεις Αρχές των Ψηφιακών Εικόνων Δειγµατοληψία και Κβαντισµός: Μια εικόνα (µπορεί να) είναι συνεχής τόσο ως προς τις συντεταγµένες x, y όσο και ως προς το πλάτος. Για να τη µετατρέψουµε
Πανεπιστήµιο Κύπρου Πολυτεχνική Σχολή
 Πανεπιστήµιο Κύπρου Πολυτεχνική Σχολή Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών ΗΜΜΥ 795: ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ Ακαδηµαϊκό έτος 2010-11 Χειµερινό Εξάµηνο Τελική εξέταση Τρίτη, 21 εκεµβρίου 2010,
Πανεπιστήµιο Κύπρου Πολυτεχνική Σχολή Τµήµα Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών ΗΜΜΥ 795: ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ Ακαδηµαϊκό έτος 2010-11 Χειµερινό Εξάµηνο Τελική εξέταση Τρίτη, 21 εκεµβρίου 2010,
οµή δικτύου ΣΧΗΜΑ 8.1
 8. ίκτυα Kohonen Το µοντέλο αυτό των δικτύων προτάθηκε το 1984 από τον Kοhonen, και αφορά διαδικασία εκµάθησης χωρίς επίβλεψη, δηλαδή δεν δίδεται καµία εξωτερική επέµβαση σχετικά µε τους στόχους που πρέπει
8. ίκτυα Kohonen Το µοντέλο αυτό των δικτύων προτάθηκε το 1984 από τον Kοhonen, και αφορά διαδικασία εκµάθησης χωρίς επίβλεψη, δηλαδή δεν δίδεται καµία εξωτερική επέµβαση σχετικά µε τους στόχους που πρέπει
ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής
 ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής Το πρόβληµα Το πρόβληµα που καλείται ο υποψήφιος διδάκτορας να επιλύσει είναι η εξαγωγή χαρακτηριστικών (feature extraction) από ένα 3 αντικείµενο,
ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής Το πρόβληµα Το πρόβληµα που καλείται ο υποψήφιος διδάκτορας να επιλύσει είναι η εξαγωγή χαρακτηριστικών (feature extraction) από ένα 3 αντικείµενο,
Ανάκτηση πολυμεσικού περιεχομένου
 Ανάκτηση πολυμεσικού περιεχομένου Ανίχνευση / αναγνώριση προσώπων Ανίχνευση / ανάγνωση κειμένου Ανίχνευση αντικειμένων Οπτικές λέξεις Δεικτοδότηση Σχέσεις ομοιότητας Κατηγοριοποίηση ειδών μουσικής Διάκριση
Ανάκτηση πολυμεσικού περιεχομένου Ανίχνευση / αναγνώριση προσώπων Ανίχνευση / ανάγνωση κειμένου Ανίχνευση αντικειμένων Οπτικές λέξεις Δεικτοδότηση Σχέσεις ομοιότητας Κατηγοριοποίηση ειδών μουσικής Διάκριση
Μετασχηµατισµοί 2 &3
 Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Κατάτµηση Εικόνων: Ανίχνευση Ακµών και Κατάτµηση µε Κατωφλίωση
 ΤΨΣ 50 Ψηφιακή Επεξεργασία Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών και Κατάτµηση µε Κατωφλίωση Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο Πειραιώς Περιεχόµενα Βιβλιογραφία
ΤΨΣ 50 Ψηφιακή Επεξεργασία Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών και Κατάτµηση µε Κατωφλίωση Τµήµα ιδακτικής της Τεχνολογίας και Ψηφιακών Συστηµάτων Πανεπιστήµιο Πειραιώς Περιεχόµενα Βιβλιογραφία
ΚΕΦΑΛΑΙΟ 4 ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟ ΟΙ ΕΥΡΕΣΗΣ ΠΡΑΓΜΑΤΙΚΩΝ Ι ΙΟΤΙΜΩΝ. 4.1 Γραµµικοί µετασχηµατισµοί-ιδιοτιµές-ιδιοδιανύσµατα
 ΚΕΦΑΛΑΙΟ 4 ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟ ΟΙ ΕΥΡΕΣΗΣ ΠΡΑΓΜΑΤΙΚΩΝ Ι ΙΟΤΙΜΩΝ 4. Γραµµικοί µετασχηµατισµοί-ιδιοτιµές-ιδιοδιανύσµατα Εστω R είναι ο γνωστός -διάστατος πραγµατικός διανυσµατικός χώρος. Μία απεικόνιση L :
ΚΕΦΑΛΑΙΟ 4 ΑΡΙΘΜΗΤΙΚΕΣ ΜΕΘΟ ΟΙ ΕΥΡΕΣΗΣ ΠΡΑΓΜΑΤΙΚΩΝ Ι ΙΟΤΙΜΩΝ 4. Γραµµικοί µετασχηµατισµοί-ιδιοτιµές-ιδιοδιανύσµατα Εστω R είναι ο γνωστός -διάστατος πραγµατικός διανυσµατικός χώρος. Μία απεικόνιση L :
ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής
 ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής Το πρόβληµα Το πρόβληµα που καλείται ο υποψήφιος διδάκτορας να επιλύσει είναι η εξαγωγή χαρακτηριστικών (feature extraction) από ένα 3 αντικείµενο,
ΕΚΘΕΣΗ ΠΡΟΟ ΟΥ Υποψήφιος ιδάκτορας: Ιωάννης Κυριαζής Το πρόβληµα Το πρόβληµα που καλείται ο υποψήφιος διδάκτορας να επιλύσει είναι η εξαγωγή χαρακτηριστικών (feature extraction) από ένα 3 αντικείµενο,
Αριθµητική Ανάλυση 1 εκεµβρίου / 43
 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Αριθµητική Ανάλυση 1 εκεµβρίου 2014 Αριθµητική Ανάλυση 1 εκεµβρίου 2014 1 / 43 Κεφ.5. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ίνεται ένας πίνακας A C n n και Ϲητούνται να προσδιορισθούν οι
Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 2010 Προκαταρκτικός διαγωνισµός στη Φυσική. Σχολείο:
 ΕΚΦΕ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 010 Προκαταρκτικός διαγωνισµός στη Φυσική Σχολείο: Ονόµατα των µαθητών της οµάδας 1) ) 3) Οι στόχοι του πειράµατος 1. Η µέτρηση της επιτάχυνσης
ΕΚΦΕ ΑΝΑΤΟΛΙΚΗΣ ΑΤΤΙΚΗΣ Ευρωπαϊκή Ολυµπιάδα Φυσικών Επιστηµών 010 Προκαταρκτικός διαγωνισµός στη Φυσική Σχολείο: Ονόµατα των µαθητών της οµάδας 1) ) 3) Οι στόχοι του πειράµατος 1. Η µέτρηση της επιτάχυνσης
ΕΛΕΓΧΟΙ ΠΡΟΣΑΡΜΟΓΗΣ & ΥΠΟΘΕΣΕΩΝ
 ΕΛΕΓΧΟΙ ΠΡΟΣΑΡΜΟΓΗΣ & ΥΠΟΘΕΣΕΩΝ Μετά από την εκτίµηση των παραµέτρων ενός προσοµοιώµατος, πρέπει να ελέγχουµε την αλήθεια της υποθέσεως που κάναµε. Είναι ορθή η υπόθεση που κάναµε? Βεβαίως συνήθως υπάρχουν
ΕΛΕΓΧΟΙ ΠΡΟΣΑΡΜΟΓΗΣ & ΥΠΟΘΕΣΕΩΝ Μετά από την εκτίµηση των παραµέτρων ενός προσοµοιώµατος, πρέπει να ελέγχουµε την αλήθεια της υποθέσεως που κάναµε. Είναι ορθή η υπόθεση που κάναµε? Βεβαίως συνήθως υπάρχουν
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοηµοσύνη Ι» 7ο Φροντιστήριο 15/1/2008
 Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοηµοσύνη Ι» 7ο Φροντιστήριο 5//008 Πρόβληµα ο Στα παρακάτω ερωτήµατα επισηµαίνουµε ότι perceptron είναι ένας νευρώνας και υποθέτουµε, όπου χρειάζεται, τη χρήση δικτύων
Ασκήσεις Φροντιστηρίου «Υπολογιστική Νοηµοσύνη Ι» 7ο Φροντιστήριο 5//008 Πρόβληµα ο Στα παρακάτω ερωτήµατα επισηµαίνουµε ότι perceptron είναι ένας νευρώνας και υποθέτουµε, όπου χρειάζεται, τη χρήση δικτύων
Όρια συναρτήσεων. ε > υπάρχει ( ) { } = ± ορίζονται αναλόγως. Η διατύπωση αυτών των ορισµών αφήνεται ως άσκηση. x y = +. = και για κάθε (, ) ( 0,0)
 Όρια συναρτήσεων.5. Ορισµός. Έστω, f : Α συνάρτηση συσσώρευσης του Α και b σηµείο. Λέµε ότι η f έχει ως όριο το διάνυσµα b καθώς το τείνει προς το και συµβολίζουµε li = ή f b f b αν και µόνο αν, για κάθε
Όρια συναρτήσεων.5. Ορισµός. Έστω, f : Α συνάρτηση συσσώρευσης του Α και b σηµείο. Λέµε ότι η f έχει ως όριο το διάνυσµα b καθώς το τείνει προς το και συµβολίζουµε li = ή f b f b αν και µόνο αν, για κάθε
( ) { } ( ) ( ( ) 2. ( )! r! e j ( ) Κίνηση στερεών σωμάτων. ω 2 2 ra. ω j. ω i. ω = ! ω! r a. 1 2 m a T = T = 1 2 i, j. I ij. r j. d 3! rρ. r! e!
 Κίνηση στερεών σωμάτων ΦΥΣ 11 - Διαλ.30 1 q Κίνηση στερεού σώµατος: Ø Υπολογισµός της κινητικής ενέργειας Ø Θεωρήσαµε ότι ένα σώµα διακριτής ή συνεχούς κατανοµής µάζας q Η κινητική ενέργεια δίνεται από
Κίνηση στερεών σωμάτων ΦΥΣ 11 - Διαλ.30 1 q Κίνηση στερεού σώµατος: Ø Υπολογισµός της κινητικής ενέργειας Ø Θεωρήσαµε ότι ένα σώµα διακριτής ή συνεχούς κατανοµής µάζας q Η κινητική ενέργεια δίνεται από
Αναγνώριση Προτύπων - Νευρωνικά ίκτυα
 ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ Αναγνώριση Προτύπων - Νευρωνικά ίκτυα ρ. Χαράλαµπος Π. Στρουθόπουλος Αναπληρωτής Καθηγητής
ΑΝΩΤΑΤΟ ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΣΕΡΡΩΝ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ Αναγνώριση Προτύπων - Νευρωνικά ίκτυα ρ. Χαράλαµπος Π. Στρουθόπουλος Αναπληρωτής Καθηγητής
ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ ΜΕ ΙΣΤΟΓΡΑΜΜΑ
 Ψηφιακή Επεξεργασία Εικόνας-ΚΕΦ. -- ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ ΜΕ ΙΣΤΟΓΡΑΜΜΑ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΝΤΑΣΕΩΣ Η επεξεργασία εικόνας µέσω του ιστογράµµατος ουσιαστικά αποτελεί µία βασική επεξεργασία εικόνας που ανήκει
Ψηφιακή Επεξεργασία Εικόνας-ΚΕΦ. -- ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ ΜΕ ΙΣΤΟΓΡΑΜΜΑ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΝΤΑΣΕΩΣ Η επεξεργασία εικόνας µέσω του ιστογράµµατος ουσιαστικά αποτελεί µία βασική επεξεργασία εικόνας που ανήκει
Ειδικές Επιστηµονικές Εργασίες
 Ειδικές Επιστηµονικές Εργασίες 2005-2006 1. Ανίχνευση προσώπων από ακολουθίες video και παρακολούθηση (face detection & tracking) Η ανίχνευση προσώπου (face detection) αποτελεί το 1 ο βήµα σε ένα αυτόµατο
Ειδικές Επιστηµονικές Εργασίες 2005-2006 1. Ανίχνευση προσώπων από ακολουθίες video και παρακολούθηση (face detection & tracking) Η ανίχνευση προσώπου (face detection) αποτελεί το 1 ο βήµα σε ένα αυτόµατο
7.5 Ενδιάμεσο επίπεδο επεξεργασίας εικόνας
 7.5 Ενδιάμεσο επίπεδο επεξεργασίας εικόνας 7.5.1 Εισαγωγή Kάθε σύστημα επεξεργασίας εικόνας έχει ένα συγκεκριμένο σκοπό λειτουργίας. Παραδείγματος χάριν, διαφορετικές απαιτήσεις θα έχει μια βιομηχανία
7.5 Ενδιάμεσο επίπεδο επεξεργασίας εικόνας 7.5.1 Εισαγωγή Kάθε σύστημα επεξεργασίας εικόνας έχει ένα συγκεκριμένο σκοπό λειτουργίας. Παραδείγματος χάριν, διαφορετικές απαιτήσεις θα έχει μια βιομηχανία
ΤΕΙ ΣΕΡΡΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ «ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ» ΔΕ. 11 ΙΟΥΝΙΟΥ 2012
 ΔΕ. ΙΟΥΝΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η ( μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάσει το συντελεστή συσχέτισης. (γράψτε ποιο χαρακτηριστικό
ΔΕ. ΙΟΥΝΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η ( μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάσει το συντελεστή συσχέτισης. (γράψτε ποιο χαρακτηριστικό
Σχήµα 3.1: Εισαγωγή shift register σε βρόγχο for-loop.
 Η δοµή «Shift register» 1. Η δοµή «Shift register» εισάγεται στο βρόγχο for-loop αλλά και σε άλλους βρόγχους που θα δούµε στη συνέχεια, όπως ο βρόγχος «While loop». Ο τρόπος εισαγωγής και λειτουργίας της
Η δοµή «Shift register» 1. Η δοµή «Shift register» εισάγεται στο βρόγχο for-loop αλλά και σε άλλους βρόγχους που θα δούµε στη συνέχεια, όπως ο βρόγχος «While loop». Ο τρόπος εισαγωγής και λειτουργίας της
ΠΕΙΡΑΜΑ Ι-β Μελέτη Φυσικού Εκκρεµούς
 ΠΕΙΡΑΜΑ Ι-β Μελέτη Φυσικού Εκκρεµούς Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε το φυσικό εκκρεµές και θα µετρήσουµε την επιτάχυνση της βαρύτητας. Θα εξετάσουµε λοιπόν πειραµατικά τα εξής: Την ταλάντωση
ΠΕΙΡΑΜΑ Ι-β Μελέτη Φυσικού Εκκρεµούς Σκοπός πειράµατος Στο πείραµα αυτό θα µελετήσουµε το φυσικό εκκρεµές και θα µετρήσουµε την επιτάχυνση της βαρύτητας. Θα εξετάσουµε λοιπόν πειραµατικά τα εξής: Την ταλάντωση
Όρια συναρτήσεων. ε > υπάρχει ( ) { } = ± ορίζονται αναλόγως. Η διατύπωση αυτών των ορισµών αφήνεται ως άσκηση. x y = +. = και για κάθε (, ) ( 0,0)
 Όρια συναρτήσεων 5 Ορισµός Έστω, : Α συνάρτηση συσσώρευσης του Α και b σηµείο Λέµε ότι η έχει ως όριο το διάνυσµα b καθώς το τείνει προς το και συµβολίζουµε li ή b b αν και µόνο αν, για κάθε ε > υπάρχει
Όρια συναρτήσεων 5 Ορισµός Έστω, : Α συνάρτηση συσσώρευσης του Α και b σηµείο Λέµε ότι η έχει ως όριο το διάνυσµα b καθώς το τείνει προς το και συµβολίζουµε li ή b b αν και µόνο αν, για κάθε ε > υπάρχει
Γυµ.Ν.Λαµψάκου Α Γυµνασίου Γεωµ.Β2.6 γωνίες από 2 παράλληλες + τέµνουσα 19/3/10 Φύλλο εργασίας
 Φύλλο εργασίας Mπορείτε να βρείτε τη γωνία κάβων; ραστηριότητα Ένα δεξαµενόπλοιο που στο σχήµα είναι στο σηµείο Β, πλέει προς την είσοδο µιας διώρυγας µε την βοήθεια δύο ρυµουλκών που απεικονίζονται µε
Φύλλο εργασίας Mπορείτε να βρείτε τη γωνία κάβων; ραστηριότητα Ένα δεξαµενόπλοιο που στο σχήµα είναι στο σηµείο Β, πλέει προς την είσοδο µιας διώρυγας µε την βοήθεια δύο ρυµουλκών που απεικονίζονται µε
Μηχανική ΙI Ροή στο χώρο των φάσεων, θεώρηµα Liouville
 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου 16/5/2000 Μηχανική ΙI Ροή στο χώρο των φάσεων, θεώρηµα Liouville Στη Χαµιλτονιανή θεώρηση η κατάσταση του συστήµατος προσδιορίζεται κάθε στιγµή από ένα και µόνο σηµείο
Τµήµα Π. Ιωάννου & Θ. Αποστολάτου 16/5/2000 Μηχανική ΙI Ροή στο χώρο των φάσεων, θεώρηµα Liouville Στη Χαµιλτονιανή θεώρηση η κατάσταση του συστήµατος προσδιορίζεται κάθε στιγµή από ένα και µόνο σηµείο
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων
 5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
Μεθοδολογία Υπερβολής
 Μεθοδολογία Υπερβολής Υπερβολή ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερή και μικρότερη από την απόσταση
Μεθοδολογία Υπερβολής Υπερβολή ονομάζεται ο γεωμετρικός τόπος των σημείων, των οποίων η απόλυτη τιμή της διαφοράς των αποστάσεων από δύο σταθερά σημεία Ε και Ε είναι σταθερή και μικρότερη από την απόσταση
Φροντιστηριακές Ασκήσεις Απεικόνισης - Αποκοπής
 Φροντιστηριακές Άσκηση Βρες τον πίνακα μετασχηματισμού που θα σχεδιάζει σημεία που περιέχονται σε ένα παράθυρο του οποίου η χαμηλότερη αριστερή γωνία είναι στο (3,3) και η ψηλότερη δεξιά γωνία είναι στο
Φροντιστηριακές Άσκηση Βρες τον πίνακα μετασχηματισμού που θα σχεδιάζει σημεία που περιέχονται σε ένα παράθυρο του οποίου η χαμηλότερη αριστερή γωνία είναι στο (3,3) και η ψηλότερη δεξιά γωνία είναι στο
4.3. Γραµµικοί ταξινοµητές
 Γραµµικοί ταξινοµητές Γραµµικός ταξινοµητής είναι ένα σύστηµα ταξινόµησης που χρησιµοποιεί γραµµικές διακριτικές συναρτήσεις Οι ταξινοµητές αυτοί αναπαρίστανται συχνά µε οµάδες κόµβων εντός των οποίων
Γραµµικοί ταξινοµητές Γραµµικός ταξινοµητής είναι ένα σύστηµα ταξινόµησης που χρησιµοποιεί γραµµικές διακριτικές συναρτήσεις Οι ταξινοµητές αυτοί αναπαρίστανται συχνά µε οµάδες κόµβων εντός των οποίων
Χαρακτηρισµός Νεοπλασµάτων στη Μαστογραφία από το Σχήµα της Παρυφής µε χρήση Νευρωνικών ικτύων
 Χαρακτηρισµός Νεοπλασµάτων στη Μαστογραφία από το Σχήµα της Παρυφής µε χρήση Νευρωνικών ικτύων Χ. Γεωργίου 1 (xgeorgio@hol.gr),. Κάβουρας 2 (cavouras@hol.gr), Ν. ηµητρόπουλος 3, Σ. Θεοδωρίδης 1 (stheodor@di.uoa.gr)
Χαρακτηρισµός Νεοπλασµάτων στη Μαστογραφία από το Σχήµα της Παρυφής µε χρήση Νευρωνικών ικτύων Χ. Γεωργίου 1 (xgeorgio@hol.gr),. Κάβουρας 2 (cavouras@hol.gr), Ν. ηµητρόπουλος 3, Σ. Θεοδωρίδης 1 (stheodor@di.uoa.gr)
4. Ο αισθητήρας (perceptron)
 4. Ο αισθητήρας (perceptron) Σκοπός: Προσδοκώµενα αποτελέσµατα: Λέξεις Κλειδιά: To µοντέλο του αισθητήρα (perceptron) είναι από τα πρώτα µοντέλα νευρωνικών δικτύων που αναπτύχθηκαν, και έδωσαν µεγάλη ώθηση
4. Ο αισθητήρας (perceptron) Σκοπός: Προσδοκώµενα αποτελέσµατα: Λέξεις Κλειδιά: To µοντέλο του αισθητήρα (perceptron) είναι από τα πρώτα µοντέλα νευρωνικών δικτύων που αναπτύχθηκαν, και έδωσαν µεγάλη ώθηση
ΘΕΑΝΩ ΕΡΙΦΥΛΗ ΜΟΣΧΟΝΑ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ
 ΘΕΑΝΩ ΕΡΙΦΥΛΗ ΜΟΣΧΟΝΑ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ Πρόβληµα µεταφοράς Η ανάπτυξη και διαµόρφωση του προβλήµατος µεταφοράς αναπτύσσεται στις σελίδες 40-45 του βιβλίου των
ΘΕΑΝΩ ΕΡΙΦΥΛΗ ΜΟΣΧΟΝΑ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ Πρόβληµα µεταφοράς Η ανάπτυξη και διαµόρφωση του προβλήµατος µεταφοράς αναπτύσσεται στις σελίδες 40-45 του βιβλίου των
Η γραφική απεικόνιση µιας κατανοµής συχνότητας µπορεί να γίνει µε δύο τρόπους, µε ιστόγραµµα και µε πολυγωνική γραµµή.
 ΠΕΜΠΤΟ ΠΑΚΕΤΟ ΣΗΜΕΙΩΣΕΩΝ ΣΤΑΤΙΣΤΙΚΑ ΙΑΓΡΑΜΜΑΤΑ Χρησιµότητα των διαγραµµάτων Η παρουσίαση των στατιστικών στοιχείων µπορεί να γίνει όχι µόνο µε πίνακες, αλλά και µε διαγράµµατα ή γραφικές απεικονίσεις.
ΠΕΜΠΤΟ ΠΑΚΕΤΟ ΣΗΜΕΙΩΣΕΩΝ ΣΤΑΤΙΣΤΙΚΑ ΙΑΓΡΑΜΜΑΤΑ Χρησιµότητα των διαγραµµάτων Η παρουσίαση των στατιστικών στοιχείων µπορεί να γίνει όχι µόνο µε πίνακες, αλλά και µε διαγράµµατα ή γραφικές απεικονίσεις.
+ cos(45 ) i + sin(45 ) j + cos(45 ) i sin(45 ) j +
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Τέταρτο Φροντιστήριο Επιµέλεια : Αναστασία Πεντάρη Υποψήφια ιδάκτωρ Ασκηση 1. Πόση είναι η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Τέταρτο Φροντιστήριο Επιµέλεια : Αναστασία Πεντάρη Υποψήφια ιδάκτωρ Ασκηση 1. Πόση είναι η
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Σημειακή επεξεργασία και μετασχηματισμοί Κατηγορίες μετασχηματισμού εικόνων Σημειακοί μετασχηματισμοί
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Σημειακή επεξεργασία και μετασχηματισμοί Κατηγορίες μετασχηματισμού εικόνων Σημειακοί μετασχηματισμοί
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ
 ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ Σ.Α.Ε. ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ ΕΚΕΜΒΡΙΟΣ 3 ) Αρχικό σήµα ( ) Στο παρακάτω σχήµα φαίνεται ένα περιοδικό σήµα ( ), το οποίο έχει ληφθεί από
ΣΧΟΛΗ Ν. ΟΚΙΜΩΝ ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ Σ.Α.Ε. ΥΠΟΛΟΓΙΣΜΟΣ ΑΝΑΠΤΥΓΜΑΤΟΣ FOURIER ΜΕ ΑΡΙΘΜΗΤΙΚΟ ΤΡΟΠΟ ΕΚΕΜΒΡΙΟΣ 3 ) Αρχικό σήµα ( ) Στο παρακάτω σχήµα φαίνεται ένα περιοδικό σήµα ( ), το οποίο έχει ληφθεί από
Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και2015 Ιδιοδιανυσµάτων 1 / 50
 Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 2 : Βελτιστοποίηση εικόνας (Image enhancement) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 2 : Βελτιστοποίηση εικόνας (Image enhancement) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΤΕΙ ΣΕΡΡΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΩΝ ΕΞΕΤΑΣΗ ΣΤΟ ΜΑΘΗΜΑ «ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ» ΠΑ. 7 ΣΕΠΤΕΜΒΡΙΟΥ 2012
 ΠΑ. 7 ΣΕΠΤΕΜΒΡΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η (3 μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάση το συντελεστή συσχέτισης. (γράψτε ποιο
ΠΑ. 7 ΣΕΠΤΕΜΒΡΙΟΥ Δίνονται τα εξής πρότυπα: [ ] [ ] [ ] [ ] Άσκηση η (3 μονάδες) Χρησιμοποιώντας το κριτήριο της ομοιότητας να απορριφθεί ένα χαρακτηριστικό με βάση το συντελεστή συσχέτισης. (γράψτε ποιο
Κεφάλαιο 6 Παράγωγος
 Σελίδα από 5 Κεφάλαιο 6 Παράγωγος Στο κεφάλαιο αυτό στόχος µας είναι να συνδέσουµε µία συγκεκριµένη συνάρτηση f ( ) µε µία δεύτερη συνάρτηση f ( ), την οποία και θα ονοµάζουµε παράγωγο της f. Η τιµή της
Σελίδα από 5 Κεφάλαιο 6 Παράγωγος Στο κεφάλαιο αυτό στόχος µας είναι να συνδέσουµε µία συγκεκριµένη συνάρτηση f ( ) µε µία δεύτερη συνάρτηση f ( ), την οποία και θα ονοµάζουµε παράγωγο της f. Η τιµή της
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 22D D σχημάτων (ευθεία
 Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Γραφικά με Η/Υ Αλγόριθμοι σχεδίασης βασικών 2D σχημάτων (ευθεία) Σχεδίαση ευθείας θί με σάρωση (παρουσίαση προβλήματος) σχεδίαση ευθείας AB, με σάρωση, όπου A=(0,1) και B=(5,4) ποιο είναι το επόμενο pixel
Μεθοδολογίες παρεµβολής σε DTM.
 Μάθηµα : Αλγοριθµικές Βάσεις στη Γεωπληροφορική ιδάσκων : Συµεών Κατσουγιαννόπουλος Μεθοδολογίες παρεµβολής σε DTM.. Μέθοδοι παρεµβολής. Η παρεµβολή σε ψηφιακό µοντέλο εδάφους (DTM) είναι η διαδικασία
Μάθηµα : Αλγοριθµικές Βάσεις στη Γεωπληροφορική ιδάσκων : Συµεών Κατσουγιαννόπουλος Μεθοδολογίες παρεµβολής σε DTM.. Μέθοδοι παρεµβολής. Η παρεµβολή σε ψηφιακό µοντέλο εδάφους (DTM) είναι η διαδικασία
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 3 : Αποκατάσταση εικόνας (Image Restoration) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 3 : Αποκατάσταση εικόνας (Image Restoration) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν
Εργαστήριο ADICV1. Image Boundary detection and filtering. Κώστας Μαριάς 13/3/2017
 Εργαστήριο ADICV1 Image Boundary detection and filtering Κώστας Μαριάς 13/3/2017 Boundary Detection 2 Γείτονες και περίγραμμα εικόνας Ορίζουμε ως V το σύνολο των τιμών εντάσεων εικόνας για να ορίσουμε
Εργαστήριο ADICV1 Image Boundary detection and filtering Κώστας Μαριάς 13/3/2017 Boundary Detection 2 Γείτονες και περίγραμμα εικόνας Ορίζουμε ως V το σύνολο των τιμών εντάσεων εικόνας για να ορίσουμε
ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ
 ΘΕΜΑ ο (.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις Πέµπτη 7 Ιανουαρίου 8 5:-8: Σχεδιάστε έναν αισθητήρα (perceptron)
ΘΕΜΑ ο (.5 µονάδες) ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΚΟΙΝΩΝΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΗΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΝΕΥΡΩΝΙΚΑ ΙΚΤΥΑ Τελικές εξετάσεις Πέµπτη 7 Ιανουαρίου 8 5:-8: Σχεδιάστε έναν αισθητήρα (perceptron)
Ε.Α.Υ. Υπολογιστική Όραση. Κατάτμηση Εικόνας
 Ε.Α.Υ. Υπολογιστική Όραση Κατάτμηση Εικόνας Γεώργιος Παπαϊωάννου 2015 ΚΑΤΩΦΛΙΩΣΗ Κατωφλίωση - Γενικά Είναι η πιο απλή μέθοδος segmentation εικόνας Χωρίζουμε την εικόνα σε 2 (binary) ή περισσότερες στάθμες
Ε.Α.Υ. Υπολογιστική Όραση Κατάτμηση Εικόνας Γεώργιος Παπαϊωάννου 2015 ΚΑΤΩΦΛΙΩΣΗ Κατωφλίωση - Γενικά Είναι η πιο απλή μέθοδος segmentation εικόνας Χωρίζουμε την εικόνα σε 2 (binary) ή περισσότερες στάθμες
Στροφορµή. υο παρατηρήσεις: 1) Η στροφορµή ενός υλικού σηµείου, που υπολογίζουµε µε βάση τα προηγούµενα, αναφέρεται. σε µια ορισµένη χρονική στιγµή.
 Στροφορµή Έστω ένα υλικό σηµείο που κινείται µε ταχύτητα υ και έστω ένα σηµείο Ο. Ορίζουµε στροφορµή του υλικού σηµείου ως προς το Ο, το εξωτερικό γινόµενο: L= r p= m r υ Όπου r η απόσταση του υλικού σηµείου
Στροφορµή Έστω ένα υλικό σηµείο που κινείται µε ταχύτητα υ και έστω ένα σηµείο Ο. Ορίζουµε στροφορµή του υλικού σηµείου ως προς το Ο, το εξωτερικό γινόµενο: L= r p= m r υ Όπου r η απόσταση του υλικού σηµείου
7 ο Εργαστήριο Θόρυβος 2Δ, Μετακίνηση, Περιστροφή
 7 ο Εργαστήριο Θόρυβος 2Δ, Μετακίνηση, Περιστροφή O θόρυβος 2Δ μας δίνει τη δυνατότητα να δημιουργίας υφής 2Δ. Στο παρακάτω παράδειγμα, γίνεται σχεδίαση γραμμών σε πλέγμα 300x300 με μεταβαλόμενη τιμή αδιαφάνειας
7 ο Εργαστήριο Θόρυβος 2Δ, Μετακίνηση, Περιστροφή O θόρυβος 2Δ μας δίνει τη δυνατότητα να δημιουργίας υφής 2Δ. Στο παρακάτω παράδειγμα, γίνεται σχεδίαση γραμμών σε πλέγμα 300x300 με μεταβαλόμενη τιμή αδιαφάνειας
ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
QR είναι ˆx τότε x ˆx. 10 ρ. Ποιά είναι η τιµή του ρ και γιατί (σύντοµη εξήγηση). P = [X. 0, X,..., X. (n 1), X. n] a(n + 1 : 1 : 1)
![QR είναι ˆx τότε x ˆx. 10 ρ. Ποιά είναι η τιµή του ρ και γιατί (σύντοµη εξήγηση). P = [X. 0, X,..., X. (n 1), X. n] a(n + 1 : 1 : 1) QR είναι ˆx τότε x ˆx. 10 ρ. Ποιά είναι η τιµή του ρ και γιατί (σύντοµη εξήγηση). P = [X. 0, X,..., X. (n 1), X. n] a(n + 1 : 1 : 1)](/thumbs/27/10724538.jpg) ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ I (22 Σεπτεµβρίου) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ 1ο ΘΕΜΑ 1. Αφού ορίσετε ακριβώς τι σηµαίνει πίσω ευσταθής υπολογισµός, να εξηγήσετε αν ο υ- πολογισµός του εσωτερικού γινοµένου δύο διανυσµάτων
ΕΠΙΣΤΗΜΟΝΙΚΟΣ ΥΠΟΛΟΓΙΣΜΟΣ I (22 Σεπτεµβρίου) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ 1ο ΘΕΜΑ 1. Αφού ορίσετε ακριβώς τι σηµαίνει πίσω ευσταθής υπολογισµός, να εξηγήσετε αν ο υ- πολογισµός του εσωτερικού γινοµένου δύο διανυσµάτων
Εντάξεις δικτύων GPS. 6.1 Εισαγωγή
 6 Εντάξεις δικτύων GPS 6.1 Εισαγωγή Oι απόλυτες (X, Y, Z ή σχετικές (ΔX, ΔY, ΔZ θέσεις των σηµείων, έτσι όπως προσδιορίζονται από τις µετρήσεις GPS, αναφέρονται στο γεωκεντρικό σύστηµα WGS 84 (Wrld Gedetic
6 Εντάξεις δικτύων GPS 6.1 Εισαγωγή Oι απόλυτες (X, Y, Z ή σχετικές (ΔX, ΔY, ΔZ θέσεις των σηµείων, έτσι όπως προσδιορίζονται από τις µετρήσεις GPS, αναφέρονται στο γεωκεντρικό σύστηµα WGS 84 (Wrld Gedetic
Κατανοµές. Η κατανοµή (distribution) µιας µεταβλητής (variable) φαίνεται από το σχήµα του ιστογράµµατος (histogram).
 Ιωάννης Παραβάντης Επίκουρος Καθηγητής Τµήµα ιεθνών και Ευρωπαϊκών Σπουδών Πανεπιστήµιο Πειραιώς Μάρτιος 2010 Κατανοµές 1. Οµοιόµορφη κατανοµή Η κατανοµή (distribution) µιας µεταβλητής (variable) φαίνεται
Ιωάννης Παραβάντης Επίκουρος Καθηγητής Τµήµα ιεθνών και Ευρωπαϊκών Σπουδών Πανεπιστήµιο Πειραιώς Μάρτιος 2010 Κατανοµές 1. Οµοιόµορφη κατανοµή Η κατανοµή (distribution) µιας µεταβλητής (variable) φαίνεται
Αλγόριθμος Ομαδοποίησης
 Αλγόριθμος Ομαδοποίησης Εμπειρίες από τη μελέτη αναλλοίωτων χαρακτηριστικών και ταξινομητών για συστήματα OCR Μορφονιός Κωνσταντίνος Αθήνα, Ιανουάριος 2002 Γενικά Ένα σύστημα OCR χρησιμοποιείται για την
Αλγόριθμος Ομαδοποίησης Εμπειρίες από τη μελέτη αναλλοίωτων χαρακτηριστικών και ταξινομητών για συστήματα OCR Μορφονιός Κωνσταντίνος Αθήνα, Ιανουάριος 2002 Γενικά Ένα σύστημα OCR χρησιμοποιείται για την
Επίλυση Γραµµικών Συστηµάτων
 Κεφάλαιο 3 Επίλυση Γραµµικών Συστηµάτων 31 Εισαγωγή Αριθµητική λύση γενικών γραµµικών συστηµάτων n n A n n x n 1 b n 1, όπου a 11 a 12 a 1n a 21 a 22 a 2n A [a i j, x a n1 a n2 a nn x n, b b 1 b 2 b n
Κεφάλαιο 3 Επίλυση Γραµµικών Συστηµάτων 31 Εισαγωγή Αριθµητική λύση γενικών γραµµικών συστηµάτων n n A n n x n 1 b n 1, όπου a 11 a 12 a 1n a 21 a 22 a 2n A [a i j, x a n1 a n2 a nn x n, b b 1 b 2 b n
ΚΕΣ 03: Αναγνώριση Προτύπων και Ανάλυση Εικόνας. KEΣ 03 Αναγνώριση Προτύπων και Ανάλυση Εικόνας. Κατάτµηση Εικόνων:
 KEΣ 3 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών Τµήµα Επιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
KEΣ 3 Αναγνώριση Προτύπων και Ανάλυση Εικόνας Κατάτµηση Εικόνων: Ανίχνευση Ακµών Τµήµα Επιστήµης και Τεχνολογίας Τηλεπικοινωνιών Πανεπιστήµιο Πελοποννήσου Περιεχόµενα Βιβλιογραφία Περιεχόµενα Ενότητας
Κεφάλαιο 4 Δείκτες Κεντρικής Τάσης
 Κεφάλαιο 4 Δείκτες Κεντρικής Τάσης 1 Οι Δείκτες Κεντρικής Τάσης Είναι αριθμητικές τιμές που δείχνουν το ΚΕΝΤΡΟ της κατανομής Η Δεσπόζουσα Τιμή (Δσπ) Η Διάμεσος (Δμ ή δ) Ο Μέσος Όρος (Μ.Ο) 2 Η Δεσπόζουσα
Κεφάλαιο 4 Δείκτες Κεντρικής Τάσης 1 Οι Δείκτες Κεντρικής Τάσης Είναι αριθμητικές τιμές που δείχνουν το ΚΕΝΤΡΟ της κατανομής Η Δεσπόζουσα Τιμή (Δσπ) Η Διάμεσος (Δμ ή δ) Ο Μέσος Όρος (Μ.Ο) 2 Η Δεσπόζουσα
Στροβιλισµός πεδίου δυνάµεων
 Στροβιλισµός πεδίου δυνάµεων Θεωρείστε ένα απειροστό απλό χωρίο στο χώρο τόσο µικρό ώστε να µπορεί να θεωρηθεί ότι βρίσκεται σε ένα επίπεδο Έστω ότι το χωρίο αυτό περικλείει εµβαδόν µέτρου Το έργο που
Στροβιλισµός πεδίου δυνάµεων Θεωρείστε ένα απειροστό απλό χωρίο στο χώρο τόσο µικρό ώστε να µπορεί να θεωρηθεί ότι βρίσκεται σε ένα επίπεδο Έστω ότι το χωρίο αυτό περικλείει εµβαδόν µέτρου Το έργο που
ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ. ΔΙΑΡΚΕΙΑ: 1 περιόδους. 28/9/2008 12:48 Όνομα: Λεκάκης Κωνσταντίνος καθ.
 ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ ΔΙΑΡΚΕΙΑ: 1 περιόδους 28/9/2008 12:48 καθ. Τεχνολογίας 28/9/2008 12:57 Προοπτικό σχέδιο με 2 Σημεία Φυγής Σημείο φυγής 1 Σημείο φυγής 2 Γωνία κτιρίου
ΘΕΜΑ : ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ΜΕ 2 Σ.Φ ΙΣΟΜΕΤΡΙΚΗ ΠΡΟΒΟΛΗ ΔΙΑΡΚΕΙΑ: 1 περιόδους 28/9/2008 12:48 καθ. Τεχνολογίας 28/9/2008 12:57 Προοπτικό σχέδιο με 2 Σημεία Φυγής Σημείο φυγής 1 Σημείο φυγής 2 Γωνία κτιρίου
Ακαδημαϊκό Έτος , Χειμερινό Εξάμηνο Διδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΕΣ 3: ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΚΑΙ ΑΝΑΛΥΣΗ ΕΙΚΟΝΑΣ Ακαδημαϊκό Έτος 7 8, Χειμερινό Εξάμηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Το παρόν
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΕΣ 3: ΑΝΑΓΝΩΡΙΣΗ ΠΡΟΤΥΠΩΝ ΚΑΙ ΑΝΑΛΥΣΗ ΕΙΚΟΝΑΣ Ακαδημαϊκό Έτος 7 8, Χειμερινό Εξάμηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Το παρόν
4. Μέθοδοι αναγνώρισης ταξινοµητές µε επόπτη
 ΑΕΙ Σερρών 4. Μέθοδοι αναγνώρισης ταξινοµητές µε επόπτη 4.. Αναγνώριση µε βάση τα κέντρα των τάξεων Είναι µια απλοϊκή µέθοδος αναγνώρισης µε επόπτη σύµφωνα µε την οποία κατά την εκµάθηση υπολογίζεται η
ΑΕΙ Σερρών 4. Μέθοδοι αναγνώρισης ταξινοµητές µε επόπτη 4.. Αναγνώριση µε βάση τα κέντρα των τάξεων Είναι µια απλοϊκή µέθοδος αναγνώρισης µε επόπτη σύµφωνα µε την οποία κατά την εκµάθηση υπολογίζεται η
Physics by Chris Simopoulos
 Στο παρακάτω σχήµα: ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΓΥΜΝΑΣΙΟΥ ΠΑΡΑ ΕΙΓΜΑ ο α) Να ορίσετε τις θέσεις των σηµείων (Α), (Β) και (Γ). β) Να υπολογίσετε τη µετατόπιση (ΑΓ). γ) Να υπολογίσετε το διάστηµα (ΑΒΓ).
Στο παρακάτω σχήµα: ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ Β ΓΥΜΝΑΣΙΟΥ ΠΑΡΑ ΕΙΓΜΑ ο α) Να ορίσετε τις θέσεις των σηµείων (Α), (Β) και (Γ). β) Να υπολογίσετε τη µετατόπιση (ΑΓ). γ) Να υπολογίσετε το διάστηµα (ΑΒΓ).
, όπου οι σταθερές προσδιορίζονται από τις αρχικές συνθήκες.
 Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
Στην περίπτωση της ταλάντωσης µε κρίσιµη απόσβεση οι δύο γραµµικώς ανεξάρτητες λύσεις εκφυλίζονται (καταλήγουν να ταυτίζονται) Στην περιοχή ασθενούς απόσβεσης ( ) δύο γραµµικώς ανεξάρτητες λύσεις είναι
( ) Κλίση και επιφάνειες στάθµης µιας συνάρτησης. x + y + z = κ ορίζει την επιφάνεια µιας σφαίρας κέντρου ( ) κ > τότε η
 Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Κεφάλαιο 6 Ιστογράμματα δορυφορικών εικόνων
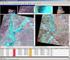 Κεφάλαιο 6 Ιστογράμματα δορυφορικών εικόνων Κωνσταντίνος Γ. Περάκης Σύνοψη Μία γενική επισκόπηση με εστίαση στη χρήση των ιστογραμμάτων στην Τηλεπισκόπηση και περιγραφές ειδικών εικόνων με τα χαρακτηριστικά
Κεφάλαιο 6 Ιστογράμματα δορυφορικών εικόνων Κωνσταντίνος Γ. Περάκης Σύνοψη Μία γενική επισκόπηση με εστίαση στη χρήση των ιστογραμμάτων στην Τηλεπισκόπηση και περιγραφές ειδικών εικόνων με τα χαρακτηριστικά
Κώδικας σχεδίασης Λογισµικής ιαγραµµατικής Οντολογίας
 Κώδικας σχεδίασης Λογισµικής ιαγραµµατικής Οντολογίας Αρχιµήδης ΙΙΙ Υποέργο 18 2013 Ενα µάγµα µπορεί να εξελιχθεί κάτω από την επίδραση τριών ειδών επιρροών. Την εξέλιξη αυτή συµβολίζουµε µε ένα απλό τόξο
Κώδικας σχεδίασης Λογισµικής ιαγραµµατικής Οντολογίας Αρχιµήδης ΙΙΙ Υποέργο 18 2013 Ενα µάγµα µπορεί να εξελιχθεί κάτω από την επίδραση τριών ειδών επιρροών. Την εξέλιξη αυτή συµβολίζουµε µε ένα απλό τόξο
Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση
 8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να:
 6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να: ορίσουµε το Μετασχηµατισµό Laplace (ML) και το Μονόπλευρο Μετασχηµατισµό Laplace (MML) και να περιγράψουµε
6. ΚΕΦΑΛΑΙΟ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ LAPLACE Όταν θα έχουµε τελειώσει το Κεφάλαιο αυτό θα µπορούµε να: ορίσουµε το Μετασχηµατισµό Laplace (ML) και το Μονόπλευρο Μετασχηµατισµό Laplace (MML) και να περιγράψουµε
Μετασχηματισμοί Μοντελοποίησης (modeling transformations)
 Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Μετασχηµατισµοί 2 & 3
 Μετασχηµατισµοί & 3 Περιγράφονται σαν σύνεση βασικών: µετατόπιση αλλαγή κλίµακαςπεριστροφή στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών Θέση
Μετασχηµατισµοί & 3 Περιγράφονται σαν σύνεση βασικών: µετατόπιση αλλαγή κλίµακαςπεριστροφή στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών Θέση
Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση
 8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα. Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
8 Υπολογισµός διπλών ολοκληρωµάτων µε διαδοχική ολοκλήρωση Υπάρχουν δύο θεµελιώδη αποτελέσµατα που µας βοηθούν να υπολογίζουµε πολλαπλά ολοκληρώµατα. Το πρώτο αποτέλεσµα σχετίζεται µε τον υπολογισµό ενός
Υπολογιστικές μέθοδοι για την ανάλυση της πληροφορίας των εικόνων και την κατανόηση του περιεχομένου
 Ανάλυση Εικόνων Εικόνα : μορφή πληροφορίας Ανάλυση : εξαγωγή γνώσης Υπολογιστικές μέθοδοι για την ανάλυση της πληροφορίας των εικόνων και την κατανόηση του περιεχομένου Θέματα ειδίκευσης Υπολογιστική Όραση
Ανάλυση Εικόνων Εικόνα : μορφή πληροφορίας Ανάλυση : εξαγωγή γνώσης Υπολογιστικές μέθοδοι για την ανάλυση της πληροφορίας των εικόνων και την κατανόηση του περιεχομένου Θέματα ειδίκευσης Υπολογιστική Όραση
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
Ερωτήσεις αντιστοίχισης
 Ερωτήσεις αντιστοίχισης 1. ** Να αντιστοιχίσετε κάθε ευθεία που η εξίσωσή της βρίσκεται στη του πίνακα (Ι) µε τον συντελεστή της που βρίσκεται στη, συµπληρώνοντας τον πίνακα (ΙΙ) (α, β 0). 1. ε 1 : y =
Ερωτήσεις αντιστοίχισης 1. ** Να αντιστοιχίσετε κάθε ευθεία που η εξίσωσή της βρίσκεται στη του πίνακα (Ι) µε τον συντελεστή της που βρίσκεται στη, συµπληρώνοντας τον πίνακα (ΙΙ) (α, β 0). 1. ε 1 : y =
Ειδικά Θέµατα Υπολογιστικής Όρασης & Γραφικής. Εµµανουήλ Ζ. Ψαράκης & Αθανάσιος Τσακαλίδης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Ειδικά Θέµατα Υπολογιστικής Όρασης & Γραφικής Εµµανουήλ Ζ. Ψαράκης & Αθανάσιος Τσακαλίδης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Σύνθεση Πανοράµατος Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή
Ειδικά Θέµατα Υπολογιστικής Όρασης & Γραφικής Εµµανουήλ Ζ. Ψαράκης & Αθανάσιος Τσακαλίδης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Σύνθεση Πανοράµατος Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 9 : Κωδικοποίηση βίντεο Πρότυπο συμπίεσης MPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 9 : Κωδικοποίηση βίντεο Πρότυπο συμπίεσης MPEG Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το
1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός.
 1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός. ( Καρτεσιανή ) επιλέχθηκε για το σχήµα. Ο αριθµός a δεν επιρρεάζει
1)Βρείτε την εξίσωση για το επίπεδο που περιέχει το σηµείο (1,-1,3) και είναι παράλληλο προς το επίπεδο 3x+y+z=a όπου a ένας αριθµός. ( Καρτεσιανή ) επιλέχθηκε για το σχήµα. Ο αριθµός a δεν επιρρεάζει
Εισαγωγή στον Προγραµµατισµό. Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
 Εισαγωγή στον Προγραµµατισµό Αριθµητική Ανάλυση (ή Επιστηµονικοί Υπολογισµοί) ιδάσκοντες: Καθηγητής Ν. Μισυρλής, Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 8 εκεµβρίου 2014 Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
Εισαγωγή στον Προγραµµατισµό Αριθµητική Ανάλυση (ή Επιστηµονικοί Υπολογισµοί) ιδάσκοντες: Καθηγητής Ν. Μισυρλής, Επίκ. Καθηγητής Φ.Τζαφέρης ΕΚΠΑ 8 εκεµβρίου 2014 Ανάλυση (ή Επιστηµονικοί8 Υπολογισµοί)
