ΘΕΜΑ Α Α1. Έστω συνεχής συνάρτηση f:[ α, β ] με παράγουσα συνάρτηση F. Τι ονομάζεται ορισμένο ολοκλήρωμα της συνάρτησης f από το α έως το β;
|
|
|
- Ολυμπιάς Κοσμόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Ανκτήθηκε πό την Εκπιδευτική Κλίμκ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 3 ΜΑΪΟΥ 013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ι ΗΜΕΡΗΣΙΑ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1. Έστω συνεχής συνάρτηση f:[, ] με πράγουσ συνάρτηση F. Τι ονομάζετι ορισμένο ολοκλήρωμ της συνάρτησης f πό το έως το ; ΤΕΛΟΣ 1ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ Μονάδες 6 Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς, δίπλ στο γράμμ που ντιστοιχεί σε κάθε πρότση, τη λέξη Σωστό, ν η πρότση είνι σωστή ή τη λέξη Λάθος, ν η πρότση είνι λνθσμένη. ) Εάν η τιμή του συντελεστή μετλητότητς είνι κάτω του 10%, ο πληθυσμός του δείγμτος θεωρείτι ομοιογενής. (Μον. ) ) Εάν οι συνρτήσεις f,g:a είνι πργωγίσιμες στο πεδίο ορισμού τους, με g(x) 0, τότε ισχύει: f ' f '(x) g(x) f(x)g '(x) (x) =. g g (x) (Μον. ) γ) Εάν μι συνάρτηση f δεν είνι συνεχής σε έν σημείο x 0 του πεδίου ορισμού της, τότε είνι πργωγίσιμη στο x 0. (Μον. )
2 Ανκτήθηκε πό την Εκπιδευτική Κλίμκ ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ δ) Ισχύει ότι: ex dx e e = + 1 με 1 κι (Μον. ) ε) ίνοντι οι συνρτήσεις f,g συνεχείς στο [,]. Αν f(x) g(x) γι κάθε x [, ], τότε f(x) dx g(x) dx. (Μον. ) Μονάδες 10 Α3. Ν μετφέρετε στο τετράδιό σς τις πρκάτω ισότητες κι ν τις συμπληρώσετε: ) ημ xdx =... (Μον. 3) ) Αν η συνάρτηση f είνι πργωγίσιμη στο κι c μί στθερά, τότε: (c f) (x)=... γ) Αν * κι x > 0, τότε: (x ) =... (Μον. 3) (Μον. 3) ΘΕΜΑ B ίνετι η συνάρτηση f:(0, + ) με τύπο: Μονάδες 9 f(x) x+ lnx, ν 0< x 1κι = x x x+ 3, ν x > 1 ΤΕΛΟΣ ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
3 Ανκτήθηκε πό την Εκπιδευτική Κλίμκ ΑΡΧΗ 3ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ Β1. Ν ρείτε το lim f(x). x 1 - Β. Ν δείξετε ότι Μονάδες 7 lim x 1 + f(x)=4. Μονάδες 10 Β3. Ν ρείτε γι ποιες τιμές του η συνάρτηση f είνι συνεχής στο x 0 =1. ΘΕΜΑ Γ Μονάδες 8 Στον πρκάτω πίνκ προυσιάζοντι οι μισθοί των υπλλήλων μίς ετιρείς (σε εκτοντάδες ): Μισθός (εκτοντάδες ) x i Συχνότητ (ριθμός υπλλήλων) ν i Σχετική συχνότητ f i % Σύνολ ν= x i ν i Γ1. Ν μετφέρετε στο τετράδιό σς τον πρπάνω πίνκ κι ν τον συμπληρώσετε. Μονάδες 5 Γ. Ν υπολογίσετε τη μέση τιμή x των μισθών των υπλλήλων. Μονάδες 5 Γ3. Τι ποσοστό υπλλήλων έχουν μισθό το πολύ 1000 ; Μονάδες 7 ΤΕΛΟΣ 3ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
4 Ανκτήθηκε πό την Εκπιδευτική Κλίμκ ΑΡΧΗ 4ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ Γ4. Ν υπολογίσετε τη δικύμνση s των μισθών των υπλλήλων της ετιρείς. ΘΕΜΑ ίνετι η συνάρτηση f(x) = (x ) (x + ), x,. Μονάδες 8 1. Ν ποδείξετε ότι η πράγωγος της συνάρτησης f είνι f(x) ' = (x )(3x+ ), x. Μονάδες 5. Ν ρείτε τον ριθμό, ν η συνάρτηση f προυσιάζει κρόττο στο x 0 =4. Μονάδες 5 3. Γι =-5, ν μελετήσετε τη συνάρτηση f ως προς τη μονοτονί κι ν ρείτε το είδος κι τις τιμές των κροτάτων. Μονάδες 8 4. ίνοντι οι συνρτήσεις g(x)=3x -1x, x κι h(x)=6x-4, x. Ν ρείτε το εμδόν του χωρίου Ω, που περικλείετι πό τις γρφικές πρστάσεις των συνρτήσεων g(x) κι h(x). Ο ΗΓΙΕΣ ΓΙΑ ΤΟΥΣ ΕΞΕΤΑΖΟΜΕΝΟΥΣ Μονάδες 7 1. Στο τετράδιο ν γράψετε μόνον τ προκτρκτικά (ημερομηνί, εξετζόμενο μάθημ). Ν μην ντιγράψετε τ θέμτ στο τετράδιο.. Ν γράψετε το ονομτεπώνυμό σς στο πάνω μέρος των φωτοντιγράφων μέσως μόλις σς πρδοθούν. εν επιτρέπετι ν γράψετε κμιά άλλη σημείωση. Κτά την ΤΕΛΟΣ 4ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
5 Ανκτήθηκε πό την Εκπιδευτική Κλίμκ ΑΡΧΗ 5ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ποχώρησή σς ν πρδώσετε μζί με το τετράδιο κι τ φωτοντίγρφ. 3. Ν πντήσετε στο τετράδιό σς σε όλ τ θέμτ. 4. Ν γράψετε τις πντήσεις σς μόνον με μπλε ή μόνον με μύρο στυλό νεξίτηλης μελάνης. 5. Κάθε πάντηση τεκμηριωμένη επιστημονικά είνι ποδεκτή. 6. ιάρκει εξέτσης: τρεις (3) ώρες μετά τη δινομή των φωτοντιγράφων. 7. Χρόνος δυντής ποχώρησης: π.μ. KΑΛΗ ΕΠΙΤΥΧΙΑ ΤΕΛΟΣ ΜΗΝΥΜΑΤΟΣ ΤΕΛΟΣ 5ΗΣ ΑΠΟ 5 ΣΕΛΙ ΕΣ
6 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 3 ΜΑΪΟΥ 013 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ι ΘΕΜΑ A A1. Θεωρί σχολικού ιλίου σελίδ 34 A.. Σωστό,. Σωστό, γ. Λάθος, δ. Λάθος ν κι Σωστό ν =, ε. Σωστό. Α3... γ. ημx dx = c f (x) = c f (x) x = x - 1 -συνx = -συν + συν ΘΕΜΑ Β Β1. im f (x) = im x + nx = - - x1 x1 + x1 x - x Β. im f (x) = im = im x1 x1 x x1 x x = x (x - 1) im x(x - 1) x x im x - 1 x1 + = x x = 4. Β3. f (1) = 1 + n1 = - + x1 x1 = 4 Γι ν είνι η f συνεχής στο x = 1 πρέπει im f (x) = im f (x) = f (1) = 0
7 ΘΕΜΑ Γ Γ1. x i v i f i % x. i v i ΣΥΝΟΛΑ ν = Γ. x v + x v + x v + x v 450 v + v + v + v x = = = 9 εκτοντάδες ευρώ Γ = 10 εκτοντάδες f 1 % + f % = 50% + 34% = 84% άρ το 84% των υπλλήλων έχουν μισθό το πολύ Γ4. x i v i x. i v i x - x i ( x - x i ) ( x - x i ) v i ΣΥΝΟΛΑ ν = (x-x 1) v 1 + (x-x ) v + (x-x 3 ) v 3 + (x-x 4 ) v4 700 s = = = 14 v + v + v + v
8 ΘΕΜΑ Δ Δ1. f (x) = (x - ) (x + ) f (x) = (x - ) (x + ) = (x - ) (x + ) + (x - ) (x + ) = (x - ) (x - ) (x + ) + (x - ) 1 = (x - ) (x + ) + (x - ) = (x - ) (x + ) + (x - ) = (x - ) (x + + x - ) = (x - ) (3x + - ) Δ. Γι ν προυσιάζει η συνάρτηση κρόττο στο x 0 = 4, πρέπει f (4) = 0 (4 - )( ) = 0 ( + 10) = = 0 = -10 = -5 Δ3. f (x) = (x - ) (x - 5) f (x) = (x - ) (3x - 1) = 3x - 6x + 4 f (x) = 0 (x - ) (3x - 1) = 0 x = ή x = 4 x f (x) f (x) H f είνι γνησίως ύξουσ στ (-, ] κι [4, +) ενώ είνι γνησίως φθίνουσ στο [, 4]. Η f προυσιάζει τοπικό μέγιστο γι x = την τιμή f () = 0 Η f προυσιάζει τοπικό ελάχιστο γι x = 4 την τιμή f (4) = -4 Δ4. g (x) - h (x) = 3x - 1x - (6x - 4) = 3x - 6x + 4 = f (x) Είνι f (x) 0 στο [, 4] πό Δ3 ερώτημ 4 4 Ε = - f (x) dx = - f (x) = - f (4) - f () = f () - f (4) = 4 τ.μ.
ΘΕΜΑ Α Α1. Έστω συνεχής συνάρτηση f:[ α, β ] με παράγουσα συνάρτηση F. Τι ονομάζεται ορισμένο ολοκλήρωμα της συνάρτησης f από το α έως το β;
![ΘΕΜΑ Α Α1. Έστω συνεχής συνάρτηση f:[ α, β ] με παράγουσα συνάρτηση F. Τι ονομάζεται ορισμένο ολοκλήρωμα της συνάρτησης f από το α έως το β; ΘΕΜΑ Α Α1. Έστω συνεχής συνάρτηση f:[ α, β ] με παράγουσα συνάρτηση F. Τι ονομάζεται ορισμένο ολοκλήρωμα της συνάρτησης f από το α έως το β;](/thumbs/81/84354683.jpg) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 3 ΜΑΪΟΥ 013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 3 ΜΑΪΟΥ 013 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 3 IOYNIOY 014 ΕΞΕΤΑΖΟΜΕΝΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 3 IOYNIOY 014 ΕΞΕΤΑΖΟΜΕΝΟ
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 4 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 4 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΟΜΑ Α Β ΤΡΙΤΗ 3 IOYNIOY 4 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΟΜΑ Α A ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΟΜΑ Α Β ΤΡΙΤΗ 3 IOYNIOY 4 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 24 ΜΑΪΟΥ 202 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 24 ΜΑΪΟΥ 202 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 3 IOYNIOY 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 3 IOYNIOY 04 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. Α.3 Πότε η ευθεία y = λέγεται οριζόντια ασύμπτωτη της γραφικής παράστασης της f στο + ; Μονάδες 3
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 4 ΜΑΪΟΥ 7 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1 o A.1 Αν z
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 4 ΜΑΪΟΥ 7 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1 o A.1 Αν z
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 1 x. Μονάδες 10 Α.2 Πότε μια συνάρτηση f λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα [α,β]; Μονάδες 5
![ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 1 x. Μονάδες 10 Α.2 Πότε μια συνάρτηση f λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα [α,β]; Μονάδες 5 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 1 x. Μονάδες 10 Α.2 Πότε μια συνάρτηση f λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα [α,β]; Μονάδες 5](/thumbs/101/148382957.jpg) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1 o A.1
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 24 ΜΑΪΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1 o A.1
είναι μιγαδικοί αριθμοί, τότε ισχύει , z 2 Μονάδες 2 β. Μία συνάρτηση f με πεδίο ορισμού Α λέμε ότι παρουσιάζει (ολικό) ελάχιστο στο x 0
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ ΜΑΪΟΥ 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ ΜΑΪΟΥ 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΘΕΜΑ Α Α1. Τι ονομάζεται διάμεσος δ ενός δείγματος ν παρατηρήσεων που έχουν διαταχθεί σε αύξουσα σειρά;
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑΔΑ A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑΔΑ Β ) ΠΕΜΠΤΗ 4 ΜΑΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ι ΗΜΕΡΗΣΙΑ ΘΕΜΑ
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑΔΑ A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙΔΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑΔΑ Β ) ΠΕΜΠΤΗ 4 ΜΑΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ι ΗΜΕΡΗΣΙΑ ΘΕΜΑ
Επαναληπτικό Διαγώνισµα Μαθηµατικών Γ Λυκείου ΕΠΑΛ
 ΘΕΜΑ Α Επνληπτικό Διγώνισµ Μθηµτικών Γ Λυκείου ΕΠΑΛ Α. Ν δώσετε τον ορισµό της συχνότητς κι της σχετικής συχνότητς µις πρτήρησης x i. (7 Μονάδες) Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς
ΘΕΜΑ Α Επνληπτικό Διγώνισµ Μθηµτικών Γ Λυκείου ΕΠΑΛ Α. Ν δώσετε τον ορισµό της συχνότητς κι της σχετικής συχνότητς µις πρτήρησης x i. (7 Μονάδες) Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς
ΜΑΘΗΜΑΤΙΚΑ ΕΠΑ.Λ. Α ΟΜΑ ΑΣ 2011 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΕΠΑ.Λ. Α ΟΜΑ ΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Α. Τι ονοµάζετι εύρος µις µετβλητής; Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς, δίπλ στο γράµµ που ντιστοιχεί σε κάθε πρότση,
ΜΑΘΗΜΑΤΙΚΑ ΕΠΑ.Λ. Α ΟΜΑ ΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α. Α. Τι ονοµάζετι εύρος µις µετβλητής; Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς, δίπλ στο γράµµ που ντιστοιχεί σε κάθε πρότση,
β) Αν υπάρχουν τα limf (x), και είναι γ) Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, τότε ισχύει: ( f g ) (x) = f (x) g (x), x
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 4 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 4 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΕΙΟΥ ΠΕΜΠΤΗ 9 ΙΟΥΝΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Γι τις ερωτήσεις 1.1-1.4 ν γράψετε στο
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΕΙΟΥ ΠΕΜΠΤΗ 9 ΙΟΥΝΙΟΥ 2005 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΗΣ ΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Γι τις ερωτήσεις 1.1-1.4 ν γράψετε στο
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 19 ΜΑΪOY 16 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Α1. Να αποδείξετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 19 ΜΑΪOY 16 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Α1. Να αποδείξετε
( ) = ( ) για κάθε. Θέμα Δ. x 2. Δίνονται οι συναρτήσεις f x
 ΔΙΑΓΩΝΙΣΜΑΤΑ Διγώνισμ Θέμ Α Α Ν ποδειχθεί ότι η συνάρτηση f = ln,, είνι πργωγίσιμη στο κι ισχύει f = Μονάδες 7 Α Πότε μί συνάρτηση f λέμε ότι είνι πργωγίσιμη σε έν σημείο του πεδίου ορισμού της; Α Πότε
ΔΙΑΓΩΝΙΣΜΑΤΑ Διγώνισμ Θέμ Α Α Ν ποδειχθεί ότι η συνάρτηση f = ln,, είνι πργωγίσιμη στο κι ισχύει f = Μονάδες 7 Α Πότε μί συνάρτηση f λέμε ότι είνι πργωγίσιμη σε έν σημείο του πεδίου ορισμού της; Α Πότε
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ' ΛΥΚΕΙΟΥ (27 /5/ 2004)
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ' ΛΥΚΕΙΟΥ (7 /5/ 4) ΘΕΜΑ ο Α. Έστω μι συνάρτηση f ορισμένη σ' έν διάστημ Δ κι έν εσωτερικό σημείο του Δ. Αν η f προυσιάζει τοπικό κρόττο στο κι είνι πργωγίσιμη
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ' ΛΥΚΕΙΟΥ (7 /5/ 4) ΘΕΜΑ ο Α. Έστω μι συνάρτηση f ορισμένη σ' έν διάστημ Δ κι έν εσωτερικό σημείο του Δ. Αν η f προυσιάζει τοπικό κρόττο στο κι είνι πργωγίσιμη
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 20 ΜΑΪΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 1 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ ΜΑΪΟΥ 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θέµ 1ο Α. Έστω µι συνεχής συνάρτηση f ορισµένη σε έν διάστηµ.
1 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ ΜΑΪΟΥ 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Θέµ 1ο Α. Έστω µι συνεχής συνάρτηση f ορισµένη σε έν διάστηµ.
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 19 ΜΑΪOY 16 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Α1. Να αποδείξετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 19 ΜΑΪOY 16 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Α1. Να αποδείξετε
ΜΑΘΗΜΑΤΙΚΑ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2006 ΕΚΦΩΝΗΣΕΙΣ
 ΘΕΜΑ o ΜΑΘΗΜΑΤΙΚΑ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 006 ΕΚΦΩΝΗΣΕΙΣ A Έστω µι συνάρτηση, η οποί είνι συνεχς σε έν διάστηµ Ν ποδείξετε ότι: Αν >0 σε κάθε εσωτερικό σηµείο του, τότε η είνι γνησίως
ΘΕΜΑ o ΜΑΘΗΜΑΤΙΚΑ Γ' ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 006 ΕΚΦΩΝΗΣΕΙΣ A Έστω µι συνάρτηση, η οποί είνι συνεχς σε έν διάστηµ Ν ποδείξετε ότι: Αν >0 σε κάθε εσωτερικό σηµείο του, τότε η είνι γνησίως
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 1 ΜΑΪOY 015 ΕΞΕΤΑΖΟΜΕΝΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 1 ΜΑΪOY 015 ΕΞΕΤΑΖΟΜΕΝΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. Μονάδες 9 B. Έστω μια συνάρτηση f και x o ένα σημείο του πεδίου ορισμού της. Πότε θα λέμε ότι η f είναι συνεχής στο x o ; Μονάδες 6
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 9 ΙΟΥΛΙΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 9 ΙΟΥΛΙΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ. 1. y - -2 x + π. f (x) = 3x, x = 1. π y = 9 x - 6. δ. f (x) = x, x0. 4. y = -9 x + 5. (2000-1ο)
 ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ 6 Α) Αν η συνάρτηση f είνι πργωγίσιµη σε έν σηµείο του πεδίου ορισµού της, ν γρφεί η εξίσωση της εφπτοµένης της γρφ πρ/σης της f στο σηµείο A(,f ( )) Α) Ν ποδείξετε ότι ν µι συνάρτηση f
ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ 6 Α) Αν η συνάρτηση f είνι πργωγίσιµη σε έν σηµείο του πεδίου ορισµού της, ν γρφεί η εξίσωση της εφπτοµένης της γρφ πρ/σης της f στο σηµείο A(,f ( )) Α) Ν ποδείξετε ότι ν µι συνάρτηση f
α) Στο μιγαδικό επίπεδο οι εικόνες δύο συζυγών μιγαδικών είναι σημεία συμμετρικά ως προς τον πραγματικό άξονα
 Α Π Α Ν Τ Η Σ Ε Ι Σ Θ Ε Μ Α Τ Ω Ν Π Α Ν Ε Λ Λ Α Δ Ι Κ Ω Ν Ε Ξ Ε Τ Α Σ Ε Ω Ν ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ 8.5. ΘΕΜΑ Α A. Έστω μι συνάρτηση f η οποί είνι συνεχής σε έν διάστημ Δ.
Α Π Α Ν Τ Η Σ Ε Ι Σ Θ Ε Μ Α Τ Ω Ν Π Α Ν Ε Λ Λ Α Δ Ι Κ Ω Ν Ε Ξ Ε Τ Α Σ Ε Ω Ν ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ 8.5. ΘΕΜΑ Α A. Έστω μι συνάρτηση f η οποί είνι συνεχής σε έν διάστημ Δ.
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 30 ΜΑΪΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΜΑΘΗΜΑΤΙΚΑ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 3 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o A. Έστω µι συνεχής συνάρτηση σ' έν διάστηµ [, ]. Αν G είνι µι πράγουσ
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 3 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o A. Έστω µι συνεχής συνάρτηση σ' έν διάστηµ [, ]. Αν G είνι µι πράγουσ
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2004
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑο Α Έστω µι συνάρτηση f ορισµένη σ' έν διάστηµ κι έν εσωτερικό σηµείο του Αν η f προυσιάζει τοπικό κρόττο στο κι είνι πργωγίσιµη
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑο Α Έστω µι συνάρτηση f ορισµένη σ' έν διάστηµ κι έν εσωτερικό σηµείο του Αν η f προυσιάζει τοπικό κρόττο στο κι είνι πργωγίσιµη
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 2004
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑο Α Έστω µι συνάρτηση f ορισµένη σ' έν διάστηµ κι έν εσωτερικό σηµείο του Αν η f προυσιάζει τοπικό κρόττο στο κι είνι πργωγίσιµη στο σηµείο
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ 4 ΘΕΜΑο Α Έστω µι συνάρτηση f ορισµένη σ' έν διάστηµ κι έν εσωτερικό σηµείο του Αν η f προυσιάζει τοπικό κρόττο στο κι είνι πργωγίσιµη στο σηµείο
ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ. 1. y - -2 x + π. f (x) = 3x, x = 1. π y = 9 x - 6. δ. f (x) = x, x0. 4. y = -9 x + 5. (2000-1ο) ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ 6 Α) Αν η συνάρτηση f είνι πργωγίσιµη σε έν σηµείο του πεδίου ορισµού της, ν γρφεί η εξίσωση της εφπτοµένης της γρφ πρ/σης της f στο σηµείο A(,f ( )) Α)
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ 6 Α) Αν η συνάρτηση f είνι πργωγίσιµη σε έν σηµείο του πεδίου ορισµού της, ν γρφεί η εξίσωση της εφπτοµένης της γρφ πρ/σης της f στο σηµείο A(,f ( )) Α)
ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2015
 ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 05 ΘΕΜΑ Α. Γι μι συνεχή συνάρτηση f ν γράψετε τις τρείς κτηγορίες σημείων, τ οποί εινι πιθνές θέσεις τοπικών κροτάτων. (6 Μονάδες). Ν χρκτηρίσετε τις προτάσεις
ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 05 ΘΕΜΑ Α. Γι μι συνεχή συνάρτηση f ν γράψετε τις τρείς κτηγορίες σημείων, τ οποί εινι πιθνές θέσεις τοπικών κροτάτων. (6 Μονάδες). Ν χρκτηρίσετε τις προτάσεις
ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ «ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ» ΕΠΑ.Λ.
 ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ «ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ» ΕΠΑ.Λ. ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ
ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ «ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ» ΕΠΑ.Λ. ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ
Σάββατο, 27 Μαΐου 2006 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ. A.1. Έστω συνάρτηση f, η οποία είναι συνεχής σε ένα διάστηµα Δ. Να αποδείξετε ότι:
 Σάββτο, 7 Μΐου 006 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o A.. Έστω συνάρτηση, η οποί είνι συνεχής σε έν διάστηµ Δ. Ν ποδείξετε ότι: Αν (>0 σε κάθε εσωτερικό σηµείο x του Δ, τότε η είνι γνησίως ύξουσ σε
Σάββτο, 7 Μΐου 006 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o A.. Έστω συνάρτηση, η οποί είνι συνεχής σε έν διάστηµ Δ. Ν ποδείξετε ότι: Αν (>0 σε κάθε εσωτερικό σηµείο x του Δ, τότε η είνι γνησίως ύξουσ σε
4o Επαναληπτικό Διαγώνισμα 2016
 wwwaskisopolisgr ΘΕΜΑ A 4o Επνληπτικό Διγώνισμ 6 Διάρκει: ώρες Α Έστω μι συνάρτηση f πργωγίσιμη σ έν διάστημ,, με εξίρεση ίσως έν σημείο του f διτηρεί πρόσημο στο,,, ν,στο οποίο όμως η f είνι συνεχής Αν
wwwaskisopolisgr ΘΕΜΑ A 4o Επνληπτικό Διγώνισμ 6 Διάρκει: ώρες Α Έστω μι συνάρτηση f πργωγίσιμη σ έν διάστημ,, με εξίρεση ίσως έν σημείο του f διτηρεί πρόσημο στο,,, ν,στο οποίο όμως η f είνι συνεχής Αν
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 21 ΜΑΪOY 2015 ΕΞΕΤΑΖΟΜΕΝΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 21 ΜΑΪOY 2015 ΕΞΕΤΑΖΟΜΕΝΟ
Α2. Πότε μία συνάρτηση f λέγεται γνησίως φθίνουσα σε ένα διάστημα του πεδίου ορισμού της; Μονάδες 3
 Βθμός: /25 Τεστ Μθημτικών Εξετζόμενος-η: Προσντολισμού, Γ Λυκείου Θεωρί 1 Κθηγητής: Ιορδάνης Χτζηνικολάου Συνρτήσεις Θέμ Α Α1. Ν ποδείξετε ότι οι γρφικές πρστάσεις C κι C των συνρτήσεων f κι f 1 είνι συμμετρικές
Βθμός: /25 Τεστ Μθημτικών Εξετζόμενος-η: Προσντολισμού, Γ Λυκείου Θεωρί 1 Κθηγητής: Ιορδάνης Χτζηνικολάου Συνρτήσεις Θέμ Α Α1. Ν ποδείξετε ότι οι γρφικές πρστάσεις C κι C των συνρτήσεων f κι f 1 είνι συμμετρικές
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Α =, Β = α. Να υπολογίσετε τον πίνακα 3Α - 4Β. Μονάδες 5. β. Να υπολογίσετε τον πίνακα Χ έτσι ώστε να ισχύει: 2Α + Χ = 3Β Μονάδες 10
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΕΣΠΕΡΙΝΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΕΣΠΕΡΙΝΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ
3ο Επαναληπτικό διαγώνισμα στα Μαθηματικά κατεύθυνσης της Γ Λυκείου Θέμα A
 3ο Επνληπτικό διγώνισμ στ Μθημτικά κτεύθυνσης της Γ Λυκείου 17-18 Θέμ A Α1 Έστω f μι συνεχής συνάρτηση σ έν διάστημ β ν ποδείξετε ότι: f t dt G β G Α Πότε μι συνάρτηση λέγετι 1-1; Α3 Πότε μι συνάρτηση
3ο Επνληπτικό διγώνισμ στ Μθημτικά κτεύθυνσης της Γ Λυκείου 17-18 Θέμ A Α1 Έστω f μι συνεχής συνάρτηση σ έν διάστημ β ν ποδείξετε ότι: f t dt G β G Α Πότε μι συνάρτηση λέγετι 1-1; Α3 Πότε μι συνάρτηση
με x1 x2 , τότε η f είναι γνησίως αύξουσα στο Α. β) Αν για μια συνάρτηση f: ισχύει ότι f x , τότε το σύνολο τιμών της δεν μπορεί να είναι της μορφής,
 Μθημτικά κτεύθυνσης Γ Λυκείου ο Διγώνισμ διάρκεις ωρών στις Συνρτήσεις κι τ Όρι Οκτώβριος Θέμ Α Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς την ένδειξη Σωστό ή Λάθος δίπλ στο
Μθημτικά κτεύθυνσης Γ Λυκείου ο Διγώνισμ διάρκεις ωρών στις Συνρτήσεις κι τ Όρι Οκτώβριος Θέμ Α Α. Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς την ένδειξη Σωστό ή Λάθος δίπλ στο
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 5 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 5 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Γι τις ερωτήσεις 1.1-1.4 ν γράψετε
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Σ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 5 ΙΟΥΝΙΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΕΞΙ (6) ΘΕΜΑ 1ο Γι τις ερωτήσεις 1.1-1.4 ν γράψετε
β ] και συνεχής στο ( a, β ], τότε η f παίρνει πάντοτε στο [ a,
![β ] και συνεχής στο ( a, β ], τότε η f παίρνει πάντοτε στο [ a, β ] και συνεχής στο ( a, β ], τότε η f παίρνει πάντοτε στο [ a,](/thumbs/53/31826077.jpg) ΕΡΩΤΗΣΕΙΣ Σ Λ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΑΔΙΚΩΝ - Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς την ένδειξη σωστό ή λάθος δίπλ στο γράμμ που ντιστοιχεί σε κάθε πρότση
ΕΡΩΤΗΣΕΙΣ Σ Λ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΠΑΝΕΛΛΑΔΙΚΩΝ - Ν χρκτηρίσετε τις προτάσεις που κολουθούν, γράφοντς στο τετράδιό σς την ένδειξη σωστό ή λάθος δίπλ στο γράμμ που ντιστοιχεί σε κάθε πρότση
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. x 100% = s. lim. x x. γ) Αν οι συναρτήσεις f, g: A είναι παραγωγίσιμες στο πεδίο ορισμού τους Α, τότε ισχύει:
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Α ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 7 ΜΑΪΟΥ 010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Α ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΠΕΜΠΤΗ 7 ΜΑΪΟΥ 010 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. Α. Έστω μία συνάρτηση f ορισμένη σε ένα διάστημα. Αν η f είναι συνεχής στο και για κάθε εσωτερικό σημείο x του ισχύει f (x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ ΜΑΪΟΥ 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ ΜΑΪΟΥ 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΙΟΥΝΙΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΑΡΑΣΚΕΥΗ 0 ΙΟΥΝΙΟΥ 014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
4ο Επαναληπτικό διαγώνισμα στα Μαθηματικά κατεύθυνσης της Γ Λυκείου Θέμα A
 4ο Επνληπτικό διγώνισμ στ Μθημτικά κτεύθυνσης της Γ Λυκείου 7-8 Θέμ A Α Έστω η συνάρτηση Ν ποδείξετε ότι η είνι πργωγίσιμη στο,, δηλδή κι ισχύει Ν ποδείξετε ότι η δεν είνι πργωγίσιμη στο μονάδες 7 A Ν
4ο Επνληπτικό διγώνισμ στ Μθημτικά κτεύθυνσης της Γ Λυκείου 7-8 Θέμ A Α Έστω η συνάρτηση Ν ποδείξετε ότι η είνι πργωγίσιμη στο,, δηλδή κι ισχύει Ν ποδείξετε ότι η δεν είνι πργωγίσιμη στο μονάδες 7 A Ν
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. v i x i. Σχετική Συχνότητα (f i )
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ HMEΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΑΥΤΟΤΕΛΩΝ ΤΜΗΜΑΤΩΝ & ΤΜΗΜΑΤΩΝ ΣΥΝ Ι ΑΣΚΑΛΙΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΣΑΒΒΑΤΟ 9 ΙΟΥΝΙΟΥ 018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ HMEΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΑΥΤΟΤΕΛΩΝ ΤΜΗΜΑΤΩΝ & ΤΜΗΜΑΤΩΝ ΣΥΝ Ι ΑΣΚΑΛΙΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΣΑΒΒΑΤΟ 9 ΙΟΥΝΙΟΥ 018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ
Επαναληπτικό Διαγώνισμα Μαθηματικών Γενικής Παιδείας Γ Λυκείου
 Επνληπτικό Διγώνισμ Μθημτικών Γενικής Πιδείς Γ Λυκείου Θέμ A Α. Ν ποδείξετε ότι η πράγωγος της συνάρτησης f(x)=x ισούτι με x, δηλδή(x ) =x. (6 μονάδες) A. Ν δώσετε τον ορισμό:. του ξιωμτικού ορισμού της
Επνληπτικό Διγώνισμ Μθημτικών Γενικής Πιδείς Γ Λυκείου Θέμ A Α. Ν ποδείξετε ότι η πράγωγος της συνάρτησης f(x)=x ισούτι με x, δηλδή(x ) =x. (6 μονάδες) A. Ν δώσετε τον ορισμό:. του ξιωμτικού ορισμού της
Τα παρακάτω είναι τα κυριότερα θεωρήματα και ορισμοί από το σχολικό βιβλίο ακολουθούμενα από δικά μας σχόλια. 1 ο ΠΡΩΤΟ. www.1proto.gr. www.1proto.
 1 Τ πρκάτω είνι τ κυριότερ θεωρήμτ κι ορισμοί πό το σχολικό βιβλίο κολουθούμεν πό δικά μς σχόλι. 1 ο ΠΡΩΤΟ 2 Συνρτήσεις Γνησίως μονότονη συνάρτηση Μι γνησίως ύξουσ ή γνησίως φθίνουσ συνάρτηση λέμε ότι
1 Τ πρκάτω είνι τ κυριότερ θεωρήμτ κι ορισμοί πό το σχολικό βιβλίο κολουθούμεν πό δικά μς σχόλι. 1 ο ΠΡΩΤΟ 2 Συνρτήσεις Γνησίως μονότονη συνάρτηση Μι γνησίως ύξουσ ή γνησίως φθίνουσ συνάρτηση λέμε ότι
Τετάρτη, 20 Μα ου 2009 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ
 Τετάρτη, Μ ου 9 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o Α. Έστω μί συνάρτηση f ορισμένη σε έν διάστημ Δ. Αν η f είνι συνεχής στο Δ κι γι κάθε εσωτερικό σημείο του Δ ισχύει f (), ν ποδείξετε ότι η f είνι
Τετάρτη, Μ ου 9 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ o Α. Έστω μί συνάρτηση f ορισμένη σε έν διάστημ Δ. Αν η f είνι συνεχής στο Δ κι γι κάθε εσωτερικό σημείο του Δ ισχύει f (), ν ποδείξετε ότι η f είνι
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
Π Α Ν Ε Λ Λ Η Ν Ι Ε Σ Μ Α Θ Η Μ Α Τ Ι Κ Α I E Π Α Λ
 Π Α Ν Ε Λ Λ Η Ν Ι Ε Σ 0 1 3 Μ Α Θ Η Μ Α Τ Ι Κ Α I E Π Α Λ Ε π ι μ ε λ ε ι α : Τ α κ η ς Τ σ α κ α λ α κ ο ς 1o ΘΕΜΑ 1 A1. Εστω συνεχης συναρτηση f : [α, ] με παραγουσα συναρτηση F. Τι ονομαζεται ορισμενο
Π Α Ν Ε Λ Λ Η Ν Ι Ε Σ 0 1 3 Μ Α Θ Η Μ Α Τ Ι Κ Α I E Π Α Λ Ε π ι μ ε λ ε ι α : Τ α κ η ς Τ σ α κ α λ α κ ο ς 1o ΘΕΜΑ 1 A1. Εστω συνεχης συναρτηση f : [α, ] με παραγουσα συναρτηση F. Τι ονομαζεται ορισμενο
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 1 x. ln = Μονάδες 10 Α.2 Πότε μια συνάρτηση f λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα [α,β]; Μονάδες 5
![ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 1 x. ln = Μονάδες 10 Α.2 Πότε μια συνάρτηση f λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα [α,β]; Μονάδες 5 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. 1 x. ln = Μονάδες 10 Α.2 Πότε μια συνάρτηση f λέμε ότι είναι συνεχής σε ένα κλειστό διάστημα [α,β]; Μονάδες 5](/thumbs/55/35946674.jpg) ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΜΑΪΟΥ 008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1 o A.1 Να
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 4 ΜΑΪΟΥ 008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ 1 o A.1 Να
ίνονται οι πραγµατικές συναρτήσεις f, g µε πεδίο ορισµού το έχουν πρώτη και δεύτερη παράγωγο και g(x) f(α) g(α) f(x) g (x) για κάθε x { α}
 1997 ΘΕΜΑΤΑ 1 ίνοντι οι πργµτικές συνρτήσεις f, g µε πεδίο ορισµού το έχουν πρώτη κι δεύτερη πράγωγο κι πργµτικός ριθµός Θέτουµε Α f() g(), που γι κάθε Έστω κι Β f () Α g () Αν φ g() είνι πργµτική συνάρτηση
1997 ΘΕΜΑΤΑ 1 ίνοντι οι πργµτικές συνρτήσεις f, g µε πεδίο ορισµού το έχουν πρώτη κι δεύτερη πράγωγο κι πργµτικός ριθµός Θέτουµε Α f() g(), που γι κάθε Έστω κι Β f () Α g () Αν φ g() είνι πργµτική συνάρτηση
ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ (Οµάδα Α) Θέµα1.Α κυκλώστε το Σ αν η πρόταση είναι σωστή και το Λ αν είναι λάθος
 ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ (Οµάδ Α) Θέµ.Α κυκλώστε το Σ ν η πρότση είνι σωστή κι το Λ ν είνι λάθος ) σχετική συχνότητ v = v ) Η µέση τιµή µις µετλητής εξρτάτι πο τις κριες τιµές γ) Η διάµεσος νφέρετι
ΕΠΑΝΑΛΗΠΤΙΚΟ ΙΑΓΩΝΙΣΜΑ ΜΑΘΗΜΑΤΙΚΩΝ (Οµάδ Α) Θέµ.Α κυκλώστε το Σ ν η πρότση είνι σωστή κι το Λ ν είνι λάθος ) σχετική συχνότητ v = v ) Η µέση τιµή µις µετλητής εξρτάτι πο τις κριες τιµές γ) Η διάµεσος νφέρετι
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 7 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Γι τις προτάσεις
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 7 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Γι τις προτάσεις
γραπτή εξέταση στo μάθημα ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΦΡΟΝΤΙΣΤΗΡΙΑ δυδικό η εξετστική περίοδος πό 9/0/5 έως 9/04/5 γρπτή εξέτση στo μάθημ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ ΛΥΚΕΙΟΥ Τμήμ: Βθμός: Ονομτεπώνυμο: Κθηγητές: Θ Ε Μ Α Α Α. Έστω μι συνάρτηση
ΦΡΟΝΤΙΣΤΗΡΙΑ δυδικό η εξετστική περίοδος πό 9/0/5 έως 9/04/5 γρπτή εξέτση στo μάθημ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ ΛΥΚΕΙΟΥ Τμήμ: Βθμός: Ονομτεπώνυμο: Κθηγητές: Θ Ε Μ Α Α Α. Έστω μι συνάρτηση
β) Αν υπάρχουν τα limf (x), και είναι γ) Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, τότε ισχύει: ( f g ) (x) = f (x) g (x), x
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 24 ΜΑΪΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 24 ΜΑΪΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ
Γ. Ε. ΛΥΚΕΙΟ 2008 ΑΛΓΕΒΡΑ ΤΑΞΗ Β
 Γ. Ε. ΛΥΚΕΙΟ 008 81 Γ. Ε. ΛΥΚΕΙΟ 008 8 Α. Ν ποδείξετε ότι ν συν( + β) 0, συν 0 κι συνβ 0 ισχύει: εφ + εφβ εφ( + β) = 1 εφ εφβ Β. Ν χρκτηρίσετε με Σ(σωστό) ή Λ(λάθος)κάθε μι πό τις πρκάτω προτάσεις:. Αν
Γ. Ε. ΛΥΚΕΙΟ 008 81 Γ. Ε. ΛΥΚΕΙΟ 008 8 Α. Ν ποδείξετε ότι ν συν( + β) 0, συν 0 κι συνβ 0 ισχύει: εφ + εφβ εφ( + β) = 1 εφ εφβ Β. Ν χρκτηρίσετε με Σ(σωστό) ή Λ(λάθος)κάθε μι πό τις πρκάτω προτάσεις:. Αν
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. Σχετική Συχνότητα (f i ) v i x i
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ
ΘΕΜΑ 1o A. Να αποδείξετε ότι για οποιαδήποτε ασυμβίβαστα μεταξύ τους ενδεχόμενα Α και Β ισχύει ότι Ρ(Α»Β)=Ρ(Α)+Ρ(Β) Μονάδες 10
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 18 MAΪΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 18 MAΪΟΥ 009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
1995 ΘΕΜΑΤΑ ίνονται οι πραγµατικοί αριθµοί κ, λ µε κ < λ και η συνάρτηση f(x)= (x κ) 5 (x λ) 3 µε x. Να αποδείξετε ότι:, για κάθε x κ και x λ.
 995 ΘΕΜΑΤΑ. ίνοντι οι πργµτικοί ριθµοί κ, λ µε κ < λ κι η συνάρτηση f() ( κ) 5 ( λ) µε. Ν ποδείξετε ότι: ) f () f() 5 κ, γι κάθε κ κι λ. λ ) Η συνάρτηση g() ln f() στρέφει τ κοίλ προς τ κάτω στο διάστηµ
995 ΘΕΜΑΤΑ. ίνοντι οι πργµτικοί ριθµοί κ, λ µε κ < λ κι η συνάρτηση f() ( κ) 5 ( λ) µε. Ν ποδείξετε ότι: ) f () f() 5 κ, γι κάθε κ κι λ. λ ) Η συνάρτηση g() ln f() στρέφει τ κοίλ προς τ κάτω στο διάστηµ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΩΝ & ΤΑΞΗΣ ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 20 ΣΕΠΤΕΜΒΡΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1.
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 20 ΣΕΠΤΕΜΒΡΙΟΥ 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1.
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΝΕΟ & ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΝΕΟ & ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 8 ΜΑΪΟΥ 06 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ ΝΕΟ & ΠΑΛΑΙΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 8 ΜΑΪΟΥ 06 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (ΝΕΟ
OPMH. κοντά στο µαθητή!
 ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 3 IOYNIOY 014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ι ΗΜΕΡΗΣΙΑ
ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΚΑΙ ΕΣΠΕΡΙΝΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α A ) ΚΑΙ ΜΑΘΗΜΑΤΩΝ ΕΙ ΙΚΟΤΗΤΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ (ΟΜΑ Α Β ) ΤΡΙΤΗ 3 IOYNIOY 014 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ι ΗΜΕΡΗΣΙΑ
Φροντιστήρια ΠΡΟΟΠΤΙΚΗ ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 7 ΙΟΥΛΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 7 ΙΟΥΛΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ
ρ3ρ ΑΠΑΝΤΗΣΕΙΣ Επιμέλεια: Τομέας Μαθηματικών της Ώθησης
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 5 ρρ ΑΠΑΝΤΗΣΕΙΣ Επιμέλει: Τομές Μθημτικών της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 5 ευτέρ, 5 Μ ου 5 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α A. Έστω μι συνάρτηση, η οποί είνι ορισμένη σε έν κλειστό
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 5 ρρ ΑΠΑΝΤΗΣΕΙΣ Επιμέλει: Τομές Μθημτικών της Ώθησης ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 5 ευτέρ, 5 Μ ου 5 Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑ Α A. Έστω μι συνάρτηση, η οποί είνι ορισμένη σε έν κλειστό
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4)
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ HMEΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΑΥΤΟΤΕΛΩΝ ΤΜΗΜΑΤΩΝ & ΤΜΗΜΑΤΩΝ ΣΥΝ Ι ΑΣΚΑΛΙΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΣΑΒΒΑΤΟ 9 ΙΟΥΝΙΟΥ 8 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ HMEΡΗΣΙΩΝ ΕΣΠΕΡΙΝΩΝ ΑΥΤΟΤΕΛΩΝ ΤΜΗΜΑΤΩΝ & ΤΜΗΜΑΤΩΝ ΣΥΝ Ι ΑΣΚΑΛΙΑΣ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΣΑΒΒΑΤΟ 9 ΙΟΥΝΙΟΥ 8 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ
στο (α, β). Μονάδες 7 A2. Έστω Α ένα μη κενό υποσύνολο του. Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α; Μονάδες 4
 ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 208 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 208 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
ίνονται οι πραγµατικές συναρτήσεις f, g που έχουν πεδίο ορισµού το σύνολο
 996 ΘΕΜΑΤΑ. ίνοντι οι πργµτικές συνρτήσεις f, g που έχουν πεδίο ορισµού το σύνολο. Αν οι f κι g έχουν συνεχείς πρώτες πργώγους κι συνδέοντι µετξύ τους µε τις σχέσεις f = g, g = - f τότε ν ποδείξετε ότι:
996 ΘΕΜΑΤΑ. ίνοντι οι πργµτικές συνρτήσεις f, g που έχουν πεδίο ορισµού το σύνολο. Αν οι f κι g έχουν συνεχείς πρώτες πργώγους κι συνδέοντι µετξύ τους µε τις σχέσεις f = g, g = - f τότε ν ποδείξετε ότι:
ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 3: Η ΣΥΝΑΡΤΗΣΗ. F(x) = f(t)dt Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β
![ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 3: Η ΣΥΝΑΡΤΗΣΗ. F(x) = f(t)dt Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 3: Η ΣΥΝΑΡΤΗΣΗ. F(x) = f(t)dt Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β](/thumbs/27/11825451.jpg) ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : Η ΣΥΝΑΡΤΗΣΗ F( = (d [Kεφ:.5 H Συνάρτηση F( = (d Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Πράδειγμ. lim e d. Ν υπολογίσετε το όριο: ( Έχουμε ( e d
ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : Η ΣΥΝΑΡΤΗΣΗ F( = (d [Kεφ:.5 H Συνάρτηση F( = (d Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Πράδειγμ. lim e d. Ν υπολογίσετε το όριο: ( Έχουμε ( e d
just ( u) Πατρόκλου 66 Ίλιον
 just f ( u) du it Πτρόκλου 66 Ίλιον 637345 6944 www.group group-aei aei.gr Νίκος Σούρµπης - - Γιώργος Βρδούκς Ν χρκτηρίσετε τ πρκάτω, σηµειώνοντς Σ (σωστό) ή Λ (λάθος). Αν z, z C, τοτε zz = zz. Η εξίσωση
just f ( u) du it Πτρόκλου 66 Ίλιον 637345 6944 www.group group-aei aei.gr Νίκος Σούρµπης - - Γιώργος Βρδούκς Ν χρκτηρίσετε τ πρκάτω, σηµειώνοντς Σ (σωστό) ή Λ (λάθος). Αν z, z C, τοτε zz = zz. Η εξίσωση
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 19 ΜΑΪOY 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Α1. Να αποδείξετε ότι η παράγωγος
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 19 ΜΑΪOY 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ (ΑΛΓΕΒΡΑ) ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ Α Α1. Να αποδείξετε ότι η παράγωγος
ΘΕΜΑ Α Α1. Έστω t 1,t 2,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν, που έχουν
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
Ο Λ Ο Κ Λ Η Ρ Ω Μ Α Τ Α
 Ο Λ Ο Κ Λ Η Ρ Ω Μ Α Τ Α ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ 4 Ν υπολογίσετε το ολοκλήρωµ: 5 + d (988) 4 Αν I v π 4 v = εϕ d, ν Ν*, τότε: ) Ν ποδείξετε ότι γι κάθε ν>, ισχύει: Iv = Iv v β) Ν υπολογίσετε το Ι 5 (99) 4 Ν βρεθεί
Ο Λ Ο Κ Λ Η Ρ Ω Μ Α Τ Α ΒΑΣΙΚΕΣ ΜΕΘΟ ΟΙ 4 Ν υπολογίσετε το ολοκλήρωµ: 5 + d (988) 4 Αν I v π 4 v = εϕ d, ν Ν*, τότε: ) Ν ποδείξετε ότι γι κάθε ν>, ισχύει: Iv = Iv v β) Ν υπολογίσετε το Ι 5 (99) 4 Ν βρεθεί
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. B. Πώς ορίζεται ο συντελεστής μεταβολής ή συντελεστής. μεταβλητότητας μιας μεταβλητής X, αν x > 0 και πώς, αν
 ΘΕΜΑ 1o ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
ΘΕΜΑ 1o ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
A. Να δείξετε ότι για δύο συμπληρωματικά ενδεχόμενα Α και Α ενός δειγματικού χώρου, ισχύει
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ o ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 7 ΙΟΥΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ o ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 7 ΙΟΥΛΙΟΥ 2009 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ , Β =
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΙΔΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΕΣΠΕΡΙΝΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙΔΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 0 ΙΟΥΝΙΟΥ 001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ 1ο
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΙΔΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΕΣΠΕΡΙΝΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙΔΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 0 ΙΟΥΝΙΟΥ 001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΡΕΙΣ (3) ΘΕΜΑ 1ο
ΘΕΜΑ 1 ο. Α1. Πότε λέμε ότι μία συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α, β]; (Μονάδες 4)
![ΘΕΜΑ 1 ο. Α1. Πότε λέμε ότι μία συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α, β]; (Μονάδες 4) ΘΕΜΑ 1 ο. Α1. Πότε λέμε ότι μία συνάρτηση f είναι συνεχής σε ένα κλειστό διάστημα [α, β]; (Μονάδες 4)](/thumbs/57/40560022.jpg) ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 4 ΠΑΡΑΣΚΕΥΗ, 22 ΑΠΡΙΛΙΟΥ 216 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ 4 ΠΑΡΑΣΚΕΥΗ, 22 ΑΠΡΙΛΙΟΥ 216 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
x, όπου c σταθερός πραγματικός αριθμός. Μονάδες 10
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ - ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 23 ΜΑΪΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ - ΕΣΠΕΡΙΝΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 23 ΜΑΪΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΣΥΝΟΛΟ
ΜΑΘΗΜΑΤΙΚA Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΕ 2002 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚA Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΕ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Οι βαθμοί των 11 μαθητών μιας τάξης ενός Τ.Ε.Ε. σε ένα μάθημα είναι: 1, 1, 9, 15, 1, 16, 17, 7, 19, 18, 17. Για τα δεδομένα αυτά: α. Να κατασκευάσετε
ΜΑΘΗΜΑΤΙΚA Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΕ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Οι βαθμοί των 11 μαθητών μιας τάξης ενός Τ.Ε.Ε. σε ένα μάθημα είναι: 1, 1, 9, 15, 1, 16, 17, 7, 19, 18, 17. Για τα δεδομένα αυτά: α. Να κατασκευάσετε
γ. H εικόνα f( ) ενός διαστήματος μέσω μιας συνεχούς και μη σταθερής συνάρτησης f είναι διάστημα. Μονάδες 2 Μονάδες 2 ε.
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 7 ΜΑΪΟΥ 006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ o A. Έστω
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΣΑΒΒΑΤΟ 7 ΜΑΪΟΥ 006 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ o A. Έστω
Θέματα. Α1. Να δώσετε τον ορισμό της συχνότητας και της σχετικής συχνότητας μιας παρατήρησης x i. Σ Λ
 Θέματα ΘΕΜΑ Α Α. Να δώσετε τον ορισμό της συχνότητας και της σχετικής συχνότητας μιας παρατήρησης x i. (7 Μονάδες) Α. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη
Θέματα ΘΕΜΑ Α Α. Να δώσετε τον ορισμό της συχνότητας και της σχετικής συχνότητας μιας παρατήρησης x i. (7 Μονάδες) Α. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας την ένδειξη
Ερωτήσεις πολλαπλής επιλογής. 1. * Αν η γραφική παράσταση µιας συνάρτησης f είναι αυτή που φαίνεται στο σχήµα, τότε λάθος είναι
 Ερωτήσεις πολλπλής επιλογής 1. * Αν η γρφική πράστση µις συνάρτησης f είνι υτή που φίνετι στο σχήµ, τότε λάθος είνι Α. lim f () = 4 B. lim f () = 1 1 1 Γ. lim f () =. f ( 1) = 1 4 0 1 1 1 E. f (1) = 4.
Ερωτήσεις πολλπλής επιλογής 1. * Αν η γρφική πράστση µις συνάρτησης f είνι υτή που φίνετι στο σχήµ, τότε λάθος είνι Α. lim f () = 4 B. lim f () = 1 1 1 Γ. lim f () =. f ( 1) = 1 4 0 1 1 1 E. f (1) = 4.
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 A ΦΑΣΗ. Ηµεροµηνία: Σάββατο 7 Ιανουαρίου 2017 ιάρκεια Εξέτασης: 2 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.ΜλΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Ηµεροµηνί: Σάββτο 7 Ινουρίου 07 ιάρκει Εξέτσης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Ν συµπληρώσετε τους τύπους: i. ii....,... =...,... β
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.ΜλΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Ηµεροµηνί: Σάββτο 7 Ινουρίου 07 ιάρκει Εξέτσης: ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Ν συµπληρώσετε τους τύπους: i. ii....,... =...,... β
ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2000-2008 1. ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ
 ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ -8 ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΘΕΜΑ Αν η συνάρτηση f είνι πργωγίσιμη σε έν σημείο του πεδίου ορισμού της, ν γρφεί η εξίσωση της εφπτομένης της γρφικής πράστσης της f στο σημείο Α(,f( ))
ΘΕΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ -8 ΘΕΜΑΤΑ ΘΕΩΡΙΑΣ ΘΕΜΑ Αν η συνάρτηση f είνι πργωγίσιμη σε έν σημείο του πεδίου ορισμού της, ν γρφεί η εξίσωση της εφπτομένης της γρφικής πράστσης της f στο σημείο Α(,f( ))
(f(x) + g(x)) = f (x) + g (x).
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1o ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΛΙΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΘΕΜΑ 1o ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 1 ΙΟΥΛΙΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα 10 Ιουνίου 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. (Ενδεικτικές Απαντήσεις)
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρ Ιουνίου 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απντήσεις) ΘΕΜΑ Α Α. () Ορισμός σχολικού βιβλίου σελ.5 (β) (i) Μι συνάρτηση
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρ Ιουνίου 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απντήσεις) ΘΕΜΑ Α Α. () Ορισμός σχολικού βιβλίου σελ.5 (β) (i) Μι συνάρτηση
x του Δ». ΘΕΜΑ Α Α1. Έστω μία συνάρτηση f και x Αν η πρόταση είναι αληθής να το αποδείξετε, ενώ αν είναι ψευδής να δώσετε κατάλληλο αντιπαράδειγμα.
 ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ (2) ΠΑΡΑΣΚΕΥΗ, 18 ΜΑΪΟΥ 218 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ
ΘΕΜΑ Α ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ (2) ΠΑΡΑΣΚΕΥΗ, 18 ΜΑΪΟΥ 218 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ
f ( x) 0 για κάθε εσωτερικό σημείο x του Δ,
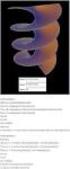 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑ.Λ. (ΟΜΑ Α Β ) ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 1 ΑΠΡΙΛΙΟΥ 13 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑ.Λ. (ΟΜΑ Α Β ) ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 1 ΑΠΡΙΛΙΟΥ 13 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ:ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ
α) Για κάθε μιγαδικό αριθμό z 0 ορίζουμε z 0 =1
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
γ) Αν μια συνάρτηση f είναι γνησίως μονότονη σε ένα διάστημα τότε είναι και 1-1 στο διάστημα αυτό.
 ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ - ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 6 ΙΟΥΝΙΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΣΥΝΟΛΟ
ΘΕΜΑ Α ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ - ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 6 ΙΟΥΝΙΟΥ 2011 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΣΥΝΟΛΟ
Α) Να αποδείξετε ότι η νιοστή παράγωγος της συνάρτησης f µπορεί να πάρει. )e όπου α ν, β ν είναι συντελεστές
 . ίνετι η συνάρτηση f() e. Α) Ν ποδείξετε ότι η νιοστή πράγωγος της συνάρτησης f µπορεί ν πάρει τη µορφή (ν) f () ( + ν + ν )e όπου ν ν είνι συντελεστές εξρτηµένοι πό το ν τους οποίους κι ν υπολογίσετε.
. ίνετι η συνάρτηση f() e. Α) Ν ποδείξετε ότι η νιοστή πράγωγος της συνάρτησης f µπορεί ν πάρει τη µορφή (ν) f () ( + ν + ν )e όπου ν ν είνι συντελεστές εξρτηµένοι πό το ν τους οποίους κι ν υπολογίσετε.
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΛΥΚΕΙΟΥ 2006 ΘΕΜΑ 23
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΛΥΚΕΙΟΥ 6 ΘΕΜΑ Αν η συνάρτηση f είνι συνεχής στο, πργωγίσιμη στο κι γι κάθε ισχύει f f ( ) d = e e e Α) Ν ποδείξετε ότι: f = e i) η f είνι πργωγίσιμη στο κι ισχύει ii) f() = e Β)
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Γ ΛΥΚΕΙΟΥ 6 ΘΕΜΑ Αν η συνάρτηση f είνι συνεχής στο, πργωγίσιμη στο κι γι κάθε ισχύει f f ( ) d = e e e Α) Ν ποδείξετε ότι: f = e i) η f είνι πργωγίσιμη στο κι ισχύει ii) f() = e Β)
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. α. Να μεταφέρετε τον παρακάτω πίνακα στο τετράδιό σας και να τον συμπληρώσετε με τη βοήθεια του παραπάνω ιστογράμματος συχνοτήτων.
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΡΙΤΗ 12 ΙΟΥΝΙΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΕΙ ΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙ ΕΥΤΗΡΙΩΝ ΤΡΙΤΗ 12 ΙΟΥΝΙΟΥ 2007 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
µε Horner 3 + x 2 = 0 (x 1)(x
 998 ΘΕΜΑΤΑ. Η συνάρτηση f: ικνοποιεί τη σχέση f(f()) +f ) Ν ποδείξετε ότι η f είνι «έν προς έν». β) Ν λύσετε την εξίσωση f( 3 + ) f(4 ),. 3 () + 3,. ) Έστω, µε f( ) f( ). Τότε f(f( )) f(f( )) κι f 3 (
998 ΘΕΜΑΤΑ. Η συνάρτηση f: ικνοποιεί τη σχέση f(f()) +f ) Ν ποδείξετε ότι η f είνι «έν προς έν». β) Ν λύσετε την εξίσωση f( 3 + ) f(4 ),. 3 () + 3,. ) Έστω, µε f( ) f( ). Τότε f(f( )) f(f( )) κι f 3 (
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. Σχετική Συχνότητα (f i ) v i x
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΙΔΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙΔΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΘΕΜΑ 1ο Δίνεται ο πίνακας συχνοτήτων
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΙΔΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΠΟΦΟΙΤΩΝ Β ΚΥΚΛΟΥ ΗΜΕΡΗΣΙΩΝ ΤΕΧΝΙΚΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΕΚΠΑΙΔΕΥΤΗΡΙΩΝ ΤΕΤΑΡΤΗ 20 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚA ΘΕΜΑ 1ο Δίνεται ο πίνακας συχνοτήτων
α) Για κάθε μιγαδικό αριθμό z 0 ορίζουμε z 0 =1
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 6 ΜΑΪΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ:
f(x ) 0 O) = 0, τότε το x
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 5 ΣΕΠΤΕΜΒΡΙΟΥ 07 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ & ΕΣΠΕΡΙΝΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 5 ΣΕΠΤΕΜΒΡΙΟΥ 07 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
