Introduction à la théorie du contrôle

Transcript

1 Introduction à la théorie du contrôle ARNAUD MÜNCH Université Blaise Pascal - Clermont-Ferrand Cours dans le cadre de l école doctorale - Hiver 216

2 Partie I - Introduction

3 Introduction générale La théorie du contrôle étudie la possibilité d agir sur un système dynamique dépendant de la variable temporelle de façon à conduire l état de ce système à un état donné à un instant donné! Soit X = X(t) une variable dynamique solution d un système dynamique : { F(X(t), X (t), X (t), ) =, t > (1) X(t = ) = X donnée initiale A l instant t=t, X(T ) = X T Soit maintenant X cible X T. On souhaite agir sur le système de façon à ce que X(t = T ) = X cible

7 Introduction générale Pour cela, on modifie l équation et on rajoute une fonction contrôle v { F (Xv (t), X v (t), X v (t), ) = v, t > X v (t = ) = X donnée initiale (2) de solution dépendante de v. Question Peut-on trouver au moins un contrôle v tel que X v (t = T ) = X cible??? Si oui, on dit que le système en X est contrôlable de façon exacte au temps t = T. Question Si le système est contrôlable au temps T, peux-t-on déterminer parmi tous les contrôles possibles celui de norme minimale.

10 Introduction générale Question Si le système n est pas contrôlable exactement au temps T, le système est-il contrôlable approximativement au temps T : pour tout ɛ >, peux-t-on trouver un contrôle v tel que : X(t = T ) X cible ɛ? (3) Question Si le système n est pas contrôlable au temps T, est-il contrôlable en temps long, c est-à-dire: X(t) X cible quand t (4) La notion de Stabilisation du système apparaît.

11 Introduction générale Question Si le système n est pas contrôlable exactement au temps T, le système est-il contrôlable approximativement au temps T : pour tout ɛ >, peux-t-on trouver un contrôle v tel que : X(t = T ) X cible ɛ? (3) Question Si le système n est pas contrôlable au temps T, est-il contrôlable en temps long, c est-à-dire: X(t) X cible quand t (4) La notion de Stabilisation du système apparaît.

12 Exemple 1: Le système masse-ressort Le système masse-ressort s écrit de la façon suivante : { mx (t) + Rx(t) =, t > x(t = ) = x, x (t = ) = x 1 (5) m - masse du ressort, R - coefficient de raideur - x(t) - position x (t) - vitesse On note l énergie du système: E(t) = 1 ) (m x (t) 2 + R x(t) 2 2 Proposition de(t) dt =, pour tout t >. Question Comment stabiliser le système?

16 Exemple 2: Le système du pendule Le système du pendule de masse m et de longueur L est donné par: { mθ (t) + mg sin θ(t) =, t > θ(t = ) = θ, θ (t = ) = θ 1 (6) θ est l angle du pendule formé avec la verticale; θ est la vitesse angulaire. Question Comment stabiliser ce système non linéaire?

17 Contrôle optimal La notion de controle optimal est un peu differente, mais très liée a la notion de contrôlabilité. Elle apparait lorsque l on minimise une certaine fonctionnelle J(v) = α X v β v 2 2 où X v est solution du système dynamique associé au controle v. Ici, il n y a pas nécessairement de contrainte sur la variable X v à un instant T >!

18 Exemple 3: Le problème de la barque Le mouvement d une barque se déplacant a vitesse constante sur une rivière où il y a un courant c(y) est modélisé par { x (t) = v cos(u(t)) + c(y(t)), x() =, y (7) (t) = v sin(u(t)), y() = où v est la vitesse et u(t), l angle de la barque par rapport à l axe (O, x), est le contrôle. Question Comment atteindre un point donné sur l autre berge? Comment l atteindre en un temps minimal?

19 Exemple 4: Un problème optimal de pèche L évolution d une population de poisson x(t) et modélisée par { x (t) =.8x(t)(1 1 6 x(t)) u(t), t >, x() = x (8) Question Politique optimale de pêche, de manière a maximiser la quantité et telle que x(t ) >? T e.3t ln(u(t))dt

20 Exemple 5: Contrôle optimal d un réservoir On veut ajouter de l eau dans un réservoir de façon à atteindre le niveau d eau h 1, en tenant compte du fait qu il faut compenser une perte d eau linéaire en temps. La modélisation est h (t) = u(t) t, h() = (9) où u est le contrôle. Question Quelle est la loi optimale permettant d atteindre l objectif en minimisant tf le temps t f final n étant pas fixé? u(t) 2 dt (1)

21 Exemple 6: Contrôle optimal d une réaction chimique Une réaction chimique est modélisée par { x 1 (t) = ux 1 + u 2 x 2, x 1 () = 1, x 2 (t) = ux 1 3u 2 x 2, x 2 () = (11) où x 1 et x 2 sont les concentrations des réactifs, et le contrôle u(t) 1. Question Quelle est la politique optimale permettant de maximiser la quantité finale x 2 (1) du second réactif? Le problème est : max u, u(t) 1 x 2 (1) (12)

22 Exemple 7: Contrôle optimal d une épidémie par vaccination On considère une population de N individus soumis à une épidémie qu on veut contrôler par vaccination. Par simplicité, on suppose qu un individu qui a été malade et soigné peut à nouveau tomber malade. Le modèle est le suivant. On note α > le taux de contamination, u(t) (contrôle) le taux de vaccination et x(t) le nombre d individus infectés. On a: x t = αx(t)(n x(t)) u(t)x(t), x() = x (13) où x N et où le controle u(t) vérife la contrainte u(t) C, (14) où C > est une constante.soit T >. On cherche à minimiser le critère: Z T C T (u) = (x(t) + βu(t))dt + γx(t ) (15) où β > et γ > sont des constantes de pondération (compromis entre économie de vaccins dépensés et minimisation du nombre d individus infectés).

25 Exemple 8: Contrôle optimal d un procédé de fermentation Considérons le procédé de fermentation : { x (t) = x(t) + u(t)(1 x(t)), x() = x, y (t) = x(t) u(t)y(t), y() = (16) où x(t) représente la concentration de sucre, y(t) la concentration d ethanol, et u(t), le contrôle, est le taux d évaporation. On suppose u(t) M, et < x < 1. Soit y 1 tel que y 1 > 1/M et y 1 > x ; on veut résoudre le problème du temps minimal pour rejoindre y(t f ) = y 1

26 Exemple 9: Contrôle optimal d un avion Considérons le mouvement d un avion, modélisé par : x (t) = v(t), v (t) = u(t) mv(t) µg c m v(t)2 (17) où x(t) est la distance au sol parcourue, v(t) est le module de la vitesse, le controle u(t) est l apport d énergie, m est la masse, et µ, c sont des coefficients aérodynamiques. Le contrôle vérifie la contrainte : < a u(t) b (18) Le but est de déterminer une trajectoire menant du point initial x() = x, v() = v au point final x(t f ) = x f, v(t f ) = v f et minimisant le coût. C(u) = tf u(t)dt

27 Exemple 9: Contrôle optimal d un avion Considérons le mouvement d un avion, modélisé par : x (t) = v(t), v (t) = u(t) mv(t) µg c m v(t)2 (17) où x(t) est la distance au sol parcourue, v(t) est le module de la vitesse, le controle u(t) est l apport d énergie, m est la masse, et µ, c sont des coefficients aérodynamiques. Le contrôle vérifie la contrainte : < a u(t) b (18) Le but est de déterminer une trajectoire menant du point initial x() = x, v() = v au point final x(t f ) = x f, v(t f ) = v f et minimisant le coût. C(u) = tf u(t)dt

28 Exemple 1: Système proies-prédateurs [dynamique des populations; systeme de Lotka-Volterra] On considère le système proies-prédateurs ( x (t) = x(t)(α βy(t)), x() = x y (t) = y(t)(γ δx(t)), y() = y (19) où x(t) est l effectif des proies, y(t) l effectif des prédateurs, α est le taux de reproduction des proies, β le taux de mortalité des proies du aux prédateurs rencontrés, γ le taux de mortalité des prédateurs, et δ le taux de reproduction des prédateurs en fonction des proies rencontrées et mangées Les deux points d equilibres sont : x(t) =, y(t) = (extinction definitive de l espèce) et x(t) = α β, y(t) = γ δ. La matrice jacobienne est donnée par α βy(t) βx(t), J(x(t), y(t)) = δy(t) δx(t) γ J(, ) admet α et γ pour valeur propres donc l équilibre est instable. J( α β, γ δ ) admet ±i αγ pour valeurs propres. Ce point fixe est donc un foyer et plus particulièrement un centre, ce qui signifie que les populations de proies et prédateurs oscillent autour de leurs valeurs en ce point fixe. «(2)

31 Exemple 11: Contrôle optimal d insectes nuisibles par des prédateurs Pour traiter une population x > d insectes nuisibles, on introduit dans l eco-système une population y > d insectes prédateurs (non nuisibles), se nourrissant des nuisibles. On suppose que les insectes prédateurs sont stériles. Le contrôle consiste en l introduction, régulière d insectes prédateurs. Le modèle s écrit: ( x (t) = x(t)(a by(t)), x() = x, y (t) = cy(t) + u(t), y() = y (21) où a > est le taux de reproduction naturelle des nuisibles, b > est un taux de prédation, c > est le taux de disparition naturelle des prédateurs.le contrôle u(t) est le taux d introduction de nouveaux prédateurs au temps t, il vérifie la contrainte u(t) M, (M > ) On cherche à minimiser, au bout d un temps T > fixé, le nombre de nuisibles, tout en cherchant a minimiser la quantité globale de predateurs introduits: Z T x(t ) + u(t)dt (22)

34 Exemple 12: Contrôle optimal d insectes nuisibles par des prédateurs (suite) On suppose que les prédateurs que l on introduit se reproduisent, de manière proportionnelle au nombre de nuisibles. Le contrôle est cette fois le taux de disparition des prédateurs. Le modèle normalisé est: où le contrôle u(t) vérifie la contrainte: ( x (t) = x(t)(1 y(t)), x() = x, y (t) = y(t)(u(t) x(t)), y() = y (23) < α u(t) β. (24) Cette fois, on cherche a résoudre le problème de joindre en temps minimal le point d équilibre x(t f ) = a, y(t f ) = 1

35 Exemple 11: Contrôle des vibrations d une corde On se donne une corde homogène élastique de longueur un. Le déplacement transversal est donné par l équation aux derivées partielles (équation des ondes) : y (x, t) c 2 y xx (x, t) = f (x, t), (x, t) (, 1) (, T ), y(, t) = y(1, t) =, t (, T ), y(x, ) = y (x), y (x, ) = y 1 (x) (25) Sans force extérieure (f = ), l énergie du système (non controlé) est donnée par : E(t) = ( y (x, t) 2 + y x (x, t) 2 )dx (26) et est constante au cours du temps; E(t) = E(). Le système est conservatif. On cherche un contrôle v tel que y(1, t) = v(t) tel que E(T ) = pour T > suffisamment grand. (T est le temps de contrôlabilité).

36 Exemple 12: Contrôle des vibrations d une corde soumise à un contact unilatéral On se donne une corde homogène élastique de longueur un. Le déplacement transversal est donné par l équation aux derivées partielles (équation des ondes): y (x, t) c 2 y xx (x, t) = f (x, t), (x, t) (, 1) (, T ), y(, t) = y(1, t) =, t (, T ), y(x, ) = y (x), y (x, ) = y 1 (x), x (, 1), y(, t), t (, T ) (27) On cherche un contrôle v tel que y(1, t) = v(t) tel que E(T ) = pour T > suffisamment grand. (T est le temps de contrôlabilité).

37 Exemple 13: Contrôle de la chaleur au sein d une poutre On se donne une corde homogène élastique de longueur un. La température de la poutre est régie par l équation de la chaleur: θ (x, t) c 2 θ xx (x, t) = f (x, t), (x, t) (, 1) (, T ), θ(, t) = θ(1, t) =, t (, T ), (28) θ(x, ) = θ (x), x (, 1), Contrairement à l équation des ondes, ce système est naturellement dissipatif: θ(t) lorsque t. On cherche un contrôle v tel que θ(1, t) = v(t) de façon à rendre la chaleur homogene au sein de la corde?

38 Exemple 14: Système de réaction-diffusion en dynamique du cancer y 1 = y 1 (x, t), y 2 = y 2 (x, t), y 3 = y 3 (x, t) On considère le système de réaction-diffusion : 8 y 1 = d 1 y 1 + a 1 (1 y1 \ k 1 )y 1 (α 1,2 y 2 + k 1,3 y 3 )y 1, (x, t) Ω (, T ), >< y 2 = d 2 y 2 + a 2 (1 y2 \ k 2 )y 2 (α 2,1 y 1 + k 2,3 y 3 )y 2, (x, t) Ω (, T ), y 3 = d 3 y 3 a 3 y 3 + u, (x, t) Ω (, T ), y i (x, ) = y i, (x), x Ω, >: y i ν =, x Ω (29) avec y 1 la densité de cellules cancéreuses, y 2 la densité de cellules saines, y 3 la concentration de médicament, u le taux d injection du médicament, variable de contrôle. On cherche u de façon à augmenter la durée de vie des cellules saines: max u Z Z y 1 (x, t)dx Ω «dt (3)

44 Retour sur le système masse-ressort Le système masse-ressort sans contrôle s écrit de la façon suivante : { mx (t) + Rx(t) =, t > x(t = ) = x, x (t = ) = x 1 (31) C est une équation différentielle du second ordre à coefficient constant. Le polynôme caractéristique est p(r) = mr 2 + R; p(r) = = 4mR < donc les racines sont r 1, r 2 = ±i 4mR R 2m = ±i m donc la solution est donnée par: R m R x(t) = x cos( m t) + x 1 R sin( m t), t >

45 Energie du système masse-ressort On définit l énergie du système par E(t) = 1 ) (m x (t) 2 + R x(t) 2, t > (32) 2 Proposition L énergie est constante: E(t) = E() Pour cela, on multiplie l équation par x (t) soit Mais (mx (t) + Rx(t))x (t) =, t > (33) x (t)x(t) = 1 d 2 dt x(t) 2, x (t)x (t) = 1 d 2 dt x (t) 2 ce qui donne = m d dt x (t) 2 + R d dt x (t) 2 = d dt E(t).

48 Contrôle du système masse-ressort Le système masse-ressort avec contrôle s écrit de la façon suivante : { mx (t) + Rx(t) = v(t), t > x(t = ) = x, x (t = ) = x 1 (34) On cherche un contrôle v tel que x(t ) = x (T ) =?? Ici, on peut construire facilement un tel contrôle v! On cherche x tel que x() = x, x () = x 1, x(t ) =, x (T ) = soit 4 contraintes à satisfaire. On cherche x de la forme x(t) = at 3 + bt 2 + ct + d = (T t) 2 (αt + β) puis β = x T 2 puis α = x 1+2T β T 2 = 2x +x 1 T T 3.

49 Retour sur le système masse-ressort x(t) = (T t)2 (2tx + tx 1 T + x T ) T 3 Il reste à définir v := mx (t) + Rx(t) soit ( 2(2x + x 1 T )t v(t) = m T 3 + 2x T 2 4(T t))(2x ) + x 1 T T 3 ( (T t) 2 ((2x + x 1 T )t + R T 3 + x ) (35) T 2 Question Comment calculer le contrôle de norme minimale T min v 2 (t)dt? (36) v Question Comment faire si on on rajoute la contrainte 1 v(t) 1?

52 Stabilisation du système masse-ressort On cherche un contrôle v explicitement en fonction de x(t)! On pose v(t) = kx (t), k > donc l équation en x devient mx (t) + Rx(t) = kx (t) Proposition d dt E(t) = k x (t) 2 <!! Question L énergie tend -t-elle vers lorsque t.

56 Stabilisation du système masse-ressort donc p(r) = mr 2 + kr + R; p(r) = = k 2 4mR < r 1 (k), r 2 (k) = k ± k 2 4mR 2 Si k 2 4mR >, les racines sont réelles négatives et x(t) = Ae ( k+ k 2 4mR) 2m t + Be ( k k 2 4mR) t 2m avec A, B solution de A + B = x et Ar 1 + Br 2 = x 1 soit, A = m(x 1 x r 2 (k)) k 2 4mR ; B = m(x r 1 (k) x 1 ) k 2 4mR et on a X(t), X (t) quand t

57 Stabilisation du système masse-ressort donc p(r) = mr 2 + kr + R; p(r) = = k 2 4mR < r 1 (k), r 2 (k) = k ± k 2 4mR 2 Si k 2 4mR >, les racines sont réelles négatives et x(t) = Ae ( k+ k 2 4mR) 2m t + Be ( k k 2 4mR) t 2m avec A, B solution de A + B = x et Ar 1 + Br 2 = x 1 soit, A = m(x 1 x r 2 (k)) k 2 4mR ; B = m(x r 1 (k) x 1 ) k 2 4mR et on a X(t), X (t) quand t

58 Stabilisation du système masse-ressort Si k 2 4mR =, racine double r 1 = k 2 et ( x(t) = x + (x 1 + kx ) 2m )t e k 2m t et à nouveau x(t), x (t) quand t. Si k 2 4mR <, r 1, r 2 = k±i 4mR k 2 2m et ) x(t) = e k 4mR k 2m (x t 2 4mR k 2 cos( t) + B sin( t) 2m 2m et à nouveau, E(t). Conclusion: Pour tout k >, décroissance exponentielle de l énergie en temps.

61 Valeur optimale de k? Si k 2 4mR >, les racines sont réelles négatives et avec x(t) = Ae ( k+ k 2 4mR) 2m t + Be ( k k 2 4mR) t 2m A = m(x 1 x r 2 (k)) k 2 4mR ; B = m(x r 1 (k) x 1 ) k 2 4mR. x(t) = x + (x 1m x Rt) k x (t) = x R k + O( 1 k 2 ) + 1 k e tk m ( x1 m + O( 1 k )), + O( 1 tk ) + e m (x1 + x 1Rt + x R + O(k 2 )), k 2 k E(t) = E() O( t2 k 2 ); La valeur de k optimale est donnée par k tel que k 2 4mR = soit k = 2 mr et le taux de décroissance exponentielle vaut alors k R 2m = m

62 Valeur optimale de k? Si k 2 4mR >, les racines sont réelles négatives et avec x(t) = Ae ( k+ k 2 4mR) 2m t + Be ( k k 2 4mR) t 2m A = m(x 1 x r 2 (k)) k 2 4mR ; B = m(x r 1 (k) x 1 ) k 2 4mR. x(t) = x + (x 1m x Rt) k x (t) = x R k + O( 1 k 2 ) + 1 k e tk m ( x1 m + O( 1 k )), + O( 1 tk ) + e m (x1 + x 1Rt + x R + O(k 2 )), k 2 k E(t) = E() O( t2 k 2 ); La valeur de k optimale est donnée par k tel que k 2 4mR = soit k = 2 mr et le taux de décroissance exponentielle vaut alors k R 2m = m

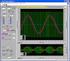
63 Application numérique du système masse-ressort : m = R = k= 4 k=2 )t(e 3 k= k=2 k= t E(t)

64 Application numérique du système masse-ressort : m = R = 1 E t E k E(t = 1) et E(t = 1) en fonction de k

65 Remarque: Problème masse-ressort - Reformulation L équation du masse ressort mx (t) + Rx(t) = prend la forme du système différentielle linéaire X (t) = AX(t) avec X(t) = ( x(t) m R x (t) ) ; A = R m R m De mème, l équation mx (t) + Rx(t) = v(t) prend la forme ( ) X (t) = AX(t) + Bv(t) B = 1 ; mr

66 Remarque: Problème masse-ressort - Reformulation L équation du masse ressort mx (t) + Rx(t) = prend la forme du système différentielle linéaire X (t) = AX(t) avec X(t) = ( x(t) m R x (t) ) ; A = R m R m De mème, l équation mx (t) + Rx(t) = v(t) prend la forme ( ) X (t) = AX(t) + Bv(t) B = 1 ; mr

67 Partie II - Contrôlabilité des systèmes différentielles linéaires de la forme { X (t) = AX(t) + Bu(t), t >, X() = X

68 Contrôlabilité de X (t) = AX(t) + Bu(t) Soit n, m N et T >. On considère le système de dimension finie: { X (t) = AX(t) + Bu(t),t (, T ), X() = x (37) avec A une matrice n n et B une matrice n m. On utilise donc m contrôle(s) pour n états. En pratique, m n. X = (X 1, X 2,, X n ) T, u = (u 1, u 2,, u m ) T, Si u L 2 (, T ; R m ), i.e. T u2 i (t)dt <, i {1,, m}, alors le système (37) est bien posé: il existe une solution unique X H 1 (, T ; R n ) donnée par la méthode de variation de la constante : X(t) = e At X + t e A(t s) Bu(s)ds, t [, T ].

69 Contrôlabilité de X (t) = AX(t) + Bu(t) Soit n, m N et T >. On considère le système de dimension finie: { X (t) = AX(t) + Bu(t),t (, T ), X() = x (37) avec A une matrice n n et B une matrice n m. On utilise donc m contrôle(s) pour n états. En pratique, m n. X = (X 1, X 2,, X n ) T, u = (u 1, u 2,, u m ) T, Si u L 2 (, T ; R m ), i.e. T u2 i (t)dt <, i {1,, m}, alors le système (37) est bien posé: il existe une solution unique X H 1 (, T ; R n ) donnée par la méthode de variation de la constante : X(t) = e At X + t e A(t s) Bu(s)ds, t [, T ].

70 Contrôlabilité de X (t) = AX(t) + Bu(t) Definition Le système (37) est exactement contrôlable au temps T > ssi pour toute donnée initiale X et finale X T, il existe un contrôle u L 2 (, T ; R m ) tel que X(T ) = X T. Remarque On peut supposer par linéarité que X T =. Si X T, on peut définir la solution Y de { Y (t) = AY (t),t (, T ), Y (T ) = X T (38) et Z = X Y solution de { Z (t) = AZ (t) + Bu(t),t (, T ), Z () = X Y () (39) X(T ) = X T si et seulement si Z (T ) =!

76 Contrôlabilité de X (t) = AX(t) + Bu(t) Definition Le système (37) est contrôlable à zéro au temps T > ssi pour toute donnée initiale X, il existe un contrôle u L 2 (, T ; R m ) tel que X(T ) =. Contrôlabilité à zéro Contrôlabilité exacte

79 Caractérisation des contrôles Lemme u est un contrôle à zéro pour la donnée initiale X si et seulement si T < u, B ϕ > dt+ < X, ϕ() >= (4) pour tout ϕ solution du problème adjoint : { ϕ (t) = A ϕ(t), t (, T ), ϕ(t ) = ϕ T R n (41)

80 Caractérisation des contrôles: démonstration X est solution de X (t) = AX(t) + Bu(t) = donc en multipliant par ϕ, < X, ϕ >=< AX, ϕ > + < Bu, ϕ > ϕ est solution de ϕ (t) = A ϕ(t) donc en multipliant par X, < ϕ, X >=< A ϕ, X > =< ϕ, AX >=< AX, ϕ > donc < X, ϕ > + < ϕ, X >=< Bu, ϕ > donc d < X, ϕ >=< Bu, ϕ > dt donc en intégrant sur (,T) < X(T ), ϕ(t ) > < X, ϕ() >= T < Bu, ϕ > dt u est un nul contrôle si et seulement X(T ) = donc on obtient

86 Caractérisation des contrôles: démonstration T < X(), ϕ() > + < u, B ϕ > dt = (42) pour tout ϕ solution du problème adjoint, et en fait pour tout ϕ T R n car la solution ϕ est entièrement déterminée par ϕ T! (42) caractérise les points critiques de la fonctionnelle J : R n R J(ϕ T ) = 1 2 T B ϕ 2 dt+ < X, ϕ() > Lemme Supposons que J admet un minimum ˆϕ T R n et soit ˆϕ la solution adjointe correspondante. Alors est un contrôle à zéro pour X. u = B ˆϕ

89 lien avec J: démonstration Si ˆϕ T est un minimum de J, alors J( ˆϕ T + hϕ T ) J( ˆϕ T ) DJ( ˆϕ T ) ϕ T = lim =, ϕ T R n h h Apres calculs, on obtient que DJ( ˆϕ T ) ϕ T = T < B ˆϕ, B ϕ > dt+ < X, ϕ() >, ϕ T R n Il en résulte que si ˆϕ T est un minimum de J, alors B ˆϕ vérifie la caractérisation des contrôles pour X et est donc un contrôle pour X.

90 Observabilité pour le système adjoint Definition Le système adjoint en ϕ est dit observable au temps T > ssi il existe c > tel que c ϕ() 2 T B ϕ 2 dt, ϕ T R n. (43) Remarque Si le système adjoint est observable, alors B ϕ(t) = t [, T ] = ϕ = Theoreme Le système en X est exactement contrôlable au temps T ssi le système adjoint en ϕ est observable : Contrôlabilité du système en X Observabilité du système adjoint en ϕ

93 Remarque sur la démonstration de l équivalence La propriété d observabilité entraine que la fonctionnelle J est coercive, c est-à-dire que lim J(ϕ T ) = +. ϕ T R n Comme la fonctionnelle J est continue, c est-à-dire J(φ T,1 ) J(φ T,2 ) lorsque φ T,1 ϕ T,2 et convexe, c est-à-dire J (φ T ), il en résulte que J admet au moins un minimum: il existe au moins un ϕ T R n tel que J ( ˆϕ T ).ϕ T =, ϕ T R n.

94 Remarque sur la démonstration de l équivalence La propriété d observabilité entraine que la fonctionnelle J est coercive, c est-à-dire que lim J(ϕ T ) = +. ϕ T R n Comme la fonctionnelle J est continue, c est-à-dire J(φ T,1 ) J(φ T,2 ) lorsque φ T,1 ϕ T,2 et convexe, c est-à-dire J (φ T ), il en résulte que J admet au moins un minimum: il existe au moins un ϕ T R n tel que J ( ˆϕ T ).ϕ T =, ϕ T R n.

95 Condition de contrôlabilité de Kalman R.E. Kalman, 193- Theoreme Le système en X est exactement contrôlable au temps T ssi rang[b, AB,, A n 1 B] = n Remarque La contrôlabilité depend de A et de B mais pas de T >. Le temps de contrôlabilité T peut donc etre arbitrairement petit.

98 Retour sur le système masse-ressort X (t) = AX(t) + Bu(t) avec X(t) = ( x(t) m R x (t) = AB = ( 1 m ) ; A = ) ; [B, AB] = R m R m ; B = ( ) 1 m ; 1 mr et on a bien que rang[b, AB] = 2 = n donc le système masse-ressort est contrôlable. ( 1 mr ) ;

101 Un autre exemple plus trivial X (t) = AX(t) + Bu(t) avec A = ( 1 1 ) ( 1 ; B = ) ; Ce système est-il contrôlable? = AB = ( 1 ) ( 1 1 ; [B, AB] = ) ; et on a rang[b, AB] = 1 n donc ce système n est pas contrôlable.

104 Calcul du contrôle pour le système masse-ressort n = 2, ϕ T = (ϕ 1,T, ϕ 2,T ) T R 2. On minimise la fonctionnelle J(ϕ T ) = 1 2 = 1 2 T T B ϕ 2 dt+ < X, ϕ() > ϕ 2 (t) 2 dt + X 1, ϕ 1 () + X 2, ϕ 2 () où ϕ est solution de ϕ (t) = A ϕ(t) soit ϕ(t) = e A (T t) ϕ T avec ( ) A (T t) (T t) = (T t) ( ) = e A (T t) cos(t t) sin(t t) = ; sin(t t) cos(t t)

108 Calcul du contrôle pour le système masse-ressort donc ϕ 2 (t) = sin(t t)ϕ 1 (T ) + cos(t t)ϕ 2 (T ), ϕ 1 () = cos(t )ϕ 1 (T ) sin(t )ϕ 2 (T ), ϕ 2 () = sin(t )ϕ 1 (T ) + cos(t )ϕ 2 (T ) (44) soit finalement J(ϕ T ) = 1 2 < Mϕ T, ϕ T > + < N(X ), ϕ T > avec M = 1 2 ( T cos(t ) sin(t ) sin 2 (T ) sin 2 (T ) T + cos(t ) sin(t ) ) ; (45) et N(X ) = ( X1, cos(t ) + X 2, sin(t ) X 1, sin(t ) + X 2, cos(t ) ) ; (46) = det(m) = T 2 + cos 2 (T ) 1 > pour tout T >.

109 Calcul du contrôle pour le système masse-ressort donc ϕ 2 (t) = sin(t t)ϕ 1 (T ) + cos(t t)ϕ 2 (T ), ϕ 1 () = cos(t )ϕ 1 (T ) sin(t )ϕ 2 (T ), ϕ 2 () = sin(t )ϕ 1 (T ) + cos(t )ϕ 2 (T ) (44) soit finalement J(ϕ T ) = 1 2 < Mϕ T, ϕ T > + < N(X ), ϕ T > avec M = 1 2 ( T cos(t ) sin(t ) sin 2 (T ) sin 2 (T ) T + cos(t ) sin(t ) ) ; (45) et N(X ) = ( X1, cos(t ) + X 2, sin(t ) X 1, sin(t ) + X 2, cos(t ) ) ; (46) = det(m) = T 2 + cos 2 (T ) 1 > pour tout T >.

110 Calcul du contrôle pour le système masse-ressort J(ϕ T ) = 1 2 < Mϕ T, ϕ T > + < N(X ), ϕ T > atteint son unique minimum en soit ˆϕ1,T ˆϕ 2,T «= 1 det(m) ˆϕ T = M 1 N(x ) T + cos(t ) sin(t ) sin 2 (T ) sin 2 (T ) T cos(t ) sin(t ) «N(X ) (47) Finalement, un contrôle est donné par u(t) = B ˆϕ(t) = ˆϕ 2 (t) avec ˆϕ solution de ˆϕ (t) = A ϕ(t) ˆ tel que ˆϕ(T ) = ˆϕ T soit u(t) = sin(t t) ˆϕ 1,T + cos(t t) ˆϕ 2,T Si la vitesse initiale X 2, est nulle, il vient simplement, u(t) = «1 sin(t t)t cos(t ) + sin(t t) sin(t ) cos(t t)t sin(t ) X 1, det(m)

Δείτε περισσότερα