Εισαγωγή. Πληροφορική
|
|
|
- Δάμαρις Γεωργίου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Πληροφορική Διδάσκων:Μ.Χατζόπουλος, Παραδόσεις:Τρίτη 4-6, Τετάρτη 1-3; (Αμφιθέατρο Α15) Πληροφορίες στην ιστοσελίδα του μαθήματος Η δομή του μαθήματος Εισαγωγή στην Επιστήμη των Υπολογιστών Προγραμματισμός Υπολογιστών με Γλώσσα C. Η Επιστήμη των Υπολογιστών J.G.Brookshear Εισαγωγή στον Προγραμματισμό με την C, Ν.Μισυρλής Διαδικαστικά Το μάθημα έχει και εργαστήριο (θα δώσετε σήμερα τα ονόματά σας για να δούμε πόσες ομάδες εργαστηρίων θα φτιάξουμε. Το λογισμικό που θα χρησιμοποιηθεί στο εργαστήριο μπορείτε να το πάρετε και σε δικό σας υπολογιστή (είναι ανοικτό λογισμικό) Θα δώσετε και ασκήσεις Η τελική βαθμολογία σας θα διαμορφωθεί από τον τύπο 0.4*(βαθμός ασκήσεων)+0.6*(βαθμός διαγωνίσματος). Όμωςγιαναπεράσετεθαπρέπεικαιταδύοναείναι>4. Εισαγωγή Ο ρόλος των Αλγορίθμων Ο ρόλος των Αλγορίθμων Ιστορική Εξέλιξη των Υπολογιστικών Μηχανών Η επιστήμη των Αλγορίθμων Έννοια της Αφαίρεσης Χωρίς αυστηρότητα ένας αλγόριθμος είναι ένα σύνολο βημάτων που καθορίζουν τον τρόπο εκτέλεσης μιας εργασίας. Η αναπαράσταση ενός αλγορίθμου ονομάζεται πρόγραμμα. Ηδιαδικασίατηςανάπτυξηςενόςπρογράμματοςσεμιαμορφή συμβατή με την μηχανή και της εισαγωγής στη μηχανή λέγεται προγραμματισμός. Λογισμικό (software)- Υλικό (hardware) Η μελέτη των αλγορίθμων ξεκίνησε σαν μαθηματικό θέμα (διαίρεση, αλγόριθμος του Ευκλείδη). Θεώρημα πληρότητας του Goedel (σε κάθε μαθηματική θεωρία που περιλαμβάνει το παραδοσιακό αριθμητικό μας σύστημα, υπάρχουν προτάσεις οι οποίες δεν μπορούν ούτε να αποδειχθούν ούτε να διαψευστούν). 1
2 Ιστορική Εξέλιξη Άβακας Μηχανές Pascal, Leibnitz, Babbage Αναπαράσταση με οπές σε χαρτί (Jacquard για αργαλειούς). Την ιδέα χρησιμοποίησε ο Herman Hollerith για αναπαράσταση πληροφοριών με την μορφή οπών σε χάρτινες κάρτες. MARK I, ABC, Colossus, ENIAC. Επιτραπέζιοι (Apple, Commodore, Healthkit, Radio Shack). Προσωπικός υπολογιστής (ΙΒΜ). Μηχανικές Υπολογιστικές Μηχανές Blaise Pascal (Pascaline) Τροχός του Leibnitz Αργαλειός Jaquard Διαφορική Μηχανή του Babbage Μηχανή Hollerith Σύγχρονοι Υπολογιστές ABC (Atanasoff Berry Computer) Z1 (Zuse, Γερμανία) Mark1 Colossus (Alan Turing) ENIAC Υπολογιστές που βασίσθηκαν στην αρχιτεκτονική von Neumann EDVAC (Πανεπιστήμιο Pensylvania) EDSAC (Alan Wilkes Πανεπιστήμιο Cambridge) Επιστήμη των Αλγορίθμων Αφαίρεση Ποια προβλήματα μπορούν να επιλυθούν με αλγοριθμικές διαδικασίες; Πως μπρεί να γίνει ευκολότερη η επινόηση αλγορίθμων; Μεποιόντρόπομπορούνναβελτιωθούνοιτεχνικές αναπαράστασης και μετάδοσης των αλγορίθμων; Με ποιόν τρόπο μπορεί να εφαρμοσθεί η γνώση μας και και η τεχνολογία για τους αλγορίθμους ώστε να δημιουργηθούν καλύτερες μηχανές; Πως μπορούν να αναλυθούν και να συγκριθούν τα χαρακτηριστικά διαφορετικών αλγορίθμων; Ηαφαίρεσηαναφέρεταιστηνδιάκρισημεταξύμεταξύτων εξωτερικών ιδιοτήτων μιας οντότητας και των λεπτομερειών της εσωτερικής της σύνθεσης. Η αφαίρεση δεν περιορίζεται μόνο στην επιστήμη και την τεχνολογία αλλά αποτελεί σημαντική τεχνική απλοποίησης με την οποία η κοινωνία έχει δημιουργήσει ένα τρόπο ζωής. Ο υπολογιστικός εξοπλισμός κατασκευάζεται από επίπεδα αφηρημένων εργαλείων. 2
3 Αποθήκευση Δεδομένων Τα μπιτ και ο τρόπος που αποθηκεύονται Κύρια Μνήμη Αποθηκευτικά μέσα Αναπαράσταση Πληροφοριών σε σχήματα μπιτ Το δυαδικό σύστημα Αποθήκευση Ακεραίων Στο εσωτερικό των σύγχρονων υπολογιστών οι πληροφορίες αποθηκεύονται σαν σειρές από 0 και 1. Τα ψηφίααυτάονομάζονταιμπιτ(bit). Παρά τον πειρασμό να συσχετισθούν με αριθμητικές τιμές στην πραγματικότητα αποτελούν σύμβολα που η σημασία τους εξαρτάται από την εφαρμογή. Η αποθήκευση ενός μπιτ σε μια μηχανή προϋποθέτει την ύπαρξη μιας συσκευής που μπορεί να βρίσκεται σε μια από δύο δυνατές καταστάσεις όπως ένας διακόπτης ( on, off ) ή άλλες συσκευές. Μοναδιαίοι και δυαδικοί τελεστές ΛΟΓΙΚΕΣ ΠΡΑΞΕΙΣ Λογικοί Τελεστές Πίνακες Αλήθειας 3
4 Τελεστής NOT Τελεστής AND Εγγενής κανόνας του τελεστή AND Τελεστής OR Εγγενής κανόνας του τελεστή OR τελεστής XOR 4
5 Εγγενής κανόνας του τελεστή XOR Είσοδος Έξοδος Είσοδος Ή τεχνολογία έχει κατά καιρούς χρησιμοποιήσει διάφορες τεχνικές για αποθήκευση μπιτ. Αυτή που χρησιμοποιείται σήμερα είναι αυτή των πυκνωτών (βρίσκεται σε δύο καταστάσεις φορτισμένος-αφόρτιστος). Η σύγχρονη τεχνολογία επιτρέπει την κατασκευή εκατομμυρίων μικροσκοπικών πυκνωτών μαζί με τα απαραίτητα κυκλώματα σε μια μοναδική συσκευή που ονομάζεται τσιπ. Οι σύγχρονες τεχνολογίες την αποθήκευση μπιτ σε συσκευές των οποίων το μέγεθος μετριέται σε άνγκστρομ. (όπως η flash memory στις φωτογραφικές μηχανές). 1 Τα διάφορα συστήματα αποθήκευσης έχουν διαφορετικούς βαθμούς πτητικότητας. 0 5
6 Δεκαεξαδικά ψηφία Σημείωση: Ένα σχήμα 4 μπιτ μπορεί να αναπαρασταθεί από ένα δεκαεξαδικό ψηφίο και το αντίστροφο. Σχήμα μπιτ Δεκαεξαδικό Ψηφίο Σχήμα μπιτ Δεκαεξ. ψηφίο 8 9 A BC D EF Μετασχηματισμός δυαδικού σε δεκαεξαδικό και αντίστροφα Βρέστε το δεκαεξαδικό ισοδύναμο του μπιτ σχήματος Κάθε ομάδα 4 bits μετατρέπεται σε ένα δεκαεξαδικό ψηφίο. Το ισοδύναμο είναι xce2. Κύρια Μνήμη ΚΥΡΙΑ ΜΝΗΜΗ 6
7 Μονάδες Μνήμης Ο συνολικός αριθμός των μοναδικά προσδιορίσιμων θέσεων στη μνήμη ονομάζεται χώρος διευθύνσεων (address space). Μονάδα--- kilobyte megabyte gigabyte terabyte petabyte exabyte Πλήθος bytes 2 10 bytes 2 20 bytes 2 30 bytes 2 40 bytes 2 50 bytes 2 60 bytes Προσέγγιση 10 3 bytes 10 6 bytes 10 9 bytes bytes bytes bytes 1 Ένας υπολογιστής έχει 32 MB (megabytes) μνήμη. Πόσα bits απαιτούνται για την διευθυνσιοδότηση κάθε byte στη μνήμη; SRAM DRAM Τύποι Μνήμης RAM Ο χώρος των διευθύνσεων της μνήμης είναι 32 MB, ή 2 25 (2 5 x 2 20 ). Αυτό σημαίνει ότι απαιτούνται log ή 25 bits, για την διευθυσιοδότηση. Τύποι Μνήμης ROM PROM EPROM EEPROM ΕΙΣΟΔΟΣ/ΕΞΟΔΟΣ ΕΞΟΔΟΣ 7
8 Φυσική Διάταξη μαγνητικού δίσκου Οργάνωση Επιφανείας ενός δίσκου Μηχανική Διευθέτηση Ταινίας Οργάνωση Επιφανείας μιας Ταινίας Δημιουργία και Χρήση CD-ROM Ταχύτητα 1x 2x 4x 6x 8x 12x 16x 24x 32x 40x Ρυθμός Ανάπτυξης 153,600 bytes per second 307,200 bytes per second 614,400 bytes per second 921,600 bytes per second 1,228,800 bytes per second 1,843,200 bytes per second 2,457,600 bytes per second 3,688,400 bytes per second 4,915,200 bytes per second 6,144,000 bytes per second Προσέγγιση 150 KB/s 300 KB/s 600 KB/s 900 KB/s 1.2 MB/s 1.8 MB/s 2.4 MB/s 3.6 MB/s 4.8 MB/s 6 MB/s 8
9 Μορφή CD-ROM ΤΑ ΔΕΔΟΜΕΝΑ ΜΕΣΑ ΣΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Διαφορετικοί τύποι δεδομένων Σημείωση: Στη πληροφορική χρησιμοποιείται ο όρος multimedia για ορισμό πληροφοριών που περιέχουν αριθμούς, κείμενο, εικόνες, ήχο, και video. Σχήμα μπιτ Παραδείγματα bit σχημάτων 9
10 Παράσταση συμβόλων με χρήση σχημάτων bit Πλήθος συμβόλων και μήκος σχήματος μπιτ Πλήθος συμβόλων ,536 Μήκος σχήματος μπιτ Αναπαράσταση της λέξης BYTE σε κωδικό ASCII ΔΕΚΑΔΙΚΟΙ ΚΑΙ ΔΥΑΔΙΚΟΙ Η αποθήκευση αριθμητικών τιμών με τη μορφή κωδικοποιημένων χαρακτήρων δεν είναι αποδοτική όταν οι πληροφορίες που πρέπει να καταγραφούν είναι καθαρά αριθμητικές Δεκαδικό Σύτημα Αν χρησιμοποιήσουμε κωδικοποίηση για ένα διψήφιο θα χρειασθούν 16 μπιτ και ο μεγαλύτερος που μπορεί να αποθηκευθεί είναι ο 99. Στο δυαδικό σύστημα αρίθμησης όμως σε 16 μπιτ μπορεί να αποθηκευθεί ένας αριθμός στο διάστημα 0 μέχρι Για τους αριθμούς χρησιμοποιούμε την δυαδική αναπαράστασή τους. 10
11 Δυαδικό Σύστημα Μέθοδοι Αναπαράστασης Εικόνων Ψηφιογραφική Μέθοδος Αναπαράστασης Μαυρόασπρων Εικόνων Αναπαράσταση έγχρωμων πιξελ Αναπαράσταση ήχου Μετατροπή δυαδικού σε δεκαδικό δυαδικός δεκαδικός 11
12 Μετατρέψτε τον δυαδικό σε δεκαδικό. Γράψτε τα μπιτ και το βάρος τους. Πολλαπλασιάστε κάθε μπιτ με το αντίστοιχο βάρος και καταχωρίστε το αποτέλεσμα. Στο τέλος προσθέστε τα αποτελέσματα. Δυαδικός Βάρη Δεκαδικός 19 Μετατρέψτε τον δεκαδικό 35 σε δυαδικό. Διαιρέστε συνεχώς τον αριθμό με το 2 και καταγράψτε το πηλίκο και το υπόλοιπο. Μετακινήστε αριστερά το πηλίκο και καταγράψτε το υπόλοιπο κάτω από κάθε πηλίκο. Σταματήστε όταν το πηλίκο είναι Dec. Δυαδικός Μετατροπή δεκαδικού σε δυαδικό Πεδίο ορισμού των ακεραίων Ταξινόμηση των ακεραίων Διάστημα τιμών μη προσημασμένων ακεραίων Πλήθος μπιτ Διάστημα τιμών ,535 12
13 Αποθήκευση του 7 σε 8 μπιτ θέση μνήμης Μετατροπή του αριθμού στον δυαδικό 111. Πρόσθεση πέντε 0 για να γίνουν συνολικά N (8) μπιτ, Ο αριθμός αποθηκεύεται στη μνήμη. Πράδειγμα Αποθήκευση του 258 σε μια θέση μνήμης 16 μπιτ Μετατροπή του αριθμού στον δυαδικό Προσθήκη 7 0 για να γίνουν συνολικά N (16) μπιτ, Ο αριθμός αποθηκεύεται στη μνήμη. αποθήκευσης μη προσημασμένων ακεραίων σε Διαφορετικούς υπολογιστές Δεκαδικός ,760 1,245,678 8-bit overflow overflow overflow 16-bit overflow Ερμηνεύστε τον σε δεκαδικό αν έχει αποθηκευθεί σαν μη προσημασμένος. Με την προηγούμενη διαδικασία είναι ο 43. Σημείωση: Διάστημα τιμών προσημασμένων ακεραίων Υπάρχουν δύο 0 στην αναπαράσταση προσήμου: ένα θετικό και ένα αρνητικό. Σε 8-bit : Πλήθος μπιτ Διάστημα ,147,483, ,147,483,647 13
14 Σημείωση: Στην αναπαράσταση προσήμου και μεγέθους, το πιο αριστερό bit καθορίζει το πρόσημο του αριθμού. Αν είναι 0, ο αριθμός είναι θετικός. Αν είναι 1, ο αριθμός είναι αρνητικός. Αποθηκεύστε τον 258 σε θέση μνήμης 16- bit χρησιμοποιώντας αναπαράσταση προσήμου και μεγέθους. Μετατροπή σε δυαδικό Προσθήκη 6 0 για σύνολο N-1 1 (15) bits, Προσθήκη ενός 1 επειδή πρόκειται για αρνητικό. Το αποτέλεσμα: αποθήκευσης ακεραίων προσήμου και μεγέθους σε διαφορετικούς υπολογιστές Δεκαδικός ,760 8-bit overflow overflow 16-bit Ερμηνεύστε στοδεκαδικόανο αριθμός έχει αποθηκευθεί ως ακέραιος προσήμου και μεγέθους. Αν αγνοήσουμε το τελευταίο αριστερό μπιτ, το υπόλοιπο είναι Στο δεκαδικό είναι ο 59. Το πιο αριστερό bit είναι 1, επομένως ο αριθμός είναι ο 59. Οι σχεδιαστές έχουν ακολουθήσεις μια διαφορετική προσέγγιση χρησιμοποιούν την αναπαράσταση συμπληρώματος προς 1. Για την αναπαράσταση των θετικών χρησιμοποιούν την αναπαράσταση των μη προσημασμένων ενώ για τους αρνητικούς το συμπλήρωμα προς 1 (προκύπτει αν όλα τα 0 του θετικού μετατραπούν σε 1 και τα 1 σε 0. Το διάστημα τιμών σε συμπλήρωμα του 1 με N bit είναι: -(2 N-1-1) (2 N-1-1) 14
15 Σημείωση: Διάστημα τιμών με συμπλήρωμα του 1 Υπάρχουν δύο 0 στην αναπαράσταση συμπληρώματος προς 1: θετικό και αρνητικό. Σε 8-bit θέση: # Bits Διάστημα ,147,483, ,147,483,647 Σημείωση: Στην παράσταση συμπληρώματος προς1, το πιο αριστερό μπιτ ορίζει το πρόσημο. Αν είναι 0, ο αριθμός είναι θετικός.αν είναι1 1, ο αριθμός είναι αρνητικός. Αποθήκευση του +7 σε μνήμη 8-bit με χρήση συμπληρώματος προς 1. Αλλαγή πρώτα του αριθμού σε δυαδικό 111. Προσθήκη 5 0 για να γίνουν συνολικά N (8) bits, Το πρόσημο, είναι θετικό. Το αποτέλεσμα είναι: Αποθηκεύστε το 258 σε 16-bit μνήμη χρησιμοποιώντας αναπαράσταση συπληρώματος 1. Πρώτα αλλάζει ο αριθμός σε δυαδικό Προσθήκη 0 για συμπλήρωση των N (16) bits, Επειδή το πρόσημο είναι αρνητικό παίρνουμε το συμπλήρωμα κάθε ψηφίου.το αποτέλεσμα είναι: αποθήκευσης με συπλήρωμα του 1 ακεραίων Σε διαφορετικούς υπολογιστές Δεκαδικός ,760 24,760 8-bit overflow overflow 16-bit
16 Μετατρέψτε τον σε δεκαδικό αν έχει αποθηκευθεί με συμπλήρωμα του 1. Το πιο αριστερό μπιτ είναι 1, επομένωνς είναι αρνητικός. Βρίσκουμε το συμπλήρωμα. Το αποτέλεσμα είναι Σε δεκαδικό είναι 09. Επομένως ο αρχικός αριθμός ήταν 9. Το συμπλήρωμα του συμπληρώματος είναι ο αρχικός αριθμός. Σημείωση: Συμπλήρωμα του 1 σημαίνει αντιστροφή όλων των μπιτ. Το συμπλήρωμα ενός θετικού είναι ο αντίστοιχος αρνητικός. Το συμπλήρωμα ενός αρνητικού είναι ο αντίστοιχος θετικός. Δύο φορές το συμπλήρωμα παίρνουμε τον αρχικό αριθμό. Σημείωση: Το πιο συνηθισμένο είναι το συμπλήρωμα του 2. Σχήμα Τιμή Σχήμα Τιμή Το διάστημα τιμών σε συμπλήρωμα του 2 με N bit είναι: Διάστημα τιμών με συπλήρωμα προς 2 -(2 N-1 ) (2 N-1-1) Πλήθος bit Range , ,767 2,147,483, ,147,483,647 16
17 Αποθήκευση αριθμών με συμπλήρωμα του 2 Σημείωση: Στην αναπαράσταση με συμπλήρωμα του 2, το πιο αριστερό bit ορίζει το πρόσημο του αριθμού. Αν είναι 0, ο αριθμός είναι θετικός. Αν είναι 1, ο αριθμός είναι αρνητικός. 1. Ο αριθμός μετατρέπεται στο δυαδικό αγνοώντας το προσημο. 2. Αν το πλήθος των μπιτ είναι μικρότερο από Ν, προστίθενται μηδενικά αριστερά του αριθμού για να συμπληρωθούν Ν μπιτ. 3. Αν το πρόσημο είναι θετικό αυτή είναι η αναπαράσταση του αριθμού. Αν το πρόσημο είναι αρνητικό μένουν ως έχουν όλα τα δεξιότερα 0 και το πρώτο 1. Τα υπόλοιπα μπιτ αντικαθίστανται με το συμπλήρωμά τους. Παρλαδειγμα Αποθηκεύστε τον +7 σε 8-bit μνήμη με χρήση συμπληρώματος του 2. Μετατροπή του αριθμού σε δυαδικό 111. Προσθήκη 5 0 για να γίνουν (8) bits, Το πρόσημο είναι θετικό άρα δεν χρειάζεται κάτι άλλο. Το αποτέλεσμα είναι: Αποθήκευση του 40 σε 16-bit μνήμη με χρήση συμπληρώματος του 2. Μετατροπή του αριθμού σε δυαδικό Προσθήκη 10 0 για συνολικά N (16) bits, Το πρόσημο είναι αρνητικό, επομένως αφήνουμε τα πιο δεξιά 0 μέχρι το πρώτο 1 (συμπεριλαμβανομένου του 1) άθικτα και παίρνουμε συμπλήρωμα των υπολοίπων. Το αποτέλεσμα είναι: αποθήκευσης σε συμπλήρωμα του 2 Ακεραίων σε διαφορετικούς υπολογιστές Σημείωση: Δεκαδιός ,760 24,760 8-bit overflow overflow 16-bit Υπάρχει μόνο ένα 0 στο συμπλήρωμα του 2: Σε 8-bit :
18 Δώστε τον σε δεκαδικό αν έχει αποθηκευθεί σε συμπλήρωμα του 2. Το πιο αριστερό ψηφίο είναι 1. Ο αριθμός είναι αρνητικός. Αφήνουμε το 10 δεξιά και συμπληρώνουμε το υπόλοιπο. Το αποτέλεσμα είναι Το συμπλήρωμα ως προς 2 είναι 10. Επομένως ο αρχικός αριθμός ήταν 10. Σημείωση: Το συμπλήρωμα του 2 μπορεί να επιτευχθεί αντιστρέφοντας όλα τα εκτός από τα πιο δεξιά μέχρι το πρώτο 1 (συμπεριλαμβανομένου). Τα συμπλήρωμα ενός είναι ο αντίστοιχος αρνητικός. Το συμπλήρωμα ενός αρνητικού είναι ο αντίστοιχος θετικός. Δύο φορές συμπλήρωμα παίρνουμε τον αρχικό. Παράσταση Ακεραίων Περιεχόμενο της μνήμης Χωρίς πρόσημο Πρόσημο-& μέγεθος Συμπλήρωμα του Συμπλήρωμα του Σημείωση: Κανόνες Πρόσθεσης Ακεραίων με Συμπλήρωμα του 2 Προσθέστε 2 μπιτ και διάδοση της μεταφοράς στην επόμενη στήλη. Αν υπάρχει μια τελική μεταφορά με την πρόσθεση της πιο αριστερής στήλης, απορρίπτεται. Προσθέστε δύο αριθμούς σε παράσταση συμπληρώματος του 2: (+17) + (+22) (+39) Μεταφορά Αποτέλεσμα Προσθέστε δύο αριθμούς σε παράσταση συμπληρώματος του 2: (+24) + (-17) (+7) Μεταφ Αποτελ
19 Προσθέστε δύο αριθμούς σε παράσταση συμπληρώματος του 2 : (+127) + (+3) (+130) Αριθμοί με συμπλήρωμα του 2 Μετα Αποτ (Λάθο( Λάθο) overflow. Σημείωση: Στις αριθμητικές πράξεις σε υπολογιστή, να θυμάστε ότι κάθε αριθμός καθώς και το αποτέλεσμα πρέπει να είναι στο επιτρεπτό διάστημα. Αφαιρέστε το 62 από το 101 σε συμπλήρωμα του 2: (+101) - (+62) (+101) + (-62) Μερ Αποτελ Η πιο αριστερή μεταφορά απορρίπτεται. ΠΛΕΟΝΑΣΜΑ Στην περίπτωση αυτή χρησιμοποιείται ένας θετικός ο οποίος ονομάζεται μαγικός. Ο μαγικός αριθμός είναι συνήθως ο (2 Ν-1 ) ή ο (2 Ν-1-1). Για την αναπαράσταση προστίθεται στον αριθμό ο μαγικός αριθμός και το αποτέλεσμα σε δυαδικό και προστίθενται μηδενικά για να υπάρχουν συνολικά Ν μπιτ. 19
20 Παραστήστε τον 25 σε πλεόνασμα _127 χρησιμοποιώντας 8-bit. Προσθέστε πρώτα το 127 για να πάρετε 102. Σε δυαδική μορφή είναι Προσθήκη ενός μπιτ για να γίνει 8 μπιτ. Η αναπαράσταση είναι Ποιος είναι ο σε πλεόνασμα_127. Μετατροπή σε δεκαδικό. Είναι 254. Αφαίρεση του 127 από τον αριθμό. Το αποτέλεσμα είναι δεκαδικό 127. ΑΝΑΠΑΡΑΣΤΑΣΗ ΚΙΝΗΤΗΣ ΥΠΟΔΙΑΣΤΟΛΗΣ Για να μετατρέψουμε ένα αριθμό κινητής υποδιαστολής σε δυαδικό: Μετατρέπουμε το ακέραιο μέρος σε δυαδικό Μετατρέπουμε το κλασματικό μέρος σε δυαδικό. Τοποθετούμε υποδιαστολή μεταξύ των δύο. Αλλαγή δεκαδικού μέρους σε δυαδικό Μετατροπή του σε δυαδικό Γράψτε το δεκαδικό μέρος αριστερά. Πολλαπλασιάζουμε συνεχώς επί 2 και εξάγουμε το ακέραιο μέρος σαν το δυαδικό ψηφίο. Σταματάμε όταν ο αριθμός
21 Να μετατραπεί το δεκαδικό 0.4 σε δυαδικό με 6 bits. Γράψτε το δεκαδικό στην αριστερή γωνία. Πολλαπλασιάστε τον αριθμό συνεχώς με 2 και βγάζετε το ακέραιο μέρος σαν δυαδικό ψηφίο. Ποτέ δεν θα πάρετε την ακριβή δυαδικά παράσταση. Σταματήστε όταν έχετε 6 bits. Παραδείγματα κανονικοποίησης Original Αρχικός Number αριθμός Μεταφορά Κανονικοποίηση +2 6 x x x x IEEE πρότυπα για κινητή υποδιαστολή Δείξτε την αναπαράσταση του κανονικοποιημένου x Το πρόσημο είναι θετικό. Η αναπαράσταση του εκθέτη 133 με υπέρβαση _127. Προσθέστε 0 δεξιά για να γίνουν 23 bits. Ο αριθμός που αποθηκεύεται στη μνήμη: Παραδείγματα αναπαράστασης κινητή υποδιαστολής Αριθμός -2 2 x x x Προσ Εκθέτης Mantissa Ποιος ο 32-bit αριθμός κινητής υποδιαστολής Το πρόσημο είναι αρνητικό. Ο εκθέτης 33 ( ). Ο αριθμός μετά την κανονικοποίηση -2-3 x
22 Μοντέλο επεξεργαστή δεδομένων Μοντέλο Προγραμματιζόμενου επεξεργαστή Το ίδιο πρόγραμμα διαφορετικά δεδομένα Ίδια δεδομένα, διαφορετικά προγράμματα von Neumann μοντέλο von NEUMANN ΜΟΝΤΕΛΟ 22
23 ΥΛΙΚΟ ΥΠΟΛΟΓΙΣΤΗ ΔΕΔΟΜΕΝΑ Πρόγραμμα και δεδομένα στη μνήμη ΛΟΓΙΣΜΙΚΟ ΥΠΟΛΟΓΙΣΤΩΝ Τα προγράμματα αποτελούνται από εντολές Βήματα Κύκλου Μηχανής 1. Εισαγωγή του πρώτου στοιχείου δεδομένων στη μνήμη 2. Εισαγωγή του δεύτερου στοιχείου δεδομένων στη μνήμη 3. Πρόσθεση των δύο και αποθήκευση στη μνήμη 4. Εμφάνιση του αποτελέσματος Πρόγραμμα ανάκληση αποκωδικοποίηση εκτέλεση 23
24 Περιεχόμενα μνήμης & καταχωρητών πριν από την εκτέλεση Περιεχόμενα μνήμης μετά από κάθε κύκλο Μετά την πρώτη εντολή Περιεχόμενα μνήμης μετά από κάθε κύκλο Μετά τη δεύτερη εντολή Μετά την Τρίτη εντολή Μάσκα Μετά την τέταρτη εντολή 24
25 απενεργοποίησης Συγκεκριμένων μπιτ Χρησιμοποιήστεμιαμάσκαγιανα απενεργοποιήσετε τα 5 πιο αριστερά μπιτ ενός σχήματος. Ελέγξτε τη μάσκα με το Η μάσκα είναι Στόχος AND Μας Αποτε Έστω ένα υδραγωγείο που παρέχει νερό σε μια πόλη μέσω 8 αντλιών. Η κατάσταση των αντλιών (ανοικτές ή κλειστές) μπορεί να παρασταθεί με ένα σχήμα 8 μπιτ. Για παράδειγμα, το σχήμα δείχνει ότι οι αντλίες 1 έως 3 (από δεξιά), 7 και 8 είναι ανοικτές ενώ οι αντλίες 4, 5, και 6 είναι κλειστές. Υποθέστε τώρα ότι κλείνει η αντλία 7. Πως παριστάνεται αυτό μέσω μιας μάσκας? Χρησιμοποιήστε τη μάσκα για σύζευξη (AND) με το σχήμα προορισμού. Το μόνο 0 bit (bit 7) στη μάσκα ακυρώνει το έβδομο bit στο στόχο. Στόχος AND Μάσκα Αποτέλεσμα ενεργοποίησης συγκεκριμένων μπιτ Χρησιμοποιήστεμιαμάσκαγιανα ενεργοποιήσετε τα 5 πιο αριστερά μπιτ ενός σχήματος. Ελέξετ τη μάσκα με το Η μάσκα είναι Στόχος OR Μάσκα Αποτέλεσμα
26 Στο παράδειγμα του υδραγωγείου, κατασκευάστε μια μάσκα που να ανοίγει την αντλία 6. αντιστροφής συγκεκριμένων μπιτ Χρησιμοποιήστε τη μάσκα Στόχος OR Μάσκα Αποτέλεσμα Χρησιμοποιήστε μάσκα για να αντιστρέψετε τα 5 πιο αριστερά bits ενός σχήματος. Ελέξτε τη μάσκα με το σχήμα Στόχος XOR Μάσκα Αποτέλεσμα ΠΡΑΞΕΙΣ ΟΛΙΣΘΗΣΗΣ Πράξεις ολίσθησης Οι πράξεις ολίσθησης χρειάζονται ιδιαίτερη προσοχή όταν το σχήμα αναπαριστά κάποιον προσημασμένο αριθμό. Μιατέτοιαπράξημπορείνα αλλάξει το πιο αριστερό μπιτ το οποίο αντιπροσωπεύει το πρόσημο. 26
27 Δείξτε πως μπορεί να διαιρεθεί ή να πολλαπλασιασθεί ένας αριθμός με το 2 με πράξεις ολίσθησης. Αν ένα bit σχήμα αναπαριστά ένα μη προσημασμένο αριθμό, μια δεξιά ολίσθηση διαιρεί τον αριθμό με 2. Το σχήμα παριστά τον 59. Στη δεξιά ολίσθηση παίρνουμε τον , που είναι ο 29. Στην αριστερή ολίσθηση, παίρνουμε , που είναι 118. Χρησιμοποιήστε ένα συνδυασμό από λογικές πράξεις και πράξεις ολίσθησης για να βρείτε την τιμή (0 ή 1) του τέταρτου bit (από δεξιά). Χρησιμοποιούμε τη μάσκα για σύζευξη (AND) μετονστόχογιανακρατήσουμετο τέταρτο bit και να ακυρώσουμε τα άλλα. (συνέχεια) Στόχος a b c d e f g h AND Μάσκα Αποτέλεσμα e Ολίσθηση του νέου σχήματος τρεις φορές προς τα δεξιά 0000e e e e ΣΥΝΔΕΣΗ ΥΠΟΣΥΣΤΗΜΑΤΩΝ Τώρα είναι πολύ εύκολο να ελέγξουμε την τιμή του νέου σχήματος. Αν η τιμή είναι 1, το αρχικό bit ήταν 1; Διαφορετικά το αρχικό μπιτ ήταν 0. Σύνδεση ΚΜΕ και μνήμης μέσω τριών διαύλων Σύνδεση συσκευών I/O με τους διαύλους 27
28 Ελεγκτής SCSI Small Computer Interface Ελεγκτής FireWire Ελεγκτής USB ΙΣΤΟΡΙΚΑ Στόχοι Ορισμός τύπων δεδομένων Κατανόηση της αποθήκευσης των δεδομένων σε υπολογιστή ΤΥΠΟΙ ΔΕΔΟΜΕΝΩΝ Κατανόηση των διαφορών μεταξύ κειμένου, αριθμού, εικόνων, video, και ήχου. Συμβολισμοί δεκαεξαδικών και οκταδικών αριθμών. 28
29 ΑΜΑΠΑΡΑΣΤΑΣΗ ΔΕΔΟΜΕΝΩΝ ΔΕΚΑΕΞΑΔΙΚΟΣ ΣΥΜΒΟΛΙΣΜΟΣ Example 2 Show the hexadecimal equivalent of the bit pattern Solution Χωρίστε το μπιτ σχήμα σε ομάδες των 4 μπιτ (από δεξιά). Στην περίπτωση αυτή, προσθέστε 2 επιπλέον 0 στα αριστερά ώστε το πλήθος των μπιτ να διαιρείται με το 4. Έτσι έχετε τον , που μεταφράζεται σε x0e2. 3 Ποιο είναι το μπιτ σχήμα του x24c? Γράψτε κάθε δεκαεξαδικό ψηφίο στο ισοδύναμο του δυαδικό που δίνει Σημείωση: ΟΚΤΑΔΙΚΟΣ ΣΥΜΒΟΛΙΣΜΟΣ Ένα σχήμα 3 μπιτ μπορεί να παρασταθεί με ένα δυαδικό ψηφίο και αντίστροφα. 29
30 Οκταδικά ψηφία Μετασχηματισμός δυαδικού σε οκταδικό και αντίστροφα Σχήμα μπιτ Οκταδικό ψηφίο Σχήμα μπιτ Οκταδικό ψηφίο Βρέστε το οκταδικό ισοδύναμο του Κάθε ομάδα 3 bits μετατρέπεται σε ένα οκταδικό ψηφίο. Το ισοδύναμο είναι 0562, o562, or Βρέστε το οκταδικό ισοδύναμο του Divide the bit pattern into 3-bit 3 groups (from the right). In this case, add two extra 0s at the left to make the number of bits divisible by 3. So you have , which is translated to Βρέστε το δεκαεξαδικό ισοδύναμο του μπιτ σχήματος Χωρίστε το μπιτ σχήμα σε ομάδες των 3 μπιτ (από δεξιά). Στην περίπτωση αυτή, προσθέστε 2 επιπλέον 0 στα αριστερά ώστε το πλήθος των μπιτ να διαιρείται με το 3. Έτσι έχετε τον , που μεταφράζεται σε Ποιο το μπιτ σχήμα του 24 8 ; Γράψτε κάθε οκταδικό ψηφίο στο ισοδύναμο δυαδικό σχήμα και έχετε
31 Στόχοι Μετατροπή ενός αριθμού από δεκαδικό σε δυαδικό και αντίστροφα. Κατανόηση των διαφορετικών αναπαραστάσεων ενός ακεραίου στον υπολογιστή: πρόσημο, 1_συμπλήρωμα συμπλήρωμα, και 2_συμπλήρωμα συμπλήρωμα.. Κατανόηση του συστήματος αποθήκευσης εκθετικής μορφής Πραγματικών αριθμών ΑΝΑΠΑΡΑΣΤΣΗ ΑΚΕΡΑΙΩΝ Κατανόηση της αποθήκευσης στον υπολογιστή με χρήση εκθέτη και mantissa. ΔΕΚΑΕΞΑΔΙΚΟΣ ΣΥΜΒΟΛΙΣΜΟΣ Αποθηκεύστε τον +7 σε 8 μπιτ θέση μνήμης χρησιμοποιώντας αναπαράσταση προσήμου και μεγέθους. Μετατροπή σε δυαδικό 111. Προσθήκη 4 μηδενικών N-1 1 (7) bits, Προσθήκη ενός επιπλέον 0 επειδή είναι θετικός. Το αποτέλεσμα είναι:
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 ΑριθμητικέςΠράξειςσεΑκέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση Ο πολλαπλασιασμός
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 ΑριθμητικέςΠράξειςσεΑκέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση Ο πολλαπλασιασμός
Εισαγωγή στην επιστήμη των υπολογιστών
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 3ο Αναπαράσταση Αριθμών www.di.uoa.gr/~organosi 1 Δεκαδικό και Δυαδικό Δεκαδικό σύστημα 2 3 Δεκαδικό και Δυαδικό Δυαδικό Σύστημα
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 3ο Αναπαράσταση Αριθμών www.di.uoa.gr/~organosi 1 Δεκαδικό και Δυαδικό Δεκαδικό σύστημα 2 3 Δεκαδικό και Δυαδικό Δυαδικό Σύστημα
Τμήμα Οικιακής Οικονομίας και Οικολογίας. Αναπαράσταση Αριθμών
 Αναπαράσταση Αριθμών Δεκαδικό και Δυαδικό Δεκαδικό σύστημα Δεκαδικό και Δυαδικό Μετατροπή Για τη μετατροπή ενός αριθμού από το δυαδικό σύστημα στο δεκαδικό, πολλαπλασιάζουμε κάθε δυαδικό ψηφίο του αριθμού
Αναπαράσταση Αριθμών Δεκαδικό και Δυαδικό Δεκαδικό σύστημα Δεκαδικό και Δυαδικό Μετατροπή Για τη μετατροπή ενός αριθμού από το δυαδικό σύστημα στο δεκαδικό, πολλαπλασιάζουμε κάθε δυαδικό ψηφίο του αριθμού
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 Αριθμητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση Ο πολλαπλασιασμός
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 Αριθμητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση Ο πολλαπλασιασμός
Εισαγωγή στην επιστήμη των υπολογιστών. Πράξεις με μπιτ
 Εισαγωγή στην επιστήμη των υπολογιστών Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 Αριθμητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση 3 Πρόσθεση στη μορφή συμπληρώματος ως προς δύο
Εισαγωγή στην επιστήμη των υπολογιστών Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 Αριθμητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση 3 Πρόσθεση στη μορφή συμπληρώματος ως προς δύο
Σύστημα Πλεονάσματος και Αναπαράσταση Αριθμών Κινητής Υποδιαστολής
 Σύστημα Πλεονάσματος και Αναπαράσταση Αριθμών Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση θετικών και αρνητικών ακεραίων σε έναν
Σύστημα Πλεονάσματος και Αναπαράσταση Αριθμών Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση θετικών και αρνητικών ακεραίων σε έναν
Σύστημα Πλεονάσματος. Αναπαράσταση Πραγματικών Αριθμών. Αριθμητικές Πράξεις σε Αριθμούς Κινητής Υποδιαστολής
 Σύστημα Πλεονάσματος Αναπαράσταση Πραγματικών Αριθμών Αριθμητικές Πράξεις σε Αριθμούς Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση
Σύστημα Πλεονάσματος Αναπαράσταση Πραγματικών Αριθμών Αριθμητικές Πράξεις σε Αριθμούς Κινητής Υποδιαστολής Σύστημα Πλεονάσματος (Excess System) - 1 Είναι μια άλλη μια μορφή αναπαράστασης για αποθήκευση
Εισαγωγή στον Προγραμματισμό
 Εισαγωγή στον Προγραμματισμό Ενότητα 3 Λειτουργίες σε Bits, Αριθμητικά Συστήματα Χρήστος Γκουμόπουλος Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Φύση υπολογιστών Η
Εισαγωγή στον Προγραμματισμό Ενότητα 3 Λειτουργίες σε Bits, Αριθμητικά Συστήματα Χρήστος Γκουμόπουλος Πανεπιστήμιο Αιγαίου Τμήμα Μηχανικών Πληροφοριακών και Επικοινωνιακών Συστημάτων Φύση υπολογιστών Η
Τμήμα Οικιακής Οικονομίας και Οικολογίας. Αναπαράσταση Αριθμών
 Αναπαράσταση Αριθμών Δεκαδικό και Δυαδικό Δεκαδικό σύστημα Δεκαδικό και Δυαδικό Μετατροπή Για τη μετατροπή ενός αριθμού από το δυαδικό σύστημα στο δεκαδικό, πολλαπλασιάζουμε κάθε δυαδικό ψηφίο του αριθμού
Αναπαράσταση Αριθμών Δεκαδικό και Δυαδικό Δεκαδικό σύστημα Δεκαδικό και Δυαδικό Μετατροπή Για τη μετατροπή ενός αριθμού από το δυαδικό σύστημα στο δεκαδικό, πολλαπλασιάζουμε κάθε δυαδικό ψηφίο του αριθμού
Εισαγωγή στην Πληροφορική & τον Προγραμματισμό
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στην Πληροφορική & τον Προγραμματισμό Ενότητα 3 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Χ. Κυτάγιας Τμήμα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Εισαγωγή στην Πληροφορική & τον Προγραμματισμό Ενότητα 3 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Χ. Κυτάγιας Τμήμα
Διδάσκων:Μ.Χατζόπουλος, Παραδόσεις:Τρίτη 4-6, Τετάρτη 1-3; (Αμφιθέατρο Α15) Πληροφορίες στην ιστοσελίδα του μαθήματος http://www.di.uoa.
 Πληροφορική 1 Διδάσκων:Μ.Χατζόπουλος, Παραδόσεις:Τρίτη 4-6, Τετάρτη 1-3; (Αμφιθέατρο Α15) Πληροφορίες στην ιστοσελίδα του μαθήματος http://www.di.uoa.gr/~organosi/ 2 Η δομή του μαθήματος Εισαγωγή στην
Πληροφορική 1 Διδάσκων:Μ.Χατζόπουλος, Παραδόσεις:Τρίτη 4-6, Τετάρτη 1-3; (Αμφιθέατρο Α15) Πληροφορίες στην ιστοσελίδα του μαθήματος http://www.di.uoa.gr/~organosi/ 2 Η δομή του μαθήματος Εισαγωγή στην
Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας. Πληροφορική Ι. Αναπαράσταση αριθμών στο δυαδικό σύστημα. Δρ.
 Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Πληροφορική Ι Αναπαράσταση αριθμών στο δυαδικό σύστημα Δρ. Γκόγκος Χρήστος Δεκαδικό σύστημα αρίθμησης Ελληνικό - Ρωμαϊκό Σύστημα αρίθμησης
Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Πληροφορική Ι Αναπαράσταση αριθμών στο δυαδικό σύστημα Δρ. Γκόγκος Χρήστος Δεκαδικό σύστημα αρίθμησης Ελληνικό - Ρωμαϊκό Σύστημα αρίθμησης
Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας. Πληροφορική Ι. Μάθημα 4 ο Πράξεις με bits. Δρ.
 Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Πληροφορική Ι Μάθημα 4 ο Πράξεις με bits Δρ. Γκόγκος Χρήστος Κατηγορίες πράξεων με bits Πράξεις με δυαδικά ψηφία Αριθμητικές πράξεις
Τμήμα Χρηματοοικονομικής & Ελεγκτικής ΤΕΙ Ηπείρου Παράρτημα Πρέβεζας Πληροφορική Ι Μάθημα 4 ο Πράξεις με bits Δρ. Γκόγκος Χρήστος Κατηγορίες πράξεων με bits Πράξεις με δυαδικά ψηφία Αριθμητικές πράξεις
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 Αριθμητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση Ο πολλαπλασιασμός
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 4ο Πράξεις με μπιτ 1 Πράξεις με μπιτ 2 Αριθμητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασμός, Διαίρεση Ο πολλαπλασιασμός
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Συστήματα αρίθμησης Δυαδικό αριθμητικό
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Συστήματα αρίθμησης Δυαδικό αριθμητικό
Πληροφορική. Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων. Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Πληροφορική Ενότητα 4 η : Κωδικοποίηση & Παράσταση Δεδομένων Ι. Ψαρομήλιγκος Τμήμα Λογιστικής & Χρηματοοικονομικής Άδειες Χρήσης
Εισαγωγή στην επιστήµη των υπολογιστών. Πράξεις µε µπιτ
 Εισαγωγή στην επιστήµη των υπολογιστών Πράξεις µε µπιτ 1 Πράξεις µε µπιτ 2 Αριθµητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασµός, Διαίρεση 3 Πρόσθεση στη µορφή συµπληρώµατος ως προς δύο
Εισαγωγή στην επιστήµη των υπολογιστών Πράξεις µε µπιτ 1 Πράξεις µε µπιτ 2 Αριθµητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασµός, Διαίρεση 3 Πρόσθεση στη µορφή συµπληρώµατος ως προς δύο
Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1 Αριθµητικό Σύστηµα! Ορίζει τον τρόπο αναπαράστασης ενός αριθµού µε διακεκριµένα σύµβολα! Ένας αριθµός αναπαρίσταται διαφορετικά σε κάθε σύστηµα,
Εισαγωγή στην επιστήµη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1 Αριθµητικό Σύστηµα! Ορίζει τον τρόπο αναπαράστασης ενός αριθµού µε διακεκριµένα σύµβολα! Ένας αριθµός αναπαρίσταται διαφορετικά σε κάθε σύστηµα,
ΠΛΗ21 Κεφάλαιο 2. ΠΛΗ21 Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: Παράσταση Προσημασμένων Αριθμών Συμπληρώματα
 Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 2 2.3.4 Παράσταση Προσημασμένων Αριθμών Συμπληρώματα Στόχοι του κεφαλαίου είναι να γνωρίσουμε: Τι είναι ένας Συμπλήρωμα ενός αριθμού πρακτικά Τι είναι Συμπλήρωμα ως
Ψηφιακά Συστήματα: Τόμος Α Κεφάλαιο: 2 2.3.4 Παράσταση Προσημασμένων Αριθμών Συμπληρώματα Στόχοι του κεφαλαίου είναι να γνωρίσουμε: Τι είναι ένας Συμπλήρωμα ενός αριθμού πρακτικά Τι είναι Συμπλήρωμα ως
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 2.1 Τύποι Δεδομένων Τα δεδομένα σήμερα συναντώνται σε διάφορες μορφές, στις οποίες περιλαμβάνονται αριθμοί,
Λύσεις Ασκήσεων ΣΕΙΡΑ 1 η. Πρόσημο και μέγεθος
 ΓΕΩΠΟΝΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΡΓΑΣΤΗΡΙΟ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΠΛΗΡΟΦΟΡΙΚΗ ΕΞΑΜΗΝΟ: 1 ο /2015-16 ΤΜΗΜΑ: ΑΓΡΟΤΙΚΗΣ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ Καθηγητής: Θ. Τσιλιγκιρίδης Άσκηση 1η Περιεχόμενα μνήμης Λύσεις
ΓΕΩΠΟΝΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΡΓΑΣΤΗΡΙΟ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΠΛΗΡΟΦΟΡΙΚΗ ΕΞΑΜΗΝΟ: 1 ο /2015-16 ΤΜΗΜΑ: ΑΓΡΟΤΙΚΗΣ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ Καθηγητής: Θ. Τσιλιγκιρίδης Άσκηση 1η Περιεχόμενα μνήμης Λύσεις
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 1 2. ΑΡΙΘΜΗΤΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΜΕΡΟΣ Α 2 Τεχνολογία
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 1 2. ΑΡΙΘΜΗΤΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΜΕΡΟΣ Α 2 Τεχνολογία
Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση
 Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση τους Κατόπιν, στην επινόηση συμβόλων για τη παράσταση
Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση τους Κατόπιν, στην επινόηση συμβόλων για τη παράσταση
Εισαγωγή στην επιστήµη των υπολογιστών. Πράξεις µε µπιτ
 Εισαγωγή στην επιστήµη των υπολογιστών Πράξεις µε µπιτ 1 Πράξεις µε µπιτ 2 Αριθµητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασµός, Διαίρεση Ο πολλαπλασιασµός και η διαίρεση στο επίπεδο του
Εισαγωγή στην επιστήµη των υπολογιστών Πράξεις µε µπιτ 1 Πράξεις µε µπιτ 2 Αριθµητικές Πράξεις σε Ακέραιους Πρόσθεση, Αφαίρεση, Πολλαπλασιασµός, Διαίρεση Ο πολλαπλασιασµός και η διαίρεση στο επίπεδο του
ΠΛΗΡΟΦΟΡΙΚΗ I Ενότητα 6
 ΠΛΗΡΟΦΟΡΙΚΗ I Ενότητα 6 ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Bits & Bytes Bit: η μικρότερη μονάδα πληροφορίας μία από δύο πιθανές καταστάσεις (ναι / όχι, αληθές / ψευδές, n / ff) κωδικοποίηση σε 0 ή 1 δυαδικό σύστημα
ΠΛΗΡΟΦΟΡΙΚΗ I Ενότητα 6 ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Bits & Bytes Bit: η μικρότερη μονάδα πληροφορίας μία από δύο πιθανές καταστάσεις (ναι / όχι, αληθές / ψευδές, n / ff) κωδικοποίηση σε 0 ή 1 δυαδικό σύστημα
µπιτ Λύση: Κάθε οµάδα των τεσσάρων µπιτ µεταφράζεται σε ένα δεκαεξαδικό ψηφίο 1100 C 1110 E Άρα το δεκαεξαδικό ισοδύναµο είναι CE2
 ! Βρείτε το δεκαεξαδικό ισοδύναµο του σχήµατος µπιτ 110011100010 Λύση: Κάθε οµάδα των τεσσάρων µπιτ µεταφράζεται σε ένα δεκαεξαδικό ψηφίο 1100 C 1110 E 0010 2 Άρα το δεκαεξαδικό ισοδύναµο είναι CE2 2 !
! Βρείτε το δεκαεξαδικό ισοδύναµο του σχήµατος µπιτ 110011100010 Λύση: Κάθε οµάδα των τεσσάρων µπιτ µεταφράζεται σε ένα δεκαεξαδικό ψηφίο 1100 C 1110 E 0010 2 Άρα το δεκαεξαδικό ισοδύναµο είναι CE2 2 !
Εισαγωγή στην πληροφορική
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 3: Δυαδικά Συστήματα Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Εισαγωγή στην πληροφορική Ενότητα 3: Δυαδικά Συστήματα Αγγελίδης Παντελής Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με Α.Μ. σε 8 & 9 11/10/07
 ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με Α.Μ. σε 8 & 9 11/10/07 Τμήμα θεωρίας: Α.Μ. 8, 9 Κάθε Πέμπτη, 11πμ-2μμ, ΑΜΦ23. Διδάσκων: Ντίνος Φερεντίνος Γραφείο 118 email: kpf3@cornell.edu Μάθημα: Θεωρία + προαιρετικό
ΠΛΗΡΟΦΟΡΙΚΗ Ι JAVA Τμήμα θεωρίας με Α.Μ. σε 8 & 9 11/10/07 Τμήμα θεωρίας: Α.Μ. 8, 9 Κάθε Πέμπτη, 11πμ-2μμ, ΑΜΦ23. Διδάσκων: Ντίνος Φερεντίνος Γραφείο 118 email: kpf3@cornell.edu Μάθημα: Θεωρία + προαιρετικό
Αριθµητική υπολογιστών
 Αριθµητική υπολογιστών Μιχάλης ρακόπουλος Υπολογιστική Επιστήµη & Τεχνολογία, #03 1 εκαδικό σύστηµα αρίθµησης Βάση το 10. 10 ψηφία: 0 1 2 3 4 5 6 7 8 9 1 δεκαδικό ψηφίο εκφράζει 1 από 10 πιθανές επιλογές
Αριθµητική υπολογιστών Μιχάλης ρακόπουλος Υπολογιστική Επιστήµη & Τεχνολογία, #03 1 εκαδικό σύστηµα αρίθµησης Βάση το 10. 10 ψηφία: 0 1 2 3 4 5 6 7 8 9 1 δεκαδικό ψηφίο εκφράζει 1 από 10 πιθανές επιλογές
Δυαδικό Σύστημα Αρίθμησης
 Δυαδικό Σύστημα Αρίθμησης Το δυαδικό σύστημα αρίθμησης χρησιμοποιεί δύο ψηφία. Το 0 και το 1. Τα ψηφία ενός αριθμού στο δυαδικό σύστημα αρίθμησης αντιστοιχίζονται σε δυνάμεις του 2. Μονάδες, δυάδες, τετράδες,
Δυαδικό Σύστημα Αρίθμησης Το δυαδικό σύστημα αρίθμησης χρησιμοποιεί δύο ψηφία. Το 0 και το 1. Τα ψηφία ενός αριθμού στο δυαδικό σύστημα αρίθμησης αντιστοιχίζονται σε δυνάμεις του 2. Μονάδες, δυάδες, τετράδες,
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης Μαθησιακοί Στόχοι Η Ενότητα 2 διαπραγματεύεται θέματα
Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης Μαθησιακοί Στόχοι Η Ενότητα 2 διαπραγματεύεται θέματα
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ. Βασικές Έννοιες Προγραμματισμού. Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Βασικές Έννοιες Προγραμματισμού Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Αριθμητικά συστήματα Υπάρχουν 10 τύποι ανθρώπων: Αυτοί
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Η/Υ Βασικές Έννοιες Προγραμματισμού Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Αριθμητικά συστήματα Υπάρχουν 10 τύποι ανθρώπων: Αυτοί
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Πληροφορική Ι. Ενότητα 3 : Αναπαράσταση αριθμών στο δυαδικό σύστημα. Δρ.
 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική Ι Ενότητα 3 : Αναπαράσταση αριθμών στο δυαδικό σύστημα Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική Ι Ενότητα 3 : Αναπαράσταση αριθμών στο δυαδικό σύστημα Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής
! Εάν ο αριθμός διαθέτει περισσότερα bits, χρησιμοποιούμε μεγαλύτερες δυνάμεις του 2. ! Προσοχή στη θέση του περισσότερο σημαντικού bit!
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές ) http://di.ionio.gr/~mistral/tp/csintro/ Αριθμοί Πράξεις με δυαδικούς αριθμούς
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές ) http://di.ionio.gr/~mistral/tp/csintro/ Αριθμοί Πράξεις με δυαδικούς αριθμούς
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή
 Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Γενικά Στοιχεία Ηλεκτρονικού Υπολογιστή 1. Ηλεκτρονικός Υπολογιστής Ο Ηλεκτρονικός Υπολογιστής είναι μια συσκευή, μεγάλη ή μικρή, που επεξεργάζεται δεδομένα και εκτελεί την εργασία του σύμφωνα με τα παρακάτω
Πράξεις με δυαδικούς αριθμούς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Πράξεις με δυαδικούς
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 25-6 Πράξεις με δυαδικούς αριθμούς (αριθμητικές πράξεις) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Πράξεις με δυαδικούς
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 3. ΑΡΙΘΜΗΤΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΜΕΡΟΣ Β Παράσταση Προσημασμένων
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Κ. Δεμέστιχας Εργαστήριο Πληροφορικής Γεωπονικό Πανεπιστήμιο Αθηνών Επικοινωνία μέσω e-mail: cdemest@aua.gr, cdemest@cn.ntua.gr 3. ΑΡΙΘΜΗΤΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΜΕΡΟΣ Β Παράσταση Προσημασμένων
Ψηφιακά Συστήματα. 1. Συστήματα Αριθμών
 Ψηφιακά Συστήματα 1. Συστήματα Αριθμών Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L.,
Ψηφιακά Συστήματα 1. Συστήματα Αριθμών Βιβλιογραφία 1. Φανουράκης Κ., Πάτσης Γ., Τσακιρίδης Ο., Θεωρία και Ασκήσεις Ψηφιακών Ηλεκτρονικών, ΜΑΡΙΑ ΠΑΡΙΚΟΥ & ΣΙΑ ΕΠΕ, 2016. [59382199] 2. Floyd Thomas L.,
Εισαγωγή στην επιστήμη των υπολογιστών. ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ και Μετατροπές Αριθμών
 Εισαγωγή στην επιστήμη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ και Μετατροπές Αριθμών 1 Αριθμητικό Σύστημα Ορίζει τον τρόπο αναπαράστασης ενός αριθμού με διακεκριμένα σύμβολα Ένας αριθμός αναπαρίσταται διαφορετικά
Εισαγωγή στην επιστήμη των υπολογιστών ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ και Μετατροπές Αριθμών 1 Αριθμητικό Σύστημα Ορίζει τον τρόπο αναπαράστασης ενός αριθμού με διακεκριμένα σύμβολα Ένας αριθμός αναπαρίσταται διαφορετικά
1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΩΝ. α i. (α i β i ) (1.3) όπου: η= το πλήθος ακεραίων ψηφίων του αριθμού Ν. n-1
 1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΩΝ 1.1 Εισαγωγή Το δεκαδικό σύστημα (Decimal System) αρίθμησης χρησιμοποιείται από τον άνθρωπο και είναι κατάλληλο βέβαια γι αυτόν, είναι όμως εντελώς ακατάλληλο για τις ηλεκτρονικές
1. ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΩΝ 1.1 Εισαγωγή Το δεκαδικό σύστημα (Decimal System) αρίθμησης χρησιμοποιείται από τον άνθρωπο και είναι κατάλληλο βέβαια γι αυτόν, είναι όμως εντελώς ακατάλληλο για τις ηλεκτρονικές
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Πληροφορική Ι. Ενότητα 4 : Πράξεις με bits. Δρ. Γκόγκος Χρήστος
 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική Ι Ενότητα 4 : Πράξεις με bits Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής & Ελεγκτικής
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Πληροφορική Ι Ενότητα 4 : Πράξεις με bits Δρ. Γκόγκος Χρήστος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Χρηματοοικονομικής & Ελεγκτικής
ΠΛΗΡΟΦΟΡΙΚΗ I. 4 η ΔΙΑΛΕΞΗ Αριθμητικά Συστήματα
 ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ - ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΣΑΓΩΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΤΟΥΡΙΣΤΙΚΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΚΑΙ ΕΠΙΧΕΙΡΗΣΕΩΝ ΦΙΛΟΞΕΝΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗ I 4 η ΔΙΑΛΕΞΗ Αριθμητικά Συστήματα ΧΑΣΑΝΗΣ ΒΑΣΙΛΕΙΟΣ
ΣΧΟΛΗ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΟΙΚΟΝΟΜΙΑΣ - ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΙΣΑΓΩΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΤΟΥΡΙΣΤΙΚΩΝ ΕΠΙΧΕΙΡΗΣΕΩΝ ΚΑΙ ΕΠΙΧΕΙΡΗΣΕΩΝ ΦΙΛΟΞΕΝΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗ I 4 η ΔΙΑΛΕΞΗ Αριθμητικά Συστήματα ΧΑΣΑΝΗΣ ΒΑΣΙΛΕΙΟΣ
Κεφάλαιο 2. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας. Περιεχόμενα. 2.1 Αριθμητικά Συστήματα. Εισαγωγή
 Κεφάλαιο. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας Περιεχόμενα. Αριθμητικά συστήματα. Μετατροπή αριθμών από ένα σύστημα σε άλλο.3 Πράξεις στο δυαδικό σύστημα.4 Πράξεις στο δεκαεξαδικό σύστημα.5
Κεφάλαιο. Συστήματα Αρίθμησης και Αναπαράσταση Πληροφορίας Περιεχόμενα. Αριθμητικά συστήματα. Μετατροπή αριθμών από ένα σύστημα σε άλλο.3 Πράξεις στο δυαδικό σύστημα.4 Πράξεις στο δεκαεξαδικό σύστημα.5
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ
 ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΗ ΔΙΟΙΚΗΣΗ ΚΑΙ ΣΤΗΝ ΟΙΚΟΝΟΜΙΑ 7 Ο ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΑΠΟΣΤΟΛΙΑ ΠΑΓΓΕ Περιεχόμενα 2 Δυαδικό Σύστημα Προσημασμένοι δυαδικοί αριθμοί Αφαίρεση
ΤΕΙ ΙΟΝΙΩΝ ΝΗΣΩΝ ΤΜΗΜΑ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΣΤΗ ΔΙΟΙΚΗΣΗ ΚΑΙ ΣΤΗΝ ΟΙΚΟΝΟΜΙΑ 7 Ο ΜΑΘΗΜΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΑΠΟΣΤΟΛΙΑ ΠΑΓΓΕ Περιεχόμενα 2 Δυαδικό Σύστημα Προσημασμένοι δυαδικοί αριθμοί Αφαίρεση
Οργάνωση Υπολογιστών
 Οργάνωση Υπολογιστών Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών 1 Άδειες Χρήσης Το παρόν υλικό
Οργάνωση Υπολογιστών Επιμέλεια: Γεώργιος Θεοδωρίδης, Επίκουρος Καθηγητής Ανδρέας Εμερετλής, Υποψήφιος Διδάκτορας Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών 1 Άδειες Χρήσης Το παρόν υλικό
Συστήματα αρίθμησης. = α n-1 *b n-1 + a n-2 *b n-2 + +a 1 b 1 + a 0 όπου τα 0 a i b-1
 Συστήματα αρίθμησης Δεκαδικό σύστημα αρίθμησης 1402 = 1000 + 400 +2 =1*10 3 + 4*10 2 + 0*10 1 + 2*10 0 Γενικά σε ένα σύστημα αρίθμησης με βάση το b N, ένας ακέραιος αριθμός με n ψηφία παριστάνεται ως:
Συστήματα αρίθμησης Δεκαδικό σύστημα αρίθμησης 1402 = 1000 + 400 +2 =1*10 3 + 4*10 2 + 0*10 1 + 2*10 0 Γενικά σε ένα σύστημα αρίθμησης με βάση το b N, ένας ακέραιος αριθμός με n ψηφία παριστάνεται ως:
Μάθημα 2: Παράσταση της Πληροφορίας
 Μάθημα 2: Παράσταση της Πληροφορίας 2.1 Παράσταση δεδομένων Κάθε υπολογιστική μηχανή αποτελείται από ηλεκτρονικά κυκλώματα που η λειτουργία τους βασίζεται στην αρχή ανοιχτό-κλειστό. Η συμπεριφορά τους
Μάθημα 2: Παράσταση της Πληροφορίας 2.1 Παράσταση δεδομένων Κάθε υπολογιστική μηχανή αποτελείται από ηλεκτρονικά κυκλώματα που η λειτουργία τους βασίζεται στην αρχή ανοιχτό-κλειστό. Η συμπεριφορά τους
Β1.1 Αναπαράσταση Δεδομένων και Χωρητικότητα Μονάδων Αποθήκευσης
 Β1.1 Αναπαράσταση Δεδομένων και Χωρητικότητα Μονάδων Αποθήκευσης Τι θα μάθουμε σήμερα: Να αναφέρουμε τον τρόπο αναπαράστασης των δεδομένων (δυαδικό σύστημα) Να αναγνωρίζουμε πώς γράμματα και σύμβολα από
Β1.1 Αναπαράσταση Δεδομένων και Χωρητικότητα Μονάδων Αποθήκευσης Τι θα μάθουμε σήμερα: Να αναφέρουμε τον τρόπο αναπαράστασης των δεδομένων (δυαδικό σύστημα) Να αναγνωρίζουμε πώς γράμματα και σύμβολα από
Ανασκόπηση στα ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 ΕΡΓΑΣΙΑ 1: Ονοματεπώνυμο: Εξάμηνο: Ανασκόπηση στα ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Α.Μ: Έτος: 1. Το δεκαδικό σύστημα Είναι φανερό ότι οι χιλιάδες, εκατοντάδες, δεκάδες, μονάδες και τα δεκαδικά ψηφία είναι δυνάμεις
ΕΡΓΑΣΙΑ 1: Ονοματεπώνυμο: Εξάμηνο: Ανασκόπηση στα ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ Α.Μ: Έτος: 1. Το δεκαδικό σύστημα Είναι φανερό ότι οι χιλιάδες, εκατοντάδες, δεκάδες, μονάδες και τα δεκαδικά ψηφία είναι δυνάμεις
Εισαγωγή στην Πληροφορική ΓΕΝΙΚΟ ΤΜΗΜΑ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ TEI ΧΑΛΚΙ ΑΣ
 Εισαγωγή στην Πληροφορική 1 Περιεχόµενα - Κωδικοποιήσεις - Αριθµητικά Συστήµατα 2 Ηλεκτρονικός Υπολογιστής Είπαµε ότι είναι, µία Ηλεκτρονική Μηχανή, που δουλεύει κάτω από τον έλεγχο εντολών αποθηκευµένων
Εισαγωγή στην Πληροφορική 1 Περιεχόµενα - Κωδικοποιήσεις - Αριθµητικά Συστήµατα 2 Ηλεκτρονικός Υπολογιστής Είπαµε ότι είναι, µία Ηλεκτρονική Μηχανή, που δουλεύει κάτω από τον έλεγχο εντολών αποθηκευµένων
Τετάρτη 5-12/11/2014. ΣΗΜΕΙΩΣΕΙΣ 3 ου και 4 ου ΜΑΘΗΜΑΤΟΣ ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΙΤΕΚΤΟΝΙΚΗ Η/Υ Α ΕΞΑΜΗΝΟ
 Τετάρτη 5-12/11/2014 ΣΗΜΕΙΩΣΕΙΣ 3 ου και 4 ου ΜΑΘΗΜΑΤΟΣ ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΙΤΕΚΤΟΝΙΚΗ Η/Υ Α ΕΞΑΜΗΝΟ ΕΚΠΑΙΔΕΥΤΗΣ: ΤΡΟΧΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ 1. Παράσταση και οργάνωση δεδομένων
Τετάρτη 5-12/11/2014 ΣΗΜΕΙΩΣΕΙΣ 3 ου και 4 ου ΜΑΘΗΜΑΤΟΣ ΕΙΔΙΚΟΤΗΤΑ: ΤΕΧΝΙΚΟΣ ΕΦΑΡΜΟΓΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΑΡΧΙΤΕΚΤΟΝΙΚΗ Η/Υ Α ΕΞΑΜΗΝΟ ΕΚΠΑΙΔΕΥΤΗΣ: ΤΡΟΧΙΔΗΣ ΠΑΝΑΓΙΩΤΗΣ 1. Παράσταση και οργάνωση δεδομένων
Εισαγωγή στην επιστήµη των υπολογιστών. Υπολογιστές και Δεδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών
 Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και Δεδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος
Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και Δεδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος
ΠΛΗΡΟΦΟΡΙΚΉ. Μάθημα 7
 ΠΛΗΡΟΦΟΡΙΚΉ Μάθημα 7 Μηχανισμός Οπτικών Δίσκων CD ROM (compact disk read only memory) Μεγάλη αποθηκευτική ικανότητα (650ΜΒ ή 700ΜΒ) Γρήγορη προσπέλαση στα δεδομένα Χαμηλή τιμή (CD) Μέσο μεταφοράς και διανομής
ΠΛΗΡΟΦΟΡΙΚΉ Μάθημα 7 Μηχανισμός Οπτικών Δίσκων CD ROM (compact disk read only memory) Μεγάλη αποθηκευτική ικανότητα (650ΜΒ ή 700ΜΒ) Γρήγορη προσπέλαση στα δεδομένα Χαμηλή τιμή (CD) Μέσο μεταφοράς και διανομής
Εισαγωγή στην επιστήµη των υπολογιστών. Αναπαράσταση Αριθµών
 Εισαγωγή στην επιστήµη των υπολογιστών Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος είναι το 10 αναπτύχθηκε τον 8
Εισαγωγή στην επιστήµη των υπολογιστών Αναπαράσταση Αριθµών 1 Δεκαδικό και Δυαδικό Σύστηµα Δύο κυρίαρχα συστήµατα στο χώρο των υπολογιστών Δεκαδικό: Η βάση του συστήµατος είναι το 10 αναπτύχθηκε τον 8
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Συστήματα αρίθμησης
 ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Συστήματα αρίθμησης Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 8 Σημειώσεις βασισμένες στο βιβλίο Το MATLAB στην Υπολογιστική
ΠΛΗΡΟΦΟΡΙΚΗ Ι Ενότητα 8: Συστήματα αρίθμησης Μιχάλης Δρακόπουλος Σχολή Θετικών επιστημών Τμήμα Μαθηματικών ΠΛΗΡΟΦΟΡΙΚΗ Ι (MATLAB) Ενότητα 8 Σημειώσεις βασισμένες στο βιβλίο Το MATLAB στην Υπολογιστική
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου
 Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Νο 01 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Αρχιτεκτονική Υπολογιστών Ασκήσεις Εργαστηρίου Ενότητα: ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ Νο 01 Δρ. Μηνάς Δασυγένης mdasyg@ieee.org Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Εργαστήριο Ψηφιακών Συστημάτων και
Υπάρχουν δύο τύποι μνήμης, η μνήμη τυχαίας προσπέλασης (Random Access Memory RAM) και η μνήμη ανάγνωσης-μόνο (Read-Only Memory ROM).
 Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Μνήμες Ένα από τα βασικά πλεονεκτήματα των ψηφιακών συστημάτων σε σχέση με τα αναλογικά, είναι η ευκολία αποθήκευσης μεγάλων ποσοτήτων πληροφοριών, είτε προσωρινά είτε μόνιμα Οι πληροφορίες αποθηκεύονται
Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση. Κεφάλαιο 3. Αριθµητική για υπολογιστές
 Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση Κεφάλαιο 3 Αριθµητική για υπολογιστές Ασκήσεις Η αρίθµηση των ασκήσεων είναι από την 4 η έκδοση του «Οργάνωση και Σχεδίαση
Οργάνωση και Σχεδίαση Υπολογιστών Η ιασύνδεση Υλικού και Λογισµικού, 4 η έκδοση Κεφάλαιο 3 Αριθµητική για υπολογιστές Ασκήσεις Η αρίθµηση των ασκήσεων είναι από την 4 η έκδοση του «Οργάνωση και Σχεδίαση
2. ΑΡΙΘΜΗΤΙΚΗ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. 2.1 Αριθμητικά συστήματα
 2. ΑΡΙΘΜΗΤΙΚΗ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ 2.1 Αριθμητικά συστήματα Κάθε πραγματικός αριθμός χ μπορεί να παρασταθεί σε ένα αριθμητικό σύστημα με βάση β>1 με μια δυναμοσειρά της μορφής, -οο * = ± Σ ψ β " (2 1) η - ν
2. ΑΡΙΘΜΗΤΙΚΗ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ 2.1 Αριθμητικά συστήματα Κάθε πραγματικός αριθμός χ μπορεί να παρασταθεί σε ένα αριθμητικό σύστημα με βάση β>1 με μια δυναμοσειρά της μορφής, -οο * = ± Σ ψ β " (2 1) η - ν
Εισαγωγή στην επιστήμη των υπολογιστών. Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων
 Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 Εισαγωγή Ο Υπολογιστής είναι μια μηχανή επεξεργασίας δεδομένων Πριν ασχοληθούμε με την επεξεργασία τους
Εισαγωγή στην επιστήμη των υπολογιστών Υπολογιστές και Δεδομένα Κεφάλαιο 2ο Αναπαράσταση Δεδομένων 1 Εισαγωγή Ο Υπολογιστής είναι μια μηχανή επεξεργασίας δεδομένων Πριν ασχοληθούμε με την επεξεργασία τους
ΑΡΙΘΜΗΤΙΚΗ ΓΙΑ ΥΠΟΛΟΓΙΣΤΕΣ
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΑΡΙΘΜΗΤΙΚΗ ΓΙΑ ΥΠΟΛΟΓΙΣΤΕΣ ΣΗΜΜΥ, 5 Ο ΕΞΑΜΗΝΟ http://www.cslab.ece.ntua.gr/courses/comparch t / / h 1 ΑΡΙΘΜΟΙ Decimal Eύκολο για τον άνθρωπο Ιδιαίτερα για την εκτέλεση αριθμητικών
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ ΑΡΙΘΜΗΤΙΚΗ ΓΙΑ ΥΠΟΛΟΓΙΣΤΕΣ ΣΗΜΜΥ, 5 Ο ΕΞΑΜΗΝΟ http://www.cslab.ece.ntua.gr/courses/comparch t / / h 1 ΑΡΙΘΜΟΙ Decimal Eύκολο για τον άνθρωπο Ιδιαίτερα για την εκτέλεση αριθμητικών
Εισαγωγή στην επιστήμη των υπολογιστών. Υλικό Υπολογιστών Κεφάλαιο 5ο Οργάνωση υπολογιστών
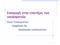 Εισαγωγή στην επιστήμη των υπολογιστών Υλικό Υπολογιστών Κεφάλαιο 5ο Οργάνωση υπολογιστών 1 Οργάνωση υπολογιστών ΚΜΕ Κύρια Μνήμη Υποσύστημα εισόδου/εξόδου 2 Κεντρική Μονάδα Επεξεργασίας (ΚΜΕ) R1 R2 ΑΛΜ
Εισαγωγή στην επιστήμη των υπολογιστών Υλικό Υπολογιστών Κεφάλαιο 5ο Οργάνωση υπολογιστών 1 Οργάνωση υπολογιστών ΚΜΕ Κύρια Μνήμη Υποσύστημα εισόδου/εξόδου 2 Κεντρική Μονάδα Επεξεργασίας (ΚΜΕ) R1 R2 ΑΛΜ
Τα µπιτ και η σηµασία τους. Σχήµα bit. ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (1/2) 1.7 Αποθήκευση κλασµάτων 1.8 Συµπίεση δεδοµένων 1.9 Σφάλµατα επικοινωνίας
 ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (1/2) ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (2/2) 1.1 Τα bits και ο τρόπος που αποθηκεύονται 1.2 Κύρια µνήµη 1.3 Αποθηκευτικά µέσα 1.4 Αναπαράσταση πληροφοριών ως σχηµάτων bits
ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (1/2) ΚΕΦΑΛΑΙΟ 1: Αποθήκευση εδοµένων (2/2) 1.1 Τα bits και ο τρόπος που αποθηκεύονται 1.2 Κύρια µνήµη 1.3 Αποθηκευτικά µέσα 1.4 Αναπαράσταση πληροφοριών ως σχηµάτων bits
Αριθμητικά Συστήματα = 3 x x x x 10 0
 Δεκαδικό Όταν αναφερόμαστε σε μία αριθμητική τιμή, απεικονίζουμε μία ποσότητα με ένα σύμβολο ή έναν συνδυασμό από σύμβολα. Το αριθμητικό σύστημα που χρησιμοποιούμε είναι το δεκαδικό. Αποτελείται από δέκα
Δεκαδικό Όταν αναφερόμαστε σε μία αριθμητική τιμή, απεικονίζουμε μία ποσότητα με ένα σύμβολο ή έναν συνδυασμό από σύμβολα. Το αριθμητικό σύστημα που χρησιμοποιούμε είναι το δεκαδικό. Αποτελείται από δέκα
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 3: Υλικό Υπολογιστών, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης Μαθησιακοί Στόχοι Η Ενότητα 3 διαπραγματεύεται θέματα που
Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 3: Υλικό Υπολογιστών, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης Μαθησιακοί Στόχοι Η Ενότητα 3 διαπραγματεύεται θέματα που
3.1 εκαδικό και υαδικό
 Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και εδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 3.1 εκαδικό και υαδικό εκαδικό σύστηµα 2 1 εκαδικό και υαδικό υαδικό Σύστηµα 3 3.2 Μετατροπή Για τη µετατροπή
Εισαγωγή στην επιστήµη των υπολογιστών Υπολογιστές και εδοµένα Κεφάλαιο 3ο Αναπαράσταση Αριθµών 1 3.1 εκαδικό και υαδικό εκαδικό σύστηµα 2 1 εκαδικό και υαδικό υαδικό Σύστηµα 3 3.2 Μετατροπή Για τη µετατροπή
Ελίνα Μακρή
 Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
Ελίνα Μακρή elmak@unipi.gr Μετατροπή Αριθμητικών Συστημάτων Πράξεις στα Αριθμητικά Συστήματα Σχεδίαση Ψηφιακών Κυκλωμάτων με Logism Άλγεβρα Boole Λογικές Πύλες (AND, OR, NOT, NAND, XOR) Flip Flops (D,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Αρχιτεκτονική-Ι. Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχιτεκτονική-Ι Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Αρχιτεκτονική-Ι Ενότητα 1: Εισαγωγή στην Αρχιτεκτονική -Ι Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
Λογική Σχεδίαση Ψηφιακών Συστημάτων
 Πανεπιστήμιο Θεσσαλίας Τμήμα Πληροφορικής Λογική Σχεδίαση Ψηφιακών Συστημάτων Σταμούλης Γεώργιος georges@uth.gr Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Δυαδικοί Αριθμοί Η γενική αναπαράσταση ενός οποιουδήποτε
Πανεπιστήμιο Θεσσαλίας Τμήμα Πληροφορικής Λογική Σχεδίαση Ψηφιακών Συστημάτων Σταμούλης Γεώργιος georges@uth.gr Δαδαλιάρης Αντώνιος dadaliaris@uth.gr Δυαδικοί Αριθμοί Η γενική αναπαράσταση ενός οποιουδήποτε
Δυαδικη παρασταση αριθμων και συμβολων
 Δυαδικη παρασταση αριθμων και συμβολων Ενα αριθμητικο συστημα χαρακτηριζεται απο την βαση r και τα συμβολα a i που παιρνουν τις τιμες 0,1,...,r-1. (a n,,a 1,a 0. a -1,a -2,,a -m ) r = =a n r n + +a 1 r+a
Δυαδικη παρασταση αριθμων και συμβολων Ενα αριθμητικο συστημα χαρακτηριζεται απο την βαση r και τα συμβολα a i που παιρνουν τις τιμες 0,1,...,r-1. (a n,,a 1,a 0. a -1,a -2,,a -m ) r = =a n r n + +a 1 r+a
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ - ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΑΞΕΙΣ
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ - ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΑΞΕΙΣ ΣΗΜΜΥ, 5 Ο ΕΞΑΜΗΝΟ http://www.cslab.ece.ntua.gr/courses/comparch 1 ΑΡΙΘΜΟΙ Decimal Eύκολο για τον άνθρωπο Ιδιαίτερα για την εκτέλεση αριθμητικών πράξεων
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ - ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΑΞΕΙΣ ΣΗΜΜΥ, 5 Ο ΕΞΑΜΗΝΟ http://www.cslab.ece.ntua.gr/courses/comparch 1 ΑΡΙΘΜΟΙ Decimal Eύκολο για τον άνθρωπο Ιδιαίτερα για την εκτέλεση αριθμητικών πράξεων
Αριθμητικά Συστήματα
 Αριθμητικά Συστήματα Οργάνωση Δεδομένων (1/2) Bits: Η μικρότερη αριθμητική μονάδα ενός υπολογιστικού συστήματος, η οποία δείχνει δύο καταστάσεις, 0 ή 1 (αληθές η ψευδές). Nibbles: Μονάδα 4 bit που παριστά
Αριθμητικά Συστήματα Οργάνωση Δεδομένων (1/2) Bits: Η μικρότερη αριθμητική μονάδα ενός υπολογιστικού συστήματος, η οποία δείχνει δύο καταστάσεις, 0 ή 1 (αληθές η ψευδές). Nibbles: Μονάδα 4 bit που παριστά
Αναπαράσταση Δεδομένων. ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική
 Αναπαράσταση Δεδομένων ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική Αναπαράσταση δεδομένων Κατάλληλη συμβολική αναπαράσταση δεδομένων, για απλοποίηση βασικών πράξεων, όπως πρόσθεση Πόσο εύκολο είναι
Αναπαράσταση Δεδομένων ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική Αναπαράσταση δεδομένων Κατάλληλη συμβολική αναπαράσταση δεδομένων, για απλοποίηση βασικών πράξεων, όπως πρόσθεση Πόσο εύκολο είναι
Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις
 Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυαδικό Σύστημα Αρίθμησης Περιεχόμενα 1 Δυαδικό
Κ15 Ψηφιακή Λογική Σχεδίαση 2: Δυαδικό Σύστημα / Αναπαραστάσεις Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Δυαδικό Σύστημα Αρίθμησης Περιεχόμενα 1 Δυαδικό
Πραγµατικοί αριθµοί κινητής υποδιαστολής Floating Point Numbers. Σ. Τσιτµηδέλης - 2010 ΤΕΙ ΧΑΛΚΙΔΑΣ
 Πραγµατικοί αριθµοί κινητής υποδιαστολής Floating Point Numbers Σ. Τσιτµηδέλης - 2010 ΤΕΙ ΧΑΛΚΙΔΑΣ Εκθετική Παράσταση (Exponential Notation) Οι επόµενες είναι ισοδύναµες παραστάσεις του 1,234 123,400.0
Πραγµατικοί αριθµοί κινητής υποδιαστολής Floating Point Numbers Σ. Τσιτµηδέλης - 2010 ΤΕΙ ΧΑΛΚΙΔΑΣ Εκθετική Παράσταση (Exponential Notation) Οι επόµενες είναι ισοδύναµες παραστάσεις του 1,234 123,400.0
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές
 Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές http://courseware.mech.ntua.gr/ml23021/ 3 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ E-mail: leo@mail.ntua.gr URL: http://users.ntua.gr/leo 1 Κωδικοποίηση & Αποκωδικοποίηση
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές http://courseware.mech.ntua.gr/ml23021/ 3 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ E-mail: leo@mail.ntua.gr URL: http://users.ntua.gr/leo 1 Κωδικοποίηση & Αποκωδικοποίηση
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 12
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 12 17 Οκτωβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 12 17 Οκτωβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
Τμήμα Μαθηματικών, ΕΚΠΑ. Ακαδ. έτος
 ½ ½ ÈÐ ÖÓ ÓÖ Á Javaµ Τμήμα Μαθηματικών, ΕΚΠΑ Ακαδ. έτος 2007 2008 ¾ È Ö Õ Ñ ÒÓ Ñ Ñ ØÓ Εισαγωγή στην πληροφορική με έμφαση σε: αρχιτεκτονική και αριθμητική υπολογιστών αλγοριθμική επίλυση προβλημάτων βασικές
½ ½ ÈÐ ÖÓ ÓÖ Á Javaµ Τμήμα Μαθηματικών, ΕΚΠΑ Ακαδ. έτος 2007 2008 ¾ È Ö Õ Ñ ÒÓ Ñ Ñ ØÓ Εισαγωγή στην πληροφορική με έμφαση σε: αρχιτεκτονική και αριθμητική υπολογιστών αλγοριθμική επίλυση προβλημάτων βασικές
Αριθμητικά Συστήματα
 Αριθμητικά Συστήματα Σε οποιοδήποτε αριθμητικό σύστημα, με βάση τον αριθμό Β, ένας ακέραιος αριθμός με πλήθος ψηφίων ν, εκφράζεται ως ακολούθως: α ν-1 α ν-2 α 1 α 0 = α ν-1 Β ν-1 + α ν-2 Β ν-2 + + α 1
Αριθμητικά Συστήματα Σε οποιοδήποτε αριθμητικό σύστημα, με βάση τον αριθμό Β, ένας ακέραιος αριθμός με πλήθος ψηφίων ν, εκφράζεται ως ακολούθως: α ν-1 α ν-2 α 1 α 0 = α ν-1 Β ν-1 + α ν-2 Β ν-2 + + α 1
Κεφάλαιο 2. Οργάνωση και διαχείριση της Πληροφορίας στον. Υπολογιστή
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 2 Οργάνωση και διαχείριση της Πληροφορίας στον Υπολογιστή Δεδομένα και Εντολές πληροφορία δεδομένα εντολές αριθμητικά δδ δεδομένα κείμενο εικόνα Επιλογή Αναπαράστασης
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΥΠΟΛΟΓΙΣΤΩΝ Κεφάλαιο 2 Οργάνωση και διαχείριση της Πληροφορίας στον Υπολογιστή Δεδομένα και Εντολές πληροφορία δεδομένα εντολές αριθμητικά δδ δεδομένα κείμενο εικόνα Επιλογή Αναπαράστασης
Αριθμητικά Συστήματα Κώδικες
 Αριθμητικά Συστήματα Κώδικες 1.1 Εισαγωγή Κεφάλαιο 1 Ένα αριθμητικό σύστημα ορίζει ένα σύνολο τιμών που χρησιμοποιούνται για την αναπαράσταση μίας ποσότητας. Ποσοτικοποιώντας τιμές και αντικείμενα και
Αριθμητικά Συστήματα Κώδικες 1.1 Εισαγωγή Κεφάλαιο 1 Ένα αριθμητικό σύστημα ορίζει ένα σύνολο τιμών που χρησιμοποιούνται για την αναπαράσταση μίας ποσότητας. Ποσοτικοποιώντας τιμές και αντικείμενα και
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων: Αριθμητική του Υπολογιστή, Αριθμητικά Συστήματα Μετατροπές, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης
Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Αποθήκευση Δεδομένων: Αριθμητική του Υπολογιστή, Αριθμητικά Συστήματα Μετατροπές, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλιγκιρίδης
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 3 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές 3 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές 3 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Αρχιτεκτονικές Υπολογιστών
 ΑΡΧΙΤΕΚΤΟΝΙΚΕΣ ΥΠΟΛΟΓΙΣΤΩΝ Μάθηµα: Αρχιτεκτονικές Υπολογιστών Αναπαράσταση εδοµένων ιδάσκων: Αναπλ. Καθ. Κ. Λαµπρινουδάκης clam@unipi.gr Αρχιτεκτονικές Υπολογιστών Aναπλ. Καθ. Κ. Λαµπρινουδάκης 1 εδοµένα
ΑΡΧΙΤΕΚΤΟΝΙΚΕΣ ΥΠΟΛΟΓΙΣΤΩΝ Μάθηµα: Αρχιτεκτονικές Υπολογιστών Αναπαράσταση εδοµένων ιδάσκων: Αναπλ. Καθ. Κ. Λαµπρινουδάκης clam@unipi.gr Αρχιτεκτονικές Υπολογιστών Aναπλ. Καθ. Κ. Λαµπρινουδάκης 1 εδοµένα
Αναπαράσταση Δεδομένων (2 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική
 Αναπαράσταση Δεδομένων (2 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική «Λογικές» πράξεις, μάσκες Πώς βρίσκουμε το υπόλοιπο μιας διαίρεσης με το 4; διαίρεση με 4 = δεξιά ολίσθηση 2 bits Το υπόλοιπο
Αναπαράσταση Δεδομένων (2 ο μέρος) ΜΥΥ-106 Εισαγωγή στους Η/Υ και στην Πληροφορική «Λογικές» πράξεις, μάσκες Πώς βρίσκουμε το υπόλοιπο μιας διαίρεσης με το 4; διαίρεση με 4 = δεξιά ολίσθηση 2 bits Το υπόλοιπο
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Λογικές πράξεις, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλικρίδης Μαθησιακοί Στόχοι Η Ενότητα 2 διαπραγματεύεται θέματα που αφορούν
Εισαγωγή στην Επιστήμη των Υπολογιστών Ενότητα 2: Λογικές πράξεις, 2ΔΩ Τμήμα: Αγροτικής Οικονομίας & Ανάπτυξης Διδάσκων: Θεόδωρος Τσιλικρίδης Μαθησιακοί Στόχοι Η Ενότητα 2 διαπραγματεύεται θέματα που αφορούν
Τμήμα Οικιακής Οικονομίας και Οικολογίας. Οργάνωση Υπολογιστών
 Οργάνωση Υπολογιστών Οργάνωση υπολογιστών ΚΜΕ Κύρια Μνήμη Υποσύστημα εισόδου/εξόδου Κεντρική Μονάδα Επεξεργασίας (ΚΜΕ) R1 R2 ΑΛΜ R3 I Καταχωρητές PC Κεντρική Μονάδα Επεξεργασίας Αριθμητική και λογική μονάδα
Οργάνωση Υπολογιστών Οργάνωση υπολογιστών ΚΜΕ Κύρια Μνήμη Υποσύστημα εισόδου/εξόδου Κεντρική Μονάδα Επεξεργασίας (ΚΜΕ) R1 R2 ΑΛΜ R3 I Καταχωρητές PC Κεντρική Μονάδα Επεξεργασίας Αριθμητική και λογική μονάδα
ΘΕΜΑ : ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ. ΔΙΑΡΚΕΙΑ: 1 περιόδους. 22/1/ :11 Όνομα: Λεκάκης Κωνσταντίνος καθ. Τεχνολογίας
 ΘΕΜΑ : ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ ΔΙΑΡΚΕΙΑ: 1 περιόδους 22/1/2010 10:11 καθ. Τεχνολογίας 22/1/2010 10:12 Παραδείγματα Τι ονομάζουμε αριθμητικό σύστημα? Το σύνολο από ψηφία (αριθμοί & χαρακτήρες). Που χρησιμεύουν
ΘΕΜΑ : ΣΥΣΤΗΜΑΤΑ ΑΡΙΘΜΗΣΗΣ ΔΙΑΡΚΕΙΑ: 1 περιόδους 22/1/2010 10:11 καθ. Τεχνολογίας 22/1/2010 10:12 Παραδείγματα Τι ονομάζουμε αριθμητικό σύστημα? Το σύνολο από ψηφία (αριθμοί & χαρακτήρες). Που χρησιμεύουν
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ
 Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ1 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1. Ποια είναι η βάση
Πρόγραμμα Επικαιροποίησης Γνώσεων Αποφοίτων ΕΝΟΤΗΤΑ Μ1 ΨΗΦΙΑΚΑ ΗΛΕΚΤΡΟΝΙΚΑ Εκπαιδευτής: Γ. Π. ΠΑΤΣΗΣ, Επικ. Καθηγητής, Τμήμα Ηλεκτρονικών Μηχανικών, ΤΕΙ Αθήνας ΑΡΙΘΜΗΤΙΚΑ ΣΥΣΤΗΜΑΤΑ 1. Ποια είναι η βάση
Συστήματα Αρίθμησης. Συστήματα Αρίθμησης 1. PDF created with FinePrint pdffactory Pro trial version
 Συστήματα Αρίθμησης Στην καθημερινή μας ζωή χρησιμοποιούμε το δεκαδικό σύστημα αρίθμησης. Στο σύστημα αυτό χρησιμοποιούμε δέκα διαφορετικά σύμβολα τα :,, 2, 3, 4, 5, 6,7 8, 9. Για τον αριθμό 32 θα χρειαστούμε
Συστήματα Αρίθμησης Στην καθημερινή μας ζωή χρησιμοποιούμε το δεκαδικό σύστημα αρίθμησης. Στο σύστημα αυτό χρησιμοποιούμε δέκα διαφορετικά σύμβολα τα :,, 2, 3, 4, 5, 6,7 8, 9. Για τον αριθμό 32 θα χρειαστούμε
Προγραμματισμός Ηλεκτρονικών Υπολογιστών 1
 Προγραμματισμός Ηλεκτρονικών Υπολογιστών 1 Ενότητα 2: Αναπαράσταση Δεδομένων Δρ. Φραγκούλης Γεώργιος Τμήμα Ηλεκτρολογίας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Προγραμματισμός Ηλεκτρονικών Υπολογιστών 1 Ενότητα 2: Αναπαράσταση Δεδομένων Δρ. Φραγκούλης Γεώργιος Τμήμα Ηλεκτρολογίας Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών Περιεχόμενα Μαθήματος Συστήματα αρίθμησης Πύλες Διάγραμμα ροής-ψευδοκώδικας Python Συστήματα Αρίθμησης Δεκαδικό σύστημα Οι άνθρωποι χρησιμοποιούν το περίφημο «θεσιακό,
Εισαγωγή στην Επιστήμη των Υπολογιστών Περιεχόμενα Μαθήματος Συστήματα αρίθμησης Πύλες Διάγραμμα ροής-ψευδοκώδικας Python Συστήματα Αρίθμησης Δεκαδικό σύστημα Οι άνθρωποι χρησιμοποιούν το περίφημο «θεσιακό,
Αριθμητικά Συστήματα
 Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση τους Τέλος, στη δημιουργία των αριθμητικών συστημάτων:
Αριθμητικά Συστήματα Η ανάγκη του ανθρώπου για μετρήσεις οδήγησε αρχικά στην επινόηση των αριθμών Κατόπιν, στην επινόηση συμβόλων για τη παράσταση τους Τέλος, στη δημιουργία των αριθμητικών συστημάτων:
Εισαγωγή στην Επιστήµη των Η/Υ
 Εισαγωγή στην Επιστήµη των Η/Υ Καθ. Κ. Κουρκουµπέτης Οι διαφάνειες βασίζονται σε µεγάλο βαθµό σε αυτές που συνοδεύονται µε το προτεινόµενο σύγγραµµα. 1 Εισαγωγή στην Επιστήµη των Η/Υ Εισαγωγή 2 ΚΕΦΑΛΑΙΟ
Εισαγωγή στην Επιστήµη των Η/Υ Καθ. Κ. Κουρκουµπέτης Οι διαφάνειες βασίζονται σε µεγάλο βαθµό σε αυτές που συνοδεύονται µε το προτεινόµενο σύγγραµµα. 1 Εισαγωγή στην Επιστήµη των Η/Υ Εισαγωγή 2 ΚΕΦΑΛΑΙΟ
Εισαγωγή στους Η/Υ. Γιώργος Δημητρίου. Μάθημα 7 και 8: Αναπαραστάσεις. Πανεπιστήμιο Θεσσαλίας - Τμήμα Πληροφορικής
 Γιώργος Δημητρίου Μάθημα 7 και 8: Αναπαραστάσεις Αναπαράσταση Πληροφορίας Η/Υ Αριθμητικά δεδομένα Σταθερής υποδιαστολής Κινητής υποδιαστολής Μη αριθμητικά δεδομένα Χαρακτήρες Ειδικοί κώδικες Εντολές Γλώσσα
Γιώργος Δημητρίου Μάθημα 7 και 8: Αναπαραστάσεις Αναπαράσταση Πληροφορίας Η/Υ Αριθμητικά δεδομένα Σταθερής υποδιαστολής Κινητής υποδιαστολής Μη αριθμητικά δεδομένα Χαρακτήρες Ειδικοί κώδικες Εντολές Γλώσσα
Ψηφιακά Κυκλώματα Ι. Μάθημα 1: Δυαδικά συστήματα - Κώδικες. Λευτέρης Καπετανάκης
 ΤΛ2002 Ψηφιακά Κυκλώματα Ι Μάθημα 1: Δυαδικά συστήματα - Κώδικες Λευτέρης Καπετανάκης ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ Άνοιξη 2011 ΤΛ-2002: L1 Slide 1 Ψηφιακά Συστήματα ΤΛ-2002:
ΤΛ2002 Ψηφιακά Κυκλώματα Ι Μάθημα 1: Δυαδικά συστήματα - Κώδικες Λευτέρης Καπετανάκης ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ Άνοιξη 2011 ΤΛ-2002: L1 Slide 1 Ψηφιακά Συστήματα ΤΛ-2002:
Κεφάλαιο 2 Η έννοια και η παράσταση της πληροφορίας στον ΗΥ. Εφ. Πληροφορικής Κεφ. 2 Καραμαούνας Πολύκαρπος 1
 Κεφάλαιο 2 Η έννοια και η παράσταση της πληροφορίας στον ΗΥ Καραμαούνας Πολύκαρπος 1 2.1Η έννοια της πληροφορίας Δεδομένα Πληροφορία Καραμαούνας Πολύκαρπος 2 2.2 ΗΥ Το βασικό εργαλείο επεξεργασίας και
Κεφάλαιο 2 Η έννοια και η παράσταση της πληροφορίας στον ΗΥ Καραμαούνας Πολύκαρπος 1 2.1Η έννοια της πληροφορίας Δεδομένα Πληροφορία Καραμαούνας Πολύκαρπος 2 2.2 ΗΥ Το βασικό εργαλείο επεξεργασίας και
Εισαγωγή στους Ηλεκτρονικούς Υπολογιστές. 5 ο Μάθημα. Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ. url:
 στους Ηλεκτρονικούς Υπολογιστές 5 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
στους Ηλεκτρονικούς Υπολογιστές 5 ο Μάθημα Λεωνίδας Αλεξόπουλος Λέκτορας ΕΜΠ email: leo@mail.ntua.gr url: http://users.ntua.gr/leo Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative
Εισαγωγή στους Η/Υ & Εφαρμογές
 Τμήμα Οικονομικών Επιστημών Εισαγωγή στους Η/Υ & Εφαρμογές Διάλεξη #2: Υπολογιστές και συστήματα αρίθμησης Β. Δασκάλου, daskalu@upatras.gr Υπολογιστής Τα κύρια συστατικά ενός υπολογιστή Πληροφορίες εισόδου
Τμήμα Οικονομικών Επιστημών Εισαγωγή στους Η/Υ & Εφαρμογές Διάλεξη #2: Υπολογιστές και συστήματα αρίθμησης Β. Δασκάλου, daskalu@upatras.gr Υπολογιστής Τα κύρια συστατικά ενός υπολογιστή Πληροφορίες εισόδου
