frontistirioproios.wordpress.com
|
|
|
- Χαρικλώ Κουβέλης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Η ΔΥΝΑΜΗ ΤΟΥ ΕΛΑΤΗΡΙΟΥ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΑΛΓΕΒΡΙΚΗ ΤΙΜΗ Ή ΜΕΤΡΟ; Στον απλό αρμονικό ταλαντωτή «ατήριο- σώμα» η δύναμη που ασκεί το ατήριο στο σώμα έχει μέτρο ανάλογο της παραμόρφωσης του ατηρίου = Δ και κατεύθυνση τέτοια ώστε να τείνει να επαναφέρει το ατήριο στη θέση του φυσικού του μήκους. Πολλές φορές όμως θέλουμε τη σχέση της δύναμης του ατηρίου με την απομάκρυνση x του ταλαντωτή = f(x). Επειδή όμως η απομάκρυνση αποτυπώνεται πάντοτε με την αλγεβρική της τιμή (-A x +A) πρέπει στη σχέση αυτή και η να δίνει την αλγεβρική τιμή της δύναμης του ατηρίου. Ο ΑΠΛΟ ΠΑΡΑΔΕΙΓΜΑ: Ένα σώμα Σ μάζας m= g εκτεί απλή αρμονική ταλάντωση δεμένο στο N άκρο ενός οριζόντιου ατηρίου σταθεράς =, το άλλο άκρο του m οποίου είναι δεμένο σε ακλόνητο σημείο. Έστω ότι ταλαντωτής έχει πλάτος ταλάντωσης A=,5mκαι την t = είναι στην ακραία θετική θέση. Αρχικά ας κάνουμε το σχήμα στο οποίο να σημειώσουμε την θέση που το ατήριο έχει το φυσικό του μήκος και την θέση ισορροπίας της ταλάντωσης. Στη περίπτωση του παραδείγματος οι δύο αυτές θέσεις συμπίπτουν. Ας σημειώσουμε δύο άξονες: Φ.Μ Θ.Ι Σ παραμορφώσεων Σ x (m) απομακρύνσεων -,5 x +,5 x(m) τον άξονα των απομακρύνσεων του ταλαντωτή xx με αρχή O(x=) την θέση ισορροπίας του ταλαντωτή (αυτό δεν είναι επιλογή αλλά υποχρέωση ) και θετική φορά της επιλογής μας έστω προς τα δεξιά τον άξονα των παραμορφώσεων του ατηρίου με αρχή Δ = την θέση του φυσικού μήκους και θετική φορά ίδια με αυτή που πήραμε για τον άξονα των απομακρύνσεων.
2 Η χρονική εξίσωση της απομάκρυνσης είναι x = Aημ ωt + π x =,5ημ t + π ( SI. )... ή x=,5συν(t) Όταν ο ταλαντωτής είναι σε μια τυχαία θέση η αλγεβρική τιμή της απομάκρυνσης x ταυτίζεται με την αλγεβρική τιμή της παραμόρφωσης. D Για τη θέση αυτή γράφουμε Σ = -Dx = -x = -x x ή ή με (-,5m x +,5m) και η χρονική εξίσωση είναι = -x ή = - συν(t). xm ( ) +,5 (Ν) π t(. s) -,5 +,5 xm ( ) -,5 (Ν) - π t(. s) - Από την σχέση αυτή φαίνεται ότι όταν ο ταλαντωτής είναι σε θετική απομάκρυνση η δύναμη του ατηρίου έχει αρνητική αλγεβρική τιμή δηλαδή φορά αρνητική. Αν τώρα θέλαμε να γράψουμε την αλγεβρική τιμή της δύναμης του ατηρίου με την παραμόρφωση του ατηρίου αυτή πρέπει να γραφεί = -Δ με Δ όμως αλγεβρική τιμή και όχι μέτρο. Γενικά αν θέλουμε η = f(δ )να δίνει την αλγεβρική τιμή της δύναμης του ατηρίου, όποιο προσανατολισμό και να πάρουμε για την και Δ, η σχέση έχει πάντοτε την μορφή = -Δ. Το ατήριο εκτός από την δύναμη που ασκεί στο σώμα ασκεί και δύναμη στον τοίχο η οποία είναι αντίθετη αυτής που ασκείται στο σώμα και για τον ίδιο προσανατολισμό έχει αλγεβρική τιμή = - =+ΚΔ!
3 3 Ο ΣΥΝΘΕΤΟ ΠΑΡΑΔΕΙΓΜΑ: Ένα σώμα Σ μάζας m= g ηρεμεί δεμένο στο πάνω άκρο ενός N κατακόρυφου ατηρίου σταθεράς =, το άλλο άκρο του οποίου είναι m δεμένο σε σώμα Σ μάζας M = 5g που είναι πάνω σε οριζόντιο δάπεδο. Απομακρύνουμε το σώμα Σ από τη θέση ισορροπίας κατακόρυφα προς τα κάτω κατά,3m και τη t = το αφήνουμε εύθερο χωρίς αρχική ταχύτητα. α) Να γραφούν οι εξισώσεις που δίνουν σε συνάρτηση με την απομάκρυνση του ταλαντωτή y αλλά και το χρόνο t, τις αλγεβρικές τιμές της δύναμης που ασκεί το ατήριο στα σώματα Σ και Σ αλλά και την δύναμη στήριξης Ν β) Να γίνουν σε κοινό διάγραμμα οι αντίστοιχες γραφικές παραστάσεις. γ) Ποιο το μέγιστο πλάτος της ταλάντωσης για να μην χάσει το Σ την επαφή του με το δάπεδο. 3 Ας κάνουμε το σχήμα στο οποίο να σημειώσουμε την θέση που το ατήριο έχει το φυσικό του μήκος και την θέση ισορροπίας της ταλάντωσης. Η θέση ισορροπίας είναι πιο χαμηλά από το φυσικό μήκος κατά Δ. Ας σημειώσουμε δύο άξονες: τον άξονα των απομακρύνσεων του ταλαντωτή yy με αρχή O(y=) την θέση ισορροπίας του ταλαντωτή (αυτό δεν είναι επιλογή αλλά υποχρέωση ) και θετική φορά της επιλογής μας έστω προς τα πάνω τον άξονα των παραμορφώσεων του ατηρίου με αρχή Δ = την θέση του φυσικού μήκους και θετική φορά ίδια με αυτή που πήραμε για τον άξονα των απομακρύνσεων. Ας προσδιορίσουμε τη θέση ισορροπίας σε σχέση με τη θέση του φυσικού μήκους του ατηρίου. Στη θέση αυτή το ατήριο έχει στατική παραμόρφωση Δ που προσδιορίζεται από την σχέση Σy= +mg = - mg = Δ =,m (αλγεβρικά και με βάση το σύστημα του άξονα των παραμορφώσεων Δ = -,m ). Θεωρούμε τον ταλαντωτή Σ σε μια τυχαία θέση Γ (προτιμάμε για φορμαλιστική ευκολία να είναι θετική) και βρίσκουμε τη σχέση των αλγεβρικών τιμών για την απομάκρυνση και την παραμόρφωση. Από το σχήμα φαίνεται ότι y y=δl + Δl y =,+ Δ y =,+ Δ () Γράφουμε την εξίσωση απομάκρυνσης του ταλαντωτή Σ y = Aημ ωt + 3π y =,3ημ t + 3π ( SI. )... ή y= -,3συν(t)
4 4 (m) y(m) ( ) ( ) +,3 Φ.Μ Δ Δ = Θ.Ι O mg y +, y Γ mg -,3 N παραμορφώσεων απομακρύνσεων Mg 4 Όταν ο ταλαντωτής Σ είναι σε μια τυχαία θέση Γ γράφουμε D D Σ y = -Dy + mg = -Dy - = -y αλγεβρικές τιμές ή ή = - y με (-,3m y +,3m). Αυτή είναι η αλγεβρική τιμή της δύναμης (για το δεδομένο σύστημα) που ασκεί το ατήριο στο Σ. και διαφορετικά και επειδή από την () ά y =,+ Δ Δ y,άρα = -(y -,) = -(y -,) = - y Η αλγεβρική τιμή της δύναμης που ασκεί το ατήριο στο Σ είναι = -+y. Η αλγεβρική τιμή της δύναμης που ασκεί δάπεδο στο Σ προσδιορίζεται από την ισορροπία αυτού
5 5 Σy = N +Mg + = Ν + Mg + = N y= N =7 - y αλγεβρικές τιμές y(m) -,3 -, -, +, +, +,3 (Ν) (Ν) N(Ν) Ν = f(y) (N) ,3 -, -, +, +, +,3 y(m) - -4 = f(y) = f(y) -6-8 Οι αντίστοιχες χρονικές εξισώσεις εξάγονται απλά, θέτοντας y= -,3συν(t). = - -,3συν(t) = +6συν(t) Όμοια = - - 6συν(t) και N =7+6συν(t) και οι αντίστοιχες γραφικές παραστάσεις φαίνονται στο παρακάτω διάγραμμα. 5 Τώρα για να χαθεί η επαφή του Σ με το δάπεδο πρέπει να η μηδενισθεί η δύναμη στήριξης Ν (ουσιαστικά η να είναι προς τα πάνω θετική στο σύστημά μας και με μέτρο μεγαλύτερο του βάρους Mg του Σ και προφανώς το ατήριο να είναι τεντωμένο πάνω από το φυσικό του μήκος ). Για να μη χαθεί η επαφή πρέπει να υπάρχει η Ν και αυτή έχει πάντοτε εφόσον υπάρχει- φορά προς τα πάνω που για το σύστημά μας έχει θετική
6 6 αλγεβρική τιμή άρα N N =7 - y y,35m Amax,35m. ( Προσοχή! πήραμε N με την λογική της αλγεβρικής τιμής και όχι του μέτρου δείτε παρακάτω που θα αλλάξουμε φορά στο σύστημα!!!) (N),5,5 = f(t) Ν = f(t) = f(t) π t(. s) 6 ΚΑΙ ΑΝ Η ΦΟΡΑ ΤΩΝ ΑΞΟΝΩΝ ΗΤΑΝ ΘΕΤΙΚΗ ΠΡΟΣ ΤΑ ΚΑΤΩ; Ας ήταν η ίδια διαδικασία... Θεωρούμε τον ταλαντωτή Σ σε μια τυχαία θέση Γ ( αφήνουμε σκόπιμα την ίδια που τώρα όμως είναι αρνητική ) και βρίσκουμε τη σχέση των αλγεβρικών τιμών για την απομάκρυνση και την παραμόρφωση. Από το σχήμα φαίνεται y ότι y=δl + Δl y =,+ Δ -y =,- Δ y=δ, Γράφουμε την εξίσωση απομάκρυνσης του ταλαντωτή Σ π.. y = Aημ ωt + y =,3ημ t + π ( SI. )... ή y=,3συν(t) Όταν ο ταλαντωτής Σ είναι σε μια τυχαία θέση Γ γράφουμε D D Σ y = -Dy + mg = -Dy + = -y αλγεβρικές τιμές ή ή
7 7 = - - y με (-,3m y +,3m). Αυτή είναι η αλγεβρική τιμή της δύναμης (για το δεδομένο σύστημα) που ασκεί το ατήριο στο Σ. και διαφορετικά και επειδή από την () ά y=δ, Δ y,άρα = -(y+,) = -(y+,) = - - y Η αλγεβρική τιμή της δύναμης που ασκεί το ατήριο στο Σ είναι = +y. Η αλγεβρική τιμή της δύναμης που ασκεί δάπεδο στο Σ προσδιορίζεται από την ισορροπία αυτού Σy = N +Mg + = Ν + Mg + = αλγεβρικές τιμές N +5++y= N = -7 - y Φ.Μ παραμορφώσεων απομακρύνσεων -,3 Δ Δ = y < O -, Θ.Ι mg y Γ mg +,3 N (m) ( ) y(m) ( ) Mg 7 y(m) -,3 -, -, +, +, +,3 (Ν) (Ν) N(Ν)
8 8 Με μια πρώτη ματιά οι εξισώσεις φαίνονται «διαφορετικές» για τα δύο συστήματα αλλά αν προσέξουμε και συγκρίνουμε τους δύο πίνακες, στην ίδια θέση έχουμε το ίδιο μέτρο για κάθε δύναμη ανεξάρτητα από το σύστημα. Ας προσέξουμε τώρα πώς μετάμε την απώλεια επαφής για το κάτω σώμα Σ. Και πάλι για να χαθεί η επαφή του Σ με το δάπεδο πρέπει να η μηδενισθεί η δύναμη στήριξης Ν (ουσιαστικά η να είναι προς τα πάνω ΑΡΝΗΤΙΚΗ στο σύστημά μας και με μέτρο μεγαλύτερο του βάρους Mg του Σ και προφανώς το ατήριο να είναι τεντωμένο πάνω από το φυσικό του μήκος ). Για να μη χαθεί η επαφή πρέπει να υπάρχει η Ν και αυτή εφόσον υπάρχει έχει πάντοτε φορά προς τα πάνω και για το σύστημά μας έχει ΑΡΝΗΤΙΚΗ αλγεβρική τιμή άρα πρέπει N (!!!) N = -7 - y y,35m Δηλαδή επαφή υπάρχει εφόσον ο ταλαντωτής Σ είναι κάτω από την θέση y,35m συνεπώς το μέγιστο πλάτος για να μην χαθεί η επαφή είναι A,35m. max 8
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
Ποιο είναι το πλάτος της ταλάντωσης ;
 Ποιο είναι το πλάτος της ταλάντωσης ; 1. Ένα σώμα είναι δεμένο στο δεξιό άκρο οριζόντιου ιδανικού ελατηρίου και στο αριστερό άκρο οριζόντιου νήματος και ηρεμεί σε ισορροπία όπως δείχνει το σχήμα. Το ελατήριο
Ποιο είναι το πλάτος της ταλάντωσης ; 1. Ένα σώμα είναι δεμένο στο δεξιό άκρο οριζόντιου ιδανικού ελατηρίου και στο αριστερό άκρο οριζόντιου νήματος και ηρεμεί σε ισορροπία όπως δείχνει το σχήμα. Το ελατήριο
w w w.k z a c h a r i a d i s.g r
 Πως αποδεικνύουμε ότι ένα σώμα εκτεί απλή αρμονική ταλάντωση Μεθοδολογία i) Βρίσκουμε την θέση ισορροπίας του σώματος και σχεδιάζουμε το σώμα σε αυτή την θέση. ii) Σχεδιάζουμε τις δυνάμεις που ενεργούν
Πως αποδεικνύουμε ότι ένα σώμα εκτεί απλή αρμονική ταλάντωση Μεθοδολογία i) Βρίσκουμε την θέση ισορροπίας του σώματος και σχεδιάζουμε το σώμα σε αυτή την θέση. ii) Σχεδιάζουμε τις δυνάμεις που ενεργούν
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24
 ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
ΕΚΦΩΝΗΣΕΙΣ ΑΣΚΗΣΕΩΝ 6 24 Εκφώνηση άσκησης 6. Ένα σώμα, μάζας m, εκτελεί απλή αρμονική ταλάντωση έχοντας ολική ενέργεια Ε. Χωρίς να αλλάξουμε τα φυσικά χαρακτηριστικά του συστήματος, προσφέρουμε στο σώμα
Ενδεικτικές Λύσεις. Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Σε µία ϕθίνουσα ταλάντωση στην οποία το πλάτος µειώνεται εκθετικά µε το χρόνο : (ϐ) όταν η σταθερά απόσβεσης b µεγαλώνει, το
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ 2. έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε σταθερό σημείο.
 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ΜΕΡΟΣ. Ένα ιδανικό ελατήριο σταθεράς = 00 N/ που έχει τον άξονα του κατακόρυφο έχει το φυσικό του μήκος και η πάνω άκρη του είναι δεμένη σε
ΠΑΡΑΔΕΙΓΜΑΤΑ ΣΤΗΝ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΜΕ ΣΩΜΑΤΑ ΣΕ ΕΠΑΦΗ. Σύστημα σωμάτων σε επαφή στο οριζόντιο επίπεδο με ελατήριο συνδεδεμένο στο ένα σώμα.
 Σύστημα σωμάτων σε επαφή στο οριζόντιο επίπεδο με ελατήριο συνδεδεμένο στο ένα σώμα.. Σώμα μάζας = 0,5 g έχει το ένα άκρο στερεωμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς = 50 / και το άλλο άκρο του βρίσκεται
Σύστημα σωμάτων σε επαφή στο οριζόντιο επίπεδο με ελατήριο συνδεδεμένο στο ένα σώμα.. Σώμα μάζας = 0,5 g έχει το ένα άκρο στερεωμένο σε οριζόντιο ιδανικό ελατήριο σταθεράς = 50 / και το άλλο άκρο του βρίσκεται
Στα ερωτήματα 1,2.3,4 του ζητήματος αυτού μια πρόταση είναι σωστή να την κυκλώσετε)
 Ζήτημα ο Στα ερωτήματα,., του ζητήματος αυτού μια πρόταση είναι σωστή να την κυκλώσετε. Ένα σώμα κάνει απλή αρμονική ταλάντωση στην οποία η απομάκρυνση είναι της μορφής χ=aημωt κάποια στιγμή t η φάση του
Ζήτημα ο Στα ερωτήματα,., του ζητήματος αυτού μια πρόταση είναι σωστή να την κυκλώσετε. Ένα σώμα κάνει απλή αρμονική ταλάντωση στην οποία η απομάκρυνση είναι της μορφής χ=aημωt κάποια στιγμή t η φάση του
Α. Για ποιο από τα δυο σώματα καταναλώσαμε περισσότερη ενέργεια;
 1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
1. Στην κάτω άκρη ενός ιδανικού ελατήριου είναι δεμένο ένα σώμα που έχει μάζα m 1 = m και ισορροπεί. Στην κάτω άκρη ενός άλλου ομοίου ελατήριου είναι δεμένο ένα άλλο σώμα που έχει μάζα m 2 = 4m και ισορροπεί.
Εκφώνηση 1. α). β). γ). Επιλέξτε τη σωστή πρόταση και αιτιολογείστε.
 Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
Εκφώνηση 1 Στο σχήμα το σώμα μάζας ισορροπεί χαμηλότερα κατά h από τη θέση φυσικού μήκους του ελατηρίου. Από τη θέση φυσικού μήκους του ελατηρίου αφήνουμε σώμα ίσης μάζας ( ) να κάνει ελεύθερη πτώση στην
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5
 ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
ΑΡΧΗ ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Ο : ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΑΥΓΟΥΣΤΟΥ 08 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 5 Στις παρακάτω ερωτήσεις έως 4 να γράψετε στο τετράδιό σας τον
T 4 T 4 T 2 Τ Τ Τ 3Τ Τ Τ 4
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 29 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σηµειακό αντικείµενο εκτελεί απλή αρµονική ταλάντωση. Η αποµάκρυνση χ από τη θέση ισορροπίας του είναι: α. ανάλογη του χρόνου. β. αρµονική συνάρτηση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 29 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ 1. Σηµειακό αντικείµενο εκτελεί απλή αρµονική ταλάντωση. Η αποµάκρυνση χ από τη θέση ισορροπίας του είναι: α. ανάλογη του χρόνου. β. αρµονική συνάρτηση
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI).
 1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
1. Η απομάκρυνση σώματος που πραγματοποιεί οριζόντια απλή αρμονική ταλάντωση δίδεται από την σχέση x = 0,2 ημ π t, (SI). Να βρείτε: α. το πλάτος της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης. β.
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ
 ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
ΤΑΛΑΝΤΩΣΗ ΚΑΙ ΚΡΟΥΣΗ 1. Κατακόρυφο ελατήριο σταθεράς k=1000 N /m έχει το κάτω άκρο του στερεωμένο σε ακίνητο σημείο. Στο πάνω άκρο του ελατηρίου έχει προσδεθεί σώμα Σ 1 μάζας m 1 =8 kg, ενώ ένα δεύτερο
7. Ένα σώμα εκτελεί Α.Α.Τ. Η σταθερά επαναφοράς συστήματος είναι.
 ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
ΚΕΦΑΛΑΙΟ 1 ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 6α. Σφαίρα μάζας ισορροπεί δεμένη στο πάνω άκρο κατακόρυφου
1. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου.
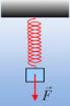 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΚΡΟΥΣΗ.. Σώμα που συγκρούεται ανελαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Σώμα μάζας = g κινείται σε λείο οριζόντιο επίπεδο με ταχύτητα υ μέτρου υ = 5 /s συγκρούεται
1. Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα.
 Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
Γενικές ασκήσεις Θέματα εξετάσεων από το 1ο κεφάλαιο ΚΕΦΑΛΑΙΟ 1 1 Ένα σώμα m=1kg εκτελεί απλή αρμονική ταλάντωση και η μεταβολή της επιτάχυνσής του σε συνάρτηση με το χρόνο, φαίνεται στο σχήμα α Να βρείτε
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 A ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Δευτέρα 7 Ιανουαρίου 09 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ημερομηνία: Δευτέρα 7 Ιανουαρίου 09 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς προτάσεις Α Α4 να γράψετε στο τετράδιό
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/11/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
γ. Πόση επιτάχυνση θα έχει το σώμα τη στιγμή που έχει απομάκρυνση 0,3 m;
 ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Γ 1. Ένα σώμα εκτελεί αρμονική ταλάντωση με εξίσωση 0,6 ημ 8 S.I.. α. Να βρείτε την περίοδο και τον αριθμό των ταλαντώσεων που εκτελεί το σώμα σε ένα λεπτό της ώρας. β. Να γράψετε τις εξισώσεις της
ΘΕΜΑ Α. Α.1. Ένα σύστηµα ελατηρίου-µάζας εκτελεί απλή αρµονική ταλάντωση πλάτους Α.
 ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α 1 Α 6 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά. Α.1. Ένα σύστηµα ελατηρίου-µάζας
ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α 1 Α 6 να γράψετε στο τετράδιο σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία τη συμπληρώνει σωστά. Α.1. Ένα σύστηµα ελατηρίου-µάζας
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ : ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση Ένα σώμα εκτελεί απλή
D α x γ. α D m x δ. m
 ΚΟΨΙΔΑΣ Η. ΔΗΜΗΤΡΙΟΣ Καθηγητς Φυσικς ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΑΝΤΙΚΕΙΜΕΝΟ: ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ (ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Διάρκεια εξέτασης: ώρες ΘΕΜΑ ο Οδηγία: Στις ερωτσεις -4 να γράψετε στο τετράδιο σας
ΚΟΨΙΔΑΣ Η. ΔΗΜΗΤΡΙΟΣ Καθηγητς Φυσικς ο ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ ΑΝΤΙΚΕΙΜΕΝΟ: ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ (ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ) Διάρκεια εξέτασης: ώρες ΘΕΜΑ ο Οδηγία: Στις ερωτσεις -4 να γράψετε στο τετράδιο σας
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Φροντιστήρια Εν-τάξη Σελίδα 1 από 6
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 11/09/2016 ΘΕΜΑ Α Να γράψετε στο τετραδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Ένα
1.1 Κινηματική προσέγγιση
 1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
1.1 Κινηματική προσέγγιση ΣΑ 1.8: Η απομάκρυνση από τη θέση ισορροπίας ενός σώματος που κάνει αατ δίνεται σε συνάρτηση με το χρόνο από τη σχέση x=10 ημ(π/4t) (x σε cm και t σε s). Να βρείτε: Α) το πλάτος
4. Σώμα Σ 1 μάζας m 1 =1kg ισορροπεί πάνω σε λείο κεκλιμένο επίπεδο που σχηματίζει με τον ορίζοντα γωνία φ=30 ο. Το σώμα Σ 1 είναι δεμένο στην άκρη
 1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
1. Δίσκος μάζας Μ=1 Kg είναι στερεωμένος στο πάνω άκρο κατακόρυφου ελατηρίου, σταθεράς k=200 N/m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο σε οριζόντιο δάπεδο. Πάνω στο δίσκο κάθεται ένα πουλί με μάζα
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση
 Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
ΚΡΙΤΗΡΙΟ ΑΞΙΟΛΟΓΗΣΗΣ στις αμείωτες μηχανικές ΤΑΛΑΝΤΩΣΕΙΣ- ΚΡΟΥΣΕΙΣ (1) ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΘΕΜΑ Α Α1.Ένα σώμα μάζας m είναι δεμένο και ισορροπεί στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k 1 του
Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις
 Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις Θέμα Α. (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Κριτήριο αξιολόγησης: Κρούσεις Αμείωτες Μηχανικές Ταλαντώσεις Θέμα Α. (Για τις ερωτήσεις Α. έως και Α.4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση
 Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
Σώματα σε επαφή και Απλή Αρμονική Ταλάντωση Σε όλες τις περιπτώσεις που θα εξετάσουμε το δάπεδο είναι λείο. Επίσης τα σύμβολα των διανυσματικών μεγεθών αντιπροσωπεύουν τις αλγεβρικές τους τιμές. Α. Η επιφάνεια
ΑΠΛΟ ΑΡΜΟΝΙΚΟ ΣΑΛΑΝΣΩΣΗ - ΤΣΗΜΑ ΕΛΑΣΗΡΙΟΤ ΩΜΑΣΟ
 ΑΠΛΟ ΑΡΜΟΝΙΚΟ ΣΑΛΑΝΣΩΣΗ - ΤΣΗΜΑ ΕΛΑΣΗΡΙΟΤ ΩΜΑΣΟ α) Ένα σώμα που μπορεί να εκτελεί απλή αρμονική ταλάντωση ονομάζεται απλός αρμονικός ταλαντωτής. Το σύστημα ελατήριο-μάζα είναι απλός αρμονικός ταλαντωτής,
ΑΠΛΟ ΑΡΜΟΝΙΚΟ ΣΑΛΑΝΣΩΣΗ - ΤΣΗΜΑ ΕΛΑΣΗΡΙΟΤ ΩΜΑΣΟ α) Ένα σώμα που μπορεί να εκτελεί απλή αρμονική ταλάντωση ονομάζεται απλός αρμονικός ταλαντωτής. Το σύστημα ελατήριο-μάζα είναι απλός αρμονικός ταλαντωτής,
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς
 Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Ε ρ ω τ ή σ ε ι ς σ τ ι ς μ η χ α ν ι κ έ ς τ α λ α ν τ ώ σ ε ι ς 1. Δύο σώματα ίδιας μάζας εκτελούν Α.Α.Τ. Στο διάγραμμα του σχήματος παριστάνεται η συνισταμένη δύναμη που ασκείται σε κάθε σώμα σε συνάρτηση
Όλα τα θέματα των πανελληνίων στις μηχανικές ταλαντώσεις έως και το 2014 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ. Ερωτήσεις Πολλαπλής Επιλογής
 έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
έως και το 04 ΣΑΛΑΝΣΩΕΙ ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΣΑΛΑΝΣΩΗ ΒΑΙΚΕ ΕΝΝΟΙΕ Ερωτήσεις Πολλαπλής Επιλογής. Να μεταφέρετε στο τετράδιό σας τον παρακάτω πίνακα που αναφέρεται στην απλή αρμονική ταλάντωση και να συμπληρώσετε
Σύνολο Σελίδων: Ενδεικτικές Λύσεις Κυριακή 30 Σεπτέµβρη Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις Κυριακή 30 Σεπτέµβρη 018 Θέµα Α Α.1. Ταλαντωτής εκτελεί ϕθίνουσα ταλάντωση µικρής απόσβεσης. Η αντιτιθέµενη δύναµη είναι
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Σύνολο Σελίδων: Ενδεικτικές Λύσεις Κυριακή 30 Σεπτέµβρη 018 Θέµα Α Α.1. Ταλαντωτής εκτελεί ϕθίνουσα ταλάντωση µικρής απόσβεσης. Η αντιτιθέµενη δύναµη είναι
2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΟ 1) ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1α έως Α4β να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) 2ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ο set - μέρος Α - Απαντήσεις ΘΕΜΑ Β Ερώτηση. Ένα σώμα εκτελεί
Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή
 Θέμα ο. Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή 4--06 Στα θέματα Α, Α, Α3,Α4 επιλέξτε το γράμμα που απαντά στην ερώτηση και γράψτε το
Θέμα ο. Διαγώνισμα στη Φυσική Θετικού Προσανατολισμού στα κεφάλαια Ταλαντώσεις-κρούσεις κύματα και Doppler. Κυριακή 4--06 Στα θέματα Α, Α, Α3,Α4 επιλέξτε το γράμμα που απαντά στην ερώτηση και γράψτε το
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
: ΣFy=0 Mg + F - KΔ. = 0 (1). Η ταλάντωση αυτή είναι απλή αρμονική και έχει σταθερά επαναφοράς D= K =10N / m ( δείξτε 0,5 0,3 0,1 0,1 0,3 0,5
 6 3.4 άντηση α) Η αρχική ταλάντωση γίνεται γύρω ό την θέση ισορροπίας που είναι κάτω ό το φυσικό μήκος κατά Δ : Σy= Mg - Δ = Δ =,m ( όπως φαίνεται στο ο σχήμα). Η δεύτερη ταλάντωση που αρχίζει μετά την
6 3.4 άντηση α) Η αρχική ταλάντωση γίνεται γύρω ό την θέση ισορροπίας που είναι κάτω ό το φυσικό μήκος κατά Δ : Σy= Mg - Δ = Δ =,m ( όπως φαίνεται στο ο σχήμα). Η δεύτερη ταλάντωση που αρχίζει μετά την
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
ΕΝΕΡΓΕΙΑ ΚΑΙ ΤΑΛΑΝΤΩΣΗ 1. Ελατήριο σταθεράς K τοποθετείται κατακόρυφα με το πάνω άκρο του στερεωμένο σε ακλόνητο σημείο. Ένα σώμα μάζας M=1 kg δένεται στο κάτω άκρο του ελατηρίου και η επιμήκυνση που προκαλεί
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 3-0-0 ΧΕΙΜΕΡΙΝΑ ΘΕΜΑ ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
3-0-0 ΧΕΙΜΕΡΙΝΑ ΘΕΜΑ ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράµµα που αντιστοιχεί στη σωστή
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ.
 1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Στ. 101) Δυο σώματα αφήνονται να κινηθούν. Δυο σώματα Σ 1 και Σ 2, ίδιας μάζας m=2kg, συγκρατιόνται σε λείο κεκλιμένο επίπεδο απέχοντας κατά D=1,5m από την κορυφή του
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 2 o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 2018: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΤΑΛΑΝΤΩΣΕΙΣ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 2 ο ΔΙΑΓΩΝΙΣΜΑ ΤΑΛΑΝΤΩΣΕΙΣ - ΘΕΜΑΤΑ ΘΕΜΑ A Στις προτάσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη
ΕΝΟΤΗΤΑ 1.2: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
ΚΕΦΑΛΑΙΟ Ο : ΜΗΧΑΝΙΚΕΣ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΕΝΟΤΗΤΑ.: ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ, ΑΡΧΙΚΗ ΦΑΣΗ, ΣΥΣΤΗΜΑ ΕΛΑΤΗΡΙΟΥ ΣΩΜΑΤΟΣ, ΟΡΜΗ) ΘΕΜΑΤΑ ΠΡΟΣ ΕΠΙΛΥΣΗ ΘΕΜΑ Β Ερώτηση. Ένα σώμα, μάζας,
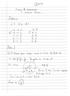 ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΟΥ ΜΕΤΑΤΡΕΠΕΤΑΙ ΣΕ ΦΘΙΝΟΥΣΑ Ένα σώμα Σ μάζας m=2kg είναι δεμένο στο ένα άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k=50n/m, το άλλο άκρο του οποίου είναι Θ.Φ.Μ στερεωμένο σε ακλόνητο
α. β. γ. δ. Μονάδες 5 α. β. γ. δ. Μονάδες 5 α. ελαστική β. ανελαστική γ. πλαστική δ. έκκεντρη
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 27/09/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4
ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ ΠΛΑΓΙΑ ΠΛΑΣΤΙΚΗ ΚΡΟΥΣΗ ΚΑΙ ΤΑΛΑΝΤΩΣΗ
 ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΠΛΑΓΙΑ ΚΡΟΥΣΗ.. Σώμα που κινείται με κάποια ταχύτητα που σχηματίζει γωνία ως προς το κεκλιμένο επίπεδο συγκρούεται πλαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Ξύλινο
ΤΑΛΑΝΤΩΣΗ ΜΕΤΑ ΑΠΟ ΠΛΑΓΙΑ ΚΡΟΥΣΗ.. Σώμα που κινείται με κάποια ταχύτητα που σχηματίζει γωνία ως προς το κεκλιμένο επίπεδο συγκρούεται πλαστικά με άλλο σώμα δεμένο στο άκρο οριζοντίου ελατηρίου. Ξύλινο
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β
 1 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β 1) Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας ma, κινούμενο με ταχύτητα υα=3 m/s κατά
1 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ ΘΕΜΑTA Β 1) Tο σώμα Β του σχήματος είναι ακίνητο πάνω σε λείο οριζόντιο δάπεδο και δεμένο στην άκρη ιδανικού ελατηρίου. Το σώμα Α, μάζας ma, κινούμενο με ταχύτητα υα=3 m/s κατά
ΔΙΑΓΩΝΙΣΜΑ 02 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
 Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 02 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και
Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 02 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ A Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1- Α4 και
ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ.
 ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. ΕΡΩΤΗΣΗ 1 Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m είναι κρεμασμένο σώμα μάζας m = 1 kg. Το σύστημα ελατήριο-σώμα εξαναγκάζεται
ΕΡΓΑΣΙΑ ΣΤΟ ΠΡΩΤΟ ΚΕΦΑΛΑΙΟ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ. ΕΡΩΤΗΣΗ 1 Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k = 400 N/m είναι κρεμασμένο σώμα μάζας m = 1 kg. Το σύστημα ελατήριο-σώμα εξαναγκάζεται
Φυσική Γ Λυκείου Κατεύθυνσης. Προτεινόμενα Θέματα
 Φυσική Γ Λυκείου Κατεύθυνσης Προτεινόμενα Θέματα Θέμα ο Ένα σώμα εκτελεί απλή αρμονική ταλάντωση πλάτους Α. Η φάση της ταλάντωσης μεταβάλλεται με το χρόνο όπως δείχνει το παρακάτω σχήμα : φ(rad) 2π π 6
Φυσική Γ Λυκείου Κατεύθυνσης Προτεινόμενα Θέματα Θέμα ο Ένα σώμα εκτελεί απλή αρμονική ταλάντωση πλάτους Α. Η φάση της ταλάντωσης μεταβάλλεται με το χρόνο όπως δείχνει το παρακάτω σχήμα : φ(rad) 2π π 6
ΔΙΑΓΩΝΙΣΜΑ 01 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α
 Σελίδα από ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ () ΘΕΜΑ Α Α. Με την πάροδο του χρόνου και καθώς τα αμορτισέρ ενός αυτοκινήτου παλιώνουν και φθείρονται:
Σελίδα από ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ () ΘΕΜΑ Α Α. Με την πάροδο του χρόνου και καθώς τα αμορτισέρ ενός αυτοκινήτου παλιώνουν και φθείρονται:
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ 2
 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ) Ένα ιδανικό ελατήριο σταθεράς 00 N/m που έχει τον άξονα του κατακόρυφο έχει το φυσικό του µήκος και η πάνω άκρη του είναι δεµένη σε σταθερό
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ ΚΑΙ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΜΕ ΑΙΤΙΟΛΟΓΗΣΗ ) Ένα ιδανικό ελατήριο σταθεράς 00 N/m που έχει τον άξονα του κατακόρυφο έχει το φυσικό του µήκος και η πάνω άκρη του είναι δεµένη σε σταθερό
2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 14 Σεπτέµβρη 2014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις. Ενδεικτικές Λύσεις. Θέµα Α
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 14 Σεπτέµβρη 014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθµό της
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Κυριακή 14 Σεπτέµβρη 014 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Στις ηµιτελείς προτάσεις Α.1 Α.4 να γράψετε στο τετράδιο σας τον αριθµό της
Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα σε κάθε αριθμό το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Μάθημα/Τάξη: Φυσική Γ Λυκείου Κεφάλαιο: Ταλαντώσεις Ονοματεπώνυμο Μαθητή: Ημερομηνία: 13-11-2017 Επιδιωκόμενος Στόχος: 80/100 Θέμα A Στις ερωτήσεις A1 - A4, να γράψετε τον αριθμό της ερώτησης και δίπλα
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις
 Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
Διαγώνισμα Φυσικής Γ Λυκείου Απλή αρμονική ταλάντωση Κρούσεις ~ Διάρκεια: 3 ώρες ~ Θέμα Α Α1. Η ορμή συστήματος δύο σωμάτων που συγκρούονται διατηρείται: α. Μόνο στην πλάγια κρούση. β. Μόνο στην έκκεντρη
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Α.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Α Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ(ΘΕΡΙΝΑ)
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ(ΘΕΡΙΝΑ) 5/01/2019 ΟΙΚΟΝΟΜΟΥ ΓΙΩΡΓΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΧΡΗΣΤΟΣ- ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ(ΘΕΡΙΝΑ) 5/01/2019 ΟΙΚΟΝΟΜΟΥ ΓΙΩΡΓΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΧΡΗΣΤΟΣ- ΤΖΑΓΚΑΡΑΚΗΣ ΓΙΑΝΝΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Ημερομηνία: Παρασκευή 27 Οκτωβρίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
ΑΠΟ /0/07 ΕΩΣ //07 η ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Παρασκευή 7 Οκτωβρίου 07 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ημιτελείς προτάσεις
2.1 Τρέχοντα Κύµατα. Οµάδα.
 2.1 Τρέχοντα Κύµατα. Οµάδα. 2.1.41. Κάποια ερωτήµατα πάνω σε µια κυµατοµορφή. Ένα εγκάρσιο αρµονικό κύµα, πλάτους 0,2m, διαδίδεται κατά µήκος ενός ελαστικού γραµµικού µέσου, από αριστερά προς τα δεξιά
2.1 Τρέχοντα Κύµατα. Οµάδα. 2.1.41. Κάποια ερωτήµατα πάνω σε µια κυµατοµορφή. Ένα εγκάρσιο αρµονικό κύµα, πλάτους 0,2m, διαδίδεται κατά µήκος ενός ελαστικού γραµµικού µέσου, από αριστερά προς τα δεξιά
Προγραμματισμένο διαγώνισμα Φυσικής κατεύθυνσης Γ Λυκείου. Ονοματεπώνυμο εξεταζόμενου:.
 Προγραμματισμένο διαγώνισμα Φυσικής κατεύθυνσης Γ Λυκείου Ονοματεπώνυμο εξεταζόμενου:. Καμιά άλλη σημείωση δεν επιτρέπεται στα θέματα τα οποία θα παραδώσετε μαζί με το γραπτό σας. Οι απαντήσεις λοιπόν
Προγραμματισμένο διαγώνισμα Φυσικής κατεύθυνσης Γ Λυκείου Ονοματεπώνυμο εξεταζόμενου:. Καμιά άλλη σημείωση δεν επιτρέπεται στα θέματα τα οποία θα παραδώσετε μαζί με το γραπτό σας. Οι απαντήσεις λοιπόν
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
17-10-11 ΑΠΟΦΟΙΤΟΙ ΣΕΙΡΑ Α Θέµα 1 ο ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΛΥΣΕΙΣ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθµό καθεµιάς από τις παρακάτω ερωτήσεις 1-4 δίπλα το γράµµα που αντιστοιχεί
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Α ΦΑΣΗ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 7 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ηµιτελείς προτάσεις Α Α4
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 7 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ηµιτελείς προτάσεις Α Α4
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 10 ΑΠΡΙΛΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6)
 ΦΥΣΙΗ Γ ΛΥΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΩΝ ΣΠΟΥΔΩΝ 10 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΦΥΣΙΗ Γ ΛΥΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΩΝ ΣΠΟΥΔΩΝ 10 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ η εξεταστική περίοδος 0-3 Σελίδα - - ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείου Τμήμα: Βαθμός: Ημερομηνία: 8-0-0 Διάρκεια: 3 ώρες Ύλη: Ταλαντώσεις Καθηγητής: ΑΤΡΕΙΔΗΣ
δυαδικό ΦΡΟΝΤΙΣΤΗΡΙΑ η εξεταστική περίοδος 0-3 Σελίδα - - ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείου Τμήμα: Βαθμός: Ημερομηνία: 8-0-0 Διάρκεια: 3 ώρες Ύλη: Ταλαντώσεις Καθηγητής: ΑΤΡΕΙΔΗΣ
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ
 Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α:. Σωστό το B.. Σωστό το Γ. 3. Σωστό το Δ. 4. Σωστά τα Α, Β, Γ. 5. Σωστό το Δ. ΘΕΜΑ Β:. Σωστό το Β. Αιτιολόγηση: Έχουµε διαδοχικά:. Σωστό το Α. D D K E U =
Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α:. Σωστό το B.. Σωστό το Γ. 3. Σωστό το Δ. 4. Σωστά τα Α, Β, Γ. 5. Σωστό το Δ. ΘΕΜΑ Β:. Σωστό το Β. Αιτιολόγηση: Έχουµε διαδοχικά:. Σωστό το Α. D D K E U =
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
ΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΣΤΙΣ ΜΗΧΑΝΙΚΕΣ ΚΑΙ ΗΛΕΚΤΡΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ Θέµα Α Στις ερωτήσεις -4 να βρείτε τη σωστή απάντηση. Α. Για κάποιο χρονικό διάστηµα t, η πολικότητα του πυκνωτή και
1ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη 12 Αυγούστου 2015 Απλή Αρµονική Ταλάντωση - Κρούσεις. Ενδεικτικές Λύσεις - Οµάδα Β.
 ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Β Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Τετάρτη Αυγούστου 05 Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις - Οµάδα Β Θέµα Α Α.. Σε µια απλή αρµονική ταλάντωση η αποµάκρυνση και η επιτάχυνση την ίδια
12ο ΓΕΛ ΠΕΙΡΑΙΑ 12/10/2010 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ
 1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
1ο ΓΕΛ ΠΕΙΡΑΙΑ 1/10/010 Ονοµατεπώνυµο: Τµήµα: Γθετ ΟΜΑΔΑ Α Διάρκεια: 45 min ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗΝ ΑΑΤ Ένα ιδανικό κατακόρυφο ελατήριο, έχει σταθερά k=400ν/m και στηρίζεται µε
Ταλάντωση συστήματος και η απώλεια επαφής.
 αλάντωση συματος και η απώλεια επαφς. Α. αλάντωσης κατακόρυφου συματος. Ένα κατακόρυφο ελατριο αθεράς είναι ερεωμένο με το κάτω άκρο του σε δάπεδο. το πάνω μέρος του ελατηρίου είναι ακλόνητα προσαρμοσμένος
αλάντωση συματος και η απώλεια επαφς. Α. αλάντωσης κατακόρυφου συματος. Ένα κατακόρυφο ελατριο αθεράς είναι ερεωμένο με το κάτω άκρο του σε δάπεδο. το πάνω μέρος του ελατηρίου είναι ακλόνητα προσαρμοσμένος
ΟΡΟΣΗΜΟ. 1ο Κριτήριο αξιολόγησης στα κεφ Θέμα 1. Κριτήρια αξιολόγησης Ταλαντώσεις - Κύματα.
 1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
1ο Κριτήριο αξιολόγησης στα κεφ. 1-2 Θέμα 1 Ποια από τις παρακάτω προτάσεις είναι σωστή; 1. Ένα σώμα μάζας m είναι δεμένο στην ελεύθερη άκρη κατακόρυφου ιδανικού ελατηρίου σταθεράς k και ηρεμεί στη θέση
Φάσμα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι.
 σύγχρονο Φάσμα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο 1. 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 2. 25ης Μαρτίου 74 Πλ. ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 3. Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ
σύγχρονο Φάσμα & Group προπαρασκευή για Α.Ε.Ι. & Τ.Ε.Ι. μαθητικό φροντιστήριο 1. 25ης Μαρτίου 111 ΠΕΤΡΟΥΠΟΛΗ 50.27.990 50.20.990 2. 25ης Μαρτίου 74 Πλ. ΠΕΤΡΟΥΠΟΛΗΣ 50.50.658 50.60.845 3. Γραβιάς 85 ΚΗΠΟΥΠΟΛΗ
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ.
 ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ. Θα μελετήσουμε τώρα συστήματα που διεγείρονται σε ταλάντωση μέσω εξωτερικής ς που μπορεί να είναι (όπως θα δούμε παρακάτω) σταθερή, μεταβλητού
ΤΑΛΑΝΤΩΣΕΙΣ ΜΕ ΕΞΩΤΕΡΙΚΗ ΔΥΝΑΜΗ ΠΟΥ ΑΡΓΟΤΕΡΑ ΜΠΟΡΕΙ ΝΑ ΚΑΤΑΡΓΗΘΕΙ. Θα μελετήσουμε τώρα συστήματα που διεγείρονται σε ταλάντωση μέσω εξωτερικής ς που μπορεί να είναι (όπως θα δούμε παρακάτω) σταθερή, μεταβλητού
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΣΕΠΤΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 ΘΕΜΑ 1 Ο : Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΘΕΜΑ 1ο. Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Ένα σώμα εκτελεί φθίνουσα αρμονική ταλάντωση με δύναμη απόσβεσης
ΘΕΜΑ ο Να γράψετε στο τετράδιό σας τον αριθμό καθεμίας από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.. Ένα σώμα εκτελεί φθίνουσα αρμονική ταλάντωση με δύναμη απόσβεσης
2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Παρασκευή 4 Σεπτέµβρη 2015 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις. Λύσεις. Θέµα Α
 2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Παρασκευή 4 Σεπτέµβρη 2015 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Λύσεις Θέµα Α Α.1. Απλός αρµονικός ταλαντωτής εκτελεί ταλάντωση πλάτους Α. ιατηρούµε σταθερό το πλάτος
2ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Παρασκευή 4 Σεπτέµβρη 2015 Το σύστηµα Ελατηρίου - Μάζας / Κρούσεις Λύσεις Θέµα Α Α.1. Απλός αρµονικός ταλαντωτής εκτελεί ταλάντωση πλάτους Α. ιατηρούµε σταθερό το πλάτος
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α
 ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Απλή Αρµονική Ταλάντωση - Κρούσεις Ενδεικτικές Λύσεις Θέµα Α Α.. Κατά την πλαστική κρούση δύο σωµάτων ισχύει ότι : (δ) η ορµή του συστήµατος των δύο σωµάτων παραµένει
ΔΙΑΓΩΝΙΣΜΑ 03 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
 Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 03 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1. Δύο σύγχρονες πηγές κυμάτων Π 1 και Π αρχίζουν τη χρονική στιγμή t=0 να ταλαντώνονται
Σελίδα 1 από 5 ΔΙΑΓΩΝΙΣΜΑ 03 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Διάρκεια: 3ώρες ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Α1. Δύο σύγχρονες πηγές κυμάτων Π 1 και Π αρχίζουν τη χρονική στιγμή t=0 να ταλαντώνονται
Α1 γ, Α2 γ, Α3 β, Α4 α, Α5 α Σ, β Λ, γ Λ, δ Σ, ε Λ. άρα. p. Έχοντας ίσες μάζες
 Λύσεις διαγωνίσματος 5 Θέμα Α Α γ, Α γ, Α β, Α4 α, Α5 α Σ, β Λ, γ Λ, δ Σ, ε Λ Θέμα Β Β. Σωστή απάντηση είναι η (γ). Στην η περίπτωση αφού το συσσωμάτωμα μετά την κρούση παραμένει ακίνητο τα σώματα πριν
Λύσεις διαγωνίσματος 5 Θέμα Α Α γ, Α γ, Α β, Α4 α, Α5 α Σ, β Λ, γ Λ, δ Σ, ε Λ Θέμα Β Β. Σωστή απάντηση είναι η (γ). Στην η περίπτωση αφού το συσσωμάτωμα μετά την κρούση παραμένει ακίνητο τα σώματα πριν
2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ
 2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ 207-208 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΝΟΕΜΒΡΙΟΥ 207 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΟΝΟΜΑΤΕΠΩΝΥΜΟ Τμήμα Γθετ.
2 ΓΕΛ ΧΑΙΔΑΡΙΟΥ 207-208 ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 26 ΝΟΕΜΒΡΙΟΥ 207 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΟΝΟΜΑΤΕΠΩΝΥΜΟ Τμήμα Γθετ.
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 frontistirioproios.wordpress.com τηλ. 69709 ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γνωστικό αντικείμενο: Αρμονικό τρέχον κύμα-συμβολή -Στάσιμο Διάρκεια h ΘΕΜΑ Α Α ) To διπλανό σχήμα παριστάνει το στιγμιότυπο
frontistirioproios.wordpress.com τηλ. 69709 ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γνωστικό αντικείμενο: Αρμονικό τρέχον κύμα-συμβολή -Στάσιμο Διάρκεια h ΘΕΜΑ Α Α ) To διπλανό σχήμα παριστάνει το στιγμιότυπο
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗΣ ΓΛ ΘΕΜΑ Α
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗΣ ΓΛ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1- Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τις συμπληρώνει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΤΑΞΗΣ ΓΛ ΘΕΜΑ Α Στις ημιτελείς προτάσεις Α1- Α5 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία τις συμπληρώνει
2.2. Συμβολή και στάσιμα κύματα.
 2.2. Συμβολή και στάσιμα κύματα. 2.2.1. Συμβολή και μέγιστο πλάτος Σε δύο σημεία μιας ευθείας ε βρίσκονται δύο σύγχρονες πηγές κυμάτων Ο 1 και Ο 2 οι οποίες παράγουν κύματα με πλάτος Α=2cm και μήκος κύματος
2.2. Συμβολή και στάσιμα κύματα. 2.2.1. Συμβολή και μέγιστο πλάτος Σε δύο σημεία μιας ευθείας ε βρίσκονται δύο σύγχρονες πηγές κυμάτων Ο 1 και Ο 2 οι οποίες παράγουν κύματα με πλάτος Α=2cm και μήκος κύματος
Ενδεικτικές Λύσεις. Θέµα Α
 3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
3ο ιαγώνισµα Γ Τάξης Ενιαίου Λυκείου Ταλαντώσεις Ενδεικτικές Λύσεις Θέµα Α Α.1. Στη σύνθεση δύο απλών αρµονικών ταλαντώσεων της ίδιας συχνότητας που γίνονται γύρω από το ίδιο σηµείο και στην ίδια διεύθυνση,
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΘΕΜΑ Β Β1. Ένας ταλαντωτής εκτελεί φθίνουσα ταλάντωση με πλάτος που μειώνεται εκθετικά με το
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2015-2016 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 08/11/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Α1 δ Α2 γ Α3 δ Α4 α Α5 β ΘΕΜΑ Β Β1 Ένας ταλαντωτής
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 2015-2016 ΜΑΘΗΜΑ / ΤΑΞΗ : ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 08/11/2015 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Α1 δ Α2 γ Α3 δ Α4 α Α5 β ΘΕΜΑ Β Β1 Ένας ταλαντωτής
. Μητρόπουλος Ταλαντώσεις Σ 1 Σ 2 V
 Ταλάντωση πάνω σε βαγονέτο Π Σ 1 Π Σ 2 V Το εικονιζόµενο βαγονέτο Σ 2 έχει πάνω του κατάλληλα στηριγµένο οριζόντιο ιδανικό ελατήριο, σταθεράς k = 1N/m. Στο άλλο άκρο του ελατηρίου είναι δεµένο σώµα Σ 1
Ταλάντωση πάνω σε βαγονέτο Π Σ 1 Π Σ 2 V Το εικονιζόµενο βαγονέτο Σ 2 έχει πάνω του κατάλληλα στηριγµένο οριζόντιο ιδανικό ελατήριο, σταθεράς k = 1N/m. Στο άλλο άκρο του ελατηρίου είναι δεµένο σώµα Σ 1
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ. ψ =0,5 ημ 2π 8t 10 x, u=8 πσυν 2π 8t 5
 ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ 1. Σ ένα σημείο Ο ενός ελαστικού μέσου υπάρχει μια πηγή κυμάτων, η οποία τη χρονική στιγμή t =0 αρχίζει να εκτελεί απλή αρμονική ταλάντωση με εξίσωση y=0,5 ημω t (y σε m, t σε sec). Στη
ΜΗΧΑΝΙΚΑ ΚΥΜΑΤΑ 1. Σ ένα σημείο Ο ενός ελαστικού μέσου υπάρχει μια πηγή κυμάτων, η οποία τη χρονική στιγμή t =0 αρχίζει να εκτελεί απλή αρμονική ταλάντωση με εξίσωση y=0,5 ημω t (y σε m, t σε sec). Στη
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ γ τάξη ενιαίου λυκείου (εξεταστέα ύλη: κρούσεις, ταλαντώσεις, εξίσωση κύματος) διάρκεια εξέτασης: 1.8sec ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ/ΜΑΘΗΤΡΙΑΣ: ΤΜΗΜΑ: ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να επιλέξετε
1.1. Μηχανικές Ταλαντώσεις. Ομάδα Ε.
 1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
1.1. Μηχανικές. Ομάδα Ε. 1.1.81. Δυο ΑΑΤ και μία Ταλάντωση. Ένα σώμα μάζας 1kg ηρεμεί σε λείο κεκλιμένο επίπεδο κλίσεως θ=30, δεμένο στο άκρο ελατηρίου σταθεράς k 1 =40Ν/m, ενώ εφάπτεται στο ε- λεύθερο
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Α) Στις ερωτήσεις 4 να σημειώσετε την σωστή. ) Σώμα εκτελεί απλή αρμονική ταλάντωση. Η συνολική δύναμη που δέχεται: (α) είναι σταθερή.
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ ο Α) Στις ερωτήσεις 4 να σημειώσετε την σωστή. ) Σώμα εκτελεί απλή αρμονική ταλάντωση. Η συνολική δύναμη που δέχεται: (α) είναι σταθερή.
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 24 ΑΠΡΙΛΙΟΥ 2018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5)
 ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που
ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 4 ΑΠΡΙΛΙΟΥ 018 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΠΕΝΤΕ (5) ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
 ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ 1. Ένα σώμα μάζας m= 2 kg εκτελεί απλή αρμονική ταλάντωση σε οριζόντια διεύθυνση. Στη θέση με απομάκρυνση x 1 =+2m το μέτρο της ταχύτητας του είναι u 1 =4m /s, ενώ στη θέση με απομάκρυνση
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ 1
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Δύο εγκάρσια κύματα
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Δύο εγκάρσια κύματα
ΤΑΛΑΝΤΩΣΕΙΣ. . Ερωτήσεις αντιστοίχισης. Σχήμα 2 από τη θέση ισορροπίας του δίνεται από την εξίσωση x = Aημωt.
 ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
ΤΑΛΑΝΤΩΣΕΙΣ. Ερωτήσεις αντιστοίχισης Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και τα κατάλληλα ζεύγη γραμμάτων - αριθμών.. Σημειακό
Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα
 Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα Θέμα Α 1) Η ιδιοσυχνότητα ενός συστήματος που εκτελεί εξαναγκασμένη ταλάντωση χωρίς τριβή είναι 20 Hz. Το πλάτος της ταλάντωσης γίνεται
Επαναληπτικό Διαγώνισμα Φυσικής Γ Λυκείου Κρούσεις-Ταλαντώσεις-Κύματα Θέμα Α 1) Η ιδιοσυχνότητα ενός συστήματος που εκτελεί εξαναγκασμένη ταλάντωση χωρίς τριβή είναι 20 Hz. Το πλάτος της ταλάντωσης γίνεται
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚ. ΘΕΤ/ΤΕΧΝ ΣΤΟ ΚΕΦ. 1 ΘΕΜΑ Α Α.1
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚ. ΘΕΤ/ΤΕΧΝ ΣΤΟ ΚΕΦ. 1 ΘΕΜΑ Α Για τις ερωτήσεις Α.1 έως και Α.4 να γράψετε τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή πρόταση. Α1) Ένα σώμα κάνει α.α.τ.
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Γ ΛΥΚ. ΘΕΤ/ΤΕΧΝ ΣΤΟ ΚΕΦ. 1 ΘΕΜΑ Α Για τις ερωτήσεις Α.1 έως και Α.4 να γράψετε τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη σωστή πρόταση. Α1) Ένα σώμα κάνει α.α.τ.
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2016 Α ΦΑΣΗ
 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Τρίτη 5 Ιανουαρίου 016 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από 1-4 να γράψετε στο τετράδιο σας
ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Ηµεροµηνία: Τρίτη 5 Ιανουαρίου 016 ιάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ερωτήσεις από 1-4 να γράψετε στο τετράδιο σας
