Απαρίθμηση ζευγών φυσικών αριθμών I. C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση
|
|
|
- Αθανας Ηλιόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι 1-1 και επί. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
2 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών II Ορισμός Μια συνάρτηση σύζευξης (pairing function) C είναι μια τεχνική αρίθμησης ζευγών για την οποία υπάρχουν οι αντίστροφες συναρτήσεις (D 1, D 2 ) που ικανοποιούν τις εξής συνθήκες για κάθε n, m, k: D 1 (C(n, m)) = n, D 2 (C(n, m)) = m, C(D 1 (k), D 2 (k)) = k Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
3 Κωδικοποίηση Απαρίθμηση n-άδων φυσικών αριθμών C 2 C, D 2 i D i C 3 (a, b, c) = C 2 (a, C 2 (b, c)) D 3 1(z) = D 2 1(z), D 3 2(z) = D 2 1(D 2 2(z)), D 3 3(z) = D 2 2(D 2 2(z))), κ.ο.κ. και γενικά για n ě 3: C n (a 1, a 2,..., a n ) = C 2 (a 1, C n 1 (a 2,..., a n )) D n 1(z) = D 2 1(z) και για i ą 1 : D n i (z) = D n 1 i 1 (D 2 2(z)) Για κωδικοποίηση πεπερασμένων ακολουθιών: C f (a 1, a 2,..., a n ) = C n+1 (n, a 1, a 2,..., a n ) κ.ο.κ. όπου n είναι το μήκος. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
4 Κωδικοποίηση Gödelization (Γκεντελοποίηση) Μέθοδος κωδικοποίησης κατα Gödel που βασίζεται στο unique factorization property των φυσικών αριθμών: Παράδειγμα G(4, 8, 3) = G(2, 0) = Και γενικά: G(a 0,..., a n ) = p a p a n+1 n Παρατήρηση: Η παραπάνω κωδικοποίηση καθώς και η αποκωδικοποίηση μπορούν να γίνουν με προγράμματα LOOP. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
5 Κωδικοποίηση Πρώτοι αριθμοί I Ορισμός Πρώτος αριθμός λέγεται ένας ακέραιος μεγαλύτερος του 1 που δεν έχει άλλους διαιρέτες εκτός από το 1 και τον εαυτό του, ειδάλλως λέγεται σύνθετος. Πρόταση Κάθε ακέραιος με α ύτερος του 1 είναι είτε πρώτος είτε ινόμενο πρώτ ν αριθμών. Θεώρημα (Ευκλείδη) Οι πρώτοι είναι άπειροι σε π ήθος. Απόδειξη. Έστω ότι οι πρώτοι είναι πεπερασμένοι σε πλήθος συγκεκριμένα p 1, p 2,..., p n τότε ο αριθμός p 1 p 2... p n + 1 δε διαιρείται από κανένα πρώτο εκ τών p 1, p 2... p n, άρα είναι πρώτος ή διαιρείται με άλλο πρώτο, κάτι που είναι άτοπο. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
6 Κωδικοποίηση Πρώτοι αριθμοί II Θεώρημα (Θεμελιώδες Θεώρημα Αριθμητικής) Κάθε αριθμός μπορεί να ραφεί με μοναδικό τρόπο σε ινόμενο πρώτ ν αριθμών (όχι απαραίτητα διαφορετικών ανά δύο). Θεώρημα (Θεώρημα Τεσσάρων τετραγώνων του Lagrange) Κάθε θετικός ακέραιος μπορεί να αναπαρασταθεί ς άθροισμα τεσσάρ ν τετρα ών ν. Εικασία (Εικασία του Goldbach) Κάθε άρτιος φυσικός με α ύτερος του δύο μπορεί να αναπαρασταθεί ς το άθροισμα δύο πρώτ ν. Ορισμός Αν ο p είναι πρώτος και ο p + 2 είναι επίσης πρώτος τότε αυτοί λέγονται δίδυμοι πρώτοι. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
7 Κωδικοποίηση Πρώτοι αριθμοί III Εικασία (Εικασία των Διδύμων Πρώτων) Υπάρχουν άπειρα το π ήθος ζευ άρια διδύμ ν πρώτ ν. Θεώρημα (Θεώρημα Πρώτων Αριθμών (de la Valee Poussin, Hadamard)) Αν με π(x) συμβο ίσουμε το π ήθος τ ν πρώτ ν αριθμών μικρότερ ν ή ίσ ν του x, τότε π(x) ÝÝÝÑ xñ8 x log x Θεώρημα (Vinogradov) Υπάρχει ακέραιος N ώστε κάθε n περιττός αριθμός με α ύτερος του N ράφεται σαν άθροισμα τριών πρώτ ν αριθμών. Η κα ύτερη ν στή τιμή του N είναι N = 3, 33 ˆ Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
8 Κωδικοποίηση Πρώτοι αριθμοί IV Πόρισμα Κάθε αριθμός με α ύτερος από την παραπάν σταθερά μπορεί να ραφτεί ς άθροισμα τεσσάρ ν πρώτ ν. Θεώρημα (Chen) Υπάρχει ακέραιος N ώστε κάθε n άρτιος αριθμός με α ύτερος του N ράφεται σαν άθροισμα ενός πρώτου και ενός ινομένου το πο ύ δύο πρώτ ν αριθμών. Παρατήρηση: Πρόσφατα(2002) οι Saxena, Kayal και Agrawal απέδειξαν ότι το πρόβλημα PRIMES είναι στο P. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
9 Κωδικοποίηση Άλλη μια συνάρτηση κωδικοποίησης Παρακάτω περιγράφουμε μια ακόμη συνάρτηση σύζευξης, C: C(n, m) = 2 n (2m + 1) 1 Υπάρχει προφανώς πρόγραμμα loop που να υπολογίζει τη C(n, m). Ως προς τις αντίστροφες συναρτήσεις D 1, D 2, αν k είναι ένας φυσικός αριθμός, αποδεικνύεται ότι υπάρχει μοναδικό ζεύγος n = D 1 (k), m = D 2 (k), ώστε: C(m, n) = k. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
10 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Program semantics (σημασιολογία): specifications, formal verification. Υπάρχουν τρεις μαθηματικοί τρόποι να μιλήσουμε για σημασιολογία: Operational semantics (λειτουργική σημασιολογία) Denotational semantics (δηλωτική σημασιολογία) Axiomatic semantics (αξιωματική σημασιολογία) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
11 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Λειτουργική σημασιολογία Ορισμοί LOOP n : το σύνολο των LOOP προγραμμάτων με μεταβλητές εκ των x 1, x 2,..., x n. Configuration είναι ένα στοιχείο του N n,συγκεκριμένα οι τιμές των μεταβλητών x 1, x 2,..., x n. Computation είναι ένα στοιχείο του (N n ) : συγκεκριμένα μια ακολουθία από διαδοχικές διαμορφώσεις. Ορισμός (Λειτουργική σημασιολογία) S o : LOOP n ˆ N n Ñ (N n ) (η S o μπορεί να οριστεί με πρωταρχική αναδρομή) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
12 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Δηλωτική σημασιολογία Ορισμός (Δηλωτική σημασιολογία) S d : LOOP n ˆ N n Ñ N n Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
13 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Αξιωματική σημασιολογία Assertions, Invariants Παράδειγμα 1: (1) x:=y; (2) for w:=1 to z do (3) x:=succ x (4) end (5) 1 y = a 1 ^ z = a 2. Βεβαίωση εισόδου. 2 y = a 1 ^ z = a 2 ^ x = a 1. 3 y = a 1 ^ z = a 2 ^ x = a 1 + w 1 ^ w ď a 2. Αναλλοίωτη βρόχου. 4 y = a 1 ^ z = a 2 ^ x = a 1 + w. 5 y = a 1 ^ z = a 2 ^ x = a 1 + a 2. Βεβαίωση εξόδου. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
14 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Αξιωματική σημασιολογία Παράδειγμα 2 (Pascal): (1) z:=0; u:=x; (2) repeat (3) z:=z+y (4) u:=u-1 (5) until u=0 (6) Βεβαιώσεις: 1 x ą 0 ^ y ą 0. Βεβαίωση εισόδου. 2 z = 0 ^ u = x ^ x ą 0 ^ y ą 0. 3 z + u y = x y ^ u ą 0. Αναλλοίωτη βρόχου. 4 (z y) + u y = x y ^ u ą 0. 5 (z y) + (u + 1) y = x y ^ u ě 0. 6 z + u y = x y ^ u ě 0 (δηλαδή z = x y ^ u = 0). Βεβαίωση εξόδου. u: συνθήκη τερματισμού (termination condition) μια γνησίως φθίνουσα συνάρτηση που εγγυάται τον τερματισμό όταν u = 0. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
15 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις LOOP-υπολογισιμότητα Ορισμός Μια συνάρτηση f: N n Ñ N λέγεται LOOP-υπολογίσιμη (LOOP-computable) εάν υπάρχει ένα LOOP n+m πρόγραμμα π(x 1,..., x n,..., x n+m ) και ένα i ď m + n έτσι ώστε για κάθε a 1, a 2,..., a n P N: f(a 1, a 2,..., a n ) = S d,i (π)[a 1,..., a n, 0,..., 0]. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
16 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις I Ορισμός Η κλάση P των πρωταρχικών αναδρομικών συναρτήσεων είναι η μικρότερη κλάση συναρτήσεων που: 1 περιέχει τις εξής αρχικές συναρτήσεις: S, P, Z, U n i (για όλα τα n και i ď n) και 2 είναι κλειστή ως προς τα σχήματα της σύνθεσης και της πρωταρχικής αναδρομής. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
17 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις II Εξηγήσεις: S(x) = x + 1, P(x + 1) = x, P(0) = 0, Z(x) = 0, U n i (x 1, x 2,..., x n ) = x i, 1 ď i ď n Σύνθεση: f(x) = h(g(x)) γενικά f(x 1, x 2,..., x n ) = h(g 1 (x 1, x 2,..., x n ),..., g m (x 1, x 2,..., x n )) Πρ ταρχική Αναδρομή: # f(0) = C f(sy) = h(y, f(y)) Γενικά: # f(x 1, x 2,..., x n, 0) = g(x 1, x 2,..., x n ) f(x 1, x 2,..., x n, Sy) = h(x 1, x 2,..., x n, y, f(x 1, x 2,..., x n, y)) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
18 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις III Παραδείγματα: 1 2 # add(x, 0) = U 1 1(x) add(x, Sy) = h(x, y, add(x, y)) # mult(x, 0) = Z(x) mult(x, Sy) = h(x, y, mult(x, y)) όπου h(x, y, z) = add(u 3 1(x, y, z), U 3 3(x, y, z)) όπου h(x, y, z) = S(U 3 3(x, y, z)) 3 mult2(x) = mult(s(s(z(x))), U 1 1(x)) # pow2(0) = 1 4 όπου h(y, z) = mult2(u 2 2(y, z)) pow2(sy) = h(y, pow2(y)) 5 Αν η g(x, y) είναι πρωταρχικά αναδρομική, τότε είναι και η f: f(x) = g(x, x) = g(u 1 1(x), U 1 1(x)) (ταυτοποίηση ορισμάτων) 6 Αν η g(x, y) είναι πρωταρχικά αναδρομική, τότε είναι και η f: f(x, y) = g(y, x) = g(u 2 2(x, y), U 2 1(x, y)) (εναλλαγή ορισμάτων) 7 abs(x y) = (x. y) + (y. x) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
19 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις IV 8 προσημοσυναρτήσεις (sg, sg) 9 eq(x, y) = sg(abs(x y)) Παρατήρηση Οι sg, sg και eq είναι χαρακτηριστικές συναρτήσεις. Ορισμός Μια σχέση R Ď N n είναι πρωταρχική αναδρομική, αν η χαρακτηριστική συνάρτηση χ R είναι πρωταρχική αναδρομική, όπου # 1, αν (x 1,..., x n ) P R χ R (x 1,..., x n ) = 0, αλλιώς Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
20 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Άλλα είδη αναδρομής I Ακολουθία Fibbonaci: $ & f(0) = 1 f(1) = 1 % f(ssn) = f(n) + f(sn) Αυτό το σχήμα είναι αναδρομή αλλά δεν είναι πρωταρχική αναδρομή! Αμοιβαία (Mutual) Πρωταρχική Αναδρομή # f 1 (0) = 1 f 1 (Sn) = f 1 (n) + f 2 (n) # f 2 (0) = 0 f 2 (Sn) = f 1 (n) f 1 : 1, 1, 2, 3, 5, 8,... f 2 : 0, 1, 1, 2, 3, 5,... Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
21 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Άλλα είδη αναδρομής II Γενικά: για j = 1,..., m: $ & f j (x 1, x 2,..., x n, 0) = g j (x 1,..., x n ) f j (x 1, x 2,..., x n, Sy) = h j (x 1,..., x n, y, f 1 (x 1, x 2,..., x n, y),... %, f m (x 1, x 2,..., x n, y)) Λήμμα Αν ό ες οι συναρτήσεις g j και h j είναι πρ ταρχικές αναδρομικές, τότε και οι συναρτήσεις f j, όπ ς ορίζονται από το παραπάν σχήμα, είναι επίσης πρ ταρχικές αναδρομικές. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
22 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Άλλα είδη αναδρομής III Απόδειξη. Χρησιμοποιούμε κωδικοποίηση και αποκωδικοποίηση κατά (π.χ.) Cantor. Σημειωτέον ότι αυτές (C m και D m i ) είναι πρωταρχικές αναδρομικές. # f(x 1, x 2,..., x n, 0) = C m (g 1 (x 1,..., x n ),..., g m (x 1,..., x n )) f(x 1, x 2,..., x n, Sy) = C m (h 1 [x 1,..., x n, y, D m 1 (f(x 1, x 2,..., x n, y)),..., D m m(f(x 1, x 2,..., x n, y))],..., h m [x 1,..., x n, y, D m 1 (f(x 1, x 2,..., x n, y)),..., D m m(f(x 1, x 2,..., x n, y))]) Η f ορίζεται με πρωταρχική αναδρομή, είναι άρα πρωταρχική αναδρομική. f j (x 1, x 2,..., x n, y) = D m j (f(x 1, x 2,..., x n, y)) και συνεπώς και οι συναρτήσεις f j είναι επίσης πρωταρχικές αναδρομικές. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
23 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων I Θεώρημα Κάθε πρ ταρχική αναδρομική συνάρτηση είναι LOOP-υπο ο ίσιμη. Απόδειξη: Με επαγωγή στη δομή της συνεπαγωγικής ακολουθίας των πρωταρχικών αναδρομικών συναρτήσεων. Παρατήρηση Η επαγωγική απόδειξη ιδιότητας σε επαγωγικό πεδίο συνεπάγεται: 1 απόδειξη της ιδιότητας για τα αρχικά στοιχεία 2 απόδειξη της ιδιότητας για νέα στοιχεία που δημιουργούνται με πράξεις κλεισίματος και με παλιά στοιχεία για τα οποία υποθέτουμε ότι έχουν την ιδιότητα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
24 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων II 1 Αρχικές συναρτήσεις αρχικές συναρτήσεις Loop-πρόγραμμα μεταβλητή εξόδου S x := succ x x P x := pred x x Z x := 0 x U n i κενό πρόγραμμα x i 2 Σχήματα κλεισίματος 1 Σύνθεση: Έστω ότι δίνονται τα m + 1 προγράμματα για: y 1 := g 1 (x 1, x 2,..., x n )... y m := g m (x 1, x 2,..., x n ) και z := h(y 1, y 2,..., y n ). Τότε η f που ορίζεται με σύνθεση από τις g 1, g 2,, g m και h, με το σχήμα δηλαδή: f(x 1, x 2,..., x n ) = h(g 1 (x 1, x 2,..., x n ),..., g m (x 1, x 2,..., x n )) μπορεί να υπολογιστεί με το εξής πρόγραμμα: y 1 := g 1 (x 1, x 2,..., x n ) ;... ; y m := g m (x 1, x 2,..., x n ) ; z := h(y 1, y 2,..., y m ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
25 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων III 2 Πρωταρχική Αναδρομή: Έστω ότι δίνονται προγράμματα για y := g(x 1,..., x n ) και y := h(x 1,..., x n, u, y). Τότε η f που ορίζεται με πρωταρχική αναδρομή από τις συναρτήσεις g και h, με το σχήμα δηλαδή: # f(x 1, x 2,..., x n, 0) = g(x 1,..., x n ) f(x 1, x 2,..., x n, Sy) = h(x 1,..., x n, y, f(x 1, x 2,..., x n, y)) μπορεί να υπολογιστεί με το εξής πρόγραμμα: z := x n+1 ; y := g(x 1, x 2,..., x n ) ; for u := 1 to z do y := h(x 1, x 2,..., x n, u 1, y) end Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
26 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων I Θεώρημα Κάθε LOOP-υπο ο ίσιμη συνάρτηση είναι πρ ταρχική αναδρομική. Απόδειξη: Με επαγωγή στη δομή των προγραμμάτων LOOP: 1 Αρχικά προγράμματα (αναθέσεις) Αρχικό πρόγρ. (αναθέσεις) Πρωτ. Αναδρ. Συναρτ. y := x i (μετ. εξόδου y) U n i (x 1, x 2,..., x n ) y := succ x i S(U n i (x 1, x 2,..., x n )) y := pred x i P(U n i (x 1, x 2,..., x n )) y := 0 Z(U n i (x 1, x 2,..., x n )) κενό π (μετ. εξόδου x j ) U n j (x 1, x 2,..., x n ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
27 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων II 2 Δομές Ελέγχου ροής προγράμματος 1 Παράθεση (;): Έστω ότι το π 1 υπολογίζει τις πρωταρχικές αναδρομικές συναρτήσεις g 1 (μεταβλητή εξόδου: x 1 ), g 2 (μεταβλητή εξόδου: x 2 ),, g n (μεταβλητή εξόδου: x n ) και ότι το π 2 υπολογίζει την πρωταρχική αναδρομική συνάρτηση h (μεταβλητή εξόδου: x j ). Τότε το πρόγραμμα π 1 ; π 2 υπολογίζει: h j (g 1 (x 1,..., x n ),..., g n (x 1,..., x n )) = f(x 1, x 2,..., x n ) που είναι πρωταρχική αναδρομική λόγω του κλεισίματος ως προς σύνθεση συναρτήσεων. 2 βρόχος for: Έστω ότι το π υπολογίζει τις πρωταρχικές αναδρομικές συναρτήσεις h 1 (μεταβλητή εξόδου: x 1 ), h 2 (μεταβλητή εξόδου: x 2 ),, h n (μεταβλητή εξόδου: x n ) και χωρίς βλάβη της γενικότητας ας υποθέσουμε ότι ούτε η μεταβλητή ελέγχου w ούτε το άνω όριο z δεν εμφανίζονται στο π (αλλιώς μετατρέψτε το π σε ισοδύναμο δες εξήγηση παρακάτω). Τότε το πρόγραμμα for w := 1 to z do π end υπολογίζει τις συναρτήσεις f j (1 ď j ď n): # f j (x 1, x 2,..., x n, 0) = U n j (x 1,..., x n ) f j (x 1, x 2,..., x n, Sz) = h j (f 1 (x 1,..., x n, z),..., f n (x 1, x 2,..., x n, z)) που είναι πρωταρχικές αναδρομές λόγω του κλεισίματος ως προς αμοιβαία πρωταρχική αναδρομή. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
28 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων III Εξήγηση: Αν η μεταβλητή ελέγχου (έστω x k ) και το άνω όριο (έστω x m ) εμφανίζονται στο π, μετατρέπουμε το πρόγραμμα for x k := 1 to x m do π end στο ακόλουθο ισοδύναμο πρόγραμμα π 1 (ισοδύναμο πρόγραμμα ως προς τις μεταβλητές x 1, x 2,, x n, του π): x k := 1; z := x m ; for w := 1 to z do (* w, z νέες μεταβλητές *) π; x k := x k + 1 end Βασιζόμενοι τώρα στις προηγούμενες αποδείξεις για την παράθεση προγραμμάτων και το βρόχο for, μπορούμε εύκολα να δείξουμε ότι κάθε μια από τις f j (1 ď j ď n) τις οποίες υπολογίζει το π 1 είναι πρωταρχική αναδρομή. Επομένως, και κάθε f j του ισοδύναμου προγράμματος for x k := 1 to x m do π end είναι πρωταρχική αναδρομική. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
29 Σταθερά σημεία Σταθερά σημεία I Ορισμοί M k = M ˆ ˆ M loooooomoooooon k φορές N M : σύνο ο τ ν ο ικών συναρτήσε ν από το M στο N. χ: χαρακτηριστική συνάρτηση στο M: χ: M Ñ t0, 1u # 1, a P S χ S : χαρακτηριστική συνάρτηση συνό ου S Ď M: χ S (a) = 0, αλλιώς Το σύνολο των χαρακτηριστικών συναρτήσεων στο M είναι ισομορφικό του δυναμοσυνόλου του M (t0, 1u M Pow(M)). Ορισμός Αν M, N αλγεβρικές δομές τότε μία συνάρτηση f: M Ñ N ονομάζεται ομομορφισμός όταν είναι 1-1 και συμβατή με τις πράξεις. Ορισμός Ένας ισομορφισμός είναι μία συνάρτηση με τις ιδιότητες: 1-1, επί, ομομορφισμού. (Επίσης ονομάζεται και αντιστοιχία.) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
30 Σταθερά σημεία Σταθερά σημεία II Λήμμα (Επανάληψης) Έστ a P N και g: N Ñ N. Υπάρχει ακριβώς μία συνάρτηση f: N Ñ N τέτοια ώστε: # Σχήμα Επανά ηψης f(0) = a (Scheme of Iteration) f(sx) = g(f(x)) ( ) Απόδειξη. Χρησιμοποιώντας επαγωγή κατασκευάζουμε διαδοχικά συναρτήσεις f 0, f 1,, f i, με dom(f i ) = t0, 1,..., iu, τέτοια ώστε f i (0) = a και f i (n + 1) = g(f i (n)), για κάθε n ă i. Όλες οι f i έχουν τις ίδιες τιμές στο κοινό πεδίο ορισμού τους (συμβολισμός f 0 Ď f 1 Ď f 2 Ď... ). Ορίζουμε: f(n) = f n P N. Η f ικανοποιεί την ( ), άρα αποδείξαμε την ύπαρξη. Έστω τώρα f 1 άλλη λύση της ( ). Η f 1 περιορισμένη σε οποιοδήποτε t0, 1,..., nu πρέπει να έχει τις ίδιες τιμές με την f n. Επομένως, f 1 (n) = f n (n) = f(n), για κάθε n P N, άρα αποδείξαμε και την μοναδικότητα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
31 Σταθερά σημεία Σταθερά σημεία III Ας δούμε την παραπάνω απόδειξη συνολοθεωρητικά. Μία συνάρτηση είναι ένα σύνολο ζευγών: F = t(x, y) y = f(x)u Ď N ˆ N. Τότε το ( ) γίνεται F = t(0, a)u Y t(x + 1, y) Dz: y = g(z) ^ (x, z) P Fu. Το δεξιό μέλος το συμβολίζουμε με τ 0 (F). Ο τελεστής τ 0 είναι το σχήμα ορισμού. Ο ισχυρισμός του λήμματος επανάληψης είναι ο εξής: F = τ 0 (F), δηλαδή το τ 0 έχει σταθερό σημείο. Το λήμμα επανάληψης είναι συνέπεια του εξής γενικότερου θεωρήματος: Ορισμός (Συνεχής τελεστής) Έστω U 0 Ď U 1 Ď U 2 Ď... μία α υσίδα (chain) υποσυνόλων του M. Λέμε ότι ο τελεστής τ : Pow(M) Ñ Pow(M) είναι συνεχής αν για κάθε αλυσίδα U 0 Ď U 1 Ď U 2 Ď... στο Pow(M) ισχύει τ( Ť tu i u) = Ť tτ(u i )u. i i Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
32 Σταθερά σημεία Σταθερά σημεία IV Θεώρημα (Σταθερού σημείου: Tarski-Knaster, Kleene) Κάθε συνεχής τε εστής τ : Pow(M) Ñ Pow(M) έχει σταθερό σημείο την F = Ť tτ i (H) i P Nu. Παράδειγμα: Έστω η συνάρτηση: # fact(0) = 1 Συνολοθεωρητικά έχουμε: fact(sn) = (n + 1) fact(n) FACT = t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P FACTu ή σύντομα: FACT = τ(fact), όπου: τ(x) = t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P Xu. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
33 Σταθερά σημεία Σταθερά σημεία V Με χρήση του θεωρήματος σταθερού σημείου λαμβάνουμε: τ 0 (H) = H τ 1 (H) = τ(h) = t(0, 1)u τ 2 (H) = τ(τ(h)) = τ(t(0, 1)u) = t(0, 1)u Y t(1, 1)u τ 3 (H) = τ(τ(τ(h))) = t(0, 1)u Y t(1, 1), (2, 2)u τ 4 (H) = τ(τ(τ(τ(h)))) = t(0, 1)u Y t(1, 1), (2, 2), (3, 6)u FACT = Ť i τ i (H) = τ 0 (H) Y τ 1 (H) Y... = t(0, 1), (1, 1), (2, 2), (3, 6),...u. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
34 Σταθερά σημεία Σταθερά σημεία VI Προκειμένου να εφαρμόσουμε βέβαια το θεώρημα σταθερού σημείου θα πρέπει να δείξουμε ότι ο τελεστής τ είναι συνεχής. Πράγματι: τ( ď i X i ) = t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P ď i X i u = t(0, 1)u Y t(n + 1, (n + 1) k) Di: (n, k) P X i u = t(0, 1)u Y ď i t(n + 1, (n + 1) k) (n, k) P X i u = ď i = ď i t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P X i u τ(x i ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
35 Σταθερά σημεία Σταθερά σημεία VII Ένας άλλος τρόπος χρήσης του θεωρήματος σταθερού σημείου είναι για να δείξουμε ότι η μικρότερη κλάση που περιέχει και είναι κλειστή ως προς ορίζει μονοσήμαντα μία κλάση P: Έστω C μία οποιαδήποτε κλάση συναρτήσεων. Έστω γ(c) η κλάση των συναρτήσεων που λαμβάνουμε αν εφαρμόσουμε μία φορά το σχήμα της σύνθεσης σε συναρτήσεις από το C. Έστω ρ(c) η κλάση των συναρτήσεων που λαμβάνουμε αν εφαρμόσουμε μία φορά το σχήμα πρωταρχικής αναδρομής σε συναρτήσεις από το C. Έστω A η κλάση των αρχικών συναρτήσεων: A = ts, P, Z, U n i u. Τότε η P είναι το ελάχιστο σταθερό σημείο της P = A Y γ(p) Y ρ(p). Το P κατασκευάζεται με επαναληπτική εφαρμογή των γ και ρ: P = A Y γ(a) Y ρ(a) Y γ(a Y γ(a) Y ρ(a)) Y ρ(a Y γ(a) Y ρ(a)) Y... Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
36 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Θεώρημα Υπάρχουν υπο ο ίσιμες συναρτήσεις που δεν είναι πρ ταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε: f(x) = φ x (x) + 1 H f είναι υπολογίσιμη. Έστω ότι η f είναι πρωταρχική αναδρομική, άρα εμφανίζεται στην παραπάνω μηχανιστική απαρίθμηση. Έστω π.χ. ότι ένας δείκτης της f είναι y, δηλαδή φ y = f. Εφάρμοσε την f σε όρισμα y: φ y (y) = f(y) = φ y (y) + 1 Άτοπο Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
37 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Παράδειγμα μιας ολικής (ορισμένης για όλους τους φυσικούς αριθμούς) υπολογίσιμης συνάρτησης που όμως δεν είναι πρωταρχική αναδρομική είναι η εξής συνάρτηση f: $ & f(x, y, 0) = Sy f(x, 0, 1) = x, f(x, 0, 2) = 0, f(x, 0, SSSn) = 1 % f(x, Sy, Sn) = f(x, f(x, y, Sn), n) H παραπάνω συνάρτηση f συγγενεύει με την περίφημη συνάρτηση του Ackermann A: $ & A(0, n) = n + 1 A(m, 0) = A(m 1, 1) % A(m, n) = A(m 1, A(m, n 1)) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
38 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Ανάγκη να επεκταθούμε απο ολικές σε μερικές συναρτήσεις Ο τρόπος να αποφύγουμε την αντίφαση (φ x (x) = φ x (x) + 1) της διαγωνιοποίησης είναι να επιτρέψουμε μερικές (partial) συναρτήσεις, δηλαδή συναρτήσεις που δεν είναι κατά ανάγκη ορισμένες για όλους τους φυσικούς αριθμούς N. Συνήθως χρησιμοποιούμε τους ακόλουθους συμβολισμούς όταν η συνάρτηση f δεν είναι ορισμένη για το όρισμα x: Η f αποκλίνει (diverges) ια το x, f(x) Ò, ή ακόμα το πρό ραμμα ια την f δεν σταματάει. Τα σχήματα σύνθεσης και πρωταρχικής αναδρομής γενικεύονται κατα προφανή τρόπο. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
39 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις I Οι assignments ακριβώς ίδιες όπως στη γλώσσα LOOP. program: Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
40 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις II Όπως είναι γνωστό, είναι δυνατόν η εκτέλεση ενός προγράμματος WHILE να μην σταματάει ποτέ. Παράδειγμα Η? x : N Ñ N, ως μερική συνάρτηση, ορίζεται (σταματάει) μόνο αν το x είναι τέλειο τετράγωνο: y := 0; z := abs(x y 2 ); while z 0 do y := y + 1; z := abs(x y 2 ) end Σημασιολογία για προγράμματα WHILE και ακολούθως η έννοια της WHILE-υπολογίσιμης συνάρτησης μπορούν να οριστούν με παρόμοιο τρόπο, όπως και για τα LOOP-προγράμματα. Η κλάση των WHILE-υπολογίσιμων συναρτήσεων συμπεριλαμβάνει και όλες τις LOOP-υπολογίσιμες συναρτήσεις. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
41 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις µ-σχήμα Θα εισαγάγουμε τώρα ένα νέο σχήμα, το µ-σχήμα ή σχήμα απεριόριστης ελαχιστοποίησης (unbounded minimization). Παράδειγμα? x = µy[abs(x y 2 ) = 0], δηλαδή το μικρότερο y, ώστε abs(x y 2 ) = 0, αν υπάρχει τέτοιο y, ειδάλλως η τιμή δεν είναι ορισμένη. Γενικώς: f(x 1,..., x n ) = µy[h(x 1,..., x n, y) = 0]. Η f μπορεί να μην είναι ορισμένη για δύο λόγους: είτε η h δεν είναι ποτέ = 0, είτε η h δεν είναι κάπου ορισμένη πριν να βρεθεί ένα y για το οποίο h = 0. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
42 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Μερικές αναδρομικές συναρτήσεις Ορισμός Η κλάση PR των μερικών αναδρομικών συναρτήσεων (partial recursive functions) είναι η μικρότερη κλάση που: α) περιλαμβάνει τις αρχικές συναρτήσεις: S, P, Z, U n i β) είναι κλειστή ως προς τη σύνθεση, την πρωταρχική αναδρομή και το µ-σχήμα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
43 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Μερικές αναδρομικές συναρτήσεις I Θεώρημα Μια μερική συνάρτηση είναι WHILE-υπο ο ίσιμη ανν είναι μερική αναδρομική. Απόδειξη (σκελετός): Με επαγωγή, παρομοίως με τις προηγούμενες αποδείξεις της ισοδυναμίας των LOOP-υπολογίσιμων και των πρωταρχικών αναδρομικών συναρτήσεων. Πρόσθετες ιδέες: ð: f(x 1,..., x n ) = µz[h(x 1,..., x n, z) = 0] μπορεί να υπολογιστεί με το πρόγραμμα: z := 0; y := h(x 1,..., x n, z) ; while y 0 do z := succ z; y := h(x 1,..., x n, z) end Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
44 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Μερικές αναδρομικές συναρτήσεις II ñ: while x k 0 do π end υπολογίζει την f i (x 1,..., x n, v(x 1,..., x n )) [σύνθεση], όπου για 1 ď i ď n: # f i (x 1,..., x n, 0) = U n i (x 1,..., x n )[αμοιβαία πρωταρχική αναδρομή] f i (x 1,..., x n, Sz) = h i (f 1 (x 1,..., x n, z),..., f n (x 1,..., x n, z)) και v(x 1,..., x n ) = µz[f k (x 1,..., x n, z) = 0] [z = αριθμός επαναλήψεων βρόχου] Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 329
Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές.
 Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
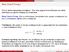 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Μη επιλυσιμότητα I. Απόδειξη. Ορίζουμε # # =
 Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Σχήματα McCarthy I. Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα:
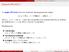 Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Μηχανές Turing (T.M) I
 Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Το 10ο πρόβλημα του Hilbert I
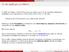 Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Περιεχόμενα 1 Πρωτοβάθμια Λογική Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων ) / 60
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
j=1 x n (i) x s (i) < ε.
 Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
> ln 1 + ln ln n = ln(1 2 3 n) = ln(n!).
 η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
i=1 i=1 i=1 (x i 1, x i +1) (x 1 1, x k +1),
 Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Φ(s(n)) = s (Φ(n)). (i) Φ(1) = a.
 1. Τα θεμελιώδη αριθμητικά συστήματα Με τον όρο θεμελιώδη αριθμητικά συστήματα εννοούμε τα σύνολα N των φυσικών αριθμών, Z των ακεραίων, Q των ρητών και R των πραγματικών. Από αυτά, το σύνολο N είναι πρωτογενές
1. Τα θεμελιώδη αριθμητικά συστήματα Με τον όρο θεμελιώδη αριθμητικά συστήματα εννοούμε τα σύνολα N των φυσικών αριθμών, Z των ακεραίων, Q των ρητών και R των πραγματικών. Από αυτά, το σύνολο N είναι πρωτογενές
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
B = {x A : f(x) = 1}.
 Θεωρία Συνόλων Χειμερινό Εξάμηνο 016 017 Λύσεις 1. Χρησιμοποιώντας την Αρχή του Περιστερώνα για τους φυσικούς αριθμούς, δείξτε ότι για κάθε πεπερασμένο σύνολο A και για κάθε f : A A, αν η f είναι 1-1 τότε
Θεωρία Συνόλων Χειμερινό Εξάμηνο 016 017 Λύσεις 1. Χρησιμοποιώντας την Αρχή του Περιστερώνα για τους φυσικούς αριθμούς, δείξτε ότι για κάθε πεπερασμένο σύνολο A και για κάθε f : A A, αν η f είναι 1-1 τότε
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Αναδρομικές Συναρτήσεις και Σχέσεις I
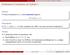 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Παραλλαγές και επεκτάσεις αυτομάτων I
 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως
Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως
* * * ( ) mod p = (a p 1. 2 ) mod p.
 Θεωρια Αριθμων Εαρινο Εξαμηνο 2016 17 Μέρος Α: Πρώτοι Αριθμοί Διάλεξη 1 Ενότητα 1. Διαιρετότητα: Διαιρετότητα, διαιρέτες, πολλαπλάσια, στοιχειώδεις ιδιότητες. Γραμμικοί Συνδυασμοί (ΓΣ). Ενότητα 2. Πρώτοι
Θεωρια Αριθμων Εαρινο Εξαμηνο 2016 17 Μέρος Α: Πρώτοι Αριθμοί Διάλεξη 1 Ενότητα 1. Διαιρετότητα: Διαιρετότητα, διαιρέτες, πολλαπλάσια, στοιχειώδεις ιδιότητες. Γραμμικοί Συνδυασμοί (ΓΣ). Ενότητα 2. Πρώτοι
Αλγόριθμοι για αυτόματα
 Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
a b b < a > < b > < a >.
 Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
Θεωρια Δακτυλιων και Modules Εαρινο Εξαμηνο 2016 17 Διάλεξη 1 Ενότητα 1. Επανάληψη: Προσθετικές ομάδες, δακτύλιοι, αντιμεταθετικοί δακτύλιοι, δακτύλιοι με μοναδιαίο στοιχείο, παραδείγματα. Συμφωνήσαμε
M. J. Lighthill. g(y) = f(x) e 2πixy dx, (1) d N. g (p) (y) =
 Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
s G 1 ). = R, Z 2 Z 3 = Z6. s, t G) s t = st. 1. H = G 4. [G : H] = a G ah = Ha.
![s G 1 ). = R, Z 2 Z 3 = Z6. s, t G) s t = st. 1. H = G 4. [G : H] = a G ah = Ha. s G 1 ). = R, Z 2 Z 3 = Z6. s, t G) s t = st. 1. H = G 4. [G : H] = a G ah = Ha.](/thumbs/91/107730007.jpg) Αλγεβρα ΙΙ Εαρινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Ομάδες-Πηλίκο: Κρατήσαμε σταθερή μια ομάδα G με ταυτοτικό το ι και μια υποομάδα H της G. Συμβολίσαμε με G 1 το G/H (το σύνολο των αριστερών συμπλόκων
Αλγεβρα ΙΙ Εαρινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Ομάδες-Πηλίκο: Κρατήσαμε σταθερή μια ομάδα G με ταυτοτικό το ι και μια υποομάδα H της G. Συμβολίσαμε με G 1 το G/H (το σύνολο των αριστερών συμπλόκων
4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ
 14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
Πεπερασμένα σώματα και Κρυπτογραφία Σύμφωνα με τις παραδόσεις του Α. Κοντογεώργη. Τσουκνίδας Ι.
 Πεπερασμένα σώματα και Κρυπτογραφία Σύμφωνα με τις παραδόσεις του Α. Κοντογεώργη Τσουκνίδας Ι. 2 Περιεχόμενα 1 Εισαγωγή στα πεπερασμένα σώματα 5 1.1 Μάθημα 1..................................... 5 1.1.1
Πεπερασμένα σώματα και Κρυπτογραφία Σύμφωνα με τις παραδόσεις του Α. Κοντογεώργη Τσουκνίδας Ι. 2 Περιεχόμενα 1 Εισαγωγή στα πεπερασμένα σώματα 5 1.1 Μάθημα 1..................................... 5 1.1.1
Σημειώσεις Λογικής I. Εαρινό Εξάμηνο Καθηγητής: Λ. Κυρούσης
 Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Α Δ Ι Θ Θ Α Ε Ι Μ : https://sites.google.com/site/maths4edu/home/algdom114
 Α Δ Ι Θ Θ Α Ε 2013-2014 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 12 Μαρτίου 2014 19:26
Α Δ Ι Θ Θ Α Ε 2013-2014 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 12 Μαρτίου 2014 19:26
 Ασκήσεις Απειροστικού Λογισμού ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Περιεχόμενα Υπακολουθίες και ακολουθίες Cuchy Σειρές πραγματικών αριθμών 3 3 Ομοιόμορφη συνέχεια 3 4 Ολοκλήρωμα
Ασκήσεις Απειροστικού Λογισμού ΙΙ Πρόχειρες Σημειώσεις Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Περιεχόμενα Υπακολουθίες και ακολουθίες Cuchy Σειρές πραγματικών αριθμών 3 3 Ομοιόμορφη συνέχεια 3 4 Ολοκλήρωμα
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
B = F i. (X \ F i ) = i I
 Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
(β ) ((X c Y ) (X c Y c )) c
 Λύσεις Ασκήσεων στα Θεμέλια των Μαθηματικών II Ρωμανός-Διογένης Μαλικιώσης Παρασκευή, 29 Οκτωβρίου 2010 Άσκηση 1. Απλοποιήστε τις ακόλουθες εκφράσεις (α ) (D c F ) c (D F ) (β ) ((X c Y ) (X c Y c )) c
Λύσεις Ασκήσεων στα Θεμέλια των Μαθηματικών II Ρωμανός-Διογένης Μαλικιώσης Παρασκευή, 29 Οκτωβρίου 2010 Άσκηση 1. Απλοποιήστε τις ακόλουθες εκφράσεις (α ) (D c F ) c (D F ) (β ) ((X c Y ) (X c Y c )) c
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΜΕΜ251 Αριθμητική Ανάλυση
 ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 03, 12 Φεβρουαρίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Επαναληπτικές μέθοδοι - Γενική θεωρία 2. Η μέθοδος του Newton
ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 03, 12 Φεβρουαρίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Επαναληπτικές μέθοδοι - Γενική θεωρία 2. Η μέθοδος του Newton
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 2: Μαθηματικό Υπόβαθρο
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 2: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Συναρτήσεις & Σχέσεις (0.2.3) Γράφοι (Γραφήματα) (0.2.4) Λέξεις και Γλώσσες (0.2.5) Αποδείξεις (0.3) 1
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 2: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Συναρτήσεις & Σχέσεις (0.2.3) Γράφοι (Γραφήματα) (0.2.4) Λέξεις και Γλώσσες (0.2.5) Αποδείξεις (0.3) 1
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 1. Μαθηματικό Υπόβαθρο 23, 26 Ιανουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 1.1. Σύνολα Ορισμός : Σύνολο μια συλλογή από αντικείμενα Στοιχεία: Μέλη συνόλου Τα στοιχεία
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 1. Μαθηματικό Υπόβαθρο 23, 26 Ιανουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 1.1. Σύνολα Ορισμός : Σύνολο μια συλλογή από αντικείμενα Στοιχεία: Μέλη συνόλου Τα στοιχεία
Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β.
 Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
Η έννοια της ακολουθίας Ξέρουμε ότι: Συνάρτηση-απεικόνιση με πεδίο ορισμού ένα σύνολο Α και πεδίο τιμών ένα σύνολο Β είναι κάθε μονοσήμαντη απεικόνιση f του Α στο Β. Δηλαδή: f : A B Η ακολουθία είναι συνάρτηση.
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
u v 4 w G 2 G 1 u v w x y z 4
 Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση: Να γνωρίζει: την αποδεικτική μέθοδο της μαθηματικής επαγωγής για την οποία πρέπει να γίνει κατανοητό ότι η αλήθεια
Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση: Να γνωρίζει: την αποδεικτική μέθοδο της μαθηματικής επαγωγής για την οποία πρέπει να γίνει κατανοητό ότι η αλήθεια
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Τα παρακάτω σύνολα θα τα θεωρήσουμε γενικά γνωστά, αν και θα δούμε πολλές από τις ιδιότητές τους: N Z Q R C
 Κεφάλαιο 1 Εισαγωγικές έννοιες Στο κεφάλαιο αυτό θα αναφερθούμε σε ορισμένες έννοιες, οι οποίες ίσως δεν έχουν άμεση σχέση με τους διανυσματικούς χώρους, όμως θα χρησιμοποιηθούν αρκετά κατά τη μελέτη τόσο
Κεφάλαιο 1 Εισαγωγικές έννοιες Στο κεφάλαιο αυτό θα αναφερθούμε σε ορισμένες έννοιες, οι οποίες ίσως δεν έχουν άμεση σχέση με τους διανυσματικούς χώρους, όμως θα χρησιμοποιηθούν αρκετά κατά τη μελέτη τόσο
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Το Θεώρημα Jordan Hölder. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Το Θεώρημα Jordan Hölder Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Το Θεώρημα Jordan Hölder 31 Προκαταρκτικές Έννοιες 311 Υποορθόθετες
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Το Θεώρημα Jordan Hölder Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Το Θεώρημα Jordan Hölder 31 Προκαταρκτικές Έννοιες 311 Υποορθόθετες
Δώδεκα Αποδείξεις του. Θεμελιώδους Θεωρήματος της Άλγεβρας
 Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Θεωρία Αναδρομικών Συναρτήσεων και Υπολογισιμότητας
 Θεωρία Αναδρομικών Συναρτήσεων και Υπολογισιμότητας Αθανάσιος Τζουβάρας ΔΙΔΑΚΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ (URL: http://users.auth.gr/~tzouvara) Θεσσαλονίκη 2007 1 Περιεχόμενα 1 Η διαισθητική προσέγγιση του αλγορίθμου
Θεωρία Αναδρομικών Συναρτήσεων και Υπολογισιμότητας Αθανάσιος Τζουβάρας ΔΙΔΑΚΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ (URL: http://users.auth.gr/~tzouvara) Θεσσαλονίκη 2007 1 Περιεχόμενα 1 Η διαισθητική προσέγγιση του αλγορίθμου
K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων
 K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Στοιχεία προτασιακής λογικής Περιεχόμενα
K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Στοιχεία προτασιακής λογικής Περιεχόμενα
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
h(x, y) = card ({ 1 i n : x i y i
 Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
Κεφάλαιο 1 Μετρικοί χώροι 1.1 Ορισμός και παραδείγματα Ορισμός 1.1.1 μετρική). Εστω X ένα μη κενό σύνολο. Μετρική στο X λέγεται κάθε συνάρτηση ρ : X X R με τις παρακάτω ιδιότητες: i) ρx, y) για κάθε x,
8. Πολλαπλές μερικές παράγωγοι
 94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό ) είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό ) είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι
 ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
sup(a + B) = sup A + sup B inf(a + B) = inf A + inf B.
 Ασκήσεις, Φυλλάδιο. Βρειτε το συνολο Φ A ολων των ανω ϕραγματων του A, και το συνολο φ A ολων των κατω ϕραγματων του A, οταν: a) A = m :, m N}, b) A = + m 2. Βρειτε το if και sup οποτε υπαρχουν) των συνολων
Ασκήσεις, Φυλλάδιο. Βρειτε το συνολο Φ A ολων των ανω ϕραγματων του A, και το συνολο φ A ολων των κατω ϕραγματων του A, οταν: a) A = m :, m N}, b) A = + m 2. Βρειτε το if και sup οποτε υπαρχουν) των συνολων
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Κατ οίκον Εργασία 1 Σκελετοί Λύσεων
 ΕΠΛ Δομές Δεδομένων και Αλγόριθμοι Σεπτέμβριος 008 Κατ οίκον Εργασία Σκελετοί Λύσεων Άσκηση Παρατηρούμε ότι ο χρόνος εκτέλεσης μέσης περίπτωσης της κάθε εντολής if ξεχωριστά: if (c mod 0) for (k ; k
ΕΠΛ Δομές Δεδομένων και Αλγόριθμοι Σεπτέμβριος 008 Κατ οίκον Εργασία Σκελετοί Λύσεων Άσκηση Παρατηρούμε ότι ο χρόνος εκτέλεσης μέσης περίπτωσης της κάθε εντολής if ξεχωριστά: if (c mod 0) for (k ; k
f(n) = a n f(n + m) = a n+m = a n a m = f(n)f(m) f(a n ) = b n f : G 1 G 2, f(a n a m ) = f(a n+m ) = b n+m = b n b m = f(a n )f(a m )
 302 14. Ταξινόµηση Κυκλικών Οµάδων και Οµάδες Αυτοµορφισµών Στην παρούσα ενότητα ϑα ταξινοµήσουµε τις κυκλικές οµάδες ως προς τη σχέση ισοµορφίας. Ε- πίσης ϑα αποδείξουµε ένα σηµαντικό κριτήριο ισοµορφίας
302 14. Ταξινόµηση Κυκλικών Οµάδων και Οµάδες Αυτοµορφισµών Στην παρούσα ενότητα ϑα ταξινοµήσουµε τις κυκλικές οµάδες ως προς τη σχέση ισοµορφίας. Ε- πίσης ϑα αποδείξουµε ένα σηµαντικό κριτήριο ισοµορφίας
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
n = r J n,r J n,s = J
 Ανάλυση Fourer και Ολοκλήρωμα Lebesgue (2011 12) 4ο Φυλλάδιο Ασκήσεων Υποδείξεις 1. Εστω E [a, b] με µ (E) = 0. Δείξτε ότι το [a, b] \ E είναι πυκνό υποσύνολο του [a, b]. Υπόδειξη. Θεωρήστε ένα μη κενό
Ανάλυση Fourer και Ολοκλήρωμα Lebesgue (2011 12) 4ο Φυλλάδιο Ασκήσεων Υποδείξεις 1. Εστω E [a, b] με µ (E) = 0. Δείξτε ότι το [a, b] \ E είναι πυκνό υποσύνολο του [a, b]. Υπόδειξη. Θεωρήστε ένα μη κενό
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
f x 0 για κάθε x και f 1
 06 4.2 Το Λήμμα του Uysoh το Λήμμα της εμφύτευσης και το θεώρημα μετρικοποίησης του Uysoh. Ο κύριος στόχος αυτής της παραγράφου είναι η απόδειξη ενός θεμελιώδους αποτελέσματος γνωστού ως το Λήμμα του Uysoh.
06 4.2 Το Λήμμα του Uysoh το Λήμμα της εμφύτευσης και το θεώρημα μετρικοποίησης του Uysoh. Ο κύριος στόχος αυτής της παραγράφου είναι η απόδειξη ενός θεμελιώδους αποτελέσματος γνωστού ως το Λήμμα του Uysoh.
x < A y f(x) < B f(y).
 Χειμερινό Εξάμηνο 2016 2017 Ασκήσεις στα Κεφάλαια 5 & 6 1. Αυτή είναι ουσιαστικά η Άσκηση 5.2 (σελ. 119), από τις σημειώσεις του Σκανδάλη. Εστω A, < καλά διατεταγμένο σύνολο και έστω στοιχείο a A. Αποδείξτε
Χειμερινό Εξάμηνο 2016 2017 Ασκήσεις στα Κεφάλαια 5 & 6 1. Αυτή είναι ουσιαστικά η Άσκηση 5.2 (σελ. 119), από τις σημειώσεις του Σκανδάλη. Εστω A, < καλά διατεταγμένο σύνολο και έστω στοιχείο a A. Αποδείξτε
f(f 1 (B)) f(f 1 (B)) B. X \ (f 1 (C)) = X \ f 1 (C) = f 1 (Y \ C) X \ (f 1 (C)) f 1 (Y \ C). f 1 (Y \ C) = f 1 (Y \ C ) = X \ f 1 (C ).
 Κεφάλαιο 4 Συναρτήσεις μεταξύ μετρικών χώρων 4.1 Συνεχείς συναρτήσεις Εστω (X, ρ) και (Y, σ) δύο μετρικοί χώροι. Στην 2.2 δώσαμε τον ορισμό της συνέχειας μιας συνάρτησης f : X Y σε κάποιο σημείο x 0 X:
Κεφάλαιο 4 Συναρτήσεις μεταξύ μετρικών χώρων 4.1 Συνεχείς συναρτήσεις Εστω (X, ρ) και (Y, σ) δύο μετρικοί χώροι. Στην 2.2 δώσαμε τον ορισμό της συνέχειας μιας συνάρτησης f : X Y σε κάποιο σημείο x 0 X:
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 2:Στοιχεία Μαθηματικής Λογικής Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 2:Στοιχεία Μαθηματικής Λογικής Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Σύνολα, Σχέσεις, Συναρτήσεις
 Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
f(x) f(c) x 1 c x 2 c
 Μαθηματικός Λογισμός Ι Φθινόπωρο 2014 Σημειώσεις 1-12-14 Μ. Ζαζάνης 1 Πραγματικές Συναρτήσεις και Ορια Εστω S R ένα υποσύνολο του R και f : S R μια συνάρτηση με πεδίο ορισμού το S και τιμές στους πραγματικούς
Μαθηματικός Λογισμός Ι Φθινόπωρο 2014 Σημειώσεις 1-12-14 Μ. Ζαζάνης 1 Πραγματικές Συναρτήσεις και Ορια Εστω S R ένα υποσύνολο του R και f : S R μια συνάρτηση με πεδίο ορισμού το S και τιμές στους πραγματικούς
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Ευθέα Γινόμενα Ομάδων. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Ευθέα Γινόμενα Ομάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Ευθέα Γινόμενα Ομάδων Για την περαιτέρω ανάπτυξη τής θεωρίας θα χρειαστούμε
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Ευθέα Γινόμενα Ομάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Ευθέα Γινόμενα Ομάδων Για την περαιτέρω ανάπτυξη τής θεωρίας θα χρειαστούμε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012) Τμήμα Θ. Αποστολάτου & Π. Ιωάννου 1 Σειρές O Ζήνων ο Ελεάτης (490-430 π.χ.) στη προσπάθειά του να υποστηρίξει
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Φυσικής Σημειώσεις Ανάλυσης Ι (ανανεωμένο στις 5 Δεκεμβρίου 2012) Τμήμα Θ. Αποστολάτου & Π. Ιωάννου 1 Σειρές O Ζήνων ο Ελεάτης (490-430 π.χ.) στη προσπάθειά του να υποστηρίξει
8. Πολλαπλές μερικές παράγωγοι
 94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
R ισούται με το μήκος του. ( πρβλ. την ιστορική σημείωση 3.27 στο τέλος
 73 3. Συμπαγείς χώροι 3. Συμπαγείς χώροι και βασικές ιδιότητες Οι συμπαγείς χώροι είναι μια από τις πιο σημαντικές κλάσεις τοπολογικών χώρων. Η κλάση των συμπαγών χώρων περιλαμβάνει τα κλειστά διαστήματα,b
73 3. Συμπαγείς χώροι 3. Συμπαγείς χώροι και βασικές ιδιότητες Οι συμπαγείς χώροι είναι μια από τις πιο σημαντικές κλάσεις τοπολογικών χώρων. Η κλάση των συμπαγών χώρων περιλαμβάνει τα κλειστά διαστήματα,b
2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί. q Z, a = b q + r.
 Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik 1994. 2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν
Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik 1994. 2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
2 ) d i = 2e 28, i=1. a b c
 ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ ΓΡΑΦΩΝ (1) Εστω G απλός γράφος, που έχει 9 κορυφές και άθροισμα βαθμών κορυφών μεγαλύτερο του 7. Αποδείξτε ότι υπάρχει μια κορυφή του G με βαθμό μεγαλύτερο ή ίσο του 4. () Αποδείξτε ότι
ΑΣΚΗΣΕΙΣ ΘΕΩΡΙΑΣ ΓΡΑΦΩΝ (1) Εστω G απλός γράφος, που έχει 9 κορυφές και άθροισμα βαθμών κορυφών μεγαλύτερο του 7. Αποδείξτε ότι υπάρχει μια κορυφή του G με βαθμό μεγαλύτερο ή ίσο του 4. () Αποδείξτε ότι
Αλγεβρικές Δομές ΙΙ. 1 Ομάδα I. Ά σ κ η σ η 1.1 Έστω R ένας δακτύλιος. Δείξτε ότι το σύνολο
 Αλγεβρικές Δομές ΙΙ 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω R ένας δακτύλιος. Δείξτε ότι το σύνολο C(R) = {a R/ax = xa, για κάθε x R} είναι υποδακτύλιος του R, και λέγεται κέντρο του δακτυλίου R. Ά σ κ η σ η 1.2
Αλγεβρικές Δομές ΙΙ 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω R ένας δακτύλιος. Δείξτε ότι το σύνολο C(R) = {a R/ax = xa, για κάθε x R} είναι υποδακτύλιος του R, και λέγεται κέντρο του δακτυλίου R. Ά σ κ η σ η 1.2
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobson
 ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
a n = sup γ n. lim inf n n n lim sup a n = lim lim inf a n = lim γ n. lim sup a n = lim β n = 0 = lim γ n = lim inf a n. 2. a n = ( 1) n, n = 1, 2...
 ΜΑΘΗΜΑΤΙΚΗ ΑΝΑΛΥΣΗ Β.ΒΛΑΧΟΥ, Α. ΣΟΥΡΜΕΛΙΔΗΣ Τμήμα Μαθηματικών, Πανεπιστήμιο Πατρών Φθινόπωρο 2013 1 Θα θέλαμε να αναφέρουμε ότι για την συγγραφή αυτών των σημειώσεων χρησιμοποιήσαμε ιδιαίτερα α)το βιβλίο
ΜΑΘΗΜΑΤΙΚΗ ΑΝΑΛΥΣΗ Β.ΒΛΑΧΟΥ, Α. ΣΟΥΡΜΕΛΙΔΗΣ Τμήμα Μαθηματικών, Πανεπιστήμιο Πατρών Φθινόπωρο 2013 1 Θα θέλαμε να αναφέρουμε ότι για την συγγραφή αυτών των σημειώσεων χρησιμοποιήσαμε ιδιαίτερα α)το βιβλίο
Ακολουθίες πραγματικών αριθμών
 ΚΕΦΑΛΑΙΟ Ακολουθίες πραγματικών αριθμών Όταν διαδοχικές τιµές που παίρνει µία μεταβλητή προσεγγίζουν απεριόριστα µία συγκεκριµένη τιµή έτσι ώστε τελικά να διαφέρουν από αυτήν λιγότερο από όσο επιθυµεί
ΚΕΦΑΛΑΙΟ Ακολουθίες πραγματικών αριθμών Όταν διαδοχικές τιµές που παίρνει µία μεταβλητή προσεγγίζουν απεριόριστα µία συγκεκριµένη τιµή έτσι ώστε τελικά να διαφέρουν από αυτήν λιγότερο από όσο επιθυµεί
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο
 Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
n 5 = 7 ε (π.χ. ορίζοντας n0 = 1+ ε συνεπώς (σύμϕωνα με τις παραπάνω ισοδυναμίες) an 5 < ε. Επομένως a n β n 23 + β n+1
 Θέμα 1 (α) Υποθέτουμε (προς απαγωγή σε άτοπο) ότι το σύνολο A έχει μέγιστο στοιχείο, έστω a = max A Τότε, εϕόσον a A, έχουμε a R Q και a M Ομως ο αριθμός μητρώου M είναι ρητός αριθμός, άρα (εϕόσον ο a
Θέμα 1 (α) Υποθέτουμε (προς απαγωγή σε άτοπο) ότι το σύνολο A έχει μέγιστο στοιχείο, έστω a = max A Τότε, εϕόσον a A, έχουμε a R Q και a M Ομως ο αριθμός μητρώου M είναι ρητός αριθμός, άρα (εϕόσον ο a
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Ρητοί αριθμοί λέγονται οι αριθμοί που έχουν ή μπορούν να πάρουν τη μορφή
 ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
Κεφάλαιο 2 ΣΥΝΑΡΤΗΣΕΙΣ ΜΙΑΣ ΜΕΤΑΒΛΗΤΗΣ. 2.1 Συνάρτηση
 Κεφάλαιο 2 ΣΥΝΑΡΤΗΣΕΙΣ ΜΙΑΣ ΜΕΤΑΒΛΗΤΗΣ 2.1 Συνάρτηση Η έννοια της συνάρτησης είναι ϐασική σ όλους τους κλάδους των µαθη- µατικών, αλλά και πολλών άλλων επιστηµών. Ο λόγος είναι, ότι µορφοποιεί τη σχέση
Κεφάλαιο 2 ΣΥΝΑΡΤΗΣΕΙΣ ΜΙΑΣ ΜΕΤΑΒΛΗΤΗΣ 2.1 Συνάρτηση Η έννοια της συνάρτησης είναι ϐασική σ όλους τους κλάδους των µαθη- µατικών, αλλά και πολλών άλλων επιστηµών. Ο λόγος είναι, ότι µορφοποιεί τη σχέση
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση
 Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αριθμήσιμα
Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αριθμήσιμα
Το βιβλίο αυτό αποτελεί τον πρώτο τόμο των Μαθηματικών Γʹ Λυκείου για τις
 wwwzitigr Πρόλογος Το βιβλίο αυτό αποτελεί τον πρώτο τόμο των Μαθηματικών Γʹ Λυκείου για τις ομάδες προσανατολισμού: ç Θετικών σπουδών ç Οικονομίας και Πληροφορικής Αναπτύσσονται διεξοδικά τα κεφάλαια:
wwwzitigr Πρόλογος Το βιβλίο αυτό αποτελεί τον πρώτο τόμο των Μαθηματικών Γʹ Λυκείου για τις ομάδες προσανατολισμού: ç Θετικών σπουδών ç Οικονομίας και Πληροφορικής Αναπτύσσονται διεξοδικά τα κεφάλαια:
Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ. 3.1 Η έννοια της παραγώγου. y = f(x) f(x 0 ), = f(x 0 + x) f(x 0 )
 Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ 3.1 Η έννοια της παραγώγου Εστω y = f(x) µία συνάρτηση, που συνδέει τις µεταβλητές ποσότητες x και y. Ενα ερώτηµα που µπορεί να προκύψει καθώς µελετούµε τις δύο αυτές ποσοτήτες είναι
Κεφάλαιο 3 ΠΑΡΑΓΩΓΟΣ 3.1 Η έννοια της παραγώγου Εστω y = f(x) µία συνάρτηση, που συνδέει τις µεταβλητές ποσότητες x και y. Ενα ερώτηµα που µπορεί να προκύψει καθώς µελετούµε τις δύο αυτές ποσοτήτες είναι
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική
Στοιχεία Κατηγορηματικής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική
Θεωρία Γραφημάτων 7η Διάλεξη
 Θεωρία Γραφημάτων 7η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 7η Διάλεξη
Θεωρία Γραφημάτων 7η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 7η Διάλεξη
