Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
|
|
|
- Ευπραξία Γιάγκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
2 Περιεχόμενα 1 Υπολογισιμότητα Ιστορία - Εισαγωγή Μαθηματικό Υπόβαθρο LOOP: Μια απλή γλώσσα προγραμματισμού Κωδικοποίηση LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σταθερά σημεία Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Μηχανές Turing και άλλα υπολογιστικά μοντέλα Σχήματα McCarthy. Στρατιγικές Υπολογισμού Θέση Church-Turing. Κανονική μορφή Kleene Μη επιλυσιμότητα. Θεωρία αναδρομικών συναρτήσεων Αναδρομικά και αναδρομικά αριθμήσιμα σύνολα Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
3 Ιστορία - Εισαγωγή Το πρόγραμμα του Leibni(t)z O Leibniz πρότεινε το εξής πρόγραμμα: 1 Να δημιουργηθεί μια τυπική γλώσσα (formal language), με την οποία να μπορούμε να περιγράψουμε όλες τις μαθηματικές έννοιες και προτάσεις. 2 Να δημιουργηθεί μια μαθηματική θεωρία (δηλαδή ένα σύνολο από αξιώματα και συμπερασματικούς κανόνες συνεπαγωγής), με την οποία να μπορούμε να αποδεικνύουμε όλες τις ορθές μαθηματικες προτάσεις. 3 Να αποδειχθεί ότι αυτή η θεωρία είναι συνεπής (consistent), (δηλαδή ότι η πρόταση A και όχι Α (A ^ A) δεν είναι δυνατόν να αποδειχθεί σ αυτή τη θεωρία). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
4 Ιστορία - Εισαγωγή Το πρόγραμμα του Leibni(t)z Gottfried Wilhelm Leibniz Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
5 Ιστορία - Εισαγωγή Υλοποίηση Γλώσσα George Boole Gottlob Frege Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
6 Ιστορία - Εισαγωγή Υλοποίηση Ενιαία θεωρία Georg Cantor Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
7 Ιστορία - Εισαγωγή Μη συνέπεια της αφελούς συνολοθεωρίας Bertrand Russel Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
8 Ιστορία - Εισαγωγή Πρόγραμμα Hilbert, Συνέπεια David Hilbert Kurt Gödel Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
9 Ιστορία - Εισαγωγή Θέση (thesis) Church-Turing Θέση (thesis) Church-Turing Όλα τα γνωστά και άγνωστα μοντέλα της έννοιας υπολογίσιμος είναι μηχανιστικά ισοδύναμα (effectively equivalent). Alonzo Church Alan Turing Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
10 Ιστορία - Εισαγωγή Άλλα υπολογιστικά μοντέλα Stephen Kleene Emil Post Andrei Andreevich Markov, jr. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
11 Ιστορία - Εισαγωγή Halting Problem Θεώρημα Το Halting Problem (HP) είναι μη αποκρίσιμο. Απόδειξη. 1 Έστω ότι π 0, π 1, π 2,... είναι μια μηχανιστική απαρίθμηση (effective enumeration) όλων των προγραμμάτων. 2 π : read(n); if π n (n) terminates then loop_forever else halt 3 Διαγωνιοποίηση. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
12 Ιστορία - Εισαγωγή Υπολογισιμότητα Ορισμός Ένα σύνολο S λέγεται αποκρίσιμο ή υπολογίσιμο ή επιλύσιμο (decidable, computable, solvable) αν και μόνο αν υπάρχει ένας αλγόριθμος που σταματάει ή μια υπολογιστική μηχανή που δίνει έξοδο ναι για κάθε είσοδο α P S και έξοδο όχι για κάθε είσοδο α R S. Ορισμός Ένα σύνολο S λέγεται καταγράψιμο (με μηχανιστική γεννήτρια) (listable, effectively generatable) αν και μόνο αν υπάρχει μια γεννήτρια διαδικασία ή μηχανή που καταγράφει όλα τα στοιχεία του S. Στην, πιθανώς άπειρη, λίστα εξόδου επιτρέπονται οι επαναλήψεις και δεν υπάρχει περιορισμός για την διάταξη των στοιχείων. Παρατήρηση Το HP δεν είναι decidable είναι όμως listable. Απόδειξη: Dovetailing. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
13 Ιστορία - Εισαγωγή Αυτοαναφορά Αυτή η πρόταση είναι ψευδής. Παράδοξό (αντινομία) του Russel: A = tx x R xu. Τότε A P A ή A R A? Τον κουρέα σε ένα χωριό που ξυρίζει όλους όσους δεν ξυρίζονται μόνοι τους, ποιός τον ξυρίζει; Μεταπαιχνίδι. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
14 Ιστορία - Εισαγωγή Διαγωνιοποίηση A : n ˆ n boolean πίνακας d i = A ii, για κάθε i, με 1 ď i ď n. D i = 1 d i, για κάθε i, με 1 ď i ď n. Το διάνυσμα D δεν εμφανίζεται ούτε ως γραμμή, ούτε ως στήλη στην πίνακα A. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
15 Ιστορία - Εισαγωγή Διαγωνιοποίηση και Halting Problem Μηχανιστική απαρίθμηση των προγραμμάτων με μία είσοδο: π 0, π 1, π 2,... Γράφουμε π x (y) Ó αν το x-οστό πρόγραμμα με είσοδο y P N τερματίζει. Διαφορετικά αν δεν τερματίζει γράφουμε π x (y) Ò. Έστω ότι υπάρχει πρόγραμμα halt(x, y) που λύνει το halting problem. π : read(n); if halt(n, n) then loop_forever else halt Di : π i = π π i (i) Óô π i (i) Ò Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
16 Ιστορία - Εισαγωγή Διαγωνιοποίηση και μη πληρότητα του Gödel Μηχανιστική απαρίθμηση των τύπων (στην αριθμητική Peano) με μία ελεύθερη μεταβλητή: ϕ 0, ϕ 1, ϕ 2,... Συνέπεια: Αν ϕ αποδείξιμος, τότε ϕ αληθής. Πληρότητα: Αν ϕ αληθής, τότε ϕ αποδείξιμος. ϕ(x) = δεν υπάρχει απόδειξη για ϕ x (x). Di : ϕ i = ϕ. ϕ i (i): δεν μπορεί να είναι ψευδής. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
17 Ιστορία - Εισαγωγή Διαγωνιοποίηση και μη πληρότητα του Gödel Θεώρημα (μη πληρότητας, Gödel) Κάθε συνεπής αξιωματικοποίηση της αριθμητικής Peano είναι μη πλήρης. Σημείωση: Δεν ισχύει το παραπάνω για την αριθμητική Presburger (που δεν έχει την πράξη *). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
18 Μαθηματικό Υπόβαθρο Μαθηματική Επαγωγή P(n): ιδιότητα του n P N. Για να δείξουμε ότι P(n) είναι αληθής για κάθε n P N αρκεί να δείξουμε: 1 Επαγωγική Βάση: η ιδιότητα ισχύει για n = 0. 2 Επαγωγικό Βήμα: η ιδιότητα κληρονομείται από το n στο n + 1 (αν είναι αληθής για n θα είναι και για n + 1). Ñ P(n + Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
19 Μαθηματικό Υπόβαθρο Συμβολοσειρές, αλφάβητα, γλώσσες Συμβολοσειρά (String) Μήκος συμβολοσειράς: w =# εμφανίσεων συμβόλων. Substring (υποσυμβολοσειρά) ε: κενή συμβολοσειρά, τ.ω. ε = 0. Πρόθεμα (prefix) Επίθεμα (suffix) *, παράθεση (concatenation) Αλφάβητο Σ Σ Γλώσσα L επί του Σ. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
20 Μαθηματικό Υπόβαθρο Σύνολα A = tx P(x)u x R A : (x P A) Σύμβολα λογικής:, ^, _, Ñ, D A Ď B P A Ñ x P B) A = B : A Ď B ^ B Ď A A B : (A = B) A Ă B (γνήσιο υποσύνολο) H (κενό σύνολο) Ένωση (union): A Y B = tx x P A _ x P Bu Τομή (intersection): A X B = tx x P A ^ x P Bu Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
21 Μαθηματικό Υπόβαθρο Σύνολα Διαφορά: AzB = tx x P A ^ x R Bu Συμμετρική Διαφορά: A B = (AzB) Y (BzA) Καρτεσιανό γινόμενο: A ˆ B = t(x, y) x P A ^ y P Bu Δυναμοσύνολο: Pow(A) = tb B Ď Au Σύνολο A B όλων των ολικών συναρτήσεων B Ñ A. A = πλήθος στοιχείων του A. Ιδιότητες (για πεπερασμένα σύνολα): A Y B ď A + B A ˆ B = A B Pow(A) = 2 A A B = A B Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
22 Μαθηματικό Υπόβαθρο Σύνολα - Αριθμησιμότητα Δύο (πιθανώς άπειρα) σύνολα A, B έχουν τον ίδιο πληθάριθμο ( A = B ) αν υπάρχει μια ένα-προς-ένα και επί απεικόνιση A Ñ B N, Z, Q, R Αριθμήσιμο σύνολο: υπάρχει μια ένα-προς-ένα και επί απεικόνιση από το N στο σύνολο αυτό. N = Z = Q N ˆ N = N (Cantor) Το R είναι μη αριθμήσιμο όπως και το διάστημα [0, 1) Pow(N) = R N Ñ N = N N = R N ˆ N Ñ N = N NˆN = N N = R N Ñ t0, 1u = Pow(N) = R Σ = N σύνολο όλων των γλωσσών L στο Σ = Pow(Σ ) = R Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
23 Μαθηματικό Υπόβαθρο Σχέσεις Ορισμός Μια διμελής σχέση R στο σύνολο A είναι ένα υποσύνολο του συνόλου A ˆ A: R Ď A ˆ A. Παρομοίως, για μία n-μελή σχέση: R Ď A ˆ... ˆ A. Για τις διμελείς σχέσεις, εισάγουμε τις παρακάτω έννοιες: R reflexive P A : (x R x) R irreflexive P A : ( (x R x)) R symmetric y P A : (x R y Ñ y R x) R asymmetric y P A : (x R y Ñ (y R x)), π.χ. ă R antisymmetric y P A : (x R y ^ y R x Ñ x = y), π.χ. ď R transitive y, z P A : (x R y ^ y R z Ñ x R z) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
24 Μαθηματικό Υπόβαθρο Σχέσεις Ορισμός R equivalence (ισοδυναμία): reflexive, symmetric, transitive. π.χ. = R partial order (μερική διάταξη): reflexive, antisymmetric, transitive. π.χ. ď, Ď Αν μια σχέση ισοδυναμίας επί του A, ονομάζουμε το σύνολο των ισοδύναμων στοιχείων με το x κλάση ισοδυναμίας του x και το σύνολο όλων των κλάσεων ισοδυναμίας συμβολίζεται με A/. Παράδειγμα Η ισοτιμία 5 είναι η σχέση ισοδυναμίας όπου x 5 y ô το 5 διαιρεί ακριβώς το x y. Οι κλάσεις ισοδυναμίας είναι: t0, 5, 10,...u, t1, 6, 11,...u, t2, 7, 12,...u, t3, 8, 13,...u, t4, 9, 14,...u Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
25 Μαθηματικό Υπόβαθρο Σχέσεις R +, transitive closure (μεταβατικό κλείσιμο) της R: η μικρότερη σχέση R 1 που περιέχει την R και είναι μεταβατική: 1 x R y ñ x R + y 2 x R + y ^ y R + z ñ x R + z 3 τίποτα άλλο δεν ανήκει στην R + εκτός από ό,τι προκύπτει από 1, 2 R, reflexive and transitive closure (ανακλαστικό και μεταβατικό κλείσιμο): R := R + Y t(x, x) x P Au Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
26 Μαθηματικό Υπόβαθρο Συναρτήσεις και Ισομορφισμοί Ορισμός Μια ολική συνάρτηση f από το σύνολο A στο σύνολο B (f : A Ñ B) είναι μία σχέση R Ď A ˆ B τέτοια ώστε για κάθε x P A να υπάρχει ακριβώς ένα y P B τέτοιο ώστε x R y. Το μοναδικό αυτό στοιχείο y για κάθε x συμβολίζουμε συνήθως ως f(x) ή fx ή f x. Ορισμός Μια μερική συνάρτηση f από το σύνολο A στο σύνολο B (f : A Ñ B) είναι μία σχέση R Ď A ˆ B τέτοια ώστε για κάθε x P A να υπάρχει το πολύ ένα y P B τέτοιο ώστε x R y. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
27 Μαθηματικό Υπόβαθρο Συναρτήσεις και Ισομορφισμοί Ορισμός Μια συνάρτηση f : A Ñ B ονομάζεται injection (μονομορφισμός ή 1-1) 1, x 2 P A : (f(x 1 ) = f(x 2 ) ñ x 1 = x 2 ) Ορισμός Μια συνάρτηση f : A Ñ B ονομάζεται surjection (επιμορφισμός ή επί) P B : Dx P A : f(x) = y Ορισμός Μια ολική συνάρτηση ονομάζεται bijection (αμφιμονοσήμαντη αντιστοιχία) όταν είναι 1-1 και επί. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
28 Μαθηματικό Υπόβαθρο Συναρτήσεις και Ισομορφισμοί Ορισμός Αλγεβρική δομή: M = xm, g 1,..., g n y, όπου M μη κενό σύνολο και g i πράξεις ή σταθερές. π.χ. N = xn, 0, Sy, R = xr, 0, +y Ορισμός Μια συνάρτηση f : M Ñ N ονομάζεται ομομορφισμός (homomorphism) όταν είναι 1-1 και συμβατή με τις πράξεις. π.χ. R + = xr +, 1, y, R = xr, 0, +y ln : R + Ñ R, ln(1) = 0, ln(a b) = ln(a) + ln(b) Ορισμός Ένας ισομορφισμός (isomorphism) είναι μια ολική συνάρτηση με τις ιδιότητες: 1-1, επί, ομομορφισμός. Παράδειγμα xn, +, y είναι ισομορφικό με xn/ 5, +, y. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
29 Μαθηματικό Υπόβαθρο Γράφοι και δένδρα Ορισμός Ένας γράφος G = (V, E) αποτελείται από ένα πεπερασμένο σύνολο V κορυφών (ή κόμβων) και από ένα σύνολο E ακμών, δηλαδή ζευγών μεταξύ των παραπάνω κορυφών. π.χ. Για τον γράφο του σχήματος ισχύει: V = t1, 2, 3, 4, 5u, E = ttx, yu x + y = 4 _ x + y = 7u Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
30 Μαθηματικό Υπόβαθρο Γράφοι και δένδρα Ορισμός (Συνεκτικότητα) Ένας γράφος ονομάζεται συνεκτικός (connected) αν υπάρχει διαδρομή από οποιαδήποτε κορυφή του γράφου προς οποιαδήποτε άλλη κορυφή. Ο γράφος του προηγούμενου παραδείγματος δεν είναι συνεκτικός. Ορισμός Ένας κατευθυνόμενος γράφος (directed graph ή digraph) είναι ένας γράφος όπου οι ακμές δεν είναι απλά ζεύγη, αλλά διατεταγμένα ζεύγη κορυφών. π.χ. { (a, b), (b, c), (c, b)}: a Ñ b Ô c Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
31 Μαθηματικό Υπόβαθρο Γράφοι και δένδρα I Ορισμός Ένας κύκλος (cycle) είναι μια κλειστή διαδρομή. Ορισμός (Ακυκλικότητα) Ένας γράφος ονομάζεται ακυκλικός (acyclic) αν δεν περιέχει κύκλους. Ορισμός Ένας γράφος ονομάζεται δένδρο (tree) αν είναι συνεκτικός και ακυκλικός. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
32 Μαθηματικό Υπόβαθρο Γράφοι και δένδρα II Ορισμός Δένδρο με ρίζα ονομάζεται ένα δένδρο το οποίο έχει ρίζα, δηλαδή έναν κόμβο που δεν έχει προηγούμενο. Επιπλέον έννοιες: πρόγονοι (predecessors), απόγονοι (successors), γονείς (parents), παιδιά (children), φύλλα (leaves), εσωτερικοί κόμβοι (internal nodes). Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
33 LOOP: Μια απλή γλώσσα προγραμματισμού Περιγραφή της LOOP Δε χρειάζονται δηλώσεις (declarations) Τέσσερα ήδη αναθέσεων (assignments) Παρατήρηση: 0. 1 = 0, (x + 1). 1 = x for loop: for i := 1 to y do end x := 0, x := y, x := y + 1, x := y. 1 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
34 LOOP: Μια απλή γλώσσα προγραμματισμού Παραδείγματα LOOP 1 Πρόγραμμα για x := y + z (δηλ. add(y, z)): x := y; for w := 1 to z do x := x + 1 end 2 x := y z (δηλ. mult(y, z)): x := 0; for w := 1 to z do x := add(x, y) end ( 3 x := y. z (δηλ. sub(y, z)): Παρατήρηση: y. z = x := y; for w := 1 to z do x := x. 1 end 4 if y = 0 then x := 0 else x := 1 (δηλ. ifnzero(y)): x := 0; z := 0; for w := 1 to y do x := z + 1 end 5 if y = 0 then x := 1 else x := 0 (δηλ. ifzero(y)): x := 0; x := x + 1; for w := 1 to y do x := 0 end # 0, y ă z y z, αλλιώς ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
35 LOOP: Μια απλή γλώσσα προγραμματισμού Συνακτικά Διαγράμματα της LOOP I Variable: Assignment: Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
36 LOOP: Μια απλή γλώσσα προγραμματισμού Συνακτικά Διαγράμματα της LOOP II Program: Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
37 LOOP: Μια απλή γλώσσα προγραμματισμού Επαγωγή και Αναδρομή Η επαγωγή είναι: Μέθοδος απόδειξης A(0): : A(n) Ñ A(n + 1): Επαγωγικό βήμα Τρόπος ορισμού επαγωγικού πεδίου Αρχικά στοιχεία (initial objects) Πράξεις για κλείσιμο (closure operations) Για κάθε επαγωγικό πεδίο μπορούμε να αποδεικνύουμε ιδιότητες των αντικειμένων χρησιμοποιώντας τη μέθοδο της επαγωγής. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
38 LOOP: Μια απλή γλώσσα προγραμματισμού Επαγωγή I Παραδείγματα: 1 N = το σύνολο των φυσικών αριθμών Αρχικό στοιχείο: 0 Πράξη για κλείσιμο: successor N = t0u Y tn + 1 n P Nu 2 Σ = το σύνολο όλων των strings του αλφάβητου Σ: αρχικά στοιχεία: ε, α για κάθε α P Σ πράξεις για κλείσιμο: concatenation 3 Σύνολο θεωρημάτων: αρχικά στοιχεία: αξιώματα πράξεις για κλείσιμο: συμπερασματικοί κανόνες (inference rules) 4 Σύνολο όρων σε μία μαθηματική θεωρία: αρχικά στοιχεία: σταθερές και μεταβλητές πράξεις για κλείσιμο: σύνθεση (composition) συναρτησιακών συμβόλων Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
39 LOOP: Μια απλή γλώσσα προγραμματισμού Επαγωγή II 5 Σύντακτικά ορθοί τύποι (καλώς, ορισμένοι, wff) σε μία θεωρία μόνο με το κατηγορηματικό σύμβολο = : αρχικά στοιχεία: σταθερές και μεταβλητές πράξεις για κλείσιμο: της μορφής Φ, Φ ^ Ψ, Φ _ Ψ, Φ Ñ Ψ, Φ Ø Ψ, όπου Φ, Ψ είναι τύποι και x είναι μεταβλητή. 6 Σύνολο προγραμμάτων LOOP: αρχικά στοιχεία: της μορφής x := 0, x := y, x := y + 1, x := y. 1 και το κενό πρόγραμμα. πράξεις για κλείσιμο: ; (παράθεση), for (βρόχος) 7 S 1 = t0u Y tn + 2 n P S 1 u 8 S 2 = t3, 5u Y t2n + m m, n P S 2 ^ n ă mu 9 S 3 = t0u Y tn + 2 n P S 3 u Y tn + 5 n P S 3 u Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
40 LOOP: Μια απλή γλώσσα προγραμματισμού Αναδρομή I Ορισμός Αναδρομικό πεδίο = Επαγωγικό πεδίο + Unique parsing Παραδείγματα: 1 N 2 Το Σ με τον παραπάνω ορισμό δεν είναι αναδρομικό. abb = conc(ab, b) = conc(a, bb) Όμως το Σ δεν είναι ουσιωδώς διφορούμενο (inherently ambiguous). Με τον παρακάτω ορισμό το Σ είναι αναδρομικό: Σ = tεu Y twα w P Σ ^ α P Σu 3 Το S 1 είναι αναδρομικό ενώ το S 3 δεν είναι. π.χ. 10 = = Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
41 LOOP: Μια απλή γλώσσα προγραμματισμού Αναδρομή II 4 A = ta, ab, bau. Το A είναι επαγωγικό πεδίο αλλά ουσιωδώς διφορούμενο (μη αναδρομικό). π.χ. aba = conc(a, ba) = conc(ab, a). Σε αναδρομικά πεδία μπορούμε να ορίζουμε μονοσήμαντα συναρτήσεις χρησιμοποιώντας τη μέθοδο της αναδρομής: " 1 0! = 1 Παραγοντικό: (n + 1)! = n! (n + 1) $ & f(0) = 1 2 Ακολουθία Fibonacci: f(1) = 1 % f(n + 2) = f(n) + f(n + 1) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
42 LOOP: Μια απλή γλώσσα προγραμματισμού Αναδρομή III 3 Συνάρτηση παρόμοια με αυτή του Ackermann: 4 # x + 0 = x x + Sy = S(x + y) f(x, y, 0) = y + 1 f(x, y, 1) = x + y = x (y φορές) f(x, y, 2) = x y = x + x + x x (y φορές) f(x, y, 3) = x y = x x x... x (y φορές) x f(x, y, 4) = x xx ή... (y φορές) # add(x, 0) = x add(x, Sy) = S(add(x, y)) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
43 LOOP: Μια απλή γλώσσα προγραμματισμού Αναδρομή IV # x 0 = 0 x Sy = x + x y # x. 0 = x x. Sy = P(x. y), όπου P(n) = n. 1 # sg(0) = 0 sg(sx) = 1 ή sg(x) = x. P(x) # sg(0) = 1 sg(sx) = 0 ή sg(x) = 1. x Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
44 LOOP: Μια απλή γλώσσα προγραμματισμού Πρωταρχική αναδρομή I Σχήμα πρωταρχικής αναδρομής (scheme of primitive recursion): " f(x, 0) = g(x) f(x, Sy) = h(x, y, f(x, y)) Ορισμός Η κλάση των primitive recursive functions (πρωταρχικά αναδρομικών συναρτήσεων) P είναι η μικρότερη κλάση συναρτήσεων που: περιέχει τις εξής αρχικές συναρτήσεις: S, P, Z, U n i (για όλα τα n, i : 1 ď i ď n) και είναι κλειστή ως προς τα σχήματα σύνθεσης και πρωταρχικής αναδρομής. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
45 LOOP: Μια απλή γλώσσα προγραμματισμού Πρωταρχική αναδρομή II Ορισμός Η κλάση των primitive recursive functions (πρωταρχικά αναδρομικών συναρτήσεων) P είναι η μικρότερη κλάση συναρτήσεων που: περιέχει τις εξής αρχικές συναρτήσεις: S, P, Z, U n i (για όλα τα n, i : 1 ď i ď n) και είναι κλειστή ως προς τα σχήματα σύνθεσης και πρωταρχικής αναδρομής. Διευκρινίσεις: S(x) = x + 1 (επόμενο) P(x) = x. 1 (προηγούμενο) (x) = 0 (μηδενική) U n i (x 1,..., x n ) = x i, 1 ď i ď n (προβολές) Σύνθεση: π.χ.: f(x, y) = g(h 1 (x, y), h 2 (x, y), h 3 (x, y)) Πρωταρχική αναδρομή: π.χ.: # f(0) = c f(sy) = h(y, f(y)) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
46 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι 1-1 και επί. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
47 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών II Ορισμός Μια συνάρτηση σύζευξης (pairing function) C είναι μια τεχνική αρίθμησης ζευγών για την οποία υπάρχουν οι αντίστροφες συναρτήσεις (D 1, D 2 ) που ικανοποιούν τις εξής συνθήκες για κάθε n, m, k: D 1 (C(n, m)) = n, D 2 (C(n, m)) = m, C(D 1 (k), D 2 (k)) = k Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
48 Κωδικοποίηση Απαρίθμηση n-άδων φυσικών αριθμών C 2 C, D 2 i D i C 3 (a, b, c) = C 2 (a, C 2 (b, c)) D 3 1(z) = D 2 1(z), D 3 2(z) = D 2 1(D 2 2(z)), D 3 3(z) = D 2 2(D 2 2(z))), κ.ο.κ. και γενικά για n ě 3: C n (a 1, a 2,..., a n ) = C 2 (a 1, C n 1 (a 2,..., a n )) D n 1(z) = D 2 1(z) και για i ą 1 : D n i (z) = D n 1 i 1 (D 2 2(z)) Για κωδικοποίηση πεπερασμένων ακολουθιών: C f (a 1, a 2,..., a n ) = C n+1 (n, a 1, a 2,..., a n ) κ.ο.κ. όπου n είναι το μήκος. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
49 Κωδικοποίηση Gödelization (Γκεντελοποίηση) Μέθοδος κωδικοποίησης κατα Gödel που βασίζεται στο unique factorization property των φυσικών αριθμών: Παράδειγμα G(4, 8, 3) = G(2, 0) = Και γενικά: G(a 0,..., a n ) = p a p a n+1 n Παρατήρηση: Η παραπάνω κωδικοποίηση καθώς και η αποκωδικοποίηση μπορούν να γίνουν με προγράμματα LOOP. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
50 Κωδικοποίηση Πρώτοι αριθμοί I Ορισμός Πρώτος αριθμός λέγεται ένας ακέραιος μεγαλύτερος του 1 που δεν έχει άλλους διαιρέτες εκτός από το 1 και τον εαυτό του, ειδάλλως λέγεται σύνθετος. Πρόταση Κάθε ακέραιος μεγαλύτερος του 1 είναι είτε πρώτος είτε γινόμενο πρώτων αριθμών. Θεώρημα (Ευκλείδη) Οι πρώτοι είναι άπειροι σε πλήθος. Απόδειξη. Έστω ότι οι πρώτοι είναι πεπερασμένοι σε πλήθος συγκεκριμένα p 1, p 2,..., p n τότε ο αριθμός p 1 p 2... p n + 1 δε διαιρείται από κανένα πρώτο εκ τών p 1, p 2... p n, άρα είναι πρώτος ή διαιρείται με άλλο πρώτο, κάτι που είναι άτοπο. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
51 Κωδικοποίηση Πρώτοι αριθμοί II Θεώρημα (Θεμελιώδες Θεώρημα Αριθμητικής) Κάθε αριθμός μπορεί να γραφεί με μοναδικό τρόπο σε γινόμενο πρώτων αριθμών (όχι απαραίτητα διαφορετικών ανά δύο). Θεώρημα (Θεώρημα Τεσσάρων τετραγώνων του Lagrange) Κάθε θετικός ακέραιος μπορεί να αναπαρασταθεί ως άθροισμα τεσσάρων τετραγώνων. Εικασία (Εικασία του Goldbach) Κάθε άρτιος φυσικός μεγαλύτερος του δύο μπορεί να αναπαρασταθεί ως το άθροισμα δύο πρώτων. Ορισμός Αν ο p είναι πρώτος και ο p + 2 είναι επίσης πρώτος τότε αυτοί λέγονται δίδυμοι πρώτοι. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
52 Κωδικοποίηση Πρώτοι αριθμοί III Εικασία (Εικασία των Διδύμων Πρώτων) Υπάρχουν άπειρα το πλήθος ζευγάρια διδύμων πρώτων. Θεώρημα (Θεώρημα Πρώτων Αριθμών (de la Valee Poussin, Hadamard)) Αν με π(x) συμβολίσουμε το πλήθος των πρώτων αριθμών μικρότερων ή ίσων του x, τότε π(x) ÝÝÝÑ xñ8 x log x Θεώρημα (Vinogradov) Υπάρχει ακέραιος N ώστε κάθε n περιττός αριθμός μεγαλύτερος του N γράφεται σαν άθροισμα τριών πρώτων αριθμών. Η καλύτερη γνωστή τιμή του N είναι N = 3, 33 ˆ Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
53 Κωδικοποίηση Πρώτοι αριθμοί IV Πόρισμα Κάθε αριθμός μεγαλύτερος από την παραπάνω σταθερά μπορεί να γραφτεί ως άθροισμα τεσσάρων πρώτων. Θεώρημα (Chen) Υπάρχει ακέραιος N ώστε κάθε n άρτιος αριθμός μεγαλύτερος του N γράφεται σαν άθροισμα ενός πρώτου και ενός γινομένου το πολύ δύο πρώτων αριθμών. Παρατήρηση: Πρόσφατα(2002) οι Saxena, Kayal και Agrawal απέδειξαν ότι το πρόβλημα PRIMES είναι στο P. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
54 Κωδικοποίηση Άλλη μια συνάρτηση κωδικοποίησης Παρακάτω περιγράφουμε μια ακόμη συνάρτηση σύζευξης, C: C(n, m) = 2 n (2m + 1) 1 Υπάρχει προφανώς πρόγραμμα loop που να υπολογίζει τη C(n, m). Ως προς τις αντίστροφες συναρτήσεις D 1, D 2, αν k είναι ένας φυσικός αριθμός, αποδεικνύεται ότι υπάρχει μοναδικό ζεύγος n = D 1 (k), m = D 2 (k), ώστε: C(m, n) = k. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
55 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Program semantics (σημασιολογία): specifications, formal verification. Υπάρχουν τρεις μαθηματικοί τρόποι να μιλήσουμε για σημασιολογία: Operational semantics (λειτουργική σημασιολογία) Denotational semantics (δηλωτική σημασιολογία) Axiomatic semantics (αξιωματική σημασιολογία) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
56 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Λειτουργική σημασιολογία Ορισμοί LOOP n : το σύνολο των LOOP προγραμμάτων με μεταβλητές εκ των x 1, x 2,..., x n. Configuration είναι ένα στοιχείο του N n,συγκεκριμένα οι τιμές των μεταβλητών x 1, x 2,..., x n. Computation είναι ένα στοιχείο του (N n ) : συγκεκριμένα μια ακολουθία από διαδοχικές διαμορφώσεις. Ορισμός (Λειτουργική σημασιολογία) S o : LOOP n ˆ N n Ñ (N n ) (η S o μπορεί να οριστεί με πρωταρχική αναδρομή) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
57 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Δηλωτική σημασιολογία Ορισμός (Δηλωτική σημασιολογία) S d : LOOP n ˆ N n Ñ N n Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
58 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Αξιωματική σημασιολογία Assertions, Invariants Παράδειγμα 1: (1) x:=y; (2) for w:=1 to z do (3) x:=succ x (4) end (5) 1 y = a 1 ^ z = a 2. Βεβαίωση εισόδου. 2 y = a 1 ^ z = a 2 ^ x = a 1. 3 y = a 1 ^ z = a 2 ^ x = a 1 + w 1 ^ w ď a 2. Αναλλοίωτη βρόχου. 4 y = a 1 ^ z = a 2 ^ x = a 1 + w. 5 y = a 1 ^ z = a 2 ^ x = a 1 + a 2. Βεβαίωση εξόδου. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
59 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Σημασιολογία προγραμμάτων LOOP Αξιωματική σημασιολογία Παράδειγμα 2 (Pascal): (1) z:=0; u:=x; (2) repeat (3) z:=z+y (4) u:=u-1 (5) until u=0 (6) Βεβαιώσεις: 1 x ą 0 ^ y ą 0. Βεβαίωση εισόδου. 2 z = 0 ^ u = x ^ x ą 0 ^ y ą 0. 3 z + u y = x y ^ u ą 0. Αναλλοίωτη βρόχου. 4 (z y) + u y = x y ^ u ą 0. 5 (z y) + (u + 1) y = x y ^ u ě 0. 6 z + u y = x y ^ u ě 0 (δηλαδή z = x y ^ u = 0). Βεβαίωση εξόδου. u: συνθήκη τερματισμού (termination condition) μια γνησίως φθίνουσα συνάρτηση που εγγυάται τον τερματισμό όταν u = 0. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
60 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις LOOP-υπολογισιμότητα Ορισμός Μια συνάρτηση f: N n Ñ N λέγεται LOOP-υπολογίσιμη (LOOP-computable) εάν υπάρχει ένα LOOP n+m πρόγραμμα (x 1,..., x n,..., x n+m ) και ένα i ď m + n έτσι ώστε για κάθε a 1, a 2,..., a n P N: f(a 1, a 2,..., a n ) = S d,i (π)[a 1,..., a n, 0,..., 0]. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
61 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις I Ορισμός Η κλάση P των πρωταρχικών αναδρομικών συναρτήσεων είναι η μικρότερη κλάση συναρτήσεων που: 1 περιέχει τις εξής αρχικές συναρτήσεις: S, P, Z, U n i (για όλα τα n και i ď n) και 2 είναι κλειστή ως προς τα σχήματα της σύνθεσης και της πρωταρχικής αναδρομής. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
62 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις II Εξηγήσεις: S(x) = x + 1, P(x + 1) = x, P(0) = 0, Z(x) = 0, U n i (x 1, x 2,..., x n ) = x i, 1 ď i ď n Σύνθεση: f(x) = h(g(x)) γενικά f(x 1, x 2,..., x n ) = h(g 1 (x 1, x 2,..., x n ),..., g m (x 1, x 2,..., x n )) Πρωταρχική Αναδρομή: # f(0) = C f(sy) = h(y, f(y)) Γενικά: # f(x 1, x 2,..., x n, 0) = g(x 1, x 2,..., x n ) f(x 1, x 2,..., x n, Sy) = h(x 1, x 2,..., x n, y, f(x 1, x 2,..., x n, y)) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
63 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις III Παραδείγματα: 1 2 # add(x, 0) = U 1 1(x) add(x, Sy) = h(x, y, add(x, y)) # mult(x, 0) = Z(x) mult(x, Sy) = h(x, y, mult(x, y)) όπου h(x, y, z) = add(u 3 1(x, y, z), U 3 3(x, y, z)) όπου h(x, y, z) = S(U 3 3(x, y, z)) 3 mult2(x) = mult(s(s(z(x))), U 1 1(x)) # pow2(0) = 1 4 όπου h(y, z) = mult2(u 2 2(y, z)) pow2(sy) = h(y, pow2(y)) 5 Αν η g(x, y) είναι πρωταρχικά αναδρομική, τότε είναι και η f: f(x) = g(x, x) = g(u 1 1(x), U 1 1(x)) (ταυτοποίηση ορισμάτων) 6 Αν η g(x, y) είναι πρωταρχικά αναδρομική, τότε είναι και η f: f(x, y) = g(y, x) = g(u 2 2(x, y), U 2 1(x, y)) (εναλλαγή ορισμάτων) 7 abs(x y) = (x. y) + (y. x) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
64 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Πρωταρχικές αναδρομικές συναρτήσεις IV 8 προσημοσυναρτήσεις (sg, sg) 9 eq(x, y) = sg(abs(x y)) Παρατήρηση Οι sg, sg και eq είναι χαρακτηριστικές συναρτήσεις. Ορισμός Μια σχέση R Ď N n είναι πρωταρχική αναδρομική, αν η χαρακτηριστική συνάρτηση χ R είναι η πρωταρχική αναδρομική, όπου # 1, αν (x 1,..., x n ) P R χ R (x 1,..., x n ) = 0, αλλιώς Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
65 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Άλλα είδη αναδρομής I Ακολουθία Fibbonaci: $ & f(0) = 1 f(1) = 1 % f(ssn) = f(n) + f(sn) Αυτό το σχήμα είναι αναδρομή αλλά δεν είναι πρωταρχική αναδρομή! Αμοιβαία (Mutual) Πρωταρχική Αναδρομή # f 1 (0) = 1 f 1 (Sn) = f 1 (n) + f 2 (n) # f 2 (0) = 0 f 2 (Sn) = f 1 (n) f 1 : 1, 1, 2, 3, 5, 8,... f 2 : 0, 1, 1, 2, 3, 5,... Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
66 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Άλλα είδη αναδρομής II Γενικά: για j = 1,..., m: $ & f j (x 1, x 2,..., x n, 0) = g j (x 1,..., x n ) f j (x 1, x 2,..., x n, Sy) = h j (x 1,..., x n, y, f 1 (x 1, x 2,..., x n, y),... %, f m (x 1, x 2,..., x n, y)) Λήμμα Αν όλες οι συναρτήσεις g j και h j είναι πρωταρχικές αναδρομικές, τότε και οι συναρτήσεις f j, όπως ορίζονται από το παραπάνω σχήμα, είναι επίσης πρωταρχικές αναδρομικές. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
67 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Άλλα είδη αναδρομής III Απόδειξη. Χρησιμοποιούμε κωδικοποίηση και αποκωδικοποίηση κατά (π.χ.) Cantor. Σημειωτέον ότι αυτές (C m και D m i ) είναι πρωταρχικές αναδρομικές. # f(x 1, x 2,..., x n, 0) = C m (g 1 (x 1,..., x n ),..., g m (x 1,..., x n )) f(x 1, x 2,..., x n, Sy) = C m (h 1 [x 1,..., x n, y, D m 1 (f(x 1, x 2,..., x n, y)),..., D m m(f(x 1, x 2,..., x n, y))],..., h m [x 1,..., x n, y, D m 1 (f(x 1, x 2,..., x n, y)),..., D m m(f(x 1, x 2,..., x n, y))]) Η f ορίζεται με πρωταρχική αναδρομή, είναι άρα πρωταρχική αναδρομική. f j (x 1, x 2,..., x n, y) = D m j (f(x 1, x 2,..., x n, y)) και συνεπώς και οι συναρτήσεις f j είναι επίσης πρωταρχικές αναδρομικές. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
68 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων I Θεώρημα Κάθε πρωταρχική αναδρομική συνάρτηση είναι LOOP-υπολογίσιμη. Απόδειξη: Με επαγωγή στη δομή της συνεπαγωγικής ακολουθίας των πρωταρχικών αναδρομικών συναρτήσεων. Παρατήρηση Η επαγωγική απόδειξη ιδιότητας σε επαγωγικό πεδίο συνεπάγεται: 1 απόδειξη της ιδιότητας για τα αρχικά στοιχεία 2 απόδειξη της ιδιότητας για νέα στοιχεία που δημιουργούνται με πράξεις κλεισίματος και με παλιά στοιχεία για τα οποία υποθέτουμε ότι έχουν την ιδιότητα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
69 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων II 1 Αρχικές συναρτήσεις αρχικές συναρτήσεις Loop-πρόγραμμα μεταβλητή εξόδου S x := succ x x P x := pred x x Z x := 0 x U n i κενό πρόγραμμα x i 2 Σχήματα κλεισίματος 1 Πρωταρχική Αναδρομή: Έστω ότι δίνονται προγράμματα για y := g(x 1,..., x n ) και y := h(x 1,..., x n, u, y). Τότε η f που ορίζεται με πρωταρχική αναδρομή από τις συναρτήσεις g και h, με το σχήμα δηλαδή: # f(x 1, x 2,..., x n, 0) = g(x 1,..., x n ) f(x 1, x 2,..., x n, Sy) = h(x 1,..., x n, y, f(x 1, x 2,..., x n, y)) μπορεί να υπολογιστεί με το εξής πρόγραμμα: z := x n+1 ; y := g(x 1, x 2,..., x n ) ; for u := 1 to z do y := h(x 1, x 2,..., x n, u 1, y) end Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
70 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων III 2 Σύνθεση: Έστω ότι δίνονται τα m + 1 προγράμματα για: y 1 := g 1 (x 1, x 2,..., x n )... y m := g m (x 1, x 2,..., x n ) και z := h(y 1, y 2,..., y n ). Τότε η f που ορίζεται με σύνθεση από τις g 1, g 2,, g m και h, με το σχήμα δηλαδή: f(x 1, x 2,..., x n ) = h(g 1 (x 1, x 2,..., x n ),..., g m (x 1, x 2,..., x n )) μπορεί να υπολογιστεί με το εξής πρόγραμμα: y 1 := g 1 (x 1, x 2,..., x n ) ;... ; y m := g m (x 1, x 2,..., x n ) ; z := h(y 1, y 2,..., y m ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
71 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων I Θεώρημα Κάθε LOOP-υπολογίσιμη συνάρτηση είναι πρωταρχική αναδρομική. Απόδειξη: Με επαγωγή στη δομή των προγραμμάτων LOOP: 1 Αρχικά προγράμματα (αναθέσεις) Αρχικό πρόγρ. (αναθέσεις) Πρωτ. Αναδρ. Συναρτ. y := x i (μετ. εξόδου y) U n i (x 1, x 2,..., x n ) y := succ x i S(U n i (x 1, x 2,..., x n )) y := pred x i P(U n i (x 1, x 2,..., x n )) y := 0 Z(U n i (x 1, x 2,..., x n )) κενό π (μετ. εξόδου x j ) U n j (x 1, x 2,..., x n ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
72 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων II 2 Δομές Ελέγχου ροής προγράμματος 1 Παράθεση (;): Έστω ότι το π 1 υπολογίζει τις πρωταρχικές αναδρομικές συναρτήσεις g 1 (μεταβλητή εξόδου: x 1 ), g 2 (μεταβλητή εξόδου: x 2 ),, g n (μεταβλητή εξόδου: x n ) και ότι το π 2 υπολογίζει την πρωταρχική αναδρομική συνάρτηση h (μεταβλητή εξόδου: x j ). Τότε το πρόγραμμα π 1 ; 2 υπολογίζει: h(g 1 (x 1,..., x n ),..., g n (x 1,..., x n )) = f(x 1, x 2,..., x n ) που είναι πρωταρχική αναδρομική λόγω του κλεισίματος ως προς σύνθεση συναρτήσεων. 2 βρόχος for: Έστω ότι το π υπολογίζει τις πρωταρχικές αναδρομικές συναρτήσεις h 1 (μεταβλητή εξόδου: x 1 ), h 2 (μεταβλητή εξόδου: x 2 ),, h n (μεταβλητή εξόδου: x n ) και χωρίς βλάβη της γενικότητας ας υποθέσουμε ότι ούτε η μεταβλητή ελέγχου w ούτε το άνω όριο z δεν εμφανίζονται στο π (αλλιώς μετατρέψτε το π σε ισοδύναμο δες εξήγηση παρακάτω). Τότε το πρόγραμμα for w := 1 to z do π end υπολογίζει τις συναρτήσεις f j (1 ď j ď n): # f j (x 1, x 2,..., x n, 0) = U n j (x 1,..., x n ) f j (x 1, x 2,..., x n, Sz) = h j (f 1 (x 1,..., x n, z),..., f n (x 1, x 2,..., x n, z)) που είναι πρωταρχικές αναδρομές λόγω του κλεισίματος ως προς αμοιβαία πρωταρχική αναδρομή. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
73 LOOP-υπολογίσιμες και πρωταρχικές αναδρομικές συναρτήσεις Ισοδυναμία πρωταρχικών αναδρομικών και LOOP συναρτήσεων III Εξήγηση: Αν η μεταβλητή ελέγχου (έστω x k ) και το άνω όριο (έστω x m ) εμφανίζονται στο π, μετατρέπουμε το πρόγραμμα for x k := 1 to x m do π end στο ακόλουθο ισοδύναμο πρόγραμμα π 1 (ισοδύναμο πρόγραμμα ως προς τις μεταβλητές x 1, x 2,, x n, του π): x k := 1; z := x m ; for w := 1 to z do (* w, z νέες μεταβλητές *) π; x k := x k + 1 end Βασιζόμενοι τώρα στις προηγούμενες αποδείξεις για την παράθεση προγραμμάτων και το βρόχο for, μπορούμε εύκολα να δείξουμε ότι κάθε μια από τις f j (1 ď j ď n) τις οποίες υπολογίζει το π 1 είναι πρωταρχική αναδρομή. Επομένως, και κάθε f j του ισοδύναμου προγράμματος for x k := 1 to x m do π end είναι πρωταρχική αναδρομική. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
74 Σταθερά σημεία Σταθερά σημεία I Ορισμοί M k = M ˆ ˆ M loooooomoooooon k φορές N M : σύνολο των ολικών συναρτήσεων από το M στο N. χ: χαρακτηριστική συνάρτηση στο M: χ: M Ñ t0, 1u # 1, a P S χ S : χαρακτηριστική συνάρτηση συνόλου S Ď M: χ S (a) = 0, αλλιώς Το σύνολο των χαρακτηριστικών συναρτήσεων στο M είναι ισομορφικό του δυναμοσυνόλου του M (t0, 1u M Pow(M)). Ορισμός Αν M, N αλγεβρικές δομές τότε μία συνάρτηση f: M Ñ N ονομάζεται ομομορφισμός όταν είναι 1-1 και συμβατή με τις πράξεις. Ορισμός Ένας ισομορφισμός είναι μία συνάρτηση με τις ιδιότητες: 1-1, επί, ομομορφισμού. (Επίσης ονομάζεται και αντιστοιχία.) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
75 Σταθερά σημεία Σταθερά σημεία II Λήμμα (Επανάληψης) Έστω a P N και g: N Ñ N. Υπάρχει ακριβώς μία συνάρτηση f: N Ñ N τέτοια ώστε: # Σχήμα Επανάληψης f(0) = a (Scheme of Iteration) f(sx) = g(f(x)) ( ) Απόδειξη. Χρησιμοποιώντας επαγωγή κατασκευάζουμε διαδοχικά συναρτήσεις f 0, f 1,, f i, με dom(f i ) = t0, 1,..., iu, τέτοια ώστε f i (0) = a και f i (n + 1) = g(f i (n)), για κάθε n ă i. Όλες οι f i έχουν τις ίδιες τιμές στο κοινό πεδίο ορισμού τους (συμβολισμός f 0 Ď f 1 Ď f 2 Ď... ). Ορίζουμε: f(n) = f n P N. Η f ικανοποιεί την ( ), άρα αποδείξαμε την ύπαρξη. Έστω τώρα f 1 άλλη λύση της ( ). Η f 1 περιορισμένη σε οποιοδήποτε t0, 1,..., nu πρέπει να έχει τις ίδιες τιμές με την f n. Επομένως, f 1 (n) = f n (n) = f(n), για κάθε n P N, άρα αποδείξαμε και την μοναδικότητα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
76 Σταθερά σημεία Σταθερά σημεία III Ας δούμε την παραπάνω απόδειξη συνολοθεωρητικά. Μία συνάρτηση είναι ένα σύνολο ζευγών: F = t(x, y) y = f(x)u Ď N ˆ N. Τότε το ( ) γίνεται F = t(0, a)u Y t(x + 1, y) Dz: y = g(z) ^ (x, z) P Fu. Το δεξιό μέλος το συμβολίζουμε με τ 0 (F). Ο τελεστής τ 0 είναι το σχήμα ορισμού. Ο ισχυρισμός του λήμματος επανάληψης είναι ο εξής: F = τ 0 (F), δηλαδή το τ 0 έχει σταθερό σημείο. Το λήμμα επανάληψης είναι συνέπεια του εξής γενικότερου θεωρήματος: Ορισμός (Συνεχής τελεστής) Έστω U 0 Ď U 1 Ď U 2 Ď... μία αλυσίδα (chain) υποσυνόλων του M. Λέμε ότι ο τελεστής τ : Pow(M) Ñ Pow(M) είναι συνεχής αν για κάθε αλυσίδα U 0 Ď U 1 Ď U 2 Ď... στο Pow(M) ισχύει τ( Ť tu i u) = Ť tτ(u i )u. i i Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
77 Σταθερά σημεία Σταθερά σημεία IV Θεώρημα (Σταθερού σημείου: Tarski-Knaster, Kleene) Κάθε συνεχής τελεστής τ : Pow(M) Ñ Pow(M) έχει σταθερό σημείο την F = Ť tτ i (H) i P Nu. Παράδειγμα: Έστω η συνάρτηση: # fact(0) = 1 Συνολοθεωρητικά έχουμε: fact(sn) = (n + 1) fact(n) FACT = t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P FACTu ή σύντομα: FACT = τ(fact), όπου: τ(x) = t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P Xu. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
78 Σταθερά σημεία Σταθερά σημεία V Με χρήση του θεωρήματος σταθερού σημείου λαμβάνουμε: τ 0 (H) = H τ 1 (H) = τ(h) = t(0, 1)u τ 2 (H) = τ(τ(h)) = τ(t(0, 1)u) = t(0, 1)u Y t(1, 1)u τ 3 (H) = τ(τ(τ(h))) = t(0, 1)u Y t(1, 1), (2, 2)u τ 4 (H) = τ(τ(τ(τ(h)))) = t(0, 1)u Y t(1, 1), (2, 2), (3, 6)u FACT = Ť i τ i (H) = τ 0 (H) Y τ 1 (H) Y... = t(0, 1), (1, 1), (2, 2), (3, 6),...u. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
79 Σταθερά σημεία Σταθερά σημεία VI Προκειμένου να εφαρμόσουμε βέβαια το θεώρημα σταθερού σημείου θα πρέπει να δείξουμε ότι ο τελεστής τ είναι συνεχής. Πράγματι: τ( ď i X i ) = t(0, 1)u Y t(n + 1, (n + 1) k) (n, k) P ď i X i u = t(0, 1)u Y t(n + 1, (n + 1) k) Di: (n, k) P X i u = t(0, 1)u Y ď i t(n + 1, (n + 1) k) : (n, k) P X i u = ď i t(0, 1)u Y t(n + 1, (n + 1) k) : (n, k) P X i u = ď i τ(x i ) Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
80 Σταθερά σημεία Σταθερά σημεία VII Ένας άλλος τρόπος χρήσης του θεωρήματος σταθερού σημείου είναι για να δείξουμε ότι η μικρότερη κλάση που περιέχει και είναι κλειστή ως προς ορίζει μονοσήμαντα μία κλάση P: Έστω C μία οποιαδήποτε κλάση συναρτήσεων. Έστω γ(c) η κλάση των συναρτήσεων που λαμβάνουμε αν εφαρμόσουμε μία φορά το σχήμα της σύνθεσης σε συναρτήσεις από το C. Έστω ρ(c) η κλάση των συναρτήσεων που λαμβάνουμε αν εφαρμόσουμε μία φορά το σχήμα πρωταρχικής αναδρομής σε συναρτήσεις από το C. Έστω A η κλάση των αρχικών συναρτήσεων: A = ts, P, Z, U n i u. Τότε η P είναι το ελάχιστο σταθερό σημείο της P = A Y γ(p) Y ρ(p). Το P κατασκευάζεται με επαναληπτική εφαρμογή των γ και ρ: P = A Y γ(a) Y ρ(a) Y γ(a Y γ(a) Y ρ(a)) Y ρ(a Y γ(a) Y ρ(a)) Y... Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 233
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
Απαρίθμηση ζευγών φυσικών αριθμών I. C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση
 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I 0 0 1 2 3 4... 1 2 3 4...... C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι
Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I 0 0 1 2 3 4... 1 2 3 4...... C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ.
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές.
 Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Μη επιλυσιμότητα I. Απόδειξη. Ορίζουμε # # =
 Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Σχήματα McCarthy I. Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα:
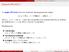 Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Μηχανές Turing (T.M) I
 Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Σύνολα, Σχέσεις, Συναρτήσεις
 Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
Κεφάλαιο 2 Σύνολα, Σχέσεις, Συναρτήσεις Τα σύνολα, οι σχέσεις και οι συναρτήσεις χρησιμοποιούνται ευρύτατα σε κάθε είδους μαθηματικές αναπαραστάσεις και μοντελοποιήσεις. Στη θεωρία υπολογισμού χρησιμεύουν,
Το 10ο πρόβλημα του Hilbert I
 Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο
 Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
Θεωρία Υπολογισμού και Πολυπλοκότητα Μαθηματικό Υπόβαθρο Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Σύνολα Συναρτήσεις και Σχέσεις Γραφήματα Λέξεις και Γλώσσες Αποδείξεις ΕΠΛ 211 Θεωρία
Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση
 Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αριθμήσιμα
Μη-Αριθμήσιμα Σύνολα, ιαγωνιοποίηση ιδάσκοντες: Φ. Αφράτη,. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αριθμήσιμα
Περιεχόμενα 1 Πρωτοβάθμια Λογική Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων ) / 60
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 1. Μαθηματικό Υπόβαθρο 23, 26 Ιανουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 1.1. Σύνολα Ορισμός : Σύνολο μια συλλογή από αντικείμενα Στοιχεία: Μέλη συνόλου Τα στοιχεία
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 1. Μαθηματικό Υπόβαθρο 23, 26 Ιανουαρίου 2007 Δρ. Παπαδοπούλου Βίκη 1 1.1. Σύνολα Ορισμός : Σύνολο μια συλλογή από αντικείμενα Στοιχεία: Μέλη συνόλου Τα στοιχεία
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 2: Μαθηματικό Υπόβαθρο
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 2: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Συναρτήσεις & Σχέσεις (0.2.3) Γράφοι (Γραφήματα) (0.2.4) Λέξεις και Γλώσσες (0.2.5) Αποδείξεις (0.3) 1
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 2: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Συναρτήσεις & Σχέσεις (0.2.3) Γράφοι (Γραφήματα) (0.2.4) Λέξεις και Γλώσσες (0.2.5) Αποδείξεις (0.3) 1
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Πρόλογος Τα πρώτα μαθήματα, σχεδόν σε όλους τους κλάδους των μαθηματικών, περιέχουν, ή θεωρούν γνωστές, εισαγωγικές έννοιες που αφορούν σύνολα, συναρτήσεις, σχέσεις ισοδυναμίας, αλγεβρικές δομές, κλπ.
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Σημειώσεις Λογικής I. Εαρινό Εξάμηνο Καθηγητής: Λ. Κυρούσης
 Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Σημειώσεις Λογικής I Εαρινό Εξάμηνο 2011-2012 Καθηγητής: Λ. Κυρούσης 2 Τελευταία ενημέρωση 28/3/2012, στις 01:37. Περιεχόμενα 1 Εισαγωγή 5 2 Προτασιακή Λογική 7 2.1 Αναδρομικοί Ορισμοί - Επαγωγικές Αποδείξεις...................
Παραλλαγές και επεκτάσεις αυτομάτων I
 Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως
Παραλλαγές, επεκτάσεις και εφαρμογές FA/REGEXP Παραλλαγές και επεκτάσεις αυτομάτων I Ορισμός Ένα two-way deterministic FA (2DFA) είναι μία πεντάδα M = (Q, Σ, δ, q 0, F), όπου τα Q, Σ, q 0 και F είναι όπως
HY118-Διακριτά Μαθηματικά
 HY118-Διακριτά Μαθηματικά Παρασκευή, 02/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
HY118-Διακριτά Μαθηματικά Παρασκευή, 02/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Α Δ Ι Θ Θ Α Ε Ι Μ : https://sites.google.com/site/maths4edu/home/algdom114
 Α Δ Ι Θ Θ Α Ε 2013-2014 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 12 Μαρτίου 2014 19:26
Α Δ Ι Θ Θ Α Ε 2013-2014 Δ : Ν. Μαρμαρίδης - Α. Μπεληγιάννης Ι Μ : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html, https://sites.google.com/site/maths4edu/home/algdom114 12 Μαρτίου 2014 19:26
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Υπολογίσιμες Συναρτήσεις
 Υπολογίσιμες Συναρτήσεις Σ Π Υ Ρ Ι Δ Ω Ν Τ Ζ Ι Μ Α Σ Δ Τ Ο Μ Ε Α Σ Τ Μ Η Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Σ Χ Ο Λ Η Θ Ε Τ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Ι Ω Α Ν Ν Ι Ν Ω Ν Υπολογίσιμες Συναρτήσεις
Υπολογίσιμες Συναρτήσεις Σ Π Υ Ρ Ι Δ Ω Ν Τ Ζ Ι Μ Α Σ Δ Τ Ο Μ Ε Α Σ Τ Μ Η Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Σ Χ Ο Λ Η Θ Ε Τ Ι Κ Ω Ν Ε Π Ι Σ Τ Η Μ Ω Ν Π Α Ν Ε Π Ι Σ Τ Η Μ Ι Ο Ι Ω Α Ν Ν Ι Ν Ω Ν Υπολογίσιμες Συναρτήσεις
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
β) 3 n < n!, n > 6 i i! = (n + 1)! 1, n 1 i=1
 Κεφάλαιο 2: Στοιχεία Λογικής - Μέθοδοι Απόδειξης 1. Να αποδειχθεί ότι οι λογικοί τύποι: (p ( (( p) q))) (p q) και p είναι λογικά ισοδύναμοι. Θέλουμε να αποδείξουμε ότι: (p ( (( p) q))) (p q) p, ή με άλλα
Κεφάλαιο 2: Στοιχεία Λογικής - Μέθοδοι Απόδειξης 1. Να αποδειχθεί ότι οι λογικοί τύποι: (p ( (( p) q))) (p q) και p είναι λογικά ισοδύναμοι. Θέλουμε να αποδείξουμε ότι: (p ( (( p) q))) (p q) p, ή με άλλα
u v 4 w G 2 G 1 u v w x y z 4
 Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Αναδρομικές Συναρτήσεις και Σχέσεις I
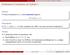 Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
Προγράμματα WHILE και μερικές αναδρομικές συναρτήσεις Αναδρομικές Συναρτήσεις και Σχέσεις I Ορισμός Η ολική συνάρτηση h( x, y) είναι κανονική (regular): @ x Dy h( x, y) = 0 Παρατήρηση Η f( x) = µy[h( x,
, για κάθε n N. και P είναι αριθμήσιμα.
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΚΡΙΤA ΜΑΘΗΜΑΤΙΚΑ Διδάσκοντες: Δ.Φωτάκης Θ. Σούλιου η Γραπτή Εργασία Ημ/νια παράδοσης 5/4/8 Θέμα (Διαδικασίες Απαρίθμησης.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΔΙΑΚΡΙΤA ΜΑΘΗΜΑΤΙΚΑ Διδάσκοντες: Δ.Φωτάκης Θ. Σούλιου η Γραπτή Εργασία Ημ/νια παράδοσης 5/4/8 Θέμα (Διαδικασίες Απαρίθμησης.
i) Για να δείξουμε την επιθυμητή ισότητα, δείχνουμε πως A B {A x : x B} και πως {A x : x B} A B. Για τον πρώτο εγκλεισμό, έστω a A B, δηλάδη a A και a
 Θεωρία Συνόλων Χειμερινό Εξάμηνο 2016 2017 Λύσεις 1. Άσκηση 1.9 (σελ. 17), από τις σημειώσεις του Σκανδάλη. Εστω A, B δεδομένα σύνολα. Θα χρησιμοποιήσουμε τα αξιώματα αλλά αναφερόμενοι, αποκλειστικά, είτε
Θεωρία Συνόλων Χειμερινό Εξάμηνο 2016 2017 Λύσεις 1. Άσκηση 1.9 (σελ. 17), από τις σημειώσεις του Σκανδάλη. Εστω A, B δεδομένα σύνολα. Θα χρησιμοποιήσουμε τα αξιώματα αλλά αναφερόμενοι, αποκλειστικά, είτε
x < A y f(x) < B f(y).
 Χειμερινό Εξάμηνο 2016 2017 Ασκήσεις στα Κεφάλαια 5 & 6 1. Αυτή είναι ουσιαστικά η Άσκηση 5.2 (σελ. 119), από τις σημειώσεις του Σκανδάλη. Εστω A, < καλά διατεταγμένο σύνολο και έστω στοιχείο a A. Αποδείξτε
Χειμερινό Εξάμηνο 2016 2017 Ασκήσεις στα Κεφάλαια 5 & 6 1. Αυτή είναι ουσιαστικά η Άσκηση 5.2 (σελ. 119), από τις σημειώσεις του Σκανδάλη. Εστω A, < καλά διατεταγμένο σύνολο και έστω στοιχείο a A. Αποδείξτε
Φ(s(n)) = s (Φ(n)). (i) Φ(1) = a.
 1. Τα θεμελιώδη αριθμητικά συστήματα Με τον όρο θεμελιώδη αριθμητικά συστήματα εννοούμε τα σύνολα N των φυσικών αριθμών, Z των ακεραίων, Q των ρητών και R των πραγματικών. Από αυτά, το σύνολο N είναι πρωτογενές
1. Τα θεμελιώδη αριθμητικά συστήματα Με τον όρο θεμελιώδη αριθμητικά συστήματα εννοούμε τα σύνολα N των φυσικών αριθμών, Z των ακεραίων, Q των ρητών και R των πραγματικών. Από αυτά, το σύνολο N είναι πρωτογενές
Αριθμήσιμα σύνολα. Μαθηματικά Πληροφορικής 5ο Μάθημα. Παραδείγματα αριθμήσιμων συνόλων. Οι ρητοί αριθμοί
 Αριθμήσιμα σύνολα Μαθηματικά Πληροφορικής 5ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Ορισμός Πόσα στοιχεία έχει το σύνολο {a, b, r, q, x}; Οσα και το σύνολο {,,, 4, 5} που είναι
Αριθμήσιμα σύνολα Μαθηματικά Πληροφορικής 5ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Ορισμός Πόσα στοιχεία έχει το σύνολο {a, b, r, q, x}; Οσα και το σύνολο {,,, 4, 5} που είναι
K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων
 K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Στοιχεία προτασιακής λογικής Περιεχόμενα
K15 Ψηφιακή Λογική Σχεδίαση 3: Προτασιακή Λογική / Θεωρία Συνόλων Γιάννης Λιαπέρδος TEI Πελοποννήσου Σχολή Τεχνολογικών Εφαρμογών Τμήμα Μηχανικών Πληροφορικής ΤΕ Στοιχεία προτασιακής λογικής Περιεχόμενα
i=1 i=1 i=1 (x i 1, x i +1) (x 1 1, x k +1),
 Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
Κεφάλαιο 6 Συμπάγεια 6.1 Ορισμός της συμπάγειας Οπως θα φανεί στην αμέσως επόμενη παράγραφο, υπάρχουν διάφοροι τρόποι με τους οποίους μπορεί κανείς να εισάγει την έννοια του συμπαγούς μετρικού χώρου. Ο
ιακριτά Μαθηµατικά Ορέστης Τελέλης Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36
 ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36 Γνωριµία ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr
ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36 Γνωριµία ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr
Δώστε έναν επαγωγικό ορισμό για το παραπάνω σύνολο παραστάσεων.
 Εισαγωγή στη Λογική Α Τάξης Σ. Κοσμαδάκης Συντακτικό τύπων Α τάξης Α Θεωρούμε δεδομένο ένα λεξιλόγιο Λ, αποτελούμενο από (1) ένα σύνολο συμβόλων για σχέσεις, { R, S,... } (2) ένα σύνολο συμβόλων για συναρτήσεις,
Εισαγωγή στη Λογική Α Τάξης Σ. Κοσμαδάκης Συντακτικό τύπων Α τάξης Α Θεωρούμε δεδομένο ένα λεξιλόγιο Λ, αποτελούμενο από (1) ένα σύνολο συμβόλων για σχέσεις, { R, S,... } (2) ένα σύνολο συμβόλων για συναρτήσεις,
Μορφές αποδείξεων. Μαθηματικά Πληροφορικής 2ο Μάθημα. Μορφές αποδείξεων (συνέχεια) Εξαντλητική μέθοδος
 Μορφές αποδείξεων Μαθηματικά Πληροφορικής ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μορφές αποδείξεων Μαθηματικά Πληροφορικής ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σχέσεις Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διμελής Σχέση Διατεταγμένο ζεύγος (α, β):
Σχέσεις Διδάσκοντες: Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διμελής Σχέση Διατεταγμένο ζεύγος (α, β):
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
B = {x A : f(x) = 1}.
 Θεωρία Συνόλων Χειμερινό Εξάμηνο 016 017 Λύσεις 1. Χρησιμοποιώντας την Αρχή του Περιστερώνα για τους φυσικούς αριθμούς, δείξτε ότι για κάθε πεπερασμένο σύνολο A και για κάθε f : A A, αν η f είναι 1-1 τότε
Θεωρία Συνόλων Χειμερινό Εξάμηνο 016 017 Λύσεις 1. Χρησιμοποιώντας την Αρχή του Περιστερώνα για τους φυσικούς αριθμούς, δείξτε ότι για κάθε πεπερασμένο σύνολο A και για κάθε f : A A, αν η f είναι 1-1 τότε
ιµελής Σχέση ιατεταγµένο ζεύγος (α, β): ύο αντικείµενα (όχι κατ ανάγκη διαφορετικά) σε καθορισµένη σειρά. Γενίκευση: διατεταγµένη τριάδα (α, β, γ), δι
 Σχέσεις ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιµελής Σχέση ιατεταγµένο ζεύγος (α, β):
Σχέσεις ιδάσκοντες: Φ. Αφράτη, Σ. Ζάχος,. Σούλιου Επιµέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιµελής Σχέση ιατεταγµένο ζεύγος (α, β):
j=1 x n (i) x s (i) < ε.
 Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
Κεφάλαιο 5 Πληρότητα 5.1 Πλήρεις μετρικοί χώροι Ορισμός 5.1.1 (πλήρης μετρικός χώρος). Ενας μετρικός χώρος (X, ρ) λέγεται πλήρης (complete) αν κάθε ρ βασική ακολουθία (x n ) στον X είναι ρ συγκλίνουσα.
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 2ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 2ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
Γνωριµία. ιακριτά Μαθηµατικά. Βιβλία Μαθήµατος. Επικοινωνία. ιδάσκων: Ορέστης Τελέλης. Ωρες γραφείου (502, Γρ.
 Γνωριµία ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη 26): ευτέρα
Γνωριµία ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη 26): ευτέρα
Λογική Πρώτης Τάξης. Γιώργος Κορφιάτης. Νοέµβριος Εθνικό Μετσόβιο Πολυτεχνείο
 Λογική Πρώτης Τάξης Γιώργος Κορφιάτης Εθνικό Μετσόβιο Πολυτεχνείο Νοέµβριος 2008 Σύνταξη Ορισµός (Σύνταξη της λογικής πρώτης τάξης) Λεξιλόγιο Σ = (Φ, Π, r) Συναρτήσεις f Φ Σχέσεις R Π r( ) η πληθικότητα
Λογική Πρώτης Τάξης Γιώργος Κορφιάτης Εθνικό Μετσόβιο Πολυτεχνείο Νοέµβριος 2008 Σύνταξη Ορισµός (Σύνταξη της λογικής πρώτης τάξης) Λεξιλόγιο Σ = (Φ, Π, r) Συναρτήσεις f Φ Σχέσεις R Π r( ) η πληθικότητα
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Πέµπτη, 09/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/9/2017
HY118- ιακριτά Μαθηµατικά Πέµπτη, 09/03/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 3/9/2017
4. Ο,τιδήποτε δεν ορίζεται με βάση τα (1) (3) δεν είναι προτασιακός τύπος.
 Κεφάλαιο 10 Μαθηματική Λογική 10.1 Προτασιακή Λογική Η γλώσσα της μαθηματικής λογικής στηρίζεται βασικά στις εργασίες του Boole και του Frege. Ο Προτασιακός Λογισμός περιλαμβάνει στο αλφάβητό του, εκτός
Κεφάλαιο 10 Μαθηματική Λογική 10.1 Προτασιακή Λογική Η γλώσσα της μαθηματικής λογικής στηρίζεται βασικά στις εργασίες του Boole και του Frege. Ο Προτασιακός Λογισμός περιλαμβάνει στο αλφάβητό του, εκτός
Σχέσεις. Διμελής Σχέση. ΣτοΊδιοΣύνολο. Αναπαράσταση
 Διμελής Σχέση Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Επιμέλεια διαφανειών: Δ. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διατεταγμένο ζεύγος (α, β): Δύο αντικείμενα
Διμελής Σχέση Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Επιμέλεια διαφανειών: Δ. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Διατεταγμένο ζεύγος (α, β): Δύο αντικείμενα
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 8: Σχέσεις - Πράξεις Δομές Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 8: Σχέσεις - Πράξεις Δομές Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 2:Στοιχεία Μαθηματικής Λογικής Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 2:Στοιχεία Μαθηματικής Λογικής Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό,
> ln 1 + ln ln n = ln(1 2 3 n) = ln(n!).
 η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
Αλγόριθμοι για αυτόματα
 Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
LÔseic Ask sewn sta Jemèlia twn Majhmatik n I
 LÔseic Ask sewn sta Jemèlia twn Majhmatik n I Rwmanìc-Diogènhc Maliki shc Tetˆrth, 6 OktwbrÐou 2010 Άσκηση 1. Για τυχόντα σύνολα A, B, C, D, να δειχθεί ότι (α ) A (B \ C) = ((A B) \ C) (A C). (β ) (A \
LÔseic Ask sewn sta Jemèlia twn Majhmatik n I Rwmanìc-Diogènhc Maliki shc Tetˆrth, 6 OktwbrÐou 2010 Άσκηση 1. Για τυχόντα σύνολα A, B, C, D, να δειχθεί ότι (α ) A (B \ C) = ((A B) \ C) (A C). (β ) (A \
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
(β ) ((X c Y ) (X c Y c )) c
 Λύσεις Ασκήσεων στα Θεμέλια των Μαθηματικών II Ρωμανός-Διογένης Μαλικιώσης Παρασκευή, 29 Οκτωβρίου 2010 Άσκηση 1. Απλοποιήστε τις ακόλουθες εκφράσεις (α ) (D c F ) c (D F ) (β ) ((X c Y ) (X c Y c )) c
Λύσεις Ασκήσεων στα Θεμέλια των Μαθηματικών II Ρωμανός-Διογένης Μαλικιώσης Παρασκευή, 29 Οκτωβρίου 2010 Άσκηση 1. Απλοποιήστε τις ακόλουθες εκφράσεις (α ) (D c F ) c (D F ) (β ) ((X c Y ) (X c Y c )) c
Σχέσεις. ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Σχέσεις ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιμελής Σχέση ιατεταγμένο ζεύγος (α, β): ύο αντικείμενα
Σχέσεις ιδάσκοντες:. Φωτάκης,. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο ιμελής Σχέση ιατεταγμένο ζεύγος (α, β): ύο αντικείμενα
Υπολογισιμότητα και Πολυπλοκότητα
 Κεφάλαιο 11 Υπολογισιμότητα και Πολυπλοκότητα 11.1 Ιστορία - Εισαγωγή Η Συλλογιστική του Αριστοτέλη αποτέλεσε την πρώτη προσπάθεια θεμελίωσης της λογικής και των μαθηματικών. Ο Leibni(t)z πρότεινε το εξής
Κεφάλαιο 11 Υπολογισιμότητα και Πολυπλοκότητα 11.1 Ιστορία - Εισαγωγή Η Συλλογιστική του Αριστοτέλη αποτέλεσε την πρώτη προσπάθεια θεμελίωσης της λογικής και των μαθηματικών. Ο Leibni(t)z πρότεινε το εξής
10.1 Υπολογίσιμες συναρτήσεις και αναδρομικά σύνολα
 Κεφάλαιο 10 Υπολογισιμότητα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 10.1 Υπολογίσιμες συναρτήσεις και αναδρομικά σύνολα Μέχρι στιγμής έχουμε δει ουσιαστικά
Κεφάλαιο 10 Υπολογισιμότητα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 10.1 Υπολογίσιμες συναρτήσεις και αναδρομικά σύνολα Μέχρι στιγμής έχουμε δει ουσιαστικά
B = F i. (X \ F i ) = i I
 Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
Κεφάλαιο 3 Τοπολογία μετρικών χώρων Ομάδα Α 3.1. Εστω (X, ρ) μετρικός χώρος και F, G υποσύνολα του X. Αν το F είναι κλειστό και το G είναι ανοικτό, δείξτε ότι το F \ G είναι κλειστό και το G \ F είναι
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Ευθέα Γινόμενα Ομάδων. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Ευθέα Γινόμενα Ομάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Ευθέα Γινόμενα Ομάδων Για την περαιτέρω ανάπτυξη τής θεωρίας θα χρειαστούμε
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Ευθέα Γινόμενα Ομάδων Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Ευθέα Γινόμενα Ομάδων Για την περαιτέρω ανάπτυξη τής θεωρίας θα χρειαστούμε
HY118-Διακριτά Μαθηματικά
 HY118-Διακριτά Μαθηματικά Πέμπτη, 01/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
HY118-Διακριτά Μαθηματικά Πέμπτη, 01/03/2018 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 02-Mar-18
ΗΥ118: Διακριτά Μαθηματικά - Εαρινό Εξάμηνο 2018 Τελική Εξέταση Ιουνίου Λύσεις
 ΗΥ118: Διακριτά Μαθηματικά - Εαρινό Εξάμηνο 018 Τελική Εξέταση Ιουνίου Λύσεις Προσοχή: Οι παρακάτω λύσεις είναι ενδεικτικές, μπορεί να υπάρχουν και άλλες που επίσης να είναι σωστές. Θέμα 1: [16 μονάδες]
ΗΥ118: Διακριτά Μαθηματικά - Εαρινό Εξάμηνο 018 Τελική Εξέταση Ιουνίου Λύσεις Προσοχή: Οι παρακάτω λύσεις είναι ενδεικτικές, μπορεί να υπάρχουν και άλλες που επίσης να είναι σωστές. Θέμα 1: [16 μονάδες]
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 1: Μαθηματικό Υπόβαθρο
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 1: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Εισαγωγικά (0.1) Σύνολα (0.2.1, 0.2.2) Συναρτήσεις & Σχέσεις (;;) (0.2.3) 1 Περιοχές που θα μελετήσουμε
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 1: Μαθηματικό Υπόβαθρο Τι θα κάνουμε σήμερα Εισαγωγικά (0.1) Σύνολα (0.2.1, 0.2.2) Συναρτήσεις & Σχέσεις (;;) (0.2.3) 1 Περιοχές που θα μελετήσουμε
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών 6
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Δώδεκα Αποδείξεις του. Θεμελιώδους Θεωρήματος της Άλγεβρας
 Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Δώδεκα Αποδείξεις του Θεμελιώδους Θεωρήματος της Άλγεβρας Mία εκδοχή της αρχικής απόδειξης του Gauss f ( z) = T ( z) + iu ( z) T = r cos φ + Ar 1 cos(( 1) φ + α) + + L cosλ U = r si φ + Ar 1 si(( 1) φ
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 3: Σύνολα Συνδυαστική Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 3: Σύνολα Συνδυαστική Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ψ φ2 = k χ φ2 = 4k χ φ1 = χ φ1 + χ φ2 + 3 = 4(k 1 + k 2 + 1) + 1 ψ φ1 = ψ φ1 + χ φ2 = k k = (k 1 + k 2 + 1) + 1
 Ασκήσεις στο μάθημα της Λογικής 15 Οκτωβρίου 2015 Άσκηση 1. Να δειχτεί ότι δεν υπάρχουν τύποι μήκους 2,3,6 αλλά κάθε άλλο (θετικό ακέραιο) μήκος είναι δυνατό (άσκηση 2, σελίδα 39) Απόδειξη. Δείχνουμε πρώτα
Ασκήσεις στο μάθημα της Λογικής 15 Οκτωβρίου 2015 Άσκηση 1. Να δειχτεί ότι δεν υπάρχουν τύποι μήκους 2,3,6 αλλά κάθε άλλο (θετικό ακέραιο) μήκος είναι δυνατό (άσκηση 2, σελίδα 39) Απόδειξη. Δείχνουμε πρώτα
Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5)
 Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στον Κατηγορηματικό Λογισμό Σύνταξη Κανόνες Συμπερασμού Σημασιολογία ΕΠΛ 412 Λογική στην
Κατηγορηματικός Λογισμός (ΗR Κεφάλαιο 2.1-2.5) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Εισαγωγή στον Κατηγορηματικό Λογισμό Σύνταξη Κανόνες Συμπερασμού Σημασιολογία ΕΠΛ 412 Λογική στην
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Αλγεβρικές Δομές Ι. 1 Ομάδα I
 Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Θεωρία Υπολογισμού. Ενότητα 3 : Γραφήματα & Αποδείξεις. Αλέξανδρος Τζάλλας
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 3 : Γραφήματα & Αποδείξεις Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Μηχανικών Πληροφορικής
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 3 : Γραφήματα & Αποδείξεις Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Μηχανικών Πληροφορικής
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Το Θεώρημα Jordan Hölder. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Το Θεώρημα Jordan Hölder Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Το Θεώρημα Jordan Hölder 31 Προκαταρκτικές Έννοιες 311 Υποορθόθετες
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Το Θεώρημα Jordan Hölder Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 3 Το Θεώρημα Jordan Hölder 31 Προκαταρκτικές Έννοιες 311 Υποορθόθετες
(a 1, b 1 ) (a 2, b 2 ) = (a 1 a 2, b 1 b 2 ).
 ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
2 n N: 0, 1,..., n A n + 1 A
 Θεωρία Υπολογισμού Ενότητα 5: Τεχνικές απόδειξης & Κλειστότητα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 5: Τεχνικές απόδειξης & Κλειστότητα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
s G 1 ). = R, Z 2 Z 3 = Z6. s, t G) s t = st. 1. H = G 4. [G : H] = a G ah = Ha.
![s G 1 ). = R, Z 2 Z 3 = Z6. s, t G) s t = st. 1. H = G 4. [G : H] = a G ah = Ha. s G 1 ). = R, Z 2 Z 3 = Z6. s, t G) s t = st. 1. H = G 4. [G : H] = a G ah = Ha.](/thumbs/91/107730007.jpg) Αλγεβρα ΙΙ Εαρινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Ομάδες-Πηλίκο: Κρατήσαμε σταθερή μια ομάδα G με ταυτοτικό το ι και μια υποομάδα H της G. Συμβολίσαμε με G 1 το G/H (το σύνολο των αριστερών συμπλόκων
Αλγεβρα ΙΙ Εαρινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Ομάδες-Πηλίκο: Κρατήσαμε σταθερή μια ομάδα G με ταυτοτικό το ι και μια υποομάδα H της G. Συμβολίσαμε με G 1 το G/H (το σύνολο των αριστερών συμπλόκων
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Στοιχεία Κατηγορηματικής Λογικής ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική Λογική
Στοιχεία Κατηγορηματικής Λογικής
 Στοιχεία Κατηγορηματικής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική
Στοιχεία Κατηγορηματικής Λογικής Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης, Δ. Σούλιου Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κατηγορηματική
Infinite Combinatorics
 Infinite Combinatorics Παναγιώτης Πατσιλινάκος ΕΜΕ 20 Ιουνίου 2017 Παναγιώτης Πατσιλινάκος (ΕΜΕ) Infinite Combinatorics 20 Ιουνίου 2017 1 / 42 1 Προαπαιτούμενα Διατακτικοί αριθμοί Πληθάριθμοι 2 Εισαγωγή
Infinite Combinatorics Παναγιώτης Πατσιλινάκος ΕΜΕ 20 Ιουνίου 2017 Παναγιώτης Πατσιλινάκος (ΕΜΕ) Infinite Combinatorics 20 Ιουνίου 2017 1 / 42 1 Προαπαιτούμενα Διατακτικοί αριθμοί Πληθάριθμοι 2 Εισαγωγή
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 4: Διατάξεις Μεταθέσεις Συνδυασμοί Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 4: Διατάξεις Μεταθέσεις Συνδυασμοί Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
HY118- ιακριτά Μαθηµατικά
 HY118- ιακριτά Μαθηµατικά Παρασκευή, 04/04/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 4/7/2017
HY118- ιακριτά Μαθηµατικά Παρασκευή, 04/04/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 4/7/2017
Τίτλος Μαθήματος: Θεωρία Ομάδων. Ενότητα: Θεωρία Sylow. Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης. Τμήμα: Μαθηματικών
 Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Θεωρία Sylow Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 2 Θεωρία Sylow 21 Τα Θεωρήματα Sylow Ορισμός 211 Μια ομάδα (G, ) τάξης p α, όπου
Τίτλος Μαθήματος: Θεωρία Ομάδων Ενότητα: Θεωρία Sylow Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης Τμήμα: Μαθηματικών Κεφάλαιο 2 Θεωρία Sylow 21 Τα Θεωρήματα Sylow Ορισμός 211 Μια ομάδα (G, ) τάξης p α, όπου
Κεφάλαιο 5 Αξιωματική Σημασιολογία και Απόδειξη Ορθότητας Προγραμμάτων
 Κεφάλαιο 5 Αξιωματική Σημασιολογία και Απόδειξη Ορθότητας Προγραμμάτων Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή Τα προγράμματα μιας (κλασικής) γλώσσας προγραμματισμού
Κεφάλαιο 5 Αξιωματική Σημασιολογία και Απόδειξη Ορθότητας Προγραμμάτων Προπτυχιακό μάθημα Αρχές Γλωσσών Προγραμματισμού Π. Ροντογιάννης 1 Εισαγωγή Τα προγράμματα μιας (κλασικής) γλώσσας προγραμματισμού
ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΕΙΣΑΓΩΓΗ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ. ΤΙ ΕΙΝΑΙ ΤΑ ΜΑΘΗΜΑΤΙΚΑ; Η επιστήμη των αριθμών Βασανιστήριο για τους μαθητές και φοιτητές Τέχνη για τους μαθηματικούς ΜΑΘΗΜΑΤΙΚΑ Α Εξάμηνο ΙΩΑΝΝΗΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΕΙΣΑΓΩΓΗ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ. ΤΙ ΕΙΝΑΙ ΤΑ ΜΑΘΗΜΑΤΙΚΑ; Η επιστήμη των αριθμών Βασανιστήριο για τους μαθητές και φοιτητές Τέχνη για τους μαθηματικούς ΜΑΘΗΜΑΤΙΚΑ Α Εξάμηνο ΙΩΑΝΝΗΣ
Τα παρακάτω σύνολα θα τα θεωρήσουμε γενικά γνωστά, αν και θα δούμε πολλές από τις ιδιότητές τους: N Z Q R C
 Κεφάλαιο 1 Εισαγωγικές έννοιες Στο κεφάλαιο αυτό θα αναφερθούμε σε ορισμένες έννοιες, οι οποίες ίσως δεν έχουν άμεση σχέση με τους διανυσματικούς χώρους, όμως θα χρησιμοποιηθούν αρκετά κατά τη μελέτη τόσο
Κεφάλαιο 1 Εισαγωγικές έννοιες Στο κεφάλαιο αυτό θα αναφερθούμε σε ορισμένες έννοιες, οι οποίες ίσως δεν έχουν άμεση σχέση με τους διανυσματικούς χώρους, όμως θα χρησιμοποιηθούν αρκετά κατά τη μελέτη τόσο
τη µέθοδο της µαθηµατικής επαγωγής για να αποδείξουµε τη Ϲητούµενη ισότητα.
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
Θεωρία Υπολογισµού Theory of Computation
 1 ο µέρος Θεωρία Υπολογισµού Theory of Computation 1 Υπολογισιµότητα - Computability o Υπολογισιµότητα (Computability) n Τι µπορεί να υπολογιστεί και τι όχι; o Υπολογιστική πολυπλοκότητα (Computational
1 ο µέρος Θεωρία Υπολογισµού Theory of Computation 1 Υπολογισιµότητα - Computability o Υπολογισιµότητα (Computability) n Τι µπορεί να υπολογιστεί και τι όχι; o Υπολογιστική πολυπλοκότητα (Computational
Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση: Να γνωρίζει: την αποδεικτική μέθοδο της μαθηματικής επαγωγής για την οποία πρέπει να γίνει κατανοητό ότι η αλήθεια
Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση: Να γνωρίζει: την αποδεικτική μέθοδο της μαθηματικής επαγωγής για την οποία πρέπει να γίνει κατανοητό ότι η αλήθεια
Μερικές διατάξεις. HY118- ιακριτά Μαθηµατικά. Μερικές διατάξεις, παράδειγµα. ιαγράµµατα Hasse: Αναπαράσταση σχέσεων µερικής διάταξης
 HY118- ιακριτά Μαθηµατικά Παρασκευή, 04/04/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 4/7/2017
HY118- ιακριτά Μαθηµατικά Παρασκευή, 04/04/2017 Αντώνης Α. Αργυρός e-mail: argyros@csd.uoc.gr Το υλικό των διαφανειών έχει βασιστεί σε διαφάνειες του Kees van Deemter, από το University of Aberdeen 4/7/2017
