Το 10ο πρόβλημα του Hilbert I
|
|
|
- Τερέντιος Μιαούλης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Το 10ο πρόβλημα του Hilbert I Το 1900 στο Παρίσι, ο David Hilbert έκανε μια ομιλία για τα 23 πιο σπουδαία μαθηματικά προβλήματα που κληρονομούσε ο 20ος αιώνας από τον 19ο. Το 10ο ήταν: Απόφανση περί επιλυσιμότητας μιας Διοφαντικής εξίσωσης δηλαδή να ευρεθεί αλγόριθμος που δεδομένου ενός πολυωνύμου με ακέραιους συντελεστές να αποφασίζει αν έχει ακέραιες ρίζες. Μία τέτοια εξίσωση D(x 1,..., x n ) = 0, όπου D πολυώνυμο με ακέραιους συντελεστές λέγεται Διοφαντική προς τιμήν του Έλληνα (Αλεξανδρινού) μαθηματικού Διόφαντου, που έζησε τον 3ο αιώνα μ.χ. Έως το 1900, υπήρχαν μέθοδοι επίλυσης (θετικής ή αρνητικής) για διάφορες υποκατηγορίες των Διοφαντικών εξισώσεων, ο Hilbert όμως ζητούσε μία καθολική μέθοδο, δηλαδή αλγόριθμο απόφασης, για όλες τις Διοφαντικές εξισώσεις. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
2 Το 10ο πρόβλημα του Hilbert II Με χρήση του θεωρήματος Lagrange (κάθε φυσικός είναι άθροισμα τεσσάρων τετραγώνων), μπορεί να δείξει κανείς ότι τα εξής δύο προβλήματα απόφασης ανάγονται το ένα στο άλλο (είναι ισοδύναμα ως προς m ): Επιλυσιμότητα Διοφαντικής εξίσωσης με ακεραίους. Επιλυσιμότητα Διοφαντικής εξίσωσης με φυσικούς. Θεώρημα (DMPR) Το 10ο πρόβλημα του Hilbert είναι μη επιλύσιμο. Και μάλιστα κατασκευαστικά: Θεώρημα Υπάρχει αλγόριθμος που, δεδομένου αλγορίθμου A που δήθεν επιλύει το 10ο πρόβλημα του Hilbert, κατασκευάζει Διοφαντική εξίσωση αντιπαράδειγμα. Δηλαδή υπάρχει ď m-αναγωγή, άρα το πρόβλημα είναι RE-πλήρες. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
3 Εικασία Davis I Ας θεωρήσουμε οικογένειες από παραμετρικές Διοφαντικές εξισώσεις: D(x 1,..., x m, a 1,..., a n ) = 0, ακέραιοι συντελεστές παράμετροι a 1,..., a n άγνωστοι x 1,..., x m. Για ποιες τιμές των παραμέτρων a i έχει η D ακέραιες ρίζες; Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
4 Εικασία Davis II Ορισμός Διοφαντικό σύνολο: t(a 1,..., a n) D(x 1,..., x m): D(x 1,..., x m, a 1,..., a n) = 0u, όπου D: Διοφαντική εξίσωση με ακέραιους συντελεστές. Παράβαλε αναδρομικά αριθμήσιμο σύνολο: t(a 1,..., a n) D(x 1,..., x m): f(x 1,..., x m, a 1,..., a n) = 0u, όπου f: αναδρομική συνάρτηση. Παρατήρηση Αν η συνάρτηση D στο ορισμό του διοφαντικού συνόλου είναι ένα πολυώνυμο ως προς τους αγνώστους x 1, x 2,..., x m τότε το σύνολο ονομάζεται πολυωνυμικά διοφαντικό σύνολο. Αν στη συνάρτηση D επιτρέπεται να υπάρχει άγνωστη μεταβλητή (x 1,..., x m ) σε εκθέτη, τότε το σύνολο ονομάζεται εκθετικά διοφαντικό. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
5 Εικασία Davis III Παράδειγμα NQ = tn n όχι τέλειο τετράγωνοu είναι διοφαντικό σύνολο διότι NQ = td D(x, y): x 2 d(y + 1) 2 1 = 0u (εξίσωση του Pell). Προφανώς κάθε Διοφαντικό σύνολο είναι (καταγράψιμο) αναδρομικά αριθμήσιμο. Παρατήρηση Και οι δύο κλάσεις D και RE είναι κλειστές ως προς ένωση και τομή όχι όμως ως προς συμπλήρωμα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
6 Εικασία Davis IV Εικασία (Davis, 1950) Κάθε αναδρομικά αριθμήσιμο σύνολο είναι διοφαντικό. Martin Davis Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
7 Εικασία Davis V Μία συνέπεια αυτής της εικασίας είναι ότι το σύνολο PRIMES είναι διοφαντικό, άρα περιγράφεται με μια πολυωνυμική εξίσωση! Το ίδιο ισχύει και για το σύνολο POWERS-OF-2. Μια άλλη συνέπεια ( Davis Normal Form, παράβαλε KNF) είναι η ύπαρξη καθολικής (universal) Διοφαντικής εξίσωσης [U n (a, k, y) = 0] που περιγράφει (με index k) κάθε r.e. [DxD(a, x) = 0 Ø Dy(U n (a, k, y) = 0] Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
8 Εικασία Davis VI Ο Martin Davis απέδειξε αμέσως: Θεώρημα (Davis Normal Form) Κάθε r.e. σύνολο περιγράφεται: ta ď z, Dx p(a, x, y, z) = 0u δηλαδή το σύνολο των παραμέτρων a ώστε όλα τα πολυώνυμα p(a, x, 0, z), p(a, x, 1, z),..., p(a, x, z, z) να έχουν ρίζα. Το ζητούμενο τώρα ήταν να απαλειφθεί ο καθολικός ποσοδείκτης για να αποδειχτεί η εικασία Davis. Αυτό έγινε μετά από τουλάχιστον 20 χρόνια. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
9 Υπολογισιμότητα J. Robinson, H. Putnam, Y. Matiyasevich I Julia Robinson Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Hilary Putnam Υπολ. & Πολυπλ. Yuri Matiyasevich Φεβρουάριος / 310
10 J. Robinson, H. Putnam, Y. Matiyasevich II Εικασία (J. Robinson) Υπάρχει διοφαντικό σύνολο ζευγαριών D τέτοιο ώστε: 1 (a, b) P D : b ď a a και D(a, b) P D : b ą a k Ορισμός Το σύνολο D = t(a, b, c) a = b c u ονομάζεται σχέση εκθετικής αυξητικότητας ή σχέση Julia Robinson. Παρατήρηση: Μέχρι την δεκαετία 1960 δεν ήταν γνωστό στους αριθμοθεωρητικούς αν υπάρχει τέτοιο σύνολο D. Η Julia Robinson (μαθήτρια του Tarski στο Berkeley) που μελετούσε την διοφαντικότητα του συνόλου POWERS-OF-2 απέδειξε το 1950 ότι η εικασία J. Robinson συνεπάγεται ότι η σχέση εκθετικής αυξητικότητας είναι διοφαντικό σύνολο. Εικασία (PAP) Υπάρχουν αριθμητικές πρόοδοι πρώτων αριθμών, αυθαιρέτου μήκους. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
11 J. Robinson, H. Putnam, Y. Matiyasevich III Ο Davis μαζί με τον φιλόσοφο (Harvard) Hilary Putnam μελέτησαν εκθετικές διοφαντικές εξισώσεις (π.χ. (x + 1) a + (y + 1) a = (z + 1) a, Fermat: μόνον για a = 1, 2) και έδειξαν το 1959 ότι: εικασία ΡΑΡ + εικασία J. Robinson ñ εικασία Davis Δυστυχώς η εικασία ΡΑΡ δεν είχε αποδειχτεί τότε. Όμως η J. Robinson κατόρθωσε να αντικαταστήσει την εικασία ΡΑΡ με κάτι σχετικό με το θεώρημα πρώτων αριθμών. Παρατήρηση Η εικασία PAP απεδείχθει το 2004 από τους Ben Green και Terence Tao και ως εκ τούτου είναι πλέον γνωστή με την ονομασία Θεώρημα Green-Tao. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
12 J. Robinson, H. Putnam, Y. Matiyasevich IV Έτσι, έχουμε: Θεώρημα (DPR) 1 Κάθε r.e. σύνολο είναι εκθετικά διοφαντικό. 2 Η εικασία J. Robinson είναι ισοδύναμη με: Κάθε r.e. σύνολο είναι (πολυωνυμικά) διοφαντικό. Παρατήρηση Η εικασία J.R. είναι ισοδύναμη με: t(a, b, a b )u είναι (πολυωνυμικά) διοφαντικό. Τέλος, ο (νεαρός, 22 ετών) Yuri Matiyasevich απέδειξε το 1970 την εικασία της J. Robinson. Έδειξε δηλαδή ότι υπάρχει σχέση που ορίζει ακριβώς την εκθετική αυξητικότητα της J. Robinson και μάλιστα η σχέση είναι t(a, b) b = Fib 2a u. Χρησιμοποίησε μια ιδιότητα των αριθμών Fibonacci που αυτός απέδειξε: Fib 2 n Fib m Ñ Fib n m. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
13 J. Robinson, H. Putnam, Y. Matiyasevich V Παρατίθενται πιο ισχυρές παραλλαγές του θεωρήματος DMPR. Θεώρημα Υπάρχει Διοφαντική εξίσωση W με μία παράμετρο a: W(a, x) = 0 έτσι ώστε το ta Dx P N m : W(a, x) = 0u είναι μη επιλύσιμο. Θεώρημα Εκτός από την παραπάνω W υπάρχει αλγόριθμος που για κάθε αλγόριθμο f μας βρίσκει ένα a f έτσι ώστε ο f να μην αποφασίζει σωστά αν η W(a f, x) έχει ρίζα. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
14 Γενικεύσεις I Παρατήρηση Αν το 10ο πρόβλημα του Hilbert είχε θετική επίλυση για ακέραιους τότε θα είχε και για ρητούς. Τώρα όμως παραμένει ανοικτό το πρόβλημα για ρητούς. Το θεώρημα DMPR έδωσε αρνητική λύση στο διάσημο 10ο Πρόβλημα του Hilbert, είναι η πιο σημαντική εφαρμογή της Λογικής στα κλασικά μαθηματικά, και ώθησε τη δημιουργία μιας καινούριας ερευνητικής περιοχής: HTP, από το αγγλικό Hilbert s Tenth Problem. Τα βασικά προβλήματα της ΗΤΡ είναι η αποκρισιμότητα των θεωριών για δομές που προκύπτουν με φυσικό τρόπο στην Άλγεβρα, τη Θεωρία Αριθμών και την Αλγεβρική Γεωμετρία. Χαρακτηριστικό της ΗΤΡ είναι ότι οι αποδείξεις δεν είναι απλές, και τείνουν να χρησιμοποιούν αποτελέσματα και μεθόδους από κλασικά μαθηματικά, έξω από τη Λογική. Και όμως, τα αποτελέσματα Θεωρίας Αριθμών που απαιτούνται για την απόδειξη του DMPR είναι σχετικά απλά κλασικές ιδιότητες της εξίσωσης Pell. Από την άλλη μεριά, το ανάλογο ερώτημα για τη δομή των ρητών αριθμών έχει αντισταθεί στις προσπάθειες πολλών διακεκριμένων μαθηματικών (από πολλούς, συναφείς κλάδους) και παραμένει το βασικό ανοικτό πρόβλημα αυτής της περιοχής: Υπάρχει αλγόριθμος που να αποφασίζει αν το τυχαίο πολυώνυμο με ρητούς συντελεστές έχει ρητές λύσεις; Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
15 Γενικεύσεις II Έτσι η περιοχή ΗΤΡ είναι ευλογημένη από ένα κλασικό θεώρημα (το DMPR), και ένα κεντρικό και (κατά γενική ομολογία) πολύ δύσκολο ανοικτό πρόβλημα και χαρακτηρίζεται από το γεγονός ότι είναι κάπου ανάμεσα στη Λογική, τη Θεωρία Αριθμών και την Αλγεβρική Γεωμετρία. Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ. & Πολυπλ. Φεβρουάριος / 310
Recursive and Recursively Enumerable sets I
 Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Recursive and Recursively Enumerable sets I Ορισμός Το σύνολο A είναι αναδρομικό ανν η χαρακτηριστική του συνάρτηση X A είναι αναδρομική. Το σύνολο A είναι αναδρομικά αριθμήσιμο (recursively enumerable)
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις.
 Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing: Όλες οι υπολογίσιμες συναρτήσεις
Τυχαιότητα (Randomness) I
 I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
I Χρησιμοποιώντας το μοντέλο δένδρων υπολογισμού, θα ορίσουμε κλάσεις πολυπλοκότητας που βασίζονται στις πιθανότητες, με βάση τυχαίες επιλογές. Αυτή η προσέγγιση είναι πολύ χρήσιμη από πρακτική άποψη,
Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές.
 Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Υπολογισιμότητα Θεώρημα Υπάρχουν υπολογίσιμες συναρτήσεις που δεν είναι πρωταρχικές αναδρομικές. Απόδειξη: Διαγωνιοποίηση. Μηχανιστική απαρίθμηση πρωταρχικών αναδρομικών συναρτήσεων: φ 0, φ 1, φ 2, Ορίζουμε:
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Στα μαθηματικά και στις άλλες επιστήμες κάνουμε συχνά υποθέσεις. Οταν δείξουμε ότι μια υπόθεση είναι αλη
 Υποθέσεις - - Θεωρήματα Μαθηματικά Πληροφορικής 1ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Στα μαθηματικά και στις άλλες επιστήμες
Υποθέσεις - - Θεωρήματα Μαθηματικά Πληροφορικής 1ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Στα μαθηματικά και στις άλλες επιστήμες
invariante Eigenschaften spezieller binärer Formen, insbesondere der
 Κουλακίδου Π. Ιστορία των Μαθηματικών Υπεύθυνη Καθηγήτρια: Χ. Χαραλάμπους Εισαγωγή David Hilbert (1862 Königsberg - 1943 Göttingen). Διδακτορικό το 1885 υπό την επίβλεψη του Ferdinand von Lindemann με
Κουλακίδου Π. Ιστορία των Μαθηματικών Υπεύθυνη Καθηγήτρια: Χ. Χαραλάμπους Εισαγωγή David Hilbert (1862 Königsberg - 1943 Göttingen). Διδακτορικό το 1885 υπό την επίβλεψη του Ferdinand von Lindemann με
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Μη επιλυσιμότητα I. Απόδειξη. Ορίζουμε # # =
 Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
Μη επιλυσιμότητα I Θεώρημα Το TOT (πρόβλημα ολικής συνάρτησης) είναι μη επιλύσιμο, δηλαδή η f δεν είναι αναδρομική όπου: 1, αν φ x είναι ολική f(x) = 0, αλλιώς Απόδειξη. Ορίζουμε h(x) = φ x (x) + 1, αν
4.6 Η ΓΡΑΜΜΙΚΗ ΔΙΟΦΑΝΤΙΚΗ ΕΞΙΣΩΣΗ
 174 46 Η ΓΡΑΜΜΙΚΗ ΔΙΟΦΑΝΤΙΚΗ ΕΞΙΣΩΣΗ Εισαγωγή Ένα από τα αρχαιότερα προβλήματα της Θεωρίας Αριθμών είναι η αναζήτηση των ακέραιων αριθμών που ικανοποιούν κάποιες δεδομένες σχέσεις Με σύγχρονη ορολογία
174 46 Η ΓΡΑΜΜΙΚΗ ΔΙΟΦΑΝΤΙΚΗ ΕΞΙΣΩΣΗ Εισαγωγή Ένα από τα αρχαιότερα προβλήματα της Θεωρίας Αριθμών είναι η αναζήτηση των ακέραιων αριθμών που ικανοποιούν κάποιες δεδομένες σχέσεις Με σύγχρονη ορολογία
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Υποθέσεις - Θεωρήματα. Μαθηματικά Πληροφορικής 1ο Μάθημα. Η χρυσή τομή. Υποθέσεις - Εικασίες
 Υποθέσεις - - Θεωρήματα Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Μαθηματικά Πληροορικής ο Μάθημα Στα μαθηματικά και στις άλλες επιστήμες κάνουμε συχνά υποθέσεις. Οταν δείξουμε ότι μια υπόθεση είναι
Υποθέσεις - - Θεωρήματα Υποθέσεις - - Θεωρήματα Υποθέσεις - Θεωρήματα Μαθηματικά Πληροορικής ο Μάθημα Στα μαθηματικά και στις άλλες επιστήμες κάνουμε συχνά υποθέσεις. Οταν δείξουμε ότι μια υπόθεση είναι
Εαρινό Εξάμηνο Χ. Χαραλάμπους ΑΠΘ
 Εαρινό εξάμηνο 2012 28.03.12 Χ. Χαραλάμπους Τι είναι αριθμητική? Τι είναι Άλγεβρα? Είναι Άλγεβρα η «Γεωμετρική Άλγεβρα»? Έκανε ο Διόφαντος Άλγεβρα? Ασχολήθηκαν με Άλγεβρα οι αρχαίοι Βαβυλώνιοι? Πολυωνυμικές
Εαρινό εξάμηνο 2012 28.03.12 Χ. Χαραλάμπους Τι είναι αριθμητική? Τι είναι Άλγεβρα? Είναι Άλγεβρα η «Γεωμετρική Άλγεβρα»? Έκανε ο Διόφαντος Άλγεβρα? Ασχολήθηκαν με Άλγεβρα οι αρχαίοι Βαβυλώνιοι? Πολυωνυμικές
y 1 (x) f(x) W (y 1, y 2 )(x) dx,
 Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
Συνήθεις Διαφορικές Εξισώσεις Ι Ασκήσεις - 07/1/017 Μέρος 1ο: Μη Ομογενείς Γραμμικές Διαφορικές Εξισώσεις Δεύτερης Τάξης Θεωρούμε τη γραμμική μή-ομογενή διαφορική εξίσωση y + p(x) y + q(x) y = f(x), x
a n = 3 n a n+1 = 3 a n, a 0 = 1
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Δηλαδή η ρητή συνάρτηση είναι πηλίκο δύο ακέραιων πολυωνύμων. Επομένως, το ζητούμενο ολοκλήρωμα είναι της μορφής
 D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
α) f(x(t), y(t)) = 0,
 Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ρητές καμπύλες Μια επίπεδη αλγεβρική καμπύλη V (f) είναι το σύνολο όλων των σημείων του επιπέδου K 2 που μηδενίζουν κάποιο συγκεκριμένο ανάγωγο πολυώνυμο f K[x, y], δηλαδή V (f) = {(x 0, y 0 ) K 2 f(x
Ενότητα 2 Πρόβλημα σελ 13-18
 Πρόβλημα Ποιό θεωρείτε το σημαντικότερο πρόβλημα της ανθρωπότητας και ποιο το σημαντικότερο πρόβλημα που χρήζει αντιμετώπισης στο σχολείο ; Με τον όρο Πρόβλημα προσδιορίζεται μια κατάσταση η οποία χρήζει
Πρόβλημα Ποιό θεωρείτε το σημαντικότερο πρόβλημα της ανθρωπότητας και ποιο το σημαντικότερο πρόβλημα που χρήζει αντιμετώπισης στο σχολείο ; Με τον όρο Πρόβλημα προσδιορίζεται μια κατάσταση η οποία χρήζει
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου. Άλγεβρα...
 Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου Άλγεβρα 1.1 Β: Δυνάμεις πραγματικών αριθμών. 1. Πως ορίζεται η δύναμη ενός πραγματικού αριθμού ; Η δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα
Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου Άλγεβρα 1.1 Β: Δυνάμεις πραγματικών αριθμών. 1. Πως ορίζεται η δύναμη ενός πραγματικού αριθμού ; Η δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα
Μηχανές Turing (T.M) I
 Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
Μηχανές Turing (T.M) I Οι βασικές λειτουργίες μιας TM είναι: Διάβασε το περιεχόμενο του τρέχοντος κυττάρου Γράψε 1 ή 0 στο τρέχον κύτταρο Κάνε τρέχον το αμέσως αριστερότερο ή το αμέσως δεξιότερο κύτταρο
2018 Φάση 2 ιαγωνίσµατα Επανάληψης ΑΛΓΕΒΡΑ. Α' Γενικού Λυκείου. Σάββατο 21 Απριλίου 2018 ιάρκεια Εξέτασης:3 ώρες ΘΕΜΑΤΑ
 ΘΕΜΑ A ΑΛΓΕΒΡΑ Α' Γενικού Λυκείου Σάββατο 1 Απριλίου 018 ιάρκεια Εξέτασης: ώρες ΘΕΜΑΤΑ Πεδίο ορισμού μιας συνάρτησης f (x) από ένα σύνολο Α σε ένα σύνολο Β ονομάζουμε το σύνολο Α, στο οποίο φαίνονται οι
ΘΕΜΑ A ΑΛΓΕΒΡΑ Α' Γενικού Λυκείου Σάββατο 1 Απριλίου 018 ιάρκεια Εξέτασης: ώρες ΘΕΜΑΤΑ Πεδίο ορισμού μιας συνάρτησης f (x) από ένα σύνολο Α σε ένα σύνολο Β ονομάζουμε το σύνολο Α, στο οποίο φαίνονται οι
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Burnside
 ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 25/9/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ
 14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
πυθαγόρειες τριάδες, τριγωνομετρία και υπολογισμός ολοκληρωμάτων.
 πυθαγόρειες τριάδες, τριγωνομετρία και υπολογισμός ολοκληρωμάτων. Αριστείδης Κοντογεώργης -Τμήμα Μαθηματικών ΕΚΠΑ Πρότυπο Λύκειο Ευαγγελικής Σχολής Σμύρνης 21 Οκτωβρίου 2015 1 το τελευταίο θεώρημα του
πυθαγόρειες τριάδες, τριγωνομετρία και υπολογισμός ολοκληρωμάτων. Αριστείδης Κοντογεώργης -Τμήμα Μαθηματικών ΕΚΠΑ Πρότυπο Λύκειο Ευαγγελικής Σχολής Σμύρνης 21 Οκτωβρίου 2015 1 το τελευταίο θεώρημα του
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ 016-17 1. Τι ονομάζεται αλγεβρική παράσταση; Ονομάζεται κάθε έκφραση που περιέχει πράξεις μεταξύ αριθμών και μεταβλητών.. Τι ονομάζεται αριθμητική τιμή αλγεβρικής
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ 016-17 1. Τι ονομάζεται αλγεβρική παράσταση; Ονομάζεται κάθε έκφραση που περιέχει πράξεις μεταξύ αριθμών και μεταβλητών.. Τι ονομάζεται αριθμητική τιμή αλγεβρικής
Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου
 Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου Άλγεβρα 1.1 Β : Δυνάμεις πραγματικών αριθμών. 1. Πως ορίζεται η δύναμη ενός πραγματικού αριθμού ; Η δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα
Ερωτήσεις θεωρίας για τα Μαθηματικά Γ γυμνασίου Άλγεβρα 1.1 Β : Δυνάμεις πραγματικών αριθμών. 1. Πως ορίζεται η δύναμη ενός πραγματικού αριθμού ; Η δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα
A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις
![A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις](/thumbs/93/111356738.jpg) ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
10.05.12 ΑΠΘ. Χαρά Χαραλάμπους Τμήμα Μαθηματικών ΑΠΘ. Ιστορία των Μαθηματικών Εαρινό Εξάμηνο 2012
 Εαρινό εξάμηνο 2012 10.05.12 Χ. Χαραλάμπους 1. Έχει κάθε πολυώνυμο ρίζα? 2. Πόσες ρίζες έχει ένα πολυώνυμο βαθμού n? 3. Μπορούμε να καθορίσουμε πότε οι ρίζες είναι ρητές, πραγματικές, θετικές, κλπ? 4.
Εαρινό εξάμηνο 2012 10.05.12 Χ. Χαραλάμπους 1. Έχει κάθε πολυώνυμο ρίζα? 2. Πόσες ρίζες έχει ένα πολυώνυμο βαθμού n? 3. Μπορούμε να καθορίσουμε πότε οι ρίζες είναι ρητές, πραγματικές, θετικές, κλπ? 4.
Σχήματα McCarthy I. Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα:
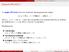 Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Σχήματα McCarthy I Το σχήμα McCarthy είναι ένα γενικότερο προγραμματιστικό σχήμα: f(x, y) = if g(...) = 0 then h(...) else k(...) όπου g(...), h(...) και k(...) είναι όροι-συναρτήσεις που κατασκευάζονται
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
(Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 2. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
f f 2 0 B f f 0 1 B 10.3 Ακρότατα υπό συνθήκες Πολλαπλασιαστές του Lagrange
 Μέγιστα και ελάχιστα 39 f f B f f yx y x xy Οι ιδιοτιμές του πίνακα Β είναι λ =-, λ =- και οι δυο αρνητικές, άρα το κρίσιμο σημείο (,) είναι σημείο τοπικού μεγίστου. Εφαρμογή 6: Στο παράδειγμα 3 ο αντίστοιχος
Μέγιστα και ελάχιστα 39 f f B f f yx y x xy Οι ιδιοτιμές του πίνακα Β είναι λ =-, λ =- και οι δυο αρνητικές, άρα το κρίσιμο σημείο (,) είναι σημείο τοπικού μεγίστου. Εφαρμογή 6: Στο παράδειγμα 3 ο αντίστοιχος
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
P(n, r) = n! P(n, r) = n r. (n r)! n r. n+r 1 r n!
 Διακριτά Μαθηματικά Σύνοψη Θεωρίας Τυπολόγιο Αναστασία Κόλλια 20/11/2016 1 / 55 Κανόνες γινομένου και αθροίσματος Κανόνας αθροίσματος: Αν ένα γεγονός μπορεί να συμβεί κατά m τρόπους και ένα άλλο γεγονός
Διακριτά Μαθηματικά Σύνοψη Θεωρίας Τυπολόγιο Αναστασία Κόλλια 20/11/2016 1 / 55 Κανόνες γινομένου και αθροίσματος Κανόνας αθροίσματος: Αν ένα γεγονός μπορεί να συμβεί κατά m τρόπους και ένα άλλο γεγονός
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
ΓΥΜΝΑΣΙΟ ΠΟΛΕΜΙΔΙΩΝ ΣΧ. ΧΡΟΝΙΑ
 ΓΥΜΝΑΣΙΟ ΠΟΛΕΜΙΔΙΩΝ ΣΧ. ΧΡΟΝΙΑ 2015-16 ΕΞΕΤΑΣΤΕΑ ΥΛΗ Α ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΕΥΧΟΣ Α ΕΝΟΤΗΤΑ 1: ΣΥΝΟΛΑ (Σελ. 25 42) Η Έννοια του Συνόλου Σχέσεις Συνόλων Πράξεις Συνόλων ΕΝΟΤΗΤΑ 2: ΑΡΙΘΜΟΙ (Σελ. 46 83)
ΓΥΜΝΑΣΙΟ ΠΟΛΕΜΙΔΙΩΝ ΣΧ. ΧΡΟΝΙΑ 2015-16 ΕΞΕΤΑΣΤΕΑ ΥΛΗ Α ΤΑΞΗΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΕΥΧΟΣ Α ΕΝΟΤΗΤΑ 1: ΣΥΝΟΛΑ (Σελ. 25 42) Η Έννοια του Συνόλου Σχέσεις Συνόλων Πράξεις Συνόλων ΕΝΟΤΗΤΑ 2: ΑΡΙΘΜΟΙ (Σελ. 46 83)
Περιεχόμενα 1 Πρωτοβάθμια Λογική Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων ) / 60
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
O n+2 = O n+1 + N n+1 = α n+1 N n+2 = O n+1. α n+2 = O n+2 + N n+2 = (O n+1 + N n+1 ) + (O n + N n ) = α n+1 + α n
 Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Σχέσεις Αναδρομής Γραμμικές Σχέσεις Αναδρομής με σταθερούς συντελεστές
Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Σχέσεις Αναδρομής Γραμμικές Σχέσεις Αναδρομής με σταθερούς συντελεστές
ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 Θ ΕΩΡΙA 10
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 04 Θ ΕΩΡΙA 0 ΘΕΜΑ A Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στην κόλλα σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 04 Θ ΕΩΡΙA 0 ΘΕΜΑ A Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στην κόλλα σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη
). Πράγματι, στο διάστημα [ x, x 1 2 ικανοποιεί τις προϋποθέσεις του Θ.Μ.Τ. Επομένως, υπάρχει ξ x 1,
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΔΕΥΤΕΡΑ 8 MAΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α A Αποδεικνύουμε το θεώρημα στην περίπτωση που
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΔΕΥΤΕΡΑ 8 MAΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α A Αποδεικνύουμε το θεώρημα στην περίπτωση που
Απαντήσεις θεωρίας Κεφάλαιο 1ο. (α μέρος)
 Μαθηματικά Γ Γυμνασίου Απαντήσεις θεωρίας Κεφάλαιο 1ο. (α μέρος) 1. Πως προσθέτουμε δυο πραγματικούς αριθμούς; Για να προσθέσουμε δύο ομόσημους αριθμούς, προσθέτουμε τις απόλυτες τιμές τους και στο άθροισμά
Μαθηματικά Γ Γυμνασίου Απαντήσεις θεωρίας Κεφάλαιο 1ο. (α μέρος) 1. Πως προσθέτουμε δυο πραγματικούς αριθμούς; Για να προσθέσουμε δύο ομόσημους αριθμούς, προσθέτουμε τις απόλυτες τιμές τους και στο άθροισμά
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να αναγνωρίζει πότε μια αλγεβρική παράσταση της πραγματικής μεταβλητής x, είναι πολυώνυμο και να διακρίνει τα στοιχεία του: όροι, συντελεστές, σταθερός
Σημειώσεις Μαθηματικών 2
 Σημειώσεις Μαθηματικών 2 Συναρτήσεις - 3 Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 3 Συνέχεια Συναρτήσεων 3.1 Όρισμός Συνεχούς Συνάρτησης Ορισμός Μια συνάρτηση f ονομάζεται συνεχής στο x 0 Df αν υπάρχει το πραγματικός
Σημειώσεις Μαθηματικών 2 Συναρτήσεις - 3 Ραφαήλ Φάνης Μαθηματικός 1 Κεφάλαιο 3 Συνέχεια Συναρτήσεων 3.1 Όρισμός Συνεχούς Συνάρτησης Ορισμός Μια συνάρτηση f ονομάζεται συνεχής στο x 0 Df αν υπάρχει το πραγματικός
ΜΕΜ251 Αριθμητική Ανάλυση
 ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
ΜΕΜ251 Αριθμητική Ανάλυση Διάλεξη 10, 12 Μαρτίου 2018 Μιχάλης Πλεξουσάκης Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Περιεχόμενα 1. Παρεμβολή 2. Παράσταση και υπολογισμός του πολυωνύμου παρεμβολής
( ) ( ) ( ) 1. α 0. Η παράσταση. Τα αποτελέσµατα σχετικά µε τις ρίζες της εξίσωσης συνοψίζονται στον παρακάτω πίνακα: Αν = 0
 IΛΥΣΗ ΕΞΙΣΩΣΗΣ Β ΒΑΘΜΟΥ ΕΞΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ Εξίσωση β βαθµού λέγεται κάθε εξίσωση της µορφής α, β, γ R µε α Η παράσταση α = β 4αγ λέγεται διακρίνουσα της εξίσωσης Τα αποτελέσµατα σχετικά µε τις ρίζες της
IΛΥΣΗ ΕΞΙΣΩΣΗΣ Β ΒΑΘΜΟΥ ΕΞΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ Εξίσωση β βαθµού λέγεται κάθε εξίσωση της µορφής α, β, γ R µε α Η παράσταση α = β 4αγ λέγεται διακρίνουσα της εξίσωσης Τα αποτελέσµατα σχετικά µε τις ρίζες της
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
ΑΠΘ. Χαρά Χαραλάμπους Τμήμα Μαθηματικών ΑΠΘ. Ιστορία των Μαθηματικών Εαρινό Εξάμηνο 2014
 Εαρινό εξάμηνο 2014 21.05.14 Χ. Χαραλάμπους Ποια είναι η πρόοδος στην Άλγεβρα την εποχή αυτή? Η Άλγεβρα μέχρι τώρα ασχολείται με εύρεση ριζών για πολυωνυμικές εξισώσεις. Χάρις στο έργα των Viete (16 ος
Εαρινό εξάμηνο 2014 21.05.14 Χ. Χαραλάμπους Ποια είναι η πρόοδος στην Άλγεβρα την εποχή αυτή? Η Άλγεβρα μέχρι τώρα ασχολείται με εύρεση ριζών για πολυωνυμικές εξισώσεις. Χάρις στο έργα των Viete (16 ος
Séminaire Grothendieck
 Séminaire Grothendieck in memoriam 28 March 928 3 November 204 Αριστείδης Κοντογεώργης 7 Φεβρουαρίου 205 Συνιστώμενη βιβλιογραφία. J.S Milne, Étale Cohomology 2. P. Deligne, SGA 4 2 Cohomologie étale Εισαγωγή
Séminaire Grothendieck in memoriam 28 March 928 3 November 204 Αριστείδης Κοντογεώργης 7 Φεβρουαρίου 205 Συνιστώμενη βιβλιογραφία. J.S Milne, Étale Cohomology 2. P. Deligne, SGA 4 2 Cohomologie étale Εισαγωγή
ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ B ΤΑΞΗΣ. χρησιμοποιήσουμε καθημερινά φαινόμενα όπως το θερμόμετρο, Θετικοί-Αρνητικοί αριθμοί.
 ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ B ΤΑΞΗΣ ΑΛΓΕΒΡΑ (50 Δ. ώρες) Περιεχόμενα Στόχοι Οδηγίες - ενδεικτικές δραστηριότητες Οι μαθητές να είναι ικανοί: Μπορούμε να ΟΙ ΑΚΕΡΑΙΟΙ ΑΡΙΘΜΟΙ χρησιμοποιήσουμε καθημερινά φαινόμενα
ΑΝΑΛΥΤΙΚΟ ΠΡΟΓΡΑΜΜΑ B ΤΑΞΗΣ ΑΛΓΕΒΡΑ (50 Δ. ώρες) Περιεχόμενα Στόχοι Οδηγίες - ενδεικτικές δραστηριότητες Οι μαθητές να είναι ικανοί: Μπορούμε να ΟΙ ΑΚΕΡΑΙΟΙ ΑΡΙΘΜΟΙ χρησιμοποιήσουμε καθημερινά φαινόμενα
n ίδια n διαφορετικά n n 0 n n n 1 n n n n 0 4
 Διακριτά Μαθηματικά Ι Επαναληπτικό Μάθημα 1 Συνδυαστική 2 Μεταξύ 2n αντικειμένων, τα n είναι ίδια. Βρείτε τον αριθμό των επιλογών n αντικειμένων από αυτά τα 2n αντικείμενα. Μεταξύ 3n + 1 αντικειμένων τα
Διακριτά Μαθηματικά Ι Επαναληπτικό Μάθημα 1 Συνδυαστική 2 Μεταξύ 2n αντικειμένων, τα n είναι ίδια. Βρείτε τον αριθμό των επιλογών n αντικειμένων από αυτά τα 2n αντικείμενα. Μεταξύ 3n + 1 αντικειμένων τα
ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 Θ ΕΩΡΙA 15
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 04 Θ ΕΩΡΙA 5 ΘΕΜΑ A Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στην κόλλα σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 04 Θ ΕΩΡΙA 5 ΘΕΜΑ A Α Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στην κόλλα σας δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση τη
Απαρίθμηση ζευγών φυσικών αριθμών I. C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση
 Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I 0 0 1 2 3 4... 1 2 3 4...... C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι
Κωδικοποίηση Απαρίθμηση ζευγών φυσικών αριθμών I 0 0 1 2 3 4... 1 2 3 4...... C(0, 0) = 0 C(2, 1) = 7 κωδικοποίηση κατά Cantor D 1 (7)=2, D 2 (7)=1 : αποκωδικοποίηση C(m, n) = (n+m)(n+m+1) 2 + m, η C είναι
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
4.3 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ & ΑΝΙΣΩΣΕΙΣ
 4.3 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ & ΑΝΙΣΩΣΕΙΣ ΘΕΩΡΙΑ. Πολυωνυµική εξίσωση Λέγεται κάθε εξίσωση της µορφής Ρ(x) = 0, όπου Ρ(x) πολυώνυµο.. Ρίζα πολυωνυµικής εξίσωσης Λέγεται κάθε ρίζα του αντίστοιχου πολυωνύµου.
4.3 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ & ΑΝΙΣΩΣΕΙΣ ΘΕΩΡΙΑ. Πολυωνυµική εξίσωση Λέγεται κάθε εξίσωση της µορφής Ρ(x) = 0, όπου Ρ(x) πολυώνυµο.. Ρίζα πολυωνυµικής εξίσωσης Λέγεται κάθε ρίζα του αντίστοιχου πολυωνύµου.
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 8. Πότε το γινόμενο δύο ή περισσοτέρων αριθμών παραγόντων είναι ίσο με το μηδέν ;
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΑ Β ΓΥΜΝΑΣΙΟΥ. ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ
 1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
1. Τι καλείται μεταβλητή; ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΑ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο ΑΛΓΕΒΡΑ Μεταβλητή είναι ένα γράμμα (π.χ., y, t, ) που το χρησιμοποιούμε για να παραστήσουμε ένα οποιοδήποτε στοιχείο ενός συνόλου..
ΓΕΝΙΚΕΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2009
 1 ΘΕΜΑ 1 Α. Σχολικό βιβλίο Σελ. 251. Β. Σχολικό βιβλίο Σελ. 213. Γ. α. Σωστό β. Σωστό γ. Λάθος δ. Λάθος ε. Λάθος ΘΕΜΑ 2 Α. α. Έστω η εικόνα του στο μιγαδικό επίπεδο. Τότε θα έχουμε: η οποία είναι η ζητούμενη
1 ΘΕΜΑ 1 Α. Σχολικό βιβλίο Σελ. 251. Β. Σχολικό βιβλίο Σελ. 213. Γ. α. Σωστό β. Σωστό γ. Λάθος δ. Λάθος ε. Λάθος ΘΕΜΑ 2 Α. α. Έστω η εικόνα του στο μιγαδικό επίπεδο. Τότε θα έχουμε: η οποία είναι η ζητούμενη
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
ψ φ2 = k χ φ2 = 4k χ φ1 = χ φ1 + χ φ2 + 3 = 4(k 1 + k 2 + 1) + 1 ψ φ1 = ψ φ1 + χ φ2 = k k = (k 1 + k 2 + 1) + 1
 Ασκήσεις στο μάθημα της Λογικής 15 Οκτωβρίου 2015 Άσκηση 1. Να δειχτεί ότι δεν υπάρχουν τύποι μήκους 2,3,6 αλλά κάθε άλλο (θετικό ακέραιο) μήκος είναι δυνατό (άσκηση 2, σελίδα 39) Απόδειξη. Δείχνουμε πρώτα
Ασκήσεις στο μάθημα της Λογικής 15 Οκτωβρίου 2015 Άσκηση 1. Να δειχτεί ότι δεν υπάρχουν τύποι μήκους 2,3,6 αλλά κάθε άλλο (θετικό ακέραιο) μήκος είναι δυνατό (άσκηση 2, σελίδα 39) Απόδειξη. Δείχνουμε πρώτα
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
Εξεταστέα ύλη μαθηματικών Α Λυκείου 2017
 Εξεταστέα ύλη μαθηματικών Α Λυκείου 2017 Α Λυκείου Γεωμετρία Κεφάλαιο 3 3.1 Είδη και στοιχεία τριγώνων 3.2 1 ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.3 2 ο Κριτήριο ισότητας
Εξεταστέα ύλη μαθηματικών Α Λυκείου 2017 Α Λυκείου Γεωμετρία Κεφάλαιο 3 3.1 Είδη και στοιχεία τριγώνων 3.2 1 ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.3 2 ο Κριτήριο ισότητας
Θεωρία Υπολογισµού Theory of Computation
 1 ο µέρος Θεωρία Υπολογισµού Theory of Computation 1 Υπολογισιµότητα - Computability o Υπολογισιµότητα (Computability) n Τι µπορεί να υπολογιστεί και τι όχι; o Υπολογιστική πολυπλοκότητα (Computational
1 ο µέρος Θεωρία Υπολογισµού Theory of Computation 1 Υπολογισιµότητα - Computability o Υπολογισιµότητα (Computability) n Τι µπορεί να υπολογιστεί και τι όχι; o Υπολογιστική πολυπλοκότητα (Computational
7. Αν υψώσουμε και τα δύο μέλη μιας εξίσωσης στον κύβο (και γενικά σε οποιαδήποτε περιττή δύναμη), τότε προκύπτει
 8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
Εαρινό Εξάμηνο Χ. Χαραλάμπους ΑΠΘ. Ιστορία των Μαθηματικών. Χαρά Χαραλάμπους Τμήμα Μαθηματικών, ΑΠΘ
 Εαρινό εξάμηνο 2011 09.05.11 Χ. Χαραλάμπους ΑΠΘ Χάρις στο έργα των Viete (16 ος αιώνας) και Descartes (17 ος αιώνας) ξεκινά η ανάπτυξη της θεωρίας των πολυωνυμικών εξισώσεων. 1. Έχει κάθε πολυώνυμο ρίζα?
Εαρινό εξάμηνο 2011 09.05.11 Χ. Χαραλάμπους ΑΠΘ Χάρις στο έργα των Viete (16 ος αιώνας) και Descartes (17 ος αιώνας) ξεκινά η ανάπτυξη της θεωρίας των πολυωνυμικών εξισώσεων. 1. Έχει κάθε πολυώνυμο ρίζα?
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
ΕΝΟΤΗΤΑ 2: Πραγματικοί Αριθμοί
 Ενδεικτικός Προγραμματισμός ΕΝΟΤΗΤΑ 2: Πραγματικοί Αριθμοί 12 περίοδοι Δείκτες επιτυχίας: Ορίζουν την έννοια της νιοστής ρίζας ενός αριθμού α και αποδεικνύουν τις ιδιότητες ριζών, όταν ν N, ν 0, 1, α R
Ενδεικτικός Προγραμματισμός ΕΝΟΤΗΤΑ 2: Πραγματικοί Αριθμοί 12 περίοδοι Δείκτες επιτυχίας: Ορίζουν την έννοια της νιοστής ρίζας ενός αριθμού α και αποδεικνύουν τις ιδιότητες ριζών, όταν ν N, ν 0, 1, α R
Κεφ. 3: Παρεμβολή. 3.1 Εισαγωγή. 3.2 Πολυωνυμική παρεμβολή Παρεμβολή Lagrange Παρεμβολή Newton. 3.3 Παρεμβολή με κυβικές splines
 Κεφ. 3: Παρεμβολή 3. Εισαγωγή 3. Πολυωνυμική παρεμβολή 3.. Παρεμβολή Lagrage 3.. Παρεμβολή Newto 3.3 Παρεμβολή με κυβικές splies 3.4 Μέθοδος ελαχίστων τετραγώνων 3.5 Παρεμβολή με ορθογώνια πολυώνυμα 3.
Κεφ. 3: Παρεμβολή 3. Εισαγωγή 3. Πολυωνυμική παρεμβολή 3.. Παρεμβολή Lagrage 3.. Παρεμβολή Newto 3.3 Παρεμβολή με κυβικές splies 3.4 Μέθοδος ελαχίστων τετραγώνων 3.5 Παρεμβολή με ορθογώνια πολυώνυμα 3.
Πολυπλοκότητα. Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης. Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης. Προσπάθεια υλοποίησης
 Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης Προσπάθεια υλοποίησης Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι
Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, εύρος ζώνης Προσπάθεια υλοποίησης Παράμετροι της αποδοτικότητας ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 2018
 ΘΕΜΑ Α ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 8 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ Α Απόδειξη
ΘΕΜΑ Α ΕΙΣΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΤΟΥ ΕΞΩΤΕΡΙΚΟΥ ΚΑΙ ΤΕΚΝΩΝ ΕΛΛΗΝΩΝ ΥΠΑΛΛΗΛΩΝ ΠΟΥ ΥΠΗΡΕΤΟΥΝ ΣΤΟ ΕΞΩΤΕΡΙΚΟ ΠΕΜΠΤΗ 6 ΣΕΠΤΕΜΒΡΙΟΥ 8 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΑΠΑΝΤΗΣΕΙΣ Α Απόδειξη
Μονώνυμα. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Μονώνυμα Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Πράξεις με μονώνυμα Ενότητα 2 η Πράξεις με μονώνυμα και πολυώνυμα Σκοπός Ο σκοπός της 2 ης ενότητας είναι να μάθουν
Μονώνυμα Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Πράξεις με μονώνυμα Ενότητα 2 η Πράξεις με μονώνυμα και πολυώνυμα Σκοπός Ο σκοπός της 2 ης ενότητας είναι να μάθουν
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 118 ερωτήσεις θεωρίας με απάντηση 324 416 ασκήσεις για λύση. 20 συνδυαστικά θέματα εξετάσεων
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ 118 ερωτήσεις θεωρίας με απάντηση 34 416 ασκήσεις για λύση ερωτήσεις κατανόησης λυμένα παραδείγματα 0 συνδυαστικά θέματα εξετάσεων Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Εισαγωγική ενότητα Το λεξιλόγιο
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ 118 ερωτήσεις θεωρίας με απάντηση 34 416 ασκήσεις για λύση ερωτήσεις κατανόησης λυμένα παραδείγματα 0 συνδυαστικά θέματα εξετάσεων Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Εισαγωγική ενότητα Το λεξιλόγιο
Άλγεβρα Α ΕΠΑΛ Εξεταστέα ύλη Από το βιβλίο «Άλγεβρα και Στοιχεία Πιθανοτήτων Α Γενικού Λυκείου» Εισαγωγικό κεφάλαιο E.2. Σύνολα Κεφ.
 Άλγεβρα Α ΕΠΑΛ Από το βιβλίο «Άλγεβρα και Στοιχεία Πιθανοτήτων Α Γενικού Λυκείου» Εισαγωγικό κεφάλαιο E.2. Σύνολα Κεφ.2ο: Οι Πραγματικοί Αριθμοί 2.1 Οι Πράξεις και οι Ιδιότητές τους 2.2 Διάταξη Πραγματικών
Άλγεβρα Α ΕΠΑΛ Από το βιβλίο «Άλγεβρα και Στοιχεία Πιθανοτήτων Α Γενικού Λυκείου» Εισαγωγικό κεφάλαιο E.2. Σύνολα Κεφ.2ο: Οι Πραγματικοί Αριθμοί 2.1 Οι Πράξεις και οι Ιδιότητές τους 2.2 Διάταξη Πραγματικών
Πρότυπα κλειστά τμήματα «ΜΕΘΟΔΟΣ» 2.6. ΘΕΩΡΗΜΑ ROLLE. Υποδείξεις Απαντήσεις Ασκήσεων. Προσδιορισμός παραμέτρων ώστε να εφαρμόζεται το θεώρημα Rolle
 Σελ.414 Πρότυπα κλειστά τμήματα «ΜΕΘΟΔΟΣ».6. ΘΕΩΡΗΜΑ ROLLE Υποδείξεις Απαντήσεις Ασκήσεων.344. α. Σωστό β. Λάθος γ. Λάθος δ. Σωστό ε. Σωστό στ. Σωστό ζ. Λάθος η. Σωστό θ. Σωστό ι. Λάθος ια. Σωστό ιβ. Σωστό
Σελ.414 Πρότυπα κλειστά τμήματα «ΜΕΘΟΔΟΣ».6. ΘΕΩΡΗΜΑ ROLLE Υποδείξεις Απαντήσεις Ασκήσεων.344. α. Σωστό β. Λάθος γ. Λάθος δ. Σωστό ε. Σωστό στ. Σωστό ζ. Λάθος η. Σωστό θ. Σωστό ι. Λάθος ια. Σωστό ιβ. Σωστό
ΑΠΘ. Χαρά Χαραλάμπους Τμήμα Μαθηματικών ΑΠΘ. Ιστορία των Μαθηματικών Εαρινό Εξάμηνο 2014
 Εαρινό εξάμηνο 2014 13.03.14 Χ. Χαραλάμπους Εντονες πυθαγόρειες επιδράσεις. Η Γεωμετρία και τα Μαθηματικά έχουν μια ξεχωριστή ξχ θέση. Ουδείς αγεωμέτρητος εισί Στον κόσμο των ιδεών τα μαθηματικά αντικείμενα
Εαρινό εξάμηνο 2014 13.03.14 Χ. Χαραλάμπους Εντονες πυθαγόρειες επιδράσεις. Η Γεωμετρία και τα Μαθηματικά έχουν μια ξεχωριστή ξχ θέση. Ουδείς αγεωμέτρητος εισί Στον κόσμο των ιδεών τα μαθηματικά αντικείμενα
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
Υπερβατικοί Αριθµοί και Θεώρηµα του Liouville
 Υπερβατικοί Αριθµοί και Θεώρηµα του Liouville Χρήστος Κονταράτος 14 Νοεµβρίου 2014 1 Περιεχόµενα 1 Εισαγωγή 3 2 Το Θεώρηµα του Liouville 4 3 Η Υπερβατικότητα του ξ 6 4 Αριθµοί του Liouville 8 2 1 Εισαγωγή
Υπερβατικοί Αριθµοί και Θεώρηµα του Liouville Χρήστος Κονταράτος 14 Νοεµβρίου 2014 1 Περιεχόµενα 1 Εισαγωγή 3 2 Το Θεώρηµα του Liouville 4 3 Η Υπερβατικότητα του ξ 6 4 Αριθµοί του Liouville 8 2 1 Εισαγωγή
ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
 9 Ιουνίου ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απαντήσεις Θεμάτων Επαναληπτικών Πανελλαδικών Εξετάσεων Εσπερινών Γενικών Λυκείων (Νέο & Παλιό Σύστημα)
9 Ιουνίου ΜΑΘΗΜΑΤΙΚΑ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ & ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Απαντήσεις Θεμάτων Επαναληπτικών Πανελλαδικών Εξετάσεων Εσπερινών Γενικών Λυκείων (Νέο & Παλιό Σύστημα)
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
~ 1 ~ ΜΙΓΑΔΙΚΟΣ ΛΟΓΙΣΜΟΣ & ΟΛΟΚΛΗΡΩΤΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ 2013 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ
 ~ ~ ΜΙΓΑΔΙΚΟΣ ΛΟΓΙΣΜΟΣ & ΟΛΟΚΛΗΡΩΤΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΘΕΜΑ α) Μια συνάρτηση f ( ) u( x, y) iv( x, y ) έχει παράγωγο σε ένα σημείο x iy αν ικανοποιούνται
~ ~ ΜΙΓΑΔΙΚΟΣ ΛΟΓΙΣΜΟΣ & ΟΛΟΚΛΗΡΩΤΙΚΟΙ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΕΞΕΤΑΣΤΙΚΗ ΠΕΡΙΟΔΟΣ ΙΑΝΟΥΑΡΙΟΥ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΘΕΜΑ α) Μια συνάρτηση f ( ) u( x, y) iv( x, y ) έχει παράγωγο σε ένα σημείο x iy αν ικανοποιούνται
Επαναληπτικές Ασκήσεις
 Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x
Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΑΣ ΔΙΟΙΚΗΣΗΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι 11 ΟΚΤΩΒΡΙΟΥ 2016 ΜΗ ΓΡΑΜΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Οικονομικές Συναρτήσεις με μεταβλητούς ρυθμούς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΑΣ ΔΙΟΙΚΗΣΗΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΜΑΘΗΜΑΤΙΚΑ Ι 11 ΟΚΤΩΒΡΙΟΥ 2016 ΜΗ ΓΡΑΜΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΕΙΣΑΓΩΓΗ Οικονομικές Συναρτήσεις με μεταβλητούς ρυθμούς
Κεφάλαιο 1: Προβλήµατα τύπου Sturm-Liouville
 Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
Κεφάλαιο : Προβλήµατα τύπου Stur-Liouvie. Ορισµός προβλήµατος Stur-Liouvie Πολλές τεχνικές επίλυσης µερικών διαφορικών εξισώσεων βασίζονται στην αναγωγή της µερικής διαφορικής εξίσωσης σε συνήθεις διαφορικές
ΚΕΦΑΛΑΙΟ 2 Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ 10 ΕΠΑΝΑΛΗΨΕΙΣ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΕΣ ΤΑΞΕΙΣ α ) Ταυτότητες 1. (a-β)(a+β)=a - b. (a ± b ) = a ± ab + b 3 3 3 3. (a ± b ) = a ± 3a b + 3ab
ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ 10 ΕΠΑΝΑΛΗΨΕΙΣ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΕΣ ΤΑΞΕΙΣ α ) Ταυτότητες 1. (a-β)(a+β)=a - b. (a ± b ) = a ± ab + b 3 3 3 3. (a ± b ) = a ± 3a b + 3ab
Εφαρμοσμένη Κρυπτογραφία Ι
 Εφαρμοσμένη Κρυπτογραφία Ι Κωνσταντίνου Ελισάβετ ekonstantinou@aegean.gr http://www.icsd.aegean.gr/ekonstantinou Η συνάρτηση φ(.) του Euler Για κάθε ακέραιο n > 0, έστω φ(n) το πλήθος των ακεραίων στο
Εφαρμοσμένη Κρυπτογραφία Ι Κωνσταντίνου Ελισάβετ ekonstantinou@aegean.gr http://www.icsd.aegean.gr/ekonstantinou Η συνάρτηση φ(.) του Euler Για κάθε ακέραιο n > 0, έστω φ(n) το πλήθος των ακεραίων στο
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity
 Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
Υπολογισιμότητα και Πολυπλοκότητα Computability and Complexity Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - ΕΜΠ Απρίλιος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab - NTUA) Υπολ
ΜΑΘΗΜΑ ΕΥΤΕΡΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ (ΟΡΙΟ ΚΑΙ ΣΥΝΕΧΕΙΑ)
 ΜΑΘΗΜΑ ΕΥΤΕΡΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ (ΟΡΙΟ ΚΑΙ ΣΥΝΕΧΕΙΑ) A. Εύρεση Πεδίου Τιµών Συναρτήσεων ίνεται η συνάρτηση h, h ( ) = 4+, [ 1,4] Να βρεθεί το πεδίο τιµών της συνάρτησης. Η λογική για
ΜΑΘΗΜΑ ΕΥΤΕΡΟ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ ΑΣΚΗΣΕΙΣ (ΟΡΙΟ ΚΑΙ ΣΥΝΕΧΕΙΑ) A. Εύρεση Πεδίου Τιµών Συναρτήσεων ίνεται η συνάρτηση h, h ( ) = 4+, [ 1,4] Να βρεθεί το πεδίο τιµών της συνάρτησης. Η λογική για
Μαθηματικά Γ Γυμνασίου. Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: 1.2-1.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες
 Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: 1.2-1.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων
Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: 1.2-1.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Μαθηματικά Γ Γυμνασίου. Επαναληπτικές Ασκήσεις στο Κεφάλαιο 1: Μονώνυμα - Πολυώνυμα - Ταυτότητες
 Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο :.2 -.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων Πολλαπλασιασμός
Μαθηματικά Γ Γυμνασίου Επαναληπτικές Ασκήσεις στο Κεφάλαιο :.2 -.5 Μονώνυμα - Πολυώνυμα - Ταυτότητες Αλγεβρικές παραστάσεις - Μονώνυμα Πράξεις με μονώνυμα Πολυώνυμα Πρόσθεση και Αφαίρεση πολυωνύμων Πολλαπλασιασμός
