x[n] = 2 cos(0.1πn) + 3 sin(0.2πn) (1) % Discrete time indices
|
|
|
- Ὅμηρ Λόντος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2018 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πρώτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις εντολές/συναρτήσεις MATLAB γράψτε : doc εντολή/συνάρτηση στο Command Window του MATLAB. Ασκηση 1 - Υπολογισµός Περιόδου (20 µ.) Εστω το σήµα διακριτού χρόνου x[n] = 2 cos(0.1πn) + 3 sin(0.2πn) (1) (Αʹ) Ας δηµιουργήσουµε στο MATLAB 50 δείγµατα του παραπάνω διακριτού σήµατος και ας εµφανίσουµε το αποτέλεσµα µε την εντολή stem, ορίζοντας κατάλληλα το διάνυσµα του διακριτού χρόνου n, να είναι από µηδέν έως 49 (σύνολο 50 χρονικές στιγµές). n = 0:49; x = 2*cos(0.1*pi*n) + 3*sin(0.2*pi*n); stem(n,x); xlabel( Samples ); title( Synthetic signal ); % Discrete time indices % Signal % Visualize i. Από το σχήµα, µπορείτε να ϐρείτε ποιά είναι περίπου η περίοδος του σήµατος ; (µην κλείσετε το γράφη- µα) ii. Υπολογίστε µε ακρίβεια την περίοδο του σήµατος σε αριθµό δειγµάτων στο χαρτί, και επιβεβαιώστε το αποτέλεσµα ελέγχοντας στο MATLAB τις τιµές του σήµατος. iii. Υπολογίσατε σωστά την περίοδο αρχικά µε το µάτι ; iv. Αν αυτό το σήµα έχει προέλθει από δειγµατοληψία ενός σήµατος συνεχούς χρόνου µε συχνότητα δειγ- µατοληψίας 200 Hz, τότε πόση είναι η περίοδος του σήµατος συνεχούς χρόνου ; (Βʹ) Ας υποθέσουµε ότι προσθέτουµε άλλη µια συνιστώσα στο παραπάνω σήµα : x[n] = 2 cos(0.1πn) + 2 cos(0.15πn) + 3 sin(0.2πn) (2) i. ηµιουργήστε 150 δείγµατα στο MATLAB. Εκτελώντας ξανά την εντολή stem για το παραπάνω σήµα, εµφανίστε το. ii. Πόση είναι η περίοδος σε αριθµό δειγµάτων ; iii. Πόση είναι η περίοδος σε δευτερόλεπτα, αν το σήµα συνεχούς χρόνου από το οποίο προήλθε δειγµατοληπτήθηκε µε συχνότητα δειγµατοληψίας 200 Hz; (Γʹ) Εστω το σήµα διακριτού χρόνου x[n] = cos(0.1π + 0.4n) (3) όπου n = 0, 1,, 99. (αʹ) Σχεδιάστε µε την εντολή stem το σήµα. (ϐʹ) Ελέγξτε το γράφηµα. Είναι το σήµα περιοδικό ; Ποιά περίοδο ϐρίσκετε µε το µάτι ; (γʹ) Επιβεβαιώστε (ή διαψέυστε) την απάντησή σας υπολογίζοντας ϑεωρητικά την περίοδο.
2 Ψηφιακή Επεξεργασία Σήµατος /Πρώτο Εργαστήριο 2 Ασκηση 2 - Κατανόηση Ενέργειας και Ισχύος (20 µ.) Υπολογίστε ϑεωρητικά και επιβεβαιώστε στο MATLAB την ενέργεια ή την ισχύ (ή τίποτε από τα δυο) των παρακάτω σηµάτων. Χρησιµοποιήστε τα hints του µαθήµατος για να γλιτώσετε πράξεις : x[n] = ( 1 2) nu[n] ( ) x[n] = 2 cos 3π 4 n x[n] = 3 n u[ n] 1, n < 0 x[n] = 0, n = 0 1, n > 0 Ενδεικτικά, σας δίνεται ο κώδικας για τον υπολογισµό της ισχύος της ϐηµατικής συνάρτησης u[n] που υπολογίσαµε στο µάθηµα : % Set time axis N = 5000; n = -N:N; % Define signal (0, n < 0 and 1, n >= 0) x = [zeros(1,n) ones(1,n)]; % Calculating Power P P = 1./(2*N+1).*sum(x.ˆ2); Το MATLAB απαντά ότι P = που είναι και η σωστή απάντηση. Ασκηση 3 - ιόρθωση σφαλµάτων (30 µ.) Τα συστήµατα DVD αποθηκεύουν τις εικόνες που αποτελούν ένα video µε µορφή σειρών από ψηφιακούς α- ϱιθµούς. Αν υπάρχει κάποιο πρόβληµα στο δισκάκι (ελαφρά γρατζουνιά, ϕθορά, σκόνη), το σύστηµα του DVD προσπαθεί να καθαρίσει το δίσκο από το πρόβληµα χρησιµοποιώντας ϕίλτρα (δηλ. συστήµατα διακριτού χρόνου που περιγράφονται ως εξισώσεις διαφορών!). Εδώ ϑα εξετάσουµε δυο τέτοια απλά συστήµατα, τα οποία ϑα ονοµάζουµε στο εξής ϕίλτρα. Το πρώτο είναι το ϕίλτρο κυλιόµενης µέσης τιµής (moving average). Συγκεκριµένα, ϑα χρησιµοποιήσουµε ένα τέτοιο ϕίλτρο τριών σηµείων (3-point Moving Average), το οποίο ϑα δούµε και στις διαλέξεις : y[n] = k= 1 x[n k] (4) Το δεύτερο είναι ένα ϕίλτρο µεσαίας τιµής (median filter), επίσης τριών σηµείων : y[n] = median(x[n + 1], x[n], x[n 1]) (5) Παρατηρήστε ότι και τα δυο ϕίλτρα απαιτούν µόνο 3 τιµές της εισόδου για να παράξουν µια τιµή της εξόδου. i. Χρησιµοποιώντας την εντολή
3 Ψηφιακή Επεξεργασία Σήµατος /Πρώτο Εργαστήριο 3 A = imread( Saturn.tif ); διαβάστε την εικόνα Saturn.tif που σας δίνεται στα αρχεία του εργαστηρίου. είτε τη µε την εντολή figure; imshow(a); Υποθέστε ότι αυτή είναι µια καθαρή εικόνα από ένα DVD δίσκο. ii. Χρησιµοποιώντας την εντολή B = imread( NoiseSaturn.tif ); διαβάστε την εικόνα NoiseSaturn.tif. είτε τη µε την εντολή figure; imshow(b); Ο ϑόρυβος που ϐλέπετε να έχει προστεθεί στην εικόνα ονοµάζεται salt and pepper noise (ϑόρυβος αλάτι και πιπέρι, λόγω της µορφής του). Υποθέστε ότι προήλθε από σφάλµα ανάγνωσης του δίσκου DVD λόγω ϕθοράς. iii. Προσπαθήστε να εφαρµόσετε τα παραπάνω ϕίλτρα για να καθαρίσετε την εικόνα B. Σκεφτείτε ότι η εικόνα είναι ένας πίνακας MxN, που σας είναι γνωστά (γράψτε [M,N] = size(b) αν ϑέλετε να τα έχετε σε µεταβλητές). Εφαρµόστε τα ϕίλτρα σας κατά γραµµές ή κατά στήλες του πίνακα. Θεωρήστε ότι κάθε γραµµή (ή στήλη) αποτελεί ένα µονοδιάστατο σήµα x[n] για τις παραπάνω εξισώσεις, το οποίο πρέπει να διατρέχετε σε τριάδες, µε µετατόπιση ένα δείγµα κάθε ϕορά. Η έξοδος y[n] ϑα είναι µια αριθµητική τιµή την οποία ϑα αποθηκεύσετε σε έναν πίνακα C, στην κατάλληλη ϑέση. Προσέξτε το type casting µεταξύ των εικόνων όταν τις απεικονίζετε. Συνίσταται να ακολουθήστε τον παρακάτω κώδικα-σκελετό που αφορά το ϕίλτρο της Σχέσης (4) εφαρµοσµένο στις γραµµές της εικόνας : % Initialize C [M,N] = size(b); C = zeros(m,n); % Cast to double for processing B = double(b); % Apply a moving average (MA) filter in every row for i = 1:M % Process rows B[i,:] for j = 2:N-1 % Why from 2 to N-1 and not from 1 to N? x = % INSERT CODE HERE - use B matrix to get % triads of data of row i y = % INSERT CODE HERE - use x vector to implement % your filter C(i,j) = y; % Store result in another matrix end end % Cast it to unsigned int C = uint8(c); % Show the result figure; imshow(c); title( MA-filtered image in rows );
4 Ψηφιακή Επεξεργασία Σήµατος /Πρώτο Εργαστήριο 4 Μπορείτε αν ϑέλετε να χρησιµοποιήσετε τις συναρτήσεις sum, mean, median, αλλά µόνο αυτές. Με ό- µοια ϕιλοσοφία ϕιλτράρετε κατά στήλες µε το ίδιο ϕίλτρο (προσέξτε το indexing στους ϐρόχους επανάληψης), και στη συνέχεια κάνετε τα ίδια για το ϕίλτρο της Σχέσης (5). Για κάθε ένα από τα δυο ϕίλτρα : iv. Παραδώστε κώδικα που παράγει δυο εικόνες του πίνακα C, µια που έχει προέλθει από ϕιλτράρισµα των γραµµών του πίνακα B, και µια που έχει προέλθει από ϕιλτράρισµα των στηλών του πίνακα B. Σχολιάστε τις παρατηρήσεις σας. Συµπεριλάβετε τις παραγόµενες εικόνες στην αναφορά σας. Εν γένει, ϑα χαρακτηρίζατε και τα δυο ϕίλτρα ως αποδοτικά ; v. Παραδώστε κώδικα που εφαρµόζει τα ϕίλτρα σας διαδοχικά (π.χ. εφαρµόστε ένα ϕίλτρο πρώτα σε γραµµές, και στο αποτέλεσµα που ϑα πάρετε εφαρµόστε το ίδιο ϕίλτρο ξανά κατά στήλες). Υλοποιήστε αυτή την προσέγγιση και µε τα δυο ϕίλτρα. Συµπεριλάβετε τις παραγόµενες εικόνες στην αναφορά σας. Παίρνετε καλύτερο αποτέλεσµα από πριν ; Σχολιάστε. vi. Χρησιµοποιήστε τη συνάρτηση filter για να γλιτώσετε το ένα for loop στον παραπάνω σκελετό-κώδικα. Γράψτε doc filter για να δείτε τη χρήση της. Γράψτε και παραδώστε κώδικα µε χρήση της filter για το ϕιλτράρισµα της εικόνας µόνο κατά γραµµές και µόνο για τη Σχέση (4). Ασκηση 4 - Ασφαλής Επικοινωνία (30 µ.) Για την ασφαλή επικοινωνία δεδοµένων µεταξύ δυο σταθµών, χρησιµοποιούµε ένα πρότυπο σήµα µήκος 50 δειγµάτων, για να το προσθέσουµε ως ϑόρυβο σε τυχαίες χρονικές στιγµές στα σήµατα που ϑέλουµε να στείλουµε. Το σήµα-πρότυπο ϐρίσκεται στο αρχείο Pat.wav, και το έχουν τόσο ο ποµπός όσο και ο δέκτης. Το σήµα που εµείς λάβαµε σε κάποια χρονική στιγµή στο δέκτη είναι το σήµα noisy.wav. Ας τα ϕορτώσουµε και ας τα ακούσουµε : [pattern, fs] = audioread( Pat.wav ); soundsc(pattern, fs); figure(1); plot(pattern); xlabel( Samples ); [noisy, fs] = audioread( noisy.wav ); soundsc(noisy, fs); figure(2); plot(noisy); xlabel( Samples ); Η εντολή plot είναι ϐολικότερη εδώ για την απεικόνιση, αλλά στην πραγµατικότητα τα σήµατά µας είναι διακριτού χρόνου (µπορείτε να το δείτε µε την εντολή stem, όπως την γνωρίζετε). Θα ϑέλαµε να ανακτήσουµε το καθαρό σήµα. Για το σκοπό αυτό, µπορούµε να χρησιµοποιήσουµε την πράξη της ετεροσυσχέτισης, η οποία ορίζεται ως φ xy [l] = + n= x[n]y[n + l] (6) Οµοια µε την πράξη της ετεροσυσχέτισης στο συνεχή χρόνο, µας αποκαλύπτει οµοιότητες και διαφορές µεταξύ των σηµάτων που συσχετίζονται. Ο δείκτης l ονοµάζεται lag, που σηµαίνει καθυστέρηση, και έχει ακριβώς όµοιο ϱόλο µε τη µεταβλητή τ στο συνεχή χρόνο 1. Η συνάρτηση [cc, lags] = xcorr(...) του MATLAB ϑα 1 Θυµηθείτε : φ xy(τ) = + x(t)y(t + τ)dt (7)
5 Ψηφιακή Επεξεργασία Σήµατος /Πρώτο Εργαστήριο 5 σας ϐοηθήσει να συσχετίσετε τα σήµατα. είτε προσεκτικά (!) το documentation της, καθώς η υλοποίηση του MATLAB διαφέρει λίγο από τον παραπάνω ορισµό, και όπως ίσως ϑυµάστε και από το συνεχή χρόνο, η ετεροσυσχέτιση είναι διαφορετική όταν συσχετίσουµε το x[n] µε το y[n] απ όταν συσχετίσουµε το y[n] µε το x[n]. Στις χρονικές τιµές των lags όπου η τιµή της ετεροσυσχέτισης είναι µεγάλη, σηµαίνει ότι εκεί έχει ϐρεθεί µεγάλη οµοιότητα του ενός σήµατος µε το άλλο. Προς ϐοήθειά σας, πληροφορείστε ότι το πρότυπο σήµα έχει προστεθεί σε 36 ϑέσεις στο σήµα noisy.wav. Αν ϐρείτε αυτές τις ϑέσεις, µπορείτε απλά να το αφαιρέσετε µε µια απλή πράξη αφαίρεσης του σήµατος προτύπου από το ϑορυβώδες σήµα. Επίσης, το σήµα που έχει σταλεί στο δέκτη περιέχει οµιλία πολύ καλής ποιότητας. Αυτό ϑα σας ϐοηθήσει να ελέγξετε τα αποτελέσµατά σας. Ο παρακάτω κώδικας ϑα σας ϐοηθήσει. Χρησιµοποιήστε το documentation του MATLAB όπου έχετε αµφι- ϐολία. [cross_corr, lags] = % INSERT CODE HERE; % Compute cross-correlation figure(3); plot(lags, cross_corr); % Plot it and check it carefully xlabel( Lags ); title( Cross-correlation ); % Using information from the plot, define a good threshold T % which separates peaks from other -not useful- data T = % INSERT CODE HERE ; % Use findpeaks to easily detect instants of high correlation % T will be used as the minimum peak height threshold [pks, locs] = findpeaks(cross_corr, lags, MinPeakHeight, T); % Check your selected peaks - did your threshold work? Did you select 36 peaks? plot(lags, cross_corr); hold on; plot(locs, pks, o ); hold off; % Check without counting peaks :) size(locs) % is it 1 x 36? % Copy noisy signal to process it clean = noisy; % Subtract pattern from noisy signal - use "clean" vector % For every lag index present in vector locs, you have % to subtract the pattern signal from the received signal % Use operator ":" to choose pieces of the signal in MATLAB % as follows: % signal(start:end) = signal(start:end) - another_signal(start:end); for i = 1:length(locs) %%%%%%%%%%%%%%%%%% % INSERT CODE HERE %%%%%%%%%%%%%%%%%% end % Listen! It should sound perfectly clear... soundsc(clean, fs); Η συνάρτηση findpeaks του MATLAB είναι πολύ ϐολική για να ϐρίσκετε κορυφές σε µια συνάρτηση, ανάλογα µε το πόσο απέχουν µεταξύ τους, µε το αν ϑέλετε να υπερβαίνουν κάποια τιµή, κλπ. Ρίξτε απλά µια µατιά στο documentation της συνάρτησης στο MATLAB για να δείτε τις δυνατότητές της, µια και η εντολή όπως δίνεται
6 Ψηφιακή Επεξεργασία Σήµατος /Πρώτο Εργαστήριο 6 στον παραπάνω κώδικα είναι πλήρης. Ελέγξτε προσεκτικά τις ϑέσεις των καθυστερήσεων (τις τιµές των locs δηλαδή) που σας επιστρέφει η findpeaks. είτε τι υπάρχει στο ϑορυβώδες σήµα σε αυτές τις χρονικές στιγµές. Για την παράδοση της άσκησης, γράψτε πλήρη αναφορά, συµπεριλαµβάνοντας απαντήσεις σε όλα τα ερωτήµατα του εργαστηρίου, καθώς και διαγράµµατα/γραφήµατα/εικόνες µε τα αποτελέσµατά σας, και συµπεριλάβετε τον κώδικα MATLAB σε ξεχωριστά.m files. Η παράδοση γίνεται αποκλειστικά µε το πρόγραµµα TURNIN. Ανάθεση : 2/10/2018 Προθεσµία : 9/10/2018, 23:59:59 (TURNIN timestamp)
x[n] = 2 cos(0.1πn) + 3 sin(0.2πn) (1) % Discrete time indices
![x[n] = 2 cos(0.1πn) + 3 sin(0.2πn) (1) % Discrete time indices x[n] = 2 cos(0.1πn) + 3 sin(0.2πn) (1) % Discrete time indices](/thumbs/57/41064774.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πρώτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πρώτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 206 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής εύτερη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 25/0/206 Ηµεροµηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 206 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής εύτερη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 25/0/206 Ηµεροµηνία
y[n] = x[n] + αx[n M], a < 1 (1) y[n] = αy[n M] + x[n], a < 1 (2)
![y[n] = x[n] + αx[n M], a < 1 (1) y[n] = αy[n M] + x[n], a < 1 (2) y[n] = x[n] + αx[n M], a < 1 (1) y[n] = αy[n M] + x[n], a < 1 (2)](/thumbs/61/45980726.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τρίτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τρίτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
y[n] = f(x[n], w[n]) (1) w[n] = f(x[n], y[n]) (2)
![y[n] = f(x[n], w[n]) (1) w[n] = f(x[n], y[n]) (2) y[n] = f(x[n], w[n]) (1) w[n] = f(x[n], y[n]) (2)](/thumbs/55/36166458.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τέταρτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τέταρτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε
x(t) = cos(2π100t + π/3) sin(2π250t + π/4) (1)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 016-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 16/3/017
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 016-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 16/3/017
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 08-9 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τρίτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 8//09
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 08-9 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τρίτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 8//09
y[n] = x[n] + αx[n M], a < 1 (1) y[n] = αy[n M] + x[n], a < 1 (2)
![y[n] = x[n] + αx[n M], a < 1 (1) y[n] = αy[n M] + x[n], a < 1 (2) y[n] = x[n] + αx[n M], a < 1 (1) y[n] = αy[n M] + x[n], a < 1 (2)](/thumbs/74/71191891.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2017 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τρίτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2017 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τρίτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
δ[n kp ], k Z (1) 1 cos πn, N 1 n N 1 + N 2 2N
![δ[n kp ], k Z (1) 1 cos πn, N 1 n N 1 + N 2 2N δ[n kp ], k Z (1) 1 cos πn, N 1 n N 1 + N 2 2N](/thumbs/66/55089135.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2015 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τέταρτο Εργαστήριο - Ηµεροµηνία : 27/11/2015 Σηµείωση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2015 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τέταρτο Εργαστήριο - Ηµεροµηνία : 27/11/2015 Σηµείωση
y[n] = x[n] + αx[n M], a < 1 (1) y[n] + αy[n M] = x[n], a < 1 (2)
![y[n] = x[n] + αx[n M], a < 1 (1) y[n] + αy[n M] = x[n], a < 1 (2) y[n] = x[n] + αx[n M], a < 1 (1) y[n] + αy[n M] = x[n], a < 1 (2)](/thumbs/93/114165677.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2018 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τρίτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2018 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Τρίτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
z(t) = 5.05e j(2πf 0t 0.209) sin 3 (5t)dt = 4 15 x(t) = 4 + cos(2π100t + π/3) cos(2π250t π/7) + 2 sin(2π300t π/4) (6)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 215-16 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 18/2/216
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 215-16 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 18/2/216
x(t) = 4 cos(2π400t π/3) + 2 cos(2π900t + π/8) + cos(2π1200t) h(t) = 2000sinc(2000t) = h(t) = 2000sinc(2000t) H(f) = rect
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 215-16 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες - Ηµεροµηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 215-16 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες - Ηµεροµηνία
H ap (z) = z m a 1 az m (1)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 206 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πέµπτο Εργαστήριο - Ηµεροµηνία : 2/2/206 Σηµείωση : Για
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 206 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πέµπτο Εργαστήριο - Ηµεροµηνία : 2/2/206 Σηµείωση : Για
H ap (z) = z m a 1 az m (1)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 207 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πέµπτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 207 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πέµπτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 2017-18 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης :
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 2017-18 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης :
x[n]z n = ) nu[n]z n z 1) n z 1 (5) ( 1 z(2z 1 1]z n +
![x[n]z n = ) nu[n]z n z 1) n z 1 (5) ( 1 z(2z 1 1]z n + x[n]z n = ) nu[n]z n z 1) n z 1 (5) ( 1 z(2z 1 1]z n +](/thumbs/65/53724700.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-7: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 6 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης : //6 Ηµεροµηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-7: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 6 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης : //6 Ηµεροµηνία
x 1 [n] = 0, αλλού x[n]e jωn X(e jω ) =
![x 1 [n] = 0, αλλού x[n]e jωn X(e jω ) = x 1 [n] = 0, αλλού x[n]e jωn X(e jω ) =](/thumbs/61/46243928.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής εύτερο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 2016 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής εύτερο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
Ψηφιακή Επεξεργασία Σήματος
 Ψηφιακή Επεξεργασία Σήματος Εργαστήριο 3 Εισαγωγή στα Σήματα Αλέξανδρος Μανουσάκης Τι είναι σήμα; Ως σήμα ορίζουμε το σύνολο των τιμών που λαμβάνει μια ποσότητα (εξαρτημένη μεταβλητή) όταν αυτή μεταβάλλεται
Ψηφιακή Επεξεργασία Σήματος Εργαστήριο 3 Εισαγωγή στα Σήματα Αλέξανδρος Μανουσάκης Τι είναι σήμα; Ως σήμα ορίζουμε το σύνολο των τιμών που λαμβάνει μια ποσότητα (εξαρτημένη μεταβλητή) όταν αυτή μεταβάλλεται
= R{(a + jb)e j2π 3 4 t } (6) a + jb = j2.707 = e j π (7) A = (9) f 0 = 3 4
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής εύτερη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης
A k s s k. H c (s) = H(z) = 1 e s kt dz 1
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 208 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πέµπτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 208 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Πέµπτο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Bonus Ασκήσεις Ηµεροµηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Bonus Ασκήσεις Ηµεροµηνία
Εξεταστική Ιανουαρίου 2007 Μάθηµα: «Σήµατα και Συστήµατα»
 Εξεταστική Ιανουαρίου 27 Μάθηµα: «Σήµατα και Συστήµατα» Θέµα 1 ο (3%) Έστω δύο διακριτά σήµατα: x(n) = {1,,, -1} και h(n) = {1,, 1} µε το πρώτο δείγµα να αντιστοιχεί σε n= και για τα δύο. Υπολογίστε τα
Εξεταστική Ιανουαρίου 27 Μάθηµα: «Σήµατα και Συστήµατα» Θέµα 1 ο (3%) Έστω δύο διακριτά σήµατα: x(n) = {1,,, -1} και h(n) = {1,, 1} µε το πρώτο δείγµα να αντιστοιχεί σε n= και για τα δύο. Υπολογίστε τα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 205-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Εβδοµη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 23/4/206
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 205-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Εβδοµη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 23/4/206
Εισαγωγή στα Σήματα. Κυριακίδης Ιωάννης 2011
 Εισαγωγή στα Σήματα Κυριακίδης Ιωάννης 2011 Τελευταία ενημέρωση: 11/11/2011 Τι είναι ένα σήμα; Ως σήμα ορίζουμε το σύνολο των τιμών που λαμβάνει μια ποσότητα (εξαρτημένη μεταβλητή) όταν αυτή μεταβάλλεται
Εισαγωγή στα Σήματα Κυριακίδης Ιωάννης 2011 Τελευταία ενημέρωση: 11/11/2011 Τι είναι ένα σήμα; Ως σήμα ορίζουμε το σύνολο των τιμών που λαμβάνει μια ποσότητα (εξαρτημένη μεταβλητή) όταν αυτή μεταβάλλεται
Εισαγωγή στη Matlab Εισαγωγή στην Αριθμητική Ανάλυση Διδάσκων: Γεώργιος Ακρίβης Βοηθός: Δημήτριος Ζαβαντής
 Εισαγωγή στη Matlab Εισαγωγή στην Αριθμητική Ανάλυση Διδάσκων: Γεώργιος Ακρίβης Βοηθός: Δημήτριος Ζαβαντής email: dzavanti@cs.uoi.gr Περιεχόμενα Τι είναι η Matlab; Ιστορικά Χρήσεις και στοιχεία της Matlab
Εισαγωγή στη Matlab Εισαγωγή στην Αριθμητική Ανάλυση Διδάσκων: Γεώργιος Ακρίβης Βοηθός: Δημήτριος Ζαβαντής email: dzavanti@cs.uoi.gr Περιεχόμενα Τι είναι η Matlab; Ιστορικά Χρήσεις και στοιχεία της Matlab
Σύντομη Αναφορά σε Βασικές Έννοιες Ψηφιακής Επεξεργασίας Σημάτων
 Πρόγραμμα Μεταπτυχιακών Σπουδών: «Τεχνολογίες και Συστήματα Ευρυζωνικών Εφαρμογών και Υπηρεσιών» Μάθημα: «Επεξεργασία Ψηφιακού Σήματος και Σχεδιασμός Υλικού» Σύντομη Αναφορά σε Βασικές Έννοιες Ψηφιακής
Πρόγραμμα Μεταπτυχιακών Σπουδών: «Τεχνολογίες και Συστήματα Ευρυζωνικών Εφαρμογών και Υπηρεσιών» Μάθημα: «Επεξεργασία Ψηφιακού Σήματος και Σχεδιασμός Υλικού» Σύντομη Αναφορά σε Βασικές Έννοιες Ψηφιακής
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18 14 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία ιάλεξη 18 14 Νοεµβρίου, 2006 Γεώργιος Έλληνας Επίκουρος Καθηγητής ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 04: ΣΥΜΠΙΕΣΗ ΚΑΙ ΜΕΤΑ ΟΣΗ ΠΟΛΥΜΕΣΩΝ Ακαδηµαϊκό Έτος 2007 2008, Χειµερινό Εξάµηνο 6 Νοεµβρίου 2007 Φροντιστηριακή Άσκηση 2: (I) Εντροπία,
u = x t t = t 0 = T = x u = = s t = = s u = u bat 1 + T c = 343 m/s 273
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-: Φυσική Ι Χειµερινό Εξάµηνο 5 ιδάσκων : Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : //5 Ηµεροµηνία Παράδοσης : 7//5 Σηµείωση : Επιτρέπεται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-: Φυσική Ι Χειµερινό Εξάµηνο 5 ιδάσκων : Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : //5 Ηµεροµηνία Παράδοσης : 7//5 Σηµείωση : Επιτρέπεται
X 1 = X1 = 1 (1) X 3 = X3 = 1 (2) X k e j2πk 1 2 t = k
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 6-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τέταρτης Σειράς Ασκήσεων Ασκηση (i) Είναι T
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 6-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τέταρτης Σειράς Ασκήσεων Ασκηση (i) Είναι T
x(t) = e 2t u(t) (4) y(t) = e t u( t) (5)
 Ηµεροµηνία Ανάθεσης : 17/5/2018 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 2017-18 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Εβδοµη Σειρά
Ηµεροµηνία Ανάθεσης : 17/5/2018 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 2017-18 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Εβδοµη Σειρά
Συστήματα Αναμονής (Queuing Systems)
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΕΜΠ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης & Βέλτιστου Σχεδιασμού Δικτύων Τηλεματικής
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ - ΕΜΠ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧ. ΥΠΟΛΟΓΙΣΤΩΝ Τομέας Επικοινωνιών, Ηλεκτρονικής & Συστημάτων Πληροφορικής Εργαστήριο Διαχείρισης & Βέλτιστου Σχεδιασμού Δικτύων Τηλεματικής
E(X(t)) = 1 k + k sin(2π) + k cos(2π) = 1 k + k 0 + k 1 = 1
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Τομέας Τηλεπικοινωνιών ΤΗΛ 2: ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΤΥΧΑΙΑ ΣΗΜΑΤΑ 4ο Εξάμηνο 2009-200 4η ΕΡΓΑΣΙΑ ΑΣΚΗΣΗ Εστω τυχαία διαδικασία X(t) =
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ Τμήμα Ηλεκτρονικών Μηχανικών και Μηχανικών Υπολογιστών Τομέας Τηλεπικοινωνιών ΤΗΛ 2: ΠΙΘΑΝΟΤΗΤΕΣ ΚΑΙ ΤΥΧΑΙΑ ΣΗΜΑΤΑ 4ο Εξάμηνο 2009-200 4η ΕΡΓΑΣΙΑ ΑΣΚΗΣΗ Εστω τυχαία διαδικασία X(t) =
x[n]e jωn (1) X(e jωkn ) x[n]e jω kn
![x[n]e jωn (1) X(e jωkn ) x[n]e jω kn x[n]e jωn (1) X(e jωkn ) x[n]e jω kn](/thumbs/96/129544675.jpg) ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 017 ιδάσκοντες : Γ Στυλιανού - Γ Καφεντζής εύτερο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος Χειµερινό Εξάµηνο 017 ιδάσκοντες : Γ Στυλιανού - Γ Καφεντζής εύτερο Εργαστήριο Σηµείωση : Για ϐοήθεια σχετικά µε τις
x(t) = 4 cos(2π600t π/3) + 2 cos(2π900t + π/8) + cos(2π1200t) (3)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες Ρήτρα τελικού : 4.0/0.0 Θέµα ο - Περιοδικά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες Ρήτρα τελικού : 4.0/0.0 Θέµα ο - Περιοδικά
Περιεχόµενα ΕΠΛ 422: στα Συστήµατα Πολυµέσων. Βιβλιογραφία. ειγµατοληψία. ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων
 Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Ψηφιακή Αναπαράσταση Σήµατος: ειγµατοληψία Βιβλιογραφία ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων Βασικές Έννοιες Επεξεργασίας Σηµάτων Ψηφιοποίηση
Περιεχόµενα ΕΠΛ 422: Συστήµατα Πολυµέσων Ψηφιακή Αναπαράσταση Σήµατος: ειγµατοληψία Βιβλιογραφία ηµιουργία ψηφιακής µορφής πληροφορίας στα Συστήµατα Πολυµέσων Βασικές Έννοιες Επεξεργασίας Σηµάτων Ψηφιοποίηση
= t2 t T 2T 3t + 9T, για t < 3T και t 2T 2T t < 3T (Σχήµα
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 016-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Συνέλιξη και Συστήµατα Σε αυτό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 016-17 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Συνέλιξη και Συστήµατα Σε αυτό
y(t) = x(t) + e x(2 t)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΕΞΕΤΑΣΗ ΠΡΟΟ ΟΥ - ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ιάρκεια : 3 ώρες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΕΞΕΤΑΣΗ ΠΡΟΟ ΟΥ - ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ιάρκεια : 3 ώρες
1 η Εργαστηριακή Άσκηση MATLAB Εισαγωγή
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. Εργαστήριο Επεξεργασία Εικόνας & Βίντεο 1 η Εργαστηριακή Άσκηση MATLAB Εισαγωγή Νικόλαος Γιαννακέας Άρτα 2018 1 Εισαγωγή Το Matlab
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΗΠΕΙΡΟΥ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ Τ.Ε. Εργαστήριο Επεξεργασία Εικόνας & Βίντεο 1 η Εργαστηριακή Άσκηση MATLAB Εισαγωγή Νικόλαος Γιαννακέας Άρτα 2018 1 Εισαγωγή Το Matlab
X(t) = A cos(2πf c t + Θ) (1) 0, αλλού. 2 cos(2πf cτ) (9)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 05-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Τυχαίες ιαδικασίες Ασκηση. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Πάτρα 2005 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Εργαστήριο Επεξεργασίας Σηµάτων Τηλεπικοινωνιών & ικτύων
 2.5 0.5 0-0.5 - -.5-2 0 50 00 50 200 250 300 350 400 450 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Πάτρα 2005 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Εργαστήριο Επεξεργασίας Σηµάτων Τηλεπικοινωνιών & ικτύων ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ
2.5 0.5 0-0.5 - -.5-2 0 50 00 50 200 250 300 350 400 450 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Πάτρα 2005 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ Η/Υ & ΠΛΗΡΟΦΟΡΙΚΗΣ Εργαστήριο Επεξεργασίας Σηµάτων Τηλεπικοινωνιών & ικτύων ΕΡΓΑΣΙΑ ΣΤΟ ΜΑΘΗΜΑ
= 5 cos(2π500t π/2) + 9 cos(2π900t + π/3) cos(2π1400t) (9) H(f) = 4.5, αλλού
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες Ρήτρα τελικού : 4.5/10.0 Θέµα 1ο - 5
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες Ρήτρα τελικού : 4.5/10.0 Θέµα 1ο - 5
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ.
 Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
Αναλογικά & Ψηφιακά Κυκλώματα ιαφάνειες Μαθήματος ρ. Μηχ. Μαραβελάκης Εμ. 1 Εισαγωγή Αναλογικό σήμα (analog signal): συνεχής συνάρτηση στην οποία η ανεξάρτητη μεταβλητή και η εξαρτημένη μεταβλητή (π.χ.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ - Ενδεικτικές Λύσεις ιάρκεια : 3 ώρες Ρήτρα τελικού :
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ - Ενδεικτικές Λύσεις ιάρκεια : 3 ώρες Ρήτρα τελικού :
3.1 Αριθμητικοί και Λογικοί Τελεστές, Μετατροπές Τύπου (Casting)
 Εργαστήριο 3: 3.1 Αριθμητικοί και Λογικοί Τελεστές, Μετατροπές Τύπου (Casting) Η C++, όπως όλες οι γλώσσες προγραμματισμού, χρησιμοποιεί τελεστές για να εκτελέσει τις αριθμητικές και λογικές λειτουργίες.
Εργαστήριο 3: 3.1 Αριθμητικοί και Λογικοί Τελεστές, Μετατροπές Τύπου (Casting) Η C++, όπως όλες οι γλώσσες προγραμματισμού, χρησιμοποιεί τελεστές για να εκτελέσει τις αριθμητικές και λογικές λειτουργίες.
LCs 2 + RCs + 1. s 1,2 = RC ± R 2 C 2 4LC 2LC. (s 2)(s 3) = A. = 4 s 3 s=2 s + 2 B = (s 2)(s 3) (s 3) s=3. = s + 2. x(t) = 4e 2t u(t) + 5e 3t u(t) (2)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 06-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Εβδοµης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 06-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Εβδοµης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
= 1 E x. f(t)x n (t)dt, n = 1, 2,, N (2) = 0, i = 1, 2,, N (3) E e = e 2 (t)dt (4) e(t) = f(t) c n x n (t) (5) f(t) cx(t) = 4 sin(t) (7)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 25-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής εύτερη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : /3/26
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 25-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής εύτερη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : /3/26
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας. Εισηγητής Αναστάσιος Κεσίδης
 Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Χωρικά φίλτρα Χωρικά φίλτρα Γενικά Σε αντίθεση με τις σημειακές πράξεις και μετασχηματισμούς, στα
Μεταπτυχιακό Πρόγραμμα «Γεωχωρικές Τεχνολογίες» Ψηφιακή Επεξεργασία Εικόνας Εισηγητής Αναστάσιος Κεσίδης Χωρικά φίλτρα Χωρικά φίλτρα Γενικά Σε αντίθεση με τις σημειακές πράξεις και μετασχηματισμούς, στα
x(t) ax 1 (t) y(t) = 1 ax 1 (t) = (1/a)y 1(t) x(t t 0 ) y(t t 0 ) =
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λύσεις Τρίτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης
0 2j e jπt e j2πkt dt (3)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τρίτη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης :
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τρίτη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης :
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Μετασχ. Laplace και Συστήµατα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 26-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις σε Μετασχ. Laplace και Συστήµατα
x(t) = 4 cos(2π600t π/3) + 2 sin(2π900t + π/4) + sin(2π1200t) (1) w(t) = y(t)z(t) = 2δ(t + 1) (2) (2 sin(2π900t + π/4) t= 1 + sin(2π1200t) )
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΕΠΑΝΑΛΗΠΤΙΚΗ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες Ρήτρα τελικού : 4.0/10.0
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-215: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής ΕΠΑΝΑΛΗΠΤΙΚΗ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ ιάρκεια : 3 ώρες Ρήτρα τελικού : 4.0/10.0
bx 2 (t). Για είσοδο ax 1(t) + bx 2 (t), η έξοδος είναι x(t t 0 ) και y(t t 0) = t t 0 x(t) ax 1 (t 1) + bx 2 (t 1) sin ax 1 (t)+
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Ασκηση. αʹ Γραµµικό: Είναι y = y = Τρίτη Σειρά Ασκήσεων
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5 ιδάσκοντες : Γ. Στυλιανού - Γ. Καφεντζής Ασκηση. αʹ Γραµµικό: Είναι y = y = Τρίτη Σειρά Ασκήσεων
x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)
![x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1) x[n] = e u[n 1] 4 x[n] = u[n 1] 4 X(z) = z 1 H(z) = (1 0.5z 1 )(1 + 4z 2 ) z 2 (βʹ) H(z) = H min (z)h lin (z) 4 z 1 1 z 1 (z 1 4 )(z 1) (1)](/thumbs/61/45634776.jpg) Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Ασκήσεις με Συστήματα στο Χώρο του Ζ Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 7 Νοεμβρίου 015 1. Υπολόγισε τον μετ. Ζ και την
Βασικά στοιχεία του MATLAB
 ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΕΡΓΑΣΤΗΡΙΟ Εξοικείωση µε το περιβάλλον του MATLAB και χρήση βασικών εντολών και τεχνικών δηµιουργίας προγραµµάτων, συναρτήσεων
ΠΟΛΥΤΕΧΝΕΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΕΡΓΑΣΤΗΡΙΟ Εξοικείωση µε το περιβάλλον του MATLAB και χρήση βασικών εντολών και τεχνικών δηµιουργίας προγραµµάτων, συναρτήσεων
y[n] 5y[n 1] + 6y[n 2] = 2x[n 1] (1) y h [n] = y h [n] = A 1 (2) n + A 2 (3) n (4) h[n] = 0, n < 0 (5) h[n] 5h[n 1] + 6h[n 2] = 2δ[n 1] (6)
![y[n] 5y[n 1] + 6y[n 2] = 2x[n 1] (1) y h [n] = y h [n] = A 1 (2) n + A 2 (3) n (4) h[n] = 0, n < 0 (5) h[n] 5h[n 1] + 6h[n 2] = 2δ[n 1] (6) y[n] 5y[n 1] + 6y[n 2] = 2x[n 1] (1) y h [n] = y h [n] = A 1 (2) n + A 2 (3) n (4) h[n] = 0, n < 0 (5) h[n] 5h[n 1] + 6h[n 2] = 2δ[n 1] (6)](/thumbs/52/30615281.jpg) Ασκήσεις σε Σήματα Συστήματα Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 9 Οκτωβρίου 015 1. Ενα αιτιατό ΓΧΑ σύστημα
Ασκήσεις σε Σήματα Συστήματα Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 9 Οκτωβρίου 015 1. Ενα αιτιατό ΓΧΑ σύστημα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 208-9 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 6/4/209
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-25: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 208-9 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 6/4/209
Εφαρµογες Της Ψηφιακης Επεξεργασιας Σηµατων. Εκτιµηση Συχνοτητων Με ΙδιοΑναλυση του Μητρωου ΑυτοΣυσχετισης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Εφαρµογες Της Ψηφιακης Επεξεργασιας Σηµατων Εκτιµηση Συχνοτητων Με ΙδιοΑναλυση του Μητρωου ΑυτοΣυσχετισης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ Η/Υ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Εφαρµογες Της Ψηφιακης Επεξεργασιας Σηµατων Εκτιµηση Συχνοτητων Με ΙδιοΑναλυση του Μητρωου ΑυτοΣυσχετισης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Σημάτων. Άσκηση 3η. Στυλιανού Ιωάννης. Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Σημάτων Άσκηση 3η Στυλιανού Ιωάννης Τμήμα Επιστήμης Υπολογιστών ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Σημάτων Άσκηση 3η Στυλιανού Ιωάννης Τμήμα Επιστήμης Υπολογιστών ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-370: Ψηφιακή Επεξεργασία Σήµατος
ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 2004., η οποία όµως µπορεί να γραφεί µε την παρακάτω µορφή: 1 e
 ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΝΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΣΥΣΤΗΜΑΤΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΝΑΛΥΣΗΣ ΗΛΕΚΤΡΙΚΩΝ ΚΥΚΛΩΜΑΤΩΝ ΜΑΘΗΜΑ: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ ΛΥΣΕΙΣ ΑΣΚΗΣΕΩΝ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΙΟΥΝΙΟΥ 4 AΣΚΗΣΗ () [ ] (.5)
Εργαστήριο ADICV1. Image Boundary detection and filtering. Κώστας Μαριάς 13/3/2017
 Εργαστήριο ADICV1 Image Boundary detection and filtering Κώστας Μαριάς 13/3/2017 Boundary Detection 2 Γείτονες και περίγραμμα εικόνας Ορίζουμε ως V το σύνολο των τιμών εντάσεων εικόνας για να ορίσουμε
Εργαστήριο ADICV1 Image Boundary detection and filtering Κώστας Μαριάς 13/3/2017 Boundary Detection 2 Γείτονες και περίγραμμα εικόνας Ορίζουμε ως V το σύνολο των τιμών εντάσεων εικόνας για να ορίσουμε
Ολοκληρωµένο Περιβάλλον Σχεδιασµού Και Επίδειξης Φίλτρων
 Ψηφιακή Επεξεργασία Σηµάτων 20 Ολοκληρωµένο Περιβάλλον Σχεδιασµού Και Επίδειξης Φίλτρων Α. Εγκατάσταση Αφού κατεβάσετε το συµπιεσµένο αρχείο µε το πρόγραµµα επίδειξης, αποσυµπιέστε το σε ένα κατάλογο µέσα
Ψηφιακή Επεξεργασία Σηµάτων 20 Ολοκληρωµένο Περιβάλλον Σχεδιασµού Και Επίδειξης Φίλτρων Α. Εγκατάσταση Αφού κατεβάσετε το συµπιεσµένο αρχείο µε το πρόγραµµα επίδειξης, αποσυµπιέστε το σε ένα κατάλογο µέσα
x(t) = 2 + cos(2πt) sin(πt) 3 cos(3πt) cos(θ + π) = cos(θ). (3)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Σειρές Fourier. Να σχεδιάσετε το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 5-6 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Σειρές Fourier. Να σχεδιάσετε το
Συστήματα Διακριτού Χρόνου (Discrete-Time Systems) Κυριακίδης Ιωάννης 2011
 Συστήματα Διακριτού Χρόνου (Discrete-Time Systems) Κυριακίδης Ιωάννης 2011 Τελευταία ενημέρωση: 11/11/2011 Πράξεις διακριτών σημάτων (υπενθύμιση) Πρόσθεση x(n) + y(n) Αφαίρεση x(n) y(n) Πολλαπλασιασμός
Συστήματα Διακριτού Χρόνου (Discrete-Time Systems) Κυριακίδης Ιωάννης 2011 Τελευταία ενημέρωση: 11/11/2011 Πράξεις διακριτών σημάτων (υπενθύμιση) Πρόσθεση x(n) + y(n) Αφαίρεση x(n) y(n) Πολλαπλασιασμός
Ακαδηµαϊκό Έτος , Χειµερινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ, ΤΜΗΜΑ Ι ΑΚΤΙΚΗΣ ΤΗΣ ΤΕΧΝΟΛΟΓΙΑΣ ΚΑΙ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΤΨΣ 50: ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ακαδηµαϊκό Έτος 005 006, Χειµερινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ Η εξέταση
3 ο ΕΡΓΑΣΤΗΡΙΟ ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα 3 ο ΕΡΓΑΣΤΗΡΙΟ ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα: ΔΟΥΛΕΥΟΝΤΑΣ ΜΕ ΣΗΜΑΤΑ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα 3 ο ΕΡΓΑΣΤΗΡΙΟ ΣΗΜΑΤΑ & ΣΥΣΤΗΜΑΤΑ Ενότητα: ΔΟΥΛΕΥΟΝΤΑΣ ΜΕ ΣΗΜΑΤΑ Aναστασία Βελώνη Τμήμα Η.Υ.Σ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Υλοποιήσεις Ψηφιακών Φίλτρων
 Ψηφιακή Επεξεργασία Σηµάτων 10 Υλοποιήσεις Ψηφιακών Φίλτρων Α. Εισαγωγή Οποιοδήποτε γραµµικό χρονικά αµετάβλητο σύστηµα διακριτού χρόνου χαρακτηρίζεται πλήρως από τη συνάρτηση µεταφοράς του η οποία έχει
Ψηφιακή Επεξεργασία Σηµάτων 10 Υλοποιήσεις Ψηφιακών Φίλτρων Α. Εισαγωγή Οποιοδήποτε γραµµικό χρονικά αµετάβλητο σύστηµα διακριτού χρόνου χαρακτηρίζεται πλήρως από τη συνάρτηση µεταφοράς του η οποία έχει
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία
 ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΑ ΘΕΜΑΤΑ ΜΑΣ ΣΗΜΕΡΑ Αναλογικά και ψηφιακά συστήματα Μετατροπή
Ακαδηµαϊκό Έτος , Εαρινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 6: ΠΡΟΣΑΡΜΟΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΤΙΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ Ακαδηµαϊκό Έτος 26 27, Εαρινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΒΕΣ 6: ΠΡΟΣΑΡΜΟΣΤΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΤΙΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΕΣ Ακαδηµαϊκό Έτος 26 27, Εαρινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το
11 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 11 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 11.1 Γενικά περί συνήθων διαφορικών εξισώσεων Μια συνήθης διαφορική εξίσωση (ΣΔΕ) 1 ης τάξης έχει τη μορφή dy d = f (, y()) όπου f(, y) γνωστή και y() άγνωστη συνάρτηση.
11 ΣΥΝΗΘΕΙΣ ΔΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ 11.1 Γενικά περί συνήθων διαφορικών εξισώσεων Μια συνήθης διαφορική εξίσωση (ΣΔΕ) 1 ης τάξης έχει τη μορφή dy d = f (, y()) όπου f(, y) γνωστή και y() άγνωστη συνάρτηση.
ΕΙΣΑΓΩΓΗ ΣΤΟ MATLAB- SIMULINK
 ΕΙΣΑΓΩΓΗ ΣΤΟ MATLAB- SIMULINK SIMULINK ρ. Γεώργιος Φ. Φραγκούλης Καθηγητής ver. 0.2 10/2012 Εισαγωγή στο Simulink Το SIMULINK είναι ένα λογισµικό πακέτο που επιτρέπει τη µοντελοποίηση, προσοµοίωση οίωση
ΕΙΣΑΓΩΓΗ ΣΤΟ MATLAB- SIMULINK SIMULINK ρ. Γεώργιος Φ. Φραγκούλης Καθηγητής ver. 0.2 10/2012 Εισαγωγή στο Simulink Το SIMULINK είναι ένα λογισµικό πακέτο που επιτρέπει τη µοντελοποίηση, προσοµοίωση οίωση
Εργαστήριο ADICV2. Image filtering. Κώστας Μαριάς
 Εργαστήριο ADICV2 Image filtering Κώστας Μαριάς Image Filtering ADICV Kostas Marias TEI Crete 2017 2 Matlab Σκοπός εργαστηρίου Θα φτιάξουμε ένα ΦΙΛΤΡΟ ΜΕΣΗΣ ΤΙΜΗΣ (mean FILTER) σε matlab Στη συνέχεια θα
Εργαστήριο ADICV2 Image filtering Κώστας Μαριάς Image Filtering ADICV Kostas Marias TEI Crete 2017 2 Matlab Σκοπός εργαστηρίου Θα φτιάξουμε ένα ΦΙΛΤΡΟ ΜΕΣΗΣ ΤΙΜΗΣ (mean FILTER) σε matlab Στη συνέχεια θα
Επεξερασία εικόνας. Μιχάλης ρακόπουλος. Υπολογιστική Επιστήµη & Τεχνολογία, #09
 Επεξερασία εικόνας Μιχάλης ρακόπουλος Υπολογιστική Επιστήµη & Τεχνολογία, #9 Επεξεργασία ήχου Βασικό ανάγνωσµα: Οι ενότητες 3. και 3.2 από το ϐιβλίο των Van Loan και Fan. Επεξεργασία ήχου Μ. ρακόπουλος
Επεξερασία εικόνας Μιχάλης ρακόπουλος Υπολογιστική Επιστήµη & Τεχνολογία, #9 Επεξεργασία ήχου Βασικό ανάγνωσµα: Οι ενότητες 3. και 3.2 από το ϐιβλίο των Van Loan και Fan. Επεξεργασία ήχου Μ. ρακόπουλος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 015-16 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τρίτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 15/3/016
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-15: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 015-16 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τρίτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 15/3/016
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών. HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής. Πρώτη Σειρά Ασκήσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 9/10/2018 Ηµεροµηνία Παράδοσης : 19/10/2018 Σηµείωση
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων Ηµεροµηνία Ανάθεσης : 9/10/2018 Ηµεροµηνία Παράδοσης : 19/10/2018 Σηµείωση
y = u i t 1 2 gt2 y = m y = 0.2 m
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ) Το χαρτονόµισµα ξεκινά από ηρεµία, u i = 0, και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2018 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ) Το χαρτονόµισµα ξεκινά από ηρεµία, u i = 0, και
400 = t2 (2) t = 15.1 s (3) 400 = (t + 1)2 (5) t = 15.3 s (6)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Θεωρούµε ως χρονικό σηµείο αναφοράς τη στιγµή που
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πρώτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. Θεωρούµε ως χρονικό σηµείο αναφοράς τη στιγµή που
x(t) = sin 2 (5πt) cos(22πt) = x 2 (t)dt
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 6-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Σειρές Fourier. Εστω το σήµα xt
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 6-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Σειρές Fourier. Εστω το σήµα xt
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ
 ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
ΣΤΟΧΑΣΤΙΚΑ ΣΗΜΑΤΑ ΚΑΙ ΕΦΑΡΜΟΓΕΣ Ακαδηµαϊκό Έτος 007-008 ιδάσκων: Ν. Παπανδρέου (Π.. 407/80) Πανεπιστήµιο Πατρών Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1η Εργαστηριακή Άσκηση Αναγνώριση
ημιουργία και διαχείριση πινάκων
 ημιουργία και διαχείριση πινάκων Για να δημιουργήσουμε έναν πίνακα στο MATLAB μπορούμε να γράψουμε A = [ 2 3 ; 7 9 0 ; - 0 5; -2-3 9 -] βλέπουμε ότι αμέσως μας επιστρέφει τον πίνακα που ορίσαμε A = 2 3
ημιουργία και διαχείριση πινάκων Για να δημιουργήσουμε έναν πίνακα στο MATLAB μπορούμε να γράψουμε A = [ 2 3 ; 7 9 0 ; - 0 5; -2-3 9 -] βλέπουμε ότι αμέσως μας επιστρέφει τον πίνακα που ορίσαμε A = 2 3
Πανεπιστήμιο Δυτικής Μακεδονίας. Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών. Ηλεκτρονική Υγεία. Εργαστήριο 10 ο : MATLAB
 Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ηλεκτρονική Υγεία Εργαστήριο 10 ο : MATLAB Αν. καθηγητής Αγγελίδης Παντελής e-mail: paggelidis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Ηλεκτρονική Υγεία Εργαστήριο 10 ο : MATLAB Αν. καθηγητής Αγγελίδης Παντελής e-mail: paggelidis@uowm.gr Τμήμα Μηχανικών Πληροφορικής και Τηλεπικοινωνιών Άδειες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 3 Ηµεροµηνία αποστολής στον φοιτητή: 3 Iανουαρίου 004. Τελική ηµεροµηνία αποστολής από τον φοιτητή: 8 Φεβρουαρίου
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ 3 Ηµεροµηνία αποστολής στον φοιτητή: 3 Iανουαρίου 004. Τελική ηµεροµηνία αποστολής από τον φοιτητή: 8 Φεβρουαρίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 06-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Μετασχηµατισµός Laplace. Εστω
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 06-7 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Λυµένες Ασκήσεις - Μετασχηµατισµός Laplace. Εστω
y[n] ay[n 1] = x[n] + βx[n 1] (6)
![y[n] ay[n 1] = x[n] + βx[n 1] (6) y[n] ay[n 1] = x[n] + βx[n 1] (6)](/thumbs/62/47574712.jpg) Ασκήσεις με το Μετασχηματισμό Fourier Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 8 Οκτωβρίου 015 1. Εστω το
Ασκήσεις με το Μετασχηματισμό Fourier Διακριτού Χρόνου Επιμέλεια: Γιώργος Π. Καφεντζης Δρ. Επιστήμης Η/Υ Πανεπιστημίου Κρήτης Δρ. Επεξεργασίας Σήματος Πανεπιστημίου Rennes 1 8 Οκτωβρίου 015 1. Εστω το
17-Φεβ-2009 ΗΜΥ Ιδιότητες Συνέλιξης Συσχέτιση
 ΗΜΥ 429 7. Ιδιότητες Συνέλιξης Συσχέτιση 1 Μαθηματικές ιδιότητες Αντιμεταθετική: a [ * b[ = b[ * a[ παρόλο που μαθηματικά ισχύει, δεν έχει φυσικό νόημα. Προσεταιριστική: ( a [ * b[ )* c[ = a[ *( b[ * c[
ΗΜΥ 429 7. Ιδιότητες Συνέλιξης Συσχέτιση 1 Μαθηματικές ιδιότητες Αντιμεταθετική: a [ * b[ = b[ * a[ παρόλο που μαθηματικά ισχύει, δεν έχει φυσικό νόημα. Προσεταιριστική: ( a [ * b[ )* c[ = a[ *( b[ * c[
Μια «ανώδυνη» εισαγωγή στο μάθημα (και στο MATLAB )
 Μια «ανώδυνη» εισαγωγή στο μάθημα (και στο MATLAB ) Μια πρώτη ιδέα για το μάθημα χωρίς καθόλου εξισώσεις!!! Περίγραμμα του μαθήματος χωρίς καθόλου εξισώσεις!!! Παραδείγματα από πραγματικές εφαρμογές ==
Μια «ανώδυνη» εισαγωγή στο μάθημα (και στο MATLAB ) Μια πρώτη ιδέα για το μάθημα χωρίς καθόλου εξισώσεις!!! Περίγραμμα του μαθήματος χωρίς καθόλου εξισώσεις!!! Παραδείγματα από πραγματικές εφαρμογές ==
Εργαστήριο Μαθηματικής Ανάλυσης Ι. Εισαγωγή στη Matlab Βασικές Συναρτήσεις-Γραφικές παραστάσεις. Πανεπιστήμιο Θεσσαλίας. Σχολή Θετικών Επιστημών
 Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής με εφαρμογές στη Βιοϊατρική Εργαστήριο Μαθηματικής Ανάλυσης Ι Εισαγωγή στη Matlab Βασικές Συναρτήσεις-Γραφικές παραστάσεις Εισαγωγή στη
Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής με εφαρμογές στη Βιοϊατρική Εργαστήριο Μαθηματικής Ανάλυσης Ι Εισαγωγή στη Matlab Βασικές Συναρτήσεις-Γραφικές παραστάσεις Εισαγωγή στη
ΗΜΥ 100 Εισαγωγή στην Τεχνολογία Διάλεξη 6
 ΗΜΥ 00 Εισαγωγή στην Τεχνολογία Διάλεξη 6 5 Σεπτεμβρίου, 0 Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα θέματά μας σήμερα Χρονικά
ΗΜΥ 00 Εισαγωγή στην Τεχνολογία Διάλεξη 6 5 Σεπτεμβρίου, 0 Δρ. Στέλιος Τιμοθέου ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ Τα θέματά μας σήμερα Χρονικά
Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II. ( ιάλεξη 12) ιδάσκων: ηµήτρης Ζεϊναλιπούρ
 Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II ( ιάλεξη 12) ιδάσκων: ηµήτρης Ζεϊναλιπούρ 12-1 Ανασκόπηση οµής Προγράµµατος µε Συναρτήσεις #include 1 void PrintMessage (); Πρότυπο ( ήλωση) Συνάρτησης (
Κεφάλαιο 3.5-3.6, 3.2: Συναρτήσεις II ( ιάλεξη 12) ιδάσκων: ηµήτρης Ζεϊναλιπούρ 12-1 Ανασκόπηση οµής Προγράµµατος µε Συναρτήσεις #include 1 void PrintMessage (); Πρότυπο ( ήλωση) Συνάρτησης (
Κυκλώματα, Σήματα και Συστήματα
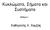 Κυκλώματα, Σήματα και Συστήματα Μάθημα 3 Καθηγητής Χ. Χαμζάς Κυκλώματα, Σήματα και Συστήματα.3- ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΕΞΙΣΩΣΕΙΣ Ένα διακριτό discree ή ψηφιακό digial σύστημα είναι μία διαδικασία προσδιορισμού
Κυκλώματα, Σήματα και Συστήματα Μάθημα 3 Καθηγητής Χ. Χαμζάς Κυκλώματα, Σήματα και Συστήματα.3- ΨΗΦΙΑΚΑ ΚΥΚΛΩΜΑΤΩΝ ΚΑΙ ΕΞΙΣΩΣΕΙΣ Ένα διακριτό discree ή ψηφιακό digial σύστημα είναι μία διαδικασία προσδιορισμού
sin(30 o ) 4 cos(60o ) = 3200 Nm 2 /C (7)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
Τυπικές χρήσεις της Matlab
 Matlab Μάθημα 1 Τι είναι η Matlab Ολοκληρωμένο Περιβάλλον Περιβάλλον ανάπτυξης Διερμηνευμένη γλώσσα Υψηλή επίδοση Ευρύτητα εφαρμογών Ευκολία διατύπωσης Cross platform (Wintel, Unix, Mac) Τυπικές χρήσεις
Matlab Μάθημα 1 Τι είναι η Matlab Ολοκληρωμένο Περιβάλλον Περιβάλλον ανάπτυξης Διερμηνευμένη γλώσσα Υψηλή επίδοση Ευρύτητα εφαρμογών Ευκολία διατύπωσης Cross platform (Wintel, Unix, Mac) Τυπικές χρήσεις
Διακριτός Μετασχηματισμός Fourier
 Διακριτός Μετασχηματισμός Fourier 1 Διακριτός Μετασχηματισμός Fourier Ο μετασχηματισμός Fourier αποτελεί τον ακρογωνιαίο λίθο της επεξεργασίας σήματος αλλά και συχνή αιτία πονοκεφάλου για όσους πρωτοασχολούνται
Διακριτός Μετασχηματισμός Fourier 1 Διακριτός Μετασχηματισμός Fourier Ο μετασχηματισμός Fourier αποτελεί τον ακρογωνιαίο λίθο της επεξεργασίας σήματος αλλά και συχνή αιτία πονοκεφάλου για όσους πρωτοασχολούνται
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Εισαγωγή. Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Εισαγωγή Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Εφαρµογές της Ψηφιακής Επεξεργασίας Σηµάτων Ακουστικά Σήµατα ü Αναγνώριση, Ανάλυση, Σύνθεση,
ΨΗΦΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΣΗΜΑΤΩΝ Εισαγωγή Εµµανουήλ Ζ. Ψαράκης Πολυτεχνική Σχολή Τµήµα Μηχανικών Η/Υ & Πληροφορικής Εφαρµογές της Ψηφιακής Επεξεργασίας Σηµάτων Ακουστικά Σήµατα ü Αναγνώριση, Ανάλυση, Σύνθεση,
e (4+j2πf)t dt (5) (0 1)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Ειστήµης Υολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Ειστήµης Υολογιστών HY-5: Εφαρµοσµένα Μαθηµατικά για Μηχανικούς Εαρινό Εξάµηνο 7-8 ιδάσκοντες : Γ. Στυλιανού, Γ. Καφεντζής Τέταρτη Σειρά Ασκήσεων - Λύσεις Ηµεροµηνία Ανάθεσης
Ψηφιακή Επεξεργασία Εικόνας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 3 : Αποκατάσταση εικόνας (Image Restoration) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ψηφιακή Επεξεργασία Εικόνας Ενότητα 3 : Αποκατάσταση εικόνας (Image Restoration) Ιωάννης Έλληνας Τμήμα Η/ΥΣ Άδειες Χρήσης Το παρόν
W = 6.34 kn (2) F = u 2 f = u2 i + 2a(x f x i ) a = u2 f u2 i 2x f. F = d U(x) (5)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-2: Φυσική Ι Χειµερινό Εξάµηνο 208 ιδάσκων : Γ. Καφεντζής Λύσεις 3ου Φροντιστηρίων Ασκηση. Επιλέγουµε ως σύστηµα τη σφάιρα. Το σύστηµα είναι µη αποµονωµένο.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-2: Φυσική Ι Χειµερινό Εξάµηνο 208 ιδάσκων : Γ. Καφεντζής Λύσεις 3ου Φροντιστηρίων Ασκηση. Επιλέγουµε ως σύστηµα τη σφάιρα. Το σύστηµα είναι µη αποµονωµένο.
Γραφικές παραστάσεις (1ο μέρος)
 ΤΕΙ ΑΘΗΝΑΣ Τμήμα Ηλεκτρονικής Φυσική των Αισθητήρων Γραφικές παραστάσεις (1ο μέρος) Σε αυτήν την ενότητα θα εξοικειωθείτε με τον τρόπο απεικόνισης γραφικών παραστάσεων στο MATLAB, και συγκεκριμένα με τις
ΤΕΙ ΑΘΗΝΑΣ Τμήμα Ηλεκτρονικής Φυσική των Αισθητήρων Γραφικές παραστάσεις (1ο μέρος) Σε αυτήν την ενότητα θα εξοικειωθείτε με τον τρόπο απεικόνισης γραφικών παραστάσεων στο MATLAB, και συγκεκριμένα με τις
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ. Ενότητα 3: Αποκατάσταση Εικόνας.
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 3: Αποκατάσταση Εικόνας Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΕΠΕΞΕΡΓΑΣΙΑ ΕΙΚΟΝΑΣ Ενότητα 3: Αποκατάσταση Εικόνας Ιωάννης Έλληνας Τμήμα Υπολογιστικών Συστημάτων Άδειες Χρήσης Το παρόν εκπαιδευτικό
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών
 HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
HMY 429: Εισαγωγή στην Επεξεργασία Ψηφιακών Σημάτων Διάλεξη 12: Δειγματοληψία και ανακατασκευή (IV) Παρεμβολή (Interpolation) Γενικά υπάρχουν πολλοί τρόποι παρεμβολής, π.χ. κυβική παρεμβολή (cubic spline
Σήματα και Συστήματα. Διάλεξη 1: Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
Σήματα και Συστήματα Διάλεξη 1: Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Σήματα 1. Σκοποί της Θεωρίας Σημάτων 2. Κατηγορίες Σημάτων 3. Χαρακτηριστικές Παράμετροι
