ΚΕΦΑΛΑΙΟ 3. ιατηρητικές δυνάµεις
|
|
|
- ŌÁĒ Ανδρέου
- 10 χρόνια πριν
- Προβολές:
Transcript
1 ΚΕΦΑΛΑΙΟ 3 ιατηρητικές δυνάµεις Στο υποκεφάλαιο.4 είδαµε ότι, για µονοδιάστατες κινήσεις στον άξονα x, όλες οι δυνάµεις της µορφής F F(x) είναι διατηρητικές. Για κίνηση λοιπόν στις τρεις διαστάσεις, µπορούµε να πούµε ότι όλες οι δυνάµεις της µορφής F F( ) F( x, είναι διατηρητικές; Με άλλα λόγια, µπορούµε να γράψοµε τον νόµο διατήρησης της ενέργειας για όλες τις δυνάµεις της µορφής F F( ) F( x, ; Θα το εξετάσοµε χρησιµοποιώντας τον εύτερο Νόµο του Νεύτωνα. Ας θεωρήσοµε υλικό σηµείο µάζας m που κινείται στον χώρο υπό την επίδραση της γενικής δύναµης F F( ) F( x,, όπου xiˆ + y ˆj + z kˆ είναι η στιγµιαία θέση του υλικού σηµείου. Συγκεκριµένα παραδείγµατα θα δούµε πιο κάτω. z m y x Ας θεωρήσοµε ότι την αρχική χρονική στιγµή t, το υλικό σηµείο ήταν στη θέση x iˆ y ˆj z kˆ + + και είχε ταχύτητα u. Βάσει του εύτερου Νόµου του Νεύτωνα γράφοµε du m F. (3.) Πολλαπλασιάζοµε (δηλαδή εσωτερικό γινόµενο) αµφότερα τα µέλη της (3.) µε την ταχύτητα u και έχοµε du m u F u. (3.) Σελίδα από 9
2 Η εξίσωση (3.) µπορεί να γραφεί ως εξής διότι d F u, (3.3) u και d du u m u. Η ποσότητα T λέγεται κινητική ενέργεια του υλικού σηµείου και η εξίσωση (3.3) γράφεται ως dt F u, (3.4) όπου η ποσότητα F u λέγεται ισχύς της δύναµης. Χωρίς λοιπόν να το καταλάβοµε, αποδείξαµε το εξής θεώρηµα: Θεώρηµα: Για δυνάµεις της µορφής F F( ), η χρονική µεταβολή της κινητικής ενέργειας του υλικού σηµείου πάνω στο οποίο ασκείται η δύναµη ισούται µε την ισχύ της δύναµης. Πολλαπλασιάζοµε αµφότερα τα µέλη της εξίσωσης (3.4) µε και έχοµε η οποία γράφεται ως dt d F, (3.5) dt F d. (3.6) Πάλι χωρίς να το καταλάβοµε, αποδείξαµε το εξής θεώρηµα: Θεώρηµα: Για δυνάµεις της µορφής F F( ), η µεταβολή της κινητικής ενέργειας του υλικού σηµείου πάνω στο οποίο ασκείται η δύναµη ισούται µε το έργο της δύναµης κατά τη µετατόπιση του υλικού σηµείου. Αν και δεν είναι απαραίτητο, την εξίσωση (3.6) τη γράφοµε ως εξής: d F d. (3.7) Σελίδα από 9
3 Παρατηρούµε ότι οι µεταβλητές είναι χωρισµένες, δηλαδή αριστερά έχοµε ταχύτητα και δεξιά θέση. Άρα µπορούµε να ολοκληρώσοµε κατά µέλη. Ολοκληρώνοµε λοιπόν το αριστερό µέλος από την αρχική ταχύτητα u µέχρι την τυχούσα ταχύτητα u και το δεξιό από την αρχική θέση µέχρι την τυχούσα θέση. Έτσι έχοµε ή u u d F( ) d, (3.8) F d, (3.9) την οποία γράφοµε ως εξής: F d σταθερά, (3.) διότι οι ποσότητες /, m, u είναι σταθερές. Τίθεται λοιπόν τώρα το ερώτηµα: Μπορούµε να ορίσοµε την ποσότητα F d (3.) ως τη δυναµική ενέργεια V ( ) (3.) του υλικού σηµείου στη θέση ; Αν ναι, τότε η εξίσωση (3.) θα ήταν ο νόµος διατήρησης της ενέργειας και όλες οι δυνάµεις F F( ) θα ήταν διατηρητικές. Όµως, αυτό δεν ισχύει. Η δυναµική ενέργεια V ( ) V ( x,, ως συνάρτηση των µεταβλητών x, z, είναι µονοσήµαντη. ηλαδή, για κάθε τριάδα αριθµών x, z µάς δίνει µια τιµή, την τιµή της δυναµικής ενέργειας σ αυτή τη θέση. Η σχέση (3.) µάς δίνει το µείον έργο που κάνει η δύναµη για µετακίνηση από το σηµείο στο σηµείο. Αν αυτό το έργο εξαρτάται από τον δρόµο που ακολουθήθηκε, τότε για διαφορετικούς δρόµους θα έχοµε διαφορετικά έργα, δηλαδή η συνάρτηση (3.) είναι πολυσήµαντη. εν µπορούµε εποµένως να εξισώσοµε µια µονοσήµαντη συνάρτηση, την (3.), µε µια πολυσήµαντη συνάρτηση, την (3.). Μπορούµε να εξισώσοµε την (3.) µε την (3.) µόνο αν η (3.) είναι κι αυτή µονοσήµαντη συνάρτηση του, δηλαδή αν το έργο της δύναµης µεταξύ των σηµείων και είναι ανεξάρτητο του δρόµου µεταξύ των δυο αυτών σηµείων. Σελίδα 3 από 9
4 Οι δυνάµεις F F( ) για τις οποίες το έργο µεταξύ δυο τυχόντων σηµείων είναι ανεξάρτητο του δρόµου λέγονται διατηρητικές ή αστρόβιλες και γι αυτές και µόνο γι αυτές µπορούµε να ορίσοµε τη δυναµική ενέργεια στο σηµείο µε τη σχέση V ( ) F d. (3.3) Για διατηρητικές δυνάµεις F F( ) µπορούµε λοιπόν να γράψοµε από τη σχέση (3.) ότι T +V σταθερά E (3.4) όπου E είναι η ολική ενέργεια. Έτσι αποδείξαµε το θεώρηµα διατήρησης της ενέργειας για διατηρητικές δυνάµεις της µορφής F F( ). Θεώρηµα: Για διατηρητικές δυνάµεις της µορφής F F( ) το άθροισµα της κινητικής και της δυναµικής ενέργειας του υλικού σηµείου είναι σταθερό κατά την κίνηση του. Από τον ορισµό που δώσαµε για την δυναµική ενέργεια, είναι προφανές ότι αυτή µηδενίζεται στην αρχική θέση διότι V ( ) F( ) d. (3.5) Ας υποθέσοµε ότι δεν θέλοµε η δυναµική ενέργεια να µηδενίζεται στην αρχική θέση, αλλά σε κάποια άλλη θέση. Τότε γράφοµε την εξίσωση (3.) ως εξής: ή F( ) d F( ) d F( ) d + F( ) d (3.6) σταθερά. (3.7) Το δεξιό µέλος της (3.7) είναι σταθερό διότι το ορισµένο ολοκλήρωµα µιας συνάρτησης είναι αριθµός. Αν τώρα ορίσοµε τη δυναµική ενέργεια ως και την ολική ενέργεια ως V ( ) F( ) d (3.8) Σελίδα 4 από 9
5 πάλι µπορούµε να γράψοµε E + F( ) d σταθερά (3.9) T +V σταθερά E, (3.) µόνο που τώρα και το E και το V έχουν διαφορετικές τιµές από πριν. Και από τον ορισµό (3.3) και από τον ορισµό (3.8) έχοµε ότι V ( x, ˆ V ( x, ˆ V ( x, F( ) i j kˆ V ( x,, (3.) x y z όπου το σύµβολο / y, / z. / x σηµαίνει µερική παράγωγος ως προς x και οµοίως για τα Με άλλα λόγια, η δυναµική ενέργεια είναι το µείον έργο της δύναµης και η δύναµη είναι το µείον ανάδελτα της δυναµικής ενέργειας. Παρατήρηση : Όπως είδαµε παραπάνω, το µηδέν της δυναµικής ενέργειας µπορούµε να το βάλοµε όπου θέλοµε και ο νόµος διατήρησης της ενέργειας ισχύει. Οι τιµές της δυναµικής ενέργειας και της ολικής ενέργειας αλλάζουν ανάλογα µε το που βάλαµε το µηδέν της δυναµικής ενέργειας. 3. Κεντρικές δυνάµεις Η πιο σηµαντική κατηγορία διατηρητικών δυνάµεων είναι οι κεντρικές δυνάµεις, που ορίζονται ως F f ( ) ˆ, (3.) όπου ˆ / / είναι το ακτινικό µοναδιαίο διάνυσµα. Είναι δηλαδή ακτινικές δυνάµεις. Όλες οι θεµελιώδεις δυνάµεις της Φύσης είναι κεντρικές (βλ. Ασκήσεις 3.3 κα 3.5). Θεώρηµα: Όλες οι κεντρικές δυνάµεις είναι διατηρητικές. Απόδειξη: Αρκεί να δείξοµε ότι το έργο που κάνουν οι κεντρικές δυνάµεις µεταξύ δυο τυχόντων σηµείων και είναι ανεξάρτητο του δρόµου που ακολουθούµε. Το έργο αυτό είναι W F d f d ( ) ˆ f ( ) d ανεξάρτητο του δρόµου, (3.3) όπου d ˆ d είναι ακτινική µετατόπιση, δηλαδή είναι η προβολή της µετατόπισης d στο ακτινικό διάνυσµα ˆ. Αποδείξαµε λοιπόν ότι το έργο της δύναµης (3.) από το τυχόν σηµείο στο τυχόν σηµείο είναι ίσο µε το έργο που κάνει η δύναµη Σελίδα 5 από 9
6 για ακτινική µετακίνηση από την επιφάνεια της σφαίρας µε ακτίνα στην επιφάνεια της σφαίρας µε ακτίνα ανεξαρτήτως της πορείας που ακολουθήσαµε. R Παράδειγµα 3.: Να σχεδιασθεί το πεδίο δυνάµεων F( ) F ˆ, όπου F Nt, R m είναι σταθερές, είναι η ακτινική απόσταση και ˆ / / είναι το µοναδιαίο ακτινικό διάνυσµα. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Να διερευνήσετε αν το πεδίο δυνάµεων είναι διατηρητικό ή όχι. Από το σχήµα και µόνο θα µπορούσατε να βγάλετε το συµπέρασµα αυτό; Λύση: Σε κάθε σηµείο η δύναµη είναι ακτινική. Για m, το µέτρο της δύναµης είναι Nt. Για m, το µέτρο της δύναµης είναι / Nt. Για 3 m, το µέτρο της δύναµης είναι /3 Nt και ούτω καθ εξής. Έτσι λοιπόν έχοµε y x Το πεδίο δυνάµεων είναι διατηρητικό ή αστρόβιλο διότι είναι κεντρικό. Το ίδιο συµπέρασµα βγάζοµε και από το σχήµα αφού το πεδίο δυνάµεων δεν στροβιλίζει, δηλαδή δεν θα µας έστριβε αν πέφταµε µέσα σ αυτό. Παράδειγµα 3.: Να σχεδιασθεί το πεδίο δυνάµεων Σελίδα 6 από 9 F ) ( F x / x ) ˆj, όπου ( F Nt, x m είναι σταθερές και ĵ είναι το µοναδιαίο διάνυσµα του άξονα y. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Παρατηρείστε ότι αυτό το πεδίο δυνάµεων δεν εξαρτάται από τις συντεταγµένες y και z, αλλά µόνο από τη συντεταγµένη x.
7 A) Να διερευνήσετε αν αυτό το πεδίο δυνάµεων είναι διατηρητικό ή όχι. Από το σχήµα και µόνο θα µπορούσατε να βγάλετε το συµπέρασµα αυτό; B) Να υπολογίσετε το έργο που κάνει το πεδίο δυνάµεων στην κλειστή διαδροµή (, ) (, ) (, ) (, ) (, ) του επιπέδου xy. Λύση: Για όλα τα σηµεία (, y ), η δύναµη είναι +. Για όλα τα σηµεία (, y ), η δύναµη είναι + κλπ. Για όλα τα σηµεία (, y), η δύναµη είναι κλπ. Έτσι έχοµε y B A x C D Α) Το πεδίο δυνάµεων δεν είναι διατηρητικό διότι, όπως θα αποδείξοµε στο ερώτηµα Β, το έργο της δύναµης σε µια κλειστή γραµµή δεν είναι ίσο µε το µηδέν. Το ίδιο συµπέρασµα βγάζοµε και από το σχήµα αφού το πεδίο δυνάµεων στροβιλίζει, δηλαδή ένα σώµα πεπερασµένων διαστάσεων θα το στρίψει κατά φορά αντίθετη των δεικτών του ωρολογίου αν πέσει µέσα. B) Τα επιµέρους έργα είναι: W AB, διότι η δύναµη είναι κάθετη στη µετατόπιση. W Joule, διότι η δύναµη είναι σταθερή και συγγραµµική µε τη BC µετατόπιση. W CD και W DA Joule. Συνεπώς το συνολικό έργο είναι W 4 Joule. Άσκηση 3.: Να σχεδιασθεί το πεδίο δυνάµεων F( ) k ˆ, όπου k Nt/m είναι σταθερά, είναι η ακτινική απόσταση και ˆ / / είναι το µοναδιαίο ακτινικό διάνυσµα. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Σελίδα 7 από 9
8 A) Να διερευνήσετε αν το πεδίο δυνάµεων είναι διατηρητικό ή όχι. Από το σχήµα και µόνο θα µπορούσατε να βγάλετε το συµπέρασµα αυτό; B) Να βρεθεί το έργο που παράγει το πεδίο δυνάµεων κατά τη µετακίνηση από το σηµείο (,, ) στο σηµείο (,, ). Άσκηση 3.: Να σχεδιασθεί το πεδίο δυνάµεων F ) ( F y / y ) iˆ, όπου ( F Nt, y m είναι σταθερές και î είναι το µοναδιαίο διάνυσµα του άξονα x. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Παρατηρείστε ότι αυτό το πεδίο δυνάµεων δεν εξαρτάται από τις συντεταγµένες x και z, αλλά µόνο από τη συντεταγµένη y. A) Να διερευνήσετε αν αυτό το πεδίο δυνάµεων είναι διατηρητικό ή όχι. Από το σχήµα και µόνο θα µπορούσατε να βγάλετε το συµπέρασµα αυτό; B) Να υπολογίσετε το έργο που κάνει το πεδίο δυνάµεων στην κλειστή διαδροµή (, ) (, ) (, ) (, ) (, ) του επιπέδου xy. Mm Άσκηση 3.3: Να σχεδιασθεί το πεδίο δυνάµεων F( ) G ˆ, που περιγράφει την έλξη της Σελήνης (σηµειακή µάζα m ) από τη Γη (σηµειακή µάζα M ), θεωρώντας ότι η Γη είναι ακίνητη στην αρχή των αξόνων. Χάριν ευκολίας, µπορείτε να θεωρήσετε ότι το γινόµενο GMm είναι ίσο µε τη µονάδα. Στον τύπο, είναι η ακτινική απόσταση της Σελήνης από τη Γη, ˆ / είναι το µοναδιαίο ακτινικό διάνυσµα και το αρνητικό πρόσηµο σηµαίνει ότι η Γη έλκει τη Σελήνη. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Α) Από το σχήµα και µόνο µπορείτε να αποφανθείτε αν το πεδίο δυνάµεων είναι διατηρητικό ή όχι; Β) Να βρεθεί το έργο που παράγει το πεδίο δυνάµεων κατά τη µετακίνηση από το σηµείο (,, ) στο σηµείο (,, ). Άσκηση 3.4: Να σχεδιασθεί το πεδίο δυνάµεων F( ) ( F x / x ) ˆj, όπου F Nt, x m είναι σταθερές και ĵ είναι το µοναδιαίο διάνυσµα του άξονα y. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Παρατηρείστε ότι αυτό το πεδίο δυνάµεων δεν εξαρτάται από τις συντεταγµένες y και z, αλλά µόνο από τη συντεταγµένη x. A) Να διερευνήσετε αν αυτό το πεδίο δυνάµεων είναι διατηρητικό ή όχι. Από το σχήµα και µόνο θα µπορούσατε να βγάλετε το συµπέρασµα αυτό; B) Να υπολογίσετε το έργο που κάνει το πεδίο δυνάµεων στην κλειστή διαδροµή ( 3, 3) ( 3, 3) ( 3, 3) (3, 3) (3, 3) του επιπέδου xy. Γ) Σχολιάστε το αποτέλεσµα που βρήκατε. Qq Άσκηση 3.5: Να σχεδιασθεί το πεδίο δυνάµεων F( ) k ˆ, που περιγράφει την άπωση σηµειακού φορτίου q από το οµόσηµο φορτίο Q, που είναι ακίνητο στην Σελίδα 8 από 9
9 αρχή των αξόνων. Χάριν ευκολίας, µπορείτε να θεωρήσετε ότι το γινόµενο kqq είναι ίσο µε τη µονάδα. Στην έκφραση του πεδίου δυνάµεων είναι η ακτινική απόσταση του φορτίου q και ˆ / είναι το µοναδιαίο ακτινικό διάνυσµα. Με άλλα λόγια, να σχεδιασθεί το διάνυσµα της δύναµης F σε διάφορες θέσεις. Χάριν ευκολίας περιοριστείτε σε σηµεία του επιπέδου xy. Α) Από το σχήµα και µόνο µπορείτε να αποφανθείτε αν το πεδίο δυνάµεων είναι διατηρητικό ή όχι; Β) Να βρεθεί το έργο που παράγει το πεδίο δυνάµεων κατά τη µετακίνηση από το σηµείο (,, 3) στο σηµείο (3,, ). Σελίδα 9 από 9
ΚΕΦΑΛΑΙΟ 8. Ροπή και Στροφορµή Μέρος δεύτερο
 ΚΕΦΑΛΑΙΟ 8 Ροπή και Στροφορµή Μέρος δεύτερο Στο προηγούµενο Κεφάλαιο εξετάσαµε την περιστροφή στερεού σώµατος περί σταθερό άξονα. Εδώ θα εξετάσοµε την εξίσωση κίνησης στερεού σώµατος γενικώς. Πριν το κάνοµε
ΚΕΦΑΛΑΙΟ 8 Ροπή και Στροφορµή Μέρος δεύτερο Στο προηγούµενο Κεφάλαιο εξετάσαµε την περιστροφή στερεού σώµατος περί σταθερό άξονα. Εδώ θα εξετάσοµε την εξίσωση κίνησης στερεού σώµατος γενικώς. Πριν το κάνοµε
ΚΕΦΑΛΑΙΟ 11. Παγκόσµια έλξη
 ΚΕΦΑΛΑΙΟ Παγκόσµια έλξη ύναµη µεταξύ υλικών σηµείων Σε ένα αδρανειακό σύστηµα συντεταγµένων θεωρούµε δυο σηµειακές µάζες και Η µάζα είναι ακίνητη στην αρχή των αξόνων και η µάζα βρίσκεται στη διανυσµατική
ΚΕΦΑΛΑΙΟ Παγκόσµια έλξη ύναµη µεταξύ υλικών σηµείων Σε ένα αδρανειακό σύστηµα συντεταγµένων θεωρούµε δυο σηµειακές µάζες και Η µάζα είναι ακίνητη στην αρχή των αξόνων και η µάζα βρίσκεται στη διανυσµατική
ΚΕΦΑΛΑΙΟ 7. Ροπή και Στροφορµή Μέρος πρώτο
 ΚΕΦΑΛΑΙΟ 7 Ροπή και Στροφορµή Μέρος πρώτο Μέχρι εδώ εξετάσαµε την κίνηση ενός υλικού σηµείου υπό την επίδραση µιας δύναµης. Τα πράγµατα αλλάζουν δραµατικά αν αντί υλικού σηµείου έχοµε ένα στερεό σώµα.
ΚΕΦΑΛΑΙΟ 7 Ροπή και Στροφορµή Μέρος πρώτο Μέχρι εδώ εξετάσαµε την κίνηση ενός υλικού σηµείου υπό την επίδραση µιας δύναµης. Τα πράγµατα αλλάζουν δραµατικά αν αντί υλικού σηµείου έχοµε ένα στερεό σώµα.
ΚΕΦΑΛΑΙΟ 2. Τρισδιάστατες κινήσεις
 ΚΕΦΑΛΑΙΟ Τρισδιάστατες κινήσεις Οι µονοδιάστατες κινήσεις είναι εύκολες αλλά ζούµε σε τρισδιάστατο χώρο Θα δούµε λοιπόν τώρα πως θα αντιµετωπίζοµε την κίνηση υλικού σηµείου στις τρεις διαστάσεις Ας θεωρήσοµε
ΚΕΦΑΛΑΙΟ Τρισδιάστατες κινήσεις Οι µονοδιάστατες κινήσεις είναι εύκολες αλλά ζούµε σε τρισδιάστατο χώρο Θα δούµε λοιπόν τώρα πως θα αντιµετωπίζοµε την κίνηση υλικού σηµείου στις τρεις διαστάσεις Ας θεωρήσοµε
ΣΗΜΕΙΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ
 ΓΕΝΙΚΗ ΦΥΣΙΚΗ Ι Ακαδηµαϊκό έτος 4-5 ΣΗΜΕΙΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ Νίκος Κυλάφης Πανεπιστήµιο Κρήτης //4 Σελίδα από 55 ΠΛΗΡΟΦΟΡΙΕΣ ΣΧΕΤΙΚΕΣ ΜΕ ΤΟ ΜΑΘΗΜΑ ΚΑΙ ΤΙΣ ΕΞΕΤΑΣΕΙΣ Το µάθηµα της Γενικής Φυσικής Ι θα γίνεται
ΓΕΝΙΚΗ ΦΥΣΙΚΗ Ι Ακαδηµαϊκό έτος 4-5 ΣΗΜΕΙΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ Νίκος Κυλάφης Πανεπιστήµιο Κρήτης //4 Σελίδα από 55 ΠΛΗΡΟΦΟΡΙΕΣ ΣΧΕΤΙΚΕΣ ΜΕ ΤΟ ΜΑΘΗΜΑ ΚΑΙ ΤΙΣ ΕΞΕΤΑΣΕΙΣ Το µάθηµα της Γενικής Φυσικής Ι θα γίνεται
ΚΕΦΑΛΑΙΟ 4. ιατήρηση ορµής
 ΚΕΦΑΛΑΙΟ 4 ιατήρηση ορµής Ας θεωρήσοµε δυο υλικά σηµεία και µε µάζες και αντιστοίχως που βρίσκονται την τυχούσα χρονική στιγµή στις αντίστοιχες διανυσµατικές ακτίνες και και έχουν αντίστοιχες ταχύτητες
ΚΕΦΑΛΑΙΟ 4 ιατήρηση ορµής Ας θεωρήσοµε δυο υλικά σηµεία και µε µάζες και αντιστοίχως που βρίσκονται την τυχούσα χρονική στιγµή στις αντίστοιχες διανυσµατικές ακτίνες και και έχουν αντίστοιχες ταχύτητες
5 η Εβδομάδα Έργο και κινητική ενέργεια. Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας
 5 η Εβδομάδα Έργο και κινητική ενέργεια Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας Ομαλή κυκλική κίνηση Κίνηση σωματίου σε κύκλο με ταχύτητα σταθερού μέτρου. Επιτάχυνση
5 η Εβδομάδα Έργο και κινητική ενέργεια Ομαλή κυκλική κίνηση Έργο δύναμης Κινητική ενέργεια Θεώρημα έργου ενέργειας Ομαλή κυκλική κίνηση Κίνηση σωματίου σε κύκλο με ταχύτητα σταθερού μέτρου. Επιτάχυνση
ΚΕΦΑΛΑΙΟ 10. Ταλαντώσεις
 ΚΕΦΑΛΑΙΟ 0 Ταλαντώσεις Στο Παράδειγµα 9 είδαµε τη µελέτη της κίνησης υλικού σηµείου µάζας, που βρίσκεται στο ένα άκρο ελατηρίου µε το άλλο άκρο του ελατηρίου σταθερό Θα επανεετάσοµε το ίδιο πρόβληµα εδώ
ΚΕΦΑΛΑΙΟ 0 Ταλαντώσεις Στο Παράδειγµα 9 είδαµε τη µελέτη της κίνησης υλικού σηµείου µάζας, που βρίσκεται στο ένα άκρο ελατηρίου µε το άλλο άκρο του ελατηρίου σταθερό Θα επανεετάσοµε το ίδιο πρόβληµα εδώ
εάν F x, x οµόρροπα εάν F x, x αντίρροπα B = T W T = W B
 4 Εργο και Ενέργεια 4.1 Εργο σε µία διάσταση Το έργο µιας σταθερής δύναµης F x, η οποία ασκείται σε ένα σώµα που κινείται σε µία διάσταση x, ορίζεται ως W = F x x Εργο ύναµης = ύναµη Μετατόπιση Εχουµε
4 Εργο και Ενέργεια 4.1 Εργο σε µία διάσταση Το έργο µιας σταθερής δύναµης F x, η οποία ασκείται σε ένα σώµα που κινείται σε µία διάσταση x, ορίζεται ως W = F x x Εργο ύναµης = ύναµη Μετατόπιση Εχουµε
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
ΚΕΦΑΛΑΙΟ 8. Ροπή και Στροφορµή Μέρος δεύτερο
 ΚΕΦΑΛΑΙΟ 8 Ροπή και Σοφορµή Μέρος δεύτερο Στο προηγούµενο Κεφάλαιο εξετάσαµε την περισοφή στερεού σώµατος περί σταθερό άξονα Εδώ θα εξετάσοµε την εξίσωση κίνησης στερεού σώµατος γενικώς Πριν το κάνοµε
ΚΕΦΑΛΑΙΟ 8 Ροπή και Σοφορµή Μέρος δεύτερο Στο προηγούµενο Κεφάλαιο εξετάσαµε την περισοφή στερεού σώµατος περί σταθερό άξονα Εδώ θα εξετάσοµε την εξίσωση κίνησης στερεού σώµατος γενικώς Πριν το κάνοµε
Βασική έννοια. Μηχανική ενέργεια.
 Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής σε άλλη. Μηχανική ενέργεια. Λύση προβλημάτων μηχανικής. α) ος νόμος Νεύτωνα,
Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής σε άλλη. Μηχανική ενέργεια. Λύση προβλημάτων μηχανικής. α) ος νόμος Νεύτωνα,
ΚΕΦΑΛΑΙΟ 4. Διατήρηση ορμής
 ΚΕΦΑΛΑΙΟ 4 Διατρηση ορμς Ας θεωρσομε δυο υλικά σημεία και, με μάζες και αντιστοίχως, που βρίσκονται την τυχούσα χρονικ στιγμ στις αντίστοιχες διανυσματικές ακτίνες r και r και έχουν αντίστοιχες ταχύτητες
ΚΕΦΑΛΑΙΟ 4 Διατρηση ορμς Ας θεωρσομε δυο υλικά σημεία και, με μάζες και αντιστοίχως, που βρίσκονται την τυχούσα χρονικ στιγμ στις αντίστοιχες διανυσματικές ακτίνες r και r και έχουν αντίστοιχες ταχύτητες
ΚΕΦΑΛΑΙΟ 5. Συστήµατα µεταβλητής µάζας
 ΚΕΦΑΛΑΙΟ 5 Συστµατα µεταβλητς µάζας Μέχρι τώρα µελετσαµε την κίνηση υλικού σηµείου µε συγκεκριµένη µάζα m, η οποία παραµένει σταθερ. Θα εξετάσοµε τώρα την περίπτωση που η µάζα δεν είναι σταθερ, αλλά µεταβάλλεται
ΚΕΦΑΛΑΙΟ 5 Συστµατα µεταβλητς µάζας Μέχρι τώρα µελετσαµε την κίνηση υλικού σηµείου µε συγκεκριµένη µάζα m, η οποία παραµένει σταθερ. Θα εξετάσοµε τώρα την περίπτωση που η µάζα δεν είναι σταθερ, αλλά µεταβάλλεται
ΕΡΓΟ -ΕΝΕΡΓΕΙΑ. Το στοιχειώδες έργο dw δύναμης F που ασκείται σε ένα σώμα κατά τη στοιχειώδη μετατόπισή του d s είναι η ποσότητα:
 ΕΡΓΟ -ΕΝΕΡΓΕΙΑ Το στοιχειώδες έργο dw δύναμης F που ασκείται σε ένα σώμα κατά τη στοιχειώδη μετατόπισή του d s είναι η ποσότητα: d F d s Παρατηρήσεις Το έργο εκφράζει την ποσότητα της ενέργειας που παράγεται
ΕΡΓΟ -ΕΝΕΡΓΕΙΑ Το στοιχειώδες έργο dw δύναμης F που ασκείται σε ένα σώμα κατά τη στοιχειώδη μετατόπισή του d s είναι η ποσότητα: d F d s Παρατηρήσεις Το έργο εκφράζει την ποσότητα της ενέργειας που παράγεται
Γενική Φυσική. Ενότητα 5: Έργο, ενέργεια. Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών
 Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής
Γενική Φυσική Γεώργιος Βούλγαρης Σχολή Θετικών Επιστημών Τμήμα Μαθηματικών Έργο - Ενέργεια Βασική έννοια. Μηχανική, Ηλεκτρομαγνητική, Χημική, Θερμική, Πυρηνική, κ.α. Δυνατότητα μετατροπής της μίας μορφής
Εργασία 3, ΦΥΕ 24, N. Κυλάφης
 Εργασία ΦΥΕ 4-4 Κυλάφης Λύσεις Άσκηση : Ένας κυκλικός δίσκος µάζας M και ακτίνας R µπορεί να περιστρέφετε χωρίς τριβές γύρω από έναν οριζόντιο άξονα που διέρχεται από το κέντρο του Ένα αβαρές νήµα είναι
Εργασία ΦΥΕ 4-4 Κυλάφης Λύσεις Άσκηση : Ένας κυκλικός δίσκος µάζας M και ακτίνας R µπορεί να περιστρέφετε χωρίς τριβές γύρω από έναν οριζόντιο άξονα που διέρχεται από το κέντρο του Ένα αβαρές νήµα είναι
ΚΕΦΑΛΑΙΟ 9. Μη αδρανειακά συστήµατα αναφοράς
 ΚΕΦΑΛΑΙΟ 9 Μη αδρανειακά συστήµατα αναφοράς Στην Εισαγωγή στη Μηχανική, πριν το Κεφάλαιο 1, είδαµε ότι ο εύτερος Νόµος του Νεύτωνα ισχύει µόνο για αδρανειακούς παρατηρητές, δηλαδή για παρατηρητές που είτε
ΚΕΦΑΛΑΙΟ 9 Μη αδρανειακά συστήµατα αναφοράς Στην Εισαγωγή στη Μηχανική, πριν το Κεφάλαιο 1, είδαµε ότι ο εύτερος Νόµος του Νεύτωνα ισχύει µόνο για αδρανειακούς παρατηρητές, δηλαδή για παρατηρητές που είτε
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 15/10/2012 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 15/1/1 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σε σώμα μάζας m = 1Kg ασκείται η δύναμη F
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 15/1/1 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗΣ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σε σώμα μάζας m = 1Kg ασκείται η δύναμη F
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ. ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέµβριος 2004 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου Θέµα 1 (25 µονάδες) Ένα εκκρεµές µήκους l κρέµεται έτσι ώστε η σηµειακή µάζα να βρίσκεται ακριβώς
ΠΑΡΑΡΤΗΜΑ Γ. Επικαμπύλια και Επιφανειακά Ολοκληρώματα. Γ.1 Επικαμπύλιο Ολοκλήρωμα
 ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
Εργασία 4, ΦΥΕ 24, N. Κυλάφης
 Εργασία ΦΥΕ - N Κυλάφης Λύσεις Άσκηση : Θεωρήστε ότι στα σηµεία υπάρχουν τέσσερα φορτία το καθένα Α Να βρεθεί το ηλεκτρικό δυναµικό που δηµιουργείται σε τυχόν σηµείο του άξονα Β Να βρεθεί η ένταση του
Εργασία ΦΥΕ - N Κυλάφης Λύσεις Άσκηση : Θεωρήστε ότι στα σηµεία υπάρχουν τέσσερα φορτία το καθένα Α Να βρεθεί το ηλεκτρικό δυναµικό που δηµιουργείται σε τυχόν σηµείο του άξονα Β Να βρεθεί η ένταση του
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους τους άξονες και.
Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους τους άξονες και.
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/2013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3//7/013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΑΠΑΝΤΗΣΕΙΣ ΓΡΑΠΤΗΣ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m=0.1 Kg κινείται σε οριζόντιο δάπεδο ευθύγραμμα με την
ΚΕΦΑΛΑΙΟ 5: ΣΥΣΤΗΜΑΤΑ ΠΟΛΛΩΝ ΣΩΜΑΤΩΝ
 ΚΕΦΑΛΑΙΟ 5: ΣΥΣΤΗΜΑΤΑ ΠΟΛΛΩΝ ΣΩΜΑΤΩΝ Στο κεφάλαιο αυτό θα ασχοληθούµε αρχικά µε ένα µεµονωµένο σύστηµα δύο σωµάτων στα οποία ασκούνται µόνο οι µεταξύ τους κεντρικές δυνάµεις, επιτρέποντας ωστόσο και την
ΚΕΦΑΛΑΙΟ 5: ΣΥΣΤΗΜΑΤΑ ΠΟΛΛΩΝ ΣΩΜΑΤΩΝ Στο κεφάλαιο αυτό θα ασχοληθούµε αρχικά µε ένα µεµονωµένο σύστηµα δύο σωµάτων στα οποία ασκούνται µόνο οι µεταξύ τους κεντρικές δυνάµεις, επιτρέποντας ωστόσο και την
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
Μηχανική ΙI Ροή στο χώρο των φάσεων, θεώρηµα Liouville
 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου 16/5/2000 Μηχανική ΙI Ροή στο χώρο των φάσεων, θεώρηµα Liouville Στη Χαµιλτονιανή θεώρηση η κατάσταση του συστήµατος προσδιορίζεται κάθε στιγµή από ένα και µόνο σηµείο
Τµήµα Π. Ιωάννου & Θ. Αποστολάτου 16/5/2000 Μηχανική ΙI Ροή στο χώρο των φάσεων, θεώρηµα Liouville Στη Χαµιλτονιανή θεώρηση η κατάσταση του συστήµατος προσδιορίζεται κάθε στιγµή από ένα και µόνο σηµείο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 05 Έργο και Κινητική Ενέργεια ΦΥΣ102 1 Όταν μια δύναμη δρα σε ένα σώμα που κινείται,
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 05 Έργο και Κινητική Ενέργεια ΦΥΣ102 1 Όταν μια δύναμη δρα σε ένα σώμα που κινείται,
1. Δυναμική Ενέργεια και Διατηρητικές Δυνάμεις
 . Δυναμική Ενέργεια και Διατηρητικές Δυνάμεις Εξετάζοντας την αιώρα παρατηρούμε ότι στα ανώτατα σημεία η ενέργεια μοιάζει να έχει αποθηκευτεί υπό κάποια άλλη μορφή, που συνδέεται με το ύψος της πάνω από
. Δυναμική Ενέργεια και Διατηρητικές Δυνάμεις Εξετάζοντας την αιώρα παρατηρούμε ότι στα ανώτατα σημεία η ενέργεια μοιάζει να έχει αποθηκευτεί υπό κάποια άλλη μορφή, που συνδέεται με το ύψος της πάνω από
Κεφάλαιο M11. Στροφορµή
 Κεφάλαιο M11 Στροφορµή Στροφορµή Η στροφορµή παίζει σηµαντικό ρόλο στη δυναµική των περιστροφών. Αρχή διατήρησης της στροφορµής Η αρχή αυτή είναι ανάλογη µε την αρχή διατήρησης της ορµής. Σύµφωνα µε την
Κεφάλαιο M11 Στροφορµή Στροφορµή Η στροφορµή παίζει σηµαντικό ρόλο στη δυναµική των περιστροφών. Αρχή διατήρησης της στροφορµής Η αρχή αυτή είναι ανάλογη µε την αρχή διατήρησης της ορµής. Σύµφωνα µε την
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέμβριος 2012
 ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέμβριος ΘΕΜΑ α) Υλικό σημείο μάζας κινείται στον άξονα Ο υπό την επίδραση του δυναμικού V=V() Αν για t=t βρίσκεται στη θέση = με ενέργεια Ε δείξτε ότι η κίνησή του δίνεται από
ΘΕΩΡΗΤΙΚΗ ΜΗΧΑΝΙΚΗ Ι Σεπτέμβριος ΘΕΜΑ α) Υλικό σημείο μάζας κινείται στον άξονα Ο υπό την επίδραση του δυναμικού V=V() Αν για t=t βρίσκεται στη θέση = με ενέργεια Ε δείξτε ότι η κίνησή του δίνεται από
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
Κεφάλαιο 5. Ενέργεια συστήματος
 Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
Μελέτη ευθύγραμμης ομαλά επιταχυνόμενης κίνησης και. του θεωρήματος μεταβολής της κινητικής ενέργειας. με τη διάταξη της αεροτροχιάς
 Εργαστηριακή Άσκηση 4 Μελέτη ευθύγραμμης ομαλά επιταχυνόμενης κίνησης και του θεωρήματος μεταβολής της κινητικής ενέργειας με τη διάταξη της αεροτροχιάς Βαρσάμης Χρήστος Στόχος: Μελέτη της ευθύγραμμης
Εργαστηριακή Άσκηση 4 Μελέτη ευθύγραμμης ομαλά επιταχυνόμενης κίνησης και του θεωρήματος μεταβολής της κινητικής ενέργειας με τη διάταξη της αεροτροχιάς Βαρσάμης Χρήστος Στόχος: Μελέτη της ευθύγραμμης
ΚΙΝΗΣΕΙΣ ΦΟΡΤΙΩΝ ΣΕ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ
 ΚΙΝΗΣΕΙΣ ΦΟΡΤΙΩΝ ΣΕ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΑΣΚΗΣΗ 1 Ακινητοποιούμε τρία σημειακά ηλεκτρικά φορτία, στις θέσεις που φαίνονται στο παρακάτω σχήμα, πάνω σε λείο οριζόντιο δάπεδο κατασκευασμένο από κάποιο μονωτικό
ΚΙΝΗΣΕΙΣ ΦΟΡΤΙΩΝ ΣΕ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΑΣΚΗΣΗ 1 Ακινητοποιούμε τρία σημειακά ηλεκτρικά φορτία, στις θέσεις που φαίνονται στο παρακάτω σχήμα, πάνω σε λείο οριζόντιο δάπεδο κατασκευασμένο από κάποιο μονωτικό
Συστήματα συντεταγμένων
 Συστήματα συντεταγμένων Χρησιμοποιούνται για την περιγραφή της θέσης ενός σημείου στον χώρο. Κοινά συστήματα συντεταγμένων: Καρτεσιανό (x, y, z) Πολικό (r, θ) Καρτεσιανό σύστημα συντεταγμένων Οι άξονες
Συστήματα συντεταγμένων Χρησιμοποιούνται για την περιγραφή της θέσης ενός σημείου στον χώρο. Κοινά συστήματα συντεταγμένων: Καρτεσιανό (x, y, z) Πολικό (r, θ) Καρτεσιανό σύστημα συντεταγμένων Οι άξονες
Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις
 Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις Έστω F=f κεντρικό πεδίο δυνάμεων. Είναι εύκολο να δείξουμε ότι F=0, δηλ. είναι διατηρητικό: F= V. Σε σφαιρικές συντεταγμένες, γενικά: V ma = F =, V maθ = Fθ =,
Ενότητα 4: Κεντρικές διατηρητικές δυνάμεις Έστω F=f κεντρικό πεδίο δυνάμεων. Είναι εύκολο να δείξουμε ότι F=0, δηλ. είναι διατηρητικό: F= V. Σε σφαιρικές συντεταγμένες, γενικά: V ma = F =, V maθ = Fθ =,
dx cos x = ln 1 + sin x 1 sin x.
 Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 17-18 Ν. Βλαχάκης 1. Εστω πεδίο δύναμης F = g () cos y ˆ + λ g() sin y ŷ, όπου λ = σταθερά και g() = 1 e π/ B C (σε κατάλληλες μονάδες). (α) Υπολογίστε πόση ενέργεια
Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 17-18 Ν. Βλαχάκης 1. Εστω πεδίο δύναμης F = g () cos y ˆ + λ g() sin y ŷ, όπου λ = σταθερά και g() = 1 e π/ B C (σε κατάλληλες μονάδες). (α) Υπολογίστε πόση ενέργεια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
Λογισμός 4 Ενότητα 18
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 18: Το Θεώρημα του Stokes. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 18: Το Θεώρημα του Stokes. Μιχ. Γ. Μαριάς Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Απαντήσεις Διαγωνισµού Μηχανικής ΙΙ Ιουνίου Ερώτηµα 2
 Απαντήσεις Διαγωνισµού Μηχανικής ΙΙ Ιουνίου 2000 Ερώτηµα 1 Βα), και, Οι εξισώσεις κίνησης είναι, Έχουµε δύο ασύζευκτους αρµονικούς ταλαντωτές συχνότητας Η Χαµιλτονιανή αυτή θα µπορούσε να περιγράφει µικρές
Απαντήσεις Διαγωνισµού Μηχανικής ΙΙ Ιουνίου 2000 Ερώτηµα 1 Βα), και, Οι εξισώσεις κίνησης είναι, Έχουµε δύο ασύζευκτους αρµονικούς ταλαντωτές συχνότητας Η Χαµιλτονιανή αυτή θα µπορούσε να περιγράφει µικρές
ΥΝΑΜΙΚΗ ΤΗΣ ΠΕΡΙΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 18/11/2011 ΚΕΦ. 10
 ΚΕΦΑΛΑΙΟ 10 ΥΝΑΜΙΚΗ ΤΗΣ ΠΕΡΙΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 1 ΕΞΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ (ΕΠΑΝΑΛΗΨΗ) Μέτρο εξωτερικού γινομένου 2 C A B C ABsin διανυσμάτων A και B Ιδιότητες εξωτερικού γινομένου A B B A εν είναι αντιμεταθετικό.
ΚΕΦΑΛΑΙΟ 10 ΥΝΑΜΙΚΗ ΤΗΣ ΠΕΡΙΣΤΡΟΦΙΚΗΣ ΚΙΝΗΣΗΣ 1 ΕΞΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ (ΕΠΑΝΑΛΗΨΗ) Μέτρο εξωτερικού γινομένου 2 C A B C ABsin διανυσμάτων A και B Ιδιότητες εξωτερικού γινομένου A B B A εν είναι αντιμεταθετικό.
Κ. Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 61. 12. Ολοκληρώµατα διανυσµατικών συναρτήσεων
 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 6 Ολοκληρώµατα διανυσµατικών συναρτήσεων Υπάρχουν διαφόρων ειδών ολοκληρώµατα διανυσµάτων, ανάλογα µε τη µορφή που έχει η ολοκληρωτέα
Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής 6 Ολοκληρώµατα διανυσµατικών συναρτήσεων Υπάρχουν διαφόρων ειδών ολοκληρώµατα διανυσµάτων, ανάλογα µε τη µορφή που έχει η ολοκληρωτέα
ιανυσµατικά πεδία Όπως έχουµε ήδη αναφέρει ένα διανυσµατικό πεδίο είναι µια συνάρτηση
 44 ιανυσµατικά πεδία Όπως έχουµε ήδη αναφέρει ένα διανυσµατικό πεδίο είναι µια συνάρτηση F : U R R. Για εµάς φυσικά µια τέτοια συνάρτηση θα θεωρείται ότι είναι τουλάχιστον συνεχής και συνήθως C και βέβαια
44 ιανυσµατικά πεδία Όπως έχουµε ήδη αναφέρει ένα διανυσµατικό πεδίο είναι µια συνάρτηση F : U R R. Για εµάς φυσικά µια τέτοια συνάρτηση θα θεωρείται ότι είναι τουλάχιστον συνεχής και συνήθως C και βέβαια
dv 2 dx v2 m z Β Ο Γ
 Μηχανική Ι Εργασία #2 Χειμερινό εξάμηνο 218-219 Ν Βλαχάκης 1 Στην άσκηση 4 της εργασίας #1 αρχικά για t = είναι φ = και η ταχύτητα του σώματος είναι v με φορά κάθετη στο νήμα ώστε αυτό να τυλίγεται στον
Μηχανική Ι Εργασία #2 Χειμερινό εξάμηνο 218-219 Ν Βλαχάκης 1 Στην άσκηση 4 της εργασίας #1 αρχικά για t = είναι φ = και η ταχύτητα του σώματος είναι v με φορά κάθετη στο νήμα ώστε αυτό να τυλίγεται στον
Στροβιλισµός πεδίου δυνάµεων
 Στροβιλισµός πεδίου δυνάµεων Θεωρείστε ένα απειροστό απλό χωρίο στο χώρο τόσο µικρό ώστε να µπορεί να θεωρηθεί ότι βρίσκεται σε ένα επίπεδο Έστω ότι το χωρίο αυτό περικλείει εµβαδόν µέτρου Το έργο που
Στροβιλισµός πεδίου δυνάµεων Θεωρείστε ένα απειροστό απλό χωρίο στο χώρο τόσο µικρό ώστε να µπορεί να θεωρηθεί ότι βρίσκεται σε ένα επίπεδο Έστω ότι το χωρίο αυτό περικλείει εµβαδόν µέτρου Το έργο που
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΕΝΟΤΗΤΑ Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕ ΙΟ Συστήµατα µονάδων Για το σχηµατισµό ενός συστήµατος µονάδων είναι απαραίτητη η εκλογή ορισµένων µεγεθών που ονοµάζονται θεµελιώδη. Στις επιστήµες χρησιµοποιείται αποκλειστικά
ΕΝΟΤΗΤΑ Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕ ΙΟ Συστήµατα µονάδων Για το σχηµατισµό ενός συστήµατος µονάδων είναι απαραίτητη η εκλογή ορισµένων µεγεθών που ονοµάζονται θεµελιώδη. Στις επιστήµες χρησιµοποιείται αποκλειστικά
Ευθύγραμμη ομαλή κίνηση
 Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
Πρόβλημα 4.9.
 Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 19//013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 υ (m/s) Σώμα μάζας m = 1Kg κινείται σε ευθύγραμμη τροχιά
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 19//013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 υ (m/s) Σώμα μάζας m = 1Kg κινείται σε ευθύγραμμη τροχιά
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3/2/2016 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3/2/2016 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ 2 ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m 0.25 Kg κινείται στο επίπεδο xy, με τις εξισώσεις κίνησης
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 3/2/2016 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ 2 ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας m 0.25 Kg κινείται στο επίπεδο xy, με τις εξισώσεις κίνησης
Ηλεκτρική δυναμική ενέργεια
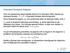 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Πώς μια μάζα αντιλαμβάνεται ότι κάπου υπάρχει μια άλλη και αλληλεπιδρά με αυτή ; Η αλληλεπίδραση μεταξύ μαζών περιγράφεται με την έννοια του πεδίου.
 ΒΑΡΥΤΙΚΟ ΠΕΔΙΟ ΓΕΝΙΚΑ Δυο σημειακές μάζες που απέχουν απόσταση r έλκονται με δύναμη που είναι ανάλογη του γινομένου των μαζών και αντίστροφα ανάλογη του τετραγώνου της απόστασής τους. Όπου G η σταθερά
ΒΑΡΥΤΙΚΟ ΠΕΔΙΟ ΓΕΝΙΚΑ Δυο σημειακές μάζες που απέχουν απόσταση r έλκονται με δύναμη που είναι ανάλογη του γινομένου των μαζών και αντίστροφα ανάλογη του τετραγώνου της απόστασής τους. Όπου G η σταθερά
1.1.3 t. t = t2 - t1 1.1.4 x2 - x1. x = x2 x1 . . 1
 1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
1 1 o Κεφάλαιο: Ευθύγραµµη Κίνηση Πώς θα µπορούσε να περιγραφεί η κίνηση ενός αγωνιστικού αυτοκινήτου; Πόσο γρήγορα κινείται η µπάλα που κλώτσησε ένας ποδοσφαιριστής; Απαντήσεις σε τέτοια ερωτήµατα δίνει
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 10//10/01 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας 1 Kg βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης 45º. Μεταξύ
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 10//10/01 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 Σώμα μάζας 1 Kg βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας κλίσης 45º. Μεταξύ
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
Η Εξίσωση Euler-Lagrange Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ. Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017 ιάρκεια Εξέτασης: 2 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Μ. Τετάρτη Απριλίου 07 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α - Α4 να γράψετε να γράψετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Μ. Τετάρτη Απριλίου 07 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α - Α4 να γράψετε να γράψετε
B' ΤΑΞΗ ΓΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΑΠΑΝΤΗΣΕΙΣ ÊÏÌÏÔÇÍÇ + +
 Επαναληπτικά Θέµατα ΟΕΦΕ 00 ΘΕΜΑ ο. β. γ. γ 4. γ. α. Λ β. Σ γ. Σ δ. Λ ε. Λ ΘΕΜΑ ο. Α. Σωστή η απάντηση () A B' ΤΑΞΗ ΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΙΚΗ ΚΑΤΕΥΘΥΝΣΗ B l w ΦΥΣΙΚΗ ΑΠΑΝΤΗΣΕΙΣ F L Ε επ, K Λ - - F
Επαναληπτικά Θέµατα ΟΕΦΕ 00 ΘΕΜΑ ο. β. γ. γ 4. γ. α. Λ β. Σ γ. Σ δ. Λ ε. Λ ΘΕΜΑ ο. Α. Σωστή η απάντηση () A B' ΤΑΞΗ ΕΝ.ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΙΚΗ ΚΑΤΕΥΘΥΝΣΗ B l w ΦΥΣΙΚΗ ΑΠΑΝΤΗΣΕΙΣ F L Ε επ, K Λ - - F
9 o Γ.Λ. ΠΕΙΡΑΙΑ ιαγώνισµα ΦΥΣΙΚΗΣ (2) 0. Καλή Επιτυχία. Ονοµατεπώνυµο:... Πειραιάς /5 / 2007
 1) Ένα σώµα εκτοξεύεται από τη βάση λείου κεκλιµένου επιπέδου µε αρχική ταχύτητα υ 0, προς τα πάνω (θέση 1) και σταµατά στη θέση (2) που βρίσκεται σε ύψος h. i) Ποια πρόταση που αναφέρεται στο έργο του
1) Ένα σώµα εκτοξεύεται από τη βάση λείου κεκλιµένου επιπέδου µε αρχική ταχύτητα υ 0, προς τα πάνω (θέση 1) και σταµατά στη θέση (2) που βρίσκεται σε ύψος h. i) Ποια πρόταση που αναφέρεται στο έργο του
GMR L = m. dx a + bx + cx. arcsin 2cx b b2 4ac. r 3. cos φ = eg. 2 = 1 c
 Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βλαχάκη, 9 Μαΐου 01 Διάρκεια εξέτασης 3 ώρες, Καλή επιτυχία bonus ερωτήματα Ονοματεπώνυμο:,
Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών, Τμήμα Φυσικής Εξετάσεις στη Μηχανική Ι, Τμήμα Κ. Τσίγκανου & Ν. Βλαχάκη, 9 Μαΐου 01 Διάρκεια εξέτασης 3 ώρες, Καλή επιτυχία bonus ερωτήματα Ονοματεπώνυμο:,
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/2014
 minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
Φυσική για Μηχανικούς Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα αυτής της
γ) να υπολογίστε το έργο για τη μετατόπιση του σώματος από τη θέση A = 10j μέχρι
 ΑΣΚΗΣΗ 4. Σε σώμα μάζας = Kg ασκείται η δύναμη F = 5j, όπου j το μοναδιαίο διάνυσμα κατακόρυφης διεύθυνσης με φορά προς τα πάνω. α) να υπολογίσετε το έργο για τη μετατόπιση του σώματος από τη θέση A =
ΑΣΚΗΣΗ 4. Σε σώμα μάζας = Kg ασκείται η δύναμη F = 5j, όπου j το μοναδιαίο διάνυσμα κατακόρυφης διεύθυνσης με φορά προς τα πάνω. α) να υπολογίσετε το έργο για τη μετατόπιση του σώματος από τη θέση A =
Κεφάλαιο M4. Κίνηση σε δύο διαστάσεις
 Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
Κεφάλαιο M4 Κίνηση σε δύο διαστάσεις Κινηµατική σε δύο διαστάσεις Θα περιγράψουµε τη διανυσµατική φύση της θέσης, της ταχύτητας, και της επιτάχυνσης µε περισσότερες λεπτοµέρειες. Θα µελετήσουµε την κίνηση
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Μηχανική Στερεού Σώματος. Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ. Από τη Φυσική της Α' Λυκείου
 ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ Ευθύγραμμη Ομαλή Κίνηση Επιμέλεια: ΑΓΚΑΝΑΚΗΣ.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός https://physicscorses.wordpress.com/ Βασικές Έννοιες Ένα σώμα καθώς κινείται περνάει από διάφορα σημεία.
Ηλεκτρομαγνητισμός. Χρήσιμες μαθηματικές έννοιες. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Χρήσιμες μαθηματικές έννοιες Νίκος Ν. Αρπατζάνης Παράγωγος ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ y y = f(x) x φ y y y = f(x) x φ y y y = f(x) φ x 1 x 1 + х x x 1 x 1 + х x x 1 x tanϕ = y x tanϕ = dy dx
Ηλεκτρομαγνητισμός Χρήσιμες μαθηματικές έννοιες Νίκος Ν. Αρπατζάνης Παράγωγος ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ y y = f(x) x φ y y y = f(x) x φ y y y = f(x) φ x 1 x 1 + х x x 1 x 1 + х x x 1 x tanϕ = y x tanϕ = dy dx
Τροχιές σωμάτων σε πεδίο Βαρύτητας. Γιώργος Νικολιδάκης
 Τροχιές σωμάτων σε πεδίο Βαρύτητας Γιώργος Νικολιδάκης 9/18/2013 1 Κωνικές Τομές Είναι καμπύλες που σχηματίζονται καθώς επίπεδα τέμνουν με διάφορες γωνίες επιφάνειες κώνων. Παραβολή Έλλειψη -κύκλος Υπερβολή
Τροχιές σωμάτων σε πεδίο Βαρύτητας Γιώργος Νικολιδάκης 9/18/2013 1 Κωνικές Τομές Είναι καμπύλες που σχηματίζονται καθώς επίπεδα τέμνουν με διάφορες γωνίες επιφάνειες κώνων. Παραβολή Έλλειψη -κύκλος Υπερβολή
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ- ΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕ Ο ΚΑΙ ΣΤΟ
 ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ- ΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕ Ο ΚΑΙ ΣΤΟ ΧΩΡΟ Στη συνέχεια θα δοθούν ορισμένες βασικές έννοιες μαθηματικών και φυσικήςμηχανικής που είναι απαραίτητες για την κατανόηση του μαθήματος
ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ Ι ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ- ΥΝΑΜΕΙΣ ΣΤΟ ΕΠΙΠΕ Ο ΚΑΙ ΣΤΟ ΧΩΡΟ Στη συνέχεια θα δοθούν ορισμένες βασικές έννοιες μαθηματικών και φυσικήςμηχανικής που είναι απαραίτητες για την κατανόηση του μαθήματος
3. ιατήρηση της ενέργειας
 3. ιατήρηση της ενέργειας Βιβλιογραφία C. Kittl, W. D. Knight, M.. Rudmn,. C. Hlmholz και. J. Moy, Μηχανική. (Πανεπιστηµιακές Εκδόσεις Ε.Μ.Π., 1998). Κεφ. 5. M. R. Spigl, Θεωρητική Μηχανική. (Εκδόσεις
3. ιατήρηση της ενέργειας Βιβλιογραφία C. Kittl, W. D. Knight, M.. Rudmn,. C. Hlmholz και. J. Moy, Μηχανική. (Πανεπιστηµιακές Εκδόσεις Ε.Μ.Π., 1998). Κεφ. 5. M. R. Spigl, Θεωρητική Μηχανική. (Εκδόσεις
ΣΥΝΤΗΡΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΕΡΓΟ Το έργο, εκφράζει την ενέργεια που μεταφέρεται από ένα σώμα σ ένα άλλο ή που μετατρέπεται από μια μορφή σε μία άλλη. Για σταθερή δύναμη δίνεται από τη σχέση W F Δx Είναι μονόμετρο μέγεθος και η μονάδα
ΕΡΓΟ Το έργο, εκφράζει την ενέργεια που μεταφέρεται από ένα σώμα σ ένα άλλο ή που μετατρέπεται από μια μορφή σε μία άλλη. Για σταθερή δύναμη δίνεται από τη σχέση W F Δx Είναι μονόμετρο μέγεθος και η μονάδα
Ποια μπορεί να είναι η κίνηση μετά την κρούση;
 Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
Ποια μπορεί να είναι η κίνηση μετά την κρούση; ή Η επιτάχυνση και ο ρυθµός µεταβολής του µέτρου της ταχύτητας. Ένα σώµα Σ ηρεµεί, δεµένο στο άκρο ενός ελατηρίου. Σε µια στιγµή συγκρούεται µε ένα άλλο κινούµενο
ΑΣΚΗΣΗ 5.1 Το διάνυσμα θέσης ενός σώματος μάζας m=0,5kgr δίνεται από τη σχέση: 3 j οπότε το μέτρο της ταχύτητας θα είναι:
 ΑΣΚΗΣΗ. Το διάνυσμα θέσης ενός σώματος μάζας =,k δίνεται από τη σχέση: 6. α Βρείτε την θέση και το μέτρο της ταχύτητας του κινητού την χρονική στιγμή. β Τι είδους κίνηση κάνει το κινητό σε κάθε άξονα;
ΑΣΚΗΣΗ. Το διάνυσμα θέσης ενός σώματος μάζας =,k δίνεται από τη σχέση: 6. α Βρείτε την θέση και το μέτρο της ταχύτητας του κινητού την χρονική στιγμή. β Τι είδους κίνηση κάνει το κινητό σε κάθε άξονα;
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Ηλεκτρικά Κυκλώματα Ι ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 Ηλεκτρικά Κυκλώματα Ι ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
Ηλεκτρικά Κυκλώματα Ι ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική.
 Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
( ) Κλίση και επιφάνειες στάθµης µιας συνάρτησης. x + y + z = κ ορίζει την επιφάνεια µιας σφαίρας κέντρου ( ) κ > τότε η
 Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
Έστω Κλίση και επιφάνειες στάθµης µιας συνάρτησης ανοικτό και σταθερά ( µε κ f ( ) ορίζει µια επιφάνεια S στον f : ) τότε η εξίσωση, ονοµάζεται συνήθως επιφάνεια στάθµης της f. εξίσωση, C συνάρτηση. Αν
A! Κινηµατική άποψη. Σχήµα 1 Σχήµα 2
 A Κινηµατική άποψη Θεωρούµε στερεό σώµα σε τυχαία κίνηση, η οποία εξέταζεται από ένα αδρα νειακό σύστηµα αναφοράς ΟXYZ. Εφοδιάζουµε το σώµα µε κινητό σύστηµα συντεταγµένων xyz ακλόνητα συνδεδεµένο µε αυτό,
A Κινηµατική άποψη Θεωρούµε στερεό σώµα σε τυχαία κίνηση, η οποία εξέταζεται από ένα αδρα νειακό σύστηµα αναφοράς ΟXYZ. Εφοδιάζουµε το σώµα µε κινητό σύστηµα συντεταγµένων xyz ακλόνητα συνδεδεµένο µε αυτό,
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2016 Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΕΚΦΩΝΗΣΕΙΣ
 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Απριλίου 6 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α Α4 να γράψετε στο απαντητικό φύλλο τον αριθµό της πρότασης
Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Κυριακή 4 Απριλίου 6 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α Α4 να γράψετε στο απαντητικό φύλλο τον αριθµό της πρότασης
x 2 = x 2 1 + x 2 2. x 2 = u 2 + x 2 3 Χρησιµοποιώντας το συµβολισµό του ανάστροφου, αυτό γράφεται x 2 = x T x. = x T x.
 Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
1η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1. Λύσεις Ασκήσεων 1 ου Κεφαλαίου
 1η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Λύσεις Ασκήσεων 1 ου Κεφαλαίου 1. Στον άξονα βρίσκονται δύο σημειακά φορτία q A = 1 μ και q Β = 45 μ, καθώς και ένα τρίτο σωματίδιο με άγνωστο φορτίο
1η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Λύσεις Ασκήσεων 1 ου Κεφαλαίου 1. Στον άξονα βρίσκονται δύο σημειακά φορτία q A = 1 μ και q Β = 45 μ, καθώς και ένα τρίτο σωματίδιο με άγνωστο φορτίο
Έργο δύναμης. Γενικά το έργο δύναμης είναι το εσωτερικό γινόμενο δύο δυανυσμάτων: της δύναμης επί την μετατόπιση
 Έργο δύναμης Γενικά το έργο δύναμης είναι το εσωτερικό γινόμενο δύο δυανυσμάτων: της δύναμης επί την μετατόπιση W F d Fd cos( θ ) θ F F cos ( θ ) d Έργο από μεταβαλλόμενη δύναμη Έστω ότι το μέτρο της δύναμης
Έργο δύναμης Γενικά το έργο δύναμης είναι το εσωτερικό γινόμενο δύο δυανυσμάτων: της δύναμης επί την μετατόπιση W F d Fd cos( θ ) θ F F cos ( θ ) d Έργο από μεταβαλλόμενη δύναμη Έστω ότι το μέτρο της δύναμης
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Εισαγωγή στις Φυσικές Επιστήμες ( ) Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1. x x. x x x ( ) + ( 20) + ( + 4) = ( + ) + ( 10 + ) + ( )
 Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Ονοματεπώνυμο Τμήμα ο Ερώτημα Να υπολογιστούν τα αόριστα ολοκληρώματα α) ( + + ) e d β) + ( + 4)( 5) 5 89 ΘΕΜΑ d Απάντηση α) θέτω u = + +και υ = e, επομένως dυ = e και du = ( + ) d. ( + + ) e d= u dυ =
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Στη φυσική, η ενέργεια είναι μια ιδιότητα των αντικειμένων που μπορεί να μεταφερθεί σε άλλα αντικείμενα ή να μετατραπεί σε διάφορες μορφές, αλλά δεν μπορεί να δημιουργηθεί
Φυσική για Μηχανικούς Εικόνα: Στη φυσική, η ενέργεια είναι μια ιδιότητα των αντικειμένων που μπορεί να μεταφερθεί σε άλλα αντικείμενα ή να μετατραπεί σε διάφορες μορφές, αλλά δεν μπορεί να δημιουργηθεί
L 2 z. 2mR 2 sin 2 mgr cos θ. 0 π/3 π/2 π L z =0.1 L z = L z =3/ 8 L z = 3-1. V eff (θ) =L z. 2 θ)-cosθ. 2 /(2sin.
 Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 15-16 Ν. Βλαχάκης 1. Σημειακό σώμα μάζας m είναι δεμένο σε αβαρές και μη εκτατό νήμα ακτίνας R και κινείται κάτω από την επίδραση του βάρους του mgẑ και της τάσης
Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 15-16 Ν. Βλαχάκης 1. Σημειακό σώμα μάζας m είναι δεμένο σε αβαρές και μη εκτατό νήμα ακτίνας R και κινείται κάτω από την επίδραση του βάρους του mgẑ και της τάσης
Τα θέματα συνεχίζονται στην πίσω σελίδα
 ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΚΑΤΕΥΘΥΝΣΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΞΕΤΑΣΤΙΚΗ ΙΑΝΟΥΑΡΙΟΥ ΑΚΑΔ. ΕΤΟΣ 16-17 Διδάσκων : Χ. Βοζίκης Τ. Ε. Ι. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΤΟΠΟΓΡΑΦΙΑΣ ΚΑΙ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΤΕ ΚΑΤΕΥΘΥΝΣΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΞΕΤΑΣΤΙΚΗ ΙΑΝΟΥΑΡΙΟΥ ΑΚΑΔ. ΕΤΟΣ 16-17 Διδάσκων : Χ. Βοζίκης Τ. Ε. Ι. ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ
