VIII. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Ángulos, perpendicularidade de rectas e planos
|
|
|
- Νάρκισσα Μαυρογένης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 VIII. ESPZO EULÍDEO TRIDIMENSIONL: Áglos perpediclaridade de rectas e plaos.- Áglo qe forma dúas rectas O áglo de dúas rectas qe se corta se defie como o meor dos áglos qe forma o plao qe determia. O áglo de dúas rectas qe se cra é o áglo formado por dúas rectas secates paralelas ás dadas. Se e so ectores direccioais das rectas r e s depededo do setido dos ectores de direcció das rectas podemos iderar os áglos o. Para asegraros qe o tomamos o áglo obtso basta esixir qe o eo sexa o egatio é dicir tomalo e alor absolto: (. arc 0. Expresió ectorial arc Expresió aalítica Dúas rectas so perpediclares cado 0 0 Dúas rectas so paralelas cado.- Áglo qe forma dos plaos Dos plaos secates forma o espao catro áglos diedros igais dos a dos. Defíese o áglo de dos plaos secates como o meor dos áglos diedros qe determia. Segdo o setido dos ectores ormais aos plaos coicidirá o o os áglos formados polos plaos e os formados polos ectores e ( ( ( ( VIII /
2 VIII / Matemáticas II XEOMETRÍ polo tato: ( 0 arc Expresió ectorial Expresió aalítica Dos plaos so perpediclares cado 0 0 Dos plaos so paralelos cado.- Áglo qe forma ha recta e plao O áglo dha recta e plao defíese como o áglo qe forma a recta coa proxecció desta sobre o plao. Sexa r a proxecció da recta r sobre o plao e sexa o ector de direcció de r e o ector característico o ormal do plao. ( - se ( ( - se e polo tato se ( se 0 arc se Expresió ectorial Expresió aalítica Uha recta e plao so perpediclares cado Uha recta e plao so paralelos cado 0 0
3 EXERIIOS. osiderado o plao : ax 0 i Disctir segdo os alores do parámetro a a súa posició relatia respecto a OXY ii alclar o alor o alores de a para qe a recta ormal (perpediclar a pasado pola orixe forme co plao OXY áglo igal a /.. Disctir segdo os alores de m a posició relatia do plao: x+my-4+m0 e a recta x t+ defiida por y t. alclar se é posible os alores de m para qe o plao e a recta for- t+ me áglo de / 6.. Qérese atar ha corda qe pasa por ha argola sitada o pto ( a dos postes r x t+ x e s de ecaciós: r y t ; s y de modo qe a loxitde da corda empregada sexa a meor posible. t+ a char os ptos sobre r e sobre s aos qe debe atarse a corda b Qe áglo forma as rectas e? 4. a char a ecació da recta qe pasado polo pto ( forme áglos igais eixes coordeados. b char a ecació do plao qe pase polo pto ( 4 e coteña á recta do apartado a. x y+ x y+ 5. Dadas as rectas r e s x 5y 4 i Estda a súa posició relatia ii Determia a ecació implícita do plao qe as coté iii alcla o áglo qe forma as rectas. 6. osidérese a recta r de R de ector director ( 0 qe pasa pola orixe. Escribir as ecaciós paramétricas de tódalas rectas qe pasa pola orixe está cotidas e x - y 0 e forma ademais áglo de 60º co r. 7. Sexa (-40 (6 e (- os tres értices d triáglo: a alcla a ecació do plao qe coté ao triáglo. b alcla o eo de cada dos tres áglos do triáglo. c alcla a área do triáglo. y 8. Dada a recta r de ecació x e o plao de ecació x y 6 0 : a calclar o áglo qe forma a recta r e o plao. b determiar a ecació cotia da recta s proxecció ortogoal de r sobre o plao. 9. Dado o plao x e a recta r x y 0 a Determiar a súa posició o espao b alclar se existe o pto P itersecció de e r. c char o áglo qe forma e r. d Dado o pto Q( 0 - de r achar o se simétrico respecto do plao e a ecació da recta simétrica a r respecto de. 0. osidera a recta r do espao dada polas ecaciós: ( a x y 0 ode a é x 0 parámetro e a recta r qe te ( - como ector director e pasa por (b - c. Determia os alores de ab e c tales qe r e r se corte a orixe formado áglo de 45º. ÁNGULOS PERPENDIULRIDDE DE RETS E PLNOS VIII /
4 . cha a ecació do plao qe coté á recta r e é paralelo á recta s; sedo y 4 r ; s x 0 0 y x 8 Determia o pto de corte do plao aterior co cada ha das rectas bisectrices dos áglos formados por dos dos eixes coordeados. x 0 x 0. osidérase as rectas r : ; s : e o plao qe pasa polos y 0 y 0 ptos ( 0 ( e ( 0. I Dar a ecació xeral o implícita de II Uha das dúas rectas corta a. Determiala e achar o pto de corte co alclar o seo do áglo qe forma dita recta e o plao III omprobar qe a otra recta é paralela a. alclar a ecació xeral do plao qe a coté e é paralelo a.. Nha oa cha de eadas frecetes pretédese trír ha casa cha plata segdo o esqema adxto. Para o tellado optase por facelo a ha soa aga ( formado plao! e as altras co respecto ao cha escollidas so: metros e e e 0 metros e. a Determiar a altra do tellado e D. b Determiar qe áglo forma a perpediclar ao tellado coa perpediclar ao cha. 4. N cbo calcla o áglo qe forma a recta coa recta qe e co pto medio do lado D y x x y 5. Dadas as rectas r : e s : ecotra ha recta x bisectri de r e s (ha recta bisectri de otras dúas pasa polo pto de itersecció de estas está o mesmo plao qe elas e forma o mesmo áglo co ambas. 6. Spoñer qe o plao coordeado 0 é espello (reflectite e ambas caras. Desde (4 parte raio de l qe reflectídose o espello ilmia o pto (0- a E qe pto do espello debe icidir o citado raio? b char a ecació xeral do plao qe coté aos raios icidete e reflectido. 7. base dha pirámide é cadrado D de metros de lado e o se értice V está sitado a ha altra de metros sobre o cetro da base. alclar o áglo qe forma os plaos V e V. 0. a Defiició e cálclo do áglo qe forma dúas rectas. odició de perpediclaridade. b Determíese o áglo qe forma a recta r e o plao de ecaciós: x : 6 x y 6 r : y 08. Estdar a posició relatia das rectas r e s e calclar o áglo qe forma. x λ x y r: s: y λ 4 x 4 λ 0. osidérese o plao o triáglo de értices (0 (0 e (--. alclar os áglos e a área deste triáglo VIII / 4 Matemáticas II XEOMETRÍ
5 6.. Áglo qe forma dúas rectas.. Determie o áglo qe forma a recta r qe pasa polo pto (-0 e tal qe o se ector director é x 6 (-0 e a recta s de ecació: 7 y Determie o ector (o ectores itarios (abc (co a>0 b>0 c>0 qe forma áglo de / 6 radiás co ector ( e áglo de / 4 radiás co w(0.. Deda as ecaciós ectorial paramétricas e implícita (o xeral d plao determiado por pto e dos ectores directores.. Dados os ptos P(4 e Q(77 determie a ecació xeral do plao qe é perpediclar ao segmeto PQ e qe pasa polo pto medio dese segmeto 4.. Áglo qe forma ha recta e plao. Determie o áglo qe forma o plao : x y 4 0 e a recta r : x y 0 y 8.. Áglo qe forma dúas rectas. odició de perpediclaridade. Determie o áglo qe forma a recta qe pasa polos ptos (0- e (0- e a recta y de ecació x.. Qe codició debe cmprir os coeficietes das ecaciós xerais de dos plaos para qe estes sexa perpediclares?. che o áglo qe forma os plaos : x y 0 e : x y ÁNGULOS PERPENDIULRIDDE DE RETS E PLNOS VIII / 5
EXERCICIOS DE REFORZO: RECTAS E PLANOS
 EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS. 3. Cal é o vector de posición da orixe de coordenadas O? Cales son as coordenadas do punto O?
 EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
VII. RECTAS E PLANOS NO ESPAZO
 VII. RETS E PLNOS NO ESPZO.- Ecuacións da recta Unha recta r no espao queda determinada por un punto, punto base, e un vector v non nulo que se chama vector director ou direccional da recta; r, v é a determinación
VII. RETS E PLNOS NO ESPZO.- Ecuacións da recta Unha recta r no espao queda determinada por un punto, punto base, e un vector v non nulo que se chama vector director ou direccional da recta; r, v é a determinación
PAU XUÑO 2011 MATEMÁTICAS II
 PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
IX. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Aplicacións ao cálculo de distancias, áreas e volumes
 IX. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Aplicacións ao cálculo de distancias, áreas e volumes 1.- Distancia entre dous puntos Se A e B son dous puntos do espazo, defínese a distancia entre A e B como o módulo
IX. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Aplicacións ao cálculo de distancias, áreas e volumes 1.- Distancia entre dous puntos Se A e B son dous puntos do espazo, defínese a distancia entre A e B como o módulo
VI. VECTORES NO ESPAZO
 VI. VECTORES NO ESPAZO.- Vectores no espazo. Operacións Sexa E o espazo de pntos ordinario o intitio da xeometría elemental. Un segmento orientado AB con orixe no pnto A e extremo no pnto B recibe o nome
VI. VECTORES NO ESPAZO.- Vectores no espazo. Operacións Sexa E o espazo de pntos ordinario o intitio da xeometría elemental. Un segmento orientado AB con orixe no pnto A e extremo no pnto B recibe o nome
PAU XUÑO 2012 MATEMÁTICAS II
 PAU Código: 6 XUÑO 01 MATEMÁTICAS II (Responder só aos exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio = 3 puntos, exercicio 3= puntos, exercicio
PAU Código: 6 XUÑO 01 MATEMÁTICAS II (Responder só aos exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio = 3 puntos, exercicio 3= puntos, exercicio
MATEMÁTICAS. (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos)
 1 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos) Opción 1. Dada a matriz a) Calcula os valores do parámetro m para os
1 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos) Opción 1. Dada a matriz a) Calcula os valores do parámetro m para os
Tema 3. Espazos métricos. Topoloxía Xeral,
 Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
PAU XUÑO 2010 MATEMÁTICAS II
 PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
1. O ESPAZO VECTORIAL DOS VECTORES LIBRES 1.1. DEFINICIÓN DE VECTOR LIBRE
 O ESPAZO VECTORIAL DOS VECTORES LIBRES DEFINICIÓN DE VECTOR LIBRE MATEMÁTICA II 06 Exames e Textos de Matemática de Pepe Sacau ten unha licenza Creative Commons Atribución Compartir igual 40 Internacional
O ESPAZO VECTORIAL DOS VECTORES LIBRES DEFINICIÓN DE VECTOR LIBRE MATEMÁTICA II 06 Exames e Textos de Matemática de Pepe Sacau ten unha licenza Creative Commons Atribución Compartir igual 40 Internacional
PAU XUÑO 2016 MATEMÁTICAS II
 PAU XUÑO 06 Código: 6 MATEMÁTICAS II (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio = 3 puntos, exercicio = 3 puntos, exercicio
PAU XUÑO 06 Código: 6 MATEMÁTICAS II (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio = 3 puntos, exercicio = 3 puntos, exercicio
LUGARES XEOMÉTRICOS. CÓNICAS
 LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
PAU XUÑO 2011 MATEMÁTICAS II
 PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
Tema: Enerxía 01/02/06 DEPARTAMENTO DE FÍSICA E QUÍMICA
 Tema: Enerxía 01/0/06 DEPARTAMENTO DE FÍSICA E QUÍMICA Nome: 1. Unha caixa de 150 kg descende dende o repouso por un plano inclinado por acción do seu peso. Se a compoñente tanxencial do peso é de 735
Tema: Enerxía 01/0/06 DEPARTAMENTO DE FÍSICA E QUÍMICA Nome: 1. Unha caixa de 150 kg descende dende o repouso por un plano inclinado por acción do seu peso. Se a compoñente tanxencial do peso é de 735
XEOMETRÍA NO ESPAZO. - Se dun vector se coñecen a orixe, o módulo, a dirección e o sentido, este está perfectamente determinado no espazo.
 XEOMETRÍA NO ESPAZO Vectores fixos Dos puntos do espazo, A e B, determinan o vector fixo AB, sendo o punto A a orixe e o punto B o extremo, é dicir, un vector no espazo é calquera segmento orientado que
XEOMETRÍA NO ESPAZO Vectores fixos Dos puntos do espazo, A e B, determinan o vector fixo AB, sendo o punto A a orixe e o punto B o extremo, é dicir, un vector no espazo é calquera segmento orientado que
Tema 1. Espazos topolóxicos. Topoloxía Xeral, 2016
 Tema 1. Espazos topolóxicos Topoloxía Xeral, 2016 Topoloxía e Espazo topolóxico Índice Topoloxía e Espazo topolóxico Exemplos de topoloxías Conxuntos pechados Topoloxías definidas por conxuntos pechados:
Tema 1. Espazos topolóxicos Topoloxía Xeral, 2016 Topoloxía e Espazo topolóxico Índice Topoloxía e Espazo topolóxico Exemplos de topoloxías Conxuntos pechados Topoloxías definidas por conxuntos pechados:
MATEMÁTICAS. (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos)
 21 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 Dada a matriz a) Calcula os valores do parámetro m para os que A ten inversa.
21 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 Dada a matriz a) Calcula os valores do parámetro m para os que A ten inversa.
XUÑO 2018 MATEMÁTICAS II
 Proba de Avaliación do Bacharelato para o Acceso áuniversidade XUÑO 218 Código: 2 MATEMÁTICAS II (Responde só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio
Proba de Avaliación do Bacharelato para o Acceso áuniversidade XUÑO 218 Código: 2 MATEMÁTICAS II (Responde só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio
ln x, d) y = (3x 5 5x 2 + 7) 8 x
 EXERCICIOS AUTOAVALIABLES: CÁLCULO DIFERENCIAL. Deriva: a) y 7 6 + 5, b) y e, c) y e) y 7 ( 5 ), f) y ln, d) y ( 5 5 + 7) 8 n e ln, g) y, h) y n. Usando a derivada da función inversa, demostra que: a)
EXERCICIOS AUTOAVALIABLES: CÁLCULO DIFERENCIAL. Deriva: a) y 7 6 + 5, b) y e, c) y e) y 7 ( 5 ), f) y ln, d) y ( 5 5 + 7) 8 n e ln, g) y, h) y n. Usando a derivada da función inversa, demostra que: a)
EXERCICIOS DE ÁLXEBRA. PAU GALICIA
 Maemáicas II EXERCICIOS DE ÁLXEBRA PAU GALICIA a) (Xuño ) Propiedades do produo de marices (só enuncialas) b) (Xuño ) Sexan M e N M + I, onde I denoa a mariz idenidade de orde n, calcule N e M 3 Son M
Maemáicas II EXERCICIOS DE ÁLXEBRA PAU GALICIA a) (Xuño ) Propiedades do produo de marices (só enuncialas) b) (Xuño ) Sexan M e N M + I, onde I denoa a mariz idenidade de orde n, calcule N e M 3 Son M
PAU XUÑO 2010 MATEMÁTICAS II
 PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Puntuación máima dos eercicios de cada opción: eercicio 1= 3 puntos, eercicio = 3 puntos, eercicio
PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Puntuación máima dos eercicios de cada opción: eercicio 1= 3 puntos, eercicio = 3 puntos, eercicio
Áreas de corpos xeométricos
 9 Áreas de corpos xeométricos Obxectivos Nesta quincena aprenderás a: Antes de empezar 1.Área dos prismas....... páx.164 Área dos prismas Calcular a área de prismas rectos de calquera número de caras.
9 Áreas de corpos xeométricos Obxectivos Nesta quincena aprenderás a: Antes de empezar 1.Área dos prismas....... páx.164 Área dos prismas Calcular a área de prismas rectos de calquera número de caras.
x 2 6º- Achar a ecuación da recta que pasa polo punto medio do segmento de extremos
 º- Dados os puntos A(,, ), B(, 4), C( 5,, ) EXERCICIOS XEOMETRÍA Acha as coodenadas dun cuato punto D coa condición que o cuadiláteo ABCD sexa un paalelogamo º- Escibi as ecuacións paaméticas, na foma
º- Dados os puntos A(,, ), B(, 4), C( 5,, ) EXERCICIOS XEOMETRÍA Acha as coodenadas dun cuato punto D coa condición que o cuadiláteo ABCD sexa un paalelogamo º- Escibi as ecuacións paaméticas, na foma
Física P.A.U. ÓPTICA 1 ÓPTICA
 Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un raio de luz de frecuencia 5 10 14 Hz incide, cun ángulo de incidencia de 30, sobre unha lámina de vidro de caras plano-paralelas de espesor
Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un raio de luz de frecuencia 5 10 14 Hz incide, cun ángulo de incidencia de 30, sobre unha lámina de vidro de caras plano-paralelas de espesor
Eletromagnetismo. Johny Carvalho Silva Universidade Federal do Rio Grande Instituto de Matemática, Física e Estatística. ...:: Solução ::...
 Eletromagnetismo Johny Carvalho Silva Universidade Federal do Rio Grande Instituto de Matemática, Física e Estatística Lista -.1 - Mostrar que a seguinte medida é invariante d 3 p p 0 onde: p 0 p + m (1)
Eletromagnetismo Johny Carvalho Silva Universidade Federal do Rio Grande Instituto de Matemática, Física e Estatística Lista -.1 - Mostrar que a seguinte medida é invariante d 3 p p 0 onde: p 0 p + m (1)
Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO. F = m a
 Física P.A.U. ELECTOMAGNETISMO 1 ELECTOMAGNETISMO INTODUCIÓN MÉTODO 1. En xeral: Debúxanse as forzas que actúan sobre o sistema. Calcúlase a resultante polo principio de superposición. Aplícase a 2ª lei
Física P.A.U. ELECTOMAGNETISMO 1 ELECTOMAGNETISMO INTODUCIÓN MÉTODO 1. En xeral: Debúxanse as forzas que actúan sobre o sistema. Calcúlase a resultante polo principio de superposición. Aplícase a 2ª lei
EQUILIBRIO QUÍMICO. 2 HI (g)
 EQUILIBRIO QUÍMICO 1- EQUILIBRIO QUÍMICO APLICADO A REACCIÓNS EN FASE GASOSA EN CONDICIÓNS IDEAIS. Se itroducimos H 2 (g) e I 2 (g) u recipiete pechado e matemos a temperatura costate podemos apreciar
EQUILIBRIO QUÍMICO 1- EQUILIBRIO QUÍMICO APLICADO A REACCIÓNS EN FASE GASOSA EN CONDICIÓNS IDEAIS. Se itroducimos H 2 (g) e I 2 (g) u recipiete pechado e matemos a temperatura costate podemos apreciar
Procedementos operatorios de unións non soldadas
 Procedementos operatorios de unións non soldadas Técnicas de montaxe de instalacións Ciclo medio de montaxe e mantemento de instalacións frigoríficas 1 de 28 Técnicas de roscado Unha rosca é unha hélice
Procedementos operatorios de unións non soldadas Técnicas de montaxe de instalacións Ciclo medio de montaxe e mantemento de instalacións frigoríficas 1 de 28 Técnicas de roscado Unha rosca é unha hélice
A circunferencia e o círculo
 10 A circunferencia e o círculo Obxectivos Nesta quincena aprenderás a: Identificar os diferentes elementos presentes na circunferencia e o círculo. Coñecer as posicións relativas de puntos, rectas e circunferencias.
10 A circunferencia e o círculo Obxectivos Nesta quincena aprenderás a: Identificar os diferentes elementos presentes na circunferencia e o círculo. Coñecer as posicións relativas de puntos, rectas e circunferencias.
TEORÍA DE XEOMETRÍA. 1º ESO
 TEORÍA DE XEOMETRÍA. 1º ESO 1. CORPOS XEOMÉTRICOS No noso entorno observamos continuamente obxectos de diversas formas: pelotas, botes, caixas, pirámides, etc. Todos estes obxectos son corpos xeométricos.
TEORÍA DE XEOMETRÍA. 1º ESO 1. CORPOS XEOMÉTRICOS No noso entorno observamos continuamente obxectos de diversas formas: pelotas, botes, caixas, pirámides, etc. Todos estes obxectos son corpos xeométricos.
Corpos xeométricos. Obxectivos. Antes de empezar. 1. Poliedros... páx. 4 Definición Elementos dun poliedro
 9 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Identificar que é un poliedro. Determinar os elementos dun poliedro: Caras, arestas e vértices. Clasificar os poliedros. Especificar cando un
9 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Identificar que é un poliedro. Determinar os elementos dun poliedro: Caras, arestas e vértices. Clasificar os poliedros. Especificar cando un
Volume dos corpos xeométricos
 11 Volume dos corpos xeométricos Obxectivos Nesta quincena aprenderás a: Comprender o concepto de medida do volume e coñecer e manexar as unidades de medida do S.M.D. Obter e aplicar expresións para o
11 Volume dos corpos xeométricos Obxectivos Nesta quincena aprenderás a: Comprender o concepto de medida do volume e coñecer e manexar as unidades de medida do S.M.D. Obter e aplicar expresións para o
Problemas xeométricos
 Problemas xeométricos Contidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores e segmentos 2. Corpos xeométricos Prismas Pirámides Troncos de pirámides
Problemas xeométricos Contidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores e segmentos 2. Corpos xeométricos Prismas Pirámides Troncos de pirámides
Exercicios de Física 02a. Campo Eléctrico
 Exercicios de Física 02a. Campo Eléctrico Problemas 1. Dúas cargas eléctricas de 3 mc están situadas en A(4,0) e B( 4,0) (en metros). Caalcula: a) o campo eléctrico en C(0,5) e en D(0,0) b) o potencial
Exercicios de Física 02a. Campo Eléctrico Problemas 1. Dúas cargas eléctricas de 3 mc están situadas en A(4,0) e B( 4,0) (en metros). Caalcula: a) o campo eléctrico en C(0,5) e en D(0,0) b) o potencial
Física P.A.U. ÓPTICA 1 ÓPTICA
 Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un raio de luz de frecuencia 5 10¹⁴ Hz incide cun ángulo de incidencia de 30 sobre unha lámina de vidro de caras plano-paralelas de espesor 10
Física P.A.U. ÓPTICA 1 ÓPTICA PROBLEMAS DIOPTRIO PLANO 1. Un raio de luz de frecuencia 5 10¹⁴ Hz incide cun ángulo de incidencia de 30 sobre unha lámina de vidro de caras plano-paralelas de espesor 10
TRAZADOS XEOMÉTRICOS FUNDAMENTAIS NO PLANO A 1. PUNTO E RECTA
 TRAZADOS XEOMÉTRICOS FUNDAMENTAIS NO PLANO 1. Punto e recta 2. Lugares xeométricos 3. Ángulos 4. Trazado de paralelas e perpendiculares con escuadro e cartabón 5. Operacións elementais 6. Trazado de ángulos
TRAZADOS XEOMÉTRICOS FUNDAMENTAIS NO PLANO 1. Punto e recta 2. Lugares xeométricos 3. Ángulos 4. Trazado de paralelas e perpendiculares con escuadro e cartabón 5. Operacións elementais 6. Trazado de ángulos
Métodos Estadísticos en la Ingeniería
 Métodos Estadísticos e la Igeiería INTERVALOS DE CONFIANZA Itervalo de cofiaza para la media µ de ua distribució ormal co variaza coocida: X ± z α/ µ = X = X i N µ X... X m.a.s. de X Nµ Itervalo de cofiaza
Métodos Estadísticos e la Igeiería INTERVALOS DE CONFIANZA Itervalo de cofiaza para la media µ de ua distribució ormal co variaza coocida: X ± z α/ µ = X = X i N µ X... X m.a.s. de X Nµ Itervalo de cofiaza
INICIACIÓN AO CÁLCULO DE DERIVADAS. APLICACIÓNS
 INICIACIÓN AO CÁLCULO DE DERIVADAS. APLICACIÓNS Páina 0 REFLEXIONA E RESOLVE Coller un autobús en marca Na gráfica seguinte, a liña vermella representa o movemento dun autobús que arranca da parada e vai,
INICIACIÓN AO CÁLCULO DE DERIVADAS. APLICACIÓNS Páina 0 REFLEXIONA E RESOLVE Coller un autobús en marca Na gráfica seguinte, a liña vermella representa o movemento dun autobús que arranca da parada e vai,
Ámbito científico tecnolóxico. Xeometría. Unidade didáctica 2. Módulo 3. Educación a distancia semipresencial
 Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 3 Unidade didáctica 2 Xeometría Índice 1. Introdución... 3 1.1 Descrición da unidade
Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 3 Unidade didáctica 2 Xeometría Índice 1. Introdución... 3 1.1 Descrición da unidade
Ano 2018 FÍSICA. SOL:a...máx. 1,00 Un son grave ten baixa frecuencia, polo que a súa lonxitude de onda é maior.
 ABAU CONVOCAT ORIA DE SET EMBRO Ano 2018 CRIT ERIOS DE AVALI ACIÓN FÍSICA (Cód. 23) Elixir e desenvolver unha das dúas opcións. As solución numéricas non acompañadas de unidades ou con unidades incorrectas...
ABAU CONVOCAT ORIA DE SET EMBRO Ano 2018 CRIT ERIOS DE AVALI ACIÓN FÍSICA (Cód. 23) Elixir e desenvolver unha das dúas opcións. As solución numéricas non acompañadas de unidades ou con unidades incorrectas...
NÚMEROS COMPLEXOS. Páxina 147 REFLEXIONA E RESOLVE. Extraer fóra da raíz. Potencias de. Como se manexa k 1? Saca fóra da raíz:
 NÚMEROS COMPLEXOS Páxina 7 REFLEXIONA E RESOLVE Extraer fóra da raíz Saca fóra da raíz: a) b) 00 a) b) 00 0 Potencias de Calcula as sucesivas potencias de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) ( ) ( ) (
NÚMEROS COMPLEXOS Páxina 7 REFLEXIONA E RESOLVE Extraer fóra da raíz Saca fóra da raíz: a) b) 00 a) b) 00 0 Potencias de Calcula as sucesivas potencias de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) ( ) ( ) (
a) Calcula m de modo que o produto escalar de a( 3, 2 ) e b( m, 5 ) sexa igual a 5. ( )
 .. MATEMÁTICAS I PENDENTES (º PARTE) a) Calcula m de modo que o produto escalar de a(, ) e b( m, 5 ) sea igual a 5. b) Calcula a proección de a sobre c, sendo c,. ( ) 5 Se (, ) e y,. Calcula: a) Un vector
.. MATEMÁTICAS I PENDENTES (º PARTE) a) Calcula m de modo que o produto escalar de a(, ) e b( m, 5 ) sea igual a 5. b) Calcula a proección de a sobre c, sendo c,. ( ) 5 Se (, ) e y,. Calcula: a) Un vector
PÁGINA 106 PÁGINA a) sen 30 = 1/2 b) cos 120 = 1/2. c) tg 135 = 1 d) cos 45 = PÁGINA 109
 PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
Exercicios de Física 04. Óptica
 Exercicios de Física 04. Óptica Problemas 1. Unha lente converxente ten unha distancia focal de 50 cm. Calcula a posición do obxecto para que a imaxe sexa: a) real e tres veces maior que o obxecto, b)
Exercicios de Física 04. Óptica Problemas 1. Unha lente converxente ten unha distancia focal de 50 cm. Calcula a posición do obxecto para que a imaxe sexa: a) real e tres veces maior que o obxecto, b)
Problemas y cuestiones de electromagnetismo
 Problemas y cuestiones de electromagnetismo 1.- Dúas cargas eléctricas puntuais de 2 e -2 µc cada unha están situadas respectivamente en (2,0) e en (-2,0) (en metros). Calcule: a) campo eléctrico en (0,0)
Problemas y cuestiones de electromagnetismo 1.- Dúas cargas eléctricas puntuais de 2 e -2 µc cada unha están situadas respectivamente en (2,0) e en (-2,0) (en metros). Calcule: a) campo eléctrico en (0,0)
ÓPTICA- A LUZ Problemas PAAU
 ÓPTICA- A LUZ Problemas PAAU XUÑO-96 CUESTION 2. opa Disponse de luz monocromática capaz de extraer electróns dun metal. A medida que medra a lonxitude de onda da luz incidente, a) os electróns emitidos
ÓPTICA- A LUZ Problemas PAAU XUÑO-96 CUESTION 2. opa Disponse de luz monocromática capaz de extraer electróns dun metal. A medida que medra a lonxitude de onda da luz incidente, a) os electróns emitidos
Física P.A.U. VIBRACIÓNS E ONDAS 1 VIBRACIÓNS E ONDAS
 Física P.A.U. VIBRACIÓNS E ONDAS 1 VIBRACIÓNS E ONDAS PROBLEMAS M.H.S.. 1. Dun resorte elástico de constante k = 500 N m -1 colga unha masa puntual de 5 kg. Estando o conxunto en equilibrio, desprázase
Física P.A.U. VIBRACIÓNS E ONDAS 1 VIBRACIÓNS E ONDAS PROBLEMAS M.H.S.. 1. Dun resorte elástico de constante k = 500 N m -1 colga unha masa puntual de 5 kg. Estando o conxunto en equilibrio, desprázase
Sheet H d-2 3D Pythagoras - Answers
 1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
1. 1.4cm 1.6cm 5cm 1cm. 5cm 1cm IGCSE Higher Sheet H7-1 4-08d-1 D Pythagoras - Answers. (i) 10.8cm (ii) 9.85cm 11.5cm 4. 7.81m 19.6m 19.0m 1. 90m 40m. 10cm 11.cm. 70.7m 4. 8.6km 5. 1600m 6. 85m 7. 6cm
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
Exame tipo. C. Problemas (Valoración: 5 puntos, 2,5 puntos cada problema)
 Exame tipo A. Proba obxectiva (Valoración: 3 puntos) 1. - Un disco de 10 cm de raio xira cunha velocidade angular de 45 revolucións por minuto. A velocidade lineal dos puntos da periferia do disco será:
Exame tipo A. Proba obxectiva (Valoración: 3 puntos) 1. - Un disco de 10 cm de raio xira cunha velocidade angular de 45 revolucións por minuto. A velocidade lineal dos puntos da periferia do disco será:
TRIGONOMETRIA. hipotenusa L 2. hipotenusa
 TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
Semellanza e trigonometría
 7 Semellanza e trigonometría Obxectivos Nesta quincena aprenderás a: Recoñecer triángulos semellantes. Calcular distancias inaccesibles, aplicando a semellanza de triángulos. Nocións básicas de trigonometría.
7 Semellanza e trigonometría Obxectivos Nesta quincena aprenderás a: Recoñecer triángulos semellantes. Calcular distancias inaccesibles, aplicando a semellanza de triángulos. Nocións básicas de trigonometría.
A proba constará de vinte cuestións tipo test. As cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta.
 Páxina 1 de 9 1. Formato da proba Formato proba constará de vinte cuestións tipo test. s cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta. Puntuación Puntuación: 0.5
Páxina 1 de 9 1. Formato da proba Formato proba constará de vinte cuestións tipo test. s cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta. Puntuación Puntuación: 0.5
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
1 La teoría de Jeans. t + (n v) = 0 (1) b) Navier-Stokes (conservación del impulso) c) Poisson
 1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
Polinomios. Obxectivos. Antes de empezar. 1.Polinomios... páx. 4 Grao. Expresión en coeficientes Valor numérico dun polinomio
 3 Polinomios Obxectivos Nesta quincena aprenderás a: Achar a expresión en coeficientes dun polinomio e operar con eles. Calcular o valor numérico dun polinomio. Recoñecer algunhas identidades notables,
3 Polinomios Obxectivos Nesta quincena aprenderás a: Achar a expresión en coeficientes dun polinomio e operar con eles. Calcular o valor numérico dun polinomio. Recoñecer algunhas identidades notables,
Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 1 Unidade didáctica 2 Xeometría
 Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 1 Unidade didáctica Xeometría Índice 1. Introdución... 3 1.1 Descrición da unidade didáctica...
Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 1 Unidade didáctica Xeometría Índice 1. Introdución... 3 1.1 Descrición da unidade didáctica...
Escenas de episodios anteriores
 Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
PAU XUÑO 2010 FÍSICA
 PAU XUÑO 1 Cóigo: 5 FÍSICA Puntuación máxima: Cuestións 4 puntos (1 caa cuestión, teórica ou practica) Problemas 6 puntos (1 caa apartao) Non se valorará a simple anotación un ítem como solución ás cuestións;
PAU XUÑO 1 Cóigo: 5 FÍSICA Puntuación máxima: Cuestións 4 puntos (1 caa cuestión, teórica ou practica) Problemas 6 puntos (1 caa apartao) Non se valorará a simple anotación un ítem como solución ás cuestións;
Onde posso encontrar o formulário para? Onde posso encontrar o formulário para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα
 - Γενικά Onde posso encontrar o formulário para? Onde posso encontrar o formulário para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Quando foi emitido seu/sua [documento]? Για να ρωτήσετε πότε έχει
- Γενικά Onde posso encontrar o formulário para? Onde posso encontrar o formulário para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Quando foi emitido seu/sua [documento]? Για να ρωτήσετε πότε έχει
ESTRUTURA ATÓMICA E CLASIFICACIÓN PERIÓDICA DOS ELEMENTOS
 Química P.A.U. ESTRUTURA ATÓMICA E CLASIFICACIÓN PERIÓDICA DOS ELEMENTOS ESTRUTURA ATÓMICA E CLASIFICACIÓN PERIÓDICA DOS ELEMENTOS CUESTIÓNS NÚMEROS CUÁNTICOS. a) Indique o significado dos números cuánticos
Química P.A.U. ESTRUTURA ATÓMICA E CLASIFICACIÓN PERIÓDICA DOS ELEMENTOS ESTRUTURA ATÓMICA E CLASIFICACIÓN PERIÓDICA DOS ELEMENTOS CUESTIÓNS NÚMEROS CUÁNTICOS. a) Indique o significado dos números cuánticos
Funcións e gráficas. Obxectivos. Antes de empezar. 1.Funcións páx. 4 Concepto Táboas e gráficas Dominio e percorrido
 9 Funcións e gráficas Obxectivos Nesta quinceer na aprenderás a: Coñecer e interpretar as funcións e as distintas formas de presentalas. Recoñecer ou dominio e ou percorrido dunha función. Determinar se
9 Funcións e gráficas Obxectivos Nesta quinceer na aprenderás a: Coñecer e interpretar as funcións e as distintas formas de presentalas. Recoñecer ou dominio e ou percorrido dunha función. Determinar se
Lógica Proposicional
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Lógica Proposicional. Justificación de la validez del razonamiento?
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Ταξίδι Τρώγοντας έξω. Τρώγοντας έξω - Στην είσοδο. Τρώγοντας έξω - Παραγγελία φαγητού
 - Στην είσοδο Eu gostaria de reservar uma mesa para _[número de pessoas]_ às _[hora]_. Για να κάνετε κράτηση Uma mesa para _[número de pessoas]_, por favor. Για να ζητήσετε τραπέζι Eu gostaria de reservar
- Στην είσοδο Eu gostaria de reservar uma mesa para _[número de pessoas]_ às _[hora]_. Για να κάνετε κράτηση Uma mesa para _[número de pessoas]_, por favor. Για να ζητήσετε τραπέζι Eu gostaria de reservar
1.- Evolución das ideas acerca da natureza da luz! Óptica xeométrica! Principio de Fermat. Camiño óptico! 3
 1.- Evolución das ideas acerca da natureza da luz! 2 2.- Óptica xeométrica! 2 2.1.- Principio de Fermat. Camiño óptico! 3 2.2.- Reflexión e refracción. Leis de Snell! 3 2.3.- Laminas plano-paralelas! 4
1.- Evolución das ideas acerca da natureza da luz! 2 2.- Óptica xeométrica! 2 2.1.- Principio de Fermat. Camiño óptico! 3 2.2.- Reflexión e refracción. Leis de Snell! 3 2.3.- Laminas plano-paralelas! 4
Da base de dados do torneio do Chess-Results Προκριματικός Όμιλος Ά Εθνικής ΕΣΣΠ Última Actualização05.05.
 Da base de dados do torneio do Chess-Results http://chess-results.com Προκριματικός Όμιλος Ά Εθνικής ΕΣΣΠ Última Actualização05.05.2011 10:57:55 Composição das equipas com resultados ronda a roda 5. ΣΟ
Da base de dados do torneio do Chess-Results http://chess-results.com Προκριματικός Όμιλος Ά Εθνικής ΕΣΣΠ Última Actualização05.05.2011 10:57:55 Composição das equipas com resultados ronda a roda 5. ΣΟ
Ονομαστική Γενική Αιτιατική Κλητική Αρσ. γλ υκοί γλ υκών γλ υκούς γλ υκοί Θηλ. γλ υκές γλ υκών γλ υκές γλ υκές Ουδ. γλ υκά γλ υκών γλ υκά γλ υκά
 Επίθετα και Μετοχές Nic o las Pe lic ioni de OLI V EI RA 1 Apresentação Modelo de declinação de adjetivos e particípios (επίθετα και μετοχές, em grego) apresentado pela universidade Thessaloniki. Só é
Επίθετα και Μετοχές Nic o las Pe lic ioni de OLI V EI RA 1 Apresentação Modelo de declinação de adjetivos e particípios (επίθετα και μετοχές, em grego) apresentado pela universidade Thessaloniki. Só é
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO
 Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO PROBLEMAS CAMPO ELECTROSTÁTICO 1. Dúas cargas eléctricas de 3 mc están situadas en A(4, 0) e B(-4, 0) (en metros). Calcula: a) O campo eléctrico en C(0,
Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO PROBLEMAS CAMPO ELECTROSTÁTICO 1. Dúas cargas eléctricas de 3 mc están situadas en A(4, 0) e B(-4, 0) (en metros). Calcula: a) O campo eléctrico en C(0,
FÍSICA. = 4π 10-7 (S.I.)).
 22 FÍSICA Elixir e desenvolver un problema e/ou cuestión de cada un dos bloques. O bloque de prácticas só ten unha opción. Puntuación máxima: Problemas, 6 puntos (1 cada apartado). Cuestións, 4 puntos
22 FÍSICA Elixir e desenvolver un problema e/ou cuestión de cada un dos bloques. O bloque de prácticas só ten unha opción. Puntuación máxima: Problemas, 6 puntos (1 cada apartado). Cuestións, 4 puntos
Da base de dados do torneio do Chess-Results
 Da base de dados do torneio do Chess-Results http://chess-results.com ΟΜΑΔΙΚΟ ΠΡΩΤΑΘΛΗΜΑ Σ.Σ. ΑΝΑΤ.ΣΤΕΡΕΑΣ & ΕΥΒΟΙΑΣ 2010 Última Actualização10.02.2010 23:56:29 Composição das equipas com resultados ronda
Da base de dados do torneio do Chess-Results http://chess-results.com ΟΜΑΔΙΚΟ ΠΡΩΤΑΘΛΗΜΑ Σ.Σ. ΑΝΑΤ.ΣΤΕΡΕΑΣ & ΕΥΒΟΙΑΣ 2010 Última Actualização10.02.2010 23:56:29 Composição das equipas com resultados ronda
MATEMÁTICAS. PRIMEIRA PARTE (Parte Común) ), cadradas de orde tres, tales que a 21
 PRIMEIRA PARTE (Parte Común) (Nesta primeira parte tódolos alumnos deben responder a tres preguntas. Unha soa pregunta de cada un dos tres bloques temáticos: Álxebra Lineal, Xeometría e Análise. A puntuación
PRIMEIRA PARTE (Parte Común) (Nesta primeira parte tódolos alumnos deben responder a tres preguntas. Unha soa pregunta de cada un dos tres bloques temáticos: Álxebra Lineal, Xeometría e Análise. A puntuación
24/10/06 MOVEMENTO HARMÓNICO SIMPLE
 NOME: CALIFICACIÓN PROBLEMAS (6 puntos) 24/10/06 MOVEMENTO HARMÓNICO SIMPLE 1. Dun resorte elástico de constante k= 500 Nm -1 colga unha masa puntual de 5 kg. Estando o conxunto en equilibrio, desprázase
NOME: CALIFICACIÓN PROBLEMAS (6 puntos) 24/10/06 MOVEMENTO HARMÓNICO SIMPLE 1. Dun resorte elástico de constante k= 500 Nm -1 colga unha masa puntual de 5 kg. Estando o conxunto en equilibrio, desprázase
Sistemas e Inecuacións
 Sistemas e Inecuacións 1. Introdución 2. Sistemas lineais 2.1 Resolución gráfica 2.2 Resolución alxébrica 3. Método de Gauss 4. Sistemas de ecuacións non lineais 5. Inecuacións 5.1 Inecuacións de 1º e
Sistemas e Inecuacións 1. Introdución 2. Sistemas lineais 2.1 Resolución gráfica 2.2 Resolución alxébrica 3. Método de Gauss 4. Sistemas de ecuacións non lineais 5. Inecuacións 5.1 Inecuacións de 1º e
Ámbito científico tecnolóxico. Ecuacións de segundo grao e sistemas de ecuacións. Módulo 3 Unidade didáctica 8
 Educación secundaria para persoas adultas Ámbito científico tecnolóxico Módulo 3 Unidade didáctica 8 Ecuacións de segundo grao e sistemas de ecuacións Páxina 1 de 45 Índice 1. Programación da unidade...3
Educación secundaria para persoas adultas Ámbito científico tecnolóxico Módulo 3 Unidade didáctica 8 Ecuacións de segundo grao e sistemas de ecuacións Páxina 1 de 45 Índice 1. Programación da unidade...3
MATEMÁTICAS APLICADAS ÁS CIENCIAS SOCIAIS
 61 MATEMÁTICAS APLICADAS ÁS CIENCIAS SOCIAIS O alumno debe resolver só un exercicio de cada un dos tres bloques temáticos Puntuación máxima de cada un dos exercicios: Álxebra 3 puntos; Análise 3,5 puntos;
61 MATEMÁTICAS APLICADAS ÁS CIENCIAS SOCIAIS O alumno debe resolver só un exercicio de cada un dos tres bloques temáticos Puntuación máxima de cada un dos exercicios: Álxebra 3 puntos; Análise 3,5 puntos;
CASE: Projeto EDW Enterprise Data Warehouse
 CASE: Projeto EDW Enterprise Data Warehouse Objetivos do Projeto Arquitetura EDW A necessidade de uma base de BI mais robusta com repositório único de informações para suportar a crescente necessidade
CASE: Projeto EDW Enterprise Data Warehouse Objetivos do Projeto Arquitetura EDW A necessidade de uma base de BI mais robusta com repositório único de informações para suportar a crescente necessidade
Caderno de traballo. Proxecto EDA 2009 Descartes na aula. Departamento de Matemáticas CPI A Xunqueira Fene
 Departamento de Matemáticas CPI A Xunqueira Fene Nome: 4º ESO Nº Páx. 1 de 36 FIGURAS SEMELLANTES 1. CONCEPTO DE SEMELLANZA Intuitivamente: Dúas figuras son SEMELLANTES se teñen a mesma forma pero distinto
Departamento de Matemáticas CPI A Xunqueira Fene Nome: 4º ESO Nº Páx. 1 de 36 FIGURAS SEMELLANTES 1. CONCEPTO DE SEMELLANZA Intuitivamente: Dúas figuras son SEMELLANTES se teñen a mesma forma pero distinto
Interferencia por división da fronte
 Tema 9 Interferencia por división da fronte No tema anterior vimos que para lograr interferencia debemos superpoñer luz procedente dunha única fonte de luz pero que recorreu camiños diferentes. Unha forma
Tema 9 Interferencia por división da fronte No tema anterior vimos que para lograr interferencia debemos superpoñer luz procedente dunha única fonte de luz pero que recorreu camiños diferentes. Unha forma
Expresións alxébricas
 5 Expresións alxébricas Obxectivos Crear expresións alxébricas a partir dun enunciado. Atopar o valor numérico dunha expresión alxébrica. Clasificar unha expresión alxébrica como monomio, binomio,... polinomio.
5 Expresións alxébricas Obxectivos Crear expresións alxébricas a partir dun enunciado. Atopar o valor numérico dunha expresión alxébrica. Clasificar unha expresión alxébrica como monomio, binomio,... polinomio.
EXERCICIOS DE REFORZO: SISTEMAS DE ECUACIÓNS LINEAIS
 EXERCICIOS DE REFORZO: SISTEMAS DE ECUACIÓNS LINEAIS. ) Clul os posiles vlores de,, pr que triz A verifique relión (A I), sendo I triz identidde de orde e triz nul de orde. ) Cl é soluión dun siste hooéneo
EXERCICIOS DE REFORZO: SISTEMAS DE ECUACIÓNS LINEAIS. ) Clul os posiles vlores de,, pr que triz A verifique relión (A I), sendo I triz identidde de orde e triz nul de orde. ) Cl é soluión dun siste hooéneo
I.E.S. CADERNO Nº 6 NOME: DATA: / / Semellanza
 Semellanza Contidos 1. Semellanza Figuras semellantes Teorema de Tales Triángulos semellantes 2. Triángulos rectángulos. Teoremas Teorema do cateto Teorema da altura Teorema de Pitágoras xeneralizado 3.
Semellanza Contidos 1. Semellanza Figuras semellantes Teorema de Tales Triángulos semellantes 2. Triángulos rectángulos. Teoremas Teorema do cateto Teorema da altura Teorema de Pitágoras xeneralizado 3.
INTERACCIÓNS GRAVITATORIA E ELECTROSTÁTICA
 INTEACCIÓNS GAVITATOIA E ELECTOSTÁTICA AS LEIS DE KEPLE O astrónomo e matemático Johannes Kepler (1571 1630) enunciou tres leis que describen o movemento planetario a partir do estudo dunha gran cantidade
INTEACCIÓNS GAVITATOIA E ELECTOSTÁTICA AS LEIS DE KEPLE O astrónomo e matemático Johannes Kepler (1571 1630) enunciou tres leis que describen o movemento planetario a partir do estudo dunha gran cantidade
Trigonometría. Obxectivos. Antes de empezar.
 7 Trigonometría Obxectivos Nesta quincena aprenderás a: Calcular as razóns trigonométricas dun ángulo. Calcular todas as razóns trigonométricas dun ángulo a partir dunha delas. Resolver triángulos rectángulos
7 Trigonometría Obxectivos Nesta quincena aprenderás a: Calcular as razóns trigonométricas dun ángulo. Calcular todas as razóns trigonométricas dun ángulo a partir dunha delas. Resolver triángulos rectángulos
a) Ao ceibar o resorte describe un MHS, polo tanto correspóndelle unha ecuación para a elongación:
 VIBRACIÓNS E ONDAS PROBLEMAS 1. Un sistema cun resorte estirado 0,03 m sóltase en t=0 deixándoo oscilar libremente, co resultado dunha oscilación cada 0, s. Calcula: a) A velocidade do extremo libre ó
VIBRACIÓNS E ONDAS PROBLEMAS 1. Un sistema cun resorte estirado 0,03 m sóltase en t=0 deixándoo oscilar libremente, co resultado dunha oscilación cada 0, s. Calcula: a) A velocidade do extremo libre ó
ANEXOS. Anexo 1. Recuento de Clase N 20
 Anexo 1. Recuento de Clase N 20 512 513 Anexo 2. Enunciados Problemas por Bloques BLOQUE N 1 Dominio temático: Geometría Plana Temas: Segmentos Congruentes; Circunferencia Problema Principal 1 Objetivo
Anexo 1. Recuento de Clase N 20 512 513 Anexo 2. Enunciados Problemas por Bloques BLOQUE N 1 Dominio temático: Geometría Plana Temas: Segmentos Congruentes; Circunferencia Problema Principal 1 Objetivo
FISICA 2º BAC 27/01/2007
 POBLEMAS 1.- Un corpo de 10 g de masa desprázase cun movemento harmónico simple de 80 Hz de frecuencia e de 1 m de amplitude. Acha: a) A enerxía potencial cando a elongación é igual a 70 cm. b) O módulo
POBLEMAS 1.- Un corpo de 10 g de masa desprázase cun movemento harmónico simple de 80 Hz de frecuencia e de 1 m de amplitude. Acha: a) A enerxía potencial cando a elongación é igual a 70 cm. b) O módulo
Inecuacións. Obxectivos
 5 Inecuacións Obxectivos Nesta quincena aprenderás a: Resolver inecuacións de primeiro e segundo grao cunha incógnita. Resolver sistemas de ecuacións cunha incógnita. Resolver de forma gráfica inecuacións
5 Inecuacións Obxectivos Nesta quincena aprenderás a: Resolver inecuacións de primeiro e segundo grao cunha incógnita. Resolver sistemas de ecuacións cunha incógnita. Resolver de forma gráfica inecuacións
Funcións e gráficas. Obxectivos. 1.Funcións reais páx. 4 Concepto de función Gráfico dunha función Dominio e percorrido Funcións definidas a anacos
 9 Funcións e gráficas Obxectivos Nesta quincena aprenderás a: Coñecer e interpretar as funcións e as distintas formas de presentalas. Recoñecer o dominio e o percorrido dunha función. Determinar se unha
9 Funcións e gráficas Obxectivos Nesta quincena aprenderás a: Coñecer e interpretar as funcións e as distintas formas de presentalas. Recoñecer o dominio e o percorrido dunha función. Determinar se unha
Filipenses 2:5-11. Filipenses
 Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
EXERCICIOS DE REFORZO: DETERMINANTES., calcula a matriz X que verifica A X = A 1 B, sendo B =
 EXERCICIOS DE REORZO: DETERMINANTES Pr A, lul riz X que verifi AX A B, sendo B ) Define enor opleenrio e duno dun eleeno nunh riz drd ) Dd riz A : i Clul o rngo, segundo os vlores de λ, de A λi, sendo
EXERCICIOS DE REORZO: DETERMINANTES Pr A, lul riz X que verifi AX A B, sendo B ) Define enor opleenrio e duno dun eleeno nunh riz drd ) Dd riz A : i Clul o rngo, segundo os vlores de λ, de A λi, sendo
Obxectivos. Resumo. titor. corpos xeométricos. Calcular as. súas áreas volumes. Terra. deles.
 8 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Distinguir as clases de corpos xeométricos. Construíloss a partir do seu desenvolvemento plano. Calcular as súas áreas e volumes. Localizar
8 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Distinguir as clases de corpos xeométricos. Construíloss a partir do seu desenvolvemento plano. Calcular as súas áreas e volumes. Localizar
Código: 25 PAU XUÑO 2014 FÍSICA OPCIÓN A OPCIÓN B
 PAU XUÑO 2014 Código: 25 FÍSICA Puntuación máxima: Cuestións 4 puntos (1 cada cuestión, teórica ou práctica). Problemas 6 puntos (1 cada apartado). Non se valorará a simple anotación dun ítem como solución
PAU XUÑO 2014 Código: 25 FÍSICA Puntuación máxima: Cuestións 4 puntos (1 cada cuestión, teórica ou práctica). Problemas 6 puntos (1 cada apartado). Non se valorará a simple anotación dun ítem como solución
Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
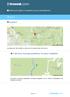 Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Números reais. Obxectivos. Antes de empezar.
 1 Números reais Obxectivos Nesta quincena aprenderás a: Clasificar os números reais en racionais e irracionais. Aproximar números con decimais ata unha orde dada. Calcular a cota de erro dunha aproximación.
1 Números reais Obxectivos Nesta quincena aprenderás a: Clasificar os números reais en racionais e irracionais. Aproximar números con decimais ata unha orde dada. Calcular a cota de erro dunha aproximación.
As Mareas INDICE. 1. Introducción 2. Forza das mareas 3. Por que temos dúas mareas ó día? 4. Predición de marea 5. Aviso para a navegación
 As Mareas INDICE 1. Introducción 2. Forza das mareas 3. Por que temos dúas mareas ó día? 4. Predición de marea 5. Aviso para a navegación Introducción A marea é a variación do nivel da superficie libre
As Mareas INDICE 1. Introducción 2. Forza das mareas 3. Por que temos dúas mareas ó día? 4. Predición de marea 5. Aviso para a navegación Introducción A marea é a variación do nivel da superficie libre
EJERCICIOS DE VIBRACIONES Y ONDAS
 EJERCICIOS DE VIBRACIONES Y ONDAS 1.- Cando un movemento ondulatorio se atopa na súa propagación cunha fenda de dimensións pequenas comparables as da súa lonxitude de onda prodúcese: a) polarización; b)
EJERCICIOS DE VIBRACIONES Y ONDAS 1.- Cando un movemento ondulatorio se atopa na súa propagación cunha fenda de dimensións pequenas comparables as da súa lonxitude de onda prodúcese: a) polarización; b)
PAAU (LOXSE) XUÑO 2005 MATEMÁTICAS APLICADAS ÁS CC. SOCIAIS
 PAAU (LOXSE) XUÑO 005 MATEMÁTICAS APLICADAS ÁS CC. SOCIAIS Código: 61 O alumno debe resolver só un exercicio de cada un dos tres bloques temáticos. Puntuación máxima de cada un dos exercicios: Álxebra
PAAU (LOXSE) XUÑO 005 MATEMÁTICAS APLICADAS ÁS CC. SOCIAIS Código: 61 O alumno debe resolver só un exercicio de cada un dos tres bloques temáticos. Puntuación máxima de cada un dos exercicios: Álxebra
