Laborator L3 3. Analiza microscopica prezentarea microscopului metalografic si a metodei de analiza
|
|
|
- Κλυταιμνήστρα Βλαστός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Laborator L3 3. Analiza microscopica prezentarea microscopului metalografic si a metodei de analiza 3.1. Aspecte teoretice Microscopul metalografic este un microscop optic, la care se analizează în lumina reflectată materialele opace, cum sunt materialele metalice, ceramice, compozite, etc. 3.2 Obiective Dupa parcurgerea acestui laborator cursantul va trebui sa: Sa cunoasca principiul de functionare a microscopului metalografic; Sa cunoasca caracteristicile optice ale microscopului metalografic; Sa cunoasca partile componente ale microscopului metalografic; Sa cunoasca metodele de lucru cu microscopul metalografic metalografic; 3.3 Principiul de funcţionare a microscopului metalografic Schema optică de principiu a unui microscop metalografic se prezintă în imaginea urmatroare observam ca aceasta este composa din două lentile: obiectivul îndreptat către obiect şi ocularul în dreptul ochiului. Lumina reflectată de obiect (suprafaţa probei metalografice) trece prin obiectiv, care formează o imagine intermediară mărită şi răsturnată. Această imagine este apoi mărită de ocular, formând o imagine virtuală vizibilă cu ochiul, sau o imagine reală proiectată pe un ecran de proiecţie, film sau placă fotografică. Pag. 1
2 3.4 Caracteristici optice ale microscopului metalografic Caracteristicile optice principale ale microscoapelor metalografice sunt: puterea de mărire; apertura obiectivului; puterea de rezoluţie; puterea de rezoluţie verticală Puterea de mărire a microscopului este dată de raportul dintre mărimea imaginii şi mărimea obiectului. Se determină ca produs al măririlor proprii ale obiectivului şi ocularului utilizate: M = Ir /O = ( Ir / Ii ) x ( Ii / O ) =Mob x Moc Mărirea obiectivului se calculează cu relaţia: Mob = L / Fob unde: L= mm este lungimea optică a tubului microscopic; Fob - distanţa focală a obiectivului (mm). Mărirea ocularului este dată de relaţia: Moc = d / Foc unde: d = 250 mm este distanţa vederii normale, de la care prin convenţie un obiect este văzut în mărime naturală; Foc-distanţa focală a ocularului (mm). Ocularele şi obiectivele au gravată pe montură mărirea proprie. Pag. 2
3 Măririle microscopului sunt în general prezentate tabelar în Cartea tehnică a aparatului, funcţie de obiectivele şi ocularele asociate. Apertura obiectivului este un indicativ al capacităţii obiectivului de a strânge razele de lumină reflectate de probă. Apertura se calculează cu relaţia: A = n sin α unde: n - indicele de refracţie al mediului dintre obiect şi obiectiv, n=1 pentru aer, n=1,518 pentru ulei de cedru; nmax=1,734 pentru lichid refrigerent (monobromnaftalină). α - semiunghiul conului de lumină, de divergenţă maximă, care pătrunde în obiectiv de la probă. Constructiv, αmax= 72 0 şi deci apertura maximă în aer este 0,95. Rezultă că obiectivele cu apertură mai mare de 0,95 trebuiesc utilizate cu lichide de imersie, cel mai des folosit fiind uleiul de cedru. Apertura este o caracteristică importantă a obiectivului care îi determină puterea de rezoluţie. De asemenea alegerea ocularului se face în corelaţie cu apertura obiectivului. Conform regulei lui Abbe, mărirea microscopului trebuie să fie cuprinsă între 500 şi 1000 ori apertura obiectivului utilizat: 500 A < M < 1000 A De exemplu, obiectivul, cu apertură 0,30 şi mărire 15x, poate realiza măriri ale microscopului între x. Rezultă că se pot asocia oculare cu măriri proprii cuprinse între 10x şi 20x. Ocularele cu măriri mai mici nu utilizează pentru că şterg din puterea de rezoluţie a obiectivului, cele cu măriri mai mari nu pot da detalii suplimentare. Puterea de rezoluţie (de separare) este definită prin distanţa d minimă dintre două puncte, pentru care obiectivul dă Pag. 3
4 imagini distincte. Se calculează cu relaţia: d = 0,61 x λ/a unde: λ este lungimea de undă a luminii folosite. λ= 0,4 µm pentru lumină albastră, 0,6 µm pentru lumină albă şi 0,8 µm pentru lumină roşie. Puterea de rezoluţie maximă (dmin) este de 0,15 µm când se foloseşte lumina albastră, imersie în lichid refrigerent şi obiective cu α maxim. Considerând puterea de rezoluţie a ochiului d1 = 0,3 mm, rezultă că mărirea maximă a microscopului metalografic este: Mmax = d1 / dmin = 2000 Puterea de rezoluţie pe verticală (adâncimea câmpului) reprezintă distanţa maximă dintre două plane paralele cu suprafaţa de observaţie, pentru care toate punctele se observă distinct. Adâncimea câmpului este invers proporţională cu apertura şi puterea de mărire. De aceea proba metalografică trebuie să prezinte suprafaţă plană, fără relief, bine lustruită şi cu atac metalografic cu atât mai slab cu cât mărirea este mai mare. 3.5 Părţi componenteale microscopului metalografic In general un microscop metalografic este format din: sistemul optic; sistemul de iluminare; sistemul mecanic de reglaj. Pag. 4
5 Sistemul optic Sistemul optic cuprinde obiectivul şi ocularul. Obiectivul este un sistem compus convergent, format dintr-o lentilă plan-convexă care realizează imaginea mărită a obiectivului şi o serie de lentile care corectează defectele primei lentile. Cele mai frecvente defecte sunt aberaţia cromatică şi de sfericitate. Aberaţia cromatică se datorează dispersiei luminii albe la trecerea prin lentilă. Indicele de refracţie este invers proporţional cu lungimea de undă. În consecinţă, se formează o serie de imagini monocromatice dispuse în plane succesive (violetă cea mai apropiată, roşie cea mai îndepărtată). Cum punerea la punct a imaginii se face pe una din imaginile monocromatice, se produce micşorarea clarităţii imaginii, deformarea ei şi colorarea marginilor. Eliminarea aberaţiei cromatice se realizează prin utilizarea luminii monocromatice şi a obiectivelor corectate. După gradul de corecţie, obiectivele sunt: - acromatice, corectate pentru zona centrală (galben verde) a spectrului, care se folosesc cu filtru galben-verde şi material fotografic ortocromatic. În lumină albă marginile unei structuri incolore au o irizaţie roşie; - apocromatice, corectate pentru întreg spectrul. Se folosesc fără filtru şi cu orice material fotografic. Imaginea nu prezintă irizaţii marginale. Pag. 5
6 Aberaţia de sfericitate este determinată de curbura suprafeţelor lentilelor şi apare în condiţiile fasciculelor largi de lumină. Razele centrale sunt mai puţin refractate decât cele marginale. Se formează o serie de imagini în plane succesive, ceea ce conduce la o luminare neuniformă. Aberaţia de sfericitate se elimină prin asocierea unei lentile concave cu alta concavă, astfel încât aberaţiile să se compenseze. Ocularul este o lentilă plan convexă, care măreşte imaginea intermediară dată de obiectiv şi corijează unele defecte optice. Ocularele pot fi: - obişnuite, tip Huygens, care nu corectează imaginea dată de obiectiv. Se asociază cu obiective acromatice; - de compensaţie, asociate cu obiective apocromatice, cărora le corectează defectele rămase. Realizează o imagine clară şi plană; - de proiecţie sau fotooculare, utilizate cu obiective apocromatice sau semiapocromatice. Asigură o imagine clară pe ecranele de proiecţie şi pe microfotografii. Pag. 6
7 Sistemul de iluminare Sistemul de iluminare se compune din sursa de lumină, diafragme, lentile, prisme, filtre de lumină. Sursa de lumină poate fi o lampă cu incandescenţă sau cu arc electric alimentată printr-un transformator de tensiune. Iluminarea probei metalice poate fi perpendiculară sau oblică. Iluminarea perpendiculară, numită şi în câmp luminos redă suprafeţele plane luminoase, iar cele înclinate întunecate. Iluminarea oblică, sub unghi de incidenţă mic, determină suprafeţe plane uşor întunecate, iar suprafeţele înclinate parţial luminoase. În cazul iluminării oblice multilaterale sub unghi mare de incidenţă, denumită în câmp întunecat suprafeţele plane apar întunecate, iar cele înclinate - luminate. Diafragmele utilizate sunt de apertură şi de câmp. Diafragma de apertură permite reglarea diametrului fasciculului de lumină şi deci a luminozităţii probei. Diafragma de câmp limitează zona analizată în câmpul ocularului. Pentru contrast maxim, se recomandă deschiderea minim permisă a diafragmelor. Lentilele şi prismele, cât şi obiectivul transmit imaginea sursei de lumină şi a diafragmei de apertură pe suprafaţa analizată. Filtrele de lumină au rolul de a îmbunătăţi calitatea imaginii. Pag. 7
8 Alegerea lor depinde de: tipul obiectivului, sursa de lumină, materialul analizat, placa fotografică. Obiectivele acromatice corectate pentru domeniul galben - verde al spectrului, necesită filtrul galben - verde. Filtrul gri neutru reduce intensitatea sursei de lumină fără a-i modifica culoarea. Filtrul bleu dă cea mai bună putere de rezoluţie vizuală. Filtrele de lumină slăbesc anumite domenii din spectrul luminii albe, fără a realiza o lumină perfect monocromatică. Astfel filtrul galben absoarbe mai puternic capătul albastru al spectrului decât pe cel roşu. Sistemul mecanic de reglaj Orice microscop prezintă un stativ pe care sunt dispuse sistemul optic, de iluminare şi măsuţa cu proba. Prin sisteme şurub piuliţă, sursa de lumină şi diafragmele au posibilităţi de centrare faţă de axul optic, ceea ce asigură o iluminare perpendiculară, uniformă. Iluminarea oblică se realizează prin dezaxarea diafragmei de apertură. În scopul punerii la punct a imaginii există sisteme de reglare rapidă şi fină a distanţei probă - obiectiv. Schimbarea câmpului analizat se poate face cu ajutorul unor şuruburi micrometrice, care deplasează masa cu proba după două direcţii perpendiculare. Măsuţa poate fi inferioară, sub obiectiv şi în acest caz proba trebuie să prezinte suprafaţa de cercetat paralelă cu suprafaţa măsuţei. În caz contrar proba se presează pe o plăcuţă în plastilină, cu ajutorul presei de mână. Se realizează astfel paralelismul suprafeţei de observaţie cu cea de aşezare şi clarul imaginii în tot câmpul. Măsuţa superioară, deasupra obiectivului permite utilizarea probelor de orice formă. 3.6 Metode optice de analiză a. Microscopia în câmp luminos, este cea mai utilizată în metalografie, pentru analiza calitativă şi cantitativă a structurii materialelor metalice (mărirea peste 100x). b. Microscopia oblică, se utilizează mai ales în analiza macroscopică (mărirea sub 100x) a materialelor metalice la stereomicroscop şi mai puţin, în analiza microscopică a structurii, pentru evidenţierea unor aspecte de relief ale suprafeţei. Pag. 8
9 c. Microscopia în câmp întunecat, are ca scop evidenţierea microreliefului suprafeţei metalografice: constituenţi structurali polifazici, incluziuni nemetalice transparente, fisuri etc., care apar puternic luminaţi pe fond întunecat. De asemenea se văd culorile naturale ale unor constituenţi structurali, la care în câmp luminos, culorile sunt denaturate prin reflexii şi absorbţii necontrolate. Astfel oxidul de cupru apare albastru în câmp luminos, în timp ce în câmp întunecat apare la culoarea naturală roşu granat. d. Microscopia în lumină polarizată foloseşte iluminarea perpendiculară cu lumină polarizată plan, prin introducerea în circuitul optic a unei prisme Nicol - polarizorul. Lumina reflectată de probă trece printr-un al doilea Nicol - analizorul. Atunci cand materialul analizat este izotrop, la pozitia incrucişată a nicolilor (planele de polarizare perpendiculare) se produce extincţia fasciculului de lumină si materialul apare întunecat. Dacă materialul analizateste puternic anizotrop (structuri cristaline necubice), la reflexia pe suprafaţa acestuia se roteşte planul de polarizare şi câmpul analizatorului apare luminat. Pentru extincţie totală trebuie rotit analizorul sau proba cu un număr de grade specific fiecărei substanţe. Pag. 9
10 Bibliografie: 1. Radulescu M., Dragan N., Hubert H., Opris C. - Atlas metalografic, Editura Tehnica, Bucuresti; 2. STAS Metalografie. Luarea şi pregătirea probelor metalografice; 3. STAS Metalografie. Microstructuri. Scări etalon pentru oţeluri. Activitati: A1 Cerinta: Sa se identifice partile de componente ale miscroscopului metalografic si metodele de analiza cu ajutorul acestuia. Etapele desfasurarii activitatii: 1. Se pune la dispozitia studentului un microscop metalografic. 2. Se studiaza partile componente ale microscopului metalografic. 3. Se identifica caracteristice optice ale microscopului. 4. Se simuleaza diverse metode de analiza. Prezentarea rezultatelor: Se intocmeste un referat care trebuie sa contina urmatoarele capitole: - Descrierea microscopului metalografic; - Caracteristicile optice ale microscopului; - Descrierea unei metode de analiza microscopica; - Concluzii. Evaluare: Activitatea este evaluata in baza referatului intocmit. Modul de punctare a activitati este: - identificarea partilor componente ale microscopului - 30 puncte; - stabilirea caracteristicilor optice ale microscopului - 30 puncte; - descrierea metodei de analiza cmicroscopica 20 puncte; - concuzii - 10 puncte Punctajul maxim este de 100 puncte si se acorda 10 puncte din oficiu. Pag. 10
Tipuri de celule sub microscopul optic
 Tipuri de celule sub microscopul optic Termenul de celulă a fost introdus de R. Hooke în cartea sa Micrographia publicată în 1665 în care descrie observaţii făcute cu microscopul şi telescopul. Microscopul
Tipuri de celule sub microscopul optic Termenul de celulă a fost introdus de R. Hooke în cartea sa Micrographia publicată în 1665 în care descrie observaţii făcute cu microscopul şi telescopul. Microscopul
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Reflexia şi refracţia luminii.
 Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Reflexia şi refracţia luminii. 1. Cu cat se deplaseaza o raza care cade sub unghiul i =30 pe o placa plan-paralela de grosime e = 8,0 mm si indicele de refractie n = 1,50, pe care o traverseaza? Caz particular
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Microscopie optica. Masuratori cu microscopul optic
 . Masuratori cu microscopul optic Tehnici de microscopie de transmisie Microscopie de baleiaj utilizand lasere Microscopie confocala Microscopie in camp apropiat Microscopie electronica Microscopie Microscopie
. Masuratori cu microscopul optic Tehnici de microscopie de transmisie Microscopie de baleiaj utilizand lasere Microscopie confocala Microscopie in camp apropiat Microscopie electronica Microscopie Microscopie
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
STUDIUL MICROSCOPULUI
 LUCRAREA NR. 6 STUDIUL MICROSCOPULUI Tema lucrării: 1) Etalonarea micrometrului ocular. 2) Măsurarea dimensiunilor unui obiect mic. 3) Determinarea aperturii numerice. 4) Determinarea grosismentului microscopului
LUCRAREA NR. 6 STUDIUL MICROSCOPULUI Tema lucrării: 1) Etalonarea micrometrului ocular. 2) Măsurarea dimensiunilor unui obiect mic. 3) Determinarea aperturii numerice. 4) Determinarea grosismentului microscopului
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25
 Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Capitolul ASAMBLAREA LAGĂRELOR LECŢIA 25 LAGĂRELE CU ALUNECARE!" 25.1.Caracteristici.Părţi componente.materiale.!" 25.2.Funcţionarea lagărelor cu alunecare.! 25.1.Caracteristici.Părţi componente.materiale.
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE
 LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE Tema lucrării: 1) Determinarea distanţei focale a unei oglinzi concave ) Determinarea distanţei focale a unei oglinzi convexe 3) Studiul
LUCRAREA NR. 3 DETERMINAREA DISTANŢEI FOCALE A OGLINZILOR SFERICE Tema lucrării: 1) Determinarea distanţei focale a unei oglinzi concave ) Determinarea distanţei focale a unei oglinzi convexe 3) Studiul
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
CUPRINS 5. Reducerea sistemelor de forţe (continuare)... 1 Cuprins..1
 CURS 5 REDUCEREA SISTEMELOR DE FORŢE (CONTINUARE) CUPRINS 5. Reducerea sistemelor de forţe (continuare)...... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 5.1. Teorema lui Varignon pentru sisteme
CURS 5 REDUCEREA SISTEMELOR DE FORŢE (CONTINUARE) CUPRINS 5. Reducerea sistemelor de forţe (continuare)...... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 5.1. Teorema lui Varignon pentru sisteme
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Metode de caracterizare structurala in stiinta nanomaterialelor: aplicatii practice
 Metode de caracterizare structurala in stiinta nanomaterialelor: aplicatii practice Utilizare de metode complementare de investigare structurala Proba investigata: SrTiO 3 sub forma de pulbere nanostructurata
Metode de caracterizare structurala in stiinta nanomaterialelor: aplicatii practice Utilizare de metode complementare de investigare structurala Proba investigata: SrTiO 3 sub forma de pulbere nanostructurata
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Difractia de electroni
 Difractia de electroni 1 Principiul lucrari Verificarea experimentala a difractiei electronilor rapizi pe straturi de grafit policristalin: observarea inelelor de interferenta ce apar pe ecranul fluorescent.
Difractia de electroni 1 Principiul lucrari Verificarea experimentala a difractiei electronilor rapizi pe straturi de grafit policristalin: observarea inelelor de interferenta ce apar pe ecranul fluorescent.
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
LUCRAREA NR. 4 DETERMINAREA INDICELUI DE REFRACŢIE AL UNUI SOLID CU AJUTORUL PRISMEI
 LUCRAREA NR. 4 DETERMINAREA INDICELUI DE REFRACŢIE AL UNUI SOLID CU AJUTORUL PRISMEI Tema lucrării: 1) Determinarea unghiului refringent al prismei. ) Determinarea indicelui de refracţie al prismei pentru
LUCRAREA NR. 4 DETERMINAREA INDICELUI DE REFRACŢIE AL UNUI SOLID CU AJUTORUL PRISMEI Tema lucrării: 1) Determinarea unghiului refringent al prismei. ) Determinarea indicelui de refracţie al prismei pentru
14. Grinzi cu zăbrele Metoda secţiunilor...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR GRINZI CU ZĂBRELE METODA SECŢIUNILOR CUPRINS. Grinzi cu zăbrele Metoda secţiunilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele Metoda secţiunilor
SEMINAR GRINZI CU ZĂBRELE METODA SECŢIUNILOR CUPRINS. Grinzi cu zăbrele Metoda secţiunilor... Cuprins... Introducere..... Aspecte teoretice..... Aplicaţii rezolvate.... Grinzi cu zăbrele Metoda secţiunilor
Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii
 Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii luminii cu substanţa. Optica geometrica este acea parte
Optica este o ramură a fizicii care studiază proprietăţile şi natura luminii, modul de producere a acesteia, şi legile propagării şi interacţiunii luminii cu substanţa. Optica geometrica este acea parte
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Continue. Answer: a. 0,25 b. 0,15 c. 0,1 d. 0,2 e. 0,3. Answer: a. 0,1 b. 0,25 c. 0,17 d. 0,02 e. 0,3
 Concurs Phi: Setul 1 - Clasa a VII-a Logout e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a VII-a» Attempt 1 1 Pentru a deplasa uniform pe orizontala un corp de masa m = 18 kg se actioneaza asupra lui
Concurs Phi: Setul 1 - Clasa a VII-a Logout e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a VII-a» Attempt 1 1 Pentru a deplasa uniform pe orizontala un corp de masa m = 18 kg se actioneaza asupra lui
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Laborator 5 INTERFEROMETRE
 Laborator 5 INTERFEROMETRE Scopul lucrarii În lucrarea de fańă sunt prezentate unele aspecte legate de interferometrie. Se prezinta functionarea unui modulator optic ce lucreaza pe baza interferentei dintre
Laborator 5 INTERFEROMETRE Scopul lucrarii În lucrarea de fańă sunt prezentate unele aspecte legate de interferometrie. Se prezinta functionarea unui modulator optic ce lucreaza pe baza interferentei dintre
3. REPREZENTAREA PLANULUI
 3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT?
 SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT? Să considerăm mai întâi (pentru a asigura o descriere fizică riguroasă) două oglinzi plane paralele M 1, M 2 (orientate după direcţia MN PQ), aparţinând spre exemplu
SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT? Să considerăm mai întâi (pentru a asigura o descriere fizică riguroasă) două oglinzi plane paralele M 1, M 2 (orientate după direcţia MN PQ), aparţinând spre exemplu
2. STATICA FLUIDELOR. 2.A. Presa hidraulică. Legea lui Arhimede
 2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
2. STATICA FLUIDELOR 2.A. Presa hidraulică. Legea lui Arhimede Aplicația 2.1 Să se determine ce masă M poate fi ridicată cu o presă hidraulică având raportul razelor pistoanelor r 1 /r 2 = 1/20, ştiind
REACŢII DE ADIŢIE NUCLEOFILĂ (AN-REACŢII) (ALDEHIDE ŞI CETONE)
 EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
EAŢII DE ADIŢIE NULEFILĂ (AN-EAŢII) (ALDEIDE ŞI ETNE) ompușii organici care conțin grupa carbonil se numesc compuși carbonilici și se clasifică în: Aldehide etone ALDEIDE: Formula generală: 3 Metanal(formaldehida
BARDAJE - Panouri sandwich
 Panourile sunt montate vertical: De jos în sus, îmbinarea este de tip nut-feder. Sensul de montaj al panourilor trebuie să fie contrar sensului dominant al vântului. Montaj panouri GAMA ALLIANCE Montaj
Panourile sunt montate vertical: De jos în sus, îmbinarea este de tip nut-feder. Sensul de montaj al panourilor trebuie să fie contrar sensului dominant al vântului. Montaj panouri GAMA ALLIANCE Montaj
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
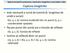 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
2CP Electropompe centrifugale cu turbina dubla
 2CP Electropompe centrifugale cu turbina dubla DOMENIUL DE UTILIZARE Capacitate de până la 450 l/min (27 m³/h) Inaltimea de pompare până la 112 m LIMITELE DE UTILIZARE Inaltimea de aspiratie manometrică
2CP Electropompe centrifugale cu turbina dubla DOMENIUL DE UTILIZARE Capacitate de până la 450 l/min (27 m³/h) Inaltimea de pompare până la 112 m LIMITELE DE UTILIZARE Inaltimea de aspiratie manometrică
LUCRAREA NR. 9 STUDIUL POLARIZĂRII ROTATORII A LUMINII
 LUCRAREA NR. 9 STUDIUL POLARIZĂRII ROTATORII A LUMINII Tema lucrării: 1) Determinarea puterii rotatorii specifice a zahărului 2) Determinarea concentraţiei unei soluţii de zahăr 3) Determinarea dispersiei
LUCRAREA NR. 9 STUDIUL POLARIZĂRII ROTATORII A LUMINII Tema lucrării: 1) Determinarea puterii rotatorii specifice a zahărului 2) Determinarea concentraţiei unei soluţii de zahăr 3) Determinarea dispersiei
* * * 57, SE 6TM, SE 7TM, SE 8TM, SE 9TM, SC , SC , SC 15007, SC 15014, SC 15015, SC , SC
 Console pentru LEA MT Cerinte Constructive Consolele sunt executate in conformitate cu proiectele S.C. Electrica S.A. * orice modificare se va face cu acordul S.C. Electrica S.A. * consolele au fost astfel
Console pentru LEA MT Cerinte Constructive Consolele sunt executate in conformitate cu proiectele S.C. Electrica S.A. * orice modificare se va face cu acordul S.C. Electrica S.A. * consolele au fost astfel
Noţiuni de optică. Ochiul uman
 Biofizică Noţiuni de optică. Ochiul uman Capitolul VII. Noţiuni de optică. Ochiul uman Vederea reprezintă unul din simţurile de bază ale lumii animale, lumina este un factor indispensabil în existenţa
Biofizică Noţiuni de optică. Ochiul uman Capitolul VII. Noţiuni de optică. Ochiul uman Vederea reprezintă unul din simţurile de bază ale lumii animale, lumina este un factor indispensabil în existenţa
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener
 Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Capitolul 14. Asamblari prin pene
 Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Capitolul 14 Asamblari prin pene T.14.1. Momentul de torsiune este transmis de la arbore la butuc prin intermediul unei pene paralele (figura 14.1). De care din cotele indicate depinde tensiunea superficiala
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Stabilizator cu diodă Zener
 LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Control confort. Variator de tensiune cu impuls Reglarea sarcinilor prin ap sare, W/VA
 Control confort Variatoare rotative electronice Variator rotativ / cap scar 40-400 W/VA Variatoare rotative 60-400W/VA MGU3.511.18 MGU3.559.18 Culoare 2 module 1 modul alb MGU3.511.18 MGU3.559.18 fi ldeş
Control confort Variatoare rotative electronice Variator rotativ / cap scar 40-400 W/VA Variatoare rotative 60-400W/VA MGU3.511.18 MGU3.559.18 Culoare 2 module 1 modul alb MGU3.511.18 MGU3.559.18 fi ldeş
Capitolul 30. Transmisii prin lant
 Capitolul 30 Transmisii prin lant T.30.1. Sa se precizeze domeniile de utilizare a transmisiilor prin lant. T.30.2. Sa se precizeze avantajele si dezavantajele transmisiilor prin lant. T.30.3. Realizati
Capitolul 30 Transmisii prin lant T.30.1. Sa se precizeze domeniile de utilizare a transmisiilor prin lant. T.30.2. Sa se precizeze avantajele si dezavantajele transmisiilor prin lant. T.30.3. Realizati
Studiu privind soluţii de climatizare eficiente energetic
 Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
Studiu privind soluţii de climatizare eficiente energetic Varianta iniţială O schemă constructivă posibilă, a unei centrale de tratare a aerului, este prezentată în figura alăturată. Baterie încălzire/răcire
SIGURANŢE CILINDRICE
 SIGURANŢE CILINDRICE SIGURANŢE CILINDRICE CH Curent nominal Caracteristici de declanşare 1-100A gg, am Aplicaţie: Siguranţele cilindrice reprezintă cea mai sigură protecţie a circuitelor electrice de control
SIGURANŢE CILINDRICE SIGURANŢE CILINDRICE CH Curent nominal Caracteristici de declanşare 1-100A gg, am Aplicaţie: Siguranţele cilindrice reprezintă cea mai sigură protecţie a circuitelor electrice de control
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
Seria Balmer. Determinarea constantei lui Rydberg
 Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
Seria Balmer. Determinarea constantei lui Rydberg Obiectivele lucrarii analiza spectrului in vizibil emis de atomii de hidrogen si determinarea lungimii de unda a liniilor serie Balmer; determinarea constantei
CUPRINS 3. Sisteme de forţe (continuare)... 1 Cuprins..1
 CURS 3 SISTEME DE FORŢE (continuare) CUPRINS 3. Sisteme de forţe (continuare)... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 3.1. Momentul forţei în raport cu un punct...2 Test de autoevaluare
CURS 3 SISTEME DE FORŢE (continuare) CUPRINS 3. Sisteme de forţe (continuare)... 1 Cuprins..1 Introducere modul.1 Obiective modul....2 3.1. Momentul forţei în raport cu un punct...2 Test de autoevaluare
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
 Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Dioda Zener şi stabilizatoare de tensiune continuă
 Laborator 2 Dioda Zener şi stabilizatoare de tensiune continuă Se vor studia dioda Zener şi stabilizatoarele de tensiune continua cu diodă Zener şi cu diodă Zener si tranzistor serie. Pentru diodă se va
Laborator 2 Dioda Zener şi stabilizatoare de tensiune continuă Se vor studia dioda Zener şi stabilizatoarele de tensiune continua cu diodă Zener şi cu diodă Zener si tranzistor serie. Pentru diodă se va
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
MODULUL VII: OPTICĂ GEOMETRICĂ
 FUNDAŢIA ÎNVĂŢĂMÂNTULUI PREUNIVERSITAR A COOPERAŢIEI MEŞTEŞUGĂREŞTI "SPIRU HARET" COLEGIUL UCECOM "SPIRU HARET" BUCUREŞTI MODULUL VII: OPTICĂ GEOMETRICĂ (SUPORT DE CURS) ŞCOALA POSTLICEALĂ CALIFICAREA:
FUNDAŢIA ÎNVĂŢĂMÂNTULUI PREUNIVERSITAR A COOPERAŢIEI MEŞTEŞUGĂREŞTI "SPIRU HARET" COLEGIUL UCECOM "SPIRU HARET" BUCUREŞTI MODULUL VII: OPTICĂ GEOMETRICĂ (SUPORT DE CURS) ŞCOALA POSTLICEALĂ CALIFICAREA:
OBIECTIVUL APARATULUI DE FOTOGRAFIAT
 Tema III OBIECTIVUL APARATULUI DE FOTOGRAFIAT 3.0 Generalitati Obiectivul este un sistem optic format din una sau mai multe lentile, cu ajutorul caruia se formeaza imaginile in planul materialului fotosensibil.
Tema III OBIECTIVUL APARATULUI DE FOTOGRAFIAT 3.0 Generalitati Obiectivul este un sistem optic format din una sau mai multe lentile, cu ajutorul caruia se formeaza imaginile in planul materialului fotosensibil.
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
