Κεφάλαιο 7 Βάσεις και ιάσταση
|
|
|
- Ανδρόνικα Μοσχοβάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε βάσεις σε τυχαίους πεπερασµένα παραγόµενους διανυσµατικούς χώρους. Το κύριο θεωρητικό αποτέλεσµα είναι ότι κάθε δυο βάσεις ενός πεπερασµένα παραγόµενου διανυσµατικού χώρου έχουν το ίδιο πλήθος στοιχείων. Το πλήθος αυτό ονοµάζεται διάσταση του διανυσµατικού χώρου. Θα µελετήσουµε πολλά σχετικά παραδείγµατα και στη συνέχεια θα δούµε την έννοια της τάξης πίνακα και µια σηµαντική εφαρµογή στα γραµµικά συστήµατα. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... ΒΑΣΕΙΣ... Ορισµός (γραµµικά ανεξάρτητα στοιχεία)... Παραδείγµατα... Ορισµός Α... Ορισµός (βάση)... Παραδείγµατα... Ορισµός (διάσταση)...5 Παραδείγµατα...5 ΤΑΞΗ ΠΙΝΑΚΑ...5 Ορισµός (χώρος γραµµών, χώρος στηλών, τάξη)...5 Παράδειγµα...5 ΘΕΜΕΛΙΩ ΕΙΣ ΓΝΩΣΕΙΣ...6 ΒΑΣΕΙΣ...6 Θεώρηµα (µέγιστο πλήθος γραµµικώς ανεξάρτητων στοιχείων)...6 Θεώρηµα (πληθάριθµος βάσης)...6 Θεώρηµα (επέκταση γραµµικώς ανεξάρτητου συνόλου σε βάση)...6 Παράδειγµα...6 Πρόταση...7 Θεώρηµα 5 (διαστάσεις υποχώρων)...7 Θεώρηµα 6 (διάσταση αθροίσµατος υποχώρων)...7 Παράδειγµα...7 ΤΑΞΗ ΠΙΝΑΚΑ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ...8 Πρόταση Παράδειγµα...8 Θεώρηµα 8 (κριτήριο συµβιβαστού γραµµικού συστήµατος)...9 Παράδειγµα...9 Θεώρηµα 9 (διάσταση λύσεων οµογενούς γραµµικού συστήµατος)... Παράδειγµα... ΧΩΡΟΙ ΜΕ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ... Θεώρηµα (ύπαρξη ορθοκανονικών βάσεων)... Παράδειγµα... ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ... Άσκηση... Άσκηση... Άσκηση... Άσκηση...5
2 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Άσκηση Άσκηση Άσκηση Άσκηση Άσκηση Άσκηση... Άσκηση... Άσκηση... Άσκηση... Άσκηση... Άσκηση 5... Άσκηση 6... Άσκηση ΑΣΚΗΣΕΙΣ...6 Άσκηση...6 Άσκηση...6 Άσκηση...6 Άσκηση...6 Άσκηση Άσκηση Άσκηση Άσκηση Άσκηση Άσκηση...8 Άσκηση...8 Άσκηση...8 Άσκηση...9 Άσκηση...9 Άσκηση Στα παρακάτω, µε V θα συµβολίζουµε ένα ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ F διανυσµατικό χώρο. ΒΑΣΕΙΣ Ορισµός (γραµµικά ανεξάρτητα στοιχεία) Έστω v,..., v. m V Τα στοιχεία αυτά λέγονται γραµµικά ανεξάρτητα πάνω από το F αν από τη σχέση av amvm=, όπου a,..., am F, έπεται ότι a =... = a m =. Σε διαφορετική περίπτωση θα λέµε ότι τα το F. v,..., vm είναι γραµµικά εξαρτηµένα πάνω από Παραδείγµατα. Στο δ.χ. τα a. ( ) v =,,, v = (,,), v = (,,) είναι γραµµικά ανεξάρτητα γιατί
3 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 av + av + av = a (,,) + a (,,) + a (,,) = (,,) a+ a + a = a = a+ a = a = a = a = b. (,,),(,,),(5,5,) είναι γραµµικά εξαρτηµένα γιατί. Στο δ.χ. F : (,,) + (,, ) (5,5, ) = (,, ). M ( ) a. Τα στοιχεία v =, v =, v =, v =, v5 =, v6 = είναι γραµµικά ανεξάρτητα γιατί av av = b. Τα στοιχεία εξαρτηµένα γιατί 6 6 a a a = a a5 a 6 a =... = a = ,, είναι γραµµικά =.. Τα στοιχεία,i του είναι γραµµικά ανεξάρτητα υπεράνω του αφού a+ bi =, a, b a= b=, αλλά είναι γραµµικά εξαρτηµένα υπεράνω του αφού i + ( ) i=.. Αν κάποιο από τα v,..., vm είναι το µηδενικό στοιχείο, τότε αυτά είναι γραµµικά εξαρτηµένα. Πράγµατι αν συνδυασµό v+ v v m =. v =, τότε έχουµε το γραµµικό Ορισµός Α Επειδή θέλουµε να επεκτείνουµε την έννοια της γραµµικής ανεξαρτησίας σε άπειρα σύνολα δίνουµε τους εξής ορισµούς.
4 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Ένα πεπερασµένο υποσύνολο { v,..., v m} του V λέγεται γραµµικά ανεξάρτητο αν τα στοιχεία v,..., vm είναι γραµµικά ανεξάρτητα. Ένα άπειρο υποσύνολο του V λέγεται γραµµικά ανεξάρτητο αν κάθε πεπερασµένο µη κενό υποσύνολό του είναι γραµµικά ανεξάρτητο. Ένα πεπερασµένο υποσύνολο { v,..., v m} του V λέγεται γραµµικά εξαρτηµένο αν τα στοιχεία v,..., vm είναι γραµµικά εξαρτηµένα. Ένα άπειρο υποσύνολο του V λέγεται γραµµικά εξαρτηµένο αν δεν είναι γραµµικά ανεξάρτητο. ηλαδή αν υπάρχει πεπερασµένο µη κενό υποσύνολο που είναι γραµµικά εξαρτηµένο. εχόµαστε ότι το κενό σύνολο είναι γραµµικά ανεξάρτητο. Ορισµός (βάση) Μια βάση του F δ.χ. V είναι ένα σύνολο στοιχείων του V που είναι γραµµικά ανεξάρτητο πάνω από το F και παράγει το V πάνω από το F. Σηµείωση Σύµφωνα µε τον προηγούµενο ορισµό ενδέχεται να έχουµε άπειρες βάσεις. Πράγµατι µια βάση του δ.χ. [ x] των πραγµατικών πολυωνύµων είναι ο σύνολο {, xx,,...}. Όµως εδώ θα µας απασχολήσουν αποκλειστικά οι δ.χ. που έχουν πεπερασµένες βάσεις. Παραδείγµατα n. Μια βάση του είναι η συνήθης βάση { } e = (,,...,),..., e n = (,,...,). ( ) e,...,, en όπου. Μια βάση του αποτελείται από τα στοιχεία M E =, E =, E =, E =, E =, E =. M n m( F ) { Eij i n, j m}. Μια βάση του είναι το σύνολο όπου σε κάθε θέση του n m πίνακα E υπάρχει το εκτός από τη θέση ( i, j) όπου υπάρχει το. ij
5 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 5 από 9. Μια βάση του [ x ] είναι το n n {,,,..., } x x x. Ορισµός (διάσταση) Έστω V ένας πεπερασµένα παραγόµενος F δ.χ.. Αποδεικνύεται ότι ο V έχει βάση και κάθε βάση του V έχει το ίδιο πλήθος στοιχείων. Ο αριθµός αυτός λέγεται η διάσταση του V και συµβολίζεται µε dim F V ή απλά dim V. Παραδείγµατα Σχετικά µε τα προηγούµενα παραδείγµατα έχουµε ( ) ( ) n dim = n, dim M = 6, dim M = nm, dim [ x] = n+. n m Στο θεωρούµε τον υπόχωρο (,,),(,,). Επειδή µια βάση αυτού είναι το {(,, ) } έχουµε dim (,,),(,,) =. n ΤΑΞΗ ΠΙΝΑΚΑ Ορισµός (χώρος γραµµών, χώρος στηλών, τάξη) Έστω A M ( F). n m m Κάθε γραµµή του Α είναι ένα στοιχείο του F. Ο χώρος γραµµών του Α είναι m ο υπόχωρος του F που παράγουν οι γραµµές του Α και συµβολίζεται µε R( A. ) Η τάξη γραµµών του Α είναι ο ακέραιος dim F R( A). n Κάθε στήλη του Α είναι ένα στοιχείο του F. Ο χώρος στηλών του Α είναι ο n υπόχωρος του F που παράγουν οι στήλες του Α και συµβολίζεται µε C( A). Η τάξη στηλών του Α είναι ο ακέραιος dim F C( A). Αποδεικνύεται ότι dim F R( A) = dim F C( A). O αριθµός αυτός ονοµάζεται η τάξη του πίνακα Α και συµβολίζεται µε r( A). Παράδειγµα Για τον πίνακα A = έχουµε ra= ( ), γιατί όπως είδαµε στο προηγούµενο παράδειγµα dim (,, ),(,, ) =.
6 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 6 από 9 ΘΕΜΕΛΙΩ ΕΙΣ ΓΝΩΣΕΙΣ ΒΑΣΕΙΣ Στο Κεφάλαιο 5, Θεώρηµα, είδαµε ότι κάθε γραµµικά ανεξάρτητο υποσύνολο του n έχει το πολύ n στοιχεία. Πιο γενικά έχουµε το εξής αποτέλεσµα. Θεώρηµα (µέγιστο πλήθος γραµµικώς ανεξάρτητων στοιχείων) Έστω V ένας δ.χ. που παράγεται από m στοιχεία, όπου m είναι ένας ακέραιος. Τότε κάθε γραµµικά ανεξάρτητο υποσύνολο του V είναι πεπερασµένο και έχει το πολύ m στοιχεία. Ξέρουµε ότι κάθε δυο βάσεις του το εξής. n έχουν το αυτό πλήθος στοιχείων. Γενικά ισχύει Θεώρηµα (πληθάριθµος βάσης) Έστω V ένας δ.χ.. Αν υπάρχει µια πεπερασµένη βάση του V που έχει n στοιχεία, τότε κάθε άλλη βάση του V έχει n στοιχεία. Θεώρηµα (επέκταση γραµµικώς ανεξάρτητου συνόλου σε βάση) Έστω V ένας πεπερασµένα παραγόµενος δ.χ. και S ένα γραµµικά ανεξάρτητο υποσύνολο του V. Τότε υπάρχει βάση του V που περιέχει το S. Από το προηγούµενο αποτέλεσµα συµπεραίνουµε ότι κάθε πεπερασµένα παραγόµενος διανυσµατικός χώρος έχει τουλάχιστον µια βάση. Παράδειγµα Εύκολα επαληθεύεται ότι τα (,,, ),(,,,),(,,,) είναι γραµµικά ανεξάρτητα στοιχεία του. Το σύνολο αυτών µπορεί να επεκταθεί σε µια βάση του µε την προσθήκη του (,,,). Πράγµατι, έχουµε Επισηµαίνουµε ότι το ίδιο συµπέρασµα αληθεύει για όλους τους δ.χ. αλλά εδώ θα ασχοληθούµε µε τους πεπερασµένα παραγόµενους δ.χ..
7 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 7 από 9 det =. Συνεπώς τα στοιχεία (,,, ),(,,,),(,,,),(,,,) αποτελούν µια βάση του σύµφωνα µε το Πόρισµα 5 του Κεφαλαίου 5. Το επόµενο αποτέλεσµα πεπερασµένα παραγόµενο διανυσµατικό χώρο. γενικεύει το Πόρισµα του Κεφαλαίου 5 σε τυχαίο Πρόταση Έστω V ένας δ.χ. µε dim V = n. Τότε. Aν ένα σύνολο { v,..., v n } µε n στοιχεία παράγει το V, τότε αυτό είναι βάση του V.. Aν ένα σύνολο { v,..., v n } µε n στοιχεία είναι γραµµικά ανεξάρτητο, τότε αυτό είναι βάση του V. Θεώρηµα 5 (διαστάσεις υποχώρων) Έστω V ένας δ.χ. µε dimv = n και U ένας υπόχωρος του V. Τότε. dimu dim V.. Αν dimu = n, τότε U = V. Θεώρηµα 6 (διάσταση αθροίσµατος υποχώρων) Έστω UW, δυο υπόχωροι ενός πεπερασµένα παραγόµενου διανυσµατικού χώρου. Τότε dim( U + W) = dimu + dimw dim U W. Παράδειγµα Έστω { U = a b } W = { a b } (,,), (,, ). Τότε µια βάση του U είναι το {(,,),(,,)} και άρα dimu =. Μια βάση του W είναι το {(,,),(,,)} και συνεπώς dimw =. Το U + W παράγεται από την ένωση των δυο προηγούµενων βάσεων η οποία τυχαίνει να είναι βάση του. Άρα U + W = και dim( U + W) = dim =. Από τη σχέση
8 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 8 από 9 έχουµε οπότε dimu W =. dim( U + W) = dimu + dimw dimu W = + dimu W, Γεωµετρικά, το U είναι το xy επίπεδο, το W είναι το xz επίπεδο και η τοµή τους είναι ο άξονας των x, όπως φαίνεται στο σχήµα. z W U W x y U ΤΑΞΗ ΠΙΝΑΚΑ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Πρόταση 7 Η τάξη ενός κλιµακωτού πίνακα είναι το πλήθος των µη µηδενικών γραµµών του. Γραµµοϊσοδύναµοι πίνακες έχουν τον ίδιο χώρο γραµµών. Γραµµοϊσοδύναµοι πίνακες έχουν την ίδια τάξη. Παράδειγµα 9 Η τάξη του A = 8 είναι ra= ( ) γιατί ο πίνακας είναι σε κλιµακωτή µορφή και υπάρχουν µη µηδενικές γραµµές. 9 Για να βρούµε την τάξη του B = 7 χρησιµοποιούµε στοιχειώδεις µετασχηµατισµούς γραµµών για να τον φέρουµε σε κλιµακωτή µορφή.
9 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 9 από 9 Αφαιρώντας την πρώτη γραµµή από τη δεύτερη βρίσκουµε τον rb ( ) = ra ( ) =. A. Άρα Τα επόµενα δυο αποτελέσµατα είναι ιδιαίτερα σηµαντικά. Θεώρηµα 8 (κριτήριο συµβιβαστού γραµµικού συστήµατος) Ένα γραµµικό σύστηµα έχει λύση αν και µόνο αν η τάξη του επαυξηµένου πίνακα του συστήµατος ισούται µε την τάξη του πίνακα των συντελεστών. Παράδειγµα Να βρεθούν οι τιµές του a για τις οποίες το επόµενο σύστηµα είναι συµβιβαστό x+ y+ z = x y+ z = x + y z = a x + y z = a Μετά από αρκετούς στοιχειώδεις µετασχηµατισµούς γραµµών, ο επαυξηµένος πίνακας a a του συστήµατος παίρνει τη µορφή B =. a + 7a + 6 Συµπεραίνουµε ότι η τάξη του πίνακα των συντελεστών είναι. Σύµφωνα µε το Θεώρηµα 8 το σύστηµα είναι συµβιβαστό αν και µόνο αν η τάξη του B είναι, δηλαδή αν και µόνο αν η τελευταία γραµµή του Β είναι µηδενική, 6 δηλαδή a =. 7
10 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Θεώρηµα 9 (διάσταση λύσεων οµογενούς γραµµικού συστήµατος) Η διάσταση του δ.χ. των λύσεων ενός οµογενούς γραµµικού συστήµατος ισούται µε τη διαφορά m r, όπου m είναι το πλήθος των αγνώστων και r είναι η τάξη του πίνακα των συντελεστών. Παράδειγµα Η διάσταση του δ.χ. των λύσεων του οµογενούς συστήµατος x+ y z+ w= x+ y z+ w= x+ y z+ w= υπολογίζεται ως εξής. Με στοιχειώδεις µετασχηµατισµούς γραµµών φέρουµε τον πίνακα των συντελεστών σε κλιµακωτή µορφή. Βρίσκουµε τον πίνακα. Αυτός έχει τάξη r =. Σύµφωνα µε το Θεώρηµα 9 η ζητούµενη διάσταση είναι m r = =. ΧΩΡΟΙ ΜΕ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ Έστω V ένας διανυσµατικός χώρος πεπερασµένης διάστασης µε εσωτερικό γινόµενο. (βλ. Κεφάλαιο 6, Ορισµός 6). Μια βάση v, v i j, i = j =., i j { v,..., v n } Θεώρηµα (ύπαρξη ορθοκανονικών βάσεων) του V λέγεται ορθοκανονική αν Κάθε διανυσµατικός χώρος πεπερασµένης διάστασης µε εσωτερικό γινόµενο έχει µια ορθοκανονική βάση. Μια αποτελεσµατική µέθοδος κατασκευής ορθοκανονικών βάσεων είναι η µέθοδος Gram-Schmidt.
11 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Μέθοδος ορθοκανονικοποίησης των Gram - Schmidt Έστω V ένας διανυσµατικός χώρος πεπερασµένης διάστασης µε εσωτερικό γινόµενο. Έστω { v,..., v n} µια βάση του V. Θέτουµε u = v v, u u = v u u v, u v, u u = v u u u u vn, un vn, u un = vn u n... u. u u n Στη συνέχεια ορίζουµε w = u,..., wn. u = u Τότε τα στοιχεία w u,..., n wn αποτελούν µια ορθοκανονική βάση του V. n Παράδειγµα Ας εφαρµόσουµε την προηγούµενη µέθοδο στη βάση { v, v, v } του, όπου v = (,,), v = (,, ), v = (,, ). εδώ είναι το σύνηθες. Θέτουµε u = v = (,,) v, u u = v u = v = (,, ) u Το εσωτερικό γινόµενο που θεωρούµε v, u v, u u = v u u = (,, ) (,, ) (,,) = (,, ). u u Τα µήκη των u, u, u είναι αντίστοιχα,,. ιαιρώντας µε αυτά βρίσκουµε την ορθοκανονική βάση (,,), (,, ),(,,). ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ Άσκηση Εξετάστε αν τα παρακάτω διανύσµατα του είναι γραµµικά ανεξάρτητα.
12 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9. (,,,),(,,,),(,,,). (,,,),(,,,),(,,,). Α τρόπος. Σύµφωνα µε τον Ορισµό εξετάζουµε αν υπάρχουν abc,, από τα οποία ένα τουλάχιστον να είναι µη µηδενικό τέτοια ώστε Έχουµε a(,,,) + b(,,,) + c(,,, ) = (,,, ). a(,,,) + b(,,,) + c(,,, ) = (,,, ) a+ b+ c= a + b + c = a c = a+ b+ c=. Μετά από µερικούς στοιχειώδεις µετασχηµατισµούς, ο επαυξηµένος πίνακας του συστήµατος παίρνει την κλιµακωτή µορφή. Από τον πίνακα αυτό συµπεραίνουµε ότι το σύστηµα έχει µοναδική λύση (την τετριµµένη). Άρα Β τρόπος. a = b= c= και τα διανύσµατα είναι γραµµικά ανεξάρτητα. Σχηµατίζουµε τον πίνακα µε γραµµές τα δοσµένα διανύσµατα και τον φέρουµε σε κλιµακωτή µορφή. Επειδή δεν υπάρχει µηδενική γραµµή στον τελευταίο πίνακα, τα δοσµένα διανύσµατα είναι γραµµικά ανεξάρτητα.. Α τρόπος. Όπως στον Α τρόπο του, από τη σχέση βρίσκουµε το σύστηµα a(,,,) + b(,,,) + c(,,,) = (,,, )
13 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 a+ b+ c= a + b + c = a c = a+ b+ c=. Μετά από µερικούς στοιχειώδεις µετασχηµατισµούς, ο επαυξηµένος πίνακας του συστήµατος παίρνει την κλιµακωτή µορφή. Από τον πίνακα αυτό συµπεραίνουµε ότι το σύστηµα έχει και άλλη λύση πέρα από την τετριµµένη. ηλαδή υπάρχουν abc,, που δεν είναι όλα µηδέν τέτοια ώστε a(,,,) + b(,,,) + c(,,,) = (,,, ). Άρα τα δοσµένα διανύσµατα είναι γραµµικά εξαρτηµένα. Β τρόπος. Σχηµατίζουµε τον πίνακα µε γραµµές τα δοσµένα διανύσµατα και τον φέρουµε σε κλιµακωτή µορφή. Επειδή υπάρχει µηδενική γραµµή στον τελευταίο πίνακα, τα δοσµένα διανύσµατα είναι γραµµικά εξαρτηµένα. Άσκηση Εξετάστε αν τα επόµενα στοιχεία του M ( ) είναι γραµµικά ανεξάρτητα 5,,. Εξετάζουµε αν υπάρχουν abc,, από τα οποία ένα τουλάχιστον να είναι µη µηδενικό και να ικανοποιούν την ισότητα 5 a + b + c = Έχουµε
14 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 5 a + b + c = a+ b+ c a b 5c = a+ b c a+ b a+ b+ c= a b 5c= a+ b c= a+ b=. Μετά από µερικούς στοιχειώδεις µετασχηµατισµούς γραµµών στον επαυξηµένο πίνακα του τελευταίου συστήµατος, φτάνουµε στην κλιµακωτή µορφή. Άµεσα συµπεραίνουµε ότι το σύστηµα έχει µη µηδενική λύση, οπότε τα δοσµένα στοιχεία είναι γραµµικά εξαρτηµένα. Άσκηση Εξετάστε αν τα παρακάτω πολυώνυµα είναι γραµµικά ανεξάρτητα στο δ.χ. [ x] των πραγµατικών πολυωνύµων βαθµού το πολύ , +, +, + x x x x x x x x + x+, x x+, x +. Ξέρουµε ότι dim [ x ] = + =. Το πλήθος των δοσµένων στοιχείων είναι και άρα από το Θεώρηµα αυτά είναι γραµµικά εξαρτηµένα.. Έστω abc,,. Έχουµε ( ) ( ) ( ) a x + x+ + b x x+ + c x + = ( a b c) x ( a b) x ( a b c) = a+ b+ c= a b = a + b + c =.
15 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 5 από 9 Το σύστηµα αυτό είναι οµογενές, τετραγωνικό και η ορίζουσα του πίνακα των συντελεστών είναι det =. Συνεπώς η µηδενική λύση είναι µοναδική. Άρα τα δοσµένα στοιχεία είναι γραµµικά ανεξάρτητα. a = b= c= Άσκηση Αν uvw,, είναι γραµµικά ανεξάρτητα στοιχεία ενός u+ v+ w,v+ 5 u+ w,u+ w Έστω είναι γραµµικά ανεξάρτητα. F δ.χ., τότε αποδείξτε ότι και τα abc,, F τέτοια ώστε a( u+ v+ w) + b( u+ 5v+ w) + c( u+ w ) =. Τότε παίρνουµε ( ) ( ) ( ) a+ b+ c u+ a+ 5b v+ a+ b+ c w=. a+ b+ c= a+ 5b= a+ b+ c=. Επειδή τα είναι γραµµικά ανεξάρτητα, όλοι οι συντελεστές της τελευταίας σχέσης οφείλουν να είναι µηδέν, οπότε uvw,, Το σύστηµα αυτό είναι οµογενές και τετραγωνικό. Επειδή η ορίζουσα det 5 = 5 που είναι βέβαια η µηδενική είναι γραµµικά ανεξάρτητα. είναι µη µηδενική, συµπεραίνουµε ότι υπάρχει µοναδική λύση a = b= c=. Άρα τα u+ v+ w,v+ 5 u+ w,u+ w Άσκηση 5 (α) Να βρεθούν οι τιµές του a για τις οποίες τα διανύσµατα (,, a),(,,),(,,) αποτελούν µια βάση του R. (β) Για τις τιµές του a που βρήκατε πριν, να εκφράστε το συνδυασµό των (,, a),(,,),(,,). (,,) ως γραµµικό (γ) Να βρεθούν οι τιµές του b για τις οποίες έχουµε (,, b) (,,),(,,).
16 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 6 από 9 (α) Επειδή η διάσταση του βρεθούν τα a τέτοια ώστε R είναι, το δοσµένο ερώτηµα ισοδυναµεί µε το να det A, όπου A = a Κεφαλαίου 5). Υπολογίζοντας βρίσκουµε ότι det A= a, οπότε a. (βλ. Πόρισµα 5 του (β) Για a, τα δοσµένα στοιχεία του R αποτελούν µια βάση. Ζητάµε να βρεθούν τα x, yzτέτοια, ώστε Το σύστηµα που προκύπτει είναι (,,) = x(,, a) + y(,,) + z(,,). x + y+ z = x z = ax + y + z =. Παρατηρούµε ότι ο πίνακας των συντελεστών είναι ο Α. Λύνοντάς το σύστηµα µε µια από τις γνωστές µεθόδους, π.χ. τον κανόνα του Cramer, βρίσκουµε ότι, a + x= y =, z =. ( a) ( a ) ( a) (γ) Ζητάµε τα b τέτοια ώστε να υπάρχουν x, y ώστε να έχουµε (,, b) = x(,,) + y(,,). Το σύστηµα που προκύπτει είναι το x+ y = x + y = x + y = b x δηλαδή είναι το B =, όπου. Από το y B = Θεώρηµα 8, το σύστηµα αυτό b έχει λύση αν και µόνο αν η τάξη του Β ισούται µε την τάξη του επαυξηµένου πίνακα C =. Η τάξη του Β είναι, γιατί ο Β είναι και υπάρχουν γραµµικά b ανεξάρτητες στήλες. Συνεπώς ζητάµε τα b ώστε rc ( ) =. Με στοιχειώδεις µετασχηµατισµούς γραµµών παίρνουµε ότι ο C είναι γραµµοϊσοδύναµος µε τον
17 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 7 από 9. Από τις γραµµές αυτού του πίνακα βλέπουµε ότι η τάξη του είναι b αν και µόνο αν η τελευταία γραµµή είναι µηδενική δηλαδή αν και µόνο αν b =. Άσκηση 6 Να βρεθεί η διάσταση και µια βάση του υπόχωρου του διανύσµατα u = (,,5, ), v= (,,, ), w= (,8,, 5). που παράγεται από τα Θεωρούµε τον πίνακα 5 A = 8 5 µε γραµµές τα δοσµένα διανύσµατα. Τότε ο υπόχωρος του που παράγεται από τα διανύσµατα uvw,, είναι ο χώρος γραµµών του Α. Μετά από µερικούς στοιχειώδεις µετασχηµατισµούς γραµµών παίρνουµε τον πίνακα 5 B = 7 9. Από την Πρόταση 7, ο χώρος γραµµών του Α ταυτίζεται µε τον χώρο γραµµών του Β και µια βάση του τελευταίου είναι {(,,5, ),(,7, 9,) }. Η ζητούµενη διάσταση είναι. Άσκηση 7 Έστω [ x] ο διανυσµατικός χώρος των πραγµατικών πολυωνύµων που έχουν βαθµό το πολύ. Αποδείξτε ότι µια βάση του [ x] είναι το σύνολο {, x, ( x ) } και βρείτε την παράσταση του παραπάνω βάσης. 5 x + x+ ως γραµµικό συνδυασµό των στοιχείων της Επειδή η διάσταση του [ x] είναι, αρκεί να αποδείξουµε ότι το σύνολο {, x, ( x ) } είναι γραµµικά ανεξάρτητο (βλ. Πρόταση ). Έχουµε
18 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 8 από 9 a + b x + c x = ( ) ( ) + ( ) + ( + ) = cx b c x a b c c = b c = a = b = c =. a b + c = Για το δεύτερο ερώτηµα, λύνουµε την εξίσωση a + b( x ) + c( x ) = + x+ 5x ως προς τα abc,,, δηλαδή την cx b c x a b c x x + ( ) + ( + ) = Αυτή ισοδυναµεί µε το σύστηµα c = 5 b c = a b + c =. Άρα a =, b=, c = 5. Τελικά + x+ 5x = + ( x ) + 5( x ). Άσκηση 8 Να βρεθεί µία βάση και η διάσταση του υπόχωρου U = X M( ) X = X M. R του ( ) Πρώτα θα βρούµε τη γενική µορφή των πινάκων Χ. Έστω X = a b. c d Τότε a b a+ b X = c d c+ d X U αν και µόνο αν και a+ c b+ d X =. Άρα έχουµε a+ c b+ d
19 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 9 από 9 a b a+ b a+ c b+ d = c d c+ d a+ c b+ d a b= a+ c a+ b= b+ d c d = a + c c+ d = b+ d b+ c= a d = a d = b+ c= b+ c= a d =. Οι λύσεις του τελευταίου συστήµατος είναι οι ( abcd,,, ) = ( d, ccd,, ), cd,. Άρα X d c =. ηλαδή c d U d c = c, d. c d Θα δείξουµε τώρα ότι µια βάση του U είναι το σύνολο,. d c Πράγµατι, αυτό παράγει το U γιατί = d + c. Επίσης τα c d στοιχεία, είναι γραµµικά ανεξάρτητα γιατί αν έχουµε λ µ λ + µ =, τότε =, οπότε λ = µ =. Η µ λ διάσταση του U είναι. Άσκηση 9 t { } Έστω ( ) U = A M A = A το υποσύνολο του M ( R) που αποτελείται από τους αντισυµµετρικούς πίνακες. Αποδείξτε ότι το U είναι υπόχωρος του να βρεθεί µια βάση και η διάστασή του. Το σύνολο U είναι βέβαια µη κενό. Έστω AB, U και λ R. Τότε M ( R). Επιπλέον
20 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 t t t ( A+ B) = A + B = A B= ( A+ B) A+ B U, t t ( λ A) =λ A =λ( A) = ( λa) λa U. Συνεπώς το U είναι υπόχωρος του Κεφαλαίου 5. M ( R) σύµφωνα µε την Πρόταση του t Επειδή το τυχαίο στοιχείο A του U ικανοποιεί A = A, βρίσκουµε ότι Θα αποδείξουµε ότι τα στοιχεία αποτελούν βάση του U. a b A= a c. b c,, Είναι σαφές ότι τα στοιχεία αυτά είναι γραµµικά ανεξάρτητα αφού λ +µ +ν = λ µ λ ν = λ = µ = ν =. µ ν Επίσης αυτά παράγουν το U γιατί a b A= a c = a + b + c. b c Τελικά, dimu =. Άσκηση Έστω { u,... u, w,..., w } m n µια βάση του διανυσµατικού χώρου V. Θέτουµε U = u,..., u, W = w,..., wn. Αποδείξτε ότι V = U W. m Επειδή κάθε στοιχείο του V είναι γραµµικός συνδυασµός των u,..., u, w,..., w m n είναι σαφές από τους ορισµούς ότι V = U + W. Για να αποδείξουµε ότι V = U W, αρκεί
21 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 να αποδείξουµε ότι U W =. Για τον σκοπό αυτό, έστω v U W. Τότε v U που σηµαίνει ότι το v είναι γραµµικός συνδυασµός των Κατά παρόµοιο τρόπο Συνεπώς από το οποίο συµπεραίνουµε ότι v=λ v λ mvm, λi R. v=µ w µ nwn, µ i R. λ v λ v µ w... µ w =, m m n n λ =... =λ =µ =... =µ =, m n u,..., um γιατί το { u,... u, w,..., w n } είναι βάση. Άρα v =, συνεπώς U W =. m, δηλαδή Άσκηση Έστω U ο υπόχωρος του υπόχωρος W του ώστε R που παράγεται από τα (,,,), (,,,). Να βρεθεί ένας = U W. Θα βρούµε δύο στοιχεία v, v R ώστε το {(,,,),(,,,), w, w} να είναι βάση του. Τότε το W = w, w θα έχει τη ζητούµενη ιδιότητα, λόγω της προηγούµενης Λυµένης Άσκησης. Θα επιλέξουµε (στην τύχη) δύο στοιχεία της συνήθους βάσης {(,,,),(,,,),(,,,),(,,,)} του. Αν η επιλογή µας δεν οδηγεί σε βάση, θα ξαναδοκιµάσουµε. Έστω w = (,,,), w = (,,,). Τότε det =. Άρα το {(,,,),(,,,), w, w } είναι βάση του R Άσκηση Έστω οι υπόχωροι του U = (,,, ),(,,,),(,,, ), W = (,,, ),(,,, ),(,,, ). Να βρεθούν οι διαστάσεις dim( U + W),dim U W..
22 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Επειδή ο χώρος U + W την κλιµακωτή µορφή του πίνακα παράγεται και από τα έξι δοσµένα στοιχεία, θα εξετάσουµε. Μετά από πολλούς στοιχειώδεις µετασχηµατισµούς γραµµών βρίσκουµε την κλιµακωτή µορφή. Επειδή υπάρχουν µη µηδενικές γραµµές, συµπεραίνουµε ότι dim( U + W) =. Για την τοµή θα εφαρµόσουµε τον τύπο του Θεωρήµατος 6 και για τον σκοπό αυτό χρειαζόµαστε τις διαστάσεις Όπως και πριν θα µετασχηµατίσουµε τους πίνακες των γεννητόρων σε κλιµακωτή µορφή. Για το U βλέπουµε ότι η κλιµακωτή µορφή του Όµοια, dim U,dim W. είναι και άρα dimu =. dimw =. Τέλος dim( U W) = dimu + dimw dim( U + W) = + =. Άσκηση Να βρεθεί µια βάση και η διάσταση του υπόχωρου του {(,, ). } U = x y z x+ y+ z = x y z = Ο U είναι ο χώρος λύσεων του συστήµατος x+ y+ z = x y z =.
23 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Αυτό ισοδυναµεί µε το x+ y+ z = y+ z = του οποίου οι λύσεις είναι ( xyz,, ) = (, zz, ), z. Άρα µια βάση του U είναι το {(,,) } και dimu =. Άσκηση Έστω οι διανυσµατικοί υπόχωροι του, {(,, ) } U = {( x, y, z) x y z = } και V = x y z x+ y+ z =. Βρείτε τη διάσταση και µια βάση για καθέναν από τους χώρους U, V, U V και U+V. Θα µπορούσαµε να βρούµε τις διαστάσεις των U,V µε τον τρόπο που είδαµε στην προηγούµενη Λυµένη Άσκηση. Ας δούµε εδώ µια άλλη µέθοδο. Επειδή έχουµε U και U ισχύει dimu σύµφωνα µε το Θεώρηµα 5. ύο διανύσµατα που ανήκουν στο U είναι τα (,,) και (,,). Παρατηρούµε ότι είναι γραµµικά ανεξάρτητα. Άρα dimu = και τα προηγούµενα διανύσµατα αποτελούν βάση του U. Mε ανάλογο τρόπο βρίσκουµε, για παράδειγµα, τη βάση του V αποτελούµενη από τα διανύσµατα (,,),(,, ). Από τα προηγούµενα τέσσερα διανύσµατα, τα πρώτα τρία είναι γραµµικά ανεξάρτητα (γιατί det ) και ανήκουν στο U+V. Επειδή ο U+V είναι υπόχωρος του έχουµε dim(u+v). Συνεπώς dim(u+v) =, και τα προαναφερθέντα τρία διανύσµατα αποτελούν βάση. Από τη σχέση dimu V dimu V = dimu + dimv dim( U + V) ου Θεωρήµατος 6 παίρνουµε =. Μένει να βρεθεί µια βάση του U V και προς τούτο αρκεί να βρούµε ένα µη µηδενικό στοιχείο του. Λύνοντας το σύστηµα x y z =, x+ y+ z = βρίσκουµε x =, και y+z =, οπότε ένα µη µηδενικό στοιχείο της τοµής είναι για παράδειγµα το (,, ). Άσκηση 5 Αφού λυθεί το σύστηµα
24 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 x+ y z+ w= x+ y z+ w= x+ y z+ w= να βρεθεί µια βάση και η διάσταση του χώρου των λύσεων. Μετά από µερικές πράξεις βρίσκουµε ότι η κλιµακωτή µορφή του πίνακα των συντελεστών είναι. w Εύκολα βρίσκουµε τις λύσεις ( xyzw,,, ) = ( y wy,,, w), yw, R. Η διάσταση του χώρου των λύσεων είναι m r = =, όπου m = πλήθος αγνώστων και r = τάξη του πίνακα των συντελεστών. Για να βρούµε µία βάση, επιλέγουµε συγκεκριµένες τιµές για τις ελεύθερες µεταβλητές y,w ώστε οι δύο λύσεις να είναι γραµµικά ανεξάρτητα στοιχεία. Για παράδειγµα από y =, w= και y =, w= παίρνουµε τη βάση {(,,,),(,,,)} Άσκηση 6 Θεωρούµε τους υπόχωρους a b a b U = a+ b=, V = a+ c= του c d c d M ( R ). Να βρεθούν οι διαστάσεις των υπόχωρων UVU,, + VU, V. Παρατηρούµε ότι κάθε στοιχείο του U είναι της µορφής a a = a + c + d. Συνεπώς τα στοιχεία c d,, παράγουν το U. Εύκολα επαληθεύεται ότι αυτά είναι γραµµικά ανεξάρτητα
25 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 5 από 9 λ + µ + ν = λ = λ = µ = ν = λ = µ = ν =. Συνεπώς µια βάση του U αποτελούν τα στοιχεία,, έχουµε dimu =. Με παρόµοιο τρόπο αποδεικνύεται ότι dimv =. και Από τους ορισµούς προκύπτει ότι a a U V M ( ) = R. Όπως πριν a d αποδεικνύεται εύκολα ότι µια βάση του U,. Άρα dimu V =. Από τον τύπο παίρνουµε dim( U + V) =. V είναι το σύνολο dimu + dimv = dim( U + V) dimu V του Θεωρήµατος 6 Άσκηση 7 Να βρεθεί µια ορθοκανονική βάση του υπόχωρου του v = (,,,), v = (,,, 5), v = (,,, ). που παράγεται από τα Σύµφωνα µε τη µέθοδο των Gram-Schmidt θέτουµε u = v = (,,,) v, u u = v u = (,,,5) (,,,) = (,,, ) u v, u v, u u = v u u = u u (,,, ) (,,,) (,,,) = (,,, ). 5 5
26 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 6 από 9 ιαιρώντας τα u, u, u µε τα µήκη τους βρίσκουµε τη ζητούµενη ορθοκανονική βάση (,,,), (,,,), (,,, ) Άσκηση.,, στο ΑΣΚΗΣΕΙΣ Εξετάστε αν τα παρακάτω στοιχεία είναι γραµµικά ανεξάρτητα. (,,, ), (,,, ), (,,, ) στο M ( ) Υπόδειξη. Βλ. Λυµένη Άσκηση.. Βλ. Λυµένη Άσκηση. Απάντηση. Είναι γραµµικά εξαρτηµένα.. Είναι γραµµικά ανεξάρτητα. Άσκηση Εξετάστε αν τα πολυώνυµα x + x+, x + x+, x + x+ αποτελούν µια βάση του [ x]. Υπόδειξη Βλ. Λυµένη Άσκηση και Πρόταση. Απάντηση Είναι βάση. Άσκηση Έστω uvw,, γραµµικά ανεξάρτητα στοιχεία ενός διανυσµατικού χώρου.. είξτε ότι τα u w, u+ v+ w,u v w είναι γραµµικά ανεξάρτητα.. είξτε ότι uvw,, = u wu, + v+ w,u v w Υπόδειξη. Βλ. Λυµένη Άσκηση.. Επειδή ισχύει u w, u+ v+ w, u v w u, v, w αρκεί να αποδειχτεί, σύµφωνα µε το Θεώρηµα 5, ότι dim uvw,, = dim u wu, + v+ w, u v w. Άσκηση. Να βρεθούν οι τιµές του a τέτοιες ώστε στο. Να βρεθούν οι τιµές του a τέτοιες ώστε στο (,,) (,,),(, a,). (,,) (,,),(, a,).
27 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 7 από 9 Υπόδειξη Βλ. Λυµένη Άσκηση 5. Απάντηση. εν υπάρχει τέτοια τιµή του a.. a =. Άσκηση 5 Να βρεθεί µια βάση και η διάσταση του υπόχωρου του (,,,),(,,, ),(,,, 5). που παράγεται από τα Υπόδειξη Βλ. Λυµένη Άσκηση 6. Απάντηση Η διάσταση είναι. Άσκηση 6 Να βρεθεί µια βάση και η διάσταση του χώρου των λύσεων του οµογενούς γραµµικού συστήµατος x+ y+ z = x+ 5y+ z = x+ 5y+ 8z =. Υπόδειξη Βλ. Λυµένη Άσκηση. Απάντηση Μια βάση είναι το {(7,, ) } και η διάσταση είναι. Άσκηση 7 t { } W = A M A = A το υποσύνολο του M ( R) που αποτελείται από τους Έστω ( ) συµµετρικούς πίνακες. Αποδείξτε ότι το W είναι υπόχωρος του βρεθεί µια βάση και η διάστασή του. Υπόδειξη Βλ. Λυµένη Άσκηση 9. Απάντηση dimw = 6. M ( R). Επιπλέον να Άσκηση 8 Θεωρούµε τους υπόχωρους { } { } U= ( xyzw,,, ) y+ z+ w=, W= ( xyzw,,, ) x+ y= z w=. Να βρεθούν οι διαστάσεις των UWU,, WU, + W. Υπόδειξη Βλ. Λυµένη Άσκηση. Απάντηση U W U W ( U W) dim =,dim =,dim =,dim + =.
28 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 8 από 9 Άσκηση 9 a b a b Θεωρούµε τους υπόχωρους U = a b=, V = a c= του c d c d M ( R ). Να βρεθούν οι διαστάσεις των υπόχωρων UVU,, + VU, V. Υπόδειξη Βλ. Λυµένη Άσκηση 6. Απάντηση U V U V ( U V) dim = dim =,dim =,dim + =. Άσκηση Αφού αποδείξτε ότι µια βάση του M ( ) είναι το σύνολο,,, να βρεθούν οι συντεταγµένες του ως 6 προς τη βάση αυτή. Υπόδειξη Από την Πρόταση αρκεί να δείξετε ότι το δοσµένο σύνολο είναι γραµµικά ανεξάρτητο. Απάντηση Οι συντεταγµένες είναι (,,5, ), δηλαδή έχουµε 6 5 = + +. Άσκηση Έστω U = {( x, y, z, w) y+ z+ w } τέτοιου ώστε U W =. Να βρεθεί µια βάση ενός υπόχωρου W του =. Υπόδειξη Βρείτε µια βάση του U και επεκτείνατε την σε βάση του Άσκηση.. Βλ. Λυµένη Άσκηση Να βρεθούν οι τάξεις των πινάκων A=, B, C = = Υπόδειξη Μετασχηµατίστε τους πίνακες σε κλιµακωτή µορφή και εφαρµόστε την Πρόταση 7. Απάντηση r( A) =, r( B) =, r( C) =.
29 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα 9 από 9 Άσκηση Αποδείξτε ότι ένας n n πίνακας είναι αντιστρέψιµος αν και µόνο αν η τάξη του είναι ίση µε n. Υπόδειξη Βλ. Θεώρηµα του Κεφαλαίου. Άλλος τρόπος: Βλ. Πόρισµα 5 Κεφάλαιο 5. Άσκηση Έστω ( ) AB, M n m F. Έστω ότι ο πίνακας A B έχει το πολύ ένα µη µηδενικό στοιχείο. Αποδείξτε ότι r( A) r( B). Υπόδειξη Εξετάστε τη διάσταση των χώρων γραµµών. Άσκηση 5 Να βρεθεί µια ορθοκανονική βάση του υπόχωρου του διανύσµατα (,,),(,,). που παράγεται από τα Υπόδειξη Βλ. Λυµένη Άσκηση 7. Απάντηση (,,), (,, )
Κεφάλαιο 4 ιανυσµατικοί Χώροι
 Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Κεφάλαιο 5 Οι χώροι. Περιεχόµενα 5.1 Ο Χώρος. 5.3 Ο Χώρος C Βάσεις Το Σύνηθες Εσωτερικό Γινόµενο Ασκήσεις
 Σελίδα 1 από 6 Κεφάλαιο 5 Οι χώροι R και C Περιεχόµενα 5.1 Ο Χώρος R Πράξεις Βάσεις Επεξεργασµένα Παραδείγµατα Ασκήσεις 5. Το Σύνηθες Εσωτερικό Γινόµενο στο Ορισµοί Ιδιότητες Επεξεργασµένα Παραδείγµατα
Σελίδα 1 από 6 Κεφάλαιο 5 Οι χώροι R και C Περιεχόµενα 5.1 Ο Χώρος R Πράξεις Βάσεις Επεξεργασµένα Παραδείγµατα Ασκήσεις 5. Το Σύνηθες Εσωτερικό Γινόµενο στο Ορισµοί Ιδιότητες Επεξεργασµένα Παραδείγµατα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
{ } ΠΛΗ 12: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι 2 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ. Απαντήσεις. 1. (15 µονάδες)
 Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 12 Οκτωβρίου 2007
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 1) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 1 Οκτωβρίου 007 Ηµεροµηνία παράδοσης της Εργασίας: 9 Νοεµβρίου 007. Πριν από την λύση κάθε άσκησης
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 1) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 1 Οκτωβρίου 007 Ηµεροµηνία παράδοσης της Εργασίας: 9 Νοεµβρίου 007. Πριν από την λύση κάθε άσκησης
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑΤΙΚΑ Ι ΕΡΓΑΣΙΑ 6 ΛΥΣΕΙΣ
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ 00- ΜΑΘΗΜΑΤΙΚΑ Ι ΕΡΓΑΣΙΑ 6 ΛΥΣΕΙΣ. (5 µον.) ίνεται ο πίνακας 0 0 A. 0 (α) (α) Να βρεθούν όλες οι ιδιοτιµές και τα ιδιοδιανύσµατα του πίνακα Α. (β) Είναι δυνατή η διαγωνιοποίηση
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ 00- ΜΑΘΗΜΑΤΙΚΑ Ι ΕΡΓΑΣΙΑ 6 ΛΥΣΕΙΣ. (5 µον.) ίνεται ο πίνακας 0 0 A. 0 (α) (α) Να βρεθούν όλες οι ιδιοτιµές και τα ιδιοδιανύσµατα του πίνακα Α. (β) Είναι δυνατή η διαγωνιοποίηση
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάµε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων. Αυτές συνδέονται µεταξύ τους µε την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάµε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων. Αυτές συνδέονται µεταξύ τους µε την έννοια της συνθετικής σειράς
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12)
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 5 Οκτωβρίου 006 Ηµεροµηνία παράδοσης της Εργασίας: 0 Νοεµβρίου 006.
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 5 Οκτωβρίου 006 Ηµεροµηνία παράδοσης της Εργασίας: 0 Νοεµβρίου 006.
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα
 Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
Βάση και Διάσταση Διανυσματικού Χώρου
 Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
ΚΕΦΑΛΑΙΟ 6 ΕΛΑΧΙΣΤΑ ΤΕΤΡΑΓΩΝΑ
 ΚΕΦΑΛΑΙΟ 6 ΕΛΑΧΙΣΤΑ ΤΕΤΡΑΓΩΝΑ 6. Βέλτιστες προσεγγίσεις σε ευκλείδειους χώρους Στο κεφάλαιο αυτό θα ασχοληθούµε µε προσεγγίσεις που ελαχιστοποιούν αποστάσεις σε διανυσµατικούς χώρους, µε νόρµα που προέρχεται
ΚΕΦΑΛΑΙΟ 6 ΕΛΑΧΙΣΤΑ ΤΕΤΡΑΓΩΝΑ 6. Βέλτιστες προσεγγίσεις σε ευκλείδειους χώρους Στο κεφάλαιο αυτό θα ασχοληθούµε µε προσεγγίσεις που ελαχιστοποιούν αποστάσεις σε διανυσµατικούς χώρους, µε νόρµα που προέρχεται
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ (Ηµεροµηνία αποστολής στον φοιτητή: Νοεµβρίου 4. Τελική ηµεροµηνία αποστολής από τον φοιτητή: εκεµβρίου 4)
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ (Ηµεροµηνία αποστολής στον φοιτητή: Νοεµβρίου 4. Τελική ηµεροµηνία αποστολής από τον φοιτητή: εκεµβρίου 4)
( ) 10 ( ) εποµ ένως. π π π π ή γενικότερα: π π. π π. π π. Άσκηση 1 (10 µον) Θεωρούµε το µιγαδικό αριθµό z= i.
 http://elern.mths.gr/, mths@mths.gr, Τηλ: 697905 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 00-0: Άσκηση (0 µον) Θεωρούµε το µιγαδικό αριθµό z= i. α) (5 µον) Βρείτε την τριγωνοµετρική µορφή του z.
http://elern.mths.gr/, mths@mths.gr, Τηλ: 697905 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 00-0: Άσκηση (0 µον) Θεωρούµε το µιγαδικό αριθµό z= i. α) (5 µον) Βρείτε την τριγωνοµετρική µορφή του z.
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Παραδείγματα (2 ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
x 2 = x 2 1 + x 2 2. x 2 = u 2 + x 2 3 Χρησιµοποιώντας το συµβολισµό του ανάστροφου, αυτό γράφεται x 2 = x T x. = x T x.
 Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων
 7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
Ευκλείδειοι Χώροι. Ορίζουµε ως R n, όπου n N, το σύνολο όλων διατεταµένων n -άδων πραγµατικών αριθµών ( x
 Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
x 2 = b 1 2x 1 + 4x 2 + x 3 = b 2. x 1 + 2x 2 + x 3 = b 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΙΙ ιαφορικός Λογισµός πολλών µεταβλητών. ιαφόριση συναρτήσεων πολλών µεταβλητών
 54 ΙΙ ιαφορικός Λογισµός πολλών µεταβλητών ιαφόριση συναρτήσεων πολλών µεταβλητών Ένας στέρεος ορισµός της παραγώγισης για συναρτήσεις πολλών µεταβλητών ανάλογος µε τον ορισµό για συναρτήσεις µιας µεταβλητής
54 ΙΙ ιαφορικός Λογισµός πολλών µεταβλητών ιαφόριση συναρτήσεων πολλών µεταβλητών Ένας στέρεος ορισµός της παραγώγισης για συναρτήσεις πολλών µεταβλητών ανάλογος µε τον ορισµό για συναρτήσεις µιας µεταβλητής
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai017/lai017html Παρασκευή 17 Νοεµβρίου 017
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai017/lai017html Παρασκευή 17 Νοεµβρίου 017
Γραµµική Αλγεβρα Ι. Ενότητα: ιανυσµατικοί χώροι. Ευάγγελος Ράπτης. Τµήµα Μαθηµατικών
 Ενότητα: ιανυσµατικοί χώροι Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα: ιανυσµατικοί χώροι Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασµένων Οµάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασµένων Οµάδων Ι Χρησιµοποιώντας το θεώρηµα του Weddebu για ηµιαπλούς δακτυλίους αναπτύσσουµε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασµένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασµένων Οµάδων Ι Χρησιµοποιώντας το θεώρηµα του Weddebu για ηµιαπλούς δακτυλίους αναπτύσσουµε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασµένων
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι. Ασκησεις - Φυλλαδιο 2
 ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 3 Μαρτίου 2016 Αν (G, ) είναι
ΑΛΓΕΒΡΙΚΕΣ ΟΜΕΣ Ι Τµηµα Β Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2016/asi2016.html Πέµπτη 3 Μαρτίου 2016 Αν (G, ) είναι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ : ΠΛΗ12 «ΜΑΘΗΜΑΤΙΚΑ Ι» Επαναληπτική Τελική Εξέταση 16 Ιουλίου 2003
 http://edueapgr/pli/pli/studetshtm Page of 6 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ : ΠΛΗ «ΜΑΘΗΜΑΤΙΚΑ Ι» Επαναληπτική Τελική Εξέταση 6 Ιουλίου Απαντήστε όλα
http://edueapgr/pli/pli/studetshtm Page of 6 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ : ΠΛΗ «ΜΑΘΗΜΑΤΙΚΑ Ι» Επαναληπτική Τελική Εξέταση 6 Ιουλίου Απαντήστε όλα
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Γραµµική Αλγεβρα Ι. Ενότητα: Γραµµικές απεικονίσεις. Ευάγγελος Ράπτης. Τµήµα Μαθηµατικών
 Ενότητα: Γραµµικές απεικονίσεις Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα: Γραµµικές απεικονίσεις Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Άσκηση 1. i) ============================================================== Α n ( 3 n 1 ) A ) 5 4. Α n 1 2 ( n n 2.
 http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6995 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 8-9: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6995 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 8-9: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης , (1)
 1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
Κεφάλαιο 3 Πίνακες. χρησιµοποιώντας µόνο την ακόλουθη διάταξη αριθµών 1 1 2 1 2 5 1 0
 Σελίδα από 53 Κεφάλαιο 3 Πίνακες Περιεχόµενα 3 Ορισµοί Επεξεργασµένα Παραδείγµατα Ασκήσεις 3 3 Πράξεις µε Πίνακες Πρόσθεση Πινάκων Πολλαπλασιασµός Πίνακα µε Αριθµό Πολλαπλασιασµός Πινάκων ιωνυµικό Ανάπτυγµα
Σελίδα από 53 Κεφάλαιο 3 Πίνακες Περιεχόµενα 3 Ορισµοί Επεξεργασµένα Παραδείγµατα Ασκήσεις 3 3 Πράξεις µε Πίνακες Πρόσθεση Πινάκων Πολλαπλασιασµός Πίνακα µε Αριθµό Πολλαπλασιασµός Πινάκων ιωνυµικό Ανάπτυγµα
Γραµµική Αλγεβρα Ι. Ενότητα: Εισαγωγικές Εννοιες. Ευάγγελος Ράπτης. Τµήµα Μαθηµατικών
 Ενότητα: Εισαγωγικές Εννοιες Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Ενότητα: Εισαγωγικές Εννοιες Ευάγγελος Ράπτης Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Kεφάλαιο 4. Συστήµατα διαφορικών εξισώσεων
 4 Εισαγωγή Kεφάλαιο 4 Συστήµατα διαφορικών εξισώσεων Εστω διανυσµατικό πεδίο F: : F=F( r), όπου r = ( x, ) και Fr είναι η ταχύτητα στο σηµείο r πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουµε τις τροχιές
4 Εισαγωγή Kεφάλαιο 4 Συστήµατα διαφορικών εξισώσεων Εστω διανυσµατικό πεδίο F: : F=F( r), όπου r = ( x, ) και Fr είναι η ταχύτητα στο σηµείο r πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουµε τις τροχιές
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2017/lai2017html Παρασκευή 15 εκεµβρίου 2017
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2017/lai2017html Παρασκευή 15 εκεµβρίου 2017
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
============================================================== Σχηµατίζουµε τον πίνακα µε στήλες τα διανύσµατα v1,v2,v3,u1,u2:
 http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
Συνεχείς συναρτήσεις πολλών µεταβλητών. ε > υπάρχει ( ) ( )
 Συνεχείς συναρτήσεις πολλών µεταβλητών 7 Η Ευκλείδεια απόσταση που ορίσαµε στον R επιτρέπει ( εκτός από τον ορισµό των ορίων συναρτήσεων και ακολουθιών και τον ορισµό της συνέχειας συναρτήσεων της µορφής
Συνεχείς συναρτήσεις πολλών µεταβλητών 7 Η Ευκλείδεια απόσταση που ορίσαµε στον R επιτρέπει ( εκτός από τον ορισµό των ορίων συναρτήσεων και ακολουθιών και τον ορισµό της συνέχειας συναρτήσεων της µορφής
[A I 3 ] [I 3 A 1 ].
![[A I 3 ] [I 3 A 1 ]. [A I 3 ] [I 3 A 1 ].](/thumbs/65/54189091.jpg) ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 7 εκεµβρίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 7 εκεµβρίου 2018 Ασκηση
Γραμμική Άλγεβρα Ι Εξέταση Φεβρουαρίου. Επώνυμο. Όνομα. ΑΜ (13 ψηφία) Σύνολο
 1 Γραμμική Άλγεβρα Ι 009-10 Εξέταση Φεβρουαρίου Επώνυμο Όνομα ΑΜ (1 ψηφία) Ημ/ία Αίθουσα 1 5 Σύνολο Α Η εξέταση αποτελείται από 5 Θέματα. Το άθροισμα των μονάδων είναι 1, το άριστα 10 και η βάση 5. Απαντήστε
1 Γραμμική Άλγεβρα Ι 009-10 Εξέταση Φεβρουαρίου Επώνυμο Όνομα ΑΜ (1 ψηφία) Ημ/ία Αίθουσα 1 5 Σύνολο Α Η εξέταση αποτελείται από 5 Θέματα. Το άθροισμα των μονάδων είναι 1, το άριστα 10 και η βάση 5. Απαντήστε
Γραµµική Αλγεβρα. Ενότητα 3 : ιανυσµατικοί Χώροι και Υπόχωροι. Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Γραµµική Αλγεβρα Ενότητα 3 : ιανυσµατικοί Χώροι και Υπόχωροι Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραµµική Αλγεβρα Ενότητα 3 : ιανυσµατικοί Χώροι και Υπόχωροι Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
βαθμού 1 με A 2. Υπολογίστε τα χαρακτηριστικά και ελάχιστα πολυώνυμα των
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai018/lai018html Παρασκευή 3 Νοεµβρίου 018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai018/lai018html Παρασκευή 3 Νοεµβρίου 018 Ασκηση
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
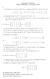 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) TEΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 4 Ιουνίου 7 Από τα κάτωθι Θέµατα καλείστε να λύσετε το ο που περιλαµβάνει ερωτήµατα από όλη την ύλη
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) TEΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 4 Ιουνίου 7 Από τα κάτωθι Θέµατα καλείστε να λύσετε το ο που περιλαµβάνει ερωτήµατα από όλη την ύλη
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΙΑΤΡΙΚΗ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΙΑΤΡΙΚΗ ΑΣΚΗΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ - Διανυσματικοί Χώροι Διδάσκουσα : Δρ Μ Αδάμ Λαμία, 6//05 Έστω = (,,), = (0,,)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΕ ΕΦΑΡΜΟΓΕΣ ΣΤΗ ΒΙΟΙΑΤΡΙΚΗ ΑΣΚΗΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ - Διανυσματικοί Χώροι Διδάσκουσα : Δρ Μ Αδάμ Λαμία, 6//05 Έστω = (,,), = (0,,)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, Αυγούστου 00 Θέμα. (μονάδες.5) α) [μονάδες: 0.5] Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, Αυγούστου 00 Θέμα. (μονάδες.5) α) [μονάδες: 0.5] Υπολογίστε
2.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 .0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
5 Γενική µορφή εξίσωσης ευθείας
 5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο
 Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
Γιώργος Πρέσβης ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΚΕΦΑΛΑΙΟ Ο : ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ ΕΠΑΝΑΛΗΨΗ Φροντιστήρια Φροντιστήρια ΜΕΘΟΔΟΛΟΓΙΑ ΑΣΚΗΣΕΩΝ 1η Κατηγορία : Εξίσωση Γραμμής 1.1 Να εξετάσετε
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι
 ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
ΚΕΦΑΛΑΙΟ 2: Ηµιαπλοί ακτύλιοι Είδαµε στο κύριο θεώρηµα του προηγούµενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισµα απλών προτύπων. Εδώ θα χαρακτηρίσουµε όλους
Αρµονική Ανάλυση. Ενότητα: L 2 -σύγκλιση σειρών Fourier. Απόστολος Γιαννόπουλος. Τµήµα Μαθηµατικών
 Ενότητα: L -σύγκλιση σειρών Fourier Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ενότητα: L -σύγκλιση σειρών Fourier Απόστολος Γιαννόπουλος Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: Ιανουαρίου 6 Ηµεροµηνία Παράδοσης της Εργασίας από
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: Ιανουαρίου 6 Ηµεροµηνία Παράδοσης της Εργασίας από
5.1 Ιδιοτιµές και Ιδιοδιανύσµατα
 Κεφάλαιο 5 Ιδιοτιµές και Ιδιοδιανύσµατα 5 Ιδιοτιµές και Ιδιοδιανύσµατα Αν ο A είναι ένας n n πίνακας και το x είναι ένα διάνυσµα στον R n, τότε το Ax είναι και αυτό ένα διάνυσµα στον R n Συνήθως δεν υπάρχει
Κεφάλαιο 5 Ιδιοτιµές και Ιδιοδιανύσµατα 5 Ιδιοτιµές και Ιδιοδιανύσµατα Αν ο A είναι ένας n n πίνακας και το x είναι ένα διάνυσµα στον R n, τότε το Ax είναι και αυτό ένα διάνυσµα στον R n Συνήθως δεν υπάρχει
Παραδείγµατα και Ασκήσεις Γραµµικής Άλγεβρας
 Περιεχόµενα και Πρόλογος Σελίδα από 4 Εναλλακτικό ιδακτικό Υλικό Θεµατική Ενότητα ΠΛΗ Παραδείγµατα και Ασκήσεις Γραµµικής Άλγεβρας Μιχάλης Μαλιάκας Μαρία Αδάµ Περιεχόµενα Κεφάλαιο Προαπαιτούµενες Έννοιες
Περιεχόµενα και Πρόλογος Σελίδα από 4 Εναλλακτικό ιδακτικό Υλικό Θεµατική Ενότητα ΠΛΗ Παραδείγµατα και Ασκήσεις Γραµµικής Άλγεβρας Μιχάλης Μαλιάκας Μαρία Αδάµ Περιεχόµενα Κεφάλαιο Προαπαιτούµενες Έννοιες
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
Η ιδέα της χρήσης διατεταγµένων Ϲευγών πραγµατικών αριθµών για την περιγραφή
 Κεφάλαιο 4 Ευκλείδιοι Χώροι 4 Ευκλείδιοι Χώροι Η ιδέα της χρήσης διατεταγµένων Ϲευγών πραγµατικών αριθµών για την περιγραφή των σηµείων στο επίπεδο και διατεταγµένων τριάδων πραγµατικών αριθµών για την
Κεφάλαιο 4 Ευκλείδιοι Χώροι 4 Ευκλείδιοι Χώροι Η ιδέα της χρήσης διατεταγµένων Ϲευγών πραγµατικών αριθµών για την περιγραφή των σηµείων στο επίπεδο και διατεταγµένων τριάδων πραγµατικών αριθµών για την
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Μάθηµα 1. Κεφάλαιο 1o: Συστήµατα. γ R παριστάνει ευθεία και καλείται γραµµική εξίσωση µε δύο αγνώστους.
 Μάθηµα 1 Κεφάλαιο 1o: Συστήµατα Θεµατικές Ενότητες: A. Συστήµατα Γραµµικών Εξισώσεων B. Συστήµατα 3x3 Α. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Ορισµοί Κάθε εξίσωση της µορφής α x+β =γ, µε α, β, γ R παριστάνει
Μάθηµα 1 Κεφάλαιο 1o: Συστήµατα Θεµατικές Ενότητες: A. Συστήµατα Γραµµικών Εξισώσεων B. Συστήµατα 3x3 Α. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Ορισµοί Κάθε εξίσωση της µορφής α x+β =γ, µε α, β, γ R παριστάνει
Παραδείγματα (2) Διανυσματικοί Χώροι
 Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Κεφάλαιο 3. Ελεύθερα Πρότυπα. στοιχείων του Μ καλείται βάση του e λ παράγει το Μ, και ii) κάθε m M γράφεται κατά µοναδικό
 Κεφάαιο 3 Εεύθερα Πρότυπα 3.1 Εεύθερα Πρότυπα Έστω Μ ένα R-πρότυπο. Μια οικογένεια Μ αν ) το σύνοο { Λ} τρόπο ως άθροισµα της µορφής πεπερασµένο πήθος από τα ( e ) στοιχείων του Μ καείται βάση του e παράγει
Κεφάαιο 3 Εεύθερα Πρότυπα 3.1 Εεύθερα Πρότυπα Έστω Μ ένα R-πρότυπο. Μια οικογένεια Μ αν ) το σύνοο { Λ} τρόπο ως άθροισµα της µορφής πεπερασµένο πήθος από τα ( e ) στοιχείων του Μ καείται βάση του e παράγει
Παράρτηµα Β. Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης [ ) ( )
 Παράρτηµα Β Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης Β1 Χώροι Baach Βάσεις Schauder Στο εξής συµβολίζουµε µε Z,, γραµµικούς (διανυσµατικούς) χώρους πάνω απ το ίδιο σώµα K = ή και γράφουµε απλά
Παράρτηµα Β Στοιχεία Θεωρίας Τελεστών και Συναρτησιακής Ανάλυσης Β1 Χώροι Baach Βάσεις Schauder Στο εξής συµβολίζουµε µε Z,, γραµµικούς (διανυσµατικούς) χώρους πάνω απ το ίδιο σώµα K = ή και γράφουµε απλά
Kεφάλαιο 4. Συστήµατα διαφορικών εξισώσεων.
 4 Εισαγωγή Kεφάλαιο 4 Συστήµατα διαφορικών εξισώσεων Εστω διανυσµατικό πεδίο F: : F=F( r), όπου r = ( x, ) και Fr είναι η ταχύτητα στο σηµείο r πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουµε τις τροχιές
4 Εισαγωγή Kεφάλαιο 4 Συστήµατα διαφορικών εξισώσεων Εστω διανυσµατικό πεδίο F: : F=F( r), όπου r = ( x, ) και Fr είναι η ταχύτητα στο σηµείο r πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουµε τις τροχιές
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
ιδασκοντες: x R y x y Q x y Q = x z Q = x z y z Q := x + Q Τετάρτη 10 Οκτωβρίου 2012
 ιδασκοντες: Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 1 Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Τετάρτη 10 Οκτωβρίου 2012 Ασκηση 1.
ιδασκοντες: Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 1 Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi.html Τετάρτη 10 Οκτωβρίου 2012 Ασκηση 1.
