[A I 3 ] [I 3 A 1 ].
|
|
|
- Παναγιώτης Αγγελίδου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x 4x x = b (α) ος τρόπος : Αν ο A είναι αντιστρέψιµος, τότε η ανηγµένη κλιµακωτή µορφή του A είναι ο I και, χρησιµοποιώντας απαλοιφή Gauss-Jordan, από τον πίνακα [A I ] παίρνουµε τον πίνακα Σχηµατίζουµε τον πίνακα [A I ] = [I A ] 6 4 Χρησιµοποιώντας απαλοιφή Gauss-Jordan, παίρνουµε ότι εναλλάσουµε την η και τη η γραµµή πολλαπλασιάζουµε την η γραµµή µε 6
2 6 Εποµένως ο A είναι αντιστρέψιµος και A = 6 6 προσθέτουµε ϕορές την η γραµµή στην η πολλαπλασιάζουµε τη η γραµµή µε πολλαπλασιάζουµε την η γραµµή µε προσθέτουµε ϕορές την η γραµµή στην η προσθέτουµε ϕορές τη η γραµµή στην η ος τρόπος : Χρησιµοποιώντας τον ορισµό της ορίζουσας ενός πίνακα παίρνουµε ότι det(a) = 6 4 = ( ) + ( ) + 6 ( 4) ( ) ( 4) 6 ( ) = = 8 Εφόσον det(a), ο πίνακας A είναι αντιστρέψιµος Χρησιµοποιώντας τον ορισµό της ορίζουσας ενός πίνακα, παίρνουµε ότι οι συµπαράγοντές του πίνακα A είναι C = ( ) + 4 = ( ) ( 4) =,
3 C = ( ) + 6 = (6 ( ) ( )) = 6, C = ( ) = 6 ( 4) ( ) =, C = ( ) + 4 = ( ( ) ( 4)) = 6, C = ( ) + = ( ) ( ) =, C = ( ) + 4 = ( ( 4) ( )) = 6, C = ( ) + = = 9, C = ( ) + 6 = ( 6) =, C = ( ) + 6 = 6 = 8 Εποµένως ο πίνακας συµπαραγόντων του A είναι ο Άρα ο προσαρτηµένος πίνακας του A είναι ο adj(a) = t = Εφόσον από όσα είπαµε, παίρνουµε ότι A = 8 A = det(a) adj(a), = Σηµείωση : () Στην πρώτη παράγραφο παραπάνω ϑα µπορούσαµε να υπολογίσου- µε την ορίζουσα του πίνακα A παίρνοντας ανάπτυγµα συµπαραγόντων : Εχουµε
4 ότι det(a) = 6 4 = = 6 ανάπτυγµα συµπαραγόντων ως προς την η γραµµή = (6 ( ) ( )) ορίζουσα πίνακα = 8 Σηµειώνουµε ότι πήραµε το ανάπτυγµα συµπαραγόντων ως προς την η γραµµή γιατί όλα τα στοιχεία της ης γραµµής εκτός από το -στοιχείο είναι () Στην πρώτη παράγραφο παραπάνω ϑα µπορούσαµε να υπολογίσουµε την ορί- Ϲουσα του πίνακα A µε αναγωγή γραµµών : Εχουµε ότι 6 4 = 6 εναλλάσουµε την η και τη 4 η γραµµή = 6 = ( 6) 4 4 = ( 6) 6 κοινός παράγοντας από την η γραµµή προσθέτουµε ϕορές την η γραµµή στην η = ( 6) ( ( )) ορίζουσα τριγωνικού πίνακα = 8 () Στην τρίτη παράγραφο παραπάνω ϑα µπορούσαµε να υπολογίσουµε τον πίνακα συµπαραγόντων του A ως εξής : Χρησιµοποιώντας τον ορισµό της ορίζουσας ενός πίνακα παίρνουµε ότι οι ελάσσονες ορίζουσες του πίνακα A είναι M = 4 = ( ) ( 4) =, 4
5 M = 6 = 6 ( ) ( ) = 6, M = 6 4 = 6 ( 4) ( ) =, M = 4 = ( ) ( 4) = 6, M = = ( ) ( ) =, M = 4 = ( 4) ( ) = 6, M = = = 9, M = 6 = 6 =, M = 6 = 6 = 8 Εποµένως ο πίνακας συµπαραγόντων του A είναι ο M M M ( 6) M M M = ( 6) 6 M M M 9 8 = (ϐ) ος τρόπος : Ο πίνακας συντελεστών του συστήµατος x = b 6x + x + x = b () x 4x x = b είναι ο A = 6 4 Από το (α) ο πίνακας A είναι αντιστρέψιµος Εποµένως, για όλα τα b, b, b στο R, το σύστηµα () έχει µοναδική λύση, την x x x = A b b b 5
6 Άρα Από το (α), A A = b b b = = b + b + b b b b b = b b b + b + b b b b Από όσα είπαµε, παίρνουµε ότι, για όλα τα b, b, b στο R, το σύστηµα () έχει µοναδική λύση, την x b + b + b x b = x b b ή x = b + b + b, x = b, x = b b ος τρόπος : Ο επαυξηµένος πίνακας του συστήµατος είναι ο x = b 6x + x + x = b () x 4x x = b b 6 b 4 b Χρησιµοποιώντας απαλοιφή Gauss-Jordan ϐρίσκουµε την ανηγµένη κλιµακωτή µορφή του Εχουµε ότι b 6 b 6 b b εναλλάσουµε την η και τη η γραµµή 4 b 4 b 6
7 b 6 b 4 b b 6 b b + b b 6 b b + b b 6 b b b b + b b b b b + b b b b b Ο τελευταίος πίνακας αντιστοιχεί στο σύστηµα πολλαπλασιάζουµε την η γραµµή µε 6 προσθέτουµε ϕορές την η γραµµή στην η πολλαπλασιάζουµε τη η γραµµή µε πολλαπλασιάζουµε την η γραµµή µε προσθέτουµε ϕορές την η γραµµή στην η προσθέτουµε ϕορές τη η γραµµή στην η x = b + b b x = b x = b b Άρα, για όλα τα b, b, b στο R, το σύστηµα () έχει µοναδική λύση, την ή x = b + b b, x = b, x = b b x = b + b + b, x = b, x = b b Σηµείωση : Στη δεύτερη και την τρίτη παράγραφο παραπάνω ϑα µπορούσαµε να δουλέψουµε και ως εξής : Χρησιµοποιώντας απαλοιφή Gauss ϐρίσκουµε την 7
8 κλιµακωτή µορφή του επαυξηµένου πίνακα του συστήµατος () Εχουµε ότι b 6 b 6 b b εναλλάσουµε την η και τη η γραµµή 4 b 4 b b 6 b 4 b b 6 b b + b b 6 b b + b b 6 b b b Ο τελευταίος πίνακας αντιστοιχεί στο σύστηµα πολλαπλασιάζουµε την η γραµµή µε 6 προσθέτουµε ϕορές την η γραµµή στην η πολλαπλασιάζουµε τη η γραµµή µε πολλαπλασιάζουµε την η γραµµή µε x + x + x = b 6 x = b x = b b Λύνουµε το σύστηµα αυτό µε προς τα πίσω αντικατάσταση : Λύνοντας ως προς τις ϐασικές µεταβλητές x, x, x παίρνουµε ότι x = b 6 x x x = b x = b b Αντικαθιστώντας την η εξίσωση στην η, παίρνουµε ότι x = b + b x x = b x = b b 8
9 Αντικαθιστώντας τη η εξίσωση στην η, παίρνουµε ότι x = b + b b x = b x = b b Άρα, για όλα τα b, b, b στο R, το σύστηµα () έχει µοναδική λύση, την x = b + b b, x = b, x = b b ή x = b + b + b, x = b, x = b b ος τρόπος : Ο πίνακας συντελεστών του συστήµατος είναι ο x = b 6x + x + x = b () x 4x x = b A = 6 4 Χρησιµοποιώντας τον ορισµό της ορίζουσας ενός πίνακα παίρνουµε ότι det(a) = 6 4 = ( ) + ( ) + 6 ( 4) ( ) ( 4) 6 ( ) = = 8 Εφόσον det(a), από τον κανόνα του Cramer παίρνουµε ότι, για όλα τα b, b, b στο R, το σύστηµα () έχει µοναδική λύση, την b b b b 6 b 6 b b 4 b 4 b x =, x =, x =
10 Χρησιµοποιώντας τον ορισµό της ορίζουσας ενός πίνακα, παίρνουµε ότι b b b 4 = = b ( ) + b + b ( 4) b b ( 4) b ( ) = 4b + 9b + + b + 6b = b + 6b + 9b, b 6 b b = = b ( ) + b ( ) + 6 b b ( ) b b 6 ( ) = 6b + + b = 6b, b 6 b 4 b = = b + b ( ) + b 6 ( 4) b ( ) b ( 4) 6 b = 6b 4b + 4b 8b = 6b 8b Από όσα είπαµε, παίρνουµε ότι, για όλα τα b, b, b στο R, το σύστηµα () έχει µοναδική λύση, την ή x = b + 6b + 9b 8, x = 6b 8, x = 6b 8b 8 x = b + b + b, x = b, x = b b Σηµείωση : () Στη δεύτερη παράγραφο παραπάνω ϑα µπορούσαµε να υπολογίσουµε την ορίζουσα του πίνακα A παίρνοντας ανάπτυγµα συµπαραγόντων, όπως στη Σηµείωση () του ου τρόπου του (α), ή µε αναγωγή γραµµών, όπως στη Σηµείωση () του ου τρόπου του (α) () Αν στο ερώτηµα (α) δουλέψαµε µε το ο τρόπο, ϑα µπορούσαµε στη δεύτερη παράγραφο παραπάνω να πάρουµε ότι det(a) = 8 χωρίς να χρειαστεί να το ξαναϋπολογίσουµε
11 () Στην τέταρτη παράγραφο παραπάνω ϑα µπορούσαµε να υπολογίσουµε τις ορίζουσες b b b 4, b 6 b b b 6 b 4 b παίρνοντας ανάπτυγµα συµπαραγόντων : Εχουµε ότι b b b 4 = = b 4 = b 4, b b + b b 4 b b ανάπτυγµα συµπαραγόντων ως προς την η γραµµή = b ( ( ) ( 4)) ( b b ) ορίζουσα πίνακα = b + 6b + 9b Σηµειώνουµε ότι πήραµε το ανάπτυγµα συµπαραγόντων ως προς την η γραµµή γιατί το -στοιχείο είναι Προφανώς ϑα µπορούσαµε να πάρουµε και το ανάπτυγµα συµπαραγόντων ως προς την η στήλη Εχουµε ότι b 6 b b = = b b b 6 = b b b ανάπτυγµα συµπαραγόντων ως προς την η γραµµή = b (6 ( ) ( )) ορίζουσα πίνακα = 6b
12 Σηµειώνουµε ότι πήραµε το ανάπτυγµα συµπαραγόντων ως προς την η γραµµή γιατί όλα τα στοιχεία της ης γραµµής εκτός από το -στοιχείο είναι Εχουµε ότι b 6 b 4 b = = b 4 b 6 b 4 b + ( ) b b = 6 b 4 b b b ανάπτυγµα συµπαραγόντων ως προς την η στήλη = 6 (b + 4b ) (b b ) ορίζουσα πίνακα = 6b 8b Σηµειώνουµε ότι πήραµε το ανάπτυγµα συµπαραγόντων ως προς την η στήλη γιατί το -στοιχείο είναι Προφανώς ϑα µπορούσαµε να πάρουµε και το ανάπτυγµα συµπαραγόντων ως προς την η γραµµή Σηµείωση : Παρατηρήστε ότι στο ο και τον ο τρόπο δεν χρησιµοποιήσαµε το αποτέλεσµα του (α) και για αυτό το λόγο χρειάστηκε να κάνουµε πολύ περισσότερη δουλειά για να καταλήξουµε στο αποτέλεσµα
13 Εστω A και B δύο n n πίνακες Αποδείξτε ότι αν το σύστηµα Ax = b είναι συµβιβαστό, για όλα τα b στον R n, και τότε B = n A B(A t ) = n, ος τρόπος : Εφόσον το σύστηµα Ax = b είναι συµβιβαστό, για όλα τα b στον R n, ο πίνακας A είναι αντιστρέψιµος Από τις ιδιότητες των αντιστρέψιµων πινάκων παίρνουµε ότι : () Εφόσον ο πίνακας A είναι αντιστρέψιµος, ο πίνακας A είναι αντιστρέψιµος (και (A ) = (A ) ) () Εφόσον ο πίνακας A είναι αντιστρέψιµος, ο πίνακας A t είναι αντιστρέψιµος (και (A t ) = (A ) t ) Εφόσον ο πίνακας A t είναι αντιστρέψιµος, ο πίνακας (A t ) είναι αντιστρέψιµος (και ((A t ) ) = ((A t ) ) = ((A ) t ) ) Χρησιµοποιώντας την αντιστρεψιµότητα των πινάκων A και (A t ) και τις ιδιότητες του πολλαπλασιασµού πινάκων, παίρνουµε ότι A B(A t ) = n (A ) (A B(A t ) ) = (A ) n (A ) (A B(A t ) ) = n αν ο T είναι m k πίνακας, τότε T k l = m l ((A ) A )(B(A ) ) = n τα του πολλαπλασιασµού t προσεταιριστική ιδιότη- πινάκων I n (B(A t ) ) = n αν ο T είναι αντιστρέψι- µος m m πίνακας, τότε T T = I m B(A t ) = n (B(A t ) )((A t ) ) = n ((A t ) ) (B(A t ) )((A t ) ) = n αν ο T είναι m k πίνακας, τότε I m T = T αν ο T είναι m k πίνακας, τότε l m T = l k B((A ) ((A ) ) ) = n τα του πολλαπλασιασµού t t προσεταιριστική ιδιότη- πινάκων BI n = n αν ο T είναι αντιστρέψι- µος m m πίνακας, τότε T T = I m
14 B = n αν ο T είναι m k πίνακας, τότε T I k = T Σηµείωση : Προφανώς ϑα µπορούσαµε, µε την ίδια λογική, πρώτα να πολλαπλασιάσουµε από δεξιά και τα δύο µέλη της A B(A t ) = n µε ((A t ) ) και να πάρουµε ότι A B = n και κατόπιν να πολλαπλασιάσουµε από αριστερά και τα δύο µέλη της A B = n µε (A ) και να πάρουµε ότι B = n ος τρόπος : Εφόσον το σύστηµα Ax = b είναι συµβιβαστό, για όλα τα b στον R n, ο πίνακας A είναι αντιστρέψιµος Από τις ιδιότητες των αντιστρέψιµων πινάκων παίρνουµε ότι : () Εφόσον ο πίνακας A είναι αντιστρέψιµος, ο πίνακας A είναι αντιστρέψιµος (και (A ) = (A ) ) () Εφόσον ο πίνακας A είναι αντιστρέψιµος, ο πίνακας A t είναι αντιστρέψιµος (και (A t ) = (A ) t ) Εφόσον ο πίνακας A t είναι αντιστρέψιµος, ο πίνακας (A t ) είναι αντιστρέψιµος (και ((A t ) ) = ((A t ) ) = ((A ) t ) ) Εφόσον ο πίνακας A είναι αντιστρέψιµος, το οµογενές σύστηµα A x = n έχει µόνο την τετριµµένη λύση Εστω y στον R n (το οποίο ταυτίζουµε µε έναν n πίνακα) Εφόσον A B(A t ) = n, χρησιµοποιώντας τις ιδιότητες του πολλαπλασιασµού πίνάκων παίρνουµε ότι A (B(A t ) y) = (A B(A t ) )y = n y = n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων αν ο T είναι m k πίνακας, τότε l m T = l k 4
15 Εποµένως, για όλα τα y στον R n, A (B(A t ) y) = n, δηλαδή το B(A t ) y είναι λύση του οµογενούς συστήµατος A x = n Εφόσον, όπως είπαµε παραπάνω, το οµογενές σύστηµα Ax = n έχει µόνο την τετριµµένη λύση, x = n, από όσα είπαµε, παίρνουµε ότι B(A t ) y = n, για όλα τα y στον R n Εστω Εφόσον για όλα τα y στον R n, B = b b b n b b b n b n b n b nn B(A t ) y = n, B(A t ) ((At ) ) B(A t ) ((At ) ) = n, = n, B(A t ) ((At ) ) 5 = n
16 Χρησιµοποιώντας τις ιδιότητες του πολλαπλασιασµού πινάκων κα την αντιστρεψιµότητα του (A t ), παίρνουµε ότι B(A t ) ((At ) ) = n B((A t ) ((A t ) ) ) = n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων BI n = n αν ο T είναι αντιστρέψιµος m m πίνακας, τότε T T = I m B = n αν ο T είναι m k πίνακας, τότε T I k = T b b b n b b b n b n b n b nn = b b b n = b = b = = b n =, 6
17 B(A t ) ((At ) ) = n B((A t ) ((A t ) ) ) = n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων BI n = n αν ο T είναι αντιστρέψιµος m m πίνακας, τότε T T = I m B = n αν ο T είναι m k πίνακας, τότε T I k = T b b b n b b b n b n b n b nn = b b b n = b = b = = b n =, 7
18 B(A t ) ((At ) ) = n B((A t ) ((A t ) ) ) = n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων BI n = n αν ο T είναι αντιστρέψιµος m m πίνακας, τότε T T = I m B = n αν ο T είναι m k πίνακας, τότε T I k = T b b b n b b b n b n b n b nn = b n b n b nn = b n = b n = = b nn = Εφόσον b ij =, για i, j n, B = 8
19 Εστω A και B δύο n n πίνακες για τους οποίους ισχύει (A t ) B A 5 (B t ) 7 = I n Αποδείξτε ότι οι A και B είναι αντιστρέψιµοι ος τρόπος : Χρησιµοποιώντας τις ιδιότητες των οριζουσών, παίρνουµε ότι (A t ) B A 5 (B t ) 7 = I n det((a t ) B A 5 (B t ) 7 ) = det( I n ) det((a t ) B A 5 (B t ) 7 ) = ( ) n det(i n ) αν ο T είναι m m πίνακας, τότε det(λt ) = λ m det(t ) det((a t ) B A 5 (B t ) 7 ) = ( ) n det(i m ) = det((a t ) B A 5 (B t ) 7 ) = ( ) n det((a t ) ) det(b ) det(a 5 ) det((b t ) 7 ) = ( ) n det(t T T k ) = det(t ) det(t ) det(t k ) det(a t ) det(b) det(a) 5 det(b t ) 7 = ( ) n det(t k ) = det(t ) k, για όλα τα k στο N det(a) det(b) det(a) 5 det(b) 7 = ( ) n det(t t ) = det(t ) det(a) 7 det(b) = ( ) n det(a) 7 det(b) det(a) 7 και det(b) det(a) και det(b) A αντιστρέψιµος και B αντιστρέψιµος T αντιστρέψιµος det(t ) ος τρόπος : Αν ο T είναι ένας m m πίνακας, τότε τα παρακάτω είναι ισοδύναµα : () Ο T είναι αντιστρέψιµος () Υπάρχει ένας m m πίνακας S τέτοιος ώστε T S = I m () Υπάρχει ένας m m πίνακας R τέτοιος ώστε RT = I m Χρησιµοποιώντας τις ιδιότητες των πράξεων πινάκων, παίρνουµε ότι (A t ) B A 5 (B t ) 7 = I n ((At ) B A 5 (B t ) 7 ) = ( I n) ((At ) B A 5 (B t ) 7 ) = ( ( ) ) I n λ(µt ) = (λµ)t ((At ) B A 5 (B t ) 7 ) = I n 9
20 ((At ) B A 5 (B t ) 7 ) = I n T = T ((At ) (B A 5 (B t ) 7 )) = I n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων (A t ) ( ) (B A 5 (B t ) 7 ) = I n λ(t S) = T (λs) ( (A t A t ) ) (B A 5 (B t ) 7 ) = I n T = T T ( A t A ( t )) (B A 5 (B t ) 7 ) = I n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων Εφόσον ( A t A ( t )) (B A 5 (B t ) 7 ) = I n, από την ισοδυναµία των () και () στην πρώτη παράγραφο (για T = A t και S = A ( t ) (B A 5 (B t ) 7 ) ) παίρνουµε ότι ο A t είναι αντιστρέψιµος Εφόσον ο A t είναι αντιστρέψιµος, από τις ιδιότητες των αντιστρέψιµων πινάκων, παίρνουµε ότι ο A είναι αντιστρέψιµος Χρησιµοποιώντας τις ιδιότητες των πράξεων πινάκων, παίρνουµε ότι (A t ) B A 5 (B t ) 7 = I n ((At ) B A 5 (B t ) 7 ) = ( I n) ((At ) B A 5 (B t ) 7 ) = ( ) ( ) I n λ(µt ) = (λµ)t ((At ) B A 5 (B t ) 7 ) = I n ((At ) B A 5 (B t ) 7 ) = I n T = T (((At ) B A 5 )(B t ) 7 προσεταιριστική ιδιότητα του ) = I n πολλαπλασιασµού πινάκων ( ) ((At ) B A 5 ) (B t ) 7 = I n λ(t S) = (λt )S ( ) ((At ) B A 5 ) ((B t ) 6 B t T ) = I k+l = T k T l, για όλους τους n k, l στο N (( ) ) ((At ) B A 5 ) (B t ) 6 B t = I n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων
21 Εφόσον (( ) ) ((At ) B A 5 ) (B t ) 6 B t = I n, ( από την ισοδυναµία των () και () (για T = B t και R = ) ((At ) B A 5 ) (B t ) 6 ) στην πρώτη παράγραφο παίρνουµε ότι ο B t είναι αντιστρέψιµος Εφόσον ο B t είναι αντιστρέψιµος, από τις ιδιότητες των αντιστρέψιµων πινάκων, παίρνουµε ότι ο B είναι αντιστρέψιµος Σηµείωση : Θα µπορούσαµε, µε την ίδια λογική, στη δεύτερη, την τρίτη, την τέταρτη και την πέµπτη παράγραφο παραπάνω να πάρουµε το ίδιο αποτέλεσµα και µε άλλους τρόπους Για παράδειγµα στη δεύτερη και την τρίτη παράγραφο ϑα µπορούσαµε να δουλέψουµε ως εξής : Χρησιµοποιώντας τις ιδιότητες των πράξεων πινάκων, παίρνουµε ότι (A t ) B A 5 (B t ) 7 = I n ((At ) B A 5 (B t ) 7 ) = ( I n) ((At ) B A 5 (B t ) 7 ) = ( ( ) ) I n λ(µt ) = (λµ)t ((At ) B A 5 (B t ) 7 ) = I n ((At ) B A 5 (B t ) 7 ) = I n T = T (At A t B A 5 (B t ) 7 ) = I n T = T T (At (A t B A 5 (B t ) 7 )) = I n προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων A ( t ) (At B A 5 (B t ) 7 ) = I n λ(t S) = T (λs) Εφόσον A ( t ) (At B A 5 (B t ) 7 ) = I n, από την ισοδυναµία των () και () στην πρώτη παράγραφο (για T = A t και S = (At B A 5 (B t ) 7 )) παίρνουµε ότι ο A t είναι αντιστρέψιµος Εφόσον ο A t είναι αντιστρέψιµος, από τις ιδιότητες των αντιστρέψιµων πινάκων, παίρνουµε ότι ο A είναι αντιστρέψιµος
22 4 Να ϐρεθεί η εξίσωση του επιπέδου που διέρχεται από τα σηµεία P (,, ), Q(,, ) και R(,, ) ος τρόπος : Εστω ότι το E είναι το επίπεδο που διέρχεται από τα σηµεία P (,, ), Q(,, ) και R(,, ) και ότι η ax + by + cz + d = (4) είναι µία εξίσωση του E (κάθε επίπεδο έχει µία εξίσωση αυτής της µορφής) Εφόσον τα σηµεία P (,, ), Q(,, ) και R(,, ) ϐρίσκονται στο επίπεδο E, οι συντεταγµένες τους πρέπει να ικανοποιούν την εξίσωση (4) Εφόσον οι συντεταγ- µένες του P (,, ) ικανοποιούν την εξίσωση (4), ϑα ισχύει ότι ή a + b + c + d = a + b + d = Εφόσον οι συντεταγµένες του Q(,, ) ικανοποιούν την εξίσωση (4), ϑα ισχύει ότι ή a + b + c + d = a + c + d = Εφόσον οι συντεταγµένες του R(,, ) ικανοποιούν την εξίσωση (4), ϑα ισχύει ότι ή a + b + c + d = a + b + c + d = Εποµένως τα a, b, c, d ικανοποιούν τις εξισώσεις a + b + d = a + c + d = a + b + c + d = (5) Λύνουµε το οµογενές σύστηµα (5) Ο πίνακας συντελεστών του είναι ο Με απαλοιφή Gauss-Jordan ϐρίσκουµε την ανηγµένη κλιµακωτή µορφή του : προσθέτουµε ϕορά την η γραµµή στη η και ϕορά την η γραµµή στην η
23 πολλαπλασιάζουµε τη η γραµµή µε προσθέτουµε ϕορά την η γραµµή στη η προσθέτουµε ϕορά τη η γραµµή στην η Το αντίστοιχο οµογενές σύστηµα είναι το a + d = b = c = Λύνουµε ώς προς τις ϐασικές µεταβλητές a, b και c και παίρνουµε a = d b = c = ίνοντας την αυθαίρετη τιµή t στην ελεύθερη µεταβλητή d, παίρνουµε ότι η λύση του συστήµατος (5) είναι Για t =, παίρνουµε a = t, b =, c =, d = t, t στο R a =, b =, c =, d = Άρα µία εξίσωση του επιπέδου που διέρχεται από τα σηµεία P (,, ), Q(,, ) και R(,, ) είναι η ( )x + y + z + = ή x + = Σηµείωση : () Στην τελευταία παράγραφο παραπάνω ϑα µπορούσαµε αντί για t = να πάρουµε οποιοδήποτε άλλο t Η εξίσωση του επίπέδου E που παίρνουµε για αυτό το t είναι ( t)x + y + z + t = ή tx + t =
24 Προφανώς, για κάθε t, έχουµε ότι tx + t = t( x + ) = x + = () Στη δεύτερη παράγραφο παραπάνω ϑα µπορούσαµε να δουλέψουµε και ως εξής : Λύνουµε το οµογενές σύστηµα (5) Ο πίνακας συντελεστών του είναι ο Με απαλοιφή Gauss ϐρίσκουµε την κλιµακωτή µορφή του προσθέτουµε ϕορά την η γραµµή στη η και ϕορά την η γραµµή στην η πολλαπλασιάζουµε τη η γραµµή µε Το αντίστοιχο οµογενές σύστηµα είναι το a + b + d = b c = c = Λύνουµε ώς προς τις ϐασικές µεταβλητές a, b και c και παίρνουµε a = d b b = c c = Αντικαθιστώντας την η εξίσωση στη η, παίρνουµε a = d b b = c = Αντικαθιστώντας τη η εξίσωση στην η, παίρνουµε a = d b = c = 4
25 ίνοντας την αυθαίρετη τιµή t στην ελεύθερη µεταβλητή d, παίρνουµε ότι η λύση του συστήµατος (5) είναι a = t, b =, c =, d = t, t στο R ος τρόπος : Εστω ότι το E είναι το επίπεδο που διέρχεται από τα σηµεία P (,, ), Q(,, ) και R(,, ) Εφόσον τα σηµεία P (,, ), Q(,, ) και R(,, ) ανήκουν στο E, τα διανύσµατα P Q και P R είναι παράλληλα στο E Εποµένως το εξωτερικό τους γινόµενο P Q P R είναι κάθετο στο E, εφόσον είναι κάθετο στο P Q και στο P R Εχουµε ότι και P Q = (,, ) = (,, ) P R = (,, ) = (,, ) Από τον ορισµό του εξωτερικού γινοµένου διανυσµάτων του -διάστατου χώρου και τον ορισµό της ορίζουσας πίνακα παίρνουµε ότι P Q P R = (,, ) (,, ) ( ) =,, = (( ), ( ), ( ) ) = (,, ) = (,, ) Άρα το επίπεδο E διέρχεται από το σηµείο P (,, ) και είναι κάθετο στο διάνυσµα P Q P R = (,, ) Εποµένως η εξίσωση σηµείου-καθέτου του είναι Προφανώς ( )(x ) + (y ) + (z ) = ( )(x ) + (y ) + (z ) = x + = Σηµείωση : () Στη δεύτερη παράγραφο παραπάνω ϑα µπορούσαµε να υπολογίσουµε το εξωτερικό γινόµενο P Q P R και ως εξής : Από τη συµβολική έκφραση του εξωτερικού γινοµένου διανυσµάτων ως ορίζουσα πίνακα, όσα γνωρίζου- µε για τον υπολογισµό οριζουσών µέσω αναπτυγµάτων συµπαραγόντων και τον ορισµό της ορίζουσας πίνακα παίρνουµε ότι P Q P R = (,, ) (,, ) 5
26 i j k = = i j + k = (( ) )i ( )j + ( ( ) )k = ( )i j + k = ( )(,, ) = (,, ) () Στην τρίτη παράγραφο παραπάνω ϑα µπορούσαµε επίσης να ϑεωρήσουµε ότι το E διέρχεται από το σηµείο Q ή R και είναι κάθετο στο διάνυσµα P Q P R Για παράδειγµα : Το επίπεδο E διέρχεται από το σηµείο R(,, ) και είναι κάθετο στο διάνυσµα P Q P R = (,, ) Εποµένως η εξίσωση σηµείου-καθέτου του είναι ( )(x ) + (y ) + (z ) = Προφανώς ( )(x ) + (y ) + (z ) = x + = () Στη δεύτερη παράγραφο παραπάνω ϑα µπορούσαµε επίσης να ϑεωρήσουµε ότι ένα από τα παρακάτω εξωτερικά γινόµενα είναι κάθετο στο E: QP P R, P Q RP, QP RP, P R P Q, P R QP, RP P Q, RP QP, QP QR, P Q QR, QP RQ, P Q RQ, QR QP, QR P Q, RQ QP, RQ P Q, RP RQ, P R RQ, RP QR, P R QR, RQ RP, RQ P R, QR RP, QR P R Στην τρίτη παράγραφο ϑα συνεχίζαµε ϑεωρώντας ότι το E διέρχεται από ένα από τα σηµεία P, Q ή R και είναι κάθετο σε ένα από τα παραπάνω διανύσµατα Για παράδειγµα : Εφόσον τα σηµεία P (,, ), Q(,, ) και R(,, ) ανήκουν στο E, τα διανύσµατα QR και P Q είναι παράλληλα στο E Εποµένως το εξωτερικό τους γινόµενο QR P Q είναι κάθετο στο E, εφόσον είναι κάθετο στο QR και στο P Q Εχουµε ότι QR = (,, ) = (,, ) και P Q = (,, ) = (,, ) Από τον ορισµό του εξωτερικού γινοµένου διανυσµάτων του -διάστατου χώρου και τον ορισµό της ορίζουσας πίνακα παίρνουµε ότι QR P Q = (,, ) (,, ) 6
27 ( ) =,, = ( ( ), ( ), ( ) ) = (,, ) = (,, ) (ϑα µπορούσαµε να υπολογίσουµε το QR P Q και όπως στο () παραπάνω) Άρα το επίπεδο E διέρχεται από το σηµείο Q(,, ) και είναι κάθετο στο διάνυσµα QR P Q = (,, ) Εποµένως η εξίσωση σηµείου-καθέτου του είναι Προφανώς (x ) + (y ) + (z ) = (x ) + (y ) + (z ) = x = x + = 7
28 5 Εξετάστε αν τα επίπεδα µε εξισώσεις x + y z + = και x + y + 8z 7 = είναι καθετα Αν το επίπεδο E είναι κάθετο στο διάνυσµα n και το επίπεδο E είναι κάθετο στο διάνυσµα n, τότε τα E και E είναι κάθετα αν και µόνο αν τα n και n είναι κάθετα Το επίπεδο µε εξίσωση ax + by + cz + d = είναι κάθετο στο διάνυσµα n = (a, b, c) Εποµένως το επίπεδο µε εξίσωση x + y z + = είναι κάθετο στο διάνυσµα n = (,, ) και το επίπεδο µε εξίσωση x + y + 8z 7 = είναι κάθετο στο διάνυσµα n = (,, 8) Εφόσον n n = (,, ) (,, 8) = + + ( ) 8 =, τα n και n είναι κάθετα Συνδυάζοντας όσα είπαµε, παίρνουµε ότι τα επίπεδα µε εξισώσεις x + y z + = και x + y + 8z 7 = είναι καθετα 8
29 6 Εξετάστε αν το σύνολο των πινάκων της µορφής [ ] a b, b a όπου οι a και b είναι τυχαίοι πραγµατικοί αριθµοί, είναι υπόχωρος του χώρου των πινάκων M Εστω W το σύνολο των πινάκων της µορφής [ ] a b, b a µε a και b τυχαίους πραγµατικούς αριθµούς Για να δείξουµε ότι το W είναι υπόχωρος του χώρου των πινάκων M, αρκεί να δείξουµε ότι το W είναι κλειστό ως προς την πρόσθεση και τον ϐαθµωτό πολλαπλασιασµό Εστω [ [ ] A = x y y x ], A = x y y x δύο στοιχεία του W Από τον ορισµό της πρόσθεσης πινάκων παίρνουµε ότι [ ] [ ] x A + A = y x + y y x y x [ ] x = + x y + y ( y ) + ( y ) x + x [ ] x = + x (y + y ) (y + y ) (x + x ) Ο πίνακας [ είναι της µορφής [ x + x (y + y ) (y + y ) (x + x ) a b ] b a (µε a = x + x και b = y + y ) Άρα ο πίνακας A + A είναι στοιχείο του W Εποµένως το W είναι κλειστό ως προς την πρόσθεση Εστω [ ] x y A = y x ένα στοιχείο του W και λ ένα ϐαθµωτό Από τον ορισµό του πολλαπλασιασµού ϐαθµωτού µε πίνακα παίρνουµε ότι [ ] x y λa = λ y x 9 ]
30 [ = [ = λx λ( y) λx (λy) λ(y) λ(x) (λy) (λx) ] ] Ο πίνακας [ λx (λy) (λy) (λx) ] είναι της µορφής [ a b ] b a (µε a = λx και b = λy) Εποµένως ο πίνακας λa είναι στοιχείο του W Άρα το W είναι κλειστό ως προς τον ϐαθµωτό πολλαπλασιασµό Εφόσον το W είναι κλειστό ως προς την πρόσθεση και τον ϐαθµωτό πολλαπλασιασµό, το W είναι υπόχωρος του χώρου των πινάκων M
31 7 Να ϐρεθεί µία ϐάση του επιπέδου W του R µε εξίσωση x + y z = Εφόσον + =, το επίπεδο W διέρχεται από την αρχή των αξόνων και άρα είναι υπόχωρος του R Προφανώς x + y z = z = x + y Εποµένως το επίπεδο W αποτελείται από όλα τα διανύσµατα w στον R της µορ- ϕής t w = s, t, s στο R Εφόσον, για όλα τα t, s στο R, t s t + s = = t t t + + s κάθε διάνυσµα του W γράφεται σαν γραµµικός συνδυασµός των διανυσµάτων, s s, και άρα τα διανύσµατα παράγουν το W Τα,,
32 είναι γραµµικά ανεξάρτητα, εφόσον κανένα δεν είναι ϐαθµωτό πολλαπλάσιο του άλλου (γιατί = λ = λ λ = και = λ = ) = λ λ Εφόσον, από όσα είπαµε, το σύνολο S =, παράγει το W και είναι γραµµικά ανεξάρτητο, το S είναι µία ϐάση για το W Σηµείωση : Προφανώς υπάρχουν και άπειρες άλλες ϐάσεις του W Για παράδειγ- µα : () Οπως είπαµε στη δεύτερη παράγραφο παραπάνω, το επίπεδο W αποτελείται από όλα τα διανύσµατα w στον R της µορφής w = t s, t, s στο R Εφόσον, για όλα τα t, s στο R, t s t + s = = t t ( ) t + s s + ( 9 ) s κάθε διάνυσµα του W γράφεται σαν γραµµικός συνδυασµός των διανυσµάτων, 9 9,
33 και άρα τα διανύσµατα παράγουν το W Τα,, είναι γραµµικά ανεξάρτητα, εφόσον κανένα δεν είναι ϐαθµωτό πολλαπλάσιο του άλλου (γιατί = λ 9 = 9λ λ 9 9 = και 9 = λ 9 = λ λ Εφόσον, από όσα είπαµε, το σύνολο S =, 9 = ) 9 παράγει το W και είναι γραµµικά ανεξάρτητο, το S είναι µία ϐάση για το W () Προφανώς x + y z = y = x + z Εποµένως το επίπεδο W αποτελείται από όλα τα διανύσµατα w στον R της µορ- ϕής t w = t + s, t, s στο R s Εφόσον, για όλα τα t, s στο R, t t + s = s t t + s s
34 = t + s κάθε διάνυσµα του W γράφεται σαν γραµµικός συνδυασµός των διανυσµάτων, και άρα τα διανύσµατα παράγουν το W Τα,, είναι γραµµικά ανεξάρτητα, εφόσον κανένα δεν είναι ϐαθµωτό πολλαπλάσιο του άλλου (γιατί = λ = =, λ λ και = λ = λ λ = ) Εφόσον, από όσα είπαµε, το σύνολο S =, παράγει το W και είναι γραµµικά ανεξάρτητο, το S είναι µία ϐάση για το W 4
35 8 Εστω A ένας αντιστρέψιµος πίνακας Άν η λ είναι µία ιδιοτιµή του A και το x είναι ένα ιδιοδιάνυσµα του A που αντιστοιχεί στην λ, αποδείξτε ότι : (α) λ (ϐ) Η λ είναι µία ιδιοτιµή του A και το x είναι ένα ιδιοδιάνυσµα του A που αντιστοιχεί στην λ (α) ος τρόπος : Εφόσον η λ είναι µία ιδιοτιµή του A, υπάρχει ένα µη µηδενικό διάνυσµα y του R n τέτοιο ώστε Ay = λy Εστω ότι λ = Τότε, από τις ιδιότητες των πράξεων διανυσµάτων στον R n, παίρνουµε ότι λy = y = Άρα υπάρχει ένα µη µηδενικό διάνυσµα y του R n τέτοιο ώστε Εποµένως το οµογενές σύστηµα Ay = Az = έχει µη τετριµµένες λύσεις και άρα ο πίνακας A δεν είναι αντιστρέψιµος Αυτό µας οδηγεί σε άτοπο, εφόσον ο A είναι αντιστρέψιµος Άρα λ ος τρόπος : Εστω ότι ο A είναι n n Εφόσον η λ είναι µία ιδιοτιµή του A, det(λi n A) = Εστω ότι λ = Τότε, από τις ιδιότητες των πράξεων πινάκων, παίρνουµε ότι και άρα λi n A = I n A = n n A = A det( A) = Από τις ιδιότητες των πράξεων πινάκων και των οριζουσών παίρνουµε ότι, εφόσον ο A είναι ένας n n πίνακας, det( A) = det(( )A) = ( ) n det(a) Εποµένως det( A) = ( ) n det(a) = det(a) = 5
36 Άρα det(a) = και εποµένως ο πίνακας A δεν είναι αντιστρέψιµος Αυτό µας οδηγεί σε άτοπο, εφόσον ο A είναι αντιστρέψιµος Άρα λ (ϐ) Εστω ότι ο A είναι n n Εφόσον η λ είναι µία ιδιοτιµή του A και το x είναι ένα ιδιοδιάνυσµα του A που αντιστοιχεί στην λ, Ax = λx Από τις ιδιότητες των πράξεων πινάκων παίρνουµε ότι, εφόσον ο A είναι αντιστρέψιµος και, από την (α), λ, Ax = λx A (Ax) = A (λx) (A A)x = A (λx) I n x = A (λx) x = A (λx) προσεταιριστική ιδιότητα του πολλαπλασιασµού πινάκων αν ο T είναι αντιστρέψι- µος m m πίνακας, τότε T T = I m αν ο T είναι m k πίνακας, τότε I m T = T x = λ(a x) T (µs) = µ(t S) λ x = λ (λ(a x)) λ x = ( λ λ ) (A x) κ(µt ) = (κµ)t λ x = (A x) λ x = A x T = T Εφόσον το x είναι ένα ιδιοδιάνυσµα του A, x 6
37 Άρα το x είναι ένα µη µηδενικό διάνυσµα του R n τέτοιο ώστε A x = λ x Εποµένως η λ είναι µία ιδιοτιµή του A και το x είναι ένα ιδιοδιάνυσµα του A που αντιστοιχεί στην λ 7
x 2 = b 1 2x 1 + 4x 2 + x 3 = b 2. x 1 + 2x 2 + x 3 = b 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ
 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ Θα ξεκινήσουµε την παρουσίαση των γραµµικών συστηµάτων µε ένα απλό παράδειγµα από τη Γεωµετρία, το οποίο ϑα µας ϐοηθήσει στην κατανόηση των συστηµάτων αυτών και των συνθηκών
5.1 Ιδιοτιµές και Ιδιοδιανύσµατα
 Κεφάλαιο 5 Ιδιοτιµές και Ιδιοδιανύσµατα 5 Ιδιοτιµές και Ιδιοδιανύσµατα Αν ο A είναι ένας n n πίνακας και το x είναι ένα διάνυσµα στον R n, τότε το Ax είναι και αυτό ένα διάνυσµα στον R n Συνήθως δεν υπάρχει
Κεφάλαιο 5 Ιδιοτιµές και Ιδιοδιανύσµατα 5 Ιδιοτιµές και Ιδιοδιανύσµατα Αν ο A είναι ένας n n πίνακας και το x είναι ένα διάνυσµα στον R n, τότε το Ax είναι και αυτό ένα διάνυσµα στον R n Συνήθως δεν υπάρχει
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Κ. Ι. ΠΑΠΑΧΡΗΣΤΟΥ. Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ. Ιδιότητες & Εφαρµογές
 Κ Ι ΠΑΠΑΧΡΗΣΤΟΥ Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ Ιδιότητες & Εφαρµογές ΠΕΙΡΑΙΑΣ 2013 ΟΡΙΖΟΥΣΕΣ Έστω 2 2 πίνακας: a b A= c d Όπως γνωρίζουµε, η ορίζουσα του Α είναι ο αριθµός a
Κ Ι ΠΑΠΑΧΡΗΣΤΟΥ Τοµέας Φυσικών Επιστηµών Σχολή Ναυτικών οκίµων ΟΡΙΖΟΥΣΕΣ Ιδιότητες & Εφαρµογές ΠΕΙΡΑΙΑΣ 2013 ΟΡΙΖΟΥΣΕΣ Έστω 2 2 πίνακας: a b A= c d Όπως γνωρίζουµε, η ορίζουσα του Α είναι ο αριθµός a
Άσκηση 1. i) ============================================================== Α n ( 3 n 1 ) A ) 5 4. Α n 1 2 ( n n 2.
 http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6995 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 8-9: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6995 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 8-9: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 12 Οκτωβρίου 2007
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 1) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 1 Οκτωβρίου 007 Ηµεροµηνία παράδοσης της Εργασίας: 9 Νοεµβρίου 007. Πριν από την λύση κάθε άσκησης
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 1) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 1 Οκτωβρίου 007 Ηµεροµηνία παράδοσης της Εργασίας: 9 Νοεµβρίου 007. Πριν από την λύση κάθε άσκησης
Κεφάλαιο 4 ιανυσµατικοί Χώροι
 Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
Επίλυση Γραµµικών Συστηµάτων
 Κεφάλαιο 3 Επίλυση Γραµµικών Συστηµάτων 31 Εισαγωγή Αριθµητική λύση γενικών γραµµικών συστηµάτων n n A n n x n 1 b n 1, όπου a 11 a 12 a 1n a 21 a 22 a 2n A [a i j, x a n1 a n2 a nn x n, b b 1 b 2 b n
Κεφάλαιο 3 Επίλυση Γραµµικών Συστηµάτων 31 Εισαγωγή Αριθµητική λύση γενικών γραµµικών συστηµάτων n n A n n x n 1 b n 1, όπου a 11 a 12 a 1n a 21 a 22 a 2n A [a i j, x a n1 a n2 a nn x n, b b 1 b 2 b n
Ευκλείδειοι Χώροι. Ορίζουµε ως R n, όπου n N, το σύνολο όλων διατεταµένων n -άδων πραγµατικών αριθµών ( x
 Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/aeligia/linearalgerai/lai07/lai07html Παρασκευή Νοεµβρίου 07 Ασκηση Αν
D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].
![D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ]. D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].](/thumbs/60/44272313.jpg) 4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων
 Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12)
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 5 Οκτωβρίου 006 Ηµεροµηνία παράδοσης της Εργασίας: 0 Νοεµβρίου 006.
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 5 Οκτωβρίου 006 Ηµεροµηνία παράδοσης της Εργασίας: 0 Νοεµβρίου 006.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 2
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai8/lai8html Παρασκευή 6 Οκτωβρίου 8 Υπενθυµίζουµε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai8/lai8html Παρασκευή 6 Οκτωβρίου 8 Υπενθυµίζουµε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 3
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
( ) 10 ( ) εποµ ένως. π π π π ή γενικότερα: π π. π π. π π. Άσκηση 1 (10 µον) Θεωρούµε το µιγαδικό αριθµό z= i.
 http://elern.mths.gr/, mths@mths.gr, Τηλ: 697905 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 00-0: Άσκηση (0 µον) Θεωρούµε το µιγαδικό αριθµό z= i. α) (5 µον) Βρείτε την τριγωνοµετρική µορφή του z.
http://elern.mths.gr/, mths@mths.gr, Τηλ: 697905 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ 00-0: Άσκηση (0 µον) Θεωρούµε το µιγαδικό αριθµό z= i. α) (5 µον) Βρείτε την τριγωνοµετρική µορφή του z.
ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ - ΠΛΗ 12,
 ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ - ΠΛΗ, - Οι παρακάτω λύσεις των ασκήσεων της 6 ης εργασίας που καλύπτει το µεγαλύτερο µέρος της ύλης της θεµατικής ενότητας ΠΛΗ) είναι αρκετά εκτεταµένες καθώς έχει δοθεί αρκετή έµφαση
ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ - ΠΛΗ, - Οι παρακάτω λύσεις των ασκήσεων της 6 ης εργασίας που καλύπτει το µεγαλύτερο µέρος της ύλης της θεµατικής ενότητας ΠΛΗ) είναι αρκετά εκτεταµένες καθώς έχει δοθεί αρκετή έµφαση
τέτοιες συναρτήσεις «πραγµατικές συναρτήσεις µε µία πραγµατική µεταβλητή». Σε αυτή
 Κεφάλαιο Ορίζουσες Η Συνάρτηση Ορίζουσα Είµαστε όλοι εξοικειωµένοι µε συναρτήσεις όπως η f(x) sin x και η f(x) x οι οποίες αντιστοιχίζουν έναν πραγµατικό αριθµό f(x) σε κάθε πραγµατική τιµή της µετα- ϐλητής
Κεφάλαιο Ορίζουσες Η Συνάρτηση Ορίζουσα Είµαστε όλοι εξοικειωµένοι µε συναρτήσεις όπως η f(x) sin x και η f(x) x οι οποίες αντιστοιχίζουν έναν πραγµατικό αριθµό f(x) σε κάθε πραγµατική τιµή της µετα- ϐλητής
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
{ } ΠΛΗ 12: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι 2 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ. Απαντήσεις. 1. (15 µονάδες)
 Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Η Ορίζουσα Gram και οι Εφαρµογές της Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 65 11 Η Ορίζουσα Gram και
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
1 x x x x 1 x x x x 1 x x x x 1 (10) B 2, B 1. (10)
 Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 8 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Βοηθος Ασκησεων: Χ. Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://www.math.uoi.gr/ abeligia/linearalgebrai/lai.html
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Εάν A = τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό. det( A) = = ( 2)4 3 1 = 8 3 = 11. τότε η ορίζουσά του πίνακα ισούται με
 Κεφάλαιο Ορίζουσες Βασικοί ορισμοί a b Εάν A τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό a b ad bc Συμβολίζουμε την ορίζουσα του πίνακα και ως A Εάν A τότε ( ) 8 Εάν a a a A a a a a a a τότε η
Κεφάλαιο Ορίζουσες Βασικοί ορισμοί a b Εάν A τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό a b ad bc Συμβολίζουμε την ορίζουσα του πίνακα και ως A Εάν A τότε ( ) 8 Εάν a a a A a a a a a a τότε η
ΚΕΦΑΛΑΙΟ 2: ΟΡΙΖΟΥΣΕΣ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ :. ΕΙΣΑΓΩΓΗ Σε κάθε τετραγωνικό πίνακα ) τάξης n θα αντιστοιχίσουμε έναν πραγματικό ( ij αριθμό, τον οποίο θα ονομάσουμε ορίζουσα του πίνακα. Η ορίζουσα θα συμβολίζεται det ή Α ή n n
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα
 Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
2 3x 5x x
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
, ορίζουμε deta = ad bc. Πρόταση Ένας πίνακας Α είναι αντιστρέψιμος τότε και μόνο αν deta 0.
 Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
1 Ορίζουσες. Άσκηση 1.1 Θεωρούμε τον πίνακα. 1 x x x x 1 x x x x 1 x x x x 1 A =
 1 Ορίζουσες Άσκηση 1.1 Θεωρούμε τον πίνακα 1 x x x x 1 x x x x 1 x x x x 1, όπου x είναι τυχόν στοιχείο του σώματος R. Να βρεθούν όλες οι τιμές του x για τις οποίες ο πίνακας A δεν είναι αντιστρέψιμος.
1 Ορίζουσες Άσκηση 1.1 Θεωρούμε τον πίνακα 1 x x x x 1 x x x x 1 x x x x 1, όπου x είναι τυχόν στοιχείο του σώματος R. Να βρεθούν όλες οι τιμές του x για τις οποίες ο πίνακας A δεν είναι αντιστρέψιμος.
Η ιδέα της χρήσης διατεταγµένων Ϲευγών πραγµατικών αριθµών για την περιγραφή
 Κεφάλαιο 4 Ευκλείδιοι Χώροι 4 Ευκλείδιοι Χώροι Η ιδέα της χρήσης διατεταγµένων Ϲευγών πραγµατικών αριθµών για την περιγραφή των σηµείων στο επίπεδο και διατεταγµένων τριάδων πραγµατικών αριθµών για την
Κεφάλαιο 4 Ευκλείδιοι Χώροι 4 Ευκλείδιοι Χώροι Η ιδέα της χρήσης διατεταγµένων Ϲευγών πραγµατικών αριθµών για την περιγραφή των σηµείων στο επίπεδο και διατεταγµένων τριάδων πραγµατικών αριθµών για την
ΚΕΦΑΛΑΙΟ 3 ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ. nn n n
 ΚΕΦΑΛΑΙΟ 3 ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ 3 Ο αλγόριθµος Gauss Eστω =,3,, µε τον όρο γραµµικά συστήµατα, εννοούµε συστήµατα εξισώσεων µε αγνώστους της µορφής: a x + + a x = b a x + + a x = b a
ΚΕΦΑΛΑΙΟ 3 ΑΡΙΘΜΗΤΙΚΗ ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ 3 Ο αλγόριθµος Gauss Eστω =,3,, µε τον όρο γραµµικά συστήµατα, εννοούµε συστήµατα εξισώσεων µε αγνώστους της µορφής: a x + + a x = b a x + + a x = b a
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
ΚΕΦΑΛΑΙΟ 1ο: ΣΥΣΤΗΜΑΤΑ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ
 ΚΕΦΑΛΑΙΟ 1ο: ΣΥΣΤΗΜΑΤΑ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ) Copyright 2015 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoo.com Αδεια χρήσης 3η Εκδοση, Ιωάννινα, Σεπτέµβριος 2015 Περιεχόµενα 1 ΣΥΣΤΗΜΑΤΑ....................................................
ΚΕΦΑΛΑΙΟ 1ο: ΣΥΣΤΗΜΑΤΑ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ) Copyright 2015 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoo.com Αδεια χρήσης 3η Εκδοση, Ιωάννινα, Σεπτέµβριος 2015 Περιεχόµενα 1 ΣΥΣΤΗΜΑΤΑ....................................................
Παραδείγματα Διανυσματικοί Χώροι
 Παραδείγματα Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού: με V και
Παραδείγματα Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού: με V και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων εξέτασης προόδου στο μάθημα «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων εξέτασης προόδου στο μάθημα «Γραμμική Άλγεβρα» (ΗΥ9) Θέμα. (μονάδες.0) Οι ορίζουσες των πινάκων ABC,, βρεθούν οι ορίζουσες των πινάκων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων εξέτασης προόδου στο μάθημα «Γραμμική Άλγεβρα» (ΗΥ9) Θέμα. (μονάδες.0) Οι ορίζουσες των πινάκων ABC,, βρεθούν οι ορίζουσες των πινάκων:
Οι πράξεις που χρειάζονται για την επίλυση αυτών των προβληµάτων (αφού είναι απλές) µπορούν να τεθούν σε µια σειρά και πάρουν µια αλγοριθµική µορφή.
 Η Αριθµητική Ανάλυση χρησιµοποιεί απλές αριθµητικές πράξεις για την επίλυση σύνθετων µαθηµατικών προβληµάτων. Τις περισσότερες φορές τα προβλήµατα αυτά είναι ή πολύ περίπλοκα ή δεν έχουν ακριβή αναλυτική
Η Αριθµητική Ανάλυση χρησιµοποιεί απλές αριθµητικές πράξεις για την επίλυση σύνθετων µαθηµατικών προβληµάτων. Τις περισσότερες φορές τα προβλήµατα αυτά είναι ή πολύ περίπλοκα ή δεν έχουν ακριβή αναλυτική
============================================================== Σχηµατίζουµε τον πίνακα µε στήλες τα διανύσµατα v1,v2,v3,u1,u2:
 http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elearn.maths.gr/, maths@maths.gr, Τηλ: 6 Ενδεικτικές απαντήσεις ης Γραπτής Εργασίας ΠΛΗ -: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
Λύση Για να είναι αντιστρέψιμος θα πρέπει η ορίζουσα του πίνακα να είναι διάφορη του μηδενός =
 7. Άσκηση 1 2 1 Εστω ο πίνακας A = 1 3 2. Να δειχθεί ότι ο πίνακας είναι αντιστρέψιμοςκαιστησυνέχειαναυπολογιστείοαντίστροφος. 1 0 1 Για να είναι αντιστρέψιμος θα πρέπει η ορίζουσα του πίνακα να είναι
7. Άσκηση 1 2 1 Εστω ο πίνακας A = 1 3 2. Να δειχθεί ότι ο πίνακας είναι αντιστρέψιμοςκαιστησυνέχειαναυπολογιστείοαντίστροφος. 1 0 1 Για να είναι αντιστρέψιμος θα πρέπει η ορίζουσα του πίνακα να είναι
Γραµµική Αλγεβρα. Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα. Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Γραµµική Αλγεβρα Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραµµική Αλγεβρα Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και2015 Ιδιοδιανυσµάτων 1 / 50
 Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
Αριθµητική Γραµµική Αλγεβρα Κεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών και Ιδιοδιανυσµάτων ΕΚΠΑ 2 Απριλίου 205 Αριθµητική Γραµµική ΑλγεβραΚεφάλαιο 4. Αριθµητικός Υπολογισµός Ιδιοτιµών 2 Απριλίου και205
5 Γενική µορφή εξίσωσης ευθείας
 5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
5 Γενική µορφή εξίσωσης ευθείας Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Κάθε ευθεία έχει εξίσωση της µορφής: Ax + By +Γ= 0, µε Α 0 ηβ 0 () και αντιστρόφως κάθε εξίσωση της µορφής () παριστάνει ευθεία γραµµή.
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΥΤΙΚΗΣ ΕΛΛΑ ΑΣ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΥΤΙΚΗΣ ΕΛΛΑ ΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ MSc PROGRAM ΑΝΑΣΚΟΠΗΣΗ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΚΟΥΓΙΑΣ ΚΑΘΗΓΗΤΗΣ ΑΝΤΙΡΡΙΟ 03-04 ΚΕΦΑΛΑΙΟ ο ΠΙΝΑΚΕΣ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ - ΟΡΙΣΜΟΙ ΛΥΜΕΝΕΣ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΥΤΙΚΗΣ ΕΛΛΑ ΑΣ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ MSc PROGRAM ΑΝΑΣΚΟΠΗΣΗ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΚΟΥΓΙΑΣ ΚΑΘΗΓΗΤΗΣ ΑΝΤΙΡΡΙΟ 03-04 ΚΕΦΑΛΑΙΟ ο ΠΙΝΑΚΕΣ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ - ΟΡΙΣΜΟΙ ΛΥΜΕΝΕΣ
Σηµειώσεις Γραµµικής Άλγεβρας
 Σηµειώσεις Γραµµικής Άλγεβρας Κεφάλαιο Συστήµατα Γραµµικών Εξισώσεων και Πίνακες Εισαγωγή στα Συστήµατα Γραµµικών Εξισώσεων Η µελέτη των συστηµάτων γραµµικών εξισώσεων και των λύσεών τους είναι ένα από
Σηµειώσεις Γραµµικής Άλγεβρας Κεφάλαιο Συστήµατα Γραµµικών Εξισώσεων και Πίνακες Εισαγωγή στα Συστήµατα Γραµµικών Εξισώσεων Η µελέτη των συστηµάτων γραµµικών εξισώσεων και των λύσεών τους είναι ένα από
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: Ιανουαρίου 6 Ηµεροµηνία Παράδοσης της Εργασίας από
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: Ιανουαρίου 6 Ηµεροµηνία Παράδοσης της Εργασίας από
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Παραδείγματα (1 ο σετ) Διανυσματικοί Χώροι
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ Τα κάτωθι προβλήµατα προέρχονται από τα κεφάλαια, και του συγγράµµατος «Γραµµική Άλγεβρα». Η ηµεροµηνία παράδοσης
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ Τα κάτωθι προβλήµατα προέρχονται από τα κεφάλαια, και του συγγράµµατος «Γραµµική Άλγεβρα». Η ηµεροµηνία παράδοσης
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα
 ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων. Μαθηµατικά Ι Ακαδ. Έτος 2009-10 1/58
 Φρ. Κουτελιέρης Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων Τηλ. 26410741964196 E-mail fkoutel@cc.uoi.gr ΜΑΘΗΜΑΤΙΚΑ Ι ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Μαθηµατικά Ι Ακαδ. Έτος 2009-10 1/58 Γραµµική άλγεβρα...... είναι τοµέας
Φρ. Κουτελιέρης Επίκουρος Καθηγητής Παν/µίου Ιωαννίνων Τηλ. 26410741964196 E-mail fkoutel@cc.uoi.gr ΜΑΘΗΜΑΤΙΚΑ Ι ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Μαθηµατικά Ι Ακαδ. Έτος 2009-10 1/58 Γραµµική άλγεβρα...... είναι τοµέας
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚH Ι (ΠΛΗ ) ΕΡΓΑΣΙΑ 6 - ΛΥΣΕΙΣ Άσκηση. (6 µον.) Ελέγξτε ποια από τα επόµενα σύνολα είναι διανυσµατικοί χώροι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚH Ι (ΠΛΗ ) ΕΡΓΑΣΙΑ 6 - ΛΥΣΕΙΣ Άσκηση. (6 µον.) Ελέγξτε ποια από τα επόµενα σύνολα είναι διανυσµατικοί χώροι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) TEΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 8 Ιουνίου 005 Από τα κάτωι Θέµατα καλείσε να λύσετε το ο που περιλαµβάνει ερωτήµατα από όλη την ύλη
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) TEΛΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 8 Ιουνίου 005 Από τα κάτωι Θέµατα καλείσε να λύσετε το ο που περιλαµβάνει ερωτήµατα από όλη την ύλη
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
Γραµµική Αλγεβρα. Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα. Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Γραµµική Αλγεβρα Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραµµική Αλγεβρα Ενότητα 6 : Ιδιοτιµές & Ιδιοδιανύσµατα Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Κεφάλαιο 9 Ιδιοτιµές και Ιδιοδιανύσµατα
 Σελίδα από 5 Κεφάλαιο 9 Ιδιοτιµές και Ιδιοδιανύσµατα 9. Ορισµοί... 9. Ιδιότητες...7 9. Θεώρηµα Cayley-Hamilto...4 9.. Εφαρµογές του Θεωρήµατος Cayley-Hamilto...6 9.4 Ελάχιστο Πολυώνυµο...5 Ασκήσεις του
Σελίδα από 5 Κεφάλαιο 9 Ιδιοτιµές και Ιδιοδιανύσµατα 9. Ορισµοί... 9. Ιδιότητες...7 9. Θεώρηµα Cayley-Hamilto...4 9.. Εφαρµογές του Θεωρήµατος Cayley-Hamilto...6 9.4 Ελάχιστο Πολυώνυµο...5 Ασκήσεις του
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai017/lai017html Παρασκευή 17 Νοεµβρίου 017
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai017/lai017html Παρασκευή 17 Νοεµβρίου 017
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ. Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες,
 ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
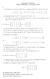 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραµµική Αλγεβρα. Ενότητα 2 : Επίλυση Γραµµικών Εξισώσεων. Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Γραµµική Αλγεβρα Ενότητα 2 : Επίλυση Γραµµικών Εξισώσεων Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραµµική Αλγεβρα Ενότητα 2 : Επίλυση Γραµµικών Εξισώσεων Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Διανύσµατα στο επίπεδο
 Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Σηµειωσεις Αναλυτικης Γεωµετριας
 Σηµειωσεις Αναλυτικης Γεωµετριας Θ. Κεχαγιας Σεπτεµβρης 009, υ.0.96 Περιεχόµενα Εισαγωγη iv Επιπεδα στον Τρισδιαστατο Χωρο. Θεωρια..................................... Λυµενες Ασκησεις..............................
Σηµειωσεις Αναλυτικης Γεωµετριας Θ. Κεχαγιας Σεπτεµβρης 009, υ.0.96 Περιεχόµενα Εισαγωγη iv Επιπεδα στον Τρισδιαστατο Χωρο. Θεωρια..................................... Λυµενες Ασκησεις..............................
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai018/lai018html Παρασκευή 3 Νοεµβρίου 018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ Λυσεις Ασκησεων - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai018/lai018html Παρασκευή 3 Νοεµβρίου 018 Ασκηση
Thanasis Kehagias, 2009
 Μέρος II Αναλυτικη Γεωµετρια 33 34 Το παρον τευχος περιεχει συντοµη ϑεωρια, λυµενες και αλυτες ασκησεις Αναλυτικης Γεωµετριας. Κατα τη γνωµη µου, για τους περισσοτερους ανθρωπους, ο µονος τροπος εξοικειωσης
Μέρος II Αναλυτικη Γεωµετρια 33 34 Το παρον τευχος περιεχει συντοµη ϑεωρια, λυµενες και αλυτες ασκησεις Αναλυτικης Γεωµετριας. Κατα τη γνωµη µου, για τους περισσοτερους ανθρωπους, ο µονος τροπος εξοικειωσης
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Θέµατα ( ικαιολογείστε πλήρως όλες τις απαντήσεις σας)
 Τµήµα Εφαρµοσµένων Μαθηµατικών Παν/µίου Κρήτης Εξεταστική περίοδος εαρινού εξαµήνου Πέµπτη, 2 Ιούνη 28 Γραµµική Αλγεβρα II ιδάσκων: Α. Τόγκας Θέµατα ( ικαιολογείστε πλήρως όλες τις απαντήσεις σας) Θέµα
Τµήµα Εφαρµοσµένων Μαθηµατικών Παν/µίου Κρήτης Εξεταστική περίοδος εαρινού εξαµήνου Πέµπτη, 2 Ιούνη 28 Γραµµική Αλγεβρα II ιδάσκων: Α. Τόγκας Θέµατα ( ικαιολογείστε πλήρως όλες τις απαντήσεις σας) Θέµα
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
!q j. = T ji Kάθε πίνακας µπορεί να γραφεί σαν άθροισµα ενός συµµετρικού και ενός αντι-συµµετρικού πίνακα
 Συστήματα με Ν βαθμούς ελευθερίας ΦΥΣ 211 - Διαλ.25 1 Ø Συστήµατα µε Ν βαθµούς ελευθερίας που βρίσκονται κοντά σε µια θέση ισσορροπίας τους συµπεριφέρονται σαν Ν ανεξάρτητοι αρµονικοί ταλαντωτές Γιατί
Συστήματα με Ν βαθμούς ελευθερίας ΦΥΣ 211 - Διαλ.25 1 Ø Συστήµατα µε Ν βαθµούς ελευθερίας που βρίσκονται κοντά σε µια θέση ισσορροπίας τους συµπεριφέρονται σαν Ν ανεξάρτητοι αρµονικοί ταλαντωτές Γιατί
AX=B (S) A A X=A B I X=A B X=A B I X=A B X=A B X=A B X X
 . Επίλυση γραμμικού συστήματος με χρήση αντιστρόφου Πρόταση Θεωρούμε ένα τετραγωνικό γραμμικό σύστημα (δηλαδή ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων) AX=B (S). Αν ο πίνακας Α είναι
. Επίλυση γραμμικού συστήματος με χρήση αντιστρόφου Πρόταση Θεωρούμε ένα τετραγωνικό γραμμικό σύστημα (δηλαδή ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων) AX=B (S). Αν ο πίνακας Α είναι
Μάθηµα 1. Κεφάλαιο 1o: Συστήµατα. γ R παριστάνει ευθεία και καλείται γραµµική εξίσωση µε δύο αγνώστους.
 Μάθηµα 1 Κεφάλαιο 1o: Συστήµατα Θεµατικές Ενότητες: A. Συστήµατα Γραµµικών Εξισώσεων B. Συστήµατα 3x3 Α. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Ορισµοί Κάθε εξίσωση της µορφής α x+β =γ, µε α, β, γ R παριστάνει
Μάθηµα 1 Κεφάλαιο 1o: Συστήµατα Θεµατικές Ενότητες: A. Συστήµατα Γραµµικών Εξισώσεων B. Συστήµατα 3x3 Α. ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ Ορισµοί Κάθε εξίσωση της µορφής α x+β =γ, µε α, β, γ R παριστάνει
11. Η έννοια του διανύσµατος 22. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο
 Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Παραουσίαση βιβλίου αθηµατικών Προσαναταλισµού Β Λυκείου. Η έννοια του διανύσµατος. Πρόσθεση & αφαίρεση διανυσµάτων 33. Βαθµωτός πολλαπλασιασµός 44. Συντεταγµένες 55. Εσωτερικό γινόµενο Παραουσίαση βιβλίου
Ορίζουσες ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. Προηγείται της Γραµµικής Αλγεβρας. Εχει ενδιαφέρουσα γεωµετρική ερµηνεία. ΛΥ.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ε. Γαλλόπουλος 1 1 Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Πολυτεχνική Σχολή, Πανεπιστήµιο Πατρών 11/5/2012 Σηµαντικό χαρακτηριστικό µέγεθος (ϐαθµωτός) για κάθε τετραγωνικό
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ε. Γαλλόπουλος 1 1 Τµήµα Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής Πολυτεχνική Σχολή, Πανεπιστήµιο Πατρών 11/5/2012 Σηµαντικό χαρακτηριστικό µέγεθος (ϐαθµωτός) για κάθε τετραγωνικό
Σημειώσεις για το μάθημα: «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α )
 Χρήστος Ι Σχοινάς Αν Καθηγητής ΔΠΘ Σημειώσεις για το μάθημα «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α ) ΞΑΝΘΗ, 008 - - - - ΚΕΦΑΛΑΙΟ ΔΙΑΝΥΣΜATA Ορισμοί και ιδιότητες Συχνά, σε διάφορα προβλήματα στα Μαθηματικά,
Χρήστος Ι Σχοινάς Αν Καθηγητής ΔΠΘ Σημειώσεις για το μάθημα «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α ) ΞΑΝΘΗ, 008 - - - - ΚΕΦΑΛΑΙΟ ΔΙΑΝΥΣΜATA Ορισμοί και ιδιότητες Συχνά, σε διάφορα προβλήματα στα Μαθηματικά,
(2) Θεωρούµε µοναδιαία διανύσµατα α, β, γ R 3, για τα οποία γνωρίζουµε ότι το διάνυσµα
 Πανεπιστηµιο Ιωαννινων σχολη θετικων επιστηµων τµηµα µαθηµατικων τοµεας αλγεβρας και γεωµετριας αναλυτικη γεωµετρια διδασκων : χρηστος κ. τατακης υποδειξεις λυσεων των θεµατων της 7.06.016 ΘΕΜΑ 1. µονάδες
Πανεπιστηµιο Ιωαννινων σχολη θετικων επιστηµων τµηµα µαθηµατικων τοµεας αλγεβρας και γεωµετριας αναλυτικη γεωµετρια διδασκων : χρηστος κ. τατακης υποδειξεις λυσεων των θεµατων της 7.06.016 ΘΕΜΑ 1. µονάδες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (2 Ιουλίου 2009) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ( Ιουλίου 009 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ I. (εκδχ. Α. Σωστό ή Λάθος: α Αν A,B R n n είναι αντιστρέψιµα, τότε το ίδιο ισχύει και για το AB. ϐ Αν A R n n, τότε A AA. γ Αν A R και συµµετρικό
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ( Ιουλίου 009 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ I. (εκδχ. Α. Σωστό ή Λάθος: α Αν A,B R n n είναι αντιστρέψιµα, τότε το ίδιο ισχύει και για το AB. ϐ Αν A R n n, τότε A AA. γ Αν A R και συµµετρικό
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU
 Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x+ y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x+ y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 00) Η Εργασία χωρίζεται σε µέρη: Το πρώτο Ασκήσεις - περιλαµβάνει
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 00) Η Εργασία χωρίζεται σε µέρη: Το πρώτο Ασκήσεις - περιλαµβάνει
1 η Εργασία Ηµεροµηνία αποστολής: 19 Νοεµβρίου 2006
 η Εργασία Ηµεροµηνία αποστολής: 9 Νοεµβρίου 6. α. Να βρεθεί η γωνία µεταξύ των διανυσµάτων a = i + j k και b = 6 i j + k. β. Να δείξετε ότι τα διανύσµατα a, b, c είναι ορθογώνια και µοναδιαία. a = ( i
η Εργασία Ηµεροµηνία αποστολής: 9 Νοεµβρίου 6. α. Να βρεθεί η γωνία µεταξύ των διανυσµάτων a = i + j k και b = 6 i j + k. β. Να δείξετε ότι τα διανύσµατα a, b, c είναι ορθογώνια και µοναδιαία. a = ( i
ΜΑΘΗΜΑΤΙΚΑ Ο.Π. ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΥΝ ΥΑΣΤΙΚΑ ΘΕΜΑΤΑ. Γιάννης Ζαµπέλης Μαθηµατικός
 ΣΥΝ ΥΑΣΤΙΚΑ ΘΕΜΑΤΑ 4 5 Γιάννης Ζαµπέλης Μαθηµατικός 867 (Αναρτήθηκε 8 4 ) ίνονται τα διανύσµατα a και b µε µέτρα, 6 αντίστοιχα και ϕ [, π] a b+ x+ a b y 5= () δίνεται η εξίσωση ( ) ( ) α) Να αποδείξετε
ΣΥΝ ΥΑΣΤΙΚΑ ΘΕΜΑΤΑ 4 5 Γιάννης Ζαµπέλης Μαθηµατικός 867 (Αναρτήθηκε 8 4 ) ίνονται τα διανύσµατα a και b µε µέτρα, 6 αντίστοιχα και ϕ [, π] a b+ x+ a b y 5= () δίνεται η εξίσωση ( ) ( ) α) Να αποδείξετε
