A New Approach to Bounded Real Lemma Representation for Linear Neutral Systems

J. of Math. (PRC) u(t k ) = I k (u(t k )), k = 1, 2,, (1.6) , [3, 4] (1.1), (1.2), (1.3), [6 8]

Vol 36 ( 216 ) No 3 J of Mah (PR) 1, 2, 3 (1, 4335) (2, 4365) (3, 431) :,,,, : ; ; ; MR(21) : 35A1; 35A2 : O17529 : A : 255-7797(216)3-591-7 1 d d [x() g(, x )] = f(, x ),, (11) x = ϕ(), [ r, ], (12) x(

Vol. 40 No Journal of Jiangxi Normal University Natural Science Jul. 2016

4 4 Vol 4 No 4 26 7 Journal of Jiangxi Normal Universiy Naural Science Jul 26-5862 26 4-349-5 3 2 6 2 67 3 3 O 77 9 A DOI 6357 /j cnki issn-5862 26 4 4 C q x' x /q G s = { α 2 - s -9 2 β 2 2 s α 2 - s

INDIRECT ADAPTIVE CONTROL

INDIREC ADAPIVE CONROL OULINE. Inroducion a. Main properies b. Running example. Adapive parameer esimaion a. Parameerized sysem model b. Linear parameric model c. Normalized gradien algorihm d. Normalized

Πραγματοποιήσιμοι Δυναμικοί Ελεγκτές σε Ουδέτερα Συστήματα με Χρονικές Καθυστερήσεις για Βιομηχανικές Εφαρμογές ΔΙΔΑΚΤΟΡΙΚΗ ΔΙΑΤΡΙΒΗ

ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΣΗΜΑΤΩΝ ΕΛΕΓΧΟΥ ΚΑΙ ΡΟΜΠΟΤΙΚΗΣ Πραγματοποιήσιμοι Δυναμικοί Ελεγκτές σε Ουδέτερα Συστήματα με Χρονικές Καθυστερήσεις

ΕΡΓΑΣΙΑ ΜΑΘΗΜΑΤΟΣ: ΘΕΩΡΙΑ ΒΕΛΤΙΣΤΟΥ ΕΛΕΓΧΟΥ ΦΙΛΤΡΟ KALMAN ΜΩΥΣΗΣ ΛΑΖΑΡΟΣ

ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΘΕΩΡΗΤΙΚΗ ΠΛΗΡΟΦΟΡΙΚΗ ΚΑΙ ΘΕΩΡΙΑ ΣΥΣΤΗΜΑΤΩΝ & ΕΛΕΓΧΟΥ ΕΡΓΑΣΙΑ ΜΑΘΗΜΑΤΟΣ: ΘΕΩΡΙΑ ΒΕΛΤΙΣΤΟΥ ΕΛΕΓΧΟΥ ΦΙΛΤΡΟ KALMAN ΜΩΥΣΗΣ

Oscillation Criteria for Nonlinear Damped Dynamic Equations on Time Scales

Oscillaion Crieria for Nonlinear Damped Dynamic Equaions on ime Scales Lynn Erbe, aher S Hassan, and Allan Peerson Absrac We presen new oscillaion crieria for he second order nonlinear damped delay dynamic

Reservoir modeling. Reservoir modelling Linear reservoirs. The linear reservoir, no input. Starting up reservoir modeling

Reservoir modeling Reservoir modelling Linear reservoirs Paul Torfs Basic equaion for one reservoir:) change in sorage = sum of inflows minus ouflows = Q in,n Q ou,n n n jus an ordinary differenial equaion

Resilient static output feedback robust H control for controlled positive systems

31 5 2014 5 DOI: 10.7641/CA.2014.30666 Control heory & Applications Vol. 31 No. 5 May 2014 H,, (, 250100), (LMI),, H,,,,, H,, ; H ; ; ; P273 A Resilient static output feedback robust H control for controlled

HMY 220: Σήματα και Συστήματα Ι

HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #3 Ιδιάζοντα σήματα Βασικές κατηγορίες συστημάτων Διασυνδέσεις συστημάτων Ιδιάζοντα σήματα (singular signals) Τα ιδιάζοντα σήματα είναι σήματα τα οποία είναι ιδεατά

Nonlinear Analysis: Modelling and Control, 2013, Vol. 18, No. 4,

Nonlinear Analysis: Modelling and Conrol, 23, Vol. 8, No. 4, 493 58 493 Exisence and uniqueness of soluions for a singular sysem of higher-order nonlinear fracional differenial equaions wih inegral boundary

Necessary and sufficient conditions for oscillation of first order nonlinear neutral differential equations

J. Mah. Anal. Appl. 321 (2006) 553 568 www.elsevier.com/locae/jmaa Necessary sufficien condiions for oscillaion of firs order nonlinear neural differenial equaions X.H. ang a,, Xiaoyan Lin b a School of

3 Frequency Domain Representation of Continuous Signals and Systems

3 Frequency Domain Represenaion of Coninuous Signals and Sysems 3. Fourier Series Represenaion of Periodic Signals............. 2 3.. Exponenial Fourier Series.................... 2 3..2 Discree Fourier

J. of Math. (PRC) Banach, , X = N(T ) R(T + ), Y = R(T ) N(T + ). Vol. 37 ( 2017 ) No. 5

Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2

Vol. 31,No JOURNAL OF CHINA UNIVERSITY OF SCIENCE AND TECHNOLOGY Feb

Ξ 31 Vol 31,No 1 2 0 0 1 2 JOURNAL OF CHINA UNIVERSITY OF SCIENCE AND TECHNOLOGY Feb 2 0 0 1 :025322778 (2001) 0120016205 (, 230026) : Q ( m 1, m 2,, m n ) k = m 1 + m 2 + + m n - n : Q ( m 1, m 2,, m

Applying Markov Decision Processes to Role-playing Game

1,a) 1 1 1 1 2011 8 25, 2012 3 2 MDPRPG RPG MDP RPG MDP RPG MDP RPG MDP RPG Applying Markov Decision Processes to Role-playing Game Yasunari Maeda 1,a) Fumitaro Goto 1 Hiroshi Masui 1 Fumito Masui 1 Masakiyo

Analiza reakcji wybranych modeli

Bank i Kredy 43 (4), 202, 85 8 www.bankikredy.nbp.pl www.bankandcredi.nbp.pl Analiza reakcji wybranych modeli 86 - - - srice - - - per capia research and developmen dynamic sochasic general equilibrium

Appendix. The solution begins with Eq. (2.15) from the text, which we repeat here for 1, (A.1)

Aenix Aenix A: The equaion o he sock rice. The soluion egins wih Eq..5 rom he ex, which we reea here or convenience as Eq.A.: [ [ E E X, A. c α where X u ε, α γ, an c α y AR. Take execaions o Eq. A. as

Oscillation criteria for two-dimensional system of non-linear ordinary differential equations

Elecronic Journal of Qualiaive Theory of Differenial Equaions 216, No. 52, 1 17; doi: 1.14232/ejqde.216.1.52 hp://www.mah.u-szeged.hu/ejqde/ Oscillaion crieria for wo-dimensional sysem of non-linear ordinary

High order interpolation function for surface contact problem

3 016 5 Journal of East China Normal University Natural Science No 3 May 016 : 1000-564101603-0009-1 1 1 1 00444; E- 00030 : Lagrange Lobatto Matlab : ; Lagrange; : O41 : A DOI: 103969/jissn1000-56410160300

6.003: Signals and Systems

6.3: Signals and Sysems Modulaion December 6, 2 Communicaions Sysems Signals are no always well mached o he media hrough which we wish o ransmi hem. signal audio video inerne applicaions elephone, radio,

6.003: Signals and Systems. Modulation

6.3: Signals and Sysems Modulaion December 6, 2 Subjec Evaluaions Your feedback is imporan o us! Please give feedback o he saff and fuure 6.3 sudens: hp://web.mi.edu/subjecevaluaion Evaluaions are open

University of Washington Department of Chemistry Chemistry 553 Spring Quarter 2010 Homework Assignment 3 Due 04/26/10

Universiy of Washingon Deparmen of Chemisry Chemisry 553 Spring Quarer 1 Homework Assignmen 3 Due 4/6/1 v e v e A s ds: a) Show ha for large 1 and, (i.e. 1 >> and >>) he velociy auocorrelaion funcion 1)

Identification of MIMO State Space Model based on MISO High-order ARX Model: Design and Application

Korean Chem. Eng. Res., Vol. 45, No. 1, February, 2007, pp. 67-72 MISO y ARX m MIMO m m : j nk kjiçlslçm Çm * 121-742 ne e 1 *LS r l 431-080 kke k (2006 11o 20p r, 2006 12o 21p }ˆ) Idenificaion of MIMO

TRM +4!5"2# 6!#!-!2&'!5$27!842//22&'9&2:1*;832<

TRM!"#$%& ' *,-./ *!#!!%!&!3,&!$-!$./!!"#$%&'*" 4!5"# 6!#!-!&'!5$7!84//&'9&:*;83< #:4

ER-Tree (Extended R*-Tree)

1-9825/22/13(4)768-6 22 Journal of Software Vol13, No4 1, 1, 2, 1 1, 1 (, 2327) 2 (, 3127) E-mail xhzhou@ustceducn,,,,,,, 1, TP311 A,,,, Elias s Rivest,Cleary Arya Mount [1] O(2 d ) Arya Mount [1] Friedman,Bentley

Lecture 6. Goals: Determine the optimal threshold, filter, signals for a binary communications problem VI-1

Lecue 6 Goals: Deemine e opimal esold, file, signals fo a binay communicaions poblem VI- Minimum Aveage Eo Pobabiliy Poblem: Find e opimum file, esold and signals o minimize e aveage eo pobabiliy. s s

Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α

Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ

Motion analysis and simulation of a stratospheric airship

32 11 Vol 32 11 2011 11 Journal of Harbin Engineering University Nov 2011 doi 10 3969 /j issn 1006-7043 2011 11 019 410073 3 2 V274 A 1006-7043 2011 11-1501-08 Motion analysis and simulation of a stratospheric

Μοντέρνα Θεωρία Ελέγχου

ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 8: Ομοιότητα και Όμοιες Περιγραφές Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative

Optimal Stopping Time to Buy an Asset When Growth Rate Is a Two-State Markov Chain

American Journa of Operaions Researc, 4, 4, 3-4 Pubise Onine May 4 in SciRes. p://www.scirp.org/journa/ajor p://x.oi.org/.436/ajor.4.433 Opima Sopping Time o Buy an Asse Wen Grow Rae Is a Two-Sae Markov

( ) ( t) ( 0) ( ) dw w. = = β. Then the solution of (1.1) is easily found to. wt = t+ t. We generalize this to the following nonlinear differential

Periodic oluion of van der Pol differenial equaion. by A. Arimoo Deparmen of Mahemaic Muahi Iniue of Technology Tokyo Japan in Seminar a Kiami Iniue of Technology January 8 9. Inroducion Le u conider a

2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.

EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.

γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000

Η Πολυεδρική Προσέγγιση στην Ανάλυση και Σύνθεση Συστηµάτων Ελέγχου. Εργαστήριο Συστηµάτων Αυτοµάτου Ελέγχου

Η Πολυεδρική Προσέγγιση στην Ανάλυση και Σύνθεση Συστηµάτων Ελέγχου Εργαστήριο Συστηµάτων Αυτοµάτου Ελέγχου Η Τετραγωνική Προσέγγιση Ευκλείδια Απόσταση (Eucldean dstance) Ευκλείδια νορµ (Eucldean norm)

Parts Manual. Trio Mobile Surgery Platform. Model 1033

Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische

η η η η GAR = 1 F RR η F RR F AR F AR F RR η F RR F AR µ µ µ µ µ µ Γ R N=mxn W T X x mean X W T x g W P x = W T (x g x mean ) X = X x mean P x = W T X d P x P i, i = 1, 2..., G M s t t

Feasible Regions Defined by Stability Constraints Based on the Argument Principle

Feasible Regions Defined by Stability Constraints Based on the Argument Principle Ken KOUNO Masahide ABE Masayuki KAWAMATA Department of Electronic Engineering, Graduate School of Engineering, Tohoku University

( ) ( ) ( ) Fourier series. ; m is an integer. r(t) is periodic (T>0), r(t+t) = r(t), t Fundamental period T 0 = smallest T. Fundamental frequency ω

Fourier series e jm when m d when m ; m is an ineger. jm jm jm jm e d e e e jm jm jm jm r( is periodi (>, r(+ r(, Fundamenal period smalles Fundamenal frequeny r ( + r ( is periodi hen M M e j M, e j,

, Snowdon. . Frahm.

- :..... ( ). :., Snowdon.. Frohrib Jennige -.[ ]...[ ] Ghannadi-Asl Zahrai..,.[ ]... Frahm Frahm [ ] Den Hartog. mzahrai@ut.ac.ir, hashemif@conwag.com . - Den Hartog g(t)=0 ω f(t)=p 0 sinωt. ω y st =P

Iterative Learning Control with a Forgetting Factor for Consensus Tracking in Multi-Agent Systems

33 E-mal: hxx@zju.edu.c :... : Ierave Learg Corol wh a Forgeg Facor for Cosesus racg Mul-Age Sysems Jgy Zheg Xogxog He Ymg Wu Zhehua Q College of Iformao Egeerg Zhejag Uversy of echology Hagzhou 33 Cha

A Control Method of Errors in Long-Term Integration

1,a) Hamilon Runge Kua Hamilonian 1/2 Runge Kua (Brouwer s law) Runge Kua Runge Kua Hamilonian 1/2 Brouwer 3 A Conrol Mehod of Errors in Long-Term Inegraion Ozawa Kazufumi 1,a) Absrac: When solving he

is the home less foreign interest rate differential (expressed as it

The model is solved algebraically, excep for a cubic roo which is solved numerically The mehod of soluion is undeermined coefficiens The noaion in his noe corresponds o he noaion in he program The model

A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3

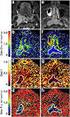大阪電気通信大学研究論集 ( 自然科学編 ) 第 51 号 A Determination Method of Diffusion-Parameter Values in the Ion-Exchange Optical Waveguides in Soda-Lime glass Made by Diluted AgNO 3 with NaNO 3 Takuya IWATA and Kiyoshi

ΕΛΕΓΧΟΣ ΚΙΝΟΥΜΕΝΗΣ ΡΟΜΠΟΤΙΚΗΣ ΔΙΑΤΑΞΗΣ ΓΙΑ ΕΡΓΑΣΙΕΣ ΜΕ ΠΕΡΙΟΡΙΣΜΕΝΗ ΚΙΝΗΣΗ

ΕΛΕΓΧΟΣ ΚΙΝΟΥΜΕΝΗΣ ΡΟΜΠΟΤΙΚΗΣ ΔΙΑΤΑΞΗΣ ΓΙΑ ΕΡΓΑΣΙΕΣ ΜΕ ΠΕΡΙΟΡΙΣΜΕΝΗ ΚΙΝΗΣΗ Φώτης Ν. Κουμπουλής Νικόλαος Δ. Κούβακας και Ιωάννης Σταθαράς Τμήμα Αυτοματισμού ΤΕΙ Χαλκίδας 34 4 Ψαχνά Ευβοίας Τμήμα Τεχνολογίας

HMY 799 1: Αναγνώριση Συστημάτων

HMY 799 : Αναγνώριση Συστημάτων Διαλέξεις 3 4 Παραμετροποιήσεις γραμμικών χρονικά αμετάβλητων συστημάτων Μοντέλα πρόβλεψης Μοναδικότητα Αναγνωρισιμότητα Τ y () = φ () θ + e () 2 Ee {()} = 0, E{ ee } =

Teor imov r. ta matem. statist. Vip. 94, 2016, stor

eor imov r. ta matem. statist. Vip. 94, 6, stor. 93 5 Abstract. e article is devoted to models of financial markets wit stocastic volatility, wic is defined by a functional of Ornstein-Ulenbeck process

Second Order Partial Differential Equations

Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y

Multiple positive periodic solutions of nonlinear functional differential system with feedback control

J. Mah. Anal. Appl. 288 (23) 819 832 www.elsevier.com/locae/jmaa Muliple posiive periodic soluions of nonlinear funcional differenial sysem wih feedback conrol Ping Liu and Yongkun Li Deparmen of Mahemaics,

Levin Lin(1992) Oh(1996),Wu(1996) Papell(1997) Im, Pesaran Shin(1996) Canzoneri, Cumby Diba(1999) Lee, Pesaran Smith(1997) FGLS SUR

EVA M, SWEEEY R 3,. ;. McDonough ; 3., 3006 ; ; F4.0 A Levin Lin(99) Im, Pesaran Shin(996) Levin Lin(99) Oh(996),Wu(996) Paell(997) Im, Pesaran Shin(996) Canzoner Cumby Diba(999) Levin Lin(99) Coe Helman(995)

Σύγχρονος Αυτόματος Έλεγχος. είναι το διάνυσμα ιδιοτιμών του πίνακα Α (Π2)

Σύγχρονος Αυτόματος Έλεγχος.Ορισμοί και Χρήσιμες Ιδιότητες (Π) (A) είναι το διάνυσμα ιδιοτιμών του πίνακα Α (Π) x x x... xn (Π3) Η «ιδιότητα του τριγώνου»: για οποιαδήποτε διανύσματα ισχύει x, y ότι x

Σύγχρονος Αυτόματος Έλεγχος. (Π3) Η «ιδιότητα του τριγώνου»: για οποιαδήποτε διανύσματα ισχύει x, y ότι

Σύγχρονος Αυτόματος Έλεγχος 1.Ορισμοί και Χρήσιμες Ιδιότητες (Π1) λ(a) είναι το διάνυσμα ιδιοτιμών του πίνακα Α (Π) x = x 1 + x +... + xn (Π3) Η «ιδιότητα του τριγώνου»: για οποιαδήποτε διανύσματα ισχύει

2002 Journal of Software

1000-9825/2002/13(02)0239-06 2002 Journal of Sofware Vol13, No2 -,, (, 100084) E-mail: shijing@mailssinghuaeducn; xingcx@singhuaeducn; dcszlz@singhuaeducn hp://dbgroupcssinghuaeducn : 10 12,, I/O -, -,,,

Numerical Analysis FMN011

Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =

Control Theory & Applications PID (, )

26 12 2009 12 : 1000 8152(2009)12 1317 08 Control Theory & Applications Vol. 26 No. 12 Dec. 2009 PID,, (, 200240) : PID (PIDNN), PID,, (BP).,, PIDNN PIDNN (MPIDNN), (CPSO) BP, MPIDNN CPSO MPIDNN CRPSO

l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R

The Euler Equations! λ 1. λ 2. λ 3. ρ ρu. E = e + u 2 /2. E + p ρ. = de /dt. = dh / dt; h = h( T ); c p. / c v. ; γ = c p. p = ( γ 1)ρe. c v.

hp://www.nd.ed/~gryggva/cfd-corse/ The Eler Eqaions The Eler Eqaions The Eler eqaions for D flow: + + p = x E E + p where Define E = e + / H = h + /; h = e + p/ Gréar Tryggvason Spring 3 Ideal Gas: p =

Nov Journal of Zhengzhou University Engineering Science Vol. 36 No FCM. A doi /j. issn

2015 11 Nov 2015 36 6 Journal of Zhengzhou University Engineering Science Vol 36 No 6 1671-6833 2015 06-0056 - 05 C 1 1 2 2 1 450001 2 461000 C FCM FCM MIA MDC MDC MIA I FCM c FCM m FCM C TP18 A doi 10

Abstract Storage Devices

Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD

Estimation of stability region for a class of switched linear systems with multiple equilibrium points

29 4 2012 4 1000 8152(2012)04 0409 06 Control Theory & Applications Vol 29 No 4 Apr 2012 12 1 (1 250061; 2 250353) ; ; ; TP273 A Estimation of stability region for a class of switched linear systems with

Probabilistic Approach to Robust Optimization

Probabilistic Approach to Robust Optimization Akiko Takeda Department of Mathematical & Computing Sciences Graduate School of Information Science and Engineering Tokyo Institute of Technology Tokyo 52-8552,

Existence of travelling wave solutions in delayed reaction diffusion systems with applications to diffusion competition systems

INSTITUTE OF PHYSICS PUBLISHING Nonlineariy 9 (2006) 253 273 NONLINEARITY doi:0.088/095-775/9/6/003 Exisence of ravelling wave soluions in delayed reacion diffusion sysems wih applicaions o diffusion compeiion

Prey-Taxis Holling-Tanner

Vol. 28 ( 2018 ) No. 1 J. of Math. (PRC) Prey-Taxis Holling-Tanner, (, 730070) : prey-taxis Holling-Tanner.,,.. : Holling-Tanner ; prey-taxis; ; MR(2010) : 35B32; 35B36 : O175.26 : A : 0255-7797(2018)01-0140-07

Positive solutions for a multi-point eigenvalue. problem involving the one dimensional

Elecronic Journal of Qualiaive Theory of Differenial Equaions 29, No. 4, -3; h://www.mah.u-szeged.hu/ejqde/ Posiive soluions for a muli-oin eigenvalue roblem involving he one dimensional -Lalacian Youyu

Anti-aliasing Prefilter (6B) Young Won Lim 6/8/12

ni-aliasing Prefiler (6B) Copyrigh (c) Young W. Lim. Permission is graned o copy, disribue and/or modify his documen under he erms of he GNU Free Documenaion License, Version. or any laer version published

Κεφάλαιο 1 Πραγματικοί Αριθμοί 1.1 Σύνολα

x + = 0 N = {,, 3....}, Z Q, b, b N c, d c, d N + b = c, b = d. N = =. < > P n P (n) P () n = P (n) P (n + ) n n + P (n) n P (n) n P n P (n) P (m) P (n) n m P (n + ) P (n) n m P n P (n) P () P (), P (),...,

Maximum likelihood estimation of state-space models

Maximum likelihood esimaion of sae-space models Florian Chevassu 1 and Juan-Pablo Orega Absrac The use of he Kalman filer for esimaion purposes is no always an easy ask despie he obvious advanages in many

= f(0) + f dt. = f. O 2 (x, u) x=(x 1,x 2,,x n ) T, f(x) =(f 1 (x), f 2 (x),, f n (x)) T. f x = A = f

2 n dx (x)+g(x)u () x n u (x), g(x) x n () +2 -a -b -b -a 3 () x,u dx x () dx () + x x + g()u + O 2 (x, u) x x x + g()u + O 2 (x, u) (2) x O 2 (x, u) x u 2 x(x,x 2,,x n ) T, (x) ( (x), 2 (x),, n (x)) T

ES440/ES911: CFD. Chapter 5. Solution of Linear Equation Systems

ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific

2 ~ 8 Hz Hz. Blondet 1 Trombetti 2-4 Symans 5. = - M p. M p. s 2 x p. s 2 x t x t. + C p. sx p. + K p. x p. C p. s 2. x tp x t.

36 2010 8 8 Vol 36 No 8 JOURNAL OF BEIJING UNIVERSITY OF TECHNOLOGY Aug 2010 Ⅰ 100124 TB 534 + 2TP 273 A 0254-0037201008 - 1091-08 20 Hz 2 ~ 8 Hz 1988 Blondet 1 Trombetti 2-4 Symans 5 2 2 1 1 1b 6 M p

Simplex Crossover for Real-coded Genetic Algolithms

Technical Papers GA Simplex Crossover for Real-coded Genetic Algolithms 47 Takahide Higuchi Shigeyoshi Tsutsui Masayuki Yamamura Interdisciplinary Graduate school of Science and Engineering, Tokyo Institute

Theory and Effectiveness Evaluation of the Chinese Government s Intervention in the Housing Market

28 1 2011 1 Saisical Research Vol. 28 No. 1 Jan. 2011 2003 6 2005 2006 2004 C812 A 1002-4565 2011 01-0027 - 09 Theory and Effeciveness Evaluaion of he Chinese Governmen s Inervenion in he Housing Marke

ACTA MATHEMATICAE APPLICATAE SINICA Nov., ( µ ) ( (

35 Þ 6 Ð Å Vol. 35 No. 6 2012 11 ACTA MATHEMATICAE APPLICATAE SINICA Nov., 2012 È ÄÎ Ç ÓÑ ( µ 266590) (E-mail: jgzhu980@yahoo.com.cn) Ð ( Æ (Í ), µ 266555) (E-mail: bbhao981@yahoo.com.cn) Þ» ½ α- Ð Æ Ä

Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee

Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset

[4-7] Rosenbrock ( ) Runge-Kutta(RK)

28 3 2011 06 CHINESE JOURNAL OF ENGINEERING MATHEMATICS Vol. 28 No. 3 June 2011 :1005-30852011)03-0335-08 2- BDF, 411105) : 1- BDF) 2- : 2- : AMS2000) 90C29 : O221.4 : A 1 ) [1,2] Petzold [3] ) ) [4-7]

ΔΙΠΛΩΜΑΤΙΚΕΣ ΕΡΓΑΣΙΕΣ

ΔΙΠΛΩΜΑΤΙΚΕΣ ΕΡΓΑΣΙΕΣ ΤΜ. ΜΗΧΑΝΙΚΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ 2018-2019 Επιβλέπουσα: Μπίμπη Ματίνα Ανάλυση της πλατφόρμας ανοιχτού κώδικα Home Assistant Το Home Assistant είναι μία πλατφόρμα ανοιχτού

16. 17. r t te 2t i t 1. 18 19 Find the derivative of the vector function. 19. r t e t cos t i e t sin t j ln t k. 31 33 Evaluate the integral.

SECTION.7 VECTOR FUNCTIONS AND SPACE CURVES.7 VECTOR FUNCTIONS AND SPACE CURVES A Click here for answers. S Click here for soluions. Copyrigh Cengage Learning. All righs reserved.. Find he domain of he

Ax = b. 7x = 21. x = 21 7 = 3.

3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3

Research on real-time inverse kinematics algorithms for 6R robots

25 6 2008 2 Control Theory & Applications Vol. 25 No. 6 Dec. 2008 : 000 852(2008)06 037 05 6R,,, (, 30027) : 6R. 6 6R6.., -, 6R., 2.03 ms, 6R. : 6R; ; ; : TP242.2 : A Research on real-time inverse kinematics

Σήματα και Συστήματα. Διάλεξη 3: Εισαγωγή στα Συστήματα. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής

Σήματα και Συστήματα Διάλεξη 3: Εισαγωγή στα Συστήματα Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Εισαγωγή στα Συστήματα 1. Ορισμός και Κατηγορίες Συστημάτων Συστήματα Συνεχούς Χρόνου Συστήματα Διακριτού

Α Ρ Ι Θ Μ Ο Σ : 6.913

Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ

P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ

P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s

Μοντέρνα Θεωρία Ελέγχου

ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 7. Ισοδύναμες Περιγραφές Συστημάτων Νίκος Καραμπετάκης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative

SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-2018 PAPER II VERSION B1

SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-8 PAPER II VERSION B [MATHEMATICS]. Ans: ( i) It is (cs5 isin5 ) ( i). Ans: i z. Ans: i i i The epressin ( i) ( ). Ans: cs i sin cs i sin

T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ

Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ

Apr Vol.26 No.2. Pure and Applied Mathematics O157.5 A (2010) (d(u)d(v)) α, 1, (1969-),,.

2010 4 26 2 Pure and Applied Matheatics Apr. 2010 Vol.26 No.2 Randić 1, 2 (1., 352100; 2., 361005) G Randić 0 R α (G) = v V (G) d(v)α, d(v) G v,α. R α,, R α. ; Randić ; O157.5 A 1008-5513(2010)02-0339-06

Quick algorithm f or computing core attribute

24 5 Vol. 24 No. 5 Cont rol an d Decision 2009 5 May 2009 : 100120920 (2009) 0520738205 1a, 2, 1b (1. a., b., 239012 ; 2., 230039) :,,.,.,. : ; ; ; : TP181 : A Quick algorithm f or computing core attribute

D-Wave D-Wave Systems Inc.

D-Wave D-Wave sems Inc. Anaol Yu. mirnov D-Wave sems Inc. Vancouver Briish Columbia HE QUANUM COMPUING COMPANY M Decoherence and Noise Conrol in rongl Driven uperconducing Quanum Bis Collaboraion: M. Grajcar

Technical Notes for Discussion of Eggertsson, What Fiscal Policy Is Effective at Zero Interest Rates? Lawrence J. Christiano

Tecnical Noes for Discussion of Eggersson Wa Fiscal Policy Is Effecive a Zero Ineres Raes? Larence J Crisiano Te model a as simulaed for e discussion is presened in e firs secion Te simulaion sraegy is

On Strong Product of Two Fuzzy Graphs

Inernaional Journal of Scienific and Research Publicaions, Volume 4, Issue 10, Ocober 014 1 ISSN 50-3153 On Srong Produc of Two Fuzzy Graphs Dr. K. Radha* Mr.S. Arumugam** * P.G & Research Deparmen of

ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:

On shift Harnack inequalities for subordinate semigroups and moment estimates for Lévy processes

Available online a www.sciencedirec.com ScienceDirec Sochasic Processes and heir Applicaions 15 (15) 3851 3878 www.elsevier.com/locae/spa On shif Harnack inequaliies for subordinae semigroups and momen

J J l 2 J T l 1 J T J T l 2 l 1 J J l 1 c 0 J J J J J l 2 l 2 J J J T J T l 1 J J T J T J T J {e n } n N {e n } n N x X {λ n } n N R x = λ n e n {e n } n N {e n : n N} e n 0 n N k 1, k 2,..., k n N λ

D-Glucosamine-derived copper catalyst for Ullmann-type C- N coupling reaction: theoretical and experimental study

Electronic Supplementary Material (ESI) for RSC Advances. This journal is The Royal Society of Chemistry 2016 D-Glucosamine-derived copper catalyst for Ullmann-type C- N coupling reaction: theoretical

New conditions for exponential stability of sampled-data systems under aperiodic sampling

33 10 2016 10 DOI: 10.7641/CTA.2016.50818 Control Theory & Applications Vol. 33 No. 10 Oct. 2016,, (, 273165) :. Lyapunov, Lyapunov.,,. Lyapunov,, Wirtinger,.. : ; ; Lyapunov; : TP273 : A New conditions

Jou rnal of M athem atical Study

38 4 2005 12 Jou rnal of M athem atical Study V ol 38 o 4 D ec 2005 α (, 361005),, (SVV ), SVV, SVV, SVV - H elm holtz, (SEM ); (SVV ); O 174 52 A 1,, 1g, ( ),, 80,, ( [ 4 ]),,,, (e g [ 1 ]),, Gibbs,,,,,,

(b) flat (continuous) fins on an array of tubes

(a) Individually finned ues () fla (coninuous) fins on an array of ues Eample Fins Fins on Segosaurus 3 Rekangulär fläns, Recangular fin. Z d f 4 Rekangulär fläns, Recangular fin. Z d f d αc d λ ( f )

Προσομοίωση Δημιουργία τυχαίων αριθμών

Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Προσομοίωση Δημιουργία τυχαίων αριθμών Άδεια Χρήσης Το παρόν εκπαιδευτικό

Center Manifold Theory and Computation Using a Forward Backward Approach

College of William and Mary W&M Publish Undergraduae Honors Theses Theses, Disseraions, & Maser Projecs 4-217 Cener Manifold Theory and Compuaion Using a Forward Backward Approach Emily E. Schaal College

w o = R 1 p. (1) R = p =. = 1

Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:

Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in

Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that