Electrodinámica Cuántica
|
|
|
- Δημόκριτος Βικελίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Electrodinámica Cuántica L 0 = ψ i m)ψ Reemplazo minimal: D µ = µ iea µ Lagrangiano de la electrodinámica cuántica. L = ψ id m)ψ 1 4 F µνf µν
2 Propagador del electrón L 0 = ψ i m)ψ + j ψ + ψ j S F x y) = S F p) = i m)ψ = j, i m)s F x y) =iδx y) d d p 2π) ds Fp)e ip.x y), p m)s F p) =i i ip + m) = p m p 2 m 2 +iε
3 Fijación de Gauge En la integral funcional, promediando sobre B µ A µ =Bx) Z = dad ψ dψdbe 1 2α B2 δ µ A µ Bx))e S Esto lleva al lagrangiano de fijación de gauge L GF = 1 2α µa µ ) 2
4 Simetría BRST δa µ = µ αx), αx) =λcx) λ 2 = 0, λcx) = Cx)λ δ = λδ BRST, δ BRST A µ = µ Cx) Cx)es el campo fantasma. Notar: δab) = δa)b + AδB) = λδ BRST A)B + Aλδ BRST B = λδ BRST AB) Si A es un fantasma, se tiene que: Imponiendo nilpotencia: δ BRST A = Aδ BRST 2 0 = δ BRST A µ = µ δ BRST Cx), δ BRST Cx)=0
5 Para tener los gauges conocidos introducimos: δ BRST C x)=bx) δ BRST Bx) = 0 C x) es el campo antifantasma. Bx) es el campo de Nakanishi-Lautrup.
6 Simetría BRST Para fijar el gauge se agrega en el lagrangiano:l GF = δ BRST F F debe tener número de fantasma -1. Sea F =C x) µ A µ + αb), L GF = αb 2 B µ A µ + C x) 2 Cx) Integrando sobre B: 2αB 0 µ A µ = 0 B 0 = µa µ 2α L GF = αb 2 0 B 0 µ A µ + C x) 2 Cx)= µa µ ) 2 + C x) 2 Cx) 4α La simetría de L GF es: δ BRST A µ = µ Cx) δ BRST Cx) = 0 δ BRST C x) = µa µ 2α
7 Propagador de Fotón L = 1 4 F µνf µν + 1 2α.A)2 + j.a, µ F µν 1 α ν.a+ j ν = 0, A ν ν µ A µ 1 α ν.a = j ν, D α ν ν µ D α µ α ) =iδα ν δx) D α ν x) = d d k 2π) d D α ν k)e ik.x k 2 D α ν +k ν k µ D α µ α Aδ ν µ +Bk ν k µ ) k 2 δ µ β k µ k β Ak 2 δ ν β Ak ν k β α ) D µ ν = i δ µ k 2 + iε ν α + 1) kµ k ν k 2 ) ν =iδα, S ν µ = k 2 δ ν µ k ν 1 ) k µ 1 + ν,aδµ +Bk ν 1ν k α µ = S µ )) ν = δ α β )+ Bk 2 k ν k β Bk 2 k ν k β ) α Ak 2 = 1, A )+Bk 2 Bk α α Bk 2 = α ) 1 α k 2 ) = 0
8 Vértice Calcular, usando la integral funcional Figura 1. L = ψ id m)ψ 1 4 F µνf µν, D µ = µ ieqa µ, L I = eqa µ ψ γ µ ψ Vértice: ieqγ µ, El electrón tiene Q= 1
9 Reglas de Feynman Figura 2. Además un loop cerrado de fermión agrega -1 y se debe calcular la traza sobre las matrices de Dirac. Ejercicio: Use la integral funcional para encontrar Figura 3.
10 Autoenergía del Fotón Π µν = ie) 2 d n p Trγ µ ip + k + m)γ ν ip+m)) [p+k) 2 m 2 + iε][p 2 m 2 + iε] ν µ
11 trazas en regularización dimensional {γ µ, γ ν } = 2η µν 1 n Trγ µ γ ν )=4η µν. Notar el 4 en cualquier número de dimensiones. Esto es Tr 1 n = 4 Trγ µ γ ν γ α γ β )=4η βµ η να 4η βν η µα +4η βα η νµ En efecto: Trγ µ γ ν γ α γ β ) = Trγ µ γ ν γ β γ α )+2η αβ Trγ µ γ ν ) = Trγ µ γ β γ ν γ α ) 2η νβ Trγ µ γ α )+2η αβ Trγ µ γ ν ) = Trγ β γ µ γ ν γ α ) +2η µβ Trγ ν γ α ) 2η νβ Trγ µ γ α )+2η αβ Trγ µ γ ν ) La traza es cíclica: 2Trγ µ γ ν γ α γ β )=2η µβ Trγ ν γ α ) 2η νβ Trγ µ γ α )+2η αβ Trγ µ γ ν )
12 Trγ µ p +k + m)γ ν p + m)) = Trγ µ p +k)γ ν p) +4m 2 η µν = p+k) α p β 4η µα η νβ η µν η αβ + η µβ η να )+4m 2 η µν =4m 2 4p 2 +p.k))η µν +4p+k) µ p ν + 4p + k) ν p µ = 4N µν
13 Autoenergía del Fotón 1 1 ab 0 = dx ax +b1 x)) 2 I γ n = 4e 2 1 dx d n p N µν 0 D 2 D =p 2 m 2 + iε)x+1 x)p+k) 2 m 2 + iε) N µν = m 2 p 2 p.k)η µν + p + k) µ p ν +µ ν) Completamos el cuadrado en el denominador: D = p 2 m 2 + iε +1 x)2p.k + k 2 ) = p + k1 x)) 2 k 2 1 x) 2 + k 2 1 x) m 2 + iε Redefinir: p p k1 x) D = p 2 +k 2 x1 x) m 2 + iε N µν = η µν m 2 p 2 k 2 1 x) 2 + k 2 1 x))+2p µ p ν 2k µ k ν x1 x) = η µν m 2 p 2 +k 2 1 x)x)+2p µ p ν 2k µ k ν x1 x) =
14 η µν m 2 p 2 +k 2 1 x)x)+ 2 n p2 η µν 2k µ k ν x1 x) = η µν m 2 p ) ) + k 2 1 x)x 2k µ k ν x1 x) = N µν n
15 Autoenergía del Fotón Integramos sobre p: d d q 1 = i 1) n 1 Γ 2 π) d q 2 + iε) n 4 π) d/2 n d 2 Γn) n 1 d n p p 2 M 2 + iε) 2 = i π 2 M 2 ) 2 n 2 p d n p 2 n p 2 M 2 +iε) 2 = i π 2 Γ 1 n M 2 ) 2 n 2 2 Se obtiene, con M 2 = k 2 x1 x) + m 2, ) 1 iε Γ 2 n ) 2 ) M 2 n 2 ) n d 2 4e 2 iπ n 1 dx 2 0 M 2 ) 2 n 2 [ Γ 2 n ) η µν m 2 + k 2 1 x)x) 2k µ k ν x1 x)) 2 +η µν 1 2 ) Γ 1 n ) M 2 n n 2 2 ]= 4e 2 iπ n 2 Γ 2 n ) 1 dx 2 0 M 2 ) 2 n 2 [η µν m 2 +k 2 1 x)x) 2k µ k ν x1 x) η µν k 2 x1 x) + m 2 )] = 8e 2 iπ n 2 Γ 2 n ) 1 dx x1 x)k 2 η 2 0 M 2 ) 2 n µν k µ k ν ) 2
16
17 Autoenergía del Electrón p+k p Figura 4.
18 Autoenergía del electrón I e n = ie) 2 i i) γ µ p+m)γ µ d n p p 2 m 2 + iε)p+k) 2 + iε) γ µ γ µ =n1 e dx γ µ γ ν γ µ = nγ ν + 2η µν γ µ = 2 n)γ ν I e n = e 2 p2 n) +nm) d n p p 2 m 2 + iε)p + k) 2 +iε) = d n p p2 n) +nm) [p 2 m 2 + iε)x + 1 x)p + k) 2 + iε)] 2 N = ip2 n) +nm D = p 2 m 2 x+iε + 2p.k1 x) +k 2 1 x)= p +k1 x)) 2 m 2 x+iε+k 2 1 x)x I n e = e dx p p k1 x) N = 2 n)k1 x) +nm 2 n)k1 x) +nm M 2 ) iπ n 2 n 2 Γ 2 n ), M 2 =m 2 x k 2 1 x)x 2 2
19 Momento Magnético Anómalo del electrón Ramond, Capítulo 8.4 Peskin, Capítulo 6
20 Lamb Shift Ramond, página 269 y problemas Peskin página 253.
21 Identidades de Ward Consideremos la integral funcional: Dφ a e isφ) Gφ) La transformación infinitesimal de φ:δφ a deja invariante la acción y la medida de integración. Realizando el cambio de variables φ a φ a +δφ a obtenemos: Dφ a e isφ) Gφ) = Dφ a e isφ) δgφ) =0 Dφ a e isφ) Gφ + δφ) δgφ) = δg δφ aδφa La ecuación en rojo es la identidad de Ward correspondiente a la simetría δφ a.
22 Identidad de Ward para la autoenergía del fotón Encontremos la identidad de Ward asociada a la simetría BRST de la electrodinámica, para GA µ,c, C )=C x)a ν y) Es decir DA µ DC DCe i S+S GF) ) µa µ x) A ν y) C x) y 2α ν Cy) 1 2α µ x D µν x y)+ ν Fx y)=0 D es el propagador vestido del fotón. En espacio de momentum se tiene: D µν k) =D 0 µν k) + D 0 µα k)π αβ k)d 0 βν k) +... Dado que ν Fx y) no tiene correcciones radiativas, la identidad se satura con el propagador del fotón libre. Por lo tanto: Esto es:k α Π αβ k) =0. k µ D 0 µα k)π αβ k)d 0 βν k)=0 k µ D 0 µα k)=ak 2 )k α
23 Identidad de Ward para la acción efectiva Esto es: Dφ a e isφ) δgφ) =0, G =e i dxj a x)φ a x) Dφ a e isφ)+i dxj a x)φ a x) dxj a x)δφ a x)=0 j a x) = δγϕ) δϕ a x) Obtenemos la identidad de Slavnov Taylor: dx<δφ a x) > j δγϕ) δϕ a x) =0 Esto dice que la acción efectiva es invariante bajo las transformaciones infinitesimales dadas por δϕ a x) = <δφ a x) > j. En general estas transformaciones difieren de las que dejan invariante la acción S. Ambas coinciden para transformaciones lineales.
24 Problema #1 Considere un campo escalar complejo, acoplado minimalmente al campo electromagnético A µ. El Lagrangiano es: L = 1 4 F µν) 2 + D µ φ) D µ φ) m 2 φ φ, F µν = µ A ν ν A µ, D µ = µ + iea µ 1- Encuentre en espacio de momentos i) el propagador del campo escalar; ii) Los vértices que describen la interacción del fotón con el campo φ.
25 2-Calcule la contribución del campo escalar a la polarización del vacío del fotón, usando regularización dimensional. Note que hay dos diagramas. Para escribir la respuesta en la forma transversal: Π µν q 2 ) =g µν q 2 q µ q ν )Πq 2 ) es conveniente sumar los dos diagramas al comienzo, poniéndolos sobre un denominador común antes de introducir parámetros de Feynman. Además use la simetría del integrando bajo el cambio de variables x >1 x. Escriba explícitamente la parte divergente y la parte finita. Explique claramente de donde viene la dependencia en µ.
26 Sol: Π1k) µν = ie) 2 F p)= i p 2 m 2 + iǫ d d p 2π) d 2p+k) µ 2p+k) ν i p +k) 2 m 2 + iǫ i p 2 m 2 +iǫ Π2k) µν = 2ie 2 d d p i 2π) d p 2 m 2 + iǫ g µν Πk) µν = e 2 d d p 2p +k) µ 2p +k) ν 2 g µν p+k) 2 m 2 ) 2π) d p 2 m 2 + iǫ)p +k) 2 m 2 = +iǫ) e 2 1 d dx d p 2p + k) µ 2p + k) ν 2g µν p+k) 2 m 2 ) 2π) d [p 2 m 2 + iǫ)x +1 x)p + k) 2 m 2 +iǫ)] 2 0 D = p 2 m x)pk + 1 x)k 2 = [p + 1 x)k] 2 + k 2 x1 x) m 2 + iǫ p >p 1 x)k:
27 N µν =2p +k 1 + 2x)) µ 2p +k 1 + 2x)) ν 2g µν p +kx) 2 m 2 ) = 4p µ p ν +k µ k ν 1 2x) 2 2g µν p 2 + k 2 x 2 m 2 ) Πk) µν = e dx d d p 2π) d 4p µ p ν + k µ k ν 1 2x) 2 2g µν p 2 + k 2 x 2 m 2 ) p 2 + k 2 x1 x) m 2 +iǫ) 2 = e 2 i 4π) d 2 Γ1 d 2 ) 0 1 dxm d 2 2 2g µν m 2 k 2 x1 x)) + k µ k ν 1 2x) 2 1 d 2 ) 2g µν [ m 2 + k 2 d 2 x1 x) +x2 1 d 2 )]
28 Coeffm 2 )=0 ǫ =2 d 2 Ck 2 g µν )=2x1 x) 2 d 2 x1 x)+x2 1 d 2 )) = 1 d )[4x1 x) 1] 2 Πk) µν =e 2 i 4π) d 2 Γ2 d 2 )k µk ν g µν k 2 1 ) 0 dxm d x) 2 2[A] +2 d=0, [A] = 1 ǫ, 1 = [e] + [A], [e] =ǫ Πk) µν = e 2 i 4π) 2Γǫ)k µk ν g µν k 2 ) PFΠk) µν = e 2 i 4π) 2k µk ν g µν k 2 ) dx dxln M 4πµ 2) ǫ 1 2x) 2 M 4πµ 2)1 2x)2 PPΠk) µν = e 2 i 1 4π) 2 ǫ k µk ν g µν k 2 ) 0 1 dx1 2x) 2
TRIGONOMETRIA. hipotenusa L 2. hipotenusa
 TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
Métodos Matemáticos en Física L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro APL)
 L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro Condiciones de contorno. Fuerzas externas aplicadas sobre una cuerda. condición que nos describe un extremo libre en una cuerda tensa. Ecuación
L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro Condiciones de contorno. Fuerzas externas aplicadas sobre una cuerda. condición que nos describe un extremo libre en una cuerda tensa. Ecuación
1 La teoría de Jeans. t + (n v) = 0 (1) b) Navier-Stokes (conservación del impulso) c) Poisson
 1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
TEMA IV: FUNCIONES HIPERGEOMETRICAS
 TEMA IV: FUNCIONES HIPERGEOMETRICAS 1. La ecuación hipergeométrica x R y α, β, γ parámetros reales. x(1 x)y + [γ (α + β + 1)x]y αβy 0 (1.1) Dividiendo en (1.1) por x(1 x) obtenemos (x 0, x 1) y + γ (α
TEMA IV: FUNCIONES HIPERGEOMETRICAS 1. La ecuación hipergeométrica x R y α, β, γ parámetros reales. x(1 x)y + [γ (α + β + 1)x]y αβy 0 (1.1) Dividiendo en (1.1) por x(1 x) obtenemos (x 0, x 1) y + γ (α
PÁGINA 106 PÁGINA a) sen 30 = 1/2 b) cos 120 = 1/2. c) tg 135 = 1 d) cos 45 = PÁGINA 109
 PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
SOLUCIONES DE LAS ACTIVIDADES Págs. 101 a 119
 Página 0. a) b) π 4 π x 0 4 π π / 0 π / x 0º 0 x π π. 0 rad 0 π π rad 0 4 π 0 π rad 0 π 0 π / 4. rad 4º 4 π π 0 π / rad 0º π π 0 π / rad 0º π 4. De izquierda a derecha: 4 80 π rad π / rad 0 Página 0. tg
Página 0. a) b) π 4 π x 0 4 π π / 0 π / x 0º 0 x π π. 0 rad 0 π π rad 0 4 π 0 π rad 0 π 0 π / 4. rad 4º 4 π π 0 π / rad 0º π π 0 π / rad 0º π 4. De izquierda a derecha: 4 80 π rad π / rad 0 Página 0. tg
La transformada de ondícula continua y algunas clases de operadores de localización
 La transformada de ondícula continua y algunas clases de operadores de localización Gerardo Ramos Vázquez Dr. Egor Maximenko Instituto Politécnico Nacional, ESFM diciembre 2016 Contenido El grupo afín
La transformada de ondícula continua y algunas clases de operadores de localización Gerardo Ramos Vázquez Dr. Egor Maximenko Instituto Politécnico Nacional, ESFM diciembre 2016 Contenido El grupo afín
την..., επειδή... Se usa cuando se cree que el punto de vista del otro es válido, pero no se concuerda completamente
 - Concordar En términos generales, coincido con X por Se usa cuando se concuerda con el punto de vista de otro Uno tiende a concordar con X ya Se usa cuando se concuerda con el punto de vista de otro Comprendo
- Concordar En términos generales, coincido con X por Se usa cuando se concuerda con el punto de vista de otro Uno tiende a concordar con X ya Se usa cuando se concuerda con el punto de vista de otro Comprendo
Section 9: Quantum Electrodynamics
 Physics 8.33 Section 9: Quantum Electrodynamics May c W. Taylor 8.33 Section 9: QED / 6 9. Feynman rules for QED Field content: A µ(x) gauge field, ψ(x) Dirac spinor Action Z» S = d x ψ(iγ µ D µ m)ψ Z
Physics 8.33 Section 9: Quantum Electrodynamics May c W. Taylor 8.33 Section 9: QED / 6 9. Feynman rules for QED Field content: A µ(x) gauge field, ψ(x) Dirac spinor Action Z» S = d x ψ(iγ µ D µ m)ψ Z
Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice de aluminio.
 HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
Lógica Proposicional
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Escenas de episodios anteriores
 Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
Filipenses 2:5-11. Filipenses
 Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
Eletromagnetismo. Johny Carvalho Silva Universidade Federal do Rio Grande Instituto de Matemática, Física e Estatística. ...:: Solução ::...
 Eletromagnetismo Johny Carvalho Silva Universidade Federal do Rio Grande Instituto de Matemática, Física e Estatística Lista -.1 - Mostrar que a seguinte medida é invariante d 3 p p 0 onde: p 0 p + m (1)
Eletromagnetismo Johny Carvalho Silva Universidade Federal do Rio Grande Instituto de Matemática, Física e Estatística Lista -.1 - Mostrar que a seguinte medida é invariante d 3 p p 0 onde: p 0 p + m (1)
8.324 Relativistic Quantum Field Theory II
 8.324 Relativistic Quantum Field Theory II MIT OpenCourseWare Lecture Notes Hong Liu, Fall 200 Lecture 2 3: GENERAL ASPECTS OF QUANTUM ELECTRODYNAMICS 3.: RENORMALIZED LAGRANGIAN Consider the Lagrangian
8.324 Relativistic Quantum Field Theory II MIT OpenCourseWare Lecture Notes Hong Liu, Fall 200 Lecture 2 3: GENERAL ASPECTS OF QUANTUM ELECTRODYNAMICS 3.: RENORMALIZED LAGRANGIAN Consider the Lagrangian
Académico Introducción
 - Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis Για να απαντήσουμε αυτή την ερώτηση, θα επικεντρωθούμε πρώτα... Para introducir un área específica
- Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis Για να απαντήσουμε αυτή την ερώτηση, θα επικεντρωθούμε πρώτα... Para introducir un área específica
Για να ρωτήσετε αν κάποιος μπορεί να σας βοηθήσει να γεμίσετε μια φόρμα
 - Γενικά Dónde tengo que pedir el formulario/impreso para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Dónde tengo que pedir el formulario/impreso para? Cuál es la fecha de expedición de su (documento)?
- Γενικά Dónde tengo que pedir el formulario/impreso para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Dónde tengo que pedir el formulario/impreso para? Cuál es la fecha de expedición de su (documento)?
Lógica Proposicional. Justificación de la validez del razonamiento?
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Problemas resueltos del teorema de Bolzano
 Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
EXERCICIOS DE REFORZO: RECTAS E PLANOS
 EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα. Adam Smith 8 Crossfield Road Selly Oak Birmingham West Midlands B29 1WQ
 - Dirección Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Jeremy Rhodes 212 Silverback Drive California Springs CA 92926 Formato
- Dirección Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Jeremy Rhodes 212 Silverback Drive California Springs CA 92926 Formato
Non-Abelian Gauge Fields
 Chapter 5 Non-Abelian Gauge Fields The simplest example starts with two Fermions Dirac particles) ψ 1, ψ 2, degenerate in mass, and hence satisfying in the absence of interactions γ 1 i + m)ψ 1 = 0, γ
Chapter 5 Non-Abelian Gauge Fields The simplest example starts with two Fermions Dirac particles) ψ 1, ψ 2, degenerate in mass, and hence satisfying in the absence of interactions γ 1 i + m)ψ 1 = 0, γ
1 Γραμμικές συναρτήσεις
 Γραμμικές συναρτήσεις Άσκηση. είξτε ότι η συνάρτηση f : R R, που ορίζεται με τη σχέση f(x, y, z) =(x y + z,x z), για κάθε (x, y, z) R, είναι μια γραμμική συνάρτηση, και να βρεθεί ο πυρήνας της. Απόδειξη.
Γραμμικές συναρτήσεις Άσκηση. είξτε ότι η συνάρτηση f : R R, που ορίζεται με τη σχέση f(x, y, z) =(x y + z,x z), για κάθε (x, y, z) R, είναι μια γραμμική συνάρτηση, και να βρεθεί ο πυρήνας της. Απόδειξη.
90 LIBERTAS SEGUNDA ÉPOCA. Introducción: La necesidad de una Reforma Institucional
 1 3 - - Abstract - - - 90 LIBERTAS SEGUNDA ÉPOCA Introducción: La necesidad de una Reforma Institucional - - - - - - - - - UNA PROPUESTA DE REFORMA MONETARIA PARA ARGENTINA 91 1 políticas establecidas
1 3 - - Abstract - - - 90 LIBERTAS SEGUNDA ÉPOCA Introducción: La necesidad de una Reforma Institucional - - - - - - - - - UNA PROPUESTA DE REFORMA MONETARIA PARA ARGENTINA 91 1 políticas establecidas
Inmigración Estudiar. Estudiar - Universidad. Indicar que quieres matricularte. Indicar que quieres matricularte en una asignatura.
 - Universidad Me gustaría matricularme en la universidad. Indicar que quieres matricularte Me quiero matricular. Indicar que quieres matricularte en una asignatura en un grado en un posgrado en un doctorado
- Universidad Me gustaría matricularme en la universidad. Indicar que quieres matricularte Me quiero matricular. Indicar que quieres matricularte en una asignatura en un grado en un posgrado en un doctorado
La experiencia de la Mesa contra el Racismo
 La experiencia de la Mesa contra el Racismo Informe Di icultad para identi icarse como discriminado Subsistencia de mecanismos individuales para enfrentar el racismo Las propuestas de las organizaciones
La experiencia de la Mesa contra el Racismo Informe Di icultad para identi icarse como discriminado Subsistencia de mecanismos individuales para enfrentar el racismo Las propuestas de las organizaciones
Quantum Electrodynamics
 Quantum Electrodynamics Ling-Fong Li Institute Slide_06 QED / 35 Quantum Electrodynamics Lagrangian density for QED, Equations of motion are Quantization Write L= L 0 + L int L = ψ x γ µ i µ ea µ ψ x mψ
Quantum Electrodynamics Ling-Fong Li Institute Slide_06 QED / 35 Quantum Electrodynamics Lagrangian density for QED, Equations of motion are Quantization Write L= L 0 + L int L = ψ x γ µ i µ ea µ ψ x mψ
FL/STEM Σχεδιασμός/Πρότυπο μαθήματος (χημεία) 2015/2016. Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1
 Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: 6η Αριθμός μαθητών στην τάξη: 8 Περιεχόμενο μαθήματος: Οξυγόνο. Θέμα: Άνθρωπος και φύση Ουσίες Προϋποθέσεις
Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: 6η Αριθμός μαθητών στην τάξη: 8 Περιεχόμενο μαθήματος: Οξυγόνο. Θέμα: Άνθρωπος και φύση Ουσίες Προϋποθέσεις
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Tema 3. Espazos métricos. Topoloxía Xeral,
 Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
PRUEBA INICIAL DE CLASIFICACIÓN CURSO Documento para adjuntar a la Solicitud de plaza
 PRUEBA INICIAL DE CLASIFICACIÓN CURSO 2017-18 Documento para adjuntar a la Solicitud de plaza Yo con DNI, número de teléfono y dirección de correo electrónico, solicitante del idioma, nivel, declaro bajo
PRUEBA INICIAL DE CLASIFICACIÓN CURSO 2017-18 Documento para adjuntar a la Solicitud de plaza Yo con DNI, número de teléfono y dirección de correo electrónico, solicitante del idioma, nivel, declaro bajo
Catálogodegrandespotencias
 www.dimotor.com Catálogogranspotencias Índice Motores grans potencias 3 Motores asíncronos trifásicos Baja Tensión y Alta tensión.... 3 Serie Y2 Baja tensión 4 Motores asíncronos trifásicos Baja Tensión
www.dimotor.com Catálogogranspotencias Índice Motores grans potencias 3 Motores asíncronos trifásicos Baja Tensión y Alta tensión.... 3 Serie Y2 Baja tensión 4 Motores asíncronos trifásicos Baja Tensión
M14/1/AYMGR/HP1/GRE/TZ0/XX
 M14/1/AYMGR/HP1/GRE/TZ0/XX 22142045 MODERN GREEK A: LANGUAGE AND LITERATURE HIGHER LEVEL PAPER 1 GREC MODERNE A : LANGUE ET LITTÉRATURE NIVEAU SUPÉRIEUR ÉPREUVE 1 GRIEGO MODERNO A: LENGUA Y LITERATURA
M14/1/AYMGR/HP1/GRE/TZ0/XX 22142045 MODERN GREEK A: LANGUAGE AND LITERATURE HIGHER LEVEL PAPER 1 GREC MODERNE A : LANGUE ET LITTÉRATURE NIVEAU SUPÉRIEUR ÉPREUVE 1 GRIEGO MODERNO A: LENGUA Y LITERATURA
Métodos Estadísticos en la Ingeniería
 Métodos Estadísticos e la Igeiería INTERVALOS DE CONFIANZA Itervalo de cofiaza para la media µ de ua distribució ormal co variaza coocida: X ± z α/ µ = X = X i N µ X... X m.a.s. de X Nµ Itervalo de cofiaza
Métodos Estadísticos e la Igeiería INTERVALOS DE CONFIANZA Itervalo de cofiaza para la media µ de ua distribució ormal co variaza coocida: X ± z α/ µ = X = X i N µ X... X m.a.s. de X Nµ Itervalo de cofiaza
T fi = 2πiδ(E f E i ) [< f V i > + 1 E i E n. < f V n > E i H 0 164/389
 164/389 Ο διαδότης του ηλεκτρονίου Από την μη σχετικιστική θεωρία είχαμε δει T fi = 2πiδ(E f E i ) < f V i > + < f V n > n i 1 < n V i > +... E i E n όπου H 0 n >= E n n >. Φορμαλιστικά μπορούμε να γράψουμε
164/389 Ο διαδότης του ηλεκτρονίου Από την μη σχετικιστική θεωρία είχαμε δει T fi = 2πiδ(E f E i ) < f V i > + < f V n > n i 1 < n V i > +... E i E n όπου H 0 n >= E n n >. Φορμαλιστικά μπορούμε να γράψουμε
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
 RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
Παρασκευή 1 Νοεμβρίου 2013 Ασκηση 1. Λύση. Παρατήρηση. Ασκηση 2. Λύση.
 (, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R
(, ) =,, = : = = ( ) = = = ( ) = = = ( ) ( ) = = ( ) = = = = (, ) =, = = =,,...,, N, (... ) ( + ) =,, ( + ) (... ) =,. ( ) = ( ) = (, ) = = { } = { } = ( ) = \ = { = } = { = }. \ = \ \ \ \ \ = = = = R
Jeux d inondation dans les graphes
 Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Η Ομάδα SL(2,C) και οι αναπαραστάσεις της
 SL(2, C) SO(3, 1) D : Λ D(Λ) SO(3, 1) 2 1 D : ±A D(π(±A)) SL(2, C) SL(2, C) SO(3, 1) SL(2, C) SO(3, 1) ξ i (, ) K i x µ p µ J µν T µν A µ ψ α J i = J i, () K i = K i, ( ) K i M 0i = (iξ i K i ) A i = 1
SL(2, C) SO(3, 1) D : Λ D(Λ) SO(3, 1) 2 1 D : ±A D(π(±A)) SL(2, C) SL(2, C) SO(3, 1) SL(2, C) SO(3, 1) ξ i (, ) K i x µ p µ J µν T µν A µ ψ α J i = J i, () K i = K i, ( ) K i M 0i = (iξ i K i ) A i = 1
CENTRIFUGAL AIR COOLED CONDENSERS CONDENSADORES DE AIRE CENTRÍFUGOS. GPC, GMC and GSC Series. Series GPC, GMC y GSC
 CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
Digestión de los lípidos
 Digestión de los lípidos El 90% de los lípidos de la dieta está conformado por triacilglicéridos. El 10% restante está compuesto por fosfolípidos, colesterol, ésteres de colesterol y ácidos grasos libres
Digestión de los lípidos El 90% de los lípidos de la dieta está conformado por triacilglicéridos. El 10% restante está compuesto por fosfolípidos, colesterol, ésteres de colesterol y ácidos grasos libres
Tema 1 : TENSIONES. Problemas resueltos F 1 S. n S. O τ F 4 F 2. Prof.: Jaime Santo Domingo Santillana E.P.S.-Zamora (U.SAL.
 Tea : TENSIONES S S u n S 4 O Probleas resuelos Prof: Jae Sano Dongo Sanllana EPS-Zaora (USL) - 8 -Las coponenes del esado de ensones en un puno son: N/ -5 N/ 8 N/ 4 N/ - N/ N/ Se pde deernar: ) Las ensones
Tea : TENSIONES S S u n S 4 O Probleas resuelos Prof: Jae Sano Dongo Sanllana EPS-Zaora (USL) - 8 -Las coponenes del esado de ensones en un puno son: N/ -5 N/ 8 N/ 4 N/ - N/ N/ Se pde deernar: ) Las ensones
Review of Generating functional and Green s functions
 Review of Generating functional and Green s functions Zhiguang Xiao March 26, 2017 Contents 1 Full Green s Function 2 Connected Green s function & Generating Functional 3 One particle irreducible Green
Review of Generating functional and Green s functions Zhiguang Xiao March 26, 2017 Contents 1 Full Green s Function 2 Connected Green s function & Generating Functional 3 One particle irreducible Green
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ
 ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο,
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο,
Ax = b. 7x = 21. x = 21 7 = 3.
 3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
Ταξίδι Υγεία. Υγεία - Έκτακτο περιστατικό. Υγεία - Στο γιατρό. Necesito ir al hospital. Παράκληση για μεταφορά στο νοσοκομείο. Me siento mal.
 - Έκτακτο περιστατικό Necesito ir al hospital. Παράκληση για μεταφορά στο νοσοκομείο Me siento mal. Necesito ver a un doctor inmediatamente! Παράκληση για άμεση γιατρική φροντίδα Ayuda! Έκκληση για άμεση
- Έκτακτο περιστατικό Necesito ir al hospital. Παράκληση για μεταφορά στο νοσοκομείο Me siento mal. Necesito ver a un doctor inmediatamente! Παράκληση για άμεση γιατρική φροντίδα Ayuda! Έκκληση για άμεση
 γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
γ 1 6 M = 0.05 F M = 0.05 F M = 0.2 F M = 0.2 F M = 0.05 F M = 0.05 F M = 0.05 F M = 0.2 F M = 0.05 F 2 2 λ τ M = 6000 M = 10000 M = 15000 M = 6000 M = 10000 M = 15000 1 6 τ = 36 1 6 τ = 102 1 6 M = 5000
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS. 3. Cal é o vector de posición da orixe de coordenadas O? Cales son as coordenadas do punto O?
 EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
LUGARES XEOMÉTRICOS. CÓNICAS
 LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
Metrología Cuántica e Información Cuántica de Fisher.
 Metrología Cuántica e Información Cuántica de Fisher. Entrelazamiento y Distinguibilidad en Interferometría Atómica. Diego Alejandro Lancheros Seminario de Óptica Cuántica. Universidad de Los Andes. Table
Metrología Cuántica e Información Cuántica de Fisher. Entrelazamiento y Distinguibilidad en Interferometría Atómica. Diego Alejandro Lancheros Seminario de Óptica Cuántica. Universidad de Los Andes. Table
Ó³ Ÿ , º 7(156).. 62Ä69. Š Œ œ ƒˆˆ ˆ ˆŠ. .. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ 2. μ ± Ê É É Ê Ò μ μ, Œμ ±
 Ó³ Ÿ. 009.. 6, º 7(156.. 6Ä69 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŒ ˆ - ˆ ƒ ˆ ˆ ˆŸ Š -Œ ˆ Šˆ ˆ.. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ μ ± Ê É É Ê Ò μ μ, Œμ ± É ÉÓ μ Ò ÕÉ Ö ²μ Í Ò - μ Ò ² É Ö ³ ÖÉÓ Ì ÒÎ ² ÖÌ, μ²ó ÊÕÐ Ì ±μ ± 4- μ Ò. This paper
Ó³ Ÿ. 009.. 6, º 7(156.. 6Ä69 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŒ ˆ - ˆ ƒ ˆ ˆ ˆŸ Š -Œ ˆ Šˆ ˆ.. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ μ ± Ê É É Ê Ò μ μ, Œμ ± É ÉÓ μ Ò ÕÉ Ö ²μ Í Ò - μ Ò ² É Ö ³ ÖÉÓ Ì ÒÎ ² ÖÌ, μ²ó ÊÕÐ Ì ±μ ± 4- μ Ò. This paper
PAU XUÑO 2010 MATEMÁTICAS II
 PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ
 Ó³ Ÿ. 2018.. 15, º 6218).. 467Ä475 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μ± μ, ÎÉμ ³μ Ë ± Í Ö ³³ É Î ±μ, μ ² μ μ ƒ ²Ó ÉÊ μ² μ ²μÉ μ É É μ Ô -
Ó³ Ÿ. 2018.. 15, º 6218).. 467Ä475 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μ± μ, ÎÉμ ³μ Ë ± Í Ö ³³ É Î ±μ, μ ² μ μ ƒ ²Ó ÉÊ μ² μ ²μÉ μ É É μ Ô -
(2), ,. 1).
 178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
.1. 8,5. µ, (=,, ) . Ρ( )... Ρ( ).
 ΡΧΗ 1Η Ε ε Γ Α Ο ΗΡ Ε Ε Ε Ε Η Ε Ο Ε Ο Ε Η 14 Ο Ο 2001 Ε Ε Ο Ε Ο Η Ε Η εε : Η Ο ΧΕ Η Ο Ο Ε εά : Ε (6) Ε Α 1ο Α.1. π µ µ ά : Ρ ( ) = Ρ ( ) Ρ ( ). 8,5 Α.2. µ π µπ µ π µ µ, (=,, ) : Ρ ( )... 1 Ρ( ) 2 Ρ( )...
ΡΧΗ 1Η Ε ε Γ Α Ο ΗΡ Ε Ε Ε Ε Η Ε Ο Ε Ο Ε Η 14 Ο Ο 2001 Ε Ε Ο Ε Ο Η Ε Η εε : Η Ο ΧΕ Η Ο Ο Ε εά : Ε (6) Ε Α 1ο Α.1. π µ µ ά : Ρ ( ) = Ρ ( ) Ρ ( ). 8,5 Α.2. µ π µπ µ π µ µ, (=,, ) : Ρ ( )... 1 Ρ( ) 2 Ρ( )...
Inmigración Documentos
 - General Πού μπορώ να βρω τη φόρμα για ; Pedir un formulario Πότε εκδόθηκε το [έγγραφο] σας; Pedir la fecha de expedición de un documento Πού εκδόθηκε το [έγγραφο] σας; Pedir el lugar de expedición de
- General Πού μπορώ να βρω τη φόρμα για ; Pedir un formulario Πότε εκδόθηκε το [έγγραφο] σας; Pedir la fecha de expedición de un documento Πού εκδόθηκε το [έγγραφο] σας; Pedir el lugar de expedición de
Inmigración Documentos
 - General Dónde tengo que pedir el formulario/impreso para? Pedir un formulario Cuál es la fecha de expedición de su (documento)? Pedir la fecha de expedición de un documento Cuál es el lugar de expedición
- General Dónde tengo que pedir el formulario/impreso para? Pedir un formulario Cuál es la fecha de expedición de su (documento)? Pedir la fecha de expedición de un documento Cuál es el lugar de expedición
Περιεχόμενα. A(x 1, x 2 )
 Περιεχόμενα A(x 1, x 2 7 Ολοκληρώματα της Μαγνητοϋδροδυναμικής και Μαγνητοϋδροδυναμικά Κύματα Σχήμα 7.1: Οι τριδιάστατες ελικοειδείς μαγνητικές γραμμές στις οποίες εφάπτεται το διάνυσμα του μαγνητικού
Περιεχόμενα A(x 1, x 2 7 Ολοκληρώματα της Μαγνητοϋδροδυναμικής και Μαγνητοϋδροδυναμικά Κύματα Σχήμα 7.1: Οι τριδιάστατες ελικοειδείς μαγνητικές γραμμές στις οποίες εφάπτεται το διάνυσμα του μαγνητικού
PROPIEDADES Y APLICACIONES DE LA FAMILIA DE DISTRIBUCIONES SKEW-NORMAL MULTIVARIADA
 PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICA DEPARTAMENTO DE ESTADÍSTICA PROPIEDADES Y APLICACIONES DE LA FAMILIA DE DISTRIBUCIONES SKEW-NORMAL MULTIVARIADA POR GABRIELA VALDÉS Tesis
PONTIFICIA UNIVERSIDAD CATÓLICA DE CHILE FACULTAD DE MATEMÁTICA DEPARTAMENTO DE ESTADÍSTICA PROPIEDADES Y APLICACIONES DE LA FAMILIA DE DISTRIBUCIONES SKEW-NORMAL MULTIVARIADA POR GABRIELA VALDÉS Tesis
Negocios Carta. Carta - Dirección
 - Dirección Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Formato de dirección
- Dirección Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Mr. J. Rhodes Rhodes & Rhodes Corp. 212 Silverback Drive California Springs CA 92926 Formato de dirección
MATRICES DE TRANSFORMACION DE COORDENADAS. 3D. ü INCLUDES. ü Cálculo de las componentes de la Matriz de rotación de tensiones (3-3)
 MATRICES DE TRANSFORMACION DE COORDENADAS. 3D ü INCLUDES In[298]:= In[301]:= In[302]:= In[303]:= Off@General::"spell"D; Off@General::"spell1"D; Off@Set::"wrsm"D; Needs@"LnearAlgebra`MatrxManpulaton`"D
MATRICES DE TRANSFORMACION DE COORDENADAS. 3D ü INCLUDES In[298]:= In[301]:= In[302]:= In[303]:= Off@General::"spell"D; Off@General::"spell1"D; Off@Set::"wrsm"D; Needs@"LnearAlgebra`MatrxManpulaton`"D
Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid. La Red de Bibliotecas de Obra Social Caja Madrid
 Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid La Red de Bibliotecas de Obra Social Caja Madrid Το ίκτυο Βιβλιοθηκών αποτελεί τµήµα ενός Χρηµατοπιστωτικού Φορέα που προορίζει ποσοστό
Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid La Red de Bibliotecas de Obra Social Caja Madrid Το ίκτυο Βιβλιοθηκών αποτελεί τµήµα ενός Χρηµατοπιστωτικού Φορέα που προορίζει ποσοστό
Ταξίδι Γενικά. Γενικά - Τα απαραίτητα. Γενικά - Συνομιλία. Παράκληση για βοήθεια. Ερώτηση σε πρόσωπο αν μιλά αγγλικά
 - Τα απαραίτητα Podría ayudarme? Παράκληση για βοήθεια Habla inglés? Ερώτηση σε πρόσωπο αν μιλά αγγλικά Habla_[idioma]_? Ερώτηση σε πρόσωπο αν μιλά ορισμένη γλώσσα No hablo_[idioma]_. Διασαφήνιση ότι δεν
- Τα απαραίτητα Podría ayudarme? Παράκληση για βοήθεια Habla inglés? Ερώτηση σε πρόσωπο αν μιλά αγγλικά Habla_[idioma]_? Ερώτηση σε πρόσωπο αν μιλά ορισμένη γλώσσα No hablo_[idioma]_. Διασαφήνιση ότι δεν
Dark matter from Dark Energy-Baryonic Matter Couplings
 Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010
Dark matter from Dark Energy-Baryonic Matter Coulings Alejandro Avilés 1,2 1 Instituto de Ciencias Nucleares, UNAM, México 2 Instituto Nacional de Investigaciones Nucleares (ININ) México January 10, 2010
TEMA 6.- BIOMOLÉCULAS ORGÁNICAS IV: ÁCIDOS NUCLEICOS
 TEMA 6.- BIMLÉCULAS RGÁNICAS IV: ÁCIDS NUCLEICS A.- Características generales de los Ácidos Nucleicos B.- Nucleótidos y derivados nucleotídicos El esqueleto covalente de los ácidos nucleicos: el enlace
TEMA 6.- BIMLÉCULAS RGÁNICAS IV: ÁCIDS NUCLEICS A.- Características generales de los Ácidos Nucleicos B.- Nucleótidos y derivados nucleotídicos El esqueleto covalente de los ácidos nucleicos: el enlace
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
 d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 5 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página PARA EMPEZAR, REFLEXIONA Y RESUELVE. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora:
5 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página PARA EMPEZAR, REFLEXIONA Y RESUELVE. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora:
Tema 7. Glúcidos. Grados de oxidación del Carbono. BIOQUÍMICA-1º de Medicina Dpto. Biología Molecular Isabel Andrés. Alqueno.
 Tema 7. Glúcidos. Funciones biológicas. Monosacáridos: nomenclatura y estereoisomería. Pentosas y hexosas. Disacáridos. Enlace glucídico. Polisacáridos de reserva: glucógeno y almidón. Polisacáridos estructurales:
Tema 7. Glúcidos. Funciones biológicas. Monosacáridos: nomenclatura y estereoisomería. Pentosas y hexosas. Disacáridos. Enlace glucídico. Polisacáridos de reserva: glucógeno y almidón. Polisacáridos estructurales:
Physics 582, Problem Set 2 Solutions
 Physics 582, Problem Set 2 Solutions TAs: Hart Goldman and Ramanjit Sohal Fall 2018 Symmetries and Conservation Laws In this problem set we return to a study of scalar electrodynamics which has the Lagrangian
Physics 582, Problem Set 2 Solutions TAs: Hart Goldman and Ramanjit Sohal Fall 2018 Symmetries and Conservation Laws In this problem set we return to a study of scalar electrodynamics which has the Lagrangian
μέλλων τελευτᾶν 0,25 puntos καὶ βουλόμενος 0,25 puntos τοὺς αὐτοῦ παῖδας ἐμπείρους εἶναι τῆς γεωργίας, 0,5 puntos
 Materia: GRIEGO II. EvAU CURSO 17/18 CRITERIOS ESPECÍFICOS DE CORRECCIÓN PROPUESTA A: EL LABRADOR Y SUS HIJOS 1.- Traducción íntegra del texto: (4 puntos). Se ponderará, ante todo: - La recta adecuación
Materia: GRIEGO II. EvAU CURSO 17/18 CRITERIOS ESPECÍFICOS DE CORRECCIÓN PROPUESTA A: EL LABRADOR Y SUS HIJOS 1.- Traducción íntegra del texto: (4 puntos). Se ponderará, ante todo: - La recta adecuación
MÉTHODES ET EXERCICES
 J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
J.-M. MONIER I G. HABERER I C. LARDON MATHS PCSI PTSI MÉTHODES ET EXERCICES 4 e édition Création graphique de la couverture : Hokus Pokus Créations Dunod, 2018 11 rue Paul Bert, 92240 Malakoff www.dunod.com
FORMULARIO DE ELASTICIDAD
 U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
Lectures on Quantum sine-gordon Models
 Lectures on Quantum sine-gordon Models Juan Mateos Guilarte, Departamento de Física Fundamental (Universidad de Salamanca IUFFyM (Universidad de Salamanca Universidade Federal de Matto Grosso Cuiabá, Brazil,
Lectures on Quantum sine-gordon Models Juan Mateos Guilarte, Departamento de Física Fundamental (Universidad de Salamanca IUFFyM (Universidad de Salamanca Universidade Federal de Matto Grosso Cuiabá, Brazil,
Conditions aux bords dans des theories conformes non unitaires
 Conditions aux bords dans des theories conformes non unitaires Jerome Dubail To cite this version: Jerome Dubail. Conditions aux bords dans des theories conformes non unitaires. Physique mathématique [math-ph].
Conditions aux bords dans des theories conformes non unitaires Jerome Dubail To cite this version: Jerome Dubail. Conditions aux bords dans des theories conformes non unitaires. Physique mathématique [math-ph].
Γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού χρονών - σύνολο
 πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση του αριθμού του οικονομικά ενεργού
πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση του αριθμού του οικονομικά ενεργού
Higgs decay to two gluons
 Higgs ecay to two gluons Eleftherios Moschanreou (a) The ecay rate An unstable particle has a probability to ecay to a certain number of final states uring a given time interval. The process of ecaying
Higgs ecay to two gluons Eleftherios Moschanreou (a) The ecay rate An unstable particle has a probability to ecay to a certain number of final states uring a given time interval. The process of ecaying
Άσκηση 2.1 Να σχεδιαστεί το διάγραµµα ροής πρωτοβάθµιας εξίσωσης της µορφής:
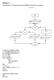 Άσκηση 2.1 Να σχεδιαστεί το διάγραµµα ροής πρωτοβάθµιας εξίσωσης της µορφής: y = bx+ c Αρχή εµφάνισε " ώσε τιµές στα b,cι διάβασε b,c b=0 c=0 x=-c/b εµφάνισε A ΥΝΑΤΗ εµφάνισε AOPIΣΤΗ εµφάνισε Λύση x=:,x
Άσκηση 2.1 Να σχεδιαστεί το διάγραµµα ροής πρωτοβάθµιας εξίσωσης της µορφής: y = bx+ c Αρχή εµφάνισε " ώσε τιµές στα b,cι διάβασε b,c b=0 c=0 x=-c/b εµφάνισε A ΥΝΑΤΗ εµφάνισε AOPIΣΤΗ εµφάνισε Λύση x=:,x
 K K 1 2 1 K M N M(2 N 1) K K K K K f f(x 1, x 2,..., x K ) = K f xk (x k ), x 1, x 2,..., x K K K K f Yk (y k x 1, x 2,..., x k ) k=1 M i, i = 1, 2 Xi n n Yi n Xn 1 Xn 2 ˆM i P (n) e = {( ˆM 1, ˆM2 )
K K 1 2 1 K M N M(2 N 1) K K K K K f f(x 1, x 2,..., x K ) = K f xk (x k ), x 1, x 2,..., x K K K K f Yk (y k x 1, x 2,..., x k ) k=1 M i, i = 1, 2 Xi n n Yi n Xn 1 Xn 2 ˆM i P (n) e = {( ˆM 1, ˆM2 )
Γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού - σύνολο
 απασχολούμενου πληθυσμού - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού υπολογίζεται με τη διαίρεση του αριθμού του ισοδύναμου πλήρως
απασχολούμενου πληθυσμού - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού υπολογίζεται με τη διαίρεση του αριθμού του ισοδύναμου πλήρως
Γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού χρονών - σύνολο
 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Ο γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση της ετήσιας αύξησης του οικονομικά ενεργού πληθυσμού
15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Ο γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση της ετήσιας αύξησης του οικονομικά ενεργού πληθυσμού
ECONOMIA MONETARIA (parte generale) Prof. Guido Ascari LEZIONE 3 LA DOMANDA DI MONETA
 ECONOMIA MONETARIA (parte generale) Prof. Guido Ascari Anno 2006-2007 2007 LEZIONE 3 LA DOMANDA DI MONETA LA DOMANDA DI MONETA Teoria Macro Micro Th.Quantitativa Th.. Keynesiana => Keynes, Tobin Th. Friedman
ECONOMIA MONETARIA (parte generale) Prof. Guido Ascari Anno 2006-2007 2007 LEZIONE 3 LA DOMANDA DI MONETA LA DOMANDA DI MONETA Teoria Macro Micro Th.Quantitativa Th.. Keynesiana => Keynes, Tobin Th. Friedman
ΠΡΟΣ: ΚΟΙΝ.: συγκρότηση Επιτροπής για την επιλογή ελευθέρων βοηθηµάτων Ισπανικής γλώσσας
 ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ----- ΕΝΙΑΙΟΣ ΙΟΙΚΗΤΙΚΟΣ ΤΟΜΕΑΣ Π/ΘΜΙΑΣ & /ΘΜΙΑΣ ΕΚΠΑΙ ΕΥΣΗΣ /ΝΣΗ ΣΠΟΥ ΩΝ /ΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΤΜΗΜΑ Α Βαθµός Ασφαλείας: Να διατηρηθεί
ΕΛΛΗΝΙΚΗ ΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ, ΠΟΛΙΤΙΣΜΟΥ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ----- ΕΝΙΑΙΟΣ ΙΟΙΚΗΤΙΚΟΣ ΤΟΜΕΑΣ Π/ΘΜΙΑΣ & /ΘΜΙΑΣ ΕΚΠΑΙ ΕΥΣΗΣ /ΝΣΗ ΣΠΟΥ ΩΝ /ΘΜΙΑΣ ΕΚΠ/ΣΗΣ ΤΜΗΜΑ Α Βαθµός Ασφαλείας: Να διατηρηθεί
4. Απαγορεύεται η χρήση υπολογιστή χειρός. Απαγορεύεται η χρήση κινητού, και ως υπολογιστή χειρός.
 ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΙΘΑΝΟΤΗΤΕΣ, ΙΩΑΝΝΗΣ ΚΟΝΤΟΓΙΑΝΝΗΣ, ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ, ΙΟΥΝΙΟΣ 207 ΟΝΟΜΑ ΦΟΙΤΗΤΗ:.............................. Οδηγίες. Συμπληρώστε το όνομά
ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ, ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΙΘΑΝΟΤΗΤΕΣ, ΙΩΑΝΝΗΣ ΚΟΝΤΟΓΙΑΝΝΗΣ, ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ, ΙΟΥΝΙΟΣ 207 ΟΝΟΜΑ ΦΟΙΤΗΤΗ:.............................. Οδηγίες. Συμπληρώστε το όνομά
Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage
 Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage José Marconi Rodrigues To cite this version: José Marconi Rodrigues. Transfert sécurisé d Images par combinaison
Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage José Marconi Rodrigues To cite this version: José Marconi Rodrigues. Transfert sécurisé d Images par combinaison
2 ÍNDICE GENERAL A Modelo de Wess Zumino Witten. 109 A.1 Propiedades del modelo de WZW B Orden normal y relaciones entre OP
 Índice General 1 Introducción. 3 2 Teor as masivas y ecuaciones de Toda no abelianas. 11 2.1 Ecuaciones de Toda no abelianas....................... 11 2.2 Teor as con acción real y positiva.......................
Índice General 1 Introducción. 3 2 Teor as masivas y ecuaciones de Toda no abelianas. 11 2.1 Ecuaciones de Toda no abelianas....................... 11 2.2 Teor as con acción real y positiva.......................
Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού χρονών - σύνολο
 Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών υπολογίζεται με
Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών υπολογίζεται με
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή ελληνικά Αξιότιμε κύριε Πρόεδρε, ισπανικά Distinguido Sr. Presidente: Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του
- Εισαγωγή ελληνικά Αξιότιμε κύριε Πρόεδρε, ισπανικά Distinguido Sr. Presidente: Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του
ε x = du dx ε(x) = ds ds = du(x) dx
 Capítulo 8 ECUCIONES DIFERENCIES Cálculo de desplazamientos Dr. Fernando Flores 8.. INTRODUCCIÓN En este capítulo se sistematizan las ecuaciones que gobiernan el comportamiento de vigas. En general se
Capítulo 8 ECUCIONES DIFERENCIES Cálculo de desplazamientos Dr. Fernando Flores 8.. INTRODUCCIÓN En este capítulo se sistematizan las ecuaciones que gobiernan el comportamiento de vigas. En general se
Ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο
 οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών υπολογίζεται με τη διαίρεση
οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών υπολογίζεται με τη διαίρεση
Œ ƒ ˆ ˆˆ. Î ± É ÉÊÉ ³..., Œµ ± ˆ ˆˆ Œ ƒ ˆ ˆˆ 1051 Ð ³ Î Ö 1051 Î ± Ö É Í Ö 1059
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2002.. 33.. 5 Š 530.145 Œ ˆ Œ ˆ Œ ƒ ˆ ˆˆ.. Œ µ µ Î ± É ÉÊÉ ³..., Œµ ± ˆ ˆˆ Œ ƒ ˆ ˆˆ 1051 Ð ³ Î Ö 1051 Î ± Ö É Í Ö 1059 µ ³µÉ Í Ö µéò 1070 ˆ Š Œ ˆ Œ ˆ 1077 ³ ɵ µ µ³ É Î Ö ³µ ²Ó 1078 ³
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2002.. 33.. 5 Š 530.145 Œ ˆ Œ ˆ Œ ƒ ˆ ˆˆ.. Œ µ µ Î ± É ÉÊÉ ³..., Œµ ± ˆ ˆˆ Œ ƒ ˆ ˆˆ 1051 Ð ³ Î Ö 1051 Î ± Ö É Í Ö 1059 µ ³µÉ Í Ö µéò 1070 ˆ Š Œ ˆ Œ ˆ 1077 ³ ɵ µ µ³ É Î Ö ³µ ²Ó 1078 ³
ΕΡΓΑΣΤΗΡΙΟ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ Η/Υ
 ΕΡΓΑΣΤΗΡΙΟ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ Η/Υ 4 ο Εξάμηνο Μαδεμλής Ιωάννης MSc Ηλεκτρονικός Φυσικός Αντικείμενο: ΠΡΟΦΙΛ ΜΑΘΗΜΑΤΟΣ Προγραμματισμός σε γλώσσα Assembly Σκοπός: Γνώση της assembly από τους απόφοιτους του τμήματος
ΕΡΓΑΣΤΗΡΙΟ ΑΡΧΙΤΕΚΤΟΝΙΚΗΣ Η/Υ 4 ο Εξάμηνο Μαδεμλής Ιωάννης MSc Ηλεκτρονικός Φυσικός Αντικείμενο: ΠΡΟΦΙΛ ΜΑΘΗΜΑΤΟΣ Προγραμματισμός σε γλώσσα Assembly Σκοπός: Γνώση της assembly από τους απόφοιτους του τμήματος
SPECIAL FUNCTIONS and POLYNOMIALS
 SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
F (x) = kx. F (x )dx. F = kx. U(x) = U(0) kx2
 F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
F (x) = kx x k F = F (x) U(0) U(x) = x F = kx 0 F (x )dx U(x) = U(0) + 1 2 kx2 x U(0) = 0 U(x) = 1 2 kx2 U(x) x 0 = 0 x 1 U(x) U(0) + U (0) x + 1 2 U (0) x 2 U (0) = 0 U(x) U(0) + 1 2 U (0) x 2 U(0) =
f(z) 1 + z a lim f (n) (0) n! = 1
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 3η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Υποθέτουμε ότι η f : C C είναι ακέραια συνάρτηση και ότι το όριο Αποδείξτε ότι η f είναι σταθερή.
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 3η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Υποθέτουμε ότι η f : C C είναι ακέραια συνάρτηση και ότι το όριο Αποδείξτε ότι η f είναι σταθερή.
TEST DE INDEPENDENCIA EN SERIES TEMPORALES
 TEST DE INDEPENDENCIA EN SERIES TEMPORALES Titulación: Doctorado en Tecnologías Industriales Alumno/a: Salvador Vera Nieto Director/a/s: José Salvador Cánovas Peña Antonio Guillamón Frutos Cartagena, 10
TEST DE INDEPENDENCIA EN SERIES TEMPORALES Titulación: Doctorado en Tecnologías Industriales Alumno/a: Salvador Vera Nieto Director/a/s: José Salvador Cánovas Peña Antonio Guillamón Frutos Cartagena, 10
υ η µ η. υ η µ υµ η υ υ υ µ υ η µ η υ. µ υ υ υ η ω µ ω µ υ η ω υ µ υ ω ω ω η ω ω., ω ω,, % #" ".µ, & ". 0, # #'
 - 1 - µ µ 1 µ µ" # 2 µ %& µ "' (µ 2 µ %& µ "' ( &% ) 3 µ %µ,, υ η µ η. υµ υ υµ ηµ υµ υ υ η µ υµ η υ υ υ µ υ η µ η υ. µ υ υ υ η ω µ ω µ υ η ω υ ω η υµ ω η υ., µ υµ µ υ ω ω ω η ω ω., ω ω ω, µω µ η µ η η
- 1 - µ µ 1 µ µ" # 2 µ %& µ "' (µ 2 µ %& µ "' ( &% ) 3 µ %µ,, υ η µ η. υµ υ υµ ηµ υµ υ υ η µ υµ η υ υ υ µ υ η µ η υ. µ υ υ υ η ω µ ω µ υ η ω υ ω η υµ ω η υ., µ υµ µ υ ω ω ω η ω ω., ω ω ω, µω µ η µ η η
Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
 Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο
 Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το μερίδιο εργοδοτουμένων με μερική ή/και προσωρινή απασχόληση
Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το μερίδιο εργοδοτουμένων με μερική ή/και προσωρινή απασχόληση
MICROMASTER Vector MIDIMASTER Vector
 s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
s MICROMASTER Vector MIDIMASTER Vector... 2 1.... 4 2. -MICROMASTER VECTOR... 5 3. -MIDIMASTER VECTOR... 16 4.... 24 5.... 28 6.... 32 7.... 54 8.... 56 9.... 61 Siemens plc 1998 G85139-H1751-U553B 1.
Council of the European Union Brussels, 24 October 2014
 Council of the European Union Brussels, 24 October 2014 Interinstitutional File: 2010/0278 (COD) 14384/14 JUR 727 ECOFIN 924 UEM 333 CODEC 2035 LEGISLATIVE ACTS AND OTHER INSTRUMENTS: CORRIGENDUM/RECTIFICATIF
Council of the European Union Brussels, 24 October 2014 Interinstitutional File: 2010/0278 (COD) 14384/14 JUR 727 ECOFIN 924 UEM 333 CODEC 2035 LEGISLATIVE ACTS AND OTHER INSTRUMENTS: CORRIGENDUM/RECTIFICATIF
