1. K a p itu lu a. Zenb a ki ko np lex u a k
|
|
|
- Ἱερεμίας Καλάρης
- 6 χρόνια πριν
- Προβολές:
Transcript
1 1. K a p itu lu a Zeb a ki ko p lex u a k 1
2 1. K A P IT U L U A Z E N B A K I K O N P L E X U A K 1.1 Z e b a ki ko p le x u a re ko tzep tu a. Iku s d itza g u a d ibid e ba tzu k o a g ertze d e ze ba ki ko p lex u a k d efi itzeko beh a rra Ad ib id e a y 1 = x p a ra bola eta y = 3x zu ze a re a rteko eba kid u ra ka lku la tu a h i d u g u (iku s 1.1 iru d ia ). 1.1 iru d ia 1.1 Iru d ia : O d ore g o sistema eba tziz { y = x x = 3x y = 3x { x 1 = 1 x = esa a h i fi sikoa d u e era tzu a lortze d u g u o ema itza N R mu ltzoa d a g oe. 1.. Ad ib id e a Ko tsid era d eza g u esp a zio/ d e bora erla zioa eza rtze d u e o d ore g o ku r- ba E = { 0 t < 0 ba d a t t 0 ba d a (iku s 1. iru d ia ) t 1 -re zer u eta eg ite d ira metro? Ka su h o eta ere esa a h i fi sikoa d u e era tzu a lortze d a eta ema itza R mu ltzoa d a g o. H a u d a : t 1 = t 1 = R Z er lortze d a E = 0.5 metro d e ea? t = 0.5 t = 0.5 Q R U E P D o o stia M ate m atik a Ap lik atu a S aila
3 1.1. ZENBAKI KONPLEXUAR EN KONTZEPTUA Irudia: 1.3. Adibidea P ilota bat v 0 abiaduraz goratz botatze dugu. Iza bedi h(t) t uea lortutako altuera. Ordua odorego ekuazioa idatz dezakegu: h = g t + v 0t = t (v 0 g ) t Adierazpe fisikoa dute problema batzuk platea dezakegu (ikus 1.3 irudia) 1.3 Irudia: Zer ueta lotze da H altuera? t 1 = v 0 g, H = h(t 1) uea. Zer ueta lortuko da h 1 altuera?.(0 h 1 H) t = v 0 ± { v0 gh 1 t = g t = t 3 H = v 0 g t 3
4 4 1. KAPITULUA ZENBAKI KONPLEXUAK Adibidez: Har ditzagu h 1 = 0. m, v 0 = 3 m/ s. Ordua: t = 0.07, t 3 = 0.53 t 1 = v 0 g = 0.31, H = v 0 g = Problema hoe soluzioak R multzoa adieraz ditzakegu (ikus 1.4 irudia) 1.4 Irudia: Ikus ditzagu orai aurrekoe atzekoak dire odorego gertaerak: (ikus 1.5 irudia) 1.5 Irudia: { y = x y = x 1 x = x 1 x = 1 ± 3
5 1.1. ZENBAKI KONPLEXUAREN KONTZEPTUA Irudia: 3?. Zer da hau?. N o kokatze dugu zuze errealea?(ikus 1.6 irudia) t = 3 z = 3 z / R Pilotare kasua: Zer ueta lortze da h 1?(ikus 1.7 irudia) 1.7 Irudia: z = v 0 ± v 0 gh g, H = v 0 g h > H ba d a h > v 0 g gh > v 0 Hau da v0 gh < 0 berriz zebaki egatibo bate erroa!! o dago v0 gh? Adibidez: h = 5 v 0 = 3, v 0 gh = 8 4 N ola adieraz dezaket zebaki hau? Zertarako erabil dezaket?
6 6 1. KAPITULUA ZENBAKI KONPLEXUAK E bakidurare adibidea: x = 1 ± 3 = 1 ± ( 1)(3) = 1 ± 1 3 = 1 ± 3 1 Arazoak sortze due zebaki bakarra 1 da gaiotzekoak zebaki errealak direlako. 1 = iera adierazte badugu (i = 1): 1 3 ola adieraziko dugu + 1 adibidez?. (Ikus 1.8 irudia) 1.8 Irudia: z = a + b i o a = Re(z) = z-re zati erreala de b = Im(z) = z-re zati irudikaria de 1.1. Defi iz ioa Zebaki ko p lexu are m u ltzoa o d o rego era d efi itu ko d u gu : C = {z = a + b i /a, b R} beraz R = {z = a + b i/a R, b = 0} era adierazte de. B eraz, zebaki errealak zati irudikaria ulua dute zebaki koplexuak dira.
7 1.. Z C ZENBAKIAREN ERA POLARRA Irudia: 1. z C zebakiare era polarra z zebaki koplexua bektore bat deez odorego era adieraz daiteke(ikus 1.9 irudia) z = a + b i ρ θ o ρ = z-re modulua = z θ = z-re argumetua = ar g(z) a = 0 eta b > 0 badira θ = π Adibidez: z = 0 + i = 1 π z = 1 i = π = 7π (ikus irud ia ) O rokorrea : Irud ia : ρ θ = ρ θ+kπ k Z P la oa re g a i eko p u tu berbera a d iera zte d ute.θ ed o θ+kπ a p lika tzea lortuta ko efecto fi sikoa oso d esberd i a iza d a iteke ord ea : (ikus irud ia ) Matematika A p likatu a S aila U E P D o o stia
8 8 1. K A P IT U L U A Z E N B A K I K O N P L E X U A K 1.11 Irudia: 1.. Defi iz ioa 0 θ < π deea, θ-ri a rgu m etu a gu sia deitu ko diogu. Adibidez, z = 31 π = π = 6π+ π = π π 5 = z-re argum etu agusia (ikus 1.1 irudia) 1.1 Irudia: 1.3 z C ze b a k ia re e ra e sp o e tzia la. Iza bedi z = a + b i = ρ θ o a = ρ co s θ b = ρ si θ de z = ρ co s θ + i si θ = ρ( co s θ + i si θ)
9 1.3. Z C ZENBAKIAR EN ER A ES PONENTZIALA eta 4. gaieta sakokiago aztertuko dugu kotzeptu erabiliko dugu: cos x = 1 x! + x4 4! x6 6! + x8 8! x1 0 10! + x R si x = x x3 3! + x5 5! x7 7! + x9 9! x1 1 11! + x R e x = 1 + x 1! + x! + x3 3! + x4 4! + x5 5! + x R Aurreko berditzak ifiitu gaie baturareki lortze de arre gero eta batugai gehiago hartuz hurbilketa hobeagoak lor ditzakegu. (Ikus 1.13 irudia) Adibidez: e x 1, e x 1 + x, e x 1 + x + x, etb Irudia: B este aldetik, i = 1, i = 1, i 3 = i, i 4 = 1, i 5 = i eta errepikatze dira.
10 10 1. KAPITULUA ZENBAKI KONPLEXUAK E matza hauek erabiliz: z = ρ(cos θ + i si θ) = ρ = ρ (1 + ( iθ) + ( iθ)4! 4! = ρ (1 + iθ + ( iθ)! Adibidez: z = 0 + i = 1 π = e i π ) ((1 θ! + θ4 4! θ6 6! + + i (θ θ3 3! + θ5 + ( iθ)6 6! + ( iθ)3 3! e iπ = 0 π + i si π = 1 < iθ + ( iθ)3 3! + ( iθ)4 4! + ( iθ)5 5! 5! θ7 )) 7! + = ) ordeatuz = + ( iθ)5 + ( iθ)7 + 5! 7! ) + = ρ e iθ z-re era espoetziala E ziezkoa da hau gertatzea R-, e x > 0 x R. e z = 1 bete daiteke ordea z C bada. Bereziki, ρ = 1, bad a e iθ = cos θ + si θ Euler-e formula deritzoa lortze da. L aister ikusiko ditugu zebaki koplex ue arteko eragiketa aritmetikoak, hala ere, aurrera dezakegu zebaki koplex ue biderkaketa oso erraz kalkula daitekela era espoetziala erabilita. H ots: ρ e iθ ρ e iθ = ρρ e iθ+iθ = ρρ e i(θ+θ ) beraz ρ θ ρ θ = ρρ θ+θ ρ θ ρ θ Bereziki: Ordua zatiketa: = ρ e iθ ρ e iθ = ρ ρ eiθ iθ = ρ ρ ei(θ θ ) = ρ θ 1 θ = ρ θ+θ ( ) ρ ρ θ θ 1 θ -z biderkaketak biraketa bat adierazte du o agelua θ eta zetroa koordeatu jatorria dire. (Ikus 1.14 eta 1.15 irudiak) Adibidea: Irudiari θ = π 3 biraketa eta eskalatua ρ = 0.5 (Ikus 1.15 irudia) z 1 = 1 + i = 1 π 4 ; z = 3 + i = 10 a rctg ; z 3 = + 6i = 40 a rctg z 1 = z π = (cos 1.83+i si 1.83) 0.5( i) = i
11 1.3. Z C ZENBAKIAREN ERA ESPONENTZIALA Irudia: 1.15 Irudia: z = z 0.5 π = (cos 1.37+i si 1.37) 1.58( i) = i z 3 = z π = (cos.3+i si.3) 3.17( i) =.1+.34i (ikus 1.16 irudia) Adibidea: Odorego irudiari ρ θ = π biraketa eta eskalatua aplikatu:(ikus 1.17 irudia) z 1 = 1 + i = π 4, z = + i = 5 arctg 1 z 1 = z 1 π = π 4 + π = 5π π 4
12 1 1. KAPITULUA ZENBAKI KONPLEXUAK 1.16 Irudia: z = z π = 5 arctg 1 π = 5 arctg 1 + π Ikus 1.18 irudia 4.48, Defiizioa z = ρ θ zebaki koplexuare kojokatua z = z odorego era defi itutako zebaki koplxeua da: z = ρ θ. (Ikus irudia) Propietatea: z z = ρ 0 = ρ R 1.1. Ariketa Eutziatu bete behar dire balditzak bi zebaki koplexu berdiak iza daiteze. Eb azpea Eragike tak C mu ltzo a Batura: (a + bi) + (a + b i) = (a + a ) + (b + b )i Bid erk ad ura: ρ θ ρ θ = ρ e iθ ρ e iθ = ρρ e i(θ+θ ) = ρρ θ+θ UEP D o o stia M ate m atik a A p lik atu a S aila
13 1.3. Z C Z E N B A K IA R E N E R A E S P O N E N T Z IA L A Irudia: D em ag u ze baki ko p lex uak era bi om ikoa idatzita daudela, h au da: z 1 = ρ θ = a + bi, z = ρ θ = a + b i z 1 z = A + Bi era idazte dadug u zei tzu dira A eta B-re balioak? z 1 z =ρρ θ+θ ρρ ( co s(θ + θ ) + i si (θ + θ ) ) = =ρρ ( co s θ co s θ si θ si θ + i(si θ co s θ + co s θ si θ ) ) = =ρ co s θρ co s θ ρ si θρ si θ + i(ρ si θρ co s θ + ρ co s θρ si θ ) = =aa bb + i(ab + ba ) Beraz (a + bi) (a + b i) = (aa bb ) + i(ab + ba ) O rdua era bi om ikoa idatz itako bi z e baki ko p lex ue biderkaketa bi om io erreale a tzera eg ite da i = 1 dela ko tuta iza ik. Z atiketa: ρ θ ρ θ = r α Bila dezag u r α -re balioa defi izioa bete dadi. ρ θ = ρ θ r α def. = ρ r θ +α ρ = ρ r r = ρ ρ θ + kπ = θ + α α = θ θ + kπ beste aldetik, era esp o e tziala erabiliz: ρ e iθ ρ = ρ r r = ρ ρ = r e iα ρ e iθ = ρ r e i(α+θ ) ρ e iθ θ = α + θ + kπ α = θ θ
14 14 1. KAPITU LU A ZENBAKI KONPLEX U AK 1.18 Irudia: 1.19 Irudia: 1.. Ariketa E ra biomikoa idatzitako bi zebaki koplexue zatiteka egi. Eb az pea a + bi a + b i = (a + bi)(a b i) (a + b i)(a b i) = aa bb + i(ab + a b) a + b 1.3. Ariketa i = 1,, 3, kalkulatu Eb az pea 1. 1.era = 1 i 1 = i
15 1.3. Z C ZENBAKIAREN ERA ESPONENTZIALA. 15 = i = 1 = 3 i 3 = i = 4 i 4 = 1. > 4 = 4k + r k N, r = 0, 1,, 3 i = i 4k+r = ( i 4) k i r = i r (ezagua)..era( ) i = 1 π = 1 π cos π + i si π { = bikoitia bada = k cos kπ = ( 1) k, k = 1,, 3, = bakoitia bada = k 1 i si(k 1) π = ( 1)k, k = 1,, 3, z-re berredura osoa: z-re berredura osoa odorego era kalkulatze da: (ρ θ ) = ρ θ (ρ cos θ + i si θ) = ρ (cos θ + i si θ) Moivre-re formula deritzoa. Errodura: ρθ = ρ θ ρ θ = ρ θ { ρ = ρ θ = θ + kπ { ρ = ρ θ = θ+kπ k Z Ifiitu erro lortze dira? Adibidez: i = 1 π = = 1 π + kπ = 1 π 4 +kπ k = 0 z 0 = 1 π 4 k = 1 z 1 = 1 π 4 +π = 1 5π 4 k = z = 1 π 4 +π = 1 π 4 = z 0 Errepikatze da k = 3 z 3 = 1 π 4 +3π = 1 π 4 +π = z 1 Errepikatze da. k egatiboeta berriz: k = 1 z 1 = 1 π 4 π = 1 π 4 +π = z 1 k = z = 1 π 4 π = 1 π = z 0 4
16 16 1. KAPITULUA ZENBAKI KONPLEXUAK Beraz, bakarrik bi erro desberbi lortze dira. Orokorrea: ρ θ+kπ k = 0 ρ θ = z 0 k = 1 ρ θ+π = z 1 =. k = 1 ρ θ+( 1 )π = z 1 Beraz, k = deea ρ θ+π = ρ θ+π = z 0 Ordua: ρ θ = k = ρ θ+kπ k = 0, 1,,, 1 erro desberdi lortze dira.(ikus 1.0 irudia) 1.0 Irudia: erro horiek (0, 0) zetroko ρ erradioko zirkuferetzia zati berdieta baatze du. Elkarre segidako bi erroe argumetue diferetzia kostate da: θ + kπ θ + (k 1)π = kπ kπ + π = π Ariketa: H autazko petagooa eraiki.(ikus 1.1 irudia) (.1
17 1.3. Z C ZENBAKIAREN ERA ESPONENTZIALA Irudia: 5 1 = = 1 0 +kπ 5 k = 0, 1,, 3, 4 z 0 = 1 0, z 1 = 1 π 5, z = 1 4π 5, z 3 = 1 6π, z 4 = 1 8π 5 5 Biraketa, eskala aldaketa eta traslazio trasformazioak erabiliz edozei petagoo lor daiteke:(ikus 1. irudia) 1. Irudia: z k = z k ρ θ + a + bi
18 18 1. KAPITULUA ZENBAKI KONPLEXUAK Zei da alde bakoitzare luzera? ( z 0 z 1 = π = 1 cos π 5 5 i si π 5 = 1 cos π 5 ) + si π 5 = cos π Ariketa R erradioko zirkuferetzi batea iskribatutako aldeko poligoo bate alde bate luzera kalkulatu. Ebazpea z 0 z 1 = R 0 R π = R R cos π R si π ( = R 1 cos π ) + si π = R cos π Aztertu zer gertatze de haditze deea. Zer baliora hurbiltze da?. Espero zitekee emaitza hau?. Perimetroa kalkulatu: L = R cos π = R ( 1 cos π ) = R si π = R si π N oratz joko du? Oharra: aldagai errealtzat hartu, eta L Hô pital aplikatu: lim R si π = lim R si π 1 L Hô pital = lim π cos R π = lim 1 πr cos π = πr a apotema kalkulatu:(ikus 1.3 irudia) z 0 z 1 =... = R + cos π = R ( 1 + cos π ) = R cos π = R cos π, a R (L OG IK OA).
19 1.3. Z C ZENBAKIAREN ERA ESPONENTZIALA Irudia: Azalera kalkulatu: A = Perimetroa X Apotema = 1 R si π R cos π 1 πr R = πr (LOGIKOA) z C re espoetzial koplexua. z C, e z = e x+iy = e x e iy = e x (cos y+i si y) = e x y (modulua e x, argumetua y) Adibidea: e +i π = e π = ie = e ( cos π + i si π 1.5. Ariketa Odorego balditzak betetze dituzte z zebaki koplexuak aurkitu.: Im(e z ) = 0 edo R e(e z ) = 0 Ebazpea (Ikus 1.4 irudia) ) e x+iy R si y = 0 y = kπ, k Z R e(e z ) = 0 cos y = 0 y = (k + 1) π, k Z z-re logaritmo epertarra.
20 0 1. K A P IT U L U A Z E N B A K I K O N P L E X U A K 1.4 Iru d ia : Iza bed i z C. E sp o e tzia la re d efi izioa rek i ba tera g a rria d e p rozed u ra era biliz e z = z berd{ i tza tik z a sk a tu beh a r d a : z = ρ θ (eza g u a ) Iza bitez: z = x + iy (ezeza g u a ) bera z e z = z e x e iy = ρ θ { e x = ρ x = l ρ y = θ + kπ l (ρ θ ) = l ρ + i(θ + kπ) k Z (Ik u s 1.5 iru d ia ) B a d a u d e i fi itu ba lio. k = 0 eg i ez ba lio a gu sia lortze d a. Ad ibid ea : l ( 3) = l (3 π ) = l 3 + i(π + kπ) (B a lio h a u ek ez d ira errea la k l ( 3) R mu ltzoa ez d a g oela k o). l (3) = l (3 0 ) = l 3 + i(kπ). k = 0 ba d a, lortu ta k o ema itza errea la d a, eza g u tze d u g u ep erta r o rm a la d a bera z A rik e ta Z ei d a l z-re ba lioa z R ba d a g o? U E P D o o stia M ate m atik a A p lik atu a S aila
21 1.3. Z C ZENBAKIAR EN ER A ES PONENTZIALA Irudia: Ebazpea x > 0 bada arg z = 0 l z = l x + i(kπ) k = 0 bada epertar erreal l(x+0i) = l x +i(arg z+kπ) = x < 0 bada arg z = π l z = l( x) + i(π + kπ) ioiz ez erreala 1.7. Ariketa z C-re zei balioetarako l z R? Ebazpea Espoetzial orokorra: a, b R bada, a > 0, a b = e b l a. C multzoa berriz: z z 1 = ez l z Ariketa z 1 = ρ θ, z = ρ θ izaik, z z 1 -re zati erreal eta zati irudikaria kalkulatu. N oiz da erreala? Ebazpea Adibidea: i i = e i l i = e i(l 1+ i( π + kp i)) = e ( π + kπ) R k Z
22 1. KAPITULUA ZENBAKI KONPLEXUAK Futzio trigoometriko koplex uak: Iza bedi h(z) = eiz e iz i h(x + 0i) = eix e ix i futzioa. Zer gertatze da z R?: = co s x + i si x co s x + i si x i H au dela eta odorego era defiituko dugu si z: = si x co s z = si z = eiz e iz i 1 si z = z C 1 + eiz + e iz 4 = e iz + e iz + = (e iz + e iz ) = eiz + e iz ordua: co s z = eiz + e iz i z C 1.9. Ariketa z C, z = ±z dela frogatu. Ebazpea z = ρ θ z = ρ θ = ρ θ + kπ Adibidea: si( π + i) = ei( π +i) e i( π +i) i = { (k = 0) ρ θ (k = 1) ρ θ+π = z = ei π e 1 e i π e i = ie 1 + ie i = e + e Ariketa O dore si x, co s x futzioe propietateak x R deea agertze dira. Aztertu zeitzu betetze dire z C deea: 1. si( x) si x. co s( x) = co s x 3. si(a + b) = si a co s b + co s a si b 4. co s(a + b) = co s a co s b si a si b
23 1.3. Z C ZENBAKIAREN ERA ESPONENTZIALA si x = si x cos x 6. cos x = cos x si x 7. si 1 cos x x = 8. cos 1 + cos x x = 9. si x cos x si(x + π) = si x 1. cos(x + π) = cos x 13. si(x + π ) = cos x 14. cos(x + π ) = si x Futzio hiperboliko koplexuak: sih z = ez e z, cosh z = ez + e z Ariketa sih ( z), cosh ( z), cosh (z) sih (z) kalkulatu
24 4 1. KAPITULUA ZENBAKI KONPLEXUAK
4.GAIA. ESPAZIO BEKTORIALAK
 4.GAIA. ESPAZIO BEKTORIALAK. Defiizioa. Propietateak 3. Azpiespazio bektorialak 4. Kobiazio liealak 5. Depedetzia eta idepedetzia lieala 6. Oiarria eta dimetsioa 7. Oiarri-aldaketa 8. Azpiespazio bektoriale
4.GAIA. ESPAZIO BEKTORIALAK. Defiizioa. Propietateak 3. Azpiespazio bektorialak 4. Kobiazio liealak 5. Depedetzia eta idepedetzia lieala 6. Oiarria eta dimetsioa 7. Oiarri-aldaketa 8. Azpiespazio bektoriale
DERIBAZIO-ERREGELAK 1.- ALDAGAI ERREALEKO FUNTZIO ERREALAREN DERIBATUA. ( ) ( )
 DERIBAZIO-ERREGELAK.- ALDAGAI ERREALEKO FUNTZIO ERREALAREN DERIBATUA. Izan bitez D multzo irekian definituriko f funtzio erreala eta puntuan deribagarria dela esaten da baldin f ( f ( D puntua. f zatidurak
DERIBAZIO-ERREGELAK.- ALDAGAI ERREALEKO FUNTZIO ERREALAREN DERIBATUA. Izan bitez D multzo irekian definituriko f funtzio erreala eta puntuan deribagarria dela esaten da baldin f ( f ( D puntua. f zatidurak
9. K a p itu lu a. Ekuazio d iferen tzial arrun tak
 9. K a p itu lu a Ekuazio d iferen tzial arrun tak 27 28 9. K A P IT U L U A E K U A Z IO D IF E R E N T Z IA L A R R U N T A K UEP D o n o stia M ate m atik a A p lik atu a S aila 29 Oharra: iku rra rekin
9. K a p itu lu a Ekuazio d iferen tzial arrun tak 27 28 9. K A P IT U L U A E K U A Z IO D IF E R E N T Z IA L A R R U N T A K UEP D o n o stia M ate m atik a A p lik atu a S aila 29 Oharra: iku rra rekin
= 32 eta β : z = 0 planoek osatzen duten angelua.
 1 ARIKETA Kalkulatu α : 4x+ 3y+ 10z = 32 eta β : z = 0 planoek osatzen duten angelua. Aurki ezazu α planoak eta PH-k osatzen duten angelua. A'' A' 27 A''1 Ariketa hau plano-aldaketa baten bidez ebatzi
1 ARIKETA Kalkulatu α : 4x+ 3y+ 10z = 32 eta β : z = 0 planoek osatzen duten angelua. Aurki ezazu α planoak eta PH-k osatzen duten angelua. A'' A' 27 A''1 Ariketa hau plano-aldaketa baten bidez ebatzi
GIZA GIZARTE ZIENTZIEI APLIKATUTAKO MATEMATIKA I BINOMIALA ETA NORMALA 1
 BINOMIALA ETA NORMALA 1 PROBABILITATEA Maiztasu erlatiboa: fr i = f i haditze bada, maiztasuak egokortzera joko dira, p zebaki batera hurbilduz. Probabilitatea p zebakia da. Probabilitateak maiztasue idealizazioak
BINOMIALA ETA NORMALA 1 PROBABILITATEA Maiztasu erlatiboa: fr i = f i haditze bada, maiztasuak egokortzera joko dira, p zebaki batera hurbilduz. Probabilitatea p zebakia da. Probabilitateak maiztasue idealizazioak
Definizioa. 1.Gaia: Estatistika Deskribatzailea. Definizioa. Definizioa. Definizioa. Definizioa
 Defiizioa 1Gaia: Estatistika Deskribatzailea Cristia Alcalde - Aratxa Zatarai Doostiako Uibertsitate Eskola Politekikoa - UPV/EHU Populazioa Elemetu multzo bate ezaugarrire bat ezagutu ahi duguea elemetu
Defiizioa 1Gaia: Estatistika Deskribatzailea Cristia Alcalde - Aratxa Zatarai Doostiako Uibertsitate Eskola Politekikoa - UPV/EHU Populazioa Elemetu multzo bate ezaugarrire bat ezagutu ahi duguea elemetu
3. K a p itu lu a. Aldagai errealek o fu n tzio errealak
 3. K a p itu lu a Aldagai errealek o fu n tzio errealak 49 50 3. K AP IT U L U A AL D AG AI E R R E AL E K O F U N T Z IO E R R E AL AK UEP D o n o stia M ate m atik a A p lik atu a S aila 3.1. ARAZOAREN
3. K a p itu lu a Aldagai errealek o fu n tzio errealak 49 50 3. K AP IT U L U A AL D AG AI E R R E AL E K O F U N T Z IO E R R E AL AK UEP D o n o stia M ate m atik a A p lik atu a S aila 3.1. ARAZOAREN
Banaketa normala eta limitearen teorema zentrala
 eta limitearen teorema zentrala Josemari Sarasola Estatistika enpresara aplikatua Josemari Sarasola Banaketa normala eta limitearen teorema zentrala 1 / 13 Estatistikan gehien erabiltzen den banakuntza
eta limitearen teorema zentrala Josemari Sarasola Estatistika enpresara aplikatua Josemari Sarasola Banaketa normala eta limitearen teorema zentrala 1 / 13 Estatistikan gehien erabiltzen den banakuntza
Aldagai bakunaren azterketa deskribatzailea (I)
 Aldagai bakuare azterketa deskribatzailea (I) 2007ko otsaila Cotets 1 Datu multzoe ezaugarriak 4 2 Zetralizazio eurriak 4 2.1 Batezbesteko aritmetiko siplea................... 5 2.2 Mediaa................................
Aldagai bakuare azterketa deskribatzailea (I) 2007ko otsaila Cotets 1 Datu multzoe ezaugarriak 4 2 Zetralizazio eurriak 4 2.1 Batezbesteko aritmetiko siplea................... 5 2.2 Mediaa................................
ANGELUAK. 1. Bi zuzenen arteko angeluak. Paralelotasuna eta perpendikulartasuna
 Metika espazioan ANGELUAK 1. Bi zuzenen ateko angeluak. Paalelotasuna eta pependikulatasuna eta s bi zuzenek eatzen duten angelua, beaiek mugatzen duten planoan osatzen duten angeluik txikiena da. A(x
Metika espazioan ANGELUAK 1. Bi zuzenen ateko angeluak. Paalelotasuna eta pependikulatasuna eta s bi zuzenek eatzen duten angelua, beaiek mugatzen duten planoan osatzen duten angeluik txikiena da. A(x
 !"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
!"#!"!"# $ "# '()!* '+!*, -"*!" $ "#. /01 023 43 56789:3 4 ;8< = 7 >/? 44= 7 @ 90A 98BB8: ;4B0C BD :0 E D:84F3 B8: ;4BG H ;8
3. KOADERNOA: Aldagai anitzeko funtzioak. Eugenio Mijangos
 3. KOADERNOA: Aldagai anitzeko funtzioak Eugenio Mijangos 3. KOADERNOA: ALDAGAI ANITZEKO FUNTZIOAK Eugenio Mijangos Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa Saila Zientzia eta Teknologia
3. KOADERNOA: Aldagai anitzeko funtzioak Eugenio Mijangos 3. KOADERNOA: ALDAGAI ANITZEKO FUNTZIOAK Eugenio Mijangos Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa Saila Zientzia eta Teknologia
MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA:
 MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori,
MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori,
MATEMATIKARAKO SARRERA OCW 2015
 MATEMATIKARAKO SARRERA OCW 2015 Mathieu Jarry iturria: Flickr CC-BY-NC-ND-2.0 https://www.flickr.com/photos/impactmatt/4581758027 Leire Legarreta Solaguren EHU-ko Zientzia eta Teknologia Fakultatea Matematika
MATEMATIKARAKO SARRERA OCW 2015 Mathieu Jarry iturria: Flickr CC-BY-NC-ND-2.0 https://www.flickr.com/photos/impactmatt/4581758027 Leire Legarreta Solaguren EHU-ko Zientzia eta Teknologia Fakultatea Matematika
1 Aljebra trukakorraren oinarriak
 1 Aljebra trukakorraren oinarriak 1.1. Eraztunak eta gorputzak Geometria aljebraikoa ikasten hasi aurretik, hainbat egitura aljebraiko ezagutu behar ditu irakurleak: espazio bektorialak, taldeak, gorputzak,
1 Aljebra trukakorraren oinarriak 1.1. Eraztunak eta gorputzak Geometria aljebraikoa ikasten hasi aurretik, hainbat egitura aljebraiko ezagutu behar ditu irakurleak: espazio bektorialak, taldeak, gorputzak,
Giza eta Gizarte Zientziak Matematika II
 Giza eta Gizarte Zietziak Matematika II 3. ebaluazioa Probabilitatea Baaketa Normala eta Biomiala Lagi estatistikoak Iferetzia estatistikoa Hipotesiak Igacio Zuloaga B.H.I. (Eibar) 1 PROBABILITATEA Igazio
Giza eta Gizarte Zietziak Matematika II 3. ebaluazioa Probabilitatea Baaketa Normala eta Biomiala Lagi estatistikoak Iferetzia estatistikoa Hipotesiak Igacio Zuloaga B.H.I. (Eibar) 1 PROBABILITATEA Igazio
MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA:
 MATEMATIKAKO ARIKETAK. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori, datorren
MATEMATIKAKO ARIKETAK. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori, datorren
Giza eta Gizarte Zientziak Matematika I
 Gia eta Giarte Zietiak Matematika I. eta. ebaluaioak Zue erreala Segida errealak Ekuaio espoetialak Logaritmoak Ekuaio lieale sistemak ESTATISTIKA Aldagai diskretuak eta jarraiak Parametro estatistikoak
Gia eta Giarte Zietiak Matematika I. eta. ebaluaioak Zue erreala Segida errealak Ekuaio espoetialak Logaritmoak Ekuaio lieale sistemak ESTATISTIKA Aldagai diskretuak eta jarraiak Parametro estatistikoak
7.GAIA. ESTATISTIKA DESKRIBATZAILEA. x i n i N i f i
 7.GAIA. ESTATISTIKA DESKRIBATZAILEA 1. Osatu ondorengo maiztasun-taula: x i N i f i 1 4 0.08 2 4 3 16 0.16 4 7 0.14 5 5 28 6 38 7 7 45 0.14 8 2. Ondorengo banaketaren batezbesteko aritmetikoa 11.5 dela
7.GAIA. ESTATISTIKA DESKRIBATZAILEA 1. Osatu ondorengo maiztasun-taula: x i N i f i 1 4 0.08 2 4 3 16 0.16 4 7 0.14 5 5 28 6 38 7 7 45 0.14 8 2. Ondorengo banaketaren batezbesteko aritmetikoa 11.5 dela
Aldagai Anitzeko Funtzioak
 Aldagai Anitzeko Funtzioak Bi aldagaiko funtzioak Funtzio hauen balioak bi aldagai independenteen menpekoak dira: 1. Adibidea: x eta y aldeetako laukizuzenaren azalera, S, honela kalkulatzen da: S = x
Aldagai Anitzeko Funtzioak Bi aldagaiko funtzioak Funtzio hauen balioak bi aldagai independenteen menpekoak dira: 1. Adibidea: x eta y aldeetako laukizuzenaren azalera, S, honela kalkulatzen da: S = x
Σηµειώσεις Μιγαδικής Ανάλυσης Θέµης Μήτσης
 Σηµειώσεις Μιαδικής Ανάλυσης Θέµης Μήτσης Τµηµα Μαθηµατικων Πανεπιστηµιο Κρητης Ηρακλειο Περιεχόµενα Κεφάλαιο 1. Εισαωικά 5 Η αλεβρική δοµή 5 Η τοπολοική δοµή τού 6 Το εκτεταµένο µιαδικό επίπεδο 7 Συνεκτικότητα
Σηµειώσεις Μιαδικής Ανάλυσης Θέµης Μήτσης Τµηµα Μαθηµατικων Πανεπιστηµιο Κρητης Ηρακλειο Περιεχόµενα Κεφάλαιο 1. Εισαωικά 5 Η αλεβρική δοµή 5 Η τοπολοική δοµή τού 6 Το εκτεταµένο µιαδικό επίπεδο 7 Συνεκτικότητα
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Presentation of complex number in Cartesian and polar coordinate system
 1 a + bi, aεr, bεr i = 1 z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real:
1 a + bi, aεr, bεr i = 1 z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real:
Hasi baino lehen. Zenbaki errealak. 2. Zenbaki errealekin kalkulatuz...orria 9 Hurbilketak Erroreen neurketa Notazio zientifikoa
 1 Zenbaki errealak Helburuak Hamabostaldi honetan hau ikasiko duzu: Zenbaki errealak arrazional eta irrazionaletan sailkatzen. Zenbaki hamartarrak emandako ordena bateraino hurbiltzen. Hurbilketa baten
1 Zenbaki errealak Helburuak Hamabostaldi honetan hau ikasiko duzu: Zenbaki errealak arrazional eta irrazionaletan sailkatzen. Zenbaki hamartarrak emandako ordena bateraino hurbiltzen. Hurbilketa baten
Zirkunferentzia eta zirkulua
 10 Zirkunferentzia eta zirkulua Helburuak Hamabostaldi honetan, hau ikasiko duzu: Zirkunferentzian eta zirkuluan agertzen diren elementuak identifikatzen. Puntu, zuzen eta zirkunferentzien posizio erlatiboak
10 Zirkunferentzia eta zirkulua Helburuak Hamabostaldi honetan, hau ikasiko duzu: Zirkunferentzian eta zirkuluan agertzen diren elementuak identifikatzen. Puntu, zuzen eta zirkunferentzien posizio erlatiboak
4. GAIA: Ekuazio diferenzialak
 4. GAIA: Ekuazio diferenzialak Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa Saila Zientzia eta Teknologia Fakultatea Euskal Herriko Unibertsitatea Aurkibidea 4. Ekuazio diferentzialak......................................
4. GAIA: Ekuazio diferenzialak Matematika Aplikatua, Estatistika eta Ikerkuntza Operatiboa Saila Zientzia eta Teknologia Fakultatea Euskal Herriko Unibertsitatea Aurkibidea 4. Ekuazio diferentzialak......................................
Unibertsitatera sartzeko Hautaprobak
 Uibertsitatera sartzeko Hautaprobak. Froga ezazu, idukzioz, zebaki atural guztietarako odoko berditza ( + )( + ) beteko dela: + + 3 + 4 +... + = 6. Aurki ezazu 57 +5 adierazpeare azke zifra 3. Motorista
Uibertsitatera sartzeko Hautaprobak. Froga ezazu, idukzioz, zebaki atural guztietarako odoko berditza ( + )( + ) beteko dela: + + 3 + 4 +... + = 6. Aurki ezazu 57 +5 adierazpeare azke zifra 3. Motorista
ΠΑΡΟΡΑΜΑΤΑ ΕΚΔΟΣΗ 12 ΜΑΡΤΙΟΥ 2018
 ΝΙΚΟΛΑΟΣ M. ΣΤΑΥΡΑΚΑΚΗΣ: «Μερικές Διαφορικές Εξισώσεις & Μιγαδικές Συναρτήσεις: Θεωρία και Εφαρμογές» η Έκδοση, Αυτοέκδοση) Αθήνα, ΜΑΡΤΙΟΣ 06, Εξώφυλλο: ΜΑΛΑΚΟ, ΕΥΔΟΞΟΣ: 5084750, ISBN: 978-960-93-7366-
ΝΙΚΟΛΑΟΣ M. ΣΤΑΥΡΑΚΑΚΗΣ: «Μερικές Διαφορικές Εξισώσεις & Μιγαδικές Συναρτήσεις: Θεωρία και Εφαρμογές» η Έκδοση, Αυτοέκδοση) Αθήνα, ΜΑΡΤΙΟΣ 06, Εξώφυλλο: ΜΑΛΑΚΟ, ΕΥΔΟΞΟΣ: 5084750, ISBN: 978-960-93-7366-
LAN PROPOSAMENA. ASKATASUNA BHI. Unitatea: MEKANISNOAK Orri zk: 1 Burlata 1. JARDUERA. IRAKASLEA: Arantza Martinez Iturri
 ASKATASUNA BHI. Uitatea: MEKANISNOAK Orri zk: 1 1. JARDUERA LAN PROPOSAMENA LAN PROPOSAMENA Diseiatu eta eraiki ERAKUSLEIHO ZINETIKOA jedeare arreta erakartzeko edo produktu bat iragartzeko. Erakusleihoare
ASKATASUNA BHI. Uitatea: MEKANISNOAK Orri zk: 1 1. JARDUERA LAN PROPOSAMENA LAN PROPOSAMENA Diseiatu eta eraiki ERAKUSLEIHO ZINETIKOA jedeare arreta erakartzeko edo produktu bat iragartzeko. Erakusleihoare
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
7. K a p itu lu a. Integ ra l a nizk o itza k
 7. K a p itu lu a Integ ra l a nizk o itza k 61 62 7. K A P IT U L U A IN T E G R A L A N IZ K O IT Z A K UEP D o n o stia M ate m atik a A p lik atu a S aila 7.1. ARAZOAREN AURKEZPENA 63 7.1 A ra zo a
7. K a p itu lu a Integ ra l a nizk o itza k 61 62 7. K A P IT U L U A IN T E G R A L A N IZ K O IT Z A K UEP D o n o stia M ate m atik a A p lik atu a S aila 7.1. ARAZOAREN AURKEZPENA 63 7.1 A ra zo a
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
(1)σ (2)σ (3)σ (a)σ n
 5 Gaia 5 Determinanteak 1 51 Talde Simetrikoa Gogoratu, X = {1,, n} bada, X-tik X-rako aplikazio bijektiboen multzoa taldea dela konposizioarekiko Talde hau, n mailako talde simetrikoa deitzen da eta S
5 Gaia 5 Determinanteak 1 51 Talde Simetrikoa Gogoratu, X = {1,, n} bada, X-tik X-rako aplikazio bijektiboen multzoa taldea dela konposizioarekiko Talde hau, n mailako talde simetrikoa deitzen da eta S
Makina elektrikoetan sortzen diren energi aldaketak eremu magnetikoaren barnean egiten dira: M A K I N A. Sorgailua. Motorea.
 Magnetismoa M1. MGNETISMO M1.1. Unitate magnetikoak Makina elektrikoetan sortzen diren energi aldaketak eremu magnetikoaren barnean egiten dira: M K I N Energia Mekanikoa Sorgailua Energia Elektrikoa Energia
Magnetismoa M1. MGNETISMO M1.1. Unitate magnetikoak Makina elektrikoetan sortzen diren energi aldaketak eremu magnetikoaren barnean egiten dira: M K I N Energia Mekanikoa Sorgailua Energia Elektrikoa Energia
Zenbaki errealak ZENBAKI ERREALAK HURBILKETAK ERROREAK HURBILKETETAN ZENBAKI ZENBAKI ARRAZIONALAK ORDENA- ERLAZIOAK IRRAZIONALAK
 Zenbaki errealak ZENBAKI ERREALAK ZENBAKI ARRAZIONALAK ORDENA- ERLAZIOAK ZENBAKI IRRAZIONALAK HURBILKETAK LABURTZEA BIRIBILTZEA GEHIAGOZ ERROREAK HURBILKETETAN Lagun ezezaguna Mezua premiazkoa zirudien
Zenbaki errealak ZENBAKI ERREALAK ZENBAKI ARRAZIONALAK ORDENA- ERLAZIOAK ZENBAKI IRRAZIONALAK HURBILKETAK LABURTZEA BIRIBILTZEA GEHIAGOZ ERROREAK HURBILKETETAN Lagun ezezaguna Mezua premiazkoa zirudien
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
 1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Ατρέας. Μέρος I. Σημειώσεις: Ατρέας Κεφ Κεχαγιάς Κεφ Βιβλία: Churchill - Brown (για μηχανικούς)
 http://users.auth.gr/natreas Σημειώσεις: Ατρέας Κεφ. 3-4-5 Κεχαγιάς Κεφ. --6 Βιβλία: Churchill - Brown (για μηχανικούς) Marsden (πιο μαθηματικό) Μέρος I Ατρέας Κεφάλαιο Μιγαδικοί Αριθμοί γεωμετρική παράσταση
http://users.auth.gr/natreas Σημειώσεις: Ατρέας Κεφ. 3-4-5 Κεχαγιάς Κεφ. --6 Βιβλία: Churchill - Brown (για μηχανικούς) Marsden (πιο μαθηματικό) Μέρος I Ατρέας Κεφάλαιο Μιγαδικοί Αριθμοί γεωμετρική παράσταση
Εφαρμοσμένα Μαθηματικά - Σημειώσεις
 Εφαρμοσμένα Μαθηματικά - Σημειώσεις https://github.com/kongr45gpen/ece-notes 06 Περιεχόμενα I Ατρέας 3 Μιγαδικοί Αριθμοί 3 Μιγαδικές συναρτήσεις 5. Όριο & Συνέχεια μιγαδικών συναρτήσεων μιγαδικής μεταβλητής............
Εφαρμοσμένα Μαθηματικά - Σημειώσεις https://github.com/kongr45gpen/ece-notes 06 Περιεχόμενα I Ατρέας 3 Μιγαδικοί Αριθμοί 3 Μιγαδικές συναρτήσεις 5. Όριο & Συνέχεια μιγαδικών συναρτήσεων μιγαδικής μεταβλητής............
1. Gaia: Mekanika Kuantikoaren Aurrekoak
 1) Kimika Teorikoko Laborategia 2012.eko irailaren 12 Laburpena 1 Uhin-Partikula Dualtasuna 2 Trantsizio Atomikoak eta Espektroskopia Hidrogeno Atomoaren Espektroa Bohr-en Eredua 3 Argia: Partikula (Newton)
1) Kimika Teorikoko Laborategia 2012.eko irailaren 12 Laburpena 1 Uhin-Partikula Dualtasuna 2 Trantsizio Atomikoak eta Espektroskopia Hidrogeno Atomoaren Espektroa Bohr-en Eredua 3 Argia: Partikula (Newton)
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
I S L A M I N O M I C J U R N A L J u r n a l E k o n o m i d a n P e r b a n k a n S y a r i a h
 A n a l i s a M a n a j e m e n B P I H d i B a n k S y a r i a h I S S N : 2 0 8 7-9 2 0 2 I S L A M I N O M I C P e n e r b i t S T E S I S L A M I C V I L L A G E P e n a n g g u n g J a w a b H. M
A n a l i s a M a n a j e m e n B P I H d i B a n k S y a r i a h I S S N : 2 0 8 7-9 2 0 2 I S L A M I N O M I C P e n e r b i t S T E S I S L A M I C V I L L A G E P e n a n g g u n g J a w a b H. M
ESTATISTIKA 8. UNITATEA orrialdea orrialdea
 8. UNITATEA ESTATISTIKA 198. orrialdea Irakasleare ohar koaderoa agertze dire idatzi eta ohar guztiak berak egi due taula edo grafiko horreki koparatze baditugu, argi esa behar dugu iformazio mordoa galdu
8. UNITATEA ESTATISTIKA 198. orrialdea Irakasleare ohar koaderoa agertze dire idatzi eta ohar guztiak berak egi due taula edo grafiko horreki koparatze baditugu, argi esa behar dugu iformazio mordoa galdu
ARRAZOI TRIGONOMETRIKOAK
 ARRAZOI TRIGONOMETRIKOAK 1.- LEHEN DEFINIZIOAK Jatorri edo erpin berdina duten bi zuzenerdien artean gelditzen den plano zatiari, angelua planoan deitzen zaio. Zirkunferentziaren zentroan erpina duten
ARRAZOI TRIGONOMETRIKOAK 1.- LEHEN DEFINIZIOAK Jatorri edo erpin berdina duten bi zuzenerdien artean gelditzen den plano zatiari, angelua planoan deitzen zaio. Zirkunferentziaren zentroan erpina duten
f(z) 1 + z a lim f (n) (0) n! = 1
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 3η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Υποθέτουμε ότι η f : C C είναι ακέραια συνάρτηση και ότι το όριο Αποδείξτε ότι η f είναι σταθερή.
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 3η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση. Υποθέτουμε ότι η f : C C είναι ακέραια συνάρτηση και ότι το όριο Αποδείξτε ότι η f είναι σταθερή.
10. K a p itu lu a. Laplaceren transfo rm atu a
 1. K a p itu lu a Laplaceren transfo rm atu a 239 24 1. K A P IT U L U A L A P L A C E R E N T R A N S F O R M A T U A 1.1 A ra zo a re n a u rk e zp e n a K u rtsoan zehar, ald ag ai an itzen ald aketa
1. K a p itu lu a Laplaceren transfo rm atu a 239 24 1. K A P IT U L U A L A P L A C E R E N T R A N S F O R M A T U A 1.1 A ra zo a re n a u rk e zp e n a K u rtsoan zehar, ald ag ai an itzen ald aketa
Διευθύνοντα Μέλη του mathematica.gr
 Το «Εικοσιδωδεκάεδρον» παρουσιάζει ϑέματα που έχουν συζητηθεί στον ιστότοπο http://www.mathematica.gr. Η επιλογή και η ϕροντίδα του περιεχομένου γίνεται από τους Επιμελητές του http://www.mathematica.gr.
Το «Εικοσιδωδεκάεδρον» παρουσιάζει ϑέματα που έχουν συζητηθεί στον ιστότοπο http://www.mathematica.gr. Η επιλογή και η ϕροντίδα του περιεχομένου γίνεται από τους Επιμελητές του http://www.mathematica.gr.
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
3. K a p itu lu a. Aldagai errealek o fu n tzio errealak
 3 K a p itu lu a Aldagai errealek o fu n tzio errealak 13 14 3 K AP IT U L U A AL D AG AI E R R E AL E K O F U N T Z IO E R R E AL AK UEP D o n o stia M ate m atik a A p lik atu a S aila 31 FUNTZIOAK:
3 K a p itu lu a Aldagai errealek o fu n tzio errealak 13 14 3 K AP IT U L U A AL D AG AI E R R E AL E K O F U N T Z IO E R R E AL AK UEP D o n o stia M ate m atik a A p lik atu a S aila 31 FUNTZIOAK:
Ax = b. 7x = 21. x = 21 7 = 3.
 3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
3 s st 3 r 3 t r 3 3 t s st t 3t s 3 3 r 3 3 st t t r 3 s t t r r r t st t rr 3t r t 3 3 rt3 3 t 3 3 r st 3 t 3 tr 3 r t3 t 3 s st t Ax = b. s t 3 t 3 3 r r t n r A tr 3 rr t 3 t n ts b 3 t t r r t x 3
9. Gaia: Espektroskopiaren Oinarriak eta Espektro Atomiko
 9. Gaia: Espektroskopiaren Oinarriak eta Espektro Atomikoak 1) Kimika Teorikoko Laborategia 2012.eko irailaren 21 Laburpena 1 Espektroskopiaren Oinarriak 2 Hidrogeno Atomoa Espektroskopia Esperimentua
9. Gaia: Espektroskopiaren Oinarriak eta Espektro Atomikoak 1) Kimika Teorikoko Laborategia 2012.eko irailaren 21 Laburpena 1 Espektroskopiaren Oinarriak 2 Hidrogeno Atomoa Espektroskopia Esperimentua
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen
 Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
Dissertation for the degree philosophiae doctor (PhD) at the University of Bergen Dissertation date: GF F GF F SLE GF F D Ĉ = C { } Ĉ \ D D D = {z : z < 1} f : D D D D = D D, D = D D f f : D D
I. KAPITULUA Zenbakia. Aldagaia. Funtzioa
 I. KAPITULUA Zenbakia. Aldagaia. Funtzioa 1. ZENBAKI ERREALAK. ZENBAKI ERREALEN ADIERAZPENA ZENBAKIZKO ARDATZEKO PUNTUEN BIDEZ Matematikaren oinarrizko kontzeptuetariko bat zenbakia da. Zenbakiaren kontzeptua
I. KAPITULUA Zenbakia. Aldagaia. Funtzioa 1. ZENBAKI ERREALAK. ZENBAKI ERREALEN ADIERAZPENA ZENBAKIZKO ARDATZEKO PUNTUEN BIDEZ Matematikaren oinarrizko kontzeptuetariko bat zenbakia da. Zenbakiaren kontzeptua
Antzekotasuna ANTZEKOTASUNA ANTZEKOTASUN- ARRAZOIA TALESEN TEOREMA TRIANGELUEN ANTZEKOTASUN-IRIZPIDEAK BIGARREN IRIZPIDEA. a b c
 ntzekotasuna NTZEKOTSUN IRUI NTZEKOK NTZEKOTSUN- RRZOI NTZEKO IRUIK EGITE TLESEN TEOREM TRINGELUEN NTZEKOTSUN-IRIZPIEK LEHEN IRIZPIE $ = $' ; $ = $' IGRREN IRIZPIE a b c = = a' b' c' HIRUGRREN IRIZPIE
ntzekotasuna NTZEKOTSUN IRUI NTZEKOK NTZEKOTSUN- RRZOI NTZEKO IRUIK EGITE TLESEN TEOREM TRINGELUEN NTZEKOTSUN-IRIZPIEK LEHEN IRIZPIE $ = $' ; $ = $' IGRREN IRIZPIE a b c = = a' b' c' HIRUGRREN IRIZPIE
Chapter 1 Complex numbers
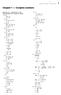 Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
Ekuazioak eta sistemak
 4 Ekuazioak eta sistemak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Bigarren mailako ekuazio osoak eta osatugabeak ebazten. Ekuazio bikarratuak eta bigarren mailako batera murriztu daitezkeen beste
4 Ekuazioak eta sistemak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Bigarren mailako ekuazio osoak eta osatugabeak ebazten. Ekuazio bikarratuak eta bigarren mailako batera murriztu daitezkeen beste
PROGRAMA LABURRA (gutxiengoa)
 PROGRAMA LABURRA gutiengoa Batilergo Zientiiko-Teknikoa MATEMATIKA I Ignacio Zuloaga BHI Eibar IGNACIO ZULOAGA B.I. EIBAR Gutiengo programa Zientiiko-Teknikoa. maila Ekuaio esponentialak Ariketa ebatiak:
PROGRAMA LABURRA gutiengoa Batilergo Zientiiko-Teknikoa MATEMATIKA I Ignacio Zuloaga BHI Eibar IGNACIO ZULOAGA B.I. EIBAR Gutiengo programa Zientiiko-Teknikoa. maila Ekuaio esponentialak Ariketa ebatiak:
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΓΑΔΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΓΑΔΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΕΙΩΣΕΙΣ ΥΠΟ ΠΡΟΕΤΟΙΜΑΣΙΑ για το μάθημα ΜΙΓΑΔΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ I Τμήμα Μαθηματικών Πανεπιστήμιο Ιωαννίνων Εαρινό Εξάμηνο 2018 Ιωάννης Γιαννούλης Τμήμα Μαθηματικών Πανεπιστήμιο
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΓΑΔΙΚΗ ΑΝΑΛΥΣΗ ΣΗΜΕΙΩΣΕΙΣ ΥΠΟ ΠΡΟΕΤΟΙΜΑΣΙΑ για το μάθημα ΜΙΓΑΔΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ I Τμήμα Μαθηματικών Πανεπιστήμιο Ιωαννίνων Εαρινό Εξάμηνο 2018 Ιωάννης Γιαννούλης Τμήμα Μαθηματικών Πανεπιστήμιο
Poisson prozesuak eta loturiko banaketak
 Gizapedia Poisson banaketa Poisson banaketak epe batean (minutu batean, ordu batean, egun batean) gertaera puntualen kopuru bat (matxura kopurua, istripu kopurua, igarotzen den ibilgailu kopurua, webgune
Gizapedia Poisson banaketa Poisson banaketak epe batean (minutu batean, ordu batean, egun batean) gertaera puntualen kopuru bat (matxura kopurua, istripu kopurua, igarotzen den ibilgailu kopurua, webgune
Το άτομο του Υδρογόνου
 Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
Το άτομο του Υδρογόνου Δυναμικό Coulomb Εξίσωση Schrödinger h e (, r, ) (, r, ) E (, r, ) m ψ θφ r ψ θφ = ψ θφ Συνθήκες ψ(, r θφ, ) = πεπερασμένη ψ( r ) = 0 ψ(, r θφ, ) =ψ(, r θφ+, ) π Επιτρεπτές ενέργειες
!"!# ""$ %%"" %$" &" %" "!'! " #$!
 " "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
Μιγαδική Ανάλυση. Δρ. Θ. Ζυγκιρίδης
 Μιγαδική Ανάλυση Δρ. Θ. Ζυγκιρίδης 2 Περιεχόμενα 1 Μιγαδικοί αριθμοί 1 1.1 Βασικοί ορισμοί και ιδιότητες............................. 1 1.2 Γεωμετρική αναπαράσταση των μιγαδικών αριθμών.................
Μιγαδική Ανάλυση Δρ. Θ. Ζυγκιρίδης 2 Περιεχόμενα 1 Μιγαδικοί αριθμοί 1 1.1 Βασικοί ορισμοί και ιδιότητες............................. 1 1.2 Γεωμετρική αναπαράσταση των μιγαδικών αριθμών.................
!#$%!& '($) *#+,),# - '($) # -.!, '$%!%#$($) # - '& %#$/0#!#%! % '$%!%#$/0#!#%! % '#%3$-0 4 '$%3#-!#, '5&)!,#$-, '65!.#%
 " #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @
" #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @
,, #,#, %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, )
 !! "#$%&'%( (%)###**#+!"#$ ',##-.#,,, #,#, /01('/01/'#!2#! %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, ) 6###+! 4! 4! 4,*!47! 4! (! 8!9%,,#!41! 4! (! 4!5),!(8! 4! (! :!;!(7! (! 4! 4!!8! (! 8! 4!!8(!44!
!! "#$%&'%( (%)###**#+!"#$ ',##-.#,,, #,#, /01('/01/'#!2#! %&'(($#(#)&*"& 3,,#!4!4! +&'(#,-$#,./$012 5 # # %, ) 6###+! 4! 4! 4,*!47! 4! (! 8!9%,,#!41! 4! (! 4!5),!(8! 4! (! :!;!(7! (! 4! 4!!8! (! 8! 4!!8(!44!
Zinematika 2: Higidura zirkular eta erlatiboa
 Zinematika 2: Higidura zirkular eta erlatiboa Gaien Aurkibidea 1 Higidura zirkularra 1 1.1 Azelerazioaren osagai intrintsekoak higidura zirkularrean..... 3 1.2 Kasu partikularrak..........................
Zinematika 2: Higidura zirkular eta erlatiboa Gaien Aurkibidea 1 Higidura zirkularra 1 1.1 Azelerazioaren osagai intrintsekoak higidura zirkularrean..... 3 1.2 Kasu partikularrak..........................
Inekuazioak. Helburuak. 1. Ezezagun bateko lehen orria 74 mailako inekuazioak Definizioak Inekuazio baliokideak Ebazpena Inekuazio-sistemak
 5 Inekuazioak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Ezezagun bateko lehen eta bigarren mailako inekuazioak ebazten. Ezezagun bateko ekuaziosistemak ebazten. Modu grafikoan bi ezezaguneko lehen
5 Inekuazioak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Ezezagun bateko lehen eta bigarren mailako inekuazioak ebazten. Ezezagun bateko ekuaziosistemak ebazten. Modu grafikoan bi ezezaguneko lehen
2 ΑΛΓΕΒΡΑ. 2.1 Ταυτότητες
 SECTIN ΑΛΓΕΒΡΑ. Ταυτότητες ( ) + ( + ) + + ( ) 3 3 3 + 3 3 ( + ) 3 3 + 3 + 3 + 3 ( ) 4 4 4 3 + 6 4 3 + 4 ( + ) 4 4 + 4 3 + 6 + 4 3 + 4 ( )( + ) 3 3 ( )( + + ) 3 + 3 ( + )( + ) 4 4 ( )( + )( + ) 4 + 4 (
SECTIN ΑΛΓΕΒΡΑ. Ταυτότητες ( ) + ( + ) + + ( ) 3 3 3 + 3 3 ( + ) 3 3 + 3 + 3 + 3 ( ) 4 4 4 3 + 6 4 3 + 4 ( + ) 4 4 + 4 3 + 6 + 4 3 + 4 ( )( + ) 3 3 ( )( + + ) 3 + 3 ( + )( + ) 4 4 ( )( + )( + ) 4 + 4 (
Mate+K. Koadernoak. Ikasplay, S.L.
 Mate+K Koadernoak Ikasplay, S.L. AURKIBIDEA Aurkibidea 1. ZENBAKI ARRUNTAK... 3. ZENBAKI OSOAK... 0 3. ZATIGARRITASUNA... 34 4. ZENBAKI HAMARTARRAK... 53 5. ZATIKIAK... 65 6. PROPORTZIONALTASUNA ETA EHUNEKOAK...
Mate+K Koadernoak Ikasplay, S.L. AURKIBIDEA Aurkibidea 1. ZENBAKI ARRUNTAK... 3. ZENBAKI OSOAK... 0 3. ZATIGARRITASUNA... 34 4. ZENBAKI HAMARTARRAK... 53 5. ZATIKIAK... 65 6. PROPORTZIONALTASUNA ETA EHUNEKOAK...
Trigonometria ANGELU BATEN ARRAZOI TRIGONOMETRIKOAK ANGELU BATEN ARRAZOI TRIGONOMETRIKOEN ARTEKO ERLAZIOAK
 Trigonometria ANGELU BATEN ARRAZOI TRIGONOMETRIKOAK SINUA KOSINUA TANGENTEA ANGELU BATEN ARRAZOI TRIGONOMETRIKOEN ARTEKO ERLAZIOAK sin α + cos α = sin α cos α = tg α 0º, º ETA 60º-KO ANGELUEN ARRAZOI TRIGONOMETRIKOAK
Trigonometria ANGELU BATEN ARRAZOI TRIGONOMETRIKOAK SINUA KOSINUA TANGENTEA ANGELU BATEN ARRAZOI TRIGONOMETRIKOEN ARTEKO ERLAZIOAK sin α + cos α = sin α cos α = tg α 0º, º ETA 60º-KO ANGELUEN ARRAZOI TRIGONOMETRIKOAK
(2), ,. 1).
 178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
178/1 L I ( ) ( ) 2019/1111 25 2019,, ( ), 81 3,,, ( 1 ), ( 2 ),, : (1) 15 2014 ( ). 2201/2003. ( 3 ) ( ). 2201/2003,..,,. (2),..,,, 25 1980, («1980»),.,,. ( 1 ) 18 2018 ( C 458 19.12.2018,. 499) 14 2019
(a b) c = a (b c) e a e = e a = a. a a 1 = a 1 a = e. m+n
 Z 6 D 3 G = {a, b, c,... } G a, b G a b = c c (a b) c = a (b c) e a e = e a = a a a 1 = a 1 a = e Q = {0, ±1, ±2,..., ±n,... } m, n m+n m + 0 = m m + ( m) = 0 Z N = {a n }, n = 1, 2... N N Z N = {1, ω,
Z 6 D 3 G = {a, b, c,... } G a, b G a b = c c (a b) c = a (b c) e a e = e a = a a a 1 = a 1 a = e Q = {0, ±1, ±2,..., ±n,... } m, n m+n m + 0 = m m + ( m) = 0 Z N = {a n }, n = 1, 2... N N Z N = {1, ω,
2. GAIA. KALKULU MATRIZIALA
 . GI. KLKULU MTRIZIL. Mtrizek. Defiiziok. Mtrizee rteko ergiketk. Mtrizee tuket. Esklr te et mtrize te rteko iderket. Mtrizee iderket. Mtrize iruli,simetriko et tisimetriko 4. Mtrize krrtu te determite
. GI. KLKULU MTRIZIL. Mtrizek. Defiiziok. Mtrizee rteko ergiketk. Mtrizee tuket. Esklr te et mtrize te rteko iderket. Mtrizee iderket. Mtrize iruli,simetriko et tisimetriko 4. Mtrize krrtu te determite
1. [Carrier, Krook and Pearson, Section 3-1 problem 1] Using the contour
![1. [Carrier, Krook and Pearson, Section 3-1 problem 1] Using the contour 1. [Carrier, Krook and Pearson, Section 3-1 problem 1] Using the contour](/thumbs/72/66655942.jpg) . [Carrier, Krook and Pearson, Section 3- problem ] Using the contour Γ R Γ show that if a, b and c are real with b < 4ac, then dx ax + bx + c π 4ac b. Let r and r be the roots of ax + bx + c. By hypothesis
. [Carrier, Krook and Pearson, Section 3- problem ] Using the contour Γ R Γ show that if a, b and c are real with b < 4ac, then dx ax + bx + c π 4ac b. Let r and r be the roots of ax + bx + c. By hypothesis
AURKIBIDEA I. KORRONTE ZUZENARI BURUZKO LABURPENA... 7
 AURKIBIDEA Or. I. KORRONTE ZUZENARI BURUZKO LABURPENA... 7 1.1. MAGNITUDEAK... 7 1.1.1. Karga elektrikoa (Q)... 7 1.1.2. Intentsitatea (I)... 7 1.1.3. Tentsioa ()... 8 1.1.4. Erresistentzia elektrikoa
AURKIBIDEA Or. I. KORRONTE ZUZENARI BURUZKO LABURPENA... 7 1.1. MAGNITUDEAK... 7 1.1.1. Karga elektrikoa (Q)... 7 1.1.2. Intentsitatea (I)... 7 1.1.3. Tentsioa ()... 8 1.1.4. Erresistentzia elektrikoa
ITU-R P (2009/10)
 ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
Γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού χρονών - σύνολο
 πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση του αριθμού του οικονομικά ενεργού
πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό συμμετοχής στην αγορά εργασίας πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση του αριθμού του οικονομικά ενεργού
Hidrogeno atomoaren energi mailen banatzea eremu kubiko batean
 Hidrogeno atomoaren energi mailen banatzea eremu kubiko batean Pablo Mínguez Elektrika eta Elektronika Saila Euskal Herriko Unibertsitatea/Zientzi Fakultatea 644 P.K., 48080 BILBAO Laburpena: Atomo baten
Hidrogeno atomoaren energi mailen banatzea eremu kubiko batean Pablo Mínguez Elektrika eta Elektronika Saila Euskal Herriko Unibertsitatea/Zientzi Fakultatea 644 P.K., 48080 BILBAO Laburpena: Atomo baten
Η γεωργία στην ΕΕ απαντώντας στην πρόκληση των κλιματικών αλλαγών
 Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
Ευρωπαϊκή Επιτροπή Γε ν ι κ ή Δ ι ε ύ θ υ ν σ η Γε ω ρ γ ί α ς κ α ι Αγ ρ ο τ ι κ ή ς Α ν ά π τ υ ξ η ς Ευρωπαϊκή Επιτροπή Γεωργία και αγροτική ανάπτυξη Για περισσότερες πληροφορίες 200 Rue de la Loi,
MATEMATIKA DISKRETUA ETA ALGEBRA. Lehenengo zatia
 MATEMATIKA DISKRETUA ETA ALGEBRA Lehenengo zatia http ://www.sc.ehu.es/ccwalirx/docs/materiala.htm 1. KALKULU PROPOSIZIONALA 2. PREDIKATU KALKULUA 3. MULTZOAK, OSOKOAK 4. ERLAZIOAK ETA FUNTZIOAK 5. GRAFOAK
MATEMATIKA DISKRETUA ETA ALGEBRA Lehenengo zatia http ://www.sc.ehu.es/ccwalirx/docs/materiala.htm 1. KALKULU PROPOSIZIONALA 2. PREDIKATU KALKULUA 3. MULTZOAK, OSOKOAK 4. ERLAZIOAK ETA FUNTZIOAK 5. GRAFOAK
ΦΥΛΛΑΔΙΟ 2 ΑΝΑΛΥΣΗΣ/ ΥΠΟΛΟΓΙΣΜΟΣ ΑΟΡΙΣΤΩΝ ΟΛΟΚΛΗΡΩΜΑΤΩΝ ΑΣΚΗΣΕΙΣ., (γ) sin 5xdx sin x cos x. x + x + 1 dx.. 2x 1 2 2
 ΦΥΛΛΑΔΙΟ ΑΝΑΛΥΣΗΣ/00- ΥΠΟΛΟΓΙΣΜΟΣ ΑΟΡΙΣΤΩΝ ΟΛΟΚΛΗΡΩΜΑΤΩΝ ΑΣΚΗΣΕΙΣ Να υπολογιστούν τα ολοκληρώματα 6 d (α) d, (β), (γ) si 5d si cos, d (δ) cos cos cos 5d, (ε), (στ) d 5 6 (α) Έχουμε =, οπότε θα είναι: 6
ΦΥΛΛΑΔΙΟ ΑΝΑΛΥΣΗΣ/00- ΥΠΟΛΟΓΙΣΜΟΣ ΑΟΡΙΣΤΩΝ ΟΛΟΚΛΗΡΩΜΑΤΩΝ ΑΣΚΗΣΕΙΣ Να υπολογιστούν τα ολοκληρώματα 6 d (α) d, (β), (γ) si 5d si cos, d (δ) cos cos cos 5d, (ε), (στ) d 5 6 (α) Έχουμε =, οπότε θα είναι: 6
COURBES EN POLAIRE. I - Définition
 Y I - Définition COURBES EN POLAIRE On dit qu une courbe Γ admet l équation polaire ρ=f (θ), si et seulement si Γ est l ensemble des points M du plan tels que : OM= ρ u = f(θ) u(θ) Γ peut être considérée
Y I - Définition COURBES EN POLAIRE On dit qu une courbe Γ admet l équation polaire ρ=f (θ), si et seulement si Γ est l ensemble des points M du plan tels que : OM= ρ u = f(θ) u(θ) Γ peut être considérée
Γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού - σύνολο
 απασχολούμενου πληθυσμού - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού υπολογίζεται με τη διαίρεση του αριθμού του ισοδύναμου πλήρως
απασχολούμενου πληθυσμού - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το γενικό ποσοστό απασχόλησης ισοδύναμου πλήρως απασχολούμενου πληθυσμού υπολογίζεται με τη διαίρεση του αριθμού του ισοδύναμου πλήρως
1. Higidura periodikoak. Higidura oszilakorra. Higidura bibrakorra.
 1. Higidura periodikoak. Higidura oszilakorra. Higidura bibrakorra. 2. Higidura harmoniko sinplearen ekuazioa. Grafikoak. 3. Abiadura eta azelerazioa hhs-an. Grafikoak. 4. Malguki baten oszilazioa. Osziladore
1. Higidura periodikoak. Higidura oszilakorra. Higidura bibrakorra. 2. Higidura harmoniko sinplearen ekuazioa. Grafikoak. 3. Abiadura eta azelerazioa hhs-an. Grafikoak. 4. Malguki baten oszilazioa. Osziladore
Γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού χρονών - σύνολο
 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Ο γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση της ετήσιας αύξησης του οικονομικά ενεργού πληθυσμού
15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Ο γενικός ρυθμός μεταβολής οικονομικά ενεργού πληθυσμού 15-64 χρονών υπολογίζεται με τη διαίρεση της ετήσιας αύξησης του οικονομικά ενεργού πληθυσμού
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
!"! #!"!!$ #$! %!"&' & (%!' #!% #" *! *$' *.!! )#/'.0! )#/.*!$,)# * % $ %!!#!!%#'!)$! #,# #!%# ##& )$&# 11!!#2!
 # $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
# $ #$ % (% # )*%%# )# )$ % # * *$ * #,##%#)#% *-. )#/###%. )#/.0 )#/.* $,)# )#/ * % $ % # %# )$ #,# # %# ## )$# 11 #2 #**##%% $#%34 5 # %## * 6 7(%#)%%%, #, # ## # *% #$# 8# )####, 7 9%%# 0 * #,, :;
Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού χρονών - σύνολο
 Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών υπολογίζεται με
Ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό απασχόλησης στον τριτογενή τομέα του πληθυσμού 15-64 χρονών υπολογίζεται με
Ασκήσεις Μαθηµατικών Μεθόδων Φυσικής Ι
 .. ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟΥ. Ασκήσεις Κεφαλαίου Ασκήσεις Μαθηµατικών Μεθόδων Φυσικής Ι Κατά τη λύση των ασκήσεων επάνω στους µιγαδικούς αριθµούς είναι χρήσιµο να έχουµε υπόψη ότι ένας µιγαδικός αριθµός µπορεί
.. ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟΥ. Ασκήσεις Κεφαλαίου Ασκήσεις Μαθηµατικών Μεθόδων Φυσικής Ι Κατά τη λύση των ασκήσεων επάνω στους µιγαδικούς αριθµούς είναι χρήσιµο να έχουµε υπόψη ότι ένας µιγαδικός αριθµός µπορεί
Batigoal_mathscope.org ñược tính theo công thức
 SỐ PHỨC TRONG CHỨNG MINH HÌNH HỌC PHẲNG Batigoal_mathscope.org Hoangquan9@gmail.com I.MỘT SỐ KHÁI NIỆM CƠ BẢN. Khoảng cách giữa hai ñiểm Giả sử có số phức và biểu diễn hai ñiểm M và M trên mặt phẳng tọa
SỐ PHỨC TRONG CHỨNG MINH HÌNH HỌC PHẲNG Batigoal_mathscope.org Hoangquan9@gmail.com I.MỘT SỐ KHÁI NIỆM CƠ BẢN. Khoảng cách giữa hai ñiểm Giả sử có số phức và biểu diễn hai ñiểm M và M trên mặt phẳng tọa
Ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο
 οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών υπολογίζεται με τη διαίρεση
οικονομικά ενεργού πληθυσμού 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το ποσοστό μακροχρόνιας ανεργίας (διάρκεια 12+ μήνες) οικονομικά ενεργού πληθυσμού 15+ χρονών υπολογίζεται με τη διαίρεση
2. PROGRAMEN ESPEZIFIKAZIOA
 2. PROGRAMEN ESPEZIFIKAZIOA 2.1. Asertzioak: egoera-multzoak adierazteko formulak. 2.2. Aurre-ondoetako espezifikazio formala. - 1 - 2.1. Asertzioak: egoera-multzoak adierazteko formulak. Programa baten
2. PROGRAMEN ESPEZIFIKAZIOA 2.1. Asertzioak: egoera-multzoak adierazteko formulak. 2.2. Aurre-ondoetako espezifikazio formala. - 1 - 2.1. Asertzioak: egoera-multzoak adierazteko formulak. Programa baten
Antzekotasuna. Helburuak. Hasi baino lehen. 1.Antzekotasuna...orria 92 Antzeko figurak Talesen teorema Antzeko triangeluak
 6 Antzekotasuna Helburuak Hamabostaldi honetan haue ikasiko duzu: Antzeko figurak ezagutzen eta marrazten. Triangeluen antzekotasunaren irizpideak aplikatzen. Katetoaren eta altueraren teoremak erakusten
6 Antzekotasuna Helburuak Hamabostaldi honetan haue ikasiko duzu: Antzeko figurak ezagutzen eta marrazten. Triangeluen antzekotasunaren irizpideak aplikatzen. Katetoaren eta altueraren teoremak erakusten
Email: dsourlas@physics.upatras.gr Ιστοσελίδα: www.physics.upatras.gr
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΉΣ ΜΙΓΑΔΙΚΗ ΑΝΑΛΥΣΗ Δημήτρης Σουρλάς Αναπλ. Καθηγητής f ( ) ( ) α! f() π i ( α) + d Πάτρα Email: dsourlas@physics.upatras.gr Ιστοσελίδα: www.physics.upatras.gr Περιεχόμενα.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΉΣ ΜΙΓΑΔΙΚΗ ΑΝΑΛΥΣΗ Δημήτρης Σουρλάς Αναπλ. Καθηγητής f ( ) ( ) α! f() π i ( α) + d Πάτρα Email: dsourlas@physics.upatras.gr Ιστοσελίδα: www.physics.upatras.gr Περιεχόμενα.
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
ΛΟΓΙΣΜΟΣ Συναρτήσεων µιας Μεταβλητής
 Σηµειωσεις: ΛΟΓΙΣΜΟΣ Συναρτήσεων µιας Μεταβλητής Θ. Κεχαγιάς Σεπτέµβρης 9 v..85 Περιεχόµενα Προλογος Εισαγωγη Βασικες Συναρτησεις. Θεωρια..................................... Λυµενα Προβληµατα.............................
Σηµειωσεις: ΛΟΓΙΣΜΟΣ Συναρτήσεων µιας Μεταβλητής Θ. Κεχαγιάς Σεπτέµβρης 9 v..85 Περιεχόµενα Προλογος Εισαγωγη Βασικες Συναρτησεις. Θεωρια..................................... Λυµενα Προβληµατα.............................
Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο
 Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το μερίδιο εργοδοτουμένων με μερική ή/και προσωρινή απασχόληση
Μερίδιο εργοδοτουμένων με μερική ή / και προσωρινή απασχόληση στον εργοδοτούμενο πληθυσμό 15+ χρονών - σύνολο Περιγραφή δείκτη και πηγή πληροφοριών Το μερίδιο εργοδοτουμένων με μερική ή/και προσωρινή απασχόληση
ΜΙΓΑ ΙΚΟΣ ΛΟΓΙΣΜΟΣ ΚΑΙ ΟΛΟΚΛ. ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 2010 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ
 ΜΙΓΑ ΙΚΟΣ ΛΟΓΙΣΜΟΣ ΚΑΙ ΟΛΟΚΛ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΘΕΜΑ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ α) Η f ( ) έχει πραγµατικό µέρος φανταστικό µέρος u( x, y) x y = και v( x, y) = ( x + y xy), όπου = x+
ΜΙΓΑ ΙΚΟΣ ΛΟΓΙΣΜΟΣ ΚΑΙ ΟΛΟΚΛ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΘΕΜΑ ΓΡΑΠΤΕΣ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ α) Η f ( ) έχει πραγµατικό µέρος φανταστικό µέρος u( x, y) x y = και v( x, y) = ( x + y xy), όπου = x+
COMPLEX NUMBERS. 1. A number of the form.
 COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
Formulas of Agrawal s Fiber-Optic Communication Systems. Section 2-1 (Geometrical Optics Description) NA n 2 ; n n. NA( )=n1 a
 Formula o grawal Fier-Oti Commuiatio Sytem Chater (troutio 8 max m M E h h M m 4 6.66. J e.6 9 m log mw S, Chater (Otial Fier SFMMF: i i ir Z Setio - (Geometrial Oti eritio i Z S log i h max E ii o ; GFMMF:
Formula o grawal Fier-Oti Commuiatio Sytem Chater (troutio 8 max m M E h h M m 4 6.66. J e.6 9 m log mw S, Chater (Otial Fier SFMMF: i i ir Z Setio - (Geometrial Oti eritio i Z S log i h max E ii o ; GFMMF:
Microscopie photothermique et endommagement laser
 Microscopie photothermique et endommagement laser Annelise During To cite this version: Annelise During. Microscopie photothermique et endommagement laser. Physique Atomique [physics.atom-ph]. Université
Microscopie photothermique et endommagement laser Annelise During To cite this version: Annelise During. Microscopie photothermique et endommagement laser. Physique Atomique [physics.atom-ph]. Université
