prin egalizarea histogramei
|
|
|
- Δείμος Παππάς
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o anumită formă dorită. 4.1 Histograma unei imagini Histograma unei imagini reprezintă frecvenţa relativă de apariţie a nivelelor de gri din imagine. Pentru o imagine f, de dimensiune M N pixeli, histograma se defineşte astfel: h(i) = 1 MN M 1 N 1 m=0 n=0 unde funcţia δ este definită în următorul mod: { 1, dacă x = y, δ(x, y) = 0, dacă x y. δ(i, f(m, n)), i = 0,.., L 1 (4.1) (4.2) Din punct de vedere statistic, putem considera valoarea fiecărui pixel al imaginii ca o realizare particulară a unei variabile aleatoare asociată nivelelor de gri, caz în care histograma reprezintă funcţia de densitate de probabilitate a acestei variabile aleatoare. Fiind o funcţie de densitate de probabilitate, histograma oricărei imagini verifică condiţia de normare: L 1 h(i) = 1 (4.3) i=0 Practic, calculul histogramei presupune parcurgerea pixel cu pixel a imaginii şi contorizarea numărului de nivele de gri întâlnite. 25
2 26 LUCRAREA 4. EGALIZAREA HISTOGRAMEI 4.2 Egalizarea histogramei Egalizarea histogramei reprezintă o operaţie de accentuare a contrastului şi are ca scop obţinerea unei histograme uniforme. Vom asocia unui pixel din imagine o variabilă aleatoare ξ. Astfel, valorile intensităţii luminoase ale pixelilor reprezintă realizări particulare ale variabilei aleatoare asociate. Vom considera că variabila aleatoare ξ are o densitate de probabilitate w ξ (x) şi o funcţie de repartiţie F ξ (x) = P {ξ x}. Vom defini în continuare variabila η, care are funcţia de repartiţie: F η (x) = x 0 p ξ (t)dt şi care va fi uniform distribuită în intervalul (0, 1). Pentru cazul discret, presupunem că nivelele x de gri ale pixelilor au valori între 0 şi L 1 (unde L este de regulă 256), având asociate probabilităţile de apariţie p ξ (x i ), unde x i = 0, 1,..., L 1. Aceste probabilităţi pot fi estimate pe baza calculului histogramei, considerând imaginea dată, ca fiind o realizare particulară a procesului aleator descris de variabila aleatoare ξ, astfel: p ξ (x i ) = h(x i) L 1 h(x i ) Noile nivele de gri, reprezentând valori discrete ale variabilei η din intervalul [0, L 1] se vor calcula cu formulele: h c (x) = i=0 x p ξ (x i ) x i =0 [ ] hc [nivel vechi ] h cmin nivel nou = int (L 1) h cmin unde h c reprezintă histograma cumulativă a imaginii, iar h cmin este valoarea minimă a histogramei cumulative Algoritmul de egalizare a histogramei Algoritmul de egalizare de histogramă, folosit în practică, poate fi descris în limbaj pseudocod astfel: Pasul 1. Se calculează histograma imaginii: pentru i = 1,..,L h[i] = 0 pentru i = 1,..,M pentru j = 1,..,N
3 4.3. OBSERVAŢII 27 nivel = imagine[i,j] h[nivel] = h[nivel] + 1 unde L este numărul de nivele de gri (256), h este histograma imaginii, iar M şi N sunt dimensiunile imaginii. Pasul 2. Se calculează histograma cumulativă a imaginii: hc[1] = h[1] pentru i = 2,..,L hc[i] = hc[i-1] + h[i] Pasul 3. Se calculează noile nivele de gri din imagine, sub forma unei transformări y = T (x) dată de formula: y = T (x) = [ ] hc[x] hc[1] (L 1) NM hc[1] astfel: pentru i = 1,..,M pentru j = 1,..,N nivel vechi = imagine[i,j] nivel nou = T(nivel vechi) imagine[i,j] = nivel nou 4.3 Observaţii Deşi la prima vedere egalizarea de histogramă ar părea că este o operaţie punctuală, din cauza formulei de calcul a noilor valori de gri, ea este totuşi o operaţie integrală, datorită faptului că pentru fiecare pixel din imagine noua valoare se calculează pe baza calculului histogramei şi, deci, pe baza valorilor tuturor pixelilor din imagine. În Figura 4.1 puteţi observa cum imaginea a fost îmbunătăţită prin egalizarea histogramei. În Figura 4.2 puteţi observa cum s-a modificat forma histogramei imaginii originale, după egalizare.
4 28 LUCRAREA 4. EGALIZAREA HISTOGRAMEI (a) (b) Figura 4.1: Egalizarea histogramei: (a) imaginea originală şi (b) imaginea rezultată. (a) (b) Figura 4.2: Histograma (a) originală şi (b) după egalizare.
5 4.3. OBSERVAŢII 29 DESFĂŞURAREA LUCRĂRII O posibilă implementare a algoritmului de egalizare a histogramei este prezentat în continuare: void ImageViewer :: egalizeaza_histograma( void ) { int i, j; int width, height; int h[ 256 ]; for( i = 0; i < 256; i++ ) h[ i ] = 0; width = image.width(); height = image.height(); //calcularea histogramei imaginii for( i = 0; i < width; i++ ) for( j = 0; j < height; j++ ) { QRgb pixel; pixel = image.pixel( i, j ); } int nivel_gri = qred( pixel ); h[ nivel_gri ]++ ; //calcularea histogramei cumulative double hc[ 256 ]; hc[ 0 ] = h[ 0 ]; for( i = 1; i < 256; i++ ) hc[ i ] = hc[ i - 1 ] + h[ i ]; QImage imag_eq( width, height, 32, 0, QImage::IgnoreEndian ); //egalizarea histogramei for( i = 0; i < width; i++ ) for( j = 0; j < height; j++ ) { QRgb pixel = image.pixel( i, j ); int nivel = qred( pixel );
6 30 LUCRAREA 4. EGALIZAREA HISTOGRAMEI int nivel_nou = (int)( ( hc[nivel] - hc[0] ) * 255 / ( width*height - hc[0] ) ); } imag_eq.setpixel( i, j, qrgb( nivel_nou, nivel_nou, nivel_nou ) ); } image = imag_eq; pm = image; update(); Problema 1. Observaţi forma histogramei pentru câteva imagini în tonuri de gri. Problema 2. Observaţi efectele egalizării de histogramă pentru diferite imagini, inclusiv pentru o imagine subexpusă şi pentru una supraexpusă. Problema 3. Modificaţi funcţia histograma imaginii astfel încât aceasta să calculeze histograma cumulativă a imaginii. Observaţi forma unei histograme cumulative. Problema 4. Justificaţi faptul că histograma cumulativă a unei imagini poate fi considerată estimatul unei funcţii de repartiţie.
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
OPERATII DE PRELUCRARE A IMAGINILOR C. VERTAN
 OPERATII DE PRELUCRARE A IMAGINILOR Prelucrare = Black Box Image In, Image Out Analiza imaginilor este Image In, Description Out Tipuri de operatii de prelucrare Clasificare dupa numarul de pixeli din
OPERATII DE PRELUCRARE A IMAGINILOR Prelucrare = Black Box Image In, Image Out Analiza imaginilor este Image In, Description Out Tipuri de operatii de prelucrare Clasificare dupa numarul de pixeli din
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Procesarea Imaginilor
 UNIVERSITATEA TRANSILVANIA DIN BRAŞOV Laurenţiu-Mihail IVANOVICI Procesarea Imaginilor Îndrumar de laborator 2006 c 2003 EDITURA UNIVERSITĂŢII TRANSILVANIA BRAŞOV Adresa: 500030 Brasov, B-dul Eroilor,
UNIVERSITATEA TRANSILVANIA DIN BRAŞOV Laurenţiu-Mihail IVANOVICI Procesarea Imaginilor Îndrumar de laborator 2006 c 2003 EDITURA UNIVERSITĂŢII TRANSILVANIA BRAŞOV Adresa: 500030 Brasov, B-dul Eroilor,
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Segmentarea imaginilor
 Lucrarea 0 Segmentarea imaginilor BREVIAR TEORETIC Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii. Fiecărui pixel i se va atribui o valoare, 0 sau, reprezentând apartenenţa
Lucrarea 0 Segmentarea imaginilor BREVIAR TEORETIC Segmentarea reprezintă împărţirea imaginii în zone de interes, după anumite criterii. Fiecărui pixel i se va atribui o valoare, 0 sau, reprezentând apartenenţa
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
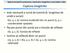
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
VARIABILE ŞI PROCESE ALEATOARE: Principii. Constantin VERTAN, Inge GAVĂT, Rodica STOIAN
 VARIABILE ŞI PROCESE ALEATOARE: Principii şi aplicaţii Constantin VERTAN, Inge GAVĂT, Rodica STOIAN 3 mai 999 Cuprins Cuvânt înainte 4 Variabile aleatoare cu valori continue 5. Funcţia de repartiţieavariabilelor
VARIABILE ŞI PROCESE ALEATOARE: Principii şi aplicaţii Constantin VERTAN, Inge GAVĂT, Rodica STOIAN 3 mai 999 Cuprins Cuvânt înainte 4 Variabile aleatoare cu valori continue 5. Funcţia de repartiţieavariabilelor
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
9 Testarea ipotezelor statistice
 9 Testarea ipotezelor statistice Un test statistic constă în obţinerea unei deducţii bazată pe o selecţie din populaţie prin testarea unei anumite ipoteze (rezultată din experienţa anterioară, din observaţii,
9 Testarea ipotezelor statistice Un test statistic constă în obţinerea unei deducţii bazată pe o selecţie din populaţie prin testarea unei anumite ipoteze (rezultată din experienţa anterioară, din observaţii,
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice
 Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Modelarea şi Simularea Sistemelor de Calcul Distribuţii ( lab. 4)
 Modelarea şi Simularea Sistemelor de Calcul Distribuţii ( lab. 4) În practică eistă nenumărate eperienţe aleatoare care au un câmp de evenimente nenumărabil şi implicit sistemul complet de evenimente aleatoare
Modelarea şi Simularea Sistemelor de Calcul Distribuţii ( lab. 4) În practică eistă nenumărate eperienţe aleatoare care au un câmp de evenimente nenumărabil şi implicit sistemul complet de evenimente aleatoare
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Statisticǎ - curs 3. 1 Seria de distribuţie a statisticilor de eşantioane 2. 2 Teorema limitǎ centralǎ 5. 3 O aplicaţie a teoremei limitǎ centralǎ 7
 Statisticǎ - curs 3 Cuprins 1 Seria de distribuţie a statisticilor de eşantioane 2 2 Teorema limitǎ centralǎ 5 3 O aplicaţie a teoremei limitǎ centralǎ 7 4 Estimarea punctualǎ a unui parametru; intervalul
Statisticǎ - curs 3 Cuprins 1 Seria de distribuţie a statisticilor de eşantioane 2 2 Teorema limitǎ centralǎ 5 3 O aplicaţie a teoremei limitǎ centralǎ 7 4 Estimarea punctualǎ a unui parametru; intervalul
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
7 Distribuţia normală
 7 Distribuţia normală Distribuţia normală este cea mai importantă distribuţie continuă, deoarece în practică multe variabile aleatoare sunt variabile aleatoare normale, sunt aproximativ variabile aleatoare
7 Distribuţia normală Distribuţia normală este cea mai importantă distribuţie continuă, deoarece în practică multe variabile aleatoare sunt variabile aleatoare normale, sunt aproximativ variabile aleatoare
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Laborator 6. Integrarea ecuaţiilor diferenţiale
 Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Procesarea imaginilor folosind logica fuzzy
 Procesarea imaginilor folosind logica fuzzy M. Ivanovici 6 noiembrie 2007 BREVIAR TEORETIC Conceptele de bază ale logicii fuzzy Logica clasică sau booleană este construită pe două valori de adevăr: adevărat
Procesarea imaginilor folosind logica fuzzy M. Ivanovici 6 noiembrie 2007 BREVIAR TEORETIC Conceptele de bază ale logicii fuzzy Logica clasică sau booleană este construită pe două valori de adevăr: adevărat
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
T R A I A N ( ) Trigonometrie. \ kπ; k. este periodică (perioada principală T * =π ), impară, nemărginită.
 Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
I3: PROBABILITǍŢI - notiţe de curs
 I3: PROBABILITǍŢI - notiţe de curs Ştefan Balint, Eva Kaslik, Simina Mariş Cuprins Experienţǎ şi evenimente aleatoare 3 2 Eveniment sigur. Eveniment imposibil 3 3 Evenimente contrare 4 4 Evenimente compatibile.
I3: PROBABILITǍŢI - notiţe de curs Ştefan Balint, Eva Kaslik, Simina Mariş Cuprins Experienţǎ şi evenimente aleatoare 3 2 Eveniment sigur. Eveniment imposibil 3 3 Evenimente contrare 4 4 Evenimente compatibile.
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE. Obiective:
 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Integrale cu parametru
 1 Integrle proprii cu prmetru 2 3 Integrle proprii cu prmetru Definiţi 1.1 Dcă f : [, b ] E R, E R este o funcţie cu propriette că pentru orice y E, funcţi de vribilă x x f (x, y) este integrbilă pe intervlul
1 Integrle proprii cu prmetru 2 3 Integrle proprii cu prmetru Definiţi 1.1 Dcă f : [, b ] E R, E R este o funcţie cu propriette că pentru orice y E, funcţi de vribilă x x f (x, y) este integrbilă pe intervlul
Tehnici de imbunatatire si restaurare a imaginilor
 Tehnici de imbunatatire si restaurare a imaginilor Tehnici de imbunatatire si restaurare a imaginilor... 1 I. Tehnici de imbunatatire si restaurare in domeniul spatial... 3 1. Conversia nivelelor de gri...
Tehnici de imbunatatire si restaurare a imaginilor Tehnici de imbunatatire si restaurare a imaginilor... 1 I. Tehnici de imbunatatire si restaurare in domeniul spatial... 3 1. Conversia nivelelor de gri...
2.2.1 Măsurători asupra semnalelor digitale
 Lucrarea 2 Măsurători asupra semnalelor digitale 2.1 Obiective Lucrarea are ca obiectiv fixarea cunoştinţelor dobândite în lucrarea anterioară: Familiarizarea cu aparatele de laborator (generatorul de
Lucrarea 2 Măsurători asupra semnalelor digitale 2.1 Obiective Lucrarea are ca obiectiv fixarea cunoştinţelor dobândite în lucrarea anterioară: Familiarizarea cu aparatele de laborator (generatorul de
I3: PROBABILITǍŢI - notiţe de curs
 I3: PROBABILITǍŢI - notiţe de curs Ştefan Balint, Eva Kaslik, Simina Mariş Cuprins Experienţǎ şi evenimente aleatoare 3 2 Eveniment sigur. Eveniment imposibil 3 3 Evenimente contrare 4 4 Evenimente compatibile.
I3: PROBABILITǍŢI - notiţe de curs Ştefan Balint, Eva Kaslik, Simina Mariş Cuprins Experienţǎ şi evenimente aleatoare 3 2 Eveniment sigur. Eveniment imposibil 3 3 Evenimente contrare 4 4 Evenimente compatibile.
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Modul de calcul al prețului polițelor RCA
 Modul de calcul al prețului polițelor RCA Componentele primei comerciale pentru o poliță RCA sunt: Prima pură Cheltuieli specifice poliței Alte cheltuieli Marja de profit Denumită și primă de risc Cheltuieli
Modul de calcul al prețului polițelor RCA Componentele primei comerciale pentru o poliță RCA sunt: Prima pură Cheltuieli specifice poliței Alte cheltuieli Marja de profit Denumită și primă de risc Cheltuieli
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Ovidiu Gabriel Avădănei, Florin Mihai Tufescu,
 vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
FLUXURI MAXIME ÎN REŢELE DE TRANSPORT. x 4
 FLUXURI MAXIME ÎN REŢELE DE TRANSPORT Se numeşte reţea de transport un graf în care fiecărui arc îi este asociat capacitatea arcului şi în care eistă un singur punct de intrare şi un singur punct de ieşire.
FLUXURI MAXIME ÎN REŢELE DE TRANSPORT Se numeşte reţea de transport un graf în care fiecărui arc îi este asociat capacitatea arcului şi în care eistă un singur punct de intrare şi un singur punct de ieşire.
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
ESTIMAREA PARAMETRILOR STATISTICI. Călinici Tudor
 ESTIMAREA PARAMETRILOR STATISTICI Călinici Tudor 1 Obiective educaţionale Înţelegerea procesului de estimare Însuşirea limbajului specific pentru inferenţa statistică Enumerarea estimatorilor fără bias
ESTIMAREA PARAMETRILOR STATISTICI Călinici Tudor 1 Obiective educaţionale Înţelegerea procesului de estimare Însuşirea limbajului specific pentru inferenţa statistică Enumerarea estimatorilor fără bias
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Concurs MATE-INFO UBB, 1 aprilie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
Sisteme de Recunoastere a Formelor Laborator 5 Histograma Orientarilor Gradientilor
 Sisteme de Recunoastere a Formelor Laborator 5 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
Sisteme de Recunoastere a Formelor Laborator 5 Histograma Orientarilor Gradientilor 1. Obiectie Descriptorii de tip histograma a orientarii gratientilor, sau descriptori HOG, sunt descriptori de trasatori
Aplicaţii ale principiului I al termodinamicii în tehnică
 Aplicaţii ale principiului I al termodinamicii în tehnică Sisteme de încălzire a locuinţelor Scopul tuturor acestor sisteme, este de a compensa pierderile de căldură prin pereţii locuinţelor şi prin sistemul
Aplicaţii ale principiului I al termodinamicii în tehnică Sisteme de încălzire a locuinţelor Scopul tuturor acestor sisteme, este de a compensa pierderile de căldură prin pereţii locuinţelor şi prin sistemul
EDITURA PARALELA 45 MATEMATICĂ DE EXCELENŢĂ. Clasa a X-a Ediţia a II-a, revizuită. pentru concursuri, olimpiade şi centre de excelenţă
 Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Subiecte Clasa a VIII-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
8. ProprietăŃi statistice ale imaginilor de intensitate
 Procesarea Imailor - aborator 8: ProprietăŃi statistice ale imailor de tensitate 8. ProprietăŃi statistice ale imailor de tensitate 8.. Introducere În această lucrare se vor prezenta prcipalele trăsături
Procesarea Imailor - aborator 8: ProprietăŃi statistice ale imailor de tensitate 8. ProprietăŃi statistice ale imailor de tensitate 8.. Introducere În această lucrare se vor prezenta prcipalele trăsături
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
LUCRAREA DE LABORATOR Nr. 9 DETERMINAREA EXPERIMENTALÃ A DISTIBUŢIEI DIMENSIUNILOR EFECTIVE ÎN INTERIORUL CÂMPULUI DE ÎMPRÃŞTIERE
 LUCRAREA DE LABORATOR Nr. 9 DETERMINAREA EXPERIMENTALÃ A DISTIBUŢIEI DIMENSIUNILOR EFECTIVE ÎN INTERIORUL CÂMPULUI DE ÎMPRÃŞTIERE 1. Scopul lucrãrii. Lucrarea are rolul de a permite cunoaşterea metodologiei
LUCRAREA DE LABORATOR Nr. 9 DETERMINAREA EXPERIMENTALÃ A DISTIBUŢIEI DIMENSIUNILOR EFECTIVE ÎN INTERIORUL CÂMPULUI DE ÎMPRÃŞTIERE 1. Scopul lucrãrii. Lucrarea are rolul de a permite cunoaşterea metodologiei
Εμπορική αλληλογραφία Ηλεκτρονική Αλληλογραφία
 - Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
- Εισαγωγή Stimate Domnule Preşedinte, Stimate Domnule Preşedinte, Εξαιρετικά επίσημη επιστολή, ο παραλήπτης έχει ένα ειδικό τίτλο ο οποίος πρέπει να χρησιμοποιηθεί αντί του ονόματος του Stimate Domnule,
Matematici speciale Seminar 10
 Matematici speciale Seminar 0 Mai 07 ii Ştiinţa se clădeşte cu fapte, aşa cum o casă se construieşte cu pietre. Dar o colecţie de fapte nu e ştiinţă, la fel cum un morman de pietre nu e o casă. Henri Poincaré
Matematici speciale Seminar 0 Mai 07 ii Ştiinţa se clădeşte cu fapte, aşa cum o casă se construieşte cu pietre. Dar o colecţie de fapte nu e ştiinţă, la fel cum un morman de pietre nu e o casă. Henri Poincaré
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Scoruri standard Curba normală (Gauss) M. Popa
 Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Lucrul mecanic. Puterea mecanică.
 1 Lucrul mecanic. Puterea mecanică. In acestă prezentare sunt discutate următoarele subiecte: Definitia lucrului mecanic al unei forţe constante Definiţia lucrului mecanic al unei forţe variabile Intepretarea
1 Lucrul mecanic. Puterea mecanică. In acestă prezentare sunt discutate următoarele subiecte: Definitia lucrului mecanic al unei forţe constante Definiţia lucrului mecanic al unei forţe variabile Intepretarea
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
