Discrete scan statistics with windows of arbitrary shape
|
|
|
- Χλόη Βέργας
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Discrete scan statistics with windows of arbitrary shape Alexandru Am rioarei National Institute of Research and Development for Biological Sciences Bucharest, Romania MΘDAL TEAM - INRIA Lille Nord Europe Lille, France The 8 th International Workshop on Applied Probability June, 206, Toronto, Canada A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP 206 / 50
2 A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
3 Introduction Framework A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
4 Introduction Framework A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Denitions and notations
5 Introduction Framework A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Preliminary notations Let T, T 2 be positive integers s T s 2 T 2 X s,s 2 T 2 T Rectangular region R 2 = [0, T ] [0, T 2 ] (X s,s 2 ) s T s 2 T 2 iid rv's Bernoulli(B(, p)) Binomial(B(n, p)) Poisson(P(λ)) Normal(N (µ, σ 2 )) X s,s 2 number of observed events in the elementary subregion r s,s 2 = [s, s ] [s 2, s 2 ]
6 Introduction Framework A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Two dimensional scan statistic Let 2 m s T s, s {, 2} be positive integers Dene for i s T s m s + and j s m s the 2-way tensor X i,i 2 R m m 2, X i,i 2 (j, j 2 ) = X i +j,i 2 +j 2 Take S : R m m 2 R to be a measurable real valued function (score function) and dene Y i,i 2 (S) = S (X i,i 2 ) Definition The two dimensional scan statistic with score function S is dened by S m,m 2 (T, T 2 ; S) = max i T m + i 2 T 2 m 2 + Y i,i 2 (S)
7 Introduction Framework A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Shape of the scanning window Let G be the geometrical shape of the scanning window (rectangle, quadrilateral, ellipse, etc) and G be its corresponding discrete form Rasterization algorithms (omputer vision): continuous shape discrete shape Line - Bresenham line algorithm ([Bresenham, 965]) Circle - Bresenham circle algorithm ([Bresenham, 977]) Bezier curves - [Foley, 995]
8 Introduction Framework Shape of the scanning window To each discrete shape G it corresponds an unique matrix (2-way tensor) A (G) = A ( G ) (of smallest size) with 0 and entries ( if there is a point and 0 otherwise): G : Circle A ( G ) : Circle A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
9 Introduction Framework Shape of the scanning window To each discrete shape G it corresponds an unique matrix (2-way tensor) A (G) = A ( G ) (of smallest size) with 0 and entries ( if there is a point and 0 otherwise): G : Annulus A ( G ) : Annulus A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
10 Introduction Framework A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Arbitrary window scan statistic Let G be a geometric shape and A = A(G) its corresponding {0, } matrix of size m m 2 Dene the score function S associated to the shape G by S (X i,i 2 ) = A X i,i 2 = Remark i +m s =i i 2 +m 2 s 2 =i 2 A(s i +, s 2 i 2 + )X s,s 2 If, in particular, the shape G is a rectangle of size m m 2 than its corresponding {0, } matrix of the same size has all the entries equal to so the score function S (X i,i 2 ) = i +m s =i i 2 +m 2 s 2 =i 2 X s,s 2 is the classical rectangular window of the two dimensional scan statistics
11 Introduction Problem A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
12 Introduction Problem A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP 206 / 50 Problem and related work
13 Introduction Problem Objective Find a good estimate for the distribution of the two dimensional discrete scan statistic with score function S Q m (T; S) = P (S m (T; S) τ) with m = (m, m 2 ) and T = (T, T 2 ) Previous work: Continuous scan statistics Rectangles: [Loader, 99], [Glaz et al, 200], [Glaz et al, 2009] Circles: [Anderson and Titterington, 997] Triangles, ellipses and other convex shapes: [Alm, 983, Alm, 997, Alm, 998], [Tango and Takahashi, 2005], [Assunção et al, 2006] Discrete scan statistics No results! A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
14 Methodology A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
15 Methodology A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 methodology for the general scan statistic
16 Methodology A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 and error bounds Theorem (Generalization of [Am rioarei, 204]) Let t, t 2 {2, 3}, Q t,t2 = P (Sm (t (m ), t 2 (m 2 ); S) τ) and L s = Ts, m s s {, 2} If ˆQt,t2 is an estimate of Qt,t2, ˆQt,t2 Qt,t2 β t,t2 and τ is such that ˆQ2,2 (τ) 0 then ( ) [ ] L P (Sm(T; S) τ) 2 ˆQ2 ˆQ3 + ˆQ2 ˆQ3 + 2( ˆQ2 ˆQ3 ) 2 E sf + E sapp, where, for t {2, 3} ) ˆQ t = (2 ˆQt,2 ˆQt,3 [ + ˆQt,2 ˆQt,3 + 2( ˆQt,2 ˆQt,3 ) 2] L2 E sf = (L )(L 2 ) (β 2,2 + β 2,3 + β 3,2 + β 3,3 ) ( ) ] 2 E sapp = (L ) [F ˆQ2 + A 2 + C 2 + (L2 )(F 2 C 2 + F 3 C 3 ) A 2 = (L 2 ) (β 2,2 + β 2,3 ) C t = (L 2 )F t ( ˆQt,2 + β t,2 ) 2
17 Methodology A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Illustration of the approximation process T 2 T R 2 Find m m 2 T T T 2 Q 2 T 2 Q 3 m 2 m 2 2(m ) 3(m ) T T T T T 2 T 2 T 2 T 2 Q 22 Q 3(m 2 ) 2(m 2 ) 23 Q 32 Q 3(m 2 ) 2(m 2 ) 33 2(m ) 2(m ) 3(m ) 3(m )
18 Methodology A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Illustration of the approximation process T 2 T R 2 First Step m m 2 T 2 T 2 T Q 2 T Q 3 m m 2(m 2 ) 3(m 2 ) T T T T T 2 T 2 T 2 T 2 Q 22 Q 3(m 2 ) 2(m ) 23 Q 32 Q 3(m 2 ) 2(m 2 ) 33 2(m ) 2(m ) 3(m ) 3(m )
19 Methodology A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Illustration of the approximation process T 2 T R 2 Second Step m m 2 T 2 T 2 T Q 2 T Q 3 m m 2(m 2 ) 3(m 2 ) T 2 T 2 T 2 T 2 T T T T Q 22 Q 3(m ) 2(m ) 23 Q 32 Q 3(m ) 2(m ) 33 2(m 2 ) 2(m 2 ) 3(m 2 ) 3(m 2 )
20 Methodology Simulation methods: Normal data A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
21 Methodology Simulation methods: Normal data A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Simulation methods for Normal data
22 Methodology Simulation methods: Normal data A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Importance sampling algorithm Test the null hypothesis of randomness against an alternative of clustering H 0 : The rv's X s,s 2 are iid N (µ, σ 2 ) H : There exists R(i, i 2 ) = [i, i + m ] [i 2, i 2 + m 2 ] R 2 where the rv's X s,s 2 N (µ, σ 2 ), µ > µ and X s,s 2 N (µ, σ 2 ) outside R(i, i 2 ) Objective Find a good estimate for P H0 (Sm(T; S) τ) We are interested in evaluating the probability P H0 (Sm(T; S) τ) = P where E i,i 2 (S) = {Y i,i 2 (S) τ} ( T m + i = T 2 m 2+ i 2= E i,i 2 (S) )
23 Methodology Simulation methods: Normal data A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Importance sampling algorithm Algorithm Importance Sampling Algorithm for Scan Statistics Begin Repeat for each k from to ITER (iterations number) : Generate uniformly the couple (i (k), i (k) 2 ) from the set {,, T m + } {,, T 2 m 2 + } { } 2: Given the couple (i (k), i (k) 2 ), generate a sample of the random eld X ~ (k) (k) = X s,s2, with s j { } {,, T j } and j {, 2}, from the conditional distribution of X given Y (k) (k) (S) τ i,i 2 3: Take c k = C( X ~ (k) ) the number of all couples (i, i 2 ) for which Ỹ i,i2 (S) τ and put ρ k (2) = c k End Repeat Return ρ(2) = ITER ρ k (2), ITER k= End Var [ ρ(2)] ITER ITER k= ( ρ k (2) ITER ρ k (2) ITER k= ) 2
24 Methodology Simulation methods: Normal data A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Importance sampling algorithm: N (µ, σ 2 ) Step 2 requires to sample: ( (S) from the tail distribution P Y i (k) (k),i 2 Y i (k) (k),i 2 for the other indices, from the conditional distribution given ) (S) τ ([Devroye, 986]) { Y i (k) (k),i 2 } (S) τ Lemma (Generalization of [Am rioarei, 204, Lemma 344]) Let N be a positive integer, X = (X, X 2,, X N ) be a vector of iid N (µ, σ 2 ) and a = (a,, a N ) R N a non zero constant vector ( a j 0 for some particular j) Then conditionally given a, X = t, the rv's X s with s j are jointly distributed as X s = a s a t µa j a a a j i j a i ( Z i µ a j a ) + Z s where Z s are iid N (µ, σ 2 ) rvs
25 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
26 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Numerical examples
27 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table : Numerical results for P(S τ): Triangle Window's shape Triangle (m = 4, m2 = 8, Nt = 33, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
28 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table : Numerical results for P(S τ): Triangle Window's shape Triangle (m = 4, m2 = 8, Nt = 33, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
29 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 2 : Numerical results for P(S τ): Rectangle Window's shape Rectangle (m =, m2 = 2, Nt = 32, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
30 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 2 : Numerical results for P(S τ): Rectangle Window's shape Rectangle (m =, m2 = 2, Nt = 32, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
31 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 3 : Numerical results for P(S τ): Quadrilateral Window's shape Quadrilateral (m = 4, m2 = 8, Nt = 3, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
32 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 3 : Numerical results for P(S τ): Quadrilateral Window's shape Quadrilateral (m = 4, m2 = 8, Nt = 3, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
33 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 4 : Numerical results for P(S τ): Circle Window's shape Circle (m = 3, m2 = 3, Nt = 29, IS = e54, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
34 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 4 : Numerical results for P(S τ): Circle Window's shape Circle (m = 3, m2 = 3, Nt = 29, IS = e54, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
35 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 5 : Numerical results for P(S τ): Ellipse Window's shape Ellipse (m = 9, m2 = 9, Nt = 35, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
36 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 5 : Numerical results for P(S τ): Ellipse Window's shape Ellipse (m = 9, m2 = 9, Nt = 35, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
37 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 6 : Numerical results for P(S τ): Ellipse2 Window's shape Ellipse2 (m = 9, m2 = 9, Nt = 35, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
38 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 6 : Numerical results for P(S τ): Ellipse2 Window's shape Ellipse2 (m = 9, m2 = 9, Nt = 35, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
39 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 7 : Numerical results for P(S τ): Annulus Window's shape Annulus (m = 7, m2 = 7, Nt = 24, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
40 Simulation study Numerical examples A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 7 : Numerical results for P(S τ): Annulus Window's shape Annulus (m = 7, m2 = 7, Nt = 24, IS = e5, IA = e6) X s,s 2 B(, 00) X s,s 2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal X s,s 2 P(025) X s,s 2 N (0, ) τ Sim AppH ETotal τ Sim AppH ETotal
41 Simulation study Power A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
42 Simulation study Power A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Power of the scan statistic test
43 Simulation study Power Power evaluation for B(, 000) model Triangular simulated cluster Rectangular simulated cluster Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Annulus (24) p Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Annulus (24) p A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
44 Simulation study Power Power evaluation for B(, 000) model Quadrilateral simulated cluster Circular simulated cluster Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Annulus (24) p Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Annulus (24) p A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
45 Simulation study Power Power evaluation for B(, 000) model Ellipsoidal simulated cluster Annular simulated cluster Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Annulus (24) p Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Annulus (24) p A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
46 Simulation study Power Power evaluation for B(5, 005) model Triangular simulated cluster Rectangular simulated cluster Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Ellipse2 (35) Annulus (24) p Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Ellipse2 (35) Annulus (24) p A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
47 Simulation study Power Power evaluation for B(5, 005) model Quadrilateral simulated cluster Circular simulated cluster Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Ellipse2 (35) Annulus (24) p Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Ellipse2 (35) Annulus (24) p A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
48 Simulation study Power Power evaluation for B(5, 005) model Ellipsoidal simulated cluster Annular simulated cluster Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Ellipse2 (35) Annulus (24) p Power Shape of the scanning window Triangle (33) Rectangle (32) Quadrillater (3) Circle (29) Ellipse (35) Ellipse2 (35) Annulus (24) p A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
49 Scan on a Cylinder Problem A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
50 Scan on a Cylinder Problem A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning the surface of a cylinder
51 Scan on a Cylinder Problem A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning the surface of a cylinder Unfolded cylinder of size T T 2 Cylinder
52 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
53 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation into a one dimensional problem
54 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, X,m2 X,T2 X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
55 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, X,m2 X,T2 X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
56 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, X,m2 X,T2 X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
57 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, Xm, X T, X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
58 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, Xm, X T, X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
59 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, Xm, X T, X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
60 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Transformation of the unfolded cylinder m2 X, X,m2 X,T2 m X m, Xm,m 2 X m,t 2 T X T, X T,m 2 X T,T 2 T2 X, Xm, X T, X,m2 Xm,m 2 XT,m 2 X,T2 X m,t 2 X T,T 2
61 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Defining the score function m2 X, X,m2 m T X m, Xm,m 2 X T, X T,m 2 The size of the scanning window is m = T m 2 (T m ) The score function is dened by S ( X i ) = A Xi where A is the corresponding {0, } vector 0 0
62 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Defining the score function m2 m T The size of the scanning window is m = T m 2 (T m ) The score function is dened by S ( X i ) = A Xi where A is the corresponding {0, } vector 0 0
63 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Defining the score function m2 m T The size of the scanning window is m = T m 2 (T m ) The score function is dened by S ( X i ) = A Xi where A is the corresponding {0, } vector 0 0
64 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Defining the score function m2 m T The size of the scanning window is m = T m 2 (T m ) The score function is dened by S ( X i ) = A Xi where A is the corresponding {0, } vector 0 0
65 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Defining the score function m2 m T The size of the scanning window is m = T m 2 (T m ) The score function is dened by S ( X i ) = A Xi where A is the corresponding {0, } vector 0 0
66 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Defining the score function m2 m T The size of the scanning window is m = T m 2 (T m ) The score function is dened by S ( X i ) = A Xi where A is the corresponding {0, } vector 0 0
67 Scan on a Cylinder A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 and error bounds Theorem [Am rioarei, 204] Let t {2, 3} and Q t = Qt (τ) = P (S m (t ( m ); S) τ) and L = T m If ˆQt is an estimate of Qt with ˆQt Qt β t and τ is such that ˆQ2 (τ) 0 then ) ) L (S P m ( T, S) τ (2 ˆQ2 ˆQ3 [ + ˆQ2 ˆQ3 + 2( ˆQ2 ˆQ3 ) 2] E total (), [ ( ) ) ] 2 E total () = (L ) β 2 + β 3 + F ˆQ2, L ( ˆQ2 + β 2 T X X m X m X2( m ) X 2 m X 3( m ) X T m 2( m ) Q 2 3( m ) Q 3
68 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Outline Introduction Framework Problem 2 Methodology Simulation methods: Normal data 3 Simulation study Numerical examples Power 4 Scanning the surface of a cylinder Problem Numerical Results 5 References
69 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Numerical examples
70 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 8 : Numerical results for P(S τ): Cylinder Cylinder: (m = 0, m 2 = 5, T = 300, T 2 = 350, IS = e4, IA = e5) X s,s2 B(, 0) Xs,s2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal
71 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 8 : Numerical results for P(S τ): Cylinder Cylinder: (m = 0, m 2 = 5, T = 300, T 2 = 350, IS = e4, IA = e5) X s,s2 B(, 0) Xs,s2 B(5, 005) τ Sim AppH ETotal τ Sim AppH ETotal
72 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 9 : Numerical results for P(S τ): Cylinder Cylinder: (m = 0, m 2 = 5, T = 300, T 2 = 350, IS = e4, IA = e5) X s,s2 P(025) τ Sim AppH ETotal
73 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Scanning a region of size T T 2 = Table 9 : Numerical results for P(S τ): Cylinder Cylinder: (m = 0, m 2 = 5, T = 300, T 2 = 350, IS = e4, IA = e5) X s,s2 P(025) τ Sim AppH ETotal
74 Scan on a Cylinder Numerical Results A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
75 References Anderson, N H and Titterington, D M (997) Some methods for investigating spatial clustering, with epidemiological applications Journal of the Royal Statistical Society: Series A (Statistics in Society), 60():8705 A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50 Alm, S E (983) On the distribution of scan statistic of poisson process In Gut, A and Helst, L, editors, Probability and Mathematical Statistics, pages 0 Upsalla University Press Alm, S E (997) On the distributions of scan statistics of a two-dimensional poisson process Advances in Applied Probability, pages 8 Alm, S E (998) and simulation of the distributions of scan statistics for poisson processes in higher dimensions Extremes, ():26 Am rioarei, A (204) s for the multidimensional discrete scan statistics PhD thesis, University of Lille
76 References Assunção, R, Costa, M, Tavares, A, and Ferreira, S (2006) Fast detection of arbitrarily shaped disease clusters Statistics in Medicine, 25(5): Bresenham, J (965) Algorithm for computer control of a digital printer IBM Systems Journal, 4() Bresenham, J (977) A linear algorithm for incremental digital display of circular arcs Communications of the ACM, 20(2):0006 Devroye, L (986) Non uniform random variate generation Springer-Verlag, New York Foley, J (995) Computer Graphics, Principles and Practice in C Addison-Wesley Professional Glaz, J, Naus, J, and Wallenstein, S (200) Scan Statistics A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
77 References Springer Glaz, J, Pozdnyakov, V, and Wallenstein, S (2009) Scan Statistics: Methods and Applications Birkhaüser Boston Loader, C R (99) Large-deviation approximations to the distribution of scan statistics Advances in Applied Probability, pages 7577 Tango, T and Takahashi, K (2005) A exibly shaped spatial scan statistic for detecting clusters Int J Health Geogr, 4: Tango, Toshiro Takahashi, Kunihiko England Int J Health Geogr 2005 May 8;4: A Am rioarei (INCDSB) Scan statistics with arbitrary shape IWAP / 50
Approximations for the distribution of the discrete scan statistics when the scanning window has arbitrary shape
Approximations for the distribution of the discrete scan statistics when the scanning window has arbitrary shape Alexandru Am rioarei National Institute of Research and Development for Biological Sciences
Other Test Constructions: Likelihood Ratio & Bayes Tests
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Biostatistics for Health Sciences Review Sheet
Biostatistics for Health Sciences Review Sheet http://mathvault.ca June 1, 2017 Contents 1 Descriptive Statistics 2 1.1 Variables.............................................. 2 1.1.1 Qualitative........................................
ST5224: Advanced Statistical Theory II
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Statistical Inference I Locally most powerful tests
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistics 104: Quantitative Methods for Economics Formula and Theorem Review
Harvard College Statistics 104: Quantitative Methods for Economics Formula and Theorem Review Tommy MacWilliam, 13 tmacwilliam@college.harvard.edu March 10, 2011 Contents 1 Introduction to Data 5 1.1 Sample
Solution Series 9. i=1 x i and i=1 x i.
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Bayesian statistics. DS GA 1002 Probability and Statistics for Data Science.
Bayesian statistics DS GA 1002 Probability and Statistics for Data Science http://www.cims.nyu.edu/~cfgranda/pages/dsga1002_fall17 Carlos Fernandez-Granda Frequentist vs Bayesian statistics In frequentist
: Monte Carlo EM 313, Louis (1982) EM, EM Newton-Raphson, /. EM, 2 Monte Carlo EM Newton-Raphson, Monte Carlo EM, Monte Carlo EM, /. 3, Monte Carlo EM
2008 6 Chinese Journal of Applied Probability and Statistics Vol.24 No.3 Jun. 2008 Monte Carlo EM 1,2 ( 1,, 200241; 2,, 310018) EM, E,,. Monte Carlo EM, EM E Monte Carlo,. EM, Monte Carlo EM,,,,. Newton-Raphson.
Μηχανική Μάθηση Hypothesis Testing
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Numerical Analysis FMN011
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Reminders: linear functions
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
2 Composition. Invertible Mappings
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
A Bonus-Malus System as a Markov Set-Chain. Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics
A Bonus-Malus System as a Markov Set-Chain Małgorzata Niemiec Warsaw School of Economics Institute of Econometrics Contents 1. Markov set-chain 2. Model of bonus-malus system 3. Example 4. Conclusions
Parametrized Surfaces
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Probability and Random Processes (Part II)
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Partial Differential Equations in Biology The boundary element method. March 26, 2013
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Fractional Colorings and Zykov Products of graphs
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
EE512: Error Control Coding
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
TMA4115 Matematikk 3
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Homework 8 Model Solution Section
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
The Simply Typed Lambda Calculus
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Example Sheet 3 Solutions
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής
Πρόβλημα 1: Αναζήτηση Ελάχιστης/Μέγιστης Τιμής Να γραφεί πρόγραμμα το οποίο δέχεται ως είσοδο μια ακολουθία S από n (n 40) ακέραιους αριθμούς και επιστρέφει ως έξοδο δύο ακολουθίες από θετικούς ακέραιους
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 651 APPENDIX B. BIBLIOGRAPHY 677 APPENDIX C. ANSWERS TO SELECTED EXERCISES 679
APPENDICES APPENDIX A. STATISTICAL TABLES AND CHARTS 1 Table I Summary of Common Probability Distributions 2 Table II Cumulative Standard Normal Distribution Table III Percentage Points, 2 of the Chi-Squared
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
5.4 The Poisson Distribution.
The worst thing you can do about a situation is nothing. Sr. O Shea Jackson 5.4 The Poisson Distribution. Description of the Poisson Distribution Discrete probability distribution. The random variable
Matrices and Determinants
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
5. Choice under Uncertainty
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
Congruence Classes of Invertible Matrices of Order 3 over F 2
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Estimation for ARMA Processes with Stable Noise. Matt Calder & Richard A. Davis Colorado State University
Estimation for ARMA Processes with Stable Noise Matt Calder & Richard A. Davis Colorado State University rdavis@stat.colostate.edu 1 ARMA processes with stable noise Review of M-estimation Examples of
6.3 Forecasting ARMA processes
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Second Order Partial Differential Equations
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
CHAPTER 12: PERIMETER, AREA, CIRCUMFERENCE, AND 12.1 INTRODUCTION TO GEOMETRIC 12.2 PERIMETER: SQUARES, RECTANGLES,
CHAPTER : PERIMETER, AREA, CIRCUMFERENCE, AND SIGNED FRACTIONS. INTRODUCTION TO GEOMETRIC MEASUREMENTS p. -3. PERIMETER: SQUARES, RECTANGLES, TRIANGLES p. 4-5.3 AREA: SQUARES, RECTANGLES, TRIANGLES p.
4.6 Autoregressive Moving Average Model ARMA(1,1)
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
ES440/ES911: CFD. Chapter 5. Solution of Linear Equation Systems
ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific
Lecture 34 Bootstrap confidence intervals
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
C.S. 430 Assignment 6, Sample Solutions
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Homework 3 Solutions
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Problem Set 3: Solutions
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg "k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +")
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data
Web-based supplementary materials for Bayesian Quantile Regression for Ordinal Longitudinal Data Rahim Alhamzawi, Haithem Taha Mohammad Ali Department of Statistics, College of Administration and Economics,
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Jordan Form of a Square Matrix
Jordan Form of a Square Matrix Josh Engwer Texas Tech University josh.engwer@ttu.edu June 3 KEY CONCEPTS & DEFINITIONS: R Set of all real numbers C Set of all complex numbers = {a + bi : a b R and i =
Abstract Storage Devices
Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Section 8.3 Trigonometric Equations
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Areas and Lengths in Polar Coordinates
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
P AND P. P : actual probability. P : risk neutral probability. Realtionship: mutual absolute continuity P P. For example:
(B t, S (t) t P AND P,..., S (p) t ): securities P : actual probability P : risk neutral probability Realtionship: mutual absolute continuity P P For example: P : ds t = µ t S t dt + σ t S t dw t P : ds
SOME PROPERTIES OF FUZZY REAL NUMBERS
Sahand Communications in Mathematical Analysis (SCMA) Vol. 3 No. 1 (2016), 21-27 http://scma.maragheh.ac.ir SOME PROPERTIES OF FUZZY REAL NUMBERS BAYAZ DARABY 1 AND JAVAD JAFARI 2 Abstract. In the mathematical
Fundamentals of Probability: A First Course. Anirban DasGupta
Fundamentals of Probability: A First Course Anirban DasGupta Contents 1 Introducing Probability 5 1.1 ExperimentsandSampleSpaces... 6 1.2 Set Theory Notation and Axioms of Probability........... 7 1.3
ER-Tree (Extended R*-Tree)
1-9825/22/13(4)768-6 22 Journal of Software Vol13, No4 1, 1, 2, 1 1, 1 (, 2327) 2 (, 3127) E-mail xhzhou@ustceducn,,,,,,, 1, TP311 A,,,, Elias s Rivest,Cleary Arya Mount [1] O(2 d ) Arya Mount [1] Friedman,Bentley
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
A summation formula ramified with hypergeometric function and involving recurrence relation
South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
Areas and Lengths in Polar Coordinates
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
FORMULAS FOR STATISTICS 1
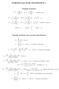FORMULAS FOR STATISTICS 1 X = 1 n Sample statistics X i or x = 1 n x i (sample mean) S 2 = 1 n 1 s 2 = 1 n 1 (X i X) 2 = 1 n 1 (x i x) 2 = 1 n 1 Xi 2 n n 1 X 2 x 2 i n n 1 x 2 or (sample variance) E(X)
Module 5. February 14, h 0min
Module 5 Stationary Time Series Models Part 2 AR and ARMA Models and Their Properties Class notes for Statistics 451: Applied Time Series Iowa State University Copyright 2015 W. Q. Meeker. February 14,
Math 6 SL Probability Distributions Practice Test Mark Scheme
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Approximation of distance between locations on earth given by latitude and longitude
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Optimal Impartial Selection
Optimal Impartial Selection Max Klimm Technische Universität Berlin Head of Junior Research Group Optimization under Uncertainty Einstein-Zentrum für Mathematik Introduction select member of a set of agents
ON NEGATIVE MOMENTS OF CERTAIN DISCRETE DISTRIBUTIONS
Pa J Statist 2009 Vol 25(2), 135-140 ON NEGTIVE MOMENTS OF CERTIN DISCRETE DISTRIBUTIONS Masood nwar 1 and Munir hmad 2 1 Department of Maematics, COMSTS Institute of Information Technology, Islamabad,
Every set of first-order formulas is equivalent to an independent set
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
New bounds for spherical two-distance sets and equiangular lines
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
An Inventory of Continuous Distributions
Appendi A An Inventory of Continuous Distributions A.1 Introduction The incomplete gamma function is given by Also, define Γ(α; ) = 1 with = G(α; ) = Z 0 Z 0 Z t α 1 e t dt, α > 0, >0 t α 1 e t dt, α >
Reflecting Brownian motion in two dimensions: Exact asymptotics for the stationary distribution
Reflecting Brownian motion in two dimensions: Exact asymptotics for the stationary distribution Jim Dai Joint work with Masakiyo Miyazawa July 8, 211 211 INFORMS APS conference at Stockholm Jim Dai (Georgia
Supplementary Appendix
Supplementary Appendix Measuring crisis risk using conditional copulas: An empirical analysis of the 2008 shipping crisis Sebastian Opitz, Henry Seidel and Alexander Szimayer Model specification Table
Bayesian modeling of inseparable space-time variation in disease risk
Bayesian modeling of inseparable space-time variation in disease risk Leonhard Knorr-Held Laina Mercer Department of Statistics UW May, 013 Motivation Ohio Lung Cancer Example Lung Cancer Mortality Rates
A Laplace Type Problem for Lattice with Cell Composed by Four Isoscele Triangles and the Test Body Rectangle
Applied Mathematical Sciences Vol. 11 2017 no. 8 361-374 HIKARI Ltd www.m-hikari.com https://doi.org/.12988/ams.2017.7113 A Laplace Type Problem for Lattice with Cell Composed by Four Isoscele Triangles
The ε-pseudospectrum of a Matrix
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Volume of a Cuboid. Volume = length x breadth x height. V = l x b x h. The formula for the volume of a cuboid is
Volume of a Cuboid The formula for the volume of a cuboid is Volume = length x breadth x height V = l x b x h Example Work out the volume of this cuboid 10 cm 15 cm V = l x b x h V = 15 x 6 x 10 V = 900cm³
557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING
Most Powerful Tests 557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING To construct and assess the quality of a statistical test, we consider the power function β(θ). Consider a
Divergence for log concave functions
Divergence or log concave unctions Umut Caglar The Euler International Mathematical Institute June 22nd, 2013 Joint work with C. Schütt and E. Werner Outline 1 Introduction 2 Main Theorem 3 -divergence
D Alembert s Solution to the Wave Equation
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Homomorphism in Intuitionistic Fuzzy Automata
International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
Mean-Variance Analysis
Mean-Variance Analysis Jan Schneider McCombs School of Business University of Texas at Austin Jan Schneider Mean-Variance Analysis Beta Representation of the Risk Premium risk premium E t [Rt t+τ ] R1
Outline Analog Communications. Lecture 05 Angle Modulation. Instantaneous Frequency and Frequency Deviation. Angle Modulation. Pierluigi SALVO ROSSI
Outline Analog Communications Lecture 05 Angle Modulation 1 PM and FM Pierluigi SALVO ROSSI Department of Industrial and Information Engineering Second University of Naples Via Roma 9, 81031 Aversa (CE),
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Theorem 8 Let φ be the most powerful size α test of H
Testing composite hypotheses Θ = Θ 0 Θ c 0 H 0 : θ Θ 0 H 1 : θ Θ c 0 Definition 16 A test φ is a uniformly most powerful (UMP) level α test for H 0 vs. H 1 if φ has level α and for any other level α test