RG analysis at higher orders in perturbativ QFTs in CMP
|
|
|
- Γῆ Βενιζέλος
- 5 χρόνια πριν
- Προβολές:
Transcript
1 RG analysis at highr ordrs in prturbativ QFTs in CMP Nikolai Zrf Institut für Thortisch Physik Univrsity of Hidlbrg Humboldt Univrsity, Brlin 2017 [arxiv: ] & [arxiv: ] Nikolai Zrf (ITP UHD) CMP HUB / 37
2 Ovrviw 1 Motivation 2 Suprconducting Landau-Ginzburg 3 Gross-Nvu-Yukawa Modl 4 Summary & Outlook Nikolai Zrf (ITP UHD) CMP HUB / 37
3 Motivation Obtain rliabl & prcis prdictions In HEP th SM (QFT with L SM ) provids collidr obsrvabls Nw physics L ral = L SM +L X? Nw physics includs ralization of SUSY? (MSSM, nmssm,...) Origin of L SM? Origin of QFTs? How to procd? Build and run LHC to find nw physics Calculat obsrvabls at highr ordr in PT Invstigat on various QFTs (may not hav HEP rlvancy) Nikolai Zrf (ITP UHD) CMP HUB / 37
4 Work in collaboration with... Univrsity of Albrta (Edmonton) Josph Macijko Chin-Hung Lin Univrsity of Hidlbrg Michal Schrr ( Köln) Luminita Mihaila Brnhard Ihrig DESY Zuthn Ptr Marquard Nikolai Zrf (ITP UHD) CMP HUB / 37
5 Whr to find QFTs? On th blackboard at th offic of my boss in Edmonton 1 γ γ 2 γ γ 3 γ γ 4 γ γ * * 5 γ γ * 6 γ γ * 7 γ γ * 8 γ γ * 9 γ γ * 10 γ γ * A.P.: Som condnsd mattr physics guy askd m how to calculat ths diagrams... Its only two loops. This should b asy for you. You can probably do it in a wk or two. Nikolai Zrf (ITP UHD) CMP HUB / 37
6 Whr to find QFTs? At th offic of Josph Macijko in Edmonton L =i ψ/ ψ + µ 2 + m 2 2 +λ h( ψ T iσ 2 ψ + h.c.). Imaginary tim Landau-Ginzburg Lagrangian with Lornzian-symmtry. ψ: 2-componnt Dirac frmion : complx Coopr pair scalar-fild / = γ µ µ. +Clifford algbra: {γ µ,γ ν } = 2g µν. (Ex.Rp.: γ 0 = σ 3,γ 1 = σ 1,γ 2 = σ 2 ) iσ2 ǫ! Invariant SU(2) tnsors:,, ( a T = σa 2 ),. Nikolai Zrf (ITP UHD) CMP HUB / 37
7 LET for Suprconductor Landau-Ginzburg Lagrangian with Lornzian-symmtry L =i ψ/ ψ + µ 2 + m 2 2 +λ h( ψ T iσ 2 ψ + h.c.). Smimtal phas Global U(1) symmtry for m 2 > 0 ψ iθ ψ, 2iθ, 0 0 = 0 = 0. Phastransition at Quantum Critical Point (QCP) for m 2 = 0 Suprconducting phas Spontanously brokn global U(1) symmtry for m 2 < = 0 0. alias non-vanishing ordr paramtr 0 " Nikolai Zrf (ITP UHD) CMP HUB / 37
8 LET for Suprconductor Landau-Ginzburg Lagrangian with Lornzian-symmtry L =i ψ/ ψ + µ 2 + m 2 2 +λ h( ψ T iσ 2 ψ + h.c.). Bhavior λ(µ), h(µ) for small scal µ/low nrgy limit in d = 2+1 = 3 dimnsions at th QCP? Rsults for MS β-function at 1-loop PT in d = 4 ǫ [Scott Thomas 05]: h 2 = h 2 /(4π) 2,λ 2 = λ 2 /(4π) 2 β h 2 = dh2 d lnµ = ǫh2 + 12h 4, β λ 2 = dλ2 d lnµ = ǫλ2 + 20λ 4 + 8h 2 λ 2 16h 4, γ ψ = d ln Z ψ d lnµ = 4h2, γ = d ln Z d lnµ = 4h2. Nikolai Zrf (ITP UHD) CMP HUB / 37
9 Rnormalization Do MS fild and coupling rdfinitions: 0 = Z, ψ ψ 0 = Z ψ ψ, λ λ 0 =µ ǫ/2 Z λ λ, h h 0 =µ ǫ/2 Z h h. Rnormalizd Landau-Ginzburg Lagrangian L =iz ψ ψ/ ψ + Z µ 2 + Z 4λ 2 µ ǫ 4 + Z ψψ hµ ǫ/2 ( ψ T iσ 2 ψ + h.c.). Z 4 =Z 2 λ Z2, Z ψψ = Z h Z Z ψ. Bar paramtrs and filds do not dpnd on µ. β, γ. dx 0 dµ = 0, X {h2,λ 2,ψ,}. Nikolai Zrf (ITP UHD) CMP HUB / 37
10 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
11 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z ψ (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
12 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z ψψ (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
13 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z 4 (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
14 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z (L = 2) Nikolai Zrf (ITP UHD) CMP HUB / 37
15 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z ψ (L = 2) Nikolai Zrf (ITP UHD) CMP HUB / 37
16 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z ψψ (L = 2) Nikolai Zrf (ITP UHD) CMP HUB / 37
17 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z 4 (L = 2) +18 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
18 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z (L = 3) +21 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
19 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z ψ (L = 3) +13 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
20 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z ψψ (L = 3) +18 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
21 How to obtain Zs? Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z Z ψ Z ψψ Z 4 Exampl Diagrams Z 4 (L = 3) +362 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
22 How to obtain Zs? Chosing massiv tadpol kinmatics Us singl IR rgulator mass M in vry dnominator Expand in small xtrnal momnta pi /M 1 All intgrals ar 1-scal tadpol intgrals Us infrard rarrangmnt [Chtyrkin,Misiak,Munz] to consistntly subtract artificial trms M 2 Nikolai Zrf (ITP UHD) CMP HUB / 37
23 How to obtain Zs? Chosing massiv tadpol kinmatics Us singl IR rgulator mass M in vry dnominator Expand in small xtrnal momnta pi /M 1 All intgrals ar 1-scal tadpol intgrals Us infrard rarrangmnt [Chtyrkin,Misiak,Munz] to consistntly subtract artificial trms M 2 Fully automatizd stup QGRAF [Noguira] q2 [Sidnstickr] xp [Sidnstickr] FORM [Vrmasrn & Co] MATAD [Stinhausr] OR CRUSHER [Marquard,Sidl] modifid majoranas.pl [Harlandr] RcalcPrfac [NZ] Nikolai Zrf (ITP UHD) CMP HUB / 37
24 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ 0 â ( 1 2 ǫαβ ψ α ψ β ) ( 1 2 ǫ γδψ γ ψ δ ) â 0 S = Nikolai Zrf (ITP UHD) CMP HUB / 37
25 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ 0 â ( 1 2 ǫαβ ψ α ψ β ) ( 1 2 ǫ γδψ γ ψ δ ) â 0 S = 1 2 Nikolai Zrf (ITP UHD) CMP HUB / 37
26 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ Gnrat diagrams with quivalnt frmions S S = 1 2 Nikolai Zrf (ITP UHD) CMP HUB / 37
27 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ Gnrat diagrams with quivalnt frmions S Chos a Dnnr currnt flow dirction & rcalculat sign of S * 0 â ( 1 2 ǫαβ ψ α ψ β ) ( 1 2 ǫ γδψ γ ψ δ ) â 0 S = 1 2 Nikolai Zrf (ITP UHD) CMP HUB / 37
28 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ Gnrat diagrams with quivalnt frmions S Chos a Dnnr currnt flow dirction & rcalculat sign of S * 0 â ( 1 2 ǫαβ ψ α ψ β ) ( 1 2 ǫ γδψ γ ψ δ ) â 0 S = Nikolai Zrf (ITP UHD) CMP HUB / 37
29 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ Gnrat diagrams with quivalnt frmions S Chos a Dnnr currnt flow dirction & rcalculat sign of S * 0 â ( 1 2 ǫαβ ψ α ψ β ) ( 1 2 ǫ γδψ γ ψ δ ) â 0 + using: S = S F = ψψ ( 1) S F. Nikolai Zrf (ITP UHD) CMP HUB / 37
30 Back in Wick s Gardn... Sign of Wick factor S is corrlatd with indx ordr in ǫ αβ Gnrat diagrams with quivalnt frmions S Chos a Dnnr currnt flow dirction & rcalculat sign of S * 0 â ( 1 2 ǫαβ ψ α ψ β ) ( 1 2 ǫ γδψ γ ψ δ ) â 0 + using: S = S F = ψψ ( 1) S F. How to trat ǫ αβ in amplituds with FORM? Nikolai Zrf (ITP UHD) CMP HUB / 37
31 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Nikolai Zrf (ITP UHD) CMP HUB / 37
32 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Nikolai Zrf (ITP UHD) CMP HUB / 37
33 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Nikolai Zrf (ITP UHD) CMP HUB / 37
34 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Nikolai Zrf (ITP UHD) CMP HUB / 37
35 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Invarianc conditions [G(ω) = xp(i a Tω a )] ǫ α1 α 2 = G(ω) γ 1 α 1 G(ω) γ 2 α 2 ǫ γ1 γ 2, ǫ β 1β 2 = ǫ δ 1δ 2 G 1 (ω) β 1 δ 1 G 1 (ω) β 2 δ 2. Nikolai Zrf (ITP UHD) CMP HUB / 37
36 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Invarianc condition ω 1,. Nikolai Zrf (ITP UHD) CMP HUB / 37
37 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Invarianc condition ω 1,. Annihilation. Nikolai Zrf (ITP UHD) CMP HUB / 37
38 How to ǫ αβ? Shorthands,,,. Ridr for sign controll Invarianc condition ω 1,. Annihilation. ǫ can b mulatd by naiv anti-commuting γ 5 : {γ µ,γ 5 } = 0. Nikolai Zrf (ITP UHD) CMP HUB / 37
39 β and 3 Loops β h 2 = ǫh h 4 +8h 2 λ 4 64h 4 λ 2 + 8h 6 h 2 = h 2 /(4π) 2,λ 2 = λ 2 /(4π) 2 40h 2 λ h 4 λ h 6 λ 2 [ ζ 3 ]h 8, β λ 2 = ǫλ λ 4 + 8h 2 λ 2 16h 4 80h 2 λ h 4 λ h 6 240λ h 2 λ 6 +[ ζ 3 ]h 4 λ 4 [ ζ 3 ]h 6 λ 2 [ ζ 3 ]h 8 +[ ζ 3 ]λ 8, γ = 4h 2 24h 4 + 8λ 4 40λ 6 60h 2 λ h 4 λ 2 +[20+192ζ 3 ]h 6, γ ψ = 4h 2 16h 4 44h 2 λ h 4 λ 2 +[192ζ 3 4]h 6. Nikolai Zrf (ITP UHD) CMP HUB / 37
40 β and 3 Loops whn λ = h: h 2 = h 2 /(4π) 2 β h 2 = ǫh h 4 48h h 8 (5+12ζ 3 ), β λ 2 = ǫh h 4 48h h 8 (5+12ζ 3 ), γ = 4h 2 16h h 6 (5+12ζ 3 ), γ ψ = 4h 2 16h h 6 (5+12ζ 3 ). Nikolai Zrf (ITP UHD) CMP HUB / 37
41 β and 3 Loops whn λ = h: h 2 = h 2 /(4π) 2 β h 2 β h 2 = ǫh h 4 48h h 8 (5+12ζ 3 ), γ = 4h 2 16h h 6 (5+12ζ 3 ),? = ( ǫ+3γ )h 2. Nikolai Zrf (ITP UHD) CMP HUB / 37
42 RG Fixd Points Sarching for IR fixd points (µ 0) at d = 3: ( ) h 2,λ 2 = (0, 0), (unstabl) ( ) h 2,λ2 = ( 0, ǫ ǫ ζ h 2 = λ2 = ǫ 12 + ǫ2 36 4ζ ǫ3. (stabl) ǫ 3 ), (unstabl) Nikolai Zrf (ITP UHD) CMP HUB / 37
43 RG Fixd Points Sarching for IR fixd points (µ 0) at d = 3: ( ) h 2,λ 2 = (0, 0), (unstabl) ( ) h 2,λ2 = ( 0, ǫ ǫ ζ h 2 = λ2 = ǫ 12 + ǫ2 36 4ζ ǫ3. (stabl) ǫ 3 ), (unstabl) Nikolai Zrf (ITP UHD) CMP HUB / 37
44 RG Fixd Points Sarching for IR fixd points (µ 0) at d = 3: ( ) h 2,λ 2 = (0, 0), (unstabl) ( ) h 2,λ2 = ( 0, ǫ ǫ ζ h 2 = λ2 = ǫ 12 + ǫ2 36 4ζ ǫ3. (stabl) ǫ 3 ), (unstabl) Nikolai Zrf (ITP UHD) CMP HUB / 37
45 RG Fixd Points Sarching for IR fixd points (µ 0) at d = 3: ( ) h 2,λ 2 = (0, 0), (unstabl) ( ) h 2,λ2 = ( 0, ǫ ǫ ζ h 2 = λ2 = ǫ 12 + ǫ2 36 4ζ ǫ3. (stabl) ǫ 3 ), (unstabl) Nikolai Zrf (ITP UHD) CMP HUB / 37
46 Emrgnt SUSY PT 3-loop RG analysis around d = 4 ǫ supports dynamically mrgnt SUSY conjctur at d = 3 Nikolai Zrf (ITP UHD) CMP HUB / 37
47 Emrgnt SUSY PT 3-loop RG analysis around d = 4 ǫ supports dynamically mrgnt SUSY conjctur at d = 3 At SUSY fixd point (λ 2 = h 2, m = 0) : ( L = d 2 θd 2 θφ Φ+ Φ(y) =(y)+ 2θψ(y)+θ 2 F(y), y µ =x µ iθγ µ θ. d 2 θ h ) 3 Φ3 + h.c., Nikolai Zrf (ITP UHD) CMP HUB / 37
48 Emrgnt SUSY PT 3-loop RG analysis around d = 4 ǫ supports dynamically mrgnt SUSY conjctur at d = 3 At SUSY fixd point (λ 2 = h 2, m = 0) : ( L = d 2 θd 2 θφ Φ+ Φ(y) =(y)+ 2θψ(y)+θ 2 F(y), y µ =x µ iθγ µ θ. d 2 θ h ) 3 Φ3 + h.c., SUSY non-rnormalization thorms Nikolai Zrf (ITP UHD) CMP HUB / 37
49 Emrgnt SUSY PT 3-loop RG analysis around d = 4 ǫ supports dynamically mrgnt SUSY conjctur at d = 3 At SUSY fixd point (λ 2 = h 2, m = 0) : ( L = d 2 θd 2 θφ Φ+ Φ(y) =(y)+ 2θψ(y)+θ 2 F(y), y µ =x µ iθγ µ θ. d 2 θ h ) 3 Φ3 + h.c., SUSY non-rnormalization thorms At th SUSY fixd point w chck: [Strasslr 03] γ = γ ψ = ǫ 3 +O(ǫ4 ). Nikolai Zrf (ITP UHD) CMP HUB / 37
50 Critical Exponnts Stability xponnt (ω 0 IR stabl/unstabl ) ω = dβ h 2(λ2 = h 2 ) dh 2 = ǫ 1 ( 1 h=h 3 ǫ ) 3 ζ 3 ǫ 3 +O(ǫ 4 ). Nikolai Zrf (ITP UHD) CMP HUB / 37
51 Critical Exponnts Stability xponnt (ω 0 IR stabl/unstabl ) ω = dβ h 2(λ2 = h 2 ) dh 2 = ǫ 1 ( 1 h=h 3 ǫ ) 3 ζ 3 ǫ 3 +O(ǫ 4 ). Corrlation lngth xponnt ν 1 =2+γ m 2, γ m 2 = d ln Z m 2 d lnµ, Z m 2m2 =m 2 0. Nikolai Zrf (ITP UHD) CMP HUB / 37
52 Critical Exponnts Stability xponnt (ω 0 IR stabl/unstabl ) ω = dβ h 2(λ2 = h 2 ) dh 2 = ǫ 1 ( 1 h=h 3 ǫ ) 3 ζ 3 ǫ 3 +O(ǫ 4 ). Corrlation lngth xponnt ν 1 =2+γ m 2, γ m 2 = d ln Z m 2 d lnµ, Z m 2m2 =m 2 0. Using Grassmannian continuation of th SUSY Lagrangian γ m = dβ h 2(λ2 = h 2 ) 2 dh 2 = 3h 2 dγ h 2(λ 2 = h 2 ) h=h dh 2. h=h Nikolai Zrf (ITP UHD) CMP HUB / 37
53 Critical Exponnts Stability xponnt (ω 0 IR stabl/unstabl ) ω = dβ h 2(λ2 = h 2 ) dh 2 = ǫ 1 ( 1 h=h 3 ǫ ) 3 ζ 3 ǫ 3 +O(ǫ 4 ). Corrlation lngth xponnt ν 1 =2+γ m 2, γ m 2 = d ln Z m 2 d lnµ, Z m 2m2 =m 2 0. Using Grassmannian continuation of th SUSY Lagrangian γ m = dβ h 2(λ2 = h 2 ) 2 dh 2 = 3h 2 dγ h 2(λ 2 = h 2 ) h=h dh 2. h=h ν = ǫ+ 1 ( 1 24 ǫ2 + 6 ζ 3 1 ) ǫ 3 +O(ǫ 4 ). 144 Nikolai Zrf (ITP UHD) CMP HUB / 37
54 Critical Exponnts Naiv xtrapolation to d = 2+1 (ǫ = 1): ν 1 loop = 0.75, ν 2 loop 0.792, ν 3 loop Bootstrap rsult [Bobv,El-Showk,Mazac,Paulos 15]: ν Nikolai Zrf (ITP UHD) CMP HUB / 37
55 Whr to find LHC Nikolai Zrf (ITP UHD) CMP HUB / 37
56 Whr to find LHC As EFT on th surfac of topological th smimtal-suprconductor QCP [S.-S.L 07] Nikolai Zrf (ITP UHD) CMP HUB / 37
57 Gauging U(1) What happns to SUSY whn thr is a dynamical photon? µ D µ = µ + ia µ : L = i ψ/dψ + D µ 2 + m h( ψ T iσ 2 ψ + h.c.) +λ F2 µν + 1 2ξ ( µa µ ) 2, F µν = µ A ν ν A µ, Nikolai Zrf (ITP UHD) CMP HUB / 37
58 Gauging U(1) What happns to SUSY whn thr is a dynamical photon? loops Nikolai Zrf (ITP UHD) CMP HUB / 37
59 Gauging U(1) What happns to SUSY whn thr is a dynamical photon? 2 G 0 h 2 = 2 Nikolai Zrf (ITP UHD) CMP HUB / 37
60 W can do for... NEW: 4-loop rsult for β and = 0 (hr for λ = h): β h 2 = β λ 2 = ǫh h 4 48h h 8 (5+12ζ 3 ) 192h 10 (9+60ζ 3 18ζ ζ 5 ), γ ψ = γ = 4h 2 16h h 6 (5+12ζ 3 ) 64h 8 (9+60ζ 3 18ζ ζ 5 ). h 2 = λ 2 limit in agrmnt with Wss-Zumino modl [Avdv,Goroshni 82] Stability? ν = ǫ+0.042ǫ ǫ ǫ 4. Asymptotic Sris: Mor sophisticatd xtrapolations to d = 3 rquird! Padé: ν [2,3] Nikolai Zrf (ITP UHD) CMP HUB / 37
61 Intrmission Upcoming nxt: Gross-Nvu-Yukawa Modl Nikolai Zrf (ITP UHD) CMP HUB / 37
62 Whr to find QFTs? In Hidlbrg, on th way to Marstall with Michal Schrr Th Gross-Nvu-Yukawa Modl: chiral Ising Univrsality Class (UC) L = ψ(/ + g)ψ (m2 2 µ )+λ4. chiral Hisnbrg UC (T a F = 1 2 σa su(2) ) L = ψ α (/ + g[t a F ]α β a)ψ β a(m 2 2 µ ) a +λ( a a ) 2. Lornzian-symmtry ψ: Dirac frmions. Rsult of lattic structur : ral spin-coupling scalar-fild / = γ µ µ. +Clifford algbra: {γ µ,γ ν } = 2g µν. Chiral symmtry (masslss frmions!) Nikolai Zrf (ITP UHD) CMP HUB / 37
63 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z, Z m 2 (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
64 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z ψ (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
65 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z ψψ (L = 1) Nikolai Zrf (ITP UHD) CMP HUB / 37
66 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z 4 (L = 1) +2 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
67 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z, Z m 2 (L = 2) Nikolai Zrf (ITP UHD) CMP HUB / 37
68 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z ψ (L = 2) Nikolai Zrf (ITP UHD) CMP HUB / 37
69 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z ψψ (L = 2) +4 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
70 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z 4 (L = 2) +86 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
71 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z, Z m 2 (L = 3) +29 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
72 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z ψ (L = 3) +24 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
73 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z ψψ (L = 3) +138 mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
74 Rlvant Diagrams Using DREG gt pols in small ǫ = 4 d of 1-PI n-point functions at L = 1, 2, 3,... loops for any kinmatics Z, Z m 2 Z ψ Z ψψ Z 4 Exampl Diagrams Z 4 (L = 3) mor... Nikolai Zrf (ITP UHD) CMP HUB / 37
75 Ising vs Hisnbrg Hisnbrg diagrams factoriz: Nikolai Zrf (ITP UHD) CMP HUB / 37
76 Ising vs Hisnbrg Hisnbrg diagrams factoriz: Calculat color amplituds for gnric Li algbra with FORM packag COLOR [Ritbrgn,Schllkns,Vrmasrn 98] Nikolai Zrf (ITP UHD) CMP HUB / 37
77 Ising vs Hisnbrg Hisnbrg diagrams factoriz: Calculat color amplituds for gnric Li algbra with FORM packag COLOR [Ritbrgn,Schllkns,Vrmasrn 98] Color structur of 4 -vrtx: L 4 = λ( a a ) 2 = λ 3 a b c d (δ ab δ cd +δ ac δ bd +δ ad δ cb ). Nikolai Zrf (ITP UHD) CMP HUB / 37
78 What dos COLOR do? Nikolai Zrf (ITP UHD) CMP HUB / 37
79 What dos COLOR do? Exploits th Li algbra (adjoint rp.: Jacobi ID),. Nikolai Zrf (ITP UHD) CMP HUB / 37
80 What dos COLOR do? Exploits th Li algbra (adjoint rp.: Jacobi ID),. to xprss scalar color amplituds ( us projctors) via,,,,,. Nikolai Zrf (ITP UHD) CMP HUB / 37
81 What dos COLOR do? Exploits th Li algbra (adjoint rp.: Jacobi ID),. to xprss scalar color amplituds ( us projctors) via,,,,,. Nikolai Zrf (ITP UHD) CMP HUB / 37
82 What dos COLOR do? Exploits th Li algbra (adjoint rp.: Jacobi ID),. to xprss scalar color amplituds ( us projctors) via,,,, & stuff that is irrducibl w.r.t to it,. Nikolai Zrf (ITP UHD) CMP HUB / 37
83 What dos COLOR do? Explicit xampls,,. It dos not us,,... Not: d aab =0, daabc =0, I 3(A) =0. Nikolai Zrf (ITP UHD) CMP HUB / 37
84 Rnormalizability Is th QFT with L = ψ α (/ + g[t a R] α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2, a rnormalizabl thory in d = 4 whn w assum that T R oby a finit dimnsional simpl Li algbra? Nikolai Zrf (ITP UHD) CMP HUB / 37
85 Rnormalizability Is th QFT with L = ψ α (/ + g[t a R] α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2, a rnormalizabl thory in d = 4 whn w assum that T R oby a finit dimnsional simpl Li algbra? Li algbra Btti numbrs A r SU(r+ 1) 2, 3,..., r+ 1 B r SO(2r+ 1) 2, 4, 6,..., 2r C r Sp(2r) 2, 4, 6,..., 2r D r SO(2r) 2, 4, 6,..., 2r 2, r G 2 2, 6 F 4 2, 6, 8, 12 E 6 2, 5, 6, 8, 9, 12 E 7 2, 6, 8, 10, 12, 14, 18 E 8 2, 8, 12, 14, 18, 20, 24, 30 Nikolai Zrf (ITP UHD) CMP HUB / 37
86 Rnormalizability Just calculat th Zs and s what happns... 1-loop: Z x = 1+ n=1 δz (n) x δz (1) x = ( g 2 (4π) 2 i+j=1 ) i ( ) j λ 1 (4π) 2 ǫ N(1,1) x,i,j, N R. Nikolai Zrf (ITP UHD) CMP HUB / 37
87 Rnormalizability Just calculat th Zs and s what happns... 2-loop: δz (2) x = ( g 2 (4π) 2 i+j=2 Z x = 1+ n=1 δz (n) x ) i ( ) j ( λ 1 (4π) 2 ǫ N(2,1) x,i,j + 1 ) ǫ 2 N(2,2) x,i,j, N R Nikolai Zrf (ITP UHD) CMP HUB / 37
88 Rnormalizability Just calculat th Zs and s what happns... Z x = 1+ n=1 δz (n) x 3-loop: δz (3) 4 = 1 ǫ ( g 2 (4π) 2 N (3,1) 4,4, 1 =N log(µ2 /M 2 )+... ) 4 ( ) 1 λ (4π) 2 N (3,1) 4,4, 1 +, Rnormalization constant Z 4 is non-local Thory is not rnormalizabl for a gnric simpl Li algbra Nikolai Zrf (ITP UHD) CMP HUB / 37
89 Rnormalizability Origin of th N (3,1) 4,4, 2 + d 44(R, R) log(µ 2 /M 2 ) 3-loop: Nikolai Zrf (ITP UHD) CMP HUB / 37
90 Rnormalizability Origin of th N (3,1) 4,4, 2 + d 44(R, R) log(µ 2 /M 2 ) 3-loop: Alrady at 1-loop color structur d abcd divrgnt: + x 1 +x 2 Nikolai Zrf (ITP UHD) CMP HUB / 37
91 Rnormalizability For simpl Li algbras which can mak up a fully symmtric d abcd th thory is not rnormalizabl Nikolai Zrf (ITP UHD) CMP HUB / 37
92 Rnormalizability For simpl Li algbras which can mak up a fully symmtric d abcd th thory is not rnormalizabl Li algbra Btti numbrs A r SU(r+ 1) 2, 3, 4,..., r+ 1 B r SO(2r+ 1) 2, 4, 6,..., 2r C r Sp(2r) 2, 4, 6,..., 2r D r SO(2r) 2, 4, 6,..., 2r 2, r G 2 2, 6 F 4 2, 6, 8, 12 E 6 2, 5, 6, 8, 9, 12 E 7 2, 6, 8, 10, 12, 14, 18 E 8 2, 8, 12, 14, 18, 20, 24, 30 Nikolai Zrf (ITP UHD) CMP HUB / 37
93 Rnormalizability For simpl Li algbras which can mak up a fully symmtric d abcd th thory is not rnormalizabl Li algbra Btti numbrs A r SU(r+ 1) 2, 3, 4,..., r+ 1 B r SO(2r+ 1) 2, 4, 6,..., 2r C r Sp(2r) 2, 4, 6,..., 2r D r SO(2r) 2, 4, 6,..., 2r 2, r G 2 2, 6 F 4 2, 6, 8, 12 E 6 2, 5, 6, 8, 9, 12 E 7 2, 6, 8, 10, 12, 14, 18 E 8 2, 8, 12, 14, 18, 20, 24, 30 For all xcptional algbras th thory is rnormalizabl Nikolai Zrf (ITP UHD) CMP HUB / 37
94 Rnormalizability For simpl Li algbras which can mak up a fully symmtric d abcd th thory is not rnormalizabl Li algbra Btti numbrs A r SU(r+ 1) 2, 3, 4,..., r+ 1 B r SO(2r+ 1) 2, 4, 6,..., 2r C r Sp(2r) 2, 4, 6,..., 2r D r SO(2r) 2, 4, 6,..., 2r 2, r G 2 2, 6 F 4 2, 6, 8, 12 E 6 2, 5, 6, 8, 9, 12 E 7 2, 6, 8, 10, 12, 14, 18 E 8 2, 8, 12, 14, 18, 20, 24, 30 For all xcptional algbras th thory is rnormalizabl For SU(N), Sp(N), SO(N) with N < 4, 4, 5 th thory is rnormalizabl. Th numbr of indpndnt fully symmtric tnsors is th rank of a simpl Li algbra Nikolai Zrf (ITP UHD) CMP HUB / 37
95 Rnormalizability Can w fix Rnormalizability for SU(4+), Sp(4+), SO(5+)? Nikolai Zrf (ITP UHD) CMP HUB / 37
96 Rnormalizability Can w fix Rnormalizability for SU(4+), Sp(4+), SO(5+)? Ys, w can! L = ψ α (/ + g[t a R ]α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2 +λ d abcd a b c d. Nikolai Zrf (ITP UHD) CMP HUB / 37
97 Rnormalizability Can w fix Rnormalizability for SU(4+), Sp(4+), SO(5+)? Ys, w can! L = ψ α (/ + g[t a R ]α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2 +λ d abcd a b c d. Calculat Zs in dp. of and for nw coupling 2-loop: Z 4 Non-trivial log(µ 2 /M 2 ) cancllation Nikolai Zrf (ITP UHD) CMP HUB / 37
98 Rnormalizability Can w fix Rnormalizability for SU(4+), Sp(4+), SO(5+)? Ys, w can! L = ψ α (/ + g[t a R ]α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2 +λ d abcd a b c d. Calculat Zs in dp. of and for nw coupling 2-loop: Z 4 Non-trivial log(µ 2 /M 2 ) cancllation 3-loop: Nikolai Zrf (ITP UHD) CMP HUB / 37
![Rnormalizability Can w fix Rnormalizability for SU(4+), Sp(4+), SO(5+)? Ys, w can! L = ψ α (/ + g[t a R ]α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2 +λ d abcd a b c d.](/docs-images/88/114585113/images/99-0.jpg "Calculat Zs in dp. of and for nw coupling 2-loop: Z 4 Non-trivial log(µ 2 /M 2 ) cancllation 3-loop: Condnsd mattr physics: T R SU(2).")
99 Rnormalizability Can w fix Rnormalizability for SU(4+), Sp(4+), SO(5+)? Ys, w can! L = ψ α (/ + g[t a R ]α β a)ψ β 1 2 a 2 µ a +λ( a a ) 2 +λ d abcd a b c d. Calculat Zs in dp. of and for nw coupling 2-loop: Z 4 Non-trivial log(µ 2 /M 2 ) cancllation 3-loop: Condnsd mattr physics: T R SU(2). Nikolai Zrf (ITP UHD) CMP HUB / 37
100 β for Ising Numbr of Frmion flavours = N, g 2 8π 2 y, λ 8π 2 λ β y = ǫy+(3+2n)y 2 +24yλ(λ y) ( N) y 3 + y ( 1152(7+5N)y 2 λ+192(91 30N)yλ ( 912ζ N(67+112N + 432ζ 3 ) ) y λ 3), β λ = ǫλ+36λ 2 + 4Nyλ Ny 2 +4Ny 3 + 7Ny 2 λ 72Nyλ 2 816λ ( 6912( ζ 3 )λ Nyλ 3 48N(72N ζ 3 )y 2 λ 2 + 2N(1736N ζ 3 )y 3 λ + N(5 628N 384ζ 3 )y 4), 2-loop rsults [Rosnstin,Kovnr,Yu 93] Nikolai Zrf (ITP UHD) CMP HUB / 37
101 Fixd Point Analysis Numbr of frmion gnrations N = 2: Ising Hisnbrg g 2 PRELIMINARY λ [from Brnhard Ihrig s dsk] Nikolai Zrf (ITP UHD) CMP HUB / 37
102 Critical Exponnts (Chiral Ising) η x = γ x (y,λ ) N = 2 : ν ǫ ǫ ǫ 3 η ψ ǫ ǫ ǫ 3 η 0.571ǫ+0.124ǫ ǫ 3 N = 1 : ν ǫ ǫ ǫ 3 η ψ 0.1ǫ ǫ ǫ 3 η 0.4ǫ+0.102ǫ ǫ 3 N = 1/4 : ν ǫ ǫ ǫ 3 η ψ 0.143ǫ ǫ ǫ 3 η 0.143ǫ ǫ ǫ 3 N = 0 : ν ǫ 0.117ǫ ǫ 3 η ψ 0.167ǫ ǫ ǫ 3 η ǫ ǫ 3 Nikolai Zrf (ITP UHD) CMP HUB / 37
103 Critical Exponnts (Chiral Ising) N = 2 1/ν η η ψ this work (Padé [2/1]) (2+ǫ), (ǫ 4, Padé)[Gracy,Luth,Schrodr 16] functional RG[Knorr 16] 0.994(2) Mont Carlo[Chandraskharan,Li 13] 1.20(1) 0.62(1) 0.38(1) N = 1 1/ν η η ψ this work (Padé [2/1]) functional RG[Knorr 16] 1.075(4) Mont Carlo[Li,Jiang, Yao 15] (3) N = 1/4 1/ν η η ψ this work (Padé [2/1]) functional RG[Hilmann,a 15] conformal bootstrap[ilisiu,a 16] Nikolai Zrf (ITP UHD) CMP HUB / 37
104 Summary & Outlook Summary QFTs ar ETs If SUSY is not found at LHC on may tak a closr look at condnsd mattr systm on a dsk Kinmatics Symmtry Dp undrstanding of symmtris is rquird Nikolai Zrf (ITP UHD) CMP HUB / 37
105 Summary & Outlook Summary Outlook QFTs ar ETs If SUSY is not found at LHC on may tak a closr look at condnsd mattr systm on a dsk Kinmatics Symmtry Dp undrstanding of symmtris is rquird Hisnbrg Mor sophisticatd RG analysis (larg ordr bhavior?) Z m 2 for GNY at 4-loop XY-Modl Nikolai Zrf (ITP UHD) CMP HUB / 37
106 To backup slids Nikolai Zrf (ITP UHD) CMP HUB
107 Suprspac d 2 θ 1 4 dθα dθ β ε αβ, d 2 θ 1 4 d θ α d θ β ε αβ, θ 2 θ α θ α = θ α ε αβ θ β, d 2 θd 2 θφ Φ = i ψ/ ψ + µ 2 + F 2. d 2 θ h 3 Φ3 = h 2 F + hψ T iσ 2 ψ. kintic trms supr potntial trms Auxiliary filds ar liminatd using EQM: F = h 2, F = h 2. Nikolai Zrf (ITP UHD) CMP HUB
Homework #6. A circular cylinder of radius R rotates about the long axis with angular velocity
Homwork #6 1. (Kittl 5.1) Cntrifug. A circular cylindr of radius R rotats about th long axis with angular vlocity ω. Th cylindr contains an idal gas of atoms of mass m at tmpratur. Find an xprssion for
Relativsitic Quantum Mechanics. 3.1 Dirac Equation Summary and notation 3.1. DIRAC EQUATION SUMMARY AND NOTATION. April 22, 2015 Lecture XXXIII
3.1. DIRAC EQUATION SUMMARY AND NOTATION April, 015 Lctur XXXIII Rlativsitic Quantum Mchanics 3.1 Dirac Equation Summary and notation W found that th two componnt spinors transform according to A = ± σ
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Pairs of Random Variables
Pairs of Random Variabls Rading: Chaptr 4. 4. Homwork: (do at last 5 out of th following problms 4..4, 4..6, 4.., 4.3.4, 4.3.5, 4.4., 4.4.4, 4.5.3, 4.6.3, 4.6.7, 4.6., 4.7.9, 4.7., 4.8.3, 4.8.7, 4.9.,
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Homework 8 Model Solution Section
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
Partial Differential Equations in Biology The boundary element method. March 26, 2013
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
α A G C T 國立交通大學生物資訊及系統生物研究所林勇欣老師
A G C T Juks and Cantor s (969) on-aramtr modl A T C G A G 0 0 0-3 C T A() A( t ) ( 3 ) ( ) A() A() ( 3 ) ( ) A( A( A( A( t ) A( 3 A( t ) ( ) A( A( Juks and Cantor s (969) on-aramtr modl A( A( t ) A( d
Example Sheet 3 Solutions
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Reminders: linear functions
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Higher spin gauge theories and their CFT duals
Higher spin gauge theories and their CFT duals E-mail: hikida@phys-h.keio.ac.jp 2 AdS Vasiliev AdS/CFT 4 Vasiliev 3 O(N) 3 Vasiliev 2 W N 1 AdS/CFT g µν Vasiliev AdS [1] AdS/CFT anti-de Sitter (AdS) (CFT)
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
Matrices and Determinants
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Higher Derivative Gravity Theories
Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
2 Composition. Invertible Mappings
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Solutions to the Schrodinger equation atomic orbitals. Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz
Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Approximation of distance between locations on earth given by latitude and longitude
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Section 8.3 Trigonometric Equations
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
( )( ) ( ) ( )( ) ( )( ) β = Chapter 5 Exercise Problems EX α So 49 β 199 EX EX EX5.4 EX5.5. (a)
hapter 5 xercise Problems X5. α β α 0.980 For α 0.980, β 49 0.980 0.995 For α 0.995, β 99 0.995 So 49 β 99 X5. O 00 O or n 3 O 40.5 β 0 X5.3 6.5 μ A 00 β ( 0)( 6.5 μa) 8 ma 5 ( 8)( 4 ) or.88 P on + 0.0065
TMA4115 Matematikk 3
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
Space-Time Symmetries
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Differential equations
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Non-Gaussianity from Lifshitz Scalar
COSMO/CosPA 200 September 27, 200 Non-Gaussianity from Lifshitz Scalar Takeshi Kobayashi (Tokyo U.) based on: arxiv:008.406 with Keisuke Izumi, Shinji Mukohyama Lifshitz scalars with z=3 obtain super-horizon,
4.6 Autoregressive Moving Average Model ARMA(1,1)
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Code Breaker. TEACHER s NOTES
TEACHER s NOTES Time: 50 minutes Learning Outcomes: To relate the genetic code to the assembly of proteins To summarize factors that lead to different types of mutations To distinguish among positive,
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
derivation of the Laplacian from rectangular to spherical coordinates
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg "k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +")
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
UV fixed-point structure of the 3d Thirring model
UV fixed-point structure of the 3d Thirring model arxiv:1006.3747 [hep-th] (PRD accepted) Lukas Janssen in collaboration with Holger Gies Friedrich-Schiller-Universität Jena Theoretisch-Physikalisches
Arithmetical applications of lagrangian interpolation. Tanguy Rivoal. Institut Fourier CNRS and Université de Grenoble 1
Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Other Test Constructions: Likelihood Ratio & Bayes Tests
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Lecture 26: Circular domains
Introductory lecture notes on Partial Differential Equations - c Anthony Peirce. Not to be copied, used, or revised without eplicit written permission from the copyright owner. 1 Lecture 6: Circular domains
Lifting Entry (continued)
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
Κύµατα παρουσία βαρύτητας
Κύµατα παουσία βαύτητας 8. Grait as in th ocan Sarantis Sofianos Dpt. of hsics, Unirsit of thns Was in th ocan Srfac grait as Short and long limit in grait as Wa charactristics Intrnal as Charactristic
From the finite to the transfinite: Λµ-terms and streams
From the finite to the transfinite: Λµ-terms and streams WIR 2014 Fanny He f.he@bath.ac.uk Alexis Saurin alexis.saurin@pps.univ-paris-diderot.fr 12 July 2014 The Λµ-calculus Syntax of Λµ t ::= x λx.t (t)u
Tridiagonal matrices. Gérard MEURANT. October, 2008
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
D-term Dynamical SUSY Breaking
D-term Dynamical SUSY Breaking Nobuhito Maru (Keio University) with H. Itoyama (Osaka City University) arxiv: 1109.76 [hep-ph] 7/6/01 @Y ITP workshop on Field Theory & String Theory Introduction SUPERSYMMETRY
Areas and Lengths in Polar Coordinates
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.
![= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.](/thumbs/93/113370452.jpg "= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.")
PHY 396 T: SUSY Solutions for problem set #1. Problem 2(a): First of all, [D α, D 2 D α D α ] = {D α, D α }D α D α {D α, D α } = {D α, D α }D α + D α {D α, D α } (S.1) = {{D α, D α }, D α }. Second, {D
Solar Neutrinos: Fluxes
Solar Neutrinos: Fluxes pp chain Sun shines by : 4 p 4 He + e + + ν e + γ Solar Standard Model Fluxes CNO cycle e + N 13 =0.707MeV He 4 C 1 C 13 p p p p N 15 N 14 He 4 O 15 O 16 e + =0.997MeV O17
Areas and Lengths in Polar Coordinates
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Statistical Inference I Locally most powerful tests
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
CRASH COURSE IN PRECALCULUS
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
SPECIAL FUNCTIONS and POLYNOMIALS
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
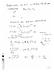Prblma dl smipian Cas i cs ω µ Cas sin cs i cs Cas fas [ ] [ ] ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ttal S S J L J J L A d I I A d I d I V d d V V d d V n J n J ˆ 0 ˆ ˆ ˆ 0 ˆ 0 ˆ ˆ ˆ 0 S S S S i i
Differentiation exercise show differential equation
Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Solutions to Exercise Sheet 5
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
ERG for a Yukawa Theory in 3 Dimensions
ERG for a Yukawa Theory in 3 Dimensions Hidenori SONODA Physics Department, Kobe University, Japan 14 September 2010 at ERG2010 Abstract We consider a theory of N Majorana fermions and a real scalar in
Depth versus Rigidity in the Design of International Trade Agreements. Leslie Johns
Depth versus Rigidity in the Design of International Trade Agreements Leslie Johns Supplemental Appendix September 3, 202 Alternative Punishment Mechanisms The one-period utility functions of the home
Prey-Taxis Holling-Tanner
Vol. 28 ( 2018 ) No. 1 J. of Math. (PRC) Prey-Taxis Holling-Tanner, (, 730070) : prey-taxis Holling-Tanner.,,.. : Holling-Tanner ; prey-taxis; ; MR(2010) : 35B32; 35B36 : O175.26 : A : 0255-7797(2018)01-0140-07
상대론적고에너지중이온충돌에서 제트입자와관련된제동복사 박가영 인하대학교 윤진희교수님, 권민정교수님
상대론적고에너지중이온충돌에서 제트입자와관련된제동복사 박가영 인하대학교 윤진희교수님, 권민정교수님 Motivation Bremsstrahlung is a major rocess losing energies while jet articles get through the medium. BUT it should be quite different from low energy
EE512: Error Control Coding
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Srednicki Chapter 55
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Potential Dividers. 46 minutes. 46 marks. Page 1 of 11
Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Προβολές και Μετασχηματισμοί Παρατήρησης
Γραφικά & Οπτικοποίηση Κεφάλαιο 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή Στα γραφικά υπάρχουν: 3Δ μοντέλα 2Δ συσκευές επισκόπησης (οθόνες & εκτυπωτές) Προοπτική απεικόνιση (προβολή): Λαμβάνει
DYNAMICAL BEHAVIORS OF A DELAYED REACTION-DIFFUSION EQUATION. Zhihao Ge
Mathmatical and Computational Applications, Vol. 5, No. 5, pp. 76-767, 00. Association for Scintific Rsarch DYNAMICAL BEHAVIORS OF A DELAYED REACTION-DIFFUSION EQUATION Zhihao G Institut of Applid Mathmatics
MathCity.org Merging man and maths
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
Every set of first-order formulas is equivalent to an independent set
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Spherical Coordinates
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Notes on the Open Economy
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Answers - Worksheet A ALGEBRA PMT. 1 a = 7 b = 11 c = 1 3. e = 0.1 f = 0.3 g = 2 h = 10 i = 3 j = d = k = 3 1. = 1 or 0.5 l =
C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Η Ομάδα SL(2,C) και οι αναπαραστάσεις της
SL(2, C) SO(3, 1) D : Λ D(Λ) SO(3, 1) 2 1 D : ±A D(π(±A)) SL(2, C) SL(2, C) SO(3, 1) SL(2, C) SO(3, 1) ξ i (, ) K i x µ p µ J µν T µν A µ ψ α J i = J i, () K i = K i, ( ) K i M 0i = (iξ i K i ) A i = 1
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
Math 6 SL Probability Distributions Practice Test Mark Scheme
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Homework 3 Solutions
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Second Order Partial Differential Equations
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
þÿ»±íº »¹ Áà  : É º±¹ Ä þÿ Á³ Ä Å : ¼¹± ºÁ¹Ä¹º ±À Ä ¼
Neapolis University HEPHAESTUS Repository School of Health Sciences http://hephaestus.nup.ac.cy Master Degree Thesis 2015 þÿ»±íº »¹ Áà  : É º±¹ Ä þÿ Á³ Ä Å : ¼¹± ºÁ¹Ä¹º ±À Ä ¼ þÿ Ä Æ Á Â, Á ÃÄ Â þÿ Á̳Á±¼¼±
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Volume of a Cuboid. Volume = length x breadth x height. V = l x b x h. The formula for the volume of a cuboid is
Volume of a Cuboid The formula for the volume of a cuboid is Volume = length x breadth x height V = l x b x h Example Work out the volume of this cuboid 10 cm 15 cm V = l x b x h V = 15 x 6 x 10 V = 900cm³
8.324 Relativistic Quantum Field Theory II
8.324 Relativistic Quantum Field Theory II MIT OpenCourseWare Lecture Notes Hong Liu, Fall 200 Lecture 2 3: GENERAL ASPECTS OF QUANTUM ELECTRODYNAMICS 3.: RENORMALIZED LAGRANGIAN Consider the Lagrangian
6. MAXIMUM LIKELIHOOD ESTIMATION
6 MAXIMUM LIKELIHOOD ESIMAION [1] Maximum Likelihood Estimator (1) Cases in which θ (unknown parameter) is scalar Notational Clarification: From now on, we denote the true value of θ as θ o hen, view θ
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
CE 530 Molecular Simulation
C 53 olecular Siulation Lecture Histogra Reweighting ethods David. Kofke Departent of Cheical ngineering SUNY uffalo kofke@eng.buffalo.edu Histogra Reweighting ethod to cobine results taken at different
Right Rear Door. Let's now finish the door hinge saga with the right rear door
Right Rear Door Let's now finish the door hinge saga with the right rear door You may have been already guessed my steps, so there is not much to describe in detail. Old upper one file:///c /Documents
Local Approximation with Kernels
Local Approximation with Kernels Thomas Hangelbroek University of Hawaii at Manoa 5th International Conference Approximation Theory, 26 work supported by: NSF DMS-43726 A cubic spline example Consider
Lifting Entry 2. Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYLAND U N I V E R S I T Y O F
ifting Entry Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYAN 1 010 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu ifting Atmospheric
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
The ε-pseudospectrum of a Matrix
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ. Θέµα:
Ε ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ Θέµα: Πολιτιστική Επικοινωνία και Τοπική ηµοσιότητα: Η αξιοποίηση των Μέσων Ενηµέρωσης, ο ρόλος των
The Finite Element Method
Th Finit Elmnt Mthod Plan (D) Truss and Fram Elmnts Rad: Sctions 4.6 and 5.4 CONTENTS Rviw of bar finit lmnt in th local coordinats Plan truss lmnt Rviw of bam finit lmnt in th local coordinats Plan fram
The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
Fractional Colorings and Zykov Products of graphs
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Hartree-Fock Theory. Solving electronic structure problem on computers
Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli
Models for Probabilistic Programs with an Adversary
Models for Probabilistic Programs with an Adversary Robert Rand, Steve Zdancewic University of Pennsylvania Probabilistic Programming Semantics 2016 Interactive Proofs 2/47 Interactive Proofs 2/47 Interactive
ES440/ES911: CFD. Chapter 5. Solution of Linear Equation Systems
ES440/ES911: CFD Chapter 5. Solution of Linear Equation Systems Dr Yongmann M. Chung http://www.eng.warwick.ac.uk/staff/ymc/es440.html Y.M.Chung@warwick.ac.uk School of Engineering & Centre for Scientific