Κύµατα παρουσία βαρύτητας
|
|
|
- Διδώ Κοσμόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Κύµατα παουσία βαύτητας 8. Grait as in th ocan Sarantis Sofianos Dpt. of hsics, Unirsit of thns Was in th ocan Srfac grait as Short and long limit in grait as Wa charactristics Intrnal as
2 Charactristic proprtis of as η λ Walngth (λ): Th distanc btn to conscti paks and Wanmbr (K) π K λ riod (Τ): Th tim it taks for to conscti paks to pass from a point in spac and Frqnc (ω) ω π T ω λ has Spd (C): Th spd of a monochromatic a C K T Grop Spd (C g ): Th spd of a a packt C g ω K Wa Enrg (Ε ): E g η Significant Wa ight (Η /3 ): Th arag hight (dobl amplitd) of th /3 largst as /3 4 η / π l Ftch: Th lngth of atr or hich a gin ind has blon λ π K K π k
3 t ( ) Ω g V dt d f t V f t V g t V Working qations Momntm Consration Mass Consration (Incomprssibl flo)
4 Th ocanic a spctrm ind as sll tsnamis long grait as tids h 4h plantar as f ks months capillar λ T s m
5 Linar grait as in barotropic flid Coriolis Trm Changs Tmporal >> ft fu T U R ot Coriolis Trm Viscosit Trms << f fl E V k F R U N >> Scaling paramtrs f p t V f p t V g p t V t () υ t () t (3) hr p g
6 () () (3) t (Continit) Εξίσωση LLCE Looking for a-lik soltions: Bondar Conditions: at gη η t at η η ( k l ω ) - D soltions cos t for simplicit ill instigat a -D (-) a Wa soltion for Laplac qation: ( k k B ) cos( k
7 Using th srfac bondar B gη condition: Using th ocan bottom bondar condition: gη k ( ) k( ) k k From qation (3): t cos k B k ( k gη cosh cosh kgη sinh[k( )] cos cosh( k ) Using th srfac bondar condition: kgη sinh cosh ( k ) ( k ) cos ω gη B gη k k [ k( )] ( k ) ( k Disprsion rlation Σχέση διασποάς η t t ( k ωt) ω η cos( k gk tanh( k ) k k cos k k η t ( k
8 Short as λ << Η (short alngth or dp ocan) > k>> Long as λ >> Η (long alngth or shallo ocan) > k<< tanh( k ) tanh( k ) k ω gk ω gk has Spd : C C g k Grop Vlocit : Disprsi ω k C g ω k C has Spd : C g Grop Vlocit : ω k Non-disprsi C g ω k C g C C g C
9 Watr parcl orbits ξ t ζ t ξ η cosh cosh( k ) smimajor ais [ k( )] ξ cosh kgη t ω cosh( k ) [ k( )] ζ sinh kgη t ω cosh( k ) cos( k sin( k [ k( )] cosh ξ η cosh( k ) [ k( )] sinh ζ η cosh( k ) [ k( )] η sinh[ k( )] ζ cosh( k ) smiminor ais sin( k cos( k ξ ζ (, ) ( ξ, ζ ) Both as dcras ith dpth Th smiminor ais is ro at bottom (-)
10 Short as λ << Η (short alngth or dp ocan) > k>> [ k( )] sinh[ k( )] k cosh cosh( k ) cosh( k ) ξ η k ζ η sin( k k cos( k Circls Both dcras ponntiall ith dpth Long as Constant λ >> Η (long alngth or shallo ocan) > k<< ξ η sin(k cosh[ k( )] ζ kη ( )cos(k sinh k k [ ( )] ( ) cosh( k ) Dcras linarl ith dpth and bcoms ro at
11 Stoks Drift If do not s th approimation (i.. th Lagrangian locit at tim t is qal ith th Elrian locit at, at tim t) (, Th Lagrangian locit L (,,t) can b dfind as th Talor sris pansion of th Elrian locit (,,t) arond, L For short grait as (dp atr limit): (,, t) (,, t) ( ) ( )..., t) η η η ω k k sin( k k cos( k cos( k raging or on priod s L η ω k k In gnral [ k( )] cos s ηωk sinh ( k ) Stoks locit
12 η η cos( k η cos( k ωt) η cos( k)cos( ωt) kgη cosh[ k( )] sin( k)sin( ωt) ω cosh( k ) Sichs Bondar condition: at και L n kl (n )π n,,,... ω λ L n πg( n ) ( n ) π tanh L L L n Wa Rfraction and th island ffct on as
13 Intrnal grait as: Lard stratification Εσωτεικά κύµατα βαύτητας: Απλή στωµάτωση Δύο στώµατα. Οι εξισώσεις Laplac για κάθε στώµα: k k i ( ) ( k ωt B ) ( k ) i( k ω t ) C k D i η a ζ b ( k ωt ) i ( k ωt ) η ζ - Οιακές συνθήκες: at at gη at η t ( η ζ ) η t g ζ ζ t Χησιµοποιώντας τις οιακές συνθήκες: ω gk ω gk [ sinh( k ) cosh( k )] ( ) sinh( k )
14 First soltion: ω gk Barotropic mod (Βαοτοπικός τόπος ταλάντωσης) Scond soltion: ω ( ) gk sinh( k ) cosh( k ) sinh( k ) In gnral: For an ocan of n lars, thr is on barotropic mod and n- baroclinic mods (a total of n mods of oscillation). Baroclinic mod (Βαοκλινικός τόπος ταλάντηωσης)
15 Intrnal as: Baroclinic mod Short as k coth( k ) ω ( ) gk sinh( k ) cosh( k ) sinh( k ) ( ) gk coth( k ) Long as k << sinh( k ) k cosh( k ) c gʹ, gk ω gʹ ( ) g ω gk η ζ k For a tpical ocanic stratificatiob: ΔΟ(kg/m 3 ), O(kg/m 3 ) g -3 g η ζ
ΔΙΑΛΕΞΗ 8 Kύματα βαρύτητας απουσία περιστροφής
 ΔΙΑΛΕΞΗ 8 Kύματα βαύτητας απουσία πειστοφής Πειεχόμενα: Χαακτηιστικά μεγέθη τν κυμάτν Εξισώσεις τν επιφανειακών κυμάτν Ποσεγγίσεις βαχέν/μακών κυμάτν Το κυματικό φάσμα Εστεικά κύματα βαύτητας Χαακτηιστικά
ΔΙΑΛΕΞΗ 8 Kύματα βαύτητας απουσία πειστοφής Πειεχόμενα: Χαακτηιστικά μεγέθη τν κυμάτν Εξισώσεις τν επιφανειακών κυμάτν Ποσεγγίσεις βαχέν/μακών κυμάτν Το κυματικό φάσμα Εστεικά κύματα βαύτητας Χαακτηιστικά
Αλληλεπίδραση θάλασσας-ατμόσφαιρας
 Αλληλεπίδραση θάλασσας-ατμόσφαιρας ΙΑΛΕΞΗ Περιεχόμενα: Ελεύθερα επιφανειακά κύματα (free-aes) ( απουσία γήινης περιστροφής) Προσεγγίσεις βραχέων/μακρών κυμάτων Ανεμογεννή κύματα (ind-aes) Κυματικά μοντέλα
Αλληλεπίδραση θάλασσας-ατμόσφαιρας ΙΑΛΕΞΗ Περιεχόμενα: Ελεύθερα επιφανειακά κύματα (free-aes) ( απουσία γήινης περιστροφής) Προσεγγίσεις βραχέων/μακρών κυμάτων Ανεμογεννή κύματα (ind-aes) Κυματικά μοντέλα
Homework #6. A circular cylinder of radius R rotates about the long axis with angular velocity
 Homwork #6 1. (Kittl 5.1) Cntrifug. A circular cylindr of radius R rotats about th long axis with angular vlocity ω. Th cylindr contains an idal gas of atoms of mass m at tmpratur. Find an xprssion for
Homwork #6 1. (Kittl 5.1) Cntrifug. A circular cylindr of radius R rotats about th long axis with angular vlocity ω. Th cylindr contains an idal gas of atoms of mass m at tmpratur. Find an xprssion for
6.4 Superposition of Linear Plane Progressive Waves
 .0 - Marine Hydrodynamics, Spring 005 Lecture.0 - Marine Hydrodynamics Lecture 6.4 Superposition of Linear Plane Progressive Waves. Oblique Plane Waves z v k k k z v k = ( k, k z ) θ (Looking up the y-ais
.0 - Marine Hydrodynamics, Spring 005 Lecture.0 - Marine Hydrodynamics Lecture 6.4 Superposition of Linear Plane Progressive Waves. Oblique Plane Waves z v k k k z v k = ( k, k z ) θ (Looking up the y-ais
STEADY, INVISCID ( potential flow, irrotational) INCOMPRESSIBLE + V Φ + i x. Ψ y = Φ. and. Ψ x
 STEADY, INVISCID ( potential flow, iotational) INCOMPRESSIBLE constant Benolli's eqation along a steamline, EQATION MOMENTM constant is a steamline the Steam Fnction is sbsititing into the continit eqation,
STEADY, INVISCID ( potential flow, iotational) INCOMPRESSIBLE constant Benolli's eqation along a steamline, EQATION MOMENTM constant is a steamline the Steam Fnction is sbsititing into the continit eqation,
wave energy Superposition of linear plane progressive waves Marine Hydrodynamics Lecture Oblique Plane Waves:
 3.0 Marine Hydrodynamics, Fall 004 Lecture 0 Copyriht c 004 MIT - Department of Ocean Enineerin, All rihts reserved. 3.0 - Marine Hydrodynamics Lecture 0 Free-surface waves: wave enery linear superposition,
3.0 Marine Hydrodynamics, Fall 004 Lecture 0 Copyriht c 004 MIT - Department of Ocean Enineerin, All rihts reserved. 3.0 - Marine Hydrodynamics Lecture 0 Free-surface waves: wave enery linear superposition,
4.4 Superposition of Linear Plane Progressive Waves
 .0 Marine Hydrodynamics, Fall 08 Lecture 6 Copyright c 08 MIT - Department of Mechanical Engineering, All rights reserved..0 - Marine Hydrodynamics Lecture 6 4.4 Superposition of Linear Plane Progressive
.0 Marine Hydrodynamics, Fall 08 Lecture 6 Copyright c 08 MIT - Department of Mechanical Engineering, All rights reserved..0 - Marine Hydrodynamics Lecture 6 4.4 Superposition of Linear Plane Progressive
Οι νόµοι διατήρησης στη Φυσική Ωκεανογραφία
 Οι όµοι διατήρησης στη Φσική Ωκεαογραφία 4. The conservation las in the ocean dnamics Sarantis Sofianos Dept. of Phsics, niversit of Athens Fndamental dnamics and the eqations for geophsical flids Oceanic
Οι όµοι διατήρησης στη Φσική Ωκεαογραφία 4. The conservation las in the ocean dnamics Sarantis Sofianos Dept. of Phsics, niversit of Athens Fndamental dnamics and the eqations for geophsical flids Oceanic
ΑΓΓΕΛΗΣ ΧΡΗΣΤΟΣ ΠΑΝΑΓΙΩΤΗΣ 6 OO ΑΓΓΕΛΙΔΗΣ ΧΑΡΙΛΑΟΣ ΧΡΗΣΤΟΣ 4 OO ΑΓΓΟΥ ΑΝΑΣΤΑΣΙΑ ΔΗΜΗΤΡΙΟΣ 6 OO ΑΔΑΜΙΔΟΥ ΕΥΑΓΓΕΛΙΑ ΑΒΡΑΑΜ 3 OO ΑΛΕΒΙΖΟΥ ΠΑΝΑΓΙΩΤΑ
 ΕΠΩΝΥΜΙΑ ΠΕΡΙΟΔΟΣ ΜΕΣΟ ΑΓΓΕΛΗΣ ΧΡΗΣΤΟΣ ΠΑΝΑΓΙΩΤΗΣ 6 OO ΑΓΓΕΛΙΔΗΣ ΧΑΡΙΛΑΟΣ ΧΡΗΣΤΟΣ 4 OO ΑΓΓΟΥ ΑΝΑΣΤΑΣΙΑ ΔΗΜΗΤΡΙΟΣ 6 OO ΑΔΑΜΙΔΟΥ ΕΥΑΓΓΕΛΙΑ ΑΒΡΑΑΜ 3 OO ΑΛΕΒΙΖΟΥ ΠΑΝΑΓΙΩΤΑ ΔΗΜΗΤΡΙΟΣ 7 OO ΑΝΑΓΝΩΣΤΟΠΟΥΛΟΥ ΖΩΙΤΣΑ
ΕΠΩΝΥΜΙΑ ΠΕΡΙΟΔΟΣ ΜΕΣΟ ΑΓΓΕΛΗΣ ΧΡΗΣΤΟΣ ΠΑΝΑΓΙΩΤΗΣ 6 OO ΑΓΓΕΛΙΔΗΣ ΧΑΡΙΛΑΟΣ ΧΡΗΣΤΟΣ 4 OO ΑΓΓΟΥ ΑΝΑΣΤΑΣΙΑ ΔΗΜΗΤΡΙΟΣ 6 OO ΑΔΑΜΙΔΟΥ ΕΥΑΓΓΕΛΙΑ ΑΒΡΑΑΜ 3 OO ΑΛΕΒΙΖΟΥ ΠΑΝΑΓΙΩΤΑ ΔΗΜΗΤΡΙΟΣ 7 OO ΑΝΑΓΝΩΣΤΟΠΟΥΛΟΥ ΖΩΙΤΣΑ
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Similarly, we may define hyperbolic functions cosh α and sinh α from the unit hyperbola
 Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Review Exercises for Chapter 7
 8 Chapter 7 Integration Techniques, L Hôpital s Rule, and Improper Integrals 8. For n, I d b For n >, I n n u n, du n n d, dv (a) d b 6 b 6 (b) (c) n d 5 d b n n b n n n d, v d 6 5 5 6 d 5 5 b d 6. b 6
8 Chapter 7 Integration Techniques, L Hôpital s Rule, and Improper Integrals 8. For n, I d b For n >, I n n u n, du n n d, dv (a) d b 6 b 6 (b) (c) n d 5 d b n n b n n n d, v d 6 5 5 6 d 5 5 b d 6. b 6
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ- ΦΥΛΛΑΔΙΟ 1(ΑΝΑΛΥΣΗ)
 ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ- ΦΥΛΛΑΔΙΟ (ΑΝΑΛΥΣΗ) Ι. Οι τριγωνομετρικές συναρτήσεις και οι αντίστροφές τους. Η συνάρτηση = sin. Η συνάρτηση sin : -, [,], = sin είναι, αφού (sin ) = cos >, για κάθε -,. Άρα
ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ- ΦΥΛΛΑΔΙΟ (ΑΝΑΛΥΣΗ) Ι. Οι τριγωνομετρικές συναρτήσεις και οι αντίστροφές τους. Η συνάρτηση = sin. Η συνάρτηση sin : -, [,], = sin είναι, αφού (sin ) = cos >, για κάθε -,. Άρα
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Lifting Entry (continued)
 ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
is like multiplying by the conversion factor of. Dividing by 2π gives you the
 Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Forced Pendulum Numerical approach
 Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
Numerical approach UiO April 8, 2014 Physical problem and equation We have a pendulum of length l, with mass m. The pendulum is subject to gravitation as well as both a forcing and linear resistance force.
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
 DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
Basic Formulas. 8. sin(x) = cos(x π 2 ) 9. sin 2 (x) =1 cos 2 (x) 10. sin(2x) = 2 sin(x)cos(x) 11. cos(2x) =2cos 2 (x) tan(x) = 1 cos(2x)
 Bsic Formuls. n d =. d b = 3. b d =. sin d = 5. cos d = 6. tn d = n n ln b ln b b cos sin ln cos 7. udv= uv vdu. sin( = cos( π 9. sin ( = cos ( 0. sin( = sin(cos(. cos( =cos (. tn( = cos( sin( 3. sin(b
Bsic Formuls. n d =. d b = 3. b d =. sin d = 5. cos d = 6. tn d = n n ln b ln b b cos sin ln cos 7. udv= uv vdu. sin( = cos( π 9. sin ( = cos ( 0. sin( = sin(cos(. cos( =cos (. tn( = cos( sin( 3. sin(b
1 String with massive end-points
 1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
1 String with massive end-points Πρόβλημα 5.11:Θεωρείστε μια χορδή μήκους, τάσης T, με δύο σημειακά σωματίδια στα άκρα της, το ένα μάζας m, και το άλλο μάζας m. α) Μελετώντας την κίνηση των άκρων βρείτε
(a) Individually finned tubes (b) flat (continuous) fins on an array of tubes
 (a) Individually finned tues () flat (continuous) fins on an array of tues Eample Fins Fins on Stegosaurus 3 Rektangulär fläns, Rectangular fin. Z t d t f 4 Rektangulär fläns, Rectangular fin. Z t d t
(a) Individually finned tues () flat (continuous) fins on an array of tues Eample Fins Fins on Stegosaurus 3 Rektangulär fläns, Rectangular fin. Z t d t f 4 Rektangulär fläns, Rectangular fin. Z t d t
Ι ΤΕΛΕΣΤΕΣ, ΤΑΥΤΟΤΗΤΕΣ, ΠΑΡΑΓΩΓΟΙ, ΣΕΙΡΕΣ, ΙΑΦΟΡΟΙ ΤΥΠΟΙ
 Ι ΤΕΛΕΣΤΕΣ, ΤΑΥΤΟΤΗΤΕΣ, ΠΑΡΑΓΩΓΟΙ, ΣΕΙΡΕΣ, ΙΑΦΟΡΟΙ ΤΥΠΟΙ TΑ TΡΙΑ ΣΥΝΗΘΗ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ O P(,, ) O φ φ φ P(, φ, ) P(,, φ) O φ (α) (β) (γ) (α) Κατεσιαό σύστηµα συτεταγµέω,,. (σχήµα (α)) (β) Σύστηµα
Ι ΤΕΛΕΣΤΕΣ, ΤΑΥΤΟΤΗΤΕΣ, ΠΑΡΑΓΩΓΟΙ, ΣΕΙΡΕΣ, ΙΑΦΟΡΟΙ ΤΥΠΟΙ TΑ TΡΙΑ ΣΥΝΗΘΗ ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ O P(,, ) O φ φ φ P(, φ, ) P(,, φ) O φ (α) (β) (γ) (α) Κατεσιαό σύστηµα συτεταγµέω,,. (σχήµα (α)) (β) Σύστηµα
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
ΔΙΑΛΕΞΗ 6 Ρεύματα παρουσία τριβής Ανεμογεννής Κυκλοφορία
 ΔΙΑΛΕΞΗ 6 Ρεύμαα παουσία ιβής Ανεμογεννής Κυκλοφοία Πειεχόμενα: Ανεμογενής κυκλοφοία Θεωία Ekman Θεωία Serdrp Ρεύμαα ου δυικού οίου g P V Ω r r r r Naier-Stokes Eqation ( ) t dt d r r r r cceleration dection
ΔΙΑΛΕΞΗ 6 Ρεύμαα παουσία ιβής Ανεμογεννής Κυκλοφοία Πειεχόμενα: Ανεμογενής κυκλοφοία Θεωία Ekman Θεωία Serdrp Ρεύμαα ου δυικού οίου g P V Ω r r r r Naier-Stokes Eqation ( ) t dt d r r r r cceleration dection
Differential equations
 Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Calculus and Differential Equations page 1 of 17 CALCULUS and DIFFERENTIAL EQUATIONS
 alculus and Diffrnial Equaions pag of 7 ALULUS and DIFFERENTIAL EQUATIONS Th following 55 qusions concrn calculus and diffrnial quaions. In his vrsion of h am, h firs choic is always h corrc on. In h acual
alculus and Diffrnial Equaions pag of 7 ALULUS and DIFFERENTIAL EQUATIONS Th following 55 qusions concrn calculus and diffrnial quaions. In his vrsion of h am, h firs choic is always h corrc on. In h acual
2 c. cos H 8. u = 50 n
 Τεχνολογικό Πανεπιστήµιο Κύπρου Σχολή Μηχανικής και Τεχνολογίας Τµήµα Πολιτικών Μηχανικών και Μηχανικών Γεωπληροφορικής (Κατεύθυνση Πολιτικών Μηχανικών / Τοπογράφων Μηχανικών και Μηχανικών Γεωπληροφορικής)
Τεχνολογικό Πανεπιστήµιο Κύπρου Σχολή Μηχανικής και Τεχνολογίας Τµήµα Πολιτικών Μηχανικών και Μηχανικών Γεωπληροφορικής (Κατεύθυνση Πολιτικών Μηχανικών / Τοπογράφων Μηχανικών και Μηχανικών Γεωπληροφορικής)
Spectrum Representation (5A) Young Won Lim 11/3/16
 Spectrum (5A) Copyright (c) 2009-2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Spectrum (5A) Copyright (c) 2009-2016 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 2012 ΘΕΜΑΤΑ Α
 ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 0 ΘΕΜΑΤΑ Α Θέµα ο. Να βρεθεί (α) η γενική λύση yy() της διαφορικής εξίσωσης y' y + καθώς και (β) η µερική λύση που διέρχεται από το σηµείο y(/). (γ) Από ποια σηµεία του επιπέδου
ΙΑΦΟΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΙΑΝΟΥΑΡΙΟΣ 0 ΘΕΜΑΤΑ Α Θέµα ο. Να βρεθεί (α) η γενική λύση yy() της διαφορικής εξίσωσης y' y + καθώς και (β) η µερική λύση που διέρχεται από το σηµείο y(/). (γ) Από ποια σηµεία του επιπέδου
G L (x) =Ax + B, G R (x) =A x + B οπότε από τις συνοριακές συνθήκες έχουμε
 1 ÈÖ Ð Ñ Για να είναι εφαρμόσιμη η μέθοδος της συνάρτησης Green, θαπρέπειηομογενής εξίσωση Ly =+ Ο.Σ.Σ. να έχει ως μοναδική λύση τη μηδενική. α) Η ομογενής εξίσωση y =έχει λύση y = A + B, από τις δεδομένες
1 ÈÖ Ð Ñ Για να είναι εφαρμόσιμη η μέθοδος της συνάρτησης Green, θαπρέπειηομογενής εξίσωση Ly =+ Ο.Σ.Σ. να έχει ως μοναδική λύση τη μηδενική. α) Η ομογενής εξίσωση y =έχει λύση y = A + B, από τις δεδομένες
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
Finite difference method for 2-D heat equation
 Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
Finite difference method for 2-D heat equation Praveen. C praveen@math.tifrbng.res.in Tata Institute of Fundamental Research Center for Applicable Mathematics Bangalore 560065 http://math.tifrbng.res.in/~praveen
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1
 General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Radiation Stress Concerned with the force (or momentum flux) exerted on the right hand side of a plane by water on the left hand side of the plane.
 upplement on Radiation tress and Wave etup/et down Radiation tress oncerned wit te force (or momentum flu) eerted on te rit and side of a plane water on te left and side of te plane. plane z "Radiation
upplement on Radiation tress and Wave etup/et down Radiation tress oncerned wit te force (or momentum flu) eerted on te rit and side of a plane water on te left and side of te plane. plane z "Radiation
Pairs of Random Variables
 Pairs of Random Variabls Rading: Chaptr 4. 4. Homwork: (do at last 5 out of th following problms 4..4, 4..6, 4.., 4.3.4, 4.3.5, 4.4., 4.4.4, 4.5.3, 4.6.3, 4.6.7, 4.6., 4.7.9, 4.7., 4.8.3, 4.8.7, 4.9.,
Pairs of Random Variabls Rading: Chaptr 4. 4. Homwork: (do at last 5 out of th following problms 4..4, 4..6, 4.., 4.3.4, 4.3.5, 4.4., 4.4.4, 4.5.3, 4.6.3, 4.6.7, 4.6., 4.7.9, 4.7., 4.8.3, 4.8.7, 4.9.,
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
LTI Systems (1A) Young Won Lim 3/21/15
 LTI Systems (1A) Copyright (c) 214 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
LTI Systems (1A) Copyright (c) 214 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version
Ρεύµατα παρουσία τριβής ανεµογενής κυκλοφορία
 Ρεύµατα παρουσία τριής ανεµογενής κυκλοφορία 6. Wind drien circulation Sarantis Sofianos Dept. of Physics, niersity of thens Ekman Theory Serdrup theory for the wind-drien circulation Stommel and Munk
Ρεύµατα παρουσία τριής ανεµογενής κυκλοφορία 6. Wind drien circulation Sarantis Sofianos Dept. of Physics, niersity of thens Ekman Theory Serdrup theory for the wind-drien circulation Stommel and Munk
Graded Refractive-Index
 Graded Refractive-Index Common Devices Methodologies for Graded Refractive Index Methodologies: Ray Optics WKB Multilayer Modelling Solution requires: some knowledge of index profile n 2 x Ray Optics for
Graded Refractive-Index Common Devices Methodologies for Graded Refractive Index Methodologies: Ray Optics WKB Multilayer Modelling Solution requires: some knowledge of index profile n 2 x Ray Optics for
α A G C T 國立交通大學生物資訊及系統生物研究所林勇欣老師
 A G C T Juks and Cantor s (969) on-aramtr modl A T C G A G 0 0 0-3 C T A() A( t ) ( 3 ) ( ) A() A() ( 3 ) ( ) A( A( A( A( t ) A( 3 A( t ) ( ) A( A( Juks and Cantor s (969) on-aramtr modl A( A( t ) A( d
A G C T Juks and Cantor s (969) on-aramtr modl A T C G A G 0 0 0-3 C T A() A( t ) ( 3 ) ( ) A() A() ( 3 ) ( ) A( A( A( A( t ) A( 3 A( t ) ( ) A( A( Juks and Cantor s (969) on-aramtr modl A( A( t ) A( d
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
γ /ω=0.2 γ /ω=1 γ /ω= (ω /g) v. (ω 2 /g)(x-l 0 ) ωt. 2m.
 Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 015-016 Ν. Βλαχάκης 1. Σώμα μάζας m και φορτίου q κινείται σε κατακόρυφο άξονα x, δεμένο σε ελατήριο σταθεράς k = mω του οποίου το άλλο άκρο είναι σταθερό. Το σύστημα
Μηχανική Ι Εργασία #7 Χειμερινό εξάμηνο 015-016 Ν. Βλαχάκης 1. Σώμα μάζας m και φορτίου q κινείται σε κατακόρυφο άξονα x, δεμένο σε ελατήριο σταθεράς k = mω του οποίου το άλλο άκρο είναι σταθερό. Το σύστημα
ECON 381 SC ASSIGNMENT 2
 ECON 8 SC ASSIGNMENT 2 JOHN HILLAS UNIVERSITY OF AUCKLAND Problem Consider a consmer with wealth w who consmes two goods which we shall call goods and 2 Let the amont of good l that the consmer consmes
ECON 8 SC ASSIGNMENT 2 JOHN HILLAS UNIVERSITY OF AUCKLAND Problem Consider a consmer with wealth w who consmes two goods which we shall call goods and 2 Let the amont of good l that the consmer consmes
Computing the Macdonald function for complex orders
 Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
Macdonald p. 1/1 Computing the Macdonald function for complex orders Walter Gautschi wxg@cs.purdue.edu Purdue University Macdonald p. 2/1 Integral representation K ν (x) = complex order ν = α + iβ e x
Faculdade de Engenharia. Transmission Lines ELECTROMAGNETIC ENGINEERING MAP TELE 2008/2009
 Facudad d Ennharia Transmission ins EECTROMAGNETC ENGNEERNG MAP TEE 8/9 Transmission ins Facudad d Ennharia transmission ins wavuids supportin TEM wavs most common typs para-pat wavuids coaxia wavuids
Facudad d Ennharia Transmission ins EECTROMAGNETC ENGNEERNG MAP TEE 8/9 Transmission ins Facudad d Ennharia transmission ins wavuids supportin TEM wavs most common typs para-pat wavuids coaxia wavuids
x L I I I II II II Ακόµα αφού η συνάρτηση στην θέση x=0 είναι συνεχής, έχουµε την παρακάτω συνθήκη. ηλαδή οι ιδιοσυναρτήσεις είναι
 Πρόβληµα ΑπειρόβαθοΚβαντικόΠηγάδι3α(ΑΚΠ3α), x > Θεωρούµε κβαντικό πηγάδι µε δυναµικό της µορφής V( x) x Να εκτιµηθούν οι ιδιοκαταστάσεις του συστήµατος για (α) c> και (β) c< Για την περίπτωση (α) να µελετηθεί
Πρόβληµα ΑπειρόβαθοΚβαντικόΠηγάδι3α(ΑΚΠ3α), x > Θεωρούµε κβαντικό πηγάδι µε δυναµικό της µορφής V( x) x Να εκτιµηθούν οι ιδιοκαταστάσεις του συστήµατος για (α) c> και (β) c< Για την περίπτωση (α) να µελετηθεί
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
General theorems of Optical Imaging systems
 Gnral thorms of Optcal Imagng sstms Tratonal Optcal Imagng Topcs Imagng qualt harp: mags a pont sourc to a pont Dstorton fr: mags a shap to a smlar shap tgmatc Imagng Imags a pont sourc to a nfntl sharp
Gnral thorms of Optcal Imagng sstms Tratonal Optcal Imagng Topcs Imagng qualt harp: mags a pont sourc to a pont Dstorton fr: mags a shap to a smlar shap tgmatc Imagng Imags a pont sourc to a nfntl sharp
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
Φυσική για Μηχανικούς Απλή Αρμονική Ταλάντωση Εικόνα: Σταγόνες νερού που πέφτουν από ύψος επάνω σε μια επιφάνεια νερού προκαλούν την ταλάντωση της επιφάνειας. Αυτές οι ταλαντώσεις σχετίζονται με κυκλικά
= 1. z n 1 = z z n = 1. f(z) = x 0. (0, 0) = lim
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 1η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση 1. Να λυθεί η εξίσωση: 4 1 + 3i. Λύση. Επειδή 1 + 3i e πi/3, οι λύσεις της εξίσωσης 4 1 + 3i
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ ΜΑΘΗΜΑΤΙΚΩΝ 1η Σειρά Ασκήσεων στη Μιγαδική Ανάλυση 1. Να λυθεί η εξίσωση: 4 1 + 3i. Λύση. Επειδή 1 + 3i e πi/3, οι λύσεις της εξίσωσης 4 1 + 3i
Oscillatory Gap Damping
 Oscillatory Gap Damping Find the damping due to the linear motion of a viscous gas in in a gap with an oscillating size: ) Find the motion in a gap due to an oscillating external force; ) Recast the solution
Oscillatory Gap Damping Find the damping due to the linear motion of a viscous gas in in a gap with an oscillating size: ) Find the motion in a gap due to an oscillating external force; ) Recast the solution
ECE 468: Digital Image Processing. Lecture 8
 ECE 468: Digital Image Processing Lecture 8 Prof. Sinisa Todorovic sinisa@eecs.oregonstate.edu 1 Image Reconstruction from Projections X-ray computed tomography: X-raying an object from different directions
ECE 468: Digital Image Processing Lecture 8 Prof. Sinisa Todorovic sinisa@eecs.oregonstate.edu 1 Image Reconstruction from Projections X-ray computed tomography: X-raying an object from different directions
ΔΙΑΛΕΞΗ 4 Βασικές εξισώσεις διατήρησης στη Φυσική Ωκεανογραφία
 ΔΙΑΛΕΞΗ 4 Βασικές εξισώσεις ιατήησης στη Φυσική Ωκεανογαφία Πειεχόµενα: q Δυνάµεις που ουν στον ωκεανό q Εξισώσεις κίνησης q Scaling q Εξίσωση συνέχειας q Εξίσωση ιατήησης της ενέγειας q Οιακές συνθήκες
ΔΙΑΛΕΞΗ 4 Βασικές εξισώσεις ιατήησης στη Φυσική Ωκεανογαφία Πειεχόµενα: q Δυνάµεις που ουν στον ωκεανό q Εξισώσεις κίνησης q Scaling q Εξίσωση συνέχειας q Εξίσωση ιατήησης της ενέγειας q Οιακές συνθήκες
= df. f (n) (x) = dn f dx n
 Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) Ορισμός Cauchy: f (ξ) = lim x ξ g(x, ξ), g(x, ξ) = f(x) f(ξ) x ξ ɛ > 0 δ(ɛ, ξ) > 0
Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) Ορισμός Cauchy: f (ξ) = lim x ξ g(x, ξ), g(x, ξ) = f(x) f(ξ) x ξ ɛ > 0 δ(ɛ, ξ) > 0
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n 1
 d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
d dx x 2 = 2x d dx x 3 = 3x 2 d dx x n = nx n1 x dx = 1 2 b2 1 2 a2 a b b x 2 dx = 1 a 3 b3 1 3 a3 b x n dx = 1 a n +1 bn +1 1 n +1 an +1 d dx d dx f (x) = 0 f (ax) = a f (ax) lim d dx f (ax) = lim 0 =
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Α Ρ Ι Θ Μ Ο Σ : 6.913
 Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Αλληλεπίδραση θάλασσας ατμόσφαιρας
 Αλληλεπίδαση θάλασσας αμόσφαιας ΔΙΑΛΕΞΗ 3 Το σώμα Ekman Πειεχόμενα: Θεωία Ekman Ανεμογενής κυκλοφοία Αποελέσμαα ης θεωίας Ekman Η γενική ανεμογεννής κυκλοφοία ου παγκόσμιου ωκεανού (θεωία Serdrp - εύμαα
Αλληλεπίδαση θάλασσας αμόσφαιας ΔΙΑΛΕΞΗ 3 Το σώμα Ekman Πειεχόμενα: Θεωία Ekman Ανεμογενής κυκλοφοία Αποελέσμαα ης θεωίας Ekman Η γενική ανεμογεννής κυκλοφοία ου παγκόσμιου ωκεανού (θεωία Serdrp - εύμαα
Higher Derivative Gravity Theories
 Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Higher Derivative Gravity Theories Black Holes in AdS space-times James Mashiyane Supervisor: Prof Kevin Goldstein University of the Witwatersrand Second Mandelstam, 20 January 2018 James Mashiyane WITS)
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
6.003: Signals and Systems. Modulation
 6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
6.003: Signals and Systems Modulation May 6, 200 Communications Systems Signals are not always well matched to the media through which we wish to transmit them. signal audio video internet applications
Τύπος TAYLOR. f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) ξ μεταξύ x και x 0. (x x 0 ) k k! f(x) = f (k) (x 0 ) + R n (x)
![Τύπος TAYLOR. f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) ξ μεταξύ x και x 0. (x x 0 ) k k! f(x) = f (k) (x 0 ) + R n (x) Τύπος TAYLOR. f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) ξ μεταξύ x και x 0. (x x 0 ) k k! f(x) = f (k) (x 0 ) + R n (x)](/thumbs/63/49057706.jpg) Τύπος TAYLOR f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) f(x) = ξ μεταξύ x και x 0 n 1 (x x 0 ) k f (k) (x 0 ) + R n (x) R n (x) = (x ξ)n p (x x 0 ) p p(n 1)! f (n) (ξ) υπόλοιπο Sclömlich-Roche
Τύπος TAYLOR f : [a, b] R f (n 1) (x) συνεχής x [a, b] f (n) (x) x (a, b) f(x) = ξ μεταξύ x και x 0 n 1 (x x 0 ) k f (k) (x 0 ) + R n (x) R n (x) = (x ξ)n p (x x 0 ) p p(n 1)! f (n) (ξ) υπόλοιπο Sclömlich-Roche
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
MathCity.org Merging man and maths
 MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
Chapter 6 BLM Answers
 Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
The Finite Element Method
 Th Finit Elmnt Mthod Plan (D) Truss and Fram Elmnts Rad: Sctions 4.6 and 5.4 CONTENTS Rviw of bar finit lmnt in th local coordinats Plan truss lmnt Rviw of bam finit lmnt in th local coordinats Plan fram
Th Finit Elmnt Mthod Plan (D) Truss and Fram Elmnts Rad: Sctions 4.6 and 5.4 CONTENTS Rviw of bar finit lmnt in th local coordinats Plan truss lmnt Rviw of bam finit lmnt in th local coordinats Plan fram
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Παράγωγος Συνάρτησης. Ορισμός Παραγώγου σε ένα σημείο. ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) f (ξ) = lim.
 Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) f (ξ) x ξ g(x, ξ), g(x, ξ) f(x) f(ξ) x ξ Ορισμός Cauchy: ɛ > 0 δ(ɛ, ξ) > 0 x x ξ
Παράγωγος Συνάρτησης Ορισμός Παραγώγου σε ένα σημείο ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ σε ένα σημείο ξ είναι το όριο (αν υπάρχει!) f (ξ) x ξ g(x, ξ), g(x, ξ) f(x) f(ξ) x ξ Ορισμός Cauchy: ɛ > 0 δ(ɛ, ξ) > 0 x x ξ
Chapter 7 Transformations of Stress and Strain
 Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
Chapter 7 Transformations of Stress and Strain INTRODUCTION Transformation of Plane Stress Mohr s Circle for Plane Stress Application of Mohr s Circle to 3D Analsis 90 60 60 0 0 50 90 Introduction 7-1
Q1a. HeavisideTheta x. Plot f, x, Pi, Pi. Simplify, n Integers
 2 M2 Fourier Series answers in Mathematica Note the function HeavisideTheta is for x>0 and 0 for x
2 M2 Fourier Series answers in Mathematica Note the function HeavisideTheta is for x>0 and 0 for x
Leaving Certificate Applied Maths Higher Level Answers
 0 Leavin Certificate Applied Maths Hiher Level Answers ) (a) (b) (i) r (ii) d (iii) m ) (a) 0 m s - 9 N of E ) (b) (i) km h - 0 S of E (ii) (iii) 90 km ) (a) (i) 0 6 (ii) h 0h s s ) (a) (i) 8 m N (ii)
0 Leavin Certificate Applied Maths Hiher Level Answers ) (a) (b) (i) r (ii) d (iii) m ) (a) 0 m s - 9 N of E ) (b) (i) km h - 0 S of E (ii) (iii) 90 km ) (a) (i) 0 6 (ii) h 0h s s ) (a) (i) 8 m N (ii)
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Potential Dividers. 46 minutes. 46 marks. Page 1 of 11
 Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Potential Dividers 46 minutes 46 marks Page 1 of 11 Q1. In the circuit shown in the figure below, the battery, of negligible internal resistance, has an emf of 30 V. The pd across the lamp is 6.0 V and
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Solutions to the Schrodinger equation atomic orbitals. Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz
 Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Review Test 3. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Boundary-Layer Flow over a Flat Plate Approximate Method
 Bounar-aer lo oer a lat Plate Approimate Metho Transition Turbulent aminar The momentum balance on a control olume o the bounar laer leas to the olloing equation: + () The approimate metho o bounar laer
Bounar-aer lo oer a lat Plate Approimate Metho Transition Turbulent aminar The momentum balance on a control olume o the bounar laer leas to the olloing equation: + () The approimate metho o bounar laer
Μετασχηματισμοί Laplace. Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Πανεπιστήμιο Θεσσαλίας
 ιαφορικές Εξισώσεις Μετασχηματισμοί Laplace Μανόλης Βάβαλης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Πανεπιστήμιο Θεσσαλίας Βόλος, 11 Μαΐου 2015 Περιεχόμενα Μετασχηματισμοί Laplace Ορισμός μετασχηματισμού
ιαφορικές Εξισώσεις Μετασχηματισμοί Laplace Μανόλης Βάβαλης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Πανεπιστήμιο Θεσσαλίας Βόλος, 11 Μαΐου 2015 Περιεχόμενα Μετασχηματισμοί Laplace Ορισμός μετασχηματισμού
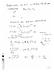 Prblma dl smipian Cas i cs ω µ Cas sin cs i cs Cas fas [ ] [ ] ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ttal S S J L J J L A d I I A d I d I V d d V V d d V n J n J ˆ 0 ˆ ˆ ˆ 0 ˆ 0 ˆ ˆ ˆ 0 S S S S i i
Prblma dl smipian Cas i cs ω µ Cas sin cs i cs Cas fas [ ] [ ] ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ttal S S J L J J L A d I I A d I d I V d d V V d d V n J n J ˆ 0 ˆ ˆ ˆ 0 ˆ 0 ˆ ˆ ˆ 0 S S S S i i
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
AΝΕΜΟΓΕΝΕΙΣ ΚΥΜΑΤΙΣΜΟΙ
 ΝΕΜΟΓΕΝΕΙΣ ΚΥΜΑΤΙΣΜΟΙ ΓΕΝΕΣΗ ΑΝΕΜΟΓΕΝΩΝ ΚΥΜΑΤΙΣΜΩΝ: Μεταφορά ενέργειας από τα κινούμενα κατώτερα ατμοσφαιρικά στρώματα στις επιφανειακές θαλάσσιες μάζες. η ενέργεια αρχικά περνά από την ατμόσφαιρα στην
ΝΕΜΟΓΕΝΕΙΣ ΚΥΜΑΤΙΣΜΟΙ ΓΕΝΕΣΗ ΑΝΕΜΟΓΕΝΩΝ ΚΥΜΑΤΙΣΜΩΝ: Μεταφορά ενέργειας από τα κινούμενα κατώτερα ατμοσφαιρικά στρώματα στις επιφανειακές θαλάσσιες μάζες. η ενέργεια αρχικά περνά από την ατμόσφαιρα στην
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 5. Exercise Solutions. Microelectronics: Circuit Analysis and Design, 4 th edition Chapter 5 EX5.1 = 1 I. = βi EX EX5.3 = = I V EX5.
 Microelectronics: ircuit nalysis and Design, 4 th edition hapter 5 y D.. Neamen xercise Solutions xercise Solutions X5. ( β ).0 β 4. β 40. 0.0085 hapter 5 β 40. α 0.999 β 4..0 0.0085.95 X5. O 00 O n 3
Microelectronics: ircuit nalysis and Design, 4 th edition hapter 5 y D.. Neamen xercise Solutions xercise Solutions X5. ( β ).0 β 4. β 40. 0.0085 hapter 5 β 40. α 0.999 β 4..0 0.0085.95 X5. O 00 O n 3
Differentiation exercise show differential equation
 Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
ΤΡΟΠΟΣ ΑΡΙΘΜΗΤΙΚΗ ΠΑΡΕΜΒΟΛΗ (INTERPOL ATION)
 . 1 (INTERPOLATION) A a 1x1 [ ] Sin[ A] [ Sin[ a]], Cos[ A] [ Cos[ a]], Tan[ A] [ Tan[ a]], Cot[ A] [ Cot[ a]]. a x + yi x, y R Sin[ a] Cosh[ y] Sin[ x] + Cos[ x] Sinh[ y] i Cos[ a] Cos[ x] Cosh[ y] Sin[
. 1 (INTERPOLATION) A a 1x1 [ ] Sin[ A] [ Sin[ a]], Cos[ A] [ Cos[ a]], Tan[ A] [ Tan[ a]], Cot[ A] [ Cot[ a]]. a x + yi x, y R Sin[ a] Cosh[ y] Sin[ x] + Cos[ x] Sinh[ y] i Cos[ a] Cos[ x] Cosh[ y] Sin[
ΕΝΙΣΧΥΣΗ ΠΛΑΚΩΝ ΚΑΙ ΔΟΚΩΝ ΣΕ ΚΑΜΨΗ ΜΕ ΜΑΝΔΥΕΣ Η ΕΛΑΣΜΑΤΑ ΣΥΝΘΕΤΩΝ ΥΛΙΚΩΝ.
 ΕΝΙΣΧΥΣΗ ΠΛΑΚΩΝ ΚΑΙ ΔΟΚΩΝ ΣΕ ΚΑΜΨΗ ΜΕ ΜΑΝΔΥΕΣ Η ΕΛΑΣΜΑΤΑ ΣΥΝΘΕΤΩΝ ΥΛΙΚΩΝ. Σύμφωνα με τον Κανονιμό Επεμβάεων, ο νέος οπλιμός υπολοίζεται έτι ώτε ε υνεραία με τον υφιτάμενο παλαιό οπλιμό να αναλαμβάνονται
ΕΝΙΣΧΥΣΗ ΠΛΑΚΩΝ ΚΑΙ ΔΟΚΩΝ ΣΕ ΚΑΜΨΗ ΜΕ ΜΑΝΔΥΕΣ Η ΕΛΑΣΜΑΤΑ ΣΥΝΘΕΤΩΝ ΥΛΙΚΩΝ. Σύμφωνα με τον Κανονιμό Επεμβάεων, ο νέος οπλιμός υπολοίζεται έτι ώτε ε υνεραία με τον υφιτάμενο παλαιό οπλιμό να αναλαμβάνονται
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
