Κοχλίες - 2 / / 34 - Παπαδόπουλος Α. Χρήστος

Transcript

1 ΚΕΦΑΛΑΙΟ 7 ΚΟΧΛΙΕΣ

2 Κοχλίες - / / 4 - Παπαδόπουλος Α. Χρήστος

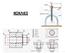
3 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ 7 Κοχλίες Οι κοχλίες διακρίνονται σε δυό κατηγορίες ως προς την αποστολή τους: τους κοχλίες συνδέσεως και τους κοχλίες κινήσεως. Οι κοχλίες συνδέσεως έχουν ως αποστολή την ασφαλή και λυόμενη (μή μόνιμη) σύνδεση, ανεξάρτητων στοιχείων μιας κατασκευής ή μηχανής μεταξύ τους. Οι κοχλίες κινήσεως μετατρέπουν την περιστροφική κίνηση του κορμού τους σε ευθύγραμμη κίνηση του περικοχλίου τους (π.χ. τόρνος, ανυψωτήρας αυτοκινήτων κλπ). 7.1 Είδη και τυποποίηση κοχλιών Ένας τυπικός κοχλίας διαμέτρου d, εξαγωνικής κεφαλής φαίνεται στο Σχήμα 7-1. Οι χαρακτηριστικές διάμετροι του κοχλία είναι: η διάμετρος d του κορμού, βάσει της οποίας τυποποιείται ο κοχλίας, η εξωτερική διάμετρος d 1 του σπειρώματος που είναι συνήθως ίση με τη d, η εσωτερική διάμετρος d του σπειρώματος που αντιστοιχεί στη μικρότερη καταπονούμενη επιφάνεια του κοχλία. Υπάρχουν κοχλίες όπου η διάμετρος του κορμού είναι ίση με την εσωτερική διάμετρο του σπειρώματος d d. Κεφαλή κοχλία Μήκος σπειρώματος dd 1 d Ονομαστικό μήκος κοχλία Περικόχλιο Σχήμα 7-1: Βασικά τμήματα κοχλία-περικοχλίου Τρία είδη κοχλιών μπορούμε να διακρίνουμε ανάλογα με τη μορφή και τη χρήση τους: (α) το σύστημα κοχλία-περικοχλίου (bolt-nut), που χρησιμοποιείται για να συνδέσει δύο ή περισσότερα αναξάρτητα στοιχεία, περνώντας τον κοχλία από τις αντίστοιχες οπές και βιδώνοντας το περικόχλιο. (β) τον βιδωτό κοχλία (screw), δηλαδή αυτόν που βιδώνεται σε τρύπα με σπείρωμα αντί του περικοχλίου, για να δημιουργήσει τη σύνδεση, και τέλος (γ) τον ακέφαλο κοχλία με σπείρωμα και στις δυο άκρες, όχι συμμετρικοί κατ ανάγκη. Σχήμα 7-: Ακέφαλοι κοχλίες Στοιχεία Μηχανών Ι - / 4

4 Κοχλίες - 4 / Σπειρώματα Η αρχή λειτουργίας του κοχλία είναι η μετατροπή της περιστροφικής κίνησης σε ευθύγραμμη, και στηρίζεται στην ύπαρξη του σπειρώματος. Το σπείρωμα λειτουργεί σαν κεκλιμένο επίπεδο γύρω από τον κορμό του κοχλία. Μπορεί να έχει μια, δυο ή τρεις αρχές (Σχήμα 7-). Με μια πλήρη περιστροφή του, πd, ο κοχλίας προχωρεί κατά L, όπου L για απλή αρχή, L για διπλή αρχή και L για τριπλή αρχή. H γωνία κλίσης του tan a L/ π d. σπειρώματος α βρίσκεται από τη σχέση: ( ) Μονή αρχή Διπλή αρχή Τριπλή αρχή α πd L L L L L L L Σχήμα 7-: Σπειρώματα με μονή, διπλή και τριπλή αρχή Τα σπειρώματα διακρίνονται σε Μετρικά (Μ) κανονικά ή λεπτά, Τραπεζοειδή (Tr), Πριονωτά (S), Τετραγωνικά, Στρογγυλά (R d ). περικόχλιο H H H Η 60 o h H 8 D 1 H 4 D 1 κοχλίας H 6 D P H P h 0.614P H H r P 6 r d d d Σχήμα 7-4: Γεωμετρία μετρικού σπειρώματος - 4 / 4 - Παπαδόπουλος Α. Χρήστος

5 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΥΠΟΣ Πίνακας 7-1: Τυποποίηση κοχλιών κανονικών μετρικών σπειρωμάτων Βήμα σπειρώματος, P Κυρία διάμετρος, d D Μέση διάμετρος, d D Εσωτερική διάμετρος κοχλία, d Εσωτερική διάμετρος περικοχλίου, D 1 Βάθος σπειρώματος, h Φορτιζόμενη επιφάνεια, A, mm M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M M Η καταπονούμενη επιφάνεια του κοχλία είναι d d A π + 4 αν η φόρτιση είναι στατική, και A π d αν είναι δυναμική 4 Στοιχεία Μηχανών Ι - 5 / 4

6 Κοχλίες - 6 / 4 - Πίνακας 7-: Τυποποίηση κοχλιών λεπτών μετρικών σπειρωμάτων - 6 / 4 - Παπαδόπουλος Α. Χρήστος

7 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Πίνακας 7-: Τυποποίηση κοχλιών Whitworth Στοιχεία Μηχανών Ι - 7 / 4

8 Κοχλίες - 8 / 4 - Πίνακας 7-4: Τυποποίηση κοχλιών τραπεζοειδών σπειρωμάτων - 8 / 4 - Παπαδόπουλος Α. Χρήστος

9 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Πίνακας 7-5: Τυποποίηση κοχλιών τραπεζοειδών σπειρωμάτων (συνέχεια) Στοιχεία Μηχανών Ι - 9 / 4

10 Κοχλίες - 10 / 4 - Πίνακας 7-6: Τυποποίηση κοχλιών στρογγυλών σπειρωμάτων - 10 / 4 - Παπαδόπουλος Α. Χρήστος

11 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Πίνακας 7-7: Τυποποίηση κοχλιών στρογγυλών σπειρωμάτων (συνέχεια) Στοιχεία Μηχανών Ι - 11 / 4

12 Κοχλίες - 1 / 4 - Πίνακας 7-8: Τυποποίηση κοχλιών στρογγυλών σπειρωμάτων (συνέχεια) - 1 / 4 - Παπαδόπουλος Α. Χρήστος

13 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Πίνακας 7-9: Τυποποίηση κοχλιών πριονωτών σπειρωμάτων Στοιχεία Μηχανών Ι - 1 / 4

14 Κοχλίες - 14 / 4-7. Κατηγορίες υλικών κοχλιών Οι χαλύβδινοι κοχλίες κατατάσσονται σε κατηγορίες ως προς την αντοχή τους. Το σύμβολο της κατηγορίας αντοχής των κοχλιών αποτελείται από δύο ψηφία, x και y, χωρισμένα με τελεία (x.y). Το πρώτο ψηφίο μας δίνει, αν πολλαπλασιαστεί με το 100, το όριο θραύσης του υλικού των κοχλιών σε MPa. Το δεύτερο ψηφίο μας δίνει το όριο διαρροής ως ποσοστό του ορίου θραύσης. Για παράδειγμα: κατηγορία (x.y) (4.8) σημαίνει: S u x*100 4* MPa, και S y (y*10)%*s u (8*10)% *400 0 MPa. Πίνακας 7-10: Μηχανικές ιδιότητες χαλύβδινων κοχλιών μετρικών σπειρωμάτων (DIN- ISO_898_art_1) ΚΑΤΗΓΟΡΙΑ ΚΟΧΛΙΑ S u S y S y0. δ u ΚΑΤΗΓΟΡΙΑ S u (% επιμήκυνση ΠΕΡΙ- (MPa) (MPa) (MPa) μετά τη θραύση) ΚΟΧΛΙΟΥ (MPa) Οι συντελεστές τριβής στους κοχλίες εξαρτώνται από την ποιότητα των επιφανειών και κατεργασίας και την λίπανση ή όχι των σπειρωμάτων. Πίνακας 7-11: Συντελεστές τριβής κοχλιών ΥΛΙΚΟ ΛΙΠΑΝΣΗ ΚΟΧΛΙΑ ΠΕΡΙΚΟΧΛΙΟΥ ΕΠΙΦΑΝΕΙΑΚΗ ΕΠΕΞΕΡΓΑΣΙΑ ΧΩΡΙΣ ΛΙΠΑΝΣΗ ΛΙΠΑΝΣΗ ΜΕ ΛΑΔΙ ΣΚΟΝΗ ΜοS Mn - Ph ΧΩΡΙΣ 0.14 έως έως έως 0.11 Zn - Ph ΧΩΡΙΣ 0.14 έως έως έως 0.1 Zn ΧΩΡΙΣ 0.15 έως έως Cd ΧΩΡΙΣ 0.08 έως έως Zn Zn 0.15 έως έως Cd Cd 0.08 έως έως / 4 - Παπαδόπουλος Α. Χρήστος

15 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ 7. Ανάλυση δυνάμεων στους κοχλίες 7..1 Ροπή σύσφιγξης σε κοχλίες Είναι χρήσιμο να συσχετίσουμε την δύναμη σύσφιγξης F u ενός περικοχλίου στον κοχλία του, με την αναπτυσσόμενη εφελκυστική δύναμη στο σώμα του κοχλία F, η οποία αναπτύσσεται λόγω της σύσφιγξης. Στο Σχήμα 7-5, μια σπείρα κοχλία αναπτύσσεται σε ορθογώνιο τρίγωνο με γωνία κεκλιμένου επιπέδου, α. Το κινούμενο πάνω της σώμα είναι το περικόχλιο πάνω στο οποίο σχεδιάζονται οι ασκούμενες δυνάμεις. (a) (β) Σχήμα 7-5: Στατική του κοχλία-περικοχλίου με τριβή κατά την σύσφιγξη κaι αποσύσφιγξη Δείχνονται εκτός των δύο προαναφερθεισών δυνάμεων και η αντίδραση Ν του κεκλιμένου σπειρώματος και η δύναμη τριβής F τ μν, όπου μ είναι ο συντελεστής τριβής μεταξύ των σπειρωμάτων κοχλία-περικοχλίου. Οι δυνάμεις σύσφιγξης και τριβής αλλάζουν φορά κατά την αποσύσφιγξη. Η ισορροπία των δυνάμεων μας δίνει για την σύσφιγξη (Σχήμα 7-5(α)), Fx Fu N sin a Fτ cosa 0 Fu N( μcosa + F y F + N cosa F τ sin a) sin a 0 F N (cos a μsin a) ενώ κατά την αποσύσφιγξη, Σχήμα 7-5(α), έχουμε: F x F y F u N sin a + F τ cosa 0 F u N ( μcosa sin a) F + N cosa + Fτ sin a 0 F N (cosa + μsin a) Αν διαιρέσουμε τις παραπάνω εξισώσεις κατά μέλη, θεωρώντας ότι ο συντελεστής τριβής αντιστοιχεί σε επιπρόσθετη γωνία ρ του κεκλιμένου επιπέδου όπου tanρ μ, μcosa ± sin a tan ρ ± tan a F u F F F tan( ρ ± α) cosa μsin a 1 tan ρ tan a όπου το άνω πρόσημο αναφέρεται στην σύσφιγξη και το κάτω πρόσημο στην αποσύσφιγξη. Η απαιτούμενη ροπή σύσφιγξης Μ σ και αποσύσφιγξης Μ α υπολογίζονται από την ανωτέρω δύναμη επί την απόσταση στην οποία αυτή εφαρμόζεται: M d F tan( ρ α) και σ + M α d F tan( ρ α) Στοιχεία Μηχανών Ι - 15 / 4

16 Κοχλίες - 16 / 4 - (α) Παραλληλεπίπεδο δυνάμεων (β) αξονική τομή Σχήμα 7-6: Η αντίδραση στο σπείρωμα λόγω της κλίσης α και θ β / του σπειρώματος Η ανάλυση που παρατέθηκε πιο πάνω ισχύει για τετραγωνικά σπειρώματα. Στην γενική περίπτωση το σπείρωμα έχει κλίση και ως προς το άλλο επίπεδο πχ τραπεζοειδές σπείρωμα, ή κανονικό μετρικό. Στο πιο πάνω σχήμα έχει σχεδιαστεί η αντίδραση του κεκλιμένου επιπέδου η Ν ΟD. Η προβολή της στο επίπεδο ΟΑC είναι η Ν cosθ n ΟC. Η δύναμη αυτή στο επόμενο σχήμα χρησιμοποιείται στην ισορροπία δυνάμεων. F F x y F u N cos θ sin a μn cos a 0 F N (cos θ sin a + μ cos a) F + N cos θ n n cos a μn sin a 0 F N (cos θ u n n cos a μ sin a) διαιρούμε κατά μέλη και αφού αντικαταστήσουμε μ tan ρ και όπου λαμβάνουμε, tan ρ tan ρ cos tan ρ + tan a Fu cosθnsin a+ μcos a cosθn tan a+ tan ρ cosθn tan ρ + tan a tan + F cosθ cos sin cos tan tan tan n a μ a θn ρ a ρ 1 tana 1 tan ρ tan a cosθ n θ n ( ρ α ) Σχήμα 7-7: Iσορροπία δυνάμεων λόγω της κλίσης α και θ β / του σπειρώματος - 16 / 4 - Παπαδόπουλος Α. Χρήστος

17 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Η σχέση των γωνιών όπως προκύπτουν από το σχήμα είναι: CD AB AB OA tanθ n tanθ cosa OC OC OA OC όπου θ β / είναι η γωνία του σπειρώματος και θ n η γωνία μεταξύ της καθέτου αντίδρασης στο κεκλιμένο κατά α και θ/ σπείρωμα σχετικά με το επίπεδο του εξεταζόμενου κεκλιμένου επιπέδου. Αρα η ροπή σύσφιγξης του κοχλία μπορεί να υπολογιστεί από την σχέση, d d M F tan ( ρ ± ) u F a Αν λάβουμε υπ' όψη μας και την τριβή μεταξύ περικοχλίου και ελάσματος, με μ π τον συντελεστή τριβής, και dm ( d1 + d π )/, όπου d π η διάμετρος του περικοχλίου, τότε η συνολική ροπή σύσφιγξης θα είναι, M ολ tan d d F m π ( ρ ± a) + μ 7.. Απόδοση κοχλιών Σαν απόδοση ενός συστήματος κοχλία περικόχλιου ορίζεται το πηλίκο της απαιτούμενης ροπής, για την σύσφιγξη ή την αποσύσφιγξη, όταν αγνοήσουμε την τριβή, πρός την απαιτούμενη ροπή όταν λάβουμε υπ' όψιν την τριβή. Ετσι οι αποδόσεις για την σύσφιγξη ή την αποσύσφιγξη δίνονται αντίστοιχα από τις σχέσεις, ΡΟΠΗ ΧΩΡΙΣ ΤΡΙΒΗ η ΡΟΠΗ ΜΕ ΤΡΙΒΗ η σ η a tan α tan cosθ + μ tan α ( α + ρ ) cosθ μcot α tan α tan cosθ ( α ρ ) cosθ μcot α n n n n + μ tan α 7.. Ευστάθεια κοχλιών Αν για την αποσύσφιγξη χρειάζεται ροπή θετική, δηλαδή τότε ο κοχλίας είναι ευσταθής (ασφαλής ως προς την αποσύσφιγξη). Μ α > 0 ή tan(ρ α) > 0 ή tan ρ tan α > 0 ή μ > tan α Αν δεν λάβουμε υπ όψη μας την γωνία κλίσης του σπειρώματος β /, και tan ρ tan a d tan ρ tan a cosθ μ tan > 1+ tan ρ tan a tan ρ cosθ 1+ tan a n cosθ n ( ρ ± a) > 0 > 0 > 0 tan a αν την λάβουμε. Η σχέση αυτή μας λέει ότι το σύστημα κοχλία-περικοχλίου είναι ασφαλές ως προς αποσύσφιγξη εφ όσον ο συντελεστής τριβής μ ή ο μ/cosθ n είναι μεγαλύτερος από την εφαπτομένη της γωνίας του σπειρώματος. n Στοιχεία Μηχανών Ι - 17 / 4

18 Κοχλίες - 18 / Κοχλίες υπό πρόταση σε στατική φόρτιση Πρόταση κοχλιών Η τιμή της πρότασης κατά Niemann είναι 1.5 φορές το στατικό φορτίο ή έως.5 φορές το δυναμικό. Μια προσεγγιστική, βασισμένη σε πειράματα, σχέση για την εκτίμηση της μέγιστης πρότασης σε ένα κοχλία διαμέτρου d cm, είναι, F i 840d k και η απαιτούμενη ροπή σύσφιγξης Μ i, M i CdF i kcm όπου C 0. για σπείρωμα χωρίς λιπαντικό C 0.18 για σπείρωμα με λιπαντικό Κοχλίες υπό πρόταση Στατική φόρτιση Ας υποθέσουμε ότι ένας κοχλίας που συνδέει δύο φλάντζες έχει υποστεί αρχική πρόταση F i. Θεωρώντας ότι ο κοχλίας δέχεται δυνάμεις ώστε να λειτουργεί στην ελαστική περιοχή σχεδιάζουμε στο Σχήμα 7-8, το διάγραμμα δύναμης παραμόρφωσης του κοχλία (αριστερά) και της φλάντζας (δεξιά). Μετά την επιβολή της πρότασης F i ο κοχλίας έχει υποστεί μια αρχική επιμήκυνση δ ib, ενώ οι συμπιεζόμενες φλάντζες μια αρχική βράχυνση δ i. Αν k b και k οι σταθερές ελατηρίου του κοχλία και των φλαντζών αντίστοιχα, τότε η πρόταση μπορεί να εκφραστεί με τις σχέσεις: F F δ, i k b i k ib δ, i Ab Eb k b L b AE k L όπου k b και k οι σταθερές ελατηρίου του κοχλία και των φλαντζών αντίστοιχα, Α b και A οι καταπονούμενες επιφάνειες κοχλία και φλαντζών αντίστοιχα, E b και E τα αντίστοιχα μέτρα ελαστικότητας και L b και L τα μήκη του εφελκυόμενου τμήματος του κοχλία και του συμπιεζόμενου πάχους των φλαντζών. Έστω τώρα ότι εφαρμόζουμε στις φλάντζες κάποιο εξωτερικό φορτίο λειτουργίας F e. Τότε ο κοχλίας θα υποστεί επιπρόσθετη επιμήκυνση κατά δ eb ενώ οι φλάντζες θα υποστούν μείωση της αρχικής τους συμπίεσης κατά δ e. Εφόσον δεν υπάρχει απομάκρυνση των φλαντζών, οι δύο μεταβολές μήκους πρέπει να είναι ίσες. Επομένως ένα μέρος της δύναμης λειτουργίας F e, η δύναμη F eb, επιμηκύνει τον κοχλία και το υπόλοιπο F e μειώνει την συμπίεση των φλαντζών / 4 - Παπαδόπουλος Α. Χρήστος

19 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ F Fb Feb Fi Feb Fe Fe Fi Fe F θb δib ΕΠΙΜΗΚΥΝΣΗ ΚΟΧΛΙΑ δeb δ δ δi ΒΡΑΧΥΝΣΗ ΦΛΑΝΤΖΑΣ θ δe Σχήμα 7-8: Διάγραμμα πρότασης σε σύστημα κοχλία-φλάντζας F e F eb + F e (α) Επίσης η επιμήκυνση του κοχλία και η βράχυνση των φλαντζών είναι ίσες, εφ όσον δεν υπάρχει αποκόλληση των φλαντζών. δ eb δ e ή F eb e (β) οπότε από τις (α) και (β) έχουμε: k F F C F k b eb e b e kb + k k F F C F C F b F k ( 1 ) e e e b e kb + k Όπως φαίνεται και από το σχήμα οι δυνάμεις που καταπονούν κοχλία και φλάντζες, όταν υπάρχει πρόταση είναι αντίστοιχα: F b F eb + F i F F i - F e Στοιχεία Μηχανών Ι - 19 / 4

20 Κοχλίες - 0 / Κοχλίες υπό πρόταση σε δυναμική φόρτιση Aν το φορτίο λειτουργίας F e είναι μεταβαλλόμενο τότε έχει μέγιστη και ελάχιστη τιμή. Ο κοχλίας θα παραλαμβάνει φορτίο από F i μέχρι F i + F eb. οπότε το μέγιστο και ελάχιστο φορτίο λειτουργίας του κοχλία θα είναι: F b (max) F eb + F i και F b (min) F i Άρα η μέση τιμή του μεταβαλλόμενου φορτίου του κοχλία, καθώς και το εύρος εναλλαγής θα είναι: F b (m) F eb / + F i και F b (r) F eb / Δύναμη, kn Σχήμα 7-9:Δυναμική φόρτιση κοχλιών υπό πρόταση H μέση τιμή της τάσης και το εύρος εναλλαγής της θα είναι: F b m m A ( ) σ και F σ r A και από την γνωστή σχέση του Soderberg, η ισοδύναμη στατική καταπόνηση θα είναι S σ σ σ y eq m + r Se Sy N ( ) br Αντίστοιχες σχέσεις ισχύουν και για τις φλάντζες. Όταν μεταξύ των συσφιγγομένων φλαντζών υπάρχει κάποιο παρέμβυσμα (ελατήρια σε σειρά), τότε η σταθερά ελατηρίου της φλάντζας υπολογίζεται από την σχέση k k k k 1 g - 0 / 4 - Παπαδόπουλος Α. Χρήστος

21 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ όπου k και k 1 οι σταθερές ελατηρίου των δύο φλαντζών. Προφανώς όταν το υλικό του παρεμβύσματος είναι κατά πολύ μαλακότερο από το υλικό των φλαντζών τότε ισχύει, k k g Σχήμα 7-10: Περαστοί κοχλίες με παρεμβύσματα Συντελεστές συγκέντρωσης τάσεων k f Οταν ένας κοχλίας υπόκειται σε δυναμική καταπόνηση, πρέπει να υπολογίζεται λαμβάνοντας υπ' όψη τον συντελεστή συγκέντρωσης τάσεων. Τα κρίσιμα σημεία για αστοχία είναι (α) το σημείο αλλαγής της διαμέτρου κάτω από την κεφαλή του κοχλία, (β) το σημείο αρχής του σπειρώματος, και (γ) κατά μήκος του σπειρώματος μέσα στο περικόχλιο. ΥΛΙΚΟ Χυτοχάλυβας Μεγαλύτερες τιμές λαμβάνονται για διάμετρο κοχλία μεγαλύτερη από 5 mm. 7.6 Τάσεις κοχλιών Για τον προσδιορισμό της διαμέτρου του κοχλία μιας κοχλιωτής σύνδεσης πρέπει να ληφθούν υπ' όψη τόσο τα στατικά όσο και τα δυναμικά φορτία. Κατά την σύσφιγξη ενός κοχλία παρουσιάζονται οι ακόλουθες τάσεις: (α) εφελκυστική τάση στον κορμό του κοχλία, (β) στρεπτική τάση στον κορμό λόγω της αντίστασης της τριβής κατά την σύσφιγξη του κοχλία, (γ) διατμητική τάση στο σπείρωμα, (δ) επιφανειακή τάση στο σπείρωμα, (ε) καμπτική τάση Στοιχεία Μηχανών Ι - 1 / 4

22 Κοχλίες - / 4 - Σχήμα 7-11: Διάγραμμα διαρκούς δυναμικής αντοχής S e για χαλύβδινους κοχλίες διαφόρων κατηγοριών στο σπείρωμα, και (στ) καμπτική τάση στον κοχλία αν η κεφαλή του κοχλία και το περικόχλιο δεν είναι ακριβώς κάθετα στον άξονα του κοχλία Εφελκυστική τάση στον κορμό του κοχλία H μέση εφελκυστική τάση σε ένα κοχλία με πρόταση F i, είναι Fi σ A s όπου η διατομή Α s είναι στατικά. π d A s 4, για δυναμικά φορτία και π dm A s όπου 4 d + d d m, για 7.6. Καμπτική τάση στον κορμό του κοχλία Αν οι εξωτερικές επιφάνειες των συνδεομένων μερών δεν είναι παράλληλες μεταξύ τους, τότε ο κοχλίας θα υποστεί καμπτική καταπόνηση. Η καμπτική τάση μπορεί να υπολογιστεί από την σχέση, δε σ L - / 4 - Παπαδόπουλος Α. Χρήστος

23 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ όπου L είναι το ενεργό μήκος του κοχλία, E το μέτρο ελαστικότητας του υλικού του κοχλία και δ η μέγιστη απόσταση μεταξύ των γωνιών του κοχλία στην διεύθυνση του άξονα Διατμητική τάση κοχλία λόγω στρέψης Η διατμητική τάση στον κορμό του κοχλία λόγω της στρεπτικής ροπής που απαιτείται για την σύσφιγξη του μπορεί να υπολογιστεί από την σχέση 16M τ π d Σύνθετη καταπόνηση Στην περίπτωση κατά την οποία θα έχουμε συνδυασμό ορθών (σ ολ ) και διατμητικών (τ ολ ) τάσεων σε μονοαξονική καταπόνηση, η ισοδύναμη (σ eq ) υπολογίζεται με την βοήθεια του κριτήριου της Μέγιστης Διατμητικής Τάσης (ΜΔΤ) ή της Θεωρίας Έργου Παραμόρφωσης (ΘΕΠ). S y σeq σολ + ατολ N όπου α για ΘΕΠ και α 4 για ΜΔΤ Διατμητική τάση σπειρώματος Η μέση διατμητική τάση στο σπείρωμα του κοχλία είναι F i τ κ π dnb όπου d η εσωτερική διάμετρος του σπειρώματος του κοχλία, n ο αριθμός των σπειρών που συνεργάζονται και b το ύψος της σπείρας στην εσωτερική διάμετρο. Επίσης η μέση διατμητική τάση στο σπείρωμα του περικοχλίου είναι, F i τ π π dnb Επιφανειακή τάση σπειρώματος Κατά τη φόρτιση ενός ζεύγους κοχλία-περικοχλίου, οι σπείρες του περικοχλίου παραλαμβάνουν τη δύναμη από τις σπείρες του κοχλία. Αν το περικόχλιο αποτελείται από n σπείρες, και έχει ύψος h π τότε επειδή το βήμα του σπειρώματος είναι P, θα ισχύει: h π n P. Επίσης η επιφάνεια του σπειρώματος που θα παραλαμβάνει τη δύναμη θα είναι: Α σ n (πd Η 1 ) όπου Η 1 το ύψος του σπειρώματος και επομένως Α σ h π (πd Η 1 ) / P Τα σπειρώματα καταπονούνται σε επιφανειακή πίεση σ b. Ο Πίνακας 7-1, περιλαμβάνει τις επιτρεπόμενες επιφανειακές πιέσεις για διάφορους συνδυασμούς υλικών σπειρωμάτων (σ b ) επ. Τότε: F F Sb σb ( σb) A h π d H / P N επ σ π ( ) 1 Από την τελευταία σχέση μπορούμε να υπολογίσουμε το απαραίτητο ύψος του περικοχλίου h π. Στοιχεία Μηχανών Ι - / 4

24 Κοχλίες - 4 / 4 - h π F ( σ ) ( dh) b π επ 1 / P Πίνακας 7-1: Επιτρεπόμενη επιφανειακή πίεση σπειρωμάτων κοχλιών-περικοχλίων KΟΧΛΙΑΣ - ΠΕΡΙΚΟΧΛΙΟ Επιτρεπόμενη επιφανειακή πίεση σ επ, (MPa) ΤΑΧΥΤΗΤΑ Χάλυβας-Χυτοσίδηρος 10 έως 170 Χαμηλή Χάλυβας-Μπρούντζος 105 έως 170 Χαμηλή Χάλυβας-Μπρούντζος 10 έως 16 Υψηλή Χάλυβας-Χυτοσίδηρος 40 έως 70 Μέτρια Χάλυβας-Μπρούντζος 50 έως 95 Μέτρια Καμπτική τάση σπειρώματος Fh i σ π d nb όπου d ( d d ) m m +, h το ύψος του δοντιού, n ο αριθμός των σπειρών μέσα στο περικόχλιο 1 και b το πλάτος του δοντιού. - 4 / 4 - Παπαδόπουλος Α. Χρήστος

25 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ 7.7 Λυμένες ασκήσεις κοχλιών ΑΣΚΗΣΗ Ενας κοχλίας μετρικού σπειρώματος Μ16, συνδέει δύο τμήματα πάχους 40 mm έκαστο, και του ιδίου υλικού μιας κατασκευής, που υφίστανται μια μεταβαλλόμενη δύναμη F e από 5 kn έως 40 kn. Ο κοχλίας και η φλάντζα είναι από το ίδιο υλικό, με S y 500 MPa και S e 0 MPa. Έστω συντελεστής συγκέντρωσης τάσης στο σπείρωμα.8. α) Είναι ασφαλής ο κοχλίας για συνεχή λειτουργία; β) Αν εφαρμόσουμε πρόταση 50 kn, είναι ασφαλής για συνεχή λειτουργία; γ) Το ίδιο αν η εφαρμοζόμενη πρόταση είναι 80 kn. F e M16 F e F e F e Σχήμα 7-1: Περαστός κοχλίας υπό πρόταση με εξωτερικό φορτίο ΛΥΣΗ: (α) Ο Πίνακας 7-1, μας δίνει για κοχλία μετρικού σπειρώματος Μ16: P mm, d 16 mm, d mm, d mm, D mm, h 1.7 mm, A 157 mm. Η εξωτερικά εφαρμοζόμενη δύναμη έχει μέση τιμή και εύρος εναλλαγής: F e ( m ).5 kn και F e ( ) 17.5kN r Κατασκευάζουμε υπό κλίμακα ένα διάγραμμα δύναμης-επιμήκυνσης (Σχήμα 7-1) όπου φαίνεται η μέση δύναμη λειτουργίας και το εύρος εναλλαγής της. Η κλίση της καμπύλης δύναμης-επιμήκυνσης είναι η σταθερά ελατηρίου του κοχλία. 5 AE ( 157mm ) (.1 10 N/mm ) b b 5 kb N/mm b 40mm Oι επιμηκύνσεις του κοχλία που αντιστοιχούν σε 5 και 40 kn είναι: Fmin Fmax ( ) N δb 5 ( ) μm k N/mm b Στοιχεία Μηχανών Ι - 5 / 4

26 Κοχλίες - 6 / 4 - Σχήμα 7-1: Διάγραμμα δύναμης-επιμήκυνσης κοχλία χωρίς πρόταση Αντίστοιχα οι αναπτυσσόμενες τάσεις θα είναι: F e( m).5 10 N σ m 14.MPa A 157mm F e( r) N ktσ r kt MPa A 157mm Κατασκευάζουμε το διάγραμμα Soderberg και τοποθετούμε το σημείο (α) που αντιστοιχεί στην πρώτη εντατική κατάσταση (σ m, σ r ) (14., 4.5). Όπως φαίνεται από το Σχήμα 7-14, δεν έχουμε ασφαλή λειτουργία. σ r 400 (α) S e 0 MPa (b) (c) S y 500 MPa σ m Σχήμα 7-14: Συνδυασμοί δυναμικών φορτίσεων ασφαλούς λειτουργίας (b) και αστοχίας (a,c) κατά Soderberg β) Αν εφαρμόσουμε αρχική πρόταση F i 50 kn, τότε ο κοχλίας θα επιμηκυνθεί κατά Fi 50000N δ b 60.7μm 5 k N/mm b - 6 / 4 - Παπαδόπουλος Α. Χρήστος

27 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Ενώ τα συμπιεζόμενα ελάσματα θα βραχυνθούν κατά Fi 50000N δ 7.58μm 6 k N/mm Σχεδιάζουμε το Σχήμα Δύναμη, kn tanφk b 8.4x10 5 N/mm Fbmax Fe5 Σχήμα 7-15: Διάγραμμα δύναμης-επιμήκυνσης κοχλία με πρόταση 50kN Ως συμπιεζόμενη επιφάνεια της φλάντζας A, δεχόμαστε τον δακτύλιο με εξωτερική διάμετρο d και εσωτερική d. π ( ) A d d 9A A 8A, οπότε: 4 C b kb AE / 1 1 k + k AE/ + 8 AE/ b AE 8AE k, και επομένως τότε η εξωτερική δύναμη F e, μοιράζεται στο τμήμα που παραλαμβάνει ο κοχλίας F eb και η φλάντζα F e : F Οπότε 1 C F 5kN.89kN και 9 eb b e Feb Fb( ) + Fi kN kn και m kb 1 F ( ) b Fe( ) CbF r r e( r) kN k + k 9 b 8 Fe (1 Cb ) Fe 5kN 1.11kN N N σ b( m) 0.9MPa και σ b ( ) 47.MPa 157mm r 157mm Στοιχεία Μηχανών Ι - 7 / 4

28 Κοχλίες - 8 / 4 - Από το διάγραμμα Soderberg η εντατική κατάσταση (σ m, σ r ) (0.9, 47.) αντιστοιχεί στο σημείο (β) και φαίνεται ότι τώρα έχουμε ασφαλή λειτουργία. γ) Αν τώρα η πρόταση γίνει 80 kn, τότε: kN F b( ) kN m και F b( r) 9 Οπότε N N σ b ( m ) 5MPa και σ b ( ) 47.MPa 157mm r 157mm Η εντατική αυτή κατάσταση (σ m, σ r ) (5, 47.), παριστάνεται από το σημείο (c) στο διάγραμμα Soderberg. Η κατάσταση είναι εκτός της γραμμής ασφαλούς λειτουργίας. - 8 / 4 - Παπαδόπουλος Α. Χρήστος

29 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ 7.7. ΑΣΚΗΣΗ Σε μια κοχλιωτή σύνδεση οι κοχλίες Μ1 συνδέουν δύο φλάντζες ίδιου υλικού και ίδιου πάχους. Οι φλάντζες έχουν μέτρο ελαστικότητας E 160 GPa. Οι κοχλίες είναι κατηγορίας 8.8 με E b 10 GPa, και υφίστανται πρόταση 6 kn. Αν η εξωτερική δύναμη κυμαίνεται από 0-1 kn ανά κοχλία, ποιός ο συντελεστής ασφαλείας των κοχλιών; ΛΥΣΗ: Αφού οι κοχλίες είναι Μ1 και κατηγορίας 8.8, ο Πίνακας 7-1, ο Πίνακας 7-10 και το Σχήμα 7-11, δίνουν: d 1 1 mm, d mm, d 9.85 mm, d / R 6 d / H 47, A 84 mm, S y, MPa, και S e 9 MPa. Fe ( ) 6.5kN m Fe ( 0 1) kn Fe ( ) 6.5kN r Ο λόγος των σταθερών ελατηρίων, φλάντζας προς κοχλία είναι: k AE L A E kb L AbEb Ab Eb 1 10 kb 1 1 C k k b + k k b Fb( ) CFe( ) + Fi kn m m Fb( ) CFe( ) ( 0.141)( 6.5) 0.9 kn r r Fb ( m) σ m A 84mm σ r σ 84mm N 0MPa N 11MPa S y m + σr Se Sy N 1 σ m σ r N S S y e Αρα ο συντελεστής ασφαλείας των κοχλιών είναι N 1.6. Στοιχεία Μηχανών Ι - 9 / 4

30 Κοχλίες - 0 / ΑΣΚΗΣΗ Σε μια κοχλιωτή σύνδεση, κοχλίες Μ1 συνδέουν δύο φλάντζες διαφορετικού υλικού ( E 100GPa και E 160 GPa 1 ) αλλά του ίδιου πάχους. Οι κοχλίες είναι χαλύβδινοι κατηγορίας 8.8. Αν η εξωτερική δύναμη μεταβάλλεται από 0 μέχρι 1 kν, βρήτε την αναγκαία πρόταση F i, ώστε ο συντελεστής ασφάλειας των κοχλιών να είναι 1.6. ΛΥΣΗ: Ο Πίνακας 7-1, για κοχλία Μ1 δίνει τα ακόλουθα στοιχεία: P 1.75 mm, d 1 1 mm, d mm, d mm, A 84 mm. Επίσης Η 0.866P x mm και r Η / / mm. Για υλικό κατηγορίας 8.8 έχουμε (Πίνακας 7-10), S u 800 MPa, S y 640 MPa και από το Σχήμα 7-11, επειδή d / r 1 / , ευρίσκουμε για το όριο διαρκούς αντοχής S e 95 MPa. Το φορτίο του κοχλία είναι: ( ) ( ) F 0 1 kn 6.5± 6.5 kn ή F e(m) 6.5 kn, F e(r) 6.5 kn e H σταθερά ελατηρίου της φλάντζας είναι: k k k 1 A E k k k k k k k L k k 1 / / Ενώ του κοχλία: k b AE b b L AE 1 k L A E A E1 m k AE b b b Ab Eb AbEb 10 L 1 1 C m Οπότε, F eb(m) CF e(m) + F i ( F i ) kn ( F i ) kn F eb(r) CF e(r) ( ) kn kn Oι ορθές τάσεις είναι ( Fi ) 10 N σ m ( Fi ) MPa π / 4 mm N σ r 15MPa π 9.85 / 4 mm Aπό Soderberg έχουμε Sy Sy σ + σ ( F ) + 15 F 1.8 kn S N m r i i e Η ζητούμενη πρόταση είναι F i 1.8 kn. - 0 / 4 - Παπαδόπουλος Α. Χρήστος

31 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ Γραφική λύση: σ r 100 S e S e /N σ r S y /N S y σ m Σχήμα 7-16: Διάγραμμα Soderberg Γραφική λύση Σχεδιάζω το διάγραμμα του Soderberg. Φέρω την (S y, S e ) και την ( N, Se N ). Aπό σ r 15 MPa, παράλληλο στην σ m, μέχρις ότου τμήσει την ευθεία ασφαλούς λειτουργίας κατά Soderberg, και από εκεί κάθετο στην σ m. Τότε σ m 00MPa. Aλλά σ m F i, οπότε F i 1.9 kn. S y Στοιχεία Μηχανών Ι - 1 / 4

32 Κοχλίες - / ΑΣΚΗΣΗ Μικρή κοχλιωτή χειροπρέσα αποτελείται από τραπεζοειδή κοχλία και ορειχάλκινο περικόχλιο. Αν o τραπεζοειδής κοχλίας έχει διάμετρο d 0 Φ, είναι από υλικό με σ επ S y / N 10 / MPa, και ο συντελεστής τριβής χάλυβα ορείχαλκου είναι μ 0.15, να βρεθούν: α) Η μέγιστη θλιπτική δύναμη F που μπορεί να φέρει ο κοχλίας, με ασφάλεια και χωρίς να υποστεί λυγισμό. β) Το ύψος του περικοχλίου. γ) Οι ροπές σύσφιγξης και αποσύσφιγξης, αμελώντας την τριβή στο Α. 800 Σχήμα 7-17: Μικρή κοχλιωτή χειροπρέσα ΛΥΣΗ: α) Από την τυποποίηση των τραπεζοειδών σπειρωμάτων (Πίνακας 7-5), έχουμε για τον Tr 0 x 4: d 1 0, d 18, d 15.5, P 4, και H 1. Η επιφάνεια που αντιστοιχεί στην εσωτερική διάμετρο d είναι A πd /4 189 mm. Η θλιπτική τάση που αντιστοιχεί σε θλιπτική δύναμη F είναι: F F σ 0.005F N/mm A 189 ( ) o Η γωνία του σπειρώματος είναι 4 tan α P/ π d 4/ π Η επιπρόσθετη κλίση του κεκλιμένου επιπέδου που ισοδυναμεί με την επίδραση της τριβής o είναι: tan ρ μ 0.15 ή ρ 8.5. Εξ αιτίας της επίδρασης της γωνίας β 0 ο του τραπεζοειδούς σπειρώματος η γωνία ρ προκύπτει: tan ρ tan8.5 tan ρ ή cos cos 0 ( β ) ( ) α επειδή ( ) ( ) o ρ 8.8. Τότε η διατμητική τάση λόγω της στρεπτικής ροπής κατά τη σύσφιγξη (αγνοώντας την τριβή στο Α) θα είναι: - / 4 - Παπαδόπουλος Α. Χρήστος

33 ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ & ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ( ) tan( + ) F( 18 ) tan( ) M F d α ρ σ τ 0.008F N/mm J / r π d /16 π 15.5 /16 ( ) ( ) ( ) σ σ + 4τ σ eq F F F επ σ επ 140 F 18157N 18kN Επομένως σύμφωνα με τον έλεγχο ταυτόχρονης θλιπτικής και στρεπτικής τάσης η μέγιστη δύναμη είναι 18 kn. Αρκεί η δύναμη αυτή να μην υπερβαίνει το κρίσιμο φορτίο λυγισμού. Διαφορετικά το κρίσιμο φορτίο λυγισμού θα είναι το άνω φράγμα της προς υπολογισμό δύναμης. Έλεγχος λυγισμού: Ο κρίσιμος βαθμός λυγηρότητας είναι: 11 E.1 10 Pa λc π π S y Pa Αν δεχθούμε τις δυσμενέστερες δυνατές οριακές συνθήκες, δηλ. άρθρωση-άρθρωση, οπότε m 1, τότε ο ισοδύναμος βαθμός λυγηρότητας της υπό εξέταση ράβδου θα είναι: λ 800 m 1 06 r 15.5/ 4. 4 I π d 4 d Όπου r είναι η ακτίνα αδρανείας, και ως διάμετρος λαμβάνεται η A 64 π d 4 μικρότερη, δηλ. η d, και ως μήκος λαμβάνεται η απόσταση των 800mm που δίνεται στο σχήμα, αν και αυτή είναι αρκετά συντηρητική παραδοχή. Επειδή λ λc ο κοχλίας θεωρείται λεπτόκορμη δοκός, και για το λυγισμό της ισχύει η εξίσωση Εuler. Επομένως το κρίσιμο φορτίο λυγισμού θα βρίσκεται στα: 11 π EA π (.1 10 N / m )( π ( m) / 4) Pcr 90N 9kN λ 06 Άρα θα έχω λυγισμό. Επομένως η μέγιστη δύναμη δεν μπορεί να είναι μεγαλύτερη από το κρίσιμο φορτίο λυγισμού, διαιρεμένο με ένα συντελεστή ασφαλείας έναντι λυγισμού. Έστω N λ 1.. Τότε, F P cr / Ν λ 7 kn β) Κατά τη φόρτιση οι σπείρες του περικοχλίου παραλαμβάνουν τη δύναμη από τις σπείρες του κοχλία και τη μεταβιβάζουν στη κατασκευή σχήματος Π. Αν το περικόχλιο αποτελείται από n σπείρες, και έχει ύψος h π τότε επειδή το βήμα του σπειρώματος είναι P 4 mm, θα ισχύει: h π n P. Επίσης η επιφάνεια του σπειρώματος που θα παραλαμβάνει τη δύναμη θα είναι: Α σ n (πd Η 1 ) και επομένως Α σ h π (πd Η 1 ) / P. Τα σπειρώματα καταπονούνται σε επιφανειακή πίεση. Έστω η επιτρεπόμενη επιφανειακή πίεση των σπειρωμάτων (σ b ) επ 10 MPa (Πίνακας 7-1). Τότε: F F σb ( σb) επ 10MPa A h π d H / P h π σ π ( ) 1 Fh 7000N 4mm 4mm ( σ ) ( π dh) 10MPa ( π 18mm mm) b επ 1 Στοιχεία Μηχανών Ι - / 4

34 Κοχλίες - 4 / 4 - Άρα το απαιτούμενο ελάχιστο ύψος του περικοχλίου, ώστε να μην έχουμε αστοχία των σπειρών σε επιφανειακή πίεση, είναι h π 4 mm. γ) Οι απαιτούμενες ροπές για τη σύσφιγξη Μ σ και αποσύσφιγξη Μ α είναι αντίστοιχα: d 18 Mσ F tan ( α + ρ ) 7kN tan ( ) 14. Nm (δεξιόστροφη) d 18 Mα F tan ( α ρ ) 7kN tan ( 4 8.8) 5. Nm (αριστερόστροφη) - 4 / 4 - Παπαδόπουλος Α. Χρήστος