ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ Γ ΛΥΚΕΙΟΥ
|
|
|
- Νύξ Παπακωνσταντίνου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 - ΟΛΗ Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΕ ΕΡΩΤΗΣΕΙΣ -ΑΠΑΝΤΗΣΕΙΣ Tι ονομάζουμε συνάρτηση ; Tι ονομάζουμε πραγματιή συνάρτηση πραγματιής μεταβλητής; Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β είναι μια διαδιασία με την οποία άθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα αριβώς στοιχείο άποιου άλλου συνόλου Β Αν Α R, Β Rη συνάρτηση λέγεται πραγματιή συνάρτηση πραγματιής μεταβλητής Tι λέγεται τιμή μίας συνάρτησης στο ; Έστω μια συνάρτηση με πεδίο ορισμού το Α Αν με τη συνάρτηση αυτή το A αντιστοιχίζεται στο y, τότε γράφουμε y αι διαβάζουμε y ίσον του Το λέγεται τιμή της στο 3 Έστω μια συνάρτηση με πεδίο ορισμού το Α Τι ονομάζεται εξαρτημένη αι τι ανεξάρτητη μεταβλητή της ; Αν με τη συνάρτηση το Aαντιστοιχίζεται στο y, τότε γράφουμε y Το γράμμα, που συμβολίζει οποιοδήποτε στοιχείο του Α, ονομάζεται ανεξάρτητη μεταβλητή, ενώ το y, που παριστάνει την τιμή της συνάρτησης στο αι εξαρτάται από την τιμή του, λέγεται εξαρτημένη μεταβλητή 4 'Έστω οι συναρτήσεις, που ορίζονται σε ένα σύνολο Α Πως ορίζονται I Το άθροισμα S ; II Η διαφορά D ; III Το γινόμενο P ; IV Το πηλίο R / ; Αν δύο συναρτήσεις, ορίζονται αι οι δύο σε ένα σύνολο Α, τότε ορίζονται αι οι συναρτήσεις: Το άθροισμα S, με S, A Η διαφορά D, με D, A Το γινόμενο P, με P, Aαι Το πηλίο R, με R, όπου Aαι 5 Έστω μια συνάρτηση με πεδίο ορισμού ένα σύνολο Α Τι ονομάζεται γραφιή παράσταση ή αμπύλη της σε ένα αρτεσιανό σύστημα συντεταγμένων Oy ; Γραφιή παράσταση ή αμπύλη της σε ένα αρτεσιανό σύστημα συντεταγμένων Oy λέγεται το σύνολο των σημείων M, για όλα τα A
2 - 6 Πότε ένα σημείο M, y του επιπέδου των αξόνων ανήει στην αμπύλη της συνάρτησης ; Ένα σημείο M, y του επιπέδου των αξόνων ανήει στην αμπύλη της, μόνο όταν y 7Τι ονομάζεται εξίσωση της γραφιής παράστασης της συνάρτησης Η εξίσωση y επαληθεύεται μόνο από τα ζεύγη, y που είναι συντεταγμένες σημείων της γραφιής παράστασης της αι λέγεται εξίσωση της γραφιής παράστασης της 8Πότε μια συνάρτηση λέγεται γνησίως αύξουσα αι πότε γνησίως φθίνουσα σε ένα διάστημα Δ του πεδίου ορισμού της; Μια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε σημεία, με < ισχύει <, 9Πότε μια συνάρτηση λέγεται γνησίως μονότονη σε ένα διάστημα Δ του πεδίου ορισμού της; Μια συνάρτηση λέγεται γνησίως φθίνουσα στο Δ, όταν για οποιαδήποτε σημεία, με < ισχύει > Τι ονομάζουμε περιοχή του ; περιοχή του ονομαζουμε ένα ανοιτό διάστημα το οποίο περιέχει το, I Πότε μια συνάρτηση με πεδίο ορισμού το Α λέμε ότι παρουσιάζει τοπιό μέγιστο στο A ; II Πότε μια συνάρτηση με πεδίο ορισμού το Α λέμε ότι παρουσιάζει τοπιό ελάχιστο A; I Μια συνάρτηση με πεδίο ορισμού το Α λέμε ότι παρουσιάζει Τοπιό μέγιστο στο A, όταν για άθε σε μια περιοχή του, αι τοπιό ελάχιστο στο A, όταν για άθε σε μια περιοχή του Μια συνάρτηση με πεδίο ορισμού το Α λέμε ότι παρουσιάζει τοπιό ελάχιστο στο A όταν για άθε σε μια περιοχή του, Τι ονομάζονται αρότατα μίας συνάρτησης ; Τα μέγιστα αι τα ελάχιστα μιας συνάρτησης, τοπιά ή ολιά, λέγονται αρότατα της συνάρτησης Ε
3 - 3 3Αν οι συναρτήσεις αι έχουν στο όρια πραγματιούς αριθμούς, δηλαδή αν l αι l µε l, l R lm l m ποια είναι τα όρια :,,,,, ν lm lm lm lm lm lm lm l l lm k kl lm ll l lm l lm ν ν l lm ν νl 4Πότε μια συνάρτηση με πεδίο ορισμού Α λέγεται συνεχής ; Ποιο είναι το χαρατηριστιό γνώρισμα μιας συνεχούς συνάρτησης σε λειστό διάστημα ; Μια συνάρτηση με πεδίο ορισμού Α λέγεται συνεχής, αν για άθε A ισχύει lm 5 Συμπληρώστε τα ενά : l m ηµ, l m εφ, lm ηµ l m ηµ, l m εφ εφ, l m e e, e l m, l m συν, l m σφ, lml n l m συν συν, l m σφ σφ, lmln l n 6 Έστω μια συνάρτηση αι ένα σημείο A, της γραφιής της παράστασης C Ποιος είναι ο συντελεστής διεύθυνσης της εφαπτομένης της C στο Α ; Ο συντελεστής διεύθυνσης της εφαπτομένης της αμπύλης που είναι η γραφιή παράσταση μιας συνάρτησης στο σημείο, θα είναι
4 - 4 7Τι ονομάζεται παράγωγος της στο ; Η συνάρτηση είναι παραγωγίσιμη στο σημείο του πεδίου ορισμού της αν,το όριο lm υπάρχει αι είναι πραγματιός αριθμός αι ονομάζεται παράγωγος της στο, συμβολίζεται με : Δηλαδή lm 8Τι ονομάζεται ρυθμός μεταβολής του y ως προς το, όταν ; Η παράγωγος της στο εφράζει το ρυθμό μεταβολής του y ως προς το, όταν 9Τι ονομάζεται παράγωγος μια συνάρτησης με πεδίο ορισμού το Α ; Έστω μια συνάρτηση με πεδίο ορισμού το Α, αι Β το σύνολο των A στα οποία η είναι παραγωγίσιμη Τότε ορίζεται μια νέα συνάρτηση, με την οποία άθε αντιστοιχίζεται στο lm Η συνάρτηση αυτή λέγεται πρώτη παράγωγος της αι συμβολίζεται με Τι ονομάζεται δεύτερη παράγωγος μια συνάρτησης ; Η παράγωγος της συνάρτησης λέγεται δεύτερη παράγωγος της αι συμβολίζεται με Να αποδείξετε ότι η παράγωγος της σταθερής συνάρτησης c είναι δηλαδή ότι c Απόδειξη Έχουμε για άθε R c c αι για, Άρα c, οπότε lm Να αποδείξετε ότι η παράγωγος της ταυτοτιής συνάρτησης είναι δηλαδή ότι Απόδειξη Έχουμε, αι για, Επομένως lm lm Άρa
5 - 5 3Να αποδείξετε ότι η παράγωγος της συνάρτησης είναι δηλαδή ότι Απόδειξη Έστω η συνάρτηση Έχουμε, αι για, Επομένως, lm Άρα lm 4Να αποδείξετε ότι : η παράγωγος της συνάρτησης είναι Απόδειξη Έστω η συνάρτηση, αι για, Έχουμε Επομένως, lm lm Άρα 5Ποιες είναι οι παράγωγοι των συναρτήσεων ημ, συν, e, ln> ; Για τις συναρτήσεις ηµ, συν ηµ συν συν ηµ, > Για την εθετιή αι τη λογαριθμιή συνάρτηση, με βάση τον αριθμό e, αποδεινύεται ότι e e αι ln
6 - 6 ΘΕΩΡΙΑ 6Να αποδείξετε ότι c c Αποδειξη Έστω η συνάρτηση c F Έχουμε c c c F F, αι για c c F F Επομένως lm lm c c F F Άρα c c 7Να αποδείξετε ότι Απόδειξη Έστω η συναρτηση F Έχουμε F F, αι για, F F Επομένως lm lm lm F F Άρα 8Ποιες είναι οι παράγωγοι των συναρτήσεων,, ; Για το γινόμενο αι το πηλίο συναρτήσεων αποδεινύεται ότι ισχύουν οι παραάτω ανόνες παραγώγισης: Αποδεινύεται ότι για την παράγωγο μιας σύνθετης συνάρτησης ισχύει:
7 - 7 9Αν μία συνάρτηση είναι παραγωγίσιμη σε ένα διάστημα Δ αι ισχύει > αντιστοίχως < για άθε εσωτεριό σημείο του Δ τι συμπεραίνουμε για την μονοτονία της στο Δ ; Αν μια συνάρτηση είναι παραγωγίσιμη σε ένα διάστημα Δ αι ισχύει > για άθε εσωτεριό σημείο του Δ, τότε η είναι γνησίως αύξουσα στο Δ Αν μια συνάρτηση είναι παραγωγίσιμη σε ένα διάστημα Δ αι ισχύει < για άθε εσωτεριό σημείο του Δ, τότε η είναι γνησίως φθίνουσα στο Δ 3Αν για μια συνάρτηση ισχύουν για α, β, > στο α, αι < στο, β αντιστοίχως για α, β, < στο α, αι > στο, β τι συμπεραίνουμε για τα αρότατα της στο α, β ; Αν για μια συνάρτηση ισχύουν για α, β, > στο α, αι < στο, β, τότε η παρουσιάζει στο διάστημα α, β για μέγιστο Αν για μια συνάρτηση ισχύουν για α, β, < στο α, αι > στο, β, τότε η παρουσιάζει στο διάστημα α, β για ελάχιστο 3 Να αποδείξετε ότι : αι εφ συν Απόδειξη ' ' Έχουμε : Άρα Έχουμε εφ ηµ ηµ συν ηµ συν συν συν συν ηµ συν συν Άρα εφ συν
8 - 8 ΣΤΑΤΙΣΤΙΚΗ ΚΕΦΑΛΑΙΟ Τι εννοούμε με τον όρο στατιστιή ; Στατιστιή είναι ένα σύνολο αρχών αι μεθοδολογιών για: το σχεδιασμό της διαδιασίας συλλογής δεδομένων τη συνοπτιή αι αποτελεσματιή παρουσίασή τους την ανάλυση αι εξαγωγή αντίστοιχων συμπερασμάτων Τι ονομάζεται πληθυσμός, δείγμα, αι πότε ένα δείγμα θα ονομάζεται αντιπροσωπευτιό ενός πληθυσμού; Ενα σύνολο το οποιο θέλουμε να εξετάσουμε τα στοιχεία του ως προς ένα ή περισσότερα χαρατηριστιά τους λέγεται πληθυσμός Καθε υποσύνολο του πληθυσμού, το οποίο αλείται δείγμα Ένα δείγμα θεωρείται αντιπροσωπευτιό ενός πληθυσμού, εάν έχει επιλεγεί ατά τέτοιο τρόπο, ώστε άθε μονάδα του πληθυσμού να έχει την ίδια δυνατότητα να επιλεγεί 3Τι ονομάζονται στη στατιστιή μεταβλητές αι τι τιμές μίας μεταβλητής; Τα χαρατηριστιά ως προς τα οποία εξετάζουμε έναν πληθυσμό λέγονται μεταβλητές varables αι τις συμβολίζουμε συνήθως με τα εφαλαία γράμματα X, Y, Z,, Οι δυνατές τιμές που μπορεί να πάρει μια μεταβλητή λέγονται τιμές της μεταβλητής 4Πως διαρίνονται οι μεταβλητές ως προς τις τιμές τους; Τις μεταβλητές τις διαρίνουμε: Σε ποιοτιές ή ατηγοριές μεταβλητές, των οποίων οι τιμές τους δεν είναι αριθμοί Σε ποσοτιές μεταβλητές, των οποίων οι τιμές είναι αριθμοί αι διαρίνονται: -Σε διαριτές μεταβλητές, που παίρνουν μόνο μεμονωμένες τιμές -Σε συνεχείς μεταβλητές, που μπορούν να πάρουν αποιαδήποτε τιμή ενός διαστήματος πραγματιών αριθμών α, β 5Τι αλείται απογραφή ; Αναφέρετε δυο μειονετήματά της Ένας τρόπος για να πάρουμε τις απαραίτητες πληροφορίες που χρειαζόμαστε για άποιο πληθυσμό είναι να εξετάσουμε όλα τα άτομα στοιχεία του πληθυσμού ως προς το χαρατηριστιό που μας ενδιαφέρει Η μέθοδος αυτή συλλογής των δεδομένων αλείται απογραφή - Σε πολλές όμως περιπτώσεις η εξέταση όλων των μονάδων του πληθυσμού είναι δύσολη ή αόμα αι αδύνατη - Επίσης ο όπος, ο χρόνος αι τα έξοδα που χρειάζονται για τη διεξαγωγή μιας απογραφής είναι πολλές φορές αρετά μεγάλα, ιδίως όταν ο πληθυσμός που εξετάζεται είναι αρετά μεγάλος
9 - 9 6 Έστω < < <, ν οι διαφορετιές τιμές μιας μεταβλητής Χ, ενός δείγματος μεγέθους v A Πως ορίζονται : α Η απόλυτη συχνότητα ν της τιμής β Η σχετιή συχνότητα της τιμής γ Η σχετιή συχνότητα% της τιμής % δ Η αθροιστιή συχνότητα N της τιμής για ποσοτιές μεταβλητές ε Η αθροιστιή σχετιή συχνότητα F της τιμής αι το αντίστοιχο ποσοστιαίο μέγεθος F% Β Συμπληρώστε τα ενά : α ν ν ν β N αι F γ N - N -, 3,, δ F - F -,, 3,, ε N αι F Α α Αν,,, είναι οι τιμές μιας μεταβλητής Χ, που αφορά τα άτομα ενός δείγματος μεγέθους v, ν Στην τιμή αντιστοιχίζεται η απόλυτη συχνότητα ν, δηλαδή ο φυσιός αριθμός που δείχνει πόσες φορές εμφανίζεται η τιμή της εξεταζόμενης μεταβλητής Χ στο σύνολο των παρατηρήσεων β Αν διαιρέσουμε τη συχνότητα ν με το μέγεθος ν του δείγματος, προύπτει η σχετιή συχνότητα της τιμής, δηλαδή ν,,,, ν γ Τις σχετιές συχνότητες τις εφράζουμε επί τοις εατό, οπότε συμβολίζονται με %, δηλαδή % δ Αθροιστιές συχνότητες εφράζουν το πλήθος των παρατηρήσεων που είναι μιρότερες ή ίσες της τιμής ε Αθροιστιές σχετιές συχνότητες F, οι οποίες εφράζουν το ποσοστό των παρατηρήσεων που είναι μιρότερες ή ίσες της τιμής Β α ν ν ν v β ν, αι F, γ ν,, 3,, δ F F, 3,, ε v v v αι k Fk 3 k 7 Να αποδείξετε ότι για τη σχετιή συχνότητα ισχύουν οι ιδιότητες : I για,,, II Απόδειξη Για τις σχετιές συχνότητες λ λ v, v,, των απλών ενδεχομένων θα έχουμε: v,,,, λ αφού v λ v Α μελος : λ v v
10 - 8 Τι ονομάζεται ατανομή συχνοτήτων μίας μεταβλητής με τιμές,,, ; Για μια μεταβλητή, το σύνολο των ζευγών, ν λέμε ότι αποτελεί την ατανομή συχνοτήτων 9 Πότε χρησιμοποιείται το ραβδόγραμμα ; Να δώσετε μία περιγραφή του Το ραβδόγραμμα χρησιμοποιείται για τη γραφιή παράσταση των τιμών μιας ποιοτιής μεταβλητής Το ραβδόγραμμα αποτελείται από ορθογώνιες στήλες που οι βάσεις τους βρίσονται πάνω στον οριζόντιο ή τον αταόρυφο άξονα Σε άθε τιμή της μεταβλητής Χ αντιστοιχεί μια ορθογώνια στήλη της οποίας το ύψος είναι ίσο με την αντίστοιχη συχνότητα ή σχετιή συχνότητα Έτσι έχουμε αντίστοιχα το ραβδόγραμμα συχνοτήτων αι το ραβδόγραμμα σχετιών συχνοτήτων Τόσο η απόσταση μεταξύ των στηλών όσο αι το μήος των βάσεών τους αθορίζονται αυθαίρετα Πότε χρησιμοποιείται το διάγραμμα συχνοτήτων; Να δώσετε μία περιγραφή του Στην περίπτωση που έχουμε μια ποσοτιή μεταβλητή αντί του ραβδογράμματος χρησιμοποιείται το διάγραμμα συχνοτήτων Αυτό μοιάζει με το ραβδόγραμμα με μόνη διαφορά ότι αντί να χρησιμοποιούμε συμπαγή ορθογώνια υψώνουμε σε άθε υποθέτοντας ότι < < < μία άθετη γραμμή με μήος ίσο προς την αντίστοιχη συχνότητα, όπως φαίνεται στο σχήμα α Μπορούμε επίσης αντί των συχνοτήτων ν στον άθετο άξονα να βάλουμε τις σχετιές συχνότητες, οπότε έχουμε το διάγραμμα σχετιών συχνοτήτων Πότε χρησιμοποιείται το πολύγωνο συχνοτήτων; Να δώσετε μία περιγραφή του Ενώνοντας τα σημεία, ν ή, έχουμε το λεγόμενο πολύγωνο συχνοτήτων ή πολύγωνο σχετιών συχνοτήτων, αντίστοιχα, που μας δίνουν μια γενιή ιδέα για τη μεταβολή της συχνότητας ή της σχετιής συχνότητας όσο μεγαλώνει η τιμή της μεταβλητής που εξετάζουμε Πότε χρησιμοποιείται το υλιό διάγραμμα; Να δώσετε μία περιγραφή του Το υλιό διάγραμμα χρησιμοποιείται για τη γραφιή παράσταση τόσο των ποιοτιών όσο αι των ποσοτιών δεδομένων, όταν οι διαφορετιές τιμές της μεταβλητής είναι σχετιά λίγες Το υλιό διάγραμμα είναι ένας υλιός δίσος χωρισμένος σε υλιούς τομείς, τα εμβαδά ή,ισοδύναμα, τα τόξα των οποίων είναι ανάλογα προς τις αντίστοιχες συχνότητες ν ή τις σχετιές συχνότητες των τιμών της μεταβλητής
11 - 3Με τι είναι ίσο το τόξο α ενός υλιού διαγραμματοσς που αντιστοιχεί στην τιμή ; Αν συμβολίσουμε με α το αντίστοιχο τόξο ενός υλιού τμήματος στο υλιό διάγραμμα συχνοτήτων, τότε: o 36 α ν 36 o για,,, ν 4 Τι είναι το σημειόγραμμα ; Όταν έχουμε λίγες παρατηρήσεις, η ατανομή τους μπορεί να περιγραφεί με το σημειόγραμμα στο οποίο οι τιμές παριστάνονται γραφιά σαν σημεία υπεράνω ενός οριζόντιου άξονα 5Τι είναι το χρονόγραμμα ή χρονολογιό διάγραμμα ; Το χρονόγραμμα ή χρονολογιό διάγραμμα χρησιμοποιείται για τη γραφιή απειόνιση της διαχρονιής εξέλιξης ενός οιονομιού, δημογραφιού ή άλλου μεγέθους Ο οριζόντιος άξονας χρησιμοποιείται συνήθως ως άξονας μέτρησης του χρόνου αι ο άθετος ως άξονας μέτρησης της εξεταζόμενης μεταβλητής 6 Τι είναι οι λάσεις αι τα όρια των λάσεων ; Τι είναι η εντριή τιμή, το πλάτος αι η συχνότητα μίας λάσης ; Κλάσεις λέγονται οι ομάδες που ταξινομούνται οι τιμές μιας μεταβλητής, ώστε άθε τιμή να ανήει σε μια λάση Όρια των λάσεων λέγονται τα άρα των λάσεων Κεντριή τιμή μιας λάσης λέγεται η τιμή του έντρου της λάσης Πλάτος μιας λάσης λέγεται η διαφορά του ατωτέρου από το ανώτερο άρο της λάσης Το πλήθος των παρατηρήσεων ν που προύπτουν από τη διαλογή για την λάση αλείται συχνότητα της λάσης αυτής ή συχνότητα της εντριής τιμής, 7 Τι είναι το ιστόγραμμα συχνοτήτων ; Πως ατασευάζεται ; Τι είναι το πολύγωνο σχετιών συχνοτήτων ; Η γραφιή παράσταση ενός πίναα συχνοτήτων με ομαδοποιημένα δεδομένα γίνεται με το ιστόγραμμα συχνοτήτων Στον οριζόντιο άξονα ενός συστήματος ορθογωνίων αξόνων σημειώνουμε, με ατάλληλη λίμαα, τα όρια των λάσεων Στη συνέχεια, ατασευάζουμε διαδοχιά ορθογώνια ιστούς, από αθένα από τα οποία έχει βάση ίση με το πλάτος της λάσης αι ύψος τέτοιο, ώστε το εμβαδόν του ορθογωνίου να ισούται με τη συχνότητα της λάσης αυτής Θεωρώντας το πλάτος c ως μονάδα μέτρησης του χαρατηριστιού στον οριζόντιο άξονα, το ύψος άθε ορθογωνίου είναι ίσο προς τη συχνότητα της αντίστοιχης λάσης, έτσι ώστε να ισχύει πάλι ότι το εμβαδόν των ορθογωνίων είναι ίσο με τις αντίστοιχες συχνότητες Επομένως, στον αταόρυφο άξονα σε ένα ιστόγραμμα συχνοτήτων βάζουμε τις συχνότητες Αν στα ιστογράμματα συχνοτήτων θεωρήσουμε δύο αόμη υποθετιές λάσεις, στην αρχή αι στο
12 - τέλος, με συχνότητα μηδέν αι στη συνέχεια ενώσουμε τα μέσα των άνω βάσεων των ορθογωνίων, σχηματίζεται το λεγόμενο πολύγωνο συχνοτήτων Το εμβαδόν του χωρίου που ορίζεται από το πολύγωνο συχνοτήτων αι τον οριζόντιο άξονα είναι ίσο με το άθροισμα των συχνοτήτων, δηλαδή με το μέγεθος του δείγματος ν Όμοια ατασευάζεται από το ιστόγραμμα σχετιών συχνοτήτων αι το πολύγωνο σχετιών συχνοτήτων με εμβαδόν ίσο με, v 8 6 4,3,5,,5,, Υ ψος σε cm Ύ ψος σε cm α β Με τον ίδιο τρόπο ατασευάζονται αι τα ιστογράμματα αθροιστιών συχνοτήτων αι αθροιστιών σχετι-ών συχνοτήτων Αν ενώσουμε σε ένα ιστόγραμμα αθροιστιών συχνοτήτων τα δεξιά άρα όχι μέσα των άνω βάσεων των ορθογωνίων με ευθύγραμμα τμήματα βρίσουμε το πολύγωνο αθροιστιών συχνοτήτων της ατανομής F,9,8,7,6,5,4,3,, Ύ ψος σε cm 8 Ποια είναι η αριθμητιή τιμή του εμβαδού του χωρίου που ορίζεται από το πολύγωνο συχνοτήτων αι τον οριζόντιο άξονα; Το εμβαδόν του χωρίου που ορίζεται από το πολύγωνο συχνοτήτων αι τον οριζόντιο άξονα είναι ίσο με το άθροισμα των συχνοτήτων, δηλαδή με το μέγεθος του δείγματος ν 9 Τι ονομάζεται αμπύλη συχνοτήτων ; Εάν υποθέσουμε ότι ο αριθμός των λάσεων για μια συνεχή μεταβλητή είναι αρετά μεγάλος τείνει στο άπειρο αι ότι το πλάτος των λάσεων είναι αρετά μιρό τείνει στο μηδέν, τότε η πολυγωνιή γραμμή συχνοτήτων τείνει να πάρει τη μορφή μιας ομαλής αμπύλης, η οποία ονομάζεται αμπύλη συχνοτήτων
13 - 3 Τι λέγεται ομοιόμορφη ατανομή αι ποια η αμπύλη συχνοτήτων της ; Όταν οι παρατηρήσεις ατανέμονται ομοιόμορφα σε ένα διάστημα [α, β],, η ατανομή λέγεται ομοιόμορφη α β γ δ Τι λέγεται ανονιή ατανομή αι ποια η αμπύλη συχνοτήτων της ; Η ατανομή β, με ωδωνοειδή μορφή λέγεται ανονιή ατανομή normal dstrbuton αι παίζει σπουδαίο ρόλο στη Στατιστιή α β γ δ Ποιά ατανομή λέγεται ασύμμετρη; Ποια είναι τα είδη ασυμμετρίας ; Σχεδιάστε τις αμπύλες συχνοτήτων τους Όταν οι παρατηρήσεις δεν είναι συμμετριά ατανεμημένες, η ατανομή λέγεται ασύμμετρη με θετιή ασυμμετρία > δ όπως στην ατανομή γ ή αρνητιή ασυμμετρία < δόπως στην ατανομή δ α β γ δ 3Τι αλούμε μέτρα θέσης ; Τα μέτρα θεσης είναι αριθμητιά μεγέθη, που να μας δίνουν τη θέση του έντρου των παρατηρήσεων στον οριζόντιο άξονα
14 - 4 4 Τι αλούμε μέτρα διασποράς ; Μέτρα διασποράς ή μέτρα μεταβλητότητας είναι αριθμητιά μεγέθη που μας δινουν τη διασπορά των παρατηρήσεων, δηλαδή πόσο αυτές ετείνονται γύρω από το έντρο τους 5 Τι αλούνται μέτρα ασυμμετρίας ; Μέτρα ασυμμετρίας είναι αριθμητια μεγεθη που αθορίζουν τη μορφή της ατανομής Κατά πόσο δηλαδή η αντίστοιχη αμπύλη συχνοτήτων είναι συμμετριή ή όχι ως προς την ευθεία, για δεδομένο σημείο του άξονα Τα μέτρα αυτά εφράζονται σε συνάρτηση με τα μέτρα θέσης αι διασποράς 6 Πως ορίζεται η μέση τιμή μίας ποσοτιής μεταβλητής Χ, σε ένα δείγμα τιμών t, t,, tν μεγέθους ν ; Όταν σε ένα δείγμα μεγέθους ν οι παρατηρήσεις μιας μεταβλητής Χ είναι t, t,, tv, τότε η μέση τιμή συμβολίζεται με αι δίνεται από τη σχέση: t t t t ν ν ν ν ν ν t 7 Πως εφράζεται η μέση τιμή μίας ποσοτιής μεταβλητής Χ, σε ένα δείγμα τιμών,,, μεγέθους ν, με αντίστοιχες συχνότητες ν,ν,, ν ; Σε μια ατανομή συχνοτήτων, αν,,, είναι οι τιμές της μεταβλητής Χ με συχνότητες v, v,, v αντίστοιχα, η μέση τιμή ορίζεται ισοδύναμα από τη σχέση: ν ν ν ν ν ν ν ν ν ν 8 Τι ονομάζουμε σταθμισμένο αριθμητιό μέσο ή σταθμιό μέσο των τιμών,,, ν με συντελεστές στάθμισης βαρύτητας w,w,, wν ; Στις περιπτώσεις που δίνεται διαφορετιή βαρύτητα έμφαση στις τιμές,,, ν ενός συνόλου δεδομένων, τότε αντί του αριθμητιού μέσου χρησιμοποιούμε τον σταθμισμένο αριθμητιό μέσο ή σταθμιό μέσο Εάν σε άθε τιμή,,, ν δώσουμε διαφορετιή βαρύτητα, που εφράζεται με τους λεγόμενους συντελεστές στάθμισης βαρύτητας w, w,, wν, τότε ο σταθμιός μέσος βρίσεται από τον τύπο:
15 - 5 w w w ν w ν ν ν w w wν w 9 Πως εφράζεται η μέση τιμή μίας ποσοτιής μεταβλητής Χ, σε ένα δείγμα τιμών,,,, μεγέθους ναπό τις τιμές της μεταβλητής αι τις σχετιές συχνότητές τους,,, ; Η μέση τιμή μίας ποσοτιής μεταβλητής Χ, σε ένα δείγμα τιμών,,,, μεγέθους ναπό τις τιμές της μεταβλητής αι τις σχετιές συχνότητές τους,,, ; ν ν 3 Πως ορίζεται η διάμεσος δ ενός δείγματος ν παρατηρήσεων οι οποίες έχουν διαταχθεί ατά αύξουσα σειρά ; Διάμεσος δ ενός δείγματος ν παρατηρήσεων οι οποίες έχουν διαταχθεί σε αύξουσα σειρά ορίζεται ως η μεσαία παρατήρηση, όταν το ν είναι περιττός αριθμός, ή ο μέσος όρος ημιάθροισμα των δύο μεσαίων παρατηρήσεων όταν το ν είναι άρτιος αριθμός 3Τι ονομάζεται εύρος ή ύμανση R μιας ατανομής ; Αναφέρατε ένα σημαντιό μειονέτημά του Το εύρος ή ύμανση R, που ορίζεται ως η διαφορά της ελάχιστης παρατήρησης από τη μέγιστη παρατήρηση, δηλαδή: Εύρος R Μεγαλύτερη παρατήρηση-μιρότερη παρατήρηση Το εύρος είναι ένα αρετά απλό μέτρο, που υπολογίζεται εύολα δε θεωρείται όμως αξιόπιστο μέτρο διασποράς, γιατί βασίζεται μόνο στις δυο αραίες παρατηρήσεις 3Δείξτε ότι ο αριθμητιός μέσος των απολίσεων των παρατηρήσεων ενός δείγματος από τη μέση τιμή του είναι ίσος με το μηδέν Απόδειξη v v v v v v v
16 - 6 33Τι ονομάζεται διαύμανση ή διασπορά s² μιας ατανομής σε ένα δείγμα τιμών t, t,, tv μεγέθους ν; Διαύμανση ή διασπορά των παρατηρήσεων t, t t 3,, t ν μιας μεταβλητής Χ αλείται ο μέσος όρος των τετραγώνων των απολίσεων των t από τη μέση τιμή τους,ορίζεται από τη σχέση ν s t ν 34Αναφέρατε ένα σημαντιό μειονέτημα της διαύμανσης εξαιτίας του οποίου προτιμάμε την θετιή ρίζα της Η διαύμανση είναι μια αξιόπιστη παράμετρος διασποράς, αλλά έχει ένα μειονέτημα Δεν εφράζεται με τις μονάδες με τις οποίες εφράζονται οι παρατηρήσεις Για παράδειγμα, αν οι παρατηρήσεις εφράζονται σε cm, η διαύμανση εφράζεται σε cm Αν όμως πάρουμε τη θετιή τετραγωνιή ρίζα της διαύμανσης, θα έχουμε ένα μέτρο διασποράς που θα εφράζεται με την ίδια μονάδα μέτρησης του χαρατηριστιού, όπως αριβώς είναι αι όλα τα άλλα μέτρα θέσης, που εξετάσαμε έως τώρα 35Τι ονομάζεται τυπιή απόλιση s μιας ατανομής ; Η ποσότητα αυτή λέγεται τυπιή απόλιση,συμβολίζεται με s αι δίνεται από τη σχέση: s s 36 Αν η μεταβλητή Χ αολουθεί την ανονιή ατανομή με μέση τιμή αι τυπιή απόλιση s, να αναφέρετε το ποσοστό των παρατηρήσεων που βρίσεται στο διάστημα s, s s, s 3s, 3s αν η αμπύλη συχνοτήτων για το χαρατηριστιό που εξετάζουμε είναι ανονιή ή περίπου ανονιή, τότε η τυπιή απόλιση s έχει τις παραάτω ιδιότητες: το 68% περίπου των παρατηρήσεων βρίσεται στο διάστημα s, s το 95% περίπου των παρατηρήσεων βρίσεται στο διάστημα s, s το 99,7% περίπου των παρατη-ρήσεων βρίσεται στο διάστημα 3s, 3s s 3s s s s s 3s 68% 95% 99,7% s
17 Ποιο είναι ατά προσέγγιση το εύρος R μίας ανονιής ατανομής ; Το εύρος εύρος R μίας ανονιής ατανομής ισούται περίπου με έξι τυπιές απολίσεις, δηλαδή R 6s 38 Πως ορίζεται ο συντελεστής μεταβολής ή συντελεστής μεταβλητότητας CV ; Ένα μέτρο το οποίο μας βοηθά στη σύγριση ομάδων τιμών, που είτε εφράζονται σε διαφορετιές μονάδες μέτρησης είτε εφράζονται στην ίδια μονάδα μέτρησης, αλλά έχουν σημαντιά διαφορετιές μέσες τιμές, είναι ο συντελεστής μεταβολής ή συντελεστής μεταβλητότητας ο οποίος ορίζεται από το λόγο: τυπιή απόλιση s CV % % µέση τιµή 39Πως συγρίνονται ως προς την ομοιογένεια δύο δείγματα Α, Β με βάση τους συντελεστές μεταβολής ; Θα λέμε ότι το δείγμα Α έχει μεγαλύτερη ομοιογένεια από ένα δείγμα Β, όταν : CV < CV A 4Πότε ένα δείγμα τιμών μιας μεταβλητής θα είναι ομοιογενές ; ένα δείγμα τιμών μιας μεταβλητής θα είναι ομοιογενές, εάν ο συντελεστής μεταβολής δεν ξεπερνά το % 4Από τα, δ, s, s, R ποια είναι μέτρα θέσης αι ποια μέτρα διασποράς ; Τα μέτρα διασποράς είναι: Το εύρος R Η διαύμανση s Η τυπιή απόλιση s Τα μέτρα θέσης είναι: Η μέση τιμή Η διάμεσος δ 4 α Αν y c τοτε ɺ : y αι S y β Αν y λ τοτε ɺ : y αι S y α y c, s y s β y c, s y c s k k για ένα δείγμα τιμών 43 Αποδείξτε τους παραάτω τύπους : s,,, μεγέθους ν, με αντίστοιχες σχετιές συχνότητες,,, Απόδειξη
18 - 8 s k v v v vk k v v vk k v v v k k v v k k v v v v v v v v v v k k k v v v v s v v v v ν v v v v ΠΙΘΑΝΟΤΗΤΕΣ ΚΕΦΑΛΑΙΟ 3 ο Πότε ένα πείραμα λέγεται πείραμα τύχης αι πότε αιτιορατιό ; Ένα πείραμα ατά το οποίο η γνώση των συνθηών άτω από τις οποίες ετελείται αθορίζει πλήρως το αποτέλεσμα λέγεται αιτιορατιό πείραμα Υπάρχουν όμως αι πειράματα των οποίων δεν μπορούμε ε των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνονται φαινομενιά τουλάχιστον άτω από τις ίδιες συνθήες Ένα τέτοιο πείραμα ονομάζεται πείραμα τύχης ατι λέγεται δειγματιός χώρος Ω ενός πειράματος τύχης ; βτι λέμε δυνατά αποτελέσματα ή δυνατές περιπτώσεις ενός πειράματος τύχης ; Όλα τα αποτελέσματα που μπορούν να εμφανιστούν σε ένα πείραμα τύχης λέγονται δυνατά αποτελέσματα ή δυνατές περιπτώσεις του πειράματος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματιός χώρος αι συμβολίζεται συνήθως με το γράμμα Ω 3 Τι λέγεται ενδεχόμενο ενός πειράματος τύχης ; Το σύνολο που έχει ως στοιχεία ένα ή περισσότερα αποτελέσματα ενός πειράματος τύχης λέγεται ενδεχόμενο ή γεγονός 4 Τι λέγεται απλό αι τι σύνθετο ενδεχόμενο ενός πειράματος τύχης ; Ένα ενδεχόμενο λέγεται απλό όταν έχει ένα μόνο στοιχείο αι σύνθετο αν έχει περισσότερα στοιχεία
19 - 9 5 Πότε λέμε ότι ένα ενδεχόμενο Α ενός πειράματος τύχης πραγματοποιείται ή συμβαίνει σε μια συγεριμένη ετέλεσή του πειράματος ; Όταν το αποτέλεσμα ενός πειράματος, σε μια συγεριμένη ετέλεσή του είναι στοιχείο ενός ενδεχομένου, τότε λέμε ότι το ενδεχόμενο αυτό πραγματοποιείται ή συμβαίνει 6Τι ονομάζονται ευνοϊές περιπτώσεις για την πραγματοποίησή ενός ενδεχομένου; Τα στοιχεία ενός ενδεχομένου λέγονται αι ευνοϊές περιπτώσεις για την πραγματοποίησή του 7Ποιο είναι το βέβαιο αι ποιο το αδύνατο ενδεχόμενο ; Ο ίδιος ο δειγματιός χώρος Ω ενός πειράματος θεωρείται ότι είναι ενδεχόμενο, το οποίο μάλιστα πραγματοποιείται πάντοτε, αφού όποιο αι αν είναι το αποτέλεσμα του πειράματος θα ανήει στο Ω Γι αυτό το Ω λέγεται βέβαιο ενδεχόμενο Δεχόμαστε αόμα ως ενδεχόμενο αι το ενό σύνολο που δεν πραγματοποιείται σε αμιά ετέλεση του πειράματος τύχης Γι αυτό λέμε ότι το είναι το αδύνατο ενδεχόμενο 8 Αν Α είναι ένα ενδεχόμενο τι συμβολίζει το NA ; Το πλήθος των στοιχείων ενός ενδεχομένου Α θα το συμβολίζουμε με A 9 Πότε πραγματοποιείται το ενδεχόμενο A ; Να παραστήσετε το A σε ένα διάγραμμα Venn Το ενδεχόμενο A, που διαβάζεται Α τομή Β ή Α αι Β αι πραγματοποιείται, όταν πραγματοποιούνται συγχρόνως τα Α αι A Ω A Πότε πραγματοποιείται το ενδεχόμενο A ; Να παραστήσετε το A σε ένα διάγραμμα Venn Το ενδεχόμενο A, που διαβάζεται Α ένωση Β ή Α ή Β αι πραγματοποιείται, όταν πραγματοποιείται ένα τουλάχιστον από τα Α, Β A Ω A
20 - Πότε πραγματοποιείται το αντίθετο ενδεχόμενο A του Α ; Να παραστήσετε το A σε ένα διάγραμμα Venn Το ενδεχόμενο A, που διαβάζεται όχι Α ή συμπληρωματιό του Α αι πραγματο-ποιείται, A A όταν δεν πραγματοποιείται το Α Το A λέγεται αι αντίθετο του Α Ω Πότε πραγματοποιείται η διαφορά A του Β από το Α ;Να παραστήσετε το A σε ένα διάγραμμα Venn Το ενδεχόμενο A, που διαβάζεται διαφορά του Β από το Α αι πραγματοποιείται, όταν πραγματοποιείται το Α αλλά όχι το Β Είναι εύολο να δούμε ότι A A Ω A A 3 Πότε δύο ενδεχόμενα Α αι Β λέγονται ασυμβίβαστα ή ξένα μεταξύ τους ; Δύο ενδεχόμενα Α αι Β λέγονται ασυμβίβαστα η ξένα μεταξύ τους ή αμοιβαίως απολειόμενα, όταν A 4 Τι ονομάζεται σχετιή συχνότητα ενός ενδεχομένου Α ; Αν σε ν ετελέσεις ενός πειράματος ένα ενδεχόμενο Α πραγματοποιείται φορές, τότε ο λόγος v ονομάζεται σχετιή συχνότητα του Α αι συμβολίζεται με A 5Έστω Ω { ω, ω,, ωλ }δειγματιός χώρος αι τα απλά ενδεχόμενα {ω},{ω},,{ωλ} τα οποία πραγματοποιούνται,,, λ φορές αντίστοιχα σε ν ετελέσεις του πειράματος με σχετιές συχνότητες,,, λ Δείξτε ότι λ Αποδειξη Από τις σχετιές συχνότητες λ λ v, v,, των απλών ενδεχομένων θα έχουμε: v λ v λ v v 6Τι ονομάζεται στατιστιή ομαλότητα ή νόμος των μεγάλων αριθμών ;
21 - Οι σχετιές συχνότητες πραγματοποίησης των ενδεχομένων ενός πειράματος σταθεροποιούνται γύρω από άποιους αριθμούς όχι πάντοτε ίδιους, αθώς ο αριθμός των δοιμών του πειράματος επαναλαμβάνεται απεριόριστα Το εμπειριό αυτό εξαγόμενο, το οποίο επιβεβαιώνεται αι θεωρητιά, ονομάζεται στατιστιή ομαλότητα ή νόμος των μεγάλων αριθμών 7Να δώσετε τον λασιό ορισμό της πιθανότητας Σε ένα πείραμα με ν ισοπίθανα αποτελέσματα η σχετιή συχνότητα ενός ενδεχομένου με στοιχεία θα τείνει στον αριθμό Γι αυτό είναι εύλογο σε ένα πείραμα με ισοπίθανα ν αποτελέσματα να ορίσουμε ως πιθανότητα του ενδεχομένου Α τον αριθμό: Πλήθος Ευνοϊών Περιπτώσεων A P A Πλήθος υνατών Περιπτώσεων Ω 8 Πως από τον λασιό ορισμό της πιθανότητας προύπτει ότι PΩ, P, PA ; Από τον λασιο ορισμό της πιθανοτητας προύπτει ότι: Ω P Ω Ω P Ω 3 Για άθε ενδεχόμενο Α ισχύει P A, αφού το πλήθος των στοιχείων ενός ενδεχομένου είναι ίσο ή μιρότερο από το πλήθος των στοιχείων του δειγματιού χώρου 9 Να δώσετε τον αξιωματιό ορισμό της πιθανότητας Έστω Ω ω, ω,, ω } ένας δειγματιός χώρος με πεπερασμένο πλήθος στοιχείων Σε άθε { ν { απλό ενδεχόμενο ω } αντιστοιχίζουμε έναν πραγματιό αριθμό, που τον συμβολίζουμε με P ω, έτσι ώστε να ισχύουν: P ω ω P ω P ων P Τον αριθμό P ω ονομάζουμε πιθανότητα του ενδεχομένου ω } Ως πιθανότητα P A ενός ενδεχομένου A α, α,, α } ορίζουμε το άθροισμα { { P α P α P α, ενώ ως πιθανότητα του αδύνατου ενδεχομένου ορίζουμε τον αριθμό P
22 - Να αποδείξετε ότι για οποιαδήποτε ασυμβίβαστα μεταξύ τους ενδεχόμενα Α αι Β ισχύε ο απλός προσθετιός νόμος : PA PA P Αποδειξη Αν A αι λ, τότε το A έχει λ στοιχεία, γιατί αλλιώς τα Α αι Β δε θα ήταν ασυμβίβαστα Δηλαδή, έχουμε A λ A Επομένως: A P A Ω A Ω A Ω Ω P A P Η ιδιότητα αυτή είναι γνωστή ως απλός προσθετιός νόμος smply addtve law αι ισχύει αι για περισσότερα από δύο ενδεχόμενα Έτσι, αν τα ενδεχόμενα Α, Β αι Γ είναι ανά δύο ασυμβίβαστα θα έχουμε P A Γ P A P P Γ Ω A A Να αποδείξετε ότι για δύο συμπληρωματιά ενδεχόμενα Α αι A ισχύει : PA PA Αποδειξη Επειδή A A, δηλαδή τα Α αι A είναι ασυμβίβαστα, έχουμε διαδοχιά, σύμφωνα με τον απλό προσθετιό νόμο: P A A P A P A P Ω P A P A A A P A P A Ω Οπότε P A P A Να αποδείξετε ότι για οποιαδήποτε ενδεχόμενα Α αι Β ισχύει ο προσθετιός νόμος : PA PA P PA Αποδειξη Για δυο ενδεχόμενα Α αι Β έχουμε A A A, αφού στο άθροισμα A το πλήθος των στοιχείων του A υπολογίζεται δυο φορές Αν διαιρέσουμε τα μέλη της με Ω έχουμε: A A A Ω Ω Ω Ω Ω A A
23 - 3 αι επομένως P A P A P P A Η ιδιότητα αυτή είναι γνωστή ως προσθετιός νόμος 3 Να αποδείξετε ότι για οποιαδήποτε ενδεχόμενα Α αι Β με Α Β ισχύει : PA P Αποδειξη Επειδή A έχουμε διαδοχιά: A A Ω Ω A P A P Ω 4 Να αποδείξετε ότι για οποιαδήποτε ενδεχόμενα Α αι Β ισχύει : PA - PA - PΑ Αποδειξη Επειδή τα ενδεχόμενα A αι A είναι ασυμβίβαστα αι A A A, έχουμε: P A P A P A A Άρα P A P A P A Ω A 5 Αποδείξτε ότι : α P[A - Β-Α] PA ΡΒ - PΑ β ΡΑ Β ΡΑ ΡΒ ΡΑ Β γ ma {PA, P } ΡΑ Β mn {, ΡΑ ΡΒ } δ ma {, PA P } ΡΑ Β mn { ΡΑ, ΡΒ } ε Αν ΡΑ ΡΒ > τότε Α, Β όχι ασυμβίβαστα Απόδειξη α A, A ξένα μεταξύ τους άρα από τον προσθετιό νόμο : P A A P A P A P A P A P P A P A P P A β P A ' P A P A P P A P A P P A γ A P P A Ma{ P, P A } P A A A P A P A
24 - 4 P A P A P P A P A P A P P A P A Mn{, P A P } δ ma {, PA P } ΡΑ Β mn { ΡΑ, ΡΒ } A A P A P A Mn{ P, P A } P A A P A P P A P A P P A P A P P A P A ma{,p A P } Ρ Α Β ε Αν ΡΑ ΡΒ > τότε Α, Β όχι ασυμβίβαστα Αν Α, Β ασυμβιβαστα τοτε P A P A P > ατοπο αρα Α, Β όχι ασυμβίβαστα
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 Οδηγός Επιβίωσης 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ : Διαφοριός Λογισμός ΚΕΦΑΛΑΙΟ : Στατιστιή Οδηγός Επιβίωσης Περιλαμβάνει: Ερωτήσεις Θεωρίας Όλες τις Αποδείξεις Χρήσιμο Τυπολόγιο ΑΜΕΡΙΚΑΝΙΚΗ
Οδηγός Επιβίωσης 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ : Διαφοριός Λογισμός ΚΕΦΑΛΑΙΟ : Στατιστιή Οδηγός Επιβίωσης Περιλαμβάνει: Ερωτήσεις Θεωρίας Όλες τις Αποδείξεις Χρήσιμο Τυπολόγιο ΑΜΕΡΙΚΑΝΙΚΗ
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ. για τα οποία ισχύει y f (x) , δηλαδή το σύνολο, x A, λέγεται γραφική παράσταση της f και συμβολίζεται συνήθως με C
 Επιμέλεια: Κ Μυλωνάκης ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΕΡΩΤΗΣΗ Τι ονομάζεται πραγματική συνάρτηση με πεδίο ορισμού το Α; Έστω Α ένα υποσύνολο του R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία
Επιμέλεια: Κ Μυλωνάκης ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΕΡΩΤΗΣΗ Τι ονομάζεται πραγματική συνάρτηση με πεδίο ορισμού το Α; Έστω Α ένα υποσύνολο του R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία
ν ν = 6. όταν είναι πραγµατικός αριθµός.
 Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
78 Ερωτήσεις Θεωρίας Στα Μαθηματικά Γενικής Παιδείας
 Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
ν ν = 6. όταν είναι πραγµατικός αριθµός.
 Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Συνάρτηση: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ λέγεται µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Γνησίως αύξουσα: σε ένα διάστηµα του πεδίου
Για το Θέμα 1 στα Μαθηματικά Γενικής Παιδείας Γ Λυκείου
 Για το Θέμα 1 στα Μαθηματικά Γενικής Παιδείας Γ Λυκείου Διαφορικός Λογισμός 1. Ισχύει f (g())) ) f ( = f (g())g () όπου f,g παραγωγίσιµες συναρτήσεις 2. Αν µια συνάρτηση f είναι παραγωγίσιµη σε ένα διάστηµα
Για το Θέμα 1 στα Μαθηματικά Γενικής Παιδείας Γ Λυκείου Διαφορικός Λογισμός 1. Ισχύει f (g())) ) f ( = f (g())g () όπου f,g παραγωγίσιµες συναρτήσεις 2. Αν µια συνάρτηση f είναι παραγωγίσιµη σε ένα διάστηµα
ΠΑΡΟΥΣΙΑΣΗ ΣΤΑΤΙΣΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ
 ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
2010-2011. 4 o Γενικό Λύκειο Χανίων Γ τάξη. Γενικής Παιδείας. Ασκήσεις για λύση
 00-0 4 o Γενιό Λύειο Χανίων Γ τάξη Μαθηματιά Γενιής Παιδείας γ Ασήσεις για λύση Επιμέλεια: Μ. Ι. Παπαγρηγοράης http://users.sch.gr/mipapagr 4 ο Γενιό Λύειο Χανίων 00 0 ΣΥΝΔΙΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑΤΙΣΤΙΚΗ
00-0 4 o Γενιό Λύειο Χανίων Γ τάξη Μαθηματιά Γενιής Παιδείας γ Ασήσεις για λύση Επιμέλεια: Μ. Ι. Παπαγρηγοράης http://users.sch.gr/mipapagr 4 ο Γενιό Λύειο Χανίων 00 0 ΣΥΝΔΙΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑΤΙΣΤΙΚΗ
ΚΕΦΑΛΑΙΟ. 1. α. Tι ονοµάζεται συνάρτηση από το σύνολο Α στο σύνολο Β; β. Tι ονοµάζεται πραγµατική συνάρτηση πραγµατικής µεταβλητής;
 Μαθηµατικά και Στοιχεία Στατιστικής ΚΕΦΑΛΑΙΟ ο 1 : ιαφορικός Λογισµός 1. α. Tι ονοµάζεται συνάρτηση από το σύνολο Α στο σύνολο Β; β. Tι ονοµάζεται πραγµατική συνάρτηση πραγµατικής µεταβλητής; 2. Έστω µια
Μαθηµατικά και Στοιχεία Στατιστικής ΚΕΦΑΛΑΙΟ ο 1 : ιαφορικός Λογισµός 1. α. Tι ονοµάζεται συνάρτηση από το σύνολο Α στο σύνολο Β; β. Tι ονοµάζεται πραγµατική συνάρτηση πραγµατικής µεταβλητής; 2. Έστω µια
Θέμα 1 ο (ΜΑΪΟΣ 2004, ΜΑΪΟΣ 2008) Να δείξετε ότι η παράγωγος της σταθερής συνάρτησης f (x) = c είναι (c) = 0. Απόδειξη
 ΕΚΔΟΣΕΙΣ ΚΕΛΑΦΑ 59 Θέμα 1 ο (ΜΑΪΟΣ 004, ΜΑΪΟΣ 008) Να δείξετε ότι η παράγωγος της σταθερής συνάρτησης f (x) = c είναι (c) = 0. Έχουμε f (x+h) - f (x) = c - c = 0 και για h 0 είναι f (x + h) - f (x) 0 m
ΕΚΔΟΣΕΙΣ ΚΕΛΑΦΑ 59 Θέμα 1 ο (ΜΑΪΟΣ 004, ΜΑΪΟΣ 008) Να δείξετε ότι η παράγωγος της σταθερής συνάρτησης f (x) = c είναι (c) = 0. Έχουμε f (x+h) - f (x) = c - c = 0 και για h 0 είναι f (x + h) - f (x) 0 m
Α. α) ίνεται η συνάρτηση F(x)=f(x)+g(x). Αν οι συναρτήσεις f, g είναι παραγωγίσιµες, να αποδείξετε ότι: F (x)=f (x)+g (x).
 Νίκος Σούρµπης - - Γιώργος Βαρβαδούκας ΘΕΜΑ ο Α. α) ίνεται η συνάρτηση F()=f()+g(). Αν οι συναρτήσεις f, g είναι παραγωγίσιµες, να αποδείξετε ότι: F ()=f ()+g (). β)να γράψετε στο τετράδιό σας τις παραγώγους
Νίκος Σούρµπης - - Γιώργος Βαρβαδούκας ΘΕΜΑ ο Α. α) ίνεται η συνάρτηση F()=f()+g(). Αν οι συναρτήσεις f, g είναι παραγωγίσιµες, να αποδείξετε ότι: F ()=f ()+g (). β)να γράψετε στο τετράδιό σας τις παραγώγους
i μιας μεταβλητής Χ είναι αρνητικός αριθμός
 ΕΡΩΤΗΣΕΙΣ Σ Λ ΠΑΝΕΛΛΑΔΙΚΩΝ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Nα χαρακτηρίσετε τις προτάσεις που ακoλουθούν γράφοντας στο τετράδιο σας την ένδειξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε
ΕΡΩΤΗΣΕΙΣ Σ Λ ΠΑΝΕΛΛΑΔΙΚΩΝ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Nα χαρακτηρίσετε τις προτάσεις που ακoλουθούν γράφοντας στο τετράδιο σας την ένδειξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε
Πληθυσμός μιας έρευνας λέγεται το σύνολο των αντικειμένων που εξετάζουμε ως προς ένα ή περισσότερα χαρακτηριστικά.
 ΣΤΑΤΙΣΤΙΚΗ Στατιστιή λέγεται ο λάδος τω Μαθηματιώ ο οποίος συγετρώει στοιχεία που ααφέροται σε έα σύολο ατιειμέω, τα ταξιομεί, αι τα παρουσιάζει σε ατάλληλη μορφή ώστε α μπορού α ααλυθού αι α ερμηευθού.
ΣΤΑΤΙΣΤΙΚΗ Στατιστιή λέγεται ο λάδος τω Μαθηματιώ ο οποίος συγετρώει στοιχεία που ααφέροται σε έα σύολο ατιειμέω, τα ταξιομεί, αι τα παρουσιάζει σε ατάλληλη μορφή ώστε α μπορού α ααλυθού αι α ερμηευθού.
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Nα χαρακτηρίσετε τις προτάσεις που ακλουθούν γράφοντας στο τετράδιο σας την ένδειξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟ ΛΑΘΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Nα χαρακτηρίσετε τις προτάσεις που ακλουθούν γράφοντας στο τετράδιο σας την ένδειξη Σωστό ή Λάθος δίπλα στο γράμμα που αντιστοιχεί σε κάθε
ΣΤΑΤΙΣΤΙΚΟΙ ΠΙΝΑΚΕΣ. ΓΕΝΙΚΟΙ (περιέχουν όλες τις πληροφορίες που προκύπτουν από μια στατιστική έρευνα) ΕΙΔΙΚΟΙ ( είναι συνοπτικοί και σαφείς )
 Πληθυσμός (populaton) ονομάζεται ένα σύνολο, τα στοιχεία του οποίου εξετάζουμε ως προς τα χαρακτηριστικά τους. Μεταβλητές (varables ) ονομάζονται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε έναν πληθυσμό.
Πληθυσμός (populaton) ονομάζεται ένα σύνολο, τα στοιχεία του οποίου εξετάζουμε ως προς τα χαρακτηριστικά τους. Μεταβλητές (varables ) ονομάζονται τα χαρακτηριστικά ως προς τα οποία εξετάζουμε έναν πληθυσμό.
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 0 ΙΟΥΝΙΟΥ 0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ Γ ΗΜΕΡΗΣΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ 0 ΙΟΥΝΙΟΥ 0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
ΣΤΑΤΙΣΤΙΚΗ Γενικές έννοιες
 ΣΤΑΤΙΣΤΙΚΗ Γειές έοιες Στατιστιή είαι ο λάδος τω μαθηματιώ, ο οποίος ως έργο έχει τη συγέτρωση στοιχείω, τη ταξιόμησή τους αι τη παρουσίασή τους σε ατάλληλη μορφή, ώστε α μπορού α ααλυθού αι α ερμηευθού
ΣΤΑΤΙΣΤΙΚΗ Γειές έοιες Στατιστιή είαι ο λάδος τω μαθηματιώ, ο οποίος ως έργο έχει τη συγέτρωση στοιχείω, τη ταξιόμησή τους αι τη παρουσίασή τους σε ατάλληλη μορφή, ώστε α μπορού α ααλυθού αι α ερμηευθού
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ 1 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1. Ένα σηµείο Α(χ, ψ) ανήκει στη γραφική παράσταση της f αν f(ψ)=χ. 2. Αν µια συνάρτηση είναι γνησίως αύξουσα σε ένα διάστηµα A,
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ Γ ΓΕΝΙΚΗΣ 1 ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1. Ένα σηµείο Α(χ, ψ) ανήκει στη γραφική παράσταση της f αν f(ψ)=χ. 2. Αν µια συνάρτηση είναι γνησίως αύξουσα σε ένα διάστηµα A,
Συναρτήσεις. Ορισμός Συνάρτησης
 Συναρτήσεις Ορισμός Συνάρτησης Συνάρτηση είναι μια διαδικασία με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Σχόλιο : Τα σύνολα Α και Β είναι
Συναρτήσεις Ορισμός Συνάρτησης Συνάρτηση είναι μια διαδικασία με την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται σε ένα ακριβώς στοιχείο κάποιου άλλου συνόλου Β. Σχόλιο : Τα σύνολα Α και Β είναι
2013-14 ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ ΕΠΙΣΗΜΑΝΣΕΙΣ ΘΕΜΑΤΑ ΤΟ Α ΘΕΜΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΘΕΜΑΤΑ. http://cutemaths.wordpress.
 3-4 ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ ΕΠΙΣΗΜΑΝΣΕΙΣ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΤΟ Α ΘΕΜΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΘΕΜΑΤΑ Βαγγέλης Α Νικολακάκης Μαθηματικός ttp://cutemats.wordpress.com/ ΛΙΓΑ ΛΟΓΙΑ Η παρούσα εργασία
3-4 ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ ΕΠΙΣΗΜΑΝΣΕΙΣ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΤΟ Α ΘΕΜΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΘΕΜΑΤΑ Βαγγέλης Α Νικολακάκης Μαθηματικός ttp://cutemats.wordpress.com/ ΛΙΓΑ ΛΟΓΙΑ Η παρούσα εργασία
F(x h) F(x) (f(x h) g(x h)) (f(x) g(x)) F(x h) F(x) f(x h) f(x) g(x h) g(x) h h h. lim lim lim f (x) g (x). h h h
 ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 3 MAΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α A1. Έστω η συνάρτηση
ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 3 MAΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α A1. Έστω η συνάρτηση
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝ. ΠΑΙΔΕΙΑΣ - Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝ. ΠΑΙΔΕΙΑΣ - Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΑ ΘΕΜΑ A A. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι f g f g,. Μονάδες 7 Α. Σε ένα πείραμα με ισοπίθανα αποτελέσματα
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝ. ΠΑΙΔΕΙΑΣ - Γ ΛΥΚΕΙΟΥ ΘΕΜΑΤΑ ΘΕΜΑ A A. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι f g f g,. Μονάδες 7 Α. Σε ένα πείραμα με ισοπίθανα αποτελέσματα
3 ΠΙΘΑΝΟΤΗΤΕΣ. ο δειγματικός χώρος του πειράματος θα είναι το σύνολο: Ω = ω, ω,..., ω }.
 3 ΠΙΘΑΝΟΤΗΤΕΣ 3.1 ΔΕΙΓΜΑΤΙΚΟΣ ΧΡΟΣ - ΕΝΔΕΧΟΜΕΝΑ Πείραμα Τύχης Ένα πείραμα του οποίου δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνεται φαινομενικά τουλάχιστον κάτω από
3 ΠΙΘΑΝΟΤΗΤΕΣ 3.1 ΔΕΙΓΜΑΤΙΚΟΣ ΧΡΟΣ - ΕΝΔΕΧΟΜΕΝΑ Πείραμα Τύχης Ένα πείραμα του οποίου δεν μπορούμε εκ των προτέρων να προβλέψουμε το αποτέλεσμα, μολονότι επαναλαμβάνεται φαινομενικά τουλάχιστον κάτω από
Θέματα. Α1. Να αποδείξετε ότι για δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω, ισχύει P(A-B)=P(A)-P( A B) (9 μονάδες)
 Θέματα Θέμα Α Α. Να αποδείξετε ότι για δύο ενδεχόμενα Α αι Β ενός δειγματιού χώρου Ω, ισχύει P(A-B)P(A)-P( A B) (9 μονάδες) Α. Να διατυπώσετε το νόμο των μεγάλων αριθμών. (6 μονάδες) Α. Να χαρατηρίσετε
Θέματα Θέμα Α Α. Να αποδείξετε ότι για δύο ενδεχόμενα Α αι Β ενός δειγματιού χώρου Ω, ισχύει P(A-B)P(A)-P( A B) (9 μονάδες) Α. Να διατυπώσετε το νόμο των μεγάλων αριθμών. (6 μονάδες) Α. Να χαρατηρίσετε
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ. ΛΥΚΕΙΟΥ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ - ΘΕΜΑ Ο Έστω η συνάρτηση f( ) =, 0 ) Να αποδείξετε ότι f ( ). f( ) =. ) Να υπολογίσετε το όριο lm f ( )+ 4. ) Να βρείτε την εξίσωση της εφαπτομένης
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ. ΛΥΚΕΙΟΥ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ - ΘΕΜΑ Ο Έστω η συνάρτηση f( ) =, 0 ) Να αποδείξετε ότι f ( ). f( ) =. ) Να υπολογίσετε το όριο lm f ( )+ 4. ) Να βρείτε την εξίσωση της εφαπτομένης
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
Α. Έστω δύο σύνολα Α και Β. Ποιά διαδικασία ονομάζεται συνάρτηση με πεδίο ορισμού το Α και πεδίο τιμών το Β;
 σελ 1 από 5 ΚΕΦΑΛΑΙΟ 1 Ο Α. Έστω δύο σύνολα Α και Β. Ποιά διαδικασία ονομάζεται συνάρτηση με πεδίο ορισμού το Α και πεδίο τιμών το Β; 1. Σ-Λ Η σχέση με:, είναι συνάρτηση. 2. Σ-Λ Η σχέση είναι συνάρτηση.
σελ 1 από 5 ΚΕΦΑΛΑΙΟ 1 Ο Α. Έστω δύο σύνολα Α και Β. Ποιά διαδικασία ονομάζεται συνάρτηση με πεδίο ορισμού το Α και πεδίο τιμών το Β; 1. Σ-Λ Η σχέση με:, είναι συνάρτηση. 2. Σ-Λ Η σχέση είναι συνάρτηση.
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο, να αποδείξετε ότι (f() + g ()) f () + g (),. Μονάδες 7 Α. Σε ένα πείραµα µε ισοπίθανα
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο, να αποδείξετε ότι (f() + g ()) f () + g (),. Μονάδες 7 Α. Σε ένα πείραµα µε ισοπίθανα
Σωστό - Λάθος Επαναληπτικές
 ΘΕΩΡΙΑ ΣΤΑΤΙΣΤΙΚΗ ΟΛΩΝ ΤΩΝ ΕΤΩΝ ημιτελές(veron 6-4-206) ΠΡΟΣΟΧΗ! Επισημαίω ότι οι λύσεις ούτε πλήρεις είαι ούτε έχου διπλοελεγχθεί τουλάχιστο μέχρι τώρα.ετσι ο ααγώστης πρέπει α έχει υπόψη του ότι μπορεί
ΘΕΩΡΙΑ ΣΤΑΤΙΣΤΙΚΗ ΟΛΩΝ ΤΩΝ ΕΤΩΝ ημιτελές(veron 6-4-206) ΠΡΟΣΟΧΗ! Επισημαίω ότι οι λύσεις ούτε πλήρεις είαι ούτε έχου διπλοελεγχθεί τουλάχιστο μέχρι τώρα.ετσι ο ααγώστης πρέπει α έχει υπόψη του ότι μπορεί
Α. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ. Πληθυσμός: Το συνόλου του οποίου τα στοιχεία εξετάζουμε ως προς ένα ή περισσότερα χαρακτηριστικά τους.
 1 Κεφάλαιο. ΣΤΑΤΙΣΤΙΚΗ Α. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στατιστική: ένα σύνολο αρχών και μεθοδολογιών για: το σχεδιασμό της διαδικασίας συλλογής δεδομένων τη συνοπτική και αποτελεσματική παρουσίασή τους την ανάλυση
1 Κεφάλαιο. ΣΤΑΤΙΣΤΙΚΗ Α. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στατιστική: ένα σύνολο αρχών και μεθοδολογιών για: το σχεδιασμό της διαδικασίας συλλογής δεδομένων τη συνοπτική και αποτελεσματική παρουσίασή τους την ανάλυση
ΣΥΝΔΥΑΣΤΙΚΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΣΥΝΔΥΑΣΤΙΚΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1.Έστω ο δειγματικός χώρος Ω = { 1,,, K,10} με ισοπίθανα απλά ενδεχόμενα. Να 4 βρείτε την πιθανότητα ώστε η συνάρτηση f ( x ) = x 4x + λ να
ΣΥΝΔΥΑΣΤΙΚΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 1.Έστω ο δειγματικός χώρος Ω = { 1,,, K,10} με ισοπίθανα απλά ενδεχόμενα. Να 4 βρείτε την πιθανότητα ώστε η συνάρτηση f ( x ) = x 4x + λ να
ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος. Ενδεχόμενα {,,..., }.
 ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Αν δηλαδή ω,,, ω2 ωκ είναι τα δυνατά αποτελέσματα ενός πειράματος
ΠΙΘΑΝΟΤΗΤΕΣ Δειγματικός Χώρος Το σύνολο των δυνατών αποτελεσμάτων λέγεται δειγματικός χώρος (sample space) και συμβολίζεται συνήθως με το γράμμα Αν δηλαδή ω,,, ω2 ωκ είναι τα δυνατά αποτελέσματα ενός πειράματος
Λύσεις των θεμάτων ΤΕΤΑΡΤΗ 23 MAΪΟΥ 2012 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΕΤΑΡΤΗ 3 MAΪΟΥ 01 Λύσεις των θεμάτων Έκδοση
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΕΤΑΡΤΗ 3 MAΪΟΥ 01 Λύσεις των θεμάτων Έκδοση
Λύσεις των θεμάτων ΔΕΥΤΕΡΑ 19 ΙΟΥΝΙΟΥ 2017 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΕΥΤΕΡΑ 19 ΙΟΥΝΙΟΥ 017 Λύσεις των θεμάτων Έκδοση η (0/06/017, 1:00) ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΕΥΤΕΡΑ 19 ΙΟΥΝΙΟΥ 017 Λύσεις των θεμάτων Έκδοση η (0/06/017, 1:00) ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ
f x g x f x g x, x του πεδίου ορισμού της; Μονάδες 4 είναι οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν και w
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α1 Αν οι συναρτήσεις f,g
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 015 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α Α1 Αν οι συναρτήσεις f,g
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 00 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΘΕΜΑ Α Α. Έστω t,t,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν,
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 00 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΘΕΜΑ Α Α. Έστω t,t,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν,
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Σημειώσεις: Σώλος Γιάννης Ορισμός Η έννοια της συνάρτησης Tι ονομάζουμε συνάρτηση ; Tι ονομάζουμε πραγματική συνάρτηση πραγματικής μεταβλητής; Μια διαδικασία με την
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ Σημειώσεις: Σώλος Γιάννης Ορισμός Η έννοια της συνάρτησης Tι ονομάζουμε συνάρτηση ; Tι ονομάζουμε πραγματική συνάρτηση πραγματικής μεταβλητής; Μια διαδικασία με την
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ. B. Πώς ορίζεται ο συντελεστής μεταβολής ή συντελεστής. μεταβλητότητας μιας μεταβλητής X, αν x > 0 και πώς, αν
 ΘΕΜΑ 1o ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
ΘΕΜΑ 1o ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2008 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΠΕΝΤΕ (5)
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2015 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 05 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιµες στο R, να αποδείξετε ότι: f + g ' = f ' + g ', R Μονάδες 7 Α. Πότε λέµε ότι µια συνάρτηση
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ. ν 1 + ν ν κ = v (1) Για τη σχετική συχνότητα ισχύουν οι ιδιότητες:
 Συχνότητα v i O φυσικός αριθμός που δείχνει πόσες φορές εμφανίζεται η τιμή x i της εξεταζόμενης μεταβλητής Χ στο σύνολο των παρατηρήσεων. Είναι φανερό ότι το άθροισμα όλων των συχνοτήτων είναι ίσο με το
Συχνότητα v i O φυσικός αριθμός που δείχνει πόσες φορές εμφανίζεται η τιμή x i της εξεταζόμενης μεταβλητής Χ στο σύνολο των παρατηρήσεων. Είναι φανερό ότι το άθροισμα όλων των συχνοτήτων είναι ίσο με το
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. Το σύνολο Α, που λέγεται πεδίο ορισµού της συνάρτησης,
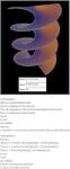 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ - ΘΕΩΡΙΑ Γιάννης Ζαμπέλης ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. Τι ονοµάζεται συνάρτηση Συνάρτηση (functon) είναι µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ - ΘΕΩΡΙΑ Γιάννης Ζαμπέλης ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. Τι ονοµάζεται συνάρτηση Συνάρτηση (functon) είναι µια διαδικασία µε την οποία κάθε στοιχείο ενός συνόλου Α αντιστοιχίζεται
ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 25 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 25 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΤΑΞΗ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 25 ΜΑΪΟΥ 2004 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι
Περιοδικό ΕΥΚΛΕΙΔΗΣ Β Ε.Μ.Ε. (Τεύχος 96) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ. f (x) s lim e. t,i 1,2,3,...
 Περιοδικό ΕΥΚΛΕΙΔΗΣ Β ΕΜΕ (Τεύχος 96) Άσκηση ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ Έστω οι παρατηρήσεις δυο δειγμάτων αντίστοιχα των μεταβλητών Χ και Ψ Δίνεται ότι η μέση τιμή
Περιοδικό ΕΥΚΛΕΙΔΗΣ Β ΕΜΕ (Τεύχος 96) Άσκηση ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΤΗΣ Γ ΛΥΚΕΙΟΥ Έστω οι παρατηρήσεις δυο δειγμάτων αντίστοιχα των μεταβλητών Χ και Ψ Δίνεται ότι η μέση τιμή
Επαναληπτικό Διαγώνισµα Μαθηµατικά Γενικής Παιδείας Γ Λυκείου
 Επαναληπτικό Διαγώνισµα Μαθηµατικά Γενικής Παιδείας Γ Λυκείου Θέµα Α A1. Για δυο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω να αποδείξετε ότι: Ρ( Α Β) = Ρ(Α) + Ρ(Β) Ρ( Α Β) Α. Πότε µια συνάρτηση f µε
Επαναληπτικό Διαγώνισµα Μαθηµατικά Γενικής Παιδείας Γ Λυκείου Θέµα Α A1. Για δυο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω να αποδείξετε ότι: Ρ( Α Β) = Ρ(Α) + Ρ(Β) Ρ( Α Β) Α. Πότε µια συνάρτηση f µε
Π Α Ν Ε Λ Λ Η Ν Ι Ε Σ 2 0 1 5 Μ Α Θ Η Μ Α Τ Ι Κ Α K A I Σ Τ Ο Ι Χ Ε Ι Α Σ Τ Α Τ Ι Σ Τ Ι Κ Η
 Π Α Ν Ε Λ Λ Η Ν Ι Ε Σ 0 Μ Α Θ Η Μ Α Τ Ι Κ Α K A I Σ Τ Ο Ι Χ Ε Ι Α Σ Τ Α Τ Ι Σ Τ Ι Κ Η Ε π ι μ ε λ ε ι α : Τ α κ η ς Τ σ α κ α λ α κ ο ς o ΘΕΜΑ Π α ν ε λ λ α δ ι κ ε ς Ε ξ ε τ α σ ε ι ς ( 0 ) A. Aν οι συναρτησεις
Π Α Ν Ε Λ Λ Η Ν Ι Ε Σ 0 Μ Α Θ Η Μ Α Τ Ι Κ Α K A I Σ Τ Ο Ι Χ Ε Ι Α Σ Τ Α Τ Ι Σ Τ Ι Κ Η Ε π ι μ ε λ ε ι α : Τ α κ η ς Τ σ α κ α λ α κ ο ς o ΘΕΜΑ Π α ν ε λ λ α δ ι κ ε ς Ε ξ ε τ α σ ε ι ς ( 0 ) A. Aν οι συναρτησεις
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2012 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο R, να αποδείξετε ότι (f() + g() )=f ()+g (), R Μονάδες 7 Α. Σε
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ Α Α. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο R, να αποδείξετε ότι (f() + g() )=f ()+g (), R Μονάδες 7 Α. Σε
(f (x) g(x)) = f (x) g(x)+f (x) g (x) (μονάδες 2)
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΔΕΥΤΕΡΑ 0 ΜΑΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ () ΘΕΜΑ Α Α.
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΚΑΙ Δ ΤΑΞΗΣ ΕΣΠΕΡΙΝΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΔΕΥΤΕΡΑ 0 ΜΑΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ () ΘΕΜΑ Α Α.
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΓΕΡΓΙΟΣ Ε. ΚΑΡΑΦΕΡΗΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ [] ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΡΙΑ: Πείραμα Τύχης Κάθε πείραμα κατά στο οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΝΕΣΤΟΡΙΟΥ ΕΠΙΜΕΛΕΙΑ : ΓΕΡΓΙΟΣ Ε. ΚΑΡΑΦΕΡΗΣ ΠΕ03 ΜΑΘΗΜΑΤΙΚΟΣ [] ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΡΙΑ: Πείραμα Τύχης Κάθε πείραμα κατά στο οποίο η γνώση των συνθηκών κάτω από τις οποίες εκτελείται καθορίζει πλήρως
Θέμα Α. Θέμα Β. ~ 1/9 ~ Πέτρος Μάρκου. % σχεδιάζουμε το πολύγωνο αθροιστικών σχετικών συχνοτήτων τοις
 01 Θέμα Α Α1. Θεωρία (απόδειξη), σελίδα 31 σχολικού βιβλίου Α. Θεωρία (ορισμός), σελίδα 18-19 σχολικού βιβλίου Α3. Θεωρία, (ορισμός), σελίδα 96 σχολικού βιβλίου Α. α) Λάθος β) Σωστό γ) Λάθος δ) Σωστό ε)
01 Θέμα Α Α1. Θεωρία (απόδειξη), σελίδα 31 σχολικού βιβλίου Α. Θεωρία (ορισμός), σελίδα 18-19 σχολικού βιβλίου Α3. Θεωρία, (ορισμός), σελίδα 96 σχολικού βιβλίου Α. α) Λάθος β) Σωστό γ) Λάθος δ) Σωστό ε)
Αν Α και Β είναι δύο ενδεχόμενα ενός δειγματικού χώρου να αποδείξετε ότι: Αν Α Β τότε Ρ(Α) Ρ(Β)
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 04 ΘΕΜΑ ο Α. Πότε δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω ονομάζονται ασυμβίβαστα;
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΕΞΕΤΑΣΕΙΣ ΠΡΟΣΟΜΟΙΩΣΗΣ 04 ΘΕΜΑ ο Α. Πότε δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω ονομάζονται ασυμβίβαστα;
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ 2ο: ΣΤΑΤΙΣΤΙΚΗ ΘΕΜΑ Α
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΤΑΤΙΣΤΙΚΗ ΘΕΜΑ Α Ερώτηση θεωρίας Τι λέγεται ιστόγραμμα αθροιστικών απολύτων σχετικών συχνοτήτων; Ιστόγραμμα αθροιστικών απολύτων ή σχετικών συχνοτήτων είναι μια σειρά από
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΣΤΑΤΙΣΤΙΚΗ ΘΕΜΑ Α Ερώτηση θεωρίας Τι λέγεται ιστόγραμμα αθροιστικών απολύτων σχετικών συχνοτήτων; Ιστόγραμμα αθροιστικών απολύτων ή σχετικών συχνοτήτων είναι μια σειρά από
4
 4 5 6 7 8 9 0 4 5 6 7 8 9 0 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ προς απάντηση Διαφορικός Λογισμός Tι ονομάζουμε συνάρτηση ; Tι ονομάζουμε πραγματική συνάρτηση πραγματικής μεταβλητής; Tι λέγεται τιμή μίας συνάρτησης f
4 5 6 7 8 9 0 4 5 6 7 8 9 0 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ προς απάντηση Διαφορικός Λογισμός Tι ονομάζουμε συνάρτηση ; Tι ονομάζουμε πραγματική συνάρτηση πραγματικής μεταβλητής; Tι λέγεται τιμή μίας συνάρτησης f
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Σ Τ Α Μ Α Θ Η Μ Α Τ Ι Κ Α Γ Ε Ν Ι Κ Η Σ Π Α Ι Δ Ε Ι Α Σ. οι τιμές μιας μεταβλητής Χ ενός δείγματος πλήθους ν με k.
 Δ Ι Α Γ Ω Ν Ι Σ Μ Α Σ Τ Α Μ Α Θ Η Μ Α Τ Ι Κ Α Γ Ε Ν Ι Κ Η Σ Π Α Ι Δ Ε Ι Α Σ ΘΕΜΑ Α A Να αποδείξετε ότι η συνάρτηση () είναι παραγωγίσιμη στο R με () Α Έστω k οι τιμές μιας μεταβλητής Χ ενός δείγματος πλήθους
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Σ Τ Α Μ Α Θ Η Μ Α Τ Ι Κ Α Γ Ε Ν Ι Κ Η Σ Π Α Ι Δ Ε Ι Α Σ ΘΕΜΑ Α A Να αποδείξετε ότι η συνάρτηση () είναι παραγωγίσιμη στο R με () Α Έστω k οι τιμές μιας μεταβλητής Χ ενός δείγματος πλήθους
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α A Να αποδείξετε ότι η συνάρτηση f () είναι παραγωγίσιμη στο R με f () Α Αν είναι οι τιμές μιας μεταβλητής Χ ενός δείγματος παρατηρήσεων μεγέθους ν ( ) να ορίσετε την
ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ Α A Να αποδείξετε ότι η συνάρτηση f () είναι παραγωγίσιμη στο R με f () Α Αν είναι οι τιμές μιας μεταβλητής Χ ενός δείγματος παρατηρήσεων μεγέθους ν ( ) να ορίσετε την
Μαθηματικός Περιηγητής σχ. έτος
 =================================================================== ΛΥΣΕΙΣ ΤΟΥ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 06 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΗΜΕΡΗΣΙΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
=================================================================== ΛΥΣΕΙΣ ΤΟΥ ΔΙΑΓΩΝΙΣΜΑΤΟΣ ΠΡΟΣΟΜΟΙΩΣΗΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ 06 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΗΜΕΡΗΣΙΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΟΜΑΔΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις
 2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
2 ΕΡΩΤΗΣΕΙΙΣ ΘΕΩΡΙΙΑΣ ΑΠΟ ΤΗΝ ΥΛΗ ΤΗΣ Β ΤΑΞΗΣ ΜΕΡΟΣ Α -- ΑΛΓΕΒΡΑ Κεφάλαιο 1 o Εξισώσεις - Ανισώσεις Α. 1 1 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2011 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΕΙΑΣ ΘΕΜΑ Ο : Α. Για δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω να αποδειχθεί ότι: Ρ(Α-Β)=Ρ(Α)-
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΕΙΑΣ ΘΕΜΑ Ο : Α. Για δύο ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω να αποδειχθεί ότι: Ρ(Α-Β)=Ρ(Α)-
ΣΤΑΤΙΣΤΙΚΗ. Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. Το χρώμα κάθε αυτοκινήτου είναι ποιοτική μεταβλητή. Σ Λ
 ΣΤΑΤΙΣΤΙΚΗ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. Το χρώμα κάθε αυτοκινήτου είναι ποιοτική μεταβλητή. Σ Λ 2. Ο αριθμός των ανθρώπων που παρακολουθούν μια συγκεκριμένη τηλεοπτική εκπομπή είναι διακριτή
ΣΤΑΤΙΣΤΙΚΗ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. Το χρώμα κάθε αυτοκινήτου είναι ποιοτική μεταβλητή. Σ Λ 2. Ο αριθμός των ανθρώπων που παρακολουθούν μια συγκεκριμένη τηλεοπτική εκπομπή είναι διακριτή
xdx και κ xdx x. Π α ν ε λ λ α δ ι κ ε ς Ε ξ ε τ α σ ε ι ς ( 1 9 8 3 8 9 ) 1 Να αποδειχθει οτι : α) Η συναρτηση f με f(x)= x ειναι γνησιως αυξουσα.
 Π α ν ε λ λ α δ ι ε ς Ε ξ ε τ α σ ε ι ς ( 9 8 3 8 9 ) Να αποδειχθει οτι : Η συναρτηση f με f() ειναι γνησιως αυξουσα. Για ισχυουν : d αι d. Η f εχει πεδιο ορισμου το Α[, ) αι ειναι συνεχης σε αυτο. Αομη
Π α ν ε λ λ α δ ι ε ς Ε ξ ε τ α σ ε ι ς ( 9 8 3 8 9 ) Να αποδειχθει οτι : Η συναρτηση f με f() ειναι γνησιως αυξουσα. Για ισχυουν : d αι d. Η f εχει πεδιο ορισμου το Α[, ) αι ειναι συνεχης σε αυτο. Αομη
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ Τι οομάζεται συάρτηση Συάρτηση uncton είαι μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α ατιστοιχίζεται σε έα αριβώς στοιχείο άποιου
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ Τι οομάζεται συάρτηση Συάρτηση uncton είαι μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α ατιστοιχίζεται σε έα αριβώς στοιχείο άποιου
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ 2016 (version ) είναι: ( ) f =
 ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ 16 (version 9-6-16) 1. A Να δώσετε τον ορισμό της παραγώγου μιας συνάρτησης σε ένα σημείο x του πεδίο ορισμού της. Απάντηση: Παράγωγος μιας συνάρτησης σε ένα σημείο x του πεδίο
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ ΙΟΥΝΙΟΥ 16 (version 9-6-16) 1. A Να δώσετε τον ορισμό της παραγώγου μιας συνάρτησης σε ένα σημείο x του πεδίο ορισμού της. Απάντηση: Παράγωγος μιας συνάρτησης σε ένα σημείο x του πεδίο
ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ σε μια σελίδα Α4 ανά έτος προσαρμοσμένα στις επιταγές του ΔΝΤ (IMF: 4o μεσοπρόθεσμο.) ( WWF:.εξοικονόμηση πόρων.
 ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ σε μια σελίδα Α4 ανά έτος προσαρμοσμένα στις επιταγές του ΔΝΤ (IMF: 4o μεσοπρόθεσμο.) ( WWF:.εξοικονόμηση πόρων.) ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ / ΣΤΑΤΙΣΤΙΚΗ 03 06 000... ΜΑΘΗΜΑΤΙΚΑ
ΘΕΜΑΤΑ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤΑΣΕΩΝ σε μια σελίδα Α4 ανά έτος προσαρμοσμένα στις επιταγές του ΔΝΤ (IMF: 4o μεσοπρόθεσμο.) ( WWF:.εξοικονόμηση πόρων.) ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΙΚΑ / ΣΤΑΤΙΣΤΙΚΗ 03 06 000... ΜΑΘΗΜΑΤΙΚΑ
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 2013 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ
 ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ Α Α. Να αποδείξετε ότι για δύο συμπληρωματικά ενδεχόμενα Α και Α ισχύει: Ρ(Α )=-Ρ(Α) Μονάδες 7 Α. Να ορίσετε το μέτρο διασποράς εύρος ή
ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ Α Α. Να αποδείξετε ότι για δύο συμπληρωματικά ενδεχόμενα Α και Α ισχύει: Ρ(Α )=-Ρ(Α) Μονάδες 7 Α. Να ορίσετε το μέτρο διασποράς εύρος ή
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α Πότε λέμε ότι η συνάρτηση είναι παραγωγίσιμη στο σημείο 0 του πεδίου ορισμού της; Α Αν οι συναρτήσεις και g είναι παραγωγίσιμες στο
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α Πότε λέμε ότι η συνάρτηση είναι παραγωγίσιμη στο σημείο 0 του πεδίου ορισμού της; Α Αν οι συναρτήσεις και g είναι παραγωγίσιμες στο
ΝΟΕΜΒΡΙΟΣ x 2. 6x x. 1B. Α) Να χαρακτηρίσετε ως σωστή (Σ) ή λανθασμένη (Λ) καθεμία από τις παρακάτω προτάσεις:
 ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Αμυραδάκη 0, Νίκαια (10-4903576) ΤΑΞΗ... Γ ΛΥΚΕΙΟΥ... ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΜΑΘΗΜΑ...ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ... ΝΟΕΜΒΡΙΟΣ 013 ΘΕΜΑ 1 Ο 1Α. α). Πότε λέμε ότι μια συνάρτηση f
ΤΕΤΡΑΚΤΥΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Αμυραδάκη 0, Νίκαια (10-4903576) ΤΑΞΗ... Γ ΛΥΚΕΙΟΥ... ΟΝΟΜΑΤΕΠΩΝΥΜΟ: ΜΑΘΗΜΑ...ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ... ΝΟΕΜΒΡΙΟΣ 013 ΘΕΜΑ 1 Ο 1Α. α). Πότε λέμε ότι μια συνάρτηση f
Γ. ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Σ Τ Α Τ Ι Σ Τ Ι Κ Η. Μαθηματικά Γενικής Παιδείας. Γ Λυκείου
 Γ. ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Σ Τ Α Τ Ι Σ Τ Ι Κ Η Μαθηματιά Γειής Παιδείας Γ Λυείου Δημήτρης Αργυράης Γεράσιμος Κουτσαδρέας Μαθηματιά Γειής Παιδείας Στατιστιή Γ. Λυείου ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
Γ. ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Σ Τ Α Τ Ι Σ Τ Ι Κ Η Μαθηματιά Γειής Παιδείας Γ Λυείου Δημήτρης Αργυράης Γεράσιμος Κουτσαδρέας Μαθηματιά Γειής Παιδείας Στατιστιή Γ. Λυείου ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 3 ΣΕΛΙΔΕΣ
 ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ ΙΟΥΝΙΟΥ 07 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΡΕΙΣ(3)
ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΕΥΤΕΡΑ ΙΟΥΝΙΟΥ 07 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΡΕΙΣ(3)
ΜΑΘΗΜΑΤΙΚΑ. 1 ο ΔΙΑΓΩΝΙΣΜΑ. ΘΕΜΑ 1 ο Δίνεται η συνάρτηση f x. Ι. Το πεδίο ορισμού της f είναι:., 1 υ -1, B. 1, Γ. -1,., 1.
 Γ ΛΥΚΕΙΟΥ-ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ ΜΑΘΗΜΑΤΙΚΑ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑ ο Δίνεται η συνάρτηση f Ι. Το πεδίο ορισμού της f είναι:., υ -, B., Γ. -,.,., ΙΙ. Το όριο f lm 0 είναι ίσο με: Α. 0 Β. Γ. Δ. Ε. Τίποτε από τα προηγούμενα
Γ ΛΥΚΕΙΟΥ-ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ ΜΑΘΗΜΑΤΙΚΑ ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑ ο Δίνεται η συνάρτηση f Ι. Το πεδίο ορισμού της f είναι:., υ -, B., Γ. -,.,., ΙΙ. Το όριο f lm 0 είναι ίσο με: Α. 0 Β. Γ. Δ. Ε. Τίποτε από τα προηγούμενα
ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ
 9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
Περιγραφική Στατιστική
 Περιγραφική Στατιστική Παναγιώτα Λάλου. Βασικές έννοιες Ορισμός: Στατιστικός πληθυσμός ονομάζεται το σύνολο των πειραματικών μονάδων π.χ άνθρωποι, ζώα, επιχειρήσεις κ.λπ, οι οποίες συμμετέχουν στην έρευνα
Περιγραφική Στατιστική Παναγιώτα Λάλου. Βασικές έννοιες Ορισμός: Στατιστικός πληθυσμός ονομάζεται το σύνολο των πειραματικών μονάδων π.χ άνθρωποι, ζώα, επιχειρήσεις κ.λπ, οι οποίες συμμετέχουν στην έρευνα
μιας παρατήρησης όπου λ. Αν για το πλήθος Ν(Ω) των σφαιρών που υπάρχουν στο κουτί ισχύει 64<Ν(Ω)<72, τότε λ
 ΘΕΜΑ Α ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΑ Β ) ΣΑΒΒΑΤΟ MAΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΕΙΑΣ Α. Για δύο ενδεχόμενα Α και Β ενός
ΘΕΜΑ Α ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΑ Β ) ΣΑΒΒΑΤΟ MAΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΕΙΑΣ Α. Για δύο ενδεχόμενα Α και Β ενός
3. Ανάπτυγμα Taylor (για συναρτήσεις δυό μεταβλητών)
 Ανάπτυγμα Taylor (για συναρτήσεις δυό μεταβλητών) Μια «πολύπλοη» συνάρτηση f, δυό μεταβλητών, μπορεί να προσεγγιστεί (στην γειτονιά ενός σημείου (,y)) από μια πολυωνιμιή συνάρτηση με την βοήθεια του αναπτύγματος
Ανάπτυγμα Taylor (για συναρτήσεις δυό μεταβλητών) Μια «πολύπλοη» συνάρτηση f, δυό μεταβλητών, μπορεί να προσεγγιστεί (στην γειτονιά ενός σημείου (,y)) από μια πολυωνιμιή συνάρτηση με την βοήθεια του αναπτύγματος
ΓΕΛ ΝΕΑΣ ΠΕΡΑΜΟΥ ΠΙΘΑΝΟΤΗΤΕΣ ΚΛΑΣΙΚΟΣ ΟΡΙΣΜΟΣ-ΛΟΓΙΣΜΟΣ. Στατιστική ομαλότητα ή Νόμος των μεγάλων αριθμών
 ΠΙΘΑΝΟΤΗΤΕΣ ΚΛΑΣΙΚΟΣ ΟΡΙΣΜΟΣ-ΛΟΓΙΣΜΟΣ Στατιστική ομαλότητα ή Νόμος των μεγάλων αριθμών Οι σχετικές συχνότητες πραγματοποίησης των ενδεχομένων ενός πειράματος σταθεροποιούνται γύρω από κάποιους αριθμούς
ΠΙΘΑΝΟΤΗΤΕΣ ΚΛΑΣΙΚΟΣ ΟΡΙΣΜΟΣ-ΛΟΓΙΣΜΟΣ Στατιστική ομαλότητα ή Νόμος των μεγάλων αριθμών Οι σχετικές συχνότητες πραγματοποίησης των ενδεχομένων ενός πειράματος σταθεροποιούνται γύρω από κάποιους αριθμούς
Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΑΡΤΗΣΕΙΣ ΓΝΗΣΙΩΣ ΑΥΞΟΥΣΑ ΣΥΝΑΡΤΗΣΗ ΓΝΗΣΙΩΣ ΦΘΙΝΟΥΣΑΣΥΝΑΡΤΗΣΗ ΤΟΠΙΚΟ ΜΕΓΙΣΤΟ ΤΟΠΙΚΟ ΕΛΑΧΙΣΤΟ
 1 Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΑΡΤΗΣΕΙΣ ΓΝΗΣΙΩΣ ΑΥΞΟΥΣΑ ΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΓΝΗΣΙΩΣ ΦΘΙΝΟΥΣΑΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΤΟΠΙΚΟ ΜΕΓΙΣΤΟ ά ( ύ ) έ
1 Η ΘΕΩΡΙΑ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΑΡΤΗΣΕΙΣ ΓΝΗΣΙΩΣ ΑΥΞΟΥΣΑ ΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΓΝΗΣΙΩΣ ΦΘΙΝΟΥΣΑΣΥΝΑΡΤΗΣΗ ά ( ύ ) έ ί ύ σ ύ ό ά, ύ ό ά 1 1 1 ΤΟΠΙΚΟ ΜΕΓΙΣΤΟ ά ( ύ ) έ
Α) Να γράψετε με τη βοήθεια των πράξεων των συνόλων το ενδεχόμενο που παριστάνει το σκιασμένο εμβαδόν σε καθένα από τα παρακάτω διαγράμματα Venn.
 Άσκηση 1 Α) Να γράψετε με τη βοήθεια των πράξεων των συνόλων το ενδεχόμενο που παριστάνει το σκιασμένο εμβαδόν σε καθένα από τα παρακάτω διαγράμματα Venn. B) Αν ( ), ( ), ( ), να εκφράσετε τις πιθανότητες
Άσκηση 1 Α) Να γράψετε με τη βοήθεια των πράξεων των συνόλων το ενδεχόμενο που παριστάνει το σκιασμένο εμβαδόν σε καθένα από τα παρακάτω διαγράμματα Venn. B) Αν ( ), ( ), ( ), να εκφράσετε τις πιθανότητες
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2010 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Έστω t, t,..., t ν οι παρατηρήσεις µιας ποσοτικής µεταβλητής Χ ενός δείγµατος µεγέθους ν, που έχουν µέση τιµή x. Σχηµατίζουµε
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 00 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Έστω t, t,..., t ν οι παρατηρήσεις µιας ποσοτικής µεταβλητής Χ ενός δείγµατος µεγέθους ν, που έχουν µέση τιµή x. Σχηµατίζουµε
F είναι ίσος µε ν. i ÏÅÖÅ ( ) h 3,f 3.
 Επαναληπτικά Θέµατα ΟΕΦΕ 0 Γ' ΤΑΞΗ ΓΕΝ. ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ A ΕΚΦΩΝΗΣΕΙΣ Α. Για δύο συµπληρωµατικά ενδεχόµενα Α και A ενός δειγµατικού χώρου Ω να P A = P A.
Επαναληπτικά Θέµατα ΟΕΦΕ 0 Γ' ΤΑΞΗ ΓΕΝ. ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΘΕΜΑ A ΕΚΦΩΝΗΣΕΙΣ Α. Για δύο συµπληρωµατικά ενδεχόµενα Α και A ενός δειγµατικού χώρου Ω να P A = P A.
1% = 100% 25 = 100. v 400. v = 6v v = 6 40 v = 240. = = 360 v v v + v + v + v = v v = 400
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 7 ΣΕΠΤΕΜΒΡΙΟΥ 000 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ ο A.. Σχολικό βιβλίο σελίδα 5 A.. α.
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΠΕΜΠΤΗ 7 ΣΕΠΤΕΜΒΡΙΟΥ 000 ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ ο A.. Σχολικό βιβλίο σελίδα 5 A.. α.
(f(x)+g(x)) =f (x)+g (x), x R
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑ ΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. Αν οι συναρτήσεις, g είναι παραγωγίσιµες στο IR, να αποδείξετε ότι (()+g()) ()+g (), R Μονάδες 7 Α.
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΠΑΝΕΛΛΑ ΙΚΩΝ ΕΞΕΤΑΣΕΩΝ 0 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Α Α. Αν οι συναρτήσεις, g είναι παραγωγίσιµες στο IR, να αποδείξετε ότι (()+g()) ()+g (), R Μονάδες 7 Α.
ΚΕΦΑΛΑΙΟ 2 ο : ΣΤΑΤΙΣΤΙΚΗ
 ΚΕΦΑΛΑΙΟ 2 ο : ΣΤΑΤΙΣΤΙΚΗ 1 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Ποιες μεταβλητές λέγονται ποσοτικές; (ΓΕΛ 2005) 2. Πότε μια ποσοτική μεταβλητή ονομάζεται διακριτή και πότε συνεχής; (ΓΕΛ 2005,2014) 3. Τι ονοµάζεται απόλυτη
ΚΕΦΑΛΑΙΟ 2 ο : ΣΤΑΤΙΣΤΙΚΗ 1 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Ποιες μεταβλητές λέγονται ποσοτικές; (ΓΕΛ 2005) 2. Πότε μια ποσοτική μεταβλητή ονομάζεται διακριτή και πότε συνεχής; (ΓΕΛ 2005,2014) 3. Τι ονοµάζεται απόλυτη
ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ- 1 o ΔΙΑΓΩΝΙΣΜΑ
 ΘΕΜΑ 1 ο Δίνεται η συνάρτηση f 1 ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ- 1 o ΔΙΑΓΩΝΙΣΜΑ Ι. Το πεδίο ορισμού της f είναι:, 1 υ -1, B. 1, Γ. -1,., 1. 1, f 1 ΙΙ. Το όριο lm είναι ίσο με: 0 Α. 0 Β. 1 Γ. -1 Δ. 1/ Ε. Τίποτε
ΘΕΜΑ 1 ο Δίνεται η συνάρτηση f 1 ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΜΑΘΗΜΑΤΙΚΑ- 1 o ΔΙΑΓΩΝΙΣΜΑ Ι. Το πεδίο ορισμού της f είναι:, 1 υ -1, B. 1, Γ. -1,., 1. 1, f 1 ΙΙ. Το όριο lm είναι ίσο με: 0 Α. 0 Β. 1 Γ. -1 Δ. 1/ Ε. Τίποτε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ 3ο: ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΜΑ Α. α) Τι λέγεται δειγματικός χώρος και τι ενδεχόμενο ενός πειράματος τύχης;
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΜΑ Α Ερώτηση θεωρίας α) Τι λέγεται δειγματικός χώρος και τι ενδεχόμενο ενός πειράματος τύχης; =. β) Για δύο συμπληρωματικά ενδεχόμενα Α και Α να αποδείξετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΠΙΘΑΝΟΤΗΤΕΣ ΘΕΜΑ Α Ερώτηση θεωρίας α) Τι λέγεται δειγματικός χώρος και τι ενδεχόμενο ενός πειράματος τύχης; =. β) Για δύο συμπληρωματικά ενδεχόμενα Α και Α να αποδείξετε
Άλγεβρα 1 ο Κεφάλαιο ... ν παράγοντες
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται δύναμη α ν με βάση τον πραγματικό αριθμό α και εκθέτη το φυσικό αριθμό >1; H δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα φυσικό αριθμό ν, συμβολίζεται
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται δύναμη α ν με βάση τον πραγματικό αριθμό α και εκθέτη το φυσικό αριθμό >1; H δύναμη με βάση έναν πραγματικό αριθμό α και εκθέτη ένα φυσικό αριθμό ν, συμβολίζεται
ΣΤΑΤΙΣΤΙΚΗ ΠΙΘΑΝΟΤΗΤΕΣ
 9/10/009 ΤΕΙ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΠΑΡΑΡΤΗΜΑ ΚΑΣΤΟΡΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ Η/Υ ΣΤΑΤΙΣΤΙΚΗ ΠΙΘΑΝΟΤΗΤΕΣ 3o ΜΑΘΗΜΑ Ι ΑΣΚΩΝ ΒΑΣΙΛΕΙΑ ΗΣ ΓΕΩΡΓΙΟΣ Emal: gasl@math.auth.gr Ιστοσελίδα Μαθήματος: users.auth.gr/gasl
9/10/009 ΤΕΙ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ ΠΑΡΑΡΤΗΜΑ ΚΑΣΤΟΡΙΑΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ Η/Υ ΣΤΑΤΙΣΤΙΚΗ ΠΙΘΑΝΟΤΗΤΕΣ 3o ΜΑΘΗΜΑ Ι ΑΣΚΩΝ ΒΑΣΙΛΕΙΑ ΗΣ ΓΕΩΡΓΙΟΣ Emal: gasl@math.auth.gr Ιστοσελίδα Μαθήματος: users.auth.gr/gasl
ΑΡΧΗ 2ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ γ) Για την παράγωγο μιας σύνθετης συνάρτησης ισχύει (f(g(x))) =f (g(x)) g (x) Μονάδες 2
 ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 4 MAΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
ΘΕΜΑ Α ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΣΑΒΒΑΤΟ 4 MAΪΟΥ 0 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 05 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ ΗΣ ΣΕΛΙΔΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΤΕΤΑΡΤΗ 0 ΜΑΪΟΥ 05 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΘΕΜΑ Α Α1. Αν οι συναρτήσεις f, g είναι παραγωγίσιμες στο, να αποδείξετε ότι ( f (x) + g(x)
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑ Α Β ) ΤΕΤΑΡΤΗ 3 ΜΑΪΟΥ 01 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΣΥΝΟΛΟ
ΘΕΜΑ Α Α1. Έστω t 1,t 2,...,t ν οι παρατηρήσεις μιας ποσοτικής μεταβλητής Χ ενός δείγματος μεγέθους ν, που έχουν
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΠΑΛ (ΟΜΑ Α Β ) ΕΥΤΕΡΑ 7 MAΪΟΥ 00 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ
P(A ) = 1 P(A). Μονάδες 7
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 20 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 20 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ:
Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η : ,
 Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η :1-0-017, 3-0-017 Διδάσκουσα: Κοντογιάννη Αριστούλα Σκοπός του μαθήματος Η παρουσίαση
Τμήμα Διοίκησης Επιχειρήσεων (Γρεβενά) Μάθημα: Στατιστική II Διάλεξη 1 η : Εισαγωγή-Επανάληψη βασικών εννοιών Εβδομάδα 1 η :1-0-017, 3-0-017 Διδάσκουσα: Κοντογιάννη Αριστούλα Σκοπός του μαθήματος Η παρουσίαση
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ
 ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΔΕΥΤΕΡΑ 0 ΜΑΪΟΥ 0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
ΑΡΧΗ ΗΣ ΣΕΛΙ ΑΣ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΔΕΥΤΕΡΑ 0 ΜΑΪΟΥ 0 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ
Γ. Ε. ΛΥΚΕΙΟ 2008 ΜΑΘ. ΚΑΙ ΣΤ. ΣΤΑΤ. ΤΑΞΗ Γ
 Γ. Ε. ΛΥΚΕΙΟ 008 43 Γ. Ε. ΛΥΚΕΙΟ 008 44 Α. Έστω f συνάρτηση με πεδίο ορισμού Α παραγωγίσιμη σε κάθε Α και c πραγματική σταθερά. Να αποδείξετε ότι: (cf ()) = cf () Μονάδες 5 Β. Να χαρακτηρίσετε με Σ (σωστό)
Γ. Ε. ΛΥΚΕΙΟ 008 43 Γ. Ε. ΛΥΚΕΙΟ 008 44 Α. Έστω f συνάρτηση με πεδίο ορισμού Α παραγωγίσιμη σε κάθε Α και c πραγματική σταθερά. Να αποδείξετε ότι: (cf ()) = cf () Μονάδες 5 Β. Να χαρακτηρίσετε με Σ (σωστό)
ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ 2 Ο «ΣΤΑΤΙΣΤΙΚΗ»
 ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ Ο «ΣΤΑΤΙΣΤΙΚΗ» Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΚΕΦΑΛΑΙΟ. ΣΤΑΤΙΣΤΙΚΗ. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στατιστική είναι ο κλάδος των εφαρμοσμένων
ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΚΕΦΑΛΑΙΟ Ο «ΣΤΑΤΙΣΤΙΚΗ» Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΚΕΦΑΛΑΙΟ. ΣΤΑΤΙΣΤΙΚΗ. ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Στατιστική είναι ο κλάδος των εφαρμοσμένων
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 2011 ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω να αποδειχθεί ότι: Ρ (Α Β ) = Ρ (Α) Ρ (Α Β ). Μονάδες 7 Α. Πότε δύο ενδεχόµενα
ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ 0 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Α. Για δύο ενδεχόµενα Α και Β ενός δειγµατικού χώρου Ω να αποδειχθεί ότι: Ρ (Α Β ) = Ρ (Α) Ρ (Α Β ). Μονάδες 7 Α. Πότε δύο ενδεχόµενα
Λύσεις των θεμάτων ΔΕΥΤΕΡΑ 19 ΙΟΥΝΙΟΥ 2017 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΕΥΤΕΡΑ 19 ΙΟΥΝΙΟΥ 017 Λύσεις των θεμάτων Έκδοση η (0/06/017, 1:00) Οι απαντήσεις και οι λύσεις
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΕΥΤΕΡΑ 19 ΙΟΥΝΙΟΥ 017 Λύσεις των θεμάτων Έκδοση η (0/06/017, 1:00) Οι απαντήσεις και οι λύσεις
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ςεδς ΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΓΙΑ ΕΞΕΤΑΣΕΙΣ ΕΠΙΜΕΛΕΙΑ Βαγγέλης Βαγγέλης Νικολακάκης Μαθηματικός
 0 ςεδς ΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΓΙΑ ΕΞΕΤΑΣΕΙΣ Βαγγέλης ΕΠΙΜΕΛΕΙΑ Βαγγέλης Νικολακάκης Μαθηματικός ΣΗΜΕΙΩΜΑ Το παραπάνω φυλλάδιο φτιάχτηκε για να προσφέρει βοήθεια κυρίως στους μαθητές
0 ςεδς ΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΙΑ ΘΕΜΑΤΑ ΓΙΑ ΕΞΕΤΑΣΕΙΣ Βαγγέλης ΕΠΙΜΕΛΕΙΑ Βαγγέλης Νικολακάκης Μαθηματικός ΣΗΜΕΙΩΜΑ Το παραπάνω φυλλάδιο φτιάχτηκε για να προσφέρει βοήθεια κυρίως στους μαθητές
ΘΕΜΑ Α Α1. Αν και είναι δύο συμπληρωματικά ενδεχόμενα ενός δειγματικού χώρου να αποδείξετε ότι για τις πιθανότητές τους ισχύει: ( ) 1 ( ).
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ() ΘΕΜΑ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β ) ΠΑΡΑΣΚΕΥΗ 0 ΜΑΪΟΥ 016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΤΕΣΣΕΡΙΣ() ΘΕΜΑ
