Απρίλιος Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6F, L = 0.4F, F = 1 kmol/s. Ζητούμενα: x Fi, x Li
|
|
|
- Ἰαρέδ Λαμέρας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας ισορροπίας Διαχωριστήρας ισορροπίας τροφοδοτείται με ρυθμό 1kmol/s, με μίγμα κανονικών υδρογονανθράκων: προπάνιο (C3), κανονικό βουτάνιο (C4) και κανονικό πεντάνιο (C5). Η πίεση είναι 6 atm. Οι εξερχόμενοι ατμοί αποτελούν το 60% της τροφοδοσίας και έχουν μοριακή σύσταση: 50% C3, 30% C4, 20% C5. Ζητούνται: α) η σύσταση της τροφοδοσίας β) η σύσταση του υγρού που εξέρχεται από τον διαχωριστήρα. Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6, L = 0.4, = 1 kmol/s. Ζητούμενα: x i, x Li V, x Vi Από το ισοζύγιο μάζας για κάθε συστατικό i βρίσκουμε: x, i =V x V, i L x L, i =0.6 x V, i 0.4 x L, i x, i =0.6 x V, i 0.4 x L, i, x i Τότε, για κάθε συστατικό i έχουμε δύο αγνώστους: τη σύσταση του υγρού και τη σύσταση της τροφοδοσίας. Χρειαζόμαστε άλλη μία συνθήκη (για κάθε συστατικό) και αυτή τη βρίσκουμε από τα δεδομένα ισορροπίας που L, x μας εκφράζονται από μια σχέση της μορφής y i = k i x Li i όπου y i είναι η σύσταση του ατμού (εδώ, με το σύμβολο i = C3, n-c4, n-c5 x Vi ) και x i είναι η σύσταση του υγρού, (εδώ, με το σύμβολο x Li ). Εδώ θεωρούμε ότι τα δεδομένα δίνονται υπό τη μορφή διαγράμματος De Priester. Επειδή κάθε ζεύγος τιμών σύστασης ατμού-υγρού αντιστοιχεί σε συγκεκριμένες συνθήκες πίεσης και θερμοκρασίας και εμείς ξέρουμε μόνο την πίεση πρέπει να κάνουμε δοκιμές για διάφορες θερμοκρασίες μέχρι να βρούμε κάποια τιμή που δίνει εύλογα αποτελέσματα. Η συνήθης μέθοδος για να το κρίνουμε αυτό σε προβλήματα τέτοιου είδους, είναι να ελέγχουμε σε κάθε δοκιμή αν τα μοριακά κλάσματα σε κάθε ένα από τα ρεύματα με άγνωστη σύσταση δίνουν άθροισμα ίσο με τη μονάδα. Αν επιλέξουμε να ελέγχουμε τα μοριακά κλάσματα της τροφοδοσίας σύμφωνα με τη σχέση που βρήκαμε πιο πάνω, τότε τα βήματα που ακολουθούμε είναι τα εξής: 1. Επιλέγουμε κάποια πιθανή θερμοκρασία της διεργασίας 2. Από το διάγραμμα De Priester βρίσκουμε τις σταθερές ισορροπίας των τριών συστατικών για τη δεδομένη πίεση και την επιλεγμένη θερμοκρασία 3. Βρίσκουμε τη σύσταση του υγρού με τη βοήθεια της σύστασης του ατμού (γνωστή) και της σταθεράς που βρήκαμε στο προηγούμενο βήμα: x Li = x Vi / k i Υπολογίζουμε το άθροισμα των μοριακών κλασμάτων που βρήκαμε. 4. Βρίσκουμε τη σύσταση της τροφοδοσίας με τη βοήθεια της σχέσης που βγάλαμε βάσει των ισοζυγίων. Υπολογίζουμε το άθροισμα των μοριακών κλασμάτων που βρήκαμε. 5. Αν τα αθροίσματα των μοριακών κλασμάτων είναι πολύ κοντά στη μονάδα τελειώσαμε, αλλιώς πάμε στο βήμα 1 για να δοκιμάσουμε άλλη θερμοκρασία.
2 Ο παρακάτω πίνακας συνοψίζει τα αποτελέσματα για θερμοκρασία 58 ο C. συστατικό x Vi k i (58 o C) x i = 0.6x Vi + 0.4x Vi /k i x Li = x Vi / k i προπάνιο βουτάνιο πεντάνιο Άρα, α) σύσταση τροφοδοσίας: x 3 = 0.37, x 4 = 0.30, x 5 = 0.33 β) σύσταση υγρού: x L3 = 0.18, x L4 = 0.30, x L5 = 0.50 Σ x i = 1.00 Σ x Li = 1.00 Πρόβλημα 2 Αριθμός θεωρητικών βαθμίδων αποστακτικής στήλης με τη μέθοδο McCabe-Thiele Ισομοριακό μίγμα τετραχλωράνθρακα και διθειάνθρακα αποστάζεται σε κλασματική στήλη συνεχούς λειτουργίας σε ατμοσφαιρική πίεση. Τροφοδοτείται ποσότητα 1500kg/h η οποία εξατμίζεται κατά 30% πριν εισέλθει στη στήλη. Η σύσταση του αποστάγματος είναι 95% διθειάνθρακας και του υπολείμματος 0.5% διθειάνθρακας (μοριακά κλάσματα). Ζητούνται: α) οι ποσότητες αποστάγματος και υπολείμματος σε kmol/h β) ο αριθμός των θεωρητικών βαθμίδων, αν ο λόγος αναρροής είναι R = 1.59 Δίνονται τα παρακάτω δεδομένα ισορροπίας για το διθειάνθρακα: Τ, ο C x y Λύση Σύνοψη δεδομένων: = 1500kg/h, P = 1 at, x = 0.5, x D = 0.95, x B = 0.05 (τα κλάσματα εκφράζονται ως προς το πτητικότερο συστατικό που είναι προφανώς ο διθειάνθρακας), εξάτμιση του 30% της τροφοδοσίας, δεδομένα ισορροπίας. Ζητούνται: D, B, N Κατ' αρχήν, επειδή η τροφοδοσία δίνεται σε μονάδες μάζας, τη μετατρέπουμε σε μονάδες kmol/h. Επειδή δεν γνωρίζουμε τη μάζα κάθε συστατικού θα βρούμε το μέσο μοριακό βάρος του μίγματος και με αυτό θα κάνουμε τη μετατροπή:, x V, x V L, x L D, x D Περιοχή Εμπλουτισμού MB = n 1 MB 1 n 2 MB 2 n 1 n 2 = x 1 MB 1 x 2 MB 2 = =115 όπου με n i συμβολίζουμε τα mol και τα μοριακά βάρη του τετραχλωράνθρακα (1) και διθειάνθρακα (2) είναι 154 και 76, αντίστοιχα. Τότε = 1500 / 115 = kmol/h V, x V Περιοχή Εξαντλήσεως Από το ισοζύγιο (ολικό και ως προς το πτητικό Β, x B
3 συστατικό) για όλη τη στήλη έχουμε: =B D x =B x B D x D Αν λύσουμε το ολικό ισοζύγιο ως προς Β (B = -D) και αντικαστήσουμε στο ισοζύγιο του πτητικού συστατικού, βρίσκουμε: D= x x B =13.04 D=6.85 kmol/h x D x B Παρόμοια, αν λύσουμε το ολικό ισοζύγιο ως προς D (D = -B) και αντικαστήσουμε στο ισοζύγιο του πτητικού συστατικού, βρίσκουμε: B= x x D =13.04 D=6.20 kmol/h x D x B β) Για τον προσδιορισμό των θεωρητικών βαθμίδων πρέπει να σχεδιάσουμε τη γραμμή ισορροπίας και τις γραμμές λειτουργίας των τμημάτων εμπλουτισμού και εξάντλησης ή, εναλλακτικά, τη γραμμή λειτουργίας του τμήματος εμπλουτισμού και τη γραμμή θερμικής κατάστασης (από το σημείο τομής των δύο διέρχεται και η τρίτη). Για τη γραμμή ισορροπίας χρησιμοποιούμε τα σημεία (x,y) που δίνονται ώστε να σχεδιάσουμε κατά προσέγγιση την καμπύλη. Όσον αφορά τις γραμμές λειτουργίας εργαζόμαστε ως εξής. Αφού έχουμε δεδομένα για την θερμική κατάσταση της τροφοδοσίας, V L συμφέρει να υπολογίσουμε τη γραμμή θερμικής κατάστασης. Συγκεκριμένα, για την εξάτμιση της τροφοδοσίας κατά 30% θα έχουμε ένα μίγμα 30% ατμών που συμβολίζουμε με V και 70% υγρού που συμβολίζουμε με L. Από αυτά, ο ατμός της τροφοδοσίας ανέρχεται και καθώς ενώνεται, V, L με το ρεύμα ατμού V που προέρχεται από τον αναβραστήρα στον πυθμένα της στήλης, δίνουν το ρεύμα ατμού V που θα βγει τελικά από την κορυφή. Παρόμοια, το ρεύμα L κατέρχεται και καθώς το συναντά το ρεύμα L του υγρού που προέρχεται από την αναρροή του συμπυκνωμένου αποστάγματος στην κορυφή της στήλης, δίνουν το ρεύμα L του υγρού που θα τροφοδοτήσει τον αναβραστήρα στον πυθμένα. Επομένως είναι προφανές ότι ισχύουν: V =V V =V 0.3 και L=L L=0.7 L V L Η θερμική κατάσταση της τροφοδοσίας δίνεται από το κλάσμα q= L L =L 0.7 L q=0.7 Η γραμμή λειτουργίας της θερμικής κατάστασης (q-line) ορίζεται ως y= q q 1 x x q 1 και επομένως η κλίση της είναι q q 1 = 7 3. Επίσης, γνωρίζουμε ότι η q-line διέρχεται από το σημείο της κύριας διαγωνίου (ευθεία y = x) που αντιστοιχεί στη σύσταση x της τροφοδοσίας. Επομένως, η q-line έχει προσδιοριστεί. Παρόμοια, η γραμμή λειτουργίας του τμήματος εμπλουτισμού έχει εξίσωση y n 1 = R R 1 x x D n R 1. Τότε, η κλίση της ευθείας είναι R/(R+1) = 1.59/( ) = 0.615, ενώ αν θέσουμε x n = 0 βρίσκουμε ότι τέμνει τον άξονα των τεταγμένων στο σημείο x D /(R + 1) = 0.95/( ) = 0.367
4 Με βάση τα παραπάνω μπορούμε να σχεδιάσουμε το διάγραμμα McCabe-Thiele από το οποίο βρίσκουμε αριθμό θεωρητικών βαθμίδων Ν = 14. Πρόβλημα 3 Κλίση της γραμμής q για διάφορες θερμικές καταστάσεις της τροφοδοσίας Να υπολογιστεί η κλίση της γραμμής q στις εξής περιπτώσεις: α) Η τροφοδοσία είναι μίγμα 20% κορεσμένου υγρού 80% ατμών στις συνθήκες τροφοδοσίας β) Η τροφοδοσία είναι υπέρθερμος ατμός και 1 mol εξατμίζεται στη βαθμίδα τροφοδοσίας για 9 mol εισερχόμενου ατμού. γ) Η τροφοδοσία είναι υπόψυκτο υγρό θερμοκρασίας 35 ο C χαμηλότερης της θερμοκρασίας βρασμού Τ ΒΡ της τροφοδοσίας. Δίνονται η ειδική θερμότητα του υγρού, C PL = 30 kj/mol και η θερμότητα εξάτμισης ΔH = kj/mol. Λύση α) Το μέρος της τροφοδοσίας που είναι ατμός, με παροχή V το 80% της συνολικής τροφοδοσίας, ανέρχεται και μαζί με τον ατμό V που προέρχεται από τον αναβραστήρα δίνουν τη ροή V που θα καταλήξει ως απόσταγμα στην κορυφή. Αντίστοιχα, το μέρος της τροφοδοσίας που είναι υγρό,
5 με παροχή L το 20% της συνολικής τροφοδοσίας, κατερχόμενο ενώνεται με την αναρροή L που προέρχεται από το συμπυκνωτήρα στην κορυφή της στήλης και δίνουν τη ροή υγρού L διαμέσου της στήλης που θα καταλήξει στον αναβραστήρα του πυθμένα. Έτσι, ισχύουν τα εξής: V L L =0.2 και L=L 0.2 άρα: q= L L = L 0.2 L =0.2, V, L Κλίση της γραμμής λειτουργίας: q q 1 = = 0.25 V L β) Εδώ έχουμε την εξής κατάσταση: όλη η τροφοδοσία είναι ατμός και ανέρχεται μαζί με τη ροή ατμού V που προέρχεται από τον αναβραστήρα, αλλά επίσης και ένα μέρος του συμπυκνώματος που κατέρχεται από την κορυφή εξατμίζεται (1 mol αυτού για 9 mol τροφοδοσίας) και ανέρχεται ως ατμός παροχής έστω V L. Τότε ισχύουν: V L V L = 9 και L=L V L q= L L L = 9 L = 1 9 V V L L Κλίση της γραμμής λειτουργίας: 1 q q 1 = 9 1 = γ) Εδώ είναι η αντίστροφη κατάσταση από την προηγούμενη. Όλη η τροφοδοσία κατερχόμενη ως υγρό ενώνεται με την υγρή αναρροή που κατέρχεται από την κορυφή της στήλης και επιπλέον συμπυκνώνεται και ένα μέρος του ανερχόμενου ατμού, έστω L V, το οποίο επίσης κατέρχεται και με τα δύο προηγούμενα δίνουν το ρεύμα L. Επειδή όμως δε μας δίνεται πόσο είναι το μέρος του ατμού που συμπυκνώνεται, θα το βρούμε με τη βοήθεια ενός ισοζυγίου θερμότητας που θα συνδυάσουμε με το ισοζύγιο μάζας. V L Ισοζύγιο μάζας: L=L L V Ισοζύγιο ενέργειας: C PL T BP T =L V H L V άρα: L V = C PL T BP T H και αντικαθιστώντας στο ισοζύγιο μάζας έχουμε: L L =q= C T T H PL BP = =1.07 H V L
6 Κλίση της γραμμής λειτουργίας: q q 1 = =15.28 Πρόβλημα 4 Θερμοκρασίες τροφοδοσίας κορυφής και πυθμένα στήλης Κορεσμένο ισομοριακό μίγμα κανονικού πεντανίου-κανονικού εξανίου διαχωρίζεται σε αποστακτική στήλη προς απόσταγμα 5% mol C6 και υπόλειμμα 5%mol C5 σε ατμοσφαιρική πίεση. α) Ποιες οι θερμοκρασίες τροφοδοσίας, αποστάγματος (πριν και μετά το συμπυκνωτήρα) και υπολείμματος για τη δεδομένη πίεση; β) Ποια η πίεση λειτουργίας ώστε να είναι δυνατή η χρήση νερού ως ψυκτικού αν το νερό έχει ανώτερη επιτρεπτή θερμοκρασία εξόδου T C 2 45 o C ; Να θεωρηθεί ότι για να έχουμε καλή λειτουργία του συμπυκνωτήρα χρειάζεται θερμοκρασιακή διαφορά τουλάχιστον ΔΤ = 10 ο C. Λύση: Σύνοψη των δεδομένων: x = 0.5 (ισομοριακό μίγμα), q = 1 (κορεσμένη τροφοδοσία), x D = 0.95, x B = 0.05, P = 1at, T C 2 45 o C, T =T DP T C 2 =10 o C (τα κλάσματα δίνονται ως προς το πτητικότερο συστατικό -πεντάνιο- και T DP = σημείο δρόσου). Ζητούμενα: T, T V, T D, T B, P για T C2. Θα στηριχτούμε από τις προφανείς σχέσεις y i = k i x i =1 και x i = y i /k i =1 (τα αθροίσματα των μοριακών κλασμάτων είναι ίσα με 1, εξ ορισμού). Για το ερώτημα (α), για πίεση Ρ = 1 at θα δοκιμάσουμε διάφορες θερμοκρασίες Τ και από το διάγραμμα De Priester (ή εν γένει δεδομένα ισορροπίας που μπορεί να υπάρχουν σε διάγραμμα, πίνακα ή υπό μορφή εξίσωσης) από τα υγρά κλάσματα x βρίσκουμε τα αέρια κλάσματα y και ελέγχουμε για ποια θερμοκρασία ισχύει y i =1 Για το ερώτημα (β), για θερμοκρασία Τ =T C 2 T δοκιμάζουμε διάφορες πιέσεις Ρ και από το διάγραμμα De Priester (ή εν γένει δεδομένα ισορροπίας) βρίσκουμε μέσω των αερίων κλασμάτων y τα υγρά κλάσματα x και ελέγχουμε για ποια πίεση ισχύει x i =1 Αναλυτικότερα: α) Θερμοκρασία τροφοδοσίας για ατμοσφαιρική πίεση. Από το διάγραμμα De Priester υπολογίζουμε τις σταθερές ισορροπίας για το πεντάνιο και το εξάνιο, k 5 και k 6 αντίστοιχα. Δοκιμάζουμε διάφορες θερμοκρασίες. Για θερμοκρασία 50 ο C βρίσκουμε : x i k i y i = K i x i n-c X 0.5 n-c X 0.5 y i =
7 Άρα, η θερμοκρασία τροφοδοσίας είναι T 50 o C. Θερμοκρασία κορυφής (υγρού αποστάγματος) Με ανάλογο τρόπο, δοκιμάζουμε διάφορες θερμοκρασίες και για θερμοκρασία 37 ο C βρίσκουμε x i k i y i = K i x i n-c X 0.95 n-c X 0.05 y i = Άρα, η θερμοκρασία του υγρού αποστάγματος είναι T D 37 o C. Θερμοκρασία κορυφής (ατμού) Εδώ, επειδή έχω να κάνω με ατμό, τα κλάσματα είναι τα y και πρέπει να βρω τα αντίστοιχα x που δίνουν άθροισμα ίσο με τη μονάδα. Για θερμοκρασία 39 ο C βρίσκω: y i k i x i = y i / k i n-c / 1.10 n-c / 0.34 x i = Άρα, η θερμοκρασία του ατμού είναι T V 39 o C. Να σημειωθεί ότι οι δύο θερμοκρασίες Tv και TD διαφέρουν επειδή έχουμε μίγμα και όχι καθαρό συστατικό (αν είχαμε καθαρή ουσία, τότε θα μπορούσαμε να έχουμε συμπύκνωση του κορεσμένου ατμού σε σταθερή θερμοκρασία). Θερμοκρασία θερμοκρασία έναρξης υγροποίησης ως προς y θερμοκρασία έναρξης βρασμού ως προς x D Η μεταβολή που συμβαίνει στο μίγμα απεικονίζεται στο διπλανό διάγραμμα θερμοκρασίας συστάσεων (οι κλίμακες δεν είναι σωστές γιατί το διάγραμμα έγινε μόνο για λόγους επίδειξης των βασικών εννοιών). Τα σημεία που αποτελούν την πράσινη γραμμή αντιπροσωπεύουν συνύπαρξη x, y ατμού και υγρού. Πάνω από την καμπύλη της ΘΕΥ έχουμε μόνο ατμό, ενώ κάτω από την καμπύλη της ΘΕΒ έχουμε μόνο υγρό. V T V =39 o C T D =37 o C
8 Θερμοκρασία πυθμένα Με ανάλογο τρόπο, δοκιμάζουμε διάφορες θερμοκρασίες και για θερμοκρασία 70 ο C βρίσκουμε x i k i y i = K i x i n-c X 2.60 n-c X 1.00 y i = Άρα, η θερμοκρασία του υπολείμματος είναι T Β 70 o C. β) Νέα πίεση λειτουργίας Με αναφορά στο διπλανό σχήμα: T =T DP T C 2 =10 o C T V =55 o C Για τη δεδομένη θερμοκρασία T V 55 o C δοκιμάζουμε διάφορες πιέσεις στο διάγραμμα De Priester για τον ατμό, ώστε να βρούμε x i =1. Για πίεση Ρ = 2.2at βρίσκουμε: y i k i x i = y i / k i n-c / 1.20 n-c / 0.42 x i = άρα, η στήλη θα λειτουργήσει σε πίεση περίπου 2.2 ατμοσφαιρών για να έχουμε τη δεδομένη θερμοκρασία του νερού ψύξης. Πρόβλημα 5 Θερμικό φορτίο συμπυκνωτήρα και αναβραστήρα Δυαδικό μίγμα Α/Β 40% mol Α, εισάγεται με παροχή = 0.1 kmol/s στο σημείο βρασμού του σε αποστακτική στήλη που λειτουργεί σε ατμοσφαιρική πίεση. Οι συστάσεις εξόδου είναι 95% Α για το απόσταγμα και 5% Α για το υπόλειμμα. Ο λόγος αναρροής είναι R = 3. Ζητούνται: θερμικό φορτίο συμπυκνωτήρα (q C ) και αναβραστήρα (q R ). Οι ενθαλπίες των ρευμάτων είναι (σε kj/mol) H = 10300, H D = 3340, H B = και η θερμοκρασία εξάτμισης του μίγματος στη θερμοκρασία κορυφής είναι ΔH v D = Λύση: Σύνοψη των δεδομένων: x = 0.4, x D = 0.95, x B = 0.05, = 0.1 kmol/s, R = 3, T = T BP (ΘΕB), H = 10300, H D = 3340, H B = 14700, ΔH v D = (όλα σε kj/mol), P = 1at. Ζητούμενα: q C, q R.
9 Για τη λύση του προβλήματος αρχίζουμε με ισοζύγιο μάζας (ολικό και συστατικών) και υπολογίζουμε τα D, V και Β. Από ισοζύγια μάζας και ενθαλπίας στο συμπυκνωτήρα βρίσκουμε το θερμικό του φορτίο, q C και με τη βοήθειά του, από ισοζύγια μάζας και ενθαλπίας στον αναβραστήρα βρίσκουμε και το δικό του θερμικό φορτίο, q R. Ολικό ισοζύγιο για όλη τη στήλη: = B + D Ισοζύγιο του Α για όλη τη στήλη: x =x D D x B B Επομένως x =x D D x B D από το οποίο βρίσκουμε: D= x x B =0.1 x D x B =0.039 άρα, D = kmol / s Με ανάλογο τρόπο για το Β βρίσκουμε: B= x x D =0.1 x D x B =0.061 άρα, D = kmol / s Ισοζύγιο για το προϊόν κορυφής: V = D + L Λόγος αναρροής: R= L L= RD D Από τις δύο παραπάνω σχέσεις προκύπτει V =D R 1 = =0.156 άρα, V = kmol / s Καταστρώνουμε τα ισοζύγια για τον συμπυκνωτήρα: Ισοζύγιο μάζας: V =L D Ισοζύγιο θερμότητας: V H V = D H D L H L q C Τα H V και H C είναι άγνωστα, αλλά: υποθέσαμε κορεσμένο υγρό (όχι περαιτέρω μεταβολή θερμοκρασίας υγρού κατά τη συμπύκνωση) τα υγρά L και το D προέρχονται από το ίδιο συμπυκνωμένο ρεύμα που εξέρχεται από το συμπυκνωτήρα, άρα H L = H D τότε, το H V διαφέρει από το H D κατά ΔH D (η ενθαλπία του ατμού είναι η ενθαλπία του κορεσμένου υγρού συν τη θερμότητα εξάτμισης).
10 Τότε, μπορούμε να ξαναγράψουμε το ισοζύγιο θερμότητας ως εξής: q C = V H D D H D L H D = V H D D L H D = V H D V H D = V H V από όπου βρίσκουμε ότι ο συμπυκνωτήρας απομακρύνει θερμότητα με ρυθμό q C = = 3691kW Τώρα, αν καταστρώσουμε ένα ισοζύγιο θερμότητας για όλη τη στήλη (ώστε να έχουμε μόνο γνωστά ρεύματα), έχουμε τα εξής: Είσοδοι θερμότητας: q R (ζητούμενο φορτίο αναφραστήρα), H Έξοδοι θερμότητας: D H D, B H B, q C Άρα έχουμε το εξής γενικό ισοζύγιο: q R H = D H D B H B q C από όπου εύκολα λύνουμε ως προς qr και με απλή αντικατάσταση των γνωστών ποσοτήτων βρίσκουμε: q R =3680 kw Στα επόμενα προβλήματα, καλείστε να σχεδιάσετε τα απαραίτητα διαγράμματα (καμπύλες ισορροπίας, γραμμές λειτουργίας κλπ) σύμφωνα με την περιγραφόμενη λύση. Πρόβλημα 6 Απαιτούμενο νερό ψύξης στο συμπυκνωτήρα και ατμός θέρμανσης στον αναβραστήρα Στήλη κλασματικής απόσταξης τροφοδοτείται με 10000kg/h μίγματος βενζολίου/τολουολίου περιεκτικότητας 40% κατά βάρος σε βενζόλιο (Β). Το απόσταγμα έχει σύσταση 96% Β και το υπόλειμμα 98% σε τολουόλιο (Τ), κατά βάρος. Η τροφοδοσία είναι κορεσμένο υγρό, η πίεση λειτουργίας 1 at και ο λόγος αναρροής είναι R = 1.1 Rmin. Η σχετική πτητικότητα είναι a B/T = 2.5 και η στήλη είναι εφοδιασμένη με ολικό συμπυκνωτήρα και συνήθη αναβραστήρα. Ζητούνται: α) παροχές αποστάγματος και υπολείμματος σε kmol/h β) αριθμός δίσκων για βαθμό απόδοσης 0.7 γ) ποιος είναι ο (θεωρητικός) δίσκος εισαγωγής της τροφοδοσίας δ) η απαιτούμενη ποσότητα νερού ψύξης (m 3 /h) αν αυτό θερμαίνεται κατά 20 ο C. ε) Ποσότητα ατμού θέρμανσης, αν αυτός είναι κορεσμένος και σε πίεση 3 atm. Δίνονται: Η ισορροπία ατμού-υγρού περιγράφεται από την προσεγγιστική σχέση y= 1 a A/B 1 x Θερμοφυσικά δεδομένα για το βενζόλιο, το τολουόλιο και τον ατμό: Ενθαλπία εξάτμισης βενζολίου H vap B = kj/kmol Σημείο βρασμού βενζολίου Τ b B =80.1 o C Ενθαλπία εξάτμισης τολουολίου H vap B = kj/kmol Σημείο βρασμού τολουολίου Τ b B =110.6 o C Ενθαλπία συμπύκνωσης ατμού H con S = kj/kmol a A/B Λύση:
11 Σύνοψη δεδομένων και αγνώστων: = kg.h 40% (B) κ.β. D =??? 96% (B) κ.β. B =??? 98% (Τ) κ.β. q = 1 (κορεσμένο υγρό τροφοδοσίας) R = 1.1Rmin =??? P = 1at, a B/T = 2.5 E = 0.7 T c2 T c1 = 20oC, P S = 3at MB T BP ( o C) ΔΗ V (kj/kmol) B T Συνοπτική περιγραφή λύσης: α) Πριν από όλα τα άλλα, μετατρέπω τα κλάσματα βάρους σε μοριακά, αφού οι άγνωστες παροχές ζητούνται σε kmol και τα θερμοφυσικά δεδομένα δίνονται επίσης σε kj/kmol. Μετά κάνω ισοζύγια μάζας για όλη τη στήλη β-γ) Κάνω το διάγραμμα ισορροπίας με τη βοήθεια της δεδομένης σχέσης, από τα δεδομένα για q (θερμική κατάσταση τροφοδοσίας) και R βρίσκω τις κλίσεις των γραμμών λειτουργίας και γραφικά βρίσκω τον αριθμό βαθμίδων και τη βαθμίδα εισαγωγής τροφοδοσίας. Επίσης, από το βαθμό απόδοσης βρίσκω και τις πραγματικές βαθμίδες δ) Κάνω ολικά ισοζύγια θερμότητας και μάζας στο συμπυκνωτήρα. ε) Ομοίως για τον αναβραστήρα. Αναλυτικότερα: α) x = =0.44, x D = =0.966, x B = = Μέσο Μοριακό Βάρος τροφοδοσίας ΜΒ = 0.44 X (1-0.44) X = 86 = / MB = / 86 = kmol/h D= x x B x D x B (βλ. πρόβλημα 5), άρα D=116.3 Ομοίως, =51.4 kmol/h B= x x D (βλ. πρόβλημα 5), άρα D=116.3 =64.9 kmol/h x D x B β) Εδώ ακολουθούμε τα εξής βήματα: β1) Από την προσεγγιστική σχέση που δίνεται στην εκφώνηση, y= x κατασκευάζουμε την καμπύλη ισορροπίας για διάφορα σημεία β2) Φέρουμε τη γραμμή-q κατακόρυφα από το σημείο x = 0.44 (= μοριακό κλάσμα βενζολίου που βρήκαμε στο (α)), επειδή κορεσμένο υγρό τροφοδοσίας σημαίνει q = 1 και κλίση γραμμής-q =. β3) Ορίζουμε το σημείο Α x D = (= σύσταση αποστάγματος που βρήκαμε στο (α)) στην κύρια διαγώνιο y = x και το ενώνουμε με το σημείο Τ όπου τέμνονται η καμπύλη ισορροπίας με τη γραμμή -q. Η ευθεία που προκύπτει είναι η γραμμή λειτουργίας του τμήματος εμπλουτισμού για τον ελάχιστο λόγο αναρροής Rmin (= άπειρες βαθμίδες). β4) Επειδή η παραπάνω γραμμή λειτουργίας υπακούει στη σχέση y= R R 1 x x D R 1, an
12 υπολογίσουμε την κλίση της R min R min 1 θα μπορέσουμε να βρούμε και το Rmin. Αλλά η κλίση της, y σημείο Α y σημείο Τ όπως προκύπτει από την κατασκευή της ευθείας είναι και επειδή το y σημείο Α y σημείο Τ σημείο Α ορίστηκε στην κύρια διαγώνιο y = x για τη σύσταση του αποστάγματος και το σημείο Τ στην καμπύλη ισορροπίας για τη σύσταση τροφοδοσίας, τελικά για την κλίση θα ισχύει R min R min 1 = x y D T = x D x =0.58 (η σύσταση y T μπορεί να υπολογιστεί είτε από τη γραφική παράσταση φέροντας την οριζόντιο από το σημείο Τ μέχρι τον άξονα των y είτε από τη σχέση που δόθηκε για την καμπύλη ισορροπίας) και από αυτά υπολογίζω Rmin = β5) Υπολογίζω τον πραγματικό λόγο αναρροής R = 1.1 Rmin = 1.53 β6) Βρίσκω την πραγματική γραμμή λειτουργίας του άνω τμήματος (τη γραμμή λειτουργίας για τον πραγματικό λόγο αναρροής): R κλίση: R 1 = =0.605 x αποτέμνουσα: D R 1 = =0.382 β7) Από την άνω γραμμή λειτουργίας που μόλις προσδιορίσαμε, βρίσκουμε το σημείο τομής Τ' με τη γραμμή-q. Αλλά αυτό είναι υποχρεωτικά και σημείο της κάτω γραμμής λειτουργίας (του τμήματος εξάντλησης). β8) Από το σημείο τομής Τ' και το σημείο Β της κύριας διαγωνίου y = x για x = x B = 0.023, ορίζουμε την κάτω γραμμή λειτουργίας. β9) Τώρα έχουμε στη διάθεσή μας το διάγραμμα που μας επιτρέπει να βρούμε το θεωρητικό αριθμό βαθμίδων που προκύπτει ότι είναι Ν = 17. β10) Οι πραγματικές βαθμίδες θα είναι ο δίσκος τροφοδοσίας + αριθμός που προκύπτει για τις υπόλοιπες βάσει του βαθμού απόδοσης. Νπ = 1 + (Ν-1)/0.7 = /0.7 = 23 γ) Από το διάγραμμα προκύπτει ότι θεωρητική βαθμίδα τροφοδοσίας = 8. δ) Επειδή θερμικό φορτίο συμπυκνωτήρα = θερμότητα για τη συμπύκνωση αποστάγματος = θερμότητα γαι αύξηση θερμοκρασίας νερού, μπορούμε να γράψουμε: V q C =V H V H D =V H D και q C =m C C P W T C2 T C 1 Επειδή το απόσταγμα έχει πολύ υψηλή περιεκτικότητα σε βενζόλιο, μπορούμε κατά προσέγγιση να χρησιμοποιήσουμε τις θερμοφυσικές ιδιότητες του βενζολίου, ενώ επίσης από το ισοζύγιο μάζας στον ολικό συμπυκνωτήρα έχουμε: V = L + D = RD + D = (R+1)D. Από τα παραπάνω προκύπτει q C = = m C => m C =4775 m 3 / h ε) Όσον αφορά τον αναβραστήρα, θεωρούμε ότι έχουμε κορεσμένο ατμό που συμπυκνώνεται εξ ολοκλήρου για να θερμάνει το υπόλειμμα που επιστρέφει ως ατμός στη στήλη. Τότε ισχύει q R =V H vap con T = m S H S. Επειδή το υπόλειμμα έχει πολύ υψηλή περιεκτικότητα σε τολουόλιο, μπορούμε κατά προσέγγιση να χρησιμοποιήσουμε τις θερμοφυσικές ιδιότητες του τολουολίου, ενώ επίσης κάνουμε την παραδοχή ότι V =V οπότε παίρνουμε m S = => ṁ S =2008.1kg / h
13 Πρόβλημα 7 Επίδραση θερμικής κατάστασης τροφοδοσίας στα θερμικά φορτία συμπυκνωτήρα και αναβραστήρα Στήλη κλασματικής απόσταξης τροφοδοτείται με μίγμα σε υγρή κατάσταση, κατά 45%mol βενζόλιο και κατά 55%mol τολουόλιο. Το προϊόν κορυφής είναι κατά 90% Β και το προϊόν πυθμένα είναι κατά 90% Τ. Ο λόγος αναρροής είναι R = 3 και η στήλη λειτουργεί σε ατμοσφαιρική πίεση. Η θερμοκρασία τροφοδοσίας είναι 48 ο C και η παροχή 100 kmol/h. Ζητούνται: α) Οι θεωρητικές βαθμίδες και η βαθμίδα τροφοδοσίας β) Οι παροχές αποστάγματος D, υπολείμματος Β, ατμών V, V, υγρού L, L σε kmol/h και ο ελάχιστος λόγος αναρροής Rmin. γ) Τα θερμικά φορτία αναβραστήρα, q R, συμπυκνωτήρα, q C, σε kw, το απαιτούμενο νερό ψύξης θερμοκρασίας εισόδου 15 ο C, ώστε η έξοδός του να είναι 37 ο C κάτω από το προϊόν κορυφής στην έξοδο του συμπυκνωτήρα. δ) Το θερμικό φορτίο του αναφραστήρα όταν η τροφοδοσία είναι: 1) κορεσμένο υγρό, 2) κορεσμένος ατμός 3) υπέρθερμος ατμός στους 130 ο C. Δίνονται: Μέσες θερμοφυσικές σταθερές στήλης: Θερμότητας εξάτμισης ΔΗ S = kj/kmol Ειδική θερμότητα υγρού CP L = 154 kj/kmolk Ειδική θερμότητα ατμού CP V = 115 kj/kmolk Ειδική θερμότητα νερού CP W = kj/kmolk Δεδομένα ισορροπίας βενζολίου: Τ, ο C x Y Λύση: Συνοψίζουμε τα βήματα που θα ακολουθήσουμε α) Υπολογίζουμε q από δεδομένα θερμότητας με τη βοήθεια των δεδομένων ισορροπίας. Κατασκευάζουμε τη γραμμή-q και τη γραμμή λειτουργίας και από αυτά τα δεδομένα, το διάγραμμα McCabe-Thiele και βρίσκουμε βαθμίδες. β) Ισοζύγια μάζας κατά τα γνωστά γ) Ισοζύγιο θερμότητας και με τη βοήθεια των δεδομένων ισορροπίας για υπολογισμό θερμοκρασίας βρασμού. T δ) για υπέρθερμο ατμό q= C T DP, PV H, για κορεσμένο υγρό q = 1, για κορεσμένο ατμό q = 0. Προκύπτει μεταβολή μόνο στο q R (όσο πιο κρύα είναι η τροφοδοσία τόσο μεγαλώνει). Αναλυτικότερα, α) Για υπόψυκτη τροφοδοσία: q= H C T T PL BP, H της τροφοδοσίας., όπου T BP, η θερμοκρασία βρασμού Από τα σημεία των δεδομένων ισορροπίας μπορούμε να κατασκευάσουμε το διάγραμμα θερμοκρασίας-σύστασης, Τ-xy, από το οποίο βλέπουμε ότι για σύσταση X = 0.45 έχουμε θερμοκρασία βρασμού T BP = 93.5 o C, οπότε βρίσκουμε q= =1.25, 28000
14 q άρα η κλίση της γραμμής θερμικής κατάστασης τροφοδοσίας είναι q 1 = 1.25 =5. Άρα, η γραμμή-q θα είναι της μορφής y = 5x + β, όπου τo β είναι άγνωστο. Αλλά η σχέση αυτή θα ισχύει και για το σημείο τομής της κύριας διαγωνίου y = x στη σύσταση της τροφοδοσίας: x =5x = 4x, οπότε τελικά βρίσκουμε για την εξίσωση της q-γραμμής: y = 5x 1.8 Η γραμμή λειτουργίας του άνω τμήματος θα διέρχεται από το σημείο (x D, x D ) και θα έχει κλίση R R 1 = 3 4 =0.75. Άρα, θα πρέπει να ισχύει x D =0.75 x D =0.25 x D = Θα μπορούσαμε επίσης να πούμε ότι η αποτέμνουσα της γραμμής λειτουργίας είναι x D R 1 = =0.225 Έτσι, η γραμμή λειτουργίας του τμήματος εμπλουτισμού είναι y = 0.75x Από το σημείο τομής των δύο γραμμών φέρουμε την ευθεία μέχρι το σημείο με συντεταγμένες (x B, x B ) και έτσι ορίζουμε τη γραμμή λειτουργίας του τμήματος εξάντλησης. Αν από τα δεδομένα ισορροπίας T-xy πάρουμε τα ζεύγη (x, y) έχουμε και την καμπύλη ισορροπίας. Έχοντας στη διάθεσή μας την καμπύλη ισορροπίας και τις γραμμές λειτουργίας, μπορούμε να υπολογίσουμε γραφικά τις θεωρητικές βαθμίδες (Ν = 7) και τη βαθμίδας εισαγωγής τροφοδοσίας (N = 3). β) Όπως έχουμε δει σε προηγούμενα προβλήματα, από ισοζύγιο μάζας για όλη τη στήλη προκύπτει ότι D= x x B =100 x D x B => D=43.75 kmol/h και B= x x D =100 x D x B => B=56.25 kmol/h Από τον ορισμό του λόγου αναρροής: L = RD = 3 X => L= kmol/h V = L + D = RD + D = (R+1)D = X (3 + 1) => V =175 kmol/h Για να υπολογίσουμε τα V, L θα λάβουμε υπ' όψιν το ποσοστό ατμού στην τροφοδοσία, (q-1) και το αντίστοιχο ποσοστό υγρού, q. Τότε ισχύει: V =V q 1 = => V =200 kmol/h L=L q = => L= kmol/h Όσον αφορά τον ελάχιστο λόγο αναρροής, η αντίστοιχη γραμμή λειτουργίας θα τέμνει τη γραμμή θερμικής κατάστασης τροφοδοσίας πάνω στη γραμμή ισορροπίας, έστω στο σημείο Τ. Γραφικά, μπορούμε να βρούμε X T 0.51 και Y T 0.72, οπότε θα ισχύει R min R min 1 = x y D T = x D x T => R min =0.85 γ) q C =V H V H D =V H D = μετατρέψω τις μονάδες σε kj / s = kw) q R =V H V H L =V H B = => q C =1361,1 kw (διαίρεσα με 3600 για να => q C = kw Από τα δεδομένα θερμοκρασίας σύστασης, Τ-xy, αν παρασταθούν γραφικά, βρίσκουμε ότι για τη
15 σύσταση του αποστάγματος x D = 0.9, προκύπτει θερμοκρασία βρασμού αποστάγματος T BP, D = 82 o C. Τότε η σχέση μεταξύ του θερμικού φορτίου του συμπυκνωτήρα και της θερμότητας που ανταλλάσσει το νερό είναι: m C C PW T C 2 T C 1 = q C m C = θεωρήσουμε πυκνότητα νερού ίση με τη μονάδα. => m C =10.8 kg/s ή περίπου 39 m 3 /h, αν δ) Από τα δεδομένα θερμοκρασίας σύστασης, Τ-xy, αν παρασταθούν γραφικά, βρίσκουμε ότι για τη σύσταση της τροφοδοσίας x Β = 0.45, προκύπτει θερμοκρασία βρασμού τροφοδοσίας T BP, Β = 100 o C. Τότε βρίσκουμε: T q= C T ΒP, PV = H => q = -0.2 (υπέρθερμος ατμός). Συνοψίζουμε αποτελέσματα για διάφορες καταστάσεις θερμικής κατάστασης τροφοδοσίας στον παρακάτω πίνακα: Κατάσταση q V (kmol/h) q C (kw) V (kmol/h) q R (kw) κορεσμένο υγρό V =V = κορεσμένος ατμός V = (0-1) 100 = υπέρθερμος ατμός V = ( ) 100 = Παρατηρούμε ότι το φορτίο του συμπυκνωτήρα, q C, είναι σταθερό ενώ το φορτίο του αναβραστήρα, q R, μεγαλώνει όσο πιο ψυχρή είναι η τροφοδοσία, επειδή πρέπει να δώσει περισσότερη θερμότητα για να παραχθεί ατμός που θα ανακυκλοφορεί από τον πυθμένα της στήλης. Πρόβλημα 8 Μέθοδος enske Underwood Gilliland Μίγμα σύστασης 20%mol σε μετα-ξυλένιο (m) και 80%mol σε ορθοξυλένιο (o) τροφοδοτείται ως κορεσμένο υγρό σε στήλη κλασματικής απόσταξης συνεχούς λειτουργίας, σε ατμοσφαιρική πίεση και για λόγο αναρροής R = 1.5Rmin. Το απόσταγμα έχει σύσταση 95% m και το απόσταγμα 5% m. Ζητείται ο αριθμός θεωρητικών βαθμίδων. Δεδομένα τάσεων ατμών καθαρών συστατικών στην ισορροπία: T, o C P o (mmhg) P o (mmhg) Λύση Από τις τιμές όπου η τάση ατμών κάθε συστατικού γίνεται ίση με την ατμοσφαιρική πίεση (= σημείο βρασμού) καθορίζω και το εύρος θερμοκρασιών που με ενδιαφέρει, γιατί ο διαχωρισμός απαιτεί το ένα συστατικό να είναι πάνω από το σημείο ζέσεώς του ενώ το άλλο κάτω από το δικό του σημείο ζέσεως. Για το εύρος αυτό, καθορίζω και τη σχετική πτητικότητα a m/o = P o m/p o o όπως φαίνεται στον επόμενο πίνακα: T, o C P o (mmhg) P o (mmhg) a m/o
16 Παρατηρώ ότι η μέση σχετική πτητικότητα a m/o, είναι περίπου 1.15 δηλαδή πολύ κοντά στη μονάδα, που σημαίνει ότι είναι δύσκολος διαχωρισμός (αυτό άλλωστε φαίνεται και από το ότι τα σημεία ζέσεως 140 και 145, των δύο συστατικών, είναι πολύ κοντά μεταξύ τους). Λόγω του δύσκολου διαχωρισμού και των λίγων δεδομένων (μόνο 4 σημεία για το εύρος μεταξύ των δύο σημείων ζέσεως), η γραφική λύση δεν ενδείκνυται. Θα καταφύγουμε στις εξισώσεις enske- Underwood και το διάγραμμα Gilliland *. Η εξίσωση enske για πλήρη αναρροή, μας δίνει τον ελάχιστο αριθμό βαθμίδων ως συνάρτηση των συστάσεων υπολείμματος-αποστάγματος και της μέσης σχετικής πτητικότητας: N min = x log D log 1 x B log log 1 x D x B = log a m/o log 1.15 =42.12 Οι εξισώσεις Underwood συσχετίζουν τον ελάχιστο λόγο αναρροής Rmin με τις συστάσεις τροφοδοσίας και αποστάγματος, τη μέση σχετική πτητικότητα και τη θερμική κατάσταση της τροφοδοσίας (στην προκειμένη περίπτωση, q = 1), μέσω μιας προσδιοριστέας παραμέτρου Θ. Underwood (1): a m/o x a m/o 1 x Underwood (2): 1 =1 q <=> R min 1= a m/o x D a m/o 1 x D 1 <=> =0 = =R min R min =1.43 Το διάγραμμα Gilliland συσχετίζει τις ποσότητες R R βρίσκουμε min R 1 = N N δίνει min N 1 = N N =69. N 1 R R min R 1 και N N min N 1. Εν προκειμένω = Για το σημείο αυτό, το διάγραμμα Gilliland * βλ. σελ. 204 από το βιβλίο του μαθήματος
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
Κεφάλαιο 4 Κλασματική Απόσταξη
 Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
(β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele
 Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ
 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
Διάλεξη 4β. Συστοιχίες διαχωρισμών
 Διάλεξη 4β Συστοιχίες διαχωρισμών Διαχωρισμός σε απλή στήλη Απλή τροφοδοσία Δύο ρεύματα εξόδου Προσκείμενα κλειδιά διαχωρισμού Στήλη με απλό αναβραστήρα και συμπυκνωτήρα Φθίνουσα πτητικότητα E () Ελαφρύ
Διάλεξη 4β Συστοιχίες διαχωρισμών Διαχωρισμός σε απλή στήλη Απλή τροφοδοσία Δύο ρεύματα εξόδου Προσκείμενα κλειδιά διαχωρισμού Στήλη με απλό αναβραστήρα και συμπυκνωτήρα Φθίνουσα πτητικότητα E () Ελαφρύ
ΣΤ' Εξάμηνο ΣΧΕΔΙΑΣΜΟΣ ΧΗΜΙΚΩΝ ΒΙΟΜΗΧΑΝΙΩΝ ΚΑΙ ΔΙΕΡΓΑΣΙΩΝ. Ερωτήσεις Επανάληψης Δεύτερο Μέρος
 ΣΤ' Εξάμηνο ΣΧΕΔΙΑΣΜΟΣ ΧΗΜΙΚΩΝ ΒΙΟΜΗΧΑΝΙΩΝ ΚΑΙ ΔΙΕΡΓΑΣΙΩΝ 2008 2009 Ερωτήσεις Επανάληψης Δεύτερο Μέρος 0 Ερώτηση: Σε αντιδραστήρα για τη μετατροπή κυκλοεξανόλης σε κυκλοεξανόνη, παρέχεται και μίγμα αντιδρώντος
ΣΤ' Εξάμηνο ΣΧΕΔΙΑΣΜΟΣ ΧΗΜΙΚΩΝ ΒΙΟΜΗΧΑΝΙΩΝ ΚΑΙ ΔΙΕΡΓΑΣΙΩΝ 2008 2009 Ερωτήσεις Επανάληψης Δεύτερο Μέρος 0 Ερώτηση: Σε αντιδραστήρα για τη μετατροπή κυκλοεξανόλης σε κυκλοεξανόνη, παρέχεται και μίγμα αντιδρώντος
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
2 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ
 ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2 ΣΗΜΑΝΤΙΚΟΙ ΟΡΟΙ Αδιαβατικό σύστημα Ισοβαρές σύστημα Ισόχωρο σύστημα Ισοθερμοκρασιακό σύστημα Μεταβλητή διαδρομής (συνάρτηση μετάβασης) Καταστατική μεταβολή (σημειακή
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2 ΣΗΜΑΝΤΙΚΟΙ ΟΡΟΙ Αδιαβατικό σύστημα Ισοβαρές σύστημα Ισόχωρο σύστημα Ισοθερμοκρασιακό σύστημα Μεταβλητή διαδρομής (συνάρτηση μετάβασης) Καταστατική μεταβολή (σημειακή
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
 ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ
 ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
Προβλήματα εκχύλισης
 Προβλήματα εκχύλισης Πηγή: Μαρίνου-Κουρή, Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, εκδ. Παπασωτηρίου, Αθήνα, 1994 1. Εκχύλιση ακετόνης από νερό με χλωροβενζόλιο σε μονοβάθμιο εκχυλιστήρα. 100 kg διαλύματος
Προβλήματα εκχύλισης Πηγή: Μαρίνου-Κουρή, Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, εκδ. Παπασωτηρίου, Αθήνα, 1994 1. Εκχύλιση ακετόνης από νερό με χλωροβενζόλιο σε μονοβάθμιο εκχυλιστήρα. 100 kg διαλύματος
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
10 Ισοζύγια Μάζας & Ενέργειας
 10 Ισοζύγια Μάζας & Ενέργειας Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή φάση, Η ανάλυση
10 Ισοζύγια Μάζας & Ενέργειας Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή φάση, Η ανάλυση
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ & ΕΝΕΡΓΕΙΑΣ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ & ΕΝΕΡΓΕΙΑΣ Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ & ΕΝΕΡΓΕΙΑΣ Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή
Κεφάλαιο 3 Απόσταξη Ισορροπίας
 Κεφάλαιο 3 Απόσταξη Ισορροπίας Σύνοψη Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου
Κεφάλαιο 3 Απόσταξη Ισορροπίας Σύνοψη Η απόσταξη ισορροπίας ή στιγμιαία απόσταξη αποτελεί μία απλή διεργασία διαχωρισμού, η εφαρμογή της οποίας βασίζεται στην ατμοποίηση μέρους της τροφοδοσίας εντός δοχείου
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης 2. Ενέργεια Ενεργοποίησης
 Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
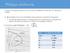 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
P. kpa T, C v, m 3 /kg u, kj/kg Περιγραφή κατάστασης και ποιότητα (αν εφαρμόζεται) , ,0 101,
 Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
. Πρόκειται για ένα σημαντικό βήμα, καθώς η παράμετρος χρόνος υποχρεωτικά μεταβάλλεται σε κάθε είδους κίνηση. Η επιλογή της χρονικής στιγμής t o
 Στις ασκήσεις Κινητικής υπάρχουν αρκετοί τρόποι για να δουλέψουμε. Ένας από αυτούς είναι με τη σωστή χρήση των εξισώσεων θέσης (κίνησης) και ταχύτητας των σωμάτων που περιγράφονται. Τα βήματα που ακολουθούμε
Στις ασκήσεις Κινητικής υπάρχουν αρκετοί τρόποι για να δουλέψουμε. Ένας από αυτούς είναι με τη σωστή χρήση των εξισώσεων θέσης (κίνησης) και ταχύτητας των σωμάτων που περιγράφονται. Τα βήματα που ακολουθούμε
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ. (χωρίς αντίδραση)
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ (χωρίς αντίδραση) 2 Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία)
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ (χωρίς αντίδραση) 2 Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία)
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
Απορρόφηση Αερίων. 1. Εισαγωγή
 1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ. Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για:
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
 Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Χημικών Μηχανικών Τομέας ΙΙ : Ανάλυσης, Σχεδιασμού και Ανάπτυξης Διεργασιών και Συστημάτων Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Χημικών Μηχανικών Τομέας ΙΙ : Ανάλυσης, Σχεδιασμού και Ανάπτυξης Διεργασιών και Συστημάτων Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ
 1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης
 ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ
 3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού
 Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
(α) (β) (γ) ή (δ) gallons/h? ΙΣΟΖΥΓΙΟ ΑΙΜΟΚΑΘΑΡΣΗΣ ΝΕΦΡΟΠΑΘΩΝ
 Πρόβλημα Α. O δευτερογενής καθαρισμός των αστικών υγρών αποβλήτων αποτελείται από δυο συνεχόμενα τμήματα, του αερισμού και της διαύγασης (κατακάθισης). Τη χώνευση / αφομοίωση επιβλαβών ουσιών από το ρεύμα
Πρόβλημα Α. O δευτερογενής καθαρισμός των αστικών υγρών αποβλήτων αποτελείται από δυο συνεχόμενα τμήματα, του αερισμού και της διαύγασης (κατακάθισης). Τη χώνευση / αφομοίωση επιβλαβών ουσιών από το ρεύμα
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι. Ενότητα 10: Ισορροπίες φάσεων. Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 0: Ισορροπίες φάσεων Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η παρουσίαση και η εξέταση της ισορροπίας ανάμεσα
ΘΕΡΜΟΔΥΝΑΜΙΚΗ Ι Ενότητα 0: Ισορροπίες φάσεων Σογομών Μπογοσιάν Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Σκοπός της ενότητας αυτής είναι η παρουσίαση και η εξέταση της ισορροπίας ανάμεσα
Κεφάλαιο 5: Διεργασίες απόσταξης
 92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
Energy resources: Technologies & Management
 Energy resources: Technologies & Management Θεωρία της καύσης Δρ Γεώργιος Σκόδρας Αναπληρωτής Καθηγητής Σκοπός της καύσης είναι η μετατροπή της χημικής ενέργειας που περιέχεται στο καύσιμο σε θερμική ενέργεια
Energy resources: Technologies & Management Θεωρία της καύσης Δρ Γεώργιος Σκόδρας Αναπληρωτής Καθηγητής Σκοπός της καύσης είναι η μετατροπή της χημικής ενέργειας που περιέχεται στο καύσιμο σε θερμική ενέργεια
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
R T ενώ σε ολοκληρωµένη, αν θεωρήσουµε ότι οι ενθαλπίες αλλαγής φάσεως είναι σταθερές στο διάστηµα θερµοκρασιών που εξετάζουµε, είναι
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων
 Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6
 Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
Αυτόματη ρύθμιση αποστακτικών στηλών
 Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ
 ΠΑΡΑΡΤΗΜΑ 3-ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ 1 Εισαγωγή Τα διαγράμματα φάσεων δεν είναι εμπειρικά σχήματα αλλά είναι ουσιαστικής σημασίας
ΠΑΡΑΡΤΗΜΑ 3-ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΠΑΡΑΡΤΗΜΑ 3 ΥΠΟΛΟΓΙΣΜΟΣ ΔΙΑΓΡΑΜΜΑΤΩΝ ΦΑΣΕΩΝ ΑΠΟ ΘΕΡΜΟΔΥΝΑΜΙΚΑ ΔΕΔΟΜΕΝΑ 1 Εισαγωγή Τα διαγράμματα φάσεων δεν είναι εμπειρικά σχήματα αλλά είναι ουσιαστικής σημασίας
ΟΛΟΚΛΗΡΩΤΙΚΑ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ
 ΟΛΟΚΛΗΡΩΤΙΚΑ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΠΟΡΕΙΑ ΠΡΟΒΛΗΜΑΤΟΣ 3 4 5 6 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ dh dt = q e A h t = h 0 e kt A 7 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ 8 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ q = Kh h t = h 0 e kt A 9 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ
ΟΛΟΚΛΗΡΩΤΙΚΑ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΠΟΡΕΙΑ ΠΡΟΒΛΗΜΑΤΟΣ 3 4 5 6 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ dh dt = q e A h t = h 0 e kt A 7 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ 8 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ q = Kh h t = h 0 e kt A 9 ΔΕΞΑΜΕΝΗ ΑΠΟΣΤΡΑΓΓΙΣΗΣ
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ
 ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΕΝΘΑΛΠΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΕΝΩΣΗΣ Ο θερμοτονισμός ή η θερμότητα της αντίδρασης εκφράζει τη μεταβολή ενέργειας λόγω της χημικής αντίδρασης Η απαιτούμενη ενέργεια για το σχηματισμό
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΕΝΘΑΛΠΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΕΝΩΣΗΣ Ο θερμοτονισμός ή η θερμότητα της αντίδρασης εκφράζει τη μεταβολή ενέργειας λόγω της χημικής αντίδρασης Η απαιτούμενη ενέργεια για το σχηματισμό
Energy resources: Technologies & Management
 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ
 ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ
 ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ 1. Έστω συνάρτηση ζήτησης με τύπο Q = 200 4P. Να βρείτε: α) Την ελαστικότητα ως προς την τιμή όταν η τιμή αυξάνεται από 10 σε 12. 1ος τρόπος Αν P 0 10 τότε Q 0 200 410
ΛΥΜΕΝΕΣ ΕΦΑΡΜΟΓΕΣ ΣΤΟ 2 ο ΚΕΦΑΛΑΙΟ 1. Έστω συνάρτηση ζήτησης με τύπο Q = 200 4P. Να βρείτε: α) Την ελαστικότητα ως προς την τιμή όταν η τιμή αυξάνεται από 10 σε 12. 1ος τρόπος Αν P 0 10 τότε Q 0 200 410
ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE
 ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστηµα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερµου ατµού σε πίεση 0 bar και θερµοκρασία 00 0 C, η δε πίεση στο συµπυκνωτή είναι 0,0 bar Να
ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστηµα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερµου ατµού σε πίεση 0 bar και θερµοκρασία 00 0 C, η δε πίεση στο συµπυκνωτή είναι 0,0 bar Να
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013
 Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Εναλλαγή θερμότητας. Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω)
 Εναλλαγή θερμότητας Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω) Σχ. 4.1 (β) Διάταξη εναλλάκτη θερμότητας καντ` αντιρροή (πάνω) και αντίστοιχο
Εναλλαγή θερμότητας Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω) Σχ. 4.1 (β) Διάταξη εναλλάκτη θερμότητας καντ` αντιρροή (πάνω) και αντίστοιχο
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
P 1 V 1 = σταθ. P 2 V 2 = σταθ.
 ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ 83 Την κατάσταση ενός αερίου μέσα σε ένα δοχείο μπορούμε να την κατανοήσουμε, άρα και να την περιγράψουμε πλήρως, αν γνωρίζουμε τις τιμές των παραμέτρων εκείνων που επηρεάζουν την συμπεριφορά
ΝΟΜΟΙ ΤΩΝ ΑΕΡΙΩΝ 83 Την κατάσταση ενός αερίου μέσα σε ένα δοχείο μπορούμε να την κατανοήσουμε, άρα και να την περιγράψουμε πλήρως, αν γνωρίζουμε τις τιμές των παραμέτρων εκείνων που επηρεάζουν την συμπεριφορά
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΜΑΘΗΜΑ: ΕΦΑΡΜΟΣΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ (Ασκήσεις πράξης) ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ
 ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
ΙΔΑΝΙΚΑ ΑΕΡΙΑ - ΕΡΓΟ 1. Να υπολογιστεί η πυκνότητα του αέρα σε πίεση 0,1 MPa και θερμοκρασία 20 ο C. (R air =0,287 kj/kgk) 2. Ποσότητα αέρα 1 kg εκτελεί τις παρακάτω διεργασίες: Διεργασία 1-2: Αδιαβατική
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
4. 1 Η ΣΥΝΑΡΤΗΣΗ Y=AX 2 ME A 0
 ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 5. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 Ορισμοί Ονομάζουμε συνάρτηση την διαδικασία με την οποία σε κάθε τιμή της μεταβλητής αντιστοιχίζουμε μια μόνο τιμή της μεταβλητής. Ονομάζουμε
ΜΕΡΟΣ Α. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 5. Η ΣΥΝΑΡΤΗΣΗ Y=AX ME A 0 Ορισμοί Ονομάζουμε συνάρτηση την διαδικασία με την οποία σε κάθε τιμή της μεταβλητής αντιστοιχίζουμε μια μόνο τιμή της μεταβλητής. Ονομάζουμε
Λύση Παραδείγματος 1. Διάγραμμα ροής διεργασίας. Εκρόφηση χλωριούχου βινυλίου από νερό στους 25 C και 850 mmhg. Είσοδος υγρού.
 Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Εφηρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 11: Μίγματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφηρμοσμένη Θερμοδυναμική Ενότητα 11: Μίγματα Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΚΕΦΑΛΑΙΟ 4 Ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 103 Α. ΠΡΩΤΟΣ ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΚΕΦΑΛΑΙΟ 4 Ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ 1. Ιδανικό αέριο εκτελεί διαδοχικά τις αντιστρεπτές μεταβολές ΑΒ, ΒΓ, ΓΑ που παριστάνονται στο ακόλουθο διάγραμμα P-V. α. Αν δίνονται Q ΑΒΓ
103 Α. ΠΡΩΤΟΣ ΘΕΡΜΟΔΥΝΑΜΙΚΟΣ ΝΟΜΟΣ ΚΕΦΑΛΑΙΟ 4 Ο ΘΕΡΜΟΔΥΝΑΜΙΚΗ 1. Ιδανικό αέριο εκτελεί διαδοχικά τις αντιστρεπτές μεταβολές ΑΒ, ΒΓ, ΓΑ που παριστάνονται στο ακόλουθο διάγραμμα P-V. α. Αν δίνονται Q ΑΒΓ
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 109 ΙΔΑΝΙΚΑ (ΤΕΛΕΙΑ) ΑΕΡΙΑ Το αέριο που οι συγκρούσεις των μορίων του είναι τελείως ελαστικές
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 109 ΙΔΑΝΙΚΑ (ΤΕΛΕΙΑ) ΑΕΡΙΑ Το αέριο που οι συγκρούσεις των μορίων του είναι τελείως ελαστικές
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
Το διάγραμμα Ρ - h ενός ψυκτικού ρευστού.
 Το διάγραμμα Ρ - h ενός ψυκτικού ρευστού. Επαρκές Σενάριο Γνωστικό αντικείμενο: Μηχανολογία (Ε.Ε.) Δημιουργός: ΚΥΡΙΑΚΟΣ ΚΟΥΡΕΝΤΖΗΣ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ
Το διάγραμμα Ρ - h ενός ψυκτικού ρευστού. Επαρκές Σενάριο Γνωστικό αντικείμενο: Μηχανολογία (Ε.Ε.) Δημιουργός: ΚΥΡΙΑΚΟΣ ΚΟΥΡΕΝΤΖΗΣ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
ΚΕΦΑΛΑΙΟ 3 Ο 3.2 Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η. (Σ) όπου α, β, α, β, είναι οι
 ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα : Εξάτμιση (2/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Ισοζύγια μάζας
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα : Εξάτμιση (2/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Ισοζύγια μάζας
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
Παντελής Μπουμπούλης, M.Sc., Ph.D. σελ. 2 math-gr.blogspot.com, bouboulis.mysch.gr
 VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
ΚΕΦΑΛΑΙΟ 2 Ο «ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ»
 ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΕΠΑΛ ΚΕΦΑΛΑΙΟ Ο «ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ» Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΚΕΦΑΛΑΙΟ ο : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Α ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Πεδίο
ΜΕΘΟΔΟΛΟΓΙΑ & ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Γ ΕΠΑΛ ΚΕΦΑΛΑΙΟ Ο «ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ» Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός ΚΕΦΑΛΑΙΟ ο : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Α ΣΥΝΑΡΤΗΣΕΙΣ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Πεδίο
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 ΥΠΟΛΟΓΙΣΜΟΙ ΠΑΡΑΜΕΤΡΩΝ ΑΕΡΙΩΝ ΡΕΥΜΑΤΩΝ Σε πολλά εργοστάσια είναι σύνηθες ένα σύστημα ελέγχου ρύπανσης να εξυπηρετεί πολλές πηγές εκπομπών. Σε τέτοιες καταστάσεις, οι παράμετροι των
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 2 ΥΠΟΛΟΓΙΣΜΟΙ ΠΑΡΑΜΕΤΡΩΝ ΑΕΡΙΩΝ ΡΕΥΜΑΤΩΝ Σε πολλά εργοστάσια είναι σύνηθες ένα σύστημα ελέγχου ρύπανσης να εξυπηρετεί πολλές πηγές εκπομπών. Σε τέτοιες καταστάσεις, οι παράμετροι των
ΑΣΚΗΣΕΙΣ ΣΥΣΚΕΥΩΝ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ. 1η ενότητα
 1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 Ακαδημαϊκό έτος 34 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Επώνυμο: Όνομα: Προσωπικός Αριθμός: Ημερομηνία: Βαθμολογία θεμάτων 3 4 5 6 7 8 9 Γενικός Βαθμός η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ "ΦΥΣΙΚΟΧΗΜΕΙΑ" ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΚΠΟΝΗΣΗ,
Ακαδημαϊκό έτος 34 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ Επώνυμο: Όνομα: Προσωπικός Αριθμός: Ημερομηνία: Βαθμολογία θεμάτων 3 4 5 6 7 8 9 Γενικός Βαθμός η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ ΣΤΗ "ΦΥΣΙΚΟΧΗΜΕΙΑ" ΟΔΗΓΙΕΣ ΓΙΑ ΤΗΝ ΕΚΠΟΝΗΣΗ,
Είδη ΙΦΥΥ δυαδικών μιγμάτων
 Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 5
 Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 5 Δευτέρα, 7 Απριλίου 2008 Τρίτη, 8 Απριλίου 2008 Σύνθεση Διεργασιών Διαχωρισμού 1 Εισαγωγή Τα βιομηχανικά προβλήματα διαχωρισμού γενικά περιλαμβάνουν
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 5 Δευτέρα, 7 Απριλίου 2008 Τρίτη, 8 Απριλίου 2008 Σύνθεση Διεργασιών Διαχωρισμού 1 Εισαγωγή Τα βιομηχανικά προβλήματα διαχωρισμού γενικά περιλαμβάνουν
Ψυχρομετρία. Εισαγωγή
 Ψυχρομετρία. Εισαγωγή Η Ψυχρομετρία ασχολείται με τη μελέτη και τη μέτρηση των περιεχόμενων υδρατμών (υγρασία) στον ατμοσφαιρικό αέρα. Κατ επέκταση, ο όρος χρησιμοποιείται συνήθως για να περιγράψει τη
Ψυχρομετρία. Εισαγωγή Η Ψυχρομετρία ασχολείται με τη μελέτη και τη μέτρηση των περιεχόμενων υδρατμών (υγρασία) στον ατμοσφαιρικό αέρα. Κατ επέκταση, ο όρος χρησιμοποιείται συνήθως για να περιγράψει τη
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ
 Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Φυσικοχημεία II, Διαλύματα Ιωάννης Πούλιος, Καθηγητής Εργ. Φυσικοχημείας Α.Π.Θ. Τηλ. 2310-997785 poulios@chem.auth.gr photocatalysisgroup.web.auth.gr ΚΡΑΜΑΤΑ Χρώμα κραμάτων αποτελούμενα από Χρυσό (Au),
Θερμοδυναμική Ενότητα 4:
 Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα - Ασκήσεις Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό
Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα - Ασκήσεις Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό
