Κεφάλαιο 5: Διεργασίες απόσταξης
|
|
|
- Ἀβειρὼν Βιλαέτης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική απόσταξη. Η κλασματική απόσταξη αποτελεί ίσως τη σημαντικότερη φυσική διεργασία και η ανάλυσή της είναι το πρότυπο για όλες τις διεργασίες που περιλαμβάνουν διαδοχικές βαθμίδες ισορροπίας. Προαπαιτούμενη γνώση Εδώ συνδυάζονται οι γνώσεις των ισοζυγίων μάζας και ενέργειας από το Κεφάλαιο 1 με τις σχέσεις ισορροπίας διφασικών μιγμάτων αερίου-υγρού από το Κεφάλαιο Απλές αποστάξεις Απόσταξη ισορροπίας H απόσταξη ισορροπίας είναι μια απλή διεργασία, που συνίσταται στην προσαγωγή ενός μίγματος σε δοχείο διαχωρισμού υγρού/ατμού, σε συνθήκες πίεσης και θερμοκρασίας που αντιστοιχούν στη διφασική περιοχή. Στις συνθήκες αυτές, η αέρια φάση εμπλουτίζεται στα πτητικά συστατικά και η υγρή φάση στα βαρύτερα. Εάν το μέγεθος του δοχείου διαχωρισμού εξασφαλίζει ικανοποιητικό χρόνο παραμονής σε επαφή των δύο φάσεων, η σύσταση των ρευμάτων εξόδου αντιστοιχεί στις συνθήκες ισορροπίας που προβλέπονται από τη θερμοδυναμική μιγμάτων (VLE). H απόσταξη ισορροπίας επιτυγχάνει μικρό σχετικά εμπλουτισμό των συγκεντρώσεων στα ρεύματα εξόδου. Βρίσκει κάποια πρακτική εφαρμογή σε διυλιστήρια στην αρχική επεξεργασία του αργού πετρελαίου, καθώς και σε διαχωρισμό μιγμάτων ενώσεων με πολύ μεγάλη διαφορά στις θερμοκρασίες βρασμού. H βασική της όμως σημασία έγκειται στο ότι αποτελεί τον θεμέλιο λίθο της κατά πολύ σημαντικότερης διεργασίας της κλασματικής απόσταξης (McCabe et al, 2001). Ένας τυπικός τρόπος πραγματοποίησης της απόσταξης ισορροπίας παρουσιάζεται στο Σχήμα 5.1. Υγρό μίγμα συστατικών προθερμαίνεται και στη συνέχεια η πίεση του μειώνεται με τη διέλευση μέσω βαλβίδας στραγγαλισμού. Το μίγμα καταλήγει σε δοχείο διαχωρισμού, από όπου παραλαμβάνονται τα ρεύματα υγρής και αέριας φάσης. Το σύστημα αυτόματου ελέγχου που απεικονίζεται στο σχήμα επιτρέπει τη διατήρηση των συνθηκών του δοχείου διαχωρισμού σε σταθερές, επιθυμητές τιμές. Έτσι, η θερμοκρασία, T, διατηρείται σταθερή χρησιμοποιώντας ως μεταβλητή χειρισμού την παροχή θερμαντικού μέσου στον εναλλάκτη προθέρμανσης, και η πίεση του δοχείου, P, διατηρείται σταθερή με χειρισμό της βαλβίδας εξόδου του αέριου ρεύματος. Τέλος, η βαλβίδα εξόδου του υγρού ρεύματος διατηρεί ικανοποιητική στάθμη στο δοχείο, έτσι ώστε να αποφεύγεται είτε η πλημμύριση με υγρό είτε η αποστράγγιση του υγρού που θα προκαλούσε διαφυγή ατμού από τη γραμμή εξόδου του υγρού Μαθηματική ανάλυση Το πρόβλημα της απόσταξης ισορροπίας μπορεί να τεθεί με διάφορους τρόπους (King, 1982). O πλέον συνηθισμένος είναι να καθορίζονται η πίεση και η θερμοκρασία του δοχείου διαχωρισμού και να ζητούνται η παροχή και η σύσταση των ρευμάτων εξόδου (απόσταξη ισορροπίας PT). Το πρόβλημα αυτό επιλύεται στη συνέχεια. Μία εναλλακτική δυνατότητα είναι να δίνεται η θερμοκρασία του δοχείου διαχωρισμού και να ζητείται η πίεση που εξασφαλίζει ότι καθορισμό ποσοστό της τροφοδοσίας ενός συστατικού απομακρύνεται με την αέρια φάση. Μία τρίτη δυνατότητα είναι η αδιαβατική (ισενθαλπική) απόσταξη ισορροπίας, όπου εξαλείφεται στο Σχήμα 5.1 ο εναλλάκτης προθέρμανσης. Στην περίπτωση αυτή γνωρίζουμε συνήθως την πίεση του δοχείου διαχωρισμού και τη θερμοκρασία της τροφοδοσίας πριν τον στραγγαλισμό, αλλά όχι τη θερμοκρασία στο δοχείο διαχωρισμού.
2 93 Αέριο προϊόν, V, yi Τροφοδοσία, F, zi ΡC LC ΤC Υγρό προϊόν, L, xi Σχήμα 5.1 Διάταξη απόσταξης ισορροπίας με σύστημα αυτόματου ελέγχου. H μαθηματική ανάλυση της απόσταξης ισορροπίας βασίζεται στα ολοκληρωτικά ισοζύγια μάζας και στα δεδομένα θερμοδυναμικής ισορροπίας. Τα τελευταία συνήθως εκφράζονται σε όρους λόγων ισορροπίας, K i, γεγονός που αντανακλά την πρακτική της πετρελαϊκής βιομηχανίας. Οι παροχές των ρευμάτων συνήθως είναι σε γραμμομόρια και οι συστάσεις x i και y i αντιπροσωπεύουν τα γραμμομοριακά κλάσματα του συστατικού i στην υγρή και την αέρια φάση αντίστοιχα. Το ισοζύγιο μάζας κάθε συστατικού δίνει x i L + y i V = z i F και με αντικατάσταση από τον ορισμό του λόγου ισορροπίας, y i = K i x i, προκύπτουν οι σχέσεις x i = z if L + K i V [5.1] [5.2α] y i = K iz i F L + K i V [5.2β] H παροχή εξόδου της κάθε φάσης βρίσκεται από την επίλυση εξίσωσης της μορφής Σx i=1 ή Σy i=1, που για i>2 απαιτεί αριθμητική διαδικασία. Από τη σκοπιά της αριθμητικής ανάλυσης καταλληλότερη αποδεικνύεται η εξίσωση Σx i-σy i=0, διατυπωμένη με τη μορφή, K i z i 1 + (K i 1)(V/F) z i 1 + (K i 1)(V/F) = 0 i i [5.3] όπου χρησιμοποιήθηκε το ολικό ισοζύγιο μάζας, F=L+V, για την απαλοιφή της παροχής υγρού, L. H αξία της παραπάνω διαμόρφωσης έγκειται στο ότι η ανεξάρτητη μεταβλητή, (V/F), περιέχεται στο γνωστό διάστημα [0,1] και ότι η προς μηδενισμό συνάρτηση είναι μονότονη (φθίνουσα). H τελευταία παρατήρηση έχει σημασία για την χρήση της μεθόδου Newton-Raphson εύρεσης ριζών μη-γραμμικής εξίσωσης, που είναι ιδιαίτερα αποτελεσματική όταν δεν μηδενίζεται η πρώτη παράγωγος της συνάρτησης. H υπολογιστική μέθοδος που περιγράφηκε παραπάνω μπορεί να εφαρμοστεί και για την ανάλυση της αδιαβατικής απόσταξης ισορροπίας, αν συμπληρωθεί με το ισοζύγιο ενέργειας και μια διαδικασία δοκιμής και σφάλματος. Ειδικότερα, το ισοζύγιο ενέργειας δίνει FH F = LH L + VH V [5.4] όπου οι ειδικές ενθαλπίες των ρευμάτων μπορούν να υπολογιστούν αν είναι γνωστές η πίεση, η θερμοκρασία και οι συστάσεις τους. H διαδικασία δοκιμής και σφάλματος περιλαμβάνει πρόβλεψη της θερμοκρασίας του
3 94 δοχείου διαχωρισμού και υπολογισμό των συστάσεων σύμφωνα με τα ανωτέρω για απόσταξη ισορροπίας PT. H αρχική πρόβλεψη της θερμοκρασίας διαφοροποιείται μέχρις ότου ικανοποιηθεί το ισοζύγιο ενέργειας Γραφική απεικόνιση της διεργασίας Στην περίπτωση απόσταξης ισορροπίας δυαδικού μίγματος, το ισοζύγιο μάζας μπορεί να παρουσιαστεί γραφικά σε διάγραμμα x,y γραμμομοριακών κλασμάτων υγρής-αέριας φάσης, παράλληλα με τα δεδομένα θερμοδυναμικής ισορροπίας (Σχήμα 5.2). Το διάγραμμα αυτό βρίσκει ευρεία εφαρμογή στην ανάλυση και της κλασματικής απόσταξης. H καμπύλη ισορροπίας προκύπτει από τα συνηθισμένα διαγράμματα σύστασηςθερμοκρασίας που περιέχουν τις καμπύλες των σημείων φυσαλίδας και δρόσου, και κάθε σημείο της αντιστοιχεί στη σύσταση ισορροπίας υγρού και ατμών σε διαφορετική θερμοκρασία. Το ισοζύγιο μάζας του ενός συστατικού (του πτητικότερου) παρίσταται στο διάγραμμα αυτό με ευθεία γραμμή που δίνεται από την εξίσωση y = L V x + zf V [5.5] H ευθεία αυτή ονομάζεται γραμμή τροφοδοσίας και διέρχεται από το σημείο της διαγωνίου που αντιστοιχεί στη σύσταση της τροφοδοσίας. Αν q=l/f παριστάνει το ποσοστό της τροφοδοσίας που παραμένει υγρό, τότε L=qF, V=(1-q)F και η κλίση της γραμμής λειτουργίας είναι ίση με q/(q-1). Παρατηρούμε ότι για q=1 η γραμμή λειτουργίας είναι κατακόρυφη και αντιστοιχεί σε ισορροπία που παράγει κορεσμένο υγρό (σημείο φυσαλίδας). Η τιμή q=0 δίνει οριζόντια γραμμή λειτουργίας και αντιστοιχεί σε κορεσμένο ατμό (σημείο δρόσου), ενώ για 0>q>1 παράγεται διφασικό προϊόν. H γραφική αυτή αναπαράσταση περιγράφει και τον δίσκο τροφοδοσίας της κλασματικής απόσταξης, όπου το μίγμα υφίσταται με την είσοδο του στη στήλη απόσταξη ισορροπίας. Σχήμα 5.2 Γραφική απεικόνιση της απόσταξης ισορροπίας δυαδικού μίγματος Διαφορική απόσταξη H διαφορική απόσταξη είναι, μεταξύ άλλων, η απόσταξη που συνήθως εκτελείται στο εργαστήριο. Περιλαμβάνει γέμισμα ενός δοχείου βρασμού με ορισμένη ποσότητα μίγματος και στη συνέχεια θέρμανση του μίγματος και συνεχή απαγωγή και συμπύκνωση των παραγόμενων ατμών (Σχήμα 5.3). H διαφορική απόσταξη
4 95 αποτελεί ένα παράδειγμα ασυνεχούς διεργασίας (batch process), καθώς δεν υπάρχει συνεχές ρεύμα τροφοδοσίας Treybal, 1980). Θερμαντήρας Απόσταγμα Σχήμα 5.3 Απλή διάταξη διαφορικής απόσταξης. Μπορεί κανείς εύκολα να διαπιστώσει ότι η σύσταση του αποστάγματος μεταβάλλεται με το χρόνο, αν σκεφτεί ότι ο ατμός που παράγεται είναι εμπλουτισμένος στα πτητικά συστατικά, και συνεπώς αφήνει υγρό υπόλειμμα σταδιακά πλουσιότερο στα βαριά συστατικά. Παρατηρήστε επίσης ότι η σταδιακή μεταβολή της σύστασης του υπολείμματος συνεπάγεται αντίστοιχη σταδιακή αύξηση με το χρόνο της θερμοκρασίας του συστήματος. Αυτή η εξάρτηση από το χρόνο (ανυπαρξία συνθηκών μόνιμης λειτουργίας) αποτελεί βασικό χαρακτηριστικό των ασυνεχών διεργασιών. Ασυνεχείς διεργασίες απαντώνται σπανιότερα από τις συνεχείς, αλλά χρησιμοποιούνται σε ορισμένες ειδικές περιπτώσεις. Τέτοιες περιπτώσεις είναι η παραγωγή ειδικών χημικών (specialty chemicals), καθώς και φαρμακευτικών και βιοχημικών προϊόντων. Γενικότερα, ασυνεχείς διεργασίες είναι κατάλληλες για την παραγωγή μικρών ποσοτήτων προϊόντων με υψηλό κόστος πρώτων υλών. Στις περιπτώσεις αυτές, η ελαχιστοποίηση του κόστους επεξεργασίας που επιτυγχάνεται με τη συνεχή λειτουργία δεν έχει σημαντική επίδραση στην τελική τιμή του προϊόντος. Αντίθετα, η ευελιξία της παραγωγικής διαδικασίας αυξάνεται σημαντικά αν η μονάδα σχεδιαστεί να λειτουργεί κατά ασυνεχή τρόπο. H μαθηματική ανάλυση της διαφορικής απόσταξης οφείλεται στον Rayleigh (1902) και επιτυγχάνει τον υπολογισμό της ποσότητας υγρού υπολείμματος στο δοχείο βρασμού ως συνάρτησης της σύστασης του (η μεταβλητή χρόνος δεν εμφανίζεται άμεσα στις εξισώσεις). Αν τη χρονική στιγμή t η ποσότητα του υγρού είναι L, και μετά παρέλευση χρόνου dt έχουν εξατμιστεί dv γραμμομόρια, τα ισοζύγια ολικής μάζας και μάζας κάθε συστατικού, με όγκο ελέγχου το υγρό υπόλειμμα, δίνουν: dv = dl [5.6α] y i dv = d(x i L) [5.6β] Στο α σκέλος της εξ. [5.6β] αγνοείται η μικρή μεταβολή της σύστασης του ατμού στο χρονικό διάστημα dt. O συνυπολογισμός της μεταβολής dy i δεν προσθέτει στην εξ. [5.6] παρά ένα διαφορικό ανώτερης τάξης, που είναι αμελητέο στο όριο dt->0. Με αντικατάσταση της εξ. [5.6β] στην [5.6α], χωρισμό μεταβλητών και ολοκλήρωση από την αρχική κατάσταση, L 0,x i0, ως την τελική, L,x i, προκύπτει η εξίσωση x i ln ( L ) = dx i L 0 x i0 y i x i [5.7]
5 96 Οι συστάσεις x i, y i συνδέονται μεταξύ τους με βάση την παραδοχή ότι ο παραγόμενος ατμός είναι κάθε στιγμή σε ισορροπία με το υγρό, και συνεπώς δίνονται από τη σχέση ισορροπίας φάσεων. Για την ειδική περίπτωση μίγματος δύο μόνον συστατικών, των οποίων η σχετική πτητικότητα δεν μεταβάλλεται πολύ στο εύρος θερμοκρασιών της διεργασίας, αντικατάσταση της εξ. [2.34] στην εξ. [5.7] δίνει το τελικό αποτέλεσμα ln ( L 1 ) = L 0 (a 12 1) [ln ( x i ) + a x 12 ln ( 1 x i0 )] i0 1 x i [5.8] Με χρήση της [5.8] μπορεί για παράδειγμα να υπολογιστεί η σύσταση σε ένα συστατικό του υπολείμματος όταν έχει εξατμιστεί ένα ορισμένο κλάσμα της αρχικής τροφοδοσίας. Αντίστοιχα, στην περίπτωση που είναι διαθέσιμα λεπτομερέστερα δεδομένα ισορροπίας (για παράδειγμα ως διάγραμμα x i, y i), μπορεί να χρησιμοποιηθεί απευθείας η εξ. [5.7] και το ολοκλήρωμα να υπολογιστεί αριθμητικά. 5.2 Κλασματική απόσταξη Οι στήλες κλασματικής απόσταξης αποτελούν τις πλέον συνηθισμένες συσκευές διαχωρισμού στη χημική βιομηχανία. Είναι οι ψηλοί πύργοι που ξεχωρίζουν εντυπωσιακά την νύχτα με τον εκτεταμένο φωτισμό των μονάδων (Σχήμα 5.4). Οι κοντύτεροι και συνήθως φαρδύτεροι πύργοι είναι οι στήλες απορρόφησης, ενώ οι χημικοί αντιδραστήρες δύσκολα διακρίνονται. Όπως έχει παρατηρηθεί (Cussler, 2009) αυτή η διαφορά μεγέθους είναι συχνά αντιπροσωπευτική και της διαφοράς κόστους. Έτσι, αν και η χημική βιομηχανία βασίζεται στις αντιδράσεις, το κύριο κόστος ενός χημικού προϊόντος συχνά καθορίζεται από τις φυσικές διεργασίες διαχωρισμού. Αντιπροσωπευτικά παραδείγματα στηλών κλασματικής απόσταξης απαντώνται στην πετρελαϊκή βιομηχανία. Με τυπικές δυναμικότητες διυλιστηρίων της τάξης των m 3 /h αργού πετρελαίου, οι βοηθητικές συσκευές της απόσταξης μπορεί να συνιστούν ολόκληρες εγκαταστάσεις. Για παράδειγμα, ο «εναλλάκτης» προθέρμανσης της τροφοδοσίας και ο αναβραστήρας μπορεί να είναι λέβητες με φλόγα, ενώ ο συμπυκνωτής να απαρτίζεται από ολόκληρη συστοιχία υδρόψυκτων ή/και αερόψυκτων εναλλακτών. Σχήμα 5.4 Εντυπωσιακή εικόνα διυλιστηρίου με νυχτερινό φωτισμό (J Nefastis, demon/ ) Διεργασίες πολλαπλών βαθμίδων επαφής H κλασματική απόσταξη, πέραν της σημασίας της για τη χημική βιομηχανία, αποτελεί το πρότυπο μιας ολόκληρης ομάδας φυσικών διεργασιών όπου η επαφή των δύο φάσεων συντελείται σε μια αλληλουχία
6 97 βαθμίδων. Για τον λόγο αυτό, η ανάλυση της έχει ιδιαίτερη βαρύτητα. Παραδείγματα άλλων τέτοιων διεργασιών (ή, καλύτερα, τέτοιας μορφής πραγματοποίησης της διεργασίας) συναντώνται από την εκχύλιση - που αφορά επαφή μη-αναμίξιμων υγρών φάσεων- έως τις διεργασίες έκπλυσης και εμπλουτισμού της εξαγωγικής μεταλλουργίας. O σχεδιασμός και η ανάλυση των διεργασιών πολλαπλών βαθμίδων επαφής βασίζονται στην παραδοχή ότι τα ρεύματα στην έξοδο κάθε βαθμίδας προσεγγίζουν τη θερμοδυναμική ισορροπία. Ως συνέπεια της παραδοχής αυτής, ο υπολογισμός των συσκευών γίνεται κυρίως με πληροφορίες από τη θερμοδυναμική που αφορούν τις συστάσεις ισορροπίας. H ανάλυση των φαινομένων μεταφοράς μάζας κατέχει δευτερεύοντα ρόλο και η σημασία τους εξαντλείται στον ορισμό και την πρόβλεψη ενός βαθμού απόδοσης κάθε βαθμίδας. O κύριος εναλλακτικός τρόπος πραγματοποίησης των φυσικών διεργασιών είναι σε συσκευές διαφορικής επαφής, όπου οι δύο φάσεις βρίσκονται σε συνεχή επαφή κατά μήκος της συσκευής και λαμβάνει χώρα μεταφορά μάζας λόγω απόκλισης των συστάσεων από τη χημική ισορροπία που προβλέπεται από τη θερμοδυναμική. Στις περιπτώσεις αυτές -τυπικό παράδειγμα των οποίων αποτελεί η απορρόφηση σε στήλες με πληρωτικό υλικό- κεντρικό ρόλο έχουν τα φαινόμενα μεταφοράς μάζας H κλασματική απόσταξη ως επέκταση της απόσταξης ισορροπίας H απόσταξη ισορροπίας που αναπτύχθηκε στο προηγούμενο κεφάλαιο επιτυγχάνει εμπλουτισμό του ρεύματος ατμού στα πτητικότερα συστατικά (και αντίστοιχα του ρεύματος υγρού στα βαρύτερα), η οποία όμως συνήθως είναι ανεπαρκής για την παραγωγή σχετικά καθαρών προϊόντων. Όπως σχολιάζει εύστοχα ο King (1982) η διαδικασία της απόσταξης ισορροπίας μπορεί καταρχήν να επαναληφθεί με μερική συμπύκνωση (με ψύξη) του ρεύματος ατμού, και μερική εξάτμιση (με θέρμανση) του ρεύματος υγρού (Σχήμα 5.5α). Με τον τρόπο αυτό δημιουργούνται δύο αλληλουχίες αποστάξεων ισορροπίας που οδηγούν τελικά σε παραγωγή καθαρών προϊόντων.
7 98 Σχήμα 5.5 (α) Δημιουργία μίας διπλής αλληλουχίας αποστάξεων ισορροπίας και (β) Απλοποίηση της αλληλουχίας ώστε να διαμορφωθεί η στήλης κλασματικής απόσταξης (King, 1982). H παραπάνω διαδικασία παρουσιάζει δύο σοβαρά προβλήματα: Απαιτεί έναν μεγάλο αριθμό εναλλακτών θερμότητας, που είναι ακριβές συσκευές. Επίσης, δημιουργεί έναν μεγάλο αριθμό ενδιάμεσων απορρευμάτων που δεν έχουν εμφανή χρησιμότητα. Στην πραγματικότητα, με την παραπάνω διαδικασία το μεγαλύτερο ποσοστό της παροχής τροφοδοσίας καταλήγει στα απορρεύματα αυτά, και μικρό μόνον μέρος της στα χρήσιμα τελικά προϊόντα. H διαδικασία βελτιώνεται εντυπωσιακά με την παρατήρηση ότι το απόρρευμα κάθε βαθμίδας ισορροπίας (ρεύμα υγρού στην πάνω αλληλουχία και ρεύμα ατμού στην κάτω) έχει περίπου την σύσταση της τροφοδοσίας της προηγούμενης βαθμίδας. Συνεπώς, μπορεί να τροφοδοτηθεί προς τα πίσω, όπως φαίνεται στο Σχήμα 5.5β, χωρίς να διαταράσσεται η διαδικασία (η εναλλακτική πχ. δυνατότητα της συλλογής όλων των απορρευμάτων και επανατροφοδοσίας τους στην αρχή, οδηγεί στην ακύρωση, λόγω της ανάμειξης, του εμπλουτισμού που έχει ήδη επιτευχθεί και δεν είναι αποτελεσματική). H παραπάνω βελτίωση έχει ως πρόσθετο θετικό αποτέλεσμα την εξαφάνιση των ενδιάμεσων εναλλακτών θερμότητας. Πράγματι, η επιστροφή υγρού απορρεύματος στην προηγούμενη βαθμίδα της πάνω αλληλουχίας δημιουργεί -σε συνδυασμό με την κανονική τροφοδοσία ατμού της βαθμίδας- το διφασικό μίγμα υγρού-ατμού που απαιτείται για τη λειτουργία της απόσταξης ισορροπίας και την επίτευξη του αντίστοιχου εμπλουτισμού. Το ίδιο συμβαίνει και στην κάτω αλληλουχία με την επιστροφή κάθε απορρεύματος ατμού στην προηγούμενη βαθμίδα. Παρατηρείστε όμως ότι, στην αλληλουχία του Σχήματος 5.5β δεν μπορούν να εξαλειφθούν οι εναλλάκτες στα δύο άκρα. O θερμαντής του κάτω άκρου εξασφαλίζει την ύπαρξη ατμού και ο ψύκτης του άνω άκρου την ύπαρξη υγρού σε όλο το μήκος της στήλης. Οι δύο αυτοί εναλλάκτες, που συνοδεύουν όλες τις αποστακτικές στήλες, είναι φυσικά ο αναβραστήρας και ο συμπυκνωτής. H απλοποίηση της παραπάνω διαδικασίας ολοκληρώνεται με την υποκατάσταση του δοχείου διαχωρισμού της κάθε βαθμίδας ισορροπίας από μία απλούστερη κατασκευή, τον δίσκο απόσταξης, και την
8 99 ενσωμάτωση των δίσκων σε ένα επιμήκες δοχείο πίεσης που αποτελεί το κέλυφος της στήλης κλασματικής απόσταξης Περιγραφή στήλης κλασματικής απόσταξης Μία τυπική στήλη κλασματικής απόσταξης εμφανίζεται στο Σχήμα 5.6, όπου περιλαμβάνονται και οι κύριες βοηθητικές συσκευές, δηλαδή ο αναβραστήρας, ο συμπυκνωτής, η αντλία και ο εναλλάκτης προθέρμανσης της τροφοδοσίας. H τροφοδοσία της στήλης εισέρχεται σε μία ενδιάμεση βαθμίδα, που η βέλτιστη θέση της προκύπτει από την ανάλυση του επόμενου κεφαλαίου. H θέση τροφοδοσίας χωρίζει τη στήλη σε δύο τμήματα, το άνω που ονομάζεται τμήμα εμπλουτισμού και το κάτω που ονομάζεται τμήμα εξάντλησης. H ονοματολογία αυτή βασίζεται στη μεταβολή σύστασης του ελαφρού συστατικού κατά μήκος της στήλης. Γενικότερα, έχει επικρατήσει ο χαρακτηρισμός της σύστασης των ρευμάτων στην απόσταξη δυαδικών μιγμάτων με βάση τη συγκέντρωση του πτητικότερου συστατικού. Ατμός παράγεται στον αναβραστήρα με μερική εξάτμιση του υγρού του πυθμένα της στήλης. H παραγωγή ατμού οδηγεί στην δημιουργία μιας μικρής υπερπίεσης στο κάτω άκρο της στήλης, που εξισορροπεί την πτώση πίεσης που απαιτείται για τη διέλευση του ατμού διαμέσου των δίσκων σε αντιρροή με το κατερχόμενο υγρό. Το υγρό υπόλειμμα του αναβραστήρα αποτελεί το προϊόν πυθμένα της στήλης. Όπως φαίνεται στο Σχήμα 5.6, η ενθαλπία του προϊόντος πυθμένα μπορεί να χρησιμοποιηθεί για την προθέρμανση της τροφοδοσίας. O ατμός που εξέρχεται από την κορυφή της στήλης τροφοδοτείται στον συμπυκνωτή όπου υφίσταται συνήθως ολική συμπύκνωση. Μέρος του συμπυκνώματος επανέρχεται στην κορυφή της στήλης για να χρησιμεύσει ως η υγρή φάση των βαθμίδων επαφής. Το υπόλοιπο αποτελεί το προϊόν κορυφής της στήλης. O λόγος της παροχής που επιστρέφει στη στήλη προς την παροχή που απομακρύνεται ονομάζεται λόγος επαναρροής, R. O λόγος επαναρροής είναι η βασική μεταβλητή χειρισμού κατά τη λειτουργία της στήλης. Μεταβάλλεται με το απλό άνοιγμα ή κλείσιμο μιας βάνας και -όπως θα φανεί από την ανάλυση του επόμενου κεφαλαίου- καθορίζει τόσο τις παροχές στο εσωτερικό της στήλης όσο και το βαθμό διαχωρισμού που επιτυγχάνεται σε δοσμένη στήλη (ή, ισοδύναμα, το πλήθος των βαθμίδων που απαιτούνται για να επιτευχθεί καθορισμένος διαχωρισμός). Προϊόν κορυφής: D, xd Τροφοδοσία: F, xf Προϊόν πυθμένα: B, xb Σχήμα 5.6 Τυπική στήλη κλασματικής απόσταξης με τα ρεύματα εισόδου-εξόδου και τις κύριες βοηθητικές συσκευές.
9 100 H επαφή της υγρής με την αέρια φάση στο εσωτερικό της στήλης επιτυγχάνεται στους δίσκους ή πατώματα. Στις περισσότερες σύγχρονες κατασκευές, οι δίσκοι είναι διάτρητες πλάκες που συγκρατούν μια στάθμη υγρού και επιτρέπουν την διέλευση του ατμού προς τα πάνω με την μορφή φυσαλίδων (Σχήμα 5.7). Το υγρό κατέρχεται λόγω βαρύτητας από τους αγωγούς καθόδου υπερχειλίζοντας το φράγμα κάθε δίσκου. H έντονη ανάμειξη υγρού/ατμού, που συνήθως οδηγεί στη δημιουργία μιας μάζας ρευστού/αφρού πάνω σε κάθε δίσκο, είναι υπεύθυνη για την παραδοχή της θερμοδυναμικής ισορροπίας στην οποία βασίζεται η μαθηματική ανάλυση της στήλης H ικανοποιητική λειτουργία των δίσκων βασίζεται στην διατήρηση κατάλληλης παροχής ατμού που επιτρέπει την διέλευση του προς τα πάνω μέσω των οπών, αλλά και την απρόσκοπτη κίνηση του υγρού προς τα κάτω μέσω των αγωγών καθόδου. Προβλήματα προκαλούνται από την πολύ μικρή παροχή ατμού (οπότε το υγρό διαφεύγει μέσω των οπών-δακρυσμός) καθώς και από την πολύ μεγάλη παροχή ατμού (οπότε το υγρό αδυνατεί να κινηθεί προς τα κάτω-πλημμύριση). H ανάλυση των προβλημάτων αυτών γίνεται κατά την εξέταση των υδραυλικών χαρακτηριστικών των δίσκων. O σχεδιασμός και η ανάλυση της στήλης κλασματικής απόσταξης που ακολουθεί απαντά σε δύο βασικά ερωτήματα. Το πρώτο αφορά το πλήθος των βαθμίδων επαφής που απαιτούνται για να ληφθούν προϊόντα κορυφής και πυθμένα ορισμένης σύστασης, και επιλύεται με συνδυασμό ισοζυγίων μάζας και δεδομένων θερμοδυναμικής ισορροπίας. Το δεύτερο ερώτημα αφορά την διάμετρο της στήλης ώστε να επεξεργάζεται ορισμένη παροχή τροφοδοσίας, και απαντάται με την εξέταση των ρευστομηχανικών χαρακτηριστικών των δίσκων. Σχήμα 5.7 (α) Παράδειγμα διάτρητου δίσκου στήλης κλασματικής απόσταξης και (β) σχηματική αναπαράσταση της ροής και ανάμιξης των δύο φάσεων στους δίσκους (H. Padleckas, File:Bubble_Cap_Trays.png ) Γραφικός σχεδιασμός στήλης κλασματικής απόσταξης Ορισμός γραμμών λειτουργίας Η ανάλυση της στήλης κλασματικής απόσταξης βασίζεται σε μια σειρά ισοζυγίων μάζας. Ο συμβολισμός που χρησιμοποιείται απεικονίζεται στο Σχήμα 5.8, όπου οι παροχές εκφράζονται σε γραμμομόρια (αντί για κιλά) και οι συγκεντρώσεις σε γραμμομοριακά κλάσματα ως προς το πτητικότερο συστατικό. Η σύμβαση αυτή είναι χρήσιμη γιατί τα δεδομένα ισορροπίας μιγμάτων υγρού-ατμού (VLE) σχεδόν πάντα εκφράζονται σε αυτές τις μονάδες. Το ολικό ισοζύγιο μάζας και το ισοζύγιο του ελαφρού συστατικού δίνουν αντίστοιχα: F = D + B Fx F = Dx D + Bx B [5.9] [5.10]
10 101 Στο εσωτερικό της στήλης, οι συστάσεις της υγρής και αέριας φάσης εκφράζονται ως x i και y i αντίστοιχα, όπου ο δείκτης i αντιστοιχεί στον δίσκο από τον οποίο απομακρύνονται τα ρεύματα. Συνεπώς, τα ρεύματα με τον ίδιο δείκτη βρίσκονται θεωρητικά σε θερμοδυναμική ισορροπία. Tα δεδομένα ισορροπίας φάσεων από τη θερμοδυναμική μιγμάτων χρησιμοποιούνται, στην ανάλυση της απόσταξης, με τη μορφή καμπύλης σε διάγραμμα x,y, και τα σημεία (x i,y i) βρίσκονται πάνω σε αυτή την καμπύλη. Το διάγραμμα x,y είναι το ίδιο που χρησιμοποιήθηκε στην γραφική απεικόνιση της απόσταξης ισορροπίας. Ln-2, xn-2 Vn-1, yn-1 ΔΙΣΚΟΣ n-1 Ln-1, xn-1 Vn, yn ΔΙΣΚΟΣ n Ln, xn Vn+1, yn+1 ΔΙΣΚΟΣ n+1 Ln+1, xn+1 Vn+2, yn+2 Σχήμα 5.8 Οι παροχές και συστάσεις των ρευμάτων υγρού και ατμού μεταξύ τριών διαδοχικών δίσκων στήλης κλασματικής απόσταξης. Οι συστάσεις των ρευμάτων υγρού και ατμού που φαίνονται στο σχήμα να περνούν το ένα δίπλα στο άλλο, συνδέονται μεταξύ τους μέσω του ισοζυγίου μάζας (στην πραγματικότητα, το υγρό ρεύμα κατέρχεται από τον αγωγό καθόδου και το ρεύμα ατμού διασχίζει τον μεταξύ των δύο δίσκων χώρο). Λαμβάνοντας τα ισοζύγια μεταξύ της κορυφής της στήλης και της νοητής τομής μεταξύ των δίσκων n και n+1, που βρίσκεται οπουδήποτε πάνω από το σημείο τροφοδοσίας, προκύπτει: V n+1 = L n + D [5.11] V n+1 y n+1 = L n x n + Dx D [5.12] Κατά την ανάλυση της στήλης γίνεται συχνά η παραδοχή ότι οι συνολικές παροχές κάθε φάσης παραμένουν αμετάβλητες από δίσκο σε δίσκο στο τμήμα εμπλουτισμού της στήλης, και επίσης αμετάβλητες (με διαφορετικές γενικά τιμές) στο τμήμα εξάντλησης. Έτσι, L 1 = = L n = L [5.13α] V 1 = = V n = V [5.13β] H παραδοχή αυτή δικαιολογείται από το γεγονός ότι σε κάθε δίσκο λαμβάνει χώρα μεταφορά μάζας σε συνθήκες ισογραμμομοριακής αντιδιάχυσης. δηλαδή, το ελαφρύτερο συστατικό διαχέεται από την κυρίως μάζα του υγρού προς τη διεπιφάνεια και την κυρίως μάζα του ατμού με τους ίδιους ρυθμούς που το βαρύτερο διαχέεται αντίστροφα. Ως αποτέλεσμα η συνολική μεταβολή γραμμομορίων κάθε φάσης είναι συνήθως πολύ μικρή.
11 102 Η ανάλυση με βάση την παραδοχή των εξ. [5.13α,β] λέγεται μεθοδολογία McCabe-Thiele (McCabe & Thiele, 1925) και αποτελεί το κύριο εργαλείο που θα χρησιμοποιήσουμε στο παρόν σύγγραμμα. Αν η παραδοχή δεν ληφθεί υπόψη τότε απαιτείται συνεκτίμηση και του ισοζυγίου ενέργειας (μέθοδος Ponchont-Savarit, Treybal, 1980) και η ανάλυση γίνεται πολυπλοκότερη. Στο πλαίσιο αυτό αξίζει να αναφερθεί η παρατήρηση ότι η ενθαλπία εξάτμισης ανά mol συστατικού είναι παρόμοια για μεγάλη ποικιλία χημικών ενώσεων. Ως συνέπεια, το αδιαβατικό ισοζύγιο ενέργειας σε κάθε δίσκο δείχνει ότι η ισογραμμομοριακή αντιδιάχυση συνεπάγεται απουσία έντονων θερμικών φαινομένων, καθώς οι ενθαλπίες εξάτμισης και συμπύκνωσης πρακτικά αλληλο-εξουδετερώνονται. Έτσι, η κατάσταση στον δίσκο περιγράφεται ικανοποιητικά από μία μόνον θερμοκρασία η οποία αντιστοιχεί στις συστάσεις ισορροπίας. Με συνδυασμό των εξ. [5.12] και [5.13] τελικά προκύπτει ότι y n+1 = L V x n + Dx D V [5.14] Η εξ. [5.14], που είναι το προϊόν ενός ισοζυγίου μάζας, έχει ιδιαίτερη σημασία. Υποδηλώνει ότι οι συστάσεις των δύο φάσεων σε κάθε τομή μεταξύ διαδοχικών δίσκων, βρίσκονται πάνω σε μια ευθεία γραμμή της οποίας η κλίση καθορίζεται από τις γραμμομοριακές παροχές των φάσεων. Η γραμμή αυτή ονομάζεται γραμμή λειτουργίας του τμήματος εμπλουτισμού, και μπορεί να παρασταθεί σε κοινό διάγραμμα x,y με τα δεδομένα ισορροπίας φάσεων. Με αντίστοιχο ισοζύγιο μάζας μεταξύ του πυθμένα και της νοητής τομής ανάμεσα στους δίσκους m και m+1, κάτω από το σημείο τροφοδοσίας, προκύπτει η εξής γραμμή λειτουργίας του τμήματος εξάντλησης: y m+1 = L V xm + Bx B V [5.15] όπου οι μεταβλητές με παύλες παριστάνουν τις γραμμομοριακές παροχές της υγρής και της αέριας φάσης κάτω από το σημείο τροφοδοσίας. Η απεικόνιση των γραμμών λειτουργίας (που είναι τα αποτελέσματα ισοζυγίων μάζας) και της καμπύλης ισορροπίας (που προέρχεται από τη θερμοδυναμική) σε κοινό διάγραμμα, θα επιτρέψει τον γραφικό προσδιορισμό των μεταβολών συγκέντρωσης που προκαλούνται σε κάθε δίσκο. Προηγουμένως όμως θα εκφράσουμε τους συντελεστές των γραμμών λειτουργίας συναρτήσει της βασικής παραμέτρου της στήλης που είναι ο λόγος επαναρροής, R=L/D. Από ολικό ισοζύγιο μάζας στον συμπυκνωτή, προκύπτει ότι V = L + D και, σε συνδυασμό με τον ορισμό του λόγου επαναρροής, R=L/D, η άνω γραμμή λειτουργίας γίνεται [5.16] y n+1 = R R + 1 x n + x D R + 1 [5.17] Αντίστοιχη μετατροπή της κάτω γραμμής λειτουργίας απαιτεί πληροφορίες σχετικά με την κατάσταση της τροφοδοσίας. Για παράδειγμα, τροφοδοσία σε συνθήκες κορεσμένου υγρού προστίθεται στην υγρή φάση και αφήνει την αέρια ανεπηρέαστη, ενώ τροφοδοσία σε διφασικές συνθήκες επαυξάνει αναλογικά την υγρή φάση κάτω από το σημείο τροφοδοσίας και την αέρια φάση πάνω από το σημείο τροφοδοσίας (ο ατμός κινείται προς τα πάνω και το υγρό προς τα κάτω). Ορισμένες εναλλακτικές καταστάσεις της τροφοδοσίας φαίνονται στο Σχήμα 5.9. Η λεπτομερέστερη ανάλυση της επίδρασης τους (που θα οδηγήσει στον ορισμό άλλης μιας γραμμής, της γραμμής τροφοδοσίας) θα γίνει στη συνέχεια στο κεφάλαιο Προς το παρόν θεωρείται ότι η τροφοδοσία εισέρχεται ως κορεσμένο υγρό, και συνεπώς οι παροχές των δύο φάσεων συνδέονται με τις σχέσεις V = V, L = L + F. Έτσι, η γραμμή λειτουργίας του τμήματος εξάντλησης γίνεται, B y m+1 = [1 + D(R + 1) ] x m Bx B D(R + 1) [5.18]
12 103 ΚΟΡΕΣΜΕΝΟ ΥΓΡΟ ΔΙΦΑΣΙΚΟ ΜΙΓΜΑ ΚΟΡΕΣΜΕΝΟΣ ΑΤΜΟΣ Σχήμα 5.9 Εναλλακτικές καταστάσεις τροφοδοσίας στήλης και η επίδραση τους στη διαφοροποίηση των παροχών πριν και μετά την τροφοδοσία Υπολογισμός πλήθους ιδανικών βαθμίδων Επόμενος στόχος μας είναι ο συνδυασμός των γραμμών λειτουργίας -που μόλις υπολογίσαμε- με την καμπύλη ισορροπίας για τον προσδιορισμό του αριθμού βαθμίδων που χρειάζονται ώστε να παραχθούν ρεύματα κορυφής και πυθμένα με τις επιθυμητές συστάσεις. Ο προσδιορισμός αυτός θα γίνει γραφικά, πάνω σε διάγραμμα συγκεντρώσεων x,y, όπως φαίνεται στο Σχήμα Παρατηρούμε καταρχάς ότι οι αντικαταστάσεις y n+1 = x n x D και y m+1 = x m x B επαληθεύουν αντίστοιχα τις εξ. [5.17] και [5.18] των δύο γραμμών λειτουργίας. Αυτό σημαίνει ότι οι γραμμές λειτουργίας τέμνουν την διαγώνιο στα σημεία με συντεταγμένες (x D, x D ) και (x Β, x Β ) αντίστοιχα. Επειδή και οι κλίσεις τους είναι γνωστές για καθορισμένη τιμή του λόγου επαναρροής, οι ευθείες μπορούν να κατασκευαστούν. Η γραφική διαδικασία προσδιορισμού των βαθμίδων ξεκινάει από πάνω δεξιά στο Σχήμα 5.10, και ειδικότερα από το σημείο (x 0, y 1 ), που αντιστοιχεί στα ρεύματα πάνω από τον πρώτο δίσκο. Παρατηρούμε ότι x 0 = y 1 = x D, λόγω του ότι ο συμπυκνωτής είναι ολικός (δηλαδή συμπυκνώνει ολόκληρη την τροφοδοσία ατμού που παραλαμβάνει) και συνεπώς η σύσταση του ατμού στην είσοδο του είναι ίδια με τη σύσταση του υγρού στην έξοδο. Από το σημείο αυτό φέρουμε μια οριζόντια γραμμή ως την καμπύλη ισορροπίας. Το νέο σημείο έχει την ίδια τεταγμένη, y 1, που είναι η συγκέντρωση εξόδου από τον πρώτο δίσκο, και συνεπώς η τετμημένη του αντιστοιχεί στη συγκέντρωση x 1. Φέροντας την κατακόρυφη ως τη γραμμή λειτουργίας, βρίσκουμε ένα νέο σημείο με τετμημένη x 1. Επειδή βρίσκεται πάνω στη γραμμή λειτουργίας, η τεταγμένη του δεν μπορεί παρά να είναι η y 2, και το σημείο αυτό αντιστοιχεί στις συστάσεις των ρευμάτων μεταξύ του πρώτου και δεύτερου δίσκου. Συνεπώς, η τριγωνική κατασκευή του σχήματος παριστάνει την μεταβολή της σύστασης που προκαλείται από την πρώτη βαθμίδα. Συνεχίζοντας με τον ίδιο τρόπο βρίσκουμε τα σημεία με συντεταγμένες (x 2, y 2 ), (x 3, y 3 ) κλπ, μέχρις ότου φτάσουμε ή ξεπεράσουμε το σημείο (x B, y B ) που αντιστοιχεί στις συνθήκες του ρεύματος πυθμένα. Το πλήθος των τριγώνων που σχηματίζονται δίνουν το πλήθος των βαθμίδων που απαιτούνται για το διαχωρισμό. Επειδή τα ρεύματα εξόδου κάθε βαθμίδας θεωρείται ότι βρίσκονται σε ισορροπία, οι βαθμίδες ονομάζονται ιδανικές. Η ανάλυση του βαθμού απόδοσης, που θα γίνει σε επόμενο κεφάλαιο, δείχνει ότι ο αριθμός των πραγματικών δίσκων που απαιτούνται είναι γενικά μεγαλύτερος από τον αριθμό ιδανικών βαθμίδων ισορροπίας. Όπως παρατηρεί ο Cussler (2009), η παραπάνω γραφική κατασκευή, που είναι η βάση της ανάλυσης McCabe-Thiele, είναι εξαιρετικά σημαντική. Παρόλο που μια γραφική κατασκευή φαίνεται εκ πρώτης όψεως αναχρονιστική στην εποχή των ηλεκτρονικών υπολογιστών, εξακολουθεί να χρησιμοποιείται ως εργαλείο από τους ειδικούς στο σχεδιασμό αποστακτικών στηλών. Ο λόγος είναι ότι το διάγραμμα αυτό συνοψίζει και συνδυάζει τις πληροφορίες από τα ισοζύγια μάζας, με τη μορφή των γραμμών λειτουργίας, και τις πληροφορίες από τη θερμοδυναμική, με τη μορφή της καμπύλης ισορροπίας. Έτσι, μας βοηθά να οργανώνουμε συστηματικά τις σκέψεις μας σχετικά με τη διεργασία Επίδραση λόγου επαναρροής και βαθμίδας τροφοδοσίας Στο διάγραμμα συγκεντρώσεων x,y, σαν αυτό του Σχήματος 5.10 μπορούν να παρασταθούν ενδιαφέρουσες οριακές καταστάσεις. Θα συζητήσουμε ορισμένες από αυτές, που βοηθούν και στην καλύτερη εξοικείωση τόσο με το διάγραμμα όσο και με τη διεργασία γενικότερα.
13 104 (x2,y2) (x1,y1) (x0,y1) y (x3,y3) (x1,y2) xd (x2,y3) κλίση: R/(R+1) xf xb x Σχήμα 5.10 Γραφική διαδικασία υπολογισμού πλήθους ιδανικών βαθμίδων αποστακτικής στήλης. Καταρχήν, η βέλτιστη θέση εισαγωγής της τροφοδοσίας. Σύμφωνα με την κατασκευή του σχήματος και τον ορισμό των γραμμών λειτουργίας, όταν συναντήσουμε την τροφοδοσία πρέπει να μεταπηδήσουμε από την πάνω στην κάτω γραμμή λειτουργίας. Ας φανταστούμε προς στιγμήν ότι τοποθετούμε την τροφοδοσία αρκετά χαμηλά στη στήλη. Η γραφική διαδικασία προσδιορισμού των βαθμίδων (ουσιαστικά, η διαδικασία υπολογισμού της μεταβολής στη σύσταση που επιτυγχάνεται στην κάθε βαθμίδα) φαίνεται για την περίπτωση αυτή στο Σχήμα Παρατηρήστε ότι οι δύο τελευταίοι δίσκοι του τμήματος εμπλουτισμού πετυχαίνουν χειρότερα αποτελέσματα όσο παραμένουμε στην πάνω γραμμή λειτουργίας. Είναι φανερό από το σχήμα ότι η μεγαλύτερη μεταβολή στη σύσταση επιτυγχάνεται αν αλλάξουμε γραμμή λειτουργίας μόλις περάσουμε το σημείο τομής των δύο γραμμών. Η θέση αυτή είναι η βέλτιστη για την εισαγωγή της τροφοδοσίας. Ένα ενδιαφέρον ερώτημα είναι ο προσδιορισμός του ελάχιστου αριθμού βαθμίδων που πετυχαίνει τον επιθυμητό διαχωρισμό. Το πλήθος των βαθμίδων φαίνεται πως ελαττώνεται όσο ο χώρος μεταξύ γραμμών λειτουργίας και καμπύλης ισορροπίας αυξάνει, άρα όσο οι γραμμές λειτουργίας προσεγγίζουν την διαγώνιο. Εξετάζοντας την κλίση των γραμμών, θα διαπιστώσετε ότι η μεταβολή αυτή συνεπάγεται αύξηση του λόγου επαναρροής. Στο όριο που ο λόγος επαναρροής τείνει στο άπειρο, οι γραμμές συμπίπτουν με τη διαγώνιο και το πλήθος των βαθμίδων που υπολογίζεται γραφικά είναι το ελάχιστο δυνατό. Εντούτοις, η λειτουργία της απόσταξης με πολύ μεγάλη επαναρροή είναι φανερά ασύμφορη. Συνεπάγεται την ύπαρξη μιας μεγάλης στήλης, της οποίας οι παροχές τροφοδοσίας και προϊόντων είναι πολύ κοντά στο μηδέν. Μια τέτοια λειτουργία θα είχε νόημα μόνον στην περίπτωση που επιθυμούμε τον καλύτερο δυνατό διαχωρισμό με δεδομένη τη στήλη. Η πρακτική σημασία του υπολογισμού έγκειται στο ότι το ελάχιστο πλήθος βαθμίδων μπορεί να χρησιμεύσει ως κριτήριο της δυσκολίας του διαχωρισμού.
14 105 Σχήμα 5.11 Επίδραση της θέσης της τροφοδοσίας στο πλήθος των βαθμίδων που απαιτούνται για ορισμένο διαχωρισμό. Ένα άλλο ενδιαφέρον ερώτημα είναι κατά πόσον υπάρχει ένας ελάχιστος λόγος επαναρροής που απαιτείται για να παράγονται προϊόντα με την επιθυμητή σύσταση. Στο κάτω-κάτω της γραφής, η επιχειρηματολογία για την εισαγωγή της επαναρροής ήταν ως τώρα ποιοτική. Ήδη όμως τα ανωτέρω αποτελέσματα, καθώς και η κεντρική θέση του λόγου επαναρροής στις εξισώσεις των γραμμών λειτουργίας, δημιουργούν την υπόνοια ότι η σημασία της πρέπει να είναι καθοριστική. Πράγματι, ελάττωση του λόγου επαναρροής ελαττώνει την κλίση της γραμμής του τμήματος εμπλουτισμού και αυξάνει την κλίση του τμήματος εξάντλησης, προσεγγίζοντας το σημείο τομής των δύο γραμμών στην καμπύλη ισορροπίας. Στο όριο σύμπτωσης, το Σχήμα 5.12 δείχνει πως απαιτείται άπειρος αριθμός βαθμίδων για την επίτευξη του επιθυμητού διαχωρισμού. Η κατάσταση αυτή αντιστοιχεί στον ελάχιστο λόγο επαναρροής, R min. y xd κλίση: R min/(r min+1) xf xb x Σχήμα 5.12 Ο σχεδιασμός της αποστακτικής στήλης στον ελάχιστο λόγο επαναρροής.
15 106 Αξίζει να αναφερθεί πως στην περίπτωση μερικών ασυνήθιστων καμπυλών ισορροπίας (διαλύματα που απέχουν πολύ από την ιδανική συμπεριφορά), η δημιουργία «μποτιλιαρίσματος» μεταξύ των γραμμών λειτουργίας και της καμπύλης ισορροπίας μπορεί να γίνει σε διαφορετική θέση. Το Σχήμα 5.13 δείχνει το παράδειγμα ενός τέτοιου μίγματος, όπου ο ελάχιστος λόγος επαναρροής προκαλείται επειδή η γραμμή λειτουργίας του τμήματος εμπλουτισμού εφάπτεται της καμπύλης ισορροπίας. y xd κλίση: R min/(r min+1) xf xb x Σχήμα 5.13 Ο ελάχιστος λόγος επαναρροής για ένα μίγμα με δεδομένο ισορροπίας που αποκλίνουν έντονα από την ιδανική συμπεριφορά Επίδραση κατάστασης τροφοδοσίας Ο σχεδιασμός της στήλης έγινε ως τώρα με την παραδοχή ότι η τροφοδοσία εισέρχεται ως κορεσμένο υγρό. Η παραδοχή αυτή μπορεί να ανασκευαστεί χωρίς μεγάλες αλλαγές στην σχεδιαστική διαδικασία. Γενικότερα, η τροφοδοσία μπορεί να είναι υπόψυκτο υγρό, κορεσμένο υγρό, μίγμα υγρού-ατμού, κορεσμένος ατμός ή υπέρθερμος ατμός. Αγνοώντας προς στιγμήν τις δύο ακραίες περιπτώσεις υπόψυκτου υγρού και υπέρθερμου ατμού και ανατρέχοντας στο Σχήμα 5.9, ορίζουμε το κλάσμα υγρού στην τροφοδοσία ως q = L L F [5.19] όπου οι παροχές υγρού αναφέρονται αντίστοιχα σε θέσεις χαμηλότερα και ψηλότερα από το σημείο τροφοδοσίας. Εύκολα προκύπτει ότι και οι αντίστοιχες παροχές ατμού συνδέονται με τη σχέση 1 q = V V F [5.20] Μπορεί να δειχθεί ότι το σημείο τομής των γραμμών λειτουργίας είναι συνάρτηση του κλάσματος υγρού q. Πράγματι, εφαρμόζοντας τις εξ. [5.14], [5.15] για το σημείο τομής τους (x τ, y τ ) που ικανοποιεί και τις δύο και αφαιρώντας κατάλληλα κατά μέλη προκύπτει τελικά η σχέση
16 107 y τ = q q 1 x τ x F q 1 [5.21] Η εξ. [5.21] ονομάζεται γραμμή τροφοδοσίας και παριστάνει τον γεωμετρικό τόπο των σημείων τομής των δύο γραμμών λειτουργίας. Παρατηρείστε επίσης ότι η εξ. [5.21] επαληθεύεται με την αντικατάσταση x τ = y τ = x F, γεγονός που σημαίνει ότι η γραμμή τροφοδοσίας τέμνει τη διαγώνιο του διαγράμματος x,y στο σημείο (x F, x F ). Με βάση τα παραπάνω, η γραφική διαδικασία σχεδιασμού της στήλης κλασματικής απόσταξης για την περίπτωση τροφοδοσίας με τυχαίο κλάσμα υγρού, μπορεί να ολοκληρωθεί ως εξής. Πρώτα κατασκευάζονται την γραμμή λειτουργίας του τμήματος εμπλουτισμού (εξ. [5.17]) και η γραμμή τροφοδοσίας (εξ. [5.21]). Το σημείο τομής των δύο καθορίζει αμέσως και την γραμμή λειτουργίας του τμήματος εξάντλησης, και συνεπώς επιτρέπει την συνέχιση της διαδικασίας όπως εκτέθηκε προηγουμένως. Στην περίπτωση που η τροφοδοσία είναι υπόψυκτο υγρό, τότε με την είσοδο στη στήλη θα έρθει στις συνθήκες κορεσμού απορροφώντας θερμότητα, δηλαδή συμπυκνώνοντας ένα μέρος του ατμού. Άρα, η αύξηση της παροχής υγρού στο κάτω τμήμα της στήλης θα είναι μεγαλύτερη από την παροχή της τροφοδοσίας (q > 1). Αντίθετα, αν η τροφοδοσία συνίσταται από υπέρθερμο ατμό, τότε με την είσοδο στη στήλη θα έρθει στις συνθήκες κορεσμού αποβάλλοντας θερμότητα, δηλαδή εξατμίζοντας ένα μέρος υγρού. Άρα η παροχή υγρού θα είναι μικρότερη κάτω σε σχέση με πάνω από το σημείο τροφοδοσίας (q < 0). Οι δύο αυτές περιπτώσεις μπορούν να συμπεριληφθούν στην ανάλυση αν το κλάσμα υγρού στην τροφοδοσία υπολογιστεί αντίστοιχα από τις σχέσεις q = 1 + C p,l(t ΣΦ Τ F ) ΔH v [5.22] q = C p,v(τ F T ΣΔ ) ΔH v [5.23] που προκύπτουν από απλά ισοζύγια ενέργειας με βάση τους παραπάνω συλλογισμούς (T ΣΦ και T ΣΔ είναι τα σημεία φυσαλίδας και δρόσου για το μίγμα της τροφοδοσίας, και ΔH v η ενθαλπία εξάτμισης) Οικονομικά στοιχεία λειτουργίας στήλης Οι βέλτιστες συνθήκες λειτουργίας της στήλης κλασματικής απόσταξης καθορίζονται -όπως και για τις άλλες συσκευές διεργασιών- με συνδυασμό τεχνικών και οικονομικών κριτηρίων. Η βασική κατάταξη των δαπανών αφορά στο κόστος προμήθειας του εξοπλισμού και στο κόστος λειτουργίας. Μεταβολή των λειτουργικών παραμέτρων έχει πάντα αντίθετα αποτελέσματα στις δύο αυτές συνιστώσες του κόστους, και συνεπώς υπάρχουν βέλτιστες τιμές. Η αντικειμενική συνάρτηση κόστους είναι συνήθως η συνολική δαπάνη ανά έτος, με το κόστος προμήθειας επιμερισμένο ως ετήσια απόσβεση. Τα τυπικά δεδομένα για στήλη κλασματικής απόσταξης παρουσιάζονται στο Σχήμα 5.14 ως συνάρτηση του λόγου επαναρροής (Peters & Timmerhaus, 1991). Το κόστος λειτουργίας συνίσταται κυρίως από τη δαπάνη θερμαντικού μέσου (πχ υδρατμού) στον αναβραστήρα, και δευτερευόντως από τη δαπάνη ψυκτικού (πχ νερού ψύξης) στο συμπυκνωτή, και αυξάνεται γραμμικά με τον λόγο επαναρροής. Αυτό γίνεται κατανοητό αν υπολογιστούν από τα ισοζύγια μάζας οι παρακάτω σχέσεις για τις παροχές ατμού στην κορυφή και τον πυθμένα της στήλης, οι οποίες είναι αντίστοιχα ανάλογες των φορτίων του συμπυκνωτή και του αναβραστήρα V = (1 + R)D [5.24α] V = (1 + R)D (1 q)f [5.24β] Το κόστος προμήθειας της στήλης αυξάνεται με το πλήθος των δίσκων και με τη διάμετρο της στήλης. Ο ελάχιστος λόγος επαναρροής συνεπάγεται άπειρο πλήθος δίσκων, και δίνει την ασυμπτωτική συμπεριφορά που φαίνεται στο αριστερό τμήμα του Σχήματος Αυξάνοντας τον λόγο επαναρροής, μειώνεται το πλήθος των δίσκων. Όμως το κόστος απόσβεσης μειώνεται βραδύτερα και πέρα από μία τιμή R αρχίζει να αυξάνεται. Αυτή η συμπεριφορά οφείλεται στην παράλληλη αύξηση της διαμέτρου της στήλης, καθώς όπως δείχνουν οι
17 Κόστος/έτος 108 εξ. [5.14α,β] αυξάνεται γραμμικά με τον λόγο επαναρροής η παροχή ατμού. Στις συνθήκες αυτές, διατήρηση μικρής διαμέτρου θα οδηγούσε σε πλημμύριση. Το συνολικό κόστος είναι το άθροισμα των δύο συνιστωσών, του κόστους προμήθειας και του κόστους λειτουργίας, και παρουσιάζει ένα πλατύ ελάχιστο στην περιοχή R = 1,2 1,6 R min. Είναι ενδιαφέρον να διερωτηθείτε προς ποια τιμή τείνουν οι σχεδιαστές στηλών σε περιόδους που η ενέργεια είναι πολύ φθηνή ή πολύ ακριβή. Σύνολο Λειτουργία Απόσβεση Rmin Ropt R Σχήμα 5.14 Ετήσιο κόστος λειτουργίας αποστακτικής στήλης ως συνάρτηση του λόγου επαναρροής Ψηφιακή ανασκόπηση μεθόδου σχεδιασμού McCabe-Thiele Η διαδικασία σχεδιασμού που εκτέθηκε στην συνοψίζεται με πολύ χρηστικό τρόπο σε φύλλο εργασίας που είναι ελεύθερα διαθέσιμο στο διαδίκτυο ( Μεταξύ των άλλων, στο αρχείο υπολογίζονται τα δεδομένα ισορροπίας μίας μεγάλης ποικιλίας δυαδικών μιγμάτων με χρήση της μεθόδου Wilson (1964) και συνεπώς λαμβάνεται υπόψη η απόκλιση από την ιδανική συμπεριφορά. Εισάγοντας τις τιμές των μεταβλητών εισόδου (πίεση λειτουργίας, συστάσεις ρευμάτων εισόδου-εξόδου, κατάσταση τροφοδοσίας, λόγος επαναρροής), το φύλλο εργασίας δίνει αμέσως το πλήθος ιδανικών βαθμίδων και την θέση της τροφοδοσίας. Οι αλλαγές σύστασης κατά μήκος της στήλης εμφανίζονται γραφικά στο γνωστό διάγραμμα (Σχήμα 5.10), με αποτέλεσμα να γίνεται εύκολα αντιληπτή η επίδραση αλλαγών στα δεδομένα. Η εξοικείωση με το φύλλο αυτό εργασίας συστήνεται ένθερμα Αναλυτικός υπολογισμός αριθμού δίσκων-εξίσωση Κremser H γραφική διαδικασία σχεδιασμού παρουσιάζει πρακτικές δυσκολίες όταν τα προϊόντα κορυφής ή/και πυθμένα είναι πολύ υψηλής καθαρότητας. Στην περίπτωση αυτή πολλές βαθμίδες συνωστίζονται στα δύο άκρα του διαγράμματος, όπου η γραφική ακρίβεια μειώνεται ραγδαία. Ευτυχώς, στις περιοχές αυτές η καμπύλη ισορροπίας είναι πρακτικά ευθεία και μπορεί να παρασταθεί με τη μορφή y = mx + b [5.25] Η εξ. [5.25] μπορεί γενικότερα να περιγράψει οποιαδήποτε δεδομένα ισορροπίας σε μια μικρή περιοχή συγκεντρώσεων, αν ο συντελεστής m ληφθεί ίσος με την κλίση της εφαπτομένης στο σημείο αυτό. Με ευθείες
18 109 τις γραμμές ισορροπίας και λειτουργίας, το πλήθος των δίσκων που απαιτούνται για ορισμένη μεταβολή συγκεντρώσεων μπορεί να υπολογιστεί αναλυτικά με βάση μία σχέση γνωστή ως εξίσωση Kremser (1930). Η εξίσωση Kremser προκύπτει από ανάλυση των ισοζυγίων μάζας γύρω από Ν διαδοχικούς δίσκους (1,2,..,Ν), όταν μεταξύ τους δεν παρεμβάλλεται εισαγωγή τροφοδοσίας ή απομάκρυνση προϊόντος. Με βάση τον γνωστό συμβολισμό του δείκτη των γραμμομοριακών κλασμάτων (Σχήμα 5.9), τα υγρά ρεύματα εισόδου/εξόδου της συστοιχίας έχουν συστάσεις x 0 /x Ν και τα αέρια y N+1 /y 1. Ισοζύγιο μάζας σε όγκο ελέγχου που περιλαμβάνει όλους τους δίσκους δίνει τη σχέση Lx 0 + Vy n+1 = Lx n + Vy 1 Αντικαθιστώντας από τη σχέση ισορροπίας, [5.25], προκύπτει τελικά ότι [5.26] y n+1 = y 1 Αy 0 + Αy n [5.27] όπου η παράμετρος Α ορίζεται ως A = L/mV και το γραμμομοριακό κλάσμα y 0 είναι η υποθετική συγκέντρωση σε ισορροπία με την x 0. Εφαρμόζοντας την εξ. [5.27] διαδοχικά για n=1, 2,..., N και μετά από αρκετές πράξεις προκύπτει η σχεδιαστική εξίσωση ln ( y Ν+1 y Ν y N = 1 y ) 0 ln A [5.28] που μας επιτρέπει να υπολογίσουμε το πλήθος των ιδανικών βαθμίδων για κάθε διεργασία (ή τμήμα διεργασίας) όπου τα δεδομένα ισορροπίας φάσεων και η γραμμή λειτουργίας παριστάνονται με ευθείες γραμμές. Η εξίσωση του Kremser μπορεί να συνδυαστεί με την γραφική διαδικασία, αν υπολογιστούν γραφικά οι βαθμίδες στο κεντρικό τμήμα του διαγράμματος x, y, και οι συγκεντρώσεις της τελευταίας γραφικής βαθμίδας χρησιμοποιηθούν στην μια άκρη της παραπάνω διαδικασίας (προφανώς, η άλλη άκρη αντιστοιχεί στην κορυφή ή τον πυθμένα της στήλης) Βαθμός απόδοσης δίσκου Ο σχεδιασμός της στήλης κλασματικής απόσταξης βασίστηκε ως το σημείο αυτό στην παραδοχή ότι τα ρεύματα που εξέρχονται από κάθε βαθμίδα βρίσκονται σε συνθήκες ισορροπίας. Για το λόγο αυτό οι βαθμίδες ονομάζονταν ιδανικές. Η προσέγγιση της ισορροπίας απαιτεί πολύ καλή ανάμιξη των δύο φάσεων και μεγάλο χρόνο επαφής, συνθήκες που δεν είναι πάντα διαθέσιμες. Έτσι, οι πραγματικοί δίσκοι χαρακτηρίζονται από ένα βαθμό απόδοσης που είναι γενικά μικρότερος του 100%. Είναι φανερό ότι η ταχύτητα προσέγγισης των συνθηκών ισορροπίας καθορίζεται από τα φαινόμενα μεταφοράς μάζας μεταξύ των δύο φάσεων. Άρα, ο υπολογισμός των βαθμών απόδοσης βασίζεται στην κατανόηση του ρυθμού μεταφοράς μάζας, που ως τώρα είχε αγνοηθεί. Με αναφορά στο Σχήμα 5.15, ο βαθμός απόδοσης κατά Murphree του δίσκου n ορίζεται ως το πηλίκο η = y n y n+1 y n y n+1 [5.29] όπου y n είναι η πραγματική σύσταση του ατμού που απομακρύνεται από τον δίσκο και y n η σύσταση σε ισορροπία με την πραγματική σύσταση x n εξόδου του υγρού. Οποιαδήποτε πρόοδος στον υπολογισμό του βαθμού απόδοσης απαιτεί την παραδοχή ενός μοντέλου για τη διαδικασία ανάμιξης των δύο φάσεων στον δίσκο. Μία δυνατή παραδοχή είναι ότι οι δύο φάσεις βρίσκονται σε συνθήκες πλήρους ανάμιξης, δηλαδή ότι οι συστάσεις του υγρού και του ατμού στο δίσκο είναι ομοιόμορφες και ίσες με τις συστάσεις των ρευμάτων εξόδου. Μια άλλη είναι πως το υγρό του δίσκου ή/και ο ατμός μεταβάλλουν τη σύστασή τους καθώς διασχίζουν τον δίσκο. Η πρώτη παραδοχή οδηγεί σε απλούστερη ανάλυση (ολοκληρωτικό και όχι διαφορικό ισοζύγιο) και περιέχει όλα τα βασικά φυσικά φαινόμενα, και για το λόγο αυτό θα την προτιμήσουμε.
19 110 yn-1 PV Δίσκος n-1 xn-1 PV+ΔPV yn hw +hw0 Δίσκος n xn yn+1 Σχήμα 5.15 Οι συστάσεις υγρού και ατμού και η πίεση ανάντη και κατάντη δύο διαδοχικών δίσκων. Επιστρέφοντας στο Σχήμα 5.15 εκτελούμε ένα ισοζύγιο μάζας για το πτητικού συστατικό, με όγκο ελέγχου τον ατμό που περιέχεται στο δίσκο. Σε μόνιμες συνθήκες, η αύξηση της παροχής του πτητικού συστατικού (παροχή εξόδου μείον παροχή εισόδου) ισούται με το ρυθμό μεταφοράς συστατικού από την υγρή φάση διαμέσου της διεπιφάνειας υγρού-ατμού. Σύμφωνα με την ανάλυση του Κεφαλαίου 3 ( 3.3) η μεταφορά μάζας μπορεί να εκφραστεί συναρτήσει του ολικού συντελεστή (με βάση τις αέριες συγκεντρώσεις) K y και συναρτήσει της ειδικής επιφάνειας, α, των δύο φάσεων (δηλαδή της διεπιφάνειας ανά μονάδα όγκου της συσκευής). Αν Α είναι η διατομή ροής του ατμού στη στήλη και δ το μέσο πάχος της υγρής στοιβάδας, τότε η συνολική παροχή της αέριας φάσης είναι VA, η συνολική διεπιφάνεια υγρού-αερίου στον δίσκο είναι αaδ, και το ισοζύγιο μάζας καταλήγει στη σχέση (VA)(y n y n+1 ) = K y (αaδ)(y n y n ) Η εξ. [5.30] καταλήγει με απλή αναδιάταξη στον εξής τύπο για το βαθμό απόδοσης [5.30] 1 η = 1 + V K y αδ [5.31] Η εξ. [5.31] περιέχει όλη τη διαισθητικά αναμενόμενη συμπεριφορά. Ο βαθμός απόδοσης είναι μικρότερος της μονάδας, και την προσεγγίζει όταν η παροχή ατμού είναι μικρή και το πάχος της υγρής στοιβάδας μεγάλο (μεγάλος χρόνος παραμονής), ή όταν ο συντελεστής μεταφοράς μάζας είναι υψηλός. Είναι ενδιαφέρον να εξετάσει κανείς την εξάρτηση του ολικού συντελεστή μεταφοράς, K y, από τη σύσταση και συνεπώς τη θέση κατά μήκος της στήλης απόσταξης. Σύμφωνα με τη θεωρία των δύο αντιστάσεων ( 3.3.2), ο ολικός συντελεστής εκφράζεται συναρτήσει των επιμέρους συντελεστών μεταφοράς κάθε φάσης από τη σχέση 1 K y = 1 k y + m k x [5.32]
20 111 όπου m είναι η τοπική κλίση της καμπύλης ισορροπίας (η ανωτέρω σχέση προκύπτει αν η ισορροπία εκφραστεί τοπικά από την εξ. [5.25]). Απλή παρατήρηση μίας τυπικής καμπύλης ισορροπίας μίγματος πτητικών υγρών δείχνει ότι ο συντελεστής m μεταβάλλεται έντονα κατά μήκος της στήλης. Είναι αρκετά μικρότερος της μονάδας στην κορυφή (όπου x 1) και μπορεί να γίνεται πολύ μεγαλύτερος της μονάδας κοντά στον πυθμένα(όπου x 1). Συνεπώς, ακόμη και αν οι επιμέρους συντελεστές μεταφοράς μάζας είναι σχεδόν σταθεροί, ο ολικός συντελεστής μεταβάλλεται έντονα. Ειδικότερα, η εξ. [5.32] δείχνει ότι κοντά στον πυθμένα αυξάνεται η σημασία της αντίστασης στο υγρό, ενώ πλησιάζοντας στην κορυφή αυξάνεται η σημασία της αντίστασης στον ατμό. Ο σχεδιασμός της στήλης κλασματικής απόσταξης, λαμβάνοντας υπόψη το βαθμό απόδοσης κάθε δίσκου, μπορεί να γίνει με την ίδια διαδικασία όπως προηγουμένως αλλά χρησιμοποιώντας μία διαφοροποιημένη καμπύλη ισορροπίας. Καταρχάς, υπολογίζεται ο ολικός συντελεστής μεταφοράς μάζας και ο βαθμός απόδοσης για διάφορες συστάσεις κατά μήκος της καμπύλης ισορροπίας, και διαμορφώνεται μια καμπύλη βαθμού απόδοσης σαν αυτή που φαίνεται στο Σχήμα Παρατηρούμε ότι στον γραφικό σχεδιασμό των ιδανικών βαθμίδων (που περιλαμβάνει διαδοχικές μετακινήσεις μεταξύ των γραμμών λειτουργίας και της καμπύλης ισορροπίας) οι κατακόρυφες αποστάσεις αντιστοιχούν με την παρούσα ορολογία στη διαφορά y n y n+1. Όμως, από τον ορισμό της εξ. [5.29], η διαφορά αυτή πολλαπλασιασμένη με τον βαθμό απόδοσης δίνει την πραγματική μεταβολή στη συγκέντρωση του ατμού που επιτυγχάνεται από τον δίσκο. Άρα, μπορούμε να κατασκευάσουμε την τροποποιημένη καμπύλη ισορροπίας πολλαπλασιάζοντας σε διάφορες θέσεις την ιδανική μεταβολή σύστασης του ατμού με τον αντίστοιχο για τη θέση βαθμό απόδοσης. Η καμπύλη αυτή απεικονίζεται διακεκομμένη στο Σχήμα Ο γραφικός σχεδιασμός μεταξύ αυτής της καμπύλης και των γραμμών λειτουργίας δίνει τώρα τον αριθμό των πραγματικών βαθμίδων. y xd Βαθμός απόδοσης Murphre xf xb x Σχήμα 5.16 Γραφικός σχεδιασμός στήλης κλασματικής απόσταξης, λαμβάνοντας υπόψη τον βαθμό απόδοσης κάθε δίσκου.
21 Υδραυλικά χαρακτηριστικά δίσκου Τα ροϊκά χαρακτηριστικά ενός τυπικού δίσκου μπορούν να σχολιαστούν με βάση το Σχήμα Η ροή του υγρού, τόσο κατά μήκος του δίσκου όσο και μεταξύ δίσκων μέσω του αγωγού καθόδου, γίνεται με τη βαρύτητα. Η ροή του ατμού προκαλείται από διαφορά πίεσης που αναπτύσσεται με τον βρασμό στον αναβραστήρα. Ο τρόπος αυτός λειτουργίας απαιτεί μια λεπτή ισορροπία συνθηκών: Πολύ μικρή ταχύτητα ατμού επιτρέπει στο υγρό να διαφεύγει από τις οπές του δίσκου (δακρυσμός). Πολύ μεγάλη ταχύτητα ατμού εμποδίζει το υγρό να κινηθεί προς τα κάτω (πλημμύριση). Ο λόγος των δύο αυτών ταχυτήτων χαρακτηρίζει την ευελιξία του δίσκου. Η κατανόηση των παραπάνω φαινομένων, και ιδιαίτερα του μηχανισμού της πλημμύρισης, απαιτεί λεπτομερέστερη εξέταση των χαρακτηριστικών πτώσης πίεσης στα δύο ρεύματα. Η πτώση πίεσης του ατμού κατά τη διέλευση από κάθε δίσκο, ΔP V, μπορεί να αναλυθεί σε μία συνεισφορά για την υπερνίκηση της υδροστατικής πίεσης του υγρού και σε μία συνεισφορά για τη ροή διαμέσου των οπών. Η τελευταία οφείλεται στην απότομη μείωση και στη συνέχεια αύξηση της διατομής ροής (συστολή/διαστολή) και είναι χονδρικά ανάλογη του τετραγώνου της ταχύτητας ροής. Εκφρασμένη σε όρους μανομετρικού ύψους, η συνολική πτώση πίεσης είναι Δh V = ΔP V = β(h gρ w + h w0 ) + u 2 0 ρ V 2 L C 0 2gρ L [5.33] όπου u 0 είναι η ταχύτητα διαμέσου των οπών, C 0 είναι η σταθερά της στένωσης, (h w + h w0 ) η ολική στάθμη του υγρού (ύψος φράγματος συν ύψος υπερχείλισης) και β η διόρθωση της πυκνότητας του ρευστού στον δίσκο, που λόγω της ανάμιξης με τις φυσαλίδες του ατμού είναι μικρότερη από του καθαρού υγρού. Το υγρό στον αγωγό καθόδου πρέπει να έχει στάθμη υψηλότερη της στάθμης του παρακείμενου υγρού στο δίσκο, ώστε να ρέει λόγω βαρύτητας. Όμως στην επιφάνεια των δύο υγρών επικρατεί η διαφορά πίεσης ΔΡ V, που οφείλεται στην πτώση πίεσης κατά τη διέλευση του ατμού διαμέσου του δίσκου (βλέπε Σχήμα 5.15). Έτσι, η διαφορά στάθμης στον αγωγό καθόδου πρέπει να είναι αρκετή ώστε να υπερνικήσει τόσο αυτή όσο και την πτώση πίεσης λόγω τριβών. Για υψηλές ταχύτητες ατμού, η πτώση πίεσης ΔΡ V οφείλεται κατά κύριο λόγο στη διέλευση διαμέσου των οπών, μια και η συνεισφορά αυτή αυξάνει με το τετράγωνο της ταχύτητας. Η μέγιστη επιτρεπτή τιμή μανομετρικού ύψους στον αγωγό καθόδου αντιστοιχεί στην απόσταση μεταξύ διαδοχικών δίσκων. Αν η πτώση πίεσης του ατμού ξεπεράσει αυτό το μανομετρικό ύψος, το υγρό γεμίζει τον αγωγό καθόδου χωρίς να ρέει και έχουμε πλημμύριση. Η επιλογή διαμέτρου στήλης ώστε να αποφευχθεί η πλημμύριση γίνεται με τη χρήση του διαγράμματος του Σχήματος 5.17, το οποίο έχει προταθεί από τον Fair (1961). Οι εναλλακτικές καμπύλες του Σχήματος 5.17 αντιστοιχούν σε διαφορετικές αποστάσεις μεταξύ δίσκων. Ο οριζόντιος άξονας είναι αδιάστατος και περιλαμβάνει τον λόγο μαζικών παροχών υγρού-αερίου και τις πυκνότητες των δύο φάσεων. Ο κατακόρυφος άξονας περιέχει την ταχύτητα πλημμύρισης, U NF, υπολογισμένη σε m/s με βάση την ελεύθερη διατομή ροής του ατμού (δηλαδή την συνολική διατομή του δίσκου μείον την διατομή του αγωγού καθόδου), καθώς την επιφανειακή τάση, σ, του υγρού σε dyn/cm. Η διαδικασία προσδιορισμού της ταχύτητας πλημμύρισης σε μία θέση κατά μήκος της στήλης περιλαμβάνει τα εξής βήματα: (α) επιλογή της κατάλληλης καμπύλης (δηλαδή της επιθυμητής απόστασης μεταξύ δίσκων). (β) Υπολογισμό της παραμέτρου του οριζόντιου άξονα x = L m ( ρ 0,5 V ) V m ρ L [5.34] όπου οι παροχές L m και V m είναι μαζικές, σε αντιδιαστολή με τις L και V που είναι γραμμομοριακές. (γ) Ανάγνωση της τιμής της παραμέτρου C SB ρ 0,5 V C BS = U NF ( ) ( 20 0,2 ρ L ρ V σ ) [5.35] και υπολογισμό από αυτήν της U NF. Η διάμετρος της στήλης επιλέγεται έτσι ώστε η ταχύτητα ατμού να μην ξεπερνά σε καμία θέση το 60-80% της ταχύτητας πλημμύρισης.
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ
 Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
Βελτιστοποίηση εναλλακτών θερμότητας
 Βελτιστοποίηση εναλλακτών θερμότητας Το πρώτο βήμα για την εύρεση των βέλτιστων διαστάσεων ή/και συνθηκών λειτουργίας, είναι ο καθορισμός του μεγέθους που θα βελτιστοποιηθεί, δηλαδή της αντικειμενικής
Βελτιστοποίηση εναλλακτών θερμότητας Το πρώτο βήμα για την εύρεση των βέλτιστων διαστάσεων ή/και συνθηκών λειτουργίας, είναι ο καθορισμός του μεγέθους που θα βελτιστοποιηθεί, δηλαδή της αντικειμενικής
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013 1 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
Αυτόματη ρύθμιση αποστακτικών στηλών
 Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
Απρίλιος Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6F, L = 0.4F, F = 1 kmol/s. Ζητούμενα: x Fi, x Li
 Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Κεφάλαιο 4 Κλασματική Απόσταξη
 Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Σφαιρικές συντεταγμένες (r, θ, φ).
 T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
T T r e r 1 T e r Σφαιρικές συντεταγμένες (r, θ, φ). 1 T e. (2.57) r sin u u e u e u e, (2.58) r r οπότε το εσωτερικό γινόμενο u.t γίνεται: T u T u T u. T ur. (2.59) r r r sin 2.5 Η ΑΡΧΗ ΔΙΑΤΗΡΗΣΗΣ ΤΗΣ
Energy resources: Technologies & Management
 Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
Πανεπιστήμιο Δυτικής Μακεδονίας Energ resources: echnologies & Management Τεχνολογίες άνθρακα Σχεδιασμός Στηλών Απορρόφησης Αερίων Δρ. Γεώργιος Σκόδρας Αν. Καθηγητής Περιεχόμενα Η διάλεξη που ακολουθεί
ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6
 Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
Υπολογισµοί του Χρόνου Ξήρανσης
 Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
ΝΟΜΟΙ ΑΕΡΙΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΑΣΚΗΣΗ 1 Μία θερμική μηχανή λειτουργεί μεταξύ των θερμοκρασιών T h 400 Κ και T c με T c < T h Η μηχανή έχει απόδοση e 0,2 και αποβάλλει στη δεξαμενή χαμηλής θερμοκρασίας θερμότητα
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Εναλλαγή θερμότητας. Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω)
 Εναλλαγή θερμότητας Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω) Σχ. 4.1 (β) Διάταξη εναλλάκτη θερμότητας καντ` αντιρροή (πάνω) και αντίστοιχο
Εναλλαγή θερμότητας Σχ. 4.1 (α) Διάταξη εναλλάκτη θερμότητας καθ` ομορροή (πάνω) και αντίστοιχο θερμοκρασιακό προφίλ (κάτω) Σχ. 4.1 (β) Διάταξη εναλλάκτη θερμότητας καντ` αντιρροή (πάνω) και αντίστοιχο
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Κεφάλαιο 4: Επιλογή σημείου παραγωγής
 Κ4.1 Μέθοδος ανάλυσης νεκρού σημείου για την επιλογή διαδικασίας παραγωγής ή σημείου παραγωγής Επιλογή διαδικασίας παραγωγής Η μέθοδος ανάλυσης νεκρού για την επιλογή διαδικασίας παραγωγής αναγνωρίζει
Κ4.1 Μέθοδος ανάλυσης νεκρού σημείου για την επιλογή διαδικασίας παραγωγής ή σημείου παραγωγής Επιλογή διαδικασίας παραγωγής Η μέθοδος ανάλυσης νεκρού για την επιλογή διαδικασίας παραγωγής αναγνωρίζει
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης
 ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΑΣΚΗΣΕΙΣ ΣΥΣΚΕΥΩΝ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ. 1η ενότητα
 1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης 2. Ενέργεια Ενεργοποίησης
 Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Χημική Κινητική Γενικές Υποδείξεις 1. Τάξη Αντίδρασης Γενικά, όταν έχουμε δεδομένα συγκέντρωσης-χρόνου και θέλουμε να βρούμε την τάξη μιας αντίδρασης, προσπαθούμε να προσαρμόσουμε τα δεδομένα σε εξισώσεις
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
5 Μετρητές παροχής. 5.1Εισαγωγή
 5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
5 Μετρητές παροχής 5.Εισαγωγή Τρεις βασικές συσκευές, με τις οποίες μπορεί να γίνει η μέτρηση της ογκομετρικής παροχής των ρευστών, είναι ο μετρητής Venturi (ή βεντουρίμετρο), ο μετρητής διαφράγματος (ή
Κεφάλαιο 4: Επιλογή σημείου παραγωγής
 Κεφάλαιο 4: Επιλογή σημείου παραγωγής Κ4.1 Μέθοδος ανάλυσης νεκρού σημείου για την επιλογή διαδικασίας παραγωγής ή σημείου παραγωγής Επιλογή διαδικασίας παραγωγής Η μέθοδος ανάλυσης νεκρού για την επιλογή
Κεφάλαιο 4: Επιλογή σημείου παραγωγής Κ4.1 Μέθοδος ανάλυσης νεκρού σημείου για την επιλογή διαδικασίας παραγωγής ή σημείου παραγωγής Επιλογή διαδικασίας παραγωγής Η μέθοδος ανάλυσης νεκρού για την επιλογή
Απορρόφηση Αερίων. 1. Εισαγωγή
 1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ
 1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
1 1 IΔΑΝΙΚΑ ΑΕΡΙΑ 1.1 ΓΕΝΙΚΑ Θα αρχίσουμε τη σειρά των μαθημάτων της Φυσικοχημείας με τη μελέτη της αέριας κατάστασης της ύλης. Η μελέτη της φύσης των αερίων αποτελεί ένα ιδανικό μέσο για την εισαγωγή
ΘΕΡΜΙΚΕΣ & ΨΥΚΤΙΚΕΣ ΜΗΧΑΝΕΣ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 www.pmoiras.weebly.om ΘΕΡΜΙΚΕΣ & ΨΥΚΤΙΚΕΣ ΜΗΧΑΝΕΣ ΘΕΩΡΙΑ Περιεχόμενα 1. Κυκλικές διαδικασίες 2. O 2ος Θερμοδυναμικός Νόμος- Φυσική Ερμηνεία 2.1 Ισοδυναμία
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 www.pmoiras.weebly.om ΘΕΡΜΙΚΕΣ & ΨΥΚΤΙΚΕΣ ΜΗΧΑΝΕΣ ΘΕΩΡΙΑ Περιεχόμενα 1. Κυκλικές διαδικασίες 2. O 2ος Θερμοδυναμικός Νόμος- Φυσική Ερμηνεία 2.1 Ισοδυναμία
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
Ο «TRANSCRITICAL» ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ ΤΟΥ CO2
 6--5 Ο «TRANSCRITICAL» ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ ΤΟΥ CO2 Στα συνηθισμένα ψυκτικά ρευστά, η απόρριψη θερμότητας γίνεται υπό σταθερά θερμοκρασία, που είναι η θερμοκρασία συμπύκνωσης του ψυκτικού ρευστού. Όπως φαίνεται
6--5 Ο «TRANSCRITICAL» ΨΥΚΤΙΚΟΣ ΚΥΚΛΟΣ ΤΟΥ CO2 Στα συνηθισμένα ψυκτικά ρευστά, η απόρριψη θερμότητας γίνεται υπό σταθερά θερμοκρασία, που είναι η θερμοκρασία συμπύκνωσης του ψυκτικού ρευστού. Όπως φαίνεται
P. kpa T, C v, m 3 /kg u, kj/kg Περιγραφή κατάστασης και ποιότητα (αν εφαρμόζεται) , ,0 101,
 Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
Ασκήσεις Άσκηση 1 Να συμπληρώσετε τα κενά κελιά στον επόμενο πίνακα των ιδιοτήτων του νερού εάν παρέχονται επαρκή δεδομένα. Στην τελευταία στήλη να περιγράψετε την κατάσταση του νερού ως υπόψυκτο υγρό,
ΔΕΙΓΜΑ ΠΡΙΝ ΤΙΣ ΔΙΟΡΘΩΣΕΙΣ - ΕΚΔΟΣΕΙΣ ΚΡΙΤΙΚΗ
 Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
Συναρτήσεις Προεπισκόπηση Κεφαλαίου Τα μαθηματικά είναι μια γλώσσα με ένα συγκεκριμένο λεξιλόγιο και πολλούς κανόνες. Πριν ξεκινήσετε το ταξίδι σας στον Απειροστικό Λογισμό, θα πρέπει να έχετε εξοικειωθεί
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
(β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele
 Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
1. Εναλλάκτες θερµότητας (Heat Exchangers)
 1. Εναλλάκτες θερµότητας (Heat Exangers) Οι εναλλάκτες θερµότητας είναι συσκευές µε τις οποίες επιτυγχάνεται η µεταφορά ενέργειας από ένα ρευστό υψηλής θερµοκρασίας σε ένα άλλο ρευστό χαµηλότερης θερµοκρασίας.
1. Εναλλάκτες θερµότητας (Heat Exangers) Οι εναλλάκτες θερµότητας είναι συσκευές µε τις οποίες επιτυγχάνεται η µεταφορά ενέργειας από ένα ρευστό υψηλής θερµοκρασίας σε ένα άλλο ρευστό χαµηλότερης θερµοκρασίας.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΛΥΜΕΝΑ ΘΕΜΑΤΑ 1 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 Θέμα 1 Επιλέγοντας το κατάλληλο διάγραμμα φάσεων για ένα πραγματικό
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Δ Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Δ Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15949 Ποσότητα ιδανικού αέριου ίση με /R mol, βρίσκεται αρχικά σε κατάσταση ισορροπίας στην οποία έχει
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Δ Θέμα ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15949 Ποσότητα ιδανικού αέριου ίση με /R mol, βρίσκεται αρχικά σε κατάσταση ισορροπίας στην οποία έχει
ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ
 ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
ΜΕΡΟΣ ΙΙ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ 36 ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΔΙΑΚΡΙΤΩΝ ΕΝΑΛΛΑΚΤΙΚΩΝ ΣΕ ΠΡΟΒΛΗΜΑΤΑ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΣΥΝΘΕΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Πολλές από τις αποφάσεις
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ. Σημειώσεις. Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ
 ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΟΡΙΑΚΟ ΣΤΡΩΜΑ: ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΘΕΩΡΗΤΙΚΗ ΑΝΑΛΥΣΗ Σημειώσεις Επιμέλεια: Άγγελος Θ. Παπαϊωάννου, Ομοτ. Καθηγητής ΕΜΠ Αθήνα, Απρίλιος 13 1. Η Έννοια του Οριακού Στρώματος Το οριακό στρώμα επινοήθηκε για
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ. Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για:
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
Ομογενή Χημικά Συστήματα
 Ομογενή Χημικά Συστήματα 1. Πειραματικός Προσδιορισμός Τάξης Αντιδράσεων 2. Συνεχείς Αντιδραστήρες (Ι) Πειραματική Μελέτη Ρυθμού Αντίδρασης Μέθοδοι Λήψης και Ερμηνείας Δεδομένων (ΙΙ) Τύποι Συνεχών Αντιδραστήρων:
Ομογενή Χημικά Συστήματα 1. Πειραματικός Προσδιορισμός Τάξης Αντιδράσεων 2. Συνεχείς Αντιδραστήρες (Ι) Πειραματική Μελέτη Ρυθμού Αντίδρασης Μέθοδοι Λήψης και Ερμηνείας Δεδομένων (ΙΙ) Τύποι Συνεχών Αντιδραστήρων:
Ιδιότητες Μιγμάτων. Μερικές Μολαρικές Ιδιότητες
 Ιδιότητες Μιγμάτων Μερικές Μολαρικές Ιδιότητες ΙΔΑΝΙΚΟ ΔΙΑΛΥΜΑ = ή διαιρεμένη διά του = x όπου όλα τα προσδιορίζονται στην ίδια T και P. = Όπου ή διαιρεμένη διά του : = x ορίζεται η μερική μολαρική ιδιότητα
Ιδιότητες Μιγμάτων Μερικές Μολαρικές Ιδιότητες ΙΔΑΝΙΚΟ ΔΙΑΛΥΜΑ = ή διαιρεμένη διά του = x όπου όλα τα προσδιορίζονται στην ίδια T και P. = Όπου ή διαιρεμένη διά του : = x ορίζεται η μερική μολαρική ιδιότητα
ΑΓΩΓΟΣ VENTURI. Σχήμα 1. Διάταξη πειραματικής συσκευής σωλήνα Venturi.
 Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 7 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΑΓΩΓΟΣ VENTURI ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Α.Ε.Ι. ΠΕΙΡΑΙΑ Τ.Τ. ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΡΕΥΣΤΩΝ 7 η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΑΓΩΓΟΣ VENTURI ΣΚΟΠΟΣ ΤΗΣ ΑΣΚΗΣΗΣ Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Εργαστήριο Μηχανικής Ρευστών. Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής
 Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Εργαστήριο Μηχανικής Ρευστών Εργασία 1 η : Πτώση πίεσης σε αγωγό κυκλικής διατομής Ονοματεπώνυμο:Κυρκιμτζής Γιώργος Σ.Τ.Ε.Φ. Οχημάτων - Εξάμηνο Γ Ημερομηνία εκτέλεσης Πειράματος : 12/4/2000 Ημερομηνία
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
1 η ΑΣΚΗΣΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΙΜΟΤΗΤΑ ΣΕ ΑΠΛΟ ΤΟΙΧΩΜΑ
 ΑEI ΠΕΙΡΑΙΑ (ΤΤ) ΣΤΕΦ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ-ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΡΓ. ΜΕΤΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ 1 η ΑΣΚΗΣΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΙΜΟΤΗΤΑ ΣΕ ΑΠΛΟ ΤΟΙΧΩΜΑ Σκοπός της άσκησης Η κατανόηση της χρήσης της εξίσωσης Fourier
ΑEI ΠΕΙΡΑΙΑ (ΤΤ) ΣΤΕΦ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ-ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΡΓ. ΜΕΤΑΔΟΣΗΣ ΘΕΡΜΟΤΗΤΑΣ 1 η ΑΣΚΗΣΗ ΜΕΤΑΔΟΣΗ ΘΕΡΜΟΤΗΤΑΣ ΜΕ ΑΓΩΓΙΜΟΤΗΤΑ ΣΕ ΑΠΛΟ ΤΟΙΧΩΜΑ Σκοπός της άσκησης Η κατανόηση της χρήσης της εξίσωσης Fourier
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών
 Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Συνήθεις διαφορικές εξισώσεις προβλήματα οριακών τιμών Οι παρούσες σημειώσεις αποτελούν βοήθημα στο μάθημα Αριθμητικές Μέθοδοι του 5 ου εξαμήνου του ΤΜΜ ημήτρης Βαλουγεώργης Καθηγητής Εργαστήριο Φυσικών
Στις εξισώσεις σχεδιασμού υπεισέρχεται ο ρυθμός της αντίδρασης. Επομένως, είναι βασικό να γνωρίζουμε την έκφραση που περιγράφει το ρυθμό.
 Βασικές Εξισώσεις Σχεδιασμού (ΣΔΟΥΚΟΣ 2-, 2-) t = n i dn i V n i R και V = n i dn i t n i R Στις εξισώσεις σχεδιασμού υπεισέρχεται ο ρυθμός της αντίδρασης. Επομένως, είναι βασικό να γνωρίζουμε την έκφραση
Βασικές Εξισώσεις Σχεδιασμού (ΣΔΟΥΚΟΣ 2-, 2-) t = n i dn i V n i R και V = n i dn i t n i R Στις εξισώσεις σχεδιασμού υπεισέρχεται ο ρυθμός της αντίδρασης. Επομένως, είναι βασικό να γνωρίζουμε την έκφραση
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013
 Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Εργαστηριακή άσκηση: Σωλήνας Venturi
 Εργαστήριο Μηχανικών των Ρευστών Τμήμα Μηχανολόγων Μηχανικών, Πανεπιστήμιο Δυτικής Αττικής Σκοπός της άσκησης Εργαστηριακή άσκηση: Σωλήνας Veturi Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Εργαστήριο Μηχανικών των Ρευστών Τμήμα Μηχανολόγων Μηχανικών, Πανεπιστήμιο Δυτικής Αττικής Σκοπός της άσκησης Εργαστηριακή άσκηση: Σωλήνας Veturi Σκοπός της άσκησης είναι η κατανόηση της χρήσης της συσκευής
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
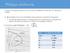 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Περιεχόμενα. Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14
 Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
Περιεχόμενα Κεφάλαιο 1 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΜΙΑ ΕΥΘΕΙΑ... 13 1.1 Οι συντεταγμένες ενός σημείου...13 1.2 Απόλυτη τιμή...14 Κεφάλαιο 2 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ ΣΕ ΕΝΑ ΕΠΙΠΕΔΟ 20 2.1 Οι συντεταγμένες
1. ΡΥΘΜΙΣΗ ΜΕ ΣΤΡΑΓΓΑΛΙΣΜΟ ΤΟΥ ΑΤΜΟΥ
 1. ΡΥΘΜΙΣΗ ΜΕ ΣΤΡΑΓΓΑΛΙΣΜΟ ΤΟΥ ΑΤΜΟΥ Ο στραγγαλισμός του ατμού υλοποιείται εξαναγκάζοντας τον ατμό, πριν παροχετευθεί στο στρόβιλο, να περάσει μέσα από κατάλληλη βαλβίδα όπου μικραίνει η διατομή διέλευσης
1. ΡΥΘΜΙΣΗ ΜΕ ΣΤΡΑΓΓΑΛΙΣΜΟ ΤΟΥ ΑΤΜΟΥ Ο στραγγαλισμός του ατμού υλοποιείται εξαναγκάζοντας τον ατμό, πριν παροχετευθεί στο στρόβιλο, να περάσει μέσα από κατάλληλη βαλβίδα όπου μικραίνει η διατομή διέλευσης
Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων
 Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία II, Διαλύματα Απλά διαγράμματα τάσης ατμών-σύστασηςιδανικών διαλυματων o P = N P P = A A A N P o B B B PA + PB = P ολ Τ=const P = Ν ολ P + N P o o A A B B Ν Α + Ν =1 o o o P = P + A N ( ολ
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 5: Διαγράμματα σημείων ζέσεως συνθέσεως Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 Σελίδα 2 1. Θεωρία
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις Άσκηση 5: Διαγράμματα σημείων ζέσεως συνθέσεως Αθανάσιος Τσεκούρας Τμήμα Χημείας 1. Θεωρία... 3 2. Μετρήσεις... 4 3. Επεξεργασία Μετρήσεων... 5 Σελίδα 2 1. Θεωρία
Θέµα 1 ο. iv) πραγµατοποιεί αντιστρεπτές µεταβολές.
 ΜΑΘΗΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ Θέµα 1 ο α) Ορισµένη ποσότητα ιδανικού αερίου πραγµατοποιεί µεταβολή AB από την κατάσταση A (p, V, T ) στην κατάσταση B (p, V 1, T ). i) Ισχύει V 1 = V. ii) Η µεταβολή παριστάνεται
ΜΑΘΗΜΑ ΟΝΟΜΑΤΕΠΩΝΥΜΟ Θέµα 1 ο α) Ορισµένη ποσότητα ιδανικού αερίου πραγµατοποιεί µεταβολή AB από την κατάσταση A (p, V, T ) στην κατάσταση B (p, V 1, T ). i) Ισχύει V 1 = V. ii) Η µεταβολή παριστάνεται
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες
 Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
Γ. Ν. Π Α Π Α Δ Α Κ Η Σ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ ( M S C ) ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΠΡΟΓΡΑΜΜΑ: Σπουδές στις Φυσικές Επιστήμες ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΦΥΕ10 (Γενικά Μαθηματικά Ι) ΠΕΡΙΕΧΕΙ ΤΙΣ
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Παραγώγιση Εισαγωγή Ορισμός 7. Αν y f x είναι μια συνάρτηση ορισμένη σε ένα διάστημα
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων
 Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΕΝΟΤΗΤΑ 3: Η ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ Η ΕΞΙΣΩΣΗ BERNOULLI ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 3 Ο : ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ ΕΝΟΤΗΤΑ 3: Η ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ Η ΕΞΙΣΩΣΗ BERNOULLI ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση 1. ΘΕΜΑ Β Στο οριζόντιο σωλήνα του διπλανού σχήματος ρέει ιδανικό υγρό. Με τον οριζόντιο
ΚΕΦΑΛΑΙΟ 3 Ο : ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ ΕΝΟΤΗΤΑ 3: Η ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΕΝΕΡΓΕΙΑΣ ΚΑΙ Η ΕΞΙΣΩΣΗ BERNOULLI ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση 1. ΘΕΜΑ Β Στο οριζόντιο σωλήνα του διπλανού σχήματος ρέει ιδανικό υγρό. Με τον οριζόντιο
Να υπολογίσετε τη μάζα 50 L βενζίνης. Δίνεται η σχετική πυκνότητά της, ως προς το νερό ρ σχ = 0,745.
 1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
1 Παράδειγμα 101 Να υπολογίσετε τη μάζα 10 m 3 πετρελαίου, στους : α) 20 ο C και β) 40 ο C. Δίνονται η πυκνότητά του στους 20 ο C ρ 20 = 845 kg/m 3 και ο συντελεστής κυβικής διαστολής του β = 9 * 10-4
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΑΤΡΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΚΑΙ ΑΕΡΟΝΑΥΠΗΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓΑΣΤΗΡΙΟ ΜΗΧΑΝΙΚΗΣ ΤΩΝ ΡΕΥΣΤΩΝ ΚΑΙ ΕΦΑΡΜΟΓΩΝ ΑΥΤΗΣ Διευθυντής: Διονύσιος-Ελευθ. Π. Μάργαρης, Αναπλ. Καθηγητής ΕΡΓΑΣΤΗΡΙΑΚΗ
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 19/02/17 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/02/7 ΕΠΙΜΕΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΗΜΕΡΟΜΗΝΙΑ: 9/02/7 ΕΠΙΜΕΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Υποθέστε ότι ο ρυθμός ροής από ένα ακροφύσιο είναι γραμμική συνάρτηση της διαφοράς στάθμης στα δύο άκρα του ακροφυσίου.
 ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
 ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
Φυσικοί μετασχηματισμοί καθαρών ουσιών
 Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
Φυσικοί μετασχηματισμοί καθαρών ουσιών Ή εξάτμιση, η τήξη και η μετατροπή του γραφίτη σε διαμάντι αποτελούν συνηθισμένα παραδείγματα αλλαγών φάσης χωρίς μεταβολή της χημικής σύστασης. Ορισμός φάσης: Μια
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας Διανύσματα Καστοριά,
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Τράπεζα θεμάτων. Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ
 ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
ΜΑΝΩΛΗ ΡΙΤΣΑ ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Τράπεζα θεμάτων Β Θέμα ΚΙΝΗΤΙΚΗ ΘΕΩΡΙΑ ΑΕΡΙΩΝ 16111 Ένα παιδί κρατάει στο χέρι του ένα μπαλόνι γεμάτο ήλιο που καταλαμβάνει όγκο 4 L (σε πίεση
μεταβάλλουμε την απόσταση h της μιας τρύπας από την επιφάνεια του υγρού (π.χ. προσθέτουμε ή αφαιρούμε υγρό) έτσι ώστε h 2 =2 Α 2
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΡΕΥΣΤΑ 1 Μια κυλινδρική δεξαμενή ακτίνας 6m και ύψους h=5m είναι γεμάτη με νερό, βρίσκεται στην κορυφή ενός πύργου ύψους 45m και χρησιμοποιείται για το πότισμα ενός χωραφιού α Ποια η παροχή
ΑΣΚΗΣΕΙΣ ΣΤΑ ΡΕΥΣΤΑ 1 Μια κυλινδρική δεξαμενή ακτίνας 6m και ύψους h=5m είναι γεμάτη με νερό, βρίσκεται στην κορυφή ενός πύργου ύψους 45m και χρησιμοποιείται για το πότισμα ενός χωραφιού α Ποια η παροχή
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. Καθηγητής Δ. Ματαράς
 ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url 0.Μεταφορά Θερμότητας σε Ρευστά Εναλλάκτης Κελύφους-Αυλών E 2 Β 2 Ατμός F C K Εξαέρωση Β Θερμό Υγρό J E D 2 Α D H Ψυχρό Υγρό Eικόνα
ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Καθηγητής Δ. Ματαράς image url 0.Μεταφορά Θερμότητας σε Ρευστά Εναλλάκτης Κελύφους-Αυλών E 2 Β 2 Ατμός F C K Εξαέρωση Β Θερμό Υγρό J E D 2 Α D H Ψυχρό Υγρό Eικόνα
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΜΑ 4
 ΘΕΜΑ 4 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15984 Ποσότητα μονατομικού ιδανικού αερίου βρίσκεται στην κατάσταση θερμοδυναμικής ισορροπίας Α (ρ0, V0, To). Το αέριο εκτελεί αρχικά ισόθερμη αντιστρεπτή μεταβολή
ΘΕΜΑ 4 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ 15984 Ποσότητα μονατομικού ιδανικού αερίου βρίσκεται στην κατάσταση θερμοδυναμικής ισορροπίας Α (ρ0, V0, To). Το αέριο εκτελεί αρχικά ισόθερμη αντιστρεπτή μεταβολή
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού
 Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος
 ΕΞ ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος ΕΞ.1 Εισαγωγή Αντικείµενο της συµπύκνωσης είναι κατά κύριο λόγο η αποµάκρυνση νερού, µε εξάτµιση, από ένα υδατικό διάλυµα που περιέχει µια ή περισσότερες διαλυµένες ουσίες,
ΕΞ ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος ΕΞ.1 Εισαγωγή Αντικείµενο της συµπύκνωσης είναι κατά κύριο λόγο η αποµάκρυνση νερού, µε εξάτµιση, από ένα υδατικό διάλυµα που περιέχει µια ή περισσότερες διαλυµένες ουσίες,
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
 ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι
 Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
Ερωτήσεις θεωρίας - Θέμα Β Εκφώνηση 1η Στο διπλανό σχήμα το έμβολο έχει βάρος Β, διατομή Α και ισορροπεί. Η δύναμη που ασκείται από το υγρό στο έμβολο είναι α) β) γ) Λύση Εκφώνηση 2η Στο διπλανό υδραυλικό
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ. ΜΕΡΟΣ Α : Άλγεβρα. Κεφάλαιο 2 ο (Προτείνεται να διατεθούν 12 διδακτικές ώρες) Ειδικότερα:
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ-ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΜΕΡΟΣ Α : Άλγεβρα Κεφάλαιο ο (Προτείνεται να διατεθούν διδακτικές ώρες) Ειδικότερα:. -. (Προτείνεται να διατεθούν 5 διδακτικές ώρες).3 (Προτείνεται να διατεθούν
