ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ, 2013
|
|
|
- Σεβαστιανός Γιάνναρης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΔΙΑΧΩΡΙΣΜΟΥ ΜΑΔ,
2 Ισορροπία Φάσεων Ανάλογα με τη φύση των συστατικών του μίγματος (ή της ολικής πίεσης του συστήματος) οι τάσεις διαφυγής υπολογίζονται - ανάλογα και με τη φάση - ως: Μη πολικά συστατικά Υψηλές πιέσεις: όπου οι συντελεστές τάσης διαφυγής υπολογίζονται με κυβικές καταστατικές εξισώσεις (π.χ. PR ή SRK). Antone με Vral με, s s v P φ φ P x f P y f L l v v φ φ = = s s l v v Pe P x f P y f ) ( φ γ φ = = l v f = f x y = K Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμούυγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων διαφυγής για όλα τα συστατικά του μίγματος: Η ποσοτική περιγραφή της ισορροπίας ατμού-υγρού εκφράζεται συνήθως με τους λόγους ισορροπίας K : Πολικά συστατικά - Χαμηλές πιέσεις: όπου : UNIFAC Van Laar, Wlson, με ) ( exp ) ( s l P P RT v Pe γ = 2
3 Οι βασικοί υπολογισμοί που ενδιαφέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο φυσαλίδας σημείο δρόσου εκτόνωση (flash) αποστακτικές στήλες 3
4 ΜΕΤΑΒΛΗΤΕΣ ΣΧΕΔΙΑΣΜΟΥ Σε κάθε φυσικό σύστημα ορίζονται: Ν Μ Ν Π : Ο συνολικός αριθμός των Μεταβλητών : Ο συνολικός αριθμός των Περιορισμών (εξισώσεων) Οι βαθμοί ελευθερίας (Ν Ε ) ή μεταβλητές σχεδιασμού ή ελεύθερες μεταβλητές είναι: ΜΕΤΑΒΛΗΤΕΣ ΣΧΕΔΙΑΣΜΟΥ 4 Ν Ε = Ν Μ Ν Π Ο καθορισμός των μεταβλητών σχεδιασμού είναι ένα από τα δυσκολότερα θέματα κατά το σχεδιασμό ενός συστήματος. Απαιτεί γνώσεις, εμπειρία και εφευρετικότητα. Συνήθως οι μεταβλητές σχεδιασμού επιλέγονται ώστε να ικανοποιούνται παράγοντες όπως: Ελαχιστοποίηση του συνολικού κόστους Ασφάλεια της εγκατάστασης Προστασία του περιβάλλοντος Ευκολία στη λειτουργία του συστήματος Ευκολία στη συντήρηση του συστήματος Προσαρμογή σε υπάρχοντα εξοπλισμό Πρόβλεψη για δυνατότητα επεκτάσεων ή μετατροπών Αλλά και ευκολία στην επίλυση του συστήματος των εξισώσεων, κ.α. Οι βέλτιστες τιμές τους προσδιορίζονται με χρήση συναρτήσεων κόστους (ή κέρδους) των οποίων επιζητούμε την ελαχιστοποίηση (ή μεγιστοποίηση).
5 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΣΥΣΤΗΜΑΤΟΣ ΣΕ Ι.Φ. Έστω ένα σύστημα Ν Φ φάσεων σε ισορροπία. Κάθε φάση περιέχει Ν Σ συστατικά. ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΣΥΣΤΗΜΑΤΟΣ ΣΕ Ι.Φ. Προσδιορισμός Μεταβλητών Ν Μ Κάθε φάση σε ορισμένη πίεση και θερμοκρασία είναι πλήρως ορισμένη όταν οριστούν οι Ν Σ -1 συστάσεις της. Άρα για το σύστημα των Ν Φ φάσεων πρέπει να οριστούν Ν Μ μεταβλητές: Ν Μ = Ν Φ (Ν Σ -1) + 2 (Το 2 για την κοινή πίεση και θερμοκρασία των φάσεων) Προσδιορισμός Περιορισμών (Εξισώσεων) Ν Π Κάθε συστατικό βρίσκεται σε ισορροπία σε όλες τις φάσεις. Άρα πρέπει να γραφούν Ν Φ -1 εξισώσεις ισορροπίας. Συνεπώς για τα Ν Σ συστατικά ο συνολικός αριθμός περιορισμών (εξισώσεων) Ν Π, είναι: Ν Π = Ν Σ (Ν Φ -1) Προσδιορισμός Μεταβλητών Σχεδιασμού Ν Ε 5 Οι βαθμοί ελευθερίας (Ν Ε ) ή μεταβλητές σχεδιασμού ή ελεύθερες μεταβλητές είναι: Ν Ε = Ν Μ Ν Π = Ν Σ Ν Φ + 2 (Κανόνας των Φάσεων του Gbbs: F=C-P+2).
6 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΜΟΝΑΔΩΝ ΟΡΙΣΜΟΙ 6 Ν Ε : Οι βαθμοί ελευθερίας (μεταβλητές σχεδιασμού) ενός απλού στοιχείου ή μονάδας Ν Μ Ν Π : Ο συνολικός αριθμός των Μεταβλητών: συστάσεις, θερμοκρασίες, πιέσεις, παροχές : Ο συνολικός αριθμός των Περιορισμών (εξισώσεων): Ισοζύγια μάζας Ισοζύγια ενέργειας Εξισώσεις ισορροπίας Ενδογενείς περιορισμοί (πχ ίδιες θερμοκρασίες ρευμάτων σε Ι.Φ)
7 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΛΗ ΜΟΝΑΔΑ ΠΕΡΙΓΡΑΦΗ ΜΕΤΑΒΛΗΤΕΣ (Ν Μ ) ΠΕΡΙΟΡΙΣΜΟΙ (Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ - ΜΕΤΑΒΛΗΤΕΣ ΣΧΕΔΙΑΣΜΟΥ (Ν Ε = Ν Μ Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ 7 ΑΠΛΟ ΡΕΥΜΑ (ΜΙΑ ΦΑΣΗ) Ν Σ ΣΥΣΤΑΤΙΚΑ ΑΝΑΜΙΚΤΗΣ ΡΕΥΜΑΤΩΝ ΔΙΑΧΩΡΙΣΤΗΣ ΡΕΥΜΑΤΟΣ Ν Σ +2 Συστάσεις (Ν Σ -1) Θερμοκρασία Πίεση Παροχή 3 (Ν Σ +2) + 1 Ν Σ + 1 Συστάσεις (Ν Σ -1), Θερμοκρασία, Πίεση, Παροχή των 3 ρευμάτων Θερμότητα (1) Ισοζύγια μάζας (N Σ ) Ισοζύγιο ενέργειας (1) 3 (Ν Σ +2) Ν Σ + 2 Συστάσεις (Ν Σ -1), Θερμοκρασία, Πίεση, Παροχή των 3 ρευμάτων Θερμότητα (1) 0 Ν Σ +2 - Ίδια σύσταση και στα 3 ρεύματα [2 (N Σ -1)] - Κοινές P, T στα ρεύματα εξόδου (2) - Ολικό ισοζύγιο μάζας (1) - Ισοζύγιο ενέργειας (1) 2 Ν Σ + 6 Ν Σ + 5
8 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΛΗ ΜΟΝΑΔΑ ΠΕΡΙΓΡΑΦΗ ΜΕΤΑΒΛΗΤΕΣ (Ν Μ ) ΠΕΡΙΟΡΙΣΜΟΙ (Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ - ΜΕΤΑΒΛΗΤΕΣ ΣΧΕΔΙΑΣΜΟΥ (Ν Ε = Ν Μ Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΔΟΧΕΙΟ ΙΣΟΡΡΟΠΙΑΣ ΦΑΣΕΩΝ ΔΙΑΧΩΡΙΣΤΗΣ ΙΣΟΡΡΟΠΙΑΣ ΦΑΣΕΩΝ 2 Ν Σ Ν Σ Συστάσεις των 2 Φάσεων: 2(Ν Σ -1) Θερμοκρασία Πίεση Εξισώσεις ισορροπίας φάσεων των συστατικών (N Σ ) Ν Σ 3 (Ν Σ +2) Ν Σ + 3 Ν Σ + 4 Συστάσεις (Ν Σ -1), Θερμοκρασία, Πίεση, Παροχή των 3 ρευμάτων: 3(Ν Σ +2) Θερμότητα (1) Ισοζύγια μάζας συστατικών (Ν Σ ) Εξισώσεις ισορροπίας φάσεων των συστατικών (N Σ ) Κοινές P, T στα ρεύματα εξόδου (2) Ισοζύγιο ενέργειας (1) Τυπικά είναι γνωστό το ρεύμα της τροφοδοσίας (Ν Σ +2) και είτε τα P,T είτε κάποιες συστάσεις ή ανακτήσεις στα προϊόντα 8
9 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΛΗ ΜΟΝΑΔΑ ΠΕΡΙΓΡΑΦΗ ΜΕΤΑΒΛΗΤΕΣ (Ν Μ ) ΠΕΡΙΟΡΙΣΜΟΙ (Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ - ΜΕΤΑΒΛΗΤΕΣ ΣΧΕΔΙΑΣΜΟΥ (Ν Ε = Ν Μ Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΟΛΙΚΟΣ ΣΥΜΠΥΝΚΩΤΗΡΑΣ ή ΑΝΑΒΡΑΣΤΗΡΑΣ ΜΕΡΙΚΟΣ ΣΥΜΠΥΝΚΩΤΗΡΑΣ ή ΑΝΑΒΡΑΣΤΗΡΑΣ (Ισοδυναμεί με διαχωριστή ισορροπίας φάσεων) 2 (Ν Σ +2) + 1 Ν Σ + 1 Συστάσεις, Τ, P, F των 2 ρευμάτων: 2(Ν Σ +2) Θερμότητα Ισοζύγια μάζας συστατικών (Ν Σ ) Ισοζύγιο ενέργειας (1) Ν Σ (Ν Σ +2) Ν Σ + 3 Ν Σ + 4 Συστάσεις (Ν Σ -1), Θερμοκρασία, Πίεση, Παροχή των 3 ρευμάτων: 3(Ν Σ +2) Θερμότητα (1) Ισοζύγια μάζας συστατικών (Ν Σ ) Εξισώσεις ισορροπίας φάσεων των συστατικών (N Σ ) Κοινές P, T στα ρεύματα εξόδου (2) Ισοζύγιο ενέργειας (1) Τυπικά είναι γνωστό το ένα ρεύμα εξόδου (Ν Σ +2) και τα P, T 9
10 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΛΗ ΜΟΝΑΔΑ ΠΕΡΙΓΡΑΦΗ ΜΕΤΑΒΛΗΤΕΣ (Ν Μ ) ΠΕΡΙΟΡΙΣΜΟΙ (Ν Π ) ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ - ΜΕΤΑΒΛΗΤΕΣ ΣΧΕΔΙΑΣΜΟΥ (Ν Ε = Ν Μ Ν Π ) 4 (Ν Σ +2) Ν Σ + 3 ΒΑΘΜΟΙ ΕΛΕΥΘΕΡΙΑΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ 10 ΒΑΘΜΙΔΑ ΙΣΟΡΡΟΠΙΑΣ ΔΙΣΚΟΣ ΤΡΟΦΟΔΟΣΙΑΣ Συστάσεις, Τ, P, F των 4 ρευμάτων: 4(Ν Σ +2) Θερμότητα (Q) Ισοζύγια μάζας συστατικών (Ν Σ ) Εξισώσεις ισορροπίας φάσεων των συστατικών (N Σ ) Κοινές P, T στα ρεύματα εξόδου (2) Ισοζύγιο ενέργειας (1) 5 (Ν Σ +2) Ν Σ + 3 Συστάσεις, Τ, P, F των 5 ρευμάτων: 5(Ν Σ +2) Θερμότητα (1) Ισοζύγια μάζας συστατικών (Ν Σ ) Εξισώσεις ισορροπίας φάσεων των συστατικών (N Σ ) Κοινές P, T στα ρεύματα εξόδου (2) Ισοζύγιο ενέργειας (1) 2 Ν Σ Ν Σ + 8
11 ΣΥΝΔΥΑΣΜΟΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΣ ΒΑΘΜΩΝ ΕΛΕΥΘΕΡΙΑΣ ΣΥΝΘΕΤΩΝ ΔΙΕΡΓΑΣΙΩΝ ΟΡΙΣΜΟΙ Ν Εολ : Οι βαθμοί ελευθερίας (μεταβλητές σχεδιασμού) της σύνθετης μονάδας Ν Α : Ο αριθμός των Αποφάσεων για το πόσες φορές επαναλαμβάνεται ένα στοιχείο ή μια απλή μονάδα. Π.χ. ορίζοντας τον αριθμό των βαθμίδων σε μια αποστακτική στήλη ή τη θέση της βαθμίδας τροφοδοσίας λαμβάνουμε μια απόφαση, δηλ Ν Α =1: Ν Π Μ : Ο συνολικός αριθμός των Μεταβλητών που ορίζονται δυο φόρες λόγω επικαλύψεων (π.χ. το ρεύμα εξόδου μιας μονάδας είναι ρεύμα εισόδου μιας άλλης) 11 Ν Εολ = ΣΝ Ε + N A - N M Π
12 ΠΥΡΓΟΣ ΑΠΟΡΡΟΦΗΣΗΣ ΜΕ ΔΙΣΚΟΥΣ 12 ΣΥΝΔΥΑΣΜΟΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΣ ΒΑΘΜΩΝ ΕΛΕΥΘΕΡΙΑΣ ΣΥΝΘΕΤΩΝ ΔΙΕΡΓΑΣΙΩΝ Αποτελείται από μια σειρά βαθμίδων ισορροπίας. Για κάθε βαθμίδα: Ν Ει = 2 Ν Σ + 6 Ορίζουμε τον αριθμό των βαθμίδων = n. Αυτό αποτελεί μια απόφαση, άρα N A =1 Για όλες τις βαθμίδες του πύργου ΣΝ Ε = n(2n Σ +6). Τα ρεύματα μεταξύ των διαδοχικών βαθμίδων μετρούνται δυο φορές (μία για κάθε βαθμίδα). Υπάρχουν n-1 χώροι μεταξύ των n βαθμίδων. Άρα τα επικαλυπτόμενα ρεύματα είναι: 2(n-1) και κάθε ρεύμα έχει (Ν Σ +2) μεταβλητές. Συνεπώς: Ν Π Μ = 2(n-1)(N Σ +2) Τελικά οι βαθμοί ελευθερίας για τον πύργο απορρόφησης (σύνθετη μονάδα) είναι: Ν Εολ = n(2ν Σ +6)+1-2(n-1)(N Σ +2) = 2Ν Σ +2n+5 Για να μπορεί να επιλυθεί ο προσομοιωτής του πύργου ορίζονται συνήθως: Αριθμός βαθμίδων: 1 Ρεύματα εισόδου (L o και V n+1 ) 2(Ν Σ +2) Απώλεια θερμότητας σε κάθε βαθμίδα (συνήθως q=0) n Πίεση σε κάθε βαθμίδα (συνήθως σταθερή) n ΣΥΝΟΛΟ 2Ν Σ +2n+5
13 ΣΥΝΔΥΑΣΜΟΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΣ ΒΑΘΜΩΝ ΕΛΕΥΘΕΡΙΑΣ ΣΥΝΘΕΤΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ 13 Χωρίζουμε τη στήλη σε έξι απλές μονάδες: 1. Ολικός συμπυκνωτήρας : Ν Ε1 =Ν Σ Διαχωριστής αναρροής : Ν Ε2 =Ν Σ Τμήμα εμπλουτισμού : Ν Ε3 =2Ν Σ +2m+5 (πύργος απορρόφησης με m βαθμίδες) 4. Βαθμίδα τροφοδοσίας : Ν Ε4 =3Ν Σ Τμήμα εξάντλησης : Ν Ε5 =2Ν Σ +2(n-m-2)+5 (πύργος απορρόφησης με [(n-1)-(m+1)] βαθμίδες) 6. Μερικός αναβραστήρας : Ν Ε6 =Ν Σ +4 ΣΝ E = 10N Σ +2n+27
14 ΣΥΝΔΥΑΣΜΟΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΣ ΒΑΘΜΩΝ ΕΛΕΥΘΕΡΙΑΣ ΣΥΝΘΕΤΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ 14 Υπάρχουν 9 ρεύματα που υπολογίζονται 2 φορές: Ν Μ Π =9(Ν Σ +2) Ο αριθμός αποφάσεων που εδώ παίρνουμε είναι: Ν Α =0 καθότι ο αριθμός των βαθμίδων στα τμήματα εμπλουτισμού και εξάντλησης έχει οριστεί κατά τον υπολογισμό των επιμέρους βαθμών ελευθερίας τους. Τελικά: Ν Εολ =ΣΝ E + Ν Α - Ν ΜΠ = 10N Σ +2n+27-9(Ν Σ +2) = Ν Σ +2n+9 Για να μπορεί να επιλυθεί ο προσομοιωτής της αποστακτικής στήλης ορίζονται συνήθως: Ρεύμα τροφοδοσίας (Ν Σ +2) Απώλεια θερμότητας σε κάθε βαθμίδα (συνήθως q=0) n-1 Απομάκρυνση θερμότητας στο διαχωριστή ρεύματος αναρροής 1 Πίεση σε κάθε βαθμίδα (συνήθως σταθερή) n Πίεση λειτουργίας (συμπυκνωτή) 1 Πίεση στο διαχωριστή ρεύματος αναρροής 1 ΣΥΝΟΛΟ Ν Σ +2n+4
15 ΣΥΝΔΥΑΣΜΟΣ ΑΠΛΩΝ ΔΙΕΡΓΑΣΙΩΝ ΚΑΙ ΥΠΟΛΟΓΙΣΜΟΣ ΒΑΘΜΩΝ ΕΛΕΥΘΕΡΙΑΣ ΣΥΝΘΕΤΩΝ ΔΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ 15 Ο ορισμός των υπόλοιπων 5 μεταβλητών εξαρτάται από το σκοπό της προσομοίωσης της στήλης: Α. Έλεγχος Δεδομένης στήλης (ελέγχουμε την ποιότητα προϊόντων για δεδομένη τροφοδοσία) Συνολικός αριθμός δίσκων 1 Θέση βαθμίδας τροφοδοσίας 1 Παροχή αποστάγματος 1 Θερμοκρασία αναρροής 1 Μέγιστη επιτρεπόμενη ροή ατμών 1 Β. Σχεδιασμός νέας αποστακτικής στήλης Ο αριθμός των δίσκων και η θέση της τροφοδοσίας είναι ζητούμενα. Αντί αυτών, όπως και αντί της παροχής αποστάγματος, μπορούμε να ορίσουμε την ανάκτηση ή τη συγκέντρωση κάποιων συστατικών στο απόσταγμα ή στο υπόλειμμα.
16 16 Αποστακτικές στήλες
17 17 Ροή ρευστών σε αποστακτική στήλη με δίσκους
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013
 Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
Ακρίβεια αποτελεσμάτων σχεδιασμού διεργασιών ΜΑΔ, 2013 1 ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ ΘΧΜ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των απαραίτητων υπολογιστικών-μεθοδολογικών
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
 ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
ΒΑΣΙΚΟΙ ΥΠΟΛΟΓΙΣΜΟΙ ΙΦ - ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαέρουν τον χημικό μηχανικό είναι οι ακόλουθοι : σημείο
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Αυτόματη ρύθμιση αποστακτικών στηλών
 Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
Αυτόματη ρύθμιση αποστακτικών στηλών Στόχοι-Αναγκαιότητα Παραγωγή προϊόντων επιθυμητών προδιαγραφών και ποσοτήτων Ασφάλεια εγκατάστασης (όρια πίεσης και θερμοκρασίας) Διατήρηση λειτουργικών συνθηκών (αποφυγή
Πρόρρηση Ισορροπίας Φάσεων. Υψηλές Πιέσεις
 Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
Πρόρρηση Ισορροπίας Φάσεων Υψηλές Πιέσεις 1 Ισορροπία Φάσεων Η βασική εξίσωση για όλους τους υπολογισμούς ισορροπίας φάσεων ατμού-υγρού είτε σε υψηλές είτε σε χαμηλές πιέσεις είναι η ισότητα των τάσεων
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Βασικές αρχές Η διεργασία της απόσταξης στηρίζεται
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Ι & ΙΙ Εργαστηριακή Άσκηση 4: ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ
 Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
Ε Θ Ν Ι Κ Ο Μ Ε Τ Σ Ο Β Ι Ο Π Ο Λ Υ Τ Ε Χ Ν Ε Ι Ο ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Σχεδιασμού, Ανάλυσης & Ανάπτυξης Διεργασιών και Συστημάτων ΕΡΓΑΣΤΗΡΙΟ ΣΧΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διευθυντής: Ι.
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ
 3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
3 Η ΣΕΙΡΑ ΜΗΧΑΝΙΚΗΣ ΚΑΙ ΑΝΑΠΤΥΞΗΣ ΔΙΕΡΓΑΣΙΩΝ - PC-LAB ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑΔΟΣΗΣ: 23.12.2015 ΑΣΚΗΣΗ 1 ΠΡΟΣΟΜΟΙΩΣΗ ΜΟΝΑΔΑΣ ΦΥΣΙΚΟΥ ΑΕΡΙΟΥ Ένα τυπικό φυσικό αέριο έχει την ακόλουθη σύσταση σε % mol: 0.5% Ν 2,
ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ Equilibrium or Flash Distillation ΑΠΟΣΤΑΞΗ ΙΣΟΡΡΟΠΙΑΣ 1. ΟΡΙΣΜΟΣ ΣΚΟΠΟΣ ΔΙΕΡΓΑΣΙΑΣ
Ογκομετρική (PVT) συμπεριφορά καθαρών ρευστών
 Ογκομετρική (PT) συμπεριφορά καθαρών ρευστών Ογκομετρική (PvT) συμπεριφορά Α.Θ Παπαϊωάννου, Θερμοδυναμική: ΤΟΜΟΣ I, Αθήνα, 007 PvT ιάγραμμα για το νερό 3 ιαγράμματα φάσεων καθαρών ουσιών Α.Θ. Παπαϊωάννου,
Ογκομετρική (PT) συμπεριφορά καθαρών ρευστών Ογκομετρική (PvT) συμπεριφορά Α.Θ Παπαϊωάννου, Θερμοδυναμική: ΤΟΜΟΣ I, Αθήνα, 007 PvT ιάγραμμα για το νερό 3 ιαγράμματα φάσεων καθαρών ουσιών Α.Θ. Παπαϊωάννου,
Οδηγίες χρήσης Aspen Plus 7.1
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Οδηγίες χρήσης Aspen Plus 7.1 Έναρξη προσομοίωσης (1/2) Έναρξη προσομοίωσης (2/2) Εμφανίζεται το ακόλουθο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Οδηγίες χρήσης Aspen Plus 7.1 Έναρξη προσομοίωσης (1/2) Έναρξη προσομοίωσης (2/2) Εμφανίζεται το ακόλουθο
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Διαφορική (batch) Rectifying column Stripping column
Είδη ΙΦΥΥ δυαδικών μιγμάτων
 Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
Είδη ΙΦΥΥ δυαδικών μιγμάτων T A X 1 X 1 ΙΦΥΥ τριαδικών μιγμάτων Τριγωνικά διαγράμματα C 0.1 0.2 0.3 0.4 0.5 P 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.6 0.7 0.8 0.9 κλάσμα βάρους του B κλάσμα βάρους του C
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Στόχος: Επεξεργασία συγκεκριμένης τροφοδοσίας (ροή
Απρίλιος Λύση: Σύνοψη των δεδομένων: P = 6at, V = 0.6F, L = 0.4F, F = 1 kmol/s. Ζητούμενα: x Fi, x Li
 Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
Φυσικές Διεργασίες Προβλήματα στην απόσταξη που λύθηκαν στην τάξη Πηγή: Δ. Μαρίνος-Κουρής, Ε. Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, Παπασωτηρίου, Αθήνα 1994 Απρίλιος 2008 Πρόβλημα 1 Διαχωριστήρας
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού
 Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Σηµειώσεις Προχωρηµένης Τεχνικής Φυσικών ιεργασιών 33 3 Βασικοί Υπολογισµοί Ισορροπίας Φάσεων Ατµών Υγρού 3.1 Εισαγωγή Οι βασικοί υπολογισµοί ισορροπίας φάσεων ατµών-υγρού που ενδιαφέρουν το χηµικό µηχανικό
Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
 Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Χημικών Μηχανικών Τομέας ΙΙ : Ανάλυσης, Σχεδιασμού και Ανάπτυξης Διεργασιών και Συστημάτων Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
Εθνικό Μετσόβιο Πολυτεχνείο Τμήμα Χημικών Μηχανικών Τομέας ΙΙ : Ανάλυσης, Σχεδιασμού και Ανάπτυξης Διεργασιών και Συστημάτων Ανάπτυξη στατικού προτύπου επίλυσης προβλημάτων αξιολόγησης αποστακτικών στηλών.
ΜΟΡΦΕΣ ΕΝΕΡΓΕΙΑΣ. ΕΝΕΡΓΕΙΑ ΔΙΕΡΓΑΣΙΩΝ (Μεταβατικές) ΕΝΕΡΓΕΙΑ ΣΥΣΤΗΜΑΤΟΣ ΕΡΓΟ ΘΕΡΜΟΤΗΤΑ
 Έργο - Θερμότητα ΜΟΡΦΕΣ ΕΝΕΡΓΕΙΑΣ ΕΝΕΡΓΕΙΑ ΔΙΕΡΓΑΣΙΩΝ (Μεταβατικές) ΕΡΓΟ ΘΕΡΜΟΤΗΤΑ ΕΝΕΡΓΕΙΑ ΣΥΣΤΗΜΑΤΟΣ ΕΞΩΤΕΡΙΚΗ (Κινητική, Δυναμική) ΕΣΩΤΕΡΙΚΗ (Εσωτερική [U], Ενθαλπία [Η]) Χαρακτηριστικά και Σύμβαση
Έργο - Θερμότητα ΜΟΡΦΕΣ ΕΝΕΡΓΕΙΑΣ ΕΝΕΡΓΕΙΑ ΔΙΕΡΓΑΣΙΩΝ (Μεταβατικές) ΕΡΓΟ ΘΕΡΜΟΤΗΤΑ ΕΝΕΡΓΕΙΑ ΣΥΣΤΗΜΑΤΟΣ ΕΞΩΤΕΡΙΚΗ (Κινητική, Δυναμική) ΕΣΩΤΕΡΙΚΗ (Εσωτερική [U], Ενθαλπία [Η]) Χαρακτηριστικά και Σύμβαση
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΛΑΣΜΑΤΙΚΗΣ ΑΠΟΣΤΑΞΗΣ Παράδειγμα 1 Μια αποστακτική στήλη διαχωρίζει μια τροφοδοσία κορεσμένου ατμού με ρυθμό ροής 100 kmol/h και σύσταση 30 mol% αιθανόλη (E), 25 mol% i- προπανόλη (i-p), 35
Τεχνοοικονομική Μελέτη
 Τμήμα Μηχανολόγων Μηχανικών Τεχνοοικονομική Μελέτη Ενότητα 10: Σχεδιασμός εγκαταστάσεων Σκόδρας Γεώργιος, Αν. Καθηγητής gskodras@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Τμήμα Μηχανολόγων Μηχανικών Τεχνοοικονομική Μελέτη Ενότητα 10: Σχεδιασμός εγκαταστάσεων Σκόδρας Γεώργιος, Αν. Καθηγητής gskodras@uowm.gr Τμήμα Μηχανολόγων Μηχανικών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ. Μ. Κροκίδα
 ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
ΜΗΧΑΝΙΚΗ ΦΥΣΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ ΙΙ Μ. Κροκίδα ΚΛΑΣΜΑΤΙΚΗ ΑΠΟΣΤΑΞΗ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΡΓ. ΣΕΔΙΑΣΜΟΥ & ΑΝΑΛΥΣΗΣ ΔΙΕΡΓΑΣΙΩΝ Ορισμός Βασικές έννοιες Απόσταξη (Distillation) είναι
Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Προχωρημένη Θερμοδυναμική Εαρινό εξάμηνο 08-09 Εισαγωγή Σε αντίθεση με τα αέρια τα οποία είναι αναμίξιμα σε όλες τις αναλογίες σε χαμηλές πιέσεις τα υγρά
Ισορροπία Υγρού-Υγρού ΠΡΟΧΩΡΗΜΕΝΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Προχωρημένη Θερμοδυναμική Εαρινό εξάμηνο 08-09 Εισαγωγή Σε αντίθεση με τα αέρια τα οποία είναι αναμίξιμα σε όλες τις αναλογίες σε χαμηλές πιέσεις τα υγρά
ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΜΗΧΑΝΙΚΗ ΚΑΙ ΑΝΑΠΤΥΞΗ ΔΙΕΡΓΑΣΙΩΝ ΟΔΗΓΙΕΣ ΕΡΓΑΣΤΗΡΙΑΚΗΣ ΑΣΚΗΣΗΣ ΥΓΡΗΣ ΕΚΧΥΛΙΣΗΣ Ελένη Παντελή, Υποψήφια Διδάκτορας Γεωργία Παππά, Δρ. Χημικός Μηχανικός
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
(β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele
 Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 2 Απόσταξη 3 (β) Εύρεση του αριθμού των θεωρητικών βαθμίδων με τη μέθοδο McCabe-Thiele Παρακάτω περιγράφουμε τα βήματα που ακολουθούμε με τη μέθοδο McCabe- Thiele για να καθορίσουμε τον αριθμό
Κεφάλαιο 4 Κλασματική Απόσταξη
 Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
Κεφάλαιο 4 Κλασματική Απόσταξη Σύνοψη Η κλασματική απόσταξη ή απλά απόσταξη αποτελεί τη διεργασία διαχωρισμού ενός πτητικού συστατικού από ένα λιγότερο πτητικό ή, γενικότερα, ενός μίγματος συστατικών που
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ
 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Κεφάλαιο Πρόλογος i Κατάλογος Σχημάτων και Εικόνων v Ενότητα 1: Εισαγωγή 1-1 1.1 Το μαθηματικό πρότυπο: ισοζύγια και άλλες σχέσεις. 1-1 1.2 Αριστοποίηση 1-2 1.3 Αλλαγή κλίμακας (scale
ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Κεφάλαιο Πρόλογος i Κατάλογος Σχημάτων και Εικόνων v Ενότητα 1: Εισαγωγή 1-1 1.1 Το μαθηματικό πρότυπο: ισοζύγια και άλλες σχέσεις. 1-1 1.2 Αριστοποίηση 1-2 1.3 Αλλαγή κλίμακας (scale
Διάλεξη 4β. Συστοιχίες διαχωρισμών
 Διάλεξη 4β Συστοιχίες διαχωρισμών Διαχωρισμός σε απλή στήλη Απλή τροφοδοσία Δύο ρεύματα εξόδου Προσκείμενα κλειδιά διαχωρισμού Στήλη με απλό αναβραστήρα και συμπυκνωτήρα Φθίνουσα πτητικότητα E () Ελαφρύ
Διάλεξη 4β Συστοιχίες διαχωρισμών Διαχωρισμός σε απλή στήλη Απλή τροφοδοσία Δύο ρεύματα εξόδου Προσκείμενα κλειδιά διαχωρισμού Στήλη με απλό αναβραστήρα και συμπυκνωτήρα Φθίνουσα πτητικότητα E () Ελαφρύ
ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΞΗΣ ΤΡΙΩΝ ΦΑΣΕΩΝ ΜΕ ΤΑΥΤΟΧΡΟΝΗ ΧΗΜΙΚΗ ΑΝΤΙΔΡΑΣΗ. Τεχνολογικής Ανάπτυξης (ΕΚΕΤΑ), Θέρμη, Θεσσαλονίκη
 ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΞΗΣ ΤΡΙΩΝ ΦΑΣΕΩΝ ΜΕ ΤΑΥΤΟΧΡΟΝΗ ΧΗΜΙΚΗ ΑΝΤΙΔΡΑΣΗ Θ. Δαμαρτζής, Π. Σεφερλής,2 Ινστιτούτο Τεχνικής Χημικών Διεργασιών (ΙΤΧΗΔ, Εθνικό Κέντρο Έρευνας και Τεχνολογικής Ανάπτυξης
ΒΕΛΤΙΣΤΟΣ ΣΧΕΔΙΑΣΜΟΣ ΔΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΞΗΣ ΤΡΙΩΝ ΦΑΣΕΩΝ ΜΕ ΤΑΥΤΟΧΡΟΝΗ ΧΗΜΙΚΗ ΑΝΤΙΔΡΑΣΗ Θ. Δαμαρτζής, Π. Σεφερλής,2 Ινστιτούτο Τεχνικής Χημικών Διεργασιών (ΙΤΧΗΔ, Εθνικό Κέντρο Έρευνας και Τεχνολογικής Ανάπτυξης
ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ (ΘΧΜ) 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ 2. ΘΕΜΕΛΙΑ
 ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ (ΘΧΜ) 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ 2. ΘΕΜΕΛΙΑ 1 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των
ΘΕΡΜΟ ΥΝΑΜΙΚΗ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ (ΘΧΜ) 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ 2. ΘΕΜΕΛΙΑ 1 1. ΣΚΟΠΟΣ και ΑΝΤΙΚΕΙΜΕΝΟ Σκοπός της θερμοδυναμικής χημικής μηχανικής είναι η παροχή των κατάλληλων θεωρητικών γνώσεων και των
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 7 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος 1 ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 7 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ
 ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
Γραμμικός Προγραμματισμός
 Γραμμικός Προγραμματισμός Εισαγωγή Το πρόβλημα του Σχεδιασμού στη Χημική Τεχνολογία και Βιομηχανία. Το συνολικό πρόβλημα του Σχεδιασμού, από μαθηματική άποψη ανάγεται σε ένα πρόβλημα επίλυσης συστήματος
Γραμμικός Προγραμματισμός Εισαγωγή Το πρόβλημα του Σχεδιασμού στη Χημική Τεχνολογία και Βιομηχανία. Το συνολικό πρόβλημα του Σχεδιασμού, από μαθηματική άποψη ανάγεται σε ένα πρόβλημα επίλυσης συστήματος
ΒΕΛΤΙΣΤΟΣ ΣΧΕ ΙΑΣΜΟΣ ΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΞΗΣ ΤΡΙΩΝ ΦΑΣΕΩΝ ΜΕ ΤΑΥΤΟΧΡΟΝΗ ΧΗΜΙΚΗ ΑΝΤΙ ΡΑΣΗ Θ. αµαρτζής 1, Π. Σεφερλής 1,2
 ΒΕΛΤΙΣΤΟΣ ΣΧΕ ΙΑΣΜΟΣ ΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΞΗΣ ΤΡΙΩΝ ΦΑΣΕΩΝ ΜΕ ΤΑΥΤΟΧΡΟΝΗ ΧΗΜΙΚΗ ΑΝΤΙ ΡΑΣΗ Θ. αµαρτζής, Π. Σεφερλής,2 Ινστιτούτο Τεχνικής Χηµικών ιεργασιών (ΙΤΧΗ ), Εθνικό Κέντρο Έρευνας και Τεχνολογικής Ανάπτυξης
ΒΕΛΤΙΣΤΟΣ ΣΧΕ ΙΑΣΜΟΣ ΙΕΡΓΑΣΙΩΝ ΑΠΟΣΤΑΞΗΣ ΤΡΙΩΝ ΦΑΣΕΩΝ ΜΕ ΤΑΥΤΟΧΡΟΝΗ ΧΗΜΙΚΗ ΑΝΤΙ ΡΑΣΗ Θ. αµαρτζής, Π. Σεφερλής,2 Ινστιτούτο Τεχνικής Χηµικών ιεργασιών (ΙΤΧΗ ), Εθνικό Κέντρο Έρευνας και Τεχνολογικής Ανάπτυξης
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6
 Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 6 Δευτέρα, 14 Απριλίου 008 Οικονομική Ανάλυση Βιομηχανιών και Διεργασιών 1 Εισαγωγή Αριστοποίηση: ενός κριτηρίου (αντικειμενικής συνάρτησης) πολυκριτηριακή
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
Έκφραση της Ισορροπίας φάσεων ατμών υγρού με τη βοήθεια του Aspen plus
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Έκφραση της Ισορροπίας φάσεων ατμών υγρού με τη βοήθεια του Aspen plus Η έννοια της ισορροπίας Εξ ορισμού
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Έκφραση της Ισορροπίας φάσεων ατμών υγρού με τη βοήθεια του Aspen plus Η έννοια της ισορροπίας Εξ ορισμού
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Μάθημα Επιλογής 8 ου εξαμήνου Διδάσκων:
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ ΚΑΙ ΒΙΟΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ
 ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ ΚΑΙ ΒΙΟΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Διδάσκοντες:Ν. Καλογεράκης Π. Παναγιωτοπούλου Γραφείο: K.9 Email: ppanagiotopoulou@isc.tuc.gr Μέρες/Ώρες διδασκαλίας: Δευτέρα (.-3.)-Τρίτη (.-3.) ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ
ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ ΚΑΙ ΒΙΟΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Διδάσκοντες:Ν. Καλογεράκης Π. Παναγιωτοπούλου Γραφείο: K.9 Email: ppanagiotopoulou@isc.tuc.gr Μέρες/Ώρες διδασκαλίας: Δευτέρα (.-3.)-Τρίτη (.-3.) ΤΕΧΝΙΚΗ ΧΗΜΙΚΩΝ
ΘΕΡΜΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. όπου το κ εξαρτάται από το υλικό και τη θερμοκρασία.
 Εισαγωγή Έστω ιδιότητα Ρ. ΘΕΡΜΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ α) Ρ = Ρ(r, t) => μη μόνιμη, μεταβατική κατάσταση. β) P = P(r), P =/= P(t) => μόνιμη κατάσταση (μη ισορροπίας). γ) P =/= P(r), P(t) σε μακροσκοπικό χωρίο =>
Εισαγωγή Έστω ιδιότητα Ρ. ΘΕΡΜΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ α) Ρ = Ρ(r, t) => μη μόνιμη, μεταβατική κατάσταση. β) P = P(r), P =/= P(t) => μόνιμη κατάσταση (μη ισορροπίας). γ) P =/= P(r), P(t) σε μακροσκοπικό χωρίο =>
Ε. Παυλάτου, 2017 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ
 1 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ Βασικές έννοιες Στοιχειομετρία-Στοιχειομετρικοί συντελεστές-στοιχειομετρική αναλογία Περιοριστικό αντιδρών Αντιδρών σε περίσσεια Μετατροπή (κλάσμα,
1 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ Βασικές έννοιες Στοιχειομετρία-Στοιχειομετρικοί συντελεστές-στοιχειομετρική αναλογία Περιοριστικό αντιδρών Αντιδρών σε περίσσεια Μετατροπή (κλάσμα,
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης 5 ο μάθημα ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών 2 Διεργασίες που περιλαμβάνουν μια
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης 5 ο μάθημα ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών 2 Διεργασίες που περιλαμβάνουν μια
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ ΑΝΑΛΥΣΗ ΚΑΙ ΣΧΕΔΙΑΣΜΟΣ ΙΔΑΝΙΚΩΝ ΑΝΤΙΔΡΑΣΤΗΡΩΝ
 Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Εισαγωγή Διαδικασία σχεδιασμού αντιδραστήρα: Καθορισμός του τύπου του αντιδραστήρα και των συνθηκών λειτουργίας. Εκτίμηση των χαρακτηριστικών για την ομαλή λειτουργία του αντιδραστήρα. μέγεθος σύσταση
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων
 Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Τεχνολογίες Εκμετάλλευσης και Αξιοποίησης Υδρογονανθράκων Μάθημα 3 ο Εισαγωγή στο διυλιστήριο Τύποι διεργασιών Απόσταξη (ατμοσφαιρική και υπό κενό) Δρ. Στέλλα Μπεζεργιάννη Διύλιση Το αργό πετρέλαιο δεν
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης
 Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Παράδειγμα 2-1. Διαχωρισμός νερού- αιθανόλης Μια αποστακτική στήλη που λειτουργεί σε πίεση 101,3 kpa, διαχωρίζει ένα μίγμα νερούαιθανόλης. Η σύσταση του μίγματος αποτελείται 40 mol% αιθανόλη και η τροφοδοσία
Πρόρρηση. Φυσικών Ιδιοτήτων Μιγμάτων
 Πρόρρηση Φυσικών Ιδιοτήτων Μιγμάτων Συντελεστής συμπιεστότητας, Ζ Αρχή Αντιστοίχων Καταστάσεων Τριών παραμέτρων Ptzer : z z (0) + ω z (1) Lee-Kesler: z (0), z (1) f(t r,p r ) Εξίσωση Ptzer Κανόνες Ανάμειξης
Πρόρρηση Φυσικών Ιδιοτήτων Μιγμάτων Συντελεστής συμπιεστότητας, Ζ Αρχή Αντιστοίχων Καταστάσεων Τριών παραμέτρων Ptzer : z z (0) + ω z (1) Lee-Kesler: z (0), z (1) f(t r,p r ) Εξίσωση Ptzer Κανόνες Ανάμειξης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Συστήματα Ανάκτησης Θερμότητας
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Συστήματα Ανάκτησης Θερμότητας Εισαγωγή Σκοπός των συστημάτων ανάκτησης θερμότητας είναι η αξιοποίηση
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Εργαστήριο Θερμοδυναμικής & Φαινομένων Μεταφοράς Συστήματα Ανάκτησης Θερμότητας Εισαγωγή Σκοπός των συστημάτων ανάκτησης θερμότητας είναι η αξιοποίηση
Πρόρρηση. Θερμοδυναμικών Ιδιοτήτων Μιγμάτων
 Πρόρρηση Θερμοδυναμικών Ιδιοτήτων Μιγμάτων 1 Χημικό Δυναμικό μ d = dg U = N V,S,N Για 1 mole καθαρής ουσίας: SdT +Vd j H = N S,,N j A = N V,T,N j G = N ( T, ) ( T,) = T T T,,N j SdT + όπου μ(t',') είναι
Πρόρρηση Θερμοδυναμικών Ιδιοτήτων Μιγμάτων 1 Χημικό Δυναμικό μ d = dg U = N V,S,N Για 1 mole καθαρής ουσίας: SdT +Vd j H = N S,,N j A = N V,T,N j G = N ( T, ) ( T,) = T T T,,N j SdT + όπου μ(t',') είναι
ΣΤ' Εξάμηνο ΣΧΕΔΙΑΣΜΟΣ ΧΗΜΙΚΩΝ ΒΙΟΜΗΧΑΝΙΩΝ ΚΑΙ ΔΙΕΡΓΑΣΙΩΝ. Ερωτήσεις Επανάληψης Δεύτερο Μέρος
 ΣΤ' Εξάμηνο ΣΧΕΔΙΑΣΜΟΣ ΧΗΜΙΚΩΝ ΒΙΟΜΗΧΑΝΙΩΝ ΚΑΙ ΔΙΕΡΓΑΣΙΩΝ 2008 2009 Ερωτήσεις Επανάληψης Δεύτερο Μέρος 0 Ερώτηση: Σε αντιδραστήρα για τη μετατροπή κυκλοεξανόλης σε κυκλοεξανόνη, παρέχεται και μίγμα αντιδρώντος
ΣΤ' Εξάμηνο ΣΧΕΔΙΑΣΜΟΣ ΧΗΜΙΚΩΝ ΒΙΟΜΗΧΑΝΙΩΝ ΚΑΙ ΔΙΕΡΓΑΣΙΩΝ 2008 2009 Ερωτήσεις Επανάληψης Δεύτερο Μέρος 0 Ερώτηση: Σε αντιδραστήρα για τη μετατροπή κυκλοεξανόλης σε κυκλοεξανόνη, παρέχεται και μίγμα αντιδρώντος
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ
 Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μηχανική και Ανάπτυξη Διεργασιών 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ ΥΓΡΗ ΕΚΧΥΛΙΣΗ Η υγρή εκχύλιση βρίσκει εφαρμογή όταν. Η σχετική πτητικότητα των συστατικών του αρχικού διαλύματος είναι κοντά στη
Μοντελοποίηση Προσομοίωση
 Μοντελοποίηση Προσομοίωση Σχεδιασμός είναι η διαδικασία μετατροπής των φυσικών νόμων σε μαθηματικές εξισώσεις είναι το κατάλληλο λογισμικό το οποίο χρησιμοποιώντας το μαθηματικό μοντέλο προβλέπει τη συμπεριφορά
Μοντελοποίηση Προσομοίωση Σχεδιασμός είναι η διαδικασία μετατροπής των φυσικών νόμων σε μαθηματικές εξισώσεις είναι το κατάλληλο λογισμικό το οποίο χρησιμοποιώντας το μαθηματικό μοντέλο προβλέπει τη συμπεριφορά
ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013
 ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 2 Αποστακτικές στήλες 3 Ροή ρευστών σε αποστακτική στήλη με δίσκους Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαφέρουν τον
ΣΧΕΔΙΑΣΜΟΣ ΑΠΟΣΤΑΚΤΙΚΩΝ ΣΤΗΛΩΝ ΜΑΔ, 2013 1 2 Αποστακτικές στήλες 3 Ροή ρευστών σε αποστακτική στήλη με δίσκους Βασικοί Υπολογισμοί Ισορροπίας Φάσεων Ατμών Υγρού Οι βασικοί υπολογισμοί που ενδιαφέρουν τον
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΑΠΟΡΡΟΦΗΣΗ ΑΕΡΙΩΝ Gas Absorption Παράγοντες που Επηρεάζουν Διεργασία Απορρόφησης Συνήθως δίνονται: Ρυθμός
ΕΤΚΛ ΕΜΠ. Τεχνολογία Πετρελαίου και Και Λιπαντικών ΕΜΠ
 Φυσικού Αερίου Στήλες Απόσταξης Πετρελαίου Ιστορικά, η παλιότερη διεργασία επεξεργασίας πετρελαίου Αποτελεί το πρώτο μόνο στάδιο της επεξεργασίας Σκοπός Ανάκτηση ελαφρών συστατικών Κλασμάτωση σε κλάσματα
Φυσικού Αερίου Στήλες Απόσταξης Πετρελαίου Ιστορικά, η παλιότερη διεργασία επεξεργασίας πετρελαίου Αποτελεί το πρώτο μόνο στάδιο της επεξεργασίας Σκοπός Ανάκτηση ελαφρών συστατικών Κλασμάτωση σε κλάσματα
ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ. Το τρίχωμα της τίγρης εμφανίζει ποικιλία χρωμάτων επειδή οι αντιδράσεις που γίνονται στα κύτταρα δεν καταλήγουν σε χημική ισορροπία.
 ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ Το τρίχωμα της τίγρης εμφανίζει ποικιλία χρωμάτων επειδή οι αντιδράσεις που γίνονται στα κύτταρα δεν καταλήγουν σε χημική ισορροπία. Δημήτρης Παπαδόπουλος, χημικός Βύρωνας, 2015 Μονόδρομες
ΧΗΜΙΚΗ ΙΣΟΡΡΟΠΙΑ Το τρίχωμα της τίγρης εμφανίζει ποικιλία χρωμάτων επειδή οι αντιδράσεις που γίνονται στα κύτταρα δεν καταλήγουν σε χημική ισορροπία. Δημήτρης Παπαδόπουλος, χημικός Βύρωνας, 2015 Μονόδρομες
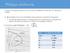
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ
 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ 13 1. ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΧΩΡΙΣΜΟΥ (γενική περιγραφή και αναγκαιότητα) 17 1.1 Φυσικές Διεργασίες Διαχωρισμού 20 1.1.1 Μια γενική εποπτεία της παραγωγικής Χημικής Βιομηχανίας 21 1.1.2 Σύντομος
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
Απορρόφηση Αερίων. 1. Εισαγωγή
 1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
1. Εισαγωγή Απορρόφηση Αερίων Πρόκειται για διαχωρισμό συστατικών από μείγμα αερίου με τη βοήθεια υγρού διαλύτη. Κινητήρια δύναμη είναι η διαφορά διαλυτότητας στο διαλύτη. Στη συνέχεια θα ασχοληθούμε με
Εξοικονόμηση Ενέργειας
 Εξοικονόμηση Ενέργειας Θεωρητικό Υπόβαθρο: Θερμοδυναμική Θερμοδυναμική: Η επιστήμη που ασχολείται με τις μετατροπές ενέργειας από μια μορφή σε μια άλλη «Κάθε παραγωγική διαδικασία βρίσκεται κάτω από τον
Εξοικονόμηση Ενέργειας Θεωρητικό Υπόβαθρο: Θερμοδυναμική Θερμοδυναμική: Η επιστήμη που ασχολείται με τις μετατροπές ενέργειας από μια μορφή σε μια άλλη «Κάθε παραγωγική διαδικασία βρίσκεται κάτω από τον
6.1 Θερμόμετρα και μέτρηση θερμοκρασίας
 ΚΕΦΑΛΑΙΟ 6 ο ΘΕΡΜΟΤΗΤΑ 6.1 Θερμόμετρα και μέτρηση θερμοκρασίας 1. Τι ονομάζεται θερμοκρασία; Το φυσικό μέγεθος που εκφράζει πόσο ζεστό ή κρύο είναι ένα σώμα ονομάζεται θερμοκρασία. 2. Πως μετράμε τη θερμοκρασία;
ΚΕΦΑΛΑΙΟ 6 ο ΘΕΡΜΟΤΗΤΑ 6.1 Θερμόμετρα και μέτρηση θερμοκρασίας 1. Τι ονομάζεται θερμοκρασία; Το φυσικό μέγεθος που εκφράζει πόσο ζεστό ή κρύο είναι ένα σώμα ονομάζεται θερμοκρασία. 2. Πως μετράμε τη θερμοκρασία;
Ισοζύγια Μάζας. 1. Eισαγωγή
 Ισοζύγια Μάζας 1. Eισαγωγή Οποιαδήποτε χηµική διεργασία όπου υπάρχουν αλληλεπιδράσεις µεταξύ δύο ή περισσότερων υλικών µπορεί να αναλυθεί µε βάση τα ισοζύγια υλικών. Γενικά, υπάρχουν δύο διαφορετικές περιπτώσεις
Ισοζύγια Μάζας 1. Eισαγωγή Οποιαδήποτε χηµική διεργασία όπου υπάρχουν αλληλεπιδράσεις µεταξύ δύο ή περισσότερων υλικών µπορεί να αναλυθεί µε βάση τα ισοζύγια υλικών. Γενικά, υπάρχουν δύο διαφορετικές περιπτώσεις
Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a 1. + α 2 Α (-a 1 ) A 1. +(-a 2
 ΠΑ- Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a A + α Α +... ------------>...+a A ή σε μορφή γραμμικής εξίσωσης a A +...+(-a ) A +(-a ) A +... 0 a Στοιχειομετρικοί συντελεστές ως προς Α (
ΠΑ- Σύνοψη ΜΗΧΑΝΙΚΗΣ ΧΗΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ Χημική αντίδραση : a A + α Α +... ------------>...+a A ή σε μορφή γραμμικής εξίσωσης a A +...+(-a ) A +(-a ) A +... 0 a Στοιχειομετρικοί συντελεστές ως προς Α (
Κεφάλαιο 5: Διεργασίες απόσταξης
 92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
92 Κεφάλαιο 5: Διεργασίες απόσταξης Σύνοψη Το κεφάλαιο αυτό συνιστά την πρώτη ολοκληρωμένη ανάλυση μίας διεργασίας. Παρουσιάζονται στην αρχή οι απλές αποστάξεις και στη συνέχεια αναλύεται διεξοδικά η κλασματική
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
 ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
ΕΝΤΡΟΠΙΑ ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ 1 ΑΣΚΗΣΗ 1 Το δοχείο του σχήματος είναι απομονωμένο (αδιαβατικά τοιχώματα). Το διάφραγμα χωρίζει το δοχείο σε δύο μέρη. Το αριστερό μέρος έχει όγκο 1 και περιέχει ιδανικό αέριο
Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού
 EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
EΘNIKO ΜEΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΙΙ: Ανάλυσης, Σχεδιασμού & Ανάπτυξης Διεργασιών & Συστημάτων Υπολογιστικές Μέθοδοι Ανάλυσης και Σχεδιασμού Εργαστηριακές Ασκήσεις Διδάσκων: Α.
Ανάκτηση Ακετόνης από ρεύμα αέρα (κεφάλαιο 12)
 Ανάκτηση Ακετόνης από ρεύμα αέρα (κεφάλαιο 12 1 Διδάσκων: Β. Ράπτης Πρόβλημα: αποβαλλόμενο ρεύμα αέρα F = 0.2kg ξηρού α./s με P F = 1 bar και T F = 80 o C περιέχει ακετόνη σε συγκέντρωση Χ F =0.1kg ακετόνης
Ανάκτηση Ακετόνης από ρεύμα αέρα (κεφάλαιο 12 1 Διδάσκων: Β. Ράπτης Πρόβλημα: αποβαλλόμενο ρεύμα αέρα F = 0.2kg ξηρού α./s με P F = 1 bar και T F = 80 o C περιέχει ακετόνη σε συγκέντρωση Χ F =0.1kg ακετόνης
Λύση Παραδείγματος 1. Διάγραμμα ροής διεργασίας. Εκρόφηση χλωριούχου βινυλίου από νερό στους 25 C και 850 mmhg. Είσοδος υγρού.
 Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Παράδειγμα 1 Μια εγκατάσταση καθαρισμού νερού απομακρύνει χλωριούχο βινύλιο (vinyl cloride) από μολυσμένα υπόγεια ύδατα σε θερμοκρασία 25 C και πίεση 850 mmhg χρησιμοποιώντας στήλη εκρόφησης κατ αντιρροή.
Υποθέστε ότι ο ρυθμός ροής από ένα ακροφύσιο είναι γραμμική συνάρτηση της διαφοράς στάθμης στα δύο άκρα του ακροφυσίου.
 ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
ΕΡΩΤΗΜΑ Δίνεται το σύστημα δεξαμενών του διπλανού σχήματος, όπου: q,q : h,h : Α : R : οι παροχές υγρού στις δύο δεξαμενές, τα ύψη του υγρού στις δύο δεξαμενές, η διατομή των δεξαμενών και η αντίσταση ροής
Υπολογισμός & Πρόρρηση. Θερμοδυναμικών Ιδιοτήτων
 Υπολογισμός & Πρόρρηση Θερμοδυναμικών Ιδιοτήτων d du d Θερμοδυναμικές Ιδιότητες d dh d d d du d d dh U A H G d d da d d dg d du dq dq d / d du dq Θεμελιώδεις Συναρτήσεις περιέχουν όλες τις πληροφορίες
Υπολογισμός & Πρόρρηση Θερμοδυναμικών Ιδιοτήτων d du d Θερμοδυναμικές Ιδιότητες d dh d d d du d d dh U A H G d d da d d dg d du dq dq d / d du dq Θεμελιώδεις Συναρτήσεις περιέχουν όλες τις πληροφορίες
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
Φυσικές Διεργασίες Πέμπτη Διάλεξη
 Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Φυσικές Διεργασίες Πέμπτη Διάλεξη Δευτέρα, 12 Μαΐου 2008 Απορρόφηση αερίων 1. Ορισμός Τι είναι απορρόφηση; Είναι μεταφορά μέσω της διεπιφάνειας αερίου-υγρού ενός συστατικού από αέριο μίγμα σε έναν υγρό
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα : Εξάτμιση (2/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Ισοζύγια μάζας
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα : Εξάτμιση (2/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Ισοζύγια μάζας
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 5
 Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 5 Δευτέρα, 7 Απριλίου 2008 Τρίτη, 8 Απριλίου 2008 Σύνθεση Διεργασιών Διαχωρισμού 1 Εισαγωγή Τα βιομηχανικά προβλήματα διαχωρισμού γενικά περιλαμβάνουν
Σχεδιασμός Χημικών Διεργασιών και Βιομηχανιών Διάλεξη 5 Δευτέρα, 7 Απριλίου 2008 Τρίτη, 8 Απριλίου 2008 Σύνθεση Διεργασιών Διαχωρισμού 1 Εισαγωγή Τα βιομηχανικά προβλήματα διαχωρισμού γενικά περιλαμβάνουν
Σεµινάριο Αυτοµάτου Ελέγχου
 ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Αυτοµατισµού Σεµινάριο Αυτοµάτου Ελέγχου Ειδικά θέµατα Ανάλυσης συστηµάτων Σύνθεσης συστηµάτων ελέγχου Μελέτης στοχαστικών συστηµάτων. Καλλιγερόπουλος Σεµινάριο Αυτοµάτου Ελέγχου Ανάλυση
ΤΕΙ ΠΕΙΡΑΙΑ Τµήµα Αυτοµατισµού Σεµινάριο Αυτοµάτου Ελέγχου Ειδικά θέµατα Ανάλυσης συστηµάτων Σύνθεσης συστηµάτων ελέγχου Μελέτης στοχαστικών συστηµάτων. Καλλιγερόπουλος Σεµινάριο Αυτοµάτου Ελέγχου Ανάλυση
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις. Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι
 Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Οι ιδιότητες των αερίων και καταστατικές εξισώσεις Θεόδωρος Λαζαρίδης Σημειώσεις για τις παραδόσεις του μαθήματος Φυσικοχημεία Ι Τι είναι αέριο; Λέμε ότι μία ουσία βρίσκεται στην αέρια κατάσταση όταν αυθόρμητα
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα 1. Θερμοδυναμική Ορισμοί. Έργο 3. Θερμότητα 4. Εσωτερική ενέργεια 5. Ο Πρώτος Θερμοδυναμικός Νόμος 6. Αντιστρεπτή
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΘΕΡΜΟΔΥΝΑΜΙΚΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Περιεχόμενα 1. Θερμοδυναμική Ορισμοί. Έργο 3. Θερμότητα 4. Εσωτερική ενέργεια 5. Ο Πρώτος Θερμοδυναμικός Νόμος 6. Αντιστρεπτή
Χειμερινό εξάμηνο
 Εξαναγκασμένη Συναγωγή Ροή Πάνω από μία Επίπεδη Επιφάνεια Τμήμα Μηχανολόγων Μηχανικών και Μηχανικών Παραγωγής ΜΜK 31 Μεταφορά Θερμότητας 1 Εξαναγκασμένη συναγωγή: Στρωτή ροή σε επίπεδες πλάκες (orced convection
Εξαναγκασμένη Συναγωγή Ροή Πάνω από μία Επίπεδη Επιφάνεια Τμήμα Μηχανολόγων Μηχανικών και Μηχανικών Παραγωγής ΜΜK 31 Μεταφορά Θερμότητας 1 Εξαναγκασμένη συναγωγή: Στρωτή ροή σε επίπεδες πλάκες (orced convection
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης
 σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
σχηματική αναπαράσταση των βασικών τμημάτων μίας βιομηχανικής εγκατάστασης Αρχές μεταφοράς μάζας Αρχές σχεδιασμού συσκευών μεταφοράς μάζας Διεργασίες μεταφοράς μάζας - Απορρόφηση - Απόσταξη - Εκχύλιση
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ
 ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Κ. Μάτης ΤΟ ΠΡΟΒΛΗΜΑ ΠΕΡΙΛΑΜΒΑΝΕΙ ΕΝΑ ΣΥΝΕΧΗ ΠΛΗΡΩΣ ΑΝΑΜΙΓΝΥΟΜΕΝΟ ΑΝΤΙΔΡΑΣΤΗΡΑ (CSTR) ΜΕ ΔΥΝΑΤΟΤΗΤΑ ΕΝΑΛΛΑΓΗΣ ΘΕΡΜΟΤΗΤΑΣ ΕΣΩΤΕΡΙΚΑ ΜΕ ΜΙΑ ΣΠΕΙΡΑ. Σημ. Η σωστή απάντηση κάθε
ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ Κ. Μάτης ΤΟ ΠΡΟΒΛΗΜΑ ΠΕΡΙΛΑΜΒΑΝΕΙ ΕΝΑ ΣΥΝΕΧΗ ΠΛΗΡΩΣ ΑΝΑΜΙΓΝΥΟΜΕΝΟ ΑΝΤΙΔΡΑΣΤΗΡΑ (CSTR) ΜΕ ΔΥΝΑΤΟΤΗΤΑ ΕΝΑΛΛΑΓΗΣ ΘΕΡΜΟΤΗΤΑΣ ΕΣΩΤΕΡΙΚΑ ΜΕ ΜΙΑ ΣΠΕΙΡΑ. Σημ. Η σωστή απάντηση κάθε
Φυσικοχημεία 2 Εργαστηριακές Ασκήσεις
 Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
Φυσικοχημεία Εργαστηριακές Ασκήσεις Άσκηση α: Συντελεστής Joule Thomson (Τζουλ Τόμσον ) Αθανάσιος Τσεκούρας Τμήμα Χημείας Θεωρία 3 Μετρήσεις 6 3 Επεξεργασία Μετρήσεων 6 Σελίδα Θεωρία Η καταστατική εξίσωση
ΑΝΩΤΕΡΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ
 ΑΝΩΤΕΡΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Διδάσκοντες: Κώστας Περράκης, Δημοσθένης Γεωργίου http://eclass.upatras.gr/ p Βιβλιογραφία Advanced Thermodynamics for Engineers, Kenneth, Jr. Wark Advanced thermodynamics engineering
ΑΝΩΤΕΡΗ ΘΕΡΜΟΔΥΝΑΜΙΚΗ Διδάσκοντες: Κώστας Περράκης, Δημοσθένης Γεωργίου http://eclass.upatras.gr/ p Βιβλιογραφία Advanced Thermodynamics for Engineers, Kenneth, Jr. Wark Advanced thermodynamics engineering
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ. Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για:
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ
 ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
ΑΕΡΙΑ ΙΔΑΝΙΚΑ ΚΑΙ ΠΡΑΓΜΑΤΙΚΑ ΑΕΡΙΑ ΝΟΜΟΣ ΤΕΛΕΙΩΝ ΑΕΡΙΩΝ O νόμος των τελείων αερίων συνδέει τις ιδιότητες ενός τελείου αερίου σε μια συγκεκριμένη κατάσταση (καταστατική εξίσωση) P V = n R T P: Απόλυτη πίεση
Ζήτημα 1 0. Επώνυμο... Όνομα... Αγρίνιο 1/3/2015. Επιλέξτε τη σωστή απάντηση
 1 Επώνυμο... Όνομα... Αγρίνιο 1/3/2015 Ζήτημα 1 0 Επιλέξτε τη σωστή απάντηση 1) Η θερμότητα που ανταλλάσει ένα αέριο με το περιβάλλον θεωρείται θετική : α) όταν προσφέρεται από το αέριο στο περιβάλλον,
1 Επώνυμο... Όνομα... Αγρίνιο 1/3/2015 Ζήτημα 1 0 Επιλέξτε τη σωστή απάντηση 1) Η θερμότητα που ανταλλάσει ένα αέριο με το περιβάλλον θεωρείται θετική : α) όταν προσφέρεται από το αέριο στο περιβάλλον,
