ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ. Κεφάλαιο 4ο: Ερωτήσεις πολλαπλής επιλογής. 1. * Το πεδίο ορισµού της συνάρτησης µε τύπο f (x) = 2 (Σχ.1) είναι. Γ το διάστηµα ( 0,
|
|
|
- Ήλιόδωρος Αγγελίδου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 4ο: ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Ερωτήσεις πολλαπλής επιλογής 1. * Το πεδίο ορισµού της συνάρτησης µε τύπο f () = 2 (Σχ.1) είναι Α. το διάστηµα [ 0, Β. το διάστηµα Γ. το σύνολο R ( 0,. το σύνολο R - {1} Ε. το σύνολο R * Σχ.1 2. * Το πεδίο ορισµού της συνάρτησης µε τύπο f () = 2 (Σχ. 2) είναι Α. το διάστηµα [ 0, Β. το σύνολο R Γ το διάστηµα ( 0,. το σύνολο R - {1} Ε. το σύνολο R * Σχ.2 165
2 3. * Η εκθετική συνάρτηση µε τύπο f () = α µε 0 < α 1 έχει πεδίο ορισµού Α. το διάστηµα [ 0, ) Β. το διάστηµα ( 0, Γ. το σύνολο R - {1}. το σύνολο R Ε. το σύνολο R * 4. * Το σύνολο τιµών της συνάρτησης µε τύπο f () = 3 (Σχ.3) είναι Α. το διάστηµα [ 0, Β. το διάστηµα ( 0, ] Γ. το διάστηµα ( 0, ). το διάστηµα Ε. το σύνολο R * ( 0, Σχ.3 5. * Το σύνολο τιµών της συνάρτησης µε τύπο f () = 1 3 (Σχ. 4) είναι Α. το διάστηµα [ 0, Β. το διάστηµα ( 0], Γ. το διάστηµα ( 0, ]. το σύνολο R * Ε. το διάστηµα ( 0, Σχ.4 6. * Η εκθετική συνάρτηση µε τύπο f () = α µε 0 < α 1 έχει σύνολο τιµών Α. το διάστηµα ( 0, Β. το διάστηµα ( 0, ] Γ. το διάστηµα ( 0, ). το διάστηµα [ 0, 166
3 Ε. το σύνολο R * 7. * Η γραφική παράσταση της συνάρτησης µε τύπο f ()= 4 (Σχ. 5) Α. έχει άξονα oυµµετρίας τον y y Β. τέµνει µόνο τον άξονα y y στο σηµείο (0,1). Γ. τον άξονα y y σε 2 σηµεία.. έχει ασύµπτωτη τον θετικό ηµιάξονα Ο Ε. τίποτα από τα προηγούµενα. Σχ.5 8. * Η γραφική παράσταση της συνάρτησης µε τύπο f () = (Σχ.6) 4 Α. έχει άξονα oυµµετρίας τον y y Β. τον άξονα y y σε 2 σηµεία. Γ. τέµνει µόνο τον άξονα y y στο σηµείο (0, 1).. έχει ασύµπτωτη τον αρνητικό ηµιάξονα Ο Ε. τίποτα από τα προηγούµενα. Σχ.6 9. * Η γραφική παράσταση της συνάρτησης µε τύπο f () = α µε 0 <α 1 Α. τέµνει µόνο τον άξονα y y στο σηµείο (0, 1) Β. έχει άξονα oυµµετρίας τον y y Γ. τον άξονα y y σε 2 σηµεία.. έχει κατακόρυφη ασύµπτωτη του y y Ε. τίποτα από τα προηγούµενα. 167
4 10. * Η συνάρτηση µε τύπο f () = (Σχ.7) είναι: 5 Α. γνησίως φθίνουσα Β. άρτια Γ. περιττή. γνησίως αύξουσα Ε. δεν είναι µονότονη Σχ * Η συνάρτηση µε τύπο f () = 5 (Σχ.8) είναι Α. γνησίως φθίνουσα Β. άρτια Γ. περιττή. γνησίως αύξουσα Ε. δεν είναι µονότονη Σχ * Η εκθετική συνάρτηση µε τύπο f () = α µε 0 < α < 1 είναι πάντοτε Α. γνησίως φθίνουσα Β. σταθερή Γ. περιοδική. γνησίως αύξουσα Ε. δεν είναι µονότονη 13. * Η εκθετική συνάρτηση µε τύπο f () = α µε α > 1 είναι πάντοτε Α. γνησίως φθίνουσα Β. άρτια Γ. περιττή. γνησίως αύξουσα Ε. δεν είναι µονότονη 168
5 14. * Στο Σχ. 9 είναι η γραφική παράσταση της συνάρτησης µε τύπο f () = 3 Σχ.9 α) Η γραφική παράσταση της συνάρτησης µε τύπο g () = 3 είναι Α. Γ. Β.. Ε. 169
6 - β) Η γραφική παράσταση της συνάρτησης µε τύπο h () = 3 είναι Α. Β. Γ.. Ε. 170
7 15. * Η γραφική παράσταση της συνάρτησης µε τύπο g () = - 2 είναι συµµετρική µε την γραφική παράσταση της f () = 2 (Σχ.11) ως προς Α. τον άξονα y y Β. την ευθεία y = Γ. την ευθεία y = -. τον άξονα Ε. κέντρο το Ο(0,0) Σχ * Η γραφική παράσταση της συνάρτησης µε τύπο g () = 5 είναι συµµετρική µε την γραφική παράσταση της f () = 5 (Σχ.12) ως προς A. τον άξονα B. τον άξονα y y Γ. την ευθεία y = 1 5. την ευθεία y = 5 Ε. κέντρο το Ο(0, 0) Σχ
8 17. * Έστω η συνάρτηση f () = 2. Ποια από τις παρακάτω προτάσεις είναι σωστή; Α. η f έχει πεδίο ορισµού το διάστηµα ( 0, Β. η f έχει σύνολο τιµών το σύνολο R Γ. η f είναι γνησίως φθίνουσα στο πεδίο ορισµού oης. η γραφική της παράσταση τέµνει τον στο σηµείο Α(0, 1) Ε. η γραφική της παράσταση έχει ασύµπτωτη τον αρνητικό ηµιάξονα των. 18. * Έστω η συνάρτηση µε τύπο f () =. Ποια από τις παρακάτω προτάσεις είναι σωστή; Α. η f είναι γνησίως αύξουσα στο R Β. η f είναι γνησίως φθίνουσα στο R 2 Γ. η f είναι γνησίως αύξουσα στο ( 0,. η γραφική παράσταση της f τέµνει τον y y στο σηµείο Μ (0, 1/2) Ε. η γραφική παράσταση της f τέµνει τον στο σηµείο Ν (1, 0) 19. * ίνεται η συνάρτηση µε τύπο f () = 2 τότε ισχύει Α. f (2) > f (3) B. f (2) < f (3) Γ. f (2) f (3). f (2) = 2f (3) E. f (2) = f (3) * ίνεται η συνάρτηση µε τύπο f () = 3 τότε ισχύει Α. f (2) < f (3) Β. f (2) f (3) Γ. f (2) > f (3). f (2) = 3f (3) E. f (2) = f (3) 21. * ίνεται η συνάρτηση µε τύπο f () = 3 τότε δεν είναι σωστή η Α. f (0,5) < f (0,8) Β. f (-2) > f (-3) Γ. f > f 5 7. f (1, 3) > f (-1, 3) E. f ( 3 ) > f ( 5 ) 172
9 22. * ίνεται η συνάρτηση µε τύπο f () = 3 τότε i f 2 2 είναι ίσος µε Α. 3 2 Β. 4 9 Γ Ε. 3 µ 23. * Αν α > 0, µ, ν θετικiί ακέραιοι µε ν 2 τότε το α ν ισούται µε Α. α α µ ν Β. α µ ν Γ. α ν µ. ν α µ Ε. τίποτα από τα προηγούµενα * Το 32 5 ισούται µε Α Β. 2 Γ Ε * Αν 3 = 27, τότε το είναι Α: 27 Β: 1/9 Γ: 0 : 3 Ε: * ίνεται η εξίσωση 2 = 16. Τότε το είναι Α. 1 ή -1 Β. 2 ή 3 Γ. -2 ή Ε. τίποτα από τα προηγούµενα * Αν 2 = 16, τότε το είναι Α. 4 Β. 1 Γ Ε * Αν f () = 2, τότε το f (f (2)) ισούται µε Α. 16 B. 8 Γ E
10 29. * Η εξίσωση = 2 έχει λύση τον αριθµό Α. -2 Β. -1 Γ Ε *Η εξίσωση = Α. έχει λύση ένα θετικό αριθµό Β. έχει λύση ένα αρνητικό αριθµό Γ. έχει λύση κάθε πραγµατικό αριθµό 0. είναι αδύνατη Ε. έχει λύση την = ίνεται η ανίσωση 3 > 1. Τότε ισχύει Α. > 2 B. = 0 Γ. < 2. 2 E. = * ίνεται η ανίσωση Τότε ισχύει A. 2 B. = -1 Γ. 1. > 1 E. > * ίνεται η ανίσωση < 625. Tότε ισχύει Α. = 3 B. 3 Γ. = 5. > 3 E. < * ίνεται η ανίσωση. Tότε ισχύει 3 81 Α. 16 B. 4 Γ. > 4. = 16 E. τίποτα από τα προηγούµενα 35. * Η ανίσωση 2 2 αληθεύει Α. Για (, 1) Β. Για (, 1] Γ. Για (,0). Για ( 1, Ε. Για κάθε R 174
11 36. * Έστω η εκθετική συνάρτηση µε τύπο f () = α µε 0 < α 1. Ποιο από τα παρακάτω σηµεία αποκλείεται να ανήκει στη γραφική παράσταση της f; A. (-2, 8), B. (0, 1), Γ. (3, -27),. (3, 2) Ε. (2, 3) 37. ** ίνονται οι συναρτήσεις f () = 2 και g() = e. Τότε ισχύει ότι Α. f (e) = g (e) B. f (e) > g(e) Γ. f (2) < g (2) 1. f g 2 1 Ε. f g ** ίνονται οι γραφικές παραστάσεις των συναρτήσεων f () = e και y = e (Σχ.13) που τέµνονται στο σηµείο Α( o,e). Το ο είναι ίσο µε Α. e B. 1 Γ e Ε. 3 2 Σχ
ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ. Κεφάλαιο 4ο: Ερωτήσεις του τύπου Σωστό - Λάθος. 1. Στο σχήμα 23 δίνεται η γραφική παράσταση της συνάρτησης
 Κεφάλαιο 4ο: ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Ερωτήσεις του τύπου Σωστό - Λάθος. Στο σχήμα δίνεται η γραφική παράσταση της συνάρτησης f( ) =. 5 Να χαρακτηρίσετε ως σωστό (Σ) ή λάθος (Λ) τις παρακάτω προτάσεις. Σχ. i)
Κεφάλαιο 4ο: ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Ερωτήσεις του τύπου Σωστό - Λάθος. Στο σχήμα δίνεται η γραφική παράσταση της συνάρτησης f( ) =. 5 Να χαρακτηρίσετε ως σωστό (Σ) ή λάθος (Λ) τις παρακάτω προτάσεις. Σχ. i)
. Το σύνολο R* E. Το σύνολο R-{1}
 Ερωτήσεις πολλαπλής επιλογής. * Το πεδίο ορισµού της συνάρτησης µε τύπο f () = log (Σχ.) είναι y y=log A. το διάστηµα [ 0, + ) Β. το διάστηµα ( 0, + ) Γ. το σύνολο R. το σύνολο R* E. το σύνολο R -{}. *
Ερωτήσεις πολλαπλής επιλογής. * Το πεδίο ορισµού της συνάρτησης µε τύπο f () = log (Σχ.) είναι y y=log A. το διάστηµα [ 0, + ) Β. το διάστηµα ( 0, + ) Γ. το σύνολο R. το σύνολο R* E. το σύνολο R -{}. *
ΕΚΘΕΤΙΚΗ ΚΑΙ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΩΣΤΑ ΛΑΘΟΣ
 ΕΚΘΕΤΙΚΗ ΚΑΙ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΩΣΤΑ ΛΑΘΟΣ 1. Στο διπλανό σχήμα δίνεται η γραφική παράσταση της συνάρτησης f( ). 1 5 Να χαρακτηρίσετε ως σωστό (Σ) ή λάθος (Λ) τις παρακάτω προτάσεις.. i) Η f έχει πεδίο
ΕΚΘΕΤΙΚΗ ΚΑΙ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΩΣΤΑ ΛΑΘΟΣ 1. Στο διπλανό σχήμα δίνεται η γραφική παράσταση της συνάρτησης f( ). 1 5 Να χαρακτηρίσετε ως σωστό (Σ) ή λάθος (Λ) τις παρακάτω προτάσεις.. i) Η f έχει πεδίο
. lim [2f (x) + 3g (x)] = 13
![. lim [2f (x) + 3g (x)] = 13 . lim [2f (x) + 3g (x)] = 13](/thumbs/91/105148515.jpg) Ερωτήσεις πολλαπλής επιλογής. * Αν η γραφική παράσταση µιας συνάρτησης f είναι αυτή που φαίνεται στο σχήµα, τότε λάθος είναι Α. f () = 4 B. f () = Γ. f () =. f ( ) = 4 E. f () = 4. * Για τη συνάρτηση f,
Ερωτήσεις πολλαπλής επιλογής. * Αν η γραφική παράσταση µιας συνάρτησης f είναι αυτή που φαίνεται στο σχήµα, τότε λάθος είναι Α. f () = 4 B. f () = Γ. f () =. f ( ) = 4 E. f () = 4. * Για τη συνάρτηση f,
5. Η γραφική παράσταση της συνάρτησης f( x) 3 x έχει ασύμπτωτη τον θετικό ημιάξονα Οx. Σ Λ., τότε ισχύει
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΣΤΡΙΤΣΙΟΥ ΕΠΙΜΕΛΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc 5 ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Σε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Σ, αν ο ισχυρισμός είναι αληθής διαφορετικά
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΣΤΡΙΤΣΙΟΥ ΕΠΙΜΕΛΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc 5 ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ Σε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Σ, αν ο ισχυρισμός είναι αληθής διαφορετικά
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
ΑΣΚΗΣΕΙΣ Β ΛΥΚΕΙΟΥ -- ΑΛΓΕΒΡΑ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Άσκηση η Γραμμικά συστήματα Δίνονται οι ευθείες : y3 και :y 5. Να βρεθεί το R, ώστε οι ευθείες να τέμνονται. Οι ευθείες και θα τέμνονται όταν το μεταξύ
3.4 ΤΡIΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. και g( x) 3x
 1 ΓΕΝΙΚΟ ΥΚΕΙΟ ΚΑΤΡΙΤΙΟΥ ΕΠΙΜΕΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc ΤΡIΓΩΝΟΜΕΤΡΙΚΕ ΥΝΑΡΤΗΕΙ 1 ε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα, αν ο ισχυρισμός είναι αληθής διαφορετικά
1 ΓΕΝΙΚΟ ΥΚΕΙΟ ΚΑΤΡΙΤΙΟΥ ΕΠΙΜΕΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc ΤΡIΓΩΝΟΜΕΤΡΙΚΕ ΥΝΑΡΤΗΕΙ 1 ε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα, αν ο ισχυρισμός είναι αληθής διαφορετικά
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις
 Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Συναρτήσεις Θεωρία Ορισμοί - Παρατηρήσεις Ορισμός: Έστω Α, Β R. Πραγματική συνάρτηση πραγματικής μεταβλητής από το σύνολο Α στο σύνολο Β ονομάζουμε την διαδικασία κατά την οποία κάθε στοιχείο του συνόλου
Ερωτήσεις πολλαπλής επιλογής. 1. * Από τα παρακάτω διαγράµµατα, γραφική παράσταση συνάρτησης είναι το
 Ερωτήσεις πολλαπλής επιλογής. * Από τα παρακάτω διαγράµµατα, γραφική παράσταση συνάρτησης είναι το διάγραµµα Α. B. Γ.. Ε. 7 . * Από τα παρακάτω διαγράµµατα δεν είναι γραφική παράσταση συνάρτησης το διάγραµµα
Ερωτήσεις πολλαπλής επιλογής. * Από τα παρακάτω διαγράµµατα, γραφική παράσταση συνάρτησης είναι το διάγραµµα Α. B. Γ.. Ε. 7 . * Από τα παρακάτω διαγράµµατα δεν είναι γραφική παράσταση συνάρτησης το διάγραµµα
Ι. Πραγματικές ΣΥΝΑΡΤΗΣΕΙΣ πραγματικής μεταβλητής (έως και ΑΝΤΙΣΤΡΟΦΗ)
 Ι. Πραγματικές ΥΝΑΡΤΗΕΙ πραγματικής μεταβλητής (έως και ΑΝΤΙΤΡΟΦΗ). Η γραφική παράσταση της συνάρτησης f βρίσκεται κάτω από τον άξονα.. Δίνεται η συνάρτηση = f (). Οι τετμημένες των σημείων τομής της C
Ι. Πραγματικές ΥΝΑΡΤΗΕΙ πραγματικής μεταβλητής (έως και ΑΝΤΙΤΡΟΦΗ). Η γραφική παράσταση της συνάρτησης f βρίσκεται κάτω από τον άξονα.. Δίνεται η συνάρτηση = f (). Οι τετμημένες των σημείων τομής της C
- 11 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 - 11 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ) 1 Να βρεθεί η σχετική θέση των γραφικών παραστάσεων των συναρτήσεων f και g γα τις οποίες ισχύει: f()+1=g()+e (Η C f κάτω
- 11 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ) 1 Να βρεθεί η σχετική θέση των γραφικών παραστάσεων των συναρτήσεων f και g γα τις οποίες ισχύει: f()+1=g()+e (Η C f κάτω
<Πεδία ορισμού ισότητα πράξεις σύνθεση>
 Συναρτήσεις 1 A Έστω μία συνάρτηση Να βρείτε το πεδίο ορισμού της συνάρτησης B Δίνεται η συνάρτηση Να βρείτε το πεδίο ορισμού των συναρτήσεων :, και Γ Να εξετάσετε
Συναρτήσεις 1 A Έστω μία συνάρτηση Να βρείτε το πεδίο ορισμού της συνάρτησης B Δίνεται η συνάρτηση Να βρείτε το πεδίο ορισμού των συναρτήσεων :, και Γ Να εξετάσετε
5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ. x, τότε ισχύει f(4) f(2). x τότε ισχύει. αν 1.
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΣΤΡΙΤΣΙΟΥ ΕΠΙΜΕΛΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc 5. ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ. Σε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Σ, αν ο ισχυρισμός είναι αληθής διαφορετικά
ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΚΑΣΤΡΙΤΣΙΟΥ ΕΠΙΜΕΛΕΙΑ: Kωνσταντόπουλος Κων/νος Μαθηματικός ΜSc 5. ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ. Σε κάθε μια από τις παρακάτω περιπτώσεις να κυκλώσετε το γράμμα Σ, αν ο ισχυρισμός είναι αληθής διαφορετικά
ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ
 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΣΥΝΟΛΑ ΕΡΩΤΗΣΕΙΣ ΤΥΠΟΥ «ΣΩΣΤΟ ΛΑΘΟΣ». {,3,5,7,... } { / = ν +, ν Ν} =. = {} 0 3. Αν Α Β τότε Α Β = Α 4. 5 {,3,5,7 } 5. Αν Α= {, 3,7} και Β= {,3} 7, τότε Α=Β 6.
2 ο Διαγώνισμα Ύλη: Συναρτήσεις
 ο Διαγώνισμα 08-9 Ύλη: Συναρτήσεις Θέμα Α Α. Θεωρήστε τον παρακάτω ισχυρισμό: «Αν μια συνάρτηση : είναι - τότε είναι και γνησίως μονότονη.» α) Να χαρακτηρίσετε τον ισχυρισμό γράφοντας στο τετράδιό σας
ο Διαγώνισμα 08-9 Ύλη: Συναρτήσεις Θέμα Α Α. Θεωρήστε τον παρακάτω ισχυρισμό: «Αν μια συνάρτηση : είναι - τότε είναι και γνησίως μονότονη.» α) Να χαρακτηρίσετε τον ισχυρισμό γράφοντας στο τετράδιό σας
Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι γνησίως αύξουσες και ποιες γνησίως φθίνουσες. i) f(x) = 1 x. ii) f(x) = 2ln(x 2) 1 = (, 1] 1 x
![Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι γνησίως αύξουσες και ποιες γνησίως φθίνουσες. i) f(x) = 1 x. ii) f(x) = 2ln(x 2) 1 = (, 1] 1 x Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι γνησίως αύξουσες και ποιες γνησίως φθίνουσες. i) f(x) = 1 x. ii) f(x) = 2ln(x 2) 1 = (, 1] 1 x](/thumbs/59/43449681.jpg) . Ασκήσεις σχολικού βιβλίου σελίδας 56 57 A µάδας. Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι γνησίως αύξουσες και ποιες γνησίως φθίνουσες. i) () = ii) () = ln( ) iii) () = e + iv) () = ( ), i)
. Ασκήσεις σχολικού βιβλίου σελίδας 56 57 A µάδας. Να βρείτε ποιες από τις παρακάτω συναρτήσεις είναι γνησίως αύξουσες και ποιες γνησίως φθίνουσες. i) () = ii) () = ln( ) iii) () = e + iv) () = ( ), i)
3.4 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 3.4 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Μια συνάρτηση με πεδίο ορισμού το σύνολο Α, λέγεται περιοδική, όταν υπάρχει πραγματικός αριθμός Τ>0 τέτοιος, ώστε για κάθε να ισχύει ότι και ( ) και ( ). Ο αριθμός Τ
3.4 ΟΙ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Μια συνάρτηση με πεδίο ορισμού το σύνολο Α, λέγεται περιοδική, όταν υπάρχει πραγματικός αριθμός Τ>0 τέτοιος, ώστε για κάθε να ισχύει ότι και ( ) και ( ). Ο αριθμός Τ
ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΕΚΘΕΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. και 1. και. με λ Z,είναι γνησίως αύξουσα στο R. f x και g x. 2 f x y f x f y g x g y.
 ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΕΚΘΕΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. Η γραφική παράσταση της συνάρτησης f (),. α) Να βρείτε την τιμή του λ R 5 β) Να βρείτε τις τιμές f και f γ) Να σχεδιάσετε τη γραφική παράσταση της f διέρχεται
ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΕΚΘΕΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. Η γραφική παράσταση της συνάρτησης f (),. α) Να βρείτε την τιμή του λ R 5 β) Να βρείτε τις τιμές f και f γ) Να σχεδιάσετε τη γραφική παράσταση της f διέρχεται
ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ
 ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Για να μελετήσουμε και να χαράξουμε τη γραφική παράταση μιας συνάρτησης ακολουθούμε τα παρακάτω βήματα: 1. Βρίσκουμε το πεδίο ορισμού της.. Εξετάζουμε την
ΜΕΛΕΤΗ ΚΑΙ ΧΑΡΑΞΗ ΓΡΑΦΙΚΗΣ ΠΑΡΑΣΤΑΣΗΣ ΣΥΝΑΡΤΗΣΗΣ Για να μελετήσουμε και να χαράξουμε τη γραφική παράταση μιας συνάρτησης ακολουθούμε τα παρακάτω βήματα: 1. Βρίσκουμε το πεδίο ορισμού της.. Εξετάζουμε την
g x είναι συνάρτηση 1 1 στο Ag = R αλλά δεν είναι γνησίως
 ΘΕΜΑ Α Α. Απόδειξη θεωρήματος σελ. 99 σχολικού βιβλίου. Α. α. Ψευδής β. Θεωρούμε τη συνάρτηση, 0 g, 0 η οποία έχει γραφική παράσταση (σχήμα σχολικού βιβλίου σελ.5): y O y=g() Η g είναι συνάρτηση στο Ag
ΘΕΜΑ Α Α. Απόδειξη θεωρήματος σελ. 99 σχολικού βιβλίου. Α. α. Ψευδής β. Θεωρούμε τη συνάρτηση, 0 g, 0 η οποία έχει γραφική παράσταση (σχήμα σχολικού βιβλίου σελ.5): y O y=g() Η g είναι συνάρτηση στο Ag
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
Κεφάλαιο 2ο: ΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 2ο ΜΕΡΟΣ
 Κεφάλαιο ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ ο ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Αν η συνάρτηση f είναι παραγωγίσιµη στο R και f (α) f (β), α, β R, α < β, τότε ισχύει f () για κάθε (α, β).. * Αν η συνάρτηση f
Κεφάλαιο ο: ΙΑΦΟΡΙΚΟ ΟΓΙΜΟ ο ΜΕΡΟ Ερωτήσεις του τύπου «ωστό - άθος» 1. * Αν η συνάρτηση f είναι παραγωγίσιµη στο R και f (α) f (β), α, β R, α < β, τότε ισχύει f () για κάθε (α, β).. * Αν η συνάρτηση f
1. Συµπλήρωσε τον πίνακα µε την κατάλληλη µαθηµατική έκφραση:
 ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ Ερωτήσεις συµπλήρωσης 1. Συµπλήρωσε τον πίνακα µε την κατάλληλη µαθηµατική έκφραση: Φυσική γλώσσα Μαθηµατική γλώσσα ύο αριθµοί x, y διαφέρουν κατά και έχουν γινόµενο x (x
ΕΡΩΤΗΣΕΙΣ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ Ερωτήσεις συµπλήρωσης 1. Συµπλήρωσε τον πίνακα µε την κατάλληλη µαθηµατική έκφραση: Φυσική γλώσσα Μαθηµατική γλώσσα ύο αριθµοί x, y διαφέρουν κατά και έχουν γινόµενο x (x
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 3: ΣΥΝΑΡΤΗΣΗ 1-1 ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση. ΘΕΜΑ Β Να
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση. ΘΕΜΑ Β Να
Ζ ΕΝΟΤΗΤΑ. Μελέτη βασικών συναρτήσεων. Ζ.1 (7.1 παρ/φος σχολικού βιβλίου) Ζ.2 (7.2 παρ/φος σχολικού βιβλίου) Ζ.3 (7.3 παρ/φος σχολικού βιβλίου) 2
 Ζ ΕΝΟΤΗΤΑ Μελέτη βασικών συναρτήσεων Ζ.1 (7.1 παρ/φος σχολικού βιβλίου) Μελέτη της συνάρτησης f(x) = αx Ζ. (7. παρ/φος σχολικού βιβλίου) Μελέτη της συνάρτησης f x α x Ζ.3 (7.3 παρ/φος σχολικού βιβλίου)
Ζ ΕΝΟΤΗΤΑ Μελέτη βασικών συναρτήσεων Ζ.1 (7.1 παρ/φος σχολικού βιβλίου) Μελέτη της συνάρτησης f(x) = αx Ζ. (7. παρ/φος σχολικού βιβλίου) Μελέτη της συνάρτησης f x α x Ζ.3 (7.3 παρ/φος σχολικού βιβλίου)
ΑΣΚΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ
 ΑΚΗΕΙ ΚΕΙΤΟΥ ΤΥΠΟΥ Α Να βάλετε σε κύκλο την σωστή απάντηση (Ερωτήσεις πολλαπλής επιλογής) Ο ρυθμός με τον οποίο μειώνεται η ακτίνα ενός κύκλου είναι,5 cm/sec Με ποιο ρυθμό μειώνεται η επιφάνειά του όταν
ΑΚΗΕΙ ΚΕΙΤΟΥ ΤΥΠΟΥ Α Να βάλετε σε κύκλο την σωστή απάντηση (Ερωτήσεις πολλαπλής επιλογής) Ο ρυθμός με τον οποίο μειώνεται η ακτίνα ενός κύκλου είναι,5 cm/sec Με ποιο ρυθμό μειώνεται η επιφάνειά του όταν
Ερωτήσεις πολλαπλής επιλογής
 Ερωτήσεις πολλαπλής επιλογής. * Το θεώρηµα µέσης τιµής του διαφορικού λογισµού για κάθε α, β R και τη συνάρτηση f () = e εξασφαλίζει την ύπαρξη ενός αριθµού κ R, ώστε να ισχύει Α. e α-β = e κ (α - β) Β.
Ερωτήσεις πολλαπλής επιλογής. * Το θεώρηµα µέσης τιµής του διαφορικού λογισµού για κάθε α, β R και τη συνάρτηση f () = e εξασφαλίζει την ύπαρξη ενός αριθµού κ R, ώστε να ισχύει Α. e α-β = e κ (α - β) Β.
2. Έστω η συνάρτηση f :[0, 6] με την παρακάτω γραφική παράσταση.
![2. Έστω η συνάρτηση f :[0, 6] με την παρακάτω γραφική παράσταση. 2. Έστω η συνάρτηση f :[0, 6] με την παρακάτω γραφική παράσταση.](/thumbs/62/47302337.jpg) . Έστω η συνάρτηση f : με την παρακάτω γραφική παράσταση. Α. Να προσδιορίσετε τα διαστήματα στα οποία η f είναι γνησίως αύξουσα, γνησίως φθίνουσα, κυρτή, κοίλη, καθώς και τα τοπικά ακρότατα και τα σημεία
. Έστω η συνάρτηση f : με την παρακάτω γραφική παράσταση. Α. Να προσδιορίσετε τα διαστήματα στα οποία η f είναι γνησίως αύξουσα, γνησίως φθίνουσα, κυρτή, κοίλη, καθώς και τα τοπικά ακρότατα και τα σημεία
5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ
 5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΘΕΩΡΙΑ. Λογαριθµική συνάρτηση µε βάση α Όταν α > f() = log α Έχει πεδίο ορισµού το (0, + ) Έχει σύνολο τιµών το R Είναι γνησίως αύξουσα Τέµνει τον άξονα των στο σηµείο (, 0) Είναι
5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΘΕΩΡΙΑ. Λογαριθµική συνάρτηση µε βάση α Όταν α > f() = log α Έχει πεδίο ορισµού το (0, + ) Έχει σύνολο τιµών το R Είναι γνησίως αύξουσα Τέµνει τον άξονα των στο σηµείο (, 0) Είναι
Ασκήσεις στη συνέχεια συναρτήσεων. τέτοια ώστε. lim. και
 Ασκήσεις στη συνέχεια συναρτήσεων Άσκηση η Να βρεθούν τα ολικά ακρότατα των συναρτήσεων ) x, 0, ) x x a x x x, x x x x Άσκηση η Αν : a, συνεχής στο, τέτοια ώστε x x και x x Να αποδείξετε ότι η συνάρτηση
Ασκήσεις στη συνέχεια συναρτήσεων Άσκηση η Να βρεθούν τα ολικά ακρότατα των συναρτήσεων ) x, 0, ) x x a x x x, x x x x Άσκηση η Αν : a, συνεχής στο, τέτοια ώστε x x και x x Να αποδείξετε ότι η συνάρτηση
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Να εξετάσετε ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασµένες.. Αν η συνάρτηση είναι συνεχής στο
ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΜΑ Ο Να εξετάσετε ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασµένες.. Αν η συνάρτηση είναι συνεχής στο
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
7.1 ΜΕΛΕΤΗ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ f ( ) 1. Μορφή της συνάρτησης f ( ) Ιδιότητες Έχει πεδίο ορισµού ολο το R Είναι άρτια, άρα συµµετρική ως προς τον άξονα y y Είναι γνησίως φθίνουσα στο διάστηµα (,0] Είναι γνησίως
( ) ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ. Σηµείωση. 2. Παραδοχή α = Ιδιότητες x. αβ = α = α ( ) x. α β. α : α = α = α
 . ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ ΘΕΩΡΙΑ. Σηµείωση Οι δυνάµεις α του κεφαλαίου έχουν βάση α > 0 και εκθέτη οποιονδήποτε πραγµατικό αριθµό.. Παραδοχή 0 α. Ιδιότητες α + α ( ) α α : α ( ) α α α αβ α β α β α β. Εκθετική
. ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ ΘΕΩΡΙΑ. Σηµείωση Οι δυνάµεις α του κεφαλαίου έχουν βάση α > 0 και εκθέτη οποιονδήποτε πραγµατικό αριθµό.. Παραδοχή 0 α. Ιδιότητες α + α ( ) α α : α ( ) α α α αβ α β α β α β. Εκθετική
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 2: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ [Κεφ. 1.3: Μονότονες Συναρτήσεις - Αντίστροφη Συνάρτηση σχολικού βιβλίου]. ΣΗΜΕΙΩΣΕΙΣ Μονοτονία
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου
 Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Βασικές Γνώσεις Μαθηματικών Α - Β Λυκείου Αριθμοί 1. ΑΡΙΘΜΟΙ Σύνολο Φυσικών αριθμών: Σύνολο Ακέραιων αριθμών: Σύνολο Ρητών αριθμών: ακέραιοι με Άρρητοι αριθμοί: είναι οι μη ρητοί π.χ. Το σύνολο Πραγματικών
Συναρτήσεις. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Άλγεβρα Κεφάλαιο 2 78 ασκήσεις. Kglykos.gr. εκδόσεις. Καλό πήξιμο. Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α
 Συναρτήσεις Κώστας Γλυκός Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / 9 / 0 1 6 Άλγεβρα Κεφάλαιο 78 ασκήσεις και τεχνικές σε 9 σελίδες εκδόσεις Καλό πήξιμο τηλ. Οικίας : 10-610.178
Συναρτήσεις Κώστας Γλυκός Ι δ ι α ί τ ε ρ α μ α θ ή μ α τ α 6 9 7. 0 0. 8 8. 8 8 Kglykos.gr / 9 / 0 1 6 Άλγεβρα Κεφάλαιο 78 ασκήσεις και τεχνικές σε 9 σελίδες εκδόσεις Καλό πήξιμο τηλ. Οικίας : 10-610.178
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ. Να εξετάσετε αν είναι ίσες οι συναρτήσεις f, g όταν: x x 2 x x. x x g x. ln x ln x 1 και
 Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
Περιορισμοί στο R. ln x,log. Β= ln Α Β Α Β Α. Σύνοψη γραφικών παραστάσεων
 στο R Πεδίο ορισμού συνάρτησης είναι η συναλήθευση των περιορισμών της συνάρτησης στο R, αν δεν έχει περιορισμούς λέμε ότι έχει πεδίο ορισμού το R. Όταν έχω πρέπει ν Α, Α Α Α Β Β ln Α, log Α Α> ln Β logα
στο R Πεδίο ορισμού συνάρτησης είναι η συναλήθευση των περιορισμών της συνάρτησης στο R, αν δεν έχει περιορισμούς λέμε ότι έχει πεδίο ορισμού το R. Όταν έχω πρέπει ν Α, Α Α Α Β Β ln Α, log Α Α> ln Β logα
ΦΥΛΛΆΔΙΟ ΑΣΚΉΣΕΩΝ 2 ΣΥΝΑΡΤΗΣΕΙΣ
 ΦΥΛΛΆΔΙΟ ΑΣΚΉΣΕΩΝ 2 ΣΥΝΑΡΤΗΣΕΙΣ 1. Να βρείτε τα πεδία ορισµού των συναρτήσεων µε τύπο: i) ii) iii) iv) v) 2. Δίνεται η συνάρτηση µε:. Να βρείτε µια περίοδο της. 3. Δίνεται η συνάρτηση µε:. Να αποδείξετε
ΦΥΛΛΆΔΙΟ ΑΣΚΉΣΕΩΝ 2 ΣΥΝΑΡΤΗΣΕΙΣ 1. Να βρείτε τα πεδία ορισµού των συναρτήσεων µε τύπο: i) ii) iii) iv) v) 2. Δίνεται η συνάρτηση µε:. Να βρείτε µια περίοδο της. 3. Δίνεται η συνάρτηση µε:. Να αποδείξετε
< και δεδομένου ότι η f είναι γνησίως μονότονη, συμπεραίνουμε ότι
 _1696 α) f ( 5) = f ( 4) = 9 Αφού
_1696 α) f ( 5) = f ( 4) = 9 Αφού
x 1 δίνει υπόλοιπο 24
 ΓΕΝΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ 3. Δίνεται το πολυώνυμο P() 6 α β το οποίο έχει παράγοντα το και όταν διαιρείται με το δίνει υπόλοιπο i. Να δείξετε ότι: α και β 6 ii. Να λύσετε την εξίσωση
ΓΕΝΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ 3. Δίνεται το πολυώνυμο P() 6 α β το οποίο έχει παράγοντα το και όταν διαιρείται με το δίνει υπόλοιπο i. Να δείξετε ότι: α και β 6 ii. Να λύσετε την εξίσωση
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ 1. Αν f συνεχής στο [α, β] είναι f ( ) d 0 f ( ) 0 2. Αν f συνεχής και γν. αύξουσα στο [α, β] ισχύει ότι: f ( ) d 0. 3. Αν f ( ) d g( ) d, ό f ( ) g( ) ά [, ]. 4. Το σύνολο τιμών
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ-ΛΑΘΟΥΣ 1. Αν f συνεχής στο [α, β] είναι f ( ) d 0 f ( ) 0 2. Αν f συνεχής και γν. αύξουσα στο [α, β] ισχύει ότι: f ( ) d 0. 3. Αν f ( ) d g( ) d, ό f ( ) g( ) ά [, ]. 4. Το σύνολο τιμών
Ερωτήσεις πολλαπλής επιλογής
 Ερωτήσεις πολλαπλής επιλογής. * Έστω µια συνάρτηση f για την οποία ισχύουν οι υποθέσεις του θεωρήµατος του Rolle στο διάστηµα [α, β]. Τότε θα υπάρχει ξ (α, β), ώστε η εφαπτοµένη της C f στο (ξ, f (ξ))
Ερωτήσεις πολλαπλής επιλογής. * Έστω µια συνάρτηση f για την οποία ισχύουν οι υποθέσεις του θεωρήµατος του Rolle στο διάστηµα [α, β]. Τότε θα υπάρχει ξ (α, β), ώστε η εφαπτοµένη της C f στο (ξ, f (ξ))
1. Το πολυώνυµο P (x) = 3 (x - 1) 2-3x είναι Α. µηδενικού βαθµού Β. πρώτου βαθµού Γ. δευτέρου βαθµού. το µηδενικό πολυώνυµο Ε.
 Ερωτήσεις πολλαπλής επιλογής 1. Το πολυώνυµο P (x) = 3 (x - 1) 2-3x 2 + 5 είναι Α. µηδενικού βαθµού Β. πρώτου βαθµού Γ. δευτέρου βαθµού. το µηδενικό πολυώνυµο Ε. τρίτου βαθµού 2. Αν το πολυώνυµο P (x)
Ερωτήσεις πολλαπλής επιλογής 1. Το πολυώνυµο P (x) = 3 (x - 1) 2-3x 2 + 5 είναι Α. µηδενικού βαθµού Β. πρώτου βαθµού Γ. δευτέρου βαθµού. το µηδενικό πολυώνυµο Ε. τρίτου βαθµού 2. Αν το πολυώνυµο P (x)
Μαθηματικά κατεύθυνσης Γ Λυκείου Διαγώνισμα διάρκειας 2 ωρών στις Συναρτήσεις
 ΘΕΜΑ Α Μαθηματικά κατεύθυνσης Γ Λυκείου Διαγώνισμα διάρκειας ωρών στις Συναρτήσεις 0 9-05 Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ).. Αν η συνάρτηση f είναι -, είναι και γνησίως
ΘΕΜΑ Α Μαθηματικά κατεύθυνσης Γ Λυκείου Διαγώνισμα διάρκειας ωρών στις Συναρτήσεις 0 9-05 Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ).. Αν η συνάρτηση f είναι -, είναι και γνησίως
Ημερομηνία: Παρασκευή 28 Οκτωβρίου 2016 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Ημερομηνία: Παρασκευή 8 Οκτωβρίου 016 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α1. Να δώσετε τους ορισμούς των: α) Γνησίως φθίνουσα συνάρτηση β) Ολικό ελάχιστο
ΤΑΞΗ: ΜΑΘΗΜΑ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Ημερομηνία: Παρασκευή 8 Οκτωβρίου 016 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α Α1. Να δώσετε τους ορισμούς των: α) Γνησίως φθίνουσα συνάρτηση β) Ολικό ελάχιστο
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ B ΛΥΚΕΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ B ΛΥΚΕΙΟΥ 1 ln 4 i Να βρείτε το πεδίο ορισμού της ii Να δείξετε ότι η παραπάνω συνάρτηση γράφεται: ln iii Να λύσετε την εξίσωση ln 5 ln 3 4 a a1 4,, a i Να βρείτε τον αριθμό
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ B ΛΥΚΕΙΟΥ 1 ln 4 i Να βρείτε το πεδίο ορισμού της ii Να δείξετε ότι η παραπάνω συνάρτηση γράφεται: ln iii Να λύσετε την εξίσωση ln 5 ln 3 4 a a1 4,, a i Να βρείτε τον αριθμό
Παραδείγµατα συναρτήσεων: f:[0,+ ) IR, f(x)=2+ x f:ir IR: f(x)=
 ΣΥΝΑΡΤΗΣΕΙΣ - 9 - ΚΕΦΑΛΑΙ ΚΕΦΑΛΑΙ ο - ΣΥΝΑΡΤΗΣΕΙΣ.. ρισµός Συνάρτηση από ένα σύνολο Α σ ένα σύνολο Β είναι ένας κανόνας µε τον οποίο κάθε στοιχείο του Α απεικονίζεται σε ένα ακριβώς στοιχείο του Β. Το
ΣΥΝΑΡΤΗΣΕΙΣ - 9 - ΚΕΦΑΛΑΙ ΚΕΦΑΛΑΙ ο - ΣΥΝΑΡΤΗΣΕΙΣ.. ρισµός Συνάρτηση από ένα σύνολο Α σ ένα σύνολο Β είναι ένας κανόνας µε τον οποίο κάθε στοιχείο του Α απεικονίζεται σε ένα ακριβώς στοιχείο του Β. Το
5.3. ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ
 5.3. Αντίστροφη συνάρτηση Έστω μια συνάρτηση f : A.Αν υποθέσουμε ότι αυτή είναι - τότε για κάθε στοιχείο y του συνόλου τιμών f (A) της f υπάρχει μοναδικό στοιχείο του πεδίου ορισμού της Α για το οποίο
5.3. Αντίστροφη συνάρτηση Έστω μια συνάρτηση f : A.Αν υποθέσουμε ότι αυτή είναι - τότε για κάθε στοιχείο y του συνόλου τιμών f (A) της f υπάρχει μοναδικό στοιχείο του πεδίου ορισμού της Α για το οποίο
ΚΕΦΑΛΑΙΟ 4 Ο ΕΚΘΕΤΙΚΗ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 4 Ο ΕΚΘΕΤΙΚΗ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 Ο ΕΚΘΕΤΙΚΗ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΙΔΙΟΤΗΤΕΣ ΔΥΝΑΜΕΩΝ Από προηγούμενες τάξεις γνωρίζουμε τις παρακάτω ιδιότητες
ΚΕΦΑΛΑΙΟ 4 Ο ΕΚΘΕΤΙΚΗ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 Ο ΕΚΘΕΤΙΚΗ ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΙΔΙΟΤΗΤΕΣ ΔΥΝΑΜΕΩΝ Από προηγούμενες τάξεις γνωρίζουμε τις παρακάτω ιδιότητες
Αν α θετικός πραγματικός αριθμός, σε κάθε x αντιστοιχεί η
 Εκθετική συνάρτηση Αν α θετικός πραγματικός αριθμός, σε κάθε αντιστοιχεί η δύναμη α. Έτσι ορίζεται η συνάρτηση : f : με f α, 0 α η οποία ονομάζεται εκθετική συνάρτηση με βάση α. Αν α, τότε έχουμε τη σταθερή
Εκθετική συνάρτηση Αν α θετικός πραγματικός αριθμός, σε κάθε αντιστοιχεί η δύναμη α. Έτσι ορίζεται η συνάρτηση : f : με f α, 0 α η οποία ονομάζεται εκθετική συνάρτηση με βάση α. Αν α, τότε έχουμε τη σταθερή
6.2 ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ
 1 6. ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ ΘΕΩΡΙΑ 1. Οι συντεταγµένες σηµείου Ο Ο άξονας τετµηµένων άξονας τεταγµένων (ΟΚ) µε πρόσηµο = α, η τετµηµένη του Μ (ΟΛ) µε πρόσηµο = β, η τεταγµένη του Μ Το ζευγάρι (α,
1 6. ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ ΘΕΩΡΙΑ 1. Οι συντεταγµένες σηµείου Ο Ο άξονας τετµηµένων άξονας τεταγµένων (ΟΚ) µε πρόσηµο = α, η τετµηµένη του Μ (ΟΛ) µε πρόσηµο = β, η τεταγµένη του Μ Το ζευγάρι (α,
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα 11 Ιουνίου 2018 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα Ιουνίου 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απαντήσεις) ΘΕΜΑ Α Α Απόδειξη θεωρήματος σελ 99 σχολικού βιβλίου
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα Ιουνίου 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απαντήσεις) ΘΕΜΑ Α Α Απόδειξη θεωρήματος σελ 99 σχολικού βιβλίου
f( x 1, x ( ) ( ) f x > f x. ( ) ( )
 MONOTONIA ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ I MONOTONIA ΣΥΝΑΡΤΗΣΕΩΝ ΘΕΩΡΙΑ Στο διπλανό σχήµα δίνεται η γραφική παράσταση µιας συνάρτησης f στο α,β Παρατηρούµε ότι διάστηµα [ ] καθώς αυξάνουν οι τιµές του
MONOTONIA ΑΚΡΟΤΑΤΑ ΣΥΜΜΕΤΡΙΕΣ ΣΥΝΑΡΤΗΣΗΣ I MONOTONIA ΣΥΝΑΡΤΗΣΕΩΝ ΘΕΩΡΙΑ Στο διπλανό σχήµα δίνεται η γραφική παράσταση µιας συνάρτησης f στο α,β Παρατηρούµε ότι διάστηµα [ ] καθώς αυξάνουν οι τιµές του
( ) Ίσες συναρτήσεις. = g, Οι συναρτήσεις f, g λέμε ότι είναι ίσες και συμβολίζουμε f. όταν: Έχουν το ίδιο πεδία ορισμού Α
 .5.. Ίσες συναρτήσεις ΣΥΝΑΡΤΗΣΕΙΣ 7 Ο ΜΑΘΗΜΑ Οι συναρτήσεις f, g λέμε ότι είναι ίσες και συμβολίζουμε f = g, Έχουν το ίδιο πεδία ορισμού Α Για κάθε x Α ισχύει f ( x) = g( x) Αν για τις συναρτήσεις: f:
.5.. Ίσες συναρτήσεις ΣΥΝΑΡΤΗΣΕΙΣ 7 Ο ΜΑΘΗΜΑ Οι συναρτήσεις f, g λέμε ότι είναι ίσες και συμβολίζουμε f = g, Έχουν το ίδιο πεδία ορισμού Α Για κάθε x Α ισχύει f ( x) = g( x) Αν για τις συναρτήσεις: f:
Ασκήσεις Επανάληψης Γ Λυκείου
 Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 3 598 Θε ματα ΟΕΦΕ - 5 Επιμέλεια Κων/νος Παπασταματίου Σελίδα
Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 3 598 Θε ματα ΟΕΦΕ - 5 Επιμέλεια Κων/νος Παπασταματίου Σελίδα
ΜΑΘΗΜΑ ΣΥΝΑΡΤΗΣΕΙΣ Σύνολο τιµών Γραφική παράσταση συνάρτησης Βασικές συναρτήσεις Ισότητα συναρτήσεων Πράξεις µε συναρτήσεις
 ΜΑΘΗΜΑ. ΣΥΝΑΡΤΗΣΕΙΣ Σύνολο τιµών Γραφική παράσταση συνάρτησης Βασικές συναρτήσεις Ισότητα συναρτήσεων Πράξεις µε συναρτήσεις Θεωρία Σχόλια Ασκήσεις ΘΕΩΡΙΑ. Ορισµός του συνόλου τιµών, κατάλληλος για τις
ΜΑΘΗΜΑ. ΣΥΝΑΡΤΗΣΕΙΣ Σύνολο τιµών Γραφική παράσταση συνάρτησης Βασικές συναρτήσεις Ισότητα συναρτήσεων Πράξεις µε συναρτήσεις Θεωρία Σχόλια Ασκήσεις ΘΕΩΡΙΑ. Ορισµός του συνόλου τιµών, κατάλληλος για τις
Συναρτήσεις. Κώστας Γλυκός ΜΑΘΗΜΑΤΙΚΟΣ. Άλγεβρα Κεφάλαιο 2 78 ασκήσεις. εκδόσεις. Καλό πήξιμο / 7 /
 Συναρτήσεις Κώστας Γλυκός Άλγεβρα Κεφάλαιο 78 ασκήσεις και τεχνικές σε 9 σελίδες ΙΙ Ι δδ ιι ι αα ίί ί ττ εε ρρ αα μμ αα θθ ήή μμ αα ττ αα 6 9 7. 0 0. 8 8. 8 8 Kgllykos..gr 0 / 7 / 0 1 8 εκδόσεις Καλό πήξιμο
Συναρτήσεις Κώστας Γλυκός Άλγεβρα Κεφάλαιο 78 ασκήσεις και τεχνικές σε 9 σελίδες ΙΙ Ι δδ ιι ι αα ίί ί ττ εε ρρ αα μμ αα θθ ήή μμ αα ττ αα 6 9 7. 0 0. 8 8. 8 8 Kgllykos..gr 0 / 7 / 0 1 8 εκδόσεις Καλό πήξιμο
α) ( ) β) ( ) γ) ( ) δ) ( ) ( ) β) ( ) ( ) δ) ( ) ( ) ( )
 Συναρτήςεισ Όριο Συνέχεια Πεδίο οριςμού ςυνάρτηςησ 1) Να βρείτε τα πεδία οριςμού των ςυναρτήςεων α) β) γ) δ) 2) Να βρείτε τα πεδία οριςμού των ςυναρτήςεων α) β) γ) δ) 3) Να βρείτε τα πεδία οριςμού των
Συναρτήςεισ Όριο Συνέχεια Πεδίο οριςμού ςυνάρτηςησ 1) Να βρείτε τα πεδία οριςμού των ςυναρτήςεων α) β) γ) δ) 2) Να βρείτε τα πεδία οριςμού των ςυναρτήςεων α) β) γ) δ) 3) Να βρείτε τα πεδία οριςμού των
ΜΑΘΗΜΑ 14 1.3 ΜΟΝΟΤΟΝΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΜΑΘΗΜΑ 4. ΜΟΝΟΤΟΝΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ Μονοτονία συνάρτησης Ακρότατα συνάρτησης Θεωρία Σχόλια Μέθοδοι Ασκήσεις ΘΕΩΡΙΑ. Ορισµός Συνάρτηση f λέγεται γνησίως αύξουσα σε διάστηµα, όταν για οποιαδήποτε,
ΜΑΘΗΜΑ 4. ΜΟΝΟΤΟΝΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ Μονοτονία συνάρτησης Ακρότατα συνάρτησης Θεωρία Σχόλια Μέθοδοι Ασκήσεις ΘΕΩΡΙΑ. Ορισµός Συνάρτηση f λέγεται γνησίως αύξουσα σε διάστηµα, όταν για οποιαδήποτε,
ΣΥΝΑΡΤΗΣΕΙΣ. 3. Μια μπάλα πέφτει από την κορυφή ενός πυργου. Το ύψος στο οποίο βρίσκετε μετά από t sec δίνεται από τη συνάρτηση f () x 75 3
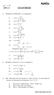 ΦΥΛ ΣΥΝΑΡΤΗΣΕΙΣ. Να βρεθούν τα Πεδία Ορισμων συναρτήσεων: i) f () 4 f () i f () 4 f () 6 5 v) f () 9 vi) f () v f () log() vi f () 4, i) f () 8, Να βρεθούν επίσης οι τιμές : n f ( 4),( f ),( f0),(),(0),(
ΦΥΛ ΣΥΝΑΡΤΗΣΕΙΣ. Να βρεθούν τα Πεδία Ορισμων συναρτήσεων: i) f () 4 f () i f () 4 f () 6 5 v) f () 9 vi) f () v f () log() vi f () 4, i) f () 8, Να βρεθούν επίσης οι τιμές : n f ( 4),( f ),( f0),(),(0),(
ΕΡΩΤΗΣΕΙΣ Σ-Λ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΕΣΠΕΡΙΝΟY. 0, τότε είναι και παραγωγίσιμη στο σημείο αυτό.
 ΕΡΩΤΗΣΕΙΣ Σ-Λ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΕΣΠΕΡΙΝΟY Αν μια συνάρτηση f είναι παραγωγίσιμη σ ένα σημείο, τότε είναι και συνεχής στο σημείο αυτό Αν μια συνάρτηση f είναι συνεχής σ ένα
ΕΡΩΤΗΣΕΙΣ Σ-Λ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΤΕΥΘΥΝΣΗΣ ΕΣΠΕΡΙΝΟY Αν μια συνάρτηση f είναι παραγωγίσιμη σ ένα σημείο, τότε είναι και συνεχής στο σημείο αυτό Αν μια συνάρτηση f είναι συνεχής σ ένα
ΣΥΝΕΠΕΙΕΣ Θ.Μ.Τ. ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ ΕΥΡΕΣΗ ΣΥΝΑΡΤΗΣΗΣ
 Ενότητα 19 ΣΥΝΕΠΕΙΕΣ Θ.Μ.Τ. ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ ΕΥΡΕΣΗ ΣΥΝΑΡΤΗΣΗΣ 1). Να βρεθεί η συνάρτηση f όταν: i) A, f ()=3 5 f(0)=1, ii) A=, f ()=συν-ημ f(π)=, Ασκήσεις για λύση - iii) A=, f ()=4e 6 f '(0)=f(0)=1,
Ενότητα 19 ΣΥΝΕΠΕΙΕΣ Θ.Μ.Τ. ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ ΕΥΡΕΣΗ ΣΥΝΑΡΤΗΣΗΣ 1). Να βρεθεί η συνάρτηση f όταν: i) A, f ()=3 5 f(0)=1, ii) A=, f ()=συν-ημ f(π)=, Ασκήσεις για λύση - iii) A=, f ()=4e 6 f '(0)=f(0)=1,
ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
5 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Εισαγωγή Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
ΣΥΝΑΡΤΗΣΕΩΝ. f3 x = και
 7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
7 ΜΕΛΕΤΗ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Στο κεφάλαιο αυτό θα δούμε πώς, με τη βοήθεια των πληροφοριών που α- ποκτήσαμε μέχρι τώρα, μπορούμε να χαράξουμε με όσο το δυνατόν μεγαλύτερη ακρίβεια τη γραφική παράσταση
ΑΣΚΗΣΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ (1o Γ Λυκείου) να ανήκουν στη γραφική παράσταση της συνάρτησης f( x)
 ΑΣΚΗΣΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ (o Γ Λυκείου).Να βρεθούν οι τιμές των α, β R ώστε: Α) τα σημεία (, ),(, ) να ανήκουν στη γραφική παράσταση της συνάρτησης α +β. Β)τα σημεία ( 0, ),( e, ) να ανήκουν στην γραφική παράσταση
ΑΣΚΗΣΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ (o Γ Λυκείου).Να βρεθούν οι τιμές των α, β R ώστε: Α) τα σημεία (, ),(, ) να ανήκουν στη γραφική παράσταση της συνάρτησης α +β. Β)τα σημεία ( 0, ),( e, ) να ανήκουν στην γραφική παράσταση
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
Α Π Α Ν Τ Η Σ Ε Ι Σ - Υ Π Ο Δ Ε Ι Ξ Ε Ι Σ Σ Τ Ι Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ
 Α Π Α Ν Τ Η Σ Ε Ι Σ - Υ Π Ο Δ Ε Ι Ξ Ε Ι Σ Σ Τ Ι Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ 60 Κεφάλαιο ο Ι. ΣΥΝΑΡΤΗΣΕΙΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ. Σ 0. i) Σ. Σ. Σ 0. ii) Σ 3. Σ 3. Σ. Σ 4. Λ 4. Λ. Λ 5.
Α Π Α Ν Τ Η Σ Ε Ι Σ - Υ Π Ο Δ Ε Ι Ξ Ε Ι Σ Σ Τ Ι Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ 60 Κεφάλαιο ο Ι. ΣΥΝΑΡΤΗΣΕΙΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ. Σ 0. i) Σ. Σ. Σ 0. ii) Σ 3. Σ 3. Σ. Σ 4. Λ 4. Λ. Λ 5.
5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ
 5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ Ασκήσεις σχολικού βιβλίου σελίδας 84 85 A Οµάδας. Στο ίδιο σύστηµα αξόνων να παραστήσετε γραφικά τις συναρτήσεις f() = log και g() = log Τι παρατηρείτε; Να δικαιολογήσετε την
5.3 ΛΟΓΑΡΙΘΜΙΚΗ ΣΥΝΑΡΤΗΣΗ Ασκήσεις σχολικού βιβλίου σελίδας 84 85 A Οµάδας. Στο ίδιο σύστηµα αξόνων να παραστήσετε γραφικά τις συναρτήσεις f() = log και g() = log Τι παρατηρείτε; Να δικαιολογήσετε την
ΟΡΙΣΜΟΣ 2 (Ισοδύναμος ορισμός που χρησιμεύει σε ασκήσεις)
 ΟΡΙΣΜΟΣ Μια συνάρτηση : A λέγεται συνάρτηση -, όταν για οποιαδήποτε, A ισχύει η συνεπαγωγή: αν, τότε ( ) ( ) ΟΡΙΣΜΟΣ (Ισοδύναμος ορισμός που χρησιμεύει σε ασκήσεις) Μια συνάρτηση : A είναι συνάρτηση -,
ΟΡΙΣΜΟΣ Μια συνάρτηση : A λέγεται συνάρτηση -, όταν για οποιαδήποτε, A ισχύει η συνεπαγωγή: αν, τότε ( ) ( ) ΟΡΙΣΜΟΣ (Ισοδύναμος ορισμός που χρησιμεύει σε ασκήσεις) Μια συνάρτηση : A είναι συνάρτηση -,
qwφιertyuiopasdfghjklzxερυυξnmηq σwωψerβνtyuςiopasdρfghjklzxcvbn mqwertyuiopasdfghjklzxcvbnφγιmλι qπςπζαwωeτrtνyuτioρνμpκaλsdfghςj
 qwφιrtyuiopasdfghjklzερυυξnmηq σwωψrβνtyuςiopasdρfghjklzcvbn mqwrtyuiopasdfghjklzcvbnφγιmλι ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ qπςπζαwωτrtνyuτioρνμpκaλsdfghςj ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ klzcvλοπbnαmqwrtyuiopasdfghjklz
qwφιrtyuiopasdfghjklzερυυξnmηq σwωψrβνtyuςiopasdρfghjklzcvbn mqwrtyuiopasdfghjklzcvbnφγιmλι ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ qπςπζαwωτrtνyuτioρνμpκaλsdfghςj ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ klzcvλοπbnαmqwrtyuiopasdfghjklz
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. 2x 1. είναι Τότε έχουμε: » τον χρησιμοποιούμε κυρίως σε θεωρητικές ασκήσεις.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΤΟ ΘΕΜΑ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ
 ΤΟ ΘΕΜΑ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΘΕΜΑ 1 Ο Α1. Έστω η συνάρτηση f ( x,,1. Nα αποδείξετε ότι η f είναι παραγωγίσιμη στο. v v 1 και ισχύει : x vx A2. Να διατυπώσετε και να ερμηνεύσετε γεωμετρικά το Θεώρημα Bolzano.
ΤΟ ΘΕΜΑ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΘΕΜΑ 1 Ο Α1. Έστω η συνάρτηση f ( x,,1. Nα αποδείξετε ότι η f είναι παραγωγίσιμη στο. v v 1 και ισχύει : x vx A2. Να διατυπώσετε και να ερμηνεύσετε γεωμετρικά το Θεώρημα Bolzano.
1. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους. 2. Να βρεθεί ο λ R ώστε f(x) = ln ( x 2 +2λx+9) να έχει πεδίο ορισμού Α = R
 ΠΕΡΙΣΤΕΡΙΟΥ Α. ΠΕΔΙΟ ΟΡΙΣΜΟΥ. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους 4 ι) () = 6 + 6 iv) () = log ( log4(- )) v) () = ii) () = iii) () = log ( + ) 5 log 4 vii) () = 5 + 4 viii) ()
ΠΕΡΙΣΤΕΡΙΟΥ Α. ΠΕΔΙΟ ΟΡΙΣΜΟΥ. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους 4 ι) () = 6 + 6 iv) () = log ( log4(- )) v) () = ii) () = iii) () = log ( + ) 5 log 4 vii) () = 5 + 4 viii) ()
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ
 ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ Ξεφυλλίζοντας τα σχολικά βιβλία της Α και Β Λυκείου θα συναντήσουμε τις παρακάτω 10 "βασικές" συναρτήσεις των οποίων τη γραφική παράσταση πρέπει να γνωρίζουμε:
4ο Επαναληπτικό διαγώνισμα στα Μαθηματικά προσανατολισμού της Γ Λυκείου
 4ο Επαναληπτικό διαγώνισμα στα Μαθηματικά προσανατολισμού της Γ Λυκείου 8-9 Θέμα A A Αν οι συναρτήσεις,g είναι παραγωγίσιμες στο, να αποδείξετε ότι η συνάρτηση και ισχύει: g g παραγωγίσιμη στο μονάδες
4ο Επαναληπτικό διαγώνισμα στα Μαθηματικά προσανατολισμού της Γ Λυκείου 8-9 Θέμα A A Αν οι συναρτήσεις,g είναι παραγωγίσιμες στο, να αποδείξετε ότι η συνάρτηση και ισχύει: g g παραγωγίσιμη στο μονάδες
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 2 ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
 Άλγεβρα Β Λυκείου, ο Κεφάλαιο ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ ΟΡΙΣΜΟΣ 1 Μια συνάρτηση ƒ λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε
Άλγεβρα Β Λυκείου, ο Κεφάλαιο ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ΙΔΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ ΟΡΙΣΜΟΣ 1 Μια συνάρτηση ƒ λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ
 9 ΧΡΟΝΙΑ ΕΜΠΕΙΡΙΑ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑΤΑ ΘΕΜΑ Α A Να αποδείξετε ότι, αν μια συνάρτηση είναι παραγωγίσιμη σε ένα σημείο 0,
9 ΧΡΟΝΙΑ ΕΜΠΕΙΡΙΑ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ ΘΕΜΑΤΑ ΘΕΜΑ Α A Να αποδείξετε ότι, αν μια συνάρτηση είναι παραγωγίσιμη σε ένα σημείο 0,
Η συνάρτηση y = αχ 2. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
Η συνάρτηση y = αχ Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd 1 Η συνάρτηση y = αχ με α 0 Μια συνάρτηση της μορφής y = α + β + γ με α 0 ονομάζεται τετραγωνική συνάρτηση.
II. Συναρτήσεις. math-gr
 II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
II Συναρτήσεις Παντελής Μπουμπούλης, MSc, PhD σελ blogspotcom, bouboulismyschgr ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική
Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ. ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος ΜΑΝΩΛΗ ΨΑΡΡΑ. Μανώλης Ψαρράς Σελίδα 1
 Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος 014-15 ΜΑΝΩΛΗ ΨΑΡΡΑ Μανώλης Ψαρράς Σελίδα 1 Α ΣΥΣΤΗΜΑΤΑ ΑΣΚΗΣΗ 1 η Να λυθούν γραφικά τα συστήματα: y y6 y 5 1 : 1 : 3 : y 6 0 y 5
Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος 014-15 ΜΑΝΩΛΗ ΨΑΡΡΑ Μανώλης Ψαρράς Σελίδα 1 Α ΣΥΣΤΗΜΑΤΑ ΑΣΚΗΣΗ 1 η Να λυθούν γραφικά τα συστήματα: y y6 y 5 1 : 1 : 3 : y 6 0 y 5
ΜΙΓΑ ΙΚΟΙ. 3. Για κάθε z 1, z 2 C ισχύει z1 + z2 = z1 + z2. 4. Για κάθε z C ισχύει z z 2 z. 5. Για κάθε µιγαδικό z ισχύει: 6.
 ΜΙΓΑ ΙΚΟΙ 1 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 1 2 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 3 Για κάθε z 1, z 2 C ισχύει z1 + z2 = z1 + z2 4 Για κάθε z C ισχύει z z 2 z 5 Για κάθε µιγαδικό z ισχύει:
ΜΙΓΑ ΙΚΟΙ 1 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 1 2 Για κάθε z 1, z 2 C ισχύει z1 z2 z1 z2 3 Για κάθε z 1, z 2 C ισχύει z1 + z2 = z1 + z2 4 Για κάθε z C ισχύει z z 2 z 5 Για κάθε µιγαδικό z ισχύει:
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες
![ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες](/thumbs/55/37062184.jpg) ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4 1. i) Να δείξετε ότι υπάρχει μοναδικό 3 3 0 1, ώστε: 3 e, 1 ln 0 + 0 = 0 ii) Δίνεται ο μιγαδικός 3 z = ln + i, > 0 a) Να βρείτε την ελάχιστη απόσταση k της εικόνας του z από την αρχή
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4 1. i) Να δείξετε ότι υπάρχει μοναδικό 3 3 0 1, ώστε: 3 e, 1 ln 0 + 0 = 0 ii) Δίνεται ο μιγαδικός 3 z = ln + i, > 0 a) Να βρείτε την ελάχιστη απόσταση k της εικόνας του z από την αρχή
Λύσεις του διαγωνίσματος στις παραγώγους
 Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ Πότε μια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της?
 ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ 4-5 Πότε μια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της? Απάντηση: Mια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της όταν
ΣΗΜΕΙΩΣΕΙΣ ΜΕΛΕΤΗΣ 4-5 Πότε μια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της? Απάντηση: Mια συνάρτηση λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της όταν
40 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ)
 Άσκηση η 4 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ) Έστω f, g είναι συνεχείς συναρτήσεις στο διάστημα, να δείξετε: Α. (Ανισότητα των Cauchy-Schwarz) Β.( Ανισότητα του Minkowski)
Άσκηση η 4 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ) Έστω f, g είναι συνεχείς συναρτήσεις στο διάστημα, να δείξετε: Α. (Ανισότητα των Cauchy-Schwarz) Β.( Ανισότητα του Minkowski)
f ( x) x EΠΙΛΕΓΜΕΝΑ ΘΕΜΑΤΑ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΛΥΚΕΙΟΥ Συναρτήσεις ( ) 1. Έστω συνάρτηση f γνησίως αύξουσα στο R τέτοια ώστε να ισχύει
 Συναρτήσεις Έστω συνάρτηση γνησίως αύξουσα στο R τέτοια ώστε να ισχύει Να δείξετε ότι (), για κάθε R ( ) +, για κάθε R Έστω συνάρτηση µε πεδίο ορισµού και σύνολο τιµών το R και τέτοια ώστε ( ) ( ) e +,
Συναρτήσεις Έστω συνάρτηση γνησίως αύξουσα στο R τέτοια ώστε να ισχύει Να δείξετε ότι (), για κάθε R ( ) +, για κάθε R Έστω συνάρτηση µε πεδίο ορισµού και σύνολο τιµών το R και τέτοια ώστε ( ) ( ) e +,
5.1. ΕΚΘΕΤΙΚΗ ΣΥΝΑΡΤΗΣΗ
 5 Δυνάμεις με άρρητο εκθέτη Αν α, β είναι θετικοί πραγματικοί αριθμοί και,,,τότε : ( ) : Εκθετική συνάρτηση Αντιστοιχίζοντας κάθε,στη δύναμη f: με f () η οποία στην περίπτωση που είναι 0
5 Δυνάμεις με άρρητο εκθέτη Αν α, β είναι θετικοί πραγματικοί αριθμοί και,,,τότε : ( ) : Εκθετική συνάρτηση Αντιστοιχίζοντας κάθε,στη δύναμη f: με f () η οποία στην περίπτωση που είναι 0
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Ε.1 I. 1. α 2 = 9 α = 3 ψ p: α 2 = 9, q: α = 3 Σύνολο αλήθειας της p: Α = {-3,3}, Σύνολο αλήθειας της q: B = {3} A B 2. α 2 = α α = 1 ψ p: α 2 = α, q: α = 1 Σύνολο
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ) Copyright 2015 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoocom Αδεια χρήσης 3η Εκδοση, Ιωάννινα, Σεπτέµβριος 2015 Περιεχόµενα 1 Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ) Copyright 2015 Αποστόλου Γιώργος Αποστόλου Γεώργιος apgeorge2004@yahoocom Αδεια χρήσης 3η Εκδοση, Ιωάννινα, Σεπτέµβριος 2015 Περιεχόµενα 1 Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ
1.1 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ 1.2 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ
 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων : π α) f() = + ηµ β) g() = + συν( ) 6 π π γ) f() = ηµ( ) δ) g() = συν( ) Να γίνει η µελέτη και η γραφική παράσταση
ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Να γίνουν οι γραφικές παραστάσεις των συναρτήσεων : π α) f() = + ηµ β) g() = + συν( ) 6 π π γ) f() = ηµ( ) δ) g() = συν( ) Να γίνει η µελέτη και η γραφική παράσταση
( 2) 1 0,. Αν ρ 1, ρ 2 οι ρίζες της (ε) και
 ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( ) α. Να βρείτε το πεδίο ορισμού της. β. Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν. γ. Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο f ( ), να δείξετε ότι αβ+=0.
ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( ) α. Να βρείτε το πεδίο ορισμού της. β. Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν. γ. Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο f ( ), να δείξετε ότι αβ+=0.
ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ Ενότητα #7: Μονοτονία- Ακρότατα-Αντιγραφή Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΟΙΚΟΝΟΜΟΛΟΓΟΥΣ Ενότητα #7: Μονοτονία- Ακρότατα-Αντιγραφή Εβελίνα Κοσσιέρη Τμήμα Λογιστικής και Χρηματοοικονομικής
ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β. 0και 4 x 3 0.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
( 2) 1 0,. Αν ρ 1, ρ 2 οι ρίζες της (ε) και
 ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( x) α Να βρείτε το πεδίο ορισμού της x x x x β Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν γ Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο x x f ( x), να δείξετε
ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( x) α Να βρείτε το πεδίο ορισμού της x x x x β Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν γ Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο x x f ( x), να δείξετε
ΠΟΛΥΩΝΥΜΑ. Κεφάλαιο 2ο: Ερωτήσεις του τύπου Σωστό-Λάθος
 Κεφάλαιο ο: ΠΟΛΥΩΝΥΜΑ Ερωτήσεις του τύπου Σωστό-Λάθος 1. * Οι πραγματικοί αριθμοί είναι σταθερά πολυώνυμα. Σ Λ. * Το σταθερό πολυώνυμο 0 λέγεται μηδενικό πολυώνυμο. Σ Λ 3. * Κάθε σταθερό και μη μηδενικό
Κεφάλαιο ο: ΠΟΛΥΩΝΥΜΑ Ερωτήσεις του τύπου Σωστό-Λάθος 1. * Οι πραγματικοί αριθμοί είναι σταθερά πολυώνυμα. Σ Λ. * Το σταθερό πολυώνυμο 0 λέγεται μηδενικό πολυώνυμο. Σ Λ 3. * Κάθε σταθερό και μη μηδενικό
Συνάρτηση f, λέγεται η διαδικασία µε βάση την. Παρατηρήσεις - Σχόλια f
 Συνάρτηση f, λέγεται η διαδικασία µε βάση την οποία σε κάθε στοιχείο χ ενός συνόλου Α αντιστοιχούµε ακριβώς ένα στοιχείο ενός άλλου συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισµού ( ή σύνολο ορισµού ) της
Συνάρτηση f, λέγεται η διαδικασία µε βάση την οποία σε κάθε στοιχείο χ ενός συνόλου Α αντιστοιχούµε ακριβώς ένα στοιχείο ενός άλλου συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισµού ( ή σύνολο ορισµού ) της
ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ. f : A R και στη συνέχεια δίνουμε τον τύπο της συνάρτησης, π.χ.
 Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
Συναρτήσεις σελ ΜΕΡΟΣ 1 ΣΥΝΑΡΤΗΣΕΙΣ Α Βασικές Έννοιες Ορισμός: Έστω Α ένα υποσύνολο του συνόλου των πραγματικών αριθμών R Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα),
ΣΧΕ ΙΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ ΤΟΥ ΜΑΘΗΤΗ ΣΤΗΝ ΑΝΑΛΥΣΗ. ( ΚΕΦΑΛΑΙΟ 1ο )
 ΣΧΕ ΙΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ ΤΟΥ ΜΑΘΗΤΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ( ΚΕΦΑΛΑΙΟ 1ο ) Τα κριτήρια αξιολόγησης που ακολουθούν είναι ενδεικτικά. Ο καθηγητής έχει τη δυνατότητα διαµόρφωσής τους σε ενιαία θέµατα, επιλογής
ΣΧΕ ΙΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ ΤΟΥ ΜΑΘΗΤΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ( ΚΕΦΑΛΑΙΟ 1ο ) Τα κριτήρια αξιολόγησης που ακολουθούν είναι ενδεικτικά. Ο καθηγητής έχει τη δυνατότητα διαµόρφωσής τους σε ενιαία θέµατα, επιλογής
