Η ΧΡΥΣΗ ΤΟΜΗ ΣΤΗ ΖΩΓΡΑΦΙΚΗ
|
|
|
- Λώτ Μακρή
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Η ΧΡΥΣΗ ΤΟΜΗ ΣΤΗ ΖΩΓΡΑΦΙΚΗ Τα µαθηµατικά και η τέχνη, αν και φαινοµενικά τουλάχιστον, αποτελούν δύο ξεχωριστά πεδία της ανθρώπινης δραστηριότητας, είναι δυνατόν να συνδυαστούν και να δώσουν δηµιουργίες οι οποίες αποτελούν αξιοθαύµαστο µείγµα εντυπωσιακής πολυπλοκότητας και εκπληκτικής οµορφιάς. Ανέκαθεν, τα µαθηµατικά έπαιζαν ένα σηµαντικό ρόλο στην εξέλιξη της τέχνης. Κατά καιρούς αναδείχθηκαν εξέχουσες µορφές, οι οποίες χρησιµοποίησαν µαθηµατικά ως το βασικό συστατικό της τέχνης τους. Πολλοί είναι οι καλλιτέχνες οι οποίοι έχουν δηµιουργήσει τα έργα τους µε την βοήθεια των µαθηµατικών και συγκεκριµένα της χρυσής τοµής, όπως για παράδειγµα, οι Λεονάρντο Ντα Βίντσι και Σαλβαντόρ Νταλί. The Bathers at Ansières του Georges Seurat Ο ΑΡΙΘΜΟΣ Φ O λόγος δύο διαδοχικών αριθµών της ακολουθίας Φιµπονάτσι ονοµάζεται Χρυσή τοµή ή Χρυσή αναλογία, συµβολίζεται µε τον αριθµό Φ και προσεγγίζει τον άρρητο αριθµό Το βιβλίο το οποίο µελετούσε τον αριθµό Φ, εικονογραφήθηκε από το γνωστό Ιταλό καλλιτέχνη Λεονάρντο Ντα Βίντσι. Ο Ντα Βίντσι, για αρκετό καιρό έδειξε ένα διακαές ενδιαφέρον για τα µαθηµατικά στην τέχνη και τη φύση και επιδόθηκε σε συστηµατικές µελέτες. Ερεύνησε τις αναλογίες του ανθρωπίνου σώµατος και ειδικότερα τις αναλογίες στο ανθρώπινο πρόσωπο όπως στα έργα του «Μόνα Λίζα» και «Άνθρωπος του Βιτρούβιου». «Ο Άνθρωπος του Βιτρούβιου» Ο Άνθρωπος του Βιτρούβιου είναι ένα διάσηµο σχέδιο µε συνοδευτικές σηµειώσεις του Λεονάρντο Ντα Βίντσι, που φτιάχτηκε περίπου το 1490 σε ένα από τα ηµερολόγιά του. Απεικονίζει µία γυµνή αντρική φιγούρα σε δύο αλληλοκαλυπτόµενες θέσεις µε τα µέλη του ανεπτυγµένα και συγχρόνως εγγεγραµµένη σε ένα κύκλο και ένα τετράγωνο. Το σχέδιο και το κείµενο συχνά ονοµάζονται Κανόνας των Αναλογιών και στηρίζεται στο "χρυσό κανόνα" του Φιµπονάτσι. Σύµφωνα µε τις σηµειώσεις του Ντα Βίντσι στο συνοδευτικό κείµενο, το σχέδιο έγινε ως µελέτη των αναλογιών του (ανδρικού) 28
2 ανθρώπινου σώµατος όπως περιγράφεται σε µια πραγµατεία του Ρωµαίου αρχιτέκτονα Βιτρούβιου, που είχε γράψει για το ανθρώπινο σώµα: µια παλάµη έχει πλάτος τεσσάρων δακτύλων ένα πόδι έχει πλάτος τέσσερις παλάµες ένας πήχης έχει πλάτος έξι παλάµες το ύψος ενός ανθρώπου είναι τέσσερις πήχεις (και άρα 24 παλάµες) µια δρασκελιά είναι τέσσερις πήχεις Το µήκος των χεριών ενός άντρα σε διάταση είναι ίσο µε το ύψος του η απόσταση από την γραµµή των µαλλιών ως την κορυφή του στήθους είναι το 1/7 του ύψους του άνδρα η απόσταση από την κορυφή του κεφαλιού ως τις θηλές είναι το 1/4 του ύψους του άνδρα το µέγιστο πλάτος των ώµων είναι το 1/4 του ύψους του άνδρα η απόσταση από το αγκώνα ως την άκρη του χεριού είναι το 1/5 του ύψους του άνδρα η απόσταση από τον αγκώνα ως την µασχάλη είναι το 1/8 του ύψους του άνδρα το µήκος του χεριού είναι 1/10 του ύψους ενός άνδρα η απόσταση από την άκρη του πηγουνιού ως την µύτη είναι το 1/3 του µήκους του προσώπου η απόσταση της γραµµής των µαλλιών ως τα φρύδια είναι το 1/3 του µήκους του προσώπου το µήκος του αυτιού είναι το 1/3 του µήκους του προσώπου. Το ίδιο το σχέδιο συχνά χρησιµοποιείται ως ένα υπονοούµενο σύµβολο της ουσιώδους συµµετρίας του ανθρώπινου σώµατος, και κατά προέκταση του σύµπαντος ως σύνολο. «Μόνα Λίζα» Ένα από τα πιο φηµισµένα και αµφιλεγόµενα έργα του Λεονάρντο Ντα Βίντσι είναι και η «Μόνα Λίζα». Ο Ντα Βίντσι ζωγράφισε το πρόσωπο της Μόνα Λίζα ώστε αυτό να χωράει τέλεια σε ένα χρυσό ορθογώνιο και δόµησε τον υπόλοιπο πίνακα γύρω από το πρόσωπο χωρίζοντάς τον επίσης σε χρυσά ορθογώνια. 29
3 Η ταυτότητα της γυναίκας στον πίνακα όµως αµφισβητείται από πολλούς και δεν είναι λίγοι εκείνοι που υποστηρίζουν ότι στον πίνακα ο Λεονάρντο ζωγράφισε τον ίδιο του τον εαυτό στη "θηλυκή" του εκδοχή καθώς ο Ντα Βίντσι ήταν υποστηρικτής της ισορροπίας ανάµεσα στο θηλυκό και το αρσενικό. «Μυστικός είπνος» Πρόκειται για µια τοιχογραφία στον τοίχο της µονής Σάντα Μαρία ντέλε Γκράτσιε που ο Λεονάρντο Ντα Βίντσι την ξεκίνησε το 1495 και την τελείωσε το Ο Μυστικός είπνος του Λεονάρντο είναι γεµάτος ανησυχητικές εκτροπές: δεν υπάρχει το Άγιο ισκοπότηρο, ούτε δείχνει το Χριστό να θεσπίζει το µυστήριο της Θείας Ευχαριστίας. Στα πρόσωπα δε των µαθητών αναγνωρίζει κανείς τα πορτραίτα επιφανών ετερόδοξων της εποχής του και το έργο ολόκληρο φαίνεται ότι µεταφέρει ένα συγκλονιστικό κρυφό µήνυµα. Παρόλα αυτά το έργο µάς εντυπωσιάζει ακόµα και σήµερα καθώς είναι µια πραγµατική και θαυµαστή µελέτη του χρυσού κανόνα". Σαλβαντόρ Νταλί και Χρυσός Λόγος Ένας ακόµα καλλιτέχνης που επηρεάστηκε από τη Χρυσή αναλογία ήταν ο Ισπανός ζωγράφος Σαλβαντόρ Νταλί ( ). Ο Νταλί συνδέθηκε µε το καλλιτεχνικό κίνηµα του υπερρεαλισµού και υπήρξε µια εκκεντρική φυσιογνωµία της σύγχρονης τέχνης. Όπως παρατηρούµε στον πίνακα του Νταλί «Θυσία του Μυστικού είπνου», οι διαστάσεις του πίνακα βρίσκονται σε Χρυσό Λόγο µεταξύ τους. Επίσης, το µέρος από ένα τεράστιο δωδεκάεδρο φαίνεται να πλέει πάνω από 30
4 το τραπέζι και να το καλύπτει (τα Πλατωνικά στερεά και ιδιαίτερα το δωδεκάεδρο σχετίζονται στενά µε το χρυσό λόγο). «Η Θυσία του Μυστικού είπνου» του Σαλβαντόρ Νταλί Έργα άλλων καλλιτεχνών που εµπνεύστηκαν από τη Χρυσή Αναλογία Η Αγία Οικογένεια του Μιχαήλ Άγγελου «Η σταύρωση» του Ραφαήλ Η γέννηση της Αφροδίτης του Μποτιτσέλι Αυτοπροσωπογραφία του Ρέµπραντ 31
5 Η ΧΡΥΣΗ ΤΟΜΗ ΣΤΗ ΓΛΥΠΤΙΚΗ Ο Μιχαήλ Άγγελος, εκτός από τη ζωγραφική, χρησιµοποίησε τη χρυσή τοµή και στη γλυπτική, όπως στο δηµιούργηµά του «αυίδ». Οι αναλογίες του αυίδ συµµορφώνονται µε τη χρυσή τοµή από τη θέση του οµφαλού σε σχέση µε το ύψος του µέχρι τη θέση των αρθρώσεων στα δάχτυλά του. Στην Αφροδίτη της Μήλου, αριστούργηµα του Αγήσανδρου ή Αλέξανδρου της Αντιοχείας, η θέση του οµφαλού επίσης χωρίζει το άγαλµα σε µέσο και άκρο λόγο. Ο «αυίδ» του Μιχαήλ Άγγελου Η «Αφροδίτη της Μήλου» Άγαλµα του «Modulor» Στη σύγχρονη εποχή, ο Le Corbusier µεταχειρίστηκε το σύστηµα της χρυσής τοµής για να σχηµατίσει το δικό του σύστηµα αναλογιών, γνωστό ως Modulor, εργαλείο µέτρησης βασισµένο στο ανθρώπινο σώµα και στα µαθηµατικά. Στο άγαλµα «Le Modulor» µε βάση τις ιδανικές διαστάσεις που πρότεινε ο Le Corbusier στο οµότιτλο βιβλίο του, ο άντρας ύψους 183 εκ., µε το σηκωµένο χέρι φτάνει τα 226 εκ., ενώ ο οµφαλός του βρίσκεται ακριβώς στη µέση, στα 113 εκ. Ο λόγος 183/113, αντιστοιχεί µε µεγάλη προσέγγιση στο χρυσό λόγο. 32
Ο Βιτρούβιος Άντρας του Λεονάρντο Ντα Βίντσι
 Ο Βιτρούβιος Άντρας του Λεονάρντο Ντα Βίντσι Ο Άνθρωπος του Βιτρούβιου είναι ένα διάσημο σχέδιο με συνοδευτικές σημειώσεις του Λεονάρντο Ντα Βίντσι, που φτιάχτηκε περίπου το 1490 σε ένα από τα ημερολόγιά
Ο Βιτρούβιος Άντρας του Λεονάρντο Ντα Βίντσι Ο Άνθρωπος του Βιτρούβιου είναι ένα διάσημο σχέδιο με συνοδευτικές σημειώσεις του Λεονάρντο Ντα Βίντσι, που φτιάχτηκε περίπου το 1490 σε ένα από τα ημερολόγιά
Σχολ. έτος Λεονάρντο Ντα Βίντσι. Γιάννης Ανθόπουλος, Εργασία στην Ιστορία
 Σχολ. έτος 2014-15 Λεονάρντο Ντα Βίντσι Γιάννης Ανθόπουλος, Β1 Εργασία στην Ιστορία Σχολ. έτος 2014-15 1 2 Leonardo da Vinci Ο Da Vinci γεννήθηκε στο Βίντσι της Ιταλίας στις 15 Απριλίου του 1452. Το πλήρες
Σχολ. έτος 2014-15 Λεονάρντο Ντα Βίντσι Γιάννης Ανθόπουλος, Β1 Εργασία στην Ιστορία Σχολ. έτος 2014-15 1 2 Leonardo da Vinci Ο Da Vinci γεννήθηκε στο Βίντσι της Ιταλίας στις 15 Απριλίου του 1452. Το πλήρες
ΛΕΟΝΑΡΝΤΟ ΝΤΑ ΒΊΝΤΣΙ 1452-1519 ΒΑΣΙΛΕΙΟΥ ΕΥΤΥΧΙΑ ΓΚΕΚΑΣ ΤΡΥΦΩΝ ΑΡΣΕΝΙΔΗΣ ΕΥΘΥΜΙΟΣ
 ΛΕΟΝΑΡΝΤΟ ΝΤΑ ΒΊΝΤΣΙ 1452-1519 ΒΑΣΙΛΕΙΟΥ ΕΥΤΥΧΙΑ ΓΚΕΚΑΣ ΤΡΥΦΩΝ ΑΡΣΕΝΙΔΗΣ ΕΥΘΥΜΙΟΣ 1 Ο Λεονάρντο ντα Βίντσι ήταν Ιταλός αρχιτέκτονας, ζωγράφος, γλύπτης, μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης
ΛΕΟΝΑΡΝΤΟ ΝΤΑ ΒΊΝΤΣΙ 1452-1519 ΒΑΣΙΛΕΙΟΥ ΕΥΤΥΧΙΑ ΓΚΕΚΑΣ ΤΡΥΦΩΝ ΑΡΣΕΝΙΔΗΣ ΕΥΘΥΜΙΟΣ 1 Ο Λεονάρντο ντα Βίντσι ήταν Ιταλός αρχιτέκτονας, ζωγράφος, γλύπτης, μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης
Λ.Ν.Β.: Μια μεγαλοφυΐα με τεράστια προσφορά στην ανθρωπότητα. Οι ανακαλύψεις του Λ.Ν.Β. γύρω από τον κόσμο της βιολογίας.
 11 0 ΓΕΛ ΠΑΤΡΑΣ Σχ. Έτος 2013-14 Τμήμα Α 2 1. Κριτήρια επιλογής θέματος Ένας παράγοντας που συνέβαλε στο να επιλέξουμε το έργο του Λεονάρντο Ντα Βίντσι είναι η φυσιογνωμία ενός ανθρώπου που ήταν μεγαλοφυής
11 0 ΓΕΛ ΠΑΤΡΑΣ Σχ. Έτος 2013-14 Τμήμα Α 2 1. Κριτήρια επιλογής θέματος Ένας παράγοντας που συνέβαλε στο να επιλέξουμε το έργο του Λεονάρντο Ντα Βίντσι είναι η φυσιογνωμία ενός ανθρώπου που ήταν μεγαλοφυής
Ο χρυσός αριθμός φ. Η συνάντηση της αισθητικής τελειότητας και των μαθηματικών
 Ο χρυσός αριθμός φ Η συνάντηση της αισθητικής τελειότητας και των μαθηματικών ΤΟ ΠΡΟΒΛΗΜΑ Το πρόβλημα της χρυσής τομής, σε απλή διατύπωση είναι το εξής: Να χωριστεί ένα τμήμα ΑΒ σε μέσο και άκρο λόγο δηλαδή
Ο χρυσός αριθμός φ Η συνάντηση της αισθητικής τελειότητας και των μαθηματικών ΤΟ ΠΡΟΒΛΗΜΑ Το πρόβλημα της χρυσής τομής, σε απλή διατύπωση είναι το εξής: Να χωριστεί ένα τμήμα ΑΒ σε μέσο και άκρο λόγο δηλαδή
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 3. ΚΛΙΜΑΚΑ ΚΑΙ ΑΝΑΛΟΓΙΕΣ
 Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 3. ΚΛΙΜΑΚΑ ΚΑΙ ΑΝΑΛΟΓΙΕΣ Η κλίμακα και οι αναλογίες έχουν άμεση σχέση με το μέγεθος των αντικειμένων που περιγράφουν. Φυσικά το μεγάλο και το μικρό μέγεθος είναι σχετικοί
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 3. ΚΛΙΜΑΚΑ ΚΑΙ ΑΝΑΛΟΓΙΕΣ Η κλίμακα και οι αναλογίες έχουν άμεση σχέση με το μέγεθος των αντικειμένων που περιγράφουν. Φυσικά το μεγάλο και το μικρό μέγεθος είναι σχετικοί
Τεχνολογία Γ Γυμνασίου
 Τεχνολογία Γ Γυμνασίου Ονοματεπώνυμο μαθήτριας: Τμήμα:Γ 2 Σχολικό έτος: 2016-2017 1 Περιεχόμενα Κεφάλαιο Σελίδες Χρονοδιάγραμμα εργασίας 3 Περίληψη 4 Παρουσίαση του προβλήματος 4,5 Υπόθεση της έρευνας
Τεχνολογία Γ Γυμνασίου Ονοματεπώνυμο μαθήτριας: Τμήμα:Γ 2 Σχολικό έτος: 2016-2017 1 Περιεχόμενα Κεφάλαιο Σελίδες Χρονοδιάγραμμα εργασίας 3 Περίληψη 4 Παρουσίαση του προβλήματος 4,5 Υπόθεση της έρευνας
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ (523)
 ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ (523) Ο ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ ΣΟΦΙΑ ΜΑΡΑ ΑΡΧΙΤΕΚΤΩΝ ΜΗΧΑΝΙΚΟΣ Ο ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ Ο Εσωτερικός σχεδιασμός είναι ο προγραμματισμός, η διάταξη και ο
ΑΡΧΙΤΕΚΤΟΝΙΚΗ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ (523) Ο ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ ΣΟΦΙΑ ΜΑΡΑ ΑΡΧΙΤΕΚΤΩΝ ΜΗΧΑΝΙΚΟΣ Ο ΣΧΕΔΙΑΣΜΟΣ ΤΩΝ ΕΣΩΤΕΡΙΚΩΝ ΧΩΡΩΝ Ο Εσωτερικός σχεδιασμός είναι ο προγραμματισμός, η διάταξη και ο
Ερευνητική εργασία Da Vinci «ΖΩΓΡΑΦΙΚΗ» 2º ΛΥΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ
 Ερευνητική εργασία Da Vinci «ΖΩΓΡΑΦΙΚΗ» 2º ΛΥΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2012-2013 Υπεύθυνοι μαθητές Τζούρι Άρτεμις Σίμος Νίκος Πέτσιος Αναστάσης Σακελλίων Γρηγόρης Υπεύθυνοι καθηγητές: Αδαμάρα Ζούλας
Ερευνητική εργασία Da Vinci «ΖΩΓΡΑΦΙΚΗ» 2º ΛΥΚΕΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΙΚΟ ΕΤΟΣ 2012-2013 Υπεύθυνοι μαθητές Τζούρι Άρτεμις Σίμος Νίκος Πέτσιος Αναστάσης Σακελλίων Γρηγόρης Υπεύθυνοι καθηγητές: Αδαμάρα Ζούλας
ΠΩΣ ΕΠΗΡΕΑΣΑΝ ΔΙΑΧΡΟΝΙΚΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΝ ΖΩΓΡΑΦΙΚΗ
 ΠΩΣ ΕΠΗΡΕΑΣΑΝ ΔΙΑΧΡΟΝΙΚΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΝ ΖΩΓΡΑΦΙΚΗ Η ΟΜΑΔΑ μας ανέλαβε το θέμα της σχέσης των Μαθηματικών με τη ΖΩΓΡΑΦΙΚΗ!!! ΠΑΡΟΥΣΙΑΣΗ-ΕΠΙΜΕΛΕΙΑ: ΓΟΥΛΑ ΕΙΡΗΝΗ, ΡΑΛΛΙΟΥ ΕΥΑΝΘΙΑ, ΤΣΙΜΗΤΡΑ ΑΓΓΕΛΙΚΗ. ΙΣΤΟΡΙΚΗ
ΠΩΣ ΕΠΗΡΕΑΣΑΝ ΔΙΑΧΡΟΝΙΚΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΝ ΖΩΓΡΑΦΙΚΗ Η ΟΜΑΔΑ μας ανέλαβε το θέμα της σχέσης των Μαθηματικών με τη ΖΩΓΡΑΦΙΚΗ!!! ΠΑΡΟΥΣΙΑΣΗ-ΕΠΙΜΕΛΕΙΑ: ΓΟΥΛΑ ΕΙΡΗΝΗ, ΡΑΛΛΙΟΥ ΕΥΑΝΘΙΑ, ΤΣΙΜΗΤΡΑ ΑΓΓΕΛΙΚΗ. ΙΣΤΟΡΙΚΗ
Η χρυσή τομή και ο χρυσός αριθμός φ
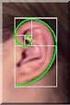 Η χρυσή τομή και ο χρυσός αριθμός φ Ο Johannes Kepler είχε πει ότι η γεωμετρία έχει δύο θησαυρούς: το Πυθαγόρειο Θεώρημα και τη Χρυσή Τομή. Το πρώτο μπορεί να συγκριθεί με μια ποσότητα χρυσού και το δεύτερο
Η χρυσή τομή και ο χρυσός αριθμός φ Ο Johannes Kepler είχε πει ότι η γεωμετρία έχει δύο θησαυρούς: το Πυθαγόρειο Θεώρημα και τη Χρυσή Τομή. Το πρώτο μπορεί να συγκριθεί με μια ποσότητα χρυσού και το δεύτερο
Γεώργιος Βασιλειάδης, Λύκειο Παιανίας «Η χρυσή τομή στα μαθηματικά, στην τέχνη, στη ζωή» 2012-2013
 Γεώργιος Βασιλειάδης, Λύκειο Παιανίας «Η χρυσή τομή στα μαθηματικά, στην τέχνη, στη ζωή» 2012-2013 Η Χρυσή τοµή στην καθηµερινότητά µας Η χρυσή τοµή δεν είναι µόνο ένας µαθηµατικός όρος, αλλά και µια
Γεώργιος Βασιλειάδης, Λύκειο Παιανίας «Η χρυσή τομή στα μαθηματικά, στην τέχνη, στη ζωή» 2012-2013 Η Χρυσή τοµή στην καθηµερινότητά µας Η χρυσή τοµή δεν είναι µόνο ένας µαθηµατικός όρος, αλλά και µια
Η γεωμετρία της ζωής. Ερευνητική εργασία Α Λυκείου 2ου ΓΕΛ ΚΑΒΑΛΑΣ
 Η γεωμετρία της ζωής Ερευνητική εργασία Α Λυκείου 2ου ΓΕΛ ΚΑΒΑΛΑΣ Τι μελετά η γεωμετρία ; Γεωμετρία είναι ο κλάδος των μαθηματικών που ασχολείται με χωρικές σχέσεις, δηλαδή με τη σύνθεση του χώρου που
Η γεωμετρία της ζωής Ερευνητική εργασία Α Λυκείου 2ου ΓΕΛ ΚΑΒΑΛΑΣ Τι μελετά η γεωμετρία ; Γεωμετρία είναι ο κλάδος των μαθηματικών που ασχολείται με χωρικές σχέσεις, δηλαδή με τη σύνθεση του χώρου που
ΧΡΥΣΗ ΤΟΜΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ
 ΧΡΥΣΗ ΤΟΜΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Χρησιμοποιήθηκε στην αρχαία Αίγυπτο και στην Πυθαγόρεια παράδοση,ο πρώτος ορισμός που έχουμε για αυτήν ανήκει στον Ευκλείδη που την ορίζει ως διαίρεση ενός ευθύγραμμου τμήματος
ΧΡΥΣΗ ΤΟΜΗ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Χρησιμοποιήθηκε στην αρχαία Αίγυπτο και στην Πυθαγόρεια παράδοση,ο πρώτος ορισμός που έχουμε για αυτήν ανήκει στον Ευκλείδη που την ορίζει ως διαίρεση ενός ευθύγραμμου τμήματος
ΛΕΟΝΑΡΝΤΟ ΝΤΑ ΒΙΝΤΣΙ ΤΕΧΝΙΚΕΣ
 ΛΕΟΝΑΡΝΤΟ ΝΤΑ ΒΙΝΤΣΙ Ο Λεονάρντο Ντα Βίντσι γεννήθηκε στην πόλη Αντσιάνο κοντά στο Βίντσι της Ιταλίας στις 15 Απριλίου του 1450 και απεβίωσε στις 2 Μαΐου του 1519 στη Γαλλία μετά την εγκατάστασή του από
ΛΕΟΝΑΡΝΤΟ ΝΤΑ ΒΙΝΤΣΙ Ο Λεονάρντο Ντα Βίντσι γεννήθηκε στην πόλη Αντσιάνο κοντά στο Βίντσι της Ιταλίας στις 15 Απριλίου του 1450 και απεβίωσε στις 2 Μαΐου του 1519 στη Γαλλία μετά την εγκατάστασή του από
Χρυσή τομή. 3.1 Εισαγωγή
 Χρυσή τομή 3.1 Εισαγωγή Ίσως όλοι έχουμε την εντύπωση πως αυτό που λέγεται λόγος χρυσής τομής, είναι μία έμπνευση των αρχαίων Ελλήνων την οποία εκμεταλλεύτηκαν για να κατασκευάσουν κτίσματα ή να δημιουργήσουν
Χρυσή τομή 3.1 Εισαγωγή Ίσως όλοι έχουμε την εντύπωση πως αυτό που λέγεται λόγος χρυσής τομής, είναι μία έμπνευση των αρχαίων Ελλήνων την οποία εκμεταλλεύτηκαν για να κατασκευάσουν κτίσματα ή να δημιουργήσουν
Υποομάδα 3 Θέμα: Χρυσός Αριθμός Φ- Χρυσή Τομή
 Α Γενικό Λύκειο Τοσιτσειο Αρσάκειο Εκάλης Ερευνητική εργασία project :Τα μαθηματικά στην Ακρόπολη Υποομάδα 3 Θέμα: Χρυσός Αριθμός Φ- Χρυσή Τομή Μέλη ομάδας: Χρήστος Παπακωνσταντίνου Βασίλης Πελωριάδης
Α Γενικό Λύκειο Τοσιτσειο Αρσάκειο Εκάλης Ερευνητική εργασία project :Τα μαθηματικά στην Ακρόπολη Υποομάδα 3 Θέμα: Χρυσός Αριθμός Φ- Χρυσή Τομή Μέλη ομάδας: Χρήστος Παπακωνσταντίνου Βασίλης Πελωριάδης
Το έργο, ο Άνθρωπος του Βιτρούβιου, που μας έδωσε το έναυσμα να το μελετήσουμε και να μας προβληματίσουν τα αποτελέσματά του.
 11 0 ΓΕΛ ΠΑΤΡΑΣ Σχ. Έτος 2013-14 Τμήμα Α 2 1.Κριτήρια επιλογής θέματος Συνεισφορά του Λεονάρντο Ντα Βίντσι στις επιστήμες και ιδιαίτερα στην ιατρική και στην ανατομία. Το έργο, ο Άνθρωπος του Βιτρούβιου,
11 0 ΓΕΛ ΠΑΤΡΑΣ Σχ. Έτος 2013-14 Τμήμα Α 2 1.Κριτήρια επιλογής θέματος Συνεισφορά του Λεονάρντο Ντα Βίντσι στις επιστήμες και ιδιαίτερα στην ιατρική και στην ανατομία. Το έργο, ο Άνθρωπος του Βιτρούβιου,
Project Α Λυκείου. Ομάδα 3 η Θέμα: Μαθηματικά στην Ακρόπολη Χρυσή τομή- ο αριθμός φ
 Project Α Λυκείου Ομάδα 3 η Θέμα: Μαθηματικά στην Ακρόπολη Χρυσή τομή- ο αριθμός φ Πιτόσκας Γιάννης Στεργίου Γιάννης Παπακωνσταντίνου Χρήστος Πελωριάδης Βασίλης ΠΑΡΘΕΝΩΝΑΣ ΚΑΙ ΧΡΥΣΗ ΤΟΜΗ ΟΡΙΣΜΟΣ ΓΙΑ ΤΗ
Project Α Λυκείου Ομάδα 3 η Θέμα: Μαθηματικά στην Ακρόπολη Χρυσή τομή- ο αριθμός φ Πιτόσκας Γιάννης Στεργίου Γιάννης Παπακωνσταντίνου Χρήστος Πελωριάδης Βασίλης ΠΑΡΘΕΝΩΝΑΣ ΚΑΙ ΧΡΥΣΗ ΤΟΜΗ ΟΡΙΣΜΟΣ ΓΙΑ ΤΗ
Ανδριοπούλου Αγγελική Σταθοπούλου Σωτηρία Χαλούλη Αλεξία Ψαράκη Κωνσταντίνα. Leonardo Da Vinci. Ανατομία Ενός Μυαλού
 Οι μαθητές με αφορμή το πολύπλευρο έργο του Λεονάρντο Ντα Βίντσι προσέγγισαν επιστημονικά και καλλιτεχνικά πεδία του ενδιαφέροντός τους σε μία προσπάθεια να «αποκωδικοποιήσουν» τον επιστήμονα και καλλιτέχνη
Οι μαθητές με αφορμή το πολύπλευρο έργο του Λεονάρντο Ντα Βίντσι προσέγγισαν επιστημονικά και καλλιτεχνικά πεδία του ενδιαφέροντός τους σε μία προσπάθεια να «αποκωδικοποιήσουν» τον επιστήμονα και καλλιτέχνη
Ο Πυθαγόρας ήταν ο πρώτος που διατύπωσε τον μαθηματικό ορισμό της αναλογίας χρησιμοποιώντας δύο ευθύγραμμα τμήματα.
 Ο ΧΡΥΣΟΣ ΑΡΙΘΜΟΣ Φ Ο Πυθαγόρας ήταν ο πρώτος που διατύπωσε τον μαθηματικό ορισμό της αναλογίας χρησιμοποιώντας δύο ευθύγραμμα τμήματα. Η σκέψη του ήταν πως αν υπάρχει ένα ευθύγραμμο τμήμα και ένα σημείο
Ο ΧΡΥΣΟΣ ΑΡΙΘΜΟΣ Φ Ο Πυθαγόρας ήταν ο πρώτος που διατύπωσε τον μαθηματικό ορισμό της αναλογίας χρησιμοποιώντας δύο ευθύγραμμα τμήματα. Η σκέψη του ήταν πως αν υπάρχει ένα ευθύγραμμο τμήμα και ένα σημείο
Υπεύθυνη καθηγήτρια: Χαρίτου Τριανταφυλιά ΠΕ03
 Υπεύθυνη καθηγήτρια: Χαρίτου Τριανταφυλιά ΠΕ03 Η ομάδα αποτελείται από τα εξής άτομα : Βασιλική Βαλλιανάτου Κρίστη Κουνάδη Ειρήνη Μαυρογιάννη Ελευθερία Μπαζίγου Κατερίνα Κουρβισιάνου Φιορένια Τουλάτου
Υπεύθυνη καθηγήτρια: Χαρίτου Τριανταφυλιά ΠΕ03 Η ομάδα αποτελείται από τα εξής άτομα : Βασιλική Βαλλιανάτου Κρίστη Κουνάδη Ειρήνη Μαυρογιάννη Ελευθερία Μπαζίγου Κατερίνα Κουρβισιάνου Φιορένια Τουλάτου
Φύση και Μαθηματικά. Η χρυσή τομή φ
 Η χρυσή τομή φ Ερευνητική Εργασία (Project) Α' Λυκείου 1ο Γενικό Λύκειο Ξάνθης 2011 2012 Συντονιστές Εκπαιδευτικοί Επαμεινώνδας Διαμαντόπουλος Βασιλική Κώττη Συμμετέχοντες Μαθητές Αναστασιάδης Κωνσταντίνος
Η χρυσή τομή φ Ερευνητική Εργασία (Project) Α' Λυκείου 1ο Γενικό Λύκειο Ξάνθης 2011 2012 Συντονιστές Εκπαιδευτικοί Επαμεινώνδας Διαμαντόπουλος Βασιλική Κώττη Συμμετέχοντες Μαθητές Αναστασιάδης Κωνσταντίνος
Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ ΦΥΣΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ
 Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ ΦΥΣΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ Επιμέλεια: Μιχαηλίσιν Άννα- Μαρία, Τζιώτης Δημήτρης, Τσάτσα Κωνσταντίνα Η συμμετρία στο φυσικό κόσμο Η συμμετρία που κατεξοχήν
Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ ΦΥΣΗ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ Η ΣΥΜΜΕΤΡΙΑ ΣΤΟ ΦΥΣΙΚΟ ΚΟΣΜΟ Επιμέλεια: Μιχαηλίσιν Άννα- Μαρία, Τζιώτης Δημήτρης, Τσάτσα Κωνσταντίνα Η συμμετρία στο φυσικό κόσμο Η συμμετρία που κατεξοχήν
Περιεχόμενα Μαθητές που συμμετείχαν στην παρούσα εργασία..3 Σκοπός της εργασίας-στόχοι-ερευνητικά ερωτήματα..4 Α. Χρυσή τομή στα μαθηματικά
 Περιεχόμενα Μαθητές που συμμετείχαν στην παρούσα εργασία..3 Σκοπός της εργασίας-στόχοι-ερευνητικά ερωτήματα..4 Α. Χρυσή τομή στα μαθηματικά.5 Μαθηματικός τύπος..5 Ιδιότητες..5 Κατασκευή με κανόνα και διαβήτη.6
Περιεχόμενα Μαθητές που συμμετείχαν στην παρούσα εργασία..3 Σκοπός της εργασίας-στόχοι-ερευνητικά ερωτήματα..4 Α. Χρυσή τομή στα μαθηματικά.5 Μαθηματικός τύπος..5 Ιδιότητες..5 Κατασκευή με κανόνα και διαβήτη.6
Παρουσίαση του μαθητή Θεοδωρίδη Γιάννη
 Παρουσίαση του μαθητή Θεοδωρίδη Γιάννη Ο Λεονάρντο ντα Βίντσι (15 Απριλίου 1452 2 Μαίου 1519) ήτανιταλός αρχιτέκτονας,ζωγράφος, γλύπτης,μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης, επιστήμονας
Παρουσίαση του μαθητή Θεοδωρίδη Γιάννη Ο Λεονάρντο ντα Βίντσι (15 Απριλίου 1452 2 Μαίου 1519) ήτανιταλός αρχιτέκτονας,ζωγράφος, γλύπτης,μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης, επιστήμονας
Ραφαέλο Σάντσιο. Raffaello Sanzio
 Ραφαέλο Σάντσιο Raffaello Sanzio Ιταλός ζωγράφος αρχιτέκτονας Γεννήθηκε στο Ουρμπίνο Μαθήτευσε στο πλευρό του πατέρα του, Τζιοβάνι Σάντι Εκπαιδεύτηκε στο εργαστήριο του Περουτζίνο Ο πατέρας του, Τζοβάνι
Ραφαέλο Σάντσιο Raffaello Sanzio Ιταλός ζωγράφος αρχιτέκτονας Γεννήθηκε στο Ουρμπίνο Μαθήτευσε στο πλευρό του πατέρα του, Τζιοβάνι Σάντι Εκπαιδεύτηκε στο εργαστήριο του Περουτζίνο Ο πατέρας του, Τζοβάνι
ίνουν ιδιαίτερη σηµασία στις λε τοµέρειες Γι αυτό το λόγο ο Μ ος θεωρείται ροάγγελος του
 ΑΝΑΓΕΝΝΗΣΗ Ο ιταλικός 15ος αιώνας ονοµάζεται κουατροτσέντο. Τα σηµαντικότερα κέντρα της Αναγέννησης στην Ιταλία είναι η Φλωρεντία, η Ρώµη, η Βενετία, το Μιλάνο. Σηµαντική όµως είναι και η εριοχή της Φλάνδρας.
ΑΝΑΓΕΝΝΗΣΗ Ο ιταλικός 15ος αιώνας ονοµάζεται κουατροτσέντο. Τα σηµαντικότερα κέντρα της Αναγέννησης στην Ιταλία είναι η Φλωρεντία, η Ρώµη, η Βενετία, το Μιλάνο. Σηµαντική όµως είναι και η εριοχή της Φλάνδρας.
Ειδικό Τεχνικό Σχέδιο
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ειδικό Τεχνικό Σχέδιο Ενότητα 6.1: Ανθρωπομετρικά στοιχεία και στοιχεία Εργονομίας στην κατοικία Δρ Σταματίνα Γ. Μαλικούτη Τμήμα
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ειδικό Τεχνικό Σχέδιο Ενότητα 6.1: Ανθρωπομετρικά στοιχεία και στοιχεία Εργονομίας στην κατοικία Δρ Σταματίνα Γ. Μαλικούτη Τμήμα
Η ΣΥΜΜΕΤΡΙΑ ΣΤΗ ΖΩΗ ΜΑΣ. Μαθήτριες: Μακρή Κωνστάντια, Μητσοτάκη Ναταλία, Πανταζοπούλου Υβόνη, Παντελή Ιωάννα
 Η ΣΥΜΜΕΤΡΙΑ ΣΤΗ ΖΩΗ ΜΑΣ Μαθήτριες: Μακρή Κωνστάντια, Μητσοτάκη Ναταλία, Πανταζοπούλου Υβόνη, Παντελή Ιωάννα Τι είναι συμμετρία; Η ΣΥΜΜΕΤΡΙΑ ΣΤΗ ΖΩΗ ΜΑΣ Η λέξη «συμμετρία» χρησιμοποιείται στην καθημερινότητα
Η ΣΥΜΜΕΤΡΙΑ ΣΤΗ ΖΩΗ ΜΑΣ Μαθήτριες: Μακρή Κωνστάντια, Μητσοτάκη Ναταλία, Πανταζοπούλου Υβόνη, Παντελή Ιωάννα Τι είναι συμμετρία; Η ΣΥΜΜΕΤΡΙΑ ΣΤΗ ΖΩΗ ΜΑΣ Η λέξη «συμμετρία» χρησιμοποιείται στην καθημερινότητα
ΤΡΕΙΣ ΚΑΙ Ο ΚΟΥΚΟΣ ΕΡΕΥΝΗΤΙΚΗ ΕΡΓΑΣΙΑ: «ΜΕΤΡΟΝ ΑΡΙΣΤΟΝ» ΣΗΜΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ
 ΕΡΕΥΝΗΤΙΚΗ ΕΡΓΑΣΙΑ: «ΜΕΤΡΟΝ ΑΡΙΣΤΟΝ» ΣΗΜΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΤΡΕΙΣ ΚΑΙ Ο ΚΟΥΚΟΣ ΦΑΙΔΡΑ ΚΟΥΡΒΙΣΙΑΝΟΥ ΒΑΣΙΛΗΣ ΚΑΤΣΑΝΤΩΝΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΗΛΙΟΠΟΥΛΟΣ ΑΝΔΡΕΑΣ ΚΑΣΙΜΑΤΗΣ Ερευνητικά Ερωτήματα Ποιοι είναι ΟΙ ΣΗΜΑΝΤΙΚΟΙ
ΕΡΕΥΝΗΤΙΚΗ ΕΡΓΑΣΙΑ: «ΜΕΤΡΟΝ ΑΡΙΣΤΟΝ» ΣΗΜΑΝΤΙΚΟΙ ΑΡΙΘΜΟΙ ΤΡΕΙΣ ΚΑΙ Ο ΚΟΥΚΟΣ ΦΑΙΔΡΑ ΚΟΥΡΒΙΣΙΑΝΟΥ ΒΑΣΙΛΗΣ ΚΑΤΣΑΝΤΩΝΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΗΛΙΟΠΟΥΛΟΣ ΑΝΔΡΕΑΣ ΚΑΣΙΜΑΤΗΣ Ερευνητικά Ερωτήματα Ποιοι είναι ΟΙ ΣΗΜΑΝΤΙΚΟΙ
ΜΟΥΣΙΚΗ & ΜΑΘΗΜΑΤΙΚΑ ΜΟΥΣΙΚΗ ΣΥΝΘΕΣΗ ΒΑΣΙΣΜΕΝΗ ΣΤΗΝ ΑΚΟΛΟΥΘΙΑ FIBONACCI
 ΜΟΥΣΙΚΗ & ΜΑΘΗΜΑΤΙΚΑ ΜΟΥΣΙΚΗ ΣΥΝΘΕΣΗ ΒΑΣΙΣΜΕΝΗ ΣΤΗΝ ΑΚΟΛΟΥΘΙΑ FIBONACCI Θωμάς Μπουλούσης & Χρήστος Παπαχρήστου Επιβλέπουσα καθηγήτρια: Χατσοπούλου Παναγιώτα 1 ο Γυμνάσιο Πεύκων Θεσσαλονίκης ΠΕΡΙΛΗΨΗ Ο
ΜΟΥΣΙΚΗ & ΜΑΘΗΜΑΤΙΚΑ ΜΟΥΣΙΚΗ ΣΥΝΘΕΣΗ ΒΑΣΙΣΜΕΝΗ ΣΤΗΝ ΑΚΟΛΟΥΘΙΑ FIBONACCI Θωμάς Μπουλούσης & Χρήστος Παπαχρήστου Επιβλέπουσα καθηγήτρια: Χατσοπούλου Παναγιώτα 1 ο Γυμνάσιο Πεύκων Θεσσαλονίκης ΠΕΡΙΛΗΨΗ Ο
Γενικά χαρακτηριστικά
 ΙΜΠΡΕΣΙΟΝΙΣΜΟΣ Γενικά χαρακτηριστικά Μικρές πινελιές που δημιουργούν παχύ στρώμα μπογιάς αποτυπώνοντας λεπτομερές. Χρήση των βασικών χρωμάτων, σπάνια χρήση του μαύρου χρώματος. Απουσία διαδοχικών επιστρώσεων
ΙΜΠΡΕΣΙΟΝΙΣΜΟΣ Γενικά χαρακτηριστικά Μικρές πινελιές που δημιουργούν παχύ στρώμα μπογιάς αποτυπώνοντας λεπτομερές. Χρήση των βασικών χρωμάτων, σπάνια χρήση του μαύρου χρώματος. Απουσία διαδοχικών επιστρώσεων
Μαθηματικά Β Γυμνασίου. Επανάληψη στη Θεωρία
 Μαθηματικά Β Γυμνασίου Επανάληψη στη Θεωρία Α.1.1: Η έννοια της μεταβλητής - Αλγεβρικές παραστάσεις Α.1.2: Εξισώσεις α βαθμού Α.1.4: Επίλυση προβλημάτων με τη χρήση εξισώσεων Α.1.5: Ανισώσεις α βαθμού
Μαθηματικά Β Γυμνασίου Επανάληψη στη Θεωρία Α.1.1: Η έννοια της μεταβλητής - Αλγεβρικές παραστάσεις Α.1.2: Εξισώσεις α βαθμού Α.1.4: Επίλυση προβλημάτων με τη χρήση εξισώσεων Α.1.5: Ανισώσεις α βαθμού
ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ
 ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ ΤΙ ΡΩΤΑΜΕ ΜΙΑ ΕΙΚΟΝΑ ; ΤΙ ΜΑΣ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΠΩΣ ΜΑΣ ΤΟ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΣΥΝΘΕΣΗ: Οργάνωση ενός συνόλου από επιμέρους στοιχεία σε μια ενιαία διάταξη Αρχική ιδέα σύνθεσης
ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ ΤΙ ΡΩΤΑΜΕ ΜΙΑ ΕΙΚΟΝΑ ; ΤΙ ΜΑΣ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΠΩΣ ΜΑΣ ΤΟ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΣΥΝΘΕΣΗ: Οργάνωση ενός συνόλου από επιμέρους στοιχεία σε μια ενιαία διάταξη Αρχική ιδέα σύνθεσης
Ε Ρ Γ Α Σ Ι Α Θέμα: «Ακολουθία Fibonacci»
 Ε Ρ Γ Α Σ Ι Α Θέμα: «Ακολουθία Fibonacci» Μάθημα: Άλγεβρα Υπεύθυνος καθηγητής: κ. Σκοτίδας Τάξη: Β Λυκείου Τμήμα Β2 Ονοματεπώνυμο: Λαμπρινή Μαρίνα Λάππα Σχολικό έτος: 2010 2011 1 ΠΕΡΙΕΧΟΜΕΝΑ 1) Ποιο πρόβλημα
Ε Ρ Γ Α Σ Ι Α Θέμα: «Ακολουθία Fibonacci» Μάθημα: Άλγεβρα Υπεύθυνος καθηγητής: κ. Σκοτίδας Τάξη: Β Λυκείου Τμήμα Β2 Ονοματεπώνυμο: Λαμπρινή Μαρίνα Λάππα Σχολικό έτος: 2010 2011 1 ΠΕΡΙΕΧΟΜΕΝΑ 1) Ποιο πρόβλημα
Ομάδες. 1 η ομάδα: Αρμονικά Κύτταρα Θέμα: Βιολογία Μαθητές: Μπάκου Εύα Μπούρλια Ελένη Πέττα Ελεονώρα Πρεβέντα Βάσω Τσόλη Στέλλα
 Ο χρυσός αριθμός Φ Ομάδες 1 η ομάδα: Αρμονικά Κύτταρα Θέμα: Βιολογία Μαθητές: Μπάκου Εύα Μπούρλια Ελένη Πέττα Ελεονώρα Πρεβέντα Βάσω Τσόλη Στέλλα 2 η ομάδα: Μικροί Εξερευνητές Θέμα: Αρχιτεκτονική Μαθητές:
Ο χρυσός αριθμός Φ Ομάδες 1 η ομάδα: Αρμονικά Κύτταρα Θέμα: Βιολογία Μαθητές: Μπάκου Εύα Μπούρλια Ελένη Πέττα Ελεονώρα Πρεβέντα Βάσω Τσόλη Στέλλα 2 η ομάδα: Μικροί Εξερευνητές Θέμα: Αρχιτεκτονική Μαθητές:
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Σχεδιασμός Προγραμμάτων
 Σχεδιασμός Προγραμμάτων Ευλυγισία & Ισορροπία Μ. Μιχαλοπούλου Δ. Π. Θράκης Διατάσεις με καρέκλα Κάθισμα σε καρέκλα και Αυτί στον ώμο (κατέβασμα του αυτιού προς τον ώμο). Το σαγόνι βλέπει τον ώμο. Κυκλικές
Σχεδιασμός Προγραμμάτων Ευλυγισία & Ισορροπία Μ. Μιχαλοπούλου Δ. Π. Θράκης Διατάσεις με καρέκλα Κάθισμα σε καρέκλα και Αυτί στον ώμο (κατέβασμα του αυτιού προς τον ώμο). Το σαγόνι βλέπει τον ώμο. Κυκλικές
Σύμβολα και σχεδιαστικά στοιχεία. Μάθημα 3
 Σύμβολα και σχεδιαστικά στοιχεία Μάθημα 3 Τα αρχιτεκτονικά σύμβολα αποτελούν μια διεθνή, συγκεκριμένη και απλή γλώσσα. Είναι προορισμένα να γίνονται κατανοητά από τον καθένα, ακόμα και από μη ειδικούς.
Σύμβολα και σχεδιαστικά στοιχεία Μάθημα 3 Τα αρχιτεκτονικά σύμβολα αποτελούν μια διεθνή, συγκεκριμένη και απλή γλώσσα. Είναι προορισμένα να γίνονται κατανοητά από τον καθένα, ακόμα και από μη ειδικούς.
Λεονάρντο Ντα Βίντσι. Μια εργασια του Νικολαου Σιδερα
 Λεονάρντο Ντα Βίντσι Μια εργασια του Νικολαου Σιδερα Ο Λεονάρντο ντα Βίντσι (15 Απριλίου 1452 2 Μαΐου 1519) ήταν Ιταλός αρχιτέκτονας, ζωγράφος, γλύπτης, μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης,
Λεονάρντο Ντα Βίντσι Μια εργασια του Νικολαου Σιδερα Ο Λεονάρντο ντα Βίντσι (15 Απριλίου 1452 2 Μαΐου 1519) ήταν Ιταλός αρχιτέκτονας, ζωγράφος, γλύπτης, μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης,
ΔΕΛΤΙΟ ΤΑΥΤΟΤΗΤΑΣ. ΟΝΟΜΑ: Στεγόσαυρος. ΣΗΜΑΣΙΑ ΟΝΟΜΑΤΟΣ: Σαύρα με οροφή. ΧΑΡΑΚΤΗΡΙΣΤΙΚΑ ΤΟΥ ΣΩΜΑΤΟΣ:
 ΟΝΟΜΑ: Στεγόσαυρος ΣΗΜΑΣΙΑ ΟΝΟΜΑΤΟΣ: Σαύρα με οροφή. Ογκώδες τετράποδο που είχε μήκος 8 10 μέτρα. Η πλάτη του καλύπτονταν από μεγάλες κεράτινες πλάκες που ξεκινούσαν μικρές από τη βάση του κεφαλιού, μεγάλωναν
ΟΝΟΜΑ: Στεγόσαυρος ΣΗΜΑΣΙΑ ΟΝΟΜΑΤΟΣ: Σαύρα με οροφή. Ογκώδες τετράποδο που είχε μήκος 8 10 μέτρα. Η πλάτη του καλύπτονταν από μεγάλες κεράτινες πλάκες που ξεκινούσαν μικρές από τη βάση του κεφαλιού, μεγάλωναν
Ειδικότητα: Ύφασµα Ένδυση
 Ειδικότητα: Ύφασµα Ένδυση Αναλυτικό Πρόγραµµα Σπουδών του Μαθήµατος Β Τάξη 1 ου Κύκλου Τ.Ε.Ε. 5 ώρες /εβδοµάδα Αθήνα, Απρίλιος 2001 Α. ΣΚΟΠΟΣ ΤΗΣ Ι ΑΣΚΑΛΙΑΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ: Μάθηµα: «Σχεδιασµός Ετοίµων Ενδυµάτων
Ειδικότητα: Ύφασµα Ένδυση Αναλυτικό Πρόγραµµα Σπουδών του Μαθήµατος Β Τάξη 1 ου Κύκλου Τ.Ε.Ε. 5 ώρες /εβδοµάδα Αθήνα, Απρίλιος 2001 Α. ΣΚΟΠΟΣ ΤΗΣ Ι ΑΣΚΑΛΙΑΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ: Μάθηµα: «Σχεδιασµός Ετοίµων Ενδυµάτων
ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΟ. «Παιχνίδι και Μαθηματικά» 1. Να συμπληρώσεις στα κουτάκια τους αριθμούς που λείπουν:
 ΑΣΚΗΣΕΙΣ ΜΕ ΠΡΑΞΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΟ «Παιχνίδι και Μαθηματικά» 1. Να συμπληρώσεις στα κουτάκια τους αριθμούς που λείπουν: : 11+ 15= 24 : 17+ 11= 16 : 11 13= 17 : 11 14= 26 i 7+
ΑΣΚΗΣΕΙΣ ΜΕ ΠΡΑΞΕΙΣ ΑΣΚΗΣΕΙΣ ΠΡΟΕΤΟΙΜΑΣΙΑΣ ΓΙΑ ΤΟ ΔΙΑΓΩΝΙΣΜΟ «Παιχνίδι και Μαθηματικά» 1. Να συμπληρώσεις στα κουτάκια τους αριθμούς που λείπουν: : 11+ 15= 24 : 17+ 11= 16 : 11 13= 17 : 11 14= 26 i 7+
1. Γενικά περί Συμμετρίας
 1. Γενικά περί Συμμετρίας ιδακτικοί στόχοι Μετά την ολοκλήρωση της μελέτης του κεφαλαίου αυτού θα μπορείτε να... o αναφέρετε τη διττή σημασία της έννοιας της συμμετρίας από την αρχαία Ελλάδα μέχρι και
1. Γενικά περί Συμμετρίας ιδακτικοί στόχοι Μετά την ολοκλήρωση της μελέτης του κεφαλαίου αυτού θα μπορείτε να... o αναφέρετε τη διττή σημασία της έννοιας της συμμετρίας από την αρχαία Ελλάδα μέχρι και
Κρόουλ. Ανάλυση τεχνικής
 Κρόουλ Ανάλυση τεχνικής (di Prampero 1986; Toussaint and Hollander 1994; Vilas-Boas et al., 2011) Γιατί είναι το crawl το γρηγορότερο στιλ; Είναι και το οικονομικότερο Περιεχόμενα Περιγραφή τεχνικής χεριών
Κρόουλ Ανάλυση τεχνικής (di Prampero 1986; Toussaint and Hollander 1994; Vilas-Boas et al., 2011) Γιατί είναι το crawl το γρηγορότερο στιλ; Είναι και το οικονομικότερο Περιεχόμενα Περιγραφή τεχνικής χεριών
"Στην αρχή το φως και η πρώτη ώρα που τα χείλη ακόμα στον πηλό δοκιμάζουν τα πράγματα του κόσμου." (Οδυσσέας Ελύτης)
 "Στην αρχή το φως και η πρώτη ώρα που τα χείλη ακόμα στον πηλό δοκιμάζουν τα πράγματα του κόσμου." (Οδυσσέας Ελύτης) Το σύμπαν δεν υπήρχε από πάντα. Γεννήθηκε κάποτε στο παρελθόν. Τη στιγμή της γέννησης
"Στην αρχή το φως και η πρώτη ώρα που τα χείλη ακόμα στον πηλό δοκιμάζουν τα πράγματα του κόσμου." (Οδυσσέας Ελύτης) Το σύμπαν δεν υπήρχε από πάντα. Γεννήθηκε κάποτε στο παρελθόν. Τη στιγμή της γέννησης
Πως η φύση παίρνει μορφή με χρυσές αναλογίες.
 3 ο ΓΕΛ ΧΑΛΑΝΔΡΙΟΥ Πως η φύση παίρνει μορφή με χρυσές αναλογίες. Ομαδα1 Νικολόπουλος Βασίλης Παχής Θοδωρής Τσιάμης Θάνος Φλέγκας Κωνσταντίνος Ομαδα2 Μαγουλά Ολίνα Μακρή Άννα Πάλλη Ευσταρτία Ντίας Στέφανος
3 ο ΓΕΛ ΧΑΛΑΝΔΡΙΟΥ Πως η φύση παίρνει μορφή με χρυσές αναλογίες. Ομαδα1 Νικολόπουλος Βασίλης Παχής Θοδωρής Τσιάμης Θάνος Φλέγκας Κωνσταντίνος Ομαδα2 Μαγουλά Ολίνα Μακρή Άννα Πάλλη Ευσταρτία Ντίας Στέφανος
Πέτερ Μπρέγκελ ( ):
 ΑΝΑΓΕΝΝΗΣΗ Πέτερ Μπρέγκελ (1525 1569) Πέτερ Μπρέγκελ (1525 1569): Ήταν ένας από τους μεγαλύτερους Ολλανδούς ζωγράφους και χαράκτες της εποχής του, πρωτοπόρος της Βορειοευρωαπαϊκής Αναγέννησης. Ασχολήθηκε
ΑΝΑΓΕΝΝΗΣΗ Πέτερ Μπρέγκελ (1525 1569) Πέτερ Μπρέγκελ (1525 1569): Ήταν ένας από τους μεγαλύτερους Ολλανδούς ζωγράφους και χαράκτες της εποχής του, πρωτοπόρος της Βορειοευρωαπαϊκής Αναγέννησης. Ασχολήθηκε
Η χρυσή τομή είναι η πιο αρμονική διαίρεση ενός ευθύγραμμου τμήματος (L) σε δύο άνισα μέρη. Τα δύο μέρη έχουν μια συγκεκριμένη μαθηματική αναλογία.
 Η χρυσή τομή είναι η πιο αρμονική διαίρεση ενός ευθύγραμμου τμήματος (L) σε δύο άνισα μέρη. Τα δύο μέρη έχουν μια συγκεκριμένη μαθηματική αναλογία. Για την ακρίβεια, ο λόγος του κοντύτερου τμήματος (b)
Η χρυσή τομή είναι η πιο αρμονική διαίρεση ενός ευθύγραμμου τμήματος (L) σε δύο άνισα μέρη. Τα δύο μέρη έχουν μια συγκεκριμένη μαθηματική αναλογία. Για την ακρίβεια, ο λόγος του κοντύτερου τμήματος (b)
ΕΚΠΑΙΔΕΥΤΙΚΕΣ ΔΡΑΣΤΗΡΙΟΤΗΤΕΣ
 Ε, τότε, παιδιά, θα έλεγα να βάλουµε όλοι το χαρτζιλίκι µας να αγοράσουµε το βιβλίο για τη µικρή µας φίλη, πρότεινε η Νάντια και όλοι συµφώνησαν. Το πολυπόθητο βιβλίο έγινε δικό της χάρη στην αγάπη των
Ε, τότε, παιδιά, θα έλεγα να βάλουµε όλοι το χαρτζιλίκι µας να αγοράσουµε το βιβλίο για τη µικρή µας φίλη, πρότεινε η Νάντια και όλοι συµφώνησαν. Το πολυπόθητο βιβλίο έγινε δικό της χάρη στην αγάπη των
Η Γκουέρνικα του Πικάσο Η απανθρωπιά, η βιαιότητα και η απόγνωση του πολέµου
 Η Γκουέρνικα του Πικάσο Η απανθρωπιά, η βιαιότητα και η απόγνωση του πολέµου Η Γκουέρνικα είναι µια έντονη διαµαρτυρία εναντίον του πολέµου και της καταστροφής που αυτός σπέρνει. Τα µήνυµα που θέλει να
Η Γκουέρνικα του Πικάσο Η απανθρωπιά, η βιαιότητα και η απόγνωση του πολέµου Η Γκουέρνικα είναι µια έντονη διαµαρτυρία εναντίον του πολέµου και της καταστροφής που αυτός σπέρνει. Τα µήνυµα που θέλει να
ΠΡΟΒΛΗΜΑΤΑ ΠΟΥ ΛΥΝΟΝΤΑΙ ΜΕ ΕΞΙΣΩΣΕΙΣ
 ΠΡΟΒΛΗΜΑΤΑ ΠΟΥ ΛΥΝΟΝΤΑΙ ΜΕ ΕΞΙΣΩΣΕΙΣ 1. Η συνδρομή για την συμμετοχή στον όμιλο κολύμβησης είναι 15 τον μήνα και 5 για κάθε φορά που χρησιμοποιούμε την πισίνα. Αν τον προηγούμενο μήνα πληρώσαμε 75, πόσες
ΠΡΟΒΛΗΜΑΤΑ ΠΟΥ ΛΥΝΟΝΤΑΙ ΜΕ ΕΞΙΣΩΣΕΙΣ 1. Η συνδρομή για την συμμετοχή στον όμιλο κολύμβησης είναι 15 τον μήνα και 5 για κάθε φορά που χρησιμοποιούμε την πισίνα. Αν τον προηγούμενο μήνα πληρώσαμε 75, πόσες
Στοιχεία Συναρτήσεων. 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: στ. x 1
 Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
Το Εικονογραφημένο Βιβλίο στην Προσχολική Εκπαίδευση
 Το Εικονογραφημένο Βιβλίο στην Προσχολική Εκπαίδευση Ενότητα 4.1: Ζωγραφική και Εικονογραφημένο Βιβλίο Αγγελική Γιαννικοπούλου Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία (ΤΕΑΠΗ) Διδακτική Πρακτική
Το Εικονογραφημένο Βιβλίο στην Προσχολική Εκπαίδευση Ενότητα 4.1: Ζωγραφική και Εικονογραφημένο Βιβλίο Αγγελική Γιαννικοπούλου Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία (ΤΕΑΠΗ) Διδακτική Πρακτική
Η µουσική και ο χορός στην αρχαία Ελλάδα
 ΥΠΟΥΡΓΕΙΟ ΠΟΛΙΤΙΣΜΟΥ, ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΑΡΧΑΙΟΤΗΤΩΝ ΚΑΙ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΔΙΕΥΘΥΝΣΗ ΜΟΥΣΕΙΩΝ TMHMA ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑΤΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ Η µουσική και ο χορός στην
ΥΠΟΥΡΓΕΙΟ ΠΟΛΙΤΙΣΜΟΥ, ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΓΕΝΙΚΗ ΔΙΕΥΘΥΝΣΗ ΑΡΧΑΙΟΤΗΤΩΝ ΚΑΙ ΠΟΛΙΤΙΣΤΙΚΗΣ ΚΛΗΡΟΝΟΜΙΑΣ ΔΙΕΥΘΥΝΣΗ ΜΟΥΣΕΙΩΝ TMHMA ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΠΡΟΓΡΑΜΜΑΤΩΝ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑΣ Η µουσική και ο χορός στην
0,1,1,2,3,5,8,13,21,34,55,89...
 ΧΡΥΣΗ ΤΟΜΗ: Β ΜΕΡΟΣ 0,1,1,2,3,5,8,13,21,34,55,89... Οι παραπάνω αριθμοί ονομάζονται Ακολουθία Fibonacci το άθροισμα των 2 προηγουμένων αριθμών ισούται με τον επόμενο αριθμό στην ακολουθία. Το πηλίκο τον
ΧΡΥΣΗ ΤΟΜΗ: Β ΜΕΡΟΣ 0,1,1,2,3,5,8,13,21,34,55,89... Οι παραπάνω αριθμοί ονομάζονται Ακολουθία Fibonacci το άθροισμα των 2 προηγουμένων αριθμών ισούται με τον επόμενο αριθμό στην ακολουθία. Το πηλίκο τον
ΕΡΓΟΝΟΜΙΑ - Λύσεις ασκήσεων στην ενότητα
 ΕΡΓΟΝΟΜΙΑ - Λύσεις ασκήσεων στην ενότητα 1. α. Να εξηγήσετε τον ρόλο του στοιχείου της προσαρμοστικότητας σε θέματα εργονομίας προϊόντων. Να αναφέρετε ένα παράδειγμα. β. Να αναφέρετε επιπτώσεις εργονομικών
ΕΡΓΟΝΟΜΙΑ - Λύσεις ασκήσεων στην ενότητα 1. α. Να εξηγήσετε τον ρόλο του στοιχείου της προσαρμοστικότητας σε θέματα εργονομίας προϊόντων. Να αναφέρετε ένα παράδειγμα. β. Να αναφέρετε επιπτώσεις εργονομικών
1 ο ΛΥΚΕΙΟ ΠΑΤΡΩΝ Ερευνητική εργασία. Εφαρμογές του «Φ» 1 ο τετράμηνο
 1 ο ΛΥΚΕΙΟ ΠΑΤΡΩΝ Ερευνητική εργασία Εφαρμογές του «Φ» 1 ο τετράμηνο 2012-13 ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ ΚΟΡΟΝΤΖΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΠΕ03 ΠΕΡΙΕΧΟΜΕΝΑ 1. Ιστορική αναδρομή 2. Αλγεβρικές ιδιότητες 3. Γεωμετρικές Ιδιότητες
1 ο ΛΥΚΕΙΟ ΠΑΤΡΩΝ Ερευνητική εργασία Εφαρμογές του «Φ» 1 ο τετράμηνο 2012-13 ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ ΚΟΡΟΝΤΖΗΣ ΚΩΝΣΤΑΝΤΙΝΟΣ ΠΕ03 ΠΕΡΙΕΧΟΜΕΝΑ 1. Ιστορική αναδρομή 2. Αλγεβρικές ιδιότητες 3. Γεωμετρικές Ιδιότητες
PROJECT Β ΤΕΤΡΑΜΗΝΟΥ ΘΕΜΑ:ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΗ ΦΥΣΗ ΚΑΙ ΣΤΗΝ ΤΕΧΝΗ ΥΠΟΘΕΜΑ:ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΗΝ ΤΕΧΝΗ
 2 ο ΓΕΛ ΡΕΘΥΜΝΟΥ Σχ. Έτος 2011-12 PROJECT Β ΤΕΤΡΑΜΗΝΟΥ ΤΑΞΗ Α' ΘΕΜΑ:ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΗ ΦΥΣΗ ΚΑΙ ΣΤΗΝ ΤΕΧΝΗ ΥΠΟΘΕΜΑ:ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΗΝ ΤΕΧΝΗ ΜΑΘΗΤΕΣ:ΚΩΣΤΗΣ ΚΑΛΑΙΤΖΙΔΑΚΗΣ ΣΤΑΜΑΤΗΣ ΜΠΡΙΛΛΑΚΗΣ ΑΝΔΡΕΑΣ ΚΑΟΥΔΗΣ
2 ο ΓΕΛ ΡΕΘΥΜΝΟΥ Σχ. Έτος 2011-12 PROJECT Β ΤΕΤΡΑΜΗΝΟΥ ΤΑΞΗ Α' ΘΕΜΑ:ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΗ ΦΥΣΗ ΚΑΙ ΣΤΗΝ ΤΕΧΝΗ ΥΠΟΘΕΜΑ:ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΣΤΗΝ ΤΕΧΝΗ ΜΑΘΗΤΕΣ:ΚΩΣΤΗΣ ΚΑΛΑΙΤΖΙΔΑΚΗΣ ΣΤΑΜΑΤΗΣ ΜΠΡΙΛΛΑΚΗΣ ΑΝΔΡΕΑΣ ΚΑΟΥΔΗΣ
Μάθετε να γράφετε 4/5. ετών. Από τελείες στη γραµµή γραµµές και διακοσµήσεις από τη γραµµή της επιστολής. να κάνετε στο σπίτι
 Υ Ο Μ Σ Η Φ Α Ρ Γ ΙΟ Α ΤΟ ΤΕΤΡ Μάθετε να γράφετε 4/5 ετών Από τελείες στη γραµµή γραµµές και διακοσµήσεις από τη γραµµή της επιστολής να κάνετε στο σπίτι 2 Από το σχολείο στο σπίτι Από το σχολείο στο σπίτι
Υ Ο Μ Σ Η Φ Α Ρ Γ ΙΟ Α ΤΟ ΤΕΤΡ Μάθετε να γράφετε 4/5 ετών Από τελείες στη γραµµή γραµµές και διακοσµήσεις από τη γραµµή της επιστολής να κάνετε στο σπίτι 2 Από το σχολείο στο σπίτι Από το σχολείο στο σπίτι
Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
 Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
Ενότητα 4 Τριγωνομετρία Στην ενότητα αυτή θα μάθουμε: Να υπολογίζουμε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Τη γωνία σε κανονική θέση και τους τριγωνομετρικούς αριθμούς γωνίας σε κανονική θέση.
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο «ΑΛΓΕΒΡΑ»
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΕΝΔΕΙΚΤΙΚΕΣ ΔΟΚΙΜΑΣΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΤΗΝ ΕΙΣΑΓΩΓΗ ΜΑΘΗΤΩΝ ΣΤΑ ΠΡΟΤΥΠΑ-ΠΕΙΡΑΜΑΤΙΚΑ ΓΥΜΝΑΣΙΑ
 ΕΝΔΕΙΚΤΙΚΕΣ ΔΟΚΙΜΑΣΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΤΗΝ ΕΙΣΑΓΩΓΗ ΜΑΘΗΤΩΝ ΣΤΑ ΠΡΟΤΥΠΑ-ΠΕΙΡΑΜΑΤΙΚΑ ΓΥΜΝΑΣΙΑ ΔΟΚΙΜΑΣΙΑ 6 1) Να εκφράσετε τον αριθμό 48 σε γινόμενο πρώτων παραγόντων με δενδροδιάγραμμα. 2) Να συγκρίνετε
ΕΝΔΕΙΚΤΙΚΕΣ ΔΟΚΙΜΑΣΙΕΣ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΤΗΝ ΕΙΣΑΓΩΓΗ ΜΑΘΗΤΩΝ ΣΤΑ ΠΡΟΤΥΠΑ-ΠΕΙΡΑΜΑΤΙΚΑ ΓΥΜΝΑΣΙΑ ΔΟΚΙΜΑΣΙΑ 6 1) Να εκφράσετε τον αριθμό 48 σε γινόμενο πρώτων παραγόντων με δενδροδιάγραμμα. 2) Να συγκρίνετε
Λύση: Οι περιορισμοί που λαμβάνονται υπόψη κατά τον σχεδιασμό των χώρων εργασίας είναι: η ύπαρξη χώρου η πρόσβαση η στάση χειρισμού η δύναμη.
 Κεφάλαιο 1: Εργονομία Σχεδιασμός και Τεχνολογία Γ Λυκείου - Λύσεις Ασκήσεων Άσκηση 1 α) Να εξηγήσετε τον ρόλο του στοιχείου της προσαρμοστικότητας σε θέματα εργονομίας προϊόντων. Να αναφέρετε ένα παράδειγμα.
Κεφάλαιο 1: Εργονομία Σχεδιασμός και Τεχνολογία Γ Λυκείου - Λύσεις Ασκήσεων Άσκηση 1 α) Να εξηγήσετε τον ρόλο του στοιχείου της προσαρμοστικότητας σε θέματα εργονομίας προϊόντων. Να αναφέρετε ένα παράδειγμα.
4η ΟΜΑΔΑ: Πρωτόπαππα Νεκταρία Κούλια Κωνσταντίνα Τσιώλης Παναγιώτης Κουτρομάνου Γεωργία
 ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΤΙΣ ΤΕΧΝΕΣ 4η ΟΜΑΔΑ: Πρωτόπαππα Νεκταρία Κούλια Κωνσταντίνα Τσιώλης Παναγιώτης Κουτρομάνου Γεωργία ΠΕΡΙΕΧΟΜΕΝΑ ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΤΗΝ ΛΟΓΟΤΕΧΝΙΑ ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΤΟΝ ΚΙΝΗΜΑΤΟΓΡΑΦΟ ΜΗΧΑΝΗ ΑΙΝΙΓΜΑ
ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΤΙΣ ΤΕΧΝΕΣ 4η ΟΜΑΔΑ: Πρωτόπαππα Νεκταρία Κούλια Κωνσταντίνα Τσιώλης Παναγιώτης Κουτρομάνου Γεωργία ΠΕΡΙΕΧΟΜΕΝΑ ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΤΗΝ ΛΟΓΟΤΕΧΝΙΑ ΚΡΥΠΤΟΓΡΑΦΙΑ ΣΤΟΝ ΚΙΝΗΜΑΤΟΓΡΑΦΟ ΜΗΧΑΝΗ ΑΙΝΙΓΜΑ
Αφιέρωμα: LeonardodaVinci
 Αφιέρωμα: LeonardodaVinci Ο Βίος και τα Έργα Ο ιταλός αρχιτέκτονας, ζωγράφος, γλύπτης, μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης και επιστήμονας LeonardodiserPierodaVinci ή αλλιώς ο γνωστός σε
Αφιέρωμα: LeonardodaVinci Ο Βίος και τα Έργα Ο ιταλός αρχιτέκτονας, ζωγράφος, γλύπτης, μουσικός, εφευρέτης, μηχανικός, ανατόμος, γεωμέτρης και επιστήμονας LeonardodiserPierodaVinci ή αλλιώς ο γνωστός σε
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 10 ο, Τμήμα Α
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2019 ΜΑΘΗΜΑΤΙΚΑ ΚΟΙΝΟΥ ΚΟΡΜΟΥ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 6, Γραφείο 102, Στρόβολος 200, Λευκωσία Τηλέφωνο: 57 2278101, Φαξ: 57 2279122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2019 ΜΑΘΗΜΑΤΙΚΑ ΚΟΙΝΟΥ ΚΟΡΜΟΥ Ημερομηνία:
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Στασίνου 6, Γραφείο 102, Στρόβολος 200, Λευκωσία Τηλέφωνο: 57 2278101, Φαξ: 57 2279122 cms@cms.org.cy, www.cms.org.cy ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2019 ΜΑΘΗΜΑΤΙΚΑ ΚΟΙΝΟΥ ΚΟΡΜΟΥ Ημερομηνία:
ΘΕΜΑ 1 ο Τα παρακάτω σχήματα έχουν χωριστεί σε ίσα τετράγωνα. Σε ποια από αυτά έχουμε γραμμοσκιάσει του σχήματος; Να κυκλώσεις το σωστό.
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Επιτροπή ιαγωνισμού του περιοδικού «Ο μικρός Ευκλείδης» 10 ος Πανελλήνιος Μαθητικός ιαγωνισμός «Παιχνίδι και Μαθηματικά» 4-3 - 2016 Για μαθητές της Ε Τάξης ημοτικού Ονοματεπώνυμο:.
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Επιτροπή ιαγωνισμού του περιοδικού «Ο μικρός Ευκλείδης» 10 ος Πανελλήνιος Μαθητικός ιαγωνισμός «Παιχνίδι και Μαθηματικά» 4-3 - 2016 Για μαθητές της Ε Τάξης ημοτικού Ονοματεπώνυμο:.
Η εκμάθηση της μετωπικής πάσας στην πετοσφαίριση
 Η εκμάθηση της μετωπικής πάσας στην πετοσφαίριση Υποδειγματικό Σενάριο Γνωστικό αντικείμενο: Φυσική αγωγή Δημιουργός: ΜΑΡΙΑ ΥΦΑΝΤΗ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ
Η εκμάθηση της μετωπικής πάσας στην πετοσφαίριση Υποδειγματικό Σενάριο Γνωστικό αντικείμενο: Φυσική αγωγή Δημιουργός: ΜΑΡΙΑ ΥΦΑΝΤΗ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. 8. Πότε το γινόμενο δύο ή περισσοτέρων αριθμών παραγόντων είναι ίσο με το μηδέν ;
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ ο : ( ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ) ΠΑΡΑΤΗΡΗΣΗ : Το κεφάλαιο αυτό περιέχει πολλά θέματα που είναι επανάληψη εννοιών που διδάχθηκαν στο Γυμνάσιο γι αυτό σ αυτές δεν θα επεκταθώ αναλυτικά
5 ος Πανελλήνιος Μαθητικός Διαγωνισμός «Παιχνίδι και Μαθηματικά»
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 106 79 ΑΘΗΝΑ Τηλ. 361653-3617784 - Fax: 364105 GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Εleftheriou Venizelou) Street GR. 106 79
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 106 79 ΑΘΗΝΑ Τηλ. 361653-3617784 - Fax: 364105 GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Εleftheriou Venizelou) Street GR. 106 79
Το πολιτιστικό πρόγραμμα με θέμα «Το ψωμί» πραγματοποιήθηκε έχοντας ως γενικό στόχο: Να γνωρίσουν οι μαθητές το ψωμί, να διαπιστώσουν για ποιο λόγο απ
 ΠΟΛΙΤΙΣΤΙΚΟ ΠΡΟΓΡΑΜΜΑ «ΤΟ ΨΩΜΙ» Δημοτικό Σχολείο Μεσοτόπου Σχολικό έτος 2009 201 0 Τάξη: Ε Υπεύθυνη εκπαιδευτικός: Παπαδοπούλου Ομορφούλα Το πολιτιστικό πρόγραμμα με θέμα «Το ψωμί» πραγματοποιήθηκε έχοντας
ΠΟΛΙΤΙΣΤΙΚΟ ΠΡΟΓΡΑΜΜΑ «ΤΟ ΨΩΜΙ» Δημοτικό Σχολείο Μεσοτόπου Σχολικό έτος 2009 201 0 Τάξη: Ε Υπεύθυνη εκπαιδευτικός: Παπαδοπούλου Ομορφούλα Το πολιτιστικό πρόγραμμα με θέμα «Το ψωμί» πραγματοποιήθηκε έχοντας
Επιπρόσθετα για την δύναμη. Από το βιβλίο «Concepts in Physics CRM Books Del Mar California 1973. Επιλογή μόνον για την εκπαίδευση των φοιτητών
 Επιπρόσθετα για την δύναμη Από το βιβλίο «Concepts in Physics CRM Books Del Mar California 1973 Επιλογή μόνον για την εκπαίδευση των φοιτητών Εικόνα : Τα πόδια της κοπέλας σπρώχνουν κάτω καθώς πατάει πάνω
Επιπρόσθετα για την δύναμη Από το βιβλίο «Concepts in Physics CRM Books Del Mar California 1973 Επιλογή μόνον για την εκπαίδευση των φοιτητών Εικόνα : Τα πόδια της κοπέλας σπρώχνουν κάτω καθώς πατάει πάνω
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ. Μηχανική Στερεού Σώματος. Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος. Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός
 ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ Μηχανική Στερεού Σώματος Ροπή Δυνάμεων & Ισορροπία Στερεού Σώματος Επιμέλεια: ΑΓΚΑΝΑΚΗΣ A.ΠΑΝΑΓΙΩΤΗΣ, Φυσικός Εισαγωγή Στην Α Λυκείου είχαμε μελετήσει τη δύναμη προκειμένου
ΠΕΡΙΓΡΑΦΗ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΔΡΑΣΗΣ
 ΠΕΡΙΓΡΑΦΗ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΔΡΑΣΗΣ Τίτλος: Αν η ομορφιά μιλούσε Προτεινόμενες τάξεις: Νήπια, Α και Β Δημοτικού Χώροι διεξαγωγής: Στο σχολείο: προετοιμασία Στο Εθνικό Αρχαιολογικό Μουσείο: έρευνα Προτεινόμενος
ΠΕΡΙΓΡΑΦΗ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΔΡΑΣΗΣ Τίτλος: Αν η ομορφιά μιλούσε Προτεινόμενες τάξεις: Νήπια, Α και Β Δημοτικού Χώροι διεξαγωγής: Στο σχολείο: προετοιμασία Στο Εθνικό Αρχαιολογικό Μουσείο: έρευνα Προτεινόμενος
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
Ο πίνακας The Agnew Clinic του Τόμας Ίκινς
 Ο πίνακας The Agnew Clinic του Τόμας Ίκινς Γεώργιος Νικ. Σχορετσανίτης 2 3 Ο πίνακας The Agnew Clinic του Τόμας Ίκινς Το 1876, ο Τόμας Ίκινς (Thomas Eakins) ολοκλήρωσε ένα πορτραίτο του John Hill Brinton
Ο πίνακας The Agnew Clinic του Τόμας Ίκινς Γεώργιος Νικ. Σχορετσανίτης 2 3 Ο πίνακας The Agnew Clinic του Τόμας Ίκινς Το 1876, ο Τόμας Ίκινς (Thomas Eakins) ολοκλήρωσε ένα πορτραίτο του John Hill Brinton
Τεχνική των επιθετικών κινήσεων. 1.Τεχνική των τρόπων κατοχής και χειρισμού της μπάλας 2. Τρόποι ρίψης της μπάλας, πάσες-σουτ
 ΤΕΧΝΙΚΗ Τεχνική των επιθετικών κινήσεων 1.Τεχνική των τρόπων κατοχής και χειρισμού της μπάλας 2. Τρόποι ρίψης της μπάλας, πάσες-σουτ 1. Τεχνική των τρόπων κατοχής και χειρισμού της μπάλας Σήκωμα της μπάλας
ΤΕΧΝΙΚΗ Τεχνική των επιθετικών κινήσεων 1.Τεχνική των τρόπων κατοχής και χειρισμού της μπάλας 2. Τρόποι ρίψης της μπάλας, πάσες-σουτ 1. Τεχνική των τρόπων κατοχής και χειρισμού της μπάλας Σήκωμα της μπάλας
5 ος Πανελλήνιος Μαθητικός Διαγωνισμός «Παιχνίδι και Μαθηματικά»
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 106 79 ΑΘΗΝΑ Τηλ. 3616532-3617784 - Fax: 3641025 e-mail : info@hms.gr www.hms.gr GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Εleftheriou
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 106 79 ΑΘΗΝΑ Τηλ. 3616532-3617784 - Fax: 3641025 e-mail : info@hms.gr www.hms.gr GREEK MATHEMATICAL SOCIETY 34, Panepistimiou (Εleftheriou
ΤΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΚΑΙ ΤΟ ΕΜΒΑΔΟ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΜΕΣΑ ΑΠΟ ΜΙΑ ΣΕΙΡΑ JAVA-APPLETS
 246 3 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΤΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΚΑΙ ΤΟ ΕΜΒΑΔΟ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΜΕΣΑ ΑΠΟ ΜΙΑ ΣΕΙΡΑ JAVA-APPLETS Φουναριωτάκης Αθανάσιος Μαθηματικός Β/θμιας Εκπαίδευσης Προσωπική ιστοσελίδα:
246 3 Ο ΣΥΝΕΔΡΙΟ ΣΤΗ ΣΥΡΟ ΤΠΕ ΣΤΗΝ ΕΚΠΑΙΔΕΥΣΗ ΤΟ ΠΥΘΑΓΟΡΕΙΟ ΘΕΩΡΗΜΑ ΚΑΙ ΤΟ ΕΜΒΑΔΟ ΚΥΚΛΙΚΟΥ ΔΙΣΚΟΥ ΜΕΣΑ ΑΠΟ ΜΙΑ ΣΕΙΡΑ JAVA-APPLETS Φουναριωτάκης Αθανάσιος Μαθηματικός Β/θμιας Εκπαίδευσης Προσωπική ιστοσελίδα:
Κανονικά πολύγωνα Τουρναβίτης Στέργιος
 Κανονικά πολύγωνα Τουρναβίτης Στέργιος Κανονικά πολύγωνα στη φύση, τέχνη, ανθρώπινες κατασκευές, Μαθηματικά Κανονικά πολύγωνα στη φύση Η κηρήθρα είναι ένα φυσικό θαύμα αρχιτεκτονικής Οι μέλισσες έχουν
Κανονικά πολύγωνα Τουρναβίτης Στέργιος Κανονικά πολύγωνα στη φύση, τέχνη, ανθρώπινες κατασκευές, Μαθηματικά Κανονικά πολύγωνα στη φύση Η κηρήθρα είναι ένα φυσικό θαύμα αρχιτεκτονικής Οι μέλισσες έχουν
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΤΑΞΗ. Κάρτες εκγύμνασης
 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΤΑΞΗ Άσκηση 1 η Κάρτες εκγύμνασης Υλικά: Ο εκπαιδευτικός ετοιμάζει 4 κάρτες με κινητικές δραστηριότητες (πχ. επικύψεις, καθίσματα, ασκήσεις χεριών, ασκήσεις ποδιών). Ο εκπαιδευτικός μοιράζει
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΤΑΞΗ Άσκηση 1 η Κάρτες εκγύμνασης Υλικά: Ο εκπαιδευτικός ετοιμάζει 4 κάρτες με κινητικές δραστηριότητες (πχ. επικύψεις, καθίσματα, ασκήσεις χεριών, ασκήσεις ποδιών). Ο εκπαιδευτικός μοιράζει
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
MERCENARY ΧΡΗΣΤΟΣ ΣΑΡΑΦΕΡΑΣ ΣΠΥΡΟΣ ΖΙΑΖΙΑΣ ΜΙΛΤΟΣ ΤΟΚΑΤΛΙΔΗΣ
 MERCENARY ΧΡΗΣΤΟΣ ΣΑΡΑΦΕΡΑΣ ΣΠΥΡΟΣ ΖΙΑΖΙΑΣ ΜΙΛΤΟΣ ΤΟΚΑΤΛΙΔΗΣ ΖΩΡΟΑΣΤΡΗΣ Ο Θεός που πίστευε, ήταν ο Ωροµάσδης (ο Θεός του φωτός και του ουρανού) Ο Ζωροάστρης καλούσε τους πιστούς να κάνουν µόνο το καλό,
MERCENARY ΧΡΗΣΤΟΣ ΣΑΡΑΦΕΡΑΣ ΣΠΥΡΟΣ ΖΙΑΖΙΑΣ ΜΙΛΤΟΣ ΤΟΚΑΤΛΙΔΗΣ ΖΩΡΟΑΣΤΡΗΣ Ο Θεός που πίστευε, ήταν ο Ωροµάσδης (ο Θεός του φωτός και του ουρανού) Ο Ζωροάστρης καλούσε τους πιστούς να κάνουν µόνο το καλό,
Όροι κλειδιά Αναγέννηση Ανθρωπισμός ανθρωπιστές οικουμενικός άνθρωπος έλληνες λόγιοι τυπογραφία γράμματα επιστήμη τέχνη
 2 Αναγέννηση και Ανθρωπισμός Όροι κλειδιά Αναγέννηση Ανθρωπισμός ανθρωπιστές οικουμενικός άνθρωπος έλληνες λόγιοι τυπογραφία γράμματα επιστήμη τέχνη Τι είναι η Αναγέννηση Η Αναγέννηση είναι ένα καλλιτεχνικό
2 Αναγέννηση και Ανθρωπισμός Όροι κλειδιά Αναγέννηση Ανθρωπισμός ανθρωπιστές οικουμενικός άνθρωπος έλληνες λόγιοι τυπογραφία γράμματα επιστήμη τέχνη Τι είναι η Αναγέννηση Η Αναγέννηση είναι ένα καλλιτεχνικό
Οι γωνιάσεις, κύριο χαρακτηριστικό του συμφυούς παραστήματος. Τα παραστήματα είναι τα τρία τέταρτα του στυλ
 ΤΟ ΜΠΡΕΤΟΝ ΚΑΙ ΟΙ ΓΩΝΙΑΣΕΙΣ ΤΟΥ Οι γωνιάσεις, κύριο χαρακτηριστικό του συμφυούς παραστήματος. Τα παραστήματα είναι τα τρία τέταρτα του στυλ Δεν σας κρύβω ότι στην προσέγγιση μου για την παρουσίαση των
ΤΟ ΜΠΡΕΤΟΝ ΚΑΙ ΟΙ ΓΩΝΙΑΣΕΙΣ ΤΟΥ Οι γωνιάσεις, κύριο χαρακτηριστικό του συμφυούς παραστήματος. Τα παραστήματα είναι τα τρία τέταρτα του στυλ Δεν σας κρύβω ότι στην προσέγγιση μου για την παρουσίαση των
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΜΑΘΗΜΑ: ΠΑΙΔΑΓΩΓΙΚΗ ΓΥΜΝΑΣΤΙΚΗ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΜΑΘΗΜΑ: ΠΑΙΔΑΓΩΓΙΚΗ ΓΥΜΝΑΣΤΙΚΗ Επικοινωνία και συνεννόηση μεταξύ καθηγητή Φ.Α και μαθητών Καλύτερη συνεργασία Εξοικονόμηση
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΦΥΣΙΚΗΣ ΑΓΩΓΗΣ ΚΑΙ ΑΘΛΗΤΙΣΜΟΥ ΜΑΘΗΜΑ: ΠΑΙΔΑΓΩΓΙΚΗ ΓΥΜΝΑΣΤΙΚΗ Επικοινωνία και συνεννόηση μεταξύ καθηγητή Φ.Α και μαθητών Καλύτερη συνεργασία Εξοικονόμηση
Κείμενο Εκκλησίας του Τιμίου Σταυρού στο Πελέντρι. Ελληνικά
 1 Κείμενο Εκκλησίας του Τιμίου Σταυρού στο Πελέντρι Ελληνικά 2 ΕΚΚΛΗΣΙΑ ΤΟΥ ΤΙΜΙΟΥ ΣΤΑΥΡΟΥ ΣΤΟ ΠΕΛΕΝΤΡΙ Η εκκλησία του Τιμίου Σταυρού στο Πελέντρι φαίνεται να χτίστηκε λίγο μετά τα μέσα του 12 ου αιώνα
1 Κείμενο Εκκλησίας του Τιμίου Σταυρού στο Πελέντρι Ελληνικά 2 ΕΚΚΛΗΣΙΑ ΤΟΥ ΤΙΜΙΟΥ ΣΤΑΥΡΟΥ ΣΤΟ ΠΕΛΕΝΤΡΙ Η εκκλησία του Τιμίου Σταυρού στο Πελέντρι φαίνεται να χτίστηκε λίγο μετά τα μέσα του 12 ου αιώνα
Βασικές Γεωμετρικές έννοιες
 Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
2 ος. Γυμνασίου. ΘΕΜΑ 1 ο Με τα. αριθμός που μπορούμε να σχηματίσουμε ώστε. Απάντηση = β) Γνωρίζουμε ότι διψήφιο τμήμα
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΡΑΡΤΗΜΑ ΗΜΑΘΙΑ ΑΣ 2 ος Ημαθιώτικος Μαθητικός Διαγωνισμός στα Μαθηματικά. «Κ. ΚΑΡΑΘΕΟΔΩΡΗ» Σάββατο 23 Ιανουαρίου 2010 Α Γυμνασίου ΘΕΜΑ 1 ο Με τα ψηφία 0, 1, 2, 3, 4, 5 σχηματίζουμ
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ ΠΑΡΑΡΤΗΜΑ ΗΜΑΘΙΑ ΑΣ 2 ος Ημαθιώτικος Μαθητικός Διαγωνισμός στα Μαθηματικά. «Κ. ΚΑΡΑΘΕΟΔΩΡΗ» Σάββατο 23 Ιανουαρίου 2010 Α Γυμνασίου ΘΕΜΑ 1 ο Με τα ψηφία 0, 1, 2, 3, 4, 5 σχηματίζουμ
Η τέχνη των Μαθηματικών και τα Μαθηματικά της τέχνης
 Η τέχνη των Μαθηματικών και τα Μαθηματικά της τέχνης Γεωμετρία και Τέχνη από την Αρχαιότητα έως σήμερα! Η έρευνά μας εστίασε στην εξελικτική πορεία της Τέχνης και τη συνεχή αλληλεπίδρασή της με θεμελιώδεις
Η τέχνη των Μαθηματικών και τα Μαθηματικά της τέχνης Γεωμετρία και Τέχνη από την Αρχαιότητα έως σήμερα! Η έρευνά μας εστίασε στην εξελικτική πορεία της Τέχνης και τη συνεχή αλληλεπίδρασή της με θεμελιώδεις
Σκοπεύουμε να επιδιορθώσουμε έναν παλιό φράχτη σε ένα αγρόκτημα και για την καταγραφή των υλικών μετράμε τις αποστάσεις ανάμεσα στους πασσάλους.
 ΜΑΘΗΜΑ 6Ο Σκοπεύουμε να επιδιορθώσουμε έναν παλιό φράχτη σε ένα αγρόκτημα και για την καταγραφή των υλικών μετράμε τις αποστάσεις ανάμεσα στους πασσάλους. Αυτές οι μετρήσεις αποκαλύπτουν ότι οι πάσσαλοι
ΜΑΘΗΜΑ 6Ο Σκοπεύουμε να επιδιορθώσουμε έναν παλιό φράχτη σε ένα αγρόκτημα και για την καταγραφή των υλικών μετράμε τις αποστάσεις ανάμεσα στους πασσάλους. Αυτές οι μετρήσεις αποκαλύπτουν ότι οι πάσσαλοι
ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ. Γεωμετρικά στερεά - Ο όγκος. Ενότητα 8. β τεύχος
 ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 49 Γεωμετρικά στερεά - Ο όγκος Ενότητα 8 β τεύχος Γεωμετρικά στερεά - Ο όγκος 49 1η Άσκηση Να αναγνωρίσεις τα γεωμετρικά στερεά που σχηματίζουν τα παρακάτω αναπτύγματα:
ΜΑΘΗΜΑΤΙΚΑ Ε ΔΗΜΟΤΙΚΟΥ ΤΕΤΡΑΔΙΟ ΕΡΓΑΣΙΩΝ 49 Γεωμετρικά στερεά - Ο όγκος Ενότητα 8 β τεύχος Γεωμετρικά στερεά - Ο όγκος 49 1η Άσκηση Να αναγνωρίσεις τα γεωμετρικά στερεά που σχηματίζουν τα παρακάτω αναπτύγματα:
σχετικά με τον ιμπρεσιονισμό
 Impressionism and Postimpressionism Ιμπρεσιονισμός και Μεταϊμπρεσσιονισμός Monet Van Gogh Σχέδιο Εργασίας: Μεγάλοι Ζωγράφοι Μαρία Κασαπίδη Ιούνιος 2007 σχετικά με τον ιμπρεσιονισμό Ο Ιμπρεσιονισμός είναι
Impressionism and Postimpressionism Ιμπρεσιονισμός και Μεταϊμπρεσσιονισμός Monet Van Gogh Σχέδιο Εργασίας: Μεγάλοι Ζωγράφοι Μαρία Κασαπίδη Ιούνιος 2007 σχετικά με τον ιμπρεσιονισμό Ο Ιμπρεσιονισμός είναι
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ. 3 2 x. β)
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
Στρατηγικές Artful thinking και παραγωγή γραπτών μαθητικών κειμένων: Ένα παράδειγμα εφαρμογής στο Τμήμα Ένταξης
 Στρατηγικές Artful thinking και παραγωγή γραπτών μαθητικών κειμένων: Ένα παράδειγμα εφαρμογής στο Τμήμα Ένταξης 7 ο ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΕΥΟΣΜΟΥ Αραμπατζής Κωνσταντίνος ΠΕ 70ΕΑΕ Με λίγα λόγια.. Ο έντεχνος
Στρατηγικές Artful thinking και παραγωγή γραπτών μαθητικών κειμένων: Ένα παράδειγμα εφαρμογής στο Τμήμα Ένταξης 7 ο ΔΗΜΟΤΙΚΟ ΣΧΟΛΕΙΟ ΕΥΟΣΜΟΥ Αραμπατζής Κωνσταντίνος ΠΕ 70ΕΑΕ Με λίγα λόγια.. Ο έντεχνος
