Σύνοψη Προηγούµενου. Κανονικές Γλώσσες (1) Προβλήµατα και Γλώσσες. Σε αυτό το µάθηµα. ιαδικαστικά του Μαθήµατος.
|
|
|
- Αμύντα Δράκος
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Σύνοψη Προηγούµενου Κανονικές Γλώσσες () ιαδικαστικά του Μαθήµατος. Ορέστης Τελέλης Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Εισαγωγή: Υπολογισιµότητα και Πολυπλοκότητα. Βασικές έννοιες, ιστορικά στοιχεία. Κάτω ϕράγµα πολυπλοκότητας της ταξινόµησης. Το πρόβληµα του τερµατισµού. Προβλήµατα Απόφασης. Ο. Τελέλης Κανονικές Γλώσσες () / 48 Ο. Τελέλης Κανονικές Γλώσσες () 2 / 48 Σε αυτό το µάθηµα Προβλήµατα και Γλώσσες Μελετάµε Προβλήµατα Απόφασης. Ζητείται ο σχεδιασµός αλγορίθµου που αποφασίζει «ΝΑΙ» ή «ΟΧΙ». Αλφάβητα, λέξεις, γλώσσες. Η (κυρίως, µη) ύπαρξη αλγορίθµου είναι αντικείµενο της Υπολογισιµότητας. Εισαγωγή στις Κανονικές Γλώσσες Regulr Lnguges Πεπερασµένα Ντετερµινιστικά Αυτόµατα. Deterministic Finite Automt DFAs Εισαγωγή στα Μη Ντετερµινιστικά Πεπερασµένα Αυτόµατα. Non-deterministic Finite Automt Οι ελάχιστες απαιτήσεις σε πόρους των δυνατών αλγορίθµων είναι αντικείµενο της Πολυπλοκότητας. Παράδειγµα: Κύκλος Hmilton σε γράφηµα. Πρόβληµα Εύρεσης: Να περιγραφεί αλγόριθµος που υπολογίζει έναν κύκλο Hmilton, σε γράφηµα εισόδου, G(V, E), αν αυτός ο κύκλος υπάρχει. 2 Πρόβληµα Απόφασης: Να περιγραφεί αλγόριθµος που, για είσοδο ένα γράφηµα G(V, E), να απαντά «ΝΑΙ» ή «ΟΧΙ», αν το G έχει, ή δεν έχει κύκλο Hmilton, αντιστοίχως. Αν λύσουµε το, αυτοµάτως έχουµε λύσει και το 2. Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 4 / 48
2 Προβλήµατα και Γλώσσες Αλφάβητο και Λέξεις Τα προβλήµατα απόφασης µπορούν να περιγραφούν µε τυπικές γλώσσες. Οι γλώσσες είναι σύνολα λέξεων. Μια λέξη είναι µια ακολουθία συµβόλων από ένα δεδοµένο αλφάβητο. Χρησιµοποιούµε λέξεις για να περιγράψουµε την είσοδο µηχανές των υπολογιστικών µας µοντέλων. εδοµένης µιας λέξης, οι µηχανές ϑα απαντούν: «ΝΑΙ», αν η λέξη ανήκει στη γλώσσα. «ΟΧΙ», διαφορετικά. Εποµένως: Γλώσσα Πρόβληµα (απόφασης) και Λέξη Είσοδος. Αλφάβητο: πεπερασµένο, µη κενό σύνολο από σύµβολα. Π.χ., Σ = {, }, Σ = {,, c }. Η ακόµα: Σ = { while, void, int, for, if... } Λέξη/Συµβολοσειρά: πεπερασµένη ακολουθία συµβόλων του αλφαβήτου Σ. Π.χ.,, c, ή ένα πρόγραµµα σε C (ή Jv, ή C++,... ) Μήκος λέξης: πλήθος συµβόλων της λέξης, συµβ. µε w. Κενή Λέξη: Λέξη µηδενικού µήκους, συµβολίζεται µε ɛ. Σ k : σύνολο λέξεων µήκους k που αποτελούνται από σύµβολα του Σ. {, } 2 = {,,, }. {,, c }2 = {, c, c, c, c, }. Σ : σύνολο όλων των λέξεων επί του Σ: Σ = k N Σk Π.χ., {, } = { ɛ,,,,,,,,,... }. Ο. Τελέλης Κανονικές Γλώσσες () 5 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 6 / 48 Πράξεις µε Λέξεις Τυπικές Γλώσσες Παράθεση των x και y: x y ή απλώς xy. Π.χ., παράθεση των και δίνει. Επανάληψη της λέξης w k ϕορές: w k = k ϕορές {}}{ w w w. Αντίστροφη w R της λέξης w: προκύπτει γράφοντας την w από το τέλος προς την αρχή. Π.χ., () R =, (cc) R = cc. Παλινδροµική λέξη w αν w = w R : π.χ., () R =. Για κάθε δύο λέξεις x και y είναι (x y) R = y R x R. Η x είναι υπολέξη της w αν w = y x z. Μπορεί να είναι y = ɛ ή z = ɛ (ή και τα δύο). Τυπική Γλώσσα L επί του αλφαβήτου Σ: Ενα συγκεκριµένο υποσύνολο του Σ. Με άπειρο ή πεπερασµένο πλήθος συµβολοσειρών (λέξεων) - αριθµήσιµο. Μερικά παραδείγµατα γλωσσών επί του αλφαβήτου Σ = {,, 2 }: L = { 2, 2, 2, 2, 2, 2 } = Σ 3 L 2 = { ɛ,,,,... } L 3 = { w Σ : το τελευταίο ψηφίο του w είναι }. L 4 = { } = (η κενή γλώσσα). L 5 = { ɛ } η γλώσσα που περιέχει µόνο την κενή λέξη. L 6 = { w : w συντακτικά ορθό πρόγραµµα σε C } = Γλώσσα C Κάθε συντακτικά ορθό πρόγραµµα είναι µία λέξη της γλώσσας. Ο. Τελέλης Κανονικές Γλώσσες () 7 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 8 / 48
3 Πράξεις µε Γλώσσες Πράξεις Συνόλων: ένωση, τοµή, διαφορά, συµπλήρωµα. Παράθεση γλωσσών L και L 2 επί του αλφαβήτου Σ : L L 2 = { w Σ : w = x x 2, για x L και x 2 L 2 } = L L2 Π.χ., αν L = {,, } και L 2 = { ɛ, }: L L 2 = {,,,,, } Παράθεση Γλώσσας µε την ίδια: L 2 = { w Σ : w = x x 2, για x L και x 2 L } Παράθεση Γλώσσας k φορές: L k = { w Σ : w = x x 2 x k, για x, x 2,..., x k L } Ο. Τελέλης Κανονικές Γλώσσες () 9 / 48 Πράξεις µε Γλώσσες Παράθεση οποιουδήποτε (πεπερασµένου) πλήθους λέξεων της L: L = L k (Παρατήρηση: k.) k N Παράδειγµα: αν L = {, }, τότε: L = { ɛ,,,,,,,,... } Αν L = { ɛ }, τότε L = { ɛ }. Αν L =, τότε L = { ɛ }. Παράθεση ϑετικού πεπερασµένου πλήθους λέξεων της L: L + = L k (Παρατήρηση: k.) k Z + Πότε είναι L = L + ; Ο. Τελέλης Κανονικές Γλώσσες () / 48 Αναπαράσταση Γλωσσών Με απλή απαρίθµηση των λέξεών τους, όταν είναι πεπερασµένες. Μέσω κοινής χαρακτηριστικής ιδιότητας που έχουν οι λέξεις: Π.χ., L = { w {, } : w έχει άρτιο πλήθος από } Π.χ., L 2 = { n n : n }. Κανονικές Γλώσσες Μέσω συνολοθεωρητικών πράξεων επί άλλων γλωσσών, π.χ., L L 2. Μέσω γραµµατικών, που αποτελούν µηχανισµούς παραγωγής λέξεων της γλώσσας. Μέσω υπολογιστικών µηχανών (ισοδύναµα: αλγορίθµων) που αποφασίζουν αν µια λέξη ανήκει στη γλώσσα ή όχι. Π.χ., ένας συντακτικός αναλυτής που αποφασίζει αν ένα πρόγραµµα C είναι ορθό ή όχι. Ο. Τελέλης Κανονικές Γλώσσες () / 48 Ο. Τελέλης Κανονικές Γλώσσες () 2 / 48
4 Πεπερασµένα Αυτόµατα Παράδειγµα: Αυτόµατη Πόρτα Μονής Κατεύθυνσης Deterministic Finite Automt (DFA ) Υπολογιστές µε πολύ µικρή µνήµη. Τα συναντάµε συχνά στην καθηµερινότητά µας. Αποτελούν τη ϐάση λειτουργίας ηλετροµηχανικών συσκευών και πολλών άλλων διεπαφών µε τις οποίες έχουµε εκτεταµένη εµπειρία. Προδιαγραφές Λειτουργίας Η πόρτα ανοίγει προς τα µέσα (δεν είναι συρόµενη). Ανοίγει όταν: εν είναι ανοιχτή. Ανιχνεύεται παρουσία έξω. εν ανιχνεύεται παρουσία µέσα (ώστε να µην χτυπήσει ο µέσα). Κλείνει όταν: Είναι ανοιχτή. εν ανιχνεύεται παρουσία πουθενά (µέσα ή έξω). Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 4 / 48 Παράδειγµα: Αυτόµατη Πόρτα Μονής Κατεύθυνσης Παράδειγµα: Αυτόµατη Πόρτα Μονής Κατεύθυνσης ΜΕΣΑ, ΠΑΝΤΟΥ, ΠΟΥΘΕΝΑ ΕΞΩ Ενας τυποποιηµένος τρόπος αναπαράστασης της πόρτας. Ενας υπολογιστής µε µνήµη it (ΑΝΟΙΚΤΑ ΚΛΕΙΣΤΑ ). ΚΛΕΙΣΤΑ ΠΟΥΘΕΝΑ ΑΝΟΙΚΤΑ ΕΞΩ, ΜΕΣΑ, ΠΑΝΤΟΥ Ενας ανελκυστήρας χρειάζεται λίγη περισσότερη µνήµη. Αλλα παραδείγµατα: οικιακές συσκευές, τµήµατα αριθµοµηχανών, ψηφιακών ϱολογιών. Πιθανοτικό αντίστοιχο των πεπερασµένων αυτοµάτων: Αλυσίδες Mrkov Ο. Τελέλης Κανονικές Γλώσσες () 5 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 6 / 48
5 Παράδειγµα Πεπερασµένου Αυτοµάτου Παράδειγµα Πεπερασµένου Αυτοµάτου q q 2 q 3 q q 2 q 3,, Παράδειγµα Εκτέλεσης για Είσοδο : ιάγραµµα Καταστάσεων Τρεις καταστάσεις, q, q 2, q 3. Αρχική Κατάσταση: q. Κατάσταση Αποδοχής: q 2. Μεταβάσεις µεταξύ καταστάσεων. q q 2 q 2 q 3 q 2 Παράδειγµα Εκτέλεσης για Είσοδο : (αποδοχή) q q q 2 q 3 q 2 q 3 q 2 Μερικές ενδεικτικές δοκιµές ακόµα: (αποδοχή),,,,, Ο. Τελέλης Κανονικές Γλώσσες () 7 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 8 / 48 Παράδειγµα Πεπερασµένου Αυτοµάτου Πεπερασµένα Αυτόµατα q q 2 q 3, Παράδειγµα Εκτέλεσης για Είσοδο : Ορισµός Μια πεντάδα (Q, Σ, δ, q, F), όπου: Q είναι ένα πεπερασµένο σύνολο καταστάσεων. 2 Σ είναι ένα πεπερασµένο σύνολο που ονοµάζεται αλφάβητο. q q 2 q 2 q 3 q 2 (αποδοχή) 3 δ : Q Σ Q είναι η συνάρτηση µεταβάσεων. Παράδειγµα Εκτέλεσης για Είσοδο : q q q 2 q 3 q 2 q 3 q 2 Μερικές ενδεικτικές δοκιµές ακόµα: (αποδοχή) 4 q Q είναι η αρχική κατάσταση. 5 F Q είναι το σύνολο των καταστάσεων αποδοχής.,,,,, Αποδέχεται τις λέξεις που τελειώνουν σε: ακολουθούµενο από άρτιο πλήθος. Ο. Τελέλης Κανονικές Γλώσσες () 8 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 9 / 48
6 Παράδειγµα Γλώσσες Αυτοµάτων q q 2 q 3, Ενα πεπερασµένο αυτόµατο M (Q, Σ, δ, q, F), όπου: Q = { q, q 2, q 3 }. 2 Σ = {, }. 3 Αρχική κατάσταση, q. 4 Καταστάσεις αποδοχής, F = {q 2 }. Συνάρτηση Μεταβάσεων, δ: δ q q q 2 q 2 q 3 q 2 q 3 q 2 q 2 Εάν A είναι το σύνολο των λέξεων που αποδέχεται το αυτόµατο M, λέµε ότι το A είναι η γλώσσα του M και γράφουµε L(M) = A. Επίσης λέµε ότι το M αποδέχεται ή αναγνωρίζει την A. Ενα αυτόµατο αναγνωρίζει / αποδέχεται την A αν αποδέχεται όλες τις λέξεις που ανήκουν στην A και µόνον αυτές. Ενα αυτόµατο αποδέχεται πολλές λέξεις, αλλά αναγνωρίζει µία µόνο γλώσσα. Αν δεν αποδέχεται καµία λέξη, τότε αναγνωρίζει την κενή γλώσσα,. Ο. Τελέλης Κανονικές Γλώσσες () 2 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 2 / 48 Παραδείγµατα () Παραδείγµατα () q q 2 Τυπική Περιγραφή: q q 2 Τυπική Περιγραφή: M 2 = ( Q = { q, q 2 }, Σ = {, }, δ, q, F = { q 2 } ) δ q q q 2 q 2 q q 2 Ποια γλώσσα αναγνωρίζει το M 2 ; Ενδεικτικές δοκιµές:,. ιαπιστώνουµε πειραµατικά ότι: L(M 2 ) = { w w τελειώνει σε }. Ο. Τελέλης Κανονικές Γλώσσες () 22 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 22 / 48
7 Παραδείγµατα (2) Παραδείγµατα (2) q q 2 q q 2 Τυπική Περιγραφή: Τυπική Περιγραφή: M 3 = ( Q = { q, q 2 }, Σ = {, }, δ, q, F = { q } ) δ q q q 2 q 2 q q 2 Ποια γλώσσα αναγνωρίζει το M 3 ; Ενδεικτικές δοκιµές:,. Ο. Τελέλης Κανονικές Γλώσσες () 23 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 23 / 48 Παραδείγµατα (2) Παραδείγµατα (ΙΙ) q q 2 s q r Τυπική Περιγραφή: M 3 = ( Q = { q, q 2 }, Σ = {, }, δ, q, F = { q } ) δ q q q 2 q 2 q q 2 q 2 r 2 Τυπική Περιγραφή: Ποια γλώσσα αναγνωρίζει το M 3 ; Ενδεικτικές δοκιµές:,. ιαπιστώνουµε πειραµατικά ότι: L(M 3 ) = { w w = ή w τελειώνει σε }. Παρατήρηση: Το M 3 αποδέχεται την κενή λέξη, ɛ. Ο. Τελέλης Κανονικές Γλώσσες () 23 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 24 / 48
8 Παραδείγµατα (ΙΙ) Παραδείγµατα (ΙΙ) s q r q 2 r 2 δ s q r q q q 2 q 2 q q 2 r r 2 r r 2 r 2 r s q r q 2 r 2 δ s q r q q q 2 q 2 q q 2 r r 2 r r 2 r 2 r Τυπική Περιγραφή: M 4 = ( Q = { s, q, q 2, r, r 2 }, Σ = {, }, δ, s, F = { q, r } ) Ποια γλώσσα αναγνωρίζει το M 4 ; Ενδεικτικές δοκιµές:,,,,,,, Τυπική Περιγραφή: M 4 = ( Q = { s, q, q 2, r, r 2 }, Σ = {, }, δ, s, F = { q, r } ) Ποια γλώσσα αναγνωρίζει το M 4 ; Ενδεικτικές δοκιµές:,,,,,,, L(M 4 ) = { w η w αρχίζει και τελειώνει µε: ή µε }. Ο. Τελέλης Κανονικές Γλώσσες () 24 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 24 / 48 Παραδείγµατα (ΙΙΙ) Παραδείγµατα (ΙΙΙ) q Τυπική Περιγραφή: M 5 = ( Q = {q, q, q 2 }, Σ = {,, 2, RESET }, δ q, F = { q } ) Αλφάβητο: Σ == {,, 2, RESET }. 2, RESET 2 Προσοχή: το RESET είναι ένα σύµβολο. Συνάρτηση µεταβάσεων, δ: q 2 q 2, RESET, RESET Ποιά είναι η τυπική περιγραφή του αυτοµάτου; Ποιά γλώσσα αναγνωρίζει; Γλώσσα που αναγνωρίζει το M 5 : δ 2 RESET q q q q 2 q q q q 2 q q q 2 q 2 q q q L(M 5 ) = { w w τελειώνει σε RESET ή ( i w i ) mod 3 = } Ο. Τελέλης Κανονικές Γλώσσες () 25 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 26 / 48
9 Ορισµός Υπολογισµού Σχεδίαση Πεπερασµένων Αυτοµάτων Εστω M = (Q, Σ, δ, q, F) πεπερασµένο αυτόµατο και w = w w 2... w n µια συµβολοσειρά εισόδου, όπου w i Σ, για i =,..., n. Το M αποδέχεται την w αν υπάρχει ακολουθία καταστάσεων r, r,..., r n Q που ικανοποιεί τις συνθήκες: r = q. 2 δ(r i, w i+ ) = r i+. 3 r n F. Ορισµός Μια γλώσσα λέγεται κανονική εάν υπάρχει πεπερασµένο αυτόµατο που την αναγνωρίζει. Υποθέτουµε ότι πρέπει να αποφασίσουµε αν µια δεδοµένη λέξη ανήκει ή όχι σε δεδοµένη γλώσσα. Μετά από κάθε σύµβολο, πρέπει να αποφαινόµαστε αν το τµήµα της λέξης που διαβάσαµε ως τώρα ανήκει ή όχι στη γλώσσα. εν µπορούµε να ϑυµόµαστε όλα τα σύµβολα που έχουµε διαβάσει. Αρκεί να ϑυµόµαστε τις κρίσιµες πληροφορίες, που εξαρτώνται από την εκάστοτε γλώσσα. Ο. Τελέλης Κανονικές Γλώσσες () 27 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 28 / 48 Παράδειγµα Σχεδίασης (α) Παράδειγµα Σχεδίασης (β) εδοµένα: Αλφάβητο εισόδου: {, }. Ζητούµενη Γλώσσα: όλες οι λέξεις µε περιττό πλήθος από. Σκεπτικό: ε µπορούµε ούτε χρειάζεται να ϑυµόµαστε το ακριβές πλήθος των. Αρκεί να ϑυµόµαστε δύο περιπτώσεις:. Εχουµε διαβάσει άρτιο πλήθος από µέχρι στιγµής. Αρχική είναι η q α : αρχικά έχουµε διαβάσει µηδέν (άρτιο) πλήθος : q α q π 2. Εχουµε διαβάσει περιττό πλήθος από µέχρι στιγµής. Εποµένως, δύο καταστάσεις: q α q π Ο. Τελέλης Κανονικές Γλώσσες () 29 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48
10 Παράδειγµα Σχεδίασης (β) Παράδειγµα Σχεδίασης (β) Αποδοχής είναι η q π : όπου ϑα έχουµε διαβάσει περιττό πλήθος : Ανάγνωση µας αφήνει στην ίδια κατάσταση: δε µεταβάλλει το πλήθος των : q α q π q α q π Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48 Παράδειγµα Σχεδίασης (β) Παράδειγµα Σχεδίασης (2α) Ανάγνωση προκαλεί µετάβαση από την κάθε κατάσταση στην άλλη: q α q π εδοµένα: Αλφάβητο εισόδου: {, }. Ζητούµενη Γλώσσα: όλες οι λέξεις που περιέχουν την υπολέξη. Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 3 / 48
11 Παράδειγµα Σχεδίασης (2β) Παράδειγµα Σχεδίασης (2γ) Σκεπτικό: Ολα τα που προηγούνται πρέπει να «αγνοηθούν». Αρχική κατάσταση q, στην οποία «αγνοούνται» τα. Το πρώτο που διαβάζεται ίσως είναι το πρώτο του. Μία κατάσταση q για το πρώτο που διαβάζουµε. Το δεύτερο που διαβάζεται ίσως είναι το δεύτερο του. Κατάσταση q όπου µεταβαίνουµε από την q µε ανάγνωση. Αν στην q διαβάσουµε, τότε αποδεχόµαστε: Κατάσταση αποδοχής q, όπου µεταβαίνουµε από την q µε ανάγνωση. Ανάγνωση στην q αποκλείει το που προηγήθηκε να ανήκει σε. q q q q Θέλουµε να αγνοήσουµε όλα τα επόµενα που µπορεί να διαβάσουµε. q q q q Ο. Τελέλης Κανονικές Γλώσσες () 32 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 33 / 48 Παράδειγµα Σχεδίασης (2γ) Παράδειγµα Σχεδίασης (2γ) Ανάγνωση στην q δε µας πειράζει (παρότι είναι το τρίτο τουλάχιστον): q q q q Ισως αυτό να είναι το «δεύτερο» της που ψάχνουµε. Εφόσον έχουµε δεί, παραµένουµε σε κατάσταση αποδοχής q :, q q q q Η λέξη ανήκει στη δεδοµένη γλώσσα, ό,τι σύµβολο κι αν ακολουθεί τα. Ο. Τελέλης Κανονικές Γλώσσες () 33 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 33 / 48
12 Παραδείγµατα Σχεδιασµού Αυτοµάτων Παραδείγµατα Σχεδιασµού Αυτοµάτων (/2) Για καθεµία από τις ακόλουθες γλώσσες, να σχεδιαστεί ένα πεπερασµένο αυτόµατο. Το σύνολο των δυαδικών συµβολοσειρών που: (α) αρχίζουν µε. (β) περιέχουν δύο συνεχόµενα. (γ) δεν περιέχουν δύο συνεχόµενα. (δ) τελειώνουν µε. (ε) περιέχουν τουλάχιστον δύο. s 3,, (α) s s s 2, (β) s s s 2, (γ) s s s 2 Ο. Τελέλης Κανονικές Γλώσσες () 34 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 35 / 48 Παραδείγµατα Σχεδιασµού Αυτοµάτων (2/2) Κανονικές Πράξεις (δ) s s s 2 Ορισµός Εστω δύο γλώσσες A και B. Ορίζουµε τις κανονικές πράξεις: Ενωση: A B = { x x A ή x B }. Παράθεση: A B = { xy x A και y B }. (ε), s s s 2 Σώρευση: A = { x x 2... x k k και κάθε x i A}. Μας ενδιαφέρει η κλειστότητα των κανονικών γλωσσών ως προς τις κανονικές πράξεις. ηλαδή, ότι αν αυτές εφαρµοστούν σε κανονικές γλώσσες, δίνουν κανονικές γλώσσες. Ο. Τελέλης Κανονικές Γλώσσες () 36 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 37 / 48
13 Κανονικές Πράξεις Θεώρηµα Αν L, L 2 κανονικές γλώσσες, η L L 2 είναι κανονική. ΑΠΟ ΕΙΚΤΙΚΗ Ι ΕΑ ίνονται κανονικές γλώσσες A, A 2. Θα δείξουµε ότι A A 2 κανονική. Για τις A, A 2 υπάρχει ένα αυτόµατο, M, M 2, που την αναγνωρίζει. Θα κατασκευάσουµε ένα αυτόµατο, M, που αναγνωρίζει την A A 2. ΑΠΟ ΕΙΚΤΙΚΗ Ι ΕΑ (συνέχεια) Πώς «ακολουθούµε» την εκτέλεση και των δύο µε πεπερασµένη µνήµη; Θα πρέπει να ϑυµόµαστε Ϲεύγη καταστάσεων. Συνεπώς, το M ϑα πρέπει να έχει Q = Q Q 2 καταστάσεις. Οι µεταβάσεις του M ϑα οδηγούν από ένα Ϲεύγος σε ένα άλλο. Καταστάσεις αποδοχής: Ϲεύγη που περιλαµβάνουν κατάσταση αποδοχής του M, ή του M 2. Θα κατασκευάσουµε το M από τα M, M 2, που προσοµοιώνει τα M, M 2. Ο. Τελέλης Κανονικές Γλώσσες () 38 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 39 / 48 Παράδειγµα Παράδειγµα q q 2, q 3 M M 2 r r 2 Ζητείται αυτόµατο M που αναγνωρίζει τη γλώσσα L(M ) L(M 2 ). Ποιές είναι οι L(M ) και L(M 2 ); Το M ϑα πρέπει να αποδέχεται µια λέξη w αν και µόνο αν: Το M ϑα έχει Q Q 2 καταστάσεις: r q r q 2 r q 3 r 2 q r 2 q 2 r 2 q 3 Μία κατάσταση για κάθε Ϲευγάρι καταστάσεων από τα M, M 2. είτε w L(M ) είτε w L(M 2 ) (είτε ανήκει και στις δύο). Ο. Τελέλης Κανονικές Γλώσσες () 4 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 4 / 48
14 Παράδειγµα Παράδειγµα Αρχική κατάσταση του M είναι το Ϲεύγος αρχικών καταστάσεων των M, M 2 : r q r q 2 r q 3 r q r q 2 r q 3 r 2 q r 2 q 2 r 2 q 3 Κατ/σεις Αποδοχής του M: Ϲεύγη µε κατ. αποδοχής είτε του M είτε του M 2. r 2 q r 2 q 2 r 2 q 3 Ο. Τελέλης Κανονικές Γλώσσες () 4 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 4 / 48 Τυπική Σύνοψη Κατασκευής Κλειστότητα ως προς Παράθεση; Σύνολο καταστάσεων: Q = Q Q 2, δηλαδή: Q = { (q, q ) q Q και q Q 2 } Συνάρτηση µεταβάσεων: Για κάθε (q, q ) Q, και Σ: ( ) ( ) δ (q, q ), = δ (q, ), δ 2 (q, ) Αρχική Κατάσταση: (q, q 2 ) (αρχικές των M, M 2 αντίστοιχα). { Καταστάσεις αποδοχής: F = (q, q ) q F ή q F 2 }: Ισοδύναµα: F = (F Q 2 ) (Q F 2 ) ( ιαφορετικό από F = F F 2 : τι δίνει αυτό;) Θεώρηµα Αν L, L 2 κανονικές γλώσσες, η L L 2 είναι κανονική. ΑΠΟ ΕΙΚΤΙΚΗ Ι ΕΑ οκιµάζουµε την προηγούµενη τεχνική (από την περίπτωση της ένωσης). Πώς να «στήσουµε» το M, από τα M, M 2, ώστε να αποδέχεται µια λέξη όταν: ένα πρώτο τµήµα της γίνεται αποδεκτό από το M, το υπόλοιπο γίνεται αποδεκτό από το M 2 ; Πρόβληµα: το M δε γνωρίζει «που να χωρίσει» την είσοδό του. Χρειαζόµαστε πιο «ισχυρό» ορισµό υπολογισµού για να συνεχίσουµε. Ο. Τελέλης Κανονικές Γλώσσες () 42 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 43 / 48
15 Μη ντετερµινισµός Εώς τώρα εξετάσαµε µόνο ντετερµινιστικά (αιτιοκρατικά) αυτόµατα. Μη ντετερµινιστικά Πεπερασµένα Αυτόµατα Non-deterministic Finite Automt NFA Κάθε µετάβαση ενός DFA καθορίζεται µονοσήµαντα µέσω της δ από: - Την τρέχουσα κατάσταση, r i, του αυτοµάτου, - το επόµενο σύµβολο εισόδου, α i+ Σ. Σε ένα NFA, η τρέχουσα κατάσταση και το επόµενο σύµβολο εισόδου µπορεί να οδηγούν ταυτόχρονα σε περισσότερες από µία µεταβάσεις!!! Κάθε ντετερµινιστικό αυτόµατο είναι τετριµένα και µη ντετερµινιστικό. Ο. Τελέλης Κανονικές Γλώσσες () 44 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 45 / 48 Παράδειγµα NFA Μη Ντετερµινιστικός Υπολογισµός Ενα NFA:,,, ɛ q q 2 q 3 q 4 ιαφορές µε τα ντετερµινιστικά πεπερασµένα αυτόµατα: Ιδιο σύµβολο σε ίδια κατάσταση = διαφορετικές µεταβάσεις. Η κενή λέξη, ɛ, µπορεί επίσης να ενεργοποιεί µεταβάσεις. Από την ίδια κατάσταση: µηδέν, µία, ή περισσότερες ɛ-µεταβάσεις. Από οποιαδήποτε κατάσταση, για οποιοδήποτε σύµβολο: µπορεί «να µην υπάρχουν» µεταβάσεις. Ενα NFA ακολουθεί από µια κατάσταση παράλληλα όλες τις µεταβάσεις, που αντιστοιχούν στο τρέχον σύµβολο εισόδου. Το NFA «διασπάται» σε πολλαπλά αντίγραφα του εαυτού του και ακολουθεί όλες τις δυνατότητες παράλληλα. Τα προηγούµενα ισχύουν και για την περίπτωση που µία ή περισσότερες µεταβάσεις από την τρέχουσα κατάσταση επιγράφονται µε το σύµβολο ɛ. Το NFA αποδέχεται την είσοδό του εάν στο τέλος της ανάγνωσης της εισόδου υπάρχει έστω και ένα αντίγραφο που ϐρίσκεται σε κατάσταση αποδοχής. Ο. Τελέλης Κανονικές Γλώσσες () 46 / 48 Ο. Τελέλης Κανονικές Γλώσσες () 47 / 48
16 Μη Ντετερµινιστικός Υπολογισµός,, NFA:, ɛ q q 2 q 3 q 4 Παράδειγµα Εκτέλεσης για Είσοδο : q q q 3 q 2 q q 3 q q 4 q 3 q 2 q q 4 q 4 q 3 q 2 q q 4 q 4 q 3 q Ο. Τελέλης Κανονικές Γλώσσες () 48 / 48
Ποιές οι θεµελιώδεις δυνατότητες και ποιοί οι εγγενείς περιορισµοί των υπολογιστών ; Τί µπορούµε και τί δε µπορούµε να υπολογίσουµε (και γιατί);
 Μοντελοποίηση του Υπολογισµού Στοιχεία Θεωρίας Υπολογισµού (): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ποιές οι θεµελιώδεις δυνατότητες
Μοντελοποίηση του Υπολογισµού Στοιχεία Θεωρίας Υπολογισµού (): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ποιές οι θεµελιώδεις δυνατότητες
Στοιχεία Θεωρίας Υπολογισµού (1): Τυπικές Γλώσσες, Γραµµατικές
 Στοιχεία Θεωρίας Υπολογισµού (1): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Υπολογισµού 1 /
Στοιχεία Θεωρίας Υπολογισµού (1): Τυπικές Γλώσσες, Γραµµατικές Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Υπολογισµού 1 /
Σύνοψη Προηγούµενου. Κανονικές Γλώσσες (3) Παραδείγµατα µε Κανονικές Εκφράσεις. Σε αυτό το µάθηµα.
 Σύνοψη Προηγούµενου Κανονικές Γλώσσες (3) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς (Ντετερµινιστική) Κλειστότητα Κανονικών Γλωσσών ως προς Ενωση. Κατασκευή: DFA
Σύνοψη Προηγούµενου Κανονικές Γλώσσες (3) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς (Ντετερµινιστική) Κλειστότητα Κανονικών Γλωσσών ως προς Ενωση. Κατασκευή: DFA
Στοιχεία Θεωρίας Υπολογισµού (2): Πεπερασµένα Αυτόµατα, Κανονικές Εκφράσεις
 Στοιχεία Θεωρίας Υπολογισµού (2): Πεπερασµένα Αυτόµατα, Κανονικές Εκφράσεις Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Υπολογισµού
Στοιχεία Θεωρίας Υπολογισµού (2): Πεπερασµένα Αυτόµατα, Κανονικές Εκφράσεις Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Υπολογισµού
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (1)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες () Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Πεπερασμένα Αυτόματα (Κεφάλαιο., Sipser) Ορισμός πεπερασμένων αυτομάτων και ορισμός του
Γενικές Παρατηρήσεις. Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα (1) Το Λήµµα της Αντλησης. Χρήση του Λήµµατος Αντλησης.
 Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
Γενικές Παρατηρήσεις Μη Κανονικές Γλώσσες - Χωρίς Συµφραζόµενα () Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Υπάρχουν µη κανονικές γλώσσες, π.χ., B = { n n n }. Αυτό
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 3: Ντετερμινιστικά Πεπερασμένα Αυτόματα (DFA)
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 3: Ντετερμινιστικά Πεπερασμένα Αυτόματα (DFA) Τι θα κάνουμε σήμερα Εισαγωγή στα Ντετερμινιστικά Πεπερασμένα Αυτόματα 14-Sep-11 Τυπικός Ορισμός Ντετερμινιστικών
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 3: Ντετερμινιστικά Πεπερασμένα Αυτόματα (DFA) Τι θα κάνουμε σήμερα Εισαγωγή στα Ντετερμινιστικά Πεπερασμένα Αυτόματα 14-Sep-11 Τυπικός Ορισμός Ντετερμινιστικών
Σύνοψη Προηγούµενου. Γλώσσες χωρίς Συµφραζόµενα (2): Αυτόµατα Στοίβας. Παραδείγµατα Σχεδιασµού CFG. Παράδειγµα 1.
 Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα 2): Αυτόµατα Στοίβας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Μη Κανονικές Γλώσσες Το Λήµµα της Αντλησης για τις
Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα 2): Αυτόµατα Στοίβας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Μη Κανονικές Γλώσσες Το Λήµµα της Αντλησης για τις
ΠΛΗ30 ΕΝΟΤΗΤΑ 3: ΚΑΝΟΝΙΚΕΣ ΓΛΩΣΣΕΣ. Μάθηµα 3.2: ηµήτρης Ψούνης
 ΠΛΗ30 ΕΝΟΤΗΤΑ 3: ΚΑΝΟΝΙΚΕΣ ΓΛΩΣΣΕΣ Μάθηµα 3.2: Ντετερµινιστικά Πεπερασµένα Αυτόµατα ηµήτρης Ψούνης 2 ΠΕΡΙΕΧΟΜΕΝΑ Α. Σκοπός του Μαθήµατος Β. Θεωρία 1. Πεπερασµένα Αυτόµατα 1. Λειτουργία και Παραδείγµατα
ΠΛΗ30 ΕΝΟΤΗΤΑ 3: ΚΑΝΟΝΙΚΕΣ ΓΛΩΣΣΕΣ Μάθηµα 3.2: Ντετερµινιστικά Πεπερασµένα Αυτόµατα ηµήτρης Ψούνης 2 ΠΕΡΙΕΧΟΜΕΝΑ Α. Σκοπός του Μαθήµατος Β. Θεωρία 1. Πεπερασµένα Αυτόµατα 1. Λειτουργία και Παραδείγµατα
Η NTM αποδέχεται αν µονοπάτι στο δέντρο που οδηγεί σε αποδοχή.
 Μη ντετερµινιστικές Μηχανές Turing - NTMs (1/6) Μηχανές Turing: Μη ντετερµινισµός, Επιλύσιµα Προβλήµατα Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς 10 εκεµβρίου 2016
Μη ντετερµινιστικές Μηχανές Turing - NTMs (1/6) Μηχανές Turing: Μη ντετερµινισµός, Επιλύσιµα Προβλήµατα Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς 10 εκεµβρίου 2016
Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L. να αναγνωρίζει (ηµιαποφασίζει) µια γλώσσα L. 1. Η TM «εκτελεί» τον απαριθµητή, E.
 Οι γλώσσες των Μηχανών Turing Αποφασισιµότητα / Αναγνωρισιµότητα Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L Αποδέχεται όταν (η είσοδος στην TM) w L. Ορέστης Τελέλης telelis@unipi.gr Τµήµα
Οι γλώσσες των Μηχανών Turing Αποφασισιµότητα / Αναγνωρισιµότητα Μια TM µπορεί ένα από τα δύο: να αποφασίζει µια γλώσσα L Αποδέχεται όταν (η είσοδος στην TM) w L. Ορέστης Τελέλης telelis@unipi.gr Τµήµα
Σε αυτό το µάθηµα. Εισαγωγή στις Μηχανές Turing. Μηχανή Turing (Turing Machine - TM) Μηχανές Turing. Παραδείγµατα Μηχανών Turing
 Σε αυτό το µάθηµα Εισαγωγή στις Μηχανές Turing Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Παραδείγµατα Μηχανών Turing Παραλλαγές: Πολυταινιακές, Μη ντετερµινιστικές
Σε αυτό το µάθηµα Εισαγωγή στις Μηχανές Turing Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Παραδείγµατα Μηχανών Turing Παραλλαγές: Πολυταινιακές, Μη ντετερµινιστικές
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 4: Μη Ντετερμινιστικά (Αντιαιτιοκρατικά) Πεπερασμένα Αυτόματα (ΝFA)
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 4: Μη Ντετερμινιστικά (Αντιαιτιοκρατικά) Πεπερασμένα Αυτόματα (ΝFA) Τι θα κάνουμε σήμερα Εισαγωγή στα Μη Ντετερμινιστικά Πεπερασμένα Αυτόματα Τυπικός
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 4: Μη Ντετερμινιστικά (Αντιαιτιοκρατικά) Πεπερασμένα Αυτόματα (ΝFA) Τι θα κάνουμε σήμερα Εισαγωγή στα Μη Ντετερμινιστικά Πεπερασμένα Αυτόματα Τυπικός
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων Λύσεις Άσκηση Ορίζουμε τη συναρμογή δύο γλωσσών Α και Β ως ΑΒ = { uv u A, v B }. (α) Έστω Α = {α,β,γ} και Β =. Να περιγράψετε τη γλώσσα ΑΒ. (β) Θεωρήστε τις γλώσσες L, M και N. Να δείξετε
Σειρά Προβλημάτων Λύσεις Άσκηση Ορίζουμε τη συναρμογή δύο γλωσσών Α και Β ως ΑΒ = { uv u A, v B }. (α) Έστω Α = {α,β,γ} και Β =. Να περιγράψετε τη γλώσσα ΑΒ. (β) Θεωρήστε τις γλώσσες L, M και N. Να δείξετε
Αποφασισιµότητα / Αναγνωρισιµότητα. Μη Επιλύσιµα Προβλήµατα. Η έννοια της αναγωγής. Τερµατίζει µια δεδοµένη TM για δεδοµένη είσοδο;
 Αποφασισιµότητα / Αναγνωρισιµότητα Ορέστης Τελέλης telelis@unipi.gr Μη Επιλύσιµα Προβλήµατα Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς 2/12/2015 Ο. Τελέλης Πανεπιστήµιο Πειραιώς Αποφασισιµότητα 2/12/2015
Αποφασισιµότητα / Αναγνωρισιµότητα Ορέστης Τελέλης telelis@unipi.gr Μη Επιλύσιµα Προβλήµατα Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς 2/12/2015 Ο. Τελέλης Πανεπιστήµιο Πειραιώς Αποφασισιµότητα 2/12/2015
Γνωριµία. Θεωρία Υπολογισµού: Εισαγωγικά. Αντικείµενο Μαθήµατος. Επικοινωνία.
 Γνωριµία Θεωρία Υπολογισµού: Εισαγωγικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη
Γνωριµία Θεωρία Υπολογισµού: Εισαγωγικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη
Σύνοψη Προηγούµενου. Γλώσσες χωρίς Συµφραζόµενα (2) Ισοδυναµία CFG και PDA. Σε αυτό το µάθηµα. Αυτόµατα Στοίβας Pushdown Automata
 Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα (2) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Αυτόµατα Στοίβας Pushdown utomata Ισοδυναµία µε τις Γλώσσες χωρίς Συµφραζόµενα:
Σύνοψη Προηγούµενου Γλώσσες χωρίς Συµφραζόµενα (2) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Αυτόµατα Στοίβας Pushdown utomata Ισοδυναµία µε τις Γλώσσες χωρίς Συµφραζόµενα:
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Επανάληψη Μαθήματος
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Επανάληψη Μαθήματος Το Μάθημα σε μια Διαφάνεια Υπολογιστικά μοντέλα Κανονικές Γλώσσες Ντετερμινιστικά Αυτόματα Μη Ντετερμινιστικά Αυτόματα Κανονικές Εκφράσεις
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Επανάληψη Μαθήματος Το Μάθημα σε μια Διαφάνεια Υπολογιστικά μοντέλα Κανονικές Γλώσσες Ντετερμινιστικά Αυτόματα Μη Ντετερμινιστικά Αυτόματα Κανονικές Εκφράσεις
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 5: Κανονικές Εκφράσεις
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 5: Κανονικές Εκφράσεις Τι θα κάνουμε σήμερα Κλειστότητα Κανονικών Πράξεων (1.2.3) Εισαγωγή στις Κανονικές Εκφράσεις Τυπικός ορισμός της κανονικής
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 5: Κανονικές Εκφράσεις Τι θα κάνουμε σήμερα Κλειστότητα Κανονικών Πράξεων (1.2.3) Εισαγωγή στις Κανονικές Εκφράσεις Τυπικός ορισμός της κανονικής
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation
 Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Αυτόματα και Υπολογιστικά Μοντέλα Automata and Models of Computation Διδάσκων: Στάθης Ζάχος Επιμέλεια Διαφανειών: Μάκης Αρσένης CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Φεβρουάριος 2017 Διδάσκων: Στάθης Ζάχος ( CoReLab
Πεπερασμένα Αυτόματα. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Πεπερασμένα Αυτόματα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πεπερασμένα Αυτόματα είναι απλούστερες
Πεπερασμένα Αυτόματα ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Πεπερασμένα Αυτόματα είναι απλούστερες
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Κανονικές Εκφράσεις (1.3) Τυπικός Ορισμός Ισοδυναμία με κανονικές γλώσσες Μη Κανονικές
Θεωρία Υπολογισμού και Πολυπλοκότητα Κανονικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Κανονικές Εκφράσεις (1.3) Τυπικός Ορισμός Ισοδυναμία με κανονικές γλώσσες Μη Κανονικές
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσhmμy 6η ενότητα: Αυτόματα, τυπικές γλώσσες, γραμματικές Επιμέλεια διαφανειών: Στάθης Ζάχος, Άρης Παγουρτζής http://www.corelab.ece.ntua.gr/courses/introcs
Κανονικές Γλώσσες. ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης. Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών
 Κανονικές Γλώσσες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κανονικές Γλώσσες Κανονική γλώσσα αν
Κανονικές Γλώσσες ιδάσκοντες: Φ. Αφράτη,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Κανονικές Γλώσσες Κανονική γλώσσα αν
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου. Θεωρία Υπολογισμού. Ενότητα 8 : Αυτόματα NFA - DFA. Αλέξανδρος Τζάλλας
 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 8 : Αυτόματα NFA - DFA Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Μηχανικών Πληροφορικής
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 8 : Αυτόματα NFA - DFA Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου Τμήμα Μηχανικών Πληροφορικής
Φροντιστήριο 10 Λύσεις
 Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 10 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {0,1} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Γνωριµία. ιακριτά Μαθηµατικά. Βιβλία Μαθήµατος. Επικοινωνία. ιδάσκων: Ορέστης Τελέλης. Ωρες γραφείου (502, Γρ.
 Γνωριµία ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη 26): ευτέρα
Γνωριµία ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr Ωρες γραφείου (502, Γρ.Λαµπράκη 26): ευτέρα
ιακριτά Μαθηµατικά Ορέστης Τελέλης Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36
 ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36 Γνωριµία ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr
ιακριτά Μαθηµατικά Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σύνολα 1 / 36 Γνωριµία ιδάσκων: Ορέστης Τελέλης e-mail: telelis@unipi.gr
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 8: Πεπερασμένα Αυτόματα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Θεωρία Υπολογισμού Ενότητα 8: Πεπερασμένα Αυτόματα Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Φροντιστήριο 9 Λύσεις
 Άσκηση 1 Φροντιστήριο 9 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {a,b} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Άσκηση 1 Φροντιστήριο 9 Λύσεις Να κατασκευάσετε μια μηχανή Turing με δύο ταινίες η οποία να αποδέχεται στην πρώτη της ταινία μια οποιαδήποτε λέξη w {a,b} * και να γράφει τη λέξη w R στη δεύτερη της ταινία.
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών 6
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Ορισµός. Εστω συναρτήσεις: f : N R και g : N R. η f(n) είναι fi( g(n) ) αν υπάρχουν σταθερές C 1, C 2 και n 0, τέτοιες ώστε:
 Συµβολισµός Ω( ) Τάξη των Συναρτήσεων () Εκτίµηση Πολυπλοκότητας Αλγορίθµων Ορέστης Τελέλης telelis@unipi.gr Ορισµός. Εστω συναρτήσεις: f : N R και g : N R η f(n) είναι Ω( g(n) ) αν υπάρχουν σταθερές C
Συµβολισµός Ω( ) Τάξη των Συναρτήσεων () Εκτίµηση Πολυπλοκότητας Αλγορίθµων Ορέστης Τελέλης telelis@unipi.gr Ορισµός. Εστω συναρτήσεις: f : N R και g : N R η f(n) είναι Ω( g(n) ) αν υπάρχουν σταθερές C
Εισαγωγή στην Επιστήμη των Υπολογιστών
 Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
Εισαγωγή στην Επιστήμη των Υπολογιστών 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές http://www.corelab.ece.ntua.gr/courses/ Αυτόματα Τρόπος κωδικοποίησης αλγορίθμων. Τρόπος περιγραφής συστημάτων πεπερασμένων
HEAD INPUT. q0 q1 CONTROL UNIT
 Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ2: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Λ, Λ 2, Λ επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις.
ΕΠΛ2: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Λ, Λ 2, Λ επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις.
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Ισοδυναµίες, Μερικές ιατάξεις
 Ισοδυναµίες, Μερικές ιατάξεις Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σχέσεις 1 / 18 Σύνοψη Προηγούµενου Σχέσεις, Ιδιότητες, Αναπαράσταση
Ισοδυναµίες, Μερικές ιατάξεις Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σχέσεις 1 / 18 Σύνοψη Προηγούµενου Σχέσεις, Ιδιότητες, Αναπαράσταση
Η δυαδική σχέση M ( «παράγει σε ένα βήμα» ) ορίζεται ως εξής: (q, w) M (q, w ), αν και μόνο αν w = σw, για κάποιο σ Σ
 Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Πεπερασμένα Αυτόματα (ΠΑ) Τα πεπερασμένα αυτόματα είναι οι απλούστερες «υπολογιστικές μηχανές». Δεν έχουν μνήμη, μόνο μία εσωτερική μονάδα με πεπερασμένο αριθμό καταστάσεων. Διαβάζουν τη συμβολοσειρά εισόδου
Αυτόματα. Παράδειγμα: πωλητής καφέ (iii) Παράδειγμα: πωλητής καφέ (iv) Εισαγωγή στην Επιστήμη των Υπολογιστών. Προδιαγραφές
 Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσ.h.m.μ.y. & Σ.Ε.Μ.Φ.Ε. http://www.corelab.ece.ntua.gr/courses/ 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές Στάθης Ζάχος Συνεργασία: Κωστής Σαγώνας Επιμέλεια:
Εισαγωγή στην Επιστήμη των Υπολογιστών 4ο εξάμηνοσ.h.m.μ.y. & Σ.Ε.Μ.Φ.Ε. http://www.corelab.ece.ntua.gr/courses/ 3η ενότητα: Αυτόματα και Τυπικές Γραμματικές Στάθης Ζάχος Συνεργασία: Κωστής Σαγώνας Επιμέλεια:
Μονοπάτια και Κυκλώµατα Euler. Στοιχεία Θεωρίας Γραφηµάτων (3,4) Παραδείγµατα. Κριτήρια Υπαρξης.
 Μονοπάτια και Κυκλώµατα Eulr Σε γράφηµα G(V, E): Στοιχεία Θεωρίας Γραφηµάτων (3,4) Ορέστης Τελέλης tllis@unipi.r Κύκλωµα Eulr: Απλό κύκλωµα που διασχίζει κάθε ακµή του G. Μονοπάτι Eulr: Απλό µονοπάτι που
Μονοπάτια και Κυκλώµατα Eulr Σε γράφηµα G(V, E): Στοιχεία Θεωρίας Γραφηµάτων (3,4) Ορέστης Τελέλης tllis@unipi.r Κύκλωµα Eulr: Απλό κύκλωµα που διασχίζει κάθε ακµή του G. Μονοπάτι Eulr: Απλό µονοπάτι που
Ανω Φράγµα στην Τάξη των Συναρτήσεων. Ρυθµός Αύξησης (Τάξη) των Συναρτήσεων. Παράδειγµα (1/2) O( g(n) ) είναι σύνολο συναρτήσεων:
 Ανω Φράγµα στην Τάξη των Συναρτήσεων Ορισµός. Εστω συναρτήσεις: f : N R και g : N R Ρυθµός Αύξησης (Τάξη) των Συναρτήσεων Ορέστης Τελέλης η (τάξη της) f(n) είναι O( g(n) ) αν υπάρχουν σταθερές C και n
Ανω Φράγµα στην Τάξη των Συναρτήσεων Ορισµός. Εστω συναρτήσεις: f : N R και g : N R Ρυθµός Αύξησης (Τάξη) των Συναρτήσεων Ορέστης Τελέλης η (τάξη της) f(n) είναι O( g(n) ) αν υπάρχουν σταθερές C και n
Σχέσεις, Ιδιότητες, Κλειστότητες
 Σχέσεις, Ιδιότητες, Κλειστότητες Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σχέσεις 1 / 26 Εισαγωγή & Ορισµοί ιµελής Σχέση R από
Σχέσεις, Ιδιότητες, Κλειστότητες Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Σχέσεις 1 / 26 Εισαγωγή & Ορισµοί ιµελής Σχέση R από
Αρχή Εγκλεισµού-Αποκλεισµού (3 σύνολα) Αρχή Εκλεισµού-Αποκλεισµού Η Τάξη των Συναρτήσεων. Εφαρµογές. Παράδειγµα 1.
 Αρχή Εγκλεισµού-Αποκλεισµού (3 σύνολα) Αρχή Εκλεισµού-Αποκλεισµού Η Τάξη των Συναρτήσεων Ορέστης Τελέλης telelis@unipi.g Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς A B C = A + B + C A B B C A C +
Αρχή Εγκλεισµού-Αποκλεισµού (3 σύνολα) Αρχή Εκλεισµού-Αποκλεισµού Η Τάξη των Συναρτήσεων Ορέστης Τελέλης telelis@unipi.g Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς A B C = A + B + C A B B C A C +
Κανονικές Γλώσσες. Κανονικές Γλώσσες. Κανονικές Γλώσσες και Αυτόματα. Κανονικές Γλώσσες και Αυτόματα
 Κανονικές Γλώσσες Κανονικές Γλώσσες Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Κανονική γλώσσα αν παράγεται από κανονική γραμματική. Παραγωγές P (V Σ) Σ * ((V Σ) ε) Παραγωγές μορφής:
Κανονικές Γλώσσες Κανονικές Γλώσσες Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Κανονική γλώσσα αν παράγεται από κανονική γραμματική. Παραγωγές P (V Σ) Σ * ((V Σ) ε) Παραγωγές μορφής:
Στοιχεία Θεωρίας Γραφηµάτων (3)
 Στοιχεία Θεωρίας Γραφηµάτων (3) Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Γραφηµάτων (3) 1 / 23 Απαρίθµηση Μονοπατιών Εστω
Στοιχεία Θεωρίας Γραφηµάτων (3) Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Γραφηµάτων (3) 1 / 23 Απαρίθµηση Μονοπατιών Εστω
Απαρίθµηση Μονοπατιών. Στοιχεία Θεωρίας Γραφηµάτων (3) Μονοπάτια και Κυκλώµατα Euler. Ορέστης Τελέλης
 Απαρίθµηση Μονοπατιών Εστω γράφηµα G(V, E) µε πίνακα γειτνίασης A Στοιχεία Θεωρίας Γραφηµάτων (3) Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ως προς µια διάταξη των
Απαρίθµηση Μονοπατιών Εστω γράφηµα G(V, E) µε πίνακα γειτνίασης A Στοιχεία Θεωρίας Γραφηµάτων (3) Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς ως προς µια διάταξη των
Στοιχεία Θεωρίας Γραφηµάτων (1)
 Στοιχεία Θεωρίας Γραφηµάτων (1) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Γραφηµάτων (1) 1 / 23 Μη κατευθυνόµενα γραφήµατα
Στοιχεία Θεωρίας Γραφηµάτων (1) Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Θεωρία Γραφηµάτων (1) 1 / 23 Μη κατευθυνόµενα γραφήµατα
Μη κατευθυνόµενα γραφήµατα. Στοιχεία Θεωρίας Γραφηµάτων (1) Υπογραφήµατα.
 Κατευθυνόµενα γραφήµατα Απλό κατευθυνόµενο Γράφηµα G είναι διατεταγµένο Ϲεύγος (V, E), µε: Στοιχεία Θεωρίας Γραφηµάτων (1) σύνολο κορυφών / κόµβων V, Ορέστης Τελέλης tllis@unipi.r Τµήµα Ψηφιακών Συστηµάτων,
Κατευθυνόµενα γραφήµατα Απλό κατευθυνόµενο Γράφηµα G είναι διατεταγµένο Ϲεύγος (V, E), µε: Στοιχεία Θεωρίας Γραφηµάτων (1) σύνολο κορυφών / κόµβων V, Ορέστης Τελέλης tllis@unipi.r Τµήµα Ψηφιακών Συστηµάτων,
3 Αναδροµή και Επαγωγή
 3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
3 Αναδροµή και Επαγωγή Η ιδέα της µαθηµατικής επαγωγής µπορεί να επεκταθεί και σε άλλες δοµές εκτός από το σύνολο των ϕυσικών N. Η ορθότητα της µαθηµατικής επαγωγής ϐασίζεται όπως ϑα δούµε λίγο αργότερα
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 1: Εισαγωγή Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 1: Εισαγωγή Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {w 1w 2 w 1 {0,1} * και w 2 = 0 k 1 m όπου k και m
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {w 1w 2 w 1 {0,1} * και w 2 = 0 k 1 m όπου k και m
Σειρά Προβλημάτων 1 Λύσεις
 ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
ΕΠΛ: Θεωρία Υπολογισμού και Πολυπλοκότητα Σειρά Προβλημάτων Λύσεις Άσκηση Θεωρείστε τις γλώσσες Α = { n n } και Β = {w η w είναι λέξη επί του αλφαβήτου {,} τ.ώ. w }. (α) Για κάθε μια από τις πιο κάτω γλώσσες
Γενικό πλάνο. Μαθηµατικά για Πληροφορική. Παράδειγµα αναδροµικού ορισµού. οµική επαγωγή ΠΑΡΑ ΕΙΓΜΑ. 3ο Μάθηµα
 Γενικό πλάνο Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 1 Παράδειγµα δοµικής επαγωγής 2 Ορισµός δοµικής
Γενικό πλάνο Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 1 Παράδειγµα δοµικής επαγωγής 2 Ορισµός δοµικής
Κατευθυνόµενα γραφήµατα. Στοιχεία Θεωρίας Γραφηµάτων (1) Πολυγραφήµατα (Multigraphs)
 Μη κατευθυνόµενα γραφήµατα Στοιχεία Θεωρίας Γραφηµάτων (1) Απλό µη κατευθυνόµενο γράφηµα G είναι διατεταγµένο Ϲεύγος (V, E) µε σύνολο κορυφών/κόµβων V Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων,
Μη κατευθυνόµενα γραφήµατα Στοιχεία Θεωρίας Γραφηµάτων (1) Απλό µη κατευθυνόµενο γράφηµα G είναι διατεταγµένο Ϲεύγος (V, E) µε σύνολο κορυφών/κόµβων V Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων,
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 Έστω αλφάβητο Σ και γλώσσες Λ 1, Λ 2 επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις. Σε περίπτωση που μια σχέση ισχύει να
Σειρά Προβλημάτων 1 Λύσεις Άσκηση 1 Έστω αλφάβητο Σ και γλώσσες Λ 1, Λ 2 επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις. Σε περίπτωση που μια σχέση ισχύει να
Μαθηµατικά για Πληροφορική
 Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 14/10/2008 1 / 24 Γενικό πλάνο 1 Παράδειγµα δοµικής επαγωγής
Μαθηµατικά για Πληροφορική 3ο Μάθηµα Ηλίας Κουτσουπιάς, Γιάννης Εµίρης Τµήµα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήµιο Αθηνών 14/10/2008 14/10/2008 1 / 24 Γενικό πλάνο 1 Παράδειγµα δοµικής επαγωγής
Θεωρία Υπολογισμού. Ενότητα 7 : Ντετερμινιστικά Πεπερασμένα Αυτόματα, Κανονικές Πράξεις. Αλέξανδρος Τζάλλας
 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 7 : Ντετερμινιστικά Πεπερασμένα Αυτόματα, Κανονικές Πράξεις Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Τμήμα Μηχανικών
Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Θεωρία Υπολογισμού Ενότητα 7 : Ντετερμινιστικά Πεπερασμένα Αυτόματα, Κανονικές Πράξεις Αλέξανδρος Τζάλλας 2 Ανοιχτά Ακαδημαϊκά Τμήμα Μηχανικών
ιαιρετότητα Στοιχεία Θεωρίας Αριθµών «Ο Αλγόριθµος της ιαίρεσης» Αριθµητική Υπολοίπων 0 r < d και a = d q +r
 ιαιρετότητα Στοιχεία Θεωρίας Αριθµών ο a διαιρεί τον b: συµβολισµός: a b Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς a b και a c a (b + c) a b a bc, για κάθε c Z +
ιαιρετότητα Στοιχεία Θεωρίας Αριθµών ο a διαιρεί τον b: συµβολισµός: a b Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς a b και a c a (b + c) a b a bc, για κάθε c Z +
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητα Ενδιάμεση Εξέταση Ημερομηνία : Κυριακή, 15 Μαρτίου 2015 Διάρκεια : 15.00 17.00 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητα Ενδιάμεση Εξέταση Ημερομηνία : Κυριακή, 15 Μαρτίου 2015 Διάρκεια : 15.00 17.00 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο:
Μεταγλωττιστές. Γιώργος Δημητρίου. Μάθημα 2 ο. Πανεπιστήμιο Θεσσαλίας - Τμήμα Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
 Γιώργος Δημητρίου Μάθημα 2 ο Αλφάβητα και Γλώσσες Αλφάβητο: Ένα μη κενό και πεπερασμένο σύνολο συμβόλων Γλώσσα: Ένα οποιοδήποτε υποσύνολο των συμβολοσειρών ενός αλφαβήτου (οι προτάσεις της γλώσσας, πχ.
Γιώργος Δημητρίου Μάθημα 2 ο Αλφάβητα και Γλώσσες Αλφάβητο: Ένα μη κενό και πεπερασμένο σύνολο συμβόλων Γλώσσα: Ένα οποιοδήποτε υποσύνολο των συμβολοσειρών ενός αλφαβήτου (οι προτάσεις της γλώσσας, πχ.
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΙΑΚΡΙΤΕΣ ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ η Γραπτή Εργασία-Ενδεικτικές Λύσεις Επιµέλεια:. Σούλιου Θέµα (Κανονικές
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΙΑΚΡΙΤΕΣ ΜΕΘΟ ΟΙ ΓΙΑ ΤΗΝ ΕΠΙΣΤΗΜΗ ΤΩΝ ΥΠΟΛΟΓΙΣΤΩΝ η Γραπτή Εργασία-Ενδεικτικές Λύσεις Επιµέλεια:. Σούλιου Θέµα (Κανονικές
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων
 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (2)
 Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Αυτόματα Στοίβας (2.2) Τυπικός Ορισμός Παραδείγματα Ισοδυναμία με Ασυμφραστικές
Θεωρία Υπολογισμού και Πολυπλοκότητα Ασυμφραστικές Γλώσσες (2) Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Αυτόματα Στοίβας (2.2) Τυπικός Ορισμός Παραδείγματα Ισοδυναμία με Ασυμφραστικές
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Λ, Λ επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις. Σε περίπτωση που μια σχέση ισχύει να το αποδείξετε,
Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Λ, Λ επί του αλφάβητου αυτού. Να διερευνήσετε κατά πόσο ισχύει κάθε μια από τις πιο κάτω σχέσεις. Σε περίπτωση που μια σχέση ισχύει να το αποδείξετε,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητα Ενδιάμεση Εξέταση Ημερομηνία : Παρασκευή, 17 Μαρτίου 2017 Διάρκεια : 9.00 10.30 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητα Ενδιάμεση Εξέταση Ημερομηνία : Παρασκευή, 17 Μαρτίου 2017 Διάρκεια : 9.00 10.30 Διδάσκουσα : Άννα Φιλίππου Ονοματεπώνυμο:
Στοιχεία Αλγορίθµων και Πολυπλοκότητας
 Στοιχεία Αλγορίθµων και Πολυπλοκότητας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Πολυπλοκότητα 1 / 16 «Ζέσταµα» Να γράψετε τις συναρτήσεις
Στοιχεία Αλγορίθµων και Πολυπλοκότητας Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Πολυπλοκότητα 1 / 16 «Ζέσταµα» Να γράψετε τις συναρτήσεις
Γραµµατικές για Κανονικές Γλώσσες
 Κανονικές Γραµµατικές Γραµµατικές για Κανονικές Γλώσσες Ταξινόµηση Γραµµατικών εξιά Παραγωγικές Γραµµατικές εξιά Παραγωγικές Γραµµατικές και NFA Αριστερά Παραγωγικές Γραµµατικές Κανονικές Γραµµατικές Γραµµατικές
Κανονικές Γραµµατικές Γραµµατικές για Κανονικές Γλώσσες Ταξινόµηση Γραµµατικών εξιά Παραγωγικές Γραµµατικές εξιά Παραγωγικές Γραµµατικές και NFA Αριστερά Παραγωγικές Γραµµατικές Κανονικές Γραµµατικές Γραµµατικές
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {1010 2 10 3 10 n 1 10 n 1 n 1}. (β) Να διατυπώσετε
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing (αυθεντικός ορισμός) η οποία να διαγιγνώσκει τη γλώσσα {1010 2 10 3 10 n 1 10 n 1 n 1}. (β) Να διατυπώσετε
Σύνοψη Προηγούµενου. Ισοδυναµίες, Μερικές ιατάξεις. Σχέσεις Ισοδυναµίας. Σχέσεις, Ιδιότητες, Αναπαράσταση. Ανακλαστικές (a, a) R
 Σύνοψη Προηγούµενου Σχέσεις, Ιδιότητες, Αναπαράσταση Ισοδυναµίες, Μερικές ιατάξεις Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ανακλαστικές (, ) R Συµµετρικές (, ) R
Σύνοψη Προηγούµενου Σχέσεις, Ιδιότητες, Αναπαράσταση Ισοδυναµίες, Μερικές ιατάξεις Ορέστης Τελέλης tllis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ανακλαστικές (, ) R Συµµετρικές (, ) R
Σειρά Προβλημάτων 3 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { a i b j c k d m i, j, k, m 0 και i + j = k + m } (β) { uxvx rev u,v,x {0,1,2} + και όλα
Άσκηση 1 Σειρά Προβλημάτων 3 Λύσεις Να δώσετε ασυμφραστικές γραμματικές που να παράγουν τις πιο κάτω γλώσσες: (α) { a i b j c k d m i, j, k, m 0 και i + j = k + m } (β) { uxvx rev u,v,x {0,1,2} + και όλα
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων
 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
771 Η - Θεωρία Υπολογισµών και Αλγορίθµων Σηµειώσεις Μέρος 2 ο ιδάσκων: Το παρόν αποτελεί σηµειώσεις που αντιστοιχούν σε µέρος των διαλέξεων για το µάθηµα 771 Η - Θεωρία Υπολογισµών και Αλγορίθµων του
1. στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι αβελιανή οµάδα, δηλαδή
 KΕΦΑΛΑΙΟ ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ιατεταγµένα σώµατα-αξίωµα πληρότητας Ένα σύνολο Σ καλείται διατεταγµένο σώµα όταν στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι
KΕΦΑΛΑΙΟ ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ιατεταγµένα σώµατα-αξίωµα πληρότητας Ένα σύνολο Σ καλείται διατεταγµένο σώµα όταν στο σύνολο Σ έχει ορισθεί η πράξη της πρόσθεσης ως προς την οποία το Σ είναι
Ισοδυναμία Αιτ. Και μη Αιτ. Π.Α.
 Ισοδυναμία Αιτ. Και μη Αιτ. Π.Α. Δύο Π.Α. Μ 1 και Μ 2 είναι ισοδύναμα ανν L(M 1 ) = L(M 2 ). Έστω Μ = (Q, Σ, q 0, Δ, F) μη Αιτ. Π.Α. Για κάθε κατάσταση q Q, ορίζουμε ως Ε(q) Q το σύνολο των καταστάσεων
Ισοδυναμία Αιτ. Και μη Αιτ. Π.Α. Δύο Π.Α. Μ 1 και Μ 2 είναι ισοδύναμα ανν L(M 1 ) = L(M 2 ). Έστω Μ = (Q, Σ, q 0, Δ, F) μη Αιτ. Π.Α. Για κάθε κατάσταση q Q, ορίζουμε ως Ε(q) Q το σύνολο των καταστάσεων
Προηγούµενο: Ανω Φράγµα στην Τάξη των Συναρτήσεων. Ρυθµός Αύξησης (Τάξη) των Συναρτήσεων. Σύνοψη Ιδιοτήτων
 Προηγούµενο: Ανω Φράγµα στην Τάξη των Συναρτήσεων Ρυθµός Αύξησης (Τάξη) των Συναρτήσεων Ορέστης Τελέλης η (τάξη της) f() είναι O( g() ) αν υπάρχουν σταθερές C και 0, τέτοιες ώστε: f() C g() για κάθε 0
Προηγούµενο: Ανω Φράγµα στην Τάξη των Συναρτήσεων Ρυθµός Αύξησης (Τάξη) των Συναρτήσεων Ορέστης Τελέλης η (τάξη της) f() είναι O( g() ) αν υπάρχουν σταθερές C και 0, τέτοιες ώστε: f() C g() για κάθε 0
Γλώσσες που περιγράφονται από Κανονικές Εκφράσεις
 Κανονικές Εκφράσεις Στοιχειώδεις Κανονικές Εκφράσεις Κανονικές Εκφράσεις Γλώσσες που περιγράφονται από Κανονικές Εκφράσεις ηµιουργία Κανονικών Εκφράσεων Παραδείγµατα Κανονικών Εκφράσεων Τις Κανονικές εκφράσεις
Κανονικές Εκφράσεις Στοιχειώδεις Κανονικές Εκφράσεις Κανονικές Εκφράσεις Γλώσσες που περιγράφονται από Κανονικές Εκφράσεις ηµιουργία Κανονικών Εκφράσεων Παραδείγµατα Κανονικών Εκφράσεων Τις Κανονικές εκφράσεις
Πιθανότητες Γεώργιος Γαλάνης Κωνσταντίνα Παναγιωτίδου
 Πιθανότητες Γεώργιος Γαλάνης Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Πράξεις Γεγονότων Σχεδιάγραµµα της Υλης Βασικές Εννοιες της Θεωρίας Πιθανοτήτων
Πιθανότητες Γεώργιος Γαλάνης Κωνσταντίνα Παναγιωτίδου Σχολή Ναυτικών οκίµων Ακ. Ετος 2018-2019 Εισαγωγικά Βασικοί Ορισµοί Πράξεις Γεγονότων Σχεδιάγραµµα της Υλης Βασικές Εννοιες της Θεωρίας Πιθανοτήτων
Ασκήσεις από παλιές εξετάσεις
 Άσκηση 2 - Τελική εξέταση 2012 Ασκήσεις από παλιές εξετάσεις (α) [10 μονάδες] Να μετατρέψετε το πιο κάτω NFA σε ένα ισοδύναμο DFA χρησιμοποιώντας την κατασκευή που μελετήσαμε στο μάθημα. a a q 0 a, ε q
Άσκηση 2 - Τελική εξέταση 2012 Ασκήσεις από παλιές εξετάσεις (α) [10 μονάδες] Να μετατρέψετε το πιο κάτω NFA σε ένα ισοδύναμο DFA χρησιμοποιώντας την κατασκευή που μελετήσαμε στο μάθημα. a a q 0 a, ε q
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 10: Ισοδυναμία ντετερμινιστικών και μη ντετερμινιστικών αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Θεωρία Υπολογισμού Ενότητα 10: Ισοδυναμία ντετερμινιστικών και μη ντετερμινιστικών αυτομάτων Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2
 Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Αλγεβρικες οµες Ι Ασκησεις - Φυλλαδιο 2 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδες Μαθηµατος : http://users.uoi.gr/abeligia/algebraicstructuresi/asi2014/asi2014.html, https://sites.google.com/site/maths4edu/home/algdom114
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { n 3 } (α) H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την επτάδα Q,
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { n 3 } (α) H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την επτάδα Q,
Μαθηµατική Επαγωγή. Ορέστης Τελέλης. Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς
 Μαθηµατική Επαγωγή Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Επαγωγή 1 / 17 Υπενθύµιση: Ακολουθίες Ακολουθία είναι συνάρτηση από
Μαθηµατική Επαγωγή Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Επαγωγή 1 / 17 Υπενθύµιση: Ακολουθίες Ακολουθία είναι συνάρτηση από
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 7: Πεπερασμένη αναπαράσταση γλωσσών Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Θεωρία Υπολογισμού Ενότητα 7: Πεπερασμένη αναπαράσταση γλωσσών Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 8: Ιδιότητες Γραμματικών χωρίς Συμφραζόμενα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 8: Ιδιότητες Γραμματικών χωρίς Συμφραζόμενα Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Φροντιστήριο 2 Λύσεις
 ΕΠΛ2: Θεωρία Υπολογισμού και Πολυπλοκότητα Άσκηση Φροντιστήριο 2 Λύσεις Ποια από τα πιο κάτω αυτόματα αποτελούν DFA επί του αλφάβητου {,}. Αιτιολογήστε τις απαντήσεις σας. (i) (ii) (iii) (iv) (v), (vi),
ΕΠΛ2: Θεωρία Υπολογισμού και Πολυπλοκότητα Άσκηση Φροντιστήριο 2 Λύσεις Ποια από τα πιο κάτω αυτόματα αποτελούν DFA επί του αλφάβητου {,}. Αιτιολογήστε τις απαντήσεις σας. (i) (ii) (iii) (iv) (v), (vi),
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Σειρά Προβλημάτων 4 Λύσεις
 Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { a 2n b n c 3n n 2 } : H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την
Άσκηση 1 Σειρά Προβλημάτων 4 Λύσεις (α) Να διατυπώσετε την τυπική περιγραφή μιας μηχανής Turing που να διαγιγνώσκει τη γλώσσα { a 2n b n c 3n n 2 } : H ζητούμενη μηχανή Turing μπορεί να διατυπωθεί ως την
KΕΦΑΛΑΙΟ 1 ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ. { 1,2,3,..., n,...
 KΕΦΑΛΑΙΟ ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ Βασικές έννοιες διαιρετότητας Θα συµβολίζουµε µε, τα σύνολα των φυσικών αριθµών και των ακεραίων αντιστοίχως: {,,3,,, } { 0,,,,, } = = ± ± ± Ορισµός Ένας φυσικός αριθµός
KΕΦΑΛΑΙΟ ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ Βασικές έννοιες διαιρετότητας Θα συµβολίζουµε µε, τα σύνολα των φυσικών αριθµών και των ακεραίων αντιστοίχως: {,,3,,, } { 0,,,,, } = = ± ± ± Ορισµός Ένας φυσικός αριθµός
Μοντελοποίηση Υπολογισμού. Γραμματικές Πεπερασμένα Αυτόματα Κανονικές Εκφράσεις
 Μοντελοποίηση Υπολογισμού Γραμματικές Πεπερασμένα Αυτόματα Κανονικές Εκφράσεις Προβλήματα - Υπολογιστές Δεδομένου ενός προβλήματος υπάρχουν 2 σημαντικά ερωτήματα: Μπορεί να επιλυθεί με χρήση υπολογιστή;
Μοντελοποίηση Υπολογισμού Γραμματικές Πεπερασμένα Αυτόματα Κανονικές Εκφράσεις Προβλήματα - Υπολογιστές Δεδομένου ενός προβλήματος υπάρχουν 2 σημαντικά ερωτήματα: Μπορεί να επιλυθεί με χρήση υπολογιστή;
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας. Διάλεξη 9: Αυτόματα Στοίβας (Pushdown Automata - PDA)
 ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 9: Αυτόματα Στοίβας (Pushdown Automata - PDA) Τι θα κάνουμε σήμερα Εισαγωγή στα Αυτόματα Στοίβας Τυπικός Ορισμός Αυτομάτου Στοίβας (2.2.1) Παραδείγματα
ΕΠΛ 211: Θεωρία Υπολογισμού και Πολυπλοκότητας Διάλεξη 9: Αυτόματα Στοίβας (Pushdown Automata - PDA) Τι θα κάνουμε σήμερα Εισαγωγή στα Αυτόματα Στοίβας Τυπικός Ορισμός Αυτομάτου Στοίβας (2.2.1) Παραδείγματα
Μηχανές Πεπερασµένων Καταστάσεων
 Μηχανές Επεξεργασίας Πληροφοριών Μηχανές Πεπερασµένων Καταστάσεων Είναι µηχανές που δέχονται ένα σύνολο από σήµατα εισόδου και παράγουν ένα αντίστοιχο σύνολο σηµάτων εξόδου Σήµατα Εισόδου Μηχανή Επεξεργασίας
Μηχανές Επεξεργασίας Πληροφοριών Μηχανές Πεπερασµένων Καταστάσεων Είναι µηχανές που δέχονται ένα σύνολο από σήµατα εισόδου και παράγουν ένα αντίστοιχο σύνολο σηµάτων εξόδου Σήµατα Εισόδου Μηχανή Επεξεργασίας
Μαθηµατική Επαγωγή. Ορέστης Τελέλης. Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς
 Μαθηµατική Επαγωγή Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Επαγωγή 1 / 20 Επιπλέον Ασκήσεις Για κάθε n 1: n i 2 = n(n + 1)(2n
Μαθηµατική Επαγωγή Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Ο. Τελέλης Πανεπιστήµιο Πειραιώς Επαγωγή 1 / 20 Επιπλέον Ασκήσεις Για κάθε n 1: n i 2 = n(n + 1)(2n
q 0 q 0.2 q 0.1 q 0.05 q 0.05 q 0.25 q 0.15 q 0.1 q 0.2 q 0.25 q 0.25 q 0.25
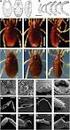 Κεφάλαιο 2 Κανονικές Γλώσσες & Πεπερασμένα Αυτόματα Σύνοψη Τα Πεπερασμένα Αυτόματα (ΠΑ) είναι το απλούστερο και το πιο ευρέως διαδεδομένο μοντέλο υπολογισμού από αυτά που θα εξετάσουμε. Είναι επίσης γνωστά
Κεφάλαιο 2 Κανονικές Γλώσσες & Πεπερασμένα Αυτόματα Σύνοψη Τα Πεπερασμένα Αυτόματα (ΠΑ) είναι το απλούστερο και το πιο ευρέως διαδεδομένο μοντέλο υπολογισμού από αυτά που θα εξετάσουμε. Είναι επίσης γνωστά
Παράδειγµα (4) Στοιχεία Θεωρίας Γραφηµάτων (2) Ορέστης Τελέλης. Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς. v 2. u 3.
 Παράδειγµα (2) s t Στοιχεία Θεωρίας Γραφηµάτων (2) w x Ορέστης Τελέλης z y tllis@unipi.r v u Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Τα δύο γραφήµατα δεν είναι ισόµορφα. Ο κόµβος (αριστερά) είναι
Παράδειγµα (2) s t Στοιχεία Θεωρίας Γραφηµάτων (2) w x Ορέστης Τελέλης z y tllis@unipi.r v u Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Τα δύο γραφήµατα δεν είναι ισόµορφα. Ο κόµβος (αριστερά) είναι
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» (ε) Κάθε συγκλίνουσα ακολουθία άρρητων αριθµών συγκλίνει σε άρρητο αριθµό.
 Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
Ασκήσεις για το µάθηµα «Ανάλυση Ι και Εφαρµογές» Κεφάλαιο : Ακολουθίες πραγµατικών αριθµών Α Οµάδα Εξετάστε αν οι παρακάτω προτάσεις είναι αληθείς ή ψευδείς αιτιολογήστε πλήρως την απάντησή σας α Κάθε
- εξίσωση που εκφράζει τον n-οστό όρο a n της ακολουθίας, - µέσω ενός ή περισσότερων όρων από τους a 0, a 1,..., a n 1, - για κάθε n n 0, όπου n 0 N.
 Αναδροµικές Σχέσεις Αναδροµικές Σχέσεις Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Αναδροµική Σχέση για την ακολουθία a n } είναι: - εξίσωση που εκφράζει τον n-οστό
Αναδροµικές Σχέσεις Αναδροµικές Σχέσεις Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς Αναδροµική Σχέση για την ακολουθία a n } είναι: - εξίσωση που εκφράζει τον n-οστό
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 10. Μηχανές Turing 20,23 Μαρτίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Μηχανές Turing: Ένα Γενικό Μοντέλο Υπολογισμού Ποια μοντέλα υπολογισμού μπορούν να δεχθούν γλώσσες
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 10. Μηχανές Turing 20,23 Μαρτίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Μηχανές Turing: Ένα Γενικό Μοντέλο Υπολογισμού Ποια μοντέλα υπολογισμού μπορούν να δεχθούν γλώσσες
Εισαγωγή στην Τοπολογία
 Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Ενότητα: Συνεκτικότητα Γεώργιος Κουµουλλής Τµήµα Μαθηµατικών Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε
Σειρά Προβλημάτων 1 Λύσεις
 Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Α, Β επί του αλφάβητου αυτού. Για κάθε μια από τις πιο κάτω περιπτώσεις να διερευνήσετε κατά πόσο Γ Δ, ή, Δ Γ, ή και τα δύο. Σε περίπτωση, που
Σειρά Προβλημάτων Λύσεις Άσκηση Έστω αλφάβητο Σ και γλώσσες Α, Β επί του αλφάβητου αυτού. Για κάθε μια από τις πιο κάτω περιπτώσεις να διερευνήσετε κατά πόσο Γ Δ, ή, Δ Γ, ή και τα δύο. Σε περίπτωση, που
