ΘΕΩΡΙΑ ΕΝΕΡΓΕΙΑΚΩΝ ΤΑΙΝΙΩΝ (Ε.Τ.) ΣΤΑ ΣΤΕΡΕΑ ΥΛΙΚΑ. Σχηματισμός και μορφή ενεργειακών ταινιών στα στερεά υλικά:
|
|
|
- Ξενοφών Αναγνωστάκης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΘΕΩΡΙΑ ΕΝΕΡΓΕΙΑΚΩΝ ΤΑΙΝΙΩΝ (Ε.Τ.) ΣΤΑ ΣΤΕΡΕΑ ΥΛΙΚΑ Σχηματισμός και μορφή ενεργειακών ταινιών στα στερεά υλικά: 1. Προσέγγιση της ισχυρής σύζευξης. Μοντέλο σχεδόν ελεύθερου ηλεκτρονίου - Οι συνέπειες του περιοδικού κρυσταλλικού δυναμικού Ταχύτητα των ηλεκτρονίων Ενεργός μάζα των ηλεκτρονίων Η θετική οπή και οι ιδιότητές της Πυκνότητα των ενεργειακών καταστάσεων σε μια ενεργειακή ταινία Φαινόμενο του Hall 1
2 ΘΕΩΡΙΑ ΕΝΕΡΓΕΙΑΚΩΝ ΤΑΙΝΙΩΝ (Ε.Τ.) Απαραίτητη για να εξηγήσουμε το μηχανισμό της ηλεκτρικής αγωγιμότητας και γιατί από τα στερεά μερικά συμπεριφέρονται σαν μέταλλα και άλλα ως ημιαγωγοί ή μονωτές Περιοχή τιμών (πειραματικές) της ειδικής ηλεκτρικής αντίστασης στη θερμοκρασία δωματίου για διάφορα υλικά που ανήκουν στις τρεις κατηγορίες υλικών: μέταλλα, ημιαγωγοί και μονωτές Ο αριθμός των διαθέσιμων ηλεκτρονίων για ηλεκτρική αγωγή σε ένα υλικό σχετίζεται με τη διευθέτηση των ηλεκτρονικών καταστάσεων (επιπέδων ή σταθμών) αναφορικά με την ενέργειά τους και με τον τρόπο που οι καταστάσεις αυτές καταλαμβάνονται από ηλεκτρόνια, δηλαδή τη λεγόμενη ηλεκτρονική δομή. Πολύπλοκη είναι η λεπτομερής μελέτη (περιέχει αρχές κβαντομηχανικής) των ενεργειακών ταινιών (Ε.Τ.) Θα παρουσιάσουμε δύο απλουστευμένα μοντέλα για το σχηματισμό και τη μορφή τους: 1. Προσέγγιση της ισχυρής σύζευξης. Μοντέλο σχεδόν ελεύθερου ηλεκτρονίου - Οι συνέπειες του περιοδικού κρυσταλλικού δυναμικού
3 1. Ενεργειακές ταινίες - προσέγγιση της ισχυρής σύζευξης (tight binding approimation) Ξεκινάει από τα μεμονωμένα άτομα και εξετάζει ποιοτικά πώς η προσέγγιση μεγάλου αριθμού ατόμων ( cm -3 ) σε απόσταση συγκρίσιμη ή μικρότερη από τη χωρική έκταση των ηλεκτρονικών κυματοσυναρτήσεων για το σχηματισμό του στερεού τροποποιεί τις κυματοσυναρτήσεις, οι οποίες σχηματίζουν ενεργειακές ταινίες (ή ζώνες) από ένα μεγάλο αριθμό καταστάσεων, τόσο κοντά σε ενέργεια η μία από την άλλη ώστε να θεωρούμε ότι είναι συνεχόμενες. Στον υπολογισμό των Ε.Τ. υποθέτουμε γραμμικό συνδυασμό των ατομικών κυματοσυναρτήσεων παίρνοντας υπόψη την περιοδική δυναμική ενέργεια του κρυστάλλου και προσεγγιστικές λύσεις της εξίσωσης Schrödingr (εκτός του ενδιαφέροντός μας) ΣΧΗΜΑΤΙΣΜΟΣ ΤΩΝ ΕΝΕΡΓΕΙΑΚΏΝ ΤΑΙΝΙΩΝ ΣΤΟ ΣΤΕΡΕΟ ΛΙΘΙΟ Ηλεκτρονική δομή ατόμου Λιθίου: 1s s p 0 Δημιουργία της ενεργειακής ταινίας (ή ζώνης) s από τα ατομικά τροχιακά s. Ονομάζεται ταινία σθένους (βρίσκονται τα ηλεκτρόνια σθένους) Η δημιουργία της ενεργειακής ταινίας (ή ζώνης) s από τα ατομικά τροχιακά s. Η ταινία δημιουργείται όταν Ν άτομα Li πλησιάζουν μεταξύ τους και σχηματίζουν το στερεό Li. Η ταινία s είναι η ταινία σθένους (βρίσκονται τα ηλεκτρόνια σθένους). Υπάρχουν Ν ηλεκτρόνια s και Ν καταστάσεις σ ολόκληρο το στερεό. Επομένως, η ταινία s είναι κατά το ήμισυ κατειλημμένη. Το ατομικό τροχιακό 1s βρίσκεται κοντά στον πυρήνα του Li και παραμένει ανεπηρέαστο στο στερεό. Στο στερεό υπάρχουν 10 άτομα νατρίου σε 1 cm 3, οπότε υπάρχουν 10 cm -3 καταστάσεις σε μια ταινία (π.χ. ταινία σθένους). Αν υποθέσουμε ότι το εύρος της είναι της τάξης 1V, η απόσταση μεταξύ των μεμονωμένων σταθμών (εφόσον ισαπέχουν) θα είναι πάρα πολύ μικρή, της τάξης 10 - V και συνεπώς θεωρούμε ότι αυτές είναι συνεχόμενες. 3
4 Καθώς τα άτομα Li πλησιάζουν από αρχικά άπειρη απόσταση, τα ατομικά τροχιακά επικαλύπτονται και δημιουργούν ταινίες. Πρώτα συμβαίνει επικάλυψη των εξωτερικών τροχιακών. Τα τροχιακά 3s δημιουργούν την ταινία 3s, τα τροχιακά p δημιουργούν την ταινία p,κ.λ.π. Οι ταινίες επικαλύπτονται και δημιουργούν μία μοναδική ταινία μέσα στην οποία η ενέργεια είναι σχεδόν συνεχής. Η τιμή της ενέργειας του επιπέδου Frmi καθορίζεται από την ενέργεια αναφοράς. Συνήθως τη μετράμε σε σχέση με τη βάση της ταινίας και ονομάζεται ενέργεια Frmi. 4
5 Η ενέργεια που αντιστοιχεί στην υψηλότερη συμπληρωμένη κατάσταση στους 0Κ ονομάζεται ενέργεια Frmi και συμβολίζεται ως E FO. Όταν αυξάνει η θερμοκρασία ορισμένα ηλεκτρόνια διεγείρονται και μεταβαίνουν σε υψηλότερα ενεργειακά επίπεδα. Η πιθανότητα που υπάρχει να βρεθεί ένα ηλεκτρόνιο σε ένα ενεργειακό επίπεδο Ε, δίνεται από τη στατιστική των σωματιδίων (Frmi-Dirac). Σημαντικές έννοιες: Ενέργεια Frmi, E FO είναι η μέγιστη ενέργεια που μπορεί να έχει ένα ηλεκτρόνιο σε ένα μέταλλο στους 0 Κ. Έργο εξόδου είναι η ελάχιστη ενέργεια που απαιτείται για να ελευθερωθεί ένα ηλεκτρόνιο από ένα μέταλλο σε θερμοκρασία απολύτου μηδενός. Είναι η ενέργεια που χωρίζει το επίπεδο Frmi από ένα επίπεδο του κενού. Για μη μεταλλλικά στερεά μεταξύ διαδοχικών ζωνών υπάρχουν χάσματα, όπως απεικονίζεται στο παρακάτω σχήμα. Οι ενέργειες που βρίσκονται στο εσωτερικό των χασμάτων ανάμεσα στις επιτρεπόμενες ζώνες (ή ταινίες) δεν είναι διαθέσιμες για κατάληψη από ηλεκτρόνια Οι ζώνες αυτές λέγονται ενεργειακά χάσματα (Enrgy gaps), και παριστάνονται με το Ε g. Το εύρος του ενεργειακού χάσματος εξαρτάται από τη φύση του ημιαγωγικού υλικού και την απόσταση ανάμεσα στα άτομα (α ο ) του στερεού. Σχηματική παράσταση της διεύρυνσης κάθε ατομικής ενεργειακής στάθμης σε μια ενεργειακή ταινία (ζώνη) ορισμένου εύρους καθώς η ενδοατομική απόσταση μικραίνει για να φτάσουμε στη χαρακτηριστική ενδοατομική απόσταση (διακεκομμένη γραμμή) του υλικού στην κατάσταση ισορροπίας. Η γραφική παράσταση της Ε ως προς είναι το γενικό διάγραμμα επίπεδης ταινίας, που δίνει την ενέργεια των επιτρεπόμενων καταστάσεων ως συνάρτηση της θέσης στον κρύσταλλο και τονίζει τη μη εντοπισμένη φύση των καταστάσεων της ταινίας που επεκτείνονται σε όλο τον κρύσταλλο. 5
6 . Μοντέλο σχεδόν ελεύθερου ηλεκτρονίου - Οι συνέπειες του περιοδικού κρυσταλλικού δυναμικού Ξεκινάμε από ελεύθερα ηλεκτρόνια στο κενό. Η εισαγωγή ασθενούς περιοδικού δυναμικού τροποποιεί τις σχέσεις ενέργειας-κυματανύσματος (επίλυση εξίσωσης Shrodingr για ηλεκτρόνιο που βρίσκεται σε περιοδικό δυναμικό του κρυστάλλου), π κυρίως σε κυματανύσματα με k = n, n=1,,3.. και δημιουργεί ενεργειακά χάσματα. a Θα δούμε τα κυριότερα συμπεράσματα: Στο πρότυπο των ελεύθερων ηλεκτρονίων, οι επιτρεπτές τιμές της ηλεκτρονικής ενέργειας E(k) είναι διακριτές και επεκτείνεται από το μηδέν ως το άπειρο: Ek h = k m Δεν διαδίδονται όμως όλα τα ηλεκτρονικά κύματα στο πλέγμα του κρυστάλλου.tα κύματα μπορούν να ανακλαστούν και να περιθλαστούν (όταν συμβάλλουν τα ανακλώμενα κύματα προσθετικά). Αυτό συμβαίνει για τιμές του k n a π =, n=1,,3., δηλ. τα ηλεκτρονικά κύματα παθαίνουν ανακλάσεις Bragg και δεν μπορούν να διαδοθούν στον κρύσταλλο. Το περιοδικό κρυσταλλικό δυναμικό ανοίγει ενεργειακά χάσματα στη συνεχή π μεταβολή του Ε(k) για k = ± (για μονοδιάστατο κρύσταλλο) a π Όταν k = ±, οι ενέργειες των κυματοσυναρτήσεων ψ C και ψ S έχουν τιμές ολικής a π ενέργειας ίσες κατά προσέγγιση με Ε S = h ( ) / m* +Δ / και a π E C = h ( ) / m* Δ /, αντίστοιχα. Δηλαδή, δύο δυνατές τιμές ενέργειας. Δεν είναι a επιτρεπτές άλλες ενέργειες ανάμεσα σε αυτές τις δύο. Οι δύο αυτές ενέργειες απέχουν κατά Δ. Το γεγονός αυτό οδηγεί σε μια ενεργειακή διαφορά Δ. Η διαφορά της π δυναμικής ενέργειας Δ, στις κυματοσυναρτήσεις ψ C και ψ S με k = ±, αποτελεί το a ενεργειακό χάσμα E του υλικού, όπως φαίνεται στο παρακάτω σχήμα. g 6
7 (α) Η ενέργεια ηλεκτρονίου ως συνάρτηση του κυματοδιανύσματος k εντός ενός π μονοδιάστατου κρυστάλλου. Στα σημεία k = ± n, υπάρχουν ασυνέχειες στην ενέργεια. a Στα σημεία αυτά τα κύματα ανακλώνται κατά Bragg μέσα στον κρύσταλλο. Δεν μπορεί για παράδειγμα για το ηλεκτρόνιο, να υπάρχει τιμή της ενέργειας μεταξύ των τιμών Ε C και Ε S. Επομένως, η περιοχή Ε S - Ε C είναι ένα ενεργειακό διάκενο (ή ενεργειακό χάσμα). Μακριά από αυτές τις τιμές του k, η συμπεριφορά της Ε-k είναι σαν τη συμπεριφορά για ένα ελεύθερο ηλεκτρόνιο. Δηλαδή στις περιοχές αυτές, η Ε αυξάνει με το k και συνδέεται με τη σχέση h E = k με μάζα m* διαφορετική της μάζας m του ελεύθερου ηλεκτρονίου στον κενό χώρο k m* Σε ένα στερεό, οι ενέργειες αυτές βρίσκονται μέσα σε μία ενεργειακή ταινία (ή ζώνη) (β). Διάγραμμα Επίπεδης Ταινίας: Η συνηθισμένη παράσταση Ε- των επιτρεπτών ταινιών (ή ζωνών) και των ενεργειακών χασμάτων στα στερεά υλικά. Η τετμημένη παριστάνει τη διεύθυνση μέσα στο υλικό (στον πραγματικό χώρο). 7
8 Απεικόνιση των ενεργειακών ταινιών (Ε.Τ.) σε μορφή α) εκτεταμένης και β) περιορισμένης ζώνης (α) (β) Απεικόνιση των ενεργειακών ταινιών (Ε.Τ.) σε μορφή: α) εκτεταμένης ζώνης, όπου φαίνονται οι 3 Ε.Τ. στις 3 Ζ.Β. (Ζώνη Brillouin) με αριθμούς και β) περιορισμένης ζώνης, όπου φαίνονται οι 3 Ε.Τ. στην 1 η Ζ.Β. Με την περιορισμένη απεικόνιση των Ε.Τ. παίρνουμε την ίδια πληροφορία που μας δίνει η εκτεταμένη απεικόνιση των Ε.Τ. (τα μεμονωμένα τμήματα του σχ. (α) έχουν μετατοπιστεί κατά πολλαπλάσιο του π/α). Σε τρισδιάστατο κρύσταλλο Αν σχεδιάσουμε την Ε(k) πρέπει να πάρουμε υπόψη τη διεύθυνση του k αφού η περίθλαση Bragg εξαρτάται από το sinθ. Για κυβικό κρύσταλλο, το ενεργειακό χάσμα κατά μήκος του άξονα, δηλαδή στη διεύθυνση θ=0 (διεύθυνση [100]) είναι στα σημεία k = ± π/α. Στη διεύθυνση θ=45 0 το ενεργειακό χάσμα είναι στα σημεία ky =± π a Η συμπεριφορά της Ε-k ενός ηλεκτρονίου σε διαφορετικές διευθύνσεις ενός κρυστάλλου. Το ενεργειακό χάσμα (ή διάκενο) στη διεύθυνση [100] είναι στο σημείο π/α, ενώ στη διεύθυνση [110] είναι στο σημείο k y = π a. 8
9 Αν στην περίπτωση των μετάλλων, λάβουμε υπόψη μας και την επικάλυψη των ενεργειακών ταινιών στις διευθύνσεις [100] και [110], τότε δεν υπάρχει ενεργειακό χάσμα. Το ηλεκτρόνιο μπορεί να έχει οποιαδήποτε ενέργεια μεταβάλλοντας απλά την κατεύθυνσή του. Αντίθετα, στην περίπτωση των ημιαγωγών υπάρχει ένα ενεργειακό χάσμα (διάκενο) λόγω της μη πλήρους επικάλυψης των ενεργειακών διακένων στις διαφορετικές κατευθύνσεις μέσα στον κρύσταλλο. 9
10 Οι βασικές διαφορές μεταξύ των μετάλλων, ημιαγωγών και μονωτών μπορούν να κατανοηθούν με βάση τη μορφή των ταινιών. Η απουσία μεταλλικής αγωγιμότητας σημαίνει ότι δεν υπάρχουν ταινίες εν μέρει κατειλημμένες από ηλεκτρόνια. Στους μονωτές κάθε ταινία είναι εντελώς πλήρης με ηλεκτρόνια ή εντελώς κενή. 1. Σχηματική αναπαράσταση των ενεργειακών ζωνών (στη μορφή επίπεδης ταινίας) για τους τρεις τύπους στερεών στους 0Κ: Σχηματική αναπαράσταση των ενεργειακών ζωνών για τους τρεις τύπους στερεών στους 0 Κ: α) ένα μέταλλο με μερικώς γεμάτη ζώνη σθένους, δηλαδή μονοσθενές μέταλλο β) ένα μέταλλο με δύο επικαλυπτόμενες μερικώς γεμάτες ζώνες, δηλαδή δισθενές μέταλλο (γ) ένα μονωτής και (δ) ένας ενδογενής ημιαγωγός ο οποίος είναι μονωτής στους 0Κ. (όπου Ε f είναι η ενέργεια Frmi) Προσοχή: Η διαφορά ανάμεσα σ ένα μονωτή και σ έναν ημιαγωγό είναι ότι Εg του μονωτή είναι >> Εg του ημιαγωγού (διαφορά ποσοτική και όχι ποιοτική) 10
11 . Mορφή ενεργειακών ταινιών με απεικόνιση Ε(k)-k, η κατάληψη αυτών από ηλεκτρόνια και η θέση της ενέργειας Frmi για: α) κανονικό μέταλλο, β) μέταλλο εξαιτίας της επικάλυψης των ταινιών και γ) μονωτή (α) (β) (γ) Mορφή ενεργειακών ταινιών και κατάληψη αυτών από ηλεκτρόνια για Τ=0Κ. α) κανονικού μετάλλου (π.χ Να), β) μετάλλου εξαιτίας της επικάλυψης των ταινιών που αντιστοιχούν στις διευθύνσεις k και k y (π.χ. Μg), και γ) μονωτή (π.χ Si). Προσοχή: Η θέση της ενέργειας Frmi είναι μέσα σε ταινία για τα μέταλλα, ενώ στους μονωτές βρίσκεται μέσα στο ενεργειακό χάσμα. 3. Mορφή ενεργειακών ταινιών με απεικόνιση g(ε)-ε, η θέση της ενέργειας Frmi και κατάληψη αυτών από ηλεκτρόνια για μέταλλο και μονωτή. Πυκνότητα ενεργειακών καταστάσεων g(e) σε συνάρτηση της Ε των ηλεκτρονίων, όπου φαίνεται το γέμισμα της ταινίας σθένους και της ταινίας αγωγιμότητας καθώς και η θέση της ενέργειας Frmi για Τ=0Κ: α) μέταλλο (π.χ. Μg) και β) μονωτής (π.χ. Si) 11
12 6 Άτομο Μg : [ 1s s p ]3s Στο στερεό μαγνήσιο το περιοδικό κρυσταλλικό δυναμικό ενεργεί κατά πολύπλοκο τρόπο ώστε να οδηγεί σε επικάλυψη των ενεργειακών ταινιών που αντιστοιχούν σε διαφορετικές διευθύνσεις μέσα στο στερεό. 6 Άτομο Si: [ 1s s p ]3s 3p Στο στερεό Si, η ψηλότερη κατειλημμένη ταινία, η ταινία σθένους, είναι υβριδική του τύπου sp 3 με τέσσερις κβαντικές καταστάσεις για κάθε άτομο και επομένως είναι πλήρης. Σε απόσταση ίση περίπου με 1V (ενεργειακό χάσμα), αρχίζει η ταινία αγωγιμότητας που είναι εντελώς κενή στις χαμηλές θερμοκρασίες για απόλυτα καθαρό στερεό πυρίτιο. Επομένως, το απόλυτα καθαρό πυρίτιο είναι άριστος μονωτής στις χαμηλές θερμοκρασίες Η θερμική διέγερση του στερεού υλικού έχει ως αποτέλεσμα ένα μικρό ποσοστό από τις κβαντικές καταστάσεις στην κορυφή της κατειλημμένης από ηλεκτρόνια ενεργειακής ταινίας του μονωτή (ταινία σθένους) να χάσουν τα ηλεκτρόνιά τους τα οποία έτσι πηγαίνουν και κατέχουν αντίστοιχο μικρό αριθμό από τις χαμηλότερες ενεργειακές ταινίες (ταινία αγωγιμότητας). Η αγωγή του ηλεκτρικού ρεύματος από τα ηλεκτρόνια της ταινίας αγωγιμότητας και από τις ισάριθμες θετικές οπές που δημιουργήθηκαν στην ταινία σθένους εξαιτίας της θερμικής διέγερσης του υλικού είναι η κατάσταση που συναντούμε σ έναν ενδογενή ημιαγωγό (intrinsic smiconductor). Η ενεργειακή διαφορά ανάμεσα στην κορυφή της ταινίας σθένους και στον πυθμένα της ταινίας αγωγιμότητας λέγεται ενδογενές ενεργειακό χάσμα. Ταχύτητα των ηλεκτρονίων Η ταχύτητα του ηλεκτρονίου μέσα στα στερεά κρυσταλλικά υλικά είναι η ω ταχύτητα ομάδας (group vlocity) και ορίζεται από τη σχέση: υg =. Μπορεί να k υπολογιστεί αν είναι γνωστή η Ε ως συνάρτηση του κυματοδιανύσματος του ηλεκτρονίου k από τη σχέση ω 1 1 Ek υg = = ( Ek) = h h Γενικά σε τρεις διαστάσεις η κίνηση του ηλεκτρονίου ισοδυναμεί με διάδοση κύματος που έχει ταχύτητα ομάδας: υ = 1 E g k k h Γεωμετρικά η ταχύτητα του ηλεκτρονίου είναι η κλίση της καμπύλης της Ε ως προς το k 1
13 Ενεργός μάζα των ηλεκτρονίων στα στερεά υλικά Στα στερεά λόγω της παρουσίας του κρυσταλλικού δυναμικού τα ηλεκτρόνια μέσα στον κρυσταλλικό πλέγμα συμπεριφέρονται σαν να έχουν διαφορετική μάζα, δηλαδή ο λόγος της δύναμης προς την επιτάχυνση ενός ηλεκτρονίου είναι διαφορετικός της αδρανειακής τους μάζας. Έτσι θα ορίσουμε την ενεργό μάζα, σε μία διάσταση, μέσα από την σχέση: _ dυ g Fεξ. = m a= m dt όπου m είναι μία σταθερά αναλογίας μεταξύ δύναμης και επιτάχυνσης και για αυτό ονομάζεται ενεργός μάζα. Η F είναι η δυναμη που εξασκείται πάνω στο ηλεκτρόνιο εξ από ένα μακροσκοπικό ηλεκτρικό πεδίο (δεν περιλαμβάνει το δυναμικό του κρυστάλλου, τις δυνάμεις που δέχεται το ηλεκτρόνιο από τα ιόντα στο στερεό). Το υ g είναι η ταχύτητα του ηλεκτρονίου παίρνοντας υπόψη τη σωματιδιακή φύση, δηλαδή η ταχύτητα ομάδας υ g της κυματοδεσμίδας που περιγράφει το ηλεκτρόνιο αυτό. Από τι εξαρτάται η ενεργός μάζα Σε μία διάσταση ορίζουμε την ενεργό μάζα m* ως h m* = d E( k) dk Όταν η σχέση διασκεδασμού των ηλεκτρονικών κυμάτων E-k είναι παραβολική (ισχύει μόνο για περιορισμένη περιοχή τιμών της ενέργειας), η m* του ηλεκτρονίου είναι ανεξάρτητη από την ενέργεια της κβαντικής κατάστασης που κατέχει, οπότε η σχέση E-k μπορεί να γραφεί με τη μορφή : k Ε= h m* Η ενεργός μάζα m* ενός ηλεκτρονίου είναι αντίστροφα ανάλογη προς την καμπυλότητα του διαγράμματος διασποράς E-k μιας ενεργειακής ταινίας. Στα σημεία d E όπου η καμπυλότητα είναι μεγάλη-μεγάλη τιμή για την παράγωγο για dk μονοδιάστατο υλικό- η ενεργός μάζα είναι μικρή, ενώ αντίθετα μικρή καμπυλότητα δείχνει μεγάλη ενεργό μάζα, όπως φαίνεται στο παρακάτω σχήμα. Η ενεργός μάζα είναι αντίστροφα ανάλογη προς την καμπυλότητα της ταινίας 13
14 Αντιπροσωπευτική μεταβολή του Ε-k σε μία ενεργειακή ταινία και της αντίστοιχης ενεργούς της μάζας m* για μονοδιάστατο υλικό δίνεται παρακάτω: α) Ενεργειακό διάγραμμα Ε-k μιας ενεργειακής ταινίας (σε μια διάσταση) β) Ενεργός μάζα m* του ηλεκτρονίου ως συνάρτηση του διανύσματος κύματος για μονοδιάστατο κρυσταλλικό υλικό Αρνητική ενεργός μάζα: σημαίνει ότι στην περιοχή αυτή του χώρου του k το κρυσταλλικό περιοδικό δυναμικό εξασκεί τόση μεγάλη δύναμη πέδησης πάνω στο ηλεκτρόνιο ώστε αυτή υπερνικάει την εξωτερική εφαρμοζόμενη δύναμη και προκαλεί επιβράδυνση (επιτάχυνση σε αντίθετη φορά απ' αυτήν που θα προκαλούσε στον ελεύθερο χώρο). Η επιτάχυνση δηλαδή που προκαλεί ένα ηλεκτρικό πεδίο σε ηλεκτρόνιο με αρνητική ενεργό μάζα, έχει την φορά που θα είχε στον ελεύθερο χώρο για ένα θετικά φορτισμένο σωματίδιο. Γενικά, η ενεργός μάζα m* ενός ηλεκτρονίου είναι δυνατό να είναι μεγαλύτερη ή μικρότερη από τη γνωστή μάζα του ελεύθερου ηλεκτρονίου m 0, γεγονός που εξαρτάται αποκλειστικά από τη μορφή του ενεργειακού διαγράμματος E- k του υλικού. Σε τρείς διαστάσεις η ενεργός μάζα θα είναι διανυσματική: Οι συνιστώσες της επιτάχυνσης είναι: a a a y z = h = h = h E E [ ( ε ) + E [ y E ( ε y ) + E E ( ε ) + ( ε ) y + y y z z ( ε )] z ( ε )] E E E [ ( ε ) + ( ε y ) + ( ε )] z z z z y z 14
15 1 Γράφοντας τη σχέση, a = [ m] ( ε ), όπου F= ε και _ ε το ηλεκτρικό πεδίο, με τη μορφή πινάκων, παίρνουμε τη σχέση: a m my mz ε a y = m y m yy m yz ε y a z mz mzy m zz ε z Οι συνιστώσες του τανυστή ενεργού μάζας του ηλεκτρονίου μέσα στο περιοδικό κρυσταλλικό δυναμικό εξισώσεις μπορούν να συντμηθούν ως εξής: _ [ m ij ] = h [ E / i j ] 1 Σε μερικά από ηλεκτρονική άποψη πολύπλοκα στερεά υλικά, οι μη διαγώνιες συνιστώσες ( m y, mz, m ym yz, mz, mzy ) του τανυστή ενεργού μάζας έχουν μεγάλες τιμές, οπότε κάτω από την επίδραση ενός ηλεκτρικού πεδίου σε μια ορισμένη διεύθυνση το ηλεκτρόνιο επιταχύνεται σε άλλη διεύθυνση. Αυτό συμβαίνει για ισοενεργειακές επιφάνειες στο χώρο k ξεκάθαρα μη σφαιρικές. Για ιδανικό ισότροπο από ηλεκτρονική άποψη στερεό υλικό, όλες οι μηδιαγώνιες συνιστώσες του τανυστή ενεργού μάζας του ηλεκτρονίου είναι ίσες με μηδέν, ενώ οι τρεις διαγώνιες συνιστώσες ( m, m yy, mzz ) είναι ίσες μεταξύ τους. Στην περίπτωση αυτή η ενεργός μάζα του ηλεκτρονίου είναι μια αριθμητική ποσότητα. Γενικά, επειδή η ενεργός μάζα εξαρτάται από τη διεύθυνση (σε σχέση με τους κρυσταλλικούς άξονες), είναι μία τανυστική ποσότητα. Όμως, συνήθως λαμβάνεται μία μέση τιμή για τις διαφορετικές κατευθύνσεις. Πρέπει να τονίσουμε ότι η χρήση της ενεργού μάζας στις διαφορετικές περιπτώσεις, όπως α) για τον υπολογισμό της πυκνότητας των καταστάσεων στις ταινίες ή β) σε υπολογισμούς μεταφοράς των φορέων κάτω από την επίδραση πεδίων (π.χ. ηλεκτρική αγωγιμότητα) ή κλίσεων στην συγκέντρωσή τους, απαιτεί διαφορετικό υπολογισμό του μέσου όρου της ενεργού μάζας και επομένως σε διαφορετικές τιμές της ενεργού μάζας των φορέων, δηλαδή των ηλεκτρονίων και οπών (θα παρουσιαστούν στις σημειώσεις Ημιαγωγοί Α και Β μέρος). Έτσι, η ενεργός μάζα που χρησιμοποιείται στους υπολογισμούς για την πυκνότητα των καταστάσεων (m*,dos), είναι διαφορετική από την ενεργό μάζα που χρησιμοποιείται στους υπολογισμούς για τη μέση ταχύτητα, ευκινησία, ταχύτητα ολίσθησης, αγωγιμότητα και γενικά για την κίνηση φορέων (m*,cond.). Αυτό γιατί η συμμετοχή των διαφόρων διεθύνσεων και κυματοδυανυσμάτων είναι διαφορετική. Η ενεργός μάζα είναι ένας σημαντικός παράγοντας στις ιδιότητες των ημιαγωγών (ταχύτητα ηλεκτρονίων, αγωγιμότητα, οπτικές ιδιότητες κ.α.), και επομένως στη λειτουργία πολλών ημιαγωγικών διατάξεων (π.χ. ταχύτητα ολοκληρωμένων κυκλωμάτων, απόδοση φωτοβολταϊκών στοιχείων και άλλα). 15
16 Τιμές ενεργού μάζας ηλεκτρονίων και οπών που σχετίζονται με την πυκνότητα καταστάσεων (m*,dos) διαφόρων ημιαγωγών Η θετική οπή και οι ιδιότητες της Οι οπές αποτελούν ένα νέο στοιχείο στην αγωγιμότητα των ημιαγωγών. Η λειτουργία του τρανζίστορ επαφών και κατ επέκταση των ολοκληρωμένων κυκλωμάτων και άλλων ημιαγωγικών διατάξεων εξαρτάται άμεσα από τη συνύπαρξη των οπών και των ηλεκτρονίων μέσα στους ημιαγωγούς. Η κίνηση της οπής στο χώρο των θέσεων και τον χώρο των ορμών κάτω από την επίδραση ηλεκτρικού πεδίου είναι συμβατή με την κίνηση ενός "ψευδοσωματίδιου" με θετικό φορτίο και θετική ενεργό μάζα. Ας εξετάσουμε την σχέση που υπάρχει ανάμεσα στις ποσότητες που χαρακτηρίζουν την οπή και εκείνες του ηλεκτρονίου που λείπει από την ταινία σθένους. Στο σχήμα, η ταινία σθένους είναι πλήρης εκτός από την κατάσταση D όπου λείπει ένα ηλεκτρόνιο. Ιδιότητες της οπής Το κυματάνυσμα της οπής είναι αντίθετο απ'αυτό του ηλεκτρονίου που λείπει. k h = k Η ενέργεια του ηλεκτρονίου αυξάνει κατά το θετικό άξονα (των ενεργειών) ενώ της οπής αυξάνει κατά τον αρνητικό άξονα 16
17 Έχει ταχύτητα ίση με την ταχύτητα του ηλεκτρονίου που λείπει 1 υ = υ = Ek h h Έχει ενεργό μάζα ίση και αντίθετη με την ενεργό μάζα του ηλεκτρονίου που λείπει m = * * h m Στην κορυφή μιας πλήρους ταινίας έχουμε: Ηλεκτρόνιο, : φορτίο -q, ενεργό μάζα - m Οπή, h: φορτίο +q, ενεργό μάζα + m * h * α=q/m*.e q/m* >0 και για το και για την h m*.α=q.e Eπιταχύνονται προς την ίδια διεύθυνση Το πεδίο θα δώσει ενέργεια στην οπή λόγω του + φορτίου Το πεδίο θα πάρει ενέργεια από το ηλεκτρόνιο λόγω του φορτίου Όμως (φορτίο) /μάζα <0 για το, ενώ για την h (φορτίο) /μάζα>0 Μόνο με την ειδική ηλεκτρική αγωγιμότητα, μπορούμε να διακρίνουμε το ηλεκτρόνιο από τη θετική οπή. (Πειραματική άσκηση ΙΙΙ, φαινόμενο Ηall) Προσοχή: Συσχέτιση ενέργειας ηλεκτρονίου και οπής Η οπή είναι μια κβαντική ενεργειακή κατάσταση της ταινίας σθένους που μπορεί να είναι κατειλημμένη από ηλεκτρόνιο αλλά δέν είναι. Το σύστημα των ηλεκτρονίων της ταινίας σθένους έχει τόσο μικρότερη ενέργεια όσο χαμηλότερες είναι οι ενέργειες των κατειλλημένων καταστάσεων άρα όσο υψηλότερα, στο ενεργειακό διάγραμμα για ηλεκτρόνια, είναι οι άδειες καταστάσεις, δηλαδή οι οπές. Επομένως, τα ηλεκτρόνια σε ψηλές τιμές ενέργειας Ε k, έχουν την τάση να πέσουν σε χαμηλότερες τιμές ενέργειας για να προσεγγίσουν την κατάσταση ισορροπίας τους, ενώ οι οπές σε χαμηλές τιμές ενέργειας Ε k, έχουν την τάση να επιπλεύσουν σε ψηλότερες τιμές ενέργειας για να προσεγγίσουν την κατάσταση ισορροπίας τους. 17
18 Πυκνότητα των ενεργειακών καταστάσεων σε μια ενεργειακή ταινία Στα στερεά το σχήμα των καμπυλών Ε(k) είναι σχεδόν παραβολική στον πυθμένα και την κορυφή της ταινίας. Στον πυθμένα (ελάχιστο) της ενεργειακής ταινίας ισχύει η σχέση: h E = ( k kmin ) m1 * * όπου m1 είναι η ενεργός μάζα του ηλεκτρονίου για τη συγκεκριμένη διεύθυνση στο χώρο του _ k. Για τα ηλεκτρόνια που βρίσκονται στην κορυφή (μέγιστο) της ενεργειακής ταινίας θα ισχύει η σχέση : h Ema E = k k m * ( ma ) όπου m * είναι η ενεργός μάζα του ηλεκτρονίου για τη συγκεκριμένη αυτή διεύθυνση στο χώρου του. Σε ενδιάμεσες περιοχές της ταινίας η πυκνότητα καταστάσεων δεν θα είναι ανάλογη του Ε 1/. Aπεικόνιση της ποιοτικής μορφής του g(e) στις ταινίες αγωγιμότητας και σθένους για ένα κυβικό κρυσταλλικό ημιαγωγό. * Σημείωση όπου m 1, m * είναι η ενεργός μάζα του ηλεκτρονίου που χρησιμοποιείται στους υπολογισμούς για την πυκνότητα των καταστάσεων (m*,dos). 18
19 Φαινόμενο του Hall Αρχικά θα εξετάσουμε το φαινόμενο του hall σε μεταλλικά υλικά και στη συνέχεια θα επεκτείνουμε αυτό στους ημιαγωγούς. Το φαινόμενο του hall φαίνεται διαγραμματικά στο παρακάτω σχήμα. Ας υποθέσουμε ότι στη διεύθυνση + ενός στερεού υλικού (π.χ. μεταλλικού σύρματος) περνάει ηλεκτρικό ρεύμα πυκνότητας J και ότι εφαρμόζεται ένα μαγνητικό πεδίο B z, κάθετα στο σύρμα στη διεύθυνση +z, θα δούμε αμέσως ότι κάτω από τις πιο πάνω συνθήκες εμφανίζεται ένα πρόσθετο ηλεκτρικό πεδίο (του Hall) ε H κάθετο τόσο στο J όσο και στο B z, δηλαδή στη διεύθυνση y. Προέλευση του ηλεκτρικού πεδίου του Hall καθώς και του φαινομένου Hall σε ένα μέταλλο. Η δύναμη Lornz F L, που παράγει τη συγκέντρωση των καθαρών φορτίων, είναι στη διεύθυνση y και έχει τιμή : F = υ B L Το ηλεκτρικό πεδίο, που οφείλεται στα καθαρά επιφανειακά φορτία, παράγει μια δύναμη F που αντιτίθεται στην πιο πάνω δύναμη Lornz H FH = FL ε H = υb ε = υ B H πυκνότητα του ρεύματος J = n υ, οπότε έχουμε: ε H 1 = J B n το ηλεκτρικό πεδίο του Hall είναι ανάλογο προς την πυκνότητα του ρεύματος (πάντοτε συμβατικό) και τη μαγνητική επαγωγή του μαγνητικού πεδίου. Ο συντελεστής αναλογίας R H = ε H J B λέγεται συντελεστής του Hall ή σταθερά του Hall και δίδεται από τη σχέση : 19
20 R H 1 = <0 n H παραπάνω σχέση δίνει τη συγκέντρωση των ηλεκτρονίων n από μετρήσεις του ηλεκτρικού πεδίου του Hall. Aυτή είναι η συνηθισμένη τεχνική που χρησιμοποιείται στον προσδιορισμό της ηλεκτρονικής συγκέντρωσης μέσα στα στερεά υλικά, στα μεταλλικά υλικά αλλά και κυρίως στους ημιαγωγούς. Τιμές του συντελεστή Hall R H (m 3 /C) για μερικά μεταλλικά υλικά και για το καθαρό (ενδογενές) πυρίτιο στη θερμοκρασία δωματίου Υλικό Li Cu Al Cd Si (καθαρό) R H 10-1, , , , Το πρόσημο του συντελεστή Hall εξαρτάται από το πρόσημο του φορτίου των φορέων της αγωγιμότητας (του ηλεκτρικού ρεύματος). Τα ηλεκτρόνια που έχουν αρνητικό φορτίο οδηγούν σε αρνητικό συντελεστή του Hall. O συντελεστής του Hall για μερικά μεταλλικά υλικά (π.χ. F,Cd, Zn) είναι θετικός, οπότε το ηλεκτρικό ρεύμα μεταφέρεται από τις οπές (έχουν θετικό φορτίο) με nh να είναι η συγκέντρωση των οπών, ισχύει: R H =+ 1 n >0 H Στην πραγματικότητα, στα μεταλλικά υλικά μαζί με τις οπές υπάρχουν πάντοτε και ισάριθμα ηλεκτρόνια. Όταν δύο ενεργειακές ταινίες επικαλύπτονται, υπάρχουν ταυτόχρονα ηλεκτρόνια στην «πάνω» ταινία και οπές στην «κάτω» ταινία, οπότε ο συντελεστής του Hall παίρνει τη μορφή : R = R σ + R σ h h ( σ + σ h ) R και Rh είναι οι συνεισφορές των επί μέρους ηλεκτρονίων και οπών, και σ και είναι οι ειδικές ηλεκτρικές αγωγιμότητες των ηλεκτρονίων και των οπών, αντίστοιχα * ( σ = n τ / m ). Αν πάρουμε n = nh, όπως συνήθως συμβαίνει στα μέταλλα, τότε R = Rh και το πρόσημο του R καθορίζεται αποκλειστικά από τα σχετικά μεγέθη των ποσοτήτων σ και σ h. Έτσι λοιπόν αν σ > σ h, αν δηλαδή τα ηλεκτρόνια έχουν μικρή ενεργό μάζα και μεγάλο μέσο ελεύθερο χρόνο ζωής, τότε κυριαρχεί η συνεισφορά των ηλεκτρονίων και ο συντελεστής του Hall είναι αρνητικός. Όταν σ h 0
21 όμως επικρατεί η αντίθετη συνθήκη ( σ < σ ), τότε κυριαρχεί η συνεισφορά των οπών και ο συντελεστής του Hall είναι θετικός. h Στους ημιαγωγούς το πρόσημο του R H μπορεί να είναι θετικό η αρνητικό ανάλογα με τους φορείς αγωγιμότητας, δηλαδή ηλεκτρόνια ή οπές. Για ημιαγωγό n- τύπου όπου οι φορείς πλειονότητας είναι τα ηλεκτρόνια, το πρόσημο του R H θα είναι αρνητικό, ενώ σε ημιαγωγό p-τύπου θα είναι θετικό λόγω του θετικού φορτίου των οπών που είναι οι φορείς πλειονότητας. Για ημιαγωγό n-τύπου και για ημιαγωγό τύπου- p έχουμε: R H 1 = <0 n R H 1 =+ >0 p το πρόσημο του συντελεστή R H δίνει πληροφορίες για τον τύπο αγωγιμότητας του ημιαγωγού. Το ενδογενές (καθαρό) πυρίτιο παρουσιάζει μεγαλύτερη τιμή για τον συντελεστη Hall σε σύγκριση με τα μέταλλα. Για ντοπαρισμένο ημιαγωγό η τιμή του R H εξαρτάται από το επίπεδο ντοπαρίσματος (δηλ.τη συγκέντρωση δοτών ή αποδεκτών). Στο παρακάτω σχήμα φαίνεται διαγραμματικά το φαινόμενο του hall για ημιαγωγό όπου υπάρχουν και οι δύο τύποι φορέων αγωγιμότητας, ηλεκτρόνια και οπές Προέλευση του ηλεκτρικού πεδίου του Hall καθώς και του φαινομένου Hall σε ημιαγωγό. Το φαινόμενο Hall έχει πλειάδα εφαρμογών σε αισθητήρες για τη μέτρηση διαφόρων φυσικών μεγεθών, όπως ένταση μαγνητικού πεδίου κ.α. Βιβλιογραφία S. Ο. Κasap. Aρχές ηλεκτρονικών υλικών και διατάξεων, Δεύτερη έκδοση, Παπασωτηρίου. 1
22 Υπενθύμιση Δομή των ενεργειακών ταινιών στα μέταλλα, ημιαγωγούς και μονωτές Απλοϊκή παράσταση: Δομή ενεργειακών ταινιών και θέση στάθμης Frmi για τις τρεις κατηγορίες υλικών Στα μέταλλα η στάθμη Frmi βρίσκεται μέσα στην ταινία σθένους που επικαλύπτεται με την ταινία αγωγιμότητας, δηλαδή τα ηλεκτρόνια σθένους είναι και ηλεκτρόνια αγωγιμότητας. Στους ημιαγωγούς και μονωτές η στάθμη Frmi βρίσκεται μέσα στο ενεργειακό χάσμα Ε G, διαφέρουν μεταξύ τους ως προς το μέγεθος του Ε G
Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς (μέρος 2)
 Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς (μέρος 2) Το μοντέλο του «άδειου πλέγματος» Βήμα 1: Στο μοντέλο του «άδειου πλέγματος» θεωρούμε ότι το ηλεκτρόνιο είναι ελεύθερο αλλά οι λύσεις της Schrödinger
Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς (μέρος 2) Το μοντέλο του «άδειου πλέγματος» Βήμα 1: Στο μοντέλο του «άδειου πλέγματος» θεωρούμε ότι το ηλεκτρόνιο είναι ελεύθερο αλλά οι λύσεις της Schrödinger
Δομή ενεργειακών ζωνών
 Ατομικό πρότυπο του Bohr Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Βασικές αρχές του προτύπου Bohr Θετικά φορτισμένος
Ατομικό πρότυπο του Bohr Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Βασικές αρχές του προτύπου Bohr Θετικά φορτισμένος
Περιεχόμενο της άσκησης
 Προαπαιτούμενες γνώσεις Ημιαγωγοί Θεωρία ζωνών Ενδογενής αγωγιμότητα Ζώνη σθένους Ζώνη αγωγιμότητας Προτεινόμενη βιβλιογραφία 1) Π.Βαρώτσος Κ.Αλεξόπουλος «Φυσική Στερεάς Κατάστασης» 2) C.Kittl, «Εισαγωγή
Προαπαιτούμενες γνώσεις Ημιαγωγοί Θεωρία ζωνών Ενδογενής αγωγιμότητα Ζώνη σθένους Ζώνη αγωγιμότητας Προτεινόμενη βιβλιογραφία 1) Π.Βαρώτσος Κ.Αλεξόπουλος «Φυσική Στερεάς Κατάστασης» 2) C.Kittl, «Εισαγωγή
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
 ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΚΕΦΑΛΑΙΟ 2ο ΗΜΙΑΓΩΓΟΙ Αγωγοί, Μονωτές, Ημιαγωγοί Κατηγοριοποίηση υλικών βάσει των ηλεκτρικών τους ιδιοτήτων: Αγωγοί (αφήνουν το ρεύμα να περάσει) Μονωτές (δεν αφήνουν το ρεύμα να
ΑΝΑΛΟΓΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΚΕΦΑΛΑΙΟ 2ο ΗΜΙΑΓΩΓΟΙ Αγωγοί, Μονωτές, Ημιαγωγοί Κατηγοριοποίηση υλικών βάσει των ηλεκτρικών τους ιδιοτήτων: Αγωγοί (αφήνουν το ρεύμα να περάσει) Μονωτές (δεν αφήνουν το ρεύμα να
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Αγωγιμότητα στα μέταλλα
 Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Η κίνηση των ατόμων σε κρυσταλλικό στερεό Θερμοκρασία 0 Θερμοκρασία 0 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo
Ηλεκτρονική δομή ημιαγωγών-περίληψη. Σχέση διασποράς για ελεύθερα ηλεκτρόνια στα μέταλλα-
 E. K. Παλούρα Οπτοηλεκτρονική_semis_summary.doc Ηλεκτρονική δομή ημιαγωγών-περίληψη Σχέση διασποράς για ελεύθερα ηλεκτρόνια στα μέταλλα- Η κυματοσυνάρτηση ψ(r) του ελεύθερου e είναι λύση της Schrödinger:
E. K. Παλούρα Οπτοηλεκτρονική_semis_summary.doc Ηλεκτρονική δομή ημιαγωγών-περίληψη Σχέση διασποράς για ελεύθερα ηλεκτρόνια στα μέταλλα- Η κυματοσυνάρτηση ψ(r) του ελεύθερου e είναι λύση της Schrödinger:
1.1 Ηλεκτρονικές ιδιότητες των στερεών. Μονωτές και αγωγοί
 1. Εισαγωγή 1.1 Ηλεκτρονικές ιδιότητες των στερεών. Μονωτές και αγωγοί Από την Ατομική Φυσική είναι γνωστό ότι οι επιτρεπόμενες ενεργειακές τιμές των ηλεκτρονίων είναι κβαντισμένες, όπως στο σχήμα 1. Σε
1. Εισαγωγή 1.1 Ηλεκτρονικές ιδιότητες των στερεών. Μονωτές και αγωγοί Από την Ατομική Φυσική είναι γνωστό ότι οι επιτρεπόμενες ενεργειακές τιμές των ηλεκτρονίων είναι κβαντισμένες, όπως στο σχήμα 1. Σε
ΗΛΕΚΤΡΟΤΕΧΝΙΚΑ Υλικα 3ο μεροσ. Θεωρητικη αναλυση
 ΗΛΕΚΤΡΟΤΕΧΝΙΚΑ Υλικα 3ο μεροσ Θεωρητικη αναλυση μεταλλα Έχουν κοινές φυσικές ιδιότητες που αποδεικνύεται πως είναι αλληλένδετες μεταξύ τους: Υψηλή φυσική αντοχή Υψηλή πυκνότητα Υψηλή ηλεκτρική και θερμική
ΗΛΕΚΤΡΟΤΕΧΝΙΚΑ Υλικα 3ο μεροσ Θεωρητικη αναλυση μεταλλα Έχουν κοινές φυσικές ιδιότητες που αποδεικνύεται πως είναι αλληλένδετες μεταξύ τους: Υψηλή φυσική αντοχή Υψηλή πυκνότητα Υψηλή ηλεκτρική και θερμική
Πυκνότητα καταστάσεων g(e)
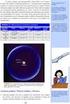 Ε. Κ. Παλούρα NF model_µέρος Πυκνότητα καταστάσεων g() Ορισµός ο αριθµός ενεργειακών καταστάσεων ανά µονάδα όγκου στην ενεργειακή περιοχή (,+d) ή αριθµός e ή τροχιακών ανά µονάδα ενέργειας g () = dn d
Ε. Κ. Παλούρα NF model_µέρος Πυκνότητα καταστάσεων g() Ορισµός ο αριθµός ενεργειακών καταστάσεων ανά µονάδα όγκου στην ενεργειακή περιοχή (,+d) ή αριθµός e ή τροχιακών ανά µονάδα ενέργειας g () = dn d
Ημιαγωγοί. Ημιαγωγοί. Ενδογενείς εξωγενείς ημιαγωγοί. Ενδογενείς ημιαγωγοί Πυρίτιο. Δομή ενεργειακών ζωνών
 Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Δομή ενεργειακών ζωνών Δεν υπάρχουν διαθέσιμες θέσεις Κενή ζώνη αγωγιμότητας
Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Δομή ενεργειακών ζωνών Δεν υπάρχουν διαθέσιμες θέσεις Κενή ζώνη αγωγιμότητας
2η Εργαστηριακή Άσκηση Εξάρτηση της ηλεκτρικής αντίστασης από τη θερμοκρασία Θεωρητικό μέρος
 2η Εργαστηριακή Άσκηση Εξάρτηση της ηλεκτρικής αντίστασης από τη θερμοκρασία Θεωρητικό μέρος Όπως είναι γνωστό από την καθημερινή εμπειρία τα περισσότερα σώματα που χρησιμοποιούνται στις ηλεκτρικές ηλεκτρονικές
2η Εργαστηριακή Άσκηση Εξάρτηση της ηλεκτρικής αντίστασης από τη θερμοκρασία Θεωρητικό μέρος Όπως είναι γνωστό από την καθημερινή εμπειρία τα περισσότερα σώματα που χρησιμοποιούνται στις ηλεκτρικές ηλεκτρονικές
ΦΩΤΟΒΟΛΤΑΪΚΑ. Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής
 ΦΩΤΟΒΟΛΤΑΪΚΑ Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής Αγωγοί- μονωτές- ημιαγωγοί Μέταλλα: Μία ζώνη μερικώς γεμάτη ή μία ζώνη επικαλύπτει την άλλη Τα ηλεκτρόνια μπορούν
ΦΩΤΟΒΟΛΤΑΪΚΑ Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής Αγωγοί- μονωτές- ημιαγωγοί Μέταλλα: Μία ζώνη μερικώς γεμάτη ή μία ζώνη επικαλύπτει την άλλη Τα ηλεκτρόνια μπορούν
Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς
 Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς Στόχος : Να εξηγήσουμε την επίδραση του δυναμικού του κρυστάλλου στις Ε- Ειδικώτερα: Το δυναμικό του κρυστάλλου 1. εισάγονται χάσματα στα σημεία όπου τέμνονται
Ελεύθερα ηλεκτρόνια στα μέταλλα-σχέση διασποράς Στόχος : Να εξηγήσουμε την επίδραση του δυναμικού του κρυστάλλου στις Ε- Ειδικώτερα: Το δυναμικό του κρυστάλλου 1. εισάγονται χάσματα στα σημεία όπου τέμνονται
ΦΩΤΟΒΟΛΤΑΪΚΑ. Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής
 ΦΩΤΟΒΟΛΤΑΪΚΑ Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής Αγωγοί- μονωτές- ημιαγωγοί Μέταλλα: Μία ζώνη μερικώς γεμάτη ή μία ζώνη επικαλύπτει την άλλη Τα ηλεκτρόνια μπορούν
ΦΩΤΟΒΟΛΤΑΪΚΑ Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής Αγωγοί- μονωτές- ημιαγωγοί Μέταλλα: Μία ζώνη μερικώς γεμάτη ή μία ζώνη επικαλύπτει την άλλη Τα ηλεκτρόνια μπορούν
Οι ηµιαγωγοι αποτελουν την πλεον χρησιµη κατηγορια υλικων απο ολα τα στερεα για εφαρµογες στα ηλεκτρονικα.
 Οι ηµιαγωγοι αποτελουν την πλεον χρησιµη κατηγορια υλικων απο ολα τα στερεα για εφαρµογες στα ηλεκτρονικα. Οι ηµιαγωγοι εχουν ηλεκτρικη ειδικη αντισταση (ή ηλεκτρικη αγωγιµοτητα) που κυµαινεται µεταξυ
Οι ηµιαγωγοι αποτελουν την πλεον χρησιµη κατηγορια υλικων απο ολα τα στερεα για εφαρµογες στα ηλεκτρονικα. Οι ηµιαγωγοι εχουν ηλεκτρικη ειδικη αντισταση (ή ηλεκτρικη αγωγιµοτητα) που κυµαινεται µεταξυ
ΝΑΝΟΥΛΙΚΑ ΚΑΙ ΝΑΝΟΤΕΧΝΟΛΟΓΙΑ ΣΤΕΛΛΑ ΚΕΝΝΟΥ ΚΑΘΗΓΗΤΡΙΑ
 ΣΤΕΛΛΑ ΚΕΝΝΟΥ ΚΑΘΗΓΗΤΡΙΑ 1 Ιδιότητες εξαρτώμενες από το μέγεθος Στην νανοκλίμακα, οι ιδιότητες εξαρτώνται δραματικά από το μέγεθος Για παράδειγμα, ΙΔΙΟΤΗΤΕΣ ΝΑΝΟΥΛΙΚΩΝ (1) Θερμικές ιδιότητες θερμοκρασία
ΣΤΕΛΛΑ ΚΕΝΝΟΥ ΚΑΘΗΓΗΤΡΙΑ 1 Ιδιότητες εξαρτώμενες από το μέγεθος Στην νανοκλίμακα, οι ιδιότητες εξαρτώνται δραματικά από το μέγεθος Για παράδειγμα, ΙΔΙΟΤΗΤΕΣ ΝΑΝΟΥΛΙΚΩΝ (1) Θερμικές ιδιότητες θερμοκρασία
ηλεκτρικό ρεύμα ampere
 Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύμα Το ηλεκτρικό ρεύμα είναι ο ρυθμός με τον οποίο διέρχεται ηλεκτρικό φορτίο από μια περιοχή του χώρου. Η μονάδα μέτρησης του ηλεκτρικού ρεύματος στο σύστημα SI είναι το ampere (A). 1 A =
Θεωρία του Sommerfeld ή jellium model (συνέχεια από το 1 ο μάθημα).
 MA8HMA _08.doc Θεωρία του Sommerfeld ή jellium model (συνέχεια από το ο μάθημα). Τα e καταλαμβάνουν ενεργειακές στάθμες σύμφωνα με την αρχή του Pauli και η κατανομή τους για Τ0 δίδεται από τη συνάρτηση
MA8HMA _08.doc Θεωρία του Sommerfeld ή jellium model (συνέχεια από το ο μάθημα). Τα e καταλαμβάνουν ενεργειακές στάθμες σύμφωνα με την αρχή του Pauli και η κατανομή τους για Τ0 δίδεται από τη συνάρτηση
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Ενεργειακές Ζώνες και Στατιστική Φορέων Φορτίου Required Text: Microelectronic Devices, Keith Leaver (2 nd Chapter) Εισαγωγή Στο προηγούμενο κεφάλαιο προσεγγίσαμε τους ημιαγωγούς
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Ενεργειακές Ζώνες και Στατιστική Φορέων Φορτίου Required Text: Microelectronic Devices, Keith Leaver (2 nd Chapter) Εισαγωγή Στο προηγούμενο κεφάλαιο προσεγγίσαμε τους ημιαγωγούς
4. Παρατηρείστε το ίχνος ενός ηλεκτρονίου (click here to select an electron
 Τα ηλεκτρόνια στα Μέταλλα Α. Χωρίς ηλεκτρικό πεδίο: 1. Τι είδους κίνηση κάνουν τα ηλεκτρόνια; Τα ηλεκτρόνια συγκρούονται μεταξύ τους; 2. Πόσα ηλεκτρόνια περνάνε προς τα δεξιά και πόσα προς τας αριστερά
Τα ηλεκτρόνια στα Μέταλλα Α. Χωρίς ηλεκτρικό πεδίο: 1. Τι είδους κίνηση κάνουν τα ηλεκτρόνια; Τα ηλεκτρόνια συγκρούονται μεταξύ τους; 2. Πόσα ηλεκτρόνια περνάνε προς τα δεξιά και πόσα προς τας αριστερά
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ
 ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Ενεργειακές Ζώνες και Στατιστική Φορέων Φορτίου Required Text: Microelectronic Devices, Keith Leaver (2 nd Chapter) Εισαγωγή Στο προηγούμενο κεφάλαιο προσεγγίσαμε τους ημιαγωγούς
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Ενεργειακές Ζώνες και Στατιστική Φορέων Φορτίου Required Text: Microelectronic Devices, Keith Leaver (2 nd Chapter) Εισαγωγή Στο προηγούμενο κεφάλαιο προσεγγίσαμε τους ημιαγωγούς
Ξεκινώντας από την εξίσωση Poisson για το δυναμικό V στο στατικό ηλεκτρικό πεδίο:
 1 2. Διοδος p-n 2.1 Επαφή p-n Στο σχήμα 2.1 εικονίζονται δύο μέρη ενός ημιαγωγού με διαφορετικού τύπου αγωγιμότητες. Αριστερά ο ημιαγωγός είναι p-τύπου και δεξια n-τύπου. Και τα δύο μέρη είναι ηλεκτρικά
1 2. Διοδος p-n 2.1 Επαφή p-n Στο σχήμα 2.1 εικονίζονται δύο μέρη ενός ημιαγωγού με διαφορετικού τύπου αγωγιμότητες. Αριστερά ο ημιαγωγός είναι p-τύπου και δεξια n-τύπου. Και τα δύο μέρη είναι ηλεκτρικά
Φυσική Στερεάς Κατάστασης η ομάδα ασκήσεων Διδάσκουσα Ε. Κ. Παλούρα
 Φυσική Στερεάς Κατάστασης -05 η ομάδα ασκήσεων. Έστω ημιαγωγός με συγκέντρωση προσμείξεων Ν>> i. Όλες οι προσμείξεις είναι ιονισμένες και ισχύει =, p= i /. Η πρόσμειξη είναι τύπου p ή? : Όλες οι προσμείξεις
Φυσική Στερεάς Κατάστασης -05 η ομάδα ασκήσεων. Έστω ημιαγωγός με συγκέντρωση προσμείξεων Ν>> i. Όλες οι προσμείξεις είναι ιονισμένες και ισχύει =, p= i /. Η πρόσμειξη είναι τύπου p ή? : Όλες οι προσμείξεις
Θεωρία Μοριακών Τροχιακών (ΜΟ)
 Θεωρία Μοριακών Τροχιακών (ΜΟ) Ετεροπυρηνικά διατομικά μόρια ή ιόντα (πολικοί δεσμοί) Το πιο ηλεκτραρνητικό στοιχείο (με ατομικά τροχιακά χαμηλότερης ενεργειακής στάθμης) συνεισφέρει περισσότερο στο δεσμικό
Θεωρία Μοριακών Τροχιακών (ΜΟ) Ετεροπυρηνικά διατομικά μόρια ή ιόντα (πολικοί δεσμοί) Το πιο ηλεκτραρνητικό στοιχείο (με ατομικά τροχιακά χαμηλότερης ενεργειακής στάθμης) συνεισφέρει περισσότερο στο δεσμικό
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ. Εργαστήριο Φυσικής IΙ. Μελέτη της απόδοσης φωτοβολταϊκού στοιχείου με χρήση υπολογιστή. 1. Σκοπός. 2. Σύντομο θεωρητικό μέρος
 ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ 1. Σκοπός Το φωτοβολταϊκό στοιχείο είναι μία διάταξη ημιαγωγών η οποία μετατρέπει την φωτεινή ενέργεια που προσπίπτει σε αυτήν σε ηλεκτρική.. Όταν αυτή φωτιστεί με φωτόνια κατάλληλης συχνότητας
ΘΕΩΡΗΤΙΚΟ ΜΕΡΟΣ 1. Σκοπός Το φωτοβολταϊκό στοιχείο είναι μία διάταξη ημιαγωγών η οποία μετατρέπει την φωτεινή ενέργεια που προσπίπτει σε αυτήν σε ηλεκτρική.. Όταν αυτή φωτιστεί με φωτόνια κατάλληλης συχνότητας
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ 2.1 ΤΟ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ
 ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ 2Η ΕΝΟΤΗΤΑ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ 2.1 ΤΟ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ Τι είναι ; Ηλεκτρικό ρεύμα ονομάζεται η προσανατολισμένη κίνηση των ηλεκτρονίων ή γενικότερα των φορτισμένων σωματιδίων Που μπορεί να
ΦΥΣΙΚΗ Γ ΓΥΜΝΑΣΙΟΥ 2Η ΕΝΟΤΗΤΑ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ 2.1 ΤΟ ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ Τι είναι ; Ηλεκτρικό ρεύμα ονομάζεται η προσανατολισμένη κίνηση των ηλεκτρονίων ή γενικότερα των φορτισμένων σωματιδίων Που μπορεί να
Περιεχόμενο της άσκησης
 Προαπαιτούμενες γνώσεις Επαφή p- Στάθμη Fermi Χαρακτηριστική ρεύματος-τάσης Ορθή και ανάστροφη πόλωση Περιεχόμενο της άσκησης Οι επαφές p- παρουσιάζουν σημαντικό ενδιαφέρον επειδή βρίσκουν εφαρμογή στη
Προαπαιτούμενες γνώσεις Επαφή p- Στάθμη Fermi Χαρακτηριστική ρεύματος-τάσης Ορθή και ανάστροφη πόλωση Περιεχόμενο της άσκησης Οι επαφές p- παρουσιάζουν σημαντικό ενδιαφέρον επειδή βρίσκουν εφαρμογή στη
Ε. Κ. ΠΑΛΟΎΡΑ Ημιαγωγοί 1. Ημιαγωγοί. Το 1931 ο Pauli δήλωσε: "One shouldn't work on. semiconductors, that is a filthy mess; who knows if they really
 Ημιαγωγοί Ανακαλύφθηκαν το 190 Το 191 ο Pauli δήλωσε: "Oe should't work o semicoductors, that is a filthy mess; who kows if they really exist!" Πιο ήταν το πρόβλημα? Οι ανεπιθύμητες προσμείξεις Το 1947
Ημιαγωγοί Ανακαλύφθηκαν το 190 Το 191 ο Pauli δήλωσε: "Oe should't work o semicoductors, that is a filthy mess; who kows if they really exist!" Πιο ήταν το πρόβλημα? Οι ανεπιθύμητες προσμείξεις Το 1947
Περιεχόμενο της άσκησης. Προτεινόμενη βιβλιογραφία. Π.Βαρώτσος, Κ.Αλεξόπουλος «Φυσική Στερεάς Κατάστασης»
 Προαπαιτούμενες γνώσεις Ενεργειακές ζώνες Πρότυπο Kroning- Penney Προτεινόμενη βιβλιογραφία Π.Βαρώτσος, Κ.Αλεξόπουλος «Φυσική Στερεάς Κατάστασης» Περιεχόμενο της άσκησης Όταν N άτομα έλθουν κοντά το ένα
Προαπαιτούμενες γνώσεις Ενεργειακές ζώνες Πρότυπο Kroning- Penney Προτεινόμενη βιβλιογραφία Π.Βαρώτσος, Κ.Αλεξόπουλος «Φυσική Στερεάς Κατάστασης» Περιεχόμενο της άσκησης Όταν N άτομα έλθουν κοντά το ένα
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ Φυσική Συμπυκνωμένης Ύλης (Ενότητα: Ημιαγωγοί) Ασκήσεις Ι. Ράπτης
 Q ολικό () ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 016-17 Φυσική Συμπυκνωμένης Ύλης (Ενότητα: Ημιαγωγοί) Ασκήσεις Ι. Ράπτης 1. Κρύσταλλος πυριτίου ( g 1.17 1170 ) νοθεύεται με προσμίξεις αρσενικού ( 40
Q ολικό () ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ 016-17 Φυσική Συμπυκνωμένης Ύλης (Ενότητα: Ημιαγωγοί) Ασκήσεις Ι. Ράπτης 1. Κρύσταλλος πυριτίου ( g 1.17 1170 ) νοθεύεται με προσμίξεις αρσενικού ( 40
ΘΕΡΜΟΚΡΑΣΙΑ Κ ΚΑΙ Η ΗΛΕΚΡΙΚΗ ΕΙΔΙΚΗ ΑΝΤΙΣΤΑΣΗ ΣΕ ΚΑΛΟ ΜΟΝΩΤΗ ΕIΝΑΙ ΤΗΣ ΤΑΞΗΣ
 ΕΝΕΡΓΕΙΑΚΕΣ ΖΩΝΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΖΩΝΕΣ ΤΟ ΠΡΟΤΥΠΟ ΤΩΝ ΕΛΕΥΘΕΡΩΝ ΗΛΕΚΤΡΟΝΙΩΝ ΟΔΗΓΕΙ ΣΤΗΝ ΚΑΤΑΝΟΗΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΙΔΙΟΤΗΤΩΝ ΤΩΝ ΜΕΤΑΛΛΩΝ OΠΩΣ ΤΗ ΘΕΡΜΙΚΗ ΑΓΩΓΙΜΟΤΗΤΑ, ΜΑΓΝΗΤΙΚΗ ΕΠΙΔΕΚΤΙΚΟΤΗΤΑ ΚΑΙ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΕΣ
ΕΝΕΡΓΕΙΑΚΕΣ ΖΩΝΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΖΩΝΕΣ ΤΟ ΠΡΟΤΥΠΟ ΤΩΝ ΕΛΕΥΘΕΡΩΝ ΗΛΕΚΤΡΟΝΙΩΝ ΟΔΗΓΕΙ ΣΤΗΝ ΚΑΤΑΝΟΗΣΗ ΤΩΝ ΦΥΣΙΚΩΝ ΙΔΙΟΤΗΤΩΝ ΤΩΝ ΜΕΤΑΛΛΩΝ OΠΩΣ ΤΗ ΘΕΡΜΙΚΗ ΑΓΩΓΙΜΟΤΗΤΑ, ΜΑΓΝΗΤΙΚΗ ΕΠΙΔΕΚΤΙΚΟΤΗΤΑ ΚΑΙ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΕΣ
αγωγοί ηµιαγωγοί µονωτές Σχήµα 1
 Η2 Μελέτη ηµιαγωγών 1. Σκοπός Στην περιοχή της επαφής δυο ηµιαγωγών τύπου p και n δηµιουργούνται ορισµένα φαινόµενα τα οποία είναι υπεύθυνα για τη συµπεριφορά της επαφής pn ή κρυσταλλοδιόδου, όπως ονοµάζεται,
Η2 Μελέτη ηµιαγωγών 1. Σκοπός Στην περιοχή της επαφής δυο ηµιαγωγών τύπου p και n δηµιουργούνται ορισµένα φαινόµενα τα οποία είναι υπεύθυνα για τη συµπεριφορά της επαφής pn ή κρυσταλλοδιόδου, όπως ονοµάζεται,
Μάθημα 23 ο. Μεταλλικός Δεσμός Θεωρία Ζωνών- Ημιαγωγοί Διαμοριακές Δυνάμεις
 Μάθημα 23 ο Μεταλλικός Δεσμός Θεωρία Ζωνών- Ημιαγωγοί Διαμοριακές Δυνάμεις Μεταλλικός Δεσμός Μοντέλο θάλασσας ηλεκτρονίων Πυρήνες σε θάλασσα e -. Μεταλλική λάμψη. Ολκιμότητα. Εφαρμογή δύναμης Γενική και
Μάθημα 23 ο Μεταλλικός Δεσμός Θεωρία Ζωνών- Ημιαγωγοί Διαμοριακές Δυνάμεις Μεταλλικός Δεσμός Μοντέλο θάλασσας ηλεκτρονίων Πυρήνες σε θάλασσα e -. Μεταλλική λάμψη. Ολκιμότητα. Εφαρμογή δύναμης Γενική και
ΗΛΕΚΤΡΟΝΙΚΑ Ι ΚΕΦΑΛΑΙΟ 1 Ο :ΗΜΙΑΓΩΓΟΙ
 ΗΛΕΚΤΡΟΝΙΚΑ Ι ΚΕΦΑΛΑΙΟ 1 Ο :ΗΜΙΑΓΩΓΟΙ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΟΜΗ. ΕΝΔΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ Δομή του ατόμου Σήμερα γνωρίζουμε ότι η ύλη αποτελείται από ενώσεις ατόμων, δημιουργώντας τις πολυάριθμες χημικές ενώσεις
ΗΛΕΚΤΡΟΝΙΚΑ Ι ΚΕΦΑΛΑΙΟ 1 Ο :ΗΜΙΑΓΩΓΟΙ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΟΜΗ. ΕΝΔΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ Δομή του ατόμου Σήμερα γνωρίζουμε ότι η ύλη αποτελείται από ενώσεις ατόμων, δημιουργώντας τις πολυάριθμες χημικές ενώσεις
ηλεκτρικό ρεύµα ampere
 Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
Ηλεκτρικό ρεύµα Το ηλεκτρικό ρεύµα είναι ο ρυθµός µε τον οποίο διέρχεται ηλεκτρικό φορτίο από µια περιοχή του χώρου. Η µονάδα µέτρησης του ηλεκτρικού ρεύµατος στο σύστηµα SI είναι το ampere (A). 1 A =
ΦΩΤΟΒΟΛΤΑΪΚΑ. Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής
 ΦΩΤΟΒΟΛΤΑΪΚΑ Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής Αγωγοί- μονωτές- ημιαγωγοί Μέταλλα: Μία ζώνη μερικώς γεμάτη ή μία ζώνη επικαλύπτει την άλλη Τα ηλεκτρόνια μπορούν
ΦΩΤΟΒΟΛΤΑΪΚΑ Γ. Λευθεριώτης Αναπλ. Καθηγητής Γ. Συρροκώστας Μεταδιδακτορικός Ερευνητής Αγωγοί- μονωτές- ημιαγωγοί Μέταλλα: Μία ζώνη μερικώς γεμάτη ή μία ζώνη επικαλύπτει την άλλη Τα ηλεκτρόνια μπορούν
7.a. Οι δεσμοί στα στερεά
 ΤΕΤΥ Σύγχρονη Φυσική Κεφ. 7-1 Κεφάλαιο 7. Στερεά Εδάφια: 7.a. Οι δεσμοί στα στερεά 7.b. Η θεωρία των ενεργειακών ζωνών 7.c. Νόθευση ημιαγωγών και εφαρμογές 7.d. Υπεραγωγοί 7.a. Οι δεσμοί στα στερεά Με
ΤΕΤΥ Σύγχρονη Φυσική Κεφ. 7-1 Κεφάλαιο 7. Στερεά Εδάφια: 7.a. Οι δεσμοί στα στερεά 7.b. Η θεωρία των ενεργειακών ζωνών 7.c. Νόθευση ημιαγωγών και εφαρμογές 7.d. Υπεραγωγοί 7.a. Οι δεσμοί στα στερεά Με
Ορθή πόλωση της επαφής p n
 Δύο τρόποι πόλωσης της επαφής p n Ορθή πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ορθή πόλωση p n Άνοδος Κάθοδος Ανάστροφη πόλωση p n Άνοδος Κάθοδος
Δύο τρόποι πόλωσης της επαφής p n Ορθή πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ορθή πόλωση p n Άνοδος Κάθοδος Ανάστροφη πόλωση p n Άνοδος Κάθοδος
Ανάστροφη πόλωση της επαφής p n
 Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n
 Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
Ανάστροφη πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων dpapageo@cc.uoi.gr http://pc164.materials.uoi.gr/dpapageo Επαφή p n Ανάστροφη πόλωση Πολώνουμε
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς
 ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Δρ. Ιούλιος Γεωργίου Required Text: Microelectronic Devices, Keith Leaver Επικοινωνία Γραφείο: Green Park, Room 406 Ηλ. Ταχυδρομείο: julio@ucy.ac.cy
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Δρ. Ιούλιος Γεωργίου Required Text: Microelectronic Devices, Keith Leaver Επικοινωνία Γραφείο: Green Park, Room 406 Ηλ. Ταχυδρομείο: julio@ucy.ac.cy
Κεφάλαια (από το βιβλίο Serway-Jewett) και αναρτημένες παρουσιάσεις
 Ύλη μαθήματος «Σύγχρονη Φυσική» Κεφάλαια (από το βιβλίο Serway-Jewett) και αναρτημένες παρουσιάσεις Σ2-Σελίδες: 673-705, (όλο το κεφάλαιο από το βιβλίο) και η παρουσίαση Σ2 που έχει αναρτηθεί στο e-class
Ύλη μαθήματος «Σύγχρονη Φυσική» Κεφάλαια (από το βιβλίο Serway-Jewett) και αναρτημένες παρουσιάσεις Σ2-Σελίδες: 673-705, (όλο το κεφάλαιο από το βιβλίο) και η παρουσίαση Σ2 που έχει αναρτηθεί στο e-class
Ορθή πόλωση της επαφής p n
 Δύο τρόποι πόλωσης της επαφής p n Ορθή πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ορθή πόλωση p n Άνοδος Κάθοδος Ανάστροφη πόλωση p n Άνοδος Κάθοδος
Δύο τρόποι πόλωσης της επαφής p n Ορθή πόλωση της επαφής p n Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ορθή πόλωση p n Άνοδος Κάθοδος Ανάστροφη πόλωση p n Άνοδος Κάθοδος
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
John Bardeen, William Schockley, Walter Bratain, Bell Labs τρανζίστορ σημειακής επαφής Γερμανίου, Bell Labs
 Ψηφιακή τεχνολογία Ε. Λοιδωρίκης Δ. Παπαγεωργίου Η εφεύρεση του τρανζίστορ Το πρώτο τρανζίστορ John rn, Willi Schocl Wltr rtin, ll Ls 948 τρανζίστορ σημειακής επαφής Γερμανίου, ll Ls 4 Τεχνολογία πυριτίου
Ψηφιακή τεχνολογία Ε. Λοιδωρίκης Δ. Παπαγεωργίου Η εφεύρεση του τρανζίστορ Το πρώτο τρανζίστορ John rn, Willi Schocl Wltr rtin, ll Ls 948 τρανζίστορ σημειακής επαφής Γερμανίου, ll Ls 4 Τεχνολογία πυριτίου
Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd Email : stvrentzou@gmail.com
 1 2.4 Παράγοντες από τους οποίους εξαρτάται η αντίσταση ενός αγωγού Λέξεις κλειδιά: ειδική αντίσταση, μικροσκοπική ερμηνεία, μεταβλητός αντισ ροοστάτης, ποτενσιόμετρο 2.4 Παράγοντες που επηρεάζουν την
1 2.4 Παράγοντες από τους οποίους εξαρτάται η αντίσταση ενός αγωγού Λέξεις κλειδιά: ειδική αντίσταση, μικροσκοπική ερμηνεία, μεταβλητός αντισ ροοστάτης, ποτενσιόμετρο 2.4 Παράγοντες που επηρεάζουν την
Διάλεξη 2. Ηλεκτροτεχνία Ι. Κυκλώματα συνεχούς και Ηλεκτρομαγνητισμός. Α. Δροσόπουλος
 Ηλεκτροτεχνία Ι Κυκλώματα συνεχούς και Ηλεκτρομαγνητισμός Α Δροσόπουλος Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Σχολή Τεχνολογικών Εφαρμογών ΤΕΙ Δυτικής Ελλάδος Α Δροσόπουλος Ηλεκτροτεχνία Ι Θεμελιώδεις έννοιες
Ηλεκτροτεχνία Ι Κυκλώματα συνεχούς και Ηλεκτρομαγνητισμός Α Δροσόπουλος Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Σχολή Τεχνολογικών Εφαρμογών ΤΕΙ Δυτικής Ελλάδος Α Δροσόπουλος Ηλεκτροτεχνία Ι Θεμελιώδεις έννοιες
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Ηλεκτρικό ρεύμα Αντίσταση - ΗΕΔ. Ηλεκτρικό ρεύμα Ένταση ηλεκτρικού ρεύματος Αντίσταση Ειδική αντίσταση Νόμος του Ohm Γραμμικοί μή γραμμικοί αγωγοί
 Ηλεκτρικό ρεύμα Αντίσταση - ΗΕΔ Ηλεκτρικό ρεύμα Ένταση ηλεκτρικού ρεύματος Αντίσταση Ειδική αντίσταση Νόμος του Ohm Γραμμικοί μή γραμμικοί αγωγοί ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ Μέχρι τώρα: Ηλεκτροστατική Δηλαδή μελετούσαμε
Ηλεκτρικό ρεύμα Αντίσταση - ΗΕΔ Ηλεκτρικό ρεύμα Ένταση ηλεκτρικού ρεύματος Αντίσταση Ειδική αντίσταση Νόμος του Ohm Γραμμικοί μή γραμμικοί αγωγοί ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ Μέχρι τώρα: Ηλεκτροστατική Δηλαδή μελετούσαμε
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ
 ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ 1 ΝΟΜΟΣ ΤΟΥ OHM (ΩΜ) Για πολλά υλικά ο λόγος της πυκνότητας του ρεύματος προς το ηλεκτρικό πεδίο είναι σταθερός και ανεξάρτητος από το ηλεκτρικό
ΗΛΕΚΤΡΟΝΙΚΑ ΣΤΟΙΧΕΙΑ & ΚΥΚΛΩΜΑΤΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΗΛΕΚΤΡΟΤΕΧΝΙΑ 1 ΝΟΜΟΣ ΤΟΥ OHM (ΩΜ) Για πολλά υλικά ο λόγος της πυκνότητας του ρεύματος προς το ηλεκτρικό πεδίο είναι σταθερός και ανεξάρτητος από το ηλεκτρικό
12. Εάν ένα κομμάτι ημιαγωγού τύπου n και ένα κομμάτι ΟΧΙ
 Πρόβλημα 1 Απαντήστε στις ερωτήσεις Σωστό 1. Οι ημιαγωγοί δεν είναι καλοί αγωγοί ούτε καλοί μονωτές. * ΝΑΙ 2. Το ιόν είναι ένα άτομο που έχει χάσει ή έχει προσλάβει ένα ΝΑΙ ή περισσότερα ηλεκτρόνια. 3.
Πρόβλημα 1 Απαντήστε στις ερωτήσεις Σωστό 1. Οι ημιαγωγοί δεν είναι καλοί αγωγοί ούτε καλοί μονωτές. * ΝΑΙ 2. Το ιόν είναι ένα άτομο που έχει χάσει ή έχει προσλάβει ένα ΝΑΙ ή περισσότερα ηλεκτρόνια. 3.
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς
 ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Μέτρηση του μ e και προσδιορισμός του προσήμου των φορέων φορτίου Πρόβλημα: προσδιορισμός
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Μέτρηση του μ e και προσδιορισμός του προσήμου των φορέων φορτίου Πρόβλημα: προσδιορισμός
Άσκηση 5 ΦΩΤΟΒΟΛΤΑΪΚΟ ΦΑΙΝΟΜΕΝΟ
 Άσκηση 5 ΦΩΤΟΒΟΛΤΑΪΚΟ ΦΑΙΝΟΜΕΝΟ 1. ΓΕΝΙΚΑ Τα ηλιακά στοιχεία χρησιμοποιούνται για τη μετατροπή του φωτός (που αποτελεί μία μορφή ηλεκτρομαγνητικής ενέργειας) σε ηλεκτρική ενέργεια. Κατασκευάζονται από
Άσκηση 5 ΦΩΤΟΒΟΛΤΑΪΚΟ ΦΑΙΝΟΜΕΝΟ 1. ΓΕΝΙΚΑ Τα ηλιακά στοιχεία χρησιμοποιούνται για τη μετατροπή του φωτός (που αποτελεί μία μορφή ηλεκτρομαγνητικής ενέργειας) σε ηλεκτρική ενέργεια. Κατασκευάζονται από
Ηλεκτρικά Κυκλώματα Ι ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 Ηλεκτρικά Κυκλώματα Ι ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
Ηλεκτρικά Κυκλώματα Ι ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1 ο :Σε κάθε μια από τις παρακάτω προτάσεις να βρείτε τη μια σωστή απάντηση: 1. Η διαφορά δυναμικού μεταξύ δύο σημείων μιας δυναμικής γραμμής, ομογενούς ηλεκτρικού
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΘΕΜΑ 1 ο :Σε κάθε μια από τις παρακάτω προτάσεις να βρείτε τη μια σωστή απάντηση: 1. Η διαφορά δυναμικού μεταξύ δύο σημείων μιας δυναμικής γραμμής, ομογενούς ηλεκτρικού
Ηλεκτρομαγνητισμός. Μαγνητικό πεδίο. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
Κεφάλαιο 3 ο. Γ. Τσιατούχας. VLSI Technology and Computer Architecture Lab. Ημιαγωγοί - ίοδος Επαφής 2
 ΗΛΕΚΤΡΟΝΙΚΗ Πανεπιστήμιο Ιωαννίνων Ημιαγωγοί Δίοδος Επαφής Κεφάλαιο 3 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας SI Techology ad Comuter Architecture ab ΗΛΕΚΤΡΟΝΙΚΗ Διάρθρωση 1. Φράγμα δυναμικού.
ΗΛΕΚΤΡΟΝΙΚΗ Πανεπιστήμιο Ιωαννίνων Ημιαγωγοί Δίοδος Επαφής Κεφάλαιο 3 ο Τμήμα Μηχανικών Η/Υ και Πληροφορικής Γ. Τσιατούχας SI Techology ad Comuter Architecture ab ΗΛΕΚΤΡΟΝΙΚΗ Διάρθρωση 1. Φράγμα δυναμικού.
ΚΕΦΑΛΑΙΟ 2: Ηλεκτρικό Ρεύμα Μέρος 1 ο
 ΚΕΦΑΛΑΙΟ 2: Ηλεκτρικό Ρεύμα Μέρος 1 ο Βασίλης Γαργανουράκης Φυσική ήγ Γυμνασίου Εισαγωγή Στο προηγούμενο κεφάλαιο μελετήσαμε τις αλληλεπιδράσεις των στατικών (ακίνητων) ηλεκτρικών φορτίων. Σε αυτό το κεφάλαιο
ΚΕΦΑΛΑΙΟ 2: Ηλεκτρικό Ρεύμα Μέρος 1 ο Βασίλης Γαργανουράκης Φυσική ήγ Γυμνασίου Εισαγωγή Στο προηγούμενο κεφάλαιο μελετήσαμε τις αλληλεπιδράσεις των στατικών (ακίνητων) ηλεκτρικών φορτίων. Σε αυτό το κεφάλαιο
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ. Ενότητα 10: ΗΜΙΑΓΩΓΟΙ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ Ενότητα 10: ΗΜΙΑΓΩΓΟΙ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ Ενότητα 10: ΗΜΙΑΓΩΓΟΙ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Μελέτη Μετασχηματιστή
 Μελέτη Μετασχηματιστή 1. Θεωρητικό μέρος Κάθε φορτίο που κινείται και κατά συνέπεια κάθε αγωγός που διαρρέεται από ρεύμα δημιουργεί γύρω του ένα μαγνητικό πεδίο. Το μαγνητικό πεδίο B με την σειρά του ασκεί
Μελέτη Μετασχηματιστή 1. Θεωρητικό μέρος Κάθε φορτίο που κινείται και κατά συνέπεια κάθε αγωγός που διαρρέεται από ρεύμα δημιουργεί γύρω του ένα μαγνητικό πεδίο. Το μαγνητικό πεδίο B με την σειρά του ασκεί
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
Φωτοδίοδος. 1.Σκοπός της άσκησης. 2.Θεωρητικό μέρος
 Φωτοδίοδος 1.Σκοπός της άσκησης Ο σκοπός της άσκησης είναι να μελετήσουμε την συμπεριφορά μιας φωτιζόμενης επαφής p-n (φωτοδίοδος) όταν αυτή είναι ορθά και ανάστροφα πολωμένη και να χαράξουμε την χαρακτηριστική
Φωτοδίοδος 1.Σκοπός της άσκησης Ο σκοπός της άσκησης είναι να μελετήσουμε την συμπεριφορά μιας φωτιζόμενης επαφής p-n (φωτοδίοδος) όταν αυτή είναι ορθά και ανάστροφα πολωμένη και να χαράξουμε την χαρακτηριστική
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε με τις αισθήσεις μας οφείλονται
1η ΠΑΡΟΥΣΙΑΣΗ. Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία
 1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
1η ΠΑΡΟΥΣΙΑΣΗ Ηλεκτρικά φορτία, ηλεκτρικές δυνάμεις και πεδία Ηλεκτρισμός και μαγνητισμός Κλάδος της Φυσικής που μελετάει τα ηλεκτρικά και τα μαγνητικά φαινόμενα. (Σχεδόν) όλα τα φαινομενα που αντιλαμβανόμαστε
Πείραμα - 6 Η ηλεκτρική αγωγιμότητα και η μέτρηση του ενεγειακού χασματος στο Γερμάνιο
 Πείραμα - 6 Η ηλεκτρική αγωγιμότητα και η μέτρηση του ενεγειακού χασματος στο Γερμάνιο 1 Η ηλεκτρική αγωγιμότητα και η μέτρηση του ενεργειακού χάσματος στο Γερμάνιο 1.1 Αρχή της άσκησης Η ηλεκτρική αγωγιμότητα
Πείραμα - 6 Η ηλεκτρική αγωγιμότητα και η μέτρηση του ενεγειακού χασματος στο Γερμάνιο 1 Η ηλεκτρική αγωγιμότητα και η μέτρηση του ενεργειακού χάσματος στο Γερμάνιο 1.1 Αρχή της άσκησης Η ηλεκτρική αγωγιμότητα
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή. Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής
 Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
Spin του πυρήνα Μαγνητική διπολική ροπή Ηλεκτρική τετραπολική ροπή Τάσος Λιόλιος Μάθημα Πυρηνικής Φυσικής Εξάρτηση του πυρηνικού δυναμικού από άλλους παράγοντες (πλην της απόστασης) Η συνάρτηση του δυναμικού
ΘΕΩΡΙΑ ΤΩΝ ΗΜΙΑΓΩΓΩΝ ΠΡΩΤΗ ΕΝΟΤΗΤΑ ΟΜΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ
 ΘΕΩΡΙΑ ΤΩΝ ΗΜΙΑΓΩΓΩΝ ΠΡΩΤΗ ΕΝΟΤΗΤΑ ΟΜΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ ΕΝΕΡΓΕΙΑΚΕΣ ΤΑΙΝΙΕΣ : Ηλεκτρονική δομή των ενεργειακών ταινιών Ε(k) διαφόρων ημιαγωγών Άμεσο και έμμεσο ενεργειακό χάσμα Ταινία αγωγιμότητας και ηλεκτρόνιαταινία
ΘΕΩΡΙΑ ΤΩΝ ΗΜΙΑΓΩΓΩΝ ΠΡΩΤΗ ΕΝΟΤΗΤΑ ΟΜΟΓΕΝΕΙΣ ΗΜΙΑΓΩΓΟΙ ΕΝΕΡΓΕΙΑΚΕΣ ΤΑΙΝΙΕΣ : Ηλεκτρονική δομή των ενεργειακών ταινιών Ε(k) διαφόρων ημιαγωγών Άμεσο και έμμεσο ενεργειακό χάσμα Ταινία αγωγιμότητας και ηλεκτρόνιαταινία
ΣΗΜΕΙΩΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ
 ΣΗΜΕΙΩΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ Κεφάλαιο 2 - Ηλεκτρικό Ρεύμα Επιμέλεια: Αγκανάκης Παναγιώτης, Φυσικός https://physicscourses.wordpress.com/ Με ποιες θεμελιώδεις έννοιες συνδέεται το ηλεκτρικό ρεύμα; Το
ΣΗΜΕΙΩΣΕΙΣ ΦΥΣΙΚΗΣ Γ ΓΥΜΝΑΣΙΟΥ Κεφάλαιο 2 - Ηλεκτρικό Ρεύμα Επιμέλεια: Αγκανάκης Παναγιώτης, Φυσικός https://physicscourses.wordpress.com/ Με ποιες θεμελιώδεις έννοιες συνδέεται το ηλεκτρικό ρεύμα; Το
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς
 ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Δρ. Ιούλιος Γεωργίου Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Τρέχον περιεχόμενο Αγωγή ηλεκτρικών φορτίων σε ημιαγωγούς
ΑΡΧΕΣ ΗΛΕΚΤΡΟΝΙΚΩΝ ΣΤΟΙΧΕΙΩΝ Αγωγιμότητα σε ημιαγωγούς Δρ. Ιούλιος Γεωργίου Required Text: Microelectronic Devices, Keith Leaver (1 st Chapter) Τρέχον περιεχόμενο Αγωγή ηλεκτρικών φορτίων σε ημιαγωγούς
ΚΕΦΑΛΑΙΟ 7 ΗΛΕΚΤΡΙΚΗ ΑΓΩΓΙΜΟΤΗΤΑ ΣΤΑ ΜΕΤΑΛΛΑ- ΑΝΤΙΣΤΑΤΕΣ
 ΚΕΦΑΛΑΙΟ 7 ΗΛΕΚΤΡΙΚΗ ΑΓΩΓΙΜΟΤΗΤΑ ΣΤΑ ΜΕΤΑΛΛΑ- ΑΝΤΙΣΤΑΤΕΣ 7.1. Εισαγωγή Στο κεφάλαιο αυτό θα εξετάσουμε την ηλεκτρική αγωγιμότητα των μεταλλικών υλικών και τους παράγοντες που την επηρεάζουν, όπως η θερμοκρασία,
ΚΕΦΑΛΑΙΟ 7 ΗΛΕΚΤΡΙΚΗ ΑΓΩΓΙΜΟΤΗΤΑ ΣΤΑ ΜΕΤΑΛΛΑ- ΑΝΤΙΣΤΑΤΕΣ 7.1. Εισαγωγή Στο κεφάλαιο αυτό θα εξετάσουμε την ηλεκτρική αγωγιμότητα των μεταλλικών υλικών και τους παράγοντες που την επηρεάζουν, όπως η θερμοκρασία,
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και
ΘΕΜΑ 1ο ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΤΡΙΤΗ 3 ΙΟΥΝΙΟΥ 2003 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και
Ασκήσεις Φασµατοσκοπίας
 Ασκήσεις Φασµατοσκοπίας Η φασµατική περιοχή στην οποία βρίσκεται µια φωτεινή ακτινοβολία χαρακτηρίζεται από την συχνότητα ν (Hz) µε την οποία ταλαντώνεται το ηλεκτρικό και το µαγνητικό πεδίο του φωτός.
Ασκήσεις Φασµατοσκοπίας Η φασµατική περιοχή στην οποία βρίσκεται µια φωτεινή ακτινοβολία χαρακτηρίζεται από την συχνότητα ν (Hz) µε την οποία ταλαντώνεται το ηλεκτρικό και το µαγνητικό πεδίο του φωτός.
ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 2
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 2: Ένωση pn Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΝΙΚΗ Ι Ενότητα 2: Ένωση pn Χατζόπουλος Αλκιβιάδης Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχ. Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό
1. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ):
 1. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ): 1) Ηλεκτρισμένα ονομάζουμε τα σώματα τα οποία, αφού τα τρίψουμε έχουν την ιδιότητα να έλκουν μικρά αντικείμενα. 2) Οι ηλεκτρικές
1. Να χαρακτηρίσετε τις παρακάτω προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ): 1) Ηλεκτρισμένα ονομάζουμε τα σώματα τα οποία, αφού τα τρίψουμε έχουν την ιδιότητα να έλκουν μικρά αντικείμενα. 2) Οι ηλεκτρικές
Κεφάλαιο 2 Χημικοί Δεσμοί
 Κεφάλαιο 2 Χημικοί Δεσμοί Σύνοψη Παρουσιάζονται οι χημικοί δεσμοί, ιοντικός, μοριακός, ατομικός, μεταλλικός. Οι ιδιότητες των υλικών τόσο οι φυσικές όσο και οι χημικές εξαρτώνται από το είδος ή τα είδη
Κεφάλαιο 2 Χημικοί Δεσμοί Σύνοψη Παρουσιάζονται οι χημικοί δεσμοί, ιοντικός, μοριακός, ατομικός, μεταλλικός. Οι ιδιότητες των υλικών τόσο οι φυσικές όσο και οι χημικές εξαρτώνται από το είδος ή τα είδη
ΓΥΜΝΑΣΙΟ ΑΓΙΟΥ ΒΑΣΙΛΕΙΟΥ ΣΤΡΟΒΟΛΟΥ ΣΧΟΛIKH ΧΡΟΝΙΑ ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2017
 ΓΥΜΝΑΣΙΟ ΑΓΙΟΥ ΑΣΙΛΕΙΟΥ ΣΤΡΟΟΛΟΥ ΣΧΟΛIKH ΧΡΟΝΙΑ 2016-2017 ΑΘΜΟΣ ΦΥΣΙΚΗΣ Αριθμητικώς:.../40 Ολογρ.:... Υπογραφή:... ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2017 ΜΑΘΗΜΑ: Φυσική ΗΜΕΡΟΜΗΝΙΑ: 26/05/2017 ΤΑΞΗ: Γ
ΓΥΜΝΑΣΙΟ ΑΓΙΟΥ ΑΣΙΛΕΙΟΥ ΣΤΡΟΟΛΟΥ ΣΧΟΛIKH ΧΡΟΝΙΑ 2016-2017 ΑΘΜΟΣ ΦΥΣΙΚΗΣ Αριθμητικώς:.../40 Ολογρ.:... Υπογραφή:... ΓΡΑΠΤΕΣ ΑΠΟΛΥΤΗΡΙΕΣ ΕΞΕΤΑΣΕΙΣ ΜΑΪΟΥ 2017 ΜΑΘΗΜΑ: Φυσική ΗΜΕΡΟΜΗΝΙΑ: 26/05/2017 ΤΑΞΗ: Γ
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Εισαγωγή στη Μικροηλεκτρονική 1. Στοιχειακοί ηµιαγωγοί
 Εισαγωγή στη Μικροηλεκτρονική 1 Στοιχειακοί ηµιαγωγοί Εισαγωγή στη Μικροηλεκτρονική Οµοιοπολικοί δεσµοί στο πυρίτιο Κρυσταλλική δοµή Πυριτίου ιάσταση κύβου για το Si: 0.543 nm Εισαγωγή στη Μικροηλεκτρονική
Εισαγωγή στη Μικροηλεκτρονική 1 Στοιχειακοί ηµιαγωγοί Εισαγωγή στη Μικροηλεκτρονική Οµοιοπολικοί δεσµοί στο πυρίτιο Κρυσταλλική δοµή Πυριτίου ιάσταση κύβου για το Si: 0.543 nm Εισαγωγή στη Μικροηλεκτρονική
ΗΜΙΑΓΩΓΟΙ. Σπύρος Νικολαΐδης Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής
 ΗΜΙΑΓΩΓΟΙ Σπύρος Νικολαΐδης Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής Ηλεκτρονικοί φλοιοί των ατόμων Σθένος και ομοιοπολικοί δεσμοί Η πρώτη ύλη με την οποία κατασκευάζονται τα περισσότερα ηλεκτρονικά
ΗΜΙΑΓΩΓΟΙ Σπύρος Νικολαΐδης Καθηγητής Τομέας Ηλεκτρονικής & ΗΥ Τμήμα Φυσικής Ηλεκτρονικοί φλοιοί των ατόμων Σθένος και ομοιοπολικοί δεσμοί Η πρώτη ύλη με την οποία κατασκευάζονται τα περισσότερα ηλεκτρονικά
2.1 Το ηλεκτρικό ρεύμα
 Κεφάλαιο 2. Ηλεκτρικό Ρέυμα 2.1 Το ηλεκτρικό ρεύμα 1. Με ποιες θεμελιώδεις έννοιες του ηλεκτρισμού συνδέεται το ηλεκτρικό ρεύμα; Το ηλεκτρικό ρεύμα συνδέεται με τις θεμελιώδεις έννοιες του ηλεκτρισμού:
Κεφάλαιο 2. Ηλεκτρικό Ρέυμα 2.1 Το ηλεκτρικό ρεύμα 1. Με ποιες θεμελιώδεις έννοιες του ηλεκτρισμού συνδέεται το ηλεκτρικό ρεύμα; Το ηλεκτρικό ρεύμα συνδέεται με τις θεμελιώδεις έννοιες του ηλεκτρισμού:
Επαφές μετάλλου ημιαγωγού
 Δίοδος Schottky Επαφές μετάλλου ημιαγωγού Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Τι είναι Ημιαγωγός Κατασκευάζεται με εξάχνωση μετάλλου το οποίο μεταφέρεται στην επιφάνεια
Δίοδος Schottky Επαφές μετάλλου ημιαγωγού Δ. Γ. Παπαγεωργίου Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Τι είναι Ημιαγωγός Κατασκευάζεται με εξάχνωση μετάλλου το οποίο μεταφέρεται στην επιφάνεια
ΘΕΜΑ 1ο 1.1 Να γράψετε στο τετράδιό σας τα φυσικά μεγέθη από τη Στήλη Ι και, δίπλα σε καθένα, τη μονάδα της Στήλης ΙΙ που αντιστοιχεί σ' αυτό.
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 5 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο 1.1 Να γράψετε στο τετράδιό σας τα φυσικά μεγέθη από τη Στήλη Ι και,
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΕΣΠΕΡΙΝΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 5 ΙΟΥΝΙΟΥ 2002 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ : ΦΥΣΙΚΗ ΘΕΜΑ 1ο 1.1 Να γράψετε στο τετράδιό σας τα φυσικά μεγέθη από τη Στήλη Ι και,
ΚΙΝΗΣΕΙΣ ΦΟΡΤΙΩΝ ΣΕ Ο.Μ.Π. 1. Στο σχήμα δίνονται δύο ομογενή μαγνητικά πεδία με εντάσεις μέτρων Β 2 =2Β 1
 1. Στο σχήμα δίνονται δύο ομογενή μαγνητικά πεδία με εντάσεις μέτρων Β 2 =2Β 1. Ένα φορτισμένο σωματίδιο μπαίνει στο πρώτο από το μέσον Ο της πλευράς ΑΓ με ταχύτητα υ 0 και αφού διαγράψει τεταρτοκύκλιο,
1. Στο σχήμα δίνονται δύο ομογενή μαγνητικά πεδία με εντάσεις μέτρων Β 2 =2Β 1. Ένα φορτισμένο σωματίδιο μπαίνει στο πρώτο από το μέσον Ο της πλευράς ΑΓ με ταχύτητα υ 0 και αφού διαγράψει τεταρτοκύκλιο,
ΒΑΣΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ Ηµιαγωγοί VLSI T echnol ogy ogy and Computer A r A chitecture Lab Γ Τσ ιατ α ο τ ύχ ύ α χ ς ΒΑΣΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ
 ΒΑΣΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ Ηµιαγωγοί VSI Techology ad Comuter Archtecture ab Ηµιαγωγοί Γ. Τσιατούχας ΒΑΣΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ Διάρθρωση. Φράγμα δυναμικού. Ενεργειακές ζώνες Ημιαγωγοί
ΒΑΣΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ Ηµιαγωγοί VSI Techology ad Comuter Archtecture ab Ηµιαγωγοί Γ. Τσιατούχας ΒΑΣΙΚΑ ΗΛΕΚΤΡΟΝΙΚΑ ΜΙΚΡΟΗΛΕΚΤΡΟΝΙΚΗ Διάρθρωση. Φράγμα δυναμικού. Ενεργειακές ζώνες Ημιαγωγοί
Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης περιγράφεται σωστά από το νόμο Coulomb
 Σημαντικό!!!!!!!! Με βάση το νόμο Coulomb υπολογίζουμε τη δύναμη ανάμεσα σε δύο φορτισμένα σωματίδια οποία είναι ακίνητα Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης
Σημαντικό!!!!!!!! Με βάση το νόμο Coulomb υπολογίζουμε τη δύναμη ανάμεσα σε δύο φορτισμένα σωματίδια οποία είναι ακίνητα Ισχύει όταν κινούνται ; Ισχύει όταν κινείται μόνο το ένα δηλαδή η δύναμη αλληλεπίδρασης
Εξεταστέα Ύλη στη Φυσική Γ Γυμνασίου
 Εξεταστέα Ύλη στη Φυσική Γ Γυμνασίου ΕΝΟΤΗΤΑ 1: Ενέργεια (Φυλλάδια) Ορισμός έργου σταθερής δύναμης που ασκείται σε ένα σώμα και έχει την ίδια διεύθυνση με την μετατόπιση του σώματος: W = Δύναμη x Μετατόπιση=
Εξεταστέα Ύλη στη Φυσική Γ Γυμνασίου ΕΝΟΤΗΤΑ 1: Ενέργεια (Φυλλάδια) Ορισμός έργου σταθερής δύναμης που ασκείται σε ένα σώμα και έχει την ίδια διεύθυνση με την μετατόπιση του σώματος: W = Δύναμη x Μετατόπιση=
http://www.electronics.teipir.gr /personalpages/papageorgas/ download/3/
 Δίοδος επαφής 1 http://www.electronics.teipir.gr /personalpages/papageorgas/ download/3/ 2 Θέματα που θα καλυφθούν Ορθή πόλωση Forward bias Ανάστροφη πόλωση Reverse bias Κατάρρευση Breakdown Ενεργειακά
Δίοδος επαφής 1 http://www.electronics.teipir.gr /personalpages/papageorgas/ download/3/ 2 Θέματα που θα καλυφθούν Ορθή πόλωση Forward bias Ανάστροφη πόλωση Reverse bias Κατάρρευση Breakdown Ενεργειακά
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
Κίνηση σε Ηλεκτρικό Πεδίο.
 Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενός ισοπλεύρου τριγώνου ΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σημειακά ηλεκτρικά φορτία 1 =2μC και 2 αντίστοιχα.
Κίνηση σε Ηλεκτρικό Πεδίο. 3.01. Έργο κατά την μετακίνηση φορτίου. Στις κορυφές Β και Γ ενός ισοπλεύρου τριγώνου ΒΓ πλευράς α= 2cm, βρίσκονται ακλόνητα δύο σημειακά ηλεκτρικά φορτία 1 =2μC και 2 αντίστοιχα.
ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση:
 Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση: Να γνωρίζει το ατοµικό πρότυπο του Bohr καθώς και τα µειονεκτήµατά του. Να υπολογίζει την ενέργεια που εκπέµπεται ή απορροφάται
Μετά το τέλος της µελέτης του 1ου κεφαλαίου, ο µαθητής θα πρέπει να είναι σε θέση: Να γνωρίζει το ατοµικό πρότυπο του Bohr καθώς και τα µειονεκτήµατά του. Να υπολογίζει την ενέργεια που εκπέµπεται ή απορροφάται
Λύση Α. Σωστή η επιλογή α. Β.
 1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
1) Αρνητικά φορτισμένο σωμάτιο κινείται σε ομογενές ηλεκτρικό πεδίο μεγάλης έκτασης. Να επιλέξετε τη σωστή πρόταση. Αν η κατεύθυνση της κίνησης του σωματίου παραμένει σταθερή, τότε: α. Συμπίπτει με την
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧ/ΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ
 ΦΥΣΙΗ ΛΥΕΙΟΥ ΘΕΤΙΗΣ Ι ΤΕΧ/ΗΣ ΤΕΥΘΥΝΣΗΣ ΘΕΜ : Στις ερωτήσεις - να γράψετε στο φύλλο απαντήσεων τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. Στις ερωτήσεις -5 να γράψετε
ΦΥΣΙΗ ΛΥΕΙΟΥ ΘΕΤΙΗΣ Ι ΤΕΧ/ΗΣ ΤΕΥΘΥΝΣΗΣ ΘΕΜ : Στις ερωτήσεις - να γράψετε στο φύλλο απαντήσεων τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. Στις ερωτήσεις -5 να γράψετε
Λυμένες ασκήσεις. Ηλεκτρική δυναμική ενέργεια
 Λυμένες ασκήσεις Ηλεκτρική δυναμική ενέργεια 1. Στις κορυφές οριζόντιου ισόπλευρου τριγώνου Α,Β,Γ πλευράς α βρίσκονται τα φόρτια,όπου. α. Ποια η δυναμική ηλεκτρική ενέργεια του συστήματος; β. Ποιο το φυσικό
Λυμένες ασκήσεις Ηλεκτρική δυναμική ενέργεια 1. Στις κορυφές οριζόντιου ισόπλευρου τριγώνου Α,Β,Γ πλευράς α βρίσκονται τα φόρτια,όπου. α. Ποια η δυναμική ηλεκτρική ενέργεια του συστήματος; β. Ποιο το φυσικό
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Β ΤΑΞΗ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 27/04/ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ & ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΕΚΦΩΝΗΣΕΙΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Β ΤΑΞΗ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 27/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ & ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ Β ΤΑΞΗ ΛΥΚΕΙΟΥ ΚΥΡΙΑΚΗ 27/04/2014 - ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ & ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ: ΕΞΙ (6) ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α Στις ερωτήσεις Α1 Α4 να γράψετε στο τετράδιο σας
Θέµατα που θα καλυφθούν
 Ηµιαγωγοί Semiconductors 1 Θέµατα που θα καλυφθούν Αγωγοί Conductors Ηµιαγωγοί Semiconductors Κρύσταλλοι πυριτίου Silicon crystals Ενδογενείς Ηµιαγωγοί Intrinsic semiconductors ύο τύποι φορέων για το ρεύµασεηµιαγωγούς
Ηµιαγωγοί Semiconductors 1 Θέµατα που θα καλυφθούν Αγωγοί Conductors Ηµιαγωγοί Semiconductors Κρύσταλλοι πυριτίου Silicon crystals Ενδογενείς Ηµιαγωγοί Intrinsic semiconductors ύο τύποι φορέων για το ρεύµασεηµιαγωγούς
ΤΕΧΝΟΛΟΓΙΑ ΥΛΙΚΩΝ ΜΑΘΗΜΑ 1 Ο ΙΔΙΟΤΗΤΕΣ ΥΛΙΚΩΝ. Δρ. M.Χανιάς Αν.Καθηγητής Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ, ΤΕΙ Ανατολικής Μακεδονίας και Θράκης
 ΤΕΧΝΟΛΟΓΙΑ ΥΛΙΚΩΝ ΜΑΘΗΜΑ 1 Ο ΙΔΙΟΤΗΤΕΣ ΥΛΙΚΩΝ Δρ. M.Χανιάς Αν.Καθηγητής Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ, ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΚΑΒΑΛΑ 018 1 1. ΕΙΣΑΓΩΓΗ ΣΤΑ ΥΛΙΚΑ. ΑΓΩΓΙΜΑ ΥΛΙΚΑ 3. ΗΜΙΑΓΩΓΟΙ
ΤΕΧΝΟΛΟΓΙΑ ΥΛΙΚΩΝ ΜΑΘΗΜΑ 1 Ο ΙΔΙΟΤΗΤΕΣ ΥΛΙΚΩΝ Δρ. M.Χανιάς Αν.Καθηγητής Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ, ΤΕΙ Ανατολικής Μακεδονίας και Θράκης ΚΑΒΑΛΑ 018 1 1. ΕΙΣΑΓΩΓΗ ΣΤΑ ΥΛΙΚΑ. ΑΓΩΓΙΜΑ ΥΛΙΚΑ 3. ΗΜΙΑΓΩΓΟΙ
