Ειςαγωγή ςτισ Συναρτήςεισ τησ PHP
|
|
|
- Κυβηλη Βλαβιανός
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ειςαγωγή ςτισ Συναρτήςεισ τησ PHP Οι ςυναρτιςεισ (functions) τθσ PHP, δθλ. αυτζσ που υπάρχουν ενςωματωμζνεσ μζςα ςτθν PHP αλλά και αυτζσ που δθμιουργοφμε μόνοι μασ, διευκολφνουν πολφ το γράψιμο του κϊδικα κακϊσ μασ δίνουν τθ δυνατότθτα να επαναχρθςιμοποιιςουμε τον κϊδικα που ζχουν γράψει κάποιοι άλλοι χριςτεσ και μποροφμε ακόμθ να κάνουμε τα δικά μασ scripts να ζχουν μικρό μζγεκοσ και να είναι ζτςι πιο εφκολα ςτθ διαχείριςι τουσ. Κακϊσ θ PHP 5 περιζχει περιςςότερεσ από ςυναρτιςεισ, μπορεί να ςκεφκοφμε ότι είναι μια πολφ εφκολθ γλϊςςα προγραμματιςμοφ, αλλά θ αλικεια είναι ότι θ κάκε ςυνάρτθςθ πρζπει να χρθςιμοποιείται με διαφορετικό τρόπο και ζτςι πρζπει να μακαίνεται ξεχωριςτά. Θα ξεκινιςουμε με τισ πιο χριςιμεσ και πιο απλζσ ςυναρτιςεισ που διακζτει θ PHP. Για να αποφφγουμε να γράφουμε τα ίδια κομμάτια κϊδικα κάκε φορά που κζλουμε να κάνουμε τθν ίδια εργαςία, θ PHP μάσ δίνει τθ δυνατότθτα να ενςωματϊςουμε κάποιον κϊδικα ςε μια ςυνάρτθςθ τθν οποία κα μποροφμε μετά να καλζςουμε από οπουδιποτε μζςα από ζνα script. Η PHP διακζτει μερικζσ εκατοντάδεσ ενςωματωμζνεσ ςυναρτήςεισ (built-in functions) για να κάνουμε πολλζσ δουλειζσ, όπωσ διάβαςμα αρχείων και χειριςμό strings μζχρι και αναηθτιςεισ ςε βάςεισ δεδομζνων και ςφνδεςθ μ ζναν IRC server. Αν διαπιςτϊςουμε ότι δεν υπάρχει κάποια ςυνάρτθςθ που τθν χρειαηόμαςτε, μποροφμε να προςκζςουμε τθ δικι μασ ς ζνα script και αυτζσ είναι γνωςτζσ ωσ οι ςυναρτήςεισ του χρήςτη (user functions). Θα δοφμε αρχικά το πϊσ μποροφμε να χρθςιμοποιιςουμε τισ ενςωματωμζνεσ ςυναρτιςεισ τθσ PHP μζςα από τα δικά μασ scripts. Η κλιςθ μιασ ςυνάρτθςθσ γίνεται πολφ απλά γράφοντασ το όνομά τθσ ακολουκοφμενο από δφο παρενκζςεισ. Πολλζσ ςυναρτιςεισ δζχονται παραμζτρουσ (parameters), δθλ. τιμζσ που χρθςιμοποιοφνται για να επθρεάςουν τθν εκτζλεςθ και φυςικά και το αποτζλεςμα τθσ ςυνάρτθςθσ. Επίςθσ, όλεσ ςχεδόν οι ςυναρτιςεισ ζχουν και μια τιμή επιςτροφήσ (return value), που είναι το αποτζλεςμα από τθν εκτζλεςθ των εντολϊν τθσ ςυνάρτθςθσ και μποροφμε μάλιςτα να χρθςιμοποιιςουμε τθν τιμι επιςτροφισ μιασ ςυνάρτθςθσ ωσ παράμετρο ς άλλεσ ςυναρτιςεισ, ωσ εξισ : func1(func2(func3(), func4())); Θα πρζπει να ζχουμε υπόψθ μασ ότι με τον όρο παράμετροι εννοοφμε τισ μεταβλθτζσ που εμφανίηονται ςτθ διλωςθ τθσ ςυνάρτθςθσ και που ορίηουν ποιεσ τιμζσ πρζπει να μεταβιβαςκοφν ςτθ ςυνάρτθςθ, ενϊ οι πραγματικζσ παράμετροι που μεταβιβάηονται όταν γίνεται θ κλιςθ μιασ ςυνάρτθςθσ αποκαλοφνται ορίςματα (arguments). Βζβαια, ουςιαςτικι διαφορά δεν υπάρχει ανάμεςα ςτουσ δφο αυτοφσ
2 όρουσ και πολλοί χρθςιμοποιοφν τουσ όρουσ «παράμετροι» και «ορίςματα» για να αναφζρονται ςτο ίδιο πράγμα. Κάτι άλλο που κα πρζπει να ζχουμε υπόψθ μασ είναι ότι ενϊ μερικζσ παράμετροι είναι υποχρεωτικζσ, δθλ. κα πρζπει να καταχωριςουμε κάποια τιμι γι αυτζσ, κάποιεσ άλλεσ είναι προαιρετικζσ, δθλ. μποροφμε να μθν γράψουμε κάτι ςτθ κζςθ τουσ. Στθν περίπτωςθ αυτι, θ PHP κα χρθςιμοποιιςει μια δικι τθσ προκακοριςμζνθ τιμι (default value). Όταν μεταβιβάηουμε μια παράμετρο ςε μια ςυνάρτθςθ, θ PHP ςτθν πραγματικότθτα χρθςιμοποιεί ζνα αντίγραφο τθσ τιμισ τθσ και αυτό ςθμαίνει ότι μποροφμε να τροποποιιςουμε τισ μεταβλθτζσ μζςα ςε μια ςυνάρτθςθ αλλά δεν κα αλλάξουν και οι αντίςτοιχεσ τιμζσ τουσ εκτόσ τθσ ςυνάρτθςθσ. Για να αλλάξουμε αυτι τθν κατάςταςθ, μποροφμε να επιλζξουμε να μεταβιβάςουμε μια μεταβλθτι με αναφορά (by reference), οπότε θ PHP μεταβιβάηει τθν πραγματικι μεταβλθτι μζςα ςτθ ςυνάρτθςθ και αυτό ςθμαίνει ότι όποιεσ αλλαγζσ κάνουμε ςτθν τιμι τθσ μεταβλθτισ κα επθρεάςουν και τθν αρχικι τιμι τθσ. Αυτό κα φανεί καλφτερα ςτο παρακάτω script : somefunc($a); somefunc($a, $b); somefunc($a, &$b); somefunc(&$a, &$b); Η πρϊτθ γραμμι του κϊδικα καλεί τθ ςυνάρτθςθ somefunc() και τθσ μεταβιβάηει ζνα αντίγραφο τθσ μεταβλθτισ $a, θ δεφτερθ γραμμι του κϊδικα μεταβιβάηει αντίγραφα των $a και $b, θ τρίτθ μεταβιβάηει ζνα αντίγραφο τθσ $a και τθν αρχικι τιμι τθσ $b και τζλοσ, θ τελευταία γραμμι κϊδικα μεταβιβάηει τισ αρχικζσ τιμζσ και τθσ $a και τθσ $b. Η μεταβίβαςθ με αναφορά (passing by reference), όπωσ ςυμβαίνει με τθ μεταβλθτι $b ςτθν 3 θ γραμμι και τισ μεταβλθτζσ $a και $b ςτθν 4 θ γραμμι κϊδικα, ςθμαίνει ότι αυτζσ οι μεταβλθτζσ μπορεί να αλλάξουν μζςα ςτθ ςυνάρτθςθ, που είναι κι ζνασ τρόποσ για να επιςτρζφουν τιμζσ οι ςυναρτιςεισ. Τα Πρωτότυπα των Συναρτήςεων Ο ςτάνταρτ τρόποσ για να περιγράψουμε τισ παραμζτρουσ που δζχεται και τθν τιμι που επιςτρζφει μια ςυνάρτθςθ είναι με το πρωτότυπο μιασ ςυνάρτθςθσ (function
3 prototype). Η κατανόθςι του είναι πολφ ςθμαντικι για τθ ςυνζχεια. Θα δοφμε αρχικά το πρωτότυπο τθσ ςυνάρτθςθσ strtoupper() : string strtoupper ( string string) Αυτό που καταλαβαίνουμε με μια πρϊτθ ματιά είναι ότι θ ςυνάρτθςθ δζχεται ζνα string ωσ παράμετρο και επιςτρζφει επίςθσ ζνα string. Μπορεί να μασ μπερδεφει θ ζκφραςθ "stringstring", που ςθμαίνει ότι ο τφποσ δεδομζνων τθσ παραμζτρου είναι string αλλά και το όνομα που δίνουμε ςτθν παράμετρο είναι επίςθσ string. Η ςυνάρτθςθ επιςτρζφει μια τιμι string και βλζπουμε ότι ο τφποσ δεδομζνων τθσ τιμισ επιςτροφισ αναγράφεται πριν από το όνομα τθσ ςυνάρτθςθσ, που αποτελεί μια ακόμα πρακτικι τθσ C. Για τισ παραμζτρουσ που μεταβιβάηονται με αναφορά (by reference), χρθςιμοποιοφμε ωσ πρόκεμα το ςφμβολο &. Θα δοφμε τϊρα το πρωτότυπο τθσ ςυνάρτθςθσ sha1() : string sha1 ( string source [, bool raw_output]) Όπωσ μποροφμε να δοφμε, θ ςυνάρτθςθ sha1() επιςτρζφει μια τιμι string, δζχεται ζνα string ωσ τθν πρϊτθ παράμετρό τθσ και μια τιμι boolean ωσ τθ δεφτερθ παράμετρό τθσ. Όμωσ, θ δεφτερθ παράμετροσ βρίςκεται ανάμεςα ςε αγκφλεσ, που ςθμαίνει ότι είναι προαιρετικι. Στα πρωτότυπα υπάρχουν δφο ειδικοί τφποι δεδομζνων, οι number και mixed. Το numberμπορεί να είναι ζνασ αρικμόσ κινθτισ υποδιαςτολισ (floating-point) ι ζνασ ακζραιοσ αρικμόσ (integer) και το mixed ςθμαίνει ότι θ ςυνάρτθςθ δζχεται ι επιςτρζφει δφο ι περιςςότερουσ τφπουσ δεδομζνων. Για παράδειγμα, ο οριςμόσ τθσ ςυνάρτθςθσ pow() είναι ο εξισ : number pow ( number base, number exp) Αυτό ςθμαίνει ότι δζχεται οποιουςδιποτε αρικμοφσ ωσ παραμζτρουσ και μπορεί να επιςτρζψει ζναν οποιονδιποτε αρικμό. Ο οριςμόσ τθσ ςυνάρτθςθσ serialize() είναι ο εξισ : string serialize ( mixed value) Η ςυνάρτθςθ serialize() εργάηεται και με αντικείμενα (objects) και με τάξεισ (classes), οπότε θ παράμετρόσ τθσ είναι του τφπου mixed. Υπάρχει και ο γνωςτόσ τφποσ δεδομζνων void, που ςθμαίνει ότι θ ςυνάρτθςθ δεν επιςτρζφει κάποια τιμι ι ότι δεν δζχεται κάποια παράμετρο ωσ είςοδο. Θα δοφμε και τον ςυμβολιςμό "...", που ςθμαίνει ότι θ ςυνάρτθςθ δζχεται ζναν μεταβλθτό αρικμό παραμζτρων. Για παράδειγμα, το πρωτότυπο τθσ ςυνάρτθςθσ isset() είναι το εξισ : bool isset ( mixed var [, mixed var [, mixed...]])
4 Η παραπάνω ςυνάρτθςθ δζχεται μία τουλάχιςτον παράμετρο ωσ είςοδο, αλλά μπορεί να δεχκεί και περιςςότερεσ κακϊσ υπάρχει ο ςυμβολιςμόσ "...". Συναρτήςεισ για τον Ζλεγχο Μεταβλητών bool isset ( mixed var [, mixed var [, mixed...]]) void unset ( mixed var [, mixed var [, mixed...]]) bool empty ( mixed var) Υπάρχουν τρεισ πολφ βαςικζσ ςυναρτιςεισ με τισ οποίεσ μποροφμε να ελζγχουμε τισ μεταβλθτζσ, οι isset(), empty() και unset(). Η ςυνάρτθςθ isset() επιςτρζφει τθν τιμι true αν θ μεταβλθτι που τθσ μεταβιβάηεται ωσ παράμετροσ ζχει ιδθ οριςκεί μζςα ςτο script, ενϊ θ ςυνάρτθςθ empty(), θ οποία δζχεται μία μόνο παράμετρο, επιςτρζφει τθν τιμι true αν θ μεταβλθτι ζχει τθν τιμι false. Για να ελζγξουμε αν μια μεταβλθτι δεν ζχει οριςκεί, μποροφμε να χρθςιμοποιιςουμε τον τελεςτι άρνθςθσ! και να δϊςουμε τθν εντολι "if(!isset($a))". Η ςυνάρτθςθ unset() διαγράφει πλιρωσ μια ιδθ υπάρχουςα μεταβλθτι, που ςθμαίνει ότι αν μετά χρθςιμοποιιςουμε τθ ςυνάρτθςθ isset(), αυτι κα επιςτρζψει τθν τιμι false. Συναρτήςεισ για τον Ζλεγχο τησ Εκτζλεςησ του Script void exit ( [mixed status]) mixed eval ( [string code_string]) void die ( [mixed status]) Η ςυνάρτθςθ exit() λαμβάνει μία μόνο προαιρετικι παράμετρο και ςταματάει αμζςωσ τθν εκτζλεςθ του script. Αν υπάρχει παράμετροσ, κα εκτελεςτεί ο κϊδικασ που αυτι περιζχει ι αν είναι string κα εμφανιςκεί το περιεχόμενό του. Η ςυνάρτθςθ die() είναι ςχεδόν ίδια με τθ ςυνάρτθςθ exit(), ενϊ θ ςυνάρτθςθ eval() λαμβάνει ζνα string ωσ παράμετρο το οποίο και εκτελεί ςαν να ιταν PHP κϊδικασ. Ακολουκοφν παραδείγματα με τισ ςυναρτιςεισ exit() και eval() : $str = "exit()"; eval($str);
5 Το παραπάνω script εκχωρεί το string "exit()" ςτθ μεταβλθτι $str και μετά μεταβιβάηει το $str ςτθ ςυνάρτθςθ eval(), θ οποία κα εκτελζςει το string ςαν να ιταν PHP κϊδικασ και ζτςι το τελικό αποτζλεςμα είναι ότι θ PHP εκτελεί τθ ςυνάρτθςθ exit() μζςω τθσ eval() και ςταματάει τθν εκτζλεςθ του script. Με τθ ςυνάρτθςθ exit() μποροφμε να τερματίςουμε τθν εκτζλεςθ ενόσ script, όπωσ για παράδειγμα : if ($a!= $blahblah) { } print "Απαγοπεύεηαι η ππόζβαζη"; exit; Η ςυνάρτθςθ die() χρθςιμοποιείται ςυνικωσ ωσ εξισ : do_some_func() OR die("η do_some_func() επέζηπετε false!"); Σφμφωνα με τον παραπάνω κϊδικα, κα κλθκεί θ ςυνάρτθςθ do_some_ func() και αν επιςτρζψει τθν τιμι false, κα κλθκεί θ ςυνάρτθςθ die() για να τερματίςει το script. Αυτό αποτελεί ζναν γριγορο και εφκολο τρόπο για να είμαςτε ςίγουροι ότι κάποιεσ ςυναρτιςεισ ζχουν εκτελεςτεί με επιτυχία πριν ςυνεχίςουμε με τον υπόλοιπο κϊδικα του script. Όπωσ ιδθ γνωρίηουμε, θ PHP κα εκτελζςει τθ δεφτερθ ςυνάρτθςθ μόνο αν θ πρϊτθ ςυνάρτθςθ επιςτρζψει τθν τιμι false. Εκείνο που πρζπει να ζχουμε υπόψθ μασ είναι ότι ο τελεςτισ, δθλ. το ιςοδφναμο του τελεςτι OR, ζχει υψθλότερθ προτεραιότθτα από τον τελεςτι OR αλλά υψθλότερθ προτεραιότθτα και από τον τελεςτι =. Αυτό κα το καταλάβουμε καλφτερα με το επόμενο παράδειγμα : $fp = fopen("somefile", "r") die("το απσείο δεν άνοιξε!"); Από μια πρϊτθ ματιά φαίνεται ίδιο με το προθγοφμενο παράδειγμα τθσ ςυνάρτθςθσ die(), δθλ. θ PHP κα προςπακιςει να φορτϊςει το αρχείο "somefile" και κα δθμιουργιςει ζναν δείκτθ αρχείου (file pointer) ςτθ μεταβλθτι $fp και αν αυτό αποτφχει, κα τερματίςει (exit) τθν εκτζλεςθ του script με το μινυμα "Το αρχείο δεν άνοιξε!". Όμωσ, δεν ςυμβαίνει κάτι τζτοιο και αυτό επειδι ο τελεςτισ ζχει υψθλότερθ προτεραιότθτα από τον τελεςτι =, είναι αυτόσ που υπολογίηεται πρϊτοσ. Ζτςι, θ PHP κα προςπακιςει πρϊτα να φορτϊςει το αρχείο somefile και αν επιτφχει, θ ςυνάρτθςθ fopen() κα επιςτρζψει ζνα resource που κα είναι true. Η ςυνάρτθςθ die() πάντα αποτιμάται ωσ true.
6 Όμωσ, επειδι θ PHP κα βραχυκυκλϊςει τον τελεςτι, όταν θ ςυνάρτθςθ fopen() επιτφχει, θ ςυνάρτθςθ die() δεν κα κλθκεί και ο τελεςτισ κα επιςτρζψει τθν τιμι 1 (true) επειδι ο τελεςτζοσ που βρίςκεται ςτα αριςτερά του (κλιςθ ςτθ ςυνάρτθςθ fopen()) επζςτρεψε τθν τιμι true. Στθν ουςία, θ PHP διαβάηει τθν παραπάνω γραμμι κϊδικα ωσ εξισ : $fp = (fopen("somefile", "r") die("το απσείο δεν άνοιξε!")); Η τιμι 1 κα εκχωρθκεί ςτθ μεταβλθτι $fp. Δεν κα κζλαμε, όμωσ, κάτι τζτοιο και ζτςι κα πρζπει να χρθςιμοποιιςουμε τον τελεςτι OR. Κακϊσ ο τελεςτισ OR ζχει χαμθλότερθ προτεραιότθτα από τον τελεςτι =, θ PHP κα διαβάςει τθ γραμμι του κϊδικα ωσ εξισ : ($fp = fopen("somefile", "r")) or die("το απσείο δεν άνοιξε!"); Αυτό ςθμαίνει ότι καλείται θ ςυνάρτθςθ fopen() και θ τιμι τθσ εκχωρείται ςτθ μεταβλθτι $fp, θ οποία μετά ςτζλνεται ςτον τελεςτι ςφγκριςθσ. Ζχουμε ανάγκθ και από τουσ δφο τελεςτζσ και OR, αλλά κα πρζπει να επιλζξουμε αυτόν που χρειαηόμαςτε κάκε φορά. Οι Συναρτήςεισ Ημερομηνίασ και Ώρασ Η PHP παριςτάνει τον χρόνο ωσ τον αρικμό των δευτερολζπτων που ζχουν παρζλκει από τθν 1 θ Ιανουαρίου του 1970 και ϊρα 00:00:00 GMT, μια θμερομθνία που είναι γνωςτι ωσ θ αρχι τθσ εποχισ του Unix (Unix epoch). Αυτόσ ο τρόποσ αποκικευςθσ θμερομθνιϊν μπορεί να μασ φαίνεται περίεργοσ αλλά είναι εξαιρετικά βολικόσ κακϊσ μποροφμε να αποκθκεφςουμε μια οποιαδιποτε θμερομθνία με τθ μορφι ενόσ ακεραίου αρικμοφ και μετά να μετατρζψουμε αυτόν τον αρικμό ςε μια μορφι θμερομθνίασ που να είναι κατανοθτι από τον άνκρωπο. Διάβαςμα τησ Τρζχουςασ Ώρασ int time ( ) mixed microtime ( [bool get_as_float]) Η PHP διακζτει μια βαςικι ςυνάρτθςθ για να διαβάςουμε τθν τρζχουςα ϊρα ςτθ μορφι epoch, τθν time(). Η ςυνάρτθςθ time() δεν δζχεται παραμζτρουσ και επιςτρζφει τθν τρζχουςα ϊρα, που είναι γνωςτι και ωσ ςφραγίδα χρόνου (timestamp). Ακολουκεί ζνα παράδειγμα :
7 print time()."<br>"; $a = time(); print $a; Το αποτζλεςμα από τθν εκτζλεςθ του παραπάνω script κα είναι το εξισ : Όπωσ βλζπουμε και από το παραπάνω παράδειγμα, μποροφμε είτε να εκτυπϊςουμε απευκείασ τθν τιμι επιςτροφισ τθσ ςυνάρτθςθσ time() ι μποροφμε να τθν αποκθκεφςουμε ςε μια μεταβλθτι και μετά να εκτυπϊςουμε τθν τιμι τθσ μεταβλθτισ. Το αποτζλεςμα είναι το ίδιο. Μποροφμε να χρθςιμοποιιςουμε τθ ςυνάρτθςθ microtime() για πιο ακριβείσ τιμζσ ϊρασ. Όταν καλείται αυτι θ ςυνάρτθςθ χωρίσ κάποια παράμετρο, επιςτρζφει τθν τρζχουςα ϊρα του ςυςτιματοσ ςε δευτερόλεπτα (seconds) και εκατομμυριοςτά του δευτερολζπτου (microseconds), με πρϊτα τα εκατομμυριοςτά του δευτερολζπτου. Για παράδειγμα : Αν δϊςουμε τθν τιμι true ωσ παράμετρο ςτθ ςυνάρτθςθ microtime(), θ PHP κα επιςτρζψει τθν ϊρα ςτθ μορφι seconds.microseconds, ωσ εξισ : Με τθ ρφκμιςθ precision ςτο αρχείο php.ini μποροφμε να ορίςουμε τον αρικμό των ςθμαντικϊν ψθφίων (significant digits) που κζλουμε να εμφανίηονται ς ζναν αρικμό κινθτισ υποδιαςτολισ (floating-point number). Δημιουργία Ημερομηνίασ από ζνα String int strtotime ( string time [, int now]) Η μετατροπι μιασ θμερομθνίασ από τθν καταχϊρθςθ ενόσ χριςτθ ςτθ μορφι Unix timestamp μπορεί να είναι επικίνδυνθ κακϊσ κάποιοι χριςτεσ καταχωροφν τισ θμερομθνίεσ με τθ μορφι θθ/μμ/εε, άλλοι με τθ μορφι εε-μμ-θθ, άλλοι με τθ μορφι θθ-μμ-εεεε κοκ. Η ςυνάρτθςθ που παρζχει θ PHP για τθ μετατροπι ενόσ string ςε μορφι timestamp, θ strtotime(), λαμβάνει δφο παραμζτρουσ : το string
8 τθσ ϊρασ και μια δεφτερθ προαιρετικι παράμετρο που μπορεί να είναι ζνα ςχετικό timestamp. Η πρϊτθ παράμετροσ είναι ςθμαντικι και κα τθν δοφμε αμζςωσ παρακάτω : print strtotime("22nd December 1979"); print strtotime("22 Dec :30"); print strtotime("1979/12/22"); Βλζπουμε ότι χρθςιμοποιιςαμε τρεισ τρόπουσ για να παραςτιςουμε τθν ίδια θμερομθνία, όπου ςτον δεφτερο τρόπο ςυμπεριλάβαμε και τθν ϊρα. Αν τρζξουμε το παραπάνω script, κα δοφμε ότι θ PHP εμφανίηει ζναν ακζραιο για τθν κάκε εντολι, όπου ο πρϊτοσ και ο τρίτοσ αρικμόσ είναι ίδιοι και ο δεφτεροσ είναι λίγο διαφορετικόσ. Αυτοί οι αρικμοί είναι οι λεγόμενεσ ςφραγίδεσ χρόνου του Unix (Unix timestamps) που αντιςτοιχοφν ςτισ θμερομθνίεσ που μεταβιβάςαμε ςτθ ςυνάρτθςθ strtotime(), θ οποία ζκανε και τθ μετατροπι. Θα πρζπει να ζχουμε υπόψθ μασ ότι θ ςυνάρτθςθ strtotime() χρθςιμοποιεί το αμερικάνικο ςτυλ για τισ θμερομθνίεσ, δθλ. βάηει πρϊτα τον μινα, όπωσ ςτθν θμερομθνία 10/11/2007, όπου κεωρεί ότι είναι 11 Οκτωβρίου και όχι 10 Νοεμβρίου. Αν θ PHP δεν μπορζςει να μετατρζψει το string ςε μορφι timestamp, κα επιςτρζψει τθν τιμι -1. Αυτό μποροφμε να το χρθςιμοποιιςουμε για να ελζγχουμε αν ζγινε ςωςτά θ μετατροπι μιασ θμερομθνίασ, ωσ εξισ : $mydate = strtotime("christmas 2006"); if ($mydate == -1) { print "Η μεηαηποπή ηηρ ημεπομηνίαρ απέηςσε!"; } else { print "Η μεηαηποπή ηηρ ημεπομηνίαρ έγινε!"; }
9 Όπωσ είδαμε νωρίτερα, θ ςυνάρτθςθ strtotime() διακζτει και μια δεφτερθ προαιρετικι παράμετρο που τθν χρθςιμοποιεί ωσ βάςθ για τον υπολογιςμό ςχετικϊν θμερομθνιϊν. Ο λόγοσ γι αυτό είναι ότι θ πρϊτθ παράμετροσ μπορεί να περιζχει ςχετικζσ τιμζσ, όπωσ "Next Sunday", "2 days" ι "1 year ago" κοκ. Σ αυτιν τθν περίπτωςθ, θ PHP πρζπει να γνωρίηει με ποια βάςθ κα υπολογίςει αυτζσ τισ ςχετικζσ τιμζσ. Ακολουκοφν μερικά παραδείγματα : print strtotime("next Sunday"); 2)); print strtotime("2 days", time() - (86400 * print strtotime("1 year ago", ); Η πρϊτθ γραμμι κα εμφανίςει το timestamp για τθν επόμενθ Κυριακι. Η δεφτερθ γραμμι κα επιςτρζψει τθν τρζχουςα ϊρα, δθλ. δφο θμζρεσ από τϊρα μείον δφο θμζρεσ (86400 = 24 Χ 60 Χ 60). Η τελευταία εντολι αφαιρεί ζνα ζτοσ από ζνα δεδομζνο timestamp. Μετατροπή Ημερομηνιών ςε String string date ( string format [, int timestamp]) Η PHP διακζτει πάρα πολλζσ επιλογζσ για να μετατρζψουμε timestamps ςε strings με τθ ςυνάρτθςθ date(). Η ςυνάρτθςθ date() δζχεται δφο παραμζτρουσ, όπου θ δεφτερθ είναι προαιρετικι. Η πρϊτθ παράμετροσ είναι ζνα ειδικό string που περιζχει κωδικοφσ μορφοποίθςθσ για το πϊσ κζλουμε να εμφανιςκεί θ θμερομθνία. Η δεφτερθ παράμετροσ είναι τοtimestamp που κζλουμε να μετατρζψουμε, όπου αν δεν δϊςουμε κάποια τιμι, θ PHP κα κεωριςει ότι κζλουμε να μετατρζψουμε το τρζχον timestamp. Η πρϊτθ παράμετροσ είναι το κλειδί και είναι ζνα string από γράμματα από μια προκακοριςμζνθ λίςτα 31 δυνατϊν τιμϊν. Αν χρθςιμοποιιςουμε άλλουσ χαρακτιρεσ ςτο string, αυτοί κα αντιγραφοφν απευκείασ μζςα ςτθ μορφοποιθμζνθ θμερομθνία. Αν κελιςουμε να ςυμπεριλάβουμε κάποιο κείμενο μζςα ςτθ μορφοποιθμζνθ θμερομθνία αλλά να μθν εκλθφκεί ωσ παράμετροσ, κα πρζπει να χρθςιμοποιιςουμε τον χαρακτιρα \ (backslash). Ακολουκεί θ ολοκλθρωμζνθ λίςτα των χαρακτιρων που χρθςιμοποιοφνται για τθ μορφοποίθςθ των θμερομθνιϊν και δεν κα πρζπει να ξεχνάμε ότι είναι case sensitive, δθλ. ξεχωρίηουν τα πεηά από τα κεφαλαία γράμματα.
10 Χαρακτήρασ Μορφοποίηςησ Περιγραφή Παράδειγμα a Το am/pm με πεηά γράμματα am ι pm A Το am/pm με κεφαλαία γράμματα AM ι PM B Swatch Internet Time 000 ζωσ 999 c Η θμερομθνία, θ ϊρα και θ ηϊνθ τθσ ϊρασ (time zone) ςφμφωνα με το ISO T09:26:55+01:00 d Ο αρικμόσ του μινα με 2 ψθφία 01 ζωσ 31 D Το όνομα τθσ θμζρασ με 3 γράμματα Mon, Thu, Sat F Το πλιρεσ όνομα του μινα January, August g G h H i Η ϊρα ςε 12ωρθ μορφι, χωρίσ μθδενικά μπροςτά Η ϊρα ςε 24ωρθ μορφι, χωρίσ μθδενικά μπροςτά Η ϊρα ςε 12ωρθ μορφι, με μθδενικά μπροςτά Η ϊρα ςε 24ωρθ μορφι, με μθδενικά μπροςτά Τα λεπτά τθσ ϊρασ με μθδενικά μπροςτά 1 ζωσ 12 0 ζωσ ζωσ ζωσ ζωσ 59 I Αν είναι ενεργι θ κερινι ϊρα 1 αν ναι, 0 αν όχι j Η θμζρα του μινα, χωρίσ μθδενικά μπροςτά 1 ζωσ 31 l Το πλιρεσ όνομα τθσ θμζρασ Monday, Saturday L Αν πρόκειται για δίςεκτο ζτοσ 1 αν ναι, 0 αν όχι m Ο αρικμόσ του μινα, με μθδενικά μπροςτά 01 ζωσ 12 M Το ςφντομο όνομα του μινα Jan, Aug n Ο αρικμόσ του μινα, χωρίσ μθδενικά μπροςτά O Η διαφορά από τθν ϊρα GMT 200 r s S Η μορφι τθσ θμερομθνίασ ςφμφωνα με το RFC-822 Τα δευτερόλεπτα τθσ ϊρασ με μθδενικά μπροςτά Το αγγλικό αρικμθτικό επίκεμα για τθν θμζρα του μινα 1 ζωσ 12 Sat, 22 Dec : ζωσ 59 st, nd, rd ι th
11 t T Ο αρικμόσ των θμερϊν που ζχει ο μινασ Η ηϊνθ τθσ ϊρασ (time zone) για τον server 28 ζωσ 31 GMT, CET, EST U Η ςφραγίδα χρόνου (Unix Timestamp) w Ο αρικμόσ τθσ θμζρασ τθσ εβδομάδασ 0 (Sunday), 6 (Saturday) W Ο αρικμόσ τθσ εβδομάδασ του ζτουσ ςφμφωνα με το ISO-8601 y Το ζτοσ με δφο ψθφία 93, 07 Y Το ζτοσ με τζςςερα ψθφία 1993, 2007 z Η θμζρα του ζτουσ 0 to 366 Z Η διαφορά τθσ ηϊνθσ ϊρασ (time zone offset) ςε δευτερόλεπτα 30 (30 θ εβδομάδα του ζτουσ) to Όπωσ μποροφμε να δοφμε, υπάρχουν πολλζσ επιλογζσ διακζςιμεσ όταν κάνουμε μετατροπι από ζνα timestamp ςε θμερομθνία. Ακολουκοφν μερικά παραδείγματα με χαρακτιρεσ μορφοποίθςθσ θμερομθνιϊν : print date("h:i"). "\n"; print "Χθερ ήηαν : ". date("l", time() ). "\n"; print "Το έηορ είναι : ". date("y"). "\n"; print date("js of F Y"). "\n"; print "Τα γενέθλιά μος είναι : " strtotime("01 Dec 2007")). " θέηορ.\n";. date("l", print date("\m\y b\i\\r\\t\h\d\a\y \i\s o\\n \a l \\t\h\i\s \ye\a\\r. ", strtotime("01 Dec 2007")). "\n"; Το αποτζλεςμα από τθν εκτζλεςθ του παραπάνω script κα είναι το εξισ : 01:31 Χθερ ήηαν : Saturday Το έηορ είναι : 2007
12 2nd of December 2007 Τα γενέθλιά μος είναι : Saturday θέηορ. My birthday is on a Saturday this year. Η πρϊτθ γραμμι είναι θ πιο βαςικι και απλά εμφανίηει τθν τρζχουςα ϊρα ςε 24ωρθ μορφι. Η δεφτερθ γραμμι είναι λίγο πιο πολφπλοκθ κακϊσ αναμειγνφει τθν ζξοδο τθσ ςυνάρτθςθσdate() μ ζνα κομμάτι κειμζνου ϊςτε να είναι πιο φυςικό το αποτζλεςμα. Κάτι ανάλογο ζχουμε και ςτθν τρίτθ γραμμι. Η τζταρτθ γραμμι εμφανίηει τθν θμερομθνία ςτθ μορφι "2nd of December 2007", όπου γράψαμε εμείσ τθ λζξθ "of". Η PHP δεν μπερδεφτθκε και αυτό γιατί το μικρό γράμμα o και το μικρό γράμμα f δεν χρθςιμοποιοφνται ςτθ μορφοποίθςθ θμερομθνιϊν τθσ ςυνάρτθςθσ date() και ζτςι εμφανίηονται ςτθν ζξοδο όπωσ ακριβϊσ είναι. Στθν πζμπτθ γραμμι ζχουμε ενϊςει τθν ζξοδο τθσ ςυνάρτθςθσ date() με δφο άλλα strings. Μποροφμε να γράψουμε τα strings και μζςα ςτθ ςυνάρτθςθ date(), όπωσ φαίνεται ςτθν ζκτθ γραμμι, αλλά αυτό είναι πολφ πιο πολφπλοκο. Στθν ζκτθ γραμμι βλζπουμε ότι ςυμπεριλάβαμε κείμενο μζςα ςτθ ςυνάρτθςθ date() αλλά αναγκαςτικαμε να χρθςιμοποιιςουμε τον χαρακτιρα \ για να μθν μπερδευτεί θ PHP και εκλάβει τα γράμματα ωσ εντολζσ μορφοποίθςθσ, όπωσ \M\y κλπ. Τα μικρά γράμματα b, o και e δεν χρθςιμοποιοφνται ςτισ εντολζσ μορφοποίθςθσ και ζτςι δεν χρειάηεται να χρθςιμοποιιςουμε τον χαρακτιρα \. Τα μικρά γράμματα r, t και n ζχουν ειδικι χριςθ ωσ χαρακτιρεσ διαφυγισ (carriage return, tab και new line αντίςτοιχα) και ζτςι αναγκαςτικαμε να χρθςιμοποιιςουμε δφο χαρακτιρεσ \\. Το ζνα backslash εμποδίηει τθν PHP από το να τα διαβάςει ωσ χαρακτιρεσ μορφοποίθςθσ θμερομθνιϊν και το άλλο εμποδίηει τθν PHP από το να τα εκλάβει ωσ χαρακτιρεσ διαφυγισ. Δημιουργία Ημερομηνιών από Συςτατικά int mktime ( [int hour [, int minute [, int second [, int month [, int day [, int year [, int is_dst]]]]]]]) Αποτελεί κοινι τακτικι να αποκθκεφουμε το ζτοσ, τον μινα και τθν θμερομθνία ςε ξεχωριςτζσ μεταβλθτζσ ϊςτε να είναι πιο εφκολθ θ ςφγκριςθ και υπάρχει μια ειδικι ςυνάρτθςθ για να δθμιουργιςουμε ζνα timestamp ςτο Unix από τα ςυςτατικά μιασ θμερομθνίασ, θ mktime(). Η ςειρά αναγραφισ των ςυςτατικϊν τθσ θμερομθνίασ ωσ ορίςματα μζςα ςτθ ςυνάρτθςθ είναι θ εξισ : hour, minute, second, month, day, year, Is_Daylight_Savings_Time. Η ϊρα (hour) κα πρζπει να είναι γραμμζνθ ςε 24ωρθ μορφι.
13 Ζτςι, για να μεταβιβάςουμε τθν ϊρα 10:30pm τθσ 3 θσ Ιουνίου του 2007, κα πρζπει να χρθςιμοποιιςουμε τθ ςυνάρτθςθ mktime() ωσ εξισ : $unixtime = mktime(22, 30, 0, 6, 3, 2007, -1); Με τθν τελευταία παράμετρο, που εδϊ είναι το -1, λζμε ςτθν PHP αν κα είναι ενεργι θ κερινι ϊρα (DST, Daylight Savings Time). Η τιμι 1 κάνει τθ κερινι ϊρα να είναι ενεργι, θ τιμι 0 τθν κάνει ανενεργι και θ τιμι -1 αφινει τθν PHP να αποφαςίςει μόνθ τθσ. Με τθ ςυνάρτθςθ mktime() μποροφμε να κάνουμε και αρικμθτικζσ πράξεισ με θμερομθνίεσ, όπωσ για παράδειγμα αν προςκζςουμε ζναν μεγάλο αρικμό ςτθν τιμι του μινα, θ PHP κα δϊςει τθν κατάλλθλθ τιμι πρϊτα ςτο ζτοσ και μετά κα υπολογίςει τον μινα. Παρόμοια, αν προςκζςουμε τον αρικμό 9990 ςτθν τιμι τθσ ϊρασ, θ PHP κα πάει μπροςτά 416 θμζρεσ. Θα πρζπει να ζχουμε υπόψθ μασ ότι ςτθν PHP είναι επικίνδυνο να βάηουμε μθδενικά μπροςτά από τισ τιμζσ που είναι μικρότερεσ από το 10 (leading zero) και αυτό γιατί οι αρικμοί αυτοί εκλαμβάνονται από τθν PHP ωσ οκταδικοί (octal numbers). Οι Μαθηματικζσ Συναρτήςεισ Η PHP διακζτει πολλζσ μακθματικζσ ςυναρτιςεισ κακϊσ και αρκετζσ ςτακερζσ (constants) για τουσ δθμοφιλείσ αρικμοφσ ϊςτε να μθν είμαςτε αναγκαςμζνοι να τουσ υπολογίηουμε εμείσ. Όλεσ ςχεδόν οι μακθματικζσ ςυναρτιςεισ μποροφν να ομαδοποιθκοφν ςε τρεισ περιοχζσ : ςτρογγυλοποίθςθσ (rounding), δθμιουργίασ τυχαίων αρικμϊν (randomisation) και μετατροπισ (conversion), όπου και ανικουν οι περιςςότερεσ. Στρογγυλοποίηςη Αριθμών float ceil ( float value) float floor ( float value) float round ( float value [, int precision]) Επειδι ςυνικωσ κζλουμε λιγότερθ ακρίβεια απ αυτιν που μασ δίνει θ PHP, μποροφμε να χρθςιμοποιιςουμε τισ εξισ ςυναρτιςεισ ςτρογγυλοποίθςθσ : ceil(), floor() και round(). Ηceil() και θ floor() λαμβάνουν μία μόνο παράμετρο, τον αρικμό που κζλουμε να ςτρογγυλοποιιςουμε. Η ςυνάρτθςθ ceil() τον ςτρογγυλοποιεί ςτον πλθςιζςτερο ακζραιο που είναι μεγαλφτεροσ από τθν τιμι του αρικμοφ, ενϊ θ
14 ςυνάρτθςθ floor() τον ςτρογγυλοποιεί ςτον πλθςιζςτερο ακζραιο που είναι μικρότεροσ από τθν τιμι του αρικμοφ. Ακολουκεί ζνα παράδειγμα : $someval = 4.9; $ceiled = ceil($someval); $floored = floor($someval); Μετά από τθν εκτζλεςθ του παραπάνω κϊδικα, θ μεταβλθτι $ceiled κα είναι ίςθ με 5 και θ μεταβλθτι $floored κα είναι ίςθ με 4. Η ςυνάρτθςθ round() λαμβάνει δφο παραμζτρουσ, τον αρικμό που κζλουμε να ςτρογγυλοποιιςουμε και το πλικοσ των δεκαδικϊν ψθφίων που κζλουμε να υπάρχουν ςτον καινοφργιο αρικμό. Ακολουκεί ζνα παράδειγμα : $a = round(4.9); // 5 $b = round(4.5); // 5 $c = round(4.4999); // 4 $d = round( , 3); // $e = round( , 4); // $f = round(1000 / 160); // 6 Όπωσ μποροφμε να δοφμε, το 4.5 ςτρογγυλοποιείται προσ τα πάνω ςτο 5, ενϊ το ςτρογγυλοποιείται προσ τα κάτω ςτο 4. Στθν τζταρτθ γραμμι βλζπουμε ότι χρθςιμοποιείται για πρϊτθ φορά και θ δεφτερθ παράμετροσ, με τθν οποία κακορίηουμε ςε πόςα δεκαδικά ψθφία κζλουμε να γίνει θ ςτρογγυλοποίθςθ. Στθν πζμπτθ γραμμι ζχουμε το αποτζλεςμα ςτθν ςτρογγυλοποίθςθ με τζςςερα δεκαδικά ψθφία και αυτό γιατί θ PHP κοιτάει το επόμενο ψθφίο για να αποφαςίςει αν κα αλλάξει τθν τιμι του τελευταίου ψθφίου. Αυτό ςθμαίνει, ότι αν ο αρικμόσ ιταν ο , θ ςτρογγυλοποίθςθ με τζςςερα δεκαδικά ψθφία κα ζδινε τον αρικμό , αλλά ςτθν προθγοφμενθ περίπτωςθ επειδι το πζμπτο ψθφίο είναι το 5, το οποίο ςτρογγυλοποιείται πάντα προσ τα
15 πάνω, ζχουμε το αποτζλεςμα Στο τελευταίο παράδειγμα, το $f, είναι μια ςυχνι κατάςταςθ που ςυναντάμε με τθ ςυνάρτθςθ round(). Για παράδειγμα, ασ υποκζςουμε ότι οργανϊνουμε ζνα ταξίδι και ζχουμε να μεταφζρουμε άτομα. Θα πρζπει να υπολογίςουμε πόςα λεωφορεία κα χρειαςκεί να νοικιάςουμε, ζτςι διαιροφμε το με το 160, που είναι θ χωρθτικότθτα του κάκε λεωφορείου, και μετά ςτρογγυλοποιοφμε το αποτζλεςμα και βλζπουμε ότι προκφπτει το 6. Το πρόβλθμα είναι ότι το πραγματικό αποτζλεςμα είναι τθσ διαίρεςθσ 1000/160 είναι το 6,25, δθλ. χρειαηόμαςτε 6 και κάτι λεωφορεία για να μεταφζρουμε τα άτομα, δθλ. ςτθν πραγματικότθτα χρειαηόμαςτε 7 λεωφορεία. Για να επιλφςουμε προβλιματα όπωσ το προθγοφμενο, κα πρζπει να χρθςιμοποιοφμε τθ ςυνάρτθςθ ceil(). Και οι τρεισ ςυναρτιςεισ ςτρογγυλοποίθςθσ είναι χριςιμεσ για τθ δουλειά που προορίηονται, ζτςι κα πρζπει να τισ γνωρίηουμε και να τισ χρθςιμοποιοφμε όλεσ. Δημιουργία Τυχαίων Αριθμών int rand ( [int min, int max]) int mt_rand ( [int min, int max]) int getrandmax ( ) int mt_getrandmax ( ) void srand ( [int seed]) void mt_srand ( [int seed]) Υπάρχουν περιπτϊςεισ που χρειαηόμαςτε τυχαίουσ αρικμοφσ ςτον κϊδικά μασ, όπωσ για να δίνουμε ςτουσ επιςκζπτεσ του Web site ζναν διαφορετικό χαιρετιςμό κάκε φορά που επιςκζπτονται τθν ιςτοςελίδα μασ ι μπορεί να κζλουμε να δθμιουργιςουμε ζνα παιχνίδι με τυχαίουσ αρικμοφσ (κλιρωςθ). Η δθμιουργία τυχαίων αρικμϊν (randomisation) είναι μια απλι και χριςιμθ διαδικαςία και υπάρχουν δφο ςυναρτιςεισ γι αυτόν τον ςκοπό, θ rand() και θ mt_rand(). Και οι δφο αυτζσ ςυναρτιςεισ κάνουν τθν ίδια δουλειά και δζχονται τισ ίδιεσ παραμζτρουσ, αλλά θ μεν rand() είναι μια βαςικι ςυνάρτθςθ δθμιουργίασ τυχαίων αρικμϊν που είναι πολφ γριγορθ αλλά όχι και πολφ τυχαία, δθλ. οι αρικμοί που δθμιουργεί είναι λίγο προβλζψιμοι. Η ςυνάρτθςθ mt_rand() από τθν άλλθ πλευρά είναι πιο περίπλοκθ, όπου τα γράμματα mtςθμαίνουν Mersenne Twister, δθλ. το όνομα του αλγορίκμου παραγωγισ τυχαίων αρικμϊν που χρθςιμοποιεί. Η ςυνάρτθςθ αυτι επιςτρζφει κακαρά τυχαίουσ αρικμοφσ αλλά είναι πιο αργι. Και οι δφο ςυναρτιςεισ χρθςιμοποιοφν δφο προαιρετικζσ παραμζτρουσ (αρικμοφσ), που είναι ο ελάχιςτοσ και ο μζγιςτοσ αρικμόσ που μπορεί να επιςτραφεί.
16 Μποροφμε είτε να μθν δϊςουμε καμία παράμετρο, οπότε θ PHP κα επιςτρζψει ζναν τυχαίο αρικμό ανάμεςα ςτο 1 και ς ζναν πολφ μεγάλο αρικμό ι μποροφμε να δϊςουμε και τουσ δφο αρικμοφσ. Ακολουκεί ζνα παράδειγμα : $random = rand(); $randrange = rand(1, 10); $mtrandrange = mt_rand(1, 100); Θα πρζπει να ζχουμε υπόψθ μασ ότι και οι δφο αρικμοί που χρθςιμοποιοφνται ωσ παράμετροι είναι πικανό να επιςτραφοφν. Δθλαδι, ο αρικμόσ $randrange μπορεί να πάρει μια οποιαδιποτε τιμι ανάμεςα ςτο 1 και το 10, με το 1 και το 10 να είναι πικανά. Όπωσ είπαμε και νωρίτερα, αν δεν περάςουμε κάποια τιμι ωσ παράμετρο ςτισ ςυναρτιςεισ rand() και mt_rand(), θ PHP κα δθμιουργιςει ζναν τυχαίο αρικμό ανάμεςα ςτο 1 και ς ζναν πολφ μεγάλο αρικμό. Για να μάκουμε ποιοσ είναι αυτόσ ο μζγιςτοσ αρικμόσ, μποροφμε να χρθςιμοποιιςουμε τθ ςυνάρτθςθ getrandmax() ι τθν αντίςτοιχθ mt_getrandmax(). Θα δοφμε τϊρα ζνα παράδειγμα για το πϊσ μποροφμε να χρθςιμοποιιςουμε τθν παραγωγι τυχαίων αρικμϊν για να δθμιουργιςουμε διάφορουσ τυχαίουσ χαιρετιςμοφσ ςτουσ επιςκζπτεσ ενόσ Web site : switch(rand(1, 6)) { case 1: case 2: case 3: case 4: $greet = 'Γεια ζαρ!'; break; $greet = 'Καλυζήπθαηε!'; break; $greet = 'Χαιπεηιζμοί!'; break;
17 $greet = 'Καλή Πλοήγηζη!'; break; case 5: $greet = 'Καλημέπα!'; break; case 6: $greet = 'Yo!'; break; } print $greet; Θα πρζπει να ζχουμε υπόψθ μασ ότι θ ταχφτθτα τθσ δθμιουργίασ τυχαίων αρικμϊν δεν εξαρτάται από το μζγεκοσ των αρικμϊν που δίνουμε ωσ παραμζτρουσ ςτθ ςυνάρτθςθ, δθλ. θ rand() είναι το ίδιο γριγορθ με τθν rand(1, 3) αλλά και με τθν rand(1, ). Οι περιςςότερεσ γεννιτριεσ τυχαίων αρικμϊν χρειάηονται ζναν ςπόρο (seed), δθλ. μια αρχικι τιμι κακϊσ οι αρικμοί που δθμιουργοφν δεν είναι ςτθν πραγματικότθτα τυχαίοι, αλλά ψευδο-τυχαίοι (pseudo-random). Η τιμι seed χρθςιμοποιείται για να παραχκεί ο πρϊτοσ αρικμόσ, μετά ο πρϊτοσ αρικμόσ χρθςιμοποιείται για να παραχκεί ο δεφτεροσ αρικμόσ, μετά ο δεφτεροσ για τον τρίτο κοκ, που ςθμαίνει ότι αν δίνουμε πάντα τθν ίδια τιμι seed κα λαμβάνουμε πάντα τθν ίδια ςειρά τυχαίων αρικμϊν. Αν τϊρα δϊςουμε ζναν τυχαίο αρικμό ωσ seed ςτθ γεννιτρια δθμιουργίασ τυχαίων αρικμϊν (random number generator), κα ζχουμε ωσ αποτζλεςμα μια κακαρι ςειρά τυχαίων αρικμϊν. Η ςυνάρτθςθ seed για τθν rand() είναι θ srand() και δζχεται μία παράμετρο, που είναι ζνασ ακζραιοσ αρικμόσ, για τθν τιμι seed. Αν χρθςιμοποιοφμε τθ ςυνάρτθςθ mt_rand(), κα πρζπει αντίςτοιχα να χρθςιμοποιιςουμε τθ ςυνάρτθςθ mt_srand(). Η ςυνάρτθςθ microtime(), που επιςτρζφει ωσ ζναν αρικμό κινθτισ υποδιαςτολισ τα εκατομμυριοςτά του δευτερολζπτου, αποτελεί μια πολφ καλι λφςθ δθμιουργίασ τυχαίου αρικμοφ για χριςθ ωσ παράμετρο seed, αρκεί να μετατραπεί το αποτζλεςμά τθσ ςε ακζραιο. Μποροφμε να μετατρζψουμε το αποτζλεςμα τθσ ςυνάρτθςθσ microtime() ςε ακζραιο, πολλαπλαςιάηοντασ το με το ζνα εκατομμφριο (10 6 ), ωσ εξισ : srand((double)microtime()* ); mt_srand((double)microtime()* ); Αν κζλουμε τϊρα να δθμιουργείται πάντα θ ίδια ςειρά τυχαίων αρικμϊν, κα πρζπει να δίνουμε τθν ίδια τιμι seed. Για παράδειγμα, ανεξάρτθτα από το πόςεσ φορζσ κα το τρζξουμε, το επόμενο script δθμιουργεί πάντα τουσ ίδιουσ τυχαίουσ αρικμοφσ :
18 mt_srand(123456); echo mt_rand(1, 100), "\n"; echo mt_rand(1, 100), "\n"; echo mt_rand(1, 100), "\n"; Οι Τριγωνομετρικζσ Συναρτήςεισ float sin ( float value) float cos ( float value) float tan ( float value) float asin ( float value) float acos ( float value) float atan ( float value) float deg2rad ( float value) float rad2deg ( float value) Για να υπολογίςουμε τουσ βαςικοφσ τριγωνομετρικοφσ αρικμοφσ του θμιτόνου (sine), ςυνθμίτονου (cosine) και εφαπτομζνθσ (tangent) μποροφμε να καλζςουμε τισ ςυναρτιςεισ sin(),cos() και tan(), ενϊ για να υπολογίςουμε το τόξο θμιτόνου (arc sine), το τόξο ςυνθμίτονου (arc cosine) και το τόξο εφαπτομζνθσ (arc tangent) μποροφμε να καλζςουμε τισ ςυναρτιςεισasin(), acos() και atan(). Και οι ζξι αυτζσ ςυναρτιςεισ δζχονται μία μόνο παράμετρο, ςυγκεκριμζνα οι τρεισ πρϊτεσ τθν τιμι τθσ γωνίασ ςε ακτίνια (radians) και οι τρεισ τελευταίεσ λαμβάνουν το αποτζλεςμα από τισ τρεισ πρϊτεσ για να επιςτρζψουν τον αρικμό των ακτινίων (radians). Για να υπολογίςουμε τθν τιμι μιασ γωνίασ ςε ακτίνια (radians) πρζπει να πολλαπλαςιάςουμε τθν τιμι τθσ ςε μοίρεσ (degrees) με τθν ςτακερά π και μετά να διαιρζςουμε με το 180. ΗPHP διακζτει τθ ςυνάρτθςθ deg2rad(), που μποροφμε να καλζςουμε για να κάνουμε τθ μετατροπι τθσ τιμισ μιασ γωνίασ από μοίρεσ ςε ακτίνια.
19 Ακολουκοφν μερικά παραδείγματα χριςθσ των παραπάνω ςυναρτιςεων : $sin1 = sin(10); $sin2 = sin(deg2rad(80)); $cos1 = cos(89); $cos2 = cos(deg2rad(9)); Αν εφαρμόςουμε τθ ςυνάρτθςθ atan() ς ζναν αρικμό και μετά εφαρμόςουμε τθ ςυνάρτθςθ tan() ςτο αποτζλεςμα που κα παραχκεί, κα επανζλκουμε ςτον αρχικό αρικμό. Ακολουκεί ζνα παράδειγμα : $sin1 = sin(deg2rad(80)); $asin1 = rad2deg(asin($sin1)); Στον παραπάνω κϊδικα, θ μεταβλθτι $asin1 κα ζχει τθν τιμι 80. Όπωσ μποροφμε να φανταςτοφμε, θ ςυνάρτθςθ rad2deg() είναι θ αντίςτροφθ τθσ ςυνάρτθςθσ deg2rad(), δθλ. μετατρζπει τθν τιμι μιασ γωνίασ από ακτίνια (radians) ςε μοίρεσ (degrees). Άλλεσ Μαθηματικζσ Συναρτήςεισ Μετατροπήσ number abs ( number value) float sqrt ( float value) number pow ( number base, number exponent) float hypot ( float num1, float num2) Υπάρχουν αρκετζσ μακθματικζσ ςυναρτιςεισ μετατροπισ αρικμϊν, από τισ οποίεσ οι ςθμαντικότερεσ είναι οι abs(), sqrt() και pow(). Η ςυνάρτθςθ abs() επιςτρζφει τθν απόλυτθ τιμι (absolute value) τθσ παραμζτρου που τθσ μεταβιβάηουμε.
20 Ακολουκεί ζνα παράδειγμα : abs(10); abs(-14); Η πρϊτθ γραμμι επιςτρζφει τθν τιμι 10 και θ δεφτερθ γραμμι τθν τιμι 14. Η ςυνάρτθςθ abs() μπορεί να δεχκεί ακεραίουσ (integers) ι και πραγματικοφσ αρικμοφσ (floats) ωσ παράμετρο και επιςτρζφει τον ίδιο τφπο : abs(10.1); abs(-14.5); Η πρϊτθ γραμμι επιςτρζφει τθν τιμι 10.1 και θ δεφτερθ γραμμι τθν τιμι Η ςυνάρτθςθ sqrt() υπολογίηει τθν τετραγωνικι ρίηα (square root) ενόσ κετικοφ αρικμοφ : print sqrt(25); print sqrt(26); Η πρϊτθ γραμμι κα επιςτρζψει τθν τιμι 5 και θ δεφτερθ γραμμι τθν τιμι Θα πρζπει να ζχουμε υπόψθ μασ ότι θ κλιςθ τθσ ςυνάρτθςθσ sqrt() κακυςτερεί τθν εκτζλεςθ του προγράμματοσ, ζτςι κα πρζπει να αποφεφγουμε τισ πολλαπλζσ κλιςεισ τθσ. Τζλοσ, θ ςυνάρτθςθ pow() δζχεται δφο παραμζτρουσ, μια βάςθ (base) και μια δφναμθ (power) ςτθν οποία κα υψωκεί θ βάςθ. Ακολουκοφν παραδείγματα : print pow(10, 2); // 100 print pow(10, 3); // 1000
21 print pow(10, 4); // print pow(-10, 4); // Οι τρεισ πρϊτεσ γραμμζσ δείχνουν το αποτζλεςμα των πολλαπλαςιαςμϊν 10 * 10, 10 * 10 * 10 και 10 * 10 * 10 * 10. Στθν τζταρτθ γραμμι ζχουμε ωσ βάςθ (πρϊτθ παράμετροσ) το -10, κάτι που θ ςυνάρτθςθ pow() το δζχεται. Η ςυνάρτθςθ pow() δζχεται ακόμθ και αρνθτικζσ δυνάμεισ για τθ δεφτερθ παράμετρο, οπότε δεν παράγει αρνθτικοφσ αλλά μικροφσ αρικμοφσ. Για παράδειγμα, θ εντολι pow(10, -1) ζχει ωσ αποτζλεςμα το 0.1, θ pow(10, -2) το 0.01, θ pow(10, -3) το κοκ. Υπάρχει και θ ςυνάρτθςθ hypot(), θ οποία λαμβάνει δφο παραμζτρουσ, X και Y, και επιςτρζφει τθν τιμι sqrt((x * X) + (Y * Y)), δθλ. το μικοσ ενόσ διανφςματοσ ι τθν υποτείνουςα (hypotenuse) ενόσ ορκογωνίου τριγϊνου. Μετατροπή Αριθμών ςε Άλλα Συςτήματα Αρίθμηςησ int bindec ( string binary_string) string decbin ( int number) string dechex ( int number) string decoct ( int number) int hexdec ( string hex_string) int octdec ( string octal_string) string base_convert ( string number, int from_base, int to_base) Μποροφμε να αλλάξουμε τθ βάςθ (base) του ςυςτιματοσ αρίκμθςθσ που χρθςιμοποιοφμε, όπωσ είναι το δεκαδικό ςφςτθμα αρίκμθςθσ όπου θ βάςθ είναι το 10. Σ ζνα ςφςτθμα αρίκμθςθσ που ζχει ωσ βάςθ το b, χρθςιμοποιοφμε τα ψθφία 0, 1,..., b-1 για να ςχθματίςουμε όλουσ τουσ δυνατοφσ αρικμοφσ του ςυςτιματοσ. Στο δεκαδικό ςφςτθμα (με βάςθ το 10) χρθςιμοποιοφμε ωσ ψθφία τουσ αρικμοφσ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 και ςτο οκταδικό ςφςτθμα (με βάςθ το 8) χρθςιμοποιοφμε ωσ ψθφία τουσ αρικμοφσ 0, 1, 2, 3, 4, 5, 6, 7. Τρία είναι τα ςυςτιματα αρίκμθςθσ, εκτόσ του δεκαδικοφ, που είναι δθμοφιλι ς όςουσ αςχολοφνται με τουσ υπολογιςτζσ, το δυαδικό (binary) με βάςθ το 2, το οκταδικό (octal) με βάςθ το 8 και το δεκαεξαδικό (hexadeci-mal) με βάςθ το 16. Στο
22 δυαδικό ςφςτθμα ζχουμε μόνο δφο ψθφία, το 0 και το 1, ενϊ ςτο δεκαεξαδικό ςφςτθμα ζχουμε 16 ψθφία, που είναι τα γνωςτά μασ 0-9 αλλά και τα A (10), B (11), C (12), D (13), E (14) και F (15). Για παράδειγμα, ασ δοφμε τον δεκαδικό αρικμό 39 ςε τζςςερα διαφορετικά ςυςτιματα αρίκμθςθσ : (δυαδικό binary) 47 (οκταδικό octal) 39 (δεκαδικό decimal) 27 (δεκαεξαδικό hexadecimal) Για να μετατρζψουμε τον δεκαεξαδικό αρικμό 27 ςε δεκαδικό, πολλαπλαςιάηουμε το ψθφίο 2 του αρικμοφ με το 16 και προςκζτουμε το 7, οπότε ζχουμε το 39. Αν ο δεκαεξαδικόσ αρικμόσ ιταν ο 2F8, κα ζπρεπε να πολλαπλαςιάςουμε το ψθφίο 2 με το 256 (256 = 16 * 16), το ψθφίο F με το 16 και να προςκζςουμε το 8, οπότε ζχουμε τον δεκαδικό αρικμό 760. Αν όλα αυτά μασ φαίνονται παράξενα, δεν κα πρζπει να ξεχνάμε ότι και ςτο δεκαδικό ςφςτθμα αρίκμθςθσ με το οποίο είμαςτε εξοικειωμζνοι, ο αρικμόσ 569 για παράδειγμα, προκφπτει αν πολλαπλαςιάςουμε το 5 με το 100 (100 = 10 * 10), μετά το 6 με το 10 και προςκζτουμε και το 9. Για τθ μετατροπι από το ζνα ςφςτθμα αρίκμθςθσ ςτο άλλο, θ PHP διακζτει αρκετζσ ςυναρτιςεισ : bindec(), decbin(), dechex(), decoct(), hexdec() και octdec(). Η δουλειά που κάνει θ κάκε ςυνάρτθςθ προκφπτει από τθν ονομαςία τθσ, όπωσ για παράδειγμα θ bindec() που μετατρζπει ζναν δυαδικό bin(ary) ςε δεκαδικό dec(imal) και θ dechex() που μετατρζπει ζναν δεκαδικό dec(imal) ςε δεκαεξαδικό hex(adecimal). Η κάκε ςυνάρτθςθ δζχεται μία μόνο παράμετρο, που είναι ο αρικμόσ που κα μετατραπεί ςτο νζο ςφςτθμα αρίκμθςθσ, όπωσ για παράδειγμα : print decbin(16); // print dechex(232); // e8 print hexdec(e8); // 232 Βλζπουμε ότι όλεσ οι παραπάνω ςυναρτιςεισ μετατρζπουν από ι προσ το δεκαδικό ςφςτθμα ς ζνα άλλο ςφςτθμα αρίκμθςθσ. Η PHP διακζτει και τθν πολφ χριςιμθ ςυνάρτθςθ base_convert() για να μποροφμε να κάνουμε μετατροπι ενόσ αρικμοφ από ζνα ςφςτθμα αρίκμθςθσ ς ζνα άλλο. Η ςυνάρτθςθ αυτι δζχεται τρεισ παραμζτρουσ, που είναι με τθ ςειρά ο αρικμόσ που κζλουμε να μετατρζψουμε, θ βάςθ του ςυςτιματοσ από το οποίο κα γίνει θ μετατροπι και θ βάςθ του ςυςτιματοσ προσ το οποίο κα γίνει θ μετατροπι.
23 Για παράδειγμα, οι επόμενεσ δφο εντολζσ είναι ιςοδφναμεσ : print decbin(16); print base_convert(16, 10, 2); Η δεφτερθ εντολι μετατρζπει τον αρικμό 16 από το δεκαδικό ςτο δυαδικό ςφςτθμα. Το μεγάλο πλεονζκτθμα τθσ ςυνάρτθςθσ base_convert() είναι ότι μποροφμε να μετατρζψουμε ζναν δυαδικό αρικμό απευκείασ ςε δεκαεξαδικό ι και να κάνουμε πιο περίεργουσ ςυνδυαςμοφσ, όπωσ μετατροπι ενόσ αρικμοφ από το οκταδικό ςτο ςφςτθμα με βάςθ το 12 (duodecimal) ι από το δεκαεξαδικό ςτο ςφςτθμα με βάςθ το 20 (vigesimal). Κάτι που ζχουμε ιδθ διαπιςτϊςει είναι ότι τα ψθφία πάνω από το 9 παριςτάνονται με γράμματα του λατινικοφ αλφαβιτου. Ζτςι, ςτο δεκαεξαδικό ςφςτθμα αρίκμθςθσ ζχουμε τα ψθφία 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E και F, ενϊ ςτο ςφςτθμα αρίκμθςθσ με βάςθ το 20 (vigesimal), ζχουμε τα ψθφία 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I και J. Με δεδομζνο το ότι υπάρχουν 10 αρικμθτικά ψθφία από το 0 ζωσ και το 9 και 26 γράμματα από το A ζωσ και το Z, θ μζγιςτθ βάςθ ςυςτιματοσ αρίκμθςθσ που μπορεί να υποςτθρίξει θphp είναι το 36. Ακολουκοφν μερικά ακόμα παραδείγματα χριςθσ τθσ ςυνάρτθςθσ base_convert() : print base_convert(556, 10, 2); // print base_convert(556, 10, 8); // 1054 print base_convert(556, 10, 20); // 17g print base_convert(556, 10, 36); // fg Όπωσ βλζπουμε, όςο μεγαλφτερθ είναι θ βάςθ του ςυςτιματοσ αρίκμθςθσ, τόςο πιο ςφντομοσ είναι ο αρικμόσ που προκφπτει. Οι Μαθηματικζσ Σταθερζσ
24 Η PHP διακζτει μερικζσ ενςωματωμζνεσ μακθματικζσ ςτακερζσ, όπωσ είναι ο γνωςτόσ αρικμόσ π (Pi), για τον οποίο υπάρχει θ ςτακερά M_PI. Για παράδειγμα, για να υπολογίςουμε το εμβαδόν ενόσ κφκλου με βάςθ τθν ακτίνα του r, ο τφποσ είναι a = pi * r 2. Στθν PHP μποροφμε να γράψουμε τον εξισ κϊδικα : $area = M_PI * ($radius * $radius); // ή $area = M_PI * pow($radius, 2); Ακολουκεί μια λίςτα με τισ πιο χριςιμεσ μακθματικζσ ςτακερζσ που διακζτει θ PHP : Σταθερά Τιμή Σημαςία M_PI Pi M_PI_ Pi/2 M_PI_ Pi/4 M_1_PI /Pi M_2_PI /Pi M_SQRTPI sqrt(m_pi) M_2_SQRTPI /sqrt(M_PI) M_SQRT sqrt(2) M_SQRT sqrt(3) M_SQRT1_ /sqrt(2)
Δείκτεσ Διαχείριςθ Μνιμθσ. Βαγγζλθσ Οικονόμου Διάλεξθ 8
 Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
Δείκτεσ Διαχείριςθ Μνιμθσ Βαγγζλθσ Οικονόμου Διάλεξθ 8 Δείκτεσ Κάκε μεταβλθτι ςχετίηεται με μία κζςθ ςτθν κφρια μνιμθ του υπολογιςτι. Κάκε κζςθ ςτθ μνιμθ ζχει τθ δικι τθσ ξεχωριςτι διεφκυνςθ. Με άμεςθ
ΘΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
Παράςταςη κινητήσ υποδιαςτολήσ ςφμφωνα με το πρότυπο ΙΕΕΕ Δρ. Χρήστος Ηλιούδης το πρότυπο ΙΕΕΕ 754 ζχει χρθςιμοποιθκεί ευρζωσ ςε πραγματικοφσ υπολογιςτζσ. Το πρότυπο αυτό κακορίηει δφο βαςικζσ μορφζσ κινθτισ
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4.1
 ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4. Να γίνει πρόγραμμα το οποίο να επιλφει το Διαγώνιο Σφςτθμα: A ι το ςφςτθμα : ι ςε μορφι εξιςώςεων το ςφςτθμα : Αλγόρικμοσ m(). Διαβάηουμε τθν τιμι του ( θ διάςταςθ του Πίνακα Α )..
ΕΡΓΑΣΗΡΙΑΚΗ ΑΚΗΗ 4. Να γίνει πρόγραμμα το οποίο να επιλφει το Διαγώνιο Σφςτθμα: A ι το ςφςτθμα : ι ςε μορφι εξιςώςεων το ςφςτθμα : Αλγόρικμοσ m(). Διαβάηουμε τθν τιμι του ( θ διάςταςθ του Πίνακα Α )..
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ. Κεφάλαιο 8 Η γλϊςςα Pascal
 ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
ΠΡΟΓΡΑΜΜΑΣΙΜΌ ΤΠΟΛΟΓΙΣΏΝ Κεφάλαιο 8 Η γλϊςςα Pascal Παράγραφοσ 8.2 Βαςικοί τφποι δεδομζνων Σα δεδομζνα ενόσ προγράμματοσ μπορεί να: είναι αποκθκευμζνα εςωτερικά ςτθν μνιμθ είναι αποκθκευμζνα εξωτερικά
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2
 Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Παράςταςη ακεραίων ςτο ςυςτημα ςυμπλήρωμα ωσ προσ 2 Δρ. Χρήζηος Ηλιούδης Μθ Προςθμαςμζνοι Ακζραιοι Εφαρμογζσ (ςε οποιαδιποτε περίπτωςθ δεν χρειάηονται αρνθτικοί αρικμοί) Καταμζτρθςθ. Διευκυνςιοδότθςθ.
Ιδιότθτεσ πεδίων Γενικζσ.
 Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
Οι ιδιότθτεσ των πεδίων διαφζρουν ανάλογα με τον τφπο δεδομζνων που επιλζγουμε. Ορίηονται ςτο κάτω μζροσ του παρακφρου ςχεδίαςθσ του πίνακα, ςτθν καρτζλα Γενικζσ. Ιδιότθτα: Μζγεκοσ πεδίου (Field size)
x n D 2 ENCODER m - σε n (m 2 n ) x 1 Παραδείγματα κωδικοποιθτϊν είναι ο κωδικοποιθτισ οκταδικοφ ςε δυαδικό και ο κωδικοποιθτισ BCD ςε δυαδικό.
 Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
Κωδικοποιητές Ο κωδικοποιθτισ (nor) είναι ζνα κφκλωμα το οποίο διακζτει n γραμμζσ εξόδου και το πολφ μζχρι m = 2 n γραμμζσ ειςόδου και (m 2 n ). Οι ζξοδοι παράγουν τθν κατάλλθλθ λζξθ ενόσ δυαδικοφ κϊδικα
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ. Φιλιοποφλου Ειρινθ
 ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
ΕΦΑΡΜΟΓΕ ΒΑΕΩΝ ΔΕΔΟΜΕΝΩΝ ΣΗ ΝΟΗΛΕΤΣΙΚΗ Φιλιοποφλου Ειρινθ Προςθήκη νζων πεδίων Ασ υποκζςουμε ότι μετά τθ δθμιουργία του πίνακα αντιλαμβανόμαςτε ότι ζχουμε ξεχάςει κάποια πεδία. Είναι ζνα πρόβλθμα το οποίο
Ένα πρόβλθμα γραμμικοφ προγραμματιςμοφ βρίςκεται ςτθν κανονικι μορφι όταν:
 Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Μζθοδος Simplex Η πλζον γνωςτι και περιςςότερο χρθςιμοποιουμζνθ μζκοδοσ για τθν επίλυςθ ενόσ γενικοφ προβλιματοσ γραμμικοφ προγραμματιςμοφ, είναι θ μζκοδοσ Simplex θ οποία αναπτφχκθκε από τον George Dantzig.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο του Άβακα Αυτζσ οι οδθγίεσ ζχουν ςτόχο λοιπόν να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο του Άβακα. Παρουςίαςη
Δομθμζνοσ Προγραμματιςμόσ. Βαγγζλθσ Οικονόμου Εργαςτιριο 9
 Δομθμζνοσ Προγραμματιςμόσ Βαγγζλθσ Οικονόμου Εργαςτιριο 9 Συναρτιςεισ Αφαιρετικότθτα ςτισ διεργαςίεσ Συνάρτθςεισ Διλωςθ, Κλιςθ και Οριςμόσ Εμβζλεια Μεταβλθτών Μεταβίβαςθ παραμζτρων ςε ςυναρτιςεισ Συναρτιςεισ
Δομθμζνοσ Προγραμματιςμόσ Βαγγζλθσ Οικονόμου Εργαςτιριο 9 Συναρτιςεισ Αφαιρετικότθτα ςτισ διεργαςίεσ Συνάρτθςεισ Διλωςθ, Κλιςθ και Οριςμόσ Εμβζλεια Μεταβλθτών Μεταβίβαςθ παραμζτρων ςε ςυναρτιςεισ Συναρτιςεισ
16. Πίνακεσ και Συναρτήςεισ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 16. Πίνακεσ και Συναρτήςεισ Ιωάννθσ Κατάκθσ Σιμερα o Κλιςθ με τιμι o Κλιςθ με αναφορά o Πίνακεσ και ςυναρτιςεισ o Παραδείγματα Ειςαγωγι o Στισ προθγοφμενεσ
5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ
 5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ Να γραφεί πρόγραμμα, το οποίο κα δίνει τισ τιμζσ 5 και 6 ςε δφο μεταβλθτζσ a και b και κα υπολογίηει και κα εμφανίηει το άκροιςμά τουσ sum. ΛΟΓΙΚΟ ΔΙΑΓΡΑΜΜΑ a 5 b 6 sum a+b sum ΑΛΓΟΡΙΘΜΟ
5 ΜΕΘΟΔΟΙ - ΠΑΡΑΜΕΤΡΟΙ Να γραφεί πρόγραμμα, το οποίο κα δίνει τισ τιμζσ 5 και 6 ςε δφο μεταβλθτζσ a και b και κα υπολογίηει και κα εμφανίηει το άκροιςμά τουσ sum. ΛΟΓΙΚΟ ΔΙΑΓΡΑΜΜΑ a 5 b 6 sum a+b sum ΑΛΓΟΡΙΘΜΟ
ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ
 ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ Οδηγός Χρήσης Εφαρμογής Ελέγχου Προσφορών Αφοφ πιςτοποιθκεί ο λογαριαςμόσ που δθμιουργιςατε ςτο πρόγραμμα ωσ Πάροχοσ Προςφορϊν, κα λάβετε ζνα e-mail με
ΗΛΕΚΣΡΟΝΙΚΗ ΤΠΗΡΕΙΑ ΑΠΟΚΣΗΗ ΑΚΑΔΗΜΑΪΚΗ ΣΑΤΣΟΣΗΣΑ Οδηγός Χρήσης Εφαρμογής Ελέγχου Προσφορών Αφοφ πιςτοποιθκεί ο λογαριαςμόσ που δθμιουργιςατε ςτο πρόγραμμα ωσ Πάροχοσ Προςφορϊν, κα λάβετε ζνα e-mail με
Παράςταςη ςυμπλήρωμα ωσ προσ 1
 Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ ΣΤ1 Προςθεςη αφαίρεςη ςτο ΣΤ1 2 ή ΣΤ1 Ονομάηουμε ςυμπλιρωμα ωσ προσ μειωμζνθ βάςθ R ενόσ μθ προςθμαςμζνου αρικμοφ Χ = ( Χ θ-1 Χ θ-2... Χ 0 ) R ζναν άλλον αρικμό Χ'
Η γλώςςα προγραμματιςμού C
 Η γλώςςα προγραμματιςμού C Οι εντολζσ επανάλθψθσ (while, do-while, for) Γενικά για τισ εντολζσ επανάλθψθσ Συχνά ςτο προγραμματιςμό είναι επικυμθτι θ πολλαπλι εκτζλεςθ μιασ ενότθτασ εντολϊν, είτε για ζνα
Η γλώςςα προγραμματιςμού C Οι εντολζσ επανάλθψθσ (while, do-while, for) Γενικά για τισ εντολζσ επανάλθψθσ Συχνά ςτο προγραμματιςμό είναι επικυμθτι θ πολλαπλι εκτζλεςθ μιασ ενότθτασ εντολϊν, είτε για ζνα
ΟΝΟΜΑΣΟΛΟΓΙΑ ΠΑΡΑΜΕΣΡΩΝ ΓΙΑ ΠΡΟΑΡΜΟΜΕΝΕ ΑΝΑΦΟΡΕ. @XXX@_<όνομα παραμζτρου> (Εμφανίηεται ςαν Caption ςτθν φόρμα των φίλτρων).
 ΟΝΟΜΑΣΟΛΟΓΙΑ ΠΑΡΑΜΕΣΡΩΝ ΓΙΑ ΠΡΟΑΡΜΟΜΕΝΕ ΑΝΑΦΟΡΕ. @XXX@_ (Εμφανίηεται ςαν Caption ςτθν φόρμα των φίλτρων). Βαςικοί παράμετροι @EDT@_ @CHK@_ @CXD@_ @CXDC@_ @CMB@_ @CHKLB@_ Παράμετροσ που
ΟΝΟΜΑΣΟΛΟΓΙΑ ΠΑΡΑΜΕΣΡΩΝ ΓΙΑ ΠΡΟΑΡΜΟΜΕΝΕ ΑΝΑΦΟΡΕ. @XXX@_ (Εμφανίηεται ςαν Caption ςτθν φόρμα των φίλτρων). Βαςικοί παράμετροι @EDT@_ @CHK@_ @CXD@_ @CXDC@_ @CMB@_ @CHKLB@_ Παράμετροσ που
17. Πολυδιάςτατοι πίνακεσ
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 17. Πολυδιάςτατοι πίνακεσ Ιωάννθσ Κατάκθσ Πολυδιάςτατοι πίνακεσ o Μζχρι τϊρα μιλοφςαμε για μονοδιάςτατουσ πίνακεσ ι int age[5]= 31,28,31,30,31; o Για παράλλθλουσ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 17. Πολυδιάςτατοι πίνακεσ Ιωάννθσ Κατάκθσ Πολυδιάςτατοι πίνακεσ o Μζχρι τϊρα μιλοφςαμε για μονοδιάςτατουσ πίνακεσ ι int age[5]= 31,28,31,30,31; o Για παράλλθλουσ
Διαχείριςθ του φακζλου "public_html" ςτο ΠΣΔ
 Διαχείριςθ του φακζλου "public_html" ςτο ΠΣΔ Οι παρακάτω οδθγίεσ αφοροφν το χριςτθ webdipe. Για διαφορετικό λογαριαςμό χρθςιμοποιιςτε κάκε φορά το αντίςτοιχο όνομα χριςτθ. = πατάμε αριςτερό κλικ ςτο Επιςκεφκείτε
Διαχείριςθ του φακζλου "public_html" ςτο ΠΣΔ Οι παρακάτω οδθγίεσ αφοροφν το χριςτθ webdipe. Για διαφορετικό λογαριαςμό χρθςιμοποιιςτε κάκε φορά το αντίςτοιχο όνομα χριςτθ. = πατάμε αριςτερό κλικ ςτο Επιςκεφκείτε
ςυςτιματα γραμμικϊν εξιςϊςεων
 κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
κεφάλαιο 7 Α ςυςτιματα γραμμικϊν εξιςϊςεων αςικζσ ζννοιεσ Γραμμικά, λζγονται τα ςυςτιματα εξιςϊςεων ςτα οποία οι άγνωςτοι εμφανίηονται ςτθν πρϊτθ δφναμθ. Σα γραμμικά ςυςτιματα με δφο εξιςϊςεισ και δφο
ΕΦΑΡΜΟΓΖσ ΒΆΕΩΝ ΔΕΔΟΜΖΝΩΝ ΚΑΙ ΔΙΑΔΙΚΣΥΟΤ. Ειρινθ Φιλιοποφλου
 ΕΦΑΡΜΟΓΖσ ΒΆΕΩΝ ΔΕΔΟΜΖΝΩΝ ΚΑΙ ΔΙΑΔΙΚΣΥΟΤ Ειρινθ Φιλιοποφλου Ειςαγωγι Ο Παγκόςμιοσ Ιςτόσ (World Wide Web - WWW) ι πιο απλά Ιςτόσ (Web) είναι μία αρχιτεκτονικι για τθν προςπζλαςθ διαςυνδεδεμζνων εγγράφων
ΕΦΑΡΜΟΓΖσ ΒΆΕΩΝ ΔΕΔΟΜΖΝΩΝ ΚΑΙ ΔΙΑΔΙΚΣΥΟΤ Ειρινθ Φιλιοποφλου Ειςαγωγι Ο Παγκόςμιοσ Ιςτόσ (World Wide Web - WWW) ι πιο απλά Ιςτόσ (Web) είναι μία αρχιτεκτονικι για τθν προςπζλαςθ διαςυνδεδεμζνων εγγράφων
Σ ΤΑΤ Ι Σ Τ Ι Κ Η. Statisticum collegium V
 Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Σ ΤΑΤ Ι Σ Τ Ι Κ Η i Statisticum collegium V Στατιςτική Συμπεραςματολογία Ι Σημειακζσ Εκτιμήςεισ Διαςτήματα Εμπιςτοςφνησ Στατιςτική Συμπεραςματολογία (Statistical Inference) Το πεδίο τθσ Στατιςτικισ Συμπεραςματολογία,
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα
 Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Δομζσ Αφαιρετικότθτα ςτα Δεδομζνα Περιεχόμενα Ζννοια δομισ Οριςμόσ δομισ Διλωςθ μεταβλθτϊν Απόδοςθ Αρχικϊν τιμϊν Αναφορά ςτα μζλθ μιασ δομισ Ζνκεςθ Δομισ Πίνακεσ Δομϊν Η ζννοια τθσ δομισ Χρθςιμοποιιςαμε
Εργαςτιριο Πικανοτιτων Σθμειϊςεισ προγραμματιςμοφ: βαςικζσ γνϊςεισ ανάπτυξθσ εφαρμογϊν. Κϊςτασ Αρβανιτάκθσ
 Εργαςτιριο Πικανοτιτων Σθμειϊςεισ προγραμματιςμοφ: βαςικζσ γνϊςεισ ανάπτυξθσ εφαρμογϊν Κϊςτασ Αρβανιτάκθσ Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Εργαςτιριο Πικανοτιτων Σθμειϊςεισ προγραμματιςμοφ: βαςικζσ γνϊςεισ ανάπτυξθσ εφαρμογϊν Κϊςτασ Αρβανιτάκθσ Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του
Περιοριςμοί μιασ Β.Δ. ςτθν Access(1/3)
 Περιοριςμοί μιασ Β.Δ. ςτθν Access(1/3) Το όνομα ενόσ πίνακα, όπωσ και κάκε άλλου αντικειμζνου, μπορεί να ζχει μζγεκοσ ζωσ 64 χαρακτιρεσ. Το όνομα ενόσ πεδίου μπορεί να ζχει μζγεκοσ ζωσ 64 χαρακτιρεσ. Κάκε
Περιοριςμοί μιασ Β.Δ. ςτθν Access(1/3) Το όνομα ενόσ πίνακα, όπωσ και κάκε άλλου αντικειμζνου, μπορεί να ζχει μζγεκοσ ζωσ 64 χαρακτιρεσ. Το όνομα ενόσ πεδίου μπορεί να ζχει μζγεκοσ ζωσ 64 χαρακτιρεσ. Κάκε
Θεςιακά ςυςτιματα αρίκμθςθσ
 Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Θεςιακά ςυςτιματα αρίκμθςθσ Δρ. Χρήστος Ηλιούδης αρικμθτικό ςφςτθμα αρίκμθςθσ (Number System) Αξία (value) παράςταςθ Οι αξίεσ (π.χ. το βάροσ μιασ ποςότθτασ μιλων) μποροφν να παραςτακοφν με πολλοφσ τρόπουσ
Ειςαγωγι ςτθν Επιςτιμθ Υπολογιςτϊν. Ειςαγωγι ςτθν Python
 Ειςαγωγι ςτθν Επιςτιμθ Υπολογιςτϊν Ειςαγωγι ςτθν Python Γ Μζροσ Modules, Αντικειμενοςτραφισ Προγραμματιςμόσ ςτθν Python, Classes, Objects, Αλλθλεπίδραςθ με αρχεία Ειςαγωγι αρκρωμάτων (modules): import
Ειςαγωγι ςτθν Επιςτιμθ Υπολογιςτϊν Ειςαγωγι ςτθν Python Γ Μζροσ Modules, Αντικειμενοςτραφισ Προγραμματιςμόσ ςτθν Python, Classes, Objects, Αλλθλεπίδραςθ με αρχεία Ειςαγωγι αρκρωμάτων (modules): import
ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 5: Αρχεία - Φάκελοι
 ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Αρχείο (File) Φάκελοσ (Folder) Διαχειριςτισ Αρχείων (File Manager) Τφποι Αρχείων Σε τι εξυπθρετεί θ οργάνωςθ των εργαςιϊν μασ ςτουσ υπολογιςτζσ; Πϊσ κα οργανϊςουμε
ΕΝΟΤΗΤΑ 2: ΕΠΙΚΟΙΝΩΝΩ ΜΕ ΤΟΝ ΥΠΟΛΟΓΙΣΤΗ Αρχείο (File) Φάκελοσ (Folder) Διαχειριςτισ Αρχείων (File Manager) Τφποι Αρχείων Σε τι εξυπθρετεί θ οργάνωςθ των εργαςιϊν μασ ςτουσ υπολογιςτζσ; Πϊσ κα οργανϊςουμε
Εργαςτιριο Βάςεων Δεδομζνων
 Εργαςτιριο Βάςεων Δεδομζνων 2010-2011 Μάθημα 1 ο 1 Ε. Σςαμούρα Σμήμα Πληροφορικήσ ΑΠΘ Σκοπόσ του 1 ου εργαςτθριακοφ μακιματοσ Σκοπόσ του πρϊτου εργαςτθριακοφ μακιματοσ είναι να μελετιςουμε ερωτιματα επιλογισ
Εργαςτιριο Βάςεων Δεδομζνων 2010-2011 Μάθημα 1 ο 1 Ε. Σςαμούρα Σμήμα Πληροφορικήσ ΑΠΘ Σκοπόσ του 1 ου εργαςτθριακοφ μακιματοσ Σκοπόσ του πρϊτου εργαςτθριακοφ μακιματοσ είναι να μελετιςουμε ερωτιματα επιλογισ
ΑΝΑΠΣΤΞΘ ΕΦΑΡΜΟΓΩΝ Ε ΠΡΟΓΡΑΜΜΑΣΙΣΙΚΟ ΠΕΡΙΒΑΛΛΟΝ 3 ο ΓΕΝΙΚΟ ΛΤΚΕΙΟ Ν. ΜΤΡΝΘ- ΕΠΙΜΕΛΕΙΑ: ΠΤΡΙΔΑΚΘ Λ.
 Ερωτήςεισ Προβλήματα Α. Σημειώςτε δεξιά από κάθε πρόταςη το γράμμα Σ αν η πρόταςη είναι ςωςτή και το γράμμα Λ αν είναι λάθοσ. 1. Θ περατότθτα ενόσ αλγορίκμου αναφζρεται ςτο γεγονόσ ότι καταλιγει ςτθ λφςθ
Ερωτήςεισ Προβλήματα Α. Σημειώςτε δεξιά από κάθε πρόταςη το γράμμα Σ αν η πρόταςη είναι ςωςτή και το γράμμα Λ αν είναι λάθοσ. 1. Θ περατότθτα ενόσ αλγορίκμου αναφζρεται ςτο γεγονόσ ότι καταλιγει ςτθ λφςθ
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ
 Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
Οδηγίεσ προσ τουσ εκπαιδευτικοφσ για το μοντζλο τησ Αριθμογραμμήσ Αυτζσ οι οδθγίεσ ζχουν ςτόχο να βοθκιςουν τουσ εκπαιδευτικοφσ να καταςκευάςουν τισ δικζσ τουσ δραςτθριότθτεσ με το μοντζλο τθσ Αρικμογραμμισ.
ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO
 ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO Το Micro Worlds Pro είναι ζνα ολοκλθρωμζνο περιβάλλον προγραμματιςμοφ. Χρθςιμοποιεί τθ γλϊςςα προγραμματιςμοφ Logo (εξελλθνιςμζνθ) Το Micro Worlds Pro περιλαμβάνει
ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ MICRO WORLDS PRO Το Micro Worlds Pro είναι ζνα ολοκλθρωμζνο περιβάλλον προγραμματιςμοφ. Χρθςιμοποιεί τθ γλϊςςα προγραμματιςμοφ Logo (εξελλθνιςμζνθ) Το Micro Worlds Pro περιλαμβάνει
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 3 ο Εργαςτιριο υγχρονιςμόσ Διεργαςιϊν
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 3 ο Εργαςτιριο υγχρονιςμόσ Διεργαςιϊν Παράλλθλεσ Διεργαςίεσ (1/5) Δφο διεργαςίεσ λζγονται «παράλλθλεσ» (concurrent) όταν υπάρχει ταυτοχρονιςμόσ, δθλαδι οι εκτελζςεισ τουσ επικαλφπτονται
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 3 ο Εργαςτιριο υγχρονιςμόσ Διεργαςιϊν Παράλλθλεσ Διεργαςίεσ (1/5) Δφο διεργαςίεσ λζγονται «παράλλθλεσ» (concurrent) όταν υπάρχει ταυτοχρονιςμόσ, δθλαδι οι εκτελζςεισ τουσ επικαλφπτονται
Διαχείριςη Αριθμοδεικτών (v.1.0.7)
 Διαχείριςη Αριθμοδεικτών (v.1.0.7) Περιεχόμενα 1. Μενοφ... 5 1.1 Αρικμοδείκτεσ.... 5 1.1.1 Δθμιουργία Αρικμοδείκτθ... 6 1.1.2 Αντιγραφι Αρικμοδείκτθ... 11 2. Παράμετροι... 12 2.1.1 Κατθγορίεσ Αρικμοδεικτϊν...
Διαχείριςη Αριθμοδεικτών (v.1.0.7) Περιεχόμενα 1. Μενοφ... 5 1.1 Αρικμοδείκτεσ.... 5 1.1.1 Δθμιουργία Αρικμοδείκτθ... 6 1.1.2 Αντιγραφι Αρικμοδείκτθ... 11 2. Παράμετροι... 12 2.1.1 Κατθγορίεσ Αρικμοδεικτϊν...
Megatron ERP Βάςη δεδομζνων Π/Φ - κατηγοριοποίηςη Databox
 Megatron ERP Βάςη δεδομζνων Π/Φ - κατηγοριοποίηςη Databox 03 05 ΙΛΤΔΑ ΠΛΗΡΟΦΟΡΙΚΗ Α.Ε. αρμά Ιηαμπζλλα Βαρλάμθσ Νίκοσ Ειςαγωγι... 1 Σι είναι το Databox...... 1 Πότε ανανεϊνεται...... 1 Μπορεί να εφαρμοςτεί
Megatron ERP Βάςη δεδομζνων Π/Φ - κατηγοριοποίηςη Databox 03 05 ΙΛΤΔΑ ΠΛΗΡΟΦΟΡΙΚΗ Α.Ε. αρμά Ιηαμπζλλα Βαρλάμθσ Νίκοσ Ειςαγωγι... 1 Σι είναι το Databox...... 1 Πότε ανανεϊνεται...... 1 Μπορεί να εφαρμοςτεί
Visual C Express - Οδηγός Χρήσης
 Visual C++ 2008 Express - Οδηγός Χρήσης Ζερβός Μιχάλης, Πρίντεζης Νίκος Σκοπόσ του οδθγοφ αυτοφ είναι να παρουςιάςει τισ βαςικζσ δυνατότθτεσ του Visual C++ 2008 Express Edition και πωσ μπορεί να χρθςιμοποιθκεί
Visual C++ 2008 Express - Οδηγός Χρήσης Ζερβός Μιχάλης, Πρίντεζης Νίκος Σκοπόσ του οδθγοφ αυτοφ είναι να παρουςιάςει τισ βαςικζσ δυνατότθτεσ του Visual C++ 2008 Express Edition και πωσ μπορεί να χρθςιμοποιθκεί
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο)
 Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Ιοφνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1.Εθνικό Τυπογραφείο... 3 1.1. Είςοδοσ... 3 1.2. Αρχική Οθόνη... 4 1.3. Διεκπεραίωςη αίτηςησ...
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Ιοφνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1.Εθνικό Τυπογραφείο... 3 1.1. Είςοδοσ... 3 1.2. Αρχική Οθόνη... 4 1.3. Διεκπεραίωςη αίτηςησ...
ΛΕΙΤΟΥΓΙΚΆ ΣΥΣΤΉΜΑΤΑ. 5 ο Εργαςτιριο Ειςαγωγι ςτθ Γραμμι Εντολϊν
 ΛΕΙΤΟΥΓΙΚΆ ΣΥΣΤΉΜΑΤΑ 5 ο Εργαςτιριο Ειςαγωγι ςτθ Γραμμι Εντολϊν Τι είναι θ Γραμμι Εντολϊν (1/6) Στουσ πρϊτουσ υπολογιςτζσ, και κυρίωσ από τθ δεκαετία του 60 και μετά, θ αλλθλεπίδραςθ του χριςτθ με τουσ
ΛΕΙΤΟΥΓΙΚΆ ΣΥΣΤΉΜΑΤΑ 5 ο Εργαςτιριο Ειςαγωγι ςτθ Γραμμι Εντολϊν Τι είναι θ Γραμμι Εντολϊν (1/6) Στουσ πρϊτουσ υπολογιςτζσ, και κυρίωσ από τθ δεκαετία του 60 και μετά, θ αλλθλεπίδραςθ του χριςτθ με τουσ
Κάνουμε κλικ ςτθν επιλογι του οριηόντιου μενοφ «Get Skype»για να κατεβάςουμε ςτον υπολογιςτι μασ το πρόγραμμα του Skype.
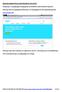 ΟΔΗΓΙΕ ΔΗΜΙΟΤΡΓΙΑ ΛΟΓΑΡΙΑΜΟΤ ΣΟ SKYPE Ανοίγουμε το πρόγραμμα περιιγθςθσ ιςτοςελίδων (εδϊ Internet Explorer). Κάνουμε κλικ ςτθ γραμμι διεφκυνςθσ του προγράμματοσ και πλθκτρολογοφμε: www.skype.com Κάνουμε
ΟΔΗΓΙΕ ΔΗΜΙΟΤΡΓΙΑ ΛΟΓΑΡΙΑΜΟΤ ΣΟ SKYPE Ανοίγουμε το πρόγραμμα περιιγθςθσ ιςτοςελίδων (εδϊ Internet Explorer). Κάνουμε κλικ ςτθ γραμμι διεφκυνςθσ του προγράμματοσ και πλθκτρολογοφμε: www.skype.com Κάνουμε
Ηλεκτρονικι Επιχειρθςιακι Δράςθ Εργαςτιριο 1
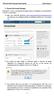 1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
1. Εγκατάςταςη Xampp Προκειμζνου να γίνει θ εγκατάςταςθ κα πρζπει πρϊτα να κατεβάςετε και εγκαταςτιςετε το XAMPP ωσ ακολοφκωσ. 1.1. Πάμε ςτθν ακόλουκθ διεφκυνςθ https://www.apachefriends.org/download.html
Πρόςβαςη και δήλωςη μαθημάτων ςτον Εφδοξο
 Πρόςβαςη και δήλωςη μαθημάτων ςτον Εφδοξο Τι πρζπει να γνωρίηω πριν ξεκινιςω τθν διαδικαςία 1. Να ζχω κωδικοφσ από τον Κζντρο Δικτφου του ΤΕΙ Ακινασ (είναι αυτοί με τουσ οποίουσ ζχω πρόςβαςθ ςτο αςφρματο
Πρόςβαςη και δήλωςη μαθημάτων ςτον Εφδοξο Τι πρζπει να γνωρίηω πριν ξεκινιςω τθν διαδικαςία 1. Να ζχω κωδικοφσ από τον Κζντρο Δικτφου του ΤΕΙ Ακινασ (είναι αυτοί με τουσ οποίουσ ζχω πρόςβαςθ ςτο αςφρματο
Modellus 4.01 Συ ντομοσ Οδηγο σ
 Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
Νίκοσ Αναςταςάκθσ 4.01 Συ ντομοσ Οδηγο σ Περιγραφή Σο είναι λογιςμικό προςομοιϊςεων που ςτθρίηει τθν λειτουργία του ςε μακθματικά μοντζλα. ε αντίκεςθ με άλλα λογιςμικά (π.χ. Interactive Physics, Crocodile
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ. ΚΕΦΑΛΑΙΟ 3: Εργονομία
 ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΕΝΟΣΗΣΑ 1: ΓΝΩΡIΖΩ ΣΟΝ ΤΠΟΛΟΓΙΣΗ Εργονομία, ωςτι ςτάςθ εργαςίασ, Εικονοςτοιχείο (pixel), Ανάλυςθ οκόνθσ (resolution), Μζγεκοσ οκόνθσ Ποιεσ επιπτϊςεισ μπορεί να ζχει θ πολφωρθ χριςθ του υπολογιςτι ςτθν
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε)
 ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε) Γραφικό Περιβάλλον Επικοινωνίασ Περιβάλλον Εντολϊν Γραμμισ (Graphical User Interface/GUI), (Command Line Interface),
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 6: Το γραφικό περιβάλλον Επικοινωνίασ (Γ.Π.Ε) Γραφικό Περιβάλλον Επικοινωνίασ Περιβάλλον Εντολϊν Γραμμισ (Graphical User Interface/GUI), (Command Line Interface),
ΕΝΟΣΘΣΑ 1: ΓΝΩΡIΗΩ ΣΟΝ ΤΠΟΛΟΓΙΣΘ Ω ΕΝΙΑΙΟ ΤΣΘΜΑ. ΚΕΦΑΛΑΙΟ 1: Ψθφιακόσ Κόςμοσ
 ΕΝΟΣΘΣΑ 1: ΓΝΩΡIΗΩ ΣΟΝ ΤΠΟΛΟΓΙΣΘ Αναλογικόσ (Analogue), Δυαδικό Ψθφίο (Binary digit, bit), Byte, Ψθφιακόσ (Digital), υςτιματα αρίκμθςθσ υχνά λζγεται ότι ηοφμε ςτθν ψθφιακι εποχι. Πολλζσ από τισ ςυςκευζσ
ΕΝΟΣΘΣΑ 1: ΓΝΩΡIΗΩ ΣΟΝ ΤΠΟΛΟΓΙΣΘ Αναλογικόσ (Analogue), Δυαδικό Ψθφίο (Binary digit, bit), Byte, Ψθφιακόσ (Digital), υςτιματα αρίκμθςθσ υχνά λζγεται ότι ηοφμε ςτθν ψθφιακι εποχι. Πολλζσ από τισ ςυςκευζσ
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο)
 Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Πάτρα, 2013 Περιεχόμενα: Ειςαγωγή... 4 1. Επιμελητήριο... Error! Bookmark not defined. 1.1 Διαχειριςτήσ Αιτήςεων Επιμελητηρίου...
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Εθνικό Τυπογραφείο) Πάτρα, 2013 Περιεχόμενα: Ειςαγωγή... 4 1. Επιμελητήριο... Error! Bookmark not defined. 1.1 Διαχειριςτήσ Αιτήςεων Επιμελητηρίου...
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Περιφέρειες)
 Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Περιφέρειες) Ιούνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1. Περιφζρεια... 3 1.1 Διαχειριςτήσ Αιτήςεων Περιφζρειασ... 3 1.1.1. Είςοδοσ... 3 1.1.2. Αρχική
Εγχειρίδιο Χρήςησ Προςωποποιημζνων Υπηρεςιών Γ.Ε.ΜΗ. (Περιφέρειες) Ιούνιοσ 2013 Περιεχόμενα: Ειςαγωγή... 3 1. Περιφζρεια... 3 1.1 Διαχειριςτήσ Αιτήςεων Περιφζρειασ... 3 1.1.1. Είςοδοσ... 3 1.1.2. Αρχική
Στα προθγοφμενα δφο εργαςτιρια είδαμε τθ δομι απόφαςθσ (ι επιλογισ ι ελζγχου ροισ). Ασ κυμθκοφμε:
 ΔΟΜΗ ΑΠΟΦΑΗ Στα προθγοφμενα δφο εργαςτιρια είδαμε τθ δομι απόφαςθσ (ι επιλογισ ι ελζγχου ροισ). Ασ κυμθκοφμε: Όταν το if που χρθςιμοποιοφμε παρζχει μόνο μία εναλλακτικι διαδρομι εκτζλεςθ, ο τφποσ δομισ
ΔΟΜΗ ΑΠΟΦΑΗ Στα προθγοφμενα δφο εργαςτιρια είδαμε τθ δομι απόφαςθσ (ι επιλογισ ι ελζγχου ροισ). Ασ κυμθκοφμε: Όταν το if που χρθςιμοποιοφμε παρζχει μόνο μία εναλλακτικι διαδρομι εκτζλεςθ, ο τφποσ δομισ
8 τριγωνομετρία. βαςικζσ ζννοιεσ. γ ςφω. εφω και γ. κεφάλαιο
 κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
κεφάλαιο 8 τριγωνομετρία Α βαςικζσ ζννοιεσ τθν τριγωνομετρία χρθςιμοποιοφμε τουσ τριγωνομετρικοφσ αρικμοφσ, οι οποίοι ορίηονται ωσ εξισ: θμω = απζναντι κάκετθ πλευρά υποτείνουςα Γ ςυνω = εφω = προςκείμενθ
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ. ΚΕΦΑΛΑΙΟ 5: Γνωριμία με το λογιςμικό του υπολογιςτι
 ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 5: Γνωριμία με το λογιςμικό του υπολογιςτι Λογιςμικό (Software), Πρόγραμμα (Programme ι Program), Προγραμματιςτισ (Programmer), Λειτουργικό Σφςτθμα (Operating
ΕΝΟΤΗΤΑ 2: ΤΟ ΛΟΓΙΣΜΙΚΟ ΤΟΥ ΥΠΟΛΟΓΙΣΤΗ ΚΕΦΑΛΑΙΟ 5: Γνωριμία με το λογιςμικό του υπολογιςτι Λογιςμικό (Software), Πρόγραμμα (Programme ι Program), Προγραμματιςτισ (Programmer), Λειτουργικό Σφςτθμα (Operating
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 7 θ Διάλεξθ Διαχείριςθ Μνιμθσ Μζροσ Γ ελιδοποίθςθ (1/10) Σόςο θ κατάτμθςθ διαμεριςμάτων ςτακεροφ μεγζκουσ όςο και θ κατάτμθςθ διαμεριςμάτων μεταβλθτοφ και άνιςου μεγζκουσ δεν κάνουν
Ανάπτυξη Εφαρμογών με Σχεςιακέσ Βάςεισ Δεδομένων
 Ανάπτυξη Εφαρμογών με Σχεςιακέσ Βάςεισ Δεδομένων Δρ. Θεοδώρου Παύλοσ theodorou@uoc.gr Περιεχόμενα Τι είναι οι Βάςεισ Δεδομζνων (DataBases) Τι είναι Σφςτθμα Διαχείριςθσ Βάςεων Δεδομζνων (DBMS) Οι Στόχοι
Ανάπτυξη Εφαρμογών με Σχεςιακέσ Βάςεισ Δεδομένων Δρ. Θεοδώρου Παύλοσ theodorou@uoc.gr Περιεχόμενα Τι είναι οι Βάςεισ Δεδομζνων (DataBases) Τι είναι Σφςτθμα Διαχείριςθσ Βάςεων Δεδομζνων (DBMS) Οι Στόχοι
Μονάδες 6. Μονάδες ΓΑΨΕ Δεν υπάρχει ρίηα 2. ΑΝ Α>0 ΤΟΤΕ 3. ΤΕΛΟΣ_ΑΝ 4. ΑΛΛΙΩΣ 5. ίηα Τ_(Α)
 50 Χρόνια ΦΡΟΝΣΙΣΗΡΙΑ ΜΕΗ ΕΚΠΑΙΔΕΤΗ ΑΒΒΑΪΔΗ-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΣΙ : Φιλολάου & Εκφαντίδου 26 : Σηλ.: 2107601470 ΔΙΑΓΩΝΙΣΜΑ : ΑΝΑΡΤΥΞΗ ΕΦΑΜΟΓΩΝ ΣΕ ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ Γϋ ΛΥΚΕΙΟΥ 2011 ΘΕΜΑ Α I. Η ςειριακι
50 Χρόνια ΦΡΟΝΣΙΣΗΡΙΑ ΜΕΗ ΕΚΠΑΙΔΕΤΗ ΑΒΒΑΪΔΗ-ΜΑΝΩΛΑΡΑΚΗ ΠΑΓΚΡΑΣΙ : Φιλολάου & Εκφαντίδου 26 : Σηλ.: 2107601470 ΔΙΑΓΩΝΙΣΜΑ : ΑΝΑΡΤΥΞΗ ΕΦΑΜΟΓΩΝ ΣΕ ΡΟΓΑΜΜΑΤΙΣΤΙΚΟ ΡΕΙΒΑΛΛΟΝ Γϋ ΛΥΚΕΙΟΥ 2011 ΘΕΜΑ Α I. Η ςειριακι
ΕΡΓΑΣΗΡΙΟ ΕΦΑΡΜΟΜΕΝΗ ΠΛΗΡΟΦΟΡΙΚΗ
 Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Στο εργαςτιριο αυτό κα δοφμε πωσ μποροφμε να προςομοιϊςουμε μια κίνθςθ χωρίσ τθ χριςθ εξειδικευμζνων εργαλείων, παρά μόνο μζςω ενόσ προγράμματοσ λογιςτικϊν φφλλων, όπωσ είναι το Calc και το Excel. Τα δφο
Σφντομεσ Οδθγίεσ Χριςθσ
 Σφντομεσ Οδθγίεσ Χριςθσ Περιεχόμενα 1. Επαφζσ... 3 2. Ημερολόγιο Επιςκζψεων... 4 3. Εκκρεμότθτεσ... 5 4. Οικονομικά... 6 5. Το 4doctors ςτο κινθτό ςου... 8 6. Υποςτιριξθ... 8 2 1. Επαφζσ Στισ «Επαφζσ»
Σφντομεσ Οδθγίεσ Χριςθσ Περιεχόμενα 1. Επαφζσ... 3 2. Ημερολόγιο Επιςκζψεων... 4 3. Εκκρεμότθτεσ... 5 4. Οικονομικά... 6 5. Το 4doctors ςτο κινθτό ςου... 8 6. Υποςτιριξθ... 8 2 1. Επαφζσ Στισ «Επαφζσ»
Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων. (v.1.0.7)
 Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων (v.1.0.7) 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ ςτθλών βιβλίου Εςόδων - Εξόδων.
Διαδικαςία Διαχείριςθσ Στθλϊν Βιβλίου Εςόδων - Εξόδων (v.1.0.7) 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ ςτθλών βιβλίου Εςόδων - Εξόδων.
Βαγγζλθσ Οικονόμου Διάλεξθ 7. Συναρτιςεισ Μζροσ 2ο
 Συναρτιςεισ Μζροσ 2 ο Βαγγζλθσ Οικονόμου Διάλεξθ 7 1 Περιεχόμενα Βιβλιοκικεσ τθσ C Μεταβίβαςθ παραμζτρων παράδειγμα swap Αναδρομικότθτα Συναρτιςεισ και Πίνακεσ 2 H βαςικι βιβλιοκικθ τθσ C Η βαςικι βιβλιοκικθ
Συναρτιςεισ Μζροσ 2 ο Βαγγζλθσ Οικονόμου Διάλεξθ 7 1 Περιεχόμενα Βιβλιοκικεσ τθσ C Μεταβίβαςθ παραμζτρων παράδειγμα swap Αναδρομικότθτα Συναρτιςεισ και Πίνακεσ 2 H βαςικι βιβλιοκικθ τθσ C Η βαςικι βιβλιοκικθ
= = 124
 Λζξεισ Κάκε μακθτισ μζςα ςτθν ομάδα κα πρζπει να ζχει μια αρικμομθχανι. Ζνασ μακθτισ κα διαβάηει φωναχτά τουσ αρικμοφσ. Οι υπόλοιποι μακθτζσ κα τουσ γράφουν ςτθν αρικμομθχανι πατϊντασ κάκε φορά το πλικτρο
Λζξεισ Κάκε μακθτισ μζςα ςτθν ομάδα κα πρζπει να ζχει μια αρικμομθχανι. Ζνασ μακθτισ κα διαβάηει φωναχτά τουσ αρικμοφσ. Οι υπόλοιποι μακθτζσ κα τουσ γράφουν ςτθν αρικμομθχανι πατϊντασ κάκε φορά το πλικτρο
Εγχειρίδιο Χρήςησ Support
 Εγχειρίδιο Χρήςησ Support Περιεχόμενα 1) Αρχικι Σελίδα...2 2) Φόρμα Σφνδεςθσ...2 3) Μετά τθ ςφνδεςθ...2 4) Λίςτα Υποκζςεων...3 5) Δθμιουργία Νζασ Υπόκεςθσ...4 6) Σελίδα Υπόκεςθσ...7 7) Αλλαγι Κωδικοφ...9
Εγχειρίδιο Χρήςησ Support Περιεχόμενα 1) Αρχικι Σελίδα...2 2) Φόρμα Σφνδεςθσ...2 3) Μετά τθ ςφνδεςθ...2 4) Λίςτα Υποκζςεων...3 5) Δθμιουργία Νζασ Υπόκεςθσ...4 6) Σελίδα Υπόκεςθσ...7 7) Αλλαγι Κωδικοφ...9
Πολυπλέκτες. 0 x 0 F = S x 0 + Sx 1 1 x 1
 Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
Πολυπλέκτες Ο πολυπλζκτθσ (multipleer - ) είναι ζνα ςυνδυαςτικό κφκλωμα που επιλζγει δυαδικι πλθροφορία μιασ από πολλζσ γραμμζσ ειςόδου και τθν κατευκφνει ςε μια και μοναδικι γραμμι εξόδου. Η επιλογι μιασ
ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση ΠΑΙΔΑΓΩΓΙΚΟ ΙΝΣΤΙΤΟΥΤΟ ΥΠΗΡΕΣΙΑ ΑΝΑΠΤΥΞΗΣ ΠΡΟΓΡΑΜΜΑΤΩΝ ΜΑΘΗΜΑΤΙΚΑ Α Γυμνασίου Ενότητα 1β: Ισότητα - Εξίσωση Συγγραφή:
Διδάςκων: Κωνςταντίνοσ τεφανίδθσ
 ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ ΧΟΛΗ ΘΕΣΙΚΩΝ ΕΠΙΣΗΜΩΝ ΣΜΗΜΑ ΕΠΙΣΗΜΗ ΤΠΟΛΟΓΙΣΩΝ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗ ΗΤ-564 ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΣΑ ΕΠΙΚΟΙΝΩΝΙΑ ΑΝΘΡΩΠΟΤ - ΜΗΧΑΝΗ Διδάςκων: Κωνςταντίνοσ τεφανίδθσ τόχοσ τθσ ςυγκεκριμζνθσ εργαςίασ
ΠΑΝΕΠΙΣΗΜΙΟ ΚΡΗΣΗ ΧΟΛΗ ΘΕΣΙΚΩΝ ΕΠΙΣΗΜΩΝ ΣΜΗΜΑ ΕΠΙΣΗΜΗ ΤΠΟΛΟΓΙΣΩΝ ΜΑΘΗΜΑ ΕΠΙΛΟΓΗ ΗΤ-564 ΠΡΟΧΩΡΗΜΕΝΑ ΘΕΜΑΣΑ ΕΠΙΚΟΙΝΩΝΙΑ ΑΝΘΡΩΠΟΤ - ΜΗΧΑΝΗ Διδάςκων: Κωνςταντίνοσ τεφανίδθσ τόχοσ τθσ ςυγκεκριμζνθσ εργαςίασ
Διαδικαζία Διατείριζης Εκηύπωζης Ιζοζσγίοσ Γενικού - Αναλσηικών Καθολικών. (v )
 Διαδικαζία Διατείριζης Εκηύπωζης Ιζοζσγίοσ Γενικού - Αναλσηικών Καθολικών (v.1. 0.7) 1 Περίλθψθ Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ Εκτφπωςθσ
Διαδικαζία Διατείριζης Εκηύπωζης Ιζοζσγίοσ Γενικού - Αναλσηικών Καθολικών (v.1. 0.7) 1 Περίλθψθ Το ςυγκεκριμζνο εγχειρίδιο δθμιουργικθκε για να βοθκιςει τθν κατανόθςθ τθσ διαδικαςίασ διαχείριςθσ Εκτφπωςθσ
Ανάπτυξη Εφαρμογών Σε Προγραμματιςτικό Περιβάλλον
 Γραπτι Εξζταςθ ςτο μάκθμα Ανάπτυξη Εφαρμογών Σε Προγραμματιςτικό Περιβάλλον Όνομα: Επϊνυμο: Τμιμα: Ημερομθνία: 20/02/11 Θζμα 1 ο Α. Να χαρακτθρίςετε κακεμιά από τισ παρακάτω προτάςεισ ωσ Σωςτι (Σ) ι Λάκοσ
Γραπτι Εξζταςθ ςτο μάκθμα Ανάπτυξη Εφαρμογών Σε Προγραμματιςτικό Περιβάλλον Όνομα: Επϊνυμο: Τμιμα: Ημερομθνία: 20/02/11 Θζμα 1 ο Α. Να χαρακτθρίςετε κακεμιά από τισ παρακάτω προτάςεισ ωσ Σωςτι (Σ) ι Λάκοσ
Joomla! - User Guide
 Joomla! - User Guide τελευταία ανανέωση: 10/10/2013 από την ICAP WEB Solutions 1 Η καταςκευι τθσ δυναμικισ ςασ ιςτοςελίδασ ζχει ολοκλθρωκεί και μπορείτε πλζον να προχωριςετε ςε αλλαγζσ ι προςκικεσ όςον
Joomla! - User Guide τελευταία ανανέωση: 10/10/2013 από την ICAP WEB Solutions 1 Η καταςκευι τθσ δυναμικισ ςασ ιςτοςελίδασ ζχει ολοκλθρωκεί και μπορείτε πλζον να προχωριςετε ςε αλλαγζσ ι προςκικεσ όςον
Περιεχόμενα. χολι Χοροφ Αντιγόνθ Βοφτου - Πολιτικι Διαχείριςθσ Cookie 1
 Περιεχόμενα Περιεχόμενα... 1 1. Ειςαγωγή... 2 1.1 Σχετικά... 2 2. Γενικέσ Πληροφορίεσ για τα Cookies... 2 2.1 Οριςμόσ... 2 2.2 Χρήςη... 3 2.3 Τφποι... 3 2.4 Έλεγχοσ... 3 3. Cookies Σχολήσ... 4 3.1 Ειςαγωγή...
Περιεχόμενα Περιεχόμενα... 1 1. Ειςαγωγή... 2 1.1 Σχετικά... 2 2. Γενικέσ Πληροφορίεσ για τα Cookies... 2 2.1 Οριςμόσ... 2 2.2 Χρήςη... 3 2.3 Τφποι... 3 2.4 Έλεγχοσ... 3 3. Cookies Σχολήσ... 4 3.1 Ειςαγωγή...
ΥΡΟΝΣΙΣΗΡΙΟ Μ. Ε. ΚΑΙ ΚΕΝΣΡΟ ΙΔΙΑΙΣΕΡΩΝ ΜΑΘΗΜΑΣΩΝ «ΚΤΡΙΣΗ» ΔΙΑΓΩΝΙΜΑ ΘΕΜΑΣΑ Β ΛΤΚΕΙΟΤ ΥΕΒΡΟΤΑΡΙΟ 2018 ΑΕΠΠ
 ΥΡΟΝΣΙΣΗΡΙΟ Μ. Ε. ΚΑΙ ΚΕΝΣΡΟ ΙΔΙΑΙΣΕΡΩΝ ΜΑΘΗΜΑΣΩΝ «ΚΤΡΙΣΗ» ΔΙΑΓΩΝΙΜΑ ΘΕΜΑΣΑ Β ΛΤΚΕΙΟΤ ΥΕΒΡΟΤΑΡΙΟ 2018 ΘΕΜΑ Α ΑΕΠΠ Α1. Για κακεμία από τισ παρακάτω προτάςεισ να χαρακτθρίςετε με ΣΩΣΤΟ ι ΛΑΘΟΣ 1. Η ζκφραςθ
ΥΡΟΝΣΙΣΗΡΙΟ Μ. Ε. ΚΑΙ ΚΕΝΣΡΟ ΙΔΙΑΙΣΕΡΩΝ ΜΑΘΗΜΑΣΩΝ «ΚΤΡΙΣΗ» ΔΙΑΓΩΝΙΜΑ ΘΕΜΑΣΑ Β ΛΤΚΕΙΟΤ ΥΕΒΡΟΤΑΡΙΟ 2018 ΘΕΜΑ Α ΑΕΠΠ Α1. Για κακεμία από τισ παρακάτω προτάςεισ να χαρακτθρίςετε με ΣΩΣΤΟ ι ΛΑΘΟΣ 1. Η ζκφραςθ
Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία).
 Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία). Από τθν τράπεηα κεμάτων Α_ΧΘΜ_0_20651 Διακζτουμε υδατικό διάλυμα (Δ1) KOH 0,1 Μ. α)να υπολογίςετε τθν % w/v περιεκτικότθτα του
Μεθολογία αςκιςεων αραίωςησ και ανάμειξησ διαλυμάτων (με τθν ίδια δ. ουςία). Από τθν τράπεηα κεμάτων Α_ΧΘΜ_0_20651 Διακζτουμε υδατικό διάλυμα (Δ1) KOH 0,1 Μ. α)να υπολογίςετε τθν % w/v περιεκτικότθτα του
Ε. ε περίπτωςθ που θ διαφορά των δφο ηαριϊν είναι 3 τότε ο παίκτθσ ξαναρίχνει μόνο ζνα ηάρι.
 1 ο Σετ Ασκήσεων Δομή Επιλογής - Επανάληψης Άςκθςθ 1θ: Ζνα παιχνίδι με ηάρια παίηεται ωσ εξισ: Α. Ο παίκτθσ αρχικά ποντάρει κάποιο ποςό και ρίχνει δφο ηάρια. Β. Ο παίκτθσ κερδίηει (το ποςό που ζχει ποντάρει)
1 ο Σετ Ασκήσεων Δομή Επιλογής - Επανάληψης Άςκθςθ 1θ: Ζνα παιχνίδι με ηάρια παίηεται ωσ εξισ: Α. Ο παίκτθσ αρχικά ποντάρει κάποιο ποςό και ρίχνει δφο ηάρια. Β. Ο παίκτθσ κερδίηει (το ποςό που ζχει ποντάρει)
Ενεργειακά Τηάκια. Πουκεβίλ 2, Ιωάννινα Τθλ. 26510.23822 www.energeiaka-ktiria.gr www.facebook.com/energeiaka.ktiria
 Ενεργειακά Τηάκια Πουκεβίλ 2, Ιωάννινα Τθλ. 26510.23822 www.facebook.com/energeiaka.ktiria Σελ. 2 Η ΕΣΑΙΡΕΙΑ Η εταιρεία Ενεργειακά Κτίρια δραςτθριοποιείται ςτθν παροχι ολοκλθρωμζνων υπθρεςιϊν και ςτθν
Ενεργειακά Τηάκια Πουκεβίλ 2, Ιωάννινα Τθλ. 26510.23822 www.facebook.com/energeiaka.ktiria Σελ. 2 Η ΕΣΑΙΡΕΙΑ Η εταιρεία Ενεργειακά Κτίρια δραςτθριοποιείται ςτθν παροχι ολοκλθρωμζνων υπθρεςιϊν και ςτθν
Multi Logo. Προγραμματιςμόσ Η/Υ με Multi Logo. Σχεδίαςη και ανάπτυξη εφαρμογήσ κίνηςησ αντικειμζνου
 Multi Logo Βαθμίδα Μάθημα Αντικείμενο Τίτλοσ Διάρκεια Μορφή Διδακτικοί ςτόχοι: Επιδιωκόμενο αποτζλεςμα: Προαπαιτούμενεσ γνώςεισ: Εργαλεία Μζςα: Γυμνάςιο Πληροφορική Προγραμματιςμόσ Η/Υ με Multi Logo Σχεδίαςη
Multi Logo Βαθμίδα Μάθημα Αντικείμενο Τίτλοσ Διάρκεια Μορφή Διδακτικοί ςτόχοι: Επιδιωκόμενο αποτζλεςμα: Προαπαιτούμενεσ γνώςεισ: Εργαλεία Μζςα: Γυμνάςιο Πληροφορική Προγραμματιςμόσ Η/Υ με Multi Logo Σχεδίαςη
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό. μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ
 Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
Πόςο εκτατό μπορεί να είναι ζνα μη εκτατό νήμα και πόςο φυςικό μπορεί να είναι ζνα μηχανικό ςτερεό. Συνιςταμζνη δφναμη versus «κατανεμημζνησ» δφναμησ Για τθν ανάδειξθ του κζματοσ κα λφνουμε κάποια προβλιματα
ΦΥΕ 14 ΑΚΑΔ. ΕΤΟΣ Η ΕΡΓΑΣΙΑ. Ημερομηνία παράδοςησ: 12 Νοεμβρίου (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 10 μονάδεσ θ κάκε μία)
 ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
ΦΥΕ ΑΚΑΔ. ΕΤΟΣ 007-008 Η ΕΡΓΑΣΙΑ Ημερομηνία παράδοςησ: Νοεμβρίου 007 (Όλεσ οι αςκιςεισ βακμολογοφνται ιςοτίμωσ με 0 μονάδεσ θ κάκε μία) Άςκηςη α) Να υπολογιςκεί θ προβολι του πάνω ςτο διάνυςμα όταν: (.
Ακολουκιακά Λογικά Κυκλώματα
 Ακολουκιακά Λογικά Κυκλώματα Τα ψθφιακά λογικά κυκλϊματα που μελετιςαμε μζχρι τϊρα ιταν ςυνδυαςτικά κυκλϊματα. Στα ςυνδυαςτικά κυκλϊματα οι ζξοδοι ςε κάκε χρονικι ςτιγμι εξαρτϊνται αποκλειςτικά και μόνο
Ακολουκιακά Λογικά Κυκλώματα Τα ψθφιακά λογικά κυκλϊματα που μελετιςαμε μζχρι τϊρα ιταν ςυνδυαςτικά κυκλϊματα. Στα ςυνδυαςτικά κυκλϊματα οι ζξοδοι ςε κάκε χρονικι ςτιγμι εξαρτϊνται αποκλειςτικά και μόνο
Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ
 Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ διαδικαςίασ αυτόματησ δημιουργίασ ςτηλών και αντιςτοίχιςησ
Αυτόματη δημιουργία στηλών Αντιστοίχηση νέων λογαριασμών ΦΠΑ 1 Περίληψη Το ςυγκεκριμζνο εγχειρίδιο δημιουργήθηκε για να βοηθήςει την κατανόηςη τησ διαδικαςίασ αυτόματησ δημιουργίασ ςτηλών και αντιςτοίχιςησ
ΗΥ101: Ειςαγωγι ςτθν Πλθροφορικι
 Παράςταςη κινητήσ υποδιαςτολήσ Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ Παράςταςη ςταθεροφ ςημείου Παράςταςη αριθμών κινητοφ ςημείου 2 Παράςταςη ςταθεροφ ςημείου Στθν παράςταςθ αρικμϊν ςτακεροφ ςθμείου (Fixed
Παράςταςη κινητήσ υποδιαςτολήσ Δρ. Χρήστος Ηλιούδης Θζματα διάλεξησ Παράςταςη ςταθεροφ ςημείου Παράςταςη αριθμών κινητοφ ςημείου 2 Παράςταςη ςταθεροφ ςημείου Στθν παράςταςθ αρικμϊν ςτακεροφ ςθμείου (Fixed
ΑΝΣΙΣΡΟΦΗ ΤΝΑΡΣΗΗ. f y x y f A αντιςτοιχίηεται ςτο μοναδικό x A για το οποίο. Παρατθριςεισ Ιδιότθτεσ τθσ αντίςτροφθσ ςυνάρτθςθσ 1. Η. f A τθσ f.
 .. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
.. Αντίςτροφθ ςυνάρτθςθ Ζςτω θ ςυνάρτθςθ : A θ οποία είναι " ". Τότε ορίηεται μια νζα ςυνάρτθςθ, θ μζςω τθσ οποίασ το κάκε ιςχφει y. : A με Η νζα αυτι ςυνάρτθςθ λζγεται αντίςτροφθ τθσ. y y A αντιςτοιχίηεται
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ. 2 ο Εργαςτιριο Διαχείριςθ Διεργαςιϊν
 ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 2 ο Εργαςτιριο Διαχείριςθ Διεργαςιϊν Τπόβακρο (1/3) τουσ παλαιότερουσ υπολογιςτζσ θ Κεντρικι Μονάδα Επεξεργαςίασ (Κ.Μ.Ε.) μποροφςε κάκε ςτιγμι να εκτελεί μόνο ζνα πρόγραμμα τουσ ςφγχρονουσ
ΛΕΙΣΟΤΡΓΙΚΆ ΤΣΉΜΑΣΑ 2 ο Εργαςτιριο Διαχείριςθ Διεργαςιϊν Τπόβακρο (1/3) τουσ παλαιότερουσ υπολογιςτζσ θ Κεντρικι Μονάδα Επεξεργαςίασ (Κ.Μ.Ε.) μποροφςε κάκε ςτιγμι να εκτελεί μόνο ζνα πρόγραμμα τουσ ςφγχρονουσ
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων
 Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
Σχεδίαςη Σφγχρονων Ακολουθιακών Κυκλωμάτων Πίνακεσ Διζγερςησ των FF Όπωσ είδαμε κατά τθ μελζτθ των FF, οι χαρακτθριςτικοί πίνακεσ δίνουν τθν τιμι τθσ επόμενθσ κατάςταςθσ κάκε FF ωσ ςυνάρτθςθ τθσ παροφςασ
ΟΔΗΓΙΕ ΔΗΜΙΟΤΡΓΙΑ ΚΑΙ ΡΤΘΜΙΗ ΔΩΡΕΑΝ ΗΛΕΚΣΡΟΝΙΚΟΤ ΣΑΧΤΔΡΟΜΕΙΟΤ ΣΟ GOOGLE (G-MAIL)
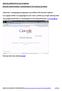 ΟΔΗΓΙΕ ΔΗΜΙΟΤΡΓΙΑ ΚΑΙ ΡΤΘΜΙΗ ΔΩΡΕΑΝ ΗΛΕΚΣΡΟΝΙΚΟΤ ΣΑΧΤΔΡΟΜΕΙΟΤ ΣΟ GOOGLE (G-MAIL) Ανοίγουμε το πρόγραμμα περιιγθςθσ ιςτοςελίδων (εδϊ Internet Explorer). Αν θ αρχικι ςελίδα του προγράμματοσ δεν είναι θ ςελίδα
ΟΔΗΓΙΕ ΔΗΜΙΟΤΡΓΙΑ ΚΑΙ ΡΤΘΜΙΗ ΔΩΡΕΑΝ ΗΛΕΚΣΡΟΝΙΚΟΤ ΣΑΧΤΔΡΟΜΕΙΟΤ ΣΟ GOOGLE (G-MAIL) Ανοίγουμε το πρόγραμμα περιιγθςθσ ιςτοςελίδων (εδϊ Internet Explorer). Αν θ αρχικι ςελίδα του προγράμματοσ δεν είναι θ ςελίδα
Άςκθςθ 1θ: Να γραφεί αλγόρικμοσ που κα δθμιουργεί με τθ βοικεια διπλοφ επαναλθπτικοφ βρόχου, τον ακόλουκο διςδιάςτατο πίνακα:
 2 ο Σετ Ασκήσεων Δομές Δεδομένων - Πίνακες Άςκθςθ 1θ: Να γραφεί αλγόρικμοσ που κα δθμιουργεί με τθ βοικεια διπλοφ επαναλθπτικοφ βρόχου, τον ακόλουκο διςδιάςτατο πίνακα: 2 3 4 5 3 4 5 6 4 5 6 7 5 6 7 8
2 ο Σετ Ασκήσεων Δομές Δεδομένων - Πίνακες Άςκθςθ 1θ: Να γραφεί αλγόρικμοσ που κα δθμιουργεί με τθ βοικεια διπλοφ επαναλθπτικοφ βρόχου, τον ακόλουκο διςδιάςτατο πίνακα: 2 3 4 5 3 4 5 6 4 5 6 7 5 6 7 8
Εγχειρίδιο Χριςθσ τθσ διαδικτυακισ εφαρμογισ «Υποβολι και παρακολοφκθςθ τθσ ζγκριςθσ Εκπαιδευτικών Πακζτων»
 Εγχειρίδιο Χριςθσ τθσ διαδικτυακισ εφαρμογισ «Υποβολι και παρακολοφκθςθ τθσ ζγκριςθσ Εκπαιδευτικών Πακζτων» Το Πλθροφοριακό Σφςτθμα τθσ δράςθσ «e-κπαιδευτείτε» ζχει ςτόχο να αυτοματοποιιςει τισ ακόλουκεσ
Εγχειρίδιο Χριςθσ τθσ διαδικτυακισ εφαρμογισ «Υποβολι και παρακολοφκθςθ τθσ ζγκριςθσ Εκπαιδευτικών Πακζτων» Το Πλθροφοριακό Σφςτθμα τθσ δράςθσ «e-κπαιδευτείτε» ζχει ςτόχο να αυτοματοποιιςει τισ ακόλουκεσ
MySchool Πρακτικζσ οδθγίεσ χριςθσ
 MySchool Πρακτικζσ οδθγίεσ χριςθσ 1) Δθμιουργία τμθμάτων (ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ, Διαχείριςθ, Διαχείριςθ τμθμάτων) Το πρώτο που πρζπει να κάνουμε ςτο MySchool είναι να δθμιουργιςουμε τα τμιματα που υπάρχουν ςτο
MySchool Πρακτικζσ οδθγίεσ χριςθσ 1) Δθμιουργία τμθμάτων (ΣΧΟΛΙΚΗ ΜΟΝΑΔΑ, Διαχείριςθ, Διαχείριςθ τμθμάτων) Το πρώτο που πρζπει να κάνουμε ςτο MySchool είναι να δθμιουργιςουμε τα τμιματα που υπάρχουν ςτο
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη
 Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Ποσοτικές Μέθοδοι Δρ. Χάϊδω Δριτσάκη MSc Τραπεζική & Χρηματοοικονομική Τεχνολογικό Εκπαιδευτικό Ίδρυμα Δυτικής Μακεδονίας Western Macedonia University of Applied Sciences Κοίλα Κοζάνης 50100 Kozani GR
Virtualization. Στο ςυγκεκριμζνο οδηγό, θα παρουςιαςτεί η ικανότητα δοκιμήσ τησ διανομήσ Ubuntu 9.04, χωρίσ την ανάγκη του format.
 Virtualization Στο ςυγκεκριμζνο οδηγό, θα παρουςιαςτεί η ικανότητα δοκιμήσ τησ διανομήσ Ubuntu 9.04, χωρίσ την ανάγκη του format. Το virtualization πρόκειται για μια τεχνολογία, θ οποία επιτρζπει το διαχωριςμό
Virtualization Στο ςυγκεκριμζνο οδηγό, θα παρουςιαςτεί η ικανότητα δοκιμήσ τησ διανομήσ Ubuntu 9.04, χωρίσ την ανάγκη του format. Το virtualization πρόκειται για μια τεχνολογία, θ οποία επιτρζπει το διαχωριςμό
SingularLogic Application. Παραμετροποίηση Galaxy Application Server
 Παραμετροποίηση Galaxy Application Server 1 Παραμετροποίηςη Galaxy Application Server Για τθν γριγορθ παραμετροποίθςθ του application server του Galaxy υπάρχει το Glx.Config.exe. Άλλο ςθμείο όπου μπορείτε
Παραμετροποίηση Galaxy Application Server 1 Παραμετροποίηςη Galaxy Application Server Για τθν γριγορθ παραμετροποίθςθ του application server του Galaxy υπάρχει το Glx.Config.exe. Άλλο ςθμείο όπου μπορείτε
Η θεωρία τησ ςτατιςτικήσ ςε ερωτήςεισ-απαντήςεισ Μέροσ 1 ον (έωσ ομαδοποίηςη δεδομένων)
 1)Πώσ ορύζεται η Στατιςτικό επιςτόμη; Στατιςτικι είναι ζνα ςφνολο αρχϊν και μεκοδολογιϊν για: το ςχεδιαςμό τθσ διαδικαςίασ ςυλλογισ δεδομζνων τθ ςυνοπτικι και αποτελεςματικι παρουςίαςι τουσ τθν ανάλυςθ
1)Πώσ ορύζεται η Στατιςτικό επιςτόμη; Στατιςτικι είναι ζνα ςφνολο αρχϊν και μεκοδολογιϊν για: το ςχεδιαςμό τθσ διαδικαςίασ ςυλλογισ δεδομζνων τθ ςυνοπτικι και αποτελεςματικι παρουςίαςι τουσ τθν ανάλυςθ
P, τότε: P και το μζςο πλικοσ των εμφανίςεων του γεγονότοσ ςτθ μονάδα του. X t το πλικοσ των εμφανίςεων του γεγονότοσ ςτο διάςτθμα. 0, t.
 Η Κατανομή oisson 1. Κατανομή oisson Ζςτω ζνα γεγονόσ, για το οποίο γνωρίηουμε ότι πραγματοποιείται κατά μζςο όρο φορζσ ςτθ μονάδα του χρόνου (ι του μικουσ ι του όγκου). Για παράδειγμα Πλικοσ τθλεφωνθμάτων
Η Κατανομή oisson 1. Κατανομή oisson Ζςτω ζνα γεγονόσ, για το οποίο γνωρίηουμε ότι πραγματοποιείται κατά μζςο όρο φορζσ ςτθ μονάδα του χρόνου (ι του μικουσ ι του όγκου). Για παράδειγμα Πλικοσ τθλεφωνθμάτων
Κατά τθν ενεργοποίθςθ τθσ ιδιότθτασ αυτισ ενδζχεται να εμφανιςτεί ζνα μινυμα ςαν αυτό τθσ παρακάτω εικόνασ. Απλά επιβεβαιϊςτε πατϊντασ ΟΚ.
 Δημιουργία Πινάκων Για τθ δθμιουργία πινάκων ςτο περιβάλλον phpmyadmin μποροφμε είτε να χρθςιμοποιιςουμε τθ φόρμα δθμιουργίασ πίνακα, είτε να εκτελζςουμε ζνα ερϊτθμα SQL Στθ παρακάτω εικόνα φαίνεται μια
Δημιουργία Πινάκων Για τθ δθμιουργία πινάκων ςτο περιβάλλον phpmyadmin μποροφμε είτε να χρθςιμοποιιςουμε τθ φόρμα δθμιουργίασ πίνακα, είτε να εκτελζςουμε ζνα ερϊτθμα SQL Στθ παρακάτω εικόνα φαίνεται μια
(Α3 1 ) Σασ δίνεται το παρακάτω αλγορικμικό τμιμα
 Μάθημα: Ανάπτυξη Εφαρμογών ςε Προγραμματιςτικό Περιβάλλον Τάξη Γ Λυκείου, Πληροφορική Οικονομικών Καθηγητής : Σιαφάκασ Γιώργοσ Ημερομηνία : 28/12/2015 Διάρκεια: 3 ώρεσ ΘΕΜΑ Α /40 (Α1) Να γράψετε ςτο τετράδιό
Μάθημα: Ανάπτυξη Εφαρμογών ςε Προγραμματιςτικό Περιβάλλον Τάξη Γ Λυκείου, Πληροφορική Οικονομικών Καθηγητής : Σιαφάκασ Γιώργοσ Ημερομηνία : 28/12/2015 Διάρκεια: 3 ώρεσ ΘΕΜΑ Α /40 (Α1) Να γράψετε ςτο τετράδιό
Ραραμετροποίθςθ ειςαγωγισ δεδομζνων περιόδων
 Παραμετροποίηςη ειςαγωγήσ δεδομζνων περιόδων 1 1 Περίληψη Το παρόν εγχειρίδιο παρουςιάηει αναλυτικά τθν παραμετροποίθςθ τθσ ειςαγωγισ αποτελεςμάτων μιςκοδοτικϊν περιόδων. 2 2 Περιεχόμενα 1 Ρερίλθψθ...2
Παραμετροποίηςη ειςαγωγήσ δεδομζνων περιόδων 1 1 Περίληψη Το παρόν εγχειρίδιο παρουςιάηει αναλυτικά τθν παραμετροποίθςθ τθσ ειςαγωγισ αποτελεςμάτων μιςκοδοτικϊν περιόδων. 2 2 Περιεχόμενα 1 Ρερίλθψθ...2
Οδηγόσ εγκατάςταςησ και ενεργοποίηςησ
 Οδηγόσ εγκατάςταςησ και ενεργοποίηςησ Ευχαριςτοφμε που επιλζξατε το memoq 4.5, το πρωτοκλαςάτο περιβάλλον μετάφραςθσ για ελεφκερουσ επαγγελματίεσ μεταφραςτζσ, μεταφραςτικά γραφεία και επιχειριςεισ. Αυτό
Οδηγόσ εγκατάςταςησ και ενεργοποίηςησ Ευχαριςτοφμε που επιλζξατε το memoq 4.5, το πρωτοκλαςάτο περιβάλλον μετάφραςθσ για ελεφκερουσ επαγγελματίεσ μεταφραςτζσ, μεταφραςτικά γραφεία και επιχειριςεισ. Αυτό
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων. 20. Αρχεία. Ιωάννθσ Κατάκθσ. ΕΠΛ 032: Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων
 Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 20. Αρχεία Ιωάννθσ Κατάκθσ Aποκικευςθ Για να αποκθκεφςουμε δεδομζνα από ζνα πρόγραμμα, πρζπει να χρθςιμοποιιςουμε τθ δευτερεφουςα μνιμθ Aποκικευςθ Η πιο ςυνθκιςμζνθ
Προγραμματιςμόσ Μεκόδων Επίλυςθσ Προβλθμάτων 20. Αρχεία Ιωάννθσ Κατάκθσ Aποκικευςθ Για να αποκθκεφςουμε δεδομζνα από ζνα πρόγραμμα, πρζπει να χρθςιμοποιιςουμε τθ δευτερεφουςα μνιμθ Aποκικευςθ Η πιο ςυνθκιςμζνθ
Λαμβάνοντασ υπόψη ότι κατά την πρόςθεςη δφο δυαδικϊν ψηφίων ιςχφει: Κρατοφμενο
 Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Αριθμητικά κυκλώματα Ημιαθροιστής (Half Adder) Ο ημιαθροιςτήσ είναι ζνα κφκλωμα το οποίο προςθζτει δφο δυαδικά ψηφία (bits) και δίνει ωσ αποτζλεςμα το άθροιςμά τουσ και το κρατοφμενο. Με βάςη αυτή την
Οδηγίες Πρόζβαζης ζηο EndNote Web. Πρόζβαζη ζηο EndNote Web
 Οδηγίες Πρόζβαζης ζηο EndNote Web Το EndNote Web είναι εργαλείο διαχείριςθσ βιβλιογραφικϊν αναφορϊν, ενςωματωμζνο ςτθ βάςθ Web of Science. Απαιτείται εγγραφι και δθμιουργία password (Sign in / Register)
Οδηγίες Πρόζβαζης ζηο EndNote Web Το EndNote Web είναι εργαλείο διαχείριςθσ βιβλιογραφικϊν αναφορϊν, ενςωματωμζνο ςτθ βάςθ Web of Science. Απαιτείται εγγραφι και δθμιουργία password (Sign in / Register)
Ρρογραμματιςμόσ Μεκόδων Επίλυςθσ Ρροβλθμάτων. 18. Αλφαριθμητικά. Ιωάννθσ Κατάκθσ. ΕΡΛ 032: Ρρογραμματιςμόσ Μεκόδων Επίλυςθσ Ρροβλθμάτων
 Ρρογραμματιςμόσ Μεκόδων Επίλυςθσ Ρροβλθμάτων 18. Αλφαριθμητικά Ιωάννθσ Κατάκθσ Αλφαρικμθτικά o Ζνα string είναι μία ακολουκία χαρακτιρων, ςθμείων ςτίξθσ κτλ Hello How are you? 121212 *Apple#123*% Σιμερα
Ρρογραμματιςμόσ Μεκόδων Επίλυςθσ Ρροβλθμάτων 18. Αλφαριθμητικά Ιωάννθσ Κατάκθσ Αλφαρικμθτικά o Ζνα string είναι μία ακολουκία χαρακτιρων, ςθμείων ςτίξθσ κτλ Hello How are you? 121212 *Apple#123*% Σιμερα
Πωσ δθμιουργώ φακζλουσ;
 Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
Πωσ δθμιουργώ φακζλουσ; Για να μπορζςετε να δθμιουργιςετε φακζλουσ ςτο χαρτοφυλάκιό ςασ ςτο Mahara κα πρζπει να μπείτε ςτο ςφςτθμα αφοφ πατιςετε πάνω ςτο ςφνδεςμο Mahara profiles από οποιοδιποτε ςελίδα
ΕΝΟΣΗΣΑ 3: ΧΡΗΗ ΕΡΓΑΛΕΙΩΝ ΕΚΦΡΑΗ ΚΑΙ ΔΗΜΙΟΤΡΓΙΑ
 ΕΝΟΣΗΣΑ 3: ΧΡΗΗ ΕΡΓΑΛΕΙΩΝ ΕΚΦΡΑΗ ΚΑΙ Επεξεργαςτισ Κειμζνου, Μορφοποίθςθ κειμζνου, Αποκικευςθ -Ανάκτθςθ εργαςίασ, Αντιγραφι - Μεταφορά κειμζνου, Γραμματοςειρά (Font), Ειςαγωγι εικόνασ ςε κείμενο Μία από
ΕΝΟΣΗΣΑ 3: ΧΡΗΗ ΕΡΓΑΛΕΙΩΝ ΕΚΦΡΑΗ ΚΑΙ Επεξεργαςτισ Κειμζνου, Μορφοποίθςθ κειμζνου, Αποκικευςθ -Ανάκτθςθ εργαςίασ, Αντιγραφι - Μεταφορά κειμζνου, Γραμματοςειρά (Font), Ειςαγωγι εικόνασ ςε κείμενο Μία από
ΜΑΘΗΜΑΤΙΚΑ ΕΠΙΠΕΔΟ 5 6 (Ε - ΣΤ Δημοτικού)
 ΕΠΙΠΕΔΟ 5 6 (Ε - ΣΤ Δημοτικού) 19 Μαρτίου 011 10:00-11:15 3 point/μονάδες 1. Ο Basil γράφει τθν λζξθ KANGAROO, ζνα γράμμα κάκε μζρα. Αρχίηει τθν Τετάρτθ. Ποια μζρα κα τελειϊςει; (A)Δευτέρα (B) Τρίτη (C)
ΕΠΙΠΕΔΟ 5 6 (Ε - ΣΤ Δημοτικού) 19 Μαρτίου 011 10:00-11:15 3 point/μονάδες 1. Ο Basil γράφει τθν λζξθ KANGAROO, ζνα γράμμα κάκε μζρα. Αρχίηει τθν Τετάρτθ. Ποια μζρα κα τελειϊςει; (A)Δευτέρα (B) Τρίτη (C)
Ονοματεπϊνυμο.. ΔΙΑΓΩΝΙΣΜΑ ΑΕΠΠ
 Ονοματεπϊνυμο.. ΔΙΑΓΩΝΙΣΜΑ ΑΕΠΠ ΘΕΜΑ 1 Ο Α) Ερωτισεις τφπου ωστοφ-λάκους 1. Κάκε βρόχος Για μπορεί να μετατραπεί σε Όσο 2. Κάκε βρόχος που υλοποιείται με τθν εντολι Όσο...επανάλαβε μπορεί να γραφεί και
Ονοματεπϊνυμο.. ΔΙΑΓΩΝΙΣΜΑ ΑΕΠΠ ΘΕΜΑ 1 Ο Α) Ερωτισεις τφπου ωστοφ-λάκους 1. Κάκε βρόχος Για μπορεί να μετατραπεί σε Όσο 2. Κάκε βρόχος που υλοποιείται με τθν εντολι Όσο...επανάλαβε μπορεί να γραφεί και
