Μερικές προαπαιτούμενες γνώσεις από τη Υυσική της Α Λυκείου
|
|
|
- Διόδωρος Κολιάτσος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Μερικές προαπαιτούμενες γνώσεις από τη Υυσική της Α Λυκείου Βαγγέλης Κολτσάκης, Υυσικός
2 ΠΕΡΙΕΦΟΜΕΝΑ Μερικές προαπαιτούμενες γνώσεις από τη Υυσική της Α Λυκείου 1 1. Η ευθύγραμμη κίνηση Πληροφορίες που μπορούμε να πάρουμε από τα διαγράμματα Η καμπυλόγραμμη κίνηση 4 3. Μερικοί ορισμοί στην κυκλική κίνηση 5 4. Νόμοι του Newton ος νόμος του Newton ος νόμος του Newton Διερεύνηση του δεύτερου νόμου (για υλικό σημείο) ος νόμος του Newton 7 5. Δυνάμεις που συναντάμε συχνά Σριβή Η δύναμη επαφής 5.3. Η τάση νήματος Δύναμη ελατηρίου 9 6. Η ορμή Η αρχή διατήρησης της ορμής (Α.Δ.Ο.) Η ισορροπία και η ευθύγραμμη ομαλή κίνηση Πως μελετάμε την ισορροπία σώματος Πως εφαρμόζουμε το θεμελιώδη νόμο της Μηχανικής στην ευθύγραμμη κίνηση Πως εφαρμόζουμε την αρχή διατήρησης της ορμής για σύστημα σωμάτων Πως εφαρμόζουμε το θεμελιώδη νόμο της Μηχανικής στην κυκλική κίνηση Έργο Ενέργεια Έργο δύναμης Κινητική ενέργεια Κ 12 K=½mu 2. Είναι η ενέργεια που έχει ένα σώμα λόγω της κίνησής του. Η κινητική ενέργεια εξαρτάται από το σύστημα αναφοράς Δυναμική ενέργεια U Αρχή διατήρησης ενέργειας (Α.Δ.Ε.) Πως εφαρμόζουμε τη Α.Δ.Ε. (Αρχή διατήρησης ενέργειας) Αρχή διατήρησης μηχανικής ενέργειας Α.Δ.Μ.Ε Πως εφαρμόζουμε τη Α.Δ.Μ.Ε. (Αρχή διατήρησης Μηχανικής ενέργειας) Πως εφαρμόζουμε το Θ.Μ.Κ.Ε. (Θεώρημα μεταβολής κινητικής ενέργειας ή θεώρημα έργου-ενέργειας) ΦΑΙΜΟ ΕΠΑΥΗ 9. ΑΝΑΚΤΚΛΩΗ Ισχύς 16 (ρυθμός παραγωγής έργου ή ρυθμός μετατροπής ενέργειας) υντελεστής απόδοσης μηχανής ΡΤΘΜΟΙ ΜΕΣΑΒΟΛΗ ΣΗ ΕΝΕΡΓΕΙΑ Μέσος ρυθμός μεταβολής τιγμιαίος ρυθμός μεταβολής Ρυθμός μεταβολής της δυναμικής ενέργειας βαρύτητας Ρυθμός μεταβολής της δυναμικής ενέργειας ελατηρίου Ρυθμός μεταβολής της κινητικής ενέργειας Ρυθμός προσφερόμενης ενέργειας Ρυθμός με τον οποίο ενέργεια του σώματος μετατρέπεται σε θερμότητα ΣΙΓΜΙΑΙΟΙ ΡΤΘΜΟΙ ΕΝΕΡΓΕΙΑ Σύποι για το έργο δύναμης 19
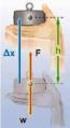
3 1. Η ευθύγραμμη κίνηση Ευθύγραμμη ομαλή ονομάζεται η κίνηση στην οποία το κινητό κινείται με σταθερή ταχύτητα u (δηλ. α) το μέτρο της ταχύτητας παραμένει σταθερό, που σημαίνει ότι το κινητό διανύει ίσες αποστάσεις σε ίσα χρονικά διαστήματα και β) η κατεύθυνση της ταχύτητας παραμένει σταθερή, που σημαίνει ότι η τροχιά είναι ευθεία γραμμή). επιτάχυνση α=0 ταχύτητα υ=δx/δt=σταθερή μετατόπιση Δx=υΔt Ευθύγραμμη ομαλά μεταβαλλόμενη ονομάζεται η κίνηση στην οποία το κινητό κινείται σε ευθύγραμμη τροχιά με σταθερή επιτάχυνση α, δηλ. το μέτρο της ταχύτητας μεταβάλλεται κατά την ίδια ποσότητα σε ίσα χρονικά διαστήματα. Ευθύγραμμη ομαλά επιταχυνόμενη ονομάζεται η κίνηση στην οποία το κινητό κινείται σε ευθύγραμμη τροχιά με σταθερή θετική επιτάχυνση (α>0), δηλ. το μέτρο της ταχύτητας αυξάνεται κατά την ίδια ποσότητα σε ίσα χρονικά διαστήματα. Ευθύγραμμη ομαλά επιβραδυνόμενη ονομάζεται η κίνηση στην οποία το κινητό κινείται σε ευθύγραμμη τροχιά με σταθερή αρνητική επιτάχυνση (α<0), δηλ. το μέτρο της ταχύτητας μειώνεται κατά την ίδια ποσότητα σε ίσα χρονικά διαστήματα. ΣΤΠΟΛΟΓΙΟ τα παρακάτω: Δx είναι η μετατόπιση (μεταβολή θέσης). Δx=x-xo και αν είναι xo=0 βάζουμε όπου Δx το x. Δt είναι το χρονικό διάστημα. Δt=t-to και αν είναι to=0 βάζουμε όπου Δt το t. Δu είναι η μεταβολή της ταχύτητας. Δu=u-uo και αν είναι uo=0 βάζουμε όπου Δu το u. Κίνηση επιτάχυνση Σαχύτητα μετατόπιση ευθύγραμμη a μέση =Δu/Δt u μέση =Δx/Δt Δx=uμέσηΔt ευθύγραμμη ομαλή ευθύγραμμη ομαλά μεταβαλλόμ ενη aστιγμιαία =Δu/Δt Δt0 uστιγμιαία =Δx/Δt Δt0 a=0 u=δx/δt=σταθερή Δx=uΔt a=δu/δt=σταθερή στην ευθύγραμμη ομαλά επιβραδυνόμενη: u uo a t 1 2 t u o a 2 uo x 2a x uo t a t 2 Πληροφορίες που μπορούμε να πάρουμε από τα διαγράμματα 1. Διάγραμμα u-t Γνωρίζουμε την ταχύτητα του κινητού σε κάθε χρονική στιγμή.
4 Αναγνωρίζουμε το είδος (ή τα είδη) της κίνησης από τη μορφή της γραμμής. Μπορούμε να βρούμε την επιτάχυνση του κινητού από τη σχέση a=δu/δt. Μπορούμε να υπολογίσουμε την μετατόπιση υπολογίζοντας εμβαδά. Σο εμβαδόν της επιφάνειας που περικλείεται από τη γραμμή και τον άξονα t ισούται αριθμητικά με το διάστημα που έχει διανύσει το κινητό. Εμβαδά κάτω από τον άξονα t είναι αρνητικά και η φυσική τους σημασία είναι ότι το κινητό κινείται προς την αρνητική φορά. 2. Διάγραμμα a-t Γνωρίζουμε την επιτάχυνση του κινητού σε κάθε χρονική στιγμή. Αναγνωρίζουμε το είδος (ή τα είδη) της κίνησης από τη μορφή της γραμμής. Μπορούμε να βρούμε τη μεταβολή της ταχύτητας του κινητού από τη σχέση Δu=aΔt. 3. Διάγραμμα x-t Γνωρίζουμε την θέση του κινητού σε κάθε χρονική στιγμή. Αναγνωρίζουμε το είδος (ή τα είδη) της κίνησης από τη μορφή της γραμμής. Μπορούμε να βρούμε την ταχύτητα του κινητού από τη σχέση u=δx/δt. 2. Η καμπυλόγραμμη κίνηση Καμπυλόγραμμη κίνηση είναι η κίνηση ενός σώματος που η τροχιά του είναι μια οποιαδήποτε καμπύλη γραμμή. Επειδή συνεχώς αλλάζει η διεύθυνση της ταχύτητας έχουμε μεταβολή του διανύσματος της ταχύτητας και συνεπώς η κίνηση χαρακτηρίζεται ως επιταχυνόμενη. Έστω σώμα κινείται σε καμπύλη τροχιά. ε κάποια χρονική στιγμή, σε κάποια θέση του κινητού, το σώμα έχει ταχύτητα u (εφαπτόμενη πάντα της τροχιάς) και επιτάχυνση a. Αναλύουμε την επιτάχυνση a του κινητού σε δυο (κάθετες μεταξύ τους) συνιστώσες. Μια, την aκ, κάθετη στην ταχύτητα, και άλλη μια, την aε, παράλληλη με την ταχύτητα (δηλ. στη διεύθυνση της εφαπτόμενης). Η κεντρομόλος επιτάχυνση aκ μεταβάλλει μόνο την κατεύθυνση της ταχύτητας του κινητού, (αναγκάζει δηλαδή το κινητό να στρίψει) και το μέτρο της δίνεται από τη σχέση aκ=u²/r, ενώ η επιτρόχιος επιτάχυνση aε μεταβάλλει μόνο το μέτρο της ταχύτητας του κινητού. Έτσι, στην ευθύγραμμη κίνηση (όπου το κινητό δεν στρίβει) είναι aκ=0, ενώ στην ομαλή κυκλική κίνηση (όπου το μέτρο της ταχύτητας παραμένει σταθερό) είναι aε=0. Αν προσθέσουμε τα δύο διανύσματα α ε α κ α υ α ε α κ υ Σελίδα 4
5 έχουμε: α=α ε+α κ. Από το Πυθαγόρειο θεώρημα βρίσκουμε το μέτρο. της ολικής επιτάχυνσης:α= α 2 α 2 ε κ 3. Μερικοί ορισμοί στην κυκλική κίνηση S είναι το τόξο που διαγράφει το σώμα εκτελώντας κυκλική ω κίνηση. Μετριέται σε m. R είναι η ακτίνα της κυκλικής υ τροχιάς. Επιβατική ακτίνα είναι η R ακτίνα που ακολουθεί το σώμα φ στην κυκλική του κίνηση. Ενώνει πάντα το σώμα με το κέντρο του κύκλου και κινείται μαζί μ αυτό. Μετριέται σε m. φ είναι η γωνία που διαγράφει η επιβατική ακτίνα καθώς ακολουθεί την κίνηση του σώματος. Με άλλα λόγια είναι η γωνία κατά την οποία στρίβει το σώμα. Μετριέται σε ακτίνια (rad). ε μερικές περιπτώσεις συμβολίζεται με Δφ. Λέγεται επίσης και γωνιακή μετατόπιση του σώματος. Σο μέτρο της επίκεντρης γωνίας φ (σε rad) είναι ο λόγος φ= S R όπου S είναι το μήκος του τόξου και R το μήκος της ακτίνας του κύκλου. 1rad δηλ. 1 ακτίνιο είναι η γωνία που αντιστοιχεί σε τόξο με μήκος S ίσο με την ακτίνα του κύκλου, δηλ. για S=R. ω είναι η γωνιακή ταχύτητα του σώματος στην κυκλική κίνηση. Είναι το πηλίκο της γωνιακής μετατόπισης Δφ προς το αντίστοιχο χρονικό διάστημα Δt. Επειδή η γωνιακή μετατόπιση μπορεί να μην είναι η ίδια για κάθε χρονικό διάστημα Δt, θεωρούμε ένα πολύ Δφ μικρό χρονικό διάστημα Δt0 και έτσι έχουμε: ω=imδt0 Δt. την ομαλή κυκλική κίνηση οι γωνιακές μετατοπίσεις που γίνονται σε ίσα χρονικά διαστήματα είναι ίσες. Έτσι λοιπόν : γωνιακή ταχύτητα στην ομαλή κυκλική κίνηση είναι το σταθερό πηλίκο Δφ Δt της γωνιακής μετατόπισης του σώματος προς τον αντίστοιχο χρόνο: ω= Δφ. Είναι διανυσματικό μέγεθος με μονάδα μέτρησης Δt το 1rad/s. Η διεύθυνση του διανύσματος της γωνιακής ταχύτητας είναι κάθετη στο επίπεδο της κίνησης, ενώ η αρχή του διανύσματος είναι το κέντρο της κυκλικής κίνησης. Δφ είναι η γωνιακή μετατόπιση και θεωρείται ίση με φ-φο, όπου φο είναι η αρχική γωνιακή θέση του σώματος που είχε τη χρονική στιγμή to. Aν to=0 και φο=0 τότε ω= φ t. Σελίδα 5
6 υ είναι η γραμμική ταχύτητα με την οποία κινείται το σώμα. Ισχύει S u στις ομαλές κινήσεις. Έτσι λοιπόν στην ομαλή κυκλική t κίνηση ισχύει ο ίδιος τύπος. Σο ΔS είναι το μήκος του τόξου που διαγράφει το σώμα σε χρονικό διάστημα Δt. Η ταχύτητα υ στην κυκλική κίνηση συχνά ονομάζεται γραμμική ταχύτητα για να αντιδιαστέλλεται με τη γωνιακή. Η ομαλή κυκλική κίνηση είναι επιταχυνόμενη αφού η ταχύτητα του κινητού αλλάζει συνεχώς διεύθυνση. Η επιτάχυνση του σώματος εξαιτίας της συνεχούς μεταβολής της διεύθυνσης της ταχύτητας 2. λέγεται κεντρομόλος επιτάχυνση ακ και ισχύει ακ= υ R ΣΤΠΟΛΟΓΙΟ Κίνηση επιτάχυνση Ταχύτητα μετατόπιση ομαλή κυκλική κεντρομόλος aκ=u 2 /R επιτρόχια aε=0 γραμμική u=δs/δt=2πr/t=2πrf=ωr γωνιακή ω=δφ/δt=2π/σ=2πf ΔS=uΔt=R.φ Δφ=ωΔt 4. Νόμοι του Newton ος νόμος του Newton (1 ος νόμος της κίνησης): F =0 u =σταθερή. Όταν ένα σώμα ηρεμεί ή κινείται με σταθερή ταχύτητα τότε η συνισταμένη των δυνάμεων που ασκούνται σε αυτό είναι ίση με μηδέν ή δεν ασκούνται σε αυτό δυνάμεις (ισχύει και αντίστροφα) ος νόμος του Newton F (2 ος νόμος της κίνησης): α = m. Η επιτάχυνση ενός σώματος έχει την κατεύθυνση της συνισταμένης δύναμης που ασκείται στο σώμα, είναι ανάλογη με την δύναμη και αντιστρόφως ανάλογη με την μάζα του σώματος. Με άλλα λόγια: F =Δ P /Δt Δ P = F Δt F =m α = m.δ u /Δt. Ο ρυθμός μεταβολής της ορμής ενός σώματος ισούται με τη συνισταμένη των δυνάμεων που ασκούνται σε αυτό. Σελίδα 6
7 4.3. Διερεύνηση του δεύτερου νόμου (για υλικό σημείο) Διερεύνηση της σχέσης F =m α (θεωρούμε την μάζα σταθερή). F =0 α =0 u =σταθερή το σώμα ηρεμεί ή κινείται ευθύγραμμα και ομαλά (1 ος νόμος) F =σταθερή α =σταθερή το σώμα εκτελεί ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση F σταθερή α σταθερή το σώμα εκτελεί μη ομαλά μεταβαλλόμενη κίνηση ος νόμος του Newton (3 ος νόμος της κίνησης): F AB=- F BA. ε κάθε δράση αναπτύσσεται μια αντίθετη αντίδραση (δηλαδή ίση κατά μέτρο αλλά με αντίθετη κατεύθυνση). Όταν ένα σώμα Α ασκεί μια δύναμη σε ένα σώμα Β, τότε και το Β ασκεί μια αντίθετη δύναμη στο σώμα Α. 5. Δυνάμεις που συναντάμε συχνά ΒΑΡΟ w=mg, με κατεύθυνση προς τα κάτω (προς το κέντρο της γης) ΣΑΗ νήματος, με κατεύθυνση από το σώμα προς το νήμα ΣΑΗ ελατηρίου, με κατεύθυνση τέτοια που να τείνει να επαναφέρει το ελατήριο στο φυσικό του μήκος F=k.Δl ΣΡΙΒΗ T=μN, με διεύθυνση παράλληλη προς τις επιφάνειες επαφής και φορά τέτοια ώστε να αντιτίθεται στην σχετική κίνηση (ολίσθηση) του σώματος. ΑΝΣΙΔΡΑΗ επαφής Ν (ή R ή Fκ), πάντοτε με διεύθυνση κάθετη στην επιφάνεια επαφής ΔΤΝΑΜΕΙ ΠΕΔΙΩΝ (γενικά) 5.1. Σριβή Σριβή είναι μια δύναμη που αντιτίθεται στην σχετική κίνηση δύο σωμάτων (ή, σωστότερα, που αντιτίθεται στην ολίσθηση ενός σώματος πάνω σε μια επιφάνεια). Έχει πάντα διεύθυνση παράλληλη με τις επιφάνειες που εφάπτονται, φορά αντίθετη με τη φορά της κίνησης και αναπτύσσεται μεταξύ των δύο επιφανειών που βρίσκονται σε επαφή. Η στατική τριβή εμφανίζεται στις επιφάνειες δύο αντικειμένων, οι οποίες βρίσκονται σε επαφή, ενώ τα αντικείμενα βρίσκονται σε σχετική ακινησία. Δεν είναι δύναμη με σταθερό μέτρο αλλά παίρνει όλες τις τιμές ανάμεσα Σελίδα 7
8 στο μηδέν και μια μέγιστη τιμή, την οριακή τριβή, που υπολογίζεται από τον τύπο: Σσ,max=μσFk. Άρα γενικά για την στατική τριβή ισχύει ότι: 0 Σσ μσ Fκ. Η τριβή ολίσθησης εμφανίζεται στις επιφάνειες δύο αντικειμένων οι οποίες βρίσκονται σε επαφή ενώ τα αντικείμενα βρίσκονται σε σχετική κίνηση. Η τριβή ολίσθησης είναι ανεξάρτητη από το εμβαδόν συνεπαφής και από τη σχετική ταχύτητα των σωμάτων, ενώ εξαρτάται από τη φύση των επιφανειών επαφής και από την κάθετη δύναμη στήριξης. Η τριβή ολίσθησης σε αντίθεση με την στατική τριβή, είναι δύναμη με σταθερό μέτρο που δίνεται από τον τύπο T=μFκ όπου μ ο συντελεστής τριβής ολίσθησης που είναι καθαρός αριθμός και εξαρτάται από τη φύση των δύο επιφανειών επαφής και Fκ η κάθετη δύναμη μεταξύ των επιφανειών. Γενικά ο συντελεστής τριβής ολίσθησης είναι μικρότερος από τον συντελεστή στατικής τριβής οπότε και η τριβή ολίσθησης είναι μικρότερη από την οριακή στατική τριβή Η δύναμη επαφής Όταν σώμα ακουμπά σε κάποια επιφάνεια, τότε δέχεται δύναμη από την επιφάνεια. Η δύναμη αυτή είναι κάθετη στην επιφάνεια και έχει φορά από την επιφάνεια προς το σώμα. Ονομάζεται συνήθως κάθετη αντίδραση ή δύναμη επαφής ή στήριξης και συμβολίζεται με Ν ή Fκ ή Α. Όταν το σώμα χάνει την επαφή του με την επιφάνεια τότε η κάθετη αντίδραση μηδενίζεται, ενώ όσο το σώμα παραμένει σε επαφή με την επιφάνεια, η κάθετη αντίδραση είναι μεγαλύτερη του μηδενός. Αν δεν υπάρχει τριβή, οι δυνάμεις επαφής μεταξύ δυο σωμάτων που εφάπτονται, είναι πάντοτε κάθετες στη διαχωριστική επιφάνεια των σωμάτων, ίσες κατά μέτρο και με αντίθετες φορές. Αν υπάρχει τριβή, οι δυνάμεις επαφής μεταξύ δυο σωμάτων που εφάπτονται, είναι πλάγιες ως προς τη διαχωριστική επιφάνεια των σωμάτων, έτσι ώστε να έχουν μια συνιστώσα (τριβή) που θα αντιτίθεται στη μεταξύ τους σχετική ολίσθηση και μια συνιστώσα κάθετη στην επιφάνεια επαφής. Αρκετές φορές όμως είναι πιο βολικό να σχεδιάζουμε εξαρχής τις δυο συνιστώσες και όχι την πλάγια δύναμη επαφής Η τάση νήματος Σα τεντωμένα νήματα ασκούν δυνάμεις ίσες και αντίθετες στα σώματα που είναι δεμένα στα άκρα τους. Σέτοια δύναμη ονομάζεται τάση νήματος, συμβολίζεται συνήθως με Σ ή Ν, έχει διεύθυνση την διεύθυνση του νήματος και φορά από το άκρο του νήματος προς το νήμα. Όσο πιο τεντωμένο είναι ένα νήμα, τόσο μεγαλύτερη είναι η τάση του. Κάθε νήμα αντέχει μέχρι ορισμένη τάση, η οποία ονομάζεται όριο θραύσης Σθρ του νήματος. Μόλις το νήμα τεντωθεί τόσο που η τάση γίνει ίση με το όριο θραύσης, το νήμα σπάει. Σελίδα 8
9 5.4. Δύναμη ελατηρίου Ιδανικό ελατήριο ονομάζεται το ελατήριο το οποίο έχει αμελητέα μάζα και υπακούει στο νόμο του Hooke. Υυσικό μήκος είναι το μήκος του ελατηρίου όταν σε αυτό δεν ασκείται καμία δύναμη. Ελατήριο παραμορφωμένο (επιμηκυμένο ή συσπειρωμένο) ασκεί στα δυο του άκρα δυο δυνάμεις ίσες και αντίθετες. Ελατήριο συσπειρωμένο απωθεί σώμα δεμένο στα άκρα του, ενώ ελατήριο επιμηκυμένο έλκει σώμα δεμένο στα άκρα του. Σέτοια δύναμη ονομάζεται τάση ελατηρίου ή δύναμη ελατηρίου Fελ, έχει πάντα διεύθυνση παράλληλη με τον άξονα του ελατηρίου και φορά τέτοια που να τείνει να επαναφέρει το ελατήριο στο φυσικό του μήκος. Σο μέτρο της δίνεται από τη σχέση Fελ=k.Δl, όπου k είναι μια σταθερά που εκφράζει το πόσο σκληρό είναι το ελατήριο και Δl είναι η παραμόρφωση του ελατηρίου. 6. Η ορμή Ορμή υλικού σημείου είναι το γινόμενο της μάζας του επί την ταχύτητά του p m u. Η ορμή είναι μέγεθος διανυσματικό με κατεύθυνση την κατεύθυνση της στιγμιαίας ταχύτητας του σώματος και μέτρο που δίνεται από τη σχέση p=m.u. Μονάδα της ορμής είναι το 1 kg m/s. Ένα σύνολο δύο ή περισσοτέρων σωμάτων που αλληλεπιδρούν μεταξύ τους με δυνάμεις δράσης αντίδρασης λέγεται σύστημα σωμάτων. Εσωτερικές ονομάζονται οι δυνάμεις που ασκούνται σε σώμα του συστήματος από άλλο σώμα που ανήκει στο σύστημα. Εξωτερικές ονομάζονται οι δυνάμεις που ασκούνται σε σώμα του συστήματος από άλλο σώμα που δεν ανήκει στο σύστημα Η αρχή διατήρησης της ορμής (Α.Δ.Ο.). Η ορμή ενός συστήματος διατηρείται σταθερή εφόσον δεν ασκούνται σε αυτό δυνάμεις εξωτερικές ή ασκούνται και έχουν μηδενική συνισταμένη (μονωμένο σύστημα) Η ισορροπία και η ευθύγραμμη ομαλή κίνηση υνθήκη ισορροπίας δυο ή περισσότερων ομοεπίπεδων δυνάμεων που ασκούνται στο ίδιο σημείο: F=0 Fx=0 και Fy=0 Σελίδα 9
10 6.3. Πως μελετάμε την ισορροπία σώματος (Ασκήσεις ισορροπίας δυο ή περισσότερων ομοεπίπεδων δυνάμεων που ασκούνται στο ίδιο σώμα (το σώμα θεωρείται ως υλικό σημείο)) 1. χεδιάζουμε το σχήμα σύμφωνα με τα δεδομένα της άσκησης 2. Βρίσκουμε και σχεδιάζουμε όλες τις δυνάμεις που ασκούνται στο σώμα 3. Επιλέγουμε ορθογώνιο σύστημα αξόνων x και y, έτσι ώστε όσο το δυνατό περισσότερες δυνάμεις να βρίσκονται πάνω στους άξονες (αρχή των αξόνων το σώμα) 4. Αναλύουμε όσες δυνάμεις δεν βρίσκονται πάνω στους δύο άξονες σε συνιστώσες πάνω στους άξονες και υπολογίζουμε τις συνιστώσες σε συνάρτηση με τα δεδομένα της άσκησης. 5. Εφαρμόζουμε τη συνθήκη ισορροπίας για κάθε άξονα: το σώμα δεν κινείται κατά τον άξονα των x, άρα Fx=0 το σώμα δεν κινείται κατά τον άξονα των y, άρα Fy=0 6. Γράφουμε και οποιαδήποτε άλλη εξίσωση προκύπτει από τα δεδομένα του προβλήματος (πχ Σ=μΝ, w=mg κλπ). 7. χηματίζουμε έτσι τουλάχιστον τόσες εξισώσεις όσοι και άγνωστοι του προβλήματος και επιλύουμε το σύστημα των εξισώσεων βρίσκοντας τα ζητούμενα μεγέθη σε συνάρτηση με τα δεδομένα μεγέθη. 8. Αντικαθιστούμε τα μέτρα των δεδομένων μεγεθών και βρίσκουμε τα μέτρα των ζητούμενων μεγεθών ή βρίσκουμε κάποιες σχέσεις που θα χρησιμοποιήσουμε στη συνέχεια της λύσης του προβλήματος Πως εφαρμόζουμε το θεμελιώδη νόμο της Μηχανικής στην ευθύγραμμη κίνηση 1. χεδιάζουμε το σχήμα σύμφωνα με τα δεδομένα της άσκησης 2. Βρίσκουμε και σχεδιάζουμε όλες τις δυνάμεις που ασκούνται στο σώμα 3. Επιλέγουμε ορθογώνιο σύστημα αξόνων x και y, έτσι ώστε ο άξονας x να είναι ο άξονας της κίνησης και ο άξονας y κάθετος στην κίνηση, και η φορά του άξονα x να είναι η ίδια με τη φορά της επιτάχυνσης (αρχή των αξόνων το σώμα). 4. Αναλύουμε όσες δυνάμεις δεν βρίσκονται πάνω στους δύο άξονες σε συνιστώσες πάνω στους άξονες και υπολογίζουμε τις συνιστώσες σε συνάρτηση με τα δεδομένα της άσκησης. 5. Εφαρμόζουμε το θεμελιώδη νόμο της Μηχανικής για κάθε άξονα: το σώμα επιταχύνεται κατά τον άξονα των x, άρα Fx=ma το σώμα δεν κινείται κατά τον άξονα των y, άρα Fy=0 (η συνθήκη Fx=ma γίνεται Fx=0 όταν το σώμα είναι ακίνητο ή κινείται με σταθερή ταχύτητα). 6. Γράφουμε και οποιαδήποτε άλλη εξίσωση προκύπτει από τα δεδομένα του προβλήματος (π.χ. w=mg, Σ=μΝ, αν το σώμα εκτελεί ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση γράφουμε τις εξισώσεις της κίνησης κλπ). 7. χηματίζουμε έτσι τουλάχιστον τόσες εξισώσεις όσοι και άγνωστοι του προβλήματος και επιλύουμε το σύστημα των εξισώσεων βρίσκοντας τα ζητούμενα μεγέθη σε συνάρτηση με τα δεδομένα μεγέθη. Σελίδα 10
11 8. Αντικαθιστούμε τα μέτρα των δεδομένων μεγεθών και βρίσκουμε τα μέτρα των ζητούμενων μεγεθών. Αν σε μια άσκηση δεν δίνεται κάποιο μέγεθος και ούτε ζητείται, αλλά πρέπει να χρησιμοποιηθεί κατά την διαδικασία επίλυσης της άσκησης, τότε το χρησιμοποιούμε ως γνωστό και πιθανότατα αυτό θα απλοποιηθεί κατά τη διάρκεια της επίλυσης της άσκησης Πως εφαρμόζουμε την αρχή διατήρησης της ορμής για σύστημα σωμάτων Φρησιμοποιούμε δυο σχήματα. το πρώτο σχήμα σχεδιάζουμε τα σώματα (με τις αρχικές ταχύτητες τους και τις αρχικές ορμές τους) αμέσως πριν την κρούση ή έκρηξη και στο δεύτερο σχήμα σχεδιάζουμε τα σώματα (με τις τελικές ταχύτητες τους και τις τελικές ορμές τους) αμέσως μετά την κρούση ή έκρηξη. Επιλέγουμε μια φορά ως θετική (όταν οι κινήσεις γίνονται πάνω σε μια ευθεία). Η φορά χρησιμεύει για να βάλουμε πρόσημα στις ταχύτητες (αλγεβρικές τιμές). Αν το πρόσημο μιας ζητούμενης ταχύτητας είναι άγνωστο, τότε θέτουμε ένα τυχαίο πρόσημο. Μετά την επίλυση της άσκησης, αν βρούμε αντίθετο πρόσημο για αυτήν την ταχύτητα, διορθώνουμε την αρχική μας επιλογή. Ισχύει P αρχ= P τελ (διανυσματικά), όπου P αρχ η ολική ορμή του συστήματος αρχικά και P τελ η ολική ορμή του συστήματος τελικά. αν ολική ορμή του συστήματος εννοούμε το άθροισμα των ορμών όλων των σωμάτων του συστήματος. Αν οι κινήσεις των σωμάτων γίνονται πάνω σε μια ευθεία, τότε η διανυσματική σχέση P αρχ= P τελ αντικαθίσταται από την αριθμητική Pαρχ=Pτελ. Αν οι κινήσεις των σωμάτων γίνονται όχι πάνω σε μια ευθεία αλλά στο επίπεδο, τότε επιλέγουμε κατάλληλα δυο κάθετους άξονες x και y και αναλύουμε όλες τις ταχύτητες των σωμάτων του συστήματος σε συνιστώσες κατά τους δυο άξονες. Η αρχή διατήρησης της ορμής ισχύει για κάθε άξονα χωριστά, δηλαδή P(x)αρχ=P(x)τελ και P(y)αρχ=P(y)τελ. Δημιουργούνται έτσι οι εξισώσεις που μας δίνουν τα ζητούμενα. Απαραίτητη προϋπόθεση είναι να μην ασκούνται στο σύστημα εξωτερικές δυνάμεις ή αν ασκούνται να έχουν μηδενική συνισταμένη. Οι ταχύτητες όλων των σωμάτων του συστήματος πρέπει να αναφέρονται στο ίδιο σύστημα αναφοράς. Η αρχή διατήρησης της ορμής συνήθως εφαρμόζεται σε ασκήσεις όπου έχουμε κρούση ή έκρηξη Πως εφαρμόζουμε το θεμελιώδη νόμο της Μηχανικής στην κυκλική κίνηση 1. χεδιάζουμε το σχήμα σύμφωνα με τα δεδομένα της άσκησης 2. Βρίσκουμε και σχεδιάζουμε όλες τις δυνάμεις που ασκούνται στο σώμα 3. Επιλέγουμε ορθογώνιο σύστημα αξόνων x και y, με αρχή των αξόνων το κινητό, έτσι ώστε ο άξονας x να είναι η διεύθυνση της ακτίνας της Σελίδα 11
12 κυκλικής τροχιάς (θετική φορά προς το κέντρο του κύκλου) και ο άξονας y η εφαπτόμενη ή η κάθετη στην κυκλική τροχιά. 4. Αναλύουμε όσες δυνάμεις δεν βρίσκονται πάνω στους δύο άξονες σε συνιστώσες πάνω στους άξονες και υπολογίζουμε τις συνιστώσες σε συνάρτηση με τα δεδομένα της άσκησης. 5. Εφαρμόζουμε τη σχέση FR=maκ FR=mu²/R, επειδή η συνισταμένη όλων των δυνάμεων με την διεύθυνση της ακτίνας είναι η κεντρομόλος δύναμη. (Γενικότερα ισχύει Fx=maκ και Fy=maε. Δηλαδή η συνισταμένη των δυνάμεων κατά την διεύθυνση της ακτίνας δημιουργεί την κεντρομόλο επιτάχυνση, ενώ η συνισταμένη των δυνάμεων κατά την διεύθυνση της εφαπτομένης δημιουργεί την επιτρόχιο επιτάχυνση. 6. Γράφουμε και οποιαδήποτε άλλη εξίσωση προκύπτει από τα δεδομένα του προβλήματος 7. χηματίζουμε έτσι τουλάχιστον τόσες εξισώσεις όσοι και άγνωστοι του προβλήματος και επιλύουμε το σύστημα των εξισώσεων βρίσκοντας τα ζητούμενα μεγέθη σε συνάρτηση με τα δεδομένα μεγέθη. 8. Αντικαθιστούμε τα μέτρα των δεδομένων μεγεθών και βρίσκουμε τα μέτρα των ζητούμενων μεγεθών. 7. Έργο Ενέργεια 7.1. Έργο δύναμης Σο έργο δύναμης εκφράζει (και ισούται με) κάποιο ποσό ενέργειας που μετατρέπεται σε άλλη μορφή ενέργειας Μια δύναμη παράγει έργο μόνον όταν μετατοπίζεται το σημείο εφαρμογής της. Δεν παράγει έργο όταν είναι κάθετη στη μετατόπιση. Σο έργο μιας δύναμης η οποία ασκείται σε ένα σώμα θεωρείται θετικό, όταν το σώμα κερδίζει ενέργεια εξαιτίας της επίδρασης αυτής της δύναμης, ενώ το έργο μιας δύναμης η οποία ασκείται σε ένα σώμα θεωρείται αρνητικό, όταν το σώμα χάνει ενέργεια εξαιτίας της επίδρασης αυτής της δύναμης Κινητική ενέργεια Κ K=½mu 2. Είναι η ενέργεια που έχει ένα σώμα λόγω της κίνησής του. Η κινητική ενέργεια εξαρτάται από το σύστημα αναφοράς Δυναμική ενέργεια U Είναι η ενέργεια που έχει ένα σώμα ή ένα σύστημα σωμάτων λόγω της θέσης ή της κατάστασης στην οποία αυτό βρίσκεται. Μερικά είδη δυναμικής ενέργειας: Σελίδα 12
13 Βαρυτική δυναμική ενέργεια Ug είναι η ενέργεια που έχει μια μάζα επειδή βρίσκεται μέσα σε πεδίο βαρύτητας. Ελαστική δυναμική ενέργεια Uελ είναι η ενέργεια που έχει ένα σώμα λόγω της ελαστικής παραμόρφωσής του. Η δυναμική ενέργεια εξαρτάται από την θέση ή την κατάσταση στην οποία έχουμε επιλέξει να είναι ίση με μηδέν. Για την βαρυτική δυναμική ενέργεια επιλέγουμε να είναι ίση με μηδέν συνήθως στην κατώτατη θέση του σώματος. Για την ελαστική δυναμική ενέργεια επιλέγουμε να είναι ίση με μηδέν συνήθως στην θέση που δεν υπάρχει παραμόρφωση Αρχή διατήρησης ενέργειας (Α.Δ.Ε.) Η συνολική ενέργεια σε ένα μονωμένο σύστημα παραμένει σταθερή. Όταν συμβαίνουν ενεργειακές μετατροπές, αυτό που συμβαίνει είναι ότι ποσά ενέργειας μετατρέπονται από μια μορφή ενέργειας σε άλλη μέσω των έργων δυνάμεων. Σο άθροισμά τους όμως παραμένει σταθερό. Η Α.Δ.Ε. μπορεί να εφαρμοστεί για την επίλυση προβλημάτων. υνήθως εφαρμόζεται σε προβλήματα στα οποία δεν είναι βολικό ή δεν είναι δυνατό να εφαρμοστεί η Α.Δ.Μ.Ε. ή το Θ.Μ.Κ.Ε Πως εφαρμόζουμε τη Α.Δ.Ε. (Αρχή διατήρησης ενέργειας) Η Α.Δ.Ε. ισχύει παντού και πάντα. Φρειάζεται όμως προσοχή ώστε να λάβουμε υπόψη όλες τις μορφές ενέργειας που εμφανίζονται στο σύστημα. Καθορίζουμε το σύστημα σωμάτων για το οποίο θα εφαρμόσουμε την ΑΔΕ Καθορίζουμε τις δυο καταστάσεις (αρχική και τελική) Εξισώνουμε τις συνολικές ενέργειες στην αρχική και τελική κατάσταση 7.6. Αρχή διατήρησης μηχανικής ενέργειας Α.Δ.Μ.Ε. υντηρητικές ή διατηρητικές δυνάμεις ονομάζονται οι δυνάμεις που το έργο τους για κλειστή διαδρομή είναι ίσο με μηδέν. Με άλλα λόγια, είναι οι δυνάμεις που το έργο τους σε μια μετατόπιση δεν εξαρτάται από την διαδρομή που ακολουθήθηκε, αλλά μόνον από την αρχική και τελική θέση. Σελίδα 13
14 Παραδείγματα συντηρητικών δυνάμεων: βάρος, δύναμη Coulomb, δύναμη ελατηρίου. Η τριβή είναι μη συντηρητική δύναμη. Μηχανική ενέργεια ενός σώματος (ή ενός συστήματος σωμάτων) ονομάζεται το άθροισμα της κινητικής και της δυναμικής ενέργειας του σώματος (ή του συστήματος). Η δράση συντηρητικών δυνάμεων δεν μεταβάλλει τη μηχανική ενέργεια. Έτσι, για το έργο συντηρητικής δύναμης ισχύει πάντα W=Uαρχ-Uτελ. Α.Δ.Μ.Ε.: Όταν σε ένα σώμα (ή σύστημα σωμάτων) παράγουν έργο μόνον συντηρητικές δυνάμεις, τότε η μηχανική ενέργεια του σώματος( ή του συστήματος σωμάτων) παραμένει σταθερή Πως εφαρμόζουμε τη Α.Δ.Μ.Ε. (Αρχή διατήρησης Μηχανικής ενέργειας) Καθορίζουμε το σώμα ή το σύστημα σωμάτων για το οποίο θα εφαρμόσουμε την ΑΔΜΕ Βεβαιωνόμαστε ότι όλες οι δυνάμεις που ασκούνται στο σώμα ή στο σύστημα είναι συντηρητικές Καθορίζουμε τις δυο θέσεις ή καταστάσεις (αρχική και τελική) Ορίζουμε αυθαίρετα το επίπεδο μηδενικής δυναμικής ενέργειας (συνήθως την χαμηλότερη από τις δύο θέσεις ή το άπειρο) χεδιάζουμε το σύστημα στην αρχική και τελική θέση ή κατάσταση Εξισώνουμε την αρχική με την τελική μηχανική ενέργεια του συστήματος 7.8. Πως εφαρμόζουμε το Θ.Μ.Κ.Ε. (Θεώρημα μεταβολής κινητικής ενέργειας ή θεώρημα έργου-ενέργειας) Θ.Μ.Κ.Ε.: W=ΔΚ. ε κάθε μετατόπιση ενός σώματος, το συνολικό έργο των δυνάμεων που ασκούνται στο σώμα ισούται με τη μεταβολή της κινητικής ενέργειας του σώματος. Σελίδα 14
15 Σο ΘΜΚΕ είναι γενικότερο από την αρχή διατήρησης της μηχανικής ενέργειας, αφού ισχύει: Για συντηρητικές και μη συντηρητικές δυνάμεις Για σταθερές και μη σταθερές δυνάμεις Για δυνάμεις που ασκούνται σε μέρος της διαδρομής ή σε ολόκληρη τη διαδρομή ενός σώματος Δηλαδή το ΘΜΚΕ ισχύει σε κάθε μετατόπιση, ανεξάρτητα από το είδος των δυνάμεων που ασκούνται. Σο ΘΜΚΕ δεν συνιστάται πάντοτε σε ασκήσεις που δίνεται ο χρόνος, αλλά συνιστάται σε ασκήσεις που δίνονται δυνάμεις, ταχύτητες, έργο δύναμης και μετατοπίσεις. την εφαρμογή του ΘΜΚΕ εφαρμόζουμε τα εξής βήματα: 1. Καθορίζουμε το σώμα (ή το σύστημα) για το οποίο θα εφαρμόσουμε το ΘΜΚΕ 2. Καθορίζουμε την αρχική και τελική θέση, ώστε να συμβολίσουμε τις ταχύτητες 3. Βάζουμε όλες τις δυνάμεις που ασκούνται στο σώμα (ή το σύστημα) κατά μήκος της διαδρομής του (προσέχοντας αν κάποια ή κάποιες δυνάμεις δεν ασκούνται σε όλη τη διαδρομή, αλλά σε μέρος της διαδρομής). Αν υπάρχει και δύναμη μεταβλητού μέτρου, υπολογίζουμε πρώτα το έργο της και μετά εφαρμόζουμε ΘΜΚΕ. Έργο συνισταμένης δυνάμεων: Ισούται με το άθροισμα των έργων των συνιστωσών δυνάμεων: WF=WF ΠΑΡΑΣΗΡΗH Όταν έχουμε κίνηση σώματος με την επίδραση σταθερής δύναμης (ή δυνάμεων) μπορούμε να δουλέψουμε με δυο τρόπους: με ΘΜΚΕ (όταν δεν χρησιμοποιούμε χρόνους κίνησης) ή με ΑΔΜΕ εφαρμόζοντας το Θεμελιώδη νόμο της μηχανικής (όταν χρησιμοποιούμε χρόνους κίνησης) Σελίδα 15
16 8. ΦΑΙΜΟ ΕΠΑΥΗ Αναγκαία συνθήκη για να χάσει ένα σώμα την επαφή του με το υποστήριγμα του: Πρέπει η κάθετη αντίδραση που δέχεται το σώμα από το υποστήριγμα να μηδενιστεί 9. ΑΝΑΚΤΚΛΩΗ Όταν σώμα διαγράφει κατακόρυφο κύκλο, ζητείται συχνά η συνθήκη που πρέπει να ισχύει ώστε το σώμα να εκτελέσει ανακύκλωση, δηλ. να φτάσει στο ψηλότερο σημείο της τροχιάς του. Οι πιο χαρακτηριστικές περιπτώσεις είναι οι ακόλουθες: Όταν το σώμα είναι δεμένο στην άκρη νήματος ώμα στο εσωτερικό κατακόρυφης σφαιρικής ή κυλινδρικής επιφάνειας ώμα στερεωμένο στο άκρο ράβδου Πρέπει στην ανώτατη θέση το νήμα να παραμένει τεντωμένο, δηλ. Σ0 Σορ=0 Πρέπει στην ανώτατη θέση το σώμα να μην χάνει την επαφή του με την επιφάνεια, δηλ. Fκάθ0 Fκάθ,ορ=0, όπου Fκάθ η αντίδραση της επιφάνειας Πρέπει στην ανώτατη θέση η ταχύτητα του σώματος να είναι θετική ή μηδέν, δηλ. u0 uορ=0 10. Ισχύς (ρυθμός παραγωγής έργου ή ρυθμός μετατροπής ενέργειας) Είναι το πηλίκο της μετατρεπόμενης ενέργειας προς το χρόνο που διάρκεσε η μετατροπή αυτή. P=ΔW/Δt. Μονάδα ισχύος:1watt=1joule/s. τιγμιαία ισχύς Pστ=limΔt0ΔW/Δt Από τη γραφική παράσταση P(t) μπορούμε να υπολογίσουμε το έργο υπολογίζοντας εμβαδά-, αφού W=Pt 11. υντελεστής απόδοσης μηχανής Κάθε μηχανή παίρνει ένα ποσό ενέργειας (δαπανώμενη ή καταναλισκόμενη) και δίνει ένα ποσό ενέργειας (ωφέλιμη). Σο πηλίκο της ωφέλιμης προς την δαπανώμενη ενέργεια το ονομάζουμε συντελεστή απόδοσης της μηχανής. α=εωφ/εδαπ=ρωφ/ρδαπ. υνήθως σε μια μηχανή έχουμε απώλειες ενέργειας Εαπ. ύμφωνα με την Α.Δ.Ε. ισχύει Εδαπ= Εωφ+ Εαπ. Ισοδύναμα ισχύει Ρδαπ= Ρωφ+ Ραπ. Σελίδα 16
17 12. ΡΤΘΜΟΙ ΜΕΣΑΒΟΛΗ ΣΗ ΕΝΕΡΓΕΙΑ Μέσος ρυθμός μεταβολής Είναι ο ρυθμός σε κάποιο χρονικό διάστημα Δt=t2-t1 και ισούται με ΔΕ/Δt=(Ε2-Ε1)/( t2-t1) τιγμιαίος ρυθμός μεταβολής Είναι ο ρυθμός σε κάποια χρονική στιγμή και ισούται με ΔΕ/Δt όπου Δt είναι στοιχειώδες χρονικό διάστημα με Δt Ρυθμός μεταβολής της δυναμικής ενέργειας βαρύτητας. Η δυναμική ενέργεια βαρύτητας μεταβάλλεται μέσω του έργου του βάρους. Σο βάρος είναι συντηρητική δύναμη, οπότε ισχύει WB=-ΔΕΔΤΝ. Άρα, ΔΕΔΤΝ/Δt=-ΔWB/Δt=-mgΔy/Δt=-mguy. Eπιλέγοντας θετική φορά για το βάρος την προς τα κάτω, έχουμε: όταν το σώμα κατεβαίνει, είναι uy>0, άρα ΔΕΔΤΝ/Δt<0, ενώ όταν το σώμα ανεβαίνει, είναι uy<0, άρα ΔΕΔΤΝ/Δt> Ρυθμός μεταβολής της δυναμικής ενέργειας ελατηρίου. Η δυναμική ενέργεια ελατηρίου μεταβάλλεται μέσω του έργου της δύναμης του ελατηρίου. Η δύναμη ελατηρίου είναι συντηρητική δύναμη, οπότε ισχύει WF,ελ=-ΔΕΔΤΝ. Άρα, ΔΕΔΤΝ/Δt=-Δ WF,ελ/ Δt=-(FελΔx/Δt)= Fελ u Ρυθμός μεταβολής της κινητικής ενέργειας. Η κινητική ενέργεια ενός σώματος μεταβάλλεται μέσω του έργου της συνισταμένης δύναμης F που ασκείται στο σώμα. (Αν η F δεν έχει την διεύθυνση της κίνησης, τότε όπου F χρησιμοποιούμε την συνιστώσα της F κατά την διεύθυνση της κίνησης). Έτσι, από το ΘΜΚΕ έχουμε: ΔΕΚΙΝ =WF, άρα ΔΕΚΙΝ/Δt=ΔWF/ Δt=FΔx/Δt=Fu Ρυθμός προσφερόμενης ενέργειας. υνήθως η ενέργεια προσφέρεται σε ένα σώμα μέσω του έργου μιας εξωτερικής δύναμης Fεξ, οπότε έχουμε ΔΕπροσφ/Δt=ΔWFεξ/Δt=FεξΔx/Δt=Fεξu. Σελίδα 17
18 12.7. Ρυθμός με τον οποίο ενέργεια του σώματος μετατρέπεται σε θερμότητα ή ρυθμός με τον οποίο το σώμα χάνει ενέργεια. τη Μηχανική, με τον όρο θερμότητα εννοείται η ενέργεια που χάνεται από το σώμα λόγω της τριβής. Έτσι, ΔQ/Δt=ΔWT/Δt=- TΔx/Δt=-Σu ΣΙΓΜΙΑΙΟΙ ΡΤΘΜΟΙ ΕΝΕΡΓΕΙΑ ΔΤΝΑΜΗ ΕΝΕΡΓΕΙΑ ΡΤΘΜΟ w Εδυν,βαρύτητας ΔΕΔΤΝ/Δt=-mguy Fελ Εδυν, ελατηρίου ΔΕΔΤΝ/Δt= Fελ u F Εκινητική ΔΕΚΙΝ/Δt=Fu Fεξ Επροσφερόμενη ΔΕπροσφ/Δt=Fεξu T Q ΔQ/Δt =-Σu Σελίδα 18
19 13. Σύποι για το έργο δύναμης ΔΤΝΑΜΗ ΕΡΓΟ ΔΤΝΑΜΗ ΜΕΣΑΣΡΕΠΕ ΣΑΙ ΕΝΕΡΓΕΙΑ Δύναμη σταθερή, σε W=F.Δx.συνφ ευθύγραμμη μετατόπιση δύναμη σταθερού μέτρου, εφαπτόμενη συνεχώς σε καμπύλη τροχιά Δύναμη σταθερής κατεύθυνσης, που το μέτρο της είναι συνάρτηση της μετατόπισης W=F.s Ισούται αριθμητικά με το εμβαδόν της επιφάνειας που περικλείεται από την γραφική Παράσταση F-x και τον άξονα x (σε διάγραμμα F-x) μηδέν Δύναμη συνεχώς κάθετη στην μετατόπιση (στην ταχύτητα) Σριβή WT =-T.s κάποιας μορφής Δύναμη που ασκείται από άνθρωπο Δύναμη πεδίου (γενικά) Δύναμη βαρυτικού πεδίου (βάρος) Δύναμη ελατηρίου WF=-ΔUδυν= Uδυν,αρχ-Uδυν,τελ Ww=-ΔUδυν= Uδυν,αρχ-Uδυν,τελ= mg(hαρχ-hτελ) (αν g=σταθ.) WFελ=-ΔUδυν= Uδυν,αρχ-Uδυν,τελ= 1/2 kδlαρχ 2-1/2 kδlτελ 2 χημική του ανθρώπου κάποιας μορφής δυναμική κάποιας μορφής βαρυτική δυναμική κάποιας μορφής ελαστική δυναμική Ε ΕΝΕΡΓΕΙΑ Θερμική ενέργεια άλλης μορφής δυναμική αν WF<0 κάποιας μορφής αν WF>0 βαρυτική δυναμική αν WΒ<0 (άνοδος) κάποιας μορφής αν WΒ>0 (κάθοδος) ελαστική δυναμική αν WFελ<0 κάποιας μορφής αν WFελ>0 ΠΑΡΑΣΗΡΗΕΙ φ είναι η γωνία που σχηματίζεται από την δύναμη και την μετατόπιση W=0 αν φ=90 ο (δύναμη κάθετη στη μετατόπιση) W>0 αν 0 ο φ<90 ο W<0 αν 90 ο <φ180 ο W=F.s αν φ=0 ο W=-F.s αν φ=180 ο όπου s το μήκος της τροχιάς εμβαδά πάνω από τον άξονα x αντιστοιχούν σε θετικό έργο, ενώ κάτω από τον άξονα σε αρνητικό Q=WT το πεδίο παίρνει ενέργεια από το υπόθεμα το υπόθεμα παίρνει ενέργεια από το πεδίο όταν η Fελ έχει φορά αντίθετη της κίνησης όταν η Fελ έχει την φορά της κίνησης Σελίδα 19
1. Κίνηση Υλικού Σημείου
 1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
1. Κίνηση Υλικού Σημείου Εισαγωγή στην Φυσική της Γ λυκείου Τροχιά: Ονομάζεται η γραμμή που συνδέει τις διαδοχικές θέσεις του κινητού. Οι κινήσεις ανάλογα με το είδος της τροχιάς διακρίνονται σε: 1. Ευθύγραμμες
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου
 Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
Προτεινόμενο διαγώνισμα Φυσικής Α Λυκείου Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Όταν ένα σώμα ισορροπεί τότε: i. Ο ρυθμός μεταβολής της ταχύτητάς του
ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ
 F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Το έργο μίας από τις δυνάμεις που ασκούνται σε ένα σώμα. α. είναι μηδέν όταν το σώμα είναι ακίνητο β. έχει πρόσημο το οποίο εξαρτάται από τη γωνία
ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Το έργο μίας από τις δυνάμεις που ασκούνται σε ένα σώμα. α. είναι μηδέν όταν το σώμα είναι ακίνητο β. έχει πρόσημο το οποίο εξαρτάται από τη γωνία
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ
 ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΔΥΝΑΜΕΙΣ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του.
ΜΗΧΑΝΙΚΗ ΕΝΟΤΗΤΑ 1. Κεφάλαιο 3 ο : Οι σπουδαιότερες. δυνάμεις στη φύση. Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 Προσδοκώμενα Αποτελέσματα Οι Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd μαθητές θα πρέπει: 1 1. Να υιοθετήσουν την άποψη ότι, σε συνθήκες έλλειψης τριβών, η δυσκολία αλλαγής
Προσδοκώμενα Αποτελέσματα Οι Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd μαθητές θα πρέπει: 1 1. Να υιοθετήσουν την άποψη ότι, σε συνθήκες έλλειψης τριβών, η δυσκολία αλλαγής
F Στεφάνου Μ. 1 Φυσικός
 F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
F 1 ΠΑΡΑΤΗΡΗΣΕΙΣ ΓΙΑ ΤΙΣ ΑΣΚΗΣΕΙΣ Όταν δίνονται οι δυνάμεις οι οποίες ασκούνται σε ένα σώμα, υπολογίζουμε τη συνισταμένη των δυνάμεων και από τη σχέση (ΣF=m.α ) την επιτάχυνσή του. Αν ασκούνται σε αρχικά
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/2014
 minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
minimath.eu Φυσική A ΛΥΚΕΙΟΥ Περικλής Πέρρος 1/1/014 minimath.eu Περιεχόμενα Κινηση 3 Ευθύγραμμη ομαλή κίνηση 4 Ευθύγραμμη ομαλά μεταβαλλόμενη κίνηση 5 Δυναμικη 7 Οι νόμοι του Νεύτωνα 7 Τριβή 8 Ομαλη κυκλικη
Ευθύγραμμη ομαλή κίνηση
 Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
Διάγραμμα s - Ευθύγραμμη Κίνηση (m) Μέση αριθμητική ταχύτητα (μονόμετρο) Μέση διανυσματική ταχύτητα Μέση επιτάχυνση 1 4 Διάγραμμα u - (sec) Απόσταση (x) ονομάζουμε την ευθεία που ενώνει την αρχική και
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ
 ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΕΝΟΤΗΤΑ 1.2 ΔΥΝΑΜΙΚΗ ΣΕ ΜΙΑ ΔΙΑΣΤΑΣΗ 1. Τι λέμε δύναμη, πως συμβολίζεται και ποια η μονάδα μέτρησής της. Δύναμη είναι η αιτία που προκαλεί τη μεταβολή της κινητικής κατάστασης των σωμάτων ή την παραμόρφωσή
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014
 1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα.
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ΣΤΕΡΕΟΎ ΣΏΜΑΤΟΣ Τα σώματα τα έχουμε αντιμετωπίσει μέχρι τώρα σαν υλικά σημεία. Το υλικό σημείο δεν έχει διαστάσεις. Έχει μόνο μάζα. Ένα υλικό σημείο μπορεί να κάνει μόνο μεταφορική
Θεώρημα μεταβολής της Κινητικής ενέργειας
 Θεώρημα μεταβολής της Κινητικής ενέργειας Λυμένες ασκήσεις Σώμα με μάζα = 2 Kg κινείται σε οριζόντιο επίπεδο με αρχική ταχύτητα υ 0 = 10 /s. Ασκείται σε αυτό οριζόντια δύναμη F = 10 N για χρόνο t = 2 s.
Θεώρημα μεταβολής της Κινητικής ενέργειας Λυμένες ασκήσεις Σώμα με μάζα = 2 Kg κινείται σε οριζόντιο επίπεδο με αρχική ταχύτητα υ 0 = 10 /s. Ασκείται σε αυτό οριζόντια δύναμη F = 10 N για χρόνο t = 2 s.
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 2014
 1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
1 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΜΕ ΝΕΟ ΣΥΣΤΗΜΑ 014 ΘΕΜΑ Α.1 Α1. Να χαρακτηρίσετε με (Σ) τις σωστές και με (Λ) τις λανθασμένες προτάσεις Στην ευθύγραμμα ομαλά επιβραδυνόμενη κίνηση: Α. Η ταχύτητα
Τυπολόγιο Κινήσεων 1. Πίνακας 1 - Τυπολόγιο Κινήσεων Τύπος Μας δίνει Παρατηρήσεις Ορισμοί βασικών μεγεθών. Ορισμός Μετατόπισης
 Τυπολόγιο Κινήσεων 1 1 Τυπολόγιο Κινήσεων Πίνακας 1 - Τυπολόγιο Κινήσεων Ορισμοί βασικών μεγεθών = 2 1 Ορισμός Μετατόπισης Αλγεβρικά, κανονικά είναι = 2 1 =, = Ορισμός ταχύτητας Διανυσματικά, αλγεβρικά
Τυπολόγιο Κινήσεων 1 1 Τυπολόγιο Κινήσεων Πίνακας 1 - Τυπολόγιο Κινήσεων Ορισμοί βασικών μεγεθών = 2 1 Ορισμός Μετατόπισης Αλγεβρικά, κανονικά είναι = 2 1 =, = Ορισμός ταχύτητας Διανυσματικά, αλγεβρικά
ΦΥΣΙΚΗ. Α Λυκείου 14/ 04 / 2019 ΘΕΜΑ Α.
 Α Λυκείου 4/ 4 / 9 ΦΥΣΙΚΗ ΘΕΜΑ Α. Α. γ, Α. β, Α3. γ, Α4. α Α5. α) Σ, β) Σ, γ) Λ, δ) Λ, ε) Λ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (β). Εφαρμόζοντας το ο νόμο του Νεύτωνα υπολογίζουμε την επιτάχυνση του συστήματος
Α Λυκείου 4/ 4 / 9 ΦΥΣΙΚΗ ΘΕΜΑ Α. Α. γ, Α. β, Α3. γ, Α4. α Α5. α) Σ, β) Σ, γ) Λ, δ) Λ, ε) Λ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (β). Εφαρμόζοντας το ο νόμο του Νεύτωνα υπολογίζουμε την επιτάχυνση του συστήματος
16. Να γίνει µετατροπή µονάδων και να συµπληρωθούν τα κενά των προτάσεων: α. οι τρεις ώρες είναι... λεπτά β. τα 400cm είναι...
 1. Ο νόµος του Hooke υποστηρίζει ότι οι ελαστικές παραµορφώσεις είναι.των...που τις προκαλούν. 2. Ο τρίτος νόµος του Νεύτωνα υποστηρίζει ότι οι δυνάµεις που αναφέρονται στο νόµο αυτό έχουν... µέτρα,......
1. Ο νόµος του Hooke υποστηρίζει ότι οι ελαστικές παραµορφώσεις είναι.των...που τις προκαλούν. 2. Ο τρίτος νόµος του Νεύτωνα υποστηρίζει ότι οι δυνάµεις που αναφέρονται στο νόµο αυτό έχουν... µέτρα,......
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ. m γ. Η μονάδα μέτρησης της επιτάχυνσης στο S.I είναι το 1.
 ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τρίτη 8 Απριλίου 04 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α - Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Ποια από τις επόμενες
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τρίτη 8 Απριλίου 04 ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α - Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Α. Ποια από τις επόμενες
ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
1 ΠΡΟΤΕΙΝΟΜΕΝΟ ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ 1 ο 1. Aν ο ρυθμός μεταβολής της ταχύτητας ενός σώματος είναι σταθερός, τότε το σώμα: (i) Ηρεμεί. (ii) Κινείται με σταθερή ταχύτητα. (iii) Κινείται με μεταβαλλόμενη
GI_V_FYSP_4_ m/s, ξεκινώντας από το σημείο Κ. Στο σημείο Λ (αντιδιαμετρικό του Κ) βρίσκεται ακίνητο σώμα Σ 2 μάζας m2 1 kg.
 Μια ράβδος μήκους R m και αμελητέας μάζας βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και μπορεί να περιστρέφεται γύρω από το σημείο Ο. Στο άλλο άκρο της είναι στερεωμένο σώμα Σ, μάζας m kg το οποίο εκτελεί
Μια ράβδος μήκους R m και αμελητέας μάζας βρίσκεται πάνω σε λείο οριζόντιο επίπεδο και μπορεί να περιστρέφεται γύρω από το σημείο Ο. Στο άλλο άκρο της είναι στερεωμένο σώμα Σ, μάζας m kg το οποίο εκτελεί
ΘΕΜΑ Α Παράδειγμα 1. Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα.
 ΘΕΜΑ Α Παράδειγμα 1 Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα. Α2. Για τον προσδιορισμό μιας δύναμης που ασκείται σε ένα σώμα απαιτείται να
ΘΕΜΑ Α Παράδειγμα 1 Α1. Ο ρυθμός μεταβολής της ταχύτητας ονομάζεται και α. μετατόπιση. β. επιτάχυνση. γ. θέση. δ. διάστημα. Α2. Για τον προσδιορισμό μιας δύναμης που ασκείται σε ένα σώμα απαιτείται να
ΚΕΦΑΛΑΙΟ 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 Σχολικό Έτος 016-017 8 ΚΕΦΑΛΑΙΟ.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 1. ΕΡΓΟ Το έργο σαν φυσικό μέγεθος εκφράζει την μεταφορά ενέργειας από ένα σώμα σε ένα άλλο ή την μετατροπή της από μια μορφή σε μια
Σχολικό Έτος 016-017 8 ΚΕΦΑΛΑΙΟ.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ 1. ΕΡΓΟ Το έργο σαν φυσικό μέγεθος εκφράζει την μεταφορά ενέργειας από ένα σώμα σε ένα άλλο ή την μετατροπή της από μια μορφή σε μια
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ
 ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σωστό ή λάθος: Η στιγμιαία ταχύτητα: α. εκφράζει τη μεταβολή της μετατόπισης β. εκφράζει το ρυθμό μεταβολής της θέσης κατά μία δεδομένη χρονική στιγμή γ. αναφέρεται σε μία δεδομένη
ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΑΘΟΥΣ 1. Σωστό ή λάθος: Η στιγμιαία ταχύτητα: α. εκφράζει τη μεταβολή της μετατόπισης β. εκφράζει το ρυθμό μεταβολής της θέσης κατά μία δεδομένη χρονική στιγμή γ. αναφέρεται σε μία δεδομένη
2 Η ΠΡΟΟΔΟΣ. Ενδεικτικές λύσεις κάποιων προβλημάτων. Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση
 2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
2 Η ΠΡΟΟΔΟΣ Ενδεικτικές λύσεις κάποιων προβλημάτων Τα νούμερα στις ασκήσεις είναι ΤΥΧΑΙΑ και ΟΧΙ αυτά της εξέταση Ένας τροχός εκκινεί από την ηρεμία και επιταχύνει με γωνιακή ταχύτητα που δίνεται από την,
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ
 ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΠΡΟΒΛΗΜΑ 1 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΚΕΦΑΛΑΙΟ Η λεπτή, ομογενής ράβδος ΟΑ του σχήματος έχει μήκος, μάζα και μπορεί να περιστρέφεται σε κατακόρυφο επίπεδο γύρω από οριζόντιο ακλόνητο άξονα (άρθρωση) που διέρχεται
ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΡΓΑΣΙΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2015 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ
 ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΡΓΑΣΙΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2015 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Οριζόντια βολή: Είναι η κίνηση (παραβολική τροχιά) που κάνει ένα σώμα το οποίο βάλλεται με οριζόντια ταχύτητα U 0 μέσα στο πεδίο βαρύτητας
ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΡΓΑΣΙΑ ΦΥΣΙΚΗΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ 2015 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Οριζόντια βολή: Είναι η κίνηση (παραβολική τροχιά) που κάνει ένα σώμα το οποίο βάλλεται με οριζόντια ταχύτητα U 0 μέσα στο πεδίο βαρύτητας
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ. Από τη Φυσική της Α' Λυκείου
 ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΒΑΣΙΚΕΣ ΚΑΙ ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ ΑΠΟ ΤΗΝ Α ΚΑΙ Β ΛΥΚΕΙΟΥ Από τη Φυσική της Α' Λυκείου Δεύτερος νόμος Νεύτωνα, και Αποδεικνύεται πειραματικά ότι: Η επιτάχυνση ενός σώματος (όταν αυτό θεωρείται
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. A.1 Μια διαφορά
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. A.1 Μια διαφορά
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ. 1. Μπορεί ένα σύστημα σωμάτων να έχει κινητική ενέργεια χωρίς να έχει ορμή; Ισχύει το ίδιο και στην περίπτωση ενός σώματος;
 ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΕΡΩΤΗΣΕΙΣ ΠΡΩΤΟΥ ΚΑΙ ΔΕΥΤΕΡΟΥ ΘΕΜΑΤΟΣ 1. Μπορεί ένα σύστημα σωμάτων να έχει κινητική ενέργεια χωρίς να έχει ορμή; Ισχύει το ίδιο και στην περίπτωση ενός σώματος; 2. Ποιο από τα παρακάτω
ΦΥΣΙΚΗ ΓΕΝΙΚΗΣ ΕΡΩΤΗΣΕΙΣ ΠΡΩΤΟΥ ΚΑΙ ΔΕΥΤΕΡΟΥ ΘΕΜΑΤΟΣ 1. Μπορεί ένα σύστημα σωμάτων να έχει κινητική ενέργεια χωρίς να έχει ορμή; Ισχύει το ίδιο και στην περίπτωση ενός σώματος; 2. Ποιο από τα παρακάτω
ΚΕΦΑΛΑΙΟ 2.1 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 ΚΕΦΑΛΑΙΟ 2.1 91 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Α. ΈΡΓΟ ΣΤΑΘΕΡΗΣ ΔΥΝΑΜΗΣ 1. Το σώμα του σχήματος μετακινείται πάνω στο οριζόντιο επίπεδο κατά x=2m. Στο σώμα εκτός του βάρους του και της αντίδρασης του
ΚΕΦΑΛΑΙΟ 2.1 91 ΔΙΑΤΗΡΗΣΗ ΤΗΣ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Α. ΈΡΓΟ ΣΤΑΘΕΡΗΣ ΔΥΝΑΜΗΣ 1. Το σώμα του σχήματος μετακινείται πάνω στο οριζόντιο επίπεδο κατά x=2m. Στο σώμα εκτός του βάρους του και της αντίδρασης του
ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ
 ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ Θέση, μετατόπιση και διάστημα Όταν ένα σημειακό αντικείμενο κινείται ευθύγραμμα, για να μελετήσουμε την κίνησή του θεωρούμε σαν σύστημα αναφοράς έναν άξονα χ χ. Στην αρχή του
ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ ΜΗΧΑΝΙΚΗΣ Θέση, μετατόπιση και διάστημα Όταν ένα σημειακό αντικείμενο κινείται ευθύγραμμα, για να μελετήσουμε την κίνησή του θεωρούμε σαν σύστημα αναφοράς έναν άξονα χ χ. Στην αρχή του
ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΣΥΝΤΗΡΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ-ΔΙΑΤΗΡΗΣΗ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ
 Φυσικό μέγεθος ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΣΥΝΤΗΡΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ-ΔΙΑΤΗΡΗΣΗ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Προηγούμενες γνώσεις Η στη φύση εμφανίζεται με διάφορες μορφές, ηλεκτρική, θερμική, αιολική, δυναμική, κινητική, χημική,
Φυσικό μέγεθος ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ ΣΥΝΤΗΡΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ-ΔΙΑΤΗΡΗΣΗ ΜΗΧΑΝΙΚΗΣ ΕΝΕΡΓΕΙΑΣ Προηγούμενες γνώσεις Η στη φύση εμφανίζεται με διάφορες μορφές, ηλεκτρική, θερμική, αιολική, δυναμική, κινητική, χημική,
Έργο-Ενέργεια Ασκήσεις Έργου-Ενέργειας Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ Μεταβλητή δύναµη και κίνηση
 2.2. Ασκήσεις Έργου-Ενέργειας. 2.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 2.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
13 Γενική Μηχανική 2 Δυνάμεις Nόμοι του Newton 15/9/2014
 3 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 5/9/04 Η Φυσική της Α Λυκείου σε 8.00 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
3 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 5/9/04 Η Φυσική της Α Λυκείου σε 8.00 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό δ. Λάθος ε. Σωστό ΘΕΜΑ B B1. Σωστή απάντηση είναι η
13 Γενική Μηχανική 2 Δυνάμεις Nόμοι του Newton 15/9/2014
 13 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 15/9/014 Η Φυσική της Α Λυκείου σε 8.100 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
13 Γενική Μηχανική Δυνάμεις Nόμοι του Newton 15/9/014 Η Φυσική της Α Λυκείου σε 8.100 sec. Η έννοια της Δύναμης Οι νόμοι της κίνησης Η έννοια της δύναμης Όταν ένα αντικείμενο αλλάζει την ταχύτητά του (είτε
ΦΥΣΙΚΗ. συστήματος των σωμάτων Α και Β, τα οποίο βρίσκονται διαρκώς σε επαφή. m m 2F. 2 3m
 Α Λυκείου 4 / 4 / 9 ΦΥΣΙΚΗ ΘΕΜΑ Α. Α. γ, ΜΟΝ5 Α. β ΜΟΝ5, Α3.γ ΜΟΝ5, Α4.α ΜΟΝ5 Α5. α)σ ΜΟΝ,β) Σ ΜΟΝ, γ) Λ ΜΟΝ, δ)λ ΜΟΝ, ε) Λ ΜΟΝ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (β).μον. Εφαρμόζοντας το ο νόμο του Νεύτωνα
Α Λυκείου 4 / 4 / 9 ΦΥΣΙΚΗ ΘΕΜΑ Α. Α. γ, ΜΟΝ5 Α. β ΜΟΝ5, Α3.γ ΜΟΝ5, Α4.α ΜΟΝ5 Α5. α)σ ΜΟΝ,β) Σ ΜΟΝ, γ) Λ ΜΟΝ, δ)λ ΜΟΝ, ε) Λ ΜΟΝ ΘΕΜΑ Β Β. Σωστή απάντηση είναι η (β).μον. Εφαρμόζοντας το ο νόμο του Νεύτωνα
ΣΥΝΤΗΡΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΕΡΓΟ Το έργο, εκφράζει την ενέργεια που μεταφέρεται από ένα σώμα σ ένα άλλο ή που μετατρέπεται από μια μορφή σε μία άλλη. Για σταθερή δύναμη δίνεται από τη σχέση W F Δx Είναι μονόμετρο μέγεθος και η μονάδα
ΕΡΓΟ Το έργο, εκφράζει την ενέργεια που μεταφέρεται από ένα σώμα σ ένα άλλο ή που μετατρέπεται από μια μορφή σε μία άλλη. Για σταθερή δύναμη δίνεται από τη σχέση W F Δx Είναι μονόμετρο μέγεθος και η μονάδα
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ. u και με μέτρο. Δt = ή και απλούστερα. Δt t t. Α. Κινήσεις. Διάστημα S Μετατόπιση Δx = x2. Ταχύτητα u.
 ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Α. Κινήσεις Διάστημα S Μετατόπιση Δ = 1 Μονόμετρο μέγεθος Εξαρτάται από τη διαδρομή που ακολουθεί το κινητό και είναι το συνολικό μήκος της τροχιάς του σώματος. Είναι πάντα θετικό Διανυσματικό
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Α. Κινήσεις Διάστημα S Μετατόπιση Δ = 1 Μονόμετρο μέγεθος Εξαρτάται από τη διαδρομή που ακολουθεί το κινητό και είναι το συνολικό μήκος της τροχιάς του σώματος. Είναι πάντα θετικό Διανυσματικό
υ r 1 F r 60 F r A 1
 2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
2.2. Ασκήσεις Έργου-Ενέργειας. 4.2.1. Θεώρηµα Μεταβολής της Κινητικής Ενέργειας. ΘΜΚΕ. Ένα σώµα µάζας m=2kg ηρεµεί σε οριζόντιο επίπεδο. Σε µια στιγµή δέχεται την επίδραση οριζόντιας δύνα- µης, το µέτρο
Επιμέλεια : Γαβριήλ Κωνσταντίνος Καθηγητής Φυσικής
 ΖΗΤΗΜΑ Ο Ερωτήσεις ΣΩΣΤΟΥ ΛΑΘΟΥΣ Σωστές διατυπώσεις Η ταχύτητα εκφράζει το ρυθμό μεταβολής της θέσης του κινητού Ο ρυθμός μεταβολής της θέσης ( ταχύτητα ) του κινητού στην Ε.Ο.. είναι σταθερός Η επιτάχυνση
ΖΗΤΗΜΑ Ο Ερωτήσεις ΣΩΣΤΟΥ ΛΑΘΟΥΣ Σωστές διατυπώσεις Η ταχύτητα εκφράζει το ρυθμό μεταβολής της θέσης του κινητού Ο ρυθμός μεταβολής της θέσης ( ταχύτητα ) του κινητού στην Ε.Ο.. είναι σταθερός Η επιτάχυνση
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα. ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 03 Νόμοι κίνησης του Νεύτωνα ΦΥΣ102 1 Δύναμη είναι: Η αιτία που προκαλεί μεταβολή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ 30/9/08 ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α5 και δίπλα το γράμμα που αντιστοιχεί στη σωστή
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΕΠΙΣΚΟΠΗΣΗ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΕΓΧΕΙΡΙΔΙΟ ΔΙΔΑΚΤΕΑΣ ΥΛΗΣ ΔΗΜΗΤΡΙΟΣ ΘΕΟΔΩΡΙΔΗΣ Κεφάλαιο 1.1 Ευθύγραμμη κίνηση 1. Τι ονομάζουμε κίνηση; Τι ονομάζουμε τροχιά; Ποια είδη τροχιών γνωρίζετε; Κίνηση ενός αντικειμένου
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ
 ΕΡΓΟ - ΕΝΕΡΓΕΙΑ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ Προσοχή στα παρακάτω!!!!! 1. Σχεδιάζουμε το σώμα σε μια θέση της κίνησής του, (κατά προτίμηση τυχαία) και σημειώνουμε εκεί όλες τις δυνάμεις που ασκούνται στο σώμα.
ΕΡΓΟ - ΕΝΕΡΓΕΙΑ ΣΤΕΦΑΝΟΥ Μ. ΦΥΣΙΚΟΣ Προσοχή στα παρακάτω!!!!! 1. Σχεδιάζουμε το σώμα σε μια θέση της κίνησής του, (κατά προτίμηση τυχαία) και σημειώνουμε εκεί όλες τις δυνάμεις που ασκούνται στο σώμα.
Ερωτήσεις του τύπου Σωστό /Λάθος
 Ερωτήσεις του τύπου Σωστό /Λάθος Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις, αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δεξιά απ αυτόν το γράμμα Σ αν την κρίνετε σωστή ή το
Ερωτήσεις του τύπου Σωστό /Λάθος Οδηγία: Για να απαντήσετε στις παρακάτω ερωτήσεις, αρκεί να γράψετε στο φύλλο απαντήσεων τον αριθμό της ερώτησης και δεξιά απ αυτόν το γράμμα Σ αν την κρίνετε σωστή ή το
1 O ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΑΣ 2015 ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΨΩΜΑΘΙΑΝΟΣ ΕΜΜΑΝΟΥΗΛ
 1 O ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΑΣ 2015 ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΨΩΜΑΘΙΑΝΟΣ ΕΜΜΑΝΟΥΗΛ ΔΥΝΑΜΗ Τις δυνάμεις τις διακρίνουμε βασικά με δύο τρόπους: Συντηρητικές Μη συντηρητικές
1 O ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΑΣ 2015 ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΨΩΜΑΘΙΑΝΟΣ ΕΜΜΑΝΟΥΗΛ ΔΥΝΑΜΗ Τις δυνάμεις τις διακρίνουμε βασικά με δύο τρόπους: Συντηρητικές Μη συντηρητικές
Περι - Φυσικής. Επαναληπτικό ιαγώνισµα Φυσικής Α Τάξης Ενιαίου Λυκείου Κυριακή 17 Μάη Θέµα Α. Ενδεικτικές Λύσεις
 Επαναληπτικό ιαγώνισµα Φυσικής Α Τάξης Ενιαίου Λυκείου Κυριακή 17 Μάη 2015 Ενδεικτικές Λύσεις Θέµα Α Α.1. Η επιτάχυνση ενός κινητού εκφράζει το : (ϐ) πόσο γρήγορα µεταβάλλεται η ταχύτητά του. Α.2. Οταν
Επαναληπτικό ιαγώνισµα Φυσικής Α Τάξης Ενιαίου Λυκείου Κυριακή 17 Μάη 2015 Ενδεικτικές Λύσεις Θέµα Α Α.1. Η επιτάχυνση ενός κινητού εκφράζει το : (ϐ) πόσο γρήγορα µεταβάλλεται η ταχύτητά του. Α.2. Οταν
ΚΕΦΑΛΑΙΟ 1 Ο ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΚΙΝΗΣΕΙΣ
 Σχολικό Έτος 016-017 1 ΚΕΦΑΛΑΙΟ 1 Ο ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΚΙΝΗΣΕΙΣ Α. ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Οριζόντια βολή, ονομάζουμε την εκτόξευση ενός σώματος από ύψος h από το έδαφος, με οριζόντια ταχύτητα u o, όταν στο σώμα επιδρά
Σχολικό Έτος 016-017 1 ΚΕΦΑΛΑΙΟ 1 Ο ΚΑΜΠΥΛΟΓΡΑΜΜΕΣ ΚΙΝΗΣΕΙΣ Α. ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ Οριζόντια βολή, ονομάζουμε την εκτόξευση ενός σώματος από ύψος h από το έδαφος, με οριζόντια ταχύτητα u o, όταν στο σώμα επιδρά
ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ
 ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ Ερωτήσεις 1. Στην ομαλή κυκλική κίνηση, α. Το μέτρο της ταχύτητας διατηρείται σταθερό. β. Η ταχύτητα διατηρείται σταθερή. γ. Το διάνυσμα της ταχύτητας υ έχει την
ΕΡΩΤΗΣΕΙΣ - ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ Ερωτήσεις 1. Στην ομαλή κυκλική κίνηση, α. Το μέτρο της ταχύτητας διατηρείται σταθερό. β. Η ταχύτητα διατηρείται σταθερή. γ. Το διάνυσμα της ταχύτητας υ έχει την
ΚΕΦΑΛΑΙΟ ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΘΕΩΡΙΑ
 ΚΕΦΑΛΑΙΟ o ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΘΕΩΡΙΑ.) Τ ι γνωρίζετε για την αρχή της ανεξαρτησίας των κινήσεων; Σε πολλές περιπτώσεις ένα σώμα εκτελεί σύνθετη κίνηση, δηλαδή συμμετέχει σε περισσότερες από μία κινήσεις. Για
ΚΕΦΑΛΑΙΟ o ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΘΕΩΡΙΑ.) Τ ι γνωρίζετε για την αρχή της ανεξαρτησίας των κινήσεων; Σε πολλές περιπτώσεις ένα σώμα εκτελεί σύνθετη κίνηση, δηλαδή συμμετέχει σε περισσότερες από μία κινήσεις. Για
ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ
 ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 19//013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 υ (m/s) Σώμα μάζας m = 1Kg κινείται σε ευθύγραμμη τροχιά
ΑΤΕΙ ΠΕΙΡΑΙΑ/ ΣΤΕΦ 19//013 ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΙΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ ΣΤΗ ΦΥΣΙΚΗ ΕΞΕΤΑΣΤΗΣ: ΒΑΡΣΑΜΗΣ ΧΡΗΣΤΟΣ ΔΙΑΡΚΕΙΑ ΩΡΕΣ ΑΣΚΗΣΗ 1 υ (m/s) Σώμα μάζας m = 1Kg κινείται σε ευθύγραμμη τροχιά
Κεφάλαιο 5. Ενέργεια συστήματος
 Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
Κεφάλαιο 5 Ενέργεια συστήματος Εισαγωγή στην ενέργεια Οι νόμοι του Νεύτωνα και οι αντίστοιχες αρχές μας επιτρέπουν να λύνουμε μια ποικιλία προβλημάτων. Ωστόσο, μερικά προβλήματα, που θεωρητικά μπορούν
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ. Ηµεροµηνία: Μ. Τετάρτη 12 Απριλίου 2017 ιάρκεια Εξέτασης: 2 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Μ. Τετάρτη Απριλίου 07 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α - Α4 να γράψετε να γράψετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 07 Ε_3.Φλ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ Ηµεροµηνία: Μ. Τετάρτη Απριλίου 07 ιάρκεια Εξέτασης: ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις Α - Α4 να γράψετε να γράψετε
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/16 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ - ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 25/09/6 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις
Physics by Chris Simopoulos
 ΟΙ ΝΟΜΟΙ ΤΟΥ ΝΕΥΤΩΝΑ - ΤΡΙΒΗ 1ος νόμος του Νεύτωνα ή νόμος της αδράνειας της ύλης. «Σε κάθε σώμα στο οποίο δεν ενεργούν δυνάμεις ή αν ενεργούν έχουν συνισταμένη μηδέν δεν μεταβάλλεται η κινητική του κατάσταση.
ΟΙ ΝΟΜΟΙ ΤΟΥ ΝΕΥΤΩΝΑ - ΤΡΙΒΗ 1ος νόμος του Νεύτωνα ή νόμος της αδράνειας της ύλης. «Σε κάθε σώμα στο οποίο δεν ενεργούν δυνάμεις ή αν ενεργούν έχουν συνισταμένη μηδέν δεν μεταβάλλεται η κινητική του κατάσταση.
5. Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με τον χρόνο.
 ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 9/0/06 ΘΕΜΑ Α Στις ερωτήσεις 7 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. Mια μικρή σφαίρα προσκρούει
ομαλή κυκλική κίνηση-κρούσεις
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΦΥΣΙΚΗ Ον/μο:.. Β Λυκείου Ύλη:Οριζόντια βολή- Γεν. Παιδεία ομαλή κυκλική κίνηση-κρούσεις 8 -- Θέμα ο : ) Ένα σώμα εκτελεί ομαλή κυκλική κίνηση και η επιβατική του ακτίνα διαγράφει γωνία
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΦΥΣΙΚΗ Ον/μο:.. Β Λυκείου Ύλη:Οριζόντια βολή- Γεν. Παιδεία ομαλή κυκλική κίνηση-κρούσεις 8 -- Θέμα ο : ) Ένα σώμα εκτελεί ομαλή κυκλική κίνηση και η επιβατική του ακτίνα διαγράφει γωνία
ΘΕΜΑ Α A1. Στις ερωτήσεις 1 9 να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση, χωρίς να αιτιολογήσετε την επιλογή σας.
 ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
ΜΑΘΗΜΑ / Προσανατολισμός / ΤΑΞΗ ΑΡΙΘΜΟΣ ΦΥΛΛΟΥ ΕΡΓΑΣΙΑΣ: ΗΜΕΡΟΜΗΝΙΑ: ΤΜΗΜΑ : ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΜΑΘΗΤΗ: ΦΥΣΙΚΗ/ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ / Γ ΛΥΚΕΙΟΥ 1 Ο ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ( ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ) ΘΕΜΑ Α A1. Στις ερωτήσεις
Φυσικά μεγέθη. Φυσική α λυκείου ΕΙΣΑΓΩΓΗ. Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα. Β.
 ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ
 1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό της καθεμιάς από τις παρακάτω προτάσεις Α1 έως Α3 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Το μέτρο της
1 ο ΔΙΑΓΩΝΙΣΜΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΘΕΜΑ Α Να γράψετε στο τετράδιό σας τον αριθμό της καθεμιάς από τις παρακάτω προτάσεις Α1 έως Α3 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση: Α1. Το μέτρο της
Όπου m είναι η μάζα του σώματος και υ η ταχύτητά του.
 1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ ΙΣΧΥΣ Η ενέργεια είναι από εκείνες τις έννοιες που δύσκολα ορίζονται στη Φυσική. Ένα σώμα μπορεί να έχει, να παίρνει ή να δίνει ενέργεια. Η ίδια η ενέργεια μπορεί να μετατρέπεται από μια
ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]
![ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%] ΚΡΟΥΣΕΙΣ. γ) Δ 64 J δ) 64%]](/thumbs/65/53613594.jpg) 1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
1. Μικρή σφαίρα Σ1, μάζας 2 kg που κινείται πάνω σε λείο επίπεδο με ταχύτητα 10 m/s συγκρούεται κεντρικά και ελαστικά με ακίνητη σφαίρα Σ2 μάζας 8 kg. Να υπολογίσετε: α) τις ταχύτητες των σωμάτων μετά
Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης
 Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης 2013 ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα
Τα Θέματα που είναι με σκούρο φόντο φέτος (2014) είναι εκτός ύλης 2013 ΘΕΜΑ Α Για τις ερωτήσεις 1 έως 4 γράψτε τον αριθμό τις ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση. 1. Για ένα
Μηχανική Στερεού Ασκήσεις Εμπέδωσης
 Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
Μηχανική Στερεού Ασκήσεις Εμπέδωσης Όπου χρειάζεται, θεωρείστε δεδομένο ότι g = 10m/s 2. 1. Μία ράβδος ΟΑ, μήκους L = 0,5m, περιστρέφεται γύρω από σταθερό άξονα που περνάει από το ένα άκρο της Ο, με σταθερή
ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 2 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ
 ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 2 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ 1. Σώμα μάζας m=15/π Kg εκτελεί ομαλή κυκλική κίνηση ακτίνας R=20/π m με φορά αντίθετη απ τους δείκτες του ρολογιού. Αν το σώμα
ΦΥΣΙΚΗ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΕΡΓΑΣΙΑ 2 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΟΜΑΛΗ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ 1. Σώμα μάζας m=15/π Kg εκτελεί ομαλή κυκλική κίνηση ακτίνας R=20/π m με φορά αντίθετη απ τους δείκτες του ρολογιού. Αν το σώμα
Δ3. Ο χρόνος από τη στιγμή που η απόστασή τους ήταν d μέχρι τη στιγμή που ακουμπά η μία την άλλη. Μονάδες 6
 ΘΕΜΑ Δ 1. Δύο αμαξοστοιχίες κινούνται κατά την ίδια φορά πάνω στην ίδια γραμμή. Η προπορευόμενη έχει ταχύτητα 54km/h και η επόμενη 72km/h. Όταν βρίσκονται σε απόσταση d, οι μηχανοδηγοί αντιλαμβάνονται
ΘΕΜΑ Δ 1. Δύο αμαξοστοιχίες κινούνται κατά την ίδια φορά πάνω στην ίδια γραμμή. Η προπορευόμενη έχει ταχύτητα 54km/h και η επόμενη 72km/h. Όταν βρίσκονται σε απόσταση d, οι μηχανοδηγοί αντιλαμβάνονται
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 2017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
5 o ΔΙΑΓΩΝΙΣΜΑ ΑΠΡΙΛΙΟΣ 017: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Α1. γ. Α. δ. Α3. γ. Α4. γ. Α5. α. Λάθος β. Λάθος γ. Σωστό
Στεφάνου Μ. 1 Φυσικός
 1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ Α. ΤΟ ΠΡΟΒΛΗΜΑ Βιομηχανική επανάσταση ατμομηχανές καύσιμα μηχανές απόδοση μιας μηχανής φως θερμότητα ηλεκτρισμός κ.τ.λ Οι δυνάμεις δεν επαρκούν πάντα στη μελέτη των αλληλεπιδράσεων Ανεπαρκείς
1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ Α. ΤΟ ΠΡΟΒΛΗΜΑ Βιομηχανική επανάσταση ατμομηχανές καύσιμα μηχανές απόδοση μιας μηχανής φως θερμότητα ηλεκτρισμός κ.τ.λ Οι δυνάμεις δεν επαρκούν πάντα στη μελέτη των αλληλεπιδράσεων Ανεπαρκείς
Φυσική Α Λυκείου. Συνδυαστικά Προβλήματα Επανάληψης. m 1
 Φυσική Α Λυκείου Συνδυαστικά Θέματα Επανάληψης, 1 Φυσική Α Λυκείου Συνδυαστικά Προβλήματα Επανάληψης 1. Τα δύο σώματα του σχήματος έχουν μάζες 1=5 Kg και = Kg και σε αυτά ασκούνται οι δυνάμεις που βλέπουμε
Φυσική Α Λυκείου Συνδυαστικά Θέματα Επανάληψης, 1 Φυσική Α Λυκείου Συνδυαστικά Προβλήματα Επανάληψης 1. Τα δύο σώματα του σχήματος έχουν μάζες 1=5 Kg και = Kg και σε αυτά ασκούνται οι δυνάμεις που βλέπουμε
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 2019
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ 019 Κινηματική ΑΣΚΗΣΗ Κ.1 Η επιτάχυνση ενός σώματος που κινείται ευθύγραμμα δίνεται από τη σχέση a = (4 t ) m s. Υπολογίστε την ταχύτητα και το διάστημα που διανύει το σώμα
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 1 o ΔΙΑΓΩΝΙΣΜΑ ΝΟΕΜΒΡΙΟΣ 2018: ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Αα. γ Αα. β Α3α. β Α4α. α Αβ. γ Αβ. δ Α3β. δ Α4β. δ Α5. Σ, Λ, Σ, Λ, Σ ΘΕΜΑ Β Β. Σωστή απάντηση η γ. Ισχύει:
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ο ΔΙΑΓΩΝΙΣΜΑ ΚΡΟΥΣΕΙΣ - ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑ Α Αα. γ Αα. β Α3α. β Α4α. α Αβ. γ Αβ. δ Α3β. δ Α4β. δ Α5. Σ, Λ, Σ, Λ, Σ ΘΕΜΑ Β Β. Σωστή απάντηση η γ. Ισχύει:
ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (ΛΥΣΕΙΣ) ΗΜΕΡΟΜΗΝΙΑ: 13/10/2013
 ΜΘΗΜ / ΤΞΗ : ΦΥΣΙΚΗ ΛΥΚΕΙΟΥ ΣΕΙΡ: (ΛΥΣΕΙΣ) ΗΜΕΡΟΜΗΝΙ: 13/1/13 ΘΕΜ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΜΘΗΜ / ΤΞΗ : ΦΥΣΙΚΗ ΛΥΚΕΙΟΥ ΣΕΙΡ: (ΛΥΣΕΙΣ) ΗΜΕΡΟΜΗΝΙ: 13/1/13 ΘΕΜ Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017
 ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017 ΚΕΦΑΛΑΙΟ 1 ο ΕΙΣΑΓΩΓΗ 1.3 Τα φυσικά μεγέθη και οι μονάδες τους 1. Ποια μεγέθη ονομάζονται θεμελιώδη; Θεμελιώδη ονομάζονται τα μεγέθη τα οποία δεν ορίζονται με
ΦΥΣΙΚΗ Β ΓΥΜΝΑΣΙΟΥ ΕΠΑΝΑΛΗΨΗ ΘΕΩΡΙΑΣ 2017 ΚΕΦΑΛΑΙΟ 1 ο ΕΙΣΑΓΩΓΗ 1.3 Τα φυσικά μεγέθη και οι μονάδες τους 1. Ποια μεγέθη ονομάζονται θεμελιώδη; Θεμελιώδη ονομάζονται τα μεγέθη τα οποία δεν ορίζονται με
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ μονόμετρα. διανυσματικά Η μάζα ενός σώματος αποτελεί το μέτρο της αδράνειάς του, πυκνότητα ενός υλικού d = m/v
 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Υπάρχουν φυσικά μεγέθη που ορίζονται πλήρως, όταν δοθεί η αριθμητική τιμή τους και λέγονται μονόμετρα.. Μονόμετρα μεγέθη είναι ο χρόνος, η μάζα, η θερμοκρασία, η πυκνότητα, η ενέργεια,
ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Υπάρχουν φυσικά μεγέθη που ορίζονται πλήρως, όταν δοθεί η αριθμητική τιμή τους και λέγονται μονόμετρα.. Μονόμετρα μεγέθη είναι ο χρόνος, η μάζα, η θερμοκρασία, η πυκνότητα, η ενέργεια,
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Α ΦΑΣΗ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 17 Ε_3.ΦλΘ(ε) ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΜΑ Α Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 17 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 17 Ε_3.ΦλΘ(ε) ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΜΑ Α Ηµεροµηνία: Πέµπτη 5 Ιανουαρίου 17 ιάρκεια Εξέτασης: ώρες ΕΚΦΩΝΗΣΕΙΣ Στις ηµιτελείς προτάσεις
Στεφάνου Μ. 1 Φυσικός
 1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ Α. ΤΟ ΠΡΟΒΛΗΜΑ Βιομηχανική επανάσταση ατμομηχανές καύσιμα μηχανές απόδοση μιας μηχανής φως θερμότητα ηλεκτρισμός κ.τ.λ Οι δυνάμεις δεν επαρκούν πάντα στη μελέτη των αλληλεπιδράσεων Ανεπαρκείς
1 ΕΡΓΟ ΕΝΕΡΓΕΙΑ Α. ΤΟ ΠΡΟΒΛΗΜΑ Βιομηχανική επανάσταση ατμομηχανές καύσιμα μηχανές απόδοση μιας μηχανής φως θερμότητα ηλεκτρισμός κ.τ.λ Οι δυνάμεις δεν επαρκούν πάντα στη μελέτη των αλληλεπιδράσεων Ανεπαρκείς
kg(χιλιόγραμμο) s(δευτερόλεπτο) Ένταση ηλεκτρικού πεδίου Α(Αμπέρ) Ένταση φωτεινής πηγής cd (καντέλα) Ποσότητα χημικής ουσίας mole(μόλ)
 ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
[50m/s, 2m/s, 1%, -10kgm/s, 1000N]
![[50m/s, 2m/s, 1%, -10kgm/s, 1000N] [50m/s, 2m/s, 1%, -10kgm/s, 1000N]](/thumbs/64/51024975.jpg) ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΚΕΦΑΛΑΙΟ 5 ο - ΜΕΡΟΣ Α : ΚΡΟΥΣΕΙΣ ΕΝΟΤΗΤΑ 1: ΚΡΟΥΣΕΙΣ 1. Σώμα ηρεμεί σε οριζόντιο επίπεδο. Βλήμα κινούμενο οριζόντια με ταχύτητα μέτρου και το με ταχύτητα, διαπερνά το σώμα χάνοντας % της κινητικής του
ΕΝΟΤΗΤΑ 1: ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β
 ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Tο γιο-γιο του σχήματος έχει ακτίνα R και αρχικά είναι ακίνητο. Την t=0 αφήνουμε ελεύθερο το δίσκο
ΚΕΦΑΛΑΙΟ 4 ο : ΜΗΧΑΝΙΚΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΕΝΟΤΗΤΑ : ΚΙΝΗΣΗ ΣΤΕΡΕΟΥ ΣΩΜΑΤΟΣ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Β Ερώτηση. Tο γιο-γιο του σχήματος έχει ακτίνα R και αρχικά είναι ακίνητο. Την t=0 αφήνουμε ελεύθερο το δίσκο
ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ Ο.Π Β Λ Γ Λ ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ
 ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ Ο.Π Β Λ Γ Λ 5//08 ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΑΠΑΝΤΗΣΕΙΣ ΦΥΣΙΚΗ Ο.Π Β Λ Γ Λ 5//08 ΧΡΗΣΤΟΣ ΚΑΡΑΒΟΚΥΡΟΣ ΙΩΑΝΝΗΣ ΤΖΑΓΚΑΡΑΚΗΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α-Α4 και δίπλα το γράμμα που αντιστοιχεί
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ
 ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ Συγγραμμικές δυνάμεις 1 ος -2 ος νόμος του Νεύτωνα 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λανθασμένες; α. Μια δύναμη μπορεί να προκαλέσει αλλαγή στην κινητική
ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ Ο.Π / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 24/09/2017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ ΕΤΟΥΣ 017-018 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΟΠ / Γ ΛΥΚΕΙΟΥ (ΘΕΡΙΝΑ) ΑΠΑΝΤΗΣΕΙΣ ΗΜΕΡΟΜΗΝΙΑ: 4/09/017 ΕΠΙΜΕΛΕΙΑ ΔΙΑΓΩΝΙΣΜΑΤΟΣ: ΑΡΧΩΝ ΜΑΡΚΟΣ ΘΕΜΑ Α Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς
γραπτή εξέταση στο μάθημα
 3η εξεταστική περίοδος από 9/03/5 έως 9/04/5 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητής: Θ Ε Μ Α Α Στις ερωτήσεις Α-Α4 να επιλέξετε τη σωστή απάντηση.
3η εξεταστική περίοδος από 9/03/5 έως 9/04/5 γραπτή εξέταση στο μάθημα ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ Τάξη: Α Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητής: Θ Ε Μ Α Α Στις ερωτήσεις Α-Α4 να επιλέξετε τη σωστή απάντηση.
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ. Ύλη: Ορμή
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. B Λυκείου Ύλη: Ορμή 13-11-2016 Θέμα 1 ο : 1) Κατά την πλαστική κρούση δύο σωμάτων: α) η κινητική ενέργεια και η ορμή του συστήματος των σωμάτων παραμένουν σταθερές β) η κινητική
ΔΙΑΓΩΝΙΣΜΑ ΣΤΗ ΦΥΣΙΚΗ Ον/μο:.. B Λυκείου Ύλη: Ορμή 13-11-2016 Θέμα 1 ο : 1) Κατά την πλαστική κρούση δύο σωμάτων: α) η κινητική ενέργεια και η ορμή του συστήματος των σωμάτων παραμένουν σταθερές β) η κινητική
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΑΙ ΤΗΝ ΟΡΜΗ 30/11/2014
 ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΑΙ ΤΗΝ ΟΡΜΗ 30//204 Ζήτημα 0 Να επιλεγεί η σωστή πρόταση ) Σώμα κινείται σε περιφέρεια κύκλου και εκτελεί ομαλή κυκλική κίνηση.τότε: α) Το μέτρο
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΣΤΗΝ ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΚΑΙ ΤΗΝ ΟΡΜΗ 30//204 Ζήτημα 0 Να επιλεγεί η σωστή πρόταση ) Σώμα κινείται σε περιφέρεια κύκλου και εκτελεί ομαλή κυκλική κίνηση.τότε: α) Το μέτρο
Εφαρμόζουμε την αρχή διατήρησης της ορμής (θετική φορά προς τα δεξιά) :
 ) Η συνολική μάζα του αρχικού σώματος είναι m =,kg. Επομένως : m = m + m, = m + 0, m = kg Οι εσωτερικές δυνάμεις που εμφανίζονται κατά την έκρηξη είναι πολύ μεγαλύτερες των εξωτερικών δυνάμεων επομένως
) Η συνολική μάζα του αρχικού σώματος είναι m =,kg. Επομένως : m = m + m, = m + 0, m = kg Οι εσωτερικές δυνάμεις που εμφανίζονται κατά την έκρηξη είναι πολύ μεγαλύτερες των εξωτερικών δυνάμεων επομένως
ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ ΠΡΟΣΠΑΘΕΙΑ ΣΑΣ ΚΙ 2014
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://wwwstudy4examsgr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΑΣΚΗΣΗ 5.1 Το διάνυσμα θέσης ενός σώματος μάζας m=0,5kgr δίνεται από τη σχέση: 3 j οπότε το μέτρο της ταχύτητας θα είναι:
 ΑΣΚΗΣΗ. Το διάνυσμα θέσης ενός σώματος μάζας =,k δίνεται από τη σχέση: 6. α Βρείτε την θέση και το μέτρο της ταχύτητας του κινητού την χρονική στιγμή. β Τι είδους κίνηση κάνει το κινητό σε κάθε άξονα;
ΑΣΚΗΣΗ. Το διάνυσμα θέσης ενός σώματος μάζας =,k δίνεται από τη σχέση: 6. α Βρείτε την θέση και το μέτρο της ταχύτητας του κινητού την χρονική στιγμή. β Τι είδους κίνηση κάνει το κινητό σε κάθε άξονα;
Διαγώνισμα Φυσικής Α Λυκείου
 Διαγώνισμα Φυσικής Α Λυκείου Δυναμιική.. Θέμα 1 ο 1. Συμπληρώστε την παρακάτω πρόταση. H αρχή της αδράνειας λέει ότι όλα ανεξαιρέτως τα σώματα εκδηλώνουν μια τάση να διατηρούν την... 2. Ένα αυτοκίνητο
Διαγώνισμα Φυσικής Α Λυκείου Δυναμιική.. Θέμα 1 ο 1. Συμπληρώστε την παρακάτω πρόταση. H αρχή της αδράνειας λέει ότι όλα ανεξαιρέτως τα σώματα εκδηλώνουν μια τάση να διατηρούν την... 2. Ένα αυτοκίνητο
Κ Ε Φ Α Λ Α Ι Ο 1ο Ε Υ Θ Υ Γ Ρ Α Μ Μ Η Κ Ι Ν Η Σ Η
 1 Σκοπός Να αποκτήσουν οι μαθητές τη δυνατότητα να απαντούν σε ερωτήματα που εμφανίζονται στην καθημερινή μας ζωή και έχουν σχέση με την ταχύτητα, την επιτάχυνση, τη θέση ή το χρόνο κίνησης ενός κινητού.
1 Σκοπός Να αποκτήσουν οι μαθητές τη δυνατότητα να απαντούν σε ερωτήματα που εμφανίζονται στην καθημερινή μας ζωή και έχουν σχέση με την ταχύτητα, την επιτάχυνση, τη θέση ή το χρόνο κίνησης ενός κινητού.
Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση
 Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση α) Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση λίγο πριν και αμέσως μετά το κόψιμο του νήματος, Η ομογενής και ισοπαχής ράβδος
Επαναληπτική άσκηση: Περιστροφή Κρούση - Κύλιση με ολίσθηση α) Το μέτρο της δύναμης που δέχεται η ράβδος από την άρθρωση λίγο πριν και αμέσως μετά το κόψιμο του νήματος, Η ομογενής και ισοπαχής ράβδος
2.1. Κυκλική κίνηση Κυκλική κίνηση. Ομάδα Β.
 2.1.. 2.1.. Ομάδα Β. 2.1.Σχέσεις μεταξύ γραμμικών και γωνιακών μεγεθών στην ΟΚΚ. Κινητό κινείται σε περιφέρεια κύκλου ακτίνας 40m με ταχύτητα μέτρου 4m/s. i) Ποια είναι η περίοδος και ποια η συχνότητά
2.1.. 2.1.. Ομάδα Β. 2.1.Σχέσεις μεταξύ γραμμικών και γωνιακών μεγεθών στην ΟΚΚ. Κινητό κινείται σε περιφέρεια κύκλου ακτίνας 40m με ταχύτητα μέτρου 4m/s. i) Ποια είναι η περίοδος και ποια η συχνότητά
ΛΥΚΕΙΟ ΑΓΙΟΥ ΣΠΥΡΙΔΩΝΑ ΣΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΛΥΚΕΙΟ ΑΓΙΟΥ ΠΥΡΙΔΩΝΑ ΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕ ΠΡΟΑΓΩΓΙΚΕ ΕΞΕΤΑΕΙ ΦΥΙΚΗ ΚΑΤΕΥΘΥΝΗ Β ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 31-05-2012 ΔΙΑΡΚΕΙΑ: 07.45 10.15 Οδηγίες 1. Το εξεταστικό δοκίμιο αποτελείται από 9 σελίδες.
ΛΥΚΕΙΟ ΑΓΙΟΥ ΠΥΡΙΔΩΝΑ ΧΟΛΙΚΗ ΧΡΟΝΙΑ 2011-2012 ΓΡΑΠΤΕ ΠΡΟΑΓΩΓΙΚΕ ΕΞΕΤΑΕΙ ΦΥΙΚΗ ΚΑΤΕΥΘΥΝΗ Β ΛΥΚΕΙΟΥ ΗΜΕΡΟΜΗΝΙΑ: 31-05-2012 ΔΙΑΡΚΕΙΑ: 07.45 10.15 Οδηγίες 1. Το εξεταστικό δοκίμιο αποτελείται από 9 σελίδες.
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση.
 ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΕΙΣΑΓΩΓΙΚΑ ΣΧΟΛΙΑ Η δύναμη που ασκείται σε ένα σώμα προκαλεί μεταβολή της ταχύτητάς του δηλαδή επιτάχυνση. Η δύναμη είναι ένα διανυσματικό μέγεθος. Όταν κατά την κίνηση ενός σώματος η δύναμη είναι μηδενική
ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΦΥΣΙΚΗ Α ΛΥΚΕΙΟΥ ΦΡΟΝΤΙΣΤΗΡΙΟ ΕΠΙΛΟΓΗ
 ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζουμε κίνηση ενός κινητού; 2. Τι ονομάζουμε τροχιά ενός κινητού; 3. Τι ονομάζουμε υλικό σημείο; 4. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Τι ονομάζουμε κίνηση ενός κινητού; 2. Τι ονομάζουμε τροχιά ενός κινητού; 3. Τι ονομάζουμε υλικό σημείο; 4. Ποια μεγέθη ονομάζονται μονόμετρα και ποια διανυσματικά;
γραπτή εξέταση στη ΦΥΣΙΚΗ B κατεύθυνσης
 η εξεταστική περίοδος από 4/0/5 έως 08//5 γραπτή εξέταση στη ΦΥΣΙΚΗ B κατεύθυνσης Τάξη: Β Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α A Στις ερωτήσεις Α-Α4 να επιλέξετε τη σωστή απάντηση.
η εξεταστική περίοδος από 4/0/5 έως 08//5 γραπτή εξέταση στη ΦΥΣΙΚΗ B κατεύθυνσης Τάξη: Β Λυκείου Τμήμα: Βαθμός: Ονοματεπώνυμο: Καθηγητές: Θ Ε Μ Α A Στις ερωτήσεις Α-Α4 να επιλέξετε τη σωστή απάντηση.
β) Ε Φ Α Ρ Μ Ο Γ Η 1 2 α)
 Ε ΦΑΡΜΟΓΗ 1 Ένα σώμα μάζας m 800g ισορροπεί ακίνητο πάνω σε λείο οριζόντιο δάπεδο, συνδεδεμένο στο ελεύθερο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς K 00N / m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο
Ε ΦΑΡΜΟΓΗ 1 Ένα σώμα μάζας m 800g ισορροπεί ακίνητο πάνω σε λείο οριζόντιο δάπεδο, συνδεδεμένο στο ελεύθερο άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς K 00N / m. Το άλλο άκρο του ελατηρίου είναι στερεωμένο
Για τις παρακάτω 3 ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
 Επαναληπτικά Θέµατα ΟΕΦΕ 007 Α ΛΥΚΕΙΟΥ Θέµα ο ΦΥΣΙΚΗ Για τις παρακάτω 3 ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε ένα σώµα
Επαναληπτικά Θέµατα ΟΕΦΕ 007 Α ΛΥΚΕΙΟΥ Θέµα ο ΦΥΣΙΚΗ Για τις παρακάτω 3 ερωτήσεις, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.. Σε ένα σώµα
ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ ΓΙΑ ΤΗ ΦΥΣΙΚΗ ΤΗΣ Γ ΛΥΚΕΙΟΥ
 Τίποτα στη ζωή δεν είναι για να το φοβόμαστε, αλλά για να το κατανοήσουμε. Marie Curie Υλικό σημείο ή σημειακό αντικείμενο: Σώμα του οποίου οι διαστάσεις θεωρούνται αμελητέες. Μονόμετρο μέγεθος: Ονομάζεται
Τίποτα στη ζωή δεν είναι για να το φοβόμαστε, αλλά για να το κατανοήσουμε. Marie Curie Υλικό σημείο ή σημειακό αντικείμενο: Σώμα του οποίου οι διαστάσεις θεωρούνται αμελητέες. Μονόμετρο μέγεθος: Ονομάζεται
