ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ
|
|
|
- Άδωνις Παπακώστας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ A u B Μέτρο Διεύθυνση Κατεύθυνση (φορά) Σημείο Εφαρμογής Διανυσματικά Μεγέθη : μετάθεση, ταχύτητα, επιτάχυνση, δύναμη Μονόμετρα Μεγέθη : χρόνος, μάζα, όγκος, θερμοκρασία, πίεση, πυκνότητα
2 u i x u k O j u u x Κατευθύνοντα συνημίτονα: α = συνθ, α = συνθ, α = συνθ συνιστώσες : u, u, u Παράσταση διανύσματος α) Μέτρο : u, (u), u και κατευθύνοντα συνημίτονα β) συνιστώσες : u, u, u u=u(u,u,u ), u=u i, i,, x u i u j u k u i, j, k u u u u, μοναδιαία διανύσματα u u u u u u u,, u u u
3 . Πράξεις Διανυσμάτων. Πρόσθεση Διανυσμάτων x i j k i j k Διανυσματικό (γεωμετρικό) άθροισμα : a a a x i j k u Αντίθετο του : (ίδιο μέτρο, αντίθετη φορά)
4 . Αφαίρεση διανυσμάτων Πρόσθεση του αντιθέτου ( ) γ =α -β, γ =α -β, γ =α -β Ίσα διανύσματα; 4
5 . Πολλαπλασιασμός διανυσμάτων α) Εσωτερικό Γινόμενο (dot product) (μονόμετρο μέγεθος) a(a,a,a ), b(b, b, b ) a b ab a b a b a b a b a a? W F s us ES 5
6 β) Εξωτερικό Γινόμενο (vector/cross/outer product) (διανυσματικό μέγεθος) a( a, a, a ), b ( b, b, b ) (,, ) (,, ) i j k M F s S B h r i( ) j( ) k( )? 6
7 γ) Δυαδικό γινόμενο (τανυστικό γινόμενο-dyadic product) a a e ia ja ka, b b e ib jb kb i i j j i j a ab ab ab a b a b b b a b a b a b a b a ab ab ab ia ib ia jb ia kb ja ib ja jb ja kb ka ib ka jb ka kb 9 συσιστώσες => μέγεθος μονόμετρο; διανυσματικό; ΔΥΑΔΙΚΗ ΟΝΤΟΤΗΤΑ => Τανυστής β Τάξης 7
8 Εφαρμογή. Δίνονται τα δύο διανύσματα a i j k b i j k Να βρεθούν το γεωμετρικό τους άθροισμα, η γεωμετρική τους διαφορά, το εσωτερικό, εξωτερικό και δυαδικό τους γινόμενο a b i j k a b i 5 j 4k a b 6 7 i j k axb 7i 7 j 7k a b ii 4ij 6ik ji 6 jj 9 jk ki kj kk 8
9 Λογισμός Διανυσμάτων - Μονόμετρες συναρτήσεις (π.χ. χρόνος, πυκνότητα, θερμοκρασία) (μεταβολές μονόμετρων ποσοτήτων στο χώρο ή το χρόνο) - Διανυσματικές συναρτήσεις (π.χ. ένταση πεδίου βαρύτητας) (μεταβολές διανυσματικών ποσοτήτων στο χώρο ή το χρόνο). Διαφορικός Λογισμός Διανυσμάτων παραγώγιση διανυσματικής ποσότητας ως προς μονόμετρη ποσότητα du du du i j k dt dt dt dt du 9
10 ΤΕΛΕΣΤΕΣ Σύμβολα μπροστά από διανυσματικές ή μονόμετρες συναρτήσεις που υποδεικνύουν πραγματοποίηση πράξεων παραγώγισης α) Διανυσματικός τελεστής ανάδελτα (nabla), (ΔΙΑΝΥΣΜΑ) i x j k x x Εφαρμόζεται σε μονόμετρες και διανυσματικές συναρτήσεις 0
11 β) Τελεστής βαθμίδα, grad (ΔΙΑΝΥΣΜΑ) U= g gradu i U x j U k U x x U ds U= U= U=μονόμετρη ποσότητα grad U = U Η βαθμίδα μεταβολής του υψομέτρου σε ένα σημείο μιας πλαγιάς είναι διάνυσμα κάθετο στην ισοϋψή στο σημείο αυτό και περιγράφει την τοπογραφική κλίση στο σημείο αυτό.
12 γ) Τελεστής απόκλιση, div (ΜΟΝΟΜΕΤΡΗ) u divu x u x u x Εφαρμόζεται σε διάνυσμα προκύπτει μονόμετρη divu u i j k iu ju ku x x x u u u x x x u 0 Σωληνοειδέ ς διάνυσμα
13 Αν θεωρήσουμε έναν ιδεατό χώρο μέσα στον οποίο πραγματοποιείται ροή ρευστού. Έστω ότι η F ( x, y, z ) είναι μια διανυσματική συνάρτηση που περιγράφει την ταχύτητα του ρευστού στη θέση ( x, y, z ) του χώρου αυτού. Απόκλιση της είναι η μεταβολή της στο χώρο. F Αν το υγρό κινείται προς τα έξω (π.χ. υπάρχουν πηγές μέσα στον ιδεατό χώρο που μελετούμε) τότε η τιμή d iv F είναι θετική και περιγράφει ποσοτικά αυτήν την διόγκωση (κίνηση προς τα έξω, εκκροή από τον ιδεατό χώρο). Αντίθετα, αν η κίνηση του υγρού είναι προς τα μέσα (π.χ. υπάρχει συνεχής τροφοδοσία από έξω προς τα μέσα και κατανάλωση ρευστού στο εσωτερικό του ιδεατού χώρου) τότε η τιμή είναι αρνητική. d iv F
14 δ) Τελεστής περιστροφή, rot ή curl (ΔΙΑΝΥΣΜΑ) i j k rotu curlu x x x u u u u u u u u u i j k x x x x x x Αν το διάνυσμα περιγράφει την ταχύτητα κίνησης ενός υγρού σε ένα ιδεατό χώρο, η διανυσματική συνάρτηση c u r l u περιγράφει το στροβιλισμό του υγρού μέσα στο χώρο αυτό u u 0 Α σ τ ρ ό β ιλ ο δ ιά ν υ σ μ α 4
15 ε) Τελεστής λαπλασιανή, (ΜΟΝΟΜΕΤΡΗ ΔΙΑΝΥΣΜΑ) U U x u i u j U x u U x k u Εφαρμογή σε μονόμετρη (U) Εφαρμογή σε διανυσματική u Φυσική σημασία: η εφαρμογή της σε μια ποσότητα δείχνει τη μεταβολή της τιμής της ποσότητας από ένα σημείο σε ένα γειτονικό του. U = U - U 0, ό U 0 = τιμή ποσότητας στο σημείο 0 U =»» στη γειτονιά του σημείου 0 5
16 Εφαρμογή. Δίνεται η μονόμετρη συνάρτηση: U = x + x - x Να βρεθούν η βαθμίδα (grad) και η λαπλασιανή της ( ) στο σημείο (0,, -) U U U grad U U i j k x x x i(x ) j(4x ) k( 6x ) 4 j 6k U U U U x x x Σε κάθε σημείο 6
17 Εφαρμογή.4 Δίνεται η διανυσματική συνάρτηση u(x,x x x,-x x x Να βρεθούν η απόκλιση (div), η περιστροφή (rot ή curl) και η λαπλασιανή της ( ) στο σημείο (, -, -) u u u divu xx xx 5 x x x u u u u u u x x x x x x rot u curl u u i j k u i u j u k u i( x x x x x ) j(x x x ) k(x x ) 8 j 4k u u u u u u u u u i j k x x x x x x x x x ) 0 0 k( x x x x ) x (x x )k 0k 7
18 Άσκηση. α) μέτρα, κατευθύνοντα συνημίτονα, γωνίες με τους άξονες β) άθροισμα, διαφορά γ) εσωτερικό, εξωτερικό, δυαδικό γινόμενο a(,, ), b(, 4,) a , 6.7, b , 9.5, a (,, ) b(, 4,) (,7,0), a b (i j k) ( i 4 j k) i 7j a (,, ) b(, 4,) (,, ), a b (i j k) ( i 4 j k) i j k ab ( ) 4 ( ) 9 i j k a b 7i j k 4 a b ii 8ij ik ji jj jk ki 4kj kk 8
19 Άσκηση. Δίνεται μονόμετρη συνάρτηση Φ = x x + x x - x x x. Να βρεθούν η βαθμίδα (grad) και η λαπλασιανή της ( ) στο σημείο (,, 0) grad j k x x x (x x x x ) (x x x x x ) j (x x x )k 4 j 6k x x x x 6x x 4 9
20 Άσκηση. Δίνεται διανυσματική συνάρτηση u ix x jx x x kx x Να βρεθούν η απόκλιση (div), η περιστροφή (rot ή curl) και η λαπλασιανή της ( ) στο σημείο (,, -) u u u divu x xx xx x x x i j k x x xx x xx x x xx x xx rot u i j k x x x x x x x x x x x x x x x x i(x x x ) j(0) k(x x x x ) k u i u j u k u u u u u u u u u u i j k x x x x x x x x x i x kx i k 0
21 . Ολοκληρωτικός Λογισμός Διανυσμάτων α) Απλό Ολοκλήρωμα Διανύσματος ds A u B B B W u dx ) u d s u dx u dx A A ( u, u, u συνιστώσες του διανύσματος u dx, dx, dx συνιστώσες του διανύσματος ds π.χ. έργο
22 β) Διπλό Ολοκλήρωμα Διανύσματος S ds u d S u d S u d S S u u d S ) εσωτερικό γινόμενο S ( u, u, u συνιστώσες του διανύσματος u ds, ds, ds συνιστώσες του διανύσματος ds u ds u ds u. ds.cos90 0 u π.χ. αν η ένταση ενός ηλεκτρικού/μαγνητικού πεδίου το διπλό ολοκλήρωμα είναι η ηλεκτρική/μαγνητική ροή του πεδίου δια μέσου της επιφάνειας S
23 γ) Τριπλό Ολοκλήρωμα Διανύσματος dv i u dv j u dv k u u V V V V dv u dv V V Μέση τιμή του διανύσματος στο χώρο του όγκου V
24 Θεώρημα της απόκλισης (Θεώρημα Gauss) V u d V u d S S Το τριπλό ολοκλήρωμα της απόκλισης διανυσματικής συνάρτησης σε όγκο V ισοδυναμεί με Το διπλό ολοκλήρωμα της διανυσματικής συνάρτησης στην επιφάνεια S που περιβάλλει τον V π.χ. Ο ρυθμός απόκλισης υγρού από όγκο V ιδεατού δοχείου = ρυθμό εκροής του από την επιφάνεια S που περιβάλλει τον όγκο (δοχείο) 4
25 Θεώρημα του Stokes S u d S u d s Το διπλό ολοκλήρωμα της περιστροφής διανύσματικής συνάρτησης σε επιφάνεια S ισοδυναμεί με Το απλό κλειστό ολοκλήρωμα της διανύσματικής συνάρτησης στη γραμμή s που περιβάλλει την S π.χ. Στροβιλισμός υγρού σε επιφάνεια S ισοδυναμεί με το μέσο στροβιλισμό υγρού κατά μήκος της γραμμής, s, που περιβάλλει την επιφάνεια S. 5
26 ΕΦΑΡΜΟΓΗ.5 Ευθύγραμμος ηλεκτρικός αγωγός ο οποίος διαρρέεται από ρεύμα έντασης i δημιουργεί μαγνητικό πεδίο έντασης Η (σε απόσταση r από τον αγωγό) η οποία εφάπτεται κύκλου ακτίνας r και έχει μέτρο ίσο με ki/r, όπου k σταθερά. Να βρεθεί το απλό ολοκλήρωμα της έντασης κατά μήκος περιφέρειας κύκλου που έχει το κέντρο του στον αγωγό και ακτίνα R. Έστω στοιχειώδες μήκος ds πάνω στον κύκλο. Τότε : ki ki ki H ds ds cos 0 ds R ki R R R (εσωτερικό γινόμενο) => H. ds. cos(0)=h. ds R H 6
27 ΕΦΑΡΜΟΓΗ.6 Η ένταση, E, του ηλεκτρικού πεδίου σε σημείο που απέχει απόσταση r από ηλεκτρικό φορτίο q έχει τη διεύθυνση της ευθείας που ενώνει το φορτίο με το σημείο () και μέτρο που δίνεται από τη σχέση E=kq/r. Να βρεθεί η ηλεκτρική ροή που περνάει από την επιφάνεια σφαίρας που έχει κέντρο το φορτίο q και ακτίνα R. () => διεύθυνση της Ε // διεύθυνση ακτίνων R => Ηλεκτρική ροή: E ds E ds cos 0 E ds όπου ds στοιχείο της επιφάνειας της σφαίρας. kq kq kq E ds ds ds 4 R 4 kq R R R S S S Άρα η συνολική ροή είναι ανεξάρτητη της επιφάνειας. 7
28 Τανυστές Τανυστής n τάξης στο χώρο των r διαστάσεων: r n συνιστώσες, κατά την αλλαγή των αξόνων υπακούει σε ορισμένο μετασχηματισμό τανυστές 0 ής τάξης, r 0 = 0 = μονόμετρα μεγέθη τανυστές ης τάξης, r = = διανυσματικά μεγέθη τανυστές ης τάξης, r = =9 τάση, ανηγμένη παραμόρφωση S ij, i,j=,, 8
29 Ιδιότητες Τανυστών Δεύτερης Τάξης Α) ΣΥΜΜΕΤΡΙΚΟΣ S ij = Sji S = S, S = S, S = S π.χ Β) ΑΝΤΙΣΥΜΜΕΤΡΙΚΟΣ (ΠΕΡΙΣΤΡΟΦΕΑΣ/ΣΤΡΟΦΕΑΣ) S = -S, S = -S, S = -S S ij = -Sji π.χ. 0 4 S = S = S = Γ) ΙΣΟΤΡΟΠΟΣ S = S = S, S = S = S = S = S = S π.χ. Στους ισότροπους τανυστές οι άξονες θεωρούνται ισοδύναμοι. Εναλλαγή των αξόνων δεν επηρεάζει τις τιμές των συνιστωσών 9
30 Ίχνος τανυστή : S + S + S Τανυστής = Συμμετρικός (με ίδιο ίχνος) + Αντισυμμετρικός () Τανυστής = Ισότροπος (με ίδιο ίχνος) + Τανυστής (με μηδενικό ίχνος) Συμμετρικός τανυστής = Ισοτροπέας + Εκτροπέας () () Λ () => Τανυστής = Ισοτροπέας + Εκτροπέας + Αντισυμμετρικός Τανυστής Kroneker, δ ij ij για i=j δ ij =, για ij δ ij =
31 Εφαρμογή Δίνεται ο τανυστής ης τάξης : Sij Να αναλυθεί σε άθροισμα ενός συμμετρικού και ενός αντισυμμετρικού τανυστή y y ij S y y y y 8 0 x x ij S x 0 x x x 0 x y 8 () () () y 6 x y 5 () () x y x 4 () (5) (6) y y x 5 (4) (6) x 9 y x (5) () (4) y 0 x y 7 (6) () x 5
32 Εφαρμογή.8 Να αναλυθεί σε άθροισμα ενός ισοτροπέα και ενός εκτροπέα 6 0 Sij Ισότροπος ομόλογα στοιχεία ίσα, ίδιο ίχνος με αρχικό Στοιχεία διαγωνίου = (++8)/ = Sij Sij Sij Sij Sij Sij Άρα:
33 Άσκηση.4 Δίνεται διανυσματική συνάρτηση Να αποδειχθεί ότι είναι αστρόβιλη u = i(x-)- jx (rot u = 0) και u ds = 0 rot u i j k u x x x u u u u u u u u u x x x x x x i j k i(0) j(0) k(0) 0 Θεώρημα Stokes: u d s ( u ) d S 0 S 0
34 Άσκηση.5 Δίνεται διανυσματική συνάρτηση u = i(x -)- jx Να αποδειχθεί ότι είναι σωληνοειδής (div u=0) και u d S = 0 S u u u x x x d iv u u 0 => Σωληνοειδής Θεώρημα της απόκλισης (θεώρημα GAUSS) u d S ( u ) d V 0 S V 0 4
35 Άσκηση.6 Να υπολογιστεί το απλό ολοκλήρωμα του διανύσματος u ix jx κατά μήκος της διαδρομής (0,0) (,0) (,) (0,) (0,0) (0,) (,) (c,d) (c,d) (c,d) (c,d) x x (a,b) (a,b) (a,b) (a,b) A u ds x.dx x.dx (0, 0) (, 0) A (0,0) (,0) (, 0) (, ) A (, ) (0, ) A (0, ) (0, 0) A4 9 9 A A A A A4 0 5
36 Άσκηση.8 Να βρεθούν τα ίχνη ενός α) στροφέα, β) εκτροπέα, γ) ισοτροπέα με ένα διαγώνιο στοιχείο -4 α) Στροφέας (αντισυμμετρικός): S ij = S ji S = S = S = 0 ίχνος = 0 β) Συμμετρικός = ισοτροπέας + εκτροπέας Ισότροπος τανυστής με ίχνος ίσο με του αρχικού και στοιχεία διαγωνίου ίσα Άρα, ίχνος εκτροπέα = 0 γ) Ισοτροπέας στοιχεία διαγωνίου ίσα, κ=-4 ίχνος =.(-4) = - 6
ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 1: Στοιχεία Διανυσματικού Λογισμού Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 1: Στοιχεία Διανυσματικού Λογισμού Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας,
ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ. Μερικές βασικές έννοιες διανυσματικού λογισμού
 ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Μερικές βασικές έννοιες διανυσματικού λογισμού ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 1. Oρισμοί Διάνυσμα ονομάζεται η μαθηματική οντότητα που έχει διεύθυνση φορά και μέτρο.
ΕΜΒΟΛΙΜΗ ΠΑΡΑΔΟΣΗ ΜΑΘΗΜΑΤΙΚΩΝ Μερικές βασικές έννοιες διανυσματικού λογισμού ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΛΟΓΙΣΜΟΥ 1. Oρισμοί Διάνυσμα ονομάζεται η μαθηματική οντότητα που έχει διεύθυνση φορά και μέτρο.
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 3 Μαρτίου 2019 1 Τανυστής Παραμόρφωσης Συνοδεύον σύστημα ονομάζεται το σύστημα συντεταγμένων ξ i το οποίο μεταβάλλεται
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 3 Μαρτίου 2019 1 Τανυστής Παραμόρφωσης Συνοδεύον σύστημα ονομάζεται το σύστημα συντεταγμένων ξ i το οποίο μεταβάλλεται
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΔΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ
 ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΣΗΜΕΙΩΣΕΙΣ ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ Σκοπός Σκοπός του κεφαλαίου είναι η ανασκόπηση βασικών μαθηματικών εργαλείων που αφορούν τη μελέτη διανυσματικών συναρτήσεων [π.χ. E(, t) ]. Τα εργαλεία αυτά είναι
ΔΥΝΑΜΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΡΕΥΣΤΩΝ
 ΔΥΝΑΜΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΡΕΥΣΤΩΝ Α. Σακελλάριος 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών Εισαγωγή Φύση και μορφή δυνάμεων/ ρυθμός παραμόρφωσης Σωματικές δυνάμεις: δυνάμεις σε όγκο ελέγχου που είναι πλήρης
ΔΥΝΑΜΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΡΕΥΣΤΩΝ Α. Σακελλάριος 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών Εισαγωγή Φύση και μορφή δυνάμεων/ ρυθμός παραμόρφωσης Σωματικές δυνάμεις: δυνάμεις σε όγκο ελέγχου που είναι πλήρης
website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Μαάιτα Τζαμάλ-Οδυσσέας 31 Μαρτίου 2019 1 Δυνάμεις μάζας και επαφής Δυνάμεις μάζας ή δυνάμεις όγκου ονομάζονται οι δυνάμεις που είναι
ΦΥΣΙΚΗ Ι. ΤΜΗΜΑ Α Ευστάθιος. Στυλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟN ΑΘΗΝΩΝ,,
 ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Ευστάθιος Στυλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟN ΑΘΗΝΩΝ,, 06 0 07 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ Πολικές Συντεταγμένες Κυλινδρικές Συντεταγμένες Σφαιρικές Συντεταγμένες Στοιχειώδεις Όγκοι ΠΑΡΑΓΩΓΙΣΗ Ιδιότητες
ΦΥΣΙΚΗ Ι ΤΜΗΜΑ Α Ευστάθιος Στυλιάρης ΠΑΝΕΠΙΣΤΗΜΙΟN ΑΘΗΝΩΝ,, 06 0 07 ΣΥΣΤΗΜΑΤΑ ΣΥΝΤΕΤΑΓΜΕΝΩΝ Πολικές Συντεταγμένες Κυλινδρικές Συντεταγμένες Σφαιρικές Συντεταγμένες Στοιχειώδεις Όγκοι ΠΑΡΑΓΩΓΙΣΗ Ιδιότητες
ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΟ ΣΥΝΕΧΕΙΑ Ορισμός. Αν τα και είναι τα μοναδιαία διανύσματα των αξόνων και αντίστοιχα η συνάρτηση που ορίζεται από τη σχέση όπου (συνιστώσες) είναι
ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ. ΔΙΑΝΥΣΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΟΡΙΟ ΣΥΝΕΧΕΙΑ Ορισμός. Αν τα και είναι τα μοναδιαία διανύσματα των αξόνων και αντίστοιχα η συνάρτηση που ορίζεται από τη σχέση όπου (συνιστώσες) είναι
ΚΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΑΠΟ ΤΗ ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ
 ΚΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΑΠΟ ΤΗ ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1. ΕΙΣΑΓΩΓΗ Γράφημα μιας πραγματικής συνάρτησης : ή ( )/ σύνολο: f Οι θέσεις του κινητού σημείου G ( x, y)/ y f( x), xa. f A y f x A είναι το M x, y, ώστε
ΚΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΑΠΟ ΤΗ ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1. ΕΙΣΑΓΩΓΗ Γράφημα μιας πραγματικής συνάρτησης : ή ( )/ σύνολο: f Οι θέσεις του κινητού σημείου G ( x, y)/ y f( x), xa. f A y f x A είναι το M x, y, ώστε
13 ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ
 ETION 1 13 ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 13.1 Ορισµοί Μεγέθη Μια ποσότητα που εκφράζεται από ένα µόνο πραγµατικό αριθµό καλείται βαθµωτό µέγεθος. Μια ποσότητα που εκφράζεται από περισσότερους από έναν πραγµατικούς
ETION 1 13 ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 13.1 Ορισµοί Μεγέθη Μια ποσότητα που εκφράζεται από ένα µόνο πραγµατικό αριθµό καλείται βαθµωτό µέγεθος. Μια ποσότητα που εκφράζεται από περισσότερους από έναν πραγµατικούς
ΔΥΝΑΜΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΡΕΥΣΤΩΝ
 ΔΥΝΑΜΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΡΕΥΣΤΩΝ Α. Παϊπέτης 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών Εισαγωγή Φύση και μορφή δυνάμεων/ ρυθμός παραμόρφωσης Σωματικές δυνάμεις: δυνάμεις σε όγκο ελέγχου που είναι πλήρης ρευστού
ΔΥΝΑΜΕΙΣ ΚΑΙ ΠΑΡΑΜΟΡΦΩΣΗ ΡΕΥΣΤΩΝ Α. Παϊπέτης 6 ο Εξάμηνο Μηχανικών Επιστήμης Υλικών Εισαγωγή Φύση και μορφή δυνάμεων/ ρυθμός παραμόρφωσης Σωματικές δυνάμεις: δυνάμεις σε όγκο ελέγχου που είναι πλήρης ρευστού
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
1.1 ΟΡΙΣΜΟΙ, ΣΤΟΙΧΕΙΩΔΗΣ ΠΡΟΣΕΓΓΙΣΗ
 Κεφάλαιο 1 ΔΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 ΟΡΙΣΜΟΙ, ΣΤΟΙΧΕΙΩΔΗΣ ΠΡΟΣΕΓΓΙΣΗ Στις θετικές επιστήμες και στις τεχνολογικές τους εφαρμογές συναντάμε συχνά μεγέθη που χαρακτηρίζονται μόνο από το μέτρο τους: τη μάζα,
Κεφάλαιο 1 ΔΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 ΟΡΙΣΜΟΙ, ΣΤΟΙΧΕΙΩΔΗΣ ΠΡΟΣΕΓΓΙΣΗ Στις θετικές επιστήμες και στις τεχνολογικές τους εφαρμογές συναντάμε συχνά μεγέθη που χαρακτηρίζονται μόνο από το μέτρο τους: τη μάζα,
Νόμος Ampere- Διανυσματικό Δυναμικό
 Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
Νόμος Ampere- Διανυσματικό Δυναμικό Δομή Διάλεξης Μαγνητικό πεδίο ευθύγραμμων αγωγών Ο στροβιλισμός και η κλίση μαγνητικού πεδίου: ο νόμος του Ampere Εφαρμογές του Νόμου του Ampere To διανυσματικό δυναμικό
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ
 Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
Μαθηματικά για μηχανικούς ΙΙ ΛΥΣΕΙΣ/ΑΠΑΝΤΗΣΕΙΣ ΑΣΚΗΣΕΩΝ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 D (, ) :9 0, 4 0 (, ) :
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ
 Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
Μαθηματικά για μηχανικούς ΙΙ ΑΣΚΗΣΕΙΣ Κεφάλαιο 1 1 Να βρείτε (και να σχεδιάσετε) το πεδίο ορισμού των πιο κάτω συναρτήσεων f (, ) 9 4 (γ) f (, ) f (, ) 16 4 1 Να υπολογίσετε το κάθε όριο αν υπάρχει ή να
ΦΥΣΙΚΑ ΜΕΓΕΘΗ Αριθμητικά ή Μονόμετρα μεγέθη: Όγκος Μάζα Χρόνος Ενέργεια κ.λ.π. Διανυσματικά μεγέθη: Μετατόπιση Δύναμη Ορμή Διανυσματικοί τελεστές
 ΦΥΣΙΚΑ ΜΕΓΕΘΗ Αριθμητικά ή Μονόμετρα μεγέθη: Όγκος Μάζα Χρόνος Ενέργεια κ.λ.π. Διανυσματικά μεγέθη: Μετατόπιση Δύναμη Ορμή Διανυσματικοί τελεστές κ.λ.π. ΔΙΑΝΥΣΜΑΤΑ Παράσταση διανύσματος ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΕΣ
ΦΥΣΙΚΑ ΜΕΓΕΘΗ Αριθμητικά ή Μονόμετρα μεγέθη: Όγκος Μάζα Χρόνος Ενέργεια κ.λ.π. Διανυσματικά μεγέθη: Μετατόπιση Δύναμη Ορμή Διανυσματικοί τελεστές κ.λ.π. ΔΙΑΝΥΣΜΑΤΑ Παράσταση διανύσματος ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΕΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Θέματα εξέτασης στο μάθημα «Μηχανική του Συνεχούς Μέσου» (ΕΜ57) Ηράκλειο, 9 Μαΐου 009 Θέμα 1 ο (μονάδες.0) Έστω ο τανυστής προβολής P= 1 n n, όπου n
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - ΤΜΗΜΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Θέματα εξέτασης στο μάθημα «Μηχανική του Συνεχούς Μέσου» (ΕΜ57) Ηράκλειο, 9 Μαΐου 009 Θέμα 1 ο (μονάδες.0) Έστω ο τανυστής προβολής P= 1 n n, όπου n
ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1
 ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1 1.1 Εισαγωγή... 1 1.2 Λύση ΔΕ, αντίστροφο πρόβλημα αυτής... 3 Ασκήσεις... 10 1.3 ΔΕ πρώτης τάξης χωριζομένων μεταβλητών... 12 Ασκήσεις... 15 1.4 Ομογενείς
ΠΕΡΙΕΧΟΜΕΝΑ KΕΦΑΛΑΙΟ 1 ΣΤΟΙΧΕΙΑ ΔΙΑΦΟΡΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 1 1.1 Εισαγωγή... 1 1.2 Λύση ΔΕ, αντίστροφο πρόβλημα αυτής... 3 Ασκήσεις... 10 1.3 ΔΕ πρώτης τάξης χωριζομένων μεταβλητών... 12 Ασκήσεις... 15 1.4 Ομογενείς
ΣΗΜΕΙΩΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΣΕ ΕΙΔΙΚΑ ΚΕΦΑΛΑΙΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΠΟΛΙΤΙΚΟΥΣ ΜΗΧΑΝΙΚΟΥΣ
 ΣΗΜΕΙΩΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΣΕ ΕΙΔΙΚΑ ΚΕΦΑΛΑΙΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΠΟΛΙΤΙΚΟΥΣ ΜΗΧΑΝΙΚΟΥΣ Νικόλαος Ι. Ιωακειμίδης Ομότιμος Καθηγητής Πολυτεχνικής Σχολής Πανεπιστημίου Πατρών ΠΑΤΡΑ 2014 ΣΗΜΕΙΩΣΕΙΣ ΚΑΙ
ΣΗΜΕΙΩΣΕΙΣ ΚΑΙ ΑΣΚΗΣΕΙΣ ΣΕ ΕΙΔΙΚΑ ΚΕΦΑΛΑΙΑ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΙΑ ΠΟΛΙΤΙΚΟΥΣ ΜΗΧΑΝΙΚΟΥΣ Νικόλαος Ι. Ιωακειμίδης Ομότιμος Καθηγητής Πολυτεχνικής Σχολής Πανεπιστημίου Πατρών ΠΑΤΡΑ 2014 ΣΗΜΕΙΩΣΕΙΣ ΚΑΙ
Η αρνητική φορά του άξονα z είναι προς τη σελίδα. Για να βρούμε το μέτρο του Β χρησιμοποιούμε την Εξ. (2.3). Στο σημείο Ρ 1 ισχύει
 ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
p = p n, (2) website:
 Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης Τμήμα Φυσικής Μηχανική Ρευστών Ιδανικά ρευστά Μαάιτα Τζαμάλ-Οδυσσέας 7 Απριλίου 2019 1 Καταστατικές εξισώσεις ιδανικού ρευστού Ιδανικό ρευστό είναι ένα υποθετικό
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
( ) ( ) ( )z. HMY Φωτονική. Διάλεξη 08 Οι εξισώσεις του Maxwell. r = A r. B r. ˆ det = Βαθμωτά και διανυσματικά μεγέθη
 HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
HMY - Φωτονική Διάλεξη 8 Οι εξισώσεις του Mawell Βαθμωτά και διανυσματικά μεγέθη Πολλαπλασιασμός Πρόσθεση διανυσμάτων Βαθμωτό: το μέγεθος που για τον προσδιορισμό του χρειάζεται μόνο το μέτρο του και η
Κ Ε Φ Α Λ Α Ι Ο ΚΑΡΤΕΣΙΑΝΟΙ ΤΑΝΥΣΤΕΣ ΠΕΡΙΛΗΨΗ ΤΟΥ ΚΕΦΑΛΑΙΟΥ
 ΠΕΡΙΛΗΨΗ ΤΟΥ ΚΕΦΑΛΑΙΟΥ 1 Κ Ε Φ Α Λ Α Ι Ο E1 ΚΑΡΤΕΣΙΑΝΟΙ ΤΑΝΥΣΤΕΣ ΠΕΡΙΛΗΨΗ ΤΟΥ ΚΕΦΑΛΑΙΟΥ Στο Κεφάλαιο αυτό Ε1 γίνεται μια πολύ απλή εισαγωγή στους Καρτεσιανούς τανυστές, δηλαδή στους τανυστές σε Καρτεσιανά
ΠΕΡΙΛΗΨΗ ΤΟΥ ΚΕΦΑΛΑΙΟΥ 1 Κ Ε Φ Α Λ Α Ι Ο E1 ΚΑΡΤΕΣΙΑΝΟΙ ΤΑΝΥΣΤΕΣ ΠΕΡΙΛΗΨΗ ΤΟΥ ΚΕΦΑΛΑΙΟΥ Στο Κεφάλαιο αυτό Ε1 γίνεται μια πολύ απλή εισαγωγή στους Καρτεσιανούς τανυστές, δηλαδή στους τανυστές σε Καρτεσιανά
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
 ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
ΚΙΝΗΜΑΤΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ ΕΙΣΑΓΩΓΗ Σκοπός της κινηματικής είναι η περιγραφή της κίνησης του ρευστού Τα αίτια που δημιούργησαν την κίνηση και η αναζήτηση των δυνάμεων που την διατηρούν είναι αντικείμενο της
Διάνυσμα: έχει μέτρο, διεύθυνση και φορά
 Διάνυσμα: έχει μέτρο, διεύθυνση και φορά Πολλά φυσικά μεγέθη είναι διανυσματικά (π.χ. δύναμη, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα, ροπή, στροφορμή ) Συμβολισμός του διανύσματος: Συμβολισμός του μέτρου
Διάνυσμα: έχει μέτρο, διεύθυνση και φορά Πολλά φυσικά μεγέθη είναι διανυσματικά (π.χ. δύναμη, ταχύτητα, επιτάχυνση, γωνιακή ταχύτητα, ροπή, στροφορμή ) Συμβολισμός του διανύσματος: Συμβολισμός του μέτρου
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου
 8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
ΦΥΕ 14 Διανύσματα. 1 Περιγραφή διανυσμάτων στο χώρο Γεωμετρική περιγραφή: Τα διανύσματα περιγράφονται σαν προσανατολισμένα ευθύγραμμα
 ΦΥΕ 4 Διανύσματα Περιγραφή διανυσμάτων στο χώρο Γεωμετρική περιγραφή: Τα διανύσματα περιγράφονται σαν προσανατολισμένα ευθύγραμμα τμήματα Δύο διανύσματα θα θεωρούμε ότι είναι ίσα, εάν έχουν το ίδιο μήκος
ΦΥΕ 4 Διανύσματα Περιγραφή διανυσμάτων στο χώρο Γεωμετρική περιγραφή: Τα διανύσματα περιγράφονται σαν προσανατολισμένα ευθύγραμμα τμήματα Δύο διανύσματα θα θεωρούμε ότι είναι ίσα, εάν έχουν το ίδιο μήκος
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Νόμος Gauss Ο νόµος του Gauss εκφράζει τη σχέση μεταξύ της συνολικής ηλεκτρικής ροής που διέρχεται από μια κλειστή επιφάνεια και του φορτίου
ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 3: Στοιχεία Θεωρίας Ελαστικότητας Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας,
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΘΕΩΡΙΑ ΜΗΧΑΝΙΚΩΝ ΤΑΛΑΝΤΩΣΕΩΝ ΚΑΙ ΕΛΑΣΤΙΚΑ ΚΥΜΑΤΑ Ενότητα 3: Στοιχεία Θεωρίας Ελαστικότητας Σκορδύλης Εμμανουήλ Καθηγητής Σεισμολογίας,
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανύσματα Ευθείες - Επίπεδα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διάνυσμα ή Διανυσματικό μέγεθος (Vector) Μέγεθος που
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανύσματα Ευθείες - Επίπεδα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διάνυσμα ή Διανυσματικό μέγεθος (Vector) Μέγεθος που
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΙΚΑ ΚΥΚΛΩΜΑΤΑ Ι ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν μια
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ 1 1. ΗΛΕΚΤΡΙΚΗ ΔΥΝΑΜΙΚΗ ΕΝΕΡΓΕΙΑ Αρχικά ας δούμε ορισμένα σημεία που αναφέρονται στο έργο, στη δυναμική ενέργεια και στη διατήρηση της ενέργειας. Πρώτον, όταν
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι. Για το 3ο εξάμηνο. ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ
 ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
ΠΡΟΣΟΧΗ : Nέα Ύλη για τις Κατατακτήριες από 2012 και μετά στην Φυσική Ι ΕΞΕΤΑΣΤΕΑ ΥΛΗ στο μάθημα ΦΥΣΙΚΗ Ι - ΜΗΧΑΝΙΚΗ 1. Κινηματική (ευθύγραμμη και καμπυλόγραμμη κίνηση) 2. Σχετική κίνηση-μετασχηματισμοί
Το βαρυτικό πεδίο της Γης.
 Το βαρυτικό πεδίο της Γης. Θα μελετήσουμε το βαρυτικό πεδίο της Γης, τόσο στο εξωτερικό της όσο και στο εσωτερικό της, χρησιμοποιώντας τη λογική μελέτης του ηλεκτροστατικού πεδίου, με την βοήθεια της ροής.
Το βαρυτικό πεδίο της Γης. Θα μελετήσουμε το βαρυτικό πεδίο της Γης, τόσο στο εξωτερικό της όσο και στο εσωτερικό της, χρησιμοποιώντας τη λογική μελέτης του ηλεκτροστατικού πεδίου, με την βοήθεια της ροής.
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Εφαρμοσμένων Μαθηματικών. «Μηχανική Συνεχούς Μέσου» (ΕΜ257) Εαρινό Εξάμηνο , Διδάσκων: Ι.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Εφαρμοσμένων Μαθηματικών «Μηχανική Συνεχούς Μέσου» (ΕΜ57) Εαρινό Εξάμηνο 008-09 Διδάσκων: Ι Τσαγράκης ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ 1 μια βάση του Ευκλείδειου χώρου E Δείξτε ότι τα διανύσματα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Εφαρμοσμένων Μαθηματικών «Μηχανική Συνεχούς Μέσου» (ΕΜ57) Εαρινό Εξάμηνο 008-09 Διδάσκων: Ι Τσαγράκης ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ 1 μια βάση του Ευκλείδειου χώρου E Δείξτε ότι τα διανύσματα
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Δ Ι Α Φ Ο Ρ Ι Κ Ο Ι Τ Ε Λ Ε Σ Τ Ε Σ
 Κλίση συνάρτησης f Δ Ι Α Φ Ο Ρ Ι Κ Ο Ι Τ Ε Λ Ε Σ Τ Ε Σ Αν σε κάθε σημείο Px, y,z ενός τμήματος Δ του χώρου μία τιμή, ορίζεται μια συνάρτηση. f x, y,z : Δ, Δ αντιστοιχίσουμε την οποία ονομάζουμε σημειακή
Κλίση συνάρτησης f Δ Ι Α Φ Ο Ρ Ι Κ Ο Ι Τ Ε Λ Ε Σ Τ Ε Σ Αν σε κάθε σημείο Px, y,z ενός τμήματος Δ του χώρου μία τιμή, ορίζεται μια συνάρτηση. f x, y,z : Δ, Δ αντιστοιχίσουμε την οποία ονομάζουμε σημειακή
 = 1 A A = A A. A A + A2 y. A = (A x, A y ) = A x î + A y ĵ. z A. 2 A + A2 z
 Οκτώβριος 2017 Ν. Τράκας ΜΑΘΗΜΑΤΙΚΟ ΒΟΗΘΗΜΑ ΔΙΑΝΥΣΜΑΤΑ Διάνυσμα: κατεύθυνση (διεύθυνση και ϕορά) και μέτρο. Συμβολισμός: A ή A. Αναπαράσταση μέσω των συνιστωσών του: A = (A x, A y ) σε 2-διαστάσεις και
Οκτώβριος 2017 Ν. Τράκας ΜΑΘΗΜΑΤΙΚΟ ΒΟΗΘΗΜΑ ΔΙΑΝΥΣΜΑΤΑ Διάνυσμα: κατεύθυνση (διεύθυνση και ϕορά) και μέτρο. Συμβολισμός: A ή A. Αναπαράσταση μέσω των συνιστωσών του: A = (A x, A y ) σε 2-διαστάσεις και
Ηλεκτρομαγνητισμός. Χρήσιμες μαθηματικές έννοιες. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Χρήσιμες μαθηματικές έννοιες Νίκος Ν. Αρπατζάνης Παράγωγος ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ y y = f(x) x φ y y y = f(x) x φ y y y = f(x) φ x 1 x 1 + х x x 1 x 1 + х x x 1 x tanϕ = y x tanϕ = dy dx
Ηλεκτρομαγνητισμός Χρήσιμες μαθηματικές έννοιες Νίκος Ν. Αρπατζάνης Παράγωγος ΓΕΩΜΕΤΡΙΚΗ ΕΡΜΗΝΕΙΑ y y = f(x) x φ y y y = f(x) x φ y y y = f(x) φ x 1 x 1 + х x x 1 x 1 + х x x 1 x tanϕ = y x tanϕ = dy dx
Δομή Διάλεξης. Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο
 Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
Ηλεκτρικό Δυναμικό Δομή Διάλεξης Ορισμός Ηλεκτρικού Δυναμικού και συσχέτιση με το Ηλεκτρικό Πεδίο Ιδιότητες ηλεκτρικού δυναμικού (χρησιμότητα σε υπολογισμούς, σημείο αναφοράς, αρχή υπέρθεσης) Διαφορικές
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES
 ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ΔΥΝΑΜΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ- ΕΞΙΣΩΣΕΙΣ NAVIER STOKES ΙΣΟΡΡΟΠΙΑ ΔΥΝΑΜΕΩΝ ΣΕ ΕΝΑΝ ΑΠΕΙΡΟΣΤΟ ΟΓΚΟ ΡΕΥΣΤΟΥ Στο κεφάλαιο αυτό θα εξετάσουμε την ισορροπία των δυνάμεων οι οποίες ασκούνται σε ένα τυχόν σωματίδιο ρευστού.
ds ds ds = τ b k t (3)
 Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
Γενικά Μαθηματικά ΙΙΙ Πρώτο σετ ασκήσεων, Λύσεις Άσκηση 1 Γνωρίζουμε ότι το εφαπτόμενο διάνυσμα ( t), ορίζεται ως: t = r = d r ds (1) και επιπλέον το διάνυσμα της καμπυλότητας ( k), ορίζεται ως: d t k
ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ I (Βασικό 3 ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ. Α. Τριγωνομετρικές Ταυτότητες
 ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ I (Βασικό 3 ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ Α. Τριγωνομετρικές Ταυτότητες Β. Αναπτύγματα σε σειρές Για
ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ I (Βασικό 3 ου Εξαμήνου) Διδάσκων : Δ.Σκαρλάτος ΜΑΘΗΜΑΤΙΚΟ ΤΥΠΟΛΟΓΙΟ Α. Τριγωνομετρικές Ταυτότητες Β. Αναπτύγματα σε σειρές Για
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
 ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. 5 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 7 ΚΕΦΑΛΑΙΟ 1: ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 15 ΚΕΦΑΛΑΙΟ 2: ΣΥΝΑΡΤΗΣΕΙΣ ΙΣΟΣΤΑΘΜΙΚΕΣ ΟΡΙΑ ΣΥΝΕΧΕΙΑ 35
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. 5 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 7 ΚΕΦΑΛΑΙΟ 1: ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 15 1. Γενικά.. 15 Επιφάνεια 15 Ευθειογενεί επιφάνειε. 15 Επιφάνειε δευτέρου βαθμού.. 16 2. Μερικέ επιφάνειε δευτέρου
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ. 5 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ 7 ΚΕΦΑΛΑΙΟ 1: ΕΠΙΦΑΝΕΙΕΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ 15 1. Γενικά.. 15 Επιφάνεια 15 Ευθειογενεί επιφάνειε. 15 Επιφάνειε δευτέρου βαθμού.. 16 2. Μερικέ επιφάνειε δευτέρου
d dx ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ
 ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ α) Η παράγωγος μιας συνάρτησης = f() σε ένα σημείο 0 εκφράζει το ρυθμό μεταβολής της συνάρτησης (ή τον παράγωγο αριθμό) στο σημείο 0. β) Γραφικά, η παράγωγος της συνάρτησης στο σημείο
ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗΣ α) Η παράγωγος μιας συνάρτησης = f() σε ένα σημείο 0 εκφράζει το ρυθμό μεταβολής της συνάρτησης (ή τον παράγωγο αριθμό) στο σημείο 0. β) Γραφικά, η παράγωγος της συνάρτησης στο σημείο
< F ( σ(h(t))), σ (h(t)) > h (t)dt.
 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ, ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ IV, /6/9 Θέμα 1. Εστω : a 1, β 1 ] R μια C 1 καμπύλη. Μια C 1 καμπύλη ρ : a, β] R λέγεται αναπαραμετρικοποίηση της αν υπάρχει h : a, β] a 1, β 1 ], 1 1 επί και
ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ, ΑΠΕΙΡΟΣΤΙΚΟΣ ΛΟΓΙΣΜΟΣ IV, /6/9 Θέμα 1. Εστω : a 1, β 1 ] R μια C 1 καμπύλη. Μια C 1 καμπύλη ρ : a, β] R λέγεται αναπαραμετρικοποίηση της αν υπάρχει h : a, β] a 1, β 1 ], 1 1 επί και
Ανασκόπηση-Μάθημα 32 Εύρεση Εμβαδού μέσω του Θεωρήματος Green- -Κυκλοφορία και εξερχόμενη ροή διανυσματικού πεδίου
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 3 Εύρεση Εμβαδού μέσω του Θεωρήματος Green- -Κυκλοφορία και εξερχόμενη ροή διανυσματικού
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Απειροστικός Λογισμός ΙΙ Γ. Καραγιώργος ykarag@aegean.gr Ανασκόπηση-Μάθημα 3 Εύρεση Εμβαδού μέσω του Θεωρήματος Green- -Κυκλοφορία και εξερχόμενη ροή διανυσματικού
ΠΑΡΑΡΤΗΜΑ Γ. Επικαμπύλια και Επιφανειακά Ολοκληρώματα. Γ.1 Επικαμπύλιο Ολοκλήρωμα
 ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΘΕΜΑ 1. Ονοματεπώνυμο. Τμήμα
 Εισαγωγή στις Φυσικές Επιστήμες (9-7-007) Ηλεκτρομαγνητισμός Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1 Α. Μια μονωτική ράβδος μήκους l φέρει ομογενώς κατανεμημένο θετικό φορτίο Q και είναι διατεταγμένη κατά μήκος του
Εισαγωγή στις Φυσικές Επιστήμες (9-7-007) Ηλεκτρομαγνητισμός Ονοματεπώνυμο Τμήμα ΘΕΜΑ 1 Α. Μια μονωτική ράβδος μήκους l φέρει ομογενώς κατανεμημένο θετικό φορτίο Q και είναι διατεταγμένη κατά μήκος του
Experiments are the only means of knowledge. Anyother is poetry and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ. Τμήμα Φαρμακευτικής Α εξάμηνο. Αριστείδης Δοκουμετζίδης. Ύλη. Διανύσματα. Πίνακες Ορίζουσες - Συστήματα. Διαφορικές εξισώσεις
 1 ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Τμήμα Φαρμακευτικής Α εξάμηνο Αριστείδης Δοκουμετζίδης Ύλη Διανύσματα Πίνακες Ορίζουσες - Συστήματα Διαφορικές εξισώσεις ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ Μία φυσική ποσότητα μπορεί να αναπαρίσταται
1 ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ Τμήμα Φαρμακευτικής Α εξάμηνο Αριστείδης Δοκουμετζίδης Ύλη Διανύσματα Πίνακες Ορίζουσες - Συστήματα Διαφορικές εξισώσεις ΔΙΑΝΥΣΜΑΤΙΚΟΣ ΛΟΓΙΣΜΟΣ Μία φυσική ποσότητα μπορεί να αναπαρίσταται
Παραµόρφωση σε Σηµείο Σώµατος. Μεταβολή του σχήµατος του στοιχείου (διατµητική παραµόρφωση)
 Παραµόρφωση σε Σηµείο Σώµατος Η ολική παραµόρφωση στερεού σώµατος στη γειτονιά ενός σηµείου, Ο, δηλαδή η συνολική παραµόρφωση ενός µικρού τµήµατος (στοιχείου) του σώµατος γύρω από το σηµείο µπορεί να αναλυθεί
Παραµόρφωση σε Σηµείο Σώµατος Η ολική παραµόρφωση στερεού σώµατος στη γειτονιά ενός σηµείου, Ο, δηλαδή η συνολική παραµόρφωση ενός µικρού τµήµατος (στοιχείου) του σώµατος γύρω από το σηµείο µπορεί να αναλυθεί
11. Βαθµίδα, Απόκλιση, Στροβιλισµός
 56 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής Βαθµίδα, Απόκλιση, Στροβιλισµός Βαθµίδα Έστω µια συνεχής βαθµωτή συνάρτηση,, Αν σε ένα σηµείο διατηρήσουµε σταθερά τα και και
56 Κ Χριστοδουλίδης: Μαθηµατικό Συµπλήρωµα για τα Εισαγωγικά Μαθήµατα Φυσικής Βαθµίδα, Απόκλιση, Στροβιλισµός Βαθµίδα Έστω µια συνεχής βαθµωτή συνάρτηση,, Αν σε ένα σηµείο διατηρήσουµε σταθερά τα και και
1 O ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΑΣ 2015 ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΨΩΜΑΘΙΑΝΟΣ ΕΜΜΑΝΟΥΗΛ
 1 O ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΑΣ 2015 ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΨΩΜΑΘΙΑΝΟΣ ΕΜΜΑΝΟΥΗΛ ΔΥΝΑΜΗ Τις δυνάμεις τις διακρίνουμε βασικά με δύο τρόπους: Συντηρητικές Μη συντηρητικές
1 O ΓΕΝΙΚΟ ΛΥΚΕΙΟ ΠΑΤΡΑΣ 2015 ΠΡΟΑΠΑΙΤΟΥΜΕΝΕΣ ΓΝΩΣΕΙΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΨΩΜΑΘΙΑΝΟΣ ΕΜΜΑΝΟΥΗΛ ΔΥΝΑΜΗ Τις δυνάμεις τις διακρίνουμε βασικά με δύο τρόπους: Συντηρητικές Μη συντηρητικές
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ. ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ 5. Εισαγωγή στη διανυσματική άλγεβρα
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ 5. Εισαγωγή στη διανυσματική άλγεβρα Φ. Καραντώνη, Δρ. Πολ. Μηχανικός Επίκουρος Καθηγήτρια 1 Σημαντική σημείωση Δεδομένου ότι θα διδαχθεί
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕΧΝΙΚΗ ΜΗΧΑΝΙΚΗ 5. Εισαγωγή στη διανυσματική άλγεβρα Φ. Καραντώνη, Δρ. Πολ. Μηχανικός Επίκουρος Καθηγήτρια 1 Σημαντική σημείωση Δεδομένου ότι θα διδαχθεί
Ηλεκτρική ροή. Εμβαδόν=Α
 Ηλεκτρική ροή Hλεκτρική ροή: φυσικό μέγεθος (μονόμετρο) που δηλώνει τον αριθμό των δυναμικών γραμών ενός ηλεκτρικού πεδίου που διαπερνούν μία επιφάνεια. Εμβαδόν=Α Για παράδειγμα, η ηλεκτρική ροή για την
Ηλεκτρική ροή Hλεκτρική ροή: φυσικό μέγεθος (μονόμετρο) που δηλώνει τον αριθμό των δυναμικών γραμών ενός ηλεκτρικού πεδίου που διαπερνούν μία επιφάνεια. Εμβαδόν=Α Για παράδειγμα, η ηλεκτρική ροή για την
Κεφάλαιο 2. Διανύσματα και Συστήματα Συντεταγμένων
 Κεφάλαιο 2 Διανύσματα και Συστήματα Συντεταγμένων Διανύσματα Διανυσματικά μεγέθη Φυσικά μεγέθη που έχουν τόσο αριθμητικές ιδιότητες όσο και ιδιότητες κατεύθυνσης. Σε αυτό το κεφάλαιο, θα ασχοληθούμε με
Κεφάλαιο 2 Διανύσματα και Συστήματα Συντεταγμένων Διανύσματα Διανυσματικά μεγέθη Φυσικά μεγέθη που έχουν τόσο αριθμητικές ιδιότητες όσο και ιδιότητες κατεύθυνσης. Σε αυτό το κεφάλαιο, θα ασχοληθούμε με
ΕΙΣΑΓΩΓΗ ΣΤΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ
 ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ Α. Ντούνης ΔΙΔΑΣΚΩΝ ΑΚΑΔ. ΥΠΟΤΡΟΦΟΣ Χ. Τσιρώνης ΕΙΣΑΓΩΓΗ ΣΤΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ ΜΑΘΗΜΑ ΔΕΥΤΕΡΟ - Διανύσματα - Πράξεις με πίνακες - Διαφορικός λογισμός (1D) ΜΑΘΗΜΑΤΙΚΟ ΥΠΟΒΑΘΡΟ
ΥΠΕΥΘΥΝΟΣ ΚΑΘΗΓΗΤΗΣ Α. Ντούνης ΔΙΔΑΣΚΩΝ ΑΚΑΔ. ΥΠΟΤΡΟΦΟΣ Χ. Τσιρώνης ΕΙΣΑΓΩΓΗ ΣΤΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ ΜΑΘΗΜΑ ΔΕΥΤΕΡΟ - Διανύσματα - Πράξεις με πίνακες - Διαφορικός λογισμός (1D) ΜΑΘΗΜΑΤΙΚΟ ΥΠΟΒΑΘΡΟ
Μ8 Η µερική παράγωγος
 Μ8 Η µερική παράγωγος Βιβλιογραφία Ι S Sokolnikoff και R M Redheffer, Μαθηµατικά για Φυσικούς και Μηχανικούς (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, Αθήνα, 1 Κεφ 5 M R Spiegel, Ανώτερα Μαθηµατικά (ΕΣΠΙ, Αθήνα 198
Μ8 Η µερική παράγωγος Βιβλιογραφία Ι S Sokolnikoff και R M Redheffer, Μαθηµατικά για Φυσικούς και Μηχανικούς (Πανεπιστηµιακές Εκδόσεις ΕΜΠ, Αθήνα, 1 Κεφ 5 M R Spiegel, Ανώτερα Μαθηµατικά (ΕΣΠΙ, Αθήνα 198
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Διανύσματα 1. Διανύσματα Πρόσθεση Διανυσμάτων Φυσική ποσότητα που περιγράφεται μόνο από ένα αριθμό ονομάζεται βαθμωτή.
 Διανύσματα 1. Διανύσματα Πρόσθεση Διανυσμάτων Φυσική ποσότητα που περιγράφεται μόνο από ένα αριθμό ονομάζεται βαθμωτή. Η διανυσματική ποσότητα έχει διεύθυνση, φορά και μέτρο. Δύο διανυσματικές ποσότητες
Διανύσματα 1. Διανύσματα Πρόσθεση Διανυσμάτων Φυσική ποσότητα που περιγράφεται μόνο από ένα αριθμό ονομάζεται βαθμωτή. Η διανυσματική ποσότητα έχει διεύθυνση, φορά και μέτρο. Δύο διανυσματικές ποσότητες
Κλασική Hλεκτροδυναμική
 Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Κλασική Hλεκτροδυναμική Ενότητα 1: Εισαγωγή Ανδρέας Τερζής Σχολή Θετικών επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι μια σύντομη επανάληψη στις βασικές έννοιες της ηλεκτροστατικής.
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
ΦΥΣΙΚΗ. Η Φυσική είναι πειραματική επιστήμη
 ΦΥΣΙΚΗ Η Φυσική είναι πειραματική επιστήμη Μέσα από το πείραμα ψάχνουμε κανονικότητες και αρχές (θεωρίες, νόμοι) ΕρώτημαΠείραμαΑποτέλεσμαΘεωρία Νόμος Φυσική 1 ΦΥΣΙΚΗ Φυσική 2 ΦΥΣΙΚΗ Η Φυσική χρησιμοποιεί
ΦΥΣΙΚΗ Η Φυσική είναι πειραματική επιστήμη Μέσα από το πείραμα ψάχνουμε κανονικότητες και αρχές (θεωρίες, νόμοι) ΕρώτημαΠείραμαΑποτέλεσμαΘεωρία Νόμος Φυσική 1 ΦΥΣΙΚΗ Φυσική 2 ΦΥΣΙΚΗ Η Φυσική χρησιμοποιεί
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ
 ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
ΔΥΝΑΜΙΚΟ ΔΙΑΦΟΡΑ ΔΥΝΑΜΙΚΟΥ Υποθέστε ότι έχουμε μερικά ακίνητα φορτισμένα σώματα (σχ.). Τα σώματα αυτά δημιουργούν γύρω τους ηλεκτρικό πεδίο. Αν σε κάποιο σημείο Α του ηλεκτρικού πεδίου τοποθετήσουμε ένα
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 1. Σχήµα 1 Σχήµα 2
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ The law of natue ae witten in the language of mathematic G.Galileo God ued beautiful mathematic in ceating the wold P.Diac ΣΥΝΤΟΜΗ ΜΑΘΗΜΑΤΙΚΗ ΕΙΣΑΓΩΓΗ Α. ΣΤΟΙΧΕΙΑ ΙΑΝΥΣΜΑΤΙΚΗΣ ΑΝΑΛΥΣΗΣ.Ροή
Μηχανική Πετρωμάτων Τάσεις
 Μηχανική Πετρωμάτων Τάσεις Δρ Παντελής Λιόλιος Σχολή Μηχανικών Ορυκτών Πόρων Πολυτεχνείο Κρήτης http://minelabmredtucgr Τελευταία ενημέρωση: 28 Φεβρουαρίου 2017 Δρ Παντελής Λιόλιος (ΠΚ) Τάσεις 28 Φεβρουαρίου
Μηχανική Πετρωμάτων Τάσεις Δρ Παντελής Λιόλιος Σχολή Μηχανικών Ορυκτών Πόρων Πολυτεχνείο Κρήτης http://minelabmredtucgr Τελευταία ενημέρωση: 28 Φεβρουαρίου 2017 Δρ Παντελής Λιόλιος (ΠΚ) Τάσεις 28 Φεβρουαρίου
πάχος 0 πλάτος 2a μήκος
 B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
0 + a = a + 0 = a, a k, a + ( a) = ( a) + a = 0, 1 a = a 1 = a, a k, a a 1 = a 1 a = 1,
 I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
Εισαγωγή στο Γήινο Πεδίο Βαρύτητας. βαρύτητας (Αρχές. Υπενθυµίζεται ότι. ιανυσµάτων. της Φυσικής Γεωδαισίας)
 Τοµέας Τοπογραφίας, Εργ. Ανώτερης Γεωδαισίας Εισαγωγή στο γήινο πεδίο βαρύτητας (Αρχές της Φυσικής Γεωδαισίας) ιδάσκοντες ηµήτρης εληκαράογλου Παρασκευάς Μήλας Γεράσιµος Μανουσάκης 7ο εξάµηνο, Ακαδ. Έτος
Τοµέας Τοπογραφίας, Εργ. Ανώτερης Γεωδαισίας Εισαγωγή στο γήινο πεδίο βαρύτητας (Αρχές της Φυσικής Γεωδαισίας) ιδάσκοντες ηµήτρης εληκαράογλου Παρασκευάς Μήλας Γεράσιµος Μανουσάκης 7ο εξάµηνο, Ακαδ. Έτος
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
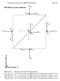 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Περιεχόμενα. Εξίσωση Συνέχειας Αστρόβιλη Ροή Εξισώσεις Κίνησης. Σειρά ΙΙ 2
 Περιεχόμενα Εξίσωση Συνέχειας Αστρόβιλη Ροή Εξισώσεις Κίνησης Σειρά ΙΙ 2 Πεδίο ταχύτητας Όγκος Ελέγχου Καρτεσιανές Συντεταγμένες w+(/)dz z y u dz u+(/ x)dx x dy dx w Σειρά ΙΙ 3 1. Εισαγωγή 1.1 Εξίσωση
Περιεχόμενα Εξίσωση Συνέχειας Αστρόβιλη Ροή Εξισώσεις Κίνησης Σειρά ΙΙ 2 Πεδίο ταχύτητας Όγκος Ελέγχου Καρτεσιανές Συντεταγμένες w+(/)dz z y u dz u+(/ x)dx x dy dx w Σειρά ΙΙ 3 1. Εισαγωγή 1.1 Εξίσωση
Βρέντζου Τίνα Φυσικός Μεταπτυχιακός τίτλος: «Σπουδές στην εκπαίδευση» ΜEd
 1 Ε Ι Σ Α Γ Ω Γ Η 1. Φ υ σ ι κ ά μ ε γ έ θ η Η Φυσική είναι η θεμελιώδης επιστήμη που εξετάζει τα φυσικά φαινόμενα που συντελούνται στο σύμπαν. Παραδείγματα φυσικών φαινομένων είναι οι κινήσεις των πλανητών,
1 Ε Ι Σ Α Γ Ω Γ Η 1. Φ υ σ ι κ ά μ ε γ έ θ η Η Φυσική είναι η θεμελιώδης επιστήμη που εξετάζει τα φυσικά φαινόμενα που συντελούνται στο σύμπαν. Παραδείγματα φυσικών φαινομένων είναι οι κινήσεις των πλανητών,
ΗΛΕΚΤΡΙΚΟ ΠΕ ΙΟ. (συνέχεια) ΝΟΜΟΣ GAUSS ΓΙΑ ΤΟ ΗΛΕΚΤΡΙΚΟ ΠΕ ΙΟ. H ηλεκτρική ροή που διέρχεται δια µέσου µιας (τυχούσας) επιφάνειας Α είναι r r
 . (συνέχεια) ΝΟΜΟΣ GAUSS ΓΙΑ ΤΟ H ηλεκτρική ροή που διέρχεται δια µέσου µιας (τυχούσας) επιφάνειας Α είναι r r Φ Ε da Ε A Το επιφανειακό ολοκλήρωµα υπολογίζεται πάνω στην επιφάνεια Α, ενώ Ε είναι η τιµή
. (συνέχεια) ΝΟΜΟΣ GAUSS ΓΙΑ ΤΟ H ηλεκτρική ροή που διέρχεται δια µέσου µιας (τυχούσας) επιφάνειας Α είναι r r Φ Ε da Ε A Το επιφανειακό ολοκλήρωµα υπολογίζεται πάνω στην επιφάνεια Α, ενώ Ε είναι η τιµή
Σφαίρα σε ράγες: Η συνάρτηση Lagrange. Ν. Παναγιωτίδης
 Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους τους άξονες και.
Σφαίρα σε ράγες: Η συνάρτηση Lagrange Ν. Παναγιωτίδης Έστω σύστημα δυο συγκλινόντων ραγών σε σχήμα Χ που πάνω τους κυλίεται σφαίρα ακτίνας. Θεωρούμε σύστημα συντεταγμένων με οριζόντιους τους άξονες και.
n, C n, διανύσματα στο χώρο Εισαγωγή
 Θα περιοριστούμε σε διανύσματα των οποίων τα στοιχεία προέρχονται από τον χώρο και τον C, χωρίς καμία δυσκολία όμως μπορούν να αναχθούν σε οποιοδήποτε χώρο K Το πρώτο διάνυσμα: Τέρματα που έχουν πέτυχει
Θα περιοριστούμε σε διανύσματα των οποίων τα στοιχεία προέρχονται από τον χώρο και τον C, χωρίς καμία δυσκολία όμως μπορούν να αναχθούν σε οποιοδήποτε χώρο K Το πρώτο διάνυσμα: Τέρματα που έχουν πέτυχει
ΦΥΣΙΚΗ. Η Φυσική είναι πειραματική επιστήμη
 ΦΥΣΙΚΗ Η Φυσική είναι πειραματική επιστήμη Μέσα από το πείραμα ψάχνουμε κανονικότητες και αρχές (θεωρίες, νόμοι) ΕρώτημαΠείραμαΑποτέλεσμαΘεωρία Νόμος Φυσική 1 ΦΥΣΙΚΗ Η Φυσική χρησιμοποιεί μοντέλα Απλοποιημένη
ΦΥΣΙΚΗ Η Φυσική είναι πειραματική επιστήμη Μέσα από το πείραμα ψάχνουμε κανονικότητες και αρχές (θεωρίες, νόμοι) ΕρώτημαΠείραμαΑποτέλεσμαΘεωρία Νόμος Φυσική 1 ΦΥΣΙΚΗ Η Φυσική χρησιμοποιεί μοντέλα Απλοποιημένη
Προτεινόμενο Διαγώνισμα Φυσικής B Λυκείου Γενικής Παιδείας
 Προτεινόμενο Διαγώνισμα Φυσικής B Λυκείου Γενικής Παιδείας Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Δύο σώματα Α και Β ( ) εκτοξεύονται ταυτόχρονα οριζόντια
Προτεινόμενο Διαγώνισμα Φυσικής B Λυκείου Γενικής Παιδείας Θέμα 1 ο Σε κάθε μια από τις παρακάτω προτάσεις 1-5 να επιλέξετε τη μια σωστή απάντηση: 1. Δύο σώματα Α και Β ( ) εκτοξεύονται ταυτόχρονα οριζόντια
Μάθημα 2 ο. Στοιχεία Θεωρίας Ελαστικότητας
 Μάθημα ο Στοιχεία Θεωρίας Ελαστικότητας Τανυστής Τάσης Τανυστής Aνηγμένης Παραμόρφωσης Σχέση Τάσης και Ανηγμένης Παραμόρφωσης Ελαστικές Σταθερές ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΕΙΣΜΟΛΟΓΙΑ Μάθημα ο: Στοιχεία Θεωρίας Ελαστικότητας
Μάθημα ο Στοιχεία Θεωρίας Ελαστικότητας Τανυστής Τάσης Τανυστής Aνηγμένης Παραμόρφωσης Σχέση Τάσης και Ανηγμένης Παραμόρφωσης Ελαστικές Σταθερές ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΕΙΣΜΟΛΟΓΙΑ Μάθημα ο: Στοιχεία Θεωρίας Ελαστικότητας
Κεφάλαιο 2. Διανύσματα και Συστήματα Συντεταγμένων
 Κεφάλαιο 2 Διανύσματα και Συστήματα Συντεταγμένων Διανύσματα Διανυσματικά μεγέθη Φυσικά μεγέθη που έχουν τόσο αριθμητικές ιδιότητες όσο και ιδιότητες κατεύθυνσης. Σε αυτό το κεφάλαιο, θα ασχοληθούμε με
Κεφάλαιο 2 Διανύσματα και Συστήματα Συντεταγμένων Διανύσματα Διανυσματικά μεγέθη Φυσικά μεγέθη που έχουν τόσο αριθμητικές ιδιότητες όσο και ιδιότητες κατεύθυνσης. Σε αυτό το κεφάλαιο, θα ασχοληθούμε με
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
ΜΑΘΗΜΑΤΙΚΑ B ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ & ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΔΙΑΝΥΣΜΑΤΑ Επιμέλεια: Άλκης Τζελέπης ΑΣΚΗΣΕΙΣ ΣΤΑ ΔΙΑΝΥΣΜΑΤΑ ΕΝΝΟΙΑ - ΠΡΑΞΕΙΣ. Αν τα διανύσματα,, σχηματίζουν τρίγωνο, να αποδείξετε ότι το ίδιο συμβαίνει
u u u u u u u u u u u x x x x
 Βασικοί συµβολισµοί και σχέσεις ϕ ϕ ui & ϕ=, ϕ, i=, ui, j= t x x u1 u1 u1 x1 x2 x u 3 1, 1 ui, j ui, j u1, 1 ui, j ui, j u u u u u u u u u u u i 2 2 2 i, j= = i, j 2, 2 i, j = i, j 2, 2 i, j = x j x1 x2
Βασικοί συµβολισµοί και σχέσεις ϕ ϕ ui & ϕ=, ϕ, i=, ui, j= t x x u1 u1 u1 x1 x2 x u 3 1, 1 ui, j ui, j u1, 1 ui, j ui, j u u u u u u u u u u u i 2 2 2 i, j= = i, j 2, 2 i, j = i, j 2, 2 i, j = x j x1 x2
Περιεχόμενα. Λίγα λόγια για τους συγγραφείς
 Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Περιεχόμενα Λίγα λόγια για τους συγγραφείς xii Εισαγωγή xiii 1 Συναρτήσεις 1 1.1 Ανασκόπηση των συναρτήσεων 1 1.2 Παράσταση συναρτήσεων 12 1.3 Τριγωνομετρικές συναρτήσεις 26 Ασκήσεις επανάληψης 34 2 Όρια
Ακουστικό Ανάλογο Μελανών Οπών
 Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Ακουστικό Ανάλογο Μελανών Οπών ιάδοση ηχητικών κυµάτων σε ρευστά. Ηχητικά κύµατα σε ακίνητο ρευστό. Εξίσωση συνέχειας: ρ t + ~ (ρ~v) =0 Εξίσωση Euler: ~v t +(~v ~ )~v = 1 ρ ~ p ( ~ Φ +...) Μικρές διαταραχές:
Λύση: Η δύναμη σε ρευματοφόρο αγωγό δίνεται από την
 1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
Κεφάλαιο Η2. Ο νόµος του Gauss
 Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
Κεφάλαιο Η2 Ο νόµος του Gauss Ο νόµος του Gauss Ο νόµος του Gauss µπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού του ηλεκτρικού πεδίου. Ο νόµος του Gauss βασίζεται στο γεγονός ότι η ηλεκτρική
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1Ο : ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ Διάνυσμα Θέσης ενός σημείου Αν θεωρήσουμε ένα οποιοδήποτε σημείο Ο του επιπέδου ως σημείο αναφοράς (ακόμα
ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ & ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1Ο : ΔΙΑΝΥΣΜΑΤΑ ΒΑΣΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ Διάνυσμα Θέσης ενός σημείου Αν θεωρήσουμε ένα οποιοδήποτε σημείο Ο του επιπέδου ως σημείο αναφοράς (ακόμα
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ
 ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
