ULAZ - IZLAZ + GENERISANJE = AKUMULACIJA U SISTEMU (3.1)
|
|
|
- Παρθενιά Μαρκόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 3. MATERIJALNI BILANSI Pri izvođenu ednačina materialnog bilansa polazi se od opšte bilansne ednačine za otvoreni sistem: ULAZ - IZLAZ + GENERISANJE AKUMULACIJA U SISTEMU (3. 3. Uupni bilans materie i omponentni bilansi Uupni bilans materie Polazeći od opšteg bilansa (3. za besonačno mali period vremena, i imaući u vidu da se masa ne generiše i ne troši u sistemu, dobiamo diferenialni blans: dm dmiz d( m miz dm 443 az - izlaz { aumai a (g čiom integraiom, dobiamo bilans za nei onačan period vremena t m m 43 iz 4 az - izlaz m { aumai a ( g m - masa oa u peridu t uđe u sistem m iz - masa oa u peridu t izađe iz sistema m - masa u sistemu Delenem diferenialnog bilansa sa infinitezimalnim periodom, dobiamo: dm dm dm ( g s iz / iz - uupni azni maseni proto, zbir protoa svih aznih strua iz - uupni izlazni maseni proto, zbir protoa svih izlaznih strua Konačno, ao razliu - iz priažemo ao algebarsi zbir protoa svih strua u sistemu, dobiamo uupni bilans materie u edinii vremena ao N S i dm ( g s i / N S - bro materialnih strua i - proto date strue ( i > za azne strue, i < za izlazne strue (3.
2 Materialni bilansi omponenata Polazeći od opšte bilansne ednačine, dobiamo bilanse omponenata besonačno malom periodu vremena : ( dm ( dm iz + R { generisan e dm,,,... N ( g ili ( mol u sistemu u i delenem sa, dobiamo omponente bilanse u edinii vremena: ( g / s dm,, iz + R,,,..., N ili (3.3 ( mol / s,,,iz uupan azni i izlazni proto omponente (maseni ili molsi R - brzina generisana omponente (g/s ili (mol/s u hem. reaiama Pod terminom generisane podrazumevamo nastaane ao pozitivno generisane (R >, ili nestaane ao negativno generisane (R < nee omponente, ao reztat odviana edne ili više hemisih reaia u sistemu. Količinu omponente u sistemu, m (g ili mol dobiamo ao proizvod uupne oličine materie u sistemu i onentraie omponente. m ( g M,,,..., N ili (3.4a ( mol M - oličina materie u sistemu (apaitet sistema - onentraia omponente u sistemu Analogno, proto omponente sa neom struom i dobiamo ao proizvod: n ( g / s, i,,..., N,,,..., N ili (3.4b i i i s n i - proto omponente sa struom i i - proto strue i - onentraia omponente u strui i ( mol / s
3 Treba imati u vidu da edinie mere za apaitet sistema i proto strua morau biti onzistentne sa ediniama mere za onentraiu omponente. Odgovaraući ili onzistentni parovi apaitet - onentraia i proto - onentraia dati su u tabeli Tab.3. Tab 3. - Odgovaraući parovi oličina (proto - onentraia apaitet sistema, M onentraia omp. u sistemu, oličina omp. m u ediniama: masa, M (g maseni udeo, (- g zapremina, (m 3 masena onentraia, (g/m 3 g molsa onentraia, C (mol/m 3 mol uupan bro molova, N (mol molsi udeo, (- mol proto strue, i onentraia omp. u strui, i omp. proto n i u ediniama : maseni, i (g/s maseni udeo, i (- (g/s zapreminsi, i (m 3 /s masena onentraia, i (g/m 3 (g/s molsa onentraia, C i (mol/m 3 (mol/s molsi i (mol/s molsi udeo, i (- (mol/s Brzina generisana omponenete, R (g/s ili mol/s se načešće dobia iz speifične brzine generisana omponente r (g/m 3 s ili (mol/ m 3 s po edinii zapremine i zapremine sistema: R r r d za sistem sa neraspodelenim param. za sistem sa raspodelenim param. (3.5a (3.5b r - speifična brzina generisana omponente, (g/m 3 s ili (mol/ m 3 s U tabeli Tab.3. dati su nei speialni slučaevi omponentnih bilansa, za sistem sa neraspodelnim parametrima, dobieni iz opšte ednačine (3.3, ednačina za određivane oličine i protoa omponente (3.5a,b i izraza (3.5a za brzinu generisana omponente u sistemu. 3
4 Tab.3. Bilans omponente u sistemu sa neraspodelenim parametrima Sistem Bilans edn. otvoren, nestaionaran sa hemisom reaiom otvoren, staionaran sa hemisom reaiom otvoren bez hemisih reaia ( g / s N dm d( M S ili i i i r + (3.6 ( mol / s NS i + i r i a staionaran b nestaionaran NS i NS i ( g / s ili (3.7 ( mol / s g s i i ( / d( M ili i i ( mol / s (3.8a (3.8b zatvoren, nestaionaran a sa reaiom b bez reaie r d onst ( M ( g / s ili ( mol / s (3.9a (3.9b eza između uupnog i omponentnih bilansa Logično e da uupni bilans materie izražen u ilogramima predstavla zbir svih omponentnih bilansnih ednačina. Zaista, ao sumiramo reimo bilanse omponenata u edinii vremena (3.3 dobiamo: N N N N dm,, iz + R ( g / s Suma brzina generisana omponenata predstavla brzinu generisana uupne mase, oa e ednaa ni, N R pa prethodna ednačina, imaući u vidu: dm d iz iz m,,,, prelazi u uupni materialni bilans (3. dm 4
5 Zalučuemo da u sistemu ednačina sastavlenom iz svih omponentnih i uupnog materialnog bilansa ima samo N nezavisnih ednačina. Tao, pri formisanu materialnog bilansa, ao reztuući sistem nezavisnih ednačina mogu se reimo odabrati : N ednačina omponentnog bilansa, ili Jednačina uupnog materialnog bilansa i bilansne ednačina, za odabranih (N - omponenata. PRIMER 3. U rezervoaru sa mešaliom nalazi se 56 l čiste vode. U ednom momentu u rezervoar počine da utiče rastvor soli onentraie 3 g/l, onstantnim protoom 84 l/min. Istovremeno, iz rezervoara ističe rastvor soli, onstantnim protoom iz 59 l/min. Kolia e onentraia soli u rezervoaru ad u nemu sadrža rastvora dostigne 84 l. Pretpostaviti da se sardža rezervoara idealno meša i da se može zanemariti promena gustine rastvora sa promenom onentraie soli (ρ onst iz iz U pitanu e otvoren sistem sa neraspodelenim parametrima u nestaionarnom stanu. Pošto nema hemise reaie bilans za so, data e ednačinom (3.8b u Tab.3. : ( d iz iz odnosno, pošto e zbog idealnog mešana sadržaa rezervoara, iz : ( d ( g / s ( iz U diferenialno ednačini ( figurišu dve funie vremena (t i (t i da bi problem bio matematiči odeređen potrebna e oš edna diferenialna ednačina sa istim funiama. To e uupan bilans mase (edn. 4.6 u Tab.4.: ρ ( ρ d ρ / iz iz odnosno, pošto e ρ onst: iz d ( g s ( m s 3 / ( Da bi dobili onretna (partiarna rešena diferenialnih ednačina ( i ( trebau nam početni uslovi, oi slede iz formaie problema: 5
6 t :, (3 Pošto dif. ednačina ( sadrži samo ednu od dve funie, prvo ćemo nu da integrišemo: t+ I, I integraiona onstanta Iz početnog uslova (3 sledi: I 3 ( + t m (4 Treba dobieno rešene zameniti u diferenialnu ednačinu (. d( d + d iz + d iz iz + ( t ( + d (5 ( t ( i rešiti e uz dat početni uslov. d I + + t ln( ln( + t + I Iz uslova: ( I ln ln što posle smene u opšte rešena i sređivana dae: odnosno: ln ln ( t + + t t (6 Traži se za ono vreme t za oe e (t 84. Iz (4: t min što naon smene u edn. (6 dae:.5 g/l Rešićemo sada isti problem, ali u bezdimenzionom obliu. Uvodimo bezdimenzione promenlive: t, θ, τ gde e τ ( s 6
7 Da bi izvršili smenu promenlivih u edn. (5 treba nam i izvod d/: d d, τ, d d I početni uslov treba izraziti preo novih promenlivih: θ : Naon smene promenlivih i sređivana, diferenialna ednačina (5 postae: d + ( f θ gde e f bezdimenzioni parametar: (7 f Rešene dif. ednačine (7 e: ( + f θ f i ima ompatniu formu od originalnog rešena (6, mada su ona, naravno, evivalentna. (8 Isoristićemo prethodni primer da se podsetimo osnovnih prinipa i primene teorie sličnosti.idimo u primeru da se ao reztat prevođena diferenialnih ednačina u bezdimenzioni obli poavio u ednačini bezdimenzioni parametar f /. Pošto rešene date ednačine zavisi od parametra f: ( θ, f on arateriše proes i dae uslov sličnosti nea dva proesa (, ( ovoga tipa : f f Naime, da se podsetimo, da za slične proese važi da su opisani istim diferenialnim ednačinama i da te ednačine imau identična rešena u bezdimenzionom obliu.u ovom, trivialnom primeru sličnosti, oi se arateriše samo ednim bezdimenzionim riteriumom f, važi dale: f f ao θ θ, onda odnosno, s obzirom na definiiu bezdimenzionih parametara i θ, ao e f f odnosno, ( ( (s onda, u vremensim momentima, oi se odnose ao: 7
8 t t τ τ ( ( ( ( ( ( ( ( (s onentraie će se odnositi ao: ( ( (s3 Relaie (s-s3 su analogne onima oe definišu sličnost u geometrii i nazivau se relaie sličnosti za posmatrana dva sistema (obeta. Tao, dva posmatrana proesa će se ponašati slično, ao i samo ao, imau ednae arateristične parametre odnosno, edna olični debalansa protoa, sa aznim protoom (relativni debalans. Ova uslov ima sasvim asan fiziči smisao, i mogli smo do nega doći i intuitivno. U ovom ednostavnom primeru, sa samo ednim araterističnim bezdimenzionim riteriumom, f, ne može se govoriti o riterialno ednačini, oa bi povezivala više riteriuma. Očigledno e iz prethodne disusie da e orisno prevesti model u bezdimenzion obli. Sama diferenialna ednačina, mada naravno ostae istog tipa, ima ompatniu formu u bezdimenzionom obliu. PRIMER 3. Ao e u prethodnom primeru, iz 84 l/min, naći onentraiu soli u rezervoaru naon min, od momenta ada e u rezervoar počeo da utiče rastvor soli. Kao e u ovom slučau f /, diferenialna ednačina (7 se reduue u: d, ( i ima rešene: e θ Ovo rešene smo mogli da dobiemo i iz rešena prethodnog problema (f ao negovu graničnu vrednost ada f. Naime lim f ( + f θ f e θ što ostavlamo čitaou da poaže. 56 Za t i τ 3 θ 84 /, / 3 5. ( , 4.99 g/l Primetimo da su u ovom slučau proesi bezuslovno slični, er e već zadovolen uslov f f (. PRIMER 3.3 DISKONTINUALNA (bath DESTILACIJA. Kod disontunualne destilaie, smeša oa se destiliše isparava u otlu za destilaiu, bez dodavana sveže smeše pa se nena oličina i sastav u otlu menau u tou vremena. Para 8
9 iz otla se ondenzue u ondenzatoru i dobieni destilat, obogaćen laše isparlivim omponentama smeše, supla., y L,, y L a Izvesti poznatu Relievu (Rayleigh ednačinu za disontinualnu destilaiu binarne smeše: L ln L d y( mol. udeo laše isparlive omponente u tečnosti u otlu y odgovaraući ravnotežni udeo laše isparlive omponente u pari L polazna oličina smeše u otlu (u momentu t L oličina (mol smeše u otlu na rau destilaie (u momentu t mol. udeo laše isparlive omponente u polazno smeši mol. udeo laše isparlive omponente u otlu na rau destilaie ( < b Potrebno e, na atmosfersom pritisu, destilisati g smeše n-heptana i n-otana, sa 5 % mol. n-heptana, do udeo heptana u destilaionom otlu ne spadne na.8. U tabeli su dati potrebni ravnotežni podai za smešu heptan-otan, gde i y označavau ravnotežne mol. udele heptana u tečnosti i pari. : y: Izračunati preostalu oličinu L smeše u otlu, ao i oličinu priuplenog destilata D i negov sastav. Ao se destilaia vrši do ne ispari 6 % od polazne oličine smeše, odrediti sastav preostale tečnosti u destilaionom otlu, oličinu i sastav priuplenog destilata na rau destilaie. 9
10 a Ao sa označimo molsi proto pare nastale lučanem tečnosti u otlu, a sa y udeo laše isparlive omponente u pari, uupni bilans i bilans laše isparlive omponente u otlu, pod pretpostavom da su para i tečnost u ravnoteži, će biti: dl (edn. 3. ( ( L d y (ed. 3.8b ( Možemo da eliminišemo vreme delenem levih i desnih strana ednačina ( i (, ( L d y( dl d L + y( dl Dobili smo dif. ednačinu oa opisue promenu sastava tečnosti u otlu, sa promenom oličine tečnosti, L u tou destilaie. Početni uslov glasi : ( L Ona razdvaa promenlive (L i i integraiom uzimaući u obzir početni uslov dobiamo: L dl L L L ln L d y( d y( b mol : mol ORIGIN: Podai: Pod : ( ( X reverse Pod : Y reverse Pod :..37 T Molese mase omponenata g M : M mol 4 g mol Poetna oliina i sastav tenosti u otlu: L : g :.5 M s : M + ( M M s 7 g L L mol : L M 9.346mol s Krana onentraia heptana u otlu: :.8
11 Definisane funie y( : y( : interp( pspline( X, Y, X, Y, Y y( X, Izraunavane L iz Relieve ednaine I : d L y( : L ep( I L.833mol Koliinu i sastav destilata dobiamo iz uupnog i omponentnog bilansa za poeta i ra destilaie: L L + D L L + D D D L L L L : D 6.5mol D : D D.596 L :.4 L Krana onentraia tenosti e resene Relieve ednaine po za zadato L i L : d y( ln L L ( : d ln y( L L ( ( :.3 : root,.39 L L D : L L D 5.67mol D : D D.64 PRIMER 3.4 Rezervoar zapremine napunen e slanom vodom onentraie.drugi rezervoar, istih dimenzia, napunen e slanom vodom onentraie <.Oba rezervoara su idealno mešana.od ednog momenta (t se u prvi rezervoar dovodi čista voda sa protoom. Iz prvog rezevoara, istim protoom, rastvor utiče u drugi rezervoar.
12 ,, a Izvesti funiu po oo se mena onentraia u drugom rezervoaru u tou vremena b Odrediti momenat u ome onentraia u drugom rezervoaru dostiže masimum. a Tražena funia e rešene matematičog modela posmatranog proesa oi se sastoi od bilansa soli u. i. rezervoaru: d d, ( (, ( Do funie ( t možemo da dođemo rešavaući posmatrani sistem dve dif. ednačine. reda na tri načina:. Prvu edn. rešimo po (, rešene zamenimo u drugu i onda e rešimo po ( t. Prvu edn. rešimo po ( t. Eliminaiom vremena nađemo funiu ( i smenom u nu ( dobiamo traženu funiu t 3. Posmatrani sistem zamenimo evivalentnom dif. ednačinom. reda po ( t, i rešimo e. Pogodno e prethodno izvršiti smenu nezavisno promenlive: t θ, gde e tzv. ontatno vremeτ ( s τ Reztat su nešto ompatnie ednačine: d d,, ( ( ( ( t. način Rešene dif. edn. ( sa datim početnim uslovom e : Negova smena u edn. ( dae linearnu dif. ednačinu: d + θ, ( ( ( θ e θ
13 dy Opšte rešene linearne dif. ednačine. reda: + p( y q( d e ao što znamo: p( d [ q( e d C] p ( d y( e +, C integraiona onstanta U posmatranom slučau: p( θ, q( θ ( θ e θ p( θ θ p( θ q( θ e ( θ e ( θ e, q( θ e θ θ ( θ e ( θ +, C Dale, tražena funia e : ( + θ θ ( θ e iz početnog uslova: C. način Delenem levih i desnih strana dif. ednačina ( i (, eliminiše se vreme (formalno se srati i dobia se dif. ednačina oa definiše zavisnost : d d, ( ( U pitanu e homogena dif. ednačina. reda i da bi e rešili uvodimo smenu: d dz z, z, + z d d Dif. ednačina prelazi u ednostavnu ednačinu oa razdvaa promenlive: dz d, z ln + C, ( z ( ln + C Iz početnog uslova dobiamo integraionu onstantu: C + ln, pa e: ( θ ( ln + ( θ ( θ i smena izraza za ( dae traženu funiu. 3. način θ Eliminisaćemo funiu ( pomoću edn. (: θ 3
14 d + d d d +, Smena u edn. ( dae sledeću homogenu dif. ednačinu drugog reda sa onstantnim oefiientima: + + Karateristična ednačina ima dva ista orena: r + r + ( r +, r, pa rešene tražimo u obliu: θ + θ ( Ce C θe θ Iz početnog uslova ( nalazimo integ. onstantu nalazimo iz početnog uslova za : ( + + C ( ( ( C, i ponovo dobiamo isti reztat. C, C. Drugu onstantu b Traženo vreme dobiamo iz uslova estremuma: θ [ ( θ + ] e d θ θ ( + θ e e θ ma, t ma τθ ma PRIMER ANALIZA KOREKTNOSTI SPECIIKACIJA Smeša omponenata A(, B( i C(3 se razdvaa u destilaiono oloni. Prodisutovati sledeće speifiaie ( označava masene udele: a g/h, 5%, 4%, 3 %, 3 6 g/h, 3 8%, 3 5%, 33 5% 4
15 b g/h, 5%, 4%, 3 %, 3 8%, 3 7%, 33 3% g/h, 5%, 4%, 3 9%, 33 %, %, 3 % a Uupan bro nezavisnih ednačina materialnog bilansa e N i ad se tome dodau sumaione ednačine za uupan bro ednačina dobiamo N N + 3. Uupan bro v promenlivih (protoi i sastavi strua e N 3 ( N +.Tao e bro stepeni slobode: d N v N N 6 v Dato e 8 podataa, ali dva od nih slede iz prethodnih na osnovu sumaionih ednačina (adan od tri udela za struu i edan od tri udela za struu 3. Dale, imamo tačno 6 nezavisnih podataa, pa e bilansni problem matematiči određen i možemo da ga rešimo: Jednačine: Uupni bilans: (a Bilans. omp.: (b Bilans. omp.: ( Sumaione ednačine za tri strue: i + i + i3, i,,3 ( Iz (a računamo g/h Iz (b : 5% Iz ( : 9.5% Iz ( : 3.5% b Od 7 podataa nezavisnih e nih 5 (dati udeli zadovolavau sumaione ednačine: proto, dva udela za struu i dva udela za struu. Problem e matematiči neodređen. Imamo 7 nezavisnih podataa pa e problem matematiči preodređen i treba ispitati nihovu onzistentnost.iz sumaionih ednačina ( dobiamo napre nedostauće udele: 3 %, 78%, 3 9% Preostae da se nađu protoi i 3 i zato su dovolna dva od tri omponentna bilansa Proveravamo da li e zadovolena treća bilansna ednačina: Pošto ednačina nie zadovolena, problem e preodređen i neoretan, t. speifiaie su neoretne. Problem oene suvišnih speifiaia nie ednostavan, ao su one reztat merena, pa sadrže neotlonive slučane greše merana. Tada preodređen problem može da bude prividno neoretan er podai su zbog grešaa merena neuslađeni. Konačan odgovor 5
16 na pitane da li su dobiena neslagana pri rešavanu preodređenog problema reztat grubih grešaa ili samo neizbežnih slučanih grešaa merena, može da pruži statističa analiza. Statističa analiza oretnosti preodređenih bilansnih problema se u prasi oristi za utvrđivane eventualnih gubitaa supstane ili energie u neom industrisom proesu 3. Simaia izotermsog fleš-isparivača i parialnog ondenzatora leš-isparivač i parialni ondenzator predstavlau ednostavne ednostepene separaione uređae U fleš-isparivač se dovodi tečna mtiomponentana smeša i zbog pada pritisa, ostvarenog pomoću prigušnog ventila, ona delimično ispari. Izlazna parna strua e obogaćena laše isparlivim, a tečna strua teže isparlivim omponentama, u odnosu na naponu smešu.usled isparavana dolazi do apsorbovana toplote i u izolovanom flešisparivaču do pada temperature, a ao se u isparivač spola dovodi ili odvodi toplota, temperature izlaznih strua zavise od dovedene (odvedene toplote. U parialni ondenzator azi parna strua i zbog odvođena toplote ona delimično ondenzue pa iz ondenzatora izlazi edna parna i edna tečna strua. Koi deo parne strue će da ondenzue zavisi od odvedene oličine toplote. Pri simaii fleš-isparivača i par. ondenzatora, pretpostave su:. Temperature i onentraie su uniformne - sistem sa neraspodelenim parametrima. reme borava i međusobni ontat faza u sistemu dovolni su da se između faza (izlaznih strua uspostavi termodinamiča ravnoteža 3. Zanemarue se pad pritisa pri istianu strua iz sistema Komponentni bilansi : 6
17 ,,...,N ( mol s (3. Sumaione ednačine (ograničena: N i, i,,3 (3. Uslovi fazne ravnoteže :, 3,,,...,N (3. Pritise (P, P i temperature (T, T smatramo poznatim (izotermsa simaia, Pretpostava e da raspolažemo relaiama za izračunavane onstanti fazne ravnoteže Uupan bro promenlivih (mol. protoi i sastavi: Uupan bro ednačina: N v ( N Bro stepeni slobode: 3 + N N + 3 v d N N N (3.3 Neophodni podai za otvorenu simaiu : proto napone smeše (N - udela omponenata u napono smeši, (a nedostaući udeo se dobia iz sumaione ednačine za naponi to Izotermsi simaioni proračun fleš-isparivača i parialnog ondenzatora se bazira na izotermsom fleš proračunu. 3.. Izotermsi fleš proračun za idealan mtiomponentan sistem Pošto onstante fazne ravnoteže ne zavise od sastava, one se izračunau. Ao edn. (3. podelimo sa : prethodno,,..., N ( pogodno e uvesti novu promenlivu: φ (3.5 7
18 oa predstavla, u slučau fleš-isparivača, deo naponog toa oi e ispario (stepen isparavana u slučau parialnog ondenzatora, deo naponog toa, oi e ostao u parnom stanu. Kada se odredi stepen isparavana φ, mogu da se izračunau protoi izlaznih strua: φ (3.6a 3 ( φ (3.6b Izračunavane stepena isparavana : Naon smene 3 u (3.4:,,..., N (3.7 3, ( φ + ali oš edna ednačina da bi problem bio matematiči određen. Još nisu isorišćene sumaione ednačine izlaznih strua. Ao se (3.7 smenu u nihovu linearnu ombinaiu: ( 3 ( 3 (3.8 dobiamo sledeću nelinearnu ednačinu, oa se oa se rešava po φ N (. ( φ + (3.9 Ona e evivalentna algebarso ednačini reda (N -, P N ( φ gde P N ( φ predstavla polinom stepena (N -. Tao se ona može rešiti analitiči za N 3. PRIMER 3.6 Tečna smeša sa 6% metana, % etana i % propana (molsi % delimično isparava u fleš-isparivaču u ome e temperatura T 7 K, a pritisa 4 bar. Na datim uslovima, ravnotežne onstante para-tečnost za metan(, etan( i propan(3 su: K., K.83, K 3.8. Izračunati oi deo tečne smeše ispari i sastave izlaznih strua. (Rešene u Mathad-u PRIMER 3.7 Mtiomponentna tečna smeša datog sastava (tabela delimično isparava u fleš-isparivaču na normalnom pritisu i temperaturi T 35 K. 8
19 omponenta mol.udeo T (K P (atm α neopentan CCl Cilohesan Benzol Etilbenzol Napone para računati pomoću Ridelove ednačine : log p ( T log P.83ϕ( T + 7log T ( α 7 ψ( T ϕ( Tr T r ln T 35 T r 6 r T r - reduovana temperatura supstane, r r r ψ( T.364ϕ( T log T a Izračunati oi deo tečne smeše ispari i sastave izlaznih strua. b Na oo temperaturi e, na datom pritisu stepen isparavana strue datog sastava, edna.3? (Rešene u Mathad-u Izračunati fleš proračunom temperaturu lučana date tečne smeše. (Rešene u Mathad-u r r r 3.. Izotermsi fleš proračun za neidealan mtiomponentan sistem Ao e sistem neidealan, proračun se ompliue čineniom da su ravnotežni odnosi funie sastava. Stepen isparavana napone smeše Φ i sastavi izlaznih strua iz flešisparivača se računau alternativno: simtanim rešavanem ednačina oe čine model deomponovanem sistema ednačina Simtano rešavane ednačina Simtano se rešavau ednačine modela :,,..., N (omp.bilansi, edn.3.4 Φ + ( Φ 3,,..., N, ( T, P,, 3 3, (uslovi fazne ravnoteže, edn. 3. ( 3,, (edn 3.8, 3 vetori molsih udela omponenata u parno i tečno strui Deomponovane sistema ednačina Sistem ednačina se deomponue na sledeći način: 9
20 u spolnem iteraionom ilusu određue se stepen isparavana rešavanem ednačine (3.9 u oviru svae iteraie, pri rešavanu (3.9, neophodne su - vrednosti i one se, pošto su funie sastava, dobiau u unutrašnem iteraionom ilusu rešavanem, metodom probe i greše (uzastopne zamene uslova fazne ravnoteže : ( T, P,, 3 3,,, N,...,, odnosno : ( T, P, (, (,,..., N 3 ili u vetorsom obliu: f ( T, P, (, ( 3 gde su vetorse funie ( i 3 ( definisane ednačinama (3.7 i (3. PRIMER 3.8 Na nisim pritisima, parna faza mtiomponentnog sistema iz prethodnog primera se može smatrati idealnim gasom, a dopunsa Gipsova funia neidealne tečne faze može opisati Redlih-Kister ovim modelom : G RT E N N C +, N - bro omponenata u sistemu C - simetrična ( N N matria binarnih parametara, sa ntom diagonalom Primenom relaie (.5, iz prethodne ednačine se dobia sledeća ednačina za izračunavane oefiienta ativnosti : ln γ N N N C, ( Cm, n m n,,..., N m n m+ m n Binarni parametri C, su funie temperature(k : B, C, A, + T gde su A,, B, onstante određene za svai od parova (, omponenata na osnovu esperimentalnih podataa. Za posmatrani sistem one imau vrednosti : Par A, ( B, K
21 Potrebno e, a Izračunati stepen isparavana posmatrane smeše, sastava datog u prethodnom primeru, na normalnom pritisu i temperaturi 35K b Odrediti temperaturu na oo e, za isti pritisa i sastav, stepen isparavana.3 (Rešene u Mathad-u leš proračun sa SRK ednačinom stana Ao se za opisivane fugaiteta obe faze oristi ednačina stana, onstante fazne ravnoteže se računau ao: L ϕˆ ( T, p, 3,,..., N ϕˆ ( T, p, Izraz za oefiient fugaiteta omponente u smeši, oi se bazira na SRK ednačini stana glasi: ln ϕˆ δ b b a a ( z ln( z B N a ( i + A b B b δ z + B ln z b, b parametar b SRK ednačine za omponentu "" i smešu datog sastava a, a parametar a SRK ednačine za omponentu "" i smešu datog sastava A, B - parametri smeše, definisani ao : P A a, B b P ( RT RT z - oefiient stišlivosti smeše, oi se dobia ao rešene ubne ednačine: z 3 z + ( A B B z AB i to ao namani realan oren, za tečnu fazu (pri računanu naveći realan oren, za parnu fazu (pri računanu Parametri a i b poedinih omponenata se računau ao : L ϕˆ ϕˆ
22 b α( T RT.8664 P r,,, [ + f ( T ] ω r, T a r, R T.4748 P T T,,, α( T r, f ω ω.76ω ω fator aentričnosti omponente Parametri a i b za smešu se računau iz parametara čistih omponenata i molsog sastava iz sledećih forma (tzv. pravila mešana : C { }, a N N (, b N a a - simetrična matria binarnih interaionih parametara, sa ntom diagonalom PRIMER 3.9 Za tečnu smešu iz Primera 3.6, za isti pritisa i sastav, a Izračunati stepen isparavana i sastave izlaznih strua. b Odrediti temperaturu da bi, za isti pritisa i sastav smeše, stepen isparavana bio.5 Za opisivane termodinamičog ponašana smeše oristiti SRK ednačinu stana. Neophodni podai: 9.6 T : 35.4 (K P : (Pa ω : b ZADACI 3. Rezervoar sadrži 3 galona rastvora soli onentraie % masenih, čia e relativna gustina u odnosu na čistu vodu.63. Radi ulanana soli, u rezervoar se uvodi čista voda sa protoom gpm (galona po minutu. Pretpostavlaući idealno mešane sadržaa rezervoara i zanemaruući efeat promene gustine rastvora sa onentraiom soli, izračunati uupnu olilinu soli u rezervoaru naon 4 časa od početa ispirana, ao e proto izlazne strue a gpm, b gpm 3. azduh u prostorii dimenzia 5 5 ft sadrži.% (zapr. CO. Radi smanena sadržaa CO, uluče se ventilatori čii e apaitet 9 fm (ubne stope u minutu. Odrediti sadrža CO u prostorii min naon ulučivana ventilaie. 3.3 Rezervoar e napunen sa 4 L rastvora soli onentraie.6 g/l.u rezervoar se od ednog momenta uvodi čista voda sa protoom L/min. Istim protoom se rastvor iz rezervoara uvodi u drugi rezervoar istih dimenzia, prethodno napunen čistom vodom. Količina rastvora u drugom rezervoaru se održava onstantnom. Pretpostavlaući idealno mešane rezervoara, potrebno e izračunati a onentraiu soli u drugom rezervoaru naon sata b masimalnu dostignutu onentraiu soli u drugom rezervoaru.
23 3.4 Dva idealno mešana rezervoara, zapremina i su povezani ao u Primeru 3.4. Oba rezervoara su prethodno napunena rastvorom soli onentraie. U prvi rezervoar se od ednog momenta uvodi čista voda sa protoom, a oličinine rasvora u oba rezervoara se održavau onstantnim. Potrebno e a Naći funiu po oo se mena onentraia soli u drugom rezervoaru, sa vremenom: t τ δt τ τ ( t e + ( e, gde e: δ τ δ ττ b Odrediti momenat u ome onentraia spadne na polovinu polazne, za sledeće podate: gal, 9gal, lb gal, gal Poazati da se rešene dobieno u a svodi na ono izvedeno u Primeru 3.4, ada se δt izednači sa (Pomoć: naći limes izraza ( e δ, ada δ, pomoću Lopitalovog pravila. 3.5 Tri idealno izmešana rezervoara ednaih zapremina su vezana u asadu: izlaz iz prethodnog e az u naredni. Početne onentraie slanih rastvora oima su napuneni su, i. 3 a Od ednog momenta u prvi od rezervoara se protoom uvodi čista voda. Izvesti sledeći izraz za funiu ( : ( t 3 3 t t t + + τ τ e t τ 3, τ b Poaži matematičom induiom da se pod opisanim uslovima izlazna onentraia iz posledneg u asadi od n identičnih rezervoara mena sa vremenom ao: min n t t n t t τ n ( t n + n + + L + e, τ τ! τ ( n! τ 3.6. Odrediti opseg u ome se smeša iz Primera 3.7, na datom pritisu, nalazi u dvofaznom stanu i to : a Koristeći za proračun tače lučana i tače rose, standardnu formaiu, datu u tab.. b Rešavanem fleš - ednačine ( Za omponente date uglovodonične smeše, na pritisu P 3 psi, ravnotežne onstante se računau iz forme: 3 3 a + at + a3t + a4t ( T T rednosti parametara u formi su date u tabeli: u R Komp mol. udeo a a 5 a 3 8 a 4 3
24 C H C H C 3H C 3H nc ic a Izračunati opseg temperatura u ome se na datom pritisu smeša nalazi u dvofaznom stanu. b Izračunati stepen isparavana smeše na temperaturi. 3.8 Izvesti proračun zadat u Primeru 3.8 ao se ao model fazne ravnoteže oristi ona baziran na SRK ednačini stana. Neophodene vrednosti fatora aentričnosti za omponente smeše, redom su : ω (.97,.94,.3,., Za smešu sa 6% neopentana, % ilohesana i % uglentetrahlorida, izračunati opseg u ome se ona, na normalnom pritisu, nalazi u dvofaznom stanu i temperaturu na oo e stepen isparavana smeše na istom pritisu, edna.5. Proračun izvesti, a Uz aprosimaiu da - vrednosti ne zavise od sastava, b Uz pretpostavu da se parna faza može smatrati idealnim gasom, a dopunsa Gipsova funia tečne faze opisati Redlih - Kisterovim modelom, Sa - vrednostima računatim iz SRK ednačine stana. 4
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
( ) π. I slučaj-štap sa zglobovima na krajevima F. Opšte rešenje diferencijalne jednačine (1): min
 Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Kritična sia izvijanja Kritična sia je ona najmanja vrednost sie pritisa pri ojoj nastupa gubita stabinosti, odnosno, pri ojoj štap iz stabine pravoinijse forme ravnoteže preazi u nestabinu rivoinijsu
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Ako je koeficijent korelacije blizak 1, ne mora značiti da su X i Y međusobno zavisne, već da postoji treća promenljiva Z od koje zavise X i Y.
 Parcialni oeficient orelacie Ao e oeficient orelacie bliza 1, ne mora značiti da su X i Y međusobno zavisne, već da postoi treća promenliva Z od oe zavise X i Y. Definiše iš se parcialni i oeficient i
Parcialni oeficient orelacie Ao e oeficient orelacie bliza 1, ne mora značiti da su X i Y međusobno zavisne, već da postoi treća promenliva Z od oe zavise X i Y. Definiše iš se parcialni i oeficient i
Signali i sustavi AUDITORNE VJEŽBE 10. Jednadžbe diferencija, primjer
 Signali i sustavi AUDITORNE VJEŽBE 0 LS&S FER ZESOI Jednadžbe diferencia Koriste se u opisu disretnog sustava modelom s ulazno izlaznim variablama. Određivane odziva sustava svodi se na problem rešavana
Signali i sustavi AUDITORNE VJEŽBE 0 LS&S FER ZESOI Jednadžbe diferencia Koriste se u opisu disretnog sustava modelom s ulazno izlaznim variablama. Određivane odziva sustava svodi se na problem rešavana
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
MEHANIKA FLUIDA. Složeni cevovodi
 MEHANIKA FLUIDA Složeni cevovoi.zaata. Iz va velia otvorena rezervoara sa istim nivoima H=0 m ističe voa roz cevi I i II istih prečnia i užina: =00mm, l=5m i magisalni cevovo užine L=00m, prečnia D=50mm.
MEHANIKA FLUIDA Složeni cevovoi.zaata. Iz va velia otvorena rezervoara sa istim nivoima H=0 m ističe voa roz cevi I i II istih prečnia i užina: =00mm, l=5m i magisalni cevovo užine L=00m, prečnia D=50mm.
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Prvi kolokvijum. y 4 dy = 0. Drugi kolokvijum. Treći kolokvijum
 27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
27. septembar 205.. Izračunati neodredjeni integral cos 3 x (sin 2 x 4)(sin 2 x + 3). 2. Izračunati zapreminu tela koje nastaje rotacijom dela površi ograničene krivama y = 3 x 2, y = x + oko x ose. 3.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK
 SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
2log. se zove numerus (logaritmand), je osnova (baza) log. log. log =
 ( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Ovo nam govori da funkcija nije ni parna ni neparna, odnosno da nije simetrična ni u odnosu na y osu ni u odnosu na
 . Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
. Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Fakultet tehničkih nauka, Softverske i informacione tehnologije, Matematika 2 KOLOKVIJUM 1. Prezime, ime, br. indeksa:
 Fakultet tehničkih nauka, Softverske i informacione tehnologije, Matematika KOLOKVIJUM 1 Prezime, ime, br. indeksa: 4.7.1 PREDISPITNE OBAVEZE sin + 1 1) lim = ) lim = 3) lim e + ) = + 3 Zaokružiti tačne
Fakultet tehničkih nauka, Softverske i informacione tehnologije, Matematika KOLOKVIJUM 1 Prezime, ime, br. indeksa: 4.7.1 PREDISPITNE OBAVEZE sin + 1 1) lim = ) lim = 3) lim e + ) = + 3 Zaokružiti tačne
MATEMATIKA 2. Grupa 1 Rexea zadataka. Prvi pismeni kolokvijum, Dragan ori
 MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
MATEMATIKA 2 Prvi pismeni kolokvijum, 14.4.2016 Grupa 1 Rexea zadataka Dragan ori Zadaci i rexea 1. unkcija f : R 2 R definisana je sa xy 2 f(x, y) = x2 + y sin 3 2 x 2, (x, y) (0, 0) + y2 0, (x, y) =
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
STACIONARAN IZOTERMSKI CEVNI REAKTOR SA JEDNOM REAKCIJOM
 STIONN IZOTEMSKI EVNI EKTO S JENOM EKIJOM U opštem slučau, bilans omponente ima stutuu: t + + t as + t ad.. t onv. dif. dif. ea. (7.74) gde su poedini dopinosi dati ednačinama (7.64a,b), (7.65)-(7.67).
STIONN IZOTEMSKI EVNI EKTO S JENOM EKIJOM U opštem slučau, bilans omponente ima stutuu: t + + t as + t ad.. t onv. dif. dif. ea. (7.74) gde su poedini dopinosi dati ednačinama (7.64a,b), (7.65)-(7.67).
DRUGI KOLOKVIJUM IZ MATEMATIKE 9x + 6y + z = 1 4x 2y + z = 1 x + 2y + 3z = 2. je neprekidna za a =
 x, y, z) 2 2 1 2. Rešiti jednačinu: 2 3 1 1 2 x = 1. x = 3. Odrediti rang matrice: rang 9x + 6y + z = 1 4x 2y + z = 1 x + 2y + 3z = 2. 2 0 1 1 1 3 1 5 2 8 14 10 3 11 13 15 = 4. Neka je A = x x N x < 7},
x, y, z) 2 2 1 2. Rešiti jednačinu: 2 3 1 1 2 x = 1. x = 3. Odrediti rang matrice: rang 9x + 6y + z = 1 4x 2y + z = 1 x + 2y + 3z = 2. 2 0 1 1 1 3 1 5 2 8 14 10 3 11 13 15 = 4. Neka je A = x x N x < 7},
Kola u ustaljenom prostoperiodičnom režimu
 Kola u ustalenom prostoperiodičnom režimu svi naponi i sve strue u kolu su prostoperiodične (sinusoidalne ili kosinusoidalne funkcie vremena sa istom kružnom učestanošću i u opštem slučau različitim fazama
Kola u ustalenom prostoperiodičnom režimu svi naponi i sve strue u kolu su prostoperiodične (sinusoidalne ili kosinusoidalne funkcie vremena sa istom kružnom učestanošću i u opštem slučau različitim fazama
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
transformacija j y i x x promatramo dva koordinatna sustava S i S sa zajedničkim ishodištem z z Homogene funkcije Ortogonalne transformacije
 promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
promatramo dva oordnatna sustava S S sa zaednčm shodštem z z y y x x blo o vetor možemo raspsat u baz, A = A x + Ay + Az = ( A ) + ( A ) + ( A ) (1) sto vred za ednčne vetore sustava S = ( ) + ( ) + (
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
MATERIJAL ZA VEŽBE. Nastavnik: prof. dr Nataša Sladoje-Matić. Asistent: dr Tibor Lukić. Godina: 2012
 MATERIJAL ZA VEŽBE Predmet: MATEMATIČKA ANALIZA Nastavnik: prof. dr Nataša Sladoje-Matić Asistent: dr Tibor Lukić Godina: 202 . Odrediti domen funkcije f ako je a) f(x) = x2 + x x(x 2) b) f(x) = sin(ln(x
MATERIJAL ZA VEŽBE Predmet: MATEMATIČKA ANALIZA Nastavnik: prof. dr Nataša Sladoje-Matić Asistent: dr Tibor Lukić Godina: 202 . Odrediti domen funkcije f ako je a) f(x) = x2 + x x(x 2) b) f(x) = sin(ln(x
Matematka 1 Zadaci za drugi kolokvijum
 Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
(y) = f (x). (x) log ϕ(x) + ψ(x) Izvodi parametarski definisane funkcije y = ψ(t)
 Izvodi Definicija. Neka je funkcija f definisana i neprekidna u okolini tačke a. Prvi izvod funkcije f u tački a je Prvi izvod funkcije f u tački : f f fa a lim. a a f lim 0 Izvodi višeg reda funkcije
Izvodi Definicija. Neka je funkcija f definisana i neprekidna u okolini tačke a. Prvi izvod funkcije f u tački a je Prvi izvod funkcije f u tački : f f fa a lim. a a f lim 0 Izvodi višeg reda funkcije
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
Pneumatski sistemi. Pneumatski sistem je tehnički sistem za pretvaranje i prenos energije, kao i za
 1 Pneumatsi sistemi Pneumatsi sistem je tehniči sistem za pretvaranje i prenos energije, ao i za upravljanje energijom. Ovo poglavlje obuhvata sledeće teme: osnovne funcije pneumatsog sistema osnovna svojstva
1 Pneumatsi sistemi Pneumatsi sistem je tehniči sistem za pretvaranje i prenos energije, ao i za upravljanje energijom. Ovo poglavlje obuhvata sledeće teme: osnovne funcije pneumatsog sistema osnovna svojstva
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Zadatak 2 Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z 3 z 4 i objasniti prelazak sa jedne na drugu granu.
 Kompleksna analiza Zadatak Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z z 4 i objasniti prelazak sa jedne na drugu granu. Zadatak Odrediti tačke grananja, Riemann-ovu
Kompleksna analiza Zadatak Odrediti tačke grananja, Riemann-ovu površ, opisati sve grane funkcije f(z) = z z 4 i objasniti prelazak sa jedne na drugu granu. Zadatak Odrediti tačke grananja, Riemann-ovu
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4 Numeričko diferenciranje
 4 Numeričko diferenciranje 7. Funkcija fx) je zadata tabelom: x 0 4 6 8 fx).17 1.5167 1.7044 3.385 5.09 7.814 Koristeći konačne razlike, zaključno sa trećim redom, odrediti tačku x minimuma funkcije fx)
4 Numeričko diferenciranje 7. Funkcija fx) je zadata tabelom: x 0 4 6 8 fx).17 1.5167 1.7044 3.385 5.09 7.814 Koristeći konačne razlike, zaključno sa trećim redom, odrediti tačku x minimuma funkcije fx)
KOPOLIMERIZACIJA. UGRADNJA VIŠE RAZLIČITIH MONOMERA u istu makromolekulu Je li stupnjevita polimerizacija tipa A 2. kopolimerizacija?
 KOPOLIERIZIJ UGRDNJ VIŠE RZLIČITIH ONOER u stu maomoleulu Je l stunevta olmezaca ta oolmezaca? ltenauć (zmenčn) oolme KOPOLIERIZIJ POLIURETNI Stunevta oolmezaca: ugadna vše azlčth monomea ste unconalnost
KOPOLIERIZIJ UGRDNJ VIŠE RZLIČITIH ONOER u stu maomoleulu Je l stunevta olmezaca ta oolmezaca? ltenauć (zmenčn) oolme KOPOLIERIZIJ POLIURETNI Stunevta oolmezaca: ugadna vše azlčth monomea ste unconalnost
Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona.
 Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona Prema osnovnoj formuli za dimenzionisanje maksimalni tangencijalni napon τ max koji se javlja u štapu mora biti manji
Dimenzionisanje štapova izloženih uvijanju na osnovu dozvoljenog tangencijalnog napona Prema osnovnoj formuli za dimenzionisanje maksimalni tangencijalni napon τ max koji se javlja u štapu mora biti manji
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Diferencijabilnost funkcije više promenljivih
 Matematiči faultet Beograd novembar 005 godine Diferencijabilnost funcije više promenljivih 1 Osnovne definicije i teoreme, primeri Diferencijabilnost je jedan od centralnih pojmova u matematičoj analizi
Matematiči faultet Beograd novembar 005 godine Diferencijabilnost funcije više promenljivih 1 Osnovne definicije i teoreme, primeri Diferencijabilnost je jedan od centralnih pojmova u matematičoj analizi
Trigonometrijske nejednačine
 Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
Trignmetrijske nejednačine T su nejednačine kd kjih se nepznata javlja ka argument trignmetrijske funkcije. Rešiti trignmetrijsku nejednačinu znači naći sve uglve kji je zadvljavaju. Prilikm traženja rešenja
ASIMPTOTE FUNKCIJA. Dakle: Asimptota je prava kojoj se funkcija približava u beskonačno dalekoj tački. Postoje tri vrste asimptota:
 ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
ASIMPTOTE FUNKCIJA Naš savet je da najpre dobro proučite granične vrednosti funkcija Neki profesori vole da asimptote funkcija ispituju kao ponašanje funkcije na krajevima oblasti definisanosti, pa kako
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
SOPSTVENE VREDNOSTI I SOPSTVENI VEKTORI LINEARNOG OPERATORA I KVADRATNE MATRICE
 1 SOPSTVENE VREDNOSTI I SOPSTVENI VEKTORI LINEARNOG OPERATORA I KVADRATNE MATRICE Neka je (V, +,, F ) vektorski prostor konačne dimenzije i neka je f : V V linearno preslikavanje. Definicija. (1) Skalar
1 SOPSTVENE VREDNOSTI I SOPSTVENI VEKTORI LINEARNOG OPERATORA I KVADRATNE MATRICE Neka je (V, +,, F ) vektorski prostor konačne dimenzije i neka je f : V V linearno preslikavanje. Definicija. (1) Skalar
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
TEORIJA BETONSKIH KONSTRUKCIJA 79
 TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
TEORIJA BETOSKIH KOSTRUKCIJA 79 Primer 1. Odrediti potrebn površin armatre za stb poznatih dimenzija, pravogaonog poprečnog preseka, opterećen momentima savijanja sled stalnog ( g ) i povremenog ( w )
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Iz poznate entropije pare izračunat ćemo sadržaj pare u točki 2, a zatim i specifičnu entalpiju stanja 2. ( ) = + 2 x2
 1. zadata Vodena para vrši promjene stanja po desnoretnom Ranineovom cilusu. Kotao proizvodi vodenu paru tlaa 150 bar i temperature 560 o C. U ondenzatoru je tla 0,06 bar, a snaga turbine je 0 MW. otrebno
1. zadata Vodena para vrši promjene stanja po desnoretnom Ranineovom cilusu. Kotao proizvodi vodenu paru tlaa 150 bar i temperature 560 o C. U ondenzatoru je tla 0,06 bar, a snaga turbine je 0 MW. otrebno
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom
 Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
MOSTOVI beleške za predavanja
 MOSTOVI beleše za predavanja. Opšta onfiguracija, generalizovana A E eletrična mreža B U ( E, Z, K ) AB = f Z n ( L,, M, f ) Z i = g, avnoteža mosta: U = 0. AB Osetljivost mosta, definicija: S m U U AB
MOSTOVI beleše za predavanja. Opšta onfiguracija, generalizovana A E eletrična mreža B U ( E, Z, K ) AB = f Z n ( L,, M, f ) Z i = g, avnoteža mosta: U = 0. AB Osetljivost mosta, definicija: S m U U AB
SKUPOVI I SKUPOVNE OPERACIJE
 SKUPOVI I SKUPOVNE OPERACIJE Ne postoji precizna definicija skupa (postoji ali nama nije zanimljiva u ovom trenutku), ali mi možemo koristiti jednu definiciju koja će nam donekle dočarati šta su zapravo
SKUPOVI I SKUPOVNE OPERACIJE Ne postoji precizna definicija skupa (postoji ali nama nije zanimljiva u ovom trenutku), ali mi možemo koristiti jednu definiciju koja će nam donekle dočarati šta su zapravo
Neodred eni integrali
 Neodred eni integrali Definicija. Za funkciju F : I R, gde je I interval, kažemo da je primitivna funkcija funkcije f : I R ako je za svako I. F () f() Teorema 1. Ako je F : I R primitivna funkcija za
Neodred eni integrali Definicija. Za funkciju F : I R, gde je I interval, kažemo da je primitivna funkcija funkcije f : I R ako je za svako I. F () f() Teorema 1. Ako je F : I R primitivna funkcija za
Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika
 Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika Rešenja. Matematičkom indukcijom dokazati da za svaki prirodan broj n važi jednakost: + 5 + + (n )(n + ) = n n +.
Univerzitet u Nišu, Prirodno-matematički fakultet Prijemni ispit za upis OAS Matematika Rešenja. Matematičkom indukcijom dokazati da za svaki prirodan broj n važi jednakost: + 5 + + (n )(n + ) = n n +.
RAVNOTEŽA TEČNO-PARA
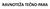 RAVNOTEŽA TEČNO-PARA Smeša dve isparljive komponente (dve tečnosti) koje se mešaju u svim odnosima: f = c p + 2 = 2 2 + 2 = 2 tečna homogena smeša+para iznad tečnosti Ako su te dve nezavisno promenjive
RAVNOTEŽA TEČNO-PARA Smeša dve isparljive komponente (dve tečnosti) koje se mešaju u svim odnosima: f = c p + 2 = 2 2 + 2 = 2 tečna homogena smeša+para iznad tečnosti Ako su te dve nezavisno promenjive
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA
 II. ODREĐIVANJE POLOŽAJA TEŽIŠTA Poožaj težišta vozia predstavja jednu od bitnih konstruktivnih karakteristika vozia s obzirom da ova konstruktivna karakteristika ima veiki uticaj na vučne karakteristike
II. ODREĐIVANJE POLOŽAJA TEŽIŠTA Poožaj težišta vozia predstavja jednu od bitnih konstruktivnih karakteristika vozia s obzirom da ova konstruktivna karakteristika ima veiki uticaj na vučne karakteristike
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
nvt 1) ukoliko su poznate struje dioda. Struja diode D 1 je I 1 = I I 2 = 8mA. Sada je = 1,2mA.
 IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
I Pismeni ispit iz matematike 1 I
 I Pismeni ispit iz matematike I 27 januar 2 I grupa (25 poena) str: Neka je A {(x, y, z): x, y, z R, x, x y, z > } i ako je operacija definisana sa (x, y, z) (u, v, w) (xu + vy, xv + uy, wz) Ispitati da
I Pismeni ispit iz matematike I 27 januar 2 I grupa (25 poena) str: Neka je A {(x, y, z): x, y, z R, x, x y, z > } i ako je operacija definisana sa (x, y, z) (u, v, w) (xu + vy, xv + uy, wz) Ispitati da
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
