H/m) električna i magnetna permeabilnost (propustljivost), koje su povezane sa brzinom elektromagnetnog talasa u
|
|
|
- ÚΑἰσχύλος Βονόρτας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 . INTERAKCIJA LASERSKOG ZRAČENJA SA MATERIJOM.1 Torija zračja crog tijla U oo odjljku lktroagto polj opisiaćo klasiči Maxwlloi [J. C. Maxwll (Maksl), ] jdačiaa i pokazaćo da s hipotza kata sjtlosti ož usti u klasiču toriju pooću dopuskog usloa za izračuaaj rgij lktroagtog polja. Izšćo Plackou forulu koja opisuj spktralu raspodjlu rgij lktroagtog zračja uutar rzoatora u trodiaičkoj raotži pri tpraturi T. Tako zračj s ož azati zračj crog tijla. Pod pojo rzoatora odj podrazuijao hoogu i izotropu dilktriču srdiu koja j zatora u koj zaprii V i koja prkido ituj i apsorbuj lktroagto zračj. Pra klasičoj toriji, gustoća rgij lktroagtog polja, opisaog jačiaa lktričog E i agtog polja H, odrđa j forulo: ( ) 1 w= εe + μ H = w d, (.1) 1 7 gdj su ε (ε = ε ε r, ε = 8,854 1 F/ ) i μ ( μ = μμr, μ = 4π 1 H/) lktriča i agta prabilost (propustljiost), koj su poza sa brzio lktroagtog talasa u razatraoj srdii forulo εμ =1 (u akuuu j ε μ c = 1). Drugi dio forul (.1) daj zu gustoć rgij w i spktral raspodjl gustoć rgij w. Mož s pokazati da j spktrala raspodjla gustoć rgij zračja w uirzala fukcija koja zaisi i od oblika rzoatora, i od prirod dilktrič srdi, ć sao od frkcij i tpratur: w = w(, T). To j pri Kirchhoffo [K. G. Kirchhoff (Kirhof), ] zako. Fukcioalu zaisost w = w(, T) aći ćo u da koraka. Pro ćo odrditi koordiatu zaisost polja u rzoatoru i aći izraz za broj različitih odoa polja (jda od j tačo odrđo rjšj talas jdači za ktor jači lktričog polja, ili, pojdostaljo rčo, od j zrak sjtlosti tačo odrđog sjra i polarizacij). Drugi korak ć biti da izračuao rgiju oda pri tpraturi T. Na osou Maxwlloih jdačia dobija s da ktor jači lktričog polja E zadooljaa talasu jdačiu: 1 E E =, (.) t gdj j Laplaco [Pirr Sio d Laplac (Laplas), ] oprator. Rjšj jdači (.) ož s dobiti razdajaj prostorih i rskih projljiih: Er (, t) = f( t) ur) (, (.) gdj u i f zadooljaaju jdači: u = k u, (.4a) d f = ω f, (.4b) dt k j kostata, a ω = k. Rjšj jdači (.4b) j: () = f ( t+ ) f t si ω ϕ, (.5) gdj su f i ϕ proizolj kostat liči. Prtpostaio da su zidoi rzoatora (praougaoog oblika, slika.1) idalo propusi, tako da j tagcijala kopota polja jdaka uli a graicaa rzoatora (atatički s to izražaa jdačio E =, gdj j orala a poršiu rzoatora). Uz taka graiči uslo, rjšj Hlholtzo [H. Hlholtz (Hlholc), ] jdači (.4a) j oblika: 11
2 y a a z Slika.1 - Praougaoi rzoator. x L ux = x cos k1x si ky si kz uy = ysi k1x cos ky si k z, (.6) uz = z si k1x si ky coskz gdj, ako žlio da graiči uslo bud zadoolj a si ajski poršiaa rzoatora, ora biti: 1 k1 = π, k = π, k = π. (.7) a a L Kokrto, za x = a j sik 1 x =, pa j uy = uz =, što s i zahtja (graiči usloo). k 1, k i k su kopot alog ktora k koji odrđuj sjr prostiraja lktroagtog talasa, pri ču j k = k1 + k + k, či j odrđa i frkcija = k /( π ). Vliči 1,, su pozitii cijli broji koji prdstaljaju broj čoroa oda stojćg talasa u sjru x, y i z, rspktio. Maxwlloa jdačia E = odi a uslo ortogoalosti polja E i alog ktora k : k =. (.8) Uslo (.8) ukazuj a to da ktor lži u rai okoitoj a k. U toj rai za izbor sjra ktora ostaju sao da stpa slobod, što odgoara dja kopotaa polarizacij polja. To zači da saki skup broja ( 1,, ) odrđuj da oda polja koja s razlikuju po polarizaciji. Sako pobuđj lktroagtog polja ož s prdstaiti u idu su takih odoa polja. Izračuajo broj odoa,, odoso aplitudu alog N ( ) rzoatora koji iaju frkciju u itralu [ ] ktora k u itralu [, π / ]. Na osou jdači (.7), očito j da su u sistu koordiata k, 1 k, k oguć rijdosti k dat ktoria koji spajaju koordiati počtak sa čori tačkaa trodizioal rštk prikaza a slici.. Pošto su liči k1, k i k poziti, to uziao sao tačk koj lž u pozitio oktatu. Broj takih tačaka jdak j jdoj osii odosa zapri sfr sa ctro u koordiato počtku, radijusa π / i zapri ltar ćlij dizija π, π i π. Uziajući u obzir da sako k odgoaraju da oda polja (da zaisa a a L sjra polarizacij), dobijao: 1 4π π 8 8π N ( ) = = V, (.9) π π π a a L gdj j V zapria rzoatora. Broj odoa u jdiici zapri i u jdiičo frkto itralu j tada: 1 dn ( ) 8π =. (.1) V d 1
3 k π / L π / L π / a π / a π / a k Slika. - Dozolj rijdosti ktora k za rzoator u obliku praougaoika. π / a Prđio sada a drugi korak ašg probla alažja w ( T), i izračuajo srdju rgiju proizoljog oda u rzoatoru a tpraturi T. U skladu sa Boltzaoo statistiko, jroatoća da rgija datog oda rzoatora lži izđu E i E + de j proporcioala E / kbt de, tako da j srdja rgija oda: kt B E de E = = kt. (.11) E E kt B de B Traža spktrala gustoća rgij ož s izračuati kao proizod broja odoa u jdiici zapri i u jdiičo frkto itralu, (.1), i srdj rgij oda E, (.11): w ( ) 1 dn 8π = E = k B T. (.1) V d To j pozata Rayligh-Jasoa [Lord Rayligh (Rjli), , i J. Jas (Džis), ] forula. Ta forula j u suprotosti sa kspritali rzultatia za lik rijdosti frkcij (za al rijdosti slagaj torij i ksprita j rlo dobro). Štaiš, postaj očigldo da ta forula ij ispraa ako s pokuša izračuati itgrala gustoća rgij w= w d. Na osou (.1), dobija s da w, što zači da klasiča torija daj ispra rzultat za zračj crog tijla. Dirgcija gustoć rgij w j pozata pod azio ultraljubičasta katastrofa. Probl j rijšio Plack uodći hipotzu o sjtlosi katia. Po toj hipotzi rgija datog oda rzoatora ož da popria proizolj rijdosti od do, kao što j to prtpostaljo pri izođju forul (.11), ć sao porcij rgij oblika E = h, gdj j pozitia cijli broj, a h ka kostata (koja j kasij azaa Plackoo kostato). Tada u (.11) ujsto itgrala iao su i rijdi: = h kt B h = E = = h kt B k 1 h. (.1) 1 h kt B 1
4 Ta forula s suštiski razlikuj od (.11). U graičo slučaju kada h, forula (.1) s sodi a (.11) (uprao lis h odgoara prlazu sa kat a klasiču toriju). Traža Plackoa forula s dobija a osou (.1) i (.1) i glasi: w 8π = h h kt B 1. (.14) Ta forula j u saglasosti sa kspritia. Na osou Placko forul (.14), za totalu gustoću rgij zračja crog tijla dobija s: 4 4 8π 8π kt B w d h x h kt B h d x dx w= = =, π kb 16 J w= a T, a= = 7, ( 5) 1, 4 15ch K (.15) 4 xdx π gdj j korišta forula =, a j idks prlaaja srdi x ( = c/ ). Čsto s ujsto 1 15 zaprisk gustoć w koristi ličia M - kscitacija ili isioa sposobost. Oa prdstalja gustoću izlazog fluksa zračja i pozaa sa gustoćo rgij w forulo (idjti zadatak.): tako da j: M = w, (.16) 4 ac 4 W M = σt, σ = = 5,67 51( 19) K. (.17) Oa rlacija prdstalja pozati Stfa-Boltzao zako [J. Stfa (Štfa), ], a kostata σ s azia Stfa-Boltzaoa kostata. Slika. Eisioa sposobost M λ zračja crog tijla kao fukcija talas duži za različit tpratur. Na slici j ozača idljia oblast spktra (osjči dio) i kria koja odgoara Vioo zakou pojraja (isprkidaa liija). 14
5 M Ekspritalo s običo jri spktrala isioa sposobost M = λ M λ = λ kao fukcija talas duži (idjti zadatk. i.). Na slici. prikazaa j zaisost od λ za čtiri različit rijdosti tpratur T. Vidio da fukcija M λ ( λ ) ia aksiu pri odrđoj rijdosti λ. Itrsuj as kaka j raspodjla gustoć rgij po talasi dužiaa M λ w λ 4 = M i kako talasa dužia koja odgoara aksialoj rijdosti w λ, λ ax, zaisi od tpratur. Rzultat t aaliz (idjti zadatak.) j Wio [W. Wi (Vi), ] zako pojraja: λ ax 1 b =, b =, ( 4) 1 K. (.18) T Udio apsorpciou spktralu sposobost ili koficijt apsorpcij zračja frkcij, A, kao odos rgij koju apsorbuj lt porši tijla u jdoj skudi u frkto itralu (, + d ), i total rgij koja pada u jdoj skudi a taj lt porši, u isto frkto itralu. Pra drugo Kirchhoffoo zakou, odos isio i apsorpcio spktral sposobosti proizoljog tijla u raotžo staju j: M = w. (.19) A 4 Za apsoluto cro tijlo (pr. šuplji rzoator sa ali otoro, slika.4; zračj koj uđ u rzoator u potpuosti s apsorbuj) j A = 1. Za stara tijla j A < 1, tako da j i itgrala isioa sposobost takih tijla aja. Kokrto, oa j M = κ M, gdj j M dato sa (.17) i odosi s a apsoluto cro tijlo, a κ j koficijt koji zaisi od rst atrijala i tpratur [pr. κ olfra ( T = 15 K) = 15, ]. λ Slika.4 - Modl apsoluto crog tijla. U opšt slučaju, od ukup rgij E (odrđ frkcij) koja pad a poršiu bilo kojg fizikalog sista, dio s rflktuj ( E r ), dio apsorbuj ( E a ), a prostali dio prođ kroz sist ( E t ). Na osou zakoa očuaja rgij j E = Er + Ea + E t, tako da, ako udo spktral koficijt rflksij ρ = E / E r, apsorpcij α = E / E a i trasisij τ = E / E t, rijdi: ρ + α + τ = 1. (.). Atoski i olkulari spktri Pozaaj atoskih i olkularih sista i jihoih spktara j ažo za shataj rada lasrskih urđaja. U opšt slučaju, ukupa rgija olkula sastoji s od čtiri dopriosa: E = E + E + Er + Et, (.1) gdj j E - lktroska rgija, uzrokoaa krtaj lktroa oko jzgra (rgija lktroskog ootača olkula), E - ibracioa rgija, pozaa sa oscilacijaa jzgara atoa koji ulaz u sasta olkula oko jihoog raotžog položaja, E r - rotacioa rgija, uzrokoaa rotacijo olkula (kao cjli), a E t - rgija traslacioog krtaja. Ergija E t s katizira, tako da ćo j isključiti iz ašg razatraja. Ostal tri rgij s katiziraju i fotoi s ituju ili apsorbuju kada sist prlazi iz jdog staja u drugo. Ergija takih fotoa j odrđa forulo: 15
6 h = ΔE + ΔE + ΔEr, (.) gdj su sa ΔE, ΔE i ΔE r ozač razlik rgija izđu lktroskih, ibracioih i rotacioih ioa, rspktio. Procijio rd liči tih rgija. Elktroska rgija ož s procijiti polazći od izraza za rgiju lktroa u atou odoika: E 1 h =, = 1,,, =, (.) a π gdj j asa lktroa, = 9, kg, a a Bohro radijus, 1 a ( ) =, Taj izraz s ož izsti polazći od Bohroih postulata ili, a strožiji ači, korištj foraliza kat haik. Odatl zaključujo da j: ( ) ΔE, (.4) a gdj j sa a ozač radijus atoa ili olkula. Korištj kat haik ož s pokazati da j razlika rgija da ibracioa ioa doatosk olkul data sa: ΔE κ 1 /, (.5) M gdj j M asa atoa, a κ koficijt lastičosti pri itrakciji da atoa [sila prilačja f = κ( r r ), r - raotži položaj]. Pojraj atoa jdog u odosu a drugi za rastojaj a doodi do izj rgij približo za ΔE, tako da ožo procijiti da j κ ΔE a, pa j: ΔE M 1 / ΔE. (.6) Pra katoj haici, rotacioa rgija doatoskog olkula j: E r = ( + ) J J 1, (.7) Ma gdj j J cijli pozitia broj (rotacioi kati broj) a Ma j ot ircij olkula (idjti zadatak 6.1). Razlika rotacioih rgija pri prlazu izđu da susjda ioa (slkcioo prailo Δ J =±1) j približo: 1/ ΔEr ΔE Ma M. (.8) Na osou forula (.4), (.6) i (.8), i toga što j / M 1 4, zaključujo da j ΔE ( 1 1) V što odgoara idljio i ultraljubičasto području talasih dužia, 4 ΔE ( 1, 1, ) V i ΔE r ( 1 1 ) V. Na slici.5 j prikaza jda prijr lktroskog spktra doatosk olkul. Ozak ispod liija spktra odos s a : - lktroski spktar, - lktrosko-ibracioi spktar i r - lktrosko-ibracioo-rotacioi spktar. Na kraju ooga odjljka utrdio k od osoih pojoa. U skladu sa zakoia kat haik, rgija lktroa zaog u atou, kao i rgija cijlog atoa, ož popriati proizolj rijdosti. Moguć diskrt rijdosti rgij E, E 1,, E, aziaju s rgtski ioia. Skup rgtskih ioa dfiiš rgtski spktar sista. Diskrtost rgtskog spktra sojsta j sako sistu itragujućih katih čstica: olkulia, joia, črsti tijlia, itd. Nio sa ajižo rgijo azia s osoi io E, a ostali ioi E1, E,, E,, E,, koji odgoaraju ći rgijaa, aziaju s pobuđi ioi. U odrđi usloia itrakcij ikročstica, lktro ož da prskoči sa jdog rgtskog ioa (pr. E ) / 16
7 a drugi io (pr. E ). Pri tako prlazu ato apsorbuj ili ituj lktroagti talas kao odrđu porciju - kat rgij - foto h. Frkcija lktroagtog talasa pri kato prlazu dfiisaa j drugi Bohroi postulato (forulisai 191. godi): E E E 1 r Slika.5 - Prijr rgtskog spktra doatosk olkul. = ( E E )/ h. (.9) Pri apsorpciji fotoa rgija atoa s poćaa za ličiu h i dolazi do katog prlaza atoa sa ižg ioa E a iši E, a pri isiji fotoa frkcij dolazi do prlaza atoa sa išg ioa E a iži io E. Frkti spktar j skup frkcija lktroagtih talasa koj ituju ili apsorbuju atoi srdi i tijso j poza sa rgtski spktro atoa. Uprao diskrtošću rgtskog spktra s i objašjaa liijski karaktr apsorpcioih i isioih spktara lktroagtih talasa. Napoio da isu ogući bilo kaki prlazi izđu različitih katih staja atoa ili olkula. Nki prlazi su dozolji, a ki zabraji. U katoj haici postoj izbora praila koja odrđuju ogućost katog prlaza iz jdog rgtskog staja u drugo. Prijo foraliza kat haik ogu s izračuati jroatoć odrđih prlaza. Nio sa kojga su prlazi zabraji izbori prailia, i koji, ako što j pobuđ, ož da postoji rlatio dugo ra, azia s tastabili io.. Širia i fora spktral liij Do sada so prtpostaljali da su rgtski ioi bskoačo uski. U skladu s ti i spktrala liija frkcij, koja odgoara prlazu sa ioa E a io E, (.9), j bskoačo uska i kažo da j joj odgoarajući lktroagti talas oohroatski. To j idalizacija. Saki rali talas lasrskog zračja j kazioohroatski, tj. to j talas sa srdjo (ctralo) frkcijo, pri kojoj j rgija lktroagtog zračja aksiala, i ko širio Δ. Frkti itral u graicaa kojga j itzitt itoaog ili apsorboaog zračja da puta aji od aksialog itzitta azia s širia spktral liij Δ. Osoi uzrok širja spktralih liija j sajj ra žiota pobuđih katih staja. Nai, u katoj haici postoji tz. Hisbrgoa [W. Hisbrg (Hajzbrg), ] rlacija odrđosti po kojoj j proizod 17
8 odrđosti rgij i ra rda liči = h /π. Kokrto, ako su τ i τ ra žiota čstic a ioia i tada j odrđost razlik ioa E E data sa (idjti sliku.6): 1 1 Δ E =Δ E +ΔE + =, (.) τ τ τ što zači da j odrđost frkcij, tj. širia spktral liij: 1 Δ. (.1) πτ Δ E ΔE g G E ΔE Δ g G idali ioi rali ioi Slika.6 - Idali i rali rgtski ioi i jiho širi. Pra to, ako j spotao rij žiota τ sp = 1/ A, širia spktral liij, uzrokoaa spotao isijo, j: A Δ,N =. (.) π To j tz. priroda širia spktral liij (idks N potič od glsk rijči atural = priroda). Da j τ sp zaista spotao rij žiota kat čstic a pobuđo iou ož s pokazati slijdćo aalizo. Broj čstica koj spotao apuštaju pobuđi rgtski io u rsko A / t t sp itralu dt j dn = A N dt, odakl j N ( t) = N ( ) = N ( ) τ, pa j τ sp rij za koj s asljost pobuđog ioa saji puta, a to j uprao dfiicija ra žiota. Priroda širia liij j običo ala. Pošto oa ij pozaa i sa kaki ajski uticaj, oa s ož jštački sajiti. Fora spktral liij koja odgoara prirodo širju j tz. Lortzoa [H. A. Lortz (Lorc), ] fora liij (slika.7), čiji atatički oblik j: 1 Δ / g L (, ) = π, (.) + Δ / ( ) ( ) pri ču su uslo oriraja i aksiala rijdost dati sa: ax ( ) ( ) ( ) g, d = 1, g = g, = / π Δ,67 / Δ. (.4) L L L 18
9 ( ) g Δ, 1 g G ax.75 g L ax.5 g ax G / g ax L /.5 Δ Gaussoa Lortzoa Slika.7 - Porđj Lortzo i Gausso for liij. Obadij kri su orira i odos s a 11 istu širiu Δ = 1, 7 1 Hz, koja odgoara poloii aksiua prirodo prošir liij 14 rubiskog lasra sa = 4, 6 1 Hz. Spotaa isija ij jdii uzrok širja spktral liij. Praktiča širia spktral liij j čsto zato ća od prirod. Širja spktralih liija s ogu podijliti a hooga i hooga. Hoogo širj, u koj spada i prirodo širj, j tako širj kod kojg s liija sakog pojdiog atoa, pa pra to i cijlog sista, širi u jdako stpu. Nasuprot to, haiza širja liija j hoog, kada o djluj a taka ači da su rzoat frkcij pojdiih atoa rasporđ u koj traci frkcija i liija cijlog sista izglda prošira i kada a širja liija pojdiih atoa. Pord prirodog širja u hoogo širj liija spada i tz. sudaro širj. Kod gasoa do takog širja dolazi uslijd sudara atoa sa drugi atoia, joia, slobodi lktroia ili zidoia rzoatora. Kod črstih tijla sudaro širj j posljdica itrakcij atoa sa rštko (kristala). Sudari arušaaju procs kohrt itrakcij atoa sa upadi lktroagti talaso. Fora liij j i u oo slučaju Lortzoa, a širia liij j odrđa srdji ro izđu da sudara τ c (glski: collisio = sudar), tačij: Δ,L Hz 1 =. (.5) πτ c Trba apouti da postoji suštiska razlika izđu sudarog širja liija i lastičih sudarih procsa koji su odgoori za prlaz bz isij ili apsorpcij fotoa. Pri lastiči sudari procsia ato prdaj soju rgiju susjdi olkulia - dolazi do rlaksacij. S drug stra, širj liija ož biti izazao i lastiči i lastiči sudaria koji dood do slučajih proja faz itoaog lktroagtog talasa. Do hoogog širja spktral liij koju ituju olkul dolazi u slučaju kada saki ato ia soju karaktrističu frkciju prlaza. Prijr j tz. Dopplroo [J. C. Dopplr (Doplr), ] širj u gasoiti aktii srdiaa. Uslijd toga što s atoi krću u različiti sjroia i sa različiti brzia, u isioo ili apsorpcioo spktru s pojaljuju a 19
10 frkcij odrđ Dopplroi poako frkcija =±. U to slučaju, u a c trodiaičkoj raotži, fora spktral liij j Gaussoa [K. F. Gauss (Gaus), ]: 1 / g l l (, ) xp G = Δ, π D D ( ) ( Δ, / ), (.6) a Dopplroa širia liij j [pri to s podrazuija Maxwlloa raspodjla čstica (atoa as M) po brziaa]: 1/ kt B,D Δ = l. (.7) Mc Dopplroo širj j aročito izražo kod gasoitih aktiih srdia, dok j kod črstih tijla oo alo jr su kod jih joi u aktioj srdii črsto zai sa kristalo rštko i ogu s u proj aproksiaciji satrati pokrti. Na slici.7 su prikaza prirodo (Lortzoa fora) i Dopplroski (Gaussoa fora) prošir spktral liij. U slučaju Gausso for liij, aalogo jdači (.4) su rlacij: 1/ ax l,99 gg(, ) d= 1, gg = gg(, ) = Δ π Δ. (.8) Kod črstih aktiih srdia začaja uzrok širja liija su hoogosti kristala i oscilacij rštk. Što j iša tpratura kristala, to su oscilacij ć. Joi s alaz u projljio polju koj ijja položaj rgtskih ioa, a ti, i širiu spktral liij. Stp toplotog širja odrđ j zo joa sa kristalo rštko. Pord oih, postoj i drugi uzroci širja liija, kao što su pr. Zao [P. Za (Za), ] i Starko [J. Stark (Štark), ] fkt. Pod djloaj ajskog agtog i lktričog polja dolazi do poaka rgtskih ioa. Npr. rgtski io E s pojra ΔE, tako da s, do tada jdisti io, pocijpa a koliko ( ) različitih podioa. Broj g stp dgracij ioa. Cijpaj rgtskog ioa (koj i doodi do jgoog širja), pod djsto agtog polja azia s Zao fkat, a cijpaj i širj ioa pod djloaj lktričog polja azia s Starko fkat. Kao i Dopplroo širj, i oa širja liija opisaa su Gaussoo raspodjlo. Razlog j to što bilo koji haiza koji izazia slučaju raspodjlu rzoatih frkcija atoa doodi do širja koj ia Gaussou foru. Nadi haizi širja liija čsto djluju istoro, pri ču su u različiti situacijaa pojdii od jih različito izraži. Čsto dolazi do kobiacij Gausso i Lortzo for liij. Nki prijri širja liija razotri su u zadatku.5..4 Vza spota i stiulisa isij i apsorpcij - Eistio trodiaički pristup Prtpostaio da iao rzoator - cro tijlo, čiji s zidoi održaaju a kostatoj tpraturi T. Kada j sist u trodiaičkoj raotži srdia uutar rzoatora s alazi u polju zračja čija j spktrala gustoća rgij data Plackoo forulo (.14). U srdii s odijaju procsi spota isij, stiulisa isij i apsorpcij. Pošto s cijli sist alazi u staju trodiaičk raotž, broj prlaza sa ižg rgtskog ioa a iši io ora biti jdak broju prlaza sa ioa a io. Ozačio jroatoću apsorpcij sa W, jroatoću stiulisa isij sa W i jroatoću spota isij sa A. Udio kostat koficijt i B (tz. Eistio koficijt B ): B W B w, W B w = =, (.9a,b) g
11 gdj j dato sa (.9). Nka su N i N raotž asljosti ioa i. Tada uslo trodiaičk raotž glasi: A N + B w N = B w N. (.4) Pra Boltzaooj statistici j: N g h = xp N g k T, (.41) B gdj su g i g statističk tži ili stpi dgracij datih ioa, tj. broji katih staja sa isti rgijaa. Tada s, a osou (.4), dobija: w = ga h kt B gb gb. (.4) Porđj (.4) sa Plackoo forulo (.14), zaključujo da j: 8π gb = gb, A = B h = B8πh. (.4a,b) Jdačia (.4a) pokazuj da su jroatoća apsorpcij i jroatoća stiulisa isij, uzrokoa zračj crog tijla, u slučaju jdak dgracij ioa ( g = g ), jdak. Jdačia (.4b) oogućaa da s izračua koficijt B A a osou pozatog kojficijta. Koficijt s ož izračuati prijo foraliza kat haik. Napoio da su pord katih prlaza sa isijo fotoa ogući i kati prlazi bz učšća fotoa. U to slučaju kat čstic itraguju sa drugi čsticaa (pr. sudari čstica). Dfiišio jroatoću prlaza bz isij fotoa kao srdji broj akata prdaj ili prija kata rgij jd čstic u jdiici ra. Ukupa jroatoća katog prlaza jroatoća prlaza uz isiju i prlaza bz isij fotoa: S B P jdaka j sui P = A + W + S. (.44) Pra foruli (.4) ličia B A rast proporcioalo sa trći stpo frkcij (u odosu a ), što zači da doprios spota isij ukupoj isiji brzo rast sa frkcijo. I zaista, u ifracroj i dalkoj ifracroj oblasti spktra spotaa isija j zaarljio ala i proladaaju spotai prlazi bz isij fotoa..5 Vjroatoća apsorpcij i stiulisa isij U oo odjljku ćo prdstaiti rzultat za jroatoću apsorpcij i stiulisa isij izd prijo poluklasič torij. Pri tako pristupu atoski sist s opisuj zakoia kat haik, a lktroagto polj upadog talasa zračja opisuj s klasičo - pooću Maxwlloih jdačia. U slučaju stiulisa isij u prisustu lasrskog polja, poluklasiča torija daj sasi zadooljaajuć rzultat. Za spotau isiju potrbo j priijiti potpuo kati pristup, tz. kato-lktrodiaičku toriju. Kato-haičko izođj pokazuj da j jroatoća apsorpcij (u jdiici ra) fotoa, + d, pri ču lktro sa ižg ioa prlazi a iši io sa frkcijo iz itrala [ ] ( h = E E ), data sa: 1
12 π μ W d = g w d. (.45), ε h (, ) U jdačii (.45) μ j odul atričog lta lktričog dipolog ota, koji zaisi od prirod srdi (idjti zadatak.6), a g(, ) j fukcija koja opisuj foru spktral liij [pr. Lortzoa fora, (.), ili Gaussoa fora, (.6)]. Fukcija g (, ) j oriraa g(, ) d= 1, a jzi kokrti oblik zaisi od haiza širja liij i ož s izračuati a osou kspritalo izjrog oblika isio liij. Širia spktral liij običo j rlo uska, tako da fukcija g(, ) ia oštar aksiu za = i poaša s kao Diracoa δ -fukcija, za koju rijdi: dx f ( x ) δ ( x x ) = f ( x ), gdj oblast itgriraja obuhata tačku x = x, a f( x ) j proizolja fukcija. Itgriraj (.45) po frkciji, u usko itralu oko (što odgoara proširoj spktraloj liiji), i koristći forulu d g(, ) w = w dobijao: W, za jroatoću apsorpcij π μ = h w. (.46) ε Na osou jdačia (.9), (.4) i (.46), zaključujo da su rijdosti Eistioih koficijata A i B dat sa: za apsorpciju: za stiulisau isiju: za spotau isiju: B B A π μ =, (.47a) ε h π g μ =, (.47b) ε h g g = = 16π 1 μ εhc g τs p,. (.47c) Jdačia (.47c) ukazuj a to da j jroatoća spota isij A proporcioala sa trći stpo frkcij prlaza sa ioa a io, pri ču koficijt proporcioalosti zaisi od karaktristika srdi. Izraz za Eistio koficijt spota isij koji so dobili porđj rzultata poluklasičog i trodiaičkog pristupa, ož s izsti i dirkti katolktrodiaički izođj (idtičost dobijih rzultata ukazuj a to da j Plackoa forula korkta i sa staoišta kat lktrodiaik). Itzitt lktroagtog talasa I prdstalja rgiju koja u jdiici ra prođ kroz jdiicu porši, okoito a sjr rg skog fluksa. O j odrđ Poytigoi [J. H. Poytig (Poitig), ] ktoro t S = E H, I = Id = E H. Uziajući u obzir da j spktrali itzitt ukupog lktroagtog talasa: I = w, (.48) a osou jdačia (.9), (.4a) i (.46), dobija s: W g π μ W I g ε h c = =, (.49) što zači da su jroatoća apsorpcij i jroatoća stiulisa isij dirkto proporcioal itzittu upadog lktroagtog talasa.
13 .6 Prsjk prlaza. Koficijti apsorpcij i pojačaja U pro poglalju dfiisali so prsjk za stiulisau isiju σ 1 izrazo (1.4): W1 = σ 1F, a prsjk za apsorpciju σ 1 sa (1.6): W1 = σ1f. Aalogo s ož dfiisati prsjk prlaza sa ioa a io, u prisustu lktroagtog polja frkcij, kao: ( ) W, / σ = F, (.5) gdj j F spktrala gustoća fluksa upadog lktroagtog talasa ( itralu h, h( + d) Fd j broj fotoa rgij u, koji u jdiici ra prođ kroz jdiicu porši okoito a ju): F = I / h. (.51) Na osou jdačia (.45), (.47a), (.48), (.5) i (.51), dobija s da j prsjk za apsorpciju: μ σ. (.5) ( ) h π h = B g(, ) = g(, ) = B, ε hc Vza prsjka za apsorpciju i prsjka za stiulisau isiju j, a osou (.47b), data sa: g σ ( ) = σ ( ). (.5) g Dakl, prsjk zaisi od osobia srdi [faktori lktroagtog talasa. Izja spktral gustoć fluksa fotoa frkcij, isij i apsorpcij u sloju dblji dz (slika 1.), j: μ / i g (, ) i frkcij upadog df, uzrokoaa procsia stiulisa g df = ( Nσ Nσ ) Fdz = σ N N Fdz. (.54) g Da biso shatili fizikali sisao prsjka prtpostaio da s si atoi alaz a iž rgtsko iou, tj. da j N = i N = N t, gdj j N t totala asljost. Tada s jdačia (.54) sodi a: df = σ. (.55) N F dz t Prtpostaio da s za saki ato ož usti fktii prsjk za apsorpciju fotoa σ a (slika.8; ako foto pad u taj prsjk, ato ga apsorbuj). Ozačio poršiu poprčog prsjka srdi kroz koju s prostir lktroagti talas sa S. Broj atoa u sloju dblji dz, koj osjtljaa taj lktroagti talas, jdak j NSdz t, a ličia σ ansdz t j ukupi prsjk apsorpcij. σ a S Slika.8 - Efktii prsjk apsorpcij σ a atoo koji s alazi u sopu lktroagtog talasa sa prsjko S. Pra to, rlatia proja broja fotoa u sloju dblji dz j: df F σ a t / = N Sdz / S. (.56)
14 Porđj (.55) i (.56) dobija s da j σ = σ, što zači da su prsjk prlaza i fktii prsjk apsorpcij jda ista ličia. Drugi paratar koji opisuj itrakciju zračja sa atrijo j koficijt α, dfiisa sa: Ako j a g α ( ) = σ ( ) N N g. (.57) N g > g N, tada paratar α karaktriš apsorpciju zračja i azia s koficijt apsorpcij. Paratar α j pogoda zbog toga što s ož posrdo izjriti. Na osou jdačia (.54) i (.57) j df = α ( ) Fdz, tako da j odos spktral gustoć fluksa fotoa koji j prošao kroz sloj dblji l i spktral gustoć fluksa fotoa koji osjtljaa srdiu dat sa F () l / F ( ) = xp ( α ( ) l). Ekspritalo jrj ooga odosa daj rijdost koficijt α za kokrtu talasu dužiu λ = / upad sjtlosti. Odgoarajući prsjk prlaza s tada ož dobiti a osou (.57), ako su pozat asljosti i stpi dgracij ioa i. U slučaju kada N g E E s srdia alazi u trodiaičkoj raotži, odos asljosti ioa j: = xp, N g kbt i, ako su pozati stpi dgracij ioa i totala asljost Nt = N + N, a osou t rlacij ogu s odrditi asljosti ioa N i N. Urđaj za jrj koficijta apsorpcij azia s apsorpcioi spktrofototar. g Ako j N < N koficijt apsorpcij α postaj gatia. U to slučaju pogodij j usti g ou ličiu - koficijt pojačaja γ : g γ ( ) = α ( ) = σ ( ) N N g. (.58) Kada j γ > lktroagti talas u srdii ć s pojačaati. Kao zaključak, ožo rći da so dfiisali tri liči koj karaktrišu prlaz: W, σ i α (odoso γ ). T liči prdstaljaju tri različita ačia da s opišu poja apsorpcij i stiulisa isij. Vjroatoća prlaza W ia jdostaa fizikali sisao [idjti jdačiu (1.): ( dn / dt) = W N i (1.5): d st 1 N1/ dt = W1N 1] i ož s jdostao izračuati prijo katohaičkog pristupa. Prsjk prlaza σ zaisi isključio od osobia dat srdi. Koficijt apsorpcij α j paratar koji s ož kspritalo izjriti. 4
Polarizacija. Procesi nastajanja polarizirane svjetlosti: a) refleksija b) raspršenje c) dvolom d) dikroizam
 Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Polarzacja Proces asajaja polarzrae svjelos: a refleksja b raspršeje c dvolom d dkrozam Freselove jedadžbe Svjelos prelaz z opčkog sredsva deksa loma 1 u sredsvo deksa loma, dolaz do: refleksje (prema
Astronomija i astrofizika Predavanje 5 Temeljne astrofizičke veličine: Zvjezdani spektri i temperatura zvijezda
 Astroomija i astrofizika Prdavaj 5 Tmlj astrofizičk vliči: vjzdai spktri i tmpratura zvijzda Astroomija i astrofizika 005 Astroomija i astrofizika 005 Spktri zvijzda i fktiv tmpratur zvijzda Astroomija
Astroomija i astrofizika Prdavaj 5 Tmlj astrofizičk vliči: vjzdai spktri i tmpratura zvijzda Astroomija i astrofizika 005 Astroomija i astrofizika 005 Spktri zvijzda i fktiv tmpratur zvijzda Astroomija
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Dvanaesti praktikum iz Analize 1
 Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
VILJUŠKARI. 1. Viljuškar se koristi za utovar standardnih euro-pool paleta na drumsko vozilo u sistemu prikazanom na slici.
 VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
VILJUŠKARI 1. Viljuškar e korii za uoar andardnih euro-pool palea na druko ozilo u ieu prikazano na lici. PALETOMAT a) Koliko reba iljuškara da bi ree uoara kaiona u koji aje palea bilo anje od 6 in, ako
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI. NEUTRALNI ELEMENT GRUPOIDA.
 KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
KOMUTATIVNI I ASOCIJATIVNI GRUPOIDI NEUTRALNI ELEMENT GRUPOIDA 1 Grupoid (G, ) je asocijativa akko važi ( x, y, z G) x (y z) = (x y) z Grupoid (G, ) je komutativa akko važi ( x, y G) x y = y x Asocijativa
Sistem sučeljnih sila
 Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
Sistm sučljnih sila Gomtrijski i analitički način slaganja sila, projkcija sil na osu i na ravan, uslovi ravnotž Sistm sučljnih sila Za sistm sila s kaž da j sučljni ukoliko sil imaju zajdničku napadnu
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
LINEARNE TRANSFORMACIJE. predavanje str. 1.
 INENE TNSFOMCIJE. prdavaj 7..6. sr.. FUNKCIJE, TNSFOMCIJE S U, OPETOI N Fukija j pravilo f koj svako lu skupa pridružuj jda i sao jda l skupa B. ko f lu a pridružuj l b, oda s piš f ( a) b i kaž s da j
INENE TNSFOMCIJE. prdavaj 7..6. sr.. FUNKCIJE, TNSFOMCIJE S U, OPETOI N Fukija j pravilo f koj svako lu skupa pridružuj jda i sao jda l skupa B. ko f lu a pridružuj l b, oda s piš f ( a) b i kaž s da j
Ovo nam govori da funkcija nije ni parna ni neparna, odnosno da nije simetrična ni u odnosu na y osu ni u odnosu na
 . Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
. Ispitati tok i skicirati grafik funkcij = Oblast dfinisanosti (domn) Ova funkcija j svuda dfinisana, jr nma razlomka a funkcija j dfinisana za svako iz skupa R. Dakl (, ). Ovo nam odmah govori da funkcija
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Dekompozicija DFT. Brzi algoritmi na bazi radix-2. Brza Furijeova transofrmacija. Tačnost izračunavanja. Kompleksna FFT OASDSP 1: 7 FFT
 OASDSP : 7 FFT Dkompozicija DFT Brzi algoritmi a bazi radix- Brza Furijova trasofrmacija Tačost izračuavaja Komplksa FFT ovi Sad, Oktobar 5 straa OASDSP : 7 FFT Brza trasformacija : itrativa dkompozicija
OASDSP : 7 FFT Dkompozicija DFT Brzi algoritmi a bazi radix- Brza Furijova trasofrmacija Tačost izračuavaja Komplksa FFT ovi Sad, Oktobar 5 straa OASDSP : 7 FFT Brza trasformacija : itrativa dkompozicija
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
10.1. Bit Error Rate Test
 .. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
.. Bt Error Rat Tst.. Bt Error Rat Tst Zadata. Izračuat otrba broj rth formacoh bta u BER tstu za,, ogršo dttovaa bta a rjmu, tao da s u sstmu sa brzoom sgalzacj od Mbs mož tvrdt da j vrovatoća grš rosa
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Elektrotehnički fakultet univerziteta u Beogradu 26. jun Katedra za Računarsku tehniku i informatiku
 Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Elektrotehički fakultet uiverziteta u Beogradu 6. ju 008. Katedra za Račuarku tehiku i iformatiku Performae račuarkih itema Rešeja zadataka..videti predavaja.. Kretaje Verovatoća Opi 4 4 Kretaje u itom
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
Granične vrednosti realnih nizova
 Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
Graiče vredosti realih izova Fukcija f : N R, gde je N skup prirodih brojeva a R skup realih brojeva, zove se iz realih brojeva ili reala iz. Opšti čla iza f je f(), N, i običo se obeležava sa f, dok se
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
 1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
Diskretizacija spektra - DFT
 OASDSP : 4. Dirtizacija igala i ptra Dirtizacija u vrmu Torma o odabiraju Izobličja u odabiraju Dirtizacija ptra - DFT ovi Sad, Otobar 5 traa OASDSP : 4. Dirtizacija igala i ptra Dirtizacija vrma : torma
OASDSP : 4. Dirtizacija igala i ptra Dirtizacija u vrmu Torma o odabiraju Izobličja u odabiraju Dirtizacija ptra - DFT ovi Sad, Otobar 5 traa OASDSP : 4. Dirtizacija igala i ptra Dirtizacija vrma : torma
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Analitička geometrija i linearna algebra. Kartezijev trodimenzionalni pravokutni koordinatni sustav čine 3 međusobno okomite osi: Ox os apscisa,
 Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
Alitičk geoetrij i lier lger Vektori KOORDINATNI SUSTAV Krteijev prvokuti koorditi sustv Krteijev trodieioli prvokuti koorditi sustv čie eđusoo okoite osi: O os pscis O os ordit O os plikt točk O ishodište
Rešenja A/2 kolokvijuma iz predmeta MERNI SISTEMI U TELEKOMUNIKACIJAMA 10. januar 2006.
 šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
šnj A/ kolokvijum iz prdmt MENI SISEMI U ELEKOMUNIKACIJAMA. jnur. Zdtk. D i prikznim urđjm mogl mriti mplitud čtvrtog hrmonik u mmorijki lok tr d ud upin ditrovn zin unkcij ( t) y co π Izlz iz urđj j td
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
( x) ( ) dy df dg. =, ( x) e = e, ( ) ' x. Zadatak 001 (Marinela, gimnazija) Nađite derivaciju funkcije f(x) = a + b x. ( ) ( )
 Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
Zadatak (Mariela, gimazija) Nađite derivaciju fukcije f() a + b c + d Rješeje Neka su f(), g(), h() fukcije ezavise varijable, a f (), g (), h () derivacije tih fukcija po Osova pravila deriviraja Derivacija
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK
 SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
SISTEMI DIFERENCIJALNIH JEDNAČINA - ZADACI NORMALNI OBLIK. Rši sism jdnačina: d 7 d d d Ršnj: Ša j idja kod ovih zadaaka? Jdnu od jdnačina difrniramo, o js nađmo izvod l jdnačin i u zamnimo drugu jdnačinu.
ZI. NEODREðENI INTEGRALI
 ZI. Nodrđni intgrali 7 ZI. NEODREðENI INTEGRALI. Antidrvacij. Pronañi tri antidrivacij funkcij.. Odrdi sv antidrivacij funkcij.. Pronañi dvij antidrivacij funkcij.. Pronañi antidrivaciju funkcij za koju
ZI. Nodrđni intgrali 7 ZI. NEODREðENI INTEGRALI. Antidrvacij. Pronañi tri antidrivacij funkcij.. Odrdi sv antidrivacij funkcij.. Pronañi dvij antidrivacij funkcij.. Pronañi antidrivaciju funkcij za koju
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
3n an = 4n3/2 +2n+ n 5n 3/2 +5n+2 n a 2 n = n 2. ( 2) n Dodatak. = 0, lim n! 2n 6n + 1
 Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
Nizovi 5 a = 5 +3+ + 6 a = 3 00 + 00 3 +5 7 a = +)+) ) 3 3 8 a = 3 +3+ + +3 9 a = 3 5 0 a = 43/ ++ 5 3/ +5+ a = + + a = + ) 3 a = + + + 4 a = 3 3 + 3 ) 5 a = +++ 6 a = + ++ 3 a = +)!++)! +3)! a = ) +3
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Općenito, iznos normalne deformacije u smjeru normale n dan je izrazom:
 Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Otporost mterijl. Zdtk ZDTK: U točki čeliče kostrukije postvlje su tri osjetil z mjereje deformij prem slii. ri opterećeju kostrukije izmjeree su reltive ormle (dužiske deformije: b ( - b 3 - -6 - ( b
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
odvodi u okoliš? Rješenje 1. zadatka Zadano: q m =0,5 kg/s p 1 =1 bar =10 5 Pa zrak w 1 = 15 m/s z = z 2 -z 1 =100 m p 2 =7 bar = Pa
 .vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
.vježba iz Terodiaike rješeja zadataka 1. Zadatak Kopresor usisava 0,5 kg/s zraka tlaka 1 bar i 0 o C, tlači ga i istiskuje u eizolirai tlači cjevovod. Na ulazo presjeku usise cijevi brzia je 15 /s. Izlazi
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
DRUGI KOLOKVIJUM IZ MATEMATIKE 9x + 6y + z = 1 4x 2y + z = 1 x + 2y + 3z = 2. je neprekidna za a =
 x, y, z) 2 2 1 2. Rešiti jednačinu: 2 3 1 1 2 x = 1. x = 3. Odrediti rang matrice: rang 9x + 6y + z = 1 4x 2y + z = 1 x + 2y + 3z = 2. 2 0 1 1 1 3 1 5 2 8 14 10 3 11 13 15 = 4. Neka je A = x x N x < 7},
x, y, z) 2 2 1 2. Rešiti jednačinu: 2 3 1 1 2 x = 1. x = 3. Odrediti rang matrice: rang 9x + 6y + z = 1 4x 2y + z = 1 x + 2y + 3z = 2. 2 0 1 1 1 3 1 5 2 8 14 10 3 11 13 15 = 4. Neka je A = x x N x < 7},
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
v = = 4 = je vektor cu u n Npr. u = je vektor s komponentama u, u. v = su jednaki ako je u Vektori u Primjer 1 Vektori u
 VEKTORSKI PROSTOR. peaaje..5. st.. VEKTORI U R atie koje imaj koje samo jea stpa (tipa ) zo se -ektoi ili kaće ektoi. Np. je ekto s kompoetama,., K, Vektoi i s jeaki ako je i i za se i,, K,. Pimje Vektoi
VEKTORSKI PROSTOR. peaaje..5. st.. VEKTORI U R atie koje imaj koje samo jea stpa (tipa ) zo se -ektoi ili kaće ektoi. Np. je ekto s kompoetama,., K, Vektoi i s jeaki ako je i i za se i,, K,. Pimje Vektoi
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
II. ANALITIČKA GEOMETRIJA PROSTORA
 II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
II. NLITIČK GEMETRIJ RSTR I. I (Točka. Ravia.) d. sc. Mia Rodić Lipaović 9./. Točka u postou ( ; i, j, k ) Kateijev pavokuti koodiati sustav k i j T T (,, ) oložaj točke u postou je jedoačo odeñe jeim
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu 2. ARITMETICKI I GEOMETRIJSKI NIZ, RED, BINOMNI POUCAK. a n ti clan aritmetickog niza
 Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
Mte Vijug: Rijesei zdci iz mtemtike z sredju skolu. ARITMETICKI I GEOMETRIJKI NIZ, RED, BINOMNI POUCAK. Aritmeticki iz Opci oblik ritmetickog iz: + - d Gdje je: prvi cl ritmetickog iz ti cl ritmetickog
!"!# ""$ %%"" %$" &" %" "!'! " #$!
 " "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Teoremi srednje vrijednosti
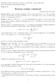 Fakultativi kolgij Studtska atjcaja iz matmatik, ak. god. 06./07. http://wb.math.pmf.uizg.hr/astava/studatj/ Tma br. 3: Tormi srdj vrijdosti Vjkoslav Kovač, 4. 3. 07. Torm Rollov torm srdj vrijdosti. Nka
Fakultativi kolgij Studtska atjcaja iz matmatik, ak. god. 06./07. http://wb.math.pmf.uizg.hr/astava/studatj/ Tma br. 3: Tormi srdj vrijdosti Vjkoslav Kovač, 4. 3. 07. Torm Rollov torm srdj vrijdosti. Nka
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Η Κβαντομηχανική. υπό ισχυρή συμπίεση
 Σημειώσεις Σ. Τραχανά Η Κβαντομηχανική υπό ισχυρή συμπίεση Σημειώσεις του Καθ. Στέφανου Τραχανά Τμ. Φυσικής, Παν/μιο Κρήτης Σημειώσεις Σ. Τραχανά Το μέλαν σώμα Ι. Τι είναι η ακτινοβολία του μέλανος σώματος
Σημειώσεις Σ. Τραχανά Η Κβαντομηχανική υπό ισχυρή συμπίεση Σημειώσεις του Καθ. Στέφανου Τραχανά Τμ. Φυσικής, Παν/μιο Κρήτης Σημειώσεις Σ. Τραχανά Το μέλαν σώμα Ι. Τι είναι η ακτινοβολία του μέλανος σώματος
Aritmetički i geometrijski niz
 Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
Zadac sa prethodh prjemh spta z matematke a Beogradskom uverztetu Artmetčk geometrjsk z. Artmetčk z. 00. FF Zbr prvh dvadeset člaova artmetčkog za čj je prv čla, a razlka A) 0 B) C) D) 880 E) 878. 000.
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
 r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
