Što je to struja (općenito)? = tok čestica kroz neku plohu u jedinici vremena -molekule tekućine struja tekućine (vode) -molekule plina struja plina
|
|
|
- Ξανθίππη Καλαμογδάρτης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Električna struja
2 Što je to struja (općenito)? = tok čestica kroz neku plohu u jedinici vremena -molekule tekućine struja tekućine (vode) -molekule plina struja plina (zraka, vjetar) -nabijene čestice električna struja
3 ELEKTRODINAMIKA Elektrostatika proučava naboje u mirovanju (ravnoteži) Elektrodinamika proučava pojave vezane uz naboje u gibanju Primjer 1: Nabijeni kondenzator spojimo ploče s vodičem pod utjecajem el. polja kondenzatora, elektroni će se gibati kroz vodič Primjer 2: Spojimo žarulju na bateriju pod utjecajem el. polja baterije, elektroni će se gibati kroz žarulju zagrijavanje nit žarulja svijetli Električna struja = usmjereno gibanje nosilaca naboja. nosilaca naboja? - elektroni u metalima - ioni u elektrolitičkim otopinama Tko tjera naboje u gibanje? Električno polje, odnosno razlika potencijala.
4 Električna struja Tko tjera naboje u gibanje? Električno polje, odnosno razlika potencijala. Ako polje koje djeluje zadržava čitavo vrijeme isti smjer (jakost polja se može mijenjati) Istosmjerna struja. Struja naboja uvijek u istom smjeru. Izmjenična struja - Ako polje koje djeluje mijenja smjer djelovanja u vremenu. Smjer struje naboja se takoñer mijenja.
5 Električna struja 2 gibanje elektrona u metalnoj žici Zašto elektroni "putuju" desno? Posljedica Franklinove teorije elektriciteta - "Fluid teče od mjesta gdje ga ima više prema mjestu gdje ga ima manje." "Smjer električne struje je smjer kojim bi se gibali pozitivno nabijeni el. naboji." Elektroni u vodiču se gibaju suprotno od smjera el. polja (el.struje). Smjer struje "od plusa ka minusu" se odnosi samo na vanjski krug struje. Unutar samog izvora, smjer struje je od negativnog prema poz. polu. I Zbog električnog polja, odnosno razlike potencijala.
6 Električna struja 2 gibanje elektrona u metalnoj žici 2 vdt Neka se svi elektroni gibaju s konstantnom brzinom v. Za vrijeme dt elektroni prevale put vdt. Koliko je elektrona za vrijeme dt prošlo vertikalnim presjekom žice? Onoliko koliko ih ima unutar volumena valjka visine vdt? n broj slobodnih elektrona u jedinici volumena žice Količina naboja koja proñe presjekom vodiča u vremenu dt? dq = nesvdt e - naboj elektrona
7 Električna struja 2 gibanje elektrona u metalnoj žici 3 dq = nesvdt vdt Jakost električne struje I = def = Količina naboja koja u jedinici vremena proñe presjekom žice. dq dq = nesvdt : dt I = = nesv [ I ] = [ A] dt Mjerna jedinica za jakost električne struje I? 1 AMPER 1 AMPER - Osnovna jedinica SI sustava 1 AMPER je jakost stalne električne struje koja prolazeći dvama usporednim, ravnim, beskonačno dugim vodičima zanemarivo malena kružnog presjeka, razmaknutim 1 m u vakuumu, uzrokuje meñu njima silu od njutna po metru duljine vodiča.
8 dq = Električna struja 2 gibanje elektrona u metalnoj žici 4 dq nesvdt I = = nesv Q C [ A] = dt = t s Praksa vrlo često se za jakost električne struje električna struja di Gustoća struje (def) J J = di J = = nev ds J = nev ds Gustoća struje J vektorska veličina proporcionalna srednjoj brzini gibanja nosilaca naboja (smjer? smjer gibanja pozitivnog naboja). I A S m [ J ] = = 2 Ako gustoća struje nije konstantna po cijelom presjeku, tada je: di = J ds I = J ds S ds vektor elementa površine, ima smjer normale na površinu
9 dq = Električna struja 2 gibanje elektrona u metalnoj žici 5 nesvdt di J = = nev J = nev ds Ako u vodiči postoje naboji različitih vrsta ukupni naboj koji proñe presjekom vodiča: ( ) dq = Sdt n q v + n q v Gibanje naboja u vodiču fizikalna stvarnost: Elektroni se sudaraju s nepokretnim česticama. Usporavanje, zaustavljanje, čak i promjena smjera. Gibanje elektrona je nepravilno. Električno polje djeluje i na jezgre i na vezane elektrone. Sile izmeñu jezgri i vezanih elektrona (izmeñu jezgri) su jače od sila el. polja. U vodiču kojim teče električna struja nema gomilanja naboja.
10 Električna struja 2 gibanje elektrona u metalnoj žici 6 dq = nesvdt I = nesv Primjer: Izračunaj srednju brzinu gibanja elektrona u bakrenoj žici promjera 0,01 m kojim teče struja jakosti 200 A. Gustoća slobodnih elektrona u bakru je n = 8, m -3. n = 8,5 10 d I = 0,01m = 200A m 28 3 v = v = I Sne 200A 1 (0,01) 2 2 8, , π m m C 4 v 4 = 1,9 10 m / s v = 0, 02 / cm s Srednja brzina iona u otopinama je još manja.
11 Ako je srednja brzina gibanja elektrona u bakrenoj žici (vodičima) reda veličine 0,02 cm/s, kako je onda moguće da žarulja na stropu zasvijetli istoga trena kada stisnemo prekidač na zidu? Električno polje, koje tjera elektrone u metalu na gibanje djelujući na njih silom, uspostavlja se duž metala jako brzo gotovo brzinom svjetlosti. Elektroni se nalaze u svakom dijelu strujnog kruga (vodiči, žarulja) i čim se uspostavi polje, oni se kolektivno počinju gibati (nije potrebno da elektron od prekidača doñe do žarulje da bi ona zasvijetlila).
12 1. Poredaj po veličini struje u ovim vodičima! 2. Je li jakost struje vektor ili skalar? 3. Je li gustoća struje vektor ili skalar?
13 Jednadžba vodljivosti Zašto se elektroni unutar vodiča gibaju? Koliko dugo će teći struja vodičem? Električno polje (odnosno gradijent potencijala na krajevima vodiča). Dok postoji el. polje, u vodiču će teći struja. Gustoća slobodnih nosilaca naboja karakteristika vodiča Djelovanje el. polja na različite vodiče različita gustoća struje Električna vodljivost (konduktivnost) (def) = Omjer gustoće struje J i jakosti el. polja E koje je tu struju uzrokovalo. σ = J E J = σ E J = σ E Jednadžba vodljivosti Ohmov zakon: proporcionalnost J i E! Veća vodljivost σ dano el. polje E tjera struju veće gustoće
14 J = σ E Jednadžba vodljivosti 2 O čemu ovisi provodnost σ? Provodnost σ je proporcionalna s gustoćom struje, a ona ovisi o gustoći slobodnih elektrona u vodiču te o brzini kojom se oni mogu gibati u vodiču. Provodnost σ danog materijala nije konstantna: ona se mijenja s temperaturom, a može ovisiti i o drugim fizikalnim uvjetima. J = σ E Primjena u praksi? Ne mjerimo ni provodnost σ ni E! I dv J = E = S dx Prelazimo na jakost el. struje i na gradijent potencijala. I dv σ S dx = [ σ ] σ AV -1 = S simens (Werner von Siemens, , njemački elektrotehničar, konstruirao prvi dinamo stroj) = [ I ] dx [ S] dv [ ] 1 1 σ = AV m [ ] = Sm = Ω m
15 Ohmov zakon Promatramo vodič duljine l i konstantnog presjeka S u kojem teče struja jakosti I. V a, V b potencijali na krajevima vodiča Neka je provodnost σ konstantna i neovisna od J konstantna je i struja I Polazimo od izraza: l 0 I dv = σ S dx V I dx = σ S dv V b σ S I = Va V l a ( ) b Idx = σ SdV ( ) Il = σ S V V b Veza izmeñu struje u vodiču i razlike potencijala na njegovim krajevima a
16 σ S I = Va V l ( ) b Ohmov zakon 2 G električna vodljivost (konduktancija) G σ S = l Za dugačak vodič stalnog presjeka vrijedi: [ G] 1 2 Sm m = = S m Električni otpor R = 1/G Recipročna vrijednost električne vodljivosti 1 l R = σ S Električna otpornost ili rezistivnost (specifični el. otpor) ρ = 1/σ l Va Vb Vab R = ρ I = = Ohmov zakon S R R Jakost struje u vodiču razmjerna je je razlici napona na njegovim krajevima. Georg Simon Ohm ( ) njemački fizičar, eksperimentalnim putem došao do zakonitosti
17 R l ρ V V ab = I = ab Ohmov zakon 3 S R Linearni vodiči (omski otpori) Materijali za koje je napon V ab linearna funkcija struje. Materijali za koje je otpor R konstantan (kod promjene struje). vodiči [ R] = R I Nelinearni vodiči Ne vrijedi gornja relacija. npr. dioda, žarulja s željeznom niti u vodiku [ V ] [ I ] V = = A = Ω El. otpor vodiča je 1 Ohm ako razlika potencijala od 1 V na njegovim krajevima uzrokuje u njemu električnu struju od 1 A. [ ] ρ = [ R][ S] [ l] = Ωm J = σ E
18 V ab Ohmov zakon 4 I = Vab = R I R Eksperimentalna provjera Ohmovog zakona? Ureñaj za mjerenje ovisnosti struje kroz vodič o naponu: Rezultati U(V) mjerenja: I(A) 0 0,23 0,46 0,69 0,92 1,15 1,37-0,23-0,47 Ι U U tgα = = I U R = I const. R se ne mijenja
19 Ovisnost električne otpornosti o temperaturi Eksperiment otpor vodiča ovisi o temperaturi Za "obične temperature" vrijedi: ρ ρ 2 = 0 + at + bt +... ρ 0 ρ 0 otpornost na 0 0 C (273 K) a, b,.. koeficijenti razvoja Obično je a >> b za male promjene temperature vrijedi: ρ = ρ 0 + at α ρ = ρ + aρ t 0 0 Označimo: ρ0 0 = + ( ) ρ ρ 1 αt 0 ρ ρ α = α - temperaturni koeficijent električne otpornosti 0 = ρ t α relativna promjena otpornosti pri 0 promjeni temperature za 1 kelvin a ρ
20 Ovisnost električne otpornosti o temperaturi 2 S obzirom na vrijednosti el. otpornosti, materijale dijelimo na: Vodiči: otpornost od 10-8 do 10-6 Ωm Izolatori: otpornost od 10 8 do Ωm Poluvodiči? Prema uvjetima u kojima se nalaze: - ponašaju se kao vodiči - ponašaju se kao izolatori (µωcm) Poluvodiči imaju α < 0 otpornost se smanjuje s temperaturom Električna otpornost materijala i temperaturni koeficijent otpora kod 20 0 C
21 Ovisnost električne otpornosti o temperaturi 3 Metali linearna ovisnost otpora vodiča o temperaturi (obične temp.) ρ = ρ 0 ( 1+ αt ) Kako se ponaša otpornost na niskim temperaturama? U blizini apsolutne nule otpornost nekih metala iščezava. Ta pojava se zove SUPRAVODLJIVOST. Kamerlingh Onnes (1911.) Mjerio otpor žive na vrlo niskim temperaturama (oko 4 K). Otkrio da postoji tzv. kritična temperatura pri kojoj se otpornost naglo smanji na nulu. Objašnjenje? Složeno (Cooperovi parovi - fizika čvrstog stanja). Ne pokazuju svi metali svojstvo supravodljivosti. Dobri kandidati su elementi s parnim brojem elektrona ρ 0
22 otpornost metala otpornost poluvodiča otpornost supravodiča levitacija magneta iznad YBa 2 Cu 3 O 7 supravodiča (T=77 K)
23 Ovisnost električne otpornosti o temperaturi 4 In Sn Hg Pb Materijal Nb 3 Sn Kritična temperatura (K) 3,4 3,7 4,2 7,2 18 Nb 3 Ga 20 LaSrCuO 4 38 YBa 2 Cu 3 O 9 90 Kritične temperature za neke materijale Supravodljivost intenzivna istraživanja u svijetu Primjene supravodljivosti Kada nema otpora, nema ni gubitaka energije (zagrijavanja vodiča). Mogućnost skladištenja energije. "Vrlo brzi vlakovi", itd. Problemi supravodljivosti Veliki utrošak energije za dobivanje i održavanje niskih temperatura. Težnje supravodljivosti Podići kritičnu temperaturu što bliže sobnoj temperaturi. novo doba za prijenos energije, elektromagnete, brza računala,
24 Primjeri za otpore koji nisu omski l Vab R = ρ I = Vab = R I S R Linearni vodiči (omski otpori) Materijali za koje je napon V ab linearna funkcija struje. Nelinearni vodiči Ne vrijedi gornja relacija. npr. dioda, žarulja s željeznom niti u vodiku Ovisnost struje i otpora diode o naponu. U-I karakteristika željeza u vodiku
25 Vrste: Otpornici U izvodu Ohmovog zakona smo dobili: l R = ρ S OTPORNIK - Vodič ili kompleks vodiča čiji je otpor znatno veći od otpora kratkih komadića žice kojima se koristimo za električne kontakte. Otpornik je elektronički element - Velika primjena u elektrotehnici. Najčešća izrada otpornika je izrada u obliku malog valjka s dvjema žicama na krajevima. Žičani Otporna žica na izolatoru od keramike ili stakla. Koriste se za veća opterećenja Slojni Na izolator (keramika) se nanese sloj odreñene otpornosti (ugljni ili metalni sloj). Promjenljivi Potenciometri. Vrijednost otpora se klizačem može mijenjati od nule do neke vrijednosti. Različiti načini izvedbe.
26 Otpornici 2 l U izvodu Ohmovog zakona smo dobili: R = ρ S Vrijednost otpora - Označavanje otpornika obojenim prstenovima ili brojem: Obični otpornik Promjenljivi otpornik
27 Otpor i otpornost otpor = karakteristika pojedinog otpornika (predmeta) otpornost = karakteristika odreñenog materijala masa gustoća
28 Model električne vodljivosti -Paul Drude ( ) model el. vodljivosti u metalima -metal = atomi (jezgre; +) + slobodni elektroni (-) E = 0 E 0 -nasumično gibanje elektrona v = 10 6 m/s slobodni elekronski plin - I = 0; nema usmjerenog gibanja elektrona -slobodni elektroni gibaju se usmjereno (driftna brzina, 10-4 m/s) zbog djelovanja el. polja (sile); -elektroni se ubrzavaju djelovanjem sile, a u sudarima s atomima gube svoju kinetičku energiju koja prelazi u energiju titranja atoma čime se povećava temperatura materijala
29 - sudari elektrona s atomima materijala (i drugim elektronima, nečistoćama, primjesama) uzrok su raspršenja elektrona, odnosno pojave električnog otpora materijala u supravodičima nema raspršenja elektrona (vezani su u Cooperove parove) raspršenje ne postoji niti u idealnoj periodičnoj rešetki - želimo izvesti izraz za driftnu brzinu: F = qe = qe a = m e m a e konačna brzina početna brzina prirast brzine zbog polja E -srednja vrijednost v i = 0, jer su elektroni u nekom početnom trenutku usmjereni nasumično srednja udaljenost izmeñu dva sudara driftna brzina (brzina zanošenja) srednji vremenski interval izmeñu dva sudara
30 -prema Drudeovom (klasičnom) modelu vodljivost/otpornost metala ne ovise o jakosti električnog polja, što znači da je zadovoljen Ohmov zakon
31 Jouleov zakon. Snaga električne struje Promatramo struju elektrona unutar vodiča. Kako se oni gibaju? elektroni niz ubrzanja, a svako završava sudarom s jezgrom ili drugim elektronom usporenje ili zaustavljanje ubrzavanje elektrona kinetička energija sudari ili zaustavljanje elektrona predaja energije česticama vezanim u materijalu Kuda ide tako dobivena energija? Jer su čestice vezane, srednji položaj čestica se ne mijenja energija ide na povećanje amplitude vibracija, tj u toplinsku energiju Vodičem kojim teče struja, kinetička energija slobodnih elektrona se pretvara u toplinsku energiju.
32 Jouleov zakon. Snaga električne struje 2 Vodičem kojim teče struja, kinetička energija slobodnih elektrona se pretvara u toplinsku energiju. Kako naći izraz za toplinsku energiju? Promatramo dijelić strujnog kruga kojim teče struja jakosti I. Za vrijeme dt će vodičem proći naboj dq = I dt dq - Količina naboja prenesena iz točke s potencijalom V a u točku s potencijalom V b. Energija koju naboj prenese: dw = dq( V V ) = Idt ( V V ) dw = I V dt : dt ab a dw P = = I V dt Snaga električne struje jednaka je produktu jakosti struje I i razlike potencijala V ab. b ab a b
33 P = I V ab Jouleov zakon. Snaga električne struje 3 Poseban slučaj Neka je vodič čisti omski otpor R Ohmov zakon Vab = I R P = I I R 2 P = I R Snaga (po def) je izvršeni rad u jedinici vremena, tj. osloboñena toplina podijeljena s vremenom. dq P = dq 2 = I R Jouleov zakon dt dt U čistom omskom otporu R sva energija el. struje I se pretvori u toplinu. Toplina stvorena u jedinici vremena je razmjerna s kvadratu struje. James Prescott Joule ( ) engleski fizičar proučavao odnose izmeñu različitih oblika energije
34 Pokusi: 1. Pad otpornosti smanjenjem temperature Na akumulator spojimo 2 žice, jednu držimo u zraku, a drugu držimo u vodi. Žice se prvo počinju grijati (usijavati), a zatim i pregore. Žica u vodi se manje žari (otpornost je manja na manjoj temperaturi). ( ) ρ = ρ 1+ αt 0 dq I 2 = R dt 2. Različite otpornosti srebra i platine: Napravimo lančić kojemu su karike (izmjenično) iz srebrne pa platinske žice jednakih debljina. Spojimo lančić na napon. Karike platine se užare, a karike srebra ne. U platini se više el. energije pretvara u toplinu jer je njena otpornost veća. 3. Osigurači Ako struja poraste preko neke granice žica pregori
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Elektrodinamika ( ) ELEKTRODINAMIKA Q t l R = ρ R R R R = W = U I t P = U I
 Elektrodinamika ELEKTRODINAMIKA Jakost električnog struje I definiramo kao količinu naboja Q koja u vremenu t prođe kroz presjek vodiča: Q I = t Gustoća struje J je omjer jakosti struje I i površine presjeka
Elektrodinamika ELEKTRODINAMIKA Jakost električnog struje I definiramo kao količinu naboja Q koja u vremenu t prođe kroz presjek vodiča: Q I = t Gustoća struje J je omjer jakosti struje I i površine presjeka
ELEKTRODINAMIKA ELEMENTI STRUJNOG KRUGA IZVOR ELEKTRIČNE ENERGIJE
 ELEKTRODINAMIKA ELEKTRIČNA STRUJA I PRIPADNE POJAVE ELEMENTI STRUJNOG KRUGA Strujni krug je sastavljen od: izvora u kojemu se neki oblik energije pretvara u električnu energiju, spojnih vodiča i trošila
ELEKTRODINAMIKA ELEKTRIČNA STRUJA I PRIPADNE POJAVE ELEMENTI STRUJNOG KRUGA Strujni krug je sastavljen od: izvora u kojemu se neki oblik energije pretvara u električnu energiju, spojnih vodiča i trošila
Elektrodinamika
 Elektrodinamika.. Gibanje električnog naboja u električnom polju.2. Električna struja.3. Električni otpor.4. Magnetska sila.5. Magnetsko polje električne struje.6. Magnetski tok.7. Elektromagnetska indukcija
Elektrodinamika.. Gibanje električnog naboja u električnom polju.2. Električna struja.3. Električni otpor.4. Magnetska sila.5. Magnetsko polje električne struje.6. Magnetski tok.7. Elektromagnetska indukcija
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
#6 Istosmjerne struje
 #6 Istosmjerne struje I Jednadžbe za istosmjerne struje II Gibbsov potencijal u vodičima predavanja 20** Drudeov model za vodljive elektrone Jouleov zakon Makroskopske jednadžbe za istosmjerne struje Gibbsov
#6 Istosmjerne struje I Jednadžbe za istosmjerne struje II Gibbsov potencijal u vodičima predavanja 20** Drudeov model za vodljive elektrone Jouleov zakon Makroskopske jednadžbe za istosmjerne struje Gibbsov
Informacije o predmetu
 Informacije o predmetu Literatura: Marinović Opća elektrotehnika i elektronika, Marinović Opća elektrotehnika i elektronika, Marinović udarska elektrotehnika (str. 45-458, Protueksplozijska zaštita) Zorić,
Informacije o predmetu Literatura: Marinović Opća elektrotehnika i elektronika, Marinović Opća elektrotehnika i elektronika, Marinović udarska elektrotehnika (str. 45-458, Protueksplozijska zaštita) Zorić,
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
kondenzatori električna struja i otpor Istosmjerni strujni krugovi
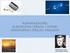 kondenzatori električna struja i otpor Istosmjerni strujni krugovi - Dva vodiča, nose jednaki naboj suprotnog predznaka - kondenzator - Vodiče nazivamo ploče kondenzatora - Između ploča kondenzatora postoji
kondenzatori električna struja i otpor Istosmjerni strujni krugovi - Dva vodiča, nose jednaki naboj suprotnog predznaka - kondenzator - Vodiče nazivamo ploče kondenzatora - Između ploča kondenzatora postoji
ELEK 3. ISTOSMJERNA ELEKTRIČNA STRUJA I STRUJNI KRUGOVI ELEKTROTEHNIKA. Doc. dr. sc. Vitomir Komen, dipl. ing. el. 1/77. Komen
 ELEKTOTEHNIKA 3. ISTOSMJENA ELEKTIČNA STUJA I STUJNI KUGOVI Doc. dr. sc. Vitomir Komen, dipl. ing. el. /77 SADŽAJ: 3. Nastajanje električne struje 3. Električni strujni krug istosmjerne struje 3.3 Električni
ELEKTOTEHNIKA 3. ISTOSMJENA ELEKTIČNA STUJA I STUJNI KUGOVI Doc. dr. sc. Vitomir Komen, dipl. ing. el. /77 SADŽAJ: 3. Nastajanje električne struje 3. Električni strujni krug istosmjerne struje 3.3 Električni
Priprema za državnu maturu
 Priprema za državnu maturu E L E K T R I Č N A S T R U J A 1. Poprečnim presjekom vodiča za 0,1 s proteče 3,125 10¹⁴ elektrona. Kolika je jakost struje koja teče vodičem? A. 0,5 ma B. 5 ma C. 0,5 A D.
Priprema za državnu maturu E L E K T R I Č N A S T R U J A 1. Poprečnim presjekom vodiča za 0,1 s proteče 3,125 10¹⁴ elektrona. Kolika je jakost struje koja teče vodičem? A. 0,5 ma B. 5 ma C. 0,5 A D.
Elektrodinamika Elektrodinamika
 1. 1.1. 1.1 1.2. 1.2 1.3. 1.3 1.4. 1.4 1.5. 1.5 1.6. 1.6 1.7. 1.7 1.8. Elektrodinamika Elektrodinamika Gibanje naboja električnog pod naboja utjecajem u električnom električnog polju polja Električna struja
1. 1.1. 1.1 1.2. 1.2 1.3. 1.3 1.4. 1.4 1.5. 1.5 1.6. 1.6 1.7. 1.7 1.8. Elektrodinamika Elektrodinamika Gibanje naboja električnog pod naboja utjecajem u električnom električnog polju polja Električna struja
Gauss, Stokes, Maxwell. Vektorski identiteti ( ),
 Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Osnove elektrotehnike I popravni parcijalni ispit VARIJANTA A
 Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
Osnove elektrotehnike I popravni parcijalni ispit 1..014. VARIJANTA A Prezime i ime: Broj indeksa: Profesorov prvi postulat: Što se ne može pročitati, ne može se ni ocijeniti. A C 1.1. Tri naelektrisanja
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Zadatak 161 (Igor, gimnazija) Koliki je promjer manganinske žice duge 31.4 m, kroz koju teče struja 0.8 A, ako je napon
 Zadatak 6 (gor, gimnazija) Koliki je promjer manganinske žice duge. m, kroz koju teče struja 0.8, ako je napon između krajeva 80 V? (električna otpornost manganina ρ = 0. 0-6 Ω m) ješenje 6 l =. m, = 0.8,
Zadatak 6 (gor, gimnazija) Koliki je promjer manganinske žice duge. m, kroz koju teče struja 0.8, ako je napon između krajeva 80 V? (električna otpornost manganina ρ = 0. 0-6 Ω m) ješenje 6 l =. m, = 0.8,
Informacije o predmetu
 Informacije o predmetu Literatura: Marinović Opća elektrotehnika i elektronika, Marinović Opća elektrotehnika i elektronika, Marinović udarska elektrotehnika (str. 45-458, Protueksplozijska zaštita) Zorić,
Informacije o predmetu Literatura: Marinović Opća elektrotehnika i elektronika, Marinović Opća elektrotehnika i elektronika, Marinović udarska elektrotehnika (str. 45-458, Protueksplozijska zaštita) Zorić,
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Metal u oscilirajućem električnom polju
 Metal u oscilirajućem električnom polju Raspršivanje elektrona na preprekama može se tretirati kao vrst sile trenja. Jednadžba gibanja elektrona: m u = e F 0 e iωt }{{} sila el. polja γ }{{ m u }, trenje
Metal u oscilirajućem električnom polju Raspršivanje elektrona na preprekama može se tretirati kao vrst sile trenja. Jednadžba gibanja elektrona: m u = e F 0 e iωt }{{} sila el. polja γ }{{ m u }, trenje
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Električne struje. Električne struje. Električne struje. Električne struje
 Električna struja (AP47-5) Elektromotorna sila (AP5-53) Omov zakon za deo provodnika i otpor provodnika (AP53-6) Omov zakon za prosto električno kolo (AP6-63) Kirhofova pravila (AP63-66) Vezivanje otpornika
Električna struja (AP47-5) Elektromotorna sila (AP5-53) Omov zakon za deo provodnika i otpor provodnika (AP53-6) Omov zakon za prosto električno kolo (AP6-63) Kirhofova pravila (AP63-66) Vezivanje otpornika
Ampèreova i Lorentzova sila zadatci za vježbu
 Ampèreova i Lorentzova sila zadatci za vježbu Sila na vodič kojim prolazi električna struja 1. Kroz horizontalno položen štap duljine 0,2 m prolazi električna struja jakosti 15 A. Štap se nalazi u horizontalnom
Ampèreova i Lorentzova sila zadatci za vježbu Sila na vodič kojim prolazi električna struja 1. Kroz horizontalno položen štap duljine 0,2 m prolazi električna struja jakosti 15 A. Štap se nalazi u horizontalnom
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
Elektrodinamika Elektrodinamika
 1. 1.1. 1.1 1.. 1. 1.3. 1.3 1.4. 1.4 1.5. 1.5 1.6. 1.6 1.7. 1.7 1.8. Elektrodinamika Elektrodinamika Gibanje naboja električnog pod naboja utjecajem u električnom električnog polju polja Električna struja
1. 1.1. 1.1 1.. 1. 1.3. 1.3 1.4. 1.4 1.5. 1.5 1.6. 1.6 1.7. 1.7 1.8. Elektrodinamika Elektrodinamika Gibanje naboja električnog pod naboja utjecajem u električnom električnog polju polja Električna struja
Podsjetnik za državnu maturu iz fizike značenje formula
 Podsjetnik za državnu maturu iz fizike značenje formula ukratko je objašnjeno značenje svih slova u formulama koje se dobiju uz ispit [u uglatim zagradama su SI mjerne jedinice] Kinetika v = brzina ( =
Podsjetnik za državnu maturu iz fizike značenje formula ukratko je objašnjeno značenje svih slova u formulama koje se dobiju uz ispit [u uglatim zagradama su SI mjerne jedinice] Kinetika v = brzina ( =
Magnetsko polje ravnog vodiča, strujne petlje i zavojnice
 Magnetske i elektromagnetske pojave_intro Svojstva magneta, Zemljin magnetizam, Oerstedov pokus, magnetsko polje ravnog vodiča, strujne petlje i zavojnice, magnetska sila na vodič, Lorentzova sila, gibanje
Magnetske i elektromagnetske pojave_intro Svojstva magneta, Zemljin magnetizam, Oerstedov pokus, magnetsko polje ravnog vodiča, strujne petlje i zavojnice, magnetska sila na vodič, Lorentzova sila, gibanje
OSNOVE ELEKTROTEHNIKE 1 POJMOVI DEFINICIJE ZADACI. Prvo obrazovno razdoblje 2014./2015. školske godine Zdravko Borić, prof.
 OSNOVE ELEKTOTEHNIKE 1 POJMOVI DEFINICIJE ZADACI Prvo obrazovno razdoblje 014./015. školske godine Zdravko Borić, prof. Zadatak za početak! Prema konvenciji, protonu se pripisuje pozitivni naboj, a elektronu
OSNOVE ELEKTOTEHNIKE 1 POJMOVI DEFINICIJE ZADACI Prvo obrazovno razdoblje 014./015. školske godine Zdravko Borić, prof. Zadatak za početak! Prema konvenciji, protonu se pripisuje pozitivni naboj, a elektronu
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Rad, energija i snaga
 Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
Rad, energija i snaga Željan Kutleša Sandra Bodrožić Rad Rad je skalarna fizikalna veličina koja opisuje djelovanje sile F na tijelo duž pomaka x. = = cos Oznaka za rad je W, a mjerna jedinica J (džul).
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Snage u kolima naizmjenične struje
 Snage u kolima naizmjenične struje U naizmjeničnim kolima struje i naponi su vremenski promjenljive veličine pa će i snaga koja se isporučuje potrošaču biti vremenski promjenljiva Ta snaga naziva se trenutna
Snage u kolima naizmjenične struje U naizmjeničnim kolima struje i naponi su vremenski promjenljive veličine pa će i snaga koja se isporučuje potrošaču biti vremenski promjenljiva Ta snaga naziva se trenutna
2. Ako je funkcija f(x) parna onda se Fourierov red funkcije f(x) reducira na Fourierov kosinusni red. f(x) cos
 . KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
. KOLOKVIJ PRIMIJENJENA MATEMATIKA FOURIEROVE TRANSFORMACIJE 1. Za periodičnu funkciju f(x) s periodom p=l Fourierov red je gdje su a,a n, b n Fourierovi koeficijenti od f(x) gdje su a =, a n =, b n =..
Popis oznaka. Elektrotehnički fakultet Osijek Stručni studij. Osnove elektrotehnike I. A el A meh. a a 1 a 2 a v a v. a v. B 1n. B 1t. B 2t.
 Popis oznaka A el A meh A a a 1 a 2 a a a x a y - rad u električnom dijelu sustaa [Ws] - mehanički rad; rad u mehaničkom dijelu sustaa [Nm], [J], [Ws] - mehanički rad [Nm], [J], [Ws] - polumjer kugle;
Popis oznaka A el A meh A a a 1 a 2 a a a x a y - rad u električnom dijelu sustaa [Ws] - mehanički rad; rad u mehaničkom dijelu sustaa [Nm], [J], [Ws] - mehanički rad [Nm], [J], [Ws] - polumjer kugle;
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika
 1. Kinematika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji
1. Kinematika Mehanika je temeljna i najstarija grana fizike koja proučava zakone gibanja i meñudjelovanja tijela. kinematika, dinamika i statika Kinematika (grč. kinein = gibati) je dio mehanike koji
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
π π ELEKTROTEHNIČKI ODJEL i) f (x) = x 3 x 2 x + 1, a = 1, b = 1;
 1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
1. Provjerite da funkcija f definirana na segmentu [a, b] zadovoljava uvjete Rolleova poučka, pa odredite barem jedan c a, b takav da je f '(c) = 0 ako je: a) f () = 1, a = 1, b = 1; b) f () = 4, a =,
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Rotacija krutog tijela
 Rotacija krutog tijela 6. Rotacija krutog tijela Djelovanje sile na tijelo promjena oblika tijela (deformacija) promjena stanja gibanja tijela Kruto tijelo pod djelovanjem vanjskih sila ne mijenja svoj
Rotacija krutog tijela 6. Rotacija krutog tijela Djelovanje sile na tijelo promjena oblika tijela (deformacija) promjena stanja gibanja tijela Kruto tijelo pod djelovanjem vanjskih sila ne mijenja svoj
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Vježba 081. ako zavojnicom teče struja jakosti 5 A? A. Rezultat: m
 Zadatak 8 (Marija, medicinska škola) Kolika je jakost magnetskog polja u unutrašnjosti zavojnice od 5 zavoja, dugačke 5 cm, ako zavojnicom teče struja jakosti A? ješenje 8 N = 5, l = 5 cm =.5 m, = A, H
Zadatak 8 (Marija, medicinska škola) Kolika je jakost magnetskog polja u unutrašnjosti zavojnice od 5 zavoja, dugačke 5 cm, ako zavojnicom teče struja jakosti A? ješenje 8 N = 5, l = 5 cm =.5 m, = A, H
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Gravitacija. Gravitacija. Newtonov zakon gravitacije. Odredivanje gravitacijske konstante. Keplerovi zakoni. Gravitacijsko polje. Troma i teška masa
 Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
Claudius Ptolemeus (100-170) - geocentrični sustav Nikola Kopernik (1473-1543) - heliocentrični sustav Tycho Brahe (1546-1601) precizno bilježio putanje nebeskih tijela 1600. Johannes Kepler (1571-1630)
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
RAČUNSKE VEŽBE IZ PREDMETA POLUPROVODNIČKE KOMPONENTE (IV semestar modul EKM) IV deo. Miloš Marjanović
 Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
Univerzitet u Nišu Elektronski fakultet RAČUNSKE VEŽBE IZ PREDMETA (IV semestar modul EKM) IV deo Miloš Marjanović MOSFET TRANZISTORI ZADATAK 35. NMOS tranzistor ima napon praga V T =2V i kroz njega protiče
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Elektricitet i magnetizam. 2. Magnetizam
 2. Magnetizam Od Oersteda do Einsteina Zimi 1819/1820 Oersted je održao predavanja iz kolegija Elektricitet, galvanizam i magnetizam U to vrijeme izgledalo je kao da elektricitet i magnetizam nemaju ništa
2. Magnetizam Od Oersteda do Einsteina Zimi 1819/1820 Oersted je održao predavanja iz kolegija Elektricitet, galvanizam i magnetizam U to vrijeme izgledalo je kao da elektricitet i magnetizam nemaju ništa
nvt 1) ukoliko su poznate struje dioda. Struja diode D 1 je I 1 = I I 2 = 8mA. Sada je = 1,2mA.
 IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
IOAE Dioda 8/9 I U kolu sa slike, diode D su identične Poznato je I=mA, I =ma, I S =fa na 7 o C i parametar n= a) Odrediti napon V I Kolika treba da bude struja I da bi izlazni napon V I iznosio 5mV? b)
5. Koliki naboj treba dati kugli mase 1 kg da ona lebdi ispod kugle s nabojem 0,07 µc na udaljenosti 5 cm?
 Coulombov zakon 1. Metalna kugla polumjera R = 10 cm nabijena je plošnom gustoćom naboja σ = 7, 95 nc/m 2. Kolika je razlika izmedu broja protona i broja elektrona u kugli? 2. Koliki je omjer gravitacijske
Coulombov zakon 1. Metalna kugla polumjera R = 10 cm nabijena je plošnom gustoćom naboja σ = 7, 95 nc/m 2. Kolika je razlika izmedu broja protona i broja elektrona u kugli? 2. Koliki je omjer gravitacijske
OSNOVI ELEKTRONIKE. Vežbe (2 časa nedeljno): mr Goran Savić
 OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
OSNOVI ELEKTRONIKE Vežbe (2 časa nedeljno): mr Goran Savić savic@el.etf.rs http://tnt.etf.rs/~si1oe Termin za konsultacije: četvrtak u 12h, kabinet 102 Referentni smerovi i polariteti 1. Odrediti vrednosti
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Elektron u periodičnom potencijalu
 Elektron u periodičnom potencijalu U Sommerfeldovom modelu elektroni se gibaju u potencijalnoj jami s ravnim dnom (kutija). Periodični potencijala od pravilne kristalne strukture pozitivnih iona se zanemaruje.
Elektron u periodičnom potencijalu U Sommerfeldovom modelu elektroni se gibaju u potencijalnoj jami s ravnim dnom (kutija). Periodični potencijala od pravilne kristalne strukture pozitivnih iona se zanemaruje.
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
SADRŽAJ. 1. Električni naboj 2. Coulombov zakon 3. Električno polje 4. Gaussov zakon 5. Potencijal elektrostatičkog polja
 ELEKTROSTATIKA 1 SADRŽAJ 1. Električni naboj 2. Coulombov zakon 3. Električno polje 4. Gaussov zakon 5. Potencijal elektrostatičkog polja 1. Električki naboj Eksperiment Stakleni štap i svilena krpa nakon
ELEKTROSTATIKA 1 SADRŽAJ 1. Električni naboj 2. Coulombov zakon 3. Električno polje 4. Gaussov zakon 5. Potencijal elektrostatičkog polja 1. Električki naboj Eksperiment Stakleni štap i svilena krpa nakon
E L E K T R I C I T E T
 Coulombov zakon E L E K T R I C I T E T 1. Dva sitna tijela jednakih naboja međusobno su udaljena 0,3 m i privlače se silom 50 μn. Koliko iznosi svaki naboj? Q = 2,2 10 ⁸ C 2. Odredi kolikom će silom međusobno
Coulombov zakon E L E K T R I C I T E T 1. Dva sitna tijela jednakih naboja međusobno su udaljena 0,3 m i privlače se silom 50 μn. Koliko iznosi svaki naboj? Q = 2,2 10 ⁸ C 2. Odredi kolikom će silom međusobno
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Elektricitet i magnetizam. 1. Elektricitet
 1. Elektricitet Podsjetnik Dodatna literatura:, E.M.Purcel. Udžbenik fizike Sveučilišta u Berkeleyu. Najelementarnije: Fizika 2. V. Paar i V. Šips. Školska knjiga. 2 Povijest elektriciteta Tales iz Mileta
1. Elektricitet Podsjetnik Dodatna literatura:, E.M.Purcel. Udžbenik fizike Sveučilišta u Berkeleyu. Najelementarnije: Fizika 2. V. Paar i V. Šips. Školska knjiga. 2 Povijest elektriciteta Tales iz Mileta
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Izvori magnetskog polja
 Izvori magnetskog polja Biot-Savartov zakon - Hans Christian Oersted 1820. g. veza elektriciteta i magnetizma: električna struja u vodiču otklanja magnetsku iglu - Jean-Baptiste Biot (1774.-1862.) i Felix
Izvori magnetskog polja Biot-Savartov zakon - Hans Christian Oersted 1820. g. veza elektriciteta i magnetizma: električna struja u vodiču otklanja magnetsku iglu - Jean-Baptiste Biot (1774.-1862.) i Felix
Dinamika tijela. a g A mg 1 3cos L 1 3cos 1
 Zadatak, Štap B duljine i mase m pridržan užetom u točki B, miruje u vertikalnoj ravnini kako je prikazano na skii. reba odrediti reakiju u ležaju u trenutku kad se presječe uže u točki B. B Rješenje:
Zadatak, Štap B duljine i mase m pridržan užetom u točki B, miruje u vertikalnoj ravnini kako je prikazano na skii. reba odrediti reakiju u ležaju u trenutku kad se presječe uže u točki B. B Rješenje:
FAKULTET PROMETNIH ZNANOSTI
 SVUČILIŠT U ZAGU FAKULTT POMTNIH ZNANOSTI predmet: Nastavnik: Prof. dr. sc. Zvonko Kavran zvonko.kavran@fpz.hr * Autorizirana predavanja 2016. 1 Pojačala - Pojačavaju ulazni signal - Zahtjev linearnost
SVUČILIŠT U ZAGU FAKULTT POMTNIH ZNANOSTI predmet: Nastavnik: Prof. dr. sc. Zvonko Kavran zvonko.kavran@fpz.hr * Autorizirana predavanja 2016. 1 Pojačala - Pojačavaju ulazni signal - Zahtjev linearnost
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
UVOD U KVANTNU TEORIJU
 UVOD U KVANTNU TEORIJU UVOD U KVANTNU TEORIJU 1.) FOTOELEKTRIČKI EFEKT 2.) LINIJSKI SPEKTRI ATOMA 3.) BOHROV MODEL ATOMA 4.) CRNO TIJELO 5.) ČESTICE I VALOVI Elektromagnetsko zračenje UVOD U KVANTNU TEORIJU
UVOD U KVANTNU TEORIJU UVOD U KVANTNU TEORIJU 1.) FOTOELEKTRIČKI EFEKT 2.) LINIJSKI SPEKTRI ATOMA 3.) BOHROV MODEL ATOMA 4.) CRNO TIJELO 5.) ČESTICE I VALOVI Elektromagnetsko zračenje UVOD U KVANTNU TEORIJU
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
UVOD U VJEŽBE IZ PODRUČJA ELEKTRIČNIH STRUJNIH KRUGOVA
 1 Mr. sc. Draga Kpan-Lisica, viši pred. UVOD U VJEŽBE IZ PODRUČJA ELEKTRIČNIH STRUJNIH KRUGOVA Pojmovi i definicije: Električna struja, električni potencijal i električni napon; Električni strujni krug;
1 Mr. sc. Draga Kpan-Lisica, viši pred. UVOD U VJEŽBE IZ PODRUČJA ELEKTRIČNIH STRUJNIH KRUGOVA Pojmovi i definicije: Električna struja, električni potencijal i električni napon; Električni strujni krug;
1. As (Amper sekunda) upotrebljava se kao mjerna jedinica za. A) jakost električne struje B) influenciju C) elektromotornu silu D) kapacitet E) naboj
 ELEKTROTEHNIKA TZ Prezime i ime GRUPA Matični br. Napomena: U tablicu upisivati slovo pod kojim smatrate da je točan odgovor. Upisivati isključivo velika štampana slova. Točan odgovor donosi jedan bod.
ELEKTROTEHNIKA TZ Prezime i ime GRUPA Matični br. Napomena: U tablicu upisivati slovo pod kojim smatrate da je točan odgovor. Upisivati isključivo velika štampana slova. Točan odgovor donosi jedan bod.
ELEKTRIČNA STRUJA KROZ TEKUĆINE. Elektrolitička disocijacija. čista destilirana voda izolator, uz npr. NaCl bolja vodljivost
 ELEKTRIČNA STRUJA KROZ TEKUĆINE Elektrolitička disocijacija čista destilirana voda izolator, uz npr. NaCl bolja vodljivost otopine kiselina, lužina ili soli = elektroliti pozitivni i negativni ioni povećavaju
ELEKTRIČNA STRUJA KROZ TEKUĆINE Elektrolitička disocijacija čista destilirana voda izolator, uz npr. NaCl bolja vodljivost otopine kiselina, lužina ili soli = elektroliti pozitivni i negativni ioni povećavaju
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
BIPOLARNI TRANZISTOR Auditorne vježbe
 BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
BPOLARN TRANZSTOR Auditorne vježbe Struje normalno polariziranog bipolarnog pnp tranzistora: p n p p - p n B0 struja emitera + n B + - + - U B B U B struja kolektora p + B0 struja baze B n + R - B0 gdje
TRIGONOMETRIJSKE FUNKCIJE I I.1.
 TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
, Zagreb. Prvi kolokvij iz Analognih sklopova i Elektroničkih sklopova
 Grupa A 29..206. agreb Prvi kolokvij Analognih sklopova i lektroničkih sklopova Kolokvij se vrednuje s ukupno 42 boda. rijednost pojedinog zadatka navedena je na kraju svakog zadatka.. a pojačalo na slici
Grupa A 29..206. agreb Prvi kolokvij Analognih sklopova i lektroničkih sklopova Kolokvij se vrednuje s ukupno 42 boda. rijednost pojedinog zadatka navedena je na kraju svakog zadatka.. a pojačalo na slici
