Riemann problems for hyperbolic systems
|
|
|
- Προκόπιος Πυλαρινός
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Riemann obems o heboic ssems A Disseaion Sbmie in aia imen FOR THE DEGREE OF MASTER OF SCIENCE IN MATHEMATICS UNDER THE ACADEMIC AUTONOMY NATIONAL INSTITUTE OF TECHNOLOGY ROURKELA TSWATI Une he Giance o DR RAJA SEKHAR TUNGALA DEPARTMENT OF MATHEMATICS NATIONAL INSTITUTE OF TECHNOLOGY ROURKELA 7698 ODISHA
2 CERTIFICATE D RAJA SEKHAR TUNGALA Assisan Poesso Deamen o Mahemaics NIT Roea-ODISHA This is o cei ha he isseaion enie Riemann obems o heboic ssems bein sbmie b TSai o he Deamen o mahemaics Naiona Insie o Technoo Roea Oisha o he aa o he eee o Mase o Science in mahemaics is a eco o bonaie eseach o caie o b hem ne m sevision an iance I am saisie ha he isseaion eo has eache he sana iin he eqiemens o he eaions eain o he nae o he eee Roea Dae: D Raja SehaTnaa Seviso
3 DECLARATION I heeb cei ha he o hich is bein esene in hesis enie RiemannPobems o heboic ssems in aia imen o he eqiemen o he aa o he Deee o Mase o Science sbmie in he Deamen o Mahemaics Naiona Insie o Technoo Roea is an ahenic eco o m o caie o ne he sevision o D Raja SehaTnaa The mae emboie in his has no been sbmie b me o he aa o an ohe eee (TSai This is o cei ha he above saemen mae b he caniae is caie o he bes o he Knoee DR RAJA SEKHAR TUNGALA Assisan Poesso Deamen o mahemaics Naiona Insie o Technoo Roea Oisha
4 4 Acnoeemens I eem i a iviee an hono o have oe in associaion ne D Raja seha Tnaa Assisan Poesso Deamen o mahemaics Naiona Insie o Technoo Roea I eess m ee sense o aie an inebeness o him o sesin me he obem an iin me hoho he isseaion Wos an inaeqae o eess m eeins o hanness o a he aena cae an aecion he has shon hie m o as in oess I han a ac membes o he Deamen o mahemaics ho have aas insie me o o ha an hee me ean ne conces in o sa a NIT Roea I o ie o hans o aens o hei nconiiona ove an so The have hee me in eve siaion hoho o ie I am ae o hei so I o ie o acco o sincee aie o M ibeanana bia o his vaabe sesions iance in cain o m ojec an his sincee he I aso han o C aa an Abhiman mahaana he eamen assisan an eon esecive o hei cooeaion an he Fina I o ie o han a o iens o hei so an he ea amih o shoe his bessin on s an main eams an asiaions TSai
5 5 Absac In his eo e eine heboic ssem an iven some eames We s he behavio o heboic ssem Lae e evise he eac soion o he Riemann Pobem o he non- inea PDE hich in heboic ssem o he enea om o consevaion as hich ovens oneimensiona isenoic maneoasnamics Las e in he soion sin hase ane anasis an ineacions o eemena aves beeen he same amiies as e as ieen amiies
6 6 INTRODUCTION The Riemann obem is eine as he iniia vae obem o he ssem ih o vae ieceise consan iniia aa The Riemann obem is a namena oo o sin he ineacion beeen aves I has ae a cena oe boh in he heoeica anasis o ssems o heboic consevaion as an in he eveomen an imemenaion o acica nmeica soions o sch ssems asica he Riemann obem ives he mico-ave sca o he o One can hin o he oaaion o he o as a se o sma scae Riemann obem beeen he ave aisin om hese Riemann obems
7 7 TALE OF CONTENTS CHAPTER : Inocion o heboic ssem Deiniion an Eames Heboic ssem o consevaion as Cach obem Riemann obem Wea soion 9 5 CHAPTER : Riemann Pobem o isenoic maneoasnamics Shoc an Raeacion aves Shocs Raeacion aves Riemann obem Ineacion o eemena aves Ineacion o aves om ieen amiies 44 Ineacion o aves om same ami 48 REFERENCES
8 8 Deiniions an Eames: Chae- Inocion o Heboic Ssems The enea om o ssem o consevaion as in sevea sace vaiabes j j j Hee be an oen sbse o R : R ; : R X R j hee The se is cae he se o saes an he ncions j j j ae cae ncions he ssem ( is ien in consevaion om he consevaion o he ea qaniies We have a simes ieenia eqaion moe o a i o: This eqaion is cae invisci e s eqaion hich is aso non as one- imensiona consevaion a hich is a o imensiona eqaion Fom his eqaion e e ooin ssem o o imensiona eqaions: R an e T Le D be an abia omain o n n n bona D o D Then i oo om ( ha be he oa ni noma o he j n j s D j D This is consevaion a in inea om This eqaion has a hsica meanin ha he Vaiaion o is eqa o he osses hoh he bona D D
9 9 Heboic Ssem o Consevaion Las: Fo a j e i ij j A be an Jacobian mai o ; j eqaion (is cae a heboic ssem I o an Ω an R he mai j A j j A has ea eienvaes ih Ineenen eienvecos λ A ie ae ih eienvecos λ A ae e eienvecos I A has ea eienvaes an coesonin inea ineenen eienvecos an i ea isinc eienvaes hen he ssem is cae sic heboic Eame: Le hen A Hee he eienvae is an eienveco is Eame: ( ( = + = ; v υ v λ v v v v
10 v v v I is heboic ssem I he eienvaes heboic ae a isinc The ssem ( is cae sic Cach Pobem: Le s s s be he aia ieenia eqaion ih iniia aa o he cve We have he sace hich conains he cve is cae Cach obem : R aone an hich have iniia vae : R o > an is he ncion o Whee an ae consans hen he Cach obem is cae Riemann obem 4 Riemann Pobem: The consevaion as is iven Le an be o saes o Ω R ; e have o ieceise smooh coninos ncion :( ( soions o ( ha connecion an :ih iniia coniion is cae Riemann obem Eame: The eqaion o as namics in Eeian cooinae: In Eeian cooinaes he Ee eqaions o a comessibe invisci i in he consevaion om + j= ( i + j= ( j = ( + δ = i j i ij
11 ( ( ( = + + = j j e e hei o = ensi veoci he ene seciic inena esse heseciic oaene e λi A e e e e
12 eienvae s ae - I A o λ λ -λ -λ -λ λ _
13 assme mie( - (4 ( ( ( is ih Coesonin eienveco Theeienvae assme
14 4 ] om eqaion in eqaion ( in
15 5 heboic a sic an i is ( an is eienveco s ae ( ( Theeienveco is omeqaion so assme 5 Wea soion: Chaaceisics cve in one-imensiona case: Le R : R be a C ncion The consevaion as ih iniia aa: 8 R R Hee be a smooh soion hich oos he above eqaions
16 6 C Le be smooh soion o Eqaion ( hen he non-consevaion om We ae a( ( Fom above eqaion e have non-consevaion om a( The chaaceisics cve o above coniion; i i be eine as he soion is inea cve o he ieenia eqaion a (9 Theoem (: Assme ha is a smooh o ( he chaaceisic cve ae saih ines aon hich is consan Poo: Consie a chaaceisic cve assin hoh he oin a soion o he oina ieenia eqaion is sin he Meho o chaaceisics so ih iniia vae C Aon a cve is consan i e above eqaion is sin b chain e so Hence he chaaceisic cves ae saih ines hose consan soes eens on he iniia vae C ( in inea cve
17 7 Eame: 4 a Soion: a e i e a he chaaceisiccves ae accoin oiniia aa a a a is smooh ncion Non-smooh Soion: an esecive Eisences o non-smooh soion: We consie conve case ie Le R sch ha i is eceasin ncion hen ae o cases o conve an concave Since hen ( ( imies ha So ha chaaceisics inesec ae inie ime an om non smooh soion Eame: 5 The es eqaion (invisci eqaion is ih iniia coniion i - i i Soion: sovin chaaceisic cve e e
18 8 ( In hese means he chaaceisics cve asses hoh he oin Then e have i i i i - e no ha i - i i - i - i A = he chaaceisic inesec i i No i is isconiniies ma eveo ae a inie ime i is noninea hen is smooh in i ( i (
19 9 Chae- Riemann Pobem o isenoic maneoasnamics Shoc an aeacion aves: When o o an isenoic invisci an eec concin comessibe i is sbjece o a ansvese maneic ie hen consevaion om can be ien as R ( Whee i ma eesen ensi veoci esse ansvesa maneic ie an enoe maneic emeabii esecive; an ae ncions in hich ae an hee an ae osiive consans an is he aiabaic consan hich ies in he ane o mos o he ases The ineenen vaiabes ae an hen hee
20 / ha i imies above eqaion can be ien as o smooh soions ssem ( can be ien as AU U ( hee he mai A is eine as A = an b c is he maneo-acosic see ih c is he oca son see an ( b hich is Aven see; AU U b c A hee
21 λ λi A ( b c λ λ λ λ λ λ λ ( λ λ λ -λ λ The eienvaes o A ae an Ths he ssem ( is sic heboic hen > Le an ae he ih eienvecos coesonin o he eienvaes an esecive We have j i hen he is chaaceisic ie is enine noninea Simia i can be shon ha he secon chaaceisic ie is noninea hen
22 The aves associae ih an chaaceisic ie i be eihe shoc o aeacion aves Shoc: Le an he e an ih han saes o eihe a shoc o a aeacion ave ae an enoes esecive; he ssem ( ae sin in Ranine Honis jm coniions he iven b 4 hee enoe he jm acoss a isconini cve an υ is he shoc see Lemma : Le S an S esecive enoe - shoc an -shoc associae ih an chaaceisic ies Le he saes cves sais U an U sais he Ranine-Honio jm coniions (4 an ( Then he shoc (5 Whee sch ha o e have o an on S his o an on S Poo: The -eiminaion o υ e have
23 ( ( ( ( ( ( ( ( ( ( ( ( Le ; on he ieeniain (5 ih esec o e obain - Ψ
24 4 hich is neaive o We can aea sho ha an ae osiive o an ψ ψ he ψ hisψ ; Le χ ψ ψψ so ha χ Since χ ψψ i oos o χ Hence o Ths o i e ieeniae aain e e ψ ψψ 4ψ on S Simia o an e have on aain ieeniain hen on S No hese shoc cves ae saisie he La eno coniions Lemma(: I saisies an hen he La coniion ho ie -shoc saisies Whis he -shoc saisies Poo: U U 6 U U U U 7 Le s consie -shoc cve o ove U On a -shoc e no ha an b Laane s mean vae heoem hee eis eiss a a b cb a cab a b ξ ξ ξ since sch ha
25 5 he since e have an is an inceasin ncion c ξ an hs ξ ξ c an i imies ha 8 ( c ξ ξ Aso since e have i imies ha ( This imies b ha b an heeoe
26 6 b (9 Fom eqaion (8 an (9 e have ( ( ( ( ( ( ( ( b c In (5 he above ineqai hos ha an hence U In same manne anohe coniion since an on -shoc e have η o some η an hence ( c ( Fhe since
27 7 b ( an hence om ( an ( e obain b c ( ( I imies ha - Fom eqaion ( an (5 im ha - - U υ an hence λ υ Las e sho ha U In his a he eqaion ( hich imin ha ( Fo -shoc cve sin (5 e have hich imies ha ( U Hence -shoc saisie La coniion; as e as a saisie b he a coniion o he -shoc No e i sho ha he ensi esse veoci maneic ie va acoss a shoc Ain eqaion ( o -shoc he e an ih saes have o saisies La coniions (6 Le s eine V - ; V an hence υ U i oos ha hen since Simia b sin secon coniion ie U U e e V imies ha
28 8 - υ v so - V hence V Fom ( e have V V Since an ae osiive boh V an V ms have same sin; since V e have V Fo -shoc he as see on he boh sies o shoc is eae han shoc see an heeoe he aices coss he om e o ih In case o -shoc ain La coniions (7 his imin V since ( U o eqivaen υ hich oos ha V an hencev In case o -shoc aices coss om ih o e Le he saes ahea o an behin he shoc be esinae he - sae an -sae esecive Then o -shoc an hencev W an V W ; o -shoc so V W an V W Ths o boh shocs e have V W an V W To his coniions saisie he eqaion (4 hos ha V V hich imies ha ; V V ; so c ( c ( he above ineqaiies oos ha an heeoe an an om ( e have ; V V
29 9 Since i oos ha V V Since o -shoc V an an i oos ha V V imies ha an so Simia o -shoc V an is imin hav V Raeacion aves: The U hich ae o he ieceise smooh coninos soions o ( sch ha U λ U( U( λn U λn U n U U λn U ( I e ae η hen he eqaion ( is a ssem o oina ieenia eqaions an i can be ien as A- I hee I is ieni mai an he ieeniain ih esec o he vaiabe is enoe b o I ( hen an become consans I hen hee eis a eienveco o he mai A coesonin o he eienvae Since i has o ea an isinc eienvaes so i has o amiies o he aeacion aves R an R hich ae -Raeacion aves an -Raeacion aves esecive; Le s consie -aeacion aves since A-I an ih e have
30 ( Whee -Riemann invaian is (4 eesens R cve Simia -Riemann invaian o he -Raeacion ave cve is eesen R cve (5 Theoem On R esecive R he Riemann invaian esecive ( is consan Lemma:Acoss-aeacion aves (esecive -aeacion aves an (esecive an i an on i chaaceisic see inceases om e han sae o ih han sae
31 Poo: Since e no ha c b is an inceasin ncion o ; o i can be ien as - These ineqaiies ae an - sho ha λ U λ U Simia e can ove λ U λ U o -aeacion aves Then he convese o -aeacion aves since U e have U so i om o -aeacion aves - (6 In he since -aeacion ave eion is consan hen e e - he eqaion (6 shos ha - hich imies ha - an Hence an Simia i can be shon ha he -aeacion aves an Inocin a ne aamee hee obain om (5 he ooin omas o shoc cves o -shoc cve an -shoc cve (Resecive aeacion cves in he em o aameeizaions Fom eqaion (5
32 θ θ i iminheeb hee ha imies so ha (7 θ θ A θ θ ( ( ( ( Fo -aeacion aves ( since -Riemann invaian is consan e have θ θ θ so ha i e se θ θ θ A A (8 Simia o -aeacion ave e have hen as e as e se
33 A A θ Ths o -ami eihe shoc o aeacion ave e have A θ A θ θ i θ i θ (9 In he simia a θ A θ A θ i θ i θ ( hee A an ; is as o eession in above eqaions (9 an ( Theoem : The R cve is conve an monoonic eceasin hie R cve is concave an monoonic inceasin Poo: We no ha -aeacion ave is i ( On ieeniain ih esec o e have -
34 4 ( We no ha c b since in he ooin eqaions Aain on ieeniain ih esec o e have cc bb cc bb cc bb cc bb cc bb We no ha b an c ae ieeniain e have so ha an hee i imies cc cc c bb b cc bb b c cc bb b c
35 5 o ho an heeoe is conve ih esec o-aeacion aves Simia e can sho o -aeacion aves No e ove ha he shoc cves ae saie ih esec o o an hese has a oo eome in Riemann invaian cooinaes heneve an Theoem : The -shoc an -shoc cve ae saie ih esec o hen an o vaes o in in he ane Poo: We have o ove ha an a hoh he oin be inesece -shoc cve in a amos one oin o his is sicien o ove he as hoh he o ieen oins on he -shoc cve an hose soe ae ieen The soe o he ine joinin ih is - an Fo he -shoc eqaion (5 ae imies ha
36 6 - - hee e ove ha an When in in an ieeniain ih esec o an e have an is aain ieeniain ih esec o e have I aso ove ha hen in an ieeniain ih esec o an e obain ( on ieeniain e have
37 7 β ( ( Le hen Then Since i above coniion ae oos ha he vaes o in e have The above eqaion o be he in -shoc an hen
38 an imin ha is a eceasin ncion o ; an his oos ha i heeoe Ths - is a eceasin ncion o ; e hence -shoc cve - is saie ih esec o as sa in same a -shoc cve an is aso a saie ih esec o 8 Lemma Π Π an he ineqaiies an ho aon -shoc an - Π Π Wih shoc esecive ih Π Π ( (4 Poo: Fom ( an (4 e have Π an Π We no ha he above heoem as on a -shoc cves Fhe as aon -shoc cves Π Π in sicien a Π i has ha Π Π Π e have In oe o ove ha Π Π < Fo a coniion -shoc cve eqaion (5 i im ha
39 9 hence he above coniion hos ha an hese imies ha Π Simia e sho ha Π Π aon -shoc cves 4 Riemann Pobem: The ssem ( be he iniia coniion as i U i U U (4 is cae as Riemann obem Whee U be he sae o he e o an U be he sae o he ih o he consan saes ae seaae b in boh aves eihe a shoc aves o aeacion ave The Riemann invaian cooinaes ae Π Π an Lemma (4: The main Π Π is one o one an he Jacobian o his main is nonzeo hen
40 4 Poo: Since Π an Π On ieeniain ih esec o e e Π Π Π Π Ths he Jacobian o he main Π Π Π Π Π Π This is one-one an ono We consie Riemann invaians as cooinae ssem Le s i ae a ane ΠΠ in ha ane e a he cves S S R an R hich ivie he ane can ino o isinc eions I II III an IV Le U ae e sae Fiin U an vain U Le s consie U beon o an o he o eion as i4 (a Fo U R S R n n U Π Π : Π Π Snn U Π Π : Π Π R n an T U S U R U n n n In an above ave cves he ane ivies ino a o eion To sove he Riemann obem consie he ave cve U m T hee U T U U m Um m cves o enie ha sace T o m n n U T An e have o vei ha o cves U T U m an so hese a o cves ae non-inesecin an he se o a sch in he ane Π Π in one-one ashion I U I a a veica ine Π Π in i4 (a Which i be inesecs S niqe a a oin U m The soion o Riemann obem is no obvios; e ain on consan sae ou m b a -shoc an hen om U m o he consan sae U b a -aeacion ave
41 4 Le U II eion a a veica ine Π Π in i4 (a hich is inesec R niqe a a oin U m The soion is oin om U an U m b R an o om U m o U b R I U III eion e eine he conce o invese shoc cve The invese cve enoe b S consiss o hose saes Π Π hich can be connece o he sae Π Π on he ih b S shoc in i4 (a These eesene om (5 b Fi 4(a Raeacion cves (R an R an shoc cves (S an S in he ane Π Π The above cve inesec he R niqe a oin U m Theeoe U can be connece ih U b R ae ooe bs Π I U IV eion (see i4(c (as om emma Π ons I aso eines in on S Π Π This mean ha he S an S i inesecin niqe a he oinu heeoe he soion consiss o -shoc an -shoc Ths e have shon ha set U m :Um T U sace in he ane Π in a one-one a Π m 4 coves he enie ha When he vacm sae i s no saisie he same coniion Lemma (4: I Π Π he vacm occs
42 4 Poo: Fom i4 (a Π m Π an Πm Π; i Π Π hen Π Π Π Π m m i i be m Π m Πm Which imin ha ha m Hence vacm occs Fi4(b ave cves in ane( Theoem (4: Assme ha an ha e ae iven iniia saes U an U hee o he Riemann obem o ssem ( Assme ha Π Π Then hee eiss a soion o he Riemann obem o ssem ( Moeove he soion is iven b - ave ooin b a -ave saisin an he soion is niqe in he cass o consan saes seaae b shoc aves an aeacion aves
43 4 i4(c -shoc ave an -shoc ave i4( vacm cve 5 Ineacion o Eemena aves: The ineacion o eemena aves obainin om he Riemann obem (4 ives ise o ne emein eemena aves An hen o jm isconiniies a an i as oos: U U i 5 U i U i The choice o U an U in he ems o U an an abia an R Wih he iniia aa e have o Riemann obem oca The is Riemann obem o he eemena ave ma ineac he secon Riemann obem o he eemena ave an he ime o ineacion a ome a ne Riemann obem a one imensiona Ee eqaion I ma be on o he ineacion o he eemena aves Hee e ie RS R i means ha a -aeacion aves o R o he is Riemann obem ineacs ih -shoc S o he secon Riemann obem o Then i ineacs o ne Riemann obem o via m S R In ieen amiies ae ossibe o ineacion o eemena aves an as e as he same ami ae esecive ( SS SR RR RS an (SS SS RS SR SR RS
44 44 5 Ineacion o Eemena aves om ieen Famiies: (a Coision o o shocs (S S : Le U is connecion o U b he - shoc S is a is Riemann obem an U is connece o b a -shoc S o he secon Riemann obem Fo a iven U e consie U an U in sch a a ha ien ( om (5 e have U in ohe a ha hen e have i 5(a S S coision Since see o -shoc o he secon Riemann obem is neaive S an see -shoc o he is Riemann obem is osiive S oveaess Then i shos ha o an abia saeu he sae U ies in he eion IV (in i4 (b I in sicien o ove ha o an Le ae in cona ha I in his hen Imin heeb ha
45 45 P P P P The above eqaion (5 is sic osiive hich is a conaicion Hence (5 ie he cve S U ae ies beo he cvess U heeoe U ies in he eion IV Ths an i oos ineacion ess isss SS ineacion ess in case o isae in i5 (a (b Coision o a shoc an aeacion (S R : Hee U SU an U R U eqaion (5 e have ie o a iven U Le U an U sch ha an om eqaion (5 e have om Since -shoc o he Riemann obem is osiive an - aeacion ave o he secon Riemann obem is neaive veoci i oos ha RoveaesS Since o an ivenu o an can be oos ha he cve U in he eion III sbseqen SR RS The come ess his case in i5 (b R ies beo he cve R U hence U ies i 5(b S R coision
46 46 (c Coision o o aeacion aves (R R : We consie R an R U U In an ohe a o a ivenu Le U an U U U sch ha an hen Since he aiin en o - aeacion ave has a osiive veoci (bone above in - ane an ha -aeacion ave has a neaive veoci (bone above ineacion i ae ace Since an I oos ha he cve R U ies above he cve R U ; hence U ies in he eion II an he ineacion ess II an he ineacion es is R R R R Then come ess in i5 (c i 5(c R R coision ( Coision o a aeacion ave an a shoc (R S : Hee R an S U U an ie o ivenu e choose U an U sch ha U U an Since he secon Riemann obem o -shoc see is ess han -aeacion ave o is Riemann obem o he see o aiin en in ( - ane an heeoe S eneaes R Fo an iven ha U I sho ha U I hen i o sho
47 47 (5 Since is a eceasin ncion ih esec o he is vaiabes o he cve S U an hen e i have Hence he eqaiies (5 hee im ha cves S (U ies above U ies in he eion I Ths he ineacion es isrs SR ; an is come ess in i 5( i 5( R S coision 5 Ineacion o Eemena aves om same ami: (a - shoc ave oveaes anohe -shoc ave (S S : We consie he siaion in hich U is connecion o U b a shoc o he is Riemann obem an U is connece o U b a - shoc o he secon Riemann obem In ohe siaion a iven e saeu he inemeiae sae U an he ih sae ih La coniions sais U U U U U U U an U ae chose sch ha (54 an ih La sabii coniions U U U U U U U (55 an
48 48 hee U U is he see o shoc connecion U o U an simia U U is he see o shoc connecin U o U Fom (54 an (55 e obaine U U U U ie he secon Riemann obem o -shoc oveaes he is Riemann obem o -shoc a a inie ime hen is ive ise o ne Riemann obem ih aa U an U To ove his obem We ms have o eemine he eion in hich U ies esec o U Le be caim ha U va ies in eion III so his have soion o he ne Riemann obem consiss o R an S In an moe a o sho ha o o caim: e have o ove ha S U ies in enie in he eion III; o ove his eqie o sho ha o - We consie on he conaicion ha - o Then he oo ha i e ae hen (56 Imin hee b ha Povin ha (57 hich is conaicion on as e han o ineqaiies (57 is osiive Hence R S S S ; an come ess in above siaion i5(a i 5(a S oveaes S
49 49 (b -shoc ave oveaes anohe - shoc ave (S S : Le U ies in a eion I so ha SS SR is simia o he evios case an is above siaion isae come ess i 5(b S oveaes R (C -shoc ave oveaes -Raeacion ave (R S : U is connece o U b - aeacion ave an he secon In case he Riemann obem o he Riemann o he U is connece o U b -shoc ie a ivenu Le U an he an R U o in ohe a o So e sho ha (58 U in sch a a ha S U ies beo o Le s eine F so ha F On ieeniain F ih esec o e obain F imin ha F F ie F an hence beo he cve RU o In anohe o sho ha i is sicien o U he cve S U o ; he sicien a he caim has S U ies S ies above
50 5 ; (59 Le s eine F So ha F F Le s consie ha o imin ha imin heeb ha ; P P P P o eqivaen P P P P (5 he e han sie o ineqai (5 is osiive hich eaves s ih a conaicion Hence o - imin ha F We eine a ne ncion o F A some oin ~ ~ inesece in U S an S U o ~ Since F an F i is inemeiae vae oe hee eiss a ~ beeen an sch ha ~ F b vie o monoonici Ths U S an S U is niqe eemine o he
51 5 inesecion an he come ess in i 5(b We isinishe hee cases o eenin on he vae o (a I ~ inee -shoc is ea as comae o - aeacion ave hen U III an he ineacion ess is RS RS (b I ~ inee o aves o is ami ineac he annihiae each ohe an ive ise o ave o secon ami henu ies on S U an he ineacion es is RS S (c I ~ an he ineacion es is RS SS on U IV; inee he -aeacion o he is Riemann obem is ea as comae o he -shoc o secon Riemann obem hich is sone oveaes an he aiin en o -aeacion ave a eece shoc S U U m an a connecion ne connecion consans sae U m on he e o U on he ih is oce The ansmie ave ae ineacion is he -shoc ha joins sae U on he e an U m on he ih i5(c R oveaes S ( - Raeacion ave oveaes -shoc ave (S R : Hee o a iven U e consie U an U sch ha U SU an U R U om eqaion (5 e have - an om eqaion (5 e have In he ane ( he see o aiin en o U U U ie is ess han -shoc see an heeoe he -aeacion ave om ih oveaes -shoc om e a inie ime We sho ha he cve R U ies beo he cve S U o ; o his e have o ha
52 5 G o Le s a ne ncion G o sho ha hen in his a i eine he o o an G o ho ha on - G ieeniain e have ha Imin heeb ha G G since G e have RU ies beo he cve R U o hen o o be G hich is G RU an S U inesec ino niqe a some oins ~ ~ G hen e ove ha Since he e han sie o his ineqaiies o is osiive so he concsion above So e sho ha o ; o sho ha o his a niqe oo has ~ sch ha ~ To sho a ne ncion e eine G G hee imin ha G i aes neaive as cose o zeo hen R U an U hee cases he vae o G ; an e no The cves ae inees niqe a he S i oos ha he inemeiae vae oe an in vie o monoonica; hee on eenin e isinish ie (i hen ~ an U IV ; he ineacion es is SR SS ; inee in sicien case he boh cves ae ineacion an hen he -aeacion ave is ea comae o he -shoc is sone hich is oce a ne eemena ave (ii hen ~ an U SU he ineacion es issr S ie ineacion o he is ami o eemena aves Gives ise o a secon ami o a ne eemena ave (iii hen ~ an U III he ineacion es is SR RS
53 5 Fi5( R oveaes S (e -Raeacion ave oveaes - shoc ave (S R : When U an U R U iven S U o he U e have consie U an an U S R ineacion aes ace in an anohe o in a U ae in a sch a ha om (5 e have S ies above he cve R U ie om (5 e have We sho ha o (5 We eine o sho ha M M Since hee imin b ha S U ies above R U On ieeniaion M since M e have M M since M i oos ha M e ove ha he R U ies above he cve R U o ; o sho ha o his i is enoh M o an he cve R U ies above he cve R U o M ; han sie o his ineqaiies is M hich o osiive e sho ha U niqe S U a oin ~ ~ o ~ M - o so ha M he e R o he inesec We eine an e consie a
54 54 consan K sch ha M o a K Then hee eiss a ~ sch ha M ~ Ths R U an S U ae inesec niqe a ~ ~ as R U an S U in a ems o monoone an he come ess shon in i5(c Hee hee cases ae ooin (i I ~ U IV he ineacion es issr SS inee he senh o R is sma comae o he eemena ave S an S annihiaes R in a inie ime The senh o he eece S is sma comae o he incien aves S an R (ii When ~ an U S( U he ineacion es issr S inee S is eae han R comae o he incien aves R ans (iii I ~ he ineacion ess issr SR ; inee R is sone hans ( -Shoc aves oveaes -Raeacion(R S : Fo a iven U e have U an S U o U hee U an R U U S U sch ha an We ove ha U R ies above he cve To sho ha e have a ne ncion (5 N o ; so ha N This in vie o he eession o an ies N Thee imin b ha Hence his es N N e sho ha U cve ; o sho i is sicien o his S U o S ies above he
55 55 o I N hen We consie hich is conaicion ha Ths i e have ha Thee imies b ha - ems o an ies o eqivaen ; his eession in (5 Which is conacion he above eqaion (5 is osiive o hence o e ove ha a oin ( ~ ~ 4 4 a SU an S U inesec niqe o ~ 4 Hee aain e isinish hee cases eenin on he vae o (i I ~ 4 U I he ineacion ess is R S SR inee he eemena ave R is sone comae o S he senh o eece S is sma comae o he incien aves S an R (ii I ~ 4 an U S U he ineacion es is R S S (iii I ~ 4 an U IV he ineacion es is R S SS ; inee S is sone han comae o he eemena ave R is eae ;
56 56 REFERENCES [] E Goesi PA Ravia Nmeica Aoimaion o Heboic Ssems o Consevaion Las Sine-Vea Ne Yo 996 [] T Raja Seha VD Shama Riemann Pobem an Eemena ave Ineacion in Isenoic Maneoasnamics Noninea Anasis: Rea Wo Aicaion ( [] YehaPinchoveJacob Rbinsein An Inocion o Paia Dieenia Eqaions Cambie Univesi Pess UK 5 [4] JKevoian Paia Dieenia Eqaions(Anaica Soion Techniqes Secon Eiion Sine-Vea Ne Yo
( ) ρ ρ + + = + d dt. ME 309 Formula Sheet. dp g dz = ρ. = f +ΣΚ and HS. +α + z = +α + z. δ =δ = δ =θ= τ =ρ =ρ. Page 1 of 7. Basic Equations.
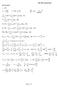 Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci
Basic Eqaions ME 9 Fomla Shee R µ F F A A ηv V el η η A Vssem ( ) V el A F F V A ( ) S B XYZ XYZ el g F F a V V A S B / XYZ el M M A V ( ) S B el ( ) Q W ev e A hee V e g ino on el V consan (o invisci
Appendix. The solution begins with Eq. (2.15) from the text, which we repeat here for 1, (A.1)
 Aenix Aenix A: The equaion o he sock rice. The soluion egins wih Eq..5 rom he ex, which we reea here or convenience as Eq.A.: [ [ E E X, A. c α where X u ε, α γ, an c α y AR. Take execaions o Eq. A. as
Aenix Aenix A: The equaion o he sock rice. The soluion egins wih Eq..5 rom he ex, which we reea here or convenience as Eq.A.: [ [ E E X, A. c α where X u ε, α γ, an c α y AR. Take execaions o Eq. A. as
SOLUTION OF EQUATIONS OF MOTION FOR THE START OF AN ELECTRIC HOIST
 Nmbe III, Vome VI, Jy OLUION O QUION O MOION OR H R O N LRI HOI Pae Vaní mmay: his conibion descibes a soion of eqaions of moion fo he sa of an eecic hois. o he cacaion hee ae sed aes fo he aca eecic hois,
Nmbe III, Vome VI, Jy OLUION O QUION O MOION OR H R O N LRI HOI Pae Vaní mmay: his conibion descibes a soion of eqaions of moion fo he sa of an eecic hois. o he cacaion hee ae sed aes fo he aca eecic hois,
( ) ( t) ( 0) ( ) dw w. = = β. Then the solution of (1.1) is easily found to. wt = t+ t. We generalize this to the following nonlinear differential
 Periodic oluion of van der Pol differenial equaion. by A. Arimoo Deparmen of Mahemaic Muahi Iniue of Technology Tokyo Japan in Seminar a Kiami Iniue of Technology January 8 9. Inroducion Le u conider a
Periodic oluion of van der Pol differenial equaion. by A. Arimoo Deparmen of Mahemaic Muahi Iniue of Technology Tokyo Japan in Seminar a Kiami Iniue of Technology January 8 9. Inroducion Le u conider a
) 2. δ δ. β β. β β β β. r k k. tll. m n Λ + +
 Techical Appedix o Hamig eposis ad Helpig Bowes: The ispaae Impac of Ba Cosolidaio (o o be published bu o be made available upo eques. eails of Poofs of Poposiios 1 ad To deive Poposiio 1 s exac ad sufficie
Techical Appedix o Hamig eposis ad Helpig Bowes: The ispaae Impac of Ba Cosolidaio (o o be published bu o be made available upo eques. eails of Poofs of Poposiios 1 ad To deive Poposiio 1 s exac ad sufficie
Analytical Expression for Hessian
 Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that
Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that
Analysis of optimal harvesting of a prey-predator fishery model with the limited sources of prey and presence of toxicity
 ES Web of Confeences 7, 68 (8) hps://doiog/5/esconf/8768 ICEIS 8 nalsis of opimal havesing of a pe-pedao fishe model wih he limied souces of pe and pesence of oici Suimin,, Sii Khabibah, and Dia nies Munawwaoh
ES Web of Confeences 7, 68 (8) hps://doiog/5/esconf/8768 ICEIS 8 nalsis of opimal havesing of a pe-pedao fishe model wih he limied souces of pe and pesence of oici Suimin,, Sii Khabibah, and Dia nies Munawwaoh
Electronic Companion to Supply Chain Dynamics and Channel Efficiency in Durable Product Pricing and Distribution
 i Eleconic Copanion o Supply Chain Dynaics and Channel Efficiency in Duable Poduc Picing and Disibuion Wei-yu Kevin Chiang College of Business Ciy Univesiy of Hong Kong wchiang@ciyueduh I Poof of Poposiion
i Eleconic Copanion o Supply Chain Dynaics and Channel Efficiency in Duable Poduc Picing and Disibuion Wei-yu Kevin Chiang College of Business Ciy Univesiy of Hong Kong wchiang@ciyueduh I Poof of Poposiion
Laplace s Equation in Spherical Polar Coördinates
 Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
= e 6t. = t 1 = t. 5 t 8L 1[ 1 = 3L 1 [ 1. L 1 [ π. = 3 π. = L 1 3s = L. = 3L 1 s t. = 3 cos(5t) sin(5t).
 Worked Soluion 95 Chaper 25: The Invere Laplace Tranform 25 a From he able: L ] e 6 6 25 c L 2 ] ] L! + 25 e L 5 2 + 25] ] L 5 2 + 5 2 in(5) 252 a L 6 + 2] L 6 ( 2)] 6L ( 2)] 6e 2 252 c L 3 8 4] 3L ] 8L
Worked Soluion 95 Chaper 25: The Invere Laplace Tranform 25 a From he able: L ] e 6 6 25 c L 2 ] ] L! + 25 e L 5 2 + 25] ] L 5 2 + 5 2 in(5) 252 a L 6 + 2] L 6 ( 2)] 6L ( 2)] 6e 2 252 c L 3 8 4] 3L ] 8L
Example 1: THE ELECTRIC DIPOLE
 Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2
Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Homomorphism of Intuitionistic Fuzzy Groups
 International Mathematical Forum, Vol. 6, 20, no. 64, 369-378 Homomorphism o Intuitionistic Fuzz Groups P. K. Sharma Department o Mathematics, D..V. College Jalandhar Cit, Punjab, India pksharma@davjalandhar.com
International Mathematical Forum, Vol. 6, 20, no. 64, 369-378 Homomorphism o Intuitionistic Fuzz Groups P. K. Sharma Department o Mathematics, D..V. College Jalandhar Cit, Punjab, India pksharma@davjalandhar.com
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
The choice of an optimal LCSCR contract involves the choice of an x L. such that the supplier chooses the LCS option when x xl
 EHNIA APPENDIX AMPANY SIMPE S SHARIN NRAS Proof of emma. he choice of an opimal SR conrac involves he choice of an such ha he supplier chooses he S opion hen and he R opion hen >. When he selecs he S opion
EHNIA APPENDIX AMPANY SIMPE S SHARIN NRAS Proof of emma. he choice of an opimal SR conrac involves he choice of an such ha he supplier chooses he S opion hen and he R opion hen >. When he selecs he S opion
On Quasi - f -Power Increasing Sequences
 Ieaioal Maheaical Fou Vol 8 203 o 8 377-386 Quasi - f -owe Iceasig Sequeces Maheda Misa G Deae of Maheaics NC College (Auooous) Jaju disha Mahedaisa2007@gailco B adhy Rolad Isiue of echoy Golahaa-76008
Ieaioal Maheaical Fou Vol 8 203 o 8 377-386 Quasi - f -owe Iceasig Sequeces Maheda Misa G Deae of Maheaics NC College (Auooous) Jaju disha Mahedaisa2007@gailco B adhy Rolad Isiue of echoy Golahaa-76008
Chapter 1 Fundamentals in Elasticity
 D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
APPENDIX A DERIVATION OF JOINT FAILURE DENSITIES
 APPENDIX A DERIVAION OF JOIN FAILRE DENSIIES I his Appedi we prese he derivaio o he eample ailre models as show i Chaper 3. Assme ha he ime ad se o ailre are relaed by he cio g ad he sochasic are o his
APPENDIX A DERIVAION OF JOIN FAILRE DENSIIES I his Appedi we prese he derivaio o he eample ailre models as show i Chaper 3. Assme ha he ime ad se o ailre are relaed by he cio g ad he sochasic are o his
The Euler Equations! λ 1. λ 2. λ 3. ρ ρu. E = e + u 2 /2. E + p ρ. = de /dt. = dh / dt; h = h( T ); c p. / c v. ; γ = c p. p = ( γ 1)ρe. c v.
 hp://www.nd.ed/~gryggva/cfd-corse/ The Eler Eqaions The Eler Eqaions The Eler eqaions for D flow: + + p = x E E + p where Define E = e + / H = h + /; h = e + p/ Gréar Tryggvason Spring 3 Ideal Gas: p =
hp://www.nd.ed/~gryggva/cfd-corse/ The Eler Eqaions The Eler Eqaions The Eler eqaions for D flow: + + p = x E E + p where Define E = e + / H = h + /; h = e + p/ Gréar Tryggvason Spring 3 Ideal Gas: p =
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Fractional Calculus. Student: Manal AL-Ali Dr. Abdalla Obeidat
 Fracional Calculu Suen: Manal AL-Ali Dr. Aballa Obeia Deignaion Deignaion mean inegraion an iffereniaion of arbirary orer, In oher ereion i mean ealing wih oeraor like,, i arbirary real or Comle value.
Fracional Calculu Suen: Manal AL-Ali Dr. Aballa Obeia Deignaion Deignaion mean inegraion an iffereniaion of arbirary orer, In oher ereion i mean ealing wih oeraor like,, i arbirary real or Comle value.
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
webpage :
 Amin Haliloic Mah Eciss E-mail : amin@shkhs wbpa : wwwshkhs/amin MATH EXERISES GRADIENT DIVERGENE URL DEL NABLA OERATOR LALAIAN OERATOR ONTINUITY AND NAVIER-STOKES EQUATIONS VETOR RODUTS I and hn scala
Amin Haliloic Mah Eciss E-mail : amin@shkhs wbpa : wwwshkhs/amin MATH EXERISES GRADIENT DIVERGENE URL DEL NABLA OERATOR LALAIAN OERATOR ONTINUITY AND NAVIER-STOKES EQUATIONS VETOR RODUTS I and hn scala
George S. A. Shaker ECE477 Understanding Reflections in Media. Reflection in Media
 Geoge S. A. Shake C477 Udesadg Reflecos Meda Refleco Meda Ths hadou ages a smplfed appoach o udesad eflecos meda. As a sude C477, you ae o equed o kow hese seps by hea. I s jus o make you udesad how some
Geoge S. A. Shake C477 Udesadg Reflecos Meda Refleco Meda Ths hadou ages a smplfed appoach o udesad eflecos meda. As a sude C477, you ae o equed o kow hese seps by hea. I s jus o make you udesad how some
Lecture 12 Modulation and Sampling
 EE 2 spring 2-22 Handou #25 Lecure 2 Modulaion and Sampling The Fourier ransform of he produc of wo signals Modulaion of a signal wih a sinusoid Sampling wih an impulse rain The sampling heorem 2 Convoluion
EE 2 spring 2-22 Handou #25 Lecure 2 Modulaion and Sampling The Fourier ransform of he produc of wo signals Modulaion of a signal wih a sinusoid Sampling wih an impulse rain The sampling heorem 2 Convoluion
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Commutative Monoids in Intuitionistic Fuzzy Sets
 Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
(a,b) Let s review the general definitions of trig functions first. (See back cover of your book) sin θ = b/r cos θ = a/r tan θ = b/a, a 0
 TRIGONOMETRIC IDENTITIES (a,b) Let s eview the geneal definitions of tig functions fist. (See back cove of you book) θ b/ θ a/ tan θ b/a, a 0 θ csc θ /b, b 0 sec θ /a, a 0 cot θ a/b, b 0 By doing some
TRIGONOMETRIC IDENTITIES (a,b) Let s eview the geneal definitions of tig functions fist. (See back cove of you book) θ b/ θ a/ tan θ b/a, a 0 θ csc θ /b, b 0 sec θ /a, a 0 cot θ a/b, b 0 By doing some
Tutorial Note - Week 09 - Solution
 Tutoial Note - Week 9 - Solution ouble Integals in Pola Coodinates. a Since + and + 5 ae cicles centeed at oigin with adius and 5, then {,θ 5, θ π } Figue. f, f cos θ, sin θ cos θ sin θ sin θ da 5 69 5
Tutoial Note - Week 9 - Solution ouble Integals in Pola Coodinates. a Since + and + 5 ae cicles centeed at oigin with adius and 5, then {,θ 5, θ π } Figue. f, f cos θ, sin θ cos θ sin θ sin θ da 5 69 5
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
F19MC2 Solutions 9 Complex Analysis
 F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
( ) ( ) ( ) Fourier series. ; m is an integer. r(t) is periodic (T>0), r(t+t) = r(t), t Fundamental period T 0 = smallest T. Fundamental frequency ω
 Fourier series e jm when m d when m ; m is an ineger. jm jm jm jm e d e e e jm jm jm jm r( is periodi (>, r(+ r(, Fundamenal period smalles Fundamenal frequeny r ( + r ( is periodi hen M M e j M, e j,
Fourier series e jm when m d when m ; m is an ineger. jm jm jm jm e d e e e jm jm jm jm r( is periodi (>, r(+ r(, Fundamenal period smalles Fundamenal frequeny r ( + r ( is periodi hen M M e j M, e j,
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Bounding Nonsplitting Enumeration Degrees
 Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
! " # " $ #% $ "! #&'() '" ( * / ) ",. #
 Ψ ƒ! " # " $ #% $ "! #&'() '" ( * +",-.'!( / ) ",. # 0# $"!"#$%# Ψ 12/345 6),78 94. ƒ 9)")1$/):0;3;::9 >'= ( ? 9 @ '&( % A! &*?9 '( B+)C*%++ &*%++C 0 4 3'+C( D'+C(%E $B B - " % B
Ψ ƒ! " # " $ #% $ "! #&'() '" ( * +",-.'!( / ) ",. # 0# $"!"#$%# Ψ 12/345 6),78 94. ƒ 9)")1$/):0;3;::9 >'= ( ? 9 @ '&( % A! &*?9 '( B+)C*%++ &*%++C 0 4 3'+C( D'+C(%E $B B - " % B
!"#$ %"&'$!&!"(!)%*+, -$!!.!$"("-#$&"%-
 !"#$ %"&$!&!"(!)%*+, -$!!.!$"("-#$&"%-.#/."0, .1%"("/+.!2$"/ 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333 4.)!$"!$-(#&!- 33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333
!"#$ %"&$!&!"(!)%*+, -$!!.!$"("-#$&"%-.#/."0, .1%"("/+.!2$"/ 3333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333 4.)!$"!$-(#&!- 33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutions to Problems on Matrix Algebra
 MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log
MATH 38061/MATH48061/MATH68061: MULTIVARIATE STATISTICS Solutios to Poblems o Matix Algeba 1 Let A be a squae diagoal matix takig the fom a 11 0 0 0 a 22 0 A 0 0 a pp The ad So, log det A t log A t log
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Η ΑΝΘΥΦΑΙΡΕΤΙΚΗ ΕΡΜΗΝΕΙΑ ΤΗΣ ΕΞΩΣΗΣ ΤΗΣ ΠΟΙΗΣΗΣ ΣΤΟ ΔΕΚΑΤΟ ΒΙΒΛΙΟ ΤΗΣ ΠΟΛΙΤΕΙΑΣ ΤΟΥ ΠΛΑΤΩΝΟΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ MΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΕΘΟΔΟΛΟΓΙΑΣ, ΙΣΤΟΡΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΉΜΩΝ ΑΓΩΓΉΣ & ΘΕΩΡΙΑΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ, ΠΑΙΔΑΓΩΓΙΚΗΣ &
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ MΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΕΘΟΔΟΛΟΓΙΑΣ, ΙΣΤΟΡΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΉΜΩΝ ΑΓΩΓΉΣ & ΘΕΩΡΙΑΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ, ΠΑΙΔΑΓΩΓΙΚΗΣ &
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Lecture 6. Goals: Determine the optimal threshold, filter, signals for a binary communications problem VI-1
 Lecue 6 Goals: Deemine e opimal esold, file, signals fo a binay communicaions poblem VI- Minimum Aveage Eo Pobabiliy Poblem: Find e opimum file, esold and signals o minimize e aveage eo pobabiliy. s s
Lecue 6 Goals: Deemine e opimal esold, file, signals fo a binay communicaions poblem VI- Minimum Aveage Eo Pobabiliy Poblem: Find e opimum file, esold and signals o minimize e aveage eo pobabiliy. s s
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Errata (Includes critical corrections only for the 1 st & 2 nd reprint)
 Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
Wedesday, May 5, 3 Erraa (Icludes criical correcios oly for he s & d repri) Advaced Egieerig Mahemaics, 7e Peer V O eil ISB: 978474 Page # Descripio 38 ie 4: chage "w v a v " "w v a v " 46 ie : chage "y
4.2 Differential Equations in Polar Coordinates
 Section 4. 4. Diffeential qations in Pola Coodinates Hee the two-dimensional Catesian elations of Chapte ae e-cast in pola coodinates. 4.. qilibim eqations in Pola Coodinates One wa of epesg the eqations
Section 4. 4. Diffeential qations in Pola Coodinates Hee the two-dimensional Catesian elations of Chapte ae e-cast in pola coodinates. 4.. qilibim eqations in Pola Coodinates One wa of epesg the eqations
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
A Two-Sided Laplace Inversion Algorithm with Computable Error Bounds and Its Applications in Financial Engineering
 Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
ω = radians per sec, t = 3 sec
 Secion. Linear and Angular Speed 7. From exercise, =. A= r A = ( 00 ) (. ) = 7,00 in 7. Since 7 is in quadran IV, he reference 7 8 7 angle is = =. In quadran IV, he cosine is posiive. Thus, 7 cos = cos
Secion. Linear and Angular Speed 7. From exercise, =. A= r A = ( 00 ) (. ) = 7,00 in 7. Since 7 is in quadran IV, he reference 7 8 7 angle is = =. In quadran IV, he cosine is posiive. Thus, 7 cos = cos
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Fundamental Equations of Fluid Mechanics
 Fundamental Equations of Fluid Mechanics 1 Calculus 1.1 Gadient of a scala s The gadient of a scala is a vecto quantit. The foms of the diffeential gadient opeato depend on the paticula geomet of inteest.
Fundamental Equations of Fluid Mechanics 1 Calculus 1.1 Gadient of a scala s The gadient of a scala is a vecto quantit. The foms of the diffeential gadient opeato depend on the paticula geomet of inteest.
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Matrix Hartree-Fock Equations for a Closed Shell System
 atix Hatee-Fock Equations fo a Closed Shell System A single deteminant wavefunction fo a system containing an even numbe of electon N) consists of N/ spatial obitals, each occupied with an α & β spin has
atix Hatee-Fock Equations fo a Closed Shell System A single deteminant wavefunction fo a system containing an even numbe of electon N) consists of N/ spatial obitals, each occupied with an α & β spin has
Đường tròn : cung dây tiếp tuyến (V1) Đường tròn cung dây tiếp tuyến. Giải.
 Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
Đường tròn cung dây tiếp tuyến BÀI 1 : Cho tam giác ABC. Đường tròn có đường kính BC cắt cạnh AB, AC lần lượt tại E, D. BD và CE cắt nhau tại H. chứng minh : 1. AH vuông góc BC (tại F thuộc BC). 2. FA.FH
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5 Ι ^ο 3 X X X. go > 'α. ο. o f Ο > = S 3. > 3 w»a. *= < ^> ^ o,2 l g f ^ 2-3 ο. χ χ. > ω. m > ο ο ο - * * ^r 2 =>^ 3^ =5 b Ο? UJ. > ο ο.
 728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
728!. -θ-cr " -;. '. UW -,2 =*- Os Os rsi Tf co co Os r4 Ι. C Ι m. Ι? U Ι. Ι os ν ) ϋ. Q- o,2 l g f 2-2 CT= ν**? 1? «δ - * * 5 Ι -ΐ j s a* " 'g cn" w *" " 1 cog 'S=o " 1= 2 5 ν s/ O / 0Q Ε!θ Ρ h o."o.
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Approximation of the Lerch zeta-function
 Approximaion of he Lerch zea-funcion Ramūna Garunkši Deparmen of Mahemaic and Informaic Vilniu Univeriy Naugarduko 4 035 Vilniu Lihuania ramunagarunki@mafvul Abrac We conider uniform in parameer approximaion
Approximaion of he Lerch zea-funcion Ramūna Garunkši Deparmen of Mahemaic and Informaic Vilniu Univeriy Naugarduko 4 035 Vilniu Lihuania ramunagarunki@mafvul Abrac We conider uniform in parameer approximaion
Similarly, we may define hyperbolic functions cosh α and sinh α from the unit hyperbola
 Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
EE101: Resonance in RLC circuits
 EE11: Resonance in RLC circuits M. B. Patil mbatil@ee.iitb.ac.in www.ee.iitb.ac.in/~sequel Deartment of Electrical Engineering Indian Institute of Technology Bombay I V R V L V C I = I m = R + jωl + 1/jωC
EE11: Resonance in RLC circuits M. B. Patil mbatil@ee.iitb.ac.in www.ee.iitb.ac.in/~sequel Deartment of Electrical Engineering Indian Institute of Technology Bombay I V R V L V C I = I m = R + jωl + 1/jωC
7 Present PERFECT Simple. 8 Present PERFECT Continuous. 9 Past PERFECT Simple. 10 Past PERFECT Continuous. 11 Future PERFECT Simple
 A/ Ονόματα και ένα παράδειγμα 1 Present Simple 7 Present PERFECT Simple 2 Present Continuous 8 Present PERFECT Continuous 3 Past Simple (+ used to) 9 Past PERFECT Simple she eats she is eating she ate
A/ Ονόματα και ένα παράδειγμα 1 Present Simple 7 Present PERFECT Simple 2 Present Continuous 8 Present PERFECT Continuous 3 Past Simple (+ used to) 9 Past PERFECT Simple she eats she is eating she ate
Chapter 6 ( )( ) 8 ( ) 1.145 0.7 ( )( ) Exercise Solutions. Microelectronics: Circuit Analysis and Design, 4 th edition Chapter 6. EX6.
 Micelectnic: icuit Analyi and Dein, 4 th editin hapte 6 y D. A. Neaen xecie Slutin xecie Slutin X6. (a ( n 0.85 0.7 80 ( 0 ( 0.000833 0. 0 Q 3.3 0. 5. β A 0. (b 3. 846 A/ 0.06 β ( 0( 0.06 0. 8 3. k Ω hapte
Micelectnic: icuit Analyi and Dein, 4 th editin hapte 6 y D. A. Neaen xecie Slutin xecie Slutin X6. (a ( n 0.85 0.7 80 ( 0 ( 0.000833 0. 0 Q 3.3 0. 5. β A 0. (b 3. 846 A/ 0.06 β ( 0( 0.06 0. 8 3. k Ω hapte
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
The one-dimensional periodic Schrödinger equation
 The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
The one-dmensonal perodc Schrödnger equaon Jordan Bell jordan.bell@gmal.com Deparmen of Mahemacs, Unversy of Torono Aprl 23, 26 Translaons and convoluon For y, le τ y f(x f(x y. To say ha f : C s unformly
Almost all short intervals containing prime numbers
 ACTA ARITHMETICA LXXVI (6 Almos all shor inervals conaining prime nmbers by Chaoha Jia (Beijing Inrocion In 37, Cramér [] conjecred ha every inerval (n, n f(n log 2 n conains a prime for some f(n as n
ACTA ARITHMETICA LXXVI (6 Almos all shor inervals conaining prime nmbers by Chaoha Jia (Beijing Inrocion In 37, Cramér [] conjecred ha every inerval (n, n f(n log 2 n conains a prime for some f(n as n
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
The Neutrix Product of the Distributions r. x λ
 ULLETIN u. Maaysia Math. Soc. Secod Seies 22 999 - of the MALAYSIAN MATHEMATICAL SOCIETY The Neuti Poduct of the Distibutios ad RIAN FISHER AND 2 FATMA AL-SIREHY Depatet of Matheatics ad Copute Sciece
ULLETIN u. Maaysia Math. Soc. Secod Seies 22 999 - of the MALAYSIAN MATHEMATICAL SOCIETY The Neuti Poduct of the Distibutios ad RIAN FISHER AND 2 FATMA AL-SIREHY Depatet of Matheatics ad Copute Sciece
University of Washington Department of Chemistry Chemistry 553 Spring Quarter 2010 Homework Assignment 3 Due 04/26/10
 Universiy of Washingon Deparmen of Chemisry Chemisry 553 Spring Quarer 1 Homework Assignmen 3 Due 4/6/1 v e v e A s ds: a) Show ha for large 1 and, (i.e. 1 >> and >>) he velociy auocorrelaion funcion 1)
Universiy of Washingon Deparmen of Chemisry Chemisry 553 Spring Quarer 1 Homework Assignmen 3 Due 4/6/1 v e v e A s ds: a) Show ha for large 1 and, (i.e. 1 >> and >>) he velociy auocorrelaion funcion 1)
21. Stresses Around a Hole (I) 21. Stresses Around a Hole (I) I Main Topics
 I Main Topics A Intoducon to stess fields and stess concentaons B An axisymmetic poblem B Stesses in a pola (cylindical) efeence fame C quaons of equilibium D Soluon of bounday value poblem fo a pessuized
I Main Topics A Intoducon to stess fields and stess concentaons B An axisymmetic poblem B Stesses in a pola (cylindical) efeence fame C quaons of equilibium D Soluon of bounday value poblem fo a pessuized
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
The Laplacian in Spherical Polar Coordinates
 Univesity of Connecticut DigitalCommons@UConn Chemisty Education Mateials Depatment of Chemisty -6-007 The Laplacian in Spheical Pola Coodinates Cal W. David Univesity of Connecticut, Cal.David@uconn.edu
Univesity of Connecticut DigitalCommons@UConn Chemisty Education Mateials Depatment of Chemisty -6-007 The Laplacian in Spheical Pola Coodinates Cal W. David Univesity of Connecticut, Cal.David@uconn.edu
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Some new generalized topologies via hereditary classes. Key Words:hereditary generalized topological space, A κ(h,µ)-sets, κµ -topology.
 Bol. Soc. Paran. Mat. (3s.) v. 30 2 (2012): 71 77. c SPM ISSN-2175-1188 on line ISSN-00378712 in press SPM: www.spm.uem.br/bspm doi:10.5269/bspm.v30i2.13793 Some new generalized topologies via hereditary
Bol. Soc. Paran. Mat. (3s.) v. 30 2 (2012): 71 77. c SPM ISSN-2175-1188 on line ISSN-00378712 in press SPM: www.spm.uem.br/bspm doi:10.5269/bspm.v30i2.13793 Some new generalized topologies via hereditary
Coefficient Inequalities for a New Subclass of K-uniformly Convex Functions
 International Journal of Computational Science and Mathematics. ISSN 0974-89 Volume, Number (00), pp. 67--75 International Research Publication House http://www.irphouse.com Coefficient Inequalities for
International Journal of Computational Science and Mathematics. ISSN 0974-89 Volume, Number (00), pp. 67--75 International Research Publication House http://www.irphouse.com Coefficient Inequalities for
ƒšˆœˆ Ÿ Œˆ ˆ ˆ ˆ Šˆ ƒˆÿ.. Ê μ Î ±μ
 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2013.. 44.. 5 ƒšˆœˆ Ÿ Œˆ ˆ ˆ ˆ Šˆ ƒˆÿ.. Ê μ Î ±μ É μë Î ± É ÉÊÉ ³.. ƒ. ±μ, ˆ É ÉÊÉ Ö μ Ë ± Š, ²³ - É, Š Ì É ˆ 1535 Œ 1537 μ² Ò Î Ö Ì É 1537 μé Í ²Ò μ² μ Ò ËÊ ±Í 1539 ² Ò ³ Éμ Ò Î É 1541
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2013.. 44.. 5 ƒšˆœˆ Ÿ Œˆ ˆ ˆ ˆ Šˆ ƒˆÿ.. Ê μ Î ±μ É μë Î ± É ÉÊÉ ³.. ƒ. ±μ, ˆ É ÉÊÉ Ö μ Ë ± Š, ²³ - É, Š Ì É ˆ 1535 Œ 1537 μ² Ò Î Ö Ì É 1537 μé Í ²Ò μ² μ Ò ËÊ ±Í 1539 ² Ò ³ Éμ Ò Î É 1541
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Probabilistic Image Processing by Extended Gauss-Markov Random Fields
 Pobablsc mage Pocessng b Eended Gauss-Makov Random Felds Kauuk anaka Munek asuda Ncolas Mon Gaduae School of nfomaon Scences ohoku Unves Japan and D. M. engon Depamen of Sascs Unves of Glasgow UK 3 Sepembe
Pobablsc mage Pocessng b Eended Gauss-Makov Random Felds Kauuk anaka Munek asuda Ncolas Mon Gaduae School of nfomaon Scences ohoku Unves Japan and D. M. engon Depamen of Sascs Unves of Glasgow UK 3 Sepembe
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
