(a,b) Let s review the general definitions of trig functions first. (See back cover of your book) sin θ = b/r cos θ = a/r tan θ = b/a, a 0
|
|
|
- Κόριννα Αναγνωστάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 TRIGONOMETRIC IDENTITIES (a,b) Let s eview the geneal definitions of tig functions fist. (See back cove of you book) θ b/ θ a/ tan θ b/a, a 0 θ csc θ /b, b 0 sec θ /a, a 0 cot θ a/b, b 0 By doing some equation manipulating we can establish the fundamental tigonometic identities: tan θ b/a Divide both the numeato, b, and the denominato, a, by and you get tan θ (b/)/(a/) θ / θ Similaly cot θ θ / θ Recipocal Identities can be established by ug the fact that /(x/y) y/x Theefoe: / θ sec θ / θ csc θ /tan θ cot θ Fom the Pythagoean Theoem, we know that a + b If we divide both sides of that equation by, we get a a + b + b θ + θ Dividing both sides by θ, we get : + θ θ + θ θ θ tan θ sec θ Dividing both sides of θ + θ by θ, we get : cot θ + θ θ + θ θ csc θ θ
2 Even-Odd Identities (- θ) - (θ) (- θ) (θ) tan(- θ) - tan(θ) csc(- θ) - csc(θ) sec(- θ) sec(θ) cot(- θ) - cot(θ) Establishing Identities Combinations of tig functions may be equal to each othe, if we can pove it. Once poven, this type of identity can be used to educe an equation down and thus educe the eos made when calculating values ug a compute. Guidelines fo Establishing Identities ) It is almost always pefeable to stat with the side containing the moe complicated expession. ) Rewite sums o diffeences of quotients as a gle quotient. 3) Sometimes, ewiting one side in tems of only es and ines will help. 4) Always keep you goal in mind. As you manipulate one side of the expession, you must keep in mind the fom of the expession on the othe side. In class, we will do p.7 Example, Example 3, Example 8
3 3.4 SUM AND DIFFERENCE FORMULAS Theoem (α+β) α β - α (α-β) α β + α NOTE: (α+β) α + β (α-β) α -β Poof of (α-β) α β + α Let s use a unit cicle so that evey point (x,y) on the cicle is the ine and e of angles in standad position (with the initial side on the positive x-axis and the teminal side with a point somewhee on the unit cicle). P ( α, α) (0,) α-β α β P ( β, ) (,0) We will use the distance fomula to stat poving ight side of the (α-β) equation. The distance fom P to P (ug the distance fomula) is d(p,p ) ( x x ) + ( y y (α β ) ) + (α )
4 α-β Now to get the left side of the equation, let s otate that pink tiangle so that it has one side on the positive x-axis. (0,) P 3 ( α-β, α-β) A (,0) Since this is the same tiangle as the pevious one (just otated), then the distance fom P to P on the pevious tiangle is the same as the distance fom P 3 to point A on this tiangle. Ug the distance fomula whee the fist point is (,0) and the second point is ( α-β, α-β) we get: ( ( α β ) ) + ( ( α ) 0) d(a,p ) β 3 Setting those two distance equations equal to each othe {d(a,p3) d(p,p )} we get: ( ( α β ) ) + ( ( α β ) 0 ) (α β ) + (α )
5 Now we can squae both sides: ( ( α β ) ) + ( ( α β ) 0 ) (α β ) + (α ) Now multiply out the squaed tems ( α β ) ( α β ) + + ( α β ) α α β + β + α α + Notice with these and tems we can apply the Pythagoean identity: θ + θ On the left side, let θ α-β and we get: ( α β ) + ( α β ) On the ight side, let θ α, and also θ β and we get: α β + α α β α Setting the ight side and left side equal to each othe we get; ( α β ) α β α Now subtacting fom both sides and then dividing both sides by - we get; (α-β) α β + α We can now pove (α+β) α β - α Use the (α-β) fomula but instead of α-β, use α-(-β) (α-(-β)) (α+β) α (-β) + α (-β) Now ou even-odd popeties [ (-θ) θ, (- θ) - θ] will become useful: (α+β) α (β) - α β β
6 Now if we ae asked to find the exact value of a tig function of an Angle, we can pehaps combine two known angles to get an exact answe Remembe that you calculato only gives appoximate values. Which angles to we know the exact values of thei tig functions? (Look at you handy Unit Cicle Diagam) θ 0 (0 o π ad ), 30 (π/6 ad ), 45 (π/4 ad ), 60 (π/3 ad ), 90 (π/ ad ) and so on.. Example Find the exact value of is not on ou Unit Cicle Diagam, but we can use the fact that , and we know the tig functions of 30 and 45. ( ) Now you do # 5 on p. 3
7 We can use the Complementay Angle Theoem to find (α-β) and (α+β) Remembe: (π/ θ) (θ) (π/ θ) (θ) (α+β) (π/ (α+β)) ((π/ α) +β)) Shift the paentheses (π/ α) β - (π/ α) α β -α Use the (α-β) fomula. Now just use the (α+β) fo (α-β) by ug this: (α-β) (α+ (-β)) α (-β) - α (-β) And ug ou even-odd popeties again, we get: (α-β) α β -α (-) α β + α Now let s do Examples 3, 5 Now you do #3 a, b, and c
8 Fomulas fo tan(α+β) and tan(α-β) Poof: tan(α+β) ( α + β ) ( α + β ) α β + α α b α Now divide both the numeato and denominato by α β. α β + α β α β α β α α β α α β tan ( α + β ) α + α β α α β + tan β tan β As befoe, we can use even-odd popeties to deive the othe fomula.. tan(α-β) tan(α+(-β)) + tan( β ) tan( β ) Recall that tan is odd so tan(-θ) -tan θ, so we get: tan β tan( α β ) Now do #3d + tan β
9 SUMMARY OF SUM AND DIFFERENCE FORMULAS (α+β) α β - α (α-β) α β + α (α+β) α β -α (α-β) α β + α tan ( α + β ) + tan β tan β tan( α β ) tan β + tan β Example 9 on p α β Remembe these ae angles
10 HOMEWORK p. 0 #,3, 9, 8 p.3 #5,9,5,3,7,9,59,63
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Section 7.7 Product-to-Sum and Sum-to-Product Formulas
 Section 7.7 Product-to-Sum and Sum-to-Product Fmulas Objective 1: Express Products as Sums To derive the Product-to-Sum Fmulas will begin by writing down the difference and sum fmulas of the cosine function:
Section 7.7 Product-to-Sum and Sum-to-Product Fmulas Objective 1: Express Products as Sums To derive the Product-to-Sum Fmulas will begin by writing down the difference and sum fmulas of the cosine function:
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
2 2 2 The correct formula for the cosine of the sum of two angles is given by the following theorem.
 5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2
![If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2 If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2](/thumbs/53/31933086.jpg) Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
If we restrict the domain of y = sin x to [ π 2, π 2
 Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
2 2 2 The correct formula for the cosine of the sum of two angles is given by the following theorem.
 5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Laplace s Equation in Spherical Polar Coördinates
 Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
Laplace s Equation in Spheical Pola Coödinates C. W. David Dated: Januay 3, 001 We stat with the pimitive definitions I. x = sin θ cos φ y = sin θ sin φ z = cos θ thei inveses = x y z θ = cos 1 z = z cos1
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Derivations of Useful Trigonometric Identities
 Derivations of Useful Trigonometric Identities Pythagorean Identity This is a basic and very useful relationship which comes directly from the definition of the trigonometric ratios of sine and cosine
Derivations of Useful Trigonometric Identities Pythagorean Identity This is a basic and very useful relationship which comes directly from the definition of the trigonometric ratios of sine and cosine
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Review Test 3. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
10/3/ revolution = 360 = 2 π radians = = x. 2π = x = 360 = : Measures of Angles and Rotations
 //.: Measures of Angles and Rotations I. Vocabulary A A. Angle the union of two rays with a common endpoint B. BA and BC C. B is the vertex. B C D. You can think of BA as the rotation of (clockwise) with
//.: Measures of Angles and Rotations I. Vocabulary A A. Angle the union of two rays with a common endpoint B. BA and BC C. B is the vertex. B C D. You can think of BA as the rotation of (clockwise) with
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Analytical Expression for Hessian
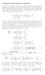 Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that
Analytical Expession fo Hessian We deive the expession of Hessian fo a binay potential the coesponding expessions wee deived in [] fo a multibody potential. In what follows, we use the convention that
Matrix Hartree-Fock Equations for a Closed Shell System
 atix Hatee-Fock Equations fo a Closed Shell System A single deteminant wavefunction fo a system containing an even numbe of electon N) consists of N/ spatial obitals, each occupied with an α & β spin has
atix Hatee-Fock Equations fo a Closed Shell System A single deteminant wavefunction fo a system containing an even numbe of electon N) consists of N/ spatial obitals, each occupied with an α & β spin has
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
MathCity.org Merging man and maths
 MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
Trigonometry 1.TRIGONOMETRIC RATIOS
 Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
Similarly, we may define hyperbolic functions cosh α and sinh α from the unit hyperbola
 Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
Universit of Hperbolic Functions The trigonometric functions cos α an cos α are efine using the unit circle + b measuring the istance α in the counter-clockwise irection along the circumference of the
9.09. # 1. Area inside the oval limaçon r = cos θ. To graph, start with θ = 0 so r = 6. Compute dr
 9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
9.9 #. Area inside the oval limaçon r = + cos. To graph, start with = so r =. Compute d = sin. Interesting points are where d vanishes, or at =,,, etc. For these values of we compute r:,,, and the values
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
F-TF Sum and Difference angle
 F-TF Sum and Difference angle formulas Alignments to Content Standards: F-TF.C.9 Task In this task, you will show how all of the sum and difference angle formulas can be derived from a single formula when
F-TF Sum and Difference angle formulas Alignments to Content Standards: F-TF.C.9 Task In this task, you will show how all of the sum and difference angle formulas can be derived from a single formula when
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Example 1: THE ELECTRIC DIPOLE
 Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2
Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2
( y) Partial Differential Equations
 Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Partial Dierential Equations Linear P.D.Es. contains no owers roducts o the deendent variables / an o its derivatives can occasionall be solved. Consider eamle ( ) a (sometimes written as a ) we can integrate
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Differentiation exercise show differential equation
 Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
Differentiation exercise show differential equation 1. If y x sin 2x, prove that x d2 y 2 2 + 2y x + 4xy 0 y x sin 2x sin 2x + 2x cos 2x 2 2cos 2x + (2 cos 2x 4x sin 2x) x d2 y 2 2 + 2y x + 4xy (2x cos
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
TRIGONOMETRIC FUNCTIONS
 Chapter TRIGONOMETRIC FUNCTIONS. Overview.. The word trigonometry is derived from the Greek words trigon and metron which means measuring the sides of a triangle. An angle is the amount of rotation of
Chapter TRIGONOMETRIC FUNCTIONS. Overview.. The word trigonometry is derived from the Greek words trigon and metron which means measuring the sides of a triangle. An angle is the amount of rotation of
e t e r Cylindrical and Spherical Coordinate Representation of grad, div, curl and 2
 Cylindical and Spheical Coodinate Repesentation of gad, div, cul and 2 Thus fa, we have descibed an abitay vecto in F as a linea combination of i, j and k, which ae unit vectos in the diection of inceasin,
Cylindical and Spheical Coodinate Repesentation of gad, div, cul and 2 Thus fa, we have descibed an abitay vecto in F as a linea combination of i, j and k, which ae unit vectos in the diection of inceasin,
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Chapter 6 BLM Answers
 Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
Chapter 6 BLM Answers BLM 6 Chapter 6 Prerequisite Skills. a) i) II ii) IV iii) III i) 5 ii) 7 iii) 7. a) 0, c) 88.,.6, 59.6 d). a) 5 + 60 n; 7 + n, c). rad + n rad; 7 9,. a) 5 6 c) 69. d) 0.88 5. a) negative
[1] P Q. Fig. 3.1
![[1] P Q. Fig. 3.1 [1] P Q. Fig. 3.1](/thumbs/79/80362156.jpg) 1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
1 (a) Define resistance....... [1] (b) The smallest conductor within a computer processing chip can be represented as a rectangular block that is one atom high, four atoms wide and twenty atoms long. One
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
dx x ψ, we should find a similar expression for rθφ L ψ. From L = R P and our knowledge of momentum operators, it follows that + e y z d
 PHYS851 Quantum Mechanics I, Fall 2009 HOMEWORK ASSIGNMENT 11 Topics Coveed: Obital angula momentum, cente-of-mass coodinates Some Key Concepts: angula degees of feedom, spheical hamonics 1. [20 pts] In
PHYS851 Quantum Mechanics I, Fall 2009 HOMEWORK ASSIGNMENT 11 Topics Coveed: Obital angula momentum, cente-of-mass coodinates Some Key Concepts: angula degees of feedom, spheical hamonics 1. [20 pts] In
Solutions to the Schrodinger equation atomic orbitals. Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz
 Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
Solutions to the Schrodinger equation atomic orbitals Ψ 1 s Ψ 2 s Ψ 2 px Ψ 2 py Ψ 2 pz ybridization Valence Bond Approach to bonding sp 3 (Ψ 2 s + Ψ 2 px + Ψ 2 py + Ψ 2 pz) sp 2 (Ψ 2 s + Ψ 2 px + Ψ 2 py)
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
Differential equations
 Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
Differential equations Differential equations: An equation inoling one dependent ariable and its deriaties w. r. t one or more independent ariables is called a differential equation. Order of differential
is like multiplying by the conversion factor of. Dividing by 2π gives you the
 Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Theoretical Competition: 12 July 2011 Question 1 Page 1 of 2
 Theoetical Competition: July Question Page of. Ένα πρόβλημα τριών σωμάτων και το LISA μ M O m EIKONA Ομοεπίπεδες τροχιές των τριών σωμάτων. Δύο μάζες Μ και m κινούνται σε κυκλικές τροχιές με ακτίνες και,
Theoetical Competition: July Question Page of. Ένα πρόβλημα τριών σωμάτων και το LISA μ M O m EIKONA Ομοεπίπεδες τροχιές των τριών σωμάτων. Δύο μάζες Μ και m κινούνται σε κυκλικές τροχιές με ακτίνες και,
Solution to Review Problems for Midterm III
 Solution to Review Problems for Mierm III Mierm III: Friday, November 19 in class Topics:.8-.11, 4.1,4. 1. Find the derivative of the following functions and simplify your answers. (a) x(ln(4x)) +ln(5
Solution to Review Problems for Mierm III Mierm III: Friday, November 19 in class Topics:.8-.11, 4.1,4. 1. Find the derivative of the following functions and simplify your answers. (a) x(ln(4x)) +ln(5
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Lecture 13 - Root Space Decomposition II
 Lecture 13 - Root Space Decomposition II October 18, 2012 1 Review First let us recall the situation. Let g be a simple algebra, with maximal toral subalgebra h (which we are calling a CSA, or Cartan Subalgebra).
Lecture 13 - Root Space Decomposition II October 18, 2012 1 Review First let us recall the situation. Let g be a simple algebra, with maximal toral subalgebra h (which we are calling a CSA, or Cartan Subalgebra).
CHAPTER 101 FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD
 CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
CHAPTER FOURIER SERIES FOR PERIODIC FUNCTIONS OF PERIOD EXERCISE 36 Page 66. Determine the Fourier series for the periodic function: f(x), when x +, when x which is periodic outside this rge of period.
1 3D Helmholtz Equation
 Deivation of the Geen s Funtions fo the Helmholtz and Wave Equations Alexande Miles Witten: Deembe 19th, 211 Last Edited: Deembe 19, 211 1 3D Helmholtz Equation A Geen s Funtion fo the 3D Helmholtz equation
Deivation of the Geen s Funtions fo the Helmholtz and Wave Equations Alexande Miles Witten: Deembe 19th, 211 Last Edited: Deembe 19, 211 1 3D Helmholtz Equation A Geen s Funtion fo the 3D Helmholtz equation
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
TMA4115 Matematikk 3
 TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
TMA4115 Matematikk 3 Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet Trondheim Spring 2010 Lecture 12: Mathematics Marvellous Matrices Andrew Stacey Norges Teknisk-Naturvitenskapelige Universitet
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
IIT JEE (2013) (Trigonomtery 1) Solutions
 L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
SOLVING CUBICS AND QUARTICS BY RADICALS
 SOLVING CUBICS AND QUARTICS BY RADICALS The purpose of this handout is to record the classical formulas expressing the roots of degree three and degree four polynomials in terms of radicals. We begin with
SOLVING CUBICS AND QUARTICS BY RADICALS The purpose of this handout is to record the classical formulas expressing the roots of degree three and degree four polynomials in terms of radicals. We begin with
Tutorial Note - Week 09 - Solution
 Tutoial Note - Week 9 - Solution ouble Integals in Pola Coodinates. a Since + and + 5 ae cicles centeed at oigin with adius and 5, then {,θ 5, θ π } Figue. f, f cos θ, sin θ cos θ sin θ sin θ da 5 69 5
Tutoial Note - Week 9 - Solution ouble Integals in Pola Coodinates. a Since + and + 5 ae cicles centeed at oigin with adius and 5, then {,θ 5, θ π } Figue. f, f cos θ, sin θ cos θ sin θ sin θ da 5 69 5
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines
![Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines Space Physics (I) [AP-3044] Lecture 1 by Ling-Hsiao Lyu Oct Lecture 1. Dipole Magnetic Field and Equations of Magnetic Field Lines](/thumbs/51/28406191.jpg) Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
Space Physics (I) [AP-344] Lectue by Ling-Hsiao Lyu Oct. 2 Lectue. Dipole Magnetic Field and Equations of Magnetic Field Lines.. Dipole Magnetic Field Since = we can define = A (.) whee A is called the
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Durbin-Levinson recursive method
 Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Durbin-Levinson recursive method A recursive method for computing ϕ n is useful because it avoids inverting large matrices; when new data are acquired, one can update predictions, instead of starting again
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
