Ultra-analytic effect of Cauchy problem for a class of kinetic equations
|
|
|
- Καλόγερος Αλεξίου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ultra-analytic effect of Cauchy problem for a class of kinetic equations Yoshinori Morimoto, Chao-Jiang Xu To cite this version: Yoshinori Morimoto, Chao-Jiang Xu. Ultra-analytic effect of Cauchy problem for a class of kinetic equations. J. Differential Equations, 9, 47, pp <hal-36863> HAL Id: hal Submitted on 17 Mar 9 HAL is a multi-disciplinary open access archive for the deposit and dissemination of scientific research documents, whether they are published or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers. L archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
2 Ultra-analytic effect of Cauchy problem for a class of kinetic equations Yoshinori MORIMOTO Graduate School of Human and Environmental Studies Kyoto University, Kyoto, , Japan Chao-Jiang XU Université de Rouen, UMR-685, Mathématiques 7681 Saint Etienne du Rouvray, France and School of Mathematics and Statistics, Wuhan University, Wuhan 437, China Abstract The smoothing effect of the Cauchy problem for a class of kinetic equations is studied. We firstly consider the spatially homogeneous nonlinear Landau equation with Maxwellian molecules and inhomogeneous linear Fokker-Planck equation to show the ultra-analytic effects of the Cauchy problem. Those smoothing effect results are optimal and similar to heat equation. In the second part, we study a model of spatially inhomogeneous linear Landau equation with Maxwellian molecules, and show the analytic effect of the Cauchy problem. Key words: Landau equation, Fokker-Planck equation, ultra-analytic effect of Cauchy problem. AMS Classification: 35A5, 35B65, 35D1, 35H, 76P5, 84C4 1. Introduction It is well known that the Cauchy problem of heat equation possesses the ultra-analytic effect phenomenon, namely, if ut, x is the solution of the following Cauchy problem : { t u x u =, x ; t > u t= = u L, then under the uniqueness hypothesis, the solution ut, = e t x u is an ultra-analytic function for any t >. We give now the definition of function spaces A s Ω where Ω is an open subset of. addresses: morimoto@math.h.kyoto-u.ac.jp Yoshinori MORIMOTO, Chao-Jiang.Xu@univ-rouen.fr Chao-Jiang XU Preprint submitted to Elsevier March 17, 9
3 Definition 1.1. For < s < +, we say that f A s Ω, if f C Ω, and there exists C >, N > such that α f L Ω C α +1 α! s, α N d, α N. If the boundary of Ω is smooth, by using Sobolev embedding theorem, we have the same type estimate with L norm replaced by any L p norm for < p +. On the whole space Ω =, it is also equivalent to e c 1 s β f L for some c > and β N d, where e c 1 s e c s 1 ux = F 1 e c ξ 1s ûξ. is the Fourier multiplier defined by If s = 1, it is usual analytic function. If s > 1, it is Gevrey class function. For < s < 1, it is called ultra-analytic function. Notice that all polynomial functions are ultra-analytic for any s >. It is obvious that if u L then, for any t > and any k N, we have ut, = e t xk u A 1 k, namely, there exists C > such that for any m N, t m km x ut, L C k m t x k m ut, L u L C k m m! C k m+1 km! 1 k, where x km = α =km,α N d α x. We say that the diffusion operators x k possess the ultra-analytic effect property if k > 1/, the analytic effect property if k = 1/ and the Gevrey effect property if < k < 1/. We study the Cauchy problem for spatially homogeneous Landau equation { āf ft = Qf, f v v f bff, v, t >, 1.1 f t= = f, where āf = ā ij f and bf = b 1 f,, b d f are defined as follows convolution is w. r.t. the variable v with ā ij f = a ij f, bj f = a ij v = vi a ij f, i, j = 1,, d, i=1 δ ij v iv j v v γ+, γ [ 3, 1]. We consider hereafter only the Maxwellian molecule case which corresponds to γ =. We introduce also the notation, for l R, L p l Rd = {f; 1 + v l/ f L p } is the weighted function space. We prove the following ultra-analytic effect results for the nonlinear Cauchy problem 1.1.
4 Theorem 1.1. Let f L L 1 Rd and < T +. If ft, x > and f L ], T[; L L 1 is a weak solution of the Cauchy problem 1.1, then for any < t < T, we have ft, A 1/, and moreover, for any < T < T, there exists c > such that for any < t T e c t v ft, L e d t f L. 1. In [17], they proved the Gevrey regularity effect of the Cauchy problem for linear spatially homogeneous non-cut-off Boltzmann equation. By a careful revision for the proof of Theorem 1. of [17], one can also prove that the solution of the Cauchy problem 1.1 in [17] belongs to A 1 α for any t >, where < α < 1 is the order of singularity of collision kernel of Boltzmann operator. Hence, if α 1/, there is also the ultra-analytic effect phenomenon. Now the above Theorem 1.1 shows that, for Landau equation, the ultra-analytic effect phenomenon holds in nonlinear case, which is an optimal regularity result. The ultra-analytic effect property is also true for the Cauchy problem of the following generalized Kolmogorov operators { t u + v x u + v α u =, x, v ; t > u t= = u L, where < α <, and the classical Kolmogorov operators is corresponding to α = 1. By Fourier transformation, the explicit solution of the above Cauchy problem is given by ût, η, ξ = e R t ξ+sη α dsû η, ξ + tη. Since there exists c α > see Lemma 3.1 below such that we have c α t ξ α + t α+1 η α t e cαt vα +t α+1 x α ut,, L, ξ + sη α ds, 1.3 i. e. ut,, A 1/α for any t >. Notice that this ultra-analytic if α > 1/ effect phenomenon is similar to heat equations of x, v variables. That is, this means v x + v α is equivalent to x α + v α by time evolution in some sense, though the equation is only transport for x variable. We consider now a more complicate equation, the Cauchy problem for linear Fokker- Planck equation : { ft + v x f = v v f + vf, x, v, t > ; 1.4 f t= = f. This equation is a natural generalization of classical Kolmogorov equation, and a simplified model of inhomogeneous Landau equation see [, 1]. The local property of 3
5 this equation is the same as classical Kolmogorov equation since the add terms v vf is a first order term, but for the studies of kinetic equation, v is velocity variable, and hence it is in whole space v. Then there occurs additional difficulty for analysis of this equation. The definition of weak solution in the function space L ], T[; L x, v L1 1 Rd x, v for the Cauchy problem is standard in the distribution sense, where for 1 p < +, l R { L p l Rd x, v = f S ; 1 + v l/ f L p x, v }. The existence of weak solution is similar to full Landau equation see [1, 13]. We get also the following ultra-analytic effect result. Theorem 1.. Let f L x, v L 1 1 x, v, < T +. Assume that f L ], T[- ; L x, v L1 1 Rd x, v is a weak solution of the Cauchy problem 1.4. Then, for any < t < T, we have ft,, A 1/. Furthermore, for any < T < T there exists c > such that for any < t T, we have e c t v+t 3 x ft,, e d t f L R. 1.5 L d Remark 1.1. The ultra-analyticity results of the above two theorems are optimal for the smoothness properties of solutions. From these results, we obtain a good understanding for the hypoellipticity of kinetic equations see [11, 14], and also the relationship, established by Villani [19] and Desvillettes-Villani [1], between the nonlinear Landau equation with Maxwellian molecules and the linear Fokker-Planck equation. We consider now the spatially inhomogeneous Landau equation { ft + v x f = Qf, f, x, v, t > ; f t= = f x, v. 1.6 The problem is now much more complicate since the solution f is the function of t, x, v variables. We consider it here only in the linearized framework around the normalized Maxwellian distribution µv = π d e v, which is the equilibrium state because Qµ, µ =. Setting f = µ + g, we consider the diffusion part of linear Landau collision operators, Qµ, g = v āµ v g bµg where ā ij µ = a ij µ = δ ij v + 1 v i v j, bj µ = vi a ij µ = vj, i, j = 1,, d. i=1 4
6 In particular, it follows that ā ij µξ i ξ j ξ, for all v, ξ. 1.7 i We then consider the following Cauchy problem { g t + v x g = v āµ v g bµg, x, v, t > ; g t= = g. 1.8 We can also look this equation as a linear model of spatially inhomogeneous Landau equation, which is much more complicate than linear Fokker-Planck equation 1.4, since the coefficients of diffusion part are now variables. The existence and C regularity of weak solution for the Cauchy problem have been considered in [1]. We prove now the following; Theorem 1.3. Let g L x, v L1 Rd x, v, < T +. Assume that g L ], T[- ; L x, v L1 Rd x, v is a weak solution of the Cauchy problem 1.8. Then, for any < t < T, we have gt,, A 1. Furthermore, for any < T < T there exist C, c > such that for any < t T, we have e ct v 1/ +t x 1/ gt,, L ec t g L R. 1.9 d In this theorem, we only consider the analytic effect result for the Cauchy problem 1.8, neglecting the symmetric term Qg, µ in the linearized operators of Landau collision operator cf.,1.15 of [1] because of the technical difficulty, see the remark in the end of section 4. There have been many results about the regularity of solutions for Boltzmann equation without angular cut-off and Landau equation, see [1,, 3, 6, 7, 9, 1, 15, 16] for the C smoothness results, and [4, 5, 8, 18, 17] for Gevrey regularity results for Boltzmann equation and Landau equation in both cases : the spatially homogeneous and inhomogeneous cases. As for the analytic and Gevrey regularities, we remark that the propagation of Gevrey regularities of solutions is investigated in [5] for full nonlinear spatially homogeneous Landau equations, including non-maxwellian molecule case, and the local Gevrey regularity for all variables t, x, v is considered in [4] for some semi-linear Fokker-Planck equations. Comparing those results, the ultra-analyticity for x, v variables showed in Theorem 1.1 is strong although the Maxwellian molecule case is only treated. As a related result for spatially homogeneous Boltzmann equation in the Maxwellian molecule case, we refer [8], where the propagation of Gevrey and ultra-analytic regularity is studied uniformly in time variable t. Throughout the present paper, we focus the smoothing effect of the Cauchy problem, and the uniform smoothness estimate near to t =. Concerning further details of the analytic and Gevrey regularities of solutions for Landau equations and Boltzmann equation without angular cut-off, we refer the introduction of [5] and references therein. 5
7 . Spatially homogeneous Landau equations We consider the Cauchy problem 1.1 and prove Theorem 1.1 in this section. We refer to the works of C. Villani [19, ] for the essential properties of homogeneous Landau equations. We suppose the existence of weak solution ft, v > in L ], T[; L 1 Rd - L. The conservation of mass, momentum and energy reads, d ft, v dt 1 v v dv. Without loss of generality, we can suppose that R ft, vdv = 1, unit mass d ft, vv j dv =, j = 1,,d; zero mean velocity R ft, v v dv = T d, unit temperature ft, vv j v k dv = T j δ jk, T j = T Then we have, T j = ft, vv jdv >, j = 1,,d; directional temperatures. j ā jk f = δ jk v + T T j v j v k ;.1 bj f = v j ;. ā jk fξ j ξ k C 1 ξ, v, ξ..3 j,k where C 1 = min 1 j d {T T j } >. Now for N > d and < δ < 1/N, c >, t >, set G δ t, ξ = e ct ξ 1 + δe c t ξ 1 + δc t ξ N. Since G δ t, L, we can use it as Fourier multiplier, denoted by G δ t, D v ft, v = F 1 G δ t, ξ ˆft, ξ. Then, for any t >, G δ t = G δ t, D v : L H N C b. The object of this section is to prove the uniform bound with respect to δ > of G δ t, D v ft, L. Since ft, L L 1 Rd is a weak solution, we can take G δ t ft, = G δ t, D v ft, H N, 6
8 as test function in the equation of 1.1, whence we have 1 d dt G δtft, L + j,k=1 = 1 t G δ t f, G δ tf LRd + + j,k=1 ā j k f vj G δ tft, v vk G δ tft, v dv vj vj ft, v G δ t ft, v dv { } ā jk f G δ t vj ft, v G δ t ā jk f vj ft, v vk G δ tft, v dv. To estimate the terms in the above equality, we prove the following two propositions. Proposition.1. We have C 1 v G δ tft L Re ā jk f vj G δ t, D v ft, v vk G δ t, D v ft, v dv..4 j,k=1 t G δ t f, G δ tf c v G δ tft L L..5 vj vj ft, v G δ t ft, vdv d G δtft L + c t v G δ tft L..6 Proof : The estimate.4 is exactly the elliptic condition.3. By using the Fourier transformation,.5 is deduced from the following calculus t G δ t, ξ = c ξ 1 Nδ G δ t, ξ 1 + δe ct ξ 1 + δc t ξ = c ξ G δ t, ξ J N,δ where To treat.6, we use J N,δ = 1 Nδ 1 + δe ct ξ 1 + δc t ξ 1. ξj G δ t, ξ = c tξ j G δ t, ξ J N,δ..7 7
9 Then, we have Re vj vj ft, v G δ t, D v ft, vdv = Re v j G δ t, D v ft, v vj G δ t, D v ft, v dv Re [G δ t, D v, v j ]ft, v vj G δ t, D v ft, v dv = d G δtft, L Re Using Fourier transformation and.7, we have that for t >, = = = R 3 R 3 [G δ t, D v, v j ]ft, v vj G δ t, D v ft, v dv. [G δ t, D v, v j ]ft, v vj G δ t, D v ft, v dv G δ t, D v v j ft, v v j G δ t, D v ft, v vj G δ t, D v ft, v dv { i ξj Gδ t, ξ ˆft, ξ G δ t, ξ i ξj ˆft, } ξ G δ t, ξ iξ j ˆft, ξdξ ξj G δ t, ξ ˆft, ξξj G δ t, ξ ˆft, ξdξ = c t ξ G δ t, ξ ˆft, ξ J N,δ dξ c t ξ G δ t, ξ ˆft, ξ dξ, which give.6. The proof of Proposition.1 is now complete. For the commutator term, the special structure of the operator implies Proposition.. j,k=1 { } ā jk f G δ t, D v vj ft, v G δ t, D v ā jk f vj ft, v vk G δ t, D v ft, v dv =. Proof : We introduce now polar coordinates on ξ by setting r = ξ and ω = ξ/ ξ S d 1. Note that / ξ j = ω j / r + r 1 Ω j where Ω j is a vector field on S d 1, and see 8
10 [14], Proposition ω j Ω j =, Ω j ω j = d 1..8 By using Fourier transformation, we have { } ā jk f G δ t, D v vj ft, v G δ t, D v ā jk f vj ft, v = j,k=1 { j,k=1 Noting, in polar coordinates on ξ, we have, denoting by Gr = G δ t, r, = = vk G δ t, D v ft, v dv [ } ξ k δ jk ξ ξk ξj, G δ t, ξ ]ξ j ˆft, ξ G δ t, ξ ˆft, ξdξ. ξ = r + d 1 r r + 1 r Ω j, [ { ω k δ jk r + d 1 } r r j,k=1 { ω k / r + r 1 Ω k ω j / r + r 1 Ω j } [ r + d 1 r r, Gr ] [ ωk / r + r 1 ω k Ω k k=1, Gr ] ω j ωj / r + r 1 Ω j ω j [ r + d 1 r r, Gr ] [ r + d 1 ], Gr r r =, where we have used.8. Then we finish the proof of Proposition.. ], Gr Remark.1. In the above proof of Proposition., we have used the polar coordinates in the dual variable of v, which is essentially related to a form of the Landau operator with Maxwellian molecules. We notice that the same relation in v variable was described by Villani [19] and Desvillettes-Villani [1]. End of proof of Theorem 1.1 : From Propositions.1 and., we get 1 d dt G δtft, L + C 1 1 c c t v G δ tft, L d G δtft, L. 9
11 For any < T < T, choose c small enough such that C 1 1 c c T. Then we get d dt G δtft, L d G δtft, L..9 Integrating the inequality.9 on ], t[, we obtain Take limit δ in.1. Then we get G δ tft, L e d t f L..1 e ct v ft, L e d t f L.11 for any < t T. We have now proved ft, A 1/ and Theorem Linear Fokker-Planck equations In the paper [19], there is an exact solution for spatially homogeneous linear Fokker- Planck equation. In the inhomogeneous case we can also obtain an exact solution of the Cauchy problem 1.4. Denote by ˆft, η, ξ = F x,v ft, x, v, the partial Fourier transformation of f with respect to x, v variable. Then, by Fourier transformation for x, v variables, the linear Fokker-Planck equation 1.4 becomes { t ˆft, η, ξ η ξ ˆft, η, ξ + ξ ξ ˆft, η, ξ = ξ ˆft, η, ξ; ˆf t= = Ff η, ξ. Therefore we obtain the exact solution Note that ˆft, ξ, η = ˆf, ξe t + η1 e t, η exp t ξe τ + η1 e τ dτ = 1 e t ξ + 1 e t ξ η + t ξe τ t + η1 e τ t dτ. t 3 + e t + e t η = X X ξ + X ξ η + log1 X X X η, where X = 1 e t t. We have for < K < /3 t ξe τ + η1 e τ dτ X1 1/K X/ ξ + 1/3 K/X 3 η. Hence for t X < 1/K, we get ft,, A 1/, so that the ultra-analytic effect holds for any t > by means of the semi-group property. But we cannot get the uniform estimate
12 We present now the proof of 1.5 which implies the ultra-analytic effect, by commutator estimates similarly as for homogeneous Landau equation. Set wt, η, ξ = ˆft, η, ξ tη. Then the Cauchy problem 1.4 is equivalent to { t wt, η, ξ = ξ tη wt, η, ξ ξ tη ξ wt, η, ξ; w t= = Ff η, ξ. 3.1 Since we need to study the function t ξ sη ds, we prove the following estimate. Lemma 3.1. For any α >, there exists a constant c α > such that t ξ sη α ds c α t ξ α + t α+1 η α. 3. Remark 3.1. If α =, we can get the above estimate by direct calculation. The following simple proof is due to Seiji Ukai. Proof : Setting s = tτ and η = tη, we see that the estimate is equivalent to 1 ξ τ η α dτ c α ξ α + η α. Since this is trivial when η =, we may assume η. If ξ < η then If ξ η then ξ τ η α dτ η α τ ξ η { ξ / η ξ αdτ 1 = η α η τ + Hence we obtain 3.. Set now η α α + 1 min 1 α+1 α + 1 ξ α + η α. α ξ / η θ 1 θα θ α+1 = dτ } τ ξ αdτ η η α α α ξ τ η α dτ ξ α 1 τ η αdτ 1 ξ α αdτ 1 τ ξ = ξ α α α + 1 ξ α + η α. t φt, η, ξ = c ξ sη ds c t3 η, 11
13 where c > is a small constant to choose later, and c is the constant in 3. with α =. Then 3. implies Let N = d + 1/4. For < δ < 1/4N and t >, set G δ = G δ t, η, ξ = φt, η, ξ c c t ξ + t 3 η. 3.3 e φt,η,ξ 1 + δe φt,η,ξ 1 + δ η + ξ N. 3.4 Since G δ t, L, we can use it as Fourier multiplier, denoted by Gδ t, D x, D v u t, x, v = F 1 η, ξ G δ t, η, ξût, η, ξ. Lemma 3.. Assume that ft, L x, v L1 1 Rd x, v for any t ], T[. Then ξ wt, η, ξ L η,ξ, and ξ tη G δ t, η, ξ wt, η, ξ, η G δ t, η, ξ wt, η, ξ, ξ G δ t, η, ξ wt, η, ξ 3.5 belong to L η,ξ for any t ], T[. Proof : Since ξj w = ifv j f, it follows from f L 1 1 x, v that ξ wt, η, ξ L η,ξ. Noting ξ tη Gδt, η, ξ, η Gδt, η, ξ L η,ξ, we see that the first two terms of 3.5 are obvious. To check the last term in 3.5, note ξj G δ t, η, ξ = c tξ j t η 1 jg δ t, η, ξ 1 + δe φt,η,ξ Nδξ j 1 + δ η + ξ G δt, η, ξ. 3.6 Then, we have ξ G δ t, η, ξ wt, η, ξ = G δ t, η, ξ ξ wt, η, ξ + ξ G δ t, η, ξ wt, η, ξ = G δ t, η, ξ ξ wt, η, ξ + 4c tξ t η δe φt,η,ξ G δt, η, ξ wt, η, ξ 4Nδξ 1 + δ η + ξ G δt, η, ξ wt, η, ξ. Since G δ t, η, ξ L x, v we have G δ t, η, ξ ξ wt, η, ξ L. Using 1 1, 1 + δe φt,η,ξ Nδξ 1 + δ η + ξ 1, 1
14 and ξ t ηg δt, η, ξ δe φt,η,ξ wt, η, ξ ξ t η G δt, η, ξ wt, η, ξ ξ tη G δ t, η, ξ wt, η, ξ + t η G δt, η, ξ wt, η, ξ L. We have proved Lemma 3. We take now G δ t, η, ξ wt, η, ξ as test function in the equation of 3.1. Then we have d dt G δt,, wt,, L + ξ tηg δ t, η, ξwt, η, ξ dηdξ = wt, η, ξ ξj ξ j tη j G δ t, η, ξ wt, η, ξ dηdξ + t G δ t,, wt,,, G δ t,, wt,,. 3.7 We prove now the following; Proposition 3.1. We have t G δ t,, w, G δ t,, w L L = c ξ tηg δ t, η, ξwt, η, ξ R dηdξ d 3 c c t η G δ t, η, ξwt, η, ξ 1 dηdξ δe φt,η,ξ Re wt, η, ξ ξj c t + c t + c 3c ξ j tη j G δ t, η, ξ wt, η, ξ dηdξ ξ tηg δ t, η, ξwt, η, ξ dηdξ + d + N δ/c G δ t,, wt,, L c c t η G δ t, η, ξwt, η, ξ 1 dηdξ δe φt,η,ξ Proof of Proposition 3.1 : The estimate 3.8 is deduced from t G δ t, η, ξ = c ξ tη 3 c t η 1 G δ t, η, ξ. 1 + δe φt,η,ξ 13
15 Since it follows from 3.6 that I = Re wt, η, ξ ξj ξ j tη j G δ t, η, ξ wt, η, ξ dηdξ = Re c t ξ j tη j ξ j t R η j G δ t, η, ξwt, η, ξ 1 dηdξ d 1 + δe φt,η,ξ we get Re Re Nδξ j ξ j tη j R 1 + δ η + ξ G δt, η, ξwt, η, ξ dηdξ d ξ j tη j ξj G δ t, η, ξwt, η, ξ G δ t, η, ξwt, η, ξdηdξ, I = c t ξ j tη j ξ j t R η j G δ t, η, ξwt, η, ξ 1 dηdξ d 1 + δe φt,η,ξ Nδξ j ξ j tη j R 1 + δ η + ξ G δt, η, ξwt, η, ξ dηdξ d + d G δt,, wt,, L = c t ξ tη G δ t, η, ξwt, η, ξ 1 dηdξ 1 + δe φt,η,ξ + c t ξ tη η G δ t, η, ξwt, η, ξ 1 dηdξ 1 + δe φt,η,ξ Nδξ j ξ j tη j R 1 + δ η + ξ G δt, η, ξwt, η, ξ dηdξ d For the last term, noting + d G δt,, wt,, L. Nδξ j ξ j tη j 1 + δ η + ξ N /c δ ξ + c ξ tη 1 + δ η + ξ N δ/c + c ξ tη we finally obtain I c t + c t 3c + c ξ tηg δ t, η, ξwt, η, ξ dηdξ + d + N δ/c G δ t,, wt,, L c c t η G δ t, η, ξwt, η, ξ 1 dηdξ. 1 + δe φt,η,ξ 14
16 Thus we have proved Proposition 3.1. End of proof of Theorem 1. : Now the equation 3.7, the estimate 3.8 and 3.9 deduce d dt G δt,, wt, L + 3c 4c t c t ξ tηg δ t, η, ξwt, η, ξ dηdξ 3c d + N δ/c G δ t,, wt,, L. Then for any < T < T choose c > depends on T small enough such that then for any < t T, which gives 3c 4c T c T 3c, d dt G δt,, wt,, L d + N δ/c G δ t,, wt,, L R, d Take δ, we have = G δ t,, wt,, L e d+n δ/c t f L. e c e c By using 3.3, we get finally R t ξ sη ds c 1t 3 η ˆft, η, ξ tη dηdξ R t ξ+t sη ds c 1t 3 η ˆft, η, ξ dηdξ e d t f L. e ct v+t3 x ft,, L e d t f L for any < t T, where c = cc >. This is the desired estimate 1.5, which implies We have thus proved Theorem 1.. ft,, A 1/. 4. Linear model of inhomogeneous Landau equations We prove now the Theorem 1.3 in this section. By the change of variables t, x, v t, x + v t, v, the Cauchy problem 1.8 is reduced to { f t = v t x āµ v t x f bµf, 4.1 f t= = g x, v, 15
17 where ft, x, v = gt, x + v t, v. Recall that and ā ij µ = a ij µ = δ ij v + 1 v i v j ; bj µ = vi a ij µ = vj ; i, j = 1,,d, i=1 ā ij µξ i ξ j ξ, for all v, ξ. i In view of this Cauchy problem, we set t Ψt, η, ξ = c ξ sη ds, for a sufficiently small c > which will be chosen later on. Then we can use the 3. with α = 1 to estimate Ψ. Set F δ t, η, ξ = e Ψ 1 + δe Ψ N for N = d + 1, < δ 1 N. If A is a first order differential operator of t, η, ξ variables then we have 1 AF δ = 1 + δe Ψ Nδ AΨF δ, 4. and δe Ψ Nδ 1. Taking F δ t, D x, D v f = F δ t f H N as a test function in the weak solution formula of 4.1, we have 1 d dt F δtf L + = v j f + j,k=1 āµ v t x F δ tf, v t x F δ tf L vj t xj F δ t f dxdv + 1 t F δ f, Fδ tf L { } ā jk µ F δ t vj t xj f F δ t ā jk µ vj t xj f We prove now the following results. vk t xk F δ tf dxdv. 16
18 Proposition 4.1. We have v t x F δ tf L āµ v t x F δ tf, v t x F δ tf. 4.3 L t F δ t f, F δ tf c v t x F δ tf L F δ tf L. 4.4 L Re v j f vj t xj F δ t f d R F δtf L d +c t v t x F δ ft L F δ ft L. 4.5 Proof : The estimate 4.3 is a direct consequence of the elliptic condition 1.7. Using the Fourier transformation and noting 4., we see that 4.4 is derived from 1 t F δ t, η, ξ = 1 + δe Ψ Nδ t ΨF δ, t Ψ = c ξ tη. For 4.5, we have firstly Re v j F δ tf R 6 vj t xj F δ tf = d F δtf L. For the commutators [v j, F δ t], using Fourier transformation, we have that for t > and ˆf = ˆft, η, ξ [F δ t, D x, D v, v j ]ft, x, v vj t xj F δ t, D x, D v ft, x, v dxdv = = = 3 F δ t, D x, D v v j ft v j F δ t, D x, D v ft vj t xj F δ t, D v ft dxdv { i ξj Fδ t, η, ξ ˆft F δ t, η, ξ i ξj ˆft } F δ t, η, ξ iξ j tη j ˆftdηdξ ξj F δ t, η, ξ ˆftξj tη j F δ t, η, ξ ˆftdηdξ c t ξ tη F δ t, η, ξ ˆft dηdξ c t v t x F δ ft L F δ ft L, where, in view of 4., we have used the fact that 1 ξj Ψt, η, ξ ξ j tη j c 3 ξ j sη j ξ sη ξ j tη j ds c t ξ tη. Thus 4.5 has been proved. 17
19 For the commutator terms, we have Proposition 4.. There exists a constant C 1 > independent of δ > such that j,k=1 { } ā jk µ F δ t vj t xj f F δ t ā jk µ vj t xj f vk t xk F δ tf C 1 { c t v t x F δ tf L + F δtf L }. 4.6 Proof : In order to prove 4.6, we introduce the polar coordinates of ξ centered at tη, that is, r = ξ tη and ω = ξ tη ξ tη Sd 1. Note again that / ξ j = ω j / r + r 1 Ω j where Ω j is a vector field on S d 1. We have again ω j Ω j =, Ω j ω j = d 1,. By means of Plancherel formula, we have j,k=1 { } ā jk µ F δ t vj t xj F δ t ā jk µ vj t xj f vk t xk F δ tf { ] = ξ k tη k [δ jk ξ ξk ξj, F δ t, η, ξ ξ j tη j ˆft } j,k=1 = J. Noting again ξ = r + d 1 r r + 1 r F δ t, η, ξ ˆftdξdη Ω l, we have with F δ t, η, r, ω = F δ t, η, r ω + tη = F δ t, η, ξ j,k=1 [ = [ { ω k δ jk r + d 1 r r + 1 r r + d 1 r l=1 l=1 Ω l { ω k r + } r 1 Ω k ω j r + r 1 Ω j ] r, Fδ 18 }, Fδ ] ω j
20 1 r Note again that [ + k=1 ω k r + r 1 ω k Ω k [ ω j Ω l, Fδ ]ω j = A 1 + A + A 3. l=1 [ A 1 + A = r + d 1 r ] r, Fδ On the other hand, we have in view of 4. A 3 = 1 r = 1 r j,l=1 j,l=1 ω j ] r + r 1 Ω j ω j, Fδ [ + r + d 1, r r F ] δ =. [ ] ω j Ω l [Ω l, Fδ ] Ω l, [Ω l, Fδ ] ω j Ωl Ψ ω j Ω l 1 + δe Ψ NδΩ lψ Ωl Ψ 1 + δe Ψ NδΩ lψ F δ Ωl Ψ + Ω l 1 + δe Ψ NδΩ lψ Fδ ω j. Putting w j = ω j Fδ w with wt, η, r, ω = ˆft, η, r ω + tη, we have J = Re J = Re r A 3 w F δ w r d 1 drdωdη η S d 1 { Ωl Ψ = Re Ω l j,l=1 η S 1 + δe Ψ NδΩ } lψ w j w j r d 1 drdωdη d 1 Ωl Ψ + j,l=1 η S 1 + δe Ψ NδΩ lψ d 1 Ωl Ψ + Ω l 1 + δe Ψ NδΩ lψ w j r d 1 drdωdη = J 1 + J. Since Ω l = Ω l + d 1ω l, the integration by parts gives Hence we obtain J = J 1 = j,l=1 η d j,l=1 η S d 1 {Ω l Ωl Ψ +d 1ω Ωl Ψ l 1+δe NδΩ lψ Ψ 1+δΨ S d 1 1+δe NδΩ lψ Ψ 1+δΨ } w j r d 1 drdωdη. { δe Ψ Nδ Ω l Ψ
21 = 1 d 1ω l 1 + δe Ψ Nδ η S d 1 { δe Ψ Nδ } Ω l Ψ w j r d 1 drdωdη Ω l Ψ 1 d δe Ψ Nδ } ω l Ω l Ψ F δ w r d 1 drdωdη. Since there exists a constant C d > such that t Ω l Ψ = c r ξ j sη j ξ sη dsω lω j c C d tr, 4.8 we have J C d {c t η l=1 l=1 r F δ w r d 1 drdωdη S d 1 } + F δ w r d 1 drdωdη, S d 1 which yields 4.6. The proof of Proposition 4. is now complete. η End of proof of Theorem 1.3 : From Propositions 4.1 and 4., there exist constants C, C 3 > independent of δ > and t > such that 1 d 1 dt F δft L + c t C v t x F δ ft L So that if 1 c t C, we have, Using the fact F δ f = 1 1+δ g, we get Take the limit δ. Then we have C 3 F δ ft L. d dt F δft L C 3 F δ ft L. 4.9 F δ ft L e C3t g L. e Ψt,η,ξ ˆft, η, ξ dηdξ e C3t g L. 4.1 On the other hand, by Lemma 3.1, there exists a c 1 > such that e Ψt,η,ξ ˆft, η, ξ R t dηdξ = e c ξ sη ds ĝt, η, ξ tη dηdξ R d R t = e c ξ+t sη ds ĝt, η, ξ dηdξ R d η ĝt, η, ξ dηdξ. e cc1t ξ +t
22 Finally, for any < T < T, choosing c > small enough such that 1 c T C, we have proved, e cc1t v1/ +t x 1/ gt, x, v dxdv e C3t g L for any < t T, which completes the proof of Theorem 1.3 with C = C 3 depending only on d. Remark 4.1. The formulas 4.7 and 4.8 show that we cannot get the ultra-analytic effect of order 1/ as in Theorem 1.. It is the same reason why we do not consider the symmetric term Qg, µ in the equation 1.8 as in [1]. Acknowledgments: Authors wish to express their hearty gratitude to Seiji Ukai who communicated Lemma 3.1. The research of the first author was supported by Grant-in- Aid for Scientific Research No , Japan Society of the Promotion of Science, and the second author would like to thank the support of Kyoto University for his visit there. References [1] R.Alexandre, Y.Morimoto, S.Ukai, C.-J.Xu and T.Yang, Uncertainty principle and kinetic equations, J. Funct. Anal [] R. Alexandre and M. Safadi, Littlewood Paley decomposition and regularity issues in Boltzmann equation homogeneous equations. I. Non cutoff case and Maxwellian molecules, Math. Models Methods Appl. Sci., [3] R. Alexandre and M. Safadi, Littlewood Paley decomposition and regularity issues in Boltzmann homogeneous equations. II. Non cutoff and non Maxwell cases. Discrete Contin. Dyn. Syst. A, [4] H. Chen, W. Li and C.-J. Xu, The Gevrey Hypoellipticity for linear and non-linear Fokker-Planck equations, to appear J. Diff. Equat. [5] H. Chen, W. Li and C.-J. Xu, Gevrey class regularity for the solution of the spatially homogeneous Landau equation, Kinetic and related models 1 8 no [6] Y. Chen, L. Desvillettes and L. He, Smoothing Effects for Classical Solutions of the Full Landau Equation, to appear in Arch. Rat. Mech. and Analysis [7] Y. Chen, Smoothness of Classical Solutions to the Vlasov-Poisson-Landau System, Kinetic and Related Models 18, no. 3, [8] L. Desvillettes, G,Furiolo and E. Terraneo, Propagation of Gevrey regularity for solutions of the Boltzmann equation for Maxwellian molecules. Trans. Amer. Math. Soc., [9] L. Desvillettes and C. Villani, On the Spatially Homogeneous Landau Equation for Hard Potentials. Part I: Existence, Uniqueness and Smoothness. Comm. Partial Differential Equations 5, no. 1-, [1] L. Desvillettes and C. Villani, On the spatially homogeneous Landau equation for hard potentials. II. H-theorem and applications. Comm. Partial Differential Equations 5, no. 1-, [11] L. Desvillettes and C. Villani, On the trend to global equilibrium in spatially inhomogeneous entropy-dissipating systems: the linear Fokker-Planck equation. Comm. Pure Appl. Math. 54 1, no. 1, 1 4. [1] L. Desvillettes and B. Wennberg, Smoothness of the solution of the spatially homogeneous Boltzmann equation without cutoff. Comm. Partial Differential Equations, [13] Y. Guo, The Landau equation in a periodic box. Comm. Math. Phys. 31, no. 3, [14] L. Hörmander, The analysis of linear partial differential operators II, Springer-Verlag, [15] Z. H. Huo, Y.Morimoto, S.Ukai and T.Yang, Regularity of entropy solutions for spatially homogeneous Boltzmann equation without Angular cutoff, Kinetic and Related Models 18, no. 3, [16] Y. Morimoto and C.-J. Xu, Hypoellipticity for a class of kinetic equations, J. Math. Kyoto Univ. 47 7,
23 [17] Y. Morimoto, S.Ukai, C.-J.Xu and T.Yang, Regularity of solutions to the spatially homogeneous Boltzmann equation without angular cutoff. Discrete Contin. Dyn. Syst. A, [18] S. Ukai, Local solutions in Gevrey classes to the nonlinear Boltzmann equation without cutoff, Japan J. Appl. Math.11984, no. 1, [19] C. Villani, On the spatially homogeneous Landau equation for Maxwellian molecules. Math. Model and Methods appl Sciences [] C. Villani, On a new class of weak solutions to the spatially homogeneous Boltzmann and Landau equations, Arch. Rational Mech. Anal., [1] C. Villani, A review of mathematical topics in collisional kinetic theory. Handbook of Fluid Mechanics. Ed. S. Friedlander, D.Serre,.
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
Jesse Maassen and Mark Lundstrom Purdue University November 25, 2013
 Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Notes on Average Scattering imes and Hall Factors Jesse Maassen and Mar Lundstrom Purdue University November 5, 13 I. Introduction 1 II. Solution of the BE 1 III. Exercises: Woring out average scattering
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
Απόκριση σε Μοναδιαία Ωστική Δύναμη (Unit Impulse) Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο. Απόστολος Σ.
 Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Απόκριση σε Δυνάμεις Αυθαίρετα Μεταβαλλόμενες με το Χρόνο The time integral of a force is referred to as impulse, is determined by and is obtained from: Newton s 2 nd Law of motion states that the action
Enzymatic Synthesis of Dithiolopyrrolone Antibiotics Using Cell-Free Extract of Saccharothrix
 Enzymatic Synthesis of Dithiolopyrrolone Antibiotics Using Cell-Free Extract of Saccharothrix algeriensis NRRL B-24137 and Biochemical Characterization of Two Pyrrothine N-Acyltransferases in This Extract.
Enzymatic Synthesis of Dithiolopyrrolone Antibiotics Using Cell-Free Extract of Saccharothrix algeriensis NRRL B-24137 and Biochemical Characterization of Two Pyrrothine N-Acyltransferases in This Extract.
Problem Set 3: Solutions
 CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
CMPSCI 69GG Applied Information Theory Fall 006 Problem Set 3: Solutions. [Cover and Thomas 7.] a Define the following notation, C I p xx; Y max X; Y C I p xx; Ỹ max I X; Ỹ We would like to show that C
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data
 Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data B. Renard, M. Lang, P. Bois To cite this version: B. Renard, M. Lang,
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data B. Renard, M. Lang, P. Bois To cite this version: B. Renard, M. Lang,
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
DYNAMICS OF CHANGE WITHIN LIVESTOCK SUB-SECTOR IN CHAD : a key-study of raw milk commodity chain in N Djamena
 DYNAMICS OF CHANGE WITHIN LIVESTOCK SUB-SECTOR IN CHAD : a key-study of raw milk commodity chain in N Djamena Koussou Mian Oudanang To cite this version: Koussou Mian Oudanang. DYNAMICS OF CHANGE WITHIN
DYNAMICS OF CHANGE WITHIN LIVESTOCK SUB-SECTOR IN CHAD : a key-study of raw milk commodity chain in N Djamena Koussou Mian Oudanang To cite this version: Koussou Mian Oudanang. DYNAMICS OF CHANGE WITHIN
Chemical and biological evaluations of an (111)in-labeled RGD-peptide targeting integrin alpha(v) beta(3) in a preclinical tumor model.
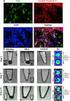 Chemical and biological evaluations of an (111)in-labeled RGD-peptide targeting integrin alpha(v) beta(3) in a preclinical tumor model. Mitra Ahmadi, Lucie Sancey, Arnaud Briat, Laurent Riou, Didier Boturyn,
Chemical and biological evaluations of an (111)in-labeled RGD-peptide targeting integrin alpha(v) beta(3) in a preclinical tumor model. Mitra Ahmadi, Lucie Sancey, Arnaud Briat, Laurent Riou, Didier Boturyn,
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Coefficient Inequalities for a New Subclass of K-uniformly Convex Functions
 International Journal of Computational Science and Mathematics. ISSN 0974-89 Volume, Number (00), pp. 67--75 International Research Publication House http://www.irphouse.com Coefficient Inequalities for
International Journal of Computational Science and Mathematics. ISSN 0974-89 Volume, Number (00), pp. 67--75 International Research Publication House http://www.irphouse.com Coefficient Inequalities for
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
derivation of the Laplacian from rectangular to spherical coordinates
 derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
derivation of the Laplacian from rectangular to spherical coordinates swapnizzle 03-03- :5:43 We begin by recognizing the familiar conversion from rectangular to spherical coordinates (note that φ is used
forms This gives Remark 1. How to remember the above formulas: Substituting these into the equation we obtain with
 Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Week 03: C lassification of S econd- Order L inear Equations In last week s lectures we have illustrated how to obtain the general solutions of first order PDEs using the method of characteristics. We
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
SCITECH Volume 13, Issue 2 RESEARCH ORGANISATION Published online: March 29, 2018
 Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
Journal of rogressive Research in Mathematics(JRM) ISSN: 2395-028 SCITECH Volume 3, Issue 2 RESEARCH ORGANISATION ublished online: March 29, 208 Journal of rogressive Research in Mathematics www.scitecresearch.com/journals
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
w o = R 1 p. (1) R = p =. = 1
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 205 ιδάσκων : Α. Μουχτάρης Τριτη Σειρά Ασκήσεων Λύσεις Ασκηση 3. 5.2 (a) From the Wiener-Hopf equation we have:
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
SPFC: a tool to improve water management and hay production in the Crau region
 SPFC: a tool to improve water management and hay production in the Crau region J.C. Mailhol, A. Merot To cite this version: J.C. Mailhol, A. Merot. SPFC: a tool to improve water management and hay production
SPFC: a tool to improve water management and hay production in the Crau region J.C. Mailhol, A. Merot To cite this version: J.C. Mailhol, A. Merot. SPFC: a tool to improve water management and hay production
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Lecture 21: Properties and robustness of LSE
 Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Lecture 21: Properties and robustness of LSE BLUE: Robustness of LSE against normality We now study properties of l τ β and σ 2 under assumption A2, i.e., without the normality assumption on ε. From Theorem
Multi-GPU numerical simulation of electromagnetic waves
 Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
Multi-GPU numerical simulation of electromagnetic waves Philippe Helluy, Thomas Strub To cite this version: Philippe Helluy, Thomas Strub. Multi-GPU numerical simulation of electromagnetic waves. ESAIM:
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)
![2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p) 2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)](/thumbs/40/21364883.jpg) Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
Homomorphism in Intuitionistic Fuzzy Automata
 International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
International Journal of Fuzzy Mathematics Systems. ISSN 2248-9940 Volume 3, Number 1 (2013), pp. 39-45 Research India Publications http://www.ripublication.com/ijfms.htm Homomorphism in Intuitionistic
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
Jie He. To cite this version: HAL Id: halshs https://halshs.archives-ouvertes.fr/halshs
 Pollution haven hypothesis and Environmental impacts of foreign direct investment: The Case of Industrial Emission of Sulfur Dioxide (SO2) in Chinese provinces Jie He To cite this version: Jie He. Pollution
Pollution haven hypothesis and Environmental impacts of foreign direct investment: The Case of Industrial Emission of Sulfur Dioxide (SO2) in Chinese provinces Jie He To cite this version: Jie He. Pollution
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques
 Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques Raphael Chenouard, Patrick Sébastian, Laurent Granvilliers To cite this version: Raphael
Solving an Air Conditioning System Problem in an Embodiment Design Context Using Constraint Satisfaction Techniques Raphael Chenouard, Patrick Sébastian, Laurent Granvilliers To cite this version: Raphael
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
MINIMAL CLOSED SETS AND MAXIMAL CLOSED SETS
 MINIMAL CLOSED SETS AND MAXIMAL CLOSED SETS FUMIE NAKAOKA AND NOBUYUKI ODA Received 20 December 2005; Revised 28 May 2006; Accepted 6 August 2006 Some properties of minimal closed sets and maximal closed
MINIMAL CLOSED SETS AND MAXIMAL CLOSED SETS FUMIE NAKAOKA AND NOBUYUKI ODA Received 20 December 2005; Revised 28 May 2006; Accepted 6 August 2006 Some properties of minimal closed sets and maximal closed
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOME PROPERTIES OF FUZZY REAL NUMBERS
 Sahand Communications in Mathematical Analysis (SCMA) Vol. 3 No. 1 (2016), 21-27 http://scma.maragheh.ac.ir SOME PROPERTIES OF FUZZY REAL NUMBERS BAYAZ DARABY 1 AND JAVAD JAFARI 2 Abstract. In the mathematical
Sahand Communications in Mathematical Analysis (SCMA) Vol. 3 No. 1 (2016), 21-27 http://scma.maragheh.ac.ir SOME PROPERTIES OF FUZZY REAL NUMBERS BAYAZ DARABY 1 AND JAVAD JAFARI 2 Abstract. In the mathematical
Srednicki Chapter 55
 Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
Srednicki Chapter 55 QFT Problems & Solutions A. George August 3, 03 Srednicki 55.. Use equations 55.3-55.0 and A i, A j ] = Π i, Π j ] = 0 (at equal times) to verify equations 55.-55.3. This is our third
n=2 In the present paper, we introduce and investigate the following two more generalized
 MATEMATIQKI VESNIK 59 (007), 65 73 UDK 517.54 originalni nauqni rad research paper SOME SUBCLASSES OF CLOSE-TO-CONVEX AND QUASI-CONVEX FUNCTIONS Zhi-Gang Wang Abstract. In the present paper, the author
MATEMATIQKI VESNIK 59 (007), 65 73 UDK 517.54 originalni nauqni rad research paper SOME SUBCLASSES OF CLOSE-TO-CONVEX AND QUASI-CONVEX FUNCTIONS Zhi-Gang Wang Abstract. In the present paper, the author
A Convolutional Neural Network Approach for Objective Video Quality Assessment
 A Convolutional Neural Network Approach for Objective Video Quality Assessment Patrick Le Callet, Christian Viard-Gaudin, Dominique Barba To cite this version: Patrick Le Callet, Christian Viard-Gaudin,
A Convolutional Neural Network Approach for Objective Video Quality Assessment Patrick Le Callet, Christian Viard-Gaudin, Dominique Barba To cite this version: Patrick Le Callet, Christian Viard-Gaudin,
STABILITY FOR RAYLEIGH-BENARD CONVECTIVE SOLUTIONS OF THE BOLTZMANN EQUATION
 STABILITY FOR RAYLEIGH-BENARD CONVECTIVE SOLUTIONS OF THE BOLTZMANN EQUATION L.Arkeryd, Chalmers, Goteborg, Sweden, R.Esposito, University of L Aquila, Italy, R.Marra, University of Rome, Italy, A.Nouri,
STABILITY FOR RAYLEIGH-BENARD CONVECTIVE SOLUTIONS OF THE BOLTZMANN EQUATION L.Arkeryd, Chalmers, Goteborg, Sweden, R.Esposito, University of L Aquila, Italy, R.Marra, University of Rome, Italy, A.Nouri,
A General Note on δ-quasi Monotone and Increasing Sequence
 International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
International Mathematical Forum, 4, 2009, no. 3, 143-149 A General Note on δ-quasi Monotone and Increasing Sequence Santosh Kr. Saxena H. N. 419, Jawaharpuri, Badaun, U.P., India Presently working in
Lecture 13 - Root Space Decomposition II
 Lecture 13 - Root Space Decomposition II October 18, 2012 1 Review First let us recall the situation. Let g be a simple algebra, with maximal toral subalgebra h (which we are calling a CSA, or Cartan Subalgebra).
Lecture 13 - Root Space Decomposition II October 18, 2012 1 Review First let us recall the situation. Let g be a simple algebra, with maximal toral subalgebra h (which we are calling a CSA, or Cartan Subalgebra).
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
The Pohozaev identity for the fractional Laplacian
 The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
DiracDelta. Notations. Primary definition. Specific values. General characteristics. Traditional name. Traditional notation
 DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
DiracDelta Notations Traditional name Dirac delta function Traditional notation x Mathematica StandardForm notation DiracDeltax Primary definition 4.03.02.000.0 x Π lim ε ; x ε0 x 2 2 ε Specific values
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Iterated trilinear fourier integrals with arbitrary symbols
 Cornell University ICM 04, Satellite Conference in Harmonic Analysis, Chosun University, Gwangju, Korea August 6, 04 Motivation the Coifman-Meyer theorem with classical paraproduct(979) B(f, f )(x) :=
Cornell University ICM 04, Satellite Conference in Harmonic Analysis, Chosun University, Gwangju, Korea August 6, 04 Motivation the Coifman-Meyer theorem with classical paraproduct(979) B(f, f )(x) :=
Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat
 Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat Pierre Coucheney, Patrick Maillé, runo Tuffin To cite this version: Pierre Coucheney, Patrick
Network Neutrality Debate and ISP Inter-Relations: Traffi c Exchange, Revenue Sharing, and Disconnection Threat Pierre Coucheney, Patrick Maillé, runo Tuffin To cite this version: Pierre Coucheney, Patrick
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Pax8 and Pax2 are specifically required at different steps of Xenopus pronephros development
 Pax8 and Pax2 are specifically required at different steps of Xenopus pronephros development Isabelle Buisson, Ronan Le Bouffant, Mélinée Futel, Jean-François Riou, Muriel Umbhauer To cite this version:
Pax8 and Pax2 are specifically required at different steps of Xenopus pronephros development Isabelle Buisson, Ronan Le Bouffant, Mélinée Futel, Jean-François Riou, Muriel Umbhauer To cite this version:
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
1. Introduction and Preliminaries.
 Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.yu/filomat Filomat 22:1 (2008), 97 106 ON δ SETS IN γ SPACES V. Renuka Devi and D. Sivaraj Abstract We
Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.yu/filomat Filomat 22:1 (2008), 97 106 ON δ SETS IN γ SPACES V. Renuka Devi and D. Sivaraj Abstract We
J. of Math. (PRC) Banach, , X = N(T ) R(T + ), Y = R(T ) N(T + ). Vol. 37 ( 2017 ) No. 5
 Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
Vol. 37 ( 2017 ) No. 5 J. of Math. (PRC) 1,2, 1, 1 (1., 225002) (2., 225009) :. I +AT +, T + = T + (I +AT + ) 1, T +. Banach Hilbert Moore-Penrose.. : ; ; Moore-Penrose ; ; MR(2010) : 47L05; 46A32 : O177.2
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
Consommation marchande et contraintes non monétaires au Canada ( )
 Consommation marchande et contraintes non monétaires au Canada (1969-2008) Julien Boelaert, François Gardes To cite this version: Julien Boelaert, François Gardes. Consommation marchande et contraintes
Consommation marchande et contraintes non monétaires au Canada (1969-2008) Julien Boelaert, François Gardes To cite this version: Julien Boelaert, François Gardes. Consommation marchande et contraintes
PROPERTIES OF CERTAIN INTEGRAL OPERATORS. a n z n (1.1)
 GEORGIAN MATHEMATICAL JOURNAL: Vol. 2, No. 5, 995, 535-545 PROPERTIES OF CERTAIN INTEGRAL OPERATORS SHIGEYOSHI OWA Abstract. Two integral operators P α and Q α for analytic functions in the open unit disk
GEORGIAN MATHEMATICAL JOURNAL: Vol. 2, No. 5, 995, 535-545 PROPERTIES OF CERTAIN INTEGRAL OPERATORS SHIGEYOSHI OWA Abstract. Two integral operators P α and Q α for analytic functions in the open unit disk
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Couplage dans les applications interactives de grande taille
 Couplage dans les applications interactives de grande taille Jean-Denis Lesage To cite this version: Jean-Denis Lesage. Couplage dans les applications interactives de grande taille. Réseaux et télécommunications
Couplage dans les applications interactives de grande taille Jean-Denis Lesage To cite this version: Jean-Denis Lesage. Couplage dans les applications interactives de grande taille. Réseaux et télécommunications
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
The semiclassical Garding inequality
 The semiclassical Garding inequality We give a proof of the semiclassical Garding inequality (Theorem 4.1 using as the only black box the Calderon-Vaillancourt Theorem. 1 Anti-Wick quantization For (q,
The semiclassical Garding inequality We give a proof of the semiclassical Garding inequality (Theorem 4.1 using as the only black box the Calderon-Vaillancourt Theorem. 1 Anti-Wick quantization For (q,
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis
 Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
 Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequality for metrics: Let (X, d) be a metric space and let x, y, z X.
 Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Math 446 Homework 3 Solutions. (1). (i): Reverse triangle inequalit for metrics: Let (X, d) be a metric space and let x,, z X. Prove that d(x, z) d(, z) d(x, ). (ii): Reverse triangle inequalit for norms:
Appendix to On the stability of a compressible axisymmetric rotating flow in a pipe. By Z. Rusak & J. H. Lee
 Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
Appendi to On the stability of a compressible aisymmetric rotating flow in a pipe By Z. Rusak & J. H. Lee Journal of Fluid Mechanics, vol. 5 4, pp. 5 4 This material has not been copy-edited or typeset
5. Choice under Uncertainty
 5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
5. Choice under Uncertainty Daisuke Oyama Microeconomics I May 23, 2018 Formulations von Neumann-Morgenstern (1944/1947) X: Set of prizes Π: Set of probability distributions on X : Preference relation
Problem Set 9 Solutions. θ + 1. θ 2 + cotθ ( ) sinθ e iφ is an eigenfunction of the ˆ L 2 operator. / θ 2. φ 2. sin 2 θ φ 2. ( ) = e iφ. = e iφ cosθ.
 Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
Chemistry 362 Dr Jean M Standard Problem Set 9 Solutions The ˆ L 2 operator is defined as Verify that the angular wavefunction Y θ,φ) Also verify that the eigenvalue is given by 2! 2 & L ˆ 2! 2 2 θ 2 +
On the Galois Group of Linear Difference-Differential Equations
 On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
Développement de virus HSV-1 (virus de l herpes simplex de type 1) oncolytiques ciblés pour traiter les carcinomes hépatocellulaires
 Développement de virus HSV-1 (virus de l herpes simplex de type 1) oncolytiques ciblés pour traiter les carcinomes hépatocellulaires Aldo Decio Pourchet To cite this version: Aldo Decio Pourchet. Développement
Développement de virus HSV-1 (virus de l herpes simplex de type 1) oncolytiques ciblés pour traiter les carcinomes hépatocellulaires Aldo Decio Pourchet To cite this version: Aldo Decio Pourchet. Développement
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.
![= {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ. = {{D α, D α }, D α }. = [D α, 4iσ µ α α D α µ ] = 4iσ µ α α [Dα, D α ] µ.](/thumbs/93/113370452.jpg) PHY 396 T: SUSY Solutions for problem set #1. Problem 2(a): First of all, [D α, D 2 D α D α ] = {D α, D α }D α D α {D α, D α } = {D α, D α }D α + D α {D α, D α } (S.1) = {{D α, D α }, D α }. Second, {D
PHY 396 T: SUSY Solutions for problem set #1. Problem 2(a): First of all, [D α, D 2 D α D α ] = {D α, D α }D α D α {D α, D α } = {D α, D α }D α + D α {D α, D α } (S.1) = {{D α, D α }, D α }. Second, {D
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
