Subset statistics in the linear IV regression model
|
|
|
- Εύφημη Λιάπης
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Dscusson Paper: 25/8 Subset statstcs n the lnear IV regresson moel Frank Klebergen (revse December 26) Amsteram School of Economcs Department of Quanttatve Economcs Roetersstraat 8 WB AMSTERDAM The Netherlans
2 Subset statstcs n the lnear IV regresson moel Frank Klebergen December 26 Abstract We show that the lmtng strbutons of subset extensons of the weak nstrument robust nstrumental varable statstcs are bounely smlar when the remanng structural parameters are estmate usng maxmum lkelhoo. They are boune from above by the lmtng strbutons whch apply when the remanng structural parameters are wellentfe an from below by the lmtng strbutons whch hol when the remanng structural parameters are completely unentfe. The lower boun strbuton oes not epen on nusance parameters an converges n case of Klebergen s (22) Lagrange multpler statstc to the lmtng strbuton uner the hgh level assumpton when the number of nstruments gets large. The power curves of the robust subset statstcs are nonstanar snce they converge to entfcaton statstcs for stant values of the parameter of nterest. The power of a test on a well-entfe parameter s therefore low at stant values when one of the remanng structural parameters s weakly entfe. It s entcal to the power of a test for a stant value of any of the other structural parameters. All subset results exten to tests on the parameters of the nclue exogenous varables. Introucton A szeable lterature currently exsts that eals wth statstcs for the lnear nstrumental varables (IV) regresson moel whose lmtng strbutons are robust to nstrument qualty, see e.g. Anerson an Rubn (949), Klebergen (22), Morera (23) an Anrews et. al. (25). These weak nstrument robust statstcs test hypotheses that are specfe on all structural parameters of the lnear IV regresson moel. Many nterestng hypotheses are, however, specfe on subsets of the structural parameters an/or on the parameters assocate wth the nclue exogenous varables. When we replace the structural parameters that are not specfe by the hypothess of nterest by estmators, the lmtng strbutons of the robust statstcs exten to tests of such Department of Economcs, Box B, Brown Unversty, Provence, RI 292, Unte States an Department of Quanttatve Economcs, Unversty of Amsteram, Roetersstraat, 8 WB Amsteram, The Netherlans, e-mal: Frank_Klebergen@brown.eu, homepage: Ths research s partly fune by the NWO research grant Emprcal Comparson of Economc Moels. I thank semnar partcpants at Montreal, Pennsylvana State, Prnceton, Rutgers an Yale Unversty, the Unversty of Pennsylvana, the 5 years of Econometrcs Conference an the UK Econometrc Stuy Group for comments an suggestons.
3 hypotheses when a hgh level entfcaton assumpton on these remanng structural parameters hols, see e.g. Stock an Wrght (2) an Klebergen (24,25). Ths hgh level assumpton s rather arbtrary an ts valty s typcally unclear. It s neee to ensure that the parameters whose values are not specfe uner the null hypothess are replace by consstent estmators so the lmtng strbutons of the weak nstrument robust statstcs reman unaltere. When the hgh level assumpton s not satsfe, the lmtng strbutons are unknown. The hgh level assumpton s avoe when we test the hypotheses usng a projecton argument whch results n conservatve tests, see Dufour an Taamout (25a,25b). We show that when we estmate the parameters that are not specfe by the hypothess of nterest by maxmum lkelhoo that the lmtng strbutons of the robust subset statstcs are bounely smlar (pvotal). They are boune from above by the lmtng strbuton whch apples when the hgh level assumpton hols an from below by the lmtng strbuton whch apples when the unspecfe parameters are completely unentfe. The lower boun strbuton oes not epen on nusance parameters an converges to the lmtng strbuton uner the hgh level assumpton when the number of nstruments gets large n case of Klebergen s (22) Lagrange multpler (KLM) statstc. The robust subset statstcs are thus conservatve when we apply the lmtng strbutons that hol uner the hgh level entfcaton assumpton. We use the conservatve crtcal values that result uner the hgh level entfcaton assumpton to compute power curves of the robust subset statstcs. These power curves show that the weak entfcaton of a partcular parameter splls over to tests on any of the other parameters. For large values of the parameter of nterest, we show that the robust subset statstcs correspon wth tests of the entfcaton of any of the structural parameters. Hence, when a partcular (combnaton of the) structural parameter(s) s weakly entfe, the power curves of tests on the structural parameters usng the robust subset statstcs converge to a rejecton frequency that s well below one when the parameter of nterest becomes large. The qualty of the entfcaton of the structural parameters whose values are not specfe uner the null hypothess are therefore of equal mportance for the power of the tests as the entfcaton of the hypothesze parameters tself. The paper s organze as follows. In the secon secton, we state the robust subset statstcs. Because the subset lkelhoo rato statstc has no close form analytcal expresson, we prove an extenson of Morera s (23) contonal lkelhoo rato statstc for tests on subsets of the structural parameters. In the thr secton, we scuss the lmtng strbutons of the robust subset statstcs when the remanng structural parameters are completely non-entfe. We show that these strbutons prove a lower boun on the lmtng strbutons of the robust subset statstcs whle the lmtng strbutons uner the hgh level entfcaton assumpton prove a upperboun. In the fourth secton, we analyse the sze an power of the subset statstcs an show that they converge to a statstc that tests for the entfcaton of any of the structural parameters when the parameter of nterest becomes large. The ffth secton llustrates some possble shapes of the p-value plots that result from the robust subset statstcs. The sxth secton extens the robust subset statstcs to statstcs that conuct tests of hypotheses specfe on the parameters of the nclue exogenous varables. It also analyses the sze an power of such tests. Fnally, the seventh secton conclues. We use the followng notaton throughout the paper: vec(a) stans for the (column) vectorzaton of the N n matrx A, vec(a) =(a...a n) for A =(a...a n ),P A = A(A A) A s 2
4 a projecton on the columns of the full rank matrx A an M A = I N P A s a projecton on the space orthogonal to A. Convergence n probablty s enote by an convergence n p strbuton by. 2 Subset statstcs n the Lnear IV Regresson Moel We conser the lnear IV regresson moel y = Xβ + Wγ + ε X = ZΠ X + V X W = ZΠ W + V W, () where y, X an W are N, N m x an N m w mensonal matrces that contan the enogenous varables, Z s a N k mensonal matrx of nstruments an m = m x + m w. The N, N m x an N m w mensonal matrces ε, V X an V W contan the sturbances. The m x, m w, k m x an k m w mensonal matrces β, γ, Π X an Π W consst of unknown parameters. We can a a set of exogenous varables to all equatons n () an the results that we obtan next reman unaltere when we replace all varables by the resuals that result from a regresson on these atonal exogenous varables. We make, analogous to Stager an Stock (997), an assumpton on the convergence of the fferent varables n (). Assumpton : hol jontly: When the sample sze N converges to nfnty, the followng convergence results a. N X. V W ) (ε. V X. V W ) Σ, wth Σ a postve efnte (m +) (m +)matrx p σ εε σ εx σ εw an Σ = σ Xε Σ XX Σ XW,σ εε :, σ εx = σ Xε : m x,σ εw = σ Wε : m w, σ Wε Σ WX Σ WW Σ XX : m x m x, Σ XW = Σ WX : m x m w, Σ WW : m w m w. b. N Z Z p Q, wth Q a postve efnte k k matrx. c. N Z (ε. V X. V W ) (ψ Zε. ψ ZX. ψ ZW ), wth ψ Zε : k, ψ ZX : k m x,ψ ZW : k m w an vec(ψ Zε. ψ ZX. ψ ZW ) N (, Σ Q). Statstcs to test jont hypotheses on β an γ, lke, for example, H : β = β an γ = γ, have been eveloppe whose (contonal) lmtng strbutons uner H an Assumpton o notepenonthevalueofπ X an Π W, see e.g. Anerson an Rubn (949), Klebergen (22) an Morera (23). These entfcaton robust statstcs can be aapte to test for hypotheses that are specfe on a subset of the parameters, for example, H : β = β. We construct such robust subset statstcs whch use the maxmum lkelhoo estmator (MLE) γ to estmate the unknown value of γ. TheMLEresultsfromthefrst orer conton (FOC) for a maxmum of 3
5 the lkelhoo. The Anerson-Rubn (AR) statstc s proportonal to the concentrate lkelhoo so we can obtan the FOC from(k tmes) the AR statstc: AR(β γ, γ) = 2 Π ˆσ εε (β ) W (β ) Z (y Xβ W γ) =, (2) where AR(β,γ)= (y Xβ ˆσ εε (β,γ) Wγ) P Z (y Xβ Wγ), ˆσ εε (β,γ)= (y Xβ N k h Wγ) M Z (y Xβ Wγ), Π W (β )=(Z Z) Z W (y Xβ W γ) ˆσ εw (β ) ˆσ εε(β an ˆσ ) εε (β )= ˆσ εε (β, γ), ˆσ εw (β )= (y Xβ N k W γ) M Z W. In orer to specfy the robust subset statstcs, we ecompose (Z Z) Z (y : X : W ) nto three components: Z (y Xβ W γ), Π W (β ) an Π h X (β )=(Z Z) Z X (y Xβ W γ) ˆσ εx(β ) ˆσ εε, (β ) ˆσ εx (β )= (y Xβ N k W γ) M Z X. Lemma : When Assumpton an H : β = β hol, Π W (β ) an Π X (β ) are gven the MLE γ nepenent of Z (y Xβ W γ) n large samples. Proof. see the Appenx. Lemma 2: When Assumpton hols an uner H : β = β, ΠW (β ) an Π X (β ) are uncorrelate wth Z (y Xβ W γ) n large samples such that E lm N Π N W (β 2 δ W ) Z (y Xβ W γ) = an E lm N Π ˆσεε (β ) N X (β 2 δ X ) Z (y Xβ W γ) =, ˆσεε (β ) (3) where δ W an δ X are such that lm N N δ W Π W Z ZΠ W = C W, lm N N δ X Π XZ ZΠ X = C X wth C W an C X m w m w an m x m x mensonal matrces of constants such that δ W an δ X are zero n case of rrelevant or weak nstruments an one n case of strong nstruments. Proof. see the Appenx. We use Lemmas an 2 to efne the robust subset statstcs whch are equal to the robust statstcs that test the jont hypothess H : β = β an γ = γ when γ equals γ. Defnton :. The AR statstc (tmes k) to test H : β = β reas AR(β )= ˆσ εε(β ) (y Xβ W γ) P Z (y Xβ W γ). (4) 2. Klebergen s (22) Lagrange multpler (KLM) statstc to test H reas, see Klebergen (24), KLM(β )= ˆσ εε(β ) (y Xβ W γ) P MZ ΠW (β ) Z Π X (β ) (y Xβ W γ). (5) For reasons of brevty, we refran from scussng ntermeate cases where nstea of normalzng Π W Z ZΠ W (or Π X Z ZΠ X ) by N δ W, we normalze a quaratc form wth respect to Π W Z ZΠ W by a agonal matrx ag(n δ W,,...,N δ w,mw ) wth fferent values of δw,,=,...,m W. These cases also have no effect on the results for the robust subset statstcs. 4
6 3. A J-statstc that tests msspecfcaton uner H reas, see Klebergen (24), 4. The lkelhoo rato (LR) statstc to test H reas, JKLM(β )= AR(β ) KLM(β ). (6) LR(β )= AR(β ) mn β AR(β), (7) where mn β AR(β) equals the smallest root of the characterstc polynomal: ˆΩ (y. X. W N k ) P Z (y. X. W ) =, (8) wth ˆΩ = N k (y. X. W ) M Z (y. X. W ). The subset LR statstc (7) can be specfe as a functon of the uncorrelate components uner H,.e.Z (y Xβ W γ) an ( Π X (β ). Π W (β )). Theorem. The LR statstc (7) equals LR(β )= AR(β ) λ mn, (9) where λ mn sthesmallestrootofthepolynomal µ ϕ λi m+ ϕ ϕ S S ϕ S S =, () wth ϕ = U (Z Z) 2 Z ˆε ˆσεε (β ), ˆε = y Xβ W γ an U an S result from a sngular value ecomposton of T (β )=(Z Z) 2 [ Π X (β ). Π W (β )]ˆΣ 2 (X : W )(X : W ).ε : T (β )=USV () n whch U : k k, U U = I k, V : m m, V V = I m, V =(VX. VW ), V X : m x m, V W : m w m; an S s a agonal k m mensonal matrx wth the sngular values n ecreasng orer on the man agonal an Ã! ˆΣ 2 (X : W )(X : W ).ε = ˆΣ 2 XX.(ε : W ) (2) ˆΣ WW.εˆΣ WX.εˆΣ 2 XX.(ε : W ) ˆΣ 2 WW.ε where ˆΣ XX.(ε : W ) = N k X M (Z : W : ˆε) X, ˆΣ WX.ε = N k W M (Z : ˆε) X, ˆΣ WW.ε = N k W M (Z : ˆε) W. Proof. see the Appenx. Theorem ffers from the ecomposton of the LR statstc gven n Klebergen (26) snce we test only a subset of the structural parameters. The estmator for the remanng structural parameters results from the FOC (2) whch puts a restrcton on the elements of the characterstc polynomal n Theorem. 5
7 Corollary. The FOC (2) for γ mples that V W S ϕ =. Proof. Snce Π W (β ) Zˆε =, ˆΣ 2 WW.ε Π W (β ) Z ˆε ˆσεε (β ) = V W S ϕ =. Corollary s mple by the FOC an the lower block trangular specfcaton of ˆΣ 2 (X : W )(X : W ).ε. If we o not use a lower block trangular specfcaton of ˆΣ 2 (X : W )(X : W ).ε, the FOC mples a more complcate restrcton on ϕ. The LR statstc that results from Theorem oes not have a close form analytcal expresson. Alongse the subset LR statstc (9), we therefore also use an approxmaton of t that has an explct expressson, see Klebergen (26). Proposton. A upperboun on the subset LR statstc (9) reas q MQLR(β )= AR(β 2 ) rk(β )+ (AR(β )+rk(β )) 2 4(AR(β ) KLM(β )) rk(β ), (3) where rk( β ) s the smallest characterstc root of ˆΣ MQLR (β )=T(β ) T (β ). Proof. see the Appenx. Unlke the subset LR statstc (9), MQLR(β ) (3) s a functon of Z (y Xβ W γ), Π X (β ) an Π W (β ) wth a close form analytcal expresson. Except for the usage of the characterstc root rk(β ), ts expresson conces wth that of Morera s (23) contonal lkelhoo rato statstc. Thus we refer to t as MQLR(β ). The MQLR statstc (3) s a quas-lr statstc that preserves the man propertes of the LR statstc: ts contonal strbuton gven rk(β ) conces wth that of AR(β ) when rk(β ) s small an wth that of KLM(β ) when rk(β ) s large. Corollary 2. The LR an MQLR statstcs are entcal when β satsfes the FOC. Proof. see the Appenx. The (contonal) lmtng strbutons of the robust subset statstcs result from the zero correlaton between Z (y Xβ Z γ) an Π X (β ), Π W (β ) n large samples that s state n Lemma 2 an from a hgh level assumpton wth respect to the rank of Π W whch mples an asymptotc normal strbuton for Z (y Xβ Z γ), Π X (β ) an Π W (β ), see Klebergen (24). The asymptotc normalty an zero correlaton mply that Z (y Xβ Z γ) an Π X (β ), Π W (β ) are nepenent n large samples. Assumpton 2: Thevalueofthek m w mensonal matrx Π W s fxe an of full rank. Theorem 2. a. Uner H an when Assumptons an 2 hol, the (contonal) lmtng strbutons of AR( β ), KLM( β ), JKLM( β ) an MQLR( β ) gven rk( β ) are characterze 6
8 by. AR(β ) ψ mx + ψ k m, 2. KLM(β ) ψ mx, 3. JKLM(β ) ψ k m, 4. MQLR(β ) rk(β ) 2 ψ mx + ψ k m rk(β )+q ψmx + ψ k m + rk(β ) 2 4ψ k m rk(β ) (4) where ψ mx an ψ k m are nepenent χ 2 (m x ) an χ 2 (k m) strbute ranom varables. b. Uner H an when Assumptons an 2 hol, the (contonal) lmtng strbuton of LR( β ) gven T (β ) s characterze by LR(β ) T (β ) ψ k m + ψ mx µ mn, (5), where µ mn sthesmallestrootofthepolynomal à λi ψk m + ψ mx m+ S ϕ mx ϕ k m ϕmx S ϕ k m S S! =, (6) wth ϕ k m a N(,I k m ) strbute ranom varable, ψ k m = ϕ k m ϕ k m; ϕ mx = M SV W ζ m wth ζ m a N(,I m ) strbute ranom varable, ψ mx = ϕ m x ϕ mx an V W an S result from the sngular value ecomposton state n Theorem. Proof. see Klebergen (24) for the proof of part a. Part b results from the ecomposton of LR(β ) n Theorem for whch Assumpton an 2 mply that ϕ M SV W ζ k wth ζ k a N(,I k ) strbute ranom varable. Part b mples that V W S ϕ mx ϕ =. k m Theorem 2 shows that the contonal lmtng strbuton of LR(β ) gven T (β ) just epens on S an V W whch result from a sngular value ecomposton. The number of unrestrcte elements of S equals m whle the number of unrestrcte elements of V =(VX. VW ) equals m(m ) snce 2 V V = I m. Hence, the number of contonng elements for the contonal lmtng strbuton of LR(β ) equals m(m +)whch s smaller than the km elements 2 of T (β ). The (contonal) lmtng strbutons n Theorem 2 hol uner Assumpton 2 whch s a hgh level assumpton that s ffcult to verfy n practce. We therefore establsh the lmtng strbutons of the fferent statstcs when Assumpton 2 fals to hol,.e. when Π W equals zero nstea of a full rank value. We show that the lmtng strbutons of the statstcs n ths extreme settng prove a lower boun for all other cases whle the lmtng strbutons from Theorem 2 prove a upper boun. 3 Lmtng strbutons of robust subset statstcs To analyse the lmtng strbutons of the robust subset statstcs n the general case, we use Lemma. Lemma states that the contonal lmtng strbutons of Z (y Xβ Z γ) an 7
9 T (β ) gven γ are nepenent. Hence, the lmtng strbutons of the robust subset statstcs epen on the strbuton of γ. We therefore analyse these lmtng strbutons for two extreme settngs of the strbuton of γ : Π W =an Π W full rank whch s alreay state n Theorem 2. We show that these extreme settngs prove lower an upper bouns on the lmtng strbutons for all other cases. Lemma 3. When Π W =an Assumpton an H hol, the FOC (2) correspons n large samples wth h γ ξ w +(ξ ε.w ξ wγ) +γ γ [ξε.w ξ wγ] =, (7) where ξ w an ξ ε.w are k an k m w mensonal nepenently stanar normal strbute matrces an γ = Σ 2 WW ( γ γ Σ WW σ Wε)σ 2 εε.w, σ εε.w = σ εε σ εw Σ wwσ wε. Proof. see the Appenx. The soluton of γ to the FOC n Lemma 3 s not unque an the MLE results as the soluton that mnmzes the AR statstc. Lemma 3 shows that γ oes not epen on any parameters beses the menson parameters k an m w.whenπ W equals zero, the strbuton of γ oes therefore not epen on any parameters as well an s a stanar Cauchy ensty, see e.g. Marano an Sawa (972) an Phllps (989). We use Lemma 3 to construct the lmtng strbutons of the robust subset statstcs to test H : β = β when Π W equals zero. Theorem 3. a. Uner Assumpton, H : β = β an when Π W equals zero:. The lmtng behavor of the AR statstc to test H : β = β s characterze by: AR(β ) +γ γ [ξ ε.w ξ wγ] [ξ ε.w ξ wγ]. (8) 2. The lmtng behavor of the KLM statstc to test H : β = β s characterze by: KLM(β ) +γ γ (ξ ε.w ξ wγ) P M [ ξ w +(ξ ε.w ξ w γ) γ +γ γ ] A (ξ ε.w ξ wγ), (9) where A s a fxe k m x mensonal matrx. 3. The lmtng behavor of the JKLM statstc s uner H characterze by: JKLM(β ) +γ γ (ξ ε.w ξ wγ) M [A : γ ξw +(ξ ε.w ξ wγ) ](ξ +γ ε.w ξ γ wγ). (2) 4. The contonal lmtng behavor of the MQLR statstc gven rk( β ) to test H : β = β reas h MQLR(β ) rk(β ) 2 +γ γ [ξ ε.w ξ wγ] [ξ ε.w ξ wγ] rk(β )+ ½ ³ +γ γ [ξ ε.w ξ wγ] [ξ ε.w ξ wγ]+rk(β ) 2 µ ¾ # (2) 4 +γ γ [ξ ε.w ξ wγ] M h 2 γ A : ξ w +(ξ ε.w ξ wγ) [ξ ε.w ξ wγ] rk(β ). +γ γ 8
10 5. The contonal lmtng strbuton of the LR statstc gven T (β ) to test H : β = β reas LR(β ) T (β ) +γ γ [ξ ε.w ξ wγ] [ξ ε.w ξ wγ] µ mn, (22) where µ mn sthesmallestrootofthepolynomal à λi +γ m+ γ [ξ ε.w ξ wγ] [ξ ε.w ξ wγ] [ξ +γγ ε.w ξ wγ] U S S U [ξ ε.w ξ wγ] S S Proof. see the Appenx. +γγ! =. (23) Fgure shows the χ 2 () strbuton functon an the lmtng strbuton functon of KLM(β ) when Π W =that results from Theorem 3 for fferent numbers of nstruments an m w = m x =. Fgure shows that the χ 2 () strbuton proves a upperboun for the lmtng strbuton functon of KLM(β ) when Π W =. It also shows that the lmtng strbuton of KLM(β ) when Π W =converges to a χ 2 () strbuton when the number of nstruments ncreases. Theorem 4. Uner H : β = β, Assumpton an when the sample sze N an the number of nstruments jontly converge to nfnty such that k/n, the lmtng behavor of KLM( β ) when Π W =s characterze by Proof. see the Appenx. KLM(β ) χ 2 (m x ). (24) Theorem 4 mples that the χ 2 strbuton becomes a better approxmaton of the lmtng strbuton of KLM(β ) when the number of nstruments gets large. The number of nstruments shoul, however, not be too large compare to the sample sze because a fferent lmtng strbuton of KLM(β ) results when t s proportonal to the sample sze, see Bekker an Klebergen (23). Fgure 2 shows the χ 2 (k m w )/(k m w ) strbuton functon an the lmtng strbuton functon of AR(β )/(k m w ) when Π W =that results from Theorem 3 for fferent number of nstruments an m w =. Fgure 2 shows that the lmtng strbuton of AR(β ) s boune by the χ 2 (k m w ) strbuton when Π W =. Fgure 2 shows that the χ 2 (k m w ) strbuton s a much more stant upperboun for the lmtng strbuton of AR(β ) than the upperboun for KLM(β ) n Fgure. The χ 2 approxmaton of the lmtng strbuton of AR(β ) when Π W =s thus a much more conservatve one than for KLM(β ). Another mportant fference wth KLM(β ) s that there s no convergence of the lmtng strbuton of AR(β ) towars a χ 2 strbuton when the number of nstruments gets large. The contonal lmtng strbutons of LR(β ) an MQLR(β ) when Π W =behave smlar to that of AR(β ) an KLM(β ) snce they are just functons of these statstcs for a gven value of the contonng statstcs. We therefore refran from showng these strbuton functons as well. Snce JKLM(β ) s also a functon of AR(β ) an KLM(β ), we also refran from showng the strbuton functon of JKLM(β ). 9
11 Dstrbuton Functon Dstrbuton Functon Fgure : (Lmtng) Dstrbuton functons of χ 2 () (sol) an KLM(β ) when Π w =,m w = m x =an k =2(otte), 5 (ashe-otte), 2 (ashe) an (ponte) Fgure 2: (Lmtng) Dstrbuton functons of χ 2 (k )/(k ) an AR(β )/(k ) when Π w =, m w = m x =an k =2(otte an ashe-otte), 2 (sol an ashe) an (sol wth trangles an sol wth plusses).
12 LemmastatesthatZ (y Xβ W γ) an ( Π X (β, γ), Π W (β, γ)) are contonal on γ nepenent n large samples. Uner Assumpton 2, γ s well entfe an the lmtng strbuton of γ s a pont mass locate at the true value γ. Hence, the contonal nepenence from Lemma extens to uncontonal nepenence when Assumpton 2 hols. Theorem 5 states that the (contonal) lmtng strbutons of the robust subset statstcs when Assumpton 2 hols, whch result from Theorem 2, prove upperbouns on ther (contonal) lmtng strbutons for general values of Π W as shown n Fgures an 2. The (contonal) lmtng strbutons uner Π W =, whch result from Theorem 3, prove a lowerboun on the (contonal) lmtng strbutons of the statstcs. Theorem 5. Uner H an when Assumpton hols, the (contonal) lmtng strbutons of the robust subset statstcs uner a full rank value of Π W prove a upperboun on the (contonal) lmtng strbutons for general values of Π W whle the (contonal) lmtng strbutons uner a zero value of Π W prove a lowerboun. Proof. see the Appenx. Theorem 5 shows that the (contonal) lmtng strbutons of the robust subset statstcs are bounely smlar. The crtcal values that result from the (contonal) lmtng strbutons n Theorem 2 can therefore be apple n general, so even for (almost) lower rank values of Π W, snce the sze of these tests s at most equal to the sze uner a full rank value of Π W. Usage of thecrtcalvaluesfromtheorem2resultsnteststhatareconservatve. 4 Sze an Power We conuct a sze an power comparson of the fferent statstcs to analyse the nfluence of the qualty of the entfcaton of γ for tests on β. We therefore conuct a smulaton experment usng () wth m x = m w =,γ=,n=5an vec(ε. V X. V W ) N(, Σ I N ). The nstruments Z are generate from a N(,I k I N ) strbuton. We compute the rejecton frequency of testng H : β =usng the robust subset statstcs an the two stage least squares (2SLS) t-statstc, to whch we refer as 2SLS(β ). The number of smulatons that we conuct equals 5. We control for the entfcaton of β an γ by specfyng Π X an Π W n accorance wth a prespecfe value of the matrx generalsaton of the concentraton parameter, see e.g. Phllps (983) an Rothenberg (984). We therefore analyse ³ the sze an power of tests on β for fferent values of Θ =(Z Z) 2 (Π X. Π W )Ω 2 XW, wth Ω XW = ΣXX Σ XW Σ WX Σ WW, whose quaratc form consttutes the matrx concentraton parameter. We specfy Θ such that only ts frst two rows have non-zero elements. Observe sze when γ s not entfe. We frst analyse the sze of the fferent statstcs for conuctng tests on β when γ s completely unentfe so Π W =. We therefore specfy Σ an Θ such that Σ equals the entty matrx an Θ =5, Θ 2 = Θ 2 = Θ 22 =. Table contans the observe sze of the fferent statstcs when we test H usng the 95% asymptotc
13 #nstr. \ stat. KLM(β ) LR(β ) MQLR(β ) AR(β ) JKLM(β ) 2SLS(β ) Table : Observe sze (n percentages) of the fferent statstcs that test H when Π w =usng the 95% (contonal) asymptotc sgnfcance level. (contonal) crtcal values that result from Theorem 2. In the Appenx we show how to obtan the contonal crtcal values for LR(β ) usng Theorem 2b when m =2. Table confrms Fgures, 2 an Theorems 4 an 5. It shows that the robust subset tests are conservatve when we use the crtcal values that result from Theorem 2. Table also confrms the convergence of the asymptotc strbuton of KLM(β ) when Π W =towars a χ 2 strbuton when the number of nstruments gets large as state n Theorem 4 an shown n Fgure. Snce KLM(β ), LR(β ), MQLR(β ) an AR(β ) are entcal when the moel s exactly entfe, so k = m =2, the sze of these statstcs conces when k = m =2an JKLM(β ) s not efne. Theszeofthe2SLSt-statstc n Table shows that t s conservatve when Π W =an Σ equals the entty matrx. Ths result s specfc for the entty covarance matrx case an, as we show later, oes not apply to general specfcatons of the covarance matrx. Power an sze for varyng levels of entfcaton. We conuct a power comparson of the fferent statstcs to analyse the nfluence of the entfcaton of γ on tests for the value of β. Except for the specfcaton of the covarance matrx Σ, we use the prevous specfcaton of the parameters. The covarance matrx Σ s specfe such that σ εε = σ XX = σ WW =, σ Xε = σ εx =.9, σ Wε = σ εw =.8 an σ XW = σ WX =.6 an the number of nstruments equals 2, k =2. SncetheKLM-statstcsproportonaltoaquaratcformoftheervatveoftheARstatstc, t s equal to zero at (local) mnma, maxma an sale ponts of the AR statstc,.e. where the FOC hols. Ths affects the power of the KLM statstc, see e.g. Klebergen (26). We therefore also compute the power of testng H usng a combnaton of the KLM an JKLM statstcs where we apply a 96% sgnfcance level for the KLM statstc an a 99% sgnfcance level for the JKLM statstc so the sze of the combne test proceure equals 5% snce the KLM an JKLM statstcs converge to nepenent ranom varables uner H.ThecombneKLM, JKLM test proceure s ncate by CJKLM. Panel shows the power curves for fferent values of the matrx concentraton parameter Θ wth Θ 2 = Θ 2 =an Table 2 shows the observe szes when we test at the 95% sgnfcance level. The value of Θ n Fgure. s such that both β an γ are well entfe. Hence all statstcs have nce shape power curves an the AR statstc s the least powerful statstc because of the larger egrees of freeom parameter of ts lmtng strbuton. The power of JKLM(β ) s rather low snce t tests the hypothess of overentfcaton whch s satsfe for all the fferent values of β. Table 2 shows that the 2SLS-statstc s sze storte n ths well entfe settng whch s ue to the large egree of enogenety. The value of Θ n Fgure.2 s such that γ s weakly entfe an β s well entfe. Fgure 2
14 Rejecton Frequency Rejecton Frequency Rejecton Frequency Rejecton Frequency Panel : Power curves of AR(β ) (ash-otte), LR(β ) (ashe-ponts), KLM(β ) (ashe), JKLM(β ) (sol-trangles), MQLR(β ) (sol), CJKLM (sol-plusses) an 2SLS(β ) (otte) for testng H : β = β β Fgure.: Strongly entfe β an γ : Fgure.2: Strongly entfe β an weakly Θ = Θ 22 =. entfe γ : Θ =, Θ 22 = β β Fgure.3: Weakly entfe β an strongly Fgure.3: Weakly entfe β an γ : entfe γ : Θ =3, Θ 22 =. Θ = Θ 22 =3..2 shows that the weak entfcaton of γ has large consequences for especally the power of tests on β. The LR statstc s the most powerful statstc n Fgure.2 but the MQLR statstc has comparable power. As shown n Table 2, except for the 2SLS t-statstc, the sze of the tests remans almost unaltere by the weak entfcaton of γ but the power s strongly affecte. Fgure.3 has a value of Θ that makes β weakly entfe an γ strongly entfe. Agan the LR statstc s the most powerful statstc but the power of the MQLR an KLM statstcs are comparable. Table 3 shows that the sze stortons of all statstcs, except the 2SLS t-statstc, s rather small. The sze of the 2SLS t-statstc s completely spurous. The specfcaton of Θ s such that all parameters are weakly entfe n Fgure.4. The power of all statstcs s therefore rather low an none of the statstcs clearly omnates the others. Because of the low egree of entfcaton, Table 2 shows that the AR statstc s rather 3
15 KLM(β ) LR(β ) MQLR(β ) JKLM(β ) CJKLM(β ) AR(β ) 2SLS(β ) Fg Fg Fg Fg Fg Fg Fg Fg Fg Fg Fg Fg Table 2: Sze of the fferent statstcs n percentages that test H at the 95% sgnfcance level. unersze whch correspons wth Table. The performance of the LR an MQLR statstcs s agan rather smlar. The sze of the 2SLS t-statstc n Table 2 s agan completely spurous. The specfcaton of the covarance matrx Σ n Panel s such that there are spll-overs between the entfcaton of β an γ that results from Θ. It s therefore ffcult to fully assess the nfluence of the weak entfcaton of γ ontheszeanpoweroftestsonβ. To analyse the nfluence of the weak entfcaton of γ on the power of tests on β n a more solate manner, we equate the covarance matrx Σ to the entty matrx. Table 2 an Panel 2 show the resultng sze an power for tests on β. Table 2 shows that the robust subset statstcs are unersze when γ s weakly entfe whch s n accorance wth Table an Theorem 5. The values of Θ n Fgure.2 an 2.2 are entcal but the robust subset statstcs are only unersze n Fgure 2.2 an not n Fgure.2. Ths results because of the fferent values of Σ that are use for Fgures.2 an 2.2 such that Π W s small for Fgure 2.2 but szeable for Fgure.2. The power curves n Panel 2 show that 2SLS(β ) s the most powerful statstc for testng H. The prevous Fgures, however, show that 2SLS(β ) s often severely sze-storte n cases when any correlaton s present whch makes ts results not trustworthy. Among the statstcs that are at most conservatve when entfcaton s weak, LR(β ) s the most powerful statstc for testng H but ts power s almost nstngushable of that of MQLR(β ). The power of LR(β ) an MQLR(β ) excee that of AR(β ) for values of β that are relatvely close to zero but are remarkably smlar to that of AR(β ) for more stant values of β. Ths argument hols n a reverse manner wth respect to KLM(β ). The level of entfcaton of β an γ s reverse n the two columns of Panel 2. In the lefthanse column, the entfcaton of γ s worse than of β an vce versa n the rght-hanse column. Table 2 therefore shows that the statstcs are somewhat unersze n the left-hanse column whle they are sze correct n the rght-hanse column. Beses the sze ssue, the power curves n the left an rght-hanse columns of Panel 2 are remarkably smlar for stant values of β. They only ffer aroun the hypothesze value of the parameter. Ths ncates that the statstcs behave n a systematc manner for stant values of β whch s state n Theorem 6. 4
16 Rejecton Frequency Rejecton Frequency Rejecton Frequency Rejecton Frequency Rejecton Frequency Rejecton Frequency Panel 2: Power curves of AR(β ) (ash-otte), LR(β ) (ashe-ponts), KLM(β ) (ashe), JKLM(β ) (sol-trangles), MQLR(β ) (sol), CJKLM (sol-plusses) an 2SLS(β ) (otte) for testng H : β = β β Fgure 2.: Θ =, Θ 22 =3. Fgure 2.2: Θ =3, Θ 22 = β β Fgure 2.3: Θ =, Θ 22 =5. Fgure 2.4: Θ =5, Θ 22 = β β Fgure 2.5: Θ =, Θ 22 =7. Fgure 2.6: Θ =7, Θ 22 =. 5
17 Theorem 6. When m x =, Assumpton hols an for tests of H : β = β for values of β that ffer substantally from the true value: a. AR( β ) equals the smallest egenvalue of ˆΩ 2 XW (X. W ) P Z (X. W )ˆΩ 2 XW, ˆΩ XW = N k (X. W ) M Z (X. W ). b. The egenvalues of ˆΣ MQLR (β )=T(β ) T (β ) are equal to the egenvalues of (y (X. W )ˆΩ ˆσXy XW ˆσ Wy )ˆσ 2 yy.(x : W ). (X. W )ˆΩ 2 XW V P Z (y (X. W )ˆΩ ˆσXy XW ˆσ Wy )ˆσ 2 yy.(x : W ). (X. W )ˆΩ 2 XW V. (25) where ˆσ Xy = N k X M Z y, ˆσ Wy = W M N k Z y, ˆσ yy = N k y M Z y, ˆσ yy.(x : W ) = ˆσ yy ˆσXy ˆσ ˆΩ ˆσXy Wy XW ˆσ Wy an V s a m m w matrx that contans the egenvectors of the largest m w egenvalues of ˆΩ 2 XW (X. W ) P Z (X. W )ˆΩ 2 XW. c. TheexpressonsoftheAR,LRanMQLRstatstcsthattestH : β = β are entcal to ther expressons that test H : α =n the moel (X. W )ˆΩ 2 XW v = εα +(X. W )ˆΩ 2 XW V δ + u ε = ZΦ ε + V ε (X. W )ˆΩ 2 XW V = ZΦ V + V V, (26) where v s a m vector that contans the egenvector of the smallest egenvalue of ˆΩ 2 XW (X. W ) P Z (X. W )ˆΩ 2 XW,ε= y Xβ Wγ wth β an γ the true values of the structural parameters so Φ ε s a k vector of zeros, α :, δ: m w an Φ V : k m w an u, V ε an V V are n, n an n m w matrces of sturbances. Proof. see the Appenx. Corollary 3. When Assumpton hols, so Φ ε equals zero, the smallest egenvalue of ˆΣ MQLR (β ) corresponswthatestforareucerankvalueof (Φ ε. Φ V ) whose rank equals at most m w an the χ 2 (k m w ) strbuton proves a upperboun on the lmtng strbuton of ths smallest egenvalue. Proof. When the rank of (Φ ε. Φ V ) equals m w, the smallest egenvalue equals a reuce rank statstc wth a χ 2 (k m w ) lmtng strbuton whch because of Theorem 5 proves an upperboun n case the rank s less than m w. 6
18 Rejecton Frequency Rejecton Frequency Panel 3: Power curves of AR(β ) (ash-otte), LR(β ) (ashe-ponts), KLM(β ) (ashe), JKLM(β ) (sol-trangles), MQLR(β ) (sol), CJKLM (sol-plusses) an 2SLS(β ) (otte) for testng H : β = β β Fgure 3.: Strongly entfe β an weakly Fgure 3.2: Weakly entfe β an strongly entfe γ : Θ =, Θ 22 =5, Θ 2 =5, entfe γ : Θ =5, Θ 22 =, Θ 2 =5, Θ 2 =5, Egenvalues Θ Θ : 3.65, 7. Θ 2 =5, Egenvalues Θ Θ : 3.65, 7. Theorem 6 shows that the power of the AR statstc equals the rejecton frequency of a rank test when the value of β gets large. The rank test to whch the AR statstc converges s entcal for all structural parameters. Hence, the power of the AR statstc for scrmnatng stant values of any structural parameter s the same. Ths explans the equalty of the rejecton frequences of the AR statstc for stant values of β n the left an rght-hanse fgures of Panel 3. The LR an MQLR statstcs are smlar to the AR statstc when the smallest egenvalue of ˆΣ MQLR (β )=T(β ) T (β ) s small. Corollary 3 shows that ths egenvalue s boune by a χ 2 (k m w ) strbute ranom varable for values of β that are stant from the true value. Ths mples that ts value s relatvely small so the LR an MQLR statstcs resemble the AR statstc at stant values of β. The power of the LR an MQLR statstcs are therefore smlar to that of the AR statstc at these stant values. The value of the LR an MQLR statstcs at stant values of β are the same for all structural parameters whch explans the equalty of the power curves n the left an rght-hanse columns of Panel 3 at such stant values. The entfcaton of β an γ s governe by the matrx concentraton parameter Θ. Beses havng values that especally entfy β an/or γ, the matrx concentraton parameter can also be such that lnear combnatons of β an γ are strong or weakly entfe. To analyse the nfluence of the strong/weak entfcaton of combnatons of β an γ on tests for β, we specfe the value of Θ such that t s close to a reuce rank one. We use the prevous non-agonal specfcaton of Σ to further sperse the entfcaton of combnatons of β an γ. Table2anPanel3showstheszeanpoweroftestsforβ when the value of Θ s close to a reuce rank one whch s reveale by the egenvalues of Θ Θ. Except for the 2SLS t-statstc, the sze of the statstcs s close to 5%. The weak entfcaton of a lnear combnaton of γ an β s such that the power of all statstcs s rather low. Fgures 3. an 3.2 show that LR(β ) an MQLR(β ) are the most powerful statstcs. 7
19 5 Confence Sets Theorem 6 shows that tests on fferent parameters become entcal when the parameters of nterest get large. Its consequences for the power curves n Panels -3 are clearly vsble an t has smlar mplcatons for the confence sets of the structural parameters. We therefore use the prevously scusse ata generatng process to compute some (one mnus the) p-value plots whch allow us to obtan the confence set of a specfc parameter. Thep-value plots are constructe by nvertng the values of the statstcs that test H : β = β for a range of values of β usng the (contonal) lmtng strbutons that result from Theorem 2. Snce these lmtng strbutons are conservatve, the coverage probablty of the resultng confence setssatmost equal to the level of the test. Panel 4 contans the one mnus p-value plots for a ata generatng process that s entcal to that of Panel 2. The Fgures n Panel 4 are such that the Fgures on the left-hanse contan the p-value plot of tests on γ whle the Fgures on the rght-hanse contan p-value plots of tests on β. The ata set use to compute the p-value plot of β an γ sthesameanonlyffers over the rows of Panel 4. Panel 4 shows that tests on β an γ fferarounthetruevalueofβ () an γ () but are entcal at stant values. Ths s exactly n lne wth Theorem 6. It shows that even when β s well entfe, confence sets of β are unboune when γ s weakly entfe. The o behavor of the p-value plot of KLM(β ) results snce t s equal to zero when the FOC hols. Fgures 4.2, 4.4 an 4.6 therefore show that KLM(β ) s equal to zero when AR(β ) s maxmal. We note that the p-value plots of KLM(β ), LR(β ), MQLR(β ) an 2SLS(β ) are equal to zero at resp. the MLE an for 2SLS(β ), the 2SLS estmator, but ths s not vsble n all of the Fgures n Panel 4 because of the specfe gr for β. The ata generatng process that s use to construct Panel 5 s entcal to that of Panel. Because of the presence of correlaton, a lnear combnaton of β an γ s weakly entfe n the Fgures n the top two rows of Panel 5 such that the p-value plots o not converge to one. The resultng 95% confence sets of β are therefore unboune for these Fgures. For stant values of β an γ, Panel 5 shows that the statstcs that conuct tests on β or γ become entcal. Panels 4 an 5 show that the stngushng features of the robust subsets statstcs for the power curves,.e. that they o not converge to one when the parameters of nterest gets large an statstcs that test hypotheses on fferent parameter become entcal for stant values of the parameter of nterest, approprately exten to confence sets. Panels -5 show that the LR an MQLR statstcs behave n an almost entcal manner. The MQLR statstc s, however, much easer to use snce ts contonal lmtng strbuton only epens on one statstc. The number of contonng statstcs for the LR statstc s equal to m(m +). The computaton of the contonal crtcal values scusse n the Appenx 2 also shows that these contonng statstcs can not be use n a straghtforwar manner. We use, for example, one mllon contonal crtcal values to compute the power curves of the LR statstcs n Panels -3 whle we use only one hunre contonal crtcal values to compute the power curves of the MQLR statstc. Thus we only use the MQLR statstc n the sequel of the paper. 8
20 One mnus p-value One mnus p-value One mnus p-value One mnus p-value One mnus p-value One mnus p-value Panel 4: One mnus p-value plots of AR (ash-otte), LR (ashe-ponts), KLM (ashe), MQLR (sol), JKLM (ponts) an 2SLS (otte) for testng β an γ, k =2, Θ 2 = Θ 2 = γ β Fgure 4.: Θ =, Θ 22 =. Fgure 4.2: Θ =, Θ 22 = γ β Fgure 4.3: Θ =3, Θ 22 =. Fgure 4.4: Θ =3, Θ 22 = γ β Fgure 4.5: Θ =5, Θ 22 =. Fgure 4.6: Θ =5, Θ 22 =. 9
21 One mnus p-value One mnus p-value One mnus p-value One mnus p-value One mnus p-value One mnus p-value Panel 5: One mnus p-value plots of AR (ash-otte), LR (ashe-ponts), KLM (ashe), MQLR (sol), JKLM (ponts) an 2SLS (otte) for testng β an γ, k =2, Θ 2 = Θ 2 = γ β Fgure 5.: Θ =, Θ 22 =. Fgure 5.2: Θ =, Θ 22 = γ β Fgure 5.3: Θ =3, Θ 22 =. Fgure 5.3: Θ =3, Θ 22 = γ β Fgure 5.5: Θ =5, Θ 22 =. Fgure 5.6: Θ =5, Θ 22 =. 2
22 6 Tests on the parameters of exogenous varables The robust subset statstcs exten to tests on the parameters of the exogenous varables that are nclue n the structural equaton. Ther expressons reman almost unaltere when X s exogenous an s spanne by the matrx of nstruments. The lnear IV regresson moel then reas y = Xβ + Wγ + ε (27) W = XΠ WX + ZΠ WZ + V W, where (X. Z) s the N (k + m x ) mensonal matrx of nstruments an Π XW an Π ZW are m x m w an k m w matrces of parameters. All other parameters are entcal to those efne for (). We are ntereste n testng H : β = β an we aapt the expressons of the statstcs from Defnton to accomoate tests of ths hypothess. Defnton 2:. The AR statstc (tmes k) to test H : β = β reas AR(β )= (y Xβ ˆσ εε (β ) W γ) P Z(y Xβ W γ), (28) wth Z =(X. Z) an γ the MLE of γ gven that β = β. 2. The KLM statstc to test H reas, KLM(β )= (y Xβ ˆσ εε(β ) W γ) P M Z ΠW (β ) X (y Xβ W γ), (29) h wth Π W (β )=( Z Z) Z W (y Xβ W γ) ˆσ εw (β ) ˆσ εε(β, ˆσ ) εε (β )= (y Xβ N k W γ) M Z(y Xβ W γ), ˆσ εw (β )= (y Xβ N k W γ) M ZW, snce Π X (β )=( Z Z) Z X = I mx, as ˆσ εx (β )= (y Xβ N k W γ) M ZX =. 3. A J-statstc that tests msspecfcaton uner H reas, JKLM(β )= AR(β ) KLM(β ). (3) 4. A quas lkelhoo rato statstc base on Morera s (23) lkelhoo rato statstc to test H reas, q MQLR(β )= AR(β 2 ) rk(β )+ (AR(β )+rk(β )) 2 4(AR(β ) KLM(β )) rk(β ), (3) where rk( β ) s the smallest egenvalue of ˆΣ MQLR = ˆΣ h 2 h WW.ε W (y Xβ Z γ) ˆσ εw (β ) PMXZ ˆσ εε W (y Xβ (β ) Z γ) ˆσ εw (β ) 2 ˆΣ ˆσ εε (β ) WW.ε. wth ˆσ εw (β )= (y Xβ N k W γ) M ZW, ˆΣ WW = W M ZW, ˆΣ N k WW.ε = ˆΣ WW ˆσ εw (β ) ˆσ εw (β ) ˆσ εε. (β ) Except for MQLR(β ), all statstcs n Defnton 2 are rect extensons of those n Defnton whenwenotethat Π X (β )= I mx, when X belongs to the set of nstruments. The alteraton of the expresson of ˆΣ MQLR for MLR(β ) partly results from M ZX = an snce only the nstruments Z entfy γ. Uner a full rank value of Π WZ, the (contonal) lmtng strbutons of the statstcs n Defnton 2 are entcal to those n Theorem 2 when k sequalto k + m x. Alongse Theorem 2, Theorems 3-5 apply to the statstcs from Theorem 2 as well. 2
23 KLM(β ) MQLR(β ) JKLM(β ) CJKLM(β ) AR(β ) 2SLS(β ) Fg Fg Fg Fg Fg Fg Table 3: Sze of the fferent statstcs n percentages that test H at the 95% sgnfcance level. Theorem 7. The (contonal) lmtng strbutons of the robust subset statstcs from Defnton 2 are boune from above by the lmtng strbuton uner a full rank value of Π WZ an from below by the lmtng strbuton uner a zero value of Π WZ. Proof. results from Theorem Sze an power propertes To llustrate the behavor of the robust subset statstcs from Defnton 2, we analyse ther sze an power propertes. We therefore conuct a smulaton experment usng (27) wth N =5, m w = m x =an k =9so the total number of nstruments equals k+m x =2. All nstruments are nepenently generate from N(,I N ) strbutons an vec(ε. V W ) s generate from a N(, Σ I N ) strbuton. The number of smulatons equals 5. The ata generatng process for the power curves n Panel 6 has Π WX =,γ=an Σ = I mw +. The specfcaton of Θ WZ =(Z M X Z) 2 Π WZ Σ 2 W n Panel 6 s such that ts frst element Θ WZ, s unequal to zero an all remanng elements of Θ WZ are equal to zero. Table 3 shows the observe sze of the fferent statstcs when we test at the 95% sgnfcance level. The parameters of the ata generatng process use for Panel 6 are specfe such that β s not partly entfe by the parameters n the equaton of W snce Π XW =an σ εw =. Panel 6 s thus comparable to Panel 2 whose ata generatng process s specfe n a smlar manner. The resultng power curves an observe szes therefore closely resemble those n Panel 2 an Table 2. Table 3 shows that the statstcs are conservatve when the entfcaton s rather low, whch s n accorance wth Theorem 7. Panel 6 shows that the rejecton frequences converge to a constant unequal to one for stant values of β when the entfcaton of γ s rather weak. Ths ncates that Theorem 6 extens to tests on subsets of the parameters. 22
24 Rejecton Frequency Rejecton Frequency Rejecton Frequency Panel 6: Power curves of AR(β ) (ashe-otte), KLM(β ) (ashe), MQLR(β ) (sol), JKLM(β ) (sol-trangles), CJKLM(sol-plusses) an 2SLS(β ) (otte) for testng H : β = β Fgure 6.: Θ WZ, =3 Fgure 6.2: Θ WZ, = β β Fgure 6.3: Θ WZ, =7 Theorem 8. When m x =, Assumpton hols, X s exogenous an for tests of H : β = β wth a value of β that ffers substantally from the true value:. AR( β ) s equal to the smallest egenvalue of ˆΣ 2 WW W P MX ZW ˆΣ 2 WW, ˆΣ WW = N k W M ZW. 2. The egenvalues of ˆΣ MQLR (β )=T (β ) T (β ) are equal to the egenvalues of (y W ˆΣ 2 WWˆσ Wy)ˆσ 2 yy.w. W ˆΣ 2 WW V P Z (y W ˆΣ 2 WWˆσ Wy)ˆσ 2 yy.w. W ˆΣ 2 WW V, (32) where V s a m m w matrx that contans the egenvectors of the largest m w egenvalues of ˆΣ 2 WW W P MX ZW ˆΣ 2 WW, ˆσ yy.w =ˆσ yy ˆσ WyˆΣ WWˆσ Wy. 23
25 3. TheexpressonsoftheAR,LRanMQLRstatstcsthattestH : β = β are entcal to ther expressons that test H : α =n the moel P MX ZW ˆΣ 2 WW v = εα + P MX ZW ˆΣ 2 WW V δ + u ε = ZΦ ε + V ε P MX ZW ˆΣ 2 WW V = ZΦ V + V V, where v s a m vector that contans the egenvector of the smallest egenvalue of ˆΣ 2 WW W P MX ZW ˆΣ 2 WW,ε= y Xβ Wγ wth β an γ thetruevaluesofthestructural parameters so Φ ε s a k vector of zeros, α :, δ: m w an Φ V : k m w an u, V ε an V V are n, n an n m w matrces of sturbances. Proof. follows from the proof of Theorem 6. (33) Corollary 4. When Assumpton hols so Φ ε equals zero, the smallest egenvalue of ˆΣ MQLR (β ) corresponswthatestforareucerankvalueof (Φ ε. Φ V ) whose rank equals at most m w an the χ 2 (k m w ) strbuton proves a upperboun on the lmtng strbuton of ths smallest egenvalue. Theorem 8 explans the convergence of the rejecton frequences n Panel 6 an mples that the behavor of MQLR(β ) s smlar to that of AR(β ) for stant values of β. Ientcal to the prevous Panels, 2SLS(β ) s the most powerful statstc n Panel 6 whle Table 3 shows that t also has lttle sze storton. Ths results because σ εw =. For non-zero values of σ εw, the sze-storton s often substantal. The parameter settngs for Panel 7 are such that β s partally entfe by the parameters n the equaton of W snce Π XW =an σ εw =.8. All remanng parameters are entcal to those n Panel 6. Because of the partal entfcaton, Table 3 shows that the statstcs are no longer conservatve when Θ WZ, s small. Because of the non-zero value of σ εw, 2SLS(β ) s now severly sze storte when Θ WZ, s small. Thus the 2SLS t-statstc can even be sze storte whenweusettotesttheparameters of the exogenous varables. Although the small value of Θ WZ, oes not affect the sze of the tests from Defnton 2, t stll strongly nfluences the power. Panel 7 shows that the power curves o not converge to one when Θ WZ, s small whch s n accorance wth Theorem 8. 7 Conclusons The lmtng strbutons of the robust subset nstrumental varable statstcs that result uner a hgh level entfcaton assumpton on the remanng structural parameters prove upperbouns on the lmtng strbuton of these statstcs n general. Lower bouns result from the lmtng strbutons uner complete entfcaton falure of the remanng parameters. For stant values of the parameter of nterest, the robust subset nstrumental varable statstcs correspon wth entfcaton statstcs. Even f the parameter of nterest s well-entfe, the power of tests on t o therefore not necessarly converge to one when the hypothesze value gets large. A smplfcaton of the LR statstc that s base on an extenson of Morera s (23) contonal 24
26 Rejecton Frequency Rejecton Frequency Rejecton Frequency Panel 7: Power curves of AR(β ) (ashe-otte), KLM(β ) (ashe), MQLR(β ) (sol), JKLM(β ) (sol-trangles), CJKLM(sol-plusses) an 2SLS(β ) (otte) for testng H : β = β Fgure 7.: Θ WZ, =3 Fgure 7.2: Θ WZ, = β β Fgure 7.3: Θ WZ, =7 lkelhoo statstc, s shown to perform equally well as the LR statstc an s much easer to use n practce. The subset AR statstc s less conservatve than the projecton base AR statstc from Dufour an Taamout (25a,b). Ths results snce the egrees of freeom parameter of ts lmtng strbuton s smaller than that of the projecton base AR statstc whle the latter s also base on the mnmal value of the AR statstc gven that H hols. In future work, we plan to exten the results from ths paper towars parameters estmate usng the generalze metho of moments. 25
27 Appenx ProofofLemma. Assumpton mples that for β = β,γ= γ, N vec(z (y Xβ Wγ ). Z X. Z W ) (I m+ Z Z)vec(Π W (γ γ ). Π X. Π W ) (ψ Zε. ψ ZX. ψ ZW ), snce y Xβ Wγ = ε + W (γ γ ). The jont lmtng strbuton of Z (y Xβ Wγ ) an Π W (β,γ )= (Z Z) Z hw (y Xβ Wγ ) ˆσ εw (β,γ ) ˆσ εε, (β,γ ) Π X (β,γ )= (Z Z) Z hx (y Xβ Wγ ) ˆσ εx(β,γ ) ˆσ εε(β,,γ ) wth ˆσ εw (β,γ )= (y Xβ N k Wγ ) M Z W, ˆσ εx (β,γ )= (y Xβ N k Wγ ) M Z X, ˆσ εε (β,γ )= (y Xβ N k Wγ ) M Z (y Xβ Wγ ), then reas N vec((z Z) Z (y Xβ Wγ ). Π X (β,γ ). Π W (β,γ )) σ εx +(γ γ ) Σ WX σ εε +2σ εw (γ γ )+(γ γ ) Σ WW (γ γ ) vec(π W (γ γ ). Π X Π W (γ γ ) σ Π W Π W (γ γ ) εw +(γ γ ) Σ WW ) σ εε +2σ εw (γ γ )+(γ γ ) Σ WW (γ γ ) (ϕ Zε. ϕ ZX. ϕ ZW ),. where ϕ Zε : k, ϕ ZX : k m x,ϕ ZW : k m w an ϕ Zε an vec(ϕ ZX. ϕ ZW ) are nepenently normal strbute ranom vectors wth mean ³ zero an covarance matrces σ εε Q an Σ (X : W )(X : W ).ε Q where Σ (X : W )(X : W ).ε = ΣXX Σ XW Σ WX Σ WW σ Xε σ Wε σ σxε εε σ Wε. The above shows that gven γ, the lmtng strbutons of Z (y Xβ Wγ ) an Π X (β,γ ), Π W (β,γ ) are nepenent. When γ s tself a ranom varable, the lmtng strbutons of Z (y Xβ Wγ ) an Π X (β,γ ), Π W (β,γ ) are nepenent contonal on the value of γ so the lmtng ensty functon can be factorze as 2 p ( N(Z Z) Z (y Xβ Wγ ),N 2 δ X Π X (β,γ ),N 2 δ W Π W (β,γ ),γ ) = p ( N(Z Z) Z (y Xβ Wγ ),N 2 δ X Π X (β,γ ),N 2 δ W Π W (β,γ ) γ )p (γ ) = p ( N(Z Z) Z (y Xβ Wγ ) γ )p (N 2 δ X ΠX (β,γ ),N 2 δ W ΠW (β,γ ) γ )p (γ ), where p (.) s the lmtng ensty functon an δ W an δ X are such that lm N N δ W Π W Z ZΠ W = C W, lm N N δ X Π XZ ZΠ X = C X wth C W an C X m w m w an m x m x mensonal matrces of constants such that δ W an δ X are zero n case of rrelevant or weak nstruments an one n case of strong nstruments. The above argument apples to any ranom γ such as, for example, the MLE γ snce, although γ s solve from Π W (β, γ) an (Z Z) Z (y Xβ W γ), all epenence between Π W (β, γ) an (Z Z) Z (y Xβ W γ) runs through γ. 2 To save on notaton, we (ncorrectly) epcte the ensty functon as a functon of ranom varables. 26
Subset statistics in the linear IV regression model
 Subset statstcs n te lnear IV regresson model Frank Klebergen Prelmnary verson. Not to be quoted wtout permsson. Abstract We sow tat te lmtng dstrbutons of subset generalzatons of te weak nstrument robust
Subset statstcs n te lnear IV regresson model Frank Klebergen Prelmnary verson. Not to be quoted wtout permsson. Abstract We sow tat te lmtng dstrbutons of subset generalzatons of te weak nstrument robust
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t tme
One and two particle density matrices for single determinant HF wavefunctions. (1) = φ 2. )β(1) ( ) ) + β(1)β * β. (1)ρ RHF
 One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
One and two partcle densty matrces for sngle determnant HF wavefunctons One partcle densty matrx Gven the Hartree-Fock wavefuncton ψ (,,3,!, = Âϕ (ϕ (ϕ (3!ϕ ( 3 The electronc energy s ψ H ψ = ϕ ( f ( ϕ
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών. ΗΥ-570: Στατιστική Επεξεργασία Σήµατος. ιδάσκων : Α. Μουχτάρης. εύτερη Σειρά Ασκήσεων.
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-570: Στατιστική Επεξεργασία Σήµατος 2015 ιδάσκων : Α. Μουχτάρης εύτερη Σειρά Ασκήσεων Λύσεις Ασκηση 1. 1. Consder the gven expresson for R 1/2 : R 1/2
8.1 The Nature of Heteroskedasticity 8.2 Using the Least Squares Estimator 8.3 The Generalized Least Squares Estimator 8.
 8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
8.1 The Nature of Heteroskedastcty 8. Usng the Least Squares Estmator 8.3 The Generalzed Least Squares Estmator 8.4 Detectng Heteroskedastcty E( y) = β+β 1 x e = y E( y ) = y β β x 1 y = β+β x + e 1 Fgure
Multi-dimensional Central Limit Theorem
 Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Mult-dmensonal Central Lmt heorem Outlne () () () t as () + () + + () () () Consder a sequence of ndependent random proceses t, t, dentcal to some ( t). Assume t 0. Defne the sum process t t t t () t ();
Exam Statistics 6 th September 2017 Solution
 Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
Exam Statstcs 6 th September 17 Soluto Maura Mezzett Exercse 1 Let (X 1,..., X be a raom sample of... raom varables. Let f θ (x be the esty fucto. Let ˆθ be the MLE of θ, θ be the true parameter, L(θ be
α & β spatial orbitals in
 The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
The atrx Hartree-Fock equatons The most common method of solvng the Hartree-Fock equatons f the spatal btals s to expand them n terms of known functons, { χ µ } µ= consder the spn-unrestrcted case. We
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit
 Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
Ordinal Arithmetic: Addition, Multiplication, Exponentiation and Limit Ting Zhang Stanford May 11, 2001 Stanford, 5/11/2001 1 Outline Ordinal Classification Ordinal Addition Ordinal Multiplication Ordinal
1 Complete Set of Grassmann States
 Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
Physcs 610 Homework 8 Solutons 1 Complete Set of Grassmann States For Θ, Θ, Θ, Θ each ndependent n-member sets of Grassmann varables, and usng the summaton conventon ΘΘ Θ Θ Θ Θ, prove the dentty e ΘΘ dθ
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
ST5224: Advanced Statistical Theory II
 ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
ST5224: Advanced Statistical Theory II 2014/2015: Semester II Tutorial 7 1. Let X be a sample from a population P and consider testing hypotheses H 0 : P = P 0 versus H 1 : P = P 1, where P j is a known
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Other Test Constructions: Likelihood Ratio & Bayes Tests
 Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Other Test Constructions: Likelihood Ratio & Bayes Tests Side-Note: So far we have seen a few approaches for creating tests such as Neyman-Pearson Lemma ( most powerful tests of H 0 : θ = θ 0 vs H 1 :
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
 Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Tridiagonal matrices. Gérard MEURANT. October, 2008
 Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
Tridiagonal matrices Gérard MEURANT October, 2008 1 Similarity 2 Cholesy factorizations 3 Eigenvalues 4 Inverse Similarity Let α 1 ω 1 β 1 α 2 ω 2 T =......... β 2 α 1 ω 1 β 1 α and β i ω i, i = 1,...,
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Variance of Trait in an Inbred Population. Variance of Trait in an Inbred Population
 Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Varance of Trat n an Inbred Populaton Revew of Mean Trat Value n Inbred Populatons We showed n the last lecture that for a populaton
Neutralino contributions to Dark Matter, LHC and future Linear Collider searches
 Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Neutralno contrbutons to Dark Matter, LHC and future Lnear Collder searches G.J. Gounars Unversty of Thessalonk, Collaboraton wth J. Layssac, P.I. Porfyrads, F.M. Renard and wth Th. Dakonds for the γz
Statistical Inference I Locally most powerful tests
 Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Statistical Inference I Locally most powerful tests Shirsendu Mukherjee Department of Statistics, Asutosh College, Kolkata, India. shirsendu st@yahoo.co.in So far we have treated the testing of one-sided
Every set of first-order formulas is equivalent to an independent set
 Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
Every set of first-order formulas is equivalent to an independent set May 6, 2008 Abstract A set of first-order formulas, whatever the cardinality of the set of symbols, is equivalent to an independent
A Class of Orthohomological Triangles
 A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
A Class of Orthohomologcal Trangles Prof. Claudu Coandă Natonal College Carol I Craova Romana. Prof. Florentn Smarandache Unversty of New Mexco Gallup USA Prof. Ion Pătraşcu Natonal College Fraţ Buzeşt
Space-Time Symmetries
 Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
4.6 Autoregressive Moving Average Model ARMA(1,1)
 84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Supplementary materials for Statistical Estimation and Testing via the Sorted l 1 Norm
 Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Sulementary materals for Statstcal Estmaton and Testng va the Sorted l Norm Małgorzata Bogdan * Ewout van den Berg Weje Su Emmanuel J. Candès October 03 Abstract In ths note we gve a roof showng that even
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in
 Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Nowhere-zero flows Let be a digraph, Abelian group. A Γ-circulation in is a mapping : such that, where, and : tail in X, head in : tail in X, head in A nowhere-zero Γ-flow is a Γ-circulation such that
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Econ 2110: Fall 2008 Suggested Solutions to Problem Set 8 questions or comments to Dan Fetter 1
 Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
Eon : Fall 8 Suggested Solutions to Problem Set 8 Email questions or omments to Dan Fetter Problem. Let X be a salar with density f(x, θ) (θx + θ) [ x ] with θ. (a) Find the most powerful level α test
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
 6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1
 Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
Main source: "Discrete-time systems and computer control" by Α. ΣΚΟΔΡΑΣ ΨΗΦΙΑΚΟΣ ΕΛΕΓΧΟΣ ΔΙΑΛΕΞΗ 4 ΔΙΑΦΑΝΕΙΑ 1 A Brief History of Sampling Research 1915 - Edmund Taylor Whittaker (1873-1956) devised a
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
C.S. 430 Assignment 6, Sample Solutions
 C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
C.S. 430 Assignment 6, Sample Solutions Paul Liu November 15, 2007 Note that these are sample solutions only; in many cases there were many acceptable answers. 1 Reynolds Problem 10.1 1.1 Normal-order
A Note on Intuitionistic Fuzzy. Equivalence Relation
 International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
International Mathematical Forum, 5, 2010, no. 67, 3301-3307 A Note on Intuitionistic Fuzzy Equivalence Relation D. K. Basnet Dept. of Mathematics, Assam University Silchar-788011, Assam, India dkbasnet@rediffmail.com
Math221: HW# 1 solutions
 Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Math: HW# solutions Andy Royston October, 5 7.5.7, 3 rd Ed. We have a n = b n = a = fxdx = xdx =, x cos nxdx = x sin nx n sin nxdx n = cos nx n = n n, x sin nxdx = x cos nx n + cos nxdx n cos n = + sin
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
A Two-Sided Laplace Inversion Algorithm with Computable Error Bounds and Its Applications in Financial Engineering
 Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
Electronic Companion A Two-Sie Laplace Inversion Algorithm with Computable Error Bouns an Its Applications in Financial Engineering Ning Cai, S. G. Kou, Zongjian Liu HKUST an Columbia University Appenix
8.324 Relativistic Quantum Field Theory II
 Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
Lecture 8.3 Relatvstc Quantum Feld Theory II Fall 00 8.3 Relatvstc Quantum Feld Theory II MIT OpenCourseWare Lecture Notes Hon Lu, Fall 00 Lecture 5.: RENORMALIZATION GROUP FLOW Consder the bare acton
LECTURE 4 : ARMA PROCESSES
 LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
LECTURE 4 : ARMA PROCESSES Movng-Average Processes The MA(q) process, s defned by (53) y(t) =µ ε(t)+µ 1 ε(t 1) + +µ q ε(t q) =µ(l)ε(t), where µ(l) =µ +µ 1 L+ +µ q L q and where ε(t) s whte nose An MA model
Appendix. Appendix I. Details used in M-step of Section 4. and expect ultimately it will close to zero. αi =α (r 1) [δq(α i ; α (r 1)
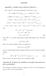 Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Appendx Appendx I. Detals used n M-step of Secton 4. Now wrte h (r) and expect ultmately t wll close to zero. and h (r) = [δq(α ; α (r) )/δα ] α =α (r 1) = [δq(α ; α (r) )/δα ] α =α (r 1) δ log L(α (r
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
F19MC2 Solutions 9 Complex Analysis
 F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
F9MC Solutions 9 Complex Analysis. (i) Let f(z) = eaz +z. Then f is ifferentiable except at z = ±i an so by Cauchy s Resiue Theorem e az z = πi[res(f,i)+res(f, i)]. +z C(,) Since + has zeros of orer at
The Simply Typed Lambda Calculus
 Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
Type Inference Instead of writing type annotations, can we use an algorithm to infer what the type annotations should be? That depends on the type system. For simple type systems the answer is yes, and
ω ω ω ω ω ω+2 ω ω+2 + ω ω ω ω+2 + ω ω+1 ω ω+2 2 ω ω ω ω ω ω ω ω+1 ω ω2 ω ω2 + ω ω ω2 + ω ω ω ω2 + ω ω+1 ω ω2 + ω ω+1 + ω ω ω ω2 + ω
 0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
0 1 2 3 4 5 6 ω ω + 1 ω + 2 ω + 3 ω + 4 ω2 ω2 + 1 ω2 + 2 ω2 + 3 ω3 ω3 + 1 ω3 + 2 ω4 ω4 + 1 ω5 ω 2 ω 2 + 1 ω 2 + 2 ω 2 + ω ω 2 + ω + 1 ω 2 + ω2 ω 2 2 ω 2 2 + 1 ω 2 2 + ω ω 2 3 ω 3 ω 3 + 1 ω 3 + ω ω 3 +
Lecture 2. Soundness and completeness of propositional logic
 Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 2 Soundness and completeness of propositional logic February 9, 2004 1 Overview Review of natural deduction. Soundness and completeness. Semantics of propositional formulas. Soundness proof. Completeness
Lecture 34 Bootstrap confidence intervals
 Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Lecture 34 Bootstrap confidence intervals Confidence Intervals θ: an unknown parameter of interest We want to find limits θ and θ such that Gt = P nˆθ θ t If G 1 1 α is known, then P θ θ = P θ θ = 1 α
Μηχανική Μάθηση Hypothesis Testing
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Μηχανική Μάθηση Hypothesis Testing Γιώργος Μπορμπουδάκης Τμήμα Επιστήμης Υπολογιστών Procedure 1. Form the null (H 0 ) and alternative (H 1 ) hypothesis 2. Consider
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Notes on the Open Economy
 Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
department listing department name αχχουντσ ϕανε βαλικτ δδσϕηασδδη σδηφγ ασκϕηλκ τεχηνιχαλ αλαν ϕουν διξ τεχηνιχαλ ϕοην µαριανι
 She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
She selects the option. Jenny starts with the al listing. This has employees listed within She drills down through the employee. The inferred ER sttricture relates this to the redcords in the databasee
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
Generalized Fibonacci-Like Polynomial and its. Determinantal Identities
 Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Int. J. Contemp. Math. Scences, Vol. 7, 01, no. 9, 1415-140 Generalzed Fbonacc-Le Polynomal and ts Determnantal Identtes V. K. Gupta 1, Yashwant K. Panwar and Ompraash Shwal 3 1 Department of Mathematcs,
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER
 ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
ORDINAL ARITHMETIC JULIAN J. SCHLÖDER Abstract. We define ordinal arithmetic and show laws of Left- Monotonicity, Associativity, Distributivity, some minor related properties and the Cantor Normal Form.
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Concrete Mathematics Exercises from 30 September 2016
 Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Concrete Mathematics Exercises from 30 September 2016 Silvio Capobianco Exercise 1.7 Let H(n) = J(n + 1) J(n). Equation (1.8) tells us that H(2n) = 2, and H(2n+1) = J(2n+2) J(2n+1) = (2J(n+1) 1) (2J(n)+1)
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr T t N n) Pr max X 1,..., X N ) t N n) Pr max
Congruence Classes of Invertible Matrices of Order 3 over F 2
 International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
International Journal of Algebra, Vol. 8, 24, no. 5, 239-246 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/.2988/ija.24.422 Congruence Classes of Invertible Matrices of Order 3 over F 2 Ligong An and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα,
 ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
ΗΥ537: Έλεγχος Πόρων και Επίδοση σε Ευρυζωνικά Δίκτυα Βασίλειος Σύρης Τμήμα Επιστήμης Υπολογιστών Πανεπιστήμιο Κρήτης Εαρινό εξάμηνο 2008 Economcs Contents The contet The basc model user utlty, rces and
2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)
![2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p) 2. Let H 1 and H 2 be Hilbert spaces and let T : H 1 H 2 be a bounded linear operator. Prove that [T (H 1 )] = N (T ). (6p)](/thumbs/40/21364883.jpg) Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
Uppsala Universitet Matematiska Institutionen Andreas Strömbergsson Prov i matematik Funktionalanalys Kurs: F3B, F4Sy, NVP 2005-03-08 Skrivtid: 9 14 Tillåtna hjälpmedel: Manuella skrivdon, Kreyszigs bok
557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING
 Most Powerful Tests 557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING To construct and assess the quality of a statistical test, we consider the power function β(θ). Consider a
Most Powerful Tests 557: MATHEMATICAL STATISTICS II RESULTS FROM CLASSICAL HYPOTHESIS TESTING To construct and assess the quality of a statistical test, we consider the power function β(θ). Consider a
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
SCHOOL OF MATHEMATICAL SCIENCES G11LMA Linear Mathematics Examination Solutions
 SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
SCHOOL OF MATHEMATICAL SCIENCES GLMA Linear Mathematics 00- Examination Solutions. (a) i. ( + 5i)( i) = (6 + 5) + (5 )i = + i. Real part is, imaginary part is. (b) ii. + 5i i ( + 5i)( + i) = ( i)( + i)
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 6/5/2006
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Ολοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα είναι μικρότεροι το 1000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Διάρκεια: 3,5 ώρες Καλή
The Probabilistic Method - Probabilistic Techniques. Lecture 7: The Janson Inequality
 The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
The Probabilistic Method - Probabilistic Techniques Lecture 7: The Janson Inequality Sotiris Nikoletseas Associate Professor Computer Engineering and Informatics Department 2014-2015 Sotiris Nikoletseas,
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
A Two Sample Test for Mean Vectors with Unequal Covariance Matrices
 A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
A Two Sample Test for Mean Vectors wth Unequal Covarance Matrces Tamae Kawasak 1 and Takash Seo 2 1 Department of Mathematcal Informaton Scence Graduate School of Scence, Tokyo Unversty of Scence, Tokyo,
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
6.3 Forecasting ARMA processes
 122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
122 CHAPTER 6. ARMA MODELS 6.3 Forecasting ARMA processes The purpose of forecasting is to predict future values of a TS based on the data collected to the present. In this section we will discuss a linear
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
ΕΙΣΑΓΩΓΗ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΑΝΑΛΥΣΗ ΕΛΕΝΑ ΦΛΟΚΑ Επίκουρος Καθηγήτρια Τµήµα Φυσικής, Τοµέας Φυσικής Περιβάλλοντος- Μετεωρολογίας ΓΕΝΙΚΟΙ ΟΡΙΣΜΟΙ Πληθυσµός Σύνολο ατόµων ή αντικειµένων στα οποία αναφέρονται
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Solution Series 9. i=1 x i and i=1 x i.
 Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
Lecturer: Prof. Dr. Mete SONER Coordinator: Yilin WANG Solution Series 9 Q1. Let α, β >, the p.d.f. of a beta distribution with parameters α and β is { Γ(α+β) Γ(α)Γ(β) f(x α, β) xα 1 (1 x) β 1 for < x
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Οικονομία. Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Οικονομία Διάλεξη 7η: Consumer Behavior Mαρίνα Μπιτσάκη Τμήμα Επιστήμης Υπολογιστών Τέλος Ενότητας Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί
The challenges of non-stable predicates
 The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
The challenges of non-stable predicates Consider a non-stable predicate Φ encoding, say, a safety property. We want to determine whether Φ holds for our program. The challenges of non-stable predicates
On a four-dimensional hyperbolic manifold with finite volume
 BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
BULETINUL ACADEMIEI DE ŞTIINŢE A REPUBLICII MOLDOVA. MATEMATICA Numbers 2(72) 3(73), 2013, Pages 80 89 ISSN 1024 7696 On a four-dimensional hyperbolic manifold with finite volume I.S.Gutsul Abstract. In
Lecture 15 - Root System Axiomatics
 Lecture 15 - Root System Axiomatics Nov 1, 01 In this lecture we examine root systems from an axiomatic point of view. 1 Reflections If v R n, then it determines a hyperplane, denoted P v, through the
Lecture 15 - Root System Axiomatics Nov 1, 01 In this lecture we examine root systems from an axiomatic point of view. 1 Reflections If v R n, then it determines a hyperplane, denoted P v, through the
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
SOLUTIONS TO MATH38181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question 1 a) The cumulative distribution function of T conditional on N n is Pr (T t N n) Pr (max (X 1,..., X N ) t N n) Pr (max
Chapter 6: Systems of Linear Differential. be continuous functions on the interval
 Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Chapter 6: Systems of Linear Differential Equations Let a (t), a 2 (t),..., a nn (t), b (t), b 2 (t),..., b n (t) be continuous functions on the interval I. The system of n first-order differential equations
Instruction Execution Times
 1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
1 C Execution Times InThisAppendix... Introduction DL330 Execution Times DL330P Execution Times DL340 Execution Times C-2 Execution Times Introduction Data Registers This appendix contains several tables
MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)
![MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3) MATH423 String Theory Solutions 4. = 0 τ = f(s). (1) dτ ds = dxµ dτ f (s) (2) dτ 2 [f (s)] 2 + dxµ. dτ f (s) (3)](/thumbs/81/84712331.jpg) 1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
1. MATH43 String Theory Solutions 4 x = 0 τ = fs). 1) = = f s) ) x = x [f s)] + f s) 3) equation of motion is x = 0 if an only if f s) = 0 i.e. fs) = As + B with A, B constants. i.e. allowe reparametrisations
Uniform Convergence of Fourier Series Michael Taylor
 Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
Uniform Convergence of Fourier Series Michael Taylor Given f L 1 T 1 ), we consider the partial sums of the Fourier series of f: N 1) S N fθ) = ˆfk)e ikθ. k= N A calculation gives the Dirichlet formula
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
= λ 1 1 e. = λ 1 =12. has the properties e 1. e 3,V(Y
 Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Stat 50 Homework Solutions Spring 005. (a λ λ λ 44 (b trace( λ + λ + λ 0 (c V (e x e e λ e e λ e (λ e by definition, the eigenvector e has the properties e λ e and e e. (d λ e e + λ e e + λ e e 8 6 4 4
Symplecticity of the Störmer-Verlet algorithm for coupling between the shallow water equations and horizontal vehicle motion
 Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Symplectcty of the Störmer-Verlet algorthm for couplng between the shallow water equatons and horzontal vehcle moton by H. Alem Ardakan & T. J. Brdges Department of Mathematcs, Unversty of Surrey, Guldford
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
