Rethinking Connes' approach to the standard model of particle physics via non-commutative geometry.
|
|
|
- Εὐκλείδης Παπακωνσταντίνου
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Rethinking Connes' approach to the standard model of particle physics via non-commutative geometry. Shane Farnsworth, joint work with Latham Boyle. Perimeter Institute for Theoretical Physics arxiv: , arxiv: , arxiv: November 02, 2014
2 Overview 1. Introduction: - The NCG Standard particle model
3 Overview 1. Introduction: - The NCG Standard particle model 2. Reformulation: - {m,g} {A,H,D} B 3. Applications: - Constraining D F - Fixing the Higgs Mass - Non-associative geometry 4. Open problems
4 Introduction: The standard model S SM = d 4 xψ /Dψ + ψφψ +F 2 +(Dφ) 2 m 2 φ φ2 + λ φ φ 4
5 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
6 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
7 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
8 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
9 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
10 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
11 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
12 Introduction: The Standard model. SU(3) SU(2) U(1) u R /3 d R 3 1 1/3 q L /6 ν R e R l L 1 2 1/2 h /2 A F = M 3 (C) H C π {H F,J F,γ F } D F S = S SM S = Tr[f (D/Λ)]+ < ψ Dψ >
13 Reformulation: WHY 1. Long obscure list of axioms
14 Reformulation: WHY 1. Long obscure list of axioms A is a real, associative, involutive, unital algebra D = D J is a unitary anti-linear operator on H γ = γ 1 = γ [a,jb J ] = 0 for all a,b A [[D,a],Jb J ] = 0 for all a,b A Ra = JL aj {D,γ} = 0...
15 Reformulation: WHY 1. Long obscure list of axioms A is a real, associative, involutive, unital algebra D = D J is a unitary anti-linear operator on H γ = γ 1 = γ [a,jb J ] = 0 for all a,b A [[D,a],Jb J ] = 0 for all a,b A Ra = JL aj {D,γ} = Too Many Higgs elds
16 Reformulation: WHY 1. Long obscure list of axioms A is a real, associative, involutive, unital algebra D = D J is a unitary anti-linear operator on H γ = γ 1 = γ [a,jb J ] = 0 for all a,b A [[D,a],Jb J ] = 0 for all a,b A Ra = JL aj {D,γ} = Too Many Higgs elds 3. Incorrect Higgs mass predicted
17 Reformulation: {A,H,J} B 0 B 0 = A H bb = (a +h)(a +h ) = aa +ah +h a + 0 b = (a +h) = a +Jh
18 Reformulation: {A,H,J} B 0 B 0 = A H bb = (a +h)(a +h ) = aa +ah +h a + 0 b = (a +h) = a +Jh
19 Reformulation: {A,H,J} B 0 B 0 = A H bb = (a +h)(a +h ) = aa +ah +h a + 0 b = (a +h) = a +Jh
20 Reformulation: {A,H,J} B 0 B 0 = A H bb = (a +h)(a +h ) = aa +ah +h a + 0 b = (a +h) = a +Jh
21 Reformulation: {A,H,J} B 0 Associativity: [b 1,b 0,b 2 ] = (b 1 b 0 )b 2 b 1 (b 0 b 2 ) = 0 (a 1 h)a 2 a 1 (ha 2 ) = [R a2,l a1 ]h = 0 [R a2,l a1 ] = 0 a i A,h H,b i B 0
22 Reformulation: {A,H,J} B 0 Associativity: [b 1,b 0,b 2 ] = (b 1 b 0 )b 2 b 1 (b 0 b 2 ) = 0 (a 1 h)a 2 a 1 (ha 2 ) = [R a2,l a1 ]h = 0 [R a2,l a1 ] = 0 a i A,h H,b i B 0 Involution: (b 1 b 0 ) = b 0 b 1 JL a1 h = R a 1 Jh R a1 = JL a 1 J a 1 A,h H,b i B 0
23 Reformulation: {A,H,D,J} B A ΩA = A Ω 1 A Ω 2 A... B = ΩA H Associativity: [ω 1,h,ω 2 ] = [R ω2,l ω1 ]h = 0 [[D,a],Jb J ] = 0 [[D,a],J[D,b ]J ] = 0...
24 Reformulation: {A,H,D,J} B A ΩA = A Ω 1 A Ω 2 A... B = ΩA H Associativity: [ω 1,h,ω 2 ] = [R ω2,l ω1 ] = 0 [[D,a],Jb J ] = 0 [[D,a],J[D,b ]J ] = 0...
25 Reformulation: {A,H,D,J} B A ΩA = A Ω 1 A Ω 2 A... B = ΩA H Associativity: [ω 1,h,ω 2 ] = [R ω2,l ω1 ] = 0 [[D,a],Jb J ] = 0 [[D,a],J[D,b ]J ] = 0...
26 Reformulation: {A,H,D,J} B A ΩA = A Ω 1 A Ω 2 A... B = ΩA H Associativity: [ω 1,h,ω 2 ] = [R ω2,l ω1 ] = 0 [[D,a],Jb J ] = 0 [[D,a],J[D,b ]J ] = 0...
27 Reformulation: {A,H,D,J} B A ΩA = A Ω 1 A Ω 2 A... B = ΩA H Associativity: [ω 1,h,ω 2 ] = [R ω2,l ω1 ] = 0 [[D,a],Jb J ] = 0 [[D,a],J[D,b] J ] = 0...
28 Applications:Too many Higgs Fields Constraints on D: D = D,{D,γ} = 0,DJ = ɛjd,[[d,a],jb J ] = 0 D 11 D 12 D 13 D 14 D 15 D 16 D 17 D 18 D 21 D 22 D 23 D 24 D 25 D 26 D 27 D 28 D 31 D 32 D 33 D 34 D 35 D 36 D 37 D 38 D 41 D 42 D 43 D 44 D 45 D 46 D 47 D 48 D F = D 51 D 52 D 53 D 54 D 55 D 56 D 57 D 58 D 61 D 62 D 63 D 64 D 65 D 66 D 67 D 68 D 71 D 72 D 73 D 74 D 75 D 76 D 77 D 78 D 81 D 82 D 83 D 84 D 85 D 86 D 87 D 88 Basis:{l R,q R,l L,q L,l R,q R,l L,q L }
29 Applications:Too many Higgs Fields Constraints on D: D = D,{D,γ} = 0,DJ = ɛjd,[[d,a],jb J ] = 0 D F = Basis:{l R,q R,l L,q L,l R,q R,l L,q L } 0 0 y l 0 m n y q n y l y q m n T yl T 0 n yq T y l y q 0 0
30 Too Many Higgs Fields [ω m,h,ω n ] = 0 [[D,a],J[D,b] J ] = 0 m = ( ) ( a b c, n = ) d b 0 0 0
31 Applications: Incorrect Higgs mass D F = 0 0 y l 0 m y q y l y q m yl T yq T y l y q 0 0 m = ( ) a 0, y l = 0 0 ( Yν α Y e β Y ν β Y e α ), y q = ( Yu α ) Y d β Y u β Y d α
32 Applications: Incorrect Higgs mass Traditional approach: symmetries = Aut(A) Symmetry Generators: δ = L a R a, where a = a A.
33 Applications: Incorrect Higgs mass Traditional approach: symmetries = Aut(A) Symmetry Generators: δ = L a R a, where a = a A. D D A = D +A+JAJ ( ) ( ) Yν α Y y l = e β Yν φ 1 Y e φ 2 Y ν β Y e α Y ν φ 2 Y e φ 1 ( ) ( ) Yu α Y y q = d β Yν φ 1 Y e φ 2 Y u β Y d α Y ν φ 2 Y e φ 1 m = ( ) ( ) a 0 a
34 Applications: Incorrect Higgs mass
35 Applications: Incorrect Higgs mass Fused algebra approach: symmetries = Aut(B) Symmetry Generators: δ = L a R a +t, where a = a A, [t,l x ] = [t,r x ] = [t,j] = [t,γ] = 0, and t = t End(H).
36 Applications: Incorrect Higgs mass Fused algebra approach: symmetries = Aut(B) Symmetry Generators: δ = L a R a +t, where a = a A, [t,l x ] = [t,r x ] = [t,j] = [t,γ] = 0, and t = t End(H). D D B = D +A+JAJ +T ( ) ( ) Yν α Y y l = e β Yν φ 1 Y e φ 2 Y ν β Y e α Y ν φ 2 Y e φ 1 ( ) ( ) Yu α Y y q = d β Yν φ 1 Y e φ 2 Y u β Y d α Y ν φ 2 Y e φ 1 m = ( ) ( ) a 0 YM σ(x)
37 Applications: Non-associative geometry [b 1,b 0,b 2 ] 0
38 Summary: {A,H,D} B
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
!#$%!& '($) *#+,),# - '($) # -.!, '$%!%#$($) # - '& %#$/0#!#%! % '$%!%#$/0#!#%! % '#%3$-0 4 '$%3#-!#, '5&)!,#$-, '65!.#%
" #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @
Higher spin gauge theories and their CFT duals
Higher spin gauge theories and their CFT duals E-mail: hikida@phys-h.keio.ac.jp 2 AdS Vasiliev AdS/CFT 4 Vasiliev 3 O(N) 3 Vasiliev 2 W N 1 AdS/CFT g µν Vasiliev AdS [1] AdS/CFT anti-de Sitter (AdS) (CFT)
ΥΠΗΡΕΣΙΕΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΧΕΙΡΙΣΗ ΑΠΟΔΟΣΗΣ ΚΑΙ ΣΤΕΛΕΧΩΣΗ
ΥΠΗΡΕΣΙΕΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΧΕΙΡΙΣΗ ΑΠΟΔΟΣΗΣ ΚΑΙ ΣΤΕΛΕΧΩΣΗ ΚΑΤΑΛΟΓΟΣ ΑΠΟΤΕΛΕΣΜΑΤΩΝ ΗΛΕΚΤΡΟΝΙΚΟΥ ΤΕΣΤ ΙΚΑΝΟΤΗΤΩΝ ΓΙΑ ΤΙΣ ΘΕΣΕΙΣ ΩΡΟΜΙΣΘΙΟΥ ΠΡΟΣΩΠΙΚΟΥ ΒΟΗΘΟΙ ΤΗΛΕΞΥΠΗΡΕΤΗΣΗΣ (ΑΡ. ΠΡΟΚΗΡΥΞΗΣ: 2/2017) (ΛΕΥΚΩΣΙΑ
SPECIAL FUNCTIONS and POLYNOMIALS
SPECIAL FUNCTIONS and POLYNOMIALS Gerard t Hooft Stefan Nobbenhuis Institute for Theoretical Physics Utrecht University, Leuvenlaan 4 3584 CC Utrecht, the Netherlands and Spinoza Institute Postbox 8.195
Takeaki Yamazaki (Toyo Univ.) 山崎丈明 ( 東洋大学 ) Oct. 24, RIMS
Takeaki Yamazaki (Toyo Univ.) 山崎丈明 ( 東洋大学 ) Oct. 24, 2017 @ RIMS Contents Introduction Generalized Karcher equation Ando-Hiai inequalities Problem Introduction PP: The set of all positive definite operators
Α Ρ Ι Θ Μ Ο Σ : 6.913
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
Geodesic Equations for the Wormhole Metric
Geodesic Equations for the Wormhole Metric Dr R Herman Physics & Physical Oceanography, UNCW February 14, 2018 The Wormhole Metric Morris and Thorne wormhole metric: [M S Morris, K S Thorne, Wormholes
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data
Statistical analysis of extreme events in a nonstationary context via a Bayesian framework. Case study with peak-over-threshold data B. Renard, M. Lang, P. Bois To cite this version: B. Renard, M. Lang,
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:
2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.
Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1
General 2 2 PT -Symmetric Matrices and Jordan Blocks 1 Qing-hai Wang National University of Singapore Quantum Physics with Non-Hermitian Operators Max-Planck-Institut für Physik komplexer Systeme Dresden,
Electronic Supplementary Information
Electronic Supplementary Information The preferred all-gauche conformations in 3-fluoro-1,2-propanediol Laize A. F. Andrade, a Josué M. Silla, a Claudimar J. Duarte, b Roberto Rittner, b Matheus P. Freitas*,a
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
Supplementary Information Chemical Partition of the Radiative Decay Rate of Luminescence of Europium Complexes
Supplementary Information Chemical Partition of the Radiative Decay Rate of Luminescence of Europium Complexes Nathalia B. D. Lima [a], José Diogo L. Dutra [a,b], Simone M. C. Gonçalves [a], Ricardo O.
SPONTANEOUS GENERATION OF GEOMETRY IN 4D
SPONTANEOUS GENERATION OF GEOMETRY IN 4D Dani Puigdomènch Dual year Russia-Spain: Particle Physics, Nuclear Physics and Astroparticle Physics 10/11/11 Based on arxiv: 1004.3664 and wor on progress. by
gr mol g lit mg lit mlit lit mol NaCl 96 NaCl HCl HCl
1 ( - ) ( ) : 5 ( CH 3 COOH ).1 0 /1M NaOH35ml CH COOH 3 = /3 gr mol 211/05 mg 3 /5mgr 210 /1gr 3 /5gr ppm.2 mg mlit mg lit g lit µg lit.3 1mol (58 /8 NaCl ) 0 /11F 14 /9ml NaCl.4 14 /9 96 0 /0149 0 /096
Non-Abelian Gauge Fields
Chapter 5 Non-Abelian Gauge Fields The simplest example starts with two Fermions Dirac particles) ψ 1, ψ 2, degenerate in mass, and hence satisfying in the absence of interactions γ 1 i + m)ψ 1 = 0, γ
6.1. Dirac Equation. Hamiltonian. Dirac Eq.
6.1. Dirac Equation Ref: M.Kaku, Quantum Field Theory, Oxford Univ Press (1993) η μν = η μν = diag(1, -1, -1, -1) p 0 = p 0 p = p i = -p i p μ p μ = p 0 p 0 + p i p i = E c 2 - p 2 = (m c) 2 H = c p 2
l 0 l 2 l 1 l 1 l 1 l 2 l 2 l 1 l p λ λ µ R N l 2 R N l 2 2 = N x i l p p R N l p N p = ( x i p ) 1 p i=1 l 2 l p p = 2 l p l 1 R N l 1 i=1 x 2 i 1 = N x i i=1 l p p p R N l 0 0 = {i x i 0} R
Hadronic Tau Decays at BaBar
Hadronic Tau Decays at BaBar Swagato Banerjee Joint Meeting of Pacific Region Particle Physics Communities (DPF006+JPS006 Honolulu, Hawaii 9 October - 3 November 006 (Page: 1 Hadronic τ decays Only lepton
UV fixed-point structure of the 3d Thirring model
UV fixed-point structure of the 3d Thirring model arxiv:1006.3747 [hep-th] (PRD accepted) Lukas Janssen in collaboration with Holger Gies Friedrich-Schiller-Universität Jena Theoretisch-Physikalisches
Commutative Monoids in Intuitionistic Fuzzy Sets
Commutative Monoids in Intuitionistic Fuzzy Sets S K Mala #1, Dr. MM Shanmugapriya *2 1 PhD Scholar in Mathematics, Karpagam University, Coimbatore, Tamilnadu- 641021 Assistant Professor of Mathematics,
Sachdev-Ye-Kitaev Model as Liouville Quantum Mechanics
Sachdev-Ye-Kitaev Model as Liouville Quantum Mechanics Dmitry Bagrets Nucl. Phys. B 9, 9 (06) arxiv: 607.00694 Alexander Altland Univ. zu Köln Alex Kamenev Univ. of Minnesota PCS IBS Workshop, Daejeon,
On the Galois Group of Linear Difference-Differential Equations
On the Galois Group of Linear Difference-Differential Equations Ruyong Feng KLMM, Chinese Academy of Sciences, China Ruyong Feng (KLMM, CAS) Galois Group 1 / 19 Contents 1 Basic Notations and Concepts
ECE 308 SIGNALS AND SYSTEMS FALL 2017 Answers to selected problems on prior years examinations
ECE 308 SIGNALS AND SYSTEMS FALL 07 Answers to selected problems on prior years examinations Answers to problems on Midterm Examination #, Spring 009. x(t) = r(t + ) r(t ) u(t ) r(t ) + r(t 3) + u(t +
Supporting Information
Electronic Supplementary Material (ESI) for ChemComm. This journal is The Royal Society of Chemistry 2015 Synthesis of 3-omosubstituted Pyrroles via Palladium- Catalyzed Intermolecular Oxidative Cyclization
4.- Littlest Higgs Model with T-parity. 5.- hhh at one loop in LHM with T-parity
1.- Introduction. 2.- Higgs physics 3.- hhh at one loop level in SM 4.- Littlest Higgs Model with T-parity 5.- hhh at one loop in LHM with T-parity 7.- Conclusions Higgs Decay modes at LHC Direct measurement
!"#$ "%&$ ##%&%'()) *..$ /. 0-1$ )$.'-
!!" !"# "%& ##%&%',-... /. -1.'- -13-',,'- '-...4 %. -5"'-1.... /..'-1.....-"..'-1.. 78::8
Solutions - Chapter 4
Solutions - Chapter Kevin S. Huang Problem.1 Unitary: Ût = 1 ī hĥt Û tût = 1 Neglect t term: 1 + hĥ ī t 1 īhĥt = 1 + hĥ ī t ī hĥt = 1 Ĥ = Ĥ Problem. Ût = lim 1 ī ] n hĥ1t 1 ī ] hĥt... 1 ī ] hĥnt 1 ī ]
Bounding Nonsplitting Enumeration Degrees
Bounding Nonsplitting Enumeration Degrees Thomas F. Kent Andrea Sorbi Università degli Studi di Siena Italia July 18, 2007 Goal: Introduce a form of Σ 0 2-permitting for the enumeration degrees. Till now,
ΑΝΑΛΥΤΙΚΟΣ ΤΙΜΟΚΑΤΑΛΟΓΟΣ BMW / MINI (Ισχύει από 15/01/2018) ΚΙΒΩΤΙΟ ΤΑΧΥΤΗΤΩΝ ΚΥΒΙΣΜΟΣ ΙΣΧΥΣ (HP)
Υ F21 LCI - Σειρά 1 3θυρη 1W11 120i ΧΚ 1.998 184 131 21.941,48 33.000 1W31 125i ΑΚ 1.998 224 130 26.407,03 42.040 1W91 M140i ΧΚ 2.998 340 179 31.878,02 52.790 1P91 M140i xdrive ΑΚ 2.998 340 169 35.428,74
SIEMENS Squirrel Cage Induction Standard Three-phase Motors
- SIEMENS Squirrel Cage Induction Standard Three-phase Motors 2 pole 3000 rpm 50Hz Rated current Power Efficiency Rated Ratio Noise Output Frame Speed Weight 3V 400V 415V factor Class 0%Load 75%Load torque
Phys624 Quantization of Scalar Fields II Homework 3. Homework 3 Solutions. 3.1: U(1) symmetry for complex scalar
Homework 3 Solutions 3.1: U(1) symmetry for complex scalar 1 3.: Two complex scalars The Lagrangian for two complex scalar fields is given by, L µ φ 1 µ φ 1 m φ 1φ 1 + µ φ µ φ m φ φ (1) This can be written
ITU-R P (2009/10)
ITU-R.45-4 (9/) % # GHz,!"# $$ # ITU-R.45-4.. (IR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.tu.t/itu-r/go/patets/e. (http://www.tu.t/publ/r-rec/e ) () ( ) BO BR BS BT F M RA S RS SA SF SM SNG TF V.ITU-R
Space-Time Symmetries
Chapter Space-Time Symmetries In classical fiel theory any continuous symmetry of the action generates a conserve current by Noether's proceure. If the Lagrangian is not invariant but only shifts by a
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3
Lecture 2: Dirac notation and a review of linear algebra Read Sakurai chapter 1, Baym chatper 3 1 State vector space and the dual space Space of wavefunctions The space of wavefunctions is the set of all
Symmetries and Feynman Rules for Ramond Sector in WZW-type Superstring Field Theories
Symmetries and Feynman Rules for Ramond Sector in WZW-type Superstring Field Theories Hiroshi Kunitomo YITP 215/3/5 @Nara Women s U. Nara arxiv:1412.5281, 153.xxxx Y TP YUKAWA INSTITUTE FOR THEORETICAL
Affine Weyl Groups. Gabriele Nebe. Summerschool GRK 1632, September Lehrstuhl D für Mathematik
Affine Weyl Groups Gabriele Nebe Lehrstuhl D für Mathematik Summerschool GRK 1632, September 2015 Crystallographic root systems. Definition A crystallographic root system Φ is a finite set of non zero
The ε-pseudospectrum of a Matrix
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
A summation formula ramified with hypergeometric function and involving recurrence relation
South Asian Journal of Mathematics 017, Vol. 7 ( 1): 1 4 www.sajm-online.com ISSN 51-151 RESEARCH ARTICLE A summation formula ramified with hypergeometric function and involving recurrence relation Salahuddin
arxiv: v1 [math.ra] 19 Dec 2017
![arxiv: v1 [math.ra] 19 Dec 2017](/thumbs/73/68347977.jpg "arxiv: v1 [math.ra] 19 Dec 2017")
TWO-DIMENSIONAL LEFT RIGHT UNITAL ALGEBRAS OVER ALGEBRAICALLY CLOSED FIELDS AND R HAHMED UBEKBAEV IRAKHIMOV 3 arxiv:7673v [mathra] 9 Dec 7 Department of Math Faculty of Science UPM Selangor Malaysia &
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ä616 Š ˆŒ CMS LHC
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2017.. 48.. 5.. 604Ä616 œ ˆ Š ˆ ˆ ˆ Š ˆŒ CMS LHC ˆ.. ƒμ²êé 1,.. ³ Éμ 1,2, 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê 2 ƒμ Ê É Ò Ê É É Ê, Ê, μ Ö É ² Ò Ê²ÓÉ ÉÒ Ô± ³ É CMS, μ²êî Ò μ μ ÒÌ - μ μ Í ±² μéò LHC
4.6 Autoregressive Moving Average Model ARMA(1,1)
84 CHAPTER 4. STATIONARY TS MODELS 4.6 Autoregressive Moving Average Model ARMA(,) This section is an introduction to a wide class of models ARMA(p,q) which we will consider in more detail later in this
Lecture 7: Overdispersion in Poisson regression
Lecture 7: Overdispersion in Poisson regression Claudia Czado TU München c (Claudia Czado, TU Munich) ZFS/IMS Göttingen 2004 0 Overview Introduction Modeling overdispersion through mixing Score test for
M p f(p, q) = (p + q) O(1)
l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
> `type/scalartype`:=proc(x) local st; return member(true,{seq(type(x,st),st=convert(_scalartypes,list))}); end proc: 3.
restart:with(clifford):with(linalg): eval(makealiases(9,'ordered')): eval(makealiases(9,'ordered')): ##read "Walshpackage.m"; ##useproduct(cmulwalsh); _default_clifford_product; Clifford:-cmulRS This worksheet
Ó³ Ÿ , º 2(214).. 171Ä176. Š Œ œ ƒˆˆ ˆ ˆŠ
Ó³ Ÿ. 218.. 15, º 2(214).. 171Ä176 Š Œ œ ƒˆˆ ˆ ˆŠ ˆ ˆ ˆ Š Š Œ Œ Ÿ ˆ Š ˆ Š ˆ ˆŠ Œ œ ˆ.. Š Ö,, 1,.. ˆ μ,,.. μ³ μ,.. ÉÓÖ μ,,.š. ʳÖ,, Í μ ²Ó Ò ² μ É ²Ó ± Ö Ò Ê É É Œˆ ˆ, Œμ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê μ ± Ê É
Fourier Analysis of Waves
Exercises for the Feynman Lectures on Physics by Richard Feynman, Et Al. Chapter 36 Fourier Analysis of Waves Detailed Work by James Pate Williams, Jr. BA, BS, MSwE, PhD From Exercises for the Feynman
Πρότυπο Αδρονίων µε Στατικά κουάρκ Ι
Πρότυπο Αδρονίων µε Στατικά κουάρκ Ι I,S: SU() group I : SU() group ΠΡΟΤΥΠΟ ΤΩΝ ΑΔΡΟΝΙΩΝ ΜΕ ΣΤΑΤΙΚΑ QUARKS QUARK ATOMS Πλήθος Βαρυονίων & Μεσονίων ~ 96 - αρχικά οι κανονικότητες (patterns) των αδρονικών
Sequent Calculi for the Modal µ-calculus over S5. Luca Alberucci, University of Berne. Logic Colloquium Berne, July 4th 2008
Sequent Calculi for the Modal µ-calculus over S5 Luca Alberucci, University of Berne Logic Colloquium Berne, July 4th 2008 Introduction Koz: Axiomatisation for the modal µ-calculus over K Axioms: All classical
Iterated trilinear fourier integrals with arbitrary symbols
Cornell University ICM 04, Satellite Conference in Harmonic Analysis, Chosun University, Gwangju, Korea August 6, 04 Motivation the Coifman-Meyer theorem with classical paraproduct(979) B(f, f )(x) :=
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ Ä ³ Éμ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ƒμ Ê É Ò Ê É É Ê, Ê, μ Ö
ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ 2018.. 49.. 4.. 1291Ä1301 Š œ Š ˆŒ CMS LHC ˆ Š ˆ ˆŠˆ ŒŠ Œˆ Œ ˆ.. ³ Éμ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ƒμ Ê É Ò Ê É É Ê, Ê, μ Ö μ É Ö ± ɱ μ μ ʲÓÉ Éμ Ô± ³ É CMS μ²óïμ³ μ μ³ ±μ²² μ μ ±Ê Ë ± ³± ³
Notes on the Open Economy
Notes on the Open Econom Ben J. Heijdra Universit of Groningen April 24 Introduction In this note we stud the two-countr model of Table.4 in more detail. restated here for convenience. The model is Table.4.
Maude 6. Maude [1] UIUC J. Meseguer. Maude. Maude SRI SRI. Maude. AC (Associative-Commutative) Maude. Maude Meseguer OBJ LTL SPIN
![Maude 6. Maude [1] UIUC J. Meseguer. Maude. Maude SRI SRI. Maude. AC (Associative-Commutative) Maude. Maude Meseguer OBJ LTL SPIN](/thumbs/84/90701332.jpg "Maude 6. Maude [1] UIUC J. Meseguer. Maude. Maude SRI SRI. Maude. AC (Associative-Commutative) Maude. Maude Meseguer OBJ LTL SPIN")
78 Maude 1 Maude [1] UIUC J. Meseguer ( 1 ) ( ) Maude Maude SRI 90 UIUC SRI Maude SRI S. Eker C++ Maude 2 Maude Meseguer OBJ 1983-84 OBJ2[3] OBJ Maude OBJ 1 CafeOBJ 3 Maude 4 Maude CafeOBJ Maude: A Computer
Non-Gaussianity from Lifshitz Scalar
COSMO/CosPA 200 September 27, 200 Non-Gaussianity from Lifshitz Scalar Takeshi Kobayashi (Tokyo U.) based on: arxiv:008.406 with Keisuke Izumi, Shinji Mukohyama Lifshitz scalars with z=3 obtain super-horizon,
Divergence for log concave functions
Divergence or log concave unctions Umut Caglar The Euler International Mathematical Institute June 22nd, 2013 Joint work with C. Schütt and E. Werner Outline 1 Introduction 2 Main Theorem 3 -divergence
Ceramic PTC Thermistor Overload Protection
FEATURES compliant CPTD type are bare disc type CPTL type are leaded Low, medium and high voltage ratings Low resistance; Small size No need to reset supply after overload No noise generated Stable over
Η ΑΝΘΥΦΑΙΡΕΤΙΚΗ ΕΡΜΗΝΕΙΑ ΤΗΣ ΕΞΩΣΗΣ ΤΗΣ ΠΟΙΗΣΗΣ ΣΤΟ ΔΕΚΑΤΟ ΒΙΒΛΙΟ ΤΗΣ ΠΟΛΙΤΕΙΑΣ ΤΟΥ ΠΛΑΤΩΝΟΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ MΑΘΗΜΑΤΙΚΩΝ ΤΜΗΜΑ ΜΕΘΟΔΟΛΟΓΙΑΣ, ΙΣΤΟΡΙΑΣ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΤΜΗΜΑ ΕΠΙΣΤΉΜΩΝ ΑΓΩΓΉΣ & ΘΕΩΡΙΑΣ ΤΗΣ ΕΠΙΣΤΗΜΗΣ ΤΜΗΜΑ ΦΙΛΟΣΟΦΙΑΣ, ΠΑΙΔΑΓΩΓΙΚΗΣ &
The Pohozaev identity for the fractional Laplacian
The Pohozaev identity for the fractional Laplacian Xavier Ros-Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya (joint work with Joaquim Serra) Xavier Ros-Oton (UPC) The Pohozaev
Computing the Gradient
FMIA F. Moukalled L. Mangani M. Darwish An Advanced Introduction with OpenFOAM and Matlab This textbook explores both the theoretical oundation o the Finite Volume Method (FVM) and its applications in
A Convolutional Neural Network Approach for Objective Video Quality Assessment
A Convolutional Neural Network Approach for Objective Video Quality Assessment Patrick Le Callet, Christian Viard-Gaudin, Dominique Barba To cite this version: Patrick Le Callet, Christian Viard-Gaudin,
Relativistic particle dynamics and deformed symmetry
Relativistic particle dynamics and deformed Poincare symmetry Department for Theoretical Physics, Ivan Franko Lviv National University XXXIII Max Born Symposium, Wroclaw Outline Lorentz-covariant deformed
A manifestly scale-invariant regularization and quantum effective operators
A manifestly scale-invariant regularization and quantum effective operators D. Ghilencea Corfu Summer Institute, Greece - 8 Sep 2015 E-print: arxiv:1508.00595 sponsored by RRC grant - project PN-II-ID-PCE-2011-3-0607
Eulerian Simulation of Large Deformations
Eulerian Simulation of Large Deformations Shayan Hoshyari April, 2018 Some Applications 1 Biomechanical Engineering 2 / 11 Some Applications 1 Biomechanical Engineering 2 Muscle Animation 2 / 11 Some Applications
Torsional Newton-Cartan gravity from a pre-newtonian expansion of GR
Torsional Newton-Cartan gravity from a pre-newtonian expansion of GR Dieter Van den Bleeken arxiv.org/submit/1828684 Supported by Bog azic i University Research Fund Grant nr 17B03P1 SCGP 10th March 2017
Terminal Contact UL Insulation Designation (provided with) style form system approval Flux tight
eatures A miniature PCB Power Relay. form A contact configuration with quick terminal type. 5KV dielectric strength, K surge voltage between coils to contact. Ideal for high rating Home Appliances of heating
8.324 Relativistic Quantum Field Theory II
8.324 Relativistic Quantum Field Theory II MIT OpenCourseWare Lecture Notes Hong Liu, Fall 200 Lecture 2 3: GENERAL ASPECTS OF QUANTUM ELECTRODYNAMICS 3.: RENORMALIZED LAGRANGIAN Consider the Lagrangian
Dong Liu State Key Laboratory of Particle Detection and Electronics University of Science and Technology of China
Dong Liu State Key Laboratory of Particle Detection and Electronics University of Science and Technology of China ISSP, Erice, 7 Outline Introduction of BESIII experiment Motivation of the study Data sample
Written Examination. Antennas and Propagation (AA ) April 26, 2017.
Written Examination Antennas and Propagation (AA. 6-7) April 6, 7. Problem ( points) Let us consider a wire antenna as in Fig. characterized by a z-oriented linear filamentary current I(z) = I cos(kz)ẑ
Κεφάλαιο 14: Πρόσθεση Στροφορμών
Κεφάλαιο 14: Πρόσθεση Στροφορμών Περιεχόμενα Κεφαλαίου Αφού δοθεί ο ορισμός ολικής στροφορμής θα γίνει η συσχέτιση της βάσης ολικής στροφορμής (jm j) με τη βάση των επιμέρους στροφορμών (m 1m ). Οι συντελεστές
Hartree-Fock Theory. Solving electronic structure problem on computers
Hartree-Foc Theory Solving electronic structure problem on computers Hartree product of non-interacting electrons mean field molecular orbitals expectations values one and two electron operators Pauli
Accounting for model errors in iterative ensemble smoothers
Accounting for model errors in iterative ensemble smoothers Geir Evensen International Research Institute of Stavanger Nansen Environmental and Remote Sensing Center The 3th EnKF Data Assimilation Workshop,
= f(0) + f dt. = f. O 2 (x, u) x=(x 1,x 2,,x n ) T, f(x) =(f 1 (x), f 2 (x),, f n (x)) T. f x = A = f
2 n dx (x)+g(x)u () x n u (x), g(x) x n () +2 -a -b -b -a 3 () x,u dx x () dx () + x x + g()u + O 2 (x, u) x x x + g()u + O 2 (x, u) (2) x O 2 (x, u) x u 2 x(x,x 2,,x n ) T, (x) ( (x), 2 (x),, n (x)) T
Arithmetical applications of lagrangian interpolation. Tanguy Rivoal. Institut Fourier CNRS and Université de Grenoble 1
Arithmetical applications of lagrangian interpolation Tanguy Rivoal Institut Fourier CNRS and Université de Grenoble Conference Diophantine and Analytic Problems in Number Theory, The 00th anniversary
W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg "k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +")
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Ó³ Ÿ , º 3(194).. 673Ä677. Š Œ œ ƒˆˆ ˆ ˆŠ. ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ±
Ó³ Ÿ. 2015.. 12, º 3(194.. 673Ä677 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŸ ˆ Šˆ ˆ ˆ Œ ˆŠ ˆ.. ³ Ì μ, ƒ.. Š ³ÒÏ,ˆ..Š Ö, Ÿ. ʲ ±μ ± Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ˆ É ÉÊÉ Ö μ Ë ± μ²ó ±μ ± ³ ʱ, Š ±μ, μ²óï μé É ² Ò Ê Ö Ö Î ² Ò Ê²ÓÉ ÉÒ,
Variational Wavefunction for the Helium Atom
Technische Universität Graz Institut für Festkörperphysik Student project Variational Wavefunction for the Helium Atom Molecular and Solid State Physics 53. submitted on: 3. November 9 by: Markus Krammer
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
arxiv: v3 [math.ra] 24 Nov 2017
![arxiv: v3 [math.ra] 24 Nov 2017](/thumbs/90/103143709.jpg "arxiv: v3 [math.ra] 24 Nov 2017")
In the name of Allah Most Gracious Most Merciful. CLASSIFICATIONS OF TWO-DIMENSIONAL JORDAN ALGEBRAS OVER THE ALGEBRAICALLY CLOSED FIELDS AND R arxiv:7.948v [math.ra] 4 Nov 7 H.AHMED U.BEKBAEV I.RAKHIMOV
D-term Dynamical SUSY Breaking
D-term Dynamical SUSY Breaking Nobuhito Maru (Keio University) with H. Itoyama (Osaka City University) arxiv: 1109.76 [hep-ph] 7/6/01 @Y ITP workshop on Field Theory & String Theory Introduction SUPERSYMMETRY
Abstract Storage Devices
Abstract Storage Devices Robert König Ueli Maurer Stefano Tessaro SOFSEM 2009 January 27, 2009 Outline 1. Motivation: Storage Devices 2. Abstract Storage Devices (ASD s) 3. Reducibility 4. Factoring ASD
AdS black disk model for small-x DIS
AdS black disk model for small-x DIS Miguel S. Costa Faculdade de Ciências da Universidade do Porto 0911.0043 [hep-th], 1001.1157 [hep-ph] Work with. Cornalba and J. Penedones Rencontres de Moriond, March
A Summary Of Linear Continuum Mechanics 1. a b = a i b i = a b cos θ. det A = ɛ ijk A 1i A 2j A 3k. e 1 e 2 e 3 a b = ɛ ijk a j b k e i =
A Summary Of Linear Continuum Mechanics 1 Vector Analysis Inner / Scalar / Dot product Norm of a vector Kronecker delta a b = a i b i = a b cos θ a = [a a] 1/2 = a 1 a 1 + a 2 a 2 + a 3 a 3 δ ij = I =
Η ανακάλυψη του Μποζονίου Higgs στο CERN
Η ανακάλυψη του Μποζονίου Higgs στο CERN - The God Particle: If the Universe Is the Answer, What Is the Question? Leon Lederman, Nobel Φυσικής 1988 Καθηγ. Ευάγγελος Γαζής (ΕΜΠ & CERN) 22 Αυγούστου 2015
Matrices and vectors. Matrix and vector. a 11 a 12 a 1n a 21 a 22 a 2n A = b 1 b 2. b m. R m n, b = = ( a ij. a m1 a m2 a mn. def
Matrices and vectors Matrix and vector a 11 a 12 a 1n a 21 a 22 a 2n A = a m1 a m2 a mn def = ( a ij ) R m n, b = b 1 b 2 b m Rm Matrix and vectors in linear equations: example E 1 : x 1 + x 2 + 3x 4 =
IL - 13 /IL - 18 ELISA PCR RT - PCR. IL - 13 IL - 18 mrna. 13 IL - 18 mrna IL - 13 /IL Th1 /Th2
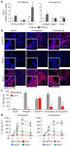344 IL - 13 /IL - 18 1 2 1 2 1 2 1 2 1 2 3 1 2 13 18 IL - 13 /IL - 18 10% / OVA /AL OH 3 5% 16 ~ 43 d 44 d ELISA BALF IL - 13 IL - 18 PCR RT - PCR IL - 13 IL - 18 mrna IL - 13 mrna 0. 01 IL - 18 mrna 0.
ΤΗΛΕΠΙΣΚΟΠΗΣΗ. Γραµµικοί Μετασχηµατισµοί (Linear Transformations) Τονισµός χαρακτηριστικών εικόνας (image enhancement)
Γραµµικοί Μετασχηµατισµοί (Linear Transformations) Τονισµός χαρακτηριστικών εικόνας (image enhancement) Συµπίεση εικόνας (image compression) Αποκατάσταση εικόνας (Image restoration) ηµήτριος. ιαµαντίδης
Review: Molecules = + + = + + Start with the full Hamiltonian. Use the Born-Oppenheimer approximation
Review: Molecules Start with the full amiltonian Ze e = + + ZZe A A B i A i me A ma ia, 4πε 0riA i< j4πε 0rij A< B4πε 0rAB Use the Born-Oppenheimer approximation elec Ze e = + + A A B i i me ia, 4πε 0riA
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Δ.Π.Μ.Σ. ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Δ.Π.Μ.Σ. ΥΠΟΛΟΓΙΣΤΙΚΗΣ ΜΗΧΑΝΙΚΗΣ Μεταπτυχιακή Εργασία Προσομοίωση Φαινομένων Μεταφοράς Θερμότητας και Μάζας στο Εσωτερικό Κτιρίων Λεκκάκης Νικόλαος Επιβλέπων: Φούντη Μαρία,
'( )*(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((( +
! " # $ %&&' '( )*(((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((( + %( ((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((((('& %('(,,
ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ. Θέµα:
Ε ΕΘΝΙΚΗ ΣΧΟΛΗ ΤΟΠΙΚΗΣ ΑΥΤΟ ΙΟΙΚΗΣΗΣ Β ΕΚΠΑΙ ΕΥΤΙΚΗ ΣΕΙΡΑ ΤΜΗΜΑ: ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΙΟΙΚΗΣΗΣ ΤΕΛΙΚΗ ΕΡΓΑΣΙΑ Θέµα: Πολιτιστική Επικοινωνία και Τοπική ηµοσιότητα: Η αξιοποίηση των Μέσων Ενηµέρωσης, ο ρόλος των
Partial Differential Equations in Biology The boundary element method. March 26, 2013
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Supporting Information. Generation Response. Physics & Chemistry of CAS, 40-1 South Beijing Road, Urumqi , China. China , USA
Supporting Information Pb 3 B 6 O 11 F 2 : A First Noncentrocentric Lead Fluoroborate with Large Second Harmonic Generation Response Hongyi Li, a Hongping Wu, a * Xin Su, a Hongwei Yu, a,b Shilie Pan,
DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM. by Zoran VARGA, Ms.C.E.
DETERMINATION OF DYNAMIC CHARACTERISTICS OF A 2DOF SYSTEM by Zoran VARGA, Ms.C.E. Euro-Apex B.V. 1990-2012 All Rights Reserved. The 2 DOF System Symbols m 1 =3m [kg] m 2 =8m m=10 [kg] l=2 [m] E=210000
Models for Probabilistic Programs with an Adversary
Models for Probabilistic Programs with an Adversary Robert Rand, Steve Zdancewic University of Pennsylvania Probabilistic Programming Semantics 2016 Interactive Proofs 2/47 Interactive Proofs 2/47 Interactive
Partial Trace and Partial Transpose
Partial Trace and Partial Transpose by José Luis Gómez-Muñoz http://homepage.cem.itesm.mx/lgomez/quantum/ jose.luis.gomez@itesm.mx This document is based on suggestions by Anirban Das Introduction This
Wavelet based matrix compression for boundary integral equations on complex geometries
1 Wavelet based matrix compression for boundary integral equations on complex geometries Ulf Kähler Chemnitz University of Technology Workshop on Fast Boundary Element Methods in Industrial Applications
EE101: Resonance in RLC circuits
EE11: Resonance in RLC circuits M. B. Patil mbatil@ee.iitb.ac.in www.ee.iitb.ac.in/~sequel Deartment of Electrical Engineering Indian Institute of Technology Bombay I V R V L V C I = I m = R + jωl + 1/jωC