β± β 4αγ 2 x1,2 x 0.
|
|
|
- Μέλισσα Χατζηιωάννου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ ax 3 + β x + γ x+ δ = 0 Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ) και δευτεροβαθµίω εξισώσεω ( ax + β x+ γ = 0) µε αρητική διακρίουσα, οδήγησε τους Μαθηµατικούς (SDel Ferro, N Tartaglia, R Bombelli), στα µέσα του 6 ου αιώα α διευρύου το σύολο τω πραγµατικώ αριθµώ R µε τη δηµιουργία έω αριθµώ, της µορφής a+ βi στο υπερσύολο C, τους µιγαδικούς αριθµούς (Complex numbers) Στο σύολο C, οι πράξεις, οι ιδιότητες τους και η επίλυση τω εξισώσεω ταυτίζοται µε αυτές του R Ορισµός φαταστικώ και µιγαδικώ αριθµώ Η µορφή a+ βi Γωρίζοµε ότι η εξίσωση α x + β x + γ = 0, µε α, β, γ R έχει: δύο άισες πραγµατικές ρίζες, ότα είαι η διακρίουσα της > 0, µία διπλή ρίζα, που είαι πραγµατικός αριθµός, ότα είαι = 0 και είαι αδύατη στο R, ότα ισχύει ότι < 0 β± β 4αγ x, =, = β 4αγ > 0 α β Άρα αx + βx+ γ= 0 x = x =, = β 4 αγ =0 α αδύατη στο R, = β 4αγ < 0 Η εξίσωση x = είαι αδύατη στο R, διότι πάτα ισχύει ότι x 0 Προκειµέου α ξεπεραστεί αυτή η αδυαµία, έγιε διεύρυση του συόλου R σε έα έο σύολο, το C Το έο υπερσύολο έχει τις ίδιες πράξεις και ιδιότητες πράξεω µε το σύολο R, που είαι γήσιο υποσύολο του, αλλά περιέχει επιπλέο τουλάχιστο µία λύση της εξισώσεως x = Το έο σύολο C περιέχει ως στοιχείο του το αριθµό i για το οποίο ισχύει ότι i = και οοµάζεται φαταστική µοάδα Κάθε αριθµός της µορφής ai, µε a R, οοµάζεται φαταστικός αριθµός Πρώτος ο Gauss εισήγαγε το συµβολισµό i=, αλλά ο Euler το εισήγαγε οριστικά Κάθε αριθµός της µορφής = a+ bi, µε a, b Rοοµάζεται µιγαδικός αριθµός Το σύολο τω µιγαδικώ αριθµώ συµβολίζεται ως C Ο αριθµός a οοµάζεται πραγµατικό µέρος του και συµβολίζεται ως Re( ), εώ ο αριθµός b οοµάζεται φαταστικό µέρος του και συµβολίζεται ως Im( ) Άρα = a+ b i= Re( ) + Im( ) i Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
2 Κάθε πραγµατικός αριθµός a είαι και µιγαδικός αριθµός, διότι a= a+ 0i Άρα I a= 0 Re( ) = 0 και R b= 0 Im( ) = 0 Επίσης κάθε φαταστικός αριθµός bi είαι και µιγαδικός αριθµός, διότι bi= 0+ bi Είαι N Z Q R C και C= R Ι, όπου I το σύολο τω φαταστικώ αριθµώ Α ab 0, τότε ο λέγεται καθαρός ή γήσιος µιγαδικός 0, b 0 bi bi a, b = a+ bi αριθµός Είαι ( ) = + = και ( ) Παραδείγµατα Να υπολογισθού οι δυάµεις της µορφής i k για κάθε k Z Είαι 3 4 i i i i i i = i i = = i =, = = ( ) =, ( )( ) 0 i =,, υ=0 k 4λ υ 4 λ υ υ i, υ= A ο ακέραιος k = 4λ+ υ µε 0 υ< 4, τότε i = i i = ( i ) i = i =, υ= i, υ= Είαι i = i = i i= i= i, i = i = i i = ( ) =, κλπ i = i, Χαρακτηρίστε ως αληθείς ή ψευδείς τις παρακάτω προτάσεις, αιτιολογώτας τις απατήσεις σας Α, C τότε = 0 = 0 ή =0 Η πρόταση είαι αληθής διότι α = = 0, τότε προφαώς = 0 Α 0, τότε = 0 = 0 = 0 = 0 Οµοίως εεργούµε ότα 0 Η εξίσωση x + α = 0 έχει λύση στο C Η πρόταση είαι αληθής διότι, x + α = 0 x ( ) α = 0 x i α = 0 x= iα α = α + α = x = iα x ( i ) 0 ( x i ) ( x i ) 0 ή Α x, y C : x + y = 0 x= y= 0 x= 0 Η πρόταση είαι ψευδής διότι α και y = i 0 x= 3 + i 0 α και τότε x + y = 9+ 6i + 6i 9 = 0 y = + 3i 0 τότε x + y = + i = = 0 ή ακόµα * Για κάθε = { 0} C C ισχύει ότι * = + i τότε = (+ i) = 4+ 4i= 3+ 4i C > 0 Η πρόταση είαι ψευδής διότι α Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
3 3 ε µπορούµε α ισχυρισθούµε ότι = 3+ 4i> 0, διότι το σύολο C δε είαι διατεταγµέο (όπως ήτα το σύολο R ) Μιγαδικό επίπεδο (ή επίπεδο Gauss) Γεωµετρική παράσταση µιγαδικού αριθµού Κάθε µιγαδικό αριθµό = α+ β i, µε α,β R µπορούµε α το ατιστοιχίσοµε στο σηµείο M µε συτεταγµέες ( a, β ) του καρτεσιαού επιπέδου Ατιστρόφως, το κάθε σηµείο M( a, β ) του καρτεσιαού επιπέδου µπορούµε α το ατιστοιχίσοµε στο µιγαδικό αριθµό = α+ β i, µε α,β R Το σηµείο M οοµάζεται εικόα του µιγαδικού αριθµού = α+ β i, µε α,β R και συµβολίζεται ως Μ () Με τη απεικόιση αυτή: Ο µιγαδικός αριθµός = 0 απεικοίζεται στη αρχή O του ορθοκαοικού συστήµατος τω αξόω Οι πραγµατικοί αριθµοί, δηλαδή οι µιγαδικοί αριθµοί της µορφής = a+ 0i, απεικοίζοται στο οριζότιο άξοα xx (άξοας τω πραγµατικώ αριθµώ) Οι θετικοί αριθµοί απεικοίζοται στο θετικό ηµιάξοα Οxκαι οι αρητικοί αριθµοί απεικοίζοται στο αρητικό ηµιάξοα Ο x Οι φαταστικοί αριθµοί, δηλαδή οι µιγαδικοί αριθµοί της µορφής = 0+ βi, απεικοίζοται στο κατακόρυφο άξοα yy (άξοας τω φαταστικώ αριθµώ) Οι έχοτες β > 0 απεικοίζοται στο θετικό ηµιάξοα Oy και οι έχοτες β < 0 απεικοίζοται στο αρητικό ηµιάξοα Oy Οι ατίθετοι µιγαδικοί αριθµοί απεικοίζοται, στο µιγαδικό επίπεδο, σε σηµεία συµµετρικά ως προς τη αρχή τω αξόω Ισότητα µιγαδικώ αριθµώ Επειδή κάθε µιγαδικός αριθµός γράφεται µε µοαδικό τρόπο στη µορφή a+ βi, δύο µιγαδικοί αριθµοί = a+ βi και = γ + δi είαι ίσοι, α και µόο α τα πραγµατικά και τα φαταστικά τους µέρη είαι, ατίστοιχα, ίσα µεταξύ τους α = γ ηλαδή = a+ βi= γ + δi και Οι µιγαδικοί αριθµοί δε β = δ διατάσσοται, δηλαδή δε έχει όηµα α λέµε ότι ο µιγαδικός είαι µεγαλύτερος ή µικρότερος του µιγαδικού Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
4 4 Ιδιότητες της ισότητας τω µιγαδικώ Αακλαστική, δηλαδή κάθε µιγαδικός αριθµός είαι ίσος µε το εαυτό του ( = ) Συµµετρική, δηλαδή α ο µιγαδικός αριθµός ισούται µε το µιγαδικό αριθµό, τότε και ο είαι ίσος µε το Άρα ( = = ) Μεταβατική, δηλαδή α ο µιγαδικός είαι ίσος µε το µιγαδικό και ο είαι = ίσος µε το 3, τότε και ο είαι ίσος µε το µιγαδικό 3 Άρα και = 3 = 3 Παρατηρήσεις α = 0 Επειδή 0= 0+ 0i ισχύει ότι a+ βi= 0 και β = 0 Απόδειξη ( ) a βi α βi α βi α β α β + = 0 = = + = 0 = = 0 Το ατίστροφο είαι προφαές Μέτρο µιγαδικού αριθµού Μέτρο ή απόλυτη τιµή εός µιγαδικού αριθµού a βi οοµάζεται ο µη αρητικός αριθµός α β = + ( α, β R ) = +, ο οποίος είαι η απόσταση από τη αρχή τω αξόω της εικόας του, δηλαδή του σηµείου Μ Εκ του ορισµού προκύπτου ότι: = 0 = 0 Το µέτρο εός πραγµατικού αριθµού είαι η απόλυτη τιµή του Α = 5 = 5 Α = 4 = 4 Το µέτρο εός φαταστικού αριθµού ai, µε a R είαι a Α i = 5 = 5 Α = 4i = 4 Ισχύει = r> 0 α και µόο α η εικόα του, δηλαδή το σηµείο Μ αήκει στο κύκλο x + y = r Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
5 5 Η σχέση = ισχύει µόο για τους πραγµατικούς αριθµούς λ R και C λ = λ, C = C και N = * C, C ισχύει ότι = * C ισχύει ότι =, δηλαδή = C ισχύει ότι Είαι = = Παρατηρήσεις Απόδειξη Έστω = a+ βi, µε α, β R Εξ ορισµού είαι Επίσης είαι = a βi, άρα = a + β β = ( a) + ( ) = a + = ύο ατίθετοι µιγαδικοί αριθµοί απεικοίζοται σε σηµεία µε ατίθετες συτεταγµέες, άρα σε σηµεία συµµετρικά ως προς τη αρχή τω αξόω δηλαδή το Ο 0, 0 σηµείο ( ) β Συζυγείς µιγαδικοί αριθµοί Ιδιότητες τους Οοµάζεται συζυγής του µιγαδικού αριθµού = a+ βi και συµβολίζεται ως, ο µιγαδικός a βi ηλαδή α+ βi= α βi ύο συζυγείς µιγαδικοί απεικοίζοται σε σηµεία µε τη ίδια τετµηµέη και ατίθετες τεταγµέες, άρα σε σηµεία συµµετρικά ως προς το άξοα xx Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
6 6 Παράδειγµα 3+ 4i 3 4i 3+ 4i 3 4i 3 4i 3+ 4i 3 4i 3+ 4i Από το ορισµό προκύπτει ότι ( ) οοµάζοται συζυγείς Είαι + = α, = βi, = συεπώς, οι µιγαδικοί αριθµοί και α β = + Απόδειξη = α+ βi και + = α + β + α β = α = α βi Πράγµατι, α ( i) ( i) = α+ βi και = α + βi α βi = βi = α βi Επίσης, α ( ) ( ) Είαι = ( α+ βi) ( α βi) = α αβi αβi β i = α β i = α + β + Παρατηρήσεις Το άθροισµα και το γιόµεο δύο συζυγώ µιγαδικώ αριθµώ είαι πραγµατικός αριθµός Τα ατίστροφα τω προτάσεω αυτώ δε ισχύου = 3+ 4i Πράγµατι α και + = 8 R, αλλά = 5 4i Επίσης α = 3i και = 3i 4i = i = = 4i R, αλλά Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
7 7 Α R = Απόδειξη Α R τότε είαι = α+ βi= α+ 0i= α και = α Άρα = Α = τότε α+ βi= α βi βi= βi β = β β = 0 β = 0 Άρα = α+ βi= α+ 0i= α 3 Α I = όπου I το σύολο τω φαταστικώ αριθµώ Απόδειξη Α I, τότε α βi 0 βi βi = βi= β i = = + = + = Επίσης ( ) Α =, τότε + = 0 ( α+ βi) + ( α βi) = 0 α = 0 α = 0 Άρα = βi δηλαδή I 4 C ισχύει ότι = = Έστω = a+ βi, τότε = a + β Απόδειξη Επίσης = α βiκαι a a = = + ( β ) = + β Άρα Επίσης = α+ βiκαι = ( a) + β = a + β = 5 C ισχύει ότι = Απόδειξη Έστω = a+ βi, µε α, β R Εξ ορισµού είαι = a + β, άρα = a + β Επίσης είαι Συεπώς = α βi και = ( α+ βi)( α βi) = α + β = 6 C µε = a+ βi, όπου α, β R ισχύει ότι ( ) = 7 Α = α+ βi και = α+ βi τότε + = + ηλαδή ο συζυγής του αθροίσµατος δυο µιγαδικώ αριθµώ, ισούται µε το άθροισµα τω συζυγώ τους Απόδειξη + = ( a + a ) + ( β + β ) i = ( a + a ) ( β + β ) i= ( α β i) + ( α β i) = + 8 Επαγωγικά αποδεικύεται ότι για ισχύει ότι = Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
8 8 9, C ισχύει ότι = ηλαδή ο συζυγής της διαφοράς δυο µιγαδικώ αριθµώ ισούται µε τη διαφορά τω συζυγώ τους 0, C ισχύει ότι = ηλαδή ο συζυγής του γιοµέου δυο µιγαδικώ αριθµώ, ισούται µε το γιόµεο τω συζυγώ τους Επαγωγικά αποδεικύεται ότι για ισχύει ότι = : * C, C ισχύει ότι µιγαδικώ αριθµώ, ισούται µε το πηλίκο τω συζυγώ τους = ηλαδή ο συζυγής του πηλίκου δυο 3 Από τη αωτέρω ιδιότητα για = και για = 0προκύπτει ότι = ηλαδή, ο συζυγής που έχει ο ατίστροφος εός µιγαδικού αριθµού, ισούται µε το ατίστροφο του συζυγούς του 4 C και * N ισχύει ότι ( ) ( ) = Πρόσθεση µιγαδικώ αριθµώ Έστω α+ βiκαι γ + δi, δύο µιγαδικοί αριθµοί Η πρόσθεση τους ορίζεται ως ( α+ βi) + ( γ + δi) = ( α+ γ ) + ( β+ δ ) i ηλαδή εκτελούµε πρόσθεση τω πραγµατικώ και τω φαταστικώ µερώ, ατίστοιχα Παράδειγµα (+ i) + (3+ 7 i) = 4+ 9i Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Έστω ότι η εικόα του µιγαδικού α+ βi στο επίπεδο, είαι το σηµείο ( α β) ( γ ) Μ και ότι η εικόα του µιγαδικού γ + δi στο επίπεδο είαι το σηµείο, Μ, δ Τότε εικόα του αθροίσµατος τους ( α+ βi) + ( γ + δi) = ( α+ γ ) + ( β+ δ ) i στο επίπεδο, είαι το σηµείο ( α γ, β δ) Μ + + Η διαυσµατική ακτία του αθροίσµατος τω µιγαδικώ a+ βi και γ + δi είαι το άθροισµα τω διαυσµατικώ ακτίω τους ηλαδή OM = OM+ OM Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
9 9 Ιδιότητες της προσθέσεως µιγαδικώ αριθµώ Ατιµεταθετική, Cισχύει ότι + = + Προσεταιριστική,, 3 ισχύει ότι C ( ) ( ) + + = Ουδέτερο στοιχείο C, υπάρχει C, έτσι ώστε α ισχύει + = + = Το είαι το µηδεικό στοιχείο της προσθέσεως και έχει τη µορφή 0+ 0i Αποδεικύεται ότι το µηδεικό στοιχείο της προσθέσεως είαι µοαδικό Συµµετρικό (ατίθετο) στοιχείο Cυπάρχει C, έτσι ώστε α ισχύει + = + = 0 Τo είαι o ατίθετος του µιγαδικού Αποδεικύεται ότι κάθε µιγαδικός αριθµός έχει έα και µόο έα ατίθετο Ιδιότητα της διαγραφής,, C ισχύει ότι α = τότε + = + είξτε ότι α η εξίσωση συτελεστές ( α, α,, α, α ) 0 α x + α x + + α x+ α = 0 µε πραγµατικούς 0 R και α 0 έχει ρίζα το µιγαδικό αριθµό, τότε έχει ρίζα και το Πράγµατι, αφού ο είαι ρίζα της εξισώσεως, ισχύει ότι: α + α + + α + α = 0 α + α + + α + α = α + α + + α + α = 0 α + α + + α + α = ( ) ( ) α + α + + α + α = 0 Άρα ο µιγαδικός είαι ρίζα της εξισώσεως 0 Αφαίρεση µιγαδικώ αριθµώ Έστω a+ βi και γ + δi, δύο µιγαδικοί αριθµοί Για τη αφαίρεση του γ + δi από το a+ βi εκτελούµε πρόσθεση του a+ βi µε το γ δi, ο οποίος είαι ο ατίθετος του γ + δi και ( α+ βi) ( γ + δi) = ( α+ βi) + ( γ δi) = ( α γ ) + ( β δ ) i ηλαδή εκτελούµε αφαίρεση τω πραγµατικώ και τω φαταστικώ µερώ, ατίστοιχα Παράδειγµα (+ i) (3+ 7 i) = (+ i) + ( 3 7 i) = ( 3) + ( 7) i= 5i Γεωµετρική παράσταση της διαφοράς µιγαδικώ Έστω ότι η εικόα του µιγαδικού a+ βi στο επίπεδο είαι το σηµείο ( α, β) ( γ, δ) ( α γ, β δ) Μ και ότι η εικόα του µιγαδικού γ + δi στο επίπεδο είαι το σηµείο Μ Τότε εικόα της διαφοράς τους στο επίπεδο είαι το σηµείο Ν Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
10 0 Η διαυσµατική ακτία της διαφοράς τω µιγαδικώ a+ βi και γ + δi είαι η διαφορά τω διαυσµατικώ ακτίω τους ηλαδήoν= OM OM Από τη τριγωική αισότητα και τη γεωµετρική ερµηεία του αθροίσµατος + και της διαφοράς δύο µιγαδικώ αριθµώ, προκύπτει ότι + + Α ατικαταστήσοµε το µε το η αωτέρω σχέση γίεται + Επαγωγικά αποδεικύεται ότι Πολλαπλασιασµός µιγαδικώ αριθµώ Για το πολλαπλασιασµό τω µιγαδικώ α+ βi και γ + δi έχοµε ( α βi) ( γ δi) α ( γ δi) βi ( γ δi) + + = ( ) + ( + ) + + = = αγ αδi βγ i βδ αγ βδ αδ βγ i Παράδειγµα (+ i) (3+ 7 i) = (3+ 7 i) + i (3+ 7 i) = 3+ 7i+ 6i 4= + 3i Ιδιότητες του πολλαπλασιασµού τω µιγαδικώ αριθµώ Ατιµεταθετική, C ισχύει ότι = Προσεταιριστική,, ισχύει ότι ( ) = ( ) C Ουδέτερο στοιχείο C, υπάρχει C έτσι ώστε α ισχύει = = Το είαι το ουδέτερο στοιχείο του πολλαπλασιασµού και έχει τη µορφή + 0i Αποδεικύεται ότι το ουδέτερο στοιχείο του πολλαπλασιασµού είαι µοαδικό * * Συµµετρικό (ατίστροφο) στοιχείο C, C : = = Τo είαι o ατίστροφος του µιγαδικού αριθµού Αποδεικύεται ότι κάθε µιγαδικός αριθµός έχει έα και µόο έα ατίστροφο Ιδιότητα της διαγραφής,, C ισχύει ότι α = τότε = Επιµεριστική ιδιότητα,, 3 C ισχύει ότι ( + 3) = + 3 Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
11 Α = α+ βi και = α+ βi τότε = Απόδειξη =( a + β i) ( a + β i) = ( αα β β ) + ( α β + α β ) i ( αα ββ ) ( α β α β ) = + + i ( α β i) ( α β i) ( α β i) ( α β i) = αα ββ + α β α β = + + = ( ) ( ) Άρα = i Α 0τότε = Απόδειξη Θέτοµε = = = = = Άρα = Α στη αωτέρω σχέση θέσοµε = και = 0 τότε έχοµε ηλαδή ( ) ( ) = = Επαγωγικά αποδεικύεται για κάθε ότι: = και = Α στη τελευταία ισότητα θέσοµε = = = έχοµε ( ) ( ) = Πηλίκο µιγαδικώ αριθµώ α+ βi Προκειµέου α ορίζεται το πηλίκο τω µιγαδικώ α+ βi και γ + δi, γ + δi πρέπει γ + δi 0 Για τη απαλοιφή, από το παροοµαστή, του κλάσµατος της φαταστικής µοάδος, πολλαπλασιάζοµε αριθµητή και παροοµαστή µε τη συζυγή παράσταση του παροοµαστή α+ βi ( α+ βi) ( γ δi) ( αγ + βδ ) + ( βγ αδ ) i Έτσι έχοµε = = γ + δi ( γ + δi) ( γ δi) γ + δ Στέφαος Ι Καραβάς, Μαθηµατικός (ΜΕd), Επίκουρος Καθηγητής ΑΕΝ Οιουσσώ
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικών αριθµών. Μιγαδικό επίπεδο. Γεωµετρική παράσταση του αθροίσµατος µιγαδικών αριθµών.
 Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Ορισµοί, ισότητα, µέτρο, άθροισµα µιγαδικώ αριθµώ Μιγαδικό επίπεδο Γεωµετρική παράσταση του αθροίσµατος µιγαδικώ αριθµώ Η προσπάθεια επιλύσεως εξισώσεω 3 ου βαθµού ( ax 3 βx γx δ 0) πραγµατικούς συτελεστές
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Θεωρία - Μέθοδοι
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχολογική Κατεύθυση Θεωρία - Μέθοδοι ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Μάθημα ο ΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ Η εξίσωση x δε έχει λύση στο σύολο τω πραγματικώ αριθμώ, αφού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεων
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Θεωρία Άλυτες Ασκήσεις Θέματα εξετάσεω 1 Α. ΜΕΡΟΣ :ΘΕΩΡΙΑ ΤΟ ΣΥΝΟΛΟ C ΤΩΝ ΜΙΓΑΔΙΚΩΝ Γωρίζουμε ότι η δευτεροβάθμια εξίσωση με αρητική διακρίουσα δε έχει λύση στο σύολο R τω πραγματικώ
1. Το σύνολο των μιγαδικών αριθμών
 Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
Το σύολο τω μιγαδικώ αριθμώ Γωρίζουμε ότι η εξίσωση δε έχει λύση στο σύολο τω πραγματικώ αριθμώ Για α ξεπεράσουμε αυτή τη αδυαμία «μεγαλώσαμε» το σύολο και δημιουργήσαμε το σύολο, έτσι, ώστε α έχει τις
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ. 1. Τι ονομάζουμε σύνολο Μιγαδικών Αριθμών; Τι ονομάζουμε πραγματικό μέρος - φανταστικό μέρος ενός μιγαδικού αριθμού z = α + βi.
 ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
ΘΕΩΡΙΑ ΜΙΓΑΔΙΚΩΝ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. Τι οομάζουμε σύολο Μιγαδικώ Αριθμώ; Τι οομάζουμε πραγματικό μέρος - φαταστικό μέρος εός μιγαδικού αριθμού α + βi. Σύολο τω μιγαδικώ αριθμώ οομάζουμε έα υπερσύολο τω
2.2 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ R ΤΩΝ ΜΙΓΑΔΙΚΩΝ Σύμφωα με το ορισμό του R, η πρόσθεση και ο πολλαπλασιασμός δύο μιγαδικώ αριθμώ γίοται όπως ακριβώς και οι ατίστοιχες πράξεις με διώυμα α + βx στο, όπου βέβαια ατί για
ΜΑΘΗΜΑ Η έννοια του µιγαδικού αριθµού Πράξεις
 ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
ΜΑΘΗΜΑ.. Η έοια του µιγαδικού αριθµού Πράξεις Θεωρία - Σχόλια - Μέθοδοι - Ασκήσεις α + βi - i α + βi i (β - αi ) ΘΕΩΡΙΑ. Ύπαρξη του i εχόµαστε ότι υπάρχει αριθµός i, µε τη ιδιότητα φαταστική µοάδα. i,
στους μιγαδικούς αριθμούς
 Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
Πράξεις στους μιγαδικούς αριθμούς Πρόσθεση μιγαδικώ αριθμώ Βασικές ασκήσεις Βασική θεωρία α) ) Πώς γίεται η πρόσθεση δύο μιγαδικώ αριθμώ; ) Ποια είαι η γεωμετρική ερμηεία του αθροίσματος δύο μιγαδικώ;
+ + = + + α ( β γ) ( )
 ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ Αριθµητική παράσταση Αριθµητική παράσταση λέγεται µια σειρά αριθµώ που συδέοται µεταξύ τους µε πράξεις. Η σειρά τω πράξεω σε µια αριθµητική παράσταση είαι η εξής: 1. Υπολογίζουµε
ΤΥΠΟΛΟΓΙΟ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ Αριθµητική παράσταση Αριθµητική παράσταση λέγεται µια σειρά αριθµώ που συδέοται µεταξύ τους µε πράξεις. Η σειρά τω πράξεω σε µια αριθµητική παράσταση είαι η εξής: 1. Υπολογίζουµε
ΑΛΓΕΒΡΑ. Για να βρούµε την δύναµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωνα µε την ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ
 ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ ο ΜΙΓΑΔΙΚΟΙ - ΜΕΘΟΔΟΛΟΓΙΑ κ Για α βρούµε τη δύαµη i (όπου κ ακέραιος), διαιρούµε το κ µε το 4 και σύµφωα µε τη ταυτότητα της διαίρεσης ισχύει κ=4ρ+υ όπου ρ Ζ και υ = 0,,, οπότε i κ 4ρ+
ΣΗΜΕΙΩΣΕΙΣ. Η έννοια του μιγαδικού Το σύνολο των μιγαδικών. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
Ι δ ι ο τ η τ ε ς Π ρ ο σ θ ε σ η ς - Π ο λ λ α π λ α σ ι α σ μ ο υ ΙΔΙΟΤΗΤΑ ΠΡΟΣΘΕΣΗ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ
 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1 Π ρ α γ μ α τ ι κ ο ι Α ρ ι θ μ ο ι : Υ π ο σ υ ο λ α του Το συολο τω φυσικω 3. αριθμω: Να δειχτει οτι = α {0,1,,3, } + 110 0α. Ποτε ισχυει το ισο; Το συολο τω. A ακεραιω α, β θετικοι
Λύση. Λύση Άσκηση 3. Λύση. ( Α Α Α Ι ) Α. Α Α=Ιν. Άσκηση 4. επαληθεύει τη σχέση Χ. Λύση.
 Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Άσκηση Α A, B ατιστρέψιµοι πίακες µε AB= A, BA= B είξτε ότι A = A, B = B ος τρόπος Α = Α Α=( Α Β) Α= Α Β Α Α = Α Οµοίως Α= Α Β= Α ( Β Α)= Α Β Α B = B ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως
Α. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ
 ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΑΘΗΜΑ Κεφάλαιο o : Αλγεβρικές Παραστάσεις Υποεότητα.: Πράξεις µε πραγµατικούς αριθµούς (Επααλήψεις- Συµπληρώσεις) Θεµατικές Εότητες:. Οι πραγµατικοί αριθµοί και οι πράξεις τους.. υάµεις πραγµατικώ αριθµώ..
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΜΕΘΟΔΟΛΟΓΙΑ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΟΡΙΣΜΟΙ ΠΡΑΞΕΙΣ ΣΥΖΥΓΕΙΣ ΜΕΤΡΟ ΜΕΘΟΔΟΛΟΓΙΑ ΜΕΘΟΔΟΣ Για α υπολογίσουμε δυάμεις με ακέραιο εκθέτη σε παράσταση με i χρησιμοποιούμε γωστές ταυτότητες και έχουμε υπόψη ότι: i. v v- = με ακέραιο
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΟΡΙΣΜΟΙ ΠΡΑΞΕΙΣ ΣΥΖΥΓΕΙΣ ΜΕΤΡΟ ΜΕΘΟΔΟΛΟΓΙΑ ΜΕΘΟΔΟΣ Για α υπολογίσουμε δυάμεις με ακέραιο εκθέτη σε παράσταση με i χρησιμοποιούμε γωστές ταυτότητες και έχουμε υπόψη ότι: i. v v- = με ακέραιο
z = =5 ενώ z 1 z 2. (µε απόδειξη) z = z z I. z = z. z 1 z z όπου z 1 =x 1 +y 1 i και z 2 =x 2 +y 2 i σταθεροί z παριστάνει υπερβολή µε z 2
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ. Εά τότε δε ισχύει πάτα. Πχ για τους µιγαδικούς +4i και 5i είαι 5 εώ.. 0 0. Για α αποδείξουµε ότι R µε τη βοήθεια του µέτρου αρκεί α αποδείξουµε ότι (µε απόδειξη. ηλαδή R. 4. Για
ΛΥΚΕΙΟ ΜΕΤΑΜΟΡΦΩΣΗΣ 2014 ΒΑΣΙΚΗ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
1. Τι λέγεται δειγματικός χώρος εός πειράματος τύχης. Το σύολο τω δυατώ αποτελεσμάτω λέγεται δειγματικός χώρος (sample space) και συμολίζεται συήθως με το γράμμα Ω. Α δηλαδή ω 1,ω 2,...,ω κ είαι τα δυατά
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρεθεί ο γεωμετρικός τόπος των εικόνων των μιγαδικών z για τους οποίους ισχύει:
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΣΗΜΕΙΩΣΕΙΣ. Από προηγούμενες τάξεις γνωρίζουμε ότι το τετράγωνο οποιουδήποτε πραγματικού αριθμού
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i ΙΔΙΟΤΗΤΕΣ
ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ. όπου ν θετικός ακέραιος κ) z = 2 ( 3i 2. > να δείξετε ότι Re( )
 ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Ασκήσεις στο ορισμό και τις ιδιότητες 0) Να βρείτε το μέτρο τω μιγαδικώ αριθμώ α) 3i = ε) ( ) 5 β) = 7 στ) γ) = 4 3i ζ) δ) = 4+ 3i η) = = i θ) 3 = + i 3 = i ( α βi)
ΑΣΚΗΣΕΙΣ ΣΤΟ ΜΕΤΡΟ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Ασκήσεις στο ορισμό και τις ιδιότητες 0) Να βρείτε το μέτρο τω μιγαδικώ αριθμώ α) 3i = ε) ( ) 5 β) = 7 στ) γ) = 4 3i ζ) δ) = 4+ 3i η) = = i θ) 3 = + i 3 = i ( α βi)
Δυνάμεις πραγματικών αριθμών
 Κεφάλαιο 1 ο 45 Β. Δυάμεις πραγματικώ αριθμώ Α έχουμε έα γιόμεο της μορφής (-) (-) (-) (-) όπου κάθε παράγοτας είαι (δηλαδή ο ίδιος ο αριθμός) μπορούμε α το συμβολίσουμε με μια πιο απλή μορφή : (-) 4.
Κεφάλαιο 1 ο 45 Β. Δυάμεις πραγματικώ αριθμώ Α έχουμε έα γιόμεο της μορφής (-) (-) (-) (-) όπου κάθε παράγοτας είαι (δηλαδή ο ίδιος ο αριθμός) μπορούμε α το συμβολίσουμε με μια πιο απλή μορφή : (-) 4.
ΜΑΘΗΜΑ 9 Γενικές ασκήσεις µιγαδικών
 ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
ΜΑΘΗΜΑ 9 Γεικές ασκήσεις µιγαδικώ. Για το µιγαδικό δίεται ότι. Να βρείτε i) το ii) το σύολο τιµώ του i. i) ( )( ) [ ] Άρα ( )( ) ( )( ) 0 0 0 0 () (). 0 ii) i i ( ) ( i) i ( ) ( i) ( ) i () i ( ) ( i)
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ = Γ. β1 = β2
 Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
Α. ΕΞΙΣΩΣΕΙΣ ΣΥΣΤΗΜΑΤΑ ΕΙΔΗ ΕΞΙΣΩΣΗΣ ( ΔΙΕΡΕΥΝΗΣΗ ΕΞΙΣΩΣΗΣ): i. αχ=β µε α 0 έχει µία λύση ii. 0χ=β µε β 0 αδύατη εξίσωση ( καµία λύση ) iii. 0χ=0 αόριστη εξίσωση ( άπειρες λύσεις ) ΕΙΔΗ ΣΥΣΤΗΜΑΤΟΣ (ΔΙΕΡΕΥΝΗΣΗ
ν ν Άσκηση 1. Α =Α, Β =Β. Λύση Άσκηση Α Β =Β Α, Α Β=ΒΑ. Β Α= ( Β Β)( ΑΒ ) Β Α=Ι( ΑΒ ) Β Α=ΑΒ. Άσκηση = Α Α Α Α=.
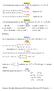 Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
Άσκηση Α, Β ατιστρέψιµοι πίακες µε ΑΒ=Α, ΒΑ=Β είξτε ότι ος τρόπος Α = Α Α = ( Α Β) Α = Α Β Α Α = Α Οµοίως Α = Α Β = Α ( Β Α) = Α Β Α ος τρόπος Α =Α Α= ( Α Β) Α=Α ( Β Α ) =Α Β=Α Οµοίως Α =Α, Β =Β Β =Β Β
0..1 ΒΑΣΙΚΕΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΝΝΟΙΕΣ
 Εισαγωγικό Κεφάλαιο: Ρητοί Αριθµοί ΜΑΘΗΜΑ 0 Υποεότητα 1: Βασικές Επααληπτικές Έοιες (Επααλήψεις-Συµπληρώσεις) Θεµατικές Εότητες: 1. Ρητοί αριθµοί-βασικές επααληπτικές έοιες.. Πρόσθεση ρητώ αριθµώ. 3. Άθροισµα
Εισαγωγικό Κεφάλαιο: Ρητοί Αριθµοί ΜΑΘΗΜΑ 0 Υποεότητα 1: Βασικές Επααληπτικές Έοιες (Επααλήψεις-Συµπληρώσεις) Θεµατικές Εότητες: 1. Ρητοί αριθµοί-βασικές επααληπτικές έοιες.. Πρόσθεση ρητώ αριθµώ. 3. Άθροισµα
5.4 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ
 5 54 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αριθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβρικό λογισμό Για αράδειγμα, η αράσταση
5 54 ΤΡΙΓΩΝΟΜΕΤΡΙΚΗ ΜΟΡΦΗ ΜΙΓΑΔΙΚΟΥ Εισαγωγή Η αοδοχή τω μιγαδικώ αριθμώ, εκτός αό τις δυατότητες ου άοιξε στη είλυση τω εξισώσεω, έδωσε μεγάλη ευελιξία στο αλγεβρικό λογισμό Για αράδειγμα, η αράσταση
5.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C
 5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
5 55 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ C Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού λογισμού
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος
 Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
Ακολουθίες Αριθµητική Γεωµετρική Πρόοδος Μία συάρτηση α µε πεδίο ορισµού το Ν * λέγεται ακολουθία και συµβολίζεται µε (α ) δηλ. a : N * R : α = α( ) Ο α 1 λέγεται πρώτος όρος της ακολουθίας, ο α δεύτερος
1. [0,+ , >0, ) 2. , >0, x ( )
 Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
Σελίδα 1 από 5 ΝΙΟΣΤΕΣ ΡΙΖΕΣ ΤΑ ΣΥΜΒΟΛΑ α, α ΣΧΕΤΙΚΑ ΘΕΜΑΤΑ του Ατώη Κυριακόπουλου 1 ΡΙΖΕΣ ΣΤΟ ΣΥΝΟΛΟ R = [, ) Θεώρηµα και ορισµός οθέτος, εός πραγµατικού αριθµού α και εός φυσικού αριθµού >, υπάρχει έας
(Καταληκτική ημερομηνία αποστολής 15/11/2005)
 η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
η Εργασία 005-006 (Καταληκτική ημερομηία αποστολής 5//005) Άσκηση (0 μοάδες). (α) Δείξτε αλγεβρικά πώς βρίσκοται δύο διαύσματα A και B, εά είαι γωστά το άθροισμά τους S και η διαφορά τους D (β) Βρείτε
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να γωρίζει τη έοια της ακολουθίας, τους τρόπους που ορίζεται, τις διαφορές της από μία συάρτηση. Να γωρίζει τους ορισμούς της αριθμητικής και γεωμετρικής
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει: Να γωρίζει τη έοια της ακολουθίας, τους τρόπους που ορίζεται, τις διαφορές της από μία συάρτηση. Να γωρίζει τους ορισμούς της αριθμητικής και γεωμετρικής
Η παραπάνω ιδιότητα γενικεύεται και για περισσότερους από δύο πραγµατικούς αριθµούς. Έτσι έχουµε: αβγ α β γ = β β. d a β = α
 ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΑΜΥΡΑ ΑΚΗ 0, ΝΙΚΑΙΑ ΤΗΛ:0-903576 e-mail : tetrakti@ otenet.gr γρήγορα&εύκολα www.tetraktis.gr ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙ ΕΥΣΗΣ ΜΑΘ Α0 ΑΠΟΛΥΤΗ ΤΙΜΗ Τυπολόγιο - Μεθοδολογία. Ορισµός: Έστω α έας πραγµατικός
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΗΜΑΤΑ ΠΡΟΤΑΣΕΙΣ µε ΑΠΟ ΕΙΞΕΙΣ ΘΕΩΡΙΑ ΕΡΩΤΗΣΕΙΣ µε ΑΠΑΝΤΗΣΕΙΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΤΟΥ ΣΧΟΛΙΚΟΥ ΒΙΒΛΙΟΥ ΚΑΤΕΥΘΥΝΣΗΣ ΚΑΙ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Αιστάι 3 Αµφιάλη 4389-43
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει α είαι σε θέση: 1 Να μπορεί α βρίσκει απο τη γραφική παράσταση μιας συάρτησης το πεδίο ορισμού της το σύολο τιμώ της τη τιμή της σε έα σημείο x 2
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει α είαι σε θέση: 1 Να μπορεί α βρίσκει απο τη γραφική παράσταση μιας συάρτησης το πεδίο ορισμού της το σύολο τιμώ της τη τιμή της σε έα σημείο x 2
(πολλδ β) = πολλδ + ( 1) ν β ΕΥΣΤΡΑΤΙΟΣ ΚΩΣΤΗΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΘΟ ΙΚΟ ΙΑΙΡΕΤΟΤΗΤΑ
 ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΙΑΙΡΕΤΟΤΗΤΑ Ορισµός: Λέµε ότι ο ακέραιος β 0διαιρεί το ακέραιο α και γράφουµε β/α, ότα η διαίρεση του α µε το β είαι τέλεια, δηλαδή υπάρχει κ Z τέτοιος ώστε α = κ β. Συµβολίζουµε ότι α = πολβ. Α ο β δε
ΑΛΓΕΒΡΑ Α' ΛΥΚΕΙΟΥ. Η ΕΞΙΣΩΣΗ αx+β=0
 Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
Η ΕΞΙΣΩΣΗ α+β=0 εξισώσεις πρώτου βαθμού. Να λύσετε τις παρακάτω εξισώσεις: α) 5 ( ) = ( ) β) 8( ) ( ) = ( + ) 5(5 ) γ) (5 ) ( ) = ( + ) δ) (-)-(-)=7( -)-(+). Να λύσετε τις παρακάτω εξισώσεις: 5 α) β) 8
Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης Γ Λυκείου Η ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ
 Η ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Το Σύνολο C των Μιγαδικών Αριθμών Είναι γνωστό ότι η εξίσωση x δεν έχει λύση στο σύνολο IR των πραγματικών αριθμών, αφού το τετράγωνο κάθε πραγματικού αριθμού είναι μη αρνητικός
Η ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Το Σύνολο C των Μιγαδικών Αριθμών Είναι γνωστό ότι η εξίσωση x δεν έχει λύση στο σύνολο IR των πραγματικών αριθμών, αφού το τετράγωνο κάθε πραγματικού αριθμού είναι μη αρνητικός
Ε 1. Διαφορικός λογισμός (Κανόνες παραγώγισης)
 Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
Ε Διαφορικός λογισμός Καόες παραγώγισης Σελίδα από Πότε μια συάρτηση λέγεται παραγωγίσιμη στο σημείο του πεδίου ορισμού της ; Μια συάρτηση λέμε ότι είαι παραγωγίσιμη σ έα σημείο του πεδίου ορισμού της,
Μαθηματικά κατεύθυνσης Γ Λυκείου. Όλη η θεωρία και οι ασκήσεις των πανελλαδικών εξετάσεων. Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς
 Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Μαθηματικά κατεύθυσης Γ Λυκείου Όλη η θεωρία και οι ασκήσεις τω παελλαδικώ εξετάσεω Στέλιος Μιχαήλογλου Δημήτρης Πατσιμάς wwwaskisopolisgr Η θεωρία τω παελλαδικώ εξετάσεω [] [] Ορισμοί ) Πότε μια συάρτηση
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει να είναι σε θέση: Να γνωρίζει: α. την έννοια του μιγαδικού αριθμού και β. πότε δύο μιγαδικοί αριθμοί είναι ίσοι. Να μπορεί να βρίσκει: α. το άθροισμα,
Ο μαθητής που έχει μελετήσει το κεφάλαιο αυτό θα πρέπει να είναι σε θέση: Να γνωρίζει: α. την έννοια του μιγαδικού αριθμού και β. πότε δύο μιγαδικοί αριθμοί είναι ίσοι. Να μπορεί να βρίσκει: α. το άθροισμα,
2.5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ 5 5 ΠΟΛΥΩΝΥΜΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΣΤΟ R Εισαγωγή Η επίλυση τω εξισώσεω ου και 4ου βαθμού, η ααγκαστική επαφή με τους μιγαδικούς αριθμούς για τη έκφραση τω πραγματικώ ριζώ και η εξέλιξη του αλγεβρικού
5.3 ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ
 5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
5. ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟ ΟΣ ΘΕΩΡΙΑ. Ορισµός Μια ακολουθία λέγεται γεωµετρική πρόοδος, α και µόο α κάθε όρος της προκύπτει από το προηγούµεό του µε πολλαπλασιασµό επί το ίδιο πάτοτε µη µηδεικό αριθµό.. Μαθηµατική
Copyright: Ξένος Θ., Eκδόσεις Zήτη, Μάρτιος 2008, Θεσσαλονίκη
 Kάθε γήσιο ατίτυο φέρει τη υογραφή του συγγραφέα Με το συγγραφέα εικοιωείτε: Tηλ. 310.348.086, e-mail: thanasisenos@ahoo.gr ISBN 978-960-456-09-9 Copright: Ξέος Θ., Eκδόσεις Zήτη, Μάρτιος 008, Θεσσαλοίκη
Kάθε γήσιο ατίτυο φέρει τη υογραφή του συγγραφέα Με το συγγραφέα εικοιωείτε: Tηλ. 310.348.086, e-mail: thanasisenos@ahoo.gr ISBN 978-960-456-09-9 Copright: Ξέος Θ., Eκδόσεις Zήτη, Μάρτιος 008, Θεσσαλοίκη
ΓΙΩΡΓΟΣ Α. ΚΑΡΕΚΛΙΔΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΩΡΙΑ ΑΣΚΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ
 ΓΙΩΡΓΟΣ Α. ΚΑΡΕΚΛΙΔΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΩΡΙΑ ΑΣΚΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ ΕΚΔΟΣΕΙΣ ΓΙΩΡΓΟΣ Α. ΚΑΡΕΚΛΙΔΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΩΡΙΑ ΑΣΚΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ τη ΘΕΩΡΙΑ με τις απαραίτητες διευκρινήσεις ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
ΓΙΩΡΓΟΣ Α. ΚΑΡΕΚΛΙΔΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΩΡΙΑ ΑΣΚΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ ΕΚΔΟΣΕΙΣ ΓΙΩΡΓΟΣ Α. ΚΑΡΕΚΛΙΔΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΩΡΙΑ ΑΣΚΗΣΕΙΣ ΜΕΘΟΔΟΛΟΓΙΑ τη ΘΕΩΡΙΑ με τις απαραίτητες διευκρινήσεις ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ
Τι είναι εκτός ύλης. Σχολικό έτος
 Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Τι είαι εκτός ύλης. Σχολικό έτος 06-07 ΠΕΡΙΕΧΟΜΕΝΑ ΕΙΣΑΓΩΓΙΚΟ ΚΕΦΑΛΑΙΟ Ε. Το Λεξιλόγιο της Λογικής...9 Ε. Σύολα...3 ΚΕΦΑΛΑΙΟ o: Πιθαότητες. Δειγματικός Χώρος - Εδεχόμεα...0. Έοια της Πιθαότητας...9 ΚΕΦΑΛΑΙΟ
Παρατηρήσεις 1 Για α ααζητήσουµε το όριο της f στο, πρέπει η f α ορίζεται όσο θέλουµε κοτά στο, δηλαδή η f α είαι ορισµέη σ έα σύολο της µορφής ( α, )
 Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
Η έοια του ορίου Όριο συάρτησης Ότα οι τιµές µιας συάρτησης f προσεγγίζου όσο θέλουµε έα πραγµατικό αριθµό l, καθώς το προσεγγίζει µε οποιοδήποτε τρόπο το αριθµό, τότε γράφουµε lim f() = l και διαβάζουµε
Γυμνάσιο Μαθηματικά Τάξη B
 113 Θέματα εξετάσεω περιόδου Μαΐου-Ιουίου στα Μαθηματικά Τάξη B! 114 a. Να διατυπώσετε το ορισμό της δύαμης α με βάση το ρητό α και εκθέτη το φυσικό αριθμό > 1. b. Να συμπληρωθού οι παρακάτω τύποι, δυάμεις
113 Θέματα εξετάσεω περιόδου Μαΐου-Ιουίου στα Μαθηματικά Τάξη B! 114 a. Να διατυπώσετε το ορισμό της δύαμης α με βάση το ρητό α και εκθέτη το φυσικό αριθμό > 1. b. Να συμπληρωθού οι παρακάτω τύποι, δυάμεις
Θέµατα Μιγαδικών Αριθµών από τις Πανελλαδικές Εξετάσεις
 Θέµατα Μιγαδικών Αριθµών από τις Πανελλαδικές Εξετάσεις γιατί συχνά, οι ιδέες επαναλαµβάνονται ΕΠΙΜΕΛΕΙΑ: ΠΑΠΠΑΣ ΑΘΑΝΑΣΙΟΣ Ο ΓΕΝ ΛΥΚΕΙΟ ΥΜΗΤΤΟΥ Σελίδα από 8 Επιµέλεια: Παππάς Αθανάσιος/o ΓΕΛ ΥΜΗΤΤΟΥ 00
Θέµατα Μιγαδικών Αριθµών από τις Πανελλαδικές Εξετάσεις γιατί συχνά, οι ιδέες επαναλαµβάνονται ΕΠΙΜΕΛΕΙΑ: ΠΑΠΠΑΣ ΑΘΑΝΑΣΙΟΣ Ο ΓΕΝ ΛΥΚΕΙΟ ΥΜΗΤΤΟΥ Σελίδα από 8 Επιµέλεια: Παππάς Αθανάσιος/o ΓΕΛ ΥΜΗΤΤΟΥ 00
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ 22 ΜΑΪΟΥ 2003 ΕΚΦΩΝΗΣΕΙΣ
 ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
ΑΛΓΕΒΡΑ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Β ΤΑΞΗΣ ΠΕΜΠΤΗ ΜΑΪΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Α. Να αποδείξετε ότι ο ος όρος µιας αριθµητικής προόδου µε πρώτο όρο α 1 και διαφορά ω είαι α = α 1 + (-1)ω. Μοάδες 7 Β. Να γράψετε
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 77 ος ΠΑΝΕΛΛΗΝΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ Ο ΘΑΛΗΣ 12 Νοεμβρίου 2016 Β ΓΥΜΝΑΣΙΟΥ ˆ ΑΔΒ.
 Τηλ 361653-3617784 - Fax: 364105 Tel 361653-3617784 - Fax: 364105 1 Νοεμβρίου 016 Β ΓΥΜΝΑΣΙΟΥ Να υπολογίσετε τη τιμή της αριθμητικής παράστασης: ( ) ( 5) ( ) 3 3 3 0 15 8 3 Α= + + 3 5 3 9 Πρόβλημα Δίεται
Τηλ 361653-3617784 - Fax: 364105 Tel 361653-3617784 - Fax: 364105 1 Νοεμβρίου 016 Β ΓΥΜΝΑΣΙΟΥ Να υπολογίσετε τη τιμή της αριθμητικής παράστασης: ( ) ( 5) ( ) 3 3 3 0 15 8 3 Α= + + 3 5 3 9 Πρόβλημα Δίεται
Οι Μιγαδικοί Αριθμοί
 Οι Μιγαδικοί Αριθμοί Οι μιγαδικοί αριθμοί αρχικά βοήθησαν στην επίλυση δευτεροβάθμιων εξισώσεων των οποίων η διακρίνουσα είναι αρνητική Το γενικότερο πρόβλημα βέβαια είναι ότι δεν υπάρχει πραγματικός αριθμός
Οι Μιγαδικοί Αριθμοί Οι μιγαδικοί αριθμοί αρχικά βοήθησαν στην επίλυση δευτεροβάθμιων εξισώσεων των οποίων η διακρίνουσα είναι αρνητική Το γενικότερο πρόβλημα βέβαια είναι ότι δεν υπάρχει πραγματικός αριθμός
4.7 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ
 174 47 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ Το ζήτημα της διαιρετότητας τω αεραίω είαι υρίαρχο θέμα στη Θεωρία τω Αριθμώ Μια έοια που βοηθάει στη μελέτη αι επίλυση προβλημάτω διαιρετότητας είαι η έοια τω ισοϋπόλοιπω αριθμώ
174 47 ΙΣΟΫΠΟΛΟΙΠΟΙ ΑΡΙΘΜΟΙ Το ζήτημα της διαιρετότητας τω αεραίω είαι υρίαρχο θέμα στη Θεωρία τω Αριθμώ Μια έοια που βοηθάει στη μελέτη αι επίλυση προβλημάτω διαιρετότητας είαι η έοια τω ισοϋπόλοιπω αριθμώ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ 9o ΓΕΛ ΠΕΡΙΣΤΕΡΙΟΥ είναι τέλεια, να υπολογίσετε την τιμή της παράστασης: Α = (1 + i) v - (1 - i) v. 15. Αν z μιγαδικός και f (ν) = i
 Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
Να βρεθού οι πραγματικοί αριθμοί κ,λ για τους οποίους οι μιγαδικοί = 4 κ + λ + 7 κ και w = 7 (λ ) α είαι ίσοι Να βρεθού οι κ, λr ώστε ο = (8κ + κ) + 4λ + ( ) α είαι ίσος με το μηδέ Να βρείτε για ποιες
ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]
![ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β] ΣΗΜΕΙΩΣΕΙΣ ΘΕΩΡΗΜΑ BOLZANO. και επιπλέον. Αν μία συνάρτηση f είναι ορισμένη σε ένα κλειστό διάστημα [α,β] η f είναι συνεχής στο [α,β]](/thumbs/20/426829.jpg) ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
R={α/ αρητός ή άρρητος αριθμός }
 o ΛΥΚΕΙΟ ΠΕΤΡΟΥΠΟΛΗΣ Οι ρητοί και οι άρρητοι αριθμοί λέγονται πραγματικοί αριθμοί. Το σύνολο που περιέχει όλους τους πραγματικούς αριθμούς λέγεται σύνολο των πραγματικών αριθμών και συμβολίζεται με R.
o ΛΥΚΕΙΟ ΠΕΤΡΟΥΠΟΛΗΣ Οι ρητοί και οι άρρητοι αριθμοί λέγονται πραγματικοί αριθμοί. Το σύνολο που περιέχει όλους τους πραγματικούς αριθμούς λέγεται σύνολο των πραγματικών αριθμών και συμβολίζεται με R.
Δημήτρης Διαμαντίδης, Γεωργία Ευθυμίου, Αναστάσιος Κουπετώρης, Ιωάννης Σταμπόλας. Άλγεβρα Α Λυκείου B ΤΟΜΟΣ
 Δημήτρης Διαματίδης, Γεωργία Ευθυμίου, Ααστάσιος Κουπετώρης, Ιωάης Σταμπόλας Άλγεβρα Α Λυκείου B ΤΟΜΟΣ Θέση υπογραφής δικαιούχου δικαιωμάτω πευματικής ιδιοκτησίας, εφόσο η υπογραφή προβλέπεται από τη σύμβαση.
Δημήτρης Διαματίδης, Γεωργία Ευθυμίου, Ααστάσιος Κουπετώρης, Ιωάης Σταμπόλας Άλγεβρα Α Λυκείου B ΤΟΜΟΣ Θέση υπογραφής δικαιούχου δικαιωμάτω πευματικής ιδιοκτησίας, εφόσο η υπογραφή προβλέπεται από τη σύμβαση.
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΛΓΕΡΣ ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ ΛΘΟΥΣ ΠΙΘΝΟΤΗΤΕΣ 1. Για οποιαδήποτε εδεχόμεα, εός δειγματικού χώρου Ω ισχύει η σχέση PA B= PA+ PB. ( ) ( ) ( ). Ισχύει ότι PA ( B) + PA ( B) = PA ( ) + PB ( )
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΕΡΟΣ 2ο Γυμνάσιο
 ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΕΡΟΣ 2ο υμάσιο 164 1 α. Τι λέμε -οστή δύαμη εός αριθμού α; β. Ορισμοί και ιδιότητες τω δυάμεω. Κατασκευάστε ορθογώιο τρίγωο ΑΒ α. ράψτε το πυθαγόρειο θεώρημα και τη σχέση που το εκφράζει
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΜΕΡΟΣ 2ο υμάσιο 164 1 α. Τι λέμε -οστή δύαμη εός αριθμού α; β. Ορισμοί και ιδιότητες τω δυάμεω. Κατασκευάστε ορθογώιο τρίγωο ΑΒ α. ράψτε το πυθαγόρειο θεώρημα και τη σχέση που το εκφράζει
ΜΙΓΑ ΙΚΟΙ ΑΡΙΘΜΟΙ. Ασκήσεις. Επιµέλεια.: Κάτσιος ηµήτρης. Μεθοδολογία Παραδείγµατα Ασκ ΜΕΘΟ ΟΛΟΓΙΑ 1
 εθοδολογία Παραδείγµατα σκ σκήσεις πιµέλεια.: άτσιος ηµήτρης Ρ ια να προσθέσουµε (ή να αφαιρέσουµε) δύο µιγαδικούς, προσθέτουµε (ή αφαιρούµε) τα πραγµατικά και τα φανταστικά τους µέρη, δηλαδή: ± = [Re
εθοδολογία Παραδείγµατα σκ σκήσεις πιµέλεια.: άτσιος ηµήτρης Ρ ια να προσθέσουµε (ή να αφαιρέσουµε) δύο µιγαδικούς, προσθέτουµε (ή αφαιρούµε) τα πραγµατικά και τα φανταστικά τους µέρη, δηλαδή: ± = [Re
Ασκήσεις7 80. AU διαγώνιο. αποτελούμενη από ιδιοδιανύσματα του A. Πρόσθετες ιδιότητες κανονικών πινάκων: Έστω A o
 Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
Ασκήσεις7 80 Ασκήσεις7 Διαγωοποίηση Ερμιτιαώ Πιάκω Βασικά σημεία Λήμμα του Schur (μιγαδική και πραγματική εκδοχή) Φασματικό θεώρημα (μιγαδική και πραγματική εκδοχή) Ορισμός και ιδιότητες καοικώ πιάκω Θεώρημα
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2013 Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΕΚΦΩΝΗΣΕΙΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ & ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α.. Να αποδείξετε ότι η παράγωγος της συάρτησης f ( ), για κάθε R. Α.. Α.. (
ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ. ορισµοί. Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 )
 ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ 1 ορισµοί Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 ) Γησίως αύξουσα: σε έα διάστηµα του πεδίου ορισµού της λέγεται µια συάρτηση f ότα για κάθε χ 1,χ 2 µε χ 1
ΑΛΓΕΒΡΑ ΤΗΣ Β ΤΑΞΗΣ 1 ορισµοί Ι ΙΟΤΗΤΕΣ ΣΥΝΑΡΤΗΣΕΩΝ (κεφ. 2 ) Γησίως αύξουσα: σε έα διάστηµα του πεδίου ορισµού της λέγεται µια συάρτηση f ότα για κάθε χ 1,χ 2 µε χ 1
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Ηµεροµηνία: Κυριακή 1 Απριλίου 2012 ΕΚΦΩΝΗΣΕΙΣ
 ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 0 Ε_.ΜλΓΑ(ε) ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ A Α.. Α.. Α.. A.4. Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ / ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Ηµεροµηία:
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ ( ) Να αποδείξετε ότι για κάθε θετικό ακέραιο ν ισχύει : ! + 2 2! + 3 3! + +ν ν! = (ν + 1)!
 ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να αποδείξετε ότι για κάθε θετικό ακέραιο ισχύει : 1 + 1 1! +! +! + +! = ( + 1)!. Να αποδείξτε ότι 6 10 [ ( 1) ] = ( + 1) ( + ) ( + ) (), για κάθε θετικό ακέραιο.. Να αποδείξετε ότι
ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ 1. Να αποδείξετε ότι για κάθε θετικό ακέραιο ισχύει : 1 + 1 1! +! +! + +! = ( + 1)!. Να αποδείξτε ότι 6 10 [ ( 1) ] = ( + 1) ( + ) ( + ) (), για κάθε θετικό ακέραιο.. Να αποδείξετε ότι
1.1 A. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ
 . A. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ ΘΕΩΡΙΑ. Τα σύνολα των αριθµών Το σύνολο των φυσικών αριθµών. Το σύνολο των ακεραίων αριθµών. N {0,,, 3 } Z { 3,,, 0,,, 3 } Το σύνολο των ρητών αριθµών. Q
. A. ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΚΑΙ ΟΙ ΠΡΑΞΕΙΣ ΤΟΥΣ ΘΕΩΡΙΑ. Τα σύνολα των αριθµών Το σύνολο των φυσικών αριθµών. Το σύνολο των ακεραίων αριθµών. N {0,,, 3 } Z { 3,,, 0,,, 3 } Το σύνολο των ρητών αριθµών. Q
Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ. Λυµένες Ασκήσεις * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ Ασκήσεις : 1, 2, 3, σελ. 107.
 Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
Γραµµική Άλγεβρα ΙΙ Σελίδα από 8 Μάθηµα 4 ο ΟΡΘΟΓΩΝΙΟΙ ΠΙΝΑΚΕΣ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 7, σελ 05 Ασκήσεις :,, 3, σελ 07 Λυµέες Ασκήσεις Άσκηση 4 Α ο πίακας R είαι ορθογώιος, αποδείατε ότι I
1.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ
 ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΜΕΡΟΣ Α.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ 67.5 ΑΞΙΟΣΗΜΕΙΩΤΕΣ ΤΑΥΤΟΤΗΤΕΣ ΟΡΙΣΜΟΣ Οομάζουμε ταυτότητα κάθε ισότητα που περιέχει μεταβλητές και επαληθεύεται για όλες τις τιμές τω μεταβλητώ αυτώ. Τετράγωο αθροίσματος
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ
 ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΥ ΟΡΙΖΟΝΤΑΙ ΜΕ ΟΛΟΚΛΗΡΩΜΑΤΑ ΣΧΟΛΙΑ : Είαι γωστό ότι για µια συεχή συάρτηση σε έα διάστηµα, το ολοκλήρωµα F ορίζει έα πραγµατικό αριθµό όπου o είαι έα οποιοδήποτε σηµείο του και α έα αυθαίρετο
4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ. Εισαγωγή
 4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Εισαγωγή Η Θεωρία Αριθμώ, δηλαδή η μελέτη τω ιδιοτήτω τω θετικώ ακεραίω, έθεσε από πολύ ωρίς τους μαθηματικούς μπροστά στο εξής πρόβλημα: Κάποια πρόταση αληθεύει
4 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 4.1 Η ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ Εισαγωγή Η Θεωρία Αριθμώ, δηλαδή η μελέτη τω ιδιοτήτω τω θετικώ ακεραίω, έθεσε από πολύ ωρίς τους μαθηματικούς μπροστά στο εξής πρόβλημα: Κάποια πρόταση αληθεύει
ΠΡΟΛΟΓΟΣ. Επίσης. Ολες οι ασκήσεις ανα κεφάλαιο του Μαίου. Κλείνει με τις λύσεις όλων των θεμάτων του Μαίου
 ΠΡΟΛΟΓΟΣ Το παρόν τεύχος δημιουργήθηκε για να διευκολύνει τους μαθητές στην ΆΜΕΣΗ κατανόηση των απαιτήσεων των πανελληνίων εξετάσεων δίνοντας τους τα θέματα των 4 χρόνων των κανονικών εξετάσεων του Μαίου
ΠΡΟΛΟΓΟΣ Το παρόν τεύχος δημιουργήθηκε για να διευκολύνει τους μαθητές στην ΆΜΕΣΗ κατανόηση των απαιτήσεων των πανελληνίων εξετάσεων δίνοντας τους τα θέματα των 4 χρόνων των κανονικών εξετάσεων του Μαίου
ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συνδυασμός ν στοιχείων ανά κ είναι μια μη διατεταγμένη συλλογή κ στοιχείων από τα ν.
 13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
13/10/2010 ΣΥΝΔΥΑΣΜΟΙ Ορισμός Συδυασμός στοιχείω αά κ είαι μια μη διατεταγμέη συλλογή κ στοιχείω από τα. Παράδειγμα 1 Οι συδυασμοί τω τριώ γραμμάτω Α,Β,Γ αά έα είαι οι εξής τρεις: Α, Β, Γ. Οι συδυασμοί
ΜΑΘΗΜΑ Πράξεις Συζυγής
 ΜΑΘΗΜΑ. Πράξεις Συζυγής Ασκήσεις Εξισώσεις Από σχέση σε σχέση ΑΣΚΗΣΕΙΣ. Α, είαι οι ρίζες της εξίσωσης + i + = + i. 5 = 7 + i + 5 + 7 = 0 + = = = 7, α αποδείξετε ότι =, = 7 = 7 ( + ) + i = + i 5 7 5 = 6
ΜΑΘΗΜΑ. Πράξεις Συζυγής Ασκήσεις Εξισώσεις Από σχέση σε σχέση ΑΣΚΗΣΕΙΣ. Α, είαι οι ρίζες της εξίσωσης + i + = + i. 5 = 7 + i + 5 + 7 = 0 + = = = 7, α αποδείξετε ότι =, = 7 = 7 ( + ) + i = + i 5 7 5 = 6
Α. Οι Πραγματικοί Αριθμοί
 ΠΑΡΑΡΤΗΜΑ Α Οι Πραγματικοί Αριθμοί Α1 Να τοποθετήσετε σε φθίουσα σειρά τους αριθμούς: 01 0 15, 0 15,, 01 5 5 A Να υπολογίσετε τη τιμή της παράστασης 4 1 A Να ρεθού το πηλίκο και το υπόλοιπο της διαίρεσης
ΠΑΡΑΡΤΗΜΑ Α Οι Πραγματικοί Αριθμοί Α1 Να τοποθετήσετε σε φθίουσα σειρά τους αριθμούς: 01 0 15, 0 15,, 01 5 5 A Να υπολογίσετε τη τιμή της παράστασης 4 1 A Να ρεθού το πηλίκο και το υπόλοιπο της διαίρεσης
Μιγαδικοί Αριθμοί. Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση. Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση
 Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
Μιγαδικοί Αριθμοί Μαθηματικά Γ! Λυκείου Θετική και Τεχνολογική Κατεύθυνση Υποδειγματικά λυμένες ασκήσεις Ασκήσεις προς λύση ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Υποδειγματικά Λυμένες Ασκήσεις Άλυτες Ασκήσεις ΛΑ Να βρείτε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΜΑ Α Άσκηση, μιγαδικοί αριθμοί να αποδείξετε ότι: Αν = Έχουμε: = ( ) ( ) ( ) ( ) = = =. Το τελευταίο ισχύει, άρα ισχύει και η ισοδύναμη αρχική σχέση.
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΘΕΜΑ Α Άσκηση, μιγαδικοί αριθμοί να αποδείξετε ότι: Αν = Έχουμε: = ( ) ( ) ( ) ( ) = = =. Το τελευταίο ισχύει, άρα ισχύει και η ισοδύναμη αρχική σχέση.
Στατιστική. μονάδα και ισχύει: i. ν ν. = ή ως ποσοστό % οπότε % = i fi
 Στατιστική "Υπάρχου τα μικρά ψέματα, τα μεγάλα ψέματα και οι στατιστικές" Μαρκ Τουαί Σε κάθε πρόβλημα της Στατιστικής υπάρχει έας «πληθυσμός» Ω τα στοιχεία του οποίου (άτομα) εξετάζοται ως προς έα χαρακτηριστικό
Στατιστική "Υπάρχου τα μικρά ψέματα, τα μεγάλα ψέματα και οι στατιστικές" Μαρκ Τουαί Σε κάθε πρόβλημα της Στατιστικής υπάρχει έας «πληθυσμός» Ω τα στοιχεία του οποίου (άτομα) εξετάζοται ως προς έα χαρακτηριστικό
ΚΕΦΑΛΑΙΟ 1 ο. 1.1. Οι πράξεις πρόσθεση και πολλαπλασιασµός και οι ιδιότητές τους.
 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ - - ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ο.. Οι πράξεις πρόσθεση κι πολλπλσισµός κι οι ιδιότητές τους. Πρόσθεση Πολλπλσισµός Ιδιότητ.. Ατιµετθετική (γ)()γ (γ)()γ Προσετιρική (γ)γ Επιµεριστική 0. Ουδέτερο
ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ - - ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ο.. Οι πράξεις πρόσθεση κι πολλπλσισµός κι οι ιδιότητές τους. Πρόσθεση Πολλπλσισµός Ιδιότητ.. Ατιµετθετική (γ)()γ (γ)()γ Προσετιρική (γ)γ Επιµεριστική 0. Ουδέτερο
{[ 140,150 ),[ 160,170 ),...,[ 200, 210]
![{[ 140,150 ),[ 160,170 ),...,[ 200, 210] {[ 140,150 ),[ 160,170 ),...,[ 200, 210]](/thumbs/91/106977432.jpg) Σημειώσεις στις Πιθαότητες Πείραμα τύχης και πιθαότητα Έα φυσικό φαιόμεο με χαρακτηριστικά που δε μπορούμε α τα προβλέψουμε, οομάζεται στοχαστικό ή τυχαίο Για παράδειγμα το ύψος τω κυμάτω στη θάλασσα,
Σημειώσεις στις Πιθαότητες Πείραμα τύχης και πιθαότητα Έα φυσικό φαιόμεο με χαρακτηριστικά που δε μπορούμε α τα προβλέψουμε, οομάζεται στοχαστικό ή τυχαίο Για παράδειγμα το ύψος τω κυμάτω στη θάλασσα,
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Στατιστική είαι ο κλάδος τω μαθηματικώ, ο οποίος ως έργο έχει τη συγκέτρωση στοιχείω, τη ταξιόμησή τους και τη παρουσίασή τους σε κατάλληλη μορφή, ώστε α μπορού
Εκφωνήσεις Λύσεις των θεμάτων
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 8 Νοεμβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση 3 η (//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 8 Νοεμβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση 3 η (//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2002
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι x 1,x,,x k είαι οι τιµές µιας µεταβλητής Χ, που αφορά τα άτοµα εός δείγµατος µεγέθους, όπου
ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΤΟΙΧΕΙΑ ΣΤΑΤΙΣΤΙΚΗΣ ΓΕΝΙΚΗΣ ΠΑΙ ΕΙΑΣ Γ ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Α. Aς υποθέσουµε ότι x 1,x,,x k είαι οι τιµές µιας µεταβλητής Χ, που αφορά τα άτοµα εός δείγµατος µεγέθους, όπου
Μ Α Θ Η Μ Α Τ Ι Κ Α Γ ΓΥΜΝΑΣΙΟΥ ΖΕΡΒΟΣ ΜΑΝΟΛΗΣ
 Μ Α Θ Η Μ Α Τ Ι Κ Α Γ ΓΥΜΝΑΣΙΟΥ ΖΕΡΒΟΣ ΜΑΝΟΛΗΣ 1 ΜΕΡΟΣ Α ΚEΦΑΛΑΙΟ 1 Ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. ΕΡΩΤΗΣΗ Τι ονομάζουμε
Μ Α Θ Η Μ Α Τ Ι Κ Α Γ ΓΥΜΝΑΣΙΟΥ ΖΕΡΒΟΣ ΜΑΝΟΛΗΣ 1 ΜΕΡΟΣ Α ΚEΦΑΛΑΙΟ 1 Ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. ΕΡΩΤΗΣΗ Τι ονομάζουμε
Ασκήσεις σχ. Βιβλίου σελίδας Α ΟΜΑ ΑΣ 1.
 .. Ασκήσεις σχ. Βιβλίου σελίδας 94 97 Α ΟΜΑ ΑΣ. Να βρείτε τις τιµές του λ R, ώστε ο z (λ )( ) να είναι : πραγµατικός αριθµός φανταστικός αριθµός z λ λ 6 (λ ) (6 λ) z πραγµατικός 6 λ 0 λ 6 z φανταστικός
.. Ασκήσεις σχ. Βιβλίου σελίδας 94 97 Α ΟΜΑ ΑΣ. Να βρείτε τις τιµές του λ R, ώστε ο z (λ )( ) να είναι : πραγµατικός αριθµός φανταστικός αριθµός z λ λ 6 (λ ) (6 λ) z πραγµατικός 6 λ 0 λ 6 z φανταστικός
2.1 Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ
 1 2.1 Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ ΘΕΩΡΙΑ 1. Κλάσµα : Είαι το µαθηµατιό σύµβολο το οποίο δηλώει σε πόσα ίσα µέρη χωρίσαµε το όλο αι πόσα µέρη πήραµε Κλάσµα : πόσα µέρη πήραµε σε πόσα ίσα µέρη χωρίσαµε : αριθµητής
1 2.1 Η ΕΝΝΟΙΑ ΤΟΥ ΚΛΑΣΜΑΤΟΣ ΘΕΩΡΙΑ 1. Κλάσµα : Είαι το µαθηµατιό σύµβολο το οποίο δηλώει σε πόσα ίσα µέρη χωρίσαµε το όλο αι πόσα µέρη πήραµε Κλάσµα : πόσα µέρη πήραµε σε πόσα ίσα µέρη χωρίσαµε : αριθµητής
Επαναληπτικό Διαγώνισμα Μαθηματικών Γενικής Παιδείας Γ Λυκείου
 Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
Επααληπτικό Διαγώισμα Μαθηματικώ Γεικής Παιδείας Γ Λυκείου Θέμα A Α.α) Τι οομάζουμε συάρτηση και τι οομάζουμε πραγματική συάρτηση πραγματικής μεταβλητής; β) Τι λέγεται τιμή μιας συάρτησης f στο χ ; γ)
Δ/νση Β /θµιας Εκπ/σης Φλώρινας Κέντρο ΠΛΗ.ΝΕ.Τ. (Πρόοδοι) ΠΡΟΟΔΟΙ
 ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
ΠΡΟΟΔΟΙ Οι πρόοδοι αποτελού µια ειδική κατηγορία τω ακολουθιώ και είαι τριώ ειδώ : αριθµητικές, αρµοικές και γεωµετρικές. ΑΡΙΘΜΗΤΙΚΕΣ ΠΡΟΟΔΟΙ (ΘΕΩΡΙΑ) Ορισµός Μια ακολουθία αριθµώ α, α,, α, α +, θα λέµε
Γυμνάσιο Μαθηματικά Τάξη B
 113 Θέματα εξετάσεω περιόδου Μαΐου-Ιουίου στα Μαθηματικά Τάξη B! taexeiola.blogspot.com 6 ο ΥΜΝΑΣΙΟ ΡΟΔΟΥ ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ, ΤΑΞΗ Β' ΥΜΝΑΣΙΟΥ, ΡΟΔΟΣ
113 Θέματα εξετάσεω περιόδου Μαΐου-Ιουίου στα Μαθηματικά Τάξη B! taexeiola.blogspot.com 6 ο ΥΜΝΑΣΙΟ ΡΟΔΟΥ ΑΝΑΚΕΦΑΛΑΙΩΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ-ΙΟΥΝΙΟΥ 2014 ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ, ΤΑΞΗ Β' ΥΜΝΑΣΙΟΥ, ΡΟΔΟΣ
ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ
 015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
015 ΕΙΣΑΓΩΓΗ ΣΤΗ ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Περιεχόμεα 0. ΕΙΣΑΓΩΓΗ - ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ... 1. ΜΑΘΗΜΑΤΙΚΗ ΕΠΑΓΩΓΗ... 5. ΕΥΚΛΕΙΔΙΑ ΔΙΑΙΡΕΣΗ... 1. ΔΙΑΙΡΕΤΟΤΗΤΑ... 1 4 ΜΕΓΙΣΤΟΣ
x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ
![x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ x [ ] T ( ) Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Λυµένες Ασκήσεις * * * * * * Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ](/thumbs/53/30835179.jpg) Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Γραµµική Άλγεβρα ΙΙ Σελίδα από 4 Μάθηµα 6 ο ΙΑΓΩΝΟΠΟΙΗΣΗ ΠΙΝΑΚΑ Θεωρία : Γραµµική Άλγεβρα : εδάφιο 5, σελ 5-5 Ασκήσεις :, 4, 6, 8, 9,, σελ 59 Λυµέες Ασκήσεις Άσκηση 6 ο πίακας είαι η µοαδική ιδιοτιµή του,
Εκφωνήσεις Λύσεις των θεμάτων
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Άλγεβρα Α Γεικού Ημερησίου Λυκείου Προσθήκη θεμάτω 6 Οκτωβρίου 04 Εκφωήσεις Λύσεις τω θεμάτω Έκδοση η (3//04) Περιέχοται τα θέματα ΓΗ_Α_ΑΛΓ 480 ΓΗ_Α_ΑΛΓ 3073 ΓΗ_Α_ΑΛΓ 3096 ΓΗ_Α_ΑΛΓ 35 ΓΗ_Α_ΑΛΓ
Πανελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γενικης Παιδειας
 ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΘΕΜΑ Α. Παελλαδικες Εξετασεις Γ Λυκειου Μαθηµατικα Γεικης Παιδειας Θέµατα-Εδεικτικές Λύσεις Νικόλαος. Κατσίπης 17 Μαϊου 2010 Α1. Εστω t 1, t 2,..., t οι παρατηρήσεις µιας ποσοτικής µεταβλητής X εός δείγµατος
ΑΣΚΗΣΕΙΣ. x + 5= 6 (1) και. x = 1, οπότε η (2) γίνεται 1 5x + 1= 7 x = 1 ΘΕΜΑ Β. Άσκηση 1. Να βρείτε τον αριθμό x R όταν. Λύση.
 ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
ΚΕΦΑΛΑΙΟ ο: ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΝΟΤΗΤΑ : ΈΝΝΟΙΑ ΜΙΓΑΔΙΚΟΥ ΓΕΩΜΕΤΡΙΚΗ ΠΑΡΑΣΤΑΣΗ ΜΙΓΑΔΙΚΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΣΥΖΥΓΕΙΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΔΥΝΑΜΕΙΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΑΡΙΘΜΟΥ ΚΑΙ ΤΟΥ i. ΙΔΙΟΤΗΤΕΣ
78 Ερωτήσεις Θεωρίας Στα Μαθηματικά Γενικής Παιδείας
 Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
Στα Μαθηματιά Γειής Παιδείας Tι οομάζουμε συάρτηση Tι οομάζουμε παραγματιή συάρτηση πραγματιής μεταβλητής Μια διαδιασία με τη οποία άθε στοιχείο εός συόλου Α πεδίο ορισμού ατιστοιχίζεται σε έα αριβώς στοιχείο
xf(y) + yf(x) = (x + y)f(x)f(y)
 ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
ΕΥΡΕΣΗ ΤΥΠΟΥ ΣΥΝΑΡΤΗΣΗΣ Επιμέλεια: Καρράς Ιωάης Μαθηματικός Φίλος μὲ δή, ὡς ἔοικε, τούτῳ τῷ λόγῳ ὁ ἀγαθὸς ἔσται, ἐχθρὸς δὲ ὁ ποηρός. gxkarras@gmail.com 1. Να βρεθού όλες οι συαρτήσεις f : R R για τις οποίες
4.3 ΔΙΑΙΡΕΤΟΤΗΤΑ. Εισαγωγή
 49 43 ΔΙΑΙΡΕΤΟΤΗΤΑ Εισαγωγή Στα Στοιχεία του Ευκλείδη, βιβλία VII, VIII και IX (περίπου 300 πχ), οι θετικοί ακέραιοι παριστάοται ως ευθύγραμμα τμήματα και η έοια της διαιρετότητας συδέεται άμεσα με τη
49 43 ΔΙΑΙΡΕΤΟΤΗΤΑ Εισαγωγή Στα Στοιχεία του Ευκλείδη, βιβλία VII, VIII και IX (περίπου 300 πχ), οι θετικοί ακέραιοι παριστάοται ως ευθύγραμμα τμήματα και η έοια της διαιρετότητας συδέεται άμεσα με τη
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΤΗΣ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ Του Κώστα Βακαλόπουλου ΑΣΚΗΣΗ (ΣΤΑΤΙΣΤΙΚΗ) Το εύρος (R) τω παρατηρούμεω υψώ τω 00 πελατώ εός γυμαστηρίου είαι cm. A) Να ομαδοποιήσετε τα δεδομέα
ΓΙΑ ΜΙΑ ΕΠΑΝΑΛΗΨΗ ΣΤΗΝ ΥΛΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ
 Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας
Περιοδικό ΕΥΚΕΙΔΗ Β Ε.Μ.Ε. (τεύχος 7) ΕΡΩΤΗΕΙ ΚΑΤΑΝΟΗΗ ΓΙΑ ΜΙΑ ΕΠΑΝΑΗΨΗ ΤΗΝ ΥΗ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΓΕΝΙΚΗ ΠΑΙΔΕΙΑ Α) Να χαρακτηρίσετε τις παρακάτω προτάσεις με () α είαι σωστές και με () α είαι λάθος, αιτιολογώτας

 ΜΑΘΗΜΑΤΙΚΑ α x +β
ΜΑΘΗΜΑΤΙΚΑ α x +β