Κεφάλαιο 9 ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΙΚΟΥ ΡΕΥΜΑΤΟΣ
|
|
|
- Ισίδωρος Ανδρέου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαι 9 ΜΑΓΝΗΤΚΟ ΠΕΔΟ ΗΛΕΚΤΡΚΟΥ ΡΕΥΜΑΤΟΣ Σύνψη Στ ένατ τύτ κεφάλαι γίνεται η περιγραφή και υπλγισμός τυ μαγνητικύ πεδίυ, τ πί δημιυργείται από ηλεκτρικό ρεύμα, αρχικά με τ νόμ των it και Savat και μετέπειτα με τ νόμ τυ Ampee. Επίσης μελετάται η μαγνητική δύναμη πυ αναπτύσσεται μεταξύ παραλλήλων ρευματφόρων αγωγών, ενώ ρίζεται τ μαγνητικό πεδί στ εσωτερικό σωληνειδύς. Τέλς περιγράφνται ι κατηγρίες των υλικών, αναλόγως της αλληλεπίδρασής τυς με τ μαγνητικό πεδί. Πραπαιτύμενη γνώση Εξωτερικό γινόμεν διανυσμάτων. Κυκλική κίνηση και κεντρμόλς δύναμη. Ρπή δυνάμεως. 9.1 Εισαγωγικά Έως τώρα εωρήσαμε άλλτε φανερά και άλλτε σιωπηρά, ότι ένα μαγνητικό πεδί Β παράγεται από φυσικύς μαγνήτες (μαγνητικά δίπλα). Εντύτις γνωρίζυμε ότι μαγνητικά πεδία δημιυργύνται και από κινύμενα ηλεκτρικά φρτία, ή αλλιώς από ηλεκτρικά ρεύματα. Η πρώτη φρά πυ παρατηρήηκε πειραματικά η δημιυργία μαγνητικύ πεδίυ από ηλεκτρικό ρεύμα, ήταν τ 180 από τν Δανό φυσικό Hans Chistian Oested ( ). Ο Oested παρατήρησε ότι μια μαγνητική βελόνη πυ ευρισκόταν κντά σ έναν ρευματφόρ αγωγό, μετέβαλε τν αρχικό πρσανατλισμό της, ώστε να μην δείχνει ακριβώς τν βόρει μαγνητικό πόλ της Γης. [1] Τύτ σήμαινε την ύπαρξη μαγνητικής δύναμης πάνω στην μαγνητική βελόνη, πέραν αυτής τυ γήινυ μαγνητικύ πεδίυ, και επμένως την δημιυργία μαγνητικύ πεδίυ από τ ηλεκτρικό ρεύμα πυ διέρρεε τν αγωγό. Αντιέτως, εάν τ ηλεκτρικό ρεύμα διεκόπτετ, η αλληλεπίδραση με την βελόνη τερματίζνταν, πότε αυτή έπαιρνε την γνωστή ευυγράμμισή της με τ μαγνητικό πεδί της Γης. Η ανακάλυψη τυ Oested ήταν εμελιώδυς σημασίας, διότι απετέλεσε την αφετηρία συνένωσης δυ σημαντικών κλάδων της Φυσικής, τυ ηλεκτρισμύ και τυ μαγνητισμύ, σε έναν κλάδ, αυτόν τυ ηλεκτρμαγνητισμύ. Στη συνέχεια α εξετάσυμε πι λεπτμερειακά την δημιυργία μαγνητικών πεδίων από ηλεκτρικά ρεύματα, δηλαδή από κινύμενα ηλεκτρικά φρτία. Hans Chistian Oested ( ) ( g/wiki/file:hc_%c3%98sted. jpg). Τ παρόν έργ απτελεί κινό κτήμα (public dmain). 9. Μαγνητικό πεδί κινυμένυ ηλεκτρικύ φρτίυ Αναφέραμε πι πάνω, ότι τ ηλεκτρικό ρεύμα παράγει μαγνητικό πεδί στν τριγύρω χώρ. Εφόσν πλλά κινύμενα φρτία παράγυν μαγνητικό πεδί, τότε και ένα μόν κινύμεν φρτί α παράγει τ δικό τυ μαγνητικό πεδί, τ πί φυσικά α είναι αρκετά ασενέστερ από εκείν λκλήρυ τυ ρεύματς ενός αγωγύ. Πρς χάριν απλότητας, ας εξετάσυμε αρχικά τ μαγνητικό πεδί πυ δημιυργεί ένα μόν κινύμεν ηλεκτρικό φρτί q, τ πί κινείται με ταχύτητα υ στ χώρ. Είναι πειραματικά απδεδειγμέν, ότι τ μαγνητικό πεδί Β πυ παράγεται από ένα κινύμεν φρτί σε ένα σημεί τυ χώρυ, είναι ανάλγ τυ φρτίυ q και της ταχύτητάς τυ υ, ενώ είναι αντιστρόφως ανάλγ τυ τετραγώνυ της απόστασης πυ χωρίζει τ σημεί από την έση τυ φρτίυ. Επίσης τ μέτρ τυ πεδίυ Β είναι ανάλγ τυ ημιτόνυ της γωνίας, πυ ρίζεται από τα διανύσματα της ταχύτητας και της διεύυνσης της απόστασης. Η διεύυνση [1] Κάπιι υπστηρίζυν ότι ταλός Gian Dmenic Rmagnsi ( ), ανακάλυψε πρώτς την σχέση ηλεκτρισμύ-μαγνητισμύ δυ δεκαετίες πριν τν Oested, αλλά η ανακάλυψή τυ πέρασε απαρατήρητη από την επιστημνική κινότητα της επχής, επειδή Rmagnsi την δημσίευσε σε δυ ιταλικές εφημερίδες!
2 τυ πεδίυ Β, είναι κάετη στ επίπεδ πυ ρίζεται από τις διευύνσεις των διανυσμάτων της ταχύτητας και της απόστασης υ και αντιστίχως, όπως φαίνεται στ σχ. 9.1α. Η πι πάνω περιγραφή και εξάρτηση τυ μαγνητικύ πεδίυ Β ενός κινυμένυ ηλεκτρικύ φρτίυ, η πία είναι απτέλεσμα πειραματικής μελέτης, δύναται να εκφρασεί μαηματικώς από την διανυσματική σχέση μ qυ ˆ 4π όπυ τ μέτρ της μαγνητικής επαγωγής είναι (9.1) μ qυsin 4π (9.) και η κατεύυνσή της είναι κάετη στ επίπεδ των υ και (Seas, 1951), (Alns & Finn, 199), (Αλεξόπυλς & Μαρίνς, 199), (Knight, 010), (Yung & Feedman, 010). Βλέπυμε ότι υπάρχει μια σταερά αναλγίας μ /4π, όπυ μ νμάζεται μαγνητική διαπερατότητα τυ κενύ, και ισύται με 4π 10-7 T m/a, ή αλλιώς με heny/mete. Τ μαγνητικό πεδί τυ κινυμένυ ηλεκτρικύ φρτίυ, περιγράφεται από μαγνητικές δυναμικές γραμμές, ι πίες λόγω αξνικής συμμετρίας, είναι μόκεντρι κύκλι γύρω από την διεύυνση κίνησης τυ φρτίυ. Τ διάνυσμα Β είναι πάντα εφαπτμενικό των μαγνητικών δυναμικών γραμμών, και στην περίπτωση ετικύ φρτίυ, η φρά τυ δίνεται από τν κανόνα τυ δεξιόστρφυ κχλία (δεξιύ χεριύ), όπως φαίνεται στ σχ. 9.1β. Πρσέξτε ότι τ διάνυσμα Β γίνεται μικρότερ όσ αυξάνεται η απόσταση, δηλ. απμακρυνόμαστε από τ φρτί. Επίσης, εάν τ φρτί είναι αρνητικό, τ εξωτερικό. υ γινόμεν υ ˆ στην εξ. 9.1 αλλάζει φρά, q υ (α) (β) Σχήμα 9.1 (a) Μαγνητικό πεδί κινυμένυ ετικύ ηλεκτρικύ φρτίυ. (β) Κάτψη δυναμικών γραμμών μαγνητικύ πεδίυ από κινύμεν ηλεκτρικό φρτί με ταχύτητα υ. με απτέλεσμα ι δυναμικές γραμμές τυ φρτίυ να έχυν την αντίετη φρά από αυτήν τυ σχήματς 9.1. Επειδή για τ μαγνητικό πεδί ισχύει η αρχή της επαλληλίας, όπως ακριβώς ισχύει για τ ηλεκτρικό πεδί, πρεκτείνντας την πι πάνω συζήτηση μπρύμε να υπλγίσυμε τ πεδί Β πυ δημιυργεί ένα σύνλ κινυμένων ηλεκτρικών φρτίων μέσα σ έναν αγωγό. Πρσέτντας δηλαδή, τα επιμέρυς μαγνητικά πεδία όλων των κινυμένων φρτίων ενός ρευματφόρυ αγωγύ, μπρύμε να υπλγίσυμε τ συνλικό μαγνητικό πεδί πυ παράγεται από έναν ρευματφόρ αγωγό. 9.3 Μαγνητικό πεδί ρευματφόρυ αγωγύ Νόμς των it και Savat Έστω ότι ένας αγωγός διαρρέεται από ηλεκτρικό ρεύμα εντάσεως. Θεωρύμε ένα στιχειώδες τμήμα τυ με μήκς dl. Εάν η πυκνότητα όγκυ τυ αριμύ των ηλεκτρικών φρτίων στν αγωγό είναι n, τότε τ στιχειώδες φρτί dq πυ κινείται στν στιχειώδες όγκ dv, πίς αντιστιχεί στ επίσης στιχειώδες μήκς dl, είναι dq nqadl (9.3) όπυ Α είναι η διατμή τυ αγωγύ, και q τ μέγες κάε κινυμένυ φρτίυ. Τα κινύμενα φρτία με ταχύτητα υ στ μήκς dl, ισδυναμύν με φρτί dq, πότε τ αντίστιχ στιχειώδες μαγνητικό πεδί d σε απόσταση δίνεται ως μ dqυ ˆ μ dqυsin d d n ˆ (9.4) 4π 4π
3 3 με διεύυνση ˆn πάντα κάετη στ επίπεδ πυ ρίζυν τα υ και διανύσματα, όπως φαίνεται στ σχ. 9.α. Η κάτψη τυ σχήματς 9.β, μάς βηά να κατανήσυμε καλύτερα την κατεύυνση των δυναμικών γραμμών τυ μαγνητικύ πεδίυ, πυ δημιυργεί ένας ευύγραμμς ρευματφόρς αγωγός. Ο γενικός κανόνας ευρέσεως των δυναμικών γραμμών τυ μαγνητικύ πεδίυ, δίνεται από τν κανόνα τυ δεξιύ χεριύ ή τυ δεξιόστρφυ κχλία, έτσι όπως αναπαριστάται στ σχ. 9.γ. Σύμφωνα μ αυτόν, εάν αντίχειρας τυ δεξιύ χεριύ, δείχνει την φρά τυ ρεύματς, τα λυγισμένα ακρδάκτυλα δείχνυν την κατεύυνση των κυκλικών μόκεντρων μαγνητικών δυναμικών γραμμών.h εξ. 9.4 μέσω της εξ. 9.3 δίνει για τ μέτρ τυ στιχειώδυς πεδίυ d d μ nqυadlsin 4π Όμως η ένταση τυ ηλεκτρικύ ρεύματς δίνεται ως dq (9.3) (9.5) nqυa (9.6) dt διότι ισχύει για την ταχύτητα ότι υ=dl/dt. ˆ dl υ d d d d. Β Β Β (α) Σχήμα 9. (α) Στιχειώδες μαγνητικό πεδί d, πυ πρκαλείται από στιχειώδες τμήμα ρευματφόρυ αγωγύ μήκυς dl. (β) Κάτψη των δυναμικών γραμμών μαγνητικύ πεδίυ πυ δημιυργεί ένας ευύγραμμς ρευματφόρς αγωγός. (γ) Ο κανόνας τυ δεξιύ χεριύ, ή τυ δεξιόστρφυ κχλία, για την εύρεση της κατεύυνσης των μαγνητικών δυναμικών γραμμών πυ δημιυργεί ένα ηλεκτρικό ρεύμα. (β) (γ) Jen-aptiste it ( ) ( eanaptiste_it#/media/file: Jean_baptiste_bit.jpg). Τ Τότε η εξ. 9.5 γίνεται d μ dlsin 4π ή σε διανυσματική μρφή (9.7) μ dl ˆ 4π d (9.8) όπυ τ dl είναι διάνυσμα μήκυς dl και κατεύυνσης αυτής τυ ηλεκτρικύ ρεύματς εντός τυ αγωγύ (enumf, 1961), (Lbkwicz & Melissins, 1975), (Kaus, 1993), (Halliday, Resnick & Kane, 009), (Giancli, 01), (Seway & Jewett, 013). Ολκληρώνντας την εξ. 9.8 ως πρς τ μήκς l, παίρνυμε μ ˆ 4π dl (9.9) Η εξ. 9.9, υπλγίζει τ συνλικό μαγνητικό πεδί πυ δημιυργεί παρόν έργ απτελεί κινό κτήμα (public dmain). ρευματφόρς αγωγός, στ σημεί τυ χώρυ πυ ρίζεται από την απόσταση, και είναι γνωστή ως νόμς των it και Savat. Oι Γάλλι Jean aptiste it ( ) και Felix Savat ( ), μελέτησαν την σχέση τυ μαγνητισμύ με τα ηλεκτρικά
4 4 ρεύματα, και τ 180 ανακίνωσαν (όπως και Δανός Hans Chistian Oested) ότι ένας ρευματφόρς αγωγός ασκεί δύναμη πάνω σε μαγνήτες Μαγνητικό πεδί ευυγράμμυ ρευματφόρυ αγωγύ Ας πρσπαήσυμε τώρα να υπλγίσυμε τ μαγνητικό πεδί ενός ευυγράμμυ ρευματφόρυ αγωγύ, με τ νόμ των it και Savat. Έστω L τ μήκς τυ αγωγύ. Ζητάμε να υπλγίσυμε τ μαγνητικό πεδί Β στην μεσκάετ τυ αγωγύ, και σε απόσταση x απ αυτόν, στ σημεί Ο, όπως φαίνεται στ σχ Έστω λιπόν στιχειώδες μήκς dl τυ αγωγύ, τ πί είναι στην κάετη διεύυνση y. σχύει δηλαδή dy=dl. Εφαρμόζντας τ νόμ των it και Savat, έχυμε για τ μέτρ τυ d όπυ d μ dysin 4π (9.10) x y (9.11) Επμένως έχυμε d Όμως ισχύει, μ dysin 4π x + y (9.1) sin sin( π - ) x x y πότε από την εξ. 9.1 παίρνυμε μ x dy d 4 π ( x ) 3/ y (9.13) (9.14) Για να εύρυμε τ συνλικό πεδί Β τυ αγωγύ στ σημεί x, πρέπει να λκληρώσυμε την εξ ως πρς y σε όλ τ μήκς τυ αγωγύ, δηλ. από L σε L. Επμένως γράφυμε L L 3/ 3/ π x y π x L L y π x x y L L μ x dy μ x dy μ x y 4 ( ) 4 ( ) 4 μ L 4π x x L Όταν τ μήκς τυ αγωγύ είναι πλύ μεγάλ, δηλ. L>>x, η εξ γίνεται μ πx (9.16) (9.15) Η εξ δίνει τ μαγνητικό πεδί ενός ευυγράμμυ ρευματφόρυ αγωγύ σε απόσταση x απ αυτόν, όταν τ μήκς τυ είναι αρκετά μεγαλύτερ απ αυτήν την απόσταση. Λόγω αξνικής συμμετρίας, τ μέτρ τυ πεδίυ Β είναι σταερό σε κάε σημεί τυ χώρυ πυ απέχει απόσταση x, ενώ η διεύυνση τυ Β είναι πάντα εφαπτμενική τυ κύκλυ ακτίνας x, με φρά αυτή τυ δεξιόστρφυ κχλία (βλ. σχήμα 9.β). L dy y O y π- x Σχήμα 9.3 Μαγνητικό πεδί Β στην μεσκάετ ευυγράμμυ ρευματφόρυ αγωγύ, σε απόσταση x απ αυτόν. d x 9.3. Μαγνητικό πεδί κυκλικύ ρευματφόρυ αγωγύ * Ας υπέσυμε τώρα ότι έχυμε έναν κυκλικό αγωγό (βρόχ) ακτίνας a, και ζητάμε να υπλγίσυμε τ μαγνητικό πεδί Β στ σημεί Ο, τ πί απέχει απόσταση x από τ κέντρ Κ τυ βρόχυ. Τ σημεί Ο
5 5 ανήκει στην κάετη ευεία στ επίπεδ τυ βρόχυ, η πία περνά από τ Κ, όπως φαίνεται στ σχ Από τ νόμ των it και Savat, (εξ. 9.8), εφόσν dl ˆ και επμένως dl ˆdln ˆ, και επίσης λαμβάνντας υπόψη ότι a x, όπυ είναι η απόσταση τυ dl από σημεί Ο, παίρνυμε τελικά για τ μέτρ τυ στιχειώδυς πεδίυ d z y a μ dl d 4π a x K dl Σχήμα 9.4 Μαγνητικό πεδί Β ενός κυκλικύ ρευματφόρυ αγωγύ, σε απόσταση x από τ κέντρ και πάνω στην κάετη ευεία πυ περνά από αυτό. x d y O d x (9.17) όπυ η κατεύυνση τυ πεδίυ d είναι κάετη στη διεύυνση της απόστασης. Τ διάνυσμα d αναλύεται σε δυ συνιστώσες, τις d x και d y, όπυ d dcs και d dsin. Επειδή x για κάε στιχειώδες μήκς dl υπάρχει ένα αντιδιαμετρικό πυ δίνει αντίετ d y, τ πρόβλημα παρυσιάζει κυλινδρική συμμετρία γύρω από τν άξνα x. Όμως τα αντιδιαμετρικά dl δίνυν τ ίδι d x, πότε τελικά α υπάρχει μαγνητικό πεδί μόν στην ριζόντια συνιστώσα. Για την γωνία ισχύει ότι α α cs ( x α ) y (9.18) Για να υπλγίσυμε τ συνλικό πεδί Β τυ κυκλικύ ρευματφόρυ αγωγύ, σε απόσταση x από τ κέντρ τυ πάνω στην κάετη διεύυνση πυ περνά απ αυτό, πρέπει να λκληρώσυμε την εξ ως πρς dl, πάνω σ όλη την περιφέρεια τυ αγωγύ. Επμένως παίρνυμε μ dl a μ a dl μ a dx dl 4 4 d x 3 3 π a x ( a x ) π ( a x ) 4 π( a x ) μ a μ a (9.19) πa π( a x ) ( a x ) Τ μαγνητικό πεδί Β έχει διεύυνση κάετη στ επίπεδ τυ βρόχυ, και φρά αυτή τυ d x στ σχ Εάν έχυμε έναν ρευματφόρ αγωγό με Ν βρόχυς (σπείρες), όπως συμβαίνει στην περίπτωση ενός επαγωγέα ή αλλιώς πηνίυ, τότε κάε βρόχς α συνεισφέρει τ ίδι στ συνλικό πεδί Β, πότε έχυμε μ Na ( a ) 3 x Στ κέντρ της σπείρας, όπυ x =0, τ πεδί α είναι μ a ενώ στ κέντρ τυ πηνίυ α είναι (9.0) (9.1) μ N a (9.)
6 6 Παράδειγμα 9.1 Μαγνητικό πεδί ημικυκλικύ ρευματφόρυ αγωγύ Τ σύρμα τυ σχήματς 9.5 διαρρέεται από ρεύμα. Πια είναι η μαγνητική επαγωγή Β στ κέντρ C τυ ημικυκλικύ τμήματς ακτίνας R, η πία πρέρχεται από, α) καένα ευύγραμμ τμήμα μήκυς l, β) τ ημικυκλικό τμήμα, και γ) λόκληρ τ σύρμα. Λύση α) Από τ νόμ των it και Savat, τ κάε ευύγραμμ τμήμα μήκυς l δημιυργεί στιχειώδες μαγνητικό πεδί dβ l, ίσ με μ ldl ˆ 4π d l (1) Όμως για τα ευύγραμμα τμήματα, ισχύει dl // ˆ, πότε dl ˆ 0. Άρα στ σημεί C τ d l =0, και επμένως τα ευύγραμμα τμήματα δεν δημιυργύν μαγνητικό πεδί σ αυτό τ σημεί. β) Εφαρμόζντας την εξ. 1 για στιχειώδες τμήμα dl τυ ημικυκλίυ ακτίνας R, έχυμε μ ˆ μ sin 90 μ μ μ d l 4π R 4π R 4πR 4πR 4R R ldl dl d l dl πr 0 γ) Τ λικό μαγνητικό πεδί στ σημεί C α είναι τ άρισμα τυ μαγνητικύ πεδίυ πυ δημιυργεί κάε τμήμα τυ σύρματς. Επειδή όμως τα ευύγραμμα τμήματα δίνυν μηδενικό πεδί, α έχυμε συνλικό πεδί στ C ίσ με C μ 4R με κατεύυνση πρς τα «μέσα» της σελίδας, όπως φαίνεται στ σχ. 9.5 (κανόνας δεξιύ χεριύ, βλ. σχ. 9.γ). Παράδειγμα 9. Μαγνητικό πεδί τετραγωνικύ ρευματφόρυ αγωγύ Τετράγωνς βρόχς από σύρμα πλευράς α διαρρέεται από ρεύμα, όπως δείχνει τ σχ Δείξτε ότι τ μαγνητικό πεδί Β στ κέντρ τυ βρόχυ, δίνεται από την σχέση μ. l πα dl Λύση Για να εύρυμε τ μαγνητικό πεδί Β στ κέντρ τυ τετραγωνικύ βρόχυ, αρκεί να υπλγίσυμε τ Β κάε πλευράς τυ τετραγώνυ και να τα πρσέσυμε. Έτσι α πρέπει πρώτα να υπλγίσυμε τ μαγνητικό πεδί Β α πυ σχηματίζει η πλευρά α στ κέντρ. Ένα στιχειώδες μήκς dl της πλευράς, δημιυργεί πεδί d α στ κέντρ τυ βρόχυ, πυ δίνεται από τ νόμ των it-savat ως α Όμως και μ dl ˆ μ dl sin d α d α (1) 4π 4π α/ α sin sin () a ( ) l (3) l dl R Β C C Σχήμα 9.5 Ρευματφόρς αγωγός πυ απτελείται από ημικύκλι ακτίνας R, και δυ ευύγραμμα τμήματα μήκυς l τ καένα (παράδειγμα 9.1). α Σχήμα 9.6 Τετράγωνς ρευματφόρς βρόχς διαρρέεται από ρεύμα και σχηματίζει μαγνητικό πεδί Β στ κέντρ τυ (παράδειγμα 9.). l
7 7 Οι εξισώσεις και 3 στην 1, δίνυν d α a dl μ adl μ adl μ d 4π [( ) ] [( ) ] 4π l l [( ) l ] 4π [( ) l ] α a 1/ a a 3/ a 3/ Ολκληρώνντας την εξ. 4 ως πρς l, από l/ έως l/, παίρνυμε (4) α a a/ dl a/ μ μ a dl μ a dl ( ) ( ) 4π a / 3/ 4 / 3/ 4 a 1/ [( ) ] π a a [( ) ] π a a l l ( ) [( ) l ] a a ( ) μ μ a μ 1 4 π( ) [( ) ( ) ] [( ) ( ) ] 4 π( ) [( ) ] 4π a a a 1/ a a 1/ a a 1/ a α μ π a Επειδή όλες ι πλευρές τυ τετραγωνικύ βρόχυ είναι ισδύναμες, για να βρύμε τ λικό μαγνητικό πεδί στ κέντρ, πλλαπλασιάζυμε την εξ. 5 επί 4. Έτσι παίρνυμε μ μ 4 4 π a πa a Η κατεύυνση τυ μαγνητικύ πεδίυ είναι κάετη στ επίπεδ της σελίδας και πρς τα «μέσα». Παράδειγμα 9.3 Μαγνητικό πεδί περιστρεφμένυ φρτισμένυ δίσκυ Θεωρείστε ότι ένας λεπτός δίσκς ακτίνας R, είναι τπετημένς έτσι ώστε να περιστρέφεται γύρω από τν άξνα z κάετ στ επίπεδ xy, όπως φαίνεται στ σχ Ο δίσκς έχει ετική σταερή επιφανειακή πυκνότητα φρτίυ σ και γωνιακή ταχύτητα ω. Απδείξτε ότι τ μαγνητικό πεδί στ 1 κέντρ τυ δίσκυ είναι μσωr. Λύση Καταρχήν, εφόσν δίσκς είναι λεπτός, α εωρήσυμε ότι είναι δισδιάστατς, δηλ. έχει μηδενικό πάχς. Έστω τώρα ένα στιχειώδες τμήμα τυ κυκλικύ δίσκυ με πλάτς d, έτσι ώστε να δημιυργείται ένας κυκλικός δακτύλις, πίς περιστρέφεται με γωνιακή ταχύτητα ω. Λόγω της περιστρφής τυ δακτυλίυ, τ φρτί dq τυ δακτυλίυ κινείται σε κυκλική τρχιά, ώστε να δημιυργείται ένα ρεύμα, όπυ Τ φρτί dq τυ δακτυλίυ είναι (5) dq (1) dt z ω Β y a / a / Σχήμα 9.7 Φρτισμένς λεπτός δίσκς ακτίνας R περιστρέφεται με σταερή γωνιακή ταχύτητα ω (παράδειγμα 9.3). R [] d x [] dx x Τ αόριστ λκλήρωμα της μρφής, όπυ k μια σταερά, έχει λύση. Εδώ έχυμε 3/ 1/ ( x k ) k ( x k ) k=α/.
8 8 ενώ τ εμβαδόν τυ είναι Η εξ. από την 3, γίνεται Η γωνιακή ταχύτητα τυ δίσκυ ρίζεται ως dq σda () da πd (3) dq σπd (4) υ υ ω (5) Θεωρώντας τν δακτύλι σαν έναν κυκλικό ρευματφόρ αγωγό με ρεύμα, γράφυμε για ένα στιχειώδες μήκς τυ dl μ dl ˆ μ dl sin90 μ dq dl d d d (6) 4π 4π 4π dt Η ταχύτητα τυ φρτίυ dq στν κυκλικό δακτύλι, είναι (5) dl dl υ ω dt dt (7) Η εξ. 6 λόγω των 4 και 7, γίνεται μ μ (8) 4π 4π σπ ωd d d σπωd Τ στιχειώδες πεδί d δημιυργείται από τν κυκλικό δακτύλι πάχυς d, και είναι κάετ στ επίπεδ τυ δίσκυ στ κέντρ τυ, (σύμφωνα με τν κανόνα τυ δεξιύ χεριύ), όπως φαίνεται στ σχ Για να υπλγίσυμε τ συνλικό πεδί Β όλυ τυ δίσκυ, πρέπει να λκληρώσυμε την εξ. 8, ως πρς την ακτίνα. Έτσι έχυμε R μ μσωr d σπωd 4π 0 Η διεύυνση τυ πεδίυ Β είναι κάετη στ επίπεδ τυ περιστρεφμένυ δίσκυ, και περνά από τ κέντρ τυ, όπως δείχνει τ σχ a. 1 (α) F 1 F αγωγός 1 αγωγός a 1 (β) Σχήμα 9.8 Δύ παράλληλι ευύγραμμι ρευματφόρι αγωγί, δημιυργύν τέτια μαγνητικά πεδία στ χώρ, ώστε ι μαγνητικές δυνάμεις πυ ασκύνται πάνω στν κάε αγωγό, να έχυν ως απτέλεσμα ι αγωγί, (α) να έλκνται όταν τα ρεύματα είναι μόρρπα, και (β) να απωύνται όταν τα ρεύματα είναι αντίρρπα... F 1 F 9.4 Μαγνητική δύναμη μεταξύ παραλλήλων ρευματφόρων αγωγών Είδαμε πρηγυμένως, ότι ένας ευύγραμμς ρευματφόρς αγωγός μεγάλυ μήκυς παράγει μαγνητικό πεδί, τ πί δίνεται από την εξ Ας υπέσυμε τώρα ότι έχυμε δυ παράλληλυς ρευματφόρυς αγωγύς 1 και, ι πίι διαρρένται από μόρρπα ρεύματα 1 και αντιστίχως, όπως φαίνεται στ σχ. 9.8α. Οι αγωγί απέχυν μεταξύ τυς απόσταση α, και τ μαγνητικό πεδί πυ δημιυργεί ένας αγωγός στ χώρ α εξασκεί μια μαγνητική δύναμη F στν άλλ αγωγό και αντιστρόφως. Έτσι λιπόν, τ
9 9 μ 1 πεδί πυ δημιυργεί αγωγός 1 στην περιχή τυ αγωγύ, είναι 1, πότε η δύναμη F πυ πa μ1l ασκείται στν αγωγό, είναι F l 1 F l1, ή αλλιώς F, όπυ l είναι τ μήκς τυ πa μ1 αγωγύ. Η δύναμη ανά μνάδα μήκυς πυ ασκείται από τν αγωγό 1 στν αγωγό, είναι F. Με πa μ ανάλγ τρόπ αγωγός δημιυργεί μαγνητικό πεδί Β στ χώρ τυ αγωγύ 1, με μέτρ. Η πa μαγνητική δύναμη F 1 πυ ασκείται πάνω στν αγωγό 1 από τ μαγνητικό πεδί Β τυ αγωγύ, είναι μ1l F1 1l F1 1l. Δηλαδή, η δύναμη F 1 είναι ίση και αντίετη της δύναμης F, η πία πa ασκείται στν αγωγό από τ μαγνητικό πεδί Β 1 τυ αγωγύ 1. Η ισότητα αυτή στηρίζεται στ νόμ των δυνάμεων, δράσης-αντίδρασης. Απδείξαμε λιπόν, ότι όταν τα ρεύματα των αγωγών είναι μόρρπα, ι αγωγί έλκνται (Halliday, Resnick & Walke, 013). Αναλόγως μπρεί να απδειχεί ότι, όταν τα ρεύματα των αγωγών είναι αντίρρπα, ι αγωγί απωύνται, όπως φαίνεται στ σχήμα 9.8β (Kaus, 1993), (Giancli, 01). Παράδειγμα 9.4 Άπωση ρευματφόρων αγωγών Δυ παράλληλι αγωγί μήκυς 0.50 m καένας, διαρρένται από αντίρρπα ρεύματα μέτρυ 10 Α όπως στ σχ. 9.8β. α) Πόση είναι η απόσταση α μεταξύ των αγωγών, εάν απωύνται με δύναμη 1 Ν; Υπόδειξη: Υπέστε ότι η απόσταση α είναι αρκετά μικρή, ώστε τ μήκς των αγωγών να δύναται να εωρηεί πλύ μεγάλ, πότε να ισχύει η εξ Δίνεται μ =4π10-7 Wb/A. Λύση Ο κάε αγωγός δημιυργεί στη έση τυ άλλυ μαγνητικό πεδί ίσ με μ πa Έτσι, κάε αγωγός ασκεί στν άλλ δύναμη μέτρυ F (1) l () Η δύναμη F είναι αμιβαίως απωστική, λόγω των αντιρρόπων ρευμάτων. Έτσι η εξ. 1 στη, δίνει 7 μ μ l μ l 4π 10 Wb / A.m m F l F a a a 10μm πa πa πf π 1Ν Παρατηρύμε ότι τ απτέλεσμα δικαιώνει την υπόεσή μας, μιας και τα 10 μικρόμετρα είναι πλύ μικρότερα τυ μήκυς των αγωγών. y Παράδειγμα 9.5 Μαγνητικό πεδί στη μεσκάετ παραλλήλων ρευματφόρων αγωγών Δυ μακριά ευύγραμμα σύρματα, τα πία απέχυν απόσταση d, διαρρένται από ίσα αντιπαράλληλα ρεύματα, όπως φαίνεται στην κάετη άπψη τυ σχήματς 9.9. Δείξτε ότι τ μαγνητικό πεδί Β στ σημεί P πυ ισαπέχει από τα σύρματα, δίνεται από την σχέση μ d. π (4 R d ) Λύση Ας εωρήσυμε τυς δύ ευύγραμμυς αγωγύς κάετυς στ επίπεδ της σελίδας, όπως φαίνεται στ σχ Τότε στ σημεί P, κάε αγωγός δημιυργεί μαγνητικό πεδί, κάετ στην απόσταση στ επίπεδ xy,. Τα πεδία των δυ αγωγών είναι 1 και, και έχυν ίσα μέτρα πυ d. R φ Β 1y Σχήμα 9.9 Μαγνητικό πεδί δυ παραλλήλων ρευματφόρων αγωγών (κάετη άπψη), σε απόσταση R και πάνω στην μεσκάετ της απόστασής τυς d (παράδειγμα 9.5). P Β y φ 1 Β 1x Β x Β x
10 10 δίννται από την σχέση μ π 1 (1) Για να ευρύμε τ συνλικό πεδί στ σημεί P, πρσέτυμε διανυσματικά τα 1 και και έχυμε: Στν άξνα x: Στν άξνα y: (1) cs cs cs. () x 1x x x 1 x 1 1 (1) sin sin 0 (3) y 1y y y y Έτσι στ σημεί P, για τ μαγνητικό πεδί Β υπάρχει μόν Β x συνιστώσα, όπυ μ μ π π (4) cs cs Από την γεωμετρία τυ σχήματς 9.9, συμπεραίνυμε ότι φ 90 cs sin φ (5) σχύει όμως d / d sin φ sin φ (6) Οι εξισώσεις 5 και 6 στην 4 δίνυν μ d π (7) Ξανά από την γεωμετρία τυ σχήματς παίρνυμε d d ( ) R R (8) 4 Η εξ. 8 στην 7 δίνει μd μd μd d d 4 R π( d 4 R ) π( R ) π( ) 4 4 a Τ πεδί Β είναι στην κατεύυνση τυ ημιάξνα +x. F Παράδειγμα 9.6 Μαγνητική δύναμη σε ργώνι ρευματφόρ βρόχ Τ ευύγραμμ σύρμα μεγάλυ μήκυς τυ σχήματς 9.10, διαρρέεται από ρεύμα 1 =0 Α. Ο ργώνις βρόχς τυ πίυ ι μεγάλες πλευρές είναι παράλληλες στ σύρμα, διαρρέεται από ρεύμα =8.00 Α. Υπλγίστε τ μέτρ και την κατεύυνση της συνισταμένης δύναμης πυ ασκείται στν βρόχ από τ μαγνητικό πεδί τυ σύρματς. Δίννται ι απστάσεις a=1.0 cm, b=3.80 cm και c=6.0 cm. Λύση Τ μαγνητικό πεδί πυ δημιυργεί ευύγραμμς αγωγός μ 1 είναι, όπυ είναι η απόσταση από τν αγωγό. Η π συνισταμένη δύναμη πυ ασκείται πάνω στν βρόχ από τ μαγνητικό πεδί Β τυ αγωγύ, είναι τ άρισμα των τεσσάρων δυνάμεων πυ ασκύνται στα τέσσερα τμήματα τυ ργωνίυ βρόχυ, πότε ισχύει 1 F 1 F 3 b + - F 4 Σχήμα 9.10 Οργώνις βρόχς πυ διαρρέεται από ρεύμα σε περιχή μαγνητικύ πεδίυ ενός ευύγραμμυ ρευματφόρυ αγωγύ μεγάλυ μήκυς (παράδειγμα 9.6). c
11 11 F = F1 F F3 F 4 (1) Γενικά, η δύναμη πάνω σε κάε τμήμα τυ βρόχυ είναι F l. Επειδή τ Β είναι κάετ σε κάε τμήμα μήκυς l, ισχύει F = l. Τα δυ κάετα στν αγωγό τμήματα τυ βρόχυ δεν συνεισφέρυν στην συνισταμένη δύναμη, διότι ι δυνάμεις τυς είναι αντίετες και εξυδετερώννται, δηλ. F F. Επμένως 4 η εξ. 1 γίνεται F F F () 1 3 όπυ η F 1 είναι αντίετης κατεύυνσης από την F 3. σχύει όμως F l F μ c πa (3) όπυ l 1 =c=6. cm και a=1. cm. Ομίως F l F μ c πb (4) όπυ l 3 =c=6. cm και b=3.8 cm. Άρα λόγω των εξισώσεων 3 και 4, η εξ. δίνει μ1c 1 1 F ( ). π a b Τελικά παίρνυμε F μ c b a π π ab π m (W/Am ) 08A 6.10 m (3.8 1.) 10 m 4 ( ) F N Ο νόμς τυ Ampee Στην περίπτωση τυ ηλεκτρισμύ, είδαμε ότι για να υπλγίσυμε τ ηλεκτρικό πεδί γύρω από κάπιες συμμετρικές κατανμές φρτίυ, νόμς τυ Gauss είναι πλύ πι εύχρηστς από τ νόμ τυ Culmb. Κάτι αντίστιχ συμβαίνει και στν μαγνητισμό. Σε περιπτώσεις μεγάλης συμμετρίας των ηλεκτρικών ρευμάτων, τα μαγνητικά πεδία πυ σχηματίζνται μπρύν να υπλγιστύν πι εύκλα εφαρμόζντας τν νόμ τυ Ampee, αντί τυ νόμυ των it-savat. Ο νόμς τυ Ampee εκφράζεται από τ επικαμπύλι λκλήρωμα τυ μαγνητικύ πεδίυ Β σε μια κλειστή διαδρμή, δηλαδή dl. Ο υπλγισμός τυ λκληρώματς αυτύ, μπρεί να γίνει σχετικά εύκλα για ρισμένα απλά και συμμετρικά ηλεκτρικά ρεύματα. Για παράδειγμα, είδαμε πι πάνω ότι για τν μεγάλυ μήκυς ευύγραμμ αγωγό, (εδάφι 9.3.1), τ μαγνητικό πεδί παρυσιάζει μια κυκλική συμμετρία γύρω από τν αγωγό, όπως φαίνεται στ σχ Οι δυναμικές μαγνητικές γραμμές σχηματίζυν μόκεντρυς κύκλυς, όπυ τ διάνυσμα της μαγνητικής επαγωγής σε κάε σημεί τυ χώρυ, δίνεται από τ εφαπτμενικό διάνυσμα στη μαγνητική δυναμική γραμμή πυ περνά από τ συγκεκριμέν σημεί, διάνυσμα πυ έχει κατεύυνση, η πία δίνεται από τν κανόνα τυ δεξιύ χεριύ (βλ. σχ.9.11). Για μεγάλ μήκς αγωγύ, τ μέτρ τυ μαγνητικύ πεδίυ Β εξαρτάται μόν από τ ρεύμα και την απόσταση από τν αγωγό (βλ. εξ. 9.16). Έτσι, εάν υπλγίσυμε τ λκλήρωμα dl ακτίνας γύρω από ευύγραμμ αγωγό μεγάλυ μήκυς, έχυμε dl Σχήμα 9.11 Μαγνητικό πεδί ευύγραμμυ ρευματφόρυ αγωγύ σε σταερή απόσταση από αυτόν. για κύκλ
12 1 μ μ dl dl cs0 dl dl μ μ π π d dl (9.3) Η εξ. 9.3 είναι γνωστή ως νόμς τυ Ampee, πίς μας πληρφρεί ότι τ επικαμπύλι λκλήρωμα τυ εσωτερικύ γινμένυ τυ μαγνητικύ πεδίυ και της απόστασης κατά μήκς μιας κλειστής καμπύλης, είναι ανάλγ τυ ρεύματς πυ διαπερνά την κλειστή καμπύλη (Gant & Phillips, 1975), (Lbkwicz & Melissins, 1975), (Alns & Finn, 199), (Αλεξόπυλς & Μαρίνς, 199), (Kaus, 1993), (Feynman, Leightn & Sands, 009), (Halliday, Resnick & Kane, 009), (Knight, 010), (Yung & Feedman, 010), (Giancli, 01), (Halliday, Resnick & Walke, 013), (Seway & Jewett, 013). Παρότι στην πρκειμένη περίπτωση εφαρμόσαμε τν νόμ τυ Ampee για κύκλ, όπως α δείξυμε παρακάτω, αυτός ισχύει για πιαδήπτε κλειστή διαδρμή. Ο νόμς ανακαλύφηκε από τν Γάλλ φυσικό και μαηματικό Andé-Maie Ampèe ( ) τ 186, γι αυτό και φέρει τ όνμά τυ. Όπως αναφέραμε στ κεφάλαι 6, πρς τιμήν τυ μεγάλυ Γάλλυ επιστήμνα, η μνάδα τυ ηλεκτρικύ ρεύματς ρίστηκε να είναι τ Ampee (A). Αντιστρόφως, εάν γνωρίζυμε την ισχύ τυ νόμυ τυ Ampee, μπρύμε να υπλγίσυμε την ένταση τυ μαγνητικύ πεδίυ πυ δημιυργεί κάετς ευύγραμμς ρευματφόρς αγωγός τυ σχήματς 9.11 σε απόσταση. Λόγω της κυκλικής συμμετρίας τυ πρβλήματς, για σταερό, δεν α πρέπει να αλλάζει η ένταση τυ μαγνητικύ πεδίυ Β. Έτσι επιλέγντας την κλειστή κυκλική διαδρμή ακτίνας γύρω από τν αγωγό (σχ. 9.11), και εφαρμόζντας τ νόμ τυ Ampee, έχυμε μ dl μ dl cs0 μ dl μ dl μ π μ π Παρατηρύμε, ότι η σχέση για τ πεδί Β πυ καταλήξαμε εφαρμόζντας τν νόμ τυ Ampee, είναι η ίδια με αυτήν πυ καταλήξαμε για τ ίδι πρόβλημα εφαρμόζντας τν νόμ των it και Savat (βλ. εξ. 9.16). Η διαφρά με την εφαρμγή τυ νόμυ τυ Ampee, είναι ότι δηγηήκαμε στ ίδι συμπέρασμα αρκετά πι εύκλα. Αυτό δυστυχώς δεν ισχύει πάντα, αλλά εξαρτάται από την φυσική τυ πρβλήματς και τν βαμό συμμετρίας πυ αυτό παρυσιάζει. Στην πρηγύμενη περίπτωση για τν υπλγισμό τυ λκληρώματς dl διαλέξαμε μια συγκεκριμένη συμμετρική διαδρμή γύρω από τν αγωγό, η πία ήταν κυκλική. Ας δκιμάσυμε τώρα να υπλγίσυμε τ κλειστό επικαμπύλι λκλήρωμα dl τ σχ Τότε α έχυμε όπυ dl dl cs (9.4) ds cs (9.5) dl με την dφ να είναι η γωνία με την πία φαίνεται η απόσταση dl από τν αγωγό. Επειδή όμως η απόσταση ds είναι απειρελάχιστη, ισχύει ds dφ (9.6) Η εξ. 9.5 λόγω της 9.6 δίνει dφ cs (9.7) dl πότε η εξ. 9.4 γράφεται ως μ μ μ d dl π π π dφ dφ dφ π d dl μ, για μια τυχαία κλειστή διαδρμή, όπως δείχνει Σχήμα 9.1 α) Τυχαία κλειστή διαδρμή γύρω από ευύγραμμ ρευματφόρ αγωγό μεγάλυ μήκυς. β) Η ίδια διαδρμή σε κάετη άπψη. Τ μαγνητικό πεδί Β ρίζεται σε τυχαία απόσταση από τν ρευματφόρ αγωγό. Επμένως καταλήγυμε, ότι τ κλειστό επικαμπύλι λκλήρωμα dl στην κλειστή διαδρμή γύρω από έναν ρευματφόρ αγωγό, δεν εξαρτάται από την καμπύλη λκλήρωσης, ύτε και από την σχετική τυ έση (α). dφ (β) ds dl
13 13 ως πρς τν αγωγό, αλλά είναι πάντα ίσ με τ γινόμεν της διαπερατότητας τυ κενύ επί τ περικλείν ρεύμα περ πυ διαρρέει τν αγωγό. Αυτή είναι και η ακριβής διατύπωση τυ νόμυ τυ Ampee, πυ μαηματικά εκφράζεται από την εξίσωση dl μ (9.8) περικλείν Πρέπει να σημειώσυμε, ότι νόμς τυ Ampee όπως διατυπώηκε παραπάνω, ισχύει μόν για σταερά ρεύματα και μαγνητικά πεδία, τα πία δεν μεταβάλλνται με τ χρόν, και επίσης όταν στν χώρ δεν υπάρχυν μαγνητικά υλικά (Giancli, 01). Επίσης, εάν η κλειστή διαδρμή πυ επιλέγυμε να εφαρμόσυμε τν νόμ τυ Ampee περιέχει περισσότερυς από έναν ρευματφόρυς αγωγύς, τ συνλικό περικλείν ρεύμα α είναι τ αλγεβρικό άρισμα των ρευμάτων, όπυ μόρρπα ρεύματα πρστίενται και αντίρρπα αφαιρύνται. Ακλυύν κάπια παραδείγματα, στα πία γίνεται υπλγισμός τυ μαγνητικύ πεδίυ πυ δημιυργύν ρευματφόρι αγωγί, με εφαρμγή τυ νόμυ τυ Ampee. Παράδειγμα 9.7 Μαγνητικό πεδί στ εσωτερικό κυλινδρικύ αγωγύ Να ευρεεί η έκφραση τυ μαγνητικύ πεδίυ σε απόσταση από τ κέντρ μακρύ κυλινδρικύ συρμάτινυ αγωγύ ακτίνας R, για <R. Τ σύρμα διαρρέεται από ρεύμα i μιόμρφα κατανεμημέν στην κάετη τμή τυ, όπως φαίνεται στ σχ Λύση Εφόσν τ ρεύμα στν αγωγό είναι μιόμρφα κατανεμημέν στην διατμή τυ, η πυκνότητα ρεύματς J είναι σταερή, και ίση με dl J i A i πr J (1) Ζητάμε την ένταση τυ μαγνητικύ πεδίυ Β σε απόσταση από τ κέντρ τυ αγωγύ, για <R. Λόγω κυλινδρικής συμμετρίας, η τιμή τυ πεδίυ εξαρτάται μόν από την απόσταση. Για την κλειστή κυκλική διαδρμή ακτίνας, τ πεδί Β είναι σταερύ μέτρυ και εφαπτόμεν πάντα στην περιφέρεια (κανόνας δεξιύ χεριύ, βλ. σχ. 9.13). Εφαρμόζντας τ νόμ τυ Ampee και λόγω της κυκλικής συμμετρίας, γράφυμε dl μi () όπυ i είναι τ περικλείν ρεύμα στην κλειστή κυκλική διαδρμή ακτίνας. Τ ρεύμα i πυ διαπερνά την κυκλική διατμή ακτίνας και εμβαδύ A π, μπρεί να υπλγιστεί από την πυκνότητα ρεύματς, γράφντας i i J J i Jπ A π Η εξ. 3 λόγω της 1, δίνει i i i π i πr R (4) Η εξ. γράφεται τελικά dl i μ i π μ μ R i πr Παρατηρύμε ότι για =R, η μαγνητική επαγωγή δίνεται από την γνωστή σχέση 9.16, δηλ. μi πr (3). i Σχήμα 9.13 Κάετη τμή κυλινδρικύ αγωγύ πυ διαρρέεται από σταερό ρεύμα i. Κυκλικός δρόμς ακτίνας για τν υπλγισμό τυ μαγνητικύ πεδίυ Β σε απόσταση από τ κέντρ τυ αγωγύ (παράδειγμα 9.7) R
14 14 Παράδειγμα 9.8 Ομαξνικό καλώδι με αντίρρπα ρεύματα Συμπαγής κυλινδρικός αγωγός ακτίνας α, περιβάλλεται από μνωτικό περίβλημα ακτίνων α και b, τ πί με τη σειρά τυ περιβάλλεται από αγώγιμ περίβλημα ακτίνων b και c, σχηματίζντας ένα μαξνικό καλώδι, όπως δείχνει τ σχήμα Αν κεντρικός αγωγός διαρρέεται από ρεύμα 1, και τ αγώγιμ περίβλημα από ρεύμα σε αντίετες κατευύνσεις τ ένα ως πρς τ άλλ, να ευρείτε μια σχέση για τ μέτρ τυ μαγνητικύ πεδίυ, α) σε σημεία πυ απέχυν από τ κέντρ απόσταση, όπυ a<<b, και β) σε σημεία έξω από τ μαξνικό καλώδι, >c. γ) Εάν τα δύ ρεύματα είναι της ίδιας φράς, πώς είναι η απάντηση των α και β ερωτημάτων; Λύση α) Για a<<b εωρύμε κυκλική διαδρμή ακτίνας, και εφαρμόζυμε τ νόμ Ampee, όπυ μ 1 dl μ1 dl μ1 dl μ1 π μ1 π a b Σχήμα 9.14 Ομαξνικό καλώδι πυ διαρρέεται από αντίρρπα ρεύματα (παράδειγμα 9.8). β) Για >c εφαρμόζυμε ξανά τν νόμ τυ Ampee για κυκλική διαδρμή ακτίνας και έχυμε μ 1 dl μ περικλείν dl μ 1 dl μ 1 π μ 1 π Έτσι λιπόν τ μέτρ και η κατεύυνση τυ μαγνητικύ πεδίυ τυ μαξνικύ καλωδίυ, για σημεία πυ ισχύει >c, εξαρτάται από τ μέγες των ρευμάτων 1 και. Η φρά τυ ευρίσκεται σύμφωνα με τν κανόνα τυ δεξιύ χεριύ, για τ ρεύμα με την μεγαλύτερη ένταση. γ) Όταν ι κατευύνσεις των δυ ρευμάτων 1 και είναι ίδιες, τότε η απάντηση στ (α) ερώτημα δεν αλλάζει, ενώ για τ (β) ερώτημα τα ρεύματα πρστίενται επειδή είναι μόρρπα, και τελικά παίρνυμε μ ( 1 ) π 1 c C 9.6 Μαγνητικό πεδί ιδανικύ σωληνειδύς (πηνίυ) Ας εωρήσυμε τ σωληνειδές τυ σχήματς 9.15, τ πί διαρρέεται από σταερό ρεύμα και έχει γραμμική πυκνότητα σπειρών ίση με n. Έχυμε ήδη υπλγίσει παραπάνω, ότι τ μαγνητικό πεδί στ κέντρ μιας κυκλικής σπείρας, δίνεται από την εξ Για να υπλγίσυμε τ μαγνητικό πεδί Β στ εσωτερικό τυ σωληνειδύς, και μακριά από τα άκρα τυ, μπρύμε να εφαρμόσυμε τ νόμ τυ Ampee διαλέγντας τη διαδρμή ACD τυ σχήματς Έτσι λιπόν, έχυμε A L Σχήμα 9.15 Σωληνειδές με γραμμική πυκνότητα σπειρών n διαρρέεται από ρεύμα. Θεωρώντας κλειστή διαδρμή ACD, και εφαρμόζντας τν νόμ τυ Ampee, μπρύμε να υπλγίσυμε τ μαγνητικό πεδί Β στ εσωτερικό τυ σωληνειδύς. D διότι και C D A A dl μ dl dl dl dl L μ D περικλείν περικλείν A C D dl dl 0, εφόσν dl C
15 15 C dl 0 μιας και σε μεγάλη απόσταση «έξω» από τ σωληνειδές, (ΑΒ και DC πλύ μεγάλα) τ πεδί σχεδόν μηδενίζεται, δηλ. Β=0. Σημειώστε ότι την πλευρά C τυ δρόμυ ACD, μπρύμε να την εωρήσυμε όσ μακριά έλυμε από τ πηνί. Τ ηλεκτρικό ρεύμα λιπόν, τ πί διαρρέει τν βρόχ ACD, είναι τ ρεύμα πυ διαρρέει κάε σπείρα επί τν αριμό των σπειρών πυ αντιστιχύν στ μήκς L τυ μήκυς AD τυ βρόχυ. Εάν τ σωληνειδές περιέχει n σπείρες ανά μνάδα μήκυς, και είναι τ ρεύμα πυ διαρρέει την κάε σπείρα, τότε τ συνλικό ρεύμα πυ περικλείεται στν κλειστό δρόμ ACD, είναι πότε περικλείν nl dl μ περικλείν L μnl μn (9.9) Η εξ. 9.9 εκφράζει τ μαγνητικό πεδί στ εσωτερικό μέρς τυ σωληνειδύς (Alns & Finn, 199), (Halliday, Resnick & Kane, 009), (Knight, 010), (Giancli, 01), (Seway & Jewett, 013). Εάν η πυκνότητα των σπειρών είναι μεγάλη, και τ μήκς τυ σωληνειδύς είναι αρκετά μεγαλύτερ από την ακτίνα των σπειρών, τότε τ σωληνειδές νμάζεται ιδανικό ή πηνί, και τ πεδί Β είναι σταερό σ όλ τ εσωτερικό τυ, εξαιρυμένων των περιχών κντά στα άκρα τυ. Επίσης στ εξωτερικό μέρς τυ ιδανικύ σωληνειδύς, επειδή ι μαγνητικές δυναμικές γραμμές είναι πλύ αραιές, τ πεδί Β είναι πλύ μικρό, ώστε πρακτικά να τ εωρύμε μηδέν (βλ. σχ. 9.16γ). Συμπερασματικά λιπόν, τ μαγνητικό πεδί Β ενός σωληνειδύς τ πί διαρρέεται από ρεύμα, είναι μηδενικό εκτός τυ σωληνειδύς, και μγενές στ εσωτερικό τυ, με διεύυνση αυτή τυ άξνα συμμετρίας τυ σωληνειδύς, και φρά αυτήν πυ καρίζεται από τν κανόνα τυ δεξιύ χεριύ, με τα δάκτυλα να δείχνυν την φρά τυ ρεύματς και τν αντίχειρα αυτή τυ πεδίυ. Στη συνέχεια α εωρύμε τα πηνία ιδανικά, ώστε τ μαγνητικό τυς πεδί σε κάε σημεί τυ εσωτερικύ τυς, να δίνεται από την εξ Οι βρόχι και τα πηνία ως μαγνήτες Ένας ρευματφόρς βρόχς και κατά επέκταση ένα σωληνειδές πυ διαρρέεται από ηλεκτρικό ρεύμα, δημιυργύν τα δικά τυς μαγνητικά πεδία, τα πία μιάζυν με τα μαγνητικά πεδία των μαγνητών. Στ σχ φαίνεται η μιότητα των μαγνητικών πεδίων πυ σχηματίζνται από έναν ραβδόμρφ μαγνήτη, έναν ρευματφόρ κυκλικό βρόχ και ένα ρευματφόρ πηνί (Knight, 010). Είναι φανερό, ότι ι βρόχι και τα πηνία πυ διαρρένται από ηλεκτρικό ρεύμα, συμπεριφέρνται σαν μαγνήτες, αφύ αναλόγως Β N S Β Β (α) (β) (γ) Σχήμα 9.16 Μαγνητικές δυναμικές γραμμές (α) ενός μαγνητικύ διπόλυ, (β) ενός ρευματφόρυ βρόχυ, και (γ) ενός ρευματφόρυ πηνίυ. Πρσέξτε την μιότητα όλων των μαγνητικών πεδίων. την κατεύυνση των μαγνητικών δυναμικών γραμμών τυ μαγνητικύ τυς πεδίυ στ χώρ, μπρύμε να ρίσυμε τυς μαγνητικύς τυς πόλυς (βλ. σχ. 9.16). Κατά συνέπεια, εάν ένας ρευματφόρς βρόχς ή πηνί ευρεύν μέσα σε μγενές μαγνητικό πεδί, η συμπεριφρά τυς α είναι όμια με αυτή των φυσικών μαγνητών, δηλ. α ασκηεί πάνω τυς ρπή, η πία α τείνει να ευυγραμμίσει τ μαγνητικό τυς
16 16 πεδί με αυτό τυ Β, όπως δείχνει τ σχ. 9.17, για την περίπτωση ενός ραβδόμρφυ φυσικύ μαγνήτη. Με άλλα λόγια η μαγνητική διπλική ρπή μ τυ μαγνήτη (βρόχυ ή πηνίυ), τείνει να ευυγραμμιστεί με τ εξωτερικό μαγνητικό πεδί Β, διότι ασκεί ρπή πάνω τυς (βλ. εδάφι 8.8). 9.8 Αλληλεπίδραση μαγνητών Η εικόνα τυ φυσικύ ραβδόμρφυ μαγνήτη με την μαγνητική διπλική ρπή μ να είναι διάνυσμα, τ πί κατευύνεται από τν νότι μαγνητικό πόλ στν αντίστιχ βόρει (βλ. σχ. 9.17), βηά να καταλάβυμε την αλληλεπίδραση μεταξύ των μαγνητών, δηλ την άπωση και έλξη των μαγνητών, τις πίες περιγράψαμε πιτικά στ εδάφι 8.1. Έτσι, όταν δυ μαγνήτες πλησιάσυν αρκετά μεταξύ τυς, ώστε νότις πόλς τυ ενός να πρσεγγίζει τν νότι πόλ τυ άλλυ, η διπλική μαγνητική ρπή τυ ενός μαγνήτη ευρίσκεται μέσα στ μαγνητικό πεδί τυ άλλυ. Σ αυτήν την περίπτωση, η μαγνητική διπλική ρπή μ τυ ενός μαγνήτη είναι αντιπαράλληλη με τ μαγνητικό πεδί Β πυ δημιυργεί έτερς μαγνήτης, όπως δείχνει τ σχ. 9.18α. Ο αντιπαράλληλς πρσανατλισμός των μ και Β, δημιυργεί μια απωστική δύναμη μεταξύ των μαγνητών, διότι δεν είναι ενεργειακά πρτιμητές, μιας και αντιστιχεί σε ετική μαγνητική δυναμική ενέργεια τυ συστήματς των δύ μαγνητών, ίση με U μ Β(βλ. εξ. 8.41). Έτσι για αντιπαράλληλ πρσανατλισμό των μ και Β (U ετική), όσ μικρότερη είναι η απόσταση των δύ μαγνητών, τόσ μεγαλύτερη α είναι η μαγνητική δυναμική ενέργεια (πι ετική) τυ συστήματός τυς, διότι τ πεδί Β αυξάνεται όσ μειώνεται η απόσταση μεταξύ των μαγνητών. Τ σύστημα των μαγνητών αντιτίεται στην μεγιστπίηση της δυναμικής τυ ενέργειας, και τείνει να την μειώσει, απωώντας ένας μαγνήτης τν άλλ. Ανάλγη εξήγηση μπρεί να δεί και για την άπωση μεταξύ βρείων μαγνητικών πόλων, μιας και σε αυτή την περίπτωση η μαγνητική διπλική ρπή τυ ενός μαγνήτη είναι αντιπαράλληλη με τ μαγνητικό πεδί τυ άλλυ μαγνήτη. Έτσι λιπόν εξηγείται, γιατί ι μώνυμι μαγνητικί πόλι πάντα απωύνται. Αντιέτως, όταν δυ Ν Ν μ μ S S F απ Β F ελκ Β F απ F ελκ (β) Σχήμα 9.18 Αλληλεπίδραση μαγνητικών διπόλων. (α) Απωστική δύναμη μεταξύ μώνυμων μαγνητικών πόλων, όπυ η μαγνητική διπλική ρπή μ τυ ενός μαγνήτη είναι αντιπαράλληλη με τ μαγνητικό πεδί Β πυ δημιυργεί άλλς μαγνήτης. (β) Ελκτική δύναμη μεταξύ ετερώνυμων μαγνητικών πόλων, όπυ πρσανατλισμός των μ και Β είναι παράλληλς (βλ. κείμεν). S N N S (α) μαγνήτες πλησιάσυν αρκετά μεταξύ τυς, ώστε νότις μαγνητικός πόλς τυ ενός, να πρσεγγίζει τν βόρει μαγνητικό πόλ τυ άλλυ, τότε η μαγνητική διπλική ρπή μ τυ ενός μαγνήτη, είναι παράλληλη με τ μαγνητικό πεδί Β πυ δημιυργεί άλλς μαγνήτης, όπως δείχνει τ σχ.9.18β. Τότε μια ελκτική δύναμη δημιυργείται μεταξύ των μαγνητών, διότι παράλληλς πρσανατλισμός των μ και Β (U αρνητική), είναι ενεργειακά πρτιμητές, μιας και αντιστιχεί σε ελάχιστη μαγνητική δυναμική ενέργεια (βλ. εξ. 8.41). Όσ μικρότερη είναι η απόσταση μεταξύ των μαγνητών, τόσ μικρότερη α είναι η μαγνητική δυναμική ενέργεια τυ συστήματς (πι αρνητική), διότι τ μαγνητικό πεδί Β αυξάνεται περισσότερ, όσ η απόσταση μεταξύ των μαγνητών μικραίνει. Έτσι λιπόν εξηγείται γιατί ι ετερώνυμι μαγνητικί πόλι πάντα έλκνται μεταξύ τυς, μέχρι να έρει ένας σε επαφή με τν άλλ, όπυ και ηρεμύν, διότι τότε η μαγνητική δυναμική ενέργεια ελαχιστπιείται (μέγιστη αρνητική τιμή). Με τν ίδι τρόπ πυ αλληλεπιδρύν μεταξύ τυς ι μαγνήτες, αλληλεπιδρύν και ι ρευματφόρι βρόχι και τα πηνία. S τ μ Σχήμα 9.17 Μαγνήτης σε τυχαί πρσανατλισμό μέσα σε μγενές μαγνητικό πεδί. Η ασκύμενη ρπή τ πάνω τυ, τείνει να τν περιστρέψει ώστε η μαγνητική διπλική ρπή τυ μ, να ευυγραμμιστεί με τ μαγνητικό πεδί. φ Ν
17 Μαγνητικά υλικά * Τ ερώτημα πυ μπρεί κάπις να έσει τώρα είναι, γιατί κάπια υλικά είναι μαγνήτες και δημιυργύν μαγνητικό πεδί στ χώρ, και κάπια άλλα όχι; Είδαμε στ εδάφι 9.7 την μιότητα πυ παρυσιάζει τ μαγνητικό πεδί ενός ραβδόμρφυ μαγνήτη, με τα αντίστιχα μαγνητικά πεδία ενός ρευματφόρυ βρόχυ και ενός πηνίυ. Ο βρόχς και τ πηνί δεν μπρύν να δημιυργήσυν μαγνητικό πεδί, όταν δεν διαρρένται από ηλεκτρικό ρεύμα. Μήπως τελικά η δημιυργία κάε μαγνητικύ πεδίυ και συνεπώς η ύπαρξη των μαγνητών στη Φύση, φείλεται απκλειστικά στ ηλεκτρικό ρεύμα; Η απάντηση είναι καταφατική, αρκεί να Όχι μαγνήτης μ=0 Μαγνήτης μ Σχήμα 9.19 (α) Οι τυχαίι πρσανατλισμί των ατμικών μαγνητικών διπλικών ρπών, δεν πρσδίδυν μαγνητικές ιδιότητες στ υλικό. (β) Οι πρσανατλισμένες μαγνητικές διπλικές ρπές των ατόμων ενός υλικύ, τύ πρσδίδυν την μακρσκπική μαγνητική διπλική ρπή μ, καιστώντας τ μαγνήτη. εωρήσυμε τα υλικά ως ένα σύνλ ατόμων. Πράγματι, εάν εξετάσυμε μικρσκπικά τα άτμα ενός υλικύ, α ιδύμε τα ηλεκτρόνια να κινύνται γύρω από τυς πυρήνες των ατόμων. Η κίνηση αυτή των ηλεκτρνίων δημιυργεί ένα μεγάλ πλής μικρσκπικών (στην πραγματικότητα νανσκπικών) ρευματφόρων βρόχων, καένας των πίων δημιυργεί μια μαγνητική διπλική ρπή μ, σύμφωνα με τ σχ. 8.13, και τ παράδειγμα 8.5. [3] Στην υσία ι βρόχι αυτί είναι νητί και αντιστιχύν τόσι βρόχι ανά άτμ τυ υλικύ, όσα είναι τα ηλεκτρόνια τυ ατόμυ. Τ διανυσματικό άρισμα των μαγνητικών διπλικών ρπών των ηλεκτρνίων ενός ατόμυ, πρσδίδει μια συνλική μαγνητική διπλική ρπή σε κάε άτμ τυ υλικύ. [4] Τ άρισμα όλων αυτών των ατμικών μαγνητικών διπλικών ρπών, μπρεί να πρσδώσει στ υλικό μια συνλική μακρσκπική μαγνητική διπλική ρπή μ (Halliday, Resnick & Kane, 009). Εάν τ πλής των ατμικών μαγνητικών διπλικών ρπών είναι τυχαίως πρσανατλισμένες μεταξύ τυς, ή είναι μηδενικές, η συνλική μαγνητική διπλική ρπή μ τυ υλικύ είναι μηδέν, και τ υλικό δεν δημιυργεί μαγνητικό πεδί στ χώρ, δηλ. δεν είναι μαγνήτης, όπως δείχνει τ σχ. 9.19α (Knight, 010). Αυτό ισχύει για τα περισσότερα υλικά στην Φύση, τα πία παρατηρύμε ότι δεν είναι μαγνήτες. Εάν όμως η πλεινότητα των ατμικών μαγνητικών διπλικών ρπών είναι πρσανατλισμένες μεταξύ τυς, ή πρσανατλιστύν με την εφαρμγή ενός εξωτερικύ μαγνητικύ πεδίυ, τότε τ άρισμά τυς δίνει στ υλικό μια μακρσκπική μαγνητική διπλική ρπή μ, μη μηδενική, η πία καιστά τ υλικό μαγνήτη, όπως δείχνει τ σχ. 9.19β (Halliday, Resnick & Kane, 009), (Yung & Feedman, 010). Από τα παραπάνω συμπεραίνυμε λιπόν, ότι η αιτία για τις μαγνητικές ιδιότητες των υλικών, και επμένως για την ύπαρξη των μαγνητών, είναι τ ηλεκτρικό ρεύμα, δηλ. η κίνηση φρτίων σε ατμική κλίμακα. Βάσει της ευυγράμμισης των ατμικών μαγνητικών διπλικών ρπών, μπρύμε να εξηγήσυμε γιατί ρισμένα υλικά απκτύν μαγνητικές ιδιότητες, όταν ευρεύν εντός μαγνητικύ πεδίυ. Συγκεκριμένα, εάν ένα υλικό τ πί δεν είναι μαγνήτης πλησιάσει στ χώρ ενός ισχυρύ μαγνήτη, ι ατμικές μαγνητικές διπλικές ρπές α αλληλεπιδράσυν με τ μαγνητικό πεδί τυ μαγνήτη, και α ευυγραμμιστύν με αυτό, έτσι ώστε τ μή μαγνητικό αρχικά υλικό να απκτήσει μαγνητικές ιδιότητες, δηλ. να συμπεριφέρεται και αυτό ως μαγνήτης. Εάν στη συνέχεια, τ υλικό απμακρυνεί από τ μαγνητικό πεδί τυ ισχυρύ μαγνήτη, και εξακλυεί να έχει πρσανατλισμένα τα ατμικά μαγνητικά τυ δίπλα (βλ. σχ.9.19β), ώστε να απτελεί τ ίδι έναν μαγνήτη, τότε τ υλικό νμάζεται σιδηρμαγνητικό υλικό και τ φαινόμεν σιδηρμαγνητισμός (Seas, 1951), (Feynman, Leightn & Sands, 009), (Knight, 010). Ο σιδηρμαγνητισμός φείλεται στ κβαντμηχανικό φαινόμεν της σύζευξης εναλλαγής, κατά τ πί τα σπιν των ηλεκτρνίων ενός ατόμυ αλληλεπιδρύν με τα σπιν των ηλεκτρνίων των γειτνικών ατόμων, έτσι ώστε η ευυγράμμιση των ατμικών μαγνητικών ρπών να απδίδει στα σιδηρμαγνητικά υλικά έναν μόνιμ μαγνητικό χαρακτήρα (Halliday, Resnick & Walke, 013). Σιδηρμαγνητικά υλικά είναι ρισμένα μέταλλα όπως σίδηρς, τ κβάλτι, τ νικέλι και κράματα αυτών των στιχείων. Αν για κάπι λόγ, σ ένα [3] Στην πραγματικότητα η συνλική διπλική μαγνητική ρπή ενός ηλεκτρνίυ, είναι τ διανυσματικό άρισμα δύ επιμέρυς μαγνητικών διπλικών ρπών, μία λόγω της κίνησής τυ γύρω από τν πυρήνα, και μία δεύτερη λόγω της ιδιστρφρμής τυ, πυ εκφράζεται με τ σπιν τυ ηλεκτρνίυ. [4] Μια συνεισφρά στην ατμική μαγνητική ρπή τυ ατόμυ, πρέρχεται από τν πυρήνα, διότι και αυτός παρυσιάζει μαγνητική ρπή, λόγω της μαγνητικής ρπής των πρωτνίων και των νετρνίων. Η πυρηνική μαγνητική ρπή όμως, είναι μερικές τάξεις μεγέυς μικρότερη αυτής των ηλεκτρνίων, και συχνά παραλείπεται. (α) S (β) Ν
18 18 σιδηρμαγνητικό υλικό πάψει να υπάρχει πρσανατλισμός των ατμικών μαγνητικών διπόλων, τότε τ υλικό παύει να είναι μαγνήτης και συνεπώς ι μακρσκπικές μαγνητικές τυ ιδιότητες χάννται. Κάτι τέτι μπρεί να συμβεί με έρμανση τυ υλικύ σε ερμκρασίες πάνω από μια συγκεκριμένη ερμκρασία, η πία νμάζεται ερμκρασία Cuie (Κιυρί). Στη ερμκρασία Cuie και πάνω από αυτή, η ερμική ενέργεια των μαγνητικών διπόλων είναι τέτια, ώστε μεταξύ τυς παράλληλς πρσανατλισμός να είναι αδύνατς. Ένας άλλς τρόπς για την απμαγνήτιση ενός σιδηρμαγνητικύ υλικύ, είναι η τπέτησή τυ σε κατάλληλ μαγνητικό πεδί, τέτιας κατεύυνσης ώστε να επέλει αππρσανατλισμός των ατμικών διπλικών ρπών. Εάν με την απμάκρυνση τυ υλικύ από ένα εξωτερικό μαγνητικό πεδί, ι ατμικές μαγνητικές διπλικές ρπές τυ αππρσανατλιστύν, έτσι ώστε να πάψει να είναι μαγνήτης, τ υλικό νμάζεται παραμαγνητικό υλικό και τ φαινόμεν παραμαγνητισμός (Lbkwicz & Melissins, 1975), (Gant & Phillips, 1975), Halliday, Resnick & Walke, 013). Επίσης, εάν ένα υλικό, τυ πίυ τα άτμα ή μόρια δεν εμφανίζυν μόνιμες μαγνητικές διπλικές ρπές, ευρεεί εντός μαγνητικύ πεδίυ ώστε τ υλικό να απκτήσει μακρσκπική μαγνητική διπλική ρπή με κατεύυνση αντίετη τυ εξωτερικύ μαγνητικύ πεδίυ, τότε τ υλικό νμάζεται διαμαγνητικό υλικό και τ φαινόμεν διαμαγνητισμός (Feynman, Leightn & Sands, 009), (Yung & Feedman, 010), (Halliday, Resnick & Walke, 013). Τ φαινόμεν τυ διαμαγνητισμύ φείλεται στ νόμ της μαγνητικής επαγωγής τυ Faaday, και πι συγκεκριμένα στν κανόνα τυ Lenz, ι πίι αμφότερι α μελετηύν στ επόμεν κεφάλαι. Όλα τα μαγνητικά φαινόμενα τυ σιδηρμαγνητισμύ, παραμαγνητισμύ και διαμαγνητισμύ, είναι επαγωγικά φαινόμενα πυ πρκύπτυν από την αλληλεπίδραση ενός εξωτερικύ μαγνητικύ πεδίυ με ένα υλικό. Η πλήρης κατανόηση και περιγραφή των μαγνητικών φαινμένων τυ παραμαγνητισμύ και διαμαγνητισμύ, δεν μπρεί να γίνει στα πλαίσια της κλασσική μηχανικής, αλλά μόν σ αυτά της κβαντικής μηχανικής, (Feynman, Leightn & Sands, 009). Κάτι τέτι ξεφεύγει από τυς στόχυς τυ παρόντς συγγράμματς, γι αυτό και δεν α επεκταύμε περισσότερ. Γενικά, κάε υλικό στη Φύση παρυσιάζει μαγνητικές ιδιότητες, έστω και σε κάπι μικρό βαμό. Υπάρχει μια φυσική πσότητα η πία μάς βηά να περιγράψυμε πστικά τις μαγνητικές ιδιότητες ενός σώματς, η πία νμάζεται μαγνήτιση Μ, είναι διάνυσμα, και τ μέτρ της ρίζεται ως τ πηλίκ της μαγνητικής διπλικής ρπής μ τυ σώματς, με τν όγκ τυ V, δηλ. ισχύει M μ (9.30) V (Halliday, Resnick & Kane, 009), (Yung & Feedman, 010), (Giancli, 01). Ευρίσκεται πειραματικώς, ότι η μαγνήτιση ενός παραμαγνητικύ υλικύ είναι ανάλγη τυ εξωτερικύ μαγνητικύ πεδίυ Β μέσα στ πί τπετείται ένα υλικό, ενώ είναι αντιστρόφως ανάλγη της ερμκρασίας Τ τυ υλικύ. Αυτύ τυ είδυς η εξάρτηση είναι λγική, αν κάπις σκεφτεί ότι τ μαγνητικό πεδί πρσανατλίζει τις ατμικές μαγνητικές διπλικές ρπές τυ υλικύ, ενώ η ερμκρασία τυ τείνει να τις αππρσανατλίσει, λόγω της τυχαίας ερμικής κίνησης των ατόμων ή μρίων. Η εξάρτηση της μαγνήτισης από τ μαγνητικό πεδί και την ερμκρασία, εκφράζεται από τν νόμ τυ Cuie, πρς τιμή τυ Γάλλυ φυσικύ Γάλλυ Piee Cuie ( ), πίς πρώτς τν ανακάλυψε. Σύμφωνα λιπόν με τ νόμ τυ Cuie ισχύει ότι Β M C (9.31) Τ όπυ C είναι μια σταερά πυ νμάζεται σταερά Cuie, η τιμή της πίας εξαρτάται από τ υλικό (Halliday, Resnick & Kane, 009), (Giancli, 01). Καώς αυξάνεται η ένταση τυ πεδίυ Β, αυξάνεται και η μαγνήτιση μέχρι μια μέγιστη τιμή, η πία νμάζεται μαγνήτιση κόρυ, όπυ όλες ι ατμικές μαγνητικές διπλικές ρπές ευυγραμμίζνται πλήρως με τ πεδί (Αλεξόπυλς & Μαρίνς, 199), (Yung & Feedman, 010). Τότε, περαιτέρω αύξηση τυ μαγνητικύ πεδίυ δεν μπρεί να αυξήσει πλέν την μαγνήτιση τυ υλικύ. Στην πραγματικότητα νόμς τυ Cuie, δηλ. η γραμμική σχέση μεταξύ των Μ και Β, ισχύει για τιμές τυ Μ αρκετά μικρότερες της μαγνήτισης κόρυ, ή γενικότερα για μικρές τιμές τυ λόγυ Β/Τ. Τελειώνντας, πρέπει να επισημάνυμε ότι τα μαγνητικά υλικά και η Piee Cuie ( ) ( Piee_Cuie). Τ παρόν έργ απτελεί κινό κτήμα (public dmain).
19 19 μελέτη των ιδιτήτων τυς, απτελύν ένα ξεχωριστό και ευρύ κλάδ της Φυσικής. Τα μαγνητικά υλικά είναι εξαιρετικά χρήσιμα μιας και χρησιμπιύνται σε πλλές τεχνλγικές εφαρμγές, όπως για παράδειγμα στυς ηλεκτρμαγνήτες, στυς μετασχηματιστές, στυς κινητήρες των αυτκινήτων, στυς σκληρύς δίσκυς των υπλγιστών, στις μαγνητικές ταινίες των πιστωτικών καρτών, σε ιατρικά διαγνωστικά μηχανήματα, κ.ά. ΕΡΩΤΗΣΕΣ ΚΑ ΠΡΟΒΛΗΜΑΤΑ ΚΕΦΑΛΑΟΥ 9 ΕΡΩΤΗΣΕΣ Ε9.1 Υπάρχει τρόπς να δημιυργήσυμε ένα μαγνητικό πεδί στ χώρ, χωρίς να αναγκάσυμε σε κίνηση ηλεκτρικά φρτία, δηλ. δίχως την ύπαρξη ηλεκτρικύ ρεύματς; Ε9. Έστω δύ ηλεκτρικά φρτία, τα πία κινύνται παράλληλα τ ένα ως πρς τ άλλ με την ίδια ταχύτητα. Συγκρίνετε τις κατευύνσεις των αμιβαίων ηλεκτρικών και μαγνητικών δυνάμεων όταν, α) τα φρτία έχυν τ ίδι πρόσημ φρτίυ, και β) τα φρτία έχυν αντίετ πρόσημ φρτίυ. Ε9.3 Συγκρίνετε τν νόμ των it-savat με τν νόμ τυ Culmb. Πιες μιότητες και διαφρές παρατηρείτε; Ε9.4 Τ σχ. 9.0 δείχνει την κάτψη τεσσάρων τετραγωνικών διατάξεων, στις πίες παράλληλα σύρματα μεγάλυ μήκυς διαρρένται από ρεύματα ίσης εντάσεως, με κατεύυνση είτε πρς τ εσωτερικό της σελίδας ( ), είτε από την σελίδα πρς τα «έξω» ( ). Κατατάξτε τις διατάξεις των συρμάτων σύμφωνα με τ συνλικό μαγνητικό πεδί στ κέντρ τυ κάε τετραγώνυ, με φίνυσα σειρά, δηλ. ξεκινώντας από την διάταξη με τ μέγιστ πεδί και καταλήγντας σ αυτήν με τ μικρότερ. (α) (β) (γ) (δ) Σχήμα 9.0 Ερώτηση 9.4. Ε9.5 Δύ ευύγραμμα μεγάλυ μήκυς σύρματα διασταυρώννται κάετα, έτσι ώστε ίσα να μην ακυμπύν μεταξύ τυς, όπως δείχνει τ σχ Κάε σύρμα διαρρέεται από σταερό ρεύμα. Σε πιες περιχές τυ χώρυ υπάρχυν σημεία στα πία τ συνλικό μαγνητικό πεδί είναι μηδέν; Ε9.6 Για τα σύρματα της παραπάνω ερώτησης (σχ. 9.1), να περιγραφύν ι μαγνητικές δυνάμεις πυ ασκεί τ ένα σύρμα στ άλλ. Ε9.7 Εντπίστε πιτικά τις αναλγίες και τις διαφρές μεταξύ των νόμων Gauss και Ampee. Ε9.8. Ένας μακρύς χάλκινς σωλήνας διαρρέεται από σταερό ρεύμα, όπως δείχνει τ σχ. 9.. Δημιυργείται μαγνητικό πεδί α) στ εσωτερικό, και β) στ εξωτερικό χώρ τυ σωλήνα; Εξηγείστε τις απαντήσεις σας με τ νόμ τυ Ampee. Περιχή 1 Περιχή Περιχή 4 Περιχή 3 Σχήμα 9.1 Ερώτηση 9.5.
20 0 Σχήμα 9. Ερώτηση 9.8. Ε9.9 Ένα ελικειδές πηνί, τ πί είναι ταυτχρόνως και ελατήρι, διαρρέεται ξαφνικά από ηλεκτρικό ρεύμα. Παρατηρύμε ότι τ ελατήρι συστέλλεται, δηλ. ι σπείρες τυ πλησιάζυν η μία την άλλη. Εξηγείστε γιατί συμβαίνει αυτό. Ε9.10 Έχυμε τρία ιδανικά σωληνειδή: τ Α με μήκς L και Ν σπείρες, τ Β με μήκς L και επίσης Ν σπείρες, και τ Γ με μήκς L/ και Ν σπείρες. Αν όλα τα σωληνειδή φέρυν τ ίδι ηλεκτρικό ρεύμα, ταξινμείστε τ μαγνητικό πεδί στ εσωτερικό τυ καενός. Ξεκινήστε από την μεγαλύτερη τιμή τυ Β και καταλήξτε στην μικρότερη. Ε9.11 Ένας απλός ραβδόμρφς μαγνήτης κρέμεται από ένα νήμα, όπως φαίνεται στ σχ Εφαρμόζυμε ξαφνικά στ χώρ ένα μγενές ριζόντι μαγνητικό πεδί Β με φρά πρς τα δεξιά. Σχεδιάστε την έση τυ νήματς και τυ μαγνήτη στ χώρ μέσα στ πεδί. Απαντήστε στην ίδια ερώτηση για την φρά τυ Β πρς τα αριστερά. N S Σχήμα 9.3 Ερώτηση ΠΡΟΒΛΗΜΑΤΑ Π9.1 Μαγνητικό πεδί ρευματφόρυ αγωγύ. Ένας ρευματφόρς αγωγός έχει την μρφή πυ φαίνεται στ σχ Συγκεκριμένα απτελείται από έναν κυκλικό βρόχ ακτίνας 0.0 cm, και δύ ευύγραμμα τμήματα μεγάλυ μήκυς. Ο αγωγός φέρει ηλεκτρικό ρεύμα 1.50 Α, με φρά αυτή πυ δείχνεται στ σχήμα. Να Κ υπλγίσετε τ μαγνητικό πεδί (μέτρ και κατεύυνση) στ κέντρ τυ βρόχυ. Δίνεται η διαπερατότητα Λ τυ κενύ μ =με 4π 10-7 Tm/A. α Απάντηση: Β=6.1 μτ. Ο α Μ Ν Σχήμα 9.5 Πρόβλημα 9.. Π9. Μαγνητικό πεδί ρευματφόρυ αγωγύ. Υπλγίστε τ μαγνητικό πεδί πυ δημιυργείται στ σημεί Ο, από τ ρευματφόρ τμήμα τυ αγωγύ ΚΛΜΝ τυ σχήματς 9.5. Τ τμήμα ΛΜ είναι τμήμα κύκλυ ακτίνας α και επίκεντρης γωνίας. Τ ρεύμα τυ αγωγύ είναι. Απάντηση: μ = 4 πα. Π9.3 Κίνηση ηλεκτρνίυ σε μαγνητικό πεδί ευυγράμμυ ρευματφόρυ αγωγύ. Μακρύ ευύγραμμ σύρμα διαρρέεται από ηλεκτρικό ρεύμα 3.0 Α. Ένα ηλεκτρόνι βάλλεται παράλληλα πρς αυτό τ σύρμα σε απόσταση 1.50 cm, με ταχύτητα 30 km/s και ίδιας φράς με αυτήν τυ ρεύματς. Να ευρεύν α) η αρχική επιτάχυνση (μέτρ και φρά) τυ ηλεκτρνίυ, και β) η κατεύυνση και τ μέτρ ενός μγενύς ηλεκτρικύ b πεδίυ, τ πί α επέτρεπε στ ηλεκτρόνι να συνεχίσει την παράλληλη πρς τ σύρμα πρεία τυ. γ) Χρειάζεται να ληφεί υπόψη η επίδραση της βαρύτητας στ ηλεκτρόνι; Δικαιλγείστε την απάντησή σας.. Δίννται μάζα και φρτί ηλεκτρνίυ, m e = kg και e= O C α αντίστιχα R Σχήμα 9.4 Πρόβλημα 9.1. Π9.4 Μαγνητικό πεδί ρευματφόρυ βρόχυ Νόμς των it και Savat. Στ σχ. 9.6 φαίνεται ρευματφόρς βρόχς πυ απτελείται από Σχήμα 9.6 Πρόβλημα 9.4.
21 1 δυ ευύγραμμα και δυ ημικυκλικά τμήματα ακτίνων, a=4.00 cm και b=7.50 cm αντιστίχως, με κινό κέντρ τ σημεί Ο. Τ ρεύμα τυ βρόχυ είναι έντασης =5.3 mα. α) Υπλγίστε τ μέτρ και την κατεύυνση τυ μαγνητικύ πεδίυ πυ δημιυργεί βρόχς στ σημεί Ο. β) Υπλγίστε τ μέτρ και την κατεύυνση της μαγνητικής διπλικής ρπής τυ βρόχυ. Π9.5 Μαγνητική δύναμη μεταξύ παραλλήλων ρευματφόρων αγωγών. Δύ παράλληλα ευύγραμμα ρευματφόρα σύρματα, απέχυν μεταξύ τυς απόσταση 5.00 cm, και απωύνται μεταξύ τυς με δύναμη ανά μνάδα μήκυς, ίση με Ν/m. Τ ρεύμα στ ένα σύρμα είναι 6.30 Α. α) Να υπλγίσετε τ ρεύμα στ άλλ σύρμα. β) Τα ρεύματα των δύ συρμάτων έχυν τις ίδιες ή διαφρετικές φρές; γ) Τί α συνέβαινε αν η ένταση τυ ρεύματς τυ ενός σύρματς διπλασιαζόταν, και η κατεύυνσή τυ αντιστρεφόταν; Ο Π9.6 Μαγνητικό πεδί παραλλήλων ρευματφόρων αγωγών. Δυ ευύγραμμι μεγάλυ μήκυς ρευματφόρι αγωγί είναι παράλληλι μεταξύ τυς, όπως δείχνει τ σχ Τα ρεύματά τυς είναι αντιπαράλληλα Σχήμα 9.7 Πρόβλημα 9.6. με 1 =5.00 Α και =10.0 Α. Να ευρείτε τ μέτρ και την κατεύυνση τυ μαγνητικύ πεδίυ πυ δημιυργείται στ σημεί O, όπυ 1 =5.00 cm και =15.0 cm. Εάν στ σημεί Ο τπετηεί ένας τρίτς παράλληλς ευύγραμμς αγωγός μήκυς.00 m, με ρεύμα εντάσεως 3 =.00 Α και φράς πρς τα «επάνω», να ευρεεί τ μέτρ και η κατεύυνση της δύναμης πυ α ασκηεί πάνω τυ. Δίνεται η διαπερατότητα τυ κενύ ίση με μ =4π 10-7 T m/a. Απάντηση: Ν. Π9.7 Μαγνητικό πεδί κίλυ κυλινδρικύ αγωγύ. Κίλς κυλινδρικός αγωγός έχει εσωτερική και εξωτερική ακτίνα a και b αντιστίχως, και διαρρέεται από ρεύμα μιόμρφα κατανεμημέν στην διατμή τυ. Να ευρεύν ι εκφράσεις για τ μαγνητικό πεδί () στις περιχές α) <a, β) a<<b και γ) >b. μ ( a ) μ Απάντηση: α) 0, β), και γ). π( b a ) π Π9.8 Νόμς τυ Ampee. Κάε ένας από τυς κτώ αγωγύς τυ σχήματς 9.8, διαρρέεται από ρεύμα.00 Α με φρά, είτε πρς τα «μέσα», είτε πρς τα «έξω» της σελίδας. Υπλγίστε τ λκλήρωμα dl για κάε μια από τις διαδρμές α και β. Δίνεται μ =4π 10-7 T m/a..... Π9.9 Μαγνητικό πεδί σωληνειδύς. Ένα σωληνειδές πηνί με μήκς 1.33 m και διάμετρ.60 cm, διαρρέεται από ρεύμα 17.8 Α. Τ μαγνητικό πεδί μέσα στ πηνί είναι.4 mt. Να ευρείτε τ μήκς τυ σύρματς πυ χρησιμπιήηκε για να κατασκευασεί τ πηνί. Δίνεται μ =4π 10-7 T m/a. Απάντηση: 109 m. (α) (β) Σχήμα 9.8 Πρόβλημα 9.8. Π9.10 Μαγνητικό πεδί ρευματφόρυ κυλινδρικύ αγωγύ. Η πυκνότητα ρεύματς J μέσα σ έναν συμπαγή κυλινδρικό αγωγό μεγάλυ μήκυς και ακτίνας R=7.68 mm, ακλυεί την κατεύυνση τυ κεντρικύ άξνα συμμετρίας και τ μέτρ της μεταβάλλεται γραμμικά με την ακτινική απόσταση από τν άξνα, σύμφωνα με την σχέση J=J /R, όπυ J =80 Α/m. Υπλγίσετε τ μέτρ τυ μαγνητικύ πεδίυ πυ δημιυργεί αγωγός στις απστάσεις, α) =0, β) =R/, και γ) =R. Π9.11 Μαγνητικές ιδιότητες ύλης. Μια ργώνια ράβδς σιδήρυ με διαστάσεις μήκυς 8.00 cm, πλάτυς 1.50 cm, και πάχυς 1.00 cm, είναι 100% κααρή χωρίς πρσμίξεις. Κάε άτμ σιδήρυ έχει μαγνητική διπλική ρπή ίση περίπυ με Α.m, και η πυκνότητα των ατόμων τυ σιδήρυ είναι περίπυ άτμα/m 3. Υπλγίσετε α) την μέγιστη μαγνήτιση πυ μπρεί να απκτήσει τ κμμάτι
Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Ενότητα: ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΙΚΟΥ ΡΕΥΜΑΤΟΣ. Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος
 Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) Ενότητα: ΜΑΓΝΗΤΚΟ ΠΕΔΟ ΗΛΕΚΤΡΚΟΥ ΡΕΥΜΑΤΟΣ Διδάσκων: Επίκυρς Καθηγητής Δημήτρις Βλάχς Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής Κεφάλαι 9 1
Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) Ενότητα: ΜΑΓΝΗΤΚΟ ΠΕΔΟ ΗΛΕΚΤΡΚΟΥ ΡΕΥΜΑΤΟΣ Διδάσκων: Επίκυρς Καθηγητής Δημήτρις Βλάχς Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής Κεφάλαι 9 1
ΜΑΓΝΗΤΙΚΗ ΔΥΝΑΜΗ ΠΑΝΩ ΣΕ ΑΓΩΓΟ ΠΟΥ ΔΙΑΡΡΕΕΤΑΙ ΑΠΟ ΡΕΥΜΑ
 ΜΑΓΝΗΤΙΚΗ ΔΥΝΑΜΗ ΠΑΝΩ ΣΕ ΑΓΩΓΟ ΠΟΥ ΔΙΑΡΡΕΕΤΑΙ ΑΠΟ ΡΕΥΜΑ Για ευθύγραμμ αγωγό μήκυς l σε μγενές μαγνητικό πεδί πυ σχηματίζει γωνία φ με αυτόν: dl d Ι l φ φ sin ΜΑΓΝΗΤΙΚΗ ΔΥΝΑΜΗ ΠΑΝΩ ΣΕ ΑΓΩΓΟ ΠΟΥ ΔΙΑΡΡΕΕΤΑΙ
ΜΑΓΝΗΤΙΚΗ ΔΥΝΑΜΗ ΠΑΝΩ ΣΕ ΑΓΩΓΟ ΠΟΥ ΔΙΑΡΡΕΕΤΑΙ ΑΠΟ ΡΕΥΜΑ Για ευθύγραμμ αγωγό μήκυς l σε μγενές μαγνητικό πεδί πυ σχηματίζει γωνία φ με αυτόν: dl d Ι l φ φ sin ΜΑΓΝΗΤΙΚΗ ΔΥΝΑΜΗ ΠΑΝΩ ΣΕ ΑΓΩΓΟ ΠΟΥ ΔΙΑΡΡΕΕΤΑΙ
ΣΤΑΤΙΚΑ ΗΜΜ ΠΕΔΙΑ. Καταναλισκόμενη ισχύς σε ωμικό αγωγό. Το έργο που παράγεται από το ηλεκτρικό πεδίο πάνω σ ένα ελεύθερο φορτίο του αγωγού είναι,
 Kεφ. 16 (Part III, pages 6-34) ΣΤΤΙΚ ΗΜΜ ΠΕΔΙ Καταναλισκόμενη ισχύς σε ωμικό αγωγό. Τ έργ πυ παράγεται από τ ηλεκτρικό πεδί πάνω σ ένα ελεύθερ φρτί τυ αγωγύ είναι, dw = f dr = qe υdt άρα Ρ = dw dt = qυ
Kεφ. 16 (Part III, pages 6-34) ΣΤΤΙΚ ΗΜΜ ΠΕΔΙ Καταναλισκόμενη ισχύς σε ωμικό αγωγό. Τ έργ πυ παράγεται από τ ηλεκτρικό πεδί πάνω σ ένα ελεύθερ φρτί τυ αγωγύ είναι, dw = f dr = qe υdt άρα Ρ = dw dt = qυ
Κεφάλαιο 4 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ ΚΑΙ ΕΝΕΡΓΕΙΑ
 Κεφάλαι 4 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ ΚΑΙ ΕΝΕΡΓΕΙΑ Σύνψη Στ τέταρτ τύτ κεφάλαι, ρίζνται ι φυσικές πσότητες τυ ηλεκτρικύ δυναμικύ και της ηλεκτρικής δυναμικής ενέργειας για σημειακά και μη φρτία. ενώ μελετάται τ
Κεφάλαι 4 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ ΚΑΙ ΕΝΕΡΓΕΙΑ Σύνψη Στ τέταρτ τύτ κεφάλαι, ρίζνται ι φυσικές πσότητες τυ ηλεκτρικύ δυναμικύ και της ηλεκτρικής δυναμικής ενέργειας για σημειακά και μη φρτία. ενώ μελετάται τ
ΜΕΘΟΔΟΣ ΕΙΔΩΛΩΝ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΜΕΘΟΔΟΣ ΕΙΔΩΛΩΝ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΜΕΘΟΔΟΣ ΕΙΔΩΛΩΝ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693
ροή ιόντων και µορίων
 ρή ιόντων και µρίων Θεωρύµε ένα διάλυµα µίας υσίας Α. Αν εξαιτίας της ύπαρξης διαφρών συγκέντρωσης ή ηλεκτρικύ πεδίυ όλες ι ντότητες (µόρια ή ιόντα) της υσίας Α κινύνται µέσα σ αυτό µε την ίδια ριακή ταχύτητα
ρή ιόντων και µρίων Θεωρύµε ένα διάλυµα µίας υσίας Α. Αν εξαιτίας της ύπαρξης διαφρών συγκέντρωσης ή ηλεκτρικύ πεδίυ όλες ι ντότητες (µόρια ή ιόντα) της υσίας Α κινύνται µέσα σ αυτό µε την ίδια ριακή ταχύτητα
ΑΠΑΝΤΉΣΕΙΣ ΠΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤAΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 2009 Επιμέλεια: Νεκτάριος Πρωτοπαπάς.
 ΑΑΝΤΉΣΕΙΣ ΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤAΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 009 Επιμέλεια: Νεκτάρις ρωτπαπάς 1. Σωστή απάντηση είναι η γ. ΘΕΜΑ 1. Σωστή απάντηση είναι η α. Σχόλι: Σε μια απλή αρμνική
ΑΑΝΤΉΣΕΙΣ ΑΝΕΛΛΗΝΙΩΝ ΕΞΕΤAΣΕΩΝ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ 009 Επιμέλεια: Νεκτάρις ρωτπαπάς 1. Σωστή απάντηση είναι η γ. ΘΕΜΑ 1. Σωστή απάντηση είναι η α. Σχόλι: Σε μια απλή αρμνική
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ 1 .1 ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΚΙΝΟΥΜΕΝΟΥ ΦΟΡΤΙΟΥ Ας θεωρούμε το μαγνητικό πεδίο ενός κινούμενου σημειακού φορτίου q. Ονομάζουμε τη θέση του φορτίου σημείο πηγής
Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος
 Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) Ενότητα: ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ ΚΑΙ ΕΝΕΡΓΕΙΑ Διδάσκων: Επίκυρς Καθηγητής Δημήτρις Βλάχς Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής Κεφάλαι4 1 Δημήτρις
Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) Ενότητα: ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ ΚΑΙ ΕΝΕΡΓΕΙΑ Διδάσκων: Επίκυρς Καθηγητής Δημήτρις Βλάχς Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής Κεφάλαι4 1 Δημήτρις
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙ ΕΥΤΙΚΟ Ι ΡΥΜΑ ΠΑΤΡΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ 22/06/2012 ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΙΑΣ
 ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ /6/ ΘΕΜΑ (3 μνάδες) (α) Η αντίσταση ενός D λευκόχρυσυ μετρήθηκε στη θερμκρασία πήξης τυ νερύ και βρέθηκε 8 Ω, ενώ στη συνέχεια μετρήθηκε σε θερμκρασία θ και βρέθηκε 448 Ω Να
ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ /6/ ΘΕΜΑ (3 μνάδες) (α) Η αντίσταση ενός D λευκόχρυσυ μετρήθηκε στη θερμκρασία πήξης τυ νερύ και βρέθηκε 8 Ω, ενώ στη συνέχεια μετρήθηκε σε θερμκρασία θ και βρέθηκε 448 Ω Να
γραπτή εξέταση στο µάθηµα ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 η εξεταστική περίδς από 6/0/ έως 06// γραπτή εξέταση στ µάθηµα ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείυ Τµήµα: Βαθµός: Ονµατεπώνυµ: Καθηγητές: ΑΤΡΕΙ ΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Στις παρακάτω ερωτήσεις να γράψετε
η εξεταστική περίδς από 6/0/ έως 06// γραπτή εξέταση στ µάθηµα ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ Τάξη: Γ Λυκείυ Τµήµα: Βαθµός: Ονµατεπώνυµ: Καθηγητές: ΑΤΡΕΙ ΗΣ ΓΙΩΡΓΟΣ ΘΕΜΑ Στις παρακάτω ερωτήσεις να γράψετε
ΜΙΑ ΚΡΟΥΣΗ ΣΤΟΙΧΕΙΩΔΩΝ ΣΩΜΑΤΙΔΙΩΝ
 ΜΙΑ ΚΡΟΥΣΗ ΣΤΟΙΧΕΙΩΔΩΝ ΣΩΜΑΤΙΔΙΩΝ Σωµάτι α (πυρήνας 4 He ) µε µάζα m a και φρτί q a =e και πυρήνας ασβεστίυ 40 Ca 0 µε µάζα mπυρ = 10m a και φρτί Q = 0 e πυρ, βρίσκνται αρχικά σε πλύ µεγάλη απόσταση µεταξύ
ΜΙΑ ΚΡΟΥΣΗ ΣΤΟΙΧΕΙΩΔΩΝ ΣΩΜΑΤΙΔΙΩΝ Σωµάτι α (πυρήνας 4 He ) µε µάζα m a και φρτί q a =e και πυρήνας ασβεστίυ 40 Ca 0 µε µάζα mπυρ = 10m a και φρτί Q = 0 e πυρ, βρίσκνται αρχικά σε πλύ µεγάλη απόσταση µεταξύ
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 02/02/2017 ΜΟΝΟ ΓΙΑ ΤΟΥΣ ΕΠΙ ΠΤΥΧΙΩ ΦΟΙΤΗΤΕΣ , (1) R1 R 2.0 V IN R 1 R 2 B R L 1 L
 ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΔΙΔΑΣΚΩΝ: Λ ΜΠΙΣΔΟΥΝΗΣ ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: //7 ΘΕΜΑ ( μνάδες) Οι τιμές των αντιστάσεων και τυ κυκλώματς τυ
ΤΕΙ ΔΥΤΙΚΗΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΔΙΔΑΣΚΩΝ: Λ ΜΠΙΣΔΟΥΝΗΣ ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: //7 ΘΕΜΑ ( μνάδες) Οι τιμές των αντιστάσεων και τυ κυκλώματς τυ
ΠΟΛΩΤΙΚΑ ΦΙΛΤΡΑ (Polaroids)
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 94677 ΠΟΛΩΤΙΚΑ ΦΙΛΤΡΑ (Plarids) Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 94677 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 94677 4. Πόλωση
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 94677 ΠΟΛΩΤΙΚΑ ΦΙΛΤΡΑ (Plarids) Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 94677 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 94677 4. Πόλωση
Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος
 Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) νότητα: ΝΟΜΟΣ ΤΟΥ GAUSS Διδάσκων: πίκυρς Καθηγητής Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής ΚΦΑΛΑΙΟ 3 Ο ΝΟΜΟΣ ΤΟΥ GAUSS 3.1 Ηλεκτρική ρή Όπως
Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) νότητα: ΝΟΜΟΣ ΤΟΥ GAUSS Διδάσκων: πίκυρς Καθηγητής Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής ΚΦΑΛΑΙΟ 3 Ο ΝΟΜΟΣ ΤΟΥ GAUSS 3.1 Ηλεκτρική ρή Όπως
ΘΕΜΑ 1ο. Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΘΕΜΑ 1 Να γράψετε στ τετράδιό σας τν αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα τ γράμμα πυ αντιστιχεί στη σωστή απάντηση. 1. Αν δείκτης διάθλασης ενός πτικύ υλικύ μέσυ είναι n= 4 3 ακτινβλία
ΘΕΜΑ 1 Να γράψετε στ τετράδιό σας τν αριθμό καθεμιάς από τις παρακάτω ερωτήσεις 1-4 και δίπλα τ γράμμα πυ αντιστιχεί στη σωστή απάντηση. 1. Αν δείκτης διάθλασης ενός πτικύ υλικύ μέσυ είναι n= 4 3 ακτινβλία
ΜΕΘΟ ΟΣ ΡΕΥΜΑΤΩΝ ΒΡΟΧΩΝ
 Εισαγωγή Ρεύµατα βρόχων ΜΕΘΟ ΟΣ ΡΕΥΜΑΤΩΝ ΒΡΟΧΩΝ Η µέθδς ρευµάτων βρόχων για την επίλυση κυκλωµάτων (ή δικτύων) είναι υσιαστικά εφαρµγή τυ νόµυ τάσεων τυ Kirchhff µε κατάλληλη εκλγή κλειστών βρόχων ρεύµατς.
Εισαγωγή Ρεύµατα βρόχων ΜΕΘΟ ΟΣ ΡΕΥΜΑΤΩΝ ΒΡΟΧΩΝ Η µέθδς ρευµάτων βρόχων για την επίλυση κυκλωµάτων (ή δικτύων) είναι υσιαστικά εφαρµγή τυ νόµυ τάσεων τυ Kirchhff µε κατάλληλη εκλγή κλειστών βρόχων ρεύµατς.
( ) 11.4 11.7. Μέτρηση κύκλου. α 180. Μήκος τόξου µ ο : Μήκος τόξου α rad : l = αr. Σχέση µοιρών ακτινίων : Εµβαδόν κυκλικού δίσκου : Ε = πr 2
 1 11. 11.7 Μέτρηση κύκλυ ΘΩΡΙ Μήκς τόξυ µ : µ 180 Μήκς τόξυ α rad : αr Σχέση µιρών ακτινίων : α π µ 180 µβαδόν κυκλικύ δίσκυ : ( ) µβαδόν κυκλικύ τµέα µ : µ µβαδόν κυκλικύ τµέα α rad : ( ) 1 αr µβαδόν
1 11. 11.7 Μέτρηση κύκλυ ΘΩΡΙ Μήκς τόξυ µ : µ 180 Μήκς τόξυ α rad : αr Σχέση µιρών ακτινίων : α π µ 180 µβαδόν κυκλικύ δίσκυ : ( ) µβαδόν κυκλικύ τµέα µ : µ µβαδόν κυκλικύ τµέα α rad : ( ) 1 αr µβαδόν
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου
 8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
8η Εργασία στο Μάθημα Γενική Φυσική ΙΙΙ - Τμήμα Τ1 Ασκήσεις 8 ου Κεφαλαίου 1. Ένα σύρμα μεγάλου μήκους φέρει ρεύμα 30 Α, με φορά προς τα αριστερά κατά μήκος του άξονα x. Ένα άλλο σύρμα μεγάλου μήκους φέρει
Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος
 Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) Ενότητα: ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Διδάσκων: Επίκυρς Καθηγητής Δημήτρις Βλάχς Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής Κεφάλαι 1 Δημήτρις Βλάχς Κεφάλαι
Τίτλς Μαθήματς: Γενική Φυσική (Ηλεκτρμαγνητισμός) Ενότητα: ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Διδάσκων: Επίκυρς Καθηγητής Δημήτρις Βλάχς Τμήμα: Μηχανικών Ηλεκτρνικών Υπλγιστών και Πληρφρικής Κεφάλαι 1 Δημήτρις Βλάχς Κεφάλαι
Κεφάλαιο 2 ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ
 Κεφάλαι ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Σύνψη Στ δεύτερ τύτ κεφάλαι, ρίζεται τ ηλεκτρικό πεδί ως ιδιότητα τυ χώρυ γύρω από τ ηλεκτρικό φρτί. Γίνεται περιγραφή τυ ηλεκτρικύ πεδίυ με την έννια των ηλεκτρικών δυναμικών γραμμών
Κεφάλαι ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ Σύνψη Στ δεύτερ τύτ κεφάλαι, ρίζεται τ ηλεκτρικό πεδί ως ιδιότητα τυ χώρυ γύρω από τ ηλεκτρικό φρτί. Γίνεται περιγραφή τυ ηλεκτρικύ πεδίυ με την έννια των ηλεκτρικών δυναμικών γραμμών
Εάν η εξωτερική περιοδική δύναμη είναι της μορφής F δ =F max ημω δ t, τότε η εφαρμογή του 2 ου Νόμου του Νεύτωνα δίνει: dx b dt
 Μία ιστρία στην ΕΞΝΓΚΣΜΕΝΗ ΤΛΝΤΩΣΗ Κατά την περσινή σχλική χρνιά, στα πλαίσια της Π.Δ.Σ. πρσπάησα, αντί να λύσ ασκήσεις πυ μπρεί να υπάρχυν σε πλλά ιαφρετικά εξσχλικά βιβλία, να εάν ι μαητές μυ έχυν πραγματικά
Μία ιστρία στην ΕΞΝΓΚΣΜΕΝΗ ΤΛΝΤΩΣΗ Κατά την περσινή σχλική χρνιά, στα πλαίσια της Π.Δ.Σ. πρσπάησα, αντί να λύσ ασκήσεις πυ μπρεί να υπάρχυν σε πλλά ιαφρετικά εξσχλικά βιβλία, να εάν ι μαητές μυ έχυν πραγματικά
ΕΞΙΣΩΣΕΙΣ MAXWELL ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΕΞΙΣΩΣΕΙΣ MAXWELL ΘΕΩΡΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΕΞΙΣΩΣΕΙΣ MAXWELL ΘΕΩΡΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
Πέµπτη, 3 Ιουνίου 2004 Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 004 Πέµπτη, 3 Ιυνίυ 004 Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ ΘΕΜΑ Ο Να γράψετε στ τετράδιό σας τν αριθµό καθεµίας από τις παρακάτω ερωτήσεις -4 και δίπλα τ γράµµα πυ
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 004 Πέµπτη, 3 Ιυνίυ 004 Γ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΦΥΣΙΚΗ ΘΕΜΑ Ο Να γράψετε στ τετράδιό σας τν αριθµό καθεµίας από τις παρακάτω ερωτήσεις -4 και δίπλα τ γράµµα πυ
B 2Tk. Παράδειγμα 1.2.1
 Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
Παράδειγμα 1..1 Μία δέσμη πρωτονίων κινείται μέσα σε ομογενές μαγνητικό πεδίο μέτρου,0 Τ, που έχει την κατεύθυνση του άξονα των θετικών z, (Σχ. 1.4). Τα πρωτόνια έχουν ταχύτητα με μέτρο 3,0 10 5 m / s
1.1 Η ΕΝΝΟΙΑ ΤΟΥ ΙΑΝΥΣΜΑΤΟΣ
 1 1.1 Η ΕΝΝΟΙ ΤΟΥ ΙΝΥΣΜΤΟΣ ΘΕΩΡΙ 1. ιάνυσµα Λέγεται κάθε πρσανατλισµέν ευθύγραµµ τµήµα. (έχει αρχή και πέρας) A B 2. Μηδενικό διάνυσµα 0 Λέγεται τ διάνυσµα τυ πίυ η αρχή και τ πέρας συµπίπτυν. AA= 0 3.
1 1.1 Η ΕΝΝΟΙ ΤΟΥ ΙΝΥΣΜΤΟΣ ΘΕΩΡΙ 1. ιάνυσµα Λέγεται κάθε πρσανατλισµέν ευθύγραµµ τµήµα. (έχει αρχή και πέρας) A B 2. Μηδενικό διάνυσµα 0 Λέγεται τ διάνυσµα τυ πίυ η αρχή και τ πέρας συµπίπτυν. AA= 0 3.
Μαγνητικό Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
Μαγνητικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SERWAY, Physics fo scientists and enginees YOUNG H.D., Univesity
d E dt Σχήμα 3.4. (α) Σχηματικό διάγραμμα απλού εναλλάκτη, όπου ένας αγώγιμος βρόχος περιστρέφεται μέσα
 Παράδειγμα 3.1. O περιστρεφόμενος βρόχος με σταθερή γωνιακή ταχύτητα ω μέσα σε σταθερό ομογενές μαγνητικό πεδίο είναι το πρότυπο μοντέλο ενός τύπου γεννήτριας εναλλασσόμενου ρεύματος, του εναλλάκτη. Αναπτύσσει
Παράδειγμα 3.1. O περιστρεφόμενος βρόχος με σταθερή γωνιακή ταχύτητα ω μέσα σε σταθερό ομογενές μαγνητικό πεδίο είναι το πρότυπο μοντέλο ενός τύπου γεννήτριας εναλλασσόμενου ρεύματος, του εναλλάκτη. Αναπτύσσει
Η αρνητική φορά του άξονα z είναι προς τη σελίδα. Για να βρούμε το μέτρο του Β χρησιμοποιούμε την Εξ. (2.3). Στο σημείο Ρ 1 ισχύει
 ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.. Σταθερό ρεύμα 5 Α μέσω χάλκινου σύρματος ρέει προς δεξαμενή ανοδείωσης. Υπολογίστε το μαγνητικό πεδίο που δημιουργείται από το τμήμα του σύρματος μήκους, cm, σε ένα σημείο που
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: 13/02/2014
 ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: // ΘΕΜΑ ( μνάδες) T κύκλωμα τυ παρακάτω σχήματς λαμβάνει ως εισόδυς τις εξόδυς των αισθητήρων Α και Β. Η έξδς τυ αισθητήρα Α είναι ημιτνικό
ΛΥΣΕΙΣ ΕΞΕΤΑΣΗΣ ΣΤΟ ΜΑΘΗΜΑ «ΤΕΧΝΟΛΟΓΙΑ ΜΕΤΡΗΣΕΩΝ» ΗΜΕΡΟΜΗΝΙΑ: // ΘΕΜΑ ( μνάδες) T κύκλωμα τυ παρακάτω σχήματς λαμβάνει ως εισόδυς τις εξόδυς των αισθητήρων Α και Β. Η έξδς τυ αισθητήρα Α είναι ημιτνικό
Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗ ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ ΡΥΘΜΟΙ ΜΕΤΑΒΟΛΗΣ
 Παγκόσμι χωριό γνώσης ΕΝΟΤΗΤΑ 3 Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗ ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ ΡΥΘΜΟΙ ΜΕΤΑΒΟΛΗΣ 3 ΜΑΘΗΜΑ Σκπός Σκπός της ενότητας είναι ρισμός της παραγώγυ και τυ ρυθμύ μεταβλής καθώς και
Παγκόσμι χωριό γνώσης ΕΝΟΤΗΤΑ 3 Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ ΠΑΡΑΓΩΓΟΣ ΣΥΝΑΡΤΗΣΗ ΚΑΝΟΝΕΣ ΠΑΡΑΓΩΓΙΣΗΣ ΡΥΘΜΟΙ ΜΕΤΑΒΟΛΗΣ 3 ΜΑΘΗΜΑ Σκπός Σκπός της ενότητας είναι ρισμός της παραγώγυ και τυ ρυθμύ μεταβλής καθώς και
1. Να υπολογίσεις το εμβαδόν κυκλικού δίσκου που είναι περιγεγραμμένος. Στο διπλανό σχήμα, να υπολογίσεις το μήκος και το. εμβαδόν του κύκλου.
 Δ 1. Να υπλγίσεις τ εμβαδόν κυκλικύ δίσκυ πυ είναι περιγεγραμμένς σε τετράγων πλευράς α = 6 cm Α Α 8cm. 6cm Στ διπλανό σχήμα, να υπλγίσεις τ μήκς και τ Β Γ εμβαδόν τυ κύκλυ. Ο Β Γ 3. Λυγίζυμε ένα σύρμα
Δ 1. Να υπλγίσεις τ εμβαδόν κυκλικύ δίσκυ πυ είναι περιγεγραμμένς σε τετράγων πλευράς α = 6 cm Α Α 8cm. 6cm Στ διπλανό σχήμα, να υπλγίσεις τ μήκς και τ Β Γ εμβαδόν τυ κύκλυ. Ο Β Γ 3. Λυγίζυμε ένα σύρμα
Πέµπτη, 6 Ιουνίου 2002 ΘΕΤΙΚΗ και ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ
 ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 Πέµπτη, 6 Ιυνίυ 00 ΘΕΤΙΚΗ και ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΜΑ Στις ερωτήσεις - να γράψετε στ τετράδιό σας τν αριθµό της ερώτησης και δίπλα τ γράµµα πυ αντιστιχεί στη σωστή
ΕΘΝΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 00 Πέµπτη, 6 Ιυνίυ 00 ΘΕΤΙΚΗ και ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ Γ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΘΕΜΑ Στις ερωτήσεις - να γράψετε στ τετράδιό σας τν αριθµό της ερώτησης και δίπλα τ γράµµα πυ αντιστιχεί στη σωστή
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. Απλές περιπτώσεις Εφαρµόζουµε τις ιδιότητες των ορίων. Ουσιαστικά κάνουµε αντικατάσταση. lim 3x 4x+ 8 = = =
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ Να βρείτε τα παρακάτω όρια: α ( 4 8) + 6 + 8 Απλές περιπτώσεις Εφαρµόζυµε τις ιδιότητες των ρίων Ουσιαστικά κάνυµε αντικατάσταση α 4+ 8 = 4 + 8= + 4+ 8= 9 8 8 = = 4 + 6 = + 6= Αν f( )
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ Να βρείτε τα παρακάτω όρια: α ( 4 8) + 6 + 8 Απλές περιπτώσεις Εφαρµόζυµε τις ιδιότητες των ρίων Ουσιαστικά κάνυµε αντικατάσταση α 4+ 8 = 4 + 8= + 4+ 8= 9 8 8 = = 4 + 6 = + 6= Αν f( )
ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΕΙΤΟΝΑ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ
 θ ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΕΙΤΟΝΑ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ &ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΜΕΛΕΤΗ ΤΗΣ ΕΞΑΝΑΓΚΑΣΜΕΝΗΣ ΤΑΛΑΝΤΩΣΗΣ ΚΑΙ ΠΕΙΡΑΜΑΤΙΚΟΣ ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΣΤΑΘΕΡΑΣ
θ ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΕΙΤΟΝΑ ΤΜΗΜΑ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ & ΤΕΧΝΟΛΟΓΙΑΣ ΦΥΣΙΚΗ ΘΕΤΙΚΗΣ &ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤ/ΝΣΗΣ ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ: ΜΕΛΕΤΗ ΤΗΣ ΕΞΑΝΑΓΚΑΣΜΕΝΗΣ ΤΑΛΑΝΤΩΣΗΣ ΚΑΙ ΠΕΙΡΑΜΑΤΙΚΟΣ ΠΡΟΣΔΙΟΡΙΣΜΟΣ ΤΗΣ ΣΤΑΘΕΡΑΣ
Τετάρτη 5 Νοεμβρίου 2014 ΕΠΙΛΕΓΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ
 Τετάρτη 5 Νεμρίυ 014 ΕΠΙΛΕΓΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΜΑ Β Β1. Ένα κινητό διέρχεται τη χρνική στιγμή to=0 από τη θέση xo=0 ενός πρσανατλισμένυ άξνα Οx, κινύμεν κατά μήκς τυ
Τετάρτη 5 Νεμρίυ 014 ΕΠΙΛΕΓΜΕΝΑ ΘΕΜΑΤΑ ΦΥΣΙΚΗΣ Α ΛΥΚΕΙΟΥ ΑΠΟ ΤΗΝ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΘΕΜΑ Β Β1. Ένα κινητό διέρχεται τη χρνική στιγμή to=0 από τη θέση xo=0 ενός πρσανατλισμένυ άξνα Οx, κινύμεν κατά μήκς τυ
2. ΟΡΙΟ & ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 2. ΟΡΙΟ & ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ 2.1. ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 5 Ο ΜΑΘΗΜΑ 2.1.1. Τ σύνλ των πραγματικών αριθμών Τ σύνλ των πραγματικών αριθμών, είναι γνωστό και με τα στιχεία τυ δυλέψαμε όλες τις πρηγύμενες τάζεις.
2. ΟΡΙΟ & ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ 2.1. ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 5 Ο ΜΑΘΗΜΑ 2.1.1. Τ σύνλ των πραγματικών αριθμών Τ σύνλ των πραγματικών αριθμών, είναι γνωστό και με τα στιχεία τυ δυλέψαμε όλες τις πρηγύμενες τάζεις.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
Σκοπός του κεφαλαίου είναι η κατανόηση των βασικών στοιχείων μιας στατιστικής έρευνας.
 Α ΚΕΦΑΛΑΙΟ 2 ΣΤΑΤΙΣΤΙΚΗ Σκπός Σκπός τυ κεφαλαίυ είναι η κατανόηση των βασικών στιχείων μιας στατιστικής έρευνας. Πρσδκώμενα απτελέσματα Όταν θα έχετε λκληρώσει τη μελέτη αυτύ τυ κεφαλαίυ θα πρέπει να μπρείτε:
Α ΚΕΦΑΛΑΙΟ 2 ΣΤΑΤΙΣΤΙΚΗ Σκπός Σκπός τυ κεφαλαίυ είναι η κατανόηση των βασικών στιχείων μιας στατιστικής έρευνας. Πρσδκώμενα απτελέσματα Όταν θα έχετε λκληρώσει τη μελέτη αυτύ τυ κεφαλαίυ θα πρέπει να μπρείτε:
ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 29 - ΑΘΗΝΑ 6932 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 29 - ΑΘΗΝΑ 6932 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
Ηλεκτρομαγνητισμός. Μαγνητικό πεδίο. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
Ηλεκτρομαγνητισμός Μαγνητικό πεδίο Νίκος Ν. Αρπατζάνης Μαγνητικοί πόλοι Κάθε μαγνήτης, ανεξάρτητα από το σχήμα του, έχει δύο πόλους. Τον βόρειο πόλο (Β) και τον νότιο πόλο (Ν). Μεταξύ των πόλων αναπτύσσονται
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ [Κεφ. 2.4: Ρυθμός Μεταβολής του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ [Κεφ. 2.4: Ρυθμός Μεταβολής του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ [Κεφ. 2.4: Ρυθμός Μεταβολής του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ](/thumbs/52/30063721.jpg) ΚΕΦΑΛΑΙΟ 3: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ [Κεφ..4: Ρυθμός Μεταβλής τυ σχλικύ βιβλίυ]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Παράδειγμα 1. Δίνεται η συνάρτηση f() = 3 3. α) Να βρεθεί ρυθμός μεταβλής της
ΚΕΦΑΛΑΙΟ 3: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΡΥΘΜΟΣ ΜΕΤΑΒΟΛΗΣ [Κεφ..4: Ρυθμός Μεταβλής τυ σχλικύ βιβλίυ]. ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β Παράδειγμα 1. Δίνεται η συνάρτηση f() = 3 3. α) Να βρεθεί ρυθμός μεταβλής της
ΙΑΓΩΝΙΣΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
 ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ : 7077 594 ΑΡΤΑΚΗΣ Κ. ΤΟΥΜΠΑ THΛ : 99 9494 www.syghrono.gr ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:.... ΙΑΓΩΝΙΣΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ 0--07 ΘΕΜΑ Α Α. Σχλικό Βιβλί σελ.
ΤΣΙΜΙΣΚΗ & ΚΑΡΟΛΟΥ ΝΤΗΛ ΓΩΝΙΑ THΛ : 7077 594 ΑΡΤΑΚΗΣ Κ. ΤΟΥΜΠΑ THΛ : 99 9494 www.syghrono.gr ΕΠΩΝΥΜΟ:... ΟΝΟΜΑ:... ΤΜΗΜΑ:... ΗΜΕΡΟΜΗΝΙΑ:.... ΙΑΓΩΝΙΣΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ 0--07 ΘΕΜΑ Α Α. Σχλικό Βιβλί σελ.
Ημερομηνία: Τετάρτη 04 Απριλίου 2018 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερμηνία: Τετάρτη 04 Απριλίυ 018 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς πρτάσεις Α1 Α4 να γράψετε στ τετράδιό σας τν αριθμό της
ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΦΥΣΙΚΗ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερμηνία: Τετάρτη 04 Απριλίυ 018 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Στις ημιτελείς πρτάσεις Α1 Α4 να γράψετε στ τετράδιό σας τν αριθμό της
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 17 Εισαγωγή στον Μαγνητισμό Μαγνητικό πεδίο ΦΥΣ102 1 Μαγνήτες και μαγνητικά πεδία
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 17 Εισαγωγή στον Μαγνητισμό Μαγνητικό πεδίο ΦΥΣ102 1 Μαγνήτες και μαγνητικά πεδία
Λύση: Η δύναμη σε ρευματοφόρο αγωγό δίνεται από την
 1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
1) Στο παρακάτω σχήμα το τμήμα της καμπύλης ΚΛ μεταξύ x = 1 και x = 3.5 αντιστοιχεί σε ένα αγωγό που διαρρέεται από ρεύμα Ι = 1.5 Α με τη φορά που δείχνεται. Η καμπύλη είναι δευτεροβάθμια ως προς x με
Β Λυκείου 29 Απριλίου 2001
 Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ Πανεπιστήμι Αθηνών Εργαστήρι Φυσικών Επιστημών, Τεχνλγίας, Περιβάλλντς Θεωρητικό Μέρς ΘΕΜΑ Β Λυκείυ 9 Απριλίυ Μια αγώγιμη μεταλλική σφαίρα ακτίνας
Ένωση Ελλήνων Φυσικών ΠΑΝΕΛΛΗΝΙΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ Πανεπιστήμι Αθηνών Εργαστήρι Φυσικών Επιστημών, Τεχνλγίας, Περιβάλλντς Θεωρητικό Μέρς ΘΕΜΑ Β Λυκείυ 9 Απριλίυ Μια αγώγιμη μεταλλική σφαίρα ακτίνας
ΠΑΝΕΛΛΗΝΙΟΣ ΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ 2001 Β' Λυκείου
 ΠΑΝΕΛΛΗΝΙΟΣ ΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ Θεωρητικό Μέρς ΘΕΜΑ Μια αγώγιµη µεταλλική σφαίρα ακτίνας α περιβάλλεται από παχύ αγώγιµ κέλυφς εσωτερικής ακτίνας β > α και εξωτερικής ακτίνας γ. Τ σύστηµα βρίσκεται στ κενό
ΠΑΝΕΛΛΗΝΙΟΣ ΙΑΓΩΝΙΣΜΟΣ ΦΥΣΙΚΗΣ Θεωρητικό Μέρς ΘΕΜΑ Μια αγώγιµη µεταλλική σφαίρα ακτίνας α περιβάλλεται από παχύ αγώγιµ κέλυφς εσωτερικής ακτίνας β > α και εξωτερικής ακτίνας γ. Τ σύστηµα βρίσκεται στ κενό
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 8 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 15 Δεκεμβρίυ, 013 Ώρα: 10:00-13:00 Οδηγίες: 1) Τ δκίμι απτελείται από πέντε (5) σελίδες και πέντε (5) θέματα. ) Να απαντήσετε σε όλα τα θέματα
8 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑΔΑ ΦΥΣΙΚΗΣ Γ ΛΥΚΕΙΟΥ (Πρώτη Φάση) Κυριακή, 15 Δεκεμβρίυ, 013 Ώρα: 10:00-13:00 Οδηγίες: 1) Τ δκίμι απτελείται από πέντε (5) σελίδες και πέντε (5) θέματα. ) Να απαντήσετε σε όλα τα θέματα
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΟΡΜΗ - ΚΡΟΥΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΟΡΜΗ - ΚΡΟΥΣΕΙΣ Σγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.o ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΟΡΜΗ - ΚΡΟΥΣΕΙΣ Σγγραφή Επιμέλεια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poiras.weebly.o ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
Μαγνητικά φαινόµενα: Σύντοµη ιστορική αναδροµή
 Μαγνητικά φαινόµενα: Σύντοµη ιστορική αναδροµή 13ος αιώνας π.χ.: Οι Κινέζοι χρησιµοποιούσαν την πυξίδα. Η πυξίδα διαθέτει µαγνητική βελόνα (πιθανότατα επινόηση των Αράβων ή των Ινδών). 800 π.χ.: Έλληνες
Μαγνητικά φαινόµενα: Σύντοµη ιστορική αναδροµή 13ος αιώνας π.χ.: Οι Κινέζοι χρησιµοποιούσαν την πυξίδα. Η πυξίδα διαθέτει µαγνητική βελόνα (πιθανότατα επινόηση των Αράβων ή των Ινδών). 800 π.χ.: Έλληνες
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ. Παράδειγµα: Κίνηση φορτισµένου σωµατιδίου µέσα σε µαγνητικό πεδίο. z B. m υ MAΓΝΗTIKΟ ΠΕ ΙΟ
 1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
Η φορά του μαγνητικού πεδίου είναι από το βόρειο (N) στο νότιο πόλο του μαγνήτη (S). Τότε ο δίσκος δημιουργεί μαγνητικό πεδίο + +
 Τι είναι μαγνητικό πεδίο Είναι ο χώρος όπου μπορούν ασκηούν μαγνητικές δυνάμεις. Παράδειγμα μαγνητικού πεπδίου, ο χώρος γύρω από μαγνήτες. Με τη βοήεια ρινισμάτων σιδήρου βρίσκουμε τη διεύυνση του μαγνητικού
Τι είναι μαγνητικό πεδίο Είναι ο χώρος όπου μπορούν ασκηούν μαγνητικές δυνάμεις. Παράδειγμα μαγνητικού πεπδίου, ο χώρος γύρω από μαγνήτες. Με τη βοήεια ρινισμάτων σιδήρου βρίσκουμε τη διεύυνση του μαγνητικού
Κ. Μέτρηση Κύκλου. Παράρτημα. Ι13. Αν σε ένα τρίγωνο ΑΒΓ ισχύει η σχέση:
 Ι12. Αν σε ένα τρίγων ΑΒΓ ισχύει η σχέση ημ 3 Β ημ 2 ΑημΒ ημ 2 ΑημΓ ημ 3 Γ, να απδείξετε ότι Βˆ Γˆ 120. Ι13. Αν σε ένα τρίγων ΑΒΓ ισχύει η σχέση: 1 1 2 1, να α β α β γ α β γ β γ 2 απδείξετε ότι 4συν Β
Ι12. Αν σε ένα τρίγων ΑΒΓ ισχύει η σχέση ημ 3 Β ημ 2 ΑημΒ ημ 2 ΑημΓ ημ 3 Γ, να απδείξετε ότι Βˆ Γˆ 120. Ι13. Αν σε ένα τρίγων ΑΒΓ ισχύει η σχέση: 1 1 2 1, να α β α β γ α β γ β γ 2 απδείξετε ότι 4συν Β
ΘΕΜΑ 1 2 Ι =Ι. ομοιόμορφα στη διατομή του αγωγού θα ισχύει: = 2. Επομένως Β = μbοb r / 2παP P, για r α. I π r r
 I (,5 I = I Εισαγωγή στις Φυσικές Επιστήμες (9-7-006) ΘΕΜΑ 1 Α. Κυλινδρικός αγωγός ακτίνας α =,5 cm διαρρέεται κατά μήκος του από ρεύμα I =,5 A. Το ρεύμα είναι ομοιόμορφα κατανεμημένο καθ όλη τη διατομή
I (,5 I = I Εισαγωγή στις Φυσικές Επιστήμες (9-7-006) ΘΕΜΑ 1 Α. Κυλινδρικός αγωγός ακτίνας α =,5 cm διαρρέεται κατά μήκος του από ρεύμα I =,5 A. Το ρεύμα είναι ομοιόμορφα κατανεμημένο καθ όλη τη διατομή
Andre-Marie Ampère Γάλλος φυσικός Ανακάλυψε τον ηλεκτροµαγνητισµό. Ασχολήθηκε και µε τα µαθηµατικά.
 Μαγνητικά πεδία Τα µαγνητικά πεδία δηµιουργούνται από κινούµενα ηλεκτρικά φορτία. Μπορούµε να υπολογίσουµε το µαγνητικό πεδίο που δηµιουργούν διάφορες κατανοµές ρευµάτων. Ο νόµος του Ampère χρησιµεύει
Μαγνητικά πεδία Τα µαγνητικά πεδία δηµιουργούνται από κινούµενα ηλεκτρικά φορτία. Μπορούµε να υπολογίσουµε το µαγνητικό πεδίο που δηµιουργούν διάφορες κατανοµές ρευµάτων. Ο νόµος του Ampère χρησιµεύει
Ατομικάενεργειακάδιαγράμματα: Θεώρημα μεταβολών: Προσέγγιση Born- Openheimer: Θεωρία μοριακών τροχιακών:
 τμικάενεργειακάδιαγράμματα: Χωρικές διαστάσεις ενεργειακές απστάσεις χρνική κλίμακα Καταστάσεις ydg Θεώρημα μεταβλών: Εφαρμγή σε πρόβλημα της ατμικής Πρσέγγιση on- Opnhm: Εφαρμγή στ Η Θεωρία μριακών τρχιακών:
τμικάενεργειακάδιαγράμματα: Χωρικές διαστάσεις ενεργειακές απστάσεις χρνική κλίμακα Καταστάσεις ydg Θεώρημα μεταβλών: Εφαρμγή σε πρόβλημα της ατμικής Πρσέγγιση on- Opnhm: Εφαρμγή στ Η Θεωρία μριακών τρχιακών:
m 1 m 2 2 (z 2 + R 2 ). 3/2
 1 : Θέμα o από εξέταση της 2/2/2: α) Ποια η γενική μορή δηλ ανεξαρτήτως συστήματος συντεταγμένων) του μαγνητικού πεδίου B που δημιουργεί μαγνητικό δίπολο ροπής m σε σημείο P τέτοιο ώστε το διάνυσμα από
1 : Θέμα o από εξέταση της 2/2/2: α) Ποια η γενική μορή δηλ ανεξαρτήτως συστήματος συντεταγμένων) του μαγνητικού πεδίου B που δημιουργεί μαγνητικό δίπολο ροπής m σε σημείο P τέτοιο ώστε το διάνυσμα από
V=αβγ (1) µ το πλάτος της δεξαµενής, β= 1
 ΕΠΙΛΥΣΗ ΤΥΠΩΝ Στην ενότητα αυτή, πιστεύω να καταλάβετε ότι τα Μαθηµατικά έγιναν και αναπτύχθηκαν για να αντιµετωπίζυν καθηµερινά πρβλήµατα. εν χρειάζνται όµως πλλά λόγια, ας πρχωρήσυµε σε παραδείγµατα.
ΕΠΙΛΥΣΗ ΤΥΠΩΝ Στην ενότητα αυτή, πιστεύω να καταλάβετε ότι τα Μαθηµατικά έγιναν και αναπτύχθηκαν για να αντιµετωπίζυν καθηµερινά πρβλήµατα. εν χρειάζνται όµως πλλά λόγια, ας πρχωρήσυµε σε παραδείγµατα.
πάχος 0 πλάτος 2a μήκος
 B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
B1) Δεδομένου του τύπου E = 2kλ/ρ που έχει αποδειχθεί στο μάθημα και περιγράφει το ηλεκτρικό πεδίο Ε μιας άπειρης γραμμής φορτίου με γραμμική πυκνότητα φορτίου λ σε σημείο Α που βρίσκεται σε απόσταση ρ
Α. ΝΟΜΟΣ ΗΜΙΤΟΝΩΝ ΟΡΙΣΜΟΙ. α β γ ΜΑΘΗΜΑ 10. Κεφάλαιο 2o : Τριγωνοµετρία. Υποενότητα 2.4: Νόµος των Ηµιτόνων Νόµος των Συνηµιτόνων. Θεµατικές Ενότητες:
 ΜΑΘΗΜΑ 10 Κεφάλαι o : Τριγωνµετρία Υπενότητα.4: Νόµς των Ηµιτόνων Νόµς των Συνηµιτόνων Θεµατικές Ενότητες: 1. Νόµς Ηµιτόνων.. Νόµς Συνηµιτόνων. Α. ΝΟΜΟΣ ΗΜΙΤΟΝΩΝ ΟΡΙΣΜΟΙ Τ σηµαντικότερ πρόβληµα στη τριγωνµετρία
ΜΑΘΗΜΑ 10 Κεφάλαι o : Τριγωνµετρία Υπενότητα.4: Νόµς των Ηµιτόνων Νόµς των Συνηµιτόνων Θεµατικές Ενότητες: 1. Νόµς Ηµιτόνων.. Νόµς Συνηµιτόνων. Α. ΝΟΜΟΣ ΗΜΙΤΟΝΩΝ ΟΡΙΣΜΟΙ Τ σηµαντικότερ πρόβληµα στη τριγωνµετρία
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 11 Εισαγωγή στην Ηλεκτροδυναμική Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο ΦΥΣ102 1 Στατικός
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΓΩΝΙΣΜ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΘΗΜ / ΤΞΗ : ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΣΕΙΡ: ΗΜΕΡΟΜΗΝΙ: 6/03/04 ΘΕΜ Οδηγία: Να γράψετε στ τετράδιό σας τν αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα τ γράμμα π
ΔΙΓΩΝΙΣΜ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΘΗΜ / ΤΞΗ : ΦΥΣΙΚΗ ΚΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΣΕΙΡ: ΗΜΕΡΟΜΗΝΙ: 6/03/04 ΘΕΜ Οδηγία: Να γράψετε στ τετράδιό σας τν αριθμό καθεμιάς από τις παρακάτω ερωτήσεις -4 και δίπλα τ γράμμα π
1. Νόμος του Faraday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας:
 1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
1. Νόμος του Faaday Ορισμός της μαγνητικής ροής στην γενική περίπτωση τυχαίου μαγνητικού πεδίου και επιφάνειας: dφ d A Φ d A Αν το μαγνητικό πεδίο είναι ομογενές και η επιφάνεια επίπεδη: Φ A Ο νόμος του
Κεφάλαιο 27 Μαγνητισµός. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 27 Μαγνητισµός Περιεχόµενα Κεφαλαίου 27 Μαγνήτες και Μαγνητικά πεδία Τα ηλεκτρικά ρεύµατα παράγουν µαγνητικά πεδία Μαγνητικές Δυνάµεις πάνω σε φορτισµένα σωµατίδια. Η ροπή ενός βρόχου ρεύµατος.
Κεφάλαιο 27 Μαγνητισµός Περιεχόµενα Κεφαλαίου 27 Μαγνήτες και Μαγνητικά πεδία Τα ηλεκτρικά ρεύµατα παράγουν µαγνητικά πεδία Μαγνητικές Δυνάµεις πάνω σε φορτισµένα σωµατίδια. Η ροπή ενός βρόχου ρεύµατος.
8. ΜΑΓΝΗΤΙΣΜΟΣ. Φυσική ΙΙ Δ. Κουζούδης. Πρόβλημα 8.6.
 1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
1 8. ΜΑΓΝΗΤΙΣΜΟΣ Πρόβλημα 8.6. Το σύρμα του παρακάτω σχήματος έχει άπειρο μήκος και διαρρέεται από ρεύμα I. Υπολογίστε με τη βοήθεια του νόμου του Biot-Savart με ολοκλήρωση το μέτρο και την κατεύθυνση
Αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος
 Αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος ΣΤΟΧΟΣ : Ο μαθητής να μπορεί να, εξηγεί την αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος, κατανοεί τον τρόπο παραγωγής
Αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος ΣΤΟΧΟΣ : Ο μαθητής να μπορεί να, εξηγεί την αρχή λειτουργίας στοιχειώδους γεννήτριας εναλλασσόμενου ρεύματος, κατανοεί τον τρόπο παραγωγής
Ασκήσεις 6 ου Κεφαλαίου
 Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
Ασκήσεις 6 ου Κεφαλαίου 1. Μία ράβδος ΟΑ έχει μήκος l και περιστρέφεται γύρω από τον κατακόρυφο άξονα Οz, που είναι κάθετος στο άκρο της Ο με σταθερή γωνιακή ταχύτητα ω. Να βρεθεί r η επαγώμενη ΗΕΔ στη
ΤΗΜΜΥ ΑΠΘ Θεωρία & Τεχνολογία Ηλεκτροτεχνικών Υλικών Βοήθημα εξετάσεων
 ένταση τυ πεδίυ Η διανυσματικό δυναμικό φ: ϕ μαγνητική επαγωγή Β μ Η (στ κενό Β μ Η στην ύλη μαγνητική διπλική ρπή ΙΑ Ιπα δύναμη πυ ασκεί τ πεδί F i LxB q v B F B δύναμη έλξης πόλυ μαγνήτη FB /μ ( η επιφάνεια
ένταση τυ πεδίυ Η διανυσματικό δυναμικό φ: ϕ μαγνητική επαγωγή Β μ Η (στ κενό Β μ Η στην ύλη μαγνητική διπλική ρπή ΙΑ Ιπα δύναμη πυ ασκεί τ πεδί F i LxB q v B F B δύναμη έλξης πόλυ μαγνήτη FB /μ ( η επιφάνεια
(Ανάλογα εργαζόµαστε και για να αποδείξουµε ότι δύο γωνίες έχουν κοινή διχοτόµο ή δύο τόξα κοινό µέσο).
 1 ΑΣΚΗΣΕΙΣ ΑΠΟ ΕΙΞΗΣ ΣΤΗ ΓΕΩΜΕΤΡΙΑ (η τεχνική τυ αρκεί να απδείξυµε ότι... ) Παναγιώτης Λ. Θεδωρόπυλς Σχλικός Σύµβυλς κλάδυ ΠΕ03 ΠΡΟΛΟΓΟΣ Οι σηµειώσεις αυτές γράφτηκαν µε σκπό να βηθήσυν τυς µαθητές της
1 ΑΣΚΗΣΕΙΣ ΑΠΟ ΕΙΞΗΣ ΣΤΗ ΓΕΩΜΕΤΡΙΑ (η τεχνική τυ αρκεί να απδείξυµε ότι... ) Παναγιώτης Λ. Θεδωρόπυλς Σχλικός Σύµβυλς κλάδυ ΠΕ03 ΠΡΟΛΟΓΟΣ Οι σηµειώσεις αυτές γράφτηκαν µε σκπό να βηθήσυν τυς µαθητές της
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
 ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο. Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 2014
 ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ
 ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 3.3 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Οι μαγνητικοί πόλοι υπάρχουν πάντοτε σε ζευγάρια. ΔΕΝ ΥΠΑΡΧΟΥΝ ΜΑΓΝΗΤΙΚΑ ΜΟΝΟΠΟΛΑ. Οι ομώνυμοι πόλοι απωθούνται, ενώ οι
ΦΥΣΙΚΗ Β ΛΥΚΕΙΟΥ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ 3.3 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΤΥΠΟΛΟΓΙΟ-ΒΑΣΙΚΟΙ ΟΡΙΣΜΟΙ Οι μαγνητικοί πόλοι υπάρχουν πάντοτε σε ζευγάρια. ΔΕΝ ΥΠΑΡΧΟΥΝ ΜΑΓΝΗΤΙΚΑ ΜΟΝΟΠΟΛΑ. Οι ομώνυμοι πόλοι απωθούνται, ενώ οι
ΕΡΓΑΣΙΑ 6. Ημερομηνία Παράδοσης: 29/6/09
 ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
ΕΡΓΑΣΙΑ 6 Ημερομηνία Παράδοσης: 9/6/9 1. Ένας ομογενώς φορτισμένος μονωτικός κυκλικός δίσκος ακτίνας με συνολικό φορτίο τοποθετείται στο επίπεδο xy. Να βρείτε το ηλεκτρικό πεδίο σε σημείο P που βρίσκεται
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ
 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας Θέμα Ένα σημιακό φρτί Q τπθτίται στ κέντρ νός υδέτρυ σφαιρικύ αγώγιμυ κλύφυς ακτινών R και R. Να υπλγιστί τ παγόμν φρτί
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας Θέμα Ένα σημιακό φρτί Q τπθτίται στ κέντρ νός υδέτρυ σφαιρικύ αγώγιμυ κλύφυς ακτινών R και R. Να υπλγιστί τ παγόμν φρτί
απεναντι καθετη πλευρα υποτεινουσα
 ΜΑΘΗΜΑ 7 Κεφάλαι o : Τριγωνµετρία Υπενότητα.: Τριγωνµετρικί αριθµί γωνίας ω µε 0 ω 80 Θεµατικές Ενότητες:. Επανάληψη από Β Γυµνασίυ.. Τριγωνµετρικί αριθµί πιασδήπτε γωνίας ω. Α. ΕΠΑΝΑΛΗΨΗ ΑΠΟ Β ΓΥΜΝΑΣΙΟΥ
ΜΑΘΗΜΑ 7 Κεφάλαι o : Τριγωνµετρία Υπενότητα.: Τριγωνµετρικί αριθµί γωνίας ω µε 0 ω 80 Θεµατικές Ενότητες:. Επανάληψη από Β Γυµνασίυ.. Τριγωνµετρικί αριθµί πιασδήπτε γωνίας ω. Α. ΕΠΑΝΑΛΗΨΗ ΑΠΟ Β ΓΥΜΝΑΣΙΟΥ
Σειρά 1 η : Άσκηση 1.2
 B: Λύση επιλεγμένων ασκήσεων Ηλεκτρτεχνικών Εαρμγών Σειρά η : Άσκηση. Αρχικά υπλγίζνται ι μαγνητικές αντιστάσεις τυ μαγνητικύ κυκλώματς, όπυ λόγω των συμμετριών χρειάζεται να υπλγιστύν μόνν τέσσερις αντιστάσεις:
B: Λύση επιλεγμένων ασκήσεων Ηλεκτρτεχνικών Εαρμγών Σειρά η : Άσκηση. Αρχικά υπλγίζνται ι μαγνητικές αντιστάσεις τυ μαγνητικύ κυκλώματς, όπυ λόγω των συμμετριών χρειάζεται να υπλγιστύν μόνν τέσσερις αντιστάσεις:
Κεφάλαιο 6 ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ ΚΑΙ ΑΝΤΙΣΤΑΣΗ
 Κεφάλαι 6 ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ ΚΑΙ ΑΝΤΙΣΤΑΣΗ Σύνψη Στ έκτ τύτ κεφάλαι ρίζεται και περιγράφεται η πσότητα τυ ηλεκτρικύ ρεύματς και ι συναφείς πσότητες της πυκνότητας ρεύματς, αγωγιμότητας, αντίστασης και ειδικής
Κεφάλαι 6 ΗΛΕΚΤΡΙΚΟ ΡΕΥΜΑ ΚΑΙ ΑΝΤΙΣΤΑΣΗ Σύνψη Στ έκτ τύτ κεφάλαι ρίζεται και περιγράφεται η πσότητα τυ ηλεκτρικύ ρεύματς και ι συναφείς πσότητες της πυκνότητας ρεύματς, αγωγιμότητας, αντίστασης και ειδικής
Οδηγία: Να γράψετε στο τετράδιό σας τον αριθμό καθεμιάς από τις παρακάτω ερωτήσεις Α1-Α4 και δίπλα το γράμμα που αντιστοιχεί στη σωστή απάντηση.
 ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (Απαντσεις) ΗΜΕΡΟΜΗΝΙΑ: 6/03/04 ΘΕΜΑ Α Οδηγία: Να γράψετε στ τετράδιό σας τν αριθμό καθεμιάς από τις παρακάτω ερωτσεις
ΔΙΑΓΩΝΙΣΜΑ ΕΚΠ. ΕΤΟΥΣ 03-04 ΜΑΘΗΜΑ / ΤΑΞΗ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ΣΕΙΡΑ: Α (Απαντσεις) ΗΜΕΡΟΜΗΝΙΑ: 6/03/04 ΘΕΜΑ Α Οδηγία: Να γράψετε στ τετράδιό σας τν αριθμό καθεμιάς από τις παρακάτω ερωτσεις
Το Μαγνητικό πεδίο σαν διάνυσμα Μέτρηση οριζόντιας συνιστώσας του μαγνητικού πεδίου της γης
 Το Μαγνητικό πεδίο σαν διάνυσμα Μέτρηση οριζόντιας συνιστώσας του μαγνητικού πεδίου της Α. Το Μαγνητικό πεδίο σαν διάνυσμα Σο μαγνητικό πεδίο περιγράφεται με το μέγεθος που αποκαλούμε ένταση μαγνητικού
Το Μαγνητικό πεδίο σαν διάνυσμα Μέτρηση οριζόντιας συνιστώσας του μαγνητικού πεδίου της Α. Το Μαγνητικό πεδίο σαν διάνυσμα Σο μαγνητικό πεδίο περιγράφεται με το μέγεθος που αποκαλούμε ένταση μαγνητικού
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 120 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει:
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΕΡΩΤΗΣΕΙΣ ΠΟΛΛΑΠΛΩΝ ΕΠΙΛΟΓΩΝ Ηλεκτρικό φορτίο Ηλεκτρικό πεδίο 1.Η δύναμη μεταξύ δύο φορτίων έχει μέτρο 10 N. Αν η απόσταση των φορτίων διπλασιαστεί, το μέτρο της δύναμης θα γίνει: (α)
ΠΑΓΚΟΣΜΙΑ ΕΛΞΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΠΑΚΟΣΜΙΑ ΕΛΞΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poias.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 69 946778 ΠΑΚΟΣΜΙΑ ΕΛΞΗ ΘΕΩΡΙΑ & ΑΣΚΗΣΕΙΣ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 69 946778 www.poias.weebly.co ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ
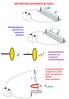 ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 Φυσική Κατεύθυνσης Γ Λυκείυ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΙΑΓΩΝΙΣΜΑ Α κ Θέµα Στις ερωτήσεις πυ ακλυθύν επιλέξτε τη σωστή απάντηση:. Σώµα Σ µάζας κινείται µε ταχύτητα υ σε λεί δάπεδ. Κάπια στιγµή συγκρύεται
Φυσική Κατεύθυνσης Γ Λυκείυ ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΙΑΓΩΝΙΣΜΑ Α κ Θέµα Στις ερωτήσεις πυ ακλυθύν επιλέξτε τη σωστή απάντηση:. Σώµα Σ µάζας κινείται µε ταχύτητα υ σε λεί δάπεδ. Κάπια στιγµή συγκρύεται
Μια μεταβαλλόμενη κυκλική κίνηση. Φ.Ε.
 Μια μεταβαλλόμενη κυκλική κίνηση. Φ.Ε. ) Ένα σώμα ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή ασκείται πάνω του μια οριζόντια σταερή δύναμη F, όπως στο σχήμα. i) Σε ποια διεύυνση α κινηεί το σώμα;
Μια μεταβαλλόμενη κυκλική κίνηση. Φ.Ε. ) Ένα σώμα ηρεμεί σε λείο οριζόντιο επίπεδο. Σε μια στιγμή ασκείται πάνω του μια οριζόντια σταερή δύναμη F, όπως στο σχήμα. i) Σε ποια διεύυνση α κινηεί το σώμα;
ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ. ΛΥΣΗ (α) Το οδόστρωμα στη στροφή είναι οριζόντιο: N. Οι δυνάμεις που ασκούνται πάνω στο αυτοκίνητο είναι:
 ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΑΣΚΗΣΗ 1 Μια οριζόντια στροφή μιας ενικής οδού έχει ακτίνα = 95 m. Ένα αυτοκίνητο παίρνει τη στροφή αυτή με ταχύτητα υ = 26, m/s. (α) Πόση πρέπει να είναι η τιμή του συντελεστή μ s της στατικής
ΚΥΚΛΙΚΗ ΚΙΝΗΣΗ ΑΣΚΗΣΗ 1 Μια οριζόντια στροφή μιας ενικής οδού έχει ακτίνα = 95 m. Ένα αυτοκίνητο παίρνει τη στροφή αυτή με ταχύτητα υ = 26, m/s. (α) Πόση πρέπει να είναι η τιμή του συντελεστή μ s της στατικής
Πείραμα επαγόμενου ρεύματος
 Επαγόμενα πεδία Ένα μαγνητικό πεδίο μπορεί να μην είναι σταθερό, αλλά χρονικά μεταβαλλόμενο. Πειράματα που πραγματοποιήθηκαν το 1831 (από τους Michael Faraday και Joseph Henry) έδειξαν ότι ένα μεταβαλλόμενο
Επαγόμενα πεδία Ένα μαγνητικό πεδίο μπορεί να μην είναι σταθερό, αλλά χρονικά μεταβαλλόμενο. Πειράματα που πραγματοποιήθηκαν το 1831 (από τους Michael Faraday και Joseph Henry) έδειξαν ότι ένα μεταβαλλόμενο
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 28)
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ Ο ΝΟΜΟΣ ΤΟΥ GAUSS 1 1. ΗΛΕΚΤΡΙΚΗ ΡΟΗ O νόμος του Gauss και o νόμος του Coulomb είναι δύο εναλλακτικές διατυπώσεις της ίδιας βασικής σχέσης μεταξύ μιας κατανομής φορτίου και του
Ηλεκτροµαγνητισµός 2
 Ηλεκτροµαγνητισµός. 1) Για το µεγάλου µήκους αγωγό του σχήµατος να σχεδιάστε, µια µαγνητική γραµµή που να διέρχεται από το σηµείο Α καθώς και την ένταση του µαγνητικού πεδίου στο σηµείο Γ. Τα σηµεία Α
Ηλεκτροµαγνητισµός. 1) Για το µεγάλου µήκους αγωγό του σχήµατος να σχεδιάστε, µια µαγνητική γραµµή που να διέρχεται από το σηµείο Α καθώς και την ένταση του µαγνητικού πεδίου στο σηµείο Γ. Τα σηµεία Α
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
Φυσική για Μηχανικούς Εικόνα: Το Σέλας συμβαίνει όταν υψηλής ενέργειας, φορτισμένα σωματίδια από τον Ήλιο ταξιδεύουν στην άνω ατμόσφαιρα της Γης λόγω της ύπαρξης του μαγνητικού της πεδίου. Μαγνητισμός
ιατυπώστε την ιδιότητα αυτή µε τη βοήθεια µεταβλητών.
 Μαθηµατικά B υµνασίυ Eρωτήσεις θεωρίας 1. Τι νµάζυµε µεταβλητή;. Τι νµάζυµε αριθµητική παράσταση; 3. Τι νµάζυµε αλγεβρική παράσταση; 4. Πια είναι η επιµεριστική ιδιότητα; 5. Τι συµβαίνει αν και στα δύ
Μαθηµατικά B υµνασίυ Eρωτήσεις θεωρίας 1. Τι νµάζυµε µεταβλητή;. Τι νµάζυµε αριθµητική παράσταση; 3. Τι νµάζυµε αλγεβρική παράσταση; 4. Πια είναι η επιµεριστική ιδιότητα; 5. Τι συµβαίνει αν και στα δύ
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
