ΔΙΑΧΕΙΡΙΣΗ ΚΑΙ ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ Λύσεις ασκήσεων Α εξεταστικής περιόδου χειμερινού εξαμήνου
|
|
|
- Χλόη Ζάρκος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΔΙΑΧΕΙΡΙΣΗ ΚΑΙ ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ Λύσεις ασκήσεων Α εξεταστικής περιόδου χειμερινού εξαμήνου 1 3 Θέμα 1 (, μον.) Δίνεται ο παρακάτω πίνακας δραστηριοτήτων έργου. 1. Να σχεδιαστεί το διασυνδεόμενο διάγραμμα Gantt του έργου (1, μον.). Να σχεδιαστεί το τοξωτό δίκτυο του έργου (1,5 μον.) 3. Να σχεδιαστεί το κομβικό δίκτυο του έργου και να προσδιοριστούν οι σχέσεις Τέλους - Έναρξης, FS(i,j), των εξαρτώμενων δραστηριοτήτων (1,5 μον.) Πίνακας Δραστηριοτήτων Έργου Δραστηριότητα Διάρκεια Σχέσεις Α Αρχή του έργου Β 3 Αρχή του έργου Γ Αρχή του έργου Δ Μετά το τέλος των Α και Β Ε 8 Μετά το τέλος των Β και Γ Ζ Μετά το τέλος της Γ Η 5 Μετά το τέλος των Δ, Ε και Ζ Θ 3 Μετά το τέλος της Η 1. Διάγραμμα Gantt: Α Β Γ Δ Διάρκεια Ε Ζ Η Θ
2 . Τοξωτό δίκτυο έργου: Α/ Β 1 / Δ/ 1 Β/3 3 5 Η/5 Θ/3 8 Γ/ Β / Ε/8 Z 1 / Ζ/ Επεξηγήσεις: Το Γεγονός 1 σηματοδοτεί την έναρξη του έργου και την ταυτόχρονη έναρξη των δραστηριοτήτων Α, Β και Γ. Το Γεγονός σηματοδοτεί το τέλος της δραστηριότητας Α και την έναρξη της δραστηριότητας Δ, μετά την ολοκλήρωση των δραστηριοτήτων Α και Β. Επειδή όμως η έναρξη της δραστηριότητας Δ προϋποθέτει το τέλος των δραστηριοτήτων Α και Β και επειδή δεν επιτρέπεται να έχουμε παράλληλες δραστηριότητες μεταξύ δύο Γεγονότων (στην περίπτωσή μας από το Γεγονός 1 στο Γεγονός ), εισάγουμε το Γεγονός 3, που σηματοδοτεί το τέλος της δραστηριότητας Β, καθώς και την πλασματική δραστηριότητα Β 1, που συνδέει τα Γεγονότα 3 και. Ομοίως, το Γεγονός σηματοδοτεί την έναρξη των δραστηριοτήτων Ε και Ζ, μετά την ολοκλήρωση των δραστηριοτήτων Β και Γ. Επειδή δεν επιτρέπεται να έχουμε παράλληλες δραστηριότητες μεταξύ δύο Γεγονότων (στην περίπτωσή μας από το Γεγονός 1 στο Γεγονός ), εισάγουμε την πλασματική δραστηριότητα Β, που συνδέει τα Γεγονότα 3 και. Το Γεγονός 5 σηματοδοτεί την ταυτόχρονη λήξη των δραστηριοτήτων Δ και Ε (1 χρονικές μονάδες μετά την έναρξη του έργου, όπως φαίνεται και από το διάγραμμα Gantt). Επίσης, το Γεγονός 5 σηματοδοτεί την έναρξη της δραστηριότητας Η, η οποία όμως προϋποθέτει την ολοκλήρωση των δραστηριοτήτων Ε και Ζ. Επειδή δεν επιτρέπεται να έχουμε παράλληλες δραστηριότητες μεταξύ δύο Γεγονότων (στην περίπτωσή μας από το Γεγονός στο Γεγονός 5), εισάγουμε το Γεγονός, που σηματοδοτεί τη λήξη της δραστηριότητας Ζ, καθώς και την πλασματική δραστηριότητα Ζ 1, που συνδέει τα Γεγονότα και 5. Το Γεγονός σηματοδοτεί το τέλος της δραστηριότητας Η και την έναρξη της δραστηριότητας Θ, μετά την ολοκλήρωση της δραστηριότητας Η. Ομοίως, το Γεγονός 8 σηματοδοτεί το τέλος της δραστηριότητας Θ και ταυτόχρονα το τέλος του έργου. Από το τοξωτό δίκτυο (αλλά και από το διάγραμμα Gantt) προκύπτει ότι η ελάχιστη διάρκεια του έργου είναι χρονικές μονάδες.
3 3. Κομβικό δίκτυο: Α FS(Α,Δ) = Δ Β 3 FS(Β,Δ) = 3 FS(Δ,Η) = FS(Β,Ε) = 1 Ε 8 Η 5 Θ 3 FS(Ε,Η) = FS(Η,Θ) = Γ FS(Γ,Ε) = FS(Γ,Ζ) = Ζ FS(Ζ,Η) = 1 Επεξηγήσεις: Το έργο αρχίζει με την ταυτόχρονη έναρξη των δραστηριοτήτων Α, Β και Γ. Η έναρξη της δραστηριότητας Δ προϋποθέτει την ολοκλήρωση των δραστηριοτήτων Α και Β. Η δραστηριότητα Α έχει διάρκεια χρονικές μονάδες και η δραστηριότητα Β έχει διάρκεια 3 χρονικές μονάδες. Επομένως, η δραστηριότητα Δ ξεκινά αμέσως μετά το τέλος της δραστηριότητας Α, οπότε έχουμε FS(Α,Δ)=, ενώ μεσολαβούν 3 χρονικές μονάδες από τη λήξη της δραστηριότητας Β μέχρι την έναρξη της δραστηριότητας Δ, οπότε έχουμε FS(Β,Δ)=3. Ομοίως, η έναρξη της δραστηριότητας Ε προϋποθέτει την ολοκλήρωση των δραστηριοτήτων Β και Γ. Η δραστηριότητα Β έχει διάρκεια 3 χρονικές μονάδες και η δραστηριότητα Γ έχει διάρκεια χρονικές μονάδες. Επομένως, η δραστηριότητα Ε ξεκινά αμέσως μετά το τέλος της δραστηριότητας Γ, οπότε έχουμε FS(Γ,Ε)=, ενώ μεσολαβεί 1 χρονική μονάδα από τη λήξη της δραστηριότητας Β μέχρι την έναρξη της δραστηριότητας Ε, οπότε έχουμε FS(Β,Ε)=1. Η δραστηριότητα Ζ ξεκινά αμέσως μετά το τέλος της Γ, οπότε έχουμε FS(Γ,Ζ)=. Η έναρξη της δραστηριότητας Η προϋποθέτει την ολοκλήρωση των δραστηριοτήτων Δ,Ε και Ζ. Όπως φαίνεται και από το διάγραμμα Gantt, το τέλος των δραστηριοτήτων Δ και Ε συμβαίνει 1 χρονικές μονάδες από την έναρξη του έργου, ενώ το τέλος της δραστηριότητας Ζ συμβαίνει 11 χρονικές μονάδες από την έναρξη του έργου. Επομένως η δραστηριότητα Η ξεκινά αμέσως μετά την ταυτόχρονη λήξη των δραστηριοτήτων Δ και Ε, οπότε έχουμε FS(Δ,Η)= και FS(Ε,Η)=, ενώ μεσολαβεί 1 χρονική μονάδα από τη λήξη της δραστηριότητας Ζ μέχρι την έναρξη της δραστηριότητας Η, οπότε έχουμε FS(Ζ,Η)=1. Τέλος, η δραστηριότητα Θ ξεκινά αμέσως μετά το τέλος της Η, οπότε έχουμε FS(Η,Θ)=.
4 Θέμα (, μον.) Στα παρακάτω σχήματα δίνονται το τοξωτό και το κομβικό δίκτυο ενός έργου. Με επίλυση του ενός από τα δύο δίκτυα να προσδιοριστεί η κρίσιμη διαδρομή. 3 Β Δ Β/ Δ/ 1 Α/ 5 Ζ/ Α Ζ Γ/5 Ε/ Γ 5 Ε Επίλυση ΤοξωτούΔικτύου: Ενωρίτεροι χρόνοι γεγονότων: Σημείωση: Ο υπολογισμός των ενωρίτερων χρόνων των γεγονότων γίνεται με σάρωση του δικτύου από αριστερά προς τα δεξιά, δηλ. από την έναρξη προς τη λήξη του έργου, θέτοντας ως ενωρίτερο χρόνο του πρώτου γεγονότος του δικτύου την τιμή μηδέν (έναρξη του έργου). ΕΧ 1 = ΕΧ = ΕΧ 1 +ΧΔ Α = + = ΕΧ 3 = ΕΧ + ΧΔ Β = + = ΕΧ = ΕΧ + ΧΔ Γ = + 5 = Στο γεγονός 5 καταλήγουν δύο διαδρομές, επομένως: ΕΧ 5 (1) = ΕΧ 3 + ΧΔ Δ = + = 1 ΕΧ 5 () = ΕΧ + ΧΔ Ε = + = 1 ΕΧ 5 = max{εχ 5 (1), ΕΧ 5 ()} = max{1, 1} = 1 ΕΧ = ΕΧ 5 + ΧΔ Ζ = 1 + = Επομένως, ο ελάχιστος χρόνος υλοποίησης του έργου είναι χρονικές μονάδες. Βραδύτεροι χρόνοι γεγονότων: Σημείωση: Ο υπολογισμός των βραδύτερων χρόνων των γεγονότων γίνεται με σάρωση του δικτύου από δεξιά προς τα αριστερά, δηλ. από το τέλος προς την αρχή του έργου. Ο βραδύτερος χρόνος για το τελικό γεγονός είναι ίσος είτε με τον τακτό χρόνο, εάν δίνεται, είτε με τον ενωρίτερο χρόνο του τελικού γεγονότος. Δεν δίνεται τακτός χρόνος. Άρα: ΒΧ = ΕΧ = ΒΧ 5 = ΒΧ ΧΔ Ζ = = 1 ΒΧ = ΒΧ 5 ΧΔ Ε = 1 = ΒΧ 3 = ΒΧ 5 ΧΔ Δ = 1 = 1 Στο γεγονός καταλήγουν δύο διαδρομές, επομένως:
5 ΒΧ (1) = ΒΧ 3 ΧΔ Β = 1 = ΒΧ () = ΒΧ ΧΔ Γ = 5 = ΒΧ = min{βχ (1), ΒΧ ()} = min{, } = ΒΧ 1 = ΒΧ ΧΔ Α = = Συνολικό περιθώριο χρόνου δραστηριοτήτων: ΣΠΧ Α = ΒΧ ΕΧ 1 ΧΔ Α = = ΣΠΧ Β = ΒΧ 3 ΕΧ ΧΔ Β = 1 = ΣΠΧ Γ = ΒΧ ΕΧ ΧΔ Γ = 5 = ΣΠΧ Δ = ΒΧ 5 ΕΧ ΧΔ Δ = 1 = ΣΠΧ Ε = ΒΧ 5 ΕΧ ΧΔ Ε = 1 = ΣΠΧ Ζ = ΒΧ ΕΧ 5 ΧΔ Ζ = 1 = Επομένως, οι δραστηριότητες Α, Γ, Ε και Ζ είναι κρίσιμες, επειδή έχουν μηδενικό συνολικό περιθώριο χρόνου, και καθορίζουν την κρίσιμη διαδρομή του έργου Α Γ Ε Ζ ή 1 5 : 3 1 Α/ 1 Δ/ Β/ Γ/5 Ε/ Ζ/ Επίλυση Κομβικού Δικτύου: Ενωρίτεροι χρόνοι δραστηριοτήτων: Σημείωση: Ο υπολογισμός των ενωρίτερων χρόνων των δραστηριοτήτων γίνεται με σάρωση του δικτύου από αριστερά προς τα δεξιά, δηλ. από την έναρξη προς τη λήξη του έργου, θέτοντας ως ενωρίτερο χρόνο της πρώτης δραστηριότητας του δικτύου την τιμή μηδέν (έναρξη του έργου). ΕΧΕ Α = ΕΧΤ Α = ΕΧΕ Α + ΧΔ Α = + = ΕΧΕ Β = ΕΧΤ Α + FS(A, B) = + = ΕΧΤ Β = ΕΧΕ Β + ΧΔ Β = + = ΕΧΕ Γ = ΕΧΤ Α + FS(Α, Γ) = + = ΕΧΤ Γ = ΕΧΕ Γ + ΧΔ Γ = + 5 =
6 ΕΧΕ Δ = ΕΧΤ Β + FS(Β, Δ) = + = ΕΧΤ Δ = ΕΧΕ Δ + ΧΔ Δ = + = 1 ΕΧΕ Ε = ΕΧΤ Γ + FS(Γ, Ε) = + = ΕΧΤ Ε = ΕΧΕ Ε + ΧΔ Ε = + = 1 Στη δραστηριότητα Ζ καταλήγουν δύο διαδρομές, επομένως: ΕΧΕ Ζ (1) = ΕΧΤ Δ + FS(Δ, Ζ) = 1 + = 1 ΕΧΕ Ζ () = ΕΧΤ Ε + FS(Ε, Ζ) = 1 + = 1 ΕΧΕ Ζ = max{εχε Ζ (1), ΕΧΕ Ζ ()} = max{1, 1} = 1 ΕΧΤ Ζ = ΕΧΕ Ζ + ΧΔ Ζ = 1 + = Επομένως, ο ελάχιστος χρόνος υλοποίησης του έργου είναι χρονικές μονάδες. Βραδύτεροι χρόνοι δραστηριοτήτων: Σημείωση: Ο υπολογισμός των βραδύτερων χρόνων των δραστηριοτήτων γίνεται με σάρωση του δικτύου από δεξιά προς τα αριστερά, δηλ. από το τέλος προς την αρχή του έργου. Ο βραδύτερος χρόνος τέλους για την τελική δραστηριότητα είναι ίσος είτε με τον τακτό χρόνο, εάν δίνεται, είτε με το μεγαλύτερο από τους ενωρίτερους χρόνους τέλους όλων των δραστηριοτήτων. Δεν δίνεται τακτός χρόνος. Άρα: ΒΧΤ Ζ = ΕΧΤ Ζ = ΒΧΕ Ζ = ΒΧΤ Ζ ΧΔ Ζ = = 1 ΒΧΤ Ε = ΒΧΕ Ζ FS(Ε, Ζ) = 1 = 1 ΒΧΕ Ε = ΒΧΤ Ε ΧΔ Ε = 1 = ΒΧΤ Δ = ΒΧΕ Ζ FS(Δ, Ζ) = 1 = 1 ΒΧΕ Δ = ΒΧΤ Δ ΧΔ Δ = 1 = 1 ΒΧΤ Γ = ΒΧΕ Ε FS(Γ, Ε) = = ΒΧΕ Γ = ΒΧΤ Γ ΧΔ Γ = 5 = ΒΧΤ Β = ΒΧΕ Δ FS(Β, Δ) = 1 = 1 ΒΧΕ Β = ΒΧΤ Β ΧΔ Β = 1 = Στη δραστηριότητα Α καταλήγουν δύο διαδρομές, επομένως: ΒΧΤ Α (1) = ΒΧΕ Β FS(Α, Β) = = ΒΧΤ Α () = ΒΧΕ Γ FS(Α, Γ) = = ΒΧΤ Α = min{βχτ Α (1), ΒΧΤ Α ()} = min{, } = BXE A = BXT A ΧΔ Α = = Περιθώρια χρόνου δραστηριοτήτων: Συνολικό περιθώριο χρόνου δραστηριοτήτων: ΣΠΧ Α = ΒΧΤ Α ΕΧΕ Α ΧΔ Α = = ΣΠΧ Β = ΒΧΤ Β ΕΧΕ Β ΧΔ Β = 1 = ΣΠΧ Γ = ΒΧΤ Γ ΕΧΕ Γ ΧΔ Γ = 5 = ΣΠΧ Δ = ΒΧΤ Δ ΕΧΕ Δ ΧΔ Δ = 1 = ΣΠΧ Ε = ΒΧΤ Ε ΕΧΕ Ε ΧΔ Ε = 1 = ΣΠΧ Ζ = ΒΧΤ Ζ ΕΧΕ Ζ ΧΔ Ζ = 1 =
7 Επομένως, οι δραστηριότητες Α, Γ, Ε και Ζ είναι κρίσιμες, επειδή έχουν μηδενικό συνολικό περιθώριο χρόνου, και καθορίζουν την κρίσιμη διαδρομή του έργου: Α Γ Ε Ζ. Σημείωση: Για τον καθορισμό της κρίσιμης διαδρομής αρκεί ο υπολογισμός του συνολικού περιθωρίου χρόνου των δραστηριοτήτων, όμως για την πληρότητα επίλυσης του δικτύου παρατίθεται και ο υπολογισμός του ελεύθερου περιθωρίου χρόνου των δραστηριοτήτων. Ελεύθερο περιθώριο χρόνου δραστηριοτήτων: ΕΠΧ Ζ = (τέλος του έργου) ΕΠΧ Ε = ΕΧΕ Ζ ΕΧΤ Ε FS(Ε, Ζ) = 1 1 = ΕΠΧ Δ =ΕΧΕ Ζ ΕΧΤ Δ FS(Δ, Ζ) = 1 1 = ΕΠΧ Γ = ΕΧΕ Ε ΕΧΤ Γ FS(Γ, Ε) = = ΕΠΧ Β = ΕΧΕ Δ ΕΧΤ Β FS(Β, Δ) = = Στη δραστηριότητα Α καταλήγουν δύο διαδρομές, επομένως: ΕΠΧ Α (1) = ΕΧΕ Β ΕΧΤ Α FS(Α, Β) = = ΕΠΧ Α () = ΕΧΕ Γ ΕΧΤ Α FS(Α, Γ) = = ΕΠΧ Α = min{επχ Α (1), ΕΠΧ Α ()} = min{, } = Β 1 Δ Α Ζ 1 1 Γ 5 Ε 1 1
Λύσεις ασκήσεων εξεταστικής περιόδου Ιανουαρίου 2017
 Λύσεις ασκήσεων εξεταστικής περιόδου Ιανουαρίου 217 Θέμα 1 (6,) Δίνεται το παρακάτω διασυνδεόμενο διάγραμμα Gantt ενός έργου. 1 2 3 5 6 7 8 9 1 12 13 Α Β Γ Δ Ε Ζ Η 1. Να συμπληρωθεί ο Πίνακας Δραστηριοτήτων
Λύσεις ασκήσεων εξεταστικής περιόδου Ιανουαρίου 217 Θέμα 1 (6,) Δίνεται το παρακάτω διασυνδεόμενο διάγραμμα Gantt ενός έργου. 1 2 3 5 6 7 8 9 1 12 13 Α Β Γ Δ Ε Ζ Η 1. Να συμπληρωθεί ο Πίνακας Δραστηριοτήτων
B Εξεταςτική Περίοδοσ Εαρινοφ Εξαμήνου Λφςη Άςκηςησ
 B Εξεταςτική Περίοδοσ Εαρινοφ Εξαμήνου 11 1 Λφςη Άςκηςησ Θέμα 1 (, μον.): Δίνεται ο παρακάτω πίνακασ δραςτθριοτιτων ζργου. Πίνακασ Δραςτηριοτήτων Έργου Δραςτηριότητα Διάρκεια Σχέςεισ Α Αρχι του ζργου Β
B Εξεταςτική Περίοδοσ Εαρινοφ Εξαμήνου 11 1 Λφςη Άςκηςησ Θέμα 1 (, μον.): Δίνεται ο παρακάτω πίνακασ δραςτθριοτιτων ζργου. Πίνακασ Δραςτηριοτήτων Έργου Δραςτηριότητα Διάρκεια Σχέςεισ Α Αρχι του ζργου Β
ΠΑΡΑΔΕΙΓΜΑΤΑ. Δραστηριότητα Αμέσως προηγούμενη Διάρκεια (ημέρες) A - 3 B A 6 Γ A 4 Δ Β, Γ 2 Ε Β 5 Ζ Γ 7 Η Δ, Ε 2
 ΠΑΡΑΔΕΙΓΜΑΤΑ 1. Εξετάζεται η κατασκευή μιας τυπικής κατοικίας. Δημιουργήστε το διάγραμμα δομής έργου (Work Breakdown Structure WBS). Συμπληρώστε τους περιορισμούς διαδοχής των εργασιών. Σχεδιάστε το δικτυωτό
ΠΑΡΑΔΕΙΓΜΑΤΑ 1. Εξετάζεται η κατασκευή μιας τυπικής κατοικίας. Δημιουργήστε το διάγραμμα δομής έργου (Work Breakdown Structure WBS). Συμπληρώστε τους περιορισμούς διαδοχής των εργασιών. Σχεδιάστε το δικτυωτό
ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ. Δρ. Βασίλης Π. Αγγελίδης Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης
 ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Δρ. Βασίλης Π. Αγγελίδης Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης Κομβικά Δίκτυα Δρ. Βασίλης Π. Αγγελίδης Διαφάνεια 2 Εισαγωγή Στα κομβικά δίκτυα οι κόμβοι
ΑΝΑΛΥΣΗ ΔΕΔΟΜΕΝΩΝ Δρ. Βασίλης Π. Αγγελίδης Τμήμα Μηχανικών Παραγωγής & Διοίκησης Δημοκρίτειο Πανεπιστήμιο Θράκης Κομβικά Δίκτυα Δρ. Βασίλης Π. Αγγελίδης Διαφάνεια 2 Εισαγωγή Στα κομβικά δίκτυα οι κόμβοι
Διαχείριση Έργων Πληροφορικής
 Διαχείριση Έργων Πληροφορικής Διαχείριση Πόρων Μ. Τσικνάκης Ε. Μανιαδή - Α. Μαριδάκη 1 Διαχείριση Χρήσης Πόρων Απαιτούμενοι πόροι στην ανάπτυξη ενός Πληροφοριακού Συστήματος: Ανθρώπινο δυναμικό (π.χ. αναλυτές,
Διαχείριση Έργων Πληροφορικής Διαχείριση Πόρων Μ. Τσικνάκης Ε. Μανιαδή - Α. Μαριδάκη 1 Διαχείριση Χρήσης Πόρων Απαιτούμενοι πόροι στην ανάπτυξη ενός Πληροφοριακού Συστήματος: Ανθρώπινο δυναμικό (π.χ. αναλυτές,
ΤΕΙ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Διοίκηση Εργοταξίου
 ΤΕΙ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Διοίκηση Εργοταξίου Διδάσκων: Γιάννης Χουλιάρας Χρονικός προγραμματισμός κατασκευής τεχνικών έργων. Μέθοδος Gantt, Μέθοδος κρίσιμης όδευσης (CPM). Επίλυση ασκήσεων
ΤΕΙ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Διοίκηση Εργοταξίου Διδάσκων: Γιάννης Χουλιάρας Χρονικός προγραμματισμός κατασκευής τεχνικών έργων. Μέθοδος Gantt, Μέθοδος κρίσιμης όδευσης (CPM). Επίλυση ασκήσεων
ΜΕΘΟΔΟΣ CPM Κατανόηση Διαδικασίας με τη Χρήση Παραδείγματος
 ΜΕΘΟΔΟΣ CPM Κατανόηση Διαδικασίας με τη Χρήση Παραδείγματος Το παράδειγμα στο οποίο θα βασιστούμε είναι το εξής: Στον παρακάτω πίνακα δίνονται οι δραστηριότητες ενός έργου, η διάρκεια τους καθώς και οι
ΜΕΘΟΔΟΣ CPM Κατανόηση Διαδικασίας με τη Χρήση Παραδείγματος Το παράδειγμα στο οποίο θα βασιστούμε είναι το εξής: Στον παρακάτω πίνακα δίνονται οι δραστηριότητες ενός έργου, η διάρκεια τους καθώς και οι
2 Ο ΜΑΘΗΜΑ ΠΡΟΒΛΗΜΑΤΑ ΧΡΟΝΟΥ-ΚΟΣΤΟΥΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ
 Διαχείριση Τεχνικών Έργων 2 Ο ΜΑΘΗΜΑ ΠΡΟΒΛΗΜΑΤΑ ΧΡΟΝΟΥ-ΚΟΣΤΟΥΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ Ορισμοί Κόστος κατασκευής: το σύνολο των δαπανών
Διαχείριση Τεχνικών Έργων 2 Ο ΜΑΘΗΜΑ ΠΡΟΒΛΗΜΑΤΑ ΧΡΟΝΟΥ-ΚΟΣΤΟΥΣ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ Ορισμοί Κόστος κατασκευής: το σύνολο των δαπανών
ΔΕΟ 40 ΤΟΜΟΣ Β ΘΕΩΡΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΔΙΚΤΥΩΝ ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ
 ΔΕΟ 40 ΤΟΜΟΣ Β ΘΕΩΡΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΔΙΚΤΥΩΝ ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ ΟΡΙΣΜΟΣ ΤΟΥ ΕΡΓΟΥ Έργο είναι μια ακολουθία μοναδικών, σύνθετων και αλληλοσυσχετιζόμενων δραστηριοτήτων που αποσκοπούν στην επίτευξη κάποιου συγκεκριμένου
ΔΕΟ 40 ΤΟΜΟΣ Β ΘΕΩΡΙΑ ΚΑΙ ΑΣΚΗΣΕΙΣ ΔΙΚΤΥΩΝ ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ ΟΡΙΣΜΟΣ ΤΟΥ ΕΡΓΟΥ Έργο είναι μια ακολουθία μοναδικών, σύνθετων και αλληλοσυσχετιζόμενων δραστηριοτήτων που αποσκοπούν στην επίτευξη κάποιου συγκεκριμένου
«Διαχείριση Έργων στη Δημόσια Διοίκηση» Ενότητα 6: Τεχνικές παρακολούθησης (μέρος 1ο) ΕΙΔΙΚΗΣ ΦΑΣΗΣ ΣΠΟΥΔΩΝ 24η ΕΚΠΑΙΔΕΥΤΙΚΗ ΣΕΙΡΑ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΚΑΙ ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ «Διαχείριση Έργων στη Δημόσια Διοίκηση» Ενότητα 6: Τεχνικές παρακολούθησης (μέρος 1ο) ΕΙΔΙΚΗΣ ΦΑΣΗΣ ΣΠΟΥΔΩΝ 24η ΕΚΠΑΙΔΕΥΤΙΚΗ ΣΕΙΡΑ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΥΠΟΥΡΓΕΙΟ ΕΣΩΤΕΡΙΚΩΝ ΚΑΙ ΔΙΟΙΚΗΤΙΚΗΣ ΑΝΑΣΥΓΚΡΟΤΗΣΗΣ «Διαχείριση Έργων στη Δημόσια Διοίκηση» Ενότητα 6: Τεχνικές παρακολούθησης (μέρος 1ο) ΕΙΔΙΚΗΣ ΦΑΣΗΣ ΣΠΟΥΔΩΝ 24η ΕΚΠΑΙΔΕΥΤΙΚΗ ΣΕΙΡΑ
ΠΡΟΤΕΙΝΟΜΕΝΗ ΑΠΑΝΤΗΣΗ 3ΗΣ ΓΡΑΠΤΗΣ ΕΡΓΑΣΙΑΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΔΕΟ 40
 ΠΡΟΤΕΙΝΟΜΕΝΗ ΑΠΑΝΤΗΣΗ 3ΗΣ ΓΡΑΠΤΗΣ ΕΡΓΑΣΙΑΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΔΕΟ 40 1 Περιεχόμενα ΘΕΜΑ 1 ο... 3 Ερώτημα 1.1.... 4 ΕΠΙΛΥΣΗ... 9 Ερώτημα 1.2.... 13 ΘΕΜΑ 2 ο... 14 Ερώτημα 2.2.... 19 ΘΕΜΑ 3 ο... 20 Ερώτημα
ΠΡΟΤΕΙΝΟΜΕΝΗ ΑΠΑΝΤΗΣΗ 3ΗΣ ΓΡΑΠΤΗΣ ΕΡΓΑΣΙΑΣ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ ΔΕΟ 40 1 Περιεχόμενα ΘΕΜΑ 1 ο... 3 Ερώτημα 1.1.... 4 ΕΠΙΛΥΣΗ... 9 Ερώτημα 1.2.... 13 ΘΕΜΑ 2 ο... 14 Ερώτημα 2.2.... 19 ΘΕΜΑ 3 ο... 20 Ερώτημα
ΕΡΓΑΛΕΙΑ ΧΡΟΝΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 ΕΡΓΑΛΕΙΑ ΧΡΟΝΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Δρ. Βασιλική Καζάνα Αναπλ. Καθηγήτρια ΤΕΙ Καβάλας, Τμήμα Δασοπονίας & Διαχείρισης Φυσικού Περιβάλλοντος Δράμας Εργαστήριο Δασικής Διαχειριστικής Τηλ. & Φαξ: 25210 60435
ΕΡΓΑΛΕΙΑ ΧΡΟΝΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Δρ. Βασιλική Καζάνα Αναπλ. Καθηγήτρια ΤΕΙ Καβάλας, Τμήμα Δασοπονίας & Διαχείρισης Φυσικού Περιβάλλοντος Δράμας Εργαστήριο Δασικής Διαχειριστικής Τηλ. & Φαξ: 25210 60435
Διοίκηση Λειτουργιών. Διοίκηση Έργων II (Δίκτυα Έργων & Χρονοπρογραμματισμός) - 6 ο μάθημα -
 Διοίκηση Λειτουργιών Διοίκηση Έργων II (Δίκτυα Έργων & Χρονοπρογραμματισμός) - 6 ο μάθημα - Θεματολογία Μορφές δικτύων έργων Χρονικός προγραμματισμός έργων Ανδρέας Νεάρχου Συμβολισμοί για δίκτυα έργων
Διοίκηση Λειτουργιών Διοίκηση Έργων II (Δίκτυα Έργων & Χρονοπρογραμματισμός) - 6 ο μάθημα - Θεματολογία Μορφές δικτύων έργων Χρονικός προγραμματισμός έργων Ανδρέας Νεάρχου Συμβολισμοί για δίκτυα έργων
ΠΕΡΙΕΧΟΜΕΝΑ ΔΙΟΙΚΗΣΗ ΛΕΙΤΟΥΡΓΙΩΝ. Διοίκηση και Προγραμματισμός Έργων
 ΔΙΟΙΚΗΣΗ ΛΕΙΤΟΥΡΓΙΩΝ Διοίκηση και Προγραμματισμός Έργων ΠΕΡΙΕΧΟΜΕΝΑ 1. Βασικές έννοιες 2. Ανάλυση του έργου και διαμόρφωση του δικτύου 3. Επίλυση δικτύου 1 1. Βασικές έννοιες Με τον όρο έργο, εκτός από
ΔΙΟΙΚΗΣΗ ΛΕΙΤΟΥΡΓΙΩΝ Διοίκηση και Προγραμματισμός Έργων ΠΕΡΙΕΧΟΜΕΝΑ 1. Βασικές έννοιες 2. Ανάλυση του έργου και διαμόρφωση του δικτύου 3. Επίλυση δικτύου 1 1. Βασικές έννοιες Με τον όρο έργο, εκτός από
ΜΕΘΟΔΟΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΩΝ
 ΤΕΙ ΚΡΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΘΟΔΟΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΚΑΠΕΛΩΝΗ ΑΘΑΝΑΣΙΑ Α.Μ. 4000 ΙΑΝΟΥΑΡΙΟΣ 2014 Μέθοδοι Διοίκησης Έργων Σελίδα 1 Copyright Aθανασία Καπελώνη, 2013 Με επιφύλαξη
ΤΕΙ ΚΡΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕΘΟΔΟΙ ΔΙΟΙΚΗΣΗΣ ΕΡΓΩΝ ΠΤΥΧΙΑΚΗ ΕΡΓΑΣΙΑ ΚΑΠΕΛΩΝΗ ΑΘΑΝΑΣΙΑ Α.Μ. 4000 ΙΑΝΟΥΑΡΙΟΣ 2014 Μέθοδοι Διοίκησης Έργων Σελίδα 1 Copyright Aθανασία Καπελώνη, 2013 Με επιφύλαξη
ΠΑΡΑΔΕΙΓΜΑΤΑ 4 ης ΟΣΣ
 ΠΑΡΑΔΕΙΓΜΑΤΑ 4 ης ΟΣΣ Τα χρονικά και οικονομικά δεδομένα ενός έργου φαίνονται στον πίνακα 1 που ακολουθεί. Πίνακας 1: Χαρακτηριστικά στοιχεία έργου ραστηριότητα Αμέσως προηγούμενη ιάρκεια (ημέρες) Μέγεθος
ΠΑΡΑΔΕΙΓΜΑΤΑ 4 ης ΟΣΣ Τα χρονικά και οικονομικά δεδομένα ενός έργου φαίνονται στον πίνακα 1 που ακολουθεί. Πίνακας 1: Χαρακτηριστικά στοιχεία έργου ραστηριότητα Αμέσως προηγούμενη ιάρκεια (ημέρες) Μέγεθος
Στοχαστικές Στρατηγικές
 Στοχαστικές Στρατηγικές 2 η ενότητα: Στοιχειώδη προβλήματα διαδρομής Τμήμα Μαθηματικών, ΠΘ καδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα γγελική Μεταδιδακτορική ερευνήτρια, ΠΘ & Πανεπιστήμιο Μακεδονίας
Στοχαστικές Στρατηγικές 2 η ενότητα: Στοιχειώδη προβλήματα διαδρομής Τμήμα Μαθηματικών, ΠΘ καδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα γγελική Μεταδιδακτορική ερευνήτρια, ΠΘ & Πανεπιστήμιο Μακεδονίας
Στοχαστικές Στρατηγικές. διαδρομής (3)
 Στοχαστικές Στρατηγικές 6 η ενότητα: Το γενικό πρόβλημα ελάχιστης διαδρομής () Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 08-09 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές 6 η ενότητα: Το γενικό πρόβλημα ελάχιστης διαδρομής () Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 08-09 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές. διαδρομής (1)
 Στοχαστικές Στρατηγικές η ενότητα: Το γενικό πρόβλημα ελάχιστης διαδρομής () Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 08-09 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές η ενότητα: Το γενικό πρόβλημα ελάχιστης διαδρομής () Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 08-09 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Project Crashing & Resource Management Assignment 3 - Λύσεις
 Project Crashing & Resource Management Assignment 3 - Λύσεις Issued: Τετάρτη, 7/6/2017 Due: Κυριακή, 18/6/2017 Άσκηση 1 - Project Crashing Έστω ότι ένα έργο Πληροφορικής αποτελείται από επτά δραστηριότητες,
Project Crashing & Resource Management Assignment 3 - Λύσεις Issued: Τετάρτη, 7/6/2017 Due: Κυριακή, 18/6/2017 Άσκηση 1 - Project Crashing Έστω ότι ένα έργο Πληροφορικής αποτελείται από επτά δραστηριότητες,
Network Analysis, CPM and PERT Assignment 2 - Λύσεις
 Network Analysis, CPM and PERT Assignment 2 - Λύσεις Άσκηση 1 - CPM Μια εταιρία έχει αναλάβει την ανάπτυξη ενός μεγάλου πληροφοριακού συστήματος. Το όλο έργο απαιτεί για την ολοκλήρωσή του την υλοποίηση
Network Analysis, CPM and PERT Assignment 2 - Λύσεις Άσκηση 1 - CPM Μια εταιρία έχει αναλάβει την ανάπτυξη ενός μεγάλου πληροφοριακού συστήματος. Το όλο έργο απαιτεί για την ολοκλήρωσή του την υλοποίηση
10/12/2012 ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ ΠΕΡΙΕΧΟΜΕΝΑ
 ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ ΔΙΑΛΕΞΗ Βεργινάδης Γιάννης Δρ. Ηλεκτρολόγος Μηχανικός και Μηχανικός Υπολογιστών ΕΜΠ ΠΕΡΙΕΧΟΜΕΝΑ 1 ΧΡΟΝΙΚΗ ΑΝΑΛΥΣΗ ΙΚΤΥΩΝ ΠΑΡΑ ΕΙΓΜΑΤΑ 1 Ανάλυση δικτύου με τη μέθοδο CPM Προσδιορισμός της
ΔΙΟΙΚΗΣΗ ΕΡΓΩΝ ΔΙΑΛΕΞΗ Βεργινάδης Γιάννης Δρ. Ηλεκτρολόγος Μηχανικός και Μηχανικός Υπολογιστών ΕΜΠ ΠΕΡΙΕΧΟΜΕΝΑ 1 ΧΡΟΝΙΚΗ ΑΝΑΛΥΣΗ ΙΚΤΥΩΝ ΠΑΡΑ ΕΙΓΜΑΤΑ 1 Ανάλυση δικτύου με τη μέθοδο CPM Προσδιορισμός της
1 Ο ΜΑΘΗΜΑ ΧΡΟΝΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ
 Διαχείριση Τεχνικών Έργων 1 Ο ΜΑΘΗΜΑ ΧΡΟΝΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ Βασικές αρχές τεχνικού έργου Σειρά
Διαχείριση Τεχνικών Έργων 1 Ο ΜΑΘΗΜΑ ΧΡΟΝΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ ΔΡ ΛΕΩΝΙΔΑΣ ΑΝΘΟΠΟΥΛΟΣ, ΕΠΙΚΟΥΡΟΣ ΚΑΘΗΓΗΤΗΣ ΤΜΗΜΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΔΙΑΧΕΙΡΙΣΗΣ ΕΡΓΩΝ ΤΕΙ ΛΑΡΙΣΑΣ Βασικές αρχές τεχνικού έργου Σειρά
Λύσεις θεμάτων Α εξεταστικής περιόδου χειμερινού εξαμήνου 2013-14 (Ιούνιος 2014)
 Λύσεις θεμάτων Α εξεταστικής περιόδου χειμερινού εξαμήνου 201314 (Ιούνιος 2014) ΘΕΜΑ 1 Ο (3,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό λειτουργικό διάγραμμα που περιγράφει ένα αναγνωριστικό αυτοκινούμενο
Λύσεις θεμάτων Α εξεταστικής περιόδου χειμερινού εξαμήνου 201314 (Ιούνιος 2014) ΘΕΜΑ 1 Ο (3,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό λειτουργικό διάγραμμα που περιγράφει ένα αναγνωριστικό αυτοκινούμενο
Λύσεις θεμάτων Α εξεταστικής περιόδου Χειμερινού εξαμήνου
 Λύσεις θεμάτων Α εξεταστικής περιόδου Χειμερινού εξαμήνου 203 4 ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος ελέγχου κλειστού βρόχου. α. Να προσδιοριστεί
Λύσεις θεμάτων Α εξεταστικής περιόδου Χειμερινού εξαμήνου 203 4 ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος ελέγχου κλειστού βρόχου. α. Να προσδιοριστεί
Στοχαστικές Στρατηγικές
 Στοχαστικές Στρατηγικές 3 η ενότητα: Στοχαστικά προβλήματα διαδρομής Μεθοδολογία (1) Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 018-019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές 3 η ενότητα: Στοχαστικά προβλήματα διαδρομής Μεθοδολογία (1) Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 018-019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Ανάλυση Χρόνου, Πόρων & Κόστους
 ΠΜΣ: «Παραγωγή και ιαχείριση Ενέργειας» ιαχείριση Ενέργειας και ιοίκηση Έργων Ανάλυση Χρόνου, Πόρων & Κόστους Επ. Καθηγητής Χάρης ούκας, Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστημάτων Αποφάσεων & ιοίκησης
ΠΜΣ: «Παραγωγή και ιαχείριση Ενέργειας» ιαχείριση Ενέργειας και ιοίκηση Έργων Ανάλυση Χρόνου, Πόρων & Κόστους Επ. Καθηγητής Χάρης ούκας, Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστημάτων Αποφάσεων & ιοίκησης
Διοίκηση Λειτουργιών. Διοίκηση Έργων II (Project Management)
 Διοίκηση Λειτουργιών Διοίκηση Έργων II (Project Management) 1 Έργο επέκτασης Νοσοκομείου Ρίου Δραστηριότητα Περιγραφή Άμεσα Προηγηθείσα Διάρκεια (βδομ.) B D E F G H Κατασκευήεσωτερικώνχώρων Αλλαγήοροφήςκαιπατώματος
Διοίκηση Λειτουργιών Διοίκηση Έργων II (Project Management) 1 Έργο επέκτασης Νοσοκομείου Ρίου Δραστηριότητα Περιγραφή Άμεσα Προηγηθείσα Διάρκεια (βδομ.) B D E F G H Κατασκευήεσωτερικώνχώρων Αλλαγήοροφήςκαιπατώματος
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX
 ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΒΑΣΙΚΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΤΗΣ ΜΕΘΟΔΟΥ SIMPLEX Θεμελιώδης αλγόριθμος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού που κάνει χρήση της θεωρίας της Γραμμικής Άλγεβρας Προτάθηκε από το Dantzig (1947) και πλέον
ΠΜΣ "Παραγωγή και ιαχείριση Ενέργειας" ιαχείριση Ενέργειας και ιοίκηση Έργων
 ιαχείριση Ενέργειας και ιοίκηση Έργων 18. Σχεδιασμός Έργων - Χρονική Ανάλυση ση ικτύων Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστημάτων Αποφάσεων & ιοίκησης Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
ιαχείριση Ενέργειας και ιοίκηση Έργων 18. Σχεδιασμός Έργων - Χρονική Ανάλυση ση ικτύων Καθηγητής Ιωάννης Ψαρράς Εργαστήριο Συστημάτων Αποφάσεων & ιοίκησης Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών
(Θέματα που θα παραδοθούν σε οποιαδήποτε άλλη ημερομηνία ή με οποιοδήποτε άλλο τρόπο δεν θα μετρήσουν βαθμολογικά) Εκσκαφή.
 7 o ΕΞΑΜΗΝΟ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ - ΑΣΚΗΣEIΣ ΓΙΑ ΣΠΙΤΙ (ΘΕΜΑ ΕΞΑΜΗΝΟΥ) ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑ ΟΣΗΣ 19- εκ- 2008 (με προφορική εξέταση) (Θέματα που θα παραδοθούν σε οποιαδήποτε άλλη ημερομηνία ή με οποιοδήποτε άλλο
7 o ΕΞΑΜΗΝΟ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ - ΑΣΚΗΣEIΣ ΓΙΑ ΣΠΙΤΙ (ΘΕΜΑ ΕΞΑΜΗΝΟΥ) ΗΜΕΡΟΜΗΝΙΑ ΠΑΡΑ ΟΣΗΣ 19- εκ- 2008 (με προφορική εξέταση) (Θέματα που θα παραδοθούν σε οποιαδήποτε άλλη ημερομηνία ή με οποιοδήποτε άλλο
Διαφορικές Εξισώσεις.
 Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y +
Διαφορικές Εξισώσεις. Εαρινό εξάμηνο 05-6. Λύσεις πρώτου φυλλαδίου ασκήσεων.. Για κάθε μία από τις παρακάτω διαφορικές εξισώσεις πείτε αν είναι γραμμική ή όχι και προσδιορίστε την τάξη της. α. y + y +
APEIROSTIKOS LOGISMOS I
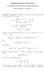 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 3. Άσκηση : Προσδιορίστε, αν υπάρχουν, τις τιμές τού a για τις οποίες οι παρακάτω συναρτήσεις είναι συνεχείς. + +, αν >
Στον παρακάτω πίνακα παρουσιάζονται οι δραστηριότητες που απατούνται για την υλοποίηση ενός μικρού έργου και η διάρκεια αυτών σε εβδομάδες.
 Εκφώνηση Στον παρακάτω πίνακα παρουσιάζονται οι δραστηριότητες που απατούνται για την υλοποίηση ενός μικρού έργου και η διάρκεια αυτών σε εβδομάδες. Activity Completion time (weeks) 1 5 2 7 3 6 4 3 5 4
Εκφώνηση Στον παρακάτω πίνακα παρουσιάζονται οι δραστηριότητες που απατούνται για την υλοποίηση ενός μικρού έργου και η διάρκεια αυτών σε εβδομάδες. Activity Completion time (weeks) 1 5 2 7 3 6 4 3 5 4
9 ΕΝΑ ΣΥΝΟΛΙΚΟ ΠΑΡΑ ΕΙΓΜΑ
 9 ΕΝΑ ΣΥΝΟΛΙΚΟ ΠΑΡΑ ΕΙΓΜΑ Στο κεφάλαιο αυτό, αναλύεται πλήρως ένα τεχνικό έργο, συγκεκριµένα αυτό της κατασκευής ενός µικρού αντλιοστασίου. Για την ανάλυση του έργου χρησιµοποιείται το πακέτο λογισµικού
9 ΕΝΑ ΣΥΝΟΛΙΚΟ ΠΑΡΑ ΕΙΓΜΑ Στο κεφάλαιο αυτό, αναλύεται πλήρως ένα τεχνικό έργο, συγκεκριµένα αυτό της κατασκευής ενός µικρού αντλιοστασίου. Για την ανάλυση του έργου χρησιµοποιείται το πακέτο λογισµικού
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΦΕΒΡΟΥΑΡΙΟΣ 2009 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΜΑ 1 ο Η Περιφέρεια Κεντρικής Μακεδονίας σχεδιάζει την ανάπτυξη ενός συστήματος αυτοκινητοδρόμων
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΦΕΒΡΟΥΑΡΙΟΣ 2009 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΜΑ 1 ο Η Περιφέρεια Κεντρικής Μακεδονίας σχεδιάζει την ανάπτυξη ενός συστήματος αυτοκινητοδρόμων
ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ ΣΤΗΝ Α ΛΥΚΕΙΟΥ
 Περιοδικό ΕΥΚΛΕΙΔΗΣ Β ΕΜΕ ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ ΣΤΗΝ Α ΛΥΚΕΙΟΥ (ΑΡΤΙΑ ΠΕΡΙΤΤΗ ΣΥΝΑΡΤΗΣΗ, ΜΟΝΟΤΟΝΙΑ ΚΑΙ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ) Κώστα Βακαλόπουλου Στο ο κεφάλαιο της Άλγεβρας της Α Λυκείου γίνεται η μελέτη των
Περιοδικό ΕΥΚΛΕΙΔΗΣ Β ΕΜΕ ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ ΣΤΗΝ Α ΛΥΚΕΙΟΥ (ΑΡΤΙΑ ΠΕΡΙΤΤΗ ΣΥΝΑΡΤΗΣΗ, ΜΟΝΟΤΟΝΙΑ ΚΑΙ ΑΚΡΟΤΑΤΑ ΣΥΝΑΡΤΗΣΗΣ) Κώστα Βακαλόπουλου Στο ο κεφάλαιο της Άλγεβρας της Α Λυκείου γίνεται η μελέτη των
Ο επόμενος πίνακας παρουσιάζει τις δραστηριότητες ενός έργου, τις σχέσεις μεταξύ τους, καθώς και τη διάρκειά τους σε εβδομάδες.
 Το Διάγραμμα Gantt Tο πλέον χρησιμοποιούμενο εργαλείο για το χρονοπρογραμματισμό ενός έργου είναι το διάγραμμα Gantt, το οποίο αναπτύχθηκε από το Η. Grantt. To διάγραμμα Gantt αποτελεί ένα γραμμικό διάγραμμα
Το Διάγραμμα Gantt Tο πλέον χρησιμοποιούμενο εργαλείο για το χρονοπρογραμματισμό ενός έργου είναι το διάγραμμα Gantt, το οποίο αναπτύχθηκε από το Η. Grantt. To διάγραμμα Gantt αποτελεί ένα γραμμικό διάγραμμα
sin ϕ = cos ϕ = tan ϕ =
 Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΜΗΧΑΝΙΚΗ 1 ΠΑΡΑ ΕΙΓΜΑ 1 ΚΑΤΑΣΚΕΥΗ ΙΑΓΡΑΜΜΑΤΩΝ MQN ΣΕ ΟΚΟ ιδάσκων: Αριστοτέλης Ε. Χαραλαµπάκης Εισαγωγή Με το παράδειγµα αυτό αναλύεται
Τ.Ε.Ι. ΠΕΙΡΑΙΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΟΜΙΚΩΝ ΕΡΓΩΝ ΜΗΧΑΝΙΚΗ 1 ΠΑΡΑ ΕΙΓΜΑ 1 ΚΑΤΑΣΚΕΥΗ ΙΑΓΡΑΜΜΑΤΩΝ MQN ΣΕ ΟΚΟ ιδάσκων: Αριστοτέλης Ε. Χαραλαµπάκης Εισαγωγή Με το παράδειγµα αυτό αναλύεται
Δομική Ανάλυση Έργων Χρονικός Προγραμματισμός Έργων. Σύνταξη-επιμέλεια παρουσίασης: Αθανάσιος Χασιακός, Στέφανος Τσινόπουλος
 ΔΙΑΧΕΙΡΙΣΗ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ Δομική Ανάλυση Έργων Χρονικός Προγραμματισμός Έργων Σύνταξη-επιμέλεια παρουσίασης: Αθανάσιος Χασιακός, Στέφανος Τσινόπουλος 1 Μέρος 1 ο : Ανάλυση δομής έργου Εισαγωγικές έννοιες
ΔΙΑΧΕΙΡΙΣΗ ΤΕΧΝΙΚΩΝ ΕΡΓΩΝ Δομική Ανάλυση Έργων Χρονικός Προγραμματισμός Έργων Σύνταξη-επιμέλεια παρουσίασης: Αθανάσιος Χασιακός, Στέφανος Τσινόπουλος 1 Μέρος 1 ο : Ανάλυση δομής έργου Εισαγωγικές έννοιες
Δικτυακή Αναπαράσταση Έργων (Δίκτυα ΑΟΑ και ΑΟΝ) & η Μέθοδος CPM. Λυμένες Ασκήσεις & Παραδείγματα
 Δικτυακή Αναπαράσταση Έργων (Δίκτυα ΑΟΑ και ΑΟΝ) & η Μέθοδος PM Λυμένες Ασκήσεις & Παραδείγματα Άσκηση σχεδίασης έργου με δίκτυο ΑΟΑ Σχεδιάστε το δίκτυο ΑΟΑ που ικανοποιεί του ακόλουθους περιορισμούς:
Δικτυακή Αναπαράσταση Έργων (Δίκτυα ΑΟΑ και ΑΟΝ) & η Μέθοδος PM Λυμένες Ασκήσεις & Παραδείγματα Άσκηση σχεδίασης έργου με δίκτυο ΑΟΑ Σχεδιάστε το δίκτυο ΑΟΑ που ικανοποιεί του ακόλουθους περιορισμούς:
2.1 ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ
 . ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ ΘΕΩΡΙΑ. Η γνησίως αύξουσα Συνάρτηση f λέγεται γνησίως αύξουσα σε ένα διάστηµα του πεδίου ορισµού της, όταν για οποιαδήποτε x, x µε x < x ισχύει : f ( x ) < f ( x ). Η
. ΜΟΝΟΤΟΝΙΑ ΑΚΡΟΤΑΤΑ - ΣΥΜΜΕΤΡΙΕΣ ΘΕΩΡΙΑ. Η γνησίως αύξουσα Συνάρτηση f λέγεται γνησίως αύξουσα σε ένα διάστηµα του πεδίου ορισµού της, όταν για οποιαδήποτε x, x µε x < x ισχύει : f ( x ) < f ( x ). Η
Φροντιστήριο #8 Ασκήσεις σε Γράφους 16/5/2017
 Φροντιστήριο #8 Ασκήσεις σε Γράφους 16/5/2017 Άσκηση 8.1: Στο παρακάτω σχήμα φαίνονται δέκα λατινικοί χαρακτήρες (A, F, K, M, R, S, T, V, X και Z) με τη μορφή γράφων. Ποιοι από αυτούς είναι ισομορφικοί;
Φροντιστήριο #8 Ασκήσεις σε Γράφους 16/5/2017 Άσκηση 8.1: Στο παρακάτω σχήμα φαίνονται δέκα λατινικοί χαρακτήρες (A, F, K, M, R, S, T, V, X και Z) με τη μορφή γράφων. Ποιοι από αυτούς είναι ισομορφικοί;
Λύσεις θεμάτων εξεταστικής περιόδου Ιανουαρίου Φεβρουαρίου 2015
 Λύσεις θεμάτων εξεταστικής περιόδου Ιανουαρίου Φεβρουαρίου 20 ΘΕΜΑ Ο (4,0 μονάδες). Να προσδιοριστεί η συνάρτηση μεταφοράς / του συστήματος που περιγράφεται από το δομικό (λειτουργικό) διάγραμμα. (2,0
Λύσεις θεμάτων εξεταστικής περιόδου Ιανουαρίου Φεβρουαρίου 20 ΘΕΜΑ Ο (4,0 μονάδες). Να προσδιοριστεί η συνάρτηση μεταφοράς / του συστήματος που περιγράφεται από το δομικό (λειτουργικό) διάγραμμα. (2,0
Φροντιστήριο #9 Ασκήσεις σε Γράφους 18/5/2018
 Φροντιστήριο #9 Ασκήσεις σε Γράφους 18/5/2018 Άσκηση 9.1: Στο παρακάτω σχήμα φαίνονται δέκα λατινικοί χαρακτήρες (A, F, K, M, R, S, T, V, X και Z) με τη μορφή γράφων. Ποιοι από αυτούς είναι ισομορφικοί;
Φροντιστήριο #9 Ασκήσεις σε Γράφους 18/5/2018 Άσκηση 9.1: Στο παρακάτω σχήμα φαίνονται δέκα λατινικοί χαρακτήρες (A, F, K, M, R, S, T, V, X και Z) με τη μορφή γράφων. Ποιοι από αυτούς είναι ισομορφικοί;
Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΕΠΤΕΜΒΡΙΟΣ 2011 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α ΘΕΜΑ 1 ο Σε ένα διαγωνισμό για την κατασκευή μίας καινούργιας γραμμής του
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΕΠΤΕΜΒΡΙΟΣ 2011 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α ΘΕΜΑ 1 ο Σε ένα διαγωνισμό για την κατασκευή μίας καινούργιας γραμμής του
MSc στη Διοίκηση και Διαχείριση Έργων και Προγραμμάτων
 MSc στη Διοίκηση και Διαχείριση Έργων και Προγραμμάτων E208 Διοίκηση Τεχνικών Έργων Διάλεξη 5: Εκτέλεση του κύκλου ζωής ενός έργου και διαχείριση των πόρων Διαχείριση χρόνου Δρ. Λεωνίδας Ανθόπουλος, Επίκουρος
MSc στη Διοίκηση και Διαχείριση Έργων και Προγραμμάτων E208 Διοίκηση Τεχνικών Έργων Διάλεξη 5: Εκτέλεση του κύκλου ζωής ενός έργου και διαχείριση των πόρων Διαχείριση χρόνου Δρ. Λεωνίδας Ανθόπουλος, Επίκουρος
Στοχαστικές Στρατηγικές
 Στοχαστικές Στρατηγικές 3 η ενότητα: Στοχαστικά προβλήματα διαδρομής Μεθοδολογία (2) Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ &
Στοχαστικές Στρατηγικές 3 η ενότητα: Στοχαστικά προβλήματα διαδρομής Μεθοδολογία (2) Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ &
Φροντιστήριο #8 Ασκήσεις σε Γράφους 24/5/2016
 Φροντιστήριο #8 Ασκήσεις σε Γράφους 24/5/2016 Άσκηση 8.1: Στο παρακάτω σχήμα φαίνονται δέκα λατινικοί χαρακτήρες (A, F, K, M, R, S, T, V, X και Z) με τη μορφή γράφων. Ποιοι από αυτούς είναι ισομορφικοί;
Φροντιστήριο #8 Ασκήσεις σε Γράφους 24/5/2016 Άσκηση 8.1: Στο παρακάτω σχήμα φαίνονται δέκα λατινικοί χαρακτήρες (A, F, K, M, R, S, T, V, X και Z) με τη μορφή γράφων. Ποιοι από αυτούς είναι ισομορφικοί;
Μάθημα: Στατική ΙΙ 9 Φεβρουαρίου 2011 Διδάσκων: Τριαντ. Κόκκινος, Ph.D. Διάρκεια εξέτασης 2:15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΑΘΗΝΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τμήμα Πολιτικών Έργων Υποδομής Μάθημα: Στατική ΙΙ 9 Φεβρουαρίου 011 Διδάσκων:, Ph.D. Διάρκεια εξέτασης :15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΑΘΗΝΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τμήμα Πολιτικών Έργων Υποδομής Μάθημα: Στατική ΙΙ 9 Φεβρουαρίου 011 Διδάσκων:, Ph.D. Διάρκεια εξέτασης :15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ
1 η Άσκηση στο Χρονοπρογραμματισμό Έργων
 1 η Άσκηση στο Χρονοπρογραμματισμό Έργων Θεωρείστε ένα έργο που απαιτεί τις δραστηριότητες του Πίνακα 1. Για κάθε δραστηριότητα αναγράφονται οι προαπαιτούμενες δραστηριότητες αν υπάρχουν, και οι εκτιμήσεις
1 η Άσκηση στο Χρονοπρογραμματισμό Έργων Θεωρείστε ένα έργο που απαιτεί τις δραστηριότητες του Πίνακα 1. Για κάθε δραστηριότητα αναγράφονται οι προαπαιτούμενες δραστηριότητες αν υπάρχουν, και οι εκτιμήσεις
Γ. Β Α Λ Α Τ Σ Ο Σ. 4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1. Γιώργος Βαλατσός Φυσικός Msc
 4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1 1. Πότε τα σώματα θεωρούνται υλικά σημεία; Αναφέρεται παραδείγματα. Στη φυσική πολλές φορές είναι απαραίτητο να μελετήσουμε τα σώματα χωρίς να λάβουμε υπόψη τις διαστάσεις τους. Αυτό
4ο ΓΥΜΝΑΣΙΟ ΛΑΜΙΑΣ 1 1. Πότε τα σώματα θεωρούνται υλικά σημεία; Αναφέρεται παραδείγματα. Στη φυσική πολλές φορές είναι απαραίτητο να μελετήσουμε τα σώματα χωρίς να λάβουμε υπόψη τις διαστάσεις τους. Αυτό
Μεθοδολογία Παραβολής
 Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
Μεθοδολογία Παραβολής Παραβολή είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από μια σταθερή ευθεία, την επονομαζόμενη διευθετούσα (δ), και από ένα σταθερό σημείο Ε που λέγεται εστία της παραβολής.
kg(χιλιόγραμμο) s(δευτερόλεπτο) Ένταση ηλεκτρικού πεδίου Α(Αμπέρ) Ένταση φωτεινής πηγής cd (καντέλα) Ποσότητα χημικής ουσίας mole(μόλ)
 ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
ΕΙΣΑΓΩΓΗ- ΦΥΣΙΚΑ ΜΕΓΕΘΗ Στα φυσικά φαινόμενα εμφανίζονται κάποιες ιδιότητες της ύλης. Για να περιγράψουμε αυτές τις ιδιότητες χρησιμοποιούμε τα φυσικά μεγέθη. Τέτοια είναι η μάζα, ο χρόνος, το ηλεκτρικό
z = c 1 x 1 + c 2 x c n x n
 Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Τεχνολογικό Εκπαιδευτικό Ιδρυμα Κεντρικής Μακεδονίας - Σέρρες Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός & Βελτιστοποίηση Δρ. Δημήτρης Βαρσάμης Καθηγητής Εφαρμογών Δρ. Δημήτρης Βαρσάμης Μάρτιος
Στοχαστικές Στρατηγικές
 Στοχαστικές Στρατηγικές 3 η ενότητα: Εισαγωγή στα στοχαστικά προβλήματα διαδρομής Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές 3 η ενότητα: Εισαγωγή στα στοχαστικά προβλήματα διαδρομής Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 2018-2019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
ΠΕΡΙΛΗΨΗ ΘΕΩΡΙΑΣ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ
 ΠΕΡΙΛΗΨΗ ΘΕΩΡΙΑΣ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ Αλγεβρική τιμή διανύσματος Όταν ένα διάνυσμα είναι παράλληλο σε έναν άξονα (δηλαδή μια ευθεία στην οποία έχουμε ορίσει θετική φορά), τότε αλγεβρική τιμή του διανύσματος
ΠΕΡΙΛΗΨΗ ΘΕΩΡΙΑΣ ΣΤΗΝ ΕΥΘΥΓΡΑΜΜΗ ΚΙΝΗΣΗ Αλγεβρική τιμή διανύσματος Όταν ένα διάνυσμα είναι παράλληλο σε έναν άξονα (δηλαδή μια ευθεία στην οποία έχουμε ορίσει θετική φορά), τότε αλγεβρική τιμή του διανύσματος
Στοχαστικές Στρατηγικές. διαδρομής (2)
 Στοχαστικές Στρατηγικές 6 η ενότητα: Το γενικό πρόβλημα ελάχιστης διαδρομής () Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 018-019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Στοχαστικές Στρατηγικές 6 η ενότητα: Το γενικό πρόβλημα ελάχιστης διαδρομής () Τμήμα Μαθηματικών, ΑΠΘ Ακαδημαϊκό έτος 018-019 Χειμερινό Εξάμηνο Παπάνα Αγγελική Μεταδιδακτορική ερευνήτρια, ΑΠΘ & Πανεπιστήμιο
Συνάρτηση f, λέγεται η διαδικασία µε βάση την. Παρατηρήσεις - Σχόλια f
 Συνάρτηση f, λέγεται η διαδικασία µε βάση την οποία σε κάθε στοιχείο χ ενός συνόλου Α αντιστοιχούµε ακριβώς ένα στοιχείο ενός άλλου συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισµού ( ή σύνολο ορισµού ) της
Συνάρτηση f, λέγεται η διαδικασία µε βάση την οποία σε κάθε στοιχείο χ ενός συνόλου Α αντιστοιχούµε ακριβώς ένα στοιχείο ενός άλλου συνόλου Β. Το σύνολο Α λέγεται πεδίο ορισµού ( ή σύνολο ορισµού ) της
Σχήμα 12-7: Σκαρίφημα άξονα με τις φορτίσεις του
 1.6.1 ΑΣΚΗΣΗ Ζητείται να υπολογιστεί ένας άξονας μετάδοσης κίνησης και ισχύος με είσοδο από την τρίτη τροχαλία του σχήματος, όπου φαίνονται οι με βασικές προδιαγραφές του προβλήματος. Ο άξονας περιστρέφεται
1.6.1 ΑΣΚΗΣΗ Ζητείται να υπολογιστεί ένας άξονας μετάδοσης κίνησης και ισχύος με είσοδο από την τρίτη τροχαλία του σχήματος, όπου φαίνονται οι με βασικές προδιαγραφές του προβλήματος. Ο άξονας περιστρέφεται
Λύσεις θεμάτων εξεταστικής περιόδου Ιανουαρίου Φεβρουαρίου 2015
 Λύσεις θεμάτων εξεταστικής περιόδου Ιανουαρίου Φεβρουαρίου 205 ΘΕΜΑ Ο (2,0 μονάδες) Ο ηλεκτρικός θερμοσίφωνας χρησιμοποιείται για τη θέρμανση νερού σε μια προκαθορισμένη επιθυμητή θερμοκρασία (θερμοκρασία
Λύσεις θεμάτων εξεταστικής περιόδου Ιανουαρίου Φεβρουαρίου 205 ΘΕΜΑ Ο (2,0 μονάδες) Ο ηλεκτρικός θερμοσίφωνας χρησιμοποιείται για τη θέρμανση νερού σε μια προκαθορισμένη επιθυμητή θερμοκρασία (θερμοκρασία
Στατιστικοί πίνακες. Δημιουργία κλάσεων
 Στατιστικοί πίνακες Δημιουργία κλάσεων Τι είναι οι κλάσεις; Κλάσεις είναι ημιανοικτά διαστήματα της μορφής [α i, b i ), τα οποία είναι ταυτόχρονα και διαδοχικά, έτσι ώστε να μην υπάρχει κάποια τιμή του
Στατιστικοί πίνακες Δημιουργία κλάσεων Τι είναι οι κλάσεις; Κλάσεις είναι ημιανοικτά διαστήματα της μορφής [α i, b i ), τα οποία είναι ταυτόχρονα και διαδοχικά, έτσι ώστε να μην υπάρχει κάποια τιμή του
ΣΥΣΤΗΜΑΤΑ ΑΠΟΦΑΣΕΩΝ ΣΤΗΝ ΠΑΡΑΓΩΓΗ Άσκηση 1. Λύση
 ΣΥΣΤΗΜΑΤΑ ΑΠΟΦΑΣΕΩΝ ΣΤΗΝ ΠΑΡΑΓΩΓΗ Άσκηση 1 Η εταιρεία Ζ εξετάζει την πιθανότητα κατασκευής ενός νέου, πρόσθετου εργοστασίου για την παραγωγή ενός νέου προϊόντος. Έτσι έχει δυο επιλογές: Η πρώτη αφορά στην
ΣΥΣΤΗΜΑΤΑ ΑΠΟΦΑΣΕΩΝ ΣΤΗΝ ΠΑΡΑΓΩΓΗ Άσκηση 1 Η εταιρεία Ζ εξετάζει την πιθανότητα κατασκευής ενός νέου, πρόσθετου εργοστασίου για την παραγωγή ενός νέου προϊόντος. Έτσι έχει δυο επιλογές: Η πρώτη αφορά στην
Α Οδηγίες: {ΑΜ} = Αριθμός Μητρώου σας, Πλήρη βαθμολογία απονέμεται μόνο σε αιτιολογημένες και σαφείς απαντήσεις με ευανάγνωστα γράμματα:
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ Τ.Ε.Ι. ΑΘΗΝΑΣ Μάθημα: ΚΕΡΑΙΕΣ ΚΑΙ ΑΣΥΡΜΑΤΕΣ ΖΕΥΞΕΙΣ Εισηγητής: Δρ. Κ. ΒΟΥΔΟΥΡΗΣ Α Οδηγίες: {ΑΜ} = Αριθμός Μητρώου σας, Πλήρη βαθμολογία απονέμεται μόνο σε αιτιολογημένες
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ Τ.Ε.Ι. ΑΘΗΝΑΣ Μάθημα: ΚΕΡΑΙΕΣ ΚΑΙ ΑΣΥΡΜΑΤΕΣ ΖΕΥΞΕΙΣ Εισηγητής: Δρ. Κ. ΒΟΥΔΟΥΡΗΣ Α Οδηγίες: {ΑΜ} = Αριθμός Μητρώου σας, Πλήρη βαθμολογία απονέμεται μόνο σε αιτιολογημένες
από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία Σχέση ελαστικότητας ζήτησης και κλίση της καμπύλης ζήτησης.
 ΕΛΑΣΤΙΚΟΤΗΤΑ ΖΗΤΗΣΗΣ Ορισμός: Η ελαστικότητα ζήτησης, ενός αγαθού ως προς την τιμή του δίνεται από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία μεταβολή της τιμής του. Δηλαδή %
ΕΛΑΣΤΙΚΟΤΗΤΑ ΖΗΤΗΣΗΣ Ορισμός: Η ελαστικότητα ζήτησης, ενός αγαθού ως προς την τιμή του δίνεται από την ποσοστιαία μεταβολή της ζητούμενης ποσότητας προς την ποσοστιαία μεταβολή της τιμής του. Δηλαδή %
Ακαδηµαϊκό Έτος , Εαρινό Εξάµηνο ιδάσκων Καθ.: Νίκος Τσαπατσούλης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΕΣ : ΑΥΤΟΜΑΤΟΣ ΕΛΕΓΧΟΣ Ακαδηµαϊκό Έτος 5 6, Εαρινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το τρέχον έγγραφο αποτελεί υπόδειγµα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ, ΤΜΗΜΑ ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΚΕΣ : ΑΥΤΟΜΑΤΟΣ ΕΛΕΓΧΟΣ Ακαδηµαϊκό Έτος 5 6, Εαρινό Εξάµηνο Καθ.: Νίκος Τσαπατσούλης ΕΡΩΤΗΣΕΙΣ ΓΙΑ ΕΠΑΝΑΛΗΨΗ Το τρέχον έγγραφο αποτελεί υπόδειγµα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΙΚΗΣ. Διάλεξη 16: O αλγόριθμος SIMPLE (συνέχεια)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΙΚΗΣ Διάλεξη 16: O αλγόριθμος SIMPLE (συνέχεια) Χειμερινό εξάμηνο 2008 Προηγούμενη παρουσίαση... Εξετάσαμε λύσεις
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΠΕΡΙΒΑΛΛΟΝΤΙΚΗΣ ΤΕΧΝΙΚΗΣ Διάλεξη 16: O αλγόριθμος SIMPLE (συνέχεια) Χειμερινό εξάμηνο 2008 Προηγούμενη παρουσίαση... Εξετάσαμε λύσεις
Συνδυασμοί αντιστάσεων και πηγών
 ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 3 Συνδυασμοί αντιστάσεων και πηγών ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ Σύνδεση σε σειρά. Παράλληλη σύνδεση Ισοδυναμία τριγώνου και αστέρα Διαιρέτης τάσης Διαιρέτης ρεύματος Πραγματικές πηγές.
ΗΛΕΚΤΡΟΤΕΧΝΙΑ Ι Κεφάλαιο 3 Συνδυασμοί αντιστάσεων και πηγών ΠΕΡΙΕΧΟΜΕΝΑ ΚΕΦΑΛΑΙΟΥ Σύνδεση σε σειρά. Παράλληλη σύνδεση Ισοδυναμία τριγώνου και αστέρα Διαιρέτης τάσης Διαιρέτης ρεύματος Πραγματικές πηγές.
7. Η ΔΥΝΑΜΙΚΗ ΤΟΥ ΕΡΓΟΣΤΑΣΙΟΥ
 7. Η ΔΥΝΑΜΙΚΗ ΤΟΥ ΕΡΓΟΣΤΑΣΙΟΥ Για να αναπτυχθούν οι βασικές έννοιες της δυναμικής του εργοστασίου εισάγουμε εδώ ορισμένους όρους πέραν αυτών που έχουν ήδη αναφερθεί σε προηγούμενα Κεφάλαια π.χ. είδος,
7. Η ΔΥΝΑΜΙΚΗ ΤΟΥ ΕΡΓΟΣΤΑΣΙΟΥ Για να αναπτυχθούν οι βασικές έννοιες της δυναμικής του εργοστασίου εισάγουμε εδώ ορισμένους όρους πέραν αυτών που έχουν ήδη αναφερθεί σε προηγούμενα Κεφάλαια π.χ. είδος,
Χρονικός Προγραμματισμός Έργων Project Scheduling. Κέντρο Εκπαίδευσης ΕΤΕΚ 69 Δρ. Σ. Χριστοδούλου και Δρ. Α. Ρουμπούτσου
 Χρονικός Προγραμματισμός Έργων Project Scheduling Κέντρο Εκπαίδευσης ΕΤΕΚ 69 Δρ. Σ. Χριστοδούλου και Δρ. Α. Ρουμπούτσου Χρονοδιαγράμματα Έργων Διαδικασία Κτίζοντας το Πρόγραμμα Έργου 1. Κατανόηση έργου/προδιαγραφών
Χρονικός Προγραμματισμός Έργων Project Scheduling Κέντρο Εκπαίδευσης ΕΤΕΚ 69 Δρ. Σ. Χριστοδούλου και Δρ. Α. Ρουμπούτσου Χρονοδιαγράμματα Έργων Διαδικασία Κτίζοντας το Πρόγραμμα Έργου 1. Κατανόηση έργου/προδιαγραφών
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Άσκηση 1. Έστω ότι η συνάρτηση f: R R είναι γνησίως αύξουσα στο R και η γραφική της παράσταση τέµνει τον άξονα y y στο. Να λύσετε την ανίσωση: f(x 9)
ΔΙΑΡΚΕΙΑ (εβδομάδες) A -- 6 B -- 2 C A 3 D B 2 E C 4 F D 1 G E,F 1 H G 6 I H 3 J H 1 K I,J 1 ΔΡΑΣΤΗΡΙΟΤΗΤΑ
 ΑΣΚΗΣΗ 1 Για την ολοκλήρωση ενός έργου απαιτείται η εκτέλεση ενός αριθμού δραστηριοτήτων. Οι δραστηριότητες αυτές, οι διάρκειές τους και οι περιορισμοί που υπάρχουν για την εκτέλεσή τους δίνονται στον
ΑΣΚΗΣΗ 1 Για την ολοκλήρωση ενός έργου απαιτείται η εκτέλεση ενός αριθμού δραστηριοτήτων. Οι δραστηριότητες αυτές, οι διάρκειές τους και οι περιορισμοί που υπάρχουν για την εκτέλεσή τους δίνονται στον
ΝΙΚΟΣ ΤΣΑΝΤΑΣ 25/11/2007. Προγραμματισμός Διαχείριση Έργων. Νίκος Τσάντας Τμήμα Μαθηματικών Πανεπιστημίου Πατρών, Ακαδημαϊκό έτος
 Επιχειρησιακή Έρευνα Προγραμματισμός ιαχείριση Έργων Νίκος Τσάντας Τμήμα Μαθηματικών Πανεπιστημίου Πατρών, Ακαδημαϊκό έτος 007-08 Προγραμματισμός Διαχείριση Έργων ΕΡΓΟ (πέρα από κάθε μεγάλη τεχνική κατασκευή)
Επιχειρησιακή Έρευνα Προγραμματισμός ιαχείριση Έργων Νίκος Τσάντας Τμήμα Μαθηματικών Πανεπιστημίου Πατρών, Ακαδημαϊκό έτος 007-08 Προγραμματισμός Διαχείριση Έργων ΕΡΓΟ (πέρα από κάθε μεγάλη τεχνική κατασκευή)
Συστήματα Αυτομάτου Ελέγχου Ι Ασκήσεις Πράξης
 ΑΝΩΤΑΤΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΤΕΧΝΟΛΟΓΙΚΟΥ ΤΟΜΕΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΑΥΤΟΜΑΤΙΣΜΟΥ Τ.Ε. ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Καθ. Εφαρμ:
ΑΝΩΤΑΤΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΠΕΙΡΑΙΑ ΤΕΧΝΟΛΟΓΙΚΟΥ ΤΟΜΕΑ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΑΥΤΟΜΑΤΙΣΜΟΥ Τ.Ε. ΣΥΣΤΗΜΑΤΑ ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ Ι ΑΣΚΗΣΕΙΣ ΠΡΑΞΗΣ Καθηγητής: Δ. ΔΗΜΟΓΙΑΝΝΟΠΟΥΛΟΣ Καθ. Εφαρμ:
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΕΠΤΕΜΒΡΙΟΣ 2008 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΜΑ 1 ο Σε μία γειτονιά, η ζήτηση ψωμιού η οποία ανέρχεται σε 1400 φραντζόλες ημερησίως,
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΣΕΠΤΕΜΒΡΙΟΣ 2008 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΘΕΜΑ 1 ο Σε μία γειτονιά, η ζήτηση ψωμιού η οποία ανέρχεται σε 1400 φραντζόλες ημερησίως,
Λύσεις θεμάτων Α εξεταστικής περιόδου εαρινού εξαμήνου (Ιούνιος 2015)
 Λύσεις θεμάτων Α εξεταστικής περιόδου εαρινού εξαμήνου 204 5 (Ιούνιος 205) ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος. α. Να προσδιοριστούν οι τιμές
Λύσεις θεμάτων Α εξεταστικής περιόδου εαρινού εξαμήνου 204 5 (Ιούνιος 205) ΘΕΜΑ Ο (4,0 μονάδες) Στο παρακάτω σχήμα δίνεται το δομικό (λειτουργικό) διάγραμμα ενός συστήματος. α. Να προσδιοριστούν οι τιμές
Ασφάλεια Πληροφοριακών Συστηµάτων. Επαναληπτικές Ασκήσεις
 Ασφάλεια Πληροφοριακών Συστηµάτων Επαναληπτικές Ασκήσεις ιάγραµµα Pareto Τα προβλήματα ασφάλειας σε δύο εξυπηρετητές μίας εταιρείας απεικονίζονται στο παρακάτω πίνακα: α/α Κωδικός Προβλήματος Συχνότητα
Ασφάλεια Πληροφοριακών Συστηµάτων Επαναληπτικές Ασκήσεις ιάγραµµα Pareto Τα προβλήματα ασφάλειας σε δύο εξυπηρετητές μίας εταιρείας απεικονίζονται στο παρακάτω πίνακα: α/α Κωδικός Προβλήματος Συχνότητα
ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ
 9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
Το κείμενο που ακολουθεί αποτελεί επεξεργασία του πρωτότυπου κειμένου του Α. Κάστωρ για την επίλυση των παραδειγμάτων κρίσιμης αλυσίδας που
 Το κείμενο που ακολουθεί αποτελεί επεξεργασία του πρωτότυπου κειμένου του Α. Κάστωρ για την επίλυση των παραδειγμάτων κρίσιμης αλυσίδας που παρουσιάστηκαν στις 19/11/2015 και 3/12/2015 στις διαλέξεις του
Το κείμενο που ακολουθεί αποτελεί επεξεργασία του πρωτότυπου κειμένου του Α. Κάστωρ για την επίλυση των παραδειγμάτων κρίσιμης αλυσίδας που παρουσιάστηκαν στις 19/11/2015 και 3/12/2015 στις διαλέξεις του
Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΙΟΥΝΙΟΣ 12 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΘΕΜΑ 1 ο Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α Μία εταιρεία παροχής ολοκληρωμένων ευρυζωνικών υπηρεσιών μελετά την
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΙΟΥΝΙΟΣ 12 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ ΘΕΜΑ 1 ο Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α Μία εταιρεία παροχής ολοκληρωμένων ευρυζωνικών υπηρεσιών μελετά την
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΣΕΠΤΕΜΒΡΙΟΥ 2005 ΘΕΜΑ 1
 ΔΕΔΟΜΕΝΑ: ΘΕΜΑ 1 Στο φορέα του σχήματος ζητούνται: α) να χαραχθούν τα διαγράμματα Μ, Q, N (3.5 μονάδες) β) η κατακόρυφη βύθιση του κόμβου 7 λόγω της φόρτισης και μιας ομοιόμορφης μείωσης της θερμοκρασίας
ΔΕΔΟΜΕΝΑ: ΘΕΜΑ 1 Στο φορέα του σχήματος ζητούνται: α) να χαραχθούν τα διαγράμματα Μ, Q, N (3.5 μονάδες) β) η κατακόρυφη βύθιση του κόμβου 7 λόγω της φόρτισης και μιας ομοιόμορφης μείωσης της θερμοκρασίας
Πληροφοριακά Συστήματα. Προγραμματισμός έργων Η μέθοδος CPM
 Πληροφοριακά Συστήματα Διοίκησης Προγραμματισμός έργων Η μέθοδος CPM Προγραμματισμός έργων Ασχολείται με τον βέλτιστο προγραμματισμό περίπλοκων έργων, ώστε να επιτευχθούν στόχοι σε σχέση με: τον χρόνο
Πληροφοριακά Συστήματα Διοίκησης Προγραμματισμός έργων Η μέθοδος CPM Προγραμματισμός έργων Ασχολείται με τον βέλτιστο προγραμματισμό περίπλοκων έργων, ώστε να επιτευχθούν στόχοι σε σχέση με: τον χρόνο
Μάθημα: Στατική ΙΙ 6 Οκτωβρίου 2011 Διδάσκων: Τριαντ. Κόκκινος, Ph.D. Διάρκεια εξέτασης 2:15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΑΘΗΝΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τμήμα Πολιτικών Έργων Υποδομής Μάθημα: Στατική ΙΙ 6 Οκτωβρίου 11 Διδάσκων:, Ph.D. Διάρκεια εξέτασης :15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΑΘΗΝΑΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ Τμήμα Πολιτικών Έργων Υποδομής Μάθημα: Στατική ΙΙ 6 Οκτωβρίου 11 Διδάσκων:, Ph.D. Διάρκεια εξέτασης :15 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΓΡΑΠΤΗ ΕΞΕΤΑΣΗ
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Α.Π.Θ. ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ
 ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Α.Π.Θ. ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Γενικές έννοιες Μία ροή χαρακτηρίζεται ανομοιόμορφη, όταν το βάθος μεταβάλλεται από διατομή σε διατομή. Η μεταβολή μπορεί να
ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ Α.Π.Θ. ΤΟΜΕΑΣ ΥΔΡΑΥΛΙΚΗΣ ΚΑΙ ΤΕΧΝΙΚΗΣ ΠΕΡΙΒΑΛΛΟΝΤΟΣ Γενικές έννοιες Μία ροή χαρακτηρίζεται ανομοιόμορφη, όταν το βάθος μεταβάλλεται από διατομή σε διατομή. Η μεταβολή μπορεί να
ΠΡΟΒΛΗΜΑΤΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΡΓΩΝ ΔΙΟΙΚΗΣΗ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΡΓΩΝ - ΠΡΟΒΛΗΜΑΤΑ
 ΠΡΟΒΛΗΜΑΤΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΡΓΩΝ 1 ΠΡΟΒΛΗΜΑ 1 Οι δραστηριότητες Χ και Ψ ενός σύνθετου έργου μηχανοργάνωσης (βλ. επόμενη σελίδα) παριστάνουν τις δύο κύριες εργασίες εγκατάστασης ενός μεγάλου
ΠΡΟΒΛΗΜΑΤΑ ΔΙΟΙΚΗΣΗΣ ΚΑΙ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΡΓΩΝ 1 ΠΡΟΒΛΗΜΑ 1 Οι δραστηριότητες Χ και Ψ ενός σύνθετου έργου μηχανοργάνωσης (βλ. επόμενη σελίδα) παριστάνουν τις δύο κύριες εργασίες εγκατάστασης ενός μεγάλου
Διαχείριση Έργων. Ενότητα 4: Διάγραμμα Gannt
 Διαχείριση Έργων Ενότητα 4: Διάγραμμα Gannt Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.) Διάγραμμα Gannt Υποενότητα
Διαχείριση Έργων Ενότητα 4: Διάγραμμα Gannt Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων (Δ.Ε.Α.Π.Τ.) Διάγραμμα Gannt Υποενότητα
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο Λύσεις έκτου φυλλαδίου ασκήσεων.
 Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
Απειροστικός Λογισμός Ι, χειμερινό εξάμηνο 208-9. Λύσεις έκτου φυλλαδίου ασκήσεων.. Παρατηρήστε ότι ο πρώτος κανόνας αλλαγής μεταβλητής εφαρμόζεται μόνο στα εφτά πρώτα όρια ενώ ο δεύτερος κανόνας εφαρμόζεται
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης
 Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 1 η Διάλεξη Ορισμός Θεωρίας Παιγνίων και Παιγνίου Κατηγοριοποίηση παιγνίων Επίλυση παιγνίου Αξία (τιμή) παιγνίου Δίκαιο παίγνιο Αναπαράσταση Παιγνίου Με πίνακα Με
Θεωρία Παιγνίων Δρ. Τασσόπουλος Ιωάννης 1 η Διάλεξη Ορισμός Θεωρίας Παιγνίων και Παιγνίου Κατηγοριοποίηση παιγνίων Επίλυση παιγνίου Αξία (τιμή) παιγνίου Δίκαιο παίγνιο Αναπαράσταση Παιγνίου Με πίνακα Με
ΕΡΓΑΣΤΗΡΙΑΚΕΣ ΑΣΚΗΣΕΙΣ C ΣΕΙΡΑ 1 η
 Δ.Π.Θ. - Πολυτεχνική Σχολή Τμήμα Μηχανικών Παραγωγής & Διοίκησης Ακαδ. έτος 2016-2017 Τομέας Συστημάτων Παραγωγής Εξάμηνο Β Αναπληρωτής Καθηγητής Στέφανος Δ. Κατσαβούνης ΜΑΘΗΜΑ : ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
Δ.Π.Θ. - Πολυτεχνική Σχολή Τμήμα Μηχανικών Παραγωγής & Διοίκησης Ακαδ. έτος 2016-2017 Τομέας Συστημάτων Παραγωγής Εξάμηνο Β Αναπληρωτής Καθηγητής Στέφανος Δ. Κατσαβούνης ΜΑΘΗΜΑ : ΔΟΜΗΜΕΝΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
ΑΣΚΗΣΗ WORD. 3. Στην ΚΕΦΑΛΙΔΑ της σελίδας εισάγετε το παρακάτω κείμενο: 5. Στην αρχή της σελίδας γράψτε το παρακάτω κείμενο:
 ΑΣΚΗΣΗ WORD 1. Ρυθμίστε τα περιθώρια της σελίδας ως εξής: Δεξιά 2,5 εκ., Αριστερά 2,5 εκ., Πάνω 3 εκ. και Κάτω 3 εκ. 2. Εισάγετε υδατογράφημα και χρώμα σελίδας όπως φαίνεται στο παρόν έγγραφο. 3. Στην
ΑΣΚΗΣΗ WORD 1. Ρυθμίστε τα περιθώρια της σελίδας ως εξής: Δεξιά 2,5 εκ., Αριστερά 2,5 εκ., Πάνω 3 εκ. και Κάτω 3 εκ. 2. Εισάγετε υδατογράφημα και χρώμα σελίδας όπως φαίνεται στο παρόν έγγραφο. 3. Στην
Τµ. Διοίκησης Επιχειρήσεων/Μεσολόγγι ΤΕΙ Δυτ. Ελλάδας ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΡΓΟΥ
 Τµ. Διοίκησης Επιχειρήσεων/Μεσολόγγι ΤΕΙ Δυτ. Ελλάδας ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΡΓΟΥ Πλάνο έργου Εργαλείο ελέγχου για την πορεία του έργου. Περιγραφή έργου Απαιτήσεις Τµηµατοποίηση έργου Χρονο-προγραµµατισµός έργου
Τµ. Διοίκησης Επιχειρήσεων/Μεσολόγγι ΤΕΙ Δυτ. Ελλάδας ΤΜΗΜΑΤΟΠΟΙΗΣΗ ΕΡΓΟΥ Πλάνο έργου Εργαλείο ελέγχου για την πορεία του έργου. Περιγραφή έργου Απαιτήσεις Τµηµατοποίηση έργου Χρονο-προγραµµατισµός έργου
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα
 Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Τμήμα Φυσικής Πανεπιστημίου Κύπρου Χειμερινό Εξάμηνο 2016/2017 ΦΥΣ102 Φυσική για Χημικούς Διδάσκων: Μάριος Κώστα ΔΙΑΛΕΞΗ 19 Ταλαντώσεις Απλή αρμονική κίνηση ΦΥΣ102 1 Ταλαντώσεις Ελατηρίου Όταν ένα αντικείμενο
Στον παρακάτω πίνακα παρουσιάζονται οι διάφορες δραστηριότητες που απαιτούνται στο πλαίσιο υλοποίησης ενός μικρού έργου:
 Εκφώνηση Στον παρακάτω πίνακα παρουσιάζονται οι διάφορες δραστηριότητες που απαιτούνται στο πλαίσιο υλοποίησης ενός μικρού έργου: Οι άμεσες σχέσεις προτεραιότητας είναι: Activity Number Activity Completion
Εκφώνηση Στον παρακάτω πίνακα παρουσιάζονται οι διάφορες δραστηριότητες που απαιτούνται στο πλαίσιο υλοποίησης ενός μικρού έργου: Οι άμεσες σχέσεις προτεραιότητας είναι: Activity Number Activity Completion
Εξέταση στο Mάθηµα: "ΘΕΩΡΙΑ ΙΚΤΥΩΝ" (5 ο εξάµηνο)
 Εξέταση στο Mάθηµα: "ΘΕΩΡΙΑ ΙΚΤΥΩΝ" (5 ο εξάµηνο) ( ιάρκεια: 3 ώρες) ΟΜΑ Α Α Ηµεροµηνία: 17 Σεπτεµβρίου 2003 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Παρατηρήσεις: Να γράψετε τον αριθµό των διφύλλων που παραδίδετε Να γράψετε το
Εξέταση στο Mάθηµα: "ΘΕΩΡΙΑ ΙΚΤΥΩΝ" (5 ο εξάµηνο) ( ιάρκεια: 3 ώρες) ΟΜΑ Α Α Ηµεροµηνία: 17 Σεπτεµβρίου 2003 ΟΝΟΜΑΤΕΠΩΝΥΜΟ: Παρατηρήσεις: Να γράψετε τον αριθµό των διφύλλων που παραδίδετε Να γράψετε το
ΕΠΩΝΥΜΟ :... ΟΝΟΜΑ :... ΒΑΘΜΟΣ:
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Μάθημα : Ανάλυση Γραμμικών Φορέων με Μητρώα ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ Διδάσκων: Μ. Γ. Σφακιανάκης ΤΜΗΜΑ ΠΟΛ/ΚΩΝ ΜΗΧ/ΚΩΝ Εξέταση : --, :-: ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΩΝ ΕΠΩΝΥΜΟ :......... ΟΝΟΜΑ :......
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Μάθημα : Ανάλυση Γραμμικών Φορέων με Μητρώα ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ Διδάσκων: Μ. Γ. Σφακιανάκης ΤΜΗΜΑ ΠΟΛ/ΚΩΝ ΜΗΧ/ΚΩΝ Εξέταση : --, :-: ΤΟΜΕΑΣ ΚΑΤΑΣΚΕΥΩΝ ΕΠΩΝΥΜΟ :......... ΟΝΟΜΑ :......
Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α
 Από ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΦΕΒΡΟΥΑΡΙΟΣ 2012 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α ΘΕΜΑ 1 ο Η UCC είναι μια μικρή εταιρεία παραγωγής εντομοκτόνων. Σε
Από ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΦΕΒΡΟΥΑΡΙΟΣ 2012 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ Ε Π Ι Χ Ε Ι Ρ Η Σ Ι Α Κ Η Ε Ρ Ε Υ Ν Α ΘΕΜΑ 1 ο Η UCC είναι μια μικρή εταιρεία παραγωγής εντομοκτόνων. Σε
dx cos x = ln 1 + sin x 1 sin x.
 Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 17-18 Ν. Βλαχάκης 1. Εστω πεδίο δύναμης F = g () cos y ˆ + λ g() sin y ŷ, όπου λ = σταθερά και g() = 1 e π/ B C (σε κατάλληλες μονάδες). (α) Υπολογίστε πόση ενέργεια
Μηχανική Ι Εργασία #5 Χειμερινό εξάμηνο 17-18 Ν. Βλαχάκης 1. Εστω πεδίο δύναμης F = g () cos y ˆ + λ g() sin y ŷ, όπου λ = σταθερά και g() = 1 e π/ B C (σε κατάλληλες μονάδες). (α) Υπολογίστε πόση ενέργεια
ΑΣΚΗΣΗ 17 ΔΕΔΟΜΕΝΑ: Δίνονται: = cm ΕΠΙΛΥΣΗ: Ερώτημα α. k = 6000kN m. Μέθοδος των Δυνάμεων:
 ΑΣΚΗΣΗ 7 ΔΕΔΟΜΕΝΑ: Στο φορέα του σχήματος ζητούνται: α) να χαραχθούν τα διαγράμματα M, Q (2.5 μονάδες) β) να υπολογιστεί το μέτρο και η φορά της κατακόρυφης μετατόπισης στο μέσο του τμήματος (23) ( μονάδα)
ΑΣΚΗΣΗ 7 ΔΕΔΟΜΕΝΑ: Στο φορέα του σχήματος ζητούνται: α) να χαραχθούν τα διαγράμματα M, Q (2.5 μονάδες) β) να υπολογιστεί το μέτρο και η φορά της κατακόρυφης μετατόπισης στο μέσο του τμήματος (23) ( μονάδα)
Προγραμματισμός & Διοίκηση Έργων
 Προγραμματισμός & Διοίκηση Έργων Διαγράμματα Gantt Κωνσταντίνος Κηρυττόπουλος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Προγραμματισμός & Διοίκηση Έργων Διαγράμματα Gantt Κωνσταντίνος Κηρυττόπουλος Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Πανεπιστήµιο Πατρών Τµήµα ιοίκησης Επιχειρήσεων. Ανδρέας Νεάρχου 2
 ιοίκηση Λειτουργιών ιοίκηση Έργων IΙΙ (Χρονοπρογραµµατισµός συνέχεια) - 7 ο µάθηµα - Άσκηση επανάληψης CPM Θεωρείστε το έργο που φαίνεται στον επόµενο πίνακα. Χρησιµοποιώντας τη µέθοδο της κρίσιµης διαδροµής
ιοίκηση Λειτουργιών ιοίκηση Έργων IΙΙ (Χρονοπρογραµµατισµός συνέχεια) - 7 ο µάθηµα - Άσκηση επανάληψης CPM Θεωρείστε το έργο που φαίνεται στον επόµενο πίνακα. Χρησιµοποιώντας τη µέθοδο της κρίσιµης διαδροµής
